1. Introduction
Not all taxes are created equal in financing public expenditures. A long-standing debate centers on capital versus labor income taxes. One strand of this literature focuses on their implications for extrinsic uncertainty unrelated to economic fundamentals, where a general wisdom holds that a government that relies on adjusting factor income tax rates to achieve budget objective may induce aggregate fluctuations driven by sunspots expectations. This was first demonstrated by Schmitt-Grohé and Uribe (Reference Schmitt-Grohé and ín Uribe1997, SGU henceforth) using a standard real business cycle model where a government in balancing its budget adjusts either labor (or capital) income tax rate or both in an equal proportion with respect to their levels.Footnote 1 Since such fiscal policy can be destabilizing even in the absence of fundamental shocks, SGU conclude that their results lend support to the view that restrictions should be imposed on the government’s ability to change factor income tax rates in order to prevent self-fulfilling instability. Their conclusion has since been reinforced by subsequent studies, most notably, Guo and Harrison (Reference Guo and Harrison2004), who show that, if a government finances public expenditures with fixed factor income tax rates, then sunspots expectations cannot be self-fulfilled and extrinsic volatility can be avoided.Footnote 2
The current paper revisits this issue of aggregate instability associated with self-fulfilling beliefs by examining the aforementioned assumption made in SGU (Reference Schmitt-Grohé and ín Uribe1997), that is, when capital and labor income tax rates are both adjusted to balance government budget, the two tax rates must be changed by the same proportion—an assumption that has been widely followed in the literature. In this paper, we relax this restriction by allowing the two individual tax rates to be adjusted in potentially different proportions. We show that this conventional wisdom may be overturned, if the rate of adjustment of the capital income tax rate is bigger than that of the labor income tax rate. How much bigger depends on country specifics and particularly on the levels of the capital and labor income tax rates. Our key conclusion here is that, adjustments in capital and labor income tax rates, if properly designed and implemented, can help achieve budget objective while also preempting self-fulfilling instability.
To help understand the intuition behind our result, let’s consider first the polar case where the labor income tax rate can be adjusted but the capital income tax rate is fixed. In this case, sunspots expectations can become self-fulfilled for empirically plausible values of the labor and capital income tax rates. When agents become optimistic about the future of the economy and contemplate to work more, the government would respond by decreasing the labor income tax rate to re-balance its budget with the rising output while continuing to be able to finance existing public expenditures. The lowered labor income tax rate would then directly incentivize the agents to indeed want to work more, and this serves to fulfill their initial optimistic expectations, resulting in an indeterminate equilibrium and endogenous business cycle fluctuations. In contrast, for the other polar case where the capital income tax rate can be adjusted but the labor income tax rate is fixed, sunspots expectations are less likely to become self-fulfilled for empirically plausible values of the capital and labor income tax rates. This is so because if agents become optimistic about the future of the economy and contemplate to invest more, the government would have to decrease the capital income tax rate in order to incentivize the agents to do so; but, with a predetermined capital stock, tax revenue from capital income would then be lower, and with only an indirect (thus generally small) general equilibrium spillover effect on the agents’ labor supply, the resultant increase in labor income tax would be insufficient to make up for the shortfall in capital income tax to finance existing public expenditures (unless the level of labor income tax rate is implausibly high). This would invalidate the agents’ initial optimistic expectations. In light of the above elaborations of the two polar cases, it is natural to conjecture that, if both tax rates can be adjusted, then the (in)stability properties of the economy will depend on the relative rates of adjustments in the two individual tax rates. We find that this is indeed the case, as reported above. We provide numerical examples to illustrate how our results may provide some useful guidance to a country’s fiscal policy practice to help ensure aggregate stability in the absence of fundamental shocks while achieving its budget objective.Footnote 3
In what follows, Section 1 describes the model. Section 3 solves the dynamic general equilibrium and reports our analytical and calibration results. Section 4 concludes.
2. The model
Our model is identical to that of SGU (Reference Schmitt-Grohé and ín Uribe1997), except that we extend their model on the assumption of how the government adjusts the factor income tax rates in balancing its budget, as will be specified in detail below. The economy consists of households, firms, and a government.
2.1. Government
Assume that government revenue includes only labor and capital income taxes, government purchases are constant, and that the government is subject to a balanced-budget requirement. The government budget constraint is then given by:
where
![]() $G$
denotes government purchases of goods,
$G$
denotes government purchases of goods,
![]() $\tau _{t}^{l}$
(
$\tau _{t}^{l}$
(
![]() $\tau _{t}^{k}$
) the labor (capital) tax rate, and
$\tau _{t}^{k}$
) the labor (capital) tax rate, and
![]() $w_{t}$
(
$w_{t}$
(
![]() $r_{t}$
) the pretax wage (rental) rate,
$r_{t}$
) the pretax wage (rental) rate,
![]() $l_{t}$
hours worked, and
$l_{t}$
hours worked, and
![]() $\delta \geq 0$
the capital depreciation rate. Here, the term
$\delta \geq 0$
the capital depreciation rate. Here, the term
![]() $-\tau _{t}^{k}\delta k_{t}$
represents a depreciation allowance.
$-\tau _{t}^{k}\delta k_{t}$
represents a depreciation allowance.
We assume in this paper that the government adjusts the tax rates to balance the budget according to
where
![]() $s\geq 0$
is a parameter. With endogenous capital and labor income tax rates, SGU (Reference Schmitt-Grohé and ín Uribe1997) restrict to the case with
$s\geq 0$
is a parameter. With endogenous capital and labor income tax rates, SGU (Reference Schmitt-Grohé and ín Uribe1997) restrict to the case with
![]() $s=1$
, that is, the two tax rates vary in the same proportion. Instead, we allow the two tax rates to change in distinct proportions, that is,
$s=1$
, that is, the two tax rates vary in the same proportion. Instead, we allow the two tax rates to change in distinct proportions, that is,
![]() $s\neq 1$
. Note that (2) also nests the two special cases examined in SGU (Reference Schmitt-Grohé and ín Uribe1997): an exogenous capital tax rate (
$s\neq 1$
. Note that (2) also nests the two special cases examined in SGU (Reference Schmitt-Grohé and ín Uribe1997): an exogenous capital tax rate (
![]() $s=0$
) and an exogenous labor tax rate (
$s=0$
) and an exogenous labor tax rate (
![]() $s=\infty$
).
$s=\infty$
).
2.2. Households
The economy is populated by a unit measure of identical infinitely lived households. The representative household chooses paths for consumption,
![]() $c_{t}$
, hours worked
$c_{t}$
, hours worked
![]() $l_{t}$
, and capital,
$l_{t}$
, and capital,
![]() $k_{t}$
, so as to maximize the present discounted value of its lifetime utility:
$k_{t}$
, so as to maximize the present discounted value of its lifetime utility:
subject to,
where
![]() $\rho \gt 0$
is the subjective discount rate and
$\rho \gt 0$
is the subjective discount rate and
![]() $\eta \gt 0$
is the a scaling parameter. The first-order conditions associated with this problem are
$\eta \gt 0$
is the a scaling parameter. The first-order conditions associated with this problem are
where
![]() $\lambda _{t}$
denotes the marginal utility of income.
$\lambda _{t}$
denotes the marginal utility of income.
2.3. Firms
The representative firm produces output
![]() $y_{t}$
, using capital and labor as inputs, with a constant returns-to-scale Cobb–Douglas production function:
$y_{t}$
, using capital and labor as inputs, with a constant returns-to-scale Cobb–Douglas production function:
Perfect competition in factor and product markets implies that factor demands are given by:
Finally, the aggregate resource constraint for the economy is given by:
2.4. Analysis of dynamics
The model’s equilibrium can be reduced to two differential equations:
along with (1)–(4), (6), and (7). In what follows, we denote the steady-state value of a variable by dropping its time index. It is straightforward to show that the dynamic system possesses a unique interior steady state. Linearizing (9)–(10) around the steady state, we obtain
 \begin{equation} \begin{pmatrix} \dot{k}_{t} \\ \dot{\lambda }_{t}\end{pmatrix}=\mathbf{J}\begin{pmatrix} k_{t}-k \\ \lambda _{t}-\lambda \end{pmatrix}\text{,} \end{equation}
\begin{equation} \begin{pmatrix} \dot{k}_{t} \\ \dot{\lambda }_{t}\end{pmatrix}=\mathbf{J}\begin{pmatrix} k_{t}-k \\ \lambda _{t}-\lambda \end{pmatrix}\text{,} \end{equation}
where J is the Jacobian matrix. The elements of
![]() $\mathbf{J}$
, denoted as
$\mathbf{J}$
, denoted as
![]() $J_{ij}$
, are given by:
$J_{ij}$
, are given by:
 \begin{align*} J_{11}&=-\alpha \epsilon _{yk}\theta _{y\lambda }\big ( 1-\tau ^{k}\big ) +\left ( \alpha \epsilon _{yk}-\delta \right ) \epsilon _{\tau \lambda }s\tau ^{k},\\ J_{12}&=\epsilon _{\lambda k}\left [ \alpha \big ( 1-\tau ^{k}\big ) \left ( 1-\theta _{yk}\right ) \epsilon _{yk}+\left ( \alpha \epsilon _{yk}-\delta \right ) \epsilon _{\tau k}s\tau ^{k}\right ], \end{align*}
\begin{align*} J_{11}&=-\alpha \epsilon _{yk}\theta _{y\lambda }\big ( 1-\tau ^{k}\big ) +\left ( \alpha \epsilon _{yk}-\delta \right ) \epsilon _{\tau \lambda }s\tau ^{k},\\ J_{12}&=\epsilon _{\lambda k}\left [ \alpha \big ( 1-\tau ^{k}\big ) \left ( 1-\theta _{yk}\right ) \epsilon _{yk}+\left ( \alpha \epsilon _{yk}-\delta \right ) \epsilon _{\tau k}s\tau ^{k}\right ], \end{align*}
where
 \begin{equation*} \theta _{\tau \lambda }\equiv -\frac {\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \left ( 1-\alpha \right ) \epsilon _{yk}}{\kappa },\theta _{\tau k}\equiv \frac {\delta \alpha \tau ^{k}-\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \alpha \epsilon _{yk}}{\kappa }, \end{equation*}
\begin{equation*} \theta _{\tau \lambda }\equiv -\frac {\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \left ( 1-\alpha \right ) \epsilon _{yk}}{\kappa },\theta _{\tau k}\equiv \frac {\delta \alpha \tau ^{k}-\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \alpha \epsilon _{yk}}{\kappa }, \end{equation*}
The expression for
![]() $\epsilon _{\lambda k}$
is not given here as its value affects neither the trace nor the determinant of
$\epsilon _{\lambda k}$
is not given here as its value affects neither the trace nor the determinant of
![]() $\mathbf{J}$
.
$\mathbf{J}$
.
While the closed-form equilibrium solutions cannot generally be obtained, for the case with
![]() $\delta =0$
, analytical results can be derived. To see this, we note that, when
$\delta =0$
, analytical results can be derived. To see this, we note that, when
![]() $\delta =0$
, the trace and determinant of
$\delta =0$
, the trace and determinant of
![]() $\mathbf{J}$
are given by:
$\mathbf{J}$
are given by:
where
 \begin{equation*} y_{\lambda }=\frac {1}{\frac {\alpha }{1-\alpha }-\frac {\tau ^{l}}{1-\tau ^{l}}\frac {\left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}},\text { }\Xi \equiv \frac {\alpha }{1-\alpha }+\frac {\left ( 1-\alpha \right ) \left ( 1-s\right ) \tau ^{l}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}\tau ^{k}, \end{equation*}
\begin{equation*} y_{\lambda }=\frac {1}{\frac {\alpha }{1-\alpha }-\frac {\tau ^{l}}{1-\tau ^{l}}\frac {\left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}},\text { }\Xi \equiv \frac {\alpha }{1-\alpha }+\frac {\left ( 1-\alpha \right ) \left ( 1-s\right ) \tau ^{l}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}\tau ^{k}, \end{equation*}
 \begin{eqnarray*} \Omega &\equiv &-\left \{ \left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] ^{2}+\left ( 1-\alpha \right ) \big ( 1-\tau ^{l}\big ) -\tau ^{k}\right \} \alpha \tau ^{k}s \\ &&-\frac{\left \{ \left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] ^{2}+\left ( 1-\alpha \right ) \big ( 1-\tau ^{l}\big ) -\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \right \} \left ( 1-\alpha \right ) \big ( 1-\tau ^{k}\big ) }{1-\tau ^{l}}\tau ^{l}. \end{eqnarray*}
\begin{eqnarray*} \Omega &\equiv &-\left \{ \left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] ^{2}+\left ( 1-\alpha \right ) \big ( 1-\tau ^{l}\big ) -\tau ^{k}\right \} \alpha \tau ^{k}s \\ &&-\frac{\left \{ \left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] ^{2}+\left ( 1-\alpha \right ) \big ( 1-\tau ^{l}\big ) -\left [ \left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}\right ] \right \} \left ( 1-\alpha \right ) \big ( 1-\tau ^{k}\big ) }{1-\tau ^{l}}\tau ^{l}. \end{eqnarray*}
The following proposition gives a necessary condition for equilibrium indeterminacy.
Proposition 1.
If
![]() $\Xi \gt 0$
, then a necessary condition for indeterminacy is that
$\Xi \gt 0$
, then a necessary condition for indeterminacy is that
where, in the interval
![]() $(0,1),$
$(0,1),$
![]() $\underline{\tau }^{l}$
is the unique root of the quadratic equation
$\underline{\tau }^{l}$
is the unique root of the quadratic equation
Proof. A necessary condition for indeterminacy is that the trace is negative, which is equivalent to
![]() $y_{\lambda }\lt 0$
if
$y_{\lambda }\lt 0$
if
![]() $\Xi \gt 0$
,Footnote 4 that is,
$\Xi \gt 0$
,Footnote 4 that is,
![]() $q\big ( \tau ^{l};\,\tau ^{k},s\big ) \gt 0$
. For
$q\big ( \tau ^{l};\,\tau ^{k},s\big ) \gt 0$
. For
![]() $\tau ^{k}\gt 0$
,
$\tau ^{k}\gt 0$
,
![]() $q\big ( \tau ^{l}=0\big ) =-\frac{s\alpha ^{2}}{1-\alpha }\tau ^{k}\lt 0$
, and
$q\big ( \tau ^{l}=0\big ) =-\frac{s\alpha ^{2}}{1-\alpha }\tau ^{k}\lt 0$
, and
![]() $q\big ( \tau ^{l}=1\big ) =1-\alpha +\alpha \tau ^{k}\gt 0$
. Thus, there exists a unique root in the interval
$q\big ( \tau ^{l}=1\big ) =1-\alpha +\alpha \tau ^{k}\gt 0$
. Thus, there exists a unique root in the interval
![]() $\underline{\tau }^{l}\in \left ( 0,1\right )$
such that
$\underline{\tau }^{l}\in \left ( 0,1\right )$
such that
![]() $q\big ( \underline{\tau }^{l}\big ) =0$
. If
$q\big ( \underline{\tau }^{l}\big ) =0$
. If
![]() $\tau ^{k}=0$
,
$\tau ^{k}=0$
,
![]() $q=(\tau ^{l}-\alpha )\tau ^{l}$
, and
$q=(\tau ^{l}-\alpha )\tau ^{l}$
, and
![]() $\underline{\tau }^{l}=\alpha$
. Thus, for all
$\underline{\tau }^{l}=\alpha$
. Thus, for all
![]() $\tau ^{l}\gt \underline{\tau }^{l}$
, we have
$\tau ^{l}\gt \underline{\tau }^{l}$
, we have
![]() $q\gt 0$
and hence
$q\gt 0$
and hence
![]() $y_{\lambda }\lt 0$
.
$y_{\lambda }\lt 0$
.
The following corollary can be readily established.
Corollary 1.
The lower bound for indeterminacy
![]() $\underline{\tau }^{l}$
in Proposition 1 is a strictly increasing function of
$\underline{\tau }^{l}$
in Proposition 1 is a strictly increasing function of
![]() $s$
.Footnote 5
$s$
.Footnote 5
Proof. From
![]() $q\big ( \underline{\tau }^{l};\,\tau ^{k},s\big ) =0$
, we have
$q\big ( \underline{\tau }^{l};\,\tau ^{k},s\big ) =0$
, we have
 \begin{align*} \frac {\partial \underline {\tau }^{l}}{\partial s}=-\frac {\dfrac {dq\big ( \underline {\tau }^{l}\big ) }{ds}}{\dfrac {dq\big ( \underline {\tau }^{l}\big ) }{d\underline {\tau }^{l}}}=\frac {\frac {\alpha ^{2}}{1-\alpha }\tau ^{k}\big ( 1-\underline {\tau }^{l}\big ) }{\left ( \underline {\tau }^{l}\right ) ^{2}+\frac {s\alpha ^{2}}{1-\alpha }\tau ^{k}}\underline {\tau }^{l}\gt 0. \\[-36pt]\end{align*}
\begin{align*} \frac {\partial \underline {\tau }^{l}}{\partial s}=-\frac {\dfrac {dq\big ( \underline {\tau }^{l}\big ) }{ds}}{\dfrac {dq\big ( \underline {\tau }^{l}\big ) }{d\underline {\tau }^{l}}}=\frac {\frac {\alpha ^{2}}{1-\alpha }\tau ^{k}\big ( 1-\underline {\tau }^{l}\big ) }{\left ( \underline {\tau }^{l}\right ) ^{2}+\frac {s\alpha ^{2}}{1-\alpha }\tau ^{k}}\underline {\tau }^{l}\gt 0. \\[-36pt]\end{align*}
We can elaborate the results in Proposition 1 and Corollary 1 in line with the intuition related to the labor market (e.g., SGU (Reference Schmitt-Grohé and ín Uribe1997)), using the log-linearized version of the labor demand function (where a variable with a hat denotes the log deviation of the variable from its steady state):
 \begin{equation*} \hat {w}_{t}^{d}=\alpha \left [ 1+\frac {\left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}\frac {\tau ^{l}}{1-\tau ^{l}}\right ] \widehat {k}_{t}-\frac {1-\alpha }{y_{\lambda }}\widehat {l}_{t}. \end{equation*}
\begin{equation*} \hat {w}_{t}^{d}=\alpha \left [ 1+\frac {\left ( 1-\alpha \right ) \tau ^{l}+\alpha \tau ^{k}}{\left ( 1-\alpha \right ) \tau ^{l}+s\alpha \tau ^{k}}\frac {\tau ^{l}}{1-\tau ^{l}}\right ] \widehat {k}_{t}-\frac {1-\alpha }{y_{\lambda }}\widehat {l}_{t}. \end{equation*}
The necessary condition for indeterminacy,
![]() $y_{\lambda }\lt 0$
, implies that the slope of the labor demand curve is positive. The larger is
$y_{\lambda }\lt 0$
, implies that the slope of the labor demand curve is positive. The larger is
![]() $s$
, the smaller is
$s$
, the smaller is
![]() $y_{\lambda }$
, thus the flatter is the labor demand curve, which makes it less likely for the labor demand curve to be steeper than the labor supply curve. Hence, indeterminacy is less likely to occur for larger value of
$y_{\lambda }$
, thus the flatter is the labor demand curve, which makes it less likely for the labor demand curve to be steeper than the labor supply curve. Hence, indeterminacy is less likely to occur for larger value of
![]() $s$
. This nexus of our paper’s results and the conventional labor market elucidation of indeterminacy is consistent with the elaboration of our model’s mechanism outlined in the introduction section based on the two polar cases, one with endogenous labor but fixed capital income tax rates (i.e.,
$s$
. This nexus of our paper’s results and the conventional labor market elucidation of indeterminacy is consistent with the elaboration of our model’s mechanism outlined in the introduction section based on the two polar cases, one with endogenous labor but fixed capital income tax rates (i.e.,
![]() $s=0$
) and the other with endogenous capital but fixed labor income tax rates (i.e.,
$s=0$
) and the other with endogenous capital but fixed labor income tax rates (i.e.,
![]() $s=\infty$
).
$s=\infty$
).
To get a quantitative feel, we calibrate the model using the same baseline parameterization as in SGU (Reference Schmitt-Grohé and ín Uribe1997), that is,
![]() $\alpha =0.3$
,
$\alpha =0.3$
,
![]() $\rho =0.04$
,
$\rho =0.04$
,
![]() $\delta =0.1$
. Fig. 1 draws the lower bounds for indeterminacy for different values of
$\delta =0.1$
. Fig. 1 draws the lower bounds for indeterminacy for different values of
![]() $s$
. The values of
$s$
. The values of
![]() $s=0$
and
$s=0$
and
![]() $1$
correspond to the two cases considered in SGU (1997), where
$1$
correspond to the two cases considered in SGU (1997), where
![]() $s=0$
corresponds to the polar case with endogenous labor but fixed capital income tax rates. To get a practical grab of our results, note that, in both cases (
$s=0$
corresponds to the polar case with endogenous labor but fixed capital income tax rates. To get a practical grab of our results, note that, in both cases (
![]() $s=0,$
$s=0,$
![]() $1$
), SGU (Reference Schmitt-Grohé and ín Uribe1997) find that the labor and capital income tax rates for the year 1988 estimated by Mendoza et al. (Reference Mendoza, Razin and Tesar1994) for USA, UK, Germany (G), Canada (C), and Japan (J), which also are the five economies studied by Giannisarou (Reference Giannisarou2007), all fall inside the range of values for which the equilibrium is indeterminate (the instability region). However, as can be seen from Fig. 1, the stability region can get larger as
$1$
), SGU (Reference Schmitt-Grohé and ín Uribe1997) find that the labor and capital income tax rates for the year 1988 estimated by Mendoza et al. (Reference Mendoza, Razin and Tesar1994) for USA, UK, Germany (G), Canada (C), and Japan (J), which also are the five economies studied by Giannisarou (Reference Giannisarou2007), all fall inside the range of values for which the equilibrium is indeterminate (the instability region). However, as can be seen from Fig. 1, the stability region can get larger as
![]() $s$
increases, and it is possible that a country in the instability region when
$s$
increases, and it is possible that a country in the instability region when
![]() $s=1$
may fall in the stability region for larger values of
$s=1$
may fall in the stability region for larger values of
![]() $s$
depending on its economic characteristics, and especially on the levels of the two tax rates.Footnote 6
$s$
depending on its economic characteristics, and especially on the levels of the two tax rates.Footnote 6
Table 1. Estimated effective tax rates
![]() $^{\textrm a}$
and threshold value of
$^{\textrm a}$
and threshold value of
![]() $s$
$s$

aEstimated effective factor income tax rates for 1988 are taken from Mendoza et al. (1994); updated estimates for 1996 areavailable at http://www.sas.upenn.edu/~egme/pp/newtaxdata.pdf.
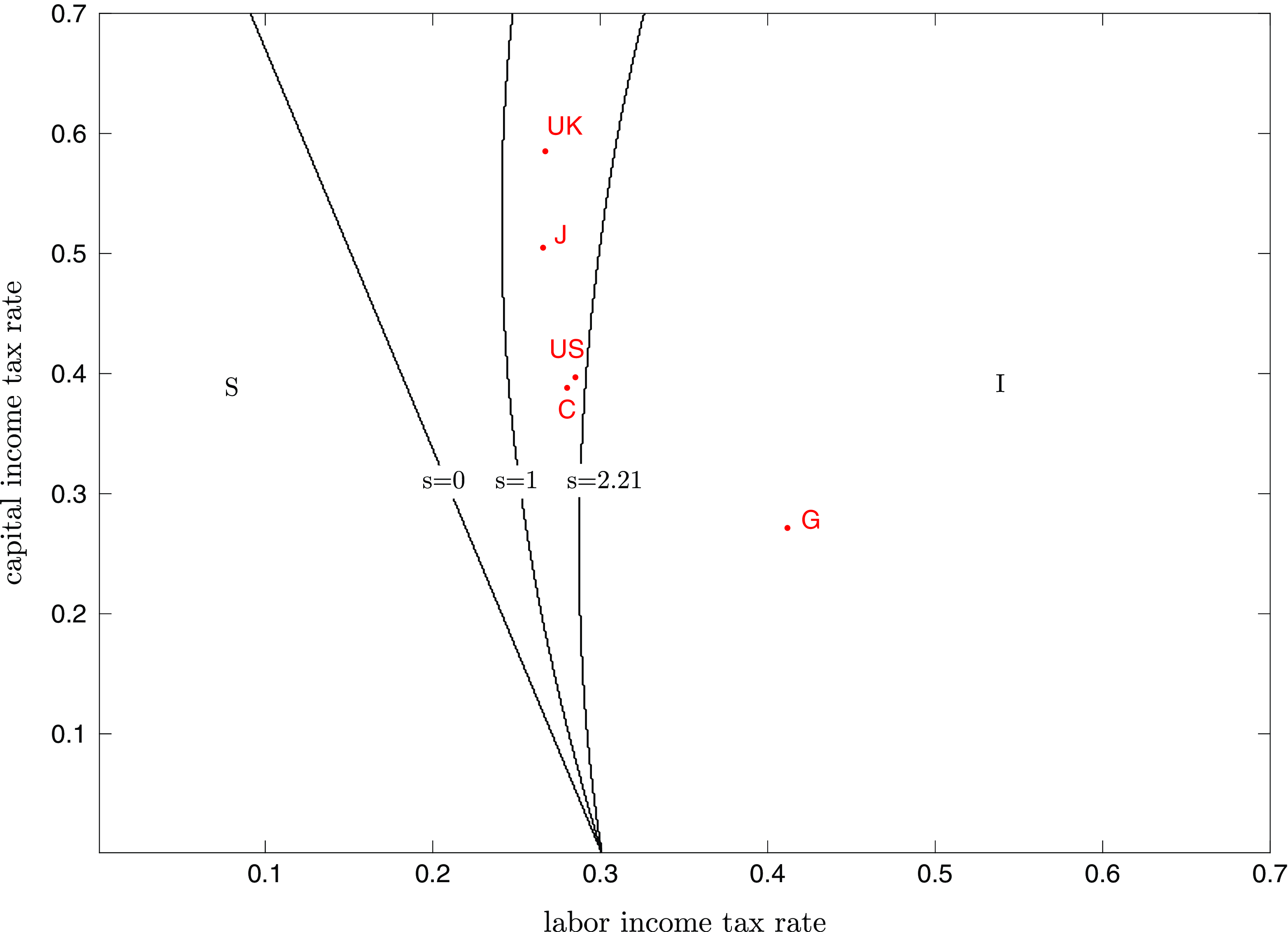
Figure 1. Adjustments of factor income tax rates and (in)stability. S—stability, I—instability. The estimated tax rates are for 1988 and taken from Mendoza et al. (Reference Mendoza, Razin and Tesar1994).
Table 1 (for the 1988 data as shown on the left side of the table) lists the threshold value of
![]() $s$
for each of the five countries (
$s$
for each of the five countries (
![]() $s_{\min }$
), above which the country falls in the stability region. As can be seen from the table, if
$s_{\min }$
), above which the country falls in the stability region. As can be seen from the table, if
![]() $s\gt 2.21$
, then except for Germany, all the other four economies fall in the stability region. The table also makes it clear that this threshold value depends on the levels of the two factor income tax rates. For example, for the case of Germany, its labor income tax rate is high whereas its capital income tax rate is low, and hence a large
$s\gt 2.21$
, then except for Germany, all the other four economies fall in the stability region. The table also makes it clear that this threshold value depends on the levels of the two factor income tax rates. For example, for the case of Germany, its labor income tax rate is high whereas its capital income tax rate is low, and hence a large
![]() $s$
is called for to ensure determinacy.Footnote 7
$s$
is called for to ensure determinacy.Footnote 7
Table 2 compares our results with those in SGU (Reference Schmitt-Grohé and ín Uribe1997), as well as those in Giannisarou (Reference Giannisarou2007) who shows that the possibility of indeterminacy can be largely mitigated if capital income tax in the model of SGU (Reference Schmitt-Grohé and ín Uribe1997) is replaced with consumption expenditure tax, that is, if the labor income and consumption tax rates are adjusted endogenously to balance government budget.
Table 2. Stability properties for different countries
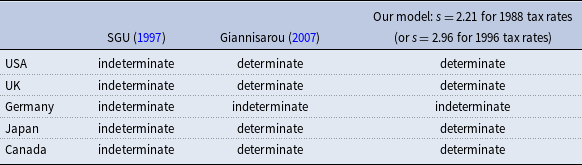
We also extend our analysis using data for the more recent years. The right side of Table 1 lists our results based on the 1996 tax rate estimates, updated by the same authors of Mendoza et al. (Reference Mendoza, Razin and Tesar1994) (available online from the authors). It is evident that the results concerning the threshold value of
![]() $s$
are generally similar to those obtained above using the 1988 tax rates. Our results based on the tax rates for the years 1995–2007 for US and some European countries estimated by Trabandt and Uhlig (Reference Trabandt and Uhlig2011) are broadly consistent: the threshold value is greater than
$s$
are generally similar to those obtained above using the 1988 tax rates. Our results based on the tax rates for the years 1995–2007 for US and some European countries estimated by Trabandt and Uhlig (Reference Trabandt and Uhlig2011) are broadly consistent: the threshold value is greater than
![]() $1$
, while its specific magnitude depends on country specifics and particularly on the levels of their capital and labor income tax rates; for example,
$1$
, while its specific magnitude depends on country specifics and particularly on the levels of their capital and labor income tax rates; for example,
![]() $(\tau ^{l},\tau ^{k},$
$(\tau ^{l},\tau ^{k},$
![]() $s_{\min })$
for USA, UK, Germany, Ireland, Portugal, and Denmark are
$s_{\min })$
for USA, UK, Germany, Ireland, Portugal, and Denmark are
![]() $(0.281,0.364,1.951)$
,
$(0.281,0.364,1.951)$
,
![]() $(0.278,0.456,1.780)$
,
$(0.278,0.456,1.780)$
,
![]() $(0.412,0.233,12.413)$
,
$(0.412,0.233,12.413)$
,
![]() $(0.268,0.207,1.235)$
,
$(0.268,0.207,1.235)$
,
![]() $(0.313,0.234,3.673)$
, and
$(0.313,0.234,3.673)$
, and
![]() $(0.474,0.506,10.091)$
, respectively. Note that for some European countries because of their tax structure and especially high labor income tax rates, the threshhold values of
$(0.474,0.506,10.091)$
, respectively. Note that for some European countries because of their tax structure and especially high labor income tax rates, the threshhold values of
![]() $s$
for them are relatively high.Footnote 8
$s$
for them are relatively high.Footnote 8
3. Concluding remarks
This paper contributes to the debate on the relative taxation of capital versus labor. It overturns a conventional wisdom that leads much research in this literature to advocate for restrictions on government’s ability to adjust factor income tax rates in achieving budget objective in order to avoid nonfundamentals-driven volatility. The main takeaway of our paper is that adjustments in capital and labor income tax rates, if properly designed and implemented, can help achieve the budget objective while at the same time preempting self-fulfilling instability. More specifically, the rate of adjustment in capital income tax rate versus that in labor income tax rate must be chosen properly, and in doing so special attention needs to be paid to the levels of the two tax rates, as well as to deep structural parameters like the elasticities of output with respect to capital and labor.
Acknowledgements
We would like to thank two anonymous referees and an Associate Editor for their helpful comments and suggestions. Xue acknowledges the support by National Science Foundation of China (Project 71988101, 72133004). All remaining errors are our own.







