No CrossRef data available.
Article contents
Commutants and complex symmetry of finite Blaschke product multiplication operator in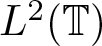 
$L^2(\mathbb{T})$
Part of:
Spaces and algebras of analytic functions
General theory of linear operators
Special classes of linear operators
Published online by Cambridge University Press: 11 January 2024
Abstract
Consider the multiplication operator MB in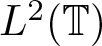 
$L^2(\mathbb{T})$, where the symbol B is a finite Blaschke product. In this article, we characterize the commutant of MB in 
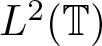$L^2(\mathbb{T})$. As an application of this characterization result, we explicitly determine the class of conjugations commuting with 
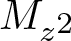$M_{z^2}$ or making 
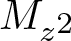$M_{z^2}$ complex symmetric by introducing a new class of conjugations in 
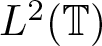$L^2(\mathbb{T})$. Moreover, we analyse their properties while keeping the whole Hardy space, model space and Beurling-type subspaces invariant. Furthermore, we extended our study concerning conjugations in the case of finite Blaschke products.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 261 - 286
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Abkar, A., Cao, G. and Zhu, K., The commutant of some shift operators, Complex Anal. Oper. Theory 14(6), (2020), .CrossRefGoogle Scholar
Bender, C., Fring, A., Günther, U. and Jones, H., Quantum physics with non-Hermitian operators, J. Phys. A: Math. Theor. 45(44), (2012), .Google Scholar
Chattopadhyay, A., Das, S., Pradhan, C. and Sarkar, S., Characterization of C-symmetric Toeplitz operators for a class of conjugations in Hardy spaces, Linear Multilinear Algebra 71(12), (2023), 2026–2048.CrossRefGoogle Scholar
Cima, J.A. Garcia, S.R. and Ross, W.T. and Wogen, W.R., Truncated Toeplitz operators: spatial isomorphism, unitary equivalence, and similarity, Indiana Univ. Math. J. 59(2), (2010), 595–620.CrossRefGoogle Scholar
Cowen, C.C. and Wahl, R.G., Commutants of finite Blaschke product multiplication operators, invariant subspaces of the shift operator. Contemp. Math., Volume 638, pp. (Amer. Math. Soc., Providence, RI, 2015).CrossRefGoogle Scholar
Cowen, C., The commutant of an analytic Toeplitz operator, Trans. Amer. Math. Soc. 239(1), (1978), 1–31.CrossRefGoogle Scholar
Cowen, C., The commutant of an analytic Toeplitz operator, II, Indiana Univ. Math. J. 29(1), (1980), 1–12.CrossRefGoogle Scholar
Cowen, M. and Douglas, R., Complex geometry and operator theory, Acta. Math. 141(3-4), (1978), 187–261.CrossRefGoogle Scholar
Câmara, M.C., Kliś-Garlicka, K. and Ptak, M., Asymmetric truncated Toeplitz operators and conjugations, Filomat 33(12), (2019), 3697–3710.CrossRefGoogle Scholar
Câmara, M.C., Kliś-Garlicka, K., Łanucha, B. and Ptak, M., Conjugations in L 2 and their invariants, Anal. Math. Phys. 10(2), (2020), .CrossRefGoogle Scholar
Câmara, M.C., Kliś-Garlicka, K., Łanucha, B. and Ptak, M., Conjugations in 
$L^2(\mathcal H)$, Integral Equations Operator Theory 92(6), (2020), .CrossRefGoogle Scholar
$L^2(\mathcal H)$, Integral Equations Operator Theory 92(6), (2020), .CrossRefGoogle ScholarDeddens, J. and Wong, T., The commutant of analytic Toeplitz operators, Trans. Amer. Math. Soc. 184(1), (1973), 261–273.CrossRefGoogle Scholar
Douglas, R., Putinar, M. and Wang, K., Reducing subspaces for analytic multipliers of the Bergman space, J. Funct. Anal. 263(6), (2012), 1744–1765.CrossRefGoogle Scholar
Fricain, E. and Mashreghi, J., The theory of H(b) spaces. New Mathematical Monographs, Volume Vol.1(20), (Cambridge University Press, Cambridge, 2016).Google Scholar
Fricain, E. and Mashreghi, J., The theory of H(b) spaces. New Mathematical Monographs, Volume 21, (Cambridge University Press, Cambridge, 2016).Google Scholar
Gallardo-Gutiérrez, E.A. and Partington, J.R., Multiplication by a finite Blaschke product on weighted Bergman spaces: commutant and reducing subspaces, J. Math. Anal. Appl. 515(1), (2022), .CrossRefGoogle Scholar
Garcia, S. R., Mashreghi, J. and Ross, W. T., Introduction to model spaces and their operators. Cambridge Studies in Advanced Mathematics, Volume 148, (Cambridge University Press, Cambridge, 2016).Google Scholar
Garcia, S.R., Prodan, E. and Putinar, M., Mathematical and physical aspects of complex symmetric operators, J. Phys. A 47(35), (2014), 1–54.CrossRefGoogle Scholar
Garcia, S.R. and Putinar, M., Complex symmetric operators and applications, Trans. Amer. Math. Soc. 358(3), (2006), 1285–1315.CrossRefGoogle Scholar
Garcia, S.R. and Putinar, M., Complex symmetric operators and applications. II, Trans. Amer. Math. Soc. 359(8), (2007), 3913–3931.CrossRefGoogle Scholar
Garcia, S.R. and Wogen, W.R., Complex symmetric partial isometries, J. Funct. Anal. 257(4), (2009), 1251–1260.CrossRefGoogle Scholar
Garcia, S.R. and Wogen, W.R., Some new classes of complex symmetric operators, Trans. Amer. Math. Soc. 362(11), (2010), 6065–6077.CrossRefGoogle Scholar
Guo, K. and Huang, H., Multiplication operators on the Bergman space. Lecture Notes in Mathematics, Volume 2145, (Springer, Heidelberg, 2015).Google Scholar
Guo, K., Sun, S., Zheng, D. and Zhong, C., Multiplication operators on the Bergman space via the Hardy space of the bidisk, J. Reine Angew. Math. 628(1), (2009), 129–168.Google Scholar
Khani Robati, B., On the commutant of multiplication operators with analytic polynomial symbols, Bull. Korean Math. Soc. 44(4), (2007), 683–689.CrossRefGoogle Scholar
Khani Robati, B. and Vaezpour, S., On the commutant of operators of multiplication by univalent functions, Proc. Amer. Math. Soc. 129(8), (2001), 2379–2383.CrossRefGoogle Scholar
Ko, E. and Lee, J.E., On complex symmetric Toeplitz operators, J. Math. Anal. Appl. 434(1), (2016), 20–34.CrossRefGoogle Scholar
Martínez-Avendaño, R.A. and Rosenthal, P., An introduction to operators on the Hardy–Hilbert space. Graduate Texts in Mathematics, Volume 237, (Springer, New York, 2007).Google Scholar
Nordgren, E., Reducing subspaces of analytic Toeplitz operators, Duke Math. J. 34(1), (1967), 175–181.CrossRefGoogle Scholar
Partington, J.R., Interpolation, identification, and sampling. London Mathematical Society Monographs, Volume 17 (The Clarendon Press, Oxford University Press, New York, 1997): New Series, .Google Scholar
Radjavi, H. and Rosenthal, P., Invariant subspaces. Ergebnisse der Mathematik und Ihrer Grenzgebiete, Band 77, (Springer-Verlag, New York-Heidelberg, 1973).Google Scholar
Seddighi, K. and Vaezpour, S., Commutant of certain multiplication operators on Hilbert spaces of analytic functions, Studia Math. 133(2), (1999), 121–130.CrossRefGoogle Scholar
Sobrino, L., Elements of Non-Relativistic Quantum Mechanics, (World Scientific Publishing Co. Inc., River Edge, NJ, 1996).CrossRefGoogle Scholar
Stessin, M. and Zhu, K., Reducing subspaces of weighted shift operators, Proc. Amer. Math. Soc. 130(9), (2002), 2631–2639.CrossRefGoogle Scholar
Sz.-Nagy, B., Foias, C., Bercovici, H. and Kérchy, L., Harmonic Analysis of Operators on Hilbert space, Universitext, Volume 2, (Springer, New York, 2010).CrossRefGoogle Scholar
Waleed Noor, S., Complex symmetry of Toeplitz operators with continuous symbols, Arch. Math.(Basel) 109(5), (2017), 455–460.CrossRefGoogle Scholar
Weinberg, S., The Quantum Theory of Fields, Volume I, (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Zhu, K., Reducing subspaces for a class of multiplication operators, J. London Math. Soc. 62(2), (2000), 553–568.CrossRefGoogle Scholar
