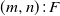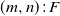1. Introduction
Redundant systems, such as k-out-of-n systems [Reference Amini-Seresht and Balakrishnan2, Reference Balakrishnan, Barmalzan and Haidari4, Reference Ding, Fang and Zhao11] and consecutive k-out-of-n systems [Reference Balakrishnan, Koutras and Milienos5, Reference Chang, Cui and Hwang7, Reference Papastavridis27], play an important role in reliability applications. The finite Markov chain imbedding approach (FMCIA), as the most efficient method for calculating reliabilities of these systems, was first proposed by Fu and Koutras [Reference Fu and Koutras12], and subsequently named as such by Koutras [Reference Koutras20]. FMCIA has since become a very useful tool in the study of distributions of runs and scans, as elaborated in the books of Balakrishnan and Koutras [Reference Balakrishnan and Koutras3] and Fu and Lou [Reference Fu and Lou14]. Through the use of FMCIA, reliabilities of a variety of redundant systems, including (linear or circular) k-out-of-
![]() $n\colon\! F/G$
systems, consecutive k-out-of-
$n\colon\! F/G$
systems, consecutive k-out-of-
![]() $n\colon\! F/G$
systems,
$n\colon\! F/G$
systems,
![]() $(n,f,k)\colon\! F/G$
systems,
$(n,f,k)\colon\! F/G$
systems,
![]() $\langle n,f,k \rangle \colon\! F/G$
systems, m-consecutive k-out-of-
$\langle n,f,k \rangle \colon\! F/G$
systems, m-consecutive k-out-of-
![]() $n\colon\! F/G$
systems, r-within-consecutive k-out-of-
$n\colon\! F/G$
systems, r-within-consecutive k-out-of-
![]() $n\colon\! F/G$
systems, and consecutive k-out-of-
$n\colon\! F/G$
systems, and consecutive k-out-of-
![]() $n\colon\! F/G$
systems with sparse d, have all been discussed in the literature; see [Reference Cui, Xu and Zhao10, Reference Yi, Cui and Gao34], for example. The efficiency of FMCIA for these systems is determined mainly by the sizes of their corresponding state space; see Table 1 for details.
$n\colon\! F/G$
systems with sparse d, have all been discussed in the literature; see [Reference Cui, Xu and Zhao10, Reference Yi, Cui and Gao34], for example. The efficiency of FMCIA for these systems is determined mainly by the sizes of their corresponding state space; see Table 1 for details.
Table 1. Efficiency of FMCIA for different one-dimensional redundant systems.

The redundant systems mentioned above are all one-dimensional systems, that is, the components in these systems are deployed either in a line or in a circle. However, there are also some two-dimensional redundant systems that are used in practice. For example, Salvia and Lasher [Reference Salvia and Lasher28] proposed a
![]() ${k^2}/{n^2}\colon\! F$
system, consisting of
${k^2}/{n^2}\colon\! F$
system, consisting of
![]() $n^2$
components in a square grid of side n, which fails if and only if there exist
$n^2$
components in a square grid of side n, which fails if and only if there exist
![]() $k^2$
failed components in a square grid of side k. Boehme et al. [Reference Boehme, Kossow and Preuss6] generalized this
$k^2$
failed components in a square grid of side k. Boehme et al. [Reference Boehme, Kossow and Preuss6] generalized this
![]() ${k^2}/{n^2}\colon\! F$
system to a linear/circular connected-X-out-of-
${k^2}/{n^2}\colon\! F$
system to a linear/circular connected-X-out-of-
![]() $(m,n)\colon\! F$
lattice system, consisting of mn elements in m rows/circles and n columns/rays, that fails if and only if there exist failed components that form a connected-X. Here, connected-(r, s) means a rectangle with r rows and s columns, and connected-(r, s)-or-(s, r) means a rectangle with r rows and s columns or with s rows and r columns; see [Reference Boehme, Kossow and Preuss6] for pertinent details. In addition, some other two-dimensional redundant systems, such as the k-within-(r, s)-out-of-(m, n) lattice system [Reference Malinowski and Preuss24], connected-
$(m,n)\colon\! F$
lattice system, consisting of mn elements in m rows/circles and n columns/rays, that fails if and only if there exist failed components that form a connected-X. Here, connected-(r, s) means a rectangle with r rows and s columns, and connected-(r, s)-or-(s, r) means a rectangle with r rows and s columns or with s rows and r columns; see [Reference Boehme, Kossow and Preuss6] for pertinent details. In addition, some other two-dimensional redundant systems, such as the k-within-(r, s)-out-of-(m, n) lattice system [Reference Malinowski and Preuss24], connected-
![]() $({r_1},{s_1})$
-or-
$({r_1},{s_1})$
-or-
![]() $({r_2},{s_2})$
-
$({r_2},{s_2})$
-
![]() $\cdots$
-
$\cdots$
-
![]() $({r_k},{s_k})$
-out-of-
$({r_k},{s_k})$
-out-of-
![]() $(m,n)\colon\! F$
lattice system [Reference Yamamoto29], and
$(m,n)\colon\! F$
lattice system [Reference Yamamoto29], and
![]() ${k^d}/{n^d}\colon\! F$
system [Reference Godbole, Potter and Sklar17], have also been studied in the literature.
${k^d}/{n^d}\colon\! F$
system [Reference Godbole, Potter and Sklar17], have also been studied in the literature.
Researchers are naturally interested in the reliability calculation of two-dimensional redundant systems, and methods for this broadly fall into three classes: efficient bounds, recursive algorithms, and FMCIA methods. For example, Salvia and Lasher [Reference Salvia and Lasher28] provided reliability bounds for a
![]() ${k^2}/{n^2}\colon\! F$
system with independent and identically distributed (i.i.d.) components, while Koutras et al. [Reference Koutras, Papadopoulos and Papastavridis21] studied the same problem in a new way without the assumption of identical distribution. Malinowski and Preuss [Reference Malinowski and Preuss24] presented reliability bounds for a linear/circular connected-(r, s)-out-of-
${k^2}/{n^2}\colon\! F$
system with independent and identically distributed (i.i.d.) components, while Koutras et al. [Reference Koutras, Papadopoulos and Papastavridis21] studied the same problem in a new way without the assumption of identical distribution. Malinowski and Preuss [Reference Malinowski and Preuss24] presented reliability bounds for a linear/circular connected-(r, s)-out-of-
![]() $(m,n)\colon\! F$
lattice system. For detailed discussions, interested readers may refer to [Reference Fu and Koutras13, Reference Godbole, Potter and Sklar17, Reference Hsieh and Chen19, Reference Yamamoto and Akiba31, Reference Yamamoto and Miyakawa33].
$(m,n)\colon\! F$
lattice system. For detailed discussions, interested readers may refer to [Reference Fu and Koutras13, Reference Godbole, Potter and Sklar17, Reference Hsieh and Chen19, Reference Yamamoto and Akiba31, Reference Yamamoto and Miyakawa33].
Even though efficient bounds provide useful information concerning the reliabilities of two-dimensional redundant systems, they are not always close enough to the exact reliabilities for specific systems. Moreover, there are many situations wherein exact reliabilities may be needed, such as in system optimization, component importance analysis, component allocation and so on [Reference Zhao, Cui, Zhao and Liu35]. In contrast to efficient bounds, recursive algorithms and FMCIA methods provide exact reliability evaluation for two-dimensional redundant systems. For example, Yamamoto and Miyakawa [Reference Yamamoto and Miyakawa32] proposed a recursive (YM) algorithm for the reliability of a linear connected-(r, s)-out-of-
![]() $(m,n)\colon\! F$
lattice system, and its generalizations to the circular case and to systems with multiple failure modes can be found in [Reference Malinowski and Preuss24, Reference Yamamoto29, Reference Yamamoto and Miyakawa33]. Lin and Zuo [Reference Lin and Zuo23] derived recursive formulas for the reliability of a linear k-within-(r, s)-out-of-
$(m,n)\colon\! F$
lattice system, and its generalizations to the circular case and to systems with multiple failure modes can be found in [Reference Malinowski and Preuss24, Reference Yamamoto29, Reference Yamamoto and Miyakawa33]. Lin and Zuo [Reference Lin and Zuo23] derived recursive formulas for the reliability of a linear k-within-(r, s)-out-of-
![]() $(m,n)\colon\! F$
lattice system, while Akiba and Yamamoto [Reference Akiba and Yamamoto1] studied the same problem for both linear and circular cases. Further discussions can be found in [Reference Habib, Yuge, Al-Seedy and Ammar18, Reference Yamamoto and Akiba30].
$(m,n)\colon\! F$
lattice system, while Akiba and Yamamoto [Reference Akiba and Yamamoto1] studied the same problem for both linear and circular cases. Further discussions can be found in [Reference Habib, Yuge, Al-Seedy and Ammar18, Reference Yamamoto and Akiba30].
FMCIA methods are actually improved versions of recursive methods, as they provide unified explicit forms for different numbers of components, and need less memory and computational time for reliability evaluation. FMCIA also has more diverse applications than just in the study of redundant systems [Reference Fu and Wu15, Reference Fu and Wu16]. Chang and Huang [Reference Chang and Huang8] investigated the reliability of a linear/circular k-within-consecutive-(r, s)-out-of-
![]() $(m,n)\colon\! F$
system using FMCIA, while Zhao et al. [Reference Zhao, Cui, Zhao and Liu35] similarly studied the reliability of a linear connected-(r, s)-out-of-
$(m,n)\colon\! F$
system using FMCIA, while Zhao et al. [Reference Zhao, Cui, Zhao and Liu35] similarly studied the reliability of a linear connected-(r, s)-out-of-
![]() $(m,n)\colon\! F$
system. Zhao et al. [Reference Zhao, Zhao and Xie36] further considered the reliability of a linear two-dimensional linear connected-k system with trinary states. Lin et al. [Reference Lin, Zeng, Zhou, Xu and Ren22] provided a lower bound for the reliability of a linear/circular k-within-consecutive-(r, s)-out-of-
$(m,n)\colon\! F$
system. Zhao et al. [Reference Zhao, Zhao and Xie36] further considered the reliability of a linear two-dimensional linear connected-k system with trinary states. Lin et al. [Reference Lin, Zeng, Zhou, Xu and Ren22] provided a lower bound for the reliability of a linear/circular k-within-consecutive-(r, s)-out-of-
![]() $(m,n)\colon\! F$
system by using FMCIA. Compared to one-dimensional systems, the efficiency of FMCIA for two-dimensional redundant systems is more complex to discuss; see Table 2. Some pertinent discussions for special cases can be found in [Reference Nakamura, Yamamoto and Shinzato25, Reference Nakamura, Yamamoto and Xiao26].
$(m,n)\colon\! F$
system by using FMCIA. Compared to one-dimensional systems, the efficiency of FMCIA for two-dimensional redundant systems is more complex to discuss; see Table 2. Some pertinent discussions for special cases can be found in [Reference Nakamura, Yamamoto and Shinzato25, Reference Nakamura, Yamamoto and Xiao26].
Table 2. Efficiency of FMCIA for different two-dimensional redundant systems.

Even though much work exists on one-dimensional consecutive k-type systems, the study of two-dimensional consecutive k-type systems is rather lacking. As an efficient method for the reliability calculation as stated above, FMCIA contributes significantly; yet, its use in the study of two-dimensional consecutive k-type systems has not been discussed much in the literature. The main problem stems from the fact that FMCIA loses its advantage as a direct method when one tries to save computational time by some implicit definitions of their state spaces. Therefore, in this work we study the reliabilities of linear two-dimensional consecutive k-type systems via FMCIA in a novel way. In fact, the adopted way is reasonable and easier to understand as it is analogous to their one-dimensional counterparts. Compared to existing FMCIA methods, the FMCIA method adopted here can be applied to different types of systems, and it will also be efficient for large systems as well. In practice, the method and results developed here would be useful in diverse problems arising from image analysis, pattern recognition, reliability theory, and minefield detection via remote sensing [Reference Chen and Glaz9].
The rest of this paper proceeds as follows. In Section 2 the reliabilities of several linear two-dimensional consecutive k-type systems, such as the linear connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system, linear l-connected-(k, r)-out-of-
$(m,n)\colon\! F$
system, linear l-connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system without overlapping, and linear l-connected-(k, r)-out-of-
$(m,n)\colon\! F$
system without overlapping, and linear l-connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system with overlapping, are all studied in detail via FMCIA, where (k, r) can be replaced by (k, r)-or-(r, k). In Section 3 some numerical examples are presented to illustrate how the reliabilities of these systems can be calculated from the theoretical results developed in Section 2. Finally, some concluding remarks, indicating possible applications of the methods developed here as well as possible future research, are made in Section 4.
$(m,n)\colon\! F$
system with overlapping, are all studied in detail via FMCIA, where (k, r) can be replaced by (k, r)-or-(r, k). In Section 3 some numerical examples are presented to illustrate how the reliabilities of these systems can be calculated from the theoretical results developed in Section 2. Finally, some concluding remarks, indicating possible applications of the methods developed here as well as possible future research, are made in Section 4.
2. FMCIA for two-dimensional consecutive systems
2.1. Linear connected-(k, r)-out-of-
 $(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system
$(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system
Consider a linear connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system [Reference Boehme, Kossow and Preuss6] that would fail if and only if there exist consecutive
$(m,n)\colon\! F$
system [Reference Boehme, Kossow and Preuss6] that would fail if and only if there exist consecutive
![]() $k\times r$
failed components among its
$k\times r$
failed components among its
![]() $m\times n$
components. As shown in Figure 1, components in the system can be denoted by
$m\times n$
components. As shown in Figure 1, components in the system can be denoted by
![]() ${x_{i,j}}\, (i = 1, \ldots ,m,\, j = 1, \ldots , n)$
according to their line number i and column number j.
${x_{i,j}}\, (i = 1, \ldots ,m,\, j = 1, \ldots , n)$
according to their line number i and column number j.

Figure 1. Labels of components according to their locations in the system.
To obtain the reliability of such a system, we assume that all the components are independent. Suppose the reliability and unreliability of component
![]() ${x_{i,j}}\,(i = 1, \ldots ,m,\, j=1,\ldots,n)$
are
${x_{i,j}}\,(i = 1, \ldots ,m,\, j=1,\ldots,n)$
are
![]() ${p_{i,j}}$
and
${p_{i,j}}$
and
![]() ${q_{i,j}} = 1 - {p_{i,j}}$
, respectively. We then define a Markov chain
${q_{i,j}} = 1 - {p_{i,j}}$
, respectively. We then define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
by adding components of the original system to an empty system column by column, where
$S = {S_W} \cup {S_F}$
by adding components of the original system to an empty system column by column, where
![]() ${S_F} = \{ {s_F}\} $
is a failure state subset and
${S_F} = \{ {s_F}\} $
is a failure state subset and
 \begin{align*}{S_W} &= \big\{ ({i_1}, \ldots ,{i_m})\colon 0 \le {i_1}, \ldots ,{i_m} \le r,\, {i_1} + \cdots + {i_k} \le kr - 1, \ldots , {i_{m - k + 1}} \\& \quad + \cdots + {i_m} \le kr - 1\big\}\\&= \big\{ ({i_1}, \ldots ,{i_m})\colon 0 \le {i_1}, \ldots ,{i_{k - 1}} \le r,\,0 \le {i_k} \le r - {I_{\{ {i_1} + \cdots + {i_{k - 1}} = (k - 1)r\} }}, \\& \quad \ldots , 0 \le {i_m} \le r - {I_{\{ {i_{m - k + 1}} + \cdots + {i_{m - 1}} = (k - 1)r\} }}\big\}\end{align*}
\begin{align*}{S_W} &= \big\{ ({i_1}, \ldots ,{i_m})\colon 0 \le {i_1}, \ldots ,{i_m} \le r,\, {i_1} + \cdots + {i_k} \le kr - 1, \ldots , {i_{m - k + 1}} \\& \quad + \cdots + {i_m} \le kr - 1\big\}\\&= \big\{ ({i_1}, \ldots ,{i_m})\colon 0 \le {i_1}, \ldots ,{i_{k - 1}} \le r,\,0 \le {i_k} \le r - {I_{\{ {i_1} + \cdots + {i_{k - 1}} = (k - 1)r\} }}, \\& \quad \ldots , 0 \le {i_m} \le r - {I_{\{ {i_{m - k + 1}} + \cdots + {i_{m - 1}} = (k - 1)r\} }}\big\}\end{align*}
is a working state subset with
![]() $I_{A}$
being an indicator function such that
$I_{A}$
being an indicator function such that
![]() $I_{A}=1$
if condition A is satisfied and
$I_{A}=1$
if condition A is satisfied and
![]() $I_{A}=0$
otherwise. Here, the only failure state
$I_{A}=0$
otherwise. Here, the only failure state
![]() ${s_F}$
means that there exist consecutive
${s_F}$
means that there exist consecutive
![]() $k \times r$
failed components in the first t columns of components, which is an absorbing state that leads to failure of the system. A working state
$k \times r$
failed components in the first t columns of components, which is an absorbing state that leads to failure of the system. A working state
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
means that in the sth line of the system
$({i_1}, \ldots ,{i_m}) \in {S_W}$
means that in the sth line of the system
![]() $(s = 1, \ldots ,m)$
, components
$(s = 1, \ldots ,m)$
, components
![]() $x_{s,t - {i_s} + 1}, \ldots ,x_{s,t}$
have all failed if
$x_{s,t - {i_s} + 1}, \ldots ,x_{s,t}$
have all failed if
![]() ${i_s} \ne 0$
and component
${i_s} \ne 0$
and component
![]() $x_{s, t - {i_s}}$
is working if
$x_{s, t - {i_s}}$
is working if
![]() ${i_s} \lt \min (t,r)$
, namely,
${i_s} \lt \min (t,r)$
, namely,
![]() $i_s$
is the number of consecutive failed components including component
$i_s$
is the number of consecutive failed components including component
![]() $x_{s,t}$
in the sth line and
$x_{s,t}$
in the sth line and
![]() $(t-r+1)$
th,
$(t-r+1)$
th,
![]() $\ldots,$
tth columns of the system.
$\ldots,$
tth columns of the system.
Note that if we add components to the system one by one instead of column by column, the meaning of a working state
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
will be different. The difference lies in the fact that when component
$({i_1}, \ldots ,{i_m}) \in {S_W}$
will be different. The difference lies in the fact that when component
![]() $x_{w,t}$
is added,
$x_{w,t}$
is added,
![]() $i_s$
is the number of consecutive failed components including component
$i_s$
is the number of consecutive failed components including component
![]() $x_{s,t-1}$
(instead of component
$x_{s,t-1}$
(instead of component
![]() $x_{s,t}$
) in the sth line and
$x_{s,t}$
) in the sth line and
![]() $(t-r+1)$
th,
$(t-r+1)$
th,
![]() $\ldots,$
$\ldots,$
![]() $(t-1)$
th columns (instead of
$(t-1)$
th columns (instead of
![]() $(t-r+1)$
th,
$(t-r+1)$
th,
![]() $\ldots,$
tth columns) of the system if
$\ldots,$
tth columns) of the system if
![]() $w+1 \le s \le m$
. For example, consider a linear connected-(2, 2)-out-of-
$w+1 \le s \le m$
. For example, consider a linear connected-(2, 2)-out-of-
![]() $(3,3)\colon\! F$
system in which components
$(3,3)\colon\! F$
system in which components
![]() $x_{1,2},x_{1,3}, x_{2,1}, x_{3,1}$
are working and all other components have failed, and state changes of the system can be seen in Figure 2 with components being added one by one.
$x_{1,2},x_{1,3}, x_{2,1}, x_{3,1}$
are working and all other components have failed, and state changes of the system can be seen in Figure 2 with components being added one by one.

Figure 2. State changes of a specific linear connected-(2, 2)-out-of-
![]() $(3,3)\colon\! F$
system.
$(3,3)\colon\! F$
system.
For convenience in computation, let us relabel the state
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
as
$({i_1}, \ldots ,{i_m}) \in {S_W}$
as
 \begin{align*}e({i_1}, \ldots ,{i_m}) &= {i_m} + 1 + \sum_{w = 1}^{m - 1} {{I_{\{ {i_w} \ge 1\} }}\sum_{{j_w} = 0}^{{i_w} - 1} {\sum_{{j_{w + 1}} = 0}^r { \cdots \sum_{{j_{w + k - 1}} = 0}^r {\sum_{{j_{w + k}} = 0}^{r - {I_{\{ {j_{w + 1}} + \cdots + {j_{w + k - 1}} = (k - 1)r\} }}} } } } }\\& \quad \cdots \sum_{{j_m} = 0}^{r - {I_{\{ {j_{m - k + 1}} + \cdots + {j_{m - 1}} = (k - 1)r\} }}} 1 ,\end{align*}
\begin{align*}e({i_1}, \ldots ,{i_m}) &= {i_m} + 1 + \sum_{w = 1}^{m - 1} {{I_{\{ {i_w} \ge 1\} }}\sum_{{j_w} = 0}^{{i_w} - 1} {\sum_{{j_{w + 1}} = 0}^r { \cdots \sum_{{j_{w + k - 1}} = 0}^r {\sum_{{j_{w + k}} = 0}^{r - {I_{\{ {j_{w + 1}} + \cdots + {j_{w + k - 1}} = (k - 1)r\} }}} } } } }\\& \quad \cdots \sum_{{j_m} = 0}^{r - {I_{\{ {j_{m - k + 1}} + \cdots + {j_{m - 1}} = (k - 1)r\} }}} 1 ,\end{align*}
and state
![]() ${s_F}$
can be relabeled as
${s_F}$
can be relabeled as
![]() $N + 1$
with N denoting the number of states in subset
$N + 1$
with N denoting the number of states in subset
![]() ${S_W}$
. For example, consider the linear connected-(2, 2)-out-of-
${S_W}$
. For example, consider the linear connected-(2, 2)-out-of-
![]() $(3,3)\colon\! F$
system in Figure 2. Its working state subset should be
$(3,3)\colon\! F$
system in Figure 2. Its working state subset should be
 \begin{align*}{S_W} &= \big\{ ({i_1}, {i_2} ,{i_3})\colon 0 \le {i_1} \le 2,\, 0\le {i_2} \le 2-I_{\{{i_1}=2\}},\, 0\le {i_3} \le 2-I_{\{{i_2}=2\}} \big\} \\&= \big\{ (0,0,0),(0,0,1),(0,0,2),(0,1,0),(0,1,1),(0,1,2),(0,2,0),(0,2,1),\\&\quad\;\;\; (1,0,0),(1,0,1),(1,0,2),(1,1,0),(1,1,1),(1,1,2),(1,2,0),(1,2,1),\\&\quad\;\;\; (2,0,0),(2,0,1),(2,0,2),(2,1,0),(2,1,1),(2,1,2)\big\}=\{1,2,\ldots,22\}.\end{align*}
\begin{align*}{S_W} &= \big\{ ({i_1}, {i_2} ,{i_3})\colon 0 \le {i_1} \le 2,\, 0\le {i_2} \le 2-I_{\{{i_1}=2\}},\, 0\le {i_3} \le 2-I_{\{{i_2}=2\}} \big\} \\&= \big\{ (0,0,0),(0,0,1),(0,0,2),(0,1,0),(0,1,1),(0,1,2),(0,2,0),(0,2,1),\\&\quad\;\;\; (1,0,0),(1,0,1),(1,0,2),(1,1,0),(1,1,1),(1,1,2),(1,2,0),(1,2,1),\\&\quad\;\;\; (2,0,0),(2,0,1),(2,0,2),(2,1,0),(2,1,1),(2,1,2)\big\}=\{1,2,\ldots,22\}.\end{align*}
With all the numbered states now arranged in ascending order, the transition matrices of the Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
can be given as
$\{ Y(t),t = 1, \ldots ,n\} $
can be given as
![]() $\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
for each step
$\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
for each step
![]() $t = 1, \ldots ,n$
, wherein the matrix
$t = 1, \ldots ,n$
, wherein the matrix
is for the transition after component
![]() ${x_{w,t}}$
gets added to the system. Then we can conclude that the elements in
${x_{w,t}}$
gets added to the system. Then we can conclude that the elements in
![]() ${\boldsymbol{A}^w}(t)$
${\boldsymbol{A}^w}(t)$
![]() $ (w = 1, \ldots ,m)$
are all zero, except that
$ (w = 1, \ldots ,m)$
are all zero, except that
![]() $a_{N + 1,N + 1}^{w,t} = 1$
, and for all
$a_{N + 1,N + 1}^{w,t} = 1$
, and for all
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
:
$({i_1}, \ldots ,{i_m}) \in {S_W}$
:
-
(1)
 $ a_{e({i_1}, \ldots ,{i_m}),e(0,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {p_{w,t}}$
,
$ a_{e({i_1}, \ldots ,{i_m}),e(0,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {p_{w,t}}$
,
 $a_{e({i_1}, \ldots ,{i_m}),e(({i_1} + 1) \wedge r,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {q_{w,t}}$
$a_{e({i_1}, \ldots ,{i_m}),e(({i_1} + 1) \wedge r,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {q_{w,t}}$
if
![]() $w = 1$
;
$w = 1$
;
-
(2)
 $ a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},0,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {p_{w,t}} $
if
$ a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},0,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {p_{w,t}} $
if
 $w \ge 2$
;
$w \ge 2$
; -
(3)
 $ a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}} $
if
$ a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}} $
if
 $2 \le w \le k - 1$
or if
$2 \le w \le k - 1$
or if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
;
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
;
-
(4)
 $a_{e({i_1}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
$a_{e({i_1}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
 ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 1$
.
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 1$
.
Note that (1) is due to the fact that failed components in the
![]() $(t - r)$
th column will not contribute to a transition to system failure after components in the tth column are added to the system if there do not exist consecutive
$(t - r)$
th column will not contribute to a transition to system failure after components in the tth column are added to the system if there do not exist consecutive
![]() $k \times r$
failed components in the first
$k \times r$
failed components in the first
![]() $t - 1$
columns of components; (2) is directly the definition of state
$t - 1$
columns of components; (2) is directly the definition of state
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
; and finally, (3) and (4) are due to the fact that a transition to system failure can only be caused by component
$({i_1}, \ldots ,{i_m}) \in {S_W}$
; and finally, (3) and (4) are due to the fact that a transition to system failure can only be caused by component
![]() ${x_{w,t}}$
if
${x_{w,t}}$
if
![]() $w \ge k$
and
$w \ge k$
and
![]() ${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
. Throughout this paper, we use
${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
. Throughout this paper, we use
![]() $a \wedge b$
to denote the smaller of the numbers a, b, and
$a \wedge b$
to denote the smaller of the numbers a, b, and
![]() $a \vee b$
to denote the larger number.
$a \vee b$
to denote the larger number.
With the above discussions on
![]() $\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
$\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
![]() $(t = 1, \ldots ,n)$
, the reliability and unreliability of such a linear connected-(k, r)-out-of-
$(t = 1, \ldots ,n)$
, the reliability and unreliability of such a linear connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system can be given as
$(m,n)\colon\! F$
system can be given as
![]() $R(m,n;\, k,r) = {\boldsymbol{\pi}} \boldsymbol{A}(1) \cdots \boldsymbol{A}(n)\boldsymbol{u}$
and
$R(m,n;\, k,r) = {\boldsymbol{\pi}} \boldsymbol{A}(1) \cdots \boldsymbol{A}(n)\boldsymbol{u}$
and
![]() $\bar R(m,n;\, k,r) = {\boldsymbol{\pi A}}(1) \cdots \boldsymbol{A}(n){\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(m,n;\, k,r) = {\boldsymbol{\pi A}}(1) \cdots \boldsymbol{A}(n){\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
Remark 2.1. Specifically, let us consider a linear connected-(k, r)-or-(r, k)-out-of-
![]() $(m,n)\colon\! F$
system
$(m,n)\colon\! F$
system
![]() $(k \lt r)$
that fails if and only if there exist consecutive
$(k \lt r)$
that fails if and only if there exist consecutive
![]() $k \times r$
or
$k \times r$
or
![]() $r \times k$
failed components in its
$r \times k$
failed components in its
![]() $m \times n$
components. Then its reliability and unreliability can be given readily from the above discussions except that (3) and (4) need to be replaced by
$m \times n$
components. Then its reliability and unreliability can be given readily from the above discussions except that (3) and (4) need to be replaced by
-
(3)
 $a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_1}, \ldots ,{i_m}),e({i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $2 \le w \le k - 1$
or if
$2 \le w \le k - 1$
or if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
-
(4)
 $a_{e({i_1}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
$a_{e({i_1}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} + {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,}}_{{i_w} \ge k- 1\}}\ge 1$
.
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} + {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,}}_{{i_w} \ge k- 1\}}\ge 1$
.
This is because for a linear connected-(k, r)-or-(r, k)-out-of-
![]() $(m,n)\colon\! F$
system, a transition to system failure can be caused by component
$(m,n)\colon\! F$
system, a transition to system failure can be caused by component
![]() ${x_{w,t}}$
not only if
${x_{w,t}}$
not only if
![]() $w \ge k$
and
$w \ge k$
and
![]() ${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, but also when
${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, but also when
![]() $w \ge r$
and
$w \ge r$
and
![]() ${i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1$
. Note that we use the same state space here for brevity since states with the pattern
${i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1$
. Note that we use the same state space here for brevity since states with the pattern
could also be in a working state right after any component in lines
![]() $s + 1, \ldots ,s + r$
is added in.
$s + 1, \ldots ,s + r$
is added in.
Remark 2.2. To reduce the memory and computational time needed for the reliability calculation of a linear connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system, we can also define a Markov chain
$(m,n)\colon\! F$
system, we can also define a Markov chain
![]() $\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
$\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
![]() $\tilde S = {\tilde S_W} \cup {S_F}$
, where a working state
$\tilde S = {\tilde S_W} \cup {S_F}$
, where a working state
![]() $({i_k}, \ldots ,{i_m})$
in the subset
$({i_k}, \ldots ,{i_m})$
in the subset
 \begin{align*}{{\tilde S}_W} &= \big\{ ({i_k}, \ldots ,{i_m})\colon 0 \le {i_k}, \ldots ,{i_m} \le r - 1,\, ({i_{l + 2}} \vee \cdots \vee {i_{(l + k) \wedge m}}){I_{\{ {i_{l + 1}} \lt {i_l}\} }} \le {i_{l + 1}} \\& \quad\; \text{with}\ l = k, \ldots ,m - 2\big\}\end{align*}
\begin{align*}{{\tilde S}_W} &= \big\{ ({i_k}, \ldots ,{i_m})\colon 0 \le {i_k}, \ldots ,{i_m} \le r - 1,\, ({i_{l + 2}} \vee \cdots \vee {i_{(l + k) \wedge m}}){I_{\{ {i_{l + 1}} \lt {i_l}\} }} \le {i_{l + 1}} \\& \quad\; \text{with}\ l = k, \ldots ,m - 2\big\}\end{align*}
means that for
![]() $s = k, \ldots ,m$
, components
$s = k, \ldots ,m$
, components
![]() ${x_{i,j}}$
${x_{i,j}}$
![]() $(i = s - k + 1, \ldots ,s,\, j = t - {i_s} + 1, \ldots ,t)$
have all failed if
$(i = s - k + 1, \ldots ,s,\, j = t - {i_s} + 1, \ldots ,t)$
have all failed if
![]() ${i_s} \ne 0$
and components
${i_s} \ne 0$
and components
![]() ${x_{i,t - {i_s}}}$
${x_{i,t - {i_s}}}$
![]() $(i = s - k + 1, \ldots ,s)$
have not all failed if
$(i = s - k + 1, \ldots ,s)$
have not all failed if
![]() ${i_s} \lt t$
. Note that
${i_s} \lt t$
. Note that
![]() ${i_{l + 1}} \lt {i_l}$
${i_{l + 1}} \lt {i_l}$
![]() $(l = k, \ldots ,m - 2)$
means component
$(l = k, \ldots ,m - 2)$
means component
![]() ${x_{l + 1,t - {i_{l + 1}}}}$
is working, which leads to the fact that
${x_{l + 1,t - {i_{l + 1}}}}$
is working, which leads to the fact that
![]() ${i_{l + 2}} \le {i_{l + 1}}, \ldots ,{i_{(l + k) \wedge m}} \le {i_{l + 1}}$
, namely,
${i_{l + 2}} \le {i_{l + 1}}, \ldots ,{i_{(l + k) \wedge m}} \le {i_{l + 1}}$
, namely,
![]() $({i_{l + 2}} \vee \cdots \vee {i_{(l + k) \wedge m}}){I_{\{ {i_{l + 1}} \lt {i_l}\} }} \le {i_{l + 1}}$
.
$({i_{l + 2}} \vee \cdots \vee {i_{(l + k) \wedge m}}){I_{\{ {i_{l + 1}} \lt {i_l}\} }} \le {i_{l + 1}}$
.
With all the states relabeled and arranged similarly, the transition matrices of the Markov chain
![]() $\{ \tilde Y(t),t = 1, \ldots ,n\} $
can be given as
$\{ \tilde Y(t),t = 1, \ldots ,n\} $
can be given as
for each step
![]() $t = 1, \ldots ,n$
, whose elements are all zero, except that
$t = 1, \ldots ,n$
, whose elements are all zero, except that
![]() $\tilde a_{\tilde N + 1,\tilde N + 1}^t = 1$
, and for all
$\tilde a_{\tilde N + 1,\tilde N + 1}^t = 1$
, and for all
![]() $({i_k}, \ldots ,{i_m}) \in {\tilde S_W}$
,
$({i_k}, \ldots ,{i_m}) \in {\tilde S_W}$
,
-
(1)
 $\tilde a_{\tilde e({i_k}, \ldots ,{i_m}),\tilde e( ({i_k} + 1){j_k}, \ldots ,({i_m} + 1){j_m})}^t = {p_{{j_k}, \ldots ,{j_m};t}}$
for all
$\tilde a_{\tilde e({i_k}, \ldots ,{i_m}),\tilde e( ({i_k} + 1){j_k}, \ldots ,({i_m} + 1){j_m})}^t = {p_{{j_k}, \ldots ,{j_m};t}}$
for all
 $({j_k}, \ldots ,{j_m}) \in \Omega $
with
$({j_k}, \ldots ,{j_m}) \in \Omega $
with
![]() $I_{\{ {i_k} + {j_k} \le r - 1,\ldots ,{i_m} + {j_m} \le r - 1\} } = 1$
;
$I_{\{ {i_k} + {j_k} \le r - 1,\ldots ,{i_m} + {j_m} \le r - 1\} } = 1$
;
-
(2)
 $\tilde a_{\tilde e({i_k}, \ldots ,{i_m}),\tilde N + 1}^t = \sum_{({j_k}, \ldots ,{j_m}) \in \Omega ,\, {I_{\{ {i_k} + {j_k} \le r - 1, \ldots ,{i_m} + {j_m} \le r - 1\} }} = 0} {{p_{{j_k}, \ldots ,{j_m};t}}} $
.
$\tilde a_{\tilde e({i_k}, \ldots ,{i_m}),\tilde N + 1}^t = \sum_{({j_k}, \ldots ,{j_m}) \in \Omega ,\, {I_{\{ {i_k} + {j_k} \le r - 1, \ldots ,{i_m} + {j_m} \le r - 1\} }} = 0} {{p_{{j_k}, \ldots ,{j_m};t}}} $
.
Here
 \begin{align*} {p_{{j_k}, \ldots ,{j_m};t}} = \sum_{{l_1}, \ldots ,{l_m} \in \{ 0,1\} ,{l_1} \times \cdots \times {l_k} = {j_k}, \ldots ,{l_{m - k + 1}} \times \cdots \times {l_m} = {j_m}} {\prod_{w = 1}^m {p_{w,t}^{1 - {l_w}}q_{w,t}^{{l_w}}} } \end{align*}
\begin{align*} {p_{{j_k}, \ldots ,{j_m};t}} = \sum_{{l_1}, \ldots ,{l_m} \in \{ 0,1\} ,{l_1} \times \cdots \times {l_k} = {j_k}, \ldots ,{l_{m - k + 1}} \times \cdots \times {l_m} = {j_m}} {\prod_{w = 1}^m {p_{w,t}^{1 - {l_w}}q_{w,t}^{{l_w}}} } \end{align*}
is the probability that for
![]() $s = k, \ldots ,m$
, components
$s = k, \ldots ,m$
, components
![]() ${x_{s - k + 1,t}}, \ldots ,{x_{s,t}}$
have all failed (if
${x_{s - k + 1,t}}, \ldots ,{x_{s,t}}$
have all failed (if
![]() ${j_s} = 1$
) or have not all failed (if
${j_s} = 1$
) or have not all failed (if
![]() ${j_s} = 0$
). Note that this method can also be applied to a linear l-connected-(k, r)-out-of-
${j_s} = 0$
). Note that this method can also be applied to a linear l-connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system without/with overlapping. The related discussions are omitted here for brevity. Compared to the main FMCIA method, the FMCIA here needs less memory and computational time for the reliability evaluation, but it cannot be applied to systems such as the linear connected-(k, r) or (r, k)-out-of-
$(m,n)\colon\! F$
system without/with overlapping. The related discussions are omitted here for brevity. Compared to the main FMCIA method, the FMCIA here needs less memory and computational time for the reliability evaluation, but it cannot be applied to systems such as the linear connected-(k, r) or (r, k)-out-of-
![]() $(m,n)\colon\! F$
system and linear l-connected-(k, r) or (r, k)-out-of-
$(m,n)\colon\! F$
system and linear l-connected-(k, r) or (r, k)-out-of-
![]() $(m,n)\colon\! F$
system without/with overlapping.
$(m,n)\colon\! F$
system without/with overlapping.
2.2. Linear l-connected-(k, r)-out-of-
 $(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system without overlapping
$(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system without overlapping
Consider a linear l-connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system without overlapping that would fail if and only if there exist l blocks of consecutive
$(m,n)\colon\! F$
system without overlapping that would fail if and only if there exist l blocks of consecutive
![]() $k \times r$
failed components without overlapping in its
$k \times r$
failed components without overlapping in its
![]() $m \times n$
components. Here, without overlapping means that the l blocks do not have any shared components. Note that in this work, blocks are searched in a given order of components, namely,
$m \times n$
components. Here, without overlapping means that the l blocks do not have any shared components. Note that in this work, blocks are searched in a given order of components, namely,
![]() $x_{1,1},\ldots, x_{m,1},x_{1,2},\ldots,x_{m,2},\ldots,x_{1,n},\ldots,x_{m,n}$
. In contrast to the one-dimensional case, there may be some missed blocks in the two-dimensional case, which is omitted for brevity. With the same assumptions as in Section 2.1, let us define a Markov chain
$x_{1,1},\ldots, x_{m,1},x_{1,2},\ldots,x_{m,2},\ldots,x_{1,n},\ldots,x_{m,n}$
. In contrast to the one-dimensional case, there may be some missed blocks in the two-dimensional case, which is omitted for brevity. With the same assumptions as in Section 2.1, let us define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, where
$S = {S_W} \cup {S_F}$
, where
![]() ${S_F} = \{ {s_F}\} $
is a failure state subset and
${S_F} = \{ {s_F}\} $
is a failure state subset and
 \begin{align*}{S_W} &= \big\{ ({i_0}, \ldots ,{i_m})\colon 0 \le {i_0} \le l - 1,\, 0 \le {i_1}, \ldots ,{i_m} \le r,{i_1} + \cdots + {i_k} \le kr - 1, \\&\quad\;\;\; \ldots , {i_{m - k + 1}} + \cdots + {i_m} \le kr - 1\big\}\\&= \big\{ ({i_0}, \ldots ,{i_m})\colon 0 \le {i_0} \le l - 1,\, 0 \le {i_1}, \ldots ,{i_{k - 1}} \le r,\\& \quad\;\;\; 0 \le {i_k} \le r -{I_{\{ {i_1} + \cdots + {i_{k - 1}} = (k - 1)r\} }},\ldots ,0 \le {i_m} \le r - {I_{\{ {i_{m - k + 1}} + \cdots + {i_{m - 1}} = (k - 1)r\} }}\big\}\end{align*}
\begin{align*}{S_W} &= \big\{ ({i_0}, \ldots ,{i_m})\colon 0 \le {i_0} \le l - 1,\, 0 \le {i_1}, \ldots ,{i_m} \le r,{i_1} + \cdots + {i_k} \le kr - 1, \\&\quad\;\;\; \ldots , {i_{m - k + 1}} + \cdots + {i_m} \le kr - 1\big\}\\&= \big\{ ({i_0}, \ldots ,{i_m})\colon 0 \le {i_0} \le l - 1,\, 0 \le {i_1}, \ldots ,{i_{k - 1}} \le r,\\& \quad\;\;\; 0 \le {i_k} \le r -{I_{\{ {i_1} + \cdots + {i_{k - 1}} = (k - 1)r\} }},\ldots ,0 \le {i_m} \le r - {I_{\{ {i_{m - k + 1}} + \cdots + {i_{m - 1}} = (k - 1)r\} }}\big\}\end{align*}
is a working state subset. Here, the only failure state
![]() ${s_F}$
means that there exist l blocks of consecutive
${s_F}$
means that there exist l blocks of consecutive
![]() $k \times r$
failed components without overlapping in the first t columns of components, which is an absorbing state that leads to failure of the system. A working state
$k \times r$
failed components without overlapping in the first t columns of components, which is an absorbing state that leads to failure of the system. A working state
![]() $({i_0}, \ldots ,{i_m}) \in {S_W}$
means that there exist
$({i_0}, \ldots ,{i_m}) \in {S_W}$
means that there exist
![]() ${i_0}$
blocks of consecutive
${i_0}$
blocks of consecutive
![]() $k \times r$
failed components without overlapping in the first t columns of components, and except that, in the sth line of the system
$k \times r$
failed components without overlapping in the first t columns of components, and except that, in the sth line of the system
![]() $(s = 1, \ldots ,m)$
, components
$(s = 1, \ldots ,m)$
, components
![]() $x_{s, t - {i_s} + 1}, \ldots ,x_{s,t}$
have all failed if
$x_{s, t - {i_s} + 1}, \ldots ,x_{s,t}$
have all failed if
![]() ${i_s} \ne 0$
and component
${i_s} \ne 0$
and component
![]() $x_{s, t - {i_s}}$
is working if
$x_{s, t - {i_s}}$
is working if
![]() ${i_s} \lt \min (t,r)$
.
${i_s} \lt \min (t,r)$
.
For ease of computation, let us relabel the state
![]() $({i_0}, \ldots ,{i_m}) \in {S_W}$
as
$({i_0}, \ldots ,{i_m}) \in {S_W}$
as
 \begin{align*}e({i_0}, \ldots ,{i_m})& = {i_m} + 1 + \sum_{w = 0}^{m - 1} {{I_{\{ {i_w} \ge 1\} }}\sum_{{j_w} = 0}^{{i_w} - 1} {\sum_{{j_{w + 1}} = 0}^r { \cdots \sum_{{j_{w + k - 1}} = 0}^r {\sum_{{j_{w + k}} = 0}^{r - {I_{\{ {j_{w + 1}} + \cdots + {j_{w + k - 1}} = (k - 1)r\} }}} } }}}\\&\quad \cdots \sum_{{j_m} = 0}^{r - {I_{\{ {j_{m - k + 1}} + \cdots + {j_{m - 1}} = (k - 1)r\} } } } 1 ,\end{align*}
\begin{align*}e({i_0}, \ldots ,{i_m})& = {i_m} + 1 + \sum_{w = 0}^{m - 1} {{I_{\{ {i_w} \ge 1\} }}\sum_{{j_w} = 0}^{{i_w} - 1} {\sum_{{j_{w + 1}} = 0}^r { \cdots \sum_{{j_{w + k - 1}} = 0}^r {\sum_{{j_{w + k}} = 0}^{r - {I_{\{ {j_{w + 1}} + \cdots + {j_{w + k - 1}} = (k - 1)r\} }}} } }}}\\&\quad \cdots \sum_{{j_m} = 0}^{r - {I_{\{ {j_{m - k + 1}} + \cdots + {j_{m - 1}} = (k - 1)r\} } } } 1 ,\end{align*}
and state
![]() ${s_F}$
can be relabeled as
${s_F}$
can be relabeled as
![]() $N + 1$
with N denoting the number of states in subset
$N + 1$
with N denoting the number of states in subset
![]() ${S_W}$
. With all the numbered states now arranged in ascending order, the transition matrices of the Markov chain
${S_W}$
. With all the numbered states now arranged in ascending order, the transition matrices of the Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
can be given as
$\{ Y(t),t = 1, \ldots ,n\} $
can be given as
![]() $\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
for each step
$\boldsymbol{A}(t) = {\boldsymbol{A}^1}(t) \cdots {\boldsymbol{A}^m}(t)$
for each step
![]() $t = 1, \ldots ,n$
, wherein the matrix
$t = 1, \ldots ,n$
, wherein the matrix
is for the transition after component
![]() ${x_{w,t}}$
is added to the system. Then we can conclude that the elements in
${x_{w,t}}$
is added to the system. Then we can conclude that the elements in
![]() ${\boldsymbol{A}^w}(t)$
${\boldsymbol{A}^w}(t)$
![]() $(w = 1, \ldots ,m)$
are all zero, except that
$(w = 1, \ldots ,m)$
are all zero, except that
![]() $a_{N + 1,N + 1}^{w,t} = 1$
, and for all
$a_{N + 1,N + 1}^{w,t} = 1$
, and for all
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
,
$({i_1}, \ldots ,{i_m}) \in {S_W}$
,
-
(1)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0},0,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {p_{w,t}}$
,
$a_{e({i_0}, \ldots ,{i_m}),e({i_0},0,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {p_{w,t}}$
,
![]() $a_{e({i_0}, \ldots ,{i_m}),e({i_0},({i_1} + 1) \wedge r,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0},({i_1} + 1) \wedge r,{i_2} \wedge (r - 1), \ldots ,{i_m} \wedge (r - 1))}^{w,t} = {q_{w,t}}$
if
![]() $w = 1$
;
$w = 1$
;
-
(2)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},0,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {p_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},0,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {p_{w,t}}$
if
 $w \ge 2$
;
$w \ge 2$
; -
(3)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $2 \le w \le k - 1$
or if
$2 \le w \le k - 1$
or if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
;
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
;
-
(4)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},\underbrace {0, \ldots ,0}_k,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},\underbrace {0, \ldots ,0}_k,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() $I_{\{ {i_0} \ne l - 1,\, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}} = 1$
;
$I_{\{ {i_0} \ne l - 1,\, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}} = 1$
;
-
(5)
 $a_{e({i_0}, \ldots ,{i_m}),N+1}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),N+1}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
 ${I_{\{ {i_0} = l - 1,\, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 1$
.
${I_{\{ {i_0} = l - 1,\, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 1$
.
Note that (1) is due to the fact that failed components in the
![]() $(t - r)$
th column will not contribute to a transition to system failure after components in the tth column are added to the system if there do not exist l blocks of consecutive
$(t - r)$
th column will not contribute to a transition to system failure after components in the tth column are added to the system if there do not exist l blocks of consecutive
![]() $k \times r$
failed components without overlapping in the first
$k \times r$
failed components without overlapping in the first
![]() $t - 1$
columns of components; (2) is similar to its counterpart in Section 2.1; and finally, (3)–(5) are due to the fact that a block of consecutive
$t - 1$
columns of components; (2) is similar to its counterpart in Section 2.1; and finally, (3)–(5) are due to the fact that a block of consecutive
![]() $k \times r$
failed components can be caused by component
$k \times r$
failed components can be caused by component
![]() ${x_{w,t}}$
only if
${x_{w,t}}$
only if
![]() $w \ge k$
and
$w \ge k$
and
![]() ${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, which leads to system failure only when
${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, which leads to system failure only when
![]() ${i_0} = l - 1$
. Note that the pattern
${i_0} = l - 1$
. Note that the pattern
in (4) is due to the fact that the required l blocks do not overlap.
Remark 2.3. Let us specifically consider a linear l-connected-(k, r)-or-(r, k)-out-of-
![]() $(m,n)\colon\! F$
system without overlapping (
$(m,n)\colon\! F$
system without overlapping (
![]() $k \lt r$
) that fails if and only if there exist l blocks of consecutive
$k \lt r$
) that fails if and only if there exist l blocks of consecutive
![]() $k \times r$
or
$k \times r$
or
![]() $r \times k$
failed components without overlapping in its
$r \times k$
failed components without overlapping in its
![]() $m \times n$
components. Then its reliability and unreliability can be given readily from the above except that (3)–(5) need to be replaced by
$m \times n$
components. Then its reliability and unreliability can be given readily from the above except that (3)–(5) need to be replaced by
-
(3)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $2 \le w \le k - 1$
or if
$2 \le w \le k - 1$
or if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
-
(4)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},\underbrace {0, \ldots ,0}_k,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},\underbrace {0, \ldots ,0}_k,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() $I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= 1$
;
$I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= 1$
;
-
(5)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - r}},\underbrace {0, \ldots ,0}_r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - r}},\underbrace {0, \ldots ,0}_r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge r$
and
$w \ge r$
and
 ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
,
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
,
![]() ${I_{\{ {i_0} \ne l - 1, \, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
${I_{\{ {i_0} \ne l - 1, \, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
-
(6)
 $a_{e({i_0}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() $({I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} + I_{\{ w\ge r, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,i_w \ge k - 1\} }){I_{\{ {i_0} = l - 1\} }} \ge 1$
.
$({I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} + I_{\{ w\ge r, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,i_w \ge k - 1\} }){I_{\{ {i_0} = l - 1\} }} \ge 1$
.
This is so because, for a linear l-connected-(k, r)-or-(r, k)-out-of-
![]() $(m,n)\colon\! F$
system (
$(m,n)\colon\! F$
system (
![]() $k \lt r$
) without overlapping, a block of consecutive
$k \lt r$
) without overlapping, a block of consecutive
![]() $k \times r$
or
$k \times r$
or
![]() $r \times k$
failed components can be caused by component
$r \times k$
failed components can be caused by component
![]() ${x_{w,t}}$
not only if
${x_{w,t}}$
not only if
![]() $w \ge k$
and
$w \ge k$
and
![]() ${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, but also when
${i_{w - k + 1}} + \cdots + {i_w} = kr - 1$
, but also when
![]() $w \ge r$
and
$w \ge r$
and
![]() ${i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k$
,
${i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k$
,
![]() ${i_w} = k - 1$
, which leads to system failure only when
${i_w} = k - 1$
, which leads to system failure only when
![]() ${i_0} = l - 1$
. To avoid overlapping, each block with consecutive
${i_0} = l - 1$
. To avoid overlapping, each block with consecutive
![]() $k \times r$
or
$k \times r$
or
![]() $r \times k$
failed components will not contribute to the next block. For a special case that a block of consecutive
$r \times k$
failed components will not contribute to the next block. For a special case that a block of consecutive
![]() $k \times r$
failed components and a block of consecutive
$k \times r$
failed components and a block of consecutive
![]() $r \times k$
components are caused by failure of component
$r \times k$
components are caused by failure of component
![]() ${x_{w,t}}$
at the same time, only one of them needs to be dealt with to avoid overlapping, which should be the former one since
${x_{w,t}}$
at the same time, only one of them needs to be dealt with to avoid overlapping, which should be the former one since
![]() $k \lt r$
and the pattern
$k \lt r$
and the pattern
in (2) has fewer zeros than the pattern
in (3).
2.3. Linear l-connected-(k, r)-out-of-
 $(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system with overlapping
$(\boldsymbol{m},\boldsymbol{n})\colon\! \boldsymbol{F}$
system with overlapping
Consider a linear l-connected-(k, r)-out-of-
![]() $(m,n)\colon\! F$
system with overlapping that would fail if and only if there exist l blocks of consecutive
$(m,n)\colon\! F$
system with overlapping that would fail if and only if there exist l blocks of consecutive
![]() $k \times r$
failed components with overlapping. Here, overlapping means that the l blocks are allowed to have some (at most
$k \times r$
failed components with overlapping. Here, overlapping means that the l blocks are allowed to have some (at most
![]() $kr - 1$
) shared components. With the same assumptions as in Section 2.1, its reliability and unreliability can be given in the same manner as in Section 2.2, except that (4) needs to be replaced by
$kr - 1$
) shared components. With the same assumptions as in Section 2.1, its reliability and unreliability can be given in the same manner as in Section 2.2, except that (4) needs to be replaced by
-
(4)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() $I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} =kr- 1\} } = 1$
.
$I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} =kr- 1\} } = 1$
.
This is because if overlapping is allowed between blocks, only the first component in a previous block needs to be dealt with to avoid generating a state with the pattern
which is not in the working subset
![]() ${S_W}$
.
${S_W}$
.
Remark 2.4. Next, let us consider a linear l-connected-(k, r)-or-(r, k)-out-of-
![]() $(m,n)\colon\! F$
system with overlapping (
$(m,n)\colon\! F$
system with overlapping (
![]() $k \lt r$
) that fails if and only if there exist l blocks of consecutive
$k \lt r$
) that fails if and only if there exist l blocks of consecutive
![]() $k \times r$
or
$k \times r$
or
![]() $r \times k$
failed components with overlapping. The derivation of its reliability is exactly the same as in Section 2.2 except that (3)–(5) need to be replaced by
$r \times k$
failed components with overlapping. The derivation of its reliability is exactly the same as in Section 2.2 except that (3)–(5) need to be replaced by
-
(3)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $2 \le w \le k - 1$
or if
$2 \le w \le k - 1$
or if
 $w \ge k$
and
$w \ge k$
and
![]() ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = {I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
-
(4)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and
![]() $I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= 1$
,
$I_{\{ {i_0} \ne l - 1, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= 1$
,
![]() ${I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
${I_{\{ w \ge r,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 0$
;
-
(5)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 1,{i_1}, \ldots ,{i_{w - 1}},({i_w} + 1) \wedge r,{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge r$
and
$w \ge r$
and
 ${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
,
${I_{\{ {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }} = 0$
,
![]() ${I_{\{ {i_0} \ne l - 1,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
${I_{\{ {i_0} \ne l - 1,{i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
-
(6)
 $a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 2,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),e({i_0} + 2,{i_1}, \ldots ,{i_{w - k}},r - 1,\underbrace {r, \ldots ,r}_{k - 1},{i_{w + 1}}, \ldots ,{i_m})}^{w,t} = {q_{w,t}}$
if
 $w \ge r$
and
$w \ge r$
and
![]() $I_{\{ {i_0} \le l - 3, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= {I_{\{ w \ge r, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
$I_{\{ {i_0} \le l - 3, \, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\}}= {I_{\{ w \ge r, {i_{w - r + 1}} \ge k, \ldots ,{i_{w - 1}} \ge k,{i_w} \ge k - 1\} }} = 1$
;
-
(7)
 $a_{e({i_0}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
$a_{e({i_0}, \ldots ,{i_m}),N + 1}^{w,t} = {q_{w,t}}$
if
 $w \ge k$
and
$w \ge k$
and  \begin{align*}& I_{\{ {i_0} = l - 1, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }\phantom{0000000000} \\& \! + I_{\{ w \ge r, {i_{w - r + 1}} \ge k, \ldots , {i_{w - 1}} \ge k, {i_w} \ge k - 1\}} \bigl(I_{\{ {i_0} = l - 1\} } + {I_{\{ {i_0} = l - 2, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }}\bigr) \ge 1.\phantom{000000000} \end{align*}
\begin{align*}& I_{\{ {i_0} = l - 1, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }\phantom{0000000000} \\& \! + I_{\{ w \ge r, {i_{w - r + 1}} \ge k, \ldots , {i_{w - 1}} \ge k, {i_w} \ge k - 1\}} \bigl(I_{\{ {i_0} = l - 1\} } + {I_{\{ {i_0} = l - 2, {i_{w - k + 1}} + \cdots + {i_w} = kr - 1\} }}\bigr) \ge 1.\phantom{000000000} \end{align*}
Note that if overlapping is allowed between blocks, only the first component in a previous
![]() $k \times r$
block needs to be dealt with for its following blocks, and no component in a previous
$k \times r$
block needs to be dealt with for its following blocks, and no component in a previous
![]() $r \times k$
block needs to be dealt with. This is because the former case will cause a state not in the working subset
$r \times k$
block needs to be dealt with. This is because the former case will cause a state not in the working subset
![]() ${S_W}$
, while the latter case does not. Moreover, for a special case when a block of consecutive
${S_W}$
, while the latter case does not. Moreover, for a special case when a block of consecutive
![]() $k \times r$
failed components and a block of consecutive
$k \times r$
failed components and a block of consecutive
![]() $r \times k$
components are caused by the failure of component
$r \times k$
components are caused by the failure of component
![]() ${x_{w,t}}$
at the same time, both blocks would contribute to the immediate or forthcoming system failure.
${x_{w,t}}$
at the same time, both blocks would contribute to the immediate or forthcoming system failure.
3. Illustrative examples
In this section, nine examples of linear two-dimensional consecutive systems are presented to illustrate the results established in Section 2, with Examples 3.1 and 3.2 being for Section 2.1, Examples 3.3 and 3.4 for Section 2.2, Examples 3.5 and 3.6 for Section 2.3, and Examples 3.7–3.9 for Remark 2.2.
Example 3.1. Consider a linear connected-(2,3)-out-of-
![]() $(3,n)\colon\! F$
system that would fail if and only if there exist consecutive
$(3,n)\colon\! F$
system that would fail if and only if there exist consecutive
![]() $2 \times 3$
failed components among its
$2 \times 3$
failed components among its
![]() $3 \times n$
components. We now assume that all the components are i.i.d. with the same reliability p and unreliability
$3 \times n$
components. We now assume that all the components are i.i.d. with the same reliability p and unreliability
![]() $q = 1 - p$
. According to the discussion in Section 2.1, we define a Markov chain
$q = 1 - p$
. According to the discussion in Section 2.1, we define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, where
$S = {S_W} \cup {S_F}$
, where
![]() ${S_F} = \{ {s_F}\} $
and
${S_F} = \{ {s_F}\} $
and
 \begin{align*}{S_W}& = \big\{ ({i_1},{i_2},{i_3})\colon 0 \le {i_1},{i_2},{i_3} \le 3, \, {i_1} + {i_2} \le 5, \, {i_2} + {i_3} \le 5\big\} \\&= \big\{ ({i_1},{i_2},{i_3})\colon 0 \le {i_1} \le 3, \, 0 \le {i_2} \le 3 - {I_{\{ {i_1} = 3\} }},\, 0 \le {i_3} \le 3 - {I_{\{ {i_2} = 3\} }}\big\} \\&= \big\{ (0,0,0),(0,0,1),(0,0,2),(0,0,3),(0,1,0),(0,1,1),(0,1,2),(0,1,3), \\&\quad\;\;\; (0,2,0),(0,2,1),(0,2,2),(0,2,3),(0,3,0),(0,3,1),(0,3,2), \\&\quad \;\;\;(1,0,0),(1,0,1),(1,0,2),(1,0,3),(1,1,0),(1,1,1),(1,1,2),(1,1,3), \\&\quad \;\;\;(1,2,0),(1,2,1),(1,2,2),(1,2,3),(1,3,0),(1,3,1),(1,3,2), \\&\quad \;\;\;(2,0,0),(2,0,1),(2,0,2),(2,0,3),(2,1,0),(2,1,1),(2,1,2),(2,1,3), \\&\quad \;\;\;(2,2,0),(2,2,1),(2,2,2),(2,2,3),(2,3,0),(2,3,1),(2,3,2),\\&\quad \;\;\;(3,0,0),(3,0,1),(3,0,2),(3,0,3),(3,1,0),(3,1,1),(3,1,2),(3,1,3), \\&\quad \;\;\;(3,2,0),(3,2,1),(3,2,2),(3,2,3)\big\}\\& \,:\!= \{ 1, \ldots ,57\} .\end{align*}
\begin{align*}{S_W}& = \big\{ ({i_1},{i_2},{i_3})\colon 0 \le {i_1},{i_2},{i_3} \le 3, \, {i_1} + {i_2} \le 5, \, {i_2} + {i_3} \le 5\big\} \\&= \big\{ ({i_1},{i_2},{i_3})\colon 0 \le {i_1} \le 3, \, 0 \le {i_2} \le 3 - {I_{\{ {i_1} = 3\} }},\, 0 \le {i_3} \le 3 - {I_{\{ {i_2} = 3\} }}\big\} \\&= \big\{ (0,0,0),(0,0,1),(0,0,2),(0,0,3),(0,1,0),(0,1,1),(0,1,2),(0,1,3), \\&\quad\;\;\; (0,2,0),(0,2,1),(0,2,2),(0,2,3),(0,3,0),(0,3,1),(0,3,2), \\&\quad \;\;\;(1,0,0),(1,0,1),(1,0,2),(1,0,3),(1,1,0),(1,1,1),(1,1,2),(1,1,3), \\&\quad \;\;\;(1,2,0),(1,2,1),(1,2,2),(1,2,3),(1,3,0),(1,3,1),(1,3,2), \\&\quad \;\;\;(2,0,0),(2,0,1),(2,0,2),(2,0,3),(2,1,0),(2,1,1),(2,1,2),(2,1,3), \\&\quad \;\;\;(2,2,0),(2,2,1),(2,2,2),(2,2,3),(2,3,0),(2,3,1),(2,3,2),\\&\quad \;\;\;(3,0,0),(3,0,1),(3,0,2),(3,0,3),(3,1,0),(3,1,1),(3,1,2),(3,1,3), \\&\quad \;\;\;(3,2,0),(3,2,1),(3,2,2),(3,2,3)\big\}\\& \,:\!= \{ 1, \ldots ,57\} .\end{align*}
Then its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, where the elements of
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, where the elements of
are all zero, except that
![]() $a_{58,58}^w = 1$
, and for all
$a_{58,58}^w = 1$
, and for all
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
,
$({i_1}, \ldots ,{i_m}) \in {S_W}$
,
-
(1)
 $a_{e({i_1},{i_2},{i_3}),e(0,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = p$
,
$a_{e({i_1},{i_2},{i_3}),e(0,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = p$
,
 $a_{e({i_1},{i_2},{i_3}),e(({i_1} + 1) \wedge 3,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = q$
;
$a_{e({i_1},{i_2},{i_3}),e(({i_1} + 1) \wedge 3,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = q$
; -
(2)
 $a_{e({i_1},{i_2},{i_3}),e({i_1},0,{i_3})}^2 = a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},0)}^3 = p$
;
$a_{e({i_1},{i_2},{i_3}),e({i_1},0,{i_3})}^2 = a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},0)}^3 = p$
; -
(3)
 $a_{({i_1},{i_2},{i_3}),e({i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
$a_{({i_1},{i_2},{i_3}),e({i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
 $({i_1},{i_2}) \ne (3,2)$
,
$({i_1},{i_2}) \ne (3,2)$
,
![]() $a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
![]() $({i_2},{i_3}) \ne (3,2)$
;
$({i_2},{i_3}) \ne (3,2)$
;
-
(4)
 $a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
$a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
 $({i_1},{i_2}) = (3,2)$
,
$({i_1},{i_2}) = (3,2)$
,
 $a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
$a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
 $({i_2},{i_3}) = (3,2)$
.
$({i_2},{i_3}) = (3,2)$
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
As the sum of reliability and unreliability of any system is 1, in the following discussion we find the results only for the unreliability, from which the reliability can then be readily found. For example, with
![]() $n = 3$
, the unreliability of a linear connected-(2,3)-out-of-
$n = 3$
, the unreliability of a linear connected-(2,3)-out-of-
![]() $(3,3)\colon\! F$
system can be given as
$(3,3)\colon\! F$
system can be given as
![]() $\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 2{q^6} - {q^9}$
, which coincides with the identity (by definition) that
$\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 2{q^6} - {q^9}$
, which coincides with the identity (by definition) that
with
![]() ${A_1}$
being the event that components
${A_1}$
being the event that components
![]() ${x_{1,1}},{x_{1,2}},{x_{1,3}},{x_{2,1}},{x_{2,2}},{x_{2,3}}$
have all failed, and
${x_{1,1}},{x_{1,2}},{x_{1,3}},{x_{2,1}},{x_{2,2}},{x_{2,3}}$
have all failed, and
![]() ${A_2}$
being the event that components
${A_2}$
being the event that components
![]() ${x_{2,1}},{x_{2,2}},{x_{2,3}},{x_{3,1}},{x_{3,2}},{x_{3,3}}$
have all failed.
${x_{2,1}},{x_{2,2}},{x_{2,3}},{x_{3,1}},{x_{3,2}},{x_{3,3}}$
have all failed.
Similarly, with
![]() $n = 4$
, the unreliability of a connected-(2,3)-out-of-
$n = 4$
, the unreliability of a connected-(2,3)-out-of-
![]() $(3,3)\colon\! F$
system can be given as
$(3,3)\colon\! F$
system can be given as
![]() $\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^6} - 2{q^8} - 2{q^9} - 2{q^{10}} + 4{q^{11}} - {q^{12}},$
which coincides with the identity (by definition) that
$\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^6} - 2{q^8} - 2{q^9} - 2{q^{10}} + 4{q^{11}} - {q^{12}},$
which coincides with the identity (by definition) that
![]() $\bar R(4) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
$\bar R(4) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
![]() ${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 3.
${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 3.

Figure 3. Events
![]() ${A_1},{A_2},{A_3},{A_4}$
for Example 3.1.
${A_1},{A_2},{A_3},{A_4}$
for Example 3.1.
Example 3.2. Consider a linear connected-(2,3)-or-(3,2)-out-of-
![]() $(3,n)\colon\! F$
system that would fail if and only if there exist consecutive
$(3,n)\colon\! F$
system that would fail if and only if there exist consecutive
![]() $2 \times 3$
or
$2 \times 3$
or
![]() $3 \times 2$
failed components among its
$3 \times 2$
failed components among its
![]() $3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.1, we can define a Markov chain
$3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.1, we can define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, the same as in Example 3.1. Its transition matrix can be given as
$S = {S_W} \cup {S_F}$
, the same as in Example 3.1. Its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as in Example 3.1, except that (3) and (4) need to be replaced by
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as in Example 3.1, except that (3) and (4) need to be replaced by
-
(3)
 $a_{({i_1},{i_2},{i_3}),e({i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
$a_{({i_1},{i_2},{i_3}),e({i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
 $({i_1},{i_2}) \ne (3,2)$
,
$({i_1},{i_2}) \ne (3,2)$
,
 $a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_1},{i_2},{i_3}),e({i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
 $({i_2},{i_3}) \ne $
$({i_2},{i_3}) \ne $
(3,2) and
![]() ${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
-
(4)
 $a_{e({i_1},{i_2},{i_3}),58}^2 = q$
if
$a_{e({i_1},{i_2},{i_3}),58}^2 = q$
if
 $({i_1},{i_2}) = (3,2)$
,
$({i_1},{i_2}) = (3,2)$
,
 $a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
$a_{e({i_1},{i_2},{i_3}),58}^3 = q$
if
 $({i_2},{i_3}) = (3,2)$
or
$({i_2},{i_3}) = (3,2)$
or
![]() ${I_{\{ {i_1} \ge 2,{i_2} \ge 2, }}_{{i_3} \ge 1\}} = 1$
.
${I_{\{ {i_1} \ge 2,{i_2} \ge 2, }}_{{i_3} \ge 1\}} = 1$
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 2$
, the unreliability of a connected-(2,3) or (3,2)-out-of-
$n = 2$
, the unreliability of a connected-(2,3) or (3,2)-out-of-
![]() $(3,2)\colon\! F$
system can be given as
$(3,2)\colon\! F$
system can be given as
![]() $\bar R(2) = {\boldsymbol{\pi }}{\boldsymbol{A}^2}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^6}$
, which coincides with the case that the system fails only when all of its components fail.
$\bar R(2) = {\boldsymbol{\pi }}{\boldsymbol{A}^2}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^6}$
, which coincides with the case that the system fails only when all of its components fail.
Similarly, with
![]() $n = 3$
, the unreliability of a linear connected-(2,3) or (3,2)-out-of-
$n = 3$
, the unreliability of a linear connected-(2,3) or (3,2)-out-of-
![]() $(3,3)\colon\! F$
system can be given as
$(3,3)\colon\! F$
system can be given as
![]() $\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^6} - 4{q^8} + {q^9}$
, which coincides with the identity (by definition) that
$\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^6} - 4{q^8} + {q^9}$
, which coincides with the identity (by definition) that
![]() $\bar R(3) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
$\bar R(3) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
![]() ${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 4.
${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 4.

Figure 4. Events
![]() ${A_1},{A_2},{A_3},{A_4}$
for Example 3.2.
${A_1},{A_2},{A_3},{A_4}$
for Example 3.2.
Example 3.3. Consider a linear 2-connected-(2,3)-out-of-
![]() $(3,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
$(3,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
![]() $2 \times 3$
failed components without overlapping among its
$2 \times 3$
failed components without overlapping among its
![]() $3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.2, we can define a Markov chain
$3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.2, we can define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, where
$S = {S_W} \cup {S_F}$
, where
![]() ${S_F} = \{ {s_F}\} $
and
${S_F} = \{ {s_F}\} $
and
 \begin{align*}{S_W}& = \{ ({i_0},{i_1},{i_2},{i_3})\colon 0 \le {i_0} \le 1, \, 0 \le {i_1},{i_2},{i_3} \le 3, \, {i_1} + {i_2} \le 5, \, {i_2} + {i_3} \le 5\} \\&= \{ ({i_0},{i_1},{i_2},{i_3})\colon 0 \le {i_0} \le 1, \, 0 \le {i_1} \le 3, \, 0 \le {i_2} \le 3 - {I_{\{ {i_1} = 3\} }},\, 0 \le {i_3} \le 3 - {I_{\{ {i_2} = 3\} }}\} \\&= \{ (0,0,0,0),(0,0,0,1),(0,0,0,2),(0,0,0,3),(0,0,1,0),(0,0,1,1),(0,0,1,2),(0,0,1,3), \\&\quad \;\;\; (0,0,2,0),(0,0,2,1),(0,0,2,2),(0,0,2,3),(0,0,3,0),(0,0,3,1),(0,0,3,2), \\&\quad \;\;\;(0,1,0,0),(0,1,0,1),(0,1,0,2),(0,1,0,3),(0,1,1,0),(0,1,1,1),(0,1,1,2),(0,1,1,3), \\&\quad \;\;\;(0,1,2,0),(0,1,2,1),(0,1,2,2),(0,1,2,3),(0,1,3,0),(0,1,3,1),(0,1,3,2), \\&\quad \;\;\;(0,2,0,0),(0,2,0,1),(0,2,0,2),(0,2,0,3),(0,2,1,0),(0,2,1,1),(0,2,1,2),(0,2,1,3), \\&\quad \;\;\;(0,2,2,0),(0,2,2,1),(0,2,2,2),(0,2,2,3),(0,2,3,0),(0,2,3,1),(0,2,3,2),\\&\quad \;\;\;(0,3,0,0),(0,3,0,1),(0,3,0,2),(0,3,0,3),(0,3,1,0),(0,3,1,1),(0,3,1,2),(0,3,1,3), \\&\quad \;\;\;(0,3,2,0),(0,3,2,1),(0,3,2,2),(0,3,2,3),\\&\quad \;\;\;(1,0,0,0),(1,0,0,1),(1,0,0,2),(1,0,0,3),(1,0,1,0),(1,0,1,1),(1,0,1,2),(1,0,1,3),\\&\quad \;\;\;(1,0,2,0),(1,0,2,1),(1,0,2,2),(1,0,2,3),(1,0,3,0),(1,0,3,1),(1,0,3,2), \\&\quad \;\;\;(1,1,0,0),(1,1,0,1),(1,1,0,2),(1,1,0,3),(1,1,1,0),(1,1,1,1),(1,1,1,2),(1,1,1,3), \\&\quad \;\;\;(1,1,2,0),(1,1,2,1),(1,1,2,2),(1,1,2,3),(1,1,3,0),(1,1,3,1),(1,1,3,2), \\&\quad \;\;\;(1,2,0,0),(1,2,0,1),(1,2,0,2),(1,2,0,3),(1,2,1,0),(1,2,1,1),(1,2,1,2),(1,2,1,3), \\&\quad \;\;\;(1,2,2,0),(1,2,2,1),(1,2,2,2),(1,2,2,3),(1,2,3,0),(1,2,3,1),(1,2,3,2), \\&\quad \;\;\;(1,3,0,0),(1,3,0,1),(1,3,0,2),(1,3,0,3),(1,3,1,0),(1,3,1,1),(1,3,1,2),(1,3,1,3), \\&\quad \;\;\;(1,3,2,0),(1,3,2,1),(1,3,2,2),(1,3,2,3)\} \\& \,:\!= \{ 1, \ldots ,114\} .\end{align*}
\begin{align*}{S_W}& = \{ ({i_0},{i_1},{i_2},{i_3})\colon 0 \le {i_0} \le 1, \, 0 \le {i_1},{i_2},{i_3} \le 3, \, {i_1} + {i_2} \le 5, \, {i_2} + {i_3} \le 5\} \\&= \{ ({i_0},{i_1},{i_2},{i_3})\colon 0 \le {i_0} \le 1, \, 0 \le {i_1} \le 3, \, 0 \le {i_2} \le 3 - {I_{\{ {i_1} = 3\} }},\, 0 \le {i_3} \le 3 - {I_{\{ {i_2} = 3\} }}\} \\&= \{ (0,0,0,0),(0,0,0,1),(0,0,0,2),(0,0,0,3),(0,0,1,0),(0,0,1,1),(0,0,1,2),(0,0,1,3), \\&\quad \;\;\; (0,0,2,0),(0,0,2,1),(0,0,2,2),(0,0,2,3),(0,0,3,0),(0,0,3,1),(0,0,3,2), \\&\quad \;\;\;(0,1,0,0),(0,1,0,1),(0,1,0,2),(0,1,0,3),(0,1,1,0),(0,1,1,1),(0,1,1,2),(0,1,1,3), \\&\quad \;\;\;(0,1,2,0),(0,1,2,1),(0,1,2,2),(0,1,2,3),(0,1,3,0),(0,1,3,1),(0,1,3,2), \\&\quad \;\;\;(0,2,0,0),(0,2,0,1),(0,2,0,2),(0,2,0,3),(0,2,1,0),(0,2,1,1),(0,2,1,2),(0,2,1,3), \\&\quad \;\;\;(0,2,2,0),(0,2,2,1),(0,2,2,2),(0,2,2,3),(0,2,3,0),(0,2,3,1),(0,2,3,2),\\&\quad \;\;\;(0,3,0,0),(0,3,0,1),(0,3,0,2),(0,3,0,3),(0,3,1,0),(0,3,1,1),(0,3,1,2),(0,3,1,3), \\&\quad \;\;\;(0,3,2,0),(0,3,2,1),(0,3,2,2),(0,3,2,3),\\&\quad \;\;\;(1,0,0,0),(1,0,0,1),(1,0,0,2),(1,0,0,3),(1,0,1,0),(1,0,1,1),(1,0,1,2),(1,0,1,3),\\&\quad \;\;\;(1,0,2,0),(1,0,2,1),(1,0,2,2),(1,0,2,3),(1,0,3,0),(1,0,3,1),(1,0,3,2), \\&\quad \;\;\;(1,1,0,0),(1,1,0,1),(1,1,0,2),(1,1,0,3),(1,1,1,0),(1,1,1,1),(1,1,1,2),(1,1,1,3), \\&\quad \;\;\;(1,1,2,0),(1,1,2,1),(1,1,2,2),(1,1,2,3),(1,1,3,0),(1,1,3,1),(1,1,3,2), \\&\quad \;\;\;(1,2,0,0),(1,2,0,1),(1,2,0,2),(1,2,0,3),(1,2,1,0),(1,2,1,1),(1,2,1,2),(1,2,1,3), \\&\quad \;\;\;(1,2,2,0),(1,2,2,1),(1,2,2,2),(1,2,2,3),(1,2,3,0),(1,2,3,1),(1,2,3,2), \\&\quad \;\;\;(1,3,0,0),(1,3,0,1),(1,3,0,2),(1,3,0,3),(1,3,1,0),(1,3,1,1),(1,3,1,2),(1,3,1,3), \\&\quad \;\;\;(1,3,2,0),(1,3,2,1),(1,3,2,2),(1,3,2,3)\} \\& \,:\!= \{ 1, \ldots ,114\} .\end{align*}
Then its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, where the elements of
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, where the elements of
are all zero, except that
![]() $a_{115, 115}^w = 1$
, and for all
$a_{115, 115}^w = 1$
, and for all
![]() $({i_1}, \ldots ,{i_m}) \in {S_W}$
,
$({i_1}, \ldots ,{i_m}) \in {S_W}$
,
-
(1)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},0,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = p$
,
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},0,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = p$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},({i_1} + 1) \wedge 3,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = q$
;
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},({i_1} + 1) \wedge 3,{i_2} \wedge 2,{i_3} \wedge 2)}^1 = q$
; -
(2)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},0,{i_3})}^2 = a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},0)}^3 = p$
;
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},0,{i_3})}^2 = a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},0)}^3 = p$
; -
(3)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
 $({i_1},{i_2}) \ne (3,2)$
,
$({i_1},{i_2}) \ne (3,2)$
,
![]() $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
![]() $({i_2},{i_3}) \ne (3,2)$
;
$({i_2},{i_3}) \ne (3,2)$
;
-
(4)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,{i_3})}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (0,3,2)$
,
$({i_0},{i_1},{i_2}) = (0,3,2)$
,
![]() $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},0,0)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},0,0)}^3 = q$
if
![]() $({i_0},{i_2},{i_3}) = (0,3,2)$
;
$({i_0},{i_2},{i_3}) = (0,3,2)$
;
-
(5)
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (1,3,2)$
,
$({i_0},{i_1},{i_2}) = (1,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
 $({i_0},{i_2},{i_3}) = (1,3,2)$
.
$({i_0},{i_2},{i_3}) = (1,3,2)$
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 6$
, the unreliability of a linear 2-connected-(2,3)-out-of-
$n = 6$
, the unreliability of a linear 2-connected-(2,3)-out-of-
![]() $(3,6)\colon\! F$
system without overlapping can be given as
$(3,6)\colon\! F$
system without overlapping can be given as
![]() $\bar R(6) = {\boldsymbol{\pi }}{\boldsymbol{A}^6}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^{12}} - 4{q^{15}} + {q^{18}}$
, which coincides with the identity (by definition) that
$\bar R(6) = {\boldsymbol{\pi }}{\boldsymbol{A}^6}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^{12}} - 4{q^{15}} + {q^{18}}$
, which coincides with the identity (by definition) that
![]() $\bar R(6) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
$\bar R(6) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
with the events
![]() ${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 5.
${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 5.

Figure 5. Events
![]() ${A_1},{A_2},{A_3},{A_4}$
for Example 3.3.
${A_1},{A_2},{A_3},{A_4}$
for Example 3.3.
Example 3.4. Consider a linear 2-connected-(2,3)-or-(3,2)-out-of-
![]() $(3,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
$(3,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
![]() $2 \times 3$
or
$2 \times 3$
or
![]() $3 \times 2$
failed components without overlapping among its
$3 \times 2$
failed components without overlapping among its
![]() $3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.2, we can define a Markov chain
$3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.2, we can define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Its transition matrix can be given as
$S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as in Example 3.3 except that (3)–(5) need to be replaced by
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as in Example 3.3 except that (3)–(5) need to be replaced by
-
(3)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
 $({i_1},{i_2}) \ne (3,2)$
,
$({i_1},{i_2}) \ne (3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
![]() $({i_2},{i_3}) \ne (3,2)$
,
$({i_2},{i_3}) \ne (3,2)$
,
![]() ${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
-
(4)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,{i_3})}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (0,3,2)$
,
$({i_0},{i_1},{i_2}) = (0,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},0,0)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},0,0)}^3 = q$
if
![]() $({i_0},{i_2},{i_3}) = (0,3,2)$
;
$({i_0},{i_2},{i_3}) = (0,3,2)$
;
-
(5)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,0)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,0,0,0)}^3 = q$
if
 $({i_0},{i_2},{i_3}) \ne (0,3,2)$
,
$({i_0},{i_2},{i_3}) \ne (0,3,2)$
,
 ${I_{\{ {i_0} = 0,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
;
${I_{\{ {i_0} = 0,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
; -
(6)
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (1,3,2)$
,
$({i_0},{i_1},{i_2}) = (1,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
 $({i_0},{i_2},{i_3}) = (1,3,2)$
or
$({i_0},{i_2},{i_3}) = (1,3,2)$
or
![]() ${I_{\{ {i_0} = 1,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
.
${I_{\{ {i_0} = 1,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
.

Figure 6. Events
![]() ${A_1}, \ldots ,{A_7}$
for Example 3.4.
${A_1}, \ldots ,{A_7}$
for Example 3.4.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 4$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
$n = 4$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
![]() $(3,4)\colon\! F$
system without overlapping can be given as
$(3,4)\colon\! F$
system without overlapping can be given as
![]() $\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^{12}}$
, which coincides with the fact that the system fails only when all of its components fail.
$\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^{12}}$
, which coincides with the fact that the system fails only when all of its components fail.
Similarly, with
![]() $n = 5$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
$n = 5$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
![]() $(3,5)\colon\! F$
system without overlapping can be given as
$(3,5)\colon\! F$
system without overlapping can be given as
![]() $\bar R(5) = {\boldsymbol{\pi }}{\boldsymbol{A}^5}{\boldsymbol{\bar{\boldsymbol{u}}}} = 7{q^{12}} - 8{q^{14}} + 2{q^{15}}$
, which coincides with the identity (by definition) that
$\bar R(5) = {\boldsymbol{\pi }}{\boldsymbol{A}^5}{\boldsymbol{\bar{\boldsymbol{u}}}} = 7{q^{12}} - 8{q^{14}} + 2{q^{15}}$
, which coincides with the identity (by definition) that
![]() $\bar R(5) = P({A_1} \cup \cdots \cup {A_7})$
with the events
$\bar R(5) = P({A_1} \cup \cdots \cup {A_7})$
with the events
![]() ${A_1}, \ldots ,{A_7}$
, as shown in Figure 6.
${A_1}, \ldots ,{A_7}$
, as shown in Figure 6.
Example 3.5. Consider a linear 2-connected-(2,3)-out-of-
![]() $(3,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
$(3,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
![]() $2 \times 3$
failed components with overlapping among its
$2 \times 3$
failed components with overlapping among its
![]() $3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.3, we can define a Markov chain
$3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.3, we can define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Then its transition matrix can be given as
$S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Then its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as Example 3.3, except that (4) needs to be replaced by
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, which is the same as Example 3.3, except that (4) needs to be replaced by
-
(4)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,2,3,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,2,3,{i_3})}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (0,3,2)$
,
$({i_0},{i_1},{i_2}) = (0,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},2,3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},2,3)}^3 = q$
if
![]() $({i_0},{i_2},{i_3}) = (0,3,2)$
.
$({i_0},{i_2},{i_3}) = (0,3,2)$
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 3$
, the unreliability of a linear 2-connected-(2,3) or (3,2)-out-of-
$n = 3$
, the unreliability of a linear 2-connected-(2,3) or (3,2)-out-of-
![]() $(3,3)\colon\! F$
system with overlapping can be given as
$(3,3)\colon\! F$
system with overlapping can be given as
![]() $\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^9}$
, which coincides with the fact that the system would fail only when all of its components fail.
$\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = {q^9}$
, which coincides with the fact that the system would fail only when all of its components fail.
Similarly, with
![]() $n = 4$
, the unreliability of a linear 2-connected-(2,3)-out-of-
$n = 4$
, the unreliability of a linear 2-connected-(2,3)-out-of-
![]() $(3,n)\colon\! F$
system with overlapping can be given as
$(3,n)\colon\! F$
system with overlapping can be given as
![]() $\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = 2{q^8} + 2{q^9} + 2{q^{10}} - 8{q^{11}} + 3{q^{12}}$
, which coincides with the identity (by definition) that
$\bar R(4) = {\boldsymbol{\pi }}{\boldsymbol{A}^4}{\boldsymbol{\bar{\boldsymbol{u}}}} = 2{q^8} + 2{q^9} + 2{q^{10}} - 8{q^{11}} + 3{q^{12}}$
, which coincides with the identity (by definition) that
![]() $\bar R(4) = P({A_1} \cup \cdots \cup {A_6})$
with the events
$\bar R(4) = P({A_1} \cup \cdots \cup {A_6})$
with the events
![]() ${A_1}, \ldots ,{A_6}$
, as shown in Figure 7.
${A_1}, \ldots ,{A_6}$
, as shown in Figure 7.

Figure 7. Events
![]() ${A_1}, \ldots ,{A_6}$
for Example 3.5.
${A_1}, \ldots ,{A_6}$
for Example 3.5.
Example 3.6. Consider a linear 2-connected-(2,3)-or-(3,2)-out-of-
![]() $(3,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
$(3,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
![]() $2 \times 3$
or
$2 \times 3$
or
![]() $3 \times 2$
failed components with overlapping among its
$3 \times 2$
failed components with overlapping among its
![]() $3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.3, we can define a Markov chain
$3 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Section 2.3, we can define a Markov chain
![]() $\{ Y(t),t = 1, \ldots ,n\} $
with state space
$\{ Y(t),t = 1, \ldots ,n\} $
with state space
![]() $S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Then its transition matrix can be given as
$S = {S_W} \cup {S_F}$
, the same as in Example 3.3. Then its transition matrix can be given as
![]() $\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, the same as in Example 3.3, except that (3)–(5) need to be replaced by
$\boldsymbol{A} = {\boldsymbol{A}^1}{\boldsymbol{A}^2}{\boldsymbol{A}^3}$
, the same as in Example 3.3, except that (3)–(5) need to be replaced by
-
(3)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},({i_2} + 1) \wedge 3,{i_3})}^2 = q$
if
 $({i_1},{i_2}) \ne (3,2)$
,
$({i_1},{i_2}) \ne (3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0},{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
![]() $({i_2},{i_3}) \ne (3,2)$
,
$({i_2},{i_3}) \ne (3,2)$
,
![]() ${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
${I_{\{ {i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 0$
;
-
(4)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,2,3,{i_3})}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,2,3,{i_3})}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (0,3,2)$
,
$({i_0},{i_1},{i_2}) = (0,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},2,3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},2,3)}^3 = q$
if
![]() $({i_0},{i_2},{i_3}) = (0,3,2)$
,
$({i_0},{i_2},{i_3}) = (0,3,2)$
,
![]() ${i_1} \le 1$
;
${i_1} \le 1$
;
-
(5)
 $a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});e({i_0} + 1,{i_1},{i_2},({i_3} + 1) \wedge 3)}^3 = q$
if
 $({i_0},{i_2},{i_3}) \ne (0,3,2)$
,
$({i_0},{i_2},{i_3}) \ne (0,3,2)$
,
 ${I_{\{ {i_0} = 0,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
;
${I_{\{ {i_0} = 0,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
; -
(6)
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^2 = q$
if
 $({i_0},{i_1},{i_2}) = (1,3,2)$
,
$({i_0},{i_1},{i_2}) = (1,3,2)$
,
 $a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
$a_{e({i_0},{i_1},{i_2},{i_3});115}^3 = q$
if
 $({i_0},{i_2},{i_3}) = (1,3,2)$
or
$({i_0},{i_2},{i_3}) = (1,3,2)$
or
![]() ${I_{\{ {i_0} = 1,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
or
${I_{\{ {i_0} = 1,{i_1} \ge 2,{i_2} \ge 2,{i_3} \ge 1\} }} = 1$
or
![]() $({i_0},{i_1},{i_2},{i_3}) = (0,2,3,2)$
.
$({i_0},{i_1},{i_2},{i_3}) = (0,2,3,2)$
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{\boldsymbol{A}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 3$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
$n = 3$
, the unreliability of a linear 2-connected-(2,3)-or-(3,2)-out-of-
![]() $(3,3)\colon\! F$
system without overlapping can be given as
$(3,3)\colon\! F$
system without overlapping can be given as
![]() $\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^8} - 3{q^9}$
, which coincides with the identity (by definition) that
$\bar R(3) = {\boldsymbol{\pi }}{\boldsymbol{A}^3}{\boldsymbol{\bar{\boldsymbol{u}}}} = 4{q^8} - 3{q^9}$
, which coincides with the identity (by definition) that
![]() $\bar R(3) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
, with the events
$\bar R(3) = P({A_1} \cup {A_2} \cup {A_3} \cup {A_4})$
, with the events
![]() ${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 8.
${A_1},{A_2},{A_3},{A_4}$
, as shown in Figure 8.

Figure 8. Events
![]() ${A_1},{A_2},{A_3},{A_4}$
for Example 3.6.
${A_1},{A_2},{A_3},{A_4}$
for Example 3.6.
The above examples are all presented by the main FMCIA method discussed in Section 2. To reduce the memory and computational time needed for the reliability calculation, the FMCIA method in Remark 2.2 is utilized for the systems considered in Examples 3.7–3.9.
Example 3.7. Consider a linear connected-(5,5)-out-of-
![]() $(9,n)\colon\! F$
system that would fail if and only if there exist consecutive
$(9,n)\colon\! F$
system that would fail if and only if there exist consecutive
![]() $5 \times 5$
failed components among its
$5 \times 5$
failed components among its
![]() $9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
$9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
![]() $\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
$\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
![]() $\tilde S = {\tilde S_W} \cup {S_F}$
, where
$\tilde S = {\tilde S_W} \cup {S_F}$
, where
 \begin{align*}{{\tilde S}_W} &= \big\{ ({i_5}, \ldots ,{i_9})\colon 0 \le {i_5} \le 4, \, 0 \le {i_6} \le 4, \, 0 \le {i_7} \le {i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}, \\&\quad\;\;\; 0 \le {i_8} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big], \\&\quad \;\;\; 0 \le {i_9} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big] \wedge \big[{i_8} + (4 - {i_8}){I_{\{ {i_8} \ge {i_7}\} }}\big]\big\} .\end{align*}
\begin{align*}{{\tilde S}_W} &= \big\{ ({i_5}, \ldots ,{i_9})\colon 0 \le {i_5} \le 4, \, 0 \le {i_6} \le 4, \, 0 \le {i_7} \le {i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}, \\&\quad\;\;\; 0 \le {i_8} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big], \\&\quad \;\;\; 0 \le {i_9} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big] \wedge \big[{i_8} + (4 - {i_8}){I_{\{ {i_8} \ge {i_7}\} }}\big]\big\} .\end{align*}
Then the transition matrix can be given as
for each step
![]() $t = 1, \ldots ,n$
, whose elements are all zero, except that
$t = 1, \ldots ,n$
, whose elements are all zero, except that
![]() ${\tilde a_{792,792}} = 1$
, and for all
${\tilde a_{792,792}} = 1$
, and for all
![]() $({i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
,
$({i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
,
-
(1)
 ${\tilde a_{\tilde e({i_5}, \ldots ,{i_9}),\tilde e(({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
${\tilde a_{\tilde e({i_5}, \ldots ,{i_9}),\tilde e(({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
 $({j_5}, \ldots ,{j_9}) \in \Omega $
with
$({j_5}, \ldots ,{j_9}) \in \Omega $
with
![]() $I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}}= 1$
;
$I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}}= 1$
;
-
(2)
 ${\tilde a_{\tilde e({i_5}, \ldots ,{i_9}),792}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.
${\tilde a_{\tilde e({i_5}, \ldots ,{i_9}),792}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.
Here,
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{{\tilde{{\boldsymbol{A}}}}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{{\tilde{{\boldsymbol{A}}}}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 5$
, the unreliability of a connected-(5,5)-out-of-
$n = 5$
, the unreliability of a connected-(5,5)-out-of-
![]() $(9,5)\colon\! F$
system is plotted in Figure 9, which coincides with the identity (by definition) that
$(9,5)\colon\! F$
system is plotted in Figure 9, which coincides with the identity (by definition) that
![]() $\bar R(5) = P({A_1} \cup \cdots \cup {A_5}) = 5{q^{25}} - 4{q^{30}}$
, with
$\bar R(5) = P({A_1} \cup \cdots \cup {A_5}) = 5{q^{25}} - 4{q^{30}}$
, with
![]() ${A_l}, \, l = 1, \ldots ,5$
, being the events that components
${A_l}, \, l = 1, \ldots ,5$
, being the events that components
![]() ${x_{i,j}} \, (l \le i \le l + 4,\,{} 1 \le j \le 5)$
have all failed.
${x_{i,j}} \, (l \le i \le l + 4,\,{} 1 \le j \le 5)$
have all failed.

Figure 9. Unreliability of the system in Example 3.7 (by definition and by FMCIA).
Example 3.8. Consider a linear 2-connected-(5,5)-out-of-
![]() $(9,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
$(9,n)\colon\! F$
system without overlapping that would fail if and only if there exist two blocks of consecutive
![]() $5 \times 5$
failed components without overlapping among its
$5 \times 5$
failed components without overlapping among its
![]() $9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
$9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
![]() $\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
$\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
![]() $\tilde S = {\tilde S_W} \cup {S_F}$
, where
$\tilde S = {\tilde S_W} \cup {S_F}$
, where
 \begin{align*}{{\tilde S}_W} &= \big\{ ({i_0},{i_5}, \ldots ,{i_9})\colon 0 \le {i_0} \le 1, 0 \le {i_5} \le 4, \, 0 \le {i_6} \le 4, \, 0 \le {i_7} \le {i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}, \\& \quad\;\;\; 0 \le {i_8} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big], \\& \quad\;\;\; 0 \le {i_9} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big] \wedge \big[{i_8} + (4 - {i_8}){I_{\{ {i_8} \ge {i_7}\} }}\big]\big\} .\end{align*}
\begin{align*}{{\tilde S}_W} &= \big\{ ({i_0},{i_5}, \ldots ,{i_9})\colon 0 \le {i_0} \le 1, 0 \le {i_5} \le 4, \, 0 \le {i_6} \le 4, \, 0 \le {i_7} \le {i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}, \\& \quad\;\;\; 0 \le {i_8} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big], \\& \quad\;\;\; 0 \le {i_9} \le \big[{i_6} + (4 - {i_6}){I_{\{ {i_6} \ge {i_5}\} }}\big] \wedge \big[{i_7} + (4 - {i_7}){I_{\{ {i_7} \ge {i_6}\} }}\big] \wedge \big[{i_8} + (4 - {i_8}){I_{\{ {i_8} \ge {i_7}\} }}\big]\big\} .\end{align*}
Then the transition matrix can be given as
for each step
![]() $t = 1, \ldots ,n$
, whose elements are all zero, except that
$t = 1, \ldots ,n$
, whose elements are all zero, except that
![]() ${\tilde a_{1583,1583}} = 1$
, and for all
${\tilde a_{1583,1583}} = 1$
, and for all
![]() $({i_0},{i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
and
$({i_0},{i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
and
![]() $\Omega $
in Example 3.7,
$\Omega $
in Example 3.7,
-
(1)
 ${\tilde a_{\tilde e({i_0},{i_5}, \ldots ,{i_9}),\tilde e({i_0},({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
${\tilde a_{\tilde e({i_0},{i_5}, \ldots ,{i_9}),\tilde e({i_0},({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
 $({j_5}, \ldots ,{j_9}) \in \Omega $
with
$({j_5}, \ldots ,{j_9}) \in \Omega $
with
![]() $I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}} = 1$
;
$I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}} = 1$
;
-
(2)
 ${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),\tilde e(1,0, \ldots ,0)}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),\tilde e(1,0, \ldots ,0)}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
 $({j_5}, \ldots ,{j_9}) \in \Omega $
with
$({j_5}, \ldots ,{j_9}) \in \Omega $
with
 ${I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0$
;
${I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0$
; -
(3)
 ${\tilde a_{\tilde e(1,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.
${\tilde a_{\tilde e(1,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 10$
, the unreliability of a 2-connected-(5,5)-out-of-
$n = 10$
, the unreliability of a 2-connected-(5,5)-out-of-
![]() $(9,10)\colon\! F$
system without overlapping is plotted in Figure 10, which coincides with the identity (by definition) that
$(9,10)\colon\! F$
system without overlapping is plotted in Figure 10, which coincides with the identity (by definition) that
with
![]() ${A_l}, \, l = 1, \ldots ,5$
, as in Example 3.7.
${A_l}, \, l = 1, \ldots ,5$
, as in Example 3.7.

Figure 10. Unreliability of the system in Example 3.8 (by definition and by FMCIA).
Example 3.9. Consider a linear 2-connected-(5,5)-out-of-
![]() $(9,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
$(9,n)\colon\! F$
system with overlapping that would fail if and only if there exist two blocks of consecutive
![]() $5 \times 5$
failed components with overlapping among its
$5 \times 5$
failed components with overlapping among its
![]() $9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
$9 \times n$
components. With the same assumptions as in Example 3.1 and the discussion in Remark 2.2, we define a Markov chain
![]() $\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
$\{ \tilde Y(t),t = 1, \ldots ,n\} $
with state space
![]() $\tilde S = {\tilde S_W} \cup {S_F}$
, the same as in Example 3.8. Then the transition matrix can be given as
$\tilde S = {\tilde S_W} \cup {S_F}$
, the same as in Example 3.8. Then the transition matrix can be given as
for each step
![]() $t = 1, \ldots ,n$
, whose elements are all zero, except that
$t = 1, \ldots ,n$
, whose elements are all zero, except that
![]() ${\tilde a_{1583,1583}} = 1$
, and for all
${\tilde a_{1583,1583}} = 1$
, and for all
![]() $({i_0},{i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
and
$({i_0},{i_5}, \ldots ,{i_9}) \in {\tilde S_W}$
and
![]() $\Omega $
in Example 3.7,
$\Omega $
in Example 3.7,
-
(1)
 ${\tilde a_{\tilde e({i_0},{i_5}, \ldots ,{i_9}),\tilde e({i_0},({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
${\tilde a_{\tilde e({i_0},{i_5}, \ldots ,{i_9}),\tilde e({i_0},({i_5} + 1){j_5}, \ldots ,({i_9} + 1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
 $({j_5}, \ldots ,{j_9}) \in \Omega $
with
$({j_5}, \ldots ,{j_9}) \in \Omega $
with
![]() $I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}} = 1$
;
$I_{\{ {i_5} + {j_5} \le 4, \ldots , {i_9} + {j_9} \le 4\}} = 1$
;
-
(2)
 ${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),\tilde e(1,({i_5}+1){j_5}, \ldots ,({i_{w - 1}}+1){j_{w - 1}},4,({i_{w + 1}}+1){i_{w + 1}}, \ldots ,({i_9}+1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),\tilde e(1,({i_5}+1){j_5}, \ldots ,({i_{w - 1}}+1){j_{w - 1}},4,({i_{w + 1}}+1){i_{w + 1}}, \ldots ,({i_9}+1){j_9})}} = {p_{{j_5}, \ldots ,{j_9}}}$
for all
![]() $({j_5}, \ldots ,{j_9}) \in \Omega $
with
$({j_5}, \ldots ,{j_9}) \in \Omega $
with
![]() $w = 5, \ldots ,9$
,
$w = 5, \ldots ,9$
,
![]() ${I_{\{{i_w} + {j_w} = 5, \, {i_s} + {j_s} \le 4\; \text{for}\ 5\le s \le 9, s \ne w\} }} = 1$
;
${I_{\{{i_w} + {j_w} = 5, \, {i_s} + {j_s} \le 4\; \text{for}\ 5\le s \le 9, s \ne w\} }} = 1$
;
-
(3)
 ${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4\} }} + \cdots + {I_{\{ {i_9} + {j_9} \le 4\} }} \le 3} {{p_{{j_5}, \ldots ,{j_9}}}} $
;
${\tilde a_{\tilde e(0,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4\} }} + \cdots + {I_{\{ {i_9} + {j_9} \le 4\} }} \le 3} {{p_{{j_5}, \ldots ,{j_9}}}} $
; -
(4)
 ${\tilde a_{\tilde e(1,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.
${\tilde a_{\tilde e(1,{i_5}, \ldots ,{i_9}),1583}} = \sum_{({j_5}, \ldots ,{j_9}) \in \Omega , \, {I_{\{ {i_5} + {j_5} \le 4, \ldots ,{i_9} + {j_9} \le 4\} }} = 0} {{p_{{j_5}, \ldots ,{j_9}}}} $
.

Figure 11. Unreliability of the system in Example 3.9 (by definition and by FMCIA).
Then the reliability and unreliability of the system can be given as
![]() $R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{u}}$
and
$R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{u}}$
and
![]() $\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
$\bar R(n) = {\boldsymbol{\pi }}{{\tilde{\boldsymbol{A}}}^n}{\boldsymbol{\bar{\boldsymbol{u}}}}$
, respectively, where
For example, with
![]() $n = 5$
, the unreliability of a 2-connected-(5,5)-out-of-
$n = 5$
, the unreliability of a 2-connected-(5,5)-out-of-
![]() $(9,5)\colon\! F$
system with overlapping is plotted in Figure 11, which coincides with the identity (by definition) that
$(9,5)\colon\! F$
system with overlapping is plotted in Figure 11, which coincides with the identity (by definition) that
 \begin{align*} \bar R(5) = P\Biggl(\bigcup_{1 \le i \ne j \le 5} {{A_i}{A_j}} \Biggr) = 4{q^{30}} - 3{q^{35}}, \end{align*}
\begin{align*} \bar R(5) = P\Biggl(\bigcup_{1 \le i \ne j \le 5} {{A_i}{A_j}} \Biggr) = 4{q^{30}} - 3{q^{35}}, \end{align*}
with
![]() ${A_l}, \, l = 1, \ldots ,5$
, as in Example 3.7.
${A_l}, \, l = 1, \ldots ,5$
, as in Example 3.7.
To demonstrate the efficiency of the proposed FMCIA method in reliability computation, unreliabilities of the nine linear two-dimensional consecutive k-type systems considered in Examples 3.1–3.9 and their average computational time from ten runs (in seconds, by MATLAB R2019 on a computer with CPU i7-5800H and 16 GB RAM) are presented in Table 3, for different sizes of systems with
![]() $p = 0.8$
. Note that in Table 3, the values within ( ) are average computational times by the main FMCIA method, and the values within [ ] are average computational times by the FMCIA method stated in Remark 2.2.
$p = 0.8$
. Note that in Table 3, the values within ( ) are average computational times by the main FMCIA method, and the values within [ ] are average computational times by the FMCIA method stated in Remark 2.2.
It can be seen from Table 3 that the proposed FMCIA method is quite efficient for large systems, since the computational time for systems with size
![]() $n = 100000$
is not much larger than the computational time for systems with size
$n = 100000$
is not much larger than the computational time for systems with size
![]() $n = 10$
; for example,
$n = 10$
; for example,
![]() $0.0824/0.0667$
seconds vs.
$0.0824/0.0667$
seconds vs.
![]() $0.0720/0.659$
seconds for Example 3.1,
$0.0720/0.659$
seconds for Example 3.1,
![]() $0.0827$
seconds vs.
$0.0827$
seconds vs.
![]() $0.0822$
seconds for Example 3.2, and so on. Moreover, the computational time does not always increase with size n, suggesting that the effect of system size might not be significant. Compared to traditional recursive algorithms and the known FMCIA methods whose computational time increase with size n quickly (see Table 3 in [Reference Zhao, Cui, Zhao and Liu35]), the FMCIA method developed here has significant computational efficiency while dealing with systems of large size.
$0.0822$
seconds for Example 3.2, and so on. Moreover, the computational time does not always increase with size n, suggesting that the effect of system size might not be significant. Compared to traditional recursive algorithms and the known FMCIA methods whose computational time increase with size n quickly (see Table 3 in [Reference Zhao, Cui, Zhao and Liu35]), the FMCIA method developed here has significant computational efficiency while dealing with systems of large size.
In contrast to the main FMCIA method, the FMCIA method explained in Remark 2.2 needs less computational time, namely,
![]() $0.0659/0.0710/0.0696/0.0666/0.0667$
seconds vs.
$0.0659/0.0710/0.0696/0.0666/0.0667$
seconds vs.
![]() $0.0720/0.0771/0.0806/0.0819/0.0824$
seconds for Example 3.1, and so on. For systems with large m and small k, the two methods require similar memory and computational time for calculation, and the difference in efficiency gets larger as k increases. For the systems in Examples 3.7–3.9, the main FMCIA method needs a computer with larger memory since MATLAB software is not able to generate matrices larger than its required dimension. On the other hand, for the systems in Examples 3.2, 3.4, and 3.6, the FMCIA method explained in Remark 2.2 is not applicable. This means that the two methods have their own advantages and disadvantages, and which one to use depends on the system type and system size.
$0.0720/0.0771/0.0806/0.0819/0.0824$
seconds for Example 3.1, and so on. For systems with large m and small k, the two methods require similar memory and computational time for calculation, and the difference in efficiency gets larger as k increases. For the systems in Examples 3.7–3.9, the main FMCIA method needs a computer with larger memory since MATLAB software is not able to generate matrices larger than its required dimension. On the other hand, for the systems in Examples 3.2, 3.4, and 3.6, the FMCIA method explained in Remark 2.2 is not applicable. This means that the two methods have their own advantages and disadvantages, and which one to use depends on the system type and system size.
4. Concluding remarks
In this work we have presented a novel way of using FMCIA in the reliability calculation of several kinds of linear two-dimensional consecutive k-type systems. Compared to existing methods, the proposed method efficiently provides exact reliabilities of these systems in a unified form, and is easy to use as a direct method. The memory and computational time needed for the main FMCIA method are
![]() ${\mathrm{O}}({N^2})$
and
${\mathrm{O}}({N^2})$
and
![]() ${\mathrm{O}}(m{N^3} + n{N^2})$
, respectively. They can be further reduced by the FMCIA method suggested in Remark 2.2 to
${\mathrm{O}}(m{N^3} + n{N^2})$
, respectively. They can be further reduced by the FMCIA method suggested in Remark 2.2 to
![]() ${\mathrm{O}}({\tilde N^2})$
and
${\mathrm{O}}({\tilde N^2})$
and
![]() ${\mathrm{O}}({2^m} \cdot {\tilde N^2} + n{\tilde N^2})$
, respectively, with
${\mathrm{O}}({2^m} \cdot {\tilde N^2} + n{\tilde N^2})$
, respectively, with
![]() $\tilde N \lt N$
. The proposed method is efficient for large systems, especially for systems with large n. The established results can be useful in many practical applications as well, such as electronic devices with connector pins, X-rays for disease cells, supervision systems with TV cameras, sensing systems with sensors, and so on [Reference Boehme, Kossow and Preuss6, Reference Salvia and Lasher28]. In addition, the present work can be generalized to the following situations.
$\tilde N \lt N$
. The proposed method is efficient for large systems, especially for systems with large n. The established results can be useful in many practical applications as well, such as electronic devices with connector pins, X-rays for disease cells, supervision systems with TV cameras, sensing systems with sensors, and so on [Reference Boehme, Kossow and Preuss6, Reference Salvia and Lasher28]. In addition, the present work can be generalized to the following situations.
-
(1) Systems with trinary, instead of binary, components can be studied.
-
(2) Only linear systems have been considered in this work, but it can be generalized to circular and toroidal systems.
-
(3) Other types of two-dimensional consecutive k-systems can be considered, such as k-within-connected-(r, s)-out-of-
 $(m,n)\colon\! F/G$
systems, systems with sparse
$(m,n)\colon\! F/G$
systems, systems with sparse
 ${\boldsymbol{d}}$
, and mixed systems with different types of failure rules.
${\boldsymbol{d}}$
, and mixed systems with different types of failure rules. -
(4) Three-dimensional consecutive k-systems can also be studied by this method, even when they have multi-state components instead of binary-state ones.
-
(5) l-connected-X-out-of-
 $(m,n)\colon\! F$
systems without/with overlapping can also be investigated when blocks are not searched in a given order, and the results in this paper might result in bounds.
$(m,n)\colon\! F$
systems without/with overlapping can also be investigated when blocks are not searched in a given order, and the results in this paper might result in bounds.
We are currently working on these problems and hope to report the findings in a future paper.
Acknowledgements
Our sincere thanks go to the Editor and the anonymous referee for their many useful comments and suggestions on an earlier version of this manuscript, which led to this much improved version.
Funding information
This work was supported by the National Natural Science Foundation of China (no. 72001016, no. 71931001, and no. 71722007), the Fundamental Research Funds for the Central Universities (buctrc202102) and the Funds for First-class Discipline Construction (XK1802-5), and the Natural Sciences and Engineering Research Council of Canada (to the second author) through an Individual Discovery Grant (RGPIN-2020-06733).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.