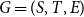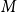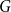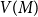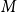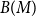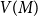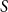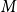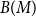1. Introduction
Let
![]() $V$
be a finite set. We will consider random subsets of
$V$
be a finite set. We will consider random subsets of
![]() $V$
. Let
$V$
. Let
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
be upward closed subsets of
$\mathcal{B}$
be upward closed subsets of
![]() $2^V$
; in other words, let
$2^V$
; in other words, let
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
be increasing events. Let
$\mathcal{B}$
be increasing events. Let
![]() $\mathcal{A}\square \mathcal{B}$
be the event that
$\mathcal{A}\square \mathcal{B}$
be the event that
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
both occur disjointly. More formally, we define
$\mathcal{B}$
both occur disjointly. More formally, we define
Let
![]() $G=(S,T,E)$
be a bipartite graph, and let
$G=(S,T,E)$
be a bipartite graph, and let
![]() $V=S\cup T$
. Let
$V=S\cup T$
. Let
![]() $\mathcal{M}$
be the set of matchings in
$\mathcal{M}$
be the set of matchings in
![]() $G$
. For a matching
$G$
. For a matching
![]() $M\in \mathcal{M}$
, let
$M\in \mathcal{M}$
, let
![]() $V(M)$
be the set of vertices covered by
$V(M)$
be the set of vertices covered by
![]() $M$
, and let
$M$
, and let
where
![]() $\Delta$
denotes the symmetric difference. Note that we have
$\Delta$
denotes the symmetric difference. Note that we have
![]() $|B(M)|=|S|$
for any matching
$|B(M)|=|S|$
for any matching
![]() $M$
.
$M$
.
Our main result is the following.
Theorem 1.1.
Let
![]() $M$
be a uniform random element of
$M$
be a uniform random element of
![]() $\mathcal{M}$
. Then
$\mathcal{M}$
. Then
![]() $B(M)$
satisfies the BK inequality for increasing events, that is, if
$B(M)$
satisfies the BK inequality for increasing events, that is, if
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are upward closed subsets of
$\mathcal{B}$
are upward closed subsets of
![]() $2^V$
, then
$2^V$
, then
For a random subset with independent marginals, the BK inequality was proved by van den Berg and Kesten [Reference van den Berg and Kesten5]. There is an extension of the notion
![]() $\mathcal{A}\square \mathcal{B}$
for arbitrary events, see Subsection 2.1. With this definition, the BK inequality holds for all events in the case of a random subset with independent marginals. This was conjectured by van den Berg and Kesten [Reference van den Berg and Kesten5], and proved by Reimer [Reference Reimer2]. Building on the results of Reimer, van den Berg and Jonasson proved that the BK inequality also holds for a uniform random
$\mathcal{A}\square \mathcal{B}$
for arbitrary events, see Subsection 2.1. With this definition, the BK inequality holds for all events in the case of a random subset with independent marginals. This was conjectured by van den Berg and Kesten [Reference van den Berg and Kesten5], and proved by Reimer [Reference Reimer2]. Building on the results of Reimer, van den Berg and Jonasson proved that the BK inequality also holds for a uniform random
![]() $k$
element subset if we only consider increasing events [Reference van den Berg and Jonasson4]. Our results extend the results in [Reference van den Berg and Jonasson4], see the discussion after Theorem 1.4. See also the paper of van den Berg and Gandolfi [Reference van den Berg and Gandolfi3] for further results.
$k$
element subset if we only consider increasing events [Reference van den Berg and Jonasson4]. Our results extend the results in [Reference van den Berg and Jonasson4], see the discussion after Theorem 1.4. See also the paper of van den Berg and Gandolfi [Reference van den Berg and Gandolfi3] for further results.
We say that an event
![]() $\mathcal{A}$
depends only on
$\mathcal{A}$
depends only on
![]() $V_0\subseteq V$
, if for any
$V_0\subseteq V$
, if for any
![]() $A,B\subseteq V$
the conditions
$A,B\subseteq V$
the conditions
![]() $A\cap V_0=B\cap V_0$
and
$A\cap V_0=B\cap V_0$
and
![]() $A\in \mathcal{A}$
imply that
$A\in \mathcal{A}$
imply that
![]() $B\in \mathcal{A}$
. Note that if
$B\in \mathcal{A}$
. Note that if
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are increasing events depending on disjoint subsets of
$\mathcal{B}$
are increasing events depending on disjoint subsets of
![]() $V$
, then
$V$
, then
![]() $\mathcal{A}\square \mathcal{B}=\mathcal{A}\cap \mathcal{B}$
. Thus, Theorem 1.1 has the following corollary.
$\mathcal{A}\square \mathcal{B}=\mathcal{A}\cap \mathcal{B}$
. Thus, Theorem 1.1 has the following corollary.
Corollary 1.2.
Let
![]() $B(M)$
be as above, then
$B(M)$
be as above, then
![]() $B(M)$
has negative associations, which means the following. Let
$B(M)$
has negative associations, which means the following. Let
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
be events depending on disjoint subsets of
$\mathcal{B}$
be events depending on disjoint subsets of
![]() $V$
. If
$V$
. If
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are both increasing or both decreasing, then
$\mathcal{B}$
are both increasing or both decreasing, then
If
![]() $\mathcal{A}$
is increasing and
$\mathcal{A}$
is increasing and
![]() $\mathcal{B}$
is decreasing, then
$\mathcal{B}$
is decreasing, then
Now we give a few extensions of Theorem 1.1. Assume that every edge
![]() $e$
of
$e$
of
![]() $G$
has a positive weight
$G$
has a positive weight
![]() $w(e)$
. For a matching
$w(e)$
. For a matching
![]() $M$
, we define the weight of
$M$
, we define the weight of
![]() $M$
as
$M$
as
![]() $w(M)=\prod _{e\in M} w(e)$
. Let
$w(M)=\prod _{e\in M} w(e)$
. Let
![]() $M$
be a random matching, where the probability of a matching is proportional to its weight. We have the following extension of Theorem 1.1.
$M$
be a random matching, where the probability of a matching is proportional to its weight. We have the following extension of Theorem 1.1.
Theorem 1.3.
Let
![]() $M$
be as above. Then
$M$
be as above. Then
![]() $B(M)$
satisfies the BK inequality for increasing events, that is, if
$B(M)$
satisfies the BK inequality for increasing events, that is, if
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are upward closed subsets of
$\mathcal{B}$
are upward closed subsets of
![]() $2^V$
, then
$2^V$
, then
Furthermore, let
![]() $V_+$
and
$V_+$
and
![]() $V_-$
be disjoint subsets of
$V_-$
be disjoint subsets of
![]() $V$
. Let
$V$
. Let
![]() $M^{\prime}$
have the same distribution as
$M^{\prime}$
have the same distribution as
![]() $M$
conditioned on the event that
$M$
conditioned on the event that
![]() $V_+\subseteq B(M)$
and
$V_+\subseteq B(M)$
and
![]() $V_-\cap B(M)=\emptyset$
. Let
$V_-\cap B(M)=\emptyset$
. Let
![]() $V^{\prime}=V\backslash (V_+\cup V_-)$
, and let
$V^{\prime}=V\backslash (V_+\cup V_-)$
, and let
![]() $B^{\prime}(M^{\prime})=B(M^{\prime})\cap V^{\prime}$
. Clearly,
$B^{\prime}(M^{\prime})=B(M^{\prime})\cap V^{\prime}$
. Clearly,
![]() $B^{\prime}(M^{\prime})$
is a random subset of
$B^{\prime}(M^{\prime})$
is a random subset of
![]() $V^{\prime}$
.
$V^{\prime}$
.
Theorem 1.4.
The random subset
![]() $B^{\prime}(M^{\prime})$
satisfies the BK inequality for increasing events.
$B^{\prime}(M^{\prime})$
satisfies the BK inequality for increasing events.
As a special case of Theorem 1.4, we can obtain the statement that a uniform random
![]() $k$
element subset of an
$k$
element subset of an
![]() $n$
element set satisfies the BK inequality for increasing event. Thus, our results generalize the result of van den Berg and Jonasson [Reference van den Berg and Jonasson4] mentioned above. Indeed, let
$n$
element set satisfies the BK inequality for increasing event. Thus, our results generalize the result of van den Berg and Jonasson [Reference van den Berg and Jonasson4] mentioned above. Indeed, let
![]() $G$
be a complete bipartite graph (with constant edge weights) such that
$G$
be a complete bipartite graph (with constant edge weights) such that
![]() $|S|=k$
and
$|S|=k$
and
![]() $|T|=n$
. If we set
$|T|=n$
. If we set
![]() $V_-=S$
and
$V_-=S$
and
![]() $V_+=\emptyset$
, then
$V_+=\emptyset$
, then
![]() $M^{\prime}$
is chosen uniformly at random from the set of matchings covering
$M^{\prime}$
is chosen uniformly at random from the set of matchings covering
![]() $S$
. By symmetry, it is clear that
$S$
. By symmetry, it is clear that
![]() $B^{\prime}(M^{\prime})$
is a uniform random
$B^{\prime}(M^{\prime})$
is a uniform random
![]() $k$
element subset of
$k$
element subset of
![]() $T$
.
$T$
.
Theorem 1.4 also has the following corollary.
Corollary 1.5.
Let
![]() $M$
be as above. Then for any subset
$M$
be as above. Then for any subset
![]() $X$
and
$X$
and
![]() $Y$
of
$Y$
of
![]() $V$
, we have
$V$
, we have
In other words, the law of
![]() $B(M)$
satisfies the negative lattice condition. See [Reference Borcea, Brändén and Liggett1], where various notions of negative dependence are discussed.
$B(M)$
satisfies the negative lattice condition. See [Reference Borcea, Brändén and Liggett1], where various notions of negative dependence are discussed.
We can also deduce the following theorem from Theorem 1.3.
Theorem 1.6.
Let
![]() $M$
be uniform random maximum size matching. Then the random subset
$M$
be uniform random maximum size matching. Then the random subset
![]() $B(M)$
satisfies the BK inequality for increasing events.
$B(M)$
satisfies the BK inequality for increasing events.
2. The proofs
2.1 The definition of
 $\mathcal{A}\square \mathcal{B}$
for arbitrary events
$\mathcal{A}\square \mathcal{B}$
for arbitrary events
Let us recall how to extend the definition of
![]() $\mathcal{A}\square \mathcal{B}$
to arbitrary events. A subset
$\mathcal{A}\square \mathcal{B}$
to arbitrary events. A subset
![]() $C$
of
$C$
of
![]() $V$
is in
$V$
is in
![]() $\mathcal{A}\square \mathcal{B}$
if and only if there are disjoint subsets
$\mathcal{A}\square \mathcal{B}$
if and only if there are disjoint subsets
![]() $V_A$
and
$V_A$
and
![]() $V_B$
of
$V_B$
of
![]() $V$
such that
$V$
such that
and
If
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are increasing, then this definition indeed coincides with our earlier definition.
$\mathcal{B}$
are increasing, then this definition indeed coincides with our earlier definition.
2.2 The proof of Theorem 1.4
In this subsection, we prove Theorem 1.4. Note that Theorem 1.1 and Theorem 1.3 can be obtained as special cases of Theorem 1.4.
Our proof will use several ideas of Berg and Jonasson [Reference van den Berg and Jonasson4].
Let
![]() $I$
be the set of tuples
$I$
be the set of tuples
![]() $(W,K,L,R)$
, where
$(W,K,L,R)$
, where
![]() $W$
is a subset of
$W$
is a subset of
![]() $V$
,
$V$
,
![]() $K$
and
$K$
and
![]() $L$
are perfect matchings in the induced subgraph
$L$
are perfect matchings in the induced subgraph
![]() $G[W]$
,
$G[W]$
,
![]() $R$
is a subgraph of
$R$
is a subgraph of
![]() $G[V\backslash W]$
consisting of vertex disjoint paths.Footnote
1
$G[V\backslash W]$
consisting of vertex disjoint paths.Footnote
1
Fix a linear ordering of the edges of
![]() $G$
. Consider an
$G$
. Consider an
![]() $i=(W,K,L,R)\in I$
. Then
$i=(W,K,L,R)\in I$
. Then
![]() $R$
is the vertex disjoint union of the paths
$R$
is the vertex disjoint union of the paths
![]() $P_1,P_2,\ldots,P_k$
, where we list the paths in increasing order of their lowest edge. We can write
$P_1,P_2,\ldots,P_k$
, where we list the paths in increasing order of their lowest edge. We can write
![]() $P_j$
as the union of the matchings
$P_j$
as the union of the matchings
![]() $M_{j,0}$
and
$M_{j,0}$
and
![]() $M_{j,1}$
. This decomposition is unique once we assume that
$M_{j,1}$
. This decomposition is unique once we assume that
![]() $M_{j,0}$
contains the lowest edge of
$M_{j,0}$
contains the lowest edge of
![]() $P_j$
. For
$P_j$
. For
![]() $\omega =(\omega _1,\omega _2,\ldots,\omega _k)\in \{0,1\}^k$
, we define the matchings
$\omega =(\omega _1,\omega _2,\ldots,\omega _k)\in \{0,1\}^k$
, we define the matchings
Moreover, we define
and
Let
![]() $H_i$
be the set of endpoints of the paths
$H_i$
be the set of endpoints of the paths
![]() $P_1,P_2,\ldots,P_k$
. Let
$P_1,P_2,\ldots,P_k$
. Let
![]() $V(R)$
be the vertex set of
$V(R)$
be the vertex set of
![]() $R$
. Let
$R$
. Let
![]() $B_i=((W\cup V(R))\Delta S)\backslash H_i$
. Let
$B_i=((W\cup V(R))\Delta S)\backslash H_i$
. Let
![]() $v_{j,0}$
and
$v_{j,0}$
and
![]() $v_{j,1}$
be the two endpoints of
$v_{j,1}$
be the two endpoints of
![]() $P_j$
. If we choose the indices in the right way, then we get that
$P_j$
. If we choose the indices in the right way, then we get that
and
This immediately implies that
 \begin{align} \big\{B(C_{i,\omega })\big|\quad \omega \in \big\{0,1\}^k\big\} & =\big\{B\big(D_{i,\omega }\big)\big|\quad \omega \in \{0,1\}^k\big\}\nonumber \\[3pt]& = \big\{B_i\cup H|\quad H\subseteq H_i\text{ and } \big|H\cap \big\{v_{j,0},v_{j,1}\big\}\big|=1\text{ for all }j=1,2,\ldots,k\big\}. \end{align}
\begin{align} \big\{B(C_{i,\omega })\big|\quad \omega \in \big\{0,1\}^k\big\} & =\big\{B\big(D_{i,\omega }\big)\big|\quad \omega \in \{0,1\}^k\big\}\nonumber \\[3pt]& = \big\{B_i\cup H|\quad H\subseteq H_i\text{ and } \big|H\cap \big\{v_{j,0},v_{j,1}\big\}\big|=1\text{ for all }j=1,2,\ldots,k\big\}. \end{align}
Let
![]() $U_i=\{v_{j,1}|\quad j=1,2,\ldots,k\}$
. We define the map
$U_i=\{v_{j,1}|\quad j=1,2,\ldots,k\}$
. We define the map
![]() $\tau _i\,:\,\mathcal{M}\to 2^{U_i}$
by
$\tau _i\,:\,\mathcal{M}\to 2^{U_i}$
by
![]() $\tau _i(M)=B(M)\cap U_i$
. It is clear from what is written above that the appropriate restriction of
$\tau _i(M)=B(M)\cap U_i$
. It is clear from what is written above that the appropriate restriction of
![]() $\tau _i$
gives a bijection from
$\tau _i$
gives a bijection from
![]() $Y_i^C$
to
$Y_i^C$
to
![]() $2^{U_i}$
, and also from
$2^{U_i}$
, and also from
![]() $Y_i^D$
to
$Y_i^D$
to
![]() $2^{U_i}$
. Moreover,
$2^{U_i}$
. Moreover,
We define
and
Lemma 2.1.
The sets
![]() $(X_i)_{i\in I^{\prime}}$
give a partition of
$(X_i)_{i\in I^{\prime}}$
give a partition of
![]() $\mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
.
$\mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
.
Proof. Let
![]() $(C,D)\in \mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
. Consider the multi-graph
$(C,D)\in \mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
. Consider the multi-graph
![]() $C\cup D$
, it is a vertex disjoint union of cycles and paths. Let
$C\cup D$
, it is a vertex disjoint union of cycles and paths. Let
![]() $R$
be the union of paths, and let
$R$
be the union of paths, and let
![]() $Q$
be the union of cycles. Let
$Q$
be the union of cycles. Let
![]() $W$
be the vertices covered by the cycles. Let
$W$
be the vertices covered by the cycles. Let
![]() $i=(W,C\cap Q,D\cap Q,R)$
. One can easily prove that
$i=(W,C\cap Q,D\cap Q,R)$
. One can easily prove that
![]() $i$
is the unique element of
$i$
is the unique element of
![]() $I^{\prime}$
such that
$I^{\prime}$
such that
![]() $(C,D)\in X_i$
.
$(C,D)\in X_i$
.
Moreover, if
![]() $i\in I^{\prime}$
, then
$i\in I^{\prime}$
, then
![]() $X_i\subset \mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
. Thus, the statement follows.
$X_i\subset \mathcal{M}^{\prime}\times \mathcal{M}^{\prime}$
. Thus, the statement follows.
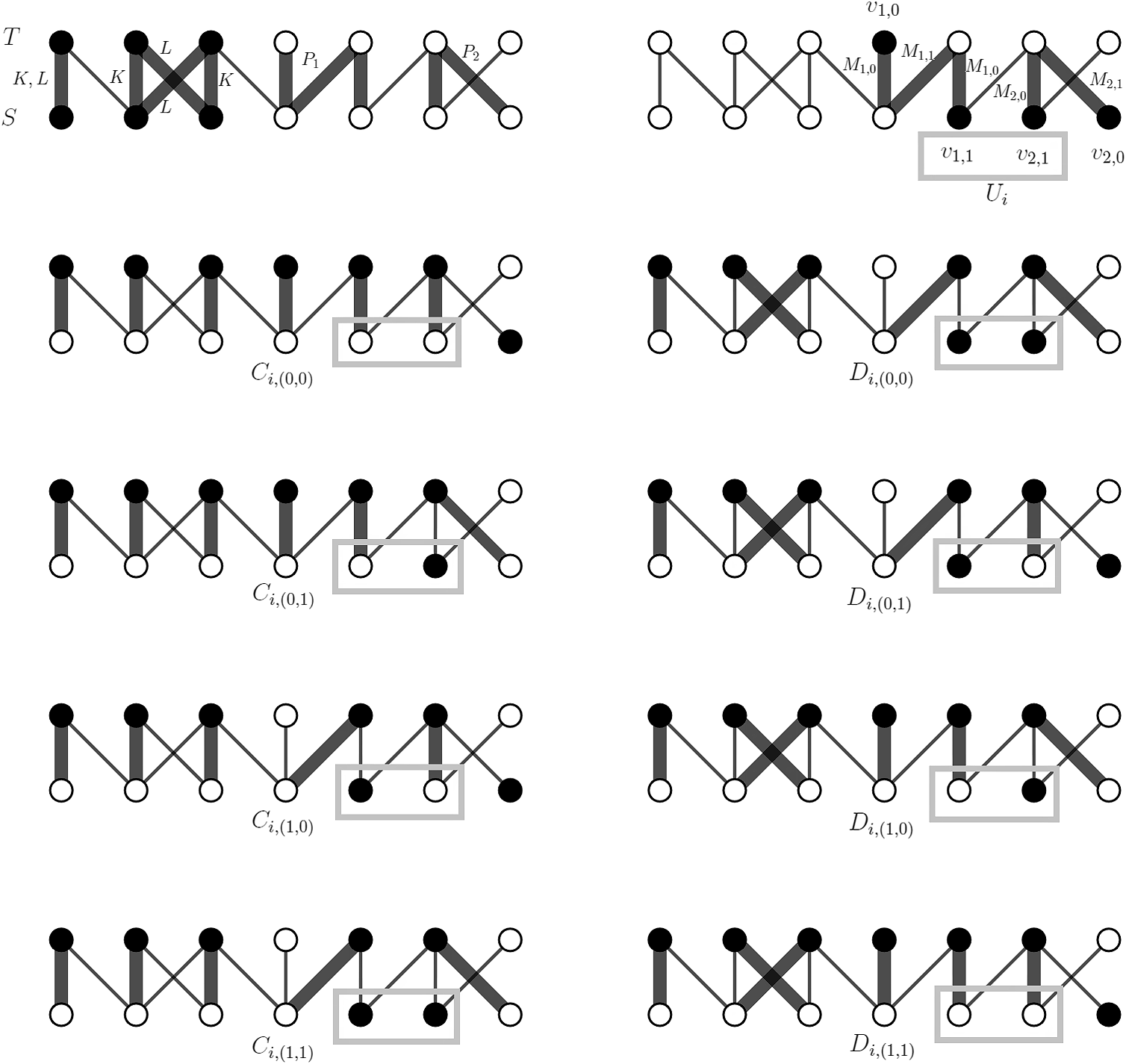
Figure 1. The first figure describes a tuple
![]() $i=(W,K,L,R)\in I$
: the vertices of
$i=(W,K,L,R)\in I$
: the vertices of
![]() $W$
are coloured black; the bold edges correspond to the edges of
$W$
are coloured black; the bold edges correspond to the edges of
![]() $K\cup L\cup R$
; the labels show the edges of the matchings
$K\cup L\cup R$
; the labels show the edges of the matchings
![]() $K,L$
and the decomposition of
$K,L$
and the decomposition of
![]() $R$
into two paths
$R$
into two paths
![]() $P_1$
and
$P_1$
and
![]() $P_2$
, and the two colour classes
$P_2$
, and the two colour classes
![]() $S$
and
$S$
and
![]() $T$
of the bipartite graphs
$T$
of the bipartite graphs
![]() $G$
. Note that the left most edge belongs to both
$G$
. Note that the left most edge belongs to both
![]() $K$
and
$K$
and
![]() $L$
. In the second figure vertices of
$L$
. In the second figure vertices of
![]() $H_i$
are coloured black; the edges of
$H_i$
are coloured black; the edges of
![]() $R=P_1\cup P_2$
are bold; the labels show the indexing of the vertices of
$R=P_1\cup P_2$
are bold; the labels show the indexing of the vertices of
![]() $H_i$
, and also the decomposition of the paths
$H_i$
, and also the decomposition of the paths
![]() $P_1$
and
$P_1$
and
![]() $P_2$
into the matchings
$P_2$
into the matchings
![]() $M_{1,0},M_{1,1}$
and
$M_{1,0},M_{1,1}$
and
![]() $M_{2,0},M_{2,1}$
. The vertical edges are in
$M_{2,0},M_{2,1}$
. The vertical edges are in
![]() $M_{1,0}$
and
$M_{1,0}$
and
![]() $M_{2,0}$
, the tilted edges are in
$M_{2,0}$
, the tilted edges are in
![]() $M_{1,1}$
and
$M_{1,1}$
and
![]() $M_{2,1}$
. (Of course, depending on the linear ordering of the edges, the labels of
$M_{2,1}$
. (Of course, depending on the linear ordering of the edges, the labels of
![]() $M_{1,0}$
and
$M_{1,0}$
and
![]() $M_{1,1}$
can be switched, we omitted the linear ordering from these figures.) We used a grey frame to indicate the elements of
$M_{1,1}$
can be switched, we omitted the linear ordering from these figures.) We used a grey frame to indicate the elements of
![]() $U_i$
. In the last four rows, the bold edges correspond to the matchings
$U_i$
. In the last four rows, the bold edges correspond to the matchings
![]() $C_{i,\omega }$
and
$C_{i,\omega }$
and
![]() $D_{i,\omega }$
as indicated. The vertices in
$D_{i,\omega }$
as indicated. The vertices in
![]() $B(C_{i,\omega })$
(and
$B(C_{i,\omega })$
(and
![]() $B(D_{i,\omega })$
) are coloured black. The grey frame again contains the vertices of
$B(D_{i,\omega })$
) are coloured black. The grey frame again contains the vertices of
![]() $U_i$
.
$U_i$
.
Given a subset
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $2^{V^{\prime}}$
, we define
$2^{V^{\prime}}$
, we define
![]() $\mathcal{M}_{\mathcal{F}}$
as
$\mathcal{M}_{\mathcal{F}}$
as
![]() $\{M\in \mathcal{M}^{\prime}| B^{\prime}(M)\in \mathcal{F}\}$
.
$\{M\in \mathcal{M}^{\prime}| B^{\prime}(M)\in \mathcal{F}\}$
.
Let
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
be upward closed subsets of
$\mathcal{B}$
be upward closed subsets of
![]() $2^{V^{\prime}}$
.
$2^{V^{\prime}}$
.
Lemma 2.2.
If for all
![]() $i\in I^{\prime}$
, we have
$i\in I^{\prime}$
, we have
then
Proof. Consider any
![]() $i\in I^{\prime}$
. If
$i\in I^{\prime}$
. If
![]() $(C_1,D_1),(C_2,D_2)\in X_i$
, then
$(C_1,D_1),(C_2,D_2)\in X_i$
, then
![]() $C_1+ D_1=C_2+ D_2$
as multisets. In particular,
$C_1+ D_1=C_2+ D_2$
as multisets. In particular,
![]() $w(C_1)w(D_1)=w(C_2)w(D_2)$
. Thus, there is a
$w(C_1)w(D_1)=w(C_2)w(D_2)$
. Thus, there is a
![]() $w_i$
such that
$w_i$
such that
![]() $w(C)w(D)=w_i$
for any
$w(C)w(D)=w_i$
for any
![]() $(C,D)\in X_i$
. Multiplying both sides of Inequality (3) by
$(C,D)\in X_i$
. Multiplying both sides of Inequality (3) by
![]() $w_i$
, we obtain that
$w_i$
, we obtain that
which is equivalent to
 \begin{equation*}\sum _{(C,D)\in \big(\mathcal {M}_{\mathcal {A}\square \mathcal {B}}\times \mathcal {M}^{\prime}\big)\cap X_i}w(C)w(D)\le \sum _{(C,D)\in (\mathcal {M}_{\mathcal {A}}\times \mathcal {M}_{\mathcal {B}})\cap X_i}w(C)w(D).\end{equation*}
\begin{equation*}\sum _{(C,D)\in \big(\mathcal {M}_{\mathcal {A}\square \mathcal {B}}\times \mathcal {M}^{\prime}\big)\cap X_i}w(C)w(D)\le \sum _{(C,D)\in (\mathcal {M}_{\mathcal {A}}\times \mathcal {M}_{\mathcal {B}})\cap X_i}w(C)w(D).\end{equation*}
Summing these inequalities for all
![]() $i\in I^{\prime}$
and using Lemma 2.1, we obtain that
$i\in I^{\prime}$
and using Lemma 2.1, we obtain that
This can be rewritten as
 \begin{equation*}\left (\sum _{M\in \mathcal {M}_{\mathcal {A}\square \mathcal {B}}}w(M)\right )\left (\sum _{M\in \mathcal {M}^{\prime}} w(M)\right )\le \left (\sum _{M\in \mathcal {M}_{\mathcal {A}}} w(M)\right )\left (\sum _{M\in \mathcal {M}_{\mathcal {B}}} w(M)\right ).\end{equation*}
\begin{equation*}\left (\sum _{M\in \mathcal {M}_{\mathcal {A}\square \mathcal {B}}}w(M)\right )\left (\sum _{M\in \mathcal {M}^{\prime}} w(M)\right )\le \left (\sum _{M\in \mathcal {M}_{\mathcal {A}}} w(M)\right )\left (\sum _{M\in \mathcal {M}_{\mathcal {B}}} w(M)\right ).\end{equation*}
Dividing both sides by
![]() $\left (\sum _{M\in \mathcal{M}^{\prime}} w(M)\right )^2$
, we obtain that
$\left (\sum _{M\in \mathcal{M}^{\prime}} w(M)\right )^2$
, we obtain that
From Lemma 2.2, it follows that it is enough to prove that for any
![]() $i\in I^{\prime}$
, we have
$i\in I^{\prime}$
, we have
For a subset
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $2^{V^{\prime}}$
and
$2^{V^{\prime}}$
and
![]() $i\in I^{\prime}$
, we define
$i\in I^{\prime}$
, we define
From Equation (1), it follows that
![]() $\big\{B^{\prime}(C)|C\in Y_i^C\big\}=\big\{B^{\prime}(D)|D\in Y_i^D\big\}$
. Therefore,
$\big\{B^{\prime}(C)|C\in Y_i^C\big\}=\big\{B^{\prime}(D)|D\in Y_i^D\big\}$
. Therefore,
![]() $\mathcal{F}^i=\big\{\tau _i(D)|D\in Y_i^D\cap \mathcal{M}_{\mathcal{F}}\big\}$
. (Note that, even for an increasing
$\mathcal{F}^i=\big\{\tau _i(D)|D\in Y_i^D\cap \mathcal{M}_{\mathcal{F}}\big\}$
. (Note that, even for an increasing
![]() $\mathcal{F}$
it might happen that
$\mathcal{F}$
it might happen that
![]() $\mathcal{F}^i$
is not increasing.) For a subset
$\mathcal{F}^i$
is not increasing.) For a subset
![]() $\mathcal{J}$
of
$\mathcal{J}$
of
![]() $2^{U_i}$
, we define
$2^{U_i}$
, we define
![]() $\overline{\mathcal{J}}=\{U_i\backslash J|J\in \mathcal{J}\}$
.
$\overline{\mathcal{J}}=\{U_i\backslash J|J\in \mathcal{J}\}$
.
Then
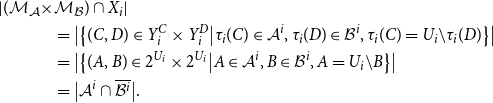 \begin{align} |(\mathcal{M}_{\mathcal{A}}\times & \mathcal{M}_{\mathcal{B}})\cap X_i|\\&= \big|\big\{(C,D)\in Y_i^C\times Y_i^D\big| \tau _i(C)\in \mathcal{A}^i,\tau _i(D)\in \mathcal{B}^i,\tau _i(C)=U_i\backslash \tau _i(D) \big\}\big|\nonumber \\&= \big|\big\{(A,B)\in 2^{U_i}\times 2^{U_i}\big|A\in \mathcal{A}^i,B\in \mathcal{B}^i,A=U_i\backslash B \big\}\big|\nonumber \\&=\big|\mathcal{A}^i\cap \overline{\mathcal{B}^i}\big|.\nonumber \end{align}
\begin{align} |(\mathcal{M}_{\mathcal{A}}\times & \mathcal{M}_{\mathcal{B}})\cap X_i|\\&= \big|\big\{(C,D)\in Y_i^C\times Y_i^D\big| \tau _i(C)\in \mathcal{A}^i,\tau _i(D)\in \mathcal{B}^i,\tau _i(C)=U_i\backslash \tau _i(D) \big\}\big|\nonumber \\&= \big|\big\{(A,B)\in 2^{U_i}\times 2^{U_i}\big|A\in \mathcal{A}^i,B\in \mathcal{B}^i,A=U_i\backslash B \big\}\big|\nonumber \\&=\big|\mathcal{A}^i\cap \overline{\mathcal{B}^i}\big|.\nonumber \end{align}
Similarly,
Lemma 2.3. We have
Proof. Let
![]() $F\in (\mathcal{A}\square \mathcal{B})^i$
, then
$F\in (\mathcal{A}\square \mathcal{B})^i$
, then
![]() $F=\tau _i(C)$
for some
$F=\tau _i(C)$
for some
![]() $C\in Y_i^C$
such that
$C\in Y_i^C$
such that
![]() $B^{\prime}(C)\in \mathcal{A}\square \mathcal{B}$
. Since
$B^{\prime}(C)\in \mathcal{A}\square \mathcal{B}$
. Since
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are upward closed, there are disjoint sets
$\mathcal{B}$
are upward closed, there are disjoint sets
![]() $V_A\in \mathcal{A}$
and
$V_A\in \mathcal{A}$
and
![]() $V_B\in \mathcal{B}$
such that
$V_B\in \mathcal{B}$
such that
![]() $B^{\prime}(C)=V_A\cup V_B$
. We define
$B^{\prime}(C)=V_A\cup V_B$
. We define
and
Since
![]() $V_A$
and
$V_A$
and
![]() $V_B$
are disjoint and
$V_B$
are disjoint and
![]() $\big|B^{\prime}(C)\cap \big\{v_{j,0},v_{j,1}\big\}\big|=1$
for all
$\big|B^{\prime}(C)\cap \big\{v_{j,0},v_{j,1}\big\}\big|=1$
for all
![]() $j$
, we obtain that
$j$
, we obtain that
![]() $U_A$
and
$U_A$
and
![]() $U_B$
are disjoint.
$U_B$
are disjoint.
Moreover, if for some
![]() $C^{\prime}\in Y_i^C$
, we have
$C^{\prime}\in Y_i^C$
, we have
![]() $\tau _i(C)\cap U_A=\tau _i(C^{\prime})\cap U_A$
, then
$\tau _i(C)\cap U_A=\tau _i(C^{\prime})\cap U_A$
, then
![]() $ V_A\subseteq B^{\prime}(C^{\prime})$
. Consequently
$ V_A\subseteq B^{\prime}(C^{\prime})$
. Consequently
![]() $B^{\prime}(C^{\prime})\in \mathcal{A}$
and
$B^{\prime}(C^{\prime})\in \mathcal{A}$
and
![]() $\tau _i(C^{\prime})\in \mathcal{A}^i$
. The analogous statement is true for
$\tau _i(C^{\prime})\in \mathcal{A}^i$
. The analogous statement is true for
![]() $V_B$
and
$V_B$
and
![]() $U_B$
. Therefore, the pair
$U_B$
. Therefore, the pair
![]() $U_A,U_B$
witnesses that
$U_A,U_B$
witnesses that
![]() $F=\tau _i(C)\in \mathcal{A}^i\square \mathcal{B}^i$
.
$F=\tau _i(C)\in \mathcal{A}^i\square \mathcal{B}^i$
.
Recall the following theorem of Reimer [Reference Reimer2]. See also [Reference van den Berg and Jonasson4].
Theorem 2.1. (Reimer) Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be subsets of
$\mathcal{Y}$
be subsets of
![]() $2^U$
, where
$2^U$
, where
![]() $U$
is a finite set. Then
$U$
is a finite set. Then
Combining Theorem 2.1 with Equations (5) and (6) and Lemma 2.3, we obtain that
This proves Inequality (4).
2.3 The proof Corollary 1.5
Let
![]() $X_0=X\backslash Y$
and
$X_0=X\backslash Y$
and
![]() $Y_0=Y\backslash X$
. Clearly the events
$Y_0=Y\backslash X$
. Clearly the events
![]() $X_0\subseteq B(M)$
and
$X_0\subseteq B(M)$
and
![]() $Y_0\subseteq B(M)$
depend on disjoint sets. Theorem 1.4 gives us
$Y_0\subseteq B(M)$
depend on disjoint sets. Theorem 1.4 gives us
and this is equivalent with the statement of the corollary.
2.4 The proof Theorem 1.6
Let
![]() $t\gt 0$
, and set all the edge weights to be equal to
$t\gt 0$
, and set all the edge weights to be equal to
![]() $t$
. Let
$t$
. Let
![]() $M_t$
be the corresponding random matching. By Theorem 1.3, if
$M_t$
be the corresponding random matching. By Theorem 1.3, if
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are increasing events, then
$\mathcal{B}$
are increasing events, then
Observe that
 \begin{align*} \lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{A}\big)&=\mathbb{P}(B(M)\in \mathcal{A}),\quad \lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{B}\big)=\mathbb{P}(B(M)\in \mathcal{B})\\&\text{ and }\lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{A}\square \mathcal{B}\big)=\mathbb{P}(B(M)\in \mathcal{A}\square \mathcal{B}). \end{align*}
\begin{align*} \lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{A}\big)&=\mathbb{P}(B(M)\in \mathcal{A}),\quad \lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{B}\big)=\mathbb{P}(B(M)\in \mathcal{B})\\&\text{ and }\lim _{t\to \infty }\mathbb{P}\big(B\big(M_t\big)\in \mathcal{A}\square \mathcal{B}\big)=\mathbb{P}(B(M)\in \mathcal{A}\square \mathcal{B}). \end{align*}
Thus, the statement follows.
Acknowledgements
The author is grateful to Péter Csikvári, Miklós Abért and the anonymous referees for their comments. The author was partially supported by the ERC Consolidator Grant 648017.