1 Introduction
A collection
![]() $(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (\mu _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
is called a random dynamical system (RDS) if the following statements hold.
$(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (\mu _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
is called a random dynamical system (RDS) if the following statements hold.
-
(1)
 $\sigma : \Omega \to \Omega $
is a
$\sigma : \Omega \to \Omega $
is a
 $\mathbb {P}$
-preserving transformation on a probability space
$\mathbb {P}$
-preserving transformation on a probability space
 $(\Omega , \mathbb {P})$
.
$(\Omega , \mathbb {P})$
. -
(2)
 $(\Delta _{\omega }, \mu _{\omega })$
is a probability space, called a fiber, at
$(\Delta _{\omega }, \mu _{\omega })$
is a probability space, called a fiber, at
 $\omega \in \Omega $
.
$\omega \in \Omega $
. -
(3)
 $F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega }$
, is called a fiber map from
$F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega }$
, is called a fiber map from
 $\Delta _{\omega }$
to
$\Delta _{\omega }$
to
 $\Delta _{\sigma \omega }$
.
$\Delta _{\sigma \omega }$
. -
(4)
 $(\mu _{\omega })_{\omega \in \Omega }$
are equivariant probability measures, namely, for almost every
$(\mu _{\omega })_{\omega \in \Omega }$
are equivariant probability measures, namely, for almost every
 $\omega \in \Omega $
, (1.1)
$\omega \in \Omega $
, (1.1) $$ \begin{align} (F_{\omega})_{*}\mu_{\omega}=\mu_{\sigma\omega}. \end{align} $$
$$ \begin{align} (F_{\omega})_{*}\mu_{\omega}=\mu_{\sigma\omega}. \end{align} $$
In this paper we only consider an invertible
![]() $\sigma : \Omega \to \Omega $
.
$\sigma : \Omega \to \Omega $
.
A decreasing series
![]() $\theta _n \searrow 0$
is called an almost sure mixing rate for the RDS if for almost every (a.e.)
$\theta _n \searrow 0$
is called an almost sure mixing rate for the RDS if for almost every (a.e.)
![]() $\omega \in \Omega $
, there is a constant
$\omega \in \Omega $
, there is a constant
![]() $C_{\omega }>0$
and a Banach space
$C_{\omega }>0$
and a Banach space
![]() $B_{\omega } \subset L^1(\Delta _{\omega }, \mu _{\omega })$
such that for any
$B_{\omega } \subset L^1(\Delta _{\omega }, \mu _{\omega })$
such that for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $ \phi _{\omega } \in B_{\omega }, \Psi _{\sigma ^n \omega } \in L^{\infty }(\Delta _{\sigma ^n \omega }, \mu _{\sigma ^n \omega })$
, there is a constant
$ \phi _{\omega } \in B_{\omega }, \Psi _{\sigma ^n \omega } \in L^{\infty }(\Delta _{\sigma ^n \omega }, \mu _{\sigma ^n \omega })$
, there is a constant
![]() $C_{\phi , \Psi }>0$
and
$C_{\phi , \Psi }>0$
and
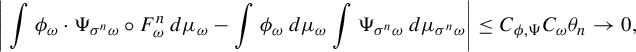 $$ \begin{align} \bigg|\int \phi_{\omega} \cdot \Psi_{\sigma^n \omega} \circ F^n_{\omega} \,d\mu_{\omega}-\int \phi_{\omega}\,d\mu_{\omega} \int \Psi_{\sigma^n \omega} \,d\mu_{\sigma^n \omega}\bigg| \le C_{\phi, \Psi} C_{\omega} \theta_n \to 0, \end{align} $$
$$ \begin{align} \bigg|\int \phi_{\omega} \cdot \Psi_{\sigma^n \omega} \circ F^n_{\omega} \,d\mu_{\omega}-\int \phi_{\omega}\,d\mu_{\omega} \int \Psi_{\sigma^n \omega} \,d\mu_{\sigma^n \omega}\bigg| \le C_{\phi, \Psi} C_{\omega} \theta_n \to 0, \end{align} $$
where
![]() $\phi (\omega , \cdot ):=\phi _{\omega }(\cdot ), \Psi (\omega , \cdot ):=\Psi _{\omega }(\cdot )$
are functions on
$\phi (\omega , \cdot ):=\phi _{\omega }(\cdot ), \Psi (\omega , \cdot ):=\Psi _{\omega }(\cdot )$
are functions on
![]() $\bigcup _{\omega \in \Omega } \{\omega \} \times \Delta _{\omega }$
. We say that an RDS has a uniform almost sure mixing rate if
$\bigcup _{\omega \in \Omega } \{\omega \} \times \Delta _{\omega }$
. We say that an RDS has a uniform almost sure mixing rate if
![]() $\operatorname *{ess~sup}_{\omega \in \Omega } C_{\omega } < \infty $
, and a non-uniform almost sure mixing rate if
$\operatorname *{ess~sup}_{\omega \in \Omega } C_{\omega } < \infty $
, and a non-uniform almost sure mixing rate if
![]() $\operatorname *{ess~sup}_{\omega \in \Omega } C_{\omega } = \infty $
.
$\operatorname *{ess~sup}_{\omega \in \Omega } C_{\omega } = \infty $
.
A random Young tower (RYT), a random extension of Young towers [Reference YoungYou99], is a powerful tool to study the almost sure mixing rate for the RDS with a weak hyperbolicity. The original one was constructed by Baladi, Benedicks, and Maume-Deschamps [Reference Baladi, Benedicks and Maume-DeschampsBBMD02] to obtain an almost sure mixing rate for independent and identically distributed (i.i.d.) translations of unimodal maps. In recent years, the RYT has been extended and used intensively. Du [Reference DuDu15] extended [Reference Baladi, Benedicks and Maume-DeschampsBBMD02] to a more general RYT and applied it to i.i.d. perturbations of a wider class of unimodal maps. Li and Vilarinho [Reference Li and VilarinhoLV18] applied the RYT [Reference Baladi, Benedicks and Maume-DeschampsBBMD02] to obtain almost sure mixing rates for i.i.d. translations of some non-uniformly expanding maps. Bahsoun, Bose, and Ruziboev [Reference Bahsoun, Bose and RuziboevBBR19] extended the RYT [Reference Baladi, Benedicks and Maume-DeschampsBBMD02, Reference DuDu15] under additional assumptions (see (P6) and (P7) in [Reference Bahsoun, Bose and RuziboevBBR19]) and obtained an almost sure mixing rate for i.i.d. perturbations of Liverani–Saussol–Vaienti (LSV) maps.
For an RDS with a uniform almost sure mixing rate, quenched limit laws have been studied by numerous authors; see [Reference Ayyer, Liverani and StenlundALS09, Reference Dragičević, Froyland, González-Tokman and VaientiDFGTV18a, Reference Dragičević, Froyland, González-Tokman and VaientiDFGTV18b, Reference Hella and LeppänenHL20, Reference Hella and StenlundHS20, Reference SuSu19a, Reference SuSu19b]. However, it is quite natural and more likely to have a RDS (e.g. the RYT) that has a non-uniform almost sure mixing rate. To the best of our knowledge, three papers [Reference Abdelkader and AiminoAA16, Reference Aimino, Nicol and VaientiANV15, Reference KiferKif98] do make progress for such RDSs: Abdelkader, Aimino, Nicol and Vaienti [Reference Abdelkader and AiminoAA16, Reference Aimino, Nicol and VaientiANV15] study an RDS with expanding average. Their approach was inspired by the paper [Reference Ayyer, Liverani and StenlundALS09], fixing a reference measure rather than finding equivariant probability measures. However, their applications are limited; see [Reference Aimino, Nicol and VaientiANV15, §7]. A different approach (assuming equivariant probability measures) is given by Kifer [Reference KiferKif98]. He proved quenched central limit theorems (QCLTs) under various technical assumptions. However, he remarks in Proposition 2.2 and Remark 6.5 of [Reference KiferKif98] that this method has to work on specific cases with explicit representations, even under the assumption that
![]() $(\Omega , \sigma )$
is Bernoulli (that is, i.i.d. perturbations).
$(\Omega , \sigma )$
is Bernoulli (that is, i.i.d. perturbations).
In this paper, we will give a different method to prove a quenched limit law, called a quenched almost sure invariance principle (QASIP; see Definition 2.1), for the RYT provided that the average measure of the tail of return times to the base of the RYT decays sufficiently fast (see the precise statement in Definition 2.2 and Theorem 2.3). QASIP convergence rates (see (2.1)) are also obtained. The QASIP implies various quenched limit laws including the QCLT.
Finally, we mention the papers [Reference Cuny, Dedecker, Korepanov and MerlevèdeCDKM20, Reference KorepanovKor18] which obtained a sharp QASIP convergence rate for deterministic Young towers (that is,
![]() $\Omega $
is a singleton).
$\Omega $
is a singleton).
The structure of the paper is as follows. In §2 we introduce conventions, which are used throughout the paper, give the necessary definitions and formulate the main results. In §3 we revisit the RYT and improve some inequalities in [Reference DuDu15]. In §4 we give several technical lemmas. In §5 we present a proof for the QASIP for the RYT. In §6 we obtain the QASIP for the RDS which can be modeled by the RYT. In §7 we apply our results to some i.i.d. perturbations of some non-uniformly expanding maps. We end our paper with a technical lemma in Appendix A.
2 Conventions, definitions and main theorems
Convention 2.1. We start with some conventions.
-
(1)
 $C_{a}$
means a constant depending on a.
$C_{a}$
means a constant depending on a. -
(2)
 $\mathbb {E}_{\mu _{\omega }} $
means the expectation with respect to (w.r.t.)
$\mathbb {E}_{\mu _{\omega }} $
means the expectation with respect to (w.r.t.)
 $\mu _{\omega }$
;
$\mu _{\omega }$
;
 $\mathbb {E}$
means the expectation of
$\mathbb {E}$
means the expectation of
 $\mathbb {P}$
.
$\mathbb {P}$
. -
(3) We do not specify the
 $\sigma $
-algebra of a measure space if it is clear from context.
$\sigma $
-algebra of a measure space if it is clear from context. -
(4)
 $a_n=O_a(b_n)$
and
$a_n=O_a(b_n)$
and
 $a_n\precsim _ab_n$
mean that
$a_n\precsim _ab_n$
mean that
 $a_n \le C_a b_n$
for a constant
$a_n \le C_a b_n$
for a constant
 $C_a>0$
and all
$C_a>0$
and all
 ${n \in \mathbb {N}}$
.
${n \in \mathbb {N}}$
. -
(5)
 $a_n=C_a^{\pm 1} b_n$
means that
$a_n=C_a^{\pm 1} b_n$
means that
 $C_a^{-1} b_n \le a_n \le C_a b_n$
for a constant
$C_a^{-1} b_n \le a_n \le C_a b_n$
for a constant
 $C_a\ge 1$
and all
$C_a\ge 1$
and all
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
. -
(6) We define
 $\phi _{\omega }(\cdot ):=\phi (\omega , \cdot )$
for any function
$\phi _{\omega }(\cdot ):=\phi (\omega , \cdot )$
for any function
 $\phi : \bigcup _{\omega \in \Omega } \{\omega \}\times \Delta _{\omega }\to \mathbb {R}$
.
$\phi : \bigcup _{\omega \in \Omega } \{\omega \}\times \Delta _{\omega }\to \mathbb {R}$
.
Definition 2.1. (QASIP and coboundary)
Consider an RDS
![]() $(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (\mu _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
and let
$(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (\mu _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
and let
![]() $\Delta :=\bigcup _{\omega \in \Omega } \{\omega \}\times \Delta _{\omega }$
. We say that a fiberwise mean zero function
$\Delta :=\bigcup _{\omega \in \Omega } \{\omega \}\times \Delta _{\omega }$
. We say that a fiberwise mean zero function
![]() $\phi : \Delta \to \mathbb {R}$
(that is,
$\phi : \Delta \to \mathbb {R}$
(that is,
![]() $\int \phi _{\omega } \,d\mu _{\omega }=0$
) has a QASIP if there is a constant
$\int \phi _{\omega } \,d\mu _{\omega }=0$
) has a QASIP if there is a constant
![]() $e \in (0,1/2)$
such that for a.e.
$e \in (0,1/2)$
such that for a.e.
![]() $\omega \in \Omega $
, there is a Brownian motion
$\omega \in \Omega $
, there is a Brownian motion
![]() $B^{\omega }$
defined on some extension of the probability space
$B^{\omega }$
defined on some extension of the probability space
![]() $(\Delta _{\omega }, \mu _{\omega })$
, say
$(\Delta _{\omega }, \mu _{\omega })$
, say
![]() ${\pmb {\Delta }}_{\omega }$
, such that
${\pmb {\Delta }}_{\omega }$
, such that
where
![]() $\sigma ^2_n(\omega ):=\int (\sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega })^2\,d\mu _{\omega } < \infty $
for all
$\sigma ^2_n(\omega ):=\int (\sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega })^2\,d\mu _{\omega } < \infty $
for all
![]() $n \ge 1$
and the constant in
$n \ge 1$
and the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
. e is called a convergence rate.
$x \in {\pmb {\Delta }}_{\omega }$
. e is called a convergence rate.
We say that
![]() $\phi $
is a coboundary if there is a function
$\phi $
is a coboundary if there is a function
![]() $g: \Delta \to \mathbb {R}$
such that for a.e.
$g: \Delta \to \mathbb {R}$
such that for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
Definition 2.2. (Random Young towers; see [Reference DuDu15])
A random Young tower
![]() $(\Delta , F)$
is constructed by the following 11 steps.
$(\Delta , F)$
is constructed by the following 11 steps.
-
(1) Fix a probability space
 $(\Lambda , \mathcal {B}, m)$
and a Bernoulli scheme
$(\Lambda , \mathcal {B}, m)$
and a Bernoulli scheme
 $(\Omega , \mathbb {P}, \sigma ):=(S^{\mathbb {Z}}, {\nu }^{\mathbb {Z}}, \sigma )$
where
$(\Omega , \mathbb {P}, \sigma ):=(S^{\mathbb {Z}}, {\nu }^{\mathbb {Z}}, \sigma )$
where
 $\nu $
is a probability on a measurable space S,
$\nu $
is a probability on a measurable space S,
 $\sigma $
is an invertible left shift on
$\sigma $
is an invertible left shift on
 $S^{\mathbb {Z}}$
and
$S^{\mathbb {Z}}$
and
 $\mathcal {B}$
is a
$\mathcal {B}$
is a
 $\sigma $
-algebra of
$\sigma $
-algebra of
 $(\Lambda ,m)$
.
$(\Lambda ,m)$
. -
(2) Assume that for a.e.
 $\omega \in \Omega $
, there is a countable partition
$\omega \in \Omega $
, there is a countable partition
 $ \mathcal {P}_{\omega } $
of a full measure subset
$ \mathcal {P}_{\omega } $
of a full measure subset
 $\mathcal {D}_{\omega }$
of
$\mathcal {D}_{\omega }$
of
 $\Lambda $
and a function
$\Lambda $
and a function
 $R_{\omega }: \Lambda \to \mathbb {N}$
such that
$R_{\omega }: \Lambda \to \mathbb {N}$
such that
 $R_{\omega }$
is constant on each
$R_{\omega }$
is constant on each
 ${U_{\omega } \in \mathcal {P}_{\omega }}$
.
${U_{\omega } \in \mathcal {P}_{\omega }}$
. -
(3) Assume that
 $R_{\omega }(x)$
is a stopping time: if
$R_{\omega }(x)$
is a stopping time: if
 $R_{\omega }(x) = n$
and
$R_{\omega }(x) = n$
and
 $\omega _i = \omega _i'$
for all
$\omega _i = \omega _i'$
for all
 $0 \le i<n$
, then
$0 \le i<n$
, then
 $R_{\omega '}(x) = n$
.
$R_{\omega '}(x) = n$
. -
(4) For a.e.
 $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $l \in \mathbb {N}$
, define
$l \in \mathbb {N}$
, define
 $\Delta _{\omega , 0}:= \Lambda \times \{0\}$
and the lth level by
$\Delta _{\omega , 0}:= \Lambda \times \{0\}$
and the lth level by  $$ \begin{align*} \Delta_{\omega, l}:= \{(x,l) : x \in \Lambda, R_{\sigma^{-l}\omega}(x)> l\}. \end{align*} $$
$$ \begin{align*} \Delta_{\omega, l}:= \{(x,l) : x \in \Lambda, R_{\sigma^{-l}\omega}(x)> l\}. \end{align*} $$
Define a tower at
 $\omega $
by
$\omega $
by  $$ \begin{align*} \Delta_{\omega}:= \bigcup_{l \ge 0} \Delta_{\omega, l}. \end{align*} $$
$$ \begin{align*} \Delta_{\omega}:= \bigcup_{l \ge 0} \Delta_{\omega, l}. \end{align*} $$
 $\Delta _{\omega }$
is endowed with a measure
$\Delta _{\omega }$
is endowed with a measure
 $m_{\omega }$
, a
$m_{\omega }$
, a
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {B}_{\omega }$
and a partition
$\mathcal {B}_{\omega }$
and a partition
 $\mathcal {Z}_{\omega }$
naturally from the probability space
$\mathcal {Z}_{\omega }$
naturally from the probability space
 $(\Lambda , \mathcal {B}, m)$
and the partitions
$(\Lambda , \mathcal {B}, m)$
and the partitions
 $(\mathcal {P}_{\sigma ^{-l}\omega })_{l\ge 0}$
.
$(\mathcal {P}_{\sigma ^{-l}\omega })_{l\ge 0}$
.
-
(5) For a.e.
 $\omega \in \Omega $
, a dynamics
$\omega \in \Omega $
, a dynamics
 $F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega } $
is defined in the following way: if
$F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega } $
is defined in the following way: if
 $R_{\sigma ^{-l}\omega }(x)> l+1$
, then
$R_{\sigma ^{-l}\omega }(x)> l+1$
, then
 $ F_{\omega }(x,l)=(x,l+1)$
; if
$ F_{\omega }(x,l)=(x,l+1)$
; if
 $R_{\sigma ^{-l}\omega }(x)= l+1$
,
$R_{\sigma ^{-l}\omega }(x)= l+1$
,
 $x \in U_{\sigma ^{-l}\omega } \in \mathcal {P}_{\sigma ^{-l}\omega }$
and
$x \in U_{\sigma ^{-l}\omega } \in \mathcal {P}_{\sigma ^{-l}\omega }$
and
 $(x,l)\in U_{\sigma ^{-l}\omega }\times \{l\} \subseteq \Delta _{\omega }$
, then
$(x,l)\in U_{\sigma ^{-l}\omega }\times \{l\} \subseteq \Delta _{\omega }$
, then
 $F_{\omega }$
maps
$F_{\omega }$
maps
 $U_{\sigma ^{-l}\omega } \times \{l\} $
bijectively onto
$U_{\sigma ^{-l}\omega } \times \{l\} $
bijectively onto
 $\Delta _{\sigma \omega , 0}$
.
$\Delta _{\sigma \omega , 0}$
. -
(6) Define
 $F_{\omega }^n:=F_{\sigma ^{n-1}\omega }\circ F_{\sigma ^{n-2}\omega } \circ \cdots \circ F_{\sigma \omega } \circ F_{\omega }$
, assume that the partition
$F_{\omega }^n:=F_{\sigma ^{n-1}\omega }\circ F_{\sigma ^{n-2}\omega } \circ \cdots \circ F_{\sigma \omega } \circ F_{\omega }$
, assume that the partition
 $\mathcal {Z}_{\omega }$
is generating for
$\mathcal {Z}_{\omega }$
is generating for
 $F_{\omega }$
in the sense that
$F_{\omega }$
in the sense that
 $\bigvee ^{\infty }_{j=0} (F^j_{\omega })^{-1}\mathcal {Z}_{\sigma ^j \omega }$
is a trivial partition into points.
$\bigvee ^{\infty }_{j=0} (F^j_{\omega })^{-1}\mathcal {Z}_{\sigma ^j \omega }$
is a trivial partition into points. -
(7) Assume that for a.e.
 $\omega \in \Omega , m_{\omega }(\Delta _{\omega })< \infty $
.
$\omega \in \Omega , m_{\omega }(\Delta _{\omega })< \infty $
. -
(8) Assume that there is an integer
 $M \in \mathbb {N}$
,
$M \in \mathbb {N}$
,
 $\{\epsilon _i> 0,i = 1,\ldots ,M\}$
and
$\{\epsilon _i> 0,i = 1,\ldots ,M\}$
and
 $\{t_i\in \mathbb {N},i= 1,\ldots ,M\}$
with
$\{t_i\in \mathbb {N},i= 1,\ldots ,M\}$
with
 $\gcd (t_i) = 1 $
such that for a.e.
$\gcd (t_i) = 1 $
such that for a.e.
 $\omega \in \Omega $
, all
$\omega \in \Omega $
, all
 $1 \le i \le M$
,
$1 \le i \le M$
,  $$ \begin{align*} m(x \in \Lambda: R_{\omega}(x) = t_i)> \epsilon_i. \end{align*} $$
$$ \begin{align*} m(x \in \Lambda: R_{\omega}(x) = t_i)> \epsilon_i. \end{align*} $$
-
(9) Extend
 $R_{\omega }$
from
$R_{\omega }$
from
 $\Delta _{\omega ,0}$
to
$\Delta _{\omega ,0}$
to
 $\Delta _{\omega }$
(still denoted by
$\Delta _{\omega }$
(still denoted by
 $R_{\omega }$
). For any
$R_{\omega }$
). For any
 $(x,l) \in \Delta _{\omega }$
, define an nth return time to
$(x,l) \in \Delta _{\omega }$
, define an nth return time to $$\begin{align*}R_{\omega}(x,l):=R_{\sigma^{-l}\omega}(x)-l,\end{align*}$$
$$\begin{align*}R_{\omega}(x,l):=R_{\sigma^{-l}\omega}(x)-l,\end{align*}$$
 $\Delta _{\omega }$
inductively: for any
$\Delta _{\omega }$
inductively: for any
 $x\in \Delta _{\omega }$
, and define a separation time
$x\in \Delta _{\omega }$
, and define a separation time $$ \begin{align*} &R^0_{\omega}(x):=0,\quad R^1_{\omega}(x):=R_{\omega}(x),\quad \ldots \quad \\ & R^n_{\omega}(x):=R^{n-1}_{\omega}(x)+R_{\sigma^{R^{n-1}_{\omega}(x)} \omega}(F_{\omega}^{R^{n-1}_{\omega}}(x)), \end{align*} $$
$$ \begin{align*} &R^0_{\omega}(x):=0,\quad R^1_{\omega}(x):=R_{\omega}(x),\quad \ldots \quad \\ & R^n_{\omega}(x):=R^{n-1}_{\omega}(x)+R_{\sigma^{R^{n-1}_{\omega}(x)} \omega}(F_{\omega}^{R^{n-1}_{\omega}}(x)), \end{align*} $$
 $s_{\omega }: \Delta _{\omega } \times \Delta _{\omega } \to \mathbb {N} \cup \{\infty \}$
by
$s_{\omega }: \Delta _{\omega } \times \Delta _{\omega } \to \mathbb {N} \cup \{\infty \}$
by  $$\begin{align*}s_{\omega}(x,y)=\inf \{n: F_{\omega}^{R^n_{\omega}(x)}(x), F_{\omega}^{R^n_{\omega}(y)}(y) \text{ lie in different elements of } \mathcal{Z}_{\sigma^{R^n_{\omega}(x)} \omega}\}.\end{align*}$$
$$\begin{align*}s_{\omega}(x,y)=\inf \{n: F_{\omega}^{R^n_{\omega}(x)}(x), F_{\omega}^{R^n_{\omega}(y)}(y) \text{ lie in different elements of } \mathcal{Z}_{\sigma^{R^n_{\omega}(x)} \omega}\}.\end{align*}$$
Assume that there are constants
 $C_{F}> 0$
and
$C_{F}> 0$
and
 $ \beta \in (0,1)$
such that for a.e.
$ \beta \in (0,1)$
such that for a.e.
 $\omega \in \Omega $
and each element
$\omega \in \Omega $
and each element
 $J_{\omega }\in \mathcal {Z}_{\omega }$
, the map
$J_{\omega }\in \mathcal {Z}_{\omega }$
, the map
 $F^{R_{\omega }}_\omega |_{J_{\omega }}$
and its inverse are non-singular w.r.t. m, and for each
$F^{R_{\omega }}_\omega |_{J_{\omega }}$
and its inverse are non-singular w.r.t. m, and for each
 $x,y \in J_{\omega }$
, (2.3)
$x,y \in J_{\omega }$
, (2.3) $$ \begin{align} \bigg|\frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}-1\bigg|\le C_F \beta^{s_{\sigma^{R_{\omega}(x)} \omega}(F^{R_{\omega}}_\omega(x), F^{R_{\omega}}_\omega(y))}. \end{align} $$
$$ \begin{align} \bigg|\frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}-1\bigg|\le C_F \beta^{s_{\sigma^{R_{\omega}(x)} \omega}(F^{R_{\omega}}_\omega(x), F^{R_{\omega}}_\omega(y))}. \end{align} $$
-
(10) Assume that there is a constant
 $C>0$
such that where
$C>0$
such that where $$ \begin{align*} \int m(x \in \Lambda: R_{\omega}(x)>n) \,d\mathbb{P} \le C \rho_n, \end{align*} $$
$$ \begin{align*} \int m(x \in \Lambda: R_{\omega}(x)>n) \,d\mathbb{P} \le C \rho_n, \end{align*} $$
 $\rho _n:= e^{-a n^{b}}$
or
$\rho _n:= e^{-a n^{b}}$
or
 $n^{-D}$
for some constants
$n^{-D}$
for some constants
 $a>0$
,
$a>0$
,
 $b \in (0,1]$
,
$b \in (0,1]$
,
 $D>4$
.
$D>4$
.
-
(11) Define a random Young tower
 $(\Delta , F)$
:
$(\Delta , F)$
:  $$ \begin{align*} \Delta:= \bigcup_{\omega \in \Omega} \{\omega\} \times \Delta_{\omega},\quad F(\omega, x):=(\sigma \omega, F_{\omega}x). \end{align*} $$
$$ \begin{align*} \Delta:= \bigcup_{\omega \in \Omega} \{\omega\} \times \Delta_{\omega},\quad F(\omega, x):=(\sigma \omega, F_{\omega}x). \end{align*} $$
Remark 2.2. For a visualization of the dynamics of the RYT, see Figure 1 in [Reference Bahsoun, Bose and RuziboevBBR19].
Definition 2.3. (Dynamical Lipschitz cones)
 $$ \begin{align*} \mathcal{F}_{\beta}^{+}:=&\bigg\{\phi: \Delta \to [0,\infty)| \text{ there is a constant } C_{\phi}>0, \text{ such that for any } J_{\omega} \in \mathcal{Z}_{\omega}, \\& \ \ \text{either } \phi_{\omega}|_{J_{\omega}}=0 \text{ or } \phi_{\omega}|_{J_{\omega}}>0, \text{ } \bigg|\log \frac{\phi_{\omega}(x)}{\phi_{\omega}(y)}\bigg| \le C_{\phi} \beta^{s_{\omega}(x,y)} \text{ for any } x,y \in J_{\omega}\bigg\}, \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\beta}^{+}:=&\bigg\{\phi: \Delta \to [0,\infty)| \text{ there is a constant } C_{\phi}>0, \text{ such that for any } J_{\omega} \in \mathcal{Z}_{\omega}, \\& \ \ \text{either } \phi_{\omega}|_{J_{\omega}}=0 \text{ or } \phi_{\omega}|_{J_{\omega}}>0, \text{ } \bigg|\log \frac{\phi_{\omega}(x)}{\phi_{\omega}(y)}\bigg| \le C_{\phi} \beta^{s_{\omega}(x,y)} \text{ for any } x,y \in J_{\omega}\bigg\}, \end{align*} $$
where
![]() $C_{\phi }$
is called a Lipschitz constant for
$C_{\phi }$
is called a Lipschitz constant for
![]() $\phi $
.
$\phi $
.
Definition 2.4. (Bounded random Lipschitz functions)
For any
![]() $p \in (1,\infty ]$
, define
$p \in (1,\infty ]$
, define
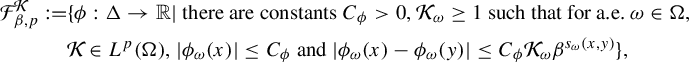 $$ \begin{align*} \mathcal{F}_{\beta,p}^{\mathcal{K}}:=&\{\phi: \Delta \to \mathbb{R}| \text{ there are constants } C_{\phi}>0, \mathcal{K}_{\omega} \ge 1 \text{ such that for a.e. } \omega \in \Omega,\\ &\mathcal{K}\in L^p(\Omega), |\phi_{\omega}(x)|\le C_{\phi} \text{ and } |\phi_{\omega}(x)- \phi_{\omega}(y)| \le C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\omega}(x,y)}\}, \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\beta,p}^{\mathcal{K}}:=&\{\phi: \Delta \to \mathbb{R}| \text{ there are constants } C_{\phi}>0, \mathcal{K}_{\omega} \ge 1 \text{ such that for a.e. } \omega \in \Omega,\\ &\mathcal{K}\in L^p(\Omega), |\phi_{\omega}(x)|\le C_{\phi} \text{ and } |\phi_{\omega}(x)- \phi_{\omega}(y)| \le C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\omega}(x,y)}\}, \end{align*} $$
where
![]() $C_{\phi }$
is also called a Lipschitz constant for
$C_{\phi }$
is also called a Lipschitz constant for
![]() $\phi $
.
$\phi $
.
Theorem 2.3. (Quenched limit laws for the RYT)
The following results hold for
![]() $(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
in Definition 2.2.
$(\Omega , \mathbb {P}, \sigma , (\Delta _{\omega })_{\omega \in \Omega }, (F_{\omega })_{\omega \in \Omega })$
in Definition 2.2.
-
(1) Equivariant probability measures (1.1)
 $(\mu _{\omega })_{\omega \in \Omega }$
exist. Define a probability
$(\mu _{\omega })_{\omega \in \Omega }$
exist. Define a probability
 $\mu $
on
$\mu $
on
 $\Delta $
by (2.4)for any measurable subset
$\Delta $
by (2.4)for any measurable subset $$ \begin{align} \mu(A):=\int \mu_{\omega}(A_{\omega}) \,d\mathbb{P} \end{align} $$
$$ \begin{align} \mu(A):=\int \mu_{\omega}(A_{\omega}) \,d\mathbb{P} \end{align} $$
 $A\subseteq \Delta $
and
$A\subseteq \Delta $
and
 $A_{\omega }:=\{x \in \Delta _{\omega }: (\omega ,x) \in A\}$
. Moreover, for any fiberwise mean zero function
$A_{\omega }:=\{x \in \Delta _{\omega }: (\omega ,x) \in A\}$
. Moreover, for any fiberwise mean zero function
 $\phi \in \mathcal {F}_{\beta ,p}^{\kern2pt\mathcal {K}}$
, suppose that
$\phi \in \mathcal {F}_{\beta ,p}^{\kern2pt\mathcal {K}}$
, suppose that
 $\rho _n$
(see Definition 2.2) is
$\rho _n$
(see Definition 2.2) is
 $ e^{-an^{b}}$
or
$ e^{-an^{b}}$
or
 ${n^{-D}}$
for some constants
${n^{-D}}$
for some constants
 $a>0$
,
$a>0$
,
 $b \in (0,1]$
and
$b \in (0,1]$
and
 $D>2+({4p}/({p-1}))$
. Then the following statements hold.
$D>2+({4p}/({p-1}))$
. Then the following statements hold.
-
(2) There is a constant
 $\Sigma ^2 \ge 0$
such that
$\Sigma ^2 \ge 0$
such that
 $\lim _{n \to \infty }({\sigma ^2_n(\omega )}/{n})=\Sigma ^2$
for a.e.
$\lim _{n \to \infty }({\sigma ^2_n(\omega )}/{n})=\Sigma ^2$
for a.e.
 $\omega \in \Omega $
.
$\omega \in \Omega $
. -
(3) If
 $\Sigma ^2>0$
, then
$\Sigma ^2>0$
, then
 $\phi $
has a QASIP (see Definition 2.1). The convergence rate is
$\phi $
has a QASIP (see Definition 2.1). The convergence rate is
 $e=\epsilon _0+1/4$
, where
$e=\epsilon _0+1/4$
, where
 $\epsilon _0 \in (0,1/4)$
satisfies the following: if
$\epsilon _0 \in (0,1/4)$
satisfies the following: if
 $\rho _n=e^{-an^b}$
, then
$\rho _n=e^{-an^b}$
, then
 $\epsilon _0>0$
can be arbitrarily small; if
$\epsilon _0>0$
can be arbitrarily small; if
 $\rho _n=n^{-D}$
, then
$\rho _n=n^{-D}$
, then
 $\epsilon _0$
can be any number in
$\epsilon _0$
can be any number in
 $(\epsilon _D, 1/4)$
, where(2.5)
$(\epsilon _D, 1/4)$
, where(2.5) $$ \begin{align} \epsilon_D=\max \bigg\{\frac{1}{4}+\frac{3\epsilon_1-2\epsilon_1^3-\epsilon_1^2}{4}, \epsilon_1, \frac{1+\epsilon_1}{4}\bigg\}-\frac{1}{4}\quad\text{and}\quad\epsilon_1=\frac{2p}{(p-1)(D-2)}. \end{align} $$
$$ \begin{align} \epsilon_D=\max \bigg\{\frac{1}{4}+\frac{3\epsilon_1-2\epsilon_1^3-\epsilon_1^2}{4}, \epsilon_1, \frac{1+\epsilon_1}{4}\bigg\}-\frac{1}{4}\quad\text{and}\quad\epsilon_1=\frac{2p}{(p-1)(D-2)}. \end{align} $$
-
(4) If
 $\Sigma ^2=0$
, then
$\Sigma ^2=0$
, then
 $\phi $
is a coboundary (see Definition 2.1), and the function g in (2.2) satisfies the following: if
$\phi $
is a coboundary (see Definition 2.1), and the function g in (2.2) satisfies the following: if
 $\rho _n=n^{-D}$
, then
$\rho _n=n^{-D}$
, then
 $g \in L^{{(D-2-\delta )(p-1)}/{(1+\delta )p}}(\Delta , \mu )$
for any sufficiently small
$g \in L^{{(D-2-\delta )(p-1)}/{(1+\delta )p}}(\Delta , \mu )$
for any sufficiently small
 $\delta>0$
such that
$\delta>0$
such that
 ${(D-2-\delta )(p-1)}/{(1+\delta )p}>4$
. In particular, if
${(D-2-\delta )(p-1)}/{(1+\delta )p}>4$
. In particular, if
 $\rho _n=e^{-a n^b}$
(which implies
$\rho _n=e^{-a n^b}$
(which implies
 $\rho _n\le n^{-D}$
for
$\rho _n\le n^{-D}$
for
 $n,D \gg 1$
), then
$n,D \gg 1$
), then
 $g \in L^{k}(\Delta , \mu )$
for all
$g \in L^{k}(\Delta , \mu )$
for all
 $k\ge 1$
.
$k\ge 1$
.
Remark 2.4. In §7, p is chosen to be
![]() $\infty $
.
$\infty $
.
Remark 2.5. For any
![]() $ n \ge 1$
, define
$ n \ge 1$
, define
![]() $S_n^{\omega }:= \sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega }$
, and
$S_n^{\omega }:= \sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega }$
, and
![]() $S^{n, \omega }$
on
$S^{n, \omega }$
on
![]() $[0,1]$
:
$[0,1]$
:
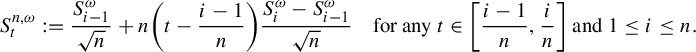 $$ \begin{align*} S^{n, \omega}_t: =\frac{S^{\omega}_{i-1}}{\sqrt n}+n\bigg(t-\frac{i-1}{n}\bigg)\frac{S^{\omega}_{i}-S^{\omega}_{i-1}}{\sqrt n} \quad\text{for any }t \in \bigg[\frac{i-1}{n},\frac{i}{n}\bigg] \text{ and } 1 \le i \le n. \end{align*} $$
$$ \begin{align*} S^{n, \omega}_t: =\frac{S^{\omega}_{i-1}}{\sqrt n}+n\bigg(t-\frac{i-1}{n}\bigg)\frac{S^{\omega}_{i}-S^{\omega}_{i-1}}{\sqrt n} \quad\text{for any }t \in \bigg[\frac{i-1}{n},\frac{i}{n}\bigg] \text{ and } 1 \le i \le n. \end{align*} $$
Then the QASIP implies the following limit laws for the RYT: for a.e.
![]() $\omega \in \Omega $
, we have the convergence (w.r.t. the probability
$\omega \in \Omega $
, we have the convergence (w.r.t. the probability
![]() $\mu _{\omega }$
)
$\mu _{\omega }$
)
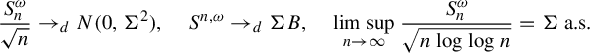 $$\begin{align*}\frac{S_n^{\omega}}{\sqrt n}\to_d N(0,\Sigma^2), \quad S^{n, \omega} \to_d\Sigma B,\quad\limsup_{n\to \infty}\frac{S_n^{\omega}}{ \sqrt{n\log\log n}}=\Sigma \text{ a.s.}\end{align*}$$
$$\begin{align*}\frac{S_n^{\omega}}{\sqrt n}\to_d N(0,\Sigma^2), \quad S^{n, \omega} \to_d\Sigma B,\quad\limsup_{n\to \infty}\frac{S_n^{\omega}}{ \sqrt{n\log\log n}}=\Sigma \text{ a.s.}\end{align*}$$
where B is a standard one-dimensional Brownian motion.
Remark 2.6. For the RYT with
![]() $\rho _n=n^{-D}$
, Du [Reference DuDu15] obtained a mixing rate (1.2)
$\rho _n=n^{-D}$
, Du [Reference DuDu15] obtained a mixing rate (1.2)
![]() $\theta _n=n^{-(D-3-\epsilon )}$
for any small
$\theta _n=n^{-(D-3-\epsilon )}$
for any small
![]() $\epsilon \in (0,1)$
when
$\epsilon \in (0,1)$
when
![]() $D>4$
(see [Reference DuDu15, Theorem 1.2.6]), while Bahsoun, Bose and Ruziboev [Reference Bahsoun, Bose and RuziboevBBR19] obtained a better
$D>4$
(see [Reference DuDu15, Theorem 1.2.6]), while Bahsoun, Bose and Ruziboev [Reference Bahsoun, Bose and RuziboevBBR19] obtained a better
![]() $\theta _n=n^{-(D-1-\epsilon )}$
for any small
$\theta _n=n^{-(D-1-\epsilon )}$
for any small
![]() $\epsilon \in (0,D-1)$
when
$\epsilon \in (0,D-1)$
when
![]() $D>1$
, under two more restrictive assumptions (P6) and (P7) in [Reference Bahsoun, Bose and RuziboevBBR19]. In this paper, we only consider the general RYT in [Reference DuDu15] for the following reasons: first, the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] is a special case of the general RYT in [Reference DuDu15] when
$D>1$
, under two more restrictive assumptions (P6) and (P7) in [Reference Bahsoun, Bose and RuziboevBBR19]. In this paper, we only consider the general RYT in [Reference DuDu15] for the following reasons: first, the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] is a special case of the general RYT in [Reference DuDu15] when
![]() $D>4$
; second, the assumptions (P6) and (P7) for the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] are not satisfied by all RDSs in our applications. We believe that the conditions
$D>4$
; second, the assumptions (P6) and (P7) for the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] are not satisfied by all RDSs in our applications. We believe that the conditions
![]() $D>4$
in [Reference DuDu15] and
$D>4$
in [Reference DuDu15] and
![]() $D>2+({4p}/({p-1}))$
in our Theorem 2.3 are technical only, and the QASIP for the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] should hold for a smaller D.
$D>2+({4p}/({p-1}))$
in our Theorem 2.3 are technical only, and the QASIP for the restrictive RYT in [Reference Bahsoun, Bose and RuziboevBBR19] should hold for a smaller D.
3 Random Young towers revisited
Lemma 3.1. (See [Reference DuDu15])
We have the following results for the RYT in Definition 2.2.
-
(1) There is a function
 $ h \in \mathcal {F}^{\kern2pt +}_{\beta }$
and a family of absolutely continuous equivariant probability measures
$ h \in \mathcal {F}^{\kern2pt +}_{\beta }$
and a family of absolutely continuous equivariant probability measures
 $\,d\mu _{\omega }:=h_{\omega }dm_{\omega } $
on
$\,d\mu _{\omega }:=h_{\omega }dm_{\omega } $
on
 $\Delta _{\omega }$
such that for a.e.
$\Delta _{\omega }$
such that for a.e.
 $\omega \in \Omega $
, (3.1)where
$\omega \in \Omega $
, (3.1)where $$ \begin{align}&(F_{\omega})_{*}\mu_{\omega}=\mu_{\sigma \omega}, \quad \operatorname*{ess~sup}_{\omega \in \Omega, x\in \Delta_{\omega}} h_{\omega}(x) < \infty,\quad h_{\omega}>0,\\ &\ \qquad(\Delta, F, \mu) \text{ is exact, mixing and ergodic}\nonumber,\end{align} $$
$$ \begin{align}&(F_{\omega})_{*}\mu_{\omega}=\mu_{\sigma \omega}, \quad \operatorname*{ess~sup}_{\omega \in \Omega, x\in \Delta_{\omega}} h_{\omega}(x) < \infty,\quad h_{\omega}>0,\\ &\ \qquad(\Delta, F, \mu) \text{ is exact, mixing and ergodic}\nonumber,\end{align} $$
 $\mu $
is the probability defined in (2.4) and
$\mu $
is the probability defined in (2.4) and
 $h_{\omega }>0$
for a.e.
$h_{\omega }>0$
for a.e.
 $\omega \in \Omega $
(that is,
$\omega \in \Omega $
(that is,
 $m_{\omega }\{h_{\omega }=0\}=0$
for a.e.
$m_{\omega }\{h_{\omega }=0\}=0$
for a.e.
 $\omega \in \Omega $
).
$\omega \in \Omega $
).
-
(2) There is an integer
 $l_0> 0$
such that for any
$l_0> 0$
such that for any
 $l \ge l_0$
, there is a constant
$l \ge l_0$
, there is a constant
 $ \epsilon _l\in (0, 1)$
such that for a.e.
$ \epsilon _l\in (0, 1)$
such that for a.e.
 $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $m_{\omega }(\Delta _{\omega , 0}\cap F_{\omega }^{-l}\Delta _{\sigma ^l \omega , 0})>\epsilon _{l}$
.
$m_{\omega }(\Delta _{\omega , 0}\cap F_{\omega }^{-l}\Delta _{\sigma ^l \omega , 0})>\epsilon _{l}$
. -
(3) Define return times on
 $\bigcup _{\omega \in \Omega }\{\omega \}\times \Delta _{\omega } \times \Delta _{\omega }$
alternatively and recursively: where
$\bigcup _{\omega \in \Omega }\{\omega \}\times \Delta _{\omega } \times \Delta _{\omega }$
alternatively and recursively: where $$ \begin{align*} &\bar{\tau}_0^\omega(x, x'):=0,\quad \bar{\tau}_1^\omega(x, x'):=R^{l_0}_{\omega}(x),\\ &\bar{\tau}_2^\omega(x, x'):=\bar{\tau}_1^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_1(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_1(x,x')} x'),\\ &\bar{\tau}_3^\omega( x, x'):=\bar{\tau}_2^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_2(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_2(x,x')} x),\\ &\bar{\tau}_4^\omega( x, x'):=\bar{\tau}_3^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_3(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_3(x,x')} x'),\ldots\\ &T^{\omega}(x, x'):=\min\{\bar{\tau}^{\omega}_i(x,x'), i \ge 1:\\ &\quad(F_{\omega}\times F_{\omega})^{\bar{\tau}^{\omega}_i(x,x')}(x,x') \in \Delta_{\sigma^{\bar{\tau}^{\omega}_i(x,x')}\omega,0}\times \Delta_{\sigma^{\bar{\tau}^{\omega}_i(x,x')}\omega,0}\},\\ &T_{0}^{\omega}:=0,\quad T_{1}^{\omega}:=T^{\omega}, \ldots\\ & T_{n}^{\omega}(x,x'):=T_{n-1}^{\omega}(x,x')+ T^{\sigma^{T^{\omega}_{n-1}(x,x')}\omega}((F_{\omega}\times F_{\omega})^{T^{\omega}_{n-1}(x,x')}(x,x')), \end{align*} $$
$$ \begin{align*} &\bar{\tau}_0^\omega(x, x'):=0,\quad \bar{\tau}_1^\omega(x, x'):=R^{l_0}_{\omega}(x),\\ &\bar{\tau}_2^\omega(x, x'):=\bar{\tau}_1^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_1(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_1(x,x')} x'),\\ &\bar{\tau}_3^\omega( x, x'):=\bar{\tau}_2^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_2(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_2(x,x')} x),\\ &\bar{\tau}_4^\omega( x, x'):=\bar{\tau}_3^\omega(x, x')+R^{l_0}_{\sigma^{\bar{\tau}^{\omega}_3(x,x')}\omega}( F_{\omega}^{\bar{\tau}^{\omega}_3(x,x')} x'),\ldots\\ &T^{\omega}(x, x'):=\min\{\bar{\tau}^{\omega}_i(x,x'), i \ge 1:\\ &\quad(F_{\omega}\times F_{\omega})^{\bar{\tau}^{\omega}_i(x,x')}(x,x') \in \Delta_{\sigma^{\bar{\tau}^{\omega}_i(x,x')}\omega,0}\times \Delta_{\sigma^{\bar{\tau}^{\omega}_i(x,x')}\omega,0}\},\\ &T_{0}^{\omega}:=0,\quad T_{1}^{\omega}:=T^{\omega}, \ldots\\ & T_{n}^{\omega}(x,x'):=T_{n-1}^{\omega}(x,x')+ T^{\sigma^{T^{\omega}_{n-1}(x,x')}\omega}((F_{\omega}\times F_{\omega})^{T^{\omega}_{n-1}(x,x')}(x,x')), \end{align*} $$
 $R^{l_0}_{\omega }(x)$
is the
$R^{l_0}_{\omega }(x)$
is the
 $l_0$
th return time of
$l_0$
th return time of
 $ x\in \Delta _{\omega }$
to the
$ x\in \Delta _{\omega }$
to the
 $0$
th level.
$0$
th level.
Let
 $\lambda _{\omega }, \lambda ^{\prime }_{\omega }$
be absolutely continuous probability measures on
$\lambda _{\omega }, \lambda ^{\prime }_{\omega }$
be absolutely continuous probability measures on
 $\Delta _{\omega }$
whose density functions are
$\Delta _{\omega }$
whose density functions are
 ${d\lambda }/{dm}, {d\lambda '}/{dm} \in \mathcal {F}^{\kern2pt +}_{\beta }$
where
${d\lambda }/{dm}, {d\lambda '}/{dm} \in \mathcal {F}^{\kern2pt +}_{\beta }$
where
 ${d\lambda }/{dm}(\omega ,\cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot ), {d\lambda '}/ {dm} (\omega ,\cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot )$
.
${d\lambda }/{dm}(\omega ,\cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot ), {d\lambda '}/ {dm} (\omega ,\cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot )$
.Then we have the following matching: there are constants
 $C=C_{\beta , F,h}>0, r \in (0,1)$
(independent of
$C=C_{\beta , F,h}>0, r \in (0,1)$
(independent of
 $\lambda , \lambda '$
) such that for a.e.
$\lambda , \lambda '$
) such that for a.e.
 $\omega \in \Omega $
, (3.2)
$\omega \in \Omega $
, (3.2) $$ \begin{align} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\lambda^{\prime}_{\omega}|:&=\int\bigg|\frac{d(F^n_{\omega})_{*}\lambda_{\omega}}{dm_{\sigma^n\omega}}-\frac{d(F^n_{\omega})_{*}\lambda^{\prime}_{\omega}}{dm_{\sigma^n\omega}}\bigg| dm_{\sigma^n\omega}\nonumber\\ &\le C \sum_{i\ge0}r^i (\lambda_{\omega} \otimes \lambda^{\prime}_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1}). \end{align} $$
$$ \begin{align} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\lambda^{\prime}_{\omega}|:&=\int\bigg|\frac{d(F^n_{\omega})_{*}\lambda_{\omega}}{dm_{\sigma^n\omega}}-\frac{d(F^n_{\omega})_{*}\lambda^{\prime}_{\omega}}{dm_{\sigma^n\omega}}\bigg| dm_{\sigma^n\omega}\nonumber\\ &\le C \sum_{i\ge0}r^i (\lambda_{\omega} \otimes \lambda^{\prime}_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1}). \end{align} $$
-
(4) If
 $\rho _n=e^{-a n^{b}}$
or
$\rho _n=e^{-a n^{b}}$
or
 ${n^{-D}}$
where
${n^{-D}}$
where
 $a>0$
,
$a>0$
,
 $b \in (0,1], D>4$
, then for any small
$b \in (0,1], D>4$
, then for any small
 $ \delta \in (0,1)$
, there is a constant
$ \delta \in (0,1)$
, there is a constant
 $C=C_{\beta ,F,\delta }>0$
and a small
$C=C_{\beta ,F,\delta }>0$
and a small
 $\alpha =\alpha _{\delta }>0$
such that (3.3)
$\alpha =\alpha _{\delta }>0$
such that (3.3) $$ \begin{align} \int (m_{\omega}\otimes m_{\omega} )(T^{\omega}_{\lfloor n^{\alpha}\rfloor}>n) \,d\mathbb{P}\le C {n^{-(D-2-\delta)}}. \end{align} $$
$$ \begin{align} \int (m_{\omega}\otimes m_{\omega} )(T^{\omega}_{\lfloor n^{\alpha}\rfloor}>n) \,d\mathbb{P}\le C {n^{-(D-2-\delta)}}. \end{align} $$
Proof. See Theorem 2.2.1 and Propositions 2.3.1, 2.3.3 and 2.3.4 of [Reference DuDu15] for the proof of (3.1). See Theorem 3.1.1 of [Reference DuDu15] for the proof of (3.2). The proof of Proposition 2.3.4 of [Reference DuDu15] showed that
![]() $h_{\omega }>0$
for a.e.
$h_{\omega }>0$
for a.e.
![]() $\omega \in \Omega $
only. It does not imply a uniform lower bound
$\omega \in \Omega $
only. It does not imply a uniform lower bound
![]() $\inf _{\omega \in \Omega , x \in \Delta _{\omega }}h_{\omega }(x)>0$
. Actually, our proofs do not require such a lower bound.
$\inf _{\omega \in \Omega , x \in \Delta _{\omega }}h_{\omega }(x)>0$
. Actually, our proofs do not require such a lower bound.
Since
![]() $\rho _n\le e^{-a n^b}$
implies
$\rho _n\le e^{-a n^b}$
implies
![]() $\rho _n\le n^{-D}$
for
$\rho _n\le n^{-D}$
for
![]() $D,n\gg 1$
, we consider
$D,n\gg 1$
, we consider
![]() $\rho _n\le n^{-D}$
only and refer to Corollary 7.1.2 of [Reference DuDu15] for the proof of (3.3).
$\rho _n\le n^{-D}$
only and refer to Corollary 7.1.2 of [Reference DuDu15] for the proof of (3.3).
Lemma 3.2. Consider the RYT in Definition 2.2. Suppose that
![]() $\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
and
$\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
and
![]() $\rho _n=e^{-a n^{b}}$
or
$\rho _n=e^{-a n^{b}}$
or
![]() ${n^{-D}}$
where
${n^{-D}}$
where
![]() $a>0$
,
$a>0$
,
![]() $b \in (0,1], D>4$
. Define a probability
$b \in (0,1], D>4$
. Define a probability
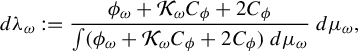 $$ \begin{align*} d\lambda_{\omega}:=\frac{\phi_{\omega}+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}{\int (\phi_{\omega}+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi})\,d\mu_{\omega}} \,d\mu_{\omega}, \end{align*} $$
$$ \begin{align*} d\lambda_{\omega}:=\frac{\phi_{\omega}+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}{\int (\phi_{\omega}+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi})\,d\mu_{\omega}} \,d\mu_{\omega}, \end{align*} $$
where
![]() $C_{\phi }$
is a Lipschitz constant for
$C_{\phi }$
is a Lipschitz constant for
![]() $\phi $
. Then for any small
$\phi $
. Then for any small
![]() $\delta \in (0,1)$
, there is a constant
$\delta \in (0,1)$
, there is a constant
![]() $C= C_{h,F,\beta ,\delta }$
such that
$C= C_{h,F,\beta ,\delta }$
such that
Proof. By (3.1) and
![]() $\mathcal {K}_{\omega } \ge 1$
,
$\mathcal {K}_{\omega } \ge 1$
,
 $$ \begin{align} \frac{d\lambda_{\omega}}{dm_{\omega}} \le \frac{C_{\phi} (3+\mathcal{K}_{\omega})}{C_{\phi} (1+\mathcal{K}_{\omega})} \operatorname*{ess~sup}_{\omega \in \Omega} h_{\omega} \le \frac{3+\mathcal{K}_{\omega}}{1+\mathcal{K}_{\omega}} C_h \le 2 C_{h}, \end{align} $$
$$ \begin{align} \frac{d\lambda_{\omega}}{dm_{\omega}} \le \frac{C_{\phi} (3+\mathcal{K}_{\omega})}{C_{\phi} (1+\mathcal{K}_{\omega})} \operatorname*{ess~sup}_{\omega \in \Omega} h_{\omega} \le \frac{3+\mathcal{K}_{\omega}}{1+\mathcal{K}_{\omega}} C_h \le 2 C_{h}, \end{align} $$
where
![]() $C_h$
is a Lipschitz constant of h. For any
$C_h$
is a Lipschitz constant of h. For any
![]() $x, y \in \Delta _{\omega }$
, using the inequality
$x, y \in \Delta _{\omega }$
, using the inequality
![]() $\log z\le z-1$
when
$\log z\le z-1$
when
![]() $z \ge 1$
, we have
$z \ge 1$
, we have
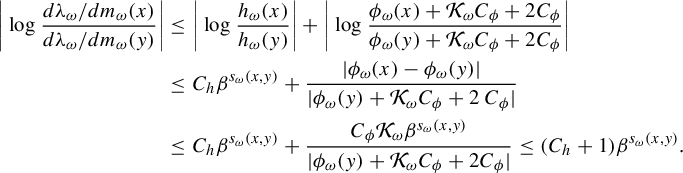 $$ \begin{align*} \bigg|\log \frac{{d\lambda_{\omega}}/{dm_{\omega}}(x)}{{d\lambda_{\omega}}/{dm_{\omega}}(y)}\bigg|&\le \bigg|\log \frac{h_{\omega}(x)}{h_{\omega}(y)}\bigg| +\bigg|\log \frac{\phi_{\omega}(x)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}{\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}\bigg|\\ &\le C_{h} \beta^{s_{\omega}(x,y)}+ \frac{|\phi_{\omega}(x)-\phi_{\omega}(y)|}{|\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 \ C_{\phi}|}\\ &\le C_{h} \beta^{s_{\omega}(x,y)}+ \frac{C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\omega}(x,y)}}{|\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}|}\le (C_{h}+1) \beta^{s_{\omega}(x,y)}. \end{align*} $$
$$ \begin{align*} \bigg|\log \frac{{d\lambda_{\omega}}/{dm_{\omega}}(x)}{{d\lambda_{\omega}}/{dm_{\omega}}(y)}\bigg|&\le \bigg|\log \frac{h_{\omega}(x)}{h_{\omega}(y)}\bigg| +\bigg|\log \frac{\phi_{\omega}(x)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}{\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}}\bigg|\\ &\le C_{h} \beta^{s_{\omega}(x,y)}+ \frac{|\phi_{\omega}(x)-\phi_{\omega}(y)|}{|\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 \ C_{\phi}|}\\ &\le C_{h} \beta^{s_{\omega}(x,y)}+ \frac{C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\omega}(x,y)}}{|\phi_{\omega}(y)+\mathcal{K}_{\omega} C_{\phi}+2 C_{\phi}|}\le (C_{h}+1) \beta^{s_{\omega}(x,y)}. \end{align*} $$
Therefore,
![]() ${d\lambda }/{dm} \in \mathcal {F}^{\kern2pt +}_{\beta }$
with a Lipschitz constant
${d\lambda }/{dm} \in \mathcal {F}^{\kern2pt +}_{\beta }$
with a Lipschitz constant
![]() $2C_{h}+1$
where
$2C_{h}+1$
where
![]() ${d\lambda }/{dm}(\omega , \cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot )$
. By (3.2) and (3.3), there are constants
${d\lambda }/{dm}(\omega , \cdot ):={d\lambda _{\omega }}/{dm_{\omega }}(\cdot )$
. By (3.2) and (3.3), there are constants
![]() $C'=C_{\beta ,F,\delta }>0$
,
$C'=C_{\beta ,F,\delta }>0$
,
![]() $\bar {C}=C_{\beta , F, h}>0$
,
$\bar {C}=C_{\beta , F, h}>0$
,
![]() $\alpha =\alpha _{\delta }$
such that
$\alpha =\alpha _{\delta }$
such that
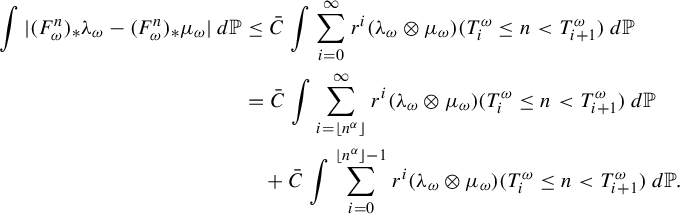 $$ \begin{align*} \int |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \,d\mathbb{P} &\le \bar{C} \int \sum_{i=0}^{\infty}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}\\ &=\bar{C} \int \sum_{i=\lfloor n^{\alpha}\rfloor}^{\infty}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}\\ & \quad + \bar{C}\int \sum_{i=0}^{\lfloor n^{\alpha}\rfloor-1}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}.\end{align*} $$
$$ \begin{align*} \int |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \,d\mathbb{P} &\le \bar{C} \int \sum_{i=0}^{\infty}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}\\ &=\bar{C} \int \sum_{i=\lfloor n^{\alpha}\rfloor}^{\infty}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}\\ & \quad + \bar{C}\int \sum_{i=0}^{\lfloor n^{\alpha}\rfloor-1}r^i (\lambda_{\omega} \otimes \mu_{\omega})(T^{\omega}_i \le n < T^{\omega}_{i+1})\,d\mathbb{P}.\end{align*} $$
By (3.5) and
![]() $r\in (0,1)$
, we can continue the estimate above as
$r\in (0,1)$
, we can continue the estimate above as
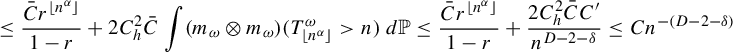 $$ \begin{align*} &\le \frac{\bar{C} r^{\lfloor n^{\alpha}\rfloor}}{1-r}+2 C^2_h \bar{C} \int (m_{\omega} \otimes m_{\omega})(T^{\omega}_{\lfloor n^{\alpha}\rfloor}>n) \,d\mathbb{P}\le \frac{\bar{C} r^{\lfloor n^{\alpha}\rfloor}}{1-r}+\frac{2C_h^2 \bar{C}C'} {n^{D-2-\delta}} \le C {n^{-(D-2-\delta)}} \end{align*} $$
$$ \begin{align*} &\le \frac{\bar{C} r^{\lfloor n^{\alpha}\rfloor}}{1-r}+2 C^2_h \bar{C} \int (m_{\omega} \otimes m_{\omega})(T^{\omega}_{\lfloor n^{\alpha}\rfloor}>n) \,d\mathbb{P}\le \frac{\bar{C} r^{\lfloor n^{\alpha}\rfloor}}{1-r}+\frac{2C_h^2 \bar{C}C'} {n^{D-2-\delta}} \le C {n^{-(D-2-\delta)}} \end{align*} $$
where the constant C depends on
![]() $\alpha _{\delta }, \delta , \beta , F, h$
.
$\alpha _{\delta }, \delta , \beta , F, h$
.
Definition 3.1. (Random transfer operators)
![]() $P_{\omega }: L^1(\Delta _{\omega }, \mu _{\omega }) \to L^1(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
is called a random transfer operator for
$P_{\omega }: L^1(\Delta _{\omega }, \mu _{\omega }) \to L^1(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
is called a random transfer operator for
![]() $F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega } $
if for any
$F_{\omega }: \Delta _{\omega } \to \Delta _{\sigma \omega } $
if for any
![]() $\Psi _{\omega } \in L^1(\Delta _{\omega }, \mu _{\omega }), \Upsilon _{\sigma \omega } \in L^{\infty }(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
,
$\Psi _{\omega } \in L^1(\Delta _{\omega }, \mu _{\omega }), \Upsilon _{\sigma \omega } \in L^{\infty }(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
,
Lemma 3.3. (Properties of random transfer operators)
Consider the RYT in Definition 2.2. The random transfer operator
![]() $P_{\omega }$
for
$P_{\omega }$
for
![]() $F_{\omega }$
has the following expression: for a.e.
$F_{\omega }$
has the following expression: for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align} (P_{\omega}\Psi_{\omega})(x)=h^{-1}_{\sigma \omega}(x)\sum_{F_{\omega}(y)=x}\frac{\Psi_{\omega}(y) h_{\omega}(y)}{JF_{\omega}(y)} \quad\text{in } L^1(\mu_{\sigma \omega}), \end{align} $$
$$ \begin{align} (P_{\omega}\Psi_{\omega})(x)=h^{-1}_{\sigma \omega}(x)\sum_{F_{\omega}(y)=x}\frac{\Psi_{\omega}(y) h_{\omega}(y)}{JF_{\omega}(y)} \quad\text{in } L^1(\mu_{\sigma \omega}), \end{align} $$
where
![]() $JF_{\omega }$
is the Jacobian of
$JF_{\omega }$
is the Jacobian of
![]() $F_{\omega }$
w.r.t. m,
$F_{\omega }$
w.r.t. m,
![]() $\Psi _{\omega }\in L^1(\Delta _{\omega }, \mu _{\omega })$
. Moreover, for any
$\Psi _{\omega }\in L^1(\Delta _{\omega }, \mu _{\omega })$
. Moreover, for any
![]() $i,k \ge 0$
, any measurable functions
$i,k \ge 0$
, any measurable functions
![]() $\Psi , \Upsilon $
on
$\Psi , \Upsilon $
on
![]() $\Delta $
, the following results hold for a.e.
$\Delta $
, the following results hold for a.e.
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
If
![]() $\Psi \in L^{\infty }(\Delta , \mu )$
, then
$\Psi \in L^{\infty }(\Delta , \mu )$
, then
If
![]() $\Psi \in L^{1}(\Delta , \mu )$
, then
$\Psi \in L^{1}(\Delta , \mu )$
, then
 $$ \begin{align} &\!\! \quad \frac{(F^{i}_{\omega})_{*}(\Psi_{\omega} \,d\mu_{\omega})}{\,d\mu_{\sigma^i \omega}}=P^i_{\omega} (\Psi_{\omega}) \quad\text{in } L^1(\mu_{\sigma^i \omega}). \end{align} $$
$$ \begin{align} &\!\! \quad \frac{(F^{i}_{\omega})_{*}(\Psi_{\omega} \,d\mu_{\omega})}{\,d\mu_{\sigma^i \omega}}=P^i_{\omega} (\Psi_{\omega}) \quad\text{in } L^1(\mu_{\sigma^i \omega}). \end{align} $$
If
![]() $\Psi , \Upsilon \in L^{2}(\Delta , \mu )$
, then
$\Psi , \Upsilon \in L^{2}(\Delta , \mu )$
, then
where
![]() $P_{\omega }^i:=P_{\sigma ^{i-1}\omega }\circ \cdots \circ P_{\sigma \omega }\circ P_{\omega }$
.
$P_{\omega }^i:=P_{\sigma ^{i-1}\omega }\circ \cdots \circ P_{\sigma \omega }\circ P_{\omega }$
.
Proof. By (3.1),
![]() $h_{\omega }>0$
for a.e.
$h_{\omega }>0$
for a.e.
![]() $\omega \in \Omega $
. Similarly to Ruelle–Perron–Frobenius operators, it is straightforward to verify (3.7)–(3.10) from Definition 3.1. To verify (3.6), let
$\omega \in \Omega $
. Similarly to Ruelle–Perron–Frobenius operators, it is straightforward to verify (3.7)–(3.10) from Definition 3.1. To verify (3.6), let
![]() $\Psi _{\omega } \in L^1(\Delta _{\omega }, \mu _{\omega }), \Upsilon _{\sigma \omega } \in L^{\infty }(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
. By Definition 3.1,
$\Psi _{\omega } \in L^1(\Delta _{\omega }, \mu _{\omega }), \Upsilon _{\sigma \omega } \in L^{\infty }(\Delta _{\sigma \omega }, \mu _{\sigma \omega })$
. By Definition 3.1,
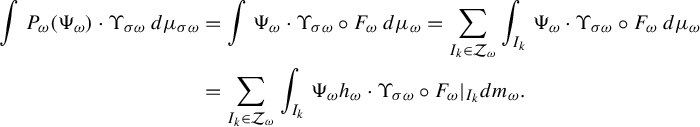 $$ \begin{align*} \int P_{\omega} (\Psi_{\omega}) \cdot \Upsilon_{\sigma \omega}\,d\mu_{\sigma \omega}&=\int \Psi_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}\,d\mu_{\omega}= \sum_{I_k \in \mathcal{Z}_{\omega}} \int_{I_k} \Psi_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}\,d\mu_{\omega} \\ &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{I_k} \Psi_{\omega} h_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}|_{I_k}dm_{\omega}. \end{align*} $$
$$ \begin{align*} \int P_{\omega} (\Psi_{\omega}) \cdot \Upsilon_{\sigma \omega}\,d\mu_{\sigma \omega}&=\int \Psi_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}\,d\mu_{\omega}= \sum_{I_k \in \mathcal{Z}_{\omega}} \int_{I_k} \Psi_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}\,d\mu_{\omega} \\ &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{I_k} \Psi_{\omega} h_{\omega} \cdot \Upsilon_{\sigma \omega} \circ F_{\omega}|_{I_k}dm_{\omega}. \end{align*} $$
Since
![]() $F_{\omega }$
is injective on
$F_{\omega }$
is injective on
![]() $I_k\in \mathcal {Z}_{\omega }$
, we can continue the calculation above as
$I_k\in \mathcal {Z}_{\omega }$
, we can continue the calculation above as
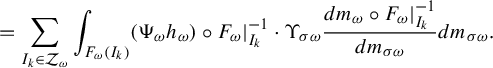 $$ \begin{align*} &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{F_{\omega}(I_k)} (\Psi_{\omega} h_{\omega}) \circ F_{\omega}|_{I_k}^{-1} \cdot \Upsilon_{\sigma \omega} \frac{dm_{\omega}\circ F_{\omega}|_{I_k}^{-1}}{dm_{\sigma \omega}} dm_{\sigma \omega}.\end{align*} $$
$$ \begin{align*} &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{F_{\omega}(I_k)} (\Psi_{\omega} h_{\omega}) \circ F_{\omega}|_{I_k}^{-1} \cdot \Upsilon_{\sigma \omega} \frac{dm_{\omega}\circ F_{\omega}|_{I_k}^{-1}}{dm_{\sigma \omega}} dm_{\sigma \omega}.\end{align*} $$
Since
![]() $h_{\sigma \omega }>0$
for a.e.
$h_{\sigma \omega }>0$
for a.e.
![]() $\omega \in \Omega $
, we can continue the calculation above as
$\omega \in \Omega $
, we can continue the calculation above as
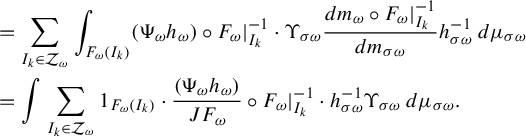 $$ \begin{align*} &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{F_{\omega}(I_k)} (\Psi_{\omega} h_{\omega}) \circ F_{\omega}|_{I_k}^{-1} \cdot \Upsilon_{\sigma \omega} \frac{dm_{\omega}\circ F_{\omega}|_{I_k}^{-1}}{dm_{\sigma \omega}} h^{-1}_{\sigma \omega} \,d\mu_{\sigma \omega}\\ &= \int \sum_{I_k \in \mathcal{Z}_{\omega}} 1_{F_{\omega}(I_k)} \cdot \frac{(\Psi_{\omega} h_{\omega}) }{JF_{\omega}}\circ F_{\omega}|_{I_k}^{-1} \cdot h^{-1}_{\sigma \omega} \Upsilon_{\sigma \omega} \,d\mu_{\sigma \omega}. \end{align*} $$
$$ \begin{align*} &=\sum_{I_k \in \mathcal{Z}_{\omega}} \int_{F_{\omega}(I_k)} (\Psi_{\omega} h_{\omega}) \circ F_{\omega}|_{I_k}^{-1} \cdot \Upsilon_{\sigma \omega} \frac{dm_{\omega}\circ F_{\omega}|_{I_k}^{-1}}{dm_{\sigma \omega}} h^{-1}_{\sigma \omega} \,d\mu_{\sigma \omega}\\ &= \int \sum_{I_k \in \mathcal{Z}_{\omega}} 1_{F_{\omega}(I_k)} \cdot \frac{(\Psi_{\omega} h_{\omega}) }{JF_{\omega}}\circ F_{\omega}|_{I_k}^{-1} \cdot h^{-1}_{\sigma \omega} \Upsilon_{\sigma \omega} \,d\mu_{\sigma \omega}. \end{align*} $$
Therefore
![]() $\sum _{I_k \in \mathcal {Z}_{\omega }} 1_{F_{\omega }(I_k)} {(\Psi _{\omega } h_{\omega }) }/{JF_{\omega }}\circ F_{\omega }|_{I_k}^{-1} h^{-1}_{\sigma \omega }$
is in
$\sum _{I_k \in \mathcal {Z}_{\omega }} 1_{F_{\omega }(I_k)} {(\Psi _{\omega } h_{\omega }) }/{JF_{\omega }}\circ F_{\omega }|_{I_k}^{-1} h^{-1}_{\sigma \omega }$
is in
![]() $L^1(\mu _{\sigma \omega })$
, finite almost everywhere on
$L^1(\mu _{\sigma \omega })$
, finite almost everywhere on
![]() $\Delta _{\sigma \omega }$
and equal to
$\Delta _{\sigma \omega }$
and equal to
![]() $P_{\omega } (\Psi _{\omega })$
in
$P_{\omega } (\Psi _{\omega })$
in
![]() $ L^1(\mu _{\sigma \omega })$
. Observe that
$ L^1(\mu _{\sigma \omega })$
. Observe that
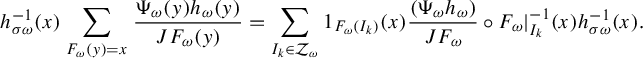 $$ \begin{align*} h^{-1}_{\sigma \omega}(x) \sum_{F_{\omega}(y)=x}\frac{\Psi_{\omega}(y) h_{\omega}(y)}{JF_{\omega}(y)}=\sum_{I_k \in \mathcal{Z}_{\omega}} 1_{F_{\omega}(I_k)}(x) \frac{(\Psi_{\omega} h_{\omega}) }{JF_{\omega}}\circ F_{\omega}|_{I_k}^{-1}(x) h^{-1}_{\sigma \omega}(x). \end{align*} $$
$$ \begin{align*} h^{-1}_{\sigma \omega}(x) \sum_{F_{\omega}(y)=x}\frac{\Psi_{\omega}(y) h_{\omega}(y)}{JF_{\omega}(y)}=\sum_{I_k \in \mathcal{Z}_{\omega}} 1_{F_{\omega}(I_k)}(x) \frac{(\Psi_{\omega} h_{\omega}) }{JF_{\omega}}\circ F_{\omega}|_{I_k}^{-1}(x) h^{-1}_{\sigma \omega}(x). \end{align*} $$
Thus our lemma holds.
Lemma 3.4. Consider the RYT in Definition 2.2. Suppose that
![]() $\rho _n=e^{-a n^{b}}$
or
$\rho _n=e^{-a n^{b}}$
or
![]() ${n^{-D}}$
where
${n^{-D}}$
where
![]() $a>0$
,
$a>0$
,
![]() $b \in (0,1], D>4$
and
$b \in (0,1], D>4$
and
![]() $\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
. Then for any small
$\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
. Then for any small
![]() $\delta \in (0,1)$
, there is a constant
$\delta \in (0,1)$
, there is a constant
![]() $C:=C_{\phi } C_{h,F,\beta , \delta ,p} \|\mathcal {K}\|_{p}$
such that
$C:=C_{\phi } C_{h,F,\beta , \delta ,p} \|\mathcal {K}\|_{p}$
such that
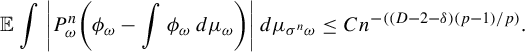 $$ \begin{align*} \mathbb{E} \int \bigg|P_{\omega}^n\bigg(\phi_{\omega}-\int \phi_{\omega}\,d\mu_{\omega}\bigg)\bigg|\,d\mu_{\sigma^n\omega} \le C n^{-((D-2-\delta) (p-1)/p)}. \end{align*} $$
$$ \begin{align*} \mathbb{E} \int \bigg|P_{\omega}^n\bigg(\phi_{\omega}-\int \phi_{\omega}\,d\mu_{\omega}\bigg)\bigg|\,d\mu_{\sigma^n\omega} \le C n^{-((D-2-\delta) (p-1)/p)}. \end{align*} $$
Proof. Let
![]() $d\lambda _{\omega }:=({\phi _{\omega }+\mathcal {K}_{\omega } C_{\phi }+2 C_{\phi }})/{\int (\phi _{\omega }+\mathcal {K}_{\omega } C_{\phi }+2 C_{\phi })\,d\mu _{\omega }} \,d\mu _{\omega }$
. By (3.9) and the Hölder inequality,
$d\lambda _{\omega }:=({\phi _{\omega }+\mathcal {K}_{\omega } C_{\phi }+2 C_{\phi }})/{\int (\phi _{\omega }+\mathcal {K}_{\omega } C_{\phi }+2 C_{\phi })\,d\mu _{\omega }} \,d\mu _{\omega }$
. By (3.9) and the Hölder inequality,
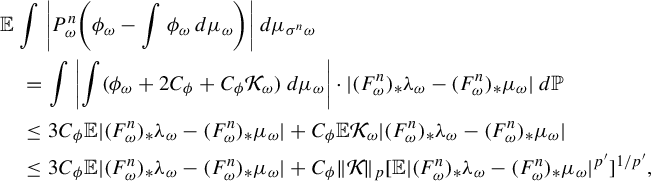 $$ \begin{align*} &\mathbb{E} \int \bigg|P_{\omega}^n\bigg(\phi_{\omega}-\int \phi_{\omega}\,d\mu_{\omega}\bigg)\bigg|\,d\mu_{\sigma^n \omega}\\ &\quad=\int \left|\int (\phi_{\omega}+2C_{\phi}+ C_{\phi} \mathcal{K}_{\omega} )\,d\mu_{\omega}\right| \cdot |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \,d\mathbb{P}\\ &\quad\le 3C_{\phi} \mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| +C_{\phi} \mathbb{E} \mathcal{K}_{\omega} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \\ &\quad\le 3C_{\phi} \mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| +C_{\phi} \|\mathcal{K}\|_{p} [\mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}|^{p'} ]^{1/p'}, \end{align*} $$
$$ \begin{align*} &\mathbb{E} \int \bigg|P_{\omega}^n\bigg(\phi_{\omega}-\int \phi_{\omega}\,d\mu_{\omega}\bigg)\bigg|\,d\mu_{\sigma^n \omega}\\ &\quad=\int \left|\int (\phi_{\omega}+2C_{\phi}+ C_{\phi} \mathcal{K}_{\omega} )\,d\mu_{\omega}\right| \cdot |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \,d\mathbb{P}\\ &\quad\le 3C_{\phi} \mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| +C_{\phi} \mathbb{E} \mathcal{K}_{\omega} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| \\ &\quad\le 3C_{\phi} \mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| +C_{\phi} \|\mathcal{K}\|_{p} [\mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}|^{p'} ]^{1/p'}, \end{align*} $$
where
![]() $1/p'=1-1/p$
. Using
$1/p'=1-1/p$
. Using
![]() $|(F^n_{\omega })_{*}\lambda _{\omega }-(F^n_{\omega })_{*}\mu _{\omega }|\le 2$
and (3.4), we continue the estimate
$|(F^n_{\omega })_{*}\lambda _{\omega }-(F^n_{\omega })_{*}\mu _{\omega }|\le 2$
and (3.4), we continue the estimate
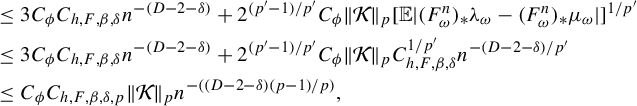 $$ \begin{align*} &\le 3C_{\phi} C_{h,F,\beta,\delta} {n^{-(D-2-\delta)}}+2^{(p'-1)/p'}C_{\phi} \|\mathcal{K}\|_{p} [\mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| ]^{1/p'}\\ &\le 3C_{\phi} C_{h,F,\beta,\delta} {n^{-(D-2-\delta)}}+2^{(p'-1)/p'}C_{\phi} \|\mathcal{K}\|_{p} C_{h,F,\beta,\delta}^{1/p'} {n^{-(D-2-\delta)/p'}}\\ &\le C_{\phi} C_{h,F,\beta, \delta,p} \|\mathcal{K}\|_{p} {n^{-((D-2-\delta) (p-1)/p)}}, \end{align*} $$
$$ \begin{align*} &\le 3C_{\phi} C_{h,F,\beta,\delta} {n^{-(D-2-\delta)}}+2^{(p'-1)/p'}C_{\phi} \|\mathcal{K}\|_{p} [\mathbb{E} |(F^n_{\omega})_{*}\lambda_{\omega}-(F^n_{\omega})_{*}\mu_{\omega}| ]^{1/p'}\\ &\le 3C_{\phi} C_{h,F,\beta,\delta} {n^{-(D-2-\delta)}}+2^{(p'-1)/p'}C_{\phi} \|\mathcal{K}\|_{p} C_{h,F,\beta,\delta}^{1/p'} {n^{-(D-2-\delta)/p'}}\\ &\le C_{\phi} C_{h,F,\beta, \delta,p} \|\mathcal{K}\|_{p} {n^{-((D-2-\delta) (p-1)/p)}}, \end{align*} $$
where the last inequality is due to
![]() $1/p'=(p-1)/p$
.
$1/p'=(p-1)/p$
.
4 Several lemmas
Lemma 4.1. Suppose that
![]() $\Psi \in L^q(\Delta , \mu )$
,
$\Psi \in L^q(\Delta , \mu )$
,
![]() $ q \ge 2$
. Then for any
$ q \ge 2$
. Then for any
![]() $\delta>0$
, for a.e.
$\delta>0$
, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
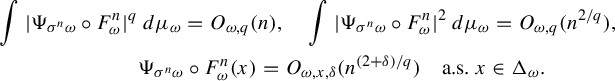 $$ \begin{align*} \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^q &\,d\mu_{\omega}=O_{\omega,q}( n),\quad \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,q}(n^{2/q}),\\ &\Psi_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{(2+\delta)/q}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
$$ \begin{align*} \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^q &\,d\mu_{\omega}=O_{\omega,q}( n),\quad \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,q}(n^{2/q}),\\ &\Psi_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{(2+\delta)/q}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
Proof. By Birkhoff’s ergodic theorem,
![]() $\lim _{n \to 0}({\sum _{i\le n}\int |\Psi _{\sigma ^i \omega } \circ F^i_{\omega }|^q \,d\mu _{\omega } }/{n})= \mathbb {E}\int \! |\Psi _{\omega } |^q \,d\mu _{\omega }< \infty $
for a.e.
$\lim _{n \to 0}({\sum _{i\le n}\int |\Psi _{\sigma ^i \omega } \circ F^i_{\omega }|^q \,d\mu _{\omega } }/{n})= \mathbb {E}\int \! |\Psi _{\omega } |^q \,d\mu _{\omega }< \infty $
for a.e.
![]() $\omega \in \Omega $
. Thus
$\omega \in \Omega $
. Thus
![]() $\int |\Psi _{\sigma ^n \omega } \circ F^n_{\omega }|^q \,d\mu _{\omega }=O_{\omega ,q}( n)$
and
$\int |\Psi _{\sigma ^n \omega } \circ F^n_{\omega }|^q \,d\mu _{\omega }=O_{\omega ,q}( n)$
and
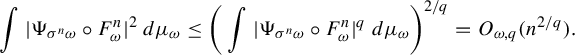 $$ \begin{align*} \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}\le \bigg(\int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^q \,d\mu_{\omega}\bigg)^{2/q} =O_{\omega,q}(n^{2/q}). \end{align*} $$
$$ \begin{align*} \int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}\le \bigg(\int |\Psi_{\sigma^n \omega} \circ F^n_{\omega}|^q \,d\mu_{\omega}\bigg)^{2/q} =O_{\omega,q}(n^{2/q}). \end{align*} $$
Since
![]() $\int |{\Psi _{\sigma ^n \omega } \circ F^n_{\omega }}/{n^{(2+\delta )/q}}|^q \,d\mu _{\omega }=O_{\omega ,q}({n}/{n^{2+\delta }})=O_{\omega ,q}({n^{-(1+\delta )}})$
, by the Borel–Cantelli lemma we have
$\int |{\Psi _{\sigma ^n \omega } \circ F^n_{\omega }}/{n^{(2+\delta )/q}}|^q \,d\mu _{\omega }=O_{\omega ,q}({n}/{n^{2+\delta }})=O_{\omega ,q}({n^{-(1+\delta )}})$
, by the Borel–Cantelli lemma we have
![]() $\Psi _{\sigma ^n \omega } \circ F^n_{\omega }(x) =O_{\omega ,x, \delta }(n^{(2+\delta )/q})$
a.s.
$\Psi _{\sigma ^n \omega } \circ F^n_{\omega }(x) =O_{\omega ,x, \delta }(n^{(2+\delta )/q})$
a.s.
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
Lemma 4.2. (Martingale convergence rates)
Suppose that
![]() $\Psi \in L^q(\Delta , \mu )$
,
$\Psi \in L^q(\Delta , \mu )$
,
![]() $q\ge 2$
, and
$q\ge 2$
, and
![]() $(\Psi _{\sigma ^n\omega }\circ F^n_{\omega })_{n \ge 0}$
is a sequence of reverse martingale differences for a.e.
$(\Psi _{\sigma ^n\omega }\circ F^n_{\omega })_{n \ge 0}$
is a sequence of reverse martingale differences for a.e.
![]() $\omega \in \Omega $
. Then for any
$\omega \in \Omega $
. Then for any
![]() $\delta>0 $
, for a.e.
$\delta>0 $
, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
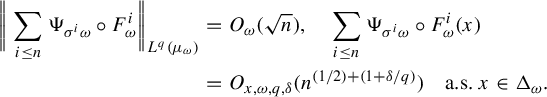 $$ \begin{align*} \bigg\|\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})} &= O_{\omega}(\sqrt{n}),\quad \sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}(x)\\ &=O_{x,\omega,q, \delta}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})} &= O_{\omega}(\sqrt{n}),\quad \sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}(x)\\ &=O_{x,\omega,q, \delta}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
Proof. By the Burkholder–Davis–Gundy inequality and Minkowski inequality, there is a constant
![]() $C_q$
such that for a.e.
$C_q$
such that for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
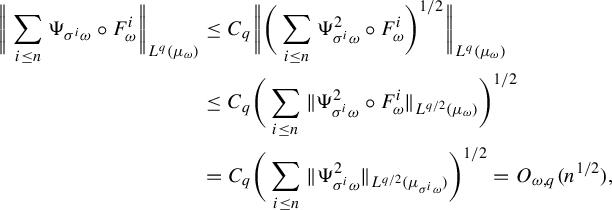 $$ \begin{align*} \bigg\|\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})} &\le C_q \bigg\|\bigg(\sum_{i \le n}\Psi^2_{\sigma^i \omega} \circ F^i_{\omega}\bigg)^{1/2}\bigg\|_{L^q{(\mu_{\omega})}} \\ &\le C_q \bigg(\sum_{i \le n}\|\Psi^2_{\sigma^i \omega}\circ F_{\omega}^i\|_{L^{q/2}(\mu_{\omega})}\bigg)^{1/2}\\ &=C_q \bigg(\sum_{i \le n}\|\Psi^2_{\sigma^i \omega}\|_{L^{q/2}(\mu_{\sigma^i\omega})}\bigg)^{1/2}= O_{\omega,q}(n^{1/2}), \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})} &\le C_q \bigg\|\bigg(\sum_{i \le n}\Psi^2_{\sigma^i \omega} \circ F^i_{\omega}\bigg)^{1/2}\bigg\|_{L^q{(\mu_{\omega})}} \\ &\le C_q \bigg(\sum_{i \le n}\|\Psi^2_{\sigma^i \omega}\circ F_{\omega}^i\|_{L^{q/2}(\mu_{\omega})}\bigg)^{1/2}\\ &=C_q \bigg(\sum_{i \le n}\|\Psi^2_{\sigma^i \omega}\|_{L^{q/2}(\mu_{\sigma^i\omega})}\bigg)^{1/2}= O_{\omega,q}(n^{1/2}), \end{align*} $$
where the last equality is due to
![]() $\mathbb {E}\|\Psi ^2_{\omega }\|_{L^{q/2}(\mu _{\omega })}\le (\mathbb {E}\int |\Psi _{\omega }|^qd\mu _{\omega })^{2/q} <\infty $
and Birkhoff’s ergodic theorem. Then for any
$\mathbb {E}\|\Psi ^2_{\omega }\|_{L^{q/2}(\mu _{\omega })}\le (\mathbb {E}\int |\Psi _{\omega }|^qd\mu _{\omega })^{2/q} <\infty $
and Birkhoff’s ergodic theorem. Then for any
![]() $\delta>0$
,
$\delta>0$
,
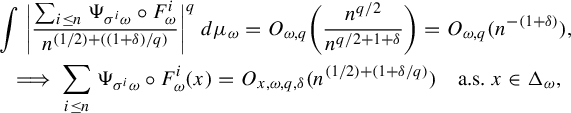 $$ \begin{gather*} \int \bigg|\frac{\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}}{n^{(1/2)+((1+\delta)/q)}}\bigg|^{q}\,d\mu_{\omega}=O_{\omega,q}\bigg(\frac{n^{q/2}}{n^{q/2+1+ \delta}}\bigg)=O_{\omega,q}({n^{-(1+ \delta)}}),\\ \implies \sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}, \end{gather*} $$
$$ \begin{gather*} \int \bigg|\frac{\sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}}{n^{(1/2)+((1+\delta)/q)}}\bigg|^{q}\,d\mu_{\omega}=O_{\omega,q}\bigg(\frac{n^{q/2}}{n^{q/2+1+ \delta}}\bigg)=O_{\omega,q}({n^{-(1+ \delta)}}),\\ \implies \sum_{i \le n}\Psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}, \end{gather*} $$
where the last equality is due to the Borel–Cantelli lemma.
Lemma 4.3. Suppose that
![]() $\psi \in L^{q}(\Delta , \mu ) $
,
$\psi \in L^{q}(\Delta , \mu ) $
,
![]() $q \ge 2$
, satisfies
$q \ge 2$
, satisfies
Then for any
![]() $\delta>0 $
, for a.e.
$\delta>0 $
, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
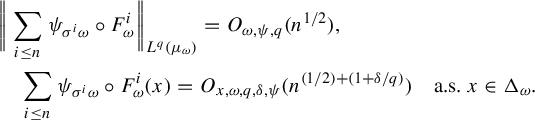 $$ \begin{align*} &\bigg\|\sum_{i \le n}\psi_{\sigma^i \omega}\circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})}=O_{\omega, \psi, q}(n^{1/2}),\\ &\quad\sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta, \psi}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
$$ \begin{align*} &\bigg\|\sum_{i \le n}\psi_{\sigma^i \omega}\circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})}=O_{\omega, \psi, q}(n^{1/2}),\\ &\quad\sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta, \psi}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
Proof. Define
![]() $g_{\omega }:= \sum _{i \ge 0} P^i_{\sigma ^{-i}\omega } ( \psi _{\sigma ^{-i} \omega })$
. This is well defined because
$g_{\omega }:= \sum _{i \ge 0} P^i_{\sigma ^{-i}\omega } ( \psi _{\sigma ^{-i} \omega })$
. This is well defined because
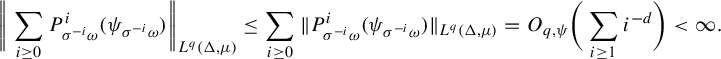 $$ \begin{align*} \bigg\|\sum_{i \ge 0} P^i_{\sigma^{-i}\omega} ( \psi_{\sigma^{-i} \omega})\bigg\|_{L^q(\Delta, \mu)}\le \sum_{i \ge 0} \|P^i_{\sigma^{-i}\omega}(\psi_{\sigma^{-i}\omega})\|_{L^{q}(\Delta, \mu)}=O_{q, \psi} \bigg(\sum_{i \ge 1} {i^{-d}}\bigg) < \infty. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i \ge 0} P^i_{\sigma^{-i}\omega} ( \psi_{\sigma^{-i} \omega})\bigg\|_{L^q(\Delta, \mu)}\le \sum_{i \ge 0} \|P^i_{\sigma^{-i}\omega}(\psi_{\sigma^{-i}\omega})\|_{L^{q}(\Delta, \mu)}=O_{q, \psi} \bigg(\sum_{i \ge 1} {i^{-d}}\bigg) < \infty. \end{align*} $$
By Lemma 4.1,
![]() $\|g_{\sigma ^n \omega } \circ F^n_{\omega }\|_{L^q(\mu _{\omega })}=O_{\omega ,q}(n^{1/q})$
. Let
$\|g_{\sigma ^n \omega } \circ F^n_{\omega }\|_{L^q(\mu _{\omega })}=O_{\omega ,q}(n^{1/q})$
. Let
![]() $\Psi _{\omega }:=\psi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
. By (3.10) we have for a.e.
$\Psi _{\omega }:=\psi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
. By (3.10) we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
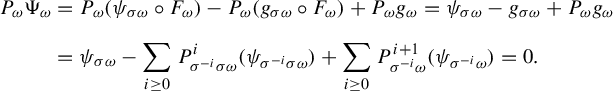 $$ \begin{align*} P_{\omega}\Psi_{\omega}&=P_{\omega}(\psi_{\sigma \omega} \circ F_{\omega}) - P_{\omega}(g_{\sigma \omega}\circ F_{\omega})+P_{\omega}g_{\omega}=\psi_{\sigma \omega}-g_{\sigma \omega}+P_{\omega}g_{\omega}\\[5pt] &=\psi_{\sigma \omega} - \sum_{i \ge 0} P^i_{\sigma^{-i}\sigma \omega} ( \psi_{\sigma^{-i} \sigma \omega})+\sum_{i \ge 0} P^{i+1}_{\sigma^{-i}\omega} ( \psi_{\sigma^{-i} \omega})=0. \end{align*} $$
$$ \begin{align*} P_{\omega}\Psi_{\omega}&=P_{\omega}(\psi_{\sigma \omega} \circ F_{\omega}) - P_{\omega}(g_{\sigma \omega}\circ F_{\omega})+P_{\omega}g_{\omega}=\psi_{\sigma \omega}-g_{\sigma \omega}+P_{\omega}g_{\omega}\\[5pt] &=\psi_{\sigma \omega} - \sum_{i \ge 0} P^i_{\sigma^{-i}\sigma \omega} ( \psi_{\sigma^{-i} \sigma \omega})+\sum_{i \ge 0} P^{i+1}_{\sigma^{-i}\omega} ( \psi_{\sigma^{-i} \omega})=0. \end{align*} $$
Then by (3.8),
![]() $\mathbb {E}_{\mu _{\omega }}[\Psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega }|(F_{\omega }^{i+1})^{-1}\mathcal {B}_{\sigma ^{i+1} \omega }]=[P_{\sigma ^i \omega }(\Psi _{\sigma ^i \omega })]\circ F_{\omega }^{i+1}=0$
, that is,
$\mathbb {E}_{\mu _{\omega }}[\Psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega }|(F_{\omega }^{i+1})^{-1}\mathcal {B}_{\sigma ^{i+1} \omega }]=[P_{\sigma ^i \omega }(\Psi _{\sigma ^i \omega })]\circ F_{\omega }^{i+1}=0$
, that is,
![]() $(\Psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
is a sequence of reverse martingale differences w.r.t.
$(\Psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
is a sequence of reverse martingale differences w.r.t.
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
. Then by Lemma 4.2, we have
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
. Then by Lemma 4.2, we have
![]() $\|\sum _{i \le n}\Psi _{\sigma ^i \omega } \circ F^i_{\omega }\|_{L^q(\mu _{\omega })} = O_{\omega }(n^{1/2})$
. Therefore,
$\|\sum _{i \le n}\Psi _{\sigma ^i \omega } \circ F^i_{\omega }\|_{L^q(\mu _{\omega })} = O_{\omega }(n^{1/2})$
. Therefore,
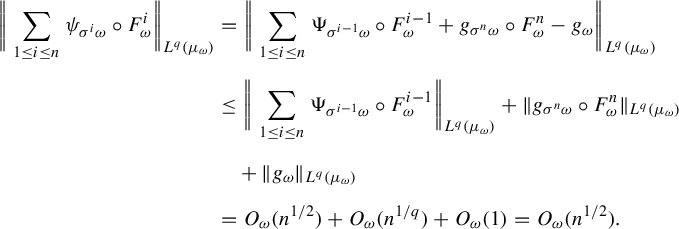 $$ \begin{align*} \bigg\|\sum_{1 \le i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})}&= \bigg\|\sum_{1 \le i \le n}\Psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+ g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\bigg\|_{L^q(\mu_{\omega})}\\[5pt] &\le \bigg\|\sum_{1 \le i \le n}\Psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^q(\mu_{\omega})} + \|g_{\sigma^n \omega} \circ F^{n}_{\omega}\|_{L^q(\mu_{\omega})}\\[5pt] &\quad +\|g_{\omega}\|_{L^q(\mu_{\omega})}\\[5pt] &=O_{\omega}(n^{1/2})+O_{\omega}(n^{1/q})+O_{\omega}(1)=O_{\omega}(n^{1/2}). \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{1 \le i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}\bigg\|_{L^q(\mu_{\omega})}&= \bigg\|\sum_{1 \le i \le n}\Psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+ g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\bigg\|_{L^q(\mu_{\omega})}\\[5pt] &\le \bigg\|\sum_{1 \le i \le n}\Psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^q(\mu_{\omega})} + \|g_{\sigma^n \omega} \circ F^{n}_{\omega}\|_{L^q(\mu_{\omega})}\\[5pt] &\quad +\|g_{\omega}\|_{L^q(\mu_{\omega})}\\[5pt] &=O_{\omega}(n^{1/2})+O_{\omega}(n^{1/q})+O_{\omega}(1)=O_{\omega}(n^{1/2}). \end{align*} $$
Then for any
![]() $\delta>0 $
,
$\delta>0 $
,
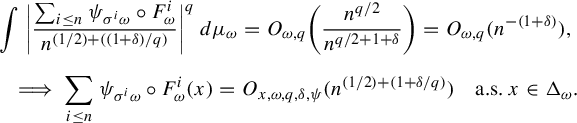 $$ \begin{gather*} \int \bigg|\frac{\sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}}{n^{(1/2)+((1+\delta)/q)}}\bigg|^{q}\,d\mu_{\omega}=O_{\omega,q}\bigg(\frac{n^{q/2}}{n^{q/2+1+ \delta}}\bigg)=O_{\omega,q}({n^{-(1+ \delta)}}),\\[5pt] \quad\implies \sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta, \psi}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{gather*} $$
$$ \begin{gather*} \int \bigg|\frac{\sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}}{n^{(1/2)+((1+\delta)/q)}}\bigg|^{q}\,d\mu_{\omega}=O_{\omega,q}\bigg(\frac{n^{q/2}}{n^{q/2+1+ \delta}}\bigg)=O_{\omega,q}({n^{-(1+ \delta)}}),\\[5pt] \quad\implies \sum_{i \le n}\psi_{\sigma^i \omega} \circ F^i_{\omega}(x)=O_{x,\omega,q, \delta, \psi}(n^{({1}/{2})+({1+\delta}/{q})}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{gather*} $$
where the last equality is due to the Borel–Cantelli lemma.
Lemma 4.4. (Regularities)
Suppose that
![]() $\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
with a Lipschitz constant
$\phi \in \mathcal {F}^{\mathcal {\kern2pt K}}_{\beta ,p}$
with a Lipschitz constant
![]() $C_{\phi }$
. Define
$C_{\phi }$
. Define
![]() $\Phi _n(\omega ,\cdot )=(P_{\omega }^n\phi _{\omega })(\cdot )$
for any
$\Phi _n(\omega ,\cdot )=(P_{\omega }^n\phi _{\omega })(\cdot )$
for any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $C_{h,F}:=C_h+e^{C_h}C_F+e^{C_h+C_F}C_h$
. Then for any
$C_{h,F}:=C_h+e^{C_h}C_F+e^{C_h+C_F}C_h$
. Then for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
Proof. By Lemma 3.3,
![]() $\|P^n_{\omega }\phi _{\omega }\|_{L^{\infty }(\mu _{\sigma ^n \omega })} < \infty $
. Suppose that
$\|P^n_{\omega }\phi _{\omega }\|_{L^{\infty }(\mu _{\sigma ^n \omega })} < \infty $
. Suppose that
![]() $x,y \in \Delta _{\sigma ^n \omega , l}$
for some
$x,y \in \Delta _{\sigma ^n \omega , l}$
for some
![]() $l \in \mathbb {N}$
and
$l \in \mathbb {N}$
and
![]() $s_{\sigma ^n \omega } (x,y)>0$
. Then by (3.6), we have
$s_{\sigma ^n \omega } (x,y)>0$
. Then by (3.6), we have
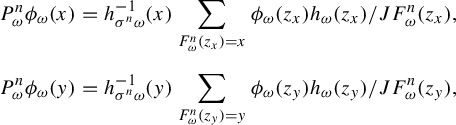 $$ \begin{align*} P^n_{\omega}\phi_{\omega}(x)&=h^{-1}_{\sigma^n \omega}(x)\sum_{F^n_{\omega}(z_x)=x}{\phi_{\omega}(z_x)} {h_{\omega}(z_x)}/{JF^n_{\omega}(z_x)}, \\[5pt] P^n_{\omega}\phi_{\omega}(y)&=h^{-1}_{\sigma^n \omega}(y)\sum_{F^n_{\omega}(z_y)=y}{\phi_{\omega}(z_y) h_{\omega}(z_y)}/{JF^n_{\omega}(z_y)}, \end{align*} $$
$$ \begin{align*} P^n_{\omega}\phi_{\omega}(x)&=h^{-1}_{\sigma^n \omega}(x)\sum_{F^n_{\omega}(z_x)=x}{\phi_{\omega}(z_x)} {h_{\omega}(z_x)}/{JF^n_{\omega}(z_x)}, \\[5pt] P^n_{\omega}\phi_{\omega}(y)&=h^{-1}_{\sigma^n \omega}(y)\sum_{F^n_{\omega}(z_y)=y}{\phi_{\omega}(z_y) h_{\omega}(z_y)}/{JF^n_{\omega}(z_y)}, \end{align*} $$
where
![]() $z_x, z_y$
are in the same element of
$z_x, z_y$
are in the same element of
![]() $\bigvee ^{n}_{j=0} (F^j_{\omega })^{-1}\mathcal {Z}_{\sigma ^j \omega }$
. Therefore,
$\bigvee ^{n}_{j=0} (F^j_{\omega })^{-1}\mathcal {Z}_{\sigma ^j \omega }$
. Therefore,
 $$ \begin{align*} |P^n_{\omega}\phi_{\omega}(x)-P^n_{\omega}\phi_{\omega}(y)|&=\bigg|\frac{1}{h_{\sigma^n \omega}(x)}\sum_{F^n_{\omega}(z_x)=x}\frac{\phi_{\omega}(z_x) h_{\omega}(z_x)}{JF^n_{\omega}(z_x)}\\[5pt]&\quad- \frac{1}{h_{\sigma^n \omega}(y)}\sum_{F^n_{\omega}(z_y)=y}\frac{\phi_{\omega}(z_y) h_{\omega}(z_y)}{JF^n_{\omega}(z_y)}\bigg|\\[5pt] &=\bigg|\frac{1}{h_{\sigma^n \omega}(x)}\sum_{F^n_{\omega}(z_x)=x}\frac{(\phi_{\omega}(z_x)-\phi_{\omega}(z_y)) h_{\omega}(z_x)}{JF^n_{\omega}(z_x)}\\[5pt] &\quad + \sum_{F^n_{\omega}(z_y)=y} \phi_{\omega}(z_y) \bigg(\frac{h_{\omega}(z_x)}{JF^n_{\omega}(z_x) h_{\sigma^n \omega}(x)}- \frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\bigg)\bigg|\\[5pt] &\le C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\sigma^n \omega}(x,y)}+C_{\phi} \sum_{F^n_{\omega}(z_y)=y} \frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\\[5pt] &\quad \times \bigg|1-\frac{h_{\omega}(z_x)}{JF^n_{\omega}(z_x) h_{\sigma^n \omega}(x)}\bigg(\frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\bigg)^{-1}\bigg|\\[5pt] &\le C_{\phi} (\mathcal{K}\circ \sigma^{-n}+C_{h,F})_{\sigma^n \omega} \beta^{s_{\sigma^n \omega}(x,y)} \end{align*} $$
$$ \begin{align*} |P^n_{\omega}\phi_{\omega}(x)-P^n_{\omega}\phi_{\omega}(y)|&=\bigg|\frac{1}{h_{\sigma^n \omega}(x)}\sum_{F^n_{\omega}(z_x)=x}\frac{\phi_{\omega}(z_x) h_{\omega}(z_x)}{JF^n_{\omega}(z_x)}\\[5pt]&\quad- \frac{1}{h_{\sigma^n \omega}(y)}\sum_{F^n_{\omega}(z_y)=y}\frac{\phi_{\omega}(z_y) h_{\omega}(z_y)}{JF^n_{\omega}(z_y)}\bigg|\\[5pt] &=\bigg|\frac{1}{h_{\sigma^n \omega}(x)}\sum_{F^n_{\omega}(z_x)=x}\frac{(\phi_{\omega}(z_x)-\phi_{\omega}(z_y)) h_{\omega}(z_x)}{JF^n_{\omega}(z_x)}\\[5pt] &\quad + \sum_{F^n_{\omega}(z_y)=y} \phi_{\omega}(z_y) \bigg(\frac{h_{\omega}(z_x)}{JF^n_{\omega}(z_x) h_{\sigma^n \omega}(x)}- \frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\bigg)\bigg|\\[5pt] &\le C_{\phi} \mathcal{K}_{\omega} \beta^{s_{\sigma^n \omega}(x,y)}+C_{\phi} \sum_{F^n_{\omega}(z_y)=y} \frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\\[5pt] &\quad \times \bigg|1-\frac{h_{\omega}(z_x)}{JF^n_{\omega}(z_x) h_{\sigma^n \omega}(x)}\bigg(\frac{h_{\omega}(z_y)}{JF^n_{\omega}(z_y) h_{\sigma^n \omega}(y)}\bigg)^{-1}\bigg|\\[5pt] &\le C_{\phi} (\mathcal{K}\circ \sigma^{-n}+C_{h,F})_{\sigma^n \omega} \beta^{s_{\sigma^n \omega}(x,y)} \end{align*} $$
where the last inequality is due to
 $|1-z_1z_2z_3|\le |1-z_1|+|z_1\|1-z_2|+|z_1\|z_2\|1-z_3|=|1-z_1|+e^{\ln |z_1|}|1-z_2|+e^{\ln |z_1|+\ln |z_2|}|1-z_3|$
,
$|1-z_1z_2z_3|\le |1-z_1|+|z_1\|1-z_2|+|z_1\|z_2\|1-z_3|=|1-z_1|+e^{\ln |z_1|}|1-z_2|+e^{\ln |z_1|+\ln |z_2|}|1-z_3|$
,
![]() $ h \in \mathcal {F}^{\kern2pt +}_{\beta }$
and (2.3).
$ h \in \mathcal {F}^{\kern2pt +}_{\beta }$
and (2.3).
5 Proof of Theorem 2.3
The equivariant probability measures
![]() $(\mu _{\omega })_{\omega \in \Omega }$
have been obtained in Lemma 3.1. Thus it remains to prove the coboundary or the QASIP and its convergence rate. In Theorem 2.3 we suppose that
$(\mu _{\omega })_{\omega \in \Omega }$
have been obtained in Lemma 3.1. Thus it remains to prove the coboundary or the QASIP and its convergence rate. In Theorem 2.3 we suppose that
![]() $\phi \in \mathcal {F}_{\beta ,p}^{\kern2pt\mathcal {K}}, \int \phi _{\omega } \,d\mu _{\omega }=0$
,
$\phi \in \mathcal {F}_{\beta ,p}^{\kern2pt\mathcal {K}}, \int \phi _{\omega } \,d\mu _{\omega }=0$
,
![]() $ \rho _n={n^{-D}}$
for some
$ \rho _n={n^{-D}}$
for some
![]() $D>2+{4 p}/({p-1})$
. In particular,
$D>2+{4 p}/({p-1})$
. In particular,
![]() $\rho _n= e^{-an^{b}}$
is a special case of
$\rho _n= e^{-an^{b}}$
is a special case of
![]() $\rho _n={n^{-D}}$
when
$\rho _n={n^{-D}}$
when
![]() $a>0, b \in (0,1]$
and
$a>0, b \in (0,1]$
and
![]() ${D, n\gg 1}$
.
${D, n\gg 1}$
.
5.1 Martingale decompositions
Lemma 5.1. (Decompositions)
Let
![]() $\delta>0$
be small such that
$\delta>0$
be small such that
![]() ${(D-2-\delta )(p-1)}/ {(\delta +1) p}>4$
, and
${(D-2-\delta )(p-1)}/ {(\delta +1) p}>4$
, and
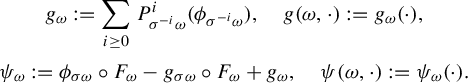 $$ \begin{gather*} g_{\omega}:= \sum_{i \ge 0} P^i_{\sigma^{-i}\omega} ( \phi_{\sigma^{-i} \omega}), \quad g(\omega,\cdot):=g_{\omega}(\cdot),\\ \psi_{\omega}:=\phi_{\sigma \omega} \circ F_{\omega} - g_{\sigma \omega}\circ F_{\omega}+g_{\omega}, \quad \psi(\omega, \cdot):=\psi_{\omega}(\cdot). \end{gather*} $$
$$ \begin{gather*} g_{\omega}:= \sum_{i \ge 0} P^i_{\sigma^{-i}\omega} ( \phi_{\sigma^{-i} \omega}), \quad g(\omega,\cdot):=g_{\omega}(\cdot),\\ \psi_{\omega}:=\phi_{\sigma \omega} \circ F_{\omega} - g_{\sigma \omega}\circ F_{\omega}+g_{\omega}, \quad \psi(\omega, \cdot):=\psi_{\omega}(\cdot). \end{gather*} $$
Then
![]() $\psi , g \in L^{{(D-2-\delta )(p-1)}/{(\delta +1) p}}(\Delta , \mu ) \subseteq L^4(\Delta , \mu )$
and for a.e.
$\psi , g \in L^{{(D-2-\delta )(p-1)}/{(\delta +1) p}}(\Delta , \mu ) \subseteq L^4(\Delta , \mu )$
and for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
namely, this is a martingale decomposition where
![]() $(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
are reverse martingale differences w.r.t.
$(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
are reverse martingale differences w.r.t.
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
for a.e.
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
for a.e.
![]() $\omega \in \Omega $
. Moreover,
$\omega \in \Omega $
. Moreover,
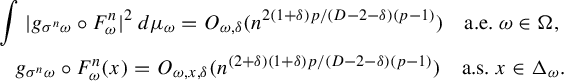 $$ \begin{align*} &\int |g_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,\delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.e. } \omega \in \Omega,\\ &\quad g_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
$$ \begin{align*} &\int |g_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,\delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.e. } \omega \in \Omega,\\ &\quad g_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
Proof. Let
![]() $q:={(D-2-\delta )(p-1)}/{(1+\delta ) p}>4$
for a small
$q:={(D-2-\delta )(p-1)}/{(1+\delta ) p}>4$
for a small
![]() $\delta>0$
. By Lemma 3.4, (3.7) and
$\delta>0$
. By Lemma 3.4, (3.7) and
![]() $\phi \in L^{\infty }(\Delta , \mu )$
,
$\phi \in L^{\infty }(\Delta , \mu )$
,
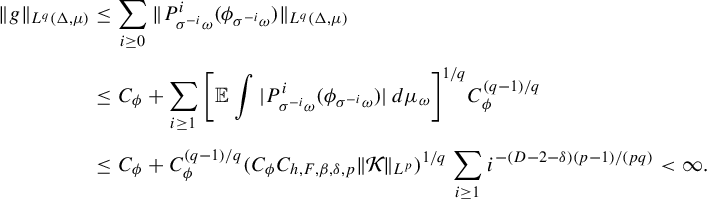 $$ \begin{align*} \|g\|_{L^{q}(\Delta, \mu)}&\le \sum_{i \ge 0} \|P^i_{\sigma^{-i}\omega}(\phi_{\sigma^{-i}\omega})\|_{L^{q}(\Delta, \mu)}\\[4pt] &\le C_{\phi}+ \sum_{i\ge 1} \bigg[\mathbb{E}\int |P^{i}_{\sigma^{-i}\omega}(\phi_{\sigma^{-i}\omega})|\,d\mu_{\omega}\bigg]^{1/q} C_{\phi}^{(q-1)/q}\\[4pt] &\le C_{\phi}+ C_{\phi}^{(q-1)/q} (C_{\phi} C_{h,F,\beta, \delta,p} \|\mathcal{K}\|_{L^p})^{1/q} \sum_{i \ge 1} {i^{-(D-2-\delta) (p-1)/(pq)}} < \infty. \end{align*} $$
$$ \begin{align*} \|g\|_{L^{q}(\Delta, \mu)}&\le \sum_{i \ge 0} \|P^i_{\sigma^{-i}\omega}(\phi_{\sigma^{-i}\omega})\|_{L^{q}(\Delta, \mu)}\\[4pt] &\le C_{\phi}+ \sum_{i\ge 1} \bigg[\mathbb{E}\int |P^{i}_{\sigma^{-i}\omega}(\phi_{\sigma^{-i}\omega})|\,d\mu_{\omega}\bigg]^{1/q} C_{\phi}^{(q-1)/q}\\[4pt] &\le C_{\phi}+ C_{\phi}^{(q-1)/q} (C_{\phi} C_{h,F,\beta, \delta,p} \|\mathcal{K}\|_{L^p})^{1/q} \sum_{i \ge 1} {i^{-(D-2-\delta) (p-1)/(pq)}} < \infty. \end{align*} $$
Then by Lemma 4.1,
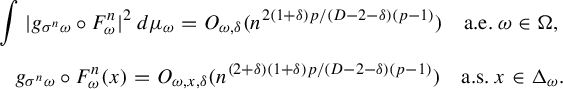 $$ \begin{align*}& \int |g_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,\delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.e. } \omega \in \Omega,\\[4pt] &\quad g_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
$$ \begin{align*}& \int |g_{\sigma^n \omega} \circ F^n_{\omega}|^2 \,d\mu_{\omega}=O_{\omega,\delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.e. } \omega \in \Omega,\\[4pt] &\quad g_{\sigma^n \omega} \circ F^n_{\omega}(x) =O_{\omega,x, \delta}(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) \quad\text{a.s. } x \in \Delta_{\omega}. \end{align*} $$
![]() $\psi \in L^{q}(\Delta , \mu )$
follows from
$\psi \in L^{q}(\Delta , \mu )$
follows from
![]() $g \in L^{q}(\Delta , \mu )$
and
$g \in L^{q}(\Delta , \mu )$
and
![]() $\phi \in \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}}$
. By (3.10),
$\phi \in \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}}$
. By (3.10),
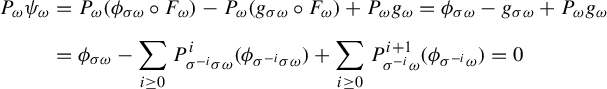 $$ \begin{align*} P_{\omega}\psi_{\omega}&=P_{\omega}(\phi_{\sigma \omega} \circ F_{\omega}) - P_{\omega}(g_{\sigma \omega}\circ F_{\omega})+P_{\omega}g_{\omega}=\phi_{\sigma \omega}-g_{\sigma \omega}+P_{\omega}g_{\omega}\\[4pt] &=\phi_{\sigma \omega} - \sum_{i \ge 0} P^i_{\sigma^{-i}\sigma \omega} ( \phi_{\sigma^{-i} \sigma \omega})+\sum_{i \ge 0} P^{i+1}_{\sigma^{-i}\omega} ( \phi_{\sigma^{-i} \omega})=0 \end{align*} $$
$$ \begin{align*} P_{\omega}\psi_{\omega}&=P_{\omega}(\phi_{\sigma \omega} \circ F_{\omega}) - P_{\omega}(g_{\sigma \omega}\circ F_{\omega})+P_{\omega}g_{\omega}=\phi_{\sigma \omega}-g_{\sigma \omega}+P_{\omega}g_{\omega}\\[4pt] &=\phi_{\sigma \omega} - \sum_{i \ge 0} P^i_{\sigma^{-i}\sigma \omega} ( \phi_{\sigma^{-i} \sigma \omega})+\sum_{i \ge 0} P^{i+1}_{\sigma^{-i}\omega} ( \phi_{\sigma^{-i} \omega})=0 \end{align*} $$
for a.e.
![]() $\omega \in \Omega $
. By (3.8),
$\omega \in \Omega $
. By (3.8),
![]() $\mathbb {E}_{\mu _{\omega }}(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega }|(F_{\omega }^{i+1})^{-1}\mathcal {B}_{\sigma ^{i+1} \omega })=[P_{\sigma ^i \omega }(\psi _{\sigma ^i \omega })]\circ F_{\omega }^{i+1}=0$
, that is,
$\mathbb {E}_{\mu _{\omega }}(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega }|(F_{\omega }^{i+1})^{-1}\mathcal {B}_{\sigma ^{i+1} \omega })=[P_{\sigma ^i \omega }(\psi _{\sigma ^i \omega })]\circ F_{\omega }^{i+1}=0$
, that is,
![]() $(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
are reverse martingale differences w.r.t.
$(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 0}$
are reverse martingale differences w.r.t.
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
.
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
.
5.2 A coboundary
Lemma 5.2. Let
![]() $\eta ^2_{n}(\omega ):=\int (\sum _{i \le n}\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })^2\,d\mu _{\omega }$
,
$\eta ^2_{n}(\omega ):=\int (\sum _{i \le n}\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })^2\,d\mu _{\omega }$
,
![]() $\Sigma ^2:=\mathbb {E}\int \psi _{\omega }^2 \,d\mu _{\omega }$
and consider any small
$\Sigma ^2:=\mathbb {E}\int \psi _{\omega }^2 \,d\mu _{\omega }$
and consider any small
![]() $\delta>0$
such that
$\delta>0$
such that
![]() ${(D-2-\delta )(p-1)}/{(\delta +1) p}>4$
. Then for a.e.
${(D-2-\delta )(p-1)}/{(\delta +1) p}>4$
. Then for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
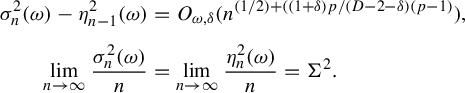 $$ \begin{align} \begin{aligned} \sigma_n^2(\omega)-\eta_{n-1}^2(\omega)&=O_{\omega, \delta}(n^{({1}/{2})+({(1+\delta) p}/{(D-2-\delta)(p-1)}}), \\[4pt] \lim_{n \to \infty}\frac{\sigma_n^2(\omega)}{n}&=\lim_{n \to \infty}\frac{\eta_n^2(\omega)}{n}=\Sigma^2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sigma_n^2(\omega)-\eta_{n-1}^2(\omega)&=O_{\omega, \delta}(n^{({1}/{2})+({(1+\delta) p}/{(D-2-\delta)(p-1)}}), \\[4pt] \lim_{n \to \infty}\frac{\sigma_n^2(\omega)}{n}&=\lim_{n \to \infty}\frac{\eta_n^2(\omega)}{n}=\Sigma^2. \end{aligned} \end{align} $$
If
![]() $\Sigma ^2>0$
, then there is a constant
$\Sigma ^2>0$
, then there is a constant
![]() $C^{\prime }_{\omega } \in [1,\infty )$
such that
$C^{\prime }_{\omega } \in [1,\infty )$
such that
![]() $\eta ^2_{n}(\omega )={C^{\prime \pm 1}_{\omega }} n$
; if
$\eta ^2_{n}(\omega )={C^{\prime \pm 1}_{\omega }} n$
; if
![]() $\Sigma ^2=0$
, then
$\Sigma ^2=0$
, then
![]() $\phi $
is a coboundary (see (2.2)), and the function g in (2.2) is in
$\phi $
is a coboundary (see (2.2)), and the function g in (2.2) is in
![]() $ L^{{(D-2-\delta )(p-1)}/{(1+\delta )p}}(\Delta , \mu )$
.
$ L^{{(D-2-\delta )(p-1)}/{(1+\delta )p}}(\Delta , \mu )$
.
Proof. Let
![]() $q:={(D-2-\delta )(p-1)}/{(1+\delta ) p}>4$
for a small
$q:={(D-2-\delta )(p-1)}/{(1+\delta ) p}>4$
for a small
![]() $\delta>0$
. By (5.1) and the Hölder inequality,
$\delta>0$
. By (5.1) and the Hölder inequality,
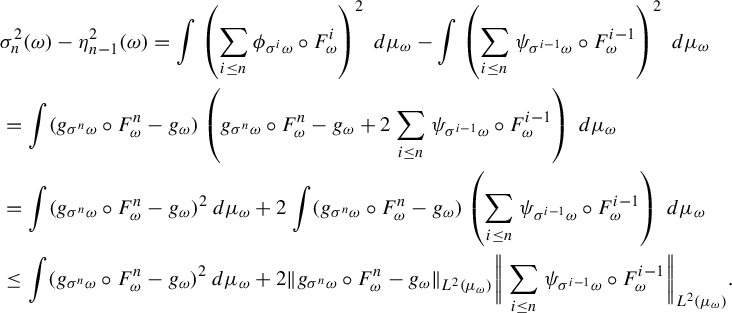 $$ \begin{align*} &\sigma_n^2(\omega)-\eta_{n-1}^2(\omega)=\int \left(\sum_{i \le n}\phi_{\sigma^i \omega} \circ F^i_{\omega}\right)^2\,d\mu_{\omega}- \int \left(\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)^2\,d\mu_{\omega}\\ &=\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}) \left( g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}+2\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)\,d\mu_{\omega}\\ &=\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})^2\,d\mu_{\omega}+2\int ( g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})\left(\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)\,d\mu_{\omega}\\ &\le\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})^2\,d\mu_{\omega}+2 \|g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\|_{L^2(\mu_{\omega})}\bigg\|\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^2(\mu_{\omega})}. \end{align*} $$
$$ \begin{align*} &\sigma_n^2(\omega)-\eta_{n-1}^2(\omega)=\int \left(\sum_{i \le n}\phi_{\sigma^i \omega} \circ F^i_{\omega}\right)^2\,d\mu_{\omega}- \int \left(\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)^2\,d\mu_{\omega}\\ &=\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}) \left( g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}+2\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)\,d\mu_{\omega}\\ &=\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})^2\,d\mu_{\omega}+2\int ( g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})\left(\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\right)\,d\mu_{\omega}\\ &\le\int (g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega})^2\,d\mu_{\omega}+2 \|g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\|_{L^2(\mu_{\omega})}\bigg\|\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^2(\mu_{\omega})}. \end{align*} $$
Using Lemmas 5.1 and 4.2, we can continue the estimate: for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
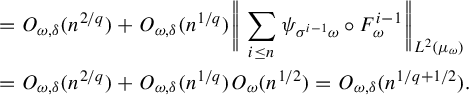 $$ \begin{align*} &= O_{\omega, \delta}(n^{2/q})+ O_{\omega, \delta}(n^{1/q}) \bigg\|\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^2(\mu_{\omega})} \\ &= O_{\omega, \delta}(n^{2/q})+ O_{\omega, \delta}(n^{1/q})O_{\omega}(n^{1/2})=O_{\omega, \delta}(n^{1/q+1/2}). \end{align*} $$
$$ \begin{align*} &= O_{\omega, \delta}(n^{2/q})+ O_{\omega, \delta}(n^{1/q}) \bigg\|\sum_{i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\bigg\|_{L^2(\mu_{\omega})} \\ &= O_{\omega, \delta}(n^{2/q})+ O_{\omega, \delta}(n^{1/q})O_{\omega}(n^{1/2})=O_{\omega, \delta}(n^{1/q+1/2}). \end{align*} $$
Using results above and applying Birkhoff’s ergodic theorem to
![]() ${\eta ^2_{n}(\omega )}/{n}$
, we have
${\eta ^2_{n}(\omega )}/{n}$
, we have
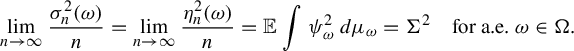 $$\begin{align*}\lim_{n \to \infty}\frac{\sigma^2_n(\omega)}{n}=\lim_{n \to \infty}\frac{\eta^2_{n}(\omega)}{n}=\mathbb{E} \int \psi^2_{\omega}\,d\mu_{\omega}=\Sigma^2 \quad\text{for a.e. } \omega \in \Omega.\end{align*}$$
$$\begin{align*}\lim_{n \to \infty}\frac{\sigma^2_n(\omega)}{n}=\lim_{n \to \infty}\frac{\eta^2_{n}(\omega)}{n}=\mathbb{E} \int \psi^2_{\omega}\,d\mu_{\omega}=\Sigma^2 \quad\text{for a.e. } \omega \in \Omega.\end{align*}$$
If
![]() $\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }>0$
, then there is a constant
$\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }>0$
, then there is a constant
![]() $C^{\prime }_{\omega }\ge 1$
such that
$C^{\prime }_{\omega }\ge 1$
such that
If
![]() $\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }=\mathbb {E}\int (\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega })^2 \,d\mu _{\omega }=0$
, then for a.e.
$\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }=\mathbb {E}\int (\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega })^2 \,d\mu _{\omega }=0$
, then for a.e.
![]() $\omega \in ~\Omega $
,
$\omega \in ~\Omega $
,
which means that
![]() $\phi $
is a coboundary. By Lemma 5.1,
$\phi $
is a coboundary. By Lemma 5.1,
![]() $g \in L^{q}(\Delta , \mu )$
.
$g \in L^{q}(\Delta , \mu )$
.
5.3 Approximations by Brownian motions
From now on, we assume (5.3), that is,
![]() $\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }>0$
.
$\Sigma ^2=\mathbb {E} \int \psi ^2_{\omega }\,d\mu _{\omega }>0$
.
Lemma 5.3. (Approximations for martingale differences)
Let
![]() $\epsilon \in (0, 1/2), \gamma :=1/(4\epsilon )$
. Define
$\epsilon \in (0, 1/2), \gamma :=1/(4\epsilon )$
. Define
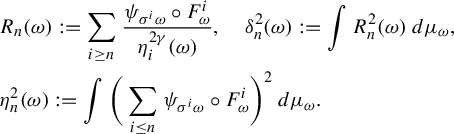 $$ \begin{align*} &R_n(\omega):=\sum_{i \ge n}\frac{\psi_{\sigma^{i} \omega} \circ F^{i}_{\omega}}{\eta^{2\gamma}_i(\omega)}, \quad \delta_n^2(\omega):=\int R^2_n(\omega) \,d\mu_{\omega}, \\ &\eta^2_{n}(\omega):=\int \bigg(\sum_{i \le n}\psi_{\sigma^{i} \omega} \circ F^{i}_{\omega}\bigg)^2\,d\mu_{\omega}. \end{align*} $$
$$ \begin{align*} &R_n(\omega):=\sum_{i \ge n}\frac{\psi_{\sigma^{i} \omega} \circ F^{i}_{\omega}}{\eta^{2\gamma}_i(\omega)}, \quad \delta_n^2(\omega):=\int R^2_n(\omega) \,d\mu_{\omega}, \\ &\eta^2_{n}(\omega):=\int \bigg(\sum_{i \le n}\psi_{\sigma^{i} \omega} \circ F^{i}_{\omega}\bigg)^2\,d\mu_{\omega}. \end{align*} $$
Then for a.e.
![]() $\omega \in \Omega $
, there is a constant
$\omega \in \Omega $
, there is a constant
![]() $C_{\omega , \gamma }\ge 1$
, a probability space
$C_{\omega , \gamma }\ge 1$
, a probability space
![]() $({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
(which is an extension of
$({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
(which is an extension of
![]() $(\Delta _{\omega }, \mu _{\omega })$
), a Brownian motion
$(\Delta _{\omega }, \mu _{\omega })$
), a Brownian motion
![]() $B^{\omega }$
and decreasing stopping times
$B^{\omega }$
and decreasing stopping times
![]() $\tau ^{\omega }_i\searrow 0$
defined on
$\tau ^{\omega }_i\searrow 0$
defined on
![]() ${\pmb {\Delta }}_{\omega }$
such that
${\pmb {\Delta }}_{\omega }$
such that
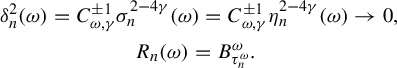 $$ \begin{align} &\delta^2_n(\omega)=C_{\omega, \gamma}^{\pm1} \sigma_n^{2-4\gamma}(\omega)=C_{\omega, \gamma}^{\pm1} \eta_n^{2-4\gamma}(\omega) \to 0, \\ &\qquad\qquad\ \,\qquad R_n(\omega)=B^{\omega}_{\tau^{\omega}_n}\nonumber. \end{align} $$
$$ \begin{align} &\delta^2_n(\omega)=C_{\omega, \gamma}^{\pm1} \sigma_n^{2-4\gamma}(\omega)=C_{\omega, \gamma}^{\pm1} \eta_n^{2-4\gamma}(\omega) \to 0, \\ &\qquad\qquad\ \,\qquad R_n(\omega)=B^{\omega}_{\tau^{\omega}_n}\nonumber. \end{align} $$
Moreover, if
then we have
 $$ \begin{align} \bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=O(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2}/{4})}) \quad\text{a.s.} \end{align} $$
$$ \begin{align} \bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=O(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2}/{4})}) \quad\text{a.s.} \end{align} $$
where the constants in
![]() $O(\cdot )$
of (5.5) and (5.6) depend on
$O(\cdot )$
of (5.5) and (5.6) depend on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
.
$x \in {\pmb {\Delta }}_{\omega }$
.
Proof. Equation (5.3) implies that there is a constant
![]() $C_{\omega } \ge 1$
such that for all
$C_{\omega } \ge 1$
such that for all
![]() $n\ge 1$
,
$n\ge 1$
,
Since
![]() $(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 1}$
are reverse martingale differences, it follows that by (5.7),
$(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 1}$
are reverse martingale differences, it follows that by (5.7),
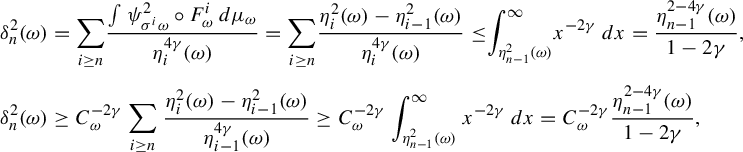 $$ \begin{align*} \delta^2_n(\omega)&=\sum_{i \ge n}\! \frac{\int \psi^2_{\sigma^{i} \omega} \circ F^{i}_{\omega}\,d\mu_{\omega}}{\eta_i^{4\gamma}(\omega)}=\sum_{i \ge n}\! \frac{\eta_i^{2}(\omega)-\eta_{i-1}^{2}(\omega)}{\eta_i^{4\gamma}(\omega)}\le\! \int_{\eta^2_{n-1}(\omega)}^{\infty}\! x^{-2\gamma} \,dx=\frac{\eta_{n-1}^{2-4\gamma}(\omega)}{1-2\gamma},\\[4pt] \delta^2_n(\omega)&\ge C_{\omega}^{-2\gamma} \sum_{i \ge n} \frac{\eta_i^{2}(\omega)-\eta_{i-1}^{2}(\omega)}{\eta_{i-1}^{4\gamma}(\omega)} \ge C_{\omega}^{-2\gamma} \int_{\eta^2_{n-1}(\omega)}^{\infty} x^{-2\gamma} \,dx = C_{\omega}^{-2\gamma} \frac{\eta_{n-1}^{2-4\gamma}(\omega)}{1-2\gamma}, \end{align*} $$
$$ \begin{align*} \delta^2_n(\omega)&=\sum_{i \ge n}\! \frac{\int \psi^2_{\sigma^{i} \omega} \circ F^{i}_{\omega}\,d\mu_{\omega}}{\eta_i^{4\gamma}(\omega)}=\sum_{i \ge n}\! \frac{\eta_i^{2}(\omega)-\eta_{i-1}^{2}(\omega)}{\eta_i^{4\gamma}(\omega)}\le\! \int_{\eta^2_{n-1}(\omega)}^{\infty}\! x^{-2\gamma} \,dx=\frac{\eta_{n-1}^{2-4\gamma}(\omega)}{1-2\gamma},\\[4pt] \delta^2_n(\omega)&\ge C_{\omega}^{-2\gamma} \sum_{i \ge n} \frac{\eta_i^{2}(\omega)-\eta_{i-1}^{2}(\omega)}{\eta_{i-1}^{4\gamma}(\omega)} \ge C_{\omega}^{-2\gamma} \int_{\eta^2_{n-1}(\omega)}^{\infty} x^{-2\gamma} \,dx = C_{\omega}^{-2\gamma} \frac{\eta_{n-1}^{2-4\gamma}(\omega)}{1-2\gamma}, \end{align*} $$
which implies (5.4) using (5.2) and (5.3). Since
![]() $(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 1}$
is a sequence of reverse martingale differences and
$(\psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega })_{i \ge 1}$
is a sequence of reverse martingale differences and
![]() $R_{n}(\omega )$
is
$R_{n}(\omega )$
is
![]() $(F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega }$
-measurable, we have that
$(F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega }$
-measurable, we have that
![]() $(R_{n}(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
$(R_{n}(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
![]() $((F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega })_{n \ge 0}$
. Therefore, by Theorem 2 of [Reference Scott and HugginsSH83], there is a probability space
$((F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega })_{n \ge 0}$
. Therefore, by Theorem 2 of [Reference Scott and HugginsSH83], there is a probability space
![]() $({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
(which is an extension of
$({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
(which is an extension of
![]() $(\Delta _{\omega }, \mu _{\omega })$
), a Brownian motion
$(\Delta _{\omega }, \mu _{\omega })$
), a Brownian motion
![]() $B^{\omega }$
, a decreasing family of stopping times
$B^{\omega }$
, a decreasing family of stopping times
![]() $\tau ^{\omega }_i\searrow 0$
defined on
$\tau ^{\omega }_i\searrow 0$
defined on
![]() ${\pmb {\Delta }}_{\omega }$
, a decreasing family of
${\pmb {\Delta }}_{\omega }$
, a decreasing family of
![]() $\sigma $
-algebras
$\sigma $
-algebras
![]() $\mathcal {G}^{\omega }_n \supseteq \sigma \{\tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
and a constant
$\mathcal {G}^{\omega }_n \supseteq \sigma \{\tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
and a constant
![]() $C_{\omega }\ge 1$
such that for any
$C_{\omega }\ge 1$
such that for any
![]() $q \ge 1$
,
$q \ge 1$
,
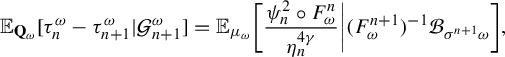 $$ \begin{align} \mathbb{E}_{\mathbf{Q}_{\omega}}[\tau^{\omega}_n-\tau^{\omega}_{n+1}|\mathcal{G}^{\omega}_{n+1}]&=\mathbb{E}_{\mu_{\omega}}\bigg[\frac{\psi_n^2 \circ F_{\omega}^{n}}{\eta_n^{4\gamma}}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg], \end{align} $$
$$ \begin{align} \mathbb{E}_{\mathbf{Q}_{\omega}}[\tau^{\omega}_n-\tau^{\omega}_{n+1}|\mathcal{G}^{\omega}_{n+1}]&=\mathbb{E}_{\mu_{\omega}}\bigg[\frac{\psi_n^2 \circ F_{\omega}^{n}}{\eta_n^{4\gamma}}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg], \end{align} $$
 $$ \begin{align} \mathbb{E}_{\mu_{\omega}}\bigg[\frac{\psi_n^{2q}\circ F^n_{\omega}}{\eta_n^{4q\gamma}}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]&= C_{\omega}^{\pm1} \mathbb{E}_{\mathbf{Q}_{\omega}}[(\tau^{\omega}_n-\tau^{\omega}_{n+1})^q|\mathcal{G}^{\omega}_{n+1}]. \end{align} $$
$$ \begin{align} \mathbb{E}_{\mu_{\omega}}\bigg[\frac{\psi_n^{2q}\circ F^n_{\omega}}{\eta_n^{4q\gamma}}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]&= C_{\omega}^{\pm1} \mathbb{E}_{\mathbf{Q}_{\omega}}[(\tau^{\omega}_n-\tau^{\omega}_{n+1})^q|\mathcal{G}^{\omega}_{n+1}]. \end{align} $$
Note that in Theorem 2 of [Reference Scott and HugginsSH83],
![]() $\sigma \{\tau ^{\omega }_i, i\geq n\}\subseteq \mathcal {G}^{\omega }_n$
only, but (5.9) and (5.10) still hold after conditioning on
$\sigma \{\tau ^{\omega }_i, i\geq n\}\subseteq \mathcal {G}^{\omega }_n$
only, but (5.9) and (5.10) still hold after conditioning on
![]() $\sigma \{\mathcal {G}^{\omega }_i, \tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
. Therefore we assume without loss of generality that
$\sigma \{\mathcal {G}^{\omega }_i, \tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
. Therefore we assume without loss of generality that
![]() $\mathcal {G}^{\omega }_n\supseteq \sigma \{\tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
.
$\mathcal {G}^{\omega }_n\supseteq \sigma \{\tau ^{\omega }_i, (F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega }, i\geq n\}$
.
By (5.8),
![]() $(B^{\omega }_{\tau ^{\omega }_i}-B^{\omega }_{\tau ^{\omega }_{i+1}}) \eta _i^{2\gamma }(\omega )=\psi _{\sigma ^i\omega }\circ F_{\omega }^i$
. Then
$(B^{\omega }_{\tau ^{\omega }_i}-B^{\omega }_{\tau ^{\omega }_{i+1}}) \eta _i^{2\gamma }(\omega )=\psi _{\sigma ^i\omega }\circ F_{\omega }^i$
. Then
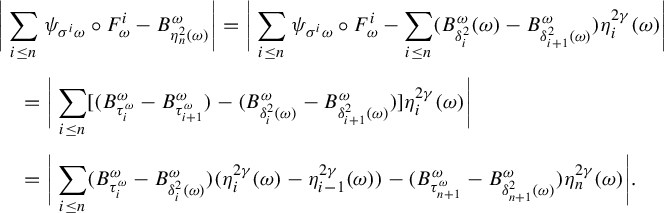 $$ \begin{align*} &\bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=\bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -\sum_{i \le n }(B^{\omega}_{\delta^{2}_i}(\omega)-B^{\omega}_{\delta^{2}_{i+1}(\omega)}) \eta_i^{2\gamma}(\omega)\bigg|\\[4pt] &\quad=\bigg|\sum_{i \leq n} [(B^{\omega}_{\tau^{\omega}_i}-B^{\omega}_{\tau^{\omega}_{i+1}})-(B^{\omega}_{\delta^{2}_i(\omega)}-B^{\omega}_{\delta^{2}_{i+1}(\omega)})] \eta_i^{2\gamma}(\omega)\bigg|\\[4pt] &\quad=\bigg|\sum_{ i \le n} (B^{\omega}_{\tau^{\omega}_i}-B^{\omega}_{\delta^{2}_{i}(\omega)}) (\eta_i^{2\gamma}(\omega)- \eta_{i-1}^{2\gamma}(\omega))- (B^{\omega}_{\tau^{\omega}_{n+1}}-B^{\omega}_{\delta^{2}_{n+1}(\omega)}) \eta_n^{2\gamma}(\omega)\bigg|. \end{align*} $$
$$ \begin{align*} &\bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=\bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -\sum_{i \le n }(B^{\omega}_{\delta^{2}_i}(\omega)-B^{\omega}_{\delta^{2}_{i+1}(\omega)}) \eta_i^{2\gamma}(\omega)\bigg|\\[4pt] &\quad=\bigg|\sum_{i \leq n} [(B^{\omega}_{\tau^{\omega}_i}-B^{\omega}_{\tau^{\omega}_{i+1}})-(B^{\omega}_{\delta^{2}_i(\omega)}-B^{\omega}_{\delta^{2}_{i+1}(\omega)})] \eta_i^{2\gamma}(\omega)\bigg|\\[4pt] &\quad=\bigg|\sum_{ i \le n} (B^{\omega}_{\tau^{\omega}_i}-B^{\omega}_{\delta^{2}_{i}(\omega)}) (\eta_i^{2\gamma}(\omega)- \eta_{i-1}^{2\gamma}(\omega))- (B^{\omega}_{\tau^{\omega}_{n+1}}-B^{\omega}_{\delta^{2}_{n+1}(\omega)}) \eta_n^{2\gamma}(\omega)\bigg|. \end{align*} $$
Since Brownian motions are locally Hölder continuous with exponent
![]() $({1-\epsilon ^2})/{2}$
, we can continue the estimate above: for a.s.
$({1-\epsilon ^2})/{2}$
, we can continue the estimate above: for a.s.
![]() $x \in {\pmb {\Delta }}_{\omega }$
,
$x \in {\pmb {\Delta }}_{\omega }$
,
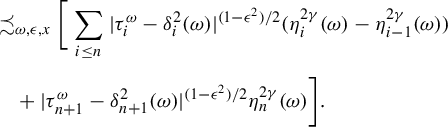 $$ \begin{align*} &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} |\tau^{\omega}_i-\delta^{2}_{i}(\omega)|^{({1-\epsilon^2})/{2}} (\eta_i^{2\gamma}(\omega)-\eta_{i-1}^{2\gamma}(\omega))\\[4pt]&\quad+|\tau^{\omega}_{n+1}-\delta^{2}_{n+1}(\omega)|^{({1-\epsilon^2})/{2}} \eta_n^{2\gamma}(\omega)\bigg].\end{align*} $$
$$ \begin{align*} &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} |\tau^{\omega}_i-\delta^{2}_{i}(\omega)|^{({1-\epsilon^2})/{2}} (\eta_i^{2\gamma}(\omega)-\eta_{i-1}^{2\gamma}(\omega))\\[4pt]&\quad+|\tau^{\omega}_{n+1}-\delta^{2}_{n+1}(\omega)|^{({1-\epsilon^2})/{2}} \eta_n^{2\gamma}(\omega)\bigg].\end{align*} $$
Using (5.5) and
![]() $\delta ^2_{n}(\omega ) \precsim _{\gamma } \eta _{n-1}^{2-4\gamma }(\omega )$
, we can continue the estimate above: for a.s.
$\delta ^2_{n}(\omega ) \precsim _{\gamma } \eta _{n-1}^{2-4\gamma }(\omega )$
, we can continue the estimate above: for a.s.
![]() $x \in {\pmb {\Delta }}_{\omega }$
,
$x \in {\pmb {\Delta }}_{\omega }$
,
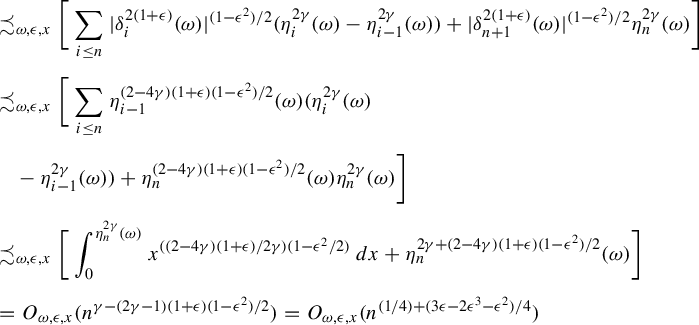 $$ \begin{align*} &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} |\delta_{i}^{2(1+\epsilon)}(\omega)|^{({1-\epsilon^2})/{2}} (\eta_i^{2\gamma}(\omega)-\eta_{i-1}^{2\gamma}(\omega))+|\delta_{n+1}^{2(1+\epsilon)}(\omega)|^{({1-\epsilon^2})/{2}} \eta_n^{2\gamma}(\omega)\bigg]\\[4pt] &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} \eta_{i-1}^{(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega) (\eta_i^{2\gamma}(\omega)\\[4pt]&\quad-\eta_{i-1}^{2\gamma}(\omega))+\eta_{n}^{(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega) \eta_n^{2\gamma}(\omega)\bigg] \\[4pt] &\precsim_{\omega, \epsilon, x}\bigg[\int_0^{\eta_n^{2\gamma}(\omega)} x^{({(2-4\gamma) (1+\epsilon) }/{2\gamma})({1-\epsilon^2}/{2})}\,dx+\eta_n^{2\gamma+(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega)\bigg] \\[4pt] &= O_{\omega, \epsilon, x}(n^{\gamma-(2\gamma-1) (1+\epsilon) (1-\epsilon^2)/2}) = O_{\omega, \epsilon, x}(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2})/{4}}) \end{align*} $$
$$ \begin{align*} &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} |\delta_{i}^{2(1+\epsilon)}(\omega)|^{({1-\epsilon^2})/{2}} (\eta_i^{2\gamma}(\omega)-\eta_{i-1}^{2\gamma}(\omega))+|\delta_{n+1}^{2(1+\epsilon)}(\omega)|^{({1-\epsilon^2})/{2}} \eta_n^{2\gamma}(\omega)\bigg]\\[4pt] &\precsim_{\omega, \epsilon, x} \bigg[\sum_{ i \le n} \eta_{i-1}^{(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega) (\eta_i^{2\gamma}(\omega)\\[4pt]&\quad-\eta_{i-1}^{2\gamma}(\omega))+\eta_{n}^{(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega) \eta_n^{2\gamma}(\omega)\bigg] \\[4pt] &\precsim_{\omega, \epsilon, x}\bigg[\int_0^{\eta_n^{2\gamma}(\omega)} x^{({(2-4\gamma) (1+\epsilon) }/{2\gamma})({1-\epsilon^2}/{2})}\,dx+\eta_n^{2\gamma+(2-4\gamma) (1+\epsilon) ({1-\epsilon^2})/{2}}(\omega)\bigg] \\[4pt] &= O_{\omega, \epsilon, x}(n^{\gamma-(2\gamma-1) (1+\epsilon) (1-\epsilon^2)/2}) = O_{\omega, \epsilon, x}(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2})/{4}}) \end{align*} $$
where the last two equalities are due to (5.7) and
![]() $\gamma =1/(4\epsilon )$
.
$\gamma =1/(4\epsilon )$
.
5.4 Proof of the QASIP for martingale differences
To prove the QASIP (5.6), we will verify (5.5) in Lemma 5.3: for some
![]() $\epsilon \in (0,1/2)$
,
$\epsilon \in (0,1/2)$
,
Lemma 5.4. (Stopping times decompositions)
The following decompositions hold:
where
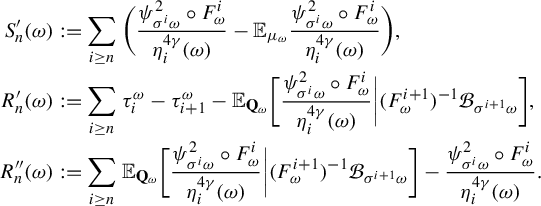 $$ \begin{align*} S^{\prime}_n(\omega):=&\sum_{i \geq n} \bigg(\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}-\mathbb{E}_{\mu_{\omega}}\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg),\\[-2pt] R_n'(\omega):=&\sum_{i \ge n} \tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg],\\[-2pt] R_n''(\omega):=&\sum_{i\ge n} \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]-\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}. \end{align*} $$
$$ \begin{align*} S^{\prime}_n(\omega):=&\sum_{i \geq n} \bigg(\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}-\mathbb{E}_{\mu_{\omega}}\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg),\\[-2pt] R_n'(\omega):=&\sum_{i \ge n} \tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg],\\[-2pt] R_n''(\omega):=&\sum_{i\ge n} \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]-\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}. \end{align*} $$
![]() $R'(\omega ),R''(\omega )\text { are reverse martingales}$
w.r.t.
$R'(\omega ),R''(\omega )\text { are reverse martingales}$
w.r.t.
![]() $( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
$( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
respectively. And for a.e.
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
respectively. And for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where the constants in
![]() $O(\cdot )$
depend on
$O(\cdot )$
depend on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
and
$x \in {\pmb {\Delta }}_{\omega }$
and
![]() $\epsilon :={2p(1+\delta )^2}/ {(p-1)(D-2-\delta )}$
for a sufficiently small
$\epsilon :={2p(1+\delta )^2}/ {(p-1)(D-2-\delta )}$
for a sufficiently small
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\epsilon \in (0,1/2)$
.
$\epsilon \in (0,1/2)$
.
Proof. It is straightforward to verify the decompositions. We will now prove that
![]() $(R_n'(\omega ))_{n \ge 0},(R_n''(\omega ))_{n\ge 0}$
are reverse martingales w.r.t.
$(R_n'(\omega ))_{n \ge 0},(R_n''(\omega ))_{n\ge 0}$
are reverse martingales w.r.t.
![]() $( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
$( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
, respectively. It is obvious that
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
, respectively. It is obvious that
![]() $R_n^{'}(\omega )$
and
$R_n^{'}(\omega )$
and
![]() $R_n^{''}(\omega )$
are measurable w.r.t.
$R_n^{''}(\omega )$
are measurable w.r.t.
![]() $( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
$( \mathcal {G}^{\omega }_i)_{i \ge 0}$
and
![]() $(F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega }$
, respectively.
$(F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega }$
, respectively.
We now study
![]() $R_n'(\omega )$
. By (5.9),
$R_n'(\omega )$
. By (5.9),
 $$ \begin{align*} &\mathbb{E}_{\mathbf{Q}_{\omega}}[ R_n'(\omega)|\mathcal{G}^{\omega}_{n+1}]\\[-1pt] &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}(\tau^{\omega}_n-\tau^{\omega}_{n+1}|\mathcal{G}^{\omega}_{n+1})-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\qquad +\sum_{i\ge n+1}\mathbb{E}_{\mathbf{Q}_{\omega}}( \tau^{\omega}_i-\tau^{\omega}_{i+1}|\mathcal{G}^{\omega}_{n+1})- \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\[-1pt] &\qquad-\mathbb{E}_{\mathbf{Q}_{\omega}} \bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\qquad +\sum_{i\ge n+1}\!\mathbb{E}_{\mathbf{Q}_{\omega}}\big[\tau^{\omega}_i-\tau^{\omega}_{i+1}\big|\mathcal{G}^{\omega}_{n+1}\big]\kern1pt{-}\kern1pt \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\kern-1.5pt\bigg\}.\end{align*} $$
$$ \begin{align*} &\mathbb{E}_{\mathbf{Q}_{\omega}}[ R_n'(\omega)|\mathcal{G}^{\omega}_{n+1}]\\[-1pt] &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}(\tau^{\omega}_n-\tau^{\omega}_{n+1}|\mathcal{G}^{\omega}_{n+1})-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\qquad +\sum_{i\ge n+1}\mathbb{E}_{\mathbf{Q}_{\omega}}( \tau^{\omega}_i-\tau^{\omega}_{i+1}|\mathcal{G}^{\omega}_{n+1})- \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\[-1pt] &\qquad-\mathbb{E}_{\mathbf{Q}_{\omega}} \bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\bigg\}\\[-1pt] &\qquad +\sum_{i\ge n+1}\!\mathbb{E}_{\mathbf{Q}_{\omega}}\big[\tau^{\omega}_i-\tau^{\omega}_{i+1}\big|\mathcal{G}^{\omega}_{n+1}\big]\kern1pt{-}\kern1pt \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|\mathcal{G}^{\omega}_{n+1}\kern-1.5pt\bigg\}.\end{align*} $$
Since
![]() $(F_{\omega }^{n+1+i})^{-1}\mathcal {B}_{\sigma ^{n+1+i} \omega } \subseteq \mathcal {G}^{\omega }_{n+1}$
and
$(F_{\omega }^{n+1+i})^{-1}\mathcal {B}_{\sigma ^{n+1+i} \omega } \subseteq \mathcal {G}^{\omega }_{n+1}$
and
![]() $\tau ^{\omega }_{n+1+i}$
is
$\tau ^{\omega }_{n+1+i}$
is
![]() $\mathcal {G}^{\omega }_{n+1}$
-measurable for any
$\mathcal {G}^{\omega }_{n+1}$
-measurable for any
![]() $i \ge 0$
, we can continue the calculation above as
$i \ge 0$
, we can continue the calculation above as
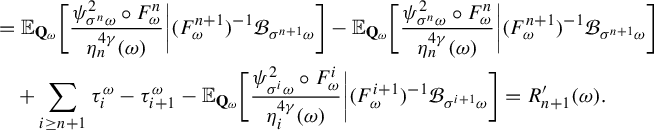 $$ \begin{align*} &=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\ &\quad +\sum_{i\ge n+1} \tau^{\omega}_i-\tau^{\omega}_{i+1}- \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[ \frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]=R^{\prime}_{n+1}(\omega). \end{align*} $$
$$ \begin{align*} &=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\ &\quad +\sum_{i\ge n+1} \tau^{\omega}_i-\tau^{\omega}_{i+1}- \mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[ \frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]=R^{\prime}_{n+1}(\omega). \end{align*} $$
Therefore
![]() $(R_n'(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
$(R_n'(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
![]() $( \mathcal {G}^{\omega }_i)_{i \ge 0}$
.
$( \mathcal {G}^{\omega }_i)_{i \ge 0}$
.
We now turn to
![]() $R_n''(\omega )$
. Since
$R_n''(\omega )$
. Since
![]() $((F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega })_{n \ge 0}$
is a decreasing filtration,
$((F_{\omega }^{n})^{-1}\mathcal {B}_{\sigma ^{n} \omega })_{n \ge 0}$
is a decreasing filtration,
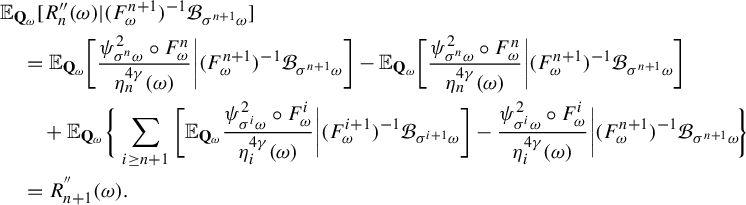 $$ \begin{align*} &\mathbb{E}_{\mathbf{Q}_{\omega}} [R_n''(\omega)|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}]\\ &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\ &\qquad +\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\sum_{i\ge n+1} \bigg[\mathbb{E}_{\mathbf{Q}_{\omega}}\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]-\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\kern-1.5pt\bigg\}\\ &\quad=R_{n+1}^{''}(\omega). \end{align*} $$
$$ \begin{align*} &\mathbb{E}_{\mathbf{Q}_{\omega}} [R_n''(\omega)|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}]\\ &\quad=\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^n \omega}^2 \circ F_{\omega}^n}{\eta_n^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\bigg]\\ &\qquad +\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg\{\sum_{i\ge n+1} \bigg[\mathbb{E}_{\mathbf{Q}_{\omega}}\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]-\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{n+1})^{-1}\mathcal{B}_{\sigma^{n+1} \omega}\kern-1.5pt\bigg\}\\ &\quad=R_{n+1}^{''}(\omega). \end{align*} $$
Therefore
![]() $(R_n''(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
$(R_n''(\omega ))_{n \ge 0}$
is a reverse martingale w.r.t.
![]() $((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
.
$((F_{\omega }^{i})^{-1}\mathcal {B}_{\sigma ^{i} \omega })_{i \ge 0}$
.
We now estimate
![]() $R_n'(\omega )$
. Let
$R_n'(\omega )$
. Let
![]() $q:={(p-1)(D-2-\delta )}/{2p(1+\delta )}>2$
,
$q:={(p-1)(D-2-\delta )}/{2p(1+\delta )}>2$
,
![]() $\epsilon :={2p(1+\delta )^2}/ {(p-1)(D-2-\delta )} \in (0, 1/2)$
for a sufficiently small
$\epsilon :={2p(1+\delta )^2}/ {(p-1)(D-2-\delta )} \in (0, 1/2)$
for a sufficiently small
![]() $\delta>0$
. By the Burkholder–Davis–Gundy inequality and Minkowski inequality, there is a constant
$\delta>0$
. By the Burkholder–Davis–Gundy inequality and Minkowski inequality, there is a constant
![]() $C_q$
such that
$C_q$
such that
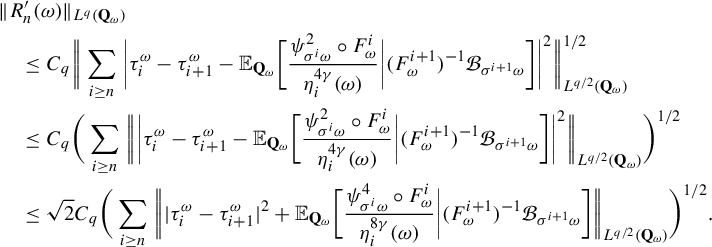 $$ \begin{align*} &\|R^{\prime}_n(\omega)\|_{L^q(\mathbf{Q}_{\omega})}\nonumber\\ &\quad\le C_q \bigg\|\sum_{i \ge n}\bigg|\tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|^2\bigg\|^{1/2}_{L^{q/2}(\mathbf{Q}_{\omega})} \nonumber\\ &\quad\le C_q \bigg(\sum_{i \ge n} \bigg\|\bigg|\tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|^2\bigg\|_{L^{q/2}(\mathbf{Q}_{\omega})}\bigg)^{1/2} \nonumber\\ &\quad\le \sqrt{2} C_q \bigg( \sum_{i \ge n} \bigg\| |\tau^{\omega}_i-\tau^{\omega}_{i+1}|^2+\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i}{\eta_i^{8\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg\|_{L^{q/2}(\mathbf{Q}_{\omega})}\bigg)^{1/2}.\nonumber \end{align*} $$
$$ \begin{align*} &\|R^{\prime}_n(\omega)\|_{L^q(\mathbf{Q}_{\omega})}\nonumber\\ &\quad\le C_q \bigg\|\sum_{i \ge n}\bigg|\tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|^2\bigg\|^{1/2}_{L^{q/2}(\mathbf{Q}_{\omega})} \nonumber\\ &\quad\le C_q \bigg(\sum_{i \ge n} \bigg\|\bigg|\tau^{\omega}_i-\tau^{\omega}_{i+1}-\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^2 \circ F_{\omega}^i}{\eta_i^{4\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg|^2\bigg\|_{L^{q/2}(\mathbf{Q}_{\omega})}\bigg)^{1/2} \nonumber\\ &\quad\le \sqrt{2} C_q \bigg( \sum_{i \ge n} \bigg\| |\tau^{\omega}_i-\tau^{\omega}_{i+1}|^2+\mathbb{E}_{\mathbf{Q}_{\omega}}\bigg[\frac{\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i}{\eta_i^{8\gamma}(\omega)}\bigg|(F_{\omega}^{i+1})^{-1}\mathcal{B}_{\sigma^{i+1} \omega}\bigg]\bigg\|_{L^{q/2}(\mathbf{Q}_{\omega})}\bigg)^{1/2}.\nonumber \end{align*} $$
Using (5.10) and the fact that
![]() $({\pmb {\Delta }}_{\omega },\mathbf {Q}_{\omega })$
is an extension of
$({\pmb {\Delta }}_{\omega },\mathbf {Q}_{\omega })$
is an extension of
![]() $(\Delta _{\omega }, \mu _{\omega })$
, we can continue the estimate above as
$(\Delta _{\omega }, \mu _{\omega })$
, we can continue the estimate above as
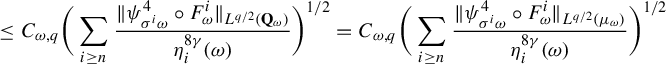 $$ \begin{align} \le C_{\omega, q} \bigg( \sum_{i \ge n} \frac{\|\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i\|_{L^{q/2}(\mathbf{Q}_{\omega})}}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2}=C_{\omega, q} \bigg( \sum_{i \ge n} \frac{\|\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i\|_{{L^{q/2}(\mu_{\omega})}}}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2} \end{align} $$
$$ \begin{align} \le C_{\omega, q} \bigg( \sum_{i \ge n} \frac{\|\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i\|_{L^{q/2}(\mathbf{Q}_{\omega})}}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2}=C_{\omega, q} \bigg( \sum_{i \ge n} \frac{\|\psi_{\sigma^i \omega}^4 \circ F_{\omega}^i\|_{{L^{q/2}(\mu_{\omega})}}}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2} \end{align} $$
for some constant
![]() $C_{\omega , q}>0$
.
$C_{\omega , q}>0$
.
Let
![]() $K_n(\omega )\kern1pt{:=} \sum _{i \leq n}\kern-1.1pt\|\psi _{\sigma ^i \omega }^4 \kern1pt{\circ}\kern1pt F_{\omega }^{i}\|_{L^{q/2}(\mu _{\omega })}$
. Then
$K_n(\omega )\kern1pt{:=} \sum _{i \leq n}\kern-1.1pt\|\psi _{\sigma ^i \omega }^4 \kern1pt{\circ}\kern1pt F_{\omega }^{i}\|_{L^{q/2}(\mu _{\omega })}$
. Then
![]() $\mathbb {E}\|\psi _{\omega }^4 \|_{L^{q/2}(\mu _{\omega })} \kern1pt{\le}\kern1pt (\mathbb {E} \kern-1.3pt\int\kern-1.3pt \psi _{\omega }^{2q} \kern1pt d\mu _{\omega })^{2/q} \kern0.8pt{<}\kern0.8pt \infty $
due to Lemma 5.1 and
$\mathbb {E}\|\psi _{\omega }^4 \|_{L^{q/2}(\mu _{\omega })} \kern1pt{\le}\kern1pt (\mathbb {E} \kern-1.3pt\int\kern-1.3pt \psi _{\omega }^{2q} \kern1pt d\mu _{\omega })^{2/q} \kern0.8pt{<}\kern0.8pt \infty $
due to Lemma 5.1 and
![]() $2/q<1$
. By Birkhoff’s ergodic theorem, for a.e.
$2/q<1$
. By Birkhoff’s ergodic theorem, for a.e.
![]() $\omega \in \Omega $
, there is a constant
$\omega \in \Omega $
, there is a constant
![]() $C_{\omega } \ge 1$
such that
$C_{\omega } \ge 1$
such that
![]() $K_{n}(\omega ) = C_{\omega }^{\pm 1} n$
for all
$K_{n}(\omega ) = C_{\omega }^{\pm 1} n$
for all
![]() $n\in \mathbb {N}$
. Using (5.3) and (5.12), we have
$n\in \mathbb {N}$
. Using (5.3) and (5.12), we have
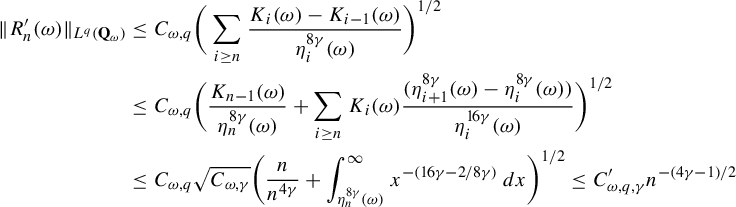 $$ \begin{align*} \|R^{\prime}_n(\omega)\|_{L^q(\mathbf{Q}_{\omega})} &\le C_{\omega,q} \bigg( \sum_{i \ge n} \frac{K_i(\omega)-K_{i-1}(\omega)}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2} \\ &\le C_{\omega, q} \bigg(\frac{K_{n-1}(\omega)}{\eta_n^{8\gamma}(\omega)} + \sum_{i \geq n} K_i(\omega) \frac{(\eta_{i+1}^{8\gamma}(\omega)-\eta_{i}^{8\gamma}(\omega))}{\eta_i^{16\gamma}(\omega)}\bigg)^{1/2}\\ &\le C_{\omega,q} \sqrt{C_{\omega,\gamma}} \bigg(\frac{n}{n^{4\gamma}} + \int_{\eta_n^{8\gamma}(\omega)}^\infty x^{-({16\gamma-2}/{8\gamma})}\,dx\bigg)^{1/2} \le C^{\prime}_{\omega, q ,\gamma} n^{-({4\gamma-1})/{2}} \end{align*} $$
$$ \begin{align*} \|R^{\prime}_n(\omega)\|_{L^q(\mathbf{Q}_{\omega})} &\le C_{\omega,q} \bigg( \sum_{i \ge n} \frac{K_i(\omega)-K_{i-1}(\omega)}{\eta_i^{8\gamma}(\omega)}\bigg)^{1/2} \\ &\le C_{\omega, q} \bigg(\frac{K_{n-1}(\omega)}{\eta_n^{8\gamma}(\omega)} + \sum_{i \geq n} K_i(\omega) \frac{(\eta_{i+1}^{8\gamma}(\omega)-\eta_{i}^{8\gamma}(\omega))}{\eta_i^{16\gamma}(\omega)}\bigg)^{1/2}\\ &\le C_{\omega,q} \sqrt{C_{\omega,\gamma}} \bigg(\frac{n}{n^{4\gamma}} + \int_{\eta_n^{8\gamma}(\omega)}^\infty x^{-({16\gamma-2}/{8\gamma})}\,dx\bigg)^{1/2} \le C^{\prime}_{\omega, q ,\gamma} n^{-({4\gamma-1})/{2}} \end{align*} $$
for some constants
![]() $C_{\omega , \gamma },C^{\prime }_{\omega , q ,\gamma }\kern-1pt >\kern-1pt 0$
. Recall that
$C_{\omega , \gamma },C^{\prime }_{\omega , q ,\gamma }\kern-1pt >\kern-1pt 0$
. Recall that
![]() $q\kern-1pt :={(p-1)(D-2-\delta )}/{2p(1+\delta )}\kern-1pt >\kern-1pt 2$
,
$q\kern-1pt :={(p-1)(D-2-\delta )}/{2p(1+\delta )}\kern-1pt >\kern-1pt 2$
,
![]() $\epsilon :={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}$
and
$\epsilon :={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}$
and
![]() $\gamma =(4\epsilon )^{-1}$
. Using (5.4), there are constants
$\gamma =(4\epsilon )^{-1}$
. Using (5.4), there are constants
![]() $C_{\omega , q, \gamma },C^{\prime \prime }_{\omega , q, \gamma }>0$
such that
$C_{\omega , q, \gamma },C^{\prime \prime }_{\omega , q, \gamma }>0$
such that
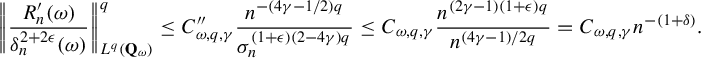 $$ \begin{align*} \bigg\|\frac{R^{\prime}_n(\omega)}{\delta_{n}^{2+2\epsilon}(\omega)}\bigg\|^q_{L^q(\mathbf{Q}_{\omega})}\le C^{\prime\prime}_{\omega, q, \gamma} \frac{n^{-({4\gamma-1}/{2})q}}{\sigma_n^{(1+\epsilon)(2-4\gamma)q}} \le C_{\omega, q, \gamma} \frac{n^{(2\gamma-1)(1+\epsilon)q}}{n^{({4\gamma-1})/{2}q}}= C_{\omega, q, \gamma} {n^{-(1+\delta)}}. \end{align*} $$
$$ \begin{align*} \bigg\|\frac{R^{\prime}_n(\omega)}{\delta_{n}^{2+2\epsilon}(\omega)}\bigg\|^q_{L^q(\mathbf{Q}_{\omega})}\le C^{\prime\prime}_{\omega, q, \gamma} \frac{n^{-({4\gamma-1}/{2})q}}{\sigma_n^{(1+\epsilon)(2-4\gamma)q}} \le C_{\omega, q, \gamma} \frac{n^{(2\gamma-1)(1+\epsilon)q}}{n^{({4\gamma-1})/{2}q}}= C_{\omega, q, \gamma} {n^{-(1+\delta)}}. \end{align*} $$
By the Borel–Cantelli lemma, we have
![]() $R_n'(\omega )=O(\delta _n^{2+2\epsilon }(\omega )) $
a.s. The estimate for
$R_n'(\omega )=O(\delta _n^{2+2\epsilon }(\omega )) $
a.s. The estimate for
![]() $R_n''(\omega )$
is similar.
$R_n''(\omega )$
is similar.
Lemma 5.5. (Estimates for
 $S^{\prime }_n(\omega )$
in (5.11))
$S^{\prime }_n(\omega )$
in (5.11))
Define
![]() $S_n(\omega ):=\sum _{i\leq n}(\psi _{\sigma ^i\omega }^2 \circ F_{\omega }^i-\int \psi _{\sigma ^i\omega }^2 \circ F_{\omega }^id\mu _{\omega })$
,
$S_n(\omega ):=\sum _{i\leq n}(\psi _{\sigma ^i\omega }^2 \circ F_{\omega }^i-\int \psi _{\sigma ^i\omega }^2 \circ F_{\omega }^id\mu _{\omega })$
,
![]() $\gamma =(4\epsilon )^{-1}$
. Suppose that
$\gamma =(4\epsilon )^{-1}$
. Suppose that
Then
![]() $ S^{\prime }_n(\omega )=O(\delta _n^{2(1+\epsilon )}(\omega )) \mu _{\omega }$
-a.s. All constants in
$ S^{\prime }_n(\omega )=O(\delta _n^{2(1+\epsilon )}(\omega )) \mu _{\omega }$
-a.s. All constants in
![]() $O(\cdot )$
here depend on
$O(\cdot )$
here depend on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() ${x \in {\Delta }_{\omega }}$
.
${x \in {\Delta }_{\omega }}$
.
Proof. Since
![]() $S^{\prime }_n(\omega ):=\sum _{i \geq n} (\psi _{\sigma ^i \omega }^2 \circ F_{\omega }^i-\mathbb {E}_{\mu _{\omega }}\psi _{\sigma ^i \omega }^2 \circ F_{\omega }^i)\eta _i^{-4\gamma }(\omega )$
, we have that
$S^{\prime }_n(\omega ):=\sum _{i \geq n} (\psi _{\sigma ^i \omega }^2 \circ F_{\omega }^i-\mathbb {E}_{\mu _{\omega }}\psi _{\sigma ^i \omega }^2 \circ F_{\omega }^i)\eta _i^{-4\gamma }(\omega )$
, we have that
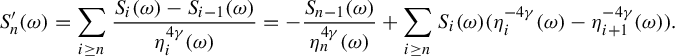 $$ \begin{align*} S^{\prime}_n(\omega)&=\sum_{i \ge n} \frac{S_i(\omega)-S_{i-1}(\omega)}{\eta_i^{4\gamma}(\omega)}=-\frac{S_{n-1}(\omega)}{\eta_n^{4\gamma}(\omega)}+\sum_{i \ge n} S_i(\omega) (\eta_i^{-4\gamma}(\omega)-\eta_{i+1}^{-4\gamma}(\omega)).\end{align*} $$
$$ \begin{align*} S^{\prime}_n(\omega)&=\sum_{i \ge n} \frac{S_i(\omega)-S_{i-1}(\omega)}{\eta_i^{4\gamma}(\omega)}=-\frac{S_{n-1}(\omega)}{\eta_n^{4\gamma}(\omega)}+\sum_{i \ge n} S_i(\omega) (\eta_i^{-4\gamma}(\omega)-\eta_{i+1}^{-4\gamma}(\omega)).\end{align*} $$
Using (5.7), we can continue the calculation above as
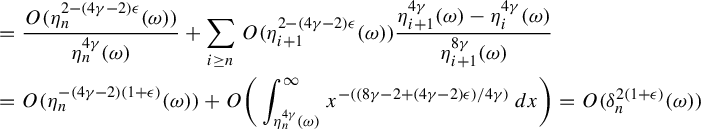 $$ \begin{align*} &= \frac{O(\eta_n^{2-(4\gamma-2)\epsilon}(\omega))}{\eta_n^{4\gamma}(\omega)}+ \sum_{i \ge n} O(\eta_{i+1}^{2-(4\gamma-2)\epsilon}(\omega)) \frac{\eta_{i+1}^{4\gamma}(\omega)-\eta_i^{4\gamma}(\omega)}{\eta_{i+1}^{8\gamma}(\omega)} \\ &= O(\eta_n^{-(4\gamma-2)(1+\epsilon)}(\omega))+O\bigg(\int^{\infty}_{\eta_n^{4\gamma}(\omega)} x^{-(({8\gamma-2+(4\gamma-2)\epsilon})/{4\gamma})}\,dx\bigg) = O(\delta_n^{2(1+\epsilon)}(\omega)) \end{align*} $$
$$ \begin{align*} &= \frac{O(\eta_n^{2-(4\gamma-2)\epsilon}(\omega))}{\eta_n^{4\gamma}(\omega)}+ \sum_{i \ge n} O(\eta_{i+1}^{2-(4\gamma-2)\epsilon}(\omega)) \frac{\eta_{i+1}^{4\gamma}(\omega)-\eta_i^{4\gamma}(\omega)}{\eta_{i+1}^{8\gamma}(\omega)} \\ &= O(\eta_n^{-(4\gamma-2)(1+\epsilon)}(\omega))+O\bigg(\int^{\infty}_{\eta_n^{4\gamma}(\omega)} x^{-(({8\gamma-2+(4\gamma-2)\epsilon})/{4\gamma})}\,dx\bigg) = O(\delta_n^{2(1+\epsilon)}(\omega)) \end{align*} $$
where the last equality is due to (5.4). All constants in
![]() $O(\cdot )$
depend on
$O(\cdot )$
depend on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
We will use Lemma 5.5 to estimate
![]() $S_n(\omega )$
to control
$S_n(\omega )$
to control
![]() $S^{\prime }_n(\omega )$
. Using
$S^{\prime }_n(\omega )$
. Using
![]() $\psi _{\omega }=\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
, we have
$\psi _{\omega }=\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
, we have
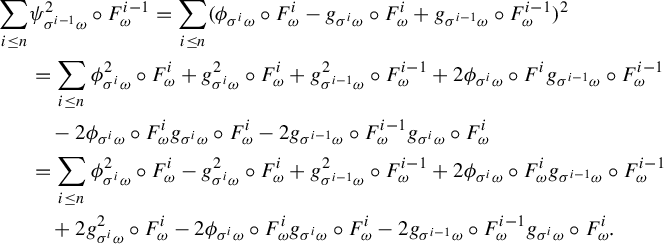 $$ \begin{align*} \sum_{i \le n}&\psi^2_{\sigma^{i-1}\omega} \circ F^{i-1}_{\omega}=\sum_{i \le n}(\phi_{\sigma^i \omega} \circ F_{\omega}^i-g_{\sigma^i \omega} \circ F^i_{\omega}+g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega})^2\\ &=\sum_{i \le n}\phi^2_{\sigma^i \omega}\circ F^i_{\omega}+g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^i \omega} \circ F^i_{\omega}-2g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega} g_{\sigma^{i} \omega} \circ F^{i}_{\omega} \\ &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad +2g^2_{\sigma^i \omega} \circ F^i_{\omega}-2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^i \omega} \circ F^i_{\omega}-2g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega} g_{\sigma^{i} \omega} \circ F^{i}_{\omega}.\end{align*} $$
$$ \begin{align*} \sum_{i \le n}&\psi^2_{\sigma^{i-1}\omega} \circ F^{i-1}_{\omega}=\sum_{i \le n}(\phi_{\sigma^i \omega} \circ F_{\omega}^i-g_{\sigma^i \omega} \circ F^i_{\omega}+g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega})^2\\ &=\sum_{i \le n}\phi^2_{\sigma^i \omega}\circ F^i_{\omega}+g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^i \omega} \circ F^i_{\omega}-2g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega} g_{\sigma^{i} \omega} \circ F^{i}_{\omega} \\ &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad +2g^2_{\sigma^i \omega} \circ F^i_{\omega}-2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^i \omega} \circ F^i_{\omega}-2g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega} g_{\sigma^{i} \omega} \circ F^{i}_{\omega}.\end{align*} $$
Using
![]() $\psi _{\omega }=\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
again, we can continue the calculation above as
$\psi _{\omega }=\phi _{\sigma \omega } \circ F_{\omega } - g_{\sigma \omega }\circ F_{\omega }+g_{\omega }$
again, we can continue the calculation above as
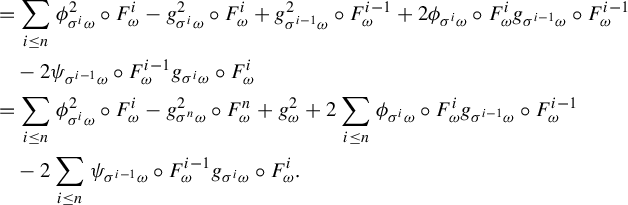 $$ \begin{align*} &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}\\ &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^n \omega} \circ F^n_{\omega}+g^2_{ \omega} +2\sum_{i\le n}\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\sum_{i\le n}\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}. \end{align*} $$
$$ \begin{align*} &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^i \omega} \circ F^i_{\omega}+g^2_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+2\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}\\ &=\sum_{i \le n} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}-g^2_{\sigma^n \omega} \circ F^n_{\omega}+g^2_{ \omega} +2\sum_{i\le n}\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\\ &\quad -2\sum_{i\le n}\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}. \end{align*} $$
Then we have
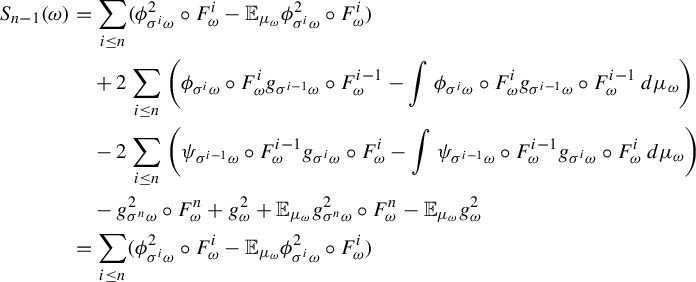 $$ \begin{align} &\hspace{-24pt}S_{n-1}(\omega)=\sum_{i \le n} (\phi^2_{\sigma^i \omega}\circ F^i_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\sigma^i \omega}\circ F^i_{\omega})\nonumber\\ &\qquad+2\sum_{i\le n}\left(\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}-\int \phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\,d\mu_{\omega}\right)\nonumber\\ &\qquad -2\sum_{i\le n}\left(\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}-\int \psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}\,d\mu_{\omega}\right)\nonumber\\ &\qquad-g^2_{\sigma^n \omega} \circ F^n_{\omega}+g^2_{ \omega} +\mathbb{E}_{\mu_{\omega}}g^2_{\sigma^n \omega} \circ F^n_{\omega}-\mathbb{E}_{\mu_{\omega}}g^2_{ \omega}\nonumber\\ &\hspace{10pt}=\sum_{i \le n} (\phi^2_{\sigma^i \omega}\circ F^i_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}) \end{align} $$
$$ \begin{align} &\hspace{-24pt}S_{n-1}(\omega)=\sum_{i \le n} (\phi^2_{\sigma^i \omega}\circ F^i_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\sigma^i \omega}\circ F^i_{\omega})\nonumber\\ &\qquad+2\sum_{i\le n}\left(\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}-\int \phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\,d\mu_{\omega}\right)\nonumber\\ &\qquad -2\sum_{i\le n}\left(\psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}-\int \psi_{\sigma^{i-1} \omega}\circ F_{\omega}^{i-1} g_{\sigma^i \omega} \circ F^i_{\omega}\,d\mu_{\omega}\right)\nonumber\\ &\qquad-g^2_{\sigma^n \omega} \circ F^n_{\omega}+g^2_{ \omega} +\mathbb{E}_{\mu_{\omega}}g^2_{\sigma^n \omega} \circ F^n_{\omega}-\mathbb{E}_{\mu_{\omega}}g^2_{ \omega}\nonumber\\ &\hspace{10pt}=\sum_{i \le n} (\phi^2_{\sigma^i \omega}\circ F^i_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\sigma^i \omega}\circ F^i_{\omega}) \end{align} $$
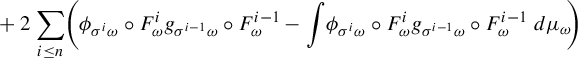 $$ \begin{align} & \hspace{35pt} +2\sum_{i\le n}\!\left(\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\kern1.5pt{-}\int\! \phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\,d\mu_{\omega}\kern-2pt\right) \end{align} $$
$$ \begin{align} & \hspace{35pt} +2\sum_{i\le n}\!\left(\phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\kern1.5pt{-}\int\! \phi_{\sigma^i \omega}\circ F_{\omega}^i g_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}\,d\mu_{\omega}\kern-2pt\right) \end{align} $$
where (5.15) is due to
To estimate
![]() $S_{n-1}(\omega )$
, we will estimate (5.13), (5.14), (5.15) and (5.16).
$S_{n-1}(\omega )$
, we will estimate (5.13), (5.14), (5.15) and (5.16).
Lemma 5.6. (Estimates for (5.16))
For a small
![]() $\delta\kern1pt{>}\kern1pt 0$
such that
$\delta\kern1pt{>}\kern1pt 0$
such that
![]() $\epsilon \kern1pt{:=}\kern1pt\max \{{2(2\kern1pt{+}\kern1pt\delta )(1\kern1pt{+}\kern1pt\delta )p} /{(D-2-\delta )(p-1)}-\tfrac 12, 0\} \in [0, 1/2)$
, we have for a.e.
$\epsilon \kern1pt{:=}\kern1pt\max \{{2(2\kern1pt{+}\kern1pt\delta )(1\kern1pt{+}\kern1pt\delta )p} /{(D-2-\delta )(p-1)}-\tfrac 12, 0\} \in [0, 1/2)$
, we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
Proof. By Lemma 5.1,
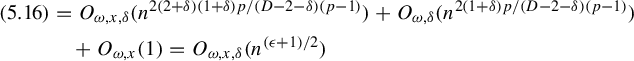 $$ \begin{align*}(5.16)&=O_{\omega,x, \delta}(n^{{2(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) +O_{\omega, \delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}})\\&\quad+O_{\omega,x}(1)=O_{\omega,x, \delta}(n^{(\epsilon+1)/2})\end{align*} $$
$$ \begin{align*}(5.16)&=O_{\omega,x, \delta}(n^{{2(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}}) +O_{\omega, \delta}(n^{{2(1+\delta)p}/{(D-2-\delta)(p-1)}})\\&\quad+O_{\omega,x}(1)=O_{\omega,x, \delta}(n^{(\epsilon+1)/2})\end{align*} $$
where
![]() ${2(2+\delta )(1+\delta )p}/{(D-2-\delta )(p-1)}\le \epsilon + 1/2$
for a sufficiently small
${2(2+\delta )(1+\delta )p}/{(D-2-\delta )(p-1)}\le \epsilon + 1/2$
for a sufficiently small
![]() $\delta>0$
.
$\delta>0$
.
Lemma 5.7. (Estimates for (5.13))
For a small
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\epsilon :={p(1+\delta )^2}/(p-1) (D-2-\delta )\in (0, 1/4)$
, we have for a.e.
$\epsilon :={p(1+\delta )^2}/(p-1) (D-2-\delta )\in (0, 1/4)$
, we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
Proof. Let
![]() $q:={(D-2-\delta )(p-1)}/{(1+\delta )p}$
. Since
$q:={(D-2-\delta )(p-1)}/{(1+\delta )p}$
. Since
![]() $\phi ^2_{(\cdot )}-\mathbb {E}_{\mu _{(\cdot )}} \phi ^2_{(\cdot )} \in L^{\infty }(\Delta , \mu ) \bigcap \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}} \subseteq L^{q}(\Delta , \mu )$
with a Lipschitz constant
$\phi ^2_{(\cdot )}-\mathbb {E}_{\mu _{(\cdot )}} \phi ^2_{(\cdot )} \in L^{\infty }(\Delta , \mu ) \bigcap \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}} \subseteq L^{q}(\Delta , \mu )$
with a Lipschitz constant
![]() $2C_{\phi }^2$
, there is a
$2C_{\phi }^2$
, there is a
![]() $C_{\phi ,q,p,h,F}>0$
by Lemma 3.4 and (3.7) such that
$C_{\phi ,q,p,h,F}>0$
by Lemma 3.4 and (3.7) such that
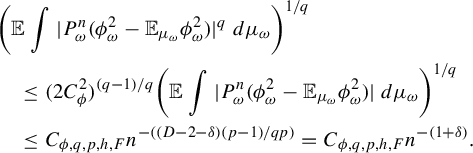 $$ \begin{align*} &\bigg(\mathbb{E} \int |P^n_{\omega}(\phi^2_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\omega})|^q \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le (2C^2_{\phi})^{(q-1)/q} \bigg(\mathbb{E} \int |P^n_{\omega}(\phi^2_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\omega})| \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le C_{\phi,q,p,h,F} {n^{-({(D-2-\delta)(p-1)}/{qp})}}= C_{\phi,q,p,h,F} {n^{-(1+\delta)}}. \end{align*} $$
$$ \begin{align*} &\bigg(\mathbb{E} \int |P^n_{\omega}(\phi^2_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\omega})|^q \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le (2C^2_{\phi})^{(q-1)/q} \bigg(\mathbb{E} \int |P^n_{\omega}(\phi^2_{\omega}-\mathbb{E}_{\mu_{\omega}} \phi^2_{\omega})| \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le C_{\phi,q,p,h,F} {n^{-({(D-2-\delta)(p-1)}/{qp})}}= C_{\phi,q,p,h,F} {n^{-(1+\delta)}}. \end{align*} $$
By Lemma 4.3, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $(5.13)=O_{\omega , x, \delta }(n^{(1/2)+(({1+\delta })/{q})})=O_{\omega , x, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
$(5.13)=O_{\omega , x, \delta }(n^{(1/2)+(({1+\delta })/{q})})=O_{\omega , x, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
Lemma 5.8. (Estimates for (5.15))
For a small
![]() $ \delta > 0$
such that
$ \delta > 0$
such that
![]() $\epsilon :={2p(1+\delta )^2}/(p-1) (D-2-\delta )\in (0,1/2)$
, we have for a.e.
$\epsilon :={2p(1+\delta )^2}/(p-1) (D-2-\delta )\in (0,1/2)$
, we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
Proof. From Lemma 5.1, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $(\psi _{\sigma ^{i} \omega }\circ F_{\omega }^{i})_{i \ge 0}$
and
$(\psi _{\sigma ^{i} \omega }\circ F_{\omega }^{i})_{i \ge 0}$
and
![]() $(\psi _{\sigma ^{i-1} \omega }\circ F_{\omega }^{i-1} \cdot g_{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 1}$
are reverse martingale differences w.r.t.
$(\psi _{\sigma ^{i-1} \omega }\circ F_{\omega }^{i-1} \cdot g_{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 1}$
are reverse martingale differences w.r.t.
![]() $((F^i_{\omega })^{-1}\mathcal {B}_{\sigma ^i \omega })_{i \ge 0}$
. Let
$((F^i_{\omega })^{-1}\mathcal {B}_{\sigma ^i \omega })_{i \ge 0}$
. Let
![]() $q:={(D-2-\delta )(p-1)}/{2(1+\delta )p}$
. By Lemma 5.1 again and the Hölder inequality,
$q:={(D-2-\delta )(p-1)}/{2(1+\delta )p}$
. By Lemma 5.1 again and the Hölder inequality,
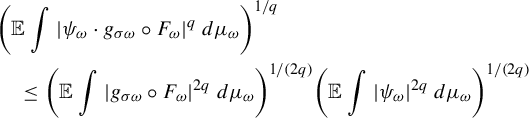 $$ \begin{align*} &\bigg(\mathbb{E} \int |\psi_{\omega}\cdot g_{\sigma \omega} \circ F_{\omega}|^q \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le \bigg(\mathbb{E} \int | g_{\sigma \omega} \circ F_{\omega}|^{2q}\,d\mu_{\omega}\bigg)^{1/(2q)}\bigg(\mathbb{E}\int |\psi_{\omega}|^{2q}\,d\mu_{\omega}\bigg)^{1/(2q)} \end{align*} $$
$$ \begin{align*} &\bigg(\mathbb{E} \int |\psi_{\omega}\cdot g_{\sigma \omega} \circ F_{\omega}|^q \,d\mu_{\omega}\bigg)^{1/q}\\ &\quad\le \bigg(\mathbb{E} \int | g_{\sigma \omega} \circ F_{\omega}|^{2q}\,d\mu_{\omega}\bigg)^{1/(2q)}\bigg(\mathbb{E}\int |\psi_{\omega}|^{2q}\,d\mu_{\omega}\bigg)^{1/(2q)} \end{align*} $$
is finite. Then by Lemma 4.2,
![]() $(5.15)=O_{x,\omega ,q, \delta }(n^{(1/2)+(({1+\delta })/{q})})=O_{x,\omega ,q, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
$(5.15)=O_{x,\omega ,q, \delta }(n^{(1/2)+(({1+\delta })/{q})})=O_{x,\omega ,q, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
Lemma 5.9. (Estimates for (5.14))
For any small
![]() $ \delta\kern-1pt >\kern-1pt 0$
such that
$ \delta\kern-1pt >\kern-1pt 0$
such that
![]() $\epsilon\kern-1pt :={2p(1+\delta )^2}/ (p-1) (D-2-\delta )\in (0,1/2)$
, we have for a.e.
$\epsilon\kern-1pt :={2p(1+\delta )^2}/ (p-1) (D-2-\delta )\in (0,1/2)$
, we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in \Delta _{\omega }$
.
$x \in \Delta _{\omega }$
.
Proof. Let
![]() $q:={(D-2-\delta )(p-1)}/{2(1+\delta )p}>2$
for a small
$q:={(D-2-\delta )(p-1)}/{2(1+\delta )p}>2$
for a small
![]() $\delta>0$
. Denote
$\delta>0$
. Denote
![]() $\Phi _{\omega }:=\phi _{\sigma \omega }\circ F_{\omega } g_{ \omega }-\int \phi _{\sigma \omega }\circ F_{\omega } g_{ \omega } \,d\mu _{\omega }$
,
$\Phi _{\omega }:=\phi _{\sigma \omega }\circ F_{\omega } g_{ \omega }-\int \phi _{\sigma \omega }\circ F_{\omega } g_{ \omega } \,d\mu _{\omega }$
,
![]() $\Phi (\omega , \cdot ):=\Phi _{\omega }(\cdot )$
. By Lemma 5.1,
$\Phi (\omega , \cdot ):=\Phi _{\omega }(\cdot )$
. By Lemma 5.1,
![]() $\|\Phi \|_{L^q(\Delta , \mu )}\le 2C_{\phi } \|g\|_{L^q(\Delta ,\mu )} <\infty $
.
$\|\Phi \|_{L^q(\Delta , \mu )}\le 2C_{\phi } \|g\|_{L^q(\Delta ,\mu )} <\infty $
.
Therefore, by the Minkowski inequality and (3.10),
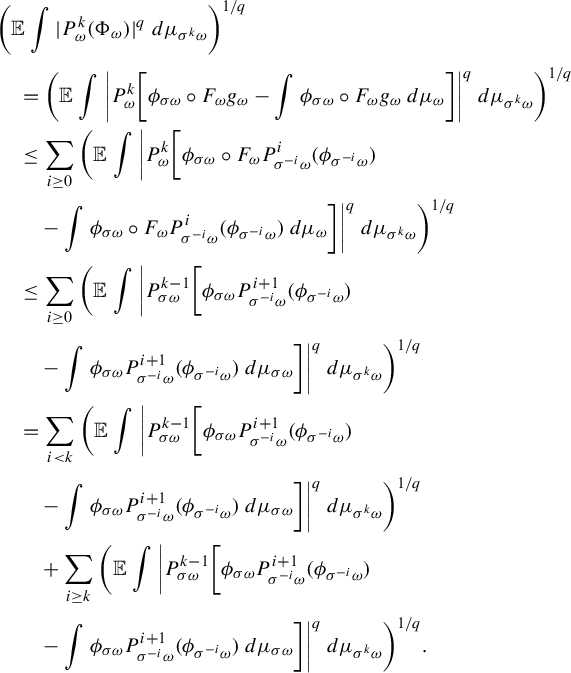 $$ \begin{align*} &\bigg(\mathbb{E}\int |P^k_{\omega}(\Phi_{\omega})|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\quad=\bigg(\mathbb{E}\int \bigg|P_{\omega}^k\bigg[\phi_{\sigma \omega}\circ F_{\omega} g_{ \omega}-\int \phi_{\sigma \omega}\circ F_{\omega} g_{ \omega}\,d\mu_{\omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad\le \sum_{i \ge 0}\bigg(\mathbb{E}\int \bigg|P_{\omega}^k\bigg[\phi_{\sigma \omega}\circ F_{\omega} P^{i}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\qquad-\int \phi_{\sigma \omega}\circ F_{\omega} P^{i}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{{1}/{q}}\\[2pt] &\quad\le \sum_{i \ge 0} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\quad=\sum_{i<k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\qquad + \sum_{i \ge k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}. \end{align*} $$
$$ \begin{align*} &\bigg(\mathbb{E}\int |P^k_{\omega}(\Phi_{\omega})|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\quad=\bigg(\mathbb{E}\int \bigg|P_{\omega}^k\bigg[\phi_{\sigma \omega}\circ F_{\omega} g_{ \omega}-\int \phi_{\sigma \omega}\circ F_{\omega} g_{ \omega}\,d\mu_{\omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad\le \sum_{i \ge 0}\bigg(\mathbb{E}\int \bigg|P_{\omega}^k\bigg[\phi_{\sigma \omega}\circ F_{\omega} P^{i}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\qquad-\int \phi_{\sigma \omega}\circ F_{\omega} P^{i}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{{1}/{q}}\\[2pt] &\quad\le \sum_{i \ge 0} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\quad=\sum_{i<k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\[2pt] &\qquad + \sum_{i \ge k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\[2pt]&\qquad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}. \end{align*} $$
By (3.7),
![]() $\|\phi _{\sigma \omega } P^{i+1}_{\sigma ^{-i}\omega }(\phi _{ \sigma ^{-i}\omega })\|_{L^{\infty }(\mu _{\sigma \omega })}\le C_{\phi }^2$
. By Definition 3.1,
$\|\phi _{\sigma \omega } P^{i+1}_{\sigma ^{-i}\omega }(\phi _{ \sigma ^{-i}\omega })\|_{L^{\infty }(\mu _{\sigma \omega })}\le C_{\phi }^2$
. By Definition 3.1,
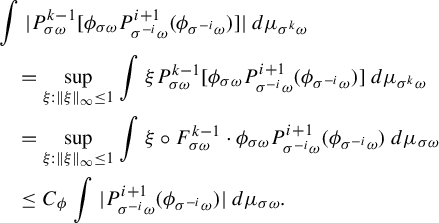 $$ \begin{align*} &\int |P_{\sigma \omega}^{k-1}[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})]| \,d\mu_{\sigma^k \omega}\\&\quad=\sup_{\xi: \|\xi\|_{\infty}\le 1}\int \xi P_{\sigma \omega}^{k-1}[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})] \,d\mu_{\sigma^k \omega}\\ &\quad=\sup_{\xi: \|\xi\|_{\infty}\le 1}\int \xi \circ F_{\sigma \omega}^{k-1}\cdot \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega}) \,d\mu_{\sigma \omega}\\ &\quad\le C_{\phi} \int |P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})| \,d\mu_{\sigma \omega}. \end{align*} $$
$$ \begin{align*} &\int |P_{\sigma \omega}^{k-1}[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})]| \,d\mu_{\sigma^k \omega}\\&\quad=\sup_{\xi: \|\xi\|_{\infty}\le 1}\int \xi P_{\sigma \omega}^{k-1}[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})] \,d\mu_{\sigma^k \omega}\\ &\quad=\sup_{\xi: \|\xi\|_{\infty}\le 1}\int \xi \circ F_{\sigma \omega}^{k-1}\cdot \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega}) \,d\mu_{\sigma \omega}\\ &\quad\le C_{\phi} \int |P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})| \,d\mu_{\sigma \omega}. \end{align*} $$
Then we can continue the estimate: there are constants
![]() $C_{\phi ,q}, C^{\prime }_{\phi ,q}>0$
such that
$C_{\phi ,q}, C^{\prime }_{\phi ,q}>0$
such that
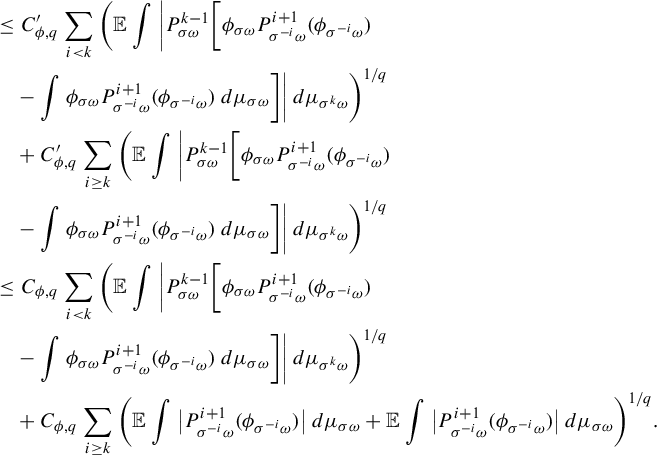 $$ \begin{align*} &\le C^{\prime}_{\phi,q} \sum_{i < k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad + C^{\prime}_{\phi,q} \sum_{i \ge k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{{1}/{q}}\\ &\le C_{\phi,q} \sum_{i < k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad+ C_{\phi, q} \sum_{i \ge k} \bigg(\mathbb{E} \int \big| P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\big|\,d\mu_{\sigma \omega}+\mathbb{E} \int \big| P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\big|\,d\mu_{\sigma \omega}\bigg)^{1/q}. \end{align*} $$
$$ \begin{align*} &\le C^{\prime}_{\phi,q} \sum_{i < k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad + C^{\prime}_{\phi,q} \sum_{i \ge k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{{1}/{q}}\\ &\le C_{\phi,q} \sum_{i < k} \bigg(\mathbb{E} \int \bigg|P_{\sigma \omega}^{k-1}\bigg[\phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\\&\quad-\int \phi_{\sigma \omega} P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\,d\mu_{\sigma \omega}\bigg]\bigg| \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\ &\quad+ C_{\phi, q} \sum_{i \ge k} \bigg(\mathbb{E} \int \big| P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\big|\,d\mu_{\sigma \omega}+\mathbb{E} \int \big| P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})\big|\,d\mu_{\sigma \omega}\bigg)^{1/q}. \end{align*} $$
To continue the estimate, we need the regularity of
![]() $\phi _{\sigma \omega } P^{i+1}_{\sigma ^{-i}\omega }(\phi _{ \sigma ^{-i}\omega })$
: by Lemma 4.4 and (3.7), for any
$\phi _{\sigma \omega } P^{i+1}_{\sigma ^{-i}\omega }(\phi _{ \sigma ^{-i}\omega })$
: by Lemma 4.4 and (3.7), for any
![]() $x,y\in \Delta _{\sigma \omega }$
,
$x,y\in \Delta _{\sigma \omega }$
,
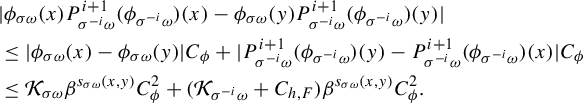 $$ \begin{align*} &|\phi_{\sigma \omega}(x) P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(x)-\phi_{\sigma \omega}(y) P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(y)|\\ &\le |\phi_{\sigma \omega}(x)-\phi_{\sigma \omega}(y)| C_{\phi}+|P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(y)-P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(x)| C_{\phi}\\ &\le \mathcal{K}_{\sigma \omega} \beta^{s_{\sigma \omega}(x,y)} C^2_{\phi}+ (\mathcal{K}_{\sigma^{-i} \omega}+C_{h,F} ) \beta^{s_{\sigma \omega}(x,y)} C^2_{\phi}. \end{align*} $$
$$ \begin{align*} &|\phi_{\sigma \omega}(x) P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(x)-\phi_{\sigma \omega}(y) P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(y)|\\ &\le |\phi_{\sigma \omega}(x)-\phi_{\sigma \omega}(y)| C_{\phi}+|P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(y)-P^{i+1}_{\sigma^{-i}\omega}(\phi_{ \sigma^{-i}\omega})(x)| C_{\phi}\\ &\le \mathcal{K}_{\sigma \omega} \beta^{s_{\sigma \omega}(x,y)} C^2_{\phi}+ (\mathcal{K}_{\sigma^{-i} \omega}+C_{h,F} ) \beta^{s_{\sigma \omega}(x,y)} C^2_{\phi}. \end{align*} $$
Thus
![]() $\phi _{(\cdot )} P^{i+1}_{\sigma ^{-(i+1)}(\cdot )}(\phi _{ \sigma ^{-(i+1)}(\cdot )}) \in \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}+\mathcal {K}\circ \sigma ^{-(i+1)}+C_{h,F}}$
with a Lipschitz constant
$\phi _{(\cdot )} P^{i+1}_{\sigma ^{-(i+1)}(\cdot )}(\phi _{ \sigma ^{-(i+1)}(\cdot )}) \in \mathcal {F}_{\beta ,p}^{\mathcal {\kern2pt K}+\mathcal {K}\circ \sigma ^{-(i+1)}+C_{h,F}}$
with a Lipschitz constant
![]() $C_{\phi }^2$
. Now we can continue our estimate: by Lemma 3.4, there is a constant
$C_{\phi }^2$
. Now we can continue our estimate: by Lemma 3.4, there is a constant
![]() $C=[C^2_{\phi } C_{h,F,\beta , \delta ,p} \|\mathcal {K}+\mathcal {K}\circ \sigma ^{-(i+1)}+C_{h,F}\|_{L^p}]^{1/q}\le [C^2_{\phi } C_{h,F,\beta , \delta ,p} (2\|\mathcal {K}\|_{L^p}+C_{h,F})]^{1/q}$
such that
$C=[C^2_{\phi } C_{h,F,\beta , \delta ,p} \|\mathcal {K}+\mathcal {K}\circ \sigma ^{-(i+1)}+C_{h,F}\|_{L^p}]^{1/q}\le [C^2_{\phi } C_{h,F,\beta , \delta ,p} (2\|\mathcal {K}\|_{L^p}+C_{h,F})]^{1/q}$
such that
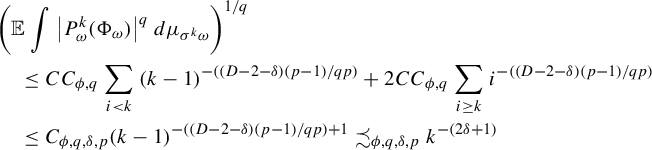 $$ \begin{align*} &\bigg(\mathbb{E}\int \big|P^k_{\omega}(\Phi_{\omega})\big|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\&\quad\le C C_{\phi, q}\sum_{i < k} {(k-1)^{-({(D-2-\delta)(p-1)}/{qp})}} +2C C_{\phi, q}\sum_{i \ge k}{i^{-({(D-2-\delta)(p-1)}/{qp})}}\\ &\quad\le C_{\phi,q,\delta,p} {(k-1)^{-({(D-2-\delta)(p-1)}/{qp})+1}}\precsim_{\phi,q,\delta,p}{k^{-(2\delta+1)}} \end{align*} $$
$$ \begin{align*} &\bigg(\mathbb{E}\int \big|P^k_{\omega}(\Phi_{\omega})\big|^q \,d\mu_{\sigma^k \omega}\bigg)^{1/q}\\&\quad\le C C_{\phi, q}\sum_{i < k} {(k-1)^{-({(D-2-\delta)(p-1)}/{qp})}} +2C C_{\phi, q}\sum_{i \ge k}{i^{-({(D-2-\delta)(p-1)}/{qp})}}\\ &\quad\le C_{\phi,q,\delta,p} {(k-1)^{-({(D-2-\delta)(p-1)}/{qp})+1}}\precsim_{\phi,q,\delta,p}{k^{-(2\delta+1)}} \end{align*} $$
for a constant
![]() $C_{\phi ,q,\delta ,p}>0$
. Therefore, by Lemma 4.3,
$C_{\phi ,q,\delta ,p}>0$
. Therefore, by Lemma 4.3,
 $\sum _{i\le n}(\phi _{\sigma ^i \omega }\circ F_{\omega }^i\cdot g_{\sigma ^{i-1} \omega } \circ F^{i-1}_{\omega }-\int \phi _{\sigma ^i \omega }\kern3pt\circ\kern3pt F_{\omega }^i\cdot g_{\sigma ^{i-1} \omega } \kern3pt\circ\kern3pt F^{i-1}_{\omega }\,d\mu _{\omega })\kern3pt =\kern3pt O_{x,\omega ,q, \delta }(n^{(1/2)+(({1+\delta })/{q})})\kern3pt =\kern3pt O_{x,\omega ,q, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
$\sum _{i\le n}(\phi _{\sigma ^i \omega }\circ F_{\omega }^i\cdot g_{\sigma ^{i-1} \omega } \circ F^{i-1}_{\omega }-\int \phi _{\sigma ^i \omega }\kern3pt\circ\kern3pt F_{\omega }^i\cdot g_{\sigma ^{i-1} \omega } \kern3pt\circ\kern3pt F^{i-1}_{\omega }\,d\mu _{\omega })\kern3pt =\kern3pt O_{x,\omega ,q, \delta }(n^{(1/2)+(({1+\delta })/{q})})\kern3pt =\kern3pt O_{x,\omega ,q, \delta }(n^{(\epsilon +1)/2}) \mu _{\omega }$
-a.s.
We now turn to the QASIP for martingale differences
![]() $(\psi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
.
$(\psi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
.
Lemma 5.10. (QASIP for
 $(\psi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
)
$(\psi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
)
For any sufficiently small
![]() $ \delta>0$
such that
$ \delta>0$
such that
![]() $\epsilon ={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}\in (0,1/2)$
, we have for a.e.
$\epsilon ={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}\in (0,1/2)$
, we have for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
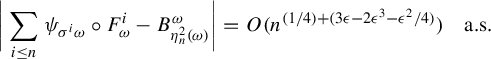 $$ \begin{align*} \bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=O(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2}/{4})}) \quad\text{a.s.} \end{align*} $$
$$ \begin{align*} \bigg|\sum_{i \leq n} \psi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\eta^2_n(\omega)}\bigg|=O(n^{({1}/{4})+({3\epsilon-2\epsilon^3-\epsilon^2}/{4})}) \quad\text{a.s.} \end{align*} $$
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
.
$x \in {\pmb {\Delta }}_{\omega }$
.
Proof. By Lemmas 5.6–5.9, we have for a small enough
![]() $\delta>0$
and a.e.
$\delta>0$
and a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
where
 $\epsilon =\max \{{2p(1+\delta )^2}/{(p-1)(D-2-\delta )}, \max \{({2(2+\delta )(1+\delta )p}/(D-2)(p- 1)) -\tfrac 12, 0\}, {p(1+\delta )^2}/{(p-1)(D-2-\delta )}\}={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}$
.
$\epsilon =\max \{{2p(1+\delta )^2}/{(p-1)(D-2-\delta )}, \max \{({2(2+\delta )(1+\delta )p}/(D-2)(p- 1)) -\tfrac 12, 0\}, {p(1+\delta )^2}/{(p-1)(D-2-\delta )}\}={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}$
.
By Lemma 5.5,
![]() $S_n'(\omega )=O_{\omega , \epsilon , x}(\delta _n^{2+2\epsilon }) \mu _{\omega }$
-a.s. By Lemma 5.4,
$S_n'(\omega )=O_{\omega , \epsilon , x}(\delta _n^{2+2\epsilon }) \mu _{\omega }$
-a.s. By Lemma 5.4,
By Lemma 5.3,
![]() $|\sum _{i \leq n} \psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega } -B^{\omega }_{\eta ^2_n(\omega )}|=O_{\omega , \epsilon , x}(n^{(1/4)+({3\epsilon -2\epsilon ^3-\epsilon ^2})/{4}})$
a.s.
$|\sum _{i \leq n} \psi _{\sigma ^{i} \omega } \circ F^{i}_{\omega } -B^{\omega }_{\eta ^2_n(\omega )}|=O_{\omega , \epsilon , x}(n^{(1/4)+({3\epsilon -2\epsilon ^3-\epsilon ^2})/{4}})$
a.s.
5.5 Proof of the QASIP for Birkhoff sums
Lemma 5.11. (QASIP for
 $(\phi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
)
$(\phi _{\sigma ^i \omega } \circ F^i_{\omega })_{i \ge 0}$
)
For a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
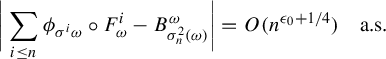 $$ \begin{align*} \bigg|\sum_{i \leq n} \phi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\sigma^2_n(\omega)}\bigg|=O(n^{\epsilon_0+1/4}) \quad\text{a.s.} \end{align*} $$
$$ \begin{align*} \bigg|\sum_{i \leq n} \phi_{\sigma^{i} \omega} \circ F^{i}_{\omega} -B^{\omega}_{\sigma^2_n(\omega)}\bigg|=O(n^{\epsilon_0+1/4}) \quad\text{a.s.} \end{align*} $$
where the constant in
![]() $O(\cdot )$
depends on
$O(\cdot )$
depends on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
.
$x \in {\pmb {\Delta }}_{\omega }$
.
If
![]() $\rho _n={n^{-D}}$
, then
$\rho _n={n^{-D}}$
, then
![]() $\epsilon _0$
is any number in
$\epsilon _0$
is any number in
![]() $(\epsilon _D, 1/4)$
, where
$(\epsilon _D, 1/4)$
, where
![]() $\epsilon _D$
is defined in (2.5). In particular, if
$\epsilon _D$
is defined in (2.5). In particular, if
![]() $\rho _n=e^{-a n^b}$
for some
$\rho _n=e^{-a n^b}$
for some
![]() $a>0, b\in (0,1]$
(which implies
$a>0, b\in (0,1]$
(which implies
![]() $\rho _n\le n^{-D}$
for
$\rho _n\le n^{-D}$
for
![]() $n,D\gg 1$
), then
$n,D\gg 1$
), then
![]() $\epsilon _D$
can be arbitrarily small, as is
$\epsilon _D$
can be arbitrarily small, as is
![]() $\epsilon _0>0$
.
$\epsilon _0>0$
.
Proof. Since
![]() $\epsilon _1={2p}/{(p-1)(D-2)}\in (0, 1/2)$
, there is a small
$\epsilon _1={2p}/{(p-1)(D-2)}\in (0, 1/2)$
, there is a small
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\epsilon ={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}\in (\epsilon _1,1/2)$
. By Lemmas 5.1 and 5.10,
$\epsilon ={2p(1+\delta )^2}/{(p-1)(D-2-\delta )}\in (\epsilon _1,1/2)$
. By Lemmas 5.1 and 5.10,
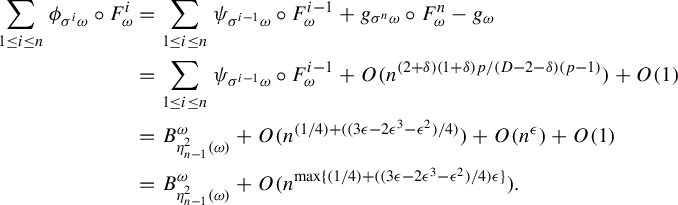 $$ \begin{align*} \sum_{1 \le i \le n}\phi_{\sigma^i \omega} \circ F^i_{\omega}&= \sum_{1\le i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+ g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\\ &=\sum_{1\le i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+O(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}})+O(1)\\ &=B^{\omega}_{\eta^2_{n-1}(\omega)}+O(n^{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4})})+O(n^{\epsilon})+O(1)\\ &=B^{\omega}_{\eta^2_{n-1}(\omega)}+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}) \epsilon\}}).\end{align*} $$
$$ \begin{align*} \sum_{1 \le i \le n}\phi_{\sigma^i \omega} \circ F^i_{\omega}&= \sum_{1\le i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+ g_{\sigma^n \omega} \circ F^{n}_{\omega}-g_{\omega}\\ &=\sum_{1\le i \le n}\psi_{\sigma^{i-1} \omega} \circ F^{i-1}_{\omega}+O(n^{{(2+\delta)(1+\delta)p}/{(D-2-\delta)(p-1)}})+O(1)\\ &=B^{\omega}_{\eta^2_{n-1}(\omega)}+O(n^{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4})})+O(n^{\epsilon})+O(1)\\ &=B^{\omega}_{\eta^2_{n-1}(\omega)}+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}) \epsilon\}}).\end{align*} $$
Using (5.2) and the basic property of Brownian motion, we can continue the estimate above as
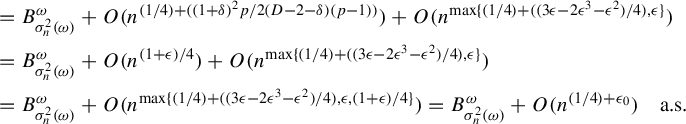 $$ \begin{align*} &=B^{\omega}_{\sigma^2_n(\omega)}+ O(n^{({1}/{4})+({(1+\delta)^2 p}/{2(D-2-\delta)(p-1)})})+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon\}})\\ &=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{({1+\epsilon})/{4}})+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon\}}) \\ &=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon, ({1+\epsilon})/{4}\}})=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{ ({1}/{4})+\epsilon_0}) \quad\text{a.s.} \end{align*} $$
$$ \begin{align*} &=B^{\omega}_{\sigma^2_n(\omega)}+ O(n^{({1}/{4})+({(1+\delta)^2 p}/{2(D-2-\delta)(p-1)})})+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon\}})\\ &=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{({1+\epsilon})/{4}})+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon\}}) \\ &=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{\max \{({1}/{4})+(({3\epsilon-2\epsilon^3-\epsilon^2})/{4}), \epsilon, ({1+\epsilon})/{4}\}})=B^{\omega}_{\sigma^2_n(\omega)}+O(n^{ ({1}/{4})+\epsilon_0}) \quad\text{a.s.} \end{align*} $$
where
![]() $\epsilon _0:=\max \{\tfrac 14+({3\epsilon -2\epsilon ^3-\epsilon ^2}/{4}), \epsilon , ({1+\epsilon })/{4}\}-\tfrac 14 \in (\epsilon _D, 1/4)$
. All constants in
$\epsilon _0:=\max \{\tfrac 14+({3\epsilon -2\epsilon ^3-\epsilon ^2}/{4}), \epsilon , ({1+\epsilon })/{4}\}-\tfrac 14 \in (\epsilon _D, 1/4)$
. All constants in
![]() $O(\cdot )$
depend on
$O(\cdot )$
depend on
![]() $\omega , \epsilon $
and
$\omega , \epsilon $
and
![]() $x \in {\pmb {\Delta }}_{\omega }$
.
$x \in {\pmb {\Delta }}_{\omega }$
.
6 Projection from towers
In this section we consider the RDS which can be described by the RYT.
Definition 6.1. (Induced random Markov maps)
We say that
![]() $(f_{\omega })_{\omega \in \Omega }$
are induced random Markov maps if they satisfy the following conditions.
$(f_{\omega })_{\omega \in \Omega }$
are induced random Markov maps if they satisfy the following conditions.
-
(1) Let
 $(\Omega , \mathbb {P}, \sigma ):=(I^{\mathbb {Z}}, {\nu }^{\mathbb {Z}}, \sigma )$
be a Bernoulli scheme where
$(\Omega , \mathbb {P}, \sigma ):=(I^{\mathbb {Z}}, {\nu }^{\mathbb {Z}}, \sigma )$
be a Bernoulli scheme where
 $(I,\nu )$
is a probability space and
$(I,\nu )$
is a probability space and
 $\sigma $
is an invertible left shift on
$\sigma $
is an invertible left shift on
 $I^{\mathbb {Z}}$
.
$I^{\mathbb {Z}}$
.
 $(M, \operatorname {Leb}, d)$
is a compact Riemannian manifold with a Riemannian volume
$(M, \operatorname {Leb}, d)$
is a compact Riemannian manifold with a Riemannian volume
 $\operatorname {Leb}$
and a Riemannian distance d.
$\operatorname {Leb}$
and a Riemannian distance d.
 $(f_{\omega })_{\omega \in \Omega }$
are non-singular random transformations w.r.t.
$(f_{\omega })_{\omega \in \Omega }$
are non-singular random transformations w.r.t.
 $\operatorname {Leb}$
on M. Define
$\operatorname {Leb}$
on M. Define
 $f_{\omega }^{n}:=f_{\sigma ^{n-1} \omega } \circ f_{\sigma ^{n-2} \omega } \circ \cdots \circ f_{\sigma \omega } \circ f_{\omega }$
.
$f_{\omega }^{n}:=f_{\sigma ^{n-1} \omega } \circ f_{\sigma ^{n-2} \omega } \circ \cdots \circ f_{\sigma \omega } \circ f_{\omega }$
. -
(2) Assume that
 $\Lambda $
is an open geodesic ball in M, with a normalized probability m inherited from
$\Lambda $
is an open geodesic ball in M, with a normalized probability m inherited from
 $\operatorname {Leb}$
.
$\operatorname {Leb}$
. -
(3) Assume that for a.e.
 $\omega \in \Omega $
, there is a countable partition
$\omega \in \Omega $
, there is a countable partition
 $ \mathcal {P}_{\omega } $
of a full measure subset
$ \mathcal {P}_{\omega } $
of a full measure subset
 $\mathcal {D}_{\omega }$
of
$\mathcal {D}_{\omega }$
of
 $\Lambda $
and a function
$\Lambda $
and a function
 $R_{\omega }: \Lambda \to \mathbb {N}$
such that
$R_{\omega }: \Lambda \to \mathbb {N}$
such that
 $R_{\omega }$
is constant on each
$R_{\omega }$
is constant on each
 $U_{\omega } \in \mathcal {P}_{\omega }$
,
$U_{\omega } \in \mathcal {P}_{\omega }$
,
 $R_{\omega }(x)$
is a stopping time (see Definition 2.2) and
$R_{\omega }(x)$
is a stopping time (see Definition 2.2) and
 $f_{\omega }^{R_{\omega }}|_{U_{\omega }}$
is a diffeomorphism from
$f_{\omega }^{R_{\omega }}|_{U_{\omega }}$
is a diffeomorphism from
 $U_{\omega }$
to
$U_{\omega }$
to
 $\Lambda $
.
$\Lambda $
. -
(4) Assume that there is an integer
 $N \in \mathbb {N}$
,
$N \in \mathbb {N}$
,
 $\{\epsilon _i> 0,i = 1,\ldots , N\}$
and
$\{\epsilon _i> 0,i = 1,\ldots , N\}$
and
 $\{t_i\in \mathbb {N},i= 1,\ldots ,N\}$
with
$\{t_i\in \mathbb {N},i= 1,\ldots ,N\}$
with
 $\gcd (t_i) = 1 $
such that for a.e.
$\gcd (t_i) = 1 $
such that for a.e.
 $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $m(x \in \Lambda : R_{\omega }(x) = t_i)> \epsilon _i$
for all
$m(x \in \Lambda : R_{\omega }(x) = t_i)> \epsilon _i$
for all
 $1 \le i \le N$
.
$1 \le i \le N$
. -
(5) Assume that there are constants
 $\beta \in (0,1)$
,
$\beta \in (0,1)$
,
 $C\ge 1$
and a function
$C\ge 1$
and a function
 $\mathcal {K} \in L^{p}(\Omega )$
(
$\mathcal {K} \in L^{p}(\Omega )$
(
 $\mathcal {K}\ge 1, p\in (1,\infty ]$
) such that for a.e.
$\mathcal {K}\ge 1, p\in (1,\infty ]$
) such that for a.e.
 $\omega \in \Omega $
, any
$\omega \in \Omega $
, any
 $U_{\omega } \in \mathcal {P}_{\omega }$
,
$U_{\omega } \in \mathcal {P}_{\omega }$
,
 $x,y \in U_{\omega }$
, and
$x,y \in U_{\omega }$
, and
 $0 \le k \le R_{\omega }|_{U_{\omega }}$
, (6.1)
$0 \le k \le R_{\omega }|_{U_{\omega }}$
, (6.1) $$ \begin{align} d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \ge \beta^{-1} d(x,y), \end{align} $$
(6.2)
$$ \begin{align} d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \ge \beta^{-1} d(x,y), \end{align} $$
(6.2) $$ \begin{align} \bigg|\log \frac{Jf_{\omega}^{R_{\omega}}(x)}{Jf_{\omega}^{R_{\omega}}(y)}\bigg| \le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)), \end{align} $$
(6.3)
$$ \begin{align} \bigg|\log \frac{Jf_{\omega}^{R_{\omega}}(x)}{Jf_{\omega}^{R_{\omega}}(y)}\bigg| \le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)), \end{align} $$
(6.3) $$ \begin{align}d(f_{\omega}^{k}(x), f_{\omega}^{k}(y)) \le C \mathcal{K}_{\sigma^k \omega} d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)). \end{align} $$
$$ \begin{align}d(f_{\omega}^{k}(x), f_{\omega}^{k}(y)) \le C \mathcal{K}_{\sigma^k \omega} d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)). \end{align} $$
-
(6) Assume that there is a constant
 $C>0$
and a decreasing sequence
$C>0$
and a decreasing sequence
 $(\rho _n)_{n \ge 1}$
such that
$(\rho _n)_{n \ge 1}$
such that  $$ \begin{align*} \int m(x \in \Lambda: R_{\omega}(x)>n) \,d\mathbb{P} \le C \rho_n \searrow 0. \end{align*} $$
$$ \begin{align*} \int m(x \in \Lambda: R_{\omega}(x)>n) \,d\mathbb{P} \le C \rho_n \searrow 0. \end{align*} $$
Theorem 6.1. (Quenched limit laws for the RDS)
Let
![]() $M_{\omega }:=M$
. Then the following statements hold for
$M_{\omega }:=M$
. Then the following statements hold for
![]() $(\Omega , \mathbb {P}, \sigma , (M_{\omega })_{\omega \in \Omega }, (f_{\omega })_{\omega \in \Omega })$
in Definition 6.1.
$(\Omega , \mathbb {P}, \sigma , (M_{\omega })_{\omega \in \Omega }, (f_{\omega })_{\omega \in \Omega })$
in Definition 6.1.
-
(1) Equivariant probability measures (1.1)
 $(\upsilon _{\omega })_{\omega \in \Omega }$
exist. Define a probability
$(\upsilon _{\omega })_{\omega \in \Omega }$
exist. Define a probability
 $\upsilon $
by for any measurable subset
$\upsilon $
by for any measurable subset $$ \begin{align*} \upsilon(A):=\int \upsilon_{\omega}(A_{\omega}) \,d\mathbb{P} \end{align*} $$
$$ \begin{align*} \upsilon(A):=\int \upsilon_{\omega}(A_{\omega}) \,d\mathbb{P} \end{align*} $$
 $A\subseteq \Omega \times M$
and
$A\subseteq \Omega \times M$
and
 $A_{\omega }:=\{x \in M: (\omega ,x) \in A\}$
. For any Hölder function
$A_{\omega }:=\{x \in M: (\omega ,x) \in A\}$
. For any Hölder function
 $\varphi $
on M with a Hölder exponent
$\varphi $
on M with a Hölder exponent
 $\gamma \in (0,1]$
, define Suppose that
$\gamma \in (0,1]$
, define Suppose that $$ \begin{gather*} {\varphi}_{\omega}:=\varphi -\int \varphi d\upsilon_{\omega}, \quad \Phi(\omega,\cdot):=\varphi_{\omega}(\cdot),\quad \sigma_n^2({\omega}): = \int\bigg(\sum_{k\le n} {\varphi}_{\sigma^k \omega} \circ f^k_{\omega} \bigg)^2 d\upsilon_{\omega}. \end{gather*} $$
$$ \begin{gather*} {\varphi}_{\omega}:=\varphi -\int \varphi d\upsilon_{\omega}, \quad \Phi(\omega,\cdot):=\varphi_{\omega}(\cdot),\quad \sigma_n^2({\omega}): = \int\bigg(\sum_{k\le n} {\varphi}_{\sigma^k \omega} \circ f^k_{\omega} \bigg)^2 d\upsilon_{\omega}. \end{gather*} $$
 $\rho _n:= e^{-a n^{b}}$
or
$\rho _n:= e^{-a n^{b}}$
or
 ${n^{-D}}$
for some constants
${n^{-D}}$
for some constants
 $a>0$
,
$a>0$
,
 $b \in (0,1]$
,
$b \in (0,1]$
,
 $D>2+({4p}/({p-\gamma }))$
,
$D>2+({4p}/({p-\gamma }))$
,
 $\gamma \in (0,1]$
. Then the following statements hold for the RDS
$\gamma \in (0,1]$
. Then the following statements hold for the RDS
 $(\Omega , \mathbb {P}, \sigma , (M_{\omega })_{\omega \in \Omega }, (\upsilon _{\omega })_{\omega \in \Omega }, (f_{\omega })_{\omega \in \Omega })$
.
$(\Omega , \mathbb {P}, \sigma , (M_{\omega })_{\omega \in \Omega }, (\upsilon _{\omega })_{\omega \in \Omega }, (f_{\omega })_{\omega \in \Omega })$
.
-
(2) There is a constant
 $\Sigma ^2 \ge 0$
such that
$\Sigma ^2 \ge 0$
such that
 $\lim _{n \to \infty }({\sigma ^2_n(\omega )}/{n})=\Sigma ^2$
a.e.
$\lim _{n \to \infty }({\sigma ^2_n(\omega )}/{n})=\Sigma ^2$
a.e.
 $\omega \in \Omega $
.
$\omega \in \Omega $
. -
(3) If
 $\Sigma ^2>0$
, then
$\Sigma ^2>0$
, then
 $\Phi $
has the QASIP (see Definition 2.1). The convergence rate is
$\Phi $
has the QASIP (see Definition 2.1). The convergence rate is
 $e=\epsilon _0+1/4$
, where
$e=\epsilon _0+1/4$
, where
 $\epsilon _0 \in (0,1/4)$
satisfies the following: if
$\epsilon _0 \in (0,1/4)$
satisfies the following: if
 $\rho _n=e^{-a n^b}$
, then
$\rho _n=e^{-a n^b}$
, then
 $\epsilon _0>0$
is any small number; if
$\epsilon _0>0$
is any small number; if
 $\rho _n={n^{-D}}$
, then
$\rho _n={n^{-D}}$
, then
 $\epsilon _0$
is any number in
$\epsilon _0$
is any number in
 $(\epsilon _D, 1/4)$
, where
$(\epsilon _D, 1/4)$
, where
 $\epsilon _D$
is defined in (2.5) with a different
$\epsilon _D$
is defined in (2.5) with a different
 $\epsilon _1={2p}/{(p-\gamma )(D-2)}$
.
$\epsilon _1={2p}/{(p-\gamma )(D-2)}$
. -
(4) If
 $\Sigma ^2=0$
, then
$\Sigma ^2=0$
, then
 $\Phi $
is a coboundary (see Definition 2.1). The function g in (2.2) satisfies the following: if
$\Phi $
is a coboundary (see Definition 2.1). The function g in (2.2) satisfies the following: if
 $\rho _n={n^{-D}}$
, then
$\rho _n={n^{-D}}$
, then
 $g \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\upsilon )$
for any small
$g \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\upsilon )$
for any small
 $\delta>0$
such that
$\delta>0$
such that
 ${(D-2-\delta )(p-\gamma )}/{(1+\delta )p}>4$
. In particular, if
${(D-2-\delta )(p-\gamma )}/{(1+\delta )p}>4$
. In particular, if
 $\rho _n=e^{-an^b}$
(which implies
$\rho _n=e^{-an^b}$
(which implies
 $\rho _n\le n^{-D}$
for
$\rho _n\le n^{-D}$
for
 $n,D \gg 1$
), then
$n,D \gg 1$
), then
 $g \in L^{k}(\upsilon )$
for all
$g \in L^{k}(\upsilon )$
for all
 $k\ge 1$
.
$k\ge 1$
.
Proof of Theorem 6.1
We identify the
![]() $0$
th levels of all
$0$
th levels of all
![]() $(\Delta _{\omega })_{\omega \in \Omega }$
with the base
$(\Delta _{\omega })_{\omega \in \Omega }$
with the base
![]() $\Lambda $
and denote
$\Lambda $
and denote
![]() $A:=\sup _{x,y \in M}d(x,y)$
. From Definition 6.1, we can construct
$A:=\sup _{x,y \in M}d(x,y)$
. From Definition 6.1, we can construct
![]() $\Delta $
and F such that
$\Delta $
and F such that
![]() $F_{\omega }^{R_{\omega }}=f_{\omega }^{R_{\omega }}$
. To show that
$F_{\omega }^{R_{\omega }}=f_{\omega }^{R_{\omega }}$
. To show that
![]() $(\Delta , F)$
is an RYT, we just need to verify the distortion (2.3) from (6.2): if the separation time for
$(\Delta , F)$
is an RYT, we just need to verify the distortion (2.3) from (6.2): if the separation time for
![]() $x,y \in \Delta _{\omega }$
is
$x,y \in \Delta _{\omega }$
is
![]() $s_{\omega }(x,y)=n$
, then for any
$s_{\omega }(x,y)=n$
, then for any
![]() $i < n$
,
$i < n$
,
![]() $ F_{\omega }^{R^i_{\omega }(x)}(x), F_{\omega }^{R^i_{\omega }(y)}(y) $
lie in the same element of
$ F_{\omega }^{R^i_{\omega }(x)}(x), F_{\omega }^{R^i_{\omega }(y)}(y) $
lie in the same element of
![]() $\mathcal {P}_{\sigma ^{R^i_{\omega }(x)} \omega }$
and
$\mathcal {P}_{\sigma ^{R^i_{\omega }(x)} \omega }$
and
![]() $ F_{\omega }^{R^n_{\omega }(x)}(x), F_{\omega }^{R^n_{\omega }(y)}(y) $
lie in different elements of
$ F_{\omega }^{R^n_{\omega }(x)}(x), F_{\omega }^{R^n_{\omega }(y)}(y) $
lie in different elements of
![]() $\mathcal {P}_{\sigma ^{R^n_{\omega }(x)} \omega }$
. By (6.1) and (6.2),
$\mathcal {P}_{\sigma ^{R^n_{\omega }(x)} \omega }$
. By (6.1) and (6.2),
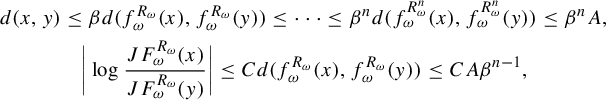 $$ \begin{gather*} d(x,y) \le \beta d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \le \cdots \le \beta^n d(f_{\omega}^{R^n_{\omega}}(x), f_{\omega}^{R^n_{\omega}}(y)) \le \beta^n A, \\ \bigg|\log \frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}\bigg|\le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \le C A \beta^{n-1}, \end{gather*} $$
$$ \begin{gather*} d(x,y) \le \beta d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \le \cdots \le \beta^n d(f_{\omega}^{R^n_{\omega}}(x), f_{\omega}^{R^n_{\omega}}(y)) \le \beta^n A, \\ \bigg|\log \frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}\bigg|\le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)) \le C A \beta^{n-1}, \end{gather*} $$
that is, there is a constant
![]() $C'>0$
such that
$C'>0$
such that
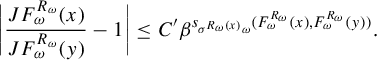 $$ \begin{align*} \bigg|\frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}-1\bigg|\le C' \beta^{s_{\sigma^{R_{\omega}(x)} \omega}(F^{R_{\omega}}_\omega(x), F^{R_{\omega}}_\omega(y))}. \end{align*} $$
$$ \begin{align*} \bigg|\frac{JF^{R_{\omega}}_\omega(x)}{JF^{R_{\omega}}_\omega(y)}-1\bigg|\le C' \beta^{s_{\sigma^{R_{\omega}(x)} \omega}(F^{R_{\omega}}_\omega(x), F^{R_{\omega}}_\omega(y))}. \end{align*} $$
Thus, by Definition 2.2 and Lemma 3.1,
![]() $(\Delta , F)$
is an RYT and there are equivariant probability measures
$(\Delta , F)$
is an RYT and there are equivariant probability measures
![]() $(\mu _{\omega })_{\omega \Omega }$
for
$(\mu _{\omega })_{\omega \Omega }$
for
![]() $(\Delta , F)$
. Define a projection
$(\Delta , F)$
. Define a projection
![]() $\pi _{\omega }: \Delta _{\omega } \to M$
by
$\pi _{\omega }: \Delta _{\omega } \to M$
by
which is a random semiconjugacy:
![]() $f_{\omega }\circ \pi _{\omega }=\pi _{\sigma \omega } \circ F_{\omega }$
. Therefore
$f_{\omega }\circ \pi _{\omega }=\pi _{\sigma \omega } \circ F_{\omega }$
. Therefore
are equivariant probability measures (see §3.1 in [Reference Bahsoun, Bose and RuziboevBBR19]).
Define functions
![]() $\phi _{\omega }:=\varphi _{\omega } \circ \pi _{\omega }$
and
$\phi _{\omega }:=\varphi _{\omega } \circ \pi _{\omega }$
and
![]() $\phi (\omega , \cdot ):=\phi _{\omega }(\cdot )$
satisfying
$\phi (\omega , \cdot ):=\phi _{\omega }(\cdot )$
satisfying
Claim.
![]() $\phi \in \mathcal {F}_{\beta ^{\gamma }, p/\gamma }^{\mathcal {\kern2pt K}^{\gamma }}$
with a Lipschitz constant
$\phi \in \mathcal {F}_{\beta ^{\gamma }, p/\gamma }^{\mathcal {\kern2pt K}^{\gamma }}$
with a Lipschitz constant
![]() $ C_{\varphi } C^{\gamma } A^{\gamma } (\beta ^{\gamma })^{-1}$
.
$ C_{\varphi } C^{\gamma } A^{\gamma } (\beta ^{\gamma })^{-1}$
.
This claim holds since for any
![]() $(x,l), (y,l) \in \Delta _{\omega }$
with
$(x,l), (y,l) \in \Delta _{\omega }$
with
![]() $s_{\omega }((x,l),(y,l))=n$
, we have, using (6.3),
$s_{\omega }((x,l),(y,l))=n$
, we have, using (6.3),
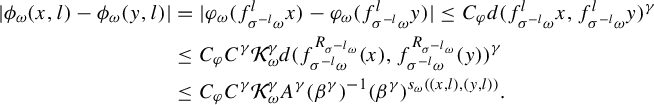 $$ \begin{align*} |\phi_{\omega}(x,l)-\phi_{\omega}(y,l)|&=|\varphi_{\omega}(f^l_{\sigma^{-l}\omega}x)-\varphi_{\omega}(f^l_{\sigma^{-l}\omega}y)|\le C_{\varphi} d(f^l_{\sigma^{-l}\omega}x, f^l_{\sigma^{-l}\omega}y)^{\gamma}\\ &\le C_{\varphi} C^{\gamma} \mathcal{K}^{\gamma}_{\omega} d(f_{\sigma^{-l}\omega}^{R_{\sigma^{-l}\omega}}(x), f_{\sigma^{-l}\omega}^{R_{\sigma^{-l}\omega}}(y))^{\gamma}\\ &\le C_{\varphi} C^{\gamma} \mathcal{K}^{\gamma}_{\omega} A^{\gamma} (\beta^{\gamma})^{-1} (\beta^{\gamma})^{s_{\omega}((x,l),(y,l))}. \end{align*} $$
$$ \begin{align*} |\phi_{\omega}(x,l)-\phi_{\omega}(y,l)|&=|\varphi_{\omega}(f^l_{\sigma^{-l}\omega}x)-\varphi_{\omega}(f^l_{\sigma^{-l}\omega}y)|\le C_{\varphi} d(f^l_{\sigma^{-l}\omega}x, f^l_{\sigma^{-l}\omega}y)^{\gamma}\\ &\le C_{\varphi} C^{\gamma} \mathcal{K}^{\gamma}_{\omega} d(f_{\sigma^{-l}\omega}^{R_{\sigma^{-l}\omega}}(x), f_{\sigma^{-l}\omega}^{R_{\sigma^{-l}\omega}}(y))^{\gamma}\\ &\le C_{\varphi} C^{\gamma} \mathcal{K}^{\gamma}_{\omega} A^{\gamma} (\beta^{\gamma})^{-1} (\beta^{\gamma})^{s_{\omega}((x,l),(y,l))}. \end{align*} $$
We now apply Theorem 2.3 to
![]() $\phi $
.
$\phi $
.
(1) There is a constant
![]() $\Sigma ^2 \ge 0$
such that
$\Sigma ^2 \ge 0$
such that
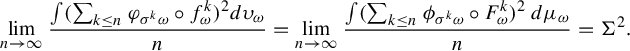 $$\begin{align*}\lim_{n \to \infty} \frac{\int(\sum_{k\le n} {\varphi}_{\sigma^k \omega} \circ f^k_{\omega} )^2 d\upsilon_{\omega}}{n}=\lim_{n \to \infty}\frac{\int(\sum_{k\le n} \phi_{\sigma^k \omega} \circ F^k_{\omega} )^2 \,d\mu_{\omega}}{n}=\Sigma^2.\end{align*}$$
$$\begin{align*}\lim_{n \to \infty} \frac{\int(\sum_{k\le n} {\varphi}_{\sigma^k \omega} \circ f^k_{\omega} )^2 d\upsilon_{\omega}}{n}=\lim_{n \to \infty}\frac{\int(\sum_{k\le n} \phi_{\sigma^k \omega} \circ F^k_{\omega} )^2 \,d\mu_{\omega}}{n}=\Sigma^2.\end{align*}$$
(2) If
![]() $\Sigma ^2>0$
, then
$\Sigma ^2>0$
, then
![]() $\phi $
has the QASIP: there is a constant
$\phi $
has the QASIP: there is a constant
![]() $e>0$
such that for a.e.
$e>0$
such that for a.e.
![]() $\omega \in \Omega $
, we have a Brownian motion
$\omega \in \Omega $
, we have a Brownian motion
![]() $\bar {B}^{\omega }$
defined on an extended probability space
$\bar {B}^{\omega }$
defined on an extended probability space
![]() $({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
and
$({\pmb {\Delta }}_{\omega }, \mathbf {Q}_{\omega })$
and
Here
![]() $\sigma _n^2(\omega )=\int (\sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega })^2 \,d\mu _{\omega }$
, and
$\sigma _n^2(\omega )=\int (\sum _{k\le n} \phi _{\sigma ^k \omega } \circ F^k_{\omega })^2 \,d\mu _{\omega }$
, and
![]() $e=1/4+\epsilon _0$
satisfies the following: if
$e=1/4+\epsilon _0$
satisfies the following: if
![]() $\rho _n=e^{-a n^b}$
, then
$\rho _n=e^{-a n^b}$
, then
![]() $\epsilon _0>0$
is any small number; if
$\epsilon _0>0$
is any small number; if
![]() $\rho _n={n^{-D}}$
, then
$\rho _n={n^{-D}}$
, then
![]() $\epsilon _0$
is any number in
$\epsilon _0$
is any number in
![]() $(\epsilon _D, 1/4)$
, where
$(\epsilon _D, 1/4)$
, where
![]() $\epsilon _D$
is defined in (2.5) with a different
$\epsilon _D$
is defined in (2.5) with a different
![]() $\epsilon _1={2p}/{(p-\gamma )(D-2)}$
.
$\epsilon _1={2p}/{(p-\gamma )(D-2)}$
.
(3) If
![]() $\Sigma ^2=0$
, then
$\Sigma ^2=0$
, then
![]() $\phi $
is a coboundary: there is a function
$\phi $
is a coboundary: there is a function
![]() $g'$
on
$g'$
on
![]() $\Delta $
such that for a.e.
$\Delta $
such that for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
in other words,
If
![]() $\rho _n={n^{-D}}$
, then
$\rho _n={n^{-D}}$
, then
![]() $g' \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\Delta , \mu )$
for a sufficiently small
$g' \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\Delta , \mu )$
for a sufficiently small
![]() $\delta>0$
such that
$\delta>0$
such that
![]() ${(D-2-\delta )(p-\gamma )}/{(1+\delta )p}>4$
.
${(D-2-\delta )(p-\gamma )}/{(1+\delta )p}>4$
.
Now we show how to project this QASIP and coboundary to the RDS. Let
![]() $\chi (\omega ,x):=(\sigma \omega , f_{\omega }(x))$
,
$\chi (\omega ,x):=(\sigma \omega , f_{\omega }(x))$
,
![]() $\chi ^*$
be its transfer operator w.r.t.
$\chi ^*$
be its transfer operator w.r.t.
![]() $\upsilon $
, and
$\upsilon $
, and
![]() $\mathcal {M}=:\bigcup _{\omega \in \Omega } (\{\omega \} \times M_{\omega })$
.
$\mathcal {M}=:\bigcup _{\omega \in \Omega } (\{\omega \} \times M_{\omega })$
.
Projection for the coboundary. We will apply Theorem 1.1 of [Reference Liverani, Ledrappier, Lewowicz and NewhouseLiv96] to the stationary system
![]() $(\mathcal {M}, \chi , \upsilon ) $
and the fiberwise mean zero function
$(\mathcal {M}, \chi , \upsilon ) $
and the fiberwise mean zero function
![]() $\Phi $
, verifying three conditions of the theorem.
$\Phi $
, verifying three conditions of the theorem.
By Lemma 3.4, there is a constant
![]() $C=C_{\phi , h,F,\beta ^{\gamma }, \delta ,p/\gamma } \|\mathcal {K}^{\gamma }\|_{L^{p/\gamma }}$
such that
$C=C_{\phi , h,F,\beta ^{\gamma }, \delta ,p/\gamma } \|\mathcal {K}^{\gamma }\|_{L^{p/\gamma }}$
such that
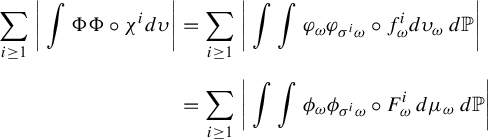 $$ \begin{align*} \sum_{i \ge 1}\bigg|\int \Phi \Phi \circ \chi^i d\upsilon\bigg|&=\sum_{i \ge 1} \bigg|\int \int \varphi_{\omega} \varphi_{\sigma^i \omega} \circ f^i_{\omega}d\upsilon_{\omega}\,d\mathbb{P}\bigg|\\[5pt] &=\sum_{i \ge 1} \bigg|\int \int \phi_{\omega} \phi_{\sigma^i \omega} \circ F^i_{\omega}\,d\mu_{\omega}\,d\mathbb{P}\bigg|\end{align*} $$
$$ \begin{align*} \sum_{i \ge 1}\bigg|\int \Phi \Phi \circ \chi^i d\upsilon\bigg|&=\sum_{i \ge 1} \bigg|\int \int \varphi_{\omega} \varphi_{\sigma^i \omega} \circ f^i_{\omega}d\upsilon_{\omega}\,d\mathbb{P}\bigg|\\[5pt] &=\sum_{i \ge 1} \bigg|\int \int \phi_{\omega} \phi_{\sigma^i \omega} \circ F^i_{\omega}\,d\mu_{\omega}\,d\mathbb{P}\bigg|\end{align*} $$
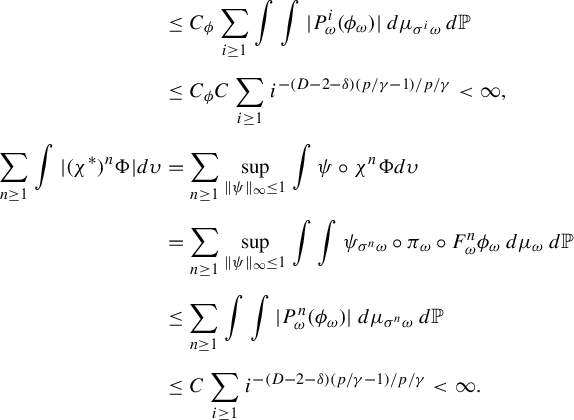 $$ \begin{align*}&\le C_{\phi} \sum_{i \ge 1} \int \int |P^i_{\omega}(\phi_{\omega})| \,d\mu_{\sigma^i\omega}\,d\mathbb{P}\\[4pt]&\le C_{\phi}C \sum_{i \ge 1} {i^{-(D-2-\delta) ({p/\gamma-1})/{p/\gamma}}} < \infty,\\[4pt] \sum_{n\ge 1}\int |(\chi^*)^n \Phi| d\upsilon&=\sum_{n\ge 1}\sup_{\|\psi\|_{\infty}\le 1}\int \psi \circ \chi^n \Phi d\upsilon\\[4pt] &=\sum_{n\ge 1}\sup_{\|\psi\|_{\infty}\le 1}\int \int \psi_{\sigma^n \omega} \circ \pi_{\omega} \circ F_{\omega}^n \phi_{\omega} \,d\mu_{\omega}\,d\mathbb{P}\\[4pt] &\le \sum_{n\ge 1} \int \int | P_{\omega}^n (\phi_{\omega})| \,d\mu_{\sigma^n\omega}\,d\mathbb{P}\\[4pt]&\le C \sum_{i \ge 1} {i^{-(D-2-\delta) ({p/\gamma-1})/{p/\gamma}}} < \infty.\end{align*} $$
$$ \begin{align*}&\le C_{\phi} \sum_{i \ge 1} \int \int |P^i_{\omega}(\phi_{\omega})| \,d\mu_{\sigma^i\omega}\,d\mathbb{P}\\[4pt]&\le C_{\phi}C \sum_{i \ge 1} {i^{-(D-2-\delta) ({p/\gamma-1})/{p/\gamma}}} < \infty,\\[4pt] \sum_{n\ge 1}\int |(\chi^*)^n \Phi| d\upsilon&=\sum_{n\ge 1}\sup_{\|\psi\|_{\infty}\le 1}\int \psi \circ \chi^n \Phi d\upsilon\\[4pt] &=\sum_{n\ge 1}\sup_{\|\psi\|_{\infty}\le 1}\int \int \psi_{\sigma^n \omega} \circ \pi_{\omega} \circ F_{\omega}^n \phi_{\omega} \,d\mu_{\omega}\,d\mathbb{P}\\[4pt] &\le \sum_{n\ge 1} \int \int | P_{\omega}^n (\phi_{\omega})| \,d\mu_{\sigma^n\omega}\,d\mathbb{P}\\[4pt]&\le C \sum_{i \ge 1} {i^{-(D-2-\delta) ({p/\gamma-1})/{p/\gamma}}} < \infty.\end{align*} $$
Using
![]() $\int \phi \phi \circ F^n \,d\mu \le C {n^{-(D-2-\delta ) (p-\gamma )/p}}\le C n^{-4}$
and following the same computations as in the proof of Corollary 3.10 of [Reference SuSu19b] (we skip this here), we have
$\int \phi \phi \circ F^n \,d\mu \le C {n^{-(D-2-\delta ) (p-\gamma )/p}}\le C n^{-4}$
and following the same computations as in the proof of Corollary 3.10 of [Reference SuSu19b] (we skip this here), we have
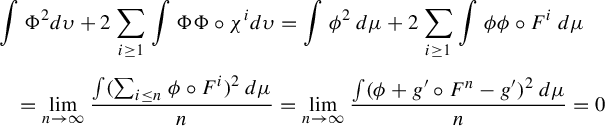 $$ \begin{align*} &\int \Phi^2 d\upsilon+2\sum_{i \ge 1}\int \Phi \Phi \circ \chi^i d\upsilon =\int \phi^2 \,d\mu+2\sum_{i \ge 1}\int \phi \phi \circ F^i \,d\mu\\[4pt] &\quad=\lim_{n \to \infty }\frac{\int (\sum_{i\le n} \phi \circ F^i )^2 \,d\mu}{n}=\lim_{n \to \infty }\frac{\int ( \phi+g'\circ F^n-g')^2 \,d\mu}{n}=0 \end{align*} $$
$$ \begin{align*} &\int \Phi^2 d\upsilon+2\sum_{i \ge 1}\int \Phi \Phi \circ \chi^i d\upsilon =\int \phi^2 \,d\mu+2\sum_{i \ge 1}\int \phi \phi \circ F^i \,d\mu\\[4pt] &\quad=\lim_{n \to \infty }\frac{\int (\sum_{i\le n} \phi \circ F^i )^2 \,d\mu}{n}=\lim_{n \to \infty }\frac{\int ( \phi+g'\circ F^n-g')^2 \,d\mu}{n}=0 \end{align*} $$
where the last two equalities are due to (6.4) and
![]() $g'\in L^4(\Delta ,\mu )$
. Therefore, by Theorem 1.1 of [Reference Liverani, Ledrappier, Lewowicz and NewhouseLiv96], there is a measurable function g on
$g'\in L^4(\Delta ,\mu )$
. Therefore, by Theorem 1.1 of [Reference Liverani, Ledrappier, Lewowicz and NewhouseLiv96], there is a measurable function g on
![]() $(\mathcal {M}, \upsilon )$
such that
$(\mathcal {M}, \upsilon )$
such that
![]() $\Phi \circ \chi = g \circ \chi -g \upsilon \text {-a.s.}$
and
$\Phi \circ \chi = g \circ \chi -g \upsilon \text {-a.s.}$
and
![]() $g:=\sum _{n \ge 0} (\chi ^{*})^n \Phi $
. Let
$g:=\sum _{n \ge 0} (\chi ^{*})^n \Phi $
. Let
![]() $q:={(D-2-\delta )(p-\gamma )}/{(1+\delta )p}$
. Using
$q:={(D-2-\delta )(p-\gamma )}/{(1+\delta )p}$
. Using
![]() $\|\Phi \|_{\infty }\le C_{\phi }$
, we have
$\|\Phi \|_{\infty }\le C_{\phi }$
, we have
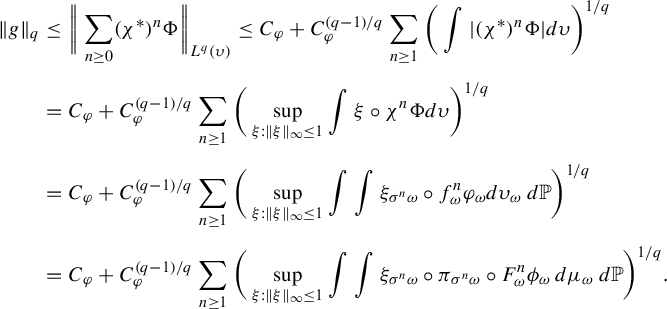 $$ \begin{align*} \|g\|_q&\le \bigg\|\sum_{n \ge 0} (\chi^{*})^n \Phi\bigg\|_{L^{q}(\upsilon)} \le C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\int |(\chi^*)^n \Phi| d\upsilon\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \xi\circ \chi^n \Phi d\upsilon\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \int \xi_{\sigma^n\omega}\circ f_{\omega}^n \varphi_{\omega} d\upsilon_{\omega}\,d\mathbb{P}\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \int \xi_{\sigma^n\omega}\circ \pi_{\sigma^n\omega}\circ F_{\omega}^n \phi_{\omega} \,d\mu_{\omega}\,d\mathbb{P}\bigg)^{1/q}.\end{align*} $$
$$ \begin{align*} \|g\|_q&\le \bigg\|\sum_{n \ge 0} (\chi^{*})^n \Phi\bigg\|_{L^{q}(\upsilon)} \le C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\int |(\chi^*)^n \Phi| d\upsilon\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \xi\circ \chi^n \Phi d\upsilon\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \int \xi_{\sigma^n\omega}\circ f_{\omega}^n \varphi_{\omega} d\upsilon_{\omega}\,d\mathbb{P}\bigg)^{1/q}\\[4pt] &=C_{\varphi}+ C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} \bigg(\sup_{\xi:\|\xi\|_{\infty}\le 1}\int \int \xi_{\sigma^n\omega}\circ \pi_{\sigma^n\omega}\circ F_{\omega}^n \phi_{\omega} \,d\mu_{\omega}\,d\mathbb{P}\bigg)^{1/q}.\end{align*} $$
By Definition 3.1,
![]() $|\xi _{\sigma ^n\omega }\circ \pi _{\sigma ^n\omega }|\le 1$
and Lemma 3.4, there is a constant
$|\xi _{\sigma ^n\omega }\circ \pi _{\sigma ^n\omega }|\le 1$
and Lemma 3.4, there is a constant
![]() $C=(C_{\phi , h,F,\beta ^{\gamma }, \delta ,p/\gamma } \|\mathcal {K}^{\gamma }\|_{L^{p/\gamma }})^{1/q}$
such that the last expression above can be estimated as
$C=(C_{\phi , h,F,\beta ^{\gamma }, \delta ,p/\gamma } \|\mathcal {K}^{\gamma }\|_{L^{p/\gamma }})^{1/q}$
such that the last expression above can be estimated as
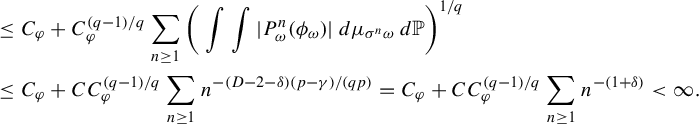 $$ \begin{align*} &\le C_{\varphi}+ C _{\varphi}^{(q-1)/q}\sum_{n\ge 1} \bigg(\int \int | P_{\omega}^n (\phi_{\omega})| \,d\mu_{\sigma^n\omega}\,d\mathbb{P}\bigg)^{1/q}\\ &\le C_{\varphi}+ C C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} {n^{-(D-2-\delta) (p-\gamma)/(qp)}}= C_{\varphi}+ C C _{\varphi}^{(q-1)/q}\sum_{n \ge 1} {n^{-(1+\delta)}} < \infty. \end{align*} $$
$$ \begin{align*} &\le C_{\varphi}+ C _{\varphi}^{(q-1)/q}\sum_{n\ge 1} \bigg(\int \int | P_{\omega}^n (\phi_{\omega})| \,d\mu_{\sigma^n\omega}\,d\mathbb{P}\bigg)^{1/q}\\ &\le C_{\varphi}+ C C _{\varphi}^{(q-1)/q} \sum_{n \ge 1} {n^{-(D-2-\delta) (p-\gamma)/(qp)}}= C_{\varphi}+ C C _{\varphi}^{(q-1)/q}\sum_{n \ge 1} {n^{-(1+\delta)}} < \infty. \end{align*} $$
Therefore
![]() $g \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\upsilon )$
.
$g \in L^{{(D-2-\delta )(p-\gamma )}/{(1+\delta )p}}(\upsilon )$
.
Projection for the QASIP. By lemma A.1, the QASIP for the RYT
implies that there is a function
![]() $H: \mathbb {R}^{\mathbb {N}}\times [0,1] \to C[0,1]$
, a uniform distribution U on
$H: \mathbb {R}^{\mathbb {N}}\times [0,1] \to C[0,1]$
, a uniform distribution U on
![]() $[0,1]$
and a Brownian motion
$[0,1]$
and a Brownian motion
![]() $\hat {B}^{\omega }:=H((\varphi _{\sigma ^k \omega } \circ f^k_{\omega } \circ \pi _{\omega })_{k \ge 1},U)$
defined on
$\hat {B}^{\omega }:=H((\varphi _{\sigma ^k \omega } \circ f^k_{\omega } \circ \pi _{\omega })_{k \ge 1},U)$
defined on
![]() $(\Delta _{\omega } \times [0,1], \mu _{\omega }\times \operatorname {Leb}_{[0,1]})$
such that for a.e.
$(\Delta _{\omega } \times [0,1], \mu _{\omega }\times \operatorname {Leb}_{[0,1]})$
such that for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align*} {\mathbf{Q}}_{\omega}&\{(( \varphi_{\sigma^k \omega} \circ f^k_{\omega} \circ \pi_{\omega})_{k \ge 1}, \bar{B}^{\omega}) \in (\cdot, \cdot) \}\\ &=(\mu_{\omega} \times \operatorname{Leb}_{[0,1]})\{(( \varphi_{\sigma^k \omega} \circ f^k_{\omega} \circ \pi_{\omega})_{k \ge 1}, \hat{B}^{\omega})\in (\cdot, \cdot)\}. \end{align*} $$
$$ \begin{align*} {\mathbf{Q}}_{\omega}&\{(( \varphi_{\sigma^k \omega} \circ f^k_{\omega} \circ \pi_{\omega})_{k \ge 1}, \bar{B}^{\omega}) \in (\cdot, \cdot) \}\\ &=(\mu_{\omega} \times \operatorname{Leb}_{[0,1]})\{(( \varphi_{\sigma^k \omega} \circ f^k_{\omega} \circ \pi_{\omega})_{k \ge 1}, \hat{B}^{\omega})\in (\cdot, \cdot)\}. \end{align*} $$
This implies that for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
Then
![]() ${B}^{\omega }:=H(( \varphi _{\sigma ^k \omega } \circ f^k_{\omega })_{k \ge 1},U)$
is also a Brownian motion defined on
${B}^{\omega }:=H(( \varphi _{\sigma ^k \omega } \circ f^k_{\omega })_{k \ge 1},U)$
is also a Brownian motion defined on
![]() $(M\times [0,1], \upsilon _{\omega }\times \operatorname {Leb}_{[0,1]})$
. Therefore, for a.e.
$(M\times [0,1], \upsilon _{\omega }\times \operatorname {Leb}_{[0,1]})$
. Therefore, for a.e.
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
and the extended probability space is
![]() ${\mathbf {M}}_{\omega }:=(M \times [0,1], \upsilon _{\omega }\times \operatorname {Leb}_{[0,1]})$
.
${\mathbf {M}}_{\omega }:=(M \times [0,1], \upsilon _{\omega }\times \operatorname {Leb}_{[0,1]})$
.
7 Applications
We will apply Theorem 6.1 to each of the following RDS, by verifying conditions (1)–(6) in Definition 6.1: i.i.d. translations of unimodal maps (satisfying the Collet–Eckmann conditions) in [Reference Baladi, Benedicks and Maume-DeschampsBBMD02]; i.i.d. translations of non-uniformly expanding maps (with a slow recurrence to singularities) in [Reference Alves and AraújoAA03, Reference Alves and VilarinhoAV13]; i.i.d. perturbations of admissible S-unimodal maps (satisfying the Collet–Eckmann conditions or summability conditions of exponent
![]() $1$
) in [Reference DuDu15]; and i.i.d. perturbations of random LSV maps with a neutral fixed point in [Reference Bahsoun, Bose and RuziboevBBR19]. Here i.i.d. means that the randomness of
$1$
) in [Reference DuDu15]; and i.i.d. perturbations of random LSV maps with a neutral fixed point in [Reference Bahsoun, Bose and RuziboevBBR19]. Here i.i.d. means that the randomness of
![]() $f_{\sigma ^i \omega }$
only depends on
$f_{\sigma ^i \omega }$
only depends on
![]() $\omega _i$
; then for any
$\omega _i$
; then for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $f_{\sigma ^n \omega }$
is independent of
$f_{\sigma ^n \omega }$
is independent of
![]() $(f_{\sigma ^i \omega })_{ i \le n-1}$
. In Definition 6.1, conditions (1), (2), (4), (6.1) and (6.2) are satisfied when the RYT is constructed. Condition (3) is also satisfied since
$(f_{\sigma ^i \omega })_{ i \le n-1}$
. In Definition 6.1, conditions (1), (2), (4), (6.1) and (6.2) are satisfied when the RYT is constructed. Condition (3) is also satisfied since
![]() $\{R_{\omega }=n\}$
is constructed inductively in these papers (it only depends on
$\{R_{\omega }=n\}$
is constructed inductively in these papers (it only depends on
![]() $(f_{\sigma ^i \omega })_{0 \le i \le n-1}$
), that is,
$(f_{\sigma ^i \omega })_{0 \le i \le n-1}$
), that is,
![]() $\{R_{\omega }=n\}$
only depends on
$\{R_{\omega }=n\}$
only depends on
![]() $\omega _0, \omega _1, \ldots , \omega _{n-1}$
. Thus it remains to verify condition (6.3):
$\omega _0, \omega _1, \ldots , \omega _{n-1}$
. Thus it remains to verify condition (6.3):
and condition (6), that is,
7.1 i.i.d. translations of unimodal maps
Condition (6.3) is due to the proof of Lemma 9.1 of [Reference Baladi, Benedicks and Maume-DeschampsBBMD02, pp. 123]. Condition (7.1) is due to Proposition 8.3 of [Reference Baladi, Benedicks and Maume-DeschampsBBMD02]. The probability measure
![]() $\nu :=\nu _{\epsilon }$
is defined as (2.1) of [Reference Baladi, Benedicks and Maume-DeschampsBBMD02, pp. 82]. The QASIP convergence rate is
$\nu :=\nu _{\epsilon }$
is defined as (2.1) of [Reference Baladi, Benedicks and Maume-DeschampsBBMD02, pp. 82]. The QASIP convergence rate is
![]() $1/4+\epsilon _0$
for any small
$1/4+\epsilon _0$
for any small
![]() $\epsilon _0>0$
.
$\epsilon _0>0$
.
7.2 i.i.d. perturbations of S-unimodal maps
Condition (7.1) is due to Theorems 8.1.2 and 8.1.4 of [Reference DuDu15]. We now verify (6.3).
-
(1) For S-unimodal maps satisfying the Collet–Eckmann conditions in [Reference DuDu15], (6.3) is due to Proposition 8.3.5 of [Reference DuDu15].
-
(2) For S-unimodal maps on interval I satisfying summability conditions of exponent
 $1$
in [Reference DuDu15], we will verify (6.3) with
$1$
in [Reference DuDu15], we will verify (6.3) with
 $\mathcal {K}\in L^{\infty }(\Omega )$
, that is, there is a constant
$\mathcal {K}\in L^{\infty }(\Omega )$
, that is, there is a constant
 $C>0$
independent of
$C>0$
independent of
 $\omega \in \Omega $
such that where
$\omega \in \Omega $
such that where $$ \begin{align*} d(f_{\omega}^{k}(x), f_{\omega}^{k}(y)) \le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)), \end{align*} $$
$$ \begin{align*} d(f_{\omega}^{k}(x), f_{\omega}^{k}(y)) \le C d(f_{\omega}^{R_{\omega}}(x), f_{\omega}^{R_{\omega}}(y)), \end{align*} $$
 $k \le R_{\omega }=n$
,
$k \le R_{\omega }=n$
,
 $x,y\in U_{\omega }(z,n):=(f_{\omega }^n)^{-1}(\widetilde {B}(\delta )) \bigcap J^{\omega }_{z,n}$
and n is a
$x,y\in U_{\omega }(z,n):=(f_{\omega }^n)^{-1}(\widetilde {B}(\delta )) \bigcap J^{\omega }_{z,n}$
and n is a
 $\theta $
-good return time of
$\theta $
-good return time of
 $(\omega , z)$
into
$(\omega , z)$
into
 $\widetilde {B}(\delta )$
. Moreover,
$\widetilde {B}(\delta )$
. Moreover,
 $f^n_{\omega }: U_{\omega }(z,n) \to \widetilde {B}(\delta )$
is a diffeomorphism,
$f^n_{\omega }: U_{\omega }(z,n) \to \widetilde {B}(\delta )$
is a diffeomorphism,
 $n-k$
is also a
$n-k$
is also a
 $\theta $
-good return time of
$\theta $
-good return time of
 $(\sigma ^k\omega , f^k_{\omega }(z))$
into
$(\sigma ^k\omega , f^k_{\omega }(z))$
into
 $\widetilde {B}(\delta )$
, and
$\widetilde {B}(\delta )$
, and
 $f^{n-k}_{\sigma ^k\omega }$
is a diffeomorphism from
$f^{n-k}_{\sigma ^k\omega }$
is a diffeomorphism from
 $f^k_{\omega }(U_{\omega }(z,n)) \subseteq U_{\sigma ^k\omega }(f^k_{\omega }(z),n-k)$
into
$f^k_{\omega }(U_{\omega }(z,n)) \subseteq U_{\sigma ^k\omega }(f^k_{\omega }(z),n-k)$
into
 $\widetilde {B}(\delta )$
(These properties can be found in Lemma 8.2.1 and Propositions 8.2.3 and 8.2.4 of [Reference DuDu15], and see Definition 8.2.2 of [Reference DuDu15] for
$\widetilde {B}(\delta )$
(These properties can be found in Lemma 8.2.1 and Propositions 8.2.3 and 8.2.4 of [Reference DuDu15], and see Definition 8.2.2 of [Reference DuDu15] for
 $\theta $
-good return times.) Equivalently, we will prove (6.3) by showing By Lemma 8.2.1 of [Reference DuDu15], for any
$\theta $
-good return times.) Equivalently, we will prove (6.3) by showing By Lemma 8.2.1 of [Reference DuDu15], for any $$ \begin{align*} |Df_{\sigma^k\omega}^{n-k}|_{f^k_{\omega}(U_{\omega}(z,n))}|\ge C^{-1}. \end{align*} $$
$$ \begin{align*} |Df_{\sigma^k\omega}^{n-k}|_{f^k_{\omega}(U_{\omega}(z,n))}|\ge C^{-1}. \end{align*} $$
 $z_1,z_2 \in U_{\sigma ^k\omega }(f^k_{\omega }(z),n-k)$
, Then for any
$z_1,z_2 \in U_{\sigma ^k\omega }(f^k_{\omega }(z),n-k)$
, Then for any $$\begin{align*}e^{-1/2}\le \frac{|Df_{\sigma^k\omega}^{n-k}(z_1)|}{|Df_{\sigma^k\omega}^{n-k}(z_2)|} \le e^{1/2}.\end{align*}$$
$$\begin{align*}e^{-1/2}\le \frac{|Df_{\sigma^k\omega}^{n-k}(z_1)|}{|Df_{\sigma^k\omega}^{n-k}(z_2)|} \le e^{1/2}.\end{align*}$$
 $z_1 \in f^k_{\omega }(U_{\omega }(z,n))$
,
$z_1 \in f^k_{\omega }(U_{\omega }(z,n))$
,  $$\begin{align*}|Df_{\sigma^k\omega}^{n-k}(z_1)|\ge e^{-1/2} \frac{|f_{\sigma^k\omega}^{n-k}[U_{\sigma^k\omega}(f^k_{\omega}(z),n-k)]|}{|U_{\sigma^k\omega}(f^k_{\omega}(z),n-k)|} \ge e^{-1/2} \frac{|\widetilde{B}(\delta)|}{|I|}=:C^{-1}.\end{align*}$$
$$\begin{align*}|Df_{\sigma^k\omega}^{n-k}(z_1)|\ge e^{-1/2} \frac{|f_{\sigma^k\omega}^{n-k}[U_{\sigma^k\omega}(f^k_{\omega}(z),n-k)]|}{|U_{\sigma^k\omega}(f^k_{\omega}(z),n-k)|} \ge e^{-1/2} \frac{|\widetilde{B}(\delta)|}{|I|}=:C^{-1}.\end{align*}$$
The probability measure
![]() $\nu :=\nu _{\epsilon }$
is defined in §8.1.1 of [Reference DuDu15, pp. 80]. The QASIP convergence rates for these two RDS are
$\nu :=\nu _{\epsilon }$
is defined in §8.1.1 of [Reference DuDu15, pp. 80]. The QASIP convergence rates for these two RDS are
![]() $1/4+\epsilon _0$
for any small
$1/4+\epsilon _0$
for any small
![]() $\epsilon _0>0$
.
$\epsilon _0>0$
.
7.3 i.i.d. translations of non-uniformly expanding maps
Condition (7.1) is due to Proposition 5.1, Theorem 2.9, and §5.2.2 of [Reference Alves and VilarinhoAV13]. Condition (6.3) is due to Proposition 4.9 of [Reference Alves and VilarinhoAV13]. The probability measure
![]() $\nu :=\theta _{\epsilon }$
is defined on p. 687 of [Reference Alves and VilarinhoAV13]. The QASIP convergence rate is
$\nu :=\theta _{\epsilon }$
is defined on p. 687 of [Reference Alves and VilarinhoAV13]. The QASIP convergence rate is
![]() $1/4+\epsilon _0$
for any small
$1/4+\epsilon _0$
for any small
![]() $\epsilon _0>0$
.
$\epsilon _0>0$
.
7.4 i.i.d. perturbations of LSV maps with a neutral fixed point
Condition (6.3) follows since LSV maps have derivatives no less than
![]() $1$
, that is,
$1$
, that is,
![]() $d(f_{\omega }^{k}(x), f_{\omega }^{k}(y)) \le d(f_{\omega }^{R_{\omega }}(x), f_{\omega }^{R_{\omega }}(y))$
. Condition (7.1) is due to Proposition 5.3 and (5.5) in [Reference Bahsoun, Bose and RuziboevBBR19] with
$d(f_{\omega }^{k}(x), f_{\omega }^{k}(y)) \le d(f_{\omega }^{R_{\omega }}(x), f_{\omega }^{R_{\omega }}(y))$
. Condition (7.1) is due to Proposition 5.3 and (5.5) in [Reference Bahsoun, Bose and RuziboevBBR19] with
![]() $\alpha _0^{-1}>6$
, that is, the QASIP holds for
$\alpha _0^{-1}>6$
, that is, the QASIP holds for
![]() $\Omega =[\alpha _0,\alpha _1]^{\mathbb {Z}}$
where
$\Omega =[\alpha _0,\alpha _1]^{\mathbb {Z}}$
where
![]() $0<\alpha _0<1/6$
and
$0<\alpha _0<1/6$
and
![]() $\alpha _1<1$
. The probability measure
$\alpha _1<1$
. The probability measure
![]() $\nu $
can be different distributions; see §5.2 of [Reference Bahsoun, Bose and RuziboevBBR19]. The QASIP convergence rate is
$\nu $
can be different distributions; see §5.2 of [Reference Bahsoun, Bose and RuziboevBBR19]. The QASIP convergence rate is
![]() $1/4+\epsilon _D+\epsilon _0$
where
$1/4+\epsilon _D+\epsilon _0$
where
![]() $D=\alpha _0^{-1}$
and
$D=\alpha _0^{-1}$
and
![]() $\epsilon _0>0$
is any small number.
$\epsilon _0>0$
is any small number.
Acknowledgements
The author warmly thanks his advisor Prof. Andrew Török for posing him one of the questions in this paper, and Prof. Ian Melbourne and the reviewer for valuable remarks and comments.
A. Appendix
Lemma A.1. (See [Reference KallenbergKal02, Theorem 6.10])
For any measurable space S and Borel space T, let
![]() $\xi $
,
$\xi $
,
![]() $\xi '$
be random elements in S and
$\xi '$
be random elements in S and
![]() $\eta $
be a random element in T such that
$\eta $
be a random element in T such that
![]() $\xi =_d \xi '$
. Then there is a random element
$\xi =_d \xi '$
. Then there is a random element
![]() $\eta '$
in T such that
$\eta '$
in T such that
![]() $(\eta , \xi ) =_d (\eta ', \xi ')$
. More precisely, there exists a measurable function
$(\eta , \xi ) =_d (\eta ', \xi ')$
. More precisely, there exists a measurable function
![]() $f: S \times [0,1] \to T$
such that
$f: S \times [0,1] \to T$
such that
![]() $\eta '=f(\xi ', U)$
where
$\eta '=f(\xi ', U)$
where
![]() $U \sim U(0,1)$
and
$U \sim U(0,1)$
and
![]() $\xi '$
are independent.
$\xi '$
are independent.
Indeed, to guarantee the independence above, we can simply extend the probability space by multiplying
![]() $([0,1], \operatorname *{Leb})$
.
$([0,1], \operatorname *{Leb})$
.













