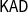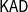1. Introduction
Kleene algebra with tests (Kozen Reference Kozen1997),
![]() $\mathsf{KAT}$
, is an algebraic framework for reasoning about equivalence and correctness of imperative programs.
$\mathsf{KAT}$
, is an algebraic framework for reasoning about equivalence and correctness of imperative programs.
![]() $\mathsf{KAT}$
comprises two-sorted algebras with a Boolean algebra of tests embedded into a Kleene algebra of programs. A Hoare-style partial correctness assertion
$\mathsf{KAT}$
comprises two-sorted algebras with a Boolean algebra of tests embedded into a Kleene algebra of programs. A Hoare-style partial correctness assertion
![]() $\{ b \} \,p\, \{ c \}$
, meaning that condition c holds after each terminating execution of program p starting in a state satisfying b, is represented in
$\{ b \} \,p\, \{ c \}$
, meaning that condition c holds after each terminating execution of program p starting in a state satisfying b, is represented in
![]() $\mathsf{KAT}$
by the equation
$\mathsf{KAT}$
by the equation
![]() $bp\bar{c} = 0$
or, equivalently,
$bp\bar{c} = 0$
or, equivalently,
![]() $bp = bpc$
. The equational theory of
$bp = bpc$
. The equational theory of
![]() $\mathsf{KAT}$
is PSPACE-complete (Cohen et al. Reference Cohen, Kozen and Smith1996). The quasi-equational theory of
$\mathsf{KAT}$
is PSPACE-complete (Cohen et al. Reference Cohen, Kozen and Smith1996). The quasi-equational theory of
![]() $\mathsf{KAT}$
is undecidable (Kozen Reference Kozen2002), but its fragment consisting of quasi-equations where the assumptions are all of the form
$\mathsf{KAT}$
is undecidable (Kozen Reference Kozen2002), but its fragment consisting of quasi-equations where the assumptions are all of the form
![]() $r = 0$
embeds into the equational theory of
$r = 0$
embeds into the equational theory of
![]() $\mathsf{KAT}$
(Kozen and Smith Reference Kozen, Smith, van Dalen and Bezem1997) and is PSPACE-complete as well.
$\mathsf{KAT}$
(Kozen and Smith Reference Kozen, Smith, van Dalen and Bezem1997) and is PSPACE-complete as well.
Kozen and Tiuryn (Reference Kozen and Tiuryn2003) extend the language of
![]() $\mathsf{KAT}$
with an implication operator
$\mathsf{KAT}$
with an implication operator
![]() $\Rightarrow$
and show that, in the resulting system
$\Rightarrow$
and show that, in the resulting system
![]() $\mathsf{S}$
, partial correctness assertions can be formalized as implicational formulas
$\mathsf{S}$
, partial correctness assertions can be formalized as implicational formulas
![]() $bp \Rightarrow c$
. They argue that the implicational rendering of partial correctness assertions has certain advantages over the equational one, for example, it facilitates a better distinction between local and global properties. Kozen and Tiuryn formulate a sequent system for
$bp \Rightarrow c$
. They argue that the implicational rendering of partial correctness assertions has certain advantages over the equational one, for example, it facilitates a better distinction between local and global properties. Kozen and Tiuryn formulate a sequent system for
![]() $\mathsf{S}$
which bears some resemblance to sequent calculi for substructural logics (Galatos et al. Reference Galatos, Jipsen, Kowalski and Ono2007). They show that their implication connective
$\mathsf{S}$
which bears some resemblance to sequent calculi for substructural logics (Galatos et al. Reference Galatos, Jipsen, Kowalski and Ono2007). They show that their implication connective
![]() $\Rightarrow$
is similar to implication in some well-known substructural logics, but that it has also many specific features not common in substructural logic. Particular combinations of Kleene algebra and substructural logics were studied in numerous works (Buszkowski Reference Buszkowski2006; Jipsen Reference Jipsen2004; Reference KozenKozen 1994b
; Kuznetsov Reference Kuznetsov2021; Palka Reference Palka2007; Pratt Reference Pratt1991). It is therefore interesting to look at the exact nature of the relation between
$\Rightarrow$
is similar to implication in some well-known substructural logics, but that it has also many specific features not common in substructural logic. Particular combinations of Kleene algebra and substructural logics were studied in numerous works (Buszkowski Reference Buszkowski2006; Jipsen Reference Jipsen2004; Reference KozenKozen 1994b
; Kuznetsov Reference Kuznetsov2021; Palka Reference Palka2007; Pratt Reference Pratt1991). It is therefore interesting to look at the exact nature of the relation between
![]() $\mathsf{S}$
and these combinations. For one, the latter are usually undecidable (Buszkowski Reference Buszkowski2006; Kuznetsov Reference Kuznetsov2021; Palka Reference Palka2007), whereas
$\mathsf{S}$
and these combinations. For one, the latter are usually undecidable (Buszkowski Reference Buszkowski2006; Kuznetsov Reference Kuznetsov2021; Palka Reference Palka2007), whereas
![]() $\mathsf{S}$
is PSPACE-complete (Kozen Reference Kozen2003).
$\mathsf{S}$
is PSPACE-complete (Kozen Reference Kozen2003).
In the conference paper (Sedlár and Wannenburg Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022), we showed that
![]() $\mathsf{S}$
embeds into a specific combination of residuated Kleene algebra and Kleene algebra with domain,
$\mathsf{S}$
embeds into a specific combination of residuated Kleene algebra and Kleene algebra with domain,
![]() $\mathsf{KAD}$
(Desharnais et al. Reference Desharnais, Möller and Struth2006; Desharnais and Struth Reference Desharnais and Struth2011). In this paper, we improve on this embedding result in two respects. First, we show that
$\mathsf{KAD}$
(Desharnais et al. Reference Desharnais, Möller and Struth2006; Desharnais and Struth Reference Desharnais and Struth2011). In this paper, we improve on this embedding result in two respects. First, we show that
![]() $\mathsf{S}$
embeds into
$\mathsf{S}$
embeds into
![]() $\mathsf{KAD}$
itself. Hence, it is not necessary to use residuated implication connectives and the adjoint to the (co)domain operator as we did in Sedlár and Wannenburg (Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022), and it is not even necessary to assume
$\mathsf{KAD}$
itself. Hence, it is not necessary to use residuated implication connectives and the adjoint to the (co)domain operator as we did in Sedlár and Wannenburg (Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022), and it is not even necessary to assume
![]() $^{*}$
-continuity of KAD to obtain the result. Second, we show that
$^{*}$
-continuity of KAD to obtain the result. Second, we show that
![]() $\mathsf{KAD}$
has an equivalent implicational formulation,
$\mathsf{KAD}$
has an equivalent implicational formulation,
![]() $\mathsf{iKAD}$
, where the antidomain operator of
$\mathsf{iKAD}$
, where the antidomain operator of
![]() $\mathsf{KAD}$
is represented using an implication operator and the constant 0. This perspective on
$\mathsf{KAD}$
is represented using an implication operator and the constant 0. This perspective on
![]() $\mathsf{KAD}$
is useful from the viewpoint of the original motivation of Sedlár and Wannenburg (Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022) which was to describe the relation of
$\mathsf{KAD}$
is useful from the viewpoint of the original motivation of Sedlár and Wannenburg (Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022) which was to describe the relation of
![]() $\mathsf{S}$
and implicational extensions of Kleene algebra. Moreover, owing to the fact that
$\mathsf{S}$
and implicational extensions of Kleene algebra. Moreover, owing to the fact that
![]() $\mathsf{KAD}$
is decidable (EXPTIME-complete, as shown in Sedlár Reference Sedlár, Glück, Santocanale and Winter2023), we obtain a (perhaps rare) example of a decidable implicational extension of Kleene algebra.
$\mathsf{KAD}$
is decidable (EXPTIME-complete, as shown in Sedlár Reference Sedlár, Glück, Santocanale and Winter2023), we obtain a (perhaps rare) example of a decidable implicational extension of Kleene algebra.
The paper is organized as follows. Section 2 recalls
![]() $\mathsf{S}$
and discusses its relation to Groenendijk and Stokhof’s Dynamic Predicate Logic (DPL) (Groenendijk and Stokhof Reference Groenendijk and Stokhof1991) and Bochman and Gabbay’s Sequential Dynamic Logic (SDL) (Bochman and Gabbay Reference Bochman and Gabbay2012). Section 3 shows that
$\mathsf{S}$
and discusses its relation to Groenendijk and Stokhof’s Dynamic Predicate Logic (DPL) (Groenendijk and Stokhof Reference Groenendijk and Stokhof1991) and Bochman and Gabbay’s Sequential Dynamic Logic (SDL) (Bochman and Gabbay Reference Bochman and Gabbay2012). Section 3 shows that
![]() $\mathsf{S}$
embeds into the equational theory of
$\mathsf{S}$
embeds into the equational theory of
![]() $\mathsf{KAD}$
. Section 4 puts forward
$\mathsf{KAD}$
. Section 4 puts forward
![]() $\mathsf{iKAD}$
, the implicational formulation of
$\mathsf{iKAD}$
, the implicational formulation of
![]() $\mathsf{KAD}$
, and discusses the main differences between
$\mathsf{KAD}$
, and discusses the main differences between
![]() $\mathsf{iKAD}$
and the standard implicational extensions of Kleene algebra.
$\mathsf{iKAD}$
and the standard implicational extensions of Kleene algebra.
2.
 $\mathsf{\mathbf{KAT}}$
and
$\mathsf{\mathbf{KAT}}$
and
 $\mathsf{\mathbf{S}}$
$\mathsf{\mathbf{S}}$
In this section, we recall
![]() $\mathsf{KAT}$
(Section 2.1) and we outline Kozen and Tiuryn’s logic
$\mathsf{KAT}$
(Section 2.1) and we outline Kozen and Tiuryn’s logic
![]() $\mathsf{S}$
(Section 2.2). We observe a connection between
$\mathsf{S}$
(Section 2.2). We observe a connection between
![]() $\mathsf{S}$
and Groenendijk and Stokhof’s DPL in Section 2.3, and we note that
$\mathsf{S}$
and Groenendijk and Stokhof’s DPL in Section 2.3, and we note that
![]() $\mathsf{S}$
is a fragment of Bochman and Gabbay’s SDL in Section 2.4.
$\mathsf{S}$
is a fragment of Bochman and Gabbay’s SDL in Section 2.4.
2.1. Kleene algebra with tests
This section recalls some basic information about Kleene algebra with tests (Kozen Reference Kozen1997; Kozen and Smith Reference Kozen, Smith, van Dalen and Bezem1997). We assume that the reader is familiar with the notion of an idempotent semiring.
Definition 1. A Kleene algebra (Reference KozenKozen 1994a
) is an idempotent semiring
![]() $(K, +, \cdot, 0, 1)$
expanded with an operation
$(K, +, \cdot, 0, 1)$
expanded with an operation
![]() $^{*} : K \to K$
such that
$^{*} : K \to K$
such that
(We define
![]() $x \leq y$
as
$x \leq y$
as
![]() $x + y = y$
and we write xy instead of
$x + y = y$
and we write xy instead of
![]() $x \cdot y$
.)
$x \cdot y$
.)
It follows from the definition that
![]() $x^{*}$
is the least element z such that
$x^{*}$
is the least element z such that
![]() $1 \leq z$
,
$1 \leq z$
,
![]() $xz \leq z $
and
$xz \leq z $
and
![]() $zx \leq z$
. A standard example of a Kleene algebra is a relational Kleene algebra where K is a set of binary relations over some set S,
$zx \leq z$
. A standard example of a Kleene algebra is a relational Kleene algebra where K is a set of binary relations over some set S,
![]() $\cdot$
is relational composition,
$\cdot$
is relational composition,
![]() $+$
is set union,
$+$
is set union,
![]() $^{*}$
is reflexive transitive closure, 1 is the identity relation on S, and 0 is the empty set. Another standard example is the Kleene algebra of regular languages over a finite alphabet where
$^{*}$
is reflexive transitive closure, 1 is the identity relation on S, and 0 is the empty set. Another standard example is the Kleene algebra of regular languages over a finite alphabet where
![]() $\cdot$
is concatenation of languages and
$\cdot$
is concatenation of languages and
![]() $^{*}$
is finite iteration (Kleene star).
$^{*}$
is finite iteration (Kleene star).
Definition 2. A Kleene algebra with tests (Kozen Reference Kozen1997) is a structure of the form:
where
-
•
 $(K, +, \cdot,\,^{*}, 0, 1)$
is a Kleene algebra,
$(K, +, \cdot,\,^{*}, 0, 1)$
is a Kleene algebra, -
•
 $B \subseteq K$
, and
$B \subseteq K$
, and
 $(B, +, \cdot, \, \bar{ }\, , 0, 1) $
is a Boolean algebra.
$(B, +, \cdot, \, \bar{ }\, , 0, 1) $
is a Boolean algebra.
(That is, we assume that B is closed under the semiring operations; the negation operator
![]() $\,^{-}$
is a partial function defined only on B.)
$\,^{-}$
is a partial function defined only on B.)
Every Kleene algebra is a Kleene algebra with tests; take
![]() $B = \{ 0, 1 \}$
and define
$B = \{ 0, 1 \}$
and define
![]() $\bar{0} = 1$
,
$\bar{0} = 1$
,
![]() $\bar{1} = 0$
. A standard example of a Kleene algebra with tests is a relational Kleene algebra expanded with a Boolean subalgebra of the negative cone, that is, the elements
$\bar{1} = 0$
. A standard example of a Kleene algebra with tests is a relational Kleene algebra expanded with a Boolean subalgebra of the negative cone, that is, the elements
![]() $x \leq 1$
, also called subidentities, which in the relational case are subsets of the identity relation. The class of Kleene algebras with tests is denoted as
$x \leq 1$
, also called subidentities, which in the relational case are subsets of the identity relation. The class of Kleene algebras with tests is denoted as
![]() $\mathsf{KAT}$
.
$\mathsf{KAT}$
.
Kleene algebras with tests are able to represent while programs and facilitate equational reasoning about their properties such as partial correctness and equivalence:
-
•
 $\mathbf{skip} = 1$
$\mathbf{skip} = 1$
-
•
 $p\,{;}\,q = pq$
$p\,{;}\,q = pq$
-
•
 $\textbf{if}\: b \: \textbf{then} \: p \: \textbf{else}\: q$
$\textbf{if}\: b \: \textbf{then} \: p \: \textbf{else}\: q$
 $= (bp) +(\bar{b}q)$
$= (bp) +(\bar{b}q)$
-
•
 $\textbf{while}\: b\: \textbf{do}\: p$
$\textbf{while}\: b\: \textbf{do}\: p$
 $= (bp)^{*}\bar{b}$
$= (bp)^{*}\bar{b}$
-
•
 $\{ b \} \,p\, \{ c \}$
corresponds to
$\{ b \} \,p\, \{ c \}$
corresponds to
 $bp\bar{c} = 0$
(equivalently,
$bp\bar{c} = 0$
(equivalently,
 $bp = bpc$
)
$bp = bpc$
)
The reader is referred to Kozen (Reference Kozen1997) and references therein for more details.
2.2 Substructural logic of partial correctness
This section outlines the logic
![]() $\mathsf{S}$
(Kozen and Tiuryn Reference Kozen and Tiuryn2003). As with
$\mathsf{S}$
(Kozen and Tiuryn Reference Kozen and Tiuryn2003). As with
![]() $\mathsf{KAT}$
, the logic
$\mathsf{KAT}$
, the logic
![]() $\mathsf{S}$
is many-sorted. Let
$\mathsf{S}$
is many-sorted. Let
![]() $\mathsf{B} = \{ \mathtt{b}_i \mid i \in \omega \}$
be the set of test variables and let
$\mathsf{B} = \{ \mathtt{b}_i \mid i \in \omega \}$
be the set of test variables and let
![]() $\mathsf{P} = \{ \mathtt{p}_i \mid i \in \omega \}$
be the set of program variables. The language of
$\mathsf{P} = \{ \mathtt{p}_i \mid i \in \omega \}$
be the set of program variables. The language of
![]() $\mathsf{S}$
,
$\mathsf{S}$
,
![]() $\mathcal{L}_{\mathsf{S}}$
, consists of the following sorts of syntactic objects:
$\mathcal{L}_{\mathsf{S}}$
, consists of the following sorts of syntactic objects:
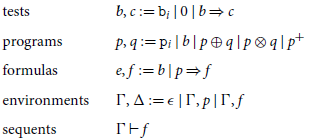
We define
![]() $1 := 0 \Rightarrow 0$
,
$1 := 0 \Rightarrow 0$
,
![]() $\neg b := b \Rightarrow 0$
and
$\neg b := b \Rightarrow 0$
and
![]() $p^{*} := 1 \oplus p^{+}$
. We will sometimes write pq instead of
$p^{*} := 1 \oplus p^{+}$
. We will sometimes write pq instead of
![]() $p \otimes q$
and
$p \otimes q$
and
![]() $\bar{b}$
instead of
$\bar{b}$
instead of
![]() $\neg b$
. Let
$\neg b$
. Let
![]() $\mathsf{E} = \mathsf{B} \cup \mathsf{P}$
and let
$\mathsf{E} = \mathsf{B} \cup \mathsf{P}$
and let
![]() $\mathcal{E}_{\mathsf{S}}$
, the set of
$\mathcal{E}_{\mathsf{S}}$
, the set of
![]() $\mathsf{S}$
-expressions, be the union of the sets of formulas, programs, and environments.
$\mathsf{S}$
-expressions, be the union of the sets of formulas, programs, and environments.
Kozen and Tiuryn (Reference Kozen and Tiuryn2003) introduce three kinds of semantics for their language: semantics based on guarded strings, traces, and binary relations, respectively. We will work only with binary relational semantics.
Definition 3. An
![]() $\mathsf{S}$
-model is a pair
$\mathsf{S}$
-model is a pair
![]() $M = (W, V)$
, where W is a non-empty set and
$M = (W, V)$
, where W is a non-empty set and
![]() $V: \mathsf{E} \to 2^{W \times W}$
such that
$V: \mathsf{E} \to 2^{W \times W}$
such that
![]() $V(\mathtt{b}) \subseteq \textrm{id}_{W}$
for all
$V(\mathtt{b}) \subseteq \textrm{id}_{W}$
for all
![]() $\mathtt{b} \in \mathsf{B}$
.
$\mathtt{b} \in \mathsf{B}$
.
For each
![]() $\mathsf{S}$
-model M, we define the M-interpretation function
$\mathsf{S}$
-model M, we define the M-interpretation function
![]() ${\texttt{[}} \, {\texttt{]}}_M : \mathcal{E}_{\mathsf{S}} \to 2^{W \times W}$
as follows:
${\texttt{[}} \, {\texttt{]}}_M : \mathcal{E}_{\mathsf{S}} \to 2^{W \times W}$
as follows:
-
•
 ${\texttt{[}} \mathtt{b} {\texttt{]}}_M = V(\mathtt{b})$
${\texttt{[}} \mathtt{b} {\texttt{]}}_M = V(\mathtt{b})$
-
•
 ${\texttt{[}} \mathtt{p} {\texttt{]}}_M = V(\mathtt{p})$
${\texttt{[}} \mathtt{p} {\texttt{]}}_M = V(\mathtt{p})$
-
•
 ${\texttt{[}} 0 {\texttt{]}}_M = \emptyset$
${\texttt{[}} 0 {\texttt{]}}_M = \emptyset$
-
•
 ${\texttt{[}} b \Rightarrow c {\texttt{]}}_M = \{ (s,s) \mid (s,s) \not\in {\texttt{[}} b {\texttt{]}}_M \text{ or } (s,s) \in {\texttt{[}} c {\texttt{]}}_M \}$
${\texttt{[}} b \Rightarrow c {\texttt{]}}_M = \{ (s,s) \mid (s,s) \not\in {\texttt{[}} b {\texttt{]}}_M \text{ or } (s,s) \in {\texttt{[}} c {\texttt{]}}_M \}$
-
•
 ${\texttt{[}} p \oplus q {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M \cup {\texttt{[}} q {\texttt{]}}_M$
${\texttt{[}} p \oplus q {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M \cup {\texttt{[}} q {\texttt{]}}_M$
-
•
 ${\texttt{[}} p \otimes q {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M \circ {\texttt{[}} q {\texttt{]}}_M$
${\texttt{[}} p \otimes q {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M \circ {\texttt{[}} q {\texttt{]}}_M$
-
•
 ${\texttt{[}} p^{+} {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M^{+}$
${\texttt{[}} p^{+} {\texttt{]}}_M = {\texttt{[}} p {\texttt{]}}_M^{+}$
-
•
 ${\texttt{[}} p \Rightarrow f {\texttt{]}}_M = \{ (s,s) \mid \forall t. (s,t) \in {\texttt{[}} p {\texttt{]}}_M \implies (t,t) \in {\texttt{[}} f {\texttt{]}}_M \}$
${\texttt{[}} p \Rightarrow f {\texttt{]}}_M = \{ (s,s) \mid \forall t. (s,t) \in {\texttt{[}} p {\texttt{]}}_M \implies (t,t) \in {\texttt{[}} f {\texttt{]}}_M \}$
-
•
 ${\texttt{[}} \varepsilon {\texttt{]}}_M = \textrm{id}_{W}$
${\texttt{[}} \varepsilon {\texttt{]}}_M = \textrm{id}_{W}$
-
•
 ${\texttt{[}} \Gamma, \Delta {\texttt{]}}_M = {\texttt{[}} \Gamma {\texttt{]}}_M \circ {\texttt{[}} \Delta {\texttt{]}}_M$
${\texttt{[}} \Gamma, \Delta {\texttt{]}}_M = {\texttt{[}} \Gamma {\texttt{]}}_M \circ {\texttt{[}} \Delta {\texttt{]}}_M$
(The symbol
![]() $^{+}$
denotes transitive closure and
$^{+}$
denotes transitive closure and
![]() $\circ$
denotes relational composition.) A sequent
$\circ$
denotes relational composition.) A sequent
![]() $\Gamma \vdash f$
is valid in M iff, for all
$\Gamma \vdash f$
is valid in M iff, for all
![]() $s,t \in W$
, if
$s,t \in W$
, if
![]() $(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
, then
$(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
, then
![]() $(t,t) \in {\texttt{[}} f {\texttt{]}}_M$
(notation:
$(t,t) \in {\texttt{[}} f {\texttt{]}}_M$
(notation:
![]() $\Gamma \vdash_M f$
).
$\Gamma \vdash_M f$
).
Observe that
![]() ${\texttt{[}} f {\texttt{]}}_M \subseteq \textrm{id}_W$
for all formulas f; if
${\texttt{[}} f {\texttt{]}}_M \subseteq \textrm{id}_W$
for all formulas f; if
![]() $(s,s) \in {\texttt{[}} f {\texttt{]}}_M$
, then we may say that formula f is true in s. Note that
$(s,s) \in {\texttt{[}} f {\texttt{]}}_M$
, then we may say that formula f is true in s. Note that
![]() ${\texttt{[}} bp \Rightarrow c {\texttt{]}}_M$
is the set of (s,s) such that, for all t, if
${\texttt{[}} bp \Rightarrow c {\texttt{]}}_M$
is the set of (s,s) such that, for all t, if
![]() $(s,s) \in {\texttt{[}} b {\texttt{]}}_M$
and
$(s,s) \in {\texttt{[}} b {\texttt{]}}_M$
and
![]() $(s,t) \in {\texttt{[}} p {\texttt{]}}_M$
, then
$(s,t) \in {\texttt{[}} p {\texttt{]}}_M$
, then
![]() $(t,t) \in {\texttt{[}} c {\texttt{]}}_M$
. Hence,
$(t,t) \in {\texttt{[}} c {\texttt{]}}_M$
. Hence,
![]() $bp \Rightarrow c$
represents a partial correctness assertion: the formula is true in s iff b is true in s and p connects s with a state t only if c is true in t.
$bp \Rightarrow c$
represents a partial correctness assertion: the formula is true in s iff b is true in s and p connects s with a state t only if c is true in t.
Fig. 1 shows the sequent proof system for
![]() $\mathsf{S}$
. A sequent
$\mathsf{S}$
. A sequent
![]() $\Gamma \vdash f$
is provable in
$\Gamma \vdash f$
is provable in
![]() $\mathsf{S}$
iff there is a finite sequence of sequents that ends with
$\mathsf{S}$
iff there is a finite sequence of sequents that ends with
![]() $\Gamma \vdash f$
each of which is either of the form (Id) or (I0) or is derived from previous sequents using some of the inference rules.
$\Gamma \vdash f$
each of which is either of the form (Id) or (I0) or is derived from previous sequents using some of the inference rules.

Figure 1: The sequent proof system for
![]() $\mathsf{S}$
.
$\mathsf{S}$
.
Theorem. (Kozen and Tiuryn Reference Kozen and Tiuryn2003).
![]() $\Gamma \vdash f$
is provable in
$\Gamma \vdash f$
is provable in
![]() $\mathsf{S}$
iff
$\mathsf{S}$
iff
![]() $\Gamma \vdash f$
is valid in all
$\Gamma \vdash f$
is valid in all
![]() $\mathsf{S}$
-models.
$\mathsf{S}$
-models.
It is evident from the semantics that
![]() $p \Rightarrow f$
corresponds to the (test of the) modal formula
$p \Rightarrow f$
corresponds to the (test of the) modal formula
![]() ${\texttt{[}} p {\texttt{]}}f$
of Propositional Dynamic Logic,
${\texttt{[}} p {\texttt{]}}f$
of Propositional Dynamic Logic,
![]() $\mathsf{PDL}$
(Fischer and Ladner Reference Fischer and Ladner1979; Harel et al. Reference Harel, Kozen and Tiuryn2000). Hence, each environment
$\mathsf{PDL}$
(Fischer and Ladner Reference Fischer and Ladner1979; Harel et al. Reference Harel, Kozen and Tiuryn2000). Hence, each environment
![]() $\Gamma$
corresponds to a program of
$\Gamma$
corresponds to a program of
![]() $\mathsf{PDL}$
and it can be shown that
$\mathsf{PDL}$
and it can be shown that
![]() $\Gamma \vdash f$
is provable in
$\Gamma \vdash f$
is provable in
![]() $\mathsf{S}$
iff
$\mathsf{S}$
iff
![]() ${\texttt{[}} \Gamma {\texttt{]}}f$
is valid in
${\texttt{[}} \Gamma {\texttt{]}}f$
is valid in
![]() $\mathsf{PDL}$
. Similarly,
$\mathsf{PDL}$
. Similarly,
![]() $ep \vdash f$
is provable in
$ep \vdash f$
is provable in
![]() $\mathsf{S}$
iff
$\mathsf{S}$
iff
![]() $e \to {\texttt{[}} p {\texttt{]}}f$
is valid in
$e \to {\texttt{[}} p {\texttt{]}}f$
is valid in
![]() $\mathsf{PDL}$
. The logic
$\mathsf{PDL}$
. The logic
![]() $\mathsf{S}$
is clearly a syntactic expansion of
$\mathsf{S}$
is clearly a syntactic expansion of
![]() $\mathsf{KAT}$
(modulo the choice of primitive operators). Kozen and Tiuryn (Reference Kozen and Tiuryn2003) show that
$\mathsf{KAT}$
(modulo the choice of primitive operators). Kozen and Tiuryn (Reference Kozen and Tiuryn2003) show that
![]() $\mathsf{KAT} \models p = q$
iff both
$\mathsf{KAT} \models p = q$
iff both
![]() $p \Rightarrow b \vdash q \Rightarrow b$
and
$p \Rightarrow b \vdash q \Rightarrow b$
and
![]() $q \Rightarrow b \vdash p \Rightarrow b$
are provable in
$q \Rightarrow b \vdash p \Rightarrow b$
are provable in
![]() $\mathsf{S}$
where b is a Boolean variable not occurring in p or q.
$\mathsf{S}$
where b is a Boolean variable not occurring in p or q.
![]() $\mathsf{S}$
can be seen as a substructural logic (Galatos et al. Reference Galatos, Jipsen, Kowalski and Ono2007; Restall Reference Restall2000). However,
$\mathsf{S}$
can be seen as a substructural logic (Galatos et al. Reference Galatos, Jipsen, Kowalski and Ono2007; Restall Reference Restall2000). However,
![]() $\mathsf{S}$
contains some rules that are unusual from the substructural logic perspective, namely, the sort-specific weakening rules (Wf) and (Wp), and the implication-formula rules (TC) and (I
$\mathsf{S}$
contains some rules that are unusual from the substructural logic perspective, namely, the sort-specific weakening rules (Wf) and (Wp), and the implication-formula rules (TC) and (I
![]() $\Rightarrow$
). It is therefore interesting to inquire how
$\Rightarrow$
). It is therefore interesting to inquire how
![]() $\mathsf{S}$
relates to mainstream substructural logics. Results of the next two sections will shed some light on the matter.
$\mathsf{S}$
relates to mainstream substructural logics. Results of the next two sections will shed some light on the matter.
2.3 Dynamic consequence and dynamic implication
It is clear from the previous section that
![]() $\mathsf{S}$
can be seen as an extension of
$\mathsf{S}$
can be seen as an extension of
![]() $\mathsf{KAT}$
that has two specific features. First,
$\mathsf{KAT}$
that has two specific features. First,
![]() $\mathsf{S}$
comes with a somewhat unusual notion of semantic entailment. In fact, the usual notion of entailment based on the subset relation would not make much sense in the present setting owing to the syntactic restriction on sequents allowing only formulas in the consequent. Second, the language of
$\mathsf{S}$
comes with a somewhat unusual notion of semantic entailment. In fact, the usual notion of entailment based on the subset relation would not make much sense in the present setting owing to the syntactic restriction on sequents allowing only formulas in the consequent. Second, the language of
![]() $\mathsf{S}$
contains an implication connective which differs semantically from the residuals of relational composition, as found in the relational semantics for Pratt’s action logic, for example. This is related to the first point since, as the reader can easily verify, the implication connective gives rise to the following semantic deduction theorem:
$\mathsf{S}$
contains an implication connective which differs semantically from the residuals of relational composition, as found in the relational semantics for Pratt’s action logic, for example. This is related to the first point since, as the reader can easily verify, the implication connective gives rise to the following semantic deduction theorem:
As a matter of fact, the entailment relation and the implication connective of
![]() $\mathsf{S}$
can be seen as restrictions of dynamic consequence and dynamic implication in
$\mathsf{S}$
can be seen as restrictions of dynamic consequence and dynamic implication in
![]() $\mathsf{DPL}$
(Groenendijk and Stokhof Reference Groenendijk and Stokhof1991). In
$\mathsf{DPL}$
(Groenendijk and Stokhof Reference Groenendijk and Stokhof1991). In
![]() $\mathsf{DPL}$
, formulas of the standard first-order language are evaluated on pairs of valuations on a relational structure. Without going into details, we just mention the operations on binary relations that give rise to semantic interpretations of dynamic negation
$\mathsf{DPL}$
, formulas of the standard first-order language are evaluated on pairs of valuations on a relational structure. Without going into details, we just mention the operations on binary relations that give rise to semantic interpretations of dynamic negation
![]() $\mathord{\sim}$
and dynamic implication
$\mathord{\sim}$
and dynamic implication
![]() $\to$
in models of
$\to$
in models of
![]() $\mathsf{DPL}$
:
$\mathsf{DPL}$
:
-
•
 $\mathord{\sim} R = \{ (s, s) \mid \neg \exists t. (s, t) \in R \}$
;
$\mathord{\sim} R = \{ (s, s) \mid \neg \exists t. (s, t) \in R \}$
; -
•
 $R \to Q = \{ (s,s) \mid \forall t. ((s, t) \in R \implies \exists u. (t, u) \in Q) \}$
.
$R \to Q = \{ (s,s) \mid \forall t. ((s, t) \in R \implies \exists u. (t, u) \in Q) \}$
.
Moreover, a formula
![]() $\varphi$
entails
$\varphi$
entails
![]() $\psi$
in
$\psi$
in
![]() $\mathsf{DPL}$
iff, for all models and all valuations s,t, if (s,t) is in the interpretation of
$\mathsf{DPL}$
iff, for all models and all valuations s,t, if (s,t) is in the interpretation of
![]() $\varphi$
, then there is u such that (t,u) is in the interpretation of
$\varphi$
, then there is u such that (t,u) is in the interpretation of
![]() $\psi$
. It is easily seen that
$\psi$
. It is easily seen that
![]() $R \to Q = \mathord{\sim} (R \circ \mathord{\sim} Q)$
, and this observation will be important later on in Section 4.
$R \to Q = \mathord{\sim} (R \circ \mathord{\sim} Q)$
, and this observation will be important later on in Section 4.
It is clear that
![]() $\mathsf{S}$
uses the same semantic clause for
$\mathsf{S}$
uses the same semantic clause for
![]() $\Rightarrow$
as
$\Rightarrow$
as
![]() $\mathsf{DPL}$
does for
$\mathsf{DPL}$
does for
![]() $\to$
with the proviso of the syntactic restriction on implicational formulas in
$\to$
with the proviso of the syntactic restriction on implicational formulas in
![]() $\mathsf{S}$
: the consequent of an implicational formula is always a formula, that is, an expression whose semantic value is a subset of the identity relation. A similar remark applies to the comparison between the notion of entailment in
$\mathsf{S}$
: the consequent of an implicational formula is always a formula, that is, an expression whose semantic value is a subset of the identity relation. A similar remark applies to the comparison between the notion of entailment in
![]() $\mathsf{S}$
and the one in
$\mathsf{S}$
and the one in
![]() $\mathsf{DPL}$
. This semantic observation entails that
$\mathsf{DPL}$
. This semantic observation entails that
![]() $\mathsf{S}$
can be seen as a fragment of a combination of relational Kleene algebra with tests with a propositional fragment of
$\mathsf{S}$
can be seen as a fragment of a combination of relational Kleene algebra with tests with a propositional fragment of
![]() $\mathsf{DPL}$
. Such a combination was studied by Bochman and Gabbay (Reference Bochman and Gabbay2012).
$\mathsf{DPL}$
. Such a combination was studied by Bochman and Gabbay (Reference Bochman and Gabbay2012).
2.4 Sequential Dynamic Logic
Bochman and Gabbay’s Sequential Dynamic Logic
![]() $\mathsf{SDL^*}$
(Bochman and Gabbay Reference Bochman and Gabbay2012) combines features of relational Kleene algebra with tests and the propositional fragment of
$\mathsf{SDL^*}$
(Bochman and Gabbay Reference Bochman and Gabbay2012) combines features of relational Kleene algebra with tests and the propositional fragment of
![]() $\mathsf{DPL}$
. In particular, it adds the dynamic negation connective
$\mathsf{DPL}$
. In particular, it adds the dynamic negation connective
![]() $\mathord{\sim}$
to
$\mathord{\sim}$
to
![]() $\mathsf{KAT}$
. Bochman and Gabbay provide a sound and weakly complete sequent system for dynamic entailment, and they observe that
$\mathsf{KAT}$
. Bochman and Gabbay provide a sound and weakly complete sequent system for dynamic entailment, and they observe that
![]() $\mathsf{SDL^*}$
bears strong resemblance to
$\mathsf{SDL^*}$
bears strong resemblance to
![]() $\mathsf{S}$
while lifting the syntactic restrictions of
$\mathsf{S}$
while lifting the syntactic restrictions of
![]() $\mathsf{S}$
. They leave a more thorough investigation of relations with
$\mathsf{S}$
. They leave a more thorough investigation of relations with
![]() $\mathsf{S}$
to another occasion. In this section, we formulate the semantics of
$\mathsf{S}$
to another occasion. In this section, we formulate the semantics of
![]() $\mathsf{SDL^*}$
and we make the straightforward observation that
$\mathsf{SDL^*}$
and we make the straightforward observation that
![]() $\mathsf{S}$
corresponds to a syntactic fragment of
$\mathsf{S}$
corresponds to a syntactic fragment of
![]() $\mathsf{SDL^*}$
.
$\mathsf{SDL^*}$
.
Formulas of the language of
![]() $\mathsf{SDL^*}$
are defined using the following grammar:
$\mathsf{SDL^*}$
are defined using the following grammar:
where
![]() $\mathtt{p} \in \mathsf{P}$
and
$\mathtt{p} \in \mathsf{P}$
and
![]() $\mathtt{b} \in \mathsf{B}$
.
$\mathtt{b} \in \mathsf{B}$
.
![]() $\mathsf{SDL^*}$
-sequents are expressions of the form
$\mathsf{SDL^*}$
-sequents are expressions of the form
![]() $\Gamma \vdash \varphi$
where
$\Gamma \vdash \varphi$
where
![]() $\Gamma$
is a finite sequence of
$\Gamma$
is a finite sequence of
![]() $\mathsf{SDL^*}$
-formulas and
$\mathsf{SDL^*}$
-formulas and
![]() $\varphi$
is a
$\varphi$
is a
![]() $\mathsf{SDL^*}$
-formula. (Bochman and Gabbay use
$\mathsf{SDL^*}$
-formula. (Bochman and Gabbay use
![]() $\land$
instead of
$\land$
instead of
![]() $\otimes$
and
$\otimes$
and
![]() $\lor$
instead of
$\lor$
instead of
![]() $\oplus$
. They do not use the constant 0; instead, their sequent system allows an empty conclusion.) Expressions of the language of
$\oplus$
. They do not use the constant 0; instead, their sequent system allows an empty conclusion.) Expressions of the language of
![]() $\mathsf{SDL^*}$
are finite sequences of
$\mathsf{SDL^*}$
are finite sequences of
![]() $\mathsf{SDL^*}$
-formulas.
$\mathsf{SDL^*}$
-formulas.
Definition 4. An
![]() $\mathsf{SDL^*}$
-model is a pair
$\mathsf{SDL^*}$
-model is a pair
![]() $M = (W, V)$
, where W is a non-empty set and
$M = (W, V)$
, where W is a non-empty set and
![]() $V: \mathsf{E} \to 2^{W \times W}$
such that
$V: \mathsf{E} \to 2^{W \times W}$
such that
![]() $V(\mathtt{b}) \subseteq \textrm{id}_{W}$
for all
$V(\mathtt{b}) \subseteq \textrm{id}_{W}$
for all
![]() $\mathtt{b} \in \mathsf{B}$
.
$\mathtt{b} \in \mathsf{B}$
.
For each
![]() $\mathsf{SDL^*}$
-model M, we define the M-interpretation function
$\mathsf{SDL^*}$
-model M, we define the M-interpretation function
![]() ${\texttt{[}} \, {\texttt{]}}_M : Fm_{\mathsf{SDL^*}} \to 2^{W \times W}$
as follows:
${\texttt{[}} \, {\texttt{]}}_M : Fm_{\mathsf{SDL^*}} \to 2^{W \times W}$
as follows:
-
•
 ${\texttt{[}} \mathtt{b} {\texttt{]}}_M = V(\mathtt{b})$
${\texttt{[}} \mathtt{b} {\texttt{]}}_M = V(\mathtt{b})$
-
•
 ${\texttt{[}} \mathtt{p} {\texttt{]}}_M = V(\mathtt{p})$
${\texttt{[}} \mathtt{p} {\texttt{]}}_M = V(\mathtt{p})$
-
•
 ${\texttt{[}} 0 {\texttt{]}}_M = \emptyset$
${\texttt{[}} 0 {\texttt{]}}_M = \emptyset$
-
•
 ${\texttt{[}} \varphi \oplus \psi {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}_M \cup {\texttt{[}} \psi {\texttt{]}}_M$
${\texttt{[}} \varphi \oplus \psi {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}_M \cup {\texttt{[}} \psi {\texttt{]}}_M$
-
•
 ${\texttt{[}} \varphi \otimes \psi {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}_M \circ {\texttt{[}} \psi {\texttt{]}}_M$
${\texttt{[}} \varphi \otimes \psi {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}_M \circ {\texttt{[}} \psi {\texttt{]}}_M$
-
•
 ${\texttt{[}} \varphi^{*} {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}^{*}_M$
${\texttt{[}} \varphi^{*} {\texttt{]}}_M = {\texttt{[}} \varphi {\texttt{]}}^{*}_M$
-
•
 ${\texttt{[}} \mathord{\sim} \varphi {\texttt{]}}_M = \{ (s, s) \mid \neg \exists t. (s, t) \in {\texttt{[}} \varphi {\texttt{]}}_M \}$
${\texttt{[}} \mathord{\sim} \varphi {\texttt{]}}_M = \{ (s, s) \mid \neg \exists t. (s, t) \in {\texttt{[}} \varphi {\texttt{]}}_M \}$
(where
![]() $R^{*}$
is the reflexive transitive closure of relation R). We define
$R^{*}$
is the reflexive transitive closure of relation R). We define
![]() ${\texttt{[}} \Gamma {\texttt{]}}_M := {\texttt{[}} \psi_1 {\texttt{]}}_M \circ \ldots \circ {\texttt{[}} \psi_n {\texttt{]}}_M$
in case
${\texttt{[}} \Gamma {\texttt{]}}_M := {\texttt{[}} \psi_1 {\texttt{]}}_M \circ \ldots \circ {\texttt{[}} \psi_n {\texttt{]}}_M$
in case
![]() $\Gamma = (\psi_1, \ldots, \psi_n)$
. If
$\Gamma = (\psi_1, \ldots, \psi_n)$
. If
![]() $\Gamma$
is empty, then
$\Gamma$
is empty, then
![]() ${\texttt{[}} \Gamma {\texttt{]}}_M = \textrm{id}_W$
. A sequent
${\texttt{[}} \Gamma {\texttt{]}}_M = \textrm{id}_W$
. A sequent
![]() $\Gamma \vdash \varphi$
is valid in M iff, for all
$\Gamma \vdash \varphi$
is valid in M iff, for all
![]() $s,t \in W$
, if
$s,t \in W$
, if
![]() $(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
, then there is u such that
$(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
, then there is u such that
![]() $(t,u) \in {\texttt{[}} \varphi {\texttt{]}}_M$
(notation:
$(t,u) \in {\texttt{[}} \varphi {\texttt{]}}_M$
(notation:
![]() $\Gamma \Vdash_M \varphi$
).
$\Gamma \Vdash_M \varphi$
).
Let
![]() $\delta : \mathcal{E}_{\mathsf{S}} \to \mathcal{E}_{\mathsf{SDL^*}}$
such that
$\delta : \mathcal{E}_{\mathsf{S}} \to \mathcal{E}_{\mathsf{SDL^*}}$
such that
![]() $\delta (\mathtt{p}) = \mathtt{p}$
,
$\delta (\mathtt{p}) = \mathtt{p}$
,
![]() $\delta(\mathtt{b}) = \mathtt{b}$
,
$\delta(\mathtt{b}) = \mathtt{b}$
,
![]() $\delta$
commutes with
$\delta$
commutes with
![]() $\oplus, \otimes$
and the environment-forming comma operator,
$\oplus, \otimes$
and the environment-forming comma operator,
![]() $\delta(p^{+}) = \delta (p) \otimes \delta (p)^{*}$
, and
$\delta(p^{+}) = \delta (p) \otimes \delta (p)^{*}$
, and
Proposition 5.
![]() $\Gamma \vdash f$
is provable in
$\Gamma \vdash f$
is provable in
![]() $\mathsf{S}$
iff
$\mathsf{S}$
iff
![]() $\delta (\Gamma) \Vdash_M \delta (f)$
for all
$\delta (\Gamma) \Vdash_M \delta (f)$
for all
![]() $\mathsf{SDL^*}$
-models M.
$\mathsf{SDL^*}$
-models M.
Proof. It is sufficient to observe that every
![]() $\mathsf{S}$
-model that is a counterexample to
$\mathsf{S}$
-model that is a counterexample to
![]() $\Gamma \vdash f$
can be turned into a
$\Gamma \vdash f$
can be turned into a
![]() $\mathsf{SDL^*}$
-model that is a counterexample to
$\mathsf{SDL^*}$
-model that is a counterexample to
![]() $\delta (\Gamma) \Vdash \delta (f)$
and vice versa. We only need to note that if
$\delta (\Gamma) \Vdash \delta (f)$
and vice versa. We only need to note that if
![]() $F \subseteq \textrm{id}_W$
, then
$F \subseteq \textrm{id}_W$
, then
Bochman and Gabbay provide a sound and weakly complete sequent system for dynamic consequence over
![]() $\mathsf{SDL^*}$
which bears strong resemblance to the sequent system for
$\mathsf{SDL^*}$
which bears strong resemblance to the sequent system for
![]() $\mathsf{S}$
and extends sequent systems for dynamic consequence over weaker languages studied earlier (Kanazawa Reference Kanazawa, Dekker and Stokhof1993; van Benthem 1995, Reference van Benthem1996; van der Does et al. Reference van der Does, Groeneveld and Veltman1997). We omit the details.
$\mathsf{S}$
and extends sequent systems for dynamic consequence over weaker languages studied earlier (Kanazawa Reference Kanazawa, Dekker and Stokhof1993; van Benthem 1995, Reference van Benthem1996; van der Does et al. Reference van der Does, Groeneveld and Veltman1997). We omit the details.
3. Embedding
 $\mathsf{\mathbf{S}}$
into
$\mathsf{\mathbf{S}}$
into
 $\mathsf{\mathbf{KAD}}$
$\mathsf{\mathbf{KAD}}$
In this section, we outline
![]() $\mathsf{KAD}$
(Section 3.1) and we prove that the set of
$\mathsf{KAD}$
(Section 3.1) and we prove that the set of
![]() $\mathsf{S}$
-provable sequents embeds into the equational theory of
$\mathsf{S}$
-provable sequents embeds into the equational theory of
![]() $\mathsf{KAD}$
(Section 3.2). We opt for a more instructive direct proof of the embedding result instead of proving the embedding via
$\mathsf{KAD}$
(Section 3.2). We opt for a more instructive direct proof of the embedding result instead of proving the embedding via
![]() $\mathsf{PDL}$
or
$\mathsf{PDL}$
or
![]() $\mathsf{SDL^*}$
.
$\mathsf{SDL^*}$
.
3.1 Kleene algebra with domain
In this section, we recall KAD. Our discussion will be brief, and the reader is referred to Desharnais et al. (Reference Desharnais, Möller and Struth2006) and Desharnais and Struth (Reference Desharnais and Struth2011) for details. We note that we assume the one-sorted version of KAD where the domain operator is defined using the primitive antidomain operator (Desharnais and Struth Reference Desharnais and Struth2011). An extension of
![]() $\mathsf{KAT}$
with a primitive domain operator (also called KAD at that time) is presented in Desharnais et al. (Reference Desharnais, Möller and Struth2006).
$\mathsf{KAT}$
with a primitive domain operator (also called KAD at that time) is presented in Desharnais et al. (Reference Desharnais, Möller and Struth2006).
The language of
![]() $\mathsf{KAD}$
,
$\mathsf{KAD}$
,
![]() $\mathcal{L}_{\mathsf{KAD}}$
, is one-sorted:
$\mathcal{L}_{\mathsf{KAD}}$
, is one-sorted:
We define
![]() $\mathsf{d}(p) := \mathsf{a} (\mathsf{a} (p))$
. A domain term is a term of the form
$\mathsf{d}(p) := \mathsf{a} (\mathsf{a} (p))$
. A domain term is a term of the form
![]() $\mathsf{d} (p)$
.
$\mathsf{d} (p)$
.
Kleene algebras with domain are expansions of Kleene algebras with a unary antidomain operator. The abstract definition below generalizes the properties of the dynamic negation operator on binary relations:
We note that, in the literature on KAD, the link between this “relational antidomain” operator and dynamic negation does not seem to have been noted yet. Relational antidomain has a natural interpretation independent of the linguistic motivations of
![]() $\mathsf{DPL}$
: if R is seen as the input–output relation determined by a program, then
$\mathsf{DPL}$
: if R is seen as the input–output relation determined by a program, then
![]() $\mathord{\sim} R$
is the input–output relation determined by the test whether the program diverges.
$\mathord{\sim} R$
is the input–output relation determined by the test whether the program diverges.
Definition 6. A KAD is a structure of the form
such that
![]() $(K, +, \cdot, \,^{*}, 0, 1)$
is a Kleene algebra,
$(K, +, \cdot, \,^{*}, 0, 1)$
is a Kleene algebra,
![]() $\mathsf{a} : K \to K$
and the following are satisfied for all
$\mathsf{a} : K \to K$
and the following are satisfied for all
![]() $x,y,z \in K$
, assuming that
$x,y,z \in K$
, assuming that
![]() $\mathsf{d} (x) := \mathsf{a} (\mathsf{a} (x))$
:
$\mathsf{d} (x) := \mathsf{a} (\mathsf{a} (x))$
:
An equation
![]() $p = q$
is valid in
$p = q$
is valid in
![]() $\mathbf{K}$
iff
$\mathbf{K}$
iff
![]() $v(p) = v(q)$
for all valuations v (that is, all homomorphisms from
$v(p) = v(q)$
for all valuations v (that is, all homomorphisms from
![]() $\mathcal{L}_{\mathsf{KAD}}$
into
$\mathcal{L}_{\mathsf{KAD}}$
into
![]() $\mathbf{K}$
).
$\mathbf{K}$
).
We will usually write
![]() $p \equiv_{\mathbf{K}} q$
to indicate that
$p \equiv_{\mathbf{K}} q$
to indicate that
![]() $p = q$
is valid in
$p = q$
is valid in
![]() $\mathbf{K}$
, and we will write
$\mathbf{K}$
, and we will write
![]() $p \equiv_{\mathsf{KAD}} q$
to indicate that the equation
$p \equiv_{\mathsf{KAD}} q$
to indicate that the equation
![]() $p = q$
belongs to the equational theory of
$p = q$
belongs to the equational theory of
![]() $\mathsf{KAD}$
(i.e. it is valid in every algebra belonging to
$\mathsf{KAD}$
(i.e. it is valid in every algebra belonging to
![]() $\mathsf{KAD}$
); the latter will often be shortened to
$\mathsf{KAD}$
); the latter will often be shortened to
![]() $p \equiv q$
if the class of algebras in question is clear from the context.
$p \equiv q$
if the class of algebras in question is clear from the context.
A standard example of a KAD is the Kleene algebra of binary relations over a set S extended with the dynamic negation operation
![]() $\mathord{\sim}$
. Note that the relational domain operation D defined by:
$\mathord{\sim}$
. Note that the relational domain operation D defined by:
is related to the projection operation familiar from relational databases. If R is seen as the input–output relation determined by a program, then D(R) is the input–output relation determined by the test whether the program halts. The Kleene algebra of regular languages over a finite alphabet
![]() $\Sigma$
can be extended to a KAD by adding
$\Sigma$
can be extended to a KAD by adding
![]() $\mathsf{a} : 2^{\Sigma^{*}} \to 2^{\Sigma^{*}}$
such that
$\mathsf{a} : 2^{\Sigma^{*}} \to 2^{\Sigma^{*}}$
such that
 \begin{align*}\mathsf{a} (L) & = \begin{cases}\{ \varepsilon \} & \text{if } L = \emptyset \\\emptyset & \text{otherwise.}\end{cases}\end{align*}
\begin{align*}\mathsf{a} (L) & = \begin{cases}\{ \varepsilon \} & \text{if } L = \emptyset \\\emptyset & \text{otherwise.}\end{cases}\end{align*}
The quasivariety of Kleene algebras with domain will be denoted as
![]() $\mathsf{KAD}$
. Not every Kleene algebra expands to a KAD (Desharnais and Struth Reference Desharnais and Struth2011), but the above example of a Kleene algebra of regular languages with domain shows that the equational theory of
$\mathsf{KAD}$
. Not every Kleene algebra expands to a KAD (Desharnais and Struth Reference Desharnais and Struth2011), but the above example of a Kleene algebra of regular languages with domain shows that the equational theory of
![]() $\mathsf{KAD}$
is a conservative extension of the equational theory of
$\mathsf{KAD}$
is a conservative extension of the equational theory of
![]() $\mathsf{KA}$
. The equational theory of
$\mathsf{KA}$
. The equational theory of
![]() $\mathsf{KAD}$
is EXPTIME-complete (Sedlár Reference Sedlár, Glück, Santocanale and Winter2023).
$\mathsf{KAD}$
is EXPTIME-complete (Sedlár Reference Sedlár, Glück, Santocanale and Winter2023).
A domain element of a KAD is an x such that
![]() $x = \mathsf{d} (y)$
for some y. In what follows, we indicate the assumption that a given x is a domain element by writing
$x = \mathsf{d} (y)$
for some y. In what follows, we indicate the assumption that a given x is a domain element by writing
![]() $\hat{x}$
. A similar notational convention is applied to domain terms.
$\hat{x}$
. A similar notational convention is applied to domain terms.
In the rest of the paper, we will often use the equalities stated in the following lemma without explicit mention.
Lemma 7. The following hold in each KAD:
-
(1)
 $\mathsf{a} (0) = 1$
and
$\mathsf{a} (0) = 1$
and
 $\mathsf{a} (1) = 0$
;
$\mathsf{a} (1) = 0$
; -
(2)
 $\mathsf{d}(0) = 0$
and
$\mathsf{d}(0) = 0$
and
 $\mathsf{d} (1) = 1$
;
$\mathsf{d} (1) = 1$
; -
(3)
 $\mathsf{d} \mathsf{a} (x) = \mathsf{a} (x)$
and
$\mathsf{d} \mathsf{a} (x) = \mathsf{a} (x)$
and
 $\mathsf{d} \mathsf{d} (x) = \mathsf{d} (x)$
;
$\mathsf{d} \mathsf{d} (x) = \mathsf{d} (x)$
; -
(4)
 $\mathsf{d} (x + y) = \mathsf{d} (x) + \mathsf{d} (y)$
;
$\mathsf{d} (x + y) = \mathsf{d} (x) + \mathsf{d} (y)$
; -
(5)
 $\mathsf{d} (x) \leq 1$
and
$\mathsf{d} (x) \leq 1$
and
 $\mathsf{a} (x) \leq 1$
;
$\mathsf{a} (x) \leq 1$
; -
(6)
 $\mathsf{a} (xy) = \mathsf{a} (x \cdot \mathsf{d} (y))$
;
$\mathsf{a} (xy) = \mathsf{a} (x \cdot \mathsf{d} (y))$
; -
(7)
 $x \leq y$
only if
$x \leq y$
only if
 $\mathsf{a} (y) \leq \mathsf{a} (x)$
;
$\mathsf{a} (y) \leq \mathsf{a} (x)$
; -
(8)
 $x = \mathsf{d} (x) x$
;
$x = \mathsf{d} (x) x$
; -
(9)
 $\mathsf{d} (x) = 0$
only if
$\mathsf{d} (x) = 0$
only if
 $x = 0$
;
$x = 0$
; -
(10)
 $x = x \hat{z}$
iff
$x = x \hat{z}$
iff
 $x \mathsf{a} (\hat{z}) = 0$
;
$x \mathsf{a} (\hat{z}) = 0$
; -
(11)
 $\hat{x}\hat{z} = \hat{z} \hat{x}$
;
$\hat{x}\hat{z} = \hat{z} \hat{x}$
;
Proof. These are well-known facts about
![]() $\mathsf{KAD}$
; see Desharnais and Struth (Reference Desharnais and Struth2011). Some items are proven explicitly in the appendix.
$\mathsf{KAD}$
; see Desharnais and Struth (Reference Desharnais and Struth2011). Some items are proven explicitly in the appendix.
Definition 8. For all
![]() $\mathbf{K}$
, we define
$\mathbf{K}$
, we define
![]() $x \trianglelefteq y $
as
$x \trianglelefteq y $
as
![]() $x = xy$
. We will write
$x = xy$
. We will write
![]() $p \trianglelefteq_{\mathsf{KAD}} q$
instead of
$p \trianglelefteq_{\mathsf{KAD}} q$
instead of
![]() $p \equiv_{\mathsf{KAD}} pq$
.
$p \equiv_{\mathsf{KAD}} pq$
.
The relation
![]() $\trianglelefteq$
is a generalization of the consequence relation of
$\trianglelefteq$
is a generalization of the consequence relation of
![]() $\mathsf{S}$
(which corresponds to the case where y is a domain element), but it does not coincide with dynamic consequence. The latter corresponds to
$\mathsf{S}$
(which corresponds to the case where y is a domain element), but it does not coincide with dynamic consequence. The latter corresponds to
![]() $x \trianglelefteq \mathsf{d} (y)$
. Note that
$x \trianglelefteq \mathsf{d} (y)$
. Note that
![]() $\trianglelefteq$
is a transitive relation and it coincides with
$\trianglelefteq$
is a transitive relation and it coincides with
![]() $\leq$
on domain elements. The following lemma states some of its further useful properties.
$\leq$
on domain elements. The following lemma states some of its further useful properties.
Lemma 9. The following hold in all
![]() $\mathbf{K}$
:
$\mathbf{K}$
:
-
(1) if
 $x \leq y$
and
$x \leq y$
and
 $\hat{z} \leq \hat{u}$
, then
$\hat{z} \leq \hat{u}$
, then
 $y \trianglelefteq \hat{z}$
only if
$y \trianglelefteq \hat{z}$
only if
 $x \trianglelefteq \hat{u}$
;
$x \trianglelefteq \hat{u}$
; -
(2) if
 $x \trianglelefteq z$
and
$x \trianglelefteq z$
and
 $y \trianglelefteq z$
, then
$y \trianglelefteq z$
, then
 $x + y \trianglelefteq z$
;
$x + y \trianglelefteq z$
;
Proof. (1) If
![]() $y = y \hat{z}$
, then
$y = y \hat{z}$
, then
![]() $\mathsf{d} (y \cdot \mathsf{a} (\hat{z})) = 0$
and so
$\mathsf{d} (y \cdot \mathsf{a} (\hat{z})) = 0$
and so
![]() $\mathsf{d} (x \cdot \mathsf{a} (\hat{u})) = 0$
since
$\mathsf{d} (x \cdot \mathsf{a} (\hat{u})) = 0$
since
![]() $x \leq z$
and
$x \leq z$
and
![]() $\hat{z} \leq \hat{u}$
. (2) If
$\hat{z} \leq \hat{u}$
. (2) If
![]() $x = xz$
and
$x = xz$
and
![]() $y = yz$
, then
$y = yz$
, then
![]() $x + y = xz + yz = (x+y)z$
.
$x + y = xz + yz = (x+y)z$
.
3.2 Embedding
 $\mathsf{\mathbf{S}}$
into Kleene algebra with domain
$\mathsf{\mathbf{S}}$
into Kleene algebra with domain
In this section, we define a translation function Tr from the language of
![]() $\mathsf{S}$
into the language of
$\mathsf{S}$
into the language of
![]() $\mathsf{KAD}$
and we show that it embeds the set of sequents provable in
$\mathsf{KAD}$
and we show that it embeds the set of sequents provable in
![]() $\mathsf{S}$
into the equational theory of
$\mathsf{S}$
into the equational theory of
![]() $\mathsf{KAD}$
.
$\mathsf{KAD}$
.
Definition 10. Let
![]() $Tr : \mathcal{E}_{\mathsf{S}} \to \mathcal{L}_{\mathsf{KAD}}$
be defined as follows:
$Tr : \mathcal{E}_{\mathsf{S}} \to \mathcal{L}_{\mathsf{KAD}}$
be defined as follows:
-
•
 $Tr (\mathtt{p}_n) = \mathtt{p}_{2n}$
$Tr (\mathtt{p}_n) = \mathtt{p}_{2n}$
-
•
 $Tr (\mathtt{b}_n) = \mathsf{d} (\mathtt{p}_{2n+1})$
$Tr (\mathtt{b}_n) = \mathsf{d} (\mathtt{p}_{2n+1})$
-
•
 $Tr (p \Rightarrow f) = \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr (f)))$
$Tr (p \Rightarrow f) = \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr (f)))$
-
•
 $Tr (p \oplus q) = Tr (p) + Tr (q)$
$Tr (p \oplus q) = Tr (p) + Tr (q)$
-
•
 $Tr (p \otimes q) = Tr (p) \cdot Tr (q)$
$Tr (p \otimes q) = Tr (p) \cdot Tr (q)$
-
•
 $Tr (p^{+}) = Tr (p) \cdot Tr (p)^{*}$
$Tr (p^{+}) = Tr (p) \cdot Tr (p)^{*}$
-
•
 $Tr (\epsilon) = 1$
$Tr (\epsilon) = 1$
-
•
 $Tr (\Gamma, \Delta) = Tr (\Gamma) \cdot Tr (\Delta)$
$Tr (\Gamma, \Delta) = Tr (\Gamma) \cdot Tr (\Delta)$
It is easily verified that, for each formula
![]() $f \in \mathcal{E}_{\mathsf{S}}$
, the term Tr (f) is equivalent to a domain term; see Lemma 15 in the appendix. Moreover, note that
$f \in \mathcal{E}_{\mathsf{S}}$
, the term Tr (f) is equivalent to a domain term; see Lemma 15 in the appendix. Moreover, note that
![]() $Tr (\bar{b}) = Tr (b \Rightarrow 0) = \mathsf{a} ( Tr (b) \cdot \mathsf{a} (0))$
is equivalent to
$Tr (\bar{b}) = Tr (b \Rightarrow 0) = \mathsf{a} ( Tr (b) \cdot \mathsf{a} (0))$
is equivalent to
![]() $\mathsf{a} (Tr (b))$
.
$\mathsf{a} (Tr (b))$
.
Theorem. For all
![]() $\Gamma, f \in \mathcal{E}_{\mathsf{S}}$
,
$\Gamma, f \in \mathcal{E}_{\mathsf{S}}$
,
Proof. To establish the implication from right to left, let us assume that
![]() $\Gamma \vdash f$
is not provable in
$\Gamma \vdash f$
is not provable in
![]() $\mathsf{S}$
. By Theorem 2.2, there is an
$\mathsf{S}$
. By Theorem 2.2, there is an
![]() $\mathsf{S}$
-model
$\mathsf{S}$
-model
![]() $M = (W, V)$
and states
$M = (W, V)$
and states
![]() $s,t \in W$
such that
$s,t \in W$
such that
![]() $(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
but
$(s,t) \in {\texttt{[}} \Gamma {\texttt{]}}_M$
but
![]() $(t,t) \not\in {\texttt{[}} f {\texttt{]}}_M$
. Equivalently,
$(t,t) \not\in {\texttt{[}} f {\texttt{]}}_M$
. Equivalently,
Define
![]() $\mathbf{K}$
as the KAD over the set of all binary relations on W, and let
$\mathbf{K}$
as the KAD over the set of all binary relations on W, and let
![]() ${\texttt{[}}\!{\texttt{[}} \, {\texttt{]}}\!{\texttt{]}}$
be the unique valuation on
${\texttt{[}}\!{\texttt{[}} \, {\texttt{]}}\!{\texttt{]}}$
be the unique valuation on
![]() $\mathbf{K}$
such that, for all
$\mathbf{K}$
such that, for all
![]() $n \in \omega$
,
$n \in \omega$
,
-
•
 ${\texttt{[}}\!{\texttt{[}} \mathtt{p}_{2n} {\texttt{]}}\!{\texttt{]}} = {\texttt{[}} \mathtt{p}_n {\texttt{]}}_M$
, and
${\texttt{[}}\!{\texttt{[}} \mathtt{p}_{2n} {\texttt{]}}\!{\texttt{]}} = {\texttt{[}} \mathtt{p}_n {\texttt{]}}_M$
, and -
•
 ${\texttt{[}}\!{\texttt{[}} \mathtt{p}_{2n+1} {\texttt{]}}\!{\texttt{]}} = {\texttt{[}} \mathtt{b}_n {\texttt{]}}_M$
.
${\texttt{[}}\!{\texttt{[}} \mathtt{p}_{2n+1} {\texttt{]}}\!{\texttt{]}} = {\texttt{[}} \mathtt{b}_n {\texttt{]}}_M$
.
It can be shown by induction on the complexity of expressions
![]() $\chi \in \mathcal{E}_{\mathsf{S}}$
that
$\chi \in \mathcal{E}_{\mathsf{S}}$
that
The base case for
![]() $\mathtt{p}_n$
holds by definition and the base case for
$\mathtt{p}_n$
holds by definition and the base case for
![]() $\mathtt{b}_n$
is established by noting that
$\mathtt{b}_n$
is established by noting that
![]() ${\texttt{[}} \mathtt{b}_n {\texttt{]}}_M = D ({\texttt{[}} \mathtt{b}_n {\texttt{]}}_M)$
since
${\texttt{[}} \mathtt{b}_n {\texttt{]}}_M = D ({\texttt{[}} \mathtt{b}_n {\texttt{]}}_M)$
since
![]() ${\texttt{[}} \mathtt{b}_n {\texttt{]}}_M \subseteq \textrm{id}_W$
, and
${\texttt{[}} \mathtt{b}_n {\texttt{]}}_M \subseteq \textrm{id}_W$
, and
![]() $D ({\texttt{[}} \mathtt{b}_n {\texttt{]}}_M) = {\texttt{[}}\!{\texttt{[}} \mathsf{d} (\mathtt{p}_{2n+1}) {\texttt{]}}\!{\texttt{]}}$
. The induction step is uneventful, perhaps with the following exception:
$D ({\texttt{[}} \mathtt{b}_n {\texttt{]}}_M) = {\texttt{[}}\!{\texttt{[}} \mathsf{d} (\mathtt{p}_{2n+1}) {\texttt{]}}\!{\texttt{]}}$
. The induction step is uneventful, perhaps with the following exception:
 \begin{align*}{\texttt{[}} p \Rightarrow f {\texttt{]}}_M & = \mathord{\sim} ({\texttt{[}} p {\texttt{]}}_M \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}_M)\\& = \mathord{\sim} ({\texttt{[}}\!{\texttt{[}} Tr (p) {\texttt{]}}\!{\texttt{]}} \circ \mathord{\sim} {\texttt{[}}\!{\texttt{[}} Tr (f) {\texttt{]}}\!{\texttt{]}})\\& = {\texttt{[}}\!{\texttt{[}} \mathsf{a} ( Tr (p) \cdot \mathsf{a} (Tr (f))) {\texttt{]}}\!{\texttt{]}}\\& = {\texttt{[}}\!{\texttt{[}} Tr (p \Rightarrow f) {\texttt{]}}\!{\texttt{]}} \, .\end{align*}
\begin{align*}{\texttt{[}} p \Rightarrow f {\texttt{]}}_M & = \mathord{\sim} ({\texttt{[}} p {\texttt{]}}_M \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}_M)\\& = \mathord{\sim} ({\texttt{[}}\!{\texttt{[}} Tr (p) {\texttt{]}}\!{\texttt{]}} \circ \mathord{\sim} {\texttt{[}}\!{\texttt{[}} Tr (f) {\texttt{]}}\!{\texttt{]}})\\& = {\texttt{[}}\!{\texttt{[}} \mathsf{a} ( Tr (p) \cdot \mathsf{a} (Tr (f))) {\texttt{]}}\!{\texttt{]}}\\& = {\texttt{[}}\!{\texttt{[}} Tr (p \Rightarrow f) {\texttt{]}}\!{\texttt{]}} \, .\end{align*}
(For a more detailed justification, see Lemma 16 in the appendix.) It follows that
Hence,
![]() $Tr (\Gamma)$
is not equivalent to
$Tr (\Gamma)$
is not equivalent to
![]() $Tr(\Gamma) \cdot Tr (f) $
in
$Tr(\Gamma) \cdot Tr (f) $
in
![]() $\mathsf{KAD}$
.
$\mathsf{KAD}$
.
The converse implication is established by induction on the length of proofs. Most of the cases of the inductive proof use only Kleene algebra; here, we prove the cases of the induction step containing implication. (The proof is carried out in more detail in the appendix; see Lemma 17.)
To establish the case corresponding to (TC), it is sufficient to show that
This is established using Lemma 9(2). The assumptions entail that
![]() $x \hat{u} y + x \mathsf{a}(\hat{u}) y \trianglelefteq \hat{z}$
, but
$x \hat{u} y + x \mathsf{a}(\hat{u}) y \trianglelefteq \hat{z}$
, but
To establish the case corresponding to (R
![]() $\Rightarrow$
), it is sufficient to show that
$\Rightarrow$
), it is sufficient to show that
If
![]() $xy = xy \hat{u}$
, then the following holds. First,
$xy = xy \hat{u}$
, then the following holds. First,
 \begin{align*}\mathsf{d} (x \mathsf{d} (y \mathsf{a} (\hat{u}))) & = \mathsf{d} (xy \mathsf{a} (\hat{u}))\\& = \mathsf{d} (xy\hat{u} \mathsf{a} (\hat{u}))\\& = 0 \, ,\end{align*}
\begin{align*}\mathsf{d} (x \mathsf{d} (y \mathsf{a} (\hat{u}))) & = \mathsf{d} (xy \mathsf{a} (\hat{u}))\\& = \mathsf{d} (xy\hat{u} \mathsf{a} (\hat{u}))\\& = 0 \, ,\end{align*}
and so
![]() $x \mathsf{d} (y \mathsf{a} (\hat{u})) = 0$
. Second,
$x \mathsf{d} (y \mathsf{a} (\hat{u})) = 0$
. Second,
 \begin{align*}x &= x \mathsf{d} (y \mathsf{a} (\hat{u})) + x \mathsf{a} (y \mathsf{a} (\hat{u}))\\& = 0 + x \mathsf{a} (y \mathsf{a} (\hat{u}))\\& = x \mathsf{a} (y \mathsf{a} (\hat{u})) \, .\end{align*}
\begin{align*}x &= x \mathsf{d} (y \mathsf{a} (\hat{u})) + x \mathsf{a} (y \mathsf{a} (\hat{u}))\\& = 0 + x \mathsf{a} (y \mathsf{a} (\hat{u}))\\& = x \mathsf{a} (y \mathsf{a} (\hat{u})) \, .\end{align*}
To establish (I
![]() $\Rightarrow$
), it is sufficient to show that
$\Rightarrow$
), it is sufficient to show that
(The desired result is then obtained using Lemma 9(1).) We reason as follows:
 \begin{align*}\mathsf{a} (x \mathsf{a} (\hat{z})) x & = \mathsf{a} (x \mathsf{a} (\hat{z})) (x \hat{z} + x \mathsf{a} (\hat{z}))\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z} + \mathsf{a} (x \mathsf{a} (\hat{z})) x \mathsf{a} (\hat{z})\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z} + 0\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z}\\& \leq x \hat{z}\end{align*}
\begin{align*}\mathsf{a} (x \mathsf{a} (\hat{z})) x & = \mathsf{a} (x \mathsf{a} (\hat{z})) (x \hat{z} + x \mathsf{a} (\hat{z}))\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z} + \mathsf{a} (x \mathsf{a} (\hat{z})) x \mathsf{a} (\hat{z})\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z} + 0\\& = \mathsf{a} (x \mathsf{a} (\hat{z})) x \hat{z}\\& \leq x \hat{z}\end{align*}
This (together with the other cases discussed in the appendix) concludes the proof of Theorem 3.2.
We note that essentially the same technique can be used to show that
![]() $\mathsf{SDL^{*}}$
embeds into
$\mathsf{SDL^{*}}$
embeds into
![]() $\mathsf{KAD}$
in the sense that
$\mathsf{KAD}$
in the sense that
![]() $\Gamma \vdash \varphi$
is valid in all
$\Gamma \vdash \varphi$
is valid in all
![]() $\mathsf{SDL^{*}}$
-models M iff
$\mathsf{SDL^{*}}$
-models M iff
![]() $\lambda (\Gamma) \trianglelefteq \mathsf{d} (\lambda(\varphi))$
is valid in
$\lambda (\Gamma) \trianglelefteq \mathsf{d} (\lambda(\varphi))$
is valid in
![]() $\mathsf{KAD}$
for a translation
$\mathsf{KAD}$
for a translation
![]() $\lambda$
that sends
$\lambda$
that sends
![]() $\mathtt{p}_n$
to
$\mathtt{p}_n$
to
![]() $\mathtt{p}_{2n}$
and
$\mathtt{p}_{2n}$
and
![]() $\mathtt{b}_n$
to
$\mathtt{b}_n$
to
![]() $\mathsf{d} (\mathtt{p}_{2n+1})$
.
$\mathsf{d} (\mathtt{p}_{2n+1})$
.
4. Implicational Kleene Algebra with Domain
In this section, we return to the main question of Sedlár and Wannenburg (Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022), namely the question of how
![]() $\mathsf{S}$
relates to substructural logics based on implicational expansions of Kleene algebra. We observe that
$\mathsf{S}$
relates to substructural logics based on implicational expansions of Kleene algebra. We observe that
![]() $\mathsf{KAD}$
itself can be seen as an implicational expansion of Kleene algebra. In particular, we introduce an extension of Kleene algebra with an implication operator which we call implicational Kleene algebra with domain,
$\mathsf{KAD}$
itself can be seen as an implicational expansion of Kleene algebra. In particular, we introduce an extension of Kleene algebra with an implication operator which we call implicational Kleene algebra with domain,
![]() $\mathsf{iKAD}$
, and we establish a mutual embedding between the equational theories of
$\mathsf{iKAD}$
, and we establish a mutual embedding between the equational theories of
![]() $\mathsf{KAD}$
and
$\mathsf{KAD}$
and
![]() $\mathsf{iKAD}$
. This mutual embedding is inspired by the mutual intertranslatability of
$\mathsf{iKAD}$
. This mutual embedding is inspired by the mutual intertranslatability of
![]() $\mathord{\sim}$
and
$\mathord{\sim}$
and
![]() $\to$
in
$\to$
in
![]() $\mathsf{DPL}$
. We discuss the similarities and differences between
$\mathsf{DPL}$
. We discuss the similarities and differences between
![]() $\mathsf{iKAD}$
and other implicational extensions of Kleene algebra (such as Pratt’s 1991 action logic).
$\mathsf{iKAD}$
and other implicational extensions of Kleene algebra (such as Pratt’s 1991 action logic).
4.1 Kleene algebra with dynamic implication
We observed in the previous section that
![]() $\mathsf{a} (x \cdot \mathsf{a} (\hat{z}))$
behaves like Kozen and Tiuryn’s implication
$\mathsf{a} (x \cdot \mathsf{a} (\hat{z}))$
behaves like Kozen and Tiuryn’s implication
![]() $x \Rightarrow \hat{z}$
. From this point of view,
$x \Rightarrow \hat{z}$
. From this point of view,
![]() $\mathsf{a} (x)$
is equivalent to “x implies 0”, that is, to
$\mathsf{a} (x)$
is equivalent to “x implies 0”, that is, to
![]() $\mathsf{a} (x \cdot \mathsf{a} (0))$
. This motivates the following question: Can we capture antidomain in terms of a primitive implication operator?
$\mathsf{a} (x \cdot \mathsf{a} (0))$
. This motivates the following question: Can we capture antidomain in terms of a primitive implication operator?
Definition 11. An iKAD is an algebra of the form:
where
![]() $(K, +, \cdot, \,^{*}, 0, 1)$
is a Kleene algebra and
$(K, +, \cdot, \,^{*}, 0, 1)$
is a Kleene algebra and
![]() $\to$
is a binary operation satisfying the following axioms:
$\to$
is a binary operation satisfying the following axioms:
We define
![]() $\mathord{\sim} x := x \to 0$
.
$\mathord{\sim} x := x \to 0$
.
The guiding example of an iKAD is a relational Kleene algebra with the dynamic implication operation of
![]() $\mathsf{DPL}$
, namely,
$\mathsf{DPL}$
, namely,
Dynamic implication expresses a test of the following liveness property: the program represented by Q has a terminating execution starting in any final state of a terminating execution of the program represented by R (we can always continue with Q after R, as put by Hollenberg Reference Hollenberg1997). In the particular instance where Q is a test, this means that Q holds after every terminating execution of R (partial correctness). Note that
![]() $R \to \emptyset$
boils down to dynamic negation of R.
$R \to \emptyset$
boils down to dynamic negation of R.
A domain element (term) is an element of the form
![]() $\mathord{\sim} \mathord{\sim} x$
(p instead of x). As before, we use the notation
$\mathord{\sim} \mathord{\sim} x$
(p instead of x). As before, we use the notation
![]() $\hat{x}$
(
$\hat{x}$
(
![]() $\hat{p}$
) to indicate that the element x (term p) is a domain element (term).
$\hat{p}$
) to indicate that the element x (term p) is a domain element (term).
Pratt’s action logic (Pratt Reference Pratt1991) is a well-known implicational extension of Kleene algebra which was studied intensively in the recent decades (Buszkowski Reference Buszkowski2006; Jipsen Reference Jipsen2004; Reference KozenKozen 1994b
; Kuznetsov Reference Kuznetsov2021; Palka Reference Palka2007). Action logic is based on residuated Kleene algebras, adding to Kleene algebras a pair of binary operations
![]() $\multimap$
and
$\multimap$
and ![]() such that
such that
As axiom (10) shows, an “axiom version” of residuation holds for
![]() $\to$
in
$\to$
in
![]() $\mathsf{iKAD}$
, bringing
$\mathsf{iKAD}$
, bringing
![]() $\to$
close to the
$\to$
close to the ![]() operator of action logic. However, it can be shown that
operator of action logic. However, it can be shown that
![]() $\to$
does not residuate with
$\to$
does not residuate with
![]() $\cdot$
. In particular, a counterexample to
$\cdot$
. In particular, a counterexample to
is a three-element Kleene algebra consisting of the linearly ordered set of elements
![]() $0 < 1 < 2$
where
$0 < 1 < 2$
where
![]() $\cdot$
is commutative and
$\cdot$
is commutative and
![]() $x \cdot 2 = 2 $
in case
$x \cdot 2 = 2 $
in case
![]() $x \neq 0$
,
$x \neq 0$
,
![]() $2^{*} = 2$
and where the following table characterizes
$2^{*} = 2$
and where the following table characterizes
![]() $\to$
:
$\to$
:
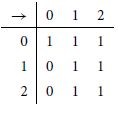
It is clear that
![]() $2 \cdot 0 \leq 0$
, but not
$2 \cdot 0 \leq 0$
, but not
![]() $2 \leq 0 \to 0$
. A similar counterexample to the converse of (13) exists. In general, it is clear that (13) should fail since
$2 \leq 0 \to 0$
. A similar counterexample to the converse of (13) exists. In general, it is clear that (13) should fail since
![]() $y \to z \leq 1$
for all y,z. We leave a more thorough comparison of iKAD and residuated Kleene algebras to another occasion.
$y \to z \leq 1$
for all y,z. We leave a more thorough comparison of iKAD and residuated Kleene algebras to another occasion.
4.2
 $\mathsf{KAD}$
and
$\mathsf{KAD}$
and
 $\mathsf{iKAD}$
$\mathsf{iKAD}$
In this section, we show that
![]() $\mathsf{KAD}$
and
$\mathsf{KAD}$
and
![]() $\mathsf{iKAD}$
are equivalent in the sense that the equational theory of one embeds into the equational theory of the other. A corollary of this result is that the equational theory of
$\mathsf{iKAD}$
are equivalent in the sense that the equational theory of one embeds into the equational theory of the other. A corollary of this result is that the equational theory of
![]() $\mathsf{iKAD}$
is decidable (EXPTIME-complete by Sedlár Reference Sedlár, Glück, Santocanale and Winter2023). This is an interesting contrast to residuated Kleene algebras (Pratt’s action logic).
$\mathsf{iKAD}$
is decidable (EXPTIME-complete by Sedlár Reference Sedlár, Glück, Santocanale and Winter2023). This is an interesting contrast to residuated Kleene algebras (Pratt’s action logic).
Definition 12. Let
![]() $\tau : \mathcal{L}_{\mathsf{KAD}} \to \mathcal{L}_{\mathsf{iKAD}}$
such that
$\tau : \mathcal{L}_{\mathsf{KAD}} \to \mathcal{L}_{\mathsf{iKAD}}$
such that
-
•
 $\tau (\mathtt{p}) = \mathtt{p}$
for all
$\tau (\mathtt{p}) = \mathtt{p}$
for all
 $\mathtt{p} \in \mathsf{P}$
;
$\mathtt{p} \in \mathsf{P}$
; -
•
 $\tau$
commutes with the Kleene algebra operators;
$\tau$
commutes with the Kleene algebra operators; -
•
 $\tau (\mathsf{a} (p)) = \tau (p) \to 0$
.
$\tau (\mathsf{a} (p)) = \tau (p) \to 0$
.
Let
![]() $\sigma : \mathcal{L}_{\mathsf{iKAD}} \to \mathcal{L}_{\mathsf{KAD}}$
such that
$\sigma : \mathcal{L}_{\mathsf{iKAD}} \to \mathcal{L}_{\mathsf{KAD}}$
such that
-
•
 $\sigma (\mathtt{p}) = \mathtt{p}$
for all
$\sigma (\mathtt{p}) = \mathtt{p}$
for all
 $\mathtt{p} \in \mathsf{P}$
;
$\mathtt{p} \in \mathsf{P}$
; -
•
 $\sigma$
commutes with the Kleene algebra operators;
$\sigma$
commutes with the Kleene algebra operators; -
•
 $\sigma (p \to q) = \mathsf{a} (\sigma (p) \cdot \mathsf{a} (\sigma (q)))$
.
$\sigma (p \to q) = \mathsf{a} (\sigma (p) \cdot \mathsf{a} (\sigma (q)))$
.
Lemma 13. The following hold:
-
(1)
 $\mathsf{KAD} \models p = q$
implies
$\mathsf{KAD} \models p = q$
implies
 $\mathsf{iKAD} \models \tau(p) = \tau(q)$
;
$\mathsf{iKAD} \models \tau(p) = \tau(q)$
; -
(2)
 $\mathsf{iKAD} \models p = q$
implies
$\mathsf{iKAD} \models p = q$
implies
 $\mathsf{KAD} \models \sigma(p) = \sigma(q)$
;
$\mathsf{KAD} \models \sigma(p) = \sigma(q)$
; -
(3)
 $\mathsf{KAD} \models p = \sigma(\tau(p))$
;
$\mathsf{KAD} \models p = \sigma(\tau(p))$
; -
(4)
 $\mathsf{iKAD} \models p = \tau(\sigma(p))$
.
$\mathsf{iKAD} \models p = \tau(\sigma(p))$
.
Proof. To prove the first item, it is sufficient to show that the translations of the antidomain axioms of
![]() $\mathsf{KAD}$
are valid in
$\mathsf{KAD}$
are valid in
![]() $\mathsf{iKAD}$
. Validity of the translations of (5) and (7) follows easily from (8) and (9), respectively. To deal with (6), it is sufficient to use the following equivalences which are established using Lemma 18 in the appendix:
$\mathsf{iKAD}$
. Validity of the translations of (5) and (7) follows easily from (8) and (9), respectively. To deal with (6), it is sufficient to use the following equivalences which are established using Lemma 18 in the appendix:
 \begin{align*}\mathord{\sim} (x \cdot \mathord{\sim}\mathord{\sim} y) & = x \to \mathord{\sim} \mathord{\sim} \mathord{\sim} y\\& = x \to \mathord{\sim} y\\& = \mathord{\sim} (xy) \, .\end{align*}
\begin{align*}\mathord{\sim} (x \cdot \mathord{\sim}\mathord{\sim} y) & = x \to \mathord{\sim} \mathord{\sim} \mathord{\sim} y\\& = x \to \mathord{\sim} y\\& = \mathord{\sim} (xy) \, .\end{align*}
To prove the second item, it is sufficient to show that the translations of the implicational axioms of
![]() $\mathsf{iKAD}$
are valid in
$\mathsf{iKAD}$
are valid in
![]() $\mathsf{KAD}$
. This is easy; see Lemma 14 in the appendix. To prove the third item, it is sufficient to observe that
$\mathsf{KAD}$
. This is easy; see Lemma 14 in the appendix. To prove the third item, it is sufficient to observe that
![]() $\mathsf{a} (x \cdot \mathsf{a} (0)) = \mathsf{a} (x)$
holds in
$\mathsf{a} (x \cdot \mathsf{a} (0)) = \mathsf{a} (x)$
holds in
![]() $\mathsf{KAD}$
. The final item is established easily using axiom (11).
$\mathsf{KAD}$
. The final item is established easily using axiom (11).
Theorem. The following hold:
-
(1) For all
 $p,q \in \mathcal{L}_{\mathsf{KAD}}$
:
$p,q \in \mathcal{L}_{\mathsf{KAD}}$
:
 $\mathsf{KAD} \models p = q$
iff
$\mathsf{KAD} \models p = q$
iff
 $\mathsf{iKAD} \models \tau(p) = \tau (q)$
;
$\mathsf{iKAD} \models \tau(p) = \tau (q)$
; -
(2) For all
 $p,q \in \mathcal{L}_{\mathsf{iKAD}}$
:
$p,q \in \mathcal{L}_{\mathsf{iKAD}}$
:
 $\mathsf{iKAD} \models p = q$
iff
$\mathsf{iKAD} \models p = q$
iff
 $\mathsf{KAD} \models \sigma(p) = \sigma (q)$
.
$\mathsf{KAD} \models \sigma(p) = \sigma (q)$
.
Proof. This is established easily using Lemma 13.
Theorem 4.2 shows that
![]() $\mathsf{S}$
embeds into a specific implicational expansion of Kleene algebra, and that this expansion is decidable (EXPTIME-complete by Sedlár Reference Sedlár, Glück, Santocanale and Winter2023).
$\mathsf{S}$
embeds into a specific implicational expansion of Kleene algebra, and that this expansion is decidable (EXPTIME-complete by Sedlár Reference Sedlár, Glück, Santocanale and Winter2023).
5. Conclusion
In this sequel to the conference paper (Sedlár and Wannenburg Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022), we have shown that Kozen and Tiuryn’s substructural logic of partial correctness
![]() $\mathsf{S}$
embeds into the equational theory of
$\mathsf{S}$
embeds into the equational theory of
![]() $\mathsf{KAD}$
. We introduced a formulation of
$\mathsf{KAD}$
. We introduced a formulation of
![]() $\mathsf{KAD}$
that replaces the antidomain operator
$\mathsf{KAD}$
that replaces the antidomain operator
![]() $\mathsf{a}$
with an implication operator
$\mathsf{a}$
with an implication operator
![]() $\to$
, thereby showing that
$\to$
, thereby showing that
![]() $\mathsf{S}$
embeds into a particular implicational expansion of Kleene algebra. We discussed the main differences between the implicational formulation of
$\mathsf{S}$
embeds into a particular implicational expansion of Kleene algebra. We discussed the main differences between the implicational formulation of
![]() $\mathsf{KAD}$
and the standard implicational expansions of Kleene algebra based on residuated semirings such as Pratt’s action logic. We hope that these results contribute to a better understanding of the place of
$\mathsf{KAD}$
and the standard implicational expansions of Kleene algebra based on residuated semirings such as Pratt’s action logic. We hope that these results contribute to a better understanding of the place of
![]() $\mathsf{S}$
in the wider context of substructural logics and implicational expansions of Kleene algebra.
$\mathsf{S}$
in the wider context of substructural logics and implicational expansions of Kleene algebra.
We also noted a close relation between KAD and the propositional fragment of DPL. One aspect of this connection is the relation of
![]() $\mathsf{S}$
to
$\mathsf{S}$
to
![]() $\mathsf{SDL^*}$
of Bochman and Gabbay which we also commented on. We note that we could obtain our embedding result via an embedding of either
$\mathsf{SDL^*}$
of Bochman and Gabbay which we also commented on. We note that we could obtain our embedding result via an embedding of either
![]() $\mathsf{PDL}$
or
$\mathsf{PDL}$
or
![]() $\mathsf{SDL^*}$
into
$\mathsf{SDL^*}$
into
![]() $\mathsf{KAD}$
, but we opted for a more instructive direct proof.
$\mathsf{KAD}$
, but we opted for a more instructive direct proof.
The connections observed in this paper and elsewhere motivate a more systematic study of algebras with (a generalization of) the dynamic negation operator. We leave such a study for another occasion.
Acknowledgements.
The author is grateful to the reviewer for their comments. Work on this paper was supported by the long-term strategic development financing of the Institute of Computer Science of the Czech Academy of Sciences (RVO:67985807).
Appendix A. A technical appendix
This appendix contains the expanded proofs of some of the results stated (or needed) in the main text.
Lemma 7. The following hold in each Kleene algebra with domain:
-
(1)
 $\mathsf{a} (0) = 1$
and
$\mathsf{a} (0) = 1$
and
 $\mathsf{a} (1) = 0$
;
$\mathsf{a} (1) = 0$
; -
(2)
 $\mathsf{d}(0) = 0$
and
$\mathsf{d}(0) = 0$
and
 $\mathsf{d} (1) = 1$
;
$\mathsf{d} (1) = 1$
; -
(3)
 $\mathsf{d} \mathsf{a} (x) = \mathsf{a} (x)$
and
$\mathsf{d} \mathsf{a} (x) = \mathsf{a} (x)$
and
 $\mathsf{d} \mathsf{d} (x) = \mathsf{d} (x)$
;
$\mathsf{d} \mathsf{d} (x) = \mathsf{d} (x)$
; -
(4)
 $\mathsf{d} (x + y) = \mathsf{d} (x) + \mathsf{d} (y)$
;
$\mathsf{d} (x + y) = \mathsf{d} (x) + \mathsf{d} (y)$
; -
(5)
 $\mathsf{d} (x) \leq 1$
and
$\mathsf{d} (x) \leq 1$
and
 $\mathsf{a} (x) \leq 1$
;
$\mathsf{a} (x) \leq 1$
; -
(6)
 $\mathsf{a} (xy) = \mathsf{a} (x \cdot \mathsf{d} (y))$
;
$\mathsf{a} (xy) = \mathsf{a} (x \cdot \mathsf{d} (y))$
; -
(7)
 $x \leq y$
only if
$x \leq y$
only if
 $\mathsf{a} (y) \leq \mathsf{a} (x)$
;
$\mathsf{a} (y) \leq \mathsf{a} (x)$
; -
(8)
 $x = \mathsf{d} (x) x$
;
$x = \mathsf{d} (x) x$
; -
(9)
 $\mathsf{d} (x) = 0$
only if
$\mathsf{d} (x) = 0$
only if
 $x = 0$
;
$x = 0$
; -
(10)
 $x = x \hat{z}$
iff
$x = x \hat{z}$
iff
 $x \mathsf{a} (\hat{z}) = 0$
;
$x \mathsf{a} (\hat{z}) = 0$
; -
(11)
 $\hat{x}\hat{z} = \hat{z} \hat{x}$
;
$\hat{x}\hat{z} = \hat{z} \hat{x}$
;
Proof. We prove some of the items explicitly. (9)
![]() $\mathsf{d} (x) = 0$
only if
$\mathsf{d} (x) = 0$
only if
![]() $\mathsf{a} (x) = 1$
. Then
$\mathsf{a} (x) = 1$
. Then
![]() $0 = \mathsf{a} (x) x = 1 x = x$
. (10) If
$0 = \mathsf{a} (x) x = 1 x = x$
. (10) If
![]() $x = x \hat{z}$
, then
$x = x \hat{z}$
, then
![]() $x \mathsf{a} (dx{z}) = x \hat{z} \mathsf{a} (\hat{z}) = 0$
. Conversely,
$x \mathsf{a} (dx{z}) = x \hat{z} \mathsf{a} (\hat{z}) = 0$
. Conversely,
![]() $x = x (\hat{z} + \mathsf{a} (\hat{z})) = x \hat{z} + x \mathsf{a}(\hat{z}) = x \hat{z} + 0 = x \hat{z}$
.
$x = x (\hat{z} + \mathsf{a} (\hat{z})) = x \hat{z} + x \mathsf{a}(\hat{z}) = x \hat{z} + 0 = x \hat{z}$
.
Lemma 14. The following hold in each Kleene algebra with domain (where
![]() $x \to y := \mathsf{a} (x \cdot \mathsf{a} (y))$
):
$x \to y := \mathsf{a} (x \cdot \mathsf{a} (y))$
):
-
(1)
 $(x \to 0)x = 0$
;
$(x \to 0)x = 0$
; -
(2)
 $(x \to y) + \mathsf{a} (x \to y) = 1$
;
$(x \to y) + \mathsf{a} (x \to y) = 1$
; -
(3)
 $(xy \to z) = (x \to (y \to z))$
;
$(xy \to z) = (x \to (y \to z))$
; -
(4)
 $(x \to y) = \mathsf{d} (x \to y)$
$(x \to y) = \mathsf{d} (x \to y)$
Proof. Item 1:
![]() $\mathsf{a} ( x \cdot \mathsf{a} (0)) x = \mathsf{a} (x 1)x = \mathsf{a} (x)x = 0$
. Item 2: if
$\mathsf{a} ( x \cdot \mathsf{a} (0)) x = \mathsf{a} (x 1)x = \mathsf{a} (x)x = 0$
. Item 2: if
![]() $z = \mathsf{a} (x \cdot \mathsf{a} (y))$
, then
$z = \mathsf{a} (x \cdot \mathsf{a} (y))$
, then
![]() $(x \to y) + \mathsf{a} (x \to y) = \mathsf{a} (z) + \mathsf{d} (z) = 1$
. Item 3:
$(x \to y) + \mathsf{a} (x \to y) = \mathsf{a} (z) + \mathsf{d} (z) = 1$
. Item 3:
![]() $(xy \to z) = \mathsf{a} (xy \cdot \mathsf{a} (z)) = \mathsf{a} (x \mathsf{d} (y \cdot \mathsf{a} (z))) = x \to (y \to z))$
. Item 4:
$(xy \to z) = \mathsf{a} (xy \cdot \mathsf{a} (z)) = \mathsf{a} (x \mathsf{d} (y \cdot \mathsf{a} (z))) = x \to (y \to z))$
. Item 4:
![]() $\mathsf{d} (x \to y) = \mathsf{d} \mathsf{a} (x \cdot \mathsf{a} (y)) = \mathsf{a} (x \cdot \mathsf{a} (y)) = x \to y$
.
$\mathsf{d} (x \to y) = \mathsf{d} \mathsf{a} (x \cdot \mathsf{a} (y)) = \mathsf{a} (x \cdot \mathsf{a} (y)) = x \to y$
.
Lemma 15. For each formula
![]() $f \in \mathcal{E}_{\mathsf{S}}$
, the term Tr (p) is equivalent to a domain term. That is,
$f \in \mathcal{E}_{\mathsf{S}}$
, the term Tr (p) is equivalent to a domain term. That is,
for some
![]() $q \in \mathcal{L}_{\mathsf{KAD}}$
.
$q \in \mathcal{L}_{\mathsf{KAD}}$
.
Proof. There are three cases to consider (it is not necessary to reason by induction on the complexity of f):
-
•
 $Tr (\mathtt{b}_n) = \mathsf{d} (\mathtt{p}_{2n+1})$
$Tr (\mathtt{b}_n) = \mathsf{d} (\mathtt{p}_{2n+1})$
-
•
 $Tr (0) = 0 \equiv \mathsf{d} (0)$
;
$Tr (0) = 0 \equiv \mathsf{d} (0)$
; -
•
 $Tr (p \Rightarrow f) = \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr(f))) \equiv \mathsf{d} \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr(f)))$
.
$Tr (p \Rightarrow f) = \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr(f))) \equiv \mathsf{d} \mathsf{a} (Tr (p) \cdot \mathsf{a} (Tr(f)))$
.
This concludes the proof.
Recall the definitions of dynamic negation (relational antidomain) and the relational domain operator, for any
![]() $R \subseteq W \times W$
:
$R \subseteq W \times W$
:
Lemma 16. The following hold in each
![]() $\mathsf{S}$
-model, assuming the above definitions of
$\mathsf{S}$
-model, assuming the above definitions of
![]() $\mathord{\sim}$
and D:
$\mathord{\sim}$
and D:
-
(1) for all f,
 ${\texttt{[}} f {\texttt{]}}_M = D {\texttt{[}} f {\texttt{]}}_M$
;
${\texttt{[}} f {\texttt{]}}_M = D {\texttt{[}} f {\texttt{]}}_M$
; -
(2) for all p and all f,
 ${\texttt{[}} p \Rightarrow f {\texttt{]}}_M = \mathord{\sim} ({\texttt{[}} p {\texttt{]}}_M \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}_M)$
.
${\texttt{[}} p \Rightarrow f {\texttt{]}}_M = \mathord{\sim} ({\texttt{[}} p {\texttt{]}}_M \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}_M)$
.
Proof. The first claim is obvious from the inspection of the semantic clauses for formulas, and the fact that
![]() $D(R) = R$
for
$D(R) = R$
for
![]() $R \subseteq \textrm{id}_W$
. The second claim is established as follows (we omit the subscript M):
$R \subseteq \textrm{id}_W$
. The second claim is established as follows (we omit the subscript M):
 \begin{align*}\mathord{\sim} ({\texttt{[}} p {\texttt{]}} \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}) & = \{ (s, s) \mid \neg\exists t. (s, t) \in ({\texttt{[}} p {\texttt{]}} \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}) \}\\ & = \{ (s, s) \mid \neg \exists t. (s, t) \in {\texttt{[}} p {\texttt{]}} \And (t, t) \in \mathord{\sim} {\texttt{[}} f {\texttt{]}} \}\\ & = \{ (s, s) \mid \forall t ( (s, t) \in {\texttt{[}} p {\texttt{]}} \implies \exists u. (t, u) \in {\texttt{[}} f {\texttt{]}} ) \}\\ & = \{ (s, s) \mid \forall t ( (s,t) \in {\texttt{[}} p {\texttt{]}} \implies (t,t) \in {\texttt{[}} f {\texttt{]}}) \}\\ & = {\texttt{[}} p \Rightarrow f {\texttt{]}}\end{align*}
\begin{align*}\mathord{\sim} ({\texttt{[}} p {\texttt{]}} \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}) & = \{ (s, s) \mid \neg\exists t. (s, t) \in ({\texttt{[}} p {\texttt{]}} \circ \mathord{\sim} {\texttt{[}} f {\texttt{]}}) \}\\ & = \{ (s, s) \mid \neg \exists t. (s, t) \in {\texttt{[}} p {\texttt{]}} \And (t, t) \in \mathord{\sim} {\texttt{[}} f {\texttt{]}} \}\\ & = \{ (s, s) \mid \forall t ( (s, t) \in {\texttt{[}} p {\texttt{]}} \implies \exists u. (t, u) \in {\texttt{[}} f {\texttt{]}} ) \}\\ & = \{ (s, s) \mid \forall t ( (s,t) \in {\texttt{[}} p {\texttt{]}} \implies (t,t) \in {\texttt{[}} f {\texttt{]}}) \}\\ & = {\texttt{[}} p \Rightarrow f {\texttt{]}}\end{align*}
Lemma 17. If
![]() $\Gamma \vdash f$
is provable in
$\Gamma \vdash f$
is provable in
![]() $\mathsf{S}$
, then
$\mathsf{S}$
, then
Proof. Induction on the length of derivations in the sequent system for
![]() $\mathsf{S}$
. Most rules are checked routinely, and the implicational rules are handled in the main text. Here, we add the proof related to the rule (I
$\mathsf{S}$
. Most rules are checked routinely, and the implicational rules are handled in the main text. Here, we add the proof related to the rule (I
![]() $^+$
), for which we used the assumption of
$^+$
), for which we used the assumption of
![]() $^{*}$
-continuity in the conference paper (Sedlár and Wannenburg Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022). In particular, we show that the quasi-equation
$^{*}$
-continuity in the conference paper (Sedlár and Wannenburg Reference Sedlár, Wannenburg, Ciabattoni, Pimentel and de Queiroz2022). In particular, we show that the quasi-equation
is valid in Kleene algebra. In order to show this, we use the fact that the following equation and two quasi-equations are valid in Kleene algebra:
For a proof of (A2), see Reference KozenKozen (1994a ), Corollary 2.5. The quasi-equation (A3) is established as follows:
To establish the quasi-equation (A4), we will show that
Then, using (4), one can infer that
![]() $ep^{+} \leq (ep)^{+}$
; conversely, one can show that
$ep^{+} \leq (ep)^{+}$
; conversely, one can show that
using the assumption
![]() $e \leq 1$
.
$e \leq 1$
.
Validity of (A8) is straightforward (since
![]() $1 \leq q^{*}$
). Validity of (A9) is established using (A2) and the assumption
$1 \leq q^{*}$
). Validity of (A9) is established using (A2) and the assumption
![]() $ep = epe$
as follows:
$ep = epe$
as follows:
 \begin{align*}(ep)^{+}p & = ep(ep)^{*}p\\& = (ep)^{*}epp\\& = (ep)^{*} epep\\& = (ep)^{+} ep\\& \leq (ep)^{+}\end{align*}
\begin{align*}(ep)^{+}p & = ep(ep)^{*}p\\& = (ep)^{*}epp\\& = (ep)^{*} epep\\& = (ep)^{+} ep\\& \leq (ep)^{+}\end{align*}
The last step is valid since
![]() $qq^{*} \leq q^{*}$
is valid in Kleene algebra. This concludes the proof of (A9) and so (A1) is established.
$qq^{*} \leq q^{*}$
is valid in Kleene algebra. This concludes the proof of (A9) and so (A1) is established.
Lemma 18. The following hold in each iKAD:
-
(1)
 $\mathord{\sim} (xy) = x \to \mathord{\sim} y$
$\mathord{\sim} (xy) = x \to \mathord{\sim} y$
-
(2)
 $\mathord{\sim} \mathord{\sim} \mathord{\sim} x = \mathord{\sim} x$
$\mathord{\sim} \mathord{\sim} \mathord{\sim} x = \mathord{\sim} x$
Proof. Item 1:
![]() $\mathord{\sim} (xy) = xy \to 0 = x \to (y \to 0) = x \to \mathord{\sim} y$
. Item 2 follows easily from axiom (11).
$\mathord{\sim} (xy) = xy \to 0 = x \to (y \to 0) = x \to \mathord{\sim} y$
. Item 2 follows easily from axiom (11).