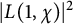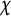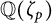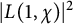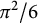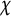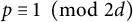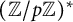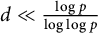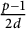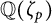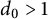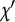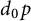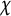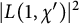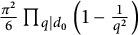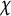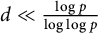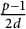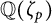1 Introduction
Let
![]() $X_f$
be the multiplicative group of the
$X_f$
be the multiplicative group of the
![]() $\phi (f)$
Dirichlet characters modulo
$\phi (f)$
Dirichlet characters modulo
![]() $f>2$
. Let
$f>2$
. Let
![]() $X_f^- =\{\chi \in X_f;\ \chi (-1)=-1\}$
be the set of the
$X_f^- =\{\chi \in X_f;\ \chi (-1)=-1\}$
be the set of the
![]() $\phi (f)/2$
odd Dirichlet characters modulo f. Let
$\phi (f)/2$
odd Dirichlet characters modulo f. Let
![]() $L(s,\chi )$
be the Dirichlet L-function associated with
$L(s,\chi )$
be the Dirichlet L-function associated with
![]() $\chi \in X_f$
. Let H denote a subgroup of index m in the multiplicative group
$\chi \in X_f$
. Let H denote a subgroup of index m in the multiplicative group
![]() $G:=({\mathbb Z}/f{\mathbb Z})^*$
. We assume that
$G:=({\mathbb Z}/f{\mathbb Z})^*$
. We assume that
![]() $-1\not \in H$
. Hence, m is even. We set
$-1\not \in H$
. Hence, m is even. We set
![]() $X_f(H) =\{\chi \in X_f;\ \chi _{/H}=1\}$
, a subgroup of order m of
$X_f(H) =\{\chi \in X_f;\ \chi _{/H}=1\}$
, a subgroup of order m of
![]() $X_f$
isomorphic to the group of Dirichlet characters of the abelian quotient group
$X_f$
isomorphic to the group of Dirichlet characters of the abelian quotient group
![]() $G/H$
of order m. Define
$G/H$
of order m. Define
![]() $X_f^-(H)=\{\chi \in X_f^-;\ \chi _{/H}=1\}$
, a set of cardinal
$X_f^-(H)=\{\chi \in X_f^-;\ \chi _{/H}=1\}$
, a set of cardinal
![]() $m/2$
. Let K be an abelian number field of degree m and prime conductor
$m/2$
. Let K be an abelian number field of degree m and prime conductor
![]() $p\geq 3$
, i.e., let K be a subfield of the cyclotomic number field
$p\geq 3$
, i.e., let K be a subfield of the cyclotomic number field
![]() ${\mathbb Q}(\zeta _p)$
(Kronecker–Weber’s theorem). The Galois group
${\mathbb Q}(\zeta _p)$
(Kronecker–Weber’s theorem). The Galois group
![]() $\mathrm {Gal}({\mathbb Q}(\zeta _p)/{\mathbb Q})$
is canonically isomorphic to the multiplicative cyclic group
$\mathrm {Gal}({\mathbb Q}(\zeta _p)/{\mathbb Q})$
is canonically isomorphic to the multiplicative cyclic group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
and
$({\mathbb Z}/p{\mathbb Z})^*$
and
![]() $H :=\mathrm {Gal}({\mathbb Q}(\zeta _p)/K)$
is a subgroup of
$H :=\mathrm {Gal}({\mathbb Q}(\zeta _p)/K)$
is a subgroup of
![]() $({\mathbb Z}/p{\mathbb Z})^*$
of index m and order
$({\mathbb Z}/p{\mathbb Z})^*$
of index m and order
Now, assume that K is imaginary. Then d is odd, m is even,
![]() $-1\not \in H$
and the set
$-1\not \in H$
and the set
is of cardinal
![]() $(p-1)/(2d) =m/2$
. Let
$(p-1)/(2d) =m/2$
. Let
![]() $K^+$
be the maximal real subfield of K of degree
$K^+$
be the maximal real subfield of K of degree
![]() $m/2$
fixed by the complex conjugation. The class number
$m/2$
fixed by the complex conjugation. The class number
![]() $h_{K^+}$
of
$h_{K^+}$
of
![]() $K^+$
divides the class number
$K^+$
divides the class number
![]() $h_K$
of K. The relative class number of K is defined by
$h_K$
of K. The relative class number of K is defined by
![]() $h_K^- =h_K/h_{K^+}$
. We refer the reader to [Reference SerreSer, Was] for such basic knowledge. The mean square value of
$h_K^- =h_K/h_{K^+}$
. We refer the reader to [Reference SerreSer, Was] for such basic knowledge. The mean square value of
![]() $L(1,\chi )$
as
$L(1,\chi )$
as
![]() $\chi $
ranges in
$\chi $
ranges in
![]() $X_f^-(H)$
is defined by
$X_f^-(H)$
is defined by
 $$ \begin{align} M(f,H) :={1\over\# X_f^-(H)}\sum_{\chi\in X_f^-(H)}\vert L(1,\chi)\vert^2. \end{align} $$
$$ \begin{align} M(f,H) :={1\over\# X_f^-(H)}\sum_{\chi\in X_f^-(H)}\vert L(1,\chi)\vert^2. \end{align} $$
The analytic class number formula and the arithmetic–geometric mean inequality give
 $$ \begin{align} h_K^- =w_K\left (\frac{p}{4\pi^2}\right )^{m/4}\prod_{\chi\in X_K^-} L(1,\chi) \leq w_K\left ({pM(p,H)\over 4\pi^2}\right )^{m/4}, \end{align} $$
$$ \begin{align} h_K^- =w_K\left (\frac{p}{4\pi^2}\right )^{m/4}\prod_{\chi\in X_K^-} L(1,\chi) \leq w_K\left ({pM(p,H)\over 4\pi^2}\right )^{m/4}, \end{align} $$
where
![]() $w_K$
is the number of complex roots of unity in K. Hence,
$w_K$
is the number of complex roots of unity in K. Hence,
![]() $w_K=2p$
for
$w_K=2p$
for
![]() $K ={\mathbb Q}(\zeta _p)$
and
$K ={\mathbb Q}(\zeta _p)$
and
![]() $w_K=2$
otherwise. In [Reference Louboutin and MunschLM21, Theorem 1.1], we proved that
$w_K=2$
otherwise. In [Reference Louboutin and MunschLM21, Theorem 1.1], we proved that
as p tends to infinity uniformly over subgroups H of
![]() $({\mathbb Z}/p{\mathbb Z})^*$
of odd order
$({\mathbb Z}/p{\mathbb Z})^*$
of odd order
![]() $d\leq \frac {\log p}{3(\log \log p)}$
Footnote
1
. Hence, by (1.2), we have
$d\leq \frac {\log p}{3(\log \log p)}$
Footnote
1
. Hence, by (1.2), we have
 $$ \begin{align} h_{K}^{-} \leq w_K\left(\frac{(1+o(1))p}{24}\right)^{(p-1)/4d}. \end{align} $$
$$ \begin{align} h_{K}^{-} \leq w_K\left(\frac{(1+o(1))p}{24}\right)^{(p-1)/4d}. \end{align} $$
In some situations, it is even possible to give an explicit formula for
![]() $M(p,H)$
implying a completely explicit bound for
$M(p,H)$
implying a completely explicit bound for
![]() $h_K^-$
. Indeed, by [Reference WalumMet, Wal] (see also (4.2)), we have
$h_K^-$
. Indeed, by [Reference WalumMet, Wal] (see also (4.2)), we have
 $$ \begin{align} M(p,\{1\}) ={\pi^2\over 6}\left (1-{1\over p}\right )\left (1-{2\over p}\right ) \leq\frac{\pi^2}{6} \ \ \ \ \ (p\geq 3). \end{align} $$
$$ \begin{align} M(p,\{1\}) ={\pi^2\over 6}\left (1-{1\over p}\right )\left (1-{2\over p}\right ) \leq\frac{\pi^2}{6} \ \ \ \ \ (p\geq 3). \end{align} $$
Hence,
 $$ \begin{align} h_{{\mathbb Q}(\zeta_p)}^- \leq 2p\left ({pM(p,\{1\})\over 4\pi^2}\right )^{(p-1)/4} \leq 2p\left ({p\over 24}\right )^{(p-1)/4}. \end{align} $$
$$ \begin{align} h_{{\mathbb Q}(\zeta_p)}^- \leq 2p\left ({pM(p,\{1\})\over 4\pi^2}\right )^{(p-1)/4} \leq 2p\left ({p\over 24}\right )^{(p-1)/4}. \end{align} $$
We refer the reader to [Reference GranvilleGra] for more information about the expected size of
![]() $h_{{\mathbb Q}(\zeta _p)}^-$
. The only other situation where a similar explicit result is known is the following one (see Theorem 6.6 for a new proof).
$h_{{\mathbb Q}(\zeta _p)}^-$
. The only other situation where a similar explicit result is known is the following one (see Theorem 6.6 for a new proof).
Theorem (SeeFootnote 2 [Reference LouboutinLou16, Theorem 1])
Let
![]() $p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
$p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
![]() $(p-1)/3$
of the cyclotomic number field
$(p-1)/3$
of the cyclotomic number field
![]() ${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. We have (compare with (
1.5
) and (
1.6
))
$({\mathbb Z}/p{\mathbb Z})^*$
. We have (compare with (
1.5
) and (
1.6
))
 $$ \begin{align} M(p,H) ={\pi^2\over 6}\left (1-{1\over p}\right ) \leq\frac{\pi^2}{6} \mbox{ and } h_K^-\leq 2\left (\frac{p}{24}\right )^{(p-1)/12}.\end{align} $$
$$ \begin{align} M(p,H) ={\pi^2\over 6}\left (1-{1\over p}\right ) \leq\frac{\pi^2}{6} \mbox{ and } h_K^-\leq 2\left (\frac{p}{24}\right )^{(p-1)/12}.\end{align} $$
In [Reference LouboutinLou94] (see also [Reference LouboutinLou11]), the following simple argument allowed to improve on (1.6). Let
![]() $d_0>1$
be a given integer. Assume that
$d_0>1$
be a given integer. Assume that
![]() $\gcd (d_0,f)=1$
. For
$\gcd (d_0,f)=1$
. For
![]() $\chi $
modulo f, let
$\chi $
modulo f, let
![]() $\chi '$
be the character modulo
$\chi '$
be the character modulo
![]() $d_0f$
induced by
$d_0f$
induced by
![]() $\chi $
. Then
$\chi $
. Then
 $$ \begin{align} L(1,\chi) =L(1,\chi')\prod_{q\mid d_0}\left (1-\frac{\chi(q)}{q}\right )^{-1} \end{align} $$
$$ \begin{align} L(1,\chi) =L(1,\chi')\prod_{q\mid d_0}\left (1-\frac{\chi(q)}{q}\right )^{-1} \end{align} $$
(throughout the paper, this notation means that q runs over the distinct prime divisors of
![]() $d_0$
). Let H be a subgroup of order d of the multiplicative group
$d_0$
). Let H be a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, with
$({\mathbb Z}/f{\mathbb Z})^*$
, with
![]() $-1\not \in H$
. We define
$-1\not \in H$
. We define
 $$ \begin{align} M_{d_0}(f,H) :={1\over\# X_f^-(H)}\sum_{\chi\in X_f^-(H)}\vert L(1,\chi')\vert^2 \end{align} $$
$$ \begin{align} M_{d_0}(f,H) :={1\over\# X_f^-(H)}\sum_{\chi\in X_f^-(H)}\vert L(1,\chi')\vert^2 \end{align} $$
andFootnote 3
 $$ \begin{align} \Pi_{d_0}(f,H) :=\prod_{q\mid d_0}\prod_{\chi\in X_f^-(H)}\left (1-\frac{\chi(q)}{q}\right ) \text{ and } D_{d_0}(f,H) :=\Pi_{d_0}(f,H)^{4/m}. \end{align} $$
$$ \begin{align} \Pi_{d_0}(f,H) :=\prod_{q\mid d_0}\prod_{\chi\in X_f^-(H)}\left (1-\frac{\chi(q)}{q}\right ) \text{ and } D_{d_0}(f,H) :=\Pi_{d_0}(f,H)^{4/m}. \end{align} $$
Clearly, there is no restriction in assuming from now on that
![]() $d_0$
is square- free. Let now H be of odd order d in the multiplicative group
$d_0$
is square- free. Let now H be of odd order d in the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. Using (1.8), we obtain (compare with (1.2))
$({\mathbb Z}/p{\mathbb Z})^*$
. Using (1.8), we obtain (compare with (1.2))
 $$ \begin{align} h_K^- =\frac{w_K}{\Pi_{d_0}(p,H)} \left (\frac{p}{4\pi^2}\right )^{m/4}\prod_{\chi\in X_K^-}L(1,\chi') \leq w_K\left (\frac{pM_{d_0}(p,H)}{4\pi^2D_{d_0}(p,H)}\right )^{m/4}. \end{align} $$
$$ \begin{align} h_K^- =\frac{w_K}{\Pi_{d_0}(p,H)} \left (\frac{p}{4\pi^2}\right )^{m/4}\prod_{\chi\in X_K^-}L(1,\chi') \leq w_K\left (\frac{pM_{d_0}(p,H)}{4\pi^2D_{d_0}(p,H)}\right )^{m/4}. \end{align} $$
Let
![]() $d=o(\log p)$
as
$d=o(\log p)$
as
![]() $p\rightarrow \infty $
. Then, by Corollary 2.4, we have
$p\rightarrow \infty $
. Then, by Corollary 2.4, we have
and we expect that
 $$ \begin{align} M_{d_0}(p,H) \sim\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \times M(p,H). \end{align} $$
$$ \begin{align} M_{d_0}(p,H) \sim\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \times M(p,H). \end{align} $$
Hence, (1.11) should indeed improve on (1.2). The aim of this paper is twofold. First, in Theorem 1.1, we give an asymptotic formula for
![]() $M_{d_0}(p,H)$
when d satisfies the same restriction as in (1.3) allowing us to improve on the bound (1.4). Second, we treat the case of groups of orders
$M_{d_0}(p,H)$
when d satisfies the same restriction as in (1.3) allowing us to improve on the bound (1.4). Second, we treat the case of groups of orders
![]() $1$
and
$1$
and
![]() $3$
for small
$3$
for small
![]() $d_0$
’s as well as the case of Mersenne primes and groups of size
$d_0$
’s as well as the case of Mersenne primes and groups of size
![]() $\approx \log p$
. In both cases, an explicit description of these subgroups allows us to obtain explicit formulas for
$\approx \log p$
. In both cases, an explicit description of these subgroups allows us to obtain explicit formulas for
![]() $M_{d_0}(p,H)$
. Our main result is the following.
$M_{d_0}(p,H)$
. Our main result is the following.
Theorem 1.1 Let
![]() $d_0\geq 1$
be a given square-free integer. As
$d_0\geq 1$
be a given square-free integer. As
![]() $p\rightarrow +\infty $
, we have the following asymptotic formula:
$p\rightarrow +\infty $
, we have the following asymptotic formula:
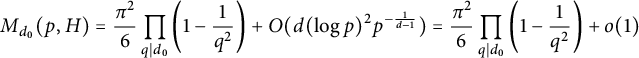 $$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{6}\prod_{q\mid d_0}\left (1-{1\over q^2}\right ) +O(d(\log p)^2 p^{-\frac{1}{d-1}}) =\frac{\pi^2}{6}\prod_{q\mid d_0}\left (1-{1\over q^2}\right ) +o(1)\end{align*} $$
$$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{6}\prod_{q\mid d_0}\left (1-{1\over q^2}\right ) +O(d(\log p)^2 p^{-\frac{1}{d-1}}) =\frac{\pi^2}{6}\prod_{q\mid d_0}\left (1-{1\over q^2}\right ) +o(1)\end{align*} $$
uniformly over subgroups H of
![]() $({\mathbb Z}/p{\mathbb Z})^*$
of odd order
$({\mathbb Z}/p{\mathbb Z})^*$
of odd order
![]() $d\leq \frac {\log p}{3(\log \log p)}.$
Moreover, let K be an imaginary abelian number field of prime conductor p and of degree
$d\leq \frac {\log p}{3(\log \log p)}.$
Moreover, let K be an imaginary abelian number field of prime conductor p and of degree
![]() $m=(p-1)/d$
. Let
$m=(p-1)/d$
. Let
![]() $C<4\pi ^2=39.478..$
be any positive constant. If p is sufficiently large and
$C<4\pi ^2=39.478..$
be any positive constant. If p is sufficiently large and
![]() $m\geq 3\frac {(p-1) \log \log p} {\log p}$
, then we have
$m\geq 3\frac {(p-1) \log \log p} {\log p}$
, then we have
 $$ \begin{align} h_K^- \leq w_K\left (\frac{p}{C}\right )^{(p-1)/4d}. \end{align} $$
$$ \begin{align} h_K^- \leq w_K\left (\frac{p}{C}\right )^{(p-1)/4d}. \end{align} $$
Remark 1.2 The second result in Theorem 1.1 improves on (1.4), (1.6), and (1.7). It follows from the first result in Theorem 1.1, and by using (1.11) and (2.2), where we take
![]() $d_0$
as the product of sufficiently many consecutive first primes.
$d_0$
as the product of sufficiently many consecutive first primes.
The special case
![]() $d_0=1$
was proved in [Reference Louboutin and MunschLM21, Theorem
$d_0=1$
was proved in [Reference Louboutin and MunschLM21, Theorem
![]() $1.1$
]. Note that the restriction on d cannot be extended further to the range
$1.1$
]. Note that the restriction on d cannot be extended further to the range
![]() $d=O(\log p)$
as shown by Theorem 5.2. Moreover, the constant C in (1.13) cannot be taken larger than
$d=O(\log p)$
as shown by Theorem 5.2. Moreover, the constant C in (1.13) cannot be taken larger than
![]() $4\pi ^2$
(see the discussion about Kummer’s conjecture in [Reference Murty and PetridisMP01].
$4\pi ^2$
(see the discussion about Kummer’s conjecture in [Reference Murty and PetridisMP01].
In the first part of the paper, the presentation goes as follows:
-
• In Section 2, we explain the condition about the prime divisors of
 $d_0$
and prove that
$d_0$
and prove that
 $D_{d_0}(p,H) =1+o(1)$
.
$D_{d_0}(p,H) =1+o(1)$
. -
• In Section 3, we review some results on Dedekind sums and prove a new bound of independent interest for Dedekind sums
 $s(h,f)$
with h being of small order modulo f (see Theorem 3.1). To do so, we use techniques from uniform distribution and discrepancy theory. Then we relate
$s(h,f)$
with h being of small order modulo f (see Theorem 3.1). To do so, we use techniques from uniform distribution and discrepancy theory. Then we relate
 $M_{d_0}(p,H)$
to twisted moments of L- functions which we further express in terms of Dedekind sums. For the sake of clarity, we first treat separately the case
$M_{d_0}(p,H)$
to twisted moments of L- functions which we further express in terms of Dedekind sums. For the sake of clarity, we first treat separately the case
 $H=\{1\}$
. Note that we found that this case is related to elementary sums of maxima that we could not estimate directly (see Section 3.4). Using our estimates on Dedekind sums, we deduce the asymptotic formula of Theorem 1.1 and the related class number bounds.
$H=\{1\}$
. Note that we found that this case is related to elementary sums of maxima that we could not estimate directly (see Section 3.4). Using our estimates on Dedekind sums, we deduce the asymptotic formula of Theorem 1.1 and the related class number bounds.
In the second part of the paper, we focus on the explicit aspects. Let us describe briefly our presentation:
-
• In Section 4.1, we establish a formula for
 $M_{d_0}(f,\{1\})$
,
$M_{d_0}(f,\{1\})$
,
 $d_0>2$
, provided that all the prime factors q of f satisfy
$d_0>2$
, provided that all the prime factors q of f satisfy
 $q\equiv \pm 1\ \ \pmod {d_0}$
. In particular, we get formulas for
$q\equiv \pm 1\ \ \pmod {d_0}$
. In particular, we get formulas for
 $M_{d_0}(f,\{1\})$
for
$M_{d_0}(f,\{1\})$
for
 $d_0\in \{1,2,3,6\}$
and
$d_0\in \{1,2,3,6\}$
and
 $\gcd (d_0,f)=1$
(such formulae become harder to come by as
$\gcd (d_0,f)=1$
(such formulae become harder to come by as
 $d_0$
gets larger). For example, for
$d_0$
gets larger). For example, for
 $p\geq 5$
and
$p\geq 5$
and
 $d_0=6$
, using Theorem 4.1, we obtain the following formula for
$d_0=6$
, using Theorem 4.1, we obtain the following formula for
 $M_6(p,\{1\})$
: which by (1.11) and Corollary 2.4 give improvements on (1.6) (see also [Reference FengFeng])
$M_6(p,\{1\})$
: which by (1.11) and Corollary 2.4 give improvements on (1.6) (see also [Reference FengFeng]) $$ \begin{align*}M_6(p,\{1\}) ={\pi^2\over 9}\left (1-\frac{c_p}{p}\right ) \leq\frac{\pi^2}{9}, \mbox{ where } c_p =\begin{cases} 1,&\mbox{if } p\equiv 1\ \ \pmod 3,\\ 0,&\mbox{if } p\equiv 2\ \ \pmod 3,\\ \end{cases}\end{align*} $$
See also [Reference LouboutinLou23, Theorem 5.2] for even better bounds. In Section 4.3, we obtain an explicit formula of the form
$$ \begin{align*}M_6(p,\{1\}) ={\pi^2\over 9}\left (1-\frac{c_p}{p}\right ) \leq\frac{\pi^2}{9}, \mbox{ where } c_p =\begin{cases} 1,&\mbox{if } p\equiv 1\ \ \pmod 3,\\ 0,&\mbox{if } p\equiv 2\ \ \pmod 3,\\ \end{cases}\end{align*} $$
See also [Reference LouboutinLou23, Theorem 5.2] for even better bounds. In Section 4.3, we obtain an explicit formula of the form $$ \begin{align*}h_{{\mathbb Q}(\zeta_p)}^- \leq 3p\left ({p\over 36}\right )^{(p-1)/4}.\end{align*} $$
(1.14)where
$$ \begin{align*}h_{{\mathbb Q}(\zeta_p)}^- \leq 3p\left ({p\over 36}\right )^{(p-1)/4}.\end{align*} $$
(1.14)where $$ \begin{align} M_{d_0}(p,H) =\frac{\pi^2}{6} \left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}(p,H)}{p}\right ){\kern-1.5pt}, \end{align} $$
$$ \begin{align} M_{d_0}(p,H) =\frac{\pi^2}{6} \left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}(p,H)}{p}\right ){\kern-1.5pt}, \end{align} $$
 $N_{d_0}(p,H)$
defined in (4.5) is an explicit average of Dedekind sums. In Proposition 4.6, we prove that
$N_{d_0}(p,H)$
defined in (4.5) is an explicit average of Dedekind sums. In Proposition 4.6, we prove that
 $N_{d_0}(p,\{1\})\in {\mathbb Q}$
depends only on p modulo
$N_{d_0}(p,\{1\})\in {\mathbb Q}$
depends only on p modulo
 $d_0$
and is easily computable.
$d_0$
and is easily computable.
-
• For
 $H\neq \{1\}$
explicit formulae for
$H\neq \{1\}$
explicit formulae for
 $M_{d_0}(p,H)$
seem difficult to come by. In Section 5, we focus on Mersenne primes
$M_{d_0}(p,H)$
seem difficult to come by. In Section 5, we focus on Mersenne primes
 $p=2^d-1$
, with d odd. We take
$p=2^d-1$
, with d odd. We take
 $H=\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of odd order d of the multiplicative group
$H=\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of odd order d of the multiplicative group
 $({\mathbb Z}/p{\mathbb Z})^*$
. For
$({\mathbb Z}/p{\mathbb Z})^*$
. For
 $d_0\in \{1,3,15\}$
, we prove in Theorem 5.4 that where
$d_0\in \{1,3,15\}$
, we prove in Theorem 5.4 that where $$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}'(p,H)}{p}\right ){\kern-1.5pt},\end{align*} $$
$$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}'(p,H)}{p}\right ){\kern-1.5pt},\end{align*} $$
 $N_{d_0}'(p,H)=a_1(p)d+a_0(p)$
with
$N_{d_0}'(p,H)=a_1(p)d+a_0(p)$
with
 $a_1(p),a_0(p)\in {\mathbb Q}$
depending only on
$a_1(p),a_0(p)\in {\mathbb Q}$
depending only on
 $p=2^d-1$
modulo
$p=2^d-1$
modulo
 $d_0$
and easily computable. In the range
$d_0$
and easily computable. In the range
 $d \gg \log p$
, we see that
$d \gg \log p$
, we see that
 $M_{d_0}(p,H)$
has a different asymptotic behavior than the one in Theorem 1.1.
$M_{d_0}(p,H)$
has a different asymptotic behavior than the one in Theorem 1.1.
-
• In Section 6, we turn to the specific case of subgroups of order
 $3$
. Writing
$3$
. Writing
 $f=a^2+ab+b^2$
not necessarily prime, and taking
$f=a^2+ab+b^2$
not necessarily prime, and taking
 $H=\{1,a/b,b/a\}$
, the subgroup of order
$H=\{1,a/b,b/a\}$
, the subgroup of order
 $3$
of the multiplicative group
$3$
of the multiplicative group
 $({\mathbb Z}/f{\mathbb Z})^*$
, we prove in Proposition 6.4 that
$({\mathbb Z}/f{\mathbb Z})^*$
, we prove in Proposition 6.4 that
 $N_{d_0}(f,H) =O(\sqrt f)$
in (1.14) for
$N_{d_0}(f,H) =O(\sqrt f)$
in (1.14) for
 $d_0\in \{1,2,3,6\}$
. To do so, we obtain bounds for the Dedekind sums stronger than the one in Theorem 3.1. Note that this cannot be expected in general for subgroups of order
$d_0\in \{1,2,3,6\}$
. To do so, we obtain bounds for the Dedekind sums stronger than the one in Theorem 3.1. Note that this cannot be expected in general for subgroups of order
 $3$
modulo composite f (see Remarks 3.4 and 6.2). Furthermore, we show that these bounds are sharp in the case of primes
$3$
modulo composite f (see Remarks 3.4 and 6.2). Furthermore, we show that these bounds are sharp in the case of primes
 $p=a^2+a+1$
, in accordance with Conjecture 7.1.
$p=a^2+a+1$
, in accordance with Conjecture 7.1.
2 Preliminaries
2.1 Algebraic considerations
Take
![]() $a\in {\mathbb Z}$
with
$a\in {\mathbb Z}$
with
![]() $\gcd (a,f)=1$
. There are infinitely many prime integers in the arithmetic progressions
$\gcd (a,f)=1$
. There are infinitely many prime integers in the arithmetic progressions
![]() $a+f{\mathbb Z}$
. Taking a prime
$a+f{\mathbb Z}$
. Taking a prime
![]() $p\in a+f{\mathbb Z}$
with
$p\in a+f{\mathbb Z}$
with
![]() $p>d_0f$
, we have
$p>d_0f$
, we have
![]() $s_{d_0}(p)=a$
, where
$s_{d_0}(p)=a$
, where
![]() $s_{d_0}:({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/f{\mathbb Z})^*$
is the canonical morphism. Therefore,
$s_{d_0}:({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/f{\mathbb Z})^*$
is the canonical morphism. Therefore,
![]() $s_{d_0}$
surjective and its kernel is of order
$s_{d_0}$
surjective and its kernel is of order
![]() $\phi (d_0)$
. Let H be a subgroup of
$\phi (d_0)$
. Let H be a subgroup of
![]() $({\mathbb Z}/f{\mathbb Z})^*$
of order d. Then
$({\mathbb Z}/f{\mathbb Z})^*$
of order d. Then
![]() $H_{d_0} =s_{d_0}^{-1}(H)$
is a subgroup of order
$H_{d_0} =s_{d_0}^{-1}(H)$
is a subgroup of order
![]() $\phi (d_0)d$
of
$\phi (d_0)d$
of
![]() $({\mathbb Z}/d_0f{\mathbb Z})^*$
and as
$({\mathbb Z}/d_0f{\mathbb Z})^*$
and as
![]() $\chi $
runs over
$\chi $
runs over
![]() $X_f^-(H)$
the
$X_f^-(H)$
the
![]() $\chi '$
’s run over
$\chi '$
’s run over
![]() $X_{d_0f}^-(H_{d_0}),$
and by (1.1) and (1.9), we have
$X_{d_0f}^-(H_{d_0}),$
and by (1.1) and (1.9), we have
The following Lemma is probably well known but we found no reference in the literature.
Lemma 2.1 Let
![]() $f>2$
. Let H be a subgroup of index
$f>2$
. Let H be a subgroup of index
![]() $m =(G:H)$
in the multiplicative group
$m =(G:H)$
in the multiplicative group
![]() $G:=({\mathbb Z}/f{\mathbb Z})^*$
. Then
$G:=({\mathbb Z}/f{\mathbb Z})^*$
. Then
![]() $\# X_f(H) =m$
and
$\# X_f(H) =m$
and
![]() $H=\cap _{\chi \in X_f(H)}\ker \chi $
. Moreover, if
$H=\cap _{\chi \in X_f(H)}\ker \chi $
. Moreover, if
![]() $-1\not \in H$
, then m is even,
$-1\not \in H$
, then m is even,
![]() $\# X_f^-(H)=m/2$
and
$\# X_f^-(H)=m/2$
and
![]() $H=\cap _{\chi \in X_f^-(H)}\ker \chi $
.
$H=\cap _{\chi \in X_f^-(H)}\ker \chi $
.
Proof Since
![]() $X_f(H)$
is isomorphic to the group of Dirichlet characters of the abelian quotient group
$X_f(H)$
is isomorphic to the group of Dirichlet characters of the abelian quotient group
![]() $G/H$
, it is of order m, by [Reference SerreSer, Chapter VI, Proposition 2]. Clearly,
$G/H$
, it is of order m, by [Reference SerreSer, Chapter VI, Proposition 2]. Clearly,
![]() $H\subseteq \cap _{\chi \in X_f(H)}\ker \chi $
. Conversely, take
$H\subseteq \cap _{\chi \in X_f(H)}\ker \chi $
. Conversely, take
![]() $g\not \in H$
, of order
$g\not \in H$
, of order
![]() $n\geq 2$
in the abelian quotient group
$n\geq 2$
in the abelian quotient group
![]() $G/H$
. Define a character
$G/H$
. Define a character
![]() $\chi $
of the subgroup
$\chi $
of the subgroup
![]() $\langle g,H\rangle $
of G generated by g and H by
$\langle g,H\rangle $
of G generated by g and H by
![]() $\chi (g^kh) =\exp (2\pi ik/n)$
,
$\chi (g^kh) =\exp (2\pi ik/n)$
,
![]() $(k,h)\in {\mathbb Z}\times H$
. It extends to a character of G still denoted
$(k,h)\in {\mathbb Z}\times H$
. It extends to a character of G still denoted
![]() $\chi $
, by [Reference SerreSer, Chapter VI, Proposition 1]. Since
$\chi $
, by [Reference SerreSer, Chapter VI, Proposition 1]. Since
![]() $g\not \in \ker \chi $
and
$g\not \in \ker \chi $
and
![]() $\chi \in X_f(H)$
, we have
$\chi \in X_f(H)$
, we have
![]() $g\not \in \cap _{\chi \in X_f(H)}\ker \chi $
, i.e.,
$g\not \in \cap _{\chi \in X_f(H)}\ker \chi $
, i.e.,
![]() $ \cap _{\chi \in X_f(H)}\ker \chi \subseteq H$
.
$ \cap _{\chi \in X_f(H)}\ker \chi \subseteq H$
.
Now, assume that
![]() $-1\not \in H$
. Set
$-1\not \in H$
. Set
![]() $H'=\langle -1,H\rangle $
, of index
$H'=\langle -1,H\rangle $
, of index
![]() $m/2$
in G. Then
$m/2$
in G. Then
![]() $X_f^-(H) =X_f(H)\setminus X_f(H')$
is indeed of order
$X_f^-(H) =X_f(H)\setminus X_f(H')$
is indeed of order
![]() $m-m/2 =m/2$
, by the first assertion. Clearly,
$m-m/2 =m/2$
, by the first assertion. Clearly,
![]() $H\subseteq \cap _{\chi \in X_f^-(H)}\ker \chi $
. Conversely, take
$H\subseteq \cap _{\chi \in X_f^-(H)}\ker \chi $
. Conversely, take
![]() $g\not \in H$
. Set
$g\not \in H$
. Set
![]() $H" :=\langle g,H\rangle =\{g^kh;\ k\in {\mathbb Z},\ h\in H\}$
, of index
$H" :=\langle g,H\rangle =\{g^kh;\ k\in {\mathbb Z},\ h\in H\}$
, of index
![]() $m"$
in G, with
$m"$
in G, with
![]() $m>m"$
. If
$m>m"$
. If
![]() $-1=g^kh\in H"$
, then clearly
$-1=g^kh\in H"$
, then clearly
![]() $\chi (g)\neq 1$
for
$\chi (g)\neq 1$
for
![]() $\chi \in X_f^-(H)$
; hence,
$\chi \in X_f^-(H)$
; hence,
![]() $g\not \in \cap _{\chi \in X_f^-(H)}\ker \chi $
. If
$g\not \in \cap _{\chi \in X_f^-(H)}\ker \chi $
. If
![]() $-1\not \in H"$
and
$-1\not \in H"$
and
![]() $\chi \in X_f^-(H)\setminus X_f^-(H")$
, a nonempty set or cardinal
$\chi \in X_f^-(H)\setminus X_f^-(H")$
, a nonempty set or cardinal
![]() $m/2-m"/2 =(H":H)/2\geq 1$
, then clearly
$m/2-m"/2 =(H":H)/2\geq 1$
, then clearly
![]() $\chi (g)\neq 1$
; hence,
$\chi (g)\neq 1$
; hence,
![]() $g\not \in \cap _{\chi \in X_f^-(H)}\ker \chi $
. Therefore,
$g\not \in \cap _{\chi \in X_f^-(H)}\ker \chi $
. Therefore,
![]() $\cap _{\chi \in X_f^-(H)}\ker \chi \subseteq H$
.
$\cap _{\chi \in X_f^-(H)}\ker \chi \subseteq H$
.
2.2 On the size of
 $\Pi _{d_0}(f,H)$
and
$\Pi _{d_0}(f,H)$
and
 $D_{d_0}(f,H)$
defined in (1.10)
$D_{d_0}(f,H)$
defined in (1.10)
Lemma 2.3 Let H be a subgroup of order
![]() $d\geq 1$
of the multiplicative group
$d\geq 1$
of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, where
$({\mathbb Z}/f{\mathbb Z})^*$
, where
![]() $f>2$
. Assume that
$f>2$
. Assume that
![]() $-1\not \in H$
. Let g be the order of a given prime integer q in the multiplicative quotient group
$-1\not \in H$
. Let g be the order of a given prime integer q in the multiplicative quotient group
![]() $({\mathbb Z}/f{\mathbb Z})^*/H$
. Let
$({\mathbb Z}/f{\mathbb Z})^*/H$
. Let
![]() $X_f(H)$
be the multiplicative group of the
$X_f(H)$
be the multiplicative group of the
![]() $\phi (f)/d$
Dirichlet characters modulo f for which
$\phi (f)/d$
Dirichlet characters modulo f for which
![]() $\chi _{/H} =1$
. Define
$\chi _{/H} =1$
. Define
![]() $X_f^-(H) = \{\chi \in X_f(H);\ \chi (-1)=-1\}$
, a set of cardinal
$X_f^-(H) = \{\chi \in X_f(H);\ \chi (-1)=-1\}$
, a set of cardinal
![]() $\phi (f)/(2d)$
. Then
$\phi (f)/(2d)$
. Then
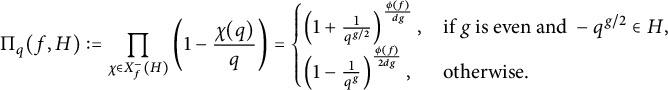 $$ \begin{align*}\Pi_{q}(f,H) :=\prod_{\chi\in X_f^-(H)}\left (1-\frac{\chi (q)}{q}\right ) =\begin{cases} \left (1+\frac{1}{q^{g/2}}\right )^{\frac{\phi(f)}{dg}},&\mbox{if } g \mbox{ is even and } -q^{g/2}\in H,\\ \left (1-\frac{1}{q^g}\right )^{\frac{\phi(f)}{2dg}},&\mbox{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}\Pi_{q}(f,H) :=\prod_{\chi\in X_f^-(H)}\left (1-\frac{\chi (q)}{q}\right ) =\begin{cases} \left (1+\frac{1}{q^{g/2}}\right )^{\frac{\phi(f)}{dg}},&\mbox{if } g \mbox{ is even and } -q^{g/2}\in H,\\ \left (1-\frac{1}{q^g}\right )^{\frac{\phi(f)}{2dg}},&\mbox{otherwise.} \end{cases}\end{align*} $$
Proof Let
![]() $\alpha $
be of order g in an abelian group A of order n. Let
$\alpha $
be of order g in an abelian group A of order n. Let
![]() $B=\langle \alpha \rangle $
be the cyclic group generated by
$B=\langle \alpha \rangle $
be the cyclic group generated by
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\hat B$
be the group of the g characters of B. Then
$\hat B$
be the group of the g characters of B. Then
![]() $P_{B}(X) :=\prod _{\chi \in \hat B} (X-\chi (\alpha )) =X^g-1$
. Now, the restriction map
$P_{B}(X) :=\prod _{\chi \in \hat B} (X-\chi (\alpha )) =X^g-1$
. Now, the restriction map
![]() $\chi \in \hat A\rightarrow \chi _{/B}\in \hat B$
is surjective, by [Reference SerreSer, Proposition 1], and of kernel isomorphic to
$\chi \in \hat A\rightarrow \chi _{/B}\in \hat B$
is surjective, by [Reference SerreSer, Proposition 1], and of kernel isomorphic to
![]() $\widehat {A/B}$
of order
$\widehat {A/B}$
of order
![]() $n/g$
, by [Reference SerreSer, Proposition 2]. Therefore,
$n/g$
, by [Reference SerreSer, Proposition 2]. Therefore,
![]() $P_{A}(X) :=\prod _{\chi \in \hat A} (X-\chi (\alpha )) =P_B(X)^{n/g} =(X^g-1)^{n/g}$
. With
$P_{A}(X) :=\prod _{\chi \in \hat A} (X-\chi (\alpha )) =P_B(X)^{n/g} =(X^g-1)^{n/g}$
. With
![]() $A=({\mathbb Z}/f{\mathbb Z})^*/H$
of order
$A=({\mathbb Z}/f{\mathbb Z})^*/H$
of order
![]() $n=\phi (f)/d$
, we have
$n=\phi (f)/d$
, we have
![]() $\hat A =X_f(H)$
and
$\hat A =X_f(H)$
and
 $$ \begin{align*}\prod_{\chi\in X_f(H)}(X-\chi (q)) =(X^g-1)^{\frac{\phi(f)}{dg}}.\end{align*} $$
$$ \begin{align*}\prod_{\chi\in X_f(H)}(X-\chi (q)) =(X^g-1)^{\frac{\phi(f)}{dg}}.\end{align*} $$
Let
![]() $H'$
be the subgroup of order
$H'$
be the subgroup of order
![]() $2d$
generated by
$2d$
generated by
![]() $-1$
and H. With
$-1$
and H. With
![]() $A'=({\mathbb Z}/f{\mathbb Z})^*/H'$
of order
$A'=({\mathbb Z}/f{\mathbb Z})^*/H'$
of order
![]() $n'=\phi (f)/(2d)$
, we have
$n'=\phi (f)/(2d)$
, we have
![]() $\hat A' =X_f(H') =X_f^+(H):=\{\chi \in X_f(H);\ \chi (-1)=+1\}$
and
$\hat A' =X_f(H') =X_f^+(H):=\{\chi \in X_f(H);\ \chi (-1)=+1\}$
and
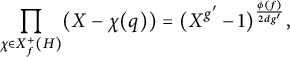 $$ \begin{align*}\prod_{\chi\in X_f^+(H)}(X-\chi (q)) =(X^{g'}-1)^{\frac{\phi(f)}{2dg'}}, \end{align*} $$
$$ \begin{align*}\prod_{\chi\in X_f^+(H)}(X-\chi (q)) =(X^{g'}-1)^{\frac{\phi(f)}{2dg'}}, \end{align*} $$
where q is of order
![]() $g'$
in
$g'$
in
![]() $A'$
.
$A'$
.
Since
![]() $X_f^-(H) =X_f(H)\setminus X_f^+(H)$
, it follows that
$X_f^-(H) =X_f(H)\setminus X_f^+(H)$
, it follows that
 $$ \begin{align*}\prod_{\chi\in X_f^-(H)} (X-\chi (q)) =\frac{(X^g-1)^{\frac{\phi(f)}{dg}}}{(X^{g'}-1)^{\frac{\phi(f)}{2dg'}}}.\end{align*} $$
$$ \begin{align*}\prod_{\chi\in X_f^-(H)} (X-\chi (q)) =\frac{(X^g-1)^{\frac{\phi(f)}{dg}}}{(X^{g'}-1)^{\frac{\phi(f)}{2dg'}}}.\end{align*} $$
Since
![]() $q^g\in H$
, we have
$q^g\in H$
, we have
![]() $q^g\in H'$
and
$q^g\in H'$
and
![]() $g'$
divides g. Since
$g'$
divides g. Since
![]() $q^{g'}\in H'=\{\pm h;\ h\in H\}$
, we have
$q^{g'}\in H'=\{\pm h;\ h\in H\}$
, we have
![]() $q^{2g'}\in H$
and g divides
$q^{2g'}\in H$
and g divides
![]() $2g'$
. Hence,
$2g'$
. Hence,
![]() $g=g'$
or
$g=g'$
or
![]() $g =2g'$
and
$g =2g'$
and
![]() $g=2g'$
if and only if g is even and
$g=2g'$
if and only if g is even and
![]() $q^{g/2}=q^{g'}\in H'\setminus H=\{-h;\ h\in H\}$
. The assertion follows.
$q^{g/2}=q^{g'}\in H'\setminus H=\{-h;\ h\in H\}$
. The assertion follows.
Corollary 2.4 Fix
![]() $d_0>1$
square-free. Let
$d_0>1$
square-free. Let
![]() $p\geq 3$
run over the prime integers that do not divide
$p\geq 3$
run over the prime integers that do not divide
![]() $d_0$
. Let H a subgroup of odd order d of the multiplicative group
$d_0$
. Let H a subgroup of odd order d of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. Then
$({\mathbb Z}/p{\mathbb Z})^*$
. Then
where
![]() $\omega (d_0)$
stands for the number of prime divisors of
$\omega (d_0)$
stands for the number of prime divisors of
![]() $d_0$
. In particular when
$d_0$
. In particular when
![]() $d =o(\log p)$
, we have
$d =o(\log p)$
, we have
Moreover,
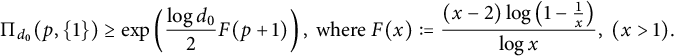 $$ \begin{align*}\Pi _{d_0}(p,\{1\}) \geq\exp\left (\frac{\log d_0}{2}F(p+1)\right ), \mbox{ where } F(x):=\frac{(x-2)\log\left (1-\frac{1}{x}\right )}{\log x},\ (x>1).\end{align*} $$
$$ \begin{align*}\Pi _{d_0}(p,\{1\}) \geq\exp\left (\frac{\log d_0}{2}F(p+1)\right ), \mbox{ where } F(x):=\frac{(x-2)\log\left (1-\frac{1}{x}\right )}{\log x},\ (x>1).\end{align*} $$
In particular,
![]() $\Pi _{6}(p,\{1\}) \geq 2/3 \,\, \mbox {for } p\geq 5.$
$\Pi _{6}(p,\{1\}) \geq 2/3 \,\, \mbox {for } p\geq 5.$
Proof Let q be a prime divisor of
![]() $d_0$
. Let g be the order of q in the multiplicative quotient group
$d_0$
. Let g be the order of q in the multiplicative quotient group
![]() $({\mathbb Z}/p{\mathbb Z})^*/H$
. Then
$({\mathbb Z}/p{\mathbb Z})^*/H$
. Then
 $$ \begin{align*}\left (1-\frac{1}{q^g}\right )^{\frac{2}{g}} \leq D_q(p,H) =\Pi_{q}(p,H)^{\frac{4d}{p-1}} \leq\left (1+\frac{1}{q^{g/2}}\right )^{\frac{4}{g}},\end{align*} $$
$$ \begin{align*}\left (1-\frac{1}{q^g}\right )^{\frac{2}{g}} \leq D_q(p,H) =\Pi_{q}(p,H)^{\frac{4d}{p-1}} \leq\left (1+\frac{1}{q^{g/2}}\right )^{\frac{4}{g}},\end{align*} $$
by (1.10) and Lemma 2.3, with
![]() $f=p$
,
$f=p$
,
![]() $\phi (f)=p-1$
and
$\phi (f)=p-1$
and
![]() $m =(p-1)/d$
. Either
$m =(p-1)/d$
. Either
![]() $q^g\equiv 1\ \ \pmod p$
, in which case
$q^g\equiv 1\ \ \pmod p$
, in which case
![]() $q^g\geq p+1$
, or
$q^g\geq p+1$
, or
![]() $q^g\equiv h\ \ \pmod p$
for some
$q^g\equiv h\ \ \pmod p$
for some
![]() $h\in \{2,\ldots ,p-1\}\cap H$
, in which case p divides
$h\in \{2,\ldots ,p-1\}\cap H$
, in which case p divides
![]() $S:=1+h+\cdots +h^{d-1}$
which satisfies
$S:=1+h+\cdots +h^{d-1}$
which satisfies
![]() $p\leq S\leq 2h^{d-1}$
. Therefore, in both cases, we have
$p\leq S\leq 2h^{d-1}$
. Therefore, in both cases, we have
![]() $q^{g}\geq (p/2)^{\frac {1}{d-1}}$
. Hence,
$q^{g}\geq (p/2)^{\frac {1}{d-1}}$
. Hence,
where we used for
![]() $x=q^{-g}$
the fact that
$x=q^{-g}$
the fact that
![]() $\log (1-x) \geq -2(\log 2)x$
in
$\log (1-x) \geq -2(\log 2)x$
in
![]() $\left [0,1/2\right ]$
,
$\left [0,1/2\right ]$
,
where we used the fact that
![]() $e^{-x} \geq 1-x$
. Therefore, we have
$e^{-x} \geq 1-x$
. Therefore, we have
 $$ \begin{align*}D_{d_0}(p,H) =\prod_{q \mid d_0}D_q(p,H) \geq 1-4(\log 2)\omega(d_0)\left(\frac{p}{2}\right)^{-1/(d-1)},\end{align*} $$
$$ \begin{align*}D_{d_0}(p,H) =\prod_{q \mid d_0}D_q(p,H) \geq 1-4(\log 2)\omega(d_0)\left(\frac{p}{2}\right)^{-1/(d-1)},\end{align*} $$
where we used the inequality
![]() $(1-x)^n \geq 1-nx$
for
$(1-x)^n \geq 1-nx$
for
![]() $x \leq 1$
and
$x \leq 1$
and
![]() $n\in \mathbb {N}$
. A similar reasoning gives an explicit upper bound
$n\in \mathbb {N}$
. A similar reasoning gives an explicit upper bound
![]() $D_{d_0}(p,H) \leq 1+ c\omega (d_0)p^{-1/2(d-1)}$
for some constant
$D_{d_0}(p,H) \leq 1+ c\omega (d_0)p^{-1/2(d-1)}$
for some constant
![]() $c>0$
. Therefore, we do get (2.2). Finally,
$c>0$
. Therefore, we do get (2.2). Finally,
![]() $p^{1/(d-1)}$
tends to infinity in the range
$p^{1/(d-1)}$
tends to infinity in the range
![]() $d =o(\log p)$
and (2.3) follows.
$d =o(\log p)$
and (2.3) follows.
Notice that if
![]() $p=2^d-1$
runs over the Mersenne primes and
$p=2^d-1$
runs over the Mersenne primes and
![]() $H=\langle 2\rangle $
, we have
$H=\langle 2\rangle $
, we have
![]() $d=O(\log p)$
but
$d=O(\log p)$
but
![]() $D_2(p,H) =\left (1-\frac {1}{2}\right )^2$
does not satisfy (2.3).
$D_2(p,H) =\left (1-\frac {1}{2}\right )^2$
does not satisfy (2.3).
Now, assume that
![]() $H=\{1\}$
. Then
$H=\{1\}$
. Then
![]() $K={\mathbb Q}(\zeta _p)$
and
$K={\mathbb Q}(\zeta _p)$
and
![]() $q^g\geq p+1$
. Hence,
$q^g\geq p+1$
. Hence,
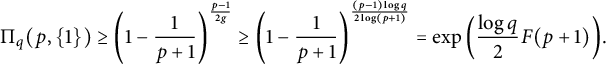 $$ \begin{align*}\Pi_q(p,\{1\}) \geq\left (1-\frac{1}{p+1}\right )^{\frac{p-1}{2g}} \geq\left (1-\frac{1}{p+1}\right )^{\frac{(p-1)\log q}{2\log (p+1)}} =\exp\left (\frac{\log q}{2}F(p+1)\right ){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}\Pi_q(p,\{1\}) \geq\left (1-\frac{1}{p+1}\right )^{\frac{p-1}{2g}} \geq\left (1-\frac{1}{p+1}\right )^{\frac{(p-1)\log q}{2\log (p+1)}} =\exp\left (\frac{\log q}{2}F(p+1)\right ){\kern-1.5pt}.\end{align*} $$
The desired lower bound easily follows.
3 Dedekind sums and mean square values of L-functions
3.1 Dedekind sums and Dedekind–Rademacher sums
The Dedekind sums is the rational number defined by
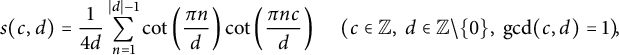 $$ \begin{align} s(c,d) ={1\over 4d}\sum_{n=1}^{\vert d\vert -1}\cot\left ({\pi n\over d}\right )\cot\left ({\pi nc\over d}\right ) \ \ \ \ \ (c\in {\mathbb Z},\ d\in {\mathbb Z}\setminus\{0\},\ \gcd (c,d)=1){\kern-1.5pt}, \end{align} $$
$$ \begin{align} s(c,d) ={1\over 4d}\sum_{n=1}^{\vert d\vert -1}\cot\left ({\pi n\over d}\right )\cot\left ({\pi nc\over d}\right ) \ \ \ \ \ (c\in {\mathbb Z},\ d\in {\mathbb Z}\setminus\{0\},\ \gcd (c,d)=1){\kern-1.5pt}, \end{align} $$
with the convention
![]() $s(c,-1)=s(c,1)=0$
for
$s(c,-1)=s(c,1)=0$
for
![]() $c\in {\mathbb Z}$
(see [Reference ApostolApo] or [Reference Rademacher and GrosswaldRG] where it is, however, assumed that
$c\in {\mathbb Z}$
(see [Reference ApostolApo] or [Reference Rademacher and GrosswaldRG] where it is, however, assumed that
![]() $d>1$
). It depends only on c mod
$d>1$
). It depends only on c mod
![]() $\vert d\vert $
and
$\vert d\vert $
and
![]() $c\mapsto s(c,d)$
can therefore be seen as a mapping from
$c\mapsto s(c,d)$
can therefore be seen as a mapping from
![]() $({\mathbb Z}/\vert d\vert {\mathbb Z})^*$
to
$({\mathbb Z}/\vert d\vert {\mathbb Z})^*$
to
![]() ${\mathbb Q}$
. Notice that
${\mathbb Q}$
. Notice that
(make the change of variables
![]() $n\mapsto nc$
in
$n\mapsto nc$
in
![]() $s(c^*,d)$
). Recall the reciprocity law for Dedekind sums
$s(c^*,d)$
). Recall the reciprocity law for Dedekind sums
In particular,
For
![]() $b,c\in {\mathbb Z},\ d\in {\mathbb Z}\setminus \{-1,0,1\}$
such that
$b,c\in {\mathbb Z},\ d\in {\mathbb Z}\setminus \{-1,0,1\}$
such that
![]() $\gcd (b,d) =\gcd (c,d)=1$
, the Dedekind–Rademacher sum is the rational number defined by
$\gcd (b,d) =\gcd (c,d)=1$
, the Dedekind–Rademacher sum is the rational number defined by
 $$ \begin{align*} s(b,c,d) ={1\over 4d}\sum_{n=1}^{\vert d\vert -1}\cot\left ({\pi nb\over d}\right )\cot\left ({\pi nc\over d}\right ){\kern-1.5pt},\end{align*} $$
$$ \begin{align*} s(b,c,d) ={1\over 4d}\sum_{n=1}^{\vert d\vert -1}\cot\left ({\pi nb\over d}\right )\cot\left ({\pi nc\over d}\right ){\kern-1.5pt},\end{align*} $$
with the convention
![]() $s(b,c,-1)=s(b,c,1)=0$
for
$s(b,c,-1)=s(b,c,1)=0$
for
![]() $b,c\in {\mathbb Z}$
. Hence,
$b,c\in {\mathbb Z}$
. Hence,
![]() $s(c,d) =s(1,c,d)$
, if
$s(c,d) =s(1,c,d)$
, if
![]() $\alpha \in ({\mathbb Z}/\vert d\vert {\mathbb Z})^*$
is represented as
$\alpha \in ({\mathbb Z}/\vert d\vert {\mathbb Z})^*$
is represented as
![]() $\alpha =b/c$
with
$\alpha =b/c$
with
![]() $\gcd (b,d)=\gcd (c,d) =1$
, then
$\gcd (b,d)=\gcd (c,d) =1$
, then
![]() $s(\alpha ,d) =s(b,c,d)$
, and
$s(\alpha ,d) =s(b,c,d)$
, and
For
![]() $\gcd ( b,c) =\gcd (c,d) =\gcd (d,b) =1$
, we have a reciprocity law for Dedekind–Rademacher sums (see [Reference RademacherRad] or [Reference Bayad and RaoujBR])
$\gcd ( b,c) =\gcd (c,d) =\gcd (d,b) =1$
, we have a reciprocity law for Dedekind–Rademacher sums (see [Reference RademacherRad] or [Reference Bayad and RaoujBR])
The Cauchy–Schwarz inequality and (3.4) yield
3.2 Nontrivial bounds on Dedekind sums
In this section, we will use the alternative definition of the Dedekind sums given by
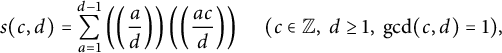 $$ \begin{align*}s(c,d) =\sum_{a=1}^{d-1} \left(\left(\frac{a}{d}\right)\right) \left(\left(\frac{ac}{d}\right)\right) \ \ \ \ \ (c\in {\mathbb Z},\ d\geq 1,\ \gcd (c,d)=1),\end{align*} $$
$$ \begin{align*}s(c,d) =\sum_{a=1}^{d-1} \left(\left(\frac{a}{d}\right)\right) \left(\left(\frac{ac}{d}\right)\right) \ \ \ \ \ (c\in {\mathbb Z},\ d\geq 1,\ \gcd (c,d)=1),\end{align*} $$
where
![]() $ \left (\left (\right )\right ):\mathbb {R} \rightarrow \mathbb {R}$
stands for the sawtooth function defined by
$ \left (\left (\right )\right ):\mathbb {R} \rightarrow \mathbb {R}$
stands for the sawtooth function defined by
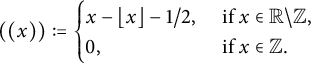 $$ \begin{align*}\left(\left(x\right)\right) := \begin{cases} x-\lfloor x\rfloor - 1/2,& \text{ if } x \in \mathbb{R} \backslash \mathbb{Z},\\ 0, &\text{ if } x \in \mathbb{Z}. \end{cases} \end{align*} $$
$$ \begin{align*}\left(\left(x\right)\right) := \begin{cases} x-\lfloor x\rfloor - 1/2,& \text{ if } x \in \mathbb{R} \backslash \mathbb{Z},\\ 0, &\text{ if } x \in \mathbb{Z}. \end{cases} \end{align*} $$
In order to prove Theorem 1.1, we need general bounds on Dedekind sums depending on the multiplicative order of the argument. This is a new type of bounds for Dedekind sums and the following result that improves upon (3.7) when the order is
![]() $o\left (\frac {\log p}{\log \log p}\right )$
might be of independent interest (see also Conjecture 7.1 for further discussions).
$o\left (\frac {\log p}{\log \log p}\right )$
might be of independent interest (see also Conjecture 7.1 for further discussions).
Theorem 3.1 Let
![]() $p>1$
be a prime integer and assume that h has order
$p>1$
be a prime integer and assume that h has order
![]() $k\geq 3$
in the multiplicative group
$k\geq 3$
in the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
We have
$({\mathbb Z}/p{\mathbb Z})^*$
We have
Remark 3.2 Let us notice that by a result of Vardi [Reference VardiVar], for any function f such that
![]() $\lim _{n\to +\infty } f(n)=+\infty $
we have
$\lim _{n\to +\infty } f(n)=+\infty $
we have
![]() $s(c,d) \ll f(d)\log d$
for almost all
$s(c,d) \ll f(d)\log d$
for almost all
![]() $(c,d)$
with
$(c,d)$
with
![]() $\gcd (c,d)=1$
. However, Dedekind sums take also very large values (see, for instance, [Reference Conrey, Fransen and KleinCEK, Reference GirstmairGir03] for more information).
$\gcd (c,d)=1$
. However, Dedekind sums take also very large values (see, for instance, [Reference Conrey, Fransen and KleinCEK, Reference GirstmairGir03] for more information).
Our proof builds from ideas of the proof of [Reference Louboutin and MunschLM21, Theorem
![]() $4.1$
] where some tools from equidistribution theory and the theory of pseudo-random generators were used. We refer for more information to [Reference KorobovKor, Nied77], or the book of Konyagin and Shparlinski [Reference Konyagin and ShparlinskiKS, Chapter
$4.1$
] where some tools from equidistribution theory and the theory of pseudo-random generators were used. We refer for more information to [Reference KorobovKor, Nied77], or the book of Konyagin and Shparlinski [Reference Konyagin and ShparlinskiKS, Chapter
![]() $12$
] (see [Reference Louboutin and MunschLM21, Section
$12$
] (see [Reference Louboutin and MunschLM21, Section
![]() $4$
] for more details and references). Let us recall some notations. For any fixed integer s, we consider the s-dimensional cube
$4$
] for more details and references). Let us recall some notations. For any fixed integer s, we consider the s-dimensional cube
![]() $I_s=\left [0,1\right ]^s$
equipped with its s-dimensional Lebesgue measure
$I_s=\left [0,1\right ]^s$
equipped with its s-dimensional Lebesgue measure
![]() $\lambda _s$
. We denote by
$\lambda _s$
. We denote by
![]() $\mathcal {B}$
the set of rectangular boxes of the form
$\mathcal {B}$
the set of rectangular boxes of the form
 $$ \begin{align*}\prod_{i=1}^{s}[\alpha_i,\beta_i) =\left\{x\in I_s, \alpha_i\leq x_i <\beta_i\right\}{\kern-1.5pt},\end{align*} $$
$$ \begin{align*}\prod_{i=1}^{s}[\alpha_i,\beta_i) =\left\{x\in I_s, \alpha_i\leq x_i <\beta_i\right\}{\kern-1.5pt},\end{align*} $$
where
![]() $0\leq \alpha _i<\beta _i\leq 1.$
If S is a finite subset of
$0\leq \alpha _i<\beta _i\leq 1.$
If S is a finite subset of
![]() $I^s$
, we define the discrepancy
$I^s$
, we define the discrepancy
![]() $D(S)$
by
$D(S)$
by
 $$ \begin{align*}D(S) =\sup_{B \in \mathcal{B}}\left\vert \frac{\# (B\cap S)}{\# S}-\lambda_s(B)\right\vert{\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}D(S) =\sup_{B \in \mathcal{B}}\left\vert \frac{\# (B\cap S)}{\# S}-\lambda_s(B)\right\vert{\kern-1.5pt}.\end{align*} $$
Let us introduce the following set of points:
 $$ \begin{align*}S_{h,p} =\left\{\left(\frac{x}{p},\frac{x h}{p}\right) \in I_2, x \bmod p\right\}{\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}S_{h,p} =\left\{\left(\frac{x}{p},\frac{x h}{p}\right) \in I_2, x \bmod p\right\}{\kern-1.5pt}.\end{align*} $$
For good choice of h, the points are equidistributed and we expect for “nice” functions f
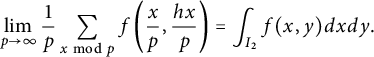 $$ \begin{align*}\lim_{p\to \infty} \frac{1}{p}\sum_{x \bmod p} f\left(\frac{x}{p},\frac{hx}{p}\right) = \int_{I_2} f(x,y)dx dy.\end{align*} $$
$$ \begin{align*}\lim_{p\to \infty} \frac{1}{p}\sum_{x \bmod p} f\left(\frac{x}{p},\frac{hx}{p}\right) = \int_{I_2} f(x,y)dx dy.\end{align*} $$
Lemma 3.3 For any h of order
![]() $k\geq 3$
, we have the following discrepancy bound:
$k\geq 3$
, we have the following discrepancy bound:
Proof It follows from the proof of [Reference Louboutin and MunschLM21, Theorem 4.1] where the bound was obtained as a consequence of Erdős–Turan inequality and tools from pseudo-random generators theory.
3.2.1 Proof of Theorem 3.1
Observe that
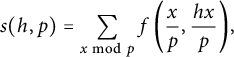 $$ \begin{align*}s(h,p)= \sum_{x \bmod p} f\left(\frac{x}{p},\frac{hx}{p}\right){\kern-1.5pt},\end{align*} $$
$$ \begin{align*}s(h,p)= \sum_{x \bmod p} f\left(\frac{x}{p},\frac{hx}{p}\right){\kern-1.5pt},\end{align*} $$
where
![]() $f(x,y)= ((x))((y))$
. By Koksma–Hlawka inequality [Reference Drmota and TichyDT, Theorem
$f(x,y)= ((x))((y))$
. By Koksma–Hlawka inequality [Reference Drmota and TichyDT, Theorem
![]() $1.14$
], we have
$1.14$
], we have
 $$ \begin{align*}\left\vert \frac{1}{p} \sum_{ x \bmod p} f\left(\frac{x}{p},\frac{x h}{p}\right) -\int_{I_{2}} f(u,v)dudv \right\vert \leq V(f)D(S_{h,p}),\end{align*} $$
$$ \begin{align*}\left\vert \frac{1}{p} \sum_{ x \bmod p} f\left(\frac{x}{p},\frac{x h}{p}\right) -\int_{I_{2}} f(u,v)dudv \right\vert \leq V(f)D(S_{h,p}),\end{align*} $$
where
![]() $V(f)$
is the Hardy–Krause variation of f. Moreover, we have
$V(f)$
is the Hardy–Krause variation of f. Moreover, we have
The readers can easily convince themselves that
![]() $V(f) \ll 1$
. Hence, the result follows from Lemma 3.3.
$V(f) \ll 1$
. Hence, the result follows from Lemma 3.3.
Remark 3.4 The same method used to bound the discrepancy leads to a similar bound for composite f. Indeed, for
![]() $h \in ({\mathbb Z}/f{\mathbb Z})^*$
of order
$h \in ({\mathbb Z}/f{\mathbb Z})^*$
of order
![]() $k\geq 3$
, we have
$k\geq 3$
, we have
![]() $s(h,f)= O\left ((\log f)^2 f/E(f)\right )$
with
$s(h,f)= O\left ((\log f)^2 f/E(f)\right )$
with
![]() $E(f)=\max \{P^{+}(f)^{1/\phi (k^*)},\textrm {rad}(f)^{1/k}\}$
where
$E(f)=\max \{P^{+}(f)^{1/\phi (k^*)},\textrm {rad}(f)^{1/k}\}$
where
![]() $P^{+}(f)$
is the largest prime factor of f,
$P^{+}(f)$
is the largest prime factor of f,
![]() $k^*$
is the order of h modulo
$k^*$
is the order of h modulo
![]() $P^+(f)$
and
$P^+(f)$
and
 $\displaystyle {\mathrm{rad}(f)=\prod _{\ell \mid f \atop \ell \textrm {prime}}\ell }$
is the radical of f. If
$\displaystyle {\mathrm{rad}(f)=\prod _{\ell \mid f \atop \ell \textrm {prime}}\ell }$
is the radical of f. If
![]() $f=h^3-1$
is square-free, then we have
$f=h^3-1$
is square-free, then we have
![]() $E(f) = f^{1/3}$
and
$E(f) = f^{1/3}$
and
![]() $s(h,f)=O\left ((\log f)^2 f^{2/3}\right )$
which is close to the truth by a logarithmic factor (see Remark 6.2).
$s(h,f)=O\left ((\log f)^2 f^{2/3}\right )$
which is close to the truth by a logarithmic factor (see Remark 6.2).
For
![]() $\gcd (b,p)=\gcd (c,p)=1$
, we recall the other definition of Dedekind–Rademacher sums
$\gcd (b,p)=\gcd (c,p)=1$
, we recall the other definition of Dedekind–Rademacher sums
 $$ \begin{align*}s(b,c,p)= \sum_{a=1}^{p-1} \left(\left(\frac{ab}{p}\right)\right) \left(\left(\frac{ac}{p}\right)\right){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}s(b,c,p)= \sum_{a=1}^{p-1} \left(\left(\frac{ab}{p}\right)\right) \left(\left(\frac{ac}{p}\right)\right){\kern-1.5pt}.\end{align*} $$
A similar argument as in the proof of Theorem 3.1 leads to a bound on these generalized sums.
Theorem 3.5 Let
![]() $q_1$
,
$q_1$
,
![]() $q_2$
and
$q_2$
and
![]() $k\geq 3$
be given natural integers. Let p run over the primes and h over the elements of order k in the multiplicative group
$k\geq 3$
be given natural integers. Let p run over the primes and h over the elements of order k in the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. Then, we have
$({\mathbb Z}/p{\mathbb Z})^*$
. Then, we have
Proof The proof follows exactly the same lines as the proof of Theorem 3.1 except for the fact that the function f is replaced by the function
![]() $g(x,y)= ((q_1 x))((q_2 y))$
. Hence, we have
$g(x,y)= ((q_1 x))((q_2 y))$
. Hence, we have
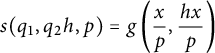 $$ \begin{align*}s(q_1,q_2 h,p)= g\left(\frac{x}{p},\frac{hx}{p}\right)\end{align*} $$
$$ \begin{align*}s(q_1,q_2 h,p)= g\left(\frac{x}{p},\frac{hx}{p}\right)\end{align*} $$
and by symmetry we remark that
Again,
![]() $V(g) \ll 1$
and the result follows from Lemma 3.3 and Koksma–Hlawka inequality.
$V(g) \ll 1$
and the result follows from Lemma 3.3 and Koksma–Hlawka inequality.
3.3 Twisted second moment of L- functions and Dedekind sums
We illustrate the link between Dedekind sums and twisted moments of L- functions by first proving Theorem 1.1 in the case
![]() $H=\{1\}$
with a stronger error term. For any integers
$H=\{1\}$
with a stronger error term. For any integers
![]() $q_1,q_2 \geq 1$
and any prime
$q_1,q_2 \geq 1$
and any prime
![]() $p\geq 3$
, we define the twisted moment
$p\geq 3$
, we define the twisted moment
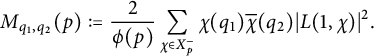 $$ \begin{align} M_{q_1,q_2}(p) :=\frac{2}{\phi(p)} \sum_{\chi \in X_p^-}\chi(q_1)\overline{\chi}(q_2)\vert L(1,\chi)\vert^2. \end{align} $$
$$ \begin{align} M_{q_1,q_2}(p) :=\frac{2}{\phi(p)} \sum_{\chi \in X_p^-}\chi(q_1)\overline{\chi}(q_2)\vert L(1,\chi)\vert^2. \end{align} $$
The following formula (see [Reference LouboutinLou94, Proposition 1]) will help us to relate L- functions to Dedekind sums:
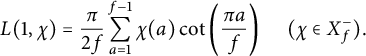 $$ \begin{align} L(1,\chi) =\frac{\pi}{2f}\sum_{a=1}^{f-1}\chi (a)\cot\left (\frac{\pi a}{f}\right ) \ \ \ \ \ (\chi\in X_f^-).\end{align} $$
$$ \begin{align} L(1,\chi) =\frac{\pi}{2f}\sum_{a=1}^{f-1}\chi (a)\cot\left (\frac{\pi a}{f}\right ) \ \ \ \ \ (\chi\in X_f^-).\end{align} $$
Theorem 3.6 Let
![]() $q_1$
and
$q_1$
and
![]() $q_2$
be given coprime integers. Then, when p goes to infinity
$q_2$
be given coprime integers. Then, when p goes to infinity
 $$ \begin{align*}M_{q_1,q_2}(p)= \frac{\pi^2}{6q_1q_2}+O_{q_1,q_2}(1/p).\end{align*} $$
$$ \begin{align*}M_{q_1,q_2}(p)= \frac{\pi^2}{6q_1q_2}+O_{q_1,q_2}(1/p).\end{align*} $$
Remark 3.7 It is worth to notice that in the case
![]() $q_2=1$
, explicit formulas are known by [Reference LouboutinLou15, Theorem
$q_2=1$
, explicit formulas are known by [Reference LouboutinLou15, Theorem
![]() $4$
] (see also [Reference Lee and LeeLee17]). This also gives a new and simpler proof of [Reference Lee and LeeLee19, Theorem
$4$
] (see also [Reference Lee and LeeLee17]). This also gives a new and simpler proof of [Reference Lee and LeeLee19, Theorem
![]() $1.1$
] in a special case.
$1.1$
] in a special case.
Proof Let us define
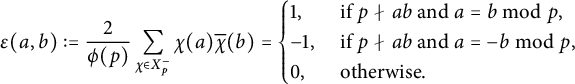 $$ \begin{align*}\epsilon(a,b) :=\frac{2}{\phi(p)}\sum_{\chi \in X_p^-}\chi(a)\overline{\chi}(b) =\begin{cases} 1,&\text{ if } p\nmid ab \text{ and } a=b \bmod p, \\ -1,&\text{ if } p\nmid ab \text{ and } a=-b \bmod p, \\ 0, &\text{ otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}\epsilon(a,b) :=\frac{2}{\phi(p)}\sum_{\chi \in X_p^-}\chi(a)\overline{\chi}(b) =\begin{cases} 1,&\text{ if } p\nmid ab \text{ and } a=b \bmod p, \\ -1,&\text{ if } p\nmid ab \text{ and } a=-b \bmod p, \\ 0, &\text{ otherwise.} \end{cases}\end{align*} $$
For p large enough, we have
![]() $\gcd (q_1,p)=\gcd (q_2,p)=1$
. Hence, using orthogonality relations and (3.9), we arrive at
$\gcd (q_1,p)=\gcd (q_2,p)=1$
. Hence, using orthogonality relations and (3.9), we arrive at
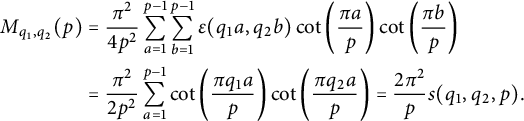 $$ \begin{align*} M_{q_1,q_2}(p) &=\frac{\pi^2}{4p^2} \sum_{a=1}^{p-1} \sum_{b=1}^{p-1}\epsilon(q_1 a,q_2 b)\cot\left(\frac{\pi a}{p}\right)\cot\left(\frac{\pi b}{p}\right) \\ & = \frac{\pi^2}{2p^2} \sum_{a=1}^{p-1}\cot\left(\frac{\pi q_1a}{p}\right)\cot\left(\frac{\pi q_2 a}{p}\right) = \frac{2\pi^2}{p}s(q_1,q_2,p). \end{align*} $$
$$ \begin{align*} M_{q_1,q_2}(p) &=\frac{\pi^2}{4p^2} \sum_{a=1}^{p-1} \sum_{b=1}^{p-1}\epsilon(q_1 a,q_2 b)\cot\left(\frac{\pi a}{p}\right)\cot\left(\frac{\pi b}{p}\right) \\ & = \frac{\pi^2}{2p^2} \sum_{a=1}^{p-1}\cot\left(\frac{\pi q_1a}{p}\right)\cot\left(\frac{\pi q_2 a}{p}\right) = \frac{2\pi^2}{p}s(q_1,q_2,p). \end{align*} $$
When
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are fixed coprime integers and p goes to infinity, we infer from (3.6) and (3.7) that
$q_2$
are fixed coprime integers and p goes to infinity, we infer from (3.6) and (3.7) that
The result follows immediately.
Corollary 3.8 Let
![]() $q_1$
and
$q_1$
and
![]() $q_2$
be given natural integers. Then, when p goes to infinity
$q_2$
be given natural integers. Then, when p goes to infinity
 $$ \begin{align*}M_{q_1,q_2}(p )=\frac{\pi^2}{6}\frac{ \gcd(q_1,q_2)^2}{q_1q_2}+O_{q_1,q_2}(1/p).\end{align*} $$
$$ \begin{align*}M_{q_1,q_2}(p )=\frac{\pi^2}{6}\frac{ \gcd(q_1,q_2)^2}{q_1q_2}+O_{q_1,q_2}(1/p).\end{align*} $$
Proof Let
![]() $\delta = \gcd (q_1,q_2)$
. We clearly have
$\delta = \gcd (q_1,q_2)$
. We clearly have
![]() $M_{q_1,q_2}(p)=M_{q_1/\delta ,q_2/\delta }(p)$
and the result follows from Theorem 3.6.
$M_{q_1,q_2}(p)=M_{q_1/\delta ,q_2/\delta }(p)$
and the result follows from Theorem 3.6.
The proof of Theorem 1.1 in the case of the trivial subgroup follows easily.
Corollary 3.9 Let
![]() $d_0$
be a given square-free integer. When p goes to infinity, we have the following asymptotic formula:
$d_0$
be a given square-free integer. When p goes to infinity, we have the following asymptotic formula:
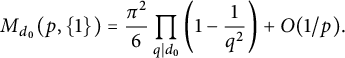 $$ \begin{align*}M_{d_0}(p,\{1\}) =\frac{\pi^2}{6}\prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)+ O(1/p).\end{align*} $$
$$ \begin{align*}M_{d_0}(p,\{1\}) =\frac{\pi^2}{6}\prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)+ O(1/p).\end{align*} $$
Proof For
![]() $\chi $
modulo p, let
$\chi $
modulo p, let
![]() $\chi '$
be the character modulo
$\chi '$
be the character modulo
![]() $d_0p$
induced by
$d_0p$
induced by
![]() $\chi $
. By (1.8) and Corollary 3.8, we have
$\chi $
. By (1.8) and Corollary 3.8, we have
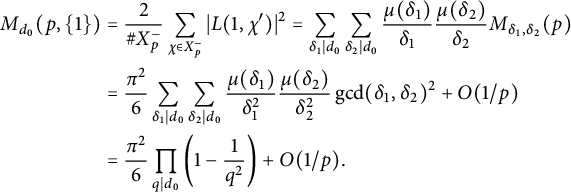 $$ \begin{align*} M_{d_0}(p,\{1\})& =\frac{2}{\# X_p^-} \sum_{\chi \in X_p^-} |L(1,\chi')|^2 =\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1}\frac{\mu(\delta_2)}{\delta_2} M_{\delta_1,\delta_2}(p) \\ &=\frac{\pi^2}{6}\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1^2} \frac{\mu(\delta_2)}{\delta_2^2}\gcd(\delta_1,\delta_2)^2 + O(1/p) \\ &=\frac{\pi^2}{6} \prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)+O(1/p). \end{align*} $$
$$ \begin{align*} M_{d_0}(p,\{1\})& =\frac{2}{\# X_p^-} \sum_{\chi \in X_p^-} |L(1,\chi')|^2 =\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1}\frac{\mu(\delta_2)}{\delta_2} M_{\delta_1,\delta_2}(p) \\ &=\frac{\pi^2}{6}\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1^2} \frac{\mu(\delta_2)}{\delta_2^2}\gcd(\delta_1,\delta_2)^2 + O(1/p) \\ &=\frac{\pi^2}{6} \prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)+O(1/p). \end{align*} $$
3.4 An interesting link with sums of maxima
Before turning to the general case of Theorem 1.1, we explain how to use Theorem 3.6 to estimate the seemingly innocuous sumFootnote
4
defined for any integers
![]() $q_1,q_2 \geq 1$
by
$q_1,q_2 \geq 1$
by
where, here and below,
![]() $q_1 x, q_2 x$
denote the representatives modulo p taken in
$q_1 x, q_2 x$
denote the representatives modulo p taken in
![]() $\left [1,p\right ]$
.
$\left [1,p\right ]$
.
Theorem 3.10 Let
![]() $q_1$
and
$q_1$
and
![]() $q_2$
be natural integers such that
$q_2$
be natural integers such that
![]() $q_1 \neq q_2$
. Then, we have the following asymptotic formula:
$q_1 \neq q_2$
. Then, we have the following asymptotic formula:
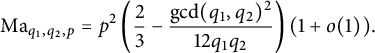 $$ \begin{align*}\text{Ma}_{q_1,q_2,p} = p^2\left(\frac{2}{3}-\frac{\gcd(q_1,q_2)^2}{12q_1q_2}\right)(1+o(1)).\end{align*} $$
$$ \begin{align*}\text{Ma}_{q_1,q_2,p} = p^2\left(\frac{2}{3}-\frac{\gcd(q_1,q_2)^2}{12q_1q_2}\right)(1+o(1)).\end{align*} $$
Remark 3.11 In the special case
![]() $q_1=1$
, we are able to evaluate the sum directly without the need of Dedekind sums and L- functions. However, we could not prove Theorem 3.10 in the general case using elementary counting methods.
$q_1=1$
, we are able to evaluate the sum directly without the need of Dedekind sums and L- functions. However, we could not prove Theorem 3.10 in the general case using elementary counting methods.
Remark 3.12 Let us notice that
![]() $\int _{0}^{1}\int _{0}^{1} \max (x,y) dx dy = 2/3$
. Hence, using the same method as in Section 3.2, we can show that if the points
$\int _{0}^{1}\int _{0}^{1} \max (x,y) dx dy = 2/3$
. Hence, using the same method as in Section 3.2, we can show that if the points
![]() $\left (\left \{\frac {x}{p}\right \},\left \{\frac {qx}{p}\right \}\right )$
are equidistributed in the square
$\left (\left \{\frac {x}{p}\right \},\left \{\frac {qx}{p}\right \}\right )$
are equidistributed in the square
![]() $[0,1]^2,$
then
$[0,1]^2,$
then
 $$ \begin{align*}\sum_{x \bmod p} \max(x,qx) \sim \frac{2}{3}p^2.\end{align*} $$
$$ \begin{align*}\sum_{x \bmod p} \max(x,qx) \sim \frac{2}{3}p^2.\end{align*} $$
For q fixed and
![]() $p \rightarrow +\infty $
, the points are not equidistributed in the square and we see that the correcting factor
$p \rightarrow +\infty $
, the points are not equidistributed in the square and we see that the correcting factor
![]() $\frac {\gcd (q_1,q_2)^2}{12q_1q_2}$
from equidistribution is related to the Dedekind sum
$\frac {\gcd (q_1,q_2)^2}{12q_1q_2}$
from equidistribution is related to the Dedekind sum
![]() $s(q_1,q_2,p)$
.
$s(q_1,q_2,p)$
.
We need the following result of [Reference Louboutin and MunschLM21, Theorem
![]() $2.1$
].
$2.1$
].
Proposition 3.13 Let
![]() $\chi $
be a primitive Dirichlet character modulo
$\chi $
be a primitive Dirichlet character modulo
![]() $f>2$
, its conductor. Set
$f>2$
, its conductor. Set
 $\displaystyle {S(k,\chi ) =\sum _{l=0}^k\chi (l)}$
. Then
$\displaystyle {S(k,\chi ) =\sum _{l=0}^k\chi (l)}$
. Then
 $$ \begin{align*}\sum_{k=1}^{f-1}\vert S(k,\chi)\vert^2 =\frac{f^2}{12}\prod_{p\mid f}\left (1-\frac{1}{p^2}\right ) +a_\chi\frac{f^2}{\pi^2}\vert L(1,\chi)\vert^2, \mbox { where } a_\chi :=\begin{cases} 0,&\mbox{if } \chi (-1)=+1,\\ 1,&\mbox{if } \chi (-1)=-1. \end{cases}\end{align*} $$
$$ \begin{align*}\sum_{k=1}^{f-1}\vert S(k,\chi)\vert^2 =\frac{f^2}{12}\prod_{p\mid f}\left (1-\frac{1}{p^2}\right ) +a_\chi\frac{f^2}{\pi^2}\vert L(1,\chi)\vert^2, \mbox { where } a_\chi :=\begin{cases} 0,&\mbox{if } \chi (-1)=+1,\\ 1,&\mbox{if } \chi (-1)=-1. \end{cases}\end{align*} $$
3.4.1 Proof of Theorem 3.10
We follow a strategy similar to the proof of [Reference Louboutin and MunschLM21, Corollary
![]() $2.2$
]. We denote by
$2.2$
]. We denote by
![]() $\chi _0$
the trivial character. Using Proposition 3.13 and recalling the definition (3.8), we arrive at
$\chi _0$
the trivial character. Using Proposition 3.13 and recalling the definition (3.8), we arrive at
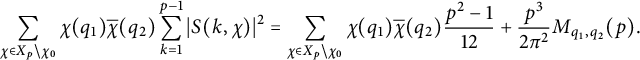 $$ \begin{align*}\sum_{\chi \in X_p \backslash \chi_0}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 = \sum_{\chi \in X_p\backslash \chi_0}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12} +\frac{p^3}{2\pi^2}M_{q_1,q_2}(p).\end{align*} $$
$$ \begin{align*}\sum_{\chi \in X_p \backslash \chi_0}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 = \sum_{\chi \in X_p\backslash \chi_0}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12} +\frac{p^3}{2\pi^2}M_{q_1,q_2}(p).\end{align*} $$
Adding the contribution of the trivial character
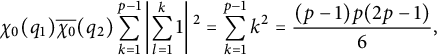 $$ \begin{align*}\chi_0(q_1)\overline{\chi_0}(q_2)\sum_{k=1}^{p-1}\left\vert\sum_{l=1}^k 1\right\vert{}^2 =\sum_{k=1}^{p-1} k^2 =\frac{(p-1)p(2p-1)}{6},\end{align*} $$
$$ \begin{align*}\chi_0(q_1)\overline{\chi_0}(q_2)\sum_{k=1}^{p-1}\left\vert\sum_{l=1}^k 1\right\vert{}^2 =\sum_{k=1}^{p-1} k^2 =\frac{(p-1)p(2p-1)}{6},\end{align*} $$
we obtain
 $$ \begin{align} \sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 =&\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12} + \frac{(p-1)p(2p-1)}{6} \nonumber \\ &+\frac{p^3}{2\pi^2}M_{q_1,q_2}(p) +O(p^2). \end{align} $$
$$ \begin{align} \sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 =&\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12} + \frac{(p-1)p(2p-1)}{6} \nonumber \\ &+\frac{p^3}{2\pi^2}M_{q_1,q_2}(p) +O(p^2). \end{align} $$
For sufficiently large p, using the fact that
![]() $q_1 \neq q_2 \bmod p$
and the orthogonality relations, we have
$q_1 \neq q_2 \bmod p$
and the orthogonality relations, we have
 $$ \begin{align*}\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12}=0.\end{align*} $$
$$ \begin{align*}\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\frac{p^2-1}{12}=0.\end{align*} $$
We now follow the method used in the proof of [Reference Louboutin and MunschLM21, Theorem
![]() $4.1$
] (see also [Reference ElmaElma]) with some needed changes to treat the left-hand side of (3.10). Again by orthogonality, we obtain
$4.1$
] (see also [Reference ElmaElma]) with some needed changes to treat the left-hand side of (3.10). Again by orthogonality, we obtain
 $$ \begin{align*} \sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 =\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\left\vert\sum_{l=1}^k\chi (l)\right\vert{}^2 \\ =\sum_{\chi \in X_p}\sum_{k=1}^{p-1}\sum_{1\leq l_1,l_2\leq k} \chi(q_1 l_1)\overline{\chi(q_2 l_2)} =(p-1)^2{\mathcal {A}}(q_1,q_2,p), \end{align*} $$
$$ \begin{align*} \sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\vert S(k,\chi)\vert^2 =\sum_{\chi \in X_p}\chi(q_1)\overline{\chi}(q_2)\sum_{k=1}^{p-1}\left\vert\sum_{l=1}^k\chi (l)\right\vert{}^2 \\ =\sum_{\chi \in X_p}\sum_{k=1}^{p-1}\sum_{1\leq l_1,l_2\leq k} \chi(q_1 l_1)\overline{\chi(q_2 l_2)} =(p-1)^2{\mathcal {A}}(q_1,q_2,p), \end{align*} $$
where
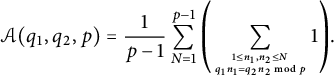 $$ \begin{align*} {\cal A}(q_1,q_2,p) =\frac{1}{p-1} \sum_{N=1}^{p-1}\left (\sum_{1 \leq n_1,n_2 \leq N \atop q_1 n_1=q_2 n_2 \bmod p} 1\right ){\kern-1.5pt}. \end{align*} $$
$$ \begin{align*} {\cal A}(q_1,q_2,p) =\frac{1}{p-1} \sum_{N=1}^{p-1}\left (\sum_{1 \leq n_1,n_2 \leq N \atop q_1 n_1=q_2 n_2 \bmod p} 1\right ){\kern-1.5pt}. \end{align*} $$
Changing the order of summation and making the change of variables
![]() $n_1=q_2m_1$
, we arrive at
$n_1=q_2m_1$
, we arrive at
By symmetry, injecting this into (3.10), we arrive at
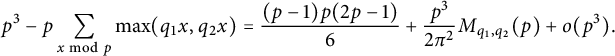 $$ \begin{align} p^3 -p\sum_{x \bmod p}\max(q_1 x,q_2 x) =\frac{(p-1)p(2p-1)}{6}+ \frac{p^3}{2\pi^2}M_{q_1,q_2}(p) +o(p^3). \end{align} $$
$$ \begin{align} p^3 -p\sum_{x \bmod p}\max(q_1 x,q_2 x) =\frac{(p-1)p(2p-1)}{6}+ \frac{p^3}{2\pi^2}M_{q_1,q_2}(p) +o(p^3). \end{align} $$
Hence, comparing the terms of order
![]() $p^3$
in the above formula (3.11) and using Corollary 3.8, we have
$p^3$
in the above formula (3.11) and using Corollary 3.8, we have
where
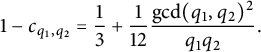 $$ \begin{align*}1-c_{q_1,q_2} =\frac{1}{3}+\frac{1}{12}\frac{\gcd(q_1,q_2)^2}{q_1 q_2}.\end{align*} $$
$$ \begin{align*}1-c_{q_1,q_2} =\frac{1}{3}+\frac{1}{12}\frac{\gcd(q_1,q_2)^2}{q_1 q_2}.\end{align*} $$
This concludes the proof.
We know turn to the general case of Theorem 1.1. Let
![]() $d_0$
be a given square-free integer such that
$d_0$
be a given square-free integer such that
![]() $\gcd (d_0,p)=1$
. For
$\gcd (d_0,p)=1$
. For
![]() $\chi $
modulo p, let
$\chi $
modulo p, let
![]() $\chi '$
be the character modulo
$\chi '$
be the character modulo
![]() $d_0p$
induced by
$d_0p$
induced by
![]() $\chi $
. Recall that we want to show for H a subgroup of
$\chi $
. Recall that we want to show for H a subgroup of
![]() $\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order
$\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order
![]() $d \ll \frac {\log p}{\log \log p}$
that
$d \ll \frac {\log p}{\log \log p}$
that
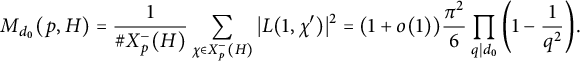 $$ \begin{align*} M_{d_0}(p,H) &=\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} |L(1,\chi')|^2 =(1+o(1))\frac{\pi^2}{6}\prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right){\kern-1.5pt}. \end{align*} $$
$$ \begin{align*} M_{d_0}(p,H) &=\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} |L(1,\chi')|^2 =(1+o(1))\frac{\pi^2}{6}\prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right){\kern-1.5pt}. \end{align*} $$
3.5 Twisted average of L- functions over subgroups
For any integers
![]() $q_1,q_2 \geq 1$
and any prime
$q_1,q_2 \geq 1$
and any prime
![]() $p\geq 3$
, we define
$p\geq 3$
, we define
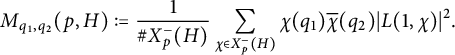 $$ \begin{align*}M_{q_1,q_2}(p,H) :=\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} \chi(q_1)\overline{\chi}(q_2)|L(1,\chi)|^2.\end{align*} $$
$$ \begin{align*}M_{q_1,q_2}(p,H) :=\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} \chi(q_1)\overline{\chi}(q_2)|L(1,\chi)|^2.\end{align*} $$
Our main result is the following.
Theorem 3.14 Let
![]() $q_1$
and
$q_1$
and
![]() $q_2$
be given coprime integers. When H runs over the subgroups of
$q_2$
be given coprime integers. When H runs over the subgroups of
![]() $\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order d, we have the following asymptotic formula:
$\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order d, we have the following asymptotic formula:
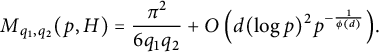 $$ \begin{align*}M_{q_1,q_2}(p,H) =\frac{\pi^2}{6q_1 q_2} + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M_{q_1,q_2}(p,H) =\frac{\pi^2}{6q_1 q_2} + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}.\end{align*} $$
Proof The proof follows the same lines as the proof of Theorem 3.6. Let us define
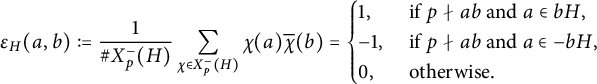 $$ \begin{align*}\epsilon_H(a,b) :=\frac{1}{\# X_p^-(H)}\sum_{\chi \in X_p^-(H)}\chi(a)\overline{\chi}(b) =\begin{cases} 1, &\text{ if } p\nmid ab \text{ and } a \in bH, \\ -1, &\text{ if } p\nmid ab \text{ and } a \in -bH, \\ 0, &\text{ otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}\epsilon_H(a,b) :=\frac{1}{\# X_p^-(H)}\sum_{\chi \in X_p^-(H)}\chi(a)\overline{\chi}(b) =\begin{cases} 1, &\text{ if } p\nmid ab \text{ and } a \in bH, \\ -1, &\text{ if } p\nmid ab \text{ and } a \in -bH, \\ 0, &\text{ otherwise.} \end{cases}\end{align*} $$
Hence, we obtain similarly
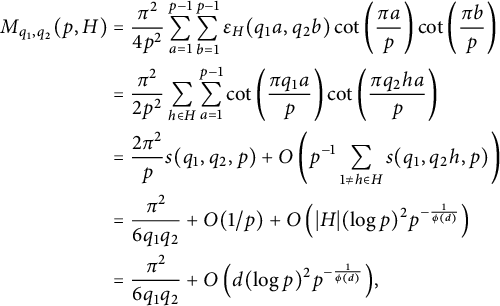 $$ \begin{align*} M_{q_1,q_2}(p,H) &=\frac{\pi^2}{4p^2} \sum_{a=1}^{p-1} \sum_{b=1}^{p-1}\epsilon_H(q_1 a,q_2 b)\cot\left(\frac{\pi a}{p}\right)\cot\left(\frac{\pi b}{p}\right) \\& = \frac{\pi^2}{2p^2}\sum_{h\in H} \sum_{a=1}^{p-1}\cot\left(\frac{\pi q_1a}{p}\right)\cot\left(\frac{\pi q_2h a}{p}\right) \\& = \frac{2\pi^2}{p}s(q_1,q_2,p)+ O\left(p^{-1}\sum_{1\neq h\in H} s(q_1,q_2h,p)\right) \\& = \frac{\pi^2}{6q_1q_2} + O(1/p) + O\left( \vert H\vert (\log p)^2p^{-\frac{1}{\phi(d)}} \right) \\& =\frac{\pi^2}{6q_1q_2} + O\left( d(\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}, \end{align*} $$
$$ \begin{align*} M_{q_1,q_2}(p,H) &=\frac{\pi^2}{4p^2} \sum_{a=1}^{p-1} \sum_{b=1}^{p-1}\epsilon_H(q_1 a,q_2 b)\cot\left(\frac{\pi a}{p}\right)\cot\left(\frac{\pi b}{p}\right) \\& = \frac{\pi^2}{2p^2}\sum_{h\in H} \sum_{a=1}^{p-1}\cot\left(\frac{\pi q_1a}{p}\right)\cot\left(\frac{\pi q_2h a}{p}\right) \\& = \frac{2\pi^2}{p}s(q_1,q_2,p)+ O\left(p^{-1}\sum_{1\neq h\in H} s(q_1,q_2h,p)\right) \\& = \frac{\pi^2}{6q_1q_2} + O(1/p) + O\left( \vert H\vert (\log p)^2p^{-\frac{1}{\phi(d)}} \right) \\& =\frac{\pi^2}{6q_1q_2} + O\left( d(\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}, \end{align*} $$
where we used Theorem 3.5 in the last line and noticed that
![]() $\phi (k)$
divides
$\phi (k)$
divides
![]() $\phi (d)$
whenever k divides d.
$\phi (d)$
whenever k divides d.
Remark 3.15 The error term is negligible as soon as
![]() $d\leq \frac {\log p}{3(\log \log p)}$
.
$d\leq \frac {\log p}{3(\log \log p)}$
.
Corollary 3.16 Let
![]() $q_1$
and
$q_1$
and
![]() $ q_2$
be given integers. When H runs over the subgroups of
$ q_2$
be given integers. When H runs over the subgroups of
![]() $\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order d, we have the following asymptotic formula:
$\left (\mathbb {Z}/p\mathbb {Z}\right )^*$
of odd order d, we have the following asymptotic formula:
 $$ \begin{align*}M_{q_1,q_2}(p,H) = \frac{\pi^2}{6}\frac{\gcd(q_1,q_2)^2}{q_1 q_2} + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M_{q_1,q_2}(p,H) = \frac{\pi^2}{6}\frac{\gcd(q_1,q_2)^2}{q_1 q_2} + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right){\kern-1.5pt}.\end{align*} $$
3.6 Proof of Theorem 1.1
As in the proof of Corollary 3.9 and using Corollary 3.16,
 $$ \begin{align*} M_{d_0}(p,H) & =\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} |L(1,\chi')|^2 =\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1}\frac{\mu(\delta_2)}{\delta_2} M_{\delta_1,\delta_2}(p,H) \\ &= \frac{\pi^2}{6} \sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1^2}\frac{\mu(\delta_2)}{\delta_2^2}\gcd(\delta_1,\delta_2)^2 + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right) \\ & = \frac{\pi^2}{6} \prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right) + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right) = (1+o(1))\frac{\pi^2}{6} \prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right) \end{align*} $$
$$ \begin{align*} M_{d_0}(p,H) & =\frac{1}{\# X_p^-(H)} \sum_{\chi \in X_p^-(H)} |L(1,\chi')|^2 =\sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1}\frac{\mu(\delta_2)}{\delta_2} M_{\delta_1,\delta_2}(p,H) \\ &= \frac{\pi^2}{6} \sum_{\delta_1 \mid d_0} \sum_{\delta_2 \mid d_0} \frac{\mu(\delta_1)}{\delta_1^2}\frac{\mu(\delta_2)}{\delta_2^2}\gcd(\delta_1,\delta_2)^2 + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right) \\ & = \frac{\pi^2}{6} \prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right) + O\left( d (\log p)^2p^{-\frac{1}{\phi(d)}} \right) = (1+o(1))\frac{\pi^2}{6} \prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right) \end{align*} $$
using the condition on d.
4 Explicit formulas for
 $M_{d_0}(f,H)$
$M_{d_0}(f,H)$
Recall that by (3.9)
 $$ \begin{align*} L(1,\chi) =\frac{\pi}{2f}\sum_{a=1}^{f-1}\chi (a)\cot\left (\frac{\pi a}{f}\right ) \ \ \ \ \ (\chi\in X_f^-). \end{align*} $$
$$ \begin{align*} L(1,\chi) =\frac{\pi}{2f}\sum_{a=1}^{f-1}\chi (a)\cot\left (\frac{\pi a}{f}\right ) \ \ \ \ \ (\chi\in X_f^-). \end{align*} $$
Hence, using the definition of Dedekind sums, we obtain (see [Reference LouboutinLou16, Proof of Theorem 2])
 $$ \begin{align} M(f,H) ={2\pi^2\over f}\sum_{\delta\mid f}\frac{\mu (\delta)}{\delta}\sum_{h\in H}s(h,f/\delta). \end{align} $$
$$ \begin{align} M(f,H) ={2\pi^2\over f}\sum_{\delta\mid f}\frac{\mu (\delta)}{\delta}\sum_{h\in H}s(h,f/\delta). \end{align} $$
4.1 A formula for
 $M_{d_0}(f,\{1\})$
for
$M_{d_0}(f,\{1\})$
for
 $d_0=1,2,3,6$
$d_0=1,2,3,6$
The first consequence of (4.1) is a short proof of [Reference LouboutinLou94, Théorèmes 2 and 3] by taking
![]() $H=\{1\}$
, the trivial subgroup of the multiplicative group
$H=\{1\}$
, the trivial subgroup of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z}^*)$
. Indeed, (4.1) and (3.4) give
$({\mathbb Z}/f{\mathbb Z}^*)$
. Indeed, (4.1) and (3.4) give
 $$ \begin{align*}M(f,\{1\}) ={2\pi^2\over f}\sum_{\delta\mid f}\frac{\mu (\delta)}{\delta}s(1,f/\delta) =\frac{\pi^2}{6}\sum_{\delta\mid f}\mu (\delta)\left (\frac{1}{\delta^2}-\frac{3}{\delta f}+\frac{2}{f^2}\right ){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M(f,\{1\}) ={2\pi^2\over f}\sum_{\delta\mid f}\frac{\mu (\delta)}{\delta}s(1,f/\delta) =\frac{\pi^2}{6}\sum_{\delta\mid f}\mu (\delta)\left (\frac{1}{\delta^2}-\frac{3}{\delta f}+\frac{2}{f^2}\right ){\kern-1.5pt}.\end{align*} $$
The arithmetic functions
![]() $f\mapsto \sum _{\delta \mid f}\mu (\delta )\delta ^k$
being multiplicative, we obtain (see also [Reference QiQi])
$f\mapsto \sum _{\delta \mid f}\mu (\delta )\delta ^k$
being multiplicative, we obtain (see also [Reference QiQi])
 $$ \begin{align} M(f,\{1\}) ={\pi^2\over 6} \times\left\{ \prod_{q\mid f}\left (1-{1\over q^2}\right )-{3\over f}\prod_{q\mid f}\left (1-{1\over q}\right ) \right\} \ \ \ \ \ (f>2). \end{align} $$
$$ \begin{align} M(f,\{1\}) ={\pi^2\over 6} \times\left\{ \prod_{q\mid f}\left (1-{1\over q^2}\right )-{3\over f}\prod_{q\mid f}\left (1-{1\over q}\right ) \right\} \ \ \ \ \ (f>2). \end{align} $$
Now, it is clear by (2.1) that for
![]() $d_0$
odd and square-free and f odd, we have
$d_0$
odd and square-free and f odd, we have
Hence, on applying (4.2) to
![]() $2f$
instead of f, we therefore obtain
$2f$
instead of f, we therefore obtain
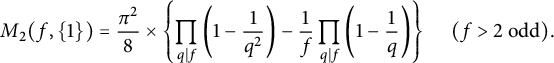 $$ \begin{align*} M_2(f,\{1\}) ={\pi^2\over 8} \times\left\{ \prod_{q\mid f}\left (1-{1\over q^2}\right )-{1\over f}\prod_{q\mid f}\left (1-{1\over q}\right ) \right\} \ \ \ \ \ (f>2 \mbox{ odd}). \end{align*} $$
$$ \begin{align*} M_2(f,\{1\}) ={\pi^2\over 8} \times\left\{ \prod_{q\mid f}\left (1-{1\over q^2}\right )-{1\over f}\prod_{q\mid f}\left (1-{1\over q}\right ) \right\} \ \ \ \ \ (f>2 \mbox{ odd}). \end{align*} $$
For
![]() $d_0\in \{3,6\}$
, the following explicit formula holds true for any f coprime with
$d_0\in \{3,6\}$
, the following explicit formula holds true for any f coprime with
![]() $d_0$
. It generalizes [Reference LouboutinLou94, Théorème 4] to composite moduli.
$d_0$
. It generalizes [Reference LouboutinLou94, Théorème 4] to composite moduli.
Theorem 4.1 Let
![]() $d_0>2$
be a given square-free integer. Set
$d_0>2$
be a given square-free integer. Set
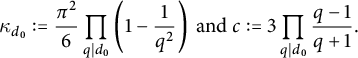 $$ \begin{align*}\kappa_{d_0} :=\frac{\pi^2}{6} \prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right ) \mbox{ and } c :=3\prod_{q\mid d_0}\frac{q-1}{q+1}.\end{align*} $$
$$ \begin{align*}\kappa_{d_0} :=\frac{\pi^2}{6} \prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right ) \mbox{ and } c :=3\prod_{q\mid d_0}\frac{q-1}{q+1}.\end{align*} $$
For
![]() $n\in {\mathbb Z}$
, set
$n\in {\mathbb Z}$
, set
![]() $\varepsilon (n) =+1$
if
$\varepsilon (n) =+1$
if
![]() $n\equiv +1\ \ \pmod {d_0}$
and
$n\equiv +1\ \ \pmod {d_0}$
and
![]() $\varepsilon (n) =-1$
if
$\varepsilon (n) =-1$
if
![]() $n\equiv -1\ \ \pmod {d_0}$
. Then, for
$n\equiv -1\ \ \pmod {d_0}$
. Then, for
![]() $f>2$
such that all its prime divisors q satisfy
$f>2$
such that all its prime divisors q satisfy
![]() $q\equiv \pm 1\ \ \pmod {d_0}$
, we have
$q\equiv \pm 1\ \ \pmod {d_0}$
, we have
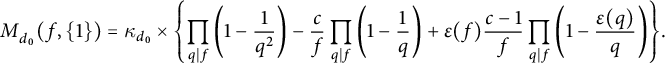 $$ \begin{align*}M_{d_0}^{}(f,\{1\}) =\kappa_{d_0} \times\left\{ \prod_{q\mid f}\left (1-\frac{1}{q^2}\right ) -\frac{c}{f}\prod_{q\mid f}\left (1-\frac{1}{q}\right ) +\varepsilon(f) \frac{c-1}{f}\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ) \right\}{\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M_{d_0}^{}(f,\{1\}) =\kappa_{d_0} \times\left\{ \prod_{q\mid f}\left (1-\frac{1}{q^2}\right ) -\frac{c}{f}\prod_{q\mid f}\left (1-\frac{1}{q}\right ) +\varepsilon(f) \frac{c-1}{f}\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ) \right\}{\kern-1.5pt}.\end{align*} $$
In particular, for
![]() $f>2$
such that all its prime divisors q satisfy
$f>2$
such that all its prime divisors q satisfy
![]() $q\equiv 1\ \ \pmod {d_0}$
, we have
$q\equiv 1\ \ \pmod {d_0}$
, we have
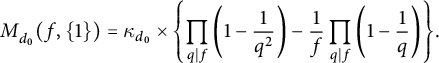 $$ \begin{align*}M_{d_0}^{}(f,\{1\}) =\kappa_{d_0} \times\left\{ \prod_{q\mid f}\left (1-\frac{1}{q^2}\right ) -\frac{1}{f}\prod_{q\mid f}\left (1-\frac{1}{q}\right ) \right\}{\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M_{d_0}^{}(f,\{1\}) =\kappa_{d_0} \times\left\{ \prod_{q\mid f}\left (1-\frac{1}{q^2}\right ) -\frac{1}{f}\prod_{q\mid f}\left (1-\frac{1}{q}\right ) \right\}{\kern-1.5pt}.\end{align*} $$
Proof With the notation of [Reference LouboutinLou11, Lemma 2], we have
![]() $M_{d_0}(f,\{1\})) =4\pi ^2S(d_0,f)$
. Hence, by [Reference LouboutinLou11, Lemmas 3 and 6], we have
$M_{d_0}(f,\{1\})) =4\pi ^2S(d_0,f)$
. Hence, by [Reference LouboutinLou11, Lemmas 3 and 6], we have
 $$ \begin{align*}M_{d_0}(f,\{1\}) =\frac{\pi^2}{6}\prod_{q\mid d_0f}\left (1-\frac{1}{q^2}\right ) -\frac{\pi^2}{2}\frac{\phi(d_0)^2\phi(f)}{d_0^2f^2} +\frac{\pi^2}{2d_0^2f}\sum_{d\mid f}\frac{\mu(d)}{d}A(d_0,f/d),\end{align*} $$
$$ \begin{align*}M_{d_0}(f,\{1\}) =\frac{\pi^2}{6}\prod_{q\mid d_0f}\left (1-\frac{1}{q^2}\right ) -\frac{\pi^2}{2}\frac{\phi(d_0)^2\phi(f)}{d_0^2f^2} +\frac{\pi^2}{2d_0^2f}\sum_{d\mid f}\frac{\mu(d)}{d}A(d_0,f/d),\end{align*} $$
where the
![]() $A(d_0,f/d)$
’s are rational numbers such that
$A(d_0,f/d)$
’s are rational numbers such that
![]() $A(d_0,f/d) =\varepsilon A(d_0,1)$
if
$A(d_0,f/d) =\varepsilon A(d_0,1)$
if
![]() $f/d\equiv \varepsilon \ \ \pmod {d_0}$
with
$f/d\equiv \varepsilon \ \ \pmod {d_0}$
with
![]() $\varepsilon \in \{\pm 1\}$
(see (4.13)). If all the prime divisors q of f satisfy
$\varepsilon \in \{\pm 1\}$
(see (4.13)). If all the prime divisors q of f satisfy
![]() $q\equiv \pm 1\ \ \pmod {d_0},$
then
$q\equiv \pm 1\ \ \pmod {d_0},$
then
![]() $f/d\equiv \varepsilon (f/d)\ \ \pmod {d_0}$
and
$f/d\equiv \varepsilon (f/d)\ \ \pmod {d_0}$
and
![]() $A(d_0,f/d) =\varepsilon (f/d)A(d_0,1) =\varepsilon (f)A(d_0,1)\varepsilon (d)$
and
$A(d_0,f/d) =\varepsilon (f/d)A(d_0,1) =\varepsilon (f)A(d_0,1)\varepsilon (d)$
and
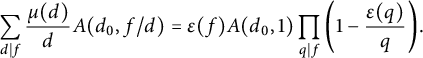 $$ \begin{align*}\sum_{d\mid f}\frac{\mu(d)}{d}A(d_0,f/d) =\varepsilon(f)A(d_0,1)\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}\sum_{d\mid f}\frac{\mu(d)}{d}A(d_0,f/d) =\varepsilon(f)A(d_0,1)\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ){\kern-1.5pt}.\end{align*} $$
Hence, we finally get
 $$ \begin{align*}M_{d_0}(f,\{1\}) =\frac{\pi^2}{6}\prod_{q\mid d_0f}\left (1-\frac{1}{q^2}\right ) -\frac{\pi^2}{2}\frac{\phi(d_0)^2\phi(f)}{d_0^2f^2} +\frac{\pi^2}{2d_0^2f}\varepsilon(f)A(d_0,1)\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}M_{d_0}(f,\{1\}) =\frac{\pi^2}{6}\prod_{q\mid d_0f}\left (1-\frac{1}{q^2}\right ) -\frac{\pi^2}{2}\frac{\phi(d_0)^2\phi(f)}{d_0^2f^2} +\frac{\pi^2}{2d_0^2f}\varepsilon(f)A(d_0,1)\prod_{q\mid f}\left (1-\frac{\varepsilon(q)}{q}\right ){\kern-1.5pt}.\end{align*} $$
The desired formula for
![]() $M_{d_0}(f,\{1\})$
follows by using the explicit formula
$M_{d_0}(f,\{1\})$
follows by using the explicit formula
 $$ \begin{align*}A(d_0,1) =\phi(d_0)^2 -\frac{d_0^2}{3}\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\end{align*} $$
$$ \begin{align*}A(d_0,1) =\phi(d_0)^2 -\frac{d_0^2}{3}\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\end{align*} $$
given in [Reference LouboutinLou11, Lemma 6].
4.2 A formula for
 $M(p,H)$
$M(p,H)$
The second immediate consequence of (4.1) and (3.4) is:
Proposition 4.2 For
![]() $f>2$
and H a subgroup of the multiplicative group
$f>2$
and H a subgroup of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, set
$({\mathbb Z}/f{\mathbb Z})^*$
, set
 $$ \begin{align} S'(H,f)=\sum_{1\neq h\in H}s(h,f) \mbox{ and } N(f,H) :=-3+\frac{2}{f}+12S'(H,f). \end{align} $$
$$ \begin{align} S'(H,f)=\sum_{1\neq h\in H}s(h,f) \mbox{ and } N(f,H) :=-3+\frac{2}{f}+12S'(H,f). \end{align} $$
Then, for
![]() $p\geq 3$
a prime and H a subgroup of odd order of the multiplicative group
$p\geq 3$
a prime and H a subgroup of odd order of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
, we have
$({\mathbb Z}/p{\mathbb Z})^*$
, we have
 $$ \begin{align} M(p,H) =\frac{\pi^2}{6} \left (1+\frac{N(p,H)}{p}\right ) =\frac{\pi^2}{6}\left (\left (1-\frac{1}{p}\right )\left (1-\frac{2}{p}\right )+\frac{12S'(H,p)}{p}\right ). \end{align} $$
$$ \begin{align} M(p,H) =\frac{\pi^2}{6} \left (1+\frac{N(p,H)}{p}\right ) =\frac{\pi^2}{6}\left (\left (1-\frac{1}{p}\right )\left (1-\frac{2}{p}\right )+\frac{12S'(H,p)}{p}\right ). \end{align} $$
Remark 4.3 In particular,
![]() $N(f,\{1\}) =-3+2/f$
and (4.4) implies (1.5). Notice also that
$N(f,\{1\}) =-3+2/f$
and (4.4) implies (1.5). Notice also that
![]() $N(p,H)\in {\mathbb Z}$
for
$N(p,H)\in {\mathbb Z}$
for
![]() $H\neq \{1\}$
, by [Reference LouboutinLou19, Theorem 6]. Moreover, by [Reference Louboutin and MunschLM21, Theorem
$H\neq \{1\}$
, by [Reference LouboutinLou19, Theorem 6]. Moreover, by [Reference Louboutin and MunschLM21, Theorem
![]() $1.1$
], the asymptotic formula
$1.1$
], the asymptotic formula
![]() $M(p,H) =\frac {\pi ^2}{6}+o(1)$
holds as p tends to infinity and H runs over the subgroup of
$M(p,H) =\frac {\pi ^2}{6}+o(1)$
holds as p tends to infinity and H runs over the subgroup of
![]() $({\mathbb Z}/p{\mathbb Z})^*$
of odd order
$({\mathbb Z}/p{\mathbb Z})^*$
of odd order
![]() $d\leq \frac {\log p}{\log \log p}$
. Hence, we have
$d\leq \frac {\log p}{\log \log p}$
. Hence, we have
![]() $N(p,H)=o(p)$
under this restriction.
$N(p,H)=o(p)$
under this restriction.
4.3 A formula for
 $M_{d_0}(p,H)$
$M_{d_0}(p,H)$
We will now derive a third consequence of (4.1): a formula for the mean square value
![]() $M_{d_0}(f,H)$
defined in (1.9) when f is prime.
$M_{d_0}(f,H)$
defined in (1.9) when f is prime.
Theorem 4.4 Let
![]() $d_0>1$
be a square-free integer. Let
$d_0>1$
be a square-free integer. Let
![]() $f>2$
be coprime with
$f>2$
be coprime with
![]() $d_0$
. Let H be a subgroup of the multiplicative group
$d_0$
. Let H be a subgroup of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Whenever
$({\mathbb Z}/f{\mathbb Z})^*$
. Whenever
![]() $\delta $
divides
$\delta $
divides
![]() $d_0$
, let
$d_0$
, let
![]() $s_\delta :({\mathbb Z}/\delta f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/f{\mathbb Z})^*$
be the canonical surjective morphism and set
$s_\delta :({\mathbb Z}/\delta f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/f{\mathbb Z})^*$
be the canonical surjective morphism and set
![]() $H_{\delta }=s_\delta ^{-1}(H)$
and
$H_{\delta }=s_\delta ^{-1}(H)$
and
![]() $H_{\delta }' =s_\delta ^{-1}(H\setminus \{1\})$
. Define the rational number
$H_{\delta }' =s_\delta ^{-1}(H\setminus \{1\})$
. Define the rational number
 $$ \begin{align} N_{d_0}(f,H) =-f +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q^2-1)} \sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta f). \end{align} $$
$$ \begin{align} N_{d_0}(f,H) =-f +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q^2-1)} \sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta f). \end{align} $$
Then, for
![]() $p\geq 3$
a prime which does not divide
$p\geq 3$
a prime which does not divide
![]() $d_0$
and H a subgroup of odd order of the multiplicative group
$d_0$
and H a subgroup of odd order of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
, we have
$({\mathbb Z}/p{\mathbb Z})^*$
, we have
 $$ \begin{align} M_{d_0}(p,H) =\frac{2\pi^2\mu(d_0)\phi(d_0)}{d_0^2p} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)} S(H_\delta,\delta p),\end{align} $$
$$ \begin{align} M_{d_0}(p,H) =\frac{2\pi^2\mu(d_0)\phi(d_0)}{d_0^2p} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)} S(H_\delta,\delta p),\end{align} $$
where
and
 $$ \begin{align} M_{d_0}(p,H) =\kappa_{d_0} \times\left ( 1 +\frac{N_{d_0}(p,H)}{p} \right ), \mbox{ where } \kappa_{d_0} :=\frac{\pi^2}{6} \prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right ). \end{align} $$
$$ \begin{align} M_{d_0}(p,H) =\kappa_{d_0} \times\left ( 1 +\frac{N_{d_0}(p,H)}{p} \right ), \mbox{ where } \kappa_{d_0} :=\frac{\pi^2}{6} \prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right ). \end{align} $$
Moreover,
 $$ \begin{align} N_{d_0}(f,H) &=-f +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(H_\delta,\delta f) \end{align} $$
$$ \begin{align} N_{d_0}(f,H) &=-f +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(H_\delta,\delta f) \end{align} $$
 $$ \begin{align} \kern66pt &=N_{d_0}(f,\{1\}) +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)} S'(H_{\delta},\delta f), \end{align} $$
$$ \begin{align} \kern66pt &=N_{d_0}(f,\{1\}) +\frac{12\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)} S'(H_{\delta},\delta f), \end{align} $$
where
Proof Using (2.1) and by making the change of variables
![]() $\delta \mapsto d_0f/\delta $
in (4.1), we obtain
$\delta \mapsto d_0f/\delta $
in (4.1), we obtain
 $$ \begin{align} M_{d_0}(f,H) =M(d_0f,H_{d_0}) ={2\pi^2\over d_0^2f^2}\sum_{\delta\mid d_0f}\delta\mu (d_0f/\delta)\sum_{h\in H_{d_0}}s(h,\delta). \end{align} $$
$$ \begin{align} M_{d_0}(f,H) =M(d_0f,H_{d_0}) ={2\pi^2\over d_0^2f^2}\sum_{\delta\mid d_0f}\delta\mu (d_0f/\delta)\sum_{h\in H_{d_0}}s(h,\delta). \end{align} $$
Since
![]() $\{\delta ;\ \delta \mid d_0p\}$
is the disjoint union of
$\{\delta ;\ \delta \mid d_0p\}$
is the disjoint union of
![]() $\{\delta ;\ \delta \mid d_0\}$
and
$\{\delta ;\ \delta \mid d_0\}$
and
![]() $\{\delta p;\ \delta \mid d_0\}$
, by (4.10), we obtain
$\{\delta p;\ \delta \mid d_0\}$
, by (4.10), we obtain
 $$ \begin{align*}M_{d_0}(p,H) =-{2\pi^2\mu(d_0)\over d_0^2p^2}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta) +{2\pi^2\mu(d_0)\over d_0^2p}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta p).\end{align*} $$
$$ \begin{align*}M_{d_0}(p,H) =-{2\pi^2\mu(d_0)\over d_0^2p^2}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta) +{2\pi^2\mu(d_0)\over d_0^2p}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta p).\end{align*} $$
Now,
![]() $S:=\sum _{h\in H_{d_0}}s(h,\delta )=0$
whenever
$S:=\sum _{h\in H_{d_0}}s(h,\delta )=0$
whenever
![]() $\delta \mid d_0$
, which gives
$\delta \mid d_0$
, which gives
 $$ \begin{align} M_{d_0}(p,H) ={2\pi^2\mu(d_0)\over d_0^2p}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta p) \end{align} $$
$$ \begin{align} M_{d_0}(p,H) ={2\pi^2\mu(d_0)\over d_0^2p}\sum_{\delta\mid d_0}\delta\mu (\delta)\sum_{h\in H_{d_0}}s(h,\delta p) \end{align} $$
and implies (4.7). Indeed, let
![]() $\sigma :({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/\delta {\mathbb Z})^*$
be the canonical surjective morphism. Its restriction
$\sigma :({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/\delta {\mathbb Z})^*$
be the canonical surjective morphism. Its restriction
![]() $\tau $
to the subgroup
$\tau $
to the subgroup
![]() $H_{d_0}$
is surjective, by the Chinese reminder theorem. Hence,
$H_{d_0}$
is surjective, by the Chinese reminder theorem. Hence,
![]() $S =(H_{d_0}:\ker \tau ) \times S'$
, where
$S =(H_{d_0}:\ker \tau ) \times S'$
, where
![]() $S':=\sum _{c\in ({\mathbb Z}/\delta {\mathbb Z})^*}s(c,\delta ) =\sum _{c\in ({\mathbb Z}/\delta {\mathbb Z})^*}s(-c,\delta ) =-S'$
yields
$S':=\sum _{c\in ({\mathbb Z}/\delta {\mathbb Z})^*}s(c,\delta ) =\sum _{c\in ({\mathbb Z}/\delta {\mathbb Z})^*}s(-c,\delta ) =-S'$
yields
![]() $S'=0$
. In the same way, whenever
$S'=0$
. In the same way, whenever
![]() $\delta \mid d_0$
, the kernel of the canonical surjective morphism
$\delta \mid d_0$
, the kernel of the canonical surjective morphism
![]() $s:({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/\delta f{\mathbb Z})^*$
being a subgroup of order
$s:({\mathbb Z}/d_0f{\mathbb Z})^*\longrightarrow ({\mathbb Z}/\delta f{\mathbb Z})^*$
being a subgroup of order
![]() $\phi (d_0f)/\phi (\delta f) =\phi (d_0)/\phi (\delta )$
, we have
$\phi (d_0f)/\phi (\delta f) =\phi (d_0)/\phi (\delta )$
, we have
 $$ \begin{align} \sum_{h\in H_{d_0}}s(h,\delta f) =\frac{\phi(d_0)}{\phi(\delta)}\sum_{h\in H_{\delta}}s(h,\delta f) \end{align} $$
$$ \begin{align} \sum_{h\in H_{d_0}}s(h,\delta f) =\frac{\phi(d_0)}{\phi(\delta)}\sum_{h\in H_{\delta}}s(h,\delta f) \end{align} $$
and (4.6) follows from (4.11) and (4.12).
Then, (4.7) is a direct consequence of (4.6) and (4.5). Finally, (4.9) is an immediate consequence of (4.5) and (4.12).
4.3.1 A new proof of Theorem 1.1
We split the sum in (4.11) into two cases depending whether
![]() $h=1$
or not. By (3.4), we have
$h=1$
or not. By (3.4), we have
![]() $s(1,\delta p)=\frac {p\delta }{12}+O(1)$
giving a contribution to the sum of order
$s(1,\delta p)=\frac {p\delta }{12}+O(1)$
giving a contribution to the sum of order
 $$ \begin{align*}\frac{\pi^2 \mu(d_0)}{6d_0^2} \sum_{\delta \mid d_0}\delta^2\mu(\delta) + O(1/p) = \frac{\pi^2}{6} \prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right)+O(1/p).\end{align*} $$
$$ \begin{align*}\frac{\pi^2 \mu(d_0)}{6d_0^2} \sum_{\delta \mid d_0}\delta^2\mu(\delta) + O(1/p) = \frac{\pi^2}{6} \prod_{q \mid d_0}\left(1-\frac{1}{q^2}\right)+O(1/p).\end{align*} $$
When
![]() $h\neq 1$
and
$h\neq 1$
and
![]() $h\in H_{d_0}$
, it is clear that the order of h modulo p is between
$h\in H_{d_0}$
, it is clear that the order of h modulo p is between
![]() $3$
and d. Hence, it follows from Theorem 3.1 (see the Remark after) that
$3$
and d. Hence, it follows from Theorem 3.1 (see the Remark after) that
![]() $s(h,\delta p)=O((\log p)^2 p^{1-\frac {1}{\phi (d)}})$
. The integer
$s(h,\delta p)=O((\log p)^2 p^{1-\frac {1}{\phi (d)}})$
. The integer
![]() $d_0$
being fixed, we can sum up these error terms and the proof is finished.
$d_0$
being fixed, we can sum up these error terms and the proof is finished.
4.4 An explicit way to compute
 $N_{d_0}(f,\{1\})$
$N_{d_0}(f,\{1\})$
Lemma 4.5 Let
![]() $d_0>1$
be a square-free integer. Let
$d_0>1$
be a square-free integer. Let
![]() $f>2$
be coprime with
$f>2$
be coprime with
![]() $d_0$
. Recall that
$d_0$
. Recall that
![]() $H_{d_0}(f) =\{h\in ({\mathbb Z}/d_0f{\mathbb Z})^*,\ h\equiv 1\ \ \pmod f\}$
and set
$H_{d_0}(f) =\{h\in ({\mathbb Z}/d_0f{\mathbb Z})^*,\ h\equiv 1\ \ \pmod f\}$
and set
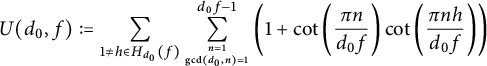 $$ \begin{align*}U(d_0,f) :=\sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0,n)=1}^{d_0f -1} \left (1+\cot\left ({\pi n\over d_0f}\right )\cot\left ({\pi nh\over d_0f}\right )\right )\end{align*} $$
$$ \begin{align*}U(d_0,f) :=\sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0,n)=1}^{d_0f -1} \left (1+\cot\left ({\pi n\over d_0f}\right )\cot\left ({\pi nh\over d_0f}\right )\right )\end{align*} $$
and
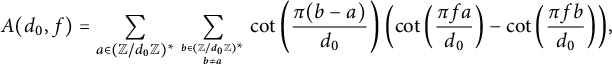 $$ \begin{align} A(d_0,f) =\sum_{a\in ({\mathbb Z}/d_0{\mathbb Z})^*} \sum_{b\in ({\mathbb Z}/d_0{\mathbb Z})^*\atop b\neq a} \cot\left (\frac{\pi (b-a)}{d_0}\right ) \left ( \cot\left (\frac{\pi fa}{d_0}\right ) -\cot\left (\frac{\pi fb}{d_0}\right ) \right ){\kern-1.5pt}, \end{align} $$
$$ \begin{align} A(d_0,f) =\sum_{a\in ({\mathbb Z}/d_0{\mathbb Z})^*} \sum_{b\in ({\mathbb Z}/d_0{\mathbb Z})^*\atop b\neq a} \cot\left (\frac{\pi (b-a)}{d_0}\right ) \left ( \cot\left (\frac{\pi fa}{d_0}\right ) -\cot\left (\frac{\pi fb}{d_0}\right ) \right ){\kern-1.5pt}, \end{align} $$
a rational number depending only on f modulo
![]() $d_0$
. Then
$d_0$
. Then
![]() $U(d_0,f) =fA(d_0,f).$
$U(d_0,f) =fA(d_0,f).$
Proof As in [Reference LouboutinLou11, Lemma 3], set
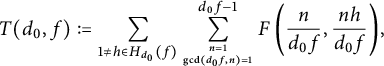 $$ \begin{align*}T(d_0,f) :=\sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0f,n)=1}^{d_0f -1} F\left (\frac{n}{d_0f},\frac{nh}{d_0f}\right ){\kern-1.5pt},\end{align*} $$
$$ \begin{align*}T(d_0,f) :=\sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0f,n)=1}^{d_0f -1} F\left (\frac{n}{d_0f},\frac{nh}{d_0f}\right ){\kern-1.5pt},\end{align*} $$
where
![]() $F(x,y)=1+\cot (\pi x)\cot (\pi y)$
. On the one hand, since
$F(x,y)=1+\cot (\pi x)\cot (\pi y)$
. On the one hand, since
![]() $\gcd (d_0f,n)=1$
if and only if
$\gcd (d_0f,n)=1$
if and only if
![]() $\gcd (d_0,n)=\gcd (f,n)=1$
and
$\gcd (d_0,n)=\gcd (f,n)=1$
and
 $\displaystyle {\sum _{d\mid f\atop d\mid n}\mu (d)}$
is equal to
$\displaystyle {\sum _{d\mid f\atop d\mid n}\mu (d)}$
is equal to
![]() $1$
if
$1$
if
![]() $\gcd (f,n)=1$
and is equal to
$\gcd (f,n)=1$
and is equal to
![]() $0$
otherwise, we have
$0$
otherwise, we have
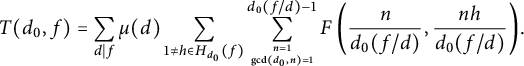 $$ \begin{align*}T(d_0,f) =\sum_{d\mid f}\mu(d) \sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0,n)=1}^{d_0(f/d) -1}F\left (\frac{n}{d_0(f/d)},\frac{nh}{d_0(f/d)}\right ){\kern-1.5pt}.\end{align*} $$
$$ \begin{align*}T(d_0,f) =\sum_{d\mid f}\mu(d) \sum_{1\neq h\in H_{d_0}(f)} \sum_{n=1\atop\gcd(d_0,n)=1}^{d_0(f/d) -1}F\left (\frac{n}{d_0(f/d)},\frac{nh}{d_0(f/d)}\right ){\kern-1.5pt}.\end{align*} $$
On the other hand, the canonical morphism
![]() $\sigma :H_{d_0}(f) \rightarrow H_{d_0}(f/d)$
is surjective and both groups have order
$\sigma :H_{d_0}(f) \rightarrow H_{d_0}(f/d)$
is surjective and both groups have order
![]() $\phi (d_0f)/\phi (f) =\phi (d_0(f/d))/\phi (f/d) =\phi (d_0)$
. Hence,
$\phi (d_0f)/\phi (f) =\phi (d_0(f/d))/\phi (f/d) =\phi (d_0)$
. Hence,
![]() $\sigma $
is bijective and
$\sigma $
is bijective and
Using [Reference LouboutinLou11, Lemma 6] and Möbius’ inversion formula, we finally do obtain
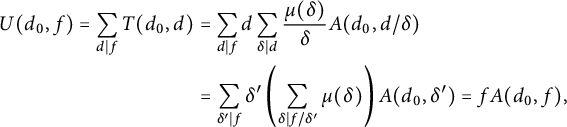 $$ \begin{align*} U(d_0,f) =\sum_{d\mid f}T(d_0,d) &=\sum_{d\mid f}d\sum_{\delta\mid d}\frac{\mu(\delta)}{\delta}A(d_0,d/\delta)\\ &=\sum_{\delta'\mid f} \delta'\left (\sum_{\delta\mid f/\delta'}\mu(\delta)\right )A(d_0,\delta') =fA(d_0,f), \end{align*} $$
$$ \begin{align*} U(d_0,f) =\sum_{d\mid f}T(d_0,d) &=\sum_{d\mid f}d\sum_{\delta\mid d}\frac{\mu(\delta)}{\delta}A(d_0,d/\delta)\\ &=\sum_{\delta'\mid f} \delta'\left (\sum_{\delta\mid f/\delta'}\mu(\delta)\right )A(d_0,\delta') =fA(d_0,f), \end{align*} $$
where we set
![]() $\delta '=d/\delta $
.
$\delta '=d/\delta $
.
Proposition 4.6 Let
![]() $d_0>1$
be a square-free integer. Set
$d_0>1$
be a square-free integer. Set
![]() $B=\prod _{q\mid d_0}(q^2-1)$
. For
$B=\prod _{q\mid d_0}(q^2-1)$
. For
![]() $f>2$
and
$f>2$
and
![]() $\gcd (d_0,f)=1,$
we have
$\gcd (d_0,f)=1,$
we have
Consequently,
![]() $N_{d_0}(f,\{1\})$
is a rational number depending only on f modulo
$N_{d_0}(f,\{1\})$
is a rational number depending only on f modulo
![]() $d_0$
.
$d_0$
.
Proof Set
![]() $H=H_{d_0}(f):=\{h\in ({\mathbb Z}/d_0f{\mathbb Z})^*,\ h\equiv 1\ \ \pmod f\}$
. By (4.5), we have
$H=H_{d_0}(f):=\{h\in ({\mathbb Z}/d_0f{\mathbb Z})^*,\ h\equiv 1\ \ \pmod f\}$
. By (4.5), we have
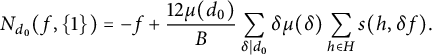 $$ \begin{align*}N_{d_0}(f,\{1\}) =-f+\frac{12\mu(d_0)}{B}\sum_{\delta\mid d_0}\delta\mu (\delta) \sum_{h\in H}s(h,\delta f).\end{align*} $$
$$ \begin{align*}N_{d_0}(f,\{1\}) =-f+\frac{12\mu(d_0)}{B}\sum_{\delta\mid d_0}\delta\mu (\delta) \sum_{h\in H}s(h,\delta f).\end{align*} $$
Using (3.4) to evaluate the contribution of
![]() $h=1$
in this expression and
$h=1$
in this expression and
![]() $\sum _{\delta \mid d_0}\mu (\delta ) =0$
, we get
$\sum _{\delta \mid d_0}\mu (\delta ) =0$
, we get
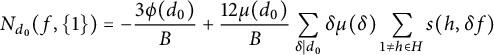 $$ \begin{align*}N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)}{B} +\frac{12\mu(d_0)}{B}\sum_{\delta\mid d_0}\delta\mu (\delta) \sum_{1\neq h\in H}s(h,\delta f)\end{align*} $$
$$ \begin{align*}N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)}{B} +\frac{12\mu(d_0)}{B}\sum_{\delta\mid d_0}\delta\mu (\delta) \sum_{1\neq h\in H}s(h,\delta f)\end{align*} $$
and
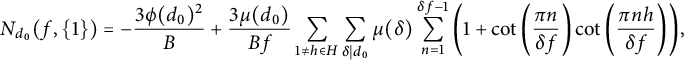 $$ \begin{align*}N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)^2}{B} +\frac{3\mu(d_0)}{Bf} \sum_{1\neq h\in H} \sum_{\delta\mid d_0}\mu (\delta) \sum_{n=1}^{\delta f -1}\left (1+\cot\left ({\pi n\over\delta f}\right )\cot\left ({\pi nh\over\delta f}\right )\right ){\kern-1.5pt},\end{align*} $$
$$ \begin{align*}N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)^2}{B} +\frac{3\mu(d_0)}{Bf} \sum_{1\neq h\in H} \sum_{\delta\mid d_0}\mu (\delta) \sum_{n=1}^{\delta f -1}\left (1+\cot\left ({\pi n\over\delta f}\right )\cot\left ({\pi nh\over\delta f}\right )\right ){\kern-1.5pt},\end{align*} $$
by (3.1) and by noticing that
![]() $\# H =\phi (d_0)$
. Therefore,
$\# H =\phi (d_0)$
. Therefore,
 $$ \begin{align} N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)^2}{B} +\frac{3}{Bf}S(d_0,f) \end{align} $$
$$ \begin{align} N_{d_0}(f,\{1\}) =-\frac{3\phi(d_0)^2}{B} +\frac{3}{Bf}S(d_0,f) \end{align} $$
(make the change of variable
![]() $\delta \mapsto d_0/\delta $
). Lemma 4.5 gives the desired result.
$\delta \mapsto d_0/\delta $
). Lemma 4.5 gives the desired result.
Remark 4.7 As a consequence, we obtain
![]() $M_{d_0}(p,\{1\}) =\frac {\pi ^2}{6}\prod _{q\mid d_0}\left (1-\frac {1}{q^2}\right ) +O(p^{-1})$
, using (4.7) and the fact that
$M_{d_0}(p,\{1\}) =\frac {\pi ^2}{6}\prod _{q\mid d_0}\left (1-\frac {1}{q^2}\right ) +O(p^{-1})$
, using (4.7) and the fact that
![]() $N_{d_0}(p,\{1\})$
depends only on p modulo
$N_{d_0}(p,\{1\})$
depends only on p modulo
![]() $d_0$
. This gives in this extreme situation another proof of Theorem 1.1 with a better error term. Moreover, in that situation, we have
$d_0$
. This gives in this extreme situation another proof of Theorem 1.1 with a better error term. Moreover, in that situation, we have
![]() $K ={\mathbb Q}(\zeta _p)$
and in (1.11) the term
$K ={\mathbb Q}(\zeta _p)$
and in (1.11) the term
![]() $\Pi _{d_0}(p,\{1\})$
is bounded from below by a constant independent of p, by Corollary 2.4.
$\Pi _{d_0}(p,\{1\})$
is bounded from below by a constant independent of p, by Corollary 2.4.
5 The case where
 $f=a^{d-1}+\cdots +a^2+a+1$
$f=a^{d-1}+\cdots +a^2+a+1$
In this specific case, we are able to obtain explicit formulas for
![]() $M_{d_0}(f,H)$
when the subgroup H is defined in terms of the parameter a defining the modulus. For a general subgroup H, it seems unrealistic to be more explicit than the formula involving Dedekind sums given in Theorem 4.4. It might be interesting to explore formulas involving continued fraction expansions in view of their link to Dedekind sums [Reference HickersonHic].
$M_{d_0}(f,H)$
when the subgroup H is defined in terms of the parameter a defining the modulus. For a general subgroup H, it seems unrealistic to be more explicit than the formula involving Dedekind sums given in Theorem 4.4. It might be interesting to explore formulas involving continued fraction expansions in view of their link to Dedekind sums [Reference HickersonHic].
5.1 Explicit formulas for
 $d_0=1,2$
$d_0=1,2$
Lemma 5.1 Let
![]() $f>1$
be a rational integer of the form
$f>1$
be a rational integer of the form
![]() $f=(a^d-1)/(a-1)$
for some
$f=(a^d-1)/(a-1)$
for some
![]() $a\neq -1,0,1$
and some odd integer
$a\neq -1,0,1$
and some odd integer
![]() $d\geq 3$
. Hence, f is odd. Set
$d\geq 3$
. Hence, f is odd. Set
![]() $H=\{a^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
$H=\{a^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Then
$({\mathbb Z}/f{\mathbb Z})^*$
. Then
and
 $$ \begin{align*}S(H_2,2f) =\begin{cases} \frac{a+1}{a-1}\times\frac{4f-(d-1)a-3d-1}{24},&\mbox{if } a \mbox{ is odd,}\\ \frac{2a-1}{a-1}\times\frac{f-(d-1)a-1}{12},&\mbox{if } a \mbox{ is even.} \end{cases}\end{align*} $$
$$ \begin{align*}S(H_2,2f) =\begin{cases} \frac{a+1}{a-1}\times\frac{4f-(d-1)a-3d-1}{24},&\mbox{if } a \mbox{ is odd,}\\ \frac{2a-1}{a-1}\times\frac{f-(d-1)a-1}{12},&\mbox{if } a \mbox{ is even.} \end{cases}\end{align*} $$
Proof We have
![]() $S(H,f) =\sum _{k=0}^{d-1}s(a^k,f)$
. Moreover,
$S(H,f) =\sum _{k=0}^{d-1}s(a^k,f)$
. Moreover,
![]() $S(H_2,2f) =\sum _{k=0}^{d-1}s(a^k,2f)$
if a is odd and
$S(H_2,2f) =\sum _{k=0}^{d-1}s(a^k,2f)$
if a is odd and
![]() $S(H_2,2f) =s(1,2f)+\sum _{k=1}^{d-1}s(a^k+f,2f)$
if a is even. Now, we claim that for
$S(H_2,2f) =s(1,2f)+\sum _{k=1}^{d-1}s(a^k+f,2f)$
if a is even. Now, we claim that for
![]() $0\leq k\leq d-1$
, we have
$0\leq k\leq d-1$
, we have
 $$ \begin{align*}s(a^k,f) =\frac{a^k}{12f}+\frac{(f^2+1)a^{-k}}{12f} +\frac{a^k+a^{-k}(a^2-2a+2)}{12(a-1)} -\frac{a(a+1)}{12(a-1)} \mbox{ whatever the parity of } a, \end{align*} $$
$$ \begin{align*}s(a^k,f) =\frac{a^k}{12f}+\frac{(f^2+1)a^{-k}}{12f} +\frac{a^k+a^{-k}(a^2-2a+2)}{12(a-1)} -\frac{a(a+1)}{12(a-1)} \mbox{ whatever the parity of } a, \end{align*} $$
 $$ \begin{align*}s(a^k,2f) =\frac{a^k}{24f}+\frac{(4f^2+1)a^{-k}}{24f} +\frac{4a^k+a^{-k}(a^2-2a+5)}{24(a-1)} -\frac{(a+1)(a+3)}{24(a-1)} \mbox{ if } a \mbox{ is odd,} \end{align*} $$
$$ \begin{align*}s(a^k,2f) =\frac{a^k}{24f}+\frac{(4f^2+1)a^{-k}}{24f} +\frac{4a^k+a^{-k}(a^2-2a+5)}{24(a-1)} -\frac{(a+1)(a+3)}{24(a-1)} \mbox{ if } a \mbox{ is odd,} \end{align*} $$
and that for
![]() $1\leq k\leq d-1$
, we have
$1\leq k\leq d-1$
, we have
 $$ \begin{align*}s(a^k+f,2f) =\frac{a^k}{24f}+\frac{(f^2+1)a^{-k}}{24f} +\frac{a^k+a^{-k}(a^2-2a+2)}{24(a-1)} -\frac{a(2a-1)}{12(a-1)} \mbox{ if } a \mbox{ is even.} \end{align*} $$
$$ \begin{align*}s(a^k+f,2f) =\frac{a^k}{24f}+\frac{(f^2+1)a^{-k}}{24f} +\frac{a^k+a^{-k}(a^2-2a+2)}{24(a-1)} -\frac{a(2a-1)}{12(a-1)} \mbox{ if } a \mbox{ is even.} \end{align*} $$
Noticing that
![]() $\sum _{k=1}^{d-1}a^k =f-1$
and
$\sum _{k=1}^{d-1}a^k =f-1$
and
![]() $\sum _{k=1}^{d-1}a^{-k} =\frac {f-1}{(a-1)f+1}$
, we then get the assertions on
$\sum _{k=1}^{d-1}a^{-k} =\frac {f-1}{(a-1)f+1}$
, we then get the assertions on
![]() $S(H,f)$
and
$S(H,f)$
and
![]() $S(H_2,2f)$
. Now, let us, for example, prove the third claim. Hence, assume that a is even and that
$S(H_2,2f)$
. Now, let us, for example, prove the third claim. Hence, assume that a is even and that
![]() $1\leq k\leq d-1$
. Then
$1\leq k\leq d-1$
. Then
![]() $f_k :=(a^k-1)/(a-1)$
is odd,
$f_k :=(a^k-1)/(a-1)$
is odd,
![]() $\mathrm {sign}(f_k)=\mathrm {sign}(a)^k$
and
$\mathrm {sign}(f_k)=\mathrm {sign}(a)^k$
and
![]() $a^k+f>0$
. First, since
$a^k+f>0$
. First, since
![]() $2f\equiv -2a^{k}\ \ \pmod {a^k+f}$
, using (3.3), we have
$2f\equiv -2a^{k}\ \ \pmod {a^k+f}$
, using (3.3), we have
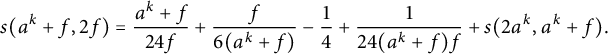 $$ \begin{align*}s(a^k+f,2f) =\frac{a^k+f}{24f} +\frac{f}{6(a^k+f)} -\frac{1}{4} +\frac{1}{24(a^k+f)f} +s(2a^{k},a^k+f).\end{align*} $$
$$ \begin{align*}s(a^k+f,2f) =\frac{a^k+f}{24f} +\frac{f}{6(a^k+f)} -\frac{1}{4} +\frac{1}{24(a^k+f)f} +s(2a^{k},a^k+f).\end{align*} $$
Second, noticing that
![]() $a^k+f\equiv f_k\ \ \pmod {2a^{k}}$
and using (3.3), we have
$a^k+f\equiv f_k\ \ \pmod {2a^{k}}$
and using (3.3), we have
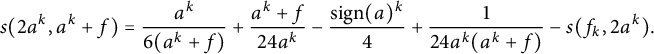 $$ \begin{align*}s(2a^{k},a^k+f) =\frac{a^{k}}{6(a^k+f)} +\frac{a^k+f}{24a^{k}} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24a^{k}(a^k+f)} -s(f_k,2a^{k}).\end{align*} $$
$$ \begin{align*}s(2a^{k},a^k+f) =\frac{a^{k}}{6(a^k+f)} +\frac{a^k+f}{24a^{k}} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24a^{k}(a^k+f)} -s(f_k,2a^{k}).\end{align*} $$
Finally, noticing that
![]() $2a^{k}\equiv 2\ \ \pmod {f_k}$
and using (3.3) and (3.4), we have
$2a^{k}\equiv 2\ \ \pmod {f_k}$
and using (3.3) and (3.4), we have
 $$ \begin{align*} s(f_k,2a^{k}) &=\frac{f_k}{24a^{k}} +\frac{a^{k}}{6f_k} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24f_ka^{k}} -s(2,f_k)\\ &=\frac{f_k}{24a^{k}} +\frac{a^{k}}{6f_k} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24f_ka^{k}} -\frac{f_k^2-6f_k+5}{24f_k}. \end{align*} $$
$$ \begin{align*} s(f_k,2a^{k}) &=\frac{f_k}{24a^{k}} +\frac{a^{k}}{6f_k} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24f_ka^{k}} -s(2,f_k)\\ &=\frac{f_k}{24a^{k}} +\frac{a^{k}}{6f_k} -\frac{\mathrm{sign}(a)^k}{4} +\frac{1}{24f_ka^{k}} -\frac{f_k^2-6f_k+5}{24f_k}. \end{align*} $$
After some simplifications, we obtain the desired formula for
![]() $s(a^k+f,2f)$
.
$s(a^k+f,2f)$
.
Notice that for
![]() $d=3$
, we obtain
$d=3$
, we obtain
![]() $S(H,f) =\frac {f-1}{12}$
, in accordance with (6.1).
$S(H,f) =\frac {f-1}{12}$
, in accordance with (6.1).
Using (4.6) and Lemma 5.1, we readily obtain:
Theorem 5.2 Let
![]() $d\geq 3$
be a prime integer. Let
$d\geq 3$
be a prime integer. Let
![]() $p\equiv 1\ \ \pmod {2d}$
be a prime integer of the form
$p\equiv 1\ \ \pmod {2d}$
be a prime integer of the form
![]() $p=(a^d-1)/(a-1)$
for some
$p=(a^d-1)/(a-1)$
for some
![]() $a\neq -1,0,1$
. Let K be the imaginary subfield of degree
$a\neq -1,0,1$
. Let K be the imaginary subfield of degree
![]() $(p-1)/d$
of the cyclotomic field
$(p-1)/d$
of the cyclotomic field
![]() ${\mathbb Q}(\zeta _p)$
. Set
${\mathbb Q}(\zeta _p)$
. Set
![]() $H=\{a^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
$H=\{a^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. We have the mean square value formulas
$({\mathbb Z}/p{\mathbb Z})^*$
. We have the mean square value formulas
 $$ \begin{align} M(p,H) =\frac{\pi^2}{6}\times\frac{a+1}{a-1}\times\left (1-\frac{(d-1)a+1}{p}\right ) \end{align} $$
$$ \begin{align} M(p,H) =\frac{\pi^2}{6}\times\frac{a+1}{a-1}\times\left (1-\frac{(d-1)a+1}{p}\right ) \end{align} $$
and
 $$ \begin{align} M_2(p,H) =\frac{\pi^2}{8}\times \begin{cases} \frac{a+1}{a-1}\times\left (1-\frac{d}{p}\right ),&\mbox{ if } a \mbox{ is odd,}\\ 1-\frac{(d-1)a+1}{p},&\mbox{ if } a \mbox{ is even.}\\ \end{cases} \end{align} $$
$$ \begin{align} M_2(p,H) =\frac{\pi^2}{8}\times \begin{cases} \frac{a+1}{a-1}\times\left (1-\frac{d}{p}\right ),&\mbox{ if } a \mbox{ is odd,}\\ 1-\frac{(d-1)a+1}{p},&\mbox{ if } a \mbox{ is even.}\\ \end{cases} \end{align} $$
Consequently, for a given d, as
![]() $p\rightarrow \infty $
, we have
$p\rightarrow \infty $
, we have
On the other hand, for a given a, as
![]() $p\rightarrow \infty $
, we have
$p\rightarrow \infty $
, we have
 $$ \begin{align*} M(p,H) =\frac{\pi^2}{6}\times\frac{a+1}{a-1}+o(1) \mbox{ and } M_2(p,H) =\begin{cases} \frac{\pi^2}{8}\times\frac{a+1}{a-1}+o(1), &\mbox{if } a \mbox{ is odd,}\\ \frac{\pi^2}{8}+o(1), &\mbox{if } a \mbox{ is even.} \end{cases} \end{align*} $$
$$ \begin{align*} M(p,H) =\frac{\pi^2}{6}\times\frac{a+1}{a-1}+o(1) \mbox{ and } M_2(p,H) =\begin{cases} \frac{\pi^2}{8}\times\frac{a+1}{a-1}+o(1), &\mbox{if } a \mbox{ is odd,}\\ \frac{\pi^2}{8}+o(1), &\mbox{if } a \mbox{ is even.} \end{cases} \end{align*} $$
Remark 5.3 Assertion (5.1) was initially provedFootnote
5
in [Reference LouboutinLou16, Theorem 5] for
![]() $d=5$
and then generalized in [Reference Louboutin and MunschLM21, Proposition 3.1] to any
$d=5$
and then generalized in [Reference Louboutin and MunschLM21, Proposition 3.1] to any
![]() $d\geq 3$
. However, (5.1) is much simpler than [Reference Louboutin and MunschLM21, equation (22)]. Notice that if p runs over the prime of the form
$d\geq 3$
. However, (5.1) is much simpler than [Reference Louboutin and MunschLM21, equation (22)]. Notice that if p runs over the prime of the form
![]() $p=(a^d-1)/(a-1)$
with
$p=(a^d-1)/(a-1)$
with
![]() $a\neq 0,2$
even then
$a\neq 0,2$
even then
![]() $M_2(p,H) =\frac {6}{8}\times \frac {a-1}{a+1}\times M(p,H)$
and the asymptotic (1.12) is not satisfied.
$M_2(p,H) =\frac {6}{8}\times \frac {a-1}{a+1}\times M(p,H)$
and the asymptotic (1.12) is not satisfied.
5.2 The case where p is a Mersenne prime and
 $d_0=1,3,15$
$d_0=1,3,15$
In the setting of Theorem 5.4, we have
![]() $2\in H$
. Hence, by Remark 2.2, we assume that
$2\in H$
. Hence, by Remark 2.2, we assume that
![]() $d_0$
is odd.
$d_0$
is odd.
Theorem 5.4 Let
![]() $p=2^d-1>3$
be a Mersenne prime. Hence, d is odd and
$p=2^d-1>3$
be a Mersenne prime. Hence, d is odd and
![]() $H=\{2^k;\ 0\leq k\leq d-1\}$
is a subgroup of odd order d of the multiplicative group
$H=\{2^k;\ 0\leq k\leq d-1\}$
is a subgroup of odd order d of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. Let K be the imaginary subfield of degree
$({\mathbb Z}/p{\mathbb Z})^*$
. Let K be the imaginary subfield of degree
![]() $m =(p-1)/d$
of
$m =(p-1)/d$
of
![]() ${\mathbb Q}(\zeta _p)$
. Then
${\mathbb Q}(\zeta _p)$
. Then
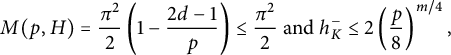 $$ \begin{align*}M(p,H) =\frac{\pi^2}{2}\left (1-\frac{2d-1}{p}\right ) \leq\frac{\pi^2}{2} \text{ and } h_K^-\leq 2\left (\frac{p}{8}\right )^{m/4},\end{align*} $$
$$ \begin{align*}M(p,H) =\frac{\pi^2}{2}\left (1-\frac{2d-1}{p}\right ) \leq\frac{\pi^2}{2} \text{ and } h_K^-\leq 2\left (\frac{p}{8}\right )^{m/4},\end{align*} $$
 $$ \begin{align*}M_3(p,H) =\frac{4\pi^2}{9}\left (1-\frac{d}{p}\right ) \leq\frac{4\pi^2}{9} \text{ and } h_K^-\leq 2\left (\frac{p}{9}\right )^{m/4},\end{align*} $$
$$ \begin{align*}M_3(p,H) =\frac{4\pi^2}{9}\left (1-\frac{d}{p}\right ) \leq\frac{4\pi^2}{9} \text{ and } h_K^-\leq 2\left (\frac{p}{9}\right )^{m/4},\end{align*} $$
and
 $$ \begin{align*}M_{15}(p,H) =\frac{32\pi^2}{75}\left (1-\frac{c_d}{48p}\right ) \leq\frac{32\pi^2}{75}, \mbox{ where } c_d =\begin{cases} 47d+1,&\mbox{if } d\equiv 1\ \ \pmod 4,\\ 17d-3,&\mbox{if } d\equiv 3\ \ \pmod 4. \end{cases}\end{align*} $$
$$ \begin{align*}M_{15}(p,H) =\frac{32\pi^2}{75}\left (1-\frac{c_d}{48p}\right ) \leq\frac{32\pi^2}{75}, \mbox{ where } c_d =\begin{cases} 47d+1,&\mbox{if } d\equiv 1\ \ \pmod 4,\\ 17d-3,&\mbox{if } d\equiv 3\ \ \pmod 4. \end{cases}\end{align*} $$
In particular, for
![]() $d\equiv 3\ \ \pmod 4$
, we have
$d\equiv 3\ \ \pmod 4$
, we have
![]() $h_K^-\leq 2\left (\frac {8p}{75}\right )^{m/4}.$
$h_K^-\leq 2\left (\frac {8p}{75}\right )^{m/4}.$
Proof By (4.6), we have
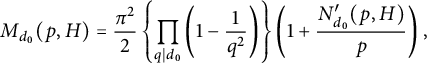 $$ \begin{align} M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}'(p,H)}{p}\right ), \end{align} $$
$$ \begin{align} M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q\mid d_0}\left (1-\frac{1}{q^2}\right )\right\} \left (1+\frac{N_{d_0}'(p,H)}{p}\right ), \end{align} $$
where for H a subgroup of odd order of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, we set
$({\mathbb Z}/f{\mathbb Z})^*$
, we set
 $$ \begin{align} N_{d_0}'(f,H) :=-f +\frac{4\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(H_\delta,\delta f). \end{align} $$
$$ \begin{align} N_{d_0}'(f,H) :=-f +\frac{4\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(H_\delta,\delta f). \end{align} $$
The formulas for
![]() $M(p,H),M_3(p,H)$
, and
$M(p,H),M_3(p,H)$
, and
![]() $M_{15}(p,H)$
follow from (5.3)) and Lemma 5.5. The upper bounds on
$M_{15}(p,H)$
follow from (5.3)) and Lemma 5.5. The upper bounds on
![]() $h_K^-$
follow from (1.11) and Lemma 2.3 according to which
$h_K^-$
follow from (1.11) and Lemma 2.3 according to which
![]() $\Pi _q(p,H)\geq 1$
if q is of even order in the quotient group
$\Pi _q(p,H)\geq 1$
if q is of even order in the quotient group
![]() $G/H$
, where
$G/H$
, where
![]() $G=({\mathbb Z}/p{\mathbb Z})^*$
, hence, if q is of even order in the group G. Now, since
$G=({\mathbb Z}/p{\mathbb Z})^*$
, hence, if q is of even order in the group G. Now, since
![]() $p\equiv 3\ \ \pmod 4$
the group G is of order
$p\equiv 3\ \ \pmod 4$
the group G is of order
![]() $p-1=2N$
with N odd and q is of even order in G if and only
$p-1=2N$
with N odd and q is of even order in G if and only
![]() $q^N=-1$
in G, i.e., if and only if the Legendre symbol
$q^N=-1$
in G, i.e., if and only if the Legendre symbol
![]() $\left (\frac {q}{p}\right )$
is equal to
$\left (\frac {q}{p}\right )$
is equal to
![]() $-1$
. Now, since
$-1$
. Now, since
![]() $p=2^d-1\equiv -1\equiv 3 \ \ \pmod 4$
for
$p=2^d-1\equiv -1\equiv 3 \ \ \pmod 4$
for
![]() $d\geq 3$
, the law of quadratic reciprocity gives
$d\geq 3$
, the law of quadratic reciprocity gives
![]() $\left (\frac {3}{p}\right ) =-\left (\frac {p}{3}\right ) =-\left (\frac {1}{3}\right ) =-1$
, as
$\left (\frac {3}{p}\right ) =-\left (\frac {p}{3}\right ) =-\left (\frac {1}{3}\right ) =-1$
, as
![]() $p\equiv (-1)^d-1\equiv -2\equiv 1\ \ \pmod 3$
. Hence,
$p\equiv (-1)^d-1\equiv -2\equiv 1\ \ \pmod 3$
. Hence,
![]() $\Pi _3(p,H)\geq 1$
. In the same way, if
$\Pi _3(p,H)\geq 1$
. In the same way, if
![]() $d\equiv 3\ \ \pmod 4$
then
$d\equiv 3\ \ \pmod 4$
then
![]() $p=2^d-1 =2\cdot 4^{\frac {d-1}{2}}-1\equiv 2\cdot (-1)^{\frac {d-1}{2}}-1\equiv -3\equiv 2\ \ \pmod 5$
and
$p=2^d-1 =2\cdot 4^{\frac {d-1}{2}}-1\equiv 2\cdot (-1)^{\frac {d-1}{2}}-1\equiv -3\equiv 2\ \ \pmod 5$
and
![]() $\left (\frac {5}{p}\right ) =\left (\frac {p}{5}\right ) =\left (\frac {2}{5}\right ) =-1$
and
$\left (\frac {5}{p}\right ) =\left (\frac {p}{5}\right ) =\left (\frac {2}{5}\right ) =-1$
and
![]() $\Pi _5(p,H)\geq 1$
.
$\Pi _5(p,H)\geq 1$
.
Lemma 5.5 Set
![]() $f=2^d-1$
and
$f=2^d-1$
and
![]() $\varepsilon _d =(-1)^{(d-1)/2}$
with
$\varepsilon _d =(-1)^{(d-1)/2}$
with
![]() $d\geq 2$
odd. Hence,
$d\geq 2$
odd. Hence,
![]() $\gcd (f,15)=1$
. Set
$\gcd (f,15)=1$
. Set
![]() $H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
$H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Then,
$({\mathbb Z}/f{\mathbb Z})^*$
. Then,
Proof The first assertion is the special case
![]() $a=2$
of Lemma 5.1. Let us now deal with the second assertion. Here,
$a=2$
of Lemma 5.1. Let us now deal with the second assertion. Here,
![]() $H_3 =\{2^k;\ 0\leq k\leq d-1\} \cup \{2^k+(-1)^kf;\ 0\leq k\leq d-1\}$
. We assume that
$H_3 =\{2^k;\ 0\leq k\leq d-1\} \cup \{2^k+(-1)^kf;\ 0\leq k\leq d-1\}$
. We assume that
![]() $0\leq k\leq d-1$
. Hence,
$0\leq k\leq d-1$
. Hence,
![]() $\mathrm {sign}(2^k+(-1)^kf)=(-1)^k$
.
$\mathrm {sign}(2^k+(-1)^kf)=(-1)^k$
.
1. Noticing that
![]() $3f\equiv -3\ \ \pmod {2^k}$
, by (3.3), we obtain
$3f\equiv -3\ \ \pmod {2^k}$
, by (3.3), we obtain
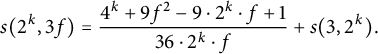 $$ \begin{align*}s(2^k,3f) =\frac{4^k+9f^2-9\cdot 2^k\cdot f+1}{36\cdot 2^k\cdot f}+s(3,2^k).\end{align*} $$
$$ \begin{align*}s(2^k,3f) =\frac{4^k+9f^2-9\cdot 2^k\cdot f+1}{36\cdot 2^k\cdot f}+s(3,2^k).\end{align*} $$
Noticing that
![]() $2^k\equiv (-1)^k\ \ \pmod 3$
, by (3.3) and (3.4), we obtain
$2^k\equiv (-1)^k\ \ \pmod 3$
, by (3.3) and (3.4), we obtain
Hence,
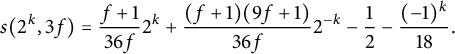 $$ \begin{align*}s(2^k,3f) =\frac{f+1}{36f}2^k +\frac{(f+1)(9f+1)}{36f}2^{-k} -\frac{1}{2} -\frac{(-1)^k}{18}.\end{align*} $$
$$ \begin{align*}s(2^k,3f) =\frac{f+1}{36f}2^k +\frac{(f+1)(9f+1)}{36f}2^{-k} -\frac{1}{2} -\frac{(-1)^k}{18}.\end{align*} $$
2. Noticing that
![]() $3f\equiv -3\cdot (-1)^k2^k\ \ \pmod {2^k+(-1)^kf}$
, by (3.3), we obtain
$3f\equiv -3\cdot (-1)^k2^k\ \ \pmod {2^k+(-1)^kf}$
, by (3.3), we obtain
 $$ \begin{align*} s(2^k+(-1)^kf,3f) =&\frac{2^k+(-1)^kf}{36f} +\frac{f}{4(2^k+(-1)^kf)} -\frac{(-1)^k}{4} +\frac{1}{36(2^k+(-1)^kf)f}\\ &+(-1)^ks(3\cdot 2^k,2^k+(-1)^kf), \end{align*} $$
$$ \begin{align*} s(2^k+(-1)^kf,3f) =&\frac{2^k+(-1)^kf}{36f} +\frac{f}{4(2^k+(-1)^kf)} -\frac{(-1)^k}{4} +\frac{1}{36(2^k+(-1)^kf)f}\\ &+(-1)^ks(3\cdot 2^k,2^k+(-1)^kf), \end{align*} $$
and noticing that
![]() $2^k+(-1)^kf\equiv (-1)^{k-1}\ \ \pmod {3\cdot 2^k}$
, by (3.3), we obtain
$2^k+(-1)^kf\equiv (-1)^{k-1}\ \ \pmod {3\cdot 2^k}$
, by (3.3), we obtain
 $$ \begin{align*} s(3\cdot 2^k,2^k+(-1)^kf) =&\frac{3\cdot 2^k}{12(2^k+(-1)^kf)} +\frac{2^k+(-1)^kf}{36\cdot 2^k} -\frac{(-1)^k}{4} \\ &+\frac{1}{36\cdot 2^k\cdot (2^k+(-1)^kf)}+(-1)^ks(1,3\cdot 2^k). \end{align*} $$
$$ \begin{align*} s(3\cdot 2^k,2^k+(-1)^kf) =&\frac{3\cdot 2^k}{12(2^k+(-1)^kf)} +\frac{2^k+(-1)^kf}{36\cdot 2^k} -\frac{(-1)^k}{4} \\ &+\frac{1}{36\cdot 2^k\cdot (2^k+(-1)^kf)}+(-1)^ks(1,3\cdot 2^k). \end{align*} $$
Using (3.4), we finally obtain
 $$ \begin{align*}s(2^k+(-1)^kf,3f) =\frac{9f+1}{36f}2^k +\frac{(f+1)^2}{36f}2^{-k} -\frac{1}{2} +\frac{(-1)^k}{18}.\end{align*} $$
$$ \begin{align*}s(2^k+(-1)^kf,3f) =\frac{9f+1}{36f}2^k +\frac{(f+1)^2}{36f}2^{-k} -\frac{1}{2} +\frac{(-1)^k}{18}.\end{align*} $$
3. Using
![]() $\sum _{k=0}^{d-1}2^k =f$
,
$\sum _{k=0}^{d-1}2^k =f$
,
![]() $\sum _{k=0}^{d-1}2^{-k}=\frac {2f}{f+1}$
and
$\sum _{k=0}^{d-1}2^{-k}=\frac {2f}{f+1}$
and
![]() $\sum _{k=0}^{d-1}(-1)^k=1$
, we obtain
$\sum _{k=0}^{d-1}(-1)^k=1$
, we obtain
 $$ \begin{align*}\sum_{k=0}^{d-1}s(2^k,3f) =\frac{19f-18d+1}{36} \mbox{ and } \sum_{k=0}^{d-1}s(2^k+(-1)^kf,3f) =\frac{11f-18d+5}{36}.\end{align*} $$
$$ \begin{align*}\sum_{k=0}^{d-1}s(2^k,3f) =\frac{19f-18d+1}{36} \mbox{ and } \sum_{k=0}^{d-1}s(2^k+(-1)^kf,3f) =\frac{11f-18d+5}{36}.\end{align*} $$
Hence, we do obtain
 $$ \begin{align*}S(H_3,3f) =\sum_{h\in H_3}s(h,3f) =\frac{19f-18d+1}{36} +\frac{11f-18d+5}{36} =\frac{5f-6d+1}{6}\end{align*} $$
$$ \begin{align*}S(H_3,3f) =\sum_{h\in H_3}s(h,3f) =\frac{19f-18d+1}{36} +\frac{11f-18d+5}{36} =\frac{5f-6d+1}{6}\end{align*} $$
and
![]() $N_3'(f,H) =-d$
, by (5.4).
$N_3'(f,H) =-d$
, by (5.4).
Let us finally deal with the third and fourth assertions. The proof involves tedious and repetitive computations. For this reason, we will restrict ourselves to a specific case. Let us, for example, give some details for the proof of (5.8) in the case that
![]() $d\equiv 1\ \ \pmod 4$
. We have
$d\equiv 1\ \ \pmod 4$
. We have
![]() $f=2^d-1\equiv 1\ \ \pmod {30}$
and
$f=2^d-1\equiv 1\ \ \pmod {30}$
and
![]() $H_{15}=\cup _{l=0}^{14}E_l$
, where
$H_{15}=\cup _{l=0}^{14}E_l$
, where
![]() $E_l := \{2^k+lf;\ 0\leq k\leq d-1,\ \gcd (2^k+l,15)=1\}$
for
$E_l := \{2^k+lf;\ 0\leq k\leq d-1,\ \gcd (2^k+l,15)=1\}$
for
![]() $0\leq l\leq 14$
. We have to compute the sums
$0\leq l\leq 14$
. We have to compute the sums
![]() $s_l:=\sum _{n\in E_l}s(n,15f)$
. Let us, for example, give some details in the case that
$s_l:=\sum _{n\in E_l}s(n,15f)$
. Let us, for example, give some details in the case that
![]() $l=1$
. We have
$l=1$
. We have
![]() $\gcd (2^k+1,15)=1$
if and only if
$\gcd (2^k+1,15)=1$
if and only if
![]() $k\equiv 0\ \ \pmod 4$
. Hence,
$k\equiv 0\ \ \pmod 4$
. Hence,
![]() $s_1=\sum _{k=0}^{(d-1)/4}s(16^{k}+f,15f)$
. Using (3.3) and (3.4), we obtain
$s_1=\sum _{k=0}^{(d-1)/4}s(16^{k}+f,15f)$
. Using (3.3) and (3.4), we obtain
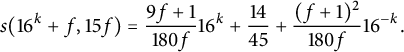 $$ \begin{align*}s(16^k+f,15f) =\frac{9f+1}{180f}16^k +\frac{14}{45} +\frac{(f+1)^2}{180f}16^{-k}.\end{align*} $$
$$ \begin{align*}s(16^k+f,15f) =\frac{9f+1}{180f}16^k +\frac{14}{45} +\frac{(f+1)^2}{180f}16^{-k}.\end{align*} $$
Finally, using
![]() $\sum _{k=0}^{(d-1)/4}16^k =\frac {8f+7}{15}$
and
$\sum _{k=0}^{(d-1)/4}16^k =\frac {8f+7}{15}$
and
![]() $\sum _{k=0}^{(d-1)/4}16^{-k} =\frac {2(8f+7)}{15(f+1)}$
, we obtain
$\sum _{k=0}^{(d-1)/4}16^{-k} =\frac {2(8f+7)}{15(f+1)}$
, we obtain
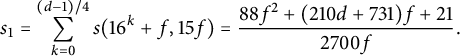 $$ \begin{align*}s_1 =\sum_{k=0}^{(d-1)/4}s(16^k+f,15f) =\frac{88f^2+(210d+731)f+21}{2700f}.\end{align*} $$
$$ \begin{align*}s_1 =\sum_{k=0}^{(d-1)/4}s(16^k+f,15f) =\frac{88f^2+(210d+731)f+21}{2700f}.\end{align*} $$
We conclude this section with the following result for
![]() $d_0 =3\times 5\times 7 =105$
, whose long proof we omit:Footnote
6
$d_0 =3\times 5\times 7 =105$
, whose long proof we omit:Footnote
6
Lemma 5.6 Set
![]() $f =2^d-1$
with
$f =2^d-1$
with
![]() $d>1$
odd. Assume
$d>1$
odd. Assume
![]() $\gcd (f,105)=1$
, i.e., that
$\gcd (f,105)=1$
, i.e., that
![]() $d\equiv 1, 5, 7, 11\ \ \pmod {12}$
. Set
$d\equiv 1, 5, 7, 11\ \ \pmod {12}$
. Set
![]() $H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
$H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Then
$({\mathbb Z}/f{\mathbb Z})^*$
. Then
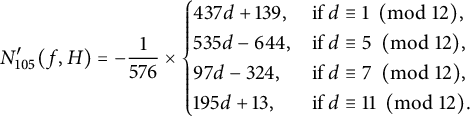 $$ \begin{align*} N_{105}'(f,H) =-\frac{1}{576} \times\begin{cases} 437d+139,&\mbox{if } d\equiv 1\ \ \pmod {12},\\ 535d-644,&\mbox{if } d\equiv 5\ \ \pmod{12},\\ 97d-324,&\mbox{if } d\equiv 7\ \ \pmod{12},\\ 195d+13,&\mbox{if } d\equiv 11\ \ \pmod {12}. \end{cases} \end{align*} $$
$$ \begin{align*} N_{105}'(f,H) =-\frac{1}{576} \times\begin{cases} 437d+139,&\mbox{if } d\equiv 1\ \ \pmod {12},\\ 535d-644,&\mbox{if } d\equiv 5\ \ \pmod{12},\\ 97d-324,&\mbox{if } d\equiv 7\ \ \pmod{12},\\ 195d+13,&\mbox{if } d\equiv 11\ \ \pmod {12}. \end{cases} \end{align*} $$
Lemmas 5.5 and 5.6 show that the following conjecture holds true for
![]() $d_0\in \{1,3,5,15,105\}$
:
$d_0\in \{1,3,5,15,105\}$
:
Conjecture 5.7 Let
![]() $d_0\geq 1$
be odd and square-free. Let N be the order of
$d_0\geq 1$
be odd and square-free. Let N be the order of
![]() $2$
in the multiplicative group
$2$
in the multiplicative group
![]() $({\mathbb Z}/d_0{\mathbb Z})^*$
. Set
$({\mathbb Z}/d_0{\mathbb Z})^*$
. Set
![]() $f =2^d-1$
with
$f =2^d-1$
with
![]() $d>1$
odd and
$d>1$
odd and
![]() $H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
$H =\{2^k;\ 0\leq k\leq d-1\}$
, a subgroup of order d of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Assume
$({\mathbb Z}/f{\mathbb Z})^*$
. Assume
![]() $\gcd (f,d_0)=1$
. Then
$\gcd (f,d_0)=1$
. Then
![]() $N_{d_0}'(f,H) =A_1(d)d+A_0(d)$
, where
$N_{d_0}'(f,H) =A_1(d)d+A_0(d)$
, where
![]() $A_1(d)$
and
$A_1(d)$
and
![]() $A_0(d)$
are rational numbers which depend only on d modulo N, i.e., only on f modulo
$A_0(d)$
are rational numbers which depend only on d modulo N, i.e., only on f modulo
![]() $d_0$
. Hence, for a prime
$d_0$
. Hence, for a prime
![]() $p\geq 3$
, we expect
$p\geq 3$
, we expect
 $$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)\right\}\left(1+\frac{A_1(d)d}{p}+\frac{A_0(d)}{p}\right),\end{align*} $$
$$ \begin{align*}M_{d_0}(p,H) =\frac{\pi^2}{2}\left\{\prod_{q \mid d_0} \left(1-\frac{1}{q^2}\right)\right\}\left(1+\frac{A_1(d)d}{p}+\frac{A_0(d)}{p}\right),\end{align*} $$
confirming again that the restriction on d in Theorem 1.1 should be sharp.
There is apparently no theoretical obstruction preventing us to prove Conjecture 5.7. Indeed, for a fixed
![]() $d_0$
, the formulas for
$d_0$
, the formulas for
![]() $A_0(d)$
and
$A_0(d)$
and
![]() $A_1(d)$
could be guessed using numerous examples on a computer algebra system. However, for large
$A_1(d)$
could be guessed using numerous examples on a computer algebra system. However, for large
![]() $d_0$
’s, the set of cases to consider grows linearly and a more unified approach seems to be required to give a complete proof.
$d_0$
’s, the set of cases to consider grows linearly and a more unified approach seems to be required to give a complete proof.
6 The case of subgroups of order
 $d=3$
$d=3$
6.1 Formulas for
 $d_0=1,2,6$
$d_0=1,2,6$
Let
![]() $p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
$p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
![]() $m=(p-1)/3$
of the cyclotomic field
$m=(p-1)/3$
of the cyclotomic field
![]() ${\mathbb Q}(\zeta _p)$
. Since p splits completely in the quadratic field
${\mathbb Q}(\zeta _p)$
. Since p splits completely in the quadratic field
![]() ${\mathbb Q}(\sqrt {-3})$
of class number one, there exists an algebraic integer
${\mathbb Q}(\sqrt {-3})$
of class number one, there exists an algebraic integer
![]() $\alpha =a+b\frac {1+\sqrt {-3}}{2}$
with
$\alpha =a+b\frac {1+\sqrt {-3}}{2}$
with
![]() $a,b\in {\mathbb Z}$
such that
$a,b\in {\mathbb Z}$
such that
![]() $p =N_{{\mathbb Q}(\sqrt {-3})/{\mathbb Q}}(\alpha ) =a^2+ab+b^2$
. Then,
$p =N_{{\mathbb Q}(\sqrt {-3})/{\mathbb Q}}(\alpha ) =a^2+ab+b^2$
. Then,
![]() $H=\{1,a/b,b/a\}$
is the unique subgroup of order
$H=\{1,a/b,b/a\}$
is the unique subgroup of order
![]() $3$
of the cyclic multiplicative group
$3$
of the cyclic multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. So we consider the integers
$({\mathbb Z}/p{\mathbb Z})^*$
. So we consider the integers
![]() $f>3$
of the form
$f>3$
of the form
![]() $f=a^2+ab+b^2$
, with
$f=a^2+ab+b^2$
, with
![]() $a,b\in {\mathbb Z}\setminus \{0\}$
and
$a,b\in {\mathbb Z}\setminus \{0\}$
and
![]() $\gcd (a,b)=1$
, which implies
$\gcd (a,b)=1$
, which implies
![]() $\gcd (a,f) =\gcd (b,f)=1$
and the oddness of f. We have the following explicit formula.
$\gcd (a,f) =\gcd (b,f)=1$
and the oddness of f. We have the following explicit formula.
Lemma 6.1 Let
![]() $f>3$
be of the form
$f>3$
be of the form
![]() $f=a^2+ab+b^2$
, with
$f=a^2+ab+b^2$
, with
![]() $a,b\in {\mathbb Z}$
and
$a,b\in {\mathbb Z}$
and
![]() $\gcd (a,b)=1$
. Set
$\gcd (a,b)=1$
. Set
![]() $H=\left \{1,a/b,b/a\right \}$
, a subgroup of order
$H=\left \{1,a/b,b/a\right \}$
, a subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Then
$({\mathbb Z}/f{\mathbb Z})^*$
. Then
Proof Noticing that
![]() $s(b,f,a) =s(b,b^2,a) =s(1,b,a) =s(b,a)$
, by (3.5), and
$s(b,f,a) =s(b,b^2,a) =s(1,b,a) =s(b,a)$
, by (3.5), and
![]() $s(f,a,b) =s(a^2,a,b) =s(a,1,b) =s(a,b)$
, and using (3.3), we obtain
$s(f,a,b) =s(a^2,a,b) =s(a,1,b) =s(a,b)$
, and using (3.3), we obtain
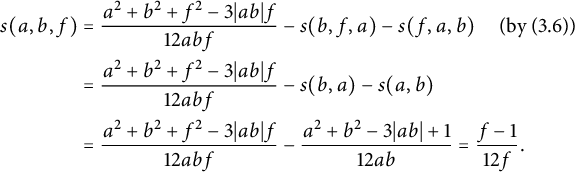 $$ \begin{align*} s(a,b,f) &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf}-s(b,f,a)-s(f,a,b) \ \ \ \ \ \text{(by (3.6))}\\ &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf} -s(b,a)-s(a,b)\\ &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf} -\frac{a^2+b^2-3\vert ab\vert+1}{12ab} =\frac{f-1}{12f}. \end{align*} $$
$$ \begin{align*} s(a,b,f) &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf}-s(b,f,a)-s(f,a,b) \ \ \ \ \ \text{(by (3.6))}\\ &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf} -s(b,a)-s(a,b)\\ &=\frac{a^2+b^2+f^2-3\vert ab\vert f}{12abf} -\frac{a^2+b^2-3\vert ab\vert+1}{12ab} =\frac{f-1}{12f}. \end{align*} $$
Finally,
![]() $S(H,f)=s(1,f)+s(a,b,f)+s(b,a,f) =s(1,f)+2s(a,b,f)$
and use (3.4) and (4.9).
$S(H,f)=s(1,f)+s(a,b,f)+s(b,a,f) =s(1,f)+2s(a,b,f)$
and use (3.4) and (4.9).
Remark 6.2 Take
![]() $f_1=A^2+AB+B^2>0$
, where
$f_1=A^2+AB+B^2>0$
, where
![]() $3\nmid f_1$
and
$3\nmid f_1$
and
![]() $\gcd (A,B)=1$
. Set
$\gcd (A,B)=1$
. Set
![]() $f=(f_1+1)^3-1$
. Then
$f=(f_1+1)^3-1$
. Then
![]() $f=a^2+ab+b^2$
, where
$f=a^2+ab+b^2$
, where
![]() $a=Af_1+A-B$
,
$a=Af_1+A-B$
,
![]() $b=Bf_1+A+2B$
and
$b=Bf_1+A+2B$
and
![]() $\gcd (a,b)=1$
. By Lemmas 6.1, we have an infinite family of moduli f for which the multiplicative group
$\gcd (a,b)=1$
. By Lemmas 6.1, we have an infinite family of moduli f for which the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
contains at the same time an element
$({\mathbb Z}/f{\mathbb Z})^*$
contains at the same time an element
![]() $h=a/b$
of order
$h=a/b$
of order
![]() $d=3$
for which
$d=3$
for which
![]() $s(h,f)$
is asymptotic to
$s(h,f)$
is asymptotic to
![]() $1/12$
and an element
$1/12$
and an element
![]() $h'=f_1+1$
of order
$h'=f_1+1$
of order
![]() $d=3$
for which
$d=3$
for which
![]() $s(h',f)$
is asymptotic to
$s(h',f)$
is asymptotic to
![]() $f^{2/3}/12$
. Indeed, by (3.3) and (3.4), for
$f^{2/3}/12$
. Indeed, by (3.3) and (3.4), for
![]() $f=(f_1+1)^3-1$
, we have
$f=(f_1+1)^3-1$
, we have
![]() $s(h',f) =\frac {h^{\prime 5}+h^{\prime 4} - 6h^{\prime 3}+6}{12f}$
.
$s(h',f) =\frac {h^{\prime 5}+h^{\prime 4} - 6h^{\prime 3}+6}{12f}$
.
To deal with the case
![]() $d_0>1$
, we notice that by (4.9), we have the following proposition.
$d_0>1$
, we notice that by (4.9), we have the following proposition.
Proposition 6.3 Let
![]() $d_0\geq 1$
be a given square-free integer. Take
$d_0\geq 1$
be a given square-free integer. Take
![]() $f>3$
odd of the form
$f>3$
odd of the form
![]() $f =a^2+ab+b^2$
, where
$f =a^2+ab+b^2$
, where
![]() $\gcd (a,b)=1$
and
$\gcd (a,b)=1$
and
![]() $\gcd (d_0,f)=1$
. Set
$\gcd (d_0,f)=1$
. Set
![]() $H=\{1,a/b,b/a\}$
, a subgroup of order
$H=\{1,a/b,b/a\}$
, a subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Let
$({\mathbb Z}/f{\mathbb Z})^*$
. Let
![]() $N_{d_0}(f,H)$
be the rational number defined in (
4.5
). Then
$N_{d_0}(f,H)$
be the rational number defined in (
4.5
). Then
 $$ \begin{align*}N_{d_0}(f,H) =N_{d_0}(f,\{1\}) +\frac{24\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(a,b,\delta f),\end{align*} $$
$$ \begin{align*}N_{d_0}(f,H) =N_{d_0}(f,\{1\}) +\frac{24\mu(d_0)}{\prod_{q\mid d_0}(q+1)} \sum_{\delta\mid d_0}\frac{\delta\mu(\delta)}{\phi(\delta)}S(a,b,\delta f),\end{align*} $$
where
![]() $N_{d_0}(f,\{1\})$
is a rational number which depends only on f modulo
$N_{d_0}(f,\{1\})$
is a rational number which depends only on f modulo
![]() $d_0$
, by Proposition 4.6, and where
$d_0$
, by Proposition 4.6, and where
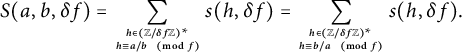 $$ \begin{align*}S(a,b,\delta f) =\sum_{h\in ({\mathbb Z}/\delta f{\mathbb Z})^*\atop h\equiv a/b\ \ \pmod f} s(h,\delta f) =\sum_{h\in ({\mathbb Z}/\delta f{\mathbb Z})^*\atop h\equiv b/a\ \ \pmod f} s(h,\delta f).\end{align*} $$
$$ \begin{align*}S(a,b,\delta f) =\sum_{h\in ({\mathbb Z}/\delta f{\mathbb Z})^*\atop h\equiv a/b\ \ \pmod f} s(h,\delta f) =\sum_{h\in ({\mathbb Z}/\delta f{\mathbb Z})^*\atop h\equiv b/a\ \ \pmod f} s(h,\delta f).\end{align*} $$
It seems that there are no explicit formulas for
![]() $S(a,b,\delta f)$
,
$S(a,b,\delta f)$
,
![]() $S(H_\delta ,\delta f)$
, or
$S(H_\delta ,\delta f)$
, or
![]() $N_\delta (f,H)$
for
$N_\delta (f,H)$
for
![]() $\delta>1$
(however, assuming that
$\delta>1$
(however, assuming that
![]() $b=1$
, we will obtain such formulas in Section 6.2 for
$b=1$
, we will obtain such formulas in Section 6.2 for
![]() $\delta \in \{2,3,6\}$
). Instead, our aim is to prove in Proposition 6.4 that
$\delta \in \{2,3,6\}$
). Instead, our aim is to prove in Proposition 6.4 that
![]() $N_\delta (f,H) =O(\sqrt f)$
for
$N_\delta (f,H) =O(\sqrt f)$
for
![]() $\delta \in \{2,3,6\}$
.
$\delta \in \{2,3,6\}$
.
Let
![]() $f>3$
be of the form
$f>3$
be of the form
![]() $f=a^2+ab+b^2$
, with
$f=a^2+ab+b^2$
, with
![]() $a,b\in {\mathbb Z}$
and
$a,b\in {\mathbb Z}$
and
![]() $\gcd (a,b)=1$
. Hence, a or b is odd. Since
$\gcd (a,b)=1$
. Hence, a or b is odd. Since
![]() $a^2+ab+b^2 =a^{\prime 2} + a'b' + b^{\prime 2} = a^{\prime \prime 2} + a" b" + b^{\prime \prime 2}$
and
$a^2+ab+b^2 =a^{\prime 2} + a'b' + b^{\prime 2} = a^{\prime \prime 2} + a" b" + b^{\prime \prime 2}$
and
![]() $a'/b' =a/b$
and
$a'/b' =a/b$
and
![]() $a"/b" =a/b$
in
$a"/b" =a/b$
in
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, where
$({\mathbb Z}/f{\mathbb Z})^*$
, where
![]() $(a',b') =(-b,a+b)$
and
$(a',b') =(-b,a+b)$
and
![]() $(a",b") =(-a-b,a)$
, we may assume that both a and b are odd. Moreover, assume that
$(a",b") =(-a-b,a)$
, we may assume that both a and b are odd. Moreover, assume that
![]() $\gcd (3,f)=1$
. If
$\gcd (3,f)=1$
. If
![]() $3\nmid ab$
, by swapping a and b as needed, which does not change neither H nor
$3\nmid ab$
, by swapping a and b as needed, which does not change neither H nor
![]() $S(a,b,H)$
, we may assume that
$S(a,b,H)$
, we may assume that
![]() $a\equiv -1\ \ \pmod 6$
and
$a\equiv -1\ \ \pmod 6$
and
![]() $b\equiv 1\ \ \pmod 6$
. If
$b\equiv 1\ \ \pmod 6$
. If
![]() $3\mid ab$
, by swapping a and b and then changing both a and b to their opposites as needed, which does not change neither H nor
$3\mid ab$
, by swapping a and b and then changing both a and b to their opposites as needed, which does not change neither H nor
![]() $S(a,b,H)$
, we may assume that
$S(a,b,H)$
, we may assume that
![]() $a\equiv 3\ \ \pmod 6$
and
$a\equiv 3\ \ \pmod 6$
and
![]() $b\equiv 1\ \ \pmod 6$
. So in Proposition 6.3, we may restrict ourselves to the integers of the form
$b\equiv 1\ \ \pmod 6$
. So in Proposition 6.3, we may restrict ourselves to the integers of the form
 $$ \begin{align} f> &3 \mbox{ is odd of the form } f=a^2+ab+b^2, \mbox{ with } a,b\in {\mathbb Z} \mbox{ odd } \mbox{ and } \gcd(a,b)=1\notag\\ &\mbox{and if } \gcd(3,f)=1 \mbox{ then } a\equiv -1\mbox{ or }3\ \ \pmod 6 \mbox{ and } b\equiv 1\ \ \pmod 6. \end{align} $$
$$ \begin{align} f> &3 \mbox{ is odd of the form } f=a^2+ab+b^2, \mbox{ with } a,b\in {\mathbb Z} \mbox{ odd } \mbox{ and } \gcd(a,b)=1\notag\\ &\mbox{and if } \gcd(3,f)=1 \mbox{ then } a\equiv -1\mbox{ or }3\ \ \pmod 6 \mbox{ and } b\equiv 1\ \ \pmod 6. \end{align} $$
Proposition 6.4 Let
![]() $\delta \in \{2,3,6\}$
be given. Let f be as in (
6.2
), with
$\delta \in \{2,3,6\}$
be given. Let f be as in (
6.2
), with
![]() $\gcd (f,\delta )=1$
. Then,
$\gcd (f,\delta )=1$
. Then,
![]() $s(h,\delta f) =O(\sqrt f)$
for any
$s(h,\delta f) =O(\sqrt f)$
for any
![]() $h\in ({\mathbb Z}/\delta f{\mathbb Z})^*$
such that
$h\in ({\mathbb Z}/\delta f{\mathbb Z})^*$
such that
![]() $h\equiv a/b\ \ \pmod f$
. Consequently, for a given
$h\equiv a/b\ \ \pmod f$
. Consequently, for a given
![]() $d_0\in \{1,2,3,6\}$
, in Proposition 6.3, we have
$d_0\in \{1,2,3,6\}$
, in Proposition 6.3, we have
![]() $N_{d_0}(f,H) =O(\sqrt f)$
, and we cannot expect great improvements on these bounds, by (
6.11
), (
6.13
), and (
6.15
).
$N_{d_0}(f,H) =O(\sqrt f)$
, and we cannot expect great improvements on these bounds, by (
6.11
), (
6.13
), and (
6.15
).
Proof First, by (6.1), we have
Second, f being odd, recalling (4.13), we have
![]() $A(2,f) =A(2,1) =0$
,
$A(2,f) =A(2,1) =0$
,
![]() $N_2(f,\{1\}) =-1$
,
$N_2(f,\{1\}) =-1$
,
and
Third, assume that
![]() $d_0\in \{3,6\}$
. Then
$d_0\in \{3,6\}$
. Then
![]() $\gcd (f,3)=1$
. Hence,
$\gcd (f,3)=1$
. Hence,
![]() $f\equiv 1\ \ \pmod 6$
. Therefore,
$f\equiv 1\ \ \pmod 6$
. Therefore,
![]() $A(3,f) =A(3,1) =4/3$
,
$A(3,f) =A(3,1) =4/3$
,
![]() $A(6,f) =A(6,1) =-4$
,
$A(6,f) =A(6,1) =-4$
,
![]() $N_3(f,\{1\}) =N_6(f,\{1\}) =-1$
,
$N_3(f,\{1\}) =N_6(f,\{1\}) =-1$
,
and
If
![]() $a\equiv -1\ \ \pmod 6$
,
$a\equiv -1\ \ \pmod 6$
,
![]() $b\equiv 1\ \ \pmod 6,$
and
$b\equiv 1\ \ \pmod 6,$
and
![]() $\delta \in \{1,2\}$
, then
$\delta \in \{1,2\}$
, then
![]() $\{h\in ({\mathbb Z}/3\delta f{\mathbb Z})^*;\ h\equiv a/b\ \ \pmod f\} =\{a/b,(a+2f)/b\}$
and
$\{h\in ({\mathbb Z}/3\delta f{\mathbb Z})^*;\ h\equiv a/b\ \ \pmod f\} =\{a/b,(a+2f)/b\}$
and
If
![]() $a\equiv 3\ \ \pmod 6$
,
$a\equiv 3\ \ \pmod 6$
,
![]() $b\equiv 1\ \ \pmod 6,$
and
$b\equiv 1\ \ \pmod 6,$
and
![]() $\delta \in \{1,2\}$
, then
$\delta \in \{1,2\}$
, then
![]() $\{h\in ({\mathbb Z}/3\delta f{\mathbb Z})^*;\ h\equiv a/b\ \ \pmod f\} =\{(a-\delta f)/b,(a+\delta f)/b\}$
and
$\{h\in ({\mathbb Z}/3\delta f{\mathbb Z})^*;\ h\equiv a/b\ \ \pmod f\} =\{(a-\delta f)/b,(a+\delta f)/b\}$
and
Let us now bound the Dedekind–Rademacher sums in (6.3)–(6.5). We will need the bounds,
Indeed,
![]() $4f-(\vert a\vert +\vert b\vert )^2 \geq 3(\vert a\vert -\vert b\vert )^2\geq 0$
and
$4f-(\vert a\vert +\vert b\vert )^2 \geq 3(\vert a\vert -\vert b\vert )^2\geq 0$
and
![]() $f\leq a^2+a^2b^2+b^2 =3a^2b^2$
.
$f\leq a^2+a^2b^2+b^2 =3a^2b^2$
.
First, we deal with the Dedekind–Rademacher sums
![]() $s(a,b,\delta f)$
in (6.3) and (6.4), where
$s(a,b,\delta f)$
in (6.3) and (6.4), where
![]() $\delta \in \{2,3,6\}$
. Here,
$\delta \in \{2,3,6\}$
. Here,
![]() $\gcd (a,b) =\gcd (a,\delta f)=\gcd (b,\delta f) =1$
. Then (3.7) and (6.6) enable us to write (3.6) as follows:
$\gcd (a,b) =\gcd (a,\delta f)=\gcd (b,\delta f) =1$
. Then (3.7) and (6.6) enable us to write (3.6) as follows:
Hence, in (6.3) and (6.4), we have
![]() $s(a,b,2f),\ s(a,b,3f),\ s(a,b,6f)=O(\sqrt f)$
.
$s(a,b,2f),\ s(a,b,3f),\ s(a,b,6f)=O(\sqrt f)$
.
Second, the remaining and more complicated Dedekind–Rademacher sums in (6.4) and (6.5) are of the form
![]() $s(a+\varepsilon \delta f,b,3\delta f)$
, where
$s(a+\varepsilon \delta f,b,3\delta f)$
, where
![]() $\varepsilon \in \{\pm 1\}$
,
$\varepsilon \in \{\pm 1\}$
,
![]() $\delta \in \{1,2\}$
and
$\delta \in \{1,2\}$
and
![]() $\gcd (a+\varepsilon \delta f,3\delta f) =\gcd (b,3\delta f)=1$
. Set
$\gcd (a+\varepsilon \delta f,3\delta f) =\gcd (b,3\delta f)=1$
. Set
![]() $\delta ' =\gcd (a+\varepsilon \delta f,b)$
. Then
$\delta ' =\gcd (a+\varepsilon \delta f,b)$
. Then
![]() $\gcd (\delta ',3\delta f)=1$
. Thus,
$\gcd (\delta ',3\delta f)=1$
. Thus,
![]() $s(a+\varepsilon \delta f,b,3\delta f)$
$s(a+\varepsilon \delta f,b,3\delta f)$
![]() $=s((a+\varepsilon \delta f)/\delta ',b/\delta ',3\delta f)$
, where now the three terms in this latter Dedekind–Rademacher are pairwise coprime. Then (3.7) and (6.6) enable us to write (3.6) as follows:
$=s((a+\varepsilon \delta f)/\delta ',b/\delta ',3\delta f)$
, where now the three terms in this latter Dedekind–Rademacher are pairwise coprime. Then (3.7) and (6.6) enable us to write (3.6) as follows:
 $$ \begin{align*} s((a+\varepsilon\delta f)/\delta',b/\delta',3\delta f) +O(\sqrt f) &+s(b/\delta',3\delta f,(a+\varepsilon\delta f)/\delta')\\ &\qquad\qquad =O(\delta^{\prime 2}/b) =O(b) =O(\sqrt f). \end{align*} $$
$$ \begin{align*} s((a+\varepsilon\delta f)/\delta',b/\delta',3\delta f) +O(\sqrt f) &+s(b/\delta',3\delta f,(a+\varepsilon\delta f)/\delta')\\ &\qquad\qquad =O(\delta^{\prime 2}/b) =O(b) =O(\sqrt f). \end{align*} $$
Now,
![]() $3\delta f\equiv -3\varepsilon a\ \ \pmod {a+\varepsilon \delta f}$
gives
$3\delta f\equiv -3\varepsilon a\ \ \pmod {a+\varepsilon \delta f}$
gives
![]() $s(b/\delta ',3\delta f,(a+\varepsilon \delta f)/\delta ') =-\varepsilon s(b/\delta ',3a,(a+\varepsilon \delta f)/\delta ')$
. Since the three rational integers in this latter Dedekind–Rademacher are pairwise coprime, the bounds (6.6) and (3.7) enable us to write (3.6) as follows:
$s(b/\delta ',3\delta f,(a+\varepsilon \delta f)/\delta ') =-\varepsilon s(b/\delta ',3a,(a+\varepsilon \delta f)/\delta ')$
. Since the three rational integers in this latter Dedekind–Rademacher are pairwise coprime, the bounds (6.6) and (3.7) enable us to write (3.6) as follows:
It follows that
![]() $s(a+\varepsilon \delta f,b,3\delta f) =s((a+\varepsilon \delta f)/\delta ',b/\delta ',3\delta f) =O(\sqrt f)$
, i.e., in (6.4) and (6.5), we have
$s(a+\varepsilon \delta f,b,3\delta f) =s((a+\varepsilon \delta f)/\delta ',b/\delta ',3\delta f) =O(\sqrt f)$
, i.e., in (6.4) and (6.5), we have
 $s(a+2f,b,6f),\ s(a-2f,b,6f),\ s(a+2f,b,3f), s(a-f,b,3f), s(a+f,b,3f) =O(\sqrt f)$
.
$s(a+2f,b,6f),\ s(a-2f,b,6f),\ s(a+2f,b,3f), s(a-f,b,3f), s(a+f,b,3f) =O(\sqrt f)$
.
Conjecture 6.5 Let
![]() $\delta $
be a given square-free integer. Let
$\delta $
be a given square-free integer. Let
![]() $f>3$
run over the odd integers of the form
$f>3$
run over the odd integers of the form
![]() $f=a^2+ab+b^2$
with
$f=a^2+ab+b^2$
with
![]() $\gcd (a,b)=1$
and
$\gcd (a,b)=1$
and
![]() $\gcd (\delta ,f)=1$
. Then
$\gcd (\delta ,f)=1$
. Then
![]() $s(h,\delta f) =O(\sqrt f)$
for any
$s(h,\delta f) =O(\sqrt f)$
for any
![]() $h\in ({\mathbb Z}/\delta f{\mathbb Z})^*$
such that
$h\in ({\mathbb Z}/\delta f{\mathbb Z})^*$
such that
![]() $h\equiv a/b\ \ \pmod f$
. Consequently, for a given square-free integer
$h\equiv a/b\ \ \pmod f$
. Consequently, for a given square-free integer
![]() $d_0$
, in Proposition 6.3, we would have
$d_0$
, in Proposition 6.3, we would have
![]() $N_{d_0}(f,H) =O(\sqrt f)$
for
$N_{d_0}(f,H) =O(\sqrt f)$
for
![]() $\gcd (d_0,f)=1$
.
$\gcd (d_0,f)=1$
.
Putting everything together, we obtain:
Theorem 6.6 Let
![]() $p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
$p\equiv 1\ \ \pmod 6$
be a prime integer. Let K be the imaginary subfield of degree
![]() $(p-1)/3$
of the cyclotomic field
$(p-1)/3$
of the cyclotomic field
![]() ${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. We have
$({\mathbb Z}/p{\mathbb Z})^*$
. We have
 $$ \begin{align*} M(p,H) ={\pi^2\over 6}\left (1+\frac{N(p,H)}{p}\right ) ={\pi^2\over 6}\left (1-\frac{1}{p}\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p}{24}\right )^{(p-1)/12}, \end{align*} $$
$$ \begin{align*} M(p,H) ={\pi^2\over 6}\left (1+\frac{N(p,H)}{p}\right ) ={\pi^2\over 6}\left (1-\frac{1}{p}\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p}{24}\right )^{(p-1)/12}, \end{align*} $$
and the following effective asymptotics and upper bounds
 $$ \begin{align} M_2(p,H) ={\pi^2\over 8}\left (1+\frac{N_2(p,H)}{p}\right ) ={\pi^2\over 8}\left (1+O(p^{-1/2})\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p+o(p)}{32}\right )^{\frac{(p-1)}{12}}, \end{align} $$
$$ \begin{align} M_2(p,H) ={\pi^2\over 8}\left (1+\frac{N_2(p,H)}{p}\right ) ={\pi^2\over 8}\left (1+O(p^{-1/2})\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p+o(p)}{32}\right )^{\frac{(p-1)}{12}}, \end{align} $$
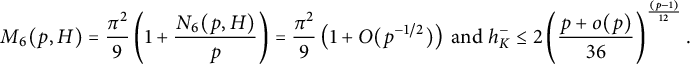 $$ \begin{align*} M_6(p,H) ={\pi^2\over 9}\left (1+\frac{N_6(p,H)}{p}\right ) ={\pi^2\over 9}\left (1+O(p^{-1/2})\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p+o(p)}{36}\right )^{\frac{(p-1)}{12}}. \end{align*} $$
$$ \begin{align*} M_6(p,H) ={\pi^2\over 9}\left (1+\frac{N_6(p,H)}{p}\right ) ={\pi^2\over 9}\left (1+O(p^{-1/2})\right ) \mbox{ and } h_K^- \leq 2\left (\frac{p+o(p)}{36}\right )^{\frac{(p-1)}{12}}. \end{align*} $$
6.2 The special case
 $p=a^2+a+1$
and
$p=a^2+a+1$
and
 $d_0=1,2,6$
$d_0=1,2,6$
Let
![]() $f>3$
be of the form
$f>3$
be of the form
![]() $f=a^2+a+1$
,
$f=a^2+a+1$
,
![]() $a\in {\mathbb Z}$
. Then
$a\in {\mathbb Z}$
. Then
![]() $\gcd (f,6)=1$
if and only if
$\gcd (f,6)=1$
if and only if
![]() $a\equiv 0,2,3,5\ \ \pmod 6$
. We define
$a\equiv 0,2,3,5\ \ \pmod 6$
. We define
![]() $c_a^{\prime }$
,
$c_a^{\prime }$
,
![]() $c_a^{\prime \prime }$
,
$c_a^{\prime \prime }$
,
![]() $c_a^{\prime \prime \prime }$
and
$c_a^{\prime \prime \prime }$
and
![]() $c_a =(-1-2c_a^{\prime } -c_a^{\prime \prime }+2c_a^{\prime \prime \prime })/12$
, as follows:
$c_a =(-1-2c_a^{\prime } -c_a^{\prime \prime }+2c_a^{\prime \prime \prime })/12$
, as follows:

Theorem 6.7 Let
![]() $p\equiv 1\ \ \pmod 6$
be a prime integer of the form
$p\equiv 1\ \ \pmod 6$
be a prime integer of the form
![]() $p=a^2+a+1$
with
$p=a^2+a+1$
with
![]() $a\in {\mathbb Z}$
. Let K be the imaginary subfield of degree
$a\in {\mathbb Z}$
. Let K be the imaginary subfield of degree
![]() $(p-1)/3$
of the cyclotomic field
$(p-1)/3$
of the cyclotomic field
![]() ${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
${\mathbb Q}(\zeta _p)$
. Let H be the subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
. We have
$({\mathbb Z}/p{\mathbb Z})^*$
. We have
 $$ \begin{align} M_2(p,H) ={\pi^2\over 8}\left (1-(-1)^{a}\frac{2a+1}{p}\right ) \end{align} $$
$$ \begin{align} M_2(p,H) ={\pi^2\over 8}\left (1-(-1)^{a}\frac{2a+1}{p}\right ) \end{align} $$
and
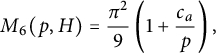 $$ \begin{align} M_6(p,H) ={\pi^2\over 9}\left (1+\frac{c_a}{p}\right ), \end{align} $$
$$ \begin{align} M_6(p,H) ={\pi^2\over 9}\left (1+\frac{c_a}{p}\right ), \end{align} $$
showing that the error term in ( 6.7 ) is optimal.
Proof The formula (6.8) is a special case of (5.2) for
![]() $d=3$
. By (4.7), we have
$d=3$
. By (4.7), we have
 $$ \begin{align*}M_6(p,H) ={\pi^2\over 9}\left (1+\frac{N_6(p,H)}{p}\right ).\end{align*} $$
$$ \begin{align*}M_6(p,H) ={\pi^2\over 9}\left (1+\frac{N_6(p,H)}{p}\right ).\end{align*} $$
Lemma 6.8 Let
![]() $f>3$
be of the form
$f>3$
be of the form
![]() $f=a^2+a+1$
,
$f=a^2+a+1$
,
![]() $a\in {\mathbb Z}$
. Set
$a\in {\mathbb Z}$
. Set
![]() $H=\{1,a,a^2\}$
, a subgroup of order
$H=\{1,a,a^2\}$
, a subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. We have
$({\mathbb Z}/f{\mathbb Z})^*$
. We have
and
Proof Apply Lemma 5.1 with
![]() $d=3$
and
$d=3$
and
![]() $f=a^2+a+1$
to get (6.10). Then, using (4.8), we get
$f=a^2+a+1$
to get (6.10). Then, using (4.8), we get
![]() $N_2(f,H) =-f-4S(H,f)+8S(H_2,2f) =\frac {2c_a^{\prime }+1}{3} =(-1)^{a-1}(2a+1)$
.
$N_2(f,H) =-f-4S(H,f)+8S(H_2,2f) =\frac {2c_a^{\prime }+1}{3} =(-1)^{a-1}(2a+1)$
.
Lemma 6.9 Let
![]() $f>3$
be of the form
$f>3$
be of the form
![]() $f=a^2+a+1$
,
$f=a^2+a+1$
,
![]() $a\in {\mathbb Z}$
. Assume that
$a\in {\mathbb Z}$
. Assume that
![]() $\gcd (f,6)=1$
, i.e., that
$\gcd (f,6)=1$
, i.e., that
![]() $a\equiv 0, 2, 3, 5\ \ \pmod 6$
. Set
$a\equiv 0, 2, 3, 5\ \ \pmod 6$
. Set
![]() $H=\{1,a,a^2\}$
, a subgroup of order
$H=\{1,a,a^2\}$
, a subgroup of order
![]() $3$
of the multiplicative group
$3$
of the multiplicative group
![]() $({\mathbb Z}/f{\mathbb Z})^*$
. Then
$({\mathbb Z}/f{\mathbb Z})^*$
. Then
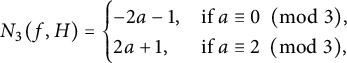 $$ \begin{align} N_3(f,H) =\begin{cases} -2a-1,&\mbox{if } a\equiv 0\ \ \pmod 3,\\ 2a+1,&\mbox{if } a\equiv 2 \ \ \pmod 3, \end{cases} \end{align} $$
$$ \begin{align} N_3(f,H) =\begin{cases} -2a-1,&\mbox{if } a\equiv 0\ \ \pmod 3,\\ 2a+1,&\mbox{if } a\equiv 2 \ \ \pmod 3, \end{cases} \end{align} $$
and
 $$ \begin{align} N_6(f,H) =\begin{cases} -2a-1,&\mbox{if } a\equiv 0\ \ \pmod 6,\\ -3,&\mbox{if } a\equiv 2,3\ \ \pmod 6,\\ 2a+1,&\mbox{if } a\equiv 5\ \ \pmod 6. \end{cases} \end{align} $$
$$ \begin{align} N_6(f,H) =\begin{cases} -2a-1,&\mbox{if } a\equiv 0\ \ \pmod 6,\\ -3,&\mbox{if } a\equiv 2,3\ \ \pmod 6,\\ 2a+1,&\mbox{if } a\equiv 5\ \ \pmod 6. \end{cases} \end{align} $$
Proof Let us, for example, detail the computation of
![]() $S(H_6,6f)$
in the case that
$S(H_6,6f)$
in the case that
![]() $a\equiv 0\ \ \pmod 6$
. We have
$a\equiv 0\ \ \pmod 6$
. We have
![]() $f\equiv 1\ \ \pmod 6$
and
$f\equiv 1\ \ \pmod 6$
and
![]() $H_6=\{1,1+4f,a+f,a+5f,a^2+f,a^2+5f\}$
. Since
$H_6=\{1,1+4f,a+f,a+5f,a^2+f,a^2+5f\}$
. Since
![]() $a^2+f =(a+f)^{-1}$
and
$a^2+f =(a+f)^{-1}$
and
![]() $a^2+5f=(a+5f)^{-1}$
in
$a^2+5f=(a+5f)^{-1}$
in
![]() $({\mathbb Z}/f{\mathbb Z})^*$
, we have
$({\mathbb Z}/f{\mathbb Z})^*$
, we have
![]() $S(H_6,6f) =s(1,6f)+s(1+4f,6f)+2s(a+f,6f)+2s(a+5f,6f)$
, by (3.2). Using (3.3) and (3.4), we obtain
$S(H_6,6f) =s(1,6f)+s(1+4f,6f)+2s(a+f,6f)+2s(a+5f,6f)$
, by (3.2). Using (3.3) and (3.4), we obtain
![]() $s(1,6f) =\frac {18f^2-9f+1}{36f}$
,
$s(1,6f) =\frac {18f^2-9f+1}{36f}$
,
![]() $s(1+4f,6f) =\frac {2f^2-13f+1}{36f}$
,
$s(1+4f,6f) =\frac {2f^2-13f+1}{36f}$
,
![]() $s(a+f,6f) =-\frac {(3a-21)f+1}{72f}$
, and
$s(a+f,6f) =-\frac {(3a-21)f+1}{72f}$
, and
![]() $s(a+5f,6f) =-\frac {(35a+19)f+1}{72f}$
. Formula (6.14) follows.
$s(a+5f,6f) =-\frac {(35a+19)f+1}{72f}$
. Formula (6.14) follows.
By (4.8), we have
and
Using (6.1), (6.10), and (6.12), we obtain
![]() $N_3(f,H) =\frac {c_a^{\prime \prime }+1}{4}$
and (6.13). Using (6.1), (6.10), (6.12), and (6.14), we obtain
$N_3(f,H) =\frac {c_a^{\prime \prime }+1}{4}$
and (6.13). Using (6.1), (6.10), (6.12), and (6.14), we obtain
![]() $N_6(f,H) =\frac {-1-2c_a^{\prime }-c_a^{\prime \prime }+2c_a^{\prime \prime \prime }}{12} =c_a$
and (6.15).
$N_6(f,H) =\frac {-1-2c_a^{\prime }-c_a^{\prime \prime }+2c_a^{\prime \prime \prime }}{12} =c_a$
and (6.15).
7 Conclusion and a conjecture
The proof of Lemma 5.1 gives for
![]() $d\geq 3$
odd and
$d\geq 3$
odd and
![]() $a\neq 0,\pm 1$
$a\neq 0,\pm 1$
 $$ \begin{align} s\left (a,\frac{a^d-1}{a-1}\right ) =\frac{(f-1)(f-a^2-1)}{12af} =O\left (f^{1-\frac{1}{d-1}}\right ). \end{align} $$
$$ \begin{align} s\left (a,\frac{a^d-1}{a-1}\right ) =\frac{(f-1)(f-a^2-1)}{12af} =O\left (f^{1-\frac{1}{d-1}}\right ). \end{align} $$
Our numerical computations suggest the following stronger version of Theorem 3.1:
Conjecture 7.1 There exists
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $d>2$
dividing
$d>2$
dividing
![]() $p-1$
and any h of order d in the multiplicative group
$p-1$
and any h of order d in the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
, we have
$({\mathbb Z}/p{\mathbb Z})^*$
, we have
Indeed, for
![]() $p\leq 2\cdot 10^5$
, we checked on a desk computer that any
$p\leq 2\cdot 10^5$
, we checked on a desk computer that any
![]() $d>2$
dividing
$d>2$
dividing
![]() $p-1$
and any h of order d in the multiplicative group
$p-1$
and any h of order d in the multiplicative group
![]() $({\mathbb Z}/p{\mathbb Z})^*$
, we have
$({\mathbb Z}/p{\mathbb Z})^*$
, we have
 $$ \begin{align*}Q(h,p) :=\frac{\vert s(h,p)\vert}{p^{1-\frac{1}{\phi(d)}}} \leq Q(2,2^7-1) =0.08903\ldots.\end{align*} $$
$$ \begin{align*}Q(h,p) :=\frac{\vert s(h,p)\vert}{p^{1-\frac{1}{\phi(d)}}} \leq Q(2,2^7-1) =0.08903\ldots.\end{align*} $$
The estimate (7.2) would allow to slightly extend the range of validity of Theorem 1.1 to
![]() $d \leq (1-\varepsilon )\frac {\log p}{\log \log p}$
. Moreover, the choice
$d \leq (1-\varepsilon )\frac {\log p}{\log \log p}$
. Moreover, the choice
![]() $a=2$
in (7.1) for which
$a=2$
in (7.1) for which
![]() $s(2,f)$
is asymptotic to
$s(2,f)$
is asymptotic to
![]() $\frac {1}{24}f$
with
$\frac {1}{24}f$
with
![]() $f=2^d-1$
shows that
$f=2^d-1$
shows that
![]() $s(h,p) =o(p)$
cannot hold true in the range
$s(h,p) =o(p)$
cannot hold true in the range
![]() $d \asymp \log p$
. Notice that we cannot expect a better bound than (7.2), by (7.1). Finally, the restriction that p be prime in (7.2) is paramount by Remark 6.2 where
$d \asymp \log p$
. Notice that we cannot expect a better bound than (7.2), by (7.1). Finally, the restriction that p be prime in (7.2) is paramount by Remark 6.2 where
![]() $s(a,f) \sim f^{2/3}/12$
for a of order
$s(a,f) \sim f^{2/3}/12$
for a of order
![]() $3$
in
$3$
in
![]() $({\mathbb Z}/(a^3-1){\mathbb Z})^*$
.
$({\mathbb Z}/(a^3-1){\mathbb Z})^*$
.