Introduction
Background
A relatively large number of the glaciers in the Svalbard archipelago are assumed to be of surge type. During the last century, nearly 100 of Svalbard’s glaciers have been observed to surge (Reference HagenHagen and others, 1993; Liestøl, 1993) and many more have features indicating past surge activity (Reference LefauconnierLefauconnier and Hagen, 1991; Reference Hamilton and DowdeswellHamilton and Dowdeswell, 1996).
General surge behaviour has been described by Reference MeierMeier and Post (1969) and Reference RaymondRaymond (1987), and surges in Svalbard have been described by Liestøl (1969), Reference SchyttSchytt (1969), Reference DowdeswellDowdeswell (1986), Reference HagenHagen (1987), Reference Dowdeswell, Hamilton and HagenDowdeswell and others (1991), Reference LefauconnierLefauconnier and Hagen (1991), and Reference HodgkinsHodgkins and Dowdeswell (1994). Surge behaviour is characterized by a rapid increase in the ice velocity, up to 101 or 102 times the speed during the quiescent period. The quiescent phase seems to be from 50 to 100 years for Svalbard glaciers and the duration of the surging phase (3-10years) tends to be longer than for glaciers in other areas (1-2 years) (Reference Dowdeswell, Hamilton and HagenDowdeswell and others, 1991). During the quiescent phase, glacier flow is too low to be in a steady state with the climate; ice is lost from the receiving area and built up in the reservoir area.
Most of the long-term mass-balance investigations in Svalbard have been carried out on small cirque glaciers at a relatively low altitude. These investigations show a negative net balance and mainly thinning in the period 1950-88 (Hagen and Liestøl, 1990). These small glaciers, such as Brøggerbreen and Lovénbreen, have only small reservoir areas, and during the most negative mass-balance years almost the entire glacier has been in the ablation area and does not accumulate sufficient mass to build up to a new-surge. Such a consistently negative mass balance has been linked to: (i) an increase in the length of the quiescent period, resulting in a reduction of the frequency and occurrence of glacier surges in Svalbard (Reference DowdeswellDowdeswell and others, 1995), or (ii) to a surge release at a lower profile and with less ice mass than previously, remains that large recent surges will be followed by surges of smaller scale (Reference LefauconnierLefauconnier and Hagen, 1991).
It is questionable whether the larger ice masses covering the higher altitudes in Svalbard show the same signs of low mass accumulation. Only sporadic measurements of mass balance have been made on the larger glaciers and ice caps with accumulation areas at higher altitudes. The exception is Kongsvegen (102 km2) where mass-balance measurements began in 1987 by the Norsk Polarinstitutt. The last time Kongsvegen surged was just before 1948 (Liestøl, 1988).
In this paper, measurements of surface mass balance, surface elevation, ice thickness and ice velocity of Kongsvegen are presented. The paper focuses on the observed changes of glacier geometry and dynamics. To test whether or not Kongsvegen is building up to a new surge, the balance flux is compared with the measured ice flux. The evolution of Kongsvegen is also compared to other surge-type glaciers in Svalbard where there are observations.
Description of Kongsvegen
Kongsvegen is situated in northwest Spitsbergen 78°51’N, 12030’E (Fig. 1). The ice flows in a northwesterly direction from an ice divide, Kongsvegpasset, at 800 m a.s.l., down to sea level in Kongsfjorden. Kongsvegen has a joint calving front with Kronebreen, which is a fast-flowing ice stream and among the most active tidewater glaciers in Svalbard (Liestøl, 1988; Reference Dowdeswell and DrewryDowdeswell, 1989). Kongsvegen’s confluence with Kronebreen is about 5 km from the calving front and a large medial moraine demarcates the boundary between them.
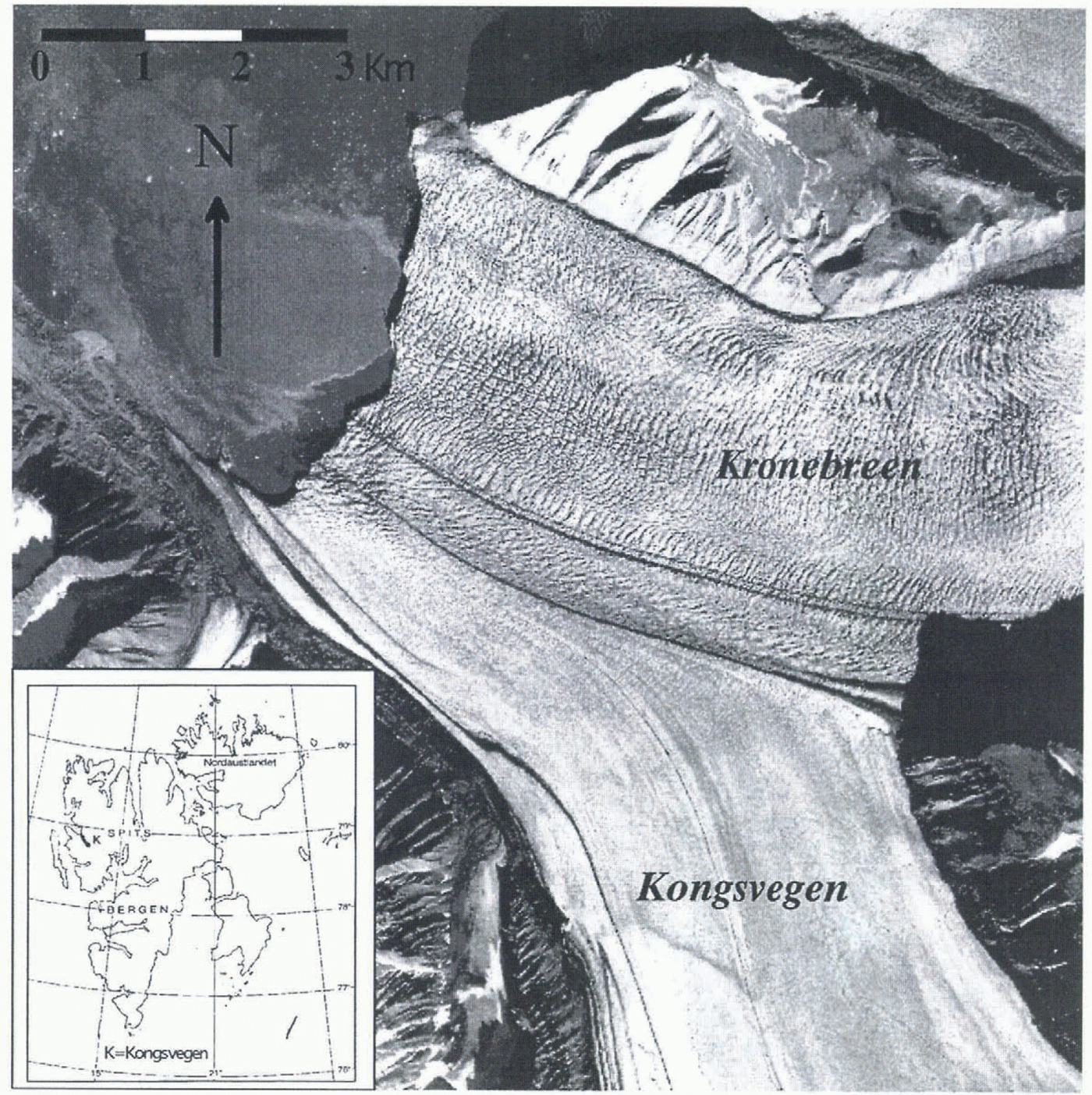
Fig. 1. Location of Kongsvegen in the inner part of Kongsfjorden, Spitsbergen. The terminus and the lower ablation area of Kongsvegen and Kronebreen in 1990 from a vertical aerial photograph (photo: ©Norst Polarinstitutt S90,6484). The width of Kongsvegen and Kronebreen (heavily crevassed) before the confluence is about 3km. Looped moraines can be seen along the western margin.
The Kongsvegen drainage basin is composed of two main tributaries named Kongsvegen and Sidevegen. Other small basins contribute to the two main streams, which can be seen by the moraine pattern on the glacier surface (Fig. 2). Based on maps from 1966, the Kongsvegen basin has an area of 102 km2 and a length of 25.8 km. In 1990, the surface slope was relatively low, from 0.50to 2.50, and the surface was relatively uniform with almost no crevasses. In the ablation area, meltwater drained in large supraglacial channels. The glacier front, ending partly on land, is almost stationary while it is partly active where it calves into Kongsfjorden.
Kongsvegen is classified as a sub-polar or polythermal glacier such as most of the glaciers in Svalbard (Reference SverdrupSverdrup, 1935; Reference SchyttSchytt, 1969; Liestøl, 1977, 1988). Kongsvegen has a 50-130m thick upper layer with sub-freezing temperatures and a temperate basal layer in the ablation area (BjÖrnsson and others, 1996). The accumulation area is temperate, while the glacier is frozen to the bed along the mountainsides in the ablation area (Liestøl, 1988; Reference BamberBamber, 1989; BjÖrnsson and others, 1996).
Kongsvegen is underlain by fine-grained sandstone mainly of Middle and Upper Carboniferous and Permian age (Reference HjelleHjelle, 1993).There also exist Devonian sand/siltstones. A Tertiary fold and thrust-belt system underlies the glacier for much of its length (Reference Dallmann, Bergh and MaherDallmann and others, 1993).
Previous work
The glacier-front positions of Kongsvegen and Kronebreen have been described by Reference VoigtVoigt (1965), Reference LefauconnierLefauconnier (1987) and Liestøl (l988). These sources indicate retreat of the glaciers interrupted by periods of glacier advances which have been related to surges. Kongsvegen surged just before 1948 and Kronebreen or a small tributary glacier most probably surged in 1869. No direct observations of those surges have been made. On air records from 1956 (NP S56 pairs 1090-99) it is, however, still possible to see crevasses formed during the 1948 surge of Kongsvegen. During this surge, the front advanced about 1.5-2 km from its mapped position in 1938 (Liestøl, 1988; Lefauconnier and others, 1994a). A new looped moraine was formed on the surface and the medial moraine between Kongsvegen and Kronebreen was pushed about 2 km to the north at the glacier front (Voigt, 1966). During the last 45years (1948-93), the glacier front has retreated more than 4km (Lefauconnier and others, 1994a) at a rate of up to about 250 ma −1 on the south shore. The glacier front is now about 10 km behind its maximum position of 1869. Figure 2 shows the total retreat between 1964 and 1990 and how the medial moraines have been pushed southwards. A lateral displacement of the medial moraine of 15-50 cm d −1 was measured along the medial moraine from Garwoodtoppen towards the front (Fig. 2) from 1962 to 1964 (Voigt, 1966).
During the last six decades, several expeditions have visited the glacier and carried out measurements of surface velocity in the frontal areas (Pillewizer, 1939, 1965; Voigt, 1965; Vivet and Lliboutry, 1978; Lefauconnier, 1987; Melvold, 1992; Lefauconnier and others, 1994a). The surface velocity at the calving front has been relatively high, 2-4 m d −1 during all the measurement periods. The surface velocities upstream of the junction between Kongsvegen and Kronebreen were measured in 1963-65 (Voigt, 1967) and 1990 (Melvold, 1992) and show that the surface velocity on Kronebreen (1-3 m d−1) is about 100 times higher than on Kongsvegen (0.7- 4.0 cm d −l). The difference in velocity has been related to the fact that Kongsvegen is partly frozen to its bed and that there is only a small amount of basal motion, while Kronebreen with its four times larger accumulation area possibly could maintain a higher ice flux and a high basal motion (Liestøl, 1988). Therefore, Kongsvegen at the present has a smooth surface while Kronebreen is heavily crevassed in its lower regions (Fig. 1).
Data Sources and Observations
Reference centre line
Measurement locations are referred to stake positions and distances along the centre-line curvilinear coordinate system with its origin ai the head (at stake S9) of the glacier (Fig. 2). The system was defined to follow closely the centre-line marker established in May 1992. Stake positions are referred to as “SI”, while between the stakes we used the "xx km site”.
Mass balance
Mass-balance investigations on Kongsvegen began in 1987 by the Norsk Polarinstitutt and have been carried out every year since then. During the observation period (1987-94), the mean summer balance has been -0.69 ± 0.28 m w.e. and the mean winter balance has been 0.78 ± 0.14 m w.e., which gives a weak positive mean net balance of 0.09 m w.e. (Fig. 3). The summer ablation shows strong annual variations. It includes an annual average of 5.1 x 10 6 m3 of mass loss due to calving (Hagen, 1996), corresponding to a mean value of 0.05 m w.e. over the whole glacier. The mean equilibrium-line altitude (ELA) is about 490 m a.s.l. with a maximum of 580ma.s.l for the most positive balance year and a minimum of 380 m a.s.l. for the most negative balance year. Figure 4 shows the specific net balance against altitude for the balance year 1992-93 (mostly negative), for the balance year 1986-87 (mostly positive) and the mean for the 9 year observation period (1987-94]. A mass-balance gradient of about 0.33 m 100 m−1 was found. As large areas of the glacier are close to the ELA, small changes in ELA elevation give large changes in mass balance. The mean accumulation-area ratio is about 61 % during the observation period.
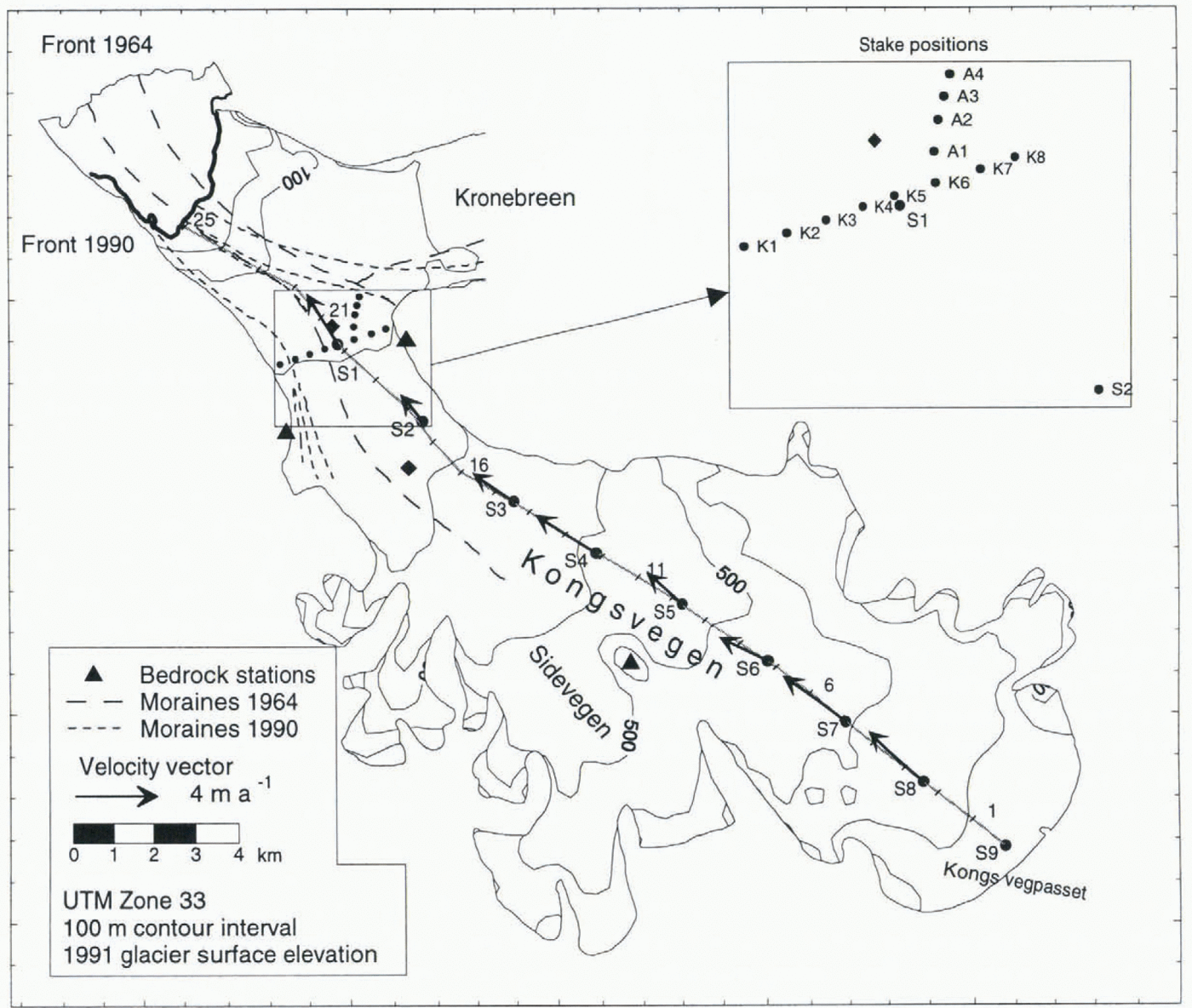
Fig. 2. Kongsvegen, showing stake positions and kilometre ticks giving distance along the centre-line coordinate system from head (taken at stake S9). Measured horizontal surface velocity is shown by velocity vectors. Positions of Voigt (1967) velocity measurements are marked by squares. The total displacement of medial moraines between Kongsvegen and Kronebreen during the 1964-90 period and the change in the calving-front position are shown. The glacier-surface elevations are interpolated from GPS data from 1991 (Eiken and others, 1997).

Fig. 3. Annual variation of the winter bw,summer bs,and net balance bn between 1987 and 1994. The observed net balance for the period 1987-94 and the estimated net balance for the period 1967-94 are shown. The mean of the series is 0.09 and 0.04 m w.e., respectively.

Fig. 4. Specific net balance against altitude for the most positive (1986-87) and most negative (1992-93) years, and the mean for the observation period 1987-94. Area against altitude distribution of Kongsvegen is also shown.
The measured positive mean net balance value of 0.09 m w.e. is somewhat higher than the negative value of -0.11 m w.e. which was estimated for the period 1964-88 by Lefauconnier and others (1994b), but is similar to their estimated values for the period 1986-88. Based on mass-balance data from Austre Brøggerbreen (1987-94) obtained from Hagen and Liestøl (1990) and Hagen (1996), we used a regression model to reconstruct the mass balance of Kongsvegen for the period 1967-94. Austre Brøggcrbreen is a small valley glacier about 15 km west of Kongsvegcn. There is a high positive correlation between the last 9 years (1987-94) net balance on Austre Brøggerbreen and Kongsvegen. The correlation coefficient is 0.924 and is statistically significant at a 0.01 % level. From the reconstructed mass-balance data (Fig. 3), the calculated mean net balance is 0.04 m w.e. On the basis of these data, we conclude that the long-term (1967-94) annual mass balance over the glacier is close to zero, supporting the conclusion of Hagen (1996) that glaciers in Svalbard covering relatively high-altitude accumulation areas are closer to balance than the lower valley glaciers closer to the coast.
Flow velocities
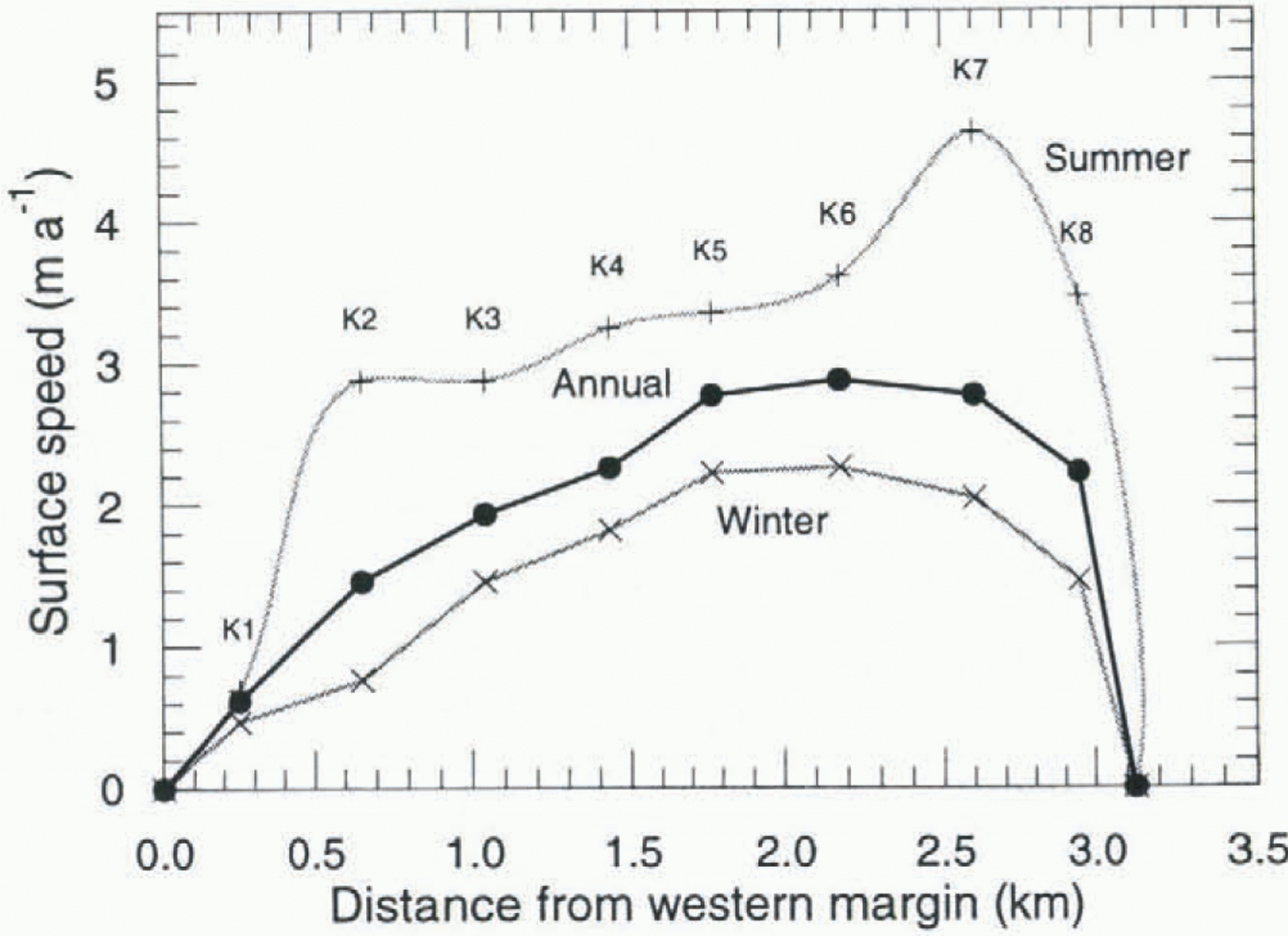
The observations of glacier motion on Kongsvegcn were made using stakes at the glacier surface. Along the longitudinal centre line, nine mass-balance stakes (S1-S9), approximately 2.5 km apart, were used. Eight stakes (K1 -K8) were placed about 350 m apart along a transverse section close to stake SI (Fig. 2). The stakes were surveyed by theodolite (Wild T2) triangulation and an electronic distance meter (Wild DI 3000) from fixed points on solid rock (Fig. 2). The S stakes along the centre line were measured in May 1991 and in May 1992, which gives only the annual speed. Stakes K1-K8 were surveyed in August 1989 and in May and August 1990, and thus provided winter and summer velocities. Four stakes (A1-A4) were also placed in a line from stake K6 towards Kronebreen (Fig. 2) and surveyed twice in May 1990.
The longitudinal variation of the annual centre-line velocity from the glacier head (stake S9) down to stake S1 (4.4km from the calving front) is shown in Figure 5 and Table 1. The annual velocities were low, from 1.41(S2) to 3.59 m a −1 (S7), and there is no clear longitudinal pattern in the velocities. The somewhat lower velocity measured at stake S2 is most probably due to a more marginal position of this stake towards the eastern valley side (Fig. 2), where the ice thickness is smaller and the drag from the valley side is higher than along the centre line.

Fig. 5. Measured annual speed along Kongsvegen during 1991-92 shown as black dots. Calculated speed by the longitudinal coupling theory for averaging lengths l = 0.9km, l-1.8km and 1=2.0km (see text). Centre-line basal shear stress calculated by longitudinal coupling theory for 1966 and 1991. Geometrical parameters are described in the text.
Table 1. Measured flow velocity in different periods for Kongsvegen. All velocity values are given in m aM-1

The variation in the velocity across the glacier close to stake SI in the lower ablation area is shown in Figure 6 and Table 1. The transverse-flow pattern, with small changes in velocity across the glacier in the central part, suggests a flat bottom form. This is probably due to small drag from the valley sides, since the glacier thickness is small compared to the width. The main error in the measured velocities is caused by rotation of the reflectors placed on the stakes, the offset from the centre of the stakes and the distance to the stakes from the bedrock stations (Melvold, 1992). The error in the velocity also depends on the measurement interval (cf. Brecher, 1969). For a time interval of 1 year, three standard errors do not exceed 0.18 m a −1 (10% of the mean) for the S stakes and 0.11 m a −1 (7.8% of the mean) for the K stakes. For shorter time intervals, the error increases to a maximum of 22% of the flow velocities.
Figure 6 shows that Kongsvegen, at least in the lower ablation area, undergoes seasonal velocity variations like some other glaciers in Svalbard (Nuttall and others, 1997), and in other areas such as Greenland (Paterson, 1961; Andreasen, 1985), Arctic Canada (Iken, 1974,1978; Hooke and others, 1983) and in Alaska (Raymond and Harrison, 1988). The summer velocity approaches double the winter velocities. As the thickness and slope change is insignificant during the melt season, the increased speed during summer must be due to enhanced basal motion. Measurements of stakes A1-A4 in May 1990 showed that the surface velocity increased even before the melt season started. This cannot be explained by increased loading of the glacier as the winter balance is less than 1 m w.e. This implies that at least some of the winter motion between 1989 and 1990 is due to basal motion. If we follow Hodge’s (1974) conclusion, this may be due to a steady increase of stored water at the glacier bed throughout the winter.
Voigt (1967) measured velocities of 7.30 ± 1.0 and 14.60 ± 1.0 m a −1, respectively close to stake SI in early and late September 1964 (Fig. 2) and about 3.65 m a−1 for a point about 500 m northwest of stake S2 during the winter 1964-65.These values are much higher than those observed in the same part of the glacier in 1991-92 (1.5-2.7 m a−1), showing a long-term deceleration in speed in the lower part of the glacier.
Surface elevation
A longitudinal profile of elevation along the centre line has been obtained from topographical maps and kinematic GPS profiles. There is an East German map of the ablation area from 1967 with 10 m contour intervals (Pillewizer, 1967). The map is based on 1964 terrestrial photography and is at a scale of 1:50 000. The only map that covers the whole glacier is the Norsk Polarinstitutt topographical map at 1:100000 (Tre Kroner, No. B7), which has a 50 m contour interval. This map is based on August 1966 air photography. As there were only small changes in elevation between the 1964 and 1966 maps compared to the uncertainty of the map elevation (±1.0 m (1964) and ±3.9 m (1966)), a composite of them was made. A digital elevation model (DEM) was then interpolated by using the methods developed by Hutchinson (1989).The elevation profile from this composite map, hereafter called the “1966 profile”, is shown in figure 7a. The measurements in the accumulation area cannot be considered to be as accurate as measurements in the ablation area due to the lower resolution of the data sources and difficulties of map-making in the featureless snow covered areas.
The elevation of the surface between the head and stake S1 was also obtained from kinematic GPS profiles for the summers of 1991 and 1995 (Eiken and others, 1997). The elevation profile from 1991 is shown in figure 7a, after transformation from WGS-84 ellipsoidal heights to ED-50 ellipsoidal heights. The 1995 profile is not shown as it was close to the 1991 profile. The accuracy of the GPS profile is less than ±0.05 m in horizontal position and ±0.10 m altitude. The surface elevation between S1 and the front was taken from a topographic map which has 25 m contour intervals and is based on the August 1990 air-photography map (Melvold, 1992). A rate-of-elevation change was obtained by comparison of the 1966 and 1990 elevations, and this was used to make a small extrapolation from 1990 to 1991. The profiles are shown in Figure 7.
The change in thickness along the centre line during the 1966-91 period was found by subtracting the profiles. This long time-scale picture of changes is shown in figure 8a together with the change found by Eiken and others (1997) between 1991 and 1995, using the 1966 profile as a datum. The mean annual changes in m w.e. for these two periods are shown in figure 8b using measured snow-density values from Lefauconnier and others (1994 b). The general trends of the two series are the same and show that a decrease in altitude in the lower part of the glacier and an increase in elevation has occurred in the upper pan of the glacier, such as expected for a surge-type glacier during it quiescent phase (e.g. Reference MeierMeier and Post, 1969; Raymond, 1987).

Fig. 7. (a) Longitudinal profile of the centre-line surface elevations in 1966 and 1991, and bed elevation. Bed elevation below 20km is extrapolated from gravimetrical data from Oelsner (1967) and bathymetry data from Lefauconnier (1987). (b) Longitudinal variations in width, shape factor, ice thickness and surface slope. Surface slope is derived from GPS measurements in 1991.
The boundary between net thickening (reservoir area) and net thinning (receiving area), defined by zero change in elevation, is situated at about 7.1 km (stake S6) from the head of the glacier between 1966 and 1991. Zero change in elevation between 1991 and 1995 occurred at 8.1 km, indicating a down-glacier migration of the boundary. In the area below stake S6 (7.1km) and the glacier front, a monotonie increase in thinning occurred. The rate of thinning was the same during both periods. In the reservoir area, the picture is not as simple as in the ablation area. From the head, there was a step-wise increase in thickness down to 2.6 km for the period 1966-91 and 4.1 km for the period 1991 -95. The thickening rate was lower during 1991-95 than during the 1966-91 period. In the area between 4.3 km and stake S6 (7.1 km), a steadily thickening occurred during both periods. The lower thickening rate in the area close to stake S9 (head)is probably caused by wind transport of snow from the ice divide. This is in agreement with the mass-balance measurements which also show some years with less accumulation close to stake S9 compared to the area 2-4 km downstream. During both periods, 1966-91 and 1991-95, the thickening rate in the upper part of the glacier is only about half of the thinning rate in the lower part (figs 7 and 8a).

Fig. 8. (a) Changes in elevation near the centre line of Kongsvegen using the 1966 profile as datum. The long time changes from 1966 to 1991 are shown together with the changes from 1991 to 1995 obtained from Eiken and others (1997). (b) The calculated annual change in elevation is derived from balance assessment and the observed rate of change from surface-elevation measurements for the two periods in m a−1 (water equivalents).
Ice thickness
Ice thickness measured by radio-echo soundings along longitudinal and transverse profiles have been used construct a map of ice thickness and bedrock topography. The radio-echo soundings used were obtained from Hagen and Sætrang (1991), BjÖrnsson and others (1996) and from measurements carried out by the present authors in spring 1995. The estimated uncertainty for the measured values of ice thickness is less than 10% and somewhat, higher for the unmeasured areas where the ice thickness was estimated by interpolation techniques using a combination of surface morphology and Hutchinson’s (1989) method. The measured ice thickness from the radio-echo soundings is in agreement with data from hot-water drilling and earlier radio-echo studies (Dowdeswell and others,1984). The bedrock elevation and ice thickness along the centre line are shown in figure 7a and b, respectively. The maximum measured ice thickness was 443 m.
Width
The width of the glacier (2-5 km) as measured from maps and air photographs has changed little between 1966 and 1992 except for the part below the confluence with Kronebreen where the glacier flow toward the northwest is dammed and pushed towards the west (Fig. 2). The variation in width along the glacier is shown in figure 7b.The width and the radio echo-sounding data show that Kongsvegen flows in a broad valley with steep sides.
Present State of the Glacier
State of balance
To evaluate the state of the glacier, the balance flux was calculated based on mass-balance measurements and compared with volume flux derived from measured velocity and cross-section areas (e.g. Bindschadler, 1984; Clarke, 1987; Dowdeswell and Collin, (1990). The balance flux and volume flux were calculated above each stake (S1-S9).
Balance fluxAs the flow velocity on Kongsvegen is only known near the glacier centre for most of its length, the flux calculation was carried out along a thin (c. 250 in wide) “stream sheet" that follows a flowline near the centre. This approach was adapted from Meier and others (1974). The balance flux across a transverse section is the integral of the net balance over the area of the basin upstream from the section:

where Qb is the balance flux at a position x from the head of the glacier along the longitudinal transects, Ws is the transverse width of the transects of the “stream sheet" and b is the net balance averaged across the width. We approximate Qb as follows

where Aj is the area of the glacier surface between the two flowlines (stream sheet) and the cross-section j,j+1 and bj is the net balance in the area spanned by Aj. The stream sheet consists of an ice volume between two flowlines a small distance apart (about 240 m at equilibrium-line altitude). The longitudinal transect was divided into ten parts by nine transverse cross-sections located at the velocity markers (S1-S9). The cross-sections were laid out roughly parallel to contours on the glacier surface and thus approximately normal to the flow. The balance flux was calculated above each cross-section by using the mean net balance bj over the last nine budget years in the altitude interval spanned by Aj. The results are shown in Figure 9. Balance fluxes were also estimated by using the most negative (1992-93) and most positive (1986-87) mass balance during the last 9 years of measurements (1986-95).
Volume fluxThe volume flux Qv which is the actual flux transported by the glacier, was obtained by:
where S is the cross-section area, ![]() is the velocity averaged over the cross-section, where us and ub are the average surface and basal velocity over the cross-section, and F is a shape factor (Nye, 1965; Paterson, 1994). Since only small changes in lateral velocity occurred over the central part (Fig. 6), the measured annual speed was assumed to be equal to the average surface velocity over the transect. As shown for the K stakes, some seasonal variation exists in the glacier velocity (Fig. 6). The summer increase in speed and part of the winter motion is probably due to enhanced basal motion. A minimum value of the contribution of basal motion is obtained by using the difference in velocity between summer and winter. Close to stake S1, the contribution from basal motion was about one-third of the annual movement (Melvold, 1992). For stakes S1-S9, no data on seasonal speed exist. To apply Equation (3)], we used the annual velocity measured at stakes S1-S9 over the year 1991-92 (Fig. 5). It is assumed that the measured velocity equals the basal motion (us = ub). In this case, the shape factor is equal to unity. The calculated volume flux gives a maximum value and is slightly overestimated by up to 15% as plug flow is assumed (Fig. 9).
is the velocity averaged over the cross-section, where us and ub are the average surface and basal velocity over the cross-section, and F is a shape factor (Nye, 1965; Paterson, 1994). Since only small changes in lateral velocity occurred over the central part (Fig. 6), the measured annual speed was assumed to be equal to the average surface velocity over the transect. As shown for the K stakes, some seasonal variation exists in the glacier velocity (Fig. 6). The summer increase in speed and part of the winter motion is probably due to enhanced basal motion. A minimum value of the contribution of basal motion is obtained by using the difference in velocity between summer and winter. Close to stake S1, the contribution from basal motion was about one-third of the annual movement (Melvold, 1992). For stakes S1-S9, no data on seasonal speed exist. To apply Equation (3)], we used the annual velocity measured at stakes S1-S9 over the year 1991-92 (Fig. 5). It is assumed that the measured velocity equals the basal motion (us = ub). In this case, the shape factor is equal to unity. The calculated volume flux gives a maximum value and is slightly overestimated by up to 15% as plug flow is assumed (Fig. 9).

Fig. 9. Ice flux along Kongsvegen from head to front. (a)Observed volume flux and estimated balance flux. (b) Volume and balance flux gradients.
Even though there are uncertainties in both the balance flux values and the volume flux, it is clear that the glacier in the period 1987-94 has transported a much smaller volume of ice than that required to maintain a stable ice-surface profile and to achieve steady state. The ratios of volume flux to balance flux were derived at the ELA and were between 0.03 and 0.20. A ratio of 1.0 means steady state. This indicates that the glacier is building up a reservoir area of ice which could be released during a surge. Based on the equation of continuity at a particular time, t, the rate of change in the cross-sectional area could be calculated by:

since Qb(0)= 0. Mass continuity thus provides a connection between gradients of volume flux and balance flux, and the rate of change in thickness. A thickening will occur when the balance-flux gradient exceeds the volume-flux gradient, and thinning occurs when the gradient of balance flux is less than gradient of volume flux (cf. Bindschadler, 1984). The change in cross-section area, S(x) = h(x)W(x), is mainly due to a change in glacier thickness, as the change in width is small.
The gradients of balance flux and volume flux were calculated along the glacier by using the estimated values of volume flux (Equation (3)]) and balance flux [Equation (2)]) at each stake (fig. 9b). The annual thickening and thinning rate above each cross-section (stakes S1-S9) was calculated (fig. 8b). The minimum and maximum change, shown as error bars in figure 8b, was obtained by using the most negative and most positive mass-balance gradients in the balance-flux calculation (Fig. 4). As can be seen from figure 8b, the calculated annual rate of change in ice thickness during the period 1991-95 is more or less in agreement with that measured. For both periods, however, the calculated thickening rate at stake S7 is higher than the measured rate. The difference may arise from: (i) data errors in the surface elevation, ice depth, surface velocity and cross-sectional area, and (ii) too high mean accumulation rates used in the flux calculation. We assume that (ii) is most likely as some deviation in the accumulation rate has been found at stake S7 for some years.
Mass balance and elevation changeThe change of surface elevation with time at a fixed position on the glacier surface gives a minimum value of the specific net balance as the change is given by dh/dt = b- ws where b is the net balance and ws is the emergence velocity (e.g. Paterson, 1994). The net balance can therefore be predicted if one knows the emergence velocity and assumes that the density does not change with depth during the period. This assumption should at least be valid in the ablation area (500 m a.s.l.). The true cumulative net balance will be more negative than estimated from the geometry changes alone in the ablation area and more positive in the accumulation area. An average emergence velocity of -0.03 m a−1 (submergence) was estimated for the area above stake S5. This uses the fact that the ice transported down-glacier at a given position must be equal to the mean downward flow of ice relative to the surface in the area above. The highest emergence (submergence) velocity estimated was -0.20 m a−1 in the area above stake S8. The low horizontal surface velocity on Kongsvegen (3.65-14.60 m a−1 in 1963-64 {Voigt, 1967), and 0.62-2.88 m a−1 in 1991-92), also indicates that the emergence velocities are low. Hence, the mean annual elevation change along the profile is more or less equal to the mean annual net balance, indicating that during the last 30 years the mass balance is the driving force for the surface-elevation changes, while the flow only plays a minor role.
Basal shear stress and ice deformation
The speed u{x) and the basal shear stress Tb beneath the centre line in 1966 and 1991 was calculated by the methods of Kamb and Echelmeyer (1986, Equations (35a and b) and (39)) from measured surface- and bed-elevation profiles and with a shape factor along the profile (Raymond and Harrison, 1988). The shape factor f was estimated from data in table IV of Nye (1965), assuming a parabolic cross-sectional shape and no basal sliding, using values of half-width w divided by the centre-line depth h along the glacier. The measured cross-sections along the glacier are close to parabolic with half-width to depth ratio between 3.6 and 18. This gives f values between 0.80 and ~l (fig. 7b). The local slope stresses (Raymond and Harrison, 1988) were calculated using the local ice thickness h(x), and shape factor f(x) at 0.05 km intervals and the slope α(x) averaged over 0.75 and 0.05 km for 1966 and 1991, respectively. The slope data α(x) (fig. 7b) were derived from profiles of surface elevations from 1966 and 1991 (fig. 7a). The difference in mean slope corresponds to the resolution of these profiles. The basal shear stress Tb was calculated using a constant value of l = 2.0 km for the longitudinal coupling length (Kamb and Echelmeyer, 1986). This corresponds to a ratio l/h of between 6 and 8 found from theoretical calculation by Kamb and Echelmeyer (1986, Fig. 5), assuming f = 1 and with a longitudinal strain rate of about 0.00024 a −1. This coupling length was found to give the best simulation of the measured velocities. Due to differences in the spatial resolution of the geometrical parameter α, the calculated stress Tb in 1966 should be smoother than that of 1991, but the large-scale picture should be correct The evolution of the basal shear stresses between 1966 and 1991 is shown in Figure 5. It can be seen that a significant change in the pattern has occurred. Above 8.6 km, Tb increased by a maximum of 10-13 kPa, mainly due to an increasing surface slope. Between 8.6 and 20.8 km down-glacier, there was a progressive decrease of Tb as the increase in surface slope was too small to compensate for the decrease in ice thickness.
The spatial pattern of annual velocity between 1991 and 1992 was investigated by calculating the speed u(x), using the 1991 datasets described above. The matching point for the 1991 calculation was taken at stake S5 (x = 9.7km) and the annual velocity (2.31 ma−1) between May 1991 and May 1992 was used as uobs(x0). A triangular weighting function was used with averaging lengths l = 0.9, 1.8 and 2.0 km. The predicted u(x) along the glacier, and the actual observed velocity at the stake positions, are shown in Figure 5. It is clear that the best match was obtained with an averaging length of 2.0 km. The calculated u(x) matches the measured velocity very well over most parts of the glacier but significant differences occurred down-glacier of stake S2 with any choice of the averaging length l. The observed velocity increased in this part of the glacier, while the calculated velocity decreased rapidly due to rapid thinning. The increase in the observed velocity is probably an effect of the confluence with the fast-flowing Kronebreen, which will affect the longitudinal force balance significantly. It could also be an effect of the tidewater terminal region of the glacier. In the area downstream from about 17 km (S2), the glacier bed lies below sea level and is subject to buoyancy as the effective water pressure (Bindschadler, 1983) will decrease as the ice thickness decreases towards the front. Thus, the observed velocity increase is probably due to an increasing contribution from basal motion as Kronebreen and the terminus area are approached.
Changes in speed with time
During the period 1966-91, the speed has decelerated in the lower part of the glacier and, in the same period, the glacier has thinned by 26 m at stake S2 and 49 m at stake SI, which will cause a reduction of internal deformation in the ice column. To determine how much of the velocity changes is due to a change in ice deformation, we estimated the deformation velocity ud from
where h is the ice thickness, Tb is the basal shear stress and K= 2A/(n+1), A and n are flow-law constants (see Paterson, 1994). To apply Equation (5)], we used a value of n = 3 (Hooke, 1981; Paterson, 1994) and the parameter K was calculated at locations S1 and S2 from the values of observed surface velocity u,Tb and h measured over the year 1991-92 (Raymond and Harrison, 1988). With a value of K equal to 0.051 bar −3 a−1 at stake S1 and 0.019 bar −3 a −1 at stake S2, the calculated internal deformation in 1966 was 6.7 and 2.9 m a −1 at stakes S1 and S2, respectively. The large spatial variation of K found may arise from: (i) different basal motion at the two locations, (ii) a more marginal position of stake S2 where the drag from the valley side is larger. We assume that (i) is the dominant contribution as it has been shown that basal motion is large close to stake S1 (Melvold, 1992). Basal motion at stake S1 will give an overestimated value of K and the predicted velocity from internal deformation will be too high. The difference between the calculated deformation speed and the measured surface. speed in 1966 shows that much of the reduction in velocity at stake S2 is due to less internal deformation. At stake S1, the change in velocity between 1966 and 1991 is mostly due to a reduction in the basal motion.
The estimated K value at stake S2 is more equal to the value of K used to predict the spatial pattern of annual velocity above, as there is a match between the predicted u(x) using the Kamb and Echelmeyer (1986) equations and the measured speed. This K value of 0.019 bar −3 a−1 is smaller than that Raymond and Harrison (1988) found on Variegated Glacier and smaller than that predicted from Paterson’s preferred parameters for temperate ice. Thus, the glacier was stiffer than Variegated Glacier and other temperate glaciers. A possible reason for this is the polythermal temperature regime in Kongsvegen with a 50-130 m thick upper layer with a sub-freezing temperature in the ablation area (BjÖrnsson and others, 1996).
Evolution of Surge-Type Glaciers in Svalbard
Surface elevation
The evolution of the geometrical changes on Kongsvegen is relatively similar to those observed on Black Rapids Glacier, Alaska (Heinrichs and others, 1996), on Bjuvbreen (Hamilton, 1992) and on Finsterwalderbreen (Nuttall and others, 1997) in Svalbard. It is less similar to the well-studied Variegated Glacier (Raymond and Harrison, 1988) and Medvezhiy Glacier in the Pamirs (Dolgoushin and Osipova, 1975; Raymond, 1987). The annual change in elevation along Kongsvegen shows that the thickening rate in the reservoir area is lower than the thinning rate in the glacier-receiving area, such as also found on Black Rapids Glacier. But the maximum thickening rate of about 1 m a −1 found is smaller than that observed in corresponding areas of Black Rapids Glacier and more than an order of magnitude less than that observed on Variegated Glacier. The same pattern of evolution, but with even lower thickening rates than on Kongsvegen, is found on Finsterwaiderbreen (0.5 m a −1) and on Bjuvbreen, Svalbard. On Scott Turnerbreen, no build up at all has been found between 1936 and 1993 (Hodgkins, 1994). The slow build-up of a Svalbard glacier is a function of the low precipitation in Svalbard. Meteorological records from western Svalbard in the period 1975-89 show a mean annual precipitation of 372 mm (Hanssen-Bauer and others, 1990). Due to large losses in the precipitation gauge, this value has been corrected up to 550 mm (Hanssen-Bauer and others, 1996), As may be expected, the mountain regions and the higher parts of the glaciers in Svalbard receive considerably more precipitation but it seldom exceeds 2-4 m of snow (Hagen and others, 1993). The net accumulation in the highest part of Kongsvegen is between 0.6 and 1.1 m w.e. a −1 (Fig. 4) and about 0.5 m w.e. a −1 on Finsterwaiderbreen (Nuttall and others, 1997). Generally, it is only 0.3-0.6 m w.e. a −1 for Svalbard glaciers (e.g. Dowdeswell and Drewry, 1989; Hagen and Liestøl, 1990). The low rate of build-up (thickening) is therefore probably common for surge-type glaciers in Svalbard. In comparison, Black Rapids Glacier in Alaska can receive between 0.9-2.25 m w.e. a −1 (Heinrichs and others, 1996), but this is much less than on Variegated Glacier in Alaska and Medvezhiy Glacier in the Pamirs (Raymond, 1987). This difference in mass building during the quiescent phase will probably cause a longer quiescent phase length in Svalbard than in the other areas. This has also been suggested by Dowdeswell and others (1991). Only four glaciers have been observed to surge twice in Svalbard: Tunabreen (203 km2) with a 50 year interval, Hambergbreen (104 km2) with a 70 year interval, Recherchebreen (146 km2) with a 107 year interval (Liestøl, 1993) and Fridtjovbreen (48.7 km2) with a 134 year interval. In addition to these observations, an extensive examination of aerial photography carried out by Hamilton (1992) shows that no glacier was observed to surge twice in Spitsbergen, during a span of almost 60 years of aerial photographic records. Other calculated return intervals from Svalbard glaciers indicate long quiescent phase periods; from 80-100 years at Usherbreen (Hagen, 1987), 90-130 years for Bjuvbreen (Hamilton, 1992) to 370-510 years for Bråsvellbreen (Solheim, 1991). In Alaska, the return interval ranges from 17 to 20 years for Variegated Glacier (Kamb and others, 1985) to 50-75 years for Black Rapids Glacier (Heinrichs and others, 1996). Surge-type glaciers in the Pamirs commonly have a quiescent phase length of 17- 20 years but the well-documented Medvezhiy Glacier has a surge cycle of 9-14years (Dolgoushin and Osipova, 1975; Raymond, 1987). This suggests that the difference in precipitation may cause differences in quiescent-phase length. This has also been proposed as a possible reason for the longer quiescent phase on Black Rapids Glacier compared to Variegated Glacier (Heinrichs and others, 1996). According to Heinrichs and others, another possible reason may be the different size of the glacier. Hamilton’s (1992) examination of Spitsbergen glaciers from aerial photography covered all sizes of glaciers for almost 60 years and indicated that size could not be the only reason for the longer quiescent-phase length in Svalbard.
As mentioned previously, the thickening rate in the reservoir area of Kongsvegen is higher than on other studied surge-type glaciers in Svalbard. The low thickening rates (or lack of it) found on surge-type glaciers in Svalbard at present has been related to the climate change that occurred in Svalbard at the end of the Little Ice Age about a 100 years ago (Reference LefauconnierLefauconnier and Hagen, 1991; Dowdeswell and others 1995). Meteorological records show that the mean annual temperature around 1940 was approximately 20 higher than at the start of the measurement series in 1911 (Hanssen-Bauer and others, 1990). The mean summer and autumn temperatures show an abrupt rise from 1910 to about 1920 (Reference LefauconnierLefauconnier and Hagen, 1991). The shift to warmer conditions has thus led to consistently negative mass balances on all the small glaciers at relatively low attitudes for which measurements are available (Hagen and Liestøl, 1990; Reference LefauconnierLefauconnier and Hagen, 1991; Hagen, 1996) and may prevent some surge-type glaciers in Svalbard from accumulating mass (Reference DowdeswellDowdeswell and others, 1995). Energy-balance modelling carried out by Fleming and others (1997) has shown that the glaciers in northwest Spitsbergen are very sensitive to climate change. The model predicted a negative shift in mass balance of 0.5 to 0.8 m w.e. a −1 for each degree of warming, depending on die area/altitude distribution of individual glaciers. As the glaciers in Svalbard generally have a low surface slope, even small changes in height of the ELA will have a large effect on the accumulation and ablation rates on the glaciers. A surge is another important factor that will affect the accumulation/ablation rates, because the area/altitude distribution will change considerably during a surge. Measurements on Usherbreen and Osbornebrecn showed a drop in the surface elevation of the reservoir area of 40—70m and more than 100 m, respectively, during the surges (Hagen, 1987; Rolstad, 1995). Thus, a smaller part of the previous accumulation area is above the present-day ELA and the glacier is less able to build up mass. This suggests that both climatic change and previous surges could cause reduction in the possibility to build up mass toward a new surge.
Due to the reduction in mass accumulated, future surges will be either: (i) delayed or prevented, causing a decrease in the frequency of glacier surges in Svalbard, as suggested by Reference DowdeswellDowdeswell and others (1995), or (ii) occur with less mass than previously which means that the surge will be smaller than earlier ones as suggested by Lefauconnier and Hagen (1991). As Kongsvegen has a higher accumulation area relative to the present-day ELA than the other glaciers studied in Svalbard, it will receive more snow and thus thicken faster than the others. This indicates that glaciers covering higher areas relative to the ELA have a greater possibility of accumulating mass under the present climate than glaciers at lower altitudes, Thus, it is likely that future surges will be delayed or surge with less mass or even not occur in the future on low-altitude glaciers. A combination of these effects will probably be the results of a possible future climatic change.
Conclusions
The main conclusions of the present analysis are summarized as follows:
(1) The measured modern ice flux on Kongsvegen is lower than required to achieve a steady state. Comparison of the present-day balance flux and volume/actual flux shows that the mass transported down to the ELA is only about 3-20% of what accumulates in the upper basin (Fig. 9). The overall similarity between the measured change and the calculated changes shows that the flux comparison is a reasonable way to evaluate the state of a glacier.
(2) The annual elevation change is more or less equal to the mean annual net balance. During the last 30years, the mass balance has been the driving force of the elevation changes (Fig. 8).
(3) The change in basal shear stress in the upper half of the glacier is mainly a result of the increased surface slope. The change down-glacier is mainly due to a decrease in ice thickness.
(4) It is not certain when Kongsvegen will surge again. But, it is certain that the glacier is building up a reservoir area of ice (Fig. 8). It is therefore likely that Kongsvegen, under the present climate, will surge some time in the future.
The evolution of Kongsvegen and other studied surge-type glaciers in Svalbard, compared to surge-type glaciers in Alaska and the Pamirs, reveals several characteristics. These can be summarized as follows:
(1) The build-up of mass in the reservoir area for surge-type glaciers seems to be slow compared to studied surge-type glaciers in Alaska and the Pamirs. The main reason for the slow build-up is the low precipitation in Svalbard compared to other regions.
(2) The low accumulation rate is probably the reason for the relatively long quiescent phase length observed in Svalbard.
(3) Under the present climate, the build-up of Kongsvegen is larger than on other observed surge-type glaciers in Svalbard. This is a result of the high accumulation area relative to the ELA compared to the others, indicating that glaciers with high-altitude areas compared to the ELA build up faster towards a new surge event and will surge with a greater mass than the others.
Acknowledgements
We wish to thank our field assistants throughout the years and the Norsk Polarinstitutt for logistical help during the field work. B. Luktvasslimo and T. Eiken deserve special thanks for help with GPS measurements and processing. We are grateful to O. Liestol, for his constructive advice during the work, and H. BjÖrnsson, for his valuable comments on an early draft of this paper. H. Madsen carried out the digitizing work. The constructive critical comments of J.A. Dowdeswell and B. Lefauconnier, and an anonymous reviewer, have resulted in significant improvements in this paper. This project received financial support from the Norsk Polarinstitutt in 1989 and 1990.