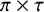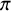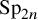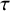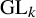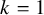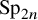1 Introduction
When Hecke developed his theory of L-functions for modular forms of integral weight, he observed that for half-integral weight, his operators (now called Hecke operators) could not ensure the existence of an Euler product expansion for the L-series ([Reference Gelbart and Piatetski-ShapiroGPS80]). In the adelic setting, these modular forms can be interpreted as functions on global double covering groups of
![]() $\operatorname {\mathrm {SL}}_2$
. The work of Weil was perhaps the first application of covering groups to the theory of modular forms. Weil constructed the double covering of the symplectic group and a geometric realization for the theta representation [Reference WeilWei64], with the intention of reformulating Siegel’s theory of what is now known as theta liftings, a goal pursued in [Reference WeilWei65]. Arbitrary rank coverings of
$\operatorname {\mathrm {SL}}_2$
. The work of Weil was perhaps the first application of covering groups to the theory of modular forms. Weil constructed the double covering of the symplectic group and a geometric realization for the theta representation [Reference WeilWei64], with the intention of reformulating Siegel’s theory of what is now known as theta liftings, a goal pursued in [Reference WeilWei65]. Arbitrary rank coverings of
![]() $\operatorname {\mathrm {SL}}_2$
and
$\operatorname {\mathrm {SL}}_2$
and
![]() $\operatorname {\mathrm {GL}}_2$
were studied by Kubota [Reference KubotaKub67, Reference KubotaKub69]. Around the same time, Moore [Reference MooreMoo68], Steinberg [Reference SteinbergSte68] and Matsumoto [Reference MatsumotoMat69] constructed covering groups for almost simple simply connected split groups and laid the foundations for their systematic study.
$\operatorname {\mathrm {GL}}_2$
were studied by Kubota [Reference KubotaKub67, Reference KubotaKub69]. Around the same time, Moore [Reference MooreMoo68], Steinberg [Reference SteinbergSte68] and Matsumoto [Reference MatsumotoMat69] constructed covering groups for almost simple simply connected split groups and laid the foundations for their systematic study.
Shimura [Reference ShimuraShi73] studied modular forms of half-integral weight and was able to address the problems observed by Hecke. He defined a new family of Hecke operators, which controlled the Euler product factorization (as in the integral case). He proceeded to produce a lift of modular forms of weight
![]() $k/2$
, where
$k/2$
, where
![]() $k\geq 3$
is an odd integer, to modular forms of weight
$k\geq 3$
is an odd integer, to modular forms of weight
![]() $k-1$
. To obtain this result, Shimura developed an integral representation involving an Eisenstein series, by generalizing the method of Rankin [Reference RankinRan39], and used it for the study of the L-series attached to a
$k-1$
. To obtain this result, Shimura developed an integral representation involving an Eisenstein series, by generalizing the method of Rankin [Reference RankinRan39], and used it for the study of the L-series attached to a
![]() $k/2$
modular form. He then applied the converse theorem of Weil [Reference WeilWei67] to produce a weight
$k/2$
modular form. He then applied the converse theorem of Weil [Reference WeilWei67] to produce a weight
![]() $k-1$
modular form. We also mention Waldspurger [Reference WaldspurgerWal80, Reference WaldspurgerWal81, Reference WaldspurgerWal90, Reference WaldspurgerWal91], who obtained local and global correspondences between representations of the double covering of
$k-1$
modular form. We also mention Waldspurger [Reference WaldspurgerWal80, Reference WaldspurgerWal81, Reference WaldspurgerWal90, Reference WaldspurgerWal91], who obtained local and global correspondences between representations of the double covering of
![]() $\operatorname {\mathrm {SL}}_2$
and the group
$\operatorname {\mathrm {SL}}_2$
and the group
![]() $\operatorname {\mathrm {SO}}_3$
, using the theta correspondence. The results of Waldspurger were generalized only recently by Gan and Ichino [Reference Gan and IchinoGI18], who described the generic part of the automorphic discrete spectrum of the double covering
$\operatorname {\mathrm {SO}}_3$
, using the theta correspondence. The results of Waldspurger were generalized only recently by Gan and Ichino [Reference Gan and IchinoGI18], who described the generic part of the automorphic discrete spectrum of the double covering
![]() $\operatorname {\mathrm {Sp}}^{(2)}_{2n}(\mathbb {A})$
of
$\operatorname {\mathrm {Sp}}^{(2)}_{2n}(\mathbb {A})$
of
![]() $\operatorname {\mathrm {Sp}}_{2n}(\mathbb {A})$
, using the theta lift of Li [Reference LiLi97] to
$\operatorname {\mathrm {Sp}}_{2n}(\mathbb {A})$
, using the theta lift of Li [Reference LiLi97] to
![]() $\operatorname {\mathrm {SO}}_{2l+1}(\mathbb {A})$
for
$\operatorname {\mathrm {SO}}_{2l+1}(\mathbb {A})$
for
![]() $l\gg n$
(which is known to be nonzero) and the work of Arthur [Reference ArthurArt13] on the endoscopic classification (for
$l\gg n$
(which is known to be nonzero) and the work of Arthur [Reference ArthurArt13] on the endoscopic classification (for
![]() $\operatorname {\mathrm {SO}}_{2l+1}$
). Other works on the theta correspondence include [Reference Kudla and RallisKR05, Reference Gan, Gross and PrasadGGP12, Reference Gan and SavinGS12] and the recent proof of the Howe duality conjecture by Gan and Takeda [Reference Gan and TakedaGT16]. Refer to [Reference Gan, Gao and WeissmanGGW18] for an historical overview of these topics.
$\operatorname {\mathrm {SO}}_{2l+1}$
). Other works on the theta correspondence include [Reference Kudla and RallisKR05, Reference Gan, Gross and PrasadGGP12, Reference Gan and SavinGS12] and the recent proof of the Howe duality conjecture by Gan and Takeda [Reference Gan and TakedaGT16]. Refer to [Reference Gan, Gao and WeissmanGGW18] for an historical overview of these topics.
In this work, we take a modest step towards a generalized Shimura lift, of genuine cuspidal automorphic representations, of covering groups of classical groups, to automorphic representations of suitable general linear groups, via an integral representation. For any
![]() $m>1$
, we construct an integral representation for the partial L-function of a pair of genuine irreducible cuspidal automorphic representations,
$m>1$
, we construct an integral representation for the partial L-function of a pair of genuine irreducible cuspidal automorphic representations,
![]() $\pi $
of the m-fold covering of
$\pi $
of the m-fold covering of
![]() $\operatorname {\mathrm {Sp}}_{2n}(\mathbb {A})$
of Matsumoto [Reference MatsumotoMat69] and
$\operatorname {\mathrm {Sp}}_{2n}(\mathbb {A})$
of Matsumoto [Reference MatsumotoMat69] and
![]() $\tau $
of the covering of
$\tau $
of the covering of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
obtained by restriction from the similar m-fold covering of
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
obtained by restriction from the similar m-fold covering of
![]() $\operatorname {\mathrm {Sp}}_{2k}(\mathbb {A})$
. We prove a global identity, which on factorizable data leads to an ‘almost Eulerian product’: an infinite product of local integrals over almost all the unramified places, multiplied by an integral over the remaining finitely many places. Then, we compute the local integrals at almost all places. Our construction is based on the doubling method of Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87] and its recent generalization in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK22, Reference Gourevitch and KaplanGK23], and we expect it to apply to a wide range of covering groups. For precise details and description see below: The linear construction is briefly recalled in § 1.1, then we describe its extension to coverings in § 1.2.
$\operatorname {\mathrm {Sp}}_{2k}(\mathbb {A})$
. We prove a global identity, which on factorizable data leads to an ‘almost Eulerian product’: an infinite product of local integrals over almost all the unramified places, multiplied by an integral over the remaining finitely many places. Then, we compute the local integrals at almost all places. Our construction is based on the doubling method of Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87] and its recent generalization in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK22, Reference Gourevitch and KaplanGK23], and we expect it to apply to a wide range of covering groups. For precise details and description see below: The linear construction is briefly recalled in § 1.1, then we describe its extension to coverings in § 1.2.
Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87] developed an integral representation for the standard automorphic L-function of an irreducible cuspidal automorphic representation of a classical group or its rank-
![]() $1$
twists. Their construction was different from other constructions for classical groups at the time ([Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Reference GinzburgGin90]), in the sense that it did not assume any global or local model. Cuspidal representations of general linear groups are always globally generic, that is, admit Whittaker–Fourier coefficients, but this is the exceptional case, for other groups cuspidal (or supercuspidal, locally) representations need not admit Whittaker models. The local theory of the integrals of [Reference Piatetski-Shapiro and RallisPSR87] was fully developed by Lapid and Rallis [Reference Lapid, Rallis, Cogdell, Jiang, Kudla, Soudry, Stanton and UnivLR05], with additional cases of groups added by Gan [Reference GanGan12] (see § 1.3 below) and Yamana [Reference YamanaYam14]. The construction of [Reference Piatetski-Shapiro and RallisPSR87], now known as the doubling method, has had numerous applications, including to the study of the theta correspondence [Reference Kudla and RallisKR94, Reference Harris, Kudla and SweetHKS96, Reference Gan and SavinGS12, Reference YamanaYam14] and to cohomological automorphic representations [Reference Böcherer and SchmidtBS00, Reference Harris, Li and SkinnerHLS05, Reference Harris, Li and SkinnerHLS06, Reference Eischen, Harris, Li and SkinnerEHLS20]. However, since it was limited to the standard L-function, it was not sufficient for the study of the functorial transfer.
$1$
twists. Their construction was different from other constructions for classical groups at the time ([Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Reference GinzburgGin90]), in the sense that it did not assume any global or local model. Cuspidal representations of general linear groups are always globally generic, that is, admit Whittaker–Fourier coefficients, but this is the exceptional case, for other groups cuspidal (or supercuspidal, locally) representations need not admit Whittaker models. The local theory of the integrals of [Reference Piatetski-Shapiro and RallisPSR87] was fully developed by Lapid and Rallis [Reference Lapid, Rallis, Cogdell, Jiang, Kudla, Soudry, Stanton and UnivLR05], with additional cases of groups added by Gan [Reference GanGan12] (see § 1.3 below) and Yamana [Reference YamanaYam14]. The construction of [Reference Piatetski-Shapiro and RallisPSR87], now known as the doubling method, has had numerous applications, including to the study of the theta correspondence [Reference Kudla and RallisKR94, Reference Harris, Kudla and SweetHKS96, Reference Gan and SavinGS12, Reference YamanaYam14] and to cohomological automorphic representations [Reference Böcherer and SchmidtBS00, Reference Harris, Li and SkinnerHLS05, Reference Harris, Li and SkinnerHLS06, Reference Eischen, Harris, Li and SkinnerEHLS20]. However, since it was limited to the standard L-function, it was not sufficient for the study of the functorial transfer.
In the recent works [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK22, Reference Gourevitch and KaplanGK23], the doubling method was generalized to produce L-functions for arbitrary pairs of irreducible cuspidal automorphic representations of a classical group and general linear group. This generalization was obtained by taking arbitrary generalized Speh representations for the inducing data of the Eisenstein series and applying an additional Fourier coefficient. The goal of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] was the basic global identity for the integral and the computation of the local integrals with unramified data, while the main focus of [Reference Cai, Friedberg and KaplanCFK22, Reference Gourevitch and KaplanGK23] was the local theory at all places. This line of work culminated in [Reference Cai, Friedberg and KaplanCFK] which obtained a global weak transfer from cuspidal automorphic representations of symplectic, split special orthogonal or split general spin groups to automorphic representations of
![]() $\operatorname {\mathrm {GL}}_N$
(for the appropriate N), via the converse theorem of Cogdell and Piatetski-Shapiro [Reference Cogdell and Piatetski-ShapiroCPS94, Reference Cogdell and Piatetski-ShapiroCPS99] (as in [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS01]). This result extended the functorial lift of [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS01, Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS04, Reference Asgari and ShahidiAS06] from globally generic representations to arbitrary ones. Let us mention that this transfer can already be obtained from Arthur’s work [Reference ArthurArt13], which involved the stable trace formula (at present, several references in [Reference ArthurArt13] remain unpublished). While there are already several works on the trace formula for covering groups, for example, Li [Reference LiLi12, Reference LiLi13, Reference LiLi14a, Reference LiLi14b, Reference LiLi15] and the recent work of Li [Reference LiLi] where he proved the stabilization of the Arthur–Selberg trace formula for
$\operatorname {\mathrm {GL}}_N$
(for the appropriate N), via the converse theorem of Cogdell and Piatetski-Shapiro [Reference Cogdell and Piatetski-ShapiroCPS94, Reference Cogdell and Piatetski-ShapiroCPS99] (as in [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS01]). This result extended the functorial lift of [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS01, Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS04, Reference Asgari and ShahidiAS06] from globally generic representations to arbitrary ones. Let us mention that this transfer can already be obtained from Arthur’s work [Reference ArthurArt13], which involved the stable trace formula (at present, several references in [Reference ArthurArt13] remain unpublished). While there are already several works on the trace formula for covering groups, for example, Li [Reference LiLi12, Reference LiLi13, Reference LiLi14a, Reference LiLi14b, Reference LiLi15] and the recent work of Li [Reference LiLi] where he proved the stabilization of the Arthur–Selberg trace formula for
![]() $\operatorname {\mathrm {Sp}}^{(2)}_{2n}(\mathbb {A})$
, at the time of writing this paper we are unaware of any full analogs of [Reference ArthurArt13] (or [Reference MokMok15]) for covering groups.
$\operatorname {\mathrm {Sp}}^{(2)}_{2n}(\mathbb {A})$
, at the time of writing this paper we are unaware of any full analogs of [Reference ArthurArt13] (or [Reference MokMok15]) for covering groups.
At present, the advantages of the generalized doubling method over other integral representations include its uniform approach (e.g., independent of the difference between the ranks of the classical group and the general linear group), the local theory which is now available at all places and the applicability to all cuspidal automorphic representations, that is, no model assumption is made. As mentioned above, this is already beneficial for linear groups, but is particularly important when considering covering groups. For covering groups the local (and thereby global) multiplicity one for Whittaker models breaks down, first and foremost, for genuine unramified principal series representations. This is one of the reasons it is intrinsically difficult to develop Eulerian integrals. The doubling construction is free of this assumption, making it suitable for extensions to covering groups.
1.1 The linear case
We briefly introduce the integrals in the linear case first, following [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19]. Let F be a number field with a ring of adeles
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $G=\operatorname {\mathrm {Sp}}_{2n}$
be the symplectic group on
$G=\operatorname {\mathrm {Sp}}_{2n}$
be the symplectic group on
![]() $2n$
variables. Let
$2n$
variables. Let
![]() $\pi $
be an irreducible cuspidal automorphic representation of
$\pi $
be an irreducible cuspidal automorphic representation of
![]() $G(\mathbb {A})$
. For any
$G(\mathbb {A})$
. For any
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $\tau $
be an irreducible cuspidal automorphic representation of
$\tau $
be an irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
. We integrate two cusp forms in the space of
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
. We integrate two cusp forms in the space of
![]() $\pi $
, against a Fourier coefficient of an Eisenstein series on
$\pi $
, against a Fourier coefficient of an Eisenstein series on
![]() $H=\operatorname {\mathrm {Sp}}_{4kn}$
with inducing data attached to
$H=\operatorname {\mathrm {Sp}}_{4kn}$
with inducing data attached to
![]() $\tau $
. The integral represents the partial L-function
$\tau $
. The integral represents the partial L-function
![]() $L^S(s,\pi \times \tau )$
, where S is a finite set of places of F outside which all data are unramified.
$L^S(s,\pi \times \tau )$
, where S is a finite set of places of F outside which all data are unramified.
For
![]() $c\geq 1$
, let
$c\geq 1$
, let
![]() $\mathcal {E}_{\tau }$
be the generalized Speh representation corresponding to c copies of
$\mathcal {E}_{\tau }$
be the generalized Speh representation corresponding to c copies of
![]() $\tau $
, constructed by Jacquet [Reference JacquetJac84]. It is the residual representation of an Eisenstein series, corresponding to a representation of
$\tau $
, constructed by Jacquet [Reference JacquetJac84]. It is the residual representation of an Eisenstein series, corresponding to a representation of
![]() $\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
parabolically induced from
$\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
parabolically induced from
![]() $|\det |^{\zeta _1}\tau \otimes \ldots \otimes |\det |^{\zeta _c}\tau $
, at the point
$|\det |^{\zeta _1}\tau \otimes \ldots \otimes |\det |^{\zeta _c}\tau $
, at the point
![]() $((c-1)/2,(c-3)/2,\ldots , (1-c)/2)$
. The main properties of
$((c-1)/2,(c-3)/2,\ldots , (1-c)/2)$
. The main properties of
![]() $\mathcal {E}_{\tau }$
, which were used in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19], were that its generic Fourier coefficient along the unipotent orbit
$\mathcal {E}_{\tau }$
, which were used in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19], were that its generic Fourier coefficient along the unipotent orbit
![]() $(k^c)$
, called a (global)
$(k^c)$
, called a (global)
![]() $(k,c)$
functional, is not identically zero and that it does not support any generic Fourier coefficient on an orbit greater than or not comparable with
$(k,c)$
functional, is not identically zero and that it does not support any generic Fourier coefficient on an orbit greater than or not comparable with
![]() $(k^c)$
. These were proved in [Reference GinzburgGin06, Reference Jiang and LiuJL13]. The local components of
$(k^c)$
. These were proved in [Reference GinzburgGin06, Reference Jiang and LiuJL13]. The local components of
![]() $\mathcal {E}_{\tau }$
admit unique
$\mathcal {E}_{\tau }$
admit unique
![]() $(k,c)$
models, which are the local analogs of the
$(k,c)$
models, which are the local analogs of the
![]() $(k,c)$
functional: This was proved in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] for the unramified components and refined in [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23] to all components. We call a representation of
$(k,c)$
functional: This was proved in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] for the unramified components and refined in [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23] to all components. We call a representation of
![]() $\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
with these properties a
$\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
with these properties a
![]() $(k,c)$
representation, or simply
$(k,c)$
representation, or simply
![]() $(k,c)$
. For the precise definition, see § 3.1.
$(k,c)$
. For the precise definition, see § 3.1.
For instance, if
![]() $c=1$
,
$c=1$
,
![]() $\mathcal {E}_{\tau }=\tau $
and since
$\mathcal {E}_{\tau }=\tau $
and since
![]() $\tau $
is cuspidal, it is globally generic, that is, admits a (nonzero) Whittaker–Fourier coefficient. In this case,
$\tau $
is cuspidal, it is globally generic, that is, admits a (nonzero) Whittaker–Fourier coefficient. In this case,
![]() $(k,c)$
models are simply Whittaker models, and indeed the local components of
$(k,c)$
models are simply Whittaker models, and indeed the local components of
![]() $\tau $
all admit unique Whittaker models.
$\tau $
all admit unique Whittaker models.
Put
![]() $c=2n$
. Let
$c=2n$
. Let
![]() $H=\operatorname {\mathrm {Sp}}_{2kc}$
,
$H=\operatorname {\mathrm {Sp}}_{2kc}$
,
![]() $B_H$
be a fixed Borel subgroup of H,
$B_H$
be a fixed Borel subgroup of H,
![]() $K_H$
be a standard maximal compact subgroup of
$K_H$
be a standard maximal compact subgroup of
![]() $H(\mathbb {A})$
and
$H(\mathbb {A})$
and
![]() $P=M_P\ltimes U_P$
be the standard Siegel parabolic subgroup of H, that is, the Levi part
$P=M_P\ltimes U_P$
be the standard Siegel parabolic subgroup of H, that is, the Levi part
![]() $M_P$
of P is isomorphic to
$M_P$
of P is isomorphic to
![]() $\operatorname {\mathrm {GL}}_{kc}$
. Consider the representation
$\operatorname {\mathrm {GL}}_{kc}$
. Consider the representation
![]() $\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{H(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
(normalized induction), where
$\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{H(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
(normalized induction), where
![]() $s\in \mathbb {C}$
. For a standard
$s\in \mathbb {C}$
. For a standard
![]() $K_H$
-finite section f of
$K_H$
-finite section f of
![]() $\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{H(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
, regarded as a complex-valued function, we have the Eisenstein series
$\operatorname {\mathrm {Ind}}_{P(\mathbb {A})}^{H(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
, regarded as a complex-valued function, we have the Eisenstein series
 $$ \begin{align} E(h;s,f)=\sum\limits_{\gamma\in P(F)\backslash H(F)}f(s,\gamma h),\qquad h\in H(\mathbb{A}). \end{align} $$
$$ \begin{align} E(h;s,f)=\sum\limits_{\gamma\in P(F)\backslash H(F)}f(s,\gamma h),\qquad h\in H(\mathbb{A}). \end{align} $$
This series is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
and admits meromorphic continuation to
$\operatorname {\mathrm {Re}}(s)\gg 0$
and admits meromorphic continuation to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
To describe the Fourier coefficient of
![]() $E(h;s,f)$
, let Q be a standard parabolic subgroup of H, whose Levi part
$E(h;s,f)$
, let Q be a standard parabolic subgroup of H, whose Levi part
![]() $M_Q$
is isomorphic to
$M_Q$
is isomorphic to
![]() $\operatorname {\mathrm {GL}}_c\times \ldots \times \operatorname {\mathrm {GL}}_c\times \operatorname {\mathrm {Sp}}_{2c}$
. Let
$\operatorname {\mathrm {GL}}_c\times \ldots \times \operatorname {\mathrm {GL}}_c\times \operatorname {\mathrm {Sp}}_{2c}$
. Let
![]() $U=U_Q$
be the unipotent radical of Q. Fix a nontrivial character
$U=U_Q$
be the unipotent radical of Q. Fix a nontrivial character
![]() $\psi $
of
$\psi $
of
![]() $F\backslash \mathbb {A}$
. One can define an automorphic character
$F\backslash \mathbb {A}$
. One can define an automorphic character
![]() $\psi _U$
of
$\psi _U$
of
![]() $U(\mathbb {A})$
such that the direct product
$U(\mathbb {A})$
such that the direct product
![]() $G(\mathbb {A})\times G(\mathbb {A})$
is embedded in the stabilizer of
$G(\mathbb {A})\times G(\mathbb {A})$
is embedded in the stabilizer of
![]() $\psi _U$
inside
$\psi _U$
inside
![]() $M_Q(\mathbb {A})$
. Denote the image of this embedding by
$M_Q(\mathbb {A})$
. Denote the image of this embedding by
![]() $(g_1,g_2)\in H(\mathbb {A})$
. By construction, the Fourier coefficient
$(g_1,g_2)\in H(\mathbb {A})$
. By construction, the Fourier coefficient
![]() $E^{U,\psi _U}(h;s,f)$
of
$E^{U,\psi _U}(h;s,f)$
of
![]() $E(h;s,f)$
along
$E(h;s,f)$
along
![]() $(U,\psi _U)$
is an automorphic function on
$(U,\psi _U)$
is an automorphic function on
![]() $G(\mathbb {A})\times G(\mathbb {A})$
.
$G(\mathbb {A})\times G(\mathbb {A})$
.
Let
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
be two cusp forms in the space of
$\varphi _2$
be two cusp forms in the space of
![]() $\pi $
. Let
$\pi $
. Let
![]() $\iota =\left (\begin {smallmatrix}& I_{c/2}\\ I_{c/2} &\end {smallmatrix}\right )$
,
$\iota =\left (\begin {smallmatrix}& I_{c/2}\\ I_{c/2} &\end {smallmatrix}\right )$
,
![]() $g\mapsto {}^{\iota }g=\iota g\iota ^{-1}$
is an outer involution of G, and denote
$g\mapsto {}^{\iota }g=\iota g\iota ^{-1}$
is an outer involution of G, and denote
![]() ${}^{\iota }\varphi _2(g)=\varphi _2({}^{\iota }g)$
.
${}^{\iota }\varphi _2(g)=\varphi _2({}^{\iota }g)$
.
The global integral in the linear setting was defined in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] by
 $$ \begin{align*} Z(s,\varphi_1,\varphi_2,f)= \int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \varphi_1(g_1)\,\overline{{}^{\iota}\varphi_2(g_2)}\, E^{U,\psi_U}((g_1,g_2);f,s)\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} Z(s,\varphi_1,\varphi_2,f)= \int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \varphi_1(g_1)\,\overline{{}^{\iota}\varphi_2(g_2)}\, E^{U,\psi_U}((g_1,g_2);f,s)\,dg_1\,dg_2. \end{align*} $$
This integral is absolutely convergent on the whole plane except perhaps at the poles of the Eisenstein series.
Let
![]() $\{\varphi _1,\varphi _2\}$
be the standard
$\{\varphi _1,\varphi _2\}$
be the standard
![]() $G(\mathbb {A})$
-invariant inner product on the space of
$G(\mathbb {A})$
-invariant inner product on the space of
![]() $\pi $
, and
$\pi $
, and
![]() $f_{W({\mathcal E}_{\tau })}(h,s)$
denote the composition of f with the
$f_{W({\mathcal E}_{\tau })}(h,s)$
denote the composition of f with the
![]() $(k,c)$
functional on
$(k,c)$
functional on
![]() $\mathcal {E}_{\tau }$
, namely
$\mathcal {E}_{\tau }$
, namely
 $$ \begin{align*} f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s)=\int\limits_{V_{(c^k)}(F)\backslash V_{(c^k)}({\mathbb{A}})} f(vh,s)\,\psi^{-1}(\mathrm{tr}(\sum_{i=1}^{k-1}v_{i,i+1}))\,dv. \end{align*} $$
$$ \begin{align*} f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s)=\int\limits_{V_{(c^k)}(F)\backslash V_{(c^k)}({\mathbb{A}})} f(vh,s)\,\psi^{-1}(\mathrm{tr}(\sum_{i=1}^{k-1}v_{i,i+1}))\,dv. \end{align*} $$
Here,
![]() $V_{(c^k)}$
is the unipotent radical of the parabolic subgroup of
$V_{(c^k)}$
is the unipotent radical of the parabolic subgroup of
![]() $\operatorname {\mathrm {GL}}_{kc}$
corresponding to the partition
$\operatorname {\mathrm {GL}}_{kc}$
corresponding to the partition
![]() $(c^k)$
,
$(c^k)$
,
![]() $v=(v_{i,j})_{1\leq i,j\leq k}$
, where
$v=(v_{i,j})_{1\leq i,j\leq k}$
, where
![]() $v_{i,j}$
are
$v_{i,j}$
are
![]() $c\times c$
blocks, and
$c\times c$
blocks, and
![]() $\mathrm {tr}$
is the trace map. The main global result of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] was that, in
$\mathrm {tr}$
is the trace map. The main global result of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] was that, in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
 $$ \begin{align} Z(s,\varphi_1,\varphi_2,f)=\int\limits_{G({\mathbb{A}})}\int\limits_{(U_P\cap U)({\mathbb{A}})} \{\varphi_1,\pi(g)\varphi_2\}f_{W({\mathcal E}_{\tau})}(\delta u_0(1,{}^{\iota}g),s) \,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} Z(s,\varphi_1,\varphi_2,f)=\int\limits_{G({\mathbb{A}})}\int\limits_{(U_P\cap U)({\mathbb{A}})} \{\varphi_1,\pi(g)\varphi_2\}f_{W({\mathcal E}_{\tau})}(\delta u_0(1,{}^{\iota}g),s) \,\psi_U(u_0)\,du_0\,dg. \end{align} $$
Here,
![]() $\delta =\left (\begin {smallmatrix}&I_{kc}\\-I_{kc}\end {smallmatrix}\right )\cdot \operatorname {\mathrm {diag}}(I_{(k-1)c},\left (\begin {smallmatrix}I_{c}&I_{c}\\&I_{c}\end {smallmatrix}\right ),I_{(k-1)c})\in H(F)$
. On factorizable data, the right-hand side (r.h.s.) can be written as an Euler product of local integrals. In fact, in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] we obtained an almost Euler product, in the sense that the places with ramified or Archimedean data appear together as one integral; the full Euler product was obtained in [Reference Cai, Friedberg and KaplanCFK22] after the uniqueness of the
$\delta =\left (\begin {smallmatrix}&I_{kc}\\-I_{kc}\end {smallmatrix}\right )\cdot \operatorname {\mathrm {diag}}(I_{(k-1)c},\left (\begin {smallmatrix}I_{c}&I_{c}\\&I_{c}\end {smallmatrix}\right ),I_{(k-1)c})\in H(F)$
. On factorizable data, the right-hand side (r.h.s.) can be written as an Euler product of local integrals. In fact, in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] we obtained an almost Euler product, in the sense that the places with ramified or Archimedean data appear together as one integral; the full Euler product was obtained in [Reference Cai, Friedberg and KaplanCFK22] after the uniqueness of the
![]() $(k,c)$
models was proved in general, in [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23].
$(k,c)$
models was proved in general, in [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23].
Now, at almost all places, the local integrals consist of unramified data. The main local result of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] was the computation of these integrals. The infinite product over the places with unramified data is
![]() $L^S(s,\pi \times \tau )$
divided by a product of partial L-functions which constitute the normalizing factor of the Eisenstein series.
$L^S(s,\pi \times \tau )$
divided by a product of partial L-functions which constitute the normalizing factor of the Eisenstein series.
The computation of the integrals with unramified data was carried out in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] through a sequence of reductions: The
![]() $G\times \operatorname {\mathrm {GL}}_k$
integral was reduced to a doubling integral for
$G\times \operatorname {\mathrm {GL}}_k$
integral was reduced to a doubling integral for
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
(also defined in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19]), then to the case of
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
(also defined in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19]), then to the case of
![]() $n=1$
, that is, to a
$n=1$
, that is, to a
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
integral. Since the representation of
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
integral. Since the representation of
![]() $\operatorname {\mathrm {GL}}_k$
is irreducible and generic (it is a local component of
$\operatorname {\mathrm {GL}}_k$
is irreducible and generic (it is a local component of
![]() $\tau $
), it is natural to compute this integral via the theory of Rankin–Selberg integrals for
$\tau $
), it is natural to compute this integral via the theory of Rankin–Selberg integrals for
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
and
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
and
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{2k}$
of [Reference Jacquet and ShalikaJS81b, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83].
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{2k}$
of [Reference Jacquet and ShalikaJS81b, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83].
1.2 Doubling for coverings
Simply put, the purpose of this work is to extend this construction to representations of covering groups of
![]() $G=\operatorname {\mathrm {Sp}}_{2n}$
. For a positive integer
$G=\operatorname {\mathrm {Sp}}_{2n}$
. For a positive integer
![]() $m>1$
, assume that F contains the full group
$m>1$
, assume that F contains the full group
![]() $\mu _m$
of m-th roots of unity, and let
$\mu _m$
of m-th roots of unity, and let
![]() $G^{(m)}(\mathbb {A})$
be the m-fold covering of
$G^{(m)}(\mathbb {A})$
be the m-fold covering of
![]() $G(\mathbb {A})$
constructed by Matsumoto [Reference MatsumotoMat69] (following [Reference MooreMoo68, Reference SteinbergSte68]), defined using a global m-th order Hilbert symbol (
$G(\mathbb {A})$
constructed by Matsumoto [Reference MatsumotoMat69] (following [Reference MooreMoo68, Reference SteinbergSte68]), defined using a global m-th order Hilbert symbol (
![]() $G^{(1)}=G$
). Then
$G^{(1)}=G$
). Then
![]() $G^{(m)}(\mathbb {A})$
is a central covering group of
$G^{(m)}(\mathbb {A})$
is a central covering group of
![]() $G(\mathbb {A})$
by
$G(\mathbb {A})$
by
![]() $\mu _m$
. Within the framework of Brylinski and Deligne [Reference Brylinski and DeligneBD01], this is the unique covering, which corresponds to the integer valued Weyl group invariant quadratic form
$\mu _m$
. Within the framework of Brylinski and Deligne [Reference Brylinski and DeligneBD01], this is the unique covering, which corresponds to the integer valued Weyl group invariant quadratic form
![]() $\mathcal {Q}$
on the cocharacter group of a maximal torus of G, which is
$\mathcal {Q}$
on the cocharacter group of a maximal torus of G, which is
![]() $1$
on the short coroots ([Reference Brylinski and DeligneBD01, Proposition 4.15]).
$1$
on the short coroots ([Reference Brylinski and DeligneBD01, Proposition 4.15]).
In the linear setting, the global construction of the doubling method is based on the restriction of the Eisenstein series or its Fourier coefficient to a function on
![]() $G(\mathbb {A})\times G(\mathbb {A})$
. Locally, we have a Jacquet functor along
$G(\mathbb {A})\times G(\mathbb {A})$
. Locally, we have a Jacquet functor along
![]() $(U(F_{\nu }),(\psi _{\nu })_U)$
applied to
$(U(F_{\nu }),(\psi _{\nu })_U)$
applied to
![]() $\operatorname {\mathrm {Ind}}_{P(F_{\nu })}^{H(F_{\nu })}((\mathcal {E}_{\tau })_{\nu }\delta _P^s)$
at each place
$\operatorname {\mathrm {Ind}}_{P(F_{\nu })}^{H(F_{\nu })}((\mathcal {E}_{\tau })_{\nu }\delta _P^s)$
at each place
![]() $\nu $
of F, and one fundamental property is that the resulting Jacquet module restricts to a multiplicity free representation of
$\nu $
of F, and one fundamental property is that the resulting Jacquet module restricts to a multiplicity free representation of
![]() $G(F_{\nu })\times G(F_{\nu })$
, outside a discrete subset of
$G(F_{\nu })\times G(F_{\nu })$
, outside a discrete subset of
![]() $s\in \mathbb {C}$
.
$s\in \mathbb {C}$
.
Restriction is much more subtle for covering groups. For a covering
![]() $\widetilde {H}$
of H and a subgroup L of H, let
$\widetilde {H}$
of H and a subgroup L of H, let
![]() $\widetilde {L}$
be the restriction of the covering to L. It is always a subgroup of
$\widetilde {L}$
be the restriction of the covering to L. It is always a subgroup of
![]() $\widetilde {H}$
, but the restriction
$\widetilde {H}$
, but the restriction
![]() $\mathrm {H}^2(H,\mu _m)\rightarrow \mathrm {H}^2(L,\mu _m)$
(
$\mathrm {H}^2(H,\mu _m)\rightarrow \mathrm {H}^2(L,\mu _m)$
(
![]() $2$
-nd cohomology for topological groups) depends on the precise embedding of L. For example, consider the
$2$
-nd cohomology for topological groups) depends on the precise embedding of L. For example, consider the
![]() $2$
-fold covering of
$2$
-fold covering of
![]() $\operatorname {\mathrm {GL}}_{2d}$
of Kazhdan and Patterson [Reference Kazhdan and PattersonKP84] over a local field: If
$\operatorname {\mathrm {GL}}_{2d}$
of Kazhdan and Patterson [Reference Kazhdan and PattersonKP84] over a local field: If
![]() $\operatorname {\mathrm {GL}}_d$
is embedded via
$\operatorname {\mathrm {GL}}_d$
is embedded via
![]() $g\mapsto \operatorname {\mathrm {diag}}(g,I_d)$
,
$g\mapsto \operatorname {\mathrm {diag}}(g,I_d)$
,
![]() $\widetilde {\operatorname {\mathrm {GL}}}_d$
is a similar
$\widetilde {\operatorname {\mathrm {GL}}}_d$
is a similar
![]() $2$
-fold covering, but for the map
$2$
-fold covering, but for the map
![]() $g\mapsto \operatorname {\mathrm {diag}}(g,g)$
,
$g\mapsto \operatorname {\mathrm {diag}}(g,g)$
,
![]() $\widetilde {\operatorname {\mathrm {GL}}}_d$
is either trivial or not even among the coverings of [Reference Kazhdan and PattersonKP84], depending on the field (it is, however, a covering of [Reference Brylinski and DeligneBD01]; see below). This means that the embedding of
$\widetilde {\operatorname {\mathrm {GL}}}_d$
is either trivial or not even among the coverings of [Reference Kazhdan and PattersonKP84], depending on the field (it is, however, a covering of [Reference Brylinski and DeligneBD01]; see below). This means that the embedding of
![]() $G\times G$
in H has to be consistent with the choice of covering group
$G\times G$
in H has to be consistent with the choice of covering group
![]() $\widetilde {G}$
on each of the factors to begin with.
$\widetilde {G}$
on each of the factors to begin with.
A second problem concerns the lift of automorphisms of linear groups to their coverings. Since the covering groups in this work are central, H certainly acts on
![]() $H^{(m)}$
by conjugation, but a trivial action might lift to a nontrivial action. For instance, the inverse image of an abelian subgroup might not be abelian, and an inverse image of the center might not be central (nor abelian). We must then verify that both copies of
$H^{(m)}$
by conjugation, but a trivial action might lift to a nontrivial action. For instance, the inverse image of an abelian subgroup might not be abelian, and an inverse image of the center might not be central (nor abelian). We must then verify that both copies of
![]() $\widetilde {G}$
commute.
$\widetilde {G}$
commute.
A third difficulty is related to local-global issues. Locally, we have the block-compatible
![]() $2$
-cocycle
$2$
-cocycle
![]() $\sigma $
of Banks et al. [Reference Banks, Levy and SepanskiBLS99], which is convenient for computations, and is compatible with restrictions in a certain strong sense. For example, the restriction of
$\sigma $
of Banks et al. [Reference Banks, Levy and SepanskiBLS99], which is convenient for computations, and is compatible with restrictions in a certain strong sense. For example, the restriction of
![]() $H^{(m)}$
to the direct factor
$H^{(m)}$
to the direct factor
![]() $\operatorname {\mathrm {Sp}}_{2c}$
of
$\operatorname {\mathrm {Sp}}_{2c}$
of
![]() $M_Q$
is
$M_Q$
is
![]() $\operatorname {\mathrm {Sp}}_{2c}^{(m)}$
. Globally, however, the product
$\operatorname {\mathrm {Sp}}_{2c}^{(m)}$
. Globally, however, the product
![]() $\prod _{\nu }\sigma _{\nu }$
is not defined on
$\prod _{\nu }\sigma _{\nu }$
is not defined on
![]() $H^{(m)}(\mathbb {A})$
, so a global
$H^{(m)}(\mathbb {A})$
, so a global
![]() $2$
-cocycle must be defined by normalizing
$2$
-cocycle must be defined by normalizing
![]() $\sigma _{\nu }$
at almost all places, but then the compatibility properties are in general lost (a similar issue was treated in [Reference TakedaTak14]).
$\sigma _{\nu }$
at almost all places, but then the compatibility properties are in general lost (a similar issue was treated in [Reference TakedaTak14]).
One precondition for the study of automorphic forms on covering groups is the splitting of the global covering over the rational points of the group. This is guaranteed, for example, for the covering group constructed using a Hilbert symbol, by the reciprocity law for the symbol. Here,
![]() $\prod _{\nu }\sigma _{\nu }$
is defined on
$\prod _{\nu }\sigma _{\nu }$
is defined on
![]() $H(F)$
, and can be used to define this (unique) splitting.
$H(F)$
, and can be used to define this (unique) splitting.
The next component to extend to the covering is
![]() $\mathcal {E}_{\tau }$
, the generalized Speh representation. Let
$\mathcal {E}_{\tau }$
, the generalized Speh representation. Let
![]() $\tau $
be a genuine irreducible cuspidal automorphic representation of a covering of
$\tau $
be a genuine irreducible cuspidal automorphic representation of a covering of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
, say,
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
, say,
![]() $\widetilde {\operatorname {\mathrm {GL}}}_k(\mathbb {A})$
. For the covering groups under consideration, the coverings are split canonically over unipotent subgroups (see [Reference SteinbergSte62, Reference MatsumotoMat69] or the general result of [Reference Mœglin and WaldspurgerMW95, Appendix I]). Therefore, the definitions of Fourier coefficients along unipotent subgroups, and locally Jacquet functors, immediately extend to covering groups. Alas, uniqueness results often break down. For example, the Fourier expansion of Shalika [Reference ShalikaSha74] implies in particular that
$\widetilde {\operatorname {\mathrm {GL}}}_k(\mathbb {A})$
. For the covering groups under consideration, the coverings are split canonically over unipotent subgroups (see [Reference SteinbergSte62, Reference MatsumotoMat69] or the general result of [Reference Mœglin and WaldspurgerMW95, Appendix I]). Therefore, the definitions of Fourier coefficients along unipotent subgroups, and locally Jacquet functors, immediately extend to covering groups. Alas, uniqueness results often break down. For example, the Fourier expansion of Shalika [Reference ShalikaSha74] implies in particular that
![]() $\tau $
is globally generic, as in the linear case, but in sharp contrast almost all of the local components of
$\tau $
is globally generic, as in the linear case, but in sharp contrast almost all of the local components of
![]() $\tau $
admit a number of Whittaker models which is polynomial in the degree of the covering (see, e.g., [Reference Kazhdan and PattersonKP84, Reference McNamaraMcN12, Reference Chinta and OffenCO13]). The reason for this is that (as already observed above) preimages of abelian subgroups need not be abelian in coverings, and in particular genuine irreducible representations of the preimage of the diagonal torus of
$\tau $
admit a number of Whittaker models which is polynomial in the degree of the covering (see, e.g., [Reference Kazhdan and PattersonKP84, Reference McNamaraMcN12, Reference Chinta and OffenCO13]). The reason for this is that (as already observed above) preimages of abelian subgroups need not be abelian in coverings, and in particular genuine irreducible representations of the preimage of the diagonal torus of
![]() $\operatorname {\mathrm {GL}}_k(F_{\nu })$
are finite-dimensional but not one-dimensional. Thus, the naive extension of
$\operatorname {\mathrm {GL}}_k(F_{\nu })$
are finite-dimensional but not one-dimensional. Thus, the naive extension of
![]() $\mathcal {E}_{\tau }$
to
$\mathcal {E}_{\tau }$
to
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{kc}(\mathbb {A})$
will not work, already for
$\widetilde {\operatorname {\mathrm {GL}}}_{kc}(\mathbb {A})$
will not work, already for
![]() $c=1$
.
$c=1$
.
Suzuki [Reference SuzukiSuz98] extended the generalized Speh representations to r-fold covering groups (of [Reference Kazhdan and PattersonKP84]), under certain global (and also local, implicitly) assumptions. Given
![]() $\tau $
as above, he produced a residual representation of an r-fold covering group
$\tau $
as above, he produced a residual representation of an r-fold covering group
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{rk}(\mathbb {A})$
, which is globally generic and admits unique Whittaker models at almost all places (at least). The idea behind his construction was the local correspondence obtained in [Reference SuzukiSuz98] between certain irreducible unramified representations of
$\widetilde {\operatorname {\mathrm {GL}}}_{rk}(\mathbb {A})$
, which is globally generic and admits unique Whittaker models at almost all places (at least). The idea behind his construction was the local correspondence obtained in [Reference SuzukiSuz98] between certain irreducible unramified representations of
![]() $\operatorname {\mathrm {GL}}_k$
and
$\operatorname {\mathrm {GL}}_k$
and
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{rk}$
(for the latter, genuine), where each unramified quasi-character
$\widetilde {\operatorname {\mathrm {GL}}}_{rk}$
(for the latter, genuine), where each unramified quasi-character
![]() $\chi _i$
was replaced with an exceptional representation (in the sense of [Reference Kazhdan and PattersonKP84]) of
$\chi _i$
was replaced with an exceptional representation (in the sense of [Reference Kazhdan and PattersonKP84]) of
![]() $\widetilde {\operatorname {\mathrm {GL}}}_r$
twisted by
$\widetilde {\operatorname {\mathrm {GL}}}_r$
twisted by
![]() $\chi _i$
. To prove the existence of the residue, the computation of the constant term from [Reference JacquetJac84] was carried out on
$\chi _i$
. To prove the existence of the residue, the computation of the constant term from [Reference JacquetJac84] was carried out on
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{rk}$
, and the analysis of the poles required several assumptions on the partial L-functions of
$\widetilde {\operatorname {\mathrm {GL}}}_{rk}$
, and the analysis of the poles required several assumptions on the partial L-functions of
![]() $\tau \times \tau ^{\vee }$
(
$\tau \times \tau ^{\vee }$
(
![]() $\tau ^{\vee }$
- the contragredient of
$\tau ^{\vee }$
- the contragredient of
![]() $\tau $
). Basically, one has to assume that the theory of automorphic L-functions of
$\tau $
). Basically, one has to assume that the theory of automorphic L-functions of
![]() $\operatorname {\mathrm {GL}}_k\times \operatorname {\mathrm {GL}}_k$
of Jacquet and Shalika [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b] can be applied to
$\operatorname {\mathrm {GL}}_k\times \operatorname {\mathrm {GL}}_k$
of Jacquet and Shalika [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b] can be applied to
![]() $\widetilde {\operatorname {\mathrm {GL}}}_k(\mathbb {A})$
.
$\widetilde {\operatorname {\mathrm {GL}}}_k(\mathbb {A})$
.
The construction of [Reference SuzukiSuz98] provides us with global
![]() $(rk,1)$
representations, that is, the case
$(rk,1)$
representations, that is, the case
![]() $c=1$
. The extension of his ideas to
$c=1$
. The extension of his ideas to
![]() $c>1$
provides a residual representation
$c>1$
provides a residual representation
![]() $\mathcal {E}_{\tau }$
of
$\mathcal {E}_{\tau }$
of
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{rkc}(\mathbb {A})$
, which is
$\widetilde {\operatorname {\mathrm {GL}}}_{rkc}(\mathbb {A})$
, which is
![]() $(rk,c)$
, and in particular all of its local unramified components admit unique models, a phenomenon which is very rare for covering groups.
$(rk,c)$
, and in particular all of its local unramified components admit unique models, a phenomenon which is very rare for covering groups.
As above, let
![]() $m>1$
be an integer, and put
$m>1$
be an integer, and put
![]() $r=m$
if m is odd, otherwise
$r=m$
if m is odd, otherwise
![]() $r=m/2$
. Let
$r=m/2$
. Let
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
be the covering of
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
be the covering of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
obtained by restriction from
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
obtained by restriction from
![]() $\operatorname {\mathrm {Sp}}_{2k}^{(m)}(\mathbb {A})$
to the Levi part of the Siegel subgroup. It is the cover of
$\operatorname {\mathrm {Sp}}_{2k}^{(m)}(\mathbb {A})$
to the Levi part of the Siegel subgroup. It is the cover of
![]() $\operatorname {\mathrm {GL}}_{k}(\mathbb {A})$
of [Reference Brylinski and DeligneBD01] defined by letting the quadratic form
$\operatorname {\mathrm {GL}}_{k}(\mathbb {A})$
of [Reference Brylinski and DeligneBD01] defined by letting the quadratic form
![]() $\mathcal {Q}$
be
$\mathcal {Q}$
be
![]() $-2$
on all the coroots, in particular it is not one of the coverings from [Reference Kazhdan and PattersonKP84]. This cover was recently introduced by Savin [Reference SavinSav] (in a local context) and also studied by Gao [Reference GaoGao18a, Reference GaoGao21]. Morally, it is an r-fold cover. For example, the quadratic Hilbert symbol composed with the determinant is a (global or local)
$-2$
on all the coroots, in particular it is not one of the coverings from [Reference Kazhdan and PattersonKP84]. This cover was recently introduced by Savin [Reference SavinSav] (in a local context) and also studied by Gao [Reference GaoGao18a, Reference GaoGao21]. Morally, it is an r-fold cover. For example, the quadratic Hilbert symbol composed with the determinant is a (global or local)
![]() $2$
-cocycle for
$2$
-cocycle for
![]() $\operatorname {\mathrm {GL}}_{k}^{(2,1)}$
. One of the useful properties of
$\operatorname {\mathrm {GL}}_{k}^{(2,1)}$
. One of the useful properties of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
is that direct factors of Levi subgroups of
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
is that direct factors of Levi subgroups of
![]() $\operatorname {\mathrm {GL}}_k(F_{\nu })$
do commute in the cover ([Reference SavinSav, Reference GaoGao18a]). Another interesting property is that the dual group of
$\operatorname {\mathrm {GL}}_k(F_{\nu })$
do commute in the cover ([Reference SavinSav, Reference GaoGao18a]). Another interesting property is that the dual group of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
(in the sense of, for example, [Reference McNamaraMcN12]) is
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
(in the sense of, for example, [Reference McNamaraMcN12]) is
![]() $\operatorname {\mathrm {GL}}_{k}(\mathbb {C})$
for all m (see [Reference GaoGao18a]). We also note that the main involution of
$\operatorname {\mathrm {GL}}_{k}(\mathbb {C})$
for all m (see [Reference GaoGao18a]). We also note that the main involution of
![]() $\operatorname {\mathrm {GL}}_{k}(F_{\nu })$
admits a trivial extension to
$\operatorname {\mathrm {GL}}_{k}(F_{\nu })$
admits a trivial extension to
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
, though this is not the only extension (cf. [Reference KableKab99]).
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(F_{\nu })$
, though this is not the only extension (cf. [Reference KableKab99]).
We mention that Gao [Reference GaoGao17, Reference GaoGao18a, Reference GaoGao21] studied the aforementioned exceptional representations, in the very general context of the covering groups of [Reference Brylinski and DeligneBD01] of split reductive groups, locally and globally (we will use his results on exceptional representations for
![]() $\operatorname {\mathrm {GL}}_{r}^{(m,r)}$
). In particular, in [Reference GaoGao21] he computed the Whittaker–Fourier coefficient of an Eisenstein series attached to a global exceptional representation, in certain cases. He then showed that this coefficient is essentially the reciprocal of a global partial L-function (as in the linear case), thereby extending a result of [Reference SuzukiSuz97]. But note that these exceptional representations afford unique Whittaker models.
$\operatorname {\mathrm {GL}}_{r}^{(m,r)}$
). In particular, in [Reference GaoGao21] he computed the Whittaker–Fourier coefficient of an Eisenstein series attached to a global exceptional representation, in certain cases. He then showed that this coefficient is essentially the reciprocal of a global partial L-function (as in the linear case), thereby extending a result of [Reference SuzukiSuz97]. But note that these exceptional representations afford unique Whittaker models.
Let
![]() $\tau $
be a genuine irreducible cuspidal automorphic representation of
$\tau $
be a genuine irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
. Let
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
. Let
![]() $c=2n$
. The representation
$c=2n$
. The representation
![]() $\mathcal {E}_{\tau }$
is the residual representation of an Eisenstein series attached to a representation of
$\mathcal {E}_{\tau }$
is the residual representation of an Eisenstein series attached to a representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
parabolically induced from
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
parabolically induced from
![]() $|\det |^{\zeta _1}\tau \otimes \ldots \otimes |\det |^{\zeta _{rc}}\tau $
, the multiresidue taken at
$|\det |^{\zeta _1}\tau \otimes \ldots \otimes |\det |^{\zeta _{rc}}\tau $
, the multiresidue taken at
![]() $((rc-1)/(2r),(rc-3)/(2r),\ldots , (1-rc)/(2r))$
. As in [Reference SuzukiSuz98], the construction is conjectural. Here, it is based on two assumptions: locally Conjecture 50 and globally Conjecture 51, which are known when
$((rc-1)/(2r),(rc-3)/(2r),\ldots , (1-rc)/(2r))$
. As in [Reference SuzukiSuz98], the construction is conjectural. Here, it is based on two assumptions: locally Conjecture 50 and globally Conjecture 51, which are known when
![]() $m=1$
(the linear case) as well as when
$m=1$
(the linear case) as well as when
![]() $m=2$
or
$m=2$
or
![]() $k=1$
(and all
$k=1$
(and all
![]() $m\geq 1$
). These are the current cases where
$m\geq 1$
). These are the current cases where
![]() $\mathcal {E}_{\tau }\ne 0$
unconditionally. In general, these conjectures are natural granted a Shimura type correspondence for coverings of general linear groups, and it is perhaps possible to study them by extending the correspondences from [Reference FlickerFli80, Reference Flicker and KazhdanFK86] which used the trace formula (see also [Reference Piatetski-ShapiroPS84]). Granted the conjectures, we prove that
$\mathcal {E}_{\tau }\ne 0$
unconditionally. In general, these conjectures are natural granted a Shimura type correspondence for coverings of general linear groups, and it is perhaps possible to study them by extending the correspondences from [Reference FlickerFli80, Reference Flicker and KazhdanFK86] which used the trace formula (see also [Reference Piatetski-ShapiroPS84]). Granted the conjectures, we prove that
![]() $\mathcal {E}_{\tau }$
is an
$\mathcal {E}_{\tau }$
is an
![]() $(rk,c)$
representation. More precisely, we prove that the residual representation of the Eisenstein series contains an irreducible
$(rk,c)$
representation. More precisely, we prove that the residual representation of the Eisenstein series contains an irreducible
![]() $(rk,c)$
subrepresentation, which is what we denote by
$(rk,c)$
subrepresentation, which is what we denote by
![]() $\mathcal {E}_{\tau }$
. See § 3.4.
$\mathcal {E}_{\tau }$
. See § 3.4.
Let
![]() $H=\operatorname {\mathrm {Sp}}_{2rkc}$
, and take the Siegel parabolic subgroup P, now with
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
, and take the Siegel parabolic subgroup P, now with
![]() $M_P=\operatorname {\mathrm {GL}}_{rkc}$
. The Eisenstein series
$M_P=\operatorname {\mathrm {GL}}_{rkc}$
. The Eisenstein series
![]() $E(h;s,f)$
is defined for a standard
$E(h;s,f)$
is defined for a standard
![]() $\widetilde {K}_H$
-finite section f of
$\widetilde {K}_H$
-finite section f of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}(\mathbb {A})}^{H^{(m)}(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
, similarly to Equation (1.1), taking into account the splitting of
$\operatorname {\mathrm {Ind}}_{\widetilde {P}(\mathbb {A})}^{H^{(m)}(\mathbb {A})}(\mathcal {E}_{\tau }\delta _P^s)$
, similarly to Equation (1.1), taking into account the splitting of
![]() $H(F)$
into
$H(F)$
into
![]() $H^{(m)}(\mathbb {A})$
. The Fourier coefficient is simple to define: The parabolic subgroup Q, U and
$H^{(m)}(\mathbb {A})$
. The Fourier coefficient is simple to define: The parabolic subgroup Q, U and
![]() $\psi _U$
are defined as above, except that
$\psi _U$
are defined as above, except that
![]() $M_Q$
consists of
$M_Q$
consists of
![]() $rk-1$
copies of
$rk-1$
copies of
![]() $\operatorname {\mathrm {GL}}_c$
instead of
$\operatorname {\mathrm {GL}}_c$
instead of
![]() $k-1$
copies, multiplied by
$k-1$
copies, multiplied by
![]() $\operatorname {\mathrm {Sp}}_{2c}$
.
$\operatorname {\mathrm {Sp}}_{2c}$
.
The group
![]() $G(\mathbb {A})\times G(\mathbb {A})$
is still embedded in the stabilizer of
$G(\mathbb {A})\times G(\mathbb {A})$
is still embedded in the stabilizer of
![]() $\psi _U$
in
$\psi _U$
in
![]() $M_Q(\mathbb {A})$
, but as explained above, we have to verify that the restriction of
$M_Q(\mathbb {A})$
, but as explained above, we have to verify that the restriction of
![]() $H^{(m)}(\mathbb {A})$
to each copy is
$H^{(m)}(\mathbb {A})$
to each copy is
![]() $G^{(m)}(\mathbb {A})$
and that they commute in
$G^{(m)}(\mathbb {A})$
and that they commute in
![]() $H^{(m)}(\mathbb {A})$
. In fact, even more care is needed because while restriction does give
$H^{(m)}(\mathbb {A})$
. In fact, even more care is needed because while restriction does give
![]() $G^{(m)}(\mathbb {A})$
, an equality in
$G^{(m)}(\mathbb {A})$
, an equality in
![]() $\mathrm {H}^2(G(\mathbb {A}),\mu _m)$
is only up to a
$\mathrm {H}^2(G(\mathbb {A}),\mu _m)$
is only up to a
![]() $2$
-coboundary. In the computation, we must be sensitive to this distinction because we have one representation
$2$
-coboundary. In the computation, we must be sensitive to this distinction because we have one representation
![]() $\pi $
of
$\pi $
of
![]() $G^{(m)}(\mathbb {A})$
, but the restrictions to each copy are only isomorphic. At least this isomorphism is canonical because
$G^{(m)}(\mathbb {A})$
, but the restrictions to each copy are only isomorphic. At least this isomorphism is canonical because
![]() $G(\mathbb {A})$
is perfect.
$G(\mathbb {A})$
is perfect.
Similarly to the linear case, we require
![]() $E^{U,\psi _U}(h;s,f)$
to be an automorphic function on
$E^{U,\psi _U}(h;s,f)$
to be an automorphic function on
![]() $G^{(m)}(\mathbb {A})\times G^{(m)}(\mathbb {A})$
. Here, we have three identifications of
$G^{(m)}(\mathbb {A})\times G^{(m)}(\mathbb {A})$
. Here, we have three identifications of
![]() $G(F)$
: One in each copy of
$G(F)$
: One in each copy of
![]() $G^{(m)}(\mathbb {A})$
, and a third one through
$G^{(m)}(\mathbb {A})$
, and a third one through
![]() $H(F)$
, and our definitions must ensure that they are all compatible.
$H(F)$
, and our definitions must ensure that they are all compatible.
In addition,
![]() ${}^{\iota }$
must lift to an involution of
${}^{\iota }$
must lift to an involution of
![]() $G^{(m)}(\mathbb {A})$
; since it is only an outer involution of G, it is not even clear such a lift exists, locally or globally, but this is in fact true.
$G^{(m)}(\mathbb {A})$
; since it is only an outer involution of G, it is not even clear such a lift exists, locally or globally, but this is in fact true.
Now, for a genuine irreducible cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $G^{(m)}(\mathbb {A})$
and a pair of cusp forms
$G^{(m)}(\mathbb {A})$
and a pair of cusp forms
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
in the space of
$\varphi _2$
in the space of
![]() $\pi $
, we define the global integral
$\pi $
, we define the global integral
![]() $Z(s,\varphi _1,\varphi _2,f)$
, which is not very different from the linear version. The first main result of this paper is the following:
$Z(s,\varphi _1,\varphi _2,f)$
, which is not very different from the linear version. The first main result of this paper is the following:
Theorem (Theorem 63).
The integral
![]() $Z(s,\varphi _1,\varphi _2,f)$
given by Equation (4.2) is well defined, absolutely convergent away from the poles of the Eisenstein series and admits meromorphic continuation to
$Z(s,\varphi _1,\varphi _2,f)$
given by Equation (4.2) is well defined, absolutely convergent away from the poles of the Eisenstein series and admits meromorphic continuation to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
This theorem and the theorem below hold unconditionally only when
![]() $r=1$
or
$r=1$
or
![]() $k=1$
(but all
$k=1$
(but all
![]() $m\geq 1$
), otherwise we need to assume Conjectures 50 and 51 in order to prove the existence and properties of
$m\geq 1$
), otherwise we need to assume Conjectures 50 and 51 in order to prove the existence and properties of
![]() $\mathcal {E}_{\tau }$
.
$\mathcal {E}_{\tau }$
.
The basic identity for this integral, which is the covering analog of Equation (1.2), is obtained using the unfolding technique of [Reference Gourevitch and KaplanGK23, § 3.2] (a preliminary version was sketched in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19]). Most of the proof in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Gourevitch and KaplanGK23] was based on arguments involving unipotent groups and the vanishing properties of
![]() $\mathcal {E}_{\tau }$
. These extend naturally to our setup, with the covering version of
$\mathcal {E}_{\tau }$
. These extend naturally to our setup, with the covering version of
![]() $\mathcal {E}_{\tau }$
. However, a crucial observation in the linear case underlying the unfolding is that the summand of
$\mathcal {E}_{\tau }$
. However, a crucial observation in the linear case underlying the unfolding is that the summand of
![]() $E^{U,\psi _U}(h;s,f)$
corresponding to the double coset
$E^{U,\psi _U}(h;s,f)$
corresponding to the double coset
![]() $P\delta (G\times G)U$
is left-invariant under the subgroup
$P\delta (G\times G)U$
is left-invariant under the subgroup
![]() $\{(g,{}^{\iota }g):g\in G(\mathbb {A})\}$
. As a rule, covering groups of H do not split over reductive subgroups of H, not even locally. Carrying out this step in
$\{(g,{}^{\iota }g):g\in G(\mathbb {A})\}$
. As a rule, covering groups of H do not split over reductive subgroups of H, not even locally. Carrying out this step in
![]() $H^{(m)}(\mathbb {A})$
requires an elaborate description of the splitting. We then deduce our global identity:
$H^{(m)}(\mathbb {A})$
requires an elaborate description of the splitting. We then deduce our global identity:
Theorem (Theorem 64).
In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
$\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
![]() $Z(s,\varphi _1,\varphi _2,f)$
is equal to Integral (4.4).
$Z(s,\varphi _1,\varphi _2,f)$
is equal to Integral (4.4).
On factorizable data, the integral (4.4) factorizes into an almost Euler product given by Equation (4.16). This is the starting point for the development of the local theory. We note that, when
![]() $r=1$
or
$r=1$
or
![]() $k=1$
, the recent results of [Reference KaplanKap23] imply that the integral (4.4) is in fact a full Euler product.
$k=1$
, the recent results of [Reference KaplanKap23] imply that the integral (4.4) is in fact a full Euler product.
The main local result here is the computation of the integrals with unramified data. The first step is to define the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals. The theory of covering groups for simply connected groups such as
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals. The theory of covering groups for simply connected groups such as
![]() $\operatorname {\mathrm {SL}}_n$
or
$\operatorname {\mathrm {SL}}_n$
or
![]() $\operatorname {\mathrm {Spin}}_n$
is considerably simpler than the general reductive case. For example, coverings for
$\operatorname {\mathrm {Spin}}_n$
is considerably simpler than the general reductive case. For example, coverings for
![]() $\operatorname {\mathrm {SL}}_n$
are unique (given a Steinberg cocycle), while coverings of
$\operatorname {\mathrm {SL}}_n$
are unique (given a Steinberg cocycle), while coverings of
![]() $\operatorname {\mathrm {GL}}_n$
are parameterized by two integers ([Reference GaoGao18a]; see also [Reference Brylinski and DeligneBD01]). As another example, at almost all places
$\operatorname {\mathrm {GL}}_n$
are parameterized by two integers ([Reference GaoGao18a]; see also [Reference Brylinski and DeligneBD01]). As another example, at almost all places
![]() $\nu $
of F,
$\nu $
of F,
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}$
is split over a maximal compact open subgroup of
$\operatorname {\mathrm {GL}}_n^{(m,r)}$
is split over a maximal compact open subgroup of
![]() $\operatorname {\mathrm {GL}}_n$
, but this splitting is not unique (as opposed to the similar splitting of
$\operatorname {\mathrm {GL}}_n$
, but this splitting is not unique (as opposed to the similar splitting of
![]() $G^{(m)}$
). In addition, the construction of the integral now involves a diagonal embedding of
$G^{(m)}$
). In addition, the construction of the integral now involves a diagonal embedding of
![]() $\operatorname {\mathrm {GL}}_n$
in
$\operatorname {\mathrm {GL}}_n$
in
![]() $\operatorname {\mathrm {GL}}_{2rkn}$
, and although
$\operatorname {\mathrm {GL}}_{2rkn}$
, and although
![]() $\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
is split over this subgroup, the splitting is not unique.
$\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
is split over this subgroup, the splitting is not unique.
The computation of the doubling integral for
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
again involves an extension of the Rankin–Selberg theory, now to
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
again involves an extension of the Rankin–Selberg theory, now to
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{2rk}^{(m,r)}$
integrals. In the absence of uniqueness for Whittaker models, it is not clear such an extension in general is feasible. However, in this work the representations of
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_{2rk}^{(m,r)}$
integrals. In the absence of uniqueness for Whittaker models, it is not clear such an extension in general is feasible. However, in this work the representations of
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_{2rk}^{(m,r)}$
do admit unique Whittaker models; for example, the representation of
$\operatorname {\mathrm {GL}}_{2rk}^{(m,r)}$
do admit unique Whittaker models; for example, the representation of
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
is a local component of
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
is a local component of
![]() $\mathcal {E}_{\tau }$
with
$\mathcal {E}_{\tau }$
with
![]() $c=1$
.
$c=1$
.
To evaluate these Rankin–Selberg type integrals, we need to express the value of the normalized unramified Whittaker function W of a specific representation of
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
attached to
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
attached to
![]() $\tau _{\nu }$
, at the identity, as a special value of an L-function, and to relate between the value of W on the diagonal elements
$\tau _{\nu }$
, at the identity, as a special value of an L-function, and to relate between the value of W on the diagonal elements
![]() $\operatorname {\mathrm {diag}}(a^{rl},I_{rk-1})$
(essentially) and the l-th complete symmetric polynomial in the Satake parameter of
$\operatorname {\mathrm {diag}}(a^{rl},I_{rk-1})$
(essentially) and the l-th complete symmetric polynomial in the Satake parameter of
![]() $\tau _{\nu }$
. In the linear case, these results are known and follow from the Casselman–Shalika formula ([Reference ShintaniShi76, Reference CasselmanCas80]). This is another aspect which is difficult to generalize to covering groups.
$\tau _{\nu }$
. In the linear case, these results are known and follow from the Casselman–Shalika formula ([Reference ShintaniShi76, Reference CasselmanCas80]). This is another aspect which is difficult to generalize to covering groups.
Perhaps the first extension of the Casselman–Shalika formula to covering groups was due to Bump, Friedberg and Hoffstein [Reference Bump, Friedberg and HoffsteinBFH91], who obtained it for the double covering of
![]() $\operatorname {\mathrm {Sp}}_{2n}$
, although this case is special because the Whittaker model is unique; more recently, their work was extended by Szpruch [Reference SzpruchSzp15] to a double covering of
$\operatorname {\mathrm {Sp}}_{2n}$
, although this case is special because the Whittaker model is unique; more recently, their work was extended by Szpruch [Reference SzpruchSzp15] to a double covering of
![]() $\operatorname {\mathrm {GSp}}_{2n}$
, where uniqueness of Whittaker models already breaks down. The Casselman–Shalika formula was extended by Chinta and Offen [Reference Chinta and OffenCO13] (using results of [Reference Kazhdan and PattersonKP84]) to the coverings of
$\operatorname {\mathrm {GSp}}_{2n}$
, where uniqueness of Whittaker models already breaks down. The Casselman–Shalika formula was extended by Chinta and Offen [Reference Chinta and OffenCO13] (using results of [Reference Kazhdan and PattersonKP84]) to the coverings of
![]() $\operatorname {\mathrm {GL}}_k$
of [Reference Kazhdan and PattersonKP84]. This formula was further extended by McNamara [Reference McNamaraMcN16] to the general coverings of unramified reductive groups of [Reference Brylinski and DeligneBD01], under the assumptions that
$\operatorname {\mathrm {GL}}_k$
of [Reference Kazhdan and PattersonKP84]. This formula was further extended by McNamara [Reference McNamaraMcN16] to the general coverings of unramified reductive groups of [Reference Brylinski and DeligneBD01], under the assumptions that
![]() $\mu _{2m}\subset F^{*}$
and
$\mu _{2m}\subset F^{*}$
and
![]() $|2m|=1$
(for the coverings of
$|2m|=1$
(for the coverings of
![]() $\operatorname {\mathrm {GL}}_k$
these assumptions were relaxed in [Reference GaoGao17]; see § 2.10). These works expressed the normalized unramified Whittaker function as a weighted sum over the Weyl group.
$\operatorname {\mathrm {GL}}_k$
these assumptions were relaxed in [Reference GaoGao17]; see § 2.10). These works expressed the normalized unramified Whittaker function as a weighted sum over the Weyl group.
A different approach, motivated by the study of Whittaker coefficients of Borel Eisenstein series on covering groups, was pursued by Brubaker et al. [Reference Brubaker, Bump and FriedbergBBF08, Reference Brubaker, Bump and FriedbergBBF11a, Reference Brubaker, Bump and FriedbergBBF11b, Reference Brubaker and FriedbergBF15]. In these works, the theory of crystal graphs was applied to express the Whittaker function as a sum over ‘decorated’ Gelfand–Tsetlin patterns.
All of these works considered general unramified principal series representations of covering groups; presumably, the loss of uniqueness for the Whittaker model has made it very difficult to further extend the linear case and relate the Whittaker function to the theory of representations of the L-group. By contrast, here we have uniqueness and it is reasonable to expect results that resemble the linear case, at least formally, and this is precisely what we obtain. To compute W we combine the Casselman–Shalika formula with the Gelfand–Tsetlin patterns description. This is perhaps the first application of Gelfand–Tsetlin patterns to the computation of local integrals which arise in the context of an integral representation. For
![]() $k\leq 2$
, the formula we seek was obtained by [Reference SuzukiSuz98], and we treat the general case. We also use a recent result of Cai [Reference CaiCai20], which enables us to argue using induction. The following is our main local result:
$k\leq 2$
, the formula we seek was obtained by [Reference SuzukiSuz98], and we treat the general case. We also use a recent result of Cai [Reference CaiCai20], which enables us to argue using induction. The following is our main local result:
Theorem (Theorem 66).
Assume
![]() $\mu _{2m}\subset F^{*}$
. The integral (4.17) with unramified data equals
$\mu _{2m}\subset F^{*}$
. The integral (4.17) with unramified data equals
 $$ \begin{align*} \frac{L_{\vartheta_{\nu}}(r\alpha s+1/2,\pi_{\nu}\times\tau_{\nu})} {[L_{\vartheta_{\nu}}(r\alpha s+rn+1/2,\tau_{\nu})]\prod\limits_{1\leq j\leq rn}L_{\vartheta_{\nu}}(2r\alpha s+2j,\tau_{\nu},\wedge^2) L_{\vartheta_{\nu}}(2r\alpha s+2j-1,\tau_{\nu},\vee^2)}. \end{align*} $$
$$ \begin{align*} \frac{L_{\vartheta_{\nu}}(r\alpha s+1/2,\pi_{\nu}\times\tau_{\nu})} {[L_{\vartheta_{\nu}}(r\alpha s+rn+1/2,\tau_{\nu})]\prod\limits_{1\leq j\leq rn}L_{\vartheta_{\nu}}(2r\alpha s+2j,\tau_{\nu},\wedge^2) L_{\vartheta_{\nu}}(2r\alpha s+2j-1,\tau_{\nu},\vee^2)}. \end{align*} $$
Here,
![]() $\alpha =rkc+1$
and
$\alpha =rkc+1$
and
![]() $L_{\vartheta _{\nu }}(r\alpha s+rn+1/2,\tau _{\nu })$
appears only for odd m.
$L_{\vartheta _{\nu }}(r\alpha s+rn+1/2,\tau _{\nu })$
appears only for odd m.
For the notation and definition of the L-factors, see § 2.8.
Note the assumption
![]() $\mu _{2m}\subset F^{*}$
. When m is even, this assumption is stronger than the condition
$\mu _{2m}\subset F^{*}$
. When m is even, this assumption is stronger than the condition
![]() $\mu _m\subset F^{*}$
needed for the existence of
$\mu _m\subset F^{*}$
needed for the existence of
![]() $G^{(m)}$
. This assumption is added throughout several parts of this work. It is needed because we use results from [Reference Brubaker, Bump and FriedbergBBF11a, Reference McNamaraMcN11, Reference GaoGao18a], where it was assumed. It also simplifies our work here, but for several claims we do provide a more general computation. See § 5.5 for more details.
$G^{(m)}$
. This assumption is added throughout several parts of this work. It is needed because we use results from [Reference Brubaker, Bump and FriedbergBBF11a, Reference McNamaraMcN11, Reference GaoGao18a], where it was assumed. It also simplifies our work here, but for several claims we do provide a more general computation. See § 5.5 for more details.
The theory of the local integrals is independent of Conjectures 50 and 51: Theorem 66 holds unconditionally with a slight modification of the construction (see Remark 88).
1.3 Further background, extensions and applications
The applicability of the doubling method to representations of
![]() $\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
was known to Piatetski-Shapiro and Rallis (see [Reference Piatetski-Shapiro and RallisPSR87, § 4.3]). The local theory of the doubling integrals of [Reference Piatetski-Shapiro and RallisPSR87] for
$\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
was known to Piatetski-Shapiro and Rallis (see [Reference Piatetski-Shapiro and RallisPSR87, § 4.3]). The local theory of the doubling integrals of [Reference Piatetski-Shapiro and RallisPSR87] for
![]() $\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
(but when
$\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
(but when
![]() $k=1$
) was developed by Gan [Reference GanGan12]. Note that
$k=1$
) was developed by Gan [Reference GanGan12]. Note that
![]() $\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
is an exceptional case, in the sense that irreducible representations do admit at most one Whittaker model. This was proved by Waldspurger [Reference WaldspurgerWal80] for
$\operatorname {\mathrm {Sp}}_{2n}^{(2)}$
is an exceptional case, in the sense that irreducible representations do admit at most one Whittaker model. This was proved by Waldspurger [Reference WaldspurgerWal80] for
![]() $n=1$
over
$n=1$
over
![]() $\mathbb {R}$
and by Szpruch [Reference SzpruchSzp07] in general (see also [Reference Bump, Friedberg and HoffsteinBFH91]). Szpruch [Reference SzpruchSzp10] then developed the Langlands–Shahidi theory for this covering. In this case, there are also integral representations, for globally generic representations by Ginzburg et al. [Reference Ginzburg, Rallis and SoudryGRS98], and for arbitrary irreducible cuspidal representations by [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11]. The local theory of the integrals of [Reference Ginzburg, Rallis and SoudryGRS98] (the generic case) was developed in [Reference KaplanKap15]. The integral presented here is the first known to the author, involving representations of
$\mathbb {R}$
and by Szpruch [Reference SzpruchSzp07] in general (see also [Reference Bump, Friedberg and HoffsteinBFH91]). Szpruch [Reference SzpruchSzp10] then developed the Langlands–Shahidi theory for this covering. In this case, there are also integral representations, for globally generic representations by Ginzburg et al. [Reference Ginzburg, Rallis and SoudryGRS98], and for arbitrary irreducible cuspidal representations by [Reference Ginzburg, Jiang, Rallis and SoudryGJRS11]. The local theory of the integrals of [Reference Ginzburg, Rallis and SoudryGRS98] (the generic case) was developed in [Reference KaplanKap15]. The integral presented here is the first known to the author, involving representations of
![]() $\operatorname {\mathrm {Sp}}_{2n}^{(m)}$
for any m.
$\operatorname {\mathrm {Sp}}_{2n}^{(m)}$
for any m.
The uniformity of the doubling method was preserved in the extension to arbitrary
![]() $k>1$
in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK22], and we expect our method and results here to generalize to coverings of other (split) classical groups and general spin groups.
$k>1$
in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK22], and we expect our method and results here to generalize to coverings of other (split) classical groups and general spin groups.
Brylinski and Deligne [Reference Brylinski and DeligneBD01] provided a general framework, functorial in nature, of covering groups for any connected reductive group. Their construction inspired numerous works on extending the Langlands program to those coverings, including [Reference SavinSav04, Reference WeissmanWei09, Reference WeissmanWei11, Reference McNamaraMcN12, Reference LiLi14a, Reference WeissmanWei14, Reference Gan and GaoGG18, Reference WeissmanWei18]. The work here can be regarded as a first attempt to launch the analytic counterpart, namely a theory of integral representations for L-functions of automorphic representations of covering groups, which also provides definitions of local factors.
The theory of Eisenstein series of Langlands (e.g., [Reference LanglandsLan67, Reference LanglandsLan76]) can be used to study the partial L-function through the constant term of the series. Gao [Reference GaoGao18b] has recently extended Langlands’ analysis of the constant term to the covering groups of [Reference Brylinski and DeligneBD01] and in particular proved the meromorphic continuation of the partial L-function (e.g., the L-function obtained here).
In the celebrated works of Cogdell et al. [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS01, Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS04] on functoriality for globally generic cuspidal representations of classical groups, the functorial lift was established via the converse theorem, for which the results on the partial L-function are not enough. One must have, among other important preliminaries, the completed L-function and its functional equation. These were only obtained by Shahidi ([Reference ShahidiSha78, Reference ShahidiSha81, Reference ShahidiSha83, Reference ShahidiSha85, Reference ShahidiSha90]) through his method of local coefficients, where uniqueness of the Whittaker model is crucial.
Unfortunately, it is difficult to extend the method of local coefficients to covering groups because local multiplicity one for Whittaker models breaks down. Consequently, it is not clear how to define the completed L-function with this approach. Nonetheless, since the dimension of the space of Whittaker functionals is finite, there have been attempts recently to define and study a generalized local coefficients matrix; see Gao et al. [Reference Gao, Shahidi, Szpruch, Akbary and GunGSS18, Reference Gao, Shahidi and SzpruchGSS23, Reference Gao, Shahidi and SzpruchGSS] and Szpruch [Reference SzpruchSzp19].
In contrast, the doubling construction can provide a definition of local factors for representations of covering groups through uniqueness properties (see [Reference Gourevitch and KaplanGK23]). In a follow-up to this work ([Reference KaplanKap]), we developed the local (ramified) theory of the integrals presented here, and, using uniqueness, defined local
![]() $\gamma $
-, L- and
$\gamma $
-, L- and
![]() $\epsilon $
-factors. We then defined a (global) completed L-function and established its functional equation. However, when
$\epsilon $
-factors. We then defined a (global) completed L-function and established its functional equation. However, when
![]() $m>2$
and
$m>2$
and
![]() $k>1$
, these definitions are still conjectural and depend on the existence and uniqueness of local
$k>1$
, these definitions are still conjectural and depend on the existence and uniqueness of local
![]() $(rk,c)$
models. These results on the models are established here when data are unramified, and it is reasonable to expect that they hold in general.
$(rk,c)$
models. These results on the models are established here when data are unramified, and it is reasonable to expect that they hold in general.
1.4 Description of the contents by section
Section 2 is devoted to preliminaries. We define the groups and provide basic notation in § 2.1. General conventions and definitions for covering groups are assembled in § 2.2. The embedding of
![]() $G\times G$
in H, which dictates most of the coverings involved, is presented in § 2.3. In § 2.4, we define the local
$G\times G$
in H, which dictates most of the coverings involved, is presented in § 2.3. In § 2.4, we define the local
![]() $2$
-cocycles. First, we recall the
$2$
-cocycles. First, we recall the
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $\operatorname {\mathrm {GL}}_{2rkc}$
of [Reference Banks, Levy and SepanskiBLS99] and describe its restriction to
$\operatorname {\mathrm {GL}}_{2rkc}$
of [Reference Banks, Levy and SepanskiBLS99] and describe its restriction to
![]() $H=\operatorname {\mathrm {Sp}}_{2rkc}$
. In Proposition 7, we write a formula for the restriction of this
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
. In Proposition 7, we write a formula for the restriction of this
![]() $2$
-cocycle to
$2$
-cocycle to
![]() $G\times G$
and, in particular, deduce that the preimages of both copies of G in
$G\times G$
and, in particular, deduce that the preimages of both copies of G in
![]() $H^{(m)}$
commute. In Corollary 9, we show that
$H^{(m)}$
commute. In Corollary 9, we show that
![]() $H^{(m)}$
is split over the group
$H^{(m)}$
is split over the group
![]() $\{(g,g):g\in G\}$
. The global counterpart of these results is described in § 2.5. The global coverings of both copies of
$\{(g,g):g\in G\}$
. The global counterpart of these results is described in § 2.5. The global coverings of both copies of
![]() $G(\mathbb {A})$
are defined using
$G(\mathbb {A})$
are defined using
![]() $H^{(m)}(\mathbb {A})$
. Corollary 11 is the global analog of Corollary 9: the splitting of
$H^{(m)}(\mathbb {A})$
. Corollary 11 is the global analog of Corollary 9: the splitting of
![]() $H^{(m)}(\mathbb {A})$
over
$H^{(m)}(\mathbb {A})$
over
![]() $\{(g,g):g\in G(\mathbb {A})\}$
. In § 2.6, we discuss the local and global extensions of the involution
$\{(g,g):g\in G(\mathbb {A})\}$
. In § 2.6, we discuss the local and global extensions of the involution
![]() ${}^{\iota }$
to the covering.
${}^{\iota }$
to the covering.
The cover
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
is studied in § 2.7. As mentioned above, this is not one of the coverings of [Reference Kazhdan and PattersonKP84]. One notable difference is that here, as opposed to the coverings of [Reference Kazhdan and PattersonKP84], preimages of direct factors of Levi subgroups do commute. Consequently, the usual tensor product is defined, and we do not need to use its metaplectic versions developed in [Reference KableKab01, Reference MezoMez04, Reference TakedaTak14, Reference TakedaTak16, Reference Kaplan, Lapid and ZouKLZ23]. While this observation simplifies numerous local arguments, one still needs to define (as in [Reference TakedaTak14, Reference TakedaTak16]) a global block-compatible
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
is studied in § 2.7. As mentioned above, this is not one of the coverings of [Reference Kazhdan and PattersonKP84]. One notable difference is that here, as opposed to the coverings of [Reference Kazhdan and PattersonKP84], preimages of direct factors of Levi subgroups do commute. Consequently, the usual tensor product is defined, and we do not need to use its metaplectic versions developed in [Reference KableKab01, Reference MezoMez04, Reference TakedaTak14, Reference TakedaTak16, Reference Kaplan, Lapid and ZouKLZ23]. While this observation simplifies numerous local arguments, one still needs to define (as in [Reference TakedaTak14, Reference TakedaTak16]) a global block-compatible
![]() $2$
-cocycle. In § 2.8, we describe the construction of unramified principal series representations and define the L-factors, using the definition of the L-group of [Reference Finkelberg and LysenkoFL10, Reference McNamaraMcN12, Reference WeissmanWei18] (see also [Reference GaoGao18a]). Section 2.10 describes the analog of the Casselman–Shalika formula for
$2$
-cocycle. In § 2.8, we describe the construction of unramified principal series representations and define the L-factors, using the definition of the L-group of [Reference Finkelberg and LysenkoFL10, Reference McNamaraMcN12, Reference WeissmanWei18] (see also [Reference GaoGao18a]). Section 2.10 describes the analog of the Casselman–Shalika formula for
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
using [Reference Kazhdan and PattersonKP84, Reference Chinta and OffenCO13] and [Reference GaoGao17].
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
using [Reference Kazhdan and PattersonKP84, Reference Chinta and OffenCO13] and [Reference GaoGao17].
Section 3 contains the definition and construction of
![]() $(rk,c)$
representations. Their definition is given in § 3.1; it is similar to the linear case. In the linear case, they satisfy an additional invariance property, with respect to the diagonal embedding
$(rk,c)$
representations. Their definition is given in § 3.1; it is similar to the linear case. In the linear case, they satisfy an additional invariance property, with respect to the diagonal embedding
![]() $\operatorname {\mathrm {SL}}_c^{\triangle }$
of
$\operatorname {\mathrm {SL}}_c^{\triangle }$
of
![]() $\operatorname {\mathrm {SL}}_c$
in
$\operatorname {\mathrm {SL}}_c$
in
![]() $\operatorname {\mathrm {GL}}_{kc}$
. This property extends to covering groups. First, we show that
$\operatorname {\mathrm {GL}}_{kc}$
. This property extends to covering groups. First, we show that
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is split over
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is split over
![]() $\operatorname {\mathrm {SL}}_{c}^{\triangle }$
, locally in Proposition 36 and globally in Corollary 38. The global invariance property is proved in Proposition 39.
$\operatorname {\mathrm {SL}}_{c}^{\triangle }$
, locally in Proposition 36 and globally in Corollary 38. The global invariance property is proved in Proposition 39.
In § 3.2, we construct local
![]() $(rk,c)$
representations, roughly denoted
$(rk,c)$
representations, roughly denoted
![]() $\Theta (\chi )$
, from exceptional representations. When
$\Theta (\chi )$
, from exceptional representations. When
![]() $c=1$
,
$c=1$
,
![]() $\Theta (\chi )$
affords a unique Whittaker model, and we prove the local results on the normalized unramified Whittaker function W (see § 3.3). In Theorem 43, we use Gelfand–Tsetlin patterns to compute the Jacquet integral on W, and in Theorem 46 we express W on
$\Theta (\chi )$
affords a unique Whittaker model, and we prove the local results on the normalized unramified Whittaker function W (see § 3.3). In Theorem 43, we use Gelfand–Tsetlin patterns to compute the Jacquet integral on W, and in Theorem 46 we express W on
![]() $\operatorname {\mathrm {diag}}(a^{rl},I_{rk-1})$
as a symmetric polynomial, by combining the weighted sum formula of § 2.10, the inductive method of Suzuki [Reference SuzukiSuz98] and a result of Cai [Reference CaiCai20].
$\operatorname {\mathrm {diag}}(a^{rl},I_{rk-1})$
as a symmetric polynomial, by combining the weighted sum formula of § 2.10, the inductive method of Suzuki [Reference SuzukiSuz98] and a result of Cai [Reference CaiCai20].
The global construction of
![]() $(rk,c)$
representations using residues of Eisenstein series is presented in § 3.4. We state Conjectures 50 and 51, under which we prove the existence of
$(rk,c)$
representations using residues of Eisenstein series is presented in § 3.4. We state Conjectures 50 and 51, under which we prove the existence of
![]() $\mathcal {E}_{\tau }$
(in Theorem 53) and that
$\mathcal {E}_{\tau }$
(in Theorem 53) and that
![]() $\mathcal {E}_{\tau }$
is an
$\mathcal {E}_{\tau }$
is an
![]() $(rk,c)$
representation (see Theorem 54). The local components of
$(rk,c)$
representation (see Theorem 54). The local components of
![]() $\mathcal {E}_{\tau }$
are described in § 3.5, where they are also related to
$\mathcal {E}_{\tau }$
are described in § 3.5, where they are also related to
![]() $\Theta (\chi )$
.
$\Theta (\chi )$
.
Section 4 is devoted to the global integral. In § 4.1, we start with gluing together our preliminaries, in order to prove that the global integral (4.2) is indeed well defined, as part of Theorem 63. In § 4.2, we carry out the unfolding process and prove Theorem 64, the main global identity. We then show how to obtain, from factorizable data, the almost Euler product (4.16). The main local result of this work: Theorem 66, namely the computation of the integrals with unramified data, is stated in this section (proved in § 5). The local study of the integrals is initiated here; see Proposition 68, and see also Proposition 70 on their equivariance properties. We define the local
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals in § 4.3.
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals in § 4.3.
The local theory of the integrals with unramified (non-Archimedean) data is developed in § 5. Theorem 66 is proved through a sequence of reductions in § 5.1 and § 5.2, eventually leading to the computation of a
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral in § 5.3. The assumption that the field contains the group
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral in § 5.3. The assumption that the field contains the group
![]() $\mu _{2m}$
is discussed in § 5.5.
$\mu _{2m}$
is discussed in § 5.5.
In Appendix A, we describe the global version of the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, as an application of the techniques developed in the body of the paper, and for possible future applications; in this work, we only use their local version. Finally for ease of reading and cross-reference, we include a list of common notation and definitions in Appendix B.
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, as an application of the techniques developed in the body of the paper, and for possible future applications; in this work, we only use their local version. Finally for ease of reading and cross-reference, we include a list of common notation and definitions in Appendix B.
2 Preliminaries
2.1 The groups
Let
![]() $\operatorname {\mathrm {Sp}}_{2l}$
denote the symplectic group, realized as the subgroup of matrices
$\operatorname {\mathrm {Sp}}_{2l}$
denote the symplectic group, realized as the subgroup of matrices
![]() $g\in \operatorname {\mathrm {SL}}_{2l}$
such that
$g\in \operatorname {\mathrm {SL}}_{2l}$
such that
![]() ${}^tg\left (\begin {smallmatrix}&J_l\\-J_l\end {smallmatrix}\right )g=\left (\begin {smallmatrix}&J_l\\-J_l\end {smallmatrix}\right )$
, where
${}^tg\left (\begin {smallmatrix}&J_l\\-J_l\end {smallmatrix}\right )g=\left (\begin {smallmatrix}&J_l\\-J_l\end {smallmatrix}\right )$
, where
![]() ${}^tg$
is the transpose of g and
${}^tg$
is the transpose of g and
![]() $J_l$
is the
$J_l$
is the
![]() $l\times l$
permutation matrix with
$l\times l$
permutation matrix with
![]() $1$
along the antidiagonal. We fix the diagonal torus
$1$
along the antidiagonal. We fix the diagonal torus
![]() $T_l$
and the Borel subgroup
$T_l$
and the Borel subgroup
![]() $B_l=T_l\ltimes N_l$
of upper triangular matrices in
$B_l=T_l\ltimes N_l$
of upper triangular matrices in
![]() $\operatorname {\mathrm {Sp}}_{2l}$
. For a parabolic subgroup P of
$\operatorname {\mathrm {Sp}}_{2l}$
. For a parabolic subgroup P of
![]() $\operatorname {\mathrm {Sp}}_{2l}$
,
$\operatorname {\mathrm {Sp}}_{2l}$
,
![]() $\delta _P$
denotes the modulus character. If U is a subgroup of
$\delta _P$
denotes the modulus character. If U is a subgroup of
![]() $N_l$
,
$N_l$
,
![]() $U^-$
denotes the opposite unipotent subgroup. Denote the Weyl group of
$U^-$
denotes the opposite unipotent subgroup. Denote the Weyl group of
![]() $T_l$
in
$T_l$
in
![]() $\operatorname {\mathrm {Sp}}_{2l}$
by
$\operatorname {\mathrm {Sp}}_{2l}$
by
![]() $W_{\operatorname {\mathrm {Sp}}_{2l}}$
.
$W_{\operatorname {\mathrm {Sp}}_{2l}}$
.
In the group
![]() $\operatorname {\mathrm {GL}}_d$
, fix the Borel subgroup
$\operatorname {\mathrm {GL}}_d$
, fix the Borel subgroup
![]() $B_{\operatorname {\mathrm {GL}}_d}=T_{\operatorname {\mathrm {GL}}_d}\ltimes N_{\operatorname {\mathrm {GL}}_d}$
of upper triangular invertible matrices, where
$B_{\operatorname {\mathrm {GL}}_d}=T_{\operatorname {\mathrm {GL}}_d}\ltimes N_{\operatorname {\mathrm {GL}}_d}$
of upper triangular invertible matrices, where
![]() $T_{\operatorname {\mathrm {GL}}_d}$
is the diagonal torus. A composition of a positive integer d is an ordered sequence of positive integers whose sum is d. For a composition
$T_{\operatorname {\mathrm {GL}}_d}$
is the diagonal torus. A composition of a positive integer d is an ordered sequence of positive integers whose sum is d. For a composition
![]() $\beta =(\beta _1,\ldots ,\beta _l)$
of d, let
$\beta =(\beta _1,\ldots ,\beta _l)$
of d, let
![]() $P_{\beta }=M_{\beta }\ltimes V_{\beta }$
denote the standard parabolic subgroup with
$P_{\beta }=M_{\beta }\ltimes V_{\beta }$
denote the standard parabolic subgroup with
![]() $M_{\beta }=\operatorname {\mathrm {GL}}_{\beta _1}\times \ldots \times \operatorname {\mathrm {GL}}_{\beta _l}$
, and
$M_{\beta }=\operatorname {\mathrm {GL}}_{\beta _1}\times \ldots \times \operatorname {\mathrm {GL}}_{\beta _l}$
, and
![]() $V_{\beta }^-$
be the opposite unipotent subgroup. A block-diagonal matrix in
$V_{\beta }^-$
be the opposite unipotent subgroup. A block-diagonal matrix in
![]() $\operatorname {\mathrm {GL}}_d$
will be denoted
$\operatorname {\mathrm {GL}}_d$
will be denoted
![]() $\operatorname {\mathrm {diag}}(a_1,\ldots ,a_l)$
(
$\operatorname {\mathrm {diag}}(a_1,\ldots ,a_l)$
(
![]() $a_i\in \operatorname {\mathrm {GL}}_{\beta _i}$
).
$a_i\in \operatorname {\mathrm {GL}}_{\beta _i}$
).
Denote the set of roots of
![]() $\operatorname {\mathrm {GL}}_d$
by
$\operatorname {\mathrm {GL}}_d$
by
![]() $\Phi _d$
, each
$\Phi _d$
, each
![]() $\alpha \in \Phi _d$
corresponds to a pair
$\alpha \in \Phi _d$
corresponds to a pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq i\ne j\leq d$
. Let
$1\leq i\ne j\leq d$
. Let
![]() $\Phi _d^+\subset \Phi _d$
denote the positive roots (defined with respect to
$\Phi _d^+\subset \Phi _d$
denote the positive roots (defined with respect to
![]() $B_{\operatorname {\mathrm {GL}}_d}$
). The simple roots are
$B_{\operatorname {\mathrm {GL}}_d}$
). The simple roots are
![]() $(i,i+1)$
,
$(i,i+1)$
,
![]() $1\leq i<d$
. The Weyl group of
$1\leq i<d$
. The Weyl group of
![]() $T_{\operatorname {\mathrm {GL}}_d}$
in
$T_{\operatorname {\mathrm {GL}}_d}$
in
![]() $\operatorname {\mathrm {GL}}_d$
is denoted
$\operatorname {\mathrm {GL}}_d$
is denoted
![]() $W_{\operatorname {\mathrm {GL}}_d}$
. Let
$W_{\operatorname {\mathrm {GL}}_d}$
. Let
![]() $\ell (w)$
be the length of
$\ell (w)$
be the length of
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
. We write
$w\in W_{\operatorname {\mathrm {GL}}_d}$
. We write
![]() $w_{\alpha }$
for the reflection along
$w_{\alpha }$
for the reflection along
![]() $\alpha $
. For
$\alpha $
. For
![]() $b\in \operatorname {\mathrm {GL}}_d$
, denote
$b\in \operatorname {\mathrm {GL}}_d$
, denote
![]() $b^{*}=J_d{}^tb^{-1}J_d$
.
$b^{*}=J_d{}^tb^{-1}J_d$
.
For two elements x and y in a group X,
![]() ${}^xy=xyx^{-1}$
, and if
${}^xy=xyx^{-1}$
, and if
![]() $Y<X$
, that is, Y is a subgroup of X, denote
$Y<X$
, that is, Y is a subgroup of X, denote
![]() ${}^xY=\{{}^{x}y:y\in Y\}$
.
${}^xY=\{{}^{x}y:y\in Y\}$
.
All fields in this work are of characteristic
![]() $0$
. Over a local field F, by convention if H is a linear algebraic group defined over F, we denote its F-points also by H, that is,
$0$
. Over a local field F, by convention if H is a linear algebraic group defined over F, we denote its F-points also by H, that is,
![]() $H=H(F)$
. When F is a number field,
$H=H(F)$
. When F is a number field,
![]() $\mathbb {A}$
denotes its ring of adeles and we write F-points or
$\mathbb {A}$
denotes its ring of adeles and we write F-points or
![]() $\mathbb {A}$
-points explicitly, for example,
$\mathbb {A}$
-points explicitly, for example,
![]() $H(\mathbb {A})$
. When the discussion applies to both local and global situations, we simply write H for both cases. For an integer m,
$H(\mathbb {A})$
. When the discussion applies to both local and global situations, we simply write H for both cases. For an integer m,
![]() $F^{*m}=\{a^m:a\in F^{*}\}$
and similarly denote
$F^{*m}=\{a^m:a\in F^{*}\}$
and similarly denote
![]() $\mathbb {A}^{*m}$
.
$\mathbb {A}^{*m}$
.
Over a local field, representations of H are assumed to be complex and smooth. When the field is Archimedean, an admissible representation is understood to be admissible Fréchet of moderate growth. If
![]() $\pi $
is a representation of a unipotent subgroup
$\pi $
is a representation of a unipotent subgroup
![]() $U<H$
on a space V, and
$U<H$
on a space V, and
![]() $\psi $
is a character of U, the Jacquet module
$\psi $
is a character of U, the Jacquet module
![]() $J_{U,\psi }(\pi )$
is the quotient
$J_{U,\psi }(\pi )$
is the quotient
![]() $V(U,\psi )\backslash V$
, where over non-Archimedean fields
$V(U,\psi )\backslash V$
, where over non-Archimedean fields
![]() $V(U,\psi )\subset V$
is the subspace spanned by all vectors of the form
$V(U,\psi )\subset V$
is the subspace spanned by all vectors of the form
![]() $\pi (u)\xi -\psi (u)\xi $
,
$\pi (u)\xi -\psi (u)\xi $
,
![]() $u\in U$
and
$u\in U$
and
![]() $\xi \in V$
, and over Archimedean fields
$\xi \in V$
, and over Archimedean fields
![]() $V(U,\psi )$
is the closure of this subspace.
$V(U,\psi )$
is the closure of this subspace.
For a local non-Archimedean field F, we let
![]() $\mathcal {O}$
denote its ring of integers,
$\mathcal {O}$
denote its ring of integers,
![]() $\mathcal {P}$
be the maximal ideal of
$\mathcal {P}$
be the maximal ideal of
![]() $\mathcal {O}$
,
$\mathcal {O}$
,
![]() $\varpi $
be a uniformizer and
$\varpi $
be a uniformizer and
![]() $|\varpi |=q^{-1}$
. Then we take a hyperspecial maximal compact subgroup
$|\varpi |=q^{-1}$
. Then we take a hyperspecial maximal compact subgroup
![]() $K_{\operatorname {\mathrm {Sp}}_{2l}}=\operatorname {\mathrm {Sp}}_{2l}(\mathcal {O})$
of
$K_{\operatorname {\mathrm {Sp}}_{2l}}=\operatorname {\mathrm {Sp}}_{2l}(\mathcal {O})$
of
![]() $\operatorname {\mathrm {Sp}}_{2l}$
, and additionally
$\operatorname {\mathrm {Sp}}_{2l}$
, and additionally
![]() $K_{\operatorname {\mathrm {SL}}_d}=\operatorname {\mathrm {SL}}_d(\mathcal {O})$
and
$K_{\operatorname {\mathrm {SL}}_d}=\operatorname {\mathrm {SL}}_d(\mathcal {O})$
and
![]() $K_{\operatorname {\mathrm {GL}}_d}=\operatorname {\mathrm {GL}}_d(\mathcal {O})$
. We also denote by
$K_{\operatorname {\mathrm {GL}}_d}=\operatorname {\mathrm {GL}}_d(\mathcal {O})$
. We also denote by
![]() $K_{\operatorname {\mathrm {Sp}}_{2l}}$
a maximal compact subgroup of
$K_{\operatorname {\mathrm {Sp}}_{2l}}$
a maximal compact subgroup of
![]() $\operatorname {\mathrm {Sp}}_{2l}$
over Archimedean fields (and similarly
$\operatorname {\mathrm {Sp}}_{2l}$
over Archimedean fields (and similarly
![]() $K_{\operatorname {\mathrm {GL}}_d}$
). In a global context, the maximal compact subgroup is
$K_{\operatorname {\mathrm {GL}}_d}$
). In a global context, the maximal compact subgroup is
![]() $K_{\operatorname {\mathrm {Sp}}_{2l}}=\prod _{\nu }K_{\operatorname {\mathrm {Sp}}_{2l},\nu }$
, where the product varies over all places of F.
$K_{\operatorname {\mathrm {Sp}}_{2l}}=\prod _{\nu }K_{\operatorname {\mathrm {Sp}}_{2l},\nu }$
, where the product varies over all places of F.
Let
![]() $\text {Mat}_{n\times l}$
be the abelian group of
$\text {Mat}_{n\times l}$
be the abelian group of
![]() $n\times l$
matrices (over a field or over
$n\times l$
matrices (over a field or over
![]() $\mathbb {A}$
), and set
$\mathbb {A}$
), and set
![]() $\text {Mat}_{n}=\text {Mat}_{n\times n}$
. The trace map is denoted
$\text {Mat}_{n}=\text {Mat}_{n\times n}$
. The trace map is denoted
![]() $\operatorname {\mathrm {tr}}$
.
$\operatorname {\mathrm {tr}}$
.
In both local and global settings, for a representation
![]() $\pi $
, say, of
$\pi $
, say, of
![]() $\operatorname {\mathrm {Sp}}_{2l}$
, its contragredient is denoted
$\operatorname {\mathrm {Sp}}_{2l}$
, its contragredient is denoted
![]() $\pi ^{\vee }$
. Induction of representations from parabolic subgroups is always assumed to be normalized. The action of a group by right-translation is denoted
$\pi ^{\vee }$
. Induction of representations from parabolic subgroups is always assumed to be normalized. The action of a group by right-translation is denoted
![]() $\cdot $
, for example, for a function f on
$\cdot $
, for example, for a function f on
![]() $\operatorname {\mathrm {Sp}}_{2l}$
and
$\operatorname {\mathrm {Sp}}_{2l}$
and
![]() $g,h\in \operatorname {\mathrm {Sp}}_{2l}$
,
$g,h\in \operatorname {\mathrm {Sp}}_{2l}$
,
![]() $h\cdot f(g)=f(gh)$
.
$h\cdot f(g)=f(gh)$
.
2.2 Covering groups
We introduce our notation for covering groups and include several general observations to be used throughout. Our basic reference is [Reference MooreMoo68]; see also [Reference Gan, Gao and WeissmanGGW18]. Let
![]() $m\geq 1$
be an integer. Let F be a local field or a number field. Fix the group
$m\geq 1$
be an integer. Let F be a local field or a number field. Fix the group
![]() $\mu _m\subset \mathbb {C}^{*}$
of m-th roots of unity. Assume that
$\mu _m\subset \mathbb {C}^{*}$
of m-th roots of unity. Assume that
![]() $F^{*}$
contains m m-th roots of unity, then we may identify the subgroup of these roots with
$F^{*}$
contains m m-th roots of unity, then we may identify the subgroup of these roots with
![]() $\mu _m$
and for simplicity write
$\mu _m$
and for simplicity write
![]() $\mu _m\subset F^{*}$
. Let
$\mu _m\subset F^{*}$
. Let
![]() $(\cdot ,\cdot )_m$
be a Hilbert symbol of order m in F (for
$(\cdot ,\cdot )_m$
be a Hilbert symbol of order m in F (for
![]() $m=1$
it is trivially
$m=1$
it is trivially
![]() $1$
), which is the product of local symbols if F is a number field ([Reference WeilWei95, Ch. IX.5]).
$1$
), which is the product of local symbols if F is a number field ([Reference WeilWei95, Ch. IX.5]).
Let G be a linear algebraic group defined over F, and denote its F-points (over a local field) or
![]() $\mathbb {A}$
-points also by G. A topological (central) covering group of G by
$\mathbb {A}$
-points also by G. A topological (central) covering group of G by
![]() $\mu _m$
is a short exact sequence of groups
$\mu _m$
is a short exact sequence of groups
where i and p are continuous,
![]() $i(\mu _m)$
is closed and belongs to the center of
$i(\mu _m)$
is closed and belongs to the center of
![]() $\widetilde {G}$
, and p induces an isomorphism
$\widetilde {G}$
, and p induces an isomorphism
![]() $i(\mu _m)\backslash \widetilde {G}\cong G$
of topological groups. We call
$i(\mu _m)\backslash \widetilde {G}\cong G$
of topological groups. We call
![]() $\widetilde {G}$
an m-fold covering group of G. A Borel measurable
$\widetilde {G}$
an m-fold covering group of G. A Borel measurable
![]() $\sigma :G\times G\rightarrow \mu _m$
such that
$\sigma :G\times G\rightarrow \mu _m$
such that
and on the identity element e of G,
![]() $\sigma (e,e)=1$
, is called a
$\sigma (e,e)=1$
, is called a
![]() $2$
-cocycle of G. In particular,
$2$
-cocycle of G. In particular,
![]() $\sigma (e,g')=\sigma (g,e)=1$
. Let
$\sigma (e,g')=\sigma (g,e)=1$
. Let
![]() $\mathrm {Z}^2(G,\mu _m)$
denote the group of
$\mathrm {Z}^2(G,\mu _m)$
denote the group of
![]() $2$
-cocycles. A Borel measurable map
$2$
-cocycles. A Borel measurable map
![]() $\eta :G\rightarrow \mu _m$
such that
$\eta :G\rightarrow \mu _m$
such that
![]() $\eta (e)=1$
is called a
$\eta (e)=1$
is called a
![]() $1$
-cochain; the corresponding
$1$
-cochain; the corresponding
![]() $2$
-coboundary is given by the function
$2$
-coboundary is given by the function
![]() $(g,g')\mapsto \eta (g)\eta (g')/\eta (gg')$
. Let
$(g,g')\mapsto \eta (g)\eta (g')/\eta (gg')$
. Let
![]() $\mathrm {C}^1(G,\mu _m)$
(resp.,
$\mathrm {C}^1(G,\mu _m)$
(resp.,
![]() $\mathrm {B}^2(G,\mu _m)$
) be the group of
$\mathrm {B}^2(G,\mu _m)$
) be the group of
![]() $1$
-cochains (resp.,
$1$
-cochains (resp.,
![]() $2$
-coboundaries). The
$2$
-coboundaries). The
![]() $2$
-nd cohomology
$2$
-nd cohomology
![]() $\mathrm {H}^2(G,\mu _m)$
is by definition
$\mathrm {H}^2(G,\mu _m)$
is by definition
![]() $\mathrm {B}^2(G,\mu _m)\backslash \mathrm {Z}^2(G,\mu _m)$
, and its elements parameterize the topological covering groups of G by
$\mathrm {B}^2(G,\mu _m)\backslash \mathrm {Z}^2(G,\mu _m)$
, and its elements parameterize the topological covering groups of G by
![]() $\mu _m$
. Given
$\mu _m$
. Given
![]() $\sigma \in \mathrm {Z}^2(G,\mu _m)$
, we can realize the group
$\sigma \in \mathrm {Z}^2(G,\mu _m)$
, we can realize the group
![]() $\widetilde {G}$
as the set of elements
$\widetilde {G}$
as the set of elements
![]() $\langle g,\epsilon \rangle $
with
$\langle g,\epsilon \rangle $
with
![]() $g\in G$
and
$g\in G$
and
![]() $\epsilon \in \mu _m$
, and the product given by
$\epsilon \in \mu _m$
, and the product given by
If
![]() $\sigma ,\rho \in \mathrm {Z}^2(G,\mu _m)$
are cohomologous, that is, equal in
$\sigma ,\rho \in \mathrm {Z}^2(G,\mu _m)$
are cohomologous, that is, equal in
![]() $\mathrm {H}^2(G,\mu _m)$
, there exists
$\mathrm {H}^2(G,\mu _m)$
, there exists
![]() $\eta \in \mathrm {C}^1(G,\mu _m)$
such that
$\eta \in \mathrm {C}^1(G,\mu _m)$
such that
In this case, replacing
![]() $\sigma $
with
$\sigma $
with
![]() $\rho $
yields an isomorphic group
$\rho $
yields an isomorphic group
![]() $\widetilde {G}$
:
$\widetilde {G}$
:
![]() $\langle g,1\rangle \mapsto \langle g,\eta (g)\rangle $
is a topological isomorphism, where the domain is realized using
$\langle g,1\rangle \mapsto \langle g,\eta (g)\rangle $
is a topological isomorphism, where the domain is realized using
![]() $\rho $
and the image by
$\rho $
and the image by
![]() $\sigma $
.
$\sigma $
.
If X is a closed subgroup of G, the restriction of
![]() $\sigma $
to
$\sigma $
to
![]() $X\times X$
will be briefly referred to as the restriction to X. This is a
$X\times X$
will be briefly referred to as the restriction to X. This is a
![]() $2$
-cocycle of X. The resulting covering
$2$
-cocycle of X. The resulting covering
![]() $\widetilde {X}$
of X, which depends on the embedding of X in G, is by definition realized using the restriction of
$\widetilde {X}$
of X, which depends on the embedding of X in G, is by definition realized using the restriction of
![]() $\sigma $
to X. A section of X is a continuous map
$\sigma $
to X. A section of X is a continuous map
![]() $x\mapsto \langle x,\eta (x)\rangle $
where
$x\mapsto \langle x,\eta (x)\rangle $
where
![]() $\eta :X\rightarrow \mu _m$
satisfies
$\eta :X\rightarrow \mu _m$
satisfies
![]() $\eta (e)=1$
, and we call it a splitting of X if it is also a homomorphism, that is,
$\eta (e)=1$
, and we call it a splitting of X if it is also a homomorphism, that is,
In this case, we say that
![]() $\widetilde {G}$
splits over X. If
$\widetilde {G}$
splits over X. If
![]() $x\mapsto \langle x,\eta (x)\rangle $
and
$x\mapsto \langle x,\eta (x)\rangle $
and
![]() $x\mapsto \langle x,\eta '(x)\rangle $
are two splittings,
$x\mapsto \langle x,\eta '(x)\rangle $
are two splittings,
![]() $x\mapsto \eta (x)\eta '(x)^{-1}$
is a homomorphism
$x\mapsto \eta (x)\eta '(x)^{-1}$
is a homomorphism
![]() $X\rightarrow \mu _m$
. There will be
$X\rightarrow \mu _m$
. There will be
![]() $2$
recurring cases where we can conclude
$2$
recurring cases where we can conclude
![]() $\eta =\eta '$
: first, if X is perfect (because then
$\eta =\eta '$
: first, if X is perfect (because then
![]() $\operatorname {\mathrm {Hom}}(X,\mu _m)$
is trivial) and, second, when X is the F- or
$\operatorname {\mathrm {Hom}}(X,\mu _m)$
is trivial) and, second, when X is the F- or
![]() $\mathbb {A}$
-points of an algebraic unipotent subgroup because such a homomorphism implies that there is a homomorphism of the local field or
$\mathbb {A}$
-points of an algebraic unipotent subgroup because such a homomorphism implies that there is a homomorphism of the local field or
![]() $\mathbb {A}$
into
$\mathbb {A}$
into
![]() $\mu _m$
, hence must be trivial.
$\mu _m$
, hence must be trivial.
With the notation of Equation (2.2), if
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
are trivial on X, that is,
$\rho $
are trivial on X, that is,
![]() $\sigma (x,x')=\rho (x,x')=1$
for all
$\sigma (x,x')=\rho (x,x')=1$
for all
![]() $x,x'\in X$
,
$x,x'\in X$
,
![]() $\eta $
becomes a homomorphism which may then also be trivial, depending on X.
$\eta $
becomes a homomorphism which may then also be trivial, depending on X.
In a local-global context,
![]() $G(\mathbb {A})$
is the restricted direct product with respect to a family of compact open subgroups
$G(\mathbb {A})$
is the restricted direct product with respect to a family of compact open subgroups
![]() $K_{G,\nu }$
defined at almost all places
$K_{G,\nu }$
defined at almost all places
![]() $\nu $
. Assume that we have a family
$\nu $
. Assume that we have a family
![]() $(\sigma _{\nu },\rho _{\nu },\eta _{\nu })$
where
$(\sigma _{\nu },\rho _{\nu },\eta _{\nu })$
where
![]() $\sigma _{\nu },\rho _{\nu }\in \mathrm {Z}^2(G(F_{\nu }),\mu _m)$
and
$\sigma _{\nu },\rho _{\nu }\in \mathrm {Z}^2(G(F_{\nu }),\mu _m)$
and
![]() $\eta _{\nu }\in \mathrm {C}^1(G(F_{\nu }),\mu _m)$
, related by Equation (2.2). If we know the r.h.s. of Equation (2.2) is trivial on
$\eta _{\nu }\in \mathrm {C}^1(G(F_{\nu }),\mu _m)$
, related by Equation (2.2). If we know the r.h.s. of Equation (2.2) is trivial on
![]() $K_{G,\nu }$
for almost all
$K_{G,\nu }$
for almost all
![]() $\nu $
, we can define
$\nu $
, we can define
![]() $\rho =\prod _{\nu }\rho _{\nu }\in \mathrm {Z}^2(G(\mathbb {A}),\mu _m)$
.
$\rho =\prod _{\nu }\rho _{\nu }\in \mathrm {Z}^2(G(\mathbb {A}),\mu _m)$
.
In the opposite direction, let
![]() $X<G$
be a closed algebraic subgroup such that
$X<G$
be a closed algebraic subgroup such that
![]() $X(\mathbb {A})$
is the restricted direct product
$X(\mathbb {A})$
is the restricted direct product
![]() $\prod ^{\prime }_{\nu } X(F_{\nu })$
with respect to a family
$\prod ^{\prime }_{\nu } X(F_{\nu })$
with respect to a family
![]() $\{X_{0,\nu }\}_{\nu }$
, where for almost all
$\{X_{0,\nu }\}_{\nu }$
, where for almost all
![]() $\nu $
,
$\nu $
,
![]() $X_{0,\nu }=X(F_{\nu })\cap K_{G,\nu }$
and there is a unique homomorphism
$X_{0,\nu }=X(F_{\nu })\cap K_{G,\nu }$
and there is a unique homomorphism
![]() $X_{0,\nu }\rightarrow \mu _m$
. Assume
$X_{0,\nu }\rightarrow \mu _m$
. Assume
![]() $\sigma ,\rho \in \mathrm {Z}^2(X(\mathbb {A}),\mu _m)$
, write
$\sigma ,\rho \in \mathrm {Z}^2(X(\mathbb {A}),\mu _m)$
, write
![]() $\sigma =\prod _{\nu }\sigma _{\nu }$
,
$\sigma =\prod _{\nu }\sigma _{\nu }$
,
![]() $\rho =\prod _{\nu }\rho _{\nu }$
, and assume that we have
$\rho =\prod _{\nu }\rho _{\nu }$
, and assume that we have
![]() $\eta _{\nu }\in \mathrm {C}^1(X(F_{\nu }),\mu _m)$
as in Equation (2.2) for all
$\eta _{\nu }\in \mathrm {C}^1(X(F_{\nu }),\mu _m)$
as in Equation (2.2) for all
![]() $\nu $
, and both
$\nu $
, and both
![]() $\rho _{\nu }$
and
$\rho _{\nu }$
and
![]() $\sigma _{\nu }$
are trivial on
$\sigma _{\nu }$
are trivial on
![]() $X_{0,\nu }$
for almost all
$X_{0,\nu }$
for almost all
![]() $\nu $
. Then almost everywhere,
$\nu $
. Then almost everywhere,
![]() $\eta _{\nu }$
becomes a homomorphism
$\eta _{\nu }$
becomes a homomorphism
![]() $X_{0,\nu }\rightarrow \mu _m$
, thus
$X_{0,\nu }\rightarrow \mu _m$
, thus
![]() $\eta _{\nu }(X_{0,\nu })=1$
. Under these assumptions, we can then define
$\eta _{\nu }(X_{0,\nu })=1$
. Under these assumptions, we can then define
![]() $\eta =\prod _{\nu }\eta _{\nu }\in \mathrm {C}^1(X(\mathbb {A}),\mu _m)$
. Moreover, if
$\eta =\prod _{\nu }\eta _{\nu }\in \mathrm {C}^1(X(\mathbb {A}),\mu _m)$
. Moreover, if
![]() $x\mapsto \langle x,\zeta (x)\rangle $
is a splitting of
$x\mapsto \langle x,\zeta (x)\rangle $
is a splitting of
![]() $X(\mathbb {A})$
in
$X(\mathbb {A})$
in
![]() $\widetilde {X}(\mathbb {A})$
realized using
$\widetilde {X}(\mathbb {A})$
realized using
![]() $\sigma $
,
$\sigma $
,
Thus,
![]() $x\mapsto \langle x,\zeta (x)/\eta (x)\rangle $
is a splitting of
$x\mapsto \langle x,\zeta (x)/\eta (x)\rangle $
is a splitting of
![]() $X(\mathbb {A})$
when
$X(\mathbb {A})$
when
![]() $\widetilde {X}(\mathbb {A})$
is realized using
$\widetilde {X}(\mathbb {A})$
is realized using
![]() $\rho $
.
$\rho $
.
Since
![]() $\mu _m$
belongs to the center of
$\mu _m$
belongs to the center of
![]() $\widetilde {G}$
, G acts on
$\widetilde {G}$
, G acts on
![]() $\widetilde {G}$
by conjugation, which is also a homeomorphism. In fact,
$\widetilde {G}$
by conjugation, which is also a homeomorphism. In fact,
![]() ${}^{\langle x,\epsilon '\rangle }\langle y,\epsilon \rangle =\langle {}^xy,\sigma (x,y)\sigma (xy,x^{-1})\sigma (x,x^{-1})^{-1}\epsilon \rangle $
(independent of
${}^{\langle x,\epsilon '\rangle }\langle y,\epsilon \rangle =\langle {}^xy,\sigma (x,y)\sigma (xy,x^{-1})\sigma (x,x^{-1})^{-1}\epsilon \rangle $
(independent of
![]() $\epsilon '$
).
$\epsilon '$
).
For a topological automorphism
![]() $\chi :G\rightarrow G$
, a lift of
$\chi :G\rightarrow G$
, a lift of
![]() $\chi $
to
$\chi $
to
![]() $G^{(m)}$
is a topological automorphism
$G^{(m)}$
is a topological automorphism
![]() $\widetilde {\chi }:G^{(m)}\rightarrow G^{(m)}$
making the following diagram commute:
$\widetilde {\chi }:G^{(m)}\rightarrow G^{(m)}$
making the following diagram commute:
 $$ \begin{align*} \begin{array}{ccccccccc} 1& \rightarrow & \mu_m & \rightarrow & G^{(m)} & \rightarrow & G & \rightarrow &1\\ & & \mathrm{id}\downarrow & & \widetilde{\chi}\downarrow & & \chi\downarrow & &\\ 1& \rightarrow & \mu_m & \rightarrow & G^{(m)} & \rightarrow & G & \rightarrow &1. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccc} 1& \rightarrow & \mu_m & \rightarrow & G^{(m)} & \rightarrow & G & \rightarrow &1\\ & & \mathrm{id}\downarrow & & \widetilde{\chi}\downarrow & & \chi\downarrow & &\\ 1& \rightarrow & \mu_m & \rightarrow & G^{(m)} & \rightarrow & G & \rightarrow &1. \end{array} \end{align*} $$
One can disregard topological considerations and consider
![]() $\chi $
and
$\chi $
and
![]() $\widetilde {\chi }$
abstractly. In this weaker sense,
$\widetilde {\chi }$
abstractly. In this weaker sense,
![]() $\operatorname {\mathrm {Hom}}(G,\mu _m)$
, where G is regarded as an abstract group, acts transitively on the set of lifts ([Reference WeissWei69, § V.1, Propositions 1, 4]; see also [Reference KableKab99, § 2]). Thus, if G is perfect and
$\operatorname {\mathrm {Hom}}(G,\mu _m)$
, where G is regarded as an abstract group, acts transitively on the set of lifts ([Reference WeissWei69, § V.1, Propositions 1, 4]; see also [Reference KableKab99, § 2]). Thus, if G is perfect and
![]() $\widetilde {\chi }$
(an abstract lift or in particular, a topological lift) exists, it is unique.
$\widetilde {\chi }$
(an abstract lift or in particular, a topological lift) exists, it is unique.
Let
![]() $\chi $
and
$\chi $
and
![]() $\widetilde {\chi }$
be as above (again, topological), and Y be a closed subgroup of G. Assume that
$\widetilde {\chi }$
be as above (again, topological), and Y be a closed subgroup of G. Assume that
![]() $y\mapsto \langle y,\eta (y)\rangle $
is the unique splitting of Y and
$y\mapsto \langle y,\eta (y)\rangle $
is the unique splitting of Y and
![]() ${}^{\chi }y\mapsto \langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle $
is a splitting of
${}^{\chi }y\mapsto \langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle $
is a splitting of
![]() ${}^{\chi }Y$
. Then
${}^{\chi }Y$
. Then
![]() $y\mapsto {}^{(\widetilde {\chi })^{-1}}\langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle $
is a splitting of Y, hence by uniqueness
$y\mapsto {}^{(\widetilde {\chi })^{-1}}\langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle $
is a splitting of Y, hence by uniqueness
![]() ${}^{(\widetilde {\chi })^{-1}}\langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle =\langle y,\eta (y)\rangle $
. We deduce that in this case
${}^{(\widetilde {\chi })^{-1}}\langle {}^{\chi }y,\eta ({}^{\chi }y)\rangle =\langle y,\eta (y)\rangle $
. We deduce that in this case
When there is no risk of confusion, we will denote
![]() $\widetilde {\chi }$
also by
$\widetilde {\chi }$
also by
![]() $\chi $
.
$\chi $
.
For a parabolic subgroup
![]() $P<G$
, induction from
$P<G$
, induction from
![]() $\widetilde {P}$
to
$\widetilde {P}$
to
![]() $\widetilde {G}$
is implicitly normalized by
$\widetilde {G}$
is implicitly normalized by
![]() $\delta _P^{1/2}$
.
$\delta _P^{1/2}$
.
Given a faithful character
![]() $\varepsilon :\mu _m\rightarrow \mathbb {C}^{*}$
, an
$\varepsilon :\mu _m\rightarrow \mathbb {C}^{*}$
, an
![]() $\varepsilon $
-genuine representation
$\varepsilon $
-genuine representation
![]() $\pi $
of
$\pi $
of
![]() $\widetilde {G}$
is a representation where
$\widetilde {G}$
is a representation where
![]() $\mu _m$
acts by
$\mu _m$
acts by
![]() $\varepsilon $
. We will usually assume that this character is fixed and omit it from the definition and notation. An
$\varepsilon $
. We will usually assume that this character is fixed and omit it from the definition and notation. An
![]() $\varepsilon ^{-1}$
-genuine representation will then be called antigenuine; for example, since
$\varepsilon ^{-1}$
-genuine representation will then be called antigenuine; for example, since
![]() $\pi $
is genuine,
$\pi $
is genuine,
![]() $\pi ^{\vee }$
is antigenuine. See [Reference Kaplan and SzpruchKS23] for the extension of several fundamental results from the theory of representations of groups G over non-Archimedean fields, to their m-fold covering groups
$\pi ^{\vee }$
is antigenuine. See [Reference Kaplan and SzpruchKS23] for the extension of several fundamental results from the theory of representations of groups G over non-Archimedean fields, to their m-fold covering groups
![]() $\widetilde {G}$
, when G is a connected reductive linear algebraic group. For example, any genuine irreducible representation of
$\widetilde {G}$
, when G is a connected reductive linear algebraic group. For example, any genuine irreducible representation of
![]() $\widetilde {G}$
is admissible ([Reference Kaplan and SzpruchKS23, Theorem 3.3]).
$\widetilde {G}$
is admissible ([Reference Kaplan and SzpruchKS23, Theorem 3.3]).
For
![]() $G=\operatorname {\mathrm {Sp}}_{2l}$
let
$G=\operatorname {\mathrm {Sp}}_{2l}$
let
![]() $G^{(m)}$
denote the m-fold covering group
$G^{(m)}$
denote the m-fold covering group
![]() $\widetilde {G}$
of G, over a local field or over
$\widetilde {G}$
of G, over a local field or over
![]() $\mathbb {A}$
, defined by [Reference MatsumotoMat69] (following [Reference MooreMoo68, Reference SteinbergSte68]) with the Steinberg symbol constructed from
$\mathbb {A}$
, defined by [Reference MatsumotoMat69] (following [Reference MooreMoo68, Reference SteinbergSte68]) with the Steinberg symbol constructed from
![]() $(\cdot ,\cdot )_m^{-1}$
. It is a locally compact group, and an l-group ([Reference Bernstein and ZelevinskyBZ76] 1.1) over local non-Archimedean fields. At almost all places
$(\cdot ,\cdot )_m^{-1}$
. It is a locally compact group, and an l-group ([Reference Bernstein and ZelevinskyBZ76] 1.1) over local non-Archimedean fields. At almost all places
![]() $\nu $
of a global field F, the covering
$\nu $
of a global field F, the covering
![]() $G^{(m)}$
of
$G^{(m)}$
of
![]() $G(F_{\nu })$
splits over
$G(F_{\nu })$
splits over
![]() $K_{G,\nu }$
([Reference MooreMoo68, Lemma 11.3] and the proof of [Reference MooreMoo68, Theorem 12.2]), uniquely because
$K_{G,\nu }$
([Reference MooreMoo68, Lemma 11.3] and the proof of [Reference MooreMoo68, Theorem 12.2]), uniquely because
![]() $K_{G,\nu }$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Since
$K_{G,\nu }$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Since
![]() $G^{(m)}$
is split canonically over a maximal unipotent subgroup (for more general statements, see [Reference SteinbergSte62, Reference MatsumotoMat69, Reference Banks, Levy and SepanskiBLS99, Reference McNamaraMcN12] and [Reference Mœglin and WaldspurgerMW95, Appendix I]), notions involving unipotent orbits transfer immediately to covering groups.
$G^{(m)}$
is split canonically over a maximal unipotent subgroup (for more general statements, see [Reference SteinbergSte62, Reference MatsumotoMat69, Reference Banks, Levy and SepanskiBLS99, Reference McNamaraMcN12] and [Reference Mœglin and WaldspurgerMW95, Appendix I]), notions involving unipotent orbits transfer immediately to covering groups.
Similarly, denote by
![]() $\operatorname {\mathrm {SL}}_{l}^{(m)}$
the m-fold covering group
$\operatorname {\mathrm {SL}}_{l}^{(m)}$
the m-fold covering group
![]() $\widetilde {\operatorname {\mathrm {SL}}}_{l}$
of
$\widetilde {\operatorname {\mathrm {SL}}}_{l}$
of
![]() $\operatorname {\mathrm {SL}}_l$
, defined using
$\operatorname {\mathrm {SL}}_l$
, defined using
![]() $(\cdot ,\cdot )_m^{-1}$
.
$(\cdot ,\cdot )_m^{-1}$
.
We point out that one can redefine, once and for all,
![]() $(\cdot ,\cdot )_m$
to be
$(\cdot ,\cdot )_m$
to be
![]() $(\cdot ,\cdot )_m^l$
for any
$(\cdot ,\cdot )_m^l$
for any
![]() $l\in \mathbb {Z}$
coprime to m, our arguments are independent of this choice (e.g.,
$l\in \mathbb {Z}$
coprime to m, our arguments are independent of this choice (e.g.,
![]() $G^{(m)}$
can be constructed from
$G^{(m)}$
can be constructed from
![]() $(\cdot ,\cdot )_m^l$
).
$(\cdot ,\cdot )_m^l$
).
Henceforth throughout most of this work, G will be the symplectic group.
2.3 Embedding
 $G\times G$
in H
$G\times G$
in H
Let n, k and m be positive integers, and set
![]() $c=2n$
. If m is even, put
$c=2n$
. If m is even, put
![]() $r=m/2$
, otherwise
$r=m/2$
, otherwise
![]() $r=m$
. Let
$r=m$
. Let
![]() $G=\operatorname {\mathrm {Sp}}_{c}$
and
$G=\operatorname {\mathrm {Sp}}_{c}$
and
![]() $H=\operatorname {\mathrm {Sp}}_{2rkc}$
. Denote by
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
. Denote by
![]() $P=M_P\ltimes U_P$
the standard maximal parabolic subgroup of H with
$P=M_P\ltimes U_P$
the standard maximal parabolic subgroup of H with
![]() $M_P=\operatorname {\mathrm {GL}}_{rkc}$
, that is, the Siegel parabolic subgroup. Let
$M_P=\operatorname {\mathrm {GL}}_{rkc}$
, that is, the Siegel parabolic subgroup. Let
![]() $Q=M_Q\ltimes U_Q$
be the standard parabolic subgroup of H, whose Levi part
$Q=M_Q\ltimes U_Q$
be the standard parabolic subgroup of H, whose Levi part
![]() $M_Q$
is isomorphic to
$M_Q$
is isomorphic to
![]() $\operatorname {\mathrm {GL}}_{c}\times \ldots \operatorname {\mathrm {GL}}_{c}\times \operatorname {\mathrm {Sp}}_{2c}$
, where
$\operatorname {\mathrm {GL}}_{c}\times \ldots \operatorname {\mathrm {GL}}_{c}\times \operatorname {\mathrm {Sp}}_{2c}$
, where
![]() $\operatorname {\mathrm {GL}}_{c}$
appears
$\operatorname {\mathrm {GL}}_{c}$
appears
![]() $rk-1$
times. Put
$rk-1$
times. Put
![]() $U=U_Q$
.
$U=U_Q$
.
For a fixed nontrivial additive character
![]() $\psi $
, which is a character of a local field F, or a character of
$\psi $
, which is a character of a local field F, or a character of
![]() $F\backslash \mathbb {A}$
when F is a number field, define a character of U as follows. In a local context, it is a character of
$F\backslash \mathbb {A}$
when F is a number field, define a character of U as follows. In a local context, it is a character of
![]() $U(F)$
, in a global context it is a character of
$U(F)$
, in a global context it is a character of
![]() $U(\mathbb {A})$
which is trivial on
$U(\mathbb {A})$
which is trivial on
![]() $U(F)$
. For
$U(F)$
. For
![]() $v\in V_{(c^{rk-1})}$
, write
$v\in V_{(c^{rk-1})}$
, write
![]() $v=(v_{i,j})_{i,j}$
, where
$v=(v_{i,j})_{i,j}$
, where
![]() $v_{i,j}\in \text {Mat}_c$
, then define
$v_{i,j}\in \text {Mat}_c$
, then define
 $$ \begin{align} \psi(v)=\psi(\sum_{i=1}^{rk-2}\operatorname{\mathrm{tr}}(v_{i,i+1})). \end{align} $$
$$ \begin{align} \psi(v)=\psi(\sum_{i=1}^{rk-2}\operatorname{\mathrm{tr}}(v_{i,i+1})). \end{align} $$
For
![]() $x\in \text {Mat}_{((rk-1)c)\times 2c}$
, if
$x\in \text {Mat}_{((rk-1)c)\times 2c}$
, if
![]() $rk>1$
, write the bottom
$rk>1$
, write the bottom
![]() $c\times 2c$
block in the form
$c\times 2c$
block in the form
Then define
The stabilizer of
![]() $\psi _U$
in
$\psi _U$
in
![]() $M_Q$
contains
$M_Q$
contains
![]() $G\times G$
. The embedding
$G\times G$
. The embedding
![]() $G\times G\hookrightarrow H$
is defined by
$G\times G\hookrightarrow H$
is defined by
Here, on the r.h.s.
![]() $g_1^{*}$
appears
$g_1^{*}$
appears
![]() $rk-1$
times. Oftentimes, it will be convenient to refer to each of the copies separately. We write for
$rk-1$
times. Oftentimes, it will be convenient to refer to each of the copies separately. We write for
![]() $g\in G$
,
$g\in G$
,
![]() $\mathfrak {e}_1(g)=(g,I_c)$
and
$\mathfrak {e}_1(g)=(g,I_c)$
and
![]() $\mathfrak {e}_2(g)=(I_c,g)$
. We call
$\mathfrak {e}_2(g)=(I_c,g)$
. We call
![]() $\mathfrak {e}_1(G)$
the left copy of G in H, and
$\mathfrak {e}_1(G)$
the left copy of G in H, and
![]() $\mathfrak {e}_2(G)$
is the right copy.
$\mathfrak {e}_2(G)$
is the right copy.
2.4 Local covering
We proceed with the notation of § 2.2 and § 2.3. Consider a local field F. Let
![]() $H^{(m)}$
denote the m-fold covering of
$H^{(m)}$
denote the m-fold covering of
![]() $H=H(F)$
of [Reference MatsumotoMat69] defined with the Steinberg symbol constructed from
$H=H(F)$
of [Reference MatsumotoMat69] defined with the Steinberg symbol constructed from
![]() $(\cdot ,\cdot )_m^{-1}$
(see also [Reference SavinSav04, p. 114]). Since H is a subgroup of
$(\cdot ,\cdot )_m^{-1}$
(see also [Reference SavinSav04, p. 114]). Since H is a subgroup of
![]() $\operatorname {\mathrm {SL}}_{2rkc}$
, it is convenient to use the
$\operatorname {\mathrm {SL}}_{2rkc}$
, it is convenient to use the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\sigma _{2rkc}$
of
$\sigma _{2rkc}$
of
![]() $\operatorname {\mathrm {GL}}_{2rkc}$
of Banks et al. [Reference Banks, Levy and SepanskiBLS99, § 3] for local computations.
$\operatorname {\mathrm {GL}}_{2rkc}$
of Banks et al. [Reference Banks, Levy and SepanskiBLS99, § 3] for local computations.
First, we recall several properties of this
![]() $2$
-cocycle, used throughout. For any integer
$2$
-cocycle, used throughout. For any integer
![]() $d>1$
, let
$d>1$
, let
![]() $\sigma _{\operatorname {\mathrm {SL}}_{d+1}}\in \mathrm {Z}^2(\operatorname {\mathrm {SL}}_{d+1},\mu _m)$
be the
$\sigma _{\operatorname {\mathrm {SL}}_{d+1}}\in \mathrm {Z}^2(\operatorname {\mathrm {SL}}_{d+1},\mu _m)$
be the
![]() $2$
-cocycle of [Reference Banks, Levy and SepanskiBLS99, § 2] which represents
$2$
-cocycle of [Reference Banks, Levy and SepanskiBLS99, § 2] which represents
![]() $\operatorname {\mathrm {SL}}_{d+1}^{(m)}$
in
$\operatorname {\mathrm {SL}}_{d+1}^{(m)}$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_{d+1},\mu _m)$
(see § 2.2). Let
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_{d+1},\mu _m)$
(see § 2.2). Let
![]() $\sigma _d$
be the
$\sigma _d$
be the
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $\operatorname {\mathrm {GL}}_d$
defined in [Reference Banks, Levy and SepanskiBLS99, § 3] for
$\operatorname {\mathrm {GL}}_d$
defined in [Reference Banks, Levy and SepanskiBLS99, § 3] for
![]() $b,b'\in \operatorname {\mathrm {GL}}_d$
by
$b,b'\in \operatorname {\mathrm {GL}}_d$
by
The image of
![]() $\operatorname {\mathrm {SL}}_d$
in
$\operatorname {\mathrm {SL}}_d$
in
![]() $\operatorname {\mathrm {SL}}_{d+1}$
under the embedding
$\operatorname {\mathrm {SL}}_{d+1}$
under the embedding
![]() $b\mapsto \operatorname {\mathrm {diag}}(b,1)$
is standard in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2], hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7] the restriction of
$b\mapsto \operatorname {\mathrm {diag}}(b,1)$
is standard in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2], hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7] the restriction of
![]() $\sigma _d$
to
$\sigma _d$
to
![]() $\operatorname {\mathrm {SL}}_d$
is
$\operatorname {\mathrm {SL}}_d$
is
![]() $\sigma _{\operatorname {\mathrm {SL}}_{d}}$
. By [Reference Banks, Levy and SepanskiBLS99, § 3, Lemma 1], for
$\sigma _{\operatorname {\mathrm {SL}}_{d}}$
. By [Reference Banks, Levy and SepanskiBLS99, § 3, Lemma 1], for
![]() $t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_d)\in T_{\operatorname {\mathrm {GL}}_d}$
and
$t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_d)\in T_{\operatorname {\mathrm {GL}}_d}$
and
![]() $t'\in T_{\operatorname {\mathrm {GL}}_d}$
(with similar notation),
$t'\in T_{\operatorname {\mathrm {GL}}_d}$
(with similar notation),
According to [Reference Banks, Levy and SepanskiBLS99, § 3, Lemma 4],
![]() $\sigma _{d}$
is trivial on
$\sigma _{d}$
is trivial on
![]() $N_{\operatorname {\mathrm {GL}}_d}$
(i.e., on
$N_{\operatorname {\mathrm {GL}}_d}$
(i.e., on
![]() $N_{\operatorname {\mathrm {GL}}_d}\times N_{\operatorname {\mathrm {GL}}_d}$
, see § 2.2), and for all
$N_{\operatorname {\mathrm {GL}}_d}\times N_{\operatorname {\mathrm {GL}}_d}$
, see § 2.2), and for all
![]() $b,b'\in \operatorname {\mathrm {GL}}_{d}$
and
$b,b'\in \operatorname {\mathrm {GL}}_{d}$
and
![]() $v,v'\in N_{\operatorname {\mathrm {GL}}_d}$
,
$v,v'\in N_{\operatorname {\mathrm {GL}}_d}$
,
It follows that if
![]() ${}^bv\in N_{\operatorname {\mathrm {GL}}_d}$
,
${}^bv\in N_{\operatorname {\mathrm {GL}}_d}$
,
Also, if
![]() $u^-\mapsto \langle u^-,\varsigma (u^-)\rangle $
is the splitting of
$u^-\mapsto \langle u^-,\varsigma (u^-)\rangle $
is the splitting of
![]() $N_{\operatorname {\mathrm {GL}}_d}^-$
and for
$N_{\operatorname {\mathrm {GL}}_d}^-$
and for
![]() $u^-\in N_{\operatorname {\mathrm {GL}}_d}^-$
we have
$u^-\in N_{\operatorname {\mathrm {GL}}_d}^-$
we have
![]() ${}^bu^-\in N_{\operatorname {\mathrm {GL}}_d}$
,
${}^bu^-\in N_{\operatorname {\mathrm {GL}}_d}$
,
This follows from Equation (2.4) with
![]() $Y=N_{\operatorname {\mathrm {GL}}_d}$
and
$Y=N_{\operatorname {\mathrm {GL}}_d}$
and
![]() $\chi ={}^b(\cdot )$
.
$\chi ={}^b(\cdot )$
.
One of the key properties of
![]() $\sigma _d$
is the block-compatibility formula [Reference Banks, Levy and SepanskiBLS99, Theorem 11]: For
$\sigma _d$
is the block-compatibility formula [Reference Banks, Levy and SepanskiBLS99, Theorem 11]: For
![]() $0<l<d$
,
$0<l<d$
,
![]() $a,a'\in \operatorname {\mathrm {GL}}_l$
and
$a,a'\in \operatorname {\mathrm {GL}}_l$
and
![]() $b,b'\in \operatorname {\mathrm {GL}}_{d-l}$
,
$b,b'\in \operatorname {\mathrm {GL}}_{d-l}$
,
We also mention that
![]() $\sigma _1$
is trivial and
$\sigma _1$
is trivial and
![]() $\sigma _2$
coincides with the
$\sigma _2$
coincides with the
![]() $2$
-cocycle of Kubota [Reference KubotaKub67]:
$2$
-cocycle of Kubota [Reference KubotaKub67]:
 $$ \begin{align} \sigma_2(g,g')=\Big(\frac{\gamma(gg')}{\gamma(g)},\frac{\gamma(gg')}{\gamma(g')\det g}\Big)_m, \qquad\gamma\left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right)=\begin{cases}c&c\ne0,\\d&c=0.\end{cases} \end{align} $$
$$ \begin{align} \sigma_2(g,g')=\Big(\frac{\gamma(gg')}{\gamma(g)},\frac{\gamma(gg')}{\gamma(g')\det g}\Big)_m, \qquad\gamma\left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right)=\begin{cases}c&c\ne0,\\d&c=0.\end{cases} \end{align} $$
In addition, there is a well-defined action of
![]() $W_{\operatorname {\mathrm {GL}}_d}$
on the genuine smooth admissible representations of
$W_{\operatorname {\mathrm {GL}}_d}$
on the genuine smooth admissible representations of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
(e.g., [Reference McNamaraMcN12, § 13.6]).
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
(e.g., [Reference McNamaraMcN12, § 13.6]).
To compute conjugations of torus elements by Weyl elements, we will repeatedly use the set
![]() $\mathfrak {W}_d\subset \operatorname {\mathrm {GL}}_d$
as in [Reference Banks, Levy and SepanskiBLS99]. For any
$\mathfrak {W}_d\subset \operatorname {\mathrm {GL}}_d$
as in [Reference Banks, Levy and SepanskiBLS99]. For any
![]() $\alpha \in \Phi _d$
,
$\alpha \in \Phi _d$
,
![]() $w_{\alpha }$
was defined to be the reflection along
$w_{\alpha }$
was defined to be the reflection along
![]() $\alpha $
. For the simple roots
$\alpha $
. For the simple roots
![]() $\alpha =(i,i+1)$
, we fix concrete representatives
$\alpha =(i,i+1)$
, we fix concrete representatives
![]() $w_{\alpha }=\operatorname {\mathrm {diag}}(I_{i-1},\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),I_{d-i-1})$
. Any
$w_{\alpha }=\operatorname {\mathrm {diag}}(I_{i-1},\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),I_{d-i-1})$
. Any
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
can be written as a product
$w\in W_{\operatorname {\mathrm {GL}}_d}$
can be written as a product
![]() $w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}$
, where each
$w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}$
, where each
![]() $w_{\alpha _i}$
is a simple reflection. Define the set
$w_{\alpha _i}$
is a simple reflection. Define the set
![]() $\mathfrak {W}_d=\{w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}:w\in W_{\operatorname {\mathrm {GL}}_d}\}\subset \operatorname {\mathrm {SL}}_d$
; it is not a group. Any permutation matrix
$\mathfrak {W}_d=\{w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}:w\in W_{\operatorname {\mathrm {GL}}_d}\}\subset \operatorname {\mathrm {SL}}_d$
; it is not a group. Any permutation matrix
![]() $w\in \operatorname {\mathrm {GL}}_d$
can be written uniquely in the form
$w\in \operatorname {\mathrm {GL}}_d$
can be written uniquely in the form
![]() $w=t_0w'$
, where
$w=t_0w'$
, where
![]() $t_0\in T_{\operatorname {\mathrm {GL}}_d}$
and its coordinates are
$t_0\in T_{\operatorname {\mathrm {GL}}_d}$
and its coordinates are
![]() $\pm 1$
, and
$\pm 1$
, and
![]() $w'\in \mathfrak {W}_d$
. For any
$w'\in \mathfrak {W}_d$
. For any
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}$
, by [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7(b), (d)],
$t\in T_{\operatorname {\mathrm {GL}}_d}$
, by [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7(b), (d)],
 $$ \begin{align} &\sigma_d(w',t)=\prod_{(i,j)=\alpha\in\Phi_d^+:w\alpha<0}(-t_j,t_i)_m. \end{align} $$
$$ \begin{align} &\sigma_d(w',t)=\prod_{(i,j)=\alpha\in\Phi_d^+:w\alpha<0}(-t_j,t_i)_m. \end{align} $$
Using Equation (2.1) (with
![]() $g={}^{w'}t$
,
$g={}^{w'}t$
,
![]() $g'=w'$
,
$g'=w'$
,
![]() $g"={w'}^{-1}$
) and because
$g"={w'}^{-1}$
) and because
![]() $\sigma ({}^{w'}t,w')=1$
,
$\sigma ({}^{w'}t,w')=1$
,
Hence, combining Equation (2.16) with Equation (2.15),
 $$ \begin{align} {}^{w'}\langle t,1\rangle=\langle {}^{w'}t,\sigma_d(w',t)\sigma_d(w't,{w'}^{-1})\sigma_d(w',{w'}^{-1})^{-1}\rangle= \langle {}^{w'}t,\prod_{(i,j)=\alpha\in\Phi_d^+:w\alpha<0}(-t_j,t_i)_m\rangle. \end{align} $$
$$ \begin{align} {}^{w'}\langle t,1\rangle=\langle {}^{w'}t,\sigma_d(w',t)\sigma_d(w't,{w'}^{-1})\sigma_d(w',{w'}^{-1})^{-1}\rangle= \langle {}^{w'}t,\prod_{(i,j)=\alpha\in\Phi_d^+:w\alpha<0}(-t_j,t_i)_m\rangle. \end{align} $$
Then
![]() ${}^{w}\langle t,1\rangle ={}^{t_0}({}^{w'}\langle t,1\rangle )$
can be computed from this and Equation (2.7). It can be a lengthy computation to find
${}^{w}\langle t,1\rangle ={}^{t_0}({}^{w'}\langle t,1\rangle )$
can be computed from this and Equation (2.7). It can be a lengthy computation to find
![]() $t_0$
; things are simplified when we know (a priori) that
$t_0$
; things are simplified when we know (a priori) that
![]() $t_0$
and
$t_0$
and
![]() ${}^{w'}t$
commute in the cover (e.g., when
${}^{w'}t$
commute in the cover (e.g., when
![]() $-1\in F^{*m}$
).
$-1\in F^{*m}$
).
Example 1. Consider the permutation matrix
![]() $w=\left (\begin {smallmatrix}&I_d\\I_d\end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_{2d}$
. Denote
$w=\left (\begin {smallmatrix}&I_d\\I_d\end {smallmatrix}\right )\in \operatorname {\mathrm {GL}}_{2d}$
. Denote
![]() $\alpha _i=(i,i+1)$
for
$\alpha _i=(i,i+1)$
for
![]() $1\leq i<2d$
. Then
$1\leq i<2d$
. Then
and the product is reduced: To see this, note that if
![]() $w_{0,d}$
is the longest Weyl element of
$w_{0,d}$
is the longest Weyl element of
![]() $W_{\operatorname {\mathrm {GL}}_d}$
,
$W_{\operatorname {\mathrm {GL}}_d}$
,
![]() $\ell (w)=\ell (w_{0,2d})-2\ell (w_{0,d})=d^2$
. Hence,
$\ell (w)=\ell (w_{0,2d})-2\ell (w_{0,d})=d^2$
. Hence,
![]() $t_0=\operatorname {\mathrm {diag}}((-1)^{d}I_{d},I_{d})$
and
$t_0=\operatorname {\mathrm {diag}}((-1)^{d}I_{d},I_{d})$
and
![]() $t_0w=w'\in \mathfrak {W}_{2d}$
.
$t_0w=w'\in \mathfrak {W}_{2d}$
.
According to the Bruhat decomposition
![]() $\operatorname {\mathrm {GL}}_d=\bigsqcup _{w"\in \mathfrak {W}_{d}}N_{\operatorname {\mathrm {GL}}_d}T_{\operatorname {\mathrm {GL}}_d}w"N_{\operatorname {\mathrm {GL}}_d}$
. For
$\operatorname {\mathrm {GL}}_d=\bigsqcup _{w"\in \mathfrak {W}_{d}}N_{\operatorname {\mathrm {GL}}_d}T_{\operatorname {\mathrm {GL}}_d}w"N_{\operatorname {\mathrm {GL}}_d}$
. For
![]() $g\in \operatorname {\mathrm {GL}}_d$
, write
$g\in \operatorname {\mathrm {GL}}_d$
, write
![]() $g=n't'w"n"$
with
$g=n't'w"n"$
with
![]() $n',n"\in N_{\operatorname {\mathrm {GL}}_d}$
,
$n',n"\in N_{\operatorname {\mathrm {GL}}_d}$
,
![]() $t'\in T_{\operatorname {\mathrm {GL}}_d}$
and
$t'\in T_{\operatorname {\mathrm {GL}}_d}$
and
![]() $w"\in \mathfrak {W}_{d}$
. Define
$w"\in \mathfrak {W}_{d}$
. Define
![]() $\mathbf {t}(g)=t'$
(see [Reference Banks, Levy and SepanskiBLS99, p. 151]). By Equations (2.8) and (2.14),
$\mathbf {t}(g)=t'$
(see [Reference Banks, Levy and SepanskiBLS99, p. 151]). By Equations (2.8) and (2.14),
As mentioned above
![]() $\mathfrak {W}_d$
is not a group. It will be convenient here to work with the following group
$\mathfrak {W}_d$
is not a group. It will be convenient here to work with the following group
![]() $\mathfrak {W}^+_d$
, defined to be the group generated by
$\mathfrak {W}^+_d$
, defined to be the group generated by
![]() $\mathfrak {W}_d$
and the diagonal matrices
$\mathfrak {W}_d$
and the diagonal matrices
![]() $\operatorname {\mathrm {diag}}(t_1,\ldots ,t_d)$
with
$\operatorname {\mathrm {diag}}(t_1,\ldots ,t_d)$
with
![]() $t_i=\pm 1$
for each i. In particular,
$t_i=\pm 1$
for each i. In particular,
![]() $\mathfrak {W}^+_d$
contains the permutation matrices.
$\mathfrak {W}^+_d$
contains the permutation matrices.
When
![]() $(-1,-1)_m=1$
in F, for example, if
$(-1,-1)_m=1$
in F, for example, if
![]() $-1\in F^{*m}$
,
$-1\in F^{*m}$
,
![]() $\sigma _{d}$
is trivial on
$\sigma _{d}$
is trivial on
![]() $\mathfrak {W}^+_d$
. This follows from the proof of [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7], noting that for
$\mathfrak {W}^+_d$
. This follows from the proof of [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7], noting that for
![]() $g\in \mathfrak {W}^+_d$
, the coordinates of
$g\in \mathfrak {W}^+_d$
, the coordinates of
![]() $\mathbf {t}(g)$
are
$\mathbf {t}(g)$
are
![]() $\pm 1$
(see also [Reference Banks, Levy and SepanskiBLS99, § 5]). In particular, if we identify
$\pm 1$
(see also [Reference Banks, Levy and SepanskiBLS99, § 5]). In particular, if we identify
![]() $W_{\operatorname {\mathrm {GL}}_d}$
with the full subgroup of permutation matrices in
$W_{\operatorname {\mathrm {GL}}_d}$
with the full subgroup of permutation matrices in
![]() $\operatorname {\mathrm {GL}}_d$
,
$\operatorname {\mathrm {GL}}_d$
,
![]() $w\mapsto \langle w,1\rangle $
is a splitting of
$w\mapsto \langle w,1\rangle $
is a splitting of
![]() $W_{\operatorname {\mathrm {GL}}_d}$
.
$W_{\operatorname {\mathrm {GL}}_d}$
.
We say that F is unramified if it is non-Archimedean,
![]() $|m|=1$
and
$|m|=1$
and
![]() $q>3$
. (If
$q>3$
. (If
![]() $m>2$
, the assumption
$m>2$
, the assumption
![]() $\mu _m\subset F^{*}$
implies
$\mu _m\subset F^{*}$
implies
![]() $q>3$
.) Assume this is the case. Since
$q>3$
.) Assume this is the case. Since
![]() $|m|=1$
, we have
$|m|=1$
, we have
![]() $(\mathcal {O}^{*},\mathcal {O}^{*})_m=1$
(see, e.g., [Reference WeilWei95, Ch. XIII.5]), whence
$(\mathcal {O}^{*},\mathcal {O}^{*})_m=1$
(see, e.g., [Reference WeilWei95, Ch. XIII.5]), whence
![]() $\sigma _d$
is trivial on
$\sigma _d$
is trivial on
![]() $T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
, that is, on torus elements with coordinates in
$T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
, that is, on torus elements with coordinates in
![]() $\mathcal {O}^{*}$
(by Equation (2.7)), and on
$\mathcal {O}^{*}$
(by Equation (2.7)), and on
![]() $\mathfrak {W}^+_d$
. By [Reference MooreMoo68, Lemma 11.3], there is a splitting of
$\mathfrak {W}^+_d$
. By [Reference MooreMoo68, Lemma 11.3], there is a splitting of
![]() $K_{\operatorname {\mathrm {SL}}_{d+1}}$
in
$K_{\operatorname {\mathrm {SL}}_{d+1}}$
in
![]() $\operatorname {\mathrm {SL}}_{d+1}^{(m)}$
, and in fact there is a unique splitting because the assumption
$\operatorname {\mathrm {SL}}_{d+1}^{(m)}$
, and in fact there is a unique splitting because the assumption
![]() $q>3$
implies that
$q>3$
implies that
![]() $K_{\operatorname {\mathrm {SL}}_{d+1}}$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Restricting to
$K_{\operatorname {\mathrm {SL}}_{d+1}}$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Restricting to
![]() $K_{\operatorname {\mathrm {GL}}_{d}}$
, we obtain a splitting of
$K_{\operatorname {\mathrm {GL}}_{d}}$
, we obtain a splitting of
![]() $K_{\operatorname {\mathrm {GL}}_{d}}$
denoted by
$K_{\operatorname {\mathrm {GL}}_{d}}$
denoted by
![]() $\langle y,\eta _d(y)\rangle $
. The splitting of
$\langle y,\eta _d(y)\rangle $
. The splitting of
![]() $K_{\operatorname {\mathrm {GL}}_{d}}$
is not unique, and note that
$K_{\operatorname {\mathrm {GL}}_{d}}$
is not unique, and note that
![]() $\sigma _d$
is not trivial on
$\sigma _d$
is not trivial on
![]() $K_{\operatorname {\mathrm {GL}}_d}$
. Since
$K_{\operatorname {\mathrm {GL}}_d}$
. Since
![]() $\sigma _d$
is trivial on
$\sigma _d$
is trivial on
![]() $N_{\operatorname {\mathrm {GL}}_{d}}(\mathcal {O})$
,
$N_{\operatorname {\mathrm {GL}}_{d}}(\mathcal {O})$
,
![]() $T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
and
$T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
and
![]() $\mathfrak {W}^+_d$
,
$\mathfrak {W}^+_d$
,
![]() $\eta _d$
is a homomorphism of these subgroups, then the explicit description of
$\eta _d$
is a homomorphism of these subgroups, then the explicit description of
![]() $\eta _2$
of [Reference KubotaKub69, p. 19], namely
$\eta _2$
of [Reference KubotaKub69, p. 19], namely
![]() $\eta _2(\left (\begin {smallmatrix}a&b\\c&d\end {smallmatrix}\right ))=1$
if
$\eta _2(\left (\begin {smallmatrix}a&b\\c&d\end {smallmatrix}\right ))=1$
if
![]() $|c|=0,1$
and
$|c|=0,1$
and
![]() $(c,d(ad-bc)^{-1})_m$
otherwise, implies (in light of Equation (2.13)) that
$(c,d(ad-bc)^{-1})_m$
otherwise, implies (in light of Equation (2.13)) that
![]() $\eta _d$
is trivial on
$\eta _d$
is trivial on
![]() $N_{\operatorname {\mathrm {GL}}_{d}}(\mathcal {O})$
,
$N_{\operatorname {\mathrm {GL}}_{d}}(\mathcal {O})$
,
![]() $T_{\operatorname {\mathrm {GL}}_d} \cap K_{\operatorname {\mathrm {GL}}_d}$
and
$T_{\operatorname {\mathrm {GL}}_d} \cap K_{\operatorname {\mathrm {GL}}_d}$
and
![]() $\mathfrak {W}^+_d$
(see [Reference Kazhdan and PattersonKP84, Proposition 0.I.3] and [Reference TakedaTak14, (1.3) and p. 183]).
$\mathfrak {W}^+_d$
(see [Reference Kazhdan and PattersonKP84, Proposition 0.I.3] and [Reference TakedaTak14, (1.3) and p. 183]).
Again, consider an arbitrary F, that is, not necessarily unramified. The image of H in
![]() $\operatorname {\mathrm {SL}}_{2rkc}$
is standard (as defined in [Reference Banks, Levy and SepanskiBLS99, p. 143]), hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7], the restriction of
$\operatorname {\mathrm {SL}}_{2rkc}$
is standard (as defined in [Reference Banks, Levy and SepanskiBLS99, p. 143]), hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7], the restriction of
![]() $\sigma _{2rkc}$
to H represents
$\sigma _{2rkc}$
to H represents
![]() $H^{(m)}$
in
$H^{(m)}$
in
![]() $\mathrm {H}^2(H,\mu _m)$
. In fact this restriction is
$\mathrm {H}^2(H,\mu _m)$
. In fact this restriction is
![]() $\sigma _{\operatorname {\mathrm {Sp}}_{2rkc}}$
of [Reference Banks, Levy and SepanskiBLS99, § 2], but the description of
$\sigma _{\operatorname {\mathrm {Sp}}_{2rkc}}$
of [Reference Banks, Levy and SepanskiBLS99, § 2], but the description of
![]() $\sigma _{2rkc}$
in [Reference Banks, Levy and SepanskiBLS99, § 3] is more convenient for matrices. When we apply Equation (2.7) to
$\sigma _{2rkc}$
in [Reference Banks, Levy and SepanskiBLS99, § 3] is more convenient for matrices. When we apply Equation (2.7) to
![]() $T_{rkc}<T_{\operatorname {\mathrm {GL}}_{2rkc}}$
, if
$T_{rkc}<T_{\operatorname {\mathrm {GL}}_{2rkc}}$
, if
![]() $t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_{rkc},t_{rkc}^{-1},\ldots ,t_{1}^{-1})\in T_{rkc}$
and
$t=\operatorname {\mathrm {diag}}(t_1,\ldots ,t_{rkc},t_{rkc}^{-1},\ldots ,t_{1}^{-1})\in T_{rkc}$
and
![]() $t'\in T_{rkc}$
(with similar notation),
$t'\in T_{rkc}$
(with similar notation),
 $$ \begin{align} \sigma_{2rkc}(t,t')=\prod_{i=1}^{rkc}(t_i,t^{\prime}_i)_m^{-1}. \end{align} $$
$$ \begin{align} \sigma_{2rkc}(t,t')=\prod_{i=1}^{rkc}(t_i,t^{\prime}_i)_m^{-1}. \end{align} $$
Since
![]() $N_{rkc}<N_{\operatorname {\mathrm {GL}}_{2rkc}}$
, we can use Equations (2.8)-(2.10) for
$N_{rkc}<N_{\operatorname {\mathrm {GL}}_{2rkc}}$
, we can use Equations (2.8)-(2.10) for
![]() $b,b'\in H$
and
$b,b'\in H$
and
![]() $v,v'\in N_{rkc}$
. When F is unramified,
$v,v'\in N_{rkc}$
. When F is unramified,
![]() $K_{H}=H(\mathcal {O})$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Regarding
$K_{H}=H(\mathcal {O})$
is perfect ([Reference MooreMoo68, Lemma 11.1]). Regarding
![]() $\eta _{2rkc}$
as a function on
$\eta _{2rkc}$
as a function on
![]() $K_H$
by restriction, it is the unique
$K_H$
by restriction, it is the unique
![]() $1$
-cochain such that
$1$
-cochain such that
Indeed, if
![]() $\eta ':K_H\rightarrow \mu _m$
is another such mapping,
$\eta ':K_H\rightarrow \mu _m$
is another such mapping,
![]() $y\mapsto \eta _{2rkc}(y)\eta '(y)^{-1}$
is a character of
$y\mapsto \eta _{2rkc}(y)\eta '(y)^{-1}$
is a character of
![]() $K_{H}$
.
$K_{H}$
.
Proposition 2. Let
![]() $w\in H\cap \mathfrak {W}^+_{2rkc}$
be a representative of an element of
$w\in H\cap \mathfrak {W}^+_{2rkc}$
be a representative of an element of
![]() $W_H$
. For any
$W_H$
. For any
![]() $t\in T_{rkc}$
,
$t\in T_{rkc}$
,
![]() ${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
.
${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
.
Proof. By Equation (2.19), it suffices to prove the result for
![]() $t=\operatorname {\mathrm {diag}}(I_{i-1},x,I_{2(rkc-i)},x^{-1},I_{i-1})$
and
$t=\operatorname {\mathrm {diag}}(I_{i-1},x,I_{2(rkc-i)},x^{-1},I_{i-1})$
and
![]() $1\leq i\leq rkc$
. Since
$1\leq i\leq rkc$
. Since
![]() $H\cap \mathfrak {W}^+_{2rkc}$
acts on
$H\cap \mathfrak {W}^+_{2rkc}$
acts on
![]() $\widetilde {T}_{rkc}$
, it is enough to consider
$\widetilde {T}_{rkc}$
, it is enough to consider
![]() $t'\in T_{rkc}$
such that
$t'\in T_{rkc}$
such that
![]() $t^{\prime }_i=\pm 1$
for all
$t^{\prime }_i=\pm 1$
for all
![]() $1\leq i\leq rkc$
, and representatives for a set of generators of
$1\leq i\leq rkc$
, and representatives for a set of generators of
![]() $W_H$
. We have
$W_H$
. We have
![]() ${}^{t'}\langle t,1\rangle =\langle t,1\rangle $
by Equation (2.19), and for the representatives we take
${}^{t'}\langle t,1\rangle =\langle t,1\rangle $
by Equation (2.19), and for the representatives we take
![]() $w=\operatorname {\mathrm {diag}}(I_{j-1},J_2,I_{2(rkc-j-1)},J_2,I_{j-1})$
for
$w=\operatorname {\mathrm {diag}}(I_{j-1},J_2,I_{2(rkc-j-1)},J_2,I_{j-1})$
for
![]() $1\leq j<rkc$
and
$1\leq j<rkc$
and
![]() $w=\operatorname {\mathrm {diag}}(I_{rkc-1},\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),I_{rkc-1})$
. We then have
$w=\operatorname {\mathrm {diag}}(I_{rkc-1},\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),I_{rkc-1})$
. We then have
![]() ${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
by Equations (2.12) and (2.13) and note that
${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
by Equations (2.12) and (2.13) and note that
![]() $(x,x)_m^2=1$
for all
$(x,x)_m^2=1$
for all
![]() $x\in F^{*}$
.
$x\in F^{*}$
.
Remark 3. The proposition does not apply to arbitrary
![]() $t\in T_{\operatorname {\mathrm {GL}}_{2rkc}}$
.
$t\in T_{\operatorname {\mathrm {GL}}_{2rkc}}$
.
Consider the involution
![]() $g\mapsto g^{*}=J_c{}^tg^{-1}J_c$
of
$g\mapsto g^{*}=J_c{}^tg^{-1}J_c$
of
![]() $\operatorname {\mathrm {GL}}_c$
. Define
$\operatorname {\mathrm {GL}}_c$
. Define
This is again a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $\operatorname {\mathrm {GL}}_c$
and of
$\operatorname {\mathrm {GL}}_c$
and of
![]() $\operatorname {\mathrm {SL}}_c$
or G by restriction because
$\operatorname {\mathrm {SL}}_c$
or G by restriction because
![]() $g\mapsto g^{*}$
is an automorphism and a homeomorphism.
$g\mapsto g^{*}$
is an automorphism and a homeomorphism.
Proposition 4. The
![]() $2$
-cocycles
$2$
-cocycles
![]() $\sigma ^{*}_{c}$
and
$\sigma ^{*}_{c}$
and
![]() $\sigma _{c}$
are cohomologous on
$\sigma _{c}$
are cohomologous on
![]() $\operatorname {\mathrm {SL}}_c$
.
$\operatorname {\mathrm {SL}}_c$
.
Proof. The proof is similar to [Reference KableKab99, Lemma 2]. Let
![]() $T_{\operatorname {\mathrm {SL}}_c}=T_{\operatorname {\mathrm {GL}}_c}\cap \operatorname {\mathrm {SL}}_c$
. By [Reference MooreMoo68, p. 54, Corollary 2], restriction
$T_{\operatorname {\mathrm {SL}}_c}=T_{\operatorname {\mathrm {GL}}_c}\cap \operatorname {\mathrm {SL}}_c$
. By [Reference MooreMoo68, p. 54, Corollary 2], restriction
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)\rightarrow \mathrm {H}^2(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
is injective. Now, by Equation (2.7), for
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)\rightarrow \mathrm {H}^2(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
is injective. Now, by Equation (2.7), for
![]() $t,t'\in T_{\operatorname {\mathrm {SL}}_c}$
,
$t,t'\in T_{\operatorname {\mathrm {SL}}_c}$
,
 $$ \begin{align*} \sigma_c(t,t')=\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1},\qquad \sigma^{*}_c(t,t')=\prod_{i=1}^{c-1}\prod_{j=i}^{c-1}(t_i,t^{\prime}_j)_m^{-1}. \end{align*} $$
$$ \begin{align*} \sigma_c(t,t')=\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1},\qquad \sigma^{*}_c(t,t')=\prod_{i=1}^{c-1}\prod_{j=i}^{c-1}(t_i,t^{\prime}_j)_m^{-1}. \end{align*} $$
Therefore, if we define
![]() $\eta \in \mathrm {C}^1(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
by
$\eta \in \mathrm {C}^1(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
by
![]() $\eta (t)=\prod _{1\leq i\leq j\leq c-1}(t_i,t_j)_m$
,
$\eta (t)=\prod _{1\leq i\leq j\leq c-1}(t_i,t_j)_m$
,
 $$ \begin{align*} \sigma_c(t,t')\sigma^{*}_c(t,t')^{-1}=\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1} \prod_{i=1}^{c-1}\prod_{j=i}^{c-1}(t_i,t^{\prime}_j)_m=\frac{\eta(tt')}{\eta(t)\eta(t')}. \end{align*} $$
$$ \begin{align*} \sigma_c(t,t')\sigma^{*}_c(t,t')^{-1}=\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1} \prod_{i=1}^{c-1}\prod_{j=i}^{c-1}(t_i,t^{\prime}_j)_m=\frac{\eta(tt')}{\eta(t)\eta(t')}. \end{align*} $$
Hence,
![]() $\sigma ^{*}_{c}=\sigma _{c}$
in
$\sigma ^{*}_{c}=\sigma _{c}$
in
![]() $\mathrm {H}^2(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
, thereby also in
$\mathrm {H}^2(T_{\operatorname {\mathrm {SL}}_c},\mu _m)$
, thereby also in
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
.
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
.
Remark 5. The involution
![]() $g\mapsto g^{*}$
is the identity on
$g\mapsto g^{*}$
is the identity on
![]() $T_n$
. Also, a slightly more careful argument will extend this proposition to
$T_n$
. Also, a slightly more careful argument will extend this proposition to
![]() $\operatorname {\mathrm {GL}}_c$
; see the proof of Proposition 20 in § 2.7.
$\operatorname {\mathrm {GL}}_c$
; see the proof of Proposition 20 in § 2.7.
We then have
![]() $\varsigma _{*,c}\in \mathrm {C}^1(\operatorname {\mathrm {SL}}_c,\mu _m)$
such that
$\varsigma _{*,c}\in \mathrm {C}^1(\operatorname {\mathrm {SL}}_c,\mu _m)$
such that
 $$ \begin{align} \sigma^{*}_{c}(b,b')=\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\sigma_{c}(b,b'),\qquad \forall b,b'\in \operatorname{\mathrm{SL}}_c. \end{align} $$
$$ \begin{align} \sigma^{*}_{c}(b,b')=\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\sigma_{c}(b,b'),\qquad \forall b,b'\in \operatorname{\mathrm{SL}}_c. \end{align} $$
We mention that
![]() $\sigma ^{*}_{c}\ne \sigma _c$
in
$\sigma ^{*}_{c}\ne \sigma _c$
in
![]() $\mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
(e.g., consider
$\mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
(e.g., consider
![]() $g=\left (\begin {smallmatrix}a&\\&a^{-1}\end {smallmatrix}\right )$
and
$g=\left (\begin {smallmatrix}a&\\&a^{-1}\end {smallmatrix}\right )$
and
![]() $g'=\left (\begin {smallmatrix}&-b^{-1}\\b\end {smallmatrix}\right )$
and use Equation (2.13)); for another example see below. We introduce a minor correction to
$g'=\left (\begin {smallmatrix}&-b^{-1}\\b\end {smallmatrix}\right )$
and use Equation (2.13)); for another example see below. We introduce a minor correction to
![]() $\sigma ^{*}_{c}$
using
$\sigma ^{*}_{c}$
using
![]() $\varsigma _{*,c}$
: Define
$\varsigma _{*,c}$
: Define
![]() $\sigma ^{*,rk}_{c}\in \mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
by
$\sigma ^{*,rk}_{c}\in \mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
by
 $$ \begin{align} \sigma^{*,rk}_{c}(b,b')=\left(\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\right)^{rk}\sigma^{*}_{c}(b,b') =\left(\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\right)^{rk+1}\sigma_{c}(b,b'). \end{align} $$
$$ \begin{align} \sigma^{*,rk}_{c}(b,b')=\left(\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\right)^{rk}\sigma^{*}_{c}(b,b') =\left(\frac{\varsigma_{*,c}(b)\varsigma_{*,c}(b')}{\varsigma_{*,c}(bb')}\right)^{rk+1}\sigma_{c}(b,b'). \end{align} $$
By definition
![]() $\sigma ^{*}_{c}=\sigma ^{*,rk}_{c}=\sigma _{c}$
in
$\sigma ^{*}_{c}=\sigma ^{*,rk}_{c}=\sigma _{c}$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
, in particular in
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
, in particular in
![]() $\mathrm {H}^2(G,\mu _m)$
. Also, if
$\mathrm {H}^2(G,\mu _m)$
. Also, if
![]() $m|rk$
(e.g., when
$m|rk$
(e.g., when
![]() $r=m$
),
$r=m$
),
![]() $\sigma ^{*,rk}_{c}=\sigma ^{*}_{c}$
in
$\sigma ^{*,rk}_{c}=\sigma ^{*}_{c}$
in
![]() $\mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
because
$\mathrm {Z}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
because
![]() $\varsigma _{*,c}^{rk}$
is trivial (being an m-th root of unity).
$\varsigma _{*,c}^{rk}$
is trivial (being an m-th root of unity).
Example 6. Consider
![]() $c=4$
,
$c=4$
,
![]() $t=\operatorname {\mathrm {diag}}(t_1,t_2,t_2^{-1},t_1^{-1})$
and
$t=\operatorname {\mathrm {diag}}(t_1,t_2,t_2^{-1},t_1^{-1})$
and
![]() $w=\operatorname {\mathrm {diag}}(1,\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),1)$
. Then
$w=\operatorname {\mathrm {diag}}(1,\left (\begin {smallmatrix}&-1\\1\end {smallmatrix}\right ),1)$
. Then
![]() $\sigma _4(w,t)=(-t_2^{-1},t_2)_m=1$
by Equation (2.15). To compute
$\sigma _4(w,t)=(-t_2^{-1},t_2)_m=1$
by Equation (2.15). To compute
![]() $\sigma _4^{*}(w,t)=\sigma _4(w^{*},t)$
, write
$\sigma _4^{*}(w,t)=\sigma _4(w^{*},t)$
, write
![]() $w^{*}=t_0w'$
, where
$w^{*}=t_0w'$
, where
![]() $t_0=\operatorname {\mathrm {diag}}(1,-1,-1,1)$
and
$t_0=\operatorname {\mathrm {diag}}(1,-1,-1,1)$
and
![]() $w'$
belongs to the set
$w'$
belongs to the set
![]() $\mathfrak {W}_4$
. By Equation (2.1),
$\mathfrak {W}_4$
. By Equation (2.1),
Now,
![]() $\sigma _4(t_0,w')=1$
and
$\sigma _4(t_0,w')=1$
and
![]() $\sigma _4(w',t)=(-t_1^{-1},t_1)_m=1$
by Equations (2.14) and (2.15), and
$\sigma _4(w',t)=(-t_1^{-1},t_1)_m=1$
by Equations (2.14) and (2.15), and
where we used [Reference Banks, Levy and SepanskiBLS99, § 3, (5)] and Equation (2.7). Therefore,
![]() $\sigma _4(w^{*},t)=(-1,t_2)_m^{-1}\ne \sigma _4(w,t)$
.
$\sigma _4(w^{*},t)=(-1,t_2)_m^{-1}\ne \sigma _4(w,t)$
.
We describe the restriction of the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\sigma _{2rkc}$
to the image of
$\sigma _{2rkc}$
to the image of
![]() $G\times G$
in H. Recall that for
$G\times G$
in H. Recall that for
![]() $g_1,g_2\in G$
,
$g_1,g_2\in G$
,
![]() $\mathfrak {e}_1(g_1)\mathfrak {e}_2(g_2)=(g_1,g_2)$
.
$\mathfrak {e}_1(g_1)\mathfrak {e}_2(g_2)=(g_1,g_2)$
.
Proposition 7. For all
![]() $g_i,g_i^{\prime }\in G$
,
$g_i,g_i^{\prime }\in G$
,
In particular,
![]() $\mathfrak {e}_1(G)$
and
$\mathfrak {e}_1(G)$
and
![]() $\mathfrak {e}_2(G)$
commute in
$\mathfrak {e}_2(G)$
commute in
![]() $H^{(m)}$
(!).
$H^{(m)}$
(!).
Proof. For
![]() $g=\left (\begin {smallmatrix} g_1 & g_2 \\ g_3 & g_4 \end {smallmatrix}\right )\in G$
with
$g=\left (\begin {smallmatrix} g_1 & g_2 \\ g_3 & g_4 \end {smallmatrix}\right )\in G$
with
![]() $g_i\in \text {Mat}_n$
, denote
$g_i\in \text {Mat}_n$
, denote
Then
![]() $\mathfrak {e}_1(g)=\mathfrak {e}_1^{\circ }(g)\mathfrak {e}_1^{\bullet }(g)$
. The subgroup
$\mathfrak {e}_1(g)=\mathfrak {e}_1^{\circ }(g)\mathfrak {e}_1^{\bullet }(g)$
. The subgroup
![]() $\mathfrak {e}_2(G)$
is standard in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7] and so is
$\mathfrak {e}_2(G)$
is standard in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7] and so is
![]() $\mathfrak {e}_1^{\bullet }(G)$
(see the proof of [Reference TakedaTak16, Lemma 3.5]), but not
$\mathfrak {e}_1^{\bullet }(G)$
(see the proof of [Reference TakedaTak16, Lemma 3.5]), but not
![]() $\mathfrak {e}_1^{\circ }(G)$
. Thus, by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7],
$\mathfrak {e}_1^{\circ }(G)$
. Thus, by [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7],
Also, by Equation (2.12),
 $$ \begin{align*} \sigma_{2rkc}((g_1,g_2),(g_1',g_2'))&=\sigma_{2rkc}( \mathfrak{e}_1^{\circ}(g_1)\mathfrak{e}_1^{\bullet}(g_1)\mathfrak{e}_2(g_2) ,\mathfrak{e}_1^{\circ}(g_1')\mathfrak{e}_1^{\bullet}(g_1')\mathfrak{e}_2(g_2'))\\ &=\prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*})\sigma_{2rkc}(\mathfrak{e}_1^{\bullet}(g_1)\mathfrak{e}_2(g_2),\mathfrak{e}_1^{\bullet}(g_1')\mathfrak{e}_2(g_2')). \end{align*} $$
$$ \begin{align*} \sigma_{2rkc}((g_1,g_2),(g_1',g_2'))&=\sigma_{2rkc}( \mathfrak{e}_1^{\circ}(g_1)\mathfrak{e}_1^{\bullet}(g_1)\mathfrak{e}_2(g_2) ,\mathfrak{e}_1^{\circ}(g_1')\mathfrak{e}_1^{\bullet}(g_1')\mathfrak{e}_2(g_2'))\\ &=\prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*})\sigma_{2rkc}(\mathfrak{e}_1^{\bullet}(g_1)\mathfrak{e}_2(g_2),\mathfrak{e}_1^{\bullet}(g_1')\mathfrak{e}_2(g_2')). \end{align*} $$
Hence,
 $$ \begin{align*} \sigma_{2rkc}((g_1,g_2),(g_1',g_2'))=\prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*})\sigma_{c}(g_1,g_1')\sigma_{c}(g_2,g_2'). \end{align*} $$
$$ \begin{align*} \sigma_{2rkc}((g_1,g_2),(g_1',g_2'))=\prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*})\sigma_{c}(g_1,g_1')\sigma_{c}(g_2,g_2'). \end{align*} $$
It remains to observe that
 $$ \begin{align*} \prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*}) & =\sigma_{c}^{2rk-2}(g_1,g_1')\left(\frac{\varsigma_{*,c}(g_1)\varsigma_{*,c}(g_1')}{\varsigma_{*,c}(g_1g_1')} \right)^{rk-1}\\ & =\sigma_{c}^{-2}(g_1,g_1')\left(\frac{\varsigma_{*,c}(g_1)\varsigma_{*,c}(g_1')}{\varsigma_{*,c}(g_1g_1')} \right)^{rk-1}. \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{rk-1}\sigma_{c}(g_1,g_1')\sigma_{c}(g_1^{*},{g_1'}^{*}) & =\sigma_{c}^{2rk-2}(g_1,g_1')\left(\frac{\varsigma_{*,c}(g_1)\varsigma_{*,c}(g_1')}{\varsigma_{*,c}(g_1g_1')} \right)^{rk-1}\\ & =\sigma_{c}^{-2}(g_1,g_1')\left(\frac{\varsigma_{*,c}(g_1)\varsigma_{*,c}(g_1')}{\varsigma_{*,c}(g_1g_1')} \right)^{rk-1}. \end{align*} $$
Here, we used the fact that
![]() $\sigma _{c}^{2r}$
is trivial because the image of
$\sigma _{c}^{2r}$
is trivial because the image of
![]() $\sigma _{c}$
is in
$\sigma _{c}$
is in
![]() $\mu _m$
.
$\mu _m$
.
We realize the left copy of G using the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\sigma _c^{*,rk}$
and the right copy using
$\sigma _c^{*,rk}$
and the right copy using
![]() $\sigma _c$
. Then by Equation (2.23), we can lift the embedding
$\sigma _c$
. Then by Equation (2.23), we can lift the embedding
![]() $G\times G \hookrightarrow H$
to an embedding (of topological groups)
$G\times G \hookrightarrow H$
to an embedding (of topological groups)
(
![]() $\mu _m^2=\mu _m\times \mu _m$
), via
$\mu _m^2=\mu _m\times \mu _m$
), via
In addition, we have
While it is more natural to work with
![]() $\sigma _c$
for both copies of
$\sigma _c$
for both copies of
![]() $G^{(m)}$
, if we realize the left copy using
$G^{(m)}$
, if we realize the left copy using
![]() $\sigma _c$
, then by Equation (2.22), the embedding (2.24) of the left copy changes into
$\sigma _c$
, then by Equation (2.22), the embedding (2.24) of the left copy changes into
which complicates matters on the
![]() $H^{(m)}$
side. We combine both alternatives. Momentarily denote the realization of
$H^{(m)}$
side. We combine both alternatives. Momentarily denote the realization of
![]() $G^{(m)}$
using
$G^{(m)}$
using
![]() $\sigma _c$
by
$\sigma _c$
by
![]() $G^{(m)}[\sigma _c]$
, and similarly denote
$G^{(m)}[\sigma _c]$
, and similarly denote
![]() $G^{(m)}[\sigma _c^{*,rk}]$
. The map
$G^{(m)}[\sigma _c^{*,rk}]$
. The map
is an isomorphism, which is canonical in the sense that it is the only isomorphism (G is perfect) which projects to the identity map of G. Dualizing, for a function
![]() $\varphi $
on
$\varphi $
on
![]() $G^{(m)}[\sigma _c]$
the function
$G^{(m)}[\sigma _c]$
the function
![]() $\varphi ^{\varsigma _{*,c}^{rk+1}}$
on
$\varphi ^{\varsigma _{*,c}^{rk+1}}$
on
![]() $G^{(m)}[\sigma _c^{*,rk}]$
is defined by
$G^{(m)}[\sigma _c^{*,rk}]$
is defined by
Proposition 8. Let
![]() $\varphi _1,\varphi _2$
be continuous genuine functions on
$\varphi _1,\varphi _2$
be continuous genuine functions on
![]() $G^{(m)}$
, realized using
$G^{(m)}$
, realized using
![]() $\sigma _c$
, and f be a continuous genuine function on
$\sigma _c$
, and f be a continuous genuine function on
![]() $H^{(m)}$
. The integral
$H^{(m)}$
. The integral
 $$ \begin{align*} \int\limits_{G\times G}\varphi_1^{\varsigma_{*,c}^{rk+1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f(\langle(g_1,g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
$$ \begin{align*} \int\limits_{G\times G}\varphi_1^{\varsigma_{*,c}^{rk+1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f(\langle(g_1,g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
is well defined in the sense that the integrand factors through
![]() $G\times G$
and the integral is a right-
$G\times G$
and the integral is a right-
![]() $(G\times G)$
-invariant functional, provided it is absolutely convergent.
$(G\times G)$
-invariant functional, provided it is absolutely convergent.
Proof. First, note that since
![]() $\varphi _i(\langle g_i,\epsilon _i\rangle )=\epsilon _i\varphi _i(\langle g_i,1\rangle )$
, and Formulas (2.24)-(2.25) imply
$\varphi _i(\langle g_i,\epsilon _i\rangle )=\epsilon _i\varphi _i(\langle g_i,1\rangle )$
, and Formulas (2.24)-(2.25) imply
the integrand factors through
![]() $G\times G$
. Also,
$G\times G$
. Also,
 $$ \begin{align*} &\varphi_1^{\varsigma_{*,c}^{rk+1}}( \langle g_1,1\rangle\langle h_1,1\rangle)=\varphi_1^{\varsigma_{*,c}^{rk+1}}(\langle g_1h_1,\sigma_{c}^{*,rk}(g_1,h_1)\rangle),\\ &\varphi_2(\langle g_2,1\rangle\langle h_2,1\rangle)=\varphi_2(\langle g_2h_2,\sigma_{c}(g_2,h_2)\rangle) \end{align*} $$
$$ \begin{align*} &\varphi_1^{\varsigma_{*,c}^{rk+1}}( \langle g_1,1\rangle\langle h_1,1\rangle)=\varphi_1^{\varsigma_{*,c}^{rk+1}}(\langle g_1h_1,\sigma_{c}^{*,rk}(g_1,h_1)\rangle),\\ &\varphi_2(\langle g_2,1\rangle\langle h_2,1\rangle)=\varphi_2(\langle g_2h_2,\sigma_{c}(g_2,h_2)\rangle) \end{align*} $$
and
Therefore, the integral is a right-
![]() $(G\times G)$
-invariant functional. This completes the proof.
$(G\times G)$
-invariant functional. This completes the proof.
Consider the subgroup
![]() $\{(g,g):g\in G\}$
of H. By Equation (2.23) and since
$\{(g,g):g\in G\}$
of H. By Equation (2.23) and since
![]() $\sigma _c=\sigma ^{*,rk}_{c}$
in
$\sigma _c=\sigma ^{*,rk}_{c}$
in
![]() $\mathrm {H}^2(G,\mu _m)$
, the restriction of
$\mathrm {H}^2(G,\mu _m)$
, the restriction of
![]() $H^{(m)}$
to this subgroup is the identity in
$H^{(m)}$
to this subgroup is the identity in
![]() $\mathrm {H}^2(G,\mu _m)$
, hence
$\mathrm {H}^2(G,\mu _m)$
, hence
![]() $H^{(m)}$
splits over
$H^{(m)}$
splits over
![]() $\{(g,g):g\in G\}$
. This splitting is unique (because G is perfect) and is defined as follows.
$\{(g,g):g\in G\}$
. This splitting is unique (because G is perfect) and is defined as follows.
Corollary 9. The map
![]() $(g,g)\mapsto \langle (g,g),\varsigma _{*,c}^{rk+1}(g)\rangle $
is the splitting of
$(g,g)\mapsto \langle (g,g),\varsigma _{*,c}^{rk+1}(g)\rangle $
is the splitting of
![]() $\{(g,g):g\in G\}$
in
$\{(g,g):g\in G\}$
in
![]() $H^{(m)}$
.
$H^{(m)}$
.
Proof. Let
![]() $g,g'\in G$
. By Proposition 7,
$g,g'\in G$
. By Proposition 7,
Now, Equation (2.22) implies that
therefore
The prescribed map is continuous because
![]() $\sigma ^{*,rk}_{c}\in \mathrm {C}^1(G,\mu _m)$
.
$\sigma ^{*,rk}_{c}\in \mathrm {C}^1(G,\mu _m)$
.
2.5 Global covering
Let F be a number field containing
![]() $\mu _m$
, and let
$\mu _m$
, and let
![]() $\nu $
be a place of F. Let
$\nu $
be a place of F. Let
![]() $\sigma _{2rkc,\nu }$
be the local
$\sigma _{2rkc,\nu }$
be the local
![]() $2$
-cocycle of § 2.4, regarded as a
$2$
-cocycle of § 2.4, regarded as a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $H(F_{\nu })$
by restriction from
$H(F_{\nu })$
by restriction from
![]() $\operatorname {\mathrm {GL}}_{2rkc}(F_{\nu })$
. Denote
$\operatorname {\mathrm {GL}}_{2rkc}(F_{\nu })$
. Denote
![]() $\sigma _{\nu }=\sigma _{2rkc,\nu }$
. The product
$\sigma _{\nu }=\sigma _{2rkc,\nu }$
. The product
![]() $\sigma =\prod _{\nu }\sigma _{\nu }$
is trivial on
$\sigma =\prod _{\nu }\sigma _{\nu }$
is trivial on
![]() $N_{rkc}(\mathbb {A})$
. It is also well defined on
$N_{rkc}(\mathbb {A})$
. It is also well defined on
![]() $B_{rkc}(\mathbb {A})$
: To see this, use Equation (2.9), Equation (2.7) and note that for
$B_{rkc}(\mathbb {A})$
: To see this, use Equation (2.9), Equation (2.7) and note that for
![]() $t\in T_{rkc}(\mathbb {A})$
, at almost all places, all coordinates of t belong to
$t\in T_{rkc}(\mathbb {A})$
, at almost all places, all coordinates of t belong to
![]() $\mathcal {O}_{\nu }^{*}$
and
$\mathcal {O}_{\nu }^{*}$
and
![]() $(\mathcal {O}_{\nu }^{*},\mathcal {O}_{\nu }^{*})_m=1$
. While it is well known that
$(\mathcal {O}_{\nu }^{*},\mathcal {O}_{\nu }^{*})_m=1$
. While it is well known that
![]() $\sigma $
is undefined on
$\sigma $
is undefined on
![]() $H(\mathbb {A})$
, we can define
$H(\mathbb {A})$
, we can define
![]() $\rho \in \mathrm {Z}^2(H(\mathbb {A}),\mu _m)$
such that at any
$\rho \in \mathrm {Z}^2(H(\mathbb {A}),\mu _m)$
such that at any
![]() $\nu $
,
$\nu $
,
![]() $\rho _{\nu }=\sigma _{\nu }$
in
$\rho _{\nu }=\sigma _{\nu }$
in
![]() $\mathrm {H}^2(H(F_{\nu }),\mu _m)$
. Thus,
$\mathrm {H}^2(H(F_{\nu }),\mu _m)$
. Thus,
![]() $\rho $
represents
$\rho $
represents
![]() $H^{(m)}(\mathbb {A})$
in
$H^{(m)}(\mathbb {A})$
in
![]() $\mathrm {H}^2(H(\mathbb {A}),\mu _m)$
(see § 2.2).
$\mathrm {H}^2(H(\mathbb {A}),\mu _m)$
(see § 2.2).
To achieve this, first note that for almost all
![]() $\nu $
there is a unique splitting
$\nu $
there is a unique splitting
![]() $y\mapsto \langle y,\eta _{\nu }(y)\rangle $
of
$y\mapsto \langle y,\eta _{\nu }(y)\rangle $
of
![]() $K_{H,\nu }$
, where
$K_{H,\nu }$
, where
![]() $\eta _{\nu }=\eta _{2rkc,\nu }$
(see § 2.4). We can extend
$\eta _{\nu }=\eta _{2rkc,\nu }$
(see § 2.4). We can extend
![]() $\eta _{\nu }$
to an element of
$\eta _{\nu }$
to an element of
![]() $\mathrm {C}^1(H(F_{\nu }),\mu _m)$
(though Equation (2.20) will no longer hold for arbitrary
$\mathrm {C}^1(H(F_{\nu }),\mu _m)$
(though Equation (2.20) will no longer hold for arbitrary
![]() $y,y'\in H(F_{\nu })$
). Now, define, for almost all
$y,y'\in H(F_{\nu })$
). Now, define, for almost all
![]() $\nu $
,
$\nu $
,
Then
![]() $\rho _{\nu }$
is trivial on
$\rho _{\nu }$
is trivial on
![]() $K_{H,\nu }$
. For the remaining places, we can simply take
$K_{H,\nu }$
. For the remaining places, we can simply take
![]() $\rho _{\nu }=\sigma _{\nu }$
and
$\rho _{\nu }=\sigma _{\nu }$
and
![]() $\eta _{\nu }=1$
. Then
$\eta _{\nu }=1$
. Then
![]() $\rho =\prod _{\nu }\rho _{\nu }$
is well defined on
$\rho =\prod _{\nu }\rho _{\nu }$
is well defined on
![]() $H(\mathbb {A})$
.
$H(\mathbb {A})$
.
We realize
![]() $H^{(m)}(\mathbb {A})$
using
$H^{(m)}(\mathbb {A})$
using
![]() $\rho $
then use the embedding
$\rho $
then use the embedding
![]() $G(\mathbb {A})\times G(\mathbb {A})\hookrightarrow H(\mathbb {A})$
to realize the
$G(\mathbb {A})\times G(\mathbb {A})\hookrightarrow H(\mathbb {A})$
to realize the
![]() $2$
-cocycles on the copies of
$2$
-cocycles on the copies of
![]() $G(\mathbb {A})$
. Let
$G(\mathbb {A})$
. Let
Now, the product on the left copy of
![]() $G^{(m)}(\mathbb {A})$
is defined by
$G^{(m)}(\mathbb {A})$
is defined by
![]() $\rho _L(g,g')$
, that is,
$\rho _L(g,g')$
, that is,
and on the right copy by
![]() $\rho _R(g,g')$
. In addition,
$\rho _R(g,g')$
. In addition,
because this holds locally by Proposition 7 (this does not mean the global version of Equation (2.23) holds with
![]() $\rho $
). Therefore, we may lift the embedding
$\rho $
). Therefore, we may lift the embedding
![]() $G(\mathbb {A})\times G(\mathbb {A}) \hookrightarrow H(\mathbb {A})$
to an embedding
$G(\mathbb {A})\times G(\mathbb {A}) \hookrightarrow H(\mathbb {A})$
to an embedding
and we obtain the global analog of the embeddings (2.24), namely,
![]() $\langle g,\epsilon \rangle \mapsto \langle \mathfrak {e}_1(g),\epsilon ^{-1}\rangle $
for the left copy and
$\langle g,\epsilon \rangle \mapsto \langle \mathfrak {e}_1(g),\epsilon ^{-1}\rangle $
for the left copy and
![]() $\langle g,\epsilon \rangle \mapsto \langle \mathfrak {e}_2(g),\epsilon \rangle $
for the right. Also, by Proposition 7,
$\langle g,\epsilon \rangle \mapsto \langle \mathfrak {e}_2(g),\epsilon \rangle $
for the right. Also, by Proposition 7,
![]() $\rho _{L,\nu }=\sigma ^{*,rk}_{c,\nu }=\sigma _{c,\nu }=\rho _{R,\nu }$
in
$\rho _{L,\nu }=\sigma ^{*,rk}_{c,\nu }=\sigma _{c,\nu }=\rho _{R,\nu }$
in
![]() $\mathrm {H}^2(G(F_{\nu }),\mu _m)$
, whence both copies of
$\mathrm {H}^2(G(F_{\nu }),\mu _m)$
, whence both copies of
![]() $G^{(m)}(\mathbb {A})$
are cohomologous.
$G^{(m)}(\mathbb {A})$
are cohomologous.
As in the local setting, we would like to explicate the relation between the copies of
![]() $G^{(m)}(\mathbb {A})$
so that we can work with the same
$G^{(m)}(\mathbb {A})$
so that we can work with the same
![]() $2$
-cocycle for both yet still use the global embedding (2.31). At any place
$2$
-cocycle for both yet still use the global embedding (2.31). At any place
![]() $\nu $
, Equation (2.23) implies that
$\nu $
, Equation (2.23) implies that
Whence by Equation (2.22),
 $$ \begin{align*} \sigma_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))=\left(\frac{\varsigma_{*,c,\nu}(gg')}{\varsigma_{*,c,\nu}(g) \varsigma_{*,c,\nu}(g')}\right)^{rk+1}\sigma_{\nu}(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}. \end{align*} $$
$$ \begin{align*} \sigma_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))=\left(\frac{\varsigma_{*,c,\nu}(gg')}{\varsigma_{*,c,\nu}(g) \varsigma_{*,c,\nu}(g')}\right)^{rk+1}\sigma_{\nu}(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}. \end{align*} $$
Then for all
![]() $\nu $
,
$\nu $
,
 $$ \begin{align*} &\rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\\&=\frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_1(g'))}{\eta_{\nu}(\mathfrak{e}_1(gg'))} \sigma_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\\ &=\frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_1(g'))}{\eta_{\nu}( \mathfrak{e}_1(gg'))}\frac{\eta_{\nu}(\mathfrak{e}_2(g))\eta_{\nu}(\mathfrak{e}_2(g'))}{\eta_{\nu}(\mathfrak{e}_2(gg'))} \left(\frac{\varsigma_{*,c,\nu}(gg')}{\varsigma_{*,c,\nu}(g)\varsigma_{*,c,\nu}(g')}\right)^{rk+1}\rho_{\nu}( \mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}. \end{align*} $$
$$ \begin{align*} &\rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\\&=\frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_1(g'))}{\eta_{\nu}(\mathfrak{e}_1(gg'))} \sigma_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\\ &=\frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_1(g'))}{\eta_{\nu}( \mathfrak{e}_1(gg'))}\frac{\eta_{\nu}(\mathfrak{e}_2(g))\eta_{\nu}(\mathfrak{e}_2(g'))}{\eta_{\nu}(\mathfrak{e}_2(gg'))} \left(\frac{\varsigma_{*,c,\nu}(gg')}{\varsigma_{*,c,\nu}(g)\varsigma_{*,c,\nu}(g')}\right)^{rk+1}\rho_{\nu}( \mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}. \end{align*} $$
Hence, if we define
![]() $\eta ^{\times }_{\nu }\in \mathrm {C}^1(G(F_{\nu }),\mu _m)$
by
$\eta ^{\times }_{\nu }\in \mathrm {C}^1(G(F_{\nu }),\mu _m)$
by
 $$ \begin{align*} \eta^{\times}_{\nu}(g)&=\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_2(g))/\varsigma_{*,c,\nu}^{rk+1}(g),\\\rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))&=\frac{\eta^{\times}_{\nu}(g)\eta^{\times}_{\nu}(g')}{\eta^{\times}_{\nu}(gg')}\rho_{\nu}(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}.\end{align*} $$
$$ \begin{align*} \eta^{\times}_{\nu}(g)&=\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_2(g))/\varsigma_{*,c,\nu}^{rk+1}(g),\\\rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))&=\frac{\eta^{\times}_{\nu}(g)\eta^{\times}_{\nu}(g')}{\eta^{\times}_{\nu}(gg')}\rho_{\nu}(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))^{-1}.\end{align*} $$
Now,
![]() $\eta ^{\times }=\prod _{\nu }\eta ^{\times }_{\nu }\in \mathrm {C}^1(G(\mathbb {A}),\mu _m)$
is well defined since for almost all
$\eta ^{\times }=\prod _{\nu }\eta ^{\times }_{\nu }\in \mathrm {C}^1(G(\mathbb {A}),\mu _m)$
is well defined since for almost all
![]() $\nu $
,
$\nu $
,
and then for these places
![]() $\eta ^{\times }_{\nu }$
becomes a homomorphism of
$\eta ^{\times }_{\nu }$
becomes a homomorphism of
![]() $K_{G,\nu }$
. Thus, we deduce the global relation, for all
$K_{G,\nu }$
. Thus, we deduce the global relation, for all
![]() $g,g'\in G(\mathbb {A})$
, that is,
$g,g'\in G(\mathbb {A})$
, that is,
Then by definition
Now, we can state the global analogs of Equations (2.27) and (2.28). First, if
![]() $G^{(m)}(\mathbb {A})[\rho _R]$
denotes the realization of
$G^{(m)}(\mathbb {A})[\rho _R]$
denotes the realization of
![]() $G^{(m)}(\mathbb {A})$
using
$G^{(m)}(\mathbb {A})$
using
![]() $\rho _R$
and similarly for
$\rho _R$
and similarly for
![]() $G^{(m)}(\mathbb {A})[\rho _L]$
, we have the (canonical) isomorphism
$G^{(m)}(\mathbb {A})[\rho _L]$
, we have the (canonical) isomorphism
Then for a function
![]() $\varphi $
on
$\varphi $
on
![]() $G^{(m)}(\mathbb {A})[\rho _R]$
, the function
$G^{(m)}(\mathbb {A})[\rho _R]$
, the function
![]() $\varphi ^{(\eta ^{\times })^{-1}}$
on
$\varphi ^{(\eta ^{\times })^{-1}}$
on
![]() $G^{(m)}(\mathbb {A})[\rho _L]$
is defined by
$G^{(m)}(\mathbb {A})[\rho _L]$
is defined by
Note that locally, ignoring the correction using
![]() $\eta _{\nu }$
,
$\eta _{\nu }$
,
![]() $(\eta _{\nu }^{\times })^{-1}(g_{\nu })$
becomes
$(\eta _{\nu }^{\times })^{-1}(g_{\nu })$
becomes
![]() $\varsigma _{*,c,\nu }^{rk+1}(g_{\nu })$
from Equation (2.28).
$\varsigma _{*,c,\nu }^{rk+1}(g_{\nu })$
from Equation (2.28).
Next, we state the analog of Proposition 8.
Proposition 10. Let
![]() $\varphi _1,\varphi _2$
be continuous genuine functions on
$\varphi _1,\varphi _2$
be continuous genuine functions on
![]() $G^{(m)}(\mathbb {A})$
, realized using
$G^{(m)}(\mathbb {A})$
, realized using
![]() $\rho _R$
, and f be a continuous genuine function on
$\rho _R$
, and f be a continuous genuine function on
![]() $H^{(m)}(\mathbb {A})$
. The integral
$H^{(m)}(\mathbb {A})$
. The integral
 $$ \begin{align*} \int\limits_{G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f( \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
$$ \begin{align*} \int\limits_{G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f( \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
is well defined: The integrand factors through
![]() $G(\mathbb {A})\times G(\mathbb {A})$
and the integral is a right-
$G(\mathbb {A})\times G(\mathbb {A})$
and the integral is a right-
![]() $(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional, if it is absolutely convergent.
$(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional, if it is absolutely convergent.
Proof. The integrand factors through
![]() $G(\mathbb {A})\times G(\mathbb {A})$
by the global analog of the embeddings (2.24). To see that it is a right-
$G(\mathbb {A})\times G(\mathbb {A})$
by the global analog of the embeddings (2.24). To see that it is a right-
![]() $(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional observe that by Equations (2.30) and (2.35),
$(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional observe that by Equations (2.30) and (2.35),
 $$ \begin{align*} &\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle\langle h_1,1\rangle)=\rho_L(g_1,h_1)\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1h_1,1\rangle)=\rho^{-1}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1h_1,1\rangle),\\ &\varphi_2(\langle g_2,1\rangle\langle h_2,1\rangle)=\rho_R(g_2,h_2)\varphi_2(\langle g_2h_2,1\rangle) =\rho(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\varphi_2(\langle 1,g_2h_2\rangle). \end{align*} $$
$$ \begin{align*} &\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle\langle h_1,1\rangle)=\rho_L(g_1,h_1)\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1h_1,1\rangle)=\rho^{-1}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1h_1,1\rangle),\\ &\varphi_2(\langle g_2,1\rangle\langle h_2,1\rangle)=\rho_R(g_2,h_2)\varphi_2(\langle g_2h_2,1\rangle) =\rho(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\varphi_2(\langle 1,g_2h_2\rangle). \end{align*} $$
Now, although Equation (2.25) no longer holds, still by Equation (2.31),
 $$ \begin{align*} &\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(h_2),1\rangle \\&= \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_2(h_2),1\rangle \\&= \rho(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\rho(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\langle \mathfrak{e}_1(g_1h_1),1\rangle\langle\mathfrak{e}_2(g_2h_2),1\rangle. \end{align*} $$
$$ \begin{align*} &\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(h_2),1\rangle \\&= \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_2(h_2),1\rangle \\&= \rho(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\rho(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\langle \mathfrak{e}_1(g_1h_1),1\rangle\langle\mathfrak{e}_2(g_2h_2),1\rangle. \end{align*} $$
We see that both
![]() $\rho (\mathfrak {e}_i(g_i),\mathfrak {e}_i(h_i))$
are cancelled (we integrate against
$\rho (\mathfrak {e}_i(g_i),\mathfrak {e}_i(h_i))$
are cancelled (we integrate against
![]() $\overline {\varphi _2}$
). The result follows.
$\overline {\varphi _2}$
). The result follows.
Now, consider the subgroup
![]() $\{(g,g):g\in G\}$
of H. Locally, the covering splits over this group (see Corollary 9), and because
$\{(g,g):g\in G\}$
of H. Locally, the covering splits over this group (see Corollary 9), and because
![]() $K_{G,\nu }$
is perfect for almost all
$K_{G,\nu }$
is perfect for almost all
![]() $\nu $
, we deduce that
$\nu $
, we deduce that
![]() $H^{(m)}(\mathbb {A})$
is split over
$H^{(m)}(\mathbb {A})$
is split over
![]() $\{(g,g):g\in G(\mathbb {A})\}$
(see § 2.2). Again, we determine the splitting.
$\{(g,g):g\in G(\mathbb {A})\}$
(see § 2.2). Again, we determine the splitting.
Corollary 11. The map
![]() $(g,g)\mapsto \langle (g,g),(\eta ^{\times })^{-1}(g)\rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))\rangle $
is the splitting of
$(g,g)\mapsto \langle (g,g),(\eta ^{\times })^{-1}(g)\rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))\rangle $
is the splitting of
![]() $\{(g,g):g\in G(\mathbb {A})\}$
in
$\{(g,g):g\in G(\mathbb {A})\}$
in
![]() $H^{(m)}(\mathbb {A})$
(!).
$H^{(m)}(\mathbb {A})$
(!).
Proof. Let
![]() $g,g'\in G(\mathbb {A})$
. Since
$g,g'\in G(\mathbb {A})$
. Since
by Equation (2.31) we have
 $$ \begin{align*} &\langle(g,g),\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle\langle(g',g'),\rho(\mathfrak{e}_1(g'),\mathfrak{e}_2(g'))\rangle\\&= \langle \mathfrak{e}_1(gg'),\rho(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\rangle \langle \mathfrak{e}_2(gg'),\rho(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))\rangle \\&=\langle (gg',gg'),\rho(\mathfrak{e}_1(gg'),\mathfrak{e}_2(gg'))\rho(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\rho(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))\rangle. \end{align*} $$
$$ \begin{align*} &\langle(g,g),\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle\langle(g',g'),\rho(\mathfrak{e}_1(g'),\mathfrak{e}_2(g'))\rangle\\&= \langle \mathfrak{e}_1(gg'),\rho(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\rangle \langle \mathfrak{e}_2(gg'),\rho(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))\rangle \\&=\langle (gg',gg'),\rho(\mathfrak{e}_1(gg'),\mathfrak{e}_2(gg'))\rho(\mathfrak{e}_1(g),\mathfrak{e}_1(g'))\rho(\mathfrak{e}_2(g),\mathfrak{e}_2(g'))\rangle. \end{align*} $$
Hence, by Equation (2.32),
 $$ \begin{align*} &\langle(g,g),(\eta^{\times})^{-1}(g)\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle\langle(g',g'),(\eta^{\times})^{-1}(g')\rho(\mathfrak{e}_1(g'),\mathfrak{e}_2(g'))\rangle \\&=\langle (gg',gg'),(\eta^{\times})^{-1}(gg')\rho(\mathfrak{e}_1(gg'),\mathfrak{e}_2(gg'))\rangle. \end{align*} $$
$$ \begin{align*} &\langle(g,g),(\eta^{\times})^{-1}(g)\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle\langle(g',g'),(\eta^{\times})^{-1}(g')\rho(\mathfrak{e}_1(g'),\mathfrak{e}_2(g'))\rangle \\&=\langle (gg',gg'),(\eta^{\times})^{-1}(gg')\rho(\mathfrak{e}_1(gg'),\mathfrak{e}_2(gg'))\rangle. \end{align*} $$
The continuity follows since
![]() $\eta ^{\times }$
and
$\eta ^{\times }$
and
![]() $g\mapsto \rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))$
belong to
$g\mapsto \rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))$
belong to
![]() $\mathrm {C}^1(G(\mathbb {A}),\mu _m)$
.
$\mathrm {C}^1(G(\mathbb {A}),\mu _m)$
.
As mentioned above,
![]() $\sigma =\prod _{\nu }\sigma _{\nu }$
is defined on certain subgroups of
$\sigma =\prod _{\nu }\sigma _{\nu }$
is defined on certain subgroups of
![]() $H(\mathbb {A})$
, for example, on
$H(\mathbb {A})$
, for example, on
![]() $N_{rkc}(\mathbb {A})$
. It is also defined on
$N_{rkc}(\mathbb {A})$
. It is also defined on
![]() $H(F)$
: Indeed for
$H(F)$
: Indeed for
![]() $h,h'\in H(F)$
,
$h,h'\in H(F)$
,
![]() $\sigma _{\nu }(h_{\nu },h^{\prime }_{\nu })=1$
for almost all
$\sigma _{\nu }(h_{\nu },h^{\prime }_{\nu })=1$
for almost all
![]() $\nu $
, because the local
$\nu $
, because the local
![]() $2$
-cocycle is written as a finite product of Hilbert symbols
$2$
-cocycle is written as a finite product of Hilbert symbols
![]() $(x,x')_{m,\nu }$
, with elements
$(x,x')_{m,\nu }$
, with elements
![]() $x,x'\in F^{*}$
that are independent of
$x,x'\in F^{*}$
that are independent of
![]() $\nu $
, and
$\nu $
, and
![]() $(x,x')_{m,\nu }=1$
for almost all
$(x,x')_{m,\nu }=1$
for almost all
![]() $\nu $
(see the proof of [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7], and also [Reference Kazhdan and PattersonKP84, § 0.2] and [Reference TakedaTak14, Proposition 1.7]). Moreover,
$\nu $
(see the proof of [Reference Banks, Levy and SepanskiBLS99, § 3, Theorem 7], and also [Reference Kazhdan and PattersonKP84, § 0.2] and [Reference TakedaTak14, Proposition 1.7]). Moreover,
![]() $\eta _{\nu }$
given by Equation (2.29) is trivial on
$\eta _{\nu }$
given by Equation (2.29) is trivial on
![]() $h_{\nu }$
for almost all
$h_{\nu }$
for almost all
![]() $\nu $
. This was shown in [Reference TakedaTak14, Proposition 1.8], and we follow the argument. Write
$\nu $
. This was shown in [Reference TakedaTak14, Proposition 1.8], and we follow the argument. Write
![]() $h=n't'w'n"$
according to the Bruhat decomposition in
$h=n't'w'n"$
according to the Bruhat decomposition in
![]() $H(F)$
, that is,
$H(F)$
, that is,
![]() $n',n"\in N_{rkc}(F)$
,
$n',n"\in N_{rkc}(F)$
,
![]() $t'\in T_{rkc}(F)$
and
$t'\in T_{rkc}(F)$
and
![]() $w'\in H(F)\cap \mathfrak {W}_{2rkc}^+$
(with
$w'\in H(F)\cap \mathfrak {W}_{2rkc}^+$
(with
![]() $\mathfrak {W}_{2rkc}^+$
defined over F). For almost all
$\mathfrak {W}_{2rkc}^+$
defined over F). For almost all
![]() $\nu $
, we have
$\nu $
, we have
![]() $n^{\prime }_{\nu },t^{\prime }_{\nu },w^{\prime }_{\nu },n^{\prime \prime }_{\nu }\in K_{G,\nu }$
, then by Equation (2.18),
$n^{\prime }_{\nu },t^{\prime }_{\nu },w^{\prime }_{\nu },n^{\prime \prime }_{\nu }\in K_{G,\nu }$
, then by Equation (2.18),
![]() $\eta _{\nu }(h_{\nu })=1$
because
$\eta _{\nu }(h_{\nu })=1$
because
![]() $\eta _{\nu }(n^{\prime }_{\nu })=\eta _{\nu }(t^{\prime }_{\nu })=\eta _{\nu }(w^{\prime }_{\nu })=\eta _{\nu }(n^{\prime \prime }_{\nu })=1$
(see § 2.4). Therefore, we can define
$\eta _{\nu }(n^{\prime }_{\nu })=\eta _{\nu }(t^{\prime }_{\nu })=\eta _{\nu }(w^{\prime }_{\nu })=\eta _{\nu }(n^{\prime \prime }_{\nu })=1$
(see § 2.4). Therefore, we can define
![]() $\eta =\prod _{\nu }\eta _{\nu }$
on
$\eta =\prod _{\nu }\eta _{\nu }$
on
![]() $H(F)$
and deduce that
$H(F)$
and deduce that
![]() $\sigma =\rho $
in
$\sigma =\rho $
in
![]() $\mathrm {H}^2(H(F),\mu _m)$
. Furthermore, because of the product formula
$\mathrm {H}^2(H(F),\mu _m)$
. Furthermore, because of the product formula
![]() $\prod _{\nu }(x,x')_{m,\nu }=1$
for any
$\prod _{\nu }(x,x')_{m,\nu }=1$
for any
![]() $x,x'\in F^{*}$
,
$x,x'\in F^{*}$
,
![]() $\sigma $
is in fact trivial on
$\sigma $
is in fact trivial on
![]() $H(F)$
, thus
$H(F)$
, thus
![]() $\langle h,\eta ^{-1}(h)\rangle $
is the splitting of
$\langle h,\eta ^{-1}(h)\rangle $
is the splitting of
![]() $H(F)$
in
$H(F)$
in
![]() $H^{(m)}(\mathbb {A})$
(see [Reference TakedaTak14, Proposition 1.7]).
$H^{(m)}(\mathbb {A})$
(see [Reference TakedaTak14, Proposition 1.7]).
Since
![]() $G(F)\times G(F)<H(F)$
, we can use
$G(F)\times G(F)<H(F)$
, we can use
![]() $\eta $
to define splittings of
$\eta $
to define splittings of
![]() $G(F)$
. A direct verification shows that
$G(F)$
. A direct verification shows that
![]() $g\mapsto \langle g,\eta (\mathfrak {e}_1(g))\rangle $
is the splitting of
$g\mapsto \langle g,\eta (\mathfrak {e}_1(g))\rangle $
is the splitting of
![]() $G(F)$
in the covering
$G(F)$
in the covering
![]() $G^{(m)}(\mathbb {A})$
realized using
$G^{(m)}(\mathbb {A})$
realized using
![]() $\rho _L$
, and
$\rho _L$
, and
![]() $g\mapsto \langle g,\eta ^{-1}(\mathfrak {e}_2(g))\rangle $
is the splitting when the covering is realized via
$g\mapsto \langle g,\eta ^{-1}(\mathfrak {e}_2(g))\rangle $
is the splitting when the covering is realized via
![]() $\rho _R$
(i.e., the right copy). Having fixed these splittings, we can now consider the spaces of automorphic forms on
$\rho _R$
(i.e., the right copy). Having fixed these splittings, we can now consider the spaces of automorphic forms on
![]() $G^{(m)}(\mathbb {A})$
and
$G^{(m)}(\mathbb {A})$
and
![]() $H^{(m)}(\mathbb {A})$
, which are in particular functions on
$H^{(m)}(\mathbb {A})$
, which are in particular functions on
![]() $G(F)\backslash G^{(m)}(\mathbb {A})$
and
$G(F)\backslash G^{(m)}(\mathbb {A})$
and
![]() $H(F)\backslash H^{(m)}(\mathbb {A})$
(resp.). We must specify whether we are considering the left or right copy of
$H(F)\backslash H^{(m)}(\mathbb {A})$
(resp.). We must specify whether we are considering the left or right copy of
![]() $G^{(m)}(\mathbb {A})$
because the
$G^{(m)}(\mathbb {A})$
because the
![]() $2$
-cocycles differ (up to a
$2$
-cocycles differ (up to a
![]() $2$
-coboundary) and so do the splittings of
$2$
-coboundary) and so do the splittings of
![]() $G(F)$
(see Equation (2.3)). Our next goal is to show that the map (2.35) preserves the notion of automorphic forms.
$G(F)$
(see Equation (2.3)). Our next goal is to show that the map (2.35) preserves the notion of automorphic forms.
Observe that Equation (2.23) also implies that
![]() $\sigma _{\nu }(\mathfrak {e}_1(g),\mathfrak {e}_2(g))=1$
for
$\sigma _{\nu }(\mathfrak {e}_1(g),\mathfrak {e}_2(g))=1$
for
![]() $g\in G(F_{\nu })$
. Therefore,
$g\in G(F_{\nu })$
. Therefore,
 $$ \begin{align} \rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_2(g))= \frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_2(g))}{\eta_{\nu}(\mathfrak{e}_1(g)\mathfrak{e}_2(g))} =\frac{\eta^{\times}_{\nu}(g)\varsigma_{*,c,\nu}^{rk+1}(g)}{\eta_{\nu}(\mathfrak{e}_1(g)\mathfrak{e}_2(g))},\qquad\forall g\in G(F_{\nu}). \end{align} $$
$$ \begin{align} \rho_{\nu}(\mathfrak{e}_1(g),\mathfrak{e}_2(g))= \frac{\eta_{\nu}(\mathfrak{e}_1(g))\eta_{\nu}(\mathfrak{e}_2(g))}{\eta_{\nu}(\mathfrak{e}_1(g)\mathfrak{e}_2(g))} =\frac{\eta^{\times}_{\nu}(g)\varsigma_{*,c,\nu}^{rk+1}(g)}{\eta_{\nu}(\mathfrak{e}_1(g)\mathfrak{e}_2(g))},\qquad\forall g\in G(F_{\nu}). \end{align} $$
Now,
![]() $\eta $
is well defined on
$\eta $
is well defined on
![]() $\{(g,g):g\in G(F)\}$
because it is defined on
$\{(g,g):g\in G(F)\}$
because it is defined on
![]() $H(F)$
;
$H(F)$
;
![]() $\rho $
is well defined on
$\rho $
is well defined on
![]() $G(F)$
since it is defined on
$G(F)$
since it is defined on
![]() $H(\mathbb {A})$
, and
$H(\mathbb {A})$
, and
![]() $\eta ^{\times }$
is well defined on
$\eta ^{\times }$
is well defined on
![]() $G(F)$
because it is defined on
$G(F)$
because it is defined on
![]() $G(\mathbb {A})$
. Thus, if
$G(\mathbb {A})$
. Thus, if
![]() $g\in G(F)$
, then for almost all
$g\in G(F)$
, then for almost all
![]() $\nu $
, by Equation (2.36),
$\nu $
, by Equation (2.36),
![]() $\varsigma _{*,c,\nu }^{rk+1}(g_{\nu })=1$
, whence
$\varsigma _{*,c,\nu }^{rk+1}(g_{\nu })=1$
, whence
![]() $\varsigma _{*,c}^{rk+1}=\prod _{\nu }\varsigma _{*,c,\nu }^{rk+1}$
is well defined on
$\varsigma _{*,c}^{rk+1}=\prod _{\nu }\varsigma _{*,c,\nu }^{rk+1}$
is well defined on
![]() $G(F)$
(if
$G(F)$
(if
![]() $m\nmid rk$
,
$m\nmid rk$
,
![]() $\varsigma _{*,c}$
might not be). Therefore, we can write globally
$\varsigma _{*,c}$
might not be). Therefore, we can write globally
 $$ \begin{align} \rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))=\frac{\eta^{\times}(g)\varsigma_{*,c}^{rk+1}(g)}{\eta(\mathfrak{e}_1(g)\mathfrak{e}_2(g))},\qquad\forall g\in G(F). \end{align} $$
$$ \begin{align} \rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))=\frac{\eta^{\times}(g)\varsigma_{*,c}^{rk+1}(g)}{\eta(\mathfrak{e}_1(g)\mathfrak{e}_2(g))},\qquad\forall g\in G(F). \end{align} $$
Proposition 12. The section
![]() $\varsigma _{*,c}^{rk+1}$
is trivial on
$\varsigma _{*,c}^{rk+1}$
is trivial on
![]() $G(F)$
.
$G(F)$
.
Proof. For each
![]() $\nu $
, raising Equation (2.21) to the power
$\nu $
, raising Equation (2.21) to the power
![]() $rk+1$
we have
$rk+1$
we have
 $$ \begin{align*} (\sigma^{*}_{c,\nu})^{rk+1}(g,g')=\left(\frac{\varsigma_{*,c,\nu}(g)\varsigma_{*,c,\nu}(g')}{\varsigma_{*,c,\nu}(gg')}\right)^{rk+1}\sigma_{c,\nu}^{rk+1}(g,g'). \end{align*} $$
$$ \begin{align*} (\sigma^{*}_{c,\nu})^{rk+1}(g,g')=\left(\frac{\varsigma_{*,c,\nu}(g)\varsigma_{*,c,\nu}(g')}{\varsigma_{*,c,\nu}(gg')}\right)^{rk+1}\sigma_{c,\nu}^{rk+1}(g,g'). \end{align*} $$
Since
![]() $\sigma _c$
is trivial on
$\sigma _c$
is trivial on
![]() $G(F)$
and
$G(F)$
and
![]() $g\mapsto g^{*}$
is an involution of
$g\mapsto g^{*}$
is an involution of
![]() $G(F)$
,
$G(F)$
,
![]() $\sigma _c^{*}$
is also trivial on
$\sigma _c^{*}$
is also trivial on
![]() $G(F)$
. Also,
$G(F)$
. Also,
![]() $\varsigma _{*,c}^{rk+1}$
is well defined on
$\varsigma _{*,c}^{rk+1}$
is well defined on
![]() $G(F)$
. Therefore, we can globalize this equality and deduce that
$G(F)$
. Therefore, we can globalize this equality and deduce that
![]() $\varsigma _{*,c}^{rk+1}:G(F)\rightarrow \mu _m$
is a homomorphism, which must be trivial because
$\varsigma _{*,c}^{rk+1}:G(F)\rightarrow \mu _m$
is a homomorphism, which must be trivial because
![]() $G(F)$
is perfect.
$G(F)$
is perfect.
Corollary 13. Let
![]() $\varphi _1$
be a continuous genuine function on
$\varphi _1$
be a continuous genuine function on
![]() $G(F)\backslash G^{(m)}(\mathbb {A})$
, where
$G(F)\backslash G^{(m)}(\mathbb {A})$
, where
![]() $G^{(m)}(\mathbb {A})$
is realized using
$G^{(m)}(\mathbb {A})$
is realized using
![]() $\rho _R$
. Then
$\rho _R$
. Then
![]() $\varphi _1^{(\eta ^{\times })^{-1}}$
is a similar function on
$\varphi _1^{(\eta ^{\times })^{-1}}$
is a similar function on
![]() $G(F)\backslash G^{(m)}(\mathbb {A})$
(realized using
$G(F)\backslash G^{(m)}(\mathbb {A})$
(realized using
![]() $\rho _L$
).
$\rho _L$
).
Proof. By Proposition 12,
![]() $\eta ^{\times }(y)=\eta (\mathfrak {e}_1(y))\eta (\mathfrak {e}_2(y))$
for all
$\eta ^{\times }(y)=\eta (\mathfrak {e}_1(y))\eta (\mathfrak {e}_2(y))$
for all
![]() $y\in G(F)$
, hence for any
$y\in G(F)$
, hence for any
![]() $h\in G^{(m)}(\mathbb {A})$
,
$h\in G^{(m)}(\mathbb {A})$
,
where we used the left-invariance of
![]() $\varphi _1$
.
$\varphi _1$
.
Proposition 14. Let
![]() $\varphi _1,\varphi _2$
be continuous genuine functions on
$\varphi _1,\varphi _2$
be continuous genuine functions on
![]() $G(F)\backslash G^{(m)}(\mathbb {A})$
, where
$G(F)\backslash G^{(m)}(\mathbb {A})$
, where
![]() $G^{(m)}(\mathbb {A})$
is realized using
$G^{(m)}(\mathbb {A})$
is realized using
![]() $\rho _R$
. Let f be a continuous genuine function on the image of
$\rho _R$
. Let f be a continuous genuine function on the image of
in
![]() $H(F)\backslash H^{(m)}(\mathbb {A})$
, with the above identifications (e.g., f on
$H(F)\backslash H^{(m)}(\mathbb {A})$
, with the above identifications (e.g., f on
![]() $H(F)\backslash H^{(m)}(\mathbb {A})$
). Then the integral
$H(F)\backslash H^{(m)}(\mathbb {A})$
). Then the integral
 $$ \begin{align*} \int\limits_{G(F)\times G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
$$ \begin{align*} \int\limits_{G(F)\times G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\overline{\varphi_2(\langle g_2,1\rangle)}f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
is well defined: The integrand factors through the quotient and the integral is a right-
![]() $(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional, provided it is absolutely convergent.
$(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional, provided it is absolutely convergent.
Proof. By Proposition 10, it remains to show that the integrand factors through the quotient. Let
![]() $y_1,y_2\in G(F)$
and
$y_1,y_2\in G(F)$
and
![]() $g_1,g_2\in G(\mathbb {A})$
. Put
$g_1,g_2\in G(\mathbb {A})$
. Put
![]() $\epsilon _i=\eta _i(\mathfrak {e}_i(y_i))$
. Then
$\epsilon _i=\eta _i(\mathfrak {e}_i(y_i))$
. Then
 $$ \begin{align*} &\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1g_1,1\rangle)\overline{\varphi_2(\langle y_2g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1g_1),1\rangle\langle\mathfrak{e}_2(y_2g_2),1\rangle) \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,1\rangle \langle g_1,1\rangle )\overline{\varphi_2(\langle y_2,1\rangle \langle g_2,1\rangle )} f( \langle\mathfrak{e}_1(y_1),1\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(y_2),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle) \overline{\varphi_2(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(y_2), \epsilon_2^{-1}\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle) \overline{\varphi_2(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_2(y_2), \epsilon_2^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\\ &=\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle) \overline{\varphi_2(\langle g_2,1\rangle)}f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber. \end{align*} $$
$$ \begin{align*} &\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1g_1,1\rangle)\overline{\varphi_2(\langle y_2g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1g_1),1\rangle\langle\mathfrak{e}_2(y_2g_2),1\rangle) \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,1\rangle \langle g_1,1\rangle )\overline{\varphi_2(\langle y_2,1\rangle \langle g_2,1\rangle )} f( \langle\mathfrak{e}_1(y_1),1\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(y_2),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle) \overline{\varphi_2(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(y_2), \epsilon_2^{-1}\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle) \overline{\varphi_2(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)}f( \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_2(y_2), \epsilon_2^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\\ &=\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle) \overline{\varphi_2(\langle g_2,1\rangle)}f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber. \end{align*} $$
For the last equality, we used the left invariance under
![]() $G(F)$
(resp.,
$G(F)$
(resp.,
![]() $H(F)$
) of
$H(F)$
) of
![]() $\varphi _i$
(resp., f) and note that this left invariance is with respect to the particular section for each copy of
$\varphi _i$
(resp., f) and note that this left invariance is with respect to the particular section for each copy of
![]() $G(F)$
.
$G(F)$
.
As explained above, on
![]() $H(F)$
we have global definitions of
$H(F)$
we have global definitions of
![]() $\sigma $
and
$\sigma $
and
![]() $\eta $
so that the global analog of Equation (2.29) is valid, and
$\eta $
so that the global analog of Equation (2.29) is valid, and
![]() $h\mapsto \langle h,\eta ^{-1}(h)\rangle $
is the splitting of
$h\mapsto \langle h,\eta ^{-1}(h)\rangle $
is the splitting of
![]() $H(F)$
under
$H(F)$
under
![]() $\rho $
. A simpler argument applies to
$\rho $
. A simpler argument applies to
![]() $N_{rkc}(\mathbb {A})$
: Since
$N_{rkc}(\mathbb {A})$
: Since
![]() $\eta _{\nu }$
is trivial on
$\eta _{\nu }$
is trivial on
![]() $N_{rkc}(\mathcal {O}_{\nu })$
for all
$N_{rkc}(\mathcal {O}_{\nu })$
for all
![]() $\nu $
where
$\nu $
where
![]() $F_{\nu }$
is unramified (see § 2.4),
$F_{\nu }$
is unramified (see § 2.4),
![]() $\eta \in \mathrm {C}^1(N_{rkc}(\mathbb {A}),\mu _m)$
, and because
$\eta \in \mathrm {C}^1(N_{rkc}(\mathbb {A}),\mu _m)$
, and because
![]() $\sigma _{\nu }$
is trivial on
$\sigma _{\nu }$
is trivial on
![]() $N_{rkc}(F_{\nu })$
for all
$N_{rkc}(F_{\nu })$
for all
![]() $\nu $
, the global analog of Equation (2.29) holds and
$\nu $
, the global analog of Equation (2.29) holds and
![]() $u\mapsto \langle u,\eta ^{-1}(u)\rangle $
is the splitting of
$u\mapsto \langle u,\eta ^{-1}(u)\rangle $
is the splitting of
![]() $N_{rkc}(\mathbb {A})$
in
$N_{rkc}(\mathbb {A})$
in
![]() $H^{(m)}(\mathbb {A})$
.
$H^{(m)}(\mathbb {A})$
.
The following lemma is the extension of Equation (2.10) to the global cover.
Lemma 15. Let
![]() $h\in H(\mathbb {A})$
,
$h\in H(\mathbb {A})$
,
![]() $v\in N_{rkc}(\mathbb {A})$
. If
$v\in N_{rkc}(\mathbb {A})$
. If
![]() ${}^hv\in N_{rkc}(\mathbb {A})$
,
${}^hv\in N_{rkc}(\mathbb {A})$
,
![]() ${}^h\langle v,\eta ^{-1}(v)\rangle =\langle {}^hv,\eta ^{-1}({}^hv)\rangle $
.
${}^h\langle v,\eta ^{-1}(v)\rangle =\langle {}^hv,\eta ^{-1}({}^hv)\rangle $
.
Proof. Let
![]() $Y<N_{rkc}$
be the unipotent subgroup generated by v. Then
$Y<N_{rkc}$
be the unipotent subgroup generated by v. Then
![]() $u\mapsto \langle u,\eta ^{-1}(u)\rangle $
(the unique splitting of
$u\mapsto \langle u,\eta ^{-1}(u)\rangle $
(the unique splitting of
![]() $N_{rkc}(\mathbb {A})$
) is also the unique splitting of
$N_{rkc}(\mathbb {A})$
) is also the unique splitting of
![]() $Y(\mathbb {A})$
. Since
$Y(\mathbb {A})$
. Since
![]() ${}^hv\in N_{rkc}(\mathbb {A})$
, we have
${}^hv\in N_{rkc}(\mathbb {A})$
, we have
![]() ${}^hY(\mathbb {A})<N_{rkc}(\mathbb {A})$
and hence
${}^hY(\mathbb {A})<N_{rkc}(\mathbb {A})$
and hence
![]() ${}^hu\mapsto \langle {}^hu,\eta ^{-1}({}^hu)\rangle $
is a splitting of
${}^hu\mapsto \langle {}^hu,\eta ^{-1}({}^hu)\rangle $
is a splitting of
![]() ${}^hY(\mathbb {A})$
. Now, the result follows from Equation (2.4) (with
${}^hY(\mathbb {A})$
. Now, the result follows from Equation (2.4) (with
![]() $\chi ={}^h(\cdot )$
).
$\chi ={}^h(\cdot )$
).
Corollary 16. For any
![]() $h\in H(F)$
and
$h\in H(F)$
and
![]() $u\in N_{rkc}(\mathbb {A})$
,
$u\in N_{rkc}(\mathbb {A})$
,
Proof. By Equation (2.8),
![]() $\sigma (h^{\prime }_{\nu },u^{\prime }_{\nu })=1$
for any
$\sigma (h^{\prime }_{\nu },u^{\prime }_{\nu })=1$
for any
![]() $h'\in H(F)$
and
$h'\in H(F)$
and
![]() $u'\in N_{rkc}(\mathbb {A})$
. Hence, Equation (2.29) gives
$u'\in N_{rkc}(\mathbb {A})$
. Hence, Equation (2.29) gives
Since the left-hand side (l.h.s.) is
![]() $1$
for almost all
$1$
for almost all
![]() $\nu $
and so are
$\nu $
and so are
![]() $\eta _{\nu }(h^{\prime }_{\nu })$
and
$\eta _{\nu }(h^{\prime }_{\nu })$
and
![]() $\eta _{\nu }(u^{\prime }_{\nu })$
, we deduce that
$\eta _{\nu }(u^{\prime }_{\nu })$
, we deduce that
![]() $\eta _{\nu }(h^{\prime }_{\nu }u^{\prime }_{\nu })=1$
almost everywhere. Therefore,
$\eta _{\nu }(h^{\prime }_{\nu }u^{\prime }_{\nu })=1$
almost everywhere. Therefore,
![]() $\eta (hu)$
is well defined and we have
$\eta (hu)$
is well defined and we have
proving the first equality. The symmetric argument (for
![]() $\rho (u,h)$
) implies the second formula.
$\rho (u,h)$
) implies the second formula.
2.6 The lift of the involution
 ${}^{\iota }$
of G
${}^{\iota }$
of G
For the construction of the integral, we will repeatedly use the outer involution
![]() ${}^{\iota }$
of G, given locally and globally by
${}^{\iota }$
of G, given locally and globally by
![]() $g\mapsto {}^{\iota }g=\iota g\iota ^{-1}$
, where
$g\mapsto {}^{\iota }g=\iota g\iota ^{-1}$
, where
![]() $\iota =\left (\begin {smallmatrix}&I_{c/2}\\I_{c/2}\end {smallmatrix}\right )$
. In this section, we discuss its lift to
$\iota =\left (\begin {smallmatrix}&I_{c/2}\\I_{c/2}\end {smallmatrix}\right )$
. In this section, we discuss its lift to
![]() $G^{(m)}$
.
$G^{(m)}$
.
First, consider the local setting and realize
![]() $G^{(m)}$
with
$G^{(m)}$
with
![]() $\sigma _c$
. Since
$\sigma _c$
. Since
![]() ${}^{\iota }$
is also a (continuous) involution of
${}^{\iota }$
is also a (continuous) involution of
![]() $\operatorname {\mathrm {GL}}_c$
, we can define
$\operatorname {\mathrm {GL}}_c$
, we can define
![]() $\sigma _c^{\iota }\in \mathrm {Z}^2(\operatorname {\mathrm {GL}}_c,\mu _m)$
by
$\sigma _c^{\iota }\in \mathrm {Z}^2(\operatorname {\mathrm {GL}}_c,\mu _m)$
by
![]() $\sigma _c^{\iota }(g,g')=\sigma _c({}^{\iota }g,{}^{\iota }g')$
for
$\sigma _c^{\iota }(g,g')=\sigma _c({}^{\iota }g,{}^{\iota }g')$
for
![]() $g,g'\in \operatorname {\mathrm {GL}}_c$
.
$g,g'\in \operatorname {\mathrm {GL}}_c$
.
Proposition 17. We have
![]() $\sigma ^{\iota }_{c}=\sigma _{c}$
in
$\sigma ^{\iota }_{c}=\sigma _{c}$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
, in particular in
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_c,\mu _m)$
, in particular in
![]() $\mathrm {H}^2(G,\mu _m)$
.
$\mathrm {H}^2(G,\mu _m)$
.
Proof. As in the proof of Proposition 4, by [Reference MooreMoo68, p. 54, Corollary 2] it is enough to consider
![]() $t,t'\in T_{\operatorname {\mathrm {SL}}_c}$
(by loc. cit. restriction
$t,t'\in T_{\operatorname {\mathrm {SL}}_c}$
(by loc. cit. restriction
![]() $\mathrm {H}^2(G,\mu _m)\rightarrow \mathrm {H}^2(T_n,\mu _m)$
is
$\mathrm {H}^2(G,\mu _m)\rightarrow \mathrm {H}^2(T_n,\mu _m)$
is
![]() $2$
-to-
$2$
-to-
![]() $1$
). By Equation (2.7),
$1$
). By Equation (2.7),
![]() $\sigma _c^{\iota }(t,t')$
equals
$\sigma _c^{\iota }(t,t')$
equals
 $$ \begin{align*} \prod_{i=n+1}^{c-1}\prod_{j=n+1}^i(t_i,t^{\prime}_j)_m^{-1} \prod_{i=n}^{c-1}\prod_{j=1}^n(t_i^{-1},t^{\prime}_j)_m\prod_{i=1}^{n-1}\prod_{j=1}^n(t_i^{-1},t^{\prime}_j)_m \prod_{i=1}^{n-1}\prod_{j=i+1}^n(t_i,t^{\prime}_j)_m =\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1}=\sigma_c(t,t'). \end{align*} $$
$$ \begin{align*} \prod_{i=n+1}^{c-1}\prod_{j=n+1}^i(t_i,t^{\prime}_j)_m^{-1} \prod_{i=n}^{c-1}\prod_{j=1}^n(t_i^{-1},t^{\prime}_j)_m\prod_{i=1}^{n-1}\prod_{j=1}^n(t_i^{-1},t^{\prime}_j)_m \prod_{i=1}^{n-1}\prod_{j=i+1}^n(t_i,t^{\prime}_j)_m =\prod_{i=1}^{c-1}\prod_{j=1}^i(t_i,t^{\prime}_j)_m^{-1}=\sigma_c(t,t'). \end{align*} $$
The result follows.
Consequently, there exists
![]() $\varsigma _{\iota ,c}\in \mathrm {C}^1(\operatorname {\mathrm {SL}}_c,\mu _m)$
such that
$\varsigma _{\iota ,c}\in \mathrm {C}^1(\operatorname {\mathrm {SL}}_c,\mu _m)$
such that
 $$ \begin{align} \sigma^{\iota}_{c}(g,g')=\frac{\varsigma_{\iota,c}(g)\varsigma_{\iota,c}(g')}{\varsigma_{\iota,c}(gg')}\sigma_{c}(g,g'),\qquad \forall g,g'\in G. \end{align} $$
$$ \begin{align} \sigma^{\iota}_{c}(g,g')=\frac{\varsigma_{\iota,c}(g)\varsigma_{\iota,c}(g')}{\varsigma_{\iota,c}(gg')}\sigma_{c}(g,g'),\qquad \forall g,g'\in G. \end{align} $$
Proposition 18. The involution
![]() ${}^{\iota }$
lifts (uniquely) to an outer involution of
${}^{\iota }$
lifts (uniquely) to an outer involution of
![]() $G^{(m)}$
, also denoted
$G^{(m)}$
, also denoted
![]() ${}^{\iota }$
, and moreover
${}^{\iota }$
, and moreover
Proof. First, we show that Equation (2.39) is an abstract automorphism of
![]() $G^{(m)}$
. Indeed, the definition of
$G^{(m)}$
. Indeed, the definition of
![]() $\sigma _c^{\iota }$
and Equation (2.38) imply
$\sigma _c^{\iota }$
and Equation (2.38) imply
 $$ \begin{align*} {}^{\iota}(\langle g,1\rangle\langle g',1\rangle) &={}^{\iota}\langle gg',\sigma_c(g,g')\rangle=\langle {}^{\iota}(gg'),\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \\&=\langle {}^{\iota}g,\sigma_c({}^{\iota}g,{}^{\iota}g')^{-1}\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \langle {}^{\iota}g',1\rangle \\&=\langle {}^{\iota}g,\sigma_c^{\iota}(g,g')^{-1}\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \langle {}^{\iota}g',1\rangle \\&=\langle {}^{\iota}g,\varsigma_{\iota,c}^{-1}(g)\rangle \langle {}^{\iota}g',\varsigma_{\iota,c}^{-1}(g')\rangle ={}^{\iota}\langle g,1\rangle {}^{\iota}\langle g',1\rangle. \end{align*} $$
$$ \begin{align*} {}^{\iota}(\langle g,1\rangle\langle g',1\rangle) &={}^{\iota}\langle gg',\sigma_c(g,g')\rangle=\langle {}^{\iota}(gg'),\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \\&=\langle {}^{\iota}g,\sigma_c({}^{\iota}g,{}^{\iota}g')^{-1}\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \langle {}^{\iota}g',1\rangle \\&=\langle {}^{\iota}g,\sigma_c^{\iota}(g,g')^{-1}\varsigma_{\iota,c}^{-1}(gg')\sigma_c(g,g')\rangle \langle {}^{\iota}g',1\rangle \\&=\langle {}^{\iota}g,\varsigma_{\iota,c}^{-1}(g)\rangle \langle {}^{\iota}g',\varsigma_{\iota,c}^{-1}(g')\rangle ={}^{\iota}\langle g,1\rangle {}^{\iota}\langle g',1\rangle. \end{align*} $$
Therefore, Equation (2.39) is an abstract lift of
![]() ${}^{\iota }$
to
${}^{\iota }$
to
![]() $G^{(m)}$
and the unique one (see § 2.2).
$G^{(m)}$
and the unique one (see § 2.2).
Since
![]() $\iota \in \operatorname {\mathrm {GL}}_c$
,
$\iota \in \operatorname {\mathrm {GL}}_c$
,
![]() ${}^{\iota }g$
is simply conjugation in
${}^{\iota }g$
is simply conjugation in
![]() $\operatorname {\mathrm {GL}}_c$
. Our realization of
$\operatorname {\mathrm {GL}}_c$
. Our realization of
![]() $G^{(m)}$
using restriction from
$G^{(m)}$
using restriction from
![]() $\sigma _c$
allows us to compute
$\sigma _c$
allows us to compute
![]() ${}^{\iota }\langle g,\epsilon \rangle =\langle {}^{\iota }g,\epsilon _g\epsilon \rangle $
by regarding
${}^{\iota }\langle g,\epsilon \rangle =\langle {}^{\iota }g,\epsilon _g\epsilon \rangle $
by regarding
![]() $\iota $
and g as elements of
$\iota $
and g as elements of
![]() $\operatorname {\mathrm {GL}}_c$
and using the formulas for
$\operatorname {\mathrm {GL}}_c$
and using the formulas for
![]() $\sigma _c$
as a
$\sigma _c$
as a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $\operatorname {\mathrm {GL}}_c$
. The lift of
$\operatorname {\mathrm {GL}}_c$
. The lift of
![]() ${}^{\iota }$
to an involution of
${}^{\iota }$
to an involution of
![]() $G^{(m)}$
is unique, hence
$G^{(m)}$
is unique, hence
![]() $\epsilon _g=\varsigma _{\iota ,c}^{-1}(g)$
. This implies that Equation (2.39) is continuous, that is, the lift is a topological automorphism.
$\epsilon _g=\varsigma _{\iota ,c}^{-1}(g)$
. This implies that Equation (2.39) is continuous, that is, the lift is a topological automorphism.
Since
![]() ${}^{\iota }$
is an involution of G, the map
${}^{\iota }$
is an involution of G, the map
is the lift of the identity map, which (by uniqueness) coincides with
![]() $\langle g,1\rangle \mapsto \langle g,1\rangle $
. Hence,
$\langle g,1\rangle \mapsto \langle g,1\rangle $
. Hence,
and
![]() ${}^{\iota }$
is a also an involution of
${}^{\iota }$
is a also an involution of
![]() $G^{(m)}$
.
$G^{(m)}$
.
Remark 19. The proposition applies to
![]() $\operatorname {\mathrm {SL}}_c^{(m)}$
as well, but this will not be needed.
$\operatorname {\mathrm {SL}}_c^{(m)}$
as well, but this will not be needed.
The embedding
![]() $\mathfrak {e}_2:G\rightarrow H$
was lifted to an embedding
$\mathfrak {e}_2:G\rightarrow H$
was lifted to an embedding
![]() $G^{(m)}\hookrightarrow H^{(m)}$
by Formula (2.24). Then we can define
$G^{(m)}\hookrightarrow H^{(m)}$
by Formula (2.24). Then we can define
![]() ${}^{\iota }$
as an involution of this image of
${}^{\iota }$
as an involution of this image of
![]() $G^{(m)}$
by
$G^{(m)}$
by
By Proposition 7,
![]() $\mathfrak {e}_2(G)$
and
$\mathfrak {e}_2(G)$
and
![]() $\mathfrak {e}_1(G)$
commute in
$\mathfrak {e}_1(G)$
commute in
![]() $H^{(m)}$
. Therefore,
$H^{(m)}$
. Therefore,
Also, by Equations (2.23) and (2.25), we can lift
![]() ${}^{\iota }$
uniquely to an involution of the image of
${}^{\iota }$
uniquely to an involution of the image of
![]() $G^{(m)}\times G^{(m)}$
in
$G^{(m)}\times G^{(m)}$
in
![]() $H^{(m)}$
, which is given by
$H^{(m)}$
, which is given by
When F is unramified,
![]() $y\mapsto \langle y,\eta _c(y)\rangle $
is the unique splitting of
$y\mapsto \langle y,\eta _c(y)\rangle $
is the unique splitting of
![]() $K_G$
in
$K_G$
in
![]() $G^{(m)}$
. Since
$G^{(m)}$
. Since
![]() ${}^{\iota }$
is in particular an automorphism of
${}^{\iota }$
is in particular an automorphism of
![]() $K_G$
, the map
$K_G$
, the map
![]() ${}^{\iota }y\mapsto \langle {}^{\iota }y,\eta _c({}^{\iota }y)\rangle $
is a splitting of
${}^{\iota }y\mapsto \langle {}^{\iota }y,\eta _c({}^{\iota }y)\rangle $
is a splitting of
![]() ${}^{\iota }K_G=K_G$
, and hence by Equation (2.4) (with
${}^{\iota }K_G=K_G$
, and hence by Equation (2.4) (with
![]() $Y=K_G$
,
$Y=K_G$
,
![]() $\chi ={}^{\iota }$
),
$\chi ={}^{\iota }$
),
Given a genuine smooth admissible representation
![]() $\pi $
of
$\pi $
of
![]() $G^{(m)}$
, the representation
$G^{(m)}$
, the representation
![]() $\pi ^{\iota }$
is defined to be the genuine representation of
$\pi ^{\iota }$
is defined to be the genuine representation of
![]() $G^{(m)}$
acting on the same space as
$G^{(m)}$
acting on the same space as
![]() $\pi $
, where the action is defined by
$\pi $
, where the action is defined by
![]() $\pi ^{\iota }(g)=\pi ({}^{\iota }g)$
. Observe that since
$\pi ^{\iota }(g)=\pi ({}^{\iota }g)$
. Observe that since
![]() ${}^{\iota }(g^{-1})=({}^{\iota }g)^{-1}$
,
${}^{\iota }(g^{-1})=({}^{\iota }g)^{-1}$
,
 $$ \begin{align*} {}^{\iota}(\langle g,1\rangle^{-1})&= {}^{\iota}\langle g^{-1},\sigma_c(g,g^{-1})^{-1}\rangle\\&= \langle {}^{\iota}(g^{-1}),\varsigma_{\iota,c}^{-1}(g^{-1})\sigma_c(g,g^{-1})^{-1}\rangle\\&= \langle {}^{\iota}g,\varsigma_{\iota,c}(g^{-1})\sigma_c(g,g^{-1})\sigma_c({}^{\iota}g,{}^{\iota}g^{-1})^{-1}\rangle^{-1}\\&= \langle {}^{\iota}g,\varsigma_{\iota,c}(g^{-1})\sigma_c(g,g^{-1})\sigma_c^{\iota}(g,g^{-1})^{-1}\rangle^{-1}= \langle {}^{\iota}g,\varsigma_{\iota,c}^{-1}(g)\rangle^{-1}= ({}^{\iota}\langle g,1\rangle)^{-1}, \end{align*} $$
$$ \begin{align*} {}^{\iota}(\langle g,1\rangle^{-1})&= {}^{\iota}\langle g^{-1},\sigma_c(g,g^{-1})^{-1}\rangle\\&= \langle {}^{\iota}(g^{-1}),\varsigma_{\iota,c}^{-1}(g^{-1})\sigma_c(g,g^{-1})^{-1}\rangle\\&= \langle {}^{\iota}g,\varsigma_{\iota,c}(g^{-1})\sigma_c(g,g^{-1})\sigma_c({}^{\iota}g,{}^{\iota}g^{-1})^{-1}\rangle^{-1}\\&= \langle {}^{\iota}g,\varsigma_{\iota,c}(g^{-1})\sigma_c(g,g^{-1})\sigma_c^{\iota}(g,g^{-1})^{-1}\rangle^{-1}= \langle {}^{\iota}g,\varsigma_{\iota,c}^{-1}(g)\rangle^{-1}= ({}^{\iota}\langle g,1\rangle)^{-1}, \end{align*} $$
where we used
![]() $\langle ({}^{\iota }g)^{-1},\epsilon ^{-1}\rangle =\langle {}^{\iota }g,\epsilon \sigma _c({}^{\iota }g,{}^{\iota }g^{-1})^{-1}\rangle ^{-1}$
for the third equality, and Equation (2.38) with
$\langle ({}^{\iota }g)^{-1},\epsilon ^{-1}\rangle =\langle {}^{\iota }g,\epsilon \sigma _c({}^{\iota }g,{}^{\iota }g^{-1})^{-1}\rangle ^{-1}$
for the third equality, and Equation (2.38) with
![]() $g'=g^{-1}$
one equality before the last (note that
$g'=g^{-1}$
one equality before the last (note that
![]() $\varsigma _{\iota ,c}(gg^{-1})=\varsigma _{\iota ,c}(I_c)=1$
). Since
$\varsigma _{\iota ,c}(gg^{-1})=\varsigma _{\iota ,c}(I_c)=1$
). Since
![]() $\pi ^{\vee }$
and
$\pi ^{\vee }$
and
![]() $(\pi ^{\vee })^{\iota }$
act on the same space and
$(\pi ^{\vee })^{\iota }$
act on the same space and
![]() ${}^{\iota }(\langle g,1\rangle ^{-1})=({}^{\iota }\langle g,1\rangle )^{-1}$
, the definition of
${}^{\iota }(\langle g,1\rangle ^{-1})=({}^{\iota }\langle g,1\rangle )^{-1}$
, the definition of
![]() $\pi ^{\vee }$
implies that
$\pi ^{\vee }$
implies that
![]() $(\pi ^{\vee })^{\iota }=(\pi ^{\iota })^{\vee }$
. Also, when
$(\pi ^{\vee })^{\iota }=(\pi ^{\iota })^{\vee }$
. Also, when
![]() $\pi $
is unramified, so is
$\pi $
is unramified, so is
![]() $\pi ^{\iota }$
.
$\pi ^{\iota }$
.
Consider the global setting. Recall the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _R$
defined by Equation (2.30), which we use for the realization of the right copy of
$\rho _R$
defined by Equation (2.30), which we use for the realization of the right copy of
![]() $G^{(m)}(\mathbb {A})$
. Define
$G^{(m)}(\mathbb {A})$
. Define
![]() $\rho _R^{\iota }(g,g')=\rho _R(^{\iota }g,^{\iota }g')$
. Since
$\rho _R^{\iota }(g,g')=\rho _R(^{\iota }g,^{\iota }g')$
. Since
![]() $\rho _{R,\nu }=\sigma _{c,\nu }=\sigma _{c,\nu }^{\iota }$
, we have
$\rho _{R,\nu }=\sigma _{c,\nu }=\sigma _{c,\nu }^{\iota }$
, we have
![]() $\rho _{R,\nu }^{\iota }=\sigma _{c,\nu }^{\iota }=\rho _{R,\nu }$
(all in
$\rho _{R,\nu }^{\iota }=\sigma _{c,\nu }^{\iota }=\rho _{R,\nu }$
(all in
![]() $\mathrm {H}^2(G(F_{\nu }),\mu _m)$
), thus there exists
$\mathrm {H}^2(G(F_{\nu }),\mu _m)$
), thus there exists
![]() $\eta _{\iota ,R}\in \mathrm {C}^1(G(\mathbb {A}),\mu _m)$
such that
$\eta _{\iota ,R}\in \mathrm {C}^1(G(\mathbb {A}),\mu _m)$
such that
 $$ \begin{align} \rho_R^{\iota}(g,g')=\frac{\eta_{\iota,R}(g)\eta_{\iota,R}(g')}{\eta_{\iota,R}(gg')}\rho_R(g,g'),\qquad \forall g,g'\in G(\mathbb{A}). \end{align} $$
$$ \begin{align} \rho_R^{\iota}(g,g')=\frac{\eta_{\iota,R}(g)\eta_{\iota,R}(g')}{\eta_{\iota,R}(gg')}\rho_R(g,g'),\qquad \forall g,g'\in G(\mathbb{A}). \end{align} $$
Repeating the arguments of Proposition 18 (now with Equation (2.45) instead of Equation (2.38)), we deduce that
is the unique abstract lift of
![]() ${}^{\iota }$
. It is also a topological lift because the local lifts are topological and by Equation (2.44). Hence, we can define
${}^{\iota }$
. It is also a topological lift because the local lifts are topological and by Equation (2.44). Hence, we can define
(cf. Equations (2.39) and (2.41)). Then Equation (2.42) holds globally and we can lift
![]() ${}^{\iota }$
(uniquely) to an involution of the image of
${}^{\iota }$
(uniquely) to an involution of the image of
![]() $G^{(m)}(\mathbb {A})\times G^{(m)}(\mathbb {A})$
in
$G^{(m)}(\mathbb {A})\times G^{(m)}(\mathbb {A})$
in
![]() $H^{(m)}(\mathbb {A})$
, by defining
$H^{(m)}(\mathbb {A})$
, by defining
We can also extend the local argument on
![]() $K_{G,\nu }$
above to
$K_{G,\nu }$
above to
![]() $G(F)$
. The unique splitting of
$G(F)$
. The unique splitting of
![]() $G(F)$
is
$G(F)$
is
![]() $y\mapsto \langle y,\eta ^{-1}(\mathfrak {e}_2(y))\rangle $
, and since
$y\mapsto \langle y,\eta ^{-1}(\mathfrak {e}_2(y))\rangle $
, and since
![]() ${}^{\iota }G(F)=G(F)$
,
${}^{\iota }G(F)=G(F)$
,
![]() ${}^{\iota }y\mapsto \langle {}^{\iota }y,\eta ^{-1}(\mathfrak {e}_2({}^{\iota }y))\rangle $
is also a splitting. Hence, by Equation (2.4),
${}^{\iota }y\mapsto \langle {}^{\iota }y,\eta ^{-1}(\mathfrak {e}_2({}^{\iota }y))\rangle $
is also a splitting. Hence, by Equation (2.4),
Now, we can define, for an automorphic function
![]() $\varphi $
on the right copy of
$\varphi $
on the right copy of
![]() $G^{(m)}(\mathbb {A})$
,
$G^{(m)}(\mathbb {A})$
,
![]() ${}^{\iota }\varphi (g)=\varphi ({}^{\iota }g)$
,
${}^{\iota }\varphi (g)=\varphi ({}^{\iota }g)$
,
![]() $g\in G^{(m)}(\mathbb {A})$
. By Equation (2.49), this function is still left-invariant under
$g\in G^{(m)}(\mathbb {A})$
. By Equation (2.49), this function is still left-invariant under
![]() $\{\langle y,\eta ^{-1}(\mathfrak {e}_2(y))\rangle :y\in G(F)\}$
, hence it is still an automorphic function on
$\{\langle y,\eta ^{-1}(\mathfrak {e}_2(y))\rangle :y\in G(F)\}$
, hence it is still an automorphic function on
![]() $G^{(m)}(\mathbb {A})$
.
$G^{(m)}(\mathbb {A})$
.
2.7 The covering
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
Recall from § 2.3 that m is a positive integer and
![]() $r=m$
for odd m, otherwise
$r=m$
for odd m, otherwise
![]() $r=m/2$
. In a local or global context,
$r=m/2$
. In a local or global context,
![]() $\widetilde {M}_P$
is the covering obtained by restriction from
$\widetilde {M}_P$
is the covering obtained by restriction from
![]() $H^{(m)}$
. Identify
$H^{(m)}$
. Identify
![]() $\operatorname {\mathrm {GL}}_{rkc}$
with
$\operatorname {\mathrm {GL}}_{rkc}$
with
![]() $M_P$
via
$M_P$
via
![]() $g\mapsto \operatorname {\mathrm {diag}}(g,g^{*})$
. Then
$g\mapsto \operatorname {\mathrm {diag}}(g,g^{*})$
. Then
![]() $\widetilde {M}_P$
can be regarded as a covering
$\widetilde {M}_P$
can be regarded as a covering
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{rkc}$
of
$\widetilde {\operatorname {\mathrm {GL}}}_{rkc}$
of
![]() $\operatorname {\mathrm {GL}}_{rkc}$
. Denote
$\operatorname {\mathrm {GL}}_{rkc}$
. Denote
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}=\widetilde {\operatorname {\mathrm {GL}}}_{rkc}$
. Restricting the map
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}=\widetilde {\operatorname {\mathrm {GL}}}_{rkc}$
. Restricting the map
![]() $g\mapsto \operatorname {\mathrm {diag}}(g,g^{*})$
to
$g\mapsto \operatorname {\mathrm {diag}}(g,g^{*})$
to
![]() $\operatorname {\mathrm {SL}}_{rkc}$
, we obtain a covering
$\operatorname {\mathrm {SL}}_{rkc}$
, we obtain a covering
![]() $\widetilde {\operatorname {\mathrm {SL}}}_{rkc}$
. Locally, by Equation (2.12) and Proposition 4,
$\widetilde {\operatorname {\mathrm {SL}}}_{rkc}$
. Locally, by Equation (2.12) and Proposition 4,
![]() $\widetilde {\operatorname {\mathrm {SL}}}_{rkc}$
is essentially the covering defined in [Reference MatsumotoMat69] with
$\widetilde {\operatorname {\mathrm {SL}}}_{rkc}$
is essentially the covering defined in [Reference MatsumotoMat69] with
![]() $(\cdot ,\cdot )_m^{-2}$
, that is, an r-fold covering (except that it is still a covering group of
$(\cdot ,\cdot )_m^{-2}$
, that is, an r-fold covering (except that it is still a covering group of
![]() $\operatorname {\mathrm {SL}}_{rkc}$
by
$\operatorname {\mathrm {SL}}_{rkc}$
by
![]() $\mu _m$
), and
$\mu _m$
), and
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is ‘morally’ an r-fold covering. To distinguish
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is ‘morally’ an r-fold covering. To distinguish
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
from the coverings of [Reference Kazhdan and PattersonKP84], and because r does not determine m, we keep both m and r in the notation.
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
from the coverings of [Reference Kazhdan and PattersonKP84], and because r does not determine m, we keep both m and r in the notation.
The group
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
was recently introduced in a local context by Savin [Reference SavinSav] (see [Reference GaoGao18a]). In this section, we describe several properties of this cover. The description does not depend on the rank of the general linear group, so we take an integer d and discuss
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
was recently introduced in a local context by Savin [Reference SavinSav] (see [Reference GaoGao18a]). In this section, we describe several properties of this cover. The description does not depend on the rank of the general linear group, so we take an integer d and discuss
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, obtained by restriction from
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, obtained by restriction from
![]() $\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
.
$\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
.
Consider the local setting first. For brevity, denote
The elements of
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
are written as pairs
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
are written as pairs
![]() $<b,\epsilon>$
with
$<b,\epsilon>$
with
![]() $b\in \operatorname {\mathrm {GL}}_d$
and
$b\in \operatorname {\mathrm {GL}}_d$
and
![]() $\epsilon \in \mu _m$
, and
$\epsilon \in \mu _m$
, and
For quick reference, we rewrite Equation (2.19) for
![]() $\sigma ^{\diamondsuit }_{d}$
,
$\sigma ^{\diamondsuit }_{d}$
,
 $$ \begin{align} \sigma^{\diamondsuit}_{d}(\operatorname{\mathrm{diag}}(t_1,\ldots,t_{d}),\operatorname{\mathrm{diag}}(t_1',\ldots,t_{d}'))=\prod_{i=1}^{d}(t_i,t^{\prime}_i)_m^{-1}. \end{align} $$
$$ \begin{align} \sigma^{\diamondsuit}_{d}(\operatorname{\mathrm{diag}}(t_1,\ldots,t_{d}),\operatorname{\mathrm{diag}}(t_1',\ldots,t_{d}'))=\prod_{i=1}^{d}(t_i,t^{\prime}_i)_m^{-1}. \end{align} $$
The properties (2.8)-(2.10) remain valid with
![]() $\sigma ^{\diamondsuit }_{d}$
instead of
$\sigma ^{\diamondsuit }_{d}$
instead of
![]() $\sigma _{d}$
because the mapping
$\sigma _{d}$
because the mapping
![]() $b\mapsto b^{*}$
(see § 2.1) is an automorphism of
$b\mapsto b^{*}$
(see § 2.1) is an automorphism of
![]() $\operatorname {\mathrm {GL}}_d$
which restricts to an automorphism of
$\operatorname {\mathrm {GL}}_d$
which restricts to an automorphism of
![]() $N_{\operatorname {\mathrm {GL}}_d}$
, and for
$N_{\operatorname {\mathrm {GL}}_d}$
, and for
![]() $v\in N_{\operatorname {\mathrm {GL}}_d}$
,
$v\in N_{\operatorname {\mathrm {GL}}_d}$
,
![]() $\operatorname {\mathrm {diag}}(v,v^{*})\in N_{\operatorname {\mathrm {GL}}_{2d}}$
. However, more care is needed with formulas involving
$\operatorname {\mathrm {diag}}(v,v^{*})\in N_{\operatorname {\mathrm {GL}}_{2d}}$
. However, more care is needed with formulas involving
![]() $w'\in \mathfrak {W}_d$
(e.g., Equations (2.14) and (2.15)) because in general it is not true that
$w'\in \mathfrak {W}_d$
(e.g., Equations (2.14) and (2.15)) because in general it is not true that
![]() $\operatorname {\mathrm {diag}}(w',{w'}^{*})\in \mathfrak {W}_{2d}$
(even if
$\operatorname {\mathrm {diag}}(w',{w'}^{*})\in \mathfrak {W}_{2d}$
(even if
![]() $w'$
represents a simple reflection), only
$w'$
represents a simple reflection), only
![]() $\operatorname {\mathrm {diag}}(w',{w'}^{*})\in \mathfrak {W}^+_{2d}$
. At any rate
$\operatorname {\mathrm {diag}}(w',{w'}^{*})\in \mathfrak {W}^+_{2d}$
. At any rate
![]() ${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
for
${}^w\langle t,1\rangle =\langle {}^wt,1\rangle $
for
![]() $w\in \mathfrak {W}^+_{d}$
(e.g., a permutation matrix) and
$w\in \mathfrak {W}^+_{d}$
(e.g., a permutation matrix) and
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}$
, by Equation (2.50) and Proposition 2.
$t\in T_{\operatorname {\mathrm {GL}}_d}$
, by Equation (2.50) and Proposition 2.
According to Equation (2.19),
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_{d}}$
is a
$\widetilde {T}_{\operatorname {\mathrm {GL}}_{d}}$
is a
![]() $2$
-step nilpotent group and its center is the preimage of the subgroup of torus elements with coordinates in
$2$
-step nilpotent group and its center is the preimage of the subgroup of torus elements with coordinates in
![]() $F^{*r}$
, unless
$F^{*r}$
, unless
![]() $r=1$
, then it is abelian. Denote
$r=1$
, then it is abelian. Denote
![]() $C_{r,d}=\{xI_d:x\in F^{*r}\}$
. By Equation (2.51),
$C_{r,d}=\{xI_d:x\in F^{*r}\}$
. By Equation (2.51),
![]() $t\in C_{r,d}$
commutes with any
$t\in C_{r,d}$
commutes with any
![]() $t'\in T_{\operatorname {\mathrm {GL}}_d}$
in
$t'\in T_{\operatorname {\mathrm {GL}}_d}$
in
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, then by Equation (2.17) and since
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, then by Equation (2.17) and since
![]() $(x,-x)_m=1$
for all
$(x,-x)_m=1$
for all
![]() $x\in F^{*}$
and also by Equations (2.8)-(2.10),
$x\in F^{*}$
and also by Equations (2.8)-(2.10),
![]() $\widetilde {C}_{r,d}$
is the center of
$\widetilde {C}_{r,d}$
is the center of
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
(as opposed to coverings of [Reference Kazhdan and PattersonKP84], here the parity of r does not play a role).
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
(as opposed to coverings of [Reference Kazhdan and PattersonKP84], here the parity of r does not play a role).
Let
![]() $\beta =(\beta _1,\ldots ,\beta _l)$
be a composition of d. For
$\beta =(\beta _1,\ldots ,\beta _l)$
be a composition of d. For
![]() $b=\operatorname {\mathrm {diag}}(b_1,\ldots ,b_l)\in M_{\beta }$
and
$b=\operatorname {\mathrm {diag}}(b_1,\ldots ,b_l)\in M_{\beta }$
and
![]() $b'\in M_{\beta }$
, by Equation (2.12) and since
$b'\in M_{\beta }$
, by Equation (2.12) and since
![]() $\det b_i^{*} = \det b_i^{-1}$
,
$\det b_i^{*} = \det b_i^{-1}$
,
 $$ \begin{align*} \sigma_{2d}(\operatorname{\mathrm{diag}}(b,b^{*}),\operatorname{\mathrm{diag}}(b',{b'}^{*}))=\prod_{i=1}^l\sigma_{2\beta_i}(\operatorname{\mathrm{diag}}(b_i,b_i^{*}),\operatorname{\mathrm{diag}}(b_i^{\prime},{b_i^{\prime}}^{*})), \end{align*} $$
$$ \begin{align*} \sigma_{2d}(\operatorname{\mathrm{diag}}(b,b^{*}),\operatorname{\mathrm{diag}}(b',{b'}^{*}))=\prod_{i=1}^l\sigma_{2\beta_i}(\operatorname{\mathrm{diag}}(b_i,b_i^{*}),\operatorname{\mathrm{diag}}(b_i^{\prime},{b_i^{\prime}}^{*})), \end{align*} $$
which we can write in the form
 $$ \begin{align} \sigma^{\diamondsuit}_{d}(b,b')=\prod_{i=1}^l\sigma^{\diamondsuit}_{\beta_i}(b_i,b_i^{\prime}). \end{align} $$
$$ \begin{align} \sigma^{\diamondsuit}_{d}(b,b')=\prod_{i=1}^l\sigma^{\diamondsuit}_{\beta_i}(b_i,b_i^{\prime}). \end{align} $$
In particular, the direct factors of
![]() $M_{\beta }$
commute in
$M_{\beta }$
commute in
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, which is a special property of this covering, as opposed to the coverings of [Reference Kazhdan and PattersonKP84]. This formula also implies that the embedding
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
, which is a special property of this covering, as opposed to the coverings of [Reference Kazhdan and PattersonKP84]. This formula also implies that the embedding
![]() $b\mapsto \operatorname {\mathrm {diag}}(I_i,b,I_{d-j-i})$
of
$b\mapsto \operatorname {\mathrm {diag}}(I_i,b,I_{d-j-i})$
of
![]() $\operatorname {\mathrm {GL}}_j$
in
$\operatorname {\mathrm {GL}}_j$
in
![]() $\operatorname {\mathrm {GL}}_{d}$
induces the same covering on
$\operatorname {\mathrm {GL}}_{d}$
induces the same covering on
![]() $\operatorname {\mathrm {GL}}_j$
, that is,
$\operatorname {\mathrm {GL}}_j$
, that is,
![]() $\widetilde {\operatorname {\mathrm {GL}}}_{j}=\operatorname {\mathrm {GL}}_{j}^{(m,r)}$
. Therefore, we can study representations induced from parabolic subgroups using the usual tensor product, when we identify
$\widetilde {\operatorname {\mathrm {GL}}}_{j}=\operatorname {\mathrm {GL}}_{j}^{(m,r)}$
. Therefore, we can study representations induced from parabolic subgroups using the usual tensor product, when we identify
 $$ \begin{align} \widetilde{M}_{\beta}=\{(\epsilon_1,\ldots,\epsilon_l)\in\mu_m^l:\prod_{i=1}^l\epsilon_i=1\}\backslash \operatorname{\mathrm{GL}}_{\beta_1}^{(m,r)}\times\ldots\times \operatorname{\mathrm{GL}}_{\beta_l}^{(m,r)}. \end{align} $$
$$ \begin{align} \widetilde{M}_{\beta}=\{(\epsilon_1,\ldots,\epsilon_l)\in\mu_m^l:\prod_{i=1}^l\epsilon_i=1\}\backslash \operatorname{\mathrm{GL}}_{\beta_1}^{(m,r)}\times\ldots\times \operatorname{\mathrm{GL}}_{\beta_l}^{(m,r)}. \end{align} $$
In particular, we can construct genuine irreducible representations of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
from d genuine irreducible representations of
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
from d genuine irreducible representations of
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}$
; to construct genuine principal series representations, we extend to
$\operatorname {\mathrm {GL}}_1^{(m,r)}$
; to construct genuine principal series representations, we extend to
![]() $\widetilde {B}_{\operatorname {\mathrm {GL}}_d}$
by letting the image of
$\widetilde {B}_{\operatorname {\mathrm {GL}}_d}$
by letting the image of
![]() $N_{\operatorname {\mathrm {GL}}_d}$
act trivially then induce as usual (see § 2.8 below).
$N_{\operatorname {\mathrm {GL}}_d}$
act trivially then induce as usual (see § 2.8 below).
If F is unramified, the splitting of
![]() $K_{\operatorname {\mathrm {GL}}_d}$
is chosen to be
$K_{\operatorname {\mathrm {GL}}_d}$
is chosen to be
![]() $y\mapsto \langle y,\eta ^{\diamondsuit }_{d}(y)\rangle $
, where
$y\mapsto \langle y,\eta ^{\diamondsuit }_{d}(y)\rangle $
, where
![]() $\eta ^{\diamondsuit }_{d}(y)=\eta _{2d}(\operatorname {\mathrm {diag}}(y,y^{*}))$
. This is compatible with the choice in
$\eta ^{\diamondsuit }_{d}(y)=\eta _{2d}(\operatorname {\mathrm {diag}}(y,y^{*}))$
. This is compatible with the choice in
![]() $\operatorname {\mathrm {Sp}}_{2d}$
: if a function on
$\operatorname {\mathrm {Sp}}_{2d}$
: if a function on
![]() $\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
is right-invariant under
$\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
is right-invariant under
![]() $\{\langle y,\eta _{2d}(y)\rangle :y\in K_{\operatorname {\mathrm {Sp}}_{2d}}\}$
, its restriction to
$\{\langle y,\eta _{2d}(y)\rangle :y\in K_{\operatorname {\mathrm {Sp}}_{2d}}\}$
, its restriction to
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
is right-invariant under
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
is right-invariant under
![]() $\{\langle y,\eta ^{\diamondsuit }_{d}(y)\rangle :y\in K_{\operatorname {\mathrm {GL}}_{d}}\}$
.
$\{\langle y,\eta ^{\diamondsuit }_{d}(y)\rangle :y\in K_{\operatorname {\mathrm {GL}}_{d}}\}$
.
Using
![]() $(b^{*})^{*}=b$
and
$(b^{*})^{*}=b$
and
![]() $(\det {b},\det {b'}^{*})_m=(\det {b}^{*},\det {b'})_m$
(because
$(\det {b},\det {b'}^{*})_m=(\det {b}^{*},\det {b'})_m$
(because
![]() $\det {b^{*}}=\det {b}^{-1}$
and
$\det {b^{*}}=\det {b}^{-1}$
and
![]() $(x^{-1},y)_m=(x,y^{-1})_m$
), Equation (2.12) implies that
$(x^{-1},y)_m=(x,y^{-1})_m$
), Equation (2.12) implies that
![]() $\sigma ^{\diamondsuit }_{d}(b^{*},{b'}^{*})=\sigma ^{\diamondsuit }_{d}(b,b')$
. Thus, the involution
$\sigma ^{\diamondsuit }_{d}(b^{*},{b'}^{*})=\sigma ^{\diamondsuit }_{d}(b,b')$
. Thus, the involution
![]() $b\mapsto b^{*}$
preserves
$b\mapsto b^{*}$
preserves
![]() $\sigma ^{\diamondsuit }_{d}$
(!), hence lifts to an abstract involution of
$\sigma ^{\diamondsuit }_{d}$
(!), hence lifts to an abstract involution of
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
by
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
by
This lift is not unique; since
![]() $\operatorname {\mathrm {Hom}}(\operatorname {\mathrm {GL}}_d,\mu _m)=\operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
, any other abstract lift of
$\operatorname {\mathrm {Hom}}(\operatorname {\mathrm {GL}}_d,\mu _m)=\operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
, any other abstract lift of
![]() ${}^{*}$
takes the form
${}^{*}$
takes the form
for some abstract
![]() $\varrho \in \operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
(see § 2.2). Since
$\varrho \in \operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
(see § 2.2). Since
![]() $F^{*m}$
is open in
$F^{*m}$
is open in
![]() $F^{*}$
, any such
$F^{*}$
, any such
![]() $\varrho $
is automatically continuous and we claim that all those lifts are topological. Indeed, let
$\varrho $
is automatically continuous and we claim that all those lifts are topological. Indeed, let
![]() $w=\left (\begin {smallmatrix}&I_d\\-I_d\end {smallmatrix}\right )\in \operatorname {\mathrm {Sp}}_{2d}$
, then one of the lifts
$w=\left (\begin {smallmatrix}&I_d\\-I_d\end {smallmatrix}\right )\in \operatorname {\mathrm {Sp}}_{2d}$
, then one of the lifts
![]() $\langle b^{*},\varrho (\det {b})\epsilon \rangle $
is a homeomorphism, namely the lift corresponding to
$\langle b^{*},\varrho (\det {b})\epsilon \rangle $
is a homeomorphism, namely the lift corresponding to
![]() ${}^{*}\langle b,\epsilon \rangle ={}^w\langle \operatorname {\mathrm {diag}}(b,b^{*}),\epsilon \rangle $
. Now, for any
${}^{*}\langle b,\epsilon \rangle ={}^w\langle \operatorname {\mathrm {diag}}(b,b^{*}),\epsilon \rangle $
. Now, for any
![]() $\varrho '\in \operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
, the map
$\varrho '\in \operatorname {\mathrm {Hom}}(F^{*},\mu _m)$
, the map
![]() $b\mapsto {\varrho '}^{-1}(\det b)\varrho (\det b)$
is in
$b\mapsto {\varrho '}^{-1}(\det b)\varrho (\det b)$
is in
![]() $\mathrm {C}^1(\operatorname {\mathrm {GL}}_d,\mu _m)$
hence
$\mathrm {C}^1(\operatorname {\mathrm {GL}}_d,\mu _m)$
hence
![]() $\langle b^{*},\varrho (\det {b})\epsilon \rangle \rightarrow \langle b^{*},\varrho '(\det {b})\epsilon \rangle $
is a homeomorphism, and therefore
$\langle b^{*},\varrho (\det {b})\epsilon \rangle \rightarrow \langle b^{*},\varrho '(\det {b})\epsilon \rangle $
is a homeomorphism, and therefore
![]() $\langle b,\epsilon \rangle \rightarrow \langle b^{*},\varrho '(\det {b})\epsilon \rangle $
is a topological lift. In particular, Equation (2.54) is topological.
$\langle b,\epsilon \rangle \rightarrow \langle b^{*},\varrho '(\det {b})\epsilon \rangle $
is a topological lift. In particular, Equation (2.54) is topological.
Since we are interested in a lift which is also an involution, we must have
![]() $\varrho ^2=1$
. Hence, if m is odd, Equation (2.54) is the only lift of
$\varrho ^2=1$
. Hence, if m is odd, Equation (2.54) is the only lift of
![]() ${}^{*}$
to an involution.
${}^{*}$
to an involution.
Fixing a lift of
![]() ${}^{*}$
, we can define for a genuine smooth representation
${}^{*}$
, we can define for a genuine smooth representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the representation
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the representation
![]() $\pi ^{*}$
, which acts on the space of
$\pi ^{*}$
, which acts on the space of
![]() $\pi $
by
$\pi $
by
![]() $\pi ^{*}(\langle b,\epsilon \rangle )=\pi ({}^{*}\langle b,\epsilon \rangle )$
. If
$\pi ^{*}(\langle b,\epsilon \rangle )=\pi ({}^{*}\langle b,\epsilon \rangle )$
. If
![]() $\pi $
is unramified and
$\pi $
is unramified and
![]() $\varrho $
is trivial on
$\varrho $
is trivial on
![]() $\mathcal {O}^{*}$
, then
$\mathcal {O}^{*}$
, then
![]() $\pi ^{*}$
is also unramified. Henceforth, we only use Equation (2.54).
$\pi ^{*}$
is also unramified. Henceforth, we only use Equation (2.54).
We mention that Kable [Reference KableKab99] studied the lifts of the main involution for the coverings of [Reference Kazhdan and PattersonKP84]; at least when
![]() $-1$
is not a square, there is no
$-1$
is not a square, there is no
![]() $2$
-cocycle which is cohomologous to (a twist of)
$2$
-cocycle which is cohomologous to (a twist of)
![]() $\sigma _d$
and fixed by any of those lifts ([Reference KableKab99, Proposition 2]).
$\sigma _d$
and fixed by any of those lifts ([Reference KableKab99, Proposition 2]).
Proposition 20. The
![]() $2$
-cocycles
$2$
-cocycles
![]() $\sigma ^{\diamondsuit }_{d}(b,b')$
and
$\sigma ^{\diamondsuit }_{d}(b,b')$
and
![]() $\sigma ^2_{d}(b,b')(\det b,\det b')_m$
are cohomologous. In particular, for
$\sigma ^2_{d}(b,b')(\det b,\det b')_m$
are cohomologous. In particular, for
![]() $m=2$
,
$m=2$
,
![]() $\sigma ^{\diamondsuit }_{d}(b,b')$
is cohomologous to the
$\sigma ^{\diamondsuit }_{d}(b,b')$
is cohomologous to the
![]() $2$
-cocycle given by
$2$
-cocycle given by
![]() $(\det b,\det b')_2$
.
$(\det b,\det b')_2$
.
Proof. First, we claim that
![]() $\sigma _d^{*}=\sigma _d$
in
$\sigma _d^{*}=\sigma _d$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {GL}}_d,\mu _m)$
. This is [Reference KableKab99, Lemma 2], but the
$\mathrm {H}^2(\operatorname {\mathrm {GL}}_d,\mu _m)$
. This is [Reference KableKab99, Lemma 2], but the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\tau $
in the notation of loc. cit. is not precisely
$\tau $
in the notation of loc. cit. is not precisely
![]() $\sigma _d$
. Briefly, as in [Reference KableKab99, § 4], for
$\sigma _d$
. Briefly, as in [Reference KableKab99, § 4], for
![]() $b_0\in \operatorname {\mathrm {SL}}_{d+1}$
put
$b_0\in \operatorname {\mathrm {SL}}_{d+1}$
put
![]() $b_0^{\circ }=\operatorname {\mathrm {diag}}(J_k,1){}^tb_0^{-1}\operatorname {\mathrm {diag}}(J_k,1)$
and
$b_0^{\circ }=\operatorname {\mathrm {diag}}(J_k,1){}^tb_0^{-1}\operatorname {\mathrm {diag}}(J_k,1)$
and
![]() $\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ }(b_0,b_0')=\sigma _{\operatorname {\mathrm {SL}}_{d+1}}(b_0^{\circ },{b_0'}^{\circ })$
. The formulas from the proof of Proposition 4 remain true with
$\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ }(b_0,b_0')=\sigma _{\operatorname {\mathrm {SL}}_{d+1}}(b_0^{\circ },{b_0'}^{\circ })$
. The formulas from the proof of Proposition 4 remain true with
![]() $(\sigma _c,\sigma _c^{*},c-1)$
replaced by
$(\sigma _c,\sigma _c^{*},c-1)$
replaced by
![]() $(\sigma _{\operatorname {\mathrm {SL}}_{d+1}},\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ },d)$
, hence
$(\sigma _{\operatorname {\mathrm {SL}}_{d+1}},\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ },d)$
, hence
![]() $\sigma _{\operatorname {\mathrm {SL}}_{d+1}}$
and
$\sigma _{\operatorname {\mathrm {SL}}_{d+1}}$
and
![]() $\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ }$
are cohomologous and note that
$\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ }$
are cohomologous and note that
![]() $\sigma _d^{*}(b,b')=\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ } (\left (\begin {smallmatrix}b\\&\det b^{-1}\end {smallmatrix}\right ), \left (\begin {smallmatrix}b'\\&\det {b'}^{-1}\end {smallmatrix}\right ))$
. Now, the proposition follows from Equations (2.50) and (2.12).
$\sigma _d^{*}(b,b')=\sigma _{\operatorname {\mathrm {SL}}_{d+1}}^{\circ } (\left (\begin {smallmatrix}b\\&\det b^{-1}\end {smallmatrix}\right ), \left (\begin {smallmatrix}b'\\&\det {b'}^{-1}\end {smallmatrix}\right ))$
. Now, the proposition follows from Equations (2.50) and (2.12).
Consider the global setting. Let
![]() $\rho _{2d}\in \mathrm {Z}^2(\operatorname {\mathrm {Sp}}_{2d}^{(m)}(\mathbb {A}),\mu _m)$
as in § 2.5. Then we may define
$\rho _{2d}\in \mathrm {Z}^2(\operatorname {\mathrm {Sp}}_{2d}^{(m)}(\mathbb {A}),\mu _m)$
as in § 2.5. Then we may define
The covering
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
is by definition realized using
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
is by definition realized using
![]() $\rho ^{\diamondsuit }_{d}$
. Since
$\rho ^{\diamondsuit }_{d}$
. Since
![]() $\rho _{2d,\nu }=\sigma _{2d,\nu }$
in
$\rho _{2d,\nu }=\sigma _{2d,\nu }$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {Sp}}_{2d}(F_{\nu }),\mu _m)$
,
$\mathrm {H}^2(\operatorname {\mathrm {Sp}}_{2d}(F_{\nu }),\mu _m)$
,
![]() $\rho ^{\diamondsuit }_{d,\nu }=\sigma ^{\diamondsuit }_{d,\nu }$
in
$\rho ^{\diamondsuit }_{d,\nu }=\sigma ^{\diamondsuit }_{d,\nu }$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {GL}}_d(F_{\nu }),\mu _m)$
and we can write
$\mathrm {H}^2(\operatorname {\mathrm {GL}}_d(F_{\nu }),\mu _m)$
and we can write
 $$ \begin{align} \rho^{\diamondsuit}_{d,\nu}(b,b')=\frac{\eta^{\diamondsuit}_{d,\nu}(b)\eta^{\diamondsuit}_{d,\nu}(b')}{\eta^{\diamondsuit}_{d,\nu}(bb')}\sigma^{\diamondsuit}_{d,\nu}(b,b'), \qquad\eta^{\diamondsuit}_{d,\nu}(b)=\eta_{2d,\nu}(\operatorname{\mathrm{diag}}(b,b^{*}))\in\mathrm{C}^1(\operatorname{\mathrm{GL}}_d(F_{\nu}),\mu_m) \end{align} $$
$$ \begin{align} \rho^{\diamondsuit}_{d,\nu}(b,b')=\frac{\eta^{\diamondsuit}_{d,\nu}(b)\eta^{\diamondsuit}_{d,\nu}(b')}{\eta^{\diamondsuit}_{d,\nu}(bb')}\sigma^{\diamondsuit}_{d,\nu}(b,b'), \qquad\eta^{\diamondsuit}_{d,\nu}(b)=\eta_{2d,\nu}(\operatorname{\mathrm{diag}}(b,b^{*}))\in\mathrm{C}^1(\operatorname{\mathrm{GL}}_d(F_{\nu}),\mu_m) \end{align} $$
(
![]() $\eta _{2d,\nu }$
was used to relate
$\eta _{2d,\nu }$
was used to relate
![]() $\rho _{2d,\nu }$
to
$\rho _{2d,\nu }$
to
![]() $\sigma _{2d,\nu }$
; see Equation (2.29)). One can then globalize Equation (2.56) on the subgroups
$\sigma _{2d,\nu }$
; see Equation (2.29)). One can then globalize Equation (2.56) on the subgroups
![]() $\operatorname {\mathrm {GL}}_d(F)$
and
$\operatorname {\mathrm {GL}}_d(F)$
and
![]() $N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
(see the paragraph before Lemma 15). We deduce that
$N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
(see the paragraph before Lemma 15). We deduce that
![]() $b\mapsto \langle b,(\eta ^{\diamondsuit }_{d})^{-1}(b)\rangle $
is a splitting of
$b\mapsto \langle b,(\eta ^{\diamondsuit }_{d})^{-1}(b)\rangle $
is a splitting of
![]() $\operatorname {\mathrm {GL}}_d(F)$
(which is not a perfect group, as opposed to
$\operatorname {\mathrm {GL}}_d(F)$
(which is not a perfect group, as opposed to
![]() $\operatorname {\mathrm {Sp}}_{2d}(F)$
), and the splitting of
$\operatorname {\mathrm {Sp}}_{2d}(F)$
), and the splitting of
![]() $N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
.
$N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
.
For example, when
![]() $m=2$
, by Proposition 20 and the quadratic reciprocity
$m=2$
, by Proposition 20 and the quadratic reciprocity
![]() $\rho ^{\diamondsuit }_d$
is cohomologous to the
$\rho ^{\diamondsuit }_d$
is cohomologous to the
![]() $2$
-cocycle given by
$2$
-cocycle given by
![]() $(\det ,\det )_2$
(with the global quadratic Hilbert symbol).
$(\det ,\det )_2$
(with the global quadratic Hilbert symbol).
Since the direct factors of
![]() $M_{\beta }$
commute locally in
$M_{\beta }$
commute locally in
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
, they also commute globally. As observed by Takeda [Reference TakedaTak14, Reference TakedaTak16] (for coverings of [Reference Kazhdan and PattersonKP84]), to define a global tensor product we also need to construct a global block-compatible
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
, they also commute globally. As observed by Takeda [Reference TakedaTak14, Reference TakedaTak16] (for coverings of [Reference Kazhdan and PattersonKP84]), to define a global tensor product we also need to construct a global block-compatible
![]() $2$
-cocycle. We closely follow his arguments.
$2$
-cocycle. We closely follow his arguments.
Define
![]() $\rho _{\beta }\in \mathrm {Z}^2(M_{\beta }(\mathbb {A}),\mu _m)$
by
$\rho _{\beta }\in \mathrm {Z}^2(M_{\beta }(\mathbb {A}),\mu _m)$
by
 $$ \begin{align} \rho_{\beta}(b,b')=\prod_{i=1}^l\rho^{\diamondsuit}_{\beta_i}(b_i,b_i^{\prime}),\qquad b=\operatorname{\mathrm{diag}}(b_1,\ldots,b_l). \end{align} $$
$$ \begin{align} \rho_{\beta}(b,b')=\prod_{i=1}^l\rho^{\diamondsuit}_{\beta_i}(b_i,b_i^{\prime}),\qquad b=\operatorname{\mathrm{diag}}(b_1,\ldots,b_l). \end{align} $$
It is block-compatible by definition. We show that
![]() $\rho _{\beta }=\rho ^{\diamondsuit }_d$
in
$\rho _{\beta }=\rho ^{\diamondsuit }_d$
in
![]() $\mathrm {H}^2(M_{\beta }(\mathbb {A}),\mu _m)$
. Let
$\mathrm {H}^2(M_{\beta }(\mathbb {A}),\mu _m)$
. Let
 $$ \begin{align} \eta_{\beta,\nu}\in\mathrm{C}^1(M_{\beta}(F_{\nu}),\mu_m),\qquad \eta_{\beta,\nu}(b)=\frac{\prod_{i=1}^l\eta^{\diamondsuit}_{\beta_i,\nu}(b_i)}{\eta^{\diamondsuit}_{d,\nu}(b)},\qquad b\in M_{\beta}(F_{\nu}). \end{align} $$
$$ \begin{align} \eta_{\beta,\nu}\in\mathrm{C}^1(M_{\beta}(F_{\nu}),\mu_m),\qquad \eta_{\beta,\nu}(b)=\frac{\prod_{i=1}^l\eta^{\diamondsuit}_{\beta_i,\nu}(b_i)}{\eta^{\diamondsuit}_{d,\nu}(b)},\qquad b\in M_{\beta}(F_{\nu}). \end{align} $$
Proposition 21. For all
![]() $\nu $
,
$\nu $
,
![]() $\rho _{\beta ,\nu }$
and
$\rho _{\beta ,\nu }$
and
![]() $\rho ^{\diamondsuit }_{d,\nu }$
are cohomologous:
$\rho ^{\diamondsuit }_{d,\nu }$
are cohomologous:
 $$ \begin{align} \rho_{\beta,\nu}(m,m')=\frac{\eta_{\beta,\nu}(m)\eta_{\beta,\nu}(m')}{\eta_{\beta,\nu}(mm')}\rho^{\diamondsuit}_{d,\nu}(m,m'). \end{align} $$
$$ \begin{align} \rho_{\beta,\nu}(m,m')=\frac{\eta_{\beta,\nu}(m)\eta_{\beta,\nu}(m')}{\eta_{\beta,\nu}(mm')}\rho^{\diamondsuit}_{d,\nu}(m,m'). \end{align} $$
Proof. Indeed,
![]() $\rho _{\beta ,\nu }(m,m')$
equals
$\rho _{\beta ,\nu }(m,m')$
equals
 $$ \begin{align*} &\prod_{i=1}^l\rho^{\diamondsuit}_{\beta_i,\nu}(m_i,m_i^{\prime}) =\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})}\sigma^{\diamondsuit}_{\beta_i,\nu}(m_i,m_i^{\prime}) =\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})}\sigma^{\diamondsuit}_{d,\nu}(m,m') \\&=\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})} \frac{\eta^{\diamondsuit}_{d,\nu}(mm')}{\eta^{\diamondsuit}_{d,\nu}(m)\eta^{\diamondsuit}_{d,\nu}(m')}\rho^{\diamondsuit}_{d,\nu}(m,m') =\frac{\eta_{\beta,\nu}(m)\eta_{\beta,\nu}(m')}{\eta_{\beta,\nu}(mm')}\rho^{\diamondsuit}_{d,\nu}(m,m'). \end{align*} $$
$$ \begin{align*} &\prod_{i=1}^l\rho^{\diamondsuit}_{\beta_i,\nu}(m_i,m_i^{\prime}) =\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})}\sigma^{\diamondsuit}_{\beta_i,\nu}(m_i,m_i^{\prime}) =\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})}\sigma^{\diamondsuit}_{d,\nu}(m,m') \\&=\prod_{i=1}^l\frac{\eta^{\diamondsuit}_{\beta_i,\nu}(m_i)\eta^{\diamondsuit}_{\beta_i,\nu}(m_i^{\prime})}{\eta^{\diamondsuit}_{\beta_i,\nu}(m_im_i^{\prime})} \frac{\eta^{\diamondsuit}_{d,\nu}(mm')}{\eta^{\diamondsuit}_{d,\nu}(m)\eta^{\diamondsuit}_{d,\nu}(m')}\rho^{\diamondsuit}_{d,\nu}(m,m') =\frac{\eta_{\beta,\nu}(m)\eta_{\beta,\nu}(m')}{\eta_{\beta,\nu}(mm')}\rho^{\diamondsuit}_{d,\nu}(m,m'). \end{align*} $$
Here, for the third equality we used Equation (2.52).
Proposition 22. The
![]() $2$
-cocycles
$2$
-cocycles
![]() $\rho _{\beta }$
and
$\rho _{\beta }$
and
![]() $\rho ^{\diamondsuit }_{d}$
are cohomologous.
$\rho ^{\diamondsuit }_{d}$
are cohomologous.
Proof. By virtue of Proposition 21, to deduce that
![]() $\rho _{\beta }=\rho ^{\diamondsuit }_{d}$
, we need to show that
$\rho _{\beta }=\rho ^{\diamondsuit }_{d}$
, we need to show that
![]() $\eta _{\beta }=\prod _{\nu }\eta _{\beta ,\nu }$
is well defined. This follows at once if we prove that for almost all
$\eta _{\beta }=\prod _{\nu }\eta _{\beta ,\nu }$
is well defined. This follows at once if we prove that for almost all
![]() $\nu $
,
$\nu $
,
Fix
![]() $\nu $
such that
$\nu $
such that
![]() $F_{\nu }$
is unramified. Since for each i,
$F_{\nu }$
is unramified. Since for each i,
![]() $\rho ^{\diamondsuit }_{\beta _i,\nu }$
is trivial on
$\rho ^{\diamondsuit }_{\beta _i,\nu }$
is trivial on
![]() $K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
, so is
$K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
, so is
![]() $\rho _{\beta ,\nu }$
, thus by Equation (2.59),
$\rho _{\beta ,\nu }$
, thus by Equation (2.59),
![]() $\eta _{\beta ,\nu }$
is a homomorphism of
$\eta _{\beta ,\nu }$
is a homomorphism of
![]() $M_{\beta }(\mathcal {O}_{\nu })$
. It is therefore enough to prove Equation (2.60) for
$M_{\beta }(\mathcal {O}_{\nu })$
. It is therefore enough to prove Equation (2.60) for
![]() $y\in K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
; in other words, we must show that
$y\in K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
; in other words, we must show that
Note that because
![]() $K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
is not perfect, it is not enough to prove that both sides give rise to a splitting of
$K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
is not perfect, it is not enough to prove that both sides give rise to a splitting of
![]() $K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
with respect to the same
$K_{\operatorname {\mathrm {GL}}_{\beta _i},\nu }$
with respect to the same
![]() $2$
-cocycle.
$2$
-cocycle.
Using the definitions, we can write the last equality in the form
Consider the embedding
![]() $\operatorname {\mathrm {Sp}}_{2\beta _i}\hookrightarrow \operatorname {\mathrm {Sp}}_{2d}$
given by
$\operatorname {\mathrm {Sp}}_{2\beta _i}\hookrightarrow \operatorname {\mathrm {Sp}}_{2d}$
given by
 $$ \begin{align} x^{\blacksquare}=\operatorname{\mathrm{diag}}(I_{\sum_{j=1}^{i-1}\beta_j}, \left(\begin{smallmatrix}x_1&&x_2\\&I_{2\sum_{j=i+1}^{l}\beta_j}\\x_3&&x_4\end{smallmatrix}\right),I_{\sum_{j=1}^{i-1}\beta_j}),\qquad x_i\in\text{Mat}_{\beta_i}, \quad x=\left(\begin{smallmatrix}x_1&x_2\\x_3&x_4\end{smallmatrix}\right)\in\operatorname{\mathrm{Sp}}_{2\beta_i}. \end{align} $$
$$ \begin{align} x^{\blacksquare}=\operatorname{\mathrm{diag}}(I_{\sum_{j=1}^{i-1}\beta_j}, \left(\begin{smallmatrix}x_1&&x_2\\&I_{2\sum_{j=i+1}^{l}\beta_j}\\x_3&&x_4\end{smallmatrix}\right),I_{\sum_{j=1}^{i-1}\beta_j}),\qquad x_i\in\text{Mat}_{\beta_i}, \quad x=\left(\begin{smallmatrix}x_1&x_2\\x_3&x_4\end{smallmatrix}\right)\in\operatorname{\mathrm{Sp}}_{2\beta_i}. \end{align} $$
The image in
![]() $\operatorname {\mathrm {Sp}}_{2d}$
is a standard group in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2], hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Lemma 5] (the strong block-compatibility of the
$\operatorname {\mathrm {Sp}}_{2d}$
is a standard group in the sense of [Reference Banks, Levy and SepanskiBLS99, § 2], hence by [Reference Banks, Levy and SepanskiBLS99, § 2, Lemma 5] (the strong block-compatibility of the
![]() $2$
-cocycle on standard subgroups),
$2$
-cocycle on standard subgroups),
Since for
![]() $x,x'\in K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
,
$x,x'\in K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
,
![]() $\rho _{2\beta _i,\nu }(x,x')=\rho _{2d,\nu }(x^{\blacksquare },{x'}^{\blacksquare })=1$
, equality (2.29) implies that
$\rho _{2\beta _i,\nu }(x,x')=\rho _{2d,\nu }(x^{\blacksquare },{x'}^{\blacksquare })=1$
, equality (2.29) implies that
 $$ \begin{align*} \frac{\eta_{2\beta_i,\nu}(xx')}{\eta_{2\beta_i,\nu}(x)\eta_{2\beta_i,\nu}(x')} =\sigma_{2\beta_i,\nu}(x,x')=\sigma_{2d,\nu}(x^{\blacksquare},{x'}^{\blacksquare})= \frac{\eta_{2d,\nu}(x^{\blacksquare}{x'}^{\blacksquare})}{\eta_{2d,\nu}(x^{\blacksquare}) \eta_{2d,\nu}({x'}^{\blacksquare})}. \end{align*} $$
$$ \begin{align*} \frac{\eta_{2\beta_i,\nu}(xx')}{\eta_{2\beta_i,\nu}(x)\eta_{2\beta_i,\nu}(x')} =\sigma_{2\beta_i,\nu}(x,x')=\sigma_{2d,\nu}(x^{\blacksquare},{x'}^{\blacksquare})= \frac{\eta_{2d,\nu}(x^{\blacksquare}{x'}^{\blacksquare})}{\eta_{2d,\nu}(x^{\blacksquare}) \eta_{2d,\nu}({x'}^{\blacksquare})}. \end{align*} $$
Thus, we obtain two splittings of
![]() $K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
, when the covering is realized using
$K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
, when the covering is realized using
![]() $\sigma _{2\beta _i,\nu }$
, and we deduce that
$\sigma _{2\beta _i,\nu }$
, and we deduce that
![]() $\eta _{2\beta _i,\nu }(x)=\eta _{2d,\nu }(x^{\blacksquare })$
on
$\eta _{2\beta _i,\nu }(x)=\eta _{2d,\nu }(x^{\blacksquare })$
on
![]() $K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
; in particular, Equation (2.61) holds, and thereby Equation (2.60).
$K_{\operatorname {\mathrm {Sp}}_{2\beta _i},\nu }$
; in particular, Equation (2.61) holds, and thereby Equation (2.60).
Now, we can define the tensor product representation of
![]() $\widetilde {M}_{\beta }(\mathbb {A})$
using the global block-compatible
$\widetilde {M}_{\beta }(\mathbb {A})$
using the global block-compatible
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _{\beta }$
, and with the global version of Equation (2.53). A genuine irreducible admissible representation of
$\rho _{\beta }$
, and with the global version of Equation (2.53). A genuine irreducible admissible representation of
![]() $\widetilde {M}_{\beta }(\mathbb {A})$
can then be written as a tensor product of genuine irreducible admissible representations of
$\widetilde {M}_{\beta }(\mathbb {A})$
can then be written as a tensor product of genuine irreducible admissible representations of
![]() $\widetilde {M}_{\beta _i}(\mathbb {A})$
. We fix an embedding of
$\widetilde {M}_{\beta _i}(\mathbb {A})$
. We fix an embedding of
![]() $M_{\beta }(F)$
in
$M_{\beta }(F)$
in
![]() $\widetilde {M}_{\beta }(\mathbb {A})$
by
$\widetilde {M}_{\beta }(\mathbb {A})$
by
 $$ \begin{align} b=\operatorname{\mathrm{diag}}(b_1,\ldots,b_l)\mapsto\prod_{i=1}^l\langle b_i,(\eta_{\beta_i}^{\diamondsuit})^{-1}(b_i)\rangle. \end{align} $$
$$ \begin{align} b=\operatorname{\mathrm{diag}}(b_1,\ldots,b_l)\mapsto\prod_{i=1}^l\langle b_i,(\eta_{\beta_i}^{\diamondsuit})^{-1}(b_i)\rangle. \end{align} $$
Then if
![]() $\tau _i$
are genuine irreducible automorphic representations of
$\tau _i$
are genuine irreducible automorphic representations of
![]() $\operatorname {\mathrm {GL}}_{\beta _i}^{(m,r)}(\mathbb {A})$
, the tensor product
$\operatorname {\mathrm {GL}}_{\beta _i}^{(m,r)}(\mathbb {A})$
, the tensor product
![]() $\otimes _{i=1}^l\tau _i$
is a genuine irreducible automorphic representation of
$\otimes _{i=1}^l\tau _i$
is a genuine irreducible automorphic representation of
![]() $\widetilde {M}_{\beta }(\mathbb {A})$
.
$\widetilde {M}_{\beta }(\mathbb {A})$
.
Let
![]() $\tau _{\beta }=\otimes _{i=1}^l\tau _i$
be a genuine automorphic representation of
$\tau _{\beta }=\otimes _{i=1}^l\tau _i$
be a genuine automorphic representation of
![]() $\widetilde {M}_{\beta }(\mathbb {A})$
. The space of
$\widetilde {M}_{\beta }(\mathbb {A})$
. The space of
is the space of genuine smooth functions
![]() $\xi $
on
$\xi $
on
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
taking values in the space of
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
taking values in the space of
![]() $\tau _{\beta }$
such that
$\tau _{\beta }$
such that
The function
![]() $\eta _{\beta }$
is included to compensate for the change of the
$\eta _{\beta }$
is included to compensate for the change of the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _d^{\diamondsuit }$
to the (cohomologous)
$\rho _d^{\diamondsuit }$
to the (cohomologous)
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _{\beta }$
on
$\rho _{\beta }$
on
![]() $M_{\beta }(\mathbb {A})$
(see [Reference TakedaTak14, p. 204]). Given a
$M_{\beta }(\mathbb {A})$
(see [Reference TakedaTak14, p. 204]). Given a
![]() $\widetilde {K}_{\operatorname {\mathrm {GL}}_d}$
-finite vector in the space of the representation (2.64), as in the linear case we can extend it to a standard section in a complex parameter
$\widetilde {K}_{\operatorname {\mathrm {GL}}_d}$
-finite vector in the space of the representation (2.64), as in the linear case we can extend it to a standard section in a complex parameter
![]() $\boldsymbol {\zeta }\in \mathbb {C}^l$
, that is, to an element of
$\boldsymbol {\zeta }\in \mathbb {C}^l$
, that is, to an element of
We redenote the new section by
![]() $\xi $
and regard it as a function on
$\xi $
and regard it as a function on
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})\times \mathbb {C}^l$
. By definition, the section
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})\times \mathbb {C}^l$
. By definition, the section
![]() $\xi $
is standard, in the sense that its restriction to
$\xi $
is standard, in the sense that its restriction to
![]() $\widetilde {K}_{\operatorname {\mathrm {GL}}_d}$
is independent of
$\widetilde {K}_{\operatorname {\mathrm {GL}}_d}$
is independent of
![]() $\boldsymbol {\zeta }$
. We may then consider the Eisenstein series
$\boldsymbol {\zeta }$
. We may then consider the Eisenstein series
 $$ \begin{align} E(g;\xi,\boldsymbol{\zeta})=\sum\limits_{y\in P_{\beta}(F)\backslash \operatorname{\mathrm{GL}}_d(F)}\xi(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle g,\boldsymbol{\zeta}). \end{align} $$
$$ \begin{align} E(g;\xi,\boldsymbol{\zeta})=\sum\limits_{y\in P_{\beta}(F)\backslash \operatorname{\mathrm{GL}}_d(F)}\xi(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle g,\boldsymbol{\zeta}). \end{align} $$
To see that the summation is formally well defined, first note that we can globalize Equation (2.58) to
![]() $y\in M_{\beta }(F)$
. Indeed, for any integer j,
$y\in M_{\beta }(F)$
. Indeed, for any integer j,
![]() $\eta _{2j}$
is defined on
$\eta _{2j}$
is defined on
![]() $\operatorname {\mathrm {Sp}}_{2j}(F)$
hence each
$\operatorname {\mathrm {Sp}}_{2j}(F)$
hence each
![]() $\eta _{\beta _i}^{\diamondsuit }$
and
$\eta _{\beta _i}^{\diamondsuit }$
and
![]() $\eta _d^{\diamondsuit }$
are defined on
$\eta _d^{\diamondsuit }$
are defined on
![]() $\operatorname {\mathrm {GL}}_{\beta _i}(F)$
and
$\operatorname {\mathrm {GL}}_{\beta _i}(F)$
and
![]() $\operatorname {\mathrm {GL}}_{d}(F)$
. Thus,
$\operatorname {\mathrm {GL}}_{d}(F)$
. Thus,
![]() $\eta _{\beta }(y)=\prod _{i=1}^l\eta ^{\diamondsuit }_{\beta _i}(y_i)/\eta ^{\diamondsuit }_{d}(y)$
. Now, by Formulas (2.65) and (2.63),
$\eta _{\beta }(y)=\prod _{i=1}^l\eta ^{\diamondsuit }_{\beta _i}(y_i)/\eta ^{\diamondsuit }_{d}(y)$
. Now, by Formulas (2.65) and (2.63),
 $$ \begin{align*} \xi(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle)&= \eta_{\beta}^{-1}(y)\tau_{\beta}(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle )\xi(\langle I_d,1\rangle)\\& =\tau_{\beta}(\langle y,\prod_{i=1}^l(\eta_{\beta_i}^{\diamondsuit})^{-1}(y_i)\rangle)\xi(\langle I_d,1\rangle) =\xi(\langle I_d,1\rangle). \end{align*} $$
$$ \begin{align*} \xi(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle)&= \eta_{\beta}^{-1}(y)\tau_{\beta}(\langle y,(\eta_{d}^{\diamondsuit})^{-1}(y)\rangle )\xi(\langle I_d,1\rangle)\\& =\tau_{\beta}(\langle y,\prod_{i=1}^l(\eta_{\beta_i}^{\diamondsuit})^{-1}(y_i)\rangle)\xi(\langle I_d,1\rangle) =\xi(\langle I_d,1\rangle). \end{align*} $$
Combining this with Corollary 16 and with Equation (2.65) for
![]() $v\in V_{\beta }(F)$
, we deduce that for any
$v\in V_{\beta }(F)$
, we deduce that for any
![]() $y\in P_{\beta }(F)$
,
$y\in P_{\beta }(F)$
,
![]() $\xi (\langle y,(\eta _{d}^{\diamondsuit })^{-1}(y)\rangle )=\xi (\langle I_d,1\rangle )$
hence
$\xi (\langle y,(\eta _{d}^{\diamondsuit })^{-1}(y)\rangle )=\xi (\langle I_d,1\rangle )$
hence
![]() $\xi (\langle y,(\eta _{d}^{\diamondsuit })^{-1}(y)\rangle g,\boldsymbol {\zeta })=\xi (g,\boldsymbol {\zeta })$
.
$\xi (\langle y,(\eta _{d}^{\diamondsuit })^{-1}(y)\rangle g,\boldsymbol {\zeta })=\xi (g,\boldsymbol {\zeta })$
.
Now, the general theory of the Eisenstein series (e.g., [Reference Mœglin and WaldspurgerMW95] where covering groups were also treated) implies, among other properties, that the sum is absolutely convergent for
![]() $\operatorname {\mathrm {Re}}(\boldsymbol {\zeta })$
in a certain cone and that the series admits meromorphic continuation.
$\operatorname {\mathrm {Re}}(\boldsymbol {\zeta })$
in a certain cone and that the series admits meromorphic continuation.
2.8 Unramified representations and L-factors
Let F be unramified (see § 2.4). Recall that
![]() $r=m$
if m is odd, otherwise
$r=m$
if m is odd, otherwise
![]() $r=m/2$
,
$r=m/2$
,
![]() $c=2n$
and
$c=2n$
and
![]() $G=\operatorname {\mathrm {Sp}}_{c}$
. The preimage of the torus
$G=\operatorname {\mathrm {Sp}}_{c}$
. The preimage of the torus
![]() $T_n$
in
$T_n$
in
![]() $G^{(m)}$
is a two-step nilpotent group (unless
$G^{(m)}$
is a two-step nilpotent group (unless
![]() $m\leq 2$
). Thus, its irreducible representations are constructed using Stone-von Neumann theory, that is, by extending a genuine character of the center to a maximal abelian subgroup, then inducing to
$m\leq 2$
). Thus, its irreducible representations are constructed using Stone-von Neumann theory, that is, by extending a genuine character of the center to a maximal abelian subgroup, then inducing to
![]() $\widetilde {T}_n$
(see, e.g., [Reference SavinSav04] and [Reference McNamaraMcN12, § 13.5–13.6]). The isomorphism class of the representation is determined by the action of the center, that is, independent of the choice of the maximal abelian subgroup and the extension.
$\widetilde {T}_n$
(see, e.g., [Reference SavinSav04] and [Reference McNamaraMcN12, § 13.5–13.6]). The isomorphism class of the representation is determined by the action of the center, that is, independent of the choice of the maximal abelian subgroup and the extension.
To make this construction uniform in n, first note that by Equations (2.19) and (2.51),
 $$ \begin{align*} \widetilde{T}_{n}=\{(\epsilon_1,\ldots,\epsilon_n)\in\mu_m^n:\prod_{i=1}^n\epsilon_i=1\}\backslash \operatorname{\mathrm{GL}}_{1}^{(m,r)}\times\ldots\times\operatorname{\mathrm{GL}}_{1}^{(m,r)}, \end{align*} $$
$$ \begin{align*} \widetilde{T}_{n}=\{(\epsilon_1,\ldots,\epsilon_n)\in\mu_m^n:\prod_{i=1}^n\epsilon_i=1\}\backslash \operatorname{\mathrm{GL}}_{1}^{(m,r)}\times\ldots\times\operatorname{\mathrm{GL}}_{1}^{(m,r)}, \end{align*} $$
where on
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
the group operation is given by
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
the group operation is given by
Thus, to construct a genuine irreducible representation of
![]() $\widetilde {T}_{n}$
, we take the tensor product of n genuine irreducible representations of
$\widetilde {T}_{n}$
, we take the tensor product of n genuine irreducible representations of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. Consider the i-th copy of
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. Consider the i-th copy of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. The center of this group is
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. The center of this group is
![]() $\widetilde {C}_{r,1}$
, which is the preimage of
$\widetilde {C}_{r,1}$
, which is the preimage of
![]() $F^{*r}$
. Let
$F^{*r}$
. Let
![]() $A=F^{*r}\mathcal {O}^{*}$
,
$A=F^{*r}\mathcal {O}^{*}$
,
![]() $\widetilde {A}$
is a maximal abelian subgroup of
$\widetilde {A}$
is a maximal abelian subgroup of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. A genuine character of
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
. A genuine character of
![]() $\widetilde {A}$
is called unramified if it is trivial on
$\widetilde {A}$
is called unramified if it is trivial on
![]() $\langle \mathcal {O}^{*},1\rangle $
. Let
$\langle \mathcal {O}^{*},1\rangle $
. Let
![]() $\mu _i$
be an unramified quasi-character of
$\mu _i$
be an unramified quasi-character of
![]() $F^{*}$
.
$F^{*}$
.
If
![]() $r=m$
,
$r=m$
,
![]() $(\cdot ,\cdot )_m$
is trivial on
$(\cdot ,\cdot )_m$
is trivial on
![]() $A\times A$
, hence we may form the genuine character of
$A\times A$
, hence we may form the genuine character of
![]() $\widetilde {A}$
by
$\widetilde {A}$
by
![]() $\varepsilon \otimes \mu _i(\langle x,\epsilon \rangle )=\varepsilon (\epsilon )\mu _i(x)$
. Then we obtain a genuine irreducible unramified representation of
$\varepsilon \otimes \mu _i(\langle x,\epsilon \rangle )=\varepsilon (\epsilon )\mu _i(x)$
. Then we obtain a genuine irreducible unramified representation of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
by (nonnormalized) induction from
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
by (nonnormalized) induction from
![]() $\widetilde {A}$
and
$\widetilde {A}$
and
![]() $\varepsilon \otimes \mu _i$
.
$\varepsilon \otimes \mu _i$
.
If
![]() $r=m/2$
, the definition depends on a choice of a root of unity, as we now explain. First, we recall the definition of the Weil factor. For a nontrivial additive character
$r=m/2$
, the definition depends on a choice of a root of unity, as we now explain. First, we recall the definition of the Weil factor. For a nontrivial additive character
![]() $\psi '$
of F and
$\psi '$
of F and
![]() $a\in F^{*}$
, let
$a\in F^{*}$
, let
![]() $\psi ^{\prime }_a(x)=\psi '(ax)$
. The Weil index of
$\psi ^{\prime }_a(x)=\psi '(ax)$
. The Weil index of
![]() $x\mapsto \psi '(x^2)$
is denoted
$x\mapsto \psi '(x^2)$
is denoted
![]() $\gamma (\psi ')$
, and the Weil factor of
$\gamma (\psi ')$
, and the Weil factor of
![]() $\psi '$
is
$\psi '$
is
![]() $\gamma _{\psi '}(a)=\gamma (\psi _a')/\gamma (\psi ')$
(see [Reference WeilWei64, p. 176] and [Reference Ranga RaoRao93]). The following formulas are well known (see, e.g., [Reference Ranga RaoRao93, Appendix]):
$\gamma _{\psi '}(a)=\gamma (\psi _a')/\gamma (\psi ')$
(see [Reference WeilWei64, p. 176] and [Reference Ranga RaoRao93]). The following formulas are well known (see, e.g., [Reference Ranga RaoRao93, Appendix]):
In particular, there are
![]() $[F^{*}:F^{*2}]=4$
(e.g., [Reference WeilWei95, p. 32]) choices for
$[F^{*}:F^{*2}]=4$
(e.g., [Reference WeilWei95, p. 32]) choices for
![]() $\gamma _{\psi '}$
, and only two are unramified, that is, trivial on
$\gamma _{\psi '}$
, and only two are unramified, that is, trivial on
![]() $\mathcal {O}^{*}$
. Also, recall the formula
$\mathcal {O}^{*}$
. Also, recall the formula
![]() $(\cdot ,\cdot )_m^{r}=(\cdot ,\cdot )_2$
relating the m-th Hilbert symbol to the quadratic one (when
$(\cdot ,\cdot )_m^{r}=(\cdot ,\cdot )_2$
relating the m-th Hilbert symbol to the quadratic one (when
![]() $r=m/2$
).
$r=m/2$
).
Now, if
![]() $r=m/2$
is odd,
$r=m/2$
is odd,
![]() $(x^r,y^r)_m=(x^r,y^r)_2$
so that
$(x^r,y^r)_m=(x^r,y^r)_2$
so that
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i$
defines a genuine character of
$\varepsilon \otimes \gamma _{\psi '}\mu _i$
defines a genuine character of
![]() $\widetilde {C}_{r,1}$
. Moreover, since
$\widetilde {C}_{r,1}$
. Moreover, since
![]() $(x^r,y)_m=(x,y)_2=(x^r,y)_2$
and both m-th and quadratic Hilbert symbols are trivial on
$(x^r,y)_m=(x,y)_2=(x^r,y)_2$
and both m-th and quadratic Hilbert symbols are trivial on
![]() $\mathcal {O}^{*}\times \mathcal {O}^{*}$
,
$\mathcal {O}^{*}\times \mathcal {O}^{*}$
,
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i$
is also a genuine character of
$\varepsilon \otimes \gamma _{\psi '}\mu _i$
is also a genuine character of
![]() $\widetilde {A}$
. We take
$\widetilde {A}$
. We take
![]() $\psi '$
such that
$\psi '$
such that
![]() $\gamma _{\psi '}$
is unramified, this choice is unique up to
$\gamma _{\psi '}$
is unramified, this choice is unique up to
![]() $\pm \gamma _{\psi '}(\varpi ^r)$
(
$\pm \gamma _{\psi '}(\varpi ^r)$
(
![]() $\gamma _{\psi '}(\varpi ^r)$
is determined up to a sign and this determines
$\gamma _{\psi '}(\varpi ^r)$
is determined up to a sign and this determines
![]() $\gamma _{\psi '}$
on A). Then
$\gamma _{\psi '}$
on A). Then
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i$
is a genuine unramified character of
$\varepsilon \otimes \gamma _{\psi '}\mu _i$
is a genuine unramified character of
![]() $\widetilde {A}$
, and we induce to
$\widetilde {A}$
, and we induce to
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
as in the case
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
as in the case
![]() $r=m$
above. For
$r=m$
above. For
![]() $m\leq 2$
,
$m\leq 2$
,
![]() $r=1$
and
$r=1$
and
![]() $A=F^{*}$
, so the induction is trivial.
$A=F^{*}$
, so the induction is trivial.
Moreover, for this case (even m, odd r) since any genuine character of
![]() $\operatorname {\mathrm {GL}}_1^{(2,1)}$
can be written in the form
$\operatorname {\mathrm {GL}}_1^{(2,1)}$
can be written in the form
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
for some
$\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
for some
![]() $\psi '$
and quasi-character
$\psi '$
and quasi-character
![]() $\mu _i^{\prime }$
of
$\mu _i^{\prime }$
of
![]() $F^{*}$
, we can write any genuine character of
$F^{*}$
, we can write any genuine character of
![]() $\widetilde {C}_{r,1}$
in the form
$\widetilde {C}_{r,1}$
in the form
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
. Since
$\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
. Since
![]() $x\mapsto (a,x)_2$
is a nongenuine character of
$x\mapsto (a,x)_2$
is a nongenuine character of
![]() $\widetilde {C}_{r,1}$
, which is unramified if
$\widetilde {C}_{r,1}$
, which is unramified if
![]() $|a|=1$
, we may a priori fix an unramified
$|a|=1$
, we may a priori fix an unramified
![]() $\gamma _{\psi '}$
(in one of two ways) then write any genuine unramified character of
$\gamma _{\psi '}$
(in one of two ways) then write any genuine unramified character of
![]() $\widetilde {C}_{r,1}$
as
$\widetilde {C}_{r,1}$
as
![]() $\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
for some unramified
$\varepsilon \otimes \gamma _{\psi '}\mu _i^{\prime }$
for some unramified
![]() $\mu _i^{\prime }$
. In addition, we will not lose any generality by taking the tensor product of n genuine irreducible representations of
$\mu _i^{\prime }$
. In addition, we will not lose any generality by taking the tensor product of n genuine irreducible representations of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
using the same
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
using the same
![]() $\psi '$
so that when
$\psi '$
so that when
![]() $\psi '$
is fixed, we can effectively parameterize the genuine unramified principal series representations using linear data.
$\psi '$
is fixed, we can effectively parameterize the genuine unramified principal series representations using linear data.
Now, consider the case of even r. Then
![]() $(x^r,y^r)_m=(x^r,y)_2=1$
so that
$(x^r,y^r)_m=(x^r,y)_2=1$
so that
![]() $\varepsilon \otimes \mu _i$
defines a genuine character of
$\varepsilon \otimes \mu _i$
defines a genuine character of
![]() $\widetilde {C}_{r,1}$
. For a fixed element
$\widetilde {C}_{r,1}$
. For a fixed element
![]() $\varpi _1\in \mathcal {O}$
with
$\varpi _1\in \mathcal {O}$
with
![]() $|\varpi _1|=q^{-1}$
, we can write any
$|\varpi _1|=q^{-1}$
, we can write any
![]() $a\in A$
uniquely in the form
$a\in A$
uniquely in the form
![]() $\varpi _1^{rl}u$
with an integer l and
$\varpi _1^{rl}u$
with an integer l and
![]() $|u|=1$
. Define
$|u|=1$
. Define
The definition is independent of the choice of
![]() $\varpi _1$
because if
$\varpi _1$
because if
![]() $\varpi =\varpi _1o$
with
$\varpi =\varpi _1o$
with
![]() $|o|=1$
,
$|o|=1$
,
![]() $\varpi _1^{rl}u=\varpi ^{rl}o^{rl}u$
, then
$\varpi _1^{rl}u=\varpi ^{rl}o^{rl}u$
, then
![]() $(\varpi _1^l,u)_2=(\varpi ^l,o^{rl}u)_2$
, since r is even. This is a (genuine) character of
$(\varpi _1^l,u)_2=(\varpi ^l,o^{rl}u)_2$
, since r is even. This is a (genuine) character of
![]() $\widetilde {A}$
because
$\widetilde {A}$
because
 $$ \begin{align*} &\varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_1}u_1,1\rangle\langle \varpi_1^{rl_2}u_2,1\rangle) =\varepsilon((\varpi_1^{l_1r}u_1,\varpi_1^{l_2r}u_2)_m^{-1}(\varpi_1^{(l_1+l_2)},u_1u_2)_2) \\&=\varepsilon((\varpi_1^{l_1},u_2)_2(u_1,\varpi_1^{l_2})_2(\varpi_1^{l_1},u_1)_2 (\varpi_1^{l_1},u_2)_2(\varpi_1^{l_2},u_1)_2(\varpi_1^{l_2},u_2)_2) \\&=\varepsilon((\varpi_1^{l_1},u_1)_2(\varpi_1^{l_2},u_2)_2)= \varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_1}u_1,1\rangle)\varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_2}u_2,1\rangle). \end{align*} $$
$$ \begin{align*} &\varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_1}u_1,1\rangle\langle \varpi_1^{rl_2}u_2,1\rangle) =\varepsilon((\varpi_1^{l_1r}u_1,\varpi_1^{l_2r}u_2)_m^{-1}(\varpi_1^{(l_1+l_2)},u_1u_2)_2) \\&=\varepsilon((\varpi_1^{l_1},u_2)_2(u_1,\varpi_1^{l_2})_2(\varpi_1^{l_1},u_1)_2 (\varpi_1^{l_1},u_2)_2(\varpi_1^{l_2},u_1)_2(\varpi_1^{l_2},u_2)_2) \\&=\varepsilon((\varpi_1^{l_1},u_1)_2(\varpi_1^{l_2},u_2)_2)= \varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_1}u_1,1\rangle)\varepsilon\otimes\gamma_{\varpi_1}(\langle \varpi_1^{rl_2}u_2,1\rangle). \end{align*} $$
It is also unramified, and trivial on
![]() $\{\langle x,1\rangle :x\in F^{*r}\}$
. Thus, we can extend
$\{\langle x,1\rangle :x\in F^{*r}\}$
. Thus, we can extend
![]() $\varepsilon \otimes \mu _i$
to a genuine unramified character of
$\varepsilon \otimes \mu _i$
to a genuine unramified character of
![]() $\widetilde {A}$
by
$\widetilde {A}$
by
(We do not claim that this extension is unique.)
To unify the notation, denote the representation of
![]() $\widetilde {A}$
by
$\widetilde {A}$
by
![]() $\varepsilon \otimes \vartheta \mu _i$
. Specifically,
$\varepsilon \otimes \vartheta \mu _i$
. Specifically,
![]() $\vartheta =1$
if m is odd;
$\vartheta =1$
if m is odd;
![]() $\vartheta =\gamma _{\psi '}$
if
$\vartheta =\gamma _{\psi '}$
if
![]() $m\equiv 2\,(4)$
(m is even, r is odd), in which case the isomorphism class of the induced representation of
$m\equiv 2\,(4)$
(m is even, r is odd), in which case the isomorphism class of the induced representation of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
depends on
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
depends on
![]() $\psi '$
; and
$\psi '$
; and
![]() $\vartheta =\gamma _{\varpi _1}$
when
$\vartheta =\gamma _{\varpi _1}$
when
![]() $m\equiv 0\,(4)$
, but then the isomorphism class of the induced representation of
$m\equiv 0\,(4)$
, but then the isomorphism class of the induced representation of
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
does not depend on the choice of extension of
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
does not depend on the choice of extension of
![]() $\varepsilon \otimes \mu _i$
to
$\varepsilon \otimes \mu _i$
to
![]() $\widetilde {A}$
and in particular, it is independent of
$\widetilde {A}$
and in particular, it is independent of
![]() $\varpi _1$
.
$\varpi _1$
.
The value
![]() $\varepsilon \otimes \vartheta \mu _i(\langle \varpi ^r,1\rangle )$
is independent of the choice of uniformizer
$\varepsilon \otimes \vartheta \mu _i(\langle \varpi ^r,1\rangle )$
is independent of the choice of uniformizer
![]() $\varpi $
except when
$\varpi $
except when
![]() $m\equiv 2\,(4)$
, in which case it depends both on this choice and on
$m\equiv 2\,(4)$
, in which case it depends both on this choice and on
![]() $\psi '$
, but only up to a sign
$\psi '$
, but only up to a sign
![]() $(\varpi ,u)_2=\pm 1$
, where
$(\varpi ,u)_2=\pm 1$
, where
![]() $|u|=1$
(use Equation (2.68)).
$|u|=1$
(use Equation (2.68)).
Denote the tensor product of n such representations, with unramified quasi-characters
![]() $\mu _1,\ldots ,\mu _n$
of
$\mu _1,\ldots ,\mu _n$
of
![]() $F^{*}$
, by
$F^{*}$
, by
![]() $\varepsilon \otimes \vartheta \mu $
(we use the same
$\varepsilon \otimes \vartheta \mu $
(we use the same
![]() $\vartheta $
for all i). Let
$\vartheta $
for all i). Let
![]() $T_{n,*}=\{t\in T_n:t_i\in A,\forall i\}$
,
$T_{n,*}=\{t\in T_n:t_i\in A,\forall i\}$
,
![]() $\widetilde {T}_{n,*}$
is a maximal abelian subgroup of
$\widetilde {T}_{n,*}$
is a maximal abelian subgroup of
![]() $\widetilde {T}_n$
. Then
$\widetilde {T}_n$
. Then
 $$ \begin{align*} \varepsilon\otimes\vartheta\mu(\langle t,\epsilon\rangle)=\varepsilon(\epsilon)\prod_{i=1}^n\vartheta(t_i)\mu_i(t_i),\qquad\forall t\in T_{n,*}. \end{align*} $$
$$ \begin{align*} \varepsilon\otimes\vartheta\mu(\langle t,\epsilon\rangle)=\varepsilon(\epsilon)\prod_{i=1}^n\vartheta(t_i)\mu_i(t_i),\qquad\forall t\in T_{n,*}. \end{align*} $$
The restriction of
![]() $\varepsilon \otimes \vartheta \mu $
to the center of
$\varepsilon \otimes \vartheta \mu $
to the center of
![]() $\widetilde {T}_n$
exhausts its genuine irreducible unramified representations; therefore, when we induce to
$\widetilde {T}_n$
exhausts its genuine irreducible unramified representations; therefore, when we induce to
![]() $\widetilde {T}_n$
we obtain all such representations of
$\widetilde {T}_n$
we obtain all such representations of
![]() $\widetilde {T}_n$
by varying
$\widetilde {T}_n$
by varying
![]() $\mu _1,\ldots ,\mu _n$
. Now, extending to
$\mu _1,\ldots ,\mu _n$
. Now, extending to
![]() $\widetilde {B}_n$
then inducing to
$\widetilde {B}_n$
then inducing to
![]() $G^{(m)}$
, we obtain the genuine unramified principal series representations
$G^{(m)}$
, we obtain the genuine unramified principal series representations
(Only the outer induction is normalized.) We usually regard elements in the space of this representation as complex-valued functions by evaluating at the identity.
The dual group of a covering group has been defined and studied in several works, for example, [Reference SavinSav04, Reference McNamaraMcN12, Reference WeissmanWei14, Reference Gan and GaoGG18, Reference WeissmanWei18]. For
![]() $G^{(m)}$
, the dual group
$G^{(m)}$
, the dual group
![]() ${G^{(m)}}^{\vee }$
is
${G^{(m)}}^{\vee }$
is
![]() $\operatorname {\mathrm {SO}}_{2n+1}(\mathbb {C})$
when m is odd and
$\operatorname {\mathrm {SO}}_{2n+1}(\mathbb {C})$
when m is odd and
![]() $\operatorname {\mathrm {Sp}}_{2n}(\mathbb {C})$
if it is even (see, e.g., [Reference LiLi20, § 5.1]). If
$\operatorname {\mathrm {Sp}}_{2n}(\mathbb {C})$
if it is even (see, e.g., [Reference LiLi20, § 5.1]). If
![]() $\pi $
is the irreducible unramified constituent of
$\pi $
is the irreducible unramified constituent of
![]() $\mathrm {I}_{G^{(m)}}(\vartheta ,\mu )$
, the Satake parameter of
$\mathrm {I}_{G^{(m)}}(\vartheta ,\mu )$
, the Satake parameter of
![]() $\pi $
is the semisimple conjugacy class in
$\pi $
is the semisimple conjugacy class in
![]() ${G^{(m)}}^{\vee }$
of
${G^{(m)}}^{\vee }$
of
 $$ \begin{align} t_{\pi,\vartheta}= \begin{cases} \operatorname{\mathrm{diag}}(\mu_1(\varpi^r),\ldots,\mu_n(\varpi^r),1,\mu_n^{-1}(\varpi^r),\ldots,\mu_1^{-1}(\varpi^r))&r=m,\\ \operatorname{\mathrm{diag}}(\mu_1(\varpi^r),\ldots,\mu_n(\varpi^r),\mu_n^{-1}(\varpi^r),\ldots,\mu_1^{-1}(\varpi^r))&r=m/2. \end{cases} \end{align} $$
$$ \begin{align} t_{\pi,\vartheta}= \begin{cases} \operatorname{\mathrm{diag}}(\mu_1(\varpi^r),\ldots,\mu_n(\varpi^r),1,\mu_n^{-1}(\varpi^r),\ldots,\mu_1^{-1}(\varpi^r))&r=m,\\ \operatorname{\mathrm{diag}}(\mu_1(\varpi^r),\ldots,\mu_n(\varpi^r),\mu_n^{-1}(\varpi^r),\ldots,\mu_1^{-1}(\varpi^r))&r=m/2. \end{cases} \end{align} $$
The parameter
![]() $t_{\pi ,\vartheta }$
depends on
$t_{\pi ,\vartheta }$
depends on
![]() $\vartheta $
only when
$\vartheta $
only when
![]() $m\equiv 2\,(4)$
since only in this case
$m\equiv 2\,(4)$
since only in this case
![]() $\vartheta $
affects the choice of
$\vartheta $
affects the choice of
![]() $\mu $
. The L-function of
$\mu $
. The L-function of
![]() $\pi $
is now defined by
$\pi $
is now defined by
Again, this function depends on
![]() $\vartheta $
only when
$\vartheta $
only when
![]() $m\equiv 2\,(4)$
.
$m\equiv 2\,(4)$
.
For the covering
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the situation is similar in light of Equations (2.53) and (2.51), with
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the situation is similar in light of Equations (2.53) and (2.51), with
![]() $T_{\operatorname {\mathrm {GL}}_d}$
instead of
$T_{\operatorname {\mathrm {GL}}_d}$
instead of
![]() $T_n$
. The maximal abelian subgroup
$T_n$
. The maximal abelian subgroup
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
of
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
is the preimage of d copies of A. For unramified quasi-characters
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
is the preimage of d copies of A. For unramified quasi-characters
![]() $\chi _1,\ldots ,\chi _d$
of
$\chi _1,\ldots ,\chi _d$
of
![]() $F^{*}$
, we denote
$F^{*}$
, we denote
![]() $\chi =\otimes _{i=1}^d\chi _i$
, then the genuine unramified principal series representation is
$\chi =\otimes _{i=1}^d\chi _i$
, then the genuine unramified principal series representation is
The following argument regarding the support of unramified functions in the space of an unramified principal series appeared in the proof of [Reference McNamaraMcN12, Lemma 2], which generalized [Reference Kazhdan and PattersonKP84, Lemma I.1.3].
Proposition 23. Let
![]() $\xi $
be an unramified (nonzero) element in
$\xi $
be an unramified (nonzero) element in
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
. Write
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
. Write
![]() $b\in \operatorname {\mathrm {GL}}_d$
in the form
$b\in \operatorname {\mathrm {GL}}_d$
in the form
![]() $b=uty$
, where
$b=uty$
, where
![]() $u\in N_{\operatorname {\mathrm {GL}}_d}$
,
$u\in N_{\operatorname {\mathrm {GL}}_d}$
,
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}$
and
$t\in T_{\operatorname {\mathrm {GL}}_d}$
and
![]() $y\in K_{\operatorname {\mathrm {GL}}_d}$
. Then
$y\in K_{\operatorname {\mathrm {GL}}_d}$
. Then
![]() $\xi (\langle b,\epsilon \rangle )\ne 0$
if and only if
$\xi (\langle b,\epsilon \rangle )\ne 0$
if and only if
![]() $t\in T_{\operatorname {\mathrm {GL}}_d,*}$
.
$t\in T_{\operatorname {\mathrm {GL}}_d,*}$
.
Proof. By the definition of the space of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
,
![]() $\xi (\langle uty,\epsilon \rangle )\ne 0$
if and only if
$\xi (\langle uty,\epsilon \rangle )\ne 0$
if and only if
![]() $\xi (\langle t,1\rangle )\ne 0$
. If
$\xi (\langle t,1\rangle )\ne 0$
. If
![]() $t\notin T_{\operatorname {\mathrm {GL}}_d,*}$
, choose
$t\notin T_{\operatorname {\mathrm {GL}}_d,*}$
, choose
![]() $t_x=\operatorname {\mathrm {diag}}(I_{i-1},x,I_{n-i})$
with
$t_x=\operatorname {\mathrm {diag}}(I_{i-1},x,I_{n-i})$
with
![]() $x\in \mathcal {O}^{*}$
such that
$x\in \mathcal {O}^{*}$
such that
![]() $(x,t_i)^2_m\ne 1$
. Then
$(x,t_i)^2_m\ne 1$
. Then
![]() $t_x\in T_{\operatorname {\mathrm {GL}}_d,*}\cap K_{\operatorname {\mathrm {GL}}_d}$
and
$t_x\in T_{\operatorname {\mathrm {GL}}_d,*}\cap K_{\operatorname {\mathrm {GL}}_d}$
and
![]() $\eta _d^{\diamondsuit }(t_x)=1$
because
$\eta _d^{\diamondsuit }(t_x)=1$
because
![]() $\eta _{2d}$
is trivial on
$\eta _{2d}$
is trivial on
![]() $T_{\operatorname {\mathrm {GL}}_{2d}}\cap K_{\operatorname {\mathrm {GL}}_{2d}}$
. Thus,
$T_{\operatorname {\mathrm {GL}}_{2d}}\cap K_{\operatorname {\mathrm {GL}}_{2d}}$
. Thus,
![]() $\langle t_x,1\rangle \in \eta _d^{\diamondsuit }(T_{\operatorname {\mathrm {GL}}_d,*}\cap K_{\operatorname {\mathrm {GL}}_d})$
whence
$\langle t_x,1\rangle \in \eta _d^{\diamondsuit }(T_{\operatorname {\mathrm {GL}}_d,*}\cap K_{\operatorname {\mathrm {GL}}_d})$
whence
![]() $(\varepsilon \otimes \vartheta \chi )(\langle t_x,1\rangle )=1$
. Now, by Equation (2.51),
$(\varepsilon \otimes \vartheta \chi )(\langle t_x,1\rangle )=1$
. Now, by Equation (2.51),
hence
![]() $\xi (\langle t,1\rangle )=0$
. Thus,
$\xi (\langle t,1\rangle )=0$
. Thus,
![]() $t\in T_{\operatorname {\mathrm {GL}}_d,*}$
and then
$t\in T_{\operatorname {\mathrm {GL}}_d,*}$
and then
![]() $\xi (\langle t,1\rangle )=\delta _{B_{\operatorname {\mathrm {GL}}_d}}^{1/2}(t)(\varepsilon \otimes \vartheta \chi )(\langle t,1\rangle )\xi (\langle I_{d},1\rangle )\ne 0$
.
$\xi (\langle t,1\rangle )=\delta _{B_{\operatorname {\mathrm {GL}}_d}}^{1/2}(t)(\varepsilon \otimes \vartheta \chi )(\langle t,1\rangle )\xi (\langle I_{d},1\rangle )\ne 0$
.
The dual group
![]() ${\operatorname {\mathrm {GL}}_d^{(m,r)}}^{\vee }$
is
${\operatorname {\mathrm {GL}}_d^{(m,r)}}^{\vee }$
is
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {C})$
([Reference GaoGao18a, § 2.3]). If
$\operatorname {\mathrm {GL}}_d(\mathbb {C})$
([Reference GaoGao18a, § 2.3]). If
![]() $\tau $
is the irreducible unramified constituent of
$\tau $
is the irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
, the Satake parameter of
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
, the Satake parameter of
![]() $\tau $
is the semisimple conjugacy class in
$\tau $
is the semisimple conjugacy class in
![]() ${\operatorname {\mathrm {GL}}_d^{(m,r)}}^{\vee }$
of
${\operatorname {\mathrm {GL}}_d^{(m,r)}}^{\vee }$
of
Then for any finite-dimensional complex representation
![]() $\sigma $
of
$\sigma $
of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {C})$
, define
$\operatorname {\mathrm {GL}}_d(\mathbb {C})$
, define
For the identity representation
![]() $\mathrm {id}:\operatorname {\mathrm {GL}}_d(\mathbb {C})\rightarrow \operatorname {\mathrm {GL}}_d(\mathbb {C})$
, denote
$\mathrm {id}:\operatorname {\mathrm {GL}}_d(\mathbb {C})\rightarrow \operatorname {\mathrm {GL}}_d(\mathbb {C})$
, denote
![]() $L_{\vartheta }(s,\tau )=L_{\vartheta }(s,\tau ,\mathrm {id})$
. In the linear case, this is the standard L-function of
$L_{\vartheta }(s,\tau )=L_{\vartheta }(s,\tau ,\mathrm {id})$
. In the linear case, this is the standard L-function of
![]() $\tau $
. If
$\tau $
. If
![]() $\tau '$
is a similar constituent of
$\tau '$
is a similar constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{d'}^{(m,r)}}(\vartheta ',\chi ')$
,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{d'}^{(m,r)}}(\vartheta ',\chi ')$
,
![]() $L_{\vartheta ,\vartheta '}(s,\tau \times \tau ')=\det (I-(t_{\tau ,\vartheta }\otimes t_{\tau ',\vartheta '})q^{-s})^{-1}$
. In particular, the definitions imply
$L_{\vartheta ,\vartheta '}(s,\tau \times \tau ')=\det (I-(t_{\tau ,\vartheta }\otimes t_{\tau ',\vartheta '})q^{-s})^{-1}$
. In particular, the definitions imply
where
![]() $\mathrm {\operatorname {\mathrm {Sym}}}^2$
(resp.,
$\mathrm {\operatorname {\mathrm {Sym}}}^2$
(resp.,
![]() $\wedge ^2$
) is the symmetric (resp., exterior) square representation.
$\wedge ^2$
) is the symmetric (resp., exterior) square representation.
Finally, assume that
![]() $\pi $
and
$\pi $
and
![]() $\tau $
are the irreducible unramified constituents of
$\tau $
are the irreducible unramified constituents of
![]() $\mathrm {I}_{G^{(m)}}(\vartheta _{\pi },\mu )$
and
$\mathrm {I}_{G^{(m)}}(\vartheta _{\pi },\mu )$
and
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi )$
. Put
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi )$
. Put
![]() $n'=2n+1$
if
$n'=2n+1$
if
![]() $r=m$
, otherwise
$r=m$
, otherwise
![]() $n'=2n$
, and regard
$n'=2n$
, and regard
![]() $t_{\pi ,\vartheta _{\pi }}$
as an element of
$t_{\pi ,\vartheta _{\pi }}$
as an element of
![]() $\operatorname {\mathrm {GL}}_{n'}(\mathbb {C})$
(see Equation (2.69)). Using the definition of the L-factor for
$\operatorname {\mathrm {GL}}_{n'}(\mathbb {C})$
(see Equation (2.69)). Using the definition of the L-factor for
![]() $\operatorname {\mathrm {GL}}_{n'}\times \operatorname {\mathrm {GL}}_d$
,
$\operatorname {\mathrm {GL}}_{n'}\times \operatorname {\mathrm {GL}}_d$
,
We extend a known identity from the linear setup, relating the L-function of
![]() $\pi \times \tau $
to the product of L-functions for representations of
$\pi \times \tau $
to the product of L-functions for representations of
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
. One can always write
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
. One can always write
![]() $\pi $
as the irreducible unramified constituent of
$\pi $
as the irreducible unramified constituent of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, where
$\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, where
![]() $\pi _n$
is the irreducible unramified constituent of
$\pi _n$
is the irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_n^{(m,r)}}(\vartheta _{\pi },\mu )$
and R is a Siegel parabolic subgroup of G. The representation
$\mathrm {I}_{\operatorname {\mathrm {GL}}_n^{(m,r)}}(\vartheta _{\pi },\mu )$
and R is a Siegel parabolic subgroup of G. The representation
![]() $\pi _n^{\vee }$
(which is antigenuine) is the irreducible unramified constituent of the unramified principal series with inducing data
$\pi _n^{\vee }$
(which is antigenuine) is the irreducible unramified constituent of the unramified principal series with inducing data
![]() $\otimes _{i=1}^d\varepsilon ^{-1}\otimes \vartheta _{\pi }^{-1}\mu ^{-1}$
, and we can define
$\otimes _{i=1}^d\varepsilon ^{-1}\otimes \vartheta _{\pi }^{-1}\mu ^{-1}$
, and we can define
![]() $L_{\vartheta _{\pi }^{-1},\vartheta _{\tau }}(s,\pi _n^{\vee }\times \tau )$
as above. By definition
$L_{\vartheta _{\pi }^{-1},\vartheta _{\tau }}(s,\pi _n^{\vee }\times \tau )$
as above. By definition
where the factor in square brackets appears only when
![]() $r=m$
or, equivalently, m is odd. Note that we have to parameterize
$r=m$
or, equivalently, m is odd. Note that we have to parameterize
![]() $\pi _n^{\vee }$
using
$\pi _n^{\vee }$
using
![]() $\vartheta _{\pi }^{-1}$
(when
$\vartheta _{\pi }^{-1}$
(when
![]() $m\equiv 2\,(4)$
) to deduce Equation (2.71).
$m\equiv 2\,(4)$
) to deduce Equation (2.71).
Assume
![]() $m\equiv 2\,(4)$
(the following remarks become trivial otherwise). Since we will usually be interested in the L-function of
$m\equiv 2\,(4)$
(the following remarks become trivial otherwise). Since we will usually be interested in the L-function of
![]() $\pi \times \tau $
, it is convenient to use one parametrization for both, and we do not lose any generality by doing so. For any two parameters
$\pi \times \tau $
, it is convenient to use one parametrization for both, and we do not lose any generality by doing so. For any two parameters
![]() $\vartheta _{\pi }$
and
$\vartheta _{\pi }$
and
![]() $\vartheta _{\tau }$
,
$\vartheta _{\tau }$
,
![]() $\vartheta _{\pi }\vartheta _{\tau }^{-1}=\vartheta $
for some quadratic unramified character
$\vartheta _{\pi }\vartheta _{\tau }^{-1}=\vartheta $
for some quadratic unramified character
![]() $\vartheta $
of
$\vartheta $
of
![]() $F^{*}$
. Now,
$F^{*}$
. Now,
![]() $t_{\tau ,\vartheta _{\tau }}=t_{\tau ,\vartheta _{\pi }\vartheta }$
, and since
$t_{\tau ,\vartheta _{\tau }}=t_{\tau ,\vartheta _{\pi }\vartheta }$
, and since
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\pi }\vartheta ,\chi )=\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\pi },\vartheta \chi )$
, we also have
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\pi }\vartheta ,\chi )=\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\pi },\vartheta \chi )$
, we also have
![]() $t_{\tau ,\vartheta _{\tau }}=t_{\vartheta \tau ,\vartheta _{\pi }}$
so that
$t_{\tau ,\vartheta _{\tau }}=t_{\vartheta \tau ,\vartheta _{\pi }}$
so that
![]() $L_{\vartheta _{\pi },\vartheta _{\tau }}(s,\pi \times \tau )= L_{\vartheta _{\pi },\vartheta _{\pi }}(s,\pi \times \vartheta \tau )$
. For brevity, denote
$L_{\vartheta _{\pi },\vartheta _{\tau }}(s,\pi \times \tau )= L_{\vartheta _{\pi },\vartheta _{\pi }}(s,\pi \times \vartheta \tau )$
. For brevity, denote
![]() $L_{\vartheta _{\pi }}(\cdots )=L_{\vartheta _{\pi },\vartheta _{\pi }}(\cdots )$
. In particular, when
$L_{\vartheta _{\pi }}(\cdots )=L_{\vartheta _{\pi },\vartheta _{\pi }}(\cdots )$
. In particular, when
![]() $\mu _{2m}\subset F^{*}$
,
$\mu _{2m}\subset F^{*}$
,
![]() $(x,x)_2=1$
for all
$(x,x)_2=1$
for all
![]() $x\in F^{*}$
and
$x\in F^{*}$
and
![]() $\gamma _{\psi '}=\gamma _{\psi '}^{-1}$
(use Equation (2.68)). Hence,
$\gamma _{\psi '}=\gamma _{\psi '}^{-1}$
(use Equation (2.68)). Hence,
![]() $\vartheta _{\pi }=\vartheta _{\pi }^{-1}$
and Equation (2.71) becomes
$\vartheta _{\pi }=\vartheta _{\pi }^{-1}$
and Equation (2.71) becomes
Example 24. Since
![]() $\mathrm {I}_{G^{(m)}}(\vartheta _{\pi },\mu )=\mathrm {I}_{G^{(m)}}(\vartheta _{\pi }\vartheta ,\vartheta \mu )$
, for
$\mathrm {I}_{G^{(m)}}(\vartheta _{\pi },\mu )=\mathrm {I}_{G^{(m)}}(\vartheta _{\pi }\vartheta ,\vartheta \mu )$
, for
![]() $n=1$
we have
$n=1$
we have
![]() $t_{\pi ,\vartheta _{\pi }}=\operatorname {\mathrm {diag}}(\mu _1(\varpi ),\mu _1^{-1}(\varpi ))$
while
$t_{\pi ,\vartheta _{\pi }}=\operatorname {\mathrm {diag}}(\mu _1(\varpi ),\mu _1^{-1}(\varpi ))$
while
![]() $t_{\pi ,\vartheta \vartheta _{\pi }}=\operatorname {\mathrm {diag}}(\vartheta \mu _1(\varpi ),\vartheta \mu _1^{-1}(\varpi ))$
.
$t_{\pi ,\vartheta \vartheta _{\pi }}=\operatorname {\mathrm {diag}}(\vartheta \mu _1(\varpi ),\vartheta \mu _1^{-1}(\varpi ))$
.
Proposition 25. With
![]() $\tau $
as above,
$\tau $
as above,
![]() $\tau ^{*}$
defined by Equation (2.54) is the irreducible unramified constituent of
$\tau ^{*}$
defined by Equation (2.54) is the irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
. Consequently,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
. Consequently,
![]() $t_{\tau ^{\vee },\vartheta _{\tau }^{-1}}=t_{\tau ^{*},\vartheta _{\tau }}$
.
$t_{\tau ^{\vee },\vartheta _{\tau }^{-1}}=t_{\tau ^{*},\vartheta _{\tau }}$
.
Proof. By definition,
![]() $\tau ^{*}$
is realized in the space of
$\tau ^{*}$
is realized in the space of
![]() $\tau $
, and
$\tau $
, and
![]() $\tau ^{*}$
is irreducible and unramified. Hence, to prove that
$\tau ^{*}$
is irreducible and unramified. Hence, to prove that
![]() $\tau ^{*}$
is the irreducible unramified constituent of
$\tau ^{*}$
is the irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
, it suffices to show that
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
, it suffices to show that
![]() $(\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ))^{*}=\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
. The representation
$(\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ))^{*}=\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ^{-1})$
. The representation
![]() $(\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ))^{*}$
is an unramified principal series, and we need to check that for all
$(\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta _{\tau },\chi ))^{*}$
is an unramified principal series, and we need to check that for all
![]() $a\in A$
,
$a\in A$
,
![]() $\vartheta _{\tau }({}^{*}\langle a,1\rangle )=\vartheta _{\tau }(\langle a,1\rangle )$
. Note that
$\vartheta _{\tau }({}^{*}\langle a,1\rangle )=\vartheta _{\tau }(\langle a,1\rangle )$
. Note that
![]() ${}^{*}\langle a,1\rangle =\langle a^{-1},1\rangle $
.
${}^{*}\langle a,1\rangle =\langle a^{-1},1\rangle $
.
This is clear if
![]() $r=m$
. If
$r=m$
. If
![]() $m\equiv 2\,(4)$
,
$m\equiv 2\,(4)$
,
![]() $\vartheta _{\tau }=\gamma _{\psi '}$
and by Equation (2.68),
$\vartheta _{\tau }=\gamma _{\psi '}$
and by Equation (2.68),
![]() $\gamma _{\psi }(a)=\gamma _{\psi }(a^{-1})$
. For the remaining case
$\gamma _{\psi }(a)=\gamma _{\psi }(a^{-1})$
. For the remaining case
![]() $\vartheta _{\tau }=\gamma _{\varpi _1}$
, if we write
$\vartheta _{\tau }=\gamma _{\varpi _1}$
, if we write
![]() $a=\varpi _1^{rl}u$
as above,
$a=\varpi _1^{rl}u$
as above,
Now,
![]() $t_{\tau ^{\vee },\vartheta _{\tau }^{-1}}=t_{\tau ^{*},\vartheta _{\tau }}$
is immediate because the inducing data for
$t_{\tau ^{\vee },\vartheta _{\tau }^{-1}}=t_{\tau ^{*},\vartheta _{\tau }}$
is immediate because the inducing data for
![]() $\tau ^{\vee }$
is
$\tau ^{\vee }$
is
![]() $\otimes _{i=1}^d\varepsilon ^{-1}\otimes \vartheta _{\tau }^{-1}\chi ^{-1}$
.
$\otimes _{i=1}^d\varepsilon ^{-1}\otimes \vartheta _{\tau }^{-1}\chi ^{-1}$
.
2.9 Whittaker functionals
Suppose that F is a local non-Archimedean field. Recall that
![]() $\psi $
is a nontrivial character of F. Define a generic character
$\psi $
is a nontrivial character of F. Define a generic character
![]() $\psi $
of
$\psi $
of
![]() $N_{\operatorname {\mathrm {GL}}_d}$
by
$N_{\operatorname {\mathrm {GL}}_d}$
by
 $$ \begin{align*} \psi(v)=\psi\left(\sum_{i=1}^{d-1}v_{i,i+1}\right). \end{align*} $$
$$ \begin{align*} \psi(v)=\psi\left(\sum_{i=1}^{d-1}v_{i,i+1}\right). \end{align*} $$
Consider a genuine unramified representation
![]() $\mathrm {I}(\vartheta ,\chi )=\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\chi )$
with the notation of § 2.8. A Whittaker functional on
$\mathrm {I}(\vartheta ,\chi )=\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\chi )$
with the notation of § 2.8. A Whittaker functional on
![]() $\mathrm {I}(\vartheta ,\chi )$
is a (nonzero) morphism in
$\mathrm {I}(\vartheta ,\chi )$
is a (nonzero) morphism in
The dimension of the vector space (2.72) is
![]() $|T_{\operatorname {\mathrm {GL}}_d,*}\backslash T_{\operatorname {\mathrm {GL}}_d}|$
, by an application of the geometric lemma of Bernstein and Zelevinsky [Reference Bernstein and ZelevinskyBZ77, Theorem 5.2] (see also [Reference Kazhdan and PattersonKP84, Lemma I.3.2]). For a function f in the space of
$|T_{\operatorname {\mathrm {GL}}_d,*}\backslash T_{\operatorname {\mathrm {GL}}_d}|$
, by an application of the geometric lemma of Bernstein and Zelevinsky [Reference Bernstein and ZelevinskyBZ77, Theorem 5.2] (see also [Reference Kazhdan and PattersonKP84, Lemma I.3.2]). For a function f in the space of
![]() $\mathrm {I}(\vartheta ,\chi )$
regarded as a complex-valued function, consider the Whittaker functional
$\mathrm {I}(\vartheta ,\chi )$
regarded as a complex-valued function, consider the Whittaker functional
![]() $\Lambda _t$
defined for each fixed
$\Lambda _t$
defined for each fixed
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}$
by
$t\in T_{\operatorname {\mathrm {GL}}_d}$
by
 $$ \begin{align*} \Lambda_t(f)=\int\limits_{N_{\operatorname{\mathrm{GL}}_d}}f(\langle t,1\rangle\langle J_d,1\rangle \langle u,1\rangle)\psi^{-1}(u)\,du. \end{align*} $$
$$ \begin{align*} \Lambda_t(f)=\int\limits_{N_{\operatorname{\mathrm{GL}}_d}}f(\langle t,1\rangle\langle J_d,1\rangle \langle u,1\rangle)\psi^{-1}(u)\,du. \end{align*} $$
Note that because in this context the
![]() $2$
-cocycle is
$2$
-cocycle is
![]() $\sigma ^{\diamondsuit }_{d}$
,
$\sigma ^{\diamondsuit }_{d}$
,
![]() $u\mapsto \langle u,1\rangle $
is the canonical splitting of
$u\mapsto \langle u,1\rangle $
is the canonical splitting of
![]() $N_{\operatorname {\mathrm {GL}}_d}$
. This integral is defined as an absolutely convergent integral for
$N_{\operatorname {\mathrm {GL}}_d}$
. This integral is defined as an absolutely convergent integral for
![]() $\operatorname {\mathrm {Re}}(\chi )$
in a certain cone, then by meromorphic continuation in general. In fact, by Banks [Reference BanksBan98a] this continuation is analytic (his argument – Bernstein’s continuation principle – is applicable to
$\operatorname {\mathrm {Re}}(\chi )$
in a certain cone, then by meromorphic continuation in general. In fact, by Banks [Reference BanksBan98a] this continuation is analytic (his argument – Bernstein’s continuation principle – is applicable to
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
as well). The functionals
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
as well). The functionals
![]() $\Lambda _t$
as t varies over the set of representatives of
$\Lambda _t$
as t varies over the set of representatives of
![]() $T_{\operatorname {\mathrm {GL}}_d,*}\backslash T_{\operatorname {\mathrm {GL}}_d}$
form a linear basis of the space (2.72) (see [Reference Kazhdan and PattersonKP84, Lemma I.3.1]). In particular, denote
$T_{\operatorname {\mathrm {GL}}_d,*}\backslash T_{\operatorname {\mathrm {GL}}_d}$
form a linear basis of the space (2.72) (see [Reference Kazhdan and PattersonKP84, Lemma I.3.1]). In particular, denote
![]() $\Lambda =\Lambda _{I_d}$
.
$\Lambda =\Lambda _{I_d}$
.
2.10 The Casselman–Shalika formula for
 $\operatorname {\mathrm {GL}}_d^{(m,r)}$
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
Assume that F is unramified and
![]() $\mu _{2m}\subset F^{*}$
, in particular
$\mu _{2m}\subset F^{*}$
, in particular
![]() $(-1,x)_m=1$
for all
$(-1,x)_m=1$
for all
![]() $x\in F^{*}$
. Fix a uniformizer
$x\in F^{*}$
. Fix a uniformizer
![]() $\varpi $
(see § 2.1). Let
$\varpi $
(see § 2.1). Let
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
be an unramified principal series representation, and denote
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
be an unramified principal series representation, and denote
While
![]() $\mathbf {x}$
is independent of
$\mathbf {x}$
is independent of
![]() $\varpi $
, the formulas in this section are developed for a given fixed
$\varpi $
, the formulas in this section are developed for a given fixed
![]() $\varpi $
. Let
$\varpi $
. Let
![]() $\xi ^0$
be the normalized unramified vector in the space of
$\xi ^0$
be the normalized unramified vector in the space of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
. For each
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
. For each
![]() $t\in \operatorname {\mathrm {GL}}_d$
, we have an unramified Whittaker function
$t\in \operatorname {\mathrm {GL}}_d$
, we have an unramified Whittaker function
![]() $W_t(g)=\Lambda _t(g\cdot \xi ^0)$
(
$W_t(g)=\Lambda _t(g\cdot \xi ^0)$
(
![]() $g\in \operatorname {\mathrm {GL}}_d^{(m,r)}$
). As in the linear case, it is clear that this function is determined by its values on
$g\in \operatorname {\mathrm {GL}}_d^{(m,r)}$
). As in the linear case, it is clear that this function is determined by its values on
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
, and the purpose of the Casselman–Shalika formula is to describe
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
, and the purpose of the Casselman–Shalika formula is to describe
![]() $W_t$
on
$W_t$
on
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
in terms of
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
in terms of
![]() $\mathbf {x}$
, t and the input (in the linear case,
$\mathbf {x}$
, t and the input (in the linear case,
![]() $\mathbf {x}$
would be replaced by the Satake parameter). As mentioned in the introduction, the metaplectic analog of the Casselman–Shalika formula [Reference Casselman and ShalikaCS80] has been developed through the works [Reference Kazhdan and PattersonKP84, Reference Bump, Friedberg and HoffsteinBFH91, Reference McNamaraMcN11, Reference Chinta and OffenCO13, Reference SzpruchSzp15, Reference McNamaraMcN16, Reference GaoGao17]. In this section, we describe this formula.
$\mathbf {x}$
would be replaced by the Satake parameter). As mentioned in the introduction, the metaplectic analog of the Casselman–Shalika formula [Reference Casselman and ShalikaCS80] has been developed through the works [Reference Kazhdan and PattersonKP84, Reference Bump, Friedberg and HoffsteinBFH91, Reference McNamaraMcN11, Reference Chinta and OffenCO13, Reference SzpruchSzp15, Reference McNamaraMcN16, Reference GaoGao17]. In this section, we describe this formula.
Suppose that the conductor of
![]() $\psi $
is
$\psi $
is
![]() $0$
, that is,
$0$
, that is,
![]() $\psi $
is unramified. Fix the Haar measure on F which is self-dual with respect to
$\psi $
is unramified. Fix the Haar measure on F which is self-dual with respect to
![]() $\psi $
, then
$\psi $
, then
![]() $\mathrm {vol}(\mathcal {O})$
(the volume of
$\mathrm {vol}(\mathcal {O})$
(the volume of
![]() $\mathcal {O}$
) is
$\mathcal {O}$
) is
![]() $1$
. Define the Gauss sum (as in, e.g., [Reference Kazhdan and PattersonKP84, Reference GaoGao18a]) by
$1$
. Define the Gauss sum (as in, e.g., [Reference Kazhdan and PattersonKP84, Reference GaoGao18a]) by
 $$ \begin{align} \mathfrak{g}(l)=\int\limits_{\mathcal{O}^{*}}(o,\varpi)_m^l\psi(\varpi^{-1}o)\,do,\qquad l\in\mathbb{Z}. \end{align} $$
$$ \begin{align} \mathfrak{g}(l)=\int\limits_{\mathcal{O}^{*}}(o,\varpi)_m^l\psi(\varpi^{-1}o)\,do,\qquad l\in\mathbb{Z}. \end{align} $$
(The integral becomes a finite sum over the cosets of
![]() $1+\mathcal {P}^a$
for
$1+\mathcal {P}^a$
for
![]() $a\gg 0$
.) Here,
$a\gg 0$
.) Here,
![]() $do$
is the restriction of the Haar measure on F, in particular
$do$
is the restriction of the Haar measure on F, in particular
![]() $\int _{\mathcal {O}^{*}}do=1-q^{-1}$
. A direct computation implies the following properties (see, e.g., [Reference GaoGao18a, § 3.2]):
$\int _{\mathcal {O}^{*}}do=1-q^{-1}$
. A direct computation implies the following properties (see, e.g., [Reference GaoGao18a, § 3.2]):
-
1. If
 $l\equiv 0\,(m)$
,
$l\equiv 0\,(m)$
,
 $\mathfrak {g}(l)=-q^{-1}$
.
$\mathfrak {g}(l)=-q^{-1}$
. -
2. Otherwise,
 $|\mathfrak {g}(l)|=q^{-1/2}$
and
$|\mathfrak {g}(l)|=q^{-1/2}$
and
 $\overline {\mathfrak {g}(l)}=\mathfrak {g}(-l)$
, hence
$\overline {\mathfrak {g}(l)}=\mathfrak {g}(-l)$
, hence
 $\mathfrak {g}(l)\mathfrak {g}(-l)=q^{-1}$
.
$\mathfrak {g}(l)\mathfrak {g}(-l)=q^{-1}$
.
For
![]() $\mathbf {a}=(a_1,\ldots ,a_d)\in \mathbb {Z}^d$
, denote
$\mathbf {a}=(a_1,\ldots ,a_d)\in \mathbb {Z}^d$
, denote
The map
![]() $\mathbf {a}\mapsto t_{\mathbf {a}}$
is a homomorphism, by Equation (2.51) and because
$\mathbf {a}\mapsto t_{\mathbf {a}}$
is a homomorphism, by Equation (2.51) and because
![]() $(\varpi ,\varpi )_m=1$
. If
$(\varpi ,\varpi )_m=1$
. If
![]() $\mathbf {b}\in \mathbb {Z}^d$
, write
$\mathbf {b}\in \mathbb {Z}^d$
, write
![]() $\mathbf {a}\equiv \mathbf {b}$
if
$\mathbf {a}\equiv \mathbf {b}$
if
![]() $\mathbf {a}-\mathbf {b}\in r\mathbb {Z}^d$
. The function
$\mathbf {a}-\mathbf {b}\in r\mathbb {Z}^d$
. The function
![]() $W_{t}$
is uniquely determined by its values on
$W_{t}$
is uniquely determined by its values on
![]() $t_{\mathbf {b}}$
. We define
$t_{\mathbf {b}}$
. We define
For
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}$
, let
$t\in T_{\operatorname {\mathrm {GL}}_d}$
, let
![]() $\mathbf {v}(t)\in \mathbb {Z}^d$
, denote the vector of valuations of t. Recall that
$\mathbf {v}(t)\in \mathbb {Z}^d$
, denote the vector of valuations of t. Recall that
![]() $T_{\operatorname {\mathrm {GL}}_d,*}<T_{\operatorname {\mathrm {GL}}_d}$
consists of the torus elements with coordinates in
$T_{\operatorname {\mathrm {GL}}_d,*}<T_{\operatorname {\mathrm {GL}}_d}$
consists of the torus elements with coordinates in
![]() $F^{*r}\mathcal {O}^{*}$
. Then for
$F^{*r}\mathcal {O}^{*}$
. Then for
![]() $t_0\in T_{\operatorname {\mathrm {GL}}_d,*}$
,
$t_0\in T_{\operatorname {\mathrm {GL}}_d,*}$
,
![]() $\mathbf {v}(t_0)\in r\mathbb {Z}^d$
.
$\mathbf {v}(t_0)\in r\mathbb {Z}^d$
.
Recall from § 2.1 that
![]() $W_{\operatorname {\mathrm {GL}}_d}$
is the Weyl group of
$W_{\operatorname {\mathrm {GL}}_d}$
is the Weyl group of
![]() $\operatorname {\mathrm {GL}}_d$
,
$\operatorname {\mathrm {GL}}_d$
,
![]() $\Phi _d$
(resp.,
$\Phi _d$
(resp.,
![]() $\Phi _d^+$
) is the set of roots (resp., positive roots) and the simple roots are
$\Phi _d^+$
) is the set of roots (resp., positive roots) and the simple roots are
![]() $(i,i+1)$
,
$(i,i+1)$
,
![]() $1\leq i<d$
. We extend the notation
$1\leq i<d$
. We extend the notation
![]() $t_{\mathbf {a}}$
to
$t_{\mathbf {a}}$
to
![]() $t_{l\alpha }$
for any
$t_{l\alpha }$
for any
![]() $l\in \mathbb {Z}$
and
$l\in \mathbb {Z}$
and
![]() $\alpha \in \Phi _d$
, regarding
$\alpha \in \Phi _d$
, regarding
![]() $\alpha $
as the natural element in
$\alpha $
as the natural element in
![]() $\mathbb {Z}^d$
.
$\mathbb {Z}^d$
.
Denote
![]() $\mathbf {x}_{\alpha }=x_ix_j^{-1}$
. Since
$\mathbf {x}_{\alpha }=x_ix_j^{-1}$
. Since
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
is a permutation on
$w\in W_{\operatorname {\mathrm {GL}}_d}$
is a permutation on
![]() $1,\ldots ,d$
, we can define
$1,\ldots ,d$
, we can define
![]() ${}^w\mathbf {x}$
by
${}^w\mathbf {x}$
by
![]() $({}^w\mathbf {x})_i=x_{w^{-1}(i)}$
. Also set for
$({}^w\mathbf {x})_i=x_{w^{-1}(i)}$
. Also set for
![]() $\mathbf {a}\in r\mathbb {Z}^d$
,
$\mathbf {a}\in r\mathbb {Z}^d$
,
![]() $\mathbf {x}(\mathbf {a})=(x_1^{a_1/r},\ldots ,x_d^{a_d/r})$
.
$\mathbf {x}(\mathbf {a})=(x_1^{a_1/r},\ldots ,x_d^{a_d/r})$
.
As in [Reference Chinta and OffenCO13, p. 425], define an action
![]() $w[\mathbf {a}]$
of
$w[\mathbf {a}]$
of
![]() $W_{\operatorname {\mathrm {GL}}_d}$
on
$W_{\operatorname {\mathrm {GL}}_d}$
on
![]() $\mathbb {Z}^d$
such that
$\mathbb {Z}^d$
such that
Recall that for any
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
and a representative
$w\in W_{\operatorname {\mathrm {GL}}_d}$
and a representative
![]() $y_w\in K_{\operatorname {\mathrm {GL}}_d}$
of w, we have a standard intertwining operator defined as follows. For
$y_w\in K_{\operatorname {\mathrm {GL}}_d}$
of w, we have a standard intertwining operator defined as follows. For
![]() $\alpha \in \Phi _d^+$
, let
$\alpha \in \Phi _d^+$
, let
![]() $U_{\alpha }<N_{\operatorname {\mathrm {GL}}_d}$
be the root subgroup of
$U_{\alpha }<N_{\operatorname {\mathrm {GL}}_d}$
be the root subgroup of
![]() $\alpha $
. Denote
$\alpha $
. Denote
 $$ \begin{align} N_w=\prod_{\{\alpha\in\Phi_d^+:w^{-1}\alpha\notin\Phi_d^+\}}U_{\alpha}. \end{align} $$
$$ \begin{align} N_w=\prod_{\{\alpha\in\Phi_d^+:w^{-1}\alpha\notin\Phi_d^+\}}U_{\alpha}. \end{align} $$
For
![]() $\xi $
in the space of
$\xi $
in the space of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
, the integral
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
, the integral
 $$ \begin{align*} M(y_w)\xi(g)=\int\limits_{N_{w}}\xi(\langle y_w,1\rangle^{-1}\langle u,1\rangle g)\,du,\qquad g\in \operatorname{\mathrm{GL}}_d^{(m,r)} \end{align*} $$
$$ \begin{align*} M(y_w)\xi(g)=\int\limits_{N_{w}}\xi(\langle y_w,1\rangle^{-1}\langle u,1\rangle g)\,du,\qquad g\in \operatorname{\mathrm{GL}}_d^{(m,r)} \end{align*} $$
is absolutely convergent when
![]() $\operatorname {\mathrm {Re}}(\chi _1)\gg \ldots \gg \operatorname {\mathrm {Re}}(\chi _d)$
and admits meromorphic continuation in the variables
$\operatorname {\mathrm {Re}}(\chi _1)\gg \ldots \gg \operatorname {\mathrm {Re}}(\chi _d)$
and admits meromorphic continuation in the variables
![]() $\chi _1,\ldots ,\chi _d$
(see, e.g., [Reference McNamaraMcN12, § 13.7], this is a straightforward extension of the results in linear case, for example, [Reference CasselmanCas80]). Since
$\chi _1,\ldots ,\chi _d$
(see, e.g., [Reference McNamaraMcN12, § 13.7], this is a straightforward extension of the results in linear case, for example, [Reference CasselmanCas80]). Since
![]() $\varepsilon \otimes \vartheta \chi $
is unramified as a genuine representation of
$\varepsilon \otimes \vartheta \chi $
is unramified as a genuine representation of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
;
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
;
![]() $\eta _d^{\diamondsuit }$
is trivial on
$\eta _d^{\diamondsuit }$
is trivial on
![]() $T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
; and
$T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
; and
![]() $\sigma _d^{\diamondsuit }(t,y_w)=1$
for any
$\sigma _d^{\diamondsuit }(t,y_w)=1$
for any
![]() $t\in T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
, the integral is independent of the choice of representative
$t\in T_{\operatorname {\mathrm {GL}}_d}\cap K_{\operatorname {\mathrm {GL}}_d}$
, the integral is independent of the choice of representative
![]() $y_w$
, hence we can simply denote
$y_w$
, hence we can simply denote
![]() $M(w)=M(y_w)$
. By Proposition 2 (recall that
$M(w)=M(y_w)$
. By Proposition 2 (recall that
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
is defined via restriction from
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
is defined via restriction from
![]() $\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
),
$\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
),
![]() ${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
as a representation of
${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
as a representation of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
, hence (away from the poles)
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
, hence (away from the poles)
In fact, we can assume that
![]() $\chi $
is regular, that is,
$\chi $
is regular, that is,
![]() ${}^{w}(\varepsilon \otimes \vartheta \chi )\ne \varepsilon \otimes \vartheta \chi $
, equivalently
${}^{w}(\varepsilon \otimes \vartheta \chi )\ne \varepsilon \otimes \vartheta \chi $
, equivalently
![]() ${}^{w}\chi \ne \chi $
as characters of
${}^{w}\chi \ne \chi $
as characters of
![]() $(F^{*r})^d$
, for all
$(F^{*r})^d$
, for all
![]() $1\ne w\in W_{\operatorname {\mathrm {GL}}_d}$
. Then the operators
$1\ne w\in W_{\operatorname {\mathrm {GL}}_d}$
. Then the operators
![]() $M(w)$
are holomorphic ([Reference McNamaraMcN12, § 13.7]). Since the Jacquet integrals
$M(w)$
are holomorphic ([Reference McNamaraMcN12, § 13.7]). Since the Jacquet integrals
![]() $\Lambda _t$
admit analytic continuation, the results of this section are true regardless of this assumption by analytic continuation.
$\Lambda _t$
admit analytic continuation, the results of this section are true regardless of this assumption by analytic continuation.
Since
![]() $M(w)\xi ^0$
is unramified, it is a constant multiple of the normalized unramified vector
$M(w)\xi ^0$
is unramified, it is a constant multiple of the normalized unramified vector
![]() $\xi _w^0$
of
$\xi _w^0$
of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,{}^w\chi )$
. The constant is given by the Gindikin–Karpelevich formula [Reference GaoGao18b, Corollary 7.4], which is the extension of [Reference CasselmanCas80, Theorem 3.1] to coverings. We have
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,{}^w\chi )$
. The constant is given by the Gindikin–Karpelevich formula [Reference GaoGao18b, Corollary 7.4], which is the extension of [Reference CasselmanCas80, Theorem 3.1] to coverings. We have
 $$ \begin{align} M(w)\xi^0(g)=\prod_{\{\alpha\in\Phi_d^+:w\alpha\notin\Phi_d^+\}}\frac{1-q^{-1}\mathbf{x}_{\alpha}}{1-\mathbf{x}_{\alpha}} \xi_w^0(g). \end{align} $$
$$ \begin{align} M(w)\xi^0(g)=\prod_{\{\alpha\in\Phi_d^+:w\alpha\notin\Phi_d^+\}}\frac{1-q^{-1}\mathbf{x}_{\alpha}}{1-\mathbf{x}_{\alpha}} \xi_w^0(g). \end{align} $$
Here, the appearance of
![]() $\mathbf {x}_{\alpha }$
in Equation (2.76) is the consequence of our definition of
$\mathbf {x}_{\alpha }$
in Equation (2.76) is the consequence of our definition of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
and the fact that
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
and the fact that
![]() ${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
; in general,
${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
; in general,
![]() $\mathbf {x}_{\alpha }$
would be replaced by the restriction of the genuine unramified character of the center of
$\mathbf {x}_{\alpha }$
would be replaced by the restriction of the genuine unramified character of the center of
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
to
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
to
![]() $\langle \operatorname {\mathrm {diag}}(I_{i-1},\varpi ^r,I_{j-i-1},\varpi ^{-r},I_{d-j}),1\rangle $
where
$\langle \operatorname {\mathrm {diag}}(I_{i-1},\varpi ^r,I_{j-i-1},\varpi ^{-r},I_{d-j}),1\rangle $
where
![]() $\alpha =(i,j)$
, and one must then show that this restriction is independent of the choice of uniformizer
$\alpha =(i,j)$
, and one must then show that this restriction is independent of the choice of uniformizer
![]() $\varpi $
(see [Reference GaoGao18b, § 7.1 and Proposition 7.3] and also [Reference Chinta and OffenCO13]).
$\varpi $
(see [Reference GaoGao18b, § 7.1 and Proposition 7.3] and also [Reference Chinta and OffenCO13]).
We also mention that [Reference GaoGao18b, Corollary 7.4] is applicable even without the assumption
![]() $\mu _{2m}\subset F^{*}$
, and since
$\mu _{2m}\subset F^{*}$
, and since
![]() ${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
, the formula (2.76) still holds.
${}^{w}(\varepsilon \otimes \vartheta \chi )=\varepsilon \otimes \vartheta ({}^w\chi )$
, the formula (2.76) still holds.
For previous extensions of the Gindikin–Karpelevich formula to coverings, see [Reference Kazhdan and PattersonKP84, Reference Bump, Friedberg and HoffsteinBFH91, Reference McNamaraMcN11, Reference Chinta and OffenCO13, Reference McNamaraMcN16, Reference KaplanKap17b].
The Casselman–Shalika formula for covering groups depends on certain coefficients which we present next, following [Reference Chinta and OffenCO13, § 4, § 5]. Given
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
, these coefficients are functions
$w\in W_{\operatorname {\mathrm {GL}}_d}$
, these coefficients are functions
![]() $(t,t')\mapsto \tau _{t,t'}(w,\vartheta ,\chi )$
(
$(t,t')\mapsto \tau _{t,t'}(w,\vartheta ,\chi )$
(
![]() $t,t'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
). Let
$t,t'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
). Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {A}'$
be two sets of representatives for
$\mathcal {A}'$
be two sets of representatives for
![]() $\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}\backslash \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
. Then for any
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}\backslash \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
. Then for any
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
, we have the following functional equation:
$w\in W_{\operatorname {\mathrm {GL}}_d}$
, we have the following functional equation:
The coefficients
![]() $\tau _{t,t'}(w,\vartheta ,\chi )$
do not depend on the choice of representative in
$\tau _{t,t'}(w,\vartheta ,\chi )$
do not depend on the choice of representative in
![]() $K_{\operatorname {\mathrm {GL}}_d}$
for w. While Equation (2.77) defines them uniquely, it is simpler to compute them inductively. First, note that for any
$K_{\operatorname {\mathrm {GL}}_d}$
for w. While Equation (2.77) defines them uniquely, it is simpler to compute them inductively. First, note that for any
![]() $t,t'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
and
$t,t'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
and
![]() $t_0,t_0'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
,
$t_0,t_0'\in \widetilde {T}_{\operatorname {\mathrm {GL}}_d,*}$
,
In particular, these coefficients do depend on the choices of representatives
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {A}'$
, and thereby on
$\mathcal {A}'$
, and thereby on
![]() $\varpi $
itself. Now, if
$\varpi $
itself. Now, if
![]() $w_1,w_2\in W_{\operatorname {\mathrm {GL}}_d}$
satisfy
$w_1,w_2\in W_{\operatorname {\mathrm {GL}}_d}$
satisfy
![]() $\ell (w_1w_2)=\ell (w_1)\ell (w_2)$
,
$\ell (w_1w_2)=\ell (w_1)\ell (w_2)$
,
 $$ \begin{align} \tau_{t,t'}(w_1w_2,\vartheta,\chi)=\sum_{\mathbf{e}\in r\mathbb{Z}^d\backslash \mathbb{Z}^d}\tau_{t,t_{\mathbf{e}}}(w_1,\vartheta,{}^{w_2}\chi)\tau_{t_{\mathbf{e}},t'}(w_2,\vartheta,\chi). \end{align} $$
$$ \begin{align} \tau_{t,t'}(w_1w_2,\vartheta,\chi)=\sum_{\mathbf{e}\in r\mathbb{Z}^d\backslash \mathbb{Z}^d}\tau_{t,t_{\mathbf{e}}}(w_1,\vartheta,{}^{w_2}\chi)\tau_{t_{\mathbf{e}},t'}(w_2,\vartheta,\chi). \end{align} $$
The sum is well defined by Equation (2.78). To determine
![]() $\tau _{t,t'}(w,\vartheta ,\chi )$
on
$\tau _{t,t'}(w,\vartheta ,\chi )$
on
![]() $w_{\alpha }$
,
$w_{\alpha }$
,
![]() $\alpha =(i,i+1)$
, write
$\alpha =(i,i+1)$
, write
Proposition 26. Let
![]() $\alpha =(i,i+1)$
,
$\alpha =(i,i+1)$
,
![]() $\mathbf {a},\mathbf {b}\in \mathbb {Z}^d$
. Then
$\mathbf {a},\mathbf {b}\in \mathbb {Z}^d$
. Then
![]() $\tau _{t_{\mathbf {a}},t_{\mathbf {b}}}^1(w_{\alpha },\vartheta ,\chi )=0$
unless
$\tau _{t_{\mathbf {a}},t_{\mathbf {b}}}^1(w_{\alpha },\vartheta ,\chi )=0$
unless
![]() $\mathbf {b}\equiv \mathbf {a}$
,
$\mathbf {b}\equiv \mathbf {a}$
,
![]() $\tau _{t_{\mathbf {a}},t_{\mathbf {b}}}^2(w_{\alpha },\vartheta ,\chi )=0$
unless
$\tau _{t_{\mathbf {a}},t_{\mathbf {b}}}^2(w_{\alpha },\vartheta ,\chi )=0$
unless
![]() $\mathbf {b}\equiv w_{\alpha }[\mathbf {a}]$
,
$\mathbf {b}\equiv w_{\alpha }[\mathbf {a}]$
,
 $$ \begin{align} &\tau_{t_{\mathbf{a}},t_{\mathbf{a}}}^1(w_{\alpha},\vartheta,\chi)=(1-q^{-1})\frac{\mathbf{x}_{\alpha}^{\lceil (a_{i+1}-a_{i})/r\rceil}}{1-\mathbf{x}_{\alpha}}, \end{align} $$
$$ \begin{align} &\tau_{t_{\mathbf{a}},t_{\mathbf{a}}}^1(w_{\alpha},\vartheta,\chi)=(1-q^{-1})\frac{\mathbf{x}_{\alpha}^{\lceil (a_{i+1}-a_{i})/r\rceil}}{1-\mathbf{x}_{\alpha}}, \end{align} $$
Here, for any
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $\lceil x \rceil $
is the smallest integer greater than or equal to x. Also, with the notation of Equation (2.78), for
$\lceil x \rceil $
is the smallest integer greater than or equal to x. Also, with the notation of Equation (2.78), for
![]() $j=1,2$
,
$j=1,2$
,
Proof. See [Reference GaoGao17, Theorem 3.6] which is based on [Reference McNamaraMcN16, § 9, § 13] (and [Reference Kazhdan and PattersonKP84, § I.1.3]), but the only assumptions on F in [Reference GaoGao17, Theorem 3.6] are that
![]() $|m|=1$
and
$|m|=1$
and
![]() $\mu _m\subset F^{*}$
.
$\mu _m\subset F^{*}$
.
Remark 27. We will only apply this proposition when
![]() $\mu _{2m}\subset F^{*}$
.
$\mu _{2m}\subset F^{*}$
.
By Equation (2.78),
![]() $\tau _{t,t'}(w,\vartheta ,\chi )$
is determined by elements
$\tau _{t,t'}(w,\vartheta ,\chi )$
is determined by elements
![]() $t=t_{\mathbf {a}}$
and
$t=t_{\mathbf {a}}$
and
![]() $t'=t_{\mathbf {b}}$
, and we define
$t'=t_{\mathbf {b}}$
, and we define
The Casselman–Shalika formula for
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
takes the following form:
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
takes the following form:
 $$ \begin{align} &W_{\mathbf{a}}(\mathbf{b},\vartheta,\chi)=\delta_{B_{\operatorname{\mathrm{GL}}_{d}}}(t_{\mathbf{b}})\sum_{w\in W_{\operatorname{\mathrm{GL}}_d}}\prod_{\{\alpha\in\Phi_d^+:w\alpha\in\Phi_d^+\}}\frac{1-q^{-1}({}^{w^{-1}}\mathbf{x})_{\alpha}} {1-({}^{w^{-1}}\mathbf{x})_{\alpha}}\tau_{\mathbf{a},\mathbf{b}^{*}}(w,\vartheta,{}^{w^{-1}}\chi). \end{align} $$
$$ \begin{align} &W_{\mathbf{a}}(\mathbf{b},\vartheta,\chi)=\delta_{B_{\operatorname{\mathrm{GL}}_{d}}}(t_{\mathbf{b}})\sum_{w\in W_{\operatorname{\mathrm{GL}}_d}}\prod_{\{\alpha\in\Phi_d^+:w\alpha\in\Phi_d^+\}}\frac{1-q^{-1}({}^{w^{-1}}\mathbf{x})_{\alpha}} {1-({}^{w^{-1}}\mathbf{x})_{\alpha}}\tau_{\mathbf{a},\mathbf{b}^{*}}(w,\vartheta,{}^{w^{-1}}\chi). \end{align} $$
We also mention the following observation of [Reference SuzukiSuz97, Remark 3.2]: For
![]() $1\ne w\in W_{\operatorname {\mathrm {GL}}_d}$
, if
$1\ne w\in W_{\operatorname {\mathrm {GL}}_d}$
, if
![]() $w=w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}$
, by definition
$w=w_{\alpha _1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}$
, by definition
![]() $\tau _{t,t'}(w,\vartheta ,\chi )=0$
unless there is
$\tau _{t,t'}(w,\vartheta ,\chi )=0$
unless there is
![]() $w'=w_{\alpha _1}^{i_1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}^{i_1}$
for some
$w'=w_{\alpha _1}^{i_1}\cdot \ldots \cdot w_{\alpha _{\ell (w)}}^{i_1}$
for some
![]() $i_1,\ldots ,i_{\ell (w)}\in \{0,1\}$
, such that
$i_1,\ldots ,i_{\ell (w)}\in \{0,1\}$
, such that
![]() $w'[\mathbf {v}(t')]\equiv \mathbf {v}(t)$
.
$w'[\mathbf {v}(t')]\equiv \mathbf {v}(t)$
.
As in Suzuki [Reference SuzukiSuz97, § 4.1] (see also [Reference SuzukiSuz98, § 7.1 (2)]), we can rewrite the summation in Equation (2.84) to obtain an iterative formula. Regard
![]() $W_{\operatorname {\mathrm {GL}}_{d-1}}$
as the subgroup of
$W_{\operatorname {\mathrm {GL}}_{d-1}}$
as the subgroup of
![]() $W_{\operatorname {\mathrm {GL}}_d}$
generated by
$W_{\operatorname {\mathrm {GL}}_d}$
generated by
![]() $w_{\alpha }$
for
$w_{\alpha }$
for
![]() $\alpha =(i,i+1)$
and
$\alpha =(i,i+1)$
and
![]() $1\leq i<d-1$
. Identify
$1\leq i<d-1$
. Identify
![]() $\chi $
with
$\chi $
with
![]() $(\chi _1,\ldots ,\chi _d)$
, where each
$(\chi _1,\ldots ,\chi _d)$
, where each
![]() $\chi _i$
is an unramified quasi-character of
$\chi _i$
is an unramified quasi-character of
![]() $F^{*}$
, then let
$F^{*}$
, then let
![]() $\chi '[i]$
denote the
$\chi '[i]$
denote the
![]() $d-1$
tuple
$d-1$
tuple
![]() $(\chi _1,\ldots ,\chi _{i-1},\chi _{i+1},\ldots ,\chi _d)$
, which then defines the representation
$(\chi _1,\ldots ,\chi _{i-1},\chi _{i+1},\ldots ,\chi _d)$
, which then defines the representation
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{d-1}^{(m,r)}}(\vartheta ,\chi '[i])$
. Also, denote
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{d-1}^{(m,r)}}(\vartheta ,\chi '[i])$
. Also, denote
![]() $\mathbf {b}=(b_1,\mathbf {b}')$
(
$\mathbf {b}=(b_1,\mathbf {b}')$
(
![]() $\mathbf {b}'\in \mathbb {Z}^{d-1}$
). For
$\mathbf {b}'\in \mathbb {Z}^{d-1}$
). For
![]() $1\leq i\leq d-1$
, let
$1\leq i\leq d-1$
, let
![]() $\omega _{i}=w_{\alpha _{d-i}}\cdot \ldots \cdot w_{\alpha _{d-1}}$
(
$\omega _{i}=w_{\alpha _{d-i}}\cdot \ldots \cdot w_{\alpha _{d-1}}$
(
![]() $\omega _{i}$
takes i positive roots of
$\omega _{i}$
takes i positive roots of
![]() $P_{(d-1,1)}$
into negative roots), and take
$P_{(d-1,1)}$
into negative roots), and take
![]() $\omega _0=I_d$
. Then we can write each
$\omega _0=I_d$
. Then we can write each
![]() $w\in W_{\operatorname {\mathrm {GL}}_d}$
uniquely in the form
$w\in W_{\operatorname {\mathrm {GL}}_d}$
uniquely in the form
![]() $w=w'\omega _{i}^{-1}$
, where
$w=w'\omega _{i}^{-1}$
, where
![]() $w'\in W_{\operatorname {\mathrm {GL}}_{d-1}}$
and
$w'\in W_{\operatorname {\mathrm {GL}}_{d-1}}$
and
![]() $0\leq i\leq d-1$
. Now, Equation (2.84) can be restated in the form
$0\leq i\leq d-1$
. Now, Equation (2.84) can be restated in the form
 $$ \begin{align} W_{\mathbf{a}}(\mathbf{b},\vartheta,\chi) &= \delta_{B_{\operatorname{\mathrm{GL}}_d}}(t_{\mathbf{b}}) \sum_{i=0}^{d-1} \prod_{j=1}^{d-i-1}\frac{1-q^{-1}\mathbf{x}_{(j,d-i)}}{1-\mathbf{x}_{(j,d-i)}} \nonumber \\ & \quad \times\sum_{\mathbf{e'}\in r\mathbb{Z}^{d-1}\backslash \mathbb{Z}^{d-1}} \tau_{\mathbf{a}^{*},(\mathbf{e'}^{*},-b_1)}(\omega_i,\vartheta,{}^{\omega_i^{-1}}\chi) \delta_{B_{\operatorname{\mathrm{GL}}_{d-1}}}^{-1}(t_{\mathbf{b'}})W_{\mathbf{e'}}(\mathbf{b'},\vartheta,\chi'[d-i]). \end{align} $$
$$ \begin{align} W_{\mathbf{a}}(\mathbf{b},\vartheta,\chi) &= \delta_{B_{\operatorname{\mathrm{GL}}_d}}(t_{\mathbf{b}}) \sum_{i=0}^{d-1} \prod_{j=1}^{d-i-1}\frac{1-q^{-1}\mathbf{x}_{(j,d-i)}}{1-\mathbf{x}_{(j,d-i)}} \nonumber \\ & \quad \times\sum_{\mathbf{e'}\in r\mathbb{Z}^{d-1}\backslash \mathbb{Z}^{d-1}} \tau_{\mathbf{a}^{*},(\mathbf{e'}^{*},-b_1)}(\omega_i,\vartheta,{}^{\omega_i^{-1}}\chi) \delta_{B_{\operatorname{\mathrm{GL}}_{d-1}}}^{-1}(t_{\mathbf{b'}})W_{\mathbf{e'}}(\mathbf{b'},\vartheta,\chi'[d-i]). \end{align} $$
Remark 28. Gao et al. [Reference Gao, Shahidi, Szpruch, Akbary and GunGSS18, Reference Gao, Shahidi and SzpruchGSS23] and Szpruch [Reference SzpruchSzp19] have recently developed a reinterpretation of the coefficients of Equation (2.77): The coefficients were presented as linear combinations of Tate
![]() $\gamma $
-factors, or ‘metaplectic’
$\gamma $
-factors, or ‘metaplectic’
![]() $\gamma $
-factors (defined in [Reference SzpruchSzp11]), where the scalars were computed via harmonic analysis on
$\gamma $
-factors (defined in [Reference SzpruchSzp11]), where the scalars were computed via harmonic analysis on
![]() $F^{*r}\backslash F^{*}$
. The determinant of their local coefficients matrix was related to the Plancherel measure and may shed new light on the Plancherel formula for covering groups.
$F^{*r}\backslash F^{*}$
. The determinant of their local coefficients matrix was related to the Plancherel measure and may shed new light on the Plancherel formula for covering groups.
2.11 Exceptional representations
We briefly describe the exceptional representations of coverings of general linear groups, which play a role in our construction. These representations were introduced by [Reference Kazhdan and PattersonKP84] (for the coverings studied there). Gao [Reference GaoGao17] extended their construction to the coverings of [Reference Brylinski and DeligneBD01] of arbitrary split connected reductive groups over non-Archimedean fields and in particular to
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
(see also [Reference GaoGao18a]).
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
(see also [Reference GaoGao18a]).
Assume that F is unramified. Define the exceptional representation
![]() $\Theta _{d,m,r,\vartheta }$
as the unique irreducible subrepresentation of
$\Theta _{d,m,r,\vartheta }$
as the unique irreducible subrepresentation of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{-1/(2r)})$
, equivalently the unique irreducible quotient of
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{-1/(2r)})$
, equivalently the unique irreducible quotient of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{1/(2r)})$
. The existence of this representation follows from the Langlands quotient theorem for covering groups ([Reference Ban and JantzenBJ13]). Also,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{1/(2r)})$
. The existence of this representation follows from the Langlands quotient theorem for covering groups ([Reference Ban and JantzenBJ13]). Also,
![]() $\Theta _{d,m,r,\vartheta }$
is unramified.
$\Theta _{d,m,r,\vartheta }$
is unramified.
Assume
![]() $\mu _{2m}\subset F^{*}$
. The representation
$\mu _{2m}\subset F^{*}$
. The representation
![]() $\Theta _{r,m,r,\vartheta }$
affords a unique (up to scaling) Whittaker functional, while
$\Theta _{r,m,r,\vartheta }$
affords a unique (up to scaling) Whittaker functional, while
![]() $\Theta _{d,m,r,\vartheta }$
does not afford any Whittaker functional for any
$\Theta _{d,m,r,\vartheta }$
does not afford any Whittaker functional for any
![]() $d>r$
. This follows from [Reference GaoGao18a, Proposition 3.5]. Specifically, the condition
$d>r$
. This follows from [Reference GaoGao18a, Proposition 3.5]. Specifically, the condition
![]() $Y_{\operatorname {\mathrm {GL}}_r,Q,n}=n_{\alpha }Y_{\operatorname {\mathrm {GL}}_r}$
in the notation of loc. cit. becomes
$Y_{\operatorname {\mathrm {GL}}_r,Q,n}=n_{\alpha }Y_{\operatorname {\mathrm {GL}}_r}$
in the notation of loc. cit. becomes
![]() $Y_{\operatorname {\mathrm {GL}}_d,Q,m}=rY_{\operatorname {\mathrm {GL}}_d}$
here, which is simple to verify directly. Note that the assumption
$Y_{\operatorname {\mathrm {GL}}_d,Q,m}=rY_{\operatorname {\mathrm {GL}}_d}$
here, which is simple to verify directly. Note that the assumption
![]() $|2|=1$
of [Reference GaoGao18a, p. 187] was not needed for [Reference GaoGao18a, Proposition 3.5] (see also the applications of [Reference GaoGao18a, Proposition 3.5] in [Reference GaoGao21]). See also [Reference Kazhdan and PattersonKP84, Theorem I.3.5] for the proof of this statement in their setting.
$|2|=1$
of [Reference GaoGao18a, p. 187] was not needed for [Reference GaoGao18a, Proposition 3.5] (see also the applications of [Reference GaoGao18a, Proposition 3.5] in [Reference GaoGao21]). See also [Reference Kazhdan and PattersonKP84, Theorem I.3.5] for the proof of this statement in their setting.
Proposition 29. Let
![]() ${}^{*}$
be defined by Equation (2.54). Then
${}^{*}$
be defined by Equation (2.54). Then
![]() $\Theta _{d,m,r,\vartheta }^{*}=\Theta _{d,m,r,\vartheta }$
.
$\Theta _{d,m,r,\vartheta }^{*}=\Theta _{d,m,r,\vartheta }$
.
Proof. By Proposition 25,
![]() $\Theta _{d,m,r,\vartheta }^{*}$
is a constituent of
$\Theta _{d,m,r,\vartheta }^{*}$
is a constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{-1/(2r)})$
, and since it is also irreducible and unramified, it coincides with
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{d}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{d}}}^{-1/(2r)})$
, and since it is also irreducible and unramified, it coincides with
![]() $\Theta _{d,m,r,\vartheta }$
.
$\Theta _{d,m,r,\vartheta }$
.
Remark 30. For exceptional representations of groups other than
![]() $\operatorname {\mathrm {GL}}_d$
, Jacquet modules may depend on
$\operatorname {\mathrm {GL}}_d$
, Jacquet modules may depend on
![]() $\vartheta $
(see, e.g., [Reference GaoGao17]).
$\vartheta $
(see, e.g., [Reference GaoGao17]).
2.12 Fourier coefficients on unipotent orbits
The unipotent orbits of
![]() $\operatorname {\mathrm {GL}}_d$
are in bijection with the partitions of d. There is a partial ordering defined on the partitions, and for two partitions
$\operatorname {\mathrm {GL}}_d$
are in bijection with the partitions of d. There is a partial ordering defined on the partitions, and for two partitions
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
, we write
$\beta '$
, we write
![]() $\beta \succsim \beta '$
if
$\beta \succsim \beta '$
if
![]() $\beta $
is greater than or not comparable with
$\beta $
is greater than or not comparable with
![]() $\beta '$
. Given a partition
$\beta '$
. Given a partition
![]() $\beta $
, there exists a corresponding unipotent subgroup
$\beta $
, there exists a corresponding unipotent subgroup
![]() $V(\beta )$
and a set of generic characters of
$V(\beta )$
and a set of generic characters of
![]() $V(\beta )$
. See [Reference GinzburgGin06, § 2] for these definitions or [Reference CarterCar93, Reference Collingwood and McGovernCM93] for the standard reference. Over a local field, for one such character
$V(\beta )$
. See [Reference GinzburgGin06, § 2] for these definitions or [Reference CarterCar93, Reference Collingwood and McGovernCM93] for the standard reference. Over a local field, for one such character
![]() $\psi $
and a smooth (complex) representation
$\psi $
and a smooth (complex) representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {\mathrm {GL}}_d$
, define
$\operatorname {\mathrm {GL}}_d$
, define
![]() $\mathcal {O}(\rho ,\beta ,\psi )=\operatorname {\mathrm {Hom}}_{V(\beta )}(\rho ,\psi )$
(continuous morphisms over Archimedean fields). The global counterpart is the Fourier coefficient
$\mathcal {O}(\rho ,\beta ,\psi )=\operatorname {\mathrm {Hom}}_{V(\beta )}(\rho ,\psi )$
(continuous morphisms over Archimedean fields). The global counterpart is the Fourier coefficient
 $$ \begin{align} \int\limits_{V(\beta)(F)\backslash V(\beta)(\mathbb{A})}\phi(v)\psi^{-1}(v)\,dv, \end{align} $$
$$ \begin{align} \int\limits_{V(\beta)(F)\backslash V(\beta)(\mathbb{A})}\phi(v)\psi^{-1}(v)\,dv, \end{align} $$
defined for an automorphic form
![]() $\phi $
in the space of an automorphic representation
$\phi $
in the space of an automorphic representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {A})$
. We then let
$\operatorname {\mathrm {GL}}_d(\mathbb {A})$
. We then let
![]() $\mathcal {O}(\rho ,\beta ,\psi )$
denote the set of Fourier coefficients as
$\mathcal {O}(\rho ,\beta ,\psi )$
denote the set of Fourier coefficients as
![]() $\phi $
varies in the space of
$\phi $
varies in the space of
![]() $\rho $
.
$\rho $
.
These notions extend to
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
and any other covering of
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
and any other covering of
![]() $\operatorname {\mathrm {GL}}_d$
from [Reference Kazhdan and PattersonKP84, Reference Brylinski and DeligneBD01] because these coverings are split canonically over a given unipotent subgroup (see § 2.2).
$\operatorname {\mathrm {GL}}_d$
from [Reference Kazhdan and PattersonKP84, Reference Brylinski and DeligneBD01] because these coverings are split canonically over a given unipotent subgroup (see § 2.2).
2.13 Semi-Whittaker coefficients
Let d be a positive integer. For a composition
![]() $\lambda $
of d, let
$\lambda $
of d, let
![]() $\psi _{\lambda }$
be the character of
$\psi _{\lambda }$
be the character of
![]() $N_{\operatorname {\mathrm {GL}}_{d}}$
which restricts to
$N_{\operatorname {\mathrm {GL}}_{d}}$
which restricts to
![]() $\psi $
on the simple root subgroups of
$\psi $
on the simple root subgroups of
![]() $M_{\lambda }$
and acts trivially otherwise. Globally, starting with a nontrivial character of
$M_{\lambda }$
and acts trivially otherwise. Globally, starting with a nontrivial character of
![]() $F\backslash \mathbb {A}$
, we obtain a character of
$F\backslash \mathbb {A}$
, we obtain a character of
![]() $N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
which is trivial on
$N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
which is trivial on
![]() $N_{\operatorname {\mathrm {GL}}_d}(F)$
. For an automorphic form
$N_{\operatorname {\mathrm {GL}}_d}(F)$
. For an automorphic form
![]() $\phi $
on
$\phi $
on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {A})$
, the global Fourier coefficients along
$\operatorname {\mathrm {GL}}_d(\mathbb {A})$
, the global Fourier coefficients along
![]() $(N_{\operatorname {\mathrm {GL}}_{d}},\psi _{\lambda })$
is given by the integral
$(N_{\operatorname {\mathrm {GL}}_{d}},\psi _{\lambda })$
is given by the integral
 $$ \begin{align} \int\limits_{N_{\operatorname{\mathrm{GL}}_d}(F)\backslash N_{\operatorname{\mathrm{GL}}_d}(\mathbb{A})}\phi(u)\psi_{\lambda}^{-1}(u) \, du. \end{align} $$
$$ \begin{align} \int\limits_{N_{\operatorname{\mathrm{GL}}_d}(F)\backslash N_{\operatorname{\mathrm{GL}}_d}(\mathbb{A})}\phi(u)\psi_{\lambda}^{-1}(u) \, du. \end{align} $$
The definition extends to autormorphic forms on
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
or any other covering of
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
or any other covering of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {A})$
from [Reference Kazhdan and PattersonKP84, Reference Brylinski and DeligneBD01], except that u is replaced by its image in the covering under the canonical splitting. These coefficients are called semi-Whittaker coefficients and are closely related to the Fourier coefficients on unipotent orbits. They were studied in both global and local contexts in several works, including [Reference Mœglin and WaldspurgerMW87, Reference Gourevitch and SahiGS13, Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b, Reference Gomez, Gourevitch and SahiGGS17, Reference CaiCai18, Reference Gomez, Gourevitch and SahiGGS21].
$\operatorname {\mathrm {GL}}_d(\mathbb {A})$
from [Reference Kazhdan and PattersonKP84, Reference Brylinski and DeligneBD01], except that u is replaced by its image in the covering under the canonical splitting. These coefficients are called semi-Whittaker coefficients and are closely related to the Fourier coefficients on unipotent orbits. They were studied in both global and local contexts in several works, including [Reference Mœglin and WaldspurgerMW87, Reference Gourevitch and SahiGS13, Reference Aizenbud, Gourevitch and SahiAGS15a, Reference Aizenbud, Gourevitch and SahiAGS15b, Reference Gomez, Gourevitch and SahiGGS17, Reference CaiCai18, Reference Gomez, Gourevitch and SahiGGS21].
Extend the partial order on partitions to compositions by comparing their underlying partitions. We will use the following two results, which are particular cases of results of Cai [Reference CaiCai18, Proposition 5.3] and [Reference CaiCai18, Proposition 5.5], respectively.
Lemma 31. Let
![]() $\mathcal {E}$
be an automorphic representation of
$\mathcal {E}$
be an automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}(\mathbb {A})$
. If Integral (2.87) is identically zero on
$\operatorname {\mathrm {GL}}_{rkc}(\mathbb {A})$
. If Integral (2.87) is identically zero on
![]() $\mathcal {E}$
for any
$\mathcal {E}$
for any
![]() $\lambda \succsim ((rk)^c)$
and is nonzero for
$\lambda \succsim ((rk)^c)$
and is nonzero for
![]() $\lambda =((rk)^c)$
, then
$\lambda =((rk)^c)$
, then
![]() $\mathcal {O}(\mathcal {E},((rk)^c),\psi )\ne 0$
.
$\mathcal {O}(\mathcal {E},((rk)^c),\psi )\ne 0$
.
Lemma 32. Let
![]() $\mathcal {E}$
be a smooth representation of
$\mathcal {E}$
be a smooth representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}$
over a local non-Archimedean field. Then
$\operatorname {\mathrm {GL}}_{rkc}$
over a local non-Archimedean field. Then
![]() $J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{\lambda }}(\mathcal {E})=0$
for all
$J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{\lambda }}(\mathcal {E})=0$
for all
![]() $\lambda \succsim ((rk)^c)$
, if and only if
$\lambda \succsim ((rk)^c)$
, if and only if
![]() $\mathcal {O}(\mathcal {E},\lambda _0,\psi )=0$
for all
$\mathcal {O}(\mathcal {E},\lambda _0,\psi )=0$
for all
![]() $\lambda _0\succsim ((rk)^c)$
. Moreover,
$\lambda _0\succsim ((rk)^c)$
. Moreover,
Remark 33. The proofs in [Reference CaiCai18] were stated for general linear groups but are based on the ‘root exchange’ technique which is also applicable to covering groups: in a global context the fundamental root exchange result is [Reference Ginzburg, Rallis and SoudryGRS11, Lemma 7.1] (following [Reference GinzburgGin90, Reference Ginzburg, Rallis and SoudryGRS01, Reference Soudry, Tilouine, Carayol, Harris and VignérasSou05]); the local version of root exchange is [Reference Ginzburg, Rallis and SoudryGRS99, § 2.2] (see also the proof of [Reference KaplanKap17a, Theorem 3.1]).
3 Representations of type
 $(rk,c)$
$(rk,c)$
3.1 Definition
Let
![]() $r,k,c\geq 1$
be integers. We use the notation of § 2.12 for the group
$r,k,c\geq 1$
be integers. We use the notation of § 2.12 for the group
![]() $\operatorname {\mathrm {GL}}_{rkc}$
. For the partition
$\operatorname {\mathrm {GL}}_{rkc}$
. For the partition
![]() $\beta =((rk)^c)$
,
$\beta =((rk)^c)$
,
![]() $V(\beta )=V_{(c^{rk})}$
(the unipotent radical of
$V(\beta )=V_{(c^{rk})}$
(the unipotent radical of
![]() $P_{(c^{rk})}$
). For
$P_{(c^{rk})}$
). For
![]() $v\in V_{(c^{rk})}$
write
$v\in V_{(c^{rk})}$
write
![]() $v=(v_{i,j})_{1\leq i,j\leq rk}$
with
$v=(v_{i,j})_{1\leq i,j\leq rk}$
with
![]() $v_{i,j}\in \text {Mat}_c$
, and define
$v_{i,j}\in \text {Mat}_c$
, and define
 $$ \begin{align} \psi(v)=\psi\left(\sum_{i=1}^{rk-1}\operatorname{\mathrm{tr}}(v_{i,i+1})\right). \end{align} $$
$$ \begin{align} \psi(v)=\psi\left(\sum_{i=1}^{rk-1}\operatorname{\mathrm{tr}}(v_{i,i+1})\right). \end{align} $$
Let
![]() $\mathcal {E}$
be a genuine smooth representation of
$\mathcal {E}$
be a genuine smooth representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field. We say that
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field. We say that
![]() $\mathcal {E}$
is an
$\mathcal {E}$
is an
![]() $(rk,c)$
representation if the following holds:
$(rk,c)$
representation if the following holds:
-
1.
 $\mathcal {O}(\mathcal {E},\beta ',\psi ')=0$
for any
$\mathcal {O}(\mathcal {E},\beta ',\psi ')=0$
for any
 $\beta '\succsim ((rk)^c)$
.
$\beta '\succsim ((rk)^c)$
. -
2. For
 $\psi $
given by Equation (3.1),
$\psi $
given by Equation (3.1),
 $\dim \mathcal {O}(\mathcal {E},((rk)^c),\psi )=1$
.
$\dim \mathcal {O}(\mathcal {E},((rk)^c),\psi )=1$
.
Any (nonzero)
![]() $\Lambda \in \mathcal {O}(\mathcal {E},((rk)^c),\psi )$
is called an
$\Lambda \in \mathcal {O}(\mathcal {E},((rk)^c),\psi )$
is called an
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\mathcal {E}$
. If
$\mathcal {E}$
. If
![]() $\mathcal {E}$
is an
$\mathcal {E}$
is an
![]() $(rk,c)$
representation, we fix one such
$(rk,c)$
representation, we fix one such
![]() $\Lambda $
and let
$\Lambda $
and let
![]() $\mathcal {W}(\mathcal {E})$
be the unique
$\mathcal {W}(\mathcal {E})$
be the unique
![]() $(rk,c)$
model of
$(rk,c)$
model of
![]() $\mathcal {E}$
with respect to
$\mathcal {E}$
with respect to
![]() $\psi $
, that is, the space spanned by functions
$\psi $
, that is, the space spanned by functions
![]() $g\mapsto \Lambda (\mathcal {E}(g)\xi )$
, where
$g\mapsto \Lambda (\mathcal {E}(g)\xi )$
, where
![]() $g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
and
$g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
and
![]() $\xi $
varies in the space of
$\xi $
varies in the space of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Now, for a genuine irreducible automorphic representation
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
,
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
,
![]() $\mathcal {E}$
is a coarse
$\mathcal {E}$
is a coarse
![]() $(rk,c)$
representation if it satisfies the following conditions:
$(rk,c)$
representation if it satisfies the following conditions:
-
1.
 $\mathcal {O}(\mathcal {E},\beta ',\psi ')=0$
for any
$\mathcal {O}(\mathcal {E},\beta ',\psi ')=0$
for any
 $\beta '\succsim ((rk)^c)$
.
$\beta '\succsim ((rk)^c)$
. -
2.
 $\mathcal {O}(\mathcal {E},((rk)^c),\psi )\ne 0$
.
$\mathcal {O}(\mathcal {E},((rk)^c),\psi )\ne 0$
.
We then call
![]() $\mathcal {E}$
an
$\mathcal {E}$
an
![]() $(rk,c)$
representation if in addition:
$(rk,c)$
representation if in addition:
-
3. All the unramified components
 $\mathcal {E}_{\nu }$
of
$\mathcal {E}_{\nu }$
of
 $\mathcal {E}$
are
$\mathcal {E}$
are
 $(rk,c)$
representations.
$(rk,c)$
representations.
If
![]() $\mathcal {E}_{\nu }$
is
$\mathcal {E}_{\nu }$
is
![]() $(rk,c)$
for some finite place
$(rk,c)$
for some finite place
![]() $\nu $
, then the local vanishing properties of
$\nu $
, then the local vanishing properties of
![]() $\mathcal {E}_{\nu }$
already imply the global vanishing for
$\mathcal {E}_{\nu }$
already imply the global vanishing for
![]() $\mathcal {E}$
by a local-global principle (see, e.g., [Reference Jacquet and RallisJR92, Proposition 1]).
$\mathcal {E}$
by a local-global principle (see, e.g., [Reference Jacquet and RallisJR92, Proposition 1]).
Remark 34. In the linear case, the generalized Speh representation of
![]() $\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
attached to an irreducible cuspidal automorphic representation of
$\operatorname {\mathrm {GL}}_{kc}(\mathbb {A})$
attached to an irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
is
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
is
![]() $(k,c)$
and all of its local components are
$(k,c)$
and all of its local components are
![]() $(k,c)$
as well (globally – [Reference GinzburgGin06, Reference Jiang and LiuJL13], locally – [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Theorem 4]).
$(k,c)$
as well (globally – [Reference GinzburgGin06, Reference Jiang and LiuJL13], locally – [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Theorem 4]).
Remark 35. These definitions make sense for any covering of
![]() $\operatorname {\mathrm {GL}}_{rkc}$
, as long as it is split canonically over
$\operatorname {\mathrm {GL}}_{rkc}$
, as long as it is split canonically over
![]() $N_{\operatorname {\mathrm {GL}}_{rkc}}$
, and in a global setting it is also split over
$N_{\operatorname {\mathrm {GL}}_{rkc}}$
, and in a global setting it is also split over
![]() $\operatorname {\mathrm {GL}}_{rkc}(F)$
.
$\operatorname {\mathrm {GL}}_{rkc}(F)$
.
For
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
with the
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
with the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _{rkc}^{\diamondsuit }$
,
$\rho _{rkc}^{\diamondsuit }$
,
![]() $\beta =((rk)^c)$
and
$\beta =((rk)^c)$
and
![]() $\psi $
given by Equation (3.1), Integral (2.86) becomes
$\psi $
given by Equation (3.1), Integral (2.86) becomes
 $$ \begin{align} \Lambda(\phi)=\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}\phi(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle)\psi^{-1}(v)\,dv. \end{align} $$
$$ \begin{align} \Lambda(\phi)=\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}\phi(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle)\psi^{-1}(v)\,dv. \end{align} $$
We call this the global
![]() $(rk,c)$
functional. If
$(rk,c)$
functional. If
![]() $\mathcal {E}$
is a coarse
$\mathcal {E}$
is a coarse
![]() $(rk,c)$
representation of
$(rk,c)$
representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, then Integral (3.2) does not vanish on the space of
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, then Integral (3.2) does not vanish on the space of
![]() $\mathcal {E}$
. The (global)
$\mathcal {E}$
. The (global)
![]() $(rk,c)$
model of
$(rk,c)$
model of
![]() $\mathcal {E}$
is then by definition the space of functions
$\mathcal {E}$
is then by definition the space of functions
![]() $g\mapsto \Lambda (\mathcal {E}(g)\phi )$
.
$g\mapsto \Lambda (\mathcal {E}(g)\phi )$
.
We also mention that for
![]() $c=1$
,
$c=1$
,
![]() $\Lambda (\phi )$
is the Whittaker–Fourier coefficient on
$\Lambda (\phi )$
is the Whittaker–Fourier coefficient on
![]() $\mathcal {E}$
and we call
$\mathcal {E}$
and we call
![]() $\mathcal {E}$
globally generic when
$\mathcal {E}$
globally generic when
![]() $\mathcal {O}(\mathcal {E},rk,\psi )\ne 0$
. If
$\mathcal {O}(\mathcal {E},rk,\psi )\ne 0$
. If
![]() $\mathcal {E}$
is an irreducible globally generic automorphic representation of
$\mathcal {E}$
is an irreducible globally generic automorphic representation of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
(the linear setting), the global condition already implies the local condition at all places.
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
(the linear setting), the global condition already implies the local condition at all places.
One may expect all the local components of an
![]() $(rk,c)$
representation to be
$(rk,c)$
representation to be
![]() $(rk,c)$
, but since we can not prove this for the
$(rk,c)$
, but since we can not prove this for the
![]() $(rk,c)$
representations we construct, we settle for uniqueness at all the unramified places. Unfortunately, in the absence of local uniqueness everywhere we do not obtain a factorizable functional; we obtain the weaker statement (3.4) below, but it can still be used to obtain results on the partial L-function. See § 4.2.
$(rk,c)$
representations we construct, we settle for uniqueness at all the unramified places. Unfortunately, in the absence of local uniqueness everywhere we do not obtain a factorizable functional; we obtain the weaker statement (3.4) below, but it can still be used to obtain results on the partial L-function. See § 4.2.
Let
![]() $\mathcal {E}$
be a global
$\mathcal {E}$
be a global
![]() $(rk,c)$
representation of
$(rk,c)$
representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. We can identify
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. We can identify
![]() $\mathcal {E}$
with the restricted tensor product
$\mathcal {E}$
with the restricted tensor product
![]() $\otimes _{\nu }'\mathcal {E}_{\nu }$
, with respect to a finite set S of places of F such that
$\otimes _{\nu }'\mathcal {E}_{\nu }$
, with respect to a finite set S of places of F such that
![]() $\mathcal {E}_{\nu }$
is unramified for all
$\mathcal {E}_{\nu }$
is unramified for all
![]() $\nu \notin S$
, and a collection
$\nu \notin S$
, and a collection
![]() $\{\xi _{\nu }^0\}_{\nu \notin S}$
of vectors where each
$\{\xi _{\nu }^0\}_{\nu \notin S}$
of vectors where each
![]() $\xi _{\nu }^0$
belongs to the space of
$\xi _{\nu }^0$
belongs to the space of
![]() $\mathcal {E}_{\nu }$
and is fixed by
$\mathcal {E}_{\nu }$
and is fixed by
![]() $\{\langle y,1\rangle :y\in K_{\operatorname {\mathrm {GL}}_{rkc},\nu }\}$
(
$\{\langle y,1\rangle :y\in K_{\operatorname {\mathrm {GL}}_{rkc},\nu }\}$
(
![]() $\rho _{rkc,\nu }^{\diamondsuit }$
is trivial on
$\rho _{rkc,\nu }^{\diamondsuit }$
is trivial on
![]() $K_{\operatorname {\mathrm {GL}}_{rkc},\nu }$
). For
$K_{\operatorname {\mathrm {GL}}_{rkc},\nu }$
). For
![]() $\nu \notin S$
,
$\nu \notin S$
,
![]() $\operatorname {\mathrm {Hom}}_{V_{(c^k)}(F_\nu )}(\mathcal {E}_\nu ,\psi _\nu )$
is one-dimensional. We fix the
$\operatorname {\mathrm {Hom}}_{V_{(c^k)}(F_\nu )}(\mathcal {E}_\nu ,\psi _\nu )$
is one-dimensional. We fix the
![]() $(rk,c)$
functional
$(rk,c)$
functional
![]() $\Lambda _{\nu }^0$
on
$\Lambda _{\nu }^0$
on
![]() $\mathcal {E}_{\nu }$
by demanding
$\mathcal {E}_{\nu }$
by demanding
![]() $\Lambda _{\nu }^0(\xi _{\nu }^0)=1$
. Denote
$\Lambda _{\nu }^0(\xi _{\nu }^0)=1$
. Denote
![]() $F_S=\prod _{\nu \in S} F_{\nu }$
. For
$F_S=\prod _{\nu \in S} F_{\nu }$
. For
![]() $g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, write
$g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, write
![]() $g=(g_{\nu })_{\nu }$
with
$g=(g_{\nu })_{\nu }$
with
![]() $g_{\nu }\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(F_{\nu })$
and set
$g_{\nu }\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(F_{\nu })$
and set
![]() $g_S=(g_{\nu })_{\nu \in S}$
. Also, let
$g_S=(g_{\nu })_{\nu \in S}$
. Also, let
![]() $\mathcal {E}_S$
and
$\mathcal {E}_S$
and
![]() $\psi _S$
denote the tensor products over the components in S. For the places in S, we can define
$\psi _S$
denote the tensor products over the components in S. For the places in S, we can define
![]() $\Lambda [S]\in {\operatorname {\mathrm {Hom}}}_{V_{(c^k)}(F_S)}(\mathcal {E}_S,\psi _S)$
by
$\Lambda [S]\in {\operatorname {\mathrm {Hom}}}_{V_{(c^k)}(F_S)}(\mathcal {E}_S,\psi _S)$
by
Then for a factorizable vector
![]() $\phi =\xi _S\otimes ^{\prime }_{\nu \notin S}\xi _{\nu }$
in the space of
$\phi =\xi _S\otimes ^{\prime }_{\nu \notin S}\xi _{\nu }$
in the space of
![]() $\otimes _{\nu }'\mathcal {E}_{\nu }$
, for all
$\otimes _{\nu }'\mathcal {E}_{\nu }$
, for all
![]() $g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
,
$g\in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
,
Here,
![]() $\Lambda _{\nu }$
is a scalar multiple of
$\Lambda _{\nu }$
is a scalar multiple of
![]() $\Lambda _{\nu }^0$
for all
$\Lambda _{\nu }^0$
for all
![]() $\nu \notin S$
. To prove this, one argues exactly as in [Reference TakedaTak14, Proposition 3.14], which is the adaptation of the decomposition result of Shalika [Reference ShalikaSha74, § 4] (see also [Reference Piatetski-ShapiroPS79] and [Reference BumpBum97, Theorem 3.5.2]).
$\nu \notin S$
. To prove this, one argues exactly as in [Reference TakedaTak14, Proposition 3.14], which is the adaptation of the decomposition result of Shalika [Reference ShalikaSha74, § 4] (see also [Reference Piatetski-ShapiroPS79] and [Reference BumpBum97, Theorem 3.5.2]).
Next, we prove that
![]() $\Lambda (\phi )$
enjoys an additional invariance property, which is important for the global construction of the integral. The stabilizer of the character (3.1) inside
$\Lambda (\phi )$
enjoys an additional invariance property, which is important for the global construction of the integral. The stabilizer of the character (3.1) inside
![]() $M_{(c^{rk})}$
is the diagonal embedding
$M_{(c^{rk})}$
is the diagonal embedding
![]() $\operatorname {\mathrm {GL}}_c^{\Delta }=\{b^{\triangle }:b\in \operatorname {\mathrm {GL}}_c\}$
in
$\operatorname {\mathrm {GL}}_c^{\Delta }=\{b^{\triangle }:b\in \operatorname {\mathrm {GL}}_c\}$
in
![]() $\operatorname {\mathrm {GL}}_{rkc}$
, where
$\operatorname {\mathrm {GL}}_{rkc}$
, where
![]() $b^{\triangle }=\operatorname {\mathrm {diag}}(b,\ldots ,b)$
. Our first step is to construct a splitting of
$b^{\triangle }=\operatorname {\mathrm {diag}}(b,\ldots ,b)$
. Our first step is to construct a splitting of
![]() $\operatorname {\mathrm {SL}}_c^{\Delta }(\mathbb {A})$
under
$\operatorname {\mathrm {SL}}_c^{\Delta }(\mathbb {A})$
under
![]() $\rho _{rkc}^{\diamondsuit }$
(for
$\rho _{rkc}^{\diamondsuit }$
(for
![]() $c=1$
,
$c=1$
,
![]() $\operatorname {\mathrm {SL}}_c$
is trivial).
$\operatorname {\mathrm {SL}}_c$
is trivial).
Proposition 36. Locally for all
![]() $b,b'\in \operatorname {\mathrm {SL}}_c$
,
$b,b'\in \operatorname {\mathrm {SL}}_c$
,
![]() $\sigma _{rkc}^{\diamondsuit }(b^{\triangle },{b'}^{\triangle })= (\varsigma _{*,c}(b)\varsigma _{*,c}(b')/\varsigma _{*,c}(bb'))^{rk}$
. Hence,
$\sigma _{rkc}^{\diamondsuit }(b^{\triangle },{b'}^{\triangle })= (\varsigma _{*,c}(b)\varsigma _{*,c}(b')/\varsigma _{*,c}(bb'))^{rk}$
. Hence,
![]() $b^{\triangle }\mapsto \langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle $
is the unique splitting of
$b^{\triangle }\mapsto \langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle $
is the unique splitting of
![]() $\operatorname {\mathrm {SL}}_c^{\triangle }$
in
$\operatorname {\mathrm {SL}}_c^{\triangle }$
in
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
, when we realize
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
, when we realize
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
using
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
using
![]() $\sigma _{rkc}^{\diamondsuit }$
.
$\sigma _{rkc}^{\diamondsuit }$
.
Proof. For
![]() $b,b'\in \operatorname {\mathrm {GL}}_c$
, by Equations (2.52), (2.50) and (2.12),
$b,b'\in \operatorname {\mathrm {GL}}_c$
, by Equations (2.52), (2.50) and (2.12),
 $$ \begin{align*} \sigma_{rkc}^{\diamondsuit}(b^{\triangle},{b'}^{\triangle})= \prod_{i=1}^{rk}\sigma_{2c}(\operatorname{\mathrm{diag}}(b,b^{*}),\operatorname{\mathrm{diag}}(b',{b'}^{*})) =\left((\det b,\det {b'})_m^{-1} \sigma_{c}(b,b')\sigma^{*}_{c}(b,b')\right)^{rk}. \end{align*} $$
$$ \begin{align*} \sigma_{rkc}^{\diamondsuit}(b^{\triangle},{b'}^{\triangle})= \prod_{i=1}^{rk}\sigma_{2c}(\operatorname{\mathrm{diag}}(b,b^{*}),\operatorname{\mathrm{diag}}(b',{b'}^{*})) =\left((\det b,\det {b'})_m^{-1} \sigma_{c}(b,b')\sigma^{*}_{c}(b,b')\right)^{rk}. \end{align*} $$
In particular, when
![]() $b,b'\in \operatorname {\mathrm {SL}}_c$
, we can apply Equation (2.21) and since
$b,b'\in \operatorname {\mathrm {SL}}_c$
, we can apply Equation (2.21) and since
![]() $\sigma _{c}^{2rk}=1$
, the r.h.s. equals
$\sigma _{c}^{2rk}=1$
, the r.h.s. equals
![]() $(\varsigma _{*,c}(b)\varsigma _{*,c}(b')/\varsigma _{*,c}(bb'))^{rk}$
. The assertion regarding the splitting follows at once.
$(\varsigma _{*,c}(b)\varsigma _{*,c}(b')/\varsigma _{*,c}(bb'))^{rk}$
. The assertion regarding the splitting follows at once.
Corollary 37. Let
![]() $\mathcal {E}$
be an
$\mathcal {E}$
be an
![]() $(rk,c)$
representation of
$(rk,c)$
representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field, and
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field, and
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\mathcal {E}$
. Then
$\mathcal {E}$
. Then
![]() $\Lambda (\mathcal {E}(\langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle )\xi )= \Lambda (\xi )$
for any
$\Lambda (\mathcal {E}(\langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle )\xi )= \Lambda (\xi )$
for any
![]() $b\in \operatorname {\mathrm {SL}}_c$
and
$b\in \operatorname {\mathrm {SL}}_c$
and
![]() $\xi $
in the space of
$\xi $
in the space of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Proof. Since
![]() $\dim \mathcal {O}(\mathcal {E},((rk)^c),\psi )=1$
, we have
$\dim \mathcal {O}(\mathcal {E},((rk)^c),\psi )=1$
, we have
![]() $\dim J_{V_{(c^{rk})},\psi }(\mathcal {E})=1$
. Hence, the stabilizer acts by a character, which is (as any character) trivial on
$\dim J_{V_{(c^{rk})},\psi }(\mathcal {E})=1$
. Hence, the stabilizer acts by a character, which is (as any character) trivial on
![]() $\{\langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle :b\in \operatorname {\mathrm {SL}}_c\}\cong \operatorname {\mathrm {SL}}_c$
.
$\{\langle b^{\triangle },\varsigma _{*,c}^{-rk}(b)\rangle :b\in \operatorname {\mathrm {SL}}_c\}\cong \operatorname {\mathrm {SL}}_c$
.
Corollary 38. For each
![]() $\nu $
and
$\nu $
and
![]() $b\in \operatorname {\mathrm {SL}}_c(F_{\nu })$
, define
$b\in \operatorname {\mathrm {SL}}_c(F_{\nu })$
, define
![]() $\eta _{rkc,\nu }^{\triangle }(b)=\eta _{rkc,\nu }^{\diamondsuit }(b^{\triangle })\varsigma _{*,c,\nu }^{rk}(b)$
. The product
$\eta _{rkc,\nu }^{\triangle }(b)=\eta _{rkc,\nu }^{\diamondsuit }(b^{\triangle })\varsigma _{*,c,\nu }^{rk}(b)$
. The product
![]() $\eta _{rkc}^{\triangle }=\prod _{\nu }\eta _{rkc,\nu }^{\triangle }$
is well defined on
$\eta _{rkc}^{\triangle }=\prod _{\nu }\eta _{rkc,\nu }^{\triangle }$
is well defined on
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
![]() $b^{\triangle }\rightarrow \langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
is the unique splitting of
$b^{\triangle }\rightarrow \langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
is the unique splitting of
![]() $\operatorname {\mathrm {SL}}_c^{\triangle }(\mathbb {A})$
in
$\operatorname {\mathrm {SL}}_c^{\triangle }(\mathbb {A})$
in
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
.
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
.
Proof. According to Equation (2.56) and Proposition 36, for all
![]() $\nu $
and
$\nu $
and
![]() $b,b'\in \operatorname {\mathrm {SL}}_c(F_{\nu })$
,
$b,b'\in \operatorname {\mathrm {SL}}_c(F_{\nu })$
,
 $$ \begin{align} \rho_{rkc,\nu}^{\diamondsuit}(b^{\triangle},{b'}^{\triangle})= \frac{\eta_{rkc,\nu}^{\triangle}(b)\eta_{rkc,\nu}^{\triangle}(b')}{\eta_{rkc,\nu}^{\triangle}(bb')}. \end{align} $$
$$ \begin{align} \rho_{rkc,\nu}^{\diamondsuit}(b^{\triangle},{b'}^{\triangle})= \frac{\eta_{rkc,\nu}^{\triangle}(b)\eta_{rkc,\nu}^{\triangle}(b')}{\eta_{rkc,\nu}^{\triangle}(bb')}. \end{align} $$
At almost all places the l.h.s. is
![]() $1$
on
$1$
on
![]() $\operatorname {\mathrm {SL}}_c(\mathcal {O}_{\nu })$
, then
$\operatorname {\mathrm {SL}}_c(\mathcal {O}_{\nu })$
, then
![]() $b\mapsto \eta _{rkc,\nu }^{\triangle }(b)$
is a homomorphism of
$b\mapsto \eta _{rkc,\nu }^{\triangle }(b)$
is a homomorphism of
![]() $\operatorname {\mathrm {SL}}_c(\mathcal {O}_{\nu })$
which is trivial. Thus,
$\operatorname {\mathrm {SL}}_c(\mathcal {O}_{\nu })$
which is trivial. Thus,
![]() $\eta _{rkc}^{\triangle }$
is well defined on
$\eta _{rkc}^{\triangle }$
is well defined on
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
. Now, globalize Equation (3.5).
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
. Now, globalize Equation (3.5).
Since both
![]() $b^{\triangle }\mapsto \langle b^{\triangle },(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })\rangle $
and
$b^{\triangle }\mapsto \langle b^{\triangle },(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })\rangle $
and
![]() $b^{\triangle }\mapsto \langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
are embeddings of
$b^{\triangle }\mapsto \langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
are embeddings of
![]() $\operatorname {\mathrm {SL}}_c^{\triangle }(F)$
into
$\operatorname {\mathrm {SL}}_c^{\triangle }(F)$
into
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, and such an embedding is unique, we have
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
, and such an embedding is unique, we have
![]() $(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })=(\eta _{rkc}^{\triangle })^{-1}(b)$
for
$(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })=(\eta _{rkc}^{\triangle })^{-1}(b)$
for
![]() $b\in \operatorname {\mathrm {SL}}_c(F)$
. The same identity holds with
$b\in \operatorname {\mathrm {SL}}_c(F)$
. The same identity holds with
![]() $b\in N_{\operatorname {\mathrm {GL}}_c}(\mathbb {A})$
, for the same reason. Note that
$b\in N_{\operatorname {\mathrm {GL}}_c}(\mathbb {A})$
, for the same reason. Note that
![]() $G<\operatorname {\mathrm {SL}}_c$
, whence the corollary also provides the unique embedding of
$G<\operatorname {\mathrm {SL}}_c$
, whence the corollary also provides the unique embedding of
![]() $G^{\triangle }(\mathbb {A})$
in
$G^{\triangle }(\mathbb {A})$
in
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
which is a lift of the embedding
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
which is a lift of the embedding
![]() $G^{\triangle }(\mathbb {A})<\operatorname {\mathrm {GL}}_{rkc}(\mathbb {A})$
.
$G^{\triangle }(\mathbb {A})<\operatorname {\mathrm {GL}}_{rkc}(\mathbb {A})$
.
Proposition 39. Let
![]() $\mathcal {E}$
be a coarse
$\mathcal {E}$
be a coarse
![]() $(rk,c)$
representation of
$(rk,c)$
representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
and
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
and
![]() $\phi $
be an automorphic form in the space of
$\phi $
be an automorphic form in the space of
![]() $\mathcal {E}$
. Then
$\mathcal {E}$
. Then
Proof. The group
![]() $\operatorname {\mathrm {SL}}_c({\mathbb {A}})$
is generated as an abstract group by its unipotent subgroups, or alternatively by
$\operatorname {\mathrm {SL}}_c({\mathbb {A}})$
is generated as an abstract group by its unipotent subgroups, or alternatively by
![]() $U_{\alpha }(\mathbb {A})$
for a single root subgroup
$U_{\alpha }(\mathbb {A})$
for a single root subgroup
![]() $U_{\alpha }<N_{\operatorname {\mathrm {GL}}_c}$
and a set of representatives in
$U_{\alpha }<N_{\operatorname {\mathrm {GL}}_c}$
and a set of representatives in
![]() $\operatorname {\mathrm {SL}}_c(F)$
for the Weyl group. Since
$\operatorname {\mathrm {SL}}_c(F)$
for the Weyl group. Since
![]() $\phi $
is an automorphic form, it is in particular left-invariant with respect to the image of
$\phi $
is an automorphic form, it is in particular left-invariant with respect to the image of
![]() $\operatorname {\mathrm {SL}}_c(F)$
under
$\operatorname {\mathrm {SL}}_c(F)$
under
![]() $b\mapsto \langle b^{\triangle },(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })\rangle =\langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
. Therefore, it suffices to prove invariance under
$b\mapsto \langle b^{\triangle },(\eta _{rkc}^{\diamondsuit })^{-1}(b^{\triangle })\rangle =\langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle $
. Therefore, it suffices to prove invariance under
![]() $\{\langle u^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(u)\rangle :u\in U_{\alpha }(\mathbb {A})\}$
. As in [Reference Friedberg and GinzburgFG16, Proposition 3], we write the Fourier expansion of
$\{\langle u^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(u)\rangle :u\in U_{\alpha }(\mathbb {A})\}$
. As in [Reference Friedberg and GinzburgFG16, Proposition 3], we write the Fourier expansion of
![]() $b\mapsto \Lambda (\langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle \cdot \phi )$
along
$b\mapsto \Lambda (\langle b^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(b)\rangle \cdot \phi )$
along
![]() $U_{\alpha }$
and observe that the coefficients corresponding to nontrivial characters all belong to
$U_{\alpha }$
and observe that the coefficients corresponding to nontrivial characters all belong to
![]() $\mathcal {O}(\mathcal {E},\beta ',\psi ')$
with
$\mathcal {O}(\mathcal {E},\beta ',\psi ')$
with
![]() $\beta '\succsim ((rk)^c)$
, hence vanish on
$\beta '\succsim ((rk)^c)$
, hence vanish on
![]() $\mathcal {E}$
by definition.
$\mathcal {E}$
by definition.
Corollary 40. Let
![]() $\mathcal {E}$
be an
$\mathcal {E}$
be an
![]() $(rk,c)$
representation of
$(rk,c)$
representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. Let S be a finite set of places of F containing (at least) the Archimedean places and the places
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. Let S be a finite set of places of F containing (at least) the Archimedean places and the places
![]() $\nu $
where
$\nu $
where
![]() $\mathcal {E}_{\nu }$
is ramified. Realize
$\mathcal {E}_{\nu }$
is ramified. Realize
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(F_{S})$
using the product
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(F_{S})$
using the product
![]() $\prod _{\nu \in S}\sigma ^{\diamondsuit }_{rkc,\nu }$
. The
$\prod _{\nu \in S}\sigma ^{\diamondsuit }_{rkc,\nu }$
. The
![]() $(rk,c)$
functional
$(rk,c)$
functional
![]() $\Lambda [S]$
defined by Equation (3.3) also satisfies, for all
$\Lambda [S]$
defined by Equation (3.3) also satisfies, for all
![]() $\xi _S$
in the space of
$\xi _S$
in the space of
![]() $\mathcal {E}_S$
,
$\mathcal {E}_S$
,
 $$ \begin{align*} \Lambda[S]\left(\left\langle b^{\triangle},\prod_{\nu\in S}\varsigma_{*,c,\nu}^{-rk}(b_{\nu})\right\rangle\cdot\xi_S\right)=\Lambda[S](\xi_S),\qquad\forall b\in \operatorname{\mathrm{SL}}_c(F_S). \end{align*} $$
$$ \begin{align*} \Lambda[S]\left(\left\langle b^{\triangle},\prod_{\nu\in S}\varsigma_{*,c,\nu}^{-rk}(b_{\nu})\right\rangle\cdot\xi_S\right)=\Lambda[S](\xi_S),\qquad\forall b\in \operatorname{\mathrm{SL}}_c(F_S). \end{align*} $$
3.2 Local construction of
 $(rk,c)$
representations
$(rk,c)$
representations
Let F be unramified, and assume
![]() $\mu _{2m}\subset F^{*}$
. In this section, we construct local unramified
$\mu _{2m}\subset F^{*}$
. In this section, we construct local unramified
![]() $(rk,c)$
representations from twisted copies of an exceptional representation.
$(rk,c)$
representations from twisted copies of an exceptional representation.
Recall the representation
![]() $\Theta _{rc,m,r,\vartheta }$
of § 2.11, which is the unique irreducible unramified subrepresentation of
$\Theta _{rc,m,r,\vartheta }$
of § 2.11, which is the unique irreducible unramified subrepresentation of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_{rc}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}^{-1/(2r)})$
. For an unramified character
$\mathrm {I}_{\operatorname {\mathrm {GL}}_{rc}^{(m,r)}}(\vartheta ,\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}^{-1/(2r)})$
. For an unramified character
![]() $\chi $
of
$\chi $
of
![]() $T_{\operatorname {\mathrm {GL}}_k}$
, write
$T_{\operatorname {\mathrm {GL}}_k}$
, write
![]() $\chi =\chi _1\otimes \ldots \otimes \chi _k$
, where
$\chi =\chi _1\otimes \ldots \otimes \chi _k$
, where
![]() $\chi _1,\ldots ,\chi _k$
are unramified quasi-characters of
$\chi _1,\ldots ,\chi _k$
are unramified quasi-characters of
![]() $F^{*}$
. Consider the unramified representation
$F^{*}$
. Consider the unramified representation
 $$ \begin{align} \Theta_{rc,m,r,\vartheta}(\chi)=\operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}( \chi_1\Theta_{rc,m,r,\vartheta}\otimes\ldots\otimes\chi_k\Theta_{rc,m,r,\vartheta}). \end{align} $$
$$ \begin{align} \Theta_{rc,m,r,\vartheta}(\chi)=\operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}( \chi_1\Theta_{rc,m,r,\vartheta}\otimes\ldots\otimes\chi_k\Theta_{rc,m,r,\vartheta}). \end{align} $$
Since
![]() $\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}(\operatorname {\mathrm {diag}}(t_1,\ldots ,t_{rc}))=\prod _{j=1}^{rc}|t_j|^{rc-2j+1}$
,
$\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}(\operatorname {\mathrm {diag}}(t_1,\ldots ,t_{rc}))=\prod _{j=1}^{rc}|t_j|^{rc-2j+1}$
,
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is a subrepresentation of
$\Theta _{rc,m,r,\vartheta }(\chi )$
is a subrepresentation of
where
![]() $\otimes _{j=1}^{rc}|~|^{-(rc-2j+1)/(2r)}=|~|^{-(rc-1)}\otimes \ldots \otimes |~|^{-(1-rc)}$
, and a quotient of
$\otimes _{j=1}^{rc}|~|^{-(rc-2j+1)/(2r)}=|~|^{-(rc-1)}\otimes \ldots \otimes |~|^{-(1-rc)}$
, and a quotient of
Since we will usually use
![]() $\chi _{\Theta ,1}$
, we denote
$\chi _{\Theta ,1}$
, we denote
![]() $\chi _{\Theta }=\chi _{\Theta ,1}$
.
$\chi _{\Theta }=\chi _{\Theta ,1}$
.
Proposition 41. The representation
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is
$\Theta _{rc,m,r,\vartheta }(\chi )$
is
![]() $(rk,c)$
.
$(rk,c)$
.
Proof. According to Lemma 32 and Remark 33, to deduce the vanishing property it is enough to prove that for any composition
![]() $\lambda \succsim ((rk)^c)$
,
$\lambda \succsim ((rk)^c)$
,
![]() $J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _\lambda }(\Theta _{rc,m,r,\vartheta }(\chi ))=0$
and to prove the result on the dimension, it is enough to show that
$J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _\lambda }(\Theta _{rc,m,r,\vartheta }(\chi ))=0$
and to prove the result on the dimension, it is enough to show that
![]() $\dim J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{((rk)^c)}}(\Theta _{rc,m,r,\vartheta }(\chi ))=1$
.
$\dim J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{((rk)^c)}}(\Theta _{rc,m,r,\vartheta }(\chi ))=1$
.
We prove vanishing first. Argue by induction on k. When
![]() $k=1$
,
$k=1$
,
![]() $\Theta _{rc,m,r,\vartheta }(\chi )=\chi _1\Theta _{rc,m,r,\vartheta }$
and the assumption on
$\Theta _{rc,m,r,\vartheta }(\chi )=\chi _1\Theta _{rc,m,r,\vartheta }$
and the assumption on
![]() $\lambda $
implies that
$\lambda $
implies that
![]() $\lambda _i>r$
for some i. Then the result follows from [Reference CaiCai19, Corollary 3.34], which was stated for the coverings of [Reference Kazhdan and PattersonKP84], but the proof is actually simpler for
$\lambda _i>r$
for some i. Then the result follows from [Reference CaiCai19, Corollary 3.34], which was stated for the coverings of [Reference Kazhdan and PattersonKP84], but the proof is actually simpler for
![]() $\operatorname {\mathrm {GL}}_{rc}^{(m,r)}$
. Indeed, the main technical difficulty handled in loc. cit. was the lack of a standard tensor product construction (the ‘metaplectic tensor product’ was used) because, for the coverings considered there, direct factors of Levi subgroups do not commute in the cover.
$\operatorname {\mathrm {GL}}_{rc}^{(m,r)}$
. Indeed, the main technical difficulty handled in loc. cit. was the lack of a standard tensor product construction (the ‘metaplectic tensor product’ was used) because, for the coverings considered there, direct factors of Levi subgroups do not commute in the cover.
For the inductive step, because the direct factors of
![]() $M_{((rk)^c)}$
do commute in
$M_{((rk)^c)}$
do commute in
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
and the tensor product is the standard one, several results from [Reference Bernstein and ZelevinskyBZ77] extend immediately to the covering, and the proof now proceeds similarly to the linear case ([Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 10]). Denote
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
and the tensor product is the standard one, several results from [Reference Bernstein and ZelevinskyBZ77] extend immediately to the covering, and the proof now proceeds similarly to the linear case ([Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 10]). Denote
![]() $\chi ^-=\chi _2\otimes \ldots \otimes \chi _k$
. Let
$\chi ^-=\chi _2\otimes \ldots \otimes \chi _k$
. Let
![]() $\times $
denote the parabolic induction functor of [Reference Bernstein and ZelevinskyBZ77]. By [Reference Bernstein and ZelevinskyBZ77, 4.14], for any composition
$\times $
denote the parabolic induction functor of [Reference Bernstein and ZelevinskyBZ77]. By [Reference Bernstein and ZelevinskyBZ77, 4.14], for any composition
![]() $\lambda $
, the (normalized) Jacquet module
$\lambda $
, the (normalized) Jacquet module
is glued from the representations
Here,
![]() $\lambda '$
and
$\lambda '$
and
![]() $\lambda "$
vary over the compositions of
$\lambda "$
vary over the compositions of
![]() $r(k-1)c$
and
$r(k-1)c$
and
![]() $rc$
, with
$rc$
, with
![]() $\lambda _i=\lambda _i^{\prime }+\lambda _i^{\prime \prime }$
for all i.
$\lambda _i=\lambda _i^{\prime }+\lambda _i^{\prime \prime }$
for all i.
Now, assuming
![]() $\lambda>((rk)^c)$
, either
$\lambda>((rk)^c)$
, either
![]() $\lambda _i^{\prime }>r(k-1)$
or
$\lambda _i^{\prime }>r(k-1)$
or
![]() $\lambda _i^{\prime \prime }> r$
, thus each constituent (3.9) vanishes by the inductive hypothesis. This proves
$\lambda _i^{\prime \prime }> r$
, thus each constituent (3.9) vanishes by the inductive hypothesis. This proves
![]() $J_{N_{\operatorname {\mathrm {GL}}_{kc}},\psi _{\lambda }}(\Theta _{rc,m,r,\vartheta }(\chi ))=0$
, hence
$J_{N_{\operatorname {\mathrm {GL}}_{kc}},\psi _{\lambda }}(\Theta _{rc,m,r,\vartheta }(\chi ))=0$
, hence
![]() $\mathcal {O}(\Theta _{rc,m,r,\vartheta }(\chi ),\beta ',\psi )=0$
for any partition
$\mathcal {O}(\Theta _{rc,m,r,\vartheta }(\chi ),\beta ',\psi )=0$
for any partition
![]() $\beta '\succsim ((rk)^c)$
.
$\beta '\succsim ((rk)^c)$
.
We turn to prove
![]() $\dim J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{((rk)^c)}}(\Theta _{rc,m,r,\vartheta }(\chi ))=1$
. For
$\dim J_{N_{\operatorname {\mathrm {GL}}_{rkc}},\psi _{((rk)^c)}}(\Theta _{rc,m,r,\vartheta }(\chi ))=1$
. For
![]() $k=1$
, the Jacquet functor factors through
$k=1$
, the Jacquet functor factors through
![]() $J_{V_{(r^c)}}$
, and
$J_{V_{(r^c)}}$
, and
![]() $J_{V_{(r^c)}}(\Theta _{rc,m,r,\vartheta })=\delta _{P_{(r^c)}}^{-1/(2r)}\Theta _{r,m,r,\vartheta }\otimes \ldots \otimes \Theta _{r,m,r,\vartheta }$
(this follows as in [Reference KableKab01, Theorem 5.1] for double coverings of [Reference Kazhdan and PattersonKP84], the proof is simpler with the standard tensor product). Thus,
$J_{V_{(r^c)}}(\Theta _{rc,m,r,\vartheta })=\delta _{P_{(r^c)}}^{-1/(2r)}\Theta _{r,m,r,\vartheta }\otimes \ldots \otimes \Theta _{r,m,r,\vartheta }$
(this follows as in [Reference KableKab01, Theorem 5.1] for double coverings of [Reference Kazhdan and PattersonKP84], the proof is simpler with the standard tensor product). Thus,
and the dimension is
![]() $1$
, since
$1$
, since
![]() $\Theta _{r,m,r,\vartheta }$
affords a unique Whittaker model (see § 2.11).
$\Theta _{r,m,r,\vartheta }$
affords a unique Whittaker model (see § 2.11).
For the general case consider the filtration described above, the only nonzero term (3.9) corresponds to
![]() $\lambda '=((r(k-1))^c)$
and
$\lambda '=((r(k-1))^c)$
and
![]() $\lambda "=(r^c)$
, and the dimension is
$\lambda "=(r^c)$
, and the dimension is
![]() $1$
using induction.
$1$
using induction.
Proposition 42. Let
![]() ${}^{*}$
be defined by Equation (2.54). Then
${}^{*}$
be defined by Equation (2.54). Then
![]() $(\Theta _{rc,m,r,\vartheta }(\chi ))^{*}=\Theta _{rc,m,r,\vartheta }(\chi ^{*})$
, where
$(\Theta _{rc,m,r,\vartheta }(\chi ))^{*}=\Theta _{rc,m,r,\vartheta }(\chi ^{*})$
, where
![]() $\chi ^{*}=\chi _k^{-1}\otimes \ldots \otimes \chi _1^{-1}$
.
$\chi ^{*}=\chi _k^{-1}\otimes \ldots \otimes \chi _1^{-1}$
.
Proof. Definitions (2.54) and (3.6) imply
 $$ \begin{align*} (\Theta_{rc,m,r,\vartheta}(\chi))^{*}=\operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}( \chi_k^{-1}\Theta_{rc,m,r,\vartheta}^{*}\otimes\ldots\otimes\chi_1^{-1}\Theta_{rc,m,r,\vartheta}^{*}). \end{align*} $$
$$ \begin{align*} (\Theta_{rc,m,r,\vartheta}(\chi))^{*}=\operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}( \chi_k^{-1}\Theta_{rc,m,r,\vartheta}^{*}\otimes\ldots\otimes\chi_1^{-1}\Theta_{rc,m,r,\vartheta}^{*}). \end{align*} $$
Now, the result follows from Proposition 29.
We also mention that one expects a local correspondence between
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
and the unramified principal series representation
$\Theta _{rc,m,r,\vartheta }(\chi )$
and the unramified principal series representation
![]() $\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
; this was studied in [Reference SuzukiSuz98] (in the context of [Reference Kazhdan and PattersonKP84]) where a partial correspondence was obtained.
$\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
; this was studied in [Reference SuzukiSuz98] (in the context of [Reference Kazhdan and PattersonKP84]) where a partial correspondence was obtained.
3.3 The representation
 $\Theta _{r,m,r,\vartheta }(\chi )$
$\Theta _{r,m,r,\vartheta }(\chi )$
We continue with the assumptions of § 3.2: F is unramified and
![]() $\mu _{2m}\subset F^{*}$
. When
$\mu _{2m}\subset F^{*}$
. When
![]() $c=1$
,
$c=1$
,
![]() $(rk,1)$
-functionals are Whittaker functionals. The representation
$(rk,1)$
-functionals are Whittaker functionals. The representation
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
is unramified, and in this section we develop the Casselman–Shalika formula for the normalized unramified vector in its space. In the following, we use the notation and results of § 2.9 and § 2.10.
$\Theta _{r,m,r,\vartheta }(\chi )$
is unramified, and in this section we develop the Casselman–Shalika formula for the normalized unramified vector in its space. In the following, we use the notation and results of § 2.9 and § 2.10.
The representation
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
is the unramified quotient of the representation (3.8), and the unramified subrepresentation of (3.7) (with
$\Theta _{r,m,r,\vartheta }(\chi )$
is the unramified quotient of the representation (3.8), and the unramified subrepresentation of (3.7) (with
![]() $c=1$
). The functionals
$c=1$
). The functionals
![]() $\Lambda _t$
form a basis of the space of Whittaker functionals on each of these genuine unramified principal series representations.
$\Lambda _t$
form a basis of the space of Whittaker functionals on each of these genuine unramified principal series representations.
On the one hand, regarding
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
as a quotient, any Whittaker functional on
$\Theta _{r,m,r,\vartheta }(\chi )$
as a quotient, any Whittaker functional on
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
extends to the representation (3.8) where it is a linear combination of functionals
$\Theta _{r,m,r,\vartheta }(\chi )$
extends to the representation (3.8) where it is a linear combination of functionals
![]() $\Lambda _t$
, but it is not clear which (if any)
$\Lambda _t$
, but it is not clear which (if any)
![]() $\Lambda _t$
factors through this quotient. On the other hand, taking the subrepresentation point of view, each
$\Lambda _t$
factors through this quotient. On the other hand, taking the subrepresentation point of view, each
![]() $\Lambda _t$
restricts to
$\Lambda _t$
restricts to
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
, but a priori there is no guarantee that a Whittaker functional on the representation (3.7) would be nonzero on a subrepresentation ((3.7) is reducible).
$\Theta _{r,m,r,\vartheta }(\chi )$
, but a priori there is no guarantee that a Whittaker functional on the representation (3.7) would be nonzero on a subrepresentation ((3.7) is reducible).
Nonetheless, we will prove that
![]() $\Lambda $
(
$\Lambda $
(
![]() $\Lambda =\Lambda _{I_{rk}}$
) is nonzero on the normalized unramified vector
$\Lambda =\Lambda _{I_{rk}}$
) is nonzero on the normalized unramified vector
![]() $\xi ^0$
in the space of the representation (3.7). Since
$\xi ^0$
in the space of the representation (3.7). Since
![]() $\xi ^0$
belongs to the space of
$\xi ^0$
belongs to the space of
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
, it follows that the
$\Theta _{r,m,r,\vartheta }(\chi )$
, it follows that the
![]() $(rk,1)$
-model
$(rk,1)$
-model
![]() $\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
(which is now the Whittaker model) can be realized using
$\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
(which is now the Whittaker model) can be realized using
![]() $\Lambda $
.
$\Lambda $
.
Regarding
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
as a subrepresentation of (3.7), denote
$\Theta _{r,m,r,\vartheta }(\chi )$
as a subrepresentation of (3.7), denote
Define for any
![]() $s\in \mathbb {C}$
,
$s\in \mathbb {C}$
,
 $$ \begin{align} C(s,\mathbf{x})= \prod_{\alpha\in\Phi_{k}^+}(1-q^{-s}\mathbf{x}_{\alpha}). \end{align} $$
$$ \begin{align} C(s,\mathbf{x})= \prod_{\alpha\in\Phi_{k}^+}(1-q^{-s}\mathbf{x}_{\alpha}). \end{align} $$
Theorem 43.
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })=\prod _{j=1}^{r}C(j,\mathbf {x})$
.
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })=\prod _{j=1}^{r}C(j,\mathbf {x})$
.
For
![]() $m=1$
, this was proved in [Reference Casselman and ShalikaCS80]; assume
$m=1$
, this was proved in [Reference Casselman and ShalikaCS80]; assume
![]() $m>1$
. Since each
$m>1$
. Since each
![]() $\alpha \in \Phi _{k}^+$
is spanned by the simple roots with positive integer coefficients, the product of factors
$\alpha \in \Phi _{k}^+$
is spanned by the simple roots with positive integer coefficients, the product of factors
![]() $C(j,\mathbf {x})$
in the statement of the theorem belongs to the unique factorization domain
$C(j,\mathbf {x})$
in the statement of the theorem belongs to the unique factorization domain
![]() $\mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
(regarding
$\mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
(regarding
![]() $\mathbf {x}_{(i,i+1)}$
as formal variables). It can also be written as the product of distinct irreducible polynomials
$\mathbf {x}_{(i,i+1)}$
as formal variables). It can also be written as the product of distinct irreducible polynomials
 $$ \begin{align} 1-q^{-l}\prod_{i_0=i}^{j-1}{\mathbf{x}_{(i_0,i_0+1)}},\qquad i<j, \qquad 1\leq l\leq r. \end{align} $$
$$ \begin{align} 1-q^{-l}\prod_{i_0=i}^{j-1}{\mathbf{x}_{(i_0,i_0+1)}},\qquad i<j, \qquad 1\leq l\leq r. \end{align} $$
The total degree of
![]() $\prod _{j=1}^{r}C(j,\mathbf {x})$
is
$\prod _{j=1}^{r}C(j,\mathbf {x})$
is
![]() $rk(k^2-1)/6$
and the monomial attaining this degree is
$rk(k^2-1)/6$
and the monomial attaining this degree is
 $$ \begin{align} (-1)^{rk(k-1)/2}q^{-r(r+1)k(k-1)/4}\prod_{i=1}^{k-1}\mathbf{x}_{(i,i+1)}^{ri(k-i)}. \end{align} $$
$$ \begin{align} (-1)^{rk(k-1)/2}q^{-r(r+1)k(k-1)/4}\prod_{i=1}^{k-1}\mathbf{x}_{(i,i+1)}^{ri(k-i)}. \end{align} $$
According to the formula of McNamara [Reference McNamaraMcN11, § 8],
![]() $\Lambda (t_{\mathbf {a}}\cdot \xi ^0)\in \mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
. First, we will show that
$\Lambda (t_{\mathbf {a}}\cdot \xi ^0)\in \mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
. First, we will show that
![]() $\prod _{j=1}^{r}C(j,\mathbf {x})$
divides
$\prod _{j=1}^{r}C(j,\mathbf {x})$
divides
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
. Then, it remains to compute the total degree of
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
. Then, it remains to compute the total degree of
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
and the monomial attaining this degree.
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
and the monomial attaining this degree.
Lemma I. The product
![]() $\prod _{j=1}^{r}C(j,\mathbf {x})$
divides
$\prod _{j=1}^{r}C(j,\mathbf {x})$
divides
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
.
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
.
Proof. We will show that each factor (3.12) divides
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, then since they are distinct irreducible polynomials, so does their product.
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, then since they are distinct irreducible polynomials, so does their product.
To prove that the factor (3.12) divides
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, it is enough to show that when
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, it is enough to show that when
![]() $\mathbf {x}_{(i,j)}=q^l$
and the variables
$\mathbf {x}_{(i,j)}=q^l$
and the variables
![]() $x_{i_0}$
for
$x_{i_0}$
for
![]() $i_0\in \{1,\ldots ,k\}-\{i\}$
are in ‘general position’,
$i_0\in \{1,\ldots ,k\}-\{i\}$
are in ‘general position’,
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })=0$
.
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })=0$
.
Assume
![]() $\mathbf {x}_{(i,j)}=q^l$
, and suppose
$\mathbf {x}_{(i,j)}=q^l$
, and suppose
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
, we will arrive at a contradiction. The representation
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
, we will arrive at a contradiction. The representation
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
is a subrepresentation of the representation (3.7), namely of
$\Theta _{r,m,r,\vartheta }(\chi )$
is a subrepresentation of the representation (3.7), namely of
 $$ \begin{align*} &\operatorname{\mathrm{Ind}}_{\widetilde{B}_{\operatorname{\mathrm{GL}}_{rk}}}^{\operatorname{\mathrm{GL}}_{rk}^{(m,r)}}\left( \operatorname{\mathrm{Ind}}_{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rk},*}}^{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rk}}}( (\varepsilon\otimes_{j=1}^{r}\vartheta\chi_1|~|^{-(r-2j+1)/(2r)})\otimes \ldots \otimes (\varepsilon\otimes_{j=1}^{r}\vartheta\chi_k|~|^{-(r-2j+1)/(2r)}))\right). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Ind}}_{\widetilde{B}_{\operatorname{\mathrm{GL}}_{rk}}}^{\operatorname{\mathrm{GL}}_{rk}^{(m,r)}}\left( \operatorname{\mathrm{Ind}}_{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rk},*}}^{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rk}}}( (\varepsilon\otimes_{j=1}^{r}\vartheta\chi_1|~|^{-(r-2j+1)/(2r)})\otimes \ldots \otimes (\varepsilon\otimes_{j=1}^{r}\vartheta\chi_k|~|^{-(r-2j+1)/(2r)}))\right). \end{align*} $$
Since
![]() $x_i=x_jq^l$
,
$x_i=x_jq^l$
,
![]() $\chi _i=\chi _j|~|^{-l/r}$
(
$\chi _i=\chi _j|~|^{-l/r}$
(
![]() $x_i=\chi _i(\varpi ^r)$
). Then the l-th genuine character of
$x_i=\chi _i(\varpi ^r)$
). Then the l-th genuine character of
![]() $\widetilde {A}$
in the block of
$\widetilde {A}$
in the block of
![]() $\chi _i$
, namely
$\chi _i$
, namely
![]() $\varepsilon \otimes \vartheta \chi _i|~|^{-(r-2l+1)/(2r)}$
, is equal to
$\varepsilon \otimes \vartheta \chi _i|~|^{-(r-2l+1)/(2r)}$
, is equal to
![]() $\varepsilon \otimes \vartheta \chi _j|~|^{-(r+1)/(2r)}$
. Together with the r genuine characters of
$\varepsilon \otimes \vartheta \chi _j|~|^{-(r+1)/(2r)}$
. Together with the r genuine characters of
![]() $\widetilde {A}$
in the block of
$\widetilde {A}$
in the block of
![]() $\chi _j$
, these
$\chi _j$
, these
![]() $r+1$
characters constitute the inducing character
$r+1$
characters constitute the inducing character
![]() $\varepsilon \otimes \vartheta \chi _j|~|^{-1/(2r)}\delta _{B_{\operatorname {\mathrm {GL}}_{r+1}}}^{-1/(2r)}$
of
$\varepsilon \otimes \vartheta \chi _j|~|^{-1/(2r)}\delta _{B_{\operatorname {\mathrm {GL}}_{r+1}}}^{-1/(2r)}$
of
![]() $\chi _j|~|^{-1/(2r)}\Theta _{r+1,m,r,\vartheta }$
.
$\chi _j|~|^{-1/(2r)}\Theta _{r+1,m,r,\vartheta }$
.
Consider the unramified principal series representation obtained by permuting the aforementioned character
![]() $\vartheta \chi _i|~|^{-(r-2l+1)/(2r)}$
to the right. Using transitivity of induction, it can be written in the form
$\vartheta \chi _i|~|^{-(r-2l+1)/(2r)}$
to the right. Using transitivity of induction, it can be written in the form
for suitable genuine unramified principal series representations
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
. Then the representation (3.14) contains
$\pi _2$
. Then the representation (3.14) contains
which is again unramified. Since
![]() $\Theta _{r+1,m,r,\vartheta }$
does not admit any Whittaker functional (see § 2.11), the representation (3.15) does not admit one either (this follows from [Reference Bernstein and ZelevinskyBZ77, Theorem 5.2]; see also [Reference BanksBan98b]). Therefore, any Whittaker functional on the representation (3.14) must vanish on the normalized unramified vector
$\Theta _{r+1,m,r,\vartheta }$
does not admit any Whittaker functional (see § 2.11), the representation (3.15) does not admit one either (this follows from [Reference Bernstein and ZelevinskyBZ77, Theorem 5.2]; see also [Reference BanksBan98b]). Therefore, any Whittaker functional on the representation (3.14) must vanish on the normalized unramified vector
![]() $\xi ^0$
in the space of (3.14) because it is contained in the representation (3.15).
$\xi ^0$
in the space of (3.14) because it is contained in the representation (3.15).
However, if
![]() $M(w)$
is the intertwining operator from the representation (3.14), regarded as an unramified principal series representation, back to the representation (3.7), then we claim that
$M(w)$
is the intertwining operator from the representation (3.14), regarded as an unramified principal series representation, back to the representation (3.7), then we claim that
![]() $M(w)$
is holomorphic, and also nonzero on
$M(w)$
is holomorphic, and also nonzero on
![]() $\xi ^0$
. To see this, decompose
$\xi ^0$
. To see this, decompose
![]() $M(w)$
into rank-
$M(w)$
into rank-
![]() $1$
intertwining operators which now take the form
$1$
intertwining operators which now take the form
 $$ \begin{align*} M(w_{\alpha}):&\mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta,\chi_{i_0}|~|^{-(r-2l_0+1)/(2r)}\otimes\chi_j|~|^{-(r+1)/(2r)})\rightarrow \\& \mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta,\chi_j|~|^{-(r+1)/(2r)}\otimes\chi_{i_0}|~|^{-(r-2l_0+1)/(2r)}), \end{align*} $$
$$ \begin{align*} M(w_{\alpha}):&\mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta,\chi_{i_0}|~|^{-(r-2l_0+1)/(2r)}\otimes\chi_j|~|^{-(r+1)/(2r)})\rightarrow \\& \mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta,\chi_j|~|^{-(r+1)/(2r)}\otimes\chi_{i_0}|~|^{-(r-2l_0+1)/(2r)}), \end{align*} $$
where either
![]() $i<i_0<j$
and
$i<i_0<j$
and
![]() $l_0>0$
, or
$l_0>0$
, or
![]() $i_0=i$
but then
$i_0=i$
but then
![]() $l_0>l$
. The inducing character is regular: For
$l_0>l$
. The inducing character is regular: For
![]() $i<i_0$
, this is because we are assuming
$i<i_0$
, this is because we are assuming
![]() $x_{i_0}$
is in general position; if
$x_{i_0}$
is in general position; if
![]() $i_0=i$
, this is because
$i_0=i$
, this is because
![]() $q^{-l_0}\mathbf {x}_{(i_0,j)}=q^{-l_0+l}$
and
$q^{-l_0}\mathbf {x}_{(i_0,j)}=q^{-l_0+l}$
and
![]() $l_0>l$
. Hence, each
$l_0>l$
. Hence, each
![]() $M(w_{\alpha })$
is holomorphic. If
$M(w_{\alpha })$
is holomorphic. If
![]() ${\xi '}^0$
(resp.,
${\xi '}^0$
(resp.,
![]() ${\xi "}^0$
) is the normalized unramified vector in the domain (resp., image) of
${\xi "}^0$
) is the normalized unramified vector in the domain (resp., image) of
![]() $M(w_{\alpha })$
, Equation (2.76) implies that
$M(w_{\alpha })$
, Equation (2.76) implies that
 $$ \begin{align*} M(w_{\alpha}){\xi'}^0=\frac{1-q^{-1-l_0}\mathbf{x}_{(i_0,j)}}{1-q^{-l_0}\mathbf{x}_{(i_0,j)}}{\xi"}^0. \end{align*} $$
$$ \begin{align*} M(w_{\alpha}){\xi'}^0=\frac{1-q^{-1-l_0}\mathbf{x}_{(i_0,j)}}{1-q^{-l_0}\mathbf{x}_{(i_0,j)}}{\xi"}^0. \end{align*} $$
This is nonzero (and well defined), again for
![]() $i<i_0$
because
$i<i_0$
because
![]() $x_{i_0}$
is in general position, and for
$x_{i_0}$
is in general position, and for
![]() $i_0=i$
the quotient equals
$i_0=i$
the quotient equals
![]() $(1-q^{-1-l_0+l})/(1-q^{-l_0+l})$
(with
$(1-q^{-1-l_0+l})/(1-q^{-l_0+l})$
(with
![]() $l_0>l$
). Hence,
$l_0>l$
). Hence,
![]() $M(w)$
is well defined so that the map
$M(w)$
is well defined so that the map
![]() $\xi \mapsto \Lambda (M(w)\xi )$
(if not identically zero) is a Whittaker functional on the representation (3.14), and also
$\xi \mapsto \Lambda (M(w)\xi )$
(if not identically zero) is a Whittaker functional on the representation (3.14), and also
![]() $M(w)\xi ^0\ne 0$
. Now, if
$M(w)\xi ^0\ne 0$
. Now, if
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
,
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
,
![]() $\Lambda (M(w)\xi ^0)\ne 0$
- contradiction.
$\Lambda (M(w)\xi ^0)\ne 0$
- contradiction.
Lemma II. The total degree of
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
is
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
is
![]() $rk(k^2-1)/6$
, and the corresponding monomial attaining this degree is the monomial (3.13).
$rk(k^2-1)/6$
, and the corresponding monomial attaining this degree is the monomial (3.13).
Proof. We use the results of [Reference Brubaker, Bump and FriedbergBBF11a, Reference McNamaraMcN11] on Gelfand–Tsetlin patterns. Recall that a (strict) Gelfand–Tsetlin pattern
![]() $\mathfrak {T}$
is a triangular array
$\mathfrak {T}$
is a triangular array
![]() $\{a_{i,j}\}$
of nonnegative integers such that
$\{a_{i,j}\}$
of nonnegative integers such that
![]() $a_{i,j}>a_{i,j+1}$
and
$a_{i,j}>a_{i,j+1}$
and
![]() $a_{i,j}\geq a_{i+1,j}\geq a_{i,j+1}$
for all
$a_{i,j}\geq a_{i+1,j}\geq a_{i,j+1}$
for all
![]() $i,j$
such that all entries exist (we enumerate the elements such that the leftmost entry at row i is
$i,j$
such that all entries exist (we enumerate the elements such that the leftmost entry at row i is
![]() $a_{i,1}$
). For each monomial of
$a_{i,1}$
). For each monomial of
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, the coefficient is read off a finite set of Gelfand–Tsetlin patterns. We briefly adapt the exposition of [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12] to the case at hand, and in particular use the parameter
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
, the coefficient is read off a finite set of Gelfand–Tsetlin patterns. We briefly adapt the exposition of [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12] to the case at hand, and in particular use the parameter
![]() $\mathbf {y}$
of our principal series representation.
$\mathbf {y}$
of our principal series representation.
Here,
![]() $1\leq i,j\leq rk$
and since we are evaluating the Whittaker function at the identity, the first row is
$1\leq i,j\leq rk$
and since we are evaluating the Whittaker function at the identity, the first row is
![]() $a_{1,j}=rk-j$
,
$a_{1,j}=rk-j$
,
![]() $1\leq j\leq rk$
. The entries at row i are
$1\leq j\leq rk$
. The entries at row i are
![]() $a_{i,1},\ldots ,a_{i,rk-i+1}$
.
$a_{i,1},\ldots ,a_{i,rk-i+1}$
.
We claim that the only patterns to consider are those where the differences
 $$ \begin{align} d_{i}=\sum_{j=1}^{rk-i+1}a_{i,j}-rk+i-1+j \end{align} $$
$$ \begin{align} d_{i}=\sum_{j=1}^{rk-i+1}a_{i,j}-rk+i-1+j \end{align} $$
are divisible by r, for all
![]() $i\geq 1$
. This condition did not appear in [Reference McNamaraMcN11, Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12], we explain how to obtain it. Since
$i\geq 1$
. This condition did not appear in [Reference McNamaraMcN11, Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12], we explain how to obtain it. Since
![]() $d_1=0$
, assume
$d_1=0$
, assume
![]() $i>1$
. The value
$i>1$
. The value
![]() $d_i$
is
$d_i$
is
![]() $k_{i-1}(\mathfrak {T})$
of [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3] (in those works the rows were enumerated starting from
$k_{i-1}(\mathfrak {T})$
of [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3] (in those works the rows were enumerated starting from
![]() $0$
). Given an element
$0$
). Given an element
![]() $\mathrm {m}$
in the root lattice of
$\mathrm {m}$
in the root lattice of
![]() $\operatorname {\mathrm {GL}}_{rk}$
, denote its representation as a combination of simple roots by
$\operatorname {\mathrm {GL}}_{rk}$
, denote its representation as a combination of simple roots by
![]() $\mathrm {m}_{\Delta }$
. To deduce that
$\mathrm {m}_{\Delta }$
. To deduce that
![]() $d_i\equiv 0\,(r)$
, we relate between [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3], freely using their notation. Denote
$d_i\equiv 0\,(r)$
, we relate between [Reference McNamaraMcN11] and [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3], freely using their notation. Denote
![]() $\mathbf {k}(\mathfrak {T})=(k_1(\mathfrak {T}),\ldots ,k_{rk-1}(\mathfrak {T}))$
. Comparing coefficients between [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, (8), Theorem 1] and [Reference McNamaraMcN11, Theorem 8.6] we see that for a given
$\mathbf {k}(\mathfrak {T})=(k_1(\mathfrak {T}),\ldots ,k_{rk-1}(\mathfrak {T}))$
. Comparing coefficients between [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, (8), Theorem 1] and [Reference McNamaraMcN11, Theorem 8.6] we see that for a given
![]() $\mathbf {k}\in \mathbb {N}^{rk-1}$
,
$\mathbf {k}\in \mathbb {N}^{rk-1}$
,
![]() $H(\varpi ^{\mathbf {k}};\lambda )$
is the sum over
$H(\varpi ^{\mathbf {k}};\lambda )$
is the sum over
![]() $\mathfrak {T}$
such that
$\mathfrak {T}$
such that
![]() $\mathbf {k}(\mathfrak {T})=\mathbf {k}$
, and
$\mathbf {k}(\mathfrak {T})=\mathbf {k}$
, and
![]() $H(\varpi ^{\mathbf {k}};\lambda )$
is also equal to the sum of products
$H(\varpi ^{\mathbf {k}};\lambda )$
is also equal to the sum of products
![]() $\sum _{(\mathrm {i},\mathrm {m})\in B(\lambda +\rho )}\prod _{\alpha \in \Phi _{rk}^+}w(\mathrm {m},\alpha )$
, where
$\sum _{(\mathrm {i},\mathrm {m})\in B(\lambda +\rho )}\prod _{\alpha \in \Phi _{rk}^+}w(\mathrm {m},\alpha )$
, where
![]() $\mathrm {m}\in \mathbb {N}^{|\Phi _{rk}^+|}$
and
$\mathrm {m}\in \mathbb {N}^{|\Phi _{rk}^+|}$
and
![]() $\mathrm {m}_{\Delta }=\mathbf {k}$
. Each summand here is obtained from an integral
$\mathrm {m}_{\Delta }=\mathbf {k}$
. Each summand here is obtained from an integral
![]() $\int _{C^{\mathrm {i}}_{\mathrm {m}}}\xi ^0(u)\psi (u)du$
, where
$\int _{C^{\mathrm {i}}_{\mathrm {m}}}\xi ^0(u)\psi (u)du$
, where
![]() $C^{\mathrm {i}}_{\mathrm {m}}\subset N_{\operatorname {\mathrm {GL}}_{rk}}^-$
(called a ‘cell’). If
$C^{\mathrm {i}}_{\mathrm {m}}\subset N_{\operatorname {\mathrm {GL}}_{rk}}^-$
(called a ‘cell’). If
![]() $\mathrm {m}\notin r\mathbb {N}^{|\Phi _{rk}^+|}$
, then for any element from
$\mathrm {m}\notin r\mathbb {N}^{|\Phi _{rk}^+|}$
, then for any element from
![]() $C^{\mathrm {i}}_{\mathrm {m}}$
, in its Iwasawa decomposition given in [Reference McNamaraMcN11, Theorem 4.5, Proposition 4.6] the torus part does not belong to
$C^{\mathrm {i}}_{\mathrm {m}}$
, in its Iwasawa decomposition given in [Reference McNamaraMcN11, Theorem 4.5, Proposition 4.6] the torus part does not belong to
![]() $T_{\operatorname {\mathrm {GL}}_{rk},*}$
. In this case,
$T_{\operatorname {\mathrm {GL}}_{rk},*}$
. In this case,
![]() $\xi ^0$
vanishes on
$\xi ^0$
vanishes on
![]() $C^{\mathrm {i}}_{\mathrm {m}}$
, by Proposition 23. Hence, only cells
$C^{\mathrm {i}}_{\mathrm {m}}$
, by Proposition 23. Hence, only cells
![]() $C^{\mathrm {i}}_{\mathrm {m}}$
with
$C^{\mathrm {i}}_{\mathrm {m}}$
with
![]() $\mathrm {m}\in r\mathbb {N}^{|\Phi _{rk}^+|}$
contribute so that
$\mathrm {m}\in r\mathbb {N}^{|\Phi _{rk}^+|}$
contribute so that
![]() $\mathbf {k}\in r\mathbb {N}^{rk-1}$
, that is,
$\mathbf {k}\in r\mathbb {N}^{rk-1}$
, that is,
![]() $r|d_i$
for all
$r|d_i$
for all
![]() $i\leq rk$
.
$i\leq rk$
.
The resulting monomial for such a pattern is
 $$ \begin{align} C\left(\,\prod_{l=1}^{k}\,\prod_{i=r(l-1)+2}^{rl}\,q^{d_i/r}\right)\left(\prod_{l=1}^{k-1}\,q^{-(r-1)d_{rl+1}/r}\right)\left(\prod_{l=1}^{k-1} \,\mathbf{x}_{(l,l+1)}^{d_{rl+1}/r}\right), \end{align} $$
$$ \begin{align} C\left(\,\prod_{l=1}^{k}\,\prod_{i=r(l-1)+2}^{rl}\,q^{d_i/r}\right)\left(\prod_{l=1}^{k-1}\,q^{-(r-1)d_{rl+1}/r}\right)\left(\prod_{l=1}^{k-1} \,\mathbf{x}_{(l,l+1)}^{d_{rl+1}/r}\right), \end{align} $$
where C is a constant to be determined below, depending on certain products of Gauss sums.
Since we are looking for the monomial of highest total degree, we consider patterns with the maximal entries
![]() $a_{rl+1,j}$
for
$a_{rl+1,j}$
for
![]() $1\leq l\leq k-1$
and
$1\leq l\leq k-1$
and
![]() $1\leq j\leq rk-(rl+1)+1=r(k-l)$
. We will show that there exists exactly one pattern satisfying this condition, with a nonzero contribution. This will imply that it is the only pattern for the highest monomial and, in turn, determine the total degree and the coefficient.
$1\leq j\leq rk-(rl+1)+1=r(k-l)$
. We will show that there exists exactly one pattern satisfying this condition, with a nonzero contribution. This will imply that it is the only pattern for the highest monomial and, in turn, determine the total degree and the coefficient.
First, note that
![]() $a_{rl+1,1}\leq rk-1$
for all
$a_{rl+1,1}\leq rk-1$
for all
![]() $1\leq l\leq k-1$
because
$1\leq l\leq k-1$
because
![]() $a_{1,1}=rk-1$
. Consider patterns such that
$a_{1,1}=rk-1$
. Consider patterns such that
![]() $a_{rl+1,1}=rk-1$
for all
$a_{rl+1,1}=rk-1$
for all
![]() $1\leq l\leq k-1$
. Since the numbers are strictly decreasing,
$1\leq l\leq k-1$
. Since the numbers are strictly decreasing,
![]() $d_{rl+1}$
will attain its maximum when
$d_{rl+1}$
will attain its maximum when
Then
![]() $d_{rl+1}=r^2l(k-l)$
, and the total degree of the monomial is
$d_{rl+1}=r^2l(k-l)$
, and the total degree of the monomial is
![]() $rk(k^2-1)/6$
as required.
$rk(k^2-1)/6$
as required.
Since at each row
![]() $rl+1$
the entries are the maximal, we see that
$rl+1$
the entries are the maximal, we see that
![]() $a_{i,j}=a_{rl+1,j}$
for all pairs
$a_{i,j}=a_{rl+1,j}$
for all pairs
![]() $(i,j)$
in the set
$(i,j)$
in the set
The remaining entries to determine are
![]() $a_{i,j}$
, where
$a_{i,j}$
, where
![]() $(i,j)$
belongs to
$(i,j)$
belongs to
This is addressed by the following claim, proved below.
Claim 44. For
![]() $(i,j)\in \mathcal {B}$
,
$(i,j)\in \mathcal {B}$
,
![]() $a_{i,j}=a_{i-1,j+1}$
.
$a_{i,j}=a_{i-1,j+1}$
.
We have shown that there is a unique pattern for the monomial of
![]() $\prod _{l=1}^{k-1}\,\mathbf {x}_{(l,l+1)}^{rl(k-l)}$
. It remains to compute its coefficient.
$\prod _{l=1}^{k-1}\,\mathbf {x}_{(l,l+1)}^{rl(k-l)}$
. It remains to compute its coefficient.
For
![]() $(i,j)\in \mathcal {B}$
with
$(i,j)\in \mathcal {B}$
with
![]() $r(l-1)+1<i<rl+1$
, a repeated application of Claim 44 shows that
$r(l-1)+1<i<rl+1$
, a repeated application of Claim 44 shows that
Now, computing
![]() $d_i$
as two summations, one over
$d_i$
as two summations, one over
![]() $1\leq j\leq r(k-l)$
for which
$1\leq j\leq r(k-l)$
for which
![]() $a_{i,j}=a_{rl+1,j}=rk-j$
, the other with
$a_{i,j}=a_{rl+1,j}=rk-j$
, the other with
![]() $j>r(k-l)$
where we use Equation (3.19), we obtain
$j>r(k-l)$
where we use Equation (3.19), we obtain
Thus
 $$ \begin{align*} \sum_{l=1}^{k}\,\sum_{i=r(l-1)+2}^{rl}d_i=r^2(r-1)k(k^2-1)/6=\sum_{l=1}^{k-1}(r-1)d_{rl+1} \end{align*} $$
$$ \begin{align*} \sum_{l=1}^{k}\,\sum_{i=r(l-1)+2}^{rl}d_i=r^2(r-1)k(k^2-1)/6=\sum_{l=1}^{k-1}(r-1)d_{rl+1} \end{align*} $$
and we conclude that the powers of q vanish in the monomial (3.17). It remains to compute C.
For
![]() $i>1$
, put
$i>1$
, put
 $$ \begin{align*} h_{i,j}=\sum_{v=j}^{rk-i+1}a_{i,v}-a_{i-1,v+1}. \end{align*} $$
$$ \begin{align*} h_{i,j}=\sum_{v=j}^{rk-i+1}a_{i,v}-a_{i-1,v+1}. \end{align*} $$
Recall the Gauss sum
![]() $\mathfrak {g}(a)$
given by Equation (2.73), where
$\mathfrak {g}(a)$
given by Equation (2.73), where
![]() $\mathfrak {g}(a)=-q^{-1}$
if
$\mathfrak {g}(a)=-q^{-1}$
if
![]() $a\equiv 0\,(m)$
otherwise
$a\equiv 0\,(m)$
otherwise
![]() $\mathfrak {g}(a)\mathfrak {g}(-a)=q^{-1}$
. The coefficient C is the product of
$\mathfrak {g}(a)\mathfrak {g}(-a)=q^{-1}$
. The coefficient C is the product of
![]() $\mathfrak {g}(2h_{i,j})$
over all
$\mathfrak {g}(2h_{i,j})$
over all
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $a_{i,j}=a_{i-1,j}$
(in particular,
$a_{i,j}=a_{i-1,j}$
(in particular,
![]() $i>1$
). This follows from [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3] and note that the
$i>1$
). This follows from [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3] and note that the
![]() $2$
-cocycle used there for a covering of
$2$
-cocycle used there for a covering of
![]() $\operatorname {\mathrm {GL}}_{rk}$
is our
$\operatorname {\mathrm {GL}}_{rk}$
is our
![]() $\sigma _{rk}$
(see [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3, (4)] and Equation (2.7)); here, we use
$\sigma _{rk}$
(see [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3, (4)] and Equation (2.7)); here, we use
![]() $\sigma _{rk}^{\diamondsuit }$
and since
$\sigma _{rk}^{\diamondsuit }$
and since
![]() $\sigma _{2}(\left (\begin {smallmatrix}t\\&t^{-1}\end {smallmatrix}\right ),\left (\begin {smallmatrix}t'\\&{t'}^{-1}\end {smallmatrix}\right ))=(t,t')_m^{-1}$
and
$\sigma _{2}(\left (\begin {smallmatrix}t\\&t^{-1}\end {smallmatrix}\right ),\left (\begin {smallmatrix}t'\\&{t'}^{-1}\end {smallmatrix}\right ))=(t,t')_m^{-1}$
and
![]() $\sigma _{2}^{\diamondsuit }(\left (\begin {smallmatrix}t\\&t^{-1}\end {smallmatrix}\right ),\left (\begin {smallmatrix}t'\\&{t'}^{-1}\end {smallmatrix}\right ))=(t,t')_m^{-2}$
, the function
$\sigma _{2}^{\diamondsuit }(\left (\begin {smallmatrix}t\\&t^{-1}\end {smallmatrix}\right ),\left (\begin {smallmatrix}t'\\&{t'}^{-1}\end {smallmatrix}\right ))=(t,t')_m^{-2}$
, the function
![]() $g(b)$
of [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3, (9)] which is
$g(b)$
of [Reference Brubaker, Bump, Chinta, Friedberg and GunnellsBBC+12, § 3.3, (9)] which is
![]() $\mathfrak {g}(b)$
here (the normalization of the measure is the same) is replaced by
$\mathfrak {g}(b)$
here (the normalization of the measure is the same) is replaced by
![]() $\mathfrak {g}(2b)$
. Also, for the pattern at hand, the set of such pairs
$\mathfrak {g}(2b)$
. Also, for the pattern at hand, the set of such pairs
![]() $(i,j)$
is
$(i,j)$
is
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Let
![]() $(i,j)\in \mathcal {G}$
with
$(i,j)\in \mathcal {G}$
with
![]() $r(l-1)+1<i\leq rl+1$
. Then for
$r(l-1)+1<i\leq rl+1$
. Then for
![]() $v\leq r(k-l)$
,
$v\leq r(k-l)$
,
![]() $a_{i,v}=rk-v$
. Claim 44 shows that
$a_{i,v}=rk-v$
. Claim 44 shows that
![]() $a_{i,v}=a_{i-1,v+1}$
when
$a_{i,v}=a_{i-1,v+1}$
when
![]() $(i,v)\in \mathcal {B}$
(i.e.,
$(i,v)\in \mathcal {B}$
(i.e.,
![]() $v>r(k-l)$
). Also, since
$v>r(k-l)$
). Also, since
![]() $(i-1,r(k-l)+1)\in \mathcal {B}$
, Equation (3.19) implies that
$(i-1,r(k-l)+1)\in \mathcal {B}$
, Equation (3.19) implies that
![]() $a_{i-1,r(k-l)+1}=r(2l-1)-i+1$
. Therefore,
$a_{i-1,r(k-l)+1}=r(2l-1)-i+1$
. Therefore,
Then for each
![]() $1\leq j\leq r(k-l)$
,
$1\leq j\leq r(k-l)$
,
 $$ \begin{align*} \prod_{i=r(l-1)+2}^{rl+1}\mathfrak{g}(2h_{i,j})=\begin{cases}-q^{-(r+1)/2}&\text{odd } r,\\ -q^{-(r+1)/2}q^{1/2}\mathfrak{g}(r)&\text{even } r.\end{cases} \end{align*} $$
$$ \begin{align*} \prod_{i=r(l-1)+2}^{rl+1}\mathfrak{g}(2h_{i,j})=\begin{cases}-q^{-(r+1)/2}&\text{odd } r,\\ -q^{-(r+1)/2}q^{1/2}\mathfrak{g}(r)&\text{even } r.\end{cases} \end{align*} $$
Note that
![]() $2a\equiv 2b\,(m)$
if and only if
$2a\equiv 2b\,(m)$
if and only if
![]() $a\equiv b\,(r)$
, and if r is even,
$a\equiv b\,(r)$
, and if r is even,
![]() $-r\equiv r\,(m)$
whence
$-r\equiv r\,(m)$
whence
![]() $(q^{1/2}\mathfrak {g}(r))^r=1$
. When we multiply over
$(q^{1/2}\mathfrak {g}(r))^r=1$
. When we multiply over
![]() $r(k-l)$
columns and
$r(k-l)$
columns and
![]() $1\leq l\leq k-1$
rows we see that C is the coefficient appearing in the monomial (3.13) (!).
$1\leq l\leq k-1$
rows we see that C is the coefficient appearing in the monomial (3.13) (!).
Proof of Claim 44.
Fix
![]() $1\leq l\leq k$
. Let
$1\leq l\leq k$
. Let
![]() $r(l-1)+1<i<rl+1$
. We split the sum
$r(l-1)+1<i<rl+1$
. We split the sum
![]() $d_i$
(given by Equation (3.16)) into two summations, one for
$d_i$
(given by Equation (3.16)) into two summations, one for
![]() $1\leq j\leq r(k-l)$
, the other for
$1\leq j\leq r(k-l)$
, the other for
![]() $j>r(k-l)$
. For the first sum, by definition
$j>r(k-l)$
. For the first sum, by definition
![]() $(i,j)\in \mathcal {G}$
so that
$(i,j)\in \mathcal {G}$
so that
![]() $a_{i,j}=a_{rl+1,j}$
, which is
$a_{i,j}=a_{rl+1,j}$
, which is
![]() $rk-j$
by Equation (3.18). Hence, this sum equals
$rk-j$
by Equation (3.18). Hence, this sum equals
![]() $r(k-l)(i-1)$
which is divisible by r so that
$r(k-l)(i-1)$
which is divisible by r so that
 $$ \begin{align*} d_i\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-rk+i-1+j\equiv0\quad(r). \end{align*} $$
$$ \begin{align*} d_i\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-rk+i-1+j\equiv0\quad(r). \end{align*} $$
Put
![]() $v=i-r(l-1)-1>0$
. According to Equation (3.18), we have in particular
$v=i-r(l-1)-1>0$
. According to Equation (3.18), we have in particular
Then for each
![]() $r(k-l)< j\leq rk-i+1$
,
$r(k-l)< j\leq rk-i+1$
,
Hence,
 $$ \begin{align} d_{i}\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-a_{r(l-1)+1,j+v}\quad(r), \end{align} $$
$$ \begin{align} d_{i}\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-a_{r(l-1)+1,j+v}\quad(r), \end{align} $$
and note that
![]() $a_{r(l-1)+1,j+v}$
is defined because in the summation
$a_{r(l-1)+1,j+v}$
is defined because in the summation
![]() $j+v\leq rk-i+1+v=rk-r(l-1)$
. Since
$j+v\leq rk-i+1+v=rk-r(l-1)$
. Since
![]() $i>r(l-1)+1$
, this is a sum of less than r integers which vanishes modulo r.
$i>r(l-1)+1$
, this is a sum of less than r integers which vanishes modulo r.
We now use induction on i to show that
![]() $a_{i,j}=a_{i-1,j+1}$
for all
$a_{i,j}=a_{i-1,j+1}$
for all
![]() $r(k-l)<j\leq rk-i+1$
. For the base case,
$r(k-l)<j\leq rk-i+1$
. For the base case,
![]() $i=r(l-1)+2$
and
$i=r(l-1)+2$
and
![]() $v=1$
. Since
$v=1$
. Since
![]() $rk-i+1<r(k-(l-1))$
, Equation (3.18) implies that for any j in the range,
$rk-i+1<r(k-(l-1))$
, Equation (3.18) implies that for any j in the range,
![]() $a_{r(l-1)+1,j}=a_{r(l-1)+1,j+1}+1$
, hence we must have
$a_{r(l-1)+1,j}=a_{r(l-1)+1,j+1}+1$
, hence we must have
![]() $a_{i,j}=a_{r(l-1)+1,j}$
or
$a_{i,j}=a_{r(l-1)+1,j}$
or
![]() $a_{r(l-1)+1,j+1}$
(according to the conditions defining the Gelfand–Tsetlin pattern). Thus, Equation (3.20) is a sum of less than r integers which are either
$a_{r(l-1)+1,j+1}$
(according to the conditions defining the Gelfand–Tsetlin pattern). Thus, Equation (3.20) is a sum of less than r integers which are either
![]() $0$
or
$0$
or
![]() $1$
and is divisible by r. We conclude
$1$
and is divisible by r. We conclude
![]() $a_{i,j}=a_{r(l-1)+1,j+1}$
for all
$a_{i,j}=a_{r(l-1)+1,j+1}$
for all
![]() $r(k-l)<j\leq rk-i+1$
.
$r(k-l)<j\leq rk-i+1$
.
For
![]() $r(l-1)+2<i<rl+1$
,
$r(l-1)+2<i<rl+1$
,
![]() $a_{i,j}-a_{r(l-1)+1,j+(i-r(l-1)-1)}$
equals
$a_{i,j}-a_{r(l-1)+1,j+(i-r(l-1)-1)}$
equals
 $$ \begin{align*} a_{i,j}+\sum_{u=1}^{i-r(l-1)-2}(-a_{i-u,j+u}+a_{i-u,j+u})-a_{r(l-1)+1,j+(i-r(l-1)-1)} =a_{i,j}-a_{i-1,j+1}, \end{align*} $$
$$ \begin{align*} a_{i,j}+\sum_{u=1}^{i-r(l-1)-2}(-a_{i-u,j+u}+a_{i-u,j+u})-a_{r(l-1)+1,j+(i-r(l-1)-1)} =a_{i,j}-a_{i-1,j+1}, \end{align*} $$
where the second equality follows from the inductive hypothesis. Therefore, Equation (3.20) becomes
 $$ \begin{align*} d_{i}\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-a_{i-1,j+1}\quad(r). \end{align*} $$
$$ \begin{align*} d_{i}\equiv\sum_{j=r(k-l)+1}^{rk-i+1}a_{i,j}-a_{i-1,j+1}\quad(r). \end{align*} $$
The inductive hypothesis also implies that
![]() $a_{i-1,j}=a_{r(l-1)+1,j+v-1}$
for any j in the range, and because
$a_{i-1,j}=a_{r(l-1)+1,j+v-1}$
for any j in the range, and because
![]() $j+v-1<r(k-(l-1))$
we can use Equation (3.18) to deduce that
$j+v-1<r(k-(l-1))$
we can use Equation (3.18) to deduce that
![]() $a_{i-1,j}=a_{i-1,j+1}+1$
. Then, as in the base case, we have
$a_{i-1,j}=a_{i-1,j+1}+1$
. Then, as in the base case, we have
![]() $a_{i,j}=a_{i-1,j}$
or
$a_{i,j}=a_{i-1,j}$
or
![]() $a_{i-1,j+1}$
for all j, and the vanishing of
$a_{i-1,j+1}$
for all j, and the vanishing of
![]() $d_i$
modulo r implies that
$d_i$
modulo r implies that
![]() $a_{i,j}=a_{i-1,j+1}$
. In this manner, we argue for each l.
$a_{i,j}=a_{i-1,j+1}$
. In this manner, we argue for each l.
Example 45. The unique Gelfand–Tsetlin pattern when
![]() $r=k=2$
(
$r=k=2$
(
![]() $m=4$
) is
$m=4$
) is
 $$ \begin{align*} \begin{array}{cccccccccc} 3&&2&&1&&0\\&3&&2&&0\\&&3&&2\\&&&2 \end{array}. \end{align*} $$
$$ \begin{align*} \begin{array}{cccccccccc} 3&&2&&1&&0\\&3&&2&&0\\&&3&&2\\&&&2 \end{array}. \end{align*} $$
Here,
![]() $\mathcal {G}=\{(2,1),(2,2),(3,1),(3,2)\}$
,
$\mathcal {G}=\{(2,1),(2,2),(3,1),(3,2)\}$
,
![]() $h_{2,1}=2$
,
$h_{2,1}=2$
,
![]() $h_{2,2}=1$
,
$h_{2,2}=1$
,
![]() $h_{3,1}=3$
,
$h_{3,1}=3$
,
![]() $h_{3,2}=2$
and
$h_{3,2}=2$
and
![]() $C=\prod _{{i,j}\in \mathcal {G}}\mathfrak {g}(2h_{i,j})=q^{-3}$
. When
$C=\prod _{{i,j}\in \mathcal {G}}\mathfrak {g}(2h_{i,j})=q^{-3}$
. When
![]() $r=k=3$
(
$r=k=3$
(
![]() $m=3$
or
$m=3$
or
![]() $6$
), the pattern is
$6$
), the pattern is
 $$ \begin{align*} \begin{array}{ccccccccccccccccc} 8&&7&&6&&5&&4&&3&&2&&1&&0\\ &8&&7&&6&&5&&4&&3&&1&&0\\ &&8&&7&&6&&5&&4&&3&&0\\ &&&8&&7&&6&&5&&4&&3\\ &&&&8&&7&&6&&4&&3\\ &&&&&8&&7&&6&&3\\ &&&&&&8&&7&&6\\ &&&&&&&7&&6\\ &&&&&&&&6 \end{array}. \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccccccccccc} 8&&7&&6&&5&&4&&3&&2&&1&&0\\ &8&&7&&6&&5&&4&&3&&1&&0\\ &&8&&7&&6&&5&&4&&3&&0\\ &&&8&&7&&6&&5&&4&&3\\ &&&&8&&7&&6&&4&&3\\ &&&&&8&&7&&6&&3\\ &&&&&&8&&7&&6\\ &&&&&&&7&&6\\ &&&&&&&&6 \end{array}. \end{align*} $$
Here,
![]() $d_4=d_7=18$
;
$d_4=d_7=18$
;
![]() $\mathcal {B}=\{(2,7),(2,8),(3,7),(5,4),(5,5),(6,4),(8,1),(8,2),(9,1)\}$
; the contribution to C of rows
$\mathcal {B}=\{(2,7),(2,8),(3,7),(5,4),(5,5),(6,4),(8,1),(8,2),(9,1)\}$
; the contribution to C of rows
![]() $2,3$
and
$2,3$
and
![]() $4$
is
$4$
is
![]() $q^{-4}$
each, and rows
$q^{-4}$
each, and rows
![]() $5,6$
and
$5,6$
and
![]() $7$
contribute
$7$
contribute
![]() $-q^{-2}$
each, for example, the product for the
$-q^{-2}$
each, for example, the product for the
![]() $7$
-th row is
$7$
-th row is
![]() $\mathfrak {g}(2\cdot 5)\cdot \mathfrak {g}(2\cdot 4)\cdot (-q^{-1})$
. Hence, the monomial of highest total degree is
$\mathfrak {g}(2\cdot 5)\cdot \mathfrak {g}(2\cdot 4)\cdot (-q^{-1})$
. Hence, the monomial of highest total degree is
![]() $-q^{-18}\mathbf {x}_{(1,2)}^6\mathbf {x}_{(2,3)}^6$
.
$-q^{-18}\mathbf {x}_{(1,2)}^6\mathbf {x}_{(2,3)}^6$
.
Define a function
![]() $\mathscr {G}:W_{\operatorname {\mathrm {GL}}_{rk-1}}\times \mathbb {Z}^{rk-1}\rightarrow \mathbb {C}^{*}$
as follows.
$\mathscr {G}:W_{\operatorname {\mathrm {GL}}_{rk-1}}\times \mathbb {Z}^{rk-1}\rightarrow \mathbb {C}^{*}$
as follows.
-
1. If w is the identity element,
 $\mathscr {G}(w,\mathbf {a})=1$
.
$\mathscr {G}(w,\mathbf {a})=1$
. -
2. For
 $w=w_{\alpha }$
with
$w=w_{\alpha }$
with
 $\alpha =(i,i+1)$
,
$\alpha =(i,i+1)$
,
 $\mathscr {G}(w_{\alpha },\mathbf {a})=q^{-a_{i+1}+a_{i}+1}\mathfrak {g}(-2(a_{i+1}-a_{i}-1))$
.
$\mathscr {G}(w_{\alpha },\mathbf {a})=q^{-a_{i+1}+a_{i}+1}\mathfrak {g}(-2(a_{i+1}-a_{i}-1))$
. -
3. If
 $\ell (w_1w_2)=\ell (w_1)+\ell (w_2)$
,
$\ell (w_1w_2)=\ell (w_1)+\ell (w_2)$
,
 $\mathscr {G}(w_1w_2,\mathbf {a})=\mathscr {G}(w_1,w_2[\mathbf {a}])\mathscr {G}(w_2,\mathbf {a})$
.
$\mathscr {G}(w_1w_2,\mathbf {a})=\mathscr {G}(w_1,w_2[\mathbf {a}])\mathscr {G}(w_2,\mathbf {a})$
.
This is similar to Suzuki [Reference SuzukiSuz97, § 3.2], but the definition of the action
![]() $w[\mathbf {a}]$
is different.
$w[\mathbf {a}]$
is different.
For the rest of this section, assume that
 $$ \begin{align} \prod_{j=1}^{r}C(j,\mathbf{x})\ne0. \end{align} $$
$$ \begin{align} \prod_{j=1}^{r}C(j,\mathbf{x})\ne0. \end{align} $$
Then according to Theorem 43, since
![]() $\Lambda (\xi ^0)=W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
,
$\Lambda (\xi ^0)=W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })\ne 0$
,
![]() $\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
can be realized using
$\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
can be realized using
![]() $\Lambda $
. Now, define the normalized unramified Whittaker function
$\Lambda $
. Now, define the normalized unramified Whittaker function
![]() $W^0$
in this model by
$W^0$
in this model by
 $$ \begin{align*} W^0(g)=\frac{\Lambda(g\cdot\xi^0)}{\Lambda(\xi^0)}. \end{align*} $$
$$ \begin{align*} W^0(g)=\frac{\Lambda(g\cdot\xi^0)}{\Lambda(\xi^0)}. \end{align*} $$
This function is determined by its values on
![]() $t_{\mathbf {b}}$
, and the notation implies that
$t_{\mathbf {b}}$
, and the notation implies that
Let
![]() $p_l(\mathbf {x})$
be the l-th complete symmetric polynomial in
$p_l(\mathbf {x})$
be the l-th complete symmetric polynomial in
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
Theorem 46. For all integers
![]() $l\geq 0$
and
$l\geq 0$
and
![]() $a\in F^{*}$
,
$a\in F^{*}$
,
Remark 47. The factor
![]() $p_l(\mathbf {x})$
is independent of the choice of uniformizer
$p_l(\mathbf {x})$
is independent of the choice of uniformizer
![]() $\varpi $
.
$\varpi $
.
Remark 48. This is a special phenomenon which reflects the deep connection between
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
and
$\Theta _{r,m,r,\vartheta }(\chi )$
and
![]() $\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
(cf. § 3.2) observed by Suzuki [Reference SuzukiSuz98, § 5.5], who proved a stronger version of Theorem 46 but when
$\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
(cf. § 3.2) observed by Suzuki [Reference SuzukiSuz98, § 5.5], who proved a stronger version of Theorem 46 but when
![]() $k\leq 2$
, for the coverings of [Reference Kazhdan and PattersonKP84]. The value
$k\leq 2$
, for the coverings of [Reference Kazhdan and PattersonKP84]. The value
![]() $p_l(\mathbf {x})$
is the one obtained from the formula of Shintani [Reference ShintaniShi76] for the normalized unramified Whittaker function of
$p_l(\mathbf {x})$
is the one obtained from the formula of Shintani [Reference ShintaniShi76] for the normalized unramified Whittaker function of
![]() $\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
on
$\operatorname {\mathrm {Ind}}_{B_{\operatorname {\mathrm {GL}}_k}}^{\operatorname {\mathrm {GL}}_k}(\chi ^r)$
on
![]() $\operatorname {\mathrm {diag}}(\varpi ^{l},I_{k-1})$
.
$\operatorname {\mathrm {diag}}(\varpi ^{l},I_{k-1})$
.
Proof. For
![]() $m=1$
this follows from [Reference ShintaniShi76]; assume
$m=1$
this follows from [Reference ShintaniShi76]; assume
![]() $m>1$
. Fix a uniformizer
$m>1$
. Fix a uniformizer
![]() $\varpi $
, and write
$\varpi $
, and write
![]() $a=\varpi ^{rl}o$
with
$a=\varpi ^{rl}o$
with
![]() $|o|=1$
. Then by Equation (2.51),
$|o|=1$
. Then by Equation (2.51),
Since
![]() $W^0$
is unramified and
$W^0$
is unramified and
![]() $\eta _{d}^{\diamondsuit }(\operatorname {\mathrm {diag}}(o,I_{rk-1}))=1$
,
$\eta _{d}^{\diamondsuit }(\operatorname {\mathrm {diag}}(o,I_{rk-1}))=1$
,
At the same time,
![]() $\vartheta (a^{rl})=(\varpi ,o)^{-rl}_m\vartheta (\varpi ^{rl})=(\varpi ,o)^{rl}_m\vartheta (\varpi ^{rl})$
because
$\vartheta (a^{rl})=(\varpi ,o)^{-rl}_m\vartheta (\varpi ^{rl})=(\varpi ,o)^{rl}_m\vartheta (\varpi ^{rl})$
because
![]() $\vartheta $
is a genuine unramified character of
$\vartheta $
is a genuine unramified character of
![]() $\widetilde {A}$
. Therefore, having fixed
$\widetilde {A}$
. Therefore, having fixed
![]() $\varpi $
, the statement of the theorem is equivalent to
$\varpi $
, the statement of the theorem is equivalent to
For
![]() $r=1$
, one can prove this using the method of [Reference ShintaniShi76], because in this case the Whittaker model is unique (e.g., by Proposition 20, the assumption
$r=1$
, one can prove this using the method of [Reference ShintaniShi76], because in this case the Whittaker model is unique (e.g., by Proposition 20, the assumption
![]() $\mu _{2m}\subset F^{*}$
and Equation (2.68), the group
$\mu _{2m}\subset F^{*}$
and Equation (2.68), the group
![]() $\operatorname {\mathrm {GL}}_{k}^{(2,1)}$
is split over
$\operatorname {\mathrm {GL}}_{k}^{(2,1)}$
is split over
![]() $\operatorname {\mathrm {GL}}_k$
). However, we will treat all
$\operatorname {\mathrm {GL}}_k$
). However, we will treat all
![]() $r\geq 1$
.
$r\geq 1$
.
Recall that
it is uniquely defined given
![]() $\chi _{\Theta }$
. According to Equation (2.85) and with the same notation,
$\chi _{\Theta }$
. According to Equation (2.85) and with the same notation,
 $$ \begin{align} W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta}) &=q^{-lr(rk-1)} \sum_{i=0}^{rk-1}\, \prod_{j=1}^{rk-i-1}\,\frac{1-q^{-1}\mathbf{y}_{(j,rk-i)}}{1-\mathbf{y}_{(j,rk-i)}} \\\nonumber&\quad \sum_{\mathbf{e'}\in r\mathbb{Z}^{rk-1}\backslash \mathbb{Z}^{rk-1}} \tau_{\mathbf{0},(\mathbf{e'}^{*},-rl)}(\omega_i,\vartheta,{}^{\omega_i^{-1}}\chi_{\Theta}) W_{\mathbf{e'}}(\mathbf{0'},\vartheta,\chi_{\Theta}'[rk-i]). \end{align} $$
$$ \begin{align} W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta}) &=q^{-lr(rk-1)} \sum_{i=0}^{rk-1}\, \prod_{j=1}^{rk-i-1}\,\frac{1-q^{-1}\mathbf{y}_{(j,rk-i)}}{1-\mathbf{y}_{(j,rk-i)}} \\\nonumber&\quad \sum_{\mathbf{e'}\in r\mathbb{Z}^{rk-1}\backslash \mathbb{Z}^{rk-1}} \tau_{\mathbf{0},(\mathbf{e'}^{*},-rl)}(\omega_i,\vartheta,{}^{\omega_i^{-1}}\chi_{\Theta}) W_{\mathbf{e'}}(\mathbf{0'},\vartheta,\chi_{\Theta}'[rk-i]). \end{align} $$
By McNamara [Reference McNamaraMcN11, § 8], the l.h.s. of Equation (3.22) belongs to
![]() $\mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
, hence we can prove the result under the assumption that
$\mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
, hence we can prove the result under the assumption that
![]() $\mathbf {x}$
is in general position. Also,
$\mathbf {x}$
is in general position. Also,
![]() $W_{\mathbf {e'}}(\mathbf {0'},\vartheta ,\chi _{\Theta }'[rk-i])\in \mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
([Reference McNamaraMcN11, § 8]). The coefficients
$W_{\mathbf {e'}}(\mathbf {0'},\vartheta ,\chi _{\Theta }'[rk-i])\in \mathbb {C}[\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k}]$
([Reference McNamaraMcN11, § 8]). The coefficients
![]() $\tau _{\ldots }(\ldots )$
may a priori have poles, but by Equations (2.78)-(2.80) and Proposition 26, when
$\tau _{\ldots }(\ldots )$
may a priori have poles, but by Equations (2.78)-(2.80) and Proposition 26, when
![]() $\mathbf {y}_{(i,j)}\ne 1$
for all
$\mathbf {y}_{(i,j)}\ne 1$
for all
![]() $i<j$
, they are holomorphic (poles can only occur from the denominator in Equation (2.81)). Hence, if the product over j vanishes, the summand is zero. Looking at
$i<j$
, they are holomorphic (poles can only occur from the denominator in Equation (2.81)). Hence, if the product over j vanishes, the summand is zero. Looking at
![]() $\mathbf {y}$
, we see that the product vanishes unless
$\mathbf {y}$
, we see that the product vanishes unless
![]() $i=r(k-u)-1$
for
$i=r(k-u)-1$
for
![]() $0\leq u\leq k-1$
. For such i, we note that
$0\leq u\leq k-1$
. For such i, we note that
![]() $\mathbf {y}_{rk-i}=x_{u+1}q^{(r-1)/2}$
and
$\mathbf {y}_{rk-i}=x_{u+1}q^{(r-1)/2}$
and
![]() $\omega _{i}(rk)=ru+1$
. Then by Equation (2.78),
$\omega _{i}(rk)=ru+1$
. Then by Equation (2.78),
Note that
![]() $\vartheta $
is either trivial on
$\vartheta $
is either trivial on
![]() $\varpi ^{-rl}$
if
$\varpi ^{-rl}$
if
![]() $m\not \equiv 2\,(4)$
, otherwise
$m\not \equiv 2\,(4)$
, otherwise
![]() $\vartheta (\varpi ^{-rl})=\vartheta (\varpi ^{rl})$
by Equation (2.68). Hence, we can write Equation (3.22) in the form
$\vartheta (\varpi ^{-rl})=\vartheta (\varpi ^{rl})$
by Equation (2.68). Hence, we can write Equation (3.22) in the form
 $$ \begin{align} &W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta})=q^{-lr(rk-1)/2+l(r-1)/2} \vartheta(\varpi^{rl})\sum_{u=0}^{k-1}\,x_{u+1}^{l}\Gamma_u, \end{align} $$
$$ \begin{align} &W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta})=q^{-lr(rk-1)/2+l(r-1)/2} \vartheta(\varpi^{rl})\sum_{u=0}^{k-1}\,x_{u+1}^{l}\Gamma_u, \end{align} $$
where
![]() $\Gamma _u=\Gamma _u(\vartheta ,\chi _{\Theta })$
equals
$\Gamma _u=\Gamma _u(\vartheta ,\chi _{\Theta })$
equals
 $$ \begin{align} \prod_{j=1}^{ru}\,\frac{1-q^{-1}\mathbf{y}_{(j,ru+1)}}{1-\mathbf{y}_{(j,ru+1)}} \sum_{\mathbf{e'}\in r\mathbb{Z}^{rk-1}\backslash \mathbb{Z}^{rk-1}} \tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r(k-u)-1},\vartheta,{}^{\omega_{r(k-u)-1}^{-1}}\chi_{\Theta}) W_{\mathbf{e'}}(\mathbf{0'},\vartheta,\chi_{\Theta}'[ru+1]). \end{align} $$
$$ \begin{align} \prod_{j=1}^{ru}\,\frac{1-q^{-1}\mathbf{y}_{(j,ru+1)}}{1-\mathbf{y}_{(j,ru+1)}} \sum_{\mathbf{e'}\in r\mathbb{Z}^{rk-1}\backslash \mathbb{Z}^{rk-1}} \tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r(k-u)-1},\vartheta,{}^{\omega_{r(k-u)-1}^{-1}}\chi_{\Theta}) W_{\mathbf{e'}}(\mathbf{0'},\vartheta,\chi_{\Theta}'[ru+1]). \end{align} $$
If
![]() $k=1$
, there is only one coefficient
$k=1$
, there is only one coefficient
![]() $\Gamma _0$
, which by Equation (3.23) is equal to
$\Gamma _0$
, which by Equation (3.23) is equal to
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
. Thus, in this case the theorem follows immediately from Equation (3.23) and Theorem 43. Now, we can take
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
. Thus, in this case the theorem follows immediately from Equation (3.23) and Theorem 43. Now, we can take
![]() $k>1$
.
$k>1$
.
The coefficients
![]() $\Gamma _u$
are independent of l,
$\Gamma _u$
are independent of l,
![]() $\Gamma _u\in \mathbb {C}(\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k})$
for each u and all of these factors are holomorphic, for
$\Gamma _u\in \mathbb {C}(\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k})$
for each u and all of these factors are holomorphic, for
![]() $\mathbf {x}$
in general position (see Equation (2.81)). Therefore, if
$\mathbf {x}$
in general position (see Equation (2.81)). Therefore, if
![]() $\sum _{u=0}^{k-1}\,x_{u+1}^{l}\Gamma _u=0$
for all l, we obtain
$\sum _{u=0}^{k-1}\,x_{u+1}^{l}\Gamma _u=0$
for all l, we obtain
![]() $\Gamma _u=0$
for all u.
$\Gamma _u=0$
for all u.
The only coefficient we can evaluate directly is
![]() $\Gamma _{k-1}$
. However, since
$\Gamma _{k-1}$
. However, since
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
admits a unique Whittaker functional (up to scaling),
$\Theta _{r,m,r,\vartheta }(\chi )$
admits a unique Whittaker functional (up to scaling),
![]() $W_{\mathbf {0}}((rl,\mathbf {0'}),\vartheta ,\chi _{\Theta })$
is invariant under any permutation of
$W_{\mathbf {0}}((rl,\mathbf {0'}),\vartheta ,\chi _{\Theta })$
is invariant under any permutation of
![]() $\chi $
. Indeed, if
$\chi $
. Indeed, if
![]() $w\in W_{\operatorname {\mathrm {GL}}_k}$
, using the Gindikin–Karpelevich formula (2.76) as in [Reference Casselman and ShalikaCS80, Lemma 5.2], one sees that
$w\in W_{\operatorname {\mathrm {GL}}_k}$
, using the Gindikin–Karpelevich formula (2.76) as in [Reference Casselman and ShalikaCS80, Lemma 5.2], one sees that
Therefore,
 $$ \begin{align*} \sum_{u=0}^{k-1}\,({}^w\mathbf{x})_{u+1}^{l}\frac{\Gamma_u(\vartheta,({}^w\chi)_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,({}^w\chi)_{\Theta})}= \sum_{u=0}^{k-1}\,(\mathbf{x})_{u+1}^{l}\frac{\Gamma_u(\vartheta,\chi_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})}. \end{align*} $$
$$ \begin{align*} \sum_{u=0}^{k-1}\,({}^w\mathbf{x})_{u+1}^{l}\frac{\Gamma_u(\vartheta,({}^w\chi)_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,({}^w\chi)_{\Theta})}= \sum_{u=0}^{k-1}\,(\mathbf{x})_{u+1}^{l}\frac{\Gamma_u(\vartheta,\chi_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})}. \end{align*} $$
As explained above and by Theorem 43, the coefficients of
![]() $x_i$
appearing on both sides belong to
$x_i$
appearing on both sides belong to
![]() $\mathbb {C}(\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k})$
and are holomorphic (simultaneously) when
$\mathbb {C}(\{\mathbf {x}_{(i,i+1)}\}_{1\leq i<k})$
and are holomorphic (simultaneously) when
![]() $\mathbf {x}$
is in general position; regarding
$\mathbf {x}$
is in general position; regarding
![]() $W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
this is nontrivial, because
$W_{\mathbf {0}}(\mathbf {0},\vartheta ,\chi _{\Theta })$
this is nontrivial, because
![]() $\mathbf {y}$
is not ‘general’, but we use Theorem 43. Thus,
$\mathbf {y}$
is not ‘general’, but we use Theorem 43. Thus,
Hence, it suffices to compute
![]() $\Gamma _{k-1}$
.
$\Gamma _{k-1}$
.
In this case, the product over
![]() $1\leq j\leq r(k-1)$
simplifies to
$1\leq j\leq r(k-1)$
simplifies to
 $$ \begin{align} \prod_{j=1}^{k-1}\,\frac{1-q^{-r}\mathbf{x}_{(j,k)}}{1-\mathbf{x}_{(j,k)}}. \end{align} $$
$$ \begin{align} \prod_{j=1}^{k-1}\,\frac{1-q^{-r}\mathbf{x}_{(j,k)}}{1-\mathbf{x}_{(j,k)}}. \end{align} $$
If
![]() $r=1$
, then the summation over
$r=1$
, then the summation over
![]() $\mathbf {e'}$
is trivial, we take
$\mathbf {e'}$
is trivial, we take
![]() $\mathbf {e'}^{*}=\mathbf {0}'$
, and
$\mathbf {e'}^{*}=\mathbf {0}'$
, and
![]() $\omega _{r(k-(k-1))-1}=I_{k}$
. Now, assume
$\omega _{r(k-(k-1))-1}=I_{k}$
. Now, assume
![]() $r>1$
. By Equation (2.79) and since
$r>1$
. By Equation (2.79) and since
![]() $\omega _{r-1}=w_{\alpha _{rk-r+1}}\cdot \ldots \cdot w_{\alpha _{rk-1}}$
is a reduced expression,
$\omega _{r-1}=w_{\alpha _{rk-r+1}}\cdot \ldots \cdot w_{\alpha _{rk-1}}$
is a reduced expression,
 $$ \begin{align*} \tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) =\sum_{\mathbf{d}\in r\mathbb{Z}^{rk}\backslash \mathbb{Z}^{rk}} \tau_{\mathbf{0},\mathbf{d}}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{\mathbf{d},(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}). \end{align*} $$
$$ \begin{align*} \tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) =\sum_{\mathbf{d}\in r\mathbb{Z}^{rk}\backslash \mathbb{Z}^{rk}} \tau_{\mathbf{0},\mathbf{d}}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{\mathbf{d},(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}). \end{align*} $$
Now,
![]() $\tau _{\mathbf {0},\mathbf {d}}(w_{\alpha _{rk-r+1}},\vartheta ,{}^{w_{\alpha _{rk-r+1}}}\chi _{\Theta })$
vanishes unless
$\tau _{\mathbf {0},\mathbf {d}}(w_{\alpha _{rk-r+1}},\vartheta ,{}^{w_{\alpha _{rk-r+1}}}\chi _{\Theta })$
vanishes unless
![]() $\mathbf {d}\equiv w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
for
$\mathbf {d}\equiv w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
for
![]() $i_{rk-r+1}\in \{0,1\}$
. Hence,
$i_{rk-r+1}\in \{0,1\}$
. Hence,
 $$ \begin{align*} &\tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+1}} \tau_{\mathbf{0},w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}]}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}), \end{align*} $$
$$ \begin{align*} &\tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+1}} \tau_{\mathbf{0},w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}]}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}), \end{align*} $$
where the sum is over
![]() $i_{rk-r+1}\in \{0,1\}$
. If
$i_{rk-r+1}\in \{0,1\}$
. If
![]() $r=2$
,
$r=2$
,
![]() $\omega _{r-2}=I_{rk}$
and
$\omega _{r-2}=I_{rk}$
and
![]() $\tau _{w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}],(\mathbf {e'}^{*},0)}(\omega _{r-2},\vartheta ,{}^{\omega _{r-1}^{-1}}\chi _{\Theta })=0$
unless
$\tau _{w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}],(\mathbf {e'}^{*},0)}(\omega _{r-2},\vartheta ,{}^{\omega _{r-1}^{-1}}\chi _{\Theta })=0$
unless
![]() $i_{rk-r+1}=i_{rk-1}=0$
, hence
$i_{rk-r+1}=i_{rk-1}=0$
, hence
![]() $\mathbf {e'}^{*}$
can be taken to be
$\mathbf {e'}^{*}$
can be taken to be
![]() $\mathbf {0}'$
. Similarly, if
$\mathbf {0}'$
. Similarly, if
![]() $r>2$
,
$r>2$
,
 $$ \begin{align*} &\tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{\mathbf{d}\in r\mathbb{Z}^{rk}\backslash \mathbb{Z}^{rk}} \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],\mathbf{d}}(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{\mathbf{d},(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+2}} \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \\&\qquad\times\tau_{w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}). \end{align*} $$
$$ \begin{align*} &\tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{\mathbf{d}\in r\mathbb{Z}^{rk}\backslash \mathbb{Z}^{rk}} \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],\mathbf{d}}(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \tau_{\mathbf{d},(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+2}} \tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \\&\qquad\times\tau_{w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],(\mathbf{e'}^{*},0)}(\omega_{r-2},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}). \end{align*} $$
Proceeding
![]() $r-2$
times, we obtain
$r-2$
times, we obtain
 $$ \begin{align} &\tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+1}}\tau_{\mathbf{0},\vartheta,w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}]}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta})\nonumber \\&\qquad\times\sum_{i_{rk-r+2}}\tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],\nonumber w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \\&\qquad\ldots\nonumber \\&\qquad\times\sum_{i_{rk-2}}\tau_{w_{\alpha_{rk-3}}^{i_{rk-3}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-2}},\vartheta,{}^{w_{\alpha_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta})\nonumber \\&\qquad\times \tau_{w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], (\mathbf{e'}^{*},0)}(w_{\alpha_{rk-1}},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}).\nonumber \end{align} $$
$$ \begin{align} &\tau_{\mathbf{0},(\mathbf{e'}^{*},0)}(\omega_{r-1},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}) \\&=\sum_{i_{rk-r+1}}\tau_{\mathbf{0},\vartheta,w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}]}(w_{\alpha_{rk-r+1}},\vartheta,{}^{w_{\alpha_{rk-r+1}}}\chi_{\Theta})\nonumber \\&\qquad\times\sum_{i_{rk-r+2}}\tau_{w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}],\nonumber w_{\alpha_{rk-r+2}}^{i_{rk-r+2}}w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-r+2}},\vartheta,{}^{w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta}) \\&\qquad\ldots\nonumber \\&\qquad\times\sum_{i_{rk-2}}\tau_{w_{\alpha_{rk-3}}^{i_{rk-3}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}] }(w_{\alpha_{rk-2}},\vartheta,{}^{w_{\alpha_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+2}}w_{\alpha_{rk-r+1}}}\chi_{\Theta})\nonumber \\&\qquad\times \tau_{w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}}[\mathbf{0}], (\mathbf{e'}^{*},0)}(w_{\alpha_{rk-1}},\vartheta,{}^{\omega_{r-1}^{-1}}\chi_{\Theta}).\nonumber \end{align} $$
Momentarily, proceed assuming
![]() $r>2$
. To compute
$r>2$
. To compute
![]() $\tau _{w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}], (\mathbf {e'}^{*},0)}(w_{\alpha _{rk-1}},\vartheta ,{}^{\omega _{r-1}^{-1}}\chi _{\Theta })$
note that since the rightmost coordinate of
$\tau _{w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}], (\mathbf {e'}^{*},0)}(w_{\alpha _{rk-1}},\vartheta ,{}^{\omega _{r-1}^{-1}}\chi _{\Theta })$
note that since the rightmost coordinate of
![]() $(\mathbf {e'}^{*},0)$
is zero,
$(\mathbf {e'}^{*},0)$
is zero,
This implies that
![]() $(\mathbf {e'}^{*},0)\equiv w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
, and we can assume that this equivalence is an equality and omit the summation over
$(\mathbf {e'}^{*},0)\equiv w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
, and we can assume that this equivalence is an equality and omit the summation over
![]() $\mathbf {e'}$
in the expression (3.24). In turn, each summand on the r.h.s. of Equation (3.27) is multiplied by
$\mathbf {e'}$
in the expression (3.24). In turn, each summand on the r.h.s. of Equation (3.27) is multiplied by
Note that
![]() $\mathbf {e'}^{*}$
is well defined because
$\mathbf {e'}^{*}$
is well defined because
![]() $rk-r+1<rk-1$
. To treat
$rk-r+1<rk-1$
. To treat
![]() $r\geq 1$
simultaneously, we fix the convention that if
$r\geq 1$
simultaneously, we fix the convention that if
![]() $rk-2<rk-r+1$
,
$rk-2<rk-r+1$
,
![]() $w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}$
is taken to be the identity.
$w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}$
is taken to be the identity.
The value of the expression (3.29) was computed by Cai [Reference CaiCai20, Theorem 8.1] (using the methods of [Reference SuzukiSuz97, Reference SuzukiSuz98]) and is equal to
 $$ \begin{align} \prod_{j=1}^{k-1}(1-q^{-r}\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r}C(j,\mathbf{x}) \mathscr{G}(w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}},\mathbf{0}'). \end{align} $$
$$ \begin{align} \prod_{j=1}^{k-1}(1-q^{-r}\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r}C(j,\mathbf{x}) \mathscr{G}(w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}},\mathbf{0}'). \end{align} $$
In fact for
![]() $r=1$
, Theorem 43 immediately implies that the expression (3.29) is equal to (3.30).
$r=1$
, Theorem 43 immediately implies that the expression (3.29) is equal to (3.30).
Next, we compute the factors appearing in Equation (3.27). Fix
![]() $1\leq l\leq r-1$
. If
$1\leq l\leq r-1$
. If
![]() $1<l<r-1$
, denote
$1<l<r-1$
, denote
for
![]() $l=r-1$
,
$l=r-1$
,
![]() $\mathbf {a}=\mathbf {0}$
and
$\mathbf {a}=\mathbf {0}$
and
![]() $\mathbf {b}=w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
; and if
$\mathbf {b}=w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
; and if
![]() $l=1$
,
$l=1$
,
![]() $\mathbf {a}=\mathbf {b}=w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
(for
$\mathbf {a}=\mathbf {b}=w_{\alpha _{rk-2}}^{i_{rk-2}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}^{i_{rk-r+1}}[\mathbf {0}]$
(for
![]() $r=2$
,
$r=2$
,
![]() $\mathbf {a}=\mathbf {b}=\mathbf {0}$
either way). The corresponding factor to evaluate is
$\mathbf {a}=\mathbf {b}=\mathbf {0}$
either way). The corresponding factor to evaluate is
If
![]() $l>1$
and
$l>1$
and
![]() $i_{rk-l}=0$
, then
$i_{rk-l}=0$
, then
![]() $\mathbf {a}=\mathbf {b}$
and
$\mathbf {a}=\mathbf {b}$
and
Similarly, for
![]() $l=1$
, we have Equation (3.28). Hence, in both cases we can use Equation (2.81) to compute (3.31). Since
$l=1$
, we have Equation (3.28). Hence, in both cases we can use Equation (2.81) to compute (3.31). Since
![]() $0\leq a_{rk-l}\leq r-1-l$
and
$0\leq a_{rk-l}\leq r-1-l$
and
![]() $a_{rk-l+1}=0$
, we obtain
$a_{rk-l+1}=0$
, we obtain
![]() $\lceil (a_{rk-l+1}-a_{rk-l})/r\rceil =0$
, the expression (3.31) equals
$\lceil (a_{rk-l+1}-a_{rk-l})/r\rceil =0$
, the expression (3.31) equals
The remaining case is
![]() $l>1$
and
$l>1$
and
![]() $i_{rk-l}=1$
. We appeal to Equation (2.82) and deduce that Equation (3.31) equals
$i_{rk-l}=1$
. We appeal to Equation (2.82) and deduce that Equation (3.31) equals
At the same time,
where we replace
![]() $w_{\alpha _{rk-l-1}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}[\mathbf {0}']$
with
$w_{\alpha _{rk-l-1}}\cdot \ldots \cdot w_{\alpha _{rk-r+1}}[\mathbf {0}']$
with
![]() $\mathbf {0}'$
if
$\mathbf {0}'$
if
![]() $l=r-1$
. Since
$l=r-1$
. Since
![]() $2(a_{rk-l+1}-a_{rk-l}-1)\equiv 0\,(m)$
if and only if
$2(a_{rk-l+1}-a_{rk-l}-1)\equiv 0\,(m)$
if and only if
![]() $a_{rk-l}+1\equiv 0\,(r)$
(
$a_{rk-l}+1\equiv 0\,(r)$
(
![]() $a_{rk-l+1}=0$
) and
$a_{rk-l+1}=0$
) and
![]() $1\leq a_{rk-l}+1\leq r-l\leq r-1$
, we deduce that
$1\leq a_{rk-l}+1\leq r-l\leq r-1$
, we deduce that
![]() $2(a_{rk-l+1}-a_{rk-l}-1)\not \equiv 0\,(m)$
hence the product of Equations (3.33) and (3.34) is
$2(a_{rk-l+1}-a_{rk-l}-1)\not \equiv 0\,(m)$
hence the product of Equations (3.33) and (3.34) is
![]() $q^{-1}$
.
$q^{-1}$
.
Now, when we combine the expressions (3.24) (for
![]() $u=k-1$
and with
$u=k-1$
and with
![]() $\mathbf {e'}$
fixed, as explained above), (3.26), (3.27), (3.31) and (3.30), we obtain
$\mathbf {e'}$
fixed, as explained above), (3.26), (3.27), (3.31) and (3.30), we obtain
 $$ \begin{align*} \Gamma_{k-1}=&\prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r} C(j,\mathbf{x}) \sum_{i_{rk-r+1},\ldots,i_{rk-2}\in\{0,1\}}\\&\prod_{l=r-1}^{1} \tau_{\mathbf{a}^l,\mathbf{b}^l}(w_{\alpha_{rk-l}},\vartheta,{}^{w_{\alpha_{rk-l}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}}\chi_{\Theta})\mathscr{G}(w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}},\mathbf{0}'). \end{align*} $$
$$ \begin{align*} \Gamma_{k-1}=&\prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r} C(j,\mathbf{x}) \sum_{i_{rk-r+1},\ldots,i_{rk-2}\in\{0,1\}}\\&\prod_{l=r-1}^{1} \tau_{\mathbf{a}^l,\mathbf{b}^l}(w_{\alpha_{rk-l}},\vartheta,{}^{w_{\alpha_{rk-l}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}}\chi_{\Theta})\mathscr{G}(w_{\alpha_{rk-2}}^{i_{rk-2}}\cdot\ldots\cdot w_{\alpha_{rk-r+1}}^{i_{rk-r+1}},\mathbf{0}'). \end{align*} $$
Using Equation (3.32), Equation (3.33) and the definition of
![]() $\mathscr {G}$
, the summation over
$\mathscr {G}$
, the summation over
![]() $i_{rk-r+1},\ldots ,i_{rk-2}$
becomes
$i_{rk-r+1},\ldots ,i_{rk-2}$
becomes
 $$ \begin{align*} \prod_{l=1}^{r-2}\left(\frac{1-q^{-1}}{1-q^{-l}}+q^{-1}\right)\frac{1-q^{-1}}{1-q^{-r+1}}= \prod_{l=1}^{r-2}\left(\frac{1-q^{-l-1}}{1-q^{-l}}\right)\frac{1-q^{-1}}{1-q^{-r+1}}=1. \end{align*} $$
$$ \begin{align*} \prod_{l=1}^{r-2}\left(\frac{1-q^{-1}}{1-q^{-l}}+q^{-1}\right)\frac{1-q^{-1}}{1-q^{-r+1}}= \prod_{l=1}^{r-2}\left(\frac{1-q^{-l-1}}{1-q^{-l}}\right)\frac{1-q^{-1}}{1-q^{-r+1}}=1. \end{align*} $$
Hence, by Theorem 43, and for
![]() $r=1$
immediately from expressions (3.24), (3.26) and (3.30),
$r=1$
immediately from expressions (3.24), (3.26) and (3.30),
 $$ \begin{align*} \Gamma_{k-1}=\prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r} C(j,\mathbf{x})= \prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta}). \end{align*} $$
$$ \begin{align*} \Gamma_{k-1}=\prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}\prod_{j=1}^{r} C(j,\mathbf{x})= \prod_{j=1}^{k-1}(1-\mathbf{x}_{(j,k)})^{-1}W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta}). \end{align*} $$
Then
![]() $W^0(t_{(rl,\mathbf {0'})})$
equals
$W^0(t_{(rl,\mathbf {0'})})$
equals
 $$ \begin{align*} \frac{W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})} &=q^{-lr(rk-1)/2+l(r-1)/2}\vartheta(\varpi^{rl})\left( \frac{x_k^l}{\prod_{j=1}^{k-1}(1-x_jx_k^{-1})}+\sum_{u=0}^{k-2}\,\frac{x_{u+1}^{l}\Gamma_u}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})}\right), \end{align*} $$
$$ \begin{align*} \frac{W_{\mathbf{0}}((rl,\mathbf{0'}),\vartheta,\chi_{\Theta})}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})} &=q^{-lr(rk-1)/2+l(r-1)/2}\vartheta(\varpi^{rl})\left( \frac{x_k^l}{\prod_{j=1}^{k-1}(1-x_jx_k^{-1})}+\sum_{u=0}^{k-2}\,\frac{x_{u+1}^{l}\Gamma_u}{W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})}\right), \end{align*} $$
and the proof of the theorem is complete by Equation (3.25) and the definition of
![]() $p_l(\mathbf {x})$
.
$p_l(\mathbf {x})$
.
Remark 49. For the cases
![]() $r=1$
or
$r=1$
or
![]() $k=1$
, [Reference CaiCai20] was not used in the proof.
$k=1$
, [Reference CaiCai20] was not used in the proof.
3.4 Global construction of
 $(rk,c)$
representations
$(rk,c)$
representations
Let
![]() $\tau $
be a genuine unitary irreducible cuspidal automorphic representation of
$\tau $
be a genuine unitary irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
(see § 2.7). We construct global
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
(see § 2.7). We construct global
![]() $(rk,c)$
representations by means of residues of Eisenstein series. As explained in the introduction, for the construction we rely on certain assumptions on local intertwining operators and global partial L-functions. We begin by stating our local and global working assumptions.
$(rk,c)$
representations by means of residues of Eisenstein series. As explained in the introduction, for the construction we rely on certain assumptions on local intertwining operators and global partial L-functions. We begin by stating our local and global working assumptions.
Let
![]() $\nu $
be a place of F. For
$\nu $
be a place of F. For
![]() $l\geq 2$
, let
$l\geq 2$
, let
![]() $\boldsymbol {\zeta }=(\zeta _1,\ldots ,\zeta _{l})\in \mathbb {C}^{l}$
, and
$\boldsymbol {\zeta }=(\zeta _1,\ldots ,\zeta _{l})\in \mathbb {C}^{l}$
, and
We have the standard intertwining operator
 $$ \begin{align*} M(w_l,\boldsymbol{\zeta}):\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{l})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{lk}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_1}\tau_{\nu}\otimes\ldots\otimes|\det|^{\zeta_l}\tau_{\nu}) \rightarrow \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{l})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{lk}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_l}\tau_{\nu}\otimes\ldots\otimes|\det|^{\zeta_1}\tau_{\nu}). \end{align*} $$
$$ \begin{align*} M(w_l,\boldsymbol{\zeta}):\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{l})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{lk}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_1}\tau_{\nu}\otimes\ldots\otimes|\det|^{\zeta_l}\tau_{\nu}) \rightarrow \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{l})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{lk}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_l}\tau_{\nu}\otimes\ldots\otimes|\det|^{\zeta_1}\tau_{\nu}). \end{align*} $$
For
![]() $\operatorname {\mathrm {Re}}(\zeta _1)\gg \ldots \gg \operatorname {\mathrm {Re}}(\zeta _l)$
, it is given by the absolutely convergent integral
$\operatorname {\mathrm {Re}}(\zeta _1)\gg \ldots \gg \operatorname {\mathrm {Re}}(\zeta _l)$
, it is given by the absolutely convergent integral
 $$ \begin{align*} M(w_l,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta})=\int\limits_{V_{(k^l)}(F_{\nu})}\xi(\langle w_l,1\rangle^{-1}\langle v,1\rangle g,\boldsymbol{\zeta})\,dv, \end{align*} $$
$$ \begin{align*} M(w_l,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta})=\int\limits_{V_{(k^l)}(F_{\nu})}\xi(\langle w_l,1\rangle^{-1}\langle v,1\rangle g,\boldsymbol{\zeta})\,dv, \end{align*} $$
and in general by meromorphic continuation. Our local conjecture is the following.
Conjecture 50. For each place
![]() $\nu $
,
$\nu $
,
![]() $M(w_2,\boldsymbol {\zeta })$
is holomorphic for
$M(w_2,\boldsymbol {\zeta })$
is holomorphic for
![]() $\operatorname {\mathrm {Re}}(\zeta _1-\zeta _2)\geq 1/r$
, and if
$\operatorname {\mathrm {Re}}(\zeta _1-\zeta _2)\geq 1/r$
, and if
![]() $1<l\leq r$
, the image of
$1<l\leq r$
, the image of
![]() $M(w_l,\boldsymbol {\zeta })$
is irreducible at
$M(w_l,\boldsymbol {\zeta })$
is irreducible at
![]() $\boldsymbol {\zeta }=((l-1)/(2r),(l-3)/(2r),\ldots ,(1-l)/(2r))$
.
$\boldsymbol {\zeta }=((l-1)/(2r),(l-3)/(2r),\ldots ,(1-l)/(2r))$
.
Globally, we define the partial L-function of
![]() $\tau \times \tau ^{\vee }$
. Let S be a finite set of places of F such that outside S all data are unramified. The set S depends only on F,
$\tau \times \tau ^{\vee }$
. Let S be a finite set of places of F such that outside S all data are unramified. The set S depends only on F,
![]() $\psi $
and
$\psi $
and
![]() $\tau $
. If
$\tau $
. If
![]() $m\equiv 2\,(4)$
, we need to fix the parametrization of the local components of
$m\equiv 2\,(4)$
, we need to fix the parametrization of the local components of
![]() $\tau $
outside S because the local L-factors depend on this parametrization (see § 2.8). Choose a nontrivial character
$\tau $
outside S because the local L-factors depend on this parametrization (see § 2.8). Choose a nontrivial character
![]() $\psi '$
of
$\psi '$
of
![]() $F\backslash \mathbb {A}$
which is unramified outside S (e.g.,
$F\backslash \mathbb {A}$
which is unramified outside S (e.g.,
![]() $\psi $
). Let
$\psi $
). Let
![]() $\vartheta =\gamma _{\psi '}=\prod _{\nu }\gamma _{\psi ^{\prime }_{\nu }}$
,
$\vartheta =\gamma _{\psi '}=\prod _{\nu }\gamma _{\psi ^{\prime }_{\nu }}$
,
![]() $\vartheta _{\nu }=\gamma _{\psi ^{\prime }_{\nu }}$
for all
$\vartheta _{\nu }=\gamma _{\psi ^{\prime }_{\nu }}$
for all
![]() $\nu $
. When
$\nu $
. When
![]() $m\not \equiv 2\,(4)$
,
$m\not \equiv 2\,(4)$
,
![]() $\vartheta $
can be ignored. Then we can define for
$\vartheta $
can be ignored. Then we can define for
![]() $s\in \mathbb {C}$
,
$s\in \mathbb {C}$
,
This product is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
and admits meromorphic continuation ([Reference LanglandsLan67, Reference LanglandsLan76, Reference Mœglin and WaldspurgerMW95] and [Reference GaoGao18b]).
$\operatorname {\mathrm {Re}}(s)\gg 0$
and admits meromorphic continuation ([Reference LanglandsLan67, Reference LanglandsLan76, Reference Mœglin and WaldspurgerMW95] and [Reference GaoGao18b]).
Conjecture 51.
![]() $L^S_{\vartheta ,\vartheta ^{-1}}(s,\tau \times \tau ^{\vee })$
has a simple pole at
$L^S_{\vartheta ,\vartheta ^{-1}}(s,\tau \times \tau ^{\vee })$
has a simple pole at
![]() $s=1$
and is holomorphic and nonzero in
$s=1$
and is holomorphic and nonzero in
![]() $\operatorname {\mathrm {Re}}(s)>1$
.
$\operatorname {\mathrm {Re}}(s)>1$
.
In the linear case (
![]() $m=1$
), both conjectures are known: The local conjecture follows from [Reference JacquetJac84, Proposition 2.1] (see also [Reference Mœglin and WaldspurgerMW89, Proposition I.10] and [Reference Jacquet and ShalikaJS81b, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference Jacquet, Shalika, Gelbert, Howe, Sarnak and AvivJS90]), and the global was proved in [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b].
$m=1$
), both conjectures are known: The local conjecture follows from [Reference JacquetJac84, Proposition 2.1] (see also [Reference Mœglin and WaldspurgerMW89, Proposition I.10] and [Reference Jacquet and ShalikaJS81b, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference Jacquet, Shalika, Gelbert, Howe, Sarnak and AvivJS90]), and the global was proved in [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b].
Proof. For
![]() $m=2$
, we can assume that the
$m=2$
, we can assume that the
![]() $2$
-cocycles for
$2$
-cocycles for
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}(F_{\nu })$
and
$\operatorname {\mathrm {GL}}_k^{(2,1)}(F_{\nu })$
and
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}(\mathbb {A})$
are given by a local or global Hilbert symbol (see Proposition 20). In this case, there is a local and global bijection between representations of
$\operatorname {\mathrm {GL}}_k^{(2,1)}(\mathbb {A})$
are given by a local or global Hilbert symbol (see Proposition 20). In this case, there is a local and global bijection between representations of
![]() $\operatorname {\mathrm {GL}}_k$
and genuine representations of
$\operatorname {\mathrm {GL}}_k$
and genuine representations of
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}$
. Specifically, for a representation
$\operatorname {\mathrm {GL}}_k^{(2,1)}$
. Specifically, for a representation
![]() $\tau _0$
of
$\tau _0$
of
![]() $\operatorname {\mathrm {GL}}_k$
, define a genuine representation of
$\operatorname {\mathrm {GL}}_k$
, define a genuine representation of
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}$
by
$\operatorname {\mathrm {GL}}_k^{(2,1)}$
by
![]() $(\gamma _{\psi '}\otimes \tau _0)(\langle g,\epsilon \rangle )=\epsilon \gamma _{\psi '}(\det g)\tau _0(g)$
, where
$(\gamma _{\psi '}\otimes \tau _0)(\langle g,\epsilon \rangle )=\epsilon \gamma _{\psi '}(\det g)\tau _0(g)$
, where
![]() $\gamma _{\psi '}$
is a local or global Weil factor. In particular, irreducible representations of
$\gamma _{\psi '}$
is a local or global Weil factor. In particular, irreducible representations of
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}(F_{\nu })$
admit at most one Whittaker model. Now, Conjecture 50 holds because we can identify between
$\operatorname {\mathrm {GL}}_k^{(2,1)}(F_{\nu })$
admit at most one Whittaker model. Now, Conjecture 50 holds because we can identify between
 $$ \begin{align*} \operatorname{\mathrm{Ind}}_{P_{(k^{2})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{2k}(F_{\nu})} (|\det|^{\zeta_1}\tau_{\nu}\otimes|\det|^{\zeta_2}\tau_{\nu})\qquad\mathrm{and}\qquad \gamma_{\psi'}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{2})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{2k}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_1}\gamma_{\psi'}\tau_{\nu}\otimes|\det|^{\zeta_2}\gamma_{\psi'}\tau_{\nu}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ind}}_{P_{(k^{2})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{2k}(F_{\nu})} (|\det|^{\zeta_1}\tau_{\nu}\otimes|\det|^{\zeta_2}\tau_{\nu})\qquad\mathrm{and}\qquad \gamma_{\psi'}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{2})}(F_{\nu})}^{\operatorname{\mathrm{GL}}_{2k}^{(m,r)}(F_{\nu})} (|\det|^{\zeta_1}\gamma_{\psi'}\tau_{\nu}\otimes|\det|^{\zeta_2}\gamma_{\psi'}\tau_{\nu}) \end{align*} $$
via
![]() $\xi \mapsto \xi _{\psi '}$
, where
$\xi \mapsto \xi _{\psi '}$
, where
![]() $\xi _{\psi '}(\langle h,\epsilon \rangle ,\boldsymbol {\zeta })=\epsilon \gamma _{\psi '}(\det h)\xi (h,\boldsymbol {\zeta })$
so that the analytic properties of the intertwining operator follow from the linear case. Globally, given a genuine unitary irreducible cuspidal automorphic representation
$\xi _{\psi '}(\langle h,\epsilon \rangle ,\boldsymbol {\zeta })=\epsilon \gamma _{\psi '}(\det h)\xi (h,\boldsymbol {\zeta })$
so that the analytic properties of the intertwining operator follow from the linear case. Globally, given a genuine unitary irreducible cuspidal automorphic representation
![]() $\tau $
of
$\tau $
of
![]() $\operatorname {\mathrm {GL}}_k^{(2,1)}(\mathbb {A})$
, there is a unique unitary irreducible cuspidal automorphic representation
$\operatorname {\mathrm {GL}}_k^{(2,1)}(\mathbb {A})$
, there is a unique unitary irreducible cuspidal automorphic representation
![]() $\tau _0$
of
$\tau _0$
of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {A})$
such that
$\operatorname {\mathrm {GL}}_k(\mathbb {A})$
such that
![]() $\gamma _{\psi '}\otimes \tau _0=\tau $
. Then using
$\gamma _{\psi '}\otimes \tau _0=\tau $
. Then using
![]() $\langle a,\epsilon \rangle ^{-1}=\langle a^{-1},\epsilon ^{-1}(a,a)_2\rangle $
and Equation (2.68) we obtain
$\langle a,\epsilon \rangle ^{-1}=\langle a^{-1},\epsilon ^{-1}(a,a)_2\rangle $
and Equation (2.68) we obtain
![]() $\gamma _{\psi '}^{-1}\otimes \tau _0^{\vee }=\tau ^{\vee }$
. Now,
$\gamma _{\psi '}^{-1}\otimes \tau _0^{\vee }=\tau ^{\vee }$
. Now,
![]() $L^S(s,\tau _0\times \tau _0^{\vee })=L^S_{\gamma _{\psi '},\gamma _{\psi '}^{-1}}(s,\tau \times \tau ^{\vee })$
and Conjecture 51 follows from [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b].
$L^S(s,\tau _0\times \tau _0^{\vee })=L^S_{\gamma _{\psi '},\gamma _{\psi '}^{-1}}(s,\tau \times \tau ^{\vee })$
and Conjecture 51 follows from [Reference Jacquet and ShalikaJS81a, Reference Jacquet and ShalikaJS81b].
When
![]() $k=1$
, the local (resp., irreducible automorphic) representations of
$k=1$
, the local (resp., irreducible automorphic) representations of
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}$
are constructed using quasi-characters of
$\operatorname {\mathrm {GL}}_1^{(m,r)}$
are constructed using quasi-characters of
![]() $F_{\nu }^{*}$
(resp., automorphic characters of
$F_{\nu }^{*}$
(resp., automorphic characters of
![]() $\mathbb {A}^{*}$
) restricted to
$\mathbb {A}^{*}$
) restricted to
![]() $F_{\nu }^{*r}$
(resp.,
$F_{\nu }^{*r}$
(resp.,
![]() $\mathbb {A}^{*r}$
), by Stone-von Neumann theory (see [Reference Kazhdan and PattersonKP84] and § 2.8; for this there is no reason to assume that data are unramified).
$\mathbb {A}^{*r}$
), by Stone-von Neumann theory (see [Reference Kazhdan and PattersonKP84] and § 2.8; for this there is no reason to assume that data are unramified).
The first statement of Conjecture 50: for p-adic fields it follows from a straightforward adaptation of [Reference Kazhdan and PattersonKP84, Proposition I.2.3 (b)]; for Archimedean fields the case
![]() $m=2$
was explained above and for
$m=2$
was explained above and for
![]() $m>2$
, the underlying field is
$m>2$
, the underlying field is
![]() $\mathbb {C}$
and the results over Archimedean fields are immediate from the linear case (
$\mathbb {C}$
and the results over Archimedean fields are immediate from the linear case (
![]() $\operatorname {\mathrm {GL}}_2^{(m,r)}(\mathbb {C})$
is split over
$\operatorname {\mathrm {GL}}_2^{(m,r)}(\mathbb {C})$
is split over
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {C})$
). Note that since
$\operatorname {\mathrm {GL}}_2(\mathbb {C})$
). Note that since
![]() $k=1$
,
$k=1$
,
![]() $\tau _{\nu }$
is now tempered so that
$\tau _{\nu }$
is now tempered so that
![]() $M(w_2,\boldsymbol {\zeta })$
is known to be holomorphic already for
$M(w_2,\boldsymbol {\zeta })$
is known to be holomorphic already for
![]() $\operatorname {\mathrm {Re}}(\zeta _1-\zeta _2)>0$
(again by [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference JacquetJac84, Reference Mœglin and WaldspurgerMW89, Reference Jacquet, Shalika, Gelbert, Howe, Sarnak and AvivJS90]).
$\operatorname {\mathrm {Re}}(\zeta _1-\zeta _2)>0$
(again by [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference JacquetJac84, Reference Mœglin and WaldspurgerMW89, Reference Jacquet, Shalika, Gelbert, Howe, Sarnak and AvivJS90]).
The irreducibility statement (
![]() $r>1$
) holds because in this case the image of
$r>1$
) holds because in this case the image of
![]() $M(w_l,\boldsymbol {\zeta })$
is the exceptional representation (see § 2.11), then over p-adic fields one can modify [Reference Kazhdan and PattersonKP84, Theorem I.2.9 (a)] to
$M(w_l,\boldsymbol {\zeta })$
is the exceptional representation (see § 2.11), then over p-adic fields one can modify [Reference Kazhdan and PattersonKP84, Theorem I.2.9 (a)] to
![]() $\operatorname {\mathrm {GL}}_l^{(m,r)}$
to obtain irreducibility, and over Archimedean fields it is a direct consequence of the Langlands quotient theorem [Reference LanglandsLan89] (
$\operatorname {\mathrm {GL}}_l^{(m,r)}$
to obtain irreducibility, and over Archimedean fields it is a direct consequence of the Langlands quotient theorem [Reference LanglandsLan89] (
![]() $r>1$
implies
$r>1$
implies
![]() $m>2$
).
$m>2$
).
Conjecture 51 again follows from the linear case.
Henceforth, until the end of this section we assume these conjectures.
We turn to describe our construction. Let
![]() $\boldsymbol {\zeta }=(\zeta _1,\ldots ,\zeta _{rc})\in \mathbb {C}^{rc}$
. As explained in § 2.7, we can construct the induced representation
$\boldsymbol {\zeta }=(\zeta _1,\ldots ,\zeta _{rc})\in \mathbb {C}^{rc}$
. As explained in § 2.7, we can construct the induced representation
For a standard
![]() $\widetilde {K}_{\operatorname {\mathrm {GL}}_{rkc}}$
-finite vector
$\widetilde {K}_{\operatorname {\mathrm {GL}}_{rkc}}$
-finite vector
![]() $\xi $
in the space of the representation (3.35), let
$\xi $
in the space of the representation (3.35), let
![]() $E(g;\xi ,\boldsymbol {\zeta })$
denote the Eisenstein series, as in Equation (2.67). Let
$E(g;\xi ,\boldsymbol {\zeta })$
denote the Eisenstein series, as in Equation (2.67). Let
In particular,
![]() $\zeta ^{(rc)}_i-\zeta ^{(rc)}_{i+1}=1/r$
for all
$\zeta ^{(rc)}_i-\zeta ^{(rc)}_{i+1}=1/r$
for all
![]() $1\leq i\leq {rc}-1$
.
$1\leq i\leq {rc}-1$
.
Consider the following multiresidue of the series at the point (3.36),
 $$ \begin{align} E_{-1}(g;\xi)= \lim\limits_{\boldsymbol{\zeta}\to\boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{rc-1}(r(\zeta_i-\zeta_{i+1})-1)E(g;\xi,\boldsymbol{\zeta}). \end{align} $$
$$ \begin{align} E_{-1}(g;\xi)= \lim\limits_{\boldsymbol{\zeta}\to\boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{rc-1}(r(\zeta_i-\zeta_{i+1})-1)E(g;\xi,\boldsymbol{\zeta}). \end{align} $$
As we explain in the proof of Theorem 53 below, our assumptions imply that this limit is finite. Let
![]() $\mathcal {L}_{\tau ,c}$
denote the residual representation generated by the functions
$\mathcal {L}_{\tau ,c}$
denote the residual representation generated by the functions
![]() $E_{-1}(\cdot ;\xi )$
, it is a genuine automorphic representation of
$E_{-1}(\cdot ;\xi )$
, it is a genuine automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}})$
. Recall that for the notion of automorphic representations of
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}})$
. Recall that for the notion of automorphic representations of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}})$
we identify
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}})$
we identify
![]() $\operatorname {\mathrm {GL}}_{rkc}(F)$
with its image under the splitting
$\operatorname {\mathrm {GL}}_{rkc}(F)$
with its image under the splitting
![]() $g\mapsto \langle g,(\eta _{rkc}^{\diamondsuit })^{-1}(g)\rangle $
.
$g\mapsto \langle g,(\eta _{rkc}^{\diamondsuit })^{-1}(g)\rangle $
.
For any
![]() $d\geq 1$
, let
$d\geq 1$
, let
![]() $C_{d}=\{xI_d:x\in \mathbb {A}^{*r}\}$
. Then
$C_{d}=\{xI_d:x\in \mathbb {A}^{*r}\}$
. Then
![]() $\widetilde {C}_{d}$
is the center of
$\widetilde {C}_{d}$
is the center of
![]() $\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
(see § 2.7). For a genuine unitary character
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
(see § 2.7). For a genuine unitary character
![]() $\varrho $
of
$\varrho $
of
![]() $\widetilde {C}_{rkc}(\mathbb {A})$
which is trivial on the subgroup of elements
$\widetilde {C}_{rkc}(\mathbb {A})$
which is trivial on the subgroup of elements
![]() $\langle xI_{rkc},(\eta _{rkc}^{\diamondsuit })^{-1}(xI_{rkc})\rangle $
with
$\langle xI_{rkc},(\eta _{rkc}^{\diamondsuit })^{-1}(xI_{rkc})\rangle $
with
![]() $x\in F^{*r}$
, let
$x\in F^{*r}$
, let
![]() $L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A}),\varrho )$
be the space of genuine square-integrable automorphic forms which translate by
$L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A}),\varrho )$
be the space of genuine square-integrable automorphic forms which translate by
![]() $\varrho $
on
$\varrho $
on
![]() $\widetilde {C}_{rkc}$
.
$\widetilde {C}_{rkc}$
.
Let
![]() $\varrho _{\tau }$
be the central character of
$\varrho _{\tau }$
be the central character of
![]() $\tau $
. Since
$\tau $
. Since
![]() $C_{rkc}<C_{rc}\times \ldots \times C_{rc}$
, the representation
$C_{rkc}<C_{rc}\times \ldots \times C_{rc}$
, the representation
![]() $\mathcal {L}_{\tau ,c}$
admits a central character, which is
$\mathcal {L}_{\tau ,c}$
admits a central character, which is
![]() $\varrho _{\tau }^{rc}$
.
$\varrho _{\tau }^{rc}$
.
Theorem 53. The limit (3.37) is finite. The genuine automorphic representation
![]() $\mathcal {L}_{\tau ,c}$
lies in the discrete spectrum of
$\mathcal {L}_{\tau ,c}$
lies in the discrete spectrum of
![]() $L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}}),\varrho _{\tau }^{rc})$
, and
$L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}}),\varrho _{\tau }^{rc})$
, and
![]() $\mathcal {L}_{\tau ,1}$
is irreducible. Furthermore, for any irreducible subrepresentation
$\mathcal {L}_{\tau ,1}$
is irreducible. Furthermore, for any irreducible subrepresentation
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() $\mathcal {L}_{\tau ,c}$
(
$\mathcal {L}_{\tau ,c}$
(
![]() $c\geq 1$
),
$c\geq 1$
),
![]() $\mathcal {E}=\otimes ^{\prime }_\nu \,\mathcal {E}_\nu $
, where for all
$\mathcal {E}=\otimes ^{\prime }_\nu \,\mathcal {E}_\nu $
, where for all
![]() $\nu $
,
$\nu $
,
![]() $\mathcal {E}_{\nu }$
is an irreducible subrepresentation of
$\mathcal {E}_{\nu }$
is an irreducible subrepresentation of
and a quotient of
and for almost all
![]() $\nu $
,
$\nu $
,
![]() $\mathcal {E}_{\nu }$
is the unique irreducible unramified subrepresentation (resp., quotient) of the representation (3.38) (resp., (3.39)).
$\mathcal {E}_{\nu }$
is the unique irreducible unramified subrepresentation (resp., quotient) of the representation (3.38) (resp., (3.39)).
Proof. The proof follows from the computation of the constant term along
![]() $V_{(k^{rc})}$
, which in the linear case was carried out by Jacquet [Reference JacquetJac84, § 2.1–2.4]. Suzuki [Reference SuzukiSuz98, § 8] extended the result of [Reference JacquetJac84] to coverings of [Reference Kazhdan and PattersonKP84] under certain restrictions (see also [Reference Kazhdan and PattersonKP84, Reference GaoGao18b]).
$V_{(k^{rc})}$
, which in the linear case was carried out by Jacquet [Reference JacquetJac84, § 2.1–2.4]. Suzuki [Reference SuzukiSuz98, § 8] extended the result of [Reference JacquetJac84] to coverings of [Reference Kazhdan and PattersonKP84] under certain restrictions (see also [Reference Kazhdan and PattersonKP84, Reference GaoGao18b]).
Briefly, according to [Reference Mœglin and WaldspurgerMW95, § II.1.7], the constant term of
![]() $E(g;\xi ,\boldsymbol {\zeta })$
along
$E(g;\xi ,\boldsymbol {\zeta })$
along
![]() $V_{(k^{rc})}$
is the sum of images of intertwining operators
$V_{(k^{rc})}$
is the sum of images of intertwining operators
![]() $M(w,\boldsymbol {\zeta })$
, where w is a representative in
$M(w,\boldsymbol {\zeta })$
, where w is a representative in
![]() $\operatorname {\mathrm {GL}}_{rkc}(F)$
of an element of
$\operatorname {\mathrm {GL}}_{rkc}(F)$
of an element of
![]() $W_{\operatorname {\mathrm {GL}}_{rkc}}$
such that
$W_{\operatorname {\mathrm {GL}}_{rkc}}$
such that
![]() ${}^wM_{(k^{rc})}=M_{(k^{rc})}$
, and
${}^wM_{(k^{rc})}=M_{(k^{rc})}$
, and
![]() $M(w,\boldsymbol {\zeta })$
is given by the meromorphic continuation of the integral
$M(w,\boldsymbol {\zeta })$
is given by the meromorphic continuation of the integral
 $$ \begin{align*} M(w,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta})=\int\limits_{({}^w(V_{(k^{rc})}(\mathbb{A}))\cap V_{(k^{rc})}(\mathbb{A}))\backslash V_{(k^{rc})}(\mathbb{A})}\xi(\langle w,(\eta_{rkc}^{\diamondsuit})^{-1}(w)\rangle^{-1}\langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle g,\boldsymbol{\zeta})\,du. \end{align*} $$
$$ \begin{align*} M(w,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta})=\int\limits_{({}^w(V_{(k^{rc})}(\mathbb{A}))\cap V_{(k^{rc})}(\mathbb{A}))\backslash V_{(k^{rc})}(\mathbb{A})}\xi(\langle w,(\eta_{rkc}^{\diamondsuit})^{-1}(w)\rangle^{-1}\langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle g,\boldsymbol{\zeta})\,du. \end{align*} $$
By Conjecture 50, the poles of these operators are of global origin and are contained in the poles of quotients of partial L-functions
 $$ \begin{align*} \frac{L^S_{\vartheta,\vartheta^{-1}}(r(\zeta_i-\zeta_j),\tau\times\tau^{\vee})} {L^S_{\vartheta,\vartheta^{-1}}(r(\zeta_i-\zeta_j)+1,\tau\times\tau^{\vee})}. \end{align*} $$
$$ \begin{align*} \frac{L^S_{\vartheta,\vartheta^{-1}}(r(\zeta_i-\zeta_j),\tau\times\tau^{\vee})} {L^S_{\vartheta,\vartheta^{-1}}(r(\zeta_i-\zeta_j)+1,\tau\times\tau^{\vee})}. \end{align*} $$
As in the linear case, these quotients are determined directly from the Gindikin–Karpelevich formula (2.76) (which is applicable also when
![]() $\mu _{2m}\not \subset F^{*}$
; see the discussion following Equation (2.76)). Using Conjecture 51 we see that all of these intertwining operators are holomorphic at the point (3.36), except the one corresponding to
$\mu _{2m}\not \subset F^{*}$
; see the discussion following Equation (2.76)). Using Conjecture 51 we see that all of these intertwining operators are holomorphic at the point (3.36), except the one corresponding to
Now, Conjecture 51 also implies that
 $$ \begin{align*} \lim\limits_{\boldsymbol{\zeta}\to \boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{{rc}-1}(r(\zeta_i-\zeta_{i+1})-1)M(w_0,\boldsymbol{\zeta})\xi \end{align*} $$
$$ \begin{align*} \lim\limits_{\boldsymbol{\zeta}\to \boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{{rc}-1}(r(\zeta_i-\zeta_{i+1})-1)M(w_0,\boldsymbol{\zeta})\xi \end{align*} $$
is finite and nonzero. When we take the limit (3.37),
 $$ \begin{align} \int\limits_{V_{(k^{rc})}(F)\backslash V_{(k^{rc})}(\mathbb{A})}E_{-1}(\langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle g;\xi)\,du=\lim\limits_{\boldsymbol{\zeta}\to \boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{{rc}-1}(r(\zeta_i-\zeta_{i+1})-1)M(w_0,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta}) \end{align} $$
$$ \begin{align} \int\limits_{V_{(k^{rc})}(F)\backslash V_{(k^{rc})}(\mathbb{A})}E_{-1}(\langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle g;\xi)\,du=\lim\limits_{\boldsymbol{\zeta}\to \boldsymbol{\zeta}^{(rc)}}\prod_{i=1}^{{rc}-1}(r(\zeta_i-\zeta_{i+1})-1)M(w_0,\boldsymbol{\zeta})\xi(g,\boldsymbol{\zeta}) \end{align} $$
and it follows that the limit (3.37) is finite and nonzero. By applying Jacquet’s criterion as stated in [Reference Mœglin and WaldspurgerMW95, Lemma I.4.11], we deduce that the automorphic forms
![]() $E_{-1}(\cdot ;\xi )$
are square-integrable, and it also follows that
$E_{-1}(\cdot ;\xi )$
are square-integrable, and it also follows that
![]() $\mathcal {L}_{\tau ,c}$
belongs to the discrete spectrum of
$\mathcal {L}_{\tau ,c}$
belongs to the discrete spectrum of
![]() $L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}}),\varrho _{\tau }^{rc})$
.
$L^2(\operatorname {\mathrm {GL}}_{rkc}(F)\backslash \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}({\mathbb {A}}),\varrho _{\tau }^{rc})$
.
Note that
![]() $\mathcal {L}_{\tau ,1}$
is irreducible, because for
$\mathcal {L}_{\tau ,1}$
is irreducible, because for
![]() $r>1$
, the image of
$r>1$
, the image of
![]() $M(w_0,\boldsymbol {\zeta })$
at
$M(w_0,\boldsymbol {\zeta })$
at
![]() $\boldsymbol {\zeta }^{(r)}$
is irreducible by Conjecture 50 (in this case
$\boldsymbol {\zeta }^{(r)}$
is irreducible by Conjecture 50 (in this case
![]() $w_0$
is
$w_0$
is
![]() $w_r$
defined above).
$w_r$
defined above).
According to Equation (3.40), the application of the constant term yields an embedding of
![]() $\mathcal {L}_{\tau ,c}$
into the image of
$\mathcal {L}_{\tau ,c}$
into the image of
![]() $M(w_0,\boldsymbol {\zeta })$
. Thus, each local component
$M(w_0,\boldsymbol {\zeta })$
. Thus, each local component
![]() $(\mathcal {L}_{\tau ,c})_{\nu }$
is embedded in the representation (3.38), and at almost all places
$(\mathcal {L}_{\tau ,c})_{\nu }$
is embedded in the representation (3.38), and at almost all places
![]() $(\mathcal {L}_{\tau ,c})_{\nu }$
and (3.38) contain an unramified constituent. Since
$(\mathcal {L}_{\tau ,c})_{\nu }$
and (3.38) contain an unramified constituent. Since
![]() $\mathcal {E}_{\nu }$
is irreducible and embeds in (3.38), at almost all places it is the unique irreducible unramified subrepresentation of (3.38). Similar reasoning applies to the assertion on the quotient of the representation (3.39).
$\mathcal {E}_{\nu }$
is irreducible and embeds in (3.38), at almost all places it is the unique irreducible unramified subrepresentation of (3.38). Similar reasoning applies to the assertion on the quotient of the representation (3.39).
We construct a coarse
![]() $(rk,c)$
representation, or an
$(rk,c)$
representation, or an
![]() $(rk,c)$
representation, from
$(rk,c)$
representation, from
![]() $\mathcal {L}_{\tau ,c}$
.
$\mathcal {L}_{\tau ,c}$
.
Theorem 54. The representation
![]() $\mathcal {L}_{\tau ,c}$
has at least one irreducible
$\mathcal {L}_{\tau ,c}$
has at least one irreducible
![]() $(rk,c)$
subrepresentation
$(rk,c)$
subrepresentation
![]() $\mathcal {E}_{\tau }$
which is a coarse
$\mathcal {E}_{\tau }$
which is a coarse
![]() $(rk,c)$
representation. Moreover, if
$(rk,c)$
representation. Moreover, if
![]() $\mu _{2m}\subset F^{*}$
, then
$\mu _{2m}\subset F^{*}$
, then
![]() $\mathcal {E}_{\tau }$
is an
$\mathcal {E}_{\tau }$
is an
![]() $(rk,c)$
representation.
$(rk,c)$
representation.
Proof. Let
![]() $\mathcal {E}$
be any irreducible subrepresentation of
$\mathcal {E}$
be any irreducible subrepresentation of
![]() $\mathcal {L}_{\tau ,c}$
. Assume for now that
$\mathcal {L}_{\tau ,c}$
. Assume for now that
![]() $\mu _{2m}\subset F^{*}$
. First, consider the local setting. By Theorem 53, at almost all places
$\mu _{2m}\subset F^{*}$
. First, consider the local setting. By Theorem 53, at almost all places
![]() $\nu $
,
$\nu $
,
![]() $\mathcal {E}_{\nu }$
is an irreducible unramified subrepresentation of (3.38). Also, assume that
$\mathcal {E}_{\nu }$
is an irreducible unramified subrepresentation of (3.38). Also, assume that
![]() $\tau _{\nu }$
is the genuine irreducible unramified constituent of
$\tau _{\nu }$
is the genuine irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. By transitivity of induction, (3.38) is a genuine unramified constituent of a principal series representation, and when we permute the inducing characters of
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. By transitivity of induction, (3.38) is a genuine unramified constituent of a principal series representation, and when we permute the inducing characters of
![]() $\tau _{\nu }$
in this full induced representation and use the formula for
$\tau _{\nu }$
in this full induced representation and use the formula for
![]() $\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}$
, we obtain the representation (3.7):
$\delta _{B_{\operatorname {\mathrm {GL}}_{rc}}}$
, we obtain the representation (3.7):
By [Reference Bernstein and ZelevinskyBZ77, Theorem 2.9],
![]() $\mathcal {E}_{\nu }$
is the unique irreducible unramified constituent of (3.7). The representation
$\mathcal {E}_{\nu }$
is the unique irreducible unramified constituent of (3.7). The representation
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is also an unramified constituent (a subrepresentation) of (3.7); see § 3.2. Therefore,
$\Theta _{rc,m,r,\vartheta }(\chi )$
is also an unramified constituent (a subrepresentation) of (3.7); see § 3.2. Therefore,
![]() $\mathcal {E}_{\nu }$
is a constituent of
$\mathcal {E}_{\nu }$
is a constituent of
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
. Since the Jacquet functor is exact, by Proposition 41 (which uses the assumption
$\Theta _{rc,m,r,\vartheta }(\chi )$
. Since the Jacquet functor is exact, by Proposition 41 (which uses the assumption
![]() $\mu _{2m}\subset F_{\nu }^{*}$
) we have
$\mu _{2m}\subset F_{\nu }^{*}$
) we have
![]() $\mathcal {O}(\mathcal {E}_{\nu },\beta ,\psi _\nu )=0$
for any
$\mathcal {O}(\mathcal {E}_{\nu },\beta ,\psi _\nu )=0$
for any
![]() $\beta \succsim ((rk)^{c})$
, and
$\beta \succsim ((rk)^{c})$
, and
![]() $\dim \mathcal {O}(\mathcal {E}_\nu ,((rk)^c),\psi _\nu )\leq 1$
.
$\dim \mathcal {O}(\mathcal {E}_\nu ,((rk)^c),\psi _\nu )\leq 1$
.
Thus, far we have not assumed anything on
![]() $\mathcal {E}$
. Next, we show that Integral (2.87) with
$\mathcal {E}$
. Next, we show that Integral (2.87) with
![]() $\lambda =((rk)^c)$
is not identically zero on
$\lambda =((rk)^c)$
is not identically zero on
![]() $\mathcal {L}_{\tau ,c}$
. For
$\mathcal {L}_{\tau ,c}$
. For
![]() $c=1$
, this is proved by adapting the argument of Friedberg and Ginzburg [Reference Friedberg and GinzburgFG17, Theorem 1] (using the irreducibility assumption of Conjecture 50 for all
$c=1$
, this is proved by adapting the argument of Friedberg and Ginzburg [Reference Friedberg and GinzburgFG17, Theorem 1] (using the irreducibility assumption of Conjecture 50 for all
![]() $1<l\leq r$
). Assume
$1<l\leq r$
). Assume
![]() $c>1$
. We claim that
$c>1$
. We claim that
 $$ \begin{align} \int\limits_{N_{\operatorname{\mathrm{GL}}_{rkc}}(F)\backslash N_{\operatorname{\mathrm{GL}}_{rkc}}(\mathbb{A})} E_{-1}( \langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle;\xi)\psi_{((rk)^c)}(u)\,du\neq 0 \end{align} $$
$$ \begin{align} \int\limits_{N_{\operatorname{\mathrm{GL}}_{rkc}}(F)\backslash N_{\operatorname{\mathrm{GL}}_{rkc}}(\mathbb{A})} E_{-1}( \langle u,(\eta_{rkc}^{\diamondsuit})^{-1}(u)\rangle;\xi)\psi_{((rk)^c)}(u)\,du\neq 0 \end{align} $$
for some
![]() $\xi $
. By definition
$\xi $
. By definition
![]() $\psi _{((rk)^c)}$
is trivial on
$\psi _{((rk)^c)}$
is trivial on
![]() $V_{((rk)^c)}$
(see § 2.13), hence Integral (3.41) factors through the constant term along
$V_{((rk)^c)}$
(see § 2.13), hence Integral (3.41) factors through the constant term along
![]() $V_{((rk)^c)}$
. This constant term can be computed as in the proof of Theorem 53, and we deduce that the mapping
$V_{((rk)^c)}$
. This constant term can be computed as in the proof of Theorem 53, and we deduce that the mapping
 $$ \begin{align*} b\mapsto \int\limits_{V_{((rk)^c)}(F)\backslash V_{((rk)^c)}(\mathbb{A})} &E_{-1}(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle b;\xi)\,dv,\qquad b\in \widetilde{M}_{((rk)^c)}(\mathbb{A}) \end{align*} $$
$$ \begin{align*} b\mapsto \int\limits_{V_{((rk)^c)}(F)\backslash V_{((rk)^c)}(\mathbb{A})} &E_{-1}(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle b;\xi)\,dv,\qquad b\in \widetilde{M}_{((rk)^c)}(\mathbb{A}) \end{align*} $$
belongs to the space of
![]() $\mathcal {L}_{\tau ,1}\otimes \ldots \otimes \mathcal {L}_{\tau ,1}$
(c times). For more details, see [Reference Jiang and LiuJL13, Lemma 4.1], where the constant term of
$\mathcal {L}_{\tau ,1}\otimes \ldots \otimes \mathcal {L}_{\tau ,1}$
(c times). For more details, see [Reference Jiang and LiuJL13, Lemma 4.1], where the constant term of
![]() $E_{-1}(g;\xi )$
in the linear case was computed along any
$E_{-1}(g;\xi )$
in the linear case was computed along any
![]() $V_{(lk,(c-l)k)}$
with
$V_{(lk,(c-l)k)}$
with
![]() $0<l<c$
.
$0<l<c$
.
Now, we note that
![]() $N_{\operatorname {\mathrm {GL}}_{rkc}}=(M_{((rk)^c)}\cap N_{\operatorname {\mathrm {GL}}_{rkc}})\ltimes V_{((rk)^c)}$
,
$N_{\operatorname {\mathrm {GL}}_{rkc}}=(M_{((rk)^c)}\cap N_{\operatorname {\mathrm {GL}}_{rkc}})\ltimes V_{((rk)^c)}$
,
![]() $M_{((rk)^c)}\cap N_{\operatorname {\mathrm {GL}}_{rkc}}$
is the direct product of c copies of
$M_{((rk)^c)}\cap N_{\operatorname {\mathrm {GL}}_{rkc}}$
is the direct product of c copies of
![]() $N_{\operatorname {\mathrm {GL}}_{rk}}$
, and
$N_{\operatorname {\mathrm {GL}}_{rk}}$
, and
![]() $\psi _{((rk)^c)}$
is the product of the
$\psi _{((rk)^c)}$
is the product of the
![]() $(rk,1)$
characters on each these copies. Therefore, the integral (3.41) becomes the product of c applications of Integral (2.87) with
$(rk,1)$
characters on each these copies. Therefore, the integral (3.41) becomes the product of c applications of Integral (2.87) with
![]() $\lambda =(rk)$
on vectors in the space of
$\lambda =(rk)$
on vectors in the space of
![]() $\mathcal {L}_{\tau ,1}$
, each of these is nonzero by the case
$\mathcal {L}_{\tau ,1}$
, each of these is nonzero by the case
![]() $c=1$
.
$c=1$
.
Since by Theorem 53 the representation
![]() $\mathcal {L}_{\tau ,1}$
is irreducible, we can conclude that Integral (2.87) with
$\mathcal {L}_{\tau ,1}$
is irreducible, we can conclude that Integral (2.87) with
![]() $\lambda =((rk)^c)$
is nonzero on
$\lambda =((rk)^c)$
is nonzero on
![]() $\mathcal {L}_{\tau ,c}$
, and we let
$\mathcal {L}_{\tau ,c}$
, and we let
![]() $\mathcal {E}_{\tau }$
be an irreducible subrepresentation of
$\mathcal {E}_{\tau }$
be an irreducible subrepresentation of
![]() $\mathcal {L}_{\tau ,c}$
on which this semi-Whittaker coefficient is nonzero. As explained above, for almost all
$\mathcal {L}_{\tau ,c}$
on which this semi-Whittaker coefficient is nonzero. As explained above, for almost all
![]() $\nu $
,
$\nu $
,
![]() $\mathcal {O}((\mathcal {E}_{\tau })_{\nu },\beta ,\psi _{\nu })=0$
for any
$\mathcal {O}((\mathcal {E}_{\tau })_{\nu },\beta ,\psi _{\nu })=0$
for any
![]() $\beta \succsim ((rk)^{c})$
, then by Lemma 32,
$\beta \succsim ((rk)^{c})$
, then by Lemma 32,
![]() $J_{N_{\operatorname {\mathrm {GL}}_{rkc}},(\psi _{\nu })_{\lambda }}((\mathcal {E}_{\tau })_{\nu })=0$
for all
$J_{N_{\operatorname {\mathrm {GL}}_{rkc}},(\psi _{\nu })_{\lambda }}((\mathcal {E}_{\tau })_{\nu })=0$
for all
![]() $\lambda \succsim ((rk)^c)$
. Hence,
$\lambda \succsim ((rk)^c)$
. Hence,
![]() $\mathcal {E}_{\tau }$
does not support any semi-Whittaker functionals with respect to
$\mathcal {E}_{\tau }$
does not support any semi-Whittaker functionals with respect to
![]() $\lambda \succsim ((rk)^c)$
(local vanishing implies global). Now, we can conclude from Lemma 31 that
$\lambda \succsim ((rk)^c)$
(local vanishing implies global). Now, we can conclude from Lemma 31 that
![]() $\mathcal {O}(\mathcal {E}_{\tau },((rk)^c),\psi )\ne 0$
. This immediately implies that
$\mathcal {O}(\mathcal {E}_{\tau },((rk)^c),\psi )\ne 0$
. This immediately implies that
![]() $\dim \mathcal {O}((\mathcal {E}_{\tau })_{\nu },((rk)^c),\psi _{\nu })>0$
for all the local components of
$\dim \mathcal {O}((\mathcal {E}_{\tau })_{\nu },((rk)^c),\psi _{\nu })>0$
for all the local components of
![]() $\mathcal {E}_{\tau }$
. Thus, for almost all
$\mathcal {E}_{\tau }$
. Thus, for almost all
![]() $\nu $
, or more precisely for all the unramified components
$\nu $
, or more precisely for all the unramified components
![]() $(\mathcal {E}_{\tau })_{\nu }$
of
$(\mathcal {E}_{\tau })_{\nu }$
of
![]() $\mathcal {E}_{\tau }$
,
$\mathcal {E}_{\tau }$
,
![]() $(\mathcal {E}_{\tau })_{\nu }$
is
$(\mathcal {E}_{\tau })_{\nu }$
is
![]() $(rk,c)$
, and also
$(rk,c)$
, and also
![]() $\mathcal {E}_{\tau }$
is
$\mathcal {E}_{\tau }$
is
![]() $(rk,c)$
(
$(rk,c)$
(
![]() $\mathcal {O}(\mathcal {E}_{\tau },\beta ,\psi )=0$
for
$\mathcal {O}(\mathcal {E}_{\tau },\beta ,\psi )=0$
for
![]() $\beta \succsim ((rk)^{c})$
follows from the local assertion).
$\beta \succsim ((rk)^{c})$
follows from the local assertion).
Finally, we consider the case where
![]() $\mu _{2m}\not \subset F^{*}$
. Since there are infinitely many places
$\mu _{2m}\not \subset F^{*}$
. Since there are infinitely many places
![]() $\nu $
such that
$\nu $
such that
![]() $\mu _{2m}\subset F_{\nu }^{*}$
, we still deduce by Proposition 41 that
$\mu _{2m}\subset F_{\nu }^{*}$
, we still deduce by Proposition 41 that
![]() $\mathcal {O}(\mathcal {E}_{\nu },\beta ,\psi _\nu )=0$
for any
$\mathcal {O}(\mathcal {E}_{\nu },\beta ,\psi _\nu )=0$
for any
![]() $\beta \succsim ((rk)^{c})$
and
$\beta \succsim ((rk)^{c})$
and
![]() $\dim \mathcal {O}(\mathcal {E}_\nu ,((rk)^c),\psi _\nu )\leq 1$
, at infinitely many places
$\dim \mathcal {O}(\mathcal {E}_\nu ,((rk)^c),\psi _\nu )\leq 1$
, at infinitely many places
![]() $\nu $
. We take
$\nu $
. We take
![]() $\mathcal {E}_{\tau }$
as above. Then Lemma 32 applied at one place
$\mathcal {E}_{\tau }$
as above. Then Lemma 32 applied at one place
![]() $\nu $
, together with Lemma 31, implies that
$\nu $
, together with Lemma 31, implies that
![]() $\mathcal {O}(\mathcal {E}_{\tau },((rk)^c),\psi )\ne 0$
. Also,
$\mathcal {O}(\mathcal {E}_{\tau },((rk)^c),\psi )\ne 0$
. Also,
![]() $\mathcal {O}(\mathcal {E}_{\tau },\beta ,\psi )=0$
for
$\mathcal {O}(\mathcal {E}_{\tau },\beta ,\psi )=0$
for
![]() $\beta \succsim ((rk)^{c})$
. Therefore, in this case
$\beta \succsim ((rk)^{c})$
. Therefore, in this case
![]() $\mathcal {E}_{\tau }$
is a coarse
$\mathcal {E}_{\tau }$
is a coarse
![]() $(rk,c)$
representation.
$(rk,c)$
representation.
When we combine Theorem 53 with the proof of Theorem 54 we obtain the following corollary.
Corollary 55. Assume
![]() $\mu _{2m}\subset F^{*}$
. Outside finitely many places
$\mu _{2m}\subset F^{*}$
. Outside finitely many places
![]() $\nu $
, the representation (3.38) (resp., (3.39)) contains a unique irreducible unramified subrepresentation (resp., quotient), which is in addition the unique
$\nu $
, the representation (3.38) (resp., (3.39)) contains a unique irreducible unramified subrepresentation (resp., quotient), which is in addition the unique
![]() $(rk,c)$
constituent of a representation
$(rk,c)$
constituent of a representation
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
for some
$\Theta _{rc,m,r,\vartheta }(\chi )$
for some
![]() $\chi $
and
$\chi $
and
![]() $\vartheta $
.
$\vartheta $
.
Proof. The fact that the representation (3.38) contains a unique irreducible unramified subrepresentation was proved in Theorem 53. In the proof of Theorem 54, we deduced that this subrepresentation is a constituent of
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
and is
$\Theta _{rc,m,r,\vartheta }(\chi )$
and is
![]() $(rk,c)$
. Since
$(rk,c)$
. Since
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is also
$\Theta _{rc,m,r,\vartheta }(\chi )$
is also
![]() $(rk,c)$
by Proposition 41, it affords precisely one irreducible
$(rk,c)$
by Proposition 41, it affords precisely one irreducible
![]() $(rk,c)$
constituent by the exactness of the Jacquet functor.
$(rk,c)$
constituent by the exactness of the Jacquet functor.
3.5 The local components of
 $\mathcal {E}_{\tau }$
$\mathcal {E}_{\tau }$
Assume
![]() $\mu _{2m}\subset F^{*}$
. We describe some properties of the local components at the unramified places of the
$\mu _{2m}\subset F^{*}$
. We describe some properties of the local components at the unramified places of the
![]() $(rk,c)$
representation produced by Theorem 54. To avoid confusion, we redenote the genuine unitary irreducible cuspidal automorphic representation of
$(rk,c)$
representation produced by Theorem 54. To avoid confusion, we redenote the genuine unitary irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
by
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
by
![]() $\tau '$
, then the
$\tau '$
, then the
![]() $(rk,c)$
representation is
$(rk,c)$
representation is
![]() $\mathcal {E}_{\tau '}$
. We let
$\mathcal {E}_{\tau '}$
. We let
![]() $\tau =\tau ^{\prime }_{\nu }$
at an unramified place
$\tau =\tau ^{\prime }_{\nu }$
at an unramified place
![]() $\nu $
; in particular, F is unramified.
$\nu $
; in particular, F is unramified.
Assume that
![]() $\tau $
is the unique irreducible unramified constituent of
$\tau $
is the unique irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. Then by Proposition 25,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. Then by Proposition 25,
![]() $\tau ^{*}$
defined by Equation (2.54) is the unique irreducible unramified constituent of
$\tau ^{*}$
defined by Equation (2.54) is the unique irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ^{-1})$
. Put
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ^{-1})$
. Put
![]() $\mathbf {x}=(x_1,\ldots ,x_d)\in \mathbb {C}^d$
,
$\mathbf {x}=(x_1,\ldots ,x_d)\in \mathbb {C}^d$
,
![]() $x_i=\chi _i(\varpi ^r)$
. By Theorem 53,
$x_i=\chi _i(\varpi ^r)$
. By Theorem 53,
![]() $(\mathcal {E}_{\tau '})_{\nu }$
is the unique irreducible unramified subrepresentation of
$(\mathcal {E}_{\tau '})_{\nu }$
is the unique irreducible unramified subrepresentation of
and we denote
![]() $\rho _c(\tau )=(\mathcal {E}_{\tau '})_{\nu }$
. The representation
$\rho _c(\tau )=(\mathcal {E}_{\tau '})_{\nu }$
. The representation
![]() $\rho _c(\tau )$
is irreducible and
$\rho _c(\tau )$
is irreducible and
![]() $(rk,c)$
, hence isomorphic to its
$(rk,c)$
, hence isomorphic to its
![]() $(rk,c)$
model
$(rk,c)$
model
![]() $\mathcal {W}(\rho _c(\tau ))$
.
$\mathcal {W}(\rho _c(\tau ))$
.
If we fix c, we can further assume that for all
![]() $0<l\leq c$
, the representation
$0<l\leq c$
, the representation
 $$ \begin{align*} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \end{align*} $$
contains a unique irreducible unramified subrepresentation
![]() $\rho _l(\tau )$
, which is furthermore an
$\rho _l(\tau )$
, which is furthermore an
![]() $(rk,l)$
representation, so that
$(rk,l)$
representation, so that
![]() $\rho _l(\tau )\cong \mathcal {W}(\rho _l(\tau ))$
. This is because we can apply Corollary 55 for all l in the given range.
$\rho _l(\tau )\cong \mathcal {W}(\rho _l(\tau ))$
. This is because we can apply Corollary 55 for all l in the given range.
Corollary 56. For any
![]() $0<l<c$
, the representation
$0<l<c$
, the representation
![]() $\rho _c(\tau )$
is embedded in
$\rho _c(\tau )$
is embedded in
Proof. By transitivity of induction, the representation (3.42) is contained in
 $$ \begin{align} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkl,rk(c-l))}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}\left( \Big(\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \right. \nonumber\\&\left. \quad \otimes \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{r(c-l)})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rk(c-l)}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{r(c-l)})}}^{-1/(2rk)})\Big) \delta_{P_{(rkl,rk(c-l))}}^{-1/(2rk)}\right). \end{align} $$
$$ \begin{align} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkl,rk(c-l))}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}\left( \Big(\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \right. \nonumber\\&\left. \quad \otimes \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{r(c-l)})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rk(c-l)}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{r(c-l)})}}^{-1/(2rk)})\Big) \delta_{P_{(rkl,rk(c-l))}}^{-1/(2rk)}\right). \end{align} $$
Therefore,
![]() $\rho _c(\tau )$
is the unique irreducible unramified subrepresentation of (3.44). The representation (3.43) is also contained in (3.44) and contains
$\rho _c(\tau )$
is the unique irreducible unramified subrepresentation of (3.44). The representation (3.43) is also contained in (3.44) and contains
![]() $\rho _c(\tau )$
because it is unramified.
$\rho _c(\tau )$
because it is unramified.
Proposition 57. Conjecture 51 implies that
Proof. If
![]() $m\equiv 2\,(4)$
, then since
$m\equiv 2\,(4)$
, then since
![]() $\vartheta $
is unitary, replacing it with the parameter
$\vartheta $
is unitary, replacing it with the parameter
![]() $(\vartheta _{\tau '})_{\nu }$
appearing in Conjecture 51 does not change the condition (3.45). Now, if the condition (3.45) does not hold at a place
$(\vartheta _{\tau '})_{\nu }$
appearing in Conjecture 51 does not change the condition (3.45). Now, if the condition (3.45) does not hold at a place
![]() $\nu $
, applying the conjecture twice, first with a finite set of places S which does not contain
$\nu $
, applying the conjecture twice, first with a finite set of places S which does not contain
![]() $\nu $
, then with
$\nu $
, then with
![]() $S\cup \nu $
, we arrive at a contradiction.
$S\cup \nu $
, we arrive at a contradiction.
By definition
![]() $L_{\vartheta ,\vartheta ^{-1}}(s,\tau \times \tau ^{\vee })=\prod _{1\leq i,j\leq k}(1-q^{-s}\chi _i\chi _j^{-1}(\varpi ^r))^{-1}$
(so if
$L_{\vartheta ,\vartheta ^{-1}}(s,\tau \times \tau ^{\vee })=\prod _{1\leq i,j\leq k}(1-q^{-s}\chi _i\chi _j^{-1}(\varpi ^r))^{-1}$
(so if
![]() $m\equiv 2\,(4)$
, replacing
$m\equiv 2\,(4)$
, replacing
![]() $(\vartheta ,\vartheta ^{-1})$
by some
$(\vartheta ,\vartheta ^{-1})$
by some
![]() $(\vartheta ',\vartheta ")$
means multiplying
$(\vartheta ',\vartheta ")$
means multiplying
![]() $\chi _i\chi _j^{-1}(\varpi ^r)$
by
$\chi _i\chi _j^{-1}(\varpi ^r)$
by
![]() $(o,\varpi ^r)_2$
for some o,
$(o,\varpi ^r)_2$
for some o,
![]() $|o|=1$
). Thus, by the condition (3.45),
$|o|=1$
). Thus, by the condition (3.45),
In particular, the condition (3.21) holds. In fact (3.46) is more natural than (3.21) because the latter only depends on
![]() $\mathbf {x}_{\alpha }$
for positive roots
$\mathbf {x}_{\alpha }$
for positive roots
![]() $\alpha $
, while the Satake parameter is defined up to a permutation.
$\alpha $
, while the Satake parameter is defined up to a permutation.
Proposition 58. If
![]() $\mathbf {x}_{\alpha }\ne 0,q$
for all
$\mathbf {x}_{\alpha }\ne 0,q$
for all
![]() $\alpha \in \Phi _k$
,
$\alpha \in \Phi _k$
,
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible.
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible.
Proof. The result follows from the analog of [Reference CasselmanCas80, Proposition 3.5] for covering groups (
![]() $\mathbf {x}_{\alpha }\ne 0$
for all
$\mathbf {x}_{\alpha }\ne 0$
for all
![]() $\alpha \in \Phi _k$
implies that
$\alpha \in \Phi _k$
implies that
![]() $\chi $
is regular); see the proof in [Reference Frahm and KaplanFK19, Proposition 2.4], which is applicable to
$\chi $
is regular); see the proof in [Reference Frahm and KaplanFK19, Proposition 2.4], which is applicable to
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}$
as well. In more detail,
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}$
as well. In more detail,
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible if and only if
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible if and only if
![]() $M(J_k)$
is an isomorphism which by virtue of Equation (2.76) is equivalent to
$M(J_k)$
is an isomorphism which by virtue of Equation (2.76) is equivalent to
 $$ \begin{align*} \prod_{\alpha\in\Phi_d^+}\frac{1-q^{-1}\mathbf{x}_{\alpha}}{1-\mathbf{x}_{\alpha}} \frac{1-q^{-1}\mathbf{x}_{-\alpha}}{1-\mathbf{x}_{-\alpha}}\ne0. \end{align*} $$
$$ \begin{align*} \prod_{\alpha\in\Phi_d^+}\frac{1-q^{-1}\mathbf{x}_{\alpha}}{1-\mathbf{x}_{\alpha}} \frac{1-q^{-1}\mathbf{x}_{-\alpha}}{1-\mathbf{x}_{-\alpha}}\ne0. \end{align*} $$
This condition holds by our assumption.
Corollary 59. Any
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is well defined and nonzero on
$\Theta _{rc,m,r,\vartheta }(\chi )$
is well defined and nonzero on
![]() $\rho _c(\tau )$
. Moreover,
$\rho _c(\tau )$
. Moreover,
![]() $\mathcal {W}(\rho _c(\tau ))\subset \mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
.
$\mathcal {W}(\rho _c(\tau ))\subset \mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
.
Proof. By Corollary 55, there are
![]() $0\subset V'\subset V\subset \Theta _{rc,m,r,\vartheta }(\chi )$
such that
$0\subset V'\subset V\subset \Theta _{rc,m,r,\vartheta }(\chi )$
such that
![]() $\rho _c(\tau )\cong V'\backslash V$
. Let
$\rho _c(\tau )\cong V'\backslash V$
. Let
![]() $\Lambda $
be an
$\Lambda $
be an
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
. Since
$\Theta _{rc,m,r,\vartheta }(\chi )$
. Since
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is
$\Theta _{rc,m,r,\vartheta }(\chi )$
is
![]() $(rk,c)$
and the Jacquet functor is exact,
$(rk,c)$
and the Jacquet functor is exact,
![]() $\Lambda $
vanishes on
$\Lambda $
vanishes on
![]() $V'$
hence is well defined on
$V'$
hence is well defined on
![]() $\rho _c(\tau )$
. If it vanishes on V, then again by exactness it must already vanish on
$\rho _c(\tau )$
. If it vanishes on V, then again by exactness it must already vanish on
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
. The second assertion follows because with the present notation we can identify
$\Theta _{rc,m,r,\vartheta }(\chi )$
. The second assertion follows because with the present notation we can identify
![]() $\mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
with
$\mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
with
![]() $\mathcal {W}(V'\backslash \Theta _{rc,m,r,\vartheta }(\chi ))$
.
$\mathcal {W}(V'\backslash \Theta _{rc,m,r,\vartheta }(\chi ))$
.
This corollary does not imply
![]() $\mathcal {W}(\rho _c(\tau ))=\mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
(the latter might be reducible).
$\mathcal {W}(\rho _c(\tau ))=\mathcal {W}(\Theta _{rc,m,r,\vartheta }(\chi ))$
(the latter might be reducible).
Proposition 60. Assume that
![]() $\mathbf {x}_{\alpha }\ne q^a$
for all
$\mathbf {x}_{\alpha }\ne q^a$
for all
![]() $\alpha \in \Phi _k^+$
and
$\alpha \in \Phi _k^+$
and
![]() $0\leq a\leq rc$
. Then
$0\leq a\leq rc$
. Then
![]() $\rho _c(\tau )\subset \Theta _{rc,m,r,\vartheta }(\chi )$
.
$\rho _c(\tau )\subset \Theta _{rc,m,r,\vartheta }(\chi )$
.
Proof. By Proposition 58,
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible; in particular,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
is irreducible; in particular,
![]() $\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
so that the representation (3.42) and thereby
$\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
so that the representation (3.42) and thereby
![]() $\rho _c(\tau )$
are subrepresentations of
$\rho _c(\tau )$
are subrepresentations of
 $$ \begin{align} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rc})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkc}}((\mathrm{I}_{\operatorname{\mathrm{GL}}_k^{(m,r)}}(\vartheta,\chi)\otimes \ldots \otimes \mathrm{I}_{\operatorname{\mathrm{GL}}_k^{(m,r)}}(\vartheta,\chi))\delta_{P_{(k^{rc})}}^{-1/(2rk)}) \\&=\notag \operatorname{\mathrm{Ind}}_{\widetilde{B}_{\operatorname{\mathrm{GL}}_{rkc}}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}\left( \operatorname{\mathrm{Ind}}_{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rkc},*}}^{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rkc}}}( (\varepsilon\otimes_{i=1}^{k}\vartheta\chi_i|~|^{-(rc-1)/(2r)})\otimes \ldots \otimes (\varepsilon\otimes_{i=1}^{k}\vartheta\chi_i|~|^{(rc-1)/(2r)}))\right). \end{align} $$
$$ \begin{align} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rc})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkc}}((\mathrm{I}_{\operatorname{\mathrm{GL}}_k^{(m,r)}}(\vartheta,\chi)\otimes \ldots \otimes \mathrm{I}_{\operatorname{\mathrm{GL}}_k^{(m,r)}}(\vartheta,\chi))\delta_{P_{(k^{rc})}}^{-1/(2rk)}) \\&=\notag \operatorname{\mathrm{Ind}}_{\widetilde{B}_{\operatorname{\mathrm{GL}}_{rkc}}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}\left( \operatorname{\mathrm{Ind}}_{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rkc},*}}^{\widetilde{T}_{\operatorname{\mathrm{GL}}_{rkc}}}( (\varepsilon\otimes_{i=1}^{k}\vartheta\chi_i|~|^{-(rc-1)/(2r)})\otimes \ldots \otimes (\varepsilon\otimes_{i=1}^{k}\vartheta\chi_i|~|^{(rc-1)/(2r)}))\right). \end{align} $$
This is an unramified principal series representation. Consider the standard intertwining operator
![]() $M(w)$
on this representation whose image is contained in the representation (3.7). We claim that
$M(w)$
on this representation whose image is contained in the representation (3.7). We claim that
![]() $M(w)$
is well defined, and moreover, it is nonzero on the normalized unramified vector
$M(w)$
is well defined, and moreover, it is nonzero on the normalized unramified vector
![]() $\xi ^0$
of Equation (3.47). Since
$\xi ^0$
of Equation (3.47). Since
![]() $\xi ^0$
also belongs to the space of
$\xi ^0$
also belongs to the space of
![]() $\rho _c(\tau )$
, it will then follow that
$\rho _c(\tau )$
, it will then follow that
![]() $M(w)$
restricts to a nonzero operator on
$M(w)$
restricts to a nonzero operator on
![]() $\rho _c(\tau )$
, which must then be an embedding because
$\rho _c(\tau )$
, which must then be an embedding because
![]() $\rho _c(\tau )$
is irreducible. Because
$\rho _c(\tau )$
is irreducible. Because
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
is also an unramified subrepresentation of (3.7), it contains
$\Theta _{rc,m,r,\vartheta }(\chi )$
is also an unramified subrepresentation of (3.7), it contains
![]() $\rho _c(\tau )$
.
$\rho _c(\tau )$
.
To show that
![]() $M(w)$
is well defined and
$M(w)$
is well defined and
![]() $M(w)\xi ^0\ne 0$
, we argue as in the proof of Theorem 43. Decompose
$M(w)\xi ^0\ne 0$
, we argue as in the proof of Theorem 43. Decompose
![]() $M(w)$
into rank-
$M(w)$
into rank-
![]() $1$
intertwining operators
$1$
intertwining operators
 $$ \begin{align*} M(w_{\alpha}):&\mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta, \chi_j|~|^{-(rc-2l'+1)/(2r)}\otimes\chi_i|~|^{-(rc-2l+1)/(2r)}) \\&\rightarrow \mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta, \chi_i|~|^{-(rc-2l+1)/(2r)}\otimes\chi_j|~|^{-(rc-2l'+1)/(2r)}), \end{align*} $$
$$ \begin{align*} M(w_{\alpha}):&\mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta, \chi_j|~|^{-(rc-2l'+1)/(2r)}\otimes\chi_i|~|^{-(rc-2l+1)/(2r)}) \\&\rightarrow \mathrm{I}_{\operatorname{\mathrm{GL}}_2^{(m,r)}}(\vartheta, \chi_i|~|^{-(rc-2l+1)/(2r)}\otimes\chi_j|~|^{-(rc-2l'+1)/(2r)}), \end{align*} $$
where
![]() $i<j$
and
$i<j$
and
![]() $1\leq l'<l\leq rc$
. Since
$1\leq l'<l\leq rc$
. Since
![]() $q^{-l'+l}\mathbf {x}_{(j,i)}\ne 1,q$
, we deduce that
$q^{-l'+l}\mathbf {x}_{(j,i)}\ne 1,q$
, we deduce that
![]() $M(w_{\alpha })$
is holomorphic and nonzero on the unramified vector (see Equation (2.76)).
$M(w_{\alpha })$
is holomorphic and nonzero on the unramified vector (see Equation (2.76)).
We mention that in the linear case, since
![]() $\tau $
is irreducible unramified and generic, it is a full induced unramified principal series; then since
$\tau $
is irreducible unramified and generic, it is a full induced unramified principal series; then since
![]() $\tau $
is also unitary, we have
$\tau $
is also unitary, we have
![]() $q^{-1/2}<|\chi _i|<q^{1/2}$
for all i by [Reference Jacquet and ShalikaJS81b, Corollary 2.5]; consequently, the linear analog of
$q^{-1/2}<|\chi _i|<q^{1/2}$
for all i by [Reference Jacquet and ShalikaJS81b, Corollary 2.5]; consequently, the linear analog of
![]() $\Theta _{rc,m,r,\vartheta }(\chi )$
which is
$\Theta _{rc,m,r,\vartheta }(\chi )$
which is
![]() $\operatorname {\mathrm {Ind}}_{P_{(c^k)}}^{\operatorname {\mathrm {GL}}_{kc}}(\chi _1\circ \det \otimes \ldots \otimes \chi _k\circ \det )$
, is irreducible ([Reference ZelevinskyZel80, Theorem 4.2]), then this is
$\operatorname {\mathrm {Ind}}_{P_{(c^k)}}^{\operatorname {\mathrm {GL}}_{kc}}(\chi _1\circ \det \otimes \ldots \otimes \chi _k\circ \det )$
, is irreducible ([Reference ZelevinskyZel80, Theorem 4.2]), then this is
![]() $\rho _c(\tau )$
. See [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, § 2.2]. In fact for any
$\rho _c(\tau )$
. See [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, § 2.2]. In fact for any
![]() $m\geq 1$
, if we further take
$m\geq 1$
, if we further take
![]() $\mathbf {x}$
in general position, then by [Reference Kaplan and SzpruchKS23, Theorem 3.8] (the extension of ‘generic irreducibility’ to covering groups)
$\mathbf {x}$
in general position, then by [Reference Kaplan and SzpruchKS23, Theorem 3.8] (the extension of ‘generic irreducibility’ to covering groups)
![]() $\Theta _{rl,m,r,\vartheta }(\chi )$
is irreducible so that
$\Theta _{rl,m,r,\vartheta }(\chi )$
is irreducible so that
![]() $\rho _l(\tau )=\Theta _{rl,m,r,\vartheta }(\chi )$
. The results of this section now hold unconditionally. Indeed, the only nontrivial result is now Corollary 56. To this end, because for the normalized Jacquet functor
$\rho _l(\tau )=\Theta _{rl,m,r,\vartheta }(\chi )$
. The results of this section now hold unconditionally. Indeed, the only nontrivial result is now Corollary 56. To this end, because for the normalized Jacquet functor
(see [Reference KableKab01, Theorem 5.1], the proof here is simpler), and since
![]() $\Theta _{rc,m,r,\vartheta }$
is irreducible,
$\Theta _{rc,m,r,\vartheta }$
is irreducible,
Denote the r.h.s. by
![]() $\Theta [rl,r(c-l)]$
, then
$\Theta [rl,r(c-l)]$
, then
 $$ \begin{align} \Theta_{rc,m,r,\vartheta}(\chi)\subset \operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}(\chi_1\Theta[rl,r(c-l)]\otimes\ldots\otimes\chi_k\Theta[rl,r(c-l)]). \end{align} $$
$$ \begin{align} \Theta_{rc,m,r,\vartheta}(\chi)\subset \operatorname{\mathrm{Ind}}_{\widetilde{P}_{((rc)^k)}}^{\operatorname{\mathrm{GL}}_{rkc}^{(m,r)}}(\chi_1\Theta[rl,r(c-l)]\otimes\ldots\otimes\chi_k\Theta[rl,r(c-l)]). \end{align} $$
When we regard
![]() $\Theta [rl,r(c-l)]$
as a subrepresentation of an unramified principal series representation, we can apply an intertwining operator
$\Theta [rl,r(c-l)]$
as a subrepresentation of an unramified principal series representation, we can apply an intertwining operator
![]() $M(w)$
to permute the inducing data of the r.h.s. of the embedding (3.48), only involving blocks corresponding to
$M(w)$
to permute the inducing data of the r.h.s. of the embedding (3.48), only involving blocks corresponding to
![]() $\chi _i$
and
$\chi _i$
and
![]() $\chi _j$
for
$\chi _j$
for
![]() $i\ne j$
. This operator will be an isomorphism (see the proofs of Propositions 58 and 60) so that
$i\ne j$
. This operator will be an isomorphism (see the proofs of Propositions 58 and 60) so that
3.6 Local decomposition of
 $(rk,c)$
functionals
$(rk,c)$
functionals
We proceed with the notation and assumptions of § 3.5. In particular, the condition (3.45) holds. In this section, we construct an
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\rho _c(\tau )$
inductively. We use the
$\rho _c(\tau )$
inductively. We use the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\sigma ^{\diamondsuit }_{rkc}$
. We will repeatedly use the fact that
$\sigma ^{\diamondsuit }_{rkc}$
. We will repeatedly use the fact that
![]() $b\mapsto \langle b,1\rangle $
is a splitting for both
$b\mapsto \langle b,1\rangle $
is a splitting for both
![]() $N_{\operatorname {\mathrm {GL}}_{rkc}}$
and the subgroup of permutation matrices in
$N_{\operatorname {\mathrm {GL}}_{rkc}}$
and the subgroup of permutation matrices in
![]() $\operatorname {\mathrm {GL}}_{rkc}$
(for the latter, because
$\operatorname {\mathrm {GL}}_{rkc}$
(for the latter, because
![]() $\mu _{2m}\subset F^{*}$
), and also recall that
$\mu _{2m}\subset F^{*}$
), and also recall that
![]() $\langle y,\eta _{rkc}^{\diamondsuit }(y)\rangle $
is the chosen splitting for
$\langle y,\eta _{rkc}^{\diamondsuit }(y)\rangle $
is the chosen splitting for
![]() $K_{\operatorname {\mathrm {GL}}_{rkc}}$
(see § 2.7).
$K_{\operatorname {\mathrm {GL}}_{rkc}}$
(see § 2.7).
Since the condition (3.21) holds, Theorem 43 implies that the Jacquet integral
![]() $\Lambda $
(see § 2.9) is an
$\Lambda $
(see § 2.9) is an
![]() $(rk,1)$
functional on
$(rk,1)$
functional on
![]() $\Theta _{r,m,r,\vartheta }(\chi )$
, thereby on
$\Theta _{r,m,r,\vartheta }(\chi )$
, thereby on
![]() $\rho _1(\tau )$
by Corollary 59.
$\rho _1(\tau )$
by Corollary 59.
Fix
![]() $0<l<c$
. By Corollary 56,
$0<l<c$
. By Corollary 56,
![]() $\rho _c(\tau )$
is a subrepresentation of the representation (3.43):
$\rho _c(\tau )$
is a subrepresentation of the representation (3.43):
We construct an
![]() $(rk,c)$
functional on (3.43) and prove that it does not vanish on
$(rk,c)$
functional on (3.43) and prove that it does not vanish on
![]() $\rho _c(\tau )$
, hence can be used to realize
$\rho _c(\tau )$
, hence can be used to realize
![]() $\mathcal {W}(\rho _c(\tau ))$
. Set
$\mathcal {W}(\rho _c(\tau ))$
. Set
 $$ \begin{align*} &\kappa=\kappa_{l,c-l}=\left(\begin{smallmatrix}I_l\\0&0&I_l\\0&0&0&0&I_l&\ddots\\&&&&&&I_l&0\\ 0&I_{c-l}\\ 0&0&0&I_{c-l}&&\ddots\\&&&&&&&I_{c-l}\end{smallmatrix}\right)\in\operatorname{\mathrm{GL}}_{rkc}\qquad (I_l \text{ and } I_{c-l} \text{ each appears } rk \text{ times}). \end{align*} $$
$$ \begin{align*} &\kappa=\kappa_{l,c-l}=\left(\begin{smallmatrix}I_l\\0&0&I_l\\0&0&0&0&I_l&\ddots\\&&&&&&I_l&0\\ 0&I_{c-l}\\ 0&0&0&I_{c-l}&&\ddots\\&&&&&&&I_{c-l}\end{smallmatrix}\right)\in\operatorname{\mathrm{GL}}_{rkc}\qquad (I_l \text{ and } I_{c-l} \text{ each appears } rk \text{ times}). \end{align*} $$
For
![]() $v=(v_{i,j})_{1\leq i,j\leq rk}\in V_{(c^{rk})}$
, write each block
$v=(v_{i,j})_{1\leq i,j\leq rk}\in V_{(c^{rk})}$
, write each block
![]() $v_{i,j}\in \text {Mat}_c$
in the form
$v_{i,j}\in \text {Mat}_c$
in the form
 $$ \begin{align} \left(\begin{smallmatrix}v_{i,j}^1&v_{i,j}^2\\v_{i,j}^3&v_{i,j}^4\end{smallmatrix}\right),\qquad v_{i,j}^1\in\text{Mat}_{l},\quad v_{i,j}^4\in\text{Mat}_{c-l}. \end{align} $$
$$ \begin{align} \left(\begin{smallmatrix}v_{i,j}^1&v_{i,j}^2\\v_{i,j}^3&v_{i,j}^4\end{smallmatrix}\right),\qquad v_{i,j}^1\in\text{Mat}_{l},\quad v_{i,j}^4\in\text{Mat}_{c-l}. \end{align} $$
Let
![]() $V_{(c^{rk})}^t<V_{(c^{rk})}$
be the subgroup obtained by deleting the blocks
$V_{(c^{rk})}^t<V_{(c^{rk})}$
be the subgroup obtained by deleting the blocks
![]() $v_{i,j}^{t'}$
for all
$v_{i,j}^{t'}$
for all
![]() $i<j$
and
$i<j$
and
![]() $t'\ne t$
, where
$t'\ne t$
, where
![]() $1\leq t\leq 4$
. Put
$1\leq t\leq 4$
. Put
![]() $V=V^3$
. Consider the following integral for
$V=V^3$
. Consider the following integral for
![]() $\xi $
in the space of (3.43):
$\xi $
in the space of (3.43):
 $$ \begin{align} \int\limits_{V}\xi(\langle \kappa,1\rangle\langle v,1\rangle)\,dv. \end{align} $$
$$ \begin{align} \int\limits_{V}\xi(\langle \kappa,1\rangle\langle v,1\rangle)\,dv. \end{align} $$
Example 61. When
![]() $c=r=k=2$
(then
$c=r=k=2$
(then
![]() $l=1$
),
$l=1$
),
 $$ \begin{align*} &\kappa_{1,1}=\left(\begin{smallmatrix}1\\&&1\\&&&&1\\&&&&&&1\\&1\\&&&1\\&&&&&1\\&&&&&&&1\end{smallmatrix}\right),\qquad V=\left\{\left(\begin{smallmatrix}1&&&&&&\\&1&v_{1,2}^3&&v_{1,3}^3&&v_{1,4}^3& \\&&1&&&&\\&&&1&v_{2,3}^3&&v_{2,4}^3&\\ &&&&1&&&\\&&&&&1&v_{3,4}^3&\\&&&&&&1\\&&&&&&&1\end{smallmatrix}\right)\right\}. \end{align*} $$
$$ \begin{align*} &\kappa_{1,1}=\left(\begin{smallmatrix}1\\&&1\\&&&&1\\&&&&&&1\\&1\\&&&1\\&&&&&1\\&&&&&&&1\end{smallmatrix}\right),\qquad V=\left\{\left(\begin{smallmatrix}1&&&&&&\\&1&v_{1,2}^3&&v_{1,3}^3&&v_{1,4}^3& \\&&1&&&&\\&&&1&v_{2,3}^3&&v_{2,4}^3&\\ &&&&1&&&\\&&&&&1&v_{3,4}^3&\\&&&&&&1\\&&&&&&&1\end{smallmatrix}\right)\right\}. \end{align*} $$
This defines an
![]() $(rk,c)$
functional, at least formally. To see this, first note that
$(rk,c)$
functional, at least formally. To see this, first note that
 $$ \begin{align*} & {}^{\kappa}V^1<\operatorname{\mathrm{diag}}(V_{(l^{rk})},I_{rk(c-l)}),\quad {}^{\kappa}V^2<V_{(rkl,rk(c-l))},\quad {}^{\kappa}V<V_{(rkl,rk(c-l))}^-,\\ &\quad {}^{\kappa}V^4<\operatorname{\mathrm{diag}}(I_{rkl},V_{((c-l)^{rk})}). \end{align*} $$
$$ \begin{align*} & {}^{\kappa}V^1<\operatorname{\mathrm{diag}}(V_{(l^{rk})},I_{rk(c-l)}),\quad {}^{\kappa}V^2<V_{(rkl,rk(c-l))},\quad {}^{\kappa}V<V_{(rkl,rk(c-l))}^-,\\ &\quad {}^{\kappa}V^4<\operatorname{\mathrm{diag}}(I_{rkl},V_{((c-l)^{rk})}). \end{align*} $$
Hence,
![]() $V^1$
and
$V^1$
and
![]() $V^4$
commute, both normalize
$V^4$
commute, both normalize
![]() $V^2$
and V, and the subgroups
$V^2$
and V, and the subgroups
![]() $V^2$
and V are abelian. Also, by Equation (2.10), for
$V^2$
and V are abelian. Also, by Equation (2.10), for
![]() $v^t\in V^t$
with
$v^t\in V^t$
with
![]() $t\ne 3$
,
$t\ne 3$
,
It follows that for
![]() $u=u^1u^4u^2u^3\in V_{(c^{rk})}$
with
$u=u^1u^4u^2u^3\in V_{(c^{rk})}$
with
![]() $u^t\in V^t$
,
$u^t\in V^t$
,
 $$ \begin{align*} \int\limits_{V}\xi(\langle \kappa,1\rangle\langle v,1\rangle\langle u,1\rangle)\,dv =\int\limits_{V}\xi(\langle {}^{\kappa}u_v^1,1\rangle\langle {}^{\kappa}u_v^4,1\rangle\langle {}^{\kappa}u_v^2,1\rangle\langle \kappa,1\rangle\langle v,1\rangle)\,dv. \end{align*} $$
$$ \begin{align*} \int\limits_{V}\xi(\langle \kappa,1\rangle\langle v,1\rangle\langle u,1\rangle)\,dv =\int\limits_{V}\xi(\langle {}^{\kappa}u_v^1,1\rangle\langle {}^{\kappa}u_v^4,1\rangle\langle {}^{\kappa}u_v^2,1\rangle\langle \kappa,1\rangle\langle v,1\rangle)\,dv. \end{align*} $$
Here, we wrote
![]() $vu=(u_v^1u_v^4u_v^2)v_u$
, where
$vu=(u_v^1u_v^4u_v^2)v_u$
, where
![]() $u_v^t\in V^t$
,
$u_v^t\in V^t$
,
![]() $v_u\in V$
, changed variables in
$v_u\in V$
, changed variables in
![]() $v_u$
, and note that since
$v_u$
, and note that since
![]() $\psi $
is a character of
$\psi $
is a character of
![]() $V_{(c^{rk})}$
which is trivial on V,
$V_{(c^{rk})}$
which is trivial on V,
![]() $\psi (u^1u^4u^2)=\psi (u_v^1u_v^4u_v^2)$
.
$\psi (u^1u^4u^2)=\psi (u_v^1u_v^4u_v^2)$
.
The
![]() $(rk,c)$
character restricted to
$(rk,c)$
character restricted to
![]() $V^1$
(resp.,
$V^1$
(resp.,
![]() $V^4$
) coincides with the
$V^4$
) coincides with the
![]() $(rk,l)$
(resp.,
$(rk,l)$
(resp.,
![]() $(rk,c-l)$
) character on
$(rk,c-l)$
) character on
![]() ${}^{\kappa }V^1$
(resp.,
${}^{\kappa }V^1$
(resp.,
![]() ${}^{\kappa }V^4$
), and moreover, the
${}^{\kappa }V^4$
), and moreover, the
![]() $(rk,c)$
character is trivial on
$(rk,c)$
character is trivial on
![]() $V^2$
. Then by the definition of the representation (3.43), vectors in the space of (3.43) transform on the left under
$V^2$
. Then by the definition of the representation (3.43), vectors in the space of (3.43) transform on the left under
![]() $\langle {}^{\kappa }V^t,1\rangle $
by the
$\langle {}^{\kappa }V^t,1\rangle $
by the
![]() $(rk,l)$
character for
$(rk,l)$
character for
![]() $t=1$
,
$t=1$
,
![]() $(rk,c-l)$
character for
$(rk,c-l)$
character for
![]() $t=4$
or trivially for
$t=4$
or trivially for
![]() $t=2$
. Since the
$t=2$
. Since the
![]() $(rk,c)$
character is also trivial on V, we conclude that Integral (3.50) is an
$(rk,c)$
character is also trivial on V, we conclude that Integral (3.50) is an
![]() $(rk,c)$
functional on (3.43).
$(rk,c)$
functional on (3.43).
Proposition 62. The integral (3.50) is absolutely convergent and nonzero on any subrepresentation of (3.43). In particular, it is an
![]() $(rk,c)$
functional on
$(rk,c)$
functional on
![]() $\rho _c(\tau )$
. Moreover, Integral (3.50) is nonzero on any nonzero unramified vector
$\rho _c(\tau )$
. Moreover, Integral (3.50) is nonzero on any nonzero unramified vector
![]() $\xi $
.
$\xi $
.
Proof. The proof is similar to the linear case ([Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Lemma 9]), where we argued using ‘root elimination’ (see, e.g., [Reference GinzburgGin90] and [Reference SoudrySou93, Proposition 6.1]). Here, we focus on the computations that are different for the covering. Let
![]() $X<{}^{\kappa ^{-1}}V_{(rkl,rk(c-l))}$
be the subgroup of matrices x such that the top right
$X<{}^{\kappa ^{-1}}V_{(rkl,rk(c-l))}$
be the subgroup of matrices x such that the top right
![]() $rkl\times rk(c-l)$
block of
$rkl\times rk(c-l)$
block of
![]() ${}^{\kappa }x$
is
${}^{\kappa }x$
is
 $$ \begin{align*} &\left(\begin{smallmatrix} 0&0 &\cdots &0\\ \vdots &x_{1,2}^3 &\ddots &\vdots\\ \vdots &\vdots &\ddots &0\\ 0&x_{1,rk}^3 &\cdots &x_{rk-1,rk}^3\end{smallmatrix}\right),\qquad x_{i,j}^3\in\text{Mat}_{l\times (c-l)}. \end{align*} $$
$$ \begin{align*} &\left(\begin{smallmatrix} 0&0 &\cdots &0\\ \vdots &x_{1,2}^3 &\ddots &\vdots\\ \vdots &\vdots &\ddots &0\\ 0&x_{1,rk}^3 &\cdots &x_{rk-1,rk}^3\end{smallmatrix}\right),\qquad x_{i,j}^3\in\text{Mat}_{l\times (c-l)}. \end{align*} $$
For each pair
![]() $i<j$
, let
$i<j$
, let
![]() $y_{i,j}$
and
$y_{i,j}$
and
![]() $x_{i,j}$
be arbitrary elements of V and X (resp.) such that
$x_{i,j}$
be arbitrary elements of V and X (resp.) such that
![]() $v_{i',j'}^3=0$
and
$v_{i',j'}^3=0$
and
![]() $x_{i',j'}^3=0$
for all
$x_{i',j'}^3=0$
for all
![]() $(i',j')\ne (i,j)$
.
$(i',j')\ne (i,j)$
.
We fix the following ordering on the pairs
![]() $(i,j)$
with
$(i,j)$
with
![]() $i<j$
. The first pair is
$i<j$
. The first pair is
![]() $(rk-1,rk)$
, next
$(rk-1,rk)$
, next
![]() $(rk-2,rk-1),(rk-3,rk-2)\ldots ,(1,2)$
. Then
$(rk-2,rk-1),(rk-3,rk-2)\ldots ,(1,2)$
. Then
![]() $(rk-2,rk),(rk-3,rk-1),\ldots ,(1,3)$
, and so on. The last three pairs are
$(rk-2,rk),(rk-3,rk-1),\ldots ,(1,3)$
, and so on. The last three pairs are
![]() $(2,rk)$
,
$(2,rk)$
,
![]() $(1,rk-1)$
and
$(1,rk-1)$
and
![]() $(1,rk)$
. Write
$(1,rk)$
. Write
![]() $(i',j')<(i,j)$
if
$(i',j')<(i,j)$
if
![]() $(i',j')$
appears after
$(i',j')$
appears after
![]() $(i,j)$
with respect to this ordering. Suppose that we have reached the pair
$(i,j)$
with respect to this ordering. Suppose that we have reached the pair
![]() $(i,j)$
. Then instead of an integral over V, we will integrate over the product of two subgroups: one generated by elements
$(i,j)$
. Then instead of an integral over V, we will integrate over the product of two subgroups: one generated by elements
![]() $y_{i.j}$
, the other denoted
$y_{i.j}$
, the other denoted
![]() $V'$
is generated by elements
$V'$
is generated by elements
![]() $y_{i',j'}$
for all
$y_{i',j'}$
for all
![]() $(i',j')<(i,j)$
.
$(i',j')<(i,j)$
.
Let
![]() $\xi $
be an arbitrary function in the space of the representation (3.43). Observe that for
$\xi $
be an arbitrary function in the space of the representation (3.43). Observe that for
![]() $v'\in V'$
,
$v'\in V'$
,
where
![]() $y_x,l_x\in N_{\operatorname {\mathrm {GL}}_{rkc}}$
,
$y_x,l_x\in N_{\operatorname {\mathrm {GL}}_{rkc}}$
,
![]() $v_{x,y}^{\prime }\in V'$
depends on
$v_{x,y}^{\prime }\in V'$
depends on
![]() $(v',x_{i,j},y_{i,j})$
,
$(v',x_{i,j},y_{i,j})$
,
![]() ${}^{\kappa }y_x\in M_{(rkl,rk(c-l))}\cap N_{\operatorname {\mathrm {GL}}_{rkc}}$
,
${}^{\kappa }y_x\in M_{(rkl,rk(c-l))}\cap N_{\operatorname {\mathrm {GL}}_{rkc}}$
,
![]() $\xi $
transforms on the left under
$\xi $
transforms on the left under
![]() $\langle {}^{\kappa }y_x,1\rangle $
by
$\langle {}^{\kappa }y_x,1\rangle $
by
![]() $\psi (\mathrm {tr}(v_{i,j}^3x_{i,j}^3))$
,
$\psi (\mathrm {tr}(v_{i,j}^3x_{i,j}^3))$
,
![]() ${}^{\kappa }l_x\in N_{\operatorname {\mathrm {GL}}_{rkc}}$
and
${}^{\kappa }l_x\in N_{\operatorname {\mathrm {GL}}_{rkc}}$
and
![]() $\xi $
is left-invariant under
$\xi $
is left-invariant under
![]() $\langle {}^{\kappa }l_x,1\rangle $
. Then by Equations (2.9) and (2.10),
$\langle {}^{\kappa }l_x,1\rangle $
. Then by Equations (2.9) and (2.10),
 $$ \begin{align} \xi(\langle\kappa,1\rangle\,{}^{x_{i,j}}\langle v'y_{i,j},1\rangle)&= \xi(\langle\kappa,1\rangle\langle y_x,1\rangle\langle l_x,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle) \\&=\xi(\langle {}^{\kappa}y_x,1\rangle\langle {}^{\kappa}l_x,1\rangle\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle)\nonumber \\&=\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3))\xi(\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle).\nonumber \end{align} $$
$$ \begin{align} \xi(\langle\kappa,1\rangle\,{}^{x_{i,j}}\langle v'y_{i,j},1\rangle)&= \xi(\langle\kappa,1\rangle\langle y_x,1\rangle\langle l_x,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle) \\&=\xi(\langle {}^{\kappa}y_x,1\rangle\langle {}^{\kappa}l_x,1\rangle\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle)\nonumber \\&=\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3))\xi(\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle).\nonumber \end{align} $$
If
![]() $x_{i,j}^3\in \text {Mat}_{l\times (c-l)}(\mathcal {O})$
, then
$x_{i,j}^3\in \text {Mat}_{l\times (c-l)}(\mathcal {O})$
, then
![]() $x_{i,j}\in K_{\operatorname {\mathrm {GL}}_{rkc}}$
and
$x_{i,j}\in K_{\operatorname {\mathrm {GL}}_{rkc}}$
and
![]() ${}^{\kappa }x_{i,j}\in V_{(rkl,rk(c-l))}(\mathcal {O})$
. Since also
${}^{\kappa }x_{i,j}\in V_{(rkl,rk(c-l))}(\mathcal {O})$
. Since also
![]() $\kappa \in K_{\operatorname {\mathrm {GL}}_{rkc}}$
,
$\kappa \in K_{\operatorname {\mathrm {GL}}_{rkc}}$
,
Depending on
![]() $\xi $
, if the coordinates of
$\xi $
, if the coordinates of
![]() $x_{i,j}^3$
are small enough,
$x_{i,j}^3$
are small enough,
![]() $\xi $
is right-invariant under
$\xi $
is right-invariant under
![]() $\langle x_{i,j},\eta _{rkc}^{\diamondsuit }(x_{i,j})\rangle $
. Combining this with Equation (3.51) and the left-invariance of
$\langle x_{i,j},\eta _{rkc}^{\diamondsuit }(x_{i,j})\rangle $
. Combining this with Equation (3.51) and the left-invariance of
![]() $\xi $
on
$\xi $
on
![]() $\langle v,1\rangle $
for
$\langle v,1\rangle $
for
![]() $v\in V_{(rkl,rk(c-l))}$
, we obtain
$v\in V_{(rkl,rk(c-l))}$
, we obtain
 $$ \begin{align} \xi(\langle\kappa,1\rangle \langle v'y_{i,j},1\rangle)&= \xi(\langle\kappa,1\rangle \langle v'y_{i,j},1\rangle\langle x_{i,j},\eta_{rkc}^{\diamondsuit}(x_{i,j})\rangle)\\\nonumber &=\xi(\langle {}^{\kappa}x_{i,j},1\rangle\langle\kappa,1\rangle {}^{x_{i,j}}\langle v'y_{i,j},1\rangle)\\\nonumber &=\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3))\xi(\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle).\nonumber \end{align} $$
$$ \begin{align} \xi(\langle\kappa,1\rangle \langle v'y_{i,j},1\rangle)&= \xi(\langle\kappa,1\rangle \langle v'y_{i,j},1\rangle\langle x_{i,j},\eta_{rkc}^{\diamondsuit}(x_{i,j})\rangle)\\\nonumber &=\xi(\langle {}^{\kappa}x_{i,j},1\rangle\langle\kappa,1\rangle {}^{x_{i,j}}\langle v'y_{i,j},1\rangle)\\\nonumber &=\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3))\xi(\langle\kappa,1\rangle\langle v_{x,y}^{\prime}y_{i,j},1\rangle).\nonumber \end{align} $$
Therefore, using Equation (3.52) and a change of variables in
![]() $v'$
,
$v'$
,
 $$ \begin{align*} \int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v'y_{i,j},1\rangle)\,dv' =\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3)) \int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v'y_{i,j},1\rangle)\,dv'. \end{align*} $$
$$ \begin{align*} \int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v'y_{i,j},1\rangle)\,dv' =\psi(\mathrm{tr}(v_{i,j}^3x_{i,j}^3)) \int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v'y_{i,j},1\rangle)\,dv'. \end{align*} $$
Now, as in the linear case ([Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Lemma 9]), these computations first imply that the integrand is a Schwartz function on V, hence Integral (3.50) is absolutely convergent. Second, it does not vanish on any subrepresentation of (3.43), in particular on
![]() $\rho _c(\tau )$
. Third, when taking an unramified vector
$\rho _c(\tau )$
. Third, when taking an unramified vector
![]() $\xi $
, we can take
$\xi $
, we can take
![]() $x_{i,j}^3$
with coordinates in
$x_{i,j}^3$
with coordinates in
![]() $\mathcal {O}^{*}$
and deduce that the
$\mathcal {O}^{*}$
and deduce that the
![]() $dv'$
-integral vanishes unless
$dv'$
-integral vanishes unless
![]() $v_{i,j}^3\in \text {Mat}_{l\times (c-l)}(\mathcal {O})$
and since in this case
$v_{i,j}^3\in \text {Mat}_{l\times (c-l)}(\mathcal {O})$
and since in this case
![]() $\xi $
is already right-invariant under
$\xi $
is already right-invariant under
![]() $\langle y_{i,j},1\rangle $
,
$\langle y_{i,j},1\rangle $
,
 $$ \begin{align*} \int\limits_{V}\xi(\langle\kappa,1\rangle\langle v,1\rangle)\,dv=\mathrm{vol}(\mathcal{O})^{l(c-l)}\int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v',1\rangle)\,dv'. \end{align*} $$
$$ \begin{align*} \int\limits_{V}\xi(\langle\kappa,1\rangle\langle v,1\rangle)\,dv=\mathrm{vol}(\mathcal{O})^{l(c-l)}\int\limits_{V'}\xi(\langle\kappa,1\rangle\langle v',1\rangle)\,dv'. \end{align*} $$
Repeating this (in the order defined above), we obtain a nonzero constant multiplied by
![]() $\xi (\langle I_{rkc},1\rangle )$
.
$\xi (\langle I_{rkc},1\rangle )$
.
It remains to show that we can actually choose an unramified
![]() $\xi $
in the space of (3.43) such that
$\xi $
in the space of (3.43) such that
![]() $\xi (\langle I_{rkc},1\rangle )\ne 0$
. We argue using induction on c. For the base case
$\xi (\langle I_{rkc},1\rangle )\ne 0$
. We argue using induction on c. For the base case
![]() $c=2$
,
$c=2$
,
![]() $\xi (\langle I_{2rk},1\rangle )=\Lambda (\xi _1)\Lambda (\xi _2)$
, where
$\xi (\langle I_{2rk},1\rangle )=\Lambda (\xi _1)\Lambda (\xi _2)$
, where
![]() $\xi _i$
are unramified vectors in the space of
$\xi _i$
are unramified vectors in the space of
![]() $\rho _1(\tau )$
such that
$\rho _1(\tau )$
such that
![]() $\xi _i(\langle I_{rk},1\rangle )\ne 0$
. Then
$\xi _i(\langle I_{rk},1\rangle )\ne 0$
. Then
![]() $\Lambda (\xi _1)\Lambda (\xi _2)\ne 0$
by Theorem 43, proving the base case. For
$\Lambda (\xi _1)\Lambda (\xi _2)\ne 0$
by Theorem 43, proving the base case. For
![]() $c>2$
, we take
$c>2$
, we take
![]() $l=1$
and obtain
$l=1$
and obtain
![]() $\xi (\langle I_{rkc},1\rangle )=\Lambda (\xi _1)\Lambda '(\xi _2)$
, where now
$\xi (\langle I_{rkc},1\rangle )=\Lambda (\xi _1)\Lambda '(\xi _2)$
, where now
![]() $\xi _2$
is an unramified vector in the space of
$\xi _2$
is an unramified vector in the space of
![]() $\rho _{c-1}(\tau )$
such that
$\rho _{c-1}(\tau )$
such that
![]() $\xi _2(\langle I_{rk(c-1)},1\rangle )\ne 0$
, and
$\xi _2(\langle I_{rk(c-1)},1\rangle )\ne 0$
, and
![]() $\Lambda '$
is an
$\Lambda '$
is an
![]() $(rk,c-1)$
functional on
$(rk,c-1)$
functional on
![]() $\rho _{c-1}(\tau )$
. By the inductive hypothesis,
$\rho _{c-1}(\tau )$
. By the inductive hypothesis,
![]() $\Lambda '(\xi _2)\ne 0$
so that
$\Lambda '(\xi _2)\ne 0$
so that
![]() $\xi (\langle I_{rkc},1\rangle )\ne 0$
.
$\xi (\langle I_{rkc},1\rangle )\ne 0$
.
3.7 Local Rankin–Selberg integrals
Assume
![]() $\mu _{2m}\subset F^{*}$
. For this section, we also assume
$\mu _{2m}\subset F^{*}$
. For this section, we also assume
![]() $rk>1$
(the case
$rk>1$
(the case
![]() $rk=1$
of Integral (3.53) below is known; see [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference GanGan12]). Let
$rk=1$
of Integral (3.53) below is known; see [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, Reference GanGan12]). Let
![]() $\tau $
be the genuine irreducible unramified constituent of
$\tau $
be the genuine irreducible unramified constituent of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m)}}(\vartheta ,\chi )$
, and recall the representation
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m)}}(\vartheta ,\chi )$
, and recall the representation
![]() $\Theta _{r,m,r,\vartheta _{\tau }}(\chi )$
of § 3.3. By Proposition 41, it admits a unique Whittker model
$\Theta _{r,m,r,\vartheta _{\tau }}(\chi )$
of § 3.3. By Proposition 41, it admits a unique Whittker model
![]() $\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
. Note that
$\mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
. Note that
![]() $\Theta _{r,m,r,\vartheta _{\tau }}(\chi )$
might be reducible. We compute a Rankin–Selberg type integral, which will appear in the final part of the reduction used for the computation of the doubling integrals with unramified data (see § 5.3). The contents of this section, however, are independent of the doubling construction.
$\Theta _{r,m,r,\vartheta _{\tau }}(\chi )$
might be reducible. We compute a Rankin–Selberg type integral, which will appear in the final part of the reduction used for the computation of the doubling integrals with unramified data (see § 5.3). The contents of this section, however, are independent of the doubling construction.
Let
![]() $\pi $
be a genuine irreducible unramified representation of
$\pi $
be a genuine irreducible unramified representation of
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}$
, and write
$\operatorname {\mathrm {GL}}_1^{(m,r)}$
, and write
![]() $\pi =\mathrm {I}_{\operatorname {\mathrm {GL}}_1^{(m,r)}}(\vartheta ,\mu )$
. The contragredient representation
$\pi =\mathrm {I}_{\operatorname {\mathrm {GL}}_1^{(m,r)}}(\vartheta ,\mu )$
. The contragredient representation
![]() $\pi ^{\vee }$
is induced from
$\pi ^{\vee }$
is induced from
![]() $\varepsilon ^{-1}\otimes \vartheta ^{-1}\mu ^{-1}$
. Let
$\varepsilon ^{-1}\otimes \vartheta ^{-1}\mu ^{-1}$
. Let
![]() $\omega $
be a matrix coefficient of
$\omega $
be a matrix coefficient of
![]() $\pi ^{\vee }$
and
$\pi ^{\vee }$
and
![]() $W\in \mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
. The integral
$W\in \mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
. The integral
 $$ \begin{align} Z(s,\omega,W)=\int\limits_{F^{*}}\omega(\langle a,1\rangle)W(\langle \operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)|a|^{s-(rk-1)/2}\,d^{*}a \end{align} $$
$$ \begin{align} Z(s,\omega,W)=\int\limits_{F^{*}}\omega(\langle a,1\rangle)W(\langle \operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)|a|^{s-(rk-1)/2}\,d^{*}a \end{align} $$
is formally well defined and absolutely convergent in a right half-plane. This can be regarded as the covering analog of the Rankin–Selberg convolution for
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
of [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, § 2.4(3)] (with the parameter
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
of [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, § 2.4(3)] (with the parameter
![]() $j=0$
). Now, assume that
$j=0$
). Now, assume that
![]() $\omega $
and W are normalized and unramified. According to Proposition 23, the integrand vanishes unless
$\omega $
and W are normalized and unramified. According to Proposition 23, the integrand vanishes unless
![]() $a\in F^{*r}$
so that
$a\in F^{*r}$
so that
 $$ \begin{align*} Z(s,\omega,W)=\int\limits_{F^{*r}}W(\langle \operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)\vartheta^{-1}(a)\mu^{-1}(a)|a|^{s-(rk-1)/2}\,d^{*}a. \end{align*} $$
$$ \begin{align*} Z(s,\omega,W)=\int\limits_{F^{*r}}W(\langle \operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)\vartheta^{-1}(a)\mu^{-1}(a)|a|^{s-(rk-1)/2}\,d^{*}a. \end{align*} $$
Assume
![]() $\int _{\mathcal {O}^{*}}d^{*}a=1$
. Since
$\int _{\mathcal {O}^{*}}d^{*}a=1$
. Since
![]() $W(\langle \operatorname {\mathrm {diag}}(a,I_{rk-1}),1\rangle )=0$
unless
$W(\langle \operatorname {\mathrm {diag}}(a,I_{rk-1}),1\rangle )=0$
unless
![]() $|a|\leq 1$
(see, e.g., [Reference Casselman and ShalikaCS80, § 6]), the
$|a|\leq 1$
(see, e.g., [Reference Casselman and ShalikaCS80, § 6]), the
![]() $d^{*}a$
-integral can be written as the infinite sum over
$d^{*}a$
-integral can be written as the infinite sum over
![]() $\varpi ^{lr}$
, where
$\varpi ^{lr}$
, where
![]() $l\geq 0$
. Let
$l\geq 0$
. Let
![]() $\mathbf {x}=(\chi _1(\varpi ^r),\ldots ,\chi _k(\varpi ^r))$
, which we identify with
$\mathbf {x}=(\chi _1(\varpi ^r),\ldots ,\chi _k(\varpi ^r))$
, which we identify with
![]() $t_{\tau ,\vartheta }=\operatorname {\mathrm {diag}}(\chi _1(\varpi ^r),\ldots ,\chi _k(\varpi ^r))$
. By Theorem 46,
$t_{\tau ,\vartheta }=\operatorname {\mathrm {diag}}(\chi _1(\varpi ^r),\ldots ,\chi _k(\varpi ^r))$
. By Theorem 46,
Also,
![]() $t_{\pi ^{\vee },\vartheta }=t_{\pi ^{\vee },\vartheta ^{-1}}=\mu ^{-1}(\varpi ^{r})$
(if
$t_{\pi ^{\vee },\vartheta }=t_{\pi ^{\vee },\vartheta ^{-1}}=\mu ^{-1}(\varpi ^{r})$
(if
![]() $m\equiv 2\,(4)$
, then
$m\equiv 2\,(4)$
, then
![]() $\vartheta ^{-1}=\vartheta $
when
$\vartheta ^{-1}=\vartheta $
when
![]() $\mu _{2m}\subset F^{*}$
). Now,
$\mu _{2m}\subset F^{*}$
). Now,
 $$ \begin{align} Z(s,\omega,W)&=\sum_{l=0}^{\infty}p_l(\mathbf{x})\mu^{-1}(\varpi^{lr})q^{-l(rs-(r-1)/2)}\\&=\nonumber \prod_{1\leq i\leq k}(1-q^{-r(s-1/2)-1/2}\chi_i(\varpi^r)\mu^{-1}(\varpi^r))^{-1}= L_{\vartheta}(r(s-1/2)+1/2,\pi^{\vee}\times\tau). \end{align} $$
$$ \begin{align} Z(s,\omega,W)&=\sum_{l=0}^{\infty}p_l(\mathbf{x})\mu^{-1}(\varpi^{lr})q^{-l(rs-(r-1)/2)}\\&=\nonumber \prod_{1\leq i\leq k}(1-q^{-r(s-1/2)-1/2}\chi_i(\varpi^r)\mu^{-1}(\varpi^r))^{-1}= L_{\vartheta}(r(s-1/2)+1/2,\pi^{\vee}\times\tau). \end{align} $$
In particular,
![]() $Z(s,\omega ,W)$
is a rational function in
$Z(s,\omega ,W)$
is a rational function in
![]() $q^{-s}$
.
$q^{-s}$
.
4 The construction
4.1 The global integral
In this section, we construct the global integral, following the linear case from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] with the necessary modifications and adjustments for the covering. Let F be a number field which contains
![]() $\mu _m$
. We use the notation and definitions of § 2.3. In particular n, k and m are integers,
$\mu _m$
. We use the notation and definitions of § 2.3. In particular n, k and m are integers,
![]() $c=2n$
,
$c=2n$
,
![]() $G=\operatorname {\mathrm {Sp}}_c$
and
$G=\operatorname {\mathrm {Sp}}_c$
and
![]() $H=\operatorname {\mathrm {Sp}}_{2rkc}$
. We also have the Siegel parabolic subgroup
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
. We also have the Siegel parabolic subgroup
![]() $P=M_P\ltimes U_P$
, the parabolic subgroup
$P=M_P\ltimes U_P$
, the parabolic subgroup
![]() $Q=M_Q\ltimes U$
and the character
$Q=M_Q\ltimes U$
and the character
![]() $\psi _U$
of U given by Equation (2.6). Then
$\psi _U$
of U given by Equation (2.6). Then
![]() $G\times G$
is embedded in H in the stabilizer of
$G\times G$
is embedded in H in the stabilizer of
![]() $\psi _U$
in
$\psi _U$
in
![]() $M_Q$
.
$M_Q$
.
As explained in § 2.5, we fix the global
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho $
on
$\rho $
on
![]() $H^{(m)}(\mathbb {A})$
. This defines the
$H^{(m)}(\mathbb {A})$
. This defines the
![]() $2$
-cocycles on each copy of
$2$
-cocycles on each copy of
![]() $G^{(m)}(\mathbb {A})$
:
$G^{(m)}(\mathbb {A})$
:
![]() $\rho _L$
on the left copy,
$\rho _L$
on the left copy,
![]() $\rho _R$
on the right, and these subgroups commute in
$\rho _R$
on the right, and these subgroups commute in
![]() $H^{(m)}(\mathbb {A})$
. It also defines an identification of
$H^{(m)}(\mathbb {A})$
. It also defines an identification of
![]() $H(F)$
in
$H(F)$
in
![]() $H^{(m)}(\mathbb {A})$
, and of
$H^{(m)}(\mathbb {A})$
, and of
![]() $G(F)$
in each copy. The notions of automorphic forms on these groups are now defined. In addition, if
$G(F)$
in each copy. The notions of automorphic forms on these groups are now defined. In addition, if
![]() $\varphi _1$
is an automorphic form on the right copy,
$\varphi _1$
is an automorphic form on the right copy,
![]() $\varphi _1\mapsto \varphi _1^{(\eta ^{\times })^{-1}}$
is an automorphic form on the left copy by Corollary 13. Also, recall the involution
$\varphi _1\mapsto \varphi _1^{(\eta ^{\times })^{-1}}$
is an automorphic form on the left copy by Corollary 13. Also, recall the involution
![]() ${}^{\iota }$
, lifted to
${}^{\iota }$
, lifted to
![]() $G^{(m)}(\mathbb {A})$
in § 2.6.
$G^{(m)}(\mathbb {A})$
in § 2.6.
Let
![]() $\tau $
be a genuine unitary irreducible cuspidal automorphic representation of
$\tau $
be a genuine unitary irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
. Here and throughout § 4, we assume that Conjectures 50 and 51 hold. Then let
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
. Here and throughout § 4, we assume that Conjectures 50 and 51 hold. Then let
![]() $\mathcal {E}_{\tau }$
be the genuine irreducible automorphic representation guaranteed by Theorem 54, which is a coarse
$\mathcal {E}_{\tau }$
be the genuine irreducible automorphic representation guaranteed by Theorem 54, which is a coarse
![]() $(rk,c)$
representation (or an
$(rk,c)$
representation (or an
![]() $(rk,c)$
representation if
$(rk,c)$
representation if
![]() $\mu _{2m}\subset F^{*}$
). Consider the representation
$\mu _{2m}\subset F^{*}$
). Consider the representation
For a standard
![]() $\widetilde {K}_H$
-finite section f in the space of this representation, the Eisenstein series
$\widetilde {K}_H$
-finite section f in the space of this representation, the Eisenstein series
![]() $E(h;f,s)$
is defined by
$E(h;f,s)$
is defined by
 $$ \begin{align} E(h;f,s)=\sum_{\gamma\in P(F)\backslash H(F)}f(\langle\gamma,\eta^{-1}(\gamma)\rangle h,s), \end{align} $$
$$ \begin{align} E(h;f,s)=\sum_{\gamma\in P(F)\backslash H(F)}f(\langle\gamma,\eta^{-1}(\gamma)\rangle h,s), \end{align} $$
which is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
and defined for a general s by meromorphic continuation.
$\operatorname {\mathrm {Re}}(s)\gg 0$
and defined for a general s by meromorphic continuation.
Let
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
be genuine irreducible cuspidal automorphic representations of
$\pi _2$
be genuine irreducible cuspidal automorphic representations of
![]() $G^{(m)}(\mathbb {A})$
, where
$G^{(m)}(\mathbb {A})$
, where
![]() $G^{(m)}(\mathbb {A})$
is realized using
$G^{(m)}(\mathbb {A})$
is realized using
![]() $\rho _R$
. Let
$\rho _R$
. Let
![]() $\varphi _i$
be a cusp form in the space of
$\varphi _i$
be a cusp form in the space of
![]() $\pi _i$
,
$\pi _i$
,
![]() $i=1,2$
. The global integral is given by
$i=1,2$
. The global integral is given by
 $$ \begin{align} Z(s,\varphi_1,\varphi_2,f)=&\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{{}^{\iota}\varphi_2(\langle g_2,1\rangle)} \\&\times E(\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle;f,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align} $$
$$ \begin{align} Z(s,\varphi_1,\varphi_2,f)=&\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{{}^{\iota}\varphi_2(\langle g_2,1\rangle)} \\&\times E(\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle;f,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align} $$
Theorem 63. Integral (4.2) is formally well defined, absolutely convergent away from the poles of the series, and admits meromorphic continuation to the plane.
Proof. Since the image of
![]() $G(F)\times G(F)$
in
$G(F)\times G(F)$
in
![]() $H(F)$
normalizes U without changing the measure, and fixes
$H(F)$
normalizes U without changing the measure, and fixes
![]() $\psi _U$
, and by Lemma 15 we have
$\psi _U$
, and by Lemma 15 we have
![]() ${}^{g}\langle u,\eta ^{-1}(u)\rangle =\langle {}^gu,\eta ^{-1}({}^gu)\rangle $
for
${}^{g}\langle u,\eta ^{-1}(u)\rangle =\langle {}^gu,\eta ^{-1}({}^gu)\rangle $
for
![]() $g=(g_1,g_2)$
, the
$g=(g_1,g_2)$
, the
![]() $du$
-integral is well defined on the domain of the outer integral. The outer integral is well defined by Proposition 14. Now, convergence and continuation follow from the rapid decay of cusp forms and from the moderate growth and meromorphic continuation of the Eisenstein series.
$du$
-integral is well defined on the domain of the outer integral. The outer integral is well defined by Proposition 14. Now, convergence and continuation follow from the rapid decay of cusp forms and from the moderate growth and meromorphic continuation of the Eisenstein series.
4.2 Obtaining the Euler product
To state the unfolding theorem, we introduce the following notation. Let
![]() $L^2(G(F)\backslash G^{(m)}(\mathbb {A}))$
be the space of genuine square-integrable automorphic forms on
$L^2(G(F)\backslash G^{(m)}(\mathbb {A}))$
be the space of genuine square-integrable automorphic forms on
![]() $G^{(m)}(\mathbb {A})$
. Denote the standard
$G^{(m)}(\mathbb {A})$
. Denote the standard
![]() $G^{(m)}(\mathbb {A})$
-invariant inner product on
$G^{(m)}(\mathbb {A})$
-invariant inner product on
![]() $L^2(G(F)\backslash G^{(m)}(\mathbb {A}))$
by
$L^2(G(F)\backslash G^{(m)}(\mathbb {A}))$
by
![]() $\{\cdot ,\cdot \}$
,
$\{\cdot ,\cdot \}$
,
 $$ \begin{align*} \{\varphi_1,\varphi_2\}= \int\limits_{G(F)\backslash G(\mathbb{A})}\varphi_1(\langle g,1\rangle)\overline{\varphi_2(\langle g,1\rangle)}\,dg. \end{align*} $$
$$ \begin{align*} \{\varphi_1,\varphi_2\}= \int\limits_{G(F)\backslash G(\mathbb{A})}\varphi_1(\langle g,1\rangle)\overline{\varphi_2(\langle g,1\rangle)}\,dg. \end{align*} $$
This integral is well defined (in the sense of Proposition 14 with one copy
![]() $G(F)\backslash G(\mathbb {A})$
) because both
$G(F)\backslash G(\mathbb {A})$
) because both
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are genuine functions. While the definition itself does not depend on the
$\varphi _2$
are genuine functions. While the definition itself does not depend on the
![]() $2$
-cocycle realizing
$2$
-cocycle realizing
![]() $G^{(m)}(\mathbb {A})$
, in the construction it will be
$G^{(m)}(\mathbb {A})$
, in the construction it will be
![]() $\rho _R$
.
$\rho _R$
.
Let
 $$ \begin{align*} &\delta=\delta_0\delta_1,\qquad \delta_0=\left(\begin{smallmatrix} &I_{rkc}\\ -I_{rkc}\end{smallmatrix}\right),\qquad \delta_1=\left(\begin{smallmatrix} I_{r(k-1)c}&&&&\\ &I_{c}&&I_c&\\ &&&I_{c}&\\ &&&&I_{r(k-1)c}\end{smallmatrix}\right),\\ &U_0=U\cap U_{P}= \left\{\left(\begin{array}{cccc}I_{(k-1)c}&&X&Z\\&I_c&&X'\\&&I_c\\&&&I_{(k-1)c}\end{array}\right)\in H\right\}\qquad\left(\begin{array}{c}{}^tZJ_{(k-1)c}-J_{(k-1)c}Z=0,\\ X'=J_{c}{}^tXJ_{(k-1)c}\end{array}\right). \end{align*} $$
$$ \begin{align*} &\delta=\delta_0\delta_1,\qquad \delta_0=\left(\begin{smallmatrix} &I_{rkc}\\ -I_{rkc}\end{smallmatrix}\right),\qquad \delta_1=\left(\begin{smallmatrix} I_{r(k-1)c}&&&&\\ &I_{c}&&I_c&\\ &&&I_{c}&\\ &&&&I_{r(k-1)c}\end{smallmatrix}\right),\\ &U_0=U\cap U_{P}= \left\{\left(\begin{array}{cccc}I_{(k-1)c}&&X&Z\\&I_c&&X'\\&&I_c\\&&&I_{(k-1)c}\end{array}\right)\in H\right\}\qquad\left(\begin{array}{c}{}^tZJ_{(k-1)c}-J_{(k-1)c}Z=0,\\ X'=J_{c}{}^tXJ_{(k-1)c}\end{array}\right). \end{align*} $$
The character
![]() $\psi _U$
restricts to a character of
$\psi _U$
restricts to a character of
![]() $U_0$
and for
$U_0$
and for
![]() $u_0\in U_0$
,
$u_0\in U_0$
,
 $$ \begin{align*} &\psi_U(u_0)=\psi(\operatorname{\mathrm{tr}}(\left(\begin{array}{cc}0&I_n\end{array}\right)X\left(\begin{array}c0\\I_n\end{array}\right))). \end{align*} $$
$$ \begin{align*} &\psi_U(u_0)=\psi(\operatorname{\mathrm{tr}}(\left(\begin{array}{cc}0&I_n\end{array}\right)X\left(\begin{array}c0\\I_n\end{array}\right))). \end{align*} $$
Recall the embedding
Also, let
![]() $f_{\mathcal {W}(\mathcal {E}_{\tau })}$
denote the composition of the section f with the
$f_{\mathcal {W}(\mathcal {E}_{\tau })}$
denote the composition of the section f with the
![]() $(rk,c)$
functional (3.2) attached to the coarse
$(rk,c)$
functional (3.2) attached to the coarse
![]() $(rk,c)$
representation
$(rk,c)$
representation
![]() $\mathcal {E}_{\tau }$
, namely
$\mathcal {E}_{\tau }$
, namely
 $$ \begin{align} f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s)=\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}f(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle h,s)\psi^{-1}(v)\,dv. \end{align} $$
$$ \begin{align} f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s)=\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}f(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle h,s)\psi^{-1}(v)\,dv. \end{align} $$
Theorem 64. Integral (4.2) is not identically zero only if
![]() $\pi _1=\pi _2=\pi $
. In this case in
$\pi _1=\pi _2=\pi $
. In this case in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, it is equal to
$\operatorname {\mathrm {Re}}(s)\gg 0$
, it is equal to
 $$ \begin{align} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1,\pi(\langle g,1\rangle)\varphi_2\}f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta u_0,\eta^{-1}(\delta u_0)\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1,\pi(\langle g,1\rangle)\varphi_2\}f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta u_0,\eta^{-1}(\delta u_0)\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \,\psi_U(u_0)\,du_0\,dg. \end{align} $$
Proof. Substituting the definition of the Eisenstein series into (4.2), Integral (4.2) becomes
 $$ \begin{align*} &\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\times \sum\limits_{\gamma\in P(F)\backslash H(F)}f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\times \sum\limits_{\gamma\in P(F)\backslash H(F)}f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
Let
![]() $R=(\mathfrak {e}_1(G)\times \mathfrak {e}_2(G))\ltimes U<Q$
. The group
$R=(\mathfrak {e}_1(G)\times \mathfrak {e}_2(G))\ltimes U<Q$
. The group
![]() $R(F)$
acts on the right on the homogenous space
$R(F)$
acts on the right on the homogenous space
![]() $P(F)\backslash H(F)$
. The stabilizer of
$P(F)\backslash H(F)$
. The stabilizer of
![]() $P(F)h$
is
$P(F)h$
is
![]() $R_{h}(F)={}^{h^{-1}}P(F)\cap R(F)$
. In
$R_{h}(F)={}^{h^{-1}}P(F)\cap R(F)$
. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, we can write the last integral as
$\operatorname {\mathrm {Re}}(s)\gg 0$
, we can write the last integral as
 $$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\times\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)} f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y,\eta^{-1}(y)\rangle\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\times\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)} f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y,\eta^{-1}(y)\rangle\langle u,\eta^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
Write
![]() $y=y_3\mathfrak {e}_1(y_1)\mathfrak {e}_1(y_2)$
for
$y=y_3\mathfrak {e}_1(y_1)\mathfrak {e}_1(y_2)$
for
![]() $y_3\in U(F)$
and
$y_3\in U(F)$
and
![]() $y_1,y_2\in G(F)$
. In
$y_1,y_2\in G(F)$
. In
![]() $H^{(m)}(\mathbb {A})$
, we can write
$H^{(m)}(\mathbb {A})$
, we can write
The group
![]() $G\times G$
normalizes U and stabilizes
$G\times G$
normalizes U and stabilizes
![]() $\psi _U$
, hence we can conjugate
$\psi _U$
, hence we can conjugate
![]() $\mathfrak {e}_1(y_1)$
and
$\mathfrak {e}_1(y_1)$
and
![]() $\mathfrak {e}_1(y_2)$
to the right, and by Lemma 15 and Equation (2.30) we obtain
$\mathfrak {e}_1(y_2)$
to the right, and by Lemma 15 and Equation (2.30) we obtain
 $$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)}\eta^{-1}(\mathfrak{e}_1(y_1))\eta^{-1}(\mathfrak{e}_2(y_2))\rho_L^{-1}(y_1,g_1)\rho_R(y_2,g_2) \\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y_3u,\eta^{-1}(y_3u)\rangle \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle,s)\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\int\limits_{U(F)\backslash U({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)}\eta^{-1}(\mathfrak{e}_1(y_1))\eta^{-1}(\mathfrak{e}_2(y_2))\rho_L^{-1}(y_1,g_1)\rho_R(y_2,g_2) \\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y_3u,\eta^{-1}(y_3u)\rangle \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle,s)\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
We also have
and using Equation (2.49),
Combining these computations, we obtain
 $$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\!\!\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\!\!\int\limits_{U(F)\backslash U({\mathbb{A}})}\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)}\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle y_2g_2,1\rangle)}\, \\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y_3u,\eta^{-1}(y_3u)\rangle\nonumber \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle,s)\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\sum\limits_{\gamma\in P(F)\backslash H(F)/R(F)}\quad\!\!\int\limits_{G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})} \quad\!\!\int\limits_{U(F)\backslash U({\mathbb{A}})}\sum\limits_{y\in R_{\gamma}(F)\backslash R(F)}\varphi_1^{(\eta^{\times})^{-1}}(\langle y_1g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle y_2g_2,1\rangle)}\, \\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle y_3u,\eta^{-1}(y_3u)\rangle\nonumber \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle,s)\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
Now, we can collapse the summation into the integral, and we reach the sum
 $$ \begin{align*} \sum_{\gamma\in P(F)\backslash H(F)/R(F)}\mathrm{I}(\gamma), \end{align*} $$
$$ \begin{align*} \sum_{\gamma\in P(F)\backslash H(F)/R(F)}\mathrm{I}(\gamma), \end{align*} $$
where
 $$ \begin{align*} \mathrm{I}(\gamma)=&\int\limits_{R_\gamma(F)\backslash R({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle u,\eta^{-1}(u)\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} \mathrm{I}(\gamma)=&\int\limits_{R_\gamma(F)\backslash R({\mathbb{A}})}\varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\\& f(\langle \gamma,\eta^{-1}(\gamma)\rangle\langle u,\eta^{-1}(u)\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
As in the linear case ([Reference Gourevitch and KaplanGK23, § 3.2]), first we show that the summands
![]() $\mathrm {I}(\gamma )$
such that
$\mathrm {I}(\gamma )$
such that
![]() $\gamma \notin P(F)\delta R(F)$
vanish. Then we prove that
$\gamma \notin P(F)\delta R(F)$
vanish. Then we prove that
![]() $\mathrm {I}(\delta )$
equals Integral (4.4) (after some modifications). We start with the vanishing. Three types of arguments were used for the proof in the linear case:
$\mathrm {I}(\delta )$
equals Integral (4.4) (after some modifications). We start with the vanishing. Three types of arguments were used for the proof in the linear case:
-
1. Using
 $\psi _U$
: Find
$\psi _U$
: Find
 $U'<U$
such that
$U'<U$
such that
 $\psi _U|_{U'}\ne 1$
and
$\psi _U|_{U'}\ne 1$
and
 ${}^{\gamma }U'<U_P$
, then
${}^{\gamma }U'<U_P$
, then
 $\mathrm {I}(\gamma )=0$
since we obtain an inner integral
$\mathrm {I}(\gamma )=0$
since we obtain an inner integral
 $\int _{U'(F)\backslash U'(\mathbb {A})}\psi _U(u')du'=0$
.
$\int _{U'(F)\backslash U'(\mathbb {A})}\psi _U(u')du'=0$
. -
2. Using the cuspidality of
 $\pi _2$
: Find a unipotent radical V of a parabolic subgroup of G such that the
$\pi _2$
: Find a unipotent radical V of a parabolic subgroup of G such that the
 $du$
-integral of f is invariant under
$du$
-integral of f is invariant under
 $\mathfrak {e}_2(V(\mathbb {A}))$
, then
$\mathfrak {e}_2(V(\mathbb {A}))$
, then
 $\mathrm {I}(\gamma )=0$
because we have an inner integral
$\mathrm {I}(\gamma )=0$
because we have an inner integral
 $\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(v)dv=0$
.
$\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(v)dv=0$
. -
3. Using the vanishing properties of the
 $(k,c)$
representation: Construct as an inner integral a generic Fourier coefficient of the
$(k,c)$
representation: Construct as an inner integral a generic Fourier coefficient of the
 $(k,c)$
representation, attached to a unipotent orbit which is greater than or not comparable with
$(k,c)$
representation, attached to a unipotent orbit which is greater than or not comparable with
 $(k^{c})$
.
$(k^{c})$
.
To extend the arguments from [Reference Gourevitch and KaplanGK23, § 3.2] to the covering case, we argue as follows. First, all occurrences of k in [Reference Gourevitch and KaplanGK23, § 3.2] are replaced with
![]() $rk$
. Second, the arguments of types (1) and (3) extend to the covering by Lemma 15 and Equation (2.4). Third, for type (2) assume V is given. Then we have an embedding
$rk$
. Second, the arguments of types (1) and (3) extend to the covering by Lemma 15 and Equation (2.4). Third, for type (2) assume V is given. Then we have an embedding
![]() $v\mapsto \langle v,\eta '(v)\rangle $
of
$v\mapsto \langle v,\eta '(v)\rangle $
of
![]() $V(\mathbb {A})$
in the right copy of
$V(\mathbb {A})$
in the right copy of
![]() $G^{(m)}(\mathbb {A})$
so that
$G^{(m)}(\mathbb {A})$
so that
![]() $\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(\langle v,\eta '(v)\rangle )dv=0$
. By Equation (2.30), we can assume that
$\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(\langle v,\eta '(v)\rangle )dv=0$
. By Equation (2.30), we can assume that
![]() $\eta '$
is obtained from a
$\eta '$
is obtained from a
![]() $1$
-cochain on
$1$
-cochain on
![]() $\mathfrak {e}_2(V(\mathbb {A}))$
, which we also denote by
$\mathfrak {e}_2(V(\mathbb {A}))$
, which we also denote by
![]() $\eta '$
. That is,
$\eta '$
. That is,
![]() $\eta '(v)=\eta '(\mathfrak {e}_2(v))$
. Now, the vanishing properties of
$\eta '(v)=\eta '(\mathfrak {e}_2(v))$
. Now, the vanishing properties of
![]() $\mathcal {E}_{\tau }$
(see § 3.1) show, as in the linear case, that the
$\mathcal {E}_{\tau }$
(see § 3.1) show, as in the linear case, that the
![]() $du$
-integral of f is invariant with respect to
$du$
-integral of f is invariant with respect to
![]() $\{\langle \mathfrak {e}_2(v),\eta '(\mathfrak {e}_2(v))\rangle :v\in V(\mathbb {A})\}$
. Hence we can obtain the inner integral
$\{\langle \mathfrak {e}_2(v),\eta '(\mathfrak {e}_2(v))\rangle :v\in V(\mathbb {A})\}$
. Hence we can obtain the inner integral
![]() $\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(\langle v,\eta '(v)\rangle )dv$
. This completes the proof that
$\int _{V(F)\backslash V(\mathbb {A})}\varphi _2(\langle v,\eta '(v)\rangle )dv$
. This completes the proof that
![]() $I(\gamma )=0$
for
$I(\gamma )=0$
for
![]() $\gamma \notin P(F)\delta R(F)$
.
$\gamma \notin P(F)\delta R(F)$
.
Finally, consider
![]() $\mathrm {I}(\delta )$
. Let
$\mathrm {I}(\delta )$
. Let
![]() $v^{\diamondsuit }=\operatorname {\mathrm {diag}}(v,v^{*})$
be the natural embedding of
$v^{\diamondsuit }=\operatorname {\mathrm {diag}}(v,v^{*})$
be the natural embedding of
![]() $V_{(c^{rk})}$
in
$V_{(c^{rk})}$
in
![]() $M_P$
and put
$M_P$
and put
![]() $V_{(c^{rk})}^{\diamondsuit }=\{v^{\diamondsuit }:v\in V_{(c^{rk})}\}$
. The stabilizer in this case is
$V_{(c^{rk})}^{\diamondsuit }=\{v^{\diamondsuit }:v\in V_{(c^{rk})}\}$
. The stabilizer in this case is
Write
For
![]() $u\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
, if
$u\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
, if
![]() ${}^{\delta }u=v^{\diamondsuit }$
with
${}^{\delta }u=v^{\diamondsuit }$
with
![]() $v\in V_{(c^{rk})}$
, then since both
$v\in V_{(c^{rk})}$
, then since both
![]() $V_{(c^{rk})}^{\diamondsuit }$
and
$V_{(c^{rk})}^{\diamondsuit }$
and
![]() ${}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
are subgroups of
${}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
are subgroups of
![]() $N_{rkc}$
, we can apply Lemma 15 and obtain
$N_{rkc}$
, we can apply Lemma 15 and obtain
Here, the second equality follows from the definitions of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. Also,
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
. Also,
![]() $\psi _U({}^{\delta ^{-1}}v^{\diamondsuit })=\psi ^{-1}(v)$
, where
$\psi _U({}^{\delta ^{-1}}v^{\diamondsuit })=\psi ^{-1}(v)$
, where
![]() $\psi $
is given by Equation (3.1). Thus
$\psi $
is given by Equation (3.1). Thus
 $$ \begin{align*} &\int\limits_{{}^{\delta^{-1}}V_{(c^{rk})}^{\diamondsuit}(F)\backslash U(\mathbb{A})} f(\langle\delta ,\eta^{-1}(\delta)\rangle\langle u,\eta^{-1}(u)\rangle,s)\,\psi_U(u)\,du\\ &=\int\limits_{U_0(\mathbb{A})} \int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})} f(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle\langle \delta ,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle ,s)\,\psi^{-1}(v)\psi_U(u_0)\,dv\,du_0 \\&=\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle ,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} &\int\limits_{{}^{\delta^{-1}}V_{(c^{rk})}^{\diamondsuit}(F)\backslash U(\mathbb{A})} f(\langle\delta ,\eta^{-1}(\delta)\rangle\langle u,\eta^{-1}(u)\rangle,s)\,\psi_U(u)\,du\\ &=\int\limits_{U_0(\mathbb{A})} \int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})} f(\langle v,(\eta_{rkc}^{\diamondsuit})^{-1}(v)\rangle\langle \delta ,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle ,s)\,\psi^{-1}(v)\psi_U(u_0)\,dv\,du_0 \\&=\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle ,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
Here, for the last equality we used Equation (4.3). We substitute this into
![]() $\mathrm {I}(\delta )$
and obtain
$\mathrm {I}(\delta )$
and obtain
 $$ \begin{align*} &\int\limits_{\{(g,{}^{\iota}g):g\in G(F)\}\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{\{(g,{}^{\iota}g):g\in G(F)\}\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
The next step is to factor this integral through
![]() $\{(g,{}^{\iota }g):g\in G(\mathbb {A})\}\cong G(\mathbb {A})$
. Multiply
$\{(g,{}^{\iota }g):g\in G(\mathbb {A})\}\cong G(\mathbb {A})$
. Multiply
![]() $g_2\mapsto g_1^{\iota }g_2$
, then
$g_2\mapsto g_1^{\iota }g_2$
, then
![]() $\{(g,{}^{\iota }g):g\in G(F)\}\mapsto \{(g,1):g\in G(F)\}=G(F)$
and the integral becomes
$\{(g,{}^{\iota }g):g\in G(F)\}\mapsto \{(g,1):g\in G(F)\}=G(F)$
and the integral becomes
 $$ \begin{align} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align} $$
$$ \begin{align} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align} $$
Then
 $$ \begin{align*} &\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1g_2,1\rangle)}\mapsto \rho_R({}^{\iota}g_1,g_2)\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1g_2),1\rangle,s) \\&\mapsto \rho_R({}^{\iota}g_1,g_2)^{-1}f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s). \end{align*} $$
$$ \begin{align*} &\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1g_2,1\rangle)}\mapsto \rho_R({}^{\iota}g_1,g_2)\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1g_2),1\rangle,s) \\&\mapsto \rho_R({}^{\iota}g_1,g_2)^{-1}f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s). \end{align*} $$
The conjugation
![]() ${}^{\iota }\langle {}^{\iota }g_1,1\rangle $
takes place in the right copy of
${}^{\iota }\langle {}^{\iota }g_1,1\rangle $
takes place in the right copy of
![]() $G^{(m)}$
so that by Equation (2.46) and because
$G^{(m)}$
so that by Equation (2.46) and because
![]() ${}^{\iota }$
is an involution,
${}^{\iota }$
is an involution,
 $$ \begin{align} &{}^{\iota}\langle {}^{\iota}g_1,\eta_{\iota,R}^{-1}(g_1)\rangle= {}^{\iota}({}^{\iota}\langle g_1,1\rangle)=\langle g_1,1\rangle,\\\nonumber &\eta_{\iota,R}(g_1)\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)} =\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}. \end{align} $$
$$ \begin{align} &{}^{\iota}\langle {}^{\iota}g_1,\eta_{\iota,R}^{-1}(g_1)\rangle= {}^{\iota}({}^{\iota}\langle g_1,1\rangle)=\langle g_1,1\rangle,\\\nonumber &\eta_{\iota,R}(g_1)\overline{\varphi_2({}^{\iota}\langle {}^{\iota}g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)} =\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}. \end{align} $$
Consequently, Integral (4.7) equals
 $$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1),\eta_{\iota,R}^{-1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_1),\eta_{\iota,R}^{-1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
Then by Equation (2.48),
Hence, the last integral equals
 $$ \begin{align} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta ,\eta^{-1}(\delta )\rangle \langle u_0,\eta^{-1}(u_0)\rangle {}^{\iota}\langle (g_1,g_1),\rho(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align} $$
$$ \begin{align} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\&f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta ,\eta^{-1}(\delta )\rangle \langle u_0,\eta^{-1}(u_0)\rangle {}^{\iota}\langle (g_1,g_1),\rho(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align} $$
Next, we see that
![]() ${}^{(g_1,{}^{\iota }g_1)^{-1}}u_0=v_{g_1}u_{g_1}$
, where
${}^{(g_1,{}^{\iota }g_1)^{-1}}u_0=v_{g_1}u_{g_1}$
, where
![]() $v_{g_1}\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }(\mathbb {A})$
and
$v_{g_1}\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }(\mathbb {A})$
and
![]() $u_{g_1}\in U_0(\mathbb {A})$
. Since
$u_{g_1}\in U_0(\mathbb {A})$
. Since
![]() $v_{g_1},u_{g_1}\in N_{rkc}(\mathbb {A})$
, by Lemma 15
$v_{g_1},u_{g_1}\in N_{rkc}(\mathbb {A})$
, by Lemma 15
Thus, the
![]() $du_0$
-integral of (4.9) becomes
$du_0$
-integral of (4.9) becomes
 $$ \begin{align*} \int\limits_{U_0(\mathbb{A})}f_{\mathcal{W}(\mathcal{E}_{\tau})} ({}^{\delta\iota}\langle (g_1,g_1),\rho(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \delta ,\eta^{-1}(\delta)\rangle \langle v_{g_1},\eta^{-1}(v_{g_1})\rangle\langle u_{g_1},\eta^{-1}(u_{g_1})\rangle ,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} \int\limits_{U_0(\mathbb{A})}f_{\mathcal{W}(\mathcal{E}_{\tau})} ({}^{\delta\iota}\langle (g_1,g_1),\rho(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \delta ,\eta^{-1}(\delta)\rangle \langle v_{g_1},\eta^{-1}(v_{g_1})\rangle\langle u_{g_1},\eta^{-1}(u_{g_1})\rangle ,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
Here,
![]() ${}^{\delta \iota }\langle (g,g),\epsilon \rangle $
denotes the composition
${}^{\delta \iota }\langle (g,g),\epsilon \rangle $
denotes the composition
![]() ${}^{\delta }({}^{\iota }\langle (g,g),\epsilon \rangle )$
; in H,
${}^{\delta }({}^{\iota }\langle (g,g),\epsilon \rangle )$
; in H,
![]() ${}^{\delta \iota }$
is the automorphism of
${}^{\delta \iota }$
is the automorphism of
![]() $G\times G$
given by
$G\times G$
given by
![]() ${}^{\delta \iota }(g,g)={}^{\delta }(g,{}^{\iota }g)$
(recall
${}^{\delta \iota }(g,g)={}^{\delta }(g,{}^{\iota }g)$
(recall
![]() $\iota \notin G$
). By Corollary 11,
$\iota \notin G$
). By Corollary 11,
![]() $(g,g)\mapsto \langle (g,g),(\eta ^{\times })^{-1}(g)\rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))\rangle $
is the embedding of the group
$(g,g)\mapsto \langle (g,g),(\eta ^{\times })^{-1}(g)\rho (\mathfrak {e}_1(g),\mathfrak {e}_2(g))\rangle $
is the embedding of the group
![]() $\{(g,g):g\in G(\mathbb {A})\}$
in
$\{(g,g):g\in G(\mathbb {A})\}$
in
![]() $H^{(m)}(\mathbb {A})$
(the lift of the embedding of
$H^{(m)}(\mathbb {A})$
(the lift of the embedding of
![]() $\{(g,g):g\in G(\mathbb {A})\}$
in
$\{(g,g):g\in G(\mathbb {A})\}$
in
![]() $H(\mathbb {A})$
).
$H(\mathbb {A})$
).
Claim 65. For any
![]() $g\in G(\mathbb {A})$
and
$g\in G(\mathbb {A})$
and
![]() $h\in H^{(m)}(\mathbb {A})$
,
$h\in H^{(m)}(\mathbb {A})$
,
The claim is proved below. It follows that Integral (4.9) equals
 $$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,\eta^{\times}(g_1)\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\& f_{\mathcal{W}(\mathcal{E}_{\tau})} (\langle \delta ,\eta^{-1}(\delta)\rangle\langle v_{g_1},\eta^{-1}(v_{g_1})\rangle\langle u_{g_1},\eta^{-1}(u_{g_1})\rangle \langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1^{(\eta^{\times})^{-1}}(\langle g_1,\eta^{\times}(g_1)\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\& f_{\mathcal{W}(\mathcal{E}_{\tau})} (\langle \delta ,\eta^{-1}(\delta)\rangle\langle v_{g_1},\eta^{-1}(v_{g_1})\rangle\langle u_{g_1},\eta^{-1}(u_{g_1})\rangle \langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
The change to the character
![]() $\psi _U$
when we change variables
$\psi _U$
when we change variables
![]() $u_{g_1}\mapsto u_0$
is cancelled by the left-equivariance property of
$u_{g_1}\mapsto u_0$
is cancelled by the left-equivariance property of
![]() $f_{\mathcal {W}(\mathcal {E}_{\tau })}$
under
$f_{\mathcal {W}(\mathcal {E}_{\tau })}$
under
![]() $v_{g_1}$
(see Equation (4.6)); this actually follows from the definition of the embedding in § 2.3. Also, by definition
$v_{g_1}$
(see Equation (4.6)); this actually follows from the definition of the embedding in § 2.3. Also, by definition
![]() $\varphi _1^{(\eta ^{\times })^{-1}}(\langle g_1,\eta ^{\times }(g_1)\rangle )= \varphi _1(\langle g_1,1\rangle )$
. We obtain
$\varphi _1^{(\eta ^{\times })^{-1}}(\langle g_1,\eta ^{\times }(g_1)\rangle )= \varphi _1(\langle g_1,1\rangle )$
. We obtain
 $$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\& f_{\mathcal{W}(\mathcal{E}_{\tau})} (\langle \delta u_0 ,\eta^{-1}(\delta u_0)\rangle \langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})} \int\limits_{U_0(\mathbb{A})} \varphi_1(\langle g_1,1\rangle)\,\overline{\varphi_2(\langle g_1,1\rangle\,{}^{\iota}\langle g_2,1\rangle)}\, \\& f_{\mathcal{W}(\mathcal{E}_{\tau})} (\langle \delta u_0 ,\eta^{-1}(\delta u_0)\rangle \langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
Here, we also used Corollary 16 to combine
![]() $\delta $
and
$\delta $
and
![]() $u_0$
. Now, factoring through
$u_0$
. Now, factoring through
![]() $\{(g,1):g\in G(\mathbb {A})\}$
, the integral becomes
$\{(g,1):g\in G(\mathbb {A})\}$
, the integral becomes
 $$ \begin{align} &\int\limits_{G(\mathbb{A})}\{\varphi_1,({}^{\iota}\langle g_2,1\rangle)\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
$$ \begin{align} &\int\limits_{G(\mathbb{A})}\{\varphi_1,({}^{\iota}\langle g_2,1\rangle)\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
Using Equation (4.8) again and since
![]() $\{\varphi _1,\langle g_2,\epsilon \rangle \cdot \varphi _2\} =\epsilon ^{-1}\{\varphi _1,\langle g_2,1\rangle \cdot \varphi _2\}$
, when we change
$\{\varphi _1,\langle g_2,\epsilon \rangle \cdot \varphi _2\} =\epsilon ^{-1}\{\varphi _1,\langle g_2,1\rangle \cdot \varphi _2\}$
, when we change
![]() $g_2\mapsto {}^{\iota }g_2$
in Integral (4.11) we obtain
$g_2\mapsto {}^{\iota }g_2$
in Integral (4.11) we obtain
 $$ \begin{align} &\int\limits_{G(\mathbb{A})}\{\varphi_1,\langle g_2,1\rangle\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2({}^{\iota}g_2),\eta_{\iota,R}^{-1}(g_2)\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
$$ \begin{align} &\int\limits_{G(\mathbb{A})}\{\varphi_1,\langle g_2,1\rangle\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2({}^{\iota}g_2),\eta_{\iota,R}^{-1}(g_2)\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
Therefore, we conclude
 $$ \begin{align} &\mathrm{I}(\delta)=\int\limits_{G(\mathbb{A})}\{\varphi_1,\langle g_2,1\rangle\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\,{}^{\iota}\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
$$ \begin{align} &\mathrm{I}(\delta)=\int\limits_{G(\mathbb{A})}\{\varphi_1,\langle g_2,1\rangle\cdot\varphi_2\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle \delta u_0,\eta^{-1}(\delta u_0)\rangle\,{}^{\iota}\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg_2. \end{align} $$
This completes the proof that Integral (4.2) is equal to the integral (4.4) in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
. Moreover, it is now clear that
$\operatorname {\mathrm {Re}}(s)\gg 0$
. Moreover, it is now clear that
![]() $\mathrm {I}(\delta )$
vanishes and thereby Integral (4.2) also vanishes, unless
$\mathrm {I}(\delta )$
vanishes and thereby Integral (4.2) also vanishes, unless
![]() $\pi _1=\pi _2=\pi $
.
$\pi _1=\pi _2=\pi $
.
Proof of Claim 65.
For
![]() $g\in G(\mathbb {A})$
, by matrix multiplication
$g\in G(\mathbb {A})$
, by matrix multiplication
![]() ${}^{\delta \iota }(g,g)=d_gl_g$
with
${}^{\delta \iota }(g,g)=d_gl_g$
with
 $$ \begin{align*} &d_g=\operatorname{\mathrm{diag}}((g^{*})^{\triangle},g^{\triangle}), \qquad g^{\triangle}=\operatorname{\mathrm{diag}}(g,\ldots,g)\in\operatorname{\mathrm{GL}}_{rkc},\\ &l_g=\left(\begin{smallmatrix}I_n&&&&-A_2\\&I_n&&-A_3\\&&I_{2(rk-1)c}\\&&&I_n\\&&&&I_n\end{smallmatrix}\right),\qquad g=\left(\begin{smallmatrix}A_1 & A_2 \\ A_3 & A_4 \end{smallmatrix}\right). \end{align*} $$
$$ \begin{align*} &d_g=\operatorname{\mathrm{diag}}((g^{*})^{\triangle},g^{\triangle}), \qquad g^{\triangle}=\operatorname{\mathrm{diag}}(g,\ldots,g)\in\operatorname{\mathrm{GL}}_{rkc},\\ &l_g=\left(\begin{smallmatrix}I_n&&&&-A_2\\&I_n&&-A_3\\&&I_{2(rk-1)c}\\&&&I_n\\&&&&I_n\end{smallmatrix}\right),\qquad g=\left(\begin{smallmatrix}A_1 & A_2 \\ A_3 & A_4 \end{smallmatrix}\right). \end{align*} $$
Then
![]() $d_g\in M_P$
, and
$d_g\in M_P$
, and
![]() $l_g,{}^{d_g}l_g\in U_P(\mathbb {A})$
. Hence, locally, for
$l_g,{}^{d_g}l_g\in U_P(\mathbb {A})$
. Hence, locally, for
![]() $g,g'\in G(F_{\nu })$
, by Equation (2.9) and Proposition 36,
$g,g'\in G(F_{\nu })$
, by Equation (2.9) and Proposition 36,
 $$ \begin{align} \sigma_{2rkc,\nu}(d_gl_g,d_{g'}l_{g'})=\sigma_{2rkc,\nu}(d_g,d_{g'})= \sigma_{rkc,\nu}^{\diamondsuit}((g^{*})^{\triangle},({g'}^{*})^{\triangle})=\left(\frac{\varsigma_{*,c,\nu}(g^{*})\varsigma_{*,c,\nu}({g'}^{*})}{\varsigma_{*,c,\nu}((gg')^{*})}\right)^{rk}. \end{align} $$
$$ \begin{align} \sigma_{2rkc,\nu}(d_gl_g,d_{g'}l_{g'})=\sigma_{2rkc,\nu}(d_g,d_{g'})= \sigma_{rkc,\nu}^{\diamondsuit}((g^{*})^{\triangle},({g'}^{*})^{\triangle})=\left(\frac{\varsigma_{*,c,\nu}(g^{*})\varsigma_{*,c,\nu}({g'}^{*})}{\varsigma_{*,c,\nu}((gg')^{*})}\right)^{rk}. \end{align} $$
Then by Equation (2.29),
![]() $\rho _{\nu }(d_gl_g,d_{g'}l_{g'})$
equals
$\rho _{\nu }(d_gl_g,d_{g'}l_{g'})$
equals
 $$ \begin{align*} &{\eta_{\nu}(d_{g}l_{g}d_{g'}l_{g'})}\left(\frac{\varsigma_{*,c,\nu}(g^{*})\varsigma_{*,c,\nu}({g'}^{*})}{\varsigma_{*,c,\nu}((gg')^{*})}\right)^{rk} =\frac{(\eta_{\nu}(d_gl_g)\varsigma_{*,c,\nu}^{rk}(g^{*}))(\eta_{\nu}(d_{g'}l_{g'})\varsigma_{*,c,\nu}^{rk}({g'}^{*}))} {\eta_{\nu}(d_{g}l_{g}d_{g'}l_{g'})\varsigma_{*,c,\nu}^{rk}((gg')^{*})}. \end{align*} $$
$$ \begin{align*} &{\eta_{\nu}(d_{g}l_{g}d_{g'}l_{g'})}\left(\frac{\varsigma_{*,c,\nu}(g^{*})\varsigma_{*,c,\nu}({g'}^{*})}{\varsigma_{*,c,\nu}((gg')^{*})}\right)^{rk} =\frac{(\eta_{\nu}(d_gl_g)\varsigma_{*,c,\nu}^{rk}(g^{*}))(\eta_{\nu}(d_{g'}l_{g'})\varsigma_{*,c,\nu}^{rk}({g'}^{*}))} {\eta_{\nu}(d_{g}l_{g}d_{g'}l_{g'})\varsigma_{*,c,\nu}^{rk}((gg')^{*})}. \end{align*} $$
Since
![]() $\rho _{\nu }$
is
$\rho _{\nu }$
is
![]() $1$
on
$1$
on
![]() $K_{H,\nu }$
for almost all
$K_{H,\nu }$
for almost all
![]() $\nu $
, and
$\nu $
, and
![]() $g\mapsto {}^{\delta \iota }(g,g)=d_gl_g$
is in particular a homomorphism of
$g\mapsto {}^{\delta \iota }(g,g)=d_gl_g$
is in particular a homomorphism of
![]() $K_{G,\nu }$
into
$K_{G,\nu }$
into
![]() $K_{H,\nu }$
, we deduce that
$K_{H,\nu }$
, we deduce that
![]() $g\mapsto \eta _{\nu }(d_gl_g)\varsigma _{*,c,\nu }^{rk}(g^{*})=1$
on
$g\mapsto \eta _{\nu }(d_gl_g)\varsigma _{*,c,\nu }^{rk}(g^{*})=1$
on
![]() $K_{G,\nu }$
(see the proof of Corollary 38). Therefore,
$K_{G,\nu }$
(see the proof of Corollary 38). Therefore,
is well defined on
![]() $\{{}^{\delta \iota }(g,g):g\in G(\mathbb {A})\}$
. Then by globalizing the identity for
$\{{}^{\delta \iota }(g,g):g\in G(\mathbb {A})\}$
. Then by globalizing the identity for
![]() $\rho _{\nu }(d_gl_g,d_{g'}l_{g'})$
, it follows that
$\rho _{\nu }(d_gl_g,d_{g'}l_{g'})$
, it follows that
is the unique splitting of
![]() $\{{}^{\delta \iota }(g,g):g\in G(\mathbb {A})\}$
(cf. Equation (3.5)). Now, by Equation (2.4), with
$\{{}^{\delta \iota }(g,g):g\in G(\mathbb {A})\}$
(cf. Equation (3.5)). Now, by Equation (2.4), with
![]() $\chi ={}^{\delta \iota }$
and
$\chi ={}^{\delta \iota }$
and
![]() $Y=\{(g,g):g\in G(\mathbb {A})\}$
,
$Y=\{(g,g):g\in G(\mathbb {A})\}$
,
Furthermore, for
![]() $g\in G(F_{\nu })$
by Equation (2.29) we have
$g\in G(F_{\nu })$
by Equation (2.29) we have
 $$ \begin{align*} \rho_{\nu}(d_g,l_g)^{-1}\eta_{\nu}^{-1}(d_gl_g)\varsigma_{*,c,\nu}^{-rk}(g^{*}) &= \eta_{\nu}^{-1}(d_g)\eta_{\nu}^{-1}(l_g)\sigma_{2rkc,\nu}^{-1}(d_g,l_g)\varsigma_{*,c,\nu}^{-rk}(g^{*})\\ &=\eta_{\nu}^{-1}(d_g)\eta_{\nu}^{-1}(l_g)\varsigma_{*,c,\nu}^{-rk}(g^{*}). \end{align*} $$
$$ \begin{align*} \rho_{\nu}(d_g,l_g)^{-1}\eta_{\nu}^{-1}(d_gl_g)\varsigma_{*,c,\nu}^{-rk}(g^{*}) &= \eta_{\nu}^{-1}(d_g)\eta_{\nu}^{-1}(l_g)\sigma_{2rkc,\nu}^{-1}(d_g,l_g)\varsigma_{*,c,\nu}^{-rk}(g^{*})\\ &=\eta_{\nu}^{-1}(d_g)\eta_{\nu}^{-1}(l_g)\varsigma_{*,c,\nu}^{-rk}(g^{*}). \end{align*} $$
Here, for the second equality we used Equation (2.8). By definition
![]() $\eta _{\nu }(d_g)=\eta _{rkc,\nu }^{\diamondsuit }((g^{*})^{\triangle })$
and then
$\eta _{\nu }(d_g)=\eta _{rkc,\nu }^{\diamondsuit }((g^{*})^{\triangle })$
and then
![]() $\eta _{\nu }(d_g)\varsigma _{*,c,\nu }^{rk}(g^{*})=\eta _{rkc,\nu }^{\triangle }(g^{*})$
(see Corollary 38), hence
$\eta _{\nu }(d_g)\varsigma _{*,c,\nu }^{rk}(g^{*})=\eta _{rkc,\nu }^{\triangle }(g^{*})$
(see Corollary 38), hence
The l.h.s. globalizes because
![]() $\rho $
is well defined and so is
$\rho $
is well defined and so is
![]() $[\eta \varsigma _{*,c}^{rk}]$
, and the r.h.s. globalizes because by Corollary 38,
$[\eta \varsigma _{*,c}^{rk}]$
, and the r.h.s. globalizes because by Corollary 38,
![]() $\eta _{rkc}^{\triangle }$
is well defined (even on
$\eta _{rkc}^{\triangle }$
is well defined (even on
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
![]() $G(\mathbb {A})<\operatorname {\mathrm {SL}}_c(\mathbb {A})$
), and
$G(\mathbb {A})<\operatorname {\mathrm {SL}}_c(\mathbb {A})$
), and
![]() $\eta $
is well defined (even on
$\eta $
is well defined (even on
![]() $N_{rkc}(\mathbb {A})$
). Consequently, for any
$N_{rkc}(\mathbb {A})$
). Consequently, for any
![]() $g\in G(\mathbb {A})$
,
$g\in G(\mathbb {A})$
,
Thus
Also, note that
![]() $\langle d_g,(\eta _{rkc}^{\triangle })^{-1}(g^{*})\rangle =\langle (g^{*})^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(g^{*})\rangle $
, when we regard
$\langle d_g,(\eta _{rkc}^{\triangle })^{-1}(g^{*})\rangle =\langle (g^{*})^{\triangle },(\eta _{rkc}^{\triangle })^{-1}(g^{*})\rangle $
, when we regard
![]() $(g^{*})^{\triangle }$
as an element of
$(g^{*})^{\triangle }$
as an element of
![]() $M_P(\mathbb {A})$
(which is also how
$M_P(\mathbb {A})$
(which is also how
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
was defined). Using Equation (4.15) and these results, we obtain
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
was defined). Using Equation (4.15) and these results, we obtain
 $$ \begin{align*} &f_{\mathcal{W}(\mathcal{E}_{\tau})} ({}^{\delta\iota}\langle (g,g),(\eta^{\times})^{-1}(g)\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle h ,s)=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle d_gl_g, [\eta\varsigma_{*,c}^{rk}]^{-1}(d_gl_g)\rangle h,s) \\&\quad=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle (g^{*})^{\triangle},(\eta_{rkc}^{\triangle})^{-1}(g^{*})\rangle\langle l_g,\eta^{-1}(l_g)\rangle h,s) =f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle l_g,\eta^{-1}(l_g)\rangle h,s) =f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s). \end{align*} $$
$$ \begin{align*} &f_{\mathcal{W}(\mathcal{E}_{\tau})} ({}^{\delta\iota}\langle (g,g),(\eta^{\times})^{-1}(g)\rho(\mathfrak{e}_1(g),\mathfrak{e}_2(g))\rangle h ,s)=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle d_gl_g, [\eta\varsigma_{*,c}^{rk}]^{-1}(d_gl_g)\rangle h,s) \\&\quad=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle (g^{*})^{\triangle},(\eta_{rkc}^{\triangle})^{-1}(g^{*})\rangle\langle l_g,\eta^{-1}(l_g)\rangle h,s) =f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle l_g,\eta^{-1}(l_g)\rangle h,s) =f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s). \end{align*} $$
Here, the third equality follows from Proposition 39, and the last by the left-invariance property of
![]() $f_{\mathcal {W}(\mathcal {E}_{\tau })}$
under
$f_{\mathcal {W}(\mathcal {E}_{\tau })}$
under
![]() $\langle u,\eta ^{-1}(u)\rangle $
for
$\langle u,\eta ^{-1}(u)\rangle $
for
![]() $u\in U_P(\mathbb {A})$
.
$u\in U_P(\mathbb {A})$
.
Now, we write Integral (4.4) as an almost Euler product (in the sense of [Reference TakedaTak14]) and derive the structure of the local integrals.
![]() $\underline {\mathrm {Assume that} \ \mu _{2m}\subset F^{*}}$
, then by Theorem 54,
$\underline {\mathrm {Assume that} \ \mu _{2m}\subset F^{*}}$
, then by Theorem 54,
![]() $\mathcal {E}_{\tau }$
is an
$\mathcal {E}_{\tau }$
is an
![]() $(rk,c)$
representation. Let S be a finite set of places of F such that for
$(rk,c)$
representation. Let S be a finite set of places of F such that for
![]() $\nu \notin S$
,
$\nu \notin S$
,
![]() $F_{\nu }$
,
$F_{\nu }$
,
![]() $\psi _{\nu }$
,
$\psi _{\nu }$
,
![]() $\tau _{\nu }$
and
$\tau _{\nu }$
and
![]() $\pi _{\nu }$
are unramified. We use the notation of § 3.1. Identify
$\pi _{\nu }$
are unramified. We use the notation of § 3.1. Identify
![]() $\mathcal {E}_{\tau }$
with
$\mathcal {E}_{\tau }$
with
![]() $(\mathcal {E}_{\tau })_S\otimes \otimes ^{\prime }_{\nu \notin S}\rho _c(\tau _{\nu })$
(
$(\mathcal {E}_{\tau })_S\otimes \otimes ^{\prime }_{\nu \notin S}\rho _c(\tau _{\nu })$
(
![]() $\rho _c(\tau _{\nu })$
was defined in § 3.5). By Equation (3.4), for a factorizable f,
$\rho _c(\tau _{\nu })$
was defined in § 3.5). By Equation (3.4), for a factorizable f,
Here,
![]() $f_{\mathcal {W}((\mathcal {E}_{\tau })_S)}$
(resp.,
$f_{\mathcal {W}((\mathcal {E}_{\tau })_S)}$
(resp.,
![]() $f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
) is a standard section in the space of
$f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
) is a standard section in the space of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}(F_S)}^{H^{(m)}(F_S)}(\mathcal {W}((\mathcal {E}_{\tau })_S)\delta _P^s)$
(resp.,
$\operatorname {\mathrm {Ind}}_{\widetilde {P}(F_S)}^{H^{(m)}(F_S)}(\mathcal {W}((\mathcal {E}_{\tau })_S)\delta _P^s)$
(resp.,
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}(F_{\nu })}^{H^{(m)}(F_{\nu })}(\mathcal {W}(\rho _c(\tau _{\nu }))\delta _P^s)$
), regarded as a complex-valued function. Moreover, at almost all
$\operatorname {\mathrm {Ind}}_{\widetilde {P}(F_{\nu })}^{H^{(m)}(F_{\nu })}(\mathcal {W}(\rho _c(\tau _{\nu }))\delta _P^s)$
), regarded as a complex-valued function. Moreover, at almost all
![]() $\nu \notin S$
, the sections
$\nu \notin S$
, the sections
![]() $f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized (
$f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized (
![]() $f_{\mathcal {W}(\rho _c(\tau _{\nu }))}(\langle I_{2rkc},1\rangle ,s)=1$
) and unramified.
$f_{\mathcal {W}(\rho _c(\tau _{\nu }))}(\langle I_{2rkc},1\rangle ,s)=1$
) and unramified.
Next, for factorizable
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
, by the uniqueness of the
$\varphi _2$
, by the uniqueness of the
![]() $G^{(m)}(F_{\nu })$
-invariant bilinear pairing on
$G^{(m)}(F_{\nu })$
-invariant bilinear pairing on
![]() $\pi _{\nu }\times \pi _{\nu }^{\vee }$
at all places, there are matrix coefficients
$\pi _{\nu }\times \pi _{\nu }^{\vee }$
at all places, there are matrix coefficients
![]() $\omega _{\nu }$
of
$\omega _{\nu }$
of
![]() $\pi _{\nu }^{\vee }$
such that at almost all places
$\pi _{\nu }^{\vee }$
such that at almost all places
![]() $\nu $
,
$\nu $
,
![]() $\omega _{\nu }$
is normalized (
$\omega _{\nu }$
is normalized (
![]() $\omega _{\nu }(\langle I_c,1\rangle )=1$
) and unramified, and for all
$\omega _{\nu }(\langle I_c,1\rangle )=1$
) and unramified, and for all
![]() $g\in G^{(m)}(\mathbb {A})$
,
$g\in G^{(m)}(\mathbb {A})$
,
Then by Theorem 64 we have an almost Euler product:
where
 $$ \begin{align} &Z_{\nu}(s,\omega_{\nu},f_{\mathcal{W}(\rho_c(\tau_{\nu}))})\\&= \int\limits_{G(F_{\nu})}\int\limits_{U_0(F_{\nu})} \omega_{\nu}(\langle g,1\rangle)f_{\mathcal{W}(\rho_c(\tau_{\nu}))}(\langle\delta_{\nu} u_0,\eta_{\nu}^{-1}(\delta_{\nu} u_0)\rangle {}^{\iota_{\nu}}\langle\mathfrak{e}_2(g),1\rangle,s) \,(\psi_{\nu})_{U}(u_0)\,du_0\,dg,\nonumber \end{align} $$
$$ \begin{align} &Z_{\nu}(s,\omega_{\nu},f_{\mathcal{W}(\rho_c(\tau_{\nu}))})\\&= \int\limits_{G(F_{\nu})}\int\limits_{U_0(F_{\nu})} \omega_{\nu}(\langle g,1\rangle)f_{\mathcal{W}(\rho_c(\tau_{\nu}))}(\langle\delta_{\nu} u_0,\eta_{\nu}^{-1}(\delta_{\nu} u_0)\rangle {}^{\iota_{\nu}}\langle\mathfrak{e}_2(g),1\rangle,s) \,(\psi_{\nu})_{U}(u_0)\,du_0\,dg,\nonumber \end{align} $$
 $$ \begin{align} &Z[S](s,\omega_S,f_{\mathcal{W}((\mathcal{E}_{\tau})_S)})\\&= \int\limits_{G(F_{S})}\int\limits_{U_0(F_{S})} \omega_{S}(\langle g,1\rangle)f_{\mathcal{W}((\mathcal{E}_{\tau})_S)}(\langle\delta_{S} u_0,\eta_{S}^{-1}(\delta_{S} u_0)\rangle {}^{\iota_{S}}\langle\mathfrak{e}_2(g),1\rangle,s) \,(\psi_{S})_{U}(u_0)\,du_0\,dg.\nonumber \end{align} $$
$$ \begin{align} &Z[S](s,\omega_S,f_{\mathcal{W}((\mathcal{E}_{\tau})_S)})\\&= \int\limits_{G(F_{S})}\int\limits_{U_0(F_{S})} \omega_{S}(\langle g,1\rangle)f_{\mathcal{W}((\mathcal{E}_{\tau})_S)}(\langle\delta_{S} u_0,\eta_{S}^{-1}(\delta_{S} u_0)\rangle {}^{\iota_{S}}\langle\mathfrak{e}_2(g),1\rangle,s) \,(\psi_{S})_{U}(u_0)\,du_0\,dg.\nonumber \end{align} $$
As mentioned in the introduction, when
![]() $r=1$
or
$r=1$
or
![]() $k=1$
(and
$k=1$
(and
![]() $\mu _{2m}\subset F^{*}$
), we can already obtain a full Euler product, that is, the r.h.s. of Equation (4.16) is the infinite product of local integrals (4.17) over all places. This is because by [Reference KaplanKap23, Proposition 15 and Theorem 17], in this case, the representations
$\mu _{2m}\subset F^{*}$
), we can already obtain a full Euler product, that is, the r.h.s. of Equation (4.16) is the infinite product of local integrals (4.17) over all places. This is because by [Reference KaplanKap23, Proposition 15 and Theorem 17], in this case, the representations
![]() $(\mathcal {E}_{\tau })_{\nu }$
are
$(\mathcal {E}_{\tau })_{\nu }$
are
![]() $(rk,c)$
for all
$(rk,c)$
for all
![]() $\nu $
.
$\nu $
.
The following is the main local result of this work: The computation of Integral (4.17) with unramified data. Its proof occupies § 5 and is independent of Conjectures 50 and 51 (see Remark 88).
Theorem 66. Assume
![]() $\mu _{2m}\subset F^{*}$
. Let
$\mu _{2m}\subset F^{*}$
. Let
![]() $\nu \notin S$
, and assume that
$\nu \notin S$
, and assume that
![]() $\omega _{\nu }$
and
$\omega _{\nu }$
and
![]() $f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized and unramified. Then
$f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized and unramified. Then
 $$ \begin{align*} &Z_{\nu}(s,\omega_{\nu},f_{\mathcal{W}(\rho_c(\tau_{\nu}))})\\&= \frac{L_{\vartheta_{\nu}}(r\alpha s+1/2,\pi_{\nu}\times\tau_{\nu})} {[L_{\vartheta_{\nu}}(r\alpha s+rn+1/2,\tau_{\nu})]\prod\limits_{1\leq j\leq rn}L_{\vartheta_{\nu}}(2r\alpha s+2j,\tau_{\nu},\wedge^2) L_{\vartheta_{\nu}}(2r\alpha s+2j-1,\tau_{\nu},\vee^2)}. \end{align*} $$
$$ \begin{align*} &Z_{\nu}(s,\omega_{\nu},f_{\mathcal{W}(\rho_c(\tau_{\nu}))})\\&= \frac{L_{\vartheta_{\nu}}(r\alpha s+1/2,\pi_{\nu}\times\tau_{\nu})} {[L_{\vartheta_{\nu}}(r\alpha s+rn+1/2,\tau_{\nu})]\prod\limits_{1\leq j\leq rn}L_{\vartheta_{\nu}}(2r\alpha s+2j,\tau_{\nu},\wedge^2) L_{\vartheta_{\nu}}(2r\alpha s+2j-1,\tau_{\nu},\vee^2)}. \end{align*} $$
Here,
![]() $\alpha =rkc+1$
,
$\alpha =rkc+1$
,
![]() $L_{\vartheta _{\nu }}(r\alpha s+rn+1/2,\tau _{\nu })$
appears only for odd m, and
$L_{\vartheta _{\nu }}(r\alpha s+rn+1/2,\tau _{\nu })$
appears only for odd m, and
![]() $\vartheta _{\nu }$
is ignored when
$\vartheta _{\nu }$
is ignored when
![]() $m\not \equiv 2\,(4)$
.
$m\not \equiv 2\,(4)$
.
Remark 67. For
![]() $m=1$
, this result was proved in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Theorem 29], and for
$m=1$
, this result was proved in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Theorem 29], and for
![]() $m=2$
and
$m=2$
and
![]() $k=1$
by Li [Reference LiLi92, Proposition 4.6] (without the assumption that
$k=1$
by Li [Reference LiLi92, Proposition 4.6] (without the assumption that
![]() $\mu _{4}\subset F^{*}$
); our proof will include these cases.
$\mu _{4}\subset F^{*}$
); our proof will include these cases.
We switch to local notation. Since Integral (4.16) also includes the integral (4.18) over the places in S, we treat a single place and a finite product of places simultaneously. Let
![]() $S'$
be an arbitrary finite set of places of F, and denote
$S'$
be an arbitrary finite set of places of F, and denote
 $$ \begin{align*} &G=G(F_{S'}), \qquad H=H(F_{S'}),\qquad U_0=U_0(F_{S'}), \qquad \delta=\delta_{S'}, \qquad \iota=\iota_{S'},\\ &\psi_U=(\psi_{S'})_U,\qquad \sigma_{2rkc}=\prod_{\nu\in S'}\sigma_{2rkc,\nu},\qquad \varsigma_{\iota,c}=\prod_{\nu\in S'}\varsigma_{\iota,c,\nu}, \qquad \varsigma_{*,c}=\prod_{\nu\in S'}\varsigma_{*,c,\nu}. \end{align*} $$
$$ \begin{align*} &G=G(F_{S'}), \qquad H=H(F_{S'}),\qquad U_0=U_0(F_{S'}), \qquad \delta=\delta_{S'}, \qquad \iota=\iota_{S'},\\ &\psi_U=(\psi_{S'})_U,\qquad \sigma_{2rkc}=\prod_{\nu\in S'}\sigma_{2rkc,\nu},\qquad \varsigma_{\iota,c}=\prod_{\nu\in S'}\varsigma_{\iota,c,\nu}, \qquad \varsigma_{*,c}=\prod_{\nu\in S'}\varsigma_{*,c,\nu}. \end{align*} $$
Realize
![]() $H^{(m)}$
using
$H^{(m)}$
using
![]() $\sigma _{2rkc}$
, and the right copy of
$\sigma _{2rkc}$
, and the right copy of
![]() $G^{(m)}$
by
$G^{(m)}$
by
![]() $\sigma _c=\prod _{\nu \in S'}\sigma _{c,\nu }$
. The local properties from § 2.4 are still applicable because
$\sigma _c=\prod _{\nu \in S'}\sigma _{c,\nu }$
. The local properties from § 2.4 are still applicable because
![]() $S'$
is finite. Let
$S'$
is finite. Let
![]() $\pi $
be a genuine irreducible admissible representation of
$\pi $
be a genuine irreducible admissible representation of
![]() $G^{(m)}$
, realized using
$G^{(m)}$
, realized using
![]() $\sigma _c$
. Assume that
$\sigma _c$
. Assume that
![]() $\mathcal {E}$
is a genuine irreducible admissible representation of
$\mathcal {E}$
is a genuine irreducible admissible representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(the cover obtained from
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(the cover obtained from
![]() $\widetilde {M}_P(F_{S'})$
) which affords an
$\widetilde {M}_P(F_{S'})$
) which affords an
![]() $(rk,c)$
functional
$(rk,c)$
functional
![]() $\Lambda $
, and such that
$\Lambda $
, and such that
Even if
![]() $\Lambda $
is unique up to scaling,
$\Lambda $
is unique up to scaling,
![]() $\mathcal {E}$
might not be
$\mathcal {E}$
might not be
![]() $(rk,c)$
because we do not assume that the first condition in the definition (
$(rk,c)$
because we do not assume that the first condition in the definition (
![]() $\mathcal {O}(\mathcal {E},\beta ',\psi )=0$
for any
$\mathcal {O}(\mathcal {E},\beta ',\psi )=0$
for any
![]() $\beta '\succsim ((rk)^c)$
) holds. Let
$\beta '\succsim ((rk)^c)$
) holds. Let
![]() $\mathcal {W}(\mathcal {E})$
be the
$\mathcal {W}(\mathcal {E})$
be the
![]() $(rk,c)$
model defined using
$(rk,c)$
model defined using
![]() $\Lambda $
.
$\Lambda $
.
For the integrals (4.17), the representations
![]() $\rho _c(\tau _{\nu })$
are
$\rho _c(\tau _{\nu })$
are
![]() $(rk,c)$
and (4.19) is satisfied by Corollary 37. If
$(rk,c)$
and (4.19) is satisfied by Corollary 37. If
![]() $S'=S$
, the functional chosen for the realization of
$S'=S$
, the functional chosen for the realization of
![]() $\mathcal {W}((\mathcal {E}_{\tau })_S)$
in Equation (4.18) also satisfies Equation (4.19), by Corollary 40.
$\mathcal {W}((\mathcal {E}_{\tau })_S)$
in Equation (4.18) also satisfies Equation (4.19), by Corollary 40.
For a matrix coefficient
![]() $\omega $
of
$\omega $
of
![]() $\pi ^{\vee }$
and a standard section
$\pi ^{\vee }$
and a standard section
![]() $f_{\mathcal {W}(\mathcal {E})}$
of
$f_{\mathcal {W}(\mathcal {E})}$
of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}}^{H^{(m)}}(\mathcal {W}(\mathcal {E})\delta _P^s)$
,
$\operatorname {\mathrm {Ind}}_{\widetilde {P}}^{H^{(m)}}(\mathcal {W}(\mathcal {E})\delta _P^s)$
,
 $$ \begin{align} &Z(s,\omega,f_{\mathcal{W}(\mathcal{E})})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle\, {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &Z(s,\omega,f_{\mathcal{W}(\mathcal{E})})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle\, {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
Note that we omitted
![]() $\eta ^{-1}(\delta u_0)$
. This is because we can use Corollary 16 to separate
$\eta ^{-1}(\delta u_0)$
. This is because we can use Corollary 16 to separate
![]() $\delta $
from
$\delta $
from
![]() $u_0$
in the global integral; then
$u_0$
in the global integral; then
![]() $\eta _{\nu }(\delta _{\nu })=1$
at almost all places; and locally when we use
$\eta _{\nu }(\delta _{\nu })=1$
at almost all places; and locally when we use
![]() $\sigma _{2krc}$
,
$\sigma _{2krc}$
,
![]() $v\mapsto \langle v,1\rangle $
is the splitting of
$v\mapsto \langle v,1\rangle $
is the splitting of
![]() $N_{rkc}$
and in particular of
$N_{rkc}$
and in particular of
![]() $U_0$
, by Equation (2.8), which also implies that
$U_0$
, by Equation (2.8), which also implies that
![]() $\langle \delta ,1\rangle \langle u_0,1\rangle =\langle \delta u_0,1\rangle $
. The map
$\langle \delta ,1\rangle \langle u_0,1\rangle =\langle \delta u_0,1\rangle $
. The map
![]() $\delta \mapsto \langle \delta ,1\rangle $
is a homomorphism when the local fields
$\delta \mapsto \langle \delta ,1\rangle $
is a homomorphism when the local fields
![]() $\{F_{\nu }\}_{\nu \in S'}$
are all unramified (see § 2.4); in general, replacing
$\{F_{\nu }\}_{\nu \in S'}$
are all unramified (see § 2.4); in general, replacing
![]() $\langle \delta ,1\rangle $
with
$\langle \delta ,1\rangle $
with
![]() $\langle \delta ,\epsilon \rangle $
simply multiplies the integral by
$\langle \delta ,\epsilon \rangle $
simply multiplies the integral by
![]() $\epsilon $
.
$\epsilon $
.
Let
![]() $S_{\infty }$
be the set of Archimedean places. Since we are now assuming that
$S_{\infty }$
be the set of Archimedean places. Since we are now assuming that
![]() $\mu _{2m}\subset F^{*}$
(this was assumed in order to obtain Equation (4.16)), this is also true locally, and in particular the Archimedean places are complex (when
$\mu _{2m}\subset F^{*}$
(this was assumed in order to obtain Equation (4.16)), this is also true locally, and in particular the Archimedean places are complex (when
![]() $m>1$
). Thus, at the Archimedean places the covering is trivial. Note that for
$m>1$
). Thus, at the Archimedean places the covering is trivial. Note that for
![]() $m=1$
, both the real and complex Archimedean fields were treated in [Reference Cai, Friedberg and KaplanCFK22].
$m=1$
, both the real and complex Archimedean fields were treated in [Reference Cai, Friedberg and KaplanCFK22].
Proposition 68. The integral
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
enjoys the following properties.
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
enjoys the following properties.
-
1. It is absolutely convergent in a right half-plane
 $\operatorname {\mathrm {Re}}(s)\gg 0$
depending only on the representations.
$\operatorname {\mathrm {Re}}(s)\gg 0$
depending only on the representations. -
2. If
 $S'\cap S_{\infty }=\emptyset $
, there exist data
$S'\cap S_{\infty }=\emptyset $
, there exist data
 $(\omega ,f_{\mathcal {W}(\mathcal {E})})$
for which
$(\omega ,f_{\mathcal {W}(\mathcal {E})})$
for which
 $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is absolutely convergent and equals
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is absolutely convergent and equals
 $1$
, for all s.
$1$
, for all s. -
3. If
 $S'\subset S_{\infty }$
, then for a given s, there exist
$S'\subset S_{\infty }$
, then for a given s, there exist
 $(\omega ,f_{\mathcal {W}(\mathcal {E})})$
, where
$(\omega ,f_{\mathcal {W}(\mathcal {E})})$
, where
 $f_{\mathcal {W}(\mathcal {E})}$
is a smooth section such that
$f_{\mathcal {W}(\mathcal {E})}$
is a smooth section such that
 $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is holomorphic and nonzero in a neighborhood of s.
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is holomorphic and nonzero in a neighborhood of s. -
4. Assume that
 $\mathcal {E}$
is a local component, or a finite tensor product of local components, of the global
$\mathcal {E}$
is a local component, or a finite tensor product of local components, of the global
 $(rk,c)$
representation obtained by Theorem 54, and for
$(rk,c)$
representation obtained by Theorem 54, and for
 $\nu \in S'\cap S_{\infty }$
,
$\nu \in S'\cap S_{\infty }$
,
 $\mathcal {E}_{\nu }$
is
$\mathcal {E}_{\nu }$
is
 $(rk,c)$
. For any s, there exist
$(rk,c)$
. For any s, there exist
 $(\omega ,f_{\mathcal {W}(\mathcal {E})})$
, where
$(\omega ,f_{\mathcal {W}(\mathcal {E})})$
, where
 $f_{\mathcal {W}(\mathcal {E})}$
is
$f_{\mathcal {W}(\mathcal {E})}$
is
 $\prod _{\nu \in S'}\widetilde {K}_{H,\nu }$
-finite such that
$\prod _{\nu \in S'}\widetilde {K}_{H,\nu }$
-finite such that
 $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is holomorphic and nonzero in a neighborhood of s.
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
is holomorphic and nonzero in a neighborhood of s.
Proof. Parts (1)–(3) were proved for linear groups in [Reference Cai, Friedberg and KaplanCFK22, Propositions 2.5, 2.6] when
![]() $|S'|=1$
. The arguments extend to covering groups and to finite products of integrals (i.e., to
$|S'|=1$
. The arguments extend to covering groups and to finite products of integrals (i.e., to
![]() $|S'|>1$
) and only depend on the equivariance property of the
$|S'|>1$
) and only depend on the equivariance property of the
![]() $(k,c)$
functional under
$(k,c)$
functional under
![]() $V_{(c^k)}$
and invariance under
$V_{(c^k)}$
and invariance under
![]() $\operatorname {\mathrm {SL}}_c^{\triangle }$
; here, we have an
$\operatorname {\mathrm {SL}}_c^{\triangle }$
; here, we have an
![]() $(rk,c)$
functional with an equivariance property under
$(rk,c)$
functional with an equivariance property under
![]() $V_{(c^{rk})}$
and the invariance property is guaranteed by assumption (4.19). In particular, for part (2) note that if we take a sufficiently small compact open neighborhood of the identity
$V_{(c^{rk})}$
and the invariance property is guaranteed by assumption (4.19). In particular, for part (2) note that if we take a sufficiently small compact open neighborhood of the identity
![]() $\mathcal {N}$
in H, then
$\mathcal {N}$
in H, then
![]() $H^{(m)}$
is split over
$H^{(m)}$
is split over
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
For the last assertion, first note that under the assumption on the Archimedean places, we can write
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
as the product of an integral (4.18) with respect to
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
as the product of an integral (4.18) with respect to
![]() $S"=S'-S_{\infty }$
and
$S"=S'-S_{\infty }$
and
![]() $|S'\cap S_{\infty }|$
local integrals over the places of
$|S'\cap S_{\infty }|$
local integrals over the places of
![]() $S'\cap S_{\infty }$
. The integral over
$S'\cap S_{\infty }$
. The integral over
![]() $S"$
can be made constant by part (2). Since we also have part (3), it remains to prove that the integrals over the Archimedean places admit meromorphic continuation to
$S"$
can be made constant by part (2). Since we also have part (3), it remains to prove that the integrals over the Archimedean places admit meromorphic continuation to
![]() $\mathbb {C}$
as functions of s, and this continuation is continuous in
$\mathbb {C}$
as functions of s, and this continuation is continuous in
![]() $\omega _{\nu }$
and
$\omega _{\nu }$
and
![]() $f_{\mathcal {W}(\mathcal {E}_{\nu })}$
.
$f_{\mathcal {W}(\mathcal {E}_{\nu })}$
.
We can now use local notation and consider a single Archimedean place. Put
This representation admits a unique Whittaker model because
![]() $\tau $
is irreducible admissible and generic. Then by Theorem 53,
$\tau $
is irreducible admissible and generic. Then by Theorem 53,
By our assumption,
![]() $\mathcal {E}$
admits a unique
$\mathcal {E}$
admits a unique
![]() $(rk,c)$
functional, hence we can realize it using a functional on the full induced representation, granted it does not vanish on
$(rk,c)$
functional, hence we can realize it using a functional on the full induced representation, granted it does not vanish on
![]() $\mathcal {E}$
. Such can be obtained inductively using the integral from § 3.5: first, construct an integral on
$\mathcal {E}$
. Such can be obtained inductively using the integral from § 3.5: first, construct an integral on
then compose it with an integral on
and so on. With this realization, we can follow the arguments from [Reference Cai, Friedberg and KaplanCFK22, § 6.10]: Using the multiplicativity arguments from [Reference Cai, Friedberg and KaplanCFK22, § 5.3.1] we reduce these continuation and continuity statements to the case of doubling integrals for
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
(whose covering version will be described here in § 4.3) and
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
(whose covering version will be described here in § 4.3) and
![]() $\operatorname {\mathrm {Sp}}_{c-2}\times \operatorname {\mathrm {GL}}_{rk}$
, then repeat the arguments on the
$\operatorname {\mathrm {Sp}}_{c-2}\times \operatorname {\mathrm {GL}}_{rk}$
, then repeat the arguments on the
![]() $\operatorname {\mathrm {Sp}}_{c-2}\times \operatorname {\mathrm {GL}}_{rk}$
integral. We obtain n doubling integrals for
$\operatorname {\mathrm {Sp}}_{c-2}\times \operatorname {\mathrm {GL}}_{rk}$
integral. We obtain n doubling integrals for
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
. Note that in [Reference Cai, Friedberg and KaplanCFK22, § 5.3.1] the multiplicativity arguments were formulated under the assumption that
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
. Note that in [Reference Cai, Friedberg and KaplanCFK22, § 5.3.1] the multiplicativity arguments were formulated under the assumption that
![]() $\tau $
is essentially tempered, but this was only needed in order to have the integral realization of the model which is similar to § 3.5 here (see [Reference Cai, Friedberg and KaplanCFK22, (1.5)]). The continuation and continuity for a
$\tau $
is essentially tempered, but this was only needed in order to have the integral realization of the model which is similar to § 3.5 here (see [Reference Cai, Friedberg and KaplanCFK22, (1.5)]). The continuation and continuity for a
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
integral with a quasi-character of
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_{rk}$
integral with a quasi-character of
![]() $F^{*}$
, and a representation of
$F^{*}$
, and a representation of
![]() $\operatorname {\mathrm {GL}}_{rk}$
which admits a unique Whittaker model, was then proved directly in [Reference Cai, Friedberg and KaplanCFK22, § 6.10]; here, the representation of
$\operatorname {\mathrm {GL}}_{rk}$
which admits a unique Whittaker model, was then proved directly in [Reference Cai, Friedberg and KaplanCFK22, § 6.10]; here, the representation of
![]() $\operatorname {\mathrm {GL}}_{rk}$
is
$\operatorname {\mathrm {GL}}_{rk}$
is
![]() $\tau ^r$
, in ibid. it was
$\tau ^r$
, in ibid. it was
![]() $\tau $
. Now, nonvanishing for a
$\tau $
. Now, nonvanishing for a
![]() $K_{H,\nu }$
-finite section follows from the continuity.
$K_{H,\nu }$
-finite section follows from the continuity.
Remark 69. Over Archimedean places, the argument is greatly simplified if we assume that
![]() $|\det |^{s'}\tau ^r$
is unitary for some
$|\det |^{s'}\tau ^r$
is unitary for some
![]() $s'\in \mathbb {R}$
. Then
$s'\in \mathbb {R}$
. Then
![]() $\mathcal {E}$
is precisely
$\mathcal {E}$
is precisely
![]() $\rho _c(\tau ^r)$
of [Reference Cai, Friedberg and KaplanCFK22],
$\rho _c(\tau ^r)$
of [Reference Cai, Friedberg and KaplanCFK22],
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() $(rk,c)$
by [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Theorem 4], and all the assertions on the integral already follow from [Reference Cai, Friedberg and KaplanCFK22]. For example, if
$(rk,c)$
by [Reference Cai, Friedberg, Gourevitch and KaplanCFGK23, Theorem 4], and all the assertions on the integral already follow from [Reference Cai, Friedberg and KaplanCFK22]. For example, if
![]() $\tau $
is a unitary irreducible representation of
$\tau $
is a unitary irreducible representation of
![]() $\operatorname {\mathrm {GL}}_k(\mathbb {C})$
and
$\operatorname {\mathrm {GL}}_k(\mathbb {C})$
and
![]() $|\chi _i|=|~|^{\alpha _i}$
with
$|\chi _i|=|~|^{\alpha _i}$
with
![]() $-1/2<r\alpha _i<1/2$
for each
$-1/2<r\alpha _i<1/2$
for each
![]() $\chi _i$
in the inducing data of
$\chi _i$
in the inducing data of
![]() $\tau $
,
$\tau $
,
![]() $\tau ^r$
is unitary; thus,
$\tau ^r$
is unitary; thus,
![]() $|\det |^{s'}\tau ^r$
is unitary (for some
$|\det |^{s'}\tau ^r$
is unitary (for some
![]() $s'\in \mathbb {R}$
) when
$s'\in \mathbb {R}$
) when
![]() $\tau $
is essentially tempered.
$\tau $
is essentially tempered.
For the following proposition and for Corollary 71, we do not assume that
![]() $\mu _{2m}\subset F^{*}$
.
$\mu _{2m}\subset F^{*}$
.
Proposition 70. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
$\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
can be regarded as a morphism in the space
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
can be regarded as a morphism in the space
Here,
![]() $J_{U,\psi _U^{-1}}(\cdots )$
is the Jacquet module with respect to U and
$J_{U,\psi _U^{-1}}(\cdots )$
is the Jacquet module with respect to U and
![]() $\psi _U^{-1}$
, regarded as a representation of
$\psi _U^{-1}$
, regarded as a representation of
![]() $G^{(m)}\times G^{(m)}$
by virtue of the embedding
$G^{(m)}\times G^{(m)}$
by virtue of the embedding
![]() $(g_1,g_2)$
.
$(g_1,g_2)$
.
Proof. First, we introduce some notation. Given
![]() $\omega $
, by definition there are vectors
$\omega $
, by definition there are vectors
![]() $\xi $
and
$\xi $
and
![]() $\xi ^{\vee }$
in the spaces of
$\xi ^{\vee }$
in the spaces of
![]() $\pi $
and
$\pi $
and
![]() $\pi ^{\vee }$
such that
$\pi ^{\vee }$
such that
![]() $\omega (g)=\pi ^{\vee }(g)\xi ^{\vee }(\xi )=\xi ^{\vee }(\pi (g^{-1})\xi )$
for
$\omega (g)=\pi ^{\vee }(g)\xi ^{\vee }(\xi )=\xi ^{\vee }(\pi (g^{-1})\xi )$
for
![]() $g\in G^{(m)}$
. Assume that
$g\in G^{(m)}$
. Assume that
![]() $\xi $
and
$\xi $
and
![]() $\xi ^{\vee }$
are given, and for
$\xi ^{\vee }$
are given, and for
![]() $g_1,g_2\in G^{(m)}$
, let
$g_1,g_2\in G^{(m)}$
, let
![]() $\omega _{g_1,g_2}$
be the matrix coefficient of
$\omega _{g_1,g_2}$
be the matrix coefficient of
![]() $\pi ^{\vee }$
defined by
$\pi ^{\vee }$
defined by
Regarding the integral as a trilinear form on
we claim that for
![]() $g_1,g_2\in G$
and
$g_1,g_2\in G$
and
![]() $u\in U$
,
$u\in U$
,
Before turning to the proof, note that while (4.22) is a priori a representation of
![]() $G^{(m)}\times G^{(m)}$
, it factors through
$G^{(m)}\times G^{(m)}$
, it factors through
![]() $G\times G$
by Formula (2.24). Also, observe that since both
$G\times G$
by Formula (2.24). Also, observe that since both
![]() $\pi $
and
$\pi $
and
![]() $\pi ^{\vee }$
(thereby
$\pi ^{\vee }$
(thereby
![]() $(\pi ^{\vee })^{\iota }$
) are defined on
$(\pi ^{\vee })^{\iota }$
) are defined on
![]() $G^{(m)}$
which is realized using
$G^{(m)}$
which is realized using
![]() $\sigma _c$
, the image of
$\sigma _c$
, the image of
![]() $\langle g_1,1\rangle $
in
$\langle g_1,1\rangle $
in
![]() $H^{(m)}$
is indeed
$H^{(m)}$
is indeed
![]() $\langle \mathfrak {e}_1(g_1),\varsigma _{*,c}^{rk+1}(g_1)\rangle $
; see the embedding (2.26). Hence, Equation (4.23) implies that
$\langle \mathfrak {e}_1(g_1),\varsigma _{*,c}^{rk+1}(g_1)\rangle $
; see the embedding (2.26). Hence, Equation (4.23) implies that
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
, as a trilinear form, factors through
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
, as a trilinear form, factors through
![]() $J_{U,\psi _U^{-1}}$
, and since
$J_{U,\psi _U^{-1}}$
, and since
![]() $(\pi ^{\vee })^{\iota }=(\pi ^{\iota })^{\vee }$
, this form can be identified with an element of the representation (4.21).
$(\pi ^{\vee })^{\iota }=(\pi ^{\iota })^{\vee }$
, this form can be identified with an element of the representation (4.21).
First, we prove (for any
![]() $\omega $
)
$\omega $
)
Starting with the l.h.s.,
 $$ \begin{align*} &Z(s,\omega,\langle u,1\rangle\cdot f_{\mathcal{W}(\mathcal{E})})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle u,1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &Z(s,\omega,\langle u,1\rangle\cdot f_{\mathcal{W}(\mathcal{E})})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle u,1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
By the definition of the embedding in § 2.3, we can write
![]() ${}^{\mathfrak {e}_2({}^{\iota }g)}u=v_gu_g$
, where
${}^{\mathfrak {e}_2({}^{\iota }g)}u=v_gu_g$
, where
![]() $v_g\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
and
$v_g\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
and
![]() $u_g\in U_0$
(also see Equation (4.5)). Then by Equations (2.10) and (2.9),
$u_g\in U_0$
(also see Equation (4.5)). Then by Equations (2.10) and (2.9),
The integral becomes
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle v_g,1\rangle\langle u_g,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg \\&=\int\limits_{G}\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}( \langle {}^{\delta}v_g,1\rangle \langle\delta u_0u_g,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle v_g,1\rangle\langle u_g,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg \\&=\int\limits_{G}\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}( \langle {}^{\delta}v_g,1\rangle \langle\delta u_0u_g,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align*} $$
where the equality follows again from Equations (2.10) and (2.9). Note that if we write
![]() ${}^{\delta }v_g={v_g'}^{\diamondsuit }$
for
${}^{\delta }v_g={v_g'}^{\diamondsuit }$
for
![]() $v_g'\in V_{(c^{rk})}$
,
$v_g'\in V_{(c^{rk})}$
,
![]() $\langle {}^{\delta }v_g,1\rangle =\langle v_g',1\rangle \in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(the local analog of Equation (4.6)). Now, as in the linear case, the definition of the embedding implies that when we change variables
$\langle {}^{\delta }v_g,1\rangle =\langle v_g',1\rangle \in \operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(the local analog of Equation (4.6)). Now, as in the linear case, the definition of the embedding implies that when we change variables
![]() $u_0\mapsto u_0u_g^{-1}$
and use the left-equivariance property of
$u_0\mapsto u_0u_g^{-1}$
and use the left-equivariance property of
![]() $f_{\mathcal {W}(\mathcal {E})}$
, we get
$f_{\mathcal {W}(\mathcal {E})}$
, we get
 $$ \begin{align*} &\psi_U^{-1}(u)\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}( \langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align*} $$
$$ \begin{align*} &\psi_U^{-1}(u)\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})}( \langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align*} $$
completing the proof of Equation (4.24).
It remains to prove Equation (4.23) where u is omitted. Then the l.h.s. of Equation (4.23) equals
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle\,{}^{\iota}\langle g_2,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle\,{}^{\iota}\langle g_2,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
By Equation (2.39) and because
![]() $\pi ^{\vee }$
is antigenuine,
$\pi ^{\vee }$
is antigenuine,
Also, by Equation (2.41), Equation (2.42) and Proposition 7,
 $$ \begin{align*} {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle &={}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2({}^{\iota}g_2),\varsigma_{\iota,c}({}^{\iota}g_2)\rangle \\&=\langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}(\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_2),\varsigma_{\iota,c}({}^{\iota}g_2)\rangle) \\&=\langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g({}^{\iota}g_2)),\sigma_c(g,{}^{\iota}g_2)\varsigma_{\iota,c}({}^{\iota}g_2)\rangle. \end{align*} $$
$$ \begin{align*} {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\langle \mathfrak{e}_2(g_2),1\rangle &={}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2({}^{\iota}g_2),\varsigma_{\iota,c}({}^{\iota}g_2)\rangle \\&=\langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}(\langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_2({}^{\iota}g_2),\varsigma_{\iota,c}({}^{\iota}g_2)\rangle) \\&=\langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g({}^{\iota}g_2)),\sigma_c(g,{}^{\iota}g_2)\varsigma_{\iota,c}({}^{\iota}g_2)\rangle. \end{align*} $$
In addition by Equation (2.40),
![]() $\varsigma _{\iota ,c}({}^{\iota }g_2)\varsigma _{\iota ,c}(g_2)=1$
(!). Hence, the integral equals
$\varsigma _{\iota ,c}({}^{\iota }g_2)\varsigma _{\iota ,c}(g_2)=1$
(!). Hence, the integral equals
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g({}^{\iota}g_2),1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g({}^{\iota}g_2)),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g({}^{\iota}g_2),1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g({}^{\iota}g_2)),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
Thus, when we change
![]() $g\mapsto g({}^{\iota }g_2)^{-1}$
we obtain
$g\mapsto g({}^{\iota }g_2)^{-1}$
we obtain
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
Next, multiply
![]() $g\mapsto g_1g$
. Then
$g\mapsto g_1g$
. Then
 $$ \begin{align*} &\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \mapsto \pi^{\vee}(\langle g_1,\sigma_c(g_1,g)^{-1}\rangle\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) =\sigma_c(g_1,g)\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\xi),\\ &{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\mapsto {}^{\iota}\langle\mathfrak{e}_2(g_1),\sigma_c(g_1,g)^{-1}\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle. \end{align*} $$
$$ \begin{align*} &\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \mapsto \pi^{\vee}(\langle g_1,\sigma_c(g_1,g)^{-1}\rangle\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) =\sigma_c(g_1,g)\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\xi),\\ &{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle\mapsto {}^{\iota}\langle\mathfrak{e}_2(g_1),\sigma_c(g_1,g)^{-1}\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle. \end{align*} $$
Note that
![]() $\omega (\langle g,1\rangle )=\pi ^{\vee }(\langle g,1\rangle )\xi ^{\vee }(\xi )$
. Then Integral (4.25) becomes
$\omega (\langle g,1\rangle )=\pi ^{\vee }(\langle g,1\rangle )\xi ^{\vee }(\xi )$
. Then Integral (4.25) becomes
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g_1),1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g_1),1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
By Equations (2.23) and (2.43),
Thus, the last integral equals
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\, {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0,1\rangle {}^{\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle\, {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
We have the local analog of Equation (4.10):
![]() ${}^{(g_1,{}^{\iota }g_1)}u_0=v_{g_1}u_{g_1}$
with
${}^{(g_1,{}^{\iota }g_1)}u_0=v_{g_1}u_{g_1}$
with
![]() $v_{g_1}\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
and
$v_{g_1}\in {}^{\delta ^{-1}}V_{(c^{rk})}^{\diamondsuit }$
and
![]() $u_{g_1}\in U_0$
, and using Equation (2.10),
$u_{g_1}\in U_0$
, and using Equation (2.10),
Then using Equations (2.8) and (2.10), the integral (4.26) equals
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( {}^{\delta\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( {}^{\delta\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align} $$
where
![]() ${}^{\delta \iota }\langle (g_1,g_1),\epsilon \rangle ={}^{\delta }({}^{\iota }\langle (g_1,g_1),\epsilon \rangle )$
and
${}^{\delta \iota }\langle (g_1,g_1),\epsilon \rangle ={}^{\delta }({}^{\iota }\langle (g_1,g_1),\epsilon \rangle )$
and
![]() ${}^{\delta \iota }(g_1,g_1)={}^{\delta }(g_1,{}^{\iota }g_1)$
.
${}^{\delta \iota }(g_1,g_1)={}^{\delta }(g_1,{}^{\iota }g_1)$
.
By Corollary 9,
![]() $(g,g)\mapsto \langle (g,g),\varsigma _{*,c}^{rk+1}(g)\rangle $
is the splitting of
$(g,g)\mapsto \langle (g,g),\varsigma _{*,c}^{rk+1}(g)\rangle $
is the splitting of
![]() $\{(g,g):g\in G\}$
in
$\{(g,g):g\in G\}$
in
![]() $H^{(m)}$
. Now, we describe the local version of Claim 65 to prove that for any
$H^{(m)}$
. Now, we describe the local version of Claim 65 to prove that for any
![]() $g\in G$
and
$g\in G$
and
![]() $h\in H^{(m)}$
,
$h\in H^{(m)}$
,
Using the notation of the proof of Claim 65,
![]() ${}^{\delta \iota }(g,g)=d_gl_g$
with
${}^{\delta \iota }(g,g)=d_gl_g$
with
![]() $d_g$
and
$d_g$
and
![]() $l_g$
described there. By Equation (4.14),
$l_g$
described there. By Equation (4.14),
 $$ \begin{align*} \sigma_{2rkc}(d_gl_g,d_{g'}l_{g'})=\sigma_{2rkc}(d_g,d_{g'})= \sigma_{rkc}^{\diamondsuit}((g^{*})^{\triangle},({g'}^{*})^{\triangle})=\left(\frac{\varsigma_{*,c}(g^{*})\varsigma_{*,c}({g'}^{*})}{\varsigma_{*,c}((gg')^{*})}\right)^{rk}. \end{align*} $$
$$ \begin{align*} \sigma_{2rkc}(d_gl_g,d_{g'}l_{g'})=\sigma_{2rkc}(d_g,d_{g'})= \sigma_{rkc}^{\diamondsuit}((g^{*})^{\triangle},({g'}^{*})^{\triangle})=\left(\frac{\varsigma_{*,c}(g^{*})\varsigma_{*,c}({g'}^{*})}{\varsigma_{*,c}((gg')^{*})}\right)^{rk}. \end{align*} $$
Hence,
![]() $d_gl_g\mapsto \langle d_gl_g,\varsigma _{*,c}^{-rk}(g^{*})\rangle $
is the unique splitting of
$d_gl_g\mapsto \langle d_gl_g,\varsigma _{*,c}^{-rk}(g^{*})\rangle $
is the unique splitting of
![]() $\{{}^{\delta \iota }(g,g):g\in G\}$
, then Corollary 9 and Equation (2.4) imply
$\{{}^{\delta \iota }(g,g):g\in G\}$
, then Corollary 9 and Equation (2.4) imply
(cf. Equation (4.15)). Now, by Equation (2.8) (recall
![]() $l_g\in U_P$
),
$l_g\in U_P$
),
where in the last equality we regard
![]() $(g^{*})^{\triangle }$
as an element of
$(g^{*})^{\triangle }$
as an element of
![]() $M_P$
. Consequently,
$M_P$
. Consequently,
 $$ \begin{align*} f_{\mathcal{W}(\mathcal{E})}({}^{\delta\iota}\langle(g,g),\varsigma_{*,c}^{rk+1}(g)\rangle h,s) &=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle (g^{*})^{\triangle},\varsigma_{*,c}^{-rk}(g^{*})\rangle\langle l_g,1\rangle h,s)\\& =f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle l_g,1\rangle h,s)=f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s), \end{align*} $$
$$ \begin{align*} f_{\mathcal{W}(\mathcal{E})}({}^{\delta\iota}\langle(g,g),\varsigma_{*,c}^{rk+1}(g)\rangle h,s) &=f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle (g^{*})^{\triangle},\varsigma_{*,c}^{-rk}(g^{*})\rangle\langle l_g,1\rangle h,s)\\& =f_{\mathcal{W}(\mathcal{E}_{\tau})}(\langle l_g,1\rangle h,s)=f_{\mathcal{W}(\mathcal{E}_{\tau})}(h,s), \end{align*} $$
where the second equality follows from Equation (4.19). This proves Equation (4.28). Returning to Integral (4.27), we have
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
Finally, when we conjugate
![]() $\langle v_{g_1} ,1\rangle $
to the left, use the left-equivariance properties of
$\langle v_{g_1} ,1\rangle $
to the left, use the left-equivariance properties of
![]() $f_{\mathcal {W}(\mathcal {E})}$
and change variables in
$f_{\mathcal {W}(\mathcal {E})}$
and change variables in
![]() $u_{g_1}$
, we obtain
$u_{g_1}$
, we obtain
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( \langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})}( \langle\delta u_0,1\rangle {}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
This completes the proof of Equation (4.23) in all cases.
Corollary 71. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, for any section
$\operatorname {\mathrm {Re}}(s)\gg 0$
, for any section
![]() $f_{\mathcal {W}(\mathcal {E})}$
and
$f_{\mathcal {W}(\mathcal {E})}$
and
![]() $g_1\in G$
,
$g_1\in G$
,
 $$ \begin{align*} &\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0 ,1\rangle\, {}^{\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle,s)\,\psi_{U}(u_0)\,du_0 =\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0 ,1\rangle,s)\,\psi_{U}(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0 ,1\rangle\, {}^{\iota}\langle(g_1,g_1),\varsigma_{*,c}^{rk+1}(g_1)\rangle,s)\,\psi_{U}(u_0)\,du_0 =\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})}(\langle\delta u_0 ,1\rangle,s)\,\psi_{U}(u_0)\,du_0. \end{align*} $$
Remark 72. Meromorphic continuation of the integrals over non-Archimedean places can be proved using Bernstein’s continuation principal (in [Reference BanksBan98a]) by combining Proposition 70 with Proposition 68 and granted that the dimension of the space (4.21) is at most
![]() $1$
outside a finite set of values of
$1$
outside a finite set of values of
![]() $q^{-s}$
. This uniqueness result requires the uniqueness of the
$q^{-s}$
. This uniqueness result requires the uniqueness of the
![]() $(rk,c)$
model, and hence we may not use it here at the ramified places. We will, however, prove the meromorphic continuation of
$(rk,c)$
model, and hence we may not use it here at the ramified places. We will, however, prove the meromorphic continuation of
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
with unramified data and when the model is unique, as part of the computation.
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})})$
with unramified data and when the model is unique, as part of the computation.
As a corollary of our results, we deduce the meromorphic continuation of the global partial L-function but under an additional assumption on the Archimedean places. Also, recall that we assume Conjectures 50 and 51, but for
![]() $r=1$
or
$r=1$
or
![]() $k=1$
these conjectures hold by Proposition 52.
$k=1$
these conjectures hold by Proposition 52.
Theorem 73. Assume
![]() $\mu _{2m}\subset F^{*}$
. Let
$\mu _{2m}\subset F^{*}$
. Let
![]() $\pi $
and
$\pi $
and
![]() $\tau $
be genuine irreducible cuspidal automorphic representations of
$\tau $
be genuine irreducible cuspidal automorphic representations of
![]() $G^{(m)}(\mathbb {A})$
and
$G^{(m)}(\mathbb {A})$
and
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and let S be a finite set of places such that for
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and let S be a finite set of places such that for
![]() $\nu \notin S$
,
$\nu \notin S$
,
![]() $F_{\nu }$
,
$F_{\nu }$
,
![]() $\psi _{\nu }$
,
$\psi _{\nu }$
,
![]() $\tau _{\nu }$
and
$\tau _{\nu }$
and
![]() $\pi _{\nu }$
are unramified. Suppose that
$\pi _{\nu }$
are unramified. Suppose that
![]() $\mathcal {E}_{\nu }$
is
$\mathcal {E}_{\nu }$
is
![]() $(rk,c)$
for all
$(rk,c)$
for all
![]() $\nu \in S_{\infty }$
, for example,
$\nu \in S_{\infty }$
, for example,
![]() $r=1$
or
$r=1$
or
![]() $k=1$
(or
$k=1$
(or
![]() $\tau _{\nu }$
is essentially tempered). Then
$\tau _{\nu }$
is essentially tempered). Then
![]() $L_{\vartheta }^S(s,\pi \times \tau )$
admits meromorphic continuation to
$L_{\vartheta }^S(s,\pi \times \tau )$
admits meromorphic continuation to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Proof. According to Theorem 64,
![]() $Z(s,\varphi _1,\varphi _2,f)$
coincides with Integral (4.4) in
$Z(s,\varphi _1,\varphi _2,f)$
coincides with Integral (4.4) in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
. Given S, we can choose the global data
$\operatorname {\mathrm {Re}}(s)\gg 0$
. Given S, we can choose the global data
![]() $\varphi _1,\varphi _2$
and f such that
$\varphi _1,\varphi _2$
and f such that
![]() $\omega _{\nu }$
and
$\omega _{\nu }$
and
![]() $f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized and unramified for all
$f_{\mathcal {W}(\rho _c(\tau _{\nu }))}$
are normalized and unramified for all
![]() $\nu \notin S$
. Then in
$\nu \notin S$
. Then in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, by Equation (4.16) and Theorem 66,
$\operatorname {\mathrm {Re}}(s)\gg 0$
, by Equation (4.16) and Theorem 66,
 $$ \begin{align*} Z(s,\varphi_1,\varphi_2,f)&=Z[S](s,\omega_S,f_{\mathcal{W}((\mathcal{E}_{\tau})_S)}) \\&\quad \times\frac{L_{\vartheta}^S(r\alpha s+1/2,\pi\times\tau)} {[L_{\vartheta}^S(r\alpha s+rn+1/2,\tau)]\prod\limits_{1\leq j\leq rn}L_{\vartheta}^S(2r\alpha s+2j,\tau,\wedge^2) L_{\vartheta}^S(2r\alpha s+2j-1,\tau,\vee^2)}. \end{align*} $$
$$ \begin{align*} Z(s,\varphi_1,\varphi_2,f)&=Z[S](s,\omega_S,f_{\mathcal{W}((\mathcal{E}_{\tau})_S)}) \\&\quad \times\frac{L_{\vartheta}^S(r\alpha s+1/2,\pi\times\tau)} {[L_{\vartheta}^S(r\alpha s+rn+1/2,\tau)]\prod\limits_{1\leq j\leq rn}L_{\vartheta}^S(2r\alpha s+2j,\tau,\wedge^2) L_{\vartheta}^S(2r\alpha s+2j-1,\tau,\vee^2)}. \end{align*} $$
(
![]() $\alpha =rkc+1$
; the factor
$\alpha =rkc+1$
; the factor
![]() $L_{\vartheta }^S(r\alpha s+rn+1/2,\tau )$
appears only when m is odd.)
$L_{\vartheta }^S(r\alpha s+rn+1/2,\tau )$
appears only when m is odd.)
The l.h.s. admits meromorphic continuation to
![]() $\mathbb {C}$
by Theorem 63. The partial L-functions appearing in the denominator on the r.h.s. admit meromorphic continuation by [Reference GaoGao18b].
$\mathbb {C}$
by Theorem 63. The partial L-functions appearing in the denominator on the r.h.s. admit meromorphic continuation by [Reference GaoGao18b].
It is therefore sufficient to prove that for any
![]() $s_0\in \mathbb {C}$
, one can further choose the global data such that
$s_0\in \mathbb {C}$
, one can further choose the global data such that
![]() $Z[S](s,\omega _S,f_{\mathcal {W}((\mathcal {E}_{\tau })_S)})$
is nonzero and holomorphic in a neighborhood of
$Z[S](s,\omega _S,f_{\mathcal {W}((\mathcal {E}_{\tau })_S)})$
is nonzero and holomorphic in a neighborhood of
![]() $s_0$
. This is possible by Proposition 68 (4). Therefore,
$s_0$
. This is possible by Proposition 68 (4). Therefore,
![]() $L_{\vartheta }^S(r\alpha s+1/2,\pi \times \tau )$
admits meromorphic continuation to
$L_{\vartheta }^S(r\alpha s+1/2,\pi \times \tau )$
admits meromorphic continuation to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Remark 74. By Gao [Reference GaoGao18b], the assertion of the theorem holds unconditionally (and even without assuming that
![]() $\mu _{2m}\subset F^{*}$
).
$\mu _{2m}\subset F^{*}$
).
4.3 The local
 $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals
The proof of Theorem 66 in § 5 involves the computation of
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, which we introduce here. The global theory of these integrals is developed in Appendix A, because for the present work they are only needed locally and when the field is unramified (for the linear case see [Reference Cai, Friedberg and KaplanCFK22]). For the purpose of their definition, we take any local field (with characteristic
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, which we introduce here. The global theory of these integrals is developed in Appendix A, because for the present work they are only needed locally and when the field is unramified (for the linear case see [Reference Cai, Friedberg and KaplanCFK22]). For the purpose of their definition, we take any local field (with characteristic
![]() $0$
) such that
$0$
) such that
![]() $\mu _{m}\subset F^{*}$
. We do not assume
$\mu _{m}\subset F^{*}$
. We do not assume
![]() $\mu _{2m}\subset F^{*}$
until Proposition 77 below. As in the symplectic case, we start with the description of the groups and embeddings, proceed with the coverings, then consider the representations and integral.
$\mu _{2m}\subset F^{*}$
until Proposition 77 below. As in the symplectic case, we start with the description of the groups and embeddings, proceed with the coverings, then consider the representations and integral.
Since the construction is similar to the construction of the
![]() $\operatorname {\mathrm {Sp}}_c^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral in § 4.1, we will use similar notation. Let
$\operatorname {\mathrm {Sp}}_c^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral in § 4.1, we will use similar notation. Let
![]() $n,k$
and m be positive integers and r be either m when m is odd, or
$n,k$
and m be positive integers and r be either m when m is odd, or
![]() $r=m/2$
otherwise. Put
$r=m/2$
otherwise. Put
![]() $c=n$
. Denote
$c=n$
. Denote
![]() $G=\operatorname {\mathrm {GL}}_c$
,
$G=\operatorname {\mathrm {GL}}_c$
,
![]() $H=\operatorname {\mathrm {GL}}_{2rkc}$
and
$H=\operatorname {\mathrm {GL}}_{2rkc}$
and
![]() $P=P_{(rkc,rkc)}$
. For the embedding
$P=P_{(rkc,rkc)}$
. For the embedding
![]() $G\times G\hookrightarrow H$
, set
$G\times G\hookrightarrow H$
, set
![]() $Q=P_{(c^{rk-1},2c,c^{rk-1})}=M_Q\ltimes U$
, then
$Q=P_{(c^{rk-1},2c,c^{rk-1})}=M_Q\ltimes U$
, then
![]() $U=V_{(c^{rk-1},2c,c^{rk-1})}$
, and define
$U=V_{(c^{rk-1},2c,c^{rk-1})}$
, and define
where
![]() $\psi (v)$
and
$\psi (v)$
and
![]() $\psi (v')$
are defined by Equation (2.5),
$\psi (v')$
are defined by Equation (2.5),
![]() $X_1$
is the bottom left
$X_1$
is the bottom left
![]() $c\times c$
block of x and
$c\times c$
block of x and
![]() $Z_1$
is the top left
$Z_1$
is the top left
![]() $c\times c$
block of z. Then
$c\times c$
block of z. Then
![]() $G\times G$
is embedded in the stabilizer of
$G\times G$
is embedded in the stabilizer of
![]() $\psi _U$
in
$\psi _U$
in
![]() $M_Q$
by
$M_Q$
by
where
![]() $g_1$
appears
$g_1$
appears
![]() $rk$
times on the left of
$rk$
times on the left of
![]() $g_2$
and
$g_2$
and
![]() $rk-1$
times on the right. Again, we denote
$rk-1$
times on the right. Again, we denote
![]() $\mathfrak {e}_1(g)=(g,I_c)$
and
$\mathfrak {e}_1(g)=(g,I_c)$
and
![]() $\mathfrak {e}_2(g)=(I_c,g)$
.
$\mathfrak {e}_2(g)=(I_c,g)$
.
Recall the covering
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}$
defined in § 2.7, which is realized using the
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
defined in § 2.7, which is realized using the
![]() $2$
-cocycle
$2$
-cocycle
We realize
![]() $H^{(m,r)}$
using
$H^{(m,r)}$
using
![]() $\sigma _{2rkc}^{\diamondsuit }$
, and both copies of
$\sigma _{2rkc}^{\diamondsuit }$
, and both copies of
![]() $G^{(m)}$
are realized using
$G^{(m)}$
are realized using
![]() $\sigma _c^{\diamondsuit }$
. By Equation (2.52), we immediately deduce that the images of
$\sigma _c^{\diamondsuit }$
. By Equation (2.52), we immediately deduce that the images of
![]() $\mathfrak {e}_1(G)$
and
$\mathfrak {e}_1(G)$
and
![]() $\mathfrak {e}_2(G)$
commute in
$\mathfrak {e}_2(G)$
commute in
![]() $H^{(m,r)}$
, and moreover for all
$H^{(m,r)}$
, and moreover for all
![]() $g_i,g_i^{\prime }\in G$
,
$g_i,g_i^{\prime }\in G$
,
(Cf. Equation (2.23).)
Thus, we can lift the embedding
![]() $G\times G \hookrightarrow H$
to an embedding of
$G\times G \hookrightarrow H$
to an embedding of
via
Equality (4.31) also implies the following identity, similar to Equation (2.25):
To define the integral we introduce the following notation. Let
 $$ \begin{align*} &\delta=\delta_0\delta_1,\qquad \delta_0=\left(\begin{smallmatrix}&I_{rkc}\\I_{rkc}\end{smallmatrix}\right),\qquad \delta_1=\left(\begin{smallmatrix}I_{(rk-1)c}\\&I_c&I_c\\&&I_c\\&&&I_{(rk-1)c}\end{smallmatrix}\right),\\ &U_0=U\cap U_P, \qquad \psi_U(u_0)=\psi(\operatorname{\mathrm{tr}}(Z_1))\qquad(u_0\in U_0). \end{align*} $$
$$ \begin{align*} &\delta=\delta_0\delta_1,\qquad \delta_0=\left(\begin{smallmatrix}&I_{rkc}\\I_{rkc}\end{smallmatrix}\right),\qquad \delta_1=\left(\begin{smallmatrix}I_{(rk-1)c}\\&I_c&I_c\\&&I_c\\&&&I_{(rk-1)c}\end{smallmatrix}\right),\\ &U_0=U\cap U_P, \qquad \psi_U(u_0)=\psi(\operatorname{\mathrm{tr}}(Z_1))\qquad(u_0\in U_0). \end{align*} $$
Here,
![]() $Z_1$
is the block defined above for
$Z_1$
is the block defined above for
![]() $u_0$
written as in Equation (4.30). Recall that
$u_0$
written as in Equation (4.30). Recall that
![]() $G^{\triangle }$
is the stabilizer in
$G^{\triangle }$
is the stabilizer in
![]() $M_{(c^{rk})}$
of the character
$M_{(c^{rk})}$
of the character
![]() $\psi $
of
$\psi $
of
![]() $V_{(c^{rk})}$
given by Equation (3.1) (now
$V_{(c^{rk})}$
given by Equation (3.1) (now
![]() $G=\operatorname {\mathrm {GL}}_c)$
. By Equation (2.52),
$G=\operatorname {\mathrm {GL}}_c)$
. By Equation (2.52),
![]() $\sigma ^{\diamondsuit }_{rkc}(g^{\triangle },{g'}^{\triangle })=\sigma _c^{\diamondsuit }(g,g')^{rk}$
. Hence,
$\sigma ^{\diamondsuit }_{rkc}(g^{\triangle },{g'}^{\triangle })=\sigma _c^{\diamondsuit }(g,g')^{rk}$
. Hence,
![]() $\sigma ^{\diamondsuit }_{2rkc}$
is trivial on
$\sigma ^{\diamondsuit }_{2rkc}$
is trivial on
![]() $\{(g,g):g\in G\}$
, and note that
$\{(g,g):g\in G\}$
, and note that
![]() $(g,g)=\operatorname {\mathrm {diag}}(g^{\triangle },g^{\triangle })$
, that is, the diagonal embedding of
$(g,g)=\operatorname {\mathrm {diag}}(g^{\triangle },g^{\triangle })$
, that is, the diagonal embedding of
![]() $2rk$
copies of G in H. Thus,
$2rk$
copies of G in H. Thus,
![]() $H^{(m,r)}$
is split over
$H^{(m,r)}$
is split over
![]() $\{(g,g):g\in G\}$
, and the trivial section is a splitting (not necessarily unique, G is not perfect).
$\{(g,g):g\in G\}$
, and the trivial section is a splitting (not necessarily unique, G is not perfect).
Let
![]() $\pi $
be a genuine irreducible admissible representation of
$\pi $
be a genuine irreducible admissible representation of
![]() $G^{(m,r)}$
, and let
$G^{(m,r)}$
, and let
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E'}$
be two genuine irreducible admissible representations of
$\mathcal {E'}$
be two genuine irreducible admissible representations of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
. Assume that
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
. Assume that
![]() $\mathcal {E}$
(resp.,
$\mathcal {E}$
(resp.,
![]() $\mathcal {E}'$
) affords an
$\mathcal {E}'$
) affords an
![]() $(rk,c)$
functional
$(rk,c)$
functional
![]() $\Lambda $
(resp.,
$\Lambda $
(resp.,
![]() $\Lambda '$
), and let
$\Lambda '$
), and let
![]() $\mathcal {W}(\mathcal {E})$
(resp.,
$\mathcal {W}(\mathcal {E})$
(resp.,
![]() $\mathcal {W}(\mathcal {E}')$
) be the
$\mathcal {W}(\mathcal {E}')$
) be the
![]() $(rk,c)$
model defined using
$(rk,c)$
model defined using
![]() $\Lambda $
(resp.,
$\Lambda $
(resp.,
![]() $\Lambda '$
). We do not assume this model is unique. The additional assumption we need for the definition of the integral is that for any
$\Lambda '$
). We do not assume this model is unique. The additional assumption we need for the definition of the integral is that for any
![]() $\xi $
(resp.,
$\xi $
(resp.,
![]() $\xi '$
) in the space of
$\xi '$
) in the space of
![]() $\mathcal {E}$
(resp.,
$\mathcal {E}$
(resp.,
![]() $\mathcal {E}'$
),
$\mathcal {E}'$
),
Let
![]() $\omega $
be a matrix coefficient of
$\omega $
be a matrix coefficient of
![]() $\pi ^{\vee }$
, and
$\pi ^{\vee }$
, and
![]() $f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
be a standard section of
$f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
be a standard section of
The integral is defined by
 $$ \begin{align} &Z(s,\omega,f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &Z(s,\omega,f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')})= \int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle)f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
Note that we do not have an involution here (
![]() $\iota =I_c$
). The analog of Proposition 68 (1)–(3) is valid here as well. For example, the integrals are absolutely convergent in a right half-plane, and for a given s, there exist data
$\iota =I_c$
). The analog of Proposition 68 (1)–(3) is valid here as well. For example, the integrals are absolutely convergent in a right half-plane, and for a given s, there exist data
![]() $(\omega ,f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')})$
for which the integral is nonzero and holomorphic in a neighborhood of s. We prove the analog of Proposition 70:
$(\omega ,f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')})$
for which the integral is nonzero and holomorphic in a neighborhood of s. We prove the analog of Proposition 70:
Proposition 75. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
$\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral
![]() $Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')})$
can be regarded as a morphism in the space
$Z(s,\omega ,f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')})$
can be regarded as a morphism in the space
Proof. Let
![]() $\omega _{g_1,g_2}$
be defined as in Proposition 70 (with
$\omega _{g_1,g_2}$
be defined as in Proposition 70 (with
![]() $\iota =I_c$
). We need to prove that for
$\iota =I_c$
). We need to prove that for
![]() $g_1,g_2\in G$
and
$g_1,g_2\in G$
and
![]() $u\in U$
,
$u\in U$
,
(Note that the analog of the representation (4.22) factors through
![]() $G\times G$
according to the embedding (4.32).)
$G\times G$
according to the embedding (4.32).)
Regarding u, the proof is very similar to the proof in Proposition 70. The definition of the embedding implies that we can write
![]() ${}^{\mathfrak {e}_2(g)}u=v_gu_g$
, with
${}^{\mathfrak {e}_2(g)}u=v_gu_g$
, with
![]() $u_g\in U_0$
but
$u_g\in U_0$
but
![]() $v_g\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
. Then we apply Equations (2.10) and (2.9) (as mentioned in § 2.7, these are still applicable with
$v_g\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
. Then we apply Equations (2.10) and (2.9) (as mentioned in § 2.7, these are still applicable with
![]() $\sigma _{2rkc}^{\diamondsuit }$
instead of
$\sigma _{2rkc}^{\diamondsuit }$
instead of
![]() $\sigma _{2rkc}$
), and check that the left-equivariance property of
$\sigma _{2rkc}$
), and check that the left-equivariance property of
![]() $f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
under
$f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
under
![]() $\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
, together with
$\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
, together with
![]() $\psi _U(u_g)$
, combines to contribute
$\psi _U(u_g)$
, combines to contribute
![]() $\psi _U^{-1}(u)$
.
$\psi _U^{-1}(u)$
.
Now, assume that u is trivial. The l.h.s. of Equation (4.37) equals
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle\langle g_2,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle\langle g_2,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \\&f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
Since
![]() $\langle \mathfrak {e}_1(g_1),1\rangle $
and
$\langle \mathfrak {e}_1(g_1),1\rangle $
and
![]() $\langle \mathfrak {e}_2(g_2),1\rangle $
commute and using Equation (4.31) (with
$\langle \mathfrak {e}_2(g_2),1\rangle $
commute and using Equation (4.31) (with
![]() $g_1=g_1'=I_c$
) and the fact that
$g_1=g_1'=I_c$
) and the fact that
![]() $\pi ^{\vee }$
is antigenuine, when we change
$\pi ^{\vee }$
is antigenuine, when we change
![]() $g\mapsto gg_2^{-1}$
we obtain
$g\mapsto gg_2^{-1}$
we obtain
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \pi^{\vee}(\langle g,1\rangle) \xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_1(g_1),1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
(The absence of
![]() $\iota $
simplifies some of the computations!) Then when we multiply
$\iota $
simplifies some of the computations!) Then when we multiply
![]() $g\mapsto g_1g$
,
$g\mapsto g_1g$
,
 $$ \begin{align*} &\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \mapsto \sigma_c^{\diamondsuit}(g_1,g)\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\xi),\\ &\langle\mathfrak{e}_2(g),1\rangle\mapsto \langle\mathfrak{e}_2(g_1),\sigma_c^{\diamondsuit}(g_1,g)^{-1}\rangle\langle\mathfrak{e}_2(g),1\rangle, \end{align*} $$
$$ \begin{align*} &\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) \mapsto \sigma_c^{\diamondsuit}(g_1,g)\pi^{\vee}(\langle g,1\rangle)\xi^{\vee}(\xi),\\ &\langle\mathfrak{e}_2(g),1\rangle\mapsto \langle\mathfrak{e}_2(g_1),\sigma_c^{\diamondsuit}(g_1,g)^{-1}\rangle\langle\mathfrak{e}_2(g),1\rangle, \end{align*} $$
and Integral (4.38) equals
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle(g_1,g_1),1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0,1\rangle \langle(g_1,g_1),1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg, \end{align} $$
where we also used Equation (4.33).
As in the proof of Proposition 70,
![]() ${}^{(g_1,g_1)}u_0=v_{g_1}u_{g_1}$
with
${}^{(g_1,g_1)}u_0=v_{g_1}u_{g_1}$
with
![]() $v_{g_1}\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
and
$v_{g_1}\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
and
![]() $u_{g_1}\in U_0$
, and using Equations (2.10) and (2.8), the integral becomes
$u_{g_1}\in U_0$
, and using Equations (2.10) and (2.8), the integral becomes
 $$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}( {}^{\delta}\langle(g_1,g_1),1\rangle \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}( {}^{\delta}\langle(g_1,g_1),1\rangle \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align} $$
We proceed by first proving
Since
![]() ${}^{\delta }(g,g)=(g,g)$
(
${}^{\delta }(g,g)=(g,g)$
(
![]() $\delta _1$
commutes with
$\delta _1$
commutes with
![]() $(g,g)$
), we can write
$(g,g)$
), we can write
![]() ${}^{\delta }\langle (g,g),\epsilon \rangle =\langle (g,g),\epsilon _g\epsilon \rangle $
, where
${}^{\delta }\langle (g,g),\epsilon \rangle =\langle (g,g),\epsilon _g\epsilon \rangle $
, where
![]() $\epsilon _g\in \mu _m$
. Then because
$\epsilon _g\in \mu _m$
. Then because
![]() $\sigma _{2rkc}^{\diamondsuit }$
is trivial on
$\sigma _{2rkc}^{\diamondsuit }$
is trivial on
![]() $\{(g,g):g\in G\}$
, the map
$\{(g,g):g\in G\}$
, the map
![]() $g\mapsto \epsilon _g$
is a character of G, hence trivial on
$g\mapsto \epsilon _g$
is a character of G, hence trivial on
![]() $\operatorname {\mathrm {SL}}_c$
. Also, since
$\operatorname {\mathrm {SL}}_c$
. Also, since
![]() $\delta ^2=I_{2rkc}$
,
$\delta ^2=I_{2rkc}$
,
![]() $\epsilon _g^2=1$
. We claim that
$\epsilon _g^2=1$
. We claim that
![]() $\epsilon _g=1$
for all
$\epsilon _g=1$
for all
![]() $g\in G$
, and it remains to show this for
$g\in G$
, and it remains to show this for
![]() $g=t\in T_{\operatorname {\mathrm {GL}}_c}$
, which follows from Proposition 2.
$g=t\in T_{\operatorname {\mathrm {GL}}_c}$
, which follows from Proposition 2.
We complete the proof of Equation (4.41). Since
![]() $\epsilon _g=1$
for all
$\epsilon _g=1$
for all
![]() $g\in G$
, we can use Equation (2.52) and obtain
$g\in G$
, we can use Equation (2.52) and obtain
Also,
![]() $\delta _{P}((g,g))=1$
. This together with Equation (4.34) proves Equation (4.41).
$\delta _{P}((g,g))=1$
. This together with Equation (4.34) proves Equation (4.41).
Returning to Integral (4.40), we have
 $$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}( \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{G}\int\limits_{U_0} \omega(\langle g,1\rangle) f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}( \langle\delta ,1\rangle \langle v_{g_1} ,1\rangle\langle u_{g_1} ,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_{U}(u_0)\,du_0\,dg. \end{align*} $$
Using the left-equivariance property of
![]() $f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
under
$f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
under
![]() $\{\langle \operatorname {\mathrm {diag}}(v,v'),1\rangle :v,v'\in V_{(c^{rk})}\}$
and changing variables in
$\{\langle \operatorname {\mathrm {diag}}(v,v'),1\rangle :v,v'\in V_{(c^{rk})}\}$
and changing variables in
![]() $u_{g_1}$
, we reach the r.h.s. of Equation (4.37), as required.
$u_{g_1}$
, we reach the r.h.s. of Equation (4.37), as required.
As a corollary of the proof, we obtain the analog of Corollary 71:
Corollary 76. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, for any section
$\operatorname {\mathrm {Re}}(s)\gg 0$
, for any section
![]() $f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
and
$f_{\mathcal {W}(\mathcal {E})\otimes \mathcal {W}(\mathcal {E}')}$
and
![]() $g_1\in G$
,
$g_1\in G$
,
 $$ \begin{align*} &\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0 ,1\rangle\, \langle(g_1,g_1),1\rangle,s)\,\psi_{U}(u_0)\,du_0 =\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0 ,1\rangle,s)\,\psi_{U}(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0 ,1\rangle\, \langle(g_1,g_1),1\rangle,s)\,\psi_{U}(u_0)\,du_0 =\int\limits_{U_0} f_{\mathcal{W}(\mathcal{E})\otimes\mathcal{W}(\mathcal{E}')}(\langle\delta u_0 ,1\rangle,s)\,\psi_{U}(u_0)\,du_0. \end{align*} $$
Proof. See Integral (4.39) and the remaining part of the proof.
Proposition 77. Assume that
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E}'$
are
$\mathcal {E}'$
are
![]() $(rk,c)$
representations. Then Equation (4.34) holds for
$(rk,c)$
representations. Then Equation (4.34) holds for
![]() $g\in \operatorname {\mathrm {SL}}_c$
. Further assume that
$g\in \operatorname {\mathrm {SL}}_c$
. Further assume that
![]() $\mathcal {E}'=\mathcal {E}^{*}$
where
$\mathcal {E}'=\mathcal {E}^{*}$
where
![]() ${}^{*}$
is given by Equation (2.54), and if m does not divide
${}^{*}$
is given by Equation (2.54), and if m does not divide
![]() $rk$
(i.e.,
$rk$
(i.e.,
![]() $r=m/2$
and k is odd) we also assume
$r=m/2$
and k is odd) we also assume
![]() $\mu _{2m}\subset F^{*}$
. Then Equation (4.34) holds for
$\mu _{2m}\subset F^{*}$
. Then Equation (4.34) holds for
![]() $g\in G$
.
$g\in G$
.
Proof. By definition
![]() $J_{V_{(c^{rk})},\psi }(\mathcal {E})$
and
$J_{V_{(c^{rk})},\psi }(\mathcal {E})$
and
![]() $J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
are one-dimensional, hence so is their tensor product. The action of the subgroup
$J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
are one-dimensional, hence so is their tensor product. The action of the subgroup
![]() $\{\langle (g,g),1\rangle :g\in G\}$
on
$\{\langle (g,g),1\rangle :g\in G\}$
on
![]() $J_{V_{(c^{rk})},\psi }(\mathcal {E})\otimes J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
is by a character, which must then be trivial when
$J_{V_{(c^{rk})},\psi }(\mathcal {E})\otimes J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
is by a character, which must then be trivial when
![]() $g\in \operatorname {\mathrm {SL}}_c$
. Since
$g\in \operatorname {\mathrm {SL}}_c$
. Since
![]() $(\Lambda \otimes \Lambda ')(\xi \otimes \xi ')=\Lambda (\xi )\otimes \Lambda '(\xi ')$
factors through the Jacquet modules (on both
$(\Lambda \otimes \Lambda ')(\xi \otimes \xi ')=\Lambda (\xi )\otimes \Lambda '(\xi ')$
factors through the Jacquet modules (on both
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E}'$
), and by Equation (2.52) for any
$\mathcal {E}'$
), and by Equation (2.52) for any
![]() $g\in G$
,
$g\in G$
,
the first assertion holds.
Assume
![]() $m|rk$
, then
$m|rk$
, then
![]() $\sigma ^{\diamondsuit }_{rkc}$
is already trivial on
$\sigma ^{\diamondsuit }_{rkc}$
is already trivial on
![]() $G^{\triangle }$
, hence
$G^{\triangle }$
, hence
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is split over
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is split over
![]() $G^{\triangle }$
. Thus,
$G^{\triangle }$
. Thus,
![]() $G^{\triangle }$
acts by a nongenuine character on
$G^{\triangle }$
acts by a nongenuine character on
![]() $J_{V_{(c^{rk})},\psi }(\mathcal {E})$
(resp.,
$J_{V_{(c^{rk})},\psi }(\mathcal {E})$
(resp.,
![]() $J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
), and we can write
$J_{V_{(c^{rk})},\psi }(\mathcal {E}')$
), and we can write
for some quasi-characters
![]() $\varrho ,\varrho '$
of
$\varrho ,\varrho '$
of
![]() $F^{*}$
. When
$F^{*}$
. When
![]() $\mathcal {E}'=\mathcal {E}^{*}$
, by Equation (2.54) we have
$\mathcal {E}'=\mathcal {E}^{*}$
, by Equation (2.54) we have
![]() $\mathcal {E}'(\langle g^{\triangle },1\rangle )=\mathcal {E}({}^{*}\langle g^{\triangle },1\rangle )=\mathcal {E}(\langle (g^{*})^{\triangle },1\rangle )$
, whence
$\mathcal {E}'(\langle g^{\triangle },1\rangle )=\mathcal {E}({}^{*}\langle g^{\triangle },1\rangle )=\mathcal {E}(\langle (g^{*})^{\triangle },1\rangle )$
, whence
This proves Equation (4.34) for all
![]() $g\in G$
.
$g\in G$
.
Now, assume that m does not divide
![]() $rk$
. Since
$rk$
. Since
![]() $H^{(m,r)}$
is split over
$H^{(m,r)}$
is split over
![]() $\{(g,g):g\in G\}$
and we already have Equation (4.34) on
$\{(g,g):g\in G\}$
and we already have Equation (4.34) on
![]() $\operatorname {\mathrm {SL}}_c$
, it suffices to prove Equation (4.34) for the subgroup
$\operatorname {\mathrm {SL}}_c$
, it suffices to prove Equation (4.34) for the subgroup
![]() $A_1=\{\operatorname {\mathrm {diag}}(a,I_{c-1}):a\in F^{*}\}$
. For any
$A_1=\{\operatorname {\mathrm {diag}}(a,I_{c-1}):a\in F^{*}\}$
. For any
![]() $t=\operatorname {\mathrm {diag}}(a,I_{c-1})\in A_1$
and
$t=\operatorname {\mathrm {diag}}(a,I_{c-1})\in A_1$
and
![]() $t'=\operatorname {\mathrm {diag}}(a',I_{c-1})\in A_1$
, by Equations (2.52) and (2.51),
$t'=\operatorname {\mathrm {diag}}(a',I_{c-1})\in A_1$
, by Equations (2.52) and (2.51),
Hence, if we fix some nontrivial additive character
![]() $\psi '$
of F, there is a quasi-character
$\psi '$
of F, there is a quasi-character
![]() $\varrho $
of
$\varrho $
of
![]() $F^{*}$
such that
$F^{*}$
such that
![]() $\Lambda (\mathcal {E}(\langle \operatorname {\mathrm {diag}}(a,I_{c-1})^{\triangle },1\rangle )\xi ')=\gamma _{\psi '}(a)\varrho (a)\Lambda (\xi ')$
.
$\Lambda (\mathcal {E}(\langle \operatorname {\mathrm {diag}}(a,I_{c-1})^{\triangle },1\rangle )\xi ')=\gamma _{\psi '}(a)\varrho (a)\Lambda (\xi ')$
.
Furthermore, taking
![]() $w=(-1)^{c(c-1)/2}J_c\in \operatorname {\mathrm {SL}}_c$
, Proposition 2 and the left invariance of
$w=(-1)^{c(c-1)/2}J_c\in \operatorname {\mathrm {SL}}_c$
, Proposition 2 and the left invariance of
![]() $\Lambda $
under
$\Lambda $
under
![]() $\langle w^{\triangle },1\rangle $
imply
$\langle w^{\triangle },1\rangle $
imply
 $$ \begin{align*} \Lambda(\mathcal{E}(\langle \operatorname{\mathrm{diag}}(a,I_{c-1})^{\triangle},1\rangle)\xi)&= \Lambda(\mathcal{E}(\langle w^{\triangle},1\rangle\langle \operatorname{\mathrm{diag}}(a,I_{c-1})^{\triangle},1\rangle)\xi)\\&= \Lambda(\mathcal{E}(\langle ({}^w\operatorname{\mathrm{diag}}(a,I_{c-1}))^{\triangle},1\rangle\langle w^{\triangle},1\rangle)\xi)\\&= \Lambda(\mathcal{E}(\langle\operatorname{\mathrm{diag}}(I_{c-1},a)^{\triangle},1\rangle\langle w^{\triangle},1\rangle)\xi). \end{align*} $$
$$ \begin{align*} \Lambda(\mathcal{E}(\langle \operatorname{\mathrm{diag}}(a,I_{c-1})^{\triangle},1\rangle)\xi)&= \Lambda(\mathcal{E}(\langle w^{\triangle},1\rangle\langle \operatorname{\mathrm{diag}}(a,I_{c-1})^{\triangle},1\rangle)\xi)\\&= \Lambda(\mathcal{E}(\langle ({}^w\operatorname{\mathrm{diag}}(a,I_{c-1}))^{\triangle},1\rangle\langle w^{\triangle},1\rangle)\xi)\\&= \Lambda(\mathcal{E}(\langle\operatorname{\mathrm{diag}}(I_{c-1},a)^{\triangle},1\rangle\langle w^{\triangle},1\rangle)\xi). \end{align*} $$
Since
![]() $\langle \operatorname {\mathrm {diag}}(I_{c-1},a)^{\triangle },1\rangle $
must transform on the left by some character, using the left invariance under
$\langle \operatorname {\mathrm {diag}}(I_{c-1},a)^{\triangle },1\rangle $
must transform on the left by some character, using the left invariance under
![]() $\langle w^{\triangle },1\rangle $
again we obtain for all
$\langle w^{\triangle },1\rangle $
again we obtain for all
![]() $a\in F^{*}$
,
$a\in F^{*}$
,
In addition by Equation (2.54),
![]() ${}^{*}\langle \operatorname {\mathrm {diag}}(a,I_{c-1})^{\triangle },1\rangle =\langle \operatorname {\mathrm {diag}}(I_{c-1},a^{-1})^{\triangle },1\rangle $
. Therefore, when
${}^{*}\langle \operatorname {\mathrm {diag}}(a,I_{c-1})^{\triangle },1\rangle =\langle \operatorname {\mathrm {diag}}(I_{c-1},a^{-1})^{\triangle },1\rangle $
. Therefore, when
![]() $\mathcal {E}'=\mathcal {E}^{*}$
,
$\mathcal {E}'=\mathcal {E}^{*}$
,
Since
![]() $\gamma _{\psi '}(a)\gamma _{\psi '}(a^{-1})=1$
(see Equation (2.68),
$\gamma _{\psi '}(a)\gamma _{\psi '}(a^{-1})=1$
(see Equation (2.68),
![]() $(a,a)_2=1$
because
$(a,a)_2=1$
because
![]() $\mu _{2m}\subset F^{*}$
) and
$\mu _{2m}\subset F^{*}$
) and
![]() $\varrho (a)\varrho (a^{-1})=1$
, again Equation (4.34) holds.
$\varrho (a)\varrho (a^{-1})=1$
, again Equation (4.34) holds.
5 Computation of the local factors with unramified data
In this section, we prove Theorem 66, namely we compute the integral (4.17) with unramified data (representations, matrix coefficient and section). Throughout, F is unramified, i.e, it is non-Archimedean,
![]() $|m|=1$
and
$|m|=1$
and
![]() $q>3$
(see § 2.4). Also, assume that
$q>3$
(see § 2.4). Also, assume that
![]() $\mu _{2m}\subset F^{*}$
in this section. We fix an unramified character
$\mu _{2m}\subset F^{*}$
in this section. We fix an unramified character
![]() $\psi $
of F, and the Haar measure on F is the one assigning
$\psi $
of F, and the Haar measure on F is the one assigning
![]() $1$
to
$1$
to
![]() $\mathcal {O}$
. The measure of the subgroups
$\mathcal {O}$
. The measure of the subgroups
![]() $K_{H}$
,
$K_{H}$
,
![]() $K_G$
and
$K_G$
and
![]() $K_{\operatorname {\mathrm {GL}}_n}$
is also normalized to be
$K_{\operatorname {\mathrm {GL}}_n}$
is also normalized to be
![]() $1$
.
$1$
.
In § 5.1, we reduce the
![]() $G^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral to the
$G^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral to the
![]() $\operatorname {\mathrm {GL}}_{n}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral (4.35). In § 5.2, we reduce the latter to the product of integrals
$\operatorname {\mathrm {GL}}_{n}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral (4.35). In § 5.2, we reduce the latter to the product of integrals
![]() $\operatorname {\mathrm {GL}}_{a}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_{a}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_{b}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
, where
$\operatorname {\mathrm {GL}}_{b}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
, where
![]() $n=a+b$
. The computation of the
$n=a+b$
. The computation of the
![]() $\operatorname {\mathrm {GL}}_{1}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals with unramified data is carried out in § 5.3. Finally, in § 5.4 we collect the previous results to conclude the proof.
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals with unramified data is carried out in § 5.3. Finally, in § 5.4 we collect the previous results to conclude the proof.
5.1 The reduction from
 $\operatorname {\mathrm {Sp}}_{c}^{(m)}$
to
$\operatorname {\mathrm {Sp}}_{c}^{(m)}$
to
 $\operatorname {\mathrm {GL}}_{n}^{(m,r)}$
$\operatorname {\mathrm {GL}}_{n}^{(m,r)}$
Let
![]() $n,k$
and m be positive integers, and put
$n,k$
and m be positive integers, and put
![]() $c=2n$
. Set
$c=2n$
. Set
![]() $r=m/2$
if m is even, otherwise
$r=m/2$
if m is even, otherwise
![]() $r=m$
. Let
$r=m$
. Let
![]() $G=\operatorname {\mathrm {Sp}}_{c}$
and
$G=\operatorname {\mathrm {Sp}}_{c}$
and
![]() $H=\operatorname {\mathrm {Sp}}_{2rkc}$
. The covering
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
. The covering
![]() $H^{(m)}$
is realized using
$H^{(m)}$
is realized using
![]() $\sigma _{2rkc}$
, the embedding
$\sigma _{2rkc}$
, the embedding
![]() $G\times G \hookrightarrow H$
given in § 2.3 is lifted to the coverings via Formula (2.24) and we fix the
$G\times G \hookrightarrow H$
given in § 2.3 is lifted to the coverings via Formula (2.24) and we fix the
![]() $2$
-cocycles on G to be
$2$
-cocycles on G to be
![]() $\sigma _c^{*,rk}$
for the left copy and
$\sigma _c^{*,rk}$
for the left copy and
![]() $\sigma _c$
for the right. For the description of the local
$\sigma _c$
for the right. For the description of the local
![]() $G^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, see § 4.2. Also, recall that the embedding of
$G^{(m)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, see § 4.2. Also, recall that the embedding of
![]() $N_H$
in
$N_H$
in
![]() $H^{(m)}$
is given by
$H^{(m)}$
is given by
![]() $v\mapsto \langle v,1\rangle $
; the canonical embedding of
$v\mapsto \langle v,1\rangle $
; the canonical embedding of
![]() $K_H$
in
$K_H$
in
![]() $H^{(m)}$
is
$H^{(m)}$
is
![]() $y\mapsto \langle y,\eta _{2rkc}(y)\rangle $
, and
$y\mapsto \langle y,\eta _{2rkc}(y)\rangle $
, and
![]() $\eta _{2rkc}$
is trivial on
$\eta _{2rkc}$
is trivial on
![]() $N_{rkc}\cap K_H$
,
$N_{rkc}\cap K_H$
,
![]() $T_{rkc}\cap K_H$
and
$T_{rkc}\cap K_H$
and
![]() $\mathfrak {W}^+_{2rkc}\cap H$
(see § 2.4).
$\mathfrak {W}^+_{2rkc}\cap H$
(see § 2.4).
Let
![]() $\pi $
be a genuine irreducible unramified representation of
$\pi $
be a genuine irreducible unramified representation of
![]() $G^{(m)}$
, where
$G^{(m)}$
, where
![]() $G^{(m)}$
is realized using
$G^{(m)}$
is realized using
![]() $\sigma _c$
, and
$\sigma _c$
, and
![]() $\tau $
be a genuine irreducible unramified representation of
$\tau $
be a genuine irreducible unramified representation of
![]() $\operatorname {\mathrm {GL}}_k^{(m,r)}$
, which is the unramified subrepresentation of
$\operatorname {\mathrm {GL}}_k^{(m,r)}$
, which is the unramified subrepresentation of
![]() $\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
(
$\mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
(
![]() $\pi $
and
$\pi $
and
![]() $\tau $
are then also admissible).
$\tau $
are then also admissible).
We assume that
![]() $\tau $
satisfies the following properties, which are plainly the restatement of several properties from § 3.5. Suppose that
$\tau $
satisfies the following properties, which are plainly the restatement of several properties from § 3.5. Suppose that
![]() $\tau $
satisfies the condition (3.45), and also assume that for all
$\tau $
satisfies the condition (3.45), and also assume that for all
![]() $0<l\leq c$
, the representation
$0<l\leq c$
, the representation
 $$ \begin{align*} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}) \end{align*} $$
contains a unique irreducible unramified
![]() $(rk,l)$
subrepresentation
$(rk,l)$
subrepresentation
![]() $\rho _l(\tau )$
. Denote the
$\rho _l(\tau )$
. Denote the
![]() $(rk,l)$
model of
$(rk,l)$
model of
![]() $\rho _l(\tau )$
by
$\rho _l(\tau )$
by
![]() $\mathcal {W}(\rho _l(\tau ))$
. It follows that Corollary 56 and Corollary 59 are applicable. Hence, we have the realization of the
$\mathcal {W}(\rho _l(\tau ))$
. It follows that Corollary 56 and Corollary 59 are applicable. Hence, we have the realization of the
![]() $(rk,c)$
functional from § 3.6, using
$(rk,c)$
functional from § 3.6, using
![]() $(rk,l)$
and
$(rk,l)$
and
![]() $(rk,c-l)$
functionals.
$(rk,c-l)$
functionals.
As proved in § 3.5, these properties are all satisfied in the context of Integral (4.17), that is, when
![]() $\tau $
is a local component at an unramified place of a genuine unitary irreducible cuspidal automorphic representation of
$\tau $
is a local component at an unramified place of a genuine unitary irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and under Conjectures 50 and 51 and the global assumption that the field contains
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and under Conjectures 50 and 51 and the global assumption that the field contains
![]() $\mu _{2m}$
. See Proposition 57.
$\mu _{2m}$
. See Proposition 57.
Let
![]() $\omega $
be the normalized unramified matrix coefficient of
$\omega $
be the normalized unramified matrix coefficient of
![]() $\pi ^{\vee }$
, and
$\pi ^{\vee }$
, and
![]() $f_{\mathcal {W}(\rho _c(\tau ))}$
be the normalized unramified standard section of
$f_{\mathcal {W}(\rho _c(\tau ))}$
be the normalized unramified standard section of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}}^{H^{(m)}}(\mathcal {W}(\rho _c(\tau ))\delta _P^s)$
, as in the statement of Theorem 66.
$\operatorname {\mathrm {Ind}}_{\widetilde {P}}^{H^{(m)}}(\mathcal {W}(\rho _c(\tau ))\delta _P^s)$
, as in the statement of Theorem 66.
We can always assume that
![]() $\pi $
is a quotient of
$\pi $
is a quotient of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, where
$\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, where
![]() $R=M_R\ltimes U_R$
is the standard Siegel parabolic subgroup of G (i.e.,
$R=M_R\ltimes U_R$
is the standard Siegel parabolic subgroup of G (i.e.,
![]() $M_R=\operatorname {\mathrm {GL}}_n$
), and
$M_R=\operatorname {\mathrm {GL}}_n$
), and
![]() $\pi _n$
is a genuine irreducible unramified representation of
$\pi _n$
is a genuine irreducible unramified representation of
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}$
. Let
$\operatorname {\mathrm {GL}}_n^{(m,r)}$
. Let
![]() ${}^{*}$
be defined by Equation (2.54). By definition,
${}^{*}$
be defined by Equation (2.54). By definition,
![]() $\tau ^{*}$
enjoys the properties of
$\tau ^{*}$
enjoys the properties of
![]() $\tau $
stated above (see also Proposition 25) so that (3.45) holds and
$\tau $
stated above (see also Proposition 25) so that (3.45) holds and
![]() $\rho _l(\tau ^{*})$
is defined for all
$\rho _l(\tau ^{*})$
is defined for all
![]() $0<l\leq c$
. Also, by Equation (2.52),
$0<l\leq c$
. Also, by Equation (2.52),
 $$ \begin{align*} (\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}))^{*} =\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau^{*}\otimes \ldots \otimes \tau^{*})\delta_{P_{(k^{rl})}}^{-1/(2rk)}), \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau\otimes \ldots \otimes \tau)\delta_{P_{(k^{rl})}}^{-1/(2rk)}))^{*} =\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(k^{rl})}}^{\operatorname{\mathrm{GL}}^{(m,r)}_{rkl}}((\tau^{*}\otimes \ldots \otimes \tau^{*})\delta_{P_{(k^{rl})}}^{-1/(2rk)}), \end{align*} $$
hence
![]() $\rho _l(\tau ^{*})=\rho _l(\tau )^{*}$
.
$\rho _l(\tau ^{*})=\rho _l(\tau )^{*}$
.
Let
![]() $\omega _n$
be the normalized unramified matrix coefficient of
$\omega _n$
be the normalized unramified matrix coefficient of
![]() $\pi _n^{\vee }$
, and
$\pi _n^{\vee }$
, and
![]() $f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))}$
be the normalized unramified standard section of
$f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))}$
be the normalized unramified standard section of
Remark 78. In the linear setting, whenever
![]() $\tau $
is irreducible,
$\tau $
is irreducible,
![]() $\tau ^{*}=\tau ^{\vee }$
. Here, it is important we use
$\tau ^{*}=\tau ^{\vee }$
. Here, it is important we use
![]() $\tau ^{*}$
, since
$\tau ^{*}$
, since
![]() $\tau ^{\vee }$
is antigenuine, then
$\tau ^{\vee }$
is antigenuine, then
![]() $\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{\vee }))$
is undefined on
$\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{\vee }))$
is undefined on
![]() $\widetilde {M}_{(rkn,rkn)}$
(see Equation (2.53)) unless the notions of genuine and antigenuine coincide, that is,
$\widetilde {M}_{(rkn,rkn)}$
(see Equation (2.53)) unless the notions of genuine and antigenuine coincide, that is,
![]() $m=2$
.
$m=2$
.
Put
![]() $\alpha =2rkc+1$
, and define
$\alpha =2rkc+1$
, and define
 $$ \begin{align} d_{\tau,\vartheta}(s)=& \left[\frac{L_{\vartheta}(r\alpha s+1/2,\tau)}{L_{\vartheta}(r\alpha s+rn+1/2,\tau)}\right] \prod_{1\leq j\leq \lfloor rn/2\rfloor} \frac{L_{\vartheta}(2r\alpha s+2j,\tau,\vee^2)}{L_{\vartheta}(2r\alpha s+2j+2rn-2\lfloor rn/2\rfloor-1,\tau,\vee^2)}\\\nonumber&\times \prod_{1\leq j\leq \lceil rn/2\rceil} \frac{L_{\vartheta}(2r\alpha s+2j-1,\tau,\wedge^2)}{L_{\vartheta}(2r\alpha s+2j+2rn-2\lceil rn/2\rceil,\tau,\wedge^2)}, \end{align} $$
$$ \begin{align} d_{\tau,\vartheta}(s)=& \left[\frac{L_{\vartheta}(r\alpha s+1/2,\tau)}{L_{\vartheta}(r\alpha s+rn+1/2,\tau)}\right] \prod_{1\leq j\leq \lfloor rn/2\rfloor} \frac{L_{\vartheta}(2r\alpha s+2j,\tau,\vee^2)}{L_{\vartheta}(2r\alpha s+2j+2rn-2\lfloor rn/2\rfloor-1,\tau,\vee^2)}\\\nonumber&\times \prod_{1\leq j\leq \lceil rn/2\rceil} \frac{L_{\vartheta}(2r\alpha s+2j-1,\tau,\wedge^2)}{L_{\vartheta}(2r\alpha s+2j+2rn-2\lceil rn/2\rceil,\tau,\wedge^2)}, \end{align} $$
where the factor in square brackets is included only when m is odd, and for
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $\lfloor x \rfloor $
denotes the largest integer smaller than or equal to x.
$\lfloor x \rfloor $
denotes the largest integer smaller than or equal to x.
Lemma 79. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
![]() $Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))})=d_{\tau ,\vartheta }(s)Z(\alpha s/(rkn),\omega _{n},f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))})$
.
$Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))})=d_{\tau ,\vartheta }(s)Z(\alpha s/(rkn),\omega _{n},f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))})$
.
Proof. We adapt the proof of the linear case [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Lemma 27]. For the purpose of computing the integral with unramified data, we may assume that
![]() $\pi =\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, then
$\pi =\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n)$
, then
![]() $\pi ^{\vee }=\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n^{\vee })$
. Let
$\pi ^{\vee }=\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m)}}(\pi _n^{\vee })$
. Let
![]() $\{,\}_{M_R}$
be the
$\{,\}_{M_R}$
be the
![]() $\widetilde {M}_R$
-invariant pairing on
$\widetilde {M}_R$
-invariant pairing on
![]() $\pi _n\times \pi _n^{\vee }$
, and choose a semi-invariant measure on
$\pi _n\times \pi _n^{\vee }$
, and choose a semi-invariant measure on
![]() $R\backslash G$
(see [Reference Bernstein and ZelevinskyBZ76, 1.21]). We can then realize the
$R\backslash G$
(see [Reference Bernstein and ZelevinskyBZ76, 1.21]). We can then realize the
![]() $G^{(m)}$
-invariant pairing on
$G^{(m)}$
-invariant pairing on
![]() $\pi \times \pi ^{\vee }$
by the integral
$\pi \times \pi ^{\vee }$
by the integral
 $$ \begin{align*} \{\varphi,\varphi^{\vee}\}=\int\limits_{R\backslash G}\{\varphi(\langle g,1\rangle),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\,dg, \end{align*} $$
$$ \begin{align*} \{\varphi,\varphi^{\vee}\}=\int\limits_{R\backslash G}\{\varphi(\langle g,1\rangle),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\,dg, \end{align*} $$
where
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{\vee }$
belong to the spaces of
$\varphi ^{\vee }$
belong to the spaces of
![]() $\pi $
and
$\pi $
and
![]() $\pi ^{\vee }$
, respectively. Using the Iwasawa decomposition
$\pi ^{\vee }$
, respectively. Using the Iwasawa decomposition
![]() $G=RK_G$
, and since
$G=RK_G$
, and since
![]() $\varphi $
is genuine and
$\varphi $
is genuine and
![]() $\varphi ^{\vee }$
is antigenuine,
$\varphi ^{\vee }$
is antigenuine,
 $$ \begin{align} \{\varphi,\varphi^{\vee}\}=\int\limits_{K_G}\{\varphi(\langle y,\eta_c(y)\rangle),\varphi^{\vee}(\langle y,\eta_c(y)\rangle)\}_{M_R}\,dy. \end{align} $$
$$ \begin{align} \{\varphi,\varphi^{\vee}\}=\int\limits_{K_G}\{\varphi(\langle y,\eta_c(y)\rangle),\varphi^{\vee}(\langle y,\eta_c(y)\rangle)\}_{M_R}\,dy. \end{align} $$
If
![]() $\varphi $
is unramified,
$\varphi $
is unramified,
![]() $\varphi (\langle y,\eta _c(y)\rangle )=\varphi (e)$
, where
$\varphi (\langle y,\eta _c(y)\rangle )=\varphi (e)$
, where
![]() $e=\langle I_{c},1\rangle $
. Since
$e=\langle I_{c},1\rangle $
. Since
![]() $\omega $
is unramified, so is
$\omega $
is unramified, so is
![]() $\varphi $
(and
$\varphi $
(and
![]() $\varphi ^{\vee }$
) and
$\varphi ^{\vee }$
) and
 $$ \begin{align*} \omega(\langle g,1\rangle)=\int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy. \end{align*} $$
$$ \begin{align*} \omega(\langle g,1\rangle)=\int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy. \end{align*} $$
Substituting this into
![]() $Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))})$
, we obtain
$Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))})$
, we obtain
 $$ \begin{align} \int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
Multiplying
![]() $g\mapsto y^{-1}g$
(we can change the order of integration when
$g\mapsto y^{-1}g$
(we can change the order of integration when
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
),
$\operatorname {\mathrm {Re}}(s)\gg 0$
),
and because
![]() $\langle y,\eta _c(y)\rangle \langle y^{-1},\eta _c(y^{-1})\rangle =e$
and
$\langle y,\eta _c(y)\rangle \langle y^{-1},\eta _c(y^{-1})\rangle =e$
and
![]() $\varphi ^{\vee }$
is antigenuine,
$\varphi ^{\vee }$
is antigenuine,
Also,
 $$ \begin{align*} & f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \\ &\quad \mapsto f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota} \langle\mathfrak{e}_2(y^{-1}g),1\rangle,s) \\ &\quad =f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota} \langle\mathfrak{e}_2(y^{-1}),\sigma_{2rkc}(\mathfrak{e}_2(y^{-1}),\mathfrak{e}_2(g))^{-1}\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s). \end{align*} $$
$$ \begin{align*} & f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \\ &\quad \mapsto f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota} \langle\mathfrak{e}_2(y^{-1}g),1\rangle,s) \\ &\quad =f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota} \langle\mathfrak{e}_2(y^{-1}),\sigma_{2rkc}(\mathfrak{e}_2(y^{-1}),\mathfrak{e}_2(g))^{-1}\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s). \end{align*} $$
Since
![]() $\sigma _{c}(y^{-1},g)=\sigma _{2rkc}(\mathfrak {e}_2(y^{-1}),\mathfrak {e}_2(g))$
by Proposition 7, and
$\sigma _{c}(y^{-1},g)=\sigma _{2rkc}(\mathfrak {e}_2(y^{-1}),\mathfrak {e}_2(g))$
by Proposition 7, and
![]() $\{\varphi ,\varphi ^{\vee }\}_{M_R}$
is bilinear, Integral (5.3) becomes
$\{\varphi ,\varphi ^{\vee }\}_{M_R}$
is bilinear, Integral (5.3) becomes
 $$ \begin{align} &\int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \nonumber \\ &\quad \times \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(y^{-1}),\eta_c(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dy\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \nonumber \\ &\quad \times \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(y^{-1}),\eta_c(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dy\,dg. \end{align} $$
The map
![]() $\mathfrak {e}_1(y)\mapsto \langle \mathfrak {e}_1(y),\eta _{2rkc}(\mathfrak {e}_1(y))\rangle $
is a splitting of
$\mathfrak {e}_1(y)\mapsto \langle \mathfrak {e}_1(y),\eta _{2rkc}(\mathfrak {e}_1(y))\rangle $
is a splitting of
![]() $\mathfrak {e}_1(K_G)$
, and according to the embedding (2.26) so is the map
$\mathfrak {e}_1(K_G)$
, and according to the embedding (2.26) so is the map
Hence, because
![]() $K_G$
is perfect,
$K_G$
is perfect,
Then since
![]() $f_{\mathcal {W}(\rho _c(\tau ))}$
is right-invariant under
$f_{\mathcal {W}(\rho _c(\tau ))}$
is right-invariant under
![]() $\langle \mathfrak {e}_1(y^{-1}),\eta _{2rkc}(\mathfrak {e}_1(y^{-1}))\rangle $
and using Proposition 7 and Equation (2.43),
$\langle \mathfrak {e}_1(y^{-1}),\eta _{2rkc}(\mathfrak {e}_1(y^{-1}))\rangle $
and using Proposition 7 and Equation (2.43),
 $$ \begin{align*} &f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(y^{-1}),\eta_c(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \\&=f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle(y^{-1},y^{-1}),\varsigma_{*,c}^{rk+1}(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s). \end{align*} $$
$$ \begin{align*} &f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(y^{-1}),\eta_c(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s) \\&=f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle(y^{-1},y^{-1}),\varsigma_{*,c}^{rk+1}(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s). \end{align*} $$
The integral over
![]() $U_0$
becomes
$U_0$
becomes
 $$ \begin{align} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle(y^{-1},y^{-1}),\varsigma_{*,c}^{rk+1}(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0. \end{align} $$
$$ \begin{align} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle \,{}^{\iota}\langle(y^{-1},y^{-1}),\varsigma_{*,c}^{rk+1}(y^{-1})\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0. \end{align} $$
Now, by Corollary 71 we can omit
![]() ${}^{\iota }\langle (y^{-1},y^{-1}),\varsigma _{*,c}^{rk+1}(y^{-1})\rangle $
from this integral, and since the measure of
${}^{\iota }\langle (y^{-1},y^{-1}),\varsigma _{*,c}^{rk+1}(y^{-1})\rangle $
from this integral, and since the measure of
![]() $K_G$
is
$K_G$
is
![]() $1$
, Integral (5.4) equals
$1$
, Integral (5.4) equals
 $$ \begin{align} \int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))}(\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
The function
![]() $a\mapsto \delta _P^{-1/2-s}(a)f_{\mathcal {W}(\rho _c(\tau ))}(ah,s)$
,
$a\mapsto \delta _P^{-1/2-s}(a)f_{\mathcal {W}(\rho _c(\tau ))}(ah,s)$
,
![]() $a\in \operatorname {\mathrm {GL}}_n^{(m,r)}$
, belongs to the
$a\in \operatorname {\mathrm {GL}}_n^{(m,r)}$
, belongs to the
![]() $(rk,c)$
model
$(rk,c)$
model
![]() $\mathcal {W}(\rho _c(\tau ))$
of
$\mathcal {W}(\rho _c(\tau ))$
of
![]() $\rho _c(\tau )$
. By Corollary 56 with
$\rho _c(\tau )$
. By Corollary 56 with
![]() $l=n=c/2$
,
$l=n=c/2$
,
Let
![]() $L=M_L\ltimes U_L$
be the standard parabolic subgroup of H with
$L=M_L\ltimes U_L$
be the standard parabolic subgroup of H with
![]() $M_L=\operatorname {\mathrm {GL}}_{rkn}\times \operatorname {\mathrm {GL}}_{rkn}=M_{(rkn,rkn)}$
. According to Proposition 62, we can realize
$M_L=\operatorname {\mathrm {GL}}_{rkn}\times \operatorname {\mathrm {GL}}_{rkn}=M_{(rkn,rkn)}$
. According to Proposition 62, we can realize
![]() $\mathcal {W}(\rho _c(\tau ))$
using Integral (3.50). Then by transitivity of induction there exists a standard unramified section
$\mathcal {W}(\rho _c(\tau ))$
using Integral (3.50). Then by transitivity of induction there exists a standard unramified section
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
on
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
on
such that, for all
![]() $h\in H^{(m)}$
,
$h\in H^{(m)}$
,
 $$ \begin{align} f_{\mathcal{W}(\rho_c(\tau))}(h,s)=\int\limits_V{f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle\kappa v,1\rangle h,s)\,dv. \end{align} $$
$$ \begin{align} f_{\mathcal{W}(\rho_c(\tau))}(h,s)=\int\limits_V{f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle\kappa v,1\rangle h,s)\,dv. \end{align} $$
Here, V and
![]() $\kappa $
are the subgroup and element given in § 3.6, implicitly identified with their images in
$\kappa $
are the subgroup and element given in § 3.6, implicitly identified with their images in
![]() $M_P$
. Moreover,
$M_P$
. Moreover,
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is normalized. Indeed, by the proof of Proposition 62 and because
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is normalized. Indeed, by the proof of Proposition 62 and because
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified and the volume of
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified and the volume of
![]() $V\cap K_{\operatorname {\mathrm {GL}}_{rkc}}$
is
$V\cap K_{\operatorname {\mathrm {GL}}_{rkc}}$
is
![]() $1$
, we obtain
$1$
, we obtain
With this modification, Integral (5.7) takes the form
 $$ \begin{align} \int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \kappa v,1\rangle\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,dv\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \kappa v,1\rangle\langle\delta u_0,1\rangle\,{}^{\iota}\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,dv\,du_0\,dg. \end{align} $$
This integral is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
as a triple integral.
$\operatorname {\mathrm {Re}}(s)\gg 0$
as a triple integral.
Next, we shift v to the right. By Equation (2.8) and since
![]() $\sigma _{2rkc}$
is trivial
$\sigma _{2rkc}$
is trivial
![]() $\mathfrak {W}^+_{2rkc}$
(see § 2.4),
$\mathfrak {W}^+_{2rkc}$
(see § 2.4),
We observe the following properties.
-
1. The element
 $\delta _0$
normalizes V, in particular
$\delta _0$
normalizes V, in particular
 ${}^{\delta _0^{-1}}\langle v,1\rangle =\langle {}^{\delta _0^{-1}}v,1\rangle $
by Equation (2.10).
${}^{\delta _0^{-1}}\langle v,1\rangle =\langle {}^{\delta _0^{-1}}v,1\rangle $
by Equation (2.10). -
2. For
 $v\in V$
,
$v\in V$
,
 ${}^v\delta _1=\delta _1u'$
with
${}^v\delta _1=\delta _1u'$
with
 $u'\in U_0$
such that
$u'\in U_0$
such that
 $\psi _U(u')=1$
; since
$\psi _U(u')=1$
; since
 $\delta _1u'\in N_{rkc}$
, by Equations (2.10) and (2.8), we have
$\delta _1u'\in N_{rkc}$
, by Equations (2.10) and (2.8), we have
 ${}^v\langle \delta _1,1\rangle =\langle \delta _1u',1\rangle =\langle \delta _1,1\rangle \langle u',1\rangle $
.
${}^v\langle \delta _1,1\rangle =\langle \delta _1u',1\rangle =\langle \delta _1,1\rangle \langle u',1\rangle $
. -
3. The elements of V normalize
 $U_0$
and fix
$U_0$
and fix
 $\psi _U|_{U_0}$
.
$\psi _U|_{U_0}$
. -
4. Since V is also a subgroup of
 $M_{(rkc-n,n)}$
and the image of
$M_{(rkc-n,n)}$
and the image of
 $v\in V$
in
$v\in V$
in
 $M_P$
takes the form
$M_P$
takes the form
 $\operatorname {\mathrm {diag}}(v',I_c,{v'}^{*})$
with
$\operatorname {\mathrm {diag}}(v',I_c,{v'}^{*})$
with
 $v'\in M_{(rkc-n,n)}$
, V and
$v'\in M_{(rkc-n,n)}$
, V and
 $\mathfrak {e}_2(G)$
commute; by Equation (2.12), this extends to
$\mathfrak {e}_2(G)$
commute; by Equation (2.12), this extends to
 $H^{(m)}$
(
$H^{(m)}$
(
 $\det v=1$
for any
$\det v=1$
for any
 $v\in V$
).
$v\in V$
). -
5. Since
 $\delta _0$
and
$\delta _0$
and
 $\kappa $
commute and
$\kappa $
commute and
 $\sigma _{2rkc}$
is trivial on
$\sigma _{2rkc}$
is trivial on
 $\mathfrak {W}^+_{2rkc}$
,
$\mathfrak {W}^+_{2rkc}$
,
 $\langle \delta _0,1\rangle $
and
$\langle \delta _0,1\rangle $
and
 $\langle \kappa ,1\rangle $
commute.
$\langle \kappa ,1\rangle $
commute. -
6. Because
 $\delta _1,{}^{\kappa }\delta _1\in N_{rkc}$
, Equation (2.10) implies that
$\delta _1,{}^{\kappa }\delta _1\in N_{rkc}$
, Equation (2.10) implies that
 ${}^{\kappa }\langle \delta _1,1\rangle =\langle {}^{\kappa }\delta _1,1\rangle $
.
${}^{\kappa }\langle \delta _1,1\rangle =\langle {}^{\kappa }\delta _1,1\rangle $
. -
7. The image of
 $\kappa $
in
$\kappa $
in
 $M_P$
takes the form
$M_P$
takes the form
 $\operatorname {\mathrm {diag}}(\kappa _0,I_c,\kappa _0^{*})$
, where
$\operatorname {\mathrm {diag}}(\kappa _0,I_c,\kappa _0^{*})$
, where
 $\kappa _0\in \operatorname {\mathrm {GL}}_{rkc-n}$
is a permutation matrix, and also
$\kappa _0\in \operatorname {\mathrm {GL}}_{rkc-n}$
is a permutation matrix, and also
 $\det g=1$
, whence Equation (2.12) implies that
$\det g=1$
, whence Equation (2.12) implies that
 $\langle \kappa ,1\rangle $
and
$\langle \kappa ,1\rangle $
and
 $\langle \mathfrak {e}_2(g),1\rangle $
commute.
$\langle \mathfrak {e}_2(g),1\rangle $
commute.
A computation shows that
 $$ \begin{align} U_0'={}^{\kappa}U_0=\left\{\left(\begin{smallmatrix}I_{rkn}&&U_1&U_2\\&I_{rkn}&U_3&U_4\\&&I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right)\in H\right\}, \end{align} $$
$$ \begin{align} U_0'={}^{\kappa}U_0=\left\{\left(\begin{smallmatrix}I_{rkn}&&U_1&U_2\\&I_{rkn}&U_3&U_4\\&&I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right)\in H\right\}, \end{align} $$
where
![]() $U_1=\left (\begin {smallmatrix}*&*\\0&*\end {smallmatrix}\right )$
with
$U_1=\left (\begin {smallmatrix}*&*\\0&*\end {smallmatrix}\right )$
with
![]() $0\in \text {Mat}_{n}$
so that
$0\in \text {Mat}_{n}$
so that
![]() $\left \{\left (\begin {smallmatrix}I_{rkn}&U_1\\&I_{rkn}\end {smallmatrix}\right )\right \}$
is the unipotent subgroup appearing in the
$\left \{\left (\begin {smallmatrix}I_{rkn}&U_1\\&I_{rkn}\end {smallmatrix}\right )\right \}$
is the unipotent subgroup appearing in the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral;
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral;
![]() $\psi _U$
is trivial on
$\psi _U$
is trivial on
![]() $U_2$
and
$U_2$
and
![]() $U_3$
, and its restriction to the coordinates of
$U_3$
, and its restriction to the coordinates of
![]() $U_1$
is the character
$U_1$
is the character
![]() $\psi _U$
for this integral;
$\psi _U$
for this integral;
![]() $U_2$
(resp.,
$U_2$
(resp.,
![]() $U_3$
) takes the form
$U_3$
) takes the form
![]() $\left (\begin {smallmatrix}*&*\\0&*\end {smallmatrix}\right )$
with
$\left (\begin {smallmatrix}*&*\\0&*\end {smallmatrix}\right )$
with
![]() $0\in \text {Mat}_n$
; and
$0\in \text {Mat}_n$
; and
![]() $U_4$
is already determined by
$U_4$
is already determined by
![]() $U_1$
and the symplectic form defining H. Regard
$U_1$
and the symplectic form defining H. Regard
![]() $\psi _U$
as a character of
$\psi _U$
as a character of
![]() $U_0'$
by
$U_0'$
by
![]() $\psi _U(u_0')=\psi _U({}^{\kappa ^{-1}}u_0')$
, for
$\psi _U(u_0')=\psi _U({}^{\kappa ^{-1}}u_0')$
, for
![]() $u_0'\in U_0'$
.
$u_0'\in U_0'$
.
We can now use Equations (1)–(7) to rewrite Integral (5.10) in the form
 $$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0',1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dg.\notag \end{align} $$
$$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0',1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dg.\notag \end{align} $$
Next, factoring this integral through
![]() $U_R$
we obtain
$U_R$
we obtain
 $$ \begin{align*} &\int\limits_{U_R\backslash G} \int\limits_{U_R} \{\varphi(e),\varphi^{\vee}(\langle z,1\rangle\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0',1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(z),1 \rangle\,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_R\backslash G} \int\limits_{U_R} \{\varphi(e),\varphi^{\vee}(\langle z,1\rangle\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0',1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(z),1 \rangle\,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
Let
![]() $U_0^{\bullet }$
be the subgroup obtained from
$U_0^{\bullet }$
be the subgroup obtained from
![]() $U_0'$
by replacing the
$U_0'$
by replacing the
![]() $0$
block of
$0$
block of
![]() $U_2$
with arbitrary coordinates such that the elements still belong in H. For
$U_2$
with arbitrary coordinates such that the elements still belong in H. For
![]() $z\in U_R$
and
$z\in U_R$
and
![]() $u_0'\in U_0'$
,
$u_0'\in U_0'$
,
where
![]() $m_z$
belongs to the subgroup
$m_z$
belongs to the subgroup
![]() $V_{((2rk-1)n,n)}$
of
$V_{((2rk-1)n,n)}$
of
![]() $\operatorname {\mathrm {GL}}_{rkc}$
and when z and
$\operatorname {\mathrm {GL}}_{rkc}$
and when z and
![]() $u_0'$
vary over
$u_0'$
vary over
![]() $U_R$
and
$U_R$
and
![]() $U_0'$
,
$U_0'$
,
![]() $u_z$
varies over
$u_z$
varies over
![]() $U_0^{\bullet }$
. Moreover,
$U_0^{\bullet }$
. Moreover,
![]() ${}^{\kappa }\delta _1,u_0',m_z,u_z\in N_{rkc}$
so that by Equations (2.10) and (2.9),
${}^{\kappa }\delta _1,u_0',m_z,u_z\in N_{rkc}$
so that by Equations (2.10) and (2.9),
After this conjugation and since
![]() $\varphi ^{\vee }(\langle z,1\rangle \langle g,1\rangle )=\varphi ^{\vee }(\langle g,1\rangle )$
, the integral equals
$\varphi ^{\vee }(\langle z,1\rangle \langle g,1\rangle )=\varphi ^{\vee }(\langle g,1\rangle )$
, the integral equals
 $$ \begin{align*} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_R} \int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))} \\&( \langle \delta_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(z),1\rangle \langle m_z,1\rangle\langle({}^{\kappa}\delta_1)u_z,1\rangle \,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_R} \int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))} \\&( \langle \delta_0,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(z),1\rangle \langle m_z,1\rangle\langle({}^{\kappa}\delta_1)u_z,1\rangle \,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
Since
![]() ${}^{\delta _0}(^{\iota }\langle \mathfrak {e}_2(z),1\rangle )\in N_{rkc}$
, by Equation (2.4) we have
${}^{\delta _0}(^{\iota }\langle \mathfrak {e}_2(z),1\rangle )\in N_{rkc}$
, by Equation (2.4) we have
![]() ${}^{\delta _0}({}^{\iota }\langle \mathfrak {e}_2(z),1\rangle )=\langle {}^{\delta _0}\mathfrak {e}_2({}^{\iota }z),1\rangle $
. Also, because
${}^{\delta _0}({}^{\iota }\langle \mathfrak {e}_2(z),1\rangle )=\langle {}^{\delta _0}\mathfrak {e}_2({}^{\iota }z),1\rangle $
. Also, because
![]() ${}^{\delta _0}m_z\in V_{(n,(2rk-1)n)}<N_{rkc}$
, by Equation (2.10) we have
${}^{\delta _0}m_z\in V_{(n,(2rk-1)n)}<N_{rkc}$
, by Equation (2.10) we have
![]() ${}^{\delta _0}\langle m_z,1\rangle =\langle {}^{\delta _0}m_z,1\rangle $
. Thus, we can further write
${}^{\delta _0}\langle m_z,1\rangle =\langle {}^{\delta _0}m_z,1\rangle $
. Thus, we can further write
 $$ \begin{align*} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_R} \int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))} \\&(\langle{}^{\delta}\mathfrak{e}_2({}^{\iota}z),1\rangle \langle {}^{\delta_0}m_z,1\rangle \langle \delta_0({}^{\kappa}\delta_1),1\rangle\langle u_z,1\rangle \,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_R} \int\limits_{U_0'} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))} \\&(\langle{}^{\delta}\mathfrak{e}_2({}^{\iota}z),1\rangle \langle {}^{\delta_0}m_z,1\rangle \langle \delta_0({}^{\kappa}\delta_1),1\rangle\langle u_z,1\rangle \,{}^{\iota} \langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0')\,dv\,du_0'\,dz\,dg. \end{align*} $$
Since
![]() ${}^{\delta }\mathfrak {e}_2({}^{\iota }z)\in U_P<U_L$
, the section is left-invariant under
${}^{\delta }\mathfrak {e}_2({}^{\iota }z)\in U_P<U_L$
, the section is left-invariant under
![]() $\langle {}^{\delta }\mathfrak {e}_2({}^{\iota }z),1\rangle $
. Now, as in the linear case ([Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, (3.21)–(3.22)]), we can change variables in
$\langle {}^{\delta }\mathfrak {e}_2({}^{\iota }z),1\rangle $
. Now, as in the linear case ([Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, (3.21)–(3.22)]), we can change variables in
![]() $u_z$
to remove the dependency on z; this affects
$u_z$
to remove the dependency on z; this affects
![]() $\psi _U$
, but the change is cancelled when we use the left-equivariance properties of
$\psi _U$
, but the change is cancelled when we use the left-equivariance properties of
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
under
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
under
![]() $\langle {}^{\delta _0}m_z,1\rangle $
. Therefore, we can combine the integrations over
$\langle {}^{\delta _0}m_z,1\rangle $
. Therefore, we can combine the integrations over
![]() $U_R$
and
$U_R$
and
![]() $U_0'$
into an integration over
$U_0'$
into an integration over
![]() $U_0^{\bullet }$
and obtain
$U_0^{\bullet }$
and obtain
 $$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0^{\bullet}} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0^{\bullet},1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0^{\bullet})\,dv\,du_0^{\bullet}\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0^{\bullet}} \int\limits_V {f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber(\langle \delta_0({}^{\kappa}\delta_1),1\rangle \langle u_0^{\bullet},1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u_0^{\bullet})\,dv\,du_0^{\bullet}\,dg. \end{align} $$
Here,
![]() $\psi _U$
was lifted to a character of
$\psi _U$
was lifted to a character of
![]() $U_0^{\bullet }$
trivially on the coordinates outside
$U_0^{\bullet }$
trivially on the coordinates outside
![]() $U_0'$
.
$U_0'$
.
Now, we decompose
![]() $\delta _0$
and write
$\delta _0$
and write
![]() $du_0^{\bullet }$
as an iterated integral. Let
$du_0^{\bullet }$
as an iterated integral. Let
![]() $\delta '=\delta _0'\delta _1'$
be the elements corresponding to the
$\delta '=\delta _0'\delta _1'$
be the elements corresponding to the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral (defined in § 4.3), regarded as elements of
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral (defined in § 4.3), regarded as elements of
![]() $M_P$
. For example,
$M_P$
. For example,
![]() $\delta _0'$
is the image of
$\delta _0'$
is the image of
![]() $\left (\begin {smallmatrix}&I_{rkn}\\I_{rkn}\end {smallmatrix}\right )$
in
$\left (\begin {smallmatrix}&I_{rkn}\\I_{rkn}\end {smallmatrix}\right )$
in
![]() $M_P$
. We can then write
$M_P$
. We can then write
 $$ \begin{align*} \delta_0=w\delta_0'w,\qquad w=\left(\begin{smallmatrix}I_{rkn}\\&&I_{rkn}\\&-I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right). \end{align*} $$
$$ \begin{align*} \delta_0=w\delta_0'w,\qquad w=\left(\begin{smallmatrix}I_{rkn}\\&&I_{rkn}\\&-I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right). \end{align*} $$
Observe that because
![]() $U_0^{\bullet }$
differs from
$U_0^{\bullet }$
differs from
![]() $U_0'$
by only one block (the bottom left
$U_0'$
by only one block (the bottom left
![]() $n\times n$
block of
$n\times n$
block of
![]() $U_2$
), one may still use Equation (5.11) to describe the elements of
$U_2$
), one may still use Equation (5.11) to describe the elements of
![]() $U_0^{\bullet }$
. For
$U_0^{\bullet }$
. For
![]() $u_0^{\bullet }\in U_0^{\bullet }$
and
$u_0^{\bullet }\in U_0^{\bullet }$
and
![]() $i\in \{2,3\}$
, let
$i\in \{2,3\}$
, let
![]() $u^i$
denote the element obtained from
$u^i$
denote the element obtained from
![]() $u_0^{\bullet }$
by zeroing out the coordinates in the blocks
$u_0^{\bullet }$
by zeroing out the coordinates in the blocks
![]() $U_j$
with
$U_j$
with
![]() $j\ne i$
and
$j\ne i$
and
![]() $u^{1,4}$
be similarly obtained by removing the coordinates in
$u^{1,4}$
be similarly obtained by removing the coordinates in
![]() $U_2$
and
$U_2$
and
![]() $U_3$
. Then we have
$U_3$
. Then we have
 $$ \begin{align} &\delta_0u_0^{\bullet}=w\cdot{}^{(\delta_{0}'w)}u^2\cdot\delta_0'\cdot {}^{w}(u^{1,4})\cdot wu^3,\nonumber\\ &\delta_0({}^{\kappa}\delta_1)u_0^{\bullet}=w\cdot{}^{(\delta_{0}'w)}u^2\cdot\delta'\cdot {}^{w}(u^{1,4})\cdot wu^3. \end{align} $$
$$ \begin{align} &\delta_0u_0^{\bullet}=w\cdot{}^{(\delta_{0}'w)}u^2\cdot\delta_0'\cdot {}^{w}(u^{1,4})\cdot wu^3,\nonumber\\ &\delta_0({}^{\kappa}\delta_1)u_0^{\bullet}=w\cdot{}^{(\delta_{0}'w)}u^2\cdot\delta'\cdot {}^{w}(u^{1,4})\cdot wu^3. \end{align} $$
Note that
![]() ${}^{\kappa }\delta _1\in U_P$
, hence commutes with
${}^{\kappa }\delta _1\in U_P$
, hence commutes with
![]() $u_0^{\bullet }$
. We can extend Equation (5.14) to
$u_0^{\bullet }$
. We can extend Equation (5.14) to
![]() $H^{(m)}$
: Indeed,
$H^{(m)}$
: Indeed,
![]() $\sigma _{2rkc}$
is trivial on
$\sigma _{2rkc}$
is trivial on
![]() $\mathfrak {W}^+_{2rkc}$
; and also
$\mathfrak {W}^+_{2rkc}$
; and also
![]() $u_0^{\bullet },{}^{(\delta _{0}'w)}u^2,{}^{w}(u^{1,4}),{}^{\kappa }\delta _1\in N_{rkc}$
so that Equation (2.10) is applicable and the elements
$u_0^{\bullet },{}^{(\delta _{0}'w)}u^2,{}^{w}(u^{1,4}),{}^{\kappa }\delta _1\in N_{rkc}$
so that Equation (2.10) is applicable and the elements
![]() ${}^{\kappa }\delta _1$
and
${}^{\kappa }\delta _1$
and
![]() $u_0^{\bullet }$
commute in
$u_0^{\bullet }$
commute in
![]() $H^{(m)}$
. Hence,
$H^{(m)}$
. Hence,
Let
![]() $U^2$
be the subgroup of elements
$U^2$
be the subgroup of elements
![]() $^{(\delta _{0}'w')}u^2$
:
$^{(\delta _{0}'w')}u^2$
:
 $$ \begin{align*} U^2=\left\{\left(\begin{smallmatrix}I_{rkn}\\&I_{rkn}&Z\\&&I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right)\in H\right\}. \end{align*} $$
$$ \begin{align*} U^2=\left\{\left(\begin{smallmatrix}I_{rkn}\\&I_{rkn}&Z\\&&I_{rkn}\\&&&I_{rkn}\end{smallmatrix}\right)\in H\right\}. \end{align*} $$
This subgroup will be used below to define an intertwining operator. Let
![]() $U^{1,4}$
be the subgroup of elements
$U^{1,4}$
be the subgroup of elements
![]() ${}^{w}(u^{1,4})$
; this is the subgroup
${}^{w}(u^{1,4})$
; this is the subgroup
![]() $U_0$
of the
$U_0$
of the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral when we identify
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral when we identify
![]() $\operatorname {\mathrm {GL}}_{2rkn}$
with
$\operatorname {\mathrm {GL}}_{2rkn}$
with
![]() $M_P$
by
$M_P$
by
![]() $b\mapsto \operatorname {\mathrm {diag}}(b,b^{*})$
. Additionally, denote the subgroup of elements
$b\mapsto \operatorname {\mathrm {diag}}(b,b^{*})$
. Additionally, denote the subgroup of elements
![]() $u^3$
by
$u^3$
by
![]() $U^3$
.
$U^3$
.
Denote the
![]() $(rk,c)$
model of
$(rk,c)$
model of
![]() $\rho _n(\tau ^{*})$
defined with respect to
$\rho _n(\tau ^{*})$
defined with respect to
![]() $\psi ^{-1}$
by
$\psi ^{-1}$
by
![]() $\mathcal {W}'(\rho _n(\tau ^{*}))$
(i.e., the character Equation (3.1) is defined using
$\mathcal {W}'(\rho _n(\tau ^{*}))$
(i.e., the character Equation (3.1) is defined using
![]() $\psi ^{-1}$
). Let
$\psi ^{-1}$
). Let
![]() $M(s)$
be the standard intertwining operator from the representation (5.8) to the representationFootnote
1
$M(s)$
be the standard intertwining operator from the representation (5.8) to the representationFootnote
1
defined by
 $$ \begin{align*} M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(h,s)= \int\limits_{U^2}{f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle w,1\rangle\langle u^2,1\rangle h,s)\,du^2. \end{align*} $$
$$ \begin{align*} M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(h,s)= \int\limits_{U^2}{f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}(\langle w,1\rangle\langle u^2,1\rangle h,s)\,du^2. \end{align*} $$
Note that the image of
![]() $M(s)$
is indeed in the space of (5.16), where
$M(s)$
is indeed in the space of (5.16), where
![]() ${}^{*}$
is defined by Equation (2.54). This is because
${}^{*}$
is defined by Equation (2.54). This is because
![]() $\mathcal {W}(\rho _n(\tau ))^{*}=\mathcal {W}'(\rho _n(\tau )^{*})=\mathcal {W}'(\rho _n(\tau ^{*}))$
, which is true for any extension of
$\mathcal {W}(\rho _n(\tau ))^{*}=\mathcal {W}'(\rho _n(\tau )^{*})=\mathcal {W}'(\rho _n(\tau ^{*}))$
, which is true for any extension of
![]() ${}^{*}$
to
${}^{*}$
to
![]() $\operatorname {\mathrm {GL}}_{rkn}^{(m,r)}$
(see § 5.1); for
$\operatorname {\mathrm {GL}}_{rkn}^{(m,r)}$
(see § 5.1); for
![]() $a\in \operatorname {\mathrm {GL}}_{rkn}$
,
$a\in \operatorname {\mathrm {GL}}_{rkn}$
,
![]() ${}^{w}\operatorname {\mathrm {diag}}(I_{rkn},a,a^{*},I_{rkn})=\operatorname {\mathrm {diag}}(I_{rkn},a^{*},a,I_{rkn})$
, hence
${}^{w}\operatorname {\mathrm {diag}}(I_{rkn},a,a^{*},I_{rkn})=\operatorname {\mathrm {diag}}(I_{rkn},a^{*},a,I_{rkn})$
, hence
![]() $\langle a,\epsilon \rangle \mapsto {}^w\langle a,\epsilon \rangle $
is a lift of
$\langle a,\epsilon \rangle \mapsto {}^w\langle a,\epsilon \rangle $
is a lift of
![]() ${}^{*}$
; to check which one, consider
${}^{*}$
; to check which one, consider
![]() $a=\operatorname {\mathrm {diag}}(a_1,I_{rkn-1})$
and now
$a=\operatorname {\mathrm {diag}}(a_1,I_{rkn-1})$
and now
by Proposition 2. The image of
![]() $M(s){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is an unramified vector in the space of (5.16), and we denote
$M(s){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is an unramified vector in the space of (5.16), and we denote
![]() $d_{\tau ,\vartheta }(s)=M(s){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}(\langle I_{2rkc},1\rangle )$
. We will prove below that
$d_{\tau ,\vartheta }(s)=M(s){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}(\langle I_{2rkc},1\rangle )$
. We will prove below that
![]() $d_{\tau ,\vartheta }(s)$
is equal to the product (5.1).
$d_{\tau ,\vartheta }(s)$
is equal to the product (5.1).
When we substitute Equation (5.15) into Integral (5.13), it becomes
 $$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U^3} \int\limits_{U^{1,4}} \int\limits_V M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,dv\,du'\,du^3\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U^3} \int\limits_{U^{1,4}} \int\limits_V M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,dv\,du'\,du^3\,dg. \end{align} $$
Here,
![]() $\psi _U$
is the restriction of the character (4.30) to
$\psi _U$
is the restriction of the character (4.30) to
![]() $U^{1,4}$
.
$U^{1,4}$
.
We proceed using the Iwasawa decomposition
![]() $G=RK_G$
. Since
$G=RK_G$
. Since
![]() $\sigma _{c}(y,y')=\sigma _{2rkc}(\mathfrak {e}_2(y),\mathfrak {e}_2(y'))$
for any
$\sigma _{c}(y,y')=\sigma _{2rkc}(\mathfrak {e}_2(y),\mathfrak {e}_2(y'))$
for any
![]() $y,y'\in K_G$
and
$y,y'\in K_G$
and
![]() $K_G$
is perfect,
$K_G$
is perfect,
![]() $\eta _{c}(y)=\eta _{2rkc}(\mathfrak {e}_2(y))$
. Then by Equation (2.44),
$\eta _{c}(y)=\eta _{2rkc}(\mathfrak {e}_2(y))$
. Then by Equation (2.44),
As explained above (Equations (4) and (7)),
![]() $\mathfrak {e}_2(G)$
commutes with
$\mathfrak {e}_2(G)$
commutes with
![]() $\kappa $
and v in
$\kappa $
and v in
![]() $H^{(m)}$
. Hence,
$H^{(m)}$
. Hence,
 $$ \begin{align*} &M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \,{}^{\iota}\langle\mathfrak{e}_2(y),\eta_{c}(y)\rangle \langle \kappa v,1\rangle ,s) \\&=M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \langle \kappa v,1\rangle\langle\mathfrak{e}_2({}^{\iota}y),\eta_{2rkc}(\mathfrak{e}_2({}^{\iota}y))\rangle,s) \\&=M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \langle \kappa v,1\rangle,s). \end{align*} $$
$$ \begin{align*} &M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \,{}^{\iota}\langle\mathfrak{e}_2(y),\eta_{c}(y)\rangle \langle \kappa v,1\rangle ,s) \\&=M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \langle \kappa v,1\rangle\langle\mathfrak{e}_2({}^{\iota}y),\eta_{2rkc}(\mathfrak{e}_2({}^{\iota}y))\rangle,s) \\&=M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(g),1 \rangle \langle \kappa v,1\rangle,s). \end{align*} $$
In addition, the vector
![]() $\varphi ^{\vee }$
is right-invariant under
$\varphi ^{\vee }$
is right-invariant under
![]() $\langle y,\eta _c(y)\rangle $
. It follows that when we write a representative g in the form
$\langle y,\eta _c(y)\rangle $
. It follows that when we write a representative g in the form
![]() $\operatorname {\mathrm {diag}}(g',{g'}^{*})y$
with
$\operatorname {\mathrm {diag}}(g',{g'}^{*})y$
with
![]() $g'\in \operatorname {\mathrm {GL}}_n$
and
$g'\in \operatorname {\mathrm {GL}}_n$
and
![]() $y\in K_G$
, the integrand is right-invariant with respect to y. Since the measure of
$y\in K_G$
, the integrand is right-invariant with respect to y. Since the measure of
![]() $K_G$
is
$K_G$
is
![]() $1$
, Integral (5.17) equals
$1$
, Integral (5.17) equals
 $$ \begin{align} &\int\limits_{\operatorname{\mathrm{GL}}_n} \{\varphi(e),\varphi^{\vee}(\langle \operatorname{\mathrm{diag}}(g',{g'}^{*}),1\rangle)\}_{M_R} \int\limits_{U^3} \int\limits_{U^{1,4}} \int\limits_V M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\delta_R^{-1}(\operatorname{\mathrm{diag}}(g',{g'}^{*}))\,dv\,du'\,du^3\,dg'. \end{align} $$
$$ \begin{align} &\int\limits_{\operatorname{\mathrm{GL}}_n} \{\varphi(e),\varphi^{\vee}(\langle \operatorname{\mathrm{diag}}(g',{g'}^{*}),1\rangle)\}_{M_R} \int\limits_{U^3} \int\limits_{U^{1,4}} \int\limits_V M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle wu^3,1\rangle \,{}^{\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1 \rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\delta_R^{-1}(\operatorname{\mathrm{diag}}(g',{g'}^{*}))\,dv\,du'\,du^3\,dg'. \end{align} $$
The function
is the normalized unramified matrix coefficient of
![]() $\pi _n^{\vee }$
, which we denoted
$\pi _n^{\vee }$
, which we denoted
![]() $\omega _n$
. When we conjugate
$\omega _n$
. When we conjugate
![]() $u^3$
by
$u^3$
by
![]() ${}^{\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(g',{g'}^{*}))$
, the measure is multiplied by
${}^{\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(g',{g'}^{*}))$
, the measure is multiplied by
![]() $|\det g'|^{(-rk+1)n}$
. Using Equations (2.8) and (2.10), we have
$|\det g'|^{(-rk+1)n}$
. Using Equations (2.8) and (2.10), we have
 $$ \begin{align} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv. \end{align} $$
$$ \begin{align} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv. \end{align} $$
Here, we also changed the integration order, which is allowed in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, and for any
$\operatorname {\mathrm {Re}}(s)\gg 0$
, and for any
![]() $g\in G$
, the notation
$g\in G$
, the notation
![]() ${}^{w\iota }\langle \mathfrak {e}_2(g),1\rangle $
stands for
${}^{w\iota }\langle \mathfrak {e}_2(g),1\rangle $
stands for
![]() ${}^{w}({}^{\iota }\langle \mathfrak {e}_2(g),1\rangle )$
.
${}^{w}({}^{\iota }\langle \mathfrak {e}_2(g),1\rangle )$
.
Let
![]() $(,)':\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n\hookrightarrow \operatorname {\mathrm {GL}}_{2rkn}$
denote the embedding in the construction of the
$(,)':\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n\hookrightarrow \operatorname {\mathrm {GL}}_{2rkn}$
denote the embedding in the construction of the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral, when
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral, when
![]() $\operatorname {\mathrm {GL}}_{2rkn}$
is identified with
$\operatorname {\mathrm {GL}}_{2rkn}$
is identified with
![]() $M_P$
as above. Now, we see that
$M_P$
as above. Now, we see that
We claim that this conjugation extends to the covering, namely
In fact, since we only need to apply this identity to the integral (5.19), it is sufficient to establish Equation (5.20) on a dense subset of
![]() $\operatorname {\mathrm {GL}}_n$
. We provide two proofs for this, both valid also when F is not unramified. The first argument shows the identity (5.20) on a dense subset without using
$\operatorname {\mathrm {GL}}_n$
. We provide two proofs for this, both valid also when F is not unramified. The first argument shows the identity (5.20) on a dense subset without using
![]() $\mu _{2m}\subset F^{*}$
. The second proves Equation (5.20) for any
$\mu _{2m}\subset F^{*}$
. The second proves Equation (5.20) for any
![]() $g'\in \operatorname {\mathrm {GL}}_n$
, under the assumption
$g'\in \operatorname {\mathrm {GL}}_n$
, under the assumption
![]() $\mu _{2m}\subset F^{*}$
(which we have throughout § 5), in which case
$\mu _{2m}\subset F^{*}$
(which we have throughout § 5), in which case
![]() $(\det g',\det g')_m=1$
.
$(\det g',\det g')_m=1$
.
The first proof: We prove Equation (5.20) on the subset
![]() $B_{\operatorname {\mathrm {GL}}_n}N_{\operatorname {\mathrm {GL}}_n}^-$
, which is dense in
$B_{\operatorname {\mathrm {GL}}_n}N_{\operatorname {\mathrm {GL}}_n}^-$
, which is dense in
![]() $\operatorname {\mathrm {GL}}_n$
. Thus,
$\operatorname {\mathrm {GL}}_n$
. Thus,
![]() $g'=v_gt_gu_g^-$
where
$g'=v_gt_gu_g^-$
where
![]() $v_g\in N_{\operatorname {\mathrm {GL}}_n}$
,
$v_g\in N_{\operatorname {\mathrm {GL}}_n}$
,
![]() $t_g\in T_{\operatorname {\mathrm {GL}}_n}$
and
$t_g\in T_{\operatorname {\mathrm {GL}}_n}$
and
![]() $u_g^-\in N_{\operatorname {\mathrm {GL}}_n}^-$
. Fix the splitting
$u_g^-\in N_{\operatorname {\mathrm {GL}}_n}^-$
. Fix the splitting
![]() $u^-\mapsto \langle u^-,\varsigma _n(u^-)\rangle $
of
$u^-\mapsto \langle u^-,\varsigma _n(u^-)\rangle $
of
![]() $N_{n}^-$
in
$N_{n}^-$
in
![]() $G^{(m)}$
and similarly fix
$G^{(m)}$
and similarly fix
![]() $\varsigma _{rkc}$
for
$\varsigma _{rkc}$
for
![]() $N_{rkc}^-$
in
$N_{rkc}^-$
in
![]() $H^{(m)}$
. As explained in § 2.6, we can compute
$H^{(m)}$
. As explained in § 2.6, we can compute
![]() $\varsigma _{\iota ,c}$
by regarding
$\varsigma _{\iota ,c}$
by regarding
![]() $\iota $
as an element of
$\iota $
as an element of
![]() $\operatorname {\mathrm {GL}}_c$
, then
$\operatorname {\mathrm {GL}}_c$
, then
![]() $w\iota $
is the element in
$w\iota $
is the element in
![]() $\operatorname {\mathrm {GL}}_{2rkc}$
given by
$\operatorname {\mathrm {GL}}_{2rkc}$
given by
![]() $w\operatorname {\mathrm {diag}}(I_{2rkc-n},\iota ,I_{2rkc-n})$
. By the analog of Equation (2.10) for
$w\operatorname {\mathrm {diag}}(I_{2rkc-n},\iota ,I_{2rkc-n})$
. By the analog of Equation (2.10) for
![]() $N_{rkc}^-$
and
$N_{rkc}^-$
and
![]() $\varsigma _{rkc}$
(use Equation (2.4)),
$\varsigma _{rkc}$
(use Equation (2.4)),
By Equations (2.23) and (2.12), for any
![]() $z_1,z_2\in N_{\operatorname {\mathrm {GL}}_n}^-$
,
$z_1,z_2\in N_{\operatorname {\mathrm {GL}}_n}^-$
,
so that because
![]() $\varsigma _n$
is canonical,
$\varsigma _n$
is canonical,
Hence, Equation (5.20) holds for
![]() $u_g^-$
.
$u_g^-$
.
Consider
![]() $t_g$
and set
$t_g$
and set
![]() $d_g=\operatorname {\mathrm {diag}}(t_g,t_g^{*})\in G$
. Write
$d_g=\operatorname {\mathrm {diag}}(t_g,t_g^{*})\in G$
. Write
![]() $\iota =\iota 't_0$
, where
$\iota =\iota 't_0$
, where
![]() $t_0=\operatorname {\mathrm {diag}}(-I_n,I_n)\in T_{\operatorname {\mathrm {GL}}_{c}}$
. Then
$t_0=\operatorname {\mathrm {diag}}(-I_n,I_n)\in T_{\operatorname {\mathrm {GL}}_{c}}$
. Then
![]() $\iota '\in \operatorname {\mathrm {Sp}}_{c}$
. First, we see that by Equation (2.7),
$\iota '\in \operatorname {\mathrm {Sp}}_{c}$
. First, we see that by Equation (2.7),
Now, since
![]() $w\iota '\in H$
and
$w\iota '\in H$
and
![]() ${}^{t_0}d_g=d_g$
, by Proposition 2 we obtain
${}^{t_0}d_g=d_g$
, by Proposition 2 we obtain
Thus, Equation (5.20) holds for
![]() $t_g$
.
$t_g$
.
Identity (5.20) also holds for
![]() $v_g$
by Equation (2.10) because
$v_g$
by Equation (2.10) because
![]() ${}^{w\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(v_g,v_g^{*}))\in N_{rkc}$
.
${}^{w\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(v_g,v_g^{*}))\in N_{rkc}$
.
Since
![]() $\sigma _c(v_g,t_gu_g^-)=1$
(by Equation (2.8)), we have shown that for
$\sigma _c(v_g,t_gu_g^-)=1$
(by Equation (2.8)), we have shown that for
![]() $g'=v_gt_gu_g^-$
,
$g'=v_gt_gu_g^-$
,
 $$ \begin{align*} &{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle\\&= \sigma_{2rkc}(\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*})))^{-1} \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(v_g,v_g^{*})),1\rangle\,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),1\rangle\\& \quad\,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*})),1\rangle\\&= \sigma_{c}(\operatorname{\mathrm{diag}}(t_g,t_g^{*}),\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*}))^{-1} \langle(I_n,v_g)',1\rangle \langle(I_n,t_g)',(\det t_g,\det t_g)_m\rangle \langle(I_n,u_g^-)',1\rangle \\&=\langle(I_n,g')',(\det g',\det g')_m\rangle. \end{align*} $$
$$ \begin{align*} &{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle\\&= \sigma_{2rkc}(\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*})))^{-1} \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(v_g,v_g^{*})),1\rangle\,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),1\rangle\\& \quad\,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*})),1\rangle\\&= \sigma_{c}(\operatorname{\mathrm{diag}}(t_g,t_g^{*}),\operatorname{\mathrm{diag}}(u_g^-,{u_g^-}^{*}))^{-1} \langle(I_n,v_g)',1\rangle \langle(I_n,t_g)',(\det t_g,\det t_g)_m\rangle \langle(I_n,u_g^-)',1\rangle \\&=\langle(I_n,g')',(\det g',\det g')_m\rangle. \end{align*} $$
Here, for the last equality we used Equation (2.12). This completes the proof of Equation (5.20) for
![]() $g'\in B_{\operatorname {\mathrm {GL}}_n}N_{\operatorname {\mathrm {GL}}_n}^-$
.
$g'\in B_{\operatorname {\mathrm {GL}}_n}N_{\operatorname {\mathrm {GL}}_n}^-$
.
The second proof: Consider any
![]() $g'\in \operatorname {\mathrm {GL}}_n$
. According to the Bruhat decomposition in
$g'\in \operatorname {\mathrm {GL}}_n$
. According to the Bruhat decomposition in
![]() $\operatorname {\mathrm {GL}}_n$
, we can write
$\operatorname {\mathrm {GL}}_n$
, we can write
![]() $g'=u_gt_gw_gv_g$
with
$g'=u_gt_gw_gv_g$
with
![]() $u_g,v_g\in N_{\operatorname {\mathrm {GL}}_n}$
,
$u_g,v_g\in N_{\operatorname {\mathrm {GL}}_n}$
,
![]() $t_g\in T_{\operatorname {\mathrm {GL}}_n}$
and
$t_g\in T_{\operatorname {\mathrm {GL}}_n}$
and
![]() $w_g$
is a permutation matrix. If
$w_g$
is a permutation matrix. If
![]() $\operatorname {\mathrm {diag}}(w_g,w_g^{*})=t_0w'$
where
$\operatorname {\mathrm {diag}}(w_g,w_g^{*})=t_0w'$
where
![]() $t_0\in T_{\operatorname {\mathrm {GL}}_c}$
and
$t_0\in T_{\operatorname {\mathrm {GL}}_c}$
and
![]() $w'\in \mathfrak {W}_c$
, then by Equations (2.1) (with
$w'\in \mathfrak {W}_c$
, then by Equations (2.1) (with
![]() $g=\operatorname {\mathrm {diag}}(t_g,t_g^{*})$
,
$g=\operatorname {\mathrm {diag}}(t_g,t_g^{*})$
,
![]() $g'=t_0$
and
$g'=t_0$
and
![]() $g"=w'$
) and (2.14),
$g"=w'$
) and (2.14),
(
![]() $\mu _{2m}\subset F^{*}$
). Hence, by Equation (2.8),
$\mu _{2m}\subset F^{*}$
). Hence, by Equation (2.8),
 $$ \begin{align} &{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle \\&=\nonumber {}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g,u_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(w_g,w_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(v_g,{v_g}^{*})),1\rangle. \end{align} $$
$$ \begin{align} &{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(g',{g'}^{*})),1\rangle \\&=\nonumber {}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(u_g,u_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(t_g,t_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(w_g,w_g^{*})),1\rangle \,{}^{w\iota}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(v_g,{v_g}^{*})),1\rangle. \end{align} $$
As above, Equation (5.20) holds for
![]() $u_g$
and
$u_g$
and
![]() $v_g$
by Equation (2.10) (
$v_g$
by Equation (2.10) (
![]() ${}^{w\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(u_g,u_g^{*}))\in N_{rkc}$
and similarly for
${}^{w\iota }\mathfrak {e}_2(\operatorname {\mathrm {diag}}(u_g,u_g^{*}))\in N_{rkc}$
and similarly for
![]() $v_g$
), and for
$v_g$
), and for
![]() $w_g$
because
$w_g$
because
![]() $\sigma _{2rkc}$
is trivial on
$\sigma _{2rkc}$
is trivial on
![]() $\mathfrak {W}^+_{2rkc}$
. Regarding
$\mathfrak {W}^+_{2rkc}$
. Regarding
![]() $t_g$
, we argue as above using Proposition 2. Therefore, Equation (5.22) becomes
$t_g$
, we argue as above using Proposition 2. Therefore, Equation (5.22) becomes
Here, for the second equality note that
![]() $\sigma _{2rkc}((I_n,t_g)',(I_n,w_g)')=1$
which follows, for example, from Equations (5.21) and (2.12), or simply by applying the arguments used for the proof of Equation (5.21) to
$\sigma _{2rkc}((I_n,t_g)',(I_n,w_g)')=1$
which follows, for example, from Equations (5.21) and (2.12), or simply by applying the arguments used for the proof of Equation (5.21) to
![]() $\sigma _{2rkc}$
. Again, we conclude Equation (5.20).
$\sigma _{2rkc}$
. Again, we conclude Equation (5.20).
Now, we substitute Equation (5.20) into Integral (5.19) and obtain
 $$ \begin{align} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle (I_n,g')',1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv. \end{align} $$
$$ \begin{align} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle (I_n,g')',1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv. \end{align} $$
Let
![]() $t=\operatorname {\mathrm {diag}}((-1)^{rk-1}I_n,\ldots ,-I_n,I_n)\in T_{\operatorname {\mathrm {GL}}_{rkn}}$
,
$t=\operatorname {\mathrm {diag}}((-1)^{rk-1}I_n,\ldots ,-I_n,I_n)\in T_{\operatorname {\mathrm {GL}}_{rkn}}$
,
![]() $t'=\operatorname {\mathrm {diag}}(t,I_{2rkn},t^{*})\in T_H$
and
$t'=\operatorname {\mathrm {diag}}(t,I_{2rkn},t^{*})\in T_H$
and
![]() $h'=\langle t',1\rangle $
. By Equation (2.52),
$h'=\langle t',1\rangle $
. By Equation (2.52),
![]() $h'$
commutes with
$h'$
commutes with
![]() $\langle (I_n,g')',1\rangle $
and
$\langle (I_n,g')',1\rangle $
and
![]() $\langle \delta _1',1\rangle $
, and
$\langle \delta _1',1\rangle $
, and
![]() $h'$
also normalizes
$h'$
also normalizes
![]() $U^{1,4}$
and stabilizes
$U^{1,4}$
and stabilizes
![]() $\psi _U(u')$
. Since
$\psi _U(u')$
. Since
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified, it is right-invariant under
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified, it is right-invariant under
![]() $h'$
(
$h'$
(
![]() $\eta _{2rkc}(t')=1$
) and also under
$\eta _{2rkc}(t')=1$
) and also under
![]() ${}^{(w\kappa )^{-1}}h'$
(since
${}^{(w\kappa )^{-1}}h'$
(since
![]() $(\mathcal {O}^{*},\mathcal {O}^{*})_m=1$
). Hence, we can replace the section in Integral (5.23) with its right-translation by
$(\mathcal {O}^{*},\mathcal {O}^{*})_m=1$
). Hence, we can replace the section in Integral (5.23) with its right-translation by
![]() ${}^{(w\kappa )^{-1}}h'$
. In addition,
${}^{(w\kappa )^{-1}}h'$
. In addition,
![]() ${}^{(w\kappa )^{-1}}h'$
normalizes V and
${}^{(w\kappa )^{-1}}h'$
normalizes V and
![]() ${}^{w^{-1}}h'$
normalizes
${}^{w^{-1}}h'$
normalizes
![]() $U^3$
(because
$U^3$
(because
![]() ${}^{(w\kappa )^{-1}}h',{}^{w^{-1}}h'\in \widetilde {T}_H$
). Put
${}^{(w\kappa )^{-1}}h',{}^{w^{-1}}h'\in \widetilde {T}_H$
). Put
![]() $h={}^{\delta _0'}h'=\langle \operatorname {\mathrm {diag}}(I_{rkn},t,t^{*},I_{rkn}),1\rangle $
. Then by Equation (2.10), the integral (5.23) equals
$h={}^{\delta _0'}h'=\langle \operatorname {\mathrm {diag}}(I_{rkn},t,t^{*},I_{rkn}),1\rangle $
. Then by Equation (2.10), the integral (5.23) equals
 $$ \begin{align*} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes\mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle (I_n,g')',1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv, \end{align*} $$
$$ \begin{align*} &\int\limits_{U^3} \int\limits_V \int\limits_{\operatorname{\mathrm{GL}}_n} \omega_n(\langle g',1\rangle) \int\limits_{U^{1,4}} |\det g'|^{(n-\alpha)/2}M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes\mathcal{W}(\rho_n(\tau))}\\&\nonumber( \langle \delta'u',1\rangle\langle (I_n,g')',1\rangle \langle wu^3,1\rangle\langle \kappa v,1\rangle ,s)\,\psi_U(u')\,du'\,dg'\,du^3\,dv, \end{align*} $$
where
![]() $\lambda (h)$
denotes left-translation by h. Note that if
$\lambda (h)$
denotes left-translation by h. Note that if
![]() $\Lambda \in \mathcal {O}(\mathcal {E},((rk)^n),\psi ^{-1})$
for an
$\Lambda \in \mathcal {O}(\mathcal {E},((rk)^n),\psi ^{-1})$
for an
![]() $(rk,n)$
representation
$(rk,n)$
representation
![]() $\mathcal {E}$
, then the functional
$\mathcal {E}$
, then the functional
![]() $\xi \mapsto \Lambda (\mathcal {E}(\langle t,1\rangle )\xi )$
belongs to
$\xi \mapsto \Lambda (\mathcal {E}(\langle t,1\rangle )\xi )$
belongs to
![]() $\mathcal {O}(\mathcal {E},((rk)^n),\psi )$
. Looking at the representation (5.16), we see that when we restrict
$\mathcal {O}(\mathcal {E},((rk)^n),\psi )$
. Looking at the representation (5.16), we see that when we restrict
![]() $M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
to
$M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
to
![]() $\widetilde {M}_P=\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
, we obtain a rational section of
$\widetilde {M}_P=\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
, we obtain a rational section of
Therefore, the inner
![]() $du'dg'$
-integral of (5.23) is the
$du'dg'$
-integral of (5.23) is the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and we can rewrite Integral (5.23) in the form
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and we can rewrite Integral (5.23) in the form
 $$ \begin{align} \int\limits_{U^3} \int\limits_V Z(\alpha s/rkn,\omega_n,(\langle wu^3,1\rangle\langle \kappa v,1\rangle)\cdot M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))})\,du^3\,dv. \end{align} $$
$$ \begin{align} \int\limits_{U^3} \int\limits_V Z(\alpha s/rkn,\omega_n,(\langle wu^3,1\rangle\langle \kappa v,1\rangle)\cdot M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))})\,du^3\,dv. \end{align} $$
As in the linear case, the next step is to show that the integral over
![]() $U^3$
vanishes unless
$U^3$
vanishes unless
![]() $v,u^3\in K_H$
. Fix the splitting
$v,u^3\in K_H$
. Fix the splitting
![]() $v^-\mapsto \langle v^-,\varsigma _{rkc}(v^-)\rangle $
for
$v^-\mapsto \langle v^-,\varsigma _{rkc}(v^-)\rangle $
for
![]() $N_{rkc}^-$
in
$N_{rkc}^-$
in
![]() $H^{(m)}$
(see above). We can write
$H^{(m)}$
(see above). We can write
 $$ \begin{align*} \langle wu^3,1\rangle\langle \kappa v,1\rangle&= {}^{w}(\langle u^3,1\rangle{}^{\kappa}\langle v,1\rangle)\langle w\kappa,1\rangle= {}^{w}(\langle u^3,1\rangle\langle {}^{\kappa}v,\varsigma_{rkc}({}^{\kappa}v)\rangle)\langle w\kappa,1\rangle \\&=\langle {}^{w}u^3,\varsigma_{rkc}({}^{w}u^3)\rangle\langle {}^{w\kappa}v,\varsigma_{rkc}({}^{w\kappa}v)\rangle)\langle w\kappa,1\rangle= \langle {}^{w}(u^3({}^{\kappa}v)),\varsigma_{rkc}({}^{w}(u^3({}^{\kappa}v)))\rangle\langle w\kappa,1\rangle. \end{align*} $$
$$ \begin{align*} \langle wu^3,1\rangle\langle \kappa v,1\rangle&= {}^{w}(\langle u^3,1\rangle{}^{\kappa}\langle v,1\rangle)\langle w\kappa,1\rangle= {}^{w}(\langle u^3,1\rangle\langle {}^{\kappa}v,\varsigma_{rkc}({}^{\kappa}v)\rangle)\langle w\kappa,1\rangle \\&=\langle {}^{w}u^3,\varsigma_{rkc}({}^{w}u^3)\rangle\langle {}^{w\kappa}v,\varsigma_{rkc}({}^{w\kappa}v)\rangle)\langle w\kappa,1\rangle= \langle {}^{w}(u^3({}^{\kappa}v)),\varsigma_{rkc}({}^{w}(u^3({}^{\kappa}v)))\rangle\langle w\kappa,1\rangle. \end{align*} $$
Here, we used the fact that
![]() ${}^{\kappa }V,{}^{w}U^3,{}^{w\kappa }V<N_{rkc}^-$
together with Equation (2.4). Since
${}^{\kappa }V,{}^{w}U^3,{}^{w\kappa }V<N_{rkc}^-$
together with Equation (2.4). Since
![]() ${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified, Integral (5.25) becomes
${f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is unramified, Integral (5.25) becomes
 $$ \begin{align*} \int\limits_{U^3} \int\limits_V Z(\alpha s/rkn,\omega_n,\langle {}^{w}(u^3({}^{\kappa}v)),\varsigma_{rkc}({}^{w}(u^3({}^{\kappa}v)))\rangle\cdot M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))})\,du^3\,dv. \end{align*} $$
$$ \begin{align*} \int\limits_{U^3} \int\limits_V Z(\alpha s/rkn,\omega_n,\langle {}^{w}(u^3({}^{\kappa}v)),\varsigma_{rkc}({}^{w}(u^3({}^{\kappa}v)))\rangle\cdot M(s)\lambda(h){f}^{\downarrow}_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau))})\,du^3\,dv. \end{align*} $$
Now, we use conjugations by elements of
![]() $N_{rkc}(\mathcal {O})$
. We briefly explain how to extend the argument from the linear setting; see the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Lemma 27] for more details, and note that all occurrences of k in the argument from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, pp. 1037–1040] should be replaced here with
$N_{rkc}(\mathcal {O})$
. We briefly explain how to extend the argument from the linear setting; see the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Lemma 27] for more details, and note that all occurrences of k in the argument from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, pp. 1037–1040] should be replaced here with
![]() $rk$
. If
$rk$
. If
![]() $x\in N_{rkc}(\mathcal {O})$
, then
$x\in N_{rkc}(\mathcal {O})$
, then
![]() $M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is right-invariant under
$M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
is right-invariant under
![]() $\langle x,1\rangle $
. Assume that
$\langle x,1\rangle $
. Assume that
![]() $z\in {}^{w}(U^3({}^{\kappa }V))$
is such that
$z\in {}^{w}(U^3({}^{\kappa }V))$
is such that
![]() ${}^{x^{-1}}z=u_xz_x$
where
${}^{x^{-1}}z=u_xz_x$
where
![]() $u_x\in P\cap N_{rkc}$
. Also assume that the projection of
$u_x\in P\cap N_{rkc}$
. Also assume that the projection of
![]() $u_x$
into
$u_x$
into
![]() $M_P$
belongs to the subgroup U appearing in the
$M_P$
belongs to the subgroup U appearing in the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and
![]() $z_x\in {}^{w}(U^3({}^{\kappa }V))$
. Then by Equation (2.8),
$z_x\in {}^{w}(U^3({}^{\kappa }V))$
. Then by Equation (2.8),
 $$ \begin{align*} {}^{x^{-1}}\langle z,\varsigma_{rkc}(z)\rangle&= \langle {}^{x^{-1}}z,\sigma_{2rkc}(x^{-1},z)\sigma_{2rkc}(x^{-1}z,x)\sigma_{2rkc}(x^{-1},x)^{-1}\varsigma_{rkc}(z)\rangle= \langle u_xz_x,\varsigma_{rkc}(z)\rangle\\&=\langle u_x,1\rangle\langle z_x,\varsigma_{rkc}(z_x)\rangle. \end{align*} $$
$$ \begin{align*} {}^{x^{-1}}\langle z,\varsigma_{rkc}(z)\rangle&= \langle {}^{x^{-1}}z,\sigma_{2rkc}(x^{-1},z)\sigma_{2rkc}(x^{-1}z,x)\sigma_{2rkc}(x^{-1},x)^{-1}\varsigma_{rkc}(z)\rangle= \langle u_xz_x,\varsigma_{rkc}(z)\rangle\\&=\langle u_x,1\rangle\langle z_x,\varsigma_{rkc}(z_x)\rangle. \end{align*} $$
Now, we can change variables
![]() $z_x\mapsto z$
, this change only involves
$z_x\mapsto z$
, this change only involves
![]() $U^3$
, and use the equivariance property of the inner integral
$U^3$
, and use the equivariance property of the inner integral
![]() $Z(\cdots )$
with respect to the subgroup U of that integral. It then follows that when we select the elements x in the correct order, the
$Z(\cdots )$
with respect to the subgroup U of that integral. It then follows that when we select the elements x in the correct order, the
![]() $du^3$
integral vanishes unless
$du^3$
integral vanishes unless
![]() $v\in K_H$
. The coordinates of
$v\in K_H$
. The coordinates of
![]() $U^3$
are also handled by choosing
$U^3$
are also handled by choosing
![]() $x\in N_{rkc}(\mathcal {O})$
in a certain order such that
$x\in N_{rkc}(\mathcal {O})$
in a certain order such that
![]() ${}^{x^{-1}}z=u_xz_x$
where
${}^{x^{-1}}z=u_xz_x$
where
![]() $u_x$
and
$u_x$
and
![]() $z_x$
are as above. The change of variables involves blocks of
$z_x$
are as above. The change of variables involves blocks of
![]() $U^3$
which have not been handled, and the vanishing follows by producing an inner integral
$U^3$
which have not been handled, and the vanishing follows by producing an inner integral
![]() $\int _{\mathcal {X}}\psi (\mathrm {tr}(xu))dx$
, where
$\int _{\mathcal {X}}\psi (\mathrm {tr}(xu))dx$
, where
![]() $\mathcal {X}<\text {Mat}_{n}(\mathcal {O})$
and u is a certain block of
$\mathcal {X}<\text {Mat}_{n}(\mathcal {O})$
and u is a certain block of
![]() $U^3$
. This integral vanishes unless
$U^3$
. This integral vanishes unless
![]() $u\in \text {Mat}_{n}(\mathcal {O})$
.
$u\in \text {Mat}_{n}(\mathcal {O})$
.
Turning back to Integral (5.25), since the measures of
![]() $U^3\cap K_H$
and
$U^3\cap K_H$
and
![]() $V\cap K_H$
are
$V\cap K_H$
are
![]() $1$
, we obtain
$1$
, we obtain
The section
![]() $M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
restricted to
$M(s)\lambda (h){f}^{\downarrow }_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ))}$
restricted to
![]() $\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
is equal to
$\operatorname {\mathrm {GL}}_{2rkn}^{(m,r)}$
is equal to
![]() $d_{\tau ,\vartheta }(s)f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))}$
(by the definition of the latter section), hence we proved that (in
$d_{\tau ,\vartheta }(s)f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau ^{*}))}$
(by the definition of the latter section), hence we proved that (in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
)
$\operatorname {\mathrm {Re}}(s)\gg 0$
)
To complete the proof of the lemma, it remains to show that
![]() $d_{\tau ,\vartheta }(s)$
is equal to the product (5.1).
$d_{\tau ,\vartheta }(s)$
is equal to the product (5.1).
Recall that
![]() $\tau \subset I_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. Identify
$\tau \subset I_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
. Identify
![]() $\operatorname {\mathrm {Sp}}_{2rkn}$
with its image in the standard Levi subgroup of H isomorphic to
$\operatorname {\mathrm {Sp}}_{2rkn}$
with its image in the standard Levi subgroup of H isomorphic to
![]() $\operatorname {\mathrm {GL}}_{rkn}\times \operatorname {\mathrm {Sp}}_{2rkn}$
. By Equation (2.12) and the definition of
$\operatorname {\mathrm {GL}}_{rkn}\times \operatorname {\mathrm {Sp}}_{2rkn}$
. By Equation (2.12) and the definition of
![]() $\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
(using restriction, see § 2.4),
$\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
(using restriction, see § 2.4),
![]() $\widetilde {\operatorname {\mathrm {Sp}}}_{2rkn}=\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
(alternatively use [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7]). Looking at the representation (5.8), we see that the restriction of
$\widetilde {\operatorname {\mathrm {Sp}}}_{2rkn}=\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
(alternatively use [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7]). Looking at the representation (5.8), we see that the restriction of
![]() $f_{\mathcal {W}(\rho _c(\tau ))}$
to
$f_{\mathcal {W}(\rho _c(\tau ))}$
to
![]() $\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
is the normalized unramified element in the space of
$\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}$
is the normalized unramified element in the space of
To compute
![]() $d_{\tau ,\vartheta }(s)$
, we deploy the Gindikin–Karpelevich formula [Reference GaoGao18b, Theorem 7.10], which includes the interpretation of the proportionality factor in terms of local Langlands–Shahidi L-factors (for unramified data), that is, using a decomposition of the adjoint action.
$d_{\tau ,\vartheta }(s)$
, we deploy the Gindikin–Karpelevich formula [Reference GaoGao18b, Theorem 7.10], which includes the interpretation of the proportionality factor in terms of local Langlands–Shahidi L-factors (for unramified data), that is, using a decomposition of the adjoint action.
The adjoint action of
![]() $\operatorname {\mathrm {GL}}_{rkn}(\mathbb {C})$
on the Lie algebra of the L-group of
$\operatorname {\mathrm {GL}}_{rkn}(\mathbb {C})$
on the Lie algebra of the L-group of
![]() $U^2$
is now either
$U^2$
is now either
![]() $\text {st}\oplus \wedge ^2$
for odd m, because then
$\text {st}\oplus \wedge ^2$
for odd m, because then
![]() ${\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}}^{\vee }=\operatorname {\mathrm {SO}}_{2rkn+1}(\mathbb {C})$
, or
${\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}}^{\vee }=\operatorname {\mathrm {SO}}_{2rkn+1}(\mathbb {C})$
, or
![]() $\wedge ^2$
if m is even, since then
$\wedge ^2$
if m is even, since then
![]() ${\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}}^{\vee }=\operatorname {\mathrm {Sp}}_{2rkn}(\mathbb {C})$
.
${\operatorname {\mathrm {Sp}}_{2rkn}^{(m)}}^{\vee }=\operatorname {\mathrm {Sp}}_{2rkn}(\mathbb {C})$
.
When m is odd, the standard representation contributes
 $$ \begin{align} \prod_{1\leq i\leq k}\prod_{1\leq j\leq rn}\frac{L_{\vartheta}(r\alpha s +j-1/2,\chi_i)}{L_{\vartheta}(r\alpha s +j+1/2,\chi_i)} =\frac{L_{\vartheta}(r\alpha s +1/2,\tau)}{L_{\vartheta}(r\alpha s +rn+1/2,\tau)}. \end{align} $$
$$ \begin{align} \prod_{1\leq i\leq k}\prod_{1\leq j\leq rn}\frac{L_{\vartheta}(r\alpha s +j-1/2,\chi_i)}{L_{\vartheta}(r\alpha s +j+1/2,\chi_i)} =\frac{L_{\vartheta}(r\alpha s +1/2,\tau)}{L_{\vartheta}(r\alpha s +rn+1/2,\tau)}. \end{align} $$
For all m, the exterior square representation contributes for each pair
![]() $1\leq i\ne i'\leq k$
,
$1\leq i\ne i'\leq k$
,
 $$ \begin{align*} \prod_{1\leq j,j'\leq rn}\frac{L_{\vartheta}(2\alpha s +j+j'-1,\chi_i\chi_{i'})}{L_{\vartheta}(2\alpha s +j+j',\chi_i\chi_{i'})}= \prod_{1\leq j\leq rn}\frac{L_{\vartheta}(2\alpha s +j,\chi_i\chi_{i'})}{L_{\vartheta}(2\alpha s +j+rn,\chi_i\chi_{i'})}, \end{align*} $$
$$ \begin{align*} \prod_{1\leq j,j'\leq rn}\frac{L_{\vartheta}(2\alpha s +j+j'-1,\chi_i\chi_{i'})}{L_{\vartheta}(2\alpha s +j+j',\chi_i\chi_{i'})}= \prod_{1\leq j\leq rn}\frac{L_{\vartheta}(2\alpha s +j,\chi_i\chi_{i'})}{L_{\vartheta}(2\alpha s +j+rn,\chi_i\chi_{i'})}, \end{align*} $$
and for
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
 $$ \begin{align*} &\prod_{1\leq j_1<rn}\, \prod_{j_1<j_2\leq rn}\frac{L_{\vartheta}(2\alpha s +j_1+j_2-1,\chi_i^2)}{L_{\vartheta}(2\alpha s +j_1+j_2,\chi_i^2)} =\prod_{1\leq j<rn} \frac{L_{\vartheta}(2\alpha s +2j,\chi_i^2)}{L_{\vartheta}(2\alpha s +j+rn,\chi_i^2)}. \end{align*} $$
$$ \begin{align*} &\prod_{1\leq j_1<rn}\, \prod_{j_1<j_2\leq rn}\frac{L_{\vartheta}(2\alpha s +j_1+j_2-1,\chi_i^2)}{L_{\vartheta}(2\alpha s +j_1+j_2,\chi_i^2)} =\prod_{1\leq j<rn} \frac{L_{\vartheta}(2\alpha s +2j,\chi_i^2)}{L_{\vartheta}(2\alpha s +j+rn,\chi_i^2)}. \end{align*} $$
(This product is by definition
![]() $1$
for
$1$
for
![]() $r=n=1$
.) Thus, when
$r=n=1$
.) Thus, when
![]() $rn$
is odd we obtain
$rn$
is odd we obtain
 $$ \begin{align} \prod_{1\leq j\leq (rn-1)/2} \frac{L_{\vartheta}(2\alpha s +2j,\tau,\vee^2)}{L_{\vartheta}(2\alpha s +2j+rn,\tau,\vee^2)} \prod_{1\leq j\leq (rn+1)/2} \frac{L_{\vartheta}(2\alpha s +2j-1,\tau,\wedge^2)}{L_{\vartheta}(2\alpha s +2j+rn-1,\tau,\wedge^2)}, \end{align} $$
$$ \begin{align} \prod_{1\leq j\leq (rn-1)/2} \frac{L_{\vartheta}(2\alpha s +2j,\tau,\vee^2)}{L_{\vartheta}(2\alpha s +2j+rn,\tau,\vee^2)} \prod_{1\leq j\leq (rn+1)/2} \frac{L_{\vartheta}(2\alpha s +2j-1,\tau,\wedge^2)}{L_{\vartheta}(2\alpha s +2j+rn-1,\tau,\wedge^2)}, \end{align} $$
and for even
![]() $rn$
,
$rn$
,
 $$ \begin{align} \prod_{1\leq j\leq rn/2} \frac{L_{\vartheta}(2\alpha s +2j,\tau,\vee^2)}{L_{\vartheta}(2\alpha s +2j+rn-1,\tau,\vee^2)} \prod_{1\leq j\leq rn/2} \frac{L_{\vartheta}(2\alpha s +2j-1,\tau,\wedge^2)}{L_{\vartheta}(2\alpha s +2j+rn,\tau,\wedge^2)}. \end{align} $$
$$ \begin{align} \prod_{1\leq j\leq rn/2} \frac{L_{\vartheta}(2\alpha s +2j,\tau,\vee^2)}{L_{\vartheta}(2\alpha s +2j+rn-1,\tau,\vee^2)} \prod_{1\leq j\leq rn/2} \frac{L_{\vartheta}(2\alpha s +2j-1,\tau,\wedge^2)}{L_{\vartheta}(2\alpha s +2j+rn,\tau,\wedge^2)}. \end{align} $$
We conclude that for even m,
![]() $d_{\tau ,\vartheta }(s)$
is either the product (5.27) or (5.28) (depending on
$d_{\tau ,\vartheta }(s)$
is either the product (5.27) or (5.28) (depending on
![]() $rn$
), and if m is odd,
$rn$
), and if m is odd,
![]() $d_{\tau ,\vartheta }(s)$
also includes the factor (5.26). In both cases, we obtain (5.1).
$d_{\tau ,\vartheta }(s)$
also includes the factor (5.26). In both cases, we obtain (5.1).
5.2 The reduction from
 $\operatorname {\mathrm {GL}}_{n}^{(m,r)}$
to
$\operatorname {\mathrm {GL}}_{n}^{(m,r)}$
to
 $\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
$\operatorname {\mathrm {GL}}_{1}^{(m,r)}$
The setup and local integral were defined in § 4.3 and we use the same notation and definitions. In particular,
![]() $c=n$
,
$c=n$
,
![]() $G=\operatorname {\mathrm {GL}}_c$
,
$G=\operatorname {\mathrm {GL}}_c$
,
![]() $H=\operatorname {\mathrm {GL}}_{2rkc}$
and
$H=\operatorname {\mathrm {GL}}_{2rkc}$
and
![]() $P=P_{(rkc,rkc)}$
. The covering
$P=P_{(rkc,rkc)}$
. The covering
![]() $H^{(m,r)}$
is realized using
$H^{(m,r)}$
is realized using
![]() $\sigma _{2rkc}^{\diamondsuit }$
and G is realized using
$\sigma _{2rkc}^{\diamondsuit }$
and G is realized using
![]() $\sigma _{c}^{\diamondsuit }$
. We have a splitting of
$\sigma _{c}^{\diamondsuit }$
. We have a splitting of
![]() $K_H$
given by
$K_H$
given by
![]() $y\mapsto \langle y,\eta _{2rkc}^{\diamondsuit }(y)\rangle $
, where
$y\mapsto \langle y,\eta _{2rkc}^{\diamondsuit }(y)\rangle $
, where
![]() $\eta _{2rkc}^{\diamondsuit }(y)=\eta _{4rkc}(\operatorname {\mathrm {diag}}(y,y^{*}))$
.
$\eta _{2rkc}^{\diamondsuit }(y)=\eta _{4rkc}(\operatorname {\mathrm {diag}}(y,y^{*}))$
.
Let
![]() $\pi $
be a genuine irreducible unramified representation of G, and let
$\pi $
be a genuine irreducible unramified representation of G, and let
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
be genuine irreducible unramified representations of
$\tau '$
be genuine irreducible unramified representations of
![]() $\operatorname {\mathrm {GL}}_k^{(m,r)}$
. We assume that
$\operatorname {\mathrm {GL}}_k^{(m,r)}$
. We assume that
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
both satisfy the properties from § 5.1; in particular, they each satisfy the condition (3.45),
$\tau '$
both satisfy the properties from § 5.1; in particular, they each satisfy the condition (3.45),
![]() $\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
,
$\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
,
![]() $\tau '\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ')$
and
$\tau '\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ')$
and
![]() $\mathcal {W}(\rho _l(\tau ))$
and
$\mathcal {W}(\rho _l(\tau ))$
and
![]() $\mathcal {W}(\rho _l(\tau '))$
are the
$\mathcal {W}(\rho _l(\tau '))$
are the
![]() $(rk,l)$
models for
$(rk,l)$
models for
![]() $0<l\leq c$
.
$0<l\leq c$
.
We further assume that the pair of representations
![]() $(\rho _l(\tau ),\rho _l(\tau '))$
satisfies Equation (4.34) for all l. Since we are already assuming the
$(\rho _l(\tau ),\rho _l(\tau '))$
satisfies Equation (4.34) for all l. Since we are already assuming the
![]() $(rk,l)$
models are unique, this condition does not depend on the functionals realizing each model. Recall that Equation (4.34) was necessary for the definition of the
$(rk,l)$
models are unique, this condition does not depend on the functionals realizing each model. Recall that Equation (4.34) was necessary for the definition of the
![]() $\operatorname {\mathrm {GL}}_{l}^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integrals. Note that since
$\operatorname {\mathrm {GL}}_{l}^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integrals. Note that since
![]() $\tau '=\tau ^{*}$
when the integrals are produced by Lemma 79, Proposition 77 guarantees that this condition holds, in the context where we will be applying the results of this section.
$\tau '=\tau ^{*}$
when the integrals are produced by Lemma 79, Proposition 77 guarantees that this condition holds, in the context where we will be applying the results of this section.
Let
![]() $\omega $
be the normalized unramified matrix coefficient of
$\omega $
be the normalized unramified matrix coefficient of
![]() $\pi ^{\vee }$
and
$\pi ^{\vee }$
and
![]() $f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
be the normalized unramified standard section of
$f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
be the normalized unramified standard section of
Write
![]() $c=a+b$
for some
$c=a+b$
for some
![]() $0<a<c$
. We can now assume that
$0<a<c$
. We can now assume that
![]() $\pi $
is a quotient of
$\pi $
is a quotient of
![]() $\operatorname {\mathrm {Ind}}_{\widetilde {P}_{(a,b)}}^{ G^{(m,r)}}(\pi _a\otimes \pi _b)$
, where
$\operatorname {\mathrm {Ind}}_{\widetilde {P}_{(a,b)}}^{ G^{(m,r)}}(\pi _a\otimes \pi _b)$
, where
![]() $\pi _a$
and
$\pi _a$
and
![]() $\pi _b$
are genuine irreducible unramified representations of
$\pi _b$
are genuine irreducible unramified representations of
![]() $\operatorname {\mathrm {GL}}_a^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_a^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_b^{(m,r)}$
. Let
$\operatorname {\mathrm {GL}}_b^{(m,r)}$
. Let
![]() $\omega _a$
and
$\omega _a$
and
![]() $\omega _b$
be the normalized unramified matrix coefficients of
$\omega _b$
be the normalized unramified matrix coefficients of
![]() $\pi _a^{\vee }$
and
$\pi _a^{\vee }$
and
![]() $\pi _b^{\vee }$
. Let
$\pi _b^{\vee }$
. Let
![]() $f_{\mathcal {W}(\rho _a(\tau ))\otimes \mathcal {W}(\rho _a(\tau '))}$
and
$f_{\mathcal {W}(\rho _a(\tau ))\otimes \mathcal {W}(\rho _a(\tau '))}$
and
![]() $f_{\mathcal {W}(\rho _b(\tau ))\otimes \mathcal {W}(\rho _b(\tau '))}$
be the normalized unramified standard sections of
$f_{\mathcal {W}(\rho _b(\tau ))\otimes \mathcal {W}(\rho _b(\tau '))}$
be the normalized unramified standard sections of
 $$ \begin{align*} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka)}}^{\operatorname{\mathrm{GL}}_{2rka}^{(m,r)}}((\mathcal{W}(\rho_a(\tau))\otimes \mathcal{W}(\rho_a(\tau')))\delta_{P_{(rka,rka)}}^s)\qquad\text{and}\\ &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkb,rkb)}}^{\operatorname{\mathrm{GL}}_{2rkb}^{(m,r)}}((\mathcal{W}(\rho_b(\tau))\otimes \mathcal{W}(\rho_b(\tau')))\delta_{P_{(rkb,rkb)}}^s). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka)}}^{\operatorname{\mathrm{GL}}_{2rka}^{(m,r)}}((\mathcal{W}(\rho_a(\tau))\otimes \mathcal{W}(\rho_a(\tau')))\delta_{P_{(rka,rka)}}^s)\qquad\text{and}\\ &\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkb,rkb)}}^{\operatorname{\mathrm{GL}}_{2rkb}^{(m,r)}}((\mathcal{W}(\rho_b(\tau))\otimes \mathcal{W}(\rho_b(\tau')))\delta_{P_{(rkb,rkb)}}^s). \end{align*} $$
Denote
![]() $\alpha =rkn$
and
$\alpha =rkn$
and
 $$ \begin{align} &d_{\tau,\tau',\vartheta,a,b}(s)=\prod_{1\leq j\leq rb}\frac{L_{\vartheta,\vartheta^{-1}}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}{L_{\vartheta,\vartheta^{-1}}(2r\alpha s+ra+j,\tau\times{\tau'}^{\vee})} =\prod_{1\leq j\leq rb}\frac{L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}{L_{\vartheta}(2r\alpha s+ra+j,\tau\times{\tau'}^{\vee})}. \end{align} $$
$$ \begin{align} &d_{\tau,\tau',\vartheta,a,b}(s)=\prod_{1\leq j\leq rb}\frac{L_{\vartheta,\vartheta^{-1}}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}{L_{\vartheta,\vartheta^{-1}}(2r\alpha s+ra+j,\tau\times{\tau'}^{\vee})} =\prod_{1\leq j\leq rb}\frac{L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}{L_{\vartheta}(2r\alpha s+ra+j,\tau\times{\tau'}^{\vee})}. \end{align} $$
Note that by Proposition 25,
![]() ${\tau '}^{*}\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,{\chi '}^{-1})$
hence
${\tau '}^{*}\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,{\chi '}^{-1})$
hence
![]() $L_{\vartheta ,\vartheta ^{-1}}(s,\tau \times {\tau '}^{\vee })=L_{\vartheta }(s,\tau \times {\tau '}^{*})$
; the second equality in Equation (5.29) holds because
$L_{\vartheta ,\vartheta ^{-1}}(s,\tau \times {\tau '}^{\vee })=L_{\vartheta }(s,\tau \times {\tau '}^{*})$
; the second equality in Equation (5.29) holds because
![]() $\mu _{2m}\subset F^{*}$
.
$\mu _{2m}\subset F^{*}$
.
The following is the analog of Lemma 79, but while there we only considered the Siegel parabolic subgroup, here we handle any maximal parabolic subgroup.
Lemma 80. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
 $$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))})\\&= d_{\tau,\tau',\vartheta,a,b}(s)Z(\alpha s/(rka),\omega_{a},f_{\mathcal{W}(\rho_a(\tau))\otimes \mathcal{W}(\rho_a(\tau'))})Z(\alpha s/(rkb),\omega_{b},f_{\mathcal{W}(\rho_b(\tau))\otimes \mathcal{W}(\rho_b(\tau'))}). \end{align*} $$
$$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))})\\&= d_{\tau,\tau',\vartheta,a,b}(s)Z(\alpha s/(rka),\omega_{a},f_{\mathcal{W}(\rho_a(\tau))\otimes \mathcal{W}(\rho_a(\tau'))})Z(\alpha s/(rkb),\omega_{b},f_{\mathcal{W}(\rho_b(\tau))\otimes \mathcal{W}(\rho_b(\tau'))}). \end{align*} $$
Proof. This proof is the adaptation of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Lemma 33] to the covering case; the arguments are similar to those used for the proof of Lemma 79 and will be described more briefly.
Assume that
![]() $\pi =\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m,r)}}(\pi _a\otimes \pi _b)$
and
$\pi =\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m,r)}}(\pi _a\otimes \pi _b)$
and
![]() $\pi ^{\vee }=\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m,r)}}(\pi _a^{\vee }\otimes \pi _b^{\vee })$
. Let
$\pi ^{\vee }=\operatorname {\mathrm {Ind}}_{\widetilde {R}}^{G^{(m,r)}}(\pi _a^{\vee }\otimes \pi _b^{\vee })$
. Let
![]() $\{,\}_{M_R}$
be the
$\{,\}_{M_R}$
be the
![]() $\widetilde {M}_R$
-invariant pairing on
$\widetilde {M}_R$
-invariant pairing on
![]() $(\pi _a\otimes \pi _b)\times (\pi _a^{\vee }\otimes \pi _b^{\vee })$
. Then we can write (cf. Equation (5.2))
$(\pi _a\otimes \pi _b)\times (\pi _a^{\vee }\otimes \pi _b^{\vee })$
. Then we can write (cf. Equation (5.2))
 $$ \begin{align*} &\{\varphi,\varphi^{\vee}\}=\int\limits_{K_G}\{\varphi(\langle y,\eta_c^{\diamondsuit}(y)\rangle),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle)\}_{M_R}\,dy,\\ &\omega(\langle g,1\rangle)=\int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy. \end{align*} $$
$$ \begin{align*} &\{\varphi,\varphi^{\vee}\}=\int\limits_{K_G}\{\varphi(\langle y,\eta_c^{\diamondsuit}(y)\rangle),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle)\}_{M_R}\,dy,\\ &\omega(\langle g,1\rangle)=\int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy. \end{align*} $$
Here,
![]() $e=\langle I_c,1\rangle $
. Thus,
$e=\langle I_c,1\rangle $
. Thus,
![]() $Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))})$
equals
$Z(s,\omega ,f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))})$
equals
 $$ \begin{align} \int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle y,\eta_c^{\diamondsuit}(y)\rangle\langle g,1\rangle)\}_{M_R}\,dy \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
(Cf. Integral (5.3).) We repeat the arguments (5.3)-(5.4), that is, multiply
![]() $g\mapsto y^{-1}g$
but use the fact that
$g\mapsto y^{-1}g$
but use the fact that
![]() $\sigma ^{\diamondsuit }_{2rkc}(\mathfrak {e}_2(g),\mathfrak {e}_2(g))=\sigma _{c}^{\diamondsuit }(g,g')$
(see Equation (4.31)) instead of Proposition 7, to obtain
$\sigma ^{\diamondsuit }_{2rkc}(\mathfrak {e}_2(g),\mathfrak {e}_2(g))=\sigma _{c}^{\diamondsuit }(g,g')$
(see Equation (4.31)) instead of Proposition 7, to obtain
 $$ \begin{align} &\int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\nonumber\int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(y^{-1}),\eta_c^{\diamondsuit}(y^{-1})\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dy\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G} \int\limits_{K_G}\{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\nonumber\int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(y^{-1}),\eta_c^{\diamondsuit}(y^{-1})\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dy\,dg. \end{align} $$
To proceed, we need to show that
![]() $(\eta _c^{\diamondsuit })^{-1}(y)=\eta _{2rkc}^{\diamondsuit }(\mathfrak {e}_1(y))$
(cf. Equation (5.5)). First, we claim that
$(\eta _c^{\diamondsuit })^{-1}(y)=\eta _{2rkc}^{\diamondsuit }(\mathfrak {e}_1(y))$
(cf. Equation (5.5)). First, we claim that
This follows as in the proof of Proposition 22: Consider the embedding
![]() $\operatorname {\mathrm {Sp}}_{2c}\hookrightarrow \operatorname {\mathrm {Sp}}_{4rkc}$
,
$\operatorname {\mathrm {Sp}}_{2c}\hookrightarrow \operatorname {\mathrm {Sp}}_{4rkc}$
,
By [Reference Banks, Levy and SepanskiBLS99, § 2, Lemma 5], since
![]() $K_{\operatorname {\mathrm {Sp}}_{2c}}$
is perfect,
$K_{\operatorname {\mathrm {Sp}}_{2c}}$
is perfect,
![]() $\eta _{2c}(x)= \eta _{4rkc}(x^{\blacksquare ,rk})$
for all
$\eta _{2c}(x)= \eta _{4rkc}(x^{\blacksquare ,rk})$
for all
![]() $x\in K_{\operatorname {\mathrm {Sp}}_{2c}}$
. This proves Equation (5.32) because by definition
$x\in K_{\operatorname {\mathrm {Sp}}_{2c}}$
. This proves Equation (5.32) because by definition
![]() $\eta _c^{\diamondsuit }(y)=\eta _{2c}(\operatorname {\mathrm {diag}}(y,y^{*}))$
and
$\eta _c^{\diamondsuit }(y)=\eta _{2c}(\operatorname {\mathrm {diag}}(y,y^{*}))$
and
Consider the following
![]() $2rk-1$
additional standard embeddings of
$2rk-1$
additional standard embeddings of
![]() $\operatorname {\mathrm {Sp}}_{2c}$
in
$\operatorname {\mathrm {Sp}}_{2c}$
in
![]() $\operatorname {\mathrm {Sp}}_{4rkc}$
, given by
$\operatorname {\mathrm {Sp}}_{4rkc}$
, given by
By [Reference Banks, Levy and SepanskiBLS99, § 2, Theorem 7], all
![]() $2rk$
images
$2rk$
images
![]() $\operatorname {\mathrm {Sp}}_{2c}^{\blacksquare ,l}$
(
$\operatorname {\mathrm {Sp}}_{2c}^{\blacksquare ,l}$
(
![]() $0\leq l<2rk$
) are commuting in
$0\leq l<2rk$
) are commuting in
![]() $\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
and
$\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
and
Therefore,
![]() $x^{\blacksquare ,l}\mapsto \langle x^{\blacksquare ,l},\eta _{2c}(x)\rangle $
is the canonical splitting of
$x^{\blacksquare ,l}\mapsto \langle x^{\blacksquare ,l},\eta _{2c}(x)\rangle $
is the canonical splitting of
![]() $K_{\operatorname {\mathrm {Sp}}_{2c}}^{\blacksquare ,l}$
in
$K_{\operatorname {\mathrm {Sp}}_{2c}}^{\blacksquare ,l}$
in
![]() $\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
. Consider the diagonal embedding
$\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
. Consider the diagonal embedding
![]() $x\mapsto x^{\times }$
of
$x\mapsto x^{\times }$
of
![]() $K_{\operatorname {\mathrm {Sp}}_{2c}}$
in the direct product of
$K_{\operatorname {\mathrm {Sp}}_{2c}}$
in the direct product of
![]() $K_{\operatorname {\mathrm {Sp}}_{2c}}^{\blacksquare ,l}$
over
$K_{\operatorname {\mathrm {Sp}}_{2c}}^{\blacksquare ,l}$
over
![]() $l\ne rk$
, that is,
$l\ne rk$
, that is,
The canonical embedding of
![]() $K_{\operatorname {\mathrm {Sp}}_{2c}}^{\times }=\{x^{\times }:x\in K_{\operatorname {\mathrm {Sp}}_{2c}}\}$
in
$K_{\operatorname {\mathrm {Sp}}_{2c}}^{\times }=\{x^{\times }:x\in K_{\operatorname {\mathrm {Sp}}_{2c}}\}$
in
![]() $\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
is
$\operatorname {\mathrm {Sp}}_{4rkc}^{(m)}$
is
![]() $x^{\times }\mapsto \langle x^{\times },\eta _{2c}^{2rk-1}(x)\rangle $
. Hence, for any
$x^{\times }\mapsto \langle x^{\times },\eta _{2c}^{2rk-1}(x)\rangle $
. Hence, for any
![]() $x\in K_{\operatorname {\mathrm {Sp}}_{2c}}$
,
$x\in K_{\operatorname {\mathrm {Sp}}_{2c}}$
,
![]() $\eta _{4rkc}(x^{\times })=\eta _{2c}^{2rk-1}(x)=\eta _{2c}^{-1}(x)$
. In particular, for
$\eta _{4rkc}(x^{\times })=\eta _{2c}^{2rk-1}(x)=\eta _{2c}^{-1}(x)$
. In particular, for
![]() $y\in K_{G}$
, since
$y\in K_{G}$
, since
(
![]() $\mathfrak {e}_1(y)=\operatorname {\mathrm {diag}}(y,\ldots ,y,I_c,y,\ldots ,y)$
, where y appears
$\mathfrak {e}_1(y)=\operatorname {\mathrm {diag}}(y,\ldots ,y,I_c,y,\ldots ,y)$
, where y appears
![]() $rk$
times on the left of
$rk$
times on the left of
![]() $I_c$
and
$I_c$
and
![]() $rk-1$
times on the right),
$rk-1$
times on the right),
Now, using the right-invariance of
![]() $f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
under
$f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
under
and Equation (4.31), the
![]() $du_0$
-integral equals (cf. Integral (5.6))
$du_0$
-integral equals (cf. Integral (5.6))
 $$ \begin{align*} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle(y^{-1},y^{-1}),1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle(y^{-1},y^{-1}),1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0. \end{align*} $$
By Corollary 76 we can remove
![]() $\langle (y^{-1},y^{-1}),1\rangle $
from this integral and Integral (5.31) equals (cf. Integral (5.7))
$\langle (y^{-1},y^{-1}),1\rangle $
from this integral and Integral (5.31) equals (cf. Integral (5.7))
 $$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
$$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U_0}f_{\mathcal{W}(\rho_c(\tau))\otimes \mathcal{W}(\rho_c(\tau'))}(\langle\delta u_0,1\rangle \langle\mathfrak{e}_2(g),1\rangle,s)\,\psi_U(u_0)\,du_0\,dg. \end{align} $$
By Corollary 56 with
![]() $l=a=c-b$
,
$l=a=c-b$
,
and similarly for
![]() $\rho _c(\tau ')$
. Set
$\rho _c(\tau ')$
. Set
![]() $L=P_{(rka,rkb,rka,rkb)}$
. We realize
$L=P_{(rka,rkb,rka,rkb)}$
. We realize
![]() $\mathcal {W}(\rho _c(\tau ))$
and
$\mathcal {W}(\rho _c(\tau ))$
and
![]() $\mathcal {W}(\rho _c(\tau '))$
using Integral (3.50), and there is a standard unramified section
$\mathcal {W}(\rho _c(\tau '))$
using Integral (3.50), and there is a standard unramified section
![]() ${f}^{\downarrow }$
of
${f}^{\downarrow }$
of
 $$ \begin{align} \operatorname{\mathrm{Ind}}_{\widetilde{L}}^{H^{(m,r)}}(& |\det|^{-b/2+\alpha s}\mathcal{W}(\rho_a(\tau))\otimes |\det|^{a/2+\alpha s}\mathcal{W}(\rho_b(\tau))\\& \otimes |\det|^{-b/2-\alpha s}\mathcal{W}(\rho_a(\tau'))\otimes |\det|^{a/2-\alpha s}\mathcal{W}(\rho_b(\tau')))\nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ind}}_{\widetilde{L}}^{H^{(m,r)}}(& |\det|^{-b/2+\alpha s}\mathcal{W}(\rho_a(\tau))\otimes |\det|^{a/2+\alpha s}\mathcal{W}(\rho_b(\tau))\\& \otimes |\det|^{-b/2-\alpha s}\mathcal{W}(\rho_a(\tau'))\otimes |\det|^{a/2-\alpha s}\mathcal{W}(\rho_b(\tau')))\nonumber \end{align} $$
such that for all
![]() $h\in H^{(m,r)}$
,
$h\in H^{(m,r)}$
,
 $$ \begin{align*} &f_{\mathcal{W}(\rho_c(\tau))\otimes\mathcal{W}(\rho_c(\tau'))}(h,s)=\int\limits_V\int\limits_V {f}^{\downarrow}(\langle\operatorname{\mathrm{diag}}(\kappa,\kappa)\operatorname{\mathrm{diag}}(v,v'),1\rangle h,s)\,dv\,dv'. \end{align*} $$
$$ \begin{align*} &f_{\mathcal{W}(\rho_c(\tau))\otimes\mathcal{W}(\rho_c(\tau'))}(h,s)=\int\limits_V\int\limits_V {f}^{\downarrow}(\langle\operatorname{\mathrm{diag}}(\kappa,\kappa)\operatorname{\mathrm{diag}}(v,v'),1\rangle h,s)\,dv\,dv'. \end{align*} $$
(Cf. the representation (5.8) and Equality (5.9).) Put
![]() $\kappa ^{\bullet }=\operatorname {\mathrm {diag}}(\kappa ,\kappa )$
. Note that we implicitly computed
$\kappa ^{\bullet }=\operatorname {\mathrm {diag}}(\kappa ,\kappa )$
. Note that we implicitly computed
which is valid by Equations (2.52) and (2.8) (recall that Equations (2.8)-(2.10) are valid for
![]() $\sigma ^{\diamondsuit }_{d}$
).
$\sigma ^{\diamondsuit }_{d}$
).
Since
![]() $f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
is normalized and
$f_{\mathcal {W}(\rho _c(\tau ))\otimes \mathcal {W}(\rho _c(\tau '))}$
is normalized and
![]() ${f}^{\downarrow }$
is unramified, the proof of Proposition 62 implies that
${f}^{\downarrow }$
is unramified, the proof of Proposition 62 implies that
![]() ${f}^{\downarrow }$
is also normalized.
${f}^{\downarrow }$
is also normalized.
The integral (5.33) becomes (cf. Integral (5.10))
 $$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0}\int\limits_{V}\int\limits_{V}{f}^{\downarrow}(\langle\kappa^{\bullet}\operatorname{\mathrm{diag}}(v,v'),1\rangle \langle\delta u_0,1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\psi_U(u_0)\,dv\,dv'\,du_0\,dg,\nonumber \end{align} $$
$$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \\&\int\limits_{U_0}\int\limits_{V}\int\limits_{V}{f}^{\downarrow}(\langle\kappa^{\bullet}\operatorname{\mathrm{diag}}(v,v'),1\rangle \langle\delta u_0,1\rangle\langle\mathfrak{e}_2(g),1\rangle,s)\psi_U(u_0)\,dv\,dv'\,du_0\,dg,\nonumber \end{align} $$
which is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
as a quadruple integral.
$\operatorname {\mathrm {Re}}(s)\gg 0$
as a quadruple integral.
Also, since
![]() $\sigma _{2rkc}^{\diamondsuit }$
is trivial on
$\sigma _{2rkc}^{\diamondsuit }$
is trivial on
![]() $\mathfrak {W}^+_{2rkc}$
(
$\mathfrak {W}^+_{2rkc}$
(
![]() $\sigma _{4rkc}$
is trivial on
$\sigma _{4rkc}$
is trivial on
![]() $\mathfrak {W}^+_{4rkc}$
) and by Equation (2.8),
$\mathfrak {W}^+_{4rkc}$
) and by Equation (2.8),
Properties (1)–(7) from the proof of Lemma 79 now take the following form:
-
1. By Equation (2.10),
 ${}^{\delta _0^{-1}}\langle \operatorname {\mathrm {diag}}(v,v'),1\rangle =\langle \operatorname {\mathrm {diag}}(v',v),1\rangle $
.
${}^{\delta _0^{-1}}\langle \operatorname {\mathrm {diag}}(v,v'),1\rangle =\langle \operatorname {\mathrm {diag}}(v',v),1\rangle $
. -
2. By Equations (2.8) and (2.10),
 ${}^{\operatorname {\mathrm {diag}}(v',v)}\langle \delta _1,1\rangle = \langle \delta _1,1\rangle \langle u',1\rangle $
, where
${}^{\operatorname {\mathrm {diag}}(v',v)}\langle \delta _1,1\rangle = \langle \delta _1,1\rangle \langle u',1\rangle $
, where
 $u'\in U_0$
and
$u'\in U_0$
and
 $\psi _U(u')=1$
.
$\psi _U(u')=1$
. -
3. The elements of both copies of V normalize
 $U_0$
and fix
$U_0$
and fix
 $\psi _U|_{U_0}$
.
$\psi _U|_{U_0}$
. -
4. Since
 $\mathfrak {e}_2(G)<\operatorname {\mathrm {diag}}(I_{rkc},\operatorname {\mathrm {GL}}_{rkc})$
, by Equation (2.52) the subgroups
$\mathfrak {e}_2(G)<\operatorname {\mathrm {diag}}(I_{rkc},\operatorname {\mathrm {GL}}_{rkc})$
, by Equation (2.52) the subgroups
 $\operatorname {\mathrm {diag}}(V,I_{rkc})$
and
$\operatorname {\mathrm {diag}}(V,I_{rkc})$
and
 $\mathfrak {e}_2(G)$
commute in
$\mathfrak {e}_2(G)$
commute in
 $H^{(m,r)}$
.
$H^{(m,r)}$
. -
5.
 $\langle \delta _0,1\rangle $
commutes with
$\langle \delta _0,1\rangle $
commutes with
 $\langle \kappa ^{\bullet },1\rangle $
.
$\langle \kappa ^{\bullet },1\rangle $
. -
6. Since
 $\delta _1,{}^{\kappa ^{\bullet }}\delta _1\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
,
$\delta _1,{}^{\kappa ^{\bullet }}\delta _1\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
,
 ${}^{\kappa ^{\bullet }}\langle \delta _1,1\rangle =\langle {}^{\kappa ^{\bullet }}\delta _1,1\rangle $
.
${}^{\kappa ^{\bullet }}\langle \delta _1,1\rangle =\langle {}^{\kappa ^{\bullet }}\delta _1,1\rangle $
. -
7. The element
 $\langle \operatorname {\mathrm {diag}}(\kappa ,I_{rkc}),1\rangle $
commutes with
$\langle \operatorname {\mathrm {diag}}(\kappa ,I_{rkc}),1\rangle $
commutes with
 $\langle \mathfrak {e}_2(G),1\rangle $
, again by Equation (2.52).
$\langle \mathfrak {e}_2(G),1\rangle $
, again by Equation (2.52).
Define
 $$ \begin{align*} U_0'={}^{\kappa^{\bullet}}U_0=\left\{\left(\begin{smallmatrix}I_{rka}&&U_1&U_2\\&I_{rkb}&U_3&U_4\\&&I_{rka}\\&&&I_{rkb}\end{smallmatrix}\right)\right\}. \end{align*} $$
$$ \begin{align*} U_0'={}^{\kappa^{\bullet}}U_0=\left\{\left(\begin{smallmatrix}I_{rka}&&U_1&U_2\\&I_{rkb}&U_3&U_4\\&&I_{rka}\\&&&I_{rkb}\end{smallmatrix}\right)\right\}. \end{align*} $$
As opposed to Equation (5.11), here
![]() $U^4$
does not depend on
$U^4$
does not depend on
![]() $U_1$
. In fact,
$U_1$
. In fact,
![]() $\left \{\left (\begin {smallmatrix}I_{rka}&U_1\\&I_{rka}\end {smallmatrix}\right )\right \}$
and
$\left \{\left (\begin {smallmatrix}I_{rka}&U_1\\&I_{rka}\end {smallmatrix}\right )\right \}$
and
![]() $\left \{\left (\begin {smallmatrix}I_{rkb}&U_4\\&I_{rkb}\end {smallmatrix}\right )\right \}$
are the unipotent subgroups corresponding to the
$\left \{\left (\begin {smallmatrix}I_{rkb}&U_4\\&I_{rkb}\end {smallmatrix}\right )\right \}$
are the unipotent subgroups corresponding to the
![]() $\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, and the restriction of
$\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, and the restriction of
![]() $\psi _U$
to the coordinates of
$\psi _U$
to the coordinates of
![]() $U_1$
and
$U_1$
and
![]() $U_4$
gives the similar character for these integrals. In addition, the bottom left
$U_4$
gives the similar character for these integrals. In addition, the bottom left
![]() $a\times b$
(resp.,
$a\times b$
(resp.,
![]() $b\times a$
) block of
$b\times a$
) block of
![]() $U_2$
(resp.,
$U_2$
(resp.,
![]() $U_3$
) is
$U_3$
) is
![]() $0$
.
$0$
.
Utilizing properties (1)–(7), Integral (5.35) equals (cf. Integral (5.12))
 $$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\int\limits_{U_0'} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0',1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\psi_U(u_0')\,dv\,dv'\,du_0'\,dg.\notag \end{align} $$
$$ \begin{align} &\int\limits_{G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\int\limits_{U_0'} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0',1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\psi_U(u_0')\,dv\,dv'\,du_0'\,dg.\notag \end{align} $$
We can factor Integral (5.36) through
![]() $U_R$
, and it becomes
$U_R$
, and it becomes
 $$ \begin{align} &\int\limits_{U_R\backslash G} \int\limits_{U_R} \{\varphi(e),\varphi^{\vee}(\langle z,1\rangle\langle g,1\rangle)\}_{M_R}\int\limits_{U_0'} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0',1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(z),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\notag\\&\psi_U(u_0')\,dv\,dv'\,du_0'\,dz\,dg.\notag \end{align} $$
$$ \begin{align} &\int\limits_{U_R\backslash G} \int\limits_{U_R} \{\varphi(e),\varphi^{\vee}(\langle z,1\rangle\langle g,1\rangle)\}_{M_R}\int\limits_{U_0'} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0',1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(z),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\notag\\&\psi_U(u_0')\,dv\,dv'\,du_0'\,dz\,dg.\notag \end{align} $$
Form the group
![]() $U_0^{\bullet }$
by letting the
$U_0^{\bullet }$
by letting the
![]() $0$
block of
$0$
block of
![]() $U_2$
in
$U_2$
in
![]() $U_0'$
take arbitrary coordinates. For
$U_0'$
take arbitrary coordinates. For
![]() $z\in U_R$
,
$z\in U_R$
,
 $$ \begin{align*} &{}^{\mathfrak{e}_2(z)^{-1}}\langle\operatorname{\mathrm{diag}}(I_{rkc},v),1\rangle= \langle\operatorname{\mathrm{diag}}(I_{rkc},v_z),1\rangle\langle\operatorname{\mathrm{diag}}(I_{rkc},v),1\rangle,\qquad v_z\in V_{(a,rkc-a)},\\ &({}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z))^{-1}\,\langle({}^{\kappa^{\bullet}}\delta_1)u_0',1\rangle\, ({}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z)) =\langle({}^{\kappa^{\bullet}}\delta_1)u_z^{\bullet},1\rangle,\\ &{}^{\delta_0}\langle{}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z),1\rangle =\langle {}^{\delta_0\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z),1\rangle, \end{align*} $$
$$ \begin{align*} &{}^{\mathfrak{e}_2(z)^{-1}}\langle\operatorname{\mathrm{diag}}(I_{rkc},v),1\rangle= \langle\operatorname{\mathrm{diag}}(I_{rkc},v_z),1\rangle\langle\operatorname{\mathrm{diag}}(I_{rkc},v),1\rangle,\qquad v_z\in V_{(a,rkc-a)},\\ &({}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z))^{-1}\,\langle({}^{\kappa^{\bullet}}\delta_1)u_0',1\rangle\, ({}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z)) =\langle({}^{\kappa^{\bullet}}\delta_1)u_z^{\bullet},1\rangle,\\ &{}^{\delta_0}\langle{}^{\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z),1\rangle =\langle {}^{\delta_0\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\mathfrak{e}_2(z),1\rangle, \end{align*} $$
where we only need to use Equations (2.8) and (2.10) throughout (
![]() $\mathfrak {e}_2(z),{}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(z)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
), and
$\mathfrak {e}_2(z),{}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(z)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
), and
![]() $u_z^{\bullet }\in U_0^{\bullet }$
depends on
$u_z^{\bullet }\in U_0^{\bullet }$
depends on
![]() $u_0$
and z. Using the equivariance property of the top left
$u_0$
and z. Using the equivariance property of the top left
![]() $(rk,a)$
functional in the inducing data of
$(rk,a)$
functional in the inducing data of
![]() ${f}^{\downarrow }$
we see that
${f}^{\downarrow }$
we see that
![]() $\langle {}^{\delta _0\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(z),1\rangle $
vanishes, without a character. Regarding
$\langle {}^{\delta _0\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(z),1\rangle $
vanishes, without a character. Regarding
![]() $v_z$
,
$v_z$
,
and
where
![]() $u_{v_z}^{\bullet }\in U_0^{\bullet }$
. When we change variables to remove the dependency on
$u_{v_z}^{\bullet }\in U_0^{\bullet }$
. When we change variables to remove the dependency on
![]() $v_z$
, the character
$v_z$
, the character
![]() $\psi _U(u_0')$
changes. Then
$\psi _U(u_0')$
changes. Then
which belongs to the subgroup
![]() $V_{(a^{rk})}$
appearing in the definition of the
$V_{(a^{rk})}$
appearing in the definition of the
![]() $(rk,a)$
functional. Again, using the equivariance property of the top left
$(rk,a)$
functional. Again, using the equivariance property of the top left
![]() $(rk,a)$
functional in the inducing data of
$(rk,a)$
functional in the inducing data of
![]() ${f}^{\downarrow }$
, the change to
${f}^{\downarrow }$
, the change to
![]() $\psi _U(u_0')$
is offset. This argument extends to the covering by Equation (2.10).
$\psi _U(u_0')$
is offset. This argument extends to the covering by Equation (2.10).
Altogether, Integral (5.37) is equal to (cf. Integral (5.13))
 $$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\int\limits_{U_0^{\bullet}} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0^{\bullet},1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\psi_U(u_0^{\bullet})\,dv\,dv'\,du_0^{\bullet}\,dg.\notag \end{align} $$
$$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R}\int\limits_{U_0^{\bullet}} \int\limits_{V}\int\limits_{V}\\&{f}^{\downarrow}(\langle\delta_0({}^{\kappa^{\bullet}}\delta_1) ,1\rangle \langle u_0^{\bullet},1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\psi_U(u_0^{\bullet})\,dv\,dv'\,du_0^{\bullet}\,dg.\notag \end{align} $$
Next, for any
![]() $l>0$
we let
$l>0$
we let
![]() $\delta _{l,0}$
and
$\delta _{l,0}$
and
![]() $\delta _{l,1}$
be the elements
$\delta _{l,1}$
be the elements
![]() $\delta _{0}$
and
$\delta _{0}$
and
![]() $\delta _{1}$
corresponding to the
$\delta _{1}$
corresponding to the
![]() $\operatorname {\mathrm {GL}}_l^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and denote
$\operatorname {\mathrm {GL}}_l^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral, and denote
![]() $\delta ^{\prime }_l=\delta _{l,0}\delta _{l,1}$
. Then
$\delta ^{\prime }_l=\delta _{l,0}\delta _{l,1}$
. Then
 $$ \begin{align*} &\delta_0=w\operatorname{\mathrm{diag}}(\delta_{a,0},\delta_{b,0})w^{-1},\qquad w=\left(\begin{array}{cccc}I_{rka}\\&&I_{rkb}\\&I_{rka}\\&&&I_{rkb}\end{array}\right) \end{align*} $$
$$ \begin{align*} &\delta_0=w\operatorname{\mathrm{diag}}(\delta_{a,0},\delta_{b,0})w^{-1},\qquad w=\left(\begin{array}{cccc}I_{rka}\\&&I_{rkb}\\&I_{rka}\\&&&I_{rkb}\end{array}\right) \end{align*} $$
and (cf. Equation (5.14))
Since
![]() $u_0^{\bullet },{}^{(\operatorname {\mathrm {diag}}(\delta _{a,0},\delta _{b,0})w^{-1})}u^2,{}^{w^{-1}}(u^1u^4),{}^{\kappa ^{\bullet }}\delta _1\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
, we can apply Equations (2.8)-(2.10) to write a similar identity in
$u_0^{\bullet },{}^{(\operatorname {\mathrm {diag}}(\delta _{a,0},\delta _{b,0})w^{-1})}u^2,{}^{w^{-1}}(u^1u^4),{}^{\kappa ^{\bullet }}\delta _1\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
, we can apply Equations (2.8)-(2.10) to write a similar identity in
![]() $H^{(m,r)}$
(cf., Equation (5.15)):
$H^{(m,r)}$
(cf., Equation (5.15)):
Let
![]() $U^2$
be the subgroup of elements
$U^2$
be the subgroup of elements
![]() ${}^{(\operatorname {\mathrm {diag}}(\delta _{a,0},\delta _{b,0})w^{-1})}u^2$
; a quick computation shows that
${}^{(\operatorname {\mathrm {diag}}(\delta _{a,0},\delta _{b,0})w^{-1})}u^2$
; a quick computation shows that
Also,
![]() $U^1$
(resp.,
$U^1$
(resp.,
![]() $U^4$
) denotes the subgroup of elements
$U^4$
) denotes the subgroup of elements
![]() ${}^{w^{-1}}u^1$
(resp.,
${}^{w^{-1}}u^1$
(resp.,
![]() ${}^{w^{-1}}u^4$
) and let
${}^{w^{-1}}u^4$
) and let
![]() $U^3$
be the subgroup of elements
$U^3$
be the subgroup of elements
![]() $u^3$
. These subgroups will play the same role as in the proof of Lemma 79: The integration over
$u^3$
. These subgroups will play the same role as in the proof of Lemma 79: The integration over
![]() $U^2$
constitutes an intertwining operator,
$U^2$
constitutes an intertwining operator,
![]() $U^1$
and
$U^1$
and
![]() $U^2$
appear in the
$U^2$
appear in the
![]() $\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, and the integral over
$\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integrals, and the integral over
![]() $U^3$
evaluates to a constant.
$U^3$
evaluates to a constant.
Let
![]() $M(s)$
be the standard intertwining operator from the representation (5.34) to
$M(s)$
be the standard intertwining operator from the representation (5.34) to
 $$ \begin{align} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka,rkb,rkb)}}^{H^{(m,r)}}(& |\det|^{-b/2+\alpha s}\mathcal{W}(\rho_a(\tau))\otimes |\det|^{-b/2-\alpha s} \mathcal{W}(\rho_a(\tau'))\\ &\notag \otimes |\det|^{a/2+\alpha s}\mathcal{W}(\rho_b(\tau)) \otimes |\det|^{a/2-\alpha s}\mathcal{W}(\rho_b(\tau')))\nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka,rkb,rkb)}}^{H^{(m,r)}}(& |\det|^{-b/2+\alpha s}\mathcal{W}(\rho_a(\tau))\otimes |\det|^{-b/2-\alpha s} \mathcal{W}(\rho_a(\tau'))\\ &\notag \otimes |\det|^{a/2+\alpha s}\mathcal{W}(\rho_b(\tau)) \otimes |\det|^{a/2-\alpha s}\mathcal{W}(\rho_b(\tau')))\nonumber \end{align} $$
(cf. the representation (5.16)), defined by
 $$ \begin{align*} M(s){f}^{\downarrow}(h,s)= \int\limits_{U^2}{f}^{\downarrow}(\langle w,1\rangle\langle u^2,1\rangle h,s)\,du^2. \end{align*} $$
$$ \begin{align*} M(s){f}^{\downarrow}(h,s)= \int\limits_{U^2}{f}^{\downarrow}(\langle w,1\rangle\langle u^2,1\rangle h,s)\,du^2. \end{align*} $$
To see that the image of
![]() $M(s)$
is indeed in the space of (5.40), we must verify that
$M(s)$
is indeed in the space of (5.40), we must verify that
Since
and similarly for
![]() $N_{\operatorname {\mathrm {GL}}_{rka}}^-$
and
$N_{\operatorname {\mathrm {GL}}_{rka}}^-$
and
![]() $N_{\operatorname {\mathrm {GL}}_{rkb}}^-$
, it remains to check torus elements where we apply Proposition 2 (recall that
$N_{\operatorname {\mathrm {GL}}_{rkb}}^-$
, it remains to check torus elements where we apply Proposition 2 (recall that
![]() $\operatorname {\mathrm {SL}}_d$
is generated by
$\operatorname {\mathrm {SL}}_d$
is generated by
![]() $N_{\operatorname {\mathrm {GL}}_d}$
and
$N_{\operatorname {\mathrm {GL}}_d}$
and
![]() $N_{\operatorname {\mathrm {GL}}_d}^-$
).
$N_{\operatorname {\mathrm {GL}}_d}^-$
).
Put
![]() $d_{\tau ,\tau ',\vartheta ,a,b}(s)=M(s){f}^{\downarrow }(\langle I_{2rkc},1\rangle ,s)$
. When we apply Equation (5.39) to Integral (5.38), we obtain (cf. Integral (5.17))
$d_{\tau ,\tau ',\vartheta ,a,b}(s)=M(s){f}^{\downarrow }(\langle I_{2rkc},1\rangle ,s)$
. When we apply Equation (5.39) to Integral (5.38), we obtain (cf. Integral (5.17))
 $$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U^3}\int\limits_{U^4}\int\limits_{U^1} \int\limits_{V}\int\limits_{V} \\&M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\&\psi_{U}(u^1)\psi_{U}(u^4) \,dv\,dv'\,du^1\,du^4\,du^3\,dg.\notag \end{align} $$
$$ \begin{align} &\int\limits_{U_R\backslash G} \{\varphi(e),\varphi^{\vee}(\langle g,1\rangle)\}_{M_R} \int\limits_{U^3}\int\limits_{U^4}\int\limits_{U^1} \int\limits_{V}\int\limits_{V} \\&M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(g),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\&\psi_{U}(u^1)\psi_{U}(u^4) \,dv\,dv'\,du^1\,du^4\,du^3\,dg.\notag \end{align} $$
Here,
![]() $\psi _{U}(u^1)$
(resp.,
$\psi _{U}(u^1)$
(resp.,
![]() $\psi _{U}(u^4)$
) is the character (4.30) restricted to the subgroup
$\psi _{U}(u^4)$
) is the character (4.30) restricted to the subgroup
![]() $U_0$
appearing in the
$U_0$
appearing in the
![]() $\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
(resp.,
$\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
(resp.,
![]() $\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
) integral.
$\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
) integral.
Next, we write the
![]() $dg$
-integral using the Iwasawa decomposition
$dg$
-integral using the Iwasawa decomposition
![]() $G=RK_G$
. As in the passage (5.17)-(5.18) but using Equation (5.32), we see that when we change variables
$G=RK_G$
. As in the passage (5.17)-(5.18) but using Equation (5.32), we see that when we change variables
![]() $g\mapsto gy$
with
$g\mapsto gy$
with
![]() $y\in K_G$
, the integrand is right-invariant with respect to y. Then Integral (5.41) equals
$y\in K_G$
, the integrand is right-invariant with respect to y. Then Integral (5.41) equals
 $$ \begin{align*} &\int\limits_{\operatorname{\mathrm{GL}}_b}\int\limits_{\operatorname{\mathrm{GL}}_a} \{\varphi(e),\varphi^{\vee}(\langle\operatorname{\mathrm{diag}}(x,y),1\rangle)\}_{M_R} \int\limits_{U^3}\int\limits_{U^4}\int\limits_{U^1} \int\limits_{V}\int\limits_{V} \\&M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(x,y)),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\&\psi_U(u^1)\psi_U(u^4) \delta_R^{-1}(\operatorname{\mathrm{diag}}(x,y))\,dv\,dv'\,du^1\,du^4\,du^3\,dx\,dy.\notag \end{align*} $$
$$ \begin{align*} &\int\limits_{\operatorname{\mathrm{GL}}_b}\int\limits_{\operatorname{\mathrm{GL}}_a} \{\varphi(e),\varphi^{\vee}(\langle\operatorname{\mathrm{diag}}(x,y),1\rangle)\}_{M_R} \int\limits_{U^3}\int\limits_{U^4}\int\limits_{U^1} \int\limits_{V}\int\limits_{V} \\&M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(x,y)),1\rangle\langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\&\psi_U(u^1)\psi_U(u^4) \delta_R^{-1}(\operatorname{\mathrm{diag}}(x,y))\,dv\,dv'\,du^1\,du^4\,du^3\,dx\,dy.\notag \end{align*} $$
The conjugation of
![]() $\operatorname {\mathrm {diag}}(I_{rkc},V)$
by
$\operatorname {\mathrm {diag}}(I_{rkc},V)$
by
![]() $\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
(on the right) multiplies
$\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
(on the right) multiplies
![]() $dv$
by
$dv$
by
![]() $|\det y|^{(rk-1)a}$
; conjugating
$|\det y|^{(rk-1)a}$
; conjugating
![]() $U^3$
by
$U^3$
by
![]() ${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
(on the right) multiplies
${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
(on the right) multiplies
![]() $du^3$
by
$du^3$
by
![]() $|\det x|^{(1-rk)b}$
; and
$|\det x|^{(1-rk)b}$
; and
 $$ \begin{align*} \langle\operatorname{\mathrm{diag}}(x,y),\epsilon\rangle&\mapsto \delta_R^{-1/2}(\operatorname{\mathrm{diag}}(x,y))\{\varphi(e),\varphi^{\vee}(\langle \operatorname{\mathrm{diag}}(x,y),\epsilon\rangle)\}_{M_R}\\ &=\epsilon|\det x|^{-b/2}|\det y|^{a/2}\omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle). \end{align*} $$
$$ \begin{align*} \langle\operatorname{\mathrm{diag}}(x,y),\epsilon\rangle&\mapsto \delta_R^{-1/2}(\operatorname{\mathrm{diag}}(x,y))\{\varphi(e),\varphi^{\vee}(\langle \operatorname{\mathrm{diag}}(x,y),\epsilon\rangle)\}_{M_R}\\ &=\epsilon|\det x|^{-b/2}|\det y|^{a/2}\omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle). \end{align*} $$
Therefore, when we shift
![]() $\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
to the left the integral becomes
$\mathfrak {e}_2(\operatorname {\mathrm {diag}}(x,y))$
to the left the integral becomes
 $$ \begin{align} &\int\limits_{V}\int\limits_{V}\int\limits_{U^3} \int\limits_{\operatorname{\mathrm{GL}}_b}\int\limits_{\operatorname{\mathrm{GL}}_a}\int\limits_{U^4}\int\limits_{U^1}\omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle |\det{x}|^{b/2-rkb}|\det{y}|^{rka-a/2}\\&\notag M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle \,{}^{w^{-1}\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(x,y)),1\rangle \\&\notag\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\ &\psi_{U}(u^1)\psi_{U}(u^4) \,du^1\,du^4\,dx\,dy\,du^3\,dv\,dv'.\notag \end{align} $$
$$ \begin{align} &\int\limits_{V}\int\limits_{V}\int\limits_{U^3} \int\limits_{\operatorname{\mathrm{GL}}_b}\int\limits_{\operatorname{\mathrm{GL}}_a}\int\limits_{U^4}\int\limits_{U^1}\omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle |\det{x}|^{b/2-rkb}|\det{y}|^{rka-a/2}\\&\notag M(s){f}^{\downarrow}( \langle \operatorname{\mathrm{diag}}(\delta^{\prime}_{a},\delta^{\prime}_{b})u^1u^4,1\rangle \,{}^{w^{-1}\operatorname{\mathrm{diag}}(I_{rkc},\kappa)}\langle\mathfrak{e}_2(\operatorname{\mathrm{diag}}(x,y)),1\rangle \\&\notag\langle w^{-1}u^3,1\rangle \langle\operatorname{\mathrm{diag}}(I_{rkc},\kappa v),1\rangle \langle\operatorname{\mathrm{diag}}(\kappa v',I_{rkc}),1\rangle,s)\nonumber\\ &\psi_{U}(u^1)\psi_{U}(u^4) \,du^1\,du^4\,dx\,dy\,du^3\,dv\,dv'.\notag \end{align} $$
(Cf. Integral (5.19).)
Denote the embedding
![]() $\operatorname {\mathrm {GL}}_l\times \operatorname {\mathrm {GL}}_l\hookrightarrow \operatorname {\mathrm {GL}}_{2rkl}$
in the construction of the
$\operatorname {\mathrm {GL}}_l\times \operatorname {\mathrm {GL}}_l\hookrightarrow \operatorname {\mathrm {GL}}_{2rkl}$
in the construction of the
![]() $\operatorname {\mathrm {GL}}_l^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral by
$\operatorname {\mathrm {GL}}_l^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integral by
![]() $(,)_l'$
, and identify
$(,)_l'$
, and identify
![]() $\operatorname {\mathrm {GL}}_{2rka}\times \operatorname {\mathrm {GL}}_{2rkb}$
with
$\operatorname {\mathrm {GL}}_{2rka}\times \operatorname {\mathrm {GL}}_{2rkb}$
with
![]() $M_{(2rka,2rkb)}$
. Then
$M_{(2rka,2rkb)}$
. Then
![]() $(x_1,x_2)_a'$
belongs to the top left
$(x_1,x_2)_a'$
belongs to the top left
![]() $\operatorname {\mathrm {GL}}_{2rka}$
block of
$\operatorname {\mathrm {GL}}_{2rka}$
block of
![]() $M_{(2rka,2rkb)}$
, and
$M_{(2rka,2rkb)}$
, and
![]() $(y_1,y_2)_b'$
to the bottom right
$(y_1,y_2)_b'$
to the bottom right
![]() $\operatorname {\mathrm {GL}}_{2rkb}$
block. We have
$\operatorname {\mathrm {GL}}_{2rkb}$
block. We have
We claim that the following analog of Equation (5.20) holds:
To this end, first observe that by Equation (2.52),
Therefore, we can consider x and y separately. Consider x first. Since
these elements commute in
![]() $H^{(m,r)}$
by Equation (2.52). It remains to check the conjugation by
$H^{(m,r)}$
by Equation (2.52). It remains to check the conjugation by
![]() $w^{-1}$
which is similar to the computation above, showing that the image of
$w^{-1}$
which is similar to the computation above, showing that the image of
![]() $M(s)$
is in the space of (5.40).
$M(s)$
is in the space of (5.40).
Regarding y, here
![]() $\operatorname {\mathrm {diag}}(I_{rkc},\kappa )$
does not commute with
$\operatorname {\mathrm {diag}}(I_{rkc},\kappa )$
does not commute with
![]() $\mathfrak {e}_2(\operatorname {\mathrm {diag}}(I_a,y))$
, but because
$\mathfrak {e}_2(\operatorname {\mathrm {diag}}(I_a,y))$
, but because
![]() $w^{-1}$
commutes with
$w^{-1}$
commutes with
![]() ${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(\operatorname {\mathrm {diag}}(I_a,y))$
. Hence, it remains to consider the conjugation of y by
${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(\operatorname {\mathrm {diag}}(I_a,y))$
. Hence, it remains to consider the conjugation of y by
![]() $\operatorname {\mathrm {diag}}(I_{rkc},\kappa )$
. For
$\operatorname {\mathrm {diag}}(I_{rkc},\kappa )$
. For
![]() $u_y^-\in N_{\operatorname {\mathrm {GL}}_b}^-$
and
$u_y^-\in N_{\operatorname {\mathrm {GL}}_b}^-$
and
![]() $v_y\in N_{\operatorname {\mathrm {GL}}_b}$
, we have
$v_y\in N_{\operatorname {\mathrm {GL}}_b}$
, we have
![]() ${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(u_y^-)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}^-$
and
${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(u_y^-)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}^-$
and
![]() ${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(v_y)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
. Hence, as with
${}^{\operatorname {\mathrm {diag}}(I_{rkc},\kappa )}\mathfrak {e}_2(v_y)\in N_{\operatorname {\mathrm {GL}}_{2rkc}}$
. Hence, as with
![]() $M(s)$
above, we reduce to the case of
$M(s)$
above, we reduce to the case of
![]() $t\in T_{\operatorname {\mathrm {GL}}_b}$
which follows from Proposition 2. This completes the proof of Equation (5.43).
$t\in T_{\operatorname {\mathrm {GL}}_b}$
which follows from Proposition 2. This completes the proof of Equation (5.43).
Now, by Equations (5.43) and (2.52), the integral (5.42) equals (cf. Integral (5.23))
 $$ \begin{align} &\int\limits_{V}\int\limits_{V}\int\limits_{U^3} \int\limits_{\operatorname{\mathrm{GL}}_b} \int\limits_{U^4} \int\limits_{\operatorname{\mathrm{GL}}_a} \int\limits_{U^1} \omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle |\det{x}|^{b/2-rkb}|\det{y}|^{rka-a/2}\\&\notag M(s){f}^{\downarrow}( \langle \delta^{\prime}_au^1,1\rangle\langle (I_a,x)_a',1\rangle \langle \delta^{\prime}_bu^4,1\rangle\langle (I_b,y)_b',1\rangle \langle w^{-1}u^3,1\rangle \langle k^{\bullet}\operatorname{\mathrm{diag}}(v',v),1\rangle,s)\nonumber\\&\psi_{U}(u^1)\psi_{U}(u^4) \,du^1\,dx\,du^4\,dy\,du^3\,dv\,dv'.\notag \end{align} $$
$$ \begin{align} &\int\limits_{V}\int\limits_{V}\int\limits_{U^3} \int\limits_{\operatorname{\mathrm{GL}}_b} \int\limits_{U^4} \int\limits_{\operatorname{\mathrm{GL}}_a} \int\limits_{U^1} \omega_a(\langle x,1\rangle)\omega_b(\langle y,1\rangle |\det{x}|^{b/2-rkb}|\det{y}|^{rka-a/2}\\&\notag M(s){f}^{\downarrow}( \langle \delta^{\prime}_au^1,1\rangle\langle (I_a,x)_a',1\rangle \langle \delta^{\prime}_bu^4,1\rangle\langle (I_b,y)_b',1\rangle \langle w^{-1}u^3,1\rangle \langle k^{\bullet}\operatorname{\mathrm{diag}}(v',v),1\rangle,s)\nonumber\\&\psi_{U}(u^1)\psi_{U}(u^4) \,du^1\,dx\,du^4\,dy\,du^3\,dv\,dv'.\notag \end{align} $$
The covering
![]() $\widetilde {M}_{(2rka,2rkb)}$
is isomorphic to the quotient of the direct product
$\widetilde {M}_{(2rka,2rkb)}$
is isomorphic to the quotient of the direct product
![]() $\operatorname {\mathrm {GL}}_{2rka}^{(m,r)}\times \operatorname {\mathrm {GL}}_{2rkb}^{(m,r)}$
by
$\operatorname {\mathrm {GL}}_{2rka}^{(m,r)}\times \operatorname {\mathrm {GL}}_{2rkb}^{(m,r)}$
by
![]() $\{(\epsilon _1,\epsilon _2)\in \mu _m^2:\epsilon _1\epsilon _2=1\}$
. According to the definition of the representation (5.40), the restriction of
$\{(\epsilon _1,\epsilon _2)\in \mu _m^2:\epsilon _1\epsilon _2=1\}$
. According to the definition of the representation (5.40), the restriction of
![]() $M(s){f}^{\downarrow }$
to
$M(s){f}^{\downarrow }$
to
![]() $\widetilde {M}_{(2rka,2rkb)}$
is a rational section of (cf. the representation (5.24))
$\widetilde {M}_{(2rka,2rkb)}$
is a rational section of (cf. the representation (5.24))
 $$ \begin{align*} &|\det|^{rkb-b/2}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka)}}^{\operatorname{\mathrm{GL}}_{2rka}^{(m,r)}} ((\mathcal{W}(\rho_a(\tau))\otimes\mathcal{W}(\rho_a(\tau')))\delta_{P_{(rka,rka)}}^{\alpha s/(rka)}) \\&\otimes|\det|^{-rka+a/2}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkb,rkb)}}^{\operatorname{\mathrm{GL}}_{2rkb}^{(m,r)}} ((\mathcal{W}(\rho_b(\tau))\otimes\mathcal{W}(\rho_b(\tau')))\delta_{P_{(rkb,rkb)}}^{\alpha s/(rkb)}). \end{align*} $$
$$ \begin{align*} &|\det|^{rkb-b/2}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rka,rka)}}^{\operatorname{\mathrm{GL}}_{2rka}^{(m,r)}} ((\mathcal{W}(\rho_a(\tau))\otimes\mathcal{W}(\rho_a(\tau')))\delta_{P_{(rka,rka)}}^{\alpha s/(rka)}) \\&\otimes|\det|^{-rka+a/2}\operatorname{\mathrm{Ind}}_{\widetilde{P}_{(rkb,rkb)}}^{\operatorname{\mathrm{GL}}_{2rkb}^{(m,r)}} ((\mathcal{W}(\rho_b(\tau))\otimes\mathcal{W}(\rho_b(\tau')))\delta_{P_{(rkb,rkb)}}^{\alpha s/(rkb)}). \end{align*} $$
The inner
![]() $du^1dx$
and
$du^1dx$
and
![]() $du^4dy$
integrals are the
$du^4dy$
integrals are the
![]() $\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
and
$\operatorname {\mathrm {GL}}_a^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
and
![]() $\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integrals, respectively. The
$\operatorname {\mathrm {GL}}_b^{(m,r)}\times \operatorname {\mathrm {GL}}_{k}^{(m,r)}$
integrals, respectively. The
![]() $du^3$
-integral is first seen to vanish unless
$du^3$
-integral is first seen to vanish unless
![]() $v,v'\in K_G$
, then since the section is unramified, the
$v,v'\in K_G$
, then since the section is unramified, the
![]() $dvdv'$
-integral equals the constant
$dvdv'$
-integral equals the constant
![]() $1$
; then the
$1$
; then the
![]() $du^3$
-integral vanishes outside
$du^3$
-integral vanishes outside
![]() $U^3\cap K_H$
, whence the whole outer integral can be separated from the integral
$U^3\cap K_H$
, whence the whole outer integral can be separated from the integral
![]() $du^1\,dx\,du^4\,dy$
, and it equals
$du^1\,dx\,du^4\,dy$
, and it equals
![]() $1$
. Finally, Integral (5.44) becomes the product
$1$
. Finally, Integral (5.44) becomes the product
where
![]() $f_{\mathcal {W}(\rho _a(\tau ))\otimes \mathcal {W}(\rho _a(\tau '))}$
and
$f_{\mathcal {W}(\rho _a(\tau ))\otimes \mathcal {W}(\rho _a(\tau '))}$
and
![]() $f_{\mathcal {W}(\rho _b(\tau ))\otimes \mathcal {W}(\rho _b(\tau '))}$
are the normalized unramified sections appearing in the statement of the lemma. The proof is complete up to the computation of
$f_{\mathcal {W}(\rho _b(\tau ))\otimes \mathcal {W}(\rho _b(\tau '))}$
are the normalized unramified sections appearing in the statement of the lemma. The proof is complete up to the computation of
![]() $d_{\tau ,\tau ',\vartheta ,a,b}(s)$
.
$d_{\tau ,\tau ',\vartheta ,a,b}(s)$
.
Put
![]() $H'=\operatorname {\mathrm {diag}}(I_{rka},\operatorname {\mathrm {GL}}_{rkc},I_{rkb})$
. The restriction of
$H'=\operatorname {\mathrm {diag}}(I_{rka},\operatorname {\mathrm {GL}}_{rkc},I_{rkb})$
. The restriction of
![]() ${f}^{\downarrow }$
(which is a section of the representation (5.34)) to
${f}^{\downarrow }$
(which is a section of the representation (5.34)) to
![]() $\widetilde {H'}=\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(see Equation (2.52)) is the normalized unramified section of the unramified representation of
$\widetilde {H'}=\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(see Equation (2.52)) is the normalized unramified section of the unramified representation of
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
induced from
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
induced from
![]() $\widetilde {P}_{(rkb,rka)}$
and
$\widetilde {P}_{(rkb,rka)}$
and
 $$ \begin{align*} &\mathrm{I}_{\operatorname{\mathrm{GL}}_{rkb}^{(m,r)}}(\vartheta,\otimes_{1\leq i\leq k,1\leq j\leq rb}\chi_i|~|^{\alpha s+(a-b)/2+j/r-1/(2r)}) \\ &\quad \otimes \mathrm{I}_{\operatorname{\mathrm{GL}}_{rka}^{(m,r)}}(\vartheta,\otimes_{1\leq i\leq k,1\leq j\leq ra}\chi_i^{\prime}|~|^{-\alpha s-c/2+j/r-1/(2r)}). \end{align*} $$
$$ \begin{align*} &\mathrm{I}_{\operatorname{\mathrm{GL}}_{rkb}^{(m,r)}}(\vartheta,\otimes_{1\leq i\leq k,1\leq j\leq rb}\chi_i|~|^{\alpha s+(a-b)/2+j/r-1/(2r)}) \\ &\quad \otimes \mathrm{I}_{\operatorname{\mathrm{GL}}_{rka}^{(m,r)}}(\vartheta,\otimes_{1\leq i\leq k,1\leq j\leq ra}\chi_i^{\prime}|~|^{-\alpha s-c/2+j/r-1/(2r)}). \end{align*} $$
The adjoint action of
![]() $\operatorname {\mathrm {GL}}_{rkb}(\mathbb {C})\times \operatorname {\mathrm {GL}}_{rka}(\mathbb {C})$
on the Lie algebra of the L-group of
$\operatorname {\mathrm {GL}}_{rkb}(\mathbb {C})\times \operatorname {\mathrm {GL}}_{rka}(\mathbb {C})$
on the Lie algebra of the L-group of
![]() $U^2$
is
$U^2$
is
![]() $\text {st}\otimes \text {st}^{\vee }$
. As in the proof of Lemma 79, the value of
$\text {st}\otimes \text {st}^{\vee }$
. As in the proof of Lemma 79, the value of
![]() $d_{\tau ,\tau ',\vartheta ,a,b}(s)$
can be computed using [Reference GaoGao18b, Theorem 7.10], and we obtain the product (5.29).
$d_{\tau ,\tau ',\vartheta ,a,b}(s)$
can be computed using [Reference GaoGao18b, Theorem 7.10], and we obtain the product (5.29).
5.3 The
 $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral
In this section we compute the
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral with unramified data. We proceed with the setup and notation of § 5.2, now with
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral with unramified data. We proceed with the setup and notation of § 5.2, now with
![]() $c=n=1$
. In particular,
$c=n=1$
. In particular,
![]() $G=\operatorname {\mathrm {GL}}_1$
,
$G=\operatorname {\mathrm {GL}}_1$
,
![]() $H=\operatorname {\mathrm {GL}}_{2rk}$
,
$H=\operatorname {\mathrm {GL}}_{2rk}$
,
![]() $P=P_{(rk,rk)}$
,
$P=P_{(rk,rk)}$
,
![]() $U_P=V_{(rk,rk)}$
,
$U_P=V_{(rk,rk)}$
,
![]() $U=V_{(1^{(rk-1)},2,1^{(rk-1)})}$
and the character
$U=V_{(1^{(rk-1)},2,1^{(rk-1)})}$
and the character
![]() $\psi _U$
given by Equation (4.30) becomes
$\psi _U$
given by Equation (4.30) becomes
 $$ \begin{align*} \psi_U\left(\left(\begin{smallmatrix}v&x&y\\&I_{2}&z\\&&v'\end{smallmatrix}\right)\right)=\psi\left(-\sum_{i=1}^{rk-2}v_{i,i+1}-x_{rk-1,1}+z_{1,1} -\sum_{i=1}^{rk-2}v^{\prime}_{i,i+1}\right), \qquad v,v'\in N_{\operatorname{\mathrm{GL}}_{rk-1}}. \end{align*} $$
$$ \begin{align*} \psi_U\left(\left(\begin{smallmatrix}v&x&y\\&I_{2}&z\\&&v'\end{smallmatrix}\right)\right)=\psi\left(-\sum_{i=1}^{rk-2}v_{i,i+1}-x_{rk-1,1}+z_{1,1} -\sum_{i=1}^{rk-2}v^{\prime}_{i,i+1}\right), \qquad v,v'\in N_{\operatorname{\mathrm{GL}}_{rk-1}}. \end{align*} $$
Also,
![]() $\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
,
$\tau \subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi )$
,
![]() $\mathcal {W}(\rho _1(\tau ))$
is the
$\mathcal {W}(\rho _1(\tau ))$
is the
![]() $(rk,1)$
model (Whittaker model) of
$(rk,1)$
model (Whittaker model) of
![]() $\rho _1(\tau )$
and similarly for
$\rho _1(\tau )$
and similarly for
![]() $\tau '$
, for example,
$\tau '$
, for example,
![]() $\tau '\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ')$
. The representations
$\tau '\subset \mathrm {I}_{\operatorname {\mathrm {GL}}_k^{(m,r)}}(\vartheta ,\chi ')$
. The representations
![]() $\rho _1(\tau )$
and
$\rho _1(\tau )$
and
![]() $\rho _1(\tau ')$
are assumed to satisfy Equation (4.34).
$\rho _1(\tau ')$
are assumed to satisfy Equation (4.34).
Let
![]() $f=f_{\mathcal {W}(\rho _1(\tau ))\otimes \mathcal {W}(\rho _1(\tau '))}$
be a standard section of
$f=f_{\mathcal {W}(\rho _1(\tau ))\otimes \mathcal {W}(\rho _1(\tau '))}$
be a standard section of
Since
![]() $c=1$
,
$c=1$
,
![]() $\pi =\operatorname {\mathrm {Ind}}_{\widetilde {A}}^{G^{(m,r)}}(\varepsilon \otimes \vartheta \mu )$
(see § 2.8), and
$\pi =\operatorname {\mathrm {Ind}}_{\widetilde {A}}^{G^{(m,r)}}(\varepsilon \otimes \vartheta \mu )$
(see § 2.8), and
![]() $\omega $
is a matrix coefficient of
$\omega $
is a matrix coefficient of
![]() $\pi ^{\vee }$
.
$\pi ^{\vee }$
.
In this section, we compute the integral
![]() $Z(s,\omega ,f)$
, when
$Z(s,\omega ,f)$
, when
![]() $\omega $
and f are normalized and unramified, by relating it to another integral ((5.52) below) which is computed using the Rankin–Selberg integral of § 3.7.
$\omega $
and f are normalized and unramified, by relating it to another integral ((5.52) below) which is computed using the Rankin–Selberg integral of § 3.7.
First, consider the
![]() $\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral (4.35), now with arbitrary
$\operatorname {\mathrm {GL}}_1^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral (4.35), now with arbitrary
![]() $\omega $
and standard section f. It is absolutely convergent, in a right half-plane independent of the data, and by Proposition 75 can be regarded as a morphism in the space (4.36) (with
$\omega $
and standard section f. It is absolutely convergent, in a right half-plane independent of the data, and by Proposition 75 can be regarded as a morphism in the space (4.36) (with
![]() $c=1$
), namely in
$c=1$
), namely in
Lemma 81. For all but a finite set of values of
![]() $q^{-s}$
, the space (5.47) is at most one-dimensional.
$q^{-s}$
, the space (5.47) is at most one-dimensional.
Proof. The proof in the linear case was given in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Lemma 35], and the situation here is similar. One can adapt that proof essentially by replacing k with
![]() $rk$
, but in fact the lemma now follows immediately from [Reference Gourevitch and KaplanGK23, Theorem 3.1] where the uniqueness of the space (4.36) outside a finite set of values of
$rk$
, but in fact the lemma now follows immediately from [Reference Gourevitch and KaplanGK23, Theorem 3.1] where the uniqueness of the space (4.36) outside a finite set of values of
![]() $q^{-s}$
was proved, for all c.
$q^{-s}$
was proved, for all c.
Corollary 82. For any rational section f,
![]() $Z(s,\omega ,f)$
admits meromorphic continuation to a rational function in
$Z(s,\omega ,f)$
admits meromorphic continuation to a rational function in
![]() $q^{-s}$
.
$q^{-s}$
.
Proof. This follows from Bernstein’s continuation principle (in [Reference BanksBan98a]) because Lemma 81 provides uniqueness and one can choose data for which the integral becomes a constant.
We denote a general element of
![]() $V_{(rk,rk)}$
by
$V_{(rk,rk)}$
by
 $$ \begin{align*} [\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]=\left(\begin{smallmatrix}I_{rk-1}&&y&z\\&1&u&x\\&&1\\&&&I_{rk-1}\end{smallmatrix}\right). \end{align*} $$
$$ \begin{align*} [\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]=\left(\begin{smallmatrix}I_{rk-1}&&y&z\\&1&u&x\\&&1\\&&&I_{rk-1}\end{smallmatrix}\right). \end{align*} $$
Then
![]() $\delta _1=[\begin {smallmatrix}0&0\\1&0\end {smallmatrix}]$
,
$\delta _1=[\begin {smallmatrix}0&0\\1&0\end {smallmatrix}]$
,
![]() $U_0$
is the subgroup
$U_0$
is the subgroup
![]() $\{[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]\}$
, where
$\{[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]\}$
, where
![]() $y,z$
and x are arbitrary, and if
$y,z$
and x are arbitrary, and if
![]() $x=(x_1,\ldots ,x_{rk-1})$
,
$x=(x_1,\ldots ,x_{rk-1})$
,
![]() $\psi _U([\begin {smallmatrix}y&z\\0&x\end {smallmatrix}])=\psi (x_1)$
.
$\psi _U([\begin {smallmatrix}y&z\\0&x\end {smallmatrix}])=\psi (x_1)$
.
We claim that the representation (5.46) admits a unique Whittaker model. This follows from the geometric lemma [Reference Bernstein and ZelevinskyBZ77, Theorem 5.2] because
![]() $\mathcal {W}(\rho _1(\tau ))\otimes \mathcal {W}(\rho _1(\tau '))$
admits a unique Whittaker model (see also [Reference BanksBan98b] for the covering groups of [Reference Kazhdan and PattersonKP84]). In fact, consider the filtration of the representation (5.46) according to the space
$\mathcal {W}(\rho _1(\tau ))\otimes \mathcal {W}(\rho _1(\tau '))$
admits a unique Whittaker model (see also [Reference BanksBan98b] for the covering groups of [Reference Kazhdan and PattersonKP84]). In fact, consider the filtration of the representation (5.46) according to the space
![]() $P\backslash H/N_H$
. Then as in the linear case one shows that, for a generic character
$P\backslash H/N_H$
. Then as in the linear case one shows that, for a generic character
![]() $\psi '$
of
$\psi '$
of
![]() $N_{H}$
,
$N_{H}$
,
![]() $\psi '|_{{}^{h^{-1}}V_{(rk,rk)}\cap N_H}\ne 1$
for any
$\psi '|_{{}^{h^{-1}}V_{(rk,rk)}\cap N_H}\ne 1$
for any
![]() $h\in H$
such that
$h\in H$
such that
![]() $PhN_H\ne P\delta _0N_H$
. This verifies condition
$PhN_H\ne P\delta _0N_H$
. This verifies condition
![]() $(\bigstar )$
of [Reference Bernstein and ZelevinskyBZ77, § 5] for all but one double coset, and it remains to consider
$(\bigstar )$
of [Reference Bernstein and ZelevinskyBZ77, § 5] for all but one double coset, and it remains to consider
![]() $\delta _0$
. In this case the statement reduces to the uniqueness of the Whittaker model for the tensor product.
$\delta _0$
. In this case the statement reduces to the uniqueness of the Whittaker model for the tensor product.
We have the standard Jacquet integral on the space of the representation (5.46), defined for a holomorphic section f by
 $$ \begin{align} \int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle ,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
$$ \begin{align} \int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle ,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
This integral is absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, and one can choose f such that Integral (5.48) is absolutely convergent and equals
$\operatorname {\mathrm {Re}}(s)\gg 0$
, and one can choose f such that Integral (5.48) is absolutely convergent and equals
![]() $1$
, for all s. Since there is (in particular) at most one Whittaker model on (5.46), Bernstein’s continuation principal ([Reference BanksBan98a]) implies that Integral (5.48) admits analytic continuation to a polynomial function in
$1$
, for all s. Since there is (in particular) at most one Whittaker model on (5.46), Bernstein’s continuation principal ([Reference BanksBan98a]) implies that Integral (5.48) admits analytic continuation to a polynomial function in
![]() $q^{-s}$
and
$q^{-s}$
and
![]() $q^s$
, that is, (5.48) belongs to
$q^s$
, that is, (5.48) belongs to
![]() $\mathbb {C}[q^{-s},q^s]$
. This continuation is not identically zero for any s. Consequently, it is a realization of the unique (up to scaling) Whittaker functional on (5.46), with respect to the character
$\mathbb {C}[q^{-s},q^s]$
. This continuation is not identically zero for any s. Consequently, it is a realization of the unique (up to scaling) Whittaker functional on (5.46), with respect to the character
 $$ \begin{align} \psi(\operatorname{\mathrm{diag}}(d,d')[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}])=\psi\left(\sum_{i=1}^{rk-1}d_{i,i+1}-u+\sum_{i=1}^{rk-1}d^{\prime}_{i,i+1}\right),\qquad d,d'\in N_{\operatorname{\mathrm{GL}}_{rk}}. \end{align} $$
$$ \begin{align} \psi(\operatorname{\mathrm{diag}}(d,d')[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}])=\psi\left(\sum_{i=1}^{rk-1}d_{i,i+1}-u+\sum_{i=1}^{rk-1}d^{\prime}_{i,i+1}\right),\qquad d,d'\in N_{\operatorname{\mathrm{GL}}_{rk}}. \end{align} $$
(This argument also proves the existence of the Whittaker model for (5.46).) The corresponding Whittaker model of the representation (5.46) is spanned by the functions
 $$ \begin{align} W_f(h,s)=\int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle h,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
$$ \begin{align} W_f(h,s)=\int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle h,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
Then by definition the Whittaker model of
![]() $\mathrm {I}(\mathcal {W}(\rho _1(\tau )),\mathcal {W}(\rho _1(\tau ')),s)^{*}$
with respect to the inverse of the character (5.49) is spanned by functions
$\mathrm {I}(\mathcal {W}(\rho _1(\tau )),\mathcal {W}(\rho _1(\tau ')),s)^{*}$
with respect to the inverse of the character (5.49) is spanned by functions
 $$ \begin{align} W_f^{*}(h,s)=W_f({}^{*}h,s)=\int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\,{}^{*}h,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
$$ \begin{align} W_f^{*}(h,s)=W_f({}^{*}h,s)=\int\limits_{V_{(rk,rk)}} f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\,{}^{*}h,s)\psi(u)\,dx\,dy\,dz\,du. \end{align} $$
If
![]() $rk>1$
, denote
$rk>1$
, denote
For
![]() $rk=1$
, we take
$rk=1$
, we take
![]() $[t,v]=w'=I_2$
. Since
$[t,v]=w'=I_2$
. Since
![]() $[t,v]\in N_{H}^-$
, we fix the splitting
$[t,v]\in N_{H}^-$
, we fix the splitting
![]() $\langle v^-,\varsigma (v^-)\rangle $
of
$\langle v^-,\varsigma (v^-)\rangle $
of
![]() $N_{H}^-$
. Then
$N_{H}^-$
. Then
![]() $[t,v]\mapsto \langle [t,v],\varsigma ([t,v])\rangle $
is the splitting of the subgroup of elements
$[t,v]\mapsto \langle [t,v],\varsigma ([t,v])\rangle $
is the splitting of the subgroup of elements
![]() $[t,v]$
, which is
$[t,v]$
, which is
![]() $\operatorname {\mathrm {diag}}(I_{rk},V_{(rk-1,1)}^-)$
. Also, let
$\operatorname {\mathrm {diag}}(I_{rk},V_{(rk-1,1)}^-)$
. Also, let
![]() $\zeta \in \mathbb {C}$
.
$\zeta \in \mathbb {C}$
.
For any matrix coefficient
![]() $\omega $
of
$\omega $
of
![]() $\pi ^{\vee }$
and a holomorphic section f of the representation (5.46), consider the integral
$\pi ^{\vee }$
and a holomorphic section f of the representation (5.46), consider the integral
 $$ \begin{align} &\Psi(\zeta,s,\omega,f)\\&\nonumber=\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a. \end{align} $$
$$ \begin{align} &\Psi(\zeta,s,\omega,f)\\&\nonumber=\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a. \end{align} $$
In the linear case, this is [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, (3.42)] (with
![]() $r=1$
), and note that in loc. cit.
$r=1$
), and note that in loc. cit.
![]() $\omega $
was replaced by
$\omega $
was replaced by
![]() $\pi ^{-1}$
because there
$\pi ^{-1}$
because there
![]() $\pi ^{\vee }$
is one-dimensional. Also, if
$\pi ^{\vee }$
is one-dimensional. Also, if
![]() $rk=1$
, the
$rk=1$
, the
![]() $dtdv$
integration is omitted.
$dtdv$
integration is omitted.
Proposition 83. The integral (5.52) is well defined, absolutely convergent in
![]() $\operatorname {\mathrm {Re}}(\zeta )\leq B\operatorname {\mathrm {Re}}(s)+D$
, where B and D are real constants depending only on
$\operatorname {\mathrm {Re}}(\zeta )\leq B\operatorname {\mathrm {Re}}(s)+D$
, where B and D are real constants depending only on
![]() $\pi $
and
$\pi $
and
![]() $\tau $
, and in this domain belongs to the space (5.47), where
$\tau $
, and in this domain belongs to the space (5.47), where
![]() $\pi $
is replaced by
$\pi $
is replaced by
![]() $|~|^{-\zeta }\pi $
. Consequently, it admits meromorphic continuation which belongs to
$|~|^{-\zeta }\pi $
. Consequently, it admits meromorphic continuation which belongs to
![]() $\mathbb {C}(q^{-\zeta },q^{-s})$
. Moreover, outside finitely many values of
$\mathbb {C}(q^{-\zeta },q^{-s})$
. Moreover, outside finitely many values of
![]() $q^{-s}$
, the continuation with
$q^{-s}$
, the continuation with
![]() $\zeta =0$
belongs to (5.47).
$\zeta =0$
belongs to (5.47).
Proof. Since
![]() $W_f$
is genuine and
$W_f$
is genuine and
![]() $\omega $
is antigenuine, the integrand factors through
$\omega $
is antigenuine, the integrand factors through
![]() $F^{*}$
. Also, by Equation (2.52),
$F^{*}$
. Also, by Equation (2.52),
and because
the
![]() $d^{*}a$
-integral is a right-
$d^{*}a$
-integral is a right-
![]() $F^{*}$
-invariant functional.
$F^{*}$
-invariant functional.
It is straightforward to prove the convergence of this integral in a domain of the form
![]() $\operatorname {\mathrm {Re}}(\zeta )\leq B\operatorname {\mathrm {Re}}(s)+D$
: The integrand vanishes unless v and t belong in (large) compact subsets, and since the Whittaker function is smooth, we reduce to an integral over
$\operatorname {\mathrm {Re}}(\zeta )\leq B\operatorname {\mathrm {Re}}(s)+D$
: The integrand vanishes unless v and t belong in (large) compact subsets, and since the Whittaker function is smooth, we reduce to an integral over
![]() $F^{*}$
. The integrand vanishes unless a is bounded from below, then the usual bounds on the exponents of
$F^{*}$
. The integrand vanishes unless a is bounded from below, then the usual bounds on the exponents of
![]() $W_f$
can be used. See [Reference Godement and JacquetGJ72, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83] for similar arguments.
$W_f$
can be used. See [Reference Godement and JacquetGJ72, Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83] for similar arguments.
Next, we prove that in
![]() $\operatorname {\mathrm {Re}}(\zeta )\ll 0$
, the integral belongs to
$\operatorname {\mathrm {Re}}(\zeta )\ll 0$
, the integral belongs to
First, we show that
Write
![]() $u\in U$
in the form
$u\in U$
in the form
![]() $u=\operatorname {\mathrm {diag}}(d,d')[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
, where
$u=\operatorname {\mathrm {diag}}(d,d')[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
, where
![]() $d,d'\in N_{\operatorname {\mathrm {GL}}_{rk}}$
. By Equation (2.52) the elements
$d,d'\in N_{\operatorname {\mathrm {GL}}_{rk}}$
. By Equation (2.52) the elements
![]() $w'$
,
$w'$
,
![]() $[t,v]$
and
$[t,v]$
and
![]() $\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
commute with
$\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
commute with
![]() $\operatorname {\mathrm {diag}}(d,I_{rk})$
in
$\operatorname {\mathrm {diag}}(d,I_{rk})$
in
![]() $H^{(m,r)}$
. Hence, because of the equivariance property of
$H^{(m,r)}$
. Hence, because of the equivariance property of
![]() $W_f$
with respect to the character (5.49), the equivariance property under
$W_f$
with respect to the character (5.49), the equivariance property under
![]() $\operatorname {\mathrm {diag}}(d,I_{rk})$
holds. Since the conjugation of
$\operatorname {\mathrm {diag}}(d,I_{rk})$
holds. Since the conjugation of
![]() $[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
by the elements
$[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
by the elements
![]() $w'$
,
$w'$
,
![]() $[t,v]$
and
$[t,v]$
and
![]() $\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
still belongs to
$\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
still belongs to
![]() $N_{H}$
(even to
$N_{H}$
(even to
![]() $V_{(rk,rk)}$
), we can use Equation (2.10) to extend this conjugation to
$V_{(rk,rk)}$
), we can use Equation (2.10) to extend this conjugation to
![]() $H^{(m,r)}$
, and since
$H^{(m,r)}$
, and since
 $$ \begin{align*} {}^{w'}[\begin{smallmatrix}y&z\\0&x\end{smallmatrix}]=\left(\begin{smallmatrix}I_{rk-1}&&z&y\\&1&x&0\\&&I_{rk-1}\\&&&1\end{smallmatrix}\right), \end{align*} $$
$$ \begin{align*} {}^{w'}[\begin{smallmatrix}y&z\\0&x\end{smallmatrix}]=\left(\begin{smallmatrix}I_{rk-1}&&z&y\\&1&x&0\\&&I_{rk-1}\\&&&1\end{smallmatrix}\right), \end{align*} $$
the equivariance property under
![]() $[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
holds as well (see Definition (5.49)). Regarding
$[\begin {smallmatrix}y&z\\0&x\end {smallmatrix}]$
holds as well (see Definition (5.49)). Regarding
![]() $d'$
, first write
$d'$
, first write
Then by Equation (2.11),
Therefore, we can change variables in t and v to obtain invariance under the first row of
![]() $d'$
, as required. Regarding
$d'$
, as required. Regarding
![]() $d"$
, here
$d"$
, here
![]() ${}^{w'}\operatorname {\mathrm {diag}}(I_{rk+1},d")\in N_{H}$
so that we can conjugate by
${}^{w'}\operatorname {\mathrm {diag}}(I_{rk+1},d")\in N_{H}$
so that we can conjugate by
![]() $w'$
without introducing a root of unity. Then
$w'$
without introducing a root of unity. Then
![]() ${}^{w'}\operatorname {\mathrm {diag}}(I_{rk+1},d")=\operatorname {\mathrm {diag}}(I_{rk},d",1)$
normalizes
${}^{w'}\operatorname {\mathrm {diag}}(I_{rk+1},d")=\operatorname {\mathrm {diag}}(I_{rk},d",1)$
normalizes
![]() $\operatorname {\mathrm {diag}}(I_{rk},V_{(rk-1,1)}^-)$
hence by the analog of Equation (2.10) (use Equation (2.4) with
$\operatorname {\mathrm {diag}}(I_{rk},V_{(rk-1,1)}^-)$
hence by the analog of Equation (2.10) (use Equation (2.4) with
![]() $Y=N_H^-$
),
$Y=N_H^-$
),
Here,
![]() $t_{d"}$
and
$t_{d"}$
and
![]() $v_{d"}$
depend on
$v_{d"}$
depend on
![]() $d"$
, and we can change variables. We see that the l.h.s. of Equation (5.54) with
$d"$
, and we can change variables. We see that the l.h.s. of Equation (5.54) with
![]() $u=\operatorname {\mathrm {diag}}(I_{rk},d')$
becomes
$u=\operatorname {\mathrm {diag}}(I_{rk},d')$
becomes
 $$ \begin{align*} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f( \langle\operatorname{\mathrm{diag}}(I_{rk},d",1),1\rangle\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\\&\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a. \end{align*} $$
$$ \begin{align*} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f( \langle\operatorname{\mathrm{diag}}(I_{rk},d",1),1\rangle\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\\&\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a. \end{align*} $$
Again, we obtain
![]() $\psi _U^{-1}(\operatorname {\mathrm {diag}}(I_{rk},d'))$
by Definition (5.49). This completes the verification of Equation (5.54).
$\psi _U^{-1}(\operatorname {\mathrm {diag}}(I_{rk},d'))$
by Definition (5.49). This completes the verification of Equation (5.54).
Write
![]() $\omega (g)=\pi ^{\vee }(g)\xi ^{\vee }(\xi )$
, where
$\omega (g)=\pi ^{\vee }(g)\xi ^{\vee }(\xi )$
, where
![]() $\xi ^{\vee }$
(resp.,
$\xi ^{\vee }$
(resp.,
![]() $\xi $
) belongs to the space of
$\xi $
) belongs to the space of
![]() $\pi ^{\vee }$
(resp.,
$\pi ^{\vee }$
(resp.,
![]() $\pi $
). Let
$\pi $
). Let
![]() $g_1,g_2\in G$
, and denote
$g_1,g_2\in G$
, and denote
![]() $\omega _{g_1,g_2}(g)=\pi ^{\vee }(gg_2)\xi ^{\vee }(\pi (g_1)\xi )$
. We turn to prove
$\omega _{g_1,g_2}(g)=\pi ^{\vee }(gg_2)\xi ^{\vee }(\pi (g_1)\xi )$
. We turn to prove
We use Proposition 2 to write
 $$ \begin{align*} &\Psi(\zeta,s,\omega_{\langle g_1,1\rangle,\langle g_2,1\rangle},(\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\cdot f)\\&= \int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle \mathfrak{e}_2(a),1\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s) \\&\quad\pi^{\vee}(\langle a,1\rangle\langle g_2,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) |a|^{\zeta}\,dt\,dv\,d^{*}a. \end{align*} $$
$$ \begin{align*} &\Psi(\zeta,s,\omega_{\langle g_1,1\rangle,\langle g_2,1\rangle},(\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\cdot f)\\&= \int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle \mathfrak{e}_2(a),1\rangle\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle,s) \\&\quad\pi^{\vee}(\langle a,1\rangle\langle g_2,1\rangle)\xi^{\vee}(\pi(\langle g_1,1\rangle)\xi) |a|^{\zeta}\,dt\,dv\,d^{*}a. \end{align*} $$
Now, changing
![]() $a\mapsto ag_2^{-1}$
then
$a\mapsto ag_2^{-1}$
then
![]() $a\mapsto g_1a$
(as in the proof of Proposition 75) and using Equation (4.31) we obtain
$a\mapsto g_1a$
(as in the proof of Proposition 75) and using Equation (4.31) we obtain
 $$ \begin{align*} &|g_1|^{\zeta}|g_2|^{-\zeta}\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle (g_1,g_1),1\rangle\langle \mathfrak{e}_2(a),1\rangle,s) \omega(\langle a,1\rangle) |a|^{\zeta}\,dt\,dv\,d^{*}a. \end{align*} $$
$$ \begin{align*} &|g_1|^{\zeta}|g_2|^{-\zeta}\int\limits_{F^{*}}\int\limits_{F^{rk-2}}\int\limits_{F} W_f(\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle (g_1,g_1),1\rangle\langle \mathfrak{e}_2(a),1\rangle,s) \omega(\langle a,1\rangle) |a|^{\zeta}\,dt\,dv\,d^{*}a. \end{align*} $$
Since
![]() $(g_1,g_1)$
belongs to the center of H, it commutes with
$(g_1,g_1)$
belongs to the center of H, it commutes with
![]() $w'$
and
$w'$
and
![]() $[t,v]$
. In
$[t,v]$
. In
![]() $H^{(m,r)}$
,
$H^{(m,r)}$
,
![]() $(g_1,g_1)$
commutes with
$(g_1,g_1)$
commutes with
![]() $w'$
by Proposition 2 and with
$w'$
by Proposition 2 and with
![]() $[v,t]$
by Equation (2.10). Then by virtue of Equation (5.51), Equation (2.10), Proposition 2 and assumption (4.34), we see that
$[v,t]$
by Equation (2.10). Then by virtue of Equation (5.51), Equation (2.10), Proposition 2 and assumption (4.34), we see that
This completes the proof of Equation (5.55), and we have thus shown that
![]() $\Psi (\zeta ,s,\omega ,f)$
belongs to the space (5.47), where
$\Psi (\zeta ,s,\omega ,f)$
belongs to the space (5.47), where
![]() $\pi $
is replaced by
$\pi $
is replaced by
![]() $|~|^{-\zeta }\pi $
.
$|~|^{-\zeta }\pi $
.
We deduce the meromorphic continuation using Bernstein’s continuation principle. In general, consider the group
![]() $\operatorname {\mathrm {GL}}_l$
, the generic character of
$\operatorname {\mathrm {GL}}_l$
, the generic character of
![]() $N_{\operatorname {\mathrm {GL}}_l}$
given by
$N_{\operatorname {\mathrm {GL}}_l}$
given by
![]() $\psi (v)=\psi (\sum _{i=1}^{l-1}v_{i,i+1})$
, and the subgroup
$\psi (v)=\psi (\sum _{i=1}^{l-1}v_{i,i+1})$
, and the subgroup
![]() $\mathscr {P}_l<P_{(l-1,1)}$
of matrices with the last row
$\mathscr {P}_l<P_{(l-1,1)}$
of matrices with the last row
![]() $(0,\ldots ,0,1)$
, that is, the so-called mirabolic subgroup. By [Reference Bernstein and ZelevinskyBZ76, 5.15], if
$(0,\ldots ,0,1)$
, that is, the so-called mirabolic subgroup. By [Reference Bernstein and ZelevinskyBZ76, 5.15], if
![]() $\vartheta $
is a smooth representation of
$\vartheta $
is a smooth representation of
![]() $\mathscr {P}_l$
affording at least one Whittaker model (a nondegenerate representation in the terminology of ibid.), then
$\mathscr {P}_l$
affording at least one Whittaker model (a nondegenerate representation in the terminology of ibid.), then
![]() $\vartheta $
admits at least one subrepresentation
$\vartheta $
admits at least one subrepresentation
![]() $\operatorname {\mathrm {ind}}_{N_{\operatorname {\mathrm {GL}}_l}}^{\mathscr {P}_l}(\psi )$
. This result extends to
$\operatorname {\mathrm {ind}}_{N_{\operatorname {\mathrm {GL}}_l}}^{\mathscr {P}_l}(\psi )$
. This result extends to
![]() $\operatorname {\mathrm {GL}}_l^{(m,r)}$
: The main points to note are that the functors
$\operatorname {\mathrm {GL}}_l^{(m,r)}$
: The main points to note are that the functors
![]() $\Psi ^-=J_{V_{(l-1,1)}}$
,
$\Psi ^-=J_{V_{(l-1,1)}}$
,
![]() $\Phi ^-=J_{V_{(l-1,1)},\psi }$
,
$\Phi ^-=J_{V_{(l-1,1)},\psi }$
,
![]() $\Psi ^+(\cdot )=\operatorname {\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{l-1}^{(m,r)}V_{(l-1,1)}}^{\widetilde {\mathscr {P}}_l}(\cdot \otimes 1)$
and
$\Psi ^+(\cdot )=\operatorname {\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{l-1}^{(m,r)}V_{(l-1,1)}}^{\widetilde {\mathscr {P}}_l}(\cdot \otimes 1)$
and
![]() $\Phi ^+(\cdot )=\operatorname {\mathrm {ind}}_{\widetilde {\mathscr {P}}_{l-1}V_{(l-1,1)}}^{\widetilde {\mathscr {P}}_l}(\cdot \otimes \psi )$
carry genuine representations into genuine representations, are still exact, and
$\Phi ^+(\cdot )=\operatorname {\mathrm {ind}}_{\widetilde {\mathscr {P}}_{l-1}V_{(l-1,1)}}^{\widetilde {\mathscr {P}}_l}(\cdot \otimes \psi )$
carry genuine representations into genuine representations, are still exact, and
![]() $\widetilde {\mathscr {P}}_l$
acts on the group of characters of
$\widetilde {\mathscr {P}}_l$
acts on the group of characters of
![]() $V_{(l-1,1)}$
with two orbits. We deduce that
$V_{(l-1,1)}$
with two orbits. We deduce that
![]() $\operatorname {\mathrm {ind}}_{N_{H}}^{\widetilde {\mathscr {P}}_{2rk}}(\psi )$
is a subrepresentation of
$\operatorname {\mathrm {ind}}_{N_{H}}^{\widetilde {\mathscr {P}}_{2rk}}(\psi )$
is a subrepresentation of
![]() $\mathrm {I}(\mathcal {W}(\rho _1(\tau )),\mathcal {W}(\rho _1(\tau ')),s)$
. Furthermore, we can redefine
$\mathrm {I}(\mathcal {W}(\rho _1(\tau )),\mathcal {W}(\rho _1(\tau ')),s)$
. Furthermore, we can redefine
![]() $\mathscr {P}_l$
to be the subgroup of
$\mathscr {P}_l$
to be the subgroup of
![]() $P_{(1,l-1)}$
with the first row
$P_{(1,l-1)}$
with the first row
![]() $(1,0,\ldots ,0)$
, and obtain similar results.
$(1,0,\ldots ,0)$
, and obtain similar results.
Therefore, we can take f such that
![]() $W_f|_{\widetilde {\mathscr {P}}_{2rk}}$
is a genuine smooth function, whose support is contained in a small compact open neighborhood of the identity (with
$W_f|_{\widetilde {\mathscr {P}}_{2rk}}$
is a genuine smooth function, whose support is contained in a small compact open neighborhood of the identity (with
![]() $\mathscr {P}_{2rk}<P_{(1,2rk-1)}$
). Since
$\mathscr {P}_{2rk}<P_{(1,2rk-1)}$
). Since
![]() $\operatorname {\mathrm {diag}}(I_{2rk-1},a)[t,v]w'$
belong to
$\operatorname {\mathrm {diag}}(I_{2rk-1},a)[t,v]w'$
belong to
![]() $\mathscr {P}_{2rk}$
, there exist data f and
$\mathscr {P}_{2rk}$
, there exist data f and
![]() $\omega $
such that
$\omega $
such that
![]() $\Psi (\zeta ,s,\omega ,f)$
is absolutely convergent and equals
$\Psi (\zeta ,s,\omega ,f)$
is absolutely convergent and equals
![]() $1$
, for all
$1$
, for all
![]() $\zeta $
and s. Now, by Lemma 81, the space (5.53) is at most one-dimensional outside finitely many values of
$\zeta $
and s. Now, by Lemma 81, the space (5.53) is at most one-dimensional outside finitely many values of
![]() $q^{-\zeta }$
and
$q^{-\zeta }$
and
![]() $q^{-s}$
(in the statement we had
$q^{-s}$
(in the statement we had
![]() $\zeta $
fixed, but the proof implies this more general result), then by Bernstein’s continuation principle ([Reference BanksBan98a]),
$\zeta $
fixed, but the proof implies this more general result), then by Bernstein’s continuation principle ([Reference BanksBan98a]),
![]() $\Psi (\zeta ,s,\omega ,f)$
admits meromorphic continuation which belongs to
$\Psi (\zeta ,s,\omega ,f)$
admits meromorphic continuation which belongs to
![]() $\mathbb {C}(q^{-\zeta },q^{-s})$
.
$\mathbb {C}(q^{-\zeta },q^{-s})$
.
For the last assertion, consider now
![]() $\Psi (0,s,\omega ,f)$
. It belongs to the space (5.47) as long as
$\Psi (0,s,\omega ,f)$
. It belongs to the space (5.47) as long as
![]() $\Psi (\zeta ,s,\omega ,f)$
is well defined for all
$\Psi (\zeta ,s,\omega ,f)$
is well defined for all
![]() $\omega $
and f when we take
$\omega $
and f when we take
![]() $\zeta =0$
. This is true by [Reference BanksBan98a], since
$\zeta =0$
. This is true by [Reference BanksBan98a], since
![]() $\Psi (\zeta ,s,\omega ,f)$
is holomorphic whenever there is a unique solution (in the terminology of ibid.), and the space (5.47) is one-dimensional outside finitely many values of
$\Psi (\zeta ,s,\omega ,f)$
is holomorphic whenever there is a unique solution (in the terminology of ibid.), and the space (5.47) is one-dimensional outside finitely many values of
![]() $q^{-s}$
.
$q^{-s}$
.
The proposition implies that both
![]() $Z(s,\omega ,f)$
and
$Z(s,\omega ,f)$
and
![]() $\Psi (0,s,\omega ,f)$
, defined by meromorphic continuation, belong to the space (5.47), hence are proportional. We can thus compute the former by first computing the latter, then finding the proportionality factor. This technique is due to Soudry [Reference SoudrySou93] and has since been used in several similar settings including [Reference SoudrySou95, Reference Ginzburg, Rallis and SoudryGRS98, Reference SoudrySou00] (see also [Reference KaplanKap12, Reference KaplanKap13, Reference KaplanKap15]).
$\Psi (0,s,\omega ,f)$
, defined by meromorphic continuation, belong to the space (5.47), hence are proportional. We can thus compute the former by first computing the latter, then finding the proportionality factor. This technique is due to Soudry [Reference SoudrySou93] and has since been used in several similar settings including [Reference SoudrySou95, Reference Ginzburg, Rallis and SoudryGRS98, Reference SoudrySou00] (see also [Reference KaplanKap12, Reference KaplanKap13, Reference KaplanKap15]).
Proposition 84. Let
![]() $\omega $
and f be the normalized unramified vectors. Then
$\omega $
and f be the normalized unramified vectors. Then
 $$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\frac{L_{\vartheta}(-r\zeta+r\alpha s+1/2,\pi\times\tau^{\vee})L_{\vartheta}(-r\zeta-r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}\qquad(\alpha=rk). \end{align*} $$
$$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\frac{L_{\vartheta}(-r\zeta+r\alpha s+1/2,\pi\times\tau^{\vee})L_{\vartheta}(-r\zeta-r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}\qquad(\alpha=rk). \end{align*} $$
Proof. Since f is unramified, so is
![]() $W_f$
. As in the linear case [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, (3.42)–(3.44)], we can use conjugations to deduce that the integrand is zero unless
$W_f$
. As in the linear case [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, (3.42)–(3.44)], we can use conjugations to deduce that the integrand is zero unless
![]() $t,v\in \mathcal {O}$
, then the
$t,v\in \mathcal {O}$
, then the
![]() $dvdt$
-integral evaluates to the constant
$dvdt$
-integral evaluates to the constant
![]() $1$
. Specifically, for any
$1$
. Specifically, for any
![]() $b\in F$
,
$b\in F$
,
 $$ \begin{align} [t,v]w'[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}]= [t,v]\left(\begin{smallmatrix}I_{rk-1}\\&1&&b\\&&I_{rk-1}&\\&&&1\end{smallmatrix}\right)w' ={}^{[t,v]}\left(\begin{smallmatrix}I_{rk-1}\\&1&&b\\&&I_{rk-1}&\\&&&1\end{smallmatrix}\right)[t,v]w' =\left(\begin{smallmatrix}I_{rk-1}\\&1&b t&-b v&b\\&&1&\\&&&I_{rk-2}\\&&&&1\end{smallmatrix}\right)[t,v]w'. \end{align} $$
$$ \begin{align} [t,v]w'[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}]= [t,v]\left(\begin{smallmatrix}I_{rk-1}\\&1&&b\\&&I_{rk-1}&\\&&&1\end{smallmatrix}\right)w' ={}^{[t,v]}\left(\begin{smallmatrix}I_{rk-1}\\&1&&b\\&&I_{rk-1}&\\&&&1\end{smallmatrix}\right)[t,v]w' =\left(\begin{smallmatrix}I_{rk-1}\\&1&b t&-b v&b\\&&1&\\&&&I_{rk-2}\\&&&&1\end{smallmatrix}\right)[t,v]w'. \end{align} $$
Since
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],{}^{w'}[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],{}^{[t,v]w'}[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]\in N_{H}$
, by Equation (2.10) we can extend Equation (5.56) to
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],{}^{w'}[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],{}^{[t,v]w'}[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]\in N_{H}$
, by Equation (2.10) we can extend Equation (5.56) to
![]() $H^{(m,r)}$
. We also have
$H^{(m,r)}$
. We also have
 $$ \begin{align} W_f\left(\left\langle \left(\begin{smallmatrix}I_{rk-1}\\&1&b t&-b v&a^{-1}b\\&&1&\\&&&I_{rk-2}\\&&&&1\end{smallmatrix}\right),1\right\rangle h, s\right)=\psi^{-1}(b t)W_f(h,s)\qquad\forall h\in H^{(m,r)}, \end{align} $$
$$ \begin{align} W_f\left(\left\langle \left(\begin{smallmatrix}I_{rk-1}\\&1&b t&-b v&a^{-1}b\\&&1&\\&&&I_{rk-2}\\&&&&1\end{smallmatrix}\right),1\right\rangle h, s\right)=\psi^{-1}(b t)W_f(h,s)\qquad\forall h\in H^{(m,r)}, \end{align} $$
and in particular independent of a. While this applies to any b, when we take
![]() $b\in \mathcal {O}^{*}$
,
$b\in \mathcal {O}^{*}$
,
![]() $W_f$
is right-invariant under
$W_f$
is right-invariant under
![]() $\langle [\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],1\rangle $
and then since
$\langle [\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],1\rangle $
and then since
![]() $\psi $
is unramified, Equation (5.57) implies that the integrand vanishes unless
$\psi $
is unramified, Equation (5.57) implies that the integrand vanishes unless
![]() $t\in \mathcal {O}$
. Then by Equation (2.11),
$t\in \mathcal {O}$
. Then by Equation (2.11),
![]() ${}^{{w'}^{-1}}\langle [t,v],\varsigma ([t,v])\rangle =\langle {}^{{w'}^{-1}}[t,v],1)\rangle $
(this holds whether t is in
${}^{{w'}^{-1}}\langle [t,v],\varsigma ([t,v])\rangle =\langle {}^{{w'}^{-1}}[t,v],1)\rangle $
(this holds whether t is in
![]() $\mathcal {O}$
or not), and since
$\mathcal {O}$
or not), and since
![]() $W_f$
is unramified,
$W_f$
is unramified,
 $$ \begin{align} &W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\\&=\nonumber W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle [t,0],\varsigma([t,0])\rangle \langle w',1\rangle,s)\\&=\nonumber W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s). \end{align} $$
$$ \begin{align} &W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle,s)\\&=\nonumber W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle [t,0],\varsigma([t,0])\rangle \langle w',1\rangle,s)\\&=\nonumber W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s). \end{align} $$
We proceed similarly, now with
 $$ \begin{align*} \mathrm{e}(o_1,\ldots,o_{rk-2})={}^{{w'}^{-1}}\operatorname{\mathrm{diag}}\ \left(I_{rk},\left(\begin{smallmatrix}1&&&&o_1\\&\ddots&&&\vdots\\&&1&0&o_{rk-2}\\&&&1&0\\&&&&1\end{smallmatrix}\right)\right),\qquad o_1,\ldots,o_{rk}\in\mathcal{O}^{*}. \end{align*} $$
$$ \begin{align*} \mathrm{e}(o_1,\ldots,o_{rk-2})={}^{{w'}^{-1}}\operatorname{\mathrm{diag}}\ \left(I_{rk},\left(\begin{smallmatrix}1&&&&o_1\\&\ddots&&&\vdots\\&&1&0&o_{rk-2}\\&&&1&0\\&&&&1\end{smallmatrix}\right)\right),\qquad o_1,\ldots,o_{rk}\in\mathcal{O}^{*}. \end{align*} $$
Starting with
![]() $i=1$
and up to
$i=1$
and up to
![]() $i=rk-2$
, we show that each coordinate of v belongs in
$i=rk-2$
, we show that each coordinate of v belongs in
![]() $\mathcal {O}$
then remove it from the integrand; the integral over this coordinate equals the volume of
$\mathcal {O}$
then remove it from the integrand; the integral over this coordinate equals the volume of
![]() $\mathcal {O}$
, which is
$\mathcal {O}$
, which is
![]() $1$
. Eventually, we remain with
$1$
. Eventually, we remain with
Thus,
 $$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\int\limits_{F^{*}}W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,d^{*}a. \end{align*} $$
$$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\int\limits_{F^{*}}W_f(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,d^{*}a. \end{align*} $$
Then by Equation (5.51) and changing
![]() $a\mapsto a^{-1}$
, the r.h.s. equals
$a\mapsto a^{-1}$
, the r.h.s. equals
 $$ \begin{align} \int\limits_{F^{*}}W_f^{*}(\langle\operatorname{\mathrm{diag}}(a,I_{2rk-1}),1\rangle,s)\omega(\langle a^{-1},1\rangle)|a|^{-\zeta+1/2-(2rk-1)/2}\,d^{*}a. \end{align} $$
$$ \begin{align} \int\limits_{F^{*}}W_f^{*}(\langle\operatorname{\mathrm{diag}}(a,I_{2rk-1}),1\rangle,s)\omega(\langle a^{-1},1\rangle)|a|^{-\zeta+1/2-(2rk-1)/2}\,d^{*}a. \end{align} $$
This integral resembles the integral (3.53) from § 3.7. To complete the proof we relate
![]() $\omega (\langle a^{-1},1\rangle )$
to the matrix coefficient appearing in Integral (3.53), and
$\omega (\langle a^{-1},1\rangle )$
to the matrix coefficient appearing in Integral (3.53), and
![]() $W_f^{*}$
to the normalized unramified Whittaker function from § 3.7.
$W_f^{*}$
to the normalized unramified Whittaker function from § 3.7.
Let
![]() $\omega {}^{*}$
be the matrix coefficient of
$\omega {}^{*}$
be the matrix coefficient of
![]() $(\pi ^{\vee })^{*}$
given by
$(\pi ^{\vee })^{*}$
given by
![]() $\omega {}^{*}(\langle a,1\rangle )=\omega ({}^{*}\langle a,1\rangle )$
, where
$\omega {}^{*}(\langle a,1\rangle )=\omega ({}^{*}\langle a,1\rangle )$
, where
![]() ${}^{*}$
is defined by Equation (2.54). Since
${}^{*}$
is defined by Equation (2.54). Since
![]() ${}^{*}\langle a,1\rangle =\langle a^{-1},1\rangle $
,
${}^{*}\langle a,1\rangle =\langle a^{-1},1\rangle $
,
![]() $\omega (\langle a^{-1},1\rangle )=\omega {}^{*}(\langle a,1\rangle )$
. Moreover, by Proposition 25 the representation
$\omega (\langle a^{-1},1\rangle )=\omega {}^{*}(\langle a,1\rangle )$
. Moreover, by Proposition 25 the representation
![]() $(\pi ^{\vee })^{*}$
is induced from
$(\pi ^{\vee })^{*}$
is induced from
![]() $\varepsilon ^{-1}\otimes \vartheta ^{-1}\mu $
, thus equal to
$\varepsilon ^{-1}\otimes \vartheta ^{-1}\mu $
, thus equal to
![]() $(\pi ^{*})^{\vee }$
.
$(\pi ^{*})^{\vee }$
.
Now, consider
![]() $W_f^{*}$
. Let
$W_f^{*}$
. Let
which is an unramified character of
![]() $T_{\operatorname {\mathrm {GL}}_{2k}}$
,
$T_{\operatorname {\mathrm {GL}}_{2k}}$
,
 $$ \begin{align*} &\mathbf{x}=(x_1,\ldots,x_k), \qquad x_i=(|~|^{rks}\chi_i)(\varpi^r),\qquad \mathbf{x}'=(x^{\prime}_1,\ldots,x^{\prime}_k),\qquad x^{\prime}_i=(|~|^{-rks}\chi^{\prime}_i)(\varpi^r),\\ &\mathbf{x}^{\bullet}=(x_1,\ldots,x_k,x^{\prime}_1,\ldots,x^{\prime}_k). \end{align*} $$
$$ \begin{align*} &\mathbf{x}=(x_1,\ldots,x_k), \qquad x_i=(|~|^{rks}\chi_i)(\varpi^r),\qquad \mathbf{x}'=(x^{\prime}_1,\ldots,x^{\prime}_k),\qquad x^{\prime}_i=(|~|^{-rks}\chi^{\prime}_i)(\varpi^r),\\ &\mathbf{x}^{\bullet}=(x_1,\ldots,x_k,x^{\prime}_1,\ldots,x^{\prime}_k). \end{align*} $$
At this point, we add the assumption that
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
are regular, which means
$\chi '$
are regular, which means
![]() $\mathbf {x}_{\alpha }\ne 1$
and
$\mathbf {x}_{\alpha }\ne 1$
and
![]() $\mathbf {x}^{\prime }_{\alpha }\ne 1$
for all
$\mathbf {x}^{\prime }_{\alpha }\ne 1$
for all
![]() $\alpha \in \Phi _k^+$
; this together with the condition (3.45) imply the condition of Proposition 60, hence
$\alpha \in \Phi _k^+$
; this together with the condition (3.45) imply the condition of Proposition 60, hence
![]() $\rho _1(\tau )\subset \Theta _{r,m,r,\vartheta }(\chi )$
and
$\rho _1(\tau )\subset \Theta _{r,m,r,\vartheta }(\chi )$
and
![]() $\rho _1(\tau ')\subset \Theta _{r,m,r,\vartheta }(\chi ')$
. Therefore,
$\rho _1(\tau ')\subset \Theta _{r,m,r,\vartheta }(\chi ')$
. Therefore,
If
![]() $f'$
is the normalized unramified function in the space of
$f'$
is the normalized unramified function in the space of
![]() $\Theta _{2r,m,r,\vartheta }(\chi ^{\bullet })$
, we have
$\Theta _{2r,m,r,\vartheta }(\chi ^{\bullet })$
, we have
Since by Theorem 43,
 $$ \begin{align*} &W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq k}(1-q^{-j}\mathbf{x}_{(i,j)}),\qquad W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi^{\prime}_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq k}(1-q^{-j}\mathbf{x}^{\prime}_{(i,j)}),\\ &W_{\mathbf{0}}(\mathbf{0},\vartheta,(\chi^{\bullet})_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq 2k}(1-q^{-j}\mathbf{x}^{\bullet}_{(i,j)}), \end{align*} $$
$$ \begin{align*} &W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq k}(1-q^{-j}\mathbf{x}_{(i,j)}),\qquad W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi^{\prime}_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq k}(1-q^{-j}\mathbf{x}^{\prime}_{(i,j)}),\\ &W_{\mathbf{0}}(\mathbf{0},\vartheta,(\chi^{\bullet})_{\Theta})=\prod_{j=1}^{r}\prod_{1\leq i<j\leq 2k}(1-q^{-j}\mathbf{x}^{\bullet}_{(i,j)}), \end{align*} $$
we obtain
 $$ \begin{align*} W_f(\langle I_{2rk},1\rangle,s)=\frac{W_{\mathbf{0}}(\mathbf{0},\vartheta,(\chi^{\bullet})_{\Theta})}{ W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta}) W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi^{\prime}_{\Theta})} =\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1}. \end{align*} $$
$$ \begin{align*} W_f(\langle I_{2rk},1\rangle,s)=\frac{W_{\mathbf{0}}(\mathbf{0},\vartheta,(\chi^{\bullet})_{\Theta})}{ W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi_{\Theta}) W_{\mathbf{0}}(\mathbf{0},\vartheta,\chi^{\prime}_{\Theta})} =\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1}. \end{align*} $$
For the last equality, also note that
![]() $\vartheta =\vartheta ^{-1}$
. This is also the value of
$\vartheta =\vartheta ^{-1}$
. This is also the value of
![]() $W_f^{*}(\langle I_{2rk},1\rangle ,s)$
, and by Proposition 42,
$W_f^{*}(\langle I_{2rk},1\rangle ,s)$
, and by Proposition 42,
![]() $(\Theta _{2r,m,r,\vartheta }(\chi ^{\bullet }))^{*}=\Theta _{2r,m,r,\vartheta }((\chi ^{\bullet })^{*})$
. Thus, if
$(\Theta _{2r,m,r,\vartheta }(\chi ^{\bullet }))^{*}=\Theta _{2r,m,r,\vartheta }((\chi ^{\bullet })^{*})$
. Thus, if
![]() $W^0$
is the normalized unramified Whittaker function of
$W^0$
is the normalized unramified Whittaker function of
![]() $\Theta _{2r,m,r,\vartheta }((\chi ^{\bullet })^{*})$
,
$\Theta _{2r,m,r,\vartheta }((\chi ^{\bullet })^{*})$
,
 $$ \begin{align*} W_f^{*}(g,s)=\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1}W^0(g) \end{align*} $$
$$ \begin{align*} W_f^{*}(g,s)=\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1}W^0(g) \end{align*} $$
and Integral (5.59) equals
 $$ \begin{align*} \prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1} Z(-\zeta+1/2,\omega^{*},W^0). \end{align*} $$
$$ \begin{align*} \prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})^{-1} Z(-\zeta+1/2,\omega^{*},W^0). \end{align*} $$
Now, by Equation (3.54) (
![]() $2rk>1$
) and since
$2rk>1$
) and since
![]() $t_{(\pi ^{*})^{\vee },\vartheta }=t_{\pi ,\vartheta }$
and still assuming
$t_{(\pi ^{*})^{\vee },\vartheta }=t_{\pi ,\vartheta }$
and still assuming
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
are regular,
$\chi '$
are regular,
 $$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\frac{L_{\vartheta}(-r\zeta+1/2-r\alpha s,\pi\times\tau^{\vee})L_{\vartheta}(-r\zeta+1/2+r\alpha s,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
$$ \begin{align*} &\Psi(\zeta,s,\omega,f)=\frac{L_{\vartheta}(-r\zeta+1/2-r\alpha s,\pi\times\tau^{\vee})L_{\vartheta}(-r\zeta+1/2+r\alpha s,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^rL_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
Finally, because
![]() $W_f$
is an analytic function of
$W_f$
is an analytic function of
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $\mathbf {x}'$
, we can remove the regularity assumption on the l.h.s., and the r.h.s. is also well defined without it. Therefore, we can drop this assumption and the proof is complete.
$\mathbf {x}'$
, we can remove the regularity assumption on the l.h.s., and the r.h.s. is also well defined without it. Therefore, we can drop this assumption and the proof is complete.
We focus momentarily on the case
![]() $rk=1$
and compute the integral
$rk=1$
and compute the integral
![]() $Z(s,\omega ,f)$
with unramified data. Assume
$Z(s,\omega ,f)$
with unramified data. Assume
![]() $m=2$
, the case
$m=2$
, the case
![]() $m=1$
was proved in [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] (for any n, and using [Reference Godement and JacquetGJ72]; here
$m=1$
was proved in [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] (for any n, and using [Reference Godement and JacquetGJ72]; here
![]() $n=1$
). By Proposition 20, we can assume that
$n=1$
). By Proposition 20, we can assume that
![]() $H^{(2,1)}$
is realized using
$H^{(2,1)}$
is realized using
![]() $(\det ,\det )_2$
(this is immediate for
$(\det ,\det )_2$
(this is immediate for
![]() $\operatorname {\mathrm {GL}}_1^{(2,1)}$
). Now, we can write
$\operatorname {\mathrm {GL}}_1^{(2,1)}$
). Now, we can write
![]() $\pi =\vartheta \otimes \mu $
(
$\pi =\vartheta \otimes \mu $
(
![]() $\mu $
is an unramified quasi-character of
$\mu $
is an unramified quasi-character of
![]() $F^{*}$
) and
$F^{*}$
) and
![]() $\pi (\langle a,\epsilon \rangle )=\vartheta (a)\mu (a)$
(see § 2.8). Similarly,
$\pi (\langle a,\epsilon \rangle )=\vartheta (a)\mu (a)$
(see § 2.8). Similarly,
![]() $\tau =\vartheta \otimes \chi $
and
$\tau =\vartheta \otimes \chi $
and
![]() $\tau '=\vartheta \otimes \chi '$
. For a section f of the space of
$\tau '=\vartheta \otimes \chi '$
. For a section f of the space of
![]() $\operatorname {\mathrm {Ind}}_{P}^{H}((\chi \otimes \chi ')\delta _P^s)$
, the section
$\operatorname {\mathrm {Ind}}_{P}^{H}((\chi \otimes \chi ')\delta _P^s)$
, the section
![]() $f_{\vartheta }(\langle h,\epsilon \rangle ,s)=\epsilon \vartheta (\det h)f(h,s)$
belongs to the space of (5.46). Then if
$f_{\vartheta }(\langle h,\epsilon \rangle ,s)=\epsilon \vartheta (\det h)f(h,s)$
belongs to the space of (5.46). Then if
![]() $\omega $
is normalized,
$\omega $
is normalized,
 $$ \begin{align} Z(s,\omega,f_{\vartheta})=\int\limits_{F^{*}}\vartheta(-a)f(\left(\begin{smallmatrix}&1\\1\end{smallmatrix}\right) \left(\begin{smallmatrix}1&1\\&1\end{smallmatrix}\right)\left(\begin{smallmatrix}1&\\&a\end{smallmatrix}\right),s)\vartheta^{-1}(a)\mu^{-1}(a)\,d^{*}a. \end{align} $$
$$ \begin{align} Z(s,\omega,f_{\vartheta})=\int\limits_{F^{*}}\vartheta(-a)f(\left(\begin{smallmatrix}&1\\1\end{smallmatrix}\right) \left(\begin{smallmatrix}1&1\\&1\end{smallmatrix}\right)\left(\begin{smallmatrix}1&\\&a\end{smallmatrix}\right),s)\vartheta^{-1}(a)\mu^{-1}(a)\,d^{*}a. \end{align} $$
(Cf. [Reference GanGan12, pp. 81–83], the constant
![]() $2$
there was needed because the integration was over the cover.) This is the linear
$2$
there was needed because the integration was over the cover.) This is the linear
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_1$
doubling integral for the representations
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_1$
doubling integral for the representations
![]() $a\mapsto \mu (a)(-1,a)_2$
of
$a\mapsto \mu (a)(-1,a)_2$
of
![]() $F^{*}$
and
$F^{*}$
and
![]() $\chi \otimes \chi '$
of
$\chi \otimes \chi '$
of
![]() $F^{*}\times F^{*}$
, and the section f (see [Reference Cai, Friedberg and KaplanCFK22, § 2.4]). For the normalized unramified f, by [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] (see also [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Proposition 34]), the r.h.s. of Equation (5.60) equals
$F^{*}\times F^{*}$
, and the section f (see [Reference Cai, Friedberg and KaplanCFK22, § 2.4]). For the normalized unramified f, by [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] (see also [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Proposition 34]), the r.h.s. of Equation (5.60) equals
 $$ \begin{align*} &\frac{(1-(-1,\varpi)_2\mu^{-1}(\varpi)\chi(\varpi)q^{-s-1/2})^{-1} (1-(-1,\varpi)_2\mu(\varpi){\chi'}^{-1}(\varpi)q^{-s-1/2})^{-1}} {(1-\chi(\varpi){\chi'}^{-1}(\varpi)q^{-2s-1})^{-1}}. \end{align*} $$
$$ \begin{align*} &\frac{(1-(-1,\varpi)_2\mu^{-1}(\varpi)\chi(\varpi)q^{-s-1/2})^{-1} (1-(-1,\varpi)_2\mu(\varpi){\chi'}^{-1}(\varpi)q^{-s-1/2})^{-1}} {(1-\chi(\varpi){\chi'}^{-1}(\varpi)q^{-2s-1})^{-1}}. \end{align*} $$
Since
![]() $(-1,\varpi )_2=1$
and
$(-1,\varpi )_2=1$
and
![]() $\vartheta =\vartheta ^{-1}$
, we obtain
$\vartheta =\vartheta ^{-1}$
, we obtain
 $$ \begin{align} Z(s,\omega,f)= \frac{L_{\vartheta}(s+1/2,\pi^{\vee}\times\tau) L_{\vartheta}(s+1/2,\pi\times{\tau'}^{\vee}) }{L_{\vartheta}(2s+1,\tau\times{\tau'}^{\vee})}. \end{align} $$
$$ \begin{align} Z(s,\omega,f)= \frac{L_{\vartheta}(s+1/2,\pi^{\vee}\times\tau) L_{\vartheta}(s+1/2,\pi\times{\tau'}^{\vee}) }{L_{\vartheta}(2s+1,\tau\times{\tau'}^{\vee})}. \end{align} $$
We proceed with the general case
![]() $rk\geq 1$
. Denote
$rk\geq 1$
. Denote
 $$ \begin{align*} L_{\pi,\tau,\vartheta}(s) =\frac{L_{\vartheta}(1/2-r\alpha s,\pi\times\tau^{\vee})} {L_{\vartheta}(1/2+r\alpha s,\pi^{\vee}\times\tau)}. \end{align*} $$
$$ \begin{align*} L_{\pi,\tau,\vartheta}(s) =\frac{L_{\vartheta}(1/2-r\alpha s,\pi\times\tau^{\vee})} {L_{\vartheta}(1/2+r\alpha s,\pi^{\vee}\times\tau)}. \end{align*} $$
Lemma 85. As meromorphic continuations
![]() $L_{\pi ,\tau ,\vartheta }(s)Z(s,\omega ,f)=\Psi (0,s,\omega ,f)$
, for any
$L_{\pi ,\tau ,\vartheta }(s)Z(s,\omega ,f)=\Psi (0,s,\omega ,f)$
, for any
![]() $\omega $
and rational section f.
$\omega $
and rational section f.
Proof. For
![]() $rk=1$
, the result already follows from Proposition 84 and Equation (5.61) (and [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] for
$rk=1$
, the result already follows from Proposition 84 and Equation (5.61) (and [Reference Piatetski-Shapiro and RallisPSR87, § 6.1] for
![]() $m=1$
) so that throughout the proof we assume
$m=1$
) so that throughout the proof we assume
![]() $rk>1$
. We adapt the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] which, as mentioned above, was based on the method of Soudry [Reference SoudrySou93, p. 70]. Our use of the Fourier inversion formula (see below) was adapted from [Reference SoudrySou95].
$rk>1$
. We adapt the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] which, as mentioned above, was based on the method of Soudry [Reference SoudrySou93, p. 70]. Our use of the Fourier inversion formula (see below) was adapted from [Reference SoudrySou95].
First, we define an action of (the ring of) Schwartz–Bruhat functions on sections, this will be used repeatedly in the proof. For a section f and a Schwartz–Bruhat function
![]() $\phi $
on F,
$\phi $
on F,
 $$ \begin{align*} \phi(f)(h,s)=\int\limits_Ff(h\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}],1\rangle,s)\phi(b)\,db. \end{align*} $$
$$ \begin{align*} \phi(f)(h,s)=\int\limits_Ff(h\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}],1\rangle,s)\phi(b)\,db. \end{align*} $$
This integral is well defined because
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]\mapsto \langle [\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],1\rangle $
is the splitting of
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]\mapsto \langle [\begin {smallmatrix}0&0\\b&0\end {smallmatrix}],1\rangle $
is the splitting of
![]() $\{[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]:b\in F\}$
. Also, observe that for each f there exists some
$\{[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]:b\in F\}$
. Also, observe that for each f there exists some
![]() $\phi $
such that
$\phi $
such that
![]() $\phi (f)=f$
: for any
$\phi (f)=f$
: for any
![]() $l>0$
,
$l>0$
,
![]() $H^{(m,r)}$
is split over the subgroup
$H^{(m,r)}$
is split over the subgroup
![]() $\mathcal {N}_l=\{[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]:b\in \mathcal {P}^l\}$
. One splitting is trivial:
$\mathcal {N}_l=\{[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]:b\in \mathcal {P}^l\}$
. One splitting is trivial:
![]() $v\mapsto \langle v,1\rangle $
. In fact, this is the only splitting, for if
$v\mapsto \langle v,1\rangle $
. In fact, this is the only splitting, for if
![]() $v\mapsto \langle v,\eta '(v)\rangle $
is another splitting, then
$v\mapsto \langle v,\eta '(v)\rangle $
is another splitting, then
![]() $\eta ':\mathcal {P}^l\rightarrow \mu _m$
is a homomorphism and since the exponent of
$\eta ':\mathcal {P}^l\rightarrow \mu _m$
is a homomorphism and since the exponent of
![]() $\mu _m$
is m and
$\mu _m$
is m and
![]() $|m|=1$
(F is unramified),
$|m|=1$
(F is unramified),
![]() $\eta '=1$
. Now, since f is smooth, there exists
$\eta '=1$
. Now, since f is smooth, there exists
![]() $l\gg 0$
such that f is right-invariant under
$l\gg 0$
such that f is right-invariant under
![]() $\{\langle v,1\rangle : v\in \mathcal {N}_l\}$
. Thus, the characteristic function
$\{\langle v,1\rangle : v\in \mathcal {N}_l\}$
. Thus, the characteristic function
![]() $\phi $
of
$\phi $
of
![]() $\mathcal {P}^l$
satisfies
$\mathcal {P}^l$
satisfies
![]() $\phi (f)=f$
. In addition, define the Fourier transform of
$\phi (f)=f$
. In addition, define the Fourier transform of
![]() $\phi $
by
$\phi $
by
![]() $\widehat {\phi }(t)=\int _F\phi (b)\psi ^{-1}(bt)db$
.
$\widehat {\phi }(t)=\int _F\phi (b)\psi ^{-1}(bt)db$
.
For
![]() $t\in F$
, let
$t\in F$
, let
![]() $\jmath (t)\in P\cap N_{H}$
be given by
$\jmath (t)\in P\cap N_{H}$
be given by
Since
![]() ${}^{\delta _0}\jmath (t)\in N_{H}$
,
${}^{\delta _0}\jmath (t)\in N_{H}$
,
![]() ${}^{\delta _0}\langle \jmath (t),1\rangle = \langle {}^{\delta _0}\jmath (t),1\rangle $
by Equation (2.10) (also
${}^{\delta _0}\langle \jmath (t),1\rangle = \langle {}^{\delta _0}\jmath (t),1\rangle $
by Equation (2.10) (also
![]() ${}^{\delta _0}\jmath (t)\in P$
). We can also use Equation (2.10) to conjugate elements of
${}^{\delta _0}\jmath (t)\in P$
). We can also use Equation (2.10) to conjugate elements of
![]() $U_P$
by
$U_P$
by
![]() $\jmath (t)$
without introducing a root of unity. Also, by Equation (2.9), for any
$\jmath (t)$
without introducing a root of unity. Also, by Equation (2.9), for any
![]() $h\in H$
,
$h\in H$
,
![]() $\langle h,1\rangle \langle \jmath (t),1\rangle =\langle h\jmath (t),1\rangle $
and
$\langle h,1\rangle \langle \jmath (t),1\rangle =\langle h\jmath (t),1\rangle $
and
![]() $\langle {}^{\delta _0}\jmath (t)h,1\rangle =\langle {}^{\delta _0}\jmath (t),1\rangle \langle h,1\rangle $
. Then for fixed
$\langle {}^{\delta _0}\jmath (t)h,1\rangle =\langle {}^{\delta _0}\jmath (t),1\rangle \langle h,1\rangle $
. Then for fixed
![]() $u,t\in F$
,
$u,t\in F$
,
Since
![]() $\int _F\psi ((u-1)t)dt=0$
unless
$\int _F\psi ((u-1)t)dt=0$
unless
![]() $u=1$
,
$u=1$
,
 $$ \begin{align} Z(s,\omega,f)= \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,dt\,du\,d^{*}a. \end{align} $$
$$ \begin{align} Z(s,\omega,f)= \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,dt\,du\,d^{*}a. \end{align} $$
Here,
![]() $x\in F^{rk-1}$
is a row,
$x\in F^{rk-1}$
is a row,
![]() $y\in F^{rk-1}$
is a column,
$y\in F^{rk-1}$
is a column,
![]() $z\in \text {Mat}_{rk-1}$
(i.e.,
$z\in \text {Mat}_{rk-1}$
(i.e.,
![]() $du_0=dxdydz$
) and
$du_0=dxdydz$
) and
![]() $u,t\in F$
. The integral (5.62) is defined in the domain of definition of
$u,t\in F$
. The integral (5.62) is defined in the domain of definition of
![]() $Z(s,\omega ,f)$
but is not absolutely convergent as a multiple integral.
$Z(s,\omega ,f)$
but is not absolutely convergent as a multiple integral.
However, we can still consider the integral obtained by formally changing
![]() $dtdu$
to
$dtdu$
to
![]() $dudt$
:
$dudt$
:
 $$ \begin{align*} Z'(s,\omega,f)= \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,du\,dt\,d^{*}a. \end{align*} $$
$$ \begin{align*} Z'(s,\omega,f)= \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,du\,dt\,d^{*}a. \end{align*} $$
As in the linear case, in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
 $$ \begin{align} \int\limits_{F^{*}}\int\limits_F\left| \int \omega(\langle a,1\rangle)f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,du\right|\,dt\,d^{*}a<\infty. \end{align} $$
$$ \begin{align} \int\limits_{F^{*}}\int\limits_F\left| \int \omega(\langle a,1\rangle)f(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)\,dx\,dy\,dz\,du\right|\,dt\,d^{*}a<\infty. \end{align} $$
See [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36, (3.48)]. To show this, we extend the argument from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] to the covering. First, note that we can find
![]() $\phi $
such that
$\phi $
such that
![]() $\phi (f)=f$
(as explained above). Second, we can conjugate
$\phi (f)=f$
(as explained above). Second, we can conjugate
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
(denoted
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
(denoted
![]() $\jmath '(b)$
in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, p. 1055]) by
$\jmath '(b)$
in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, p. 1055]) by
![]() $\mathfrak {e}_2(a)$
and
$\mathfrak {e}_2(a)$
and
![]() $\jmath (t)$
and also conjugate
$\jmath (t)$
and also conjugate
![]() $\jmath (t)$
by
$\jmath (t)$
by
![]() $\mathfrak {e}_2(a)$
, without introducing a root of unity.
$\mathfrak {e}_2(a)$
, without introducing a root of unity.
Now,
![]() $Z'(s,\omega ,f)$
is convergent in the sense of Inequality (5.63) in a right half-plane, where it also belongs to the space (5.47). Thus, by Lemma 81 the integrals
$Z'(s,\omega ,f)$
is convergent in the sense of Inequality (5.63) in a right half-plane, where it also belongs to the space (5.47). Thus, by Lemma 81 the integrals
![]() $Z'(s,\omega ,f)$
and
$Z'(s,\omega ,f)$
and
![]() $Z(s,\omega ,f)$
are proportional in
$Z(s,\omega ,f)$
are proportional in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
. The proportionality factor is
$\operatorname {\mathrm {Re}}(s)\gg 0$
. The proportionality factor is
![]() $1$
: This was shown in the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] using a section of the form
$1$
: This was shown in the proof of [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] using a section of the form
![]() $\phi (f)$
, conjugations of elements
$\phi (f)$
, conjugations of elements
![]() $\jmath (t)$
and
$\jmath (t)$
and
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
which extend to the covering, and the Fourier inversion formula
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
which extend to the covering, and the Fourier inversion formula
![]() $\int _F\widehat {\phi }(t)\psi (aut)dt=\phi (au)$
. We deduce that
$\int _F\widehat {\phi }(t)\psi (aut)dt=\phi (au)$
. We deduce that
![]() $Z'(s,\omega ,f)=Z(s,\omega ,f)$
. In particular, by Corollary 82,
$Z'(s,\omega ,f)=Z(s,\omega ,f)$
. In particular, by Corollary 82,
![]() $Z'(s,\omega ,f)$
admits meromorphic continuation which belongs to
$Z'(s,\omega ,f)$
admits meromorphic continuation which belongs to
![]() $\mathbb {C}(q^{-s})$
. In the remaining part of the proof, we show that
$\mathbb {C}(q^{-s})$
. In the remaining part of the proof, we show that
using a specific substitution.
Let
![]() $\omega $
be the normalized unramified matrix coefficient. Let
$\omega $
be the normalized unramified matrix coefficient. Let
![]() $W\in \mathcal {W}(\rho _1(\tau ))$
be the normalized unramified function, and take a small compact open neighborhood
$W\in \mathcal {W}(\rho _1(\tau ))$
be the normalized unramified function, and take a small compact open neighborhood
![]() $\mathcal {N}<K_{H}$
of the identity. Choose
$\mathcal {N}<K_{H}$
of the identity. Choose
![]() $f'$
in the space of (5.46) such that
$f'$
in the space of (5.46) such that
![]() $\langle \delta _0,1\rangle \cdot f'$
is right-invariant under
$\langle \delta _0,1\rangle \cdot f'$
is right-invariant under
![]() $\{\langle y,\eta ^{\diamondsuit }_{2rk}(y)\rangle :y\in \mathcal {N}\}$
, supported in the preimage of
$\{\langle y,\eta ^{\diamondsuit }_{2rk}(y)\rangle :y\in \mathcal {N}\}$
, supported in the preimage of
![]() $P\mathcal {N}$
in
$P\mathcal {N}$
in
![]() $H^{(m,r)}$
, and for all
$H^{(m,r)}$
, and for all
![]() $a\in \operatorname {\mathrm {GL}}_{rk}$
,
$a\in \operatorname {\mathrm {GL}}_{rk}$
,
Then take
![]() $f=\phi (f')$
such that
$f=\phi (f')$
such that
 $$ \begin{align} \int\limits_Ff'(h\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\,dt=f'(h,s),\qquad\forall h,s. \end{align} $$
$$ \begin{align} \int\limits_Ff'(h\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\,dt=f'(h,s),\qquad\forall h,s. \end{align} $$
The arguments used above to show that we can find
![]() $\phi $
such that
$\phi $
such that
![]() $\phi (f)=f$
can be repeated with
$\phi (f)=f$
can be repeated with
![]() $\jmath (t)$
instead of
$\jmath (t)$
instead of
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
(
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
(
![]() $\jmath (t)\in N_{H}$
), hence the condition (5.66) is satisfied for a suitable
$\jmath (t)\in N_{H}$
), hence the condition (5.66) is satisfied for a suitable
![]() $\phi $
.
$\phi $
.
Starting with the l.h.s. of Equation (5.64),
![]() $Z'(s,\omega ,f)$
equals
$Z'(s,\omega ,f)$
equals
 $$ \begin{align*} & \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}] ,1\rangle,s)\phi(b)\psi(x_1)\,db\,dx\,dy\,dz\,du\,dt\,d^{*}a. \end{align*} $$
$$ \begin{align*} & \int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}]\jmath(t),1\rangle\langle\mathfrak{e}_2(a),1\rangle\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}] ,1\rangle,s)\phi(b)\psi(x_1)\,db\,dx\,dy\,dz\,du\,dt\,d^{*}a. \end{align*} $$
As in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36], after several manipulations including a change in the order of integration, conjugating
![]() $\langle \jmath (t),1\rangle $
by
$\langle \jmath (t),1\rangle $
by
![]() $\mathfrak {e}_2(a)^{-1}$
, then conjugating
$\mathfrak {e}_2(a)^{-1}$
, then conjugating
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
by
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
by
![]() $\jmath (t)$
and
$\jmath (t)$
and
![]() $\mathfrak {e}_2(a)$
and changing variables in
$\mathfrak {e}_2(a)$
and changing variables in
![]() $x_1$
and u, we obtain
$x_1$
and u, we obtain
![]() $\psi ^{-1}(bt)$
. We then integrate first over b and obtain
$\psi ^{-1}(bt)$
. We then integrate first over b and obtain
 $$ \begin{align*} &\int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\mathfrak{e}_2(a),1\rangle\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\psi(x_1)|a|\,dx\,dy\,dz\,du\,dt\,d^{*}a \\&=\int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)|a|\,dx\,dy\,dz\,du\,d^{*}a. \end{align*} $$
$$ \begin{align*} &\int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\mathfrak{e}_2(a),1\rangle\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\psi(x_1)|a|\,dx\,dy\,dz\,du\,dt\,d^{*}a \\&=\int\limits_{F^{*}}\omega(\langle a,1\rangle) \int f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\mathfrak{e}_2(a),1\rangle,s)\psi(x_1)|a|\,dx\,dy\,dz\,du\,d^{*}a. \end{align*} $$
Here, for the equality we first integrated over t then used Equation (5.66). Now, conjugate
![]() $[\begin {smallmatrix}y&z\\u&x\end {smallmatrix}]$
by
$[\begin {smallmatrix}y&z\\u&x\end {smallmatrix}]$
by
![]() $\mathfrak {e}_2(a)^{-1}$
(multiplying the measure by
$\mathfrak {e}_2(a)^{-1}$
(multiplying the measure by
![]() $|a|^{-rk}$
), and
$|a|^{-rk}$
), and
![]() $\langle \mathfrak {e}_2(a),1\rangle $
by
$\langle \mathfrak {e}_2(a),1\rangle $
by
![]() $\delta _0$
. By Proposition 2,
$\delta _0$
. By Proposition 2,
![]() ${}^{\delta _0}\langle \mathfrak {e}_2(a),1\rangle =\langle {}^{\delta _0}\mathfrak {e}_2(a),1\rangle $
. Then as in the linear case, the assumption on the support of
${}^{\delta _0}\langle \mathfrak {e}_2(a),1\rangle =\langle {}^{\delta _0}\mathfrak {e}_2(a),1\rangle $
. Then as in the linear case, the assumption on the support of
![]() $\langle \delta _0,1\rangle \cdot f'$
implies that the integrand vanishes unless the coordinates of
$\langle \delta _0,1\rangle \cdot f'$
implies that the integrand vanishes unless the coordinates of
![]() $x,y,z$
and u are small (independently of a). Let D be the volume assigned to
$x,y,z$
and u are small (independently of a). Let D be the volume assigned to
![]() $V_{(rk,rk)}\cap \mathcal {N}$
by the measure
$V_{(rk,rk)}\cap \mathcal {N}$
by the measure
![]() $dx\,dy\,dz\,du$
. Thus, using Equation (5.65) we obtain
$dx\,dy\,dz\,du$
. Thus, using Equation (5.65) we obtain
 $$ \begin{align*} &D\int\limits_{F^{*}}\omega(\langle a,1\rangle)W(\langle\operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)|a|^{rks+1/2-(rk-1)/2}\,d^{*}a=DZ(rks+1/2,\omega,W), \end{align*} $$
$$ \begin{align*} &D\int\limits_{F^{*}}\omega(\langle a,1\rangle)W(\langle\operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)|a|^{rks+1/2-(rk-1)/2}\,d^{*}a=DZ(rks+1/2,\omega,W), \end{align*} $$
where
![]() $Z(rks+1/2,\omega ,W)$
is defined by Integral (3.53) and note that
$Z(rks+1/2,\omega ,W)$
is defined by Integral (3.53) and note that
![]() $\mathcal {W}(\rho _1(\tau ))\subset \mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
by Corollary 59 (with
$\mathcal {W}(\rho _1(\tau ))\subset \mathcal {W}(\Theta _{r,m,r,\vartheta }(\chi ))$
by Corollary 59 (with
![]() $c=1$
). Since
$c=1$
). Since
![]() $\omega $
and W are the normalized unramified vectors, by Equation (3.54),
$\omega $
and W are the normalized unramified vectors, by Equation (3.54),
Turning to the r.h.s. of Equation (5.64), we first compute
![]() $\Psi (\zeta ,s,\omega ,f)$
in
$\Psi (\zeta ,s,\omega ,f)$
in
![]() $\operatorname {\mathrm {Re}}(\zeta )\ll 0$
. In this case, adapting the proof from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] takes a bit more care, for the following reasons. First, we use a lower triangular unipotent subgroup (the subgroup of
$\operatorname {\mathrm {Re}}(\zeta )\ll 0$
. In this case, adapting the proof from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Claim 36] takes a bit more care, for the following reasons. First, we use a lower triangular unipotent subgroup (the subgroup of
![]() $[v,t]$
). Second, while it was sufficient in ibid. to obtain an arbitrary Rankin–Selberg integral of
$[v,t]$
). Second, while it was sufficient in ibid. to obtain an arbitrary Rankin–Selberg integral of
![]() $\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
(since the
$\operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_k$
(since the
![]() $\gamma $
-factor of
$\gamma $
-factor of
![]() $\pi ^{-1}\times \tau $
of [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83] could be used), here we must evaluate the integral explicitly (as above, using Equation (3.54)), which means we must also compute the integral over
$\pi ^{-1}\times \tau $
of [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83] could be used), here we must evaluate the integral explicitly (as above, using Equation (3.54)), which means we must also compute the integral over
![]() $[v,t]$
. To start,
$[v,t]$
. To start,
 $$ \begin{align*} \Psi(\zeta,s,\omega,f)&= \int\limits_{F^{*}}\int W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}],1\rangle,s)\phi(b)\\&\quad\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,db\,dt\,dv\,d^{*}a. \end{align*} $$
$$ \begin{align*} \Psi(\zeta,s,\omega,f)&= \int\limits_{F^{*}}\int W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [t,v],\varsigma([t,v])\rangle \langle w',1\rangle\langle[\begin{smallmatrix}0&0\\b&0\end{smallmatrix}],1\rangle,s)\phi(b)\\&\quad\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,db\,dt\,dv\,d^{*}a. \end{align*} $$
Here,
![]() $b\in F$
,
$b\in F$
,
![]() $t\in F$
and
$t\in F$
and
![]() $v\in F^{rk-2}$
. As we have seen in the proof of Proposition 84 ((5.56)-(5.57)), we can conjugate
$v\in F^{rk-2}$
. As we have seen in the proof of Proposition 84 ((5.56)-(5.57)), we can conjugate
![]() $[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
to the left and obtain the character
$[\begin {smallmatrix}0&0\\b&0\end {smallmatrix}]$
to the left and obtain the character
![]() $\psi ^{-1}(b t)$
, then as in Equation (5.58) (though Equation (5.57) no longer implies that
$\psi ^{-1}(b t)$
, then as in Equation (5.58) (though Equation (5.57) no longer implies that
![]() $t\in \mathcal {O}$
, because
$t\in \mathcal {O}$
, because
![]() $f'$
is not unramified) and using
$f'$
is not unramified) and using
![]() ${}^{{w'}^{-1}}[t,0]=\jmath (t)$
, the integral becomes
${}^{{w'}^{-1}}[t,0]=\jmath (t)$
, the integral becomes
 $$ \begin{align*} &\int\limits_{F^{*}}\int W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle\langle\jmath(t),1\rangle,s)\psi^{-1}(bt)\phi(b)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\\&\quad\,db\,dt\,dv\,d^{*}a\\&\! = \int\limits_{F^{*}}\int \!\! W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a \\& \!= \int\limits_{F^{*}}\int\!\! W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dv\,d^{*}a, \end{align*} $$
$$ \begin{align*} &\int\limits_{F^{*}}\int W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle\langle\jmath(t),1\rangle,s)\psi^{-1}(bt)\phi(b)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\\&\quad\,db\,dt\,dv\,d^{*}a\\&\! = \int\limits_{F^{*}}\int \!\! W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle\langle\jmath(t),1\rangle,s)\widehat{\phi}(t)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dt\,dv\,d^{*}a \\& \!= \int\limits_{F^{*}}\int\!\! W_{f'}(\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)|a|^{\zeta+rk-1}\,dv\,d^{*}a, \end{align*} $$
where the second equality follows from Equation (5.66). Substituting Equation (5.51) into the last integral, we obtain
 $$ \begin{align} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}} \int\limits_{V_{(rk,rk)}} f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)\psi(u)|a|^{\zeta+rk-1}\\&\,dx\,dy\,dz\,du\,dv\,d^{*}a.\nonumber \end{align} $$
$$ \begin{align} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}} \int\limits_{V_{(rk,rk)}} f'(\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle\langle\operatorname{\mathrm{diag}}(I_{2rk-1},a),1\rangle\langle [0,v],\varsigma([0,v])\rangle \langle w',1\rangle,s)\omega(\langle a,1\rangle)\psi(u)|a|^{\zeta+rk-1}\\&\,dx\,dy\,dz\,du\,dv\,d^{*}a.\nonumber \end{align} $$
This formal step will be justified by the argument below. Since
![]() $\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
,
$\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
,
![]() $[0,v]$
and
$[0,v]$
and
![]() $w'$
all normalize
$w'$
all normalize
![]() $V_{(rk,rk)}$
, and also (using Proposition 2)
$V_{(rk,rk)}$
, and also (using Proposition 2)
we can shift
![]() $\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
,
$\operatorname {\mathrm {diag}}(I_{2rk-1},a)$
,
![]() $[0,v]$
and
$[0,v]$
and
![]() $w'$
to the left and obtain
$w'$
to the left and obtain
 $$ \begin{align*} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}} \int\limits_{V_{(rk,rk)}} f'(\langle{}^{\delta_0}\operatorname{\mathrm{diag}}(a,I_{2rk-1}),1\rangle \langle {}^{\delta_0}[0,v],\varsigma({}^{\delta_0}[0,v])\rangle \langle{}^{\delta_0}w',1\rangle\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle ,s)\omega(\langle a,1\rangle)\psi(u)\\&|a|^{\zeta-1}\,dx\,dy\,dz\,du\,dv\,d^{*}a. \end{align*} $$
$$ \begin{align*} &\int\limits_{F^{*}}\int\limits_{F^{rk-2}} \int\limits_{V_{(rk,rk)}} f'(\langle{}^{\delta_0}\operatorname{\mathrm{diag}}(a,I_{2rk-1}),1\rangle \langle {}^{\delta_0}[0,v],\varsigma({}^{\delta_0}[0,v])\rangle \langle{}^{\delta_0}w',1\rangle\langle\delta_0[\begin{smallmatrix}y&z\\u&x\end{smallmatrix}],1\rangle ,s)\omega(\langle a,1\rangle)\psi(u)\\&|a|^{\zeta-1}\,dx\,dy\,dz\,du\,dv\,d^{*}a. \end{align*} $$
Now, as with
![]() $Z'(s,\omega ,f)$
, the coordinates of
$Z'(s,\omega ,f)$
, the coordinates of
![]() $x,y,z$
and u are small (due to the choice of support for
$x,y,z$
and u are small (due to the choice of support for
![]() $\langle \delta _0,1\rangle \cdot f'$
), and since
$\langle \delta _0,1\rangle \cdot f'$
), and since
![]() $\langle \delta _0,1\rangle \cdot f'$
is right-invariant under
$\langle \delta _0,1\rangle \cdot f'$
is right-invariant under
![]() $\{\langle y,1\rangle :y\in \mathcal {N}\cap N_H\}$
(
$\{\langle y,1\rangle :y\in \mathcal {N}\cap N_H\}$
(
![]() $\eta ^{\diamondsuit }_{2rk}$
is trivial on
$\eta ^{\diamondsuit }_{2rk}$
is trivial on
![]() $K_H\cap N_H$
), we can use Equation (5.65) to obtain
$K_H\cap N_H$
), we can use Equation (5.65) to obtain
 $$ \begin{align} &D\int\limits_{F^{*}}\int\limits_{F^{rk-2}} W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle \langle\left(\begin{smallmatrix}1\\&I_{rk-2}\\&v&1\end{smallmatrix}\right),\varsigma'(\left(\begin{smallmatrix}1\\&I_{rk-2}\\&v&1\end{smallmatrix}\right))\rangle \langle\left(\begin{smallmatrix}&I_{rk-1}\\1&\end{smallmatrix}\right),1\rangle)\\&\omega(\langle a,1\rangle)|a|^{\zeta+rks-3/2+rk-(rk-1)/2}\,dv\,d^{*}a.\nonumber \end{align} $$
$$ \begin{align} &D\int\limits_{F^{*}}\int\limits_{F^{rk-2}} W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle \langle\left(\begin{smallmatrix}1\\&I_{rk-2}\\&v&1\end{smallmatrix}\right),\varsigma'(\left(\begin{smallmatrix}1\\&I_{rk-2}\\&v&1\end{smallmatrix}\right))\rangle \langle\left(\begin{smallmatrix}&I_{rk-1}\\1&\end{smallmatrix}\right),1\rangle)\\&\omega(\langle a,1\rangle)|a|^{\zeta+rks-3/2+rk-(rk-1)/2}\,dv\,d^{*}a.\nonumber \end{align} $$
Here,
![]() $v\mapsto \langle v,\varsigma '(v)\rangle $
is the embedding of
$v\mapsto \langle v,\varsigma '(v)\rangle $
is the embedding of
![]() $N_{\operatorname {\mathrm {GL}}_{rk}}^-$
in
$N_{\operatorname {\mathrm {GL}}_{rk}}^-$
in
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
. This also justifies the passage to (5.68), because the argument on the support can be applied to
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
. This also justifies the passage to (5.68), because the argument on the support can be applied to
![]() $|f'|$
, then Integral (5.68) is absolutely convergent as a multiple integral in
$|f'|$
, then Integral (5.68) is absolutely convergent as a multiple integral in
![]() $\operatorname {\mathrm {Re}}(\zeta )\ll 0$
, since this is true for Integral (5.69) (see [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, § 2]).
$\operatorname {\mathrm {Re}}(\zeta )\ll 0$
, since this is true for Integral (5.69) (see [Reference Jacquet, Piatetski-Shapiro and ShalikaJPSS83, § 2]).
Next, we show that the coordinates of v belong in
![]() $\mathcal {O}$
(assuming
$\mathcal {O}$
(assuming
![]() $rk>2$
). Put
$rk>2$
). Put
![]() $v=(v_1,\ldots ,v_{rk-2})$
. For simplicity, redenote
$v=(v_1,\ldots ,v_{rk-2})$
. For simplicity, redenote
![]() $[0,v]=\operatorname {\mathrm {diag}}(1,\left (\begin {smallmatrix}I_{rk-2}\\v&1\end {smallmatrix}\right ))$
and
$[0,v]=\operatorname {\mathrm {diag}}(1,\left (\begin {smallmatrix}I_{rk-2}\\v&1\end {smallmatrix}\right ))$
and
![]() $w'=\left (\begin {smallmatrix}&I_{rk-1}\\1&\end {smallmatrix}\right )$
. Let
$w'=\left (\begin {smallmatrix}&I_{rk-1}\\1&\end {smallmatrix}\right )$
. Let
![]() $\mathrm {e}(o_1)=\operatorname {\mathrm {diag}}(\left (\begin {smallmatrix}1\\o_1&1\end {smallmatrix}\right ),I_{rk-2})$
, for
$\mathrm {e}(o_1)=\operatorname {\mathrm {diag}}(\left (\begin {smallmatrix}1\\o_1&1\end {smallmatrix}\right ),I_{rk-2})$
, for
![]() $o_1\in \mathcal {O}$
. Then W is right-invariant under the elements
$o_1\in \mathcal {O}$
. Then W is right-invariant under the elements
![]() $\langle \mathrm {e}(o_1),\eta ^{\diamondsuit }_{rk}(\mathrm {e}(o_1))\rangle $
. Since
$\langle \mathrm {e}(o_1),\eta ^{\diamondsuit }_{rk}(\mathrm {e}(o_1))\rangle $
. Since
![]() $y\mapsto \langle y,\eta ^{\diamondsuit }_{rk}(y)\rangle $
is a splitting of
$y\mapsto \langle y,\eta ^{\diamondsuit }_{rk}(y)\rangle $
is a splitting of
![]() $K_{\operatorname {\mathrm {GL}}_{rk}}$
in
$K_{\operatorname {\mathrm {GL}}_{rk}}$
in
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
; there is a unique splitting of
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
; there is a unique splitting of
![]() $\mathrm {e}(\mathcal {O})$
in
$\mathrm {e}(\mathcal {O})$
in
![]() $\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
(the exponent of
$\operatorname {\mathrm {GL}}_{rk}^{(m,r)}$
(the exponent of
![]() $\mu _m$
is m and
$\mu _m$
is m and
![]() $|m|=1$
); and
$|m|=1$
); and
![]() ${}^{w'}\mathrm {e}(\mathcal {O})\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, Equation (2.4) implies that
${}^{w'}\mathrm {e}(\mathcal {O})\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, Equation (2.4) implies that
We also have
![]() ${}^{[0,v]w'}\mathrm {e}(o_1)\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, therefore
${}^{[0,v]w'}\mathrm {e}(o_1)\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, therefore
 $$ \begin{align*} &W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle)\\&= W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle\langle\mathrm{e}(o_1),\eta^{\diamondsuit}_{rk}(\mathrm{e}(o_1))\rangle) \\&= W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle\left(\begin{smallmatrix}1&-o_1v&o_1\\&I_{rk-2}\\&&1\end{smallmatrix}\right),1\rangle \langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle) \\&=\psi^{-1}(o_1v_1)W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle \langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle). \end{align*} $$
$$ \begin{align*} &W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle)\\&= W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle\langle\mathrm{e}(o_1),\eta^{\diamondsuit}_{rk}(\mathrm{e}(o_1))\rangle) \\&= W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle\langle\left(\begin{smallmatrix}1&-o_1v&o_1\\&I_{rk-2}\\&&1\end{smallmatrix}\right),1\rangle \langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle) \\&=\psi^{-1}(o_1v_1)W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle \langle[0,v],\varsigma'([0,v])\rangle\langle w',1\rangle). \end{align*} $$
Taking
![]() $o_1\in \mathcal {O}^{*}$
, we deduce that the integrand of (5.69) vanishes unless
$o_1\in \mathcal {O}^{*}$
, we deduce that the integrand of (5.69) vanishes unless
![]() $v_1\in \mathcal {O}$
. Then since
$v_1\in \mathcal {O}$
. Then since
![]() ${}^{{w'}^{-1}}[0,v]\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, we can argue as in Equation (5.58) to show that
${}^{{w'}^{-1}}[0,v]\in N_{\operatorname {\mathrm {GL}}_{rk}}$
, we can argue as in Equation (5.58) to show that
![]() $v_1$
can be omitted from the integrand, and we remain with the measure of
$v_1$
can be omitted from the integrand, and we remain with the measure of
![]() $\mathcal {O}$
which equals
$\mathcal {O}$
which equals
![]() $1$
. We proceed similarly (assuming
$1$
. We proceed similarly (assuming
![]() $rk>3$
), with
$rk>3$
), with
 $$ \begin{align*} \mathrm{e}(o_2,\ldots,o_{rk-2})=\left(\begin{smallmatrix}1\\0&1\\o_2&&1\\\vdots&&&\ddots\\o_{rk-2}&&&&1\\0&&&&&1\end{smallmatrix}\right), \end{align*} $$
$$ \begin{align*} \mathrm{e}(o_2,\ldots,o_{rk-2})=\left(\begin{smallmatrix}1\\0&1\\o_2&&1\\\vdots&&&\ddots\\o_{rk-2}&&&&1\\0&&&&&1\end{smallmatrix}\right), \end{align*} $$
in increasing order (
![]() $o_2\in \mathcal {O}^{*}$
and the remaining coordinates zero to show that
$o_2\in \mathcal {O}^{*}$
and the remaining coordinates zero to show that
![]() $v_2\in \mathcal {O}$
, etc.). Hence, Integral (5.69) equals
$v_2\in \mathcal {O}$
, etc.). Hence, Integral (5.69) equals
 $$ \begin{align*} &D\int\limits_{F^{*}}W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle)\omega(\langle a,1\rangle)|a|^{\zeta+rks-3/2+rk-(rk-1)/2}\,d^{*}a. \end{align*} $$
$$ \begin{align*} &D\int\limits_{F^{*}}W(\langle\operatorname{\mathrm{diag}}(I_{rk-1},a),1\rangle)\omega(\langle a,1\rangle)|a|^{\zeta+rks-3/2+rk-(rk-1)/2}\,d^{*}a. \end{align*} $$
As in the proof of Proposition 84 and by Equation (3.54), this integral equals
 $$ \begin{align*} &D\int\limits_{F^{*}}W^{*}(\langle\operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)\omega^{*}(\langle a,1\rangle)|a|^{-\zeta-rks+1/2-(rk-1)/2}\,d^{*}a\\& =DZ(-\zeta-rks+1/2,\omega^{*},W^{*}) =DL_{\vartheta}(-r\zeta-r\alpha s+1/2,\pi\times\tau^{\vee}). \end{align*} $$
$$ \begin{align*} &D\int\limits_{F^{*}}W^{*}(\langle\operatorname{\mathrm{diag}}(a,I_{rk-1}),1\rangle)\omega^{*}(\langle a,1\rangle)|a|^{-\zeta-rks+1/2-(rk-1)/2}\,d^{*}a\\& =DZ(-\zeta-rks+1/2,\omega^{*},W^{*}) =DL_{\vartheta}(-r\zeta-r\alpha s+1/2,\pi\times\tau^{\vee}). \end{align*} $$
Note that
![]() $W^{*}$
is indeed normalized, unramified and belongs to
$W^{*}$
is indeed normalized, unramified and belongs to
where the second equality follows from Proposition 42. We obtain
in
![]() $\mathbb {C}(q^{-\zeta },q^{-s})$
. Now, taking
$\mathbb {C}(q^{-\zeta },q^{-s})$
. Now, taking
![]() $\zeta =0$
, we deduce that
$\zeta =0$
, we deduce that
Comparing this to Equation (5.67) and using the definition of
![]() $L_{\pi ,\tau ,\vartheta }(s)$
we conclude Equation (5.64).
$L_{\pi ,\tau ,\vartheta }(s)$
we conclude Equation (5.64).
As a corollary, we finally obtain the computation of the integral with unramified data:
Corollary 86. Let
![]() $\omega $
and f be the normalized unramified vectors. Then
$\omega $
and f be the normalized unramified vectors. Then
 $$ \begin{align*} Z(s,\omega,f) =\frac{L_{\vartheta}(r\alpha s+1/2,\pi^{\vee}\times\tau)L_{\vartheta}(r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^{r}L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
$$ \begin{align*} Z(s,\omega,f) =\frac{L_{\vartheta}(r\alpha s+1/2,\pi^{\vee}\times\tau)L_{\vartheta}(r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^{r}L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
5.4 Concluding the computation
Theorem 87. Let
![]() $\pi $
be a genuine irreducible unramified representation of
$\pi $
be a genuine irreducible unramified representation of
![]() $\operatorname {\mathrm {GL}}_n$
, and
$\operatorname {\mathrm {GL}}_n$
, and
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
be genuine irreducible unramified representations of
$\tau '$
be genuine irreducible unramified representations of
![]() $\operatorname {\mathrm {GL}}_k^{(m,r)}$
. Assume that the conditions on
$\operatorname {\mathrm {GL}}_k^{(m,r)}$
. Assume that the conditions on
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
from § 5.2 hold. Let
$\tau '$
from § 5.2 hold. Let
![]() $\omega $
and
$\omega $
and
![]() $f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau '))}$
be normalized and unramified. Put
$f_{\mathcal {W}(\rho _n(\tau ))\otimes \mathcal {W}(\rho _n(\tau '))}$
be normalized and unramified. Put
![]() $\alpha =rkn$
. Then
$\alpha =rkn$
. Then
 $$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau'))})= \frac{L_{\vartheta}(r\alpha s+1/2,\pi^{\vee}\times\tau)L_{\vartheta}(r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^{rn}L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
$$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_n(\tau))\otimes \mathcal{W}(\rho_n(\tau'))})= \frac{L_{\vartheta}(r\alpha s+1/2,\pi^{\vee}\times\tau)L_{\vartheta}(r\alpha s+1/2,\pi\times{\tau'}^{\vee})}{\prod_{j=1}^{rn}L_{\vartheta}(2r\alpha s+j,\tau\times{\tau'}^{\vee})}. \end{align*} $$
Proof. The proof is by induction on n. The base case
![]() $n=1$
is Corollary 86. Assuming the result for
$n=1$
is Corollary 86. Assuming the result for
![]() $n-1$
, we deduce the result for n by applying Lemma 80 with
$n-1$
, we deduce the result for n by applying Lemma 80 with
![]() $a=1$
and
$a=1$
and
![]() $b=n-1$
, using the base case for
$b=n-1$
, using the base case for
![]() $n=1$
and the induction hypothesis on
$n=1$
and the induction hypothesis on
![]() $n-1$
and combining this with Equation (5.29). For more details, see [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Theorem 28], proved in exactly the same way.
$n-1$
and combining this with Equation (5.29). For more details, see [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Theorem 28], proved in exactly the same way.
Proof of Theorem 66.
Using local notation, let
![]() $\omega $
and
$\omega $
and
![]() $f_{\mathcal {W}(\rho _c(\tau ))}$
be normalized and unramified. Also, recall that
$f_{\mathcal {W}(\rho _c(\tau ))}$
be normalized and unramified. Also, recall that
![]() $\alpha =rkc+1$
. We need to show that
$\alpha =rkc+1$
. We need to show that
 $$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_c(\tau))})= \frac{L_{\vartheta}(r\alpha s+1/2,\pi\times\tau)} {[L_{\vartheta}(r\alpha s+rn+1/2,\tau)]\prod\limits_{1\leq j\leq rn}L_{\vartheta}(2r\alpha s+2j,\tau,\wedge^2) L_{\vartheta}(2r\alpha s+2j-1,\tau,\vee^2)}. \end{align*} $$
$$ \begin{align*} &Z(s,\omega,f_{\mathcal{W}(\rho_c(\tau))})= \frac{L_{\vartheta}(r\alpha s+1/2,\pi\times\tau)} {[L_{\vartheta}(r\alpha s+rn+1/2,\tau)]\prod\limits_{1\leq j\leq rn}L_{\vartheta}(2r\alpha s+2j,\tau,\wedge^2) L_{\vartheta}(2r\alpha s+2j-1,\tau,\vee^2)}. \end{align*} $$
Here,
![]() $L_{\vartheta }(r\alpha s+rn+1/2,\tau )$
appears only for odd m. The first step is to apply Lemma 79:
$L_{\vartheta }(r\alpha s+rn+1/2,\tau )$
appears only for odd m. The first step is to apply Lemma 79:
For the
![]() $\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral on the r.h.s., the representation
$\operatorname {\mathrm {GL}}_n^{(m,r)}\times \operatorname {\mathrm {GL}}_k^{(m,r)}$
integral on the r.h.s., the representation
![]() $\tau '$
is
$\tau '$
is
![]() $\tau ^{*}$
. As noted in §§ 5.1–5.2, in the local-global setup of Theorem 66, both
$\tau ^{*}$
. As noted in §§ 5.1–5.2, in the local-global setup of Theorem 66, both
![]() $\tau $
and
$\tau $
and
![]() $\tau ^{*}$
satisfy all the assumptions from § 5.1 and § 5.2. Hence, we can proceed to apply Theorem 87. We also have
$\tau ^{*}$
satisfy all the assumptions from § 5.1 and § 5.2. Hence, we can proceed to apply Theorem 87. We also have
![]() $L_{\vartheta }(s,\tau \times {\tau ^{*}}^{\vee })= L_{\vartheta }(s,\tau \times \tau )$
, because by Proposition 25 and since
$L_{\vartheta }(s,\tau \times {\tau ^{*}}^{\vee })= L_{\vartheta }(s,\tau \times \tau )$
, because by Proposition 25 and since
![]() $\vartheta =\vartheta ^{-1}$
,
$\vartheta =\vartheta ^{-1}$
,
![]() $t_{(\tau ^{*})^{\vee },\vartheta }= t_{(\tau ^{*})^{*},\vartheta }=t_{\tau ,\vartheta }$
. The result follows when we combine this with Equations (5.1), (2.70) and (2.71).
$t_{(\tau ^{*})^{\vee },\vartheta }= t_{(\tau ^{*})^{*},\vartheta }=t_{\tau ,\vartheta }$
. The result follows when we combine this with Equations (5.1), (2.70) and (2.71).
Remark 88. As mentioned in the introduction, the local theory can be stated independently of the conjectures of § 3.4. In this case, define
![]() $\rho _l(\tau )=\Theta _{rl,m,r,\vartheta }(\chi )$
, and the computation of the integrals with unramified data remains valid in the sense of meromorphic continuation in
$\rho _l(\tau )=\Theta _{rl,m,r,\vartheta }(\chi )$
, and the computation of the integrals with unramified data remains valid in the sense of meromorphic continuation in
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
5.5 The assumption
 $\mu _{2m}\subset F^{*}$
$\mu _{2m}\subset F^{*}$
When
![]() $2|m$
, the assumption that
$2|m$
, the assumption that
![]() $\mu _{2m}\subset F^{*}$
is stronger than the necessary assumption that
$\mu _{2m}\subset F^{*}$
is stronger than the necessary assumption that
![]() $\mu _{m}\subset F^{*}$
. We list the main places where it was used:
$\mu _{m}\subset F^{*}$
. We list the main places where it was used:
-
1. The computations of the normalized unramified Whittaker function (§ 3.3, especially Theorem 43), where we used results from [Reference Brubaker, Bump and FriedbergBBF11a, Reference McNamaraMcN11].
-
2. The properties of the local components of the global representation
 $\mathcal {E}_{\tau }$
(§ 3.2). Here, we used [Reference GaoGao18a, Proposition 3.5] for the properties of the exceptional representations
$\mathcal {E}_{\tau }$
(§ 3.2). Here, we used [Reference GaoGao18a, Proposition 3.5] for the properties of the exceptional representations
 $\Theta _{d,m,r,\vartheta }$
.
$\Theta _{d,m,r,\vartheta }$
. -
3. The invariance property (4.34) when
 $m\nmid rk$
(Proposition 77).
$m\nmid rk$
(Proposition 77).
We expect that this assumption can be removed. Our evidence for this are as follows.
-
• The partial L-function was studied in [Reference GaoGao18b] without this assumption, although in that case the unramified computation was carried out using the Gindikin–Karpelevich formula, which is based on uniqueness also for covering groups.
-
• The doubling method for
 $\operatorname {\mathrm {Sp}}_c^{(2)}\times \widetilde {\operatorname {\mathrm {GL}}}_1$
(the case
$\operatorname {\mathrm {Sp}}_c^{(2)}\times \widetilde {\operatorname {\mathrm {GL}}}_1$
(the case
 $m=2$
,
$m=2$
,
 $k=1$
) was developed in [Reference GanGan12] and also included in [Reference YamanaYam14], without the assumption that
$k=1$
) was developed in [Reference GanGan12] and also included in [Reference YamanaYam14], without the assumption that
 $\mu _4\subset F^{*}$
. In this case, it is straightforward to remove the assumption
$\mu _4\subset F^{*}$
. In this case, it is straightforward to remove the assumption
 $\mu _4\subset F^{*}$
from this work as well, the main reason being that we have Proposition 20 and the bijection described in the proof of Proposition 52.
$\mu _4\subset F^{*}$
from this work as well, the main reason being that we have Proposition 20 and the bijection described in the proof of Proposition 52. -
• In the local-global context, for a number field F, there are infinitely many places
 $\nu $
such that
$\nu $
such that
 $\mu _{2m}\subset F_{\nu }^{*}$
, hinting that if an almost Euler product of unramified L-factors can be obtained, its form is essentially determined by the computation with this stronger assumption.
$\mu _{2m}\subset F_{\nu }^{*}$
, hinting that if an almost Euler product of unramified L-factors can be obtained, its form is essentially determined by the computation with this stronger assumption. -
• The majority of the computations in this work were performed without this assumption.
To remove this assumption, the place to start would be the results of [Reference Brubaker, Bump and FriedbergBBF11a, Reference McNamaraMcN11] on Gelfand–Tsetlin patterns. We also mention that in order to generalize Proposition 77 (when
![]() $m\nmid rk$
), one may need to replace Equation (2.54) with another lift, affecting several places in the construction.
$m\nmid rk$
), one may need to replace Equation (2.54) with another lift, affecting several places in the construction.
A The global
 $\operatorname {\mathrm {GL}}_c^{(m,r)}(\mathbb {A})\times \operatorname {\mathrm {GL}}_k^{(m,r)}(\mathbb {A})$
integral
$\operatorname {\mathrm {GL}}_c^{(m,r)}(\mathbb {A})\times \operatorname {\mathrm {GL}}_k^{(m,r)}(\mathbb {A})$
integral
Let F be a number field containing
![]() $\mu _{m}$
. We use the definitions and notation of § 2.5 and § 2.7. Recall that
$\mu _{m}$
. We use the definitions and notation of § 2.5 and § 2.7. Recall that
![]() $\rho _{2d}$
is the global
$\rho _{2d}$
is the global
![]() $2$
-cocycle for
$2$
-cocycle for
![]() $\operatorname {\mathrm {Sp}}_{2d}^{(m)}(\mathbb {A})$
, and
$\operatorname {\mathrm {Sp}}_{2d}^{(m)}(\mathbb {A})$
, and
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
is by definition realized using
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
is by definition realized using
![]() $\rho ^{\diamondsuit }_{d}$
. Then
$\rho ^{\diamondsuit }_{d}$
. Then
![]() $y\mapsto \langle y,(\eta ^{\diamondsuit }_{d})^{-1}(y)\rangle $
is the embedding of
$y\mapsto \langle y,(\eta ^{\diamondsuit }_{d})^{-1}(y)\rangle $
is the embedding of
![]() $N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
in
$N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
in
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. It is also an embedding of
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. It is also an embedding of
![]() $\operatorname {\mathrm {GL}}_d(F)$
in
$\operatorname {\mathrm {GL}}_d(F)$
in
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
which we fix and use to define automorphic forms on
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
which we fix and use to define automorphic forms on
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. We also defined a global block-compatible
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. We also defined a global block-compatible
![]() $2$
-cocycle
$2$
-cocycle
![]() $\rho _{\beta }$
. By Propositions 21 and 22,
$\rho _{\beta }$
. By Propositions 21 and 22,
![]() $\eta _{\beta }=\prod _{\nu }\eta _{\beta ,\nu }$
is well defined on
$\eta _{\beta }=\prod _{\nu }\eta _{\beta ,\nu }$
is well defined on
![]() $M_{\beta }(\mathbb {A})$
and
$M_{\beta }(\mathbb {A})$
and
 $$ \begin{align} \rho_{\beta}(m,m')=\frac{\eta_{\beta}(m)\eta_{\beta}(m')}{\eta_{\beta}(mm')}\rho^{\diamondsuit}_{d}(m,m'). \end{align} $$
$$ \begin{align} \rho_{\beta}(m,m')=\frac{\eta_{\beta}(m)\eta_{\beta}(m')}{\eta_{\beta}(mm')}\rho^{\diamondsuit}_{d}(m,m'). \end{align} $$
Let
![]() $G=\operatorname {\mathrm {GL}}_c$
and
$G=\operatorname {\mathrm {GL}}_c$
and
![]() $H=\operatorname {\mathrm {GL}}_{2rkc}$
. We use the notation and definitions of § 4.3 in a global setup. Define additional
$H=\operatorname {\mathrm {GL}}_{2rkc}$
. We use the notation and definitions of § 4.3 in a global setup. Define additional
![]() $2$
-cocycles for
$2$
-cocycles for
![]() $G^{(m,r)}(\mathbb {A})$
as follows:
$G^{(m,r)}(\mathbb {A})$
as follows:
Since Equation (4.31) implies that
![]() $\sigma ^{\diamondsuit }_{2rkc,\nu }(\mathfrak {e}_1(g),\mathfrak {e}_1(g'))^{-1}=\sigma ^{\diamondsuit }_{c,\nu }(g,g')$
,
$\sigma ^{\diamondsuit }_{2rkc,\nu }(\mathfrak {e}_1(g),\mathfrak {e}_1(g'))^{-1}=\sigma ^{\diamondsuit }_{c,\nu }(g,g')$
,
![]() $\rho _{L,\nu }=\sigma _{c,\nu }^{\diamondsuit }=\rho _{R,\nu }$
in
$\rho _{L,\nu }=\sigma _{c,\nu }^{\diamondsuit }=\rho _{R,\nu }$
in
![]() $\mathrm {H}^2(G(F_{\nu }),\mu _m)$
, whence the induced coverings on both copies of
$\mathrm {H}^2(G(F_{\nu }),\mu _m)$
, whence the induced coverings on both copies of
![]() $G(\mathbb {A})$
are isomorphic to the covering
$G(\mathbb {A})$
are isomorphic to the covering
![]() $G^{(m,r)}(\mathbb {A})$
(realized as explained above, with
$G^{(m,r)}(\mathbb {A})$
(realized as explained above, with
![]() $\rho _c^{\diamondsuit }$
). Let
$\rho _c^{\diamondsuit }$
). Let
![]() $G^{(m,r)}(\mathbb {A})[\rho _L]$
and
$G^{(m,r)}(\mathbb {A})[\rho _L]$
and
![]() $G^{(m,r)}(\mathbb {A})[\rho _R]$
denote the realizations of
$G^{(m,r)}(\mathbb {A})[\rho _R]$
denote the realizations of
![]() $G^{(m,r)}(\mathbb {A})$
using
$G^{(m,r)}(\mathbb {A})$
using
![]() $\rho _L$
and
$\rho _L$
and
![]() $\rho _R$
(resp.). We have global embeddings analogous to the embeddings (4.32):
$\rho _R$
(resp.). We have global embeddings analogous to the embeddings (4.32):
According to the local relation (2.52), globally
Thus, as in the local case (see § 4.3), the embedding
![]() $G(\mathbb {A})\times G(\mathbb {A}) \hookrightarrow H(\mathbb {A})$
lifts to an embedding
$G(\mathbb {A})\times G(\mathbb {A}) \hookrightarrow H(\mathbb {A})$
lifts to an embedding
To relate between
![]() $G^{(m,r)}(\mathbb {A})[\rho _L]$
,
$G^{(m,r)}(\mathbb {A})[\rho _L]$
,
![]() $G^{(m,r)}(\mathbb {A})[\rho _R]$
and
$G^{(m,r)}(\mathbb {A})[\rho _R]$
and
![]() $G^{(m,r)}(\mathbb {A})=G^{(m,r)}(\mathbb {A})[\rho ^{\diamondsuit }_{c}]$
, observe that because
$G^{(m,r)}(\mathbb {A})=G^{(m,r)}(\mathbb {A})[\rho ^{\diamondsuit }_{c}]$
, observe that because
![]() $\rho _{(c^{2rk})}=\rho ^{\diamondsuit }_{2rkc}$
in
$\rho _{(c^{2rk})}=\rho ^{\diamondsuit }_{2rkc}$
in
![]() $\mathrm {H}^2(M_{(c^{2rk})}(\mathbb {A}),\mu _m)$
and also
$\mathrm {H}^2(M_{(c^{2rk})}(\mathbb {A}),\mu _m)$
and also
when we use Equations (A.1) and (A.2) we obtain
 $$ \begin{align*} &G^{(m,r)}(\mathbb{A})[\rho_L]\rightarrow G^{(m,r)}(\mathbb{A}),\qquad \langle g,\epsilon\rangle\mapsto \langle g,\eta_{(c^{2rk})}(\mathfrak{e}_1(g))\epsilon\rangle,\\ &G^{(m,r)}(\mathbb{A})[\rho_R]\rightarrow G^{(m,r)}(\mathbb{A}),\qquad \langle g,\epsilon\rangle\mapsto \langle g,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g))\epsilon\rangle. \end{align*} $$
$$ \begin{align*} &G^{(m,r)}(\mathbb{A})[\rho_L]\rightarrow G^{(m,r)}(\mathbb{A}),\qquad \langle g,\epsilon\rangle\mapsto \langle g,\eta_{(c^{2rk})}(\mathfrak{e}_1(g))\epsilon\rangle,\\ &G^{(m,r)}(\mathbb{A})[\rho_R]\rightarrow G^{(m,r)}(\mathbb{A}),\qquad \langle g,\epsilon\rangle\mapsto \langle g,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g))\epsilon\rangle. \end{align*} $$
Dualizing, for a function
![]() $\varphi $
on
$\varphi $
on
![]() $G^{(m,r)}(\mathbb {A})$
we have the following functions
$G^{(m,r)}(\mathbb {A})$
we have the following functions
![]() $\varphi ^{L}$
and
$\varphi ^{L}$
and
![]() $\varphi ^{R}$
on
$\varphi ^{R}$
on
![]() $G^{(m)}(\mathbb {A})[\rho _L]$
and
$G^{(m)}(\mathbb {A})[\rho _L]$
and
![]() $G^{(m)}(\mathbb {A})[\rho _R]$
,
$G^{(m)}(\mathbb {A})[\rho _R]$
,
Proposition A.1. Let
![]() $\varphi _1,\varphi _2$
be continuous functions on
$\varphi _1,\varphi _2$
be continuous functions on
![]() $G(F)\backslash G^{(m,r)}(\mathbb {A})$
such that
$G(F)\backslash G^{(m,r)}(\mathbb {A})$
such that
![]() $\varphi _1$
is genuine and
$\varphi _1$
is genuine and
![]() $\varphi _2$
is antigenuine, and f be a continuous genuine function on the image of
$\varphi _2$
is antigenuine, and f be a continuous genuine function on the image of
in
![]() $H(F)\backslash H^{(m,r)}(\mathbb {A})$
(e.g., f on
$H(F)\backslash H^{(m,r)}(\mathbb {A})$
(e.g., f on
![]() $H(F)\backslash H^{(m,r)}(\mathbb {A})$
). Then
$H(F)\backslash H^{(m,r)}(\mathbb {A})$
). Then
 $$ \begin{align*} \int\limits_{G(F)\times G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
$$ \begin{align*} \int\limits_{G(F)\times G(F)\backslash G(\mathbb{A})\times G(\mathbb{A})}\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,dg_1\,dg_2 \end{align*} $$
is well defined, provided it is absolutely convergent. (To ensure convergence one typically deals with the center of
![]() $G(\mathbb {A})$
.)
$G(\mathbb {A})$
.)
Proof. The integrand is well defined on
![]() $G(\mathbb {A})\times G(\mathbb {A})$
by Definitions (A.3)-(A.4). Specifically, if we replace the section
$G(\mathbb {A})\times G(\mathbb {A})$
by Definitions (A.3)-(A.4). Specifically, if we replace the section
![]() $g_1\mapsto \langle g_1,1\rangle $
of
$g_1\mapsto \langle g_1,1\rangle $
of
![]() $G(\mathbb {A})\rightarrow G^{(m,r)}(\mathbb {A})[\rho _L]$
with
$G(\mathbb {A})\rightarrow G^{(m,r)}(\mathbb {A})[\rho _L]$
with
![]() $g_1\mapsto \langle g_1,\epsilon _{g_1}\rangle $
and similarly take a section
$g_1\mapsto \langle g_1,\epsilon _{g_1}\rangle $
and similarly take a section
![]() $g_2\mapsto \langle g_2,\epsilon ^{\prime }_{g_2}\rangle $
of
$g_2\mapsto \langle g_2,\epsilon ^{\prime }_{g_2}\rangle $
of
![]() $G(\mathbb {A})\rightarrow G^{(m,r)}(\mathbb {A})[\rho _R]$
, the integrand does not change:
$G(\mathbb {A})\rightarrow G^{(m,r)}(\mathbb {A})[\rho _R]$
, the integrand does not change:
 $$ \begin{align*} &\varphi_1^{L}(\langle g_1,\epsilon_{g_1}\rangle)\varphi_2^{R}(\langle g_2,\epsilon^{\prime}_{g_2}\rangle)f(\langle\mathfrak{e}_1(g_1),\epsilon_{g_1}^{-1}\rangle\langle\mathfrak{e}^{\prime}_2(g_2),\epsilon^{\prime}_{g_2}\rangle) \\ &=\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle). \end{align*} $$
$$ \begin{align*} &\varphi_1^{L}(\langle g_1,\epsilon_{g_1}\rangle)\varphi_2^{R}(\langle g_2,\epsilon^{\prime}_{g_2}\rangle)f(\langle\mathfrak{e}_1(g_1),\epsilon_{g_1}^{-1}\rangle\langle\mathfrak{e}^{\prime}_2(g_2),\epsilon^{\prime}_{g_2}\rangle) \\ &=\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle). \end{align*} $$
Then Equations (A.2) and (A.5) imply that the integral is formally a right-
![]() $(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional:
$(G(\mathbb {A})\times G(\mathbb {A}))$
-invariant functional:
 $$ \begin{align*} &\varphi_1^{L}(\langle g_1,1\rangle\langle h_1,1\rangle)=\rho_L(g_1,h_1)\varphi_1^{L}(\langle g_1h_1,1\rangle)=(\rho_{2rkc}^{\diamondsuit})^{-1}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\varphi_1^{L}(\langle g_1h_1,1\rangle),\\ &\varphi_2^{R}(\langle g_2,1\rangle\langle h_2,1\rangle)=\rho_R(g_2,h_2)^{-1}\varphi_2^{R}(\langle g_2h_2,1\rangle) =(\rho_{2rkc}^{\diamondsuit})^{-1}(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\varphi_2^{R}(\langle 1,g_2h_2\rangle),\\ &f(\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(h_2),1\rangle)\\ &\quad= \rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))f(\langle \mathfrak{e}_1(g_1h_1),1\rangle\langle\mathfrak{e}_2(g_2h_2),1\rangle). \end{align*} $$
$$ \begin{align*} &\varphi_1^{L}(\langle g_1,1\rangle\langle h_1,1\rangle)=\rho_L(g_1,h_1)\varphi_1^{L}(\langle g_1h_1,1\rangle)=(\rho_{2rkc}^{\diamondsuit})^{-1}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\varphi_1^{L}(\langle g_1h_1,1\rangle),\\ &\varphi_2^{R}(\langle g_2,1\rangle\langle h_2,1\rangle)=\rho_R(g_2,h_2)^{-1}\varphi_2^{R}(\langle g_2h_2,1\rangle) =(\rho_{2rkc}^{\diamondsuit})^{-1}(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))\varphi_2^{R}(\langle 1,g_2h_2\rangle),\\ &f(\langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle \langle \mathfrak{e}_1(h_1),1\rangle\langle \mathfrak{e}_2(h_2),1\rangle)\\ &\quad= \rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_1(h_1))\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_2(g_2),\mathfrak{e}_2(h_2))f(\langle \mathfrak{e}_1(g_1h_1),1\rangle\langle\mathfrak{e}_2(g_2h_2),1\rangle). \end{align*} $$
Finally, we show that the integrand factors through the quotient. Let
![]() $y_1,y_2\in G(F)$
,
$y_1,y_2\in G(F)$
,
![]() $\epsilon _i=\eta _{2rkc}^{\diamondsuit }(\mathfrak {e}_i(y_i))$
and
$\epsilon _i=\eta _{2rkc}^{\diamondsuit }(\mathfrak {e}_i(y_i))$
and
![]() $g_1,g_2\in G(\mathbb {A})$
. The crucial point here is that
$g_1,g_2\in G(\mathbb {A})$
. The crucial point here is that
![]() $\eta _c^{\diamondsuit }$
is well defined on
$\eta _c^{\diamondsuit }$
is well defined on
![]() $G(F)$
, hence Equation (2.58) globalizes and
$G(F)$
, hence Equation (2.58) globalizes and
![]() $\eta _{2rkc}^{\diamondsuit }(b)\eta _{(c^{2rk})}(b)=\prod _{i=1}^{2rk} \eta _{c}^{\diamondsuit }(b_i)$
so that
$\eta _{2rkc}^{\diamondsuit }(b)\eta _{(c^{2rk})}(b)=\prod _{i=1}^{2rk} \eta _{c}^{\diamondsuit }(b_i)$
so that
 $$ \begin{align*} \epsilon_1\eta_{(c^{2rk})}(\mathfrak{e}_1(y_1))=\prod_{i=1}^{2rk-1} (\eta_{c}^{\diamondsuit})(y_1)=(\eta_{c}^{\diamondsuit})^{-1}(y_1),\quad \epsilon_2\eta_{(c^{2rk})}(\mathfrak{e}_2(y_2))=\eta_{c}^{\diamondsuit}(y_2). \end{align*} $$
$$ \begin{align*} \epsilon_1\eta_{(c^{2rk})}(\mathfrak{e}_1(y_1))=\prod_{i=1}^{2rk-1} (\eta_{c}^{\diamondsuit})(y_1)=(\eta_{c}^{\diamondsuit})^{-1}(y_1),\quad \epsilon_2\eta_{(c^{2rk})}(\mathfrak{e}_2(y_2))=\eta_{c}^{\diamondsuit}(y_2). \end{align*} $$
Combining this with Equation (A.6), we have
 $$ \begin{align*} \varphi_1^{L}(\langle y_1,\epsilon_1\rangle\langle g_1,1\rangle)&= \varphi_1(\langle y_1,\epsilon_1\eta_{(c^{2rk})}(\mathfrak{e}_1(y_1))\rangle\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\rangle) \\&=\varphi_1(\langle y_1,(\eta_{c}^{\diamondsuit})^{-1}(y_1)\rangle\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\rangle) =\varphi_1^L(\langle g_1,1\rangle),\\ \varphi_2^{R}(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)&= \varphi_2(\langle y_2,\epsilon_2^{-1}\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(y_2)\rangle\langle g_2,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g_2))\rangle) \\&=\varphi_2(\langle y_2,(\eta_{c}^{\diamondsuit})^{-1}(y_2)\rangle\langle g_2,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g_2))\rangle) =\varphi_2^R(\langle g_2,1\rangle). \end{align*} $$
$$ \begin{align*} \varphi_1^{L}(\langle y_1,\epsilon_1\rangle\langle g_1,1\rangle)&= \varphi_1(\langle y_1,\epsilon_1\eta_{(c^{2rk})}(\mathfrak{e}_1(y_1))\rangle\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\rangle) \\&=\varphi_1(\langle y_1,(\eta_{c}^{\diamondsuit})^{-1}(y_1)\rangle\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\rangle) =\varphi_1^L(\langle g_1,1\rangle),\\ \varphi_2^{R}(\langle y_2,\epsilon_2^{-1}\rangle\langle g_2,1\rangle)&= \varphi_2(\langle y_2,\epsilon_2^{-1}\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(y_2)\rangle\langle g_2,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g_2))\rangle) \\&=\varphi_2(\langle y_2,(\eta_{c}^{\diamondsuit})^{-1}(y_2)\rangle\langle g_2,\eta_{(c^{2rk})}^{-1}(\mathfrak{e}_2(g_2))\rangle) =\varphi_2^R(\langle g_2,1\rangle). \end{align*} $$
Therefore,
 $$ \begin{align} &\varphi_1^{L}(\langle y_1g_1,1\rangle)\varphi_2^R(\langle y_2g_2,1\rangle)f (\langle\mathfrak{e}_1(y_1g_1),1\rangle\langle\mathfrak{e}_2(y_2g_2),1\rangle)\\ &=\varphi_1^{L}(\langle y_1,1\rangle \langle g_1,1\rangle )\varphi_2^{R}(\langle y_2,1\rangle \langle g_2,1\rangle ) f( \nonumber \langle\mathfrak{e}_1(y_1),1\rangle\langle\mathfrak{e}_2(y_2),1\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{L}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle )\varphi_2^{R}(\langle y_2,\epsilon_2^{-1}\rangle \langle g_2,1\rangle ) f(\nonumber \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_2(y_2),\epsilon_2^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber\\ &=\varphi_1^{L}(\langle g_1,1\rangle)\nonumber \varphi_2^R(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber. \end{align} $$
$$ \begin{align} &\varphi_1^{L}(\langle y_1g_1,1\rangle)\varphi_2^R(\langle y_2g_2,1\rangle)f (\langle\mathfrak{e}_1(y_1g_1),1\rangle\langle\mathfrak{e}_2(y_2g_2),1\rangle)\\ &=\varphi_1^{L}(\langle y_1,1\rangle \langle g_1,1\rangle )\varphi_2^{R}(\langle y_2,1\rangle \langle g_2,1\rangle ) f( \nonumber \langle\mathfrak{e}_1(y_1),1\rangle\langle\mathfrak{e}_2(y_2),1\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber \\&=\varphi_1^{L}(\langle y_1,\epsilon_1\rangle \langle g_1,1\rangle )\varphi_2^{R}(\langle y_2,\epsilon_2^{-1}\rangle \langle g_2,1\rangle ) f(\nonumber \langle\mathfrak{e}_1(y_1),\epsilon_1^{-1}\rangle\langle\mathfrak{e}_2(y_2),\epsilon_2^{-1}\rangle\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber\\ &=\varphi_1^{L}(\langle g_1,1\rangle)\nonumber \varphi_2^R(\langle g_2,1\rangle)f(\langle\mathfrak{e}_1(g_1),1\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\nonumber. \end{align} $$
This completes the proof.
Recall the local lift of the involution
![]() ${}^{*}$
to
${}^{*}$
to
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(F_{\nu })$
given by Equation (2.54). This involution also has a global lift to an involution of
$\operatorname {\mathrm {GL}}_d^{(m,r)}(F_{\nu })$
given by Equation (2.54). This involution also has a global lift to an involution of
![]() $\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. To see this, first consider
$\operatorname {\mathrm {GL}}_d^{(m,r)}(\mathbb {A})$
. To see this, first consider
![]() ${}^{*}$
as an involution of
${}^{*}$
as an involution of
![]() $\operatorname {\mathrm {SL}}_{2d}$
. Then argue as in § 2.6 and observe that the analog of Proposition 17, namely that
$\operatorname {\mathrm {SL}}_{2d}$
. Then argue as in § 2.6 and observe that the analog of Proposition 17, namely that
![]() $\sigma ^{*}_{2d}=\sigma _{2d}$
in
$\sigma ^{*}_{2d}=\sigma _{2d}$
in
![]() $\mathrm {H}^2(\operatorname {\mathrm {SL}}_{2d}(F_{\nu }),\mu _m)$
, was obtained in Proposition 4. We do not know, however, if the global lift of
$\mathrm {H}^2(\operatorname {\mathrm {SL}}_{2d}(F_{\nu }),\mu _m)$
, was obtained in Proposition 4. We do not know, however, if the global lift of
![]() ${}^{*}$
restricts to the local involutions (2.54) at all places, except when m is odd in which case it does because then Equation (2.54) is the unique lift which is an involution (see § 2.7).
${}^{*}$
restricts to the local involutions (2.54) at all places, except when m is odd in which case it does because then Equation (2.54) is the unique lift which is an involution (see § 2.7).
We turn to construct the global integral, following the linear case from [Reference Cai, Friedberg and KaplanCFK22]. Recall that
![]() $P=M_P\ltimes U_P$
(
$P=M_P\ltimes U_P$
(
![]() $P=P_{(rkc,rkc)}$
). Let
$P=P_{(rkc,rkc)}$
). Let
![]() $\tau _0$
be a genuine irreducible cuspidal automorphic representation of
$\tau _0$
be a genuine irreducible cuspidal automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and
$\operatorname {\mathrm {GL}}_{k}^{(m,r)}(\mathbb {A})$
, and
![]() $\mathcal {E}_{\tau _0}$
be the coarse
$\mathcal {E}_{\tau _0}$
be the coarse
![]() $(rk,c)$
representation defined in § 3.4 by Theorem 54. Recall that for the existence of
$(rk,c)$
representation defined in § 3.4 by Theorem 54. Recall that for the existence of
![]() $\mathcal {E}_{\tau _0}$
we assume Conjectures 50 and 51, but we do not need to assume that
$\mathcal {E}_{\tau _0}$
we assume Conjectures 50 and 51, but we do not need to assume that
![]() $\mu _{2m}\subset F^{*}$
.
$\mu _{2m}\subset F^{*}$
.
Realize the covering
![]() $\widetilde {M}_P(\mathbb {A})$
using
$\widetilde {M}_P(\mathbb {A})$
using
![]() $\rho _{(rkc,rkc)}$
, then we can define the genuine automorphic representation
$\rho _{(rkc,rkc)}$
, then we can define the genuine automorphic representation
![]() $\mathcal {E}_{\tau _0}\otimes \mathcal {E}_{\tau _0^{*}}$
of
$\mathcal {E}_{\tau _0}\otimes \mathcal {E}_{\tau _0^{*}}$
of
![]() $\widetilde {M}_P(\mathbb {A})$
. The space of the induced representation
$\widetilde {M}_P(\mathbb {A})$
. The space of the induced representation
is the space of genuine smooth functions f on
![]() $H^{(m,r)}(\mathbb {A})$
taking values in the space of
$H^{(m,r)}(\mathbb {A})$
taking values in the space of
![]() $\mathcal {E}_{\tau _0}\otimes \mathcal {E}_{\tau _0^{*}}$
such that
$\mathcal {E}_{\tau _0}\otimes \mathcal {E}_{\tau _0^{*}}$
such that
for all
![]() $b\in M_{P}(\mathbb {A})$
,
$b\in M_{P}(\mathbb {A})$
,
![]() $u\in U_P(\mathbb {A})$
and
$u\in U_P(\mathbb {A})$
and
![]() $h\in H^{(m,r)}(\mathbb {A})$
. We regard these functions as complex-valued by evaluating at the identity.
$h\in H^{(m,r)}(\mathbb {A})$
. We regard these functions as complex-valued by evaluating at the identity.
According to Equations (2.20) and (2.29), when
![]() $F_{\nu }$
is unramified,
$F_{\nu }$
is unramified,
![]() $y\mapsto \langle y,1\rangle $
is an embedding of
$y\mapsto \langle y,1\rangle $
is an embedding of
![]() $K_{H,\nu }$
(resp.,
$K_{H,\nu }$
(resp.,
![]() $K_{G,\nu }$
) in
$K_{G,\nu }$
) in
![]() $H^{(m,r)}(\mathbb {A})$
(resp.,
$H^{(m,r)}(\mathbb {A})$
(resp.,
![]() $G^{(m,r)}(\mathbb {A})$
), which is compatible with our local choices. See the paragraph following Equation (2.53). Hence,
$G^{(m,r)}(\mathbb {A})$
), which is compatible with our local choices. See the paragraph following Equation (2.53). Hence,
![]() $y\mapsto \langle y,1\rangle $
is an embedding of
$y\mapsto \langle y,1\rangle $
is an embedding of
![]() $\prod _{\nu \notin S}K_{H,\nu }$
in
$\prod _{\nu \notin S}K_{H,\nu }$
in
![]() $H^{(m,r)}(\mathbb {A})$
for any set S such that
$H^{(m,r)}(\mathbb {A})$
for any set S such that
![]() $F_{\nu }$
is unramified for all
$F_{\nu }$
is unramified for all
![]() $\nu \notin S$
.
$\nu \notin S$
.
Let f be a standard
![]() $\widetilde {K}_H$
-finite section in the space of the representation (A.8). Define in
$\widetilde {K}_H$
-finite section in the space of the representation (A.8). Define in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
 $$ \begin{align} E(h;s,f)=\sum_{y\in P(F)\backslash H(F)}f(s,\langle y,(\eta_{2rkc}^{\diamondsuit})^{-1}(y)\rangle h),\qquad h\in H^{(m,r)}(\mathbb{A}) \end{align} $$
$$ \begin{align} E(h;s,f)=\sum_{y\in P(F)\backslash H(F)}f(s,\langle y,(\eta_{2rkc}^{\diamondsuit})^{-1}(y)\rangle h),\qquad h\in H^{(m,r)}(\mathbb{A}) \end{align} $$
and in general by meromorphic continuation. Let
 $$ \begin{align*} E^{U,\psi_U}(h;s,f)= \int\limits_{U(F)\backslash U({\mathbb{A}})} E(\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle h;s,f)\,\psi_U(u)\,du. \end{align*} $$
$$ \begin{align*} E^{U,\psi_U}(h;s,f)= \int\limits_{U(F)\backslash U({\mathbb{A}})} E(\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle h;s,f)\,\psi_U(u)\,du. \end{align*} $$
Let
![]() $\pi $
be a genuine irreducible cuspidal automorphic representation of
$\pi $
be a genuine irreducible cuspidal automorphic representation of
![]() $G^{(m,r)}(\mathbb {A})$
,
$G^{(m,r)}(\mathbb {A})$
,
![]() $\varphi _1$
be a cusp form in the space of
$\varphi _1$
be a cusp form in the space of
![]() $\pi $
and
$\pi $
and
![]() $\varphi _2$
be a cusp form in the space of
$\varphi _2$
be a cusp form in the space of
![]() $\pi ^{\vee }$
(if
$\pi ^{\vee }$
(if
![]() $\pi $
is unitary,
$\pi $
is unitary,
![]() $\pi ^{\vee }=\overline {\pi }$
). Since
$\pi ^{\vee }=\overline {\pi }$
). Since
![]() $G\times G$
normalizes U and stabilizes
$G\times G$
normalizes U and stabilizes
![]() $\psi _U$
, by Lemma 15, and also
$\psi _U$
, by Lemma 15, and also
![]() $G(F)\times G(F)$
stabilizes
$G(F)\times G(F)$
stabilizes
![]() $du$
, we deduce that
$du$
, we deduce that
![]() $E^{U,\psi _U}(\cdot ;s,f)$
is an automorphic function on the image of
$E^{U,\psi _U}(\cdot ;s,f)$
is an automorphic function on the image of
in
![]() $H(F)\backslash H^{(m,r)}(\mathbb {A})$
. Thus, we can define the global integral as in Proposition A.1 once we take care of convergence.
$H(F)\backslash H^{(m,r)}(\mathbb {A})$
. Thus, we can define the global integral as in Proposition A.1 once we take care of convergence.
Let
![]() $C_{r,c}(\mathbb {A})=\{xI_{c}:x\in \mathbb {A}^{*r}\}$
,
$C_{r,c}(\mathbb {A})=\{xI_{c}:x\in \mathbb {A}^{*r}\}$
,
![]() $\widetilde {C}_{r,c}(\mathbb {A})$
is the center of
$\widetilde {C}_{r,c}(\mathbb {A})$
is the center of
![]() $G^{(m,r)}(\mathbb {A})$
. The product
$G^{(m,r)}(\mathbb {A})$
. The product
is invariant under multiplication
![]() $(g_1,g_2)\mapsto (zg_1,zg_2)$
for
$(g_1,g_2)\mapsto (zg_1,zg_2)$
for
![]() $z\in \widetilde {C}_{r,c}(\mathbb {A})$
. Since the index of
$z\in \widetilde {C}_{r,c}(\mathbb {A})$
. Since the index of
![]() $C_{r,c}(\mathbb {A})$
in the center
$C_{r,c}(\mathbb {A})$
in the center
![]() $C_{G}(\mathbb {A})$
of
$C_{G}(\mathbb {A})$
of
![]() $G(\mathbb {A})$
is infinite, dividing by
$G(\mathbb {A})$
is infinite, dividing by
![]() $\widetilde {C}_{r,c}(\mathbb {A})$
is not enough, one must consider a larger subgroup
$\widetilde {C}_{r,c}(\mathbb {A})$
is not enough, one must consider a larger subgroup
![]() $C'$
. We argue as in [Reference Bump and GinzburgBG92, pp. 159–160]. Let
$C'$
. We argue as in [Reference Bump and GinzburgBG92, pp. 159–160]. Let
![]() $S'$
be a finite set of places of F such that for
$S'$
be a finite set of places of F such that for
![]() $\nu \notin S'$
,
$\nu \notin S'$
,
![]() $F_{\nu }$
is unramified,
$F_{\nu }$
is unramified,
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are right-invariant under
$\varphi _2$
are right-invariant under
![]() $\{\langle y,1\rangle :y\in K_{G,\nu }\}$
, and f (and thereby
$\{\langle y,1\rangle :y\in K_{G,\nu }\}$
, and f (and thereby
![]() $E^{U,\psi _U}(\cdot ;s,f)$
) is right-invariant under
$E^{U,\psi _U}(\cdot ;s,f)$
) is right-invariant under
![]() $\{\langle y,1\rangle :y\in K_{H,\nu }\}$
. Take
$\{\langle y,1\rangle :y\in K_{H,\nu }\}$
. Take
![]() $C_0'=\{xI_{c}:x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}$
, then
$C_0'=\{xI_{c}:x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}$
, then
![]() $C_{r,c}(\mathbb {A})<C_0'$
,
$C_{r,c}(\mathbb {A})<C_0'$
,
![]() $[C_{G}(\mathbb {A}):C_0']<\infty $
and the product (A.11) is invariant under
$[C_{G}(\mathbb {A}):C_0']<\infty $
and the product (A.11) is invariant under
![]() $(g_1,g_2)\mapsto (zg_1,zg_2)$
for
$(g_1,g_2)\mapsto (zg_1,zg_2)$
for
![]() $z\in C_0'$
. Let
$z\in C_0'$
. Let
![]() $C'=\{(xI_c,xI_c):x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}<G(\mathbb {A})\times G(\mathbb {A})$
. Additionally, take a compactly supported Schwartz function
$C'=\{(xI_c,xI_c):x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}<G(\mathbb {A})\times G(\mathbb {A})$
. Additionally, take a compactly supported Schwartz function
![]() $\varrho $
on
$\varrho $
on
![]() $\mathbb {R}^{*}_{>0}$
.
$\mathbb {R}^{*}_{>0}$
.
The global integral is first ‘approximated’ by the following integral:
 $$ \begin{align} Z(s,\varphi_1,\varphi_2,f,\varrho)=&\int\limits_{C'G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^R(\langle g_2,1\rangle)\\ &\times E^{U,\psi_U}(\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle;s,f)\varrho(|\det(g_2g_1^{-1})|)\,dg_1\,dg_2. \end{align} $$
$$ \begin{align} Z(s,\varphi_1,\varphi_2,f,\varrho)=&\int\limits_{C'G(F)\times G(F)\backslash G({\mathbb{A}})\times G({\mathbb{A}})}\, \varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^R(\langle g_2,1\rangle)\\ &\times E^{U,\psi_U}(\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle;s,f)\varrho(|\det(g_2g_1^{-1})|)\,dg_1\,dg_2. \end{align} $$
(Cf., [Reference Cai, Friedberg and KaplanCFK22, § 2.4] and [Reference Piatetski-Shapiro and RallisPSR87, § 4.2].) At the end of the appendix, we explain how to remove the dependency on
![]() $\varrho $
in order to define the global integral
$\varrho $
in order to define the global integral
![]() $Z(s,\varphi _1,\varphi _2,f)$
.
$Z(s,\varphi _1,\varphi _2,f)$
.
Theorem A.2. The integral (A.12) is formally well defined, absolutely convergent away from the poles of the series and admits meromorphic continuation to
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Proof. The integral is well defined by the discussion above and by Proposition A.1. Convergence and continuation follow from the rapid decay of cusp forms and moderate growth and meromorphic continuation of the Eisenstein series and the presence of
![]() $\varrho $
(see also [Reference Piatetski-Shapiro and RallisPSR87, § 4.2]).
$\varrho $
(see also [Reference Piatetski-Shapiro and RallisPSR87, § 4.2]).
Next, we prove the basic identity for Integral (A.12), but under the assumption that at each place
![]() $\nu $
of F,
$\nu $
of F,
![]() $(\mathcal {E}_{\tau _0})_{\nu }$
admits a unique
$(\mathcal {E}_{\tau _0})_{\nu }$
admits a unique
![]() $(rk,c)$
model. This assumption implies that
$(rk,c)$
model. This assumption implies that
![]() $(\mathcal {E}_{\tau _0^{*}})_{\nu }$
also admits a unique
$(\mathcal {E}_{\tau _0^{*}})_{\nu }$
also admits a unique
![]() $(rk,c)$
model for all
$(rk,c)$
model for all
![]() $\nu $
.
$\nu $
.
Recall that the
![]() $(rk,c)$
functional
$(rk,c)$
functional
![]() $\Lambda $
was defined by Integral (3.2). The global
$\Lambda $
was defined by Integral (3.2). The global
![]() $(rk,c)$
model
$(rk,c)$
model
![]() $\mathcal {W}(\mathcal {E}_{\tau _0})$
is the space spanned by
$\mathcal {W}(\mathcal {E}_{\tau _0})$
is the space spanned by
![]() $\Lambda (\xi )$
as
$\Lambda (\xi )$
as
![]() $\xi $
varies in the space of
$\xi $
varies in the space of
![]() $\mathcal {E}_{\tau _0}$
. We then have the similar functional
$\mathcal {E}_{\tau _0}$
. We then have the similar functional
![]() $\Lambda ^{*}$
and model
$\Lambda ^{*}$
and model
![]() $\mathcal {W}(\mathcal {E}_{\tau _0^{*}})$
for
$\mathcal {W}(\mathcal {E}_{\tau _0^{*}})$
for
![]() $\mathcal {E}_{\tau _0^{*}}$
. Note that our local uniqueness assumption (at all places) implies that
$\mathcal {E}_{\tau _0^{*}}$
. Note that our local uniqueness assumption (at all places) implies that
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda ^{*}$
are factorizable. Put
$\Lambda ^{*}$
are factorizable. Put
![]() $\mathcal {W}=\mathcal {W}(\mathcal {E}_{\tau _0})\otimes \mathcal {W}(\mathcal {E}_{\tau _0^{*}})$
. Let
$\mathcal {W}=\mathcal {W}(\mathcal {E}_{\tau _0})\otimes \mathcal {W}(\mathcal {E}_{\tau _0^{*}})$
. Let
![]() $f_{\mathcal {W}}$
be the composition of f with
$f_{\mathcal {W}}$
be the composition of f with
![]() $\Lambda \otimes \Lambda ^{*}$
:
$\Lambda \otimes \Lambda ^{*}$
:
 $$ \begin{align*} f_{\mathcal{W}}(s,h)=&\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})} \int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}\\&\quad f(s,\langle \operatorname{\mathrm{diag}}(v,v'),(\eta_{2rkc}^{\diamondsuit})^{-1}(\operatorname{\mathrm{diag}}(v,v'))\rangle h)\psi^{-1}(v)\psi^{-1}(v')\,dv\,dv'.\nonumber \end{align*} $$
$$ \begin{align*} f_{\mathcal{W}}(s,h)=&\int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})} \int\limits_{V_{(c^{rk})}(F)\backslash V_{(c^{rk})}(\mathbb{A})}\\&\quad f(s,\langle \operatorname{\mathrm{diag}}(v,v'),(\eta_{2rkc}^{\diamondsuit})^{-1}(\operatorname{\mathrm{diag}}(v,v'))\rangle h)\psi^{-1}(v)\psi^{-1}(v')\,dv\,dv'.\nonumber \end{align*} $$
Further let
 $$ \begin{align*} \{\varphi_1^R,\varphi_2^R\}= \int\limits_{C_0'G(F)\backslash G(\mathbb{A})}\varphi_1^R(\langle g,1\rangle)\varphi_2^R(\langle g,1\rangle)\,dg. \end{align*} $$
$$ \begin{align*} \{\varphi_1^R,\varphi_2^R\}= \int\limits_{C_0'G(F)\backslash G(\mathbb{A})}\varphi_1^R(\langle g,1\rangle)\varphi_2^R(\langle g,1\rangle)\,dg. \end{align*} $$
Theorem A.3. Assume that m is odd and that
![]() $(\mathcal {E}_{\tau _0})_{\nu }$
admits a unique
$(\mathcal {E}_{\tau _0})_{\nu }$
admits a unique
![]() $(rk,c)$
model for all
$(rk,c)$
model for all
![]() $\nu $
. In
$\nu $
. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral (A.12) equals
$\operatorname {\mathrm {Re}}(s)\gg 0$
, the integral (A.12) equals
 $$ \begin{align} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1^R,\pi(\langle g,1\rangle)\varphi_2^R\}f_{\mathcal{W}}(s,\langle\delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle \langle\mathfrak{e}_2(g),1\rangle) \,\psi_U(u_0)\varrho(|\det(g)|)\,du_0\,dg. \end{align} $$
$$ \begin{align} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1^R,\pi(\langle g,1\rangle)\varphi_2^R\}f_{\mathcal{W}}(s,\langle\delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle \langle\mathfrak{e}_2(g),1\rangle) \,\psi_U(u_0)\varrho(|\det(g)|)\,du_0\,dg. \end{align} $$
Remark A.1. The assumptions on m and
![]() $(\mathcal {E}_{\tau _0})_{\nu }$
in the statement of the theorem are only needed for Proposition 77, which is used for the proof of Lemma A.4 below. The assumption
$(\mathcal {E}_{\tau _0})_{\nu }$
in the statement of the theorem are only needed for Proposition 77, which is used for the proof of Lemma A.4 below. The assumption
![]() $2\nmid m$
guarantees that at the local places the lift
$2\nmid m$
guarantees that at the local places the lift
![]() ${}^{*}$
is given by Equation (2.54). Moreover, since this assumption implies that
${}^{*}$
is given by Equation (2.54). Moreover, since this assumption implies that
![]() $\mu _{2m}\subset F^{*}$
, the proposition is applicable also when
$\mu _{2m}\subset F^{*}$
, the proposition is applicable also when
![]() $m\nmid rk$
.
$m\nmid rk$
.
Proof. Let
![]() $D=(G\times G)\ltimes U<Q$
and for
$D=(G\times G)\ltimes U<Q$
and for
![]() $h\in H$
,
$h\in H$
,
![]() $D_h={}^{h^{-1}}P\cap D$
. To lighten the notation, set
$D_h={}^{h^{-1}}P\cap D$
. To lighten the notation, set
![]() $G^{\times }(\mathbb {A})=G(\mathbb {A})\times G(\mathbb {A})$
. In
$G^{\times }(\mathbb {A})=G(\mathbb {A})\times G(\mathbb {A})$
. In
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
,
$\operatorname {\mathrm {Re}}(s)\gg 0$
,
![]() $Z(s,\varphi _1,\varphi _2,f)$
equals
$Z(s,\varphi _1,\varphi _2,f)$
equals
 $$ \begin{align*} &\sum\limits_{h\in P(F)\backslash H(F)/D(F)}\quad\!\int\limits_{C'G^{\times}(F)\backslash G^{\times}(\mathbb{A})} \quad\!\int\limits_{U(F)\backslash U({\mathbb{A}})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)\,\sum\limits_{y\in D_{h}(F)\backslash D(F)} \\&\times f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle y,(\eta_{2rkc}^{\diamondsuit})^{-1}(y)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\sum\limits_{h\in P(F)\backslash H(F)/D(F)}\quad\!\int\limits_{C'G^{\times}(F)\backslash G^{\times}(\mathbb{A})} \quad\!\int\limits_{U(F)\backslash U({\mathbb{A}})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle)\,\sum\limits_{y\in D_{h}(F)\backslash D(F)} \\&\times f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle y,(\eta_{2rkc}^{\diamondsuit})^{-1}(y)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
(See the argument for
![]() $\operatorname {\mathrm {Sp}}_c^{(m)}(\mathbb {A})$
in § 4.2.) Write
$\operatorname {\mathrm {Sp}}_c^{(m)}(\mathbb {A})$
in § 4.2.) Write
![]() $y=y_0\mathfrak {e}_1(y_1)\mathfrak {e}_1(y_2)$
with
$y=y_0\mathfrak {e}_1(y_1)\mathfrak {e}_1(y_2)$
with
![]() $y_0\in U(F)$
and
$y_0\in U(F)$
and
![]() $y_1,y_2\in G(F)$
. Since
$y_1,y_2\in G(F)$
. Since
![]() $H^{(m,r)}(\mathbb {A})$
is split over
$H^{(m,r)}(\mathbb {A})$
is split over
![]() $H(F)$
with respect to
$H(F)$
with respect to
![]() $h\mapsto \langle h,(\eta _{2rkc}^{\diamondsuit })^{-1}(h)\rangle $
, using the global analog of Equation (2.8) (see Corollary 16), the fact that
$h\mapsto \langle h,(\eta _{2rkc}^{\diamondsuit })^{-1}(h)\rangle $
, using the global analog of Equation (2.8) (see Corollary 16), the fact that
![]() $G(F)\times G(F)$
normalizes U and stabilizes
$G(F)\times G(F)$
normalizes U and stabilizes
![]() $\psi _U$
and
$\psi _U$
and
![]() $du$
, and reversing Equation (A.7), we obtain
$du$
, and reversing Equation (A.7), we obtain
 $$ \begin{align*} &\sum\limits_{h\in P(F)\backslash H(F)/D(F)}\,\int\limits_{C'G^{\times}(F)\backslash G^{\times}(\mathbb{A})} \,\int\limits_{U(F)\backslash U({\mathbb{A}})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle y_1g_1,1\rangle)\varphi_2^{R}(\langle y_2g_2,1\rangle)\,\sum\limits_{y\in D_{h}(F)\backslash D(F)} \\ &\times f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle y_0u,(\eta_{2rkc}^{\diamondsuit})^{-1}(y_0u)\rangle\nonumber \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\sum\limits_{h\in P(F)\backslash H(F)/D(F)}\,\int\limits_{C'G^{\times}(F)\backslash G^{\times}(\mathbb{A})} \,\int\limits_{U(F)\backslash U({\mathbb{A}})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle y_1g_1,1\rangle)\varphi_2^{R}(\langle y_2g_2,1\rangle)\,\sum\limits_{y\in D_{h}(F)\backslash D(F)} \\ &\times f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle y_0u,(\eta_{2rkc}^{\diamondsuit})^{-1}(y_0u)\rangle\nonumber \langle \mathfrak{e}_1(y_1g_1),1\rangle\langle \mathfrak{e}_2(y_2g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
Thus, when we collapse the inner sum into the integral we have
![]() $\sum _{h\in P(F)\backslash H(F)/D(F)}\mathrm {I}(h)$
, where
$\sum _{h\in P(F)\backslash H(F)/D(F)}\mathrm {I}(h)$
, where
 $$ \begin{align*} \mathrm{I}(h)= &\int\limits_{C'D_h(F)\backslash D(\mathbb{A})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle) \\ &f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} \mathrm{I}(h)= &\int\limits_{C'D_h(F)\backslash D(\mathbb{A})}\varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle) \\ &f(s,\langle h,(\eta_{2rkc}^{\diamondsuit})^{-1}(h)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u)\,du\,dg_1\,dg_2. \end{align*} $$
For all h such that
![]() $PhD\ne P\delta D$
,
$PhD\ne P\delta D$
,
![]() $\mathrm {I}(h)=0$
. This follows from [Reference Gourevitch and KaplanGK23, Theorems 2.1, 3.1] as explained in [Reference Gourevitch and KaplanGK23, § 3.2] (with
$\mathrm {I}(h)=0$
. This follows from [Reference Gourevitch and KaplanGK23, Theorems 2.1, 3.1] as explained in [Reference Gourevitch and KaplanGK23, § 3.2] (with
![]() $(k,c)$
of [Reference Gourevitch and KaplanGK23, § 3.1] replaced by
$(k,c)$
of [Reference Gourevitch and KaplanGK23, § 3.1] replaced by
![]() $(rk,c)$
here). In particular, as noted in [Reference Gourevitch and KaplanGK23, § 3.2], one has to use the constant term computation of
$(rk,c)$
here). In particular, as noted in [Reference Gourevitch and KaplanGK23, § 3.2], one has to use the constant term computation of
![]() $\mathcal {E}_{\tau _0}$
given in the linear setting by [Reference Jiang and LiuJL16, Lemma 4.1], which can be carried out for
$\mathcal {E}_{\tau _0}$
given in the linear setting by [Reference Jiang and LiuJL16, Lemma 4.1], which can be carried out for
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
(with
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
(with
![]() $a=rk$
in the notation of [Reference Jiang and LiuJL16, Lemma 4.1]).
$a=rk$
in the notation of [Reference Jiang and LiuJL16, Lemma 4.1]).
Now, we consider the remaining summand
![]() $\mathrm {I}(\delta )$
and show that it is equal to Integral (A.13). Denote an element in the direct product
$\mathrm {I}(\delta )$
and show that it is equal to Integral (A.13). Denote an element in the direct product
![]() $G\times G$
by
$G\times G$
by
![]() $[g,g']$
and set
$[g,g']$
and set
![]() $G^{\triangle }=\{[g,g]:g\in G\}$
. We have
$G^{\triangle }=\{[g,g]:g\in G\}$
. We have
 $$ \begin{align*} &D_{\delta}=G^{\triangle}\ltimes{}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})}),\\ &U={}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})})\ltimes(U\cap U_P)={}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})})\ltimes U_0. \end{align*} $$
$$ \begin{align*} &D_{\delta}=G^{\triangle}\ltimes{}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})}),\\ &U={}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})})\ltimes(U\cap U_P)={}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})},V_{(c^{rk})})\ltimes U_0. \end{align*} $$
(
![]() $\delta $
does not normalize
$\delta $
does not normalize
![]() $\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
.) For
$\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
.) For
![]() $u\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
, set
$u\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
, set
![]() ${}^{\delta }u=\operatorname {\mathrm {diag}}(v,v')$
. Then because both
${}^{\delta }u=\operatorname {\mathrm {diag}}(v,v')$
. Then because both
![]() $\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
and
$\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
and
![]() ${}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
are subgroups of
${}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})},V_{(c^{rk})})$
are subgroups of
![]() $N_{2rkc}$
, by Lemma 15 and Corollary 16, we obtain
$N_{2rkc}$
, by Lemma 15 and Corollary 16, we obtain
Since Equation (2.58) implies that
when we combine Equation (A.14) with Equation (A.9) and also use the fact that
![]() $\psi _U({}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(v,v'))$
equals the product of
$\psi _U({}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(v,v'))$
equals the product of
![]() $(rk,c)$
characters
$(rk,c)$
characters
![]() $\psi ^{-1}(v)\psi ^{-1}(v')$
, we deduce that
$\psi ^{-1}(v)\psi ^{-1}(v')$
, we deduce that
 $$ \begin{align*} &\int\limits_{{}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})}(F),V_{(c^{rk})}(F))\backslash U(\mathbb{A})} f(s,\langle\delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle)\,\psi_U(u)\,du \\ &\quad=\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle )\,\psi_U(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} &\int\limits_{{}^{\delta^{-1}}\operatorname{\mathrm{diag}}(V_{(c^{rk})}(F),V_{(c^{rk})}(F))\backslash U(\mathbb{A})} f(s,\langle\delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u,(\eta_{2rkc}^{\diamondsuit})^{-1}(u)\rangle)\,\psi_U(u)\,du \\ &\quad=\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,\langle\delta,\eta^{-1}(\delta)\rangle\langle u_0,\eta^{-1}(u_0)\rangle )\,\psi_U(u_0)\,du_0. \end{align*} $$
Now,
![]() $\mathrm {I}(\delta )$
equals
$\mathrm {I}(\delta )$
equals
 $$ \begin{align*} &\int\limits_{(C'\,G^{\triangle}(F))\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle) \\&f_{\mathcal{W}}(s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} &\int\limits_{(C'\,G^{\triangle}(F))\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det(g_2g_1^{-1})|)\varphi_1^{L}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_2,1\rangle) \\&f_{\mathcal{W}}(s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2. \end{align*} $$
Next, change variables
![]() $g_2\mapsto g_1g_2$
, then
$g_2\mapsto g_1g_2$
, then
![]() $G^{\triangle }$
is mapped into
$G^{\triangle }$
is mapped into
![]() $\{[g,I_c]:g\in G(F)\}$
which we identify with
$\{[g,I_c]:g\in G(F)\}$
which we identify with
![]() $G(F)$
, and
$G(F)$
, and
![]() $C'\mapsto \{[xI_c,I_c]:x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}=C_0'$
. Also, apply Definition (A.6) to
$C'\mapsto \{[xI_c,I_c]:x\in F^{*}\mathbb {A}^{*r}\prod _{\nu \notin S'}\mathcal {O}^{*}_{\nu }\}=C_0'$
. Also, apply Definition (A.6) to
![]() $\varphi _1^{L}$
to pass to
$\varphi _1^{L}$
to pass to
![]() $\varphi _1^{R}$
. Then
$\varphi _1^{R}$
. Then
 $$ \begin{align*} \mathrm{I}(\delta)= &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\eta_{(c^{2rk})}(\mathfrak{e}_2(g_1))\rangle)\varphi_2^{R}(\langle g_1g_2,1\rangle)\\ &f_{\mathcal{W}}(s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_1g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2. \end{align*} $$
$$ \begin{align*} \mathrm{I}(\delta)= &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,\eta_{(c^{2rk})}(\mathfrak{e}_1(g_1))\eta_{(c^{2rk})}(\mathfrak{e}_2(g_1))\rangle)\varphi_2^{R}(\langle g_1g_2,1\rangle)\\ &f_{\mathcal{W}}(s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle \mathfrak{e}_1(g_1),1\rangle\langle \mathfrak{e}_2(g_1g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2. \end{align*} $$
Separating
![]() $\langle g_1g_2,1\rangle $
in
$\langle g_1g_2,1\rangle $
in
![]() $G^{(m,r)}(\mathbb {A})[\rho _R]$
and
$G^{(m,r)}(\mathbb {A})[\rho _R]$
and
![]() $\langle \mathfrak {e}_2(g_1g_2),1\rangle $
in
$\langle \mathfrak {e}_2(g_1g_2),1\rangle $
in
![]() $H^{(m,r)}(\mathbb {A})$
, the integral becomes
$H^{(m,r)}(\mathbb {A})$
, the integral becomes
 $$ \begin{align} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})}\varrho(|\det g_2|) \varphi_1^{R}(\langle g_1,\prod_{i=1}^2\eta_{(c^{2rk})}(\mathfrak{e}_i(g_1))\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle)\\&f_{\mathcal{W}}(s, \langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle (g_1,g_1),\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,d(\cdots).\nonumber \end{align} $$
$$ \begin{align} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})}\varrho(|\det g_2|) \varphi_1^{R}(\langle g_1,\prod_{i=1}^2\eta_{(c^{2rk})}(\mathfrak{e}_i(g_1))\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle)\\&f_{\mathcal{W}}(s, \langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(u_0)\rangle\nonumber \langle (g_1,g_1),\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,d(\cdots).\nonumber \end{align} $$
When we apply Equation (A.1) with
![]() $\beta =(c^{2rk})$
,
$\beta =(c^{2rk})$
,
![]() $m=\mathfrak {e}_1(g_1)$
and
$m=\mathfrak {e}_1(g_1)$
and
![]() $m'=\mathfrak {e}_2(g_1)$
, then use Equation (2.57),
$m'=\mathfrak {e}_2(g_1)$
, then use Equation (2.57),
 $$ \begin{align*} \prod_{i=1}^2\eta_{(c^{2rk})}(\mathfrak{e}_i(g_1))\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1)) &=\rho_{(c^{2rk})}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\eta_{(c^{2rk})}((g_1,g_1))\\ &=\eta_{(c^{2rk})}((g_1,g_1))\,(!). \end{align*} $$
$$ \begin{align*} \prod_{i=1}^2\eta_{(c^{2rk})}(\mathfrak{e}_i(g_1))\rho_{2rkc}^{\diamondsuit}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1)) &=\rho_{(c^{2rk})}(\mathfrak{e}_1(g_1),\mathfrak{e}_2(g_1))\eta_{(c^{2rk})}((g_1,g_1))\\ &=\eta_{(c^{2rk})}((g_1,g_1))\,(!). \end{align*} $$
Conjugate
![]() $U_0(\mathbb {A})$
by
$U_0(\mathbb {A})$
by
![]() $(g_1,g_1)$
,
$(g_1,g_1)$
,
![]() ${}^{(g_1,g_1)^{-1}}u_0=v_{g_1}u_{g_1}$
with
${}^{(g_1,g_1)^{-1}}u_0=v_{g_1}u_{g_1}$
with
![]() $v_{g_1}\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})}(\mathbb {A}),V_{(c^{rk})}(\mathbb {A}))$
and
$v_{g_1}\in {}^{\delta ^{-1}}\operatorname {\mathrm {diag}}(V_{(c^{rk})}(\mathbb {A}),V_{(c^{rk})}(\mathbb {A}))$
and
![]() $u_{g_1}\in U_0(\mathbb {A})$
. Since
$u_{g_1}\in U_0(\mathbb {A})$
. Since
![]() $u_0,v_{g_1},u_{g_1}\in N_{rkc}(\mathbb {A})$
, by Lemma 15, we can write this in
$u_0,v_{g_1},u_{g_1}\in N_{rkc}(\mathbb {A})$
, by Lemma 15, we can write this in
![]() $H^{(m,r)}(\mathbb {A})$
and the
$H^{(m,r)}(\mathbb {A})$
and the
![]() $du_0$
-integral of (A.15) equals
$du_0$
-integral of (A.15) equals
 $$ \begin{align*} &\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,{}^{\delta}\langle (g_1,g_1),\eta_{(c^{2rk})}((g_1,g_1))\rangle\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\\&\langle v_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(v_{g_1})\rangle\langle u_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(u_{g_1})\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0. \end{align*} $$
$$ \begin{align*} &\int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,{}^{\delta}\langle (g_1,g_1),\eta_{(c^{2rk})}((g_1,g_1))\rangle\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\\&\langle v_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(v_{g_1})\rangle\langle u_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(u_{g_1})\rangle\langle\mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0. \end{align*} $$
Lemma A.4. For any
![]() $g\in G(\mathbb {A})$
and
$g\in G(\mathbb {A})$
and
![]() $h\in H^{(m,r)}(\mathbb {A})$
,
$h\in H^{(m,r)}(\mathbb {A})$
,
Before proving the lemma, we deduce that Integral (A.15) equals
 $$ \begin{align*} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle)\\&f_{\mathcal{W}} (s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle v_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(v_{g_1})\rangle\langle u_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(u_{g_1})\rangle\nonumber \langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle)\\&f_{\mathcal{W}} (s,\langle \delta,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta)\rangle\langle v_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(v_{g_1})\rangle\langle u_{g_1},(\eta_{2rkc}^{\diamondsuit})^{-1}(u_{g_1})\rangle\nonumber \langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
Changing variables
![]() $u_{g_1}\mapsto u_0$
, the change to
$u_{g_1}\mapsto u_0$
, the change to
![]() $\psi _U$
is cancelled by the left-equivariance property of
$\psi _U$
is cancelled by the left-equivariance property of
![]() $f_{\mathcal {W}}$
under
$f_{\mathcal {W}}$
under
![]() $v_{g_1}$
(see Equation (A.14)). One can also combine
$v_{g_1}$
(see Equation (A.14)). One can also combine
![]() $\delta $
and
$\delta $
and
![]() $u_0$
in
$u_0$
in
![]() $H^{(m,r)}(\mathbb {A})$
(see Corollary 16). The integral equals
$H^{(m,r)}(\mathbb {A})$
(see Corollary 16). The integral equals
 $$ \begin{align*} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle) \\&f_{\mathcal{W}}(s,\langle \delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle\nonumber \langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
$$ \begin{align*} &\int\limits_{C_0'G(F)\backslash G^{\times}(\mathbb{A})} \quad\int\limits_{U_0(\mathbb{A})} \varrho(|\det g_2|)\varphi_1^{R}(\langle g_1,1\rangle)\varphi_2^{R}(\langle g_1,1\rangle\langle g_2,1\rangle) \\&f_{\mathcal{W}}(s,\langle \delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle\nonumber \langle \mathfrak{e}_2(g_2),1\rangle)\,\psi_U(u_0)\,du_0\,dg_1\,dg_2.\nonumber \end{align*} $$
Finally, factoring through
![]() $\{[g,I_c]:g\in G(\mathbb {A})\}$
(which contains
$\{[g,I_c]:g\in G(\mathbb {A})\}$
(which contains
![]() $C_0'$
) and using the definition of
$C_0'$
) and using the definition of
![]() $\{\varphi _1^R,\varphi _2^R\}$
we conclude that
$\{\varphi _1^R,\varphi _2^R\}$
we conclude that
![]() $\mathrm {I}(\delta )$
equals
$\mathrm {I}(\delta )$
equals
 $$ \begin{align*} &\int\limits_{G(\mathbb{A})}\{\varphi_1^R,\pi(\langle g_2,1\rangle)\varphi_2^R\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,\langle \delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\varrho(|\det g_2|)\,\psi_U(u_0)\,du_0\,dg_2. \end{align*} $$
$$ \begin{align*} &\int\limits_{G(\mathbb{A})}\{\varphi_1^R,\pi(\langle g_2,1\rangle)\varphi_2^R\} \int\limits_{U_0(\mathbb{A})} f_{\mathcal{W}}(s,\langle \delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle\langle \mathfrak{e}_2(g_2),1\rangle)\varrho(|\det g_2|)\,\psi_U(u_0)\,du_0\,dg_2. \end{align*} $$
Therefore, the integrals (A.12) and (A.13) are equal in
![]() $\operatorname {\mathrm {Re}}(s)\gg 0$
.
$\operatorname {\mathrm {Re}}(s)\gg 0$
.
Proof of Lemma A.4.
Let
![]() $g\in G(\mathbb {A})$
. First, observe that
$g\in G(\mathbb {A})$
. First, observe that
![]() ${}^{\delta }(g,g)=(g,g)$
. Moreover we have
${}^{\delta }(g,g)=(g,g)$
. Moreover we have
![]() ${}^{\delta }\langle (g,g),1\rangle =\langle (g,g),1\rangle $
, because at each place
${}^{\delta }\langle (g,g),1\rangle =\langle (g,g),1\rangle $
, because at each place
![]() $\nu $
,
$\nu $
,
![]() $\langle \delta _{\nu },1\rangle $
and
$\langle \delta _{\nu },1\rangle $
and
![]() $\langle (g_{\nu },g_{\nu }),1\rangle $
commute in
$\langle (g_{\nu },g_{\nu }),1\rangle $
commute in
![]() $G^{(m,r)}(F_{\nu })$
by the proof of Proposition 75 (for the proof we used
$G^{(m,r)}(F_{\nu })$
by the proof of Proposition 75 (for the proof we used
![]() $\sigma _{c,\nu }^{\diamondsuit }$
, this property holds for any isomorphic covering, in particular with
$\sigma _{c,\nu }^{\diamondsuit }$
, this property holds for any isomorphic covering, in particular with
![]() $\rho _{c,\nu }^{\diamondsuit }$
). Hence, we need to show that
$\rho _{c,\nu }^{\diamondsuit }$
). Hence, we need to show that
![]() $f_{\mathcal {W}}$
is left-invariant under
$f_{\mathcal {W}}$
is left-invariant under
![]() $\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle $
. Now, by Equation (A.9),
$\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle $
. Now, by Equation (A.9),
Recall that
![]() $\widetilde {M}_P(\mathbb {A})$
is realized using
$\widetilde {M}_P(\mathbb {A})$
is realized using
![]() $\rho _{(rkc,rkc)}$
. Identity (A.1) implies that for
$\rho _{(rkc,rkc)}$
. Identity (A.1) implies that for
![]() $g'\in G(\mathbb {A})$
,
$g'\in G(\mathbb {A})$
,
 $$ \begin{align*} &\rho_{(rkc,rkc)}((g,g),(g',g'))\eta_{(rkc,rkc)}^{-1}((g,g))\eta_{(rkc,rkc)}^{-1}((g',g'))\\&= \eta_{(rkc,rkc)}^{-1}((gg',gg'))\rho_{2rkc}^{\diamondsuit}((g,g),(g',g')). \end{align*} $$
$$ \begin{align*} &\rho_{(rkc,rkc)}((g,g),(g',g'))\eta_{(rkc,rkc)}^{-1}((g,g))\eta_{(rkc,rkc)}^{-1}((g',g'))\\&= \eta_{(rkc,rkc)}^{-1}((gg',gg'))\rho_{2rkc}^{\diamondsuit}((g,g),(g',g')). \end{align*} $$
In addition,
![]() $\rho _{(c^{2rk})}((g,g),(g',g'))=\rho _c^{\diamondsuit }(g,g')^{2rk}=1$
, whence Equation (A.1) also shows that
$\rho _{(c^{2rk})}((g,g),(g',g'))=\rho _c^{\diamondsuit }(g,g')^{2rk}=1$
, whence Equation (A.1) also shows that
Combining these identities,
 $$ \begin{align*} &\langle (g,g),\eta_{(rkc,rkc)}^{-1}((g,g))\eta_{(c^{2rk})}((g,g))\rangle \langle (g',g'),\eta_{(rkc,rkc)}^{-1}((g',g'))\eta_{(c^{2rk})}((g',g'))\rangle\\&= \langle (gg',gg'),\eta_{(rkc,rkc)}^{-1}((gg',gg'))\eta_{(c^{2rk})}((gg',gg'))\rangle. \end{align*} $$
$$ \begin{align*} &\langle (g,g),\eta_{(rkc,rkc)}^{-1}((g,g))\eta_{(c^{2rk})}((g,g))\rangle \langle (g',g'),\eta_{(rkc,rkc)}^{-1}((g',g'))\eta_{(c^{2rk})}((g',g'))\rangle\\&= \langle (gg',gg'),\eta_{(rkc,rkc)}^{-1}((gg',gg'))\eta_{(c^{2rk})}((gg',gg'))\rangle. \end{align*} $$
Thus,
![]() $(g,g)\mapsto \langle (g,g),\eta _{(rkc,rkc)}^{-1}((g,g))\eta _{(c^{2rk})}((g,g))\rangle $
is an embedding in
$(g,g)\mapsto \langle (g,g),\eta _{(rkc,rkc)}^{-1}((g,g))\eta _{(c^{2rk})}((g,g))\rangle $
is an embedding in
![]() $\widetilde {M}_P(\mathbb {A})$
. Hence, we can consider separately
$\widetilde {M}_P(\mathbb {A})$
. Hence, we can consider separately
![]() $g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
$g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
and
![]() $g=\operatorname {\mathrm {diag}}(t,I_{c-1})\in T_{G}(\mathbb {A})$
. We provide a global argument for
$g=\operatorname {\mathrm {diag}}(t,I_{c-1})\in T_{G}(\mathbb {A})$
. We provide a global argument for
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
.
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
.
Let
![]() $g\mapsto d_g=\operatorname {\mathrm {diag}}(g,\ldots ,g)$
denote the diagonal embedding of G in
$g\mapsto d_g=\operatorname {\mathrm {diag}}(g,\ldots ,g)$
denote the diagonal embedding of G in
![]() $\operatorname {\mathrm {GL}}_{rkc}$
. By Corollary 38,
$\operatorname {\mathrm {GL}}_{rkc}$
. By Corollary 38,
![]() $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
is split over
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
is split over
![]() $\{d_g:g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})\}$
, and because
$\{d_g:g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})\}$
, and because
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
is perfect, this splitting is unique and we denote it by
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
is perfect, this splitting is unique and we denote it by
![]() $d_g\mapsto \langle d_g,\operatorname {\mathrm {o}}(d_g)\rangle $
(
$d_g\mapsto \langle d_g,\operatorname {\mathrm {o}}(d_g)\rangle $
(
![]() $\operatorname {\mathrm {o}}(d_g)$
was explicitly given in the corollary with respect to
$\operatorname {\mathrm {o}}(d_g)$
was explicitly given in the corollary with respect to
![]() $\rho _{rkc}^{\diamondsuit }$
). Then because
$\rho _{rkc}^{\diamondsuit }$
). Then because
![]() $\rho _{(rkc,rkc)}((g,g),(g',g'))=\rho _{rkc}^{\diamondsuit }(g,g')^2$
, the map
$\rho _{(rkc,rkc)}((g,g),(g',g'))=\rho _{rkc}^{\diamondsuit }(g,g')^2$
, the map
is the embedding of
![]() $\{(g,g):g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})\}$
in
$\{(g,g):g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})\}$
in
![]() $\widetilde {M}_P(\mathbb {A})$
, and coincides with the embedding in the previous paragraph (restricted to
$\widetilde {M}_P(\mathbb {A})$
, and coincides with the embedding in the previous paragraph (restricted to
![]() $\operatorname {\mathrm {SL}}_c(\mathbb {A})$
). Thus, for all
$\operatorname {\mathrm {SL}}_c(\mathbb {A})$
). Thus, for all
![]() $g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
,
$g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
,
Now, according to Proposition 39 (applied twice),
This, together with Equations (A.16) and (A.17), shows that
![]() $f_{\mathcal {W}}$
is left-invariant under
$f_{\mathcal {W}}$
is left-invariant under
![]() $\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle $
for
$\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle $
for
![]() $g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
.
$g\in \operatorname {\mathrm {SL}}_c(\mathbb {A})$
.
It remains to consider
![]() $\operatorname {\mathrm {diag}}(t,I_{c-1})$
, but our argument will apply to all
$\operatorname {\mathrm {diag}}(t,I_{c-1})$
, but our argument will apply to all
![]() $g\in G(\mathbb {A})$
. By our uniqueness assumption, both
$g\in G(\mathbb {A})$
. By our uniqueness assumption, both
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda ^{*}$
are factorizable. Thus, it is enough to consider a factorizable
$\Lambda ^{*}$
are factorizable. Thus, it is enough to consider a factorizable
![]() $f_{\mathcal {W}}=\prod _{\nu }f_{\mathcal {W}_{\nu }}$
, where
$f_{\mathcal {W}}=\prod _{\nu }f_{\mathcal {W}_{\nu }}$
, where
![]() $f_{\mathcal {W}_{\nu }}$
is a section of
$f_{\mathcal {W}_{\nu }}$
is a section of
and show that for each
![]() $\nu $
,
$\nu $
,
![]() $f_{\mathcal {W}_{\nu }}$
is left-invariant under
$f_{\mathcal {W}_{\nu }}$
is left-invariant under
![]() $\langle (g_{\nu },g_{\nu }),\eta _{(c^{2rk}),\nu }((g_{\nu },g_{\nu }))\rangle $
,
$\langle (g_{\nu },g_{\nu }),\eta _{(c^{2rk}),\nu }((g_{\nu },g_{\nu }))\rangle $
,
![]() $g_{\nu }\in G(F_{\nu })$
.
$g_{\nu }\in G(F_{\nu })$
.
We will deduce this from Proposition 77, which is applicable by the assumptions in the statement of Theorem A.3. We switch to local notation and omit
![]() $\nu $
. The local analog of Equation (A.16) (which follows from Equation (A.9) for a factorizable section) takes the same form, with local notation:
$\nu $
. The local analog of Equation (A.16) (which follows from Equation (A.9) for a factorizable section) takes the same form, with local notation:
Since
![]() $\eta _{c}^{\diamondsuit }((g,g))^{2rk}=1$
, by Equation (2.58) we have
$\eta _{c}^{\diamondsuit }((g,g))^{2rk}=1$
, by Equation (2.58) we have
![]() $\eta _{(c^{2rk})}((g,g))=\eta _{2rkc}^{\diamondsuit }((g,g))^{-1}$
(use
$\eta _{(c^{2rk})}((g,g))=\eta _{2rkc}^{\diamondsuit }((g,g))^{-1}$
(use
![]() $\beta =(c^{2rk})$
) and also
$\beta =(c^{2rk})$
) and also
![]() $\eta _{(rkc,rkc)}((g,g))=\eta _{rkc}^{\diamondsuit }(d_{g})^2\eta _{2rkc}^{\diamondsuit }((g,g))^{-1}$
, hence
$\eta _{(rkc,rkc)}((g,g))=\eta _{rkc}^{\diamondsuit }(d_{g})^2\eta _{2rkc}^{\diamondsuit }((g,g))^{-1}$
, hence
As an element of
![]() $\widetilde {M}_P$
(realized using
$\widetilde {M}_P$
(realized using
![]() $\rho _{(rkc,rkc)}$
),
$\rho _{(rkc,rkc)}$
),
The map
![]() $\langle b,\epsilon \rangle \mapsto \langle b,\eta _{rkc}^{\diamondsuit }(b)\epsilon \rangle $
is the isomorphism
$\langle b,\epsilon \rangle \mapsto \langle b,\eta _{rkc}^{\diamondsuit }(b)\epsilon \rangle $
is the isomorphism
![]() $G[\rho _c^{\diamondsuit }]\rightarrow G[\sigma _c^{\diamondsuit }]$
(see Equation (2.29)). Now, by Proposition 77 we have Equation (4.34), implying that
$G[\rho _c^{\diamondsuit }]\rightarrow G[\sigma _c^{\diamondsuit }]$
(see Equation (2.29)). Now, by Proposition 77 we have Equation (4.34), implying that
![]() $f_{\mathcal {W}}(s,\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle h)=f_{\mathcal {W}}(s,h)$
as required.
$f_{\mathcal {W}}(s,\langle (g,g),\eta _{(c^{2rk})}((g,g))\rangle h)=f_{\mathcal {W}}(s,h)$
as required.
Remark A.5. One can construct the integral (A.12) with cusp forms
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
in the spaces of
$\varphi _2$
in the spaces of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2^{\vee }$
for genuine irreducible cuspidal automorphic representations
$\pi _2^{\vee }$
for genuine irreducible cuspidal automorphic representations
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
. The proof of the theorem implies that
$\pi _2$
. The proof of the theorem implies that
![]() $\mathrm {I}(\delta )$
and thereby Integral (A.12) both vanish, unless
$\mathrm {I}(\delta )$
and thereby Integral (A.12) both vanish, unless
![]() $\pi _1=\pi _2=\pi $
.
$\pi _1=\pi _2=\pi $
.
As explained in [Reference Piatetski-Shapiro and RallisPSR87, § 4.2], one can choose a right half-plane which is independent of
![]() $\varrho $
, where Integral (A.13) is absolutely convergent. Now, if we define
$\varrho $
, where Integral (A.13) is absolutely convergent. Now, if we define
![]() $Z(s,\varphi _1,\varphi _2,f)=\lim \limits _{l\to \infty }Z(s,\varphi _1,\varphi _2,f,\varrho _l)$
for a nondecreasing sequence
$Z(s,\varphi _1,\varphi _2,f)=\lim \limits _{l\to \infty }Z(s,\varphi _1,\varphi _2,f,\varrho _l)$
for a nondecreasing sequence
![]() $\varrho _l\rightarrow 1$
, then in this half-plane by the monotone convergence theorem
$\varrho _l\rightarrow 1$
, then in this half-plane by the monotone convergence theorem
![]() $Z(s,\varphi _1,\varphi _2,f)$
equals
$Z(s,\varphi _1,\varphi _2,f)$
equals
 $$ \begin{align*} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1^R,\pi(\langle g,1\rangle)\varphi_2^R\}f_{\mathcal{W}}(s,\langle\delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle \langle\mathfrak{e}_2(g),1\rangle) \,\psi_U(u_0)\,du_0\,dg. \end{align*} $$
$$ \begin{align*} \int\limits_{G({\mathbb{A}})}\int\limits_{U_0({\mathbb{A}})} \{\varphi_1^R,\pi(\langle g,1\rangle)\varphi_2^R\}f_{\mathcal{W}}(s,\langle\delta u_0,(\eta_{2rkc}^{\diamondsuit})^{-1}(\delta u_0)\rangle \langle\mathfrak{e}_2(g),1\rangle) \,\psi_U(u_0)\,du_0\,dg. \end{align*} $$
Assume that m is odd and also assume
![]() $r=1$
or
$r=1$
or
![]() $k=1$
. As mentioned after Equation (4.18), by [Reference KaplanKap23, Proposition 15 and Theorem 17] the representations
$k=1$
. As mentioned after Equation (4.18), by [Reference KaplanKap23, Proposition 15 and Theorem 17] the representations
![]() $(\mathcal {E}_{\tau _0})_{\nu }$
are
$(\mathcal {E}_{\tau _0})_{\nu }$
are
![]() $(rk,c)$
for all
$(rk,c)$
for all
![]() $\nu $
. Hence, Theorem A.3 is applicable and as in § 4.2 when we take factorizable data, the integral
$\nu $
. Hence, Theorem A.3 is applicable and as in § 4.2 when we take factorizable data, the integral
![]() $Z(s,\varphi _1,\varphi _2,f)$
is Eulerian and the local integrals with unramified data are given by Theorem 87.
$Z(s,\varphi _1,\varphi _2,f)$
is Eulerian and the local integrals with unramified data are given by Theorem 87.
B List of common notation and definitions
-
• F – a local field of characteristic
 $0$
, or a number field; § 2.1.
$0$
, or a number field; § 2.1. -
• G – usually
 $\operatorname {\mathrm {Sp}}_{2n}$
; § 2.1.
$\operatorname {\mathrm {Sp}}_{2n}$
; § 2.1. -
•
 $J_l$
– the permutation matrix in
$J_l$
– the permutation matrix in
 $\operatorname {\mathrm {GL}}_l$
with
$\operatorname {\mathrm {GL}}_l$
with
 $1$
along the antidiagonal; § 2.1.
$1$
along the antidiagonal; § 2.1. -
•
 $B_l=T_l\ltimes N_l$
– the fixed Borel subgroup of
$B_l=T_l\ltimes N_l$
– the fixed Borel subgroup of
 $\operatorname {\mathrm {Sp}}_{2l}$
, where
$\operatorname {\mathrm {Sp}}_{2l}$
, where
 $T_l$
is the torus; § 2.1.
$T_l$
is the torus; § 2.1. -
•
 $W_{G}$
– the Weyl group of G; § 2.1.
$W_{G}$
– the Weyl group of G; § 2.1. -
•
 $B_{\operatorname {\mathrm {GL}}_d}=T_{\operatorname {\mathrm {GL}}_d}\ltimes N_{\operatorname {\mathrm {GL}}_d}$
– the Borel subgroup of upper triangular invertible matrices; § 2.1.
$B_{\operatorname {\mathrm {GL}}_d}=T_{\operatorname {\mathrm {GL}}_d}\ltimes N_{\operatorname {\mathrm {GL}}_d}$
– the Borel subgroup of upper triangular invertible matrices; § 2.1. -
•
 $P_{\beta }=M_{\beta }\ltimes V_{\beta }$
– a standard parabolic subgroup of
$P_{\beta }=M_{\beta }\ltimes V_{\beta }$
– a standard parabolic subgroup of
 $\operatorname {\mathrm {GL}}_d$
, where
$\operatorname {\mathrm {GL}}_d$
, where
 $\beta $
is a composition of d; § 2.1.
$\beta $
is a composition of d; § 2.1. -
•
 $\Phi _d$
,
$\Phi _d$
,
 $\Phi _d^+$
– simple and positive roots of
$\Phi _d^+$
– simple and positive roots of
 $\operatorname {\mathrm {GL}}_d$
, usually regarded as pairs
$\operatorname {\mathrm {GL}}_d$
, usually regarded as pairs
 $(i,j)$
; § 2.1.
$(i,j)$
; § 2.1. -
•
 $W_{\operatorname {\mathrm {GL}}_d}$
– the Weyl group of
$W_{\operatorname {\mathrm {GL}}_d}$
– the Weyl group of
 $\operatorname {\mathrm {GL}}_d$
; § 2.1.
$\operatorname {\mathrm {GL}}_d$
; § 2.1. -
•
 $\ell (w)$
– the length of
$\ell (w)$
– the length of
 $w\in W_{\operatorname {\mathrm {GL}}_d}$
; § 2.1.
$w\in W_{\operatorname {\mathrm {GL}}_d}$
; § 2.1. -
•
 $b^{*}=J_d{}^tb^{-1}J_d$
for
$b^{*}=J_d{}^tb^{-1}J_d$
for
 $b\in \operatorname {\mathrm {GL}}_d$
(
$b\in \operatorname {\mathrm {GL}}_d$
(
 ${}^tb$
– the transpose of b); § 2.1.
${}^tb$
– the transpose of b); § 2.1. -
•
 ${}^xy=xyx^{-1}$
; § 2.1.
${}^xy=xyx^{-1}$
; § 2.1. -
•
 $\mathcal {O}$
,
$\mathcal {O}$
,
 $\mathcal {P}$
,
$\mathcal {P}$
,
 $\varpi $
, q – p-adic fields,
$\varpi $
, q – p-adic fields,
 $\mathcal {O}$
is the ring of integers,
$\mathcal {O}$
is the ring of integers,
 $\varpi \in \mathcal {O}$
,
$\varpi \in \mathcal {O}$
,
 $|\varpi |=q^{-1}$
and
$|\varpi |=q^{-1}$
and
 $\mathcal {P}=\varpi \mathcal {O}$
; § 2.1.
$\mathcal {P}=\varpi \mathcal {O}$
; § 2.1. -
•
 $K_G$
– over p-adic fields
$K_G$
– over p-adic fields
 $K_G=G(\mathcal {O})$
, globally a maximal compact subgroup of
$K_G=G(\mathcal {O})$
, globally a maximal compact subgroup of
 $G(\mathbb {A})$
; § 2.1.
$G(\mathbb {A})$
; § 2.1. -
•
 $\mu _m$
– the m-th roots of unity; § 2.2.
$\mu _m$
– the m-th roots of unity; § 2.2. -
•
 $(\cdot ,\cdot )_m$
– a fixed Hilbert symbol of order m; § 2.2.
$(\cdot ,\cdot )_m$
– a fixed Hilbert symbol of order m; § 2.2. -
•
 $G^{(m)}$
– the m-fold covering of G when G is a symplectic group; § 2.2.
$G^{(m)}$
– the m-fold covering of G when G is a symplectic group; § 2.2. -
•
 $\langle g,\epsilon \rangle $
– a general element of a covering group; § 2.2.
$\langle g,\epsilon \rangle $
– a general element of a covering group; § 2.2. -
•
 $\widetilde {X}$
– when a covering of G is fixed and
$\widetilde {X}$
– when a covering of G is fixed and
 $X<G$
, the covering obtained by restriction; § 2.2.
$X<G$
, the covering obtained by restriction; § 2.2. -
•
 $\varepsilon $
– a fixed faithful character of
$\varepsilon $
– a fixed faithful character of
 $\mu _m$
used to define genuine representations; § 2.2.
$\mu _m$
used to define genuine representations; § 2.2. -
• c –
 $c=2n$
except when the integrals for
$c=2n$
except when the integrals for
 $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
are considered, then
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_k$
are considered, then
 $c=n$
; § 2.3.
$c=n$
; § 2.3. -
•
 $r=m$
if m is odd, otherwise
$r=m$
if m is odd, otherwise
 $r=m/2$
; § 2.3.
$r=m/2$
; § 2.3. -
• H – usually
 $\operatorname {\mathrm {Sp}}_{2rkc}$
; § 2.3.
$\operatorname {\mathrm {Sp}}_{2rkc}$
; § 2.3. -
•
 $P=M_P\ltimes U_P$
– the Siegel parabolic subgroup of H; § 2.3.
$P=M_P\ltimes U_P$
– the Siegel parabolic subgroup of H; § 2.3. -
•
 $Q=M_Q\ltimes U$
– a standard parabolic subgroup of H,
$Q=M_Q\ltimes U$
– a standard parabolic subgroup of H,
 $G\times G$
is embedded in
$G\times G$
is embedded in
 $M_Q$
as the stabilizer of a character
$M_Q$
as the stabilizer of a character
 $\psi _U$
of U; § 2.3.
$\psi _U$
of U; § 2.3. -
•
 $\psi $
– a nontrivial additive character of a local field or of
$\psi $
– a nontrivial additive character of a local field or of
 $F\backslash \mathbb {A}$
; § 2.3.
$F\backslash \mathbb {A}$
; § 2.3. -
•
 $\psi _U$
– the character of U stabilized by
$\psi _U$
– the character of U stabilized by
 $G\times G$
; Equation (2.6).
$G\times G$
; Equation (2.6). -
•
 $(g_1,g_2)$
,
$(g_1,g_2)$
,
 $\mathfrak {e}_i$
– the embedding
$\mathfrak {e}_i$
– the embedding
 $G\times G\hookrightarrow H$
,
$G\times G\hookrightarrow H$
,
 $\mathfrak {e}_1(g)=(g,I_c)$
and
$\mathfrak {e}_1(g)=(g,I_c)$
and
 $\mathfrak {e}_2(g)=(I_c,g)$
; § 2.3.
$\mathfrak {e}_2(g)=(I_c,g)$
; § 2.3. -
•
 $\sigma _{2rkc}$
,
$\sigma _{2rkc}$
,
 $\sigma _{d}$
– the
$\sigma _{d}$
– the
 $2$
-cocycle of [Reference Banks, Levy and SepanskiBLS99] for
$2$
-cocycle of [Reference Banks, Levy and SepanskiBLS99] for
 $\operatorname {\mathrm {GL}}_{2rkc}$
,
$\operatorname {\mathrm {GL}}_{2rkc}$
,
 $\operatorname {\mathrm {GL}}_d$
, which we can compute explicitly in many cases, but does not globalize. In a local-global context we denote
$\operatorname {\mathrm {GL}}_d$
, which we can compute explicitly in many cases, but does not globalize. In a local-global context we denote
 $\sigma _{2rkc,\nu }$
or
$\sigma _{2rkc,\nu }$
or
 $\sigma _{\nu }$
; § 2.4.
$\sigma _{\nu }$
; § 2.4. -
•
 $\mathfrak {W}_d$
– a set of representatives for
$\mathfrak {W}_d$
– a set of representatives for
 $W_{\operatorname {\mathrm {GL}}_d}$
constructed in [Reference Banks, Levy and SepanskiBLS99], and used for
$W_{\operatorname {\mathrm {GL}}_d}$
constructed in [Reference Banks, Levy and SepanskiBLS99], and used for
 $\sigma _d$
; § 2.4.
$\sigma _d$
; § 2.4. -
•
 $\mathfrak {W}^+_d$
– a group containing
$\mathfrak {W}^+_d$
– a group containing
 $\mathfrak {W}_d$
and diagonal matrices whose coordinates are
$\mathfrak {W}_d$
and diagonal matrices whose coordinates are
 $\pm 1$
; § 2.4.
$\pm 1$
; § 2.4. -
• F is unramified – F is non-Archimedean,
 $|m|=1$
and
$|m|=1$
and
 $q>3$
; § 2.4.
$q>3$
; § 2.4. -
•
 $\eta _d$
– in a purely local context and when F is unramified,
$\eta _d$
– in a purely local context and when F is unramified,
 $\langle y,\eta _d(y)\rangle $
is a splitting of
$\langle y,\eta _d(y)\rangle $
is a splitting of
 $K_{\operatorname {\mathrm {GL}}_{d}}$
, and in particular
$K_{\operatorname {\mathrm {GL}}_{d}}$
, and in particular
 $\langle y,\eta _{2rkc}(y)\rangle $
is the canonical splitting of
$\langle y,\eta _{2rkc}(y)\rangle $
is the canonical splitting of
 $K_{H}$
; § 2.4.
$K_{H}$
; § 2.4. -
•
 $\sigma ^{*}_{c}$
,
$\sigma ^{*}_{c}$
,
 $\sigma ^{*,rk}_{c}$
,
$\sigma ^{*,rk}_{c}$
,
 $\varsigma _{*,c}$
: In a local context
$\varsigma _{*,c}$
: In a local context
 $\sigma ^{*}_{c}$
and
$\sigma ^{*}_{c}$
and
 $\sigma ^{*,rk}_{c}$
are
$\sigma ^{*,rk}_{c}$
are
 $2$
-cocycles of
$2$
-cocycles of
 $\operatorname {\mathrm {GL}}_c$
, cohomologous to
$\operatorname {\mathrm {GL}}_c$
, cohomologous to
 $\sigma _c$
and
$\sigma _c$
and
 $\sigma ^{*}_{c}(g,g')=\sigma _{c}(g^{*},{g'}^{*})$
where
$\sigma ^{*}_{c}(g,g')=\sigma _{c}(g^{*},{g'}^{*})$
where
 $g^{*}=J_c{}^tg^{-1}J_c$
. The
$g^{*}=J_c{}^tg^{-1}J_c$
. The
 $1$
-cochain relating
$1$
-cochain relating
 $\sigma _c$
to
$\sigma _c$
to
 $\sigma _c^{*}$
is
$\sigma _c^{*}$
is
 $\varsigma _{*,c}$
; Equation (2.21), Equation (2.22), § 2.4, Proposition 20.
$\varsigma _{*,c}$
; Equation (2.21), Equation (2.22), § 2.4, Proposition 20. -
•
 $\varphi \mapsto \varphi ^{\varsigma _{*,c}^{rk+1}}$
– the local mapping, of functions on the right copy of
$\varphi \mapsto \varphi ^{\varsigma _{*,c}^{rk+1}}$
– the local mapping, of functions on the right copy of
 $G^{(m)}$
to functions on the left copy, when the left copy is realized using the
$G^{(m)}$
to functions on the left copy, when the left copy is realized using the
 $2$
-cocycle
$2$
-cocycle
 $\sigma _c^{*,rk}$
; Equation (2.28).
$\sigma _c^{*,rk}$
; Equation (2.28). -
•
 $\rho $
– the
$\rho $
– the
 $2$
-cocycle for
$2$
-cocycle for
 $H(\mathbb {A})$
,
$H(\mathbb {A})$
,
 $\rho _{\nu }$
is its local component which is cohomologous to
$\rho _{\nu }$
is its local component which is cohomologous to
 $\sigma _{\nu }$
where
$\sigma _{\nu }$
where
 $\eta _{\nu }$
is the
$\eta _{\nu }$
is the
 $1$
-cochain. We write
$1$
-cochain. We write
 $\rho _{2l}$
for this
$\rho _{2l}$
for this
 $2$
-cocycle on
$2$
-cocycle on
 $\operatorname {\mathrm {Sp}}_{2l}(\mathbb {A})$
; Equation (2.29), § 2.5.
$\operatorname {\mathrm {Sp}}_{2l}(\mathbb {A})$
; Equation (2.29), § 2.5. -
•
 $\eta $
– the global
$\eta $
– the global
 $1$
-cochain
$1$
-cochain
 $\eta =\prod _{\nu }\eta _{\nu }$
, which is well defined on
$\eta =\prod _{\nu }\eta _{\nu }$
, which is well defined on
 $H(F)$
but not on
$H(F)$
but not on
 $H(\mathbb {A})$
; Equation (2.29), § 2.5.
$H(\mathbb {A})$
; Equation (2.29), § 2.5. -
•
 $\rho _L$
and
$\rho _L$
and
 $\rho _R$
– the global
$\rho _R$
– the global
 $2$
-cocycles for the left and right copies of
$2$
-cocycles for the left and right copies of
 $\operatorname {\mathrm {Sp}}_{c}(\mathbb {A})$
in
$\operatorname {\mathrm {Sp}}_{c}(\mathbb {A})$
in
 $H(\mathbb {A})$
; Equation (2.30).
$H(\mathbb {A})$
; Equation (2.30). -
•
 $\varphi \mapsto \varphi ^{(\eta ^{\times })^{-1}}$
– the global version of
$\varphi \mapsto \varphi ^{(\eta ^{\times })^{-1}}$
– the global version of
 $\varphi \mapsto \varphi ^{\varsigma _{*,c}^{rk+1}}$
(from the right copy to the left); Equation (2.35).
$\varphi \mapsto \varphi ^{\varsigma _{*,c}^{rk+1}}$
(from the right copy to the left); Equation (2.35). -
•
 $\sigma $
– globally this is the product of
$\sigma $
– globally this is the product of
 $2$
-cocycles
$2$
-cocycles
 $\sigma _{\nu }$
(usually
$\sigma _{\nu }$
(usually
 $\sigma _{2rkc,\nu }$
), for example, on
$\sigma _{2rkc,\nu }$
), for example, on
 $H(F)$
; § 2.5.
$H(F)$
; § 2.5. -
•
 $\langle h,\eta ^{-1}(h)\rangle $
– the splitting of
$\langle h,\eta ^{-1}(h)\rangle $
– the splitting of
 $H(F)$
, used for the definition of automorphic forms; § 2.5.
$H(F)$
, used for the definition of automorphic forms; § 2.5. -
•
 $\langle g,\eta (\mathfrak {e}_1(g))\rangle $
,
$\langle g,\eta (\mathfrak {e}_1(g))\rangle $
,
 $\langle g,\eta ^{-1}(\mathfrak {e}_2(g))\rangle $
– the splittings of
$\langle g,\eta ^{-1}(\mathfrak {e}_2(g))\rangle $
– the splittings of
 $G(F)$
in the two realizations of
$G(F)$
in the two realizations of
 $G^{(m)}(\mathbb {A})$
; § 2.5.
$G^{(m)}(\mathbb {A})$
; § 2.5. -
•
 $\eta ^{\times }$
– a
$\eta ^{\times }$
– a
 $1$
-cochain relating between the coverings on both copies of
$1$
-cochain relating between the coverings on both copies of
 $G(\mathbb {A})$
in
$G(\mathbb {A})$
in
 $H^{(m)}(\mathbb {A})$
; § 2.5.
$H^{(m)}(\mathbb {A})$
; § 2.5. -
•
 ${}^{\iota }$
– the involution
${}^{\iota }$
– the involution
 $g\mapsto {}^{\iota }g$
of G,
$g\mapsto {}^{\iota }g$
of G,
 $\iota =\left (\begin {smallmatrix}&I_{c/2}\\I_{c/2}\end {smallmatrix}\right )$
, lifted to
$\iota =\left (\begin {smallmatrix}&I_{c/2}\\I_{c/2}\end {smallmatrix}\right )$
, lifted to
 $G^{(m)}$
locally and globally; § 2.6.
$G^{(m)}$
locally and globally; § 2.6. -
•
 $\varsigma _{\iota ,c}$
– the
$\varsigma _{\iota ,c}$
– the
 $1$
-cochain used for the local lift of
$1$
-cochain used for the local lift of
 $\iota $
to
$\iota $
to
 $G^{(m)}$
; Equation (2.38), Equation (2.39).
$G^{(m)}$
; Equation (2.38), Equation (2.39). -
•
 $\pi ^{\iota }$
– for a representation
$\pi ^{\iota }$
– for a representation
 $\pi $
of
$\pi $
of
 $G^{(m)}$
,
$G^{(m)}$
,
 $\pi ^{\iota }$
acts on the space of
$\pi ^{\iota }$
acts on the space of
 $\pi $
by
$\pi $
by
 $\pi ^{\iota }(g)=\pi ({}^{\iota }g)$
; § 2.6.
$\pi ^{\iota }(g)=\pi ({}^{\iota }g)$
; § 2.6. -
•
 $\eta _{\iota ,R}$
– the global analog of
$\eta _{\iota ,R}$
– the global analog of
 $\varsigma _{\iota ,c}$
; Equation (2.45).
$\varsigma _{\iota ,c}$
; Equation (2.45). -
•
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(or
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
(or
 $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
) –
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
) –
 $\operatorname {\mathrm {GL}}_{rkc}$
is embedded in
$\operatorname {\mathrm {GL}}_{rkc}$
is embedded in
 $H=\operatorname {\mathrm {Sp}}_{2rkc}$
by
$H=\operatorname {\mathrm {Sp}}_{2rkc}$
by
 $\{\operatorname {\mathrm {diag}}(g,g^{*}):g\in \operatorname {\mathrm {GL}}_{rkc}\}$
,
$\{\operatorname {\mathrm {diag}}(g,g^{*}):g\in \operatorname {\mathrm {GL}}_{rkc}\}$
,
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is the covering obtained by restriction from
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
is the covering obtained by restriction from
 $H^{(m)}$
. Similarly for
$H^{(m)}$
. Similarly for
 $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
using
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
using
 $\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
; § 2.7.
$\operatorname {\mathrm {Sp}}_{2d}^{(m)}$
; § 2.7. -
•
 $C_{r,d}=\{xI_d:x\in F^{*r}\}$
,
$C_{r,d}=\{xI_d:x\in F^{*r}\}$
,
 $\widetilde {C}_{r,d}$
is the center of
$\widetilde {C}_{r,d}$
is the center of
 $\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.7.
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.7. -
•
 $\sigma ^{\diamondsuit }_{d}$
– the local
$\sigma ^{\diamondsuit }_{d}$
– the local
 $2$
-cocycle of
$2$
-cocycle of
 $\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
,
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}$
,
 $\sigma ^{\diamondsuit }_{d}(b,b')=\sigma _{2d}(\operatorname {\mathrm {diag}}(b,b^{*}),\operatorname {\mathrm {diag}}(b',{b'}^{*}))$
; Equation (2.50).
$\sigma ^{\diamondsuit }_{d}(b,b')=\sigma _{2d}(\operatorname {\mathrm {diag}}(b,b^{*}),\operatorname {\mathrm {diag}}(b',{b'}^{*}))$
; Equation (2.50). -
•
 $\rho ^{\diamondsuit }_{d}$
– the global
$\rho ^{\diamondsuit }_{d}$
– the global
 $2$
-cocycle of
$2$
-cocycle of
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
defined using
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
defined using
 $\rho _{2d}$
, locally
$\rho _{2d}$
, locally
 $\rho ^{\diamondsuit }_{d,\nu }$
; Equation (2.55).
$\rho ^{\diamondsuit }_{d,\nu }$
; Equation (2.55). -
•
 ${}^{*}\langle b,1\rangle $
– an involution of
${}^{*}\langle b,1\rangle $
– an involution of
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field; Equation (2.54).
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
over a local field; Equation (2.54). -
•
 $\pi ^{*}$
– for a representation
$\pi ^{*}$
– for a representation
 $\pi $
of
$\pi $
of
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
,
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}$
,
 $\pi ^{*}$
acts on the space of
$\pi ^{*}$
acts on the space of
 $\pi $
by
$\pi $
by
 $\pi ^{*}(b)=\pi (b^{*})$
; Equation (2.54).
$\pi ^{*}(b)=\pi (b^{*})$
; Equation (2.54). -
•
 $\eta _{d}^{\diamondsuit }$
– the local
$\eta _{d}^{\diamondsuit }$
– the local
 $1$
-cochain relating between
$1$
-cochain relating between
 $\rho ^{\diamondsuit }_{d}$
and
$\rho ^{\diamondsuit }_{d}$
and
 $\sigma ^{\diamondsuit }_{d}$
; Equation (2.56).
$\sigma ^{\diamondsuit }_{d}$
; Equation (2.56). -
•
 $(\eta ^{\diamondsuit }_{d})^{-1}(b)$
– the
$(\eta ^{\diamondsuit }_{d})^{-1}(b)$
– the
 $1$
-cochain used to define embeddings of
$1$
-cochain used to define embeddings of
 $\operatorname {\mathrm {GL}}_d(F)$
and
$\operatorname {\mathrm {GL}}_d(F)$
and
 $N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
in
$N_{\operatorname {\mathrm {GL}}_d}(\mathbb {A})$
in
 $\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
; § 2.7.
$\operatorname {\mathrm {GL}}_{d}^{(m,r)}(\mathbb {A})$
; § 2.7. -
•
 $\rho _{\beta }$
– a global block-compatible
$\rho _{\beta }$
– a global block-compatible
 $2$
-cocycle on
$2$
-cocycle on
 $M_{\beta }(\mathbb {A})$
,
$M_{\beta }(\mathbb {A})$
,
 $\rho _{\beta }(b,b')=\prod _{i=1}^l\rho ^{\diamondsuit }_{\beta _i}(b_i,b_i^{\prime })$
; Equation (2.57).
$\rho _{\beta }(b,b')=\prod _{i=1}^l\rho ^{\diamondsuit }_{\beta _i}(b_i,b_i^{\prime })$
; Equation (2.57). -
•
 $\eta _{\beta }$
,
$\eta _{\beta }$
,
 $\eta _{\beta ,\nu }$
– the
$\eta _{\beta ,\nu }$
– the
 $1$
-cochain relating between
$1$
-cochain relating between
 $\rho _{\beta }$
(resp.,
$\rho _{\beta }$
(resp.,
 $\rho _{\beta ,\nu }$
) and
$\rho _{\beta ,\nu }$
) and
 $\rho _d^{\diamondsuit }$
(resp.,
$\rho _d^{\diamondsuit }$
(resp.,
 $\rho _{d,\nu }^{\diamondsuit }$
); Equation (2.58).
$\rho _{d,\nu }^{\diamondsuit }$
); Equation (2.58). -
• A –
 $A=F^{*r}\mathcal {O}^{*}$
is a maximal abelian subgroup of
$A=F^{*r}\mathcal {O}^{*}$
is a maximal abelian subgroup of
 $\operatorname {\mathrm {GL}}_1^{(m,r)}$
; § 2.8.
$\operatorname {\mathrm {GL}}_1^{(m,r)}$
; § 2.8. -
•
 $\gamma _{\psi }$
– the Weil factor; Equation (2.68), § 2.8.
$\gamma _{\psi }$
– the Weil factor; Equation (2.68), § 2.8. -
•
 $T_{d,*}$
,
$T_{d,*}$
,
 $T_{\operatorname {\mathrm {GL}}_d,*}$
– the image in
$T_{\operatorname {\mathrm {GL}}_d,*}$
– the image in
 $T_d$
,
$T_d$
,
 $T_{\operatorname {\mathrm {GL}}_d}$
of certain maximal abelian subgroups of
$T_{\operatorname {\mathrm {GL}}_d}$
of certain maximal abelian subgroups of
 $\widetilde {T}_{d}$
,
$\widetilde {T}_{d}$
,
 $\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
; § 2.8.
$\widetilde {T}_{\operatorname {\mathrm {GL}}_d}$
; § 2.8. -
•
 $\mathrm {I}_{G^{(m)}}(\vartheta ,\mu )$
,
$\mathrm {I}_{G^{(m)}}(\vartheta ,\mu )$
,
 $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
– unramified principal series representations; § 2.8.
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
– unramified principal series representations; § 2.8. -
•
 $t_{\pi }$
,
$t_{\pi }$
,
 $t_{\tau }$
– Satake parameters for representations
$t_{\tau }$
– Satake parameters for representations
 $\pi $
and
$\pi $
and
 $\tau $
; Equation (2.69), § 2.8.
$\tau $
; Equation (2.69), § 2.8. -
•
 $L_{\vartheta }(s,\tau ,\sigma )$
,
$L_{\vartheta }(s,\tau ,\sigma )$
,
 $L_{\vartheta ,\vartheta '}(s,\tau \times \tau ')$
,
$L_{\vartheta ,\vartheta '}(s,\tau \times \tau ')$
,
 $L_{\vartheta _{\pi },\vartheta _{\tau }}(s,\pi \times \tau )$
– unramified L-factors; § 2.8.
$L_{\vartheta _{\pi },\vartheta _{\tau }}(s,\pi \times \tau )$
– unramified L-factors; § 2.8. -
•
 $\Lambda _t$
,
$\Lambda _t$
,
 $\Lambda $
– the Whittaker functional on
$\Lambda $
– the Whittaker functional on
 $\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
given by a Jacquet integral with left-translation by t,
$\mathrm {I}_{\operatorname {\mathrm {GL}}_d^{(m,r)}}(\vartheta ,\chi )$
given by a Jacquet integral with left-translation by t,
 $\Lambda =\Lambda _{I_d}$
; § 2.9.
$\Lambda =\Lambda _{I_d}$
; § 2.9. -
•
 $\xi ^0$
– a normalized unramified vector in a space of a principal series representation; § 2.10.
$\xi ^0$
– a normalized unramified vector in a space of a principal series representation; § 2.10. -
•
 $\mathfrak {g}$
– a Gauss sum,
$\mathfrak {g}$
– a Gauss sum,
 $\mathfrak {g}(l)=-q^{-1}$
when
$\mathfrak {g}(l)=-q^{-1}$
when
 $l\equiv 0\,(m)$
; Equation (2.73).
$l\equiv 0\,(m)$
; Equation (2.73). -
•
 $\mathbf {x}$
– the vector defining the Satake parameter of an unramified principal series representation of
$\mathbf {x}$
– the vector defining the Satake parameter of an unramified principal series representation of
 $\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.10.
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.10. -
•
 $\mathbf {a}^{*}=(-a_1,\ldots ,-a_d)$
, where
$\mathbf {a}^{*}=(-a_1,\ldots ,-a_d)$
, where
 $\mathbf {a}=(a_1,\ldots ,a_d)\in \mathbb {Z}^d$
; § 2.10.
$\mathbf {a}=(a_1,\ldots ,a_d)\in \mathbb {Z}^d$
; § 2.10. -
•
 $\varpi ^{\mathbf {a}}=\operatorname {\mathrm {diag}}(\varpi ^{a_1},\ldots ,\varpi ^{a_d})$
,
$\varpi ^{\mathbf {a}}=\operatorname {\mathrm {diag}}(\varpi ^{a_1},\ldots ,\varpi ^{a_d})$
,
 $t_{\mathbf {a}}=\langle \varpi ^{\mathbf {a}},1\rangle $
; § 2.10.
$t_{\mathbf {a}}=\langle \varpi ^{\mathbf {a}},1\rangle $
; § 2.10. -
•
 $\equiv $
on
$\equiv $
on
 $\mathbb {Z}^d$
– for
$\mathbb {Z}^d$
– for
 $\mathbf {a},\mathbf {b}\in \mathbb {Z}^d$
,
$\mathbf {a},\mathbf {b}\in \mathbb {Z}^d$
,
 $\mathbf {a}\equiv \mathbf {b}$
if
$\mathbf {a}\equiv \mathbf {b}$
if
 $\mathbf {a}-\mathbf {b}\in r\mathbb {Z}^d$
; § 2.10.
$\mathbf {a}-\mathbf {b}\in r\mathbb {Z}^d$
; § 2.10. -
•
 $W_{\mathbf {a}}(\mathbf {b},\vartheta ,\chi )=\Lambda _{t_{\mathbf {a}}}(t_{\mathbf {b}}\cdot \xi ^0)$
– the value of
$W_{\mathbf {a}}(\mathbf {b},\vartheta ,\chi )=\Lambda _{t_{\mathbf {a}}}(t_{\mathbf {b}}\cdot \xi ^0)$
– the value of
 $\Lambda _{t_{\mathbf {a}}}$
on the right-translation of
$\Lambda _{t_{\mathbf {a}}}$
on the right-translation of
 $\xi ^0$
by
$\xi ^0$
by
 $t_{\mathbf {b}}$
; Equation (2.74), Equation (2.84).
$t_{\mathbf {b}}$
; Equation (2.74), Equation (2.84). -
•
 $\mathbf {v}(t)$
– the valuations vector of a torus element t; § 2.10.
$\mathbf {v}(t)$
– the valuations vector of a torus element t; § 2.10. -
•
 $\mathbf {x}_{\alpha }=x_ix_j^{-1}$
; § 2.10.
$\mathbf {x}_{\alpha }=x_ix_j^{-1}$
; § 2.10. -
•
 ${}^w\mathbf {x}$
– the action of
${}^w\mathbf {x}$
– the action of
 $W_{\operatorname {\mathrm {GL}}_d}$
on
$W_{\operatorname {\mathrm {GL}}_d}$
on
 $\mathbf {x}$
,
$\mathbf {x}$
,
 $({}^w\mathbf {x})_i=x_{w^{-1}(i)}$
; § 2.10.
$({}^w\mathbf {x})_i=x_{w^{-1}(i)}$
; § 2.10. -
•
 $\mathbf {x}(\mathbf {a})=(x_1^{a_1/r},\ldots ,x_d^{a_d/r})$
for
$\mathbf {x}(\mathbf {a})=(x_1^{a_1/r},\ldots ,x_d^{a_d/r})$
for
 $\mathbf {a}\in r\mathbb {Z}^d$
; § 2.10.
$\mathbf {a}\in r\mathbb {Z}^d$
; § 2.10. -
•
 $w[\mathbf {a}]$
,
$w[\mathbf {a}]$
,
 $w_{\alpha }[\mathbf {a}]$
– an action of
$w_{\alpha }[\mathbf {a}]$
– an action of
 $W_{\operatorname {\mathrm {GL}}_d}$
on
$W_{\operatorname {\mathrm {GL}}_d}$
on
 $\mathbb {Z}^d$
; § 2.10.
$\mathbb {Z}^d$
; § 2.10. -
•
 $M(w_{\alpha })$
,
$M(w_{\alpha })$
,
 $M(w)$
– an intertwining operator between genuine unramified principal series; § 2.10.
$M(w)$
– an intertwining operator between genuine unramified principal series; § 2.10. -
•
 $\tau _{t,t'}$
,
$\tau _{t,t'}$
,
 $\tau _{t,t'}^1$
,
$\tau _{t,t'}^1$
,
 $\tau _{t,t'}^2$
– the coefficients appearing in the Casselman–Shalika formula for coverings of
$\tau _{t,t'}^2$
– the coefficients appearing in the Casselman–Shalika formula for coverings of
 $\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the notation
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
, the notation
 $\tau _{\mathbf {a},\mathbf {b}}$
is also used; Equations (2.77)-(2.80), Proposition 26, Equation (2.81), Equation (2.82).
$\tau _{\mathbf {a},\mathbf {b}}$
is also used; Equations (2.77)-(2.80), Proposition 26, Equation (2.81), Equation (2.82). -
•
 $\lceil x \rceil $
– the smallest integer greater than or equal to x; Proposition 26.
$\lceil x \rceil $
– the smallest integer greater than or equal to x; Proposition 26. -
•
 $\Theta _{d,m,r,\vartheta }$
– an exceptional representation of
$\Theta _{d,m,r,\vartheta }$
– an exceptional representation of
 $\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.11.
$\operatorname {\mathrm {GL}}_d^{(m,r)}$
; § 2.11. -
•
 $\beta \succsim \beta '$
– the partition
$\beta \succsim \beta '$
– the partition
 $\beta $
is greater than or not comparable with the partition
$\beta $
is greater than or not comparable with the partition
 $\beta '$
; § 2.12.
$\beta '$
; § 2.12. -
•
 $\mathcal {O}(\rho ,\beta ,\psi )$
– locally
$\mathcal {O}(\rho ,\beta ,\psi )$
– locally
 $\operatorname {\mathrm {Hom}}_{V(\beta )}(\rho ,\psi )$
, globally a set of Fourier coefficients; Integral (2.86), § 2.12.
$\operatorname {\mathrm {Hom}}_{V(\beta )}(\rho ,\psi )$
, globally a set of Fourier coefficients; Integral (2.86), § 2.12. -
•
 $\psi _{\lambda }$
– a (possibly degenerate) character of
$\psi _{\lambda }$
– a (possibly degenerate) character of
 $N_{\operatorname {\mathrm {GL}}_d}$
defined for a composition
$N_{\operatorname {\mathrm {GL}}_d}$
defined for a composition
 $\lambda $
of d; § 2.13.
$\lambda $
of d; § 2.13. -
•
 $W^0$
– the normalized unramified Whittaker function in the space of
$W^0$
– the normalized unramified Whittaker function in the space of
 $\mathcal {W}(\Theta _{r,m,r,\vartheta })$
; § 3.3.
$\mathcal {W}(\Theta _{r,m,r,\vartheta })$
; § 3.3. -
•
 $p_l(\mathbf {x})$
– the l-th complete symmetric polynomial in
$p_l(\mathbf {x})$
– the l-th complete symmetric polynomial in
 $\mathbf {x}$
; § 3.3.
$\mathbf {x}$
; § 3.3. -
•
 $\Lambda [S]$
– an
$\Lambda [S]$
– an
 $(rk,c)$
functional over a finite set of Archimedean or ramified places S; Equation (3.3).
$(rk,c)$
functional over a finite set of Archimedean or ramified places S; Equation (3.3). -
•
 $\eta _{rkc}^{\triangle }$
– the
$\eta _{rkc}^{\triangle }$
– the
 $1$
-cochain used to define the embedding of
$1$
-cochain used to define the embedding of
 $\operatorname {\mathrm {SL}}_c^{\triangle }(\mathbb {A})$
in
$\operatorname {\mathrm {SL}}_c^{\triangle }(\mathbb {A})$
in
 $\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
; Corollary 38.
$\operatorname {\mathrm {GL}}_{rkc}^{(m,r)}(\mathbb {A})$
; Corollary 38. -
•
 $\Theta _{rc,m,r,\vartheta }(\chi )$
– a representation parabolically induced from the tensor of k copies of exceptional representations
$\Theta _{rc,m,r,\vartheta }(\chi )$
– a representation parabolically induced from the tensor of k copies of exceptional representations
 $\Theta _{rc,m,r,\vartheta }$
, each twisted by
$\Theta _{rc,m,r,\vartheta }$
, each twisted by
 $\chi _i$
; Equation (3.6).
$\chi _i$
; Equation (3.6). -
•
 $\chi _{\Theta ,c}$
,
$\chi _{\Theta ,c}$
,
 $\chi _{\Theta }$
– the ‘linear part’ of the inducing character of
$\chi _{\Theta }$
– the ‘linear part’ of the inducing character of
 $\Theta _{rc,m,r,\vartheta }(\chi )$
as a subrepresentation,
$\Theta _{rc,m,r,\vartheta }(\chi )$
as a subrepresentation,
 $\chi _{\Theta }=\chi _{\Theta ,1}$
; the representation (3.7).
$\chi _{\Theta }=\chi _{\Theta ,1}$
; the representation (3.7). -
•
 $\rho _c(\tau )$
– the local component of the
$\rho _c(\tau )$
– the local component of the
 $(rk,c)$
representation
$(rk,c)$
representation
 $\mathcal {E}_{\tau }$
at an unramified place; § 3.5.
$\mathcal {E}_{\tau }$
at an unramified place; § 3.5. -
•
 $\mathcal {W}(\rho _c(\tau ))$
– the
$\mathcal {W}(\rho _c(\tau ))$
– the
 $(rk,c)$
model of
$(rk,c)$
model of
 $\rho _c(\tau )$
; § 3.5.
$\rho _c(\tau )$
; § 3.5. -
•
 $\{\varphi _1,\varphi _2\}$
- the
$\{\varphi _1,\varphi _2\}$
- the
 $G(\mathbb {A})$
-invariant pairing; § 4.2.
$G(\mathbb {A})$
-invariant pairing; § 4.2. -
•
 $f_{\mathcal {W}(\mathcal {E}_{\tau })}$
,
$f_{\mathcal {W}(\mathcal {E}_{\tau })}$
,
 $f_{\mathcal {W}(\mathcal {E})}$
- globally the composition of a section f with the
$f_{\mathcal {W}(\mathcal {E})}$
- globally the composition of a section f with the
 $(rk,c)$
functional, locally a section taking values in the
$(rk,c)$
functional, locally a section taking values in the
 $(rk,c)$
model; Equation (4.3), § 4.2.
$(rk,c)$
model; Equation (4.3), § 4.2. -
•
 $\lfloor x \rfloor $
– the largest integer smaller than or equal to x; Equation (5.1).
$\lfloor x \rfloor $
– the largest integer smaller than or equal to x; Equation (5.1).
Acknowledgements
We thank Yuanqing Cai for making a preliminary version of his results available to us, Solomon Friedberg for numerous fruitful conversations about this work and David Ginzburg for his help with the proof of Theorem 43. We are very happy to thank Mikhail Borovoi, Gautam Chinta, Wee Teck Gan, Dmitry Gourevitch, Erez Lapid, Peter McNamara, Gordan Savin, Michael Schein and Dani Szpruch for valuable and inspiring discussions. Finally, we are grateful to the referees for their interest in this work and helpful suggestions and remarks, which helped improve the presentation.
Competing interests
The authors have no competing interest to declare.
Funding statement
This research was supported by the ISRAEL SCIENCE FOUNDATION (grant numbers 376/21 and 421/17).