1 Introduction
The interaction between dendritic cells (DCs) and cytotoxic T lymphocytes (CTLs) plays a pivotal role in the immune response to cancer. DCs recognise the antigens expressed by cancer cells and present them to CTLs, which then become selectively activated against those antigens [Reference Waldman, Fritz and Lenardo28,Reference Wculek, Cueto, Mujal, Melero, Krummel and Sancho29]. Growing experimental evidence indicates that activation of CTLs via antigen presentation by DCs can bring about a switch in CTL migration modes [Reference Boissonnas, Fetler, Zeelenberg, Hugues and Amigorena5,Reference Krummel, Bartumeus and Gérard17]. In fact, while CTLs in the pre-activation state move in a non-local search pattern, which enables them to rapidly scan DCs for the presence of possible tumour antigens, the search pattern of activated CTLs is more localised. This allows activated CTLs to stay within a confined area for longer, thus facilitating their encounter with tumour cells expressing the antigens they have been activated against.
Stochastic individual-based models of immune response to cancer taking explicitly into account this difference in movement between CTLs have recently been developed [Reference Macfarlane, Chaplain and Lorenzi19,Reference Macfarlane, Lorenzi and Chaplain20]. In these models, cell motion is described as a space-jump process [Reference Othmer, Dunbar and Alt22]. In particular, CTLs in the pre-activation state undergo a space-jump process consistent with a Lévy walk, whereas a space-jump process corresponding to Brownian motion is used to describe the movement of activated CTLs. Such individual-based models enable representation of biological processes at the level of single cells and account for possible stochastic variability in cell dynamics, which allow for greater adaptability and higher accuracy in mathematical modelling. However, as the numerical exploration of these models requires large computational times for clinically relevant cell numbers (e.g. cell numbers of orders of magnitude between
![]() $10^6$
and
$10^6$
and
![]() $10^9$
[Reference Azizi, Carr, Plitas, Cornish, Konopacki, Prabhakaran, Nainys, Wu, Kiseliovas, Setty, Choi, Fromme, Dao, McKenney, Wasti, Kadaveru, Mazutis, Rudensky and Pe’er3]) and the models are not analytically tractable, it is desirable to derive corresponding deterministic continuum models in a suitable limit.
$10^9$
[Reference Azizi, Carr, Plitas, Cornish, Konopacki, Prabhakaran, Nainys, Wu, Kiseliovas, Setty, Choi, Fromme, Dao, McKenney, Wasti, Kadaveru, Mazutis, Rudensky and Pe’er3]) and the models are not analytically tractable, it is desirable to derive corresponding deterministic continuum models in a suitable limit.
In this paper, integrating the ideas proposed in [Reference Macfarlane, Chaplain and Lorenzi19,Reference Macfarlane, Lorenzi and Chaplain20] with the modelling approach presented in [Reference Estrada-Rodriguez and Gimperlein11,Reference Estrada-Rodriguez, Gimperlein and Painter12], we develop a kinetic model for the switch in CTL migration modes that is caused by activation through interactions with DCs. Cells are grouped into three populations: CTLs in the pre-activation state (i.e. inactive CTLs), activated CTLs and DCs. In the model, DCs are assumed to present a given tumour antigen on their surface so that they can activate inactive CTLs by contact. Since the focus of this study is on the mathematical modelling of the change in CTL migration mode upon activation, we do not take into account biological processes involving cell division and death. Furthermore, for simplicity, we do not consider the occurrence of molecular processes leading activated CTLs to re-enter a pre-activation state [Reference Wherry and Kurachi30].
The model is formulated as a coupled system of balance equations for the one-particle distribution functions of the three cell populations. CTL activation is modelled as a process of population switching among CTLs induced by binary interactions between inactive CTLs and DCs. Moreover, cell motion is represented as a velocity-jump process [Reference Othmer, Dunbar and Alt22], with the running time of inactive CTLs following a long-tailed distribution, which is consistent with a Lévy walk [Reference Estrada-Rodriguez and Gimperlein11,Reference Estrada-Rodriguez, Gimperlein and Painter12], and the running time of activated CTLs following a Poisson distribution, which corresponds to Brownian motion. Using a method similar to that previously employed in [Reference Estrada-Rodriguez and Gimperlein11], we formally show that the macroscopic limit of this model comprises a coupled system of balance equations for the cell densities, whereby activated CTL movement is described via a classical diffusion term, whilst a fractional diffusion term describes the movement of CTLs in the pre-activation state.
The paper is organised as follows. In Section 2, we introduce the modelling strategies and the main assumptions used to describe the spatio-temporal dynamics of CTLs and DCs at the scale of single cells, which provide a microscopic representation of the biological system. In Section 3, we present the kinetic model, which constitutes a mesoscopic analogue of the underlying microscopic scale model. In Section 4, we derive the macroscopic limit of a suitably rescaled version of the kinetic model. Section 5 concludes the paper providing a brief overview of possible research perspectives.
2 Description of the system at the microscopic scale
Biological system and cell populations
We label the three cell populations by a letter
![]() $h \in \{A,D,I\}$
, that is, activated CTLs are labelled by
$h \in \{A,D,I\}$
, that is, activated CTLs are labelled by
![]() $h=A$
, DCs are labelled by
$h=A$
, DCs are labelled by
![]() $h=D$
and inactive CTLs are labelled by
$h=D$
and inactive CTLs are labelled by
![]() $h=I$
. We let the total number of cells in the system be denoted by
$h=I$
. We let the total number of cells in the system be denoted by
![]() $N = N_D + N_T$
, where
$N = N_D + N_T$
, where
![]() $N_D \in \mathbb{N}$
is the number of DCs and
$N_D \in \mathbb{N}$
is the number of DCs and
![]() $N_T \in \mathbb{N}$
is the total number of CTLs. Moreover, we describe the number of inactive and activated CTLs in the system at time
$N_T \in \mathbb{N}$
is the total number of CTLs. Moreover, we describe the number of inactive and activated CTLs in the system at time
![]() $t \in \mathbb{R}_+$
by means of the functions
$t \in \mathbb{R}_+$
by means of the functions
![]() $N_I(t)$
and
$N_I(t)$
and
![]() $N_A(t)$
, respectively, with
$N_A(t)$
, respectively, with
![]() $N_I(t) + N_A(t) = N_T$
for all t.
$N_I(t) + N_A(t) = N_T$
for all t.
Mathematical representation of individual cells
Every individual cell is modelled as a sphere of diameter
![]() $\varrho \in \mathbb{R}^*_+$
and is labelled by an index
$\varrho \in \mathbb{R}^*_+$
and is labelled by an index
![]() $i = 1, \ldots, N$
. The phase-space state of the
$i = 1, \ldots, N$
. The phase-space state of the
![]() $i{\rm th}$
cell is represented by a pair
$i{\rm th}$
cell is represented by a pair
![]() $(\mathbf{x}_i, \mathbf{v}_i)$
, where the vector
$(\mathbf{x}_i, \mathbf{v}_i)$
, where the vector
![]() $\mathbf{x}_i\in \mathbb{R}^n$
describes the position of the centre of the cell and the vector
$\mathbf{x}_i\in \mathbb{R}^n$
describes the position of the centre of the cell and the vector
![]() $\mathbf{v}_i\in {\rm V} \subset \mathbb{R}^n$
, with
$\mathbf{v}_i\in {\rm V} \subset \mathbb{R}^n$
, with
![]() ${\rm V} \;:=\;\{\mathbf{v}_i\in\mathbb{R}^n:\ |\mathbf{v}_i|=1 \}$
(i.e. V is the unit n-sphere), represents the direction of the cell velocity. Moreover, the magnitude of the cell velocity is assumed to be constant and is denoted by
${\rm V} \;:=\;\{\mathbf{v}_i\in\mathbb{R}^n:\ |\mathbf{v}_i|=1 \}$
(i.e. V is the unit n-sphere), represents the direction of the cell velocity. Moreover, the magnitude of the cell velocity is assumed to be constant and is denoted by
![]() $c \in \mathbb{R}^*_+$
. The value of
$c \in \mathbb{R}^*_+$
. The value of
![]() $n=1,2,3$
depends on the biological scenario under study.
$n=1,2,3$
depends on the biological scenario under study.
2.1 Description of cell motion
Velocity-jump process
We describe the motion of a cell labelled by an index i as a run-and-tumble process with run time
![]() $\tau_i \in \mathbb{R}^*_+$
and running probability
$\tau_i \in \mathbb{R}^*_+$
and running probability
![]() $\psi(\mathbf{x}_i,\tau_i)$
, where
$\psi(\mathbf{x}_i,\tau_i)$
, where
![]() $0< \psi(\cdot,\cdot) \leqslant 1$
and
$0< \psi(\cdot,\cdot) \leqslant 1$
and
![]() $\partial_{\tau_i}\psi(\cdot,\cdot) \leqslant 0$
. The running probability
$\partial_{\tau_i}\psi(\cdot,\cdot) \leqslant 0$
. The running probability
![]() $\psi(\mathbf{x}_i,\tau_i)$
correlates with the stopping rate
$\psi(\mathbf{x}_i,\tau_i)$
correlates with the stopping rate
![]() $\beta(\mathbf{x}_i,\tau_i)$
through the relations given by the following definition [Reference Estrada-Rodriguez and Gimperlein11]:
$\beta(\mathbf{x}_i,\tau_i)$
through the relations given by the following definition [Reference Estrada-Rodriguez and Gimperlein11]:
Hence, starting at position
![]() $\mathbf{x}_i$
at time t, the
$\mathbf{x}_i$
at time t, the
![]() $i{\rm th}$
cell will continue moving along a straight path in the direction given by the vector
$i{\rm th}$
cell will continue moving along a straight path in the direction given by the vector
![]() $\mathbf{v}_i$
with constant speed c for a period of time
$\mathbf{v}_i$
with constant speed c for a period of time
![]() $\tau_i$
, after which it may stop with rate
$\tau_i$
, after which it may stop with rate
![]() $\beta(\mathbf{x}_i,\tau_i)$
. The cell will then instantaneously resume moving in a new randomly selected direction given by a vector
$\beta(\mathbf{x}_i,\tau_i)$
. The cell will then instantaneously resume moving in a new randomly selected direction given by a vector
![]() $\bar{\mathbf{v}}_i$
, which is prescribed by a turning kernel
$\bar{\mathbf{v}}_i$
, which is prescribed by a turning kernel
![]() $\ell(\mathbf{x}_i,t,\mathbf{v}_i;\bar{\mathbf{v}}_i)$
, that is, cells undergo a velocity-jump process [Reference Othmer, Dunbar and Alt22].
$\ell(\mathbf{x}_i,t,\mathbf{v}_i;\bar{\mathbf{v}}_i)$
, that is, cells undergo a velocity-jump process [Reference Othmer, Dunbar and Alt22].
Running probability
The running probability
![]() $\psi(\mathbf{x}_i,\tau_i)$
determines the distribution of the running time
$\psi(\mathbf{x}_i,\tau_i)$
determines the distribution of the running time
![]() $\tau_i$
and depends on the way in which the
$\tau_i$
and depends on the way in which the
![]() $i{\rm th}$
cell moves. Note that the running probability is here assumed to be independent from the cell velocity
$i{\rm th}$
cell moves. Note that the running probability is here assumed to be independent from the cell velocity
![]() $\mathbf{v}_i$
. On the basis of experimental evidence reported in [Reference Boissonnas, Fetler, Zeelenberg, Hugues and Amigorena5,Reference Engelhardt, Boldajipour, Beemiller, Pandurangi, Sorensen, Werb, Egeblad and Krummel10], we assume that inactive CTLs move in a non-local search pattern corresponding to trajectories that are characterised by a strong presence of long runs, which enable them to cover larger areas. On the other hand, activated CTLs and DCs
Footnote 1
move in a more localised search pattern. In particular, building upon the modelling approach presented in [Reference Macfarlane, Lorenzi and Chaplain20], we describe the motion of activated CTLs and DCs as a Brownian motion, whereas we let inactive CTLs undergo superdiffusive motion consistent with a Lévy walk, whereby the mean square displacement grows nonlinearly with time. In particular, the mean square displacement at time t is proportional to
$\mathbf{v}_i$
. On the basis of experimental evidence reported in [Reference Boissonnas, Fetler, Zeelenberg, Hugues and Amigorena5,Reference Engelhardt, Boldajipour, Beemiller, Pandurangi, Sorensen, Werb, Egeblad and Krummel10], we assume that inactive CTLs move in a non-local search pattern corresponding to trajectories that are characterised by a strong presence of long runs, which enable them to cover larger areas. On the other hand, activated CTLs and DCs
Footnote 1
move in a more localised search pattern. In particular, building upon the modelling approach presented in [Reference Macfarlane, Lorenzi and Chaplain20], we describe the motion of activated CTLs and DCs as a Brownian motion, whereas we let inactive CTLs undergo superdiffusive motion consistent with a Lévy walk, whereby the mean square displacement grows nonlinearly with time. In particular, the mean square displacement at time t is proportional to
![]() $t^{{2}/{\alpha}}$
, where
$t^{{2}/{\alpha}}$
, where
![]() $\alpha \in (1,2)$
is the Lévy exponent. We recall that
$\alpha \in (1,2)$
is the Lévy exponent. We recall that
![]() $\alpha=1$
and
$\alpha=1$
and
![]() $\alpha=2$
would correspond to ballistic motion (i.e. a form of motion whereby the mean square displacement at time t is proportional to
$\alpha=2$
would correspond to ballistic motion (i.e. a form of motion whereby the mean square displacement at time t is proportional to
![]() $t^2$
) and classical diffusion, respectively.
$t^2$
) and classical diffusion, respectively.
Under these assumptions, if the
![]() $i{\rm th}$
cell belongs to population A or population D, we let the value of the running time
$i{\rm th}$
cell belongs to population A or population D, we let the value of the running time
![]() $\tau_i$
follow a Poisson distribution [Reference Othmer and Hillen23]. Hence, under the additional simplifying assumption that cells in populations A and D are characterised by the same stopping rate, which is assumed to be constant and thus modelled by a parameter
$\tau_i$
follow a Poisson distribution [Reference Othmer and Hillen23]. Hence, under the additional simplifying assumption that cells in populations A and D are characterised by the same stopping rate, which is assumed to be constant and thus modelled by a parameter
![]() $b \in \mathbb{R}^*_+$
, we use the following definition of the running probability:
$b \in \mathbb{R}^*_+$
, we use the following definition of the running probability:
On the other hand, if the
![]() $i{\rm th}$
cell belongs to population I, we let the value of the running time
$i{\rm th}$
cell belongs to population I, we let the value of the running time
![]() $\tau_i$
follow a long-tailed distribution, and we define the running probability along the lines of [Reference Estrada-Rodriguez and Gimperlein11] as:
$\tau_i$
follow a long-tailed distribution, and we define the running probability along the lines of [Reference Estrada-Rodriguez and Gimperlein11] as:
Here, the function
![]() $\tau_0(\mathbf{x}_i) \geqslant 0$
captures possible spatial inhomogeneities in the running time distribution.
$\tau_0(\mathbf{x}_i) \geqslant 0$
captures possible spatial inhomogeneities in the running time distribution.
Turning kernel and turning operator
We consider the case where the new direction of cell motion given by
![]() $\bar{\mathbf{v}}_i$
is symmetrically distributed with respect to the original direction given by
$\bar{\mathbf{v}}_i$
is symmetrically distributed with respect to the original direction given by
![]() $\mathbf{v}_i$
and, therefore, we let the turning kernel
$\mathbf{v}_i$
and, therefore, we let the turning kernel
![]() $\ell(\mathbf{x}_i,t,\mathbf{v}_i;\bar{\mathbf{v}}_i)$
satisfy the following assumptions [Reference Alt2]:
$\ell(\mathbf{x}_i,t,\mathbf{v}_i;\bar{\mathbf{v}}_i)$
satisfy the following assumptions [Reference Alt2]:
where
![]() $\mathbf{e}_1 = (1, 0, \ldots, 0) \in \mathbb{R}^n$
is a unit vector.
$\mathbf{e}_1 = (1, 0, \ldots, 0) \in \mathbb{R}^n$
is a unit vector.
Moreover, we let the integral operator
![]() $\mathcal{T}$
be a turning operator such that for all test functions
$\mathcal{T}$
be a turning operator such that for all test functions
![]() $\phi(\mathbf{v}_i)$
:
$\phi(\mathbf{v}_i)$
:
where
![]() $\ell$
is the turning kernel defined via (2.4). Since
$\ell$
is the turning kernel defined via (2.4). Since
![]() $\displaystyle{\int_{\rm V} \ell(\cdot,\cdot,\cdot;\bar{\mathbf{v}}_i) \mathop{}\!\mathrm{d} \bar{\mathbf{v}}_i =1}$
, we have
$\displaystyle{\int_{\rm V} \ell(\cdot,\cdot,\cdot;\bar{\mathbf{v}}_i) \mathop{}\!\mathrm{d} \bar{\mathbf{v}}_i =1}$
, we have
where
![]() $\unicode{x1D7D9}$
is the identity operator.
$\unicode{x1D7D9}$
is the identity operator.
Finally, we recall that in n-dimensions the surface area of the unit sphere
![]() ${\rm V} $
is
${\rm V} $
is
 \begin{equation}|{\rm V}|=\begin{cases}\dfrac{2\pi^{{n}/{2}}}{\Gamma\left(\frac{n}{2}\right)} \ , & \text{for } {n} \text{ even},\\[9pt]\dfrac{\pi^{{n}/{2}}}{\Gamma\left(\frac{n}{2}+1\right)} \ , & \text{for } {n} \text{ odd}\end{cases}\end{equation}
\begin{equation}|{\rm V}|=\begin{cases}\dfrac{2\pi^{{n}/{2}}}{\Gamma\left(\frac{n}{2}\right)} \ , & \text{for } {n} \text{ even},\\[9pt]\dfrac{\pi^{{n}/{2}}}{\Gamma\left(\frac{n}{2}+1\right)} \ , & \text{for } {n} \text{ odd}\end{cases}\end{equation}
where
![]() $\Gamma(\cdot)$
is the Gamma function, and we also recall some useful properties of the spectrum of the turning operator
$\Gamma(\cdot)$
is the Gamma function, and we also recall some useful properties of the spectrum of the turning operator
![]() $\mathcal{T}$
[Reference Alt2]:
$\mathcal{T}$
[Reference Alt2]:
Lemma 1 If the turning kernel
![]() $\ell(\cdot,\cdot,|\bar{\mathbf{v}}_i-\mathbf{v}_i|)$
is continuous, then
$\ell(\cdot,\cdot,|\bar{\mathbf{v}}_i-\mathbf{v}_i|)$
is continuous, then
![]() $\mathcal{T}$
is a symmetric compact operator. In particular, there exists an orthonormal basis of
$\mathcal{T}$
is a symmetric compact operator. In particular, there exists an orthonormal basis of
![]() $L^2({\rm V})$
consisting of eigenfunctions
$L^2({\rm V})$
consisting of eigenfunctions
![]() $\{ \phi_k,\ k\geqslant 0\}$
of
$\{ \phi_k,\ k\geqslant 0\}$
of
![]() $\mathcal{T}$
. Using the notation
$\mathcal{T}$
. Using the notation
![]() $\mathbf{v}_i=({v}_0^i,{v}^i_1,\dots,{v}^i_{n-1}) \in {\rm V}$
, we have
$\mathbf{v}_i=({v}_0^i,{v}^i_1,\dots,{v}^i_{n-1}) \in {\rm V}$
, we have
 \begin{align*}\begin{aligned}\phi_{0}(\mathbf{v}_i) & =\frac{1}{|{\rm V}|} & & \text{is an eigenfunction associated with the eigenvalue} & & \iota_{0}=1,\\[5pt]\phi_{1}^j(\mathbf{v}_i) & =\frac{n{v}^i_j}{|{\rm V}|} & & \text{are eigenfunctions associated with the eigenvalue:} & &\end{aligned}\end{align*}
\begin{align*}\begin{aligned}\phi_{0}(\mathbf{v}_i) & =\frac{1}{|{\rm V}|} & & \text{is an eigenfunction associated with the eigenvalue} & & \iota_{0}=1,\\[5pt]\phi_{1}^j(\mathbf{v}_i) & =\frac{n{v}^i_j}{|{\rm V}|} & & \text{are eigenfunctions associated with the eigenvalue:} & &\end{aligned}\end{align*}
where
![]() $\mathbf{e} = (1, 1, \ldots, 1) \in \mathbb{R}^n$
is the vector with all components equal to 1. Moreover, any function
$\mathbf{e} = (1, 1, \ldots, 1) \in \mathbb{R}^n$
is the vector with all components equal to 1. Moreover, any function
![]() $p_i\in L^2(\mathbb{R}^n\times \mathbb{R}_+\times {\rm V})$
admits a unique decomposition of the form:
$p_i\in L^2(\mathbb{R}^n\times \mathbb{R}_+\times {\rm V})$
admits a unique decomposition of the form:
where
![]() $\hat{z}$
is orthogonal to all linear polynomials in
$\hat{z}$
is orthogonal to all linear polynomials in
![]() $\mathbf{v}_i$
,
$\mathbf{v}_i$
,
and
![]() ${w}_i = ({w}^i_0, \dots, {w}^i_{n-1})$
.
${w}_i = ({w}^i_0, \dots, {w}^i_{n-1})$
.
2.2 Description of the interactions between cells
Building on previous work on individual-based models of interaction dynamics between DCs and CTLs [Reference Macfarlane, Chaplain and Lorenzi19,Reference Macfarlane, Lorenzi and Chaplain20], we consider only the effects of binary cell–cell interactions, thus neglecting interactions that involve more than two cells.
Moreover, given that the focus of this work is on modelling the switch in T cell migration modes mediated by interactions between inactive CTLs and DCs, we explicitly model the effects of interactions between cells of population I and cells of population D, while for simplicity, we neglect the effects of intrapopulation cell–cell interactions and interactions between cells of population I and cells of population A.
Furthermore, the spatial dynamics of DCs are primarily affected by interactions with inactive CTLs [Reference Bousso6,Reference Gardner and Ruffell14,Reference Rothoeft, Balkow, Krummen, Beissert, Varga, Loser, Oberbanscheidt, van den Boom and Grabbe26]. Hence, for simplicity, we explicitly model the effect of interactions between cells of population D and cells of population A on the motion of A cells, while we neglect the effect of these interactions on the motion of D cells, since we take it to be negligible compared to that of interactions with cells of population I.
On the basis of these considerations, we incorporate into the model only the effects of interactions between pairs of cells that are summarised by the schematics in Figure 1, which correspond to the following definitions and assumptions.
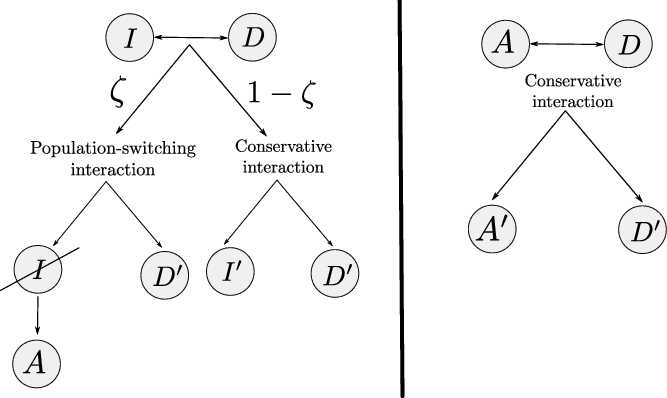
Figure 1. Schematics of cell–cell interactions corresponding to Assumptions 1 and 2. Prime symbols indicate a change in cell velocity upon interaction.
Definition 2.1 (Conservative interactions) Conservative interactions are those that preserve the number of cells in every population and only modify the velocity of the cells according to (2.11). Otherwise, the interaction is a population-switching interaction.
Definition 2.2 (Population-switching interactions) Population-switching interactions are those that lead a cell to enter a different population. These interactions are destructive for the original population of the cell and creative for the population in which the cell will be upon interaction.
Assumption 1
(Interactions between inactive CTLs and DCs) We model activation of CTLs upon interaction with DCs by assuming that, when a cell in population I interacts with a cell in population D, the I cell switches from population I to population A (i.e. the interaction is population-switching in the sense of Definition 2.2) with probability
![]() $\zeta \in (0,1)$
. For simplicity, we assume that the I cell enters population A without changing its velocity. If activation does not occur, event that happens with probability
$\zeta \in (0,1)$
. For simplicity, we assume that the I cell enters population A without changing its velocity. If activation does not occur, event that happens with probability
![]() $1-\zeta$
, the I cell remains in the same population (i.e. the interaction is conservative in the sense of Definition 2.1) and acquires the post-interaction velocity defined via (2.11). Upon interaction, the D cell always acquires a post-interaction velocity defined as in (2.11).
$1-\zeta$
, the I cell remains in the same population (i.e. the interaction is conservative in the sense of Definition 2.1) and acquires the post-interaction velocity defined via (2.11). Upon interaction, the D cell always acquires a post-interaction velocity defined as in (2.11).
Assumption 2 (Interactions between activated CTLs and DCs) We assume that when a cell in population A interacts with a cell in population D, the A cell remains in the same population and acquires the post-interaction velocity defined via (2.11), and the interaction is conservative in the sense of Definition 2.1. As explained above, we do not take into account the effect of interactions between cells of population D and cells of population A on the motion of the D cells.
We allow interactions between a cell i in the phase-space state
![]() $(\mathbf{x}_i, \mathbf{v}_i)$
and a cell j in the phase-space state
$(\mathbf{x}_i, \mathbf{v}_i)$
and a cell j in the phase-space state
![]() $(\mathbf{x}_j, \mathbf{v}_j)$
to occur when the cell j is in the domain of interaction of the cell i, which is defined as the set:
$(\mathbf{x}_j, \mathbf{v}_j)$
to occur when the cell j is in the domain of interaction of the cell i, which is defined as the set:
where
![]() ${\rm B}_\varrho(\mathbf{x}_i)$
denotes the ball of radius
${\rm B}_\varrho(\mathbf{x}_i)$
denotes the ball of radius
![]() $\varrho$
centred at
$\varrho$
centred at
![]() $\mathbf{x}_i$
(see the schematics in Figure 2). If a cell i acquires a new velocity upon interaction with a cell j, the new velocity is defined, for simplicity, as the following post-interaction velocity:
$\mathbf{x}_i$
(see the schematics in Figure 2). If a cell i acquires a new velocity upon interaction with a cell j, the new velocity is defined, for simplicity, as the following post-interaction velocity:
where
![]() $\nu$
is the normal vector at the point of interaction (i.e.
$\nu$
is the normal vector at the point of interaction (i.e.
![]() $\nu$
is the unit normal that points outward from
$\nu$
is the unit normal that points outward from
![]() $\Omega_j(\mathbf{x}_i)$
and inward to
$\Omega_j(\mathbf{x}_i)$
and inward to
![]() ${\rm B}_\varrho(\mathbf{x}_i)$
) [Reference Cercignani, Illner and Pulvirenti7].
${\rm B}_\varrho(\mathbf{x}_i)$
) [Reference Cercignani, Illner and Pulvirenti7].
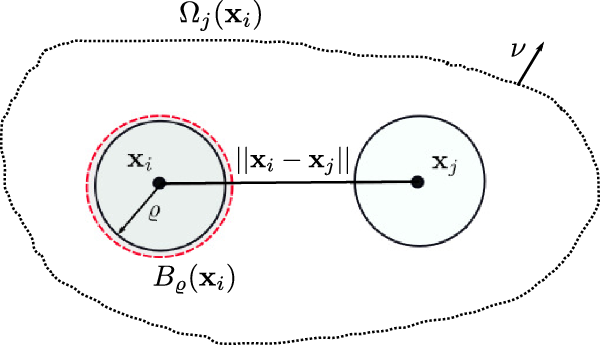
Figure 2. Schematics of the interaction domain defined in (2.10).
Remark 1 Definition (2.11) relies on the observation that, although binary collisions between cells are not elastic in nature, they may result in cell outgoing trajectories compatible with those observed in elastic collisions [Reference Albrecht-Buehler1,Reference Löber, Ziebert and Aranson18].
3 Mesoscopic scale model
In this section, we derive the mesoscopic scale model corresponding to the microscopic scale description presented in Section 2, which comprises a system of transport equations for the one-particle distribution functions of inactive CTLs, activated CTLs and DCs.
3.1 Preliminaries, assumptions and notation
The state of the system at time t is described by the N-particle distribution function
![]() $f^N\left(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N\right)$
[Reference Cercignani, Illner and Pulvirenti7,Reference Villani27]. In the case where cell dynamics at the microscopic scale obey the rules presented in Section 2, the evolution of
$f^N\left(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N\right)$
[Reference Cercignani, Illner and Pulvirenti7,Reference Villani27]. In the case where cell dynamics at the microscopic scale obey the rules presented in Section 2, the evolution of
![]() $f^N$
is governed by the following transport equation [Reference Kennard16]:
$f^N$
is governed by the following transport equation [Reference Kennard16]:
posed on
![]() $\Omega^{N} \times \mathbb{R}^*_+ \times {\rm V}^{N} \times \mathbb{R}^{* N}_+$
, with
$\Omega^{N} \times \mathbb{R}^*_+ \times {\rm V}^{N} \times \mathbb{R}^{* N}_+$
, with
We consider the transport equation (3.1) subject to smooth, compactly supported initial conditions at
![]() $t=0$
, boundary conditions corresponding to elastic interactions on
$t=0$
, boundary conditions corresponding to elastic interactions on
![]() $\partial\Omega^{N}$
, and suitable Dirichlet boundary conditions at
$\partial\Omega^{N}$
, and suitable Dirichlet boundary conditions at
![]() $\tau_i=0$
linked to the running probability
$\tau_i=0$
linked to the running probability
![]() $\psi$
for
$\psi$
for
![]() $i=1,\ldots,N$
. In the mathematical framework given by (3.1), the probability of finding at position
$i=1,\ldots,N$
. In the mathematical framework given by (3.1), the probability of finding at position
![]() $\mathbf{x}_1$
and at time t the cell labelled by the index 1 that is moving in direction
$\mathbf{x}_1$
and at time t the cell labelled by the index 1 that is moving in direction
![]() $\mathbf{v}_1$
for a period of time
$\mathbf{v}_1$
for a period of time
![]() $\tau_1$
is related to the one-particle marginal:
$\tau_1$
is related to the one-particle marginal:
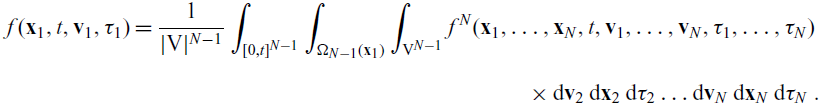 \begin{align*}{f}(\mathbf{x}_1,t,\mathbf{v}_1,\tau_1)&= \frac{1}{|{\rm V}|^{{ N-1}}}\int_{[0,t]^{{ N-1}}}\int_{\Omega_{N-1}(\mathbf{x}_1)}\int_{{\rm V}^{{ N-1}}}f^{{ N}}(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N)\nonumber\\[5pt] &\ \times\mathop{}\!\mathrm{d}\mathbf{v}_{2} \mathop{}\!\mathrm{d}\mathbf{x}_{2} \mathop{}\!\mathrm{d}\tau_{2} \ldots \mathop{}\!\mathrm{d} \mathbf{v}_{N} \mathop{}\!\mathrm{d} \mathbf{x}_{N} \mathop{}\!\mathrm{d} \tau_{N}\ .\end{align*}
\begin{align*}{f}(\mathbf{x}_1,t,\mathbf{v}_1,\tau_1)&= \frac{1}{|{\rm V}|^{{ N-1}}}\int_{[0,t]^{{ N-1}}}\int_{\Omega_{N-1}(\mathbf{x}_1)}\int_{{\rm V}^{{ N-1}}}f^{{ N}}(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N)\nonumber\\[5pt] &\ \times\mathop{}\!\mathrm{d}\mathbf{v}_{2} \mathop{}\!\mathrm{d}\mathbf{x}_{2} \mathop{}\!\mathrm{d}\tau_{2} \ldots \mathop{}\!\mathrm{d} \mathbf{v}_{N} \mathop{}\!\mathrm{d} \mathbf{x}_{N} \mathop{}\!\mathrm{d} \tau_{N}\ .\end{align*}
Here,
![]() $|{\rm V}|$
denotes the surface area of the unit sphere V and
$|{\rm V}|$
denotes the surface area of the unit sphere V and
![]() $\Omega_{N-1}(\mathbf{x}_1)\;:=\; \{(\mathbf{x}_{2}, \ldots,\mathbf{x}_{N}) \in \mathbb{R}^{n \times N-1} : (\mathbf{x}_1,\mathbf{x}_{2},\ldots,\mathbf{x}_{N})\in\Omega^{N} \}$
.
$\Omega_{N-1}(\mathbf{x}_1)\;:=\; \{(\mathbf{x}_{2}, \ldots,\mathbf{x}_{N}) \in \mathbb{R}^{n \times N-1} : (\mathbf{x}_1,\mathbf{x}_{2},\ldots,\mathbf{x}_{N})\in\Omega^{N} \}$
.
A comprehensive description of cell dynamics would in principle require considering possible interactions between all cells. However, as mentioned earlier, building on previous work on the mathematical modelling of the interaction dynamics between DCs and CTLs [Reference Macfarlane, Chaplain and Lorenzi19,Reference Macfarlane, Lorenzi and Chaplain20], we consider only the effect of binary cell–cell interactions, thus neglecting interactions that involve more than two cells. Therefore, as per the scaling and assumptions introduced in Section 4.1, which are similar to those typically considered in low-density regimes [Reference Cercignani, Illner and Pulvirenti7,Reference Othmer, Dunbar and Alt22,Reference Villani27], we truncate the hierarchy of equations corresponding to (3.1) at the second order by integrating out cells
![]() $3, \ldots ,N$
from the N-particle distribution function
$3, \ldots ,N$
from the N-particle distribution function
![]() $f^N\left(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N\right)$
.
$f^N\left(\mathbf{x}_1, \ldots, \mathbf{x}_N, t, \mathbf{v}_1, \ldots, \mathbf{v}_N, \mathbf{\tau}_1, \ldots, \mathbf{\tau}_N\right)$
.
Two-particle distribution functions
Let
![]() $f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})$
with
$f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})$
with
![]() $h, k \in \{A,D,I\}$
and
$h, k \in \{A,D,I\}$
and
![]() $k \neq h$
denote the two-particle distribution function associated with:
$k \neq h$
denote the two-particle distribution function associated with:
-
– a cell of population h in the generic phase-space state
 $(\mathbf{x}_h,\mathbf{v}_h) \in \mathbb{R}^n \times {\rm V}$
, with generic run time
$(\mathbf{x}_h,\mathbf{v}_h) \in \mathbb{R}^n \times {\rm V}$
, with generic run time
 $\tau_h \in [0,t]$
and stopping rate
$\tau_h \in [0,t]$
and stopping rate
 $ \beta_h(\mathbf{x}_h,\tau_h)$
defined via (2.1);
$ \beta_h(\mathbf{x}_h,\tau_h)$
defined via (2.1); -
– a cell of population k in the generic phase-space state
 $(\mathbf{x}_k,\mathbf{v}_k) \in \mathbb{R}^n \times {\rm V}$
, with generic run time
$(\mathbf{x}_k,\mathbf{v}_k) \in \mathbb{R}^n \times {\rm V}$
, with generic run time
 $\tau_k \in [0,t]$
and stopping rate
$\tau_k \in [0,t]$
and stopping rate
 $ \beta_k(\mathbf{x}_k,\tau_k)$
defined via (2.1).
$ \beta_k(\mathbf{x}_k,\tau_k)$
defined via (2.1).
Truncating the hierarchy of equations corresponding to (3.1) at the second order, we obtain the following transport equation for
![]() $f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})$
:
$f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})$
:
posed on
![]() $\Omega^2 \times \mathbb{R}_+ \times {\rm V}^{2} \times \mathbb{R}^{* 2}_+$
, with
$\Omega^2 \times \mathbb{R}_+ \times {\rm V}^{2} \times \mathbb{R}^{* 2}_+$
, with
This equation is subject to a smooth, compactly supported initial condition at
![]() $t=0$
, specular reflective boundary conditions corresponding to elastic interactions on
$t=0$
, specular reflective boundary conditions corresponding to elastic interactions on
![]() $\partial \Omega^2$
, and with boundary conditions at
$\partial \Omega^2$
, and with boundary conditions at
![]() $\tau_k=0$
and
$\tau_k=0$
and
![]() $\tau_h=0$
given by:
$\tau_h=0$
given by:
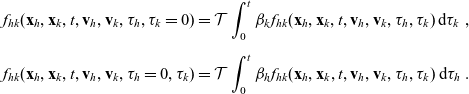 \begin{equation}\begin{aligned} f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,\tau_k=0)&=\mathcal{T}\int_0^t\beta_kf_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})\mathop{}\!\mathrm{d} \tau_k\ ,\\[5pt] f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h=0,\tau_k)&=\mathcal{T}\int_0^t\beta_hf_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})\mathop{}\!\mathrm{d} \tau_h\ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned} f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,\tau_k=0)&=\mathcal{T}\int_0^t\beta_kf_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})\mathop{}\!\mathrm{d} \tau_k\ ,\\[5pt] f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h=0,\tau_k)&=\mathcal{T}\int_0^t\beta_hf_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,{\tau_k})\mathop{}\!\mathrm{d} \tau_h\ .\end{aligned}\end{equation}
One-particle distribution functions
Given the two-particle distribution function:
the one-particle distribution function of population h is given by:
with the set
![]() $\Omega_k(\mathbf{x}_h)$
defined via (2.10). The function
$\Omega_k(\mathbf{x}_h)$
defined via (2.10). The function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
describes the density of cells of population h which at position
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
describes the density of cells of population h which at position
![]() $\mathbf{x}_h$
and time t move with velocity
$\mathbf{x}_h$
and time t move with velocity
![]() $\mathbf{v}_h$
(i.e. the quantity
$\mathbf{v}_h$
(i.e. the quantity
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h) \mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{x}_h$
is the number of cells of population h in the volume element
$p_h(\mathbf{x}_h,t,\mathbf{v}_h) \mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{x}_h$
is the number of cells of population h in the volume element
![]() $ \mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{x}_h$
centred at the point
$ \mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{x}_h$
centred at the point
![]() $(\mathbf{x}_h, \mathbf{v}_h)$
of the phase space). Moreover, we will consider the weighted two-particle distribution function given by:
$(\mathbf{x}_h, \mathbf{v}_h)$
of the phase space). Moreover, we will consider the weighted two-particle distribution function given by:
and the weighted one-particle distribution function given by:
Here,
![]() $|{\rm V}|$
denotes the surface area of the unit sphere V.
$|{\rm V}|$
denotes the surface area of the unit sphere V.
3.2 Derivation of a system of transport equations
Transport equations for two-particle distribution functions
The dynamics of the two-particle distribution functions
![]() $f_{ID}$
and
$f_{ID}$
and
![]() $f_{AD}$
are governed by the following specific forms of transport equation (3.2):
$f_{AD}$
are governed by the following specific forms of transport equation (3.2):
which are posed on
![]() $\Omega^2 \times \mathbb{R}^*_+ \times {\rm V}^{2} \times \mathbb{R}^{* 2}_+$
. The boundary conditions at
$\Omega^2 \times \mathbb{R}^*_+ \times {\rm V}^{2} \times \mathbb{R}^{* 2}_+$
. The boundary conditions at
![]() $\tau_A=0,\ \tau_D=0$
and
$\tau_A=0,\ \tau_D=0$
and
![]() $\tau_I=0$
are analogous to (3.4). Starting from transport equations (3.9)–(3.10) and using the method employed in [Reference Estrada-Rodriguez and Gimperlein11], it is possible to show (see 6) that the two-particle distribution functions
$\tau_I=0$
are analogous to (3.4). Starting from transport equations (3.9)–(3.10) and using the method employed in [Reference Estrada-Rodriguez and Gimperlein11], it is possible to show (see 6) that the two-particle distribution functions
![]() $\tilde{\tilde{f}}_{ID}$
and
$\tilde{\tilde{f}}_{ID}$
and
![]() $\tilde{\tilde{f}}_{AD}$
given by (3.5) satisfy the following transport equations:
$\tilde{\tilde{f}}_{AD}$
given by (3.5) satisfy the following transport equations:
posed on
![]() $\Omega^2 \times \mathbb{R}^*_+ \times {\rm V}^{2}$
. Here,
$\Omega^2 \times \mathbb{R}^*_+ \times {\rm V}^{2}$
. Here,
![]() $\mathcal{T}_I$
,
$\mathcal{T}_I$
,
![]() $\mathcal{T}_D$
and
$\mathcal{T}_D$
and
![]() $\mathcal{T}_A$
are the turning operators defined via (2.5), and
$\mathcal{T}_A$
are the turning operators defined via (2.5), and
![]() $\tilde{\tilde{f}}^{\beta_h}_{hk}$
and
$\tilde{\tilde{f}}^{\beta_h}_{hk}$
and
![]() $\tilde{\tilde{f}}^{\beta_k}_{hk}$
are the weighted two-particle distribution functions given by (3.7).
$\tilde{\tilde{f}}^{\beta_k}_{hk}$
are the weighted two-particle distribution functions given by (3.7).
Remark 2 Notice that the equation describing the evolution of the one-particle distribution function
![]() $p_D$
will be derived from the transport equation (3.11) for the two-particle distribution function
$p_D$
will be derived from the transport equation (3.11) for the two-particle distribution function
![]() $\tilde{\tilde{f}}_{ID}$
by integrating the variables corresponding to the I cell and using the interaction rules described in Assumption 1.
$\tilde{\tilde{f}}_{ID}$
by integrating the variables corresponding to the I cell and using the interaction rules described in Assumption 1.
Transport equation for
![]() $p_h$
$p_h$
Starting from transport equation (3.2) and building upon the method presented in [Reference Estrada-Rodriguez and Gimperlein11], it is possible to show (see 7) that the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
given by (3.6) satisfies the following transport equation:
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
given by (3.6) satisfies the following transport equation:
Here, the turning operator
![]() $\mathcal{T}_h$
is defined via (2.5), the weighted one-particle distribution function
$\mathcal{T}_h$
is defined via (2.5), the weighted one-particle distribution function
![]() $p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given by (3.8) and
$p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given by (3.8) and
In (3.14),
![]() $\nu$
is the unit normal defined in (2.11) and
$\nu$
is the unit normal defined in (2.11) and
![]() $\mathop{}\!\mathrm{d} \sigma$
denotes the surface element.
$\mathop{}\!\mathrm{d} \sigma$
denotes the surface element.
The first term on the right-hand side of transport equation (3.13) represents the rate of change of the one-particle distribution function due to cell movement, while the term
![]() $\mathcal{Q}_{hk}$
is the rate of change due to interactions between cells. The specific forms of these terms depend, respectively, on the way in which cells move and the interactions they undergo, as discussed in the remainder of this section.
$\mathcal{Q}_{hk}$
is the rate of change due to interactions between cells. The specific forms of these terms depend, respectively, on the way in which cells move and the interactions they undergo, as discussed in the remainder of this section.
Expressions for
![]() $p^{\beta_h}_{h}$
$p^{\beta_h}_{h}$
The specific form of the first term on the right-hand side of transport equation (3.13) depends on the expression for
![]() $p^{\beta_h}_{h}$
which, in turn, will depend on the definition of the stopping rate
$p^{\beta_h}_{h}$
which, in turn, will depend on the definition of the stopping rate
![]() $\beta_h$
.
$\beta_h$
.
When cells move in a local search pattern (i.e. for
![]() $h=A$
and
$h=A$
and
![]() $h=D$
), the stopping rate
$h=D$
), the stopping rate
![]() $\beta_h$
is defined via (2.1) and (2.2). In this case, inserting the definition of
$\beta_h$
is defined via (2.1) and (2.2). In this case, inserting the definition of
![]() $\beta_h$
into (3.8) yields
$\beta_h$
into (3.8) yields
On the other hand, when cells move in a non-local search pattern (i.e. for
![]() $h=I$
), the stopping rate
$h=I$
), the stopping rate
![]() $\beta_h$
is defined via (2.1) and (2.3). In this case, it is possible to show (see 8) that
$\beta_h$
is defined via (2.1) and (2.3). In this case, it is possible to show (see 8) that
where
![]() $\mathcal{B}$
is a convolution operator such that
$\mathcal{B}$
is a convolution operator such that
with B being defined through its Laplace transform in time
![]() $\hat{B}$
as:
$\hat{B}$
as:
Here,
![]() $\lambda$
is the Laplace variable,
$\lambda$
is the Laplace variable,
![]() $\hat{\varphi}_h$
and
$\hat{\varphi}_h$
and
![]() $\hat{\psi}_h$
are the Laplace transforms in
$\hat{\psi}_h$
are the Laplace transforms in
![]() $\tau_h$
of the functions
$\tau_h$
of the functions
![]() $\varphi_h$
and
$\varphi_h$
and
![]() $\psi_h$
defined via (2.3), and the parameter b is defined via (2.2).
$\psi_h$
defined via (2.3), and the parameter b is defined via (2.2).
Expressions for
![]() $\mathcal{Q}_{hk}$
$\mathcal{Q}_{hk}$
Following [Reference Estrada-Rodriguez and Gimperlein11,Reference Franz, Taylor-King, Yates and Erban13], we first note that when a cell in the phase-space state
![]() $({\bf x}_h, {\bf v}_h)$
interacts with a cell in the phase-space state
$({\bf x}_h, {\bf v}_h)$
interacts with a cell in the phase-space state
![]() $({\bf x}_k, {\bf v}_k)$
, we have
$({\bf x}_k, {\bf v}_k)$
, we have
![]() $|{\bf x}_h - {\bf x}_k| = \varrho$
. Hence, the normal vector at the point of physical contact between the interacting cells,
$|{\bf x}_h - {\bf x}_k| = \varrho$
. Hence, the normal vector at the point of physical contact between the interacting cells,
![]() $\nu \in {\rm V}$
, defined via (2.11) can be written as
$\nu \in {\rm V}$
, defined via (2.11) can be written as
![]() $\nu=(\mathbf{x}_h-\mathbf{x}_k)/\varrho$
, that is,
$\nu=(\mathbf{x}_h-\mathbf{x}_k)/\varrho$
, that is,
![]() $\mathbf{x}_k=\mathbf{x}_h-\nu\varrho$
. As a result, using the fact that
$\mathbf{x}_k=\mathbf{x}_h-\nu\varrho$
. As a result, using the fact that
![]() ${\rm B}_\varrho = \varrho {\rm V}$
along with the change of variable
${\rm B}_\varrho = \varrho {\rm V}$
along with the change of variable
![]() $\nu \mapsto -\nu$
, we rewrite (3.14) as:
$\nu \mapsto -\nu$
, we rewrite (3.14) as:
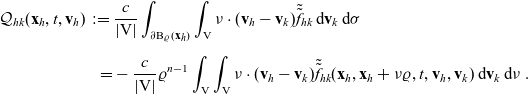 \begin{align}\mathcal{Q}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h) \;:=\; & \frac{c}{|{{\rm V}}|}\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk} \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\sigma \nonumber \\[5pt] = & -\frac{c}{|{{\rm V}}|}\varrho^{n-1}\int_{{\rm V}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ .\end{align}
\begin{align}\mathcal{Q}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h) \;:=\; & \frac{c}{|{{\rm V}}|}\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk} \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\sigma \nonumber \\[5pt] = & -\frac{c}{|{{\rm V}}|}\varrho^{n-1}\int_{{\rm V}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ .\end{align}
Following [Reference Estrada-Rodriguez and Gimperlein11], we also note that
![]() ${\rm V} \equiv {\rm V}^+_{hk}\cup {\rm V}^-_{hk}$
with
${\rm V} \equiv {\rm V}^+_{hk}\cup {\rm V}^-_{hk}$
with
 \begin{equation}\begin{aligned}{\rm V}^+_{hk} &\;:=\; \{\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)>0 \}\ , \\[5pt]{\rm V}^-_{hk} &\;:=\; \{\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)<0 \} \equiv \{-\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)>0 \}\ .\end{aligned}\end{equation}
\begin{equation}\begin{aligned}{\rm V}^+_{hk} &\;:=\; \{\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)>0 \}\ , \\[5pt]{\rm V}^-_{hk} &\;:=\; \{\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)<0 \} \equiv \{-\nu \in {\rm V} : \nu\cdot(\mathbf{v}_h-\mathbf{v}_k)>0 \}\ .\end{aligned}\end{equation}
Therefore, a cell moving in direction
![]() ${\bf v}_h$
and a cell moving in direction
${\bf v}_h$
and a cell moving in direction
![]() ${\bf v}_k$
will move towards each other if
${\bf v}_k$
will move towards each other if
![]() $\nu \in {\rm V}^+$
and away from each other if
$\nu \in {\rm V}^+$
and away from each other if
![]() $\nu \in {\rm V}^-$
.
$\nu \in {\rm V}^-$
.
Under Assumptions 1–2, denoting the post-interaction directions corresponding to
![]() $\mathbf{v}_h$
and
$\mathbf{v}_h$
and
![]() $\mathbf{v}_k$
by
$\mathbf{v}_k$
by
![]() $\mathbf{v}'_{\!h}$
and
$\mathbf{v}'_{\!h}$
and
![]() $\mathbf{v}'_{\!k}$
, which are defined via (2.11), we consider two different types of interactions between cells: conservative interactions (cf. Definition 2.1), between a cell of population h and a cell of population k, whereby both cells remain in their original populations upon interaction and acquire the post-interaction velocities; population-switching interactions (cf. Definition 2.2), between a cell in population h and a cell in population k, whereby the h cell switches from its original population to a different one upon interaction.
$\mathbf{v}'_{\!k}$
, which are defined via (2.11), we consider two different types of interactions between cells: conservative interactions (cf. Definition 2.1), between a cell of population h and a cell of population k, whereby both cells remain in their original populations upon interaction and acquire the post-interaction velocities; population-switching interactions (cf. Definition 2.2), between a cell in population h and a cell in population k, whereby the h cell switches from its original population to a different one upon interaction.
From (3.19), we define the rate of change of the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to conservative interactions as:
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to conservative interactions as:
 \begin{align} \mathcal{K}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h) & \;:=\;-\frac{c}{|{{\rm V}}|}\varrho^{n-1} \, N_k(t) \, \left[\int_{{\rm V}^+_{hk}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\right.\nonumber\\[5pt] & \qquad \left.+\int_{{\rm V}^-_{hk}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\right]\nonumber\\[5pt] &=\frac{c}{|{{\rm V}}|}\varrho^{n-1} \, N_k(t) \, \int_{{\rm V}_{hk}^+}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\Bigl[\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h-\nu\varrho,t,\mathbf{v}'_h,\mathbf{v}'_k)\nonumber\\[5pt] &\qquad -\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\Bigr]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ , \end{align}
\begin{align} \mathcal{K}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h) & \;:=\;-\frac{c}{|{{\rm V}}|}\varrho^{n-1} \, N_k(t) \, \left[\int_{{\rm V}^+_{hk}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\right.\nonumber\\[5pt] & \qquad \left.+\int_{{\rm V}^-_{hk}}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\right]\nonumber\\[5pt] &=\frac{c}{|{{\rm V}}|}\varrho^{n-1} \, N_k(t) \, \int_{{\rm V}_{hk}^+}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\Bigl[\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h-\nu\varrho,t,\mathbf{v}'_h,\mathbf{v}'_k)\nonumber\\[5pt] &\qquad -\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h+\nu\varrho,t,\mathbf{v}_h,\mathbf{v}_k)\Bigr]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ , \end{align}
with
![]() $N_k(t)$
being the number of cells in population k at time t. The second equality in (3.21) is obtained by using the normal vector
$N_k(t)$
being the number of cells in population k at time t. The second equality in (3.21) is obtained by using the normal vector
![]() $-\nu$
and the post-interaction directions
$-\nu$
and the post-interaction directions
![]() $\mathbf{v}_h'$
and
$\mathbf{v}_h'$
and
![]() $\mathbf{v}_k'$
in
$\mathbf{v}_k'$
in
![]() $\tilde{\tilde{f}}_{hk}$
over the set
$\tilde{\tilde{f}}_{hk}$
over the set
![]() ${\rm V}_{hk}^-$
. Notice that the following property holds
${\rm V}_{hk}^-$
. Notice that the following property holds
which ensures that the density of cells in population h will be preserved in the course of such interactions.
Moreover, based on~(3.19) and~(3.21), we define the rate of change of the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to population-switching interactions leading the cell to leave population h as:
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to population-switching interactions leading the cell to leave population h as:
Analogously, we define the rate of change of
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to population-switching interactions leading a cell to leave a generic population
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
due to population-switching interactions leading a cell to leave a generic population
![]() $l \neq h$
and enter population h as:
$l \neq h$
and enter population h as:
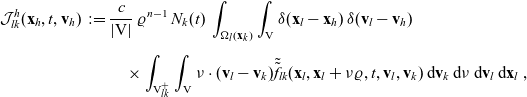 \begin{align}\mathcal{J}^h_{lk}(\mathbf{x}_h,t,\mathbf{v}_h) \;:=\; &\dfrac{c}{|{\rm V}|} \, \varrho^{n-1} \, N_k(t) \, \int_{ \Omega_l(\mathbf{x}_k)}\int_{\rm V} \delta(\mathbf{x}_l - \mathbf{x}_h) \, \delta(\mathbf{v}_l - \mathbf{v}_h)\nonumber \\[5pt]&\quad\times \int_{{\rm V}^+_{lk}}\int_{\rm V}\nu\cdot(\mathbf{v}_l-\mathbf{v}_k) \tilde{\tilde{f}}_{lk}(\mathbf{x}_l,\mathbf{x}_l+\nu\varrho, t, \mathbf{v}_l,\mathbf{v}_k) \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_l\mathop{}\!\mathrm{d}\mathbf{x}_l \ ,\end{align}
\begin{align}\mathcal{J}^h_{lk}(\mathbf{x}_h,t,\mathbf{v}_h) \;:=\; &\dfrac{c}{|{\rm V}|} \, \varrho^{n-1} \, N_k(t) \, \int_{ \Omega_l(\mathbf{x}_k)}\int_{\rm V} \delta(\mathbf{x}_l - \mathbf{x}_h) \, \delta(\mathbf{v}_l - \mathbf{v}_h)\nonumber \\[5pt]&\quad\times \int_{{\rm V}^+_{lk}}\int_{\rm V}\nu\cdot(\mathbf{v}_l-\mathbf{v}_k) \tilde{\tilde{f}}_{lk}(\mathbf{x}_l,\mathbf{x}_l+\nu\varrho, t, \mathbf{v}_l,\mathbf{v}_k) \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_l\mathop{}\!\mathrm{d}\mathbf{x}_l \ ,\end{align}
with
![]() $\delta({\mathbf{z}} - {\mathbf{z}}^*)$
being the Dirac delta distribution centred at
$\delta({\mathbf{z}} - {\mathbf{z}}^*)$
being the Dirac delta distribution centred at
![]() ${\mathbf{z}}^*$
. Definition (3.24) ensures that the density of cells that leave population l due to such interactions will appear in population h. In fact, we have
${\mathbf{z}}^*$
. Definition (3.24) ensures that the density of cells that leave population l due to such interactions will appear in population h. In fact, we have
In summary, the term
![]() $\mathcal{Q}_{hk}$
in transport equation (3.13) is defined in terms of (3.21)–(3.24) in different possible ways depending on the cell–cell interactions that are considered.
$\mathcal{Q}_{hk}$
in transport equation (3.13) is defined in terms of (3.21)–(3.24) in different possible ways depending on the cell–cell interactions that are considered.
Under Assumptions 1–2 and definitions (3.21), (3.23) and (3.24), the rates of change of the one-particle distribution functions
![]() $p_I(\mathbf{x}_I,t,\mathbf{v}_I)$
,
$p_I(\mathbf{x}_I,t,\mathbf{v}_I)$
,
![]() $p_A(\mathbf{x}_A,t,\mathbf{v}_A)$
and
$p_A(\mathbf{x}_A,t,\mathbf{v}_A)$
and
![]() $p_D(\mathbf{x}_D,t,\mathbf{v}_D)$
due to cell–cell interactions will be, respectively,
$p_D(\mathbf{x}_D,t,\mathbf{v}_D)$
due to cell–cell interactions will be, respectively,
Substituting (3.15), (3.16) and (3.25)–(3.27) into transport equation (3.13), we obtain the following transport equations for
![]() $p_I(\mathbf{x}_I,t,\mathbf{v}_I)$
,
$p_I(\mathbf{x}_I,t,\mathbf{v}_I)$
,
![]() $p_A(\mathbf{x}_A,t,\mathbf{v}_A)$
and
$p_A(\mathbf{x}_A,t,\mathbf{v}_A)$
and
![]() $p_D(\mathbf{x}_D,t,\mathbf{v}_D)$
:
$p_D(\mathbf{x}_D,t,\mathbf{v}_D)$
:
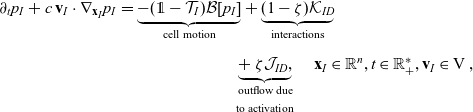 \begin{align} \partial_tp_I+c \, \mathbf{v}_I\cdot\nabla_{\mathbf{x}_I}p_I =&\underbrace{-(\unicode{x1D7D9}-\mathcal{T}_I)\mathcal{B}[p_I]}_{{\scriptsize{\rm cell\ motion}}} + \underbrace{(1-\zeta)\mathcal{K}_{ID}}_{{\scriptsize{\rm interactions}}} \nonumber \\[5pt] & \qquad \qquad \qquad \underbrace{{+} \, \zeta \mathcal{J}_{ID},}_{\substack{{\scriptsize{\rm outflow\ due}}\\[5pt] {\scriptsize{\rm to\ activation}}}} \quad \mathbf{x}_I \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_I \in {\rm V} \ , \end{align}
\begin{align} \partial_tp_I+c \, \mathbf{v}_I\cdot\nabla_{\mathbf{x}_I}p_I =&\underbrace{-(\unicode{x1D7D9}-\mathcal{T}_I)\mathcal{B}[p_I]}_{{\scriptsize{\rm cell\ motion}}} + \underbrace{(1-\zeta)\mathcal{K}_{ID}}_{{\scriptsize{\rm interactions}}} \nonumber \\[5pt] & \qquad \qquad \qquad \underbrace{{+} \, \zeta \mathcal{J}_{ID},}_{\substack{{\scriptsize{\rm outflow\ due}}\\[5pt] {\scriptsize{\rm to\ activation}}}} \quad \mathbf{x}_I \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_I \in {\rm V} \ , \end{align}
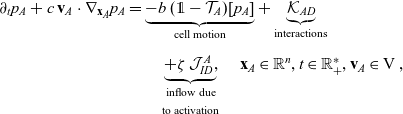 \begin{align} \partial_t{p}_A+c \, \mathbf{v}_A\cdot\nabla_{\mathbf{x}_A}{p}_A=& \underbrace{-b \, (\unicode{x1D7D9}-\mathcal{T}_A)[p_{A}]}_{{\scriptsize{\rm cell\ motion}}} + \underbrace{\mathcal{K}_{AD}}_{{\scriptsize{\rm interactions}}} \nonumber \\[5pt] & \quad \underbrace{+ \zeta \, \mathcal{J}^A_{ID},}_{\substack{{\scriptsize{\rm inflow\ due}}\\[5pt] {\scriptsize{\rm to\ activation}}}} \quad \mathbf{x}_A \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_A \in {\rm V}\ , \end{align}
\begin{align} \partial_t{p}_A+c \, \mathbf{v}_A\cdot\nabla_{\mathbf{x}_A}{p}_A=& \underbrace{-b \, (\unicode{x1D7D9}-\mathcal{T}_A)[p_{A}]}_{{\scriptsize{\rm cell\ motion}}} + \underbrace{\mathcal{K}_{AD}}_{{\scriptsize{\rm interactions}}} \nonumber \\[5pt] & \quad \underbrace{+ \zeta \, \mathcal{J}^A_{ID},}_{\substack{{\scriptsize{\rm inflow\ due}}\\[5pt] {\scriptsize{\rm to\ activation}}}} \quad \mathbf{x}_A \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_A \in {\rm V}\ , \end{align}
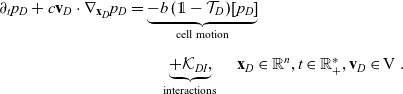 \begin{align} \partial_t {p}_D +c\mathbf{v}_D\cdot\nabla_{\mathbf{x}_D}{p}_D = &\underbrace{-b \, (\unicode{x1D7D9}-\mathcal{T}_D)[p_{D}]}_{{\scriptsize{\rm cell\ motion}}} \nonumber \\[5pt] & \quad \underbrace{+\mathcal{K}_{DI},}_{{\scriptsize{\rm interactions}}} \quad \mathbf{x}_D \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_D \in {\rm V} \ . \end{align}
\begin{align} \partial_t {p}_D +c\mathbf{v}_D\cdot\nabla_{\mathbf{x}_D}{p}_D = &\underbrace{-b \, (\unicode{x1D7D9}-\mathcal{T}_D)[p_{D}]}_{{\scriptsize{\rm cell\ motion}}} \nonumber \\[5pt] & \quad \underbrace{+\mathcal{K}_{DI},}_{{\scriptsize{\rm interactions}}} \quad \mathbf{x}_D \in \mathbb{R}^n, t \in \mathbb{R}^*_+,\mathbf{v}_D \in {\rm V} \ . \end{align}
The terms on the right-hand sides of (3.28)–(3.30) represent the rate of change of the one-particle distributions due to the biophysical phenomena specified below each term.
4 Macroscopic scale model
In this section, we derive a macroscopic system of equations corresponding to the mescoscopic scale model given by transport equations (3.28)–(3.30). Such a model consists of a coupled system of balance equations for the macroscopic densities of inactive CTLs, activated CTLs and DCs.
4.1 Preliminaries, assumptions and notation
Scaling
We assume the mean run time
![]() $\bar \tau$
to be small compared to the characteristic temporal scale for the dynamics of the macroscopic cell densities, which is represented by the parameter
$\bar \tau$
to be small compared to the characteristic temporal scale for the dynamics of the macroscopic cell densities, which is represented by the parameter
![]() $T \in \mathbb{R}^*_+$
, that is, we make the assumption:
$T \in \mathbb{R}^*_+$
, that is, we make the assumption:
Moreover, we let
![]() $X \in \mathbb{R}^*_+$
represent the characteristic spatial scale for the dynamics of the macroscopic cell densities and introduce the rescaled quantities:
$X \in \mathbb{R}^*_+$
represent the characteristic spatial scale for the dynamics of the macroscopic cell densities and introduce the rescaled quantities:
As similarly done in [Reference Alt2,Reference Estrada-Rodriguez and Gimperlein11], in order to obtain a mathematical model for the dynamics of the cells at the macroscopic scale, we consider the scaling:
with
Throughout the rest of the paper, we will drop the carets from (4.1) and we will study two-dimensional cell dynamics (i.e. we assume
![]() $n=2$
).
$n=2$
).
Furthermore, noting that the diameter of the cells is small compared to the characteristic spatial scale for the dynamics of the macroscopic cell densities, and considering a biological scenario where the number of cells in the system is large and activation of CTL occurs with a small probability
![]() $\zeta$
, we assume
$\zeta$
, we assume
In particular, we will be focussing on a biological scenario corresponding to the following assumptions:
Notice that
![]() $\xi-\vartheta<0$
when
$\xi-\vartheta<0$
when
![]() $\alpha<3/2$
. In the case where cells follow a Brownian motion (i.e. for
$\alpha<3/2$
. In the case where cells follow a Brownian motion (i.e. for
![]() $h=A$
and
$h=A$
and
![]() $h=D$
) we have
$h=D$
) we have
![]() $\alpha=2$
and, therefore,
$\alpha=2$
and, therefore,
![]() $\xi-\vartheta=1-\gamma=1/2$
. Under scaling (4.1) definitions (2.3) become
$\xi-\vartheta=1-\gamma=1/2$
. Under scaling (4.1) definitions (2.3) become
Moreover, under assumption (4.3) on
![]() $\varrho$
we have
$\varrho$
we have
‘Molecular chaos’ assumption
Considering a biological scenario where cell densities are sufficiently low, we assume the velocities of any two cells which are about to interact to be uncorrelated, that is, we make the so-called ‘molecular chaos’ assumption, which holds at low densities and is commonly used in kinetic theory [Reference Cercignani, Illner and Pulvirenti7,Reference Othmer, Dunbar and Alt22,Reference Villani27]. Under this assumption, the two-particle distribution function
![]() $\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h \pm\varepsilon^{\unicode{x03BE}}\nu,t,\mathbf{v}_h,\mathbf{v}_k)$
can be approximately expressed as the product of the corresponding one-particle distribution functions, that is,
$\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_h \pm\varepsilon^{\unicode{x03BE}}\nu,t,\mathbf{v}_h,\mathbf{v}_k)$
can be approximately expressed as the product of the corresponding one-particle distribution functions, that is,
We draw the attention of the reader to the fact that, throughout the rest of the paper, superscripts and subscripts related to the scaling should not be confused with cell population indices.
Under scaling (4.1) and assumptions (4.3), using (4.6), (4.7) and assuming
![]() $n=2$
, the interaction terms defined via (3.21), (3.23) and (3.24) read as:
$n=2$
, the interaction terms defined via (3.21), (3.23) and (3.24) read as:
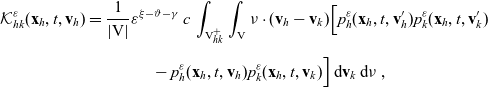 \begin{align} \mathcal{K}_{hk}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)& = \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \,c \, \int_{{\rm V}_{hk}^+}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\Bigl[p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}'_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}'_k) \nonumber\\[5pt] &\qquad\qquad - p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k)\Bigr]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ ,\end{align}
\begin{align} \mathcal{K}_{hk}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)& = \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \,c \, \int_{{\rm V}_{hk}^+}\int_{\rm V}\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\Bigl[p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}'_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}'_k) \nonumber\\[5pt] &\qquad\qquad - p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k)\Bigr]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu\ ,\end{align}
and
 \begin{align}{}_{\varepsilon}\mathcal{J}^h_{lk }(\mathbf{x}_h,t,\mathbf{v}_h) = &\dfrac{1}{|{\rm V}|} \, \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{ \Omega_l(\mathbf{x}_k)}\int_{\rm V} \delta(\mathbf{x}_l - \mathbf{x}_h) \, \delta(\mathbf{v}_l - \mathbf{v}_h)\nonumber \\[5pt]&\quad\times \int_{{\rm V}^+_{lk}}\int_{\rm V}\nu\cdot(\mathbf{v}_l-\mathbf{v}_k) p_{l}^\varepsilon(\mathbf{x}_l,t,{\bf v}_l) p_{k}^\varepsilon(\mathbf{x}_l,t,{\bf v}_k) \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_l\mathop{}\!\mathrm{d}\mathbf{x}_l \ .\end{align}
\begin{align}{}_{\varepsilon}\mathcal{J}^h_{lk }(\mathbf{x}_h,t,\mathbf{v}_h) = &\dfrac{1}{|{\rm V}|} \, \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{ \Omega_l(\mathbf{x}_k)}\int_{\rm V} \delta(\mathbf{x}_l - \mathbf{x}_h) \, \delta(\mathbf{v}_l - \mathbf{v}_h)\nonumber \\[5pt]&\quad\times \int_{{\rm V}^+_{lk}}\int_{\rm V}\nu\cdot(\mathbf{v}_l-\mathbf{v}_k) p_{l}^\varepsilon(\mathbf{x}_l,t,{\bf v}_l) p_{k}^\varepsilon(\mathbf{x}_l,t,{\bf v}_k) \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_l\mathop{}\!\mathrm{d}\mathbf{x}_l \ .\end{align}
Expansion of
![]() $p_{h}^\varepsilon$
and macroscopic cell quantities
$p_{h}^\varepsilon$
and macroscopic cell quantities
Exploiting the results established by Lemma 1 in the case where
![]() $n=2$
, we expand the one-particle distribution function
$n=2$
, we expand the one-particle distribution function
![]() $p_{h}^\varepsilon$
in terms of its zeroth moment
$p_{h}^\varepsilon$
in terms of its zeroth moment
![]() $\rho_{h}^\varepsilon$
(i.e. the macroscopic cell density) and its first moment
$\rho_{h}^\varepsilon$
(i.e. the macroscopic cell density) and its first moment
![]() $w_{h}^\varepsilon$
(i.e. the local macroscopic direction of cell motion). This is possible because, as one can see from the right-hand side of transport equation (4.13), the interaction terms are of higher order in
$w_{h}^\varepsilon$
(i.e. the local macroscopic direction of cell motion). This is possible because, as one can see from the right-hand side of transport equation (4.13), the interaction terms are of higher order in
![]() $\varepsilon$
(cf. the scaling used in (4.8)–(4.10)) and, therefore, we can write
$\varepsilon$
(cf. the scaling used in (4.8)–(4.10)) and, therefore, we can write
where
We refer the reader to [Reference Othmer and Hillen23,Reference Othmer, Maini and Murray24] and the seminal work [Reference Alt2] for a complete derivation in the case of no interactions and to [Reference Estrada-Rodriguez and Gimperlein11,Reference Franz, Taylor-King, Yates and Erban13] for the case of velocity-jump models with interacting particles. The appropriate choice of scaling for the local macroscopic direction of motion is found by first inserting (4.11) into (4.13) and then integrating over V in order to obtain a suitable macroscopic equation (see transport equation (4.2)).
4.2 Derivation of a macroscopic scale system
Transport equation for
![]() $p_{h}^\varepsilon$
$p_{h}^\varepsilon$
Under scaling (4.1) and assumptions (4.3), using (4.6) and (4.7) and assuming
![]() $n=2$
, we rewrite transport equation (3.13) for the one-particle distribution function
$n=2$
, we rewrite transport equation (3.13) for the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
as:
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
as:
where
![]() $\mathcal{Q}_{hk}^\varepsilon$
is defined in terms of
$\mathcal{Q}_{hk}^\varepsilon$
is defined in terms of
![]() $\mathcal{K}_{hk}^\varepsilon$
,
$\mathcal{K}_{hk}^\varepsilon$
,
![]() $ \mathcal{J}_{hk}^\varepsilon$
and
$ \mathcal{J}_{hk}^\varepsilon$
and
![]() ${}_{\varepsilon}\mathcal{J}^h_{lk}$
as per (3.25)–(3.27), that is,
${}_{\varepsilon}\mathcal{J}^h_{lk}$
as per (3.25)–(3.27), that is,
and
We recall that in the case where cells move in a local search pattern (i.e. for
![]() $h=A$
and
$h=A$
and
![]() $h=D$
),
$h=D$
),
![]() $\beta_h$
is defined via (2.1) and (2.2), and thus
$\beta_h$
is defined via (2.1) and (2.2), and thus
![]() ${}_{\varepsilon}p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given as in (3.15). On the other hand, in the case where cells move in a non-local search pattern (i.e. for
${}_{\varepsilon}p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given as in (3.15). On the other hand, in the case where cells move in a non-local search pattern (i.e. for
![]() $h=I$
),
$h=I$
),
![]() $\beta_h$
is defined via (2.1) and (2.3), and thus
$\beta_h$
is defined via (2.1) and (2.3), and thus
![]() ${}_{\varepsilon}p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given by (3.16)
${}_{\varepsilon}p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
is given by (3.16)
with
As before,
![]() $B^{\varepsilon}$
is defined through its Laplace transform in time
$B^{\varepsilon}$
is defined through its Laplace transform in time
![]() $\hat{B}^{\varepsilon}$
and, in particular, under assumptions (4.2), we make the approximation:
$\hat{B}^{\varepsilon}$
and, in particular, under assumptions (4.2), we make the approximation:
Using the properties of the Laplace transform of a convolution, we write
with
Analogous calculations are fully detailed in 8. Substituting the expressions of
![]() $\hat{\varphi}_{h}^\varepsilon$
and
$\hat{\varphi}_{h}^\varepsilon$
and
![]() $\hat{\psi}_{h}^\varepsilon$
into (4.17), calculations similar to those carried out in [Reference Estrada-Rodriguez and Gimperlein11,Reference Estrada-Rodriguez, Gimperlein and Painter12] allow one to show that
$\hat{\psi}_{h}^\varepsilon$
into (4.17), calculations similar to those carried out in [Reference Estrada-Rodriguez and Gimperlein11,Reference Estrada-Rodriguez, Gimperlein and Painter12] allow one to show that
 \begin{align} \hat{B}^\varepsilon&(\mathbf{x}_h,\varepsilon^{1-\gamma}c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})= \frac{\alpha-1}{d_{\varepsilon}}-\frac{\varepsilon^{1-\gamma}}{2-\alpha}c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h}\nonumber\\[5pt] &-d_{\varepsilon}^{\alpha-2}\varepsilon^{(1-\gamma)(\alpha-1)}(c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})^{\alpha-1}(\alpha-1)^2\Gamma(-\alpha+1)+\mathcal{O}(d_{\varepsilon}^{\alpha-1}\lambda^\alpha)\ \ .\end{align}
\begin{align} \hat{B}^\varepsilon&(\mathbf{x}_h,\varepsilon^{1-\gamma}c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})= \frac{\alpha-1}{d_{\varepsilon}}-\frac{\varepsilon^{1-\gamma}}{2-\alpha}c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h}\nonumber\\[5pt] &-d_{\varepsilon}^{\alpha-2}\varepsilon^{(1-\gamma)(\alpha-1)}(c\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})^{\alpha-1}(\alpha-1)^2\Gamma(-\alpha+1)+\mathcal{O}(d_{\varepsilon}^{\alpha-1}\lambda^\alpha)\ \ .\end{align}
In (4.18),
![]() $d_{\varepsilon}(\mathbf{x}_h) \;:=\; \tau_0(\mathbf{x}_h) \, \varepsilon^{\mu}$
, where
$d_{\varepsilon}(\mathbf{x}_h) \;:=\; \tau_0(\mathbf{x}_h) \, \varepsilon^{\mu}$
, where
![]() $\tau_0(\mathbf{x}_h)$
is defined via (2.3).
$\tau_0(\mathbf{x}_h)$
is defined via (2.3).
Transport equations for
![]() $\rho_{I}^\varepsilon$
,
$\rho_{I}^\varepsilon$
,
![]() $\rho_{A}^\varepsilon$
and
$\rho_{A}^\varepsilon$
and
![]() $\rho_{D}^\varepsilon$
$\rho_{D}^\varepsilon$
Integrating both sides of transport equation (4.13) with respect to
![]() ${\bf v}_h$
over the set V and using the fact that the turning operator
${\bf v}_h$
over the set V and using the fact that the turning operator
![]() $\mathcal{T}_h$
satisfies (2.6), we find that the macroscopic cell density
$\mathcal{T}_h$
satisfies (2.6), we find that the macroscopic cell density
![]() $\rho_{h}^\varepsilon(\mathbf{x}_h,t)$
given by (4.12) satisfies the following transport equation:
$\rho_{h}^\varepsilon(\mathbf{x}_h,t)$
given by (4.12) satisfies the following transport equation:
Moreover, substituting the expressions for
![]() $p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
and
$p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
and
![]() $p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)$
given by (4.11) into the definitions of
$p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)$
given by (4.11) into the definitions of
![]() $\mathcal{K}_{hk}^\varepsilon$
,
$\mathcal{K}_{hk}^\varepsilon$
,
![]() $ \mathcal{J}_{hk}^\varepsilon$
and
$ \mathcal{J}_{hk}^\varepsilon$
and
![]() ${}_{\varepsilon}\mathcal{J}^l_{hk}$
given by (4.8)–(4.10), we find
${}_{\varepsilon}\mathcal{J}^l_{hk}$
given by (4.8)–(4.10), we find
and, neglecting higher-order terms, we also obtain
where M is given by:
Notice that relation (4.19) is obtained using property (3.22).
In conclusion, using (4.19) and (4.20) along with (4.14)–(4.16), from transport equation (4.2) we obtain the following equations for the macroscopic cell densities
![]() $\rho_{I}^\varepsilon(\mathbf{x}_I,t)$
,
$\rho_{I}^\varepsilon(\mathbf{x}_I,t)$
,
![]() $\rho_{A}^\varepsilon(\mathbf{x}_A,t)$
and
$\rho_{A}^\varepsilon(\mathbf{x}_A,t)$
and
![]() $\rho_{D}^\varepsilon(\mathbf{x}_D,t)$
:
$\rho_{D}^\varepsilon(\mathbf{x}_D,t)$
:
Here, we have used the scaling relations in (4.4) for the parameter
![]() $\kappa$
. On the right-hand side of (4.22), we have the density of cells that are leaving the state I (due to interactions with cells in the population D) and are appearing in the new state A in (4.23).
$\kappa$
. On the right-hand side of (4.22), we have the density of cells that are leaving the state I (due to interactions with cells in the population D) and are appearing in the new state A in (4.23).
Transport equations for
![]() $w_{I}^\varepsilon$
,
$w_{I}^\varepsilon$
,
![]() $w_{A}^\varepsilon$
and
$w_{A}^\varepsilon$
and
![]() $w_{D}^\varepsilon$
$w_{D}^\varepsilon$
Multiplying both sides of transport equation (4.13) by
![]() ${\bf v}_h$
and then integrating both sides of the resulting equation with respect to
${\bf v}_h$
and then integrating both sides of the resulting equation with respect to
![]() ${\bf v}_h$
over the set V, we find that the local macroscopic direction of cell motion
${\bf v}_h$
over the set V, we find that the local macroscopic direction of cell motion
![]() $w_{h}^\varepsilon(\mathbf{x}_h,t)$
given by (4.12) satisfies the following transport equation:
$w_{h}^\varepsilon(\mathbf{x}_h,t)$
given by (4.12) satisfies the following transport equation:
 \begin{align} \varepsilon^{1+\gamma}2\partial_tw_{h}^\varepsilon +\varepsilon^{1-\gamma} c\nabla_{\mathbf{x}_h}\int_{\rm V}\mathbf{v}_h\otimes\mathbf{v}_h \, {p}_{h}^\varepsilon\mathop{}\!\mathrm{d}\mathbf{v}_h = &- \int_{\rm V} \mathbf{v}_h (\unicode{x1D7D9}-\mathcal{T}_h)\left[{}_{\varepsilon}p^{\beta_h}_{h}\right] \mathop{}\!\mathrm{d}\mathbf{v}_h \nonumber \\[5pt] & + \int_{\rm V} \mathbf{v}_h \, \mathcal{Q}_{hk}^\varepsilon \mathop{}\!\mathrm{d}\mathbf{v}_h \ . \end{align}
\begin{align} \varepsilon^{1+\gamma}2\partial_tw_{h}^\varepsilon +\varepsilon^{1-\gamma} c\nabla_{\mathbf{x}_h}\int_{\rm V}\mathbf{v}_h\otimes\mathbf{v}_h \, {p}_{h}^\varepsilon\mathop{}\!\mathrm{d}\mathbf{v}_h = &- \int_{\rm V} \mathbf{v}_h (\unicode{x1D7D9}-\mathcal{T}_h)\left[{}_{\varepsilon}p^{\beta_h}_{h}\right] \mathop{}\!\mathrm{d}\mathbf{v}_h \nonumber \\[5pt] & + \int_{\rm V} \mathbf{v}_h \, \mathcal{Q}_{hk}^\varepsilon \mathop{}\!\mathrm{d}\mathbf{v}_h \ . \end{align}
In the case where
![]() $\beta_h$
is defined via (2.1) and (2.2), using (4.11) and (3.15), and the properties of the turning operator
$\beta_h$
is defined via (2.1) and (2.2), using (4.11) and (3.15), and the properties of the turning operator
![]() $\mathcal{T}_h$
established by Lemma 1, we find that the first term on the right-hand side of (4.2) is given by:
$\mathcal{T}_h$
established by Lemma 1, we find that the first term on the right-hand side of (4.2) is given by:
Here,
![]() $\iota_1(\mathbf{x}_h,t)$
is the first non-zero eigenvalue of the turning operator
$\iota_1(\mathbf{x}_h,t)$
is the first non-zero eigenvalue of the turning operator
![]() $\mathcal{T}_h$
, which is given by (2.8). On the other hand, when
$\mathcal{T}_h$
, which is given by (2.8). On the other hand, when
![]() $\beta_h$
is defined via (2.1) and (2.3), using (4.11) and (3.16) and the properties of the turning operator
$\beta_h$
is defined via (2.1) and (2.3), using (4.11) and (3.16) and the properties of the turning operator
![]() $\mathcal{T}_h$
established by Lemma 1, it was proved in [Reference Estrada-Rodriguez, Gimperlein and Painter12] that the following approximate expression of the first term on the right-hand side of (4.2) holds
$\mathcal{T}_h$
established by Lemma 1, it was proved in [Reference Estrada-Rodriguez, Gimperlein and Painter12] that the following approximate expression of the first term on the right-hand side of (4.2) holds
where
Notice that
![]() $g_\alpha(\cdot,\cdot)>0$
since
$g_\alpha(\cdot,\cdot)>0$
since
![]() $\sin(\pi\alpha)<0$
for
$\sin(\pi\alpha)<0$
for
![]() $\alpha\in(1,2)$
and
$\alpha\in(1,2)$
and
![]() $4\iota_1-|{ {\rm V}}|<0$
by using (2.7) for
$4\iota_1-|{ {\rm V}}|<0$
by using (2.7) for
![]() $n=2$
and recalling that
$n=2$
and recalling that
![]() $\iota_1<1$
.
$\iota_1<1$
.
Moreover, as similarly done in [Reference Estrada-Rodriguez and Gimperlein11], using the fact that
![]() $(\cdot)':{\rm V}\mapsto {\rm V}$
is a bijection and
$(\cdot)':{\rm V}\mapsto {\rm V}$
is a bijection and
![]() $\mathbf{v}_h'\cdot\nu=-\mathbf{v}_h\cdot\nu$
, whence
$\mathbf{v}_h'\cdot\nu=-\mathbf{v}_h\cdot\nu$
, whence
![]() $\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)=-\nu\cdot(\mathbf{v}_h'-\mathbf{v}_k')$
, we find
$\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)=-\nu\cdot(\mathbf{v}_h'-\mathbf{v}_k')$
, we find
 \begin{align}\int_{\rm V} & \mathbf{v}_h \, \mathcal{K}_{hk}^\varepsilon \, \mathop{}\!\mathrm{d}\mathbf{v}_h \nonumber \\[5pt]& = \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \left(\int_{\rm V} \int_{\rm V} \int_{{\rm V}^+_{hk}} {\bf v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h') p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k') \nu\cdot(\mathbf{v}_h-\mathbf{v}_k) \mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{v}_h \right. \nonumber\\[5pt] &\left.- \int_{\rm V} \int_{\rm V} \int_{{\rm V}^+_{hk}} {\bf v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k) \nu\cdot(\mathbf{v}_h-\mathbf{v}_k) \, \mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{v}_h \right) \nonumber\\[5pt]&=- \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}(\mathbf{v}'_h)'p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h')p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k')\nu\cdot(\mathbf{v}_h'-\mathbf{v}_k')\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h'\mathop{}\!\mathrm{d}\mathbf{v}_k'\nonumber\\[5pt] &\ \ \ -\int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}\mathbf{v}_h p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\nonumber{}\\[5pt] &= \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}(\mathbf{v}_h'-\mathbf{v}_h)p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\nonumber\\[5pt] & =- \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \frac{4}{3}\int_{\rm V}\int_{\rm V}|\mathbf{v}_h-\mathbf{v}_k| \, \mathbf{v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h) \, p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\ . \end{align}
\begin{align}\int_{\rm V} & \mathbf{v}_h \, \mathcal{K}_{hk}^\varepsilon \, \mathop{}\!\mathrm{d}\mathbf{v}_h \nonumber \\[5pt]& = \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \left(\int_{\rm V} \int_{\rm V} \int_{{\rm V}^+_{hk}} {\bf v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h') p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k') \nu\cdot(\mathbf{v}_h-\mathbf{v}_k) \mathop{}\!\mathrm{d}\nu \mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{v}_h \right. \nonumber\\[5pt] &\left.- \int_{\rm V} \int_{\rm V} \int_{{\rm V}^+_{hk}} {\bf v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,{\bf v}_h) p_{k}^\varepsilon(\mathbf{x}_h,t,{\bf v}_k) \nu\cdot(\mathbf{v}_h-\mathbf{v}_k) \, \mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{v}_h \right) \nonumber\\[5pt]&=- \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}(\mathbf{v}'_h)'p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h')p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k')\nu\cdot(\mathbf{v}_h'-\mathbf{v}_k')\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h'\mathop{}\!\mathrm{d}\mathbf{v}_k'\nonumber\\[5pt] &\ \ \ -\int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}\mathbf{v}_h p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\nonumber{}\\[5pt] &= \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \int_{\rm V}\int_{\rm V}\int_{{\rm V}^+_{hk}}(\mathbf{v}_h'-\mathbf{v}_h)p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\nu\cdot(\mathbf{v}_h-\mathbf{v}_k)\mathop{}\!\mathrm{d}\nu\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\nonumber\\[5pt] & =- \frac{1}{|{{\rm V}}|} \varepsilon^{\xi -\vartheta - \gamma} \, c \, \frac{4}{3}\int_{\rm V}\int_{\rm V}|\mathbf{v}_h-\mathbf{v}_k| \, \mathbf{v}_h \, p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h) \, p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)\mathop{}\!\mathrm{d}\mathbf{v}_h\mathop{}\!\mathrm{d}\mathbf{v}_k\ . \end{align}
The last equality in (4.28) is obtained using the fact that
![]() $\mathbf{v}_h'-\mathbf{v}_h=-2(\mathbf{v}_h\cdot\nu)\nu$
. Substituting the expressions for
$\mathbf{v}_h'-\mathbf{v}_h=-2(\mathbf{v}_h\cdot\nu)\nu$
. Substituting the expressions for
![]() $p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
and
$p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
and
![]() $p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)$
given by (4.11) into (4.28) and into definitions (4.9) and (4.10) of
$p_{k}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_k)$
given by (4.11) into (4.28) and into definitions (4.9) and (4.10) of
![]() $ \mathcal{J}_{hk}^\varepsilon$
and
$ \mathcal{J}_{hk}^\varepsilon$
and
![]() ${}_{\varepsilon}\mathcal{J}^h_{lk}$
, neglecting higher-order terms we find
${}_{\varepsilon}\mathcal{J}^h_{lk}$
, neglecting higher-order terms we find
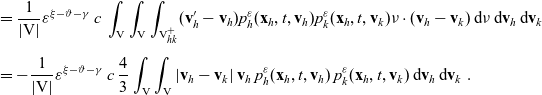 \begin{equation} \int_{\rm V} \mathbf{v}_h \, \mathcal{K}_{hk}^\varepsilon \mathop{}\!\mathrm{d}\mathbf{v}_h = - \varepsilon^{\xi -\vartheta} \, c \, \frac{8}{3} \, \dfrac{1}{|{\rm V}|^3} \, q_h \, \rho_k^\varepsilon w_h^\varepsilon\ , \end{equation}
\begin{equation} \int_{\rm V} \mathbf{v}_h \, \mathcal{K}_{hk}^\varepsilon \mathop{}\!\mathrm{d}\mathbf{v}_h = - \varepsilon^{\xi -\vartheta} \, c \, \frac{8}{3} \, \dfrac{1}{|{\rm V}|^3} \, q_h \, \rho_k^\varepsilon w_h^\varepsilon\ , \end{equation}
and
where
![]() $q_h$
and
$q_h$
and
![]() $\tilde{q}_h$
are defined as:
$\tilde{q}_h$
are defined as:
Finally, substituting the expression of
![]() $p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
into the second term on the left-hand side of (4.2) and neglecting higher-order terms yields
$p_{h}^\varepsilon(\mathbf{x}_h,t,\mathbf{v}_h)$
into the second term on the left-hand side of (4.2) and neglecting higher-order terms yields
with
![]() $C_h$
being defined as:
$C_h$
being defined as:
In conclusion, using (3.15) and (3.16), (4.29), (4.30) and (4.32) along with (4.14)–(4.16), from transport equation (4.2) we obtain the following transport equations for the local macroscopic directions of cell motion
![]() $w_{I}^\varepsilon(\mathbf{x}_I,t)$
,
$w_{I}^\varepsilon(\mathbf{x}_I,t)$
,
![]() $w_{A}^\varepsilon(\mathbf{x}_A,t)$
and
$w_{A}^\varepsilon(\mathbf{x}_A,t)$
and
![]() $w_{D}^\varepsilon(\mathbf{x}_D,t)$
:
$w_{D}^\varepsilon(\mathbf{x}_D,t)$
:
 \begin{align} \varepsilon^{1+\gamma}2\partial_tw_{A}^\varepsilon+\varepsilon^{1-\gamma} &C_A \, \nabla_{\mathbf{x}_A} \rho_{A}^\varepsilon = -\frac{2\varepsilon^\gamma}{|{\rm V}|} b{ (1-\iota_1)}w_{A}^\varepsilon \nonumber\\[5pt] & - \varepsilon^{\unicode{x03BE}-\vartheta} \, c \, \left(\frac{8}{3}\frac{1}{|{\rm V}|^3} q_A \, \rho_{D}^\varepsilon w_{A}^\varepsilon- {\frac{2c}{|{\rm V}|^2}\tilde{q}_A\rho_D^\varepsilon w_A^\varepsilon}\right) \ , \quad \mathbf{x}_A \in \mathbb{R}^2, t \in \mathbb{R}^*_+ \ , \end{align}
\begin{align} \varepsilon^{1+\gamma}2\partial_tw_{A}^\varepsilon+\varepsilon^{1-\gamma} &C_A \, \nabla_{\mathbf{x}_A} \rho_{A}^\varepsilon = -\frac{2\varepsilon^\gamma}{|{\rm V}|} b{ (1-\iota_1)}w_{A}^\varepsilon \nonumber\\[5pt] & - \varepsilon^{\unicode{x03BE}-\vartheta} \, c \, \left(\frac{8}{3}\frac{1}{|{\rm V}|^3} q_A \, \rho_{D}^\varepsilon w_{A}^\varepsilon- {\frac{2c}{|{\rm V}|^2}\tilde{q}_A\rho_D^\varepsilon w_A^\varepsilon}\right) \ , \quad \mathbf{x}_A \in \mathbb{R}^2, t \in \mathbb{R}^*_+ \ , \end{align}
and
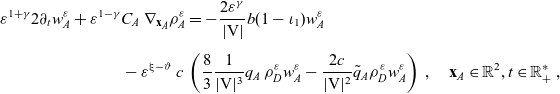 \begin{align} \varepsilon^{\gamma+1}2\partial_t w_{D}^\varepsilon +\varepsilon^{1-\gamma} C_D \, \nabla_{\mathbf{x}_D} & \rho_{D}^\varepsilon = -\frac{2\varepsilon^{\gamma}}{|{\rm V}|} b(\iota_1-1)w_{D}^\varepsilon\nonumber\\[5pt] & - \varepsilon^{\unicode{x03BE}-\vartheta} \, c \, \frac{8}{3} \frac{1}{|{\rm V}|^3} q_D \, \rho_{I}^\varepsilon w_{D}^\varepsilon \ , \quad \mathbf{x}_D \in \mathbb{R}^2, t \in \mathbb{R}^*_+ \ .\end{align}
\begin{align} \varepsilon^{\gamma+1}2\partial_t w_{D}^\varepsilon +\varepsilon^{1-\gamma} C_D \, \nabla_{\mathbf{x}_D} & \rho_{D}^\varepsilon = -\frac{2\varepsilon^{\gamma}}{|{\rm V}|} b(\iota_1-1)w_{D}^\varepsilon\nonumber\\[5pt] & - \varepsilon^{\unicode{x03BE}-\vartheta} \, c \, \frac{8}{3} \frac{1}{|{\rm V}|^3} q_D \, \rho_{I}^\varepsilon w_{D}^\varepsilon \ , \quad \mathbf{x}_D \in \mathbb{R}^2, t \in \mathbb{R}^*_+ \ .\end{align}
Macroscopic scale model
Noting that
![]() $1-\dfrac{\gamma}{\alpha-1} < 1 -\gamma$
since
$1-\dfrac{\gamma}{\alpha-1} < 1 -\gamma$
since
![]() $\alpha \in (1,2)$
and using assumptions (4.4) for the scaling parameters, letting
$\alpha \in (1,2)$
and using assumptions (4.4) for the scaling parameters, letting
![]() $\varepsilon \to 0$
in (4.34)–(4.36), we formally find the following expressions for the leading-order terms
$\varepsilon \to 0$
in (4.34)–(4.36), we formally find the following expressions for the leading-order terms
![]() $w_I({\bf x},t)$
,
$w_I({\bf x},t)$
,
![]() $w_A({\bf x},t)$
and
$w_A({\bf x},t)$
and
![]() $w_D({\bf x},t)$
of the asymptotic expansions for the local macroscopic directions of cell motion
$w_D({\bf x},t)$
of the asymptotic expansions for the local macroscopic directions of cell motion
![]() $w_{I \varepsilon}({\bf x},t)$
,
$w_{I \varepsilon}({\bf x},t)$
,
![]() $w_{A \varepsilon}({\bf x},t)$
and
$w_{A \varepsilon}({\bf x},t)$
and
![]() $w_{D \varepsilon}({\bf x},t)$
:
$w_{D \varepsilon}({\bf x},t)$
:
-
– From (4.34) and choosing the scaling parameters as
 $1-\frac{\gamma}{\alpha-1}=\xi-\vartheta$
, we have (4.39)
$1-\frac{\gamma}{\alpha-1}=\xi-\vartheta$
, we have (4.39) \begin{equation} w_I=-\frac{g_{\alpha}}{H_I}\nabla_{\mathbf{x}}^{\alpha-1}\rho_I\ , \quad \text{where} \quad H_I \;:=\;\frac{2(\alpha-1)(1-\iota_1)}{\tau_0|{\rm V}|}+\frac{8c}{|3{\rm V}|^3}q_I\rho_D>0\ . \end{equation}
\begin{equation} w_I=-\frac{g_{\alpha}}{H_I}\nabla_{\mathbf{x}}^{\alpha-1}\rho_I\ , \quad \text{where} \quad H_I \;:=\;\frac{2(\alpha-1)(1-\iota_1)}{\tau_0|{\rm V}|}+\frac{8c}{|3{\rm V}|^3}q_I\rho_D>0\ . \end{equation}
-
– From (4.35) and choosing
 $\xi-\vartheta=\gamma$
in agreement with (4.4), we obtain (4.40)
$\xi-\vartheta=\gamma$
in agreement with (4.4), we obtain (4.40) \begin{equation} w_A=-\frac{C_A}{H_A}\nabla_{\mathbf{x}}\rho_A\ , \quad \text{where}\quad H_A \;:=\;\frac{2b}{|{\rm V}|}(1-\iota_1)+\frac{8c}{3|{\rm V}|^3}q_A\rho_D>0\ . \end{equation}
\begin{equation} w_A=-\frac{C_A}{H_A}\nabla_{\mathbf{x}}\rho_A\ , \quad \text{where}\quad H_A \;:=\;\frac{2b}{|{\rm V}|}(1-\iota_1)+\frac{8c}{3|{\rm V}|^3}q_A\rho_D>0\ . \end{equation}
-
– Finally, using the same scaling rules as in the previous case, we obtain from (4.36)
(4.41) \begin{equation} w_D=-\frac{C_D}{H_D}\nabla_{\mathbf{x}}\rho_D\ ,\quad \text{where}\quad H_D \;:=\;\frac{2b}{|{\rm V}|}(1-\iota_1)+\frac{8c}{3|{\rm V}|^3}q_D\rho_I>0\ .\end{equation}
\begin{equation} w_D=-\frac{C_D}{H_D}\nabla_{\mathbf{x}}\rho_D\ ,\quad \text{where}\quad H_D \;:=\;\frac{2b}{|{\rm V}|}(1-\iota_1)+\frac{8c}{3|{\rm V}|^3}q_D\rho_I>0\ .\end{equation}
Furthermore, under assumptions (4.4), letting
![]() $\varepsilon \to 0$
in (4.22)–(4.24) and using(4.37)–(4.39), we formally obtain the following balance equations for the leading-order terms
$\varepsilon \to 0$
in (4.22)–(4.24) and using(4.37)–(4.39), we formally obtain the following balance equations for the leading-order terms
![]() $\rho_I({\bf x},t)$
,
$\rho_I({\bf x},t)$
,
![]() $\rho_A({\bf x},t)$
and
$\rho_A({\bf x},t)$
and
![]() $\rho_D({\bf x},t)$
of the asymptotic expansions for the macroscopic cell densities
$\rho_D({\bf x},t)$
of the asymptotic expansions for the macroscopic cell densities
![]() $\rho_{I}^\varepsilon({\bf x},t)$
,
$\rho_{I}^\varepsilon({\bf x},t)$
,
![]() $\rho_{A}^\varepsilon({\bf x},t)$
and
$\rho_{A}^\varepsilon({\bf x},t)$
and
![]() $\rho_{D}^\varepsilon({\bf x},t)$
:
$\rho_{D}^\varepsilon({\bf x},t)$
:
where
Remark 3 Notice that the the functions
![]() $D_I$
,
$D_I$
,
![]() $D_A$
and
$D_A$
and
![]() $D_D$
are strictly positive. Moreover, the dependence of these functions on the cell densities follows from conservative interactions between cells of different populations, while population-switching interactions do not affect their values.
$D_D$
are strictly positive. Moreover, the dependence of these functions on the cell densities follows from conservative interactions between cells of different populations, while population-switching interactions do not affect their values.
Considerations on the macroscopic scale model (4.40)–(4.42)
The functions
![]() $\rho_I({\bf x},t)$
,
$\rho_I({\bf x},t)$
,
![]() $\rho_A({\bf x},t)$
and
$\rho_A({\bf x},t)$
and
![]() $\rho_D({\bf x},t)$
model, respectively, the density of CTLs in the pre-activation state, activated CTLs and DCs presenting a tumour antigen on their surface at position x and time t. The spatio-temporal coevolution of CTLs and DCs is modelled through the coupled system of balance equations (4.40)–(4.42), which governs the dynamics of the cell density functions.
$\rho_D({\bf x},t)$
model, respectively, the density of CTLs in the pre-activation state, activated CTLs and DCs presenting a tumour antigen on their surface at position x and time t. The spatio-temporal coevolution of CTLs and DCs is modelled through the coupled system of balance equations (4.40)–(4.42), which governs the dynamics of the cell density functions.
The mathematical model defined by (4.40)–(4.42) provides a macroscopic description of cell dynamics that takes explicitly into account the effects of cell–cell interactions and the characteristics of cell motion that are encapsulated in the parameters c (i.e. the magnitude of the cell velocity, which is assumed to be constant),
![]() $\alpha$
(i.e. the characteristic exponent of the long-tailed distribution followed by the running time of CTLs in the pre-activation state) and b (i.e. the characteristic exponent of the Poisson distribution followed by the running time of activated CTLs and DCs).
$\alpha$
(i.e. the characteristic exponent of the long-tailed distribution followed by the running time of CTLs in the pre-activation state) and b (i.e. the characteristic exponent of the Poisson distribution followed by the running time of activated CTLs and DCs).
This model effectively captures the fact that interactions between DCs presenting a tumour antigen on their surface and CTLs in the pre-activation state lead to CTL activation. In particular, the term on the right-hand side of (4.40) models the decay in the density of CTLs in the pre-activation state at position x and time t due to contact interactions with DCs which result in CTL activation, while the term on the right-hand side of (4.41) models the corresponding growth in the density of activated CTLs. As one would expect, these two terms differ only in their signs and are proportional to the product between the cell density functions
![]() $\rho_{I}({\bf x},t)$
and
$\rho_{I}({\bf x},t)$
and
![]() $\rho_{D}({\bf x},t)$
. The factor of proportionality a increases with the value of the parameter c. This is coherent with the observation that higher cell motilities may increase the encounter rate of CTLs in the pre-activation state with DCs.
$\rho_{D}({\bf x},t)$
. The factor of proportionality a increases with the value of the parameter c. This is coherent with the observation that higher cell motilities may increase the encounter rate of CTLs in the pre-activation state with DCs.
The model captures also the fact that CTLs in the pre-activation state move in a non-local search pattern, while the search pattern of activated CTLs is more localised. In fact, the rate of change of the density of CTLs in the pre-activation state due to cell movement (i.e. the second term on the left-hand side of (4.40)) is a fractional diffusion term, while that of the density of activated CTLs (i.e. the second term on the left-hand side of (4.41)) is a classical diffusion term. The function modelling the diffusivity of CTLs in the pre-activation state (i.e. the function
![]() $D_I$
) and the function modelling the diffusivity of activated CTLs (i.e. the function
$D_I$
) and the function modelling the diffusivity of activated CTLs (i.e. the function
![]() $D_A$
) are proportional to the parameter c. This is coherent with the observation that, ceteris paribus, a higher magnitude of the cell velocity correlates with a higher cell motility. Both
$D_A$
) are proportional to the parameter c. This is coherent with the observation that, ceteris paribus, a higher magnitude of the cell velocity correlates with a higher cell motility. Both
![]() $D_I$
and
$D_I$
and
![]() $D_A$
are monotonically decreasing functions of the cell density function
$D_A$
are monotonically decreasing functions of the cell density function
![]() $\rho_{D}({\bf x},t)$
, which means that, all else being equal, the higher the density of DCs at a given position, the lower the diffusivity of CTLs. This reflects the fact that higher densities of DCs will make it more likely that interactions between CTLs and DCs occur and, since these interactions force CTLs to change their direction of movement at the mesoscopic scale, this will ultimately result in a lower cell diffusivity at the macroscopic scale. Moreover,
$\rho_{D}({\bf x},t)$
, which means that, all else being equal, the higher the density of DCs at a given position, the lower the diffusivity of CTLs. This reflects the fact that higher densities of DCs will make it more likely that interactions between CTLs and DCs occur and, since these interactions force CTLs to change their direction of movement at the mesoscopic scale, this will ultimately result in a lower cell diffusivity at the macroscopic scale. Moreover,
![]() $D_A$
is an increasing function of b. This is coherent with the fact that larger values of this parameter correspond to larger mean values of the cell running times.
$D_A$
is an increasing function of b. This is coherent with the fact that larger values of this parameter correspond to larger mean values of the cell running times.
The fact that the right-hand side of (4.42) is zero translates in mathematical terms the idea that we are not taking into account the effects of division and death of DCs. Moreover, coherently with the fact that the motion of DCs is here described as a Brownian motion, the rate of change of the density of DCs due to cell movement (i.e. the second term on the left-hand side of (4.42)) is a classical diffusion term. Considerations analogous to those made above about the dependence of the function
![]() $D_A$
on the parameters c and b apply to the function modelling the diffusivity of DCs (i.e. the function
$D_A$
on the parameters c and b apply to the function modelling the diffusivity of DCs (i.e. the function
![]() $D_D$
) as well. Furthermore, considerations similar to those made above about the dependence of
$D_D$
) as well. Furthermore, considerations similar to those made above about the dependence of
![]() $D_I$
on the density function
$D_I$
on the density function
![]() $\rho_{D}({\bf x},t)$
hold for the dependence of
$\rho_{D}({\bf x},t)$
hold for the dependence of
![]() $D_D$
on the density function
$D_D$
on the density function
![]() $\rho_{I}({\bf x},t)$
.
$\rho_{I}({\bf x},t)$
.
5 Research perspectives
The modelling approach for the switch between cell migration modes presented here could be generalised by including additional cellular phenomena involved in the immune response to cancer, and considering other aspects of immune cell movement as well. For the case of movement in bacteria, a recent work in this direction is [Reference Perthame, Sun and Tang25], where the switch in type of movement, that is, the switch between Lévy and Brownian strategies, was determined by chemical pathways internal to the bacteria.
With reference to the mathematical modelling of the immune response to cancer, a natural generalisation would be to include a population of cancer cells and allow activated CTLs to induce death in cancer cells via binary interactions. Moreover, the recognition phase of the adaptive immune response to cancer could be modelled by splitting the population of DCs into a subpopulation of cells with no tumour antigens on their surface and a subpopulation of cells presenting some antigen – which would move in a non-local and in a more localised search pattern, respectively [Reference Engelhardt, Boldajipour, Beemiller, Pandurangi, Sorensen, Werb, Egeblad and Krummel10] – and letting DCs switch from one subpopulation to the other via binary interactions with cancer cells [Reference Waldman, Fritz and Lenardo28,Reference Wculek, Cueto, Mujal, Melero, Krummel and Sancho29]. The strategy we have used here to model non-conservative cell–cell interactions may prove useful to the development of both generalisations of our modelling approach.
In regard to the mathematical modelling of other aspects of immune cell movement, our modelling approach could be extended to represent other switches in T cell migration patterns observed in the immune response to different pathogens, which are driven by possible chemotactic cues and by the conditions of the surrounding microenvironment [Reference Krummel, Bartumeus and Gérard17]. Moreover, further generalisations of the modelling approach could be developed in relation to experimental results indicating that T cells can also undergo subdiffusive [Reference Worbs, Mempel, Bölter, von Andrian and Förster32] and fully ballistic [Reference Witt, Raychaudhuri, Schaefer, Chakraborty and Robey31] migration.
In general, it would be interesting to apply the modelling approach presented in this paper and its possible developments to other biological and ecological contexts whereby switch from non-local to localised migration patterns has been reported [Reference Bartumeus, Peters, Pueyo, Marrasé and Catalan4,Reference de Jager, Bartumeus, Kölzsch, Weissing, Hengeveld, Nolet, Herman and van de Koppel8,Reference De Knegt, Hengeveld, Van Langevelde, De Boer and Kirkman9,Reference Humphries, Queiroz, Dyer, Pade, Musyl, Schaefer, Fuller, Brunnschweiler, Doyle, Houghton, Hays, Jones, Noble, Wearmouth, Southall and Sims15,Reference Nolet and Mooij21].
We conclude by remarking that, as previously noted, although they may result in cell outgoing trajectories compatible with those observed in elastic collisions, binary collisions between cells are not elastic in nature. Hence, it will be necessary to go beyond the definition of post-collision velocities used here in order to have a more biophysically faithful representation of cell–cell interactions. This is beyond the scope of the present work, which is primarily focused on modelling the switch in T cell migration modes mediated by interactions between inactive CTLs and DCs. Moreover, the formal approach employed in this article to derive a macroscopic limit of the mesoscopic model relies on the assumption that cell densities are sufficiently low so that cell velocities can be assumed to be uncorrelated. As such, it may lead to an inaccurate mean field representation of the dynamics of the underlying biological system in cases where cell densities are not sufficiently low, or cell–cell interactions introduce a stronger correlation between cell velocities. Therefore, another fruitful avenue of research would lie in extending this formal approach to these more complex cases by identifying alternative ways of obtaining a closed system of coupled equations for the macroscopic cell densities starting from the corresponding kinetic model.
Acknowledgements
T.L. gratefully acknowledges support from the MIUR grant ‘Dipartimenti di Eccellenza 2018-2022’.
Conflict of interests
The authors declare that they have no competing interests.
Appendix A Derivation of transport equations (3.11)–(3.12)
Using the method presented in [Reference Estrada-Rodriguez and Gimperlein11], we show how to derive a transport equation for the two-particle distribution function
![]() $\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
starting from transport equation (3.2) for the two-particle distribution function
$\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
starting from transport equation (3.2) for the two-particle distribution function
![]() $f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,\tau_k)$
.
$f_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k,\tau_h,\tau_k)$
.
We first introduce the notation:
and
and then note that, when
![]() $\beta_h$
and
$\beta_h$
and
![]() $\beta_k$
are given by (2.1) with
$\beta_k$
are given by (2.1) with
![]() $\psi_h$
and
$\psi_h$
and
![]() $\psi_k$
defined via (2.2) or (2.3), the solutions of (3.2) subject to the initial and boundary conditions considered here are such that
$\psi_k$
defined via (2.2) or (2.3), the solutions of (3.2) subject to the initial and boundary conditions considered here are such that
![]() $\tilde{f}_{\tau_h}$
decays monotonically as
$\tilde{f}_{\tau_h}$
decays monotonically as
![]() $\tau_h$
increases, and
$\tau_h$
increases, and
![]() $\tilde{f}_{\tau_k}$
exhibits an analogous behaviour. Hence, integrating (3.2) with respect to
$\tilde{f}_{\tau_k}$
exhibits an analogous behaviour. Hence, integrating (3.2) with respect to
![]() $(\tau_h, \tau_k)$
over
$(\tau_h, \tau_k)$
over
![]() $(0,t)^2$
with t large enough so that
$(0,t)^2$
with t large enough so that
![]() $\tilde{f}_{\tau_h}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k, \tau_h=t)$
is negligible compared to
$\tilde{f}_{\tau_h}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k, \tau_h=t)$
is negligible compared to
![]() $\tilde{f}^0_{\tau_h}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
and
$\tilde{f}^0_{\tau_h}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
and
![]() $\tilde{f}_{\tau_k}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k, \tau_k=t)$
is negligible compared to
$\tilde{f}_{\tau_k}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k, \tau_k=t)$
is negligible compared to
![]() $\tilde{f}_{\tau_k}^0(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
, with
$\tilde{f}_{\tau_k}^0(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
, with
and
we obtain the following transport equation for
![]() $\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
:
$\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
:
which can be rewritten as:
with
![]() $\tilde{\tilde{f}}^{\beta_h}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
and
$\tilde{\tilde{f}}^{\beta_h}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
and
![]() $\tilde{\tilde{f}}^{\beta_k}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
given by (3.7).
$\tilde{\tilde{f}}^{\beta_k}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
given by (3.7).
When cell movement at the microscopic scale obeys the rules presented in Section 2, we have
with the turning operators
![]() $\mathcal{T}_h$
and
$\mathcal{T}_h$
and
![]() $\mathcal{T}_k$
being defined via (2.5). The first two terms on the right-hand side of (A1) describe the density of cells that stop with rates
$\mathcal{T}_k$
being defined via (2.5). The first two terms on the right-hand side of (A1) describe the density of cells that stop with rates
![]() $\beta_h$
and
$\beta_h$
and
![]() $\beta_k$
. The initial conditions at
$\beta_k$
. The initial conditions at
![]() $\tau_{h}=0$
and
$\tau_{h}=0$
and
![]() $\tau_k=0$
(i.e. at the beginning of a new run phase) given by (A2) describes how the cells will resume their motion in a new direction dictated by the turning operators
$\tau_k=0$
(i.e. at the beginning of a new run phase) given by (A2) describes how the cells will resume their motion in a new direction dictated by the turning operators
![]() $\mathcal{T}_h$
and
$\mathcal{T}_h$
and
![]() $\mathcal{T}_k$
, respectively.
$\mathcal{T}_k$
, respectively.
Substituting the expressions for
![]() $\tilde{f}^0_{\tau_h}$
and
$\tilde{f}^0_{\tau_h}$
and
![]() $\tilde{f}^0_{\tau_k}$
given by (A2) into transport equation (A1) yields
$\tilde{f}^0_{\tau_k}$
given by (A2) into transport equation (A1) yields
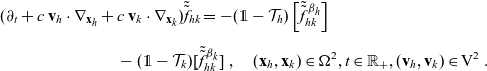 \begin{align} (\partial_t&+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h} +c \, \mathbf{v}_k\cdot\nabla_{\mathbf{x}_k})\tilde{\tilde{f}}_{hk} =-(\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right] \nonumber\\[5pt] &\quad\quad\quad\quad\quad\quad-(\unicode{x1D7D9}-\mathcal{T}_k)[\tilde{\tilde{f}}^{\beta_k}_{hk}] \ , \quad ({\bf x}_h,{\bf x}_k) \in \Omega^{2}, t \in \mathbb{R}_+, ({\bf v}_h,{\bf v}_k) \in {\rm V}^2 \ .\end{align}
\begin{align} (\partial_t&+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h} +c \, \mathbf{v}_k\cdot\nabla_{\mathbf{x}_k})\tilde{\tilde{f}}_{hk} =-(\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right] \nonumber\\[5pt] &\quad\quad\quad\quad\quad\quad-(\unicode{x1D7D9}-\mathcal{T}_k)[\tilde{\tilde{f}}^{\beta_k}_{hk}] \ , \quad ({\bf x}_h,{\bf x}_k) \in \Omega^{2}, t \in \mathbb{R}_+, ({\bf v}_h,{\bf v}_k) \in {\rm V}^2 \ .\end{align}
Remark 4 Since we consider transport equation (3.2) complemented with a smooth, compactly supported initial condition, the initial condition for transport equation (A3) will be a smooth, compactly supported function as well. Therefore, the two-particle distribution function
![]() $\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
will have compact support on
$\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
will have compact support on
![]() $\Omega^{2} \times {\rm V}^{2}$
for all
$\Omega^{2} \times {\rm V}^{2}$
for all
![]() $t \in \mathbb{R}^*_+$
.
$t \in \mathbb{R}^*_+$
.
Appendix B Derivation of the equation for the one-particle distribution
Transport equation (3.13) for the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
can derived from transport equation (A3) for the two-particle distribution function
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
can derived from transport equation (A3) for the two-particle distribution function
![]() $\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
in six steps as previously done in [Reference Estrada-Rodriguez and Gimperlein11].
$\tilde{\tilde{f}}_{hk}(\mathbf{x}_h,\mathbf{x}_k,t,\mathbf{v}_h,\mathbf{v}_k)$
in six steps as previously done in [Reference Estrada-Rodriguez and Gimperlein11].
-
I. We integrate transport equation (A3) with respect to
 $(\mathbf{x}_k,\mathbf{v}_k)$
over the set
$(\mathbf{x}_k,\mathbf{v}_k)$
over the set
 $\Omega_k(\mathbf{x}_h)\times {\rm V}$
and multiply both sides of the resulting equation by
$\Omega_k(\mathbf{x}_h)\times {\rm V}$
and multiply both sides of the resulting equation by
 $|{\rm V}|^{-1}$
to obtain (B1)
$|{\rm V}|^{-1}$
to obtain (B1) \begin{align} |{\rm V}|^{-1} \int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\partial_t&+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h} +c \, \mathbf{v}_k\cdot\nabla_{\mathbf{x}_k})\,\tilde{\tilde{f}}_{hk} \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k = \nonumber\\[5pt] & - |{\rm V}|^{-1} \int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right] \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k \nonumber\\[5pt] & - |{\rm V}|^{-1}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\unicode{x1D7D9}-\mathcal{T}_k)\left[\tilde{\tilde{f}}^{\beta_k}_{hk}\right] \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k \ .\end{align}
\begin{align} |{\rm V}|^{-1} \int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\partial_t&+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h} +c \, \mathbf{v}_k\cdot\nabla_{\mathbf{x}_k})\,\tilde{\tilde{f}}_{hk} \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k = \nonumber\\[5pt] & - |{\rm V}|^{-1} \int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right] \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k \nonumber\\[5pt] & - |{\rm V}|^{-1}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V} (\unicode{x1D7D9}-\mathcal{T}_k)\left[\tilde{\tilde{f}}^{\beta_k}_{hk}\right] \mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k \ .\end{align}
-
II. Using the fact that
 $p_h$
is given by (3.6) and integrals with respect to
$p_h$
is given by (3.6) and integrals with respect to
 $\mathbf{x}_k$
and
$\mathbf{x}_k$
and
 $\mathbf{v}_k$
commute, we rewrite the first term on the left-hand side of (B1) as:
$\mathbf{v}_k$
commute, we rewrite the first term on the left-hand side of (B1) as:  \begin{equation*} |{\rm V}|^{-1} \partial_t\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{x}_k =\partial_tp_h\ .\end{equation*}
\begin{equation*} |{\rm V}|^{-1} \partial_t\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k \mathop{}\!\mathrm{d}\mathbf{x}_k =\partial_tp_h\ .\end{equation*}
-
III. Using Reynold’s transport theorem in the variable
 $\mathbf{x}_h$
, we rewrite the second term on the left-hand side of (B1) as: Here,
$\mathbf{x}_h$
, we rewrite the second term on the left-hand side of (B1) as: Here, \begin{align*} |{\rm V}|^{-1} c\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})&\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k=|{\rm V}|^{-1} c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h}p_h\nonumber\\[5pt] &- |{\rm V}|^{-1} c\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_h \cdot \nu)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d} \sigma\ .\end{align*}
\begin{align*} |{\rm V}|^{-1} c\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})&\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k=|{\rm V}|^{-1} c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h}p_h\nonumber\\[5pt] &- |{\rm V}|^{-1} c\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_h \cdot \nu)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d} \sigma\ .\end{align*}
 $\nu$
is the unit normal to
$\nu$
is the unit normal to
 $\partial \Omega_k(\mathbf{x}_h)$
that points outward from
$\partial \Omega_k(\mathbf{x}_h)$
that points outward from
 $\Omega_k(\mathbf{x}_h)$
and inward to
$\Omega_k(\mathbf{x}_h)$
and inward to
 ${\rm B}_\varrho(\mathbf{x}_i)$
, and
${\rm B}_\varrho(\mathbf{x}_i)$
, and
 $\mathop{}\!\mathrm{d} \sigma$
denotes the surface element.
$\mathop{}\!\mathrm{d} \sigma$
denotes the surface element.
-
IV. Since
 $\tilde{\tilde{f}}_{hk}$
has compact support on
$\tilde{\tilde{f}}_{hk}$
has compact support on
 $\Omega^{2} \times \mathbb{\rm V}^{2}$
(vid. Remark 4), we use the divergence theorem and rewrite the third term on the left-hand side of (B1) as:
$\Omega^{2} \times \mathbb{\rm V}^{2}$
(vid. Remark 4), we use the divergence theorem and rewrite the third term on the left-hand side of (B1) as:  \begin{equation*} |{\rm V}|^{-1} c\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\left(\mathbf{v}_k\cdot\nabla_{\mathbf{x}_k}\right)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k = |{\rm V}|^{-1} c\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_k \cdot \nu)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d} \sigma \ .\end{equation*}
\begin{equation*} |{\rm V}|^{-1} c\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\left(\mathbf{v}_k\cdot\nabla_{\mathbf{x}_k}\right)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k = |{\rm V}|^{-1} c\int_{\partial {\rm B}_\varrho(\mathbf{x}_h)}\int_{\rm V}(\mathbf{v}_k \cdot \nu)\tilde{\tilde{f}}_{hk}\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d} \sigma \ .\end{equation*}
-
V. Changing order of integration, we rewrite the first term on the right-hand side of (B1) as:
with \begin{equation*} - |{\rm V}|^{-1}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}(\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k=-(\unicode{x1D7D9}-\mathcal{T}_h)[p^{\beta_h}_{h}] \ ,\end{equation*}
\begin{equation*} - |{\rm V}|^{-1}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}(\unicode{x1D7D9}-\mathcal{T}_h)\left[\tilde{\tilde{f}}^{\beta_h}_{hk}\right]\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k=-(\unicode{x1D7D9}-\mathcal{T}_h)[p^{\beta_h}_{h}] \ ,\end{equation*}
 $p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
given by (3.8).
$p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
given by (3.8).
-
VI. Since
 $\mathcal{T}_k$
satisfies (2.6), the second term on the right-hand side of (B1) is identically zero.
$\mathcal{T}_k$
satisfies (2.6), the second term on the right-hand side of (B1) is identically zero.
Taken together, the results obtained in Steps (1)–(6) allow one to conclude that the one-particle distribution function
![]() $p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
satisfies the following transport equation:
$p_h(\mathbf{x}_h,t,\mathbf{v}_h)$
satisfies the following transport equation:
with the weighted one-particle distribution function
![]() $p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
being given by (3.8) and the term
$p^{\beta_h}_{h}(\mathbf{x}_h,t,\mathbf{v}_h)$
being given by (3.8) and the term
![]() $\mathcal{Q}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h)$
being defined according to (3.14).
$\mathcal{Q}_{hk}(\mathbf{x}_h,t,\mathbf{v}_h)$
being defined according to (3.14).
Appendix C Derivation of the non-local trajectory term
In the case where
![]() $\beta_h$
is defined via (2.1) and (2.3) (i.e. for
$\beta_h$
is defined via (2.1) and (2.3) (i.e. for
![]() $h=I$
) and
$h=I$
) and
![]() $\beta_k$
is defined via (2.1) and (2.2) (i.e. for
$\beta_k$
is defined via (2.1) and (2.2) (i.e. for
![]() $k=D$
), applying the method of characteristics to (3.2) and using the fact that
$k=D$
), applying the method of characteristics to (3.2) and using the fact that
![]() $\dfrac{\psi_k(\cdot,\tau_k)}{\psi_k(\cdot,\tau_k-\tau_h)} = e^{-b\tau_h}$
one finds [Reference Estrada-Rodriguez and Gimperlein11]
$\dfrac{\psi_k(\cdot,\tau_k)}{\psi_k(\cdot,\tau_k-\tau_h)} = e^{-b\tau_h}$
one finds [Reference Estrada-Rodriguez and Gimperlein11]
Introducing the notation:
and substituting (C1) into (3.8) gives
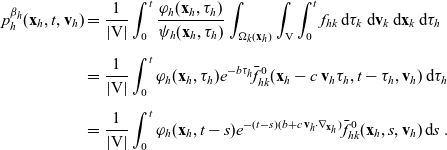 \begin{align}p^{\beta_h}_h(\mathbf{x}_h,t,\mathbf{v}_h)&=\dfrac{1}{|{{\rm V}}|}\int_0^t\frac{\varphi_h(\mathbf{x}_h,\tau_h)}{\psi_h(\mathbf{x}_h,\tau_h)}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\int_0^tf_{hk}\mathop{}\!\mathrm{d}\tau_k\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k\mathop{}\!\mathrm{d}\tau_h\nonumber\\[5pt] &= \dfrac{1}{|{{\rm V}}|} \int_0^t\varphi_h(\mathbf{x}_h,\tau_h)e^{-b\tau_h}\bar{f}_{hk}^0(\mathbf{x}_h-c \, \mathbf{v}_h\tau_h,t-\tau_h,\mathbf{v}_h)\mathop{}\!\mathrm{d}\tau_h\nonumber\\[5pt] & = \dfrac{1}{|{{\rm V}}|} \int_0^t\varphi_h(\mathbf{x}_h,t-s)e^{-(t-s)(b+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})}\bar{f}_{hk}^0(\mathbf{x}_h,s,\mathbf{v}_h)\mathop{}\!\mathrm{d} s\ . \end{align}
\begin{align}p^{\beta_h}_h(\mathbf{x}_h,t,\mathbf{v}_h)&=\dfrac{1}{|{{\rm V}}|}\int_0^t\frac{\varphi_h(\mathbf{x}_h,\tau_h)}{\psi_h(\mathbf{x}_h,\tau_h)}\int_{\Omega_k(\mathbf{x}_h)}\int_{\rm V}\int_0^tf_{hk}\mathop{}\!\mathrm{d}\tau_k\mathop{}\!\mathrm{d}\mathbf{v}_k\mathop{}\!\mathrm{d}\mathbf{x}_k\mathop{}\!\mathrm{d}\tau_h\nonumber\\[5pt] &= \dfrac{1}{|{{\rm V}}|} \int_0^t\varphi_h(\mathbf{x}_h,\tau_h)e^{-b\tau_h}\bar{f}_{hk}^0(\mathbf{x}_h-c \, \mathbf{v}_h\tau_h,t-\tau_h,\mathbf{v}_h)\mathop{}\!\mathrm{d}\tau_h\nonumber\\[5pt] & = \dfrac{1}{|{{\rm V}}|} \int_0^t\varphi_h(\mathbf{x}_h,t-s)e^{-(t-s)(b+c \, \mathbf{v}_h\cdot\nabla_{\mathbf{x}_h})}\bar{f}_{hk}^0(\mathbf{x}_h,s,\mathbf{v}_h)\mathop{}\!\mathrm{d} s\ . \end{align}
The last equality in (C2) is obtained using the change of variables
![]() $s=t-\tau_h$
along with the following Taylor expansion:
$s=t-\tau_h$
along with the following Taylor expansion:
 \begin{align} e^{-(t-s)c\mathbf{v}\cdot\nabla}f(\mathbf{x})&=\sum_{m=0}^\infty\frac{(-(t-s) \, c \, \mathbf{v}\cdot\nabla)^m}{m!}f(\mathbf{x})\nonumber\\[5pt] & =\sum_{m=0}^\infty\frac{1}{m!}(-(t-s) \, c \, \mathbf{v})^m\nabla^mf(\mathbf{x})=f(\mathbf{x}-(t-s) \, c \, \mathbf{v})\ .\nonumber\end{align}
\begin{align} e^{-(t-s)c\mathbf{v}\cdot\nabla}f(\mathbf{x})&=\sum_{m=0}^\infty\frac{(-(t-s) \, c \, \mathbf{v}\cdot\nabla)^m}{m!}f(\mathbf{x})\nonumber\\[5pt] & =\sum_{m=0}^\infty\frac{1}{m!}(-(t-s) \, c \, \mathbf{v})^m\nabla^mf(\mathbf{x})=f(\mathbf{x}-(t-s) \, c \, \mathbf{v})\ .\nonumber\end{align}
Hence, the Laplace transform in time of
![]() $p^{\beta_h}_h(\mathbf{x}_h,t,\mathbf{v}_h)$
is
$p^{\beta_h}_h(\mathbf{x}_h,t,\mathbf{v}_h)$
is
Here,
![]() $\lambda$
is the Laplace variable, and
$\lambda$
is the Laplace variable, and
![]() $\hat{\varphi}_h$
and
$\hat{\varphi}_h$
and
![]() $\hat{\bar{f}}_{hk}^0$
are the Laplace transforms in time of the functions
$\hat{\bar{f}}_{hk}^0$
are the Laplace transforms in time of the functions
![]() $\varphi_h$
and
$\varphi_h$
and
![]() $\bar{f}_{hk}^0$
. Moreover, substituting (C1) into (3.6) and computing the Laplace transform in time yields
$\bar{f}_{hk}^0$
. Moreover, substituting (C1) into (3.6) and computing the Laplace transform in time yields
with
![]() $\hat{\psi}_h$
being the Laplace transform of the function
$\hat{\psi}_h$
being the Laplace transform of the function
![]() $\psi_h$
. The latter equation gives
$\psi_h$
. The latter equation gives
Substituting such an expression for
![]() $\hat{\bar{f}}_{hk}^0$
into (C3) ones sees that (C2) can be written as:
$\hat{\bar{f}}_{hk}^0$
into (C3) ones sees that (C2) can be written as:
with the integral operator
![]() $\mathcal{B}$
being defined according to (3.17).
$\mathcal{B}$
being defined according to (3.17).








