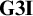1. Introduction
In his doctoral thesis [Reference Gentzen8, Reference Gentzen9], Gentzen introduced sequent calculi for classical and intuitionistic logic. In particular, he solved the decision problem for intuitionistic propositional logic (
$\mathbf {Int}$
) with a calculus that he called
$\mathbf {LI}$
.Footnote
1
However, Gentzen’s original calculus lacked some desirable properties, such as invertibility of its rules, that would avoid the need for backtracking. Ever since then, many other approaches were proposed; we refer to [Reference Dyckhoff, Kahle, Strahm and Studer4] for an extended survey.
The labelled calculus
$\mathbf {G3I}$
by Dyckhoff and Negri [Reference Dyckhoff and Negri5, Reference Negri, Dimitracopoulos, Newelski, Normann and Steel14, Reference Negri and von Plato17] reported in Table 1 solves the problem of backtracking but doesn’t yet have the property of termination, see, for instance, the example of Peirce’s Law in Section 3.3. In order to solve this problem, Negri [Reference Negri, Galmiche and Larchey-Wendling15, Reference Negri16] showed how to add a loop-checking mechanism to ensure termination. However, it is desirable to avoid loop-checking since its effect on complexity is not clear.
Table 1 The sequent calculus
$\mathbf {G3I}$
. Rule R
$\supset $
has the condition that y is fresh.
Corsi [Reference Corsi, Ballo and Franchella2, Reference Corsi and Tassi3] presented a calculus for
$\mathbf {Int}$
which fulfils the termination property. The key to get termination is the addition of the following rule:
This rule is logically equivalent to the formula
$B\supset (A\supset B),$
which is called the principle of a fortiori.
In this paper, we consider the labelled calculus
$\mathbf {G3I}$
instead, and show that a way to reach termination consists in modifying its rule R
$\supset $
as follows:
Although the idea comes from a similar terminating procedure [Reference Dyckhoff and Negri6] for the calculus
$\mathbf {G3Grz}$
for the provability logic
$\mathbf {Grz}$
, into which
$\mathbf {Int}$
is embeddable as detailed in Section 4, we notice that what we do is actually incorporating a fortiori into R
$\supset $
.
2. Structural properties
Consider the sequent calculi
$\mathbf {G3I}$
and
${\mathbf {G3I}}_{\mathbf {t}}$
as presented in Tables 1 and 2, respectively.
Table 2 The sequent calculus
${\mathbf {G3I}}_{\mathbf {t}}$
.
Theorem 2.1.
$\mathbf {G3I}$
and
${\mathbf {G3I}}_{\mathbf {t}}$
are equivalent in the sense that
$$\begin{align*}\mathbf{G3I}\vdash\Gamma\rightarrow\Delta \quad\text{if and only if}\quad {\mathbf{G3I}}_{\mathbf{t}}\vdash\Gamma\rightarrow\Delta. \end{align*}$$
Proof Suppose that
$\mathbf {G3I}\vdash \Gamma \rightarrow \Delta $
. We transform the given derivation into one in
${\mathbf {G3I}}_{\mathbf {t}}$
by using height-preserving weakening to add whenever needed the extra formula of the form
$y\colon B\supset (A\supset B)$
in the premiss of R
$\supset $
. So
${\mathbf {G3I}}_{\mathbf {t}}\vdash \Gamma \rightarrow \Delta $
.
Conversely, if
${\mathbf {G3I}}_{\mathbf {t}}\vdash \Gamma \rightarrow \Delta $
, consider the steps of R
$\supset _t$
:
By a Cut with the extra (derivable) sequent
$\rightarrow y\colon B\supset (A\supset B)$
, we turn it into premisses of R
$\supset $
with the same conclusions:
We conclude by admissibility of Cut in
$\mathbf {G3I}$
.
Theorem 2.2. All the structural properties hold for
${\mathbf {G3I}}_{\mathbf {t}}$
. In particular,
-
(i) All the sequents of the following form are derivable in
${\mathbf {G3I}}_{\mathbf {t}}$
:-
(a)
$x\leqslant y,x\colon A,\Gamma \rightarrow \Delta ,y\colon A$
, -
(b)
$x\colon A,\Gamma \rightarrow \Delta ,x\colon A$
.
-
-
(ii) If
${\mathbf {G3I}}_{\mathbf {t}}\vdash \Gamma \rightarrow \Delta $
, then
${\mathbf {G3I}}_{\mathbf {t}}\vdash \Gamma (x/y)\rightarrow \Delta (x/y)$
with the same derivation height. -
(iii) The rules of weakening,
are height-preserving admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
-
(iv) All rules of
${\mathbf {G3I}}_{\mathbf {t}}$
are height-preserving invertible. -
(v) The rules of contraction,
are height-preserving admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
Proof The proofs are similar to those of [Reference Negri and von Plato17, Lemmas 12.25–12.29 and Theorems 12.27–12.29].
We will see later that also the rule of cut,
is admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
(Corollary 3.8). However, the proof that we are going to give is not syntactical. On the other hand, this formulation of the calculus permits a completeness proof (Theorem 3.5) that yields at the same time a semantic proof of admissibility of Cut, the finite model property and a constructive decision procedure.
Remark 2.3. As a consequence of admissibility of LW, rule R
$\supset $
of
$\mathbf {G3I}$
is admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
We now prove a few lemmata that will be useful later.
Lemma 2.4. The rule
is admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
Proof We prove it by induction on the height of the derivation of the premiss.
$n=0$
: The only nontrivial case is the one in which the premiss is an initial sequent and
$x\colon A$
is principal. In this case, we can write the sequent as
$$\begin{align*}x\leqslant y,w\leqslant x,w\colon A,\Gamma'\rightarrow\Delta,x\colon A,\end{align*}$$
where
$\Gamma \equiv w\leqslant x,w\colon A,\Gamma '$
. Observe that the sequent
$$\begin{align*}w\leqslant y,x\leqslant y,w\leqslant x,w\colon A,\Gamma'\rightarrow\Delta,y\colon A \end{align*}$$
is initial. By the rule Trans
$_\leqslant $
, we get a derivation of
$$\begin{align*}x\leqslant y,w\leqslant x,w\colon A,\Gamma'\rightarrow\Delta,y\colon A,\end{align*}$$
which is just
$x\leqslant y,\Gamma \rightarrow \Delta ,y\colon A$
, as wanted.
$n>0$
: The only nontrivial cases are those in which the last rule applied is a right rule and
$x\colon A$
is principal. If the last rule applied is R
$\wedge $
and
$A\equiv B\wedge C$
, then we have
We can apply the induction hypothesis to the premisses and get
$$ \begin{align*} x\leqslant y,\Gamma\rightarrow\Delta,y\colon B, \\ x\leqslant y,\Gamma\rightarrow\Delta,y\colon C. \end{align*} $$
We conclude by an application of R
$\wedge $
. If the last rule applied is R
$\vee $
and
$A\equiv B\vee C$
, then we have
We can apply the induction hypothesis to the premiss and get
$$ \begin{align*} x\leqslant y,\Gamma\rightarrow\Delta,y\colon B,y\colon C. \end{align*} $$
We conclude by an application of R
$\vee $
. If the last rule applied is R
$\supset _t$
and
$A\equiv B\supset C$
, then we have
We can apply hp-weakening to the premiss and get
$$\begin{align*}y\leqslant z,x\leqslant z,x\leqslant y,z\colon C\supset (B\supset C),z\colon B,\Gamma\rightarrow\Delta,z\colon C, \end{align*}$$
which, by an application of transitivity leads to
$$\begin{align*}y\leqslant z,x\leqslant y,z\colon C\supset (B\supset C),z\colon B,\Gamma\rightarrow\Delta,z\colon C. \end{align*}$$
We conclude with an application of R
$\supset _t$
.
Lemma 2.5. The rule
is admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
Proof We prove it by induction on the height of the derivation of the premiss.
$n=0$
: The only nontrivial case is the one in which the premiss is an initial sequent and
$y\colon A$
is principal. In this case, we can write the sequent as
$$\begin{align*}x\leqslant y,y\leqslant z,x\colon A,y\colon A,\Gamma'\rightarrow\Delta',z\colon A,\end{align*}$$
where
$\Gamma \equiv y\leqslant z,\Gamma '$
and
$\Delta \equiv \Delta ',z\colon A$
. Observe that the sequent
$$ \begin{align*}x\leqslant y,y\leqslant z,x\leqslant z,x\colon A,\Gamma'\rightarrow\Delta',z\colon A\end{align*} $$
is initial. By transitivity, we get a derivation of
$$\begin{align*}x\leqslant y,y\leqslant z,x\colon A,\Gamma'\rightarrow\Delta',z\colon A,\end{align*}$$
which is just
$x\leqslant y,x\colon A,\Gamma \rightarrow \Delta $
, as wanted.
$n>0$
: The only nontrivial cases are those in which the last rule applied is a left rule and
$y\colon A$
is principal. If the last rule applied is L
$\wedge $
and
$A\equiv B\wedge C$
, then we have
Then, by hp-invertibility of L
$\wedge $
, we get
$$\begin{align*}x\leqslant y,x\colon B,x\colon C,y\colon B,y\colon C,\Gamma\rightarrow\Delta, \end{align*}$$
to which the induction hypothesis can be applied:
$$\begin{align*}x\leqslant y,x\colon B,x\colon C,\Gamma\rightarrow\Delta. \end{align*}$$
We conclude by an application of L
$\wedge $
. If the last rule applied is L
$\vee $
and
$A\equiv B\vee C$
, then we have
Then, by hp-invertibility of L
$\vee $
, we get
$$ \begin{align*} x\leqslant y,x\colon B,y\colon B,\Gamma&\rightarrow\Delta, \\ x\leqslant y,x\colon C,y\colon C,\Gamma&\rightarrow\Delta, \end{align*} $$
to which the induction hypothesis can be applied:
$$ \begin{align*} x\leqslant y,x\colon B,\Gamma&\rightarrow\Delta, \\ x\leqslant y,x\colon C,\Gamma&\rightarrow\Delta. \end{align*} $$
We conclude by an application of L
$\vee $
. If the last rule applied is L
$\supset $
and
$A\equiv B\supset C$
, then we have
where
$\Gamma \equiv y\leqslant z,\Gamma '$
. Then we can apply the induction hypothesis to the premisses:
$$ \begin{align*} x\leqslant y,x\colon B\supset C,y\leqslant z,\Gamma'&\rightarrow\Delta,z\colon B, \\ x\leqslant y,x\colon B\supset C,z\colon C,y\leqslant z,\Gamma'&\rightarrow\Delta. \end{align*} $$
By hp-weakening, these lead to
$$ \begin{align*} x\leqslant z,x\leqslant y,x\colon B\supset C,y\leqslant z,\Gamma'&\rightarrow\Delta,z\colon B, \\ x\leqslant z,x\leqslant y,x\colon B\supset C,z\colon C,y\leqslant z,\Gamma'&\rightarrow\Delta. \end{align*} $$
Now we can apply L
$\supset $
in order to get
$$\begin{align*}x\leqslant z,x\leqslant y,x\colon B\supset C,y\leqslant z,\Gamma'\rightarrow\Delta. \end{align*}$$
We conclude by an application of transitivity.
Lemma 2.6. The rule
is admissible.
Proof The direction from conclusion to premiss is just an instance of weakening. For the other direction, we apply invertibility of R
$\supset _t$
(we notice that the inverse rule does not have the condition on the eigenvariable, but it can be done on an arbitrary label) to get
3. Soundness and completeness
3.1. Semantics
A Kripke model [Reference Kripke11]
$(X,R,{\mathit {val}})$
is a set X together with an accessibility relation R, i.e., a binary relation between elements of X, and a valuation
${\mathit {val}}$
, i.e., a function assigning one of the truth values
$0$
or
$1$
to an element x of X and an atomic formula P. The usual notation for
${\mathit {val}}(x,P)=1$
is
$x\Vdash P$
. In Kripke models for intuitionistic logic, the accessibility relation is a preorder, i.e., it is reflexive
$$\begin{align*}\forall x(xR x) \end{align*}$$
and transitive
$$\begin{align*}\forall x\forall y\forall z(zRy\,\,\&\,\,yR x\Rightarrow zR x), \end{align*}$$
and therefore it is denoted by the usual symbol
$\leqslant $
for a preorder. For convenience, we assume to have equality
$=$
and a binary relation
$<$
on X which is transitive and irreflexive, i.e.,
$$\begin{align*}\forall x(x\nless x), \end{align*}$$
and we define
$\leqslant $
as its reflexive closure:
$$\begin{align*}x\leqslant y\iff (x<y\text{ or }x=y). \end{align*}$$
As usual, we denote by
$\geqslant $
the inverse relation of
$\leqslant $
; i.e.,
$$\begin{align*}x\geqslant y\iff y\leqslant x. \end{align*}$$
The inductive definition of truth of a proposition in
$\mathbf {Int}$
in terms of Kripke semantics is:
$$ \begin{align*} &x\nVdash\bot. \\&x\Vdash A\wedge B\text{ if and only if }x\Vdash A\text{ and }x\Vdash B. \\&x\Vdash A\vee B\text{ if and only if }x\Vdash A\text{ or }x\Vdash B. \\&x\Vdash A\supset B\text{ if and only if }y\Vdash A\Rightarrow y\Vdash B\text{ for all }y\text{ such that }x\leqslant y. \end{align*} $$
Let
$x\in X$
. We say that
$\leqslant $
satisfies the semantic a fortiori property for x if
$$\begin{align} \forall y\geqslant x(y\Vdash B\supset(A\supset B)\,\&\,y\Vdash A\Rightarrow y\Vdash B). \end{align} $$
Let R be a relation on X. An infinite R-sequence is a sequence
$(x_i)_{i\in \mathbb {N}}$
of elements of X such that
$x_iRx_{i+1}$
for all
$i\in \mathbb {N}$
. An infinite R-sequence
$(x_i)_{i\in \mathbb {N}}$
is convergent if there is
$i\in \mathbb {N}$
such that
$x_j=x_i$
for all
$j>i$
. We say that R is Noetherian—for short, R satisfies Noeth—if every infinite R-sequence converges.
Lemma 3.1. Let
$x\in X$
. If
$\leqslant $
is Noetherian and satisfies SAF
$_x$
, then
$$\begin{align*}\forall y>x(y\Vdash B\supset(A\supset B)).\end{align*}$$
Proof Notice that the relation
$<$
is transitive, irreflexive, and Noetherian. Therefore it follows that its inverse
$>$
satisfies the Gödel–Löb Induction (see [Reference Fellin, Negri, Schuster, Olivetti, Verbrugge, Negri and Sandu7, Proposition 4.2 and Theorem 4.3]), that is,
$$ \begin{align} \forall x(\forall y>x(\forall z>y\,Ez\Rightarrow Ey)&\Rightarrow\forall y>x\,Ey) \end{align} $$
for any given predicate
$E(x)$
on X. Therefore, if we let
$E(x)\equiv x\Vdash B\supset (A\supset B)$
, it suffices to show that
$$ \begin{align} \forall y>x(\forall z>y(z\Vdash B\supset(A\supset B))\Rightarrow y\Vdash B\supset(A\supset B)). \end{align} $$
So let
$y>x$
such that
$$ \begin{align} \forall z>y(z\Vdash B\supset(A\supset B)). \end{align} $$
We claim that
$y\Vdash B\supset (A\supset B)$
, i.e.,
$$ \begin{align} \forall z\geqslant y(z\Vdash B\Rightarrow z\Vdash A\supset B). \end{align} $$
So let
$z\geqslant y$
such that
$z\Vdash B$
. We have to prove
$z\Vdash A\supset B$
, i.e.,
$$ \begin{align} \forall w\geqslant z(w\Vdash A\Rightarrow w\Vdash B). \end{align} $$
So let
$w\geqslant z$
such that
$w\Vdash A$
. The claim is
$w\Vdash B$
.
-
• If
$w=z$
, then we already know that
$z\Vdash B$
. -
• If
$w>z$
, then by transitivity
$w>y$
and by (2) we get
$w\Vdash B\supset (A\supset B)$
. Since
$w\Vdash A$
and by transitivity
$w\geqslant x$
, we can apply SAF
$_x$
and derive
$w\Vdash B$
.
Now unroll the proof to get claims (4), (3), and (1), and thus the main claim.
Lemma 3.2. Fix
$x\in X$
. If
$\leqslant $
is Noetherian and satisfies SAF
$_x$
, then
$x\Vdash B\supset (A\supset B)$
.
Proof The claim is equivalent to
$$ \begin{align} \forall y\geqslant x(y\Vdash B\Rightarrow y\Vdash A\supset B). \end{align} $$
Fix
$y\geqslant x$
such that
$y\Vdash B$
. We claim that
$y\Vdash A\supset B$
, i.e.,
$$ \begin{align} \forall z\geqslant y(z\Vdash A\Rightarrow z\Vdash B). \end{align} $$
Fix
$z\geqslant y$
such that
$z\Vdash A$
. We need to prove that
$z\Vdash B$
.
-
• If
$z=y$
, then we already know that
$y\Vdash B$
. -
• If
$z>y$
, then by transitivity
$z>x$
and by Lemma 3.1 we get
$z\Vdash B\supset (A\supset B)$
. Since
$z\Vdash A$
and by transitivity
$z\geqslant x$
, we can apply SAF
$_x$
and derive
$z\Vdash B$
.
Now unroll the proof to get claims (6) and (5), and thus the main claim.
Lemma 3.3 (Semantic Lemma).
Fix
$x\in X$
. If
$\leqslant $
is Noetherian, then the following are equivalent:
-
(i) SAF
$_x$
. -
(ii)
$\forall y\geqslant x(y\Vdash A\Rightarrow y\Vdash B)$
.
Proof (ii)
$\Rightarrow $
(i): A fortiori.
(i)
$\Rightarrow $
(ii): Fix
$y\geqslant x$
such that
$y\Vdash A$
. We claim that
$y\Vdash B$
.
-
• If
$y=x$
, then by Lemma 3.2 we get that
$x\Vdash B\supset (A\supset B)$
. -
• If
$y>x$
, then by Lemma 3.1 we get that
$y\Vdash B\supset (A\supset B)$
.
In either case we have
$y\Vdash B\supset (A\supset B)$
and
$y\Vdash A$
, thus we can apply SAF
$_x$
and get
$y\Vdash B$
.
3.2. Proof search
Consider the proof search procedure as defined in [Reference Dyckhoff and Negri6]. We have the analogous of 5.3–6:
Theorem 3.4 (Soundness).
If
$\mathbf {G3I_t}\vdash \Gamma \rightarrow \Delta $
, then
$\Gamma \rightarrow \Delta $
is valid in every reflexive transitive and Noetherian frame.
Proof If
$\mathbf {G3I}_{\mathbf {t}}\vdash \Gamma \rightarrow \Delta $
, then
$\mathbf {G3I}\vdash \Gamma \rightarrow \Delta $
and therefore
$\Gamma \rightarrow \Delta $
is valid in every reflexive transitive frame, a fortiori in every Noetherian one.
Theorem 3.5. Let
$\Gamma \rightarrow \Delta $
be a sequent in the language of
${\mathbf {G3I}}_{\mathbf {t}}$
. Then it is decidable whether it is derivable in
${\mathbf {G3I}}_{\mathbf {t}}$
. If it is not derivable, the failed proof search gives a finite countermodel to the sequent on a reflexive, transitive, and Noetherian frame.
Proof We adapt the proof of [Reference Dyckhoff and Negri6, Theorem 5.4], which in turn is an adaptation to labelled sequents of the method of reduction trees detailed for Gentzen’s LK by Takeuti [Reference Takeuti20, Chapter 1, Paragraph 8].
For an arbitrary sequent
$\Gamma \rightarrow \Delta $
in the language of
${\mathbf {G3I}}_{\mathbf {t}}$
we apply, whenever possible, root-first the rules of
$\mathbf {G3I}_{\mathbf {t}}$
, in a given order. The procedure will construct either a derivation in
${\mathbf {G3I}}_{\mathbf {t}}$
or a countermodel.
1. Construction of the reduction tree: The reduction tree is defined inductively in stages as follows: Stage
$0$
has
$\Gamma \rightarrow \Delta $
at the root of the tree. For each branch, stage
$n> 0$
has two cases:
Case I: If the top-sequent is either an initial sequent or has some
$x\colon A$
, not necessarily atomic, on both left and right, or is a conclusion of L
$\bot $
, the construction of the branch ends.
Case II: Otherwise we continue the construction of the branch by writing, above its top-sequent, other sequents that are obtained by applying root-first the rules of
${\mathbf {G3I}}_{\mathbf {t}}$
(except L
$\bot $
) whenever possible, in a given order and under suitable conditions.
There are eight different stages: one for each logical rule, Ref
$_\leqslant $
and Trans. At stage
$8+1$
we repeat stage
$1$
, at stage
$8+2$
we repeat stage
$2$
, and so on until an initial sequent, or a conclusion of L
$\bot $
, or a saturated branch (defined below) is found. In applying root-first the rules, we also copy their principal formulas in the premisses. All such copied formulas, except the principal formula of L
$\supset $
, need not be analysed again and are thus marked as overlined. For instance:
These marked formulas are only auxiliary, and will thus be removed at the end of the procedure to get the reduction tree.
The stages for the rules other than R
$\supset _t$
are similar to those in [Reference Negri and von Plato17, Theorem 11.28].
For formulas of the form
$y\colon A\supset B$
in the succedent, we apply rule R
$\supset _t$
. However, if the sequent contains
$x\leqslant y,x\colon B\supset (A\supset B),y\colon A$
in the antecedent and
$y\colon B$
in the succedent, we remove it. This is justified by Lemma 2.6.
Finally, we consider the cases of the frame rules Ref
$_\leqslant $
and Trans. As detailed in [Reference Dyckhoff and Negri5, Reference Dyckhoff and Negri6], it is enough to instantiate Ref
$_\leqslant $
only on terms in the top-sequent.
Observe also that, because of height-preserving admissibility of contraction, once a rule has been considered, it need not be instantiated again on the same principal formulas (for L
$\supset $
such principal formulas are pairs of the form
$x\leqslant y,x\colon A\supset B$
and it need not be applied whenever its application produces a duplication of labelled formulas or relational atoms.
To show that the procedure terminates, it is enough to show that every branch in the reduction tree for a sequent
$\Gamma \rightarrow \Delta $
is finite. Every branch contains one or more chains of labels
${x}_{1}\leqslant y_1,\dots ,x_m\leqslant y_m,\dots $
; each label that was not already in the endsequent is introduced by a step of R
$\supset _t$
. By inspection of the rules of
${\mathbf {G3I}}_{\mathbf {t}}$
, it is clear that all the formulas that occur in the branch are subformulas of
$\Gamma ,\Delta $
or formulas of the form
$A\supset (B\supset A)$
for some subformula
$B\supset A$
of
$\Gamma ,\Delta $
. To ensure that all proper chains of labels in the reduction tree are finite, it is therefore enough to prove that rule R
$\supset _t$
need not be applied twice to the same formula along a chain of labels.
Suppose that we have a chain
$x_0\leqslant {x}_{1},\dots ,x_{n-1}\leqslant x_n$
in the antecedent and
$x_0\colon A\supset B,x_n\colon A\supset B$
in the succedent of a branch in the proof search and that R
$\supset _t$
has been applied to
$x_0\colon A\supset B$
. We need to show that there is no need to apply R
$\supset _t$
to
$x_n\colon A\supset B$
. Suppose for simplicity that we have a chain of length
$2$
, with
$x_0\equiv x,{x}_{1}\equiv y,{x}_{2}\equiv z$
:
and assume that the top-sequent is closed under all the available rules (excluding R
$\supset _t$
) of the reduction procedure. We observe that in the application of L
$\supset $
on
$y\colon B\supset (A\supset B)$
and
$y\leqslant z$
, the right premiss with
$z\colon A\supset B$
both on the left and right is derivable, therefore we only consider the left premiss with
$z\colon B$
is in the succedent. So we have that
$y\colon A$
(as marked) is in the antecedent from the first step of R
$\supset _t$
below, and
$\Delta '$
contains
$z\colon B$
is in the succedent from the application of L
$\supset $
on
$y\colon B\supset (A\supset B)$
and
$y\leqslant z$
(we consider only the left premiss since the right premiss with
$z\colon A\supset B$
both on the left and right is derivable). So we can apply Lemma 2.6 and discard
$z\colon A\supset B$
.
We can conclude that all the chains of labels in the tree are finite. To conclude that the branch is finite, it is enough to observe that it contains only a finite number of such chains (the number of chains is bounded by a function of the number of disjunctions or commas in the positive part of the endsequent). The general case, where the chain is longer than just
$x\leqslant y,y\leqslant z$
, is similar.
A branch which either ends in an initial sequent or in a sequent with the same labelled formula, even compound, in both the antecedent and succedent, or at the conclusion of L
$\bot $
, or has a top-sequent amenable to any of the reduction steps, is called unsaturated. Every other branch is said to be saturated.
2. Construction of the countermodel: If the reduction tree for
$\Gamma \rightarrow \Delta $
is not a derivation, it has at least one saturated branch. Let
$\Gamma ^*\rightarrow \Delta ^*$
be the union (respectively, of the antecedents and succedents) of all the sequents
$\Gamma _i\rightarrow \Delta _i$
of the branch up to its top-sequent. We define a Kripke model that forces all the formulas in
$\Gamma ^*$
and no formula in
$\Delta ^*$
and is therefore a countermodel to the sequent
$\Gamma \rightarrow \Delta $
.
Consider the frame X, the nodes of which are the labels that appear in the relational atoms in
$\Gamma ^*$
and the order on which is given by these relational atoms. Clearly, the construction of the reduction tree imposes the frame properties on the countermodel: Ref
$_\leqslant $
and Trans
$_\leqslant $
hold because the branch is saturated. Moreover, any label that appears in the sequent will appear in a relational atom (and thus in the frame X), because the rule Ref
$_\leqslant $
has been applied. Noetherianity clearly holds because all the strictly ascending chains in the countermodel are finite by construction.
On the frame
$(X,\leqslant )$
we define the following valuation: for each labelled atomic formula
$x\colon P$
in
$\Gamma ^*$
we stipulate that
$x\Vdash P$
. Since the top-sequent is not initial, for all labelled atomic formulas
$y\colon Q$
in
$\Delta ^*$
we infer that
$y\nVdash Q$
. We then show by induction on
$size(A)$
that
$x\Vdash A$
if
$x\colon A$
is in
$\Gamma ^*$
and that
$x\nVdash A$
if
$x\colon A$
is in
$\Delta ^*$
. Therefore we have a countermodel to the endsequent
$\Gamma \rightarrow \Delta $
.
-
– If A is atomic, then the claim holds by the definition of the model.
-
– If
$A\equiv \bot $
, it cannot be in
$\Gamma ^*$
, by definition of saturated branch: so
$x\nVdash A$
. -
– If
$A\equiv B\wedge C$
is in
$\Gamma ^*$
, then by the saturation of the branch we also have
$x\colon B$
and
$x\colon C$
in
$\Gamma ^*$
. By the induction hypothesis,
$x\Vdash B$
and
$x\Vdash C$
, and therefore
$x\Vdash B\wedge C$
. -
– If
$A\equiv B\wedge C$
is in
$\Delta ^*$
, then by the saturation of the branch either
$x\colon B$
or
$x\colon C$
in
$\Delta ^*$
. By the induction hypothesis,
$x\nVdash B$
or
$x\nVdash C$
, and therefore
$x\nVdash B\wedge C$
. -
– If
$A\equiv B\vee C$
is in
$\Gamma ^*$
, then by the saturation of the branch either
$x\colon B$
or
$x\colon C$
in
$\Gamma ^*$
. By the induction hypothesis,
$x\Vdash B$
or
$x\Vdash C$
, and therefore
$x\Vdash B\vee C$
. -
– If
$A\equiv B\vee C$
is in
$\Delta ^*$
, then by the saturation of the branch we also have
$x\colon B$
and
$x\colon C$
in
$\Delta ^*$
. By the induction hypothesis,
$x\nVdash B$
and
$x\nVdash C$
, and therefore
$x\nVdash B\vee C$
. -
– If
$A\equiv B\supset C$
is in
$\Gamma ^*$
, then for any occurrence of
$x\leqslant y$
in
$\Gamma ^*$
we find, by saturation and by the construction of the reduction tree, either an occurrence of
$y\colon B$
in
$\Delta ^*$
or an occurrence of
$y\colon C$
in
$\Gamma ^*$
. By the induction hypothesis, in the former case
$y\nVdash B$
, and in the latter
$y\Vdash C$
, so in both cases
$x\Vdash B\supset C$
. -
– If
$A\equiv B\supset C$
is in
$\Delta ^*$
, we consider the step where it is analysed. If
$x\colon C$
is in the succedent of that step (or any succedent below it), then by the induction hypothesis
$x\Vdash B$
. Since
$x\leqslant x$
is also in
$\Gamma ^*$
by construction of the reduction tree, it follows that
$x\Vdash B\supset C$
. Otherwise there is
$x\leqslant y$
in
$\Gamma ^*$
and
$y\colon C$
in
$\Delta ^*$
. By the induction hypothesis
$y\nVdash C$
, and therefore
$x\nVdash A$
.
Corollary 3.6. If a sequent
$\Gamma \rightarrow \Delta $
is valid in every reflexive, transitive, and Noetherian frame, then it is derivable in
${\mathbf {G3I}}_{\mathbf {t}}$
.
Corollary 3.7. A formula A is provable in
$\mathbf {Int}$
if and only if the sequent
$\rightarrow x\colon A$
is derivable in
${\mathbf {G3I}}_{\mathbf {t}}$
for some (or any) label x.
Corollary 3.8. The rule of cut,
is admissible in
${\mathbf {G3I}}_{\mathbf {t}}$
.
The proof of Theorem 3.5 is also of interest because it establishes the finite model property for
$\mathbf {Int}$
and gives a constructive decision procedure for it, i.e., an algorithm that, given a sequent, constructs either a derivation or a countermodel.
3.3. An example: Peirce’s Law
Consider Peirce’s Law:
$$ \begin{align*} ((P\supset Q)\supset P)\supset P. \end{align*} $$
If we try to do a derivation of
$\rightarrow x\colon ((P\supset Q)\supset P)\supset P$
in
$\mathbf {G3I}$
, we get
We see that the left branch is generating a loop and therefore does not terminate. If we try to do a derivation of
$\rightarrow x\colon ((P\supset Q)\supset P)\supset P$
in
${\mathbf {G3I}}_{\mathbf {t}}$
instead, we get
This time, the proof search algorithm defined in the proof of Theorem 3.5 tells us that the top-sequent of the left branch need not be further analysed, and it helps us in constructing a countermodel:
Let’s check that actually
$x\nVdash ((P\supset Q)\supset P)\supset P$
, which is equivalent to the statement that
$$\begin{align*}\forall {x}_{1}\geqslant x(\forall {x}_{2}\geqslant {x}_{1}(\forall x_3\geqslant {x}_{2}(x_3\Vdash P\Rightarrow x_3\Vdash Q)\Rightarrow {x}_{2}\Vdash P)\Rightarrow {x}_{1}\Vdash P)\end{align*}$$
does not hold. We check that this does not hold for
${x}_{1}\equiv y$
. Since
$y\nVdash P$
, we just need to show that
$$\begin{align*}\forall {x}_{2}\geqslant y(\forall x_3\geqslant {x}_{2}(x_3\Vdash P\Rightarrow x_3\Vdash Q)\Rightarrow {x}_{2}\Vdash P).\end{align*}$$
We have two cases: if
${x}_{2}\equiv y$
, then our claim follows from
$y\leqslant z$
and
$z\Vdash P\nRightarrow z\Vdash Q$
; if
${x}_{2}\equiv z$
, then our claim follows a fortiori from
$z\Vdash P$
.
4. Embedding into Grzegorczyk logic
We recall that modal logic is obtained by adding the modal operator
$\square $
to the language of propositional logic, and the inductive clauses for valuations of modal formulas are the following:
$$ \begin{align*} &x\nVdash\bot. \\&x\Vdash A\supset B\text{ if and only if }x\Vdash A\Rightarrow x\Vdash B. \\&x\Vdash A\wedge B\text{ if and only if }x\Vdash A\text{ and }x\Vdash B. \\&x\Vdash A\vee B\text{ if and only if }x\Vdash A\text{ or }x\Vdash B. \\&x\Vdash\square A\text{ if and only if }\forall y(x\leqslant y\Rightarrow y\Vdash A). \end{align*} $$
The provability logic
$\mathbf {Grz}$
(Grzegorczyk logic) [Reference Avron1, Reference Dyckhoff and Negri6, Reference Grzegorczyk10] is an extension of basic modal logic K with the additional schemata
$$ \begin{align} \square A\supset A, \end{align} $$
$$ \begin{align} \square A\supset\square\square A, \end{align} $$
$$ \begin{align} \square(G(A)\supset A)\supset A, \end{align} $$
where
$G(A)\equiv \square (A\supset \square A)$
.
$\mathbf {Grz}$
is characterised by reflexive, transitive, and Noetherian frames [Reference Dyckhoff and Negri6]. The sequent calculus
$\mathbf {G3Grz}$
for
$\mathbf {Grz}$
(see Table 3) satisfies all usual structural rules, including hp-invertibility of its rules [Reference Dyckhoff and Negri6].
Table 3 The sequent calculus
$\mathbf {G3Grz}$
. Rule R
$\square $
Z has the condition that y is fresh.
As shown in [Reference Dyckhoff and Negri6], an indirect decision procedure for
$\mathbf {Int}$
is obtained through faithfulness of the embedding of
$\mathbf {Int}$
into
$\mathbf {Grz}$
via the translation
$\_^\square $
inductively defined as
$$ \begin{align*} P^\square&\equiv\square P, \\ \bot^\square&\equiv\bot, \\ (A\wedge B)^\square&\equiv A^\square\wedge B^\square, \\ (A\vee B)^\square&\equiv A^\square\vee B^\square, \\ (A\supset B)^\square&\equiv\square(A^\square\supset B^\square). \end{align*} $$
Remark 4.1. The translation of R
$\supset _t$
is the following:
If we set
$A\equiv \top $
, this is equivalent to
which is an instance of R
$\square Z$
, the rule that allows decidability in the calculus
$\mathbf {G3Grz}$
for Grzegorczyk logic.
We now want to give a proof of faithfulness alternative to the one is given in [Reference Dyckhoff and Negri6] by using
${\mathbf {G3I}}_{\mathbf {t}}$
in place of
$\mathbf {G3I}$
. We first need a few lemmata:
Lemma 4.2. If there is a derivation in
$\mathbf {G3Grz}$
of height n of
$$ \begin{align} {x\colon A\supset B,\Gamma\rightarrow\Delta}, \end{align} $$
then there are derivations of height at most n of
$$ \begin{align} \Gamma&\rightarrow\Delta,x\colon A \end{align} $$
$$ \begin{align} x\colon B,\Gamma&\rightarrow\Delta. \end{align} $$
If, moreover,
$x\colon A\supset B$
is used as the principal formula somewhere in the given derivation of (7), then the derivations of (8) and (9) have height at most
$n-1$
.
Proof We slightly modify the usual argument for hp-invertibility of L
$\supset $
(see, e.g., [Reference Negri13, Proposition 4.11]). The proof proceeds by induction on n.
$n=0$
: Trivial.
$n>0$
: If
$x\colon A\supset B$
is principal in the last rule applied in the derivation of (7), then the two branches are derivations of (8) and (9) of height at most
$n-1$
. If it is not principal and the last rule applied is
$rule$
, then we proceed as usual by applying the induction hypothesis to the previous step(s) followed by
$rule$
.
Lemma 4.3. The rule
with the condition that the top-sequent is saturated under transitivity, is hp-admissible in
$\mathbf {G3Grz}$
.
Proof We prove it by induction on the height of the derivation of the premiss, with a subinduction on the length of A.
$n=0$
: Trivial.
$n>0$
: The only nontrivial cases are those in which the last rule applied is a left rule and
$y\colon A^\square $
is principal. Cases L
$\wedge $
and L
$\vee $
are dealt with as in Lemma 2.5, and L
$\square $
as in [Reference Dyckhoff and Negri6, Lemma 3.14]. The assumption of saturation under transitivity makes the application of Trans
$_\leqslant $
in [Reference Dyckhoff and Negri6, Lemma 3.14] unnecessary, thus ensuring height preservation.
Lemma 4.4. The rule
with the condition that the top-sequent is saturated under transitivity, is hp-admissible in
$\mathbf {G3Grz}$
.
Proof Suppose that there is a derivation of
$$ \begin{align} x\colon A^\square,x\colon\square((A^\square\supset B)\supset C),\Gamma\rightarrow\Delta \end{align} $$
of height n. We prove by induction on n that there is a derivation of
$$ \begin{align} x\colon A^\square,x\colon\square(B\supset C),\Gamma\rightarrow\Delta \end{align} $$
of height n.
$n=0$
: All cases are trivial.
$n>0$
: The cases in which the principal formula is in
$\Gamma $
or
$\Delta $
are trivial.
Suppose that the principal formula is
$x\colon A^\square $
, and consider the case in which
$A\equiv A_1\wedge A_2$
, which means that we have a derivation
We can apply hp-weakening to the premiss and get
$$\begin{align*}x\colon A^\square,x\colon A_1^\square,x\colon A_2^\square,x\colon\square((A^\square\supset B)\supset C),\Gamma\rightarrow\Delta, \end{align*}$$
to which we can apply the induction hypothesis:
$$\begin{align*}x\colon A^\square,x\colon A_1^\square,x\colon A_2^\square,x\colon\square(B\supset C),\Gamma\rightarrow\Delta. \end{align*}$$
We conclude by L
$\wedge $
and contraction.
Suppose that the principal formula is
$x\colon A^\square $
, and consider the case in which
$A\equiv A_1\vee A_2$
, which means that we have a derivation
We can apply hp-weakening to the premisses and get
$$ \begin{align*} x\colon A^\square,x\colon A_1^\square,x\colon\square((A^\square\supset B)\supset C),\Gamma\rightarrow\Delta, \\ x\colon A^\square,x\colon A_2^\square,x\colon\square((A^\square\supset B)\supset C),\Gamma\rightarrow\Delta, \end{align*} $$
to which we can apply the induction hypothesis:
$$ \begin{align*} x\colon A^\square,x\colon A_1^\square,x\colon\square(B\supset C),\Gamma\rightarrow\Delta, \\ x\colon A^\square,x\colon A_2^\square,x\colon\square(B\supset C),\Gamma\rightarrow\Delta. \end{align*} $$
We conclude by L
$\vee $
and contraction.
Suppose that the principal formula is
$x\colon A^\square $
, and consider the case in which
$A\equiv A_1\supset A_2$
or
$A\equiv P$
, which means that we have a derivation
where
$\Gamma \equiv x\leqslant y,\Gamma '$
. We can apply the induction hypothesis to the premiss:
$$ \begin{align*} y\colon A,x\colon A^\square,x\colon\square(B\supset C),x\leqslant y,\Gamma'\rightarrow\Delta. \end{align*} $$
We conclude by L
$\supset $
.
Now suppose that the principal formula is
$x\colon \square ((A^\square \supset B)\supset C)$
. This means that we have
where
$\Gamma \equiv x\leqslant y,\Gamma '$
. We can assume that
$y\colon (A^\square \supset B)\supset C$
is used as the principal formula somewhere above this instance of L
$\square $
: if not, then we could find a derivation of (10) without this instance of L
$\square $
, this would have smaller height and therefore we could apply the induction hypothesis to it. By applying hp-weakening to the premiss, we obtain a derivation of
$$\begin{align*}y\colon A^\square,y\colon (A^\square\supset B)\supset C,x\colon A^\square,x\colon\square((A^\square\supset B)\supset C),x\leqslant y,\Gamma'\rightarrow\Delta \end{align*}$$
of height
$n-1$
and such that
$y\colon (A^\square \supset B)\supset C$
is used as the principal formula somewhere above. Now by Lemma 4.2 on invertibility of L
$\supset $
we get derivations of
$$ \begin{align} y\colon C,y\colon A^\square,x\colon A^\square,x\colon\square((A^\square\supset B)\supset C),x\leqslant y,\Gamma'&\rightarrow\Delta, \end{align} $$
$$ \begin{align} y\colon A^\square,x\colon A^\square,x\colon\square((A^\square\supset B)\supset C),x\leqslant y,\Gamma'&\rightarrow\Delta,y\colon A^\square\supset B, \end{align} $$
both of height
$n-2$
. Now we can apply the induction hypothesis to (12) and get a derivation of
$$ \begin{align} y\colon C,y\colon A^\square,x\colon A^\square,x\colon\square(B\supset C),x\leqslant y,\Gamma'\rightarrow\Delta \end{align} $$
of height
$n-2$
. By applying hp-invertibility of R
$\supset $
and hp-contraction to (13), we get a derivation of
$$\begin{align*}y\colon A^\square,x\colon A^\square,x\colon\square((A^\square\supset B)\supset C),x\leqslant y,\Gamma'\rightarrow\Delta,y\colon B \end{align*}$$
of height
$n-2$
, to which we can apply the induction hypothesis and get a derivation of
$$ \begin{align} y\colon A^\square,x\colon A^\square,x\colon\square(B\supset C),x\leqslant y,\Gamma'\rightarrow\Delta,y\colon B \end{align} $$
of height
$n-2$
. Now we can apply L
$\supset $
to (14) and (15) and get a derivation of
$$\begin{align*}y\colon B\supset C,y\colon A^\square,x\colon A^\square,x\colon\square(B\supset C),x\leqslant y,\Gamma'\rightarrow\Delta \end{align*}$$
of height
$n-1$
, which by an application of L
$\square $
gives a derivation of
$$\begin{align*}y\colon A^\square,x\colon A^\square,x\colon\square(B\supset C),x\leqslant y,\Gamma'\rightarrow\Delta \end{align*}$$
of height n. We conclude by Lemma 4.3.
Now we are able to prove faithfulness:
Theorem 4.5 (Faithfulness).
Let
$\Gamma ,\Delta $
be multisets of labelled formulas in the language of
${\mathbf {G3I}}_{\mathbf {t}}$
,
$\Gamma ',\Delta '$
multisets of labelled atomic formulas, with
$\Gamma '$
possibly containing also relational atoms. If
$$\begin{align*}\mathbf{G3Grz}\vdash\Gamma^\square,\Gamma'\rightarrow\Delta^\square, \Delta', \end{align*}$$
then
$$\begin{align*}{\mathbf{G3I}}_{\mathbf{t}}\vdash\Gamma,\Gamma'\rightarrow\Delta,\Delta'. \end{align*}$$
Proof By induction on the height of the derivation of
$\Gamma ^\square ,\Gamma '\rightarrow \Delta ^\square ,\Delta '$
. We assume that
$\Gamma ^\square ,\Gamma '\rightarrow \Delta ^\square ,\Delta '$
is saturated under transitivity: this can be done without loss of generality since it is equivalent to apply Trans
$_\leqslant $
in the proof search as soon as possible, which is innocuous because the rule operates on labels already introduced.
$n=0$
: If it is an initial sequent or the conclusion of L
$\bot $
, then it can be translated smoothly into the corresponding initial sequent or rule in
${\mathbf {G3I}}_{\mathbf {t}}$
.
$n>0$
: First, notice that rules for
$\supset $
cannot produce a sequent of this form. If it is the conclusion of a rule for
$\bot ,\wedge ,\vee $
, then it can be translated smoothly into the corresponding initial sequent or rule in
${\mathbf {G3I}}_{\mathbf {t}}$
. If it is derived by a modal rule, then the principal formula can be of the form
$\square P$
or of the form
$\square (A^\square \supset B^\square )$
. We have four cases:
-
– If
$\square P$
is principal on the left, we have (with
$\Gamma =x:P,\Gamma "$
) which, using the induction hypothesis, is translated into the admissible
${\mathbf {G3I}}_{\mathbf {t}}$
step -
– If
$\square P$
is principal on the right, we have (with
$\Delta =x:P,\Delta "$
) which, as seen in Remark 4.1, is the translation of a step of rule R
$\supset _t$
with
$\top \supset P$
as the principal formula.
-
– If
$\square (A^\square \supset B^\square )$
is principal on the left, we have (with
$\Gamma =A\!\supset \! B,\Gamma "$
and
$\Gamma '=x\leqslant y,\Gamma "'$
) from which, by hp-invertibility of L
$\supset $
in
$\mathbf {G3Grz}$
we have to which the induction hypothesis applies:
$$ \begin{align*} \mathbf{G3Grz}&\vdash x\leqslant y,y\colon B^\square,x\colon\square(A^\square\supset B^\square),\Gamma^{\prime\prime}\square,\Gamma"'\rightarrow\Delta^\square,\Delta', \\ \mathbf{G3Grz}&\vdash x\leqslant y,x\colon\square(A^\square\supset B^\square),\Gamma^{\prime\prime}\square,\Gamma"'\rightarrow\Delta^\square,y\colon A^\square,\Delta', \end{align*} $$
We conclude by an application of L
$$ \begin{align*} {\mathbf{G3I}}_{\mathbf{t}} &\vdash x\leqslant y,y\colon B,x\colon A\supset B,\Gamma",\Gamma"'\rightarrow\Delta,\Delta', \\ {\mathbf{G3I}}_{\mathbf{t}} & \vdash x\leqslant y,x\colon A\supset B,\Gamma",\Gamma"'\rightarrow\Delta,y\colon A,\Delta'. \end{align*} $$
$\supset $
.
-
– If
$\square (A^\square \supset B^\square )$
is principal on the right, we have (with
$\Delta =x:A\!\supset \! B,\Delta "$
) from which, by hp-invertibility of R
$\supset $
in
$\mathbf {G3Grz}$
we have By Lemma 4.4, it follows that
$$ \begin{align*} \mathbf{G3Grz}&\vdash x\leqslant y,y\colon G(A^\square\supset B^\square),y\colon A^\square,\Gamma^\square,\Gamma'\rightarrow\Delta^{\prime\prime}\square,y\colon B^\square,\Delta'. \end{align*} $$
to which the induction hypothesis applies:
$$ \begin{align*} \mathbf{G3Grz}&\vdash x\leqslant y,y\colon \square(B^\square\supset\square(A^\square\supset B^\square)),y\colon A^\square,\Gamma^{\prime\prime}\square,\Gamma'\rightarrow\Delta^{\prime\prime}\square,y\colon B^\square,\Delta', \end{align*} $$
We conclude by R
$$ \begin{align*} {\mathbf{G3I}}_{\mathbf{t}} &\vdash x\leqslant y,y\colon B\supset(A\supset B),y\colon A,\Gamma,\Gamma'\rightarrow\Delta",y\colon B,\Delta'. \end{align*} $$
$\supset _t$
.
5. Future work
Since the logic
$\mathbf {Grz}$
studied in the present paper is characterised by reflexive, transitive, and Noetherian frames, we also plan to use the approach of [Reference Fellin, Negri, Schuster, Olivetti, Verbrugge, Negri and Sandu7] to define a variant of induction principle, which we may dub Grzegorczyk induction corresponding to rule R
$\square $
Z:
$$\begin{align*}\forall x\left[\forall y\leqslant x(GE(y)\Longrightarrow E(y))\Longrightarrow\forall y\leqslant x\,\,E(y)\right], \end{align*}$$
where
$GE(y)$
is an abbreviation for
$\forall z\leqslant y(E(z)\Longrightarrow \forall w\leqslant z\,\,E(w))$
. This can be considered a weak form of induction compatible with reflexivity, and may give a different perspective of the semantics of both
$\mathbf {Grz}$
and
$\mathbf {Int}$
and may give some insights on the properties of the accessibility relation.
We then plan to extend the approach of this paper to extensions of Int, such as intermediate logics [Reference Dyckhoff and Negri5, Reference Negri16], modal intuitionistic logic [Reference Maffezioli, Naibo and Negri12] and possibly bi-intuitionistic logic [Reference Pinto and Uustalu18].
Acknowledgements
Both authors are members of the “Gruppo Nazionale per le Strutture Algebriche, Geometriche e le loro Applicazioni” (GNSAGA) of the Istituto Nazionale di Alta Matematica (INdAM). Last but not least, the authors are grateful to Giovanna Corsi, Eugenio Orlandelli, Mario Piazza, Matteo Tesi, and Tarmo Uustalu for their interest and valuable suggestions.
Funding
Support for this research was granted by the projects “Reducing complexity in algebra, logic, combinatorics—REDCOM” belonging to the programme “Ricerca Scientifica di Eccellenza 2018” of the Fondazione Cariverona, “Infinity and Intensionality: Towards A New Synthesis” funded by the Research Council of Norway, and “Modalities in Substructural Logics: Theory, Methods and Applications – MOSAIC”, funded by the Community Research and Development Information Service (CORDIS) of the European Commission. The research by Sara Negri was supported in part by the MIUR Excellence Department Project awarded to Dipartimento di Matematica, Università di Genova, CUP D33C23001110001.
Open access
