Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Zhonghua
and
Pan, Ende
2019.
Sum of interpolated finite multiple harmonic q-series.
Journal of Number Theory,
Vol. 201,
Issue. ,
p.
148.
Kaneko, Masanobu
2019.
An introduction to classical and finite multiple zeta values.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
103.
Takeyama, Yoshihiro
2020.
Derivations on the algebra of multiple harmonic q-series and their applications.
The Ramanujan Journal,
Vol. 52,
Issue. 1,
p.
41.
Komori, Yasushi
2021.
Finite multiple zeta values, symmetric multiple zeta values and unified multiple zeta functions.
Tohoku Mathematical Journal,
Vol. 73,
Issue. 2,
MURAHARA, Hideki
and
ONO, Masataka
2021.
Yamamoto's Interpolation of Finite Multiple Zeta and Zeta-star Values.
Tokyo Journal of Mathematics,
Vol. 44,
Issue. 2,
Tasaka, Koji
2021.
Finite and symmetric colored multiple zeta values and multiple harmonic q-series at roots of unity.
Selecta Mathematica,
Vol. 27,
Issue. 2,
Harada, Ryotaro
2021.
Alternating multizeta values in positive characteristic.
Mathematische Zeitschrift,
Vol. 298,
Issue. 3-4,
p.
1263.
BACHMANN, Henrik
TAKEYAMA, Yoshihiro
and
TASAKA, Koji
2021.
Finite and symmetric Mordell–Tornheim multiple zeta values.
Journal of the Mathematical Society of Japan,
Vol. 73,
Issue. 4,
HESSAMI PILEHROOD, Khodabakhsh
HESSAMI PILEHROOD, Tatiana
and
TAURASO, Roberto
2022.
On 3-2-1 values of finite multiple harmonic $q$-series at roots of unity.
Journal of the Mathematical Society of Japan,
Vol. 74,
Issue. 3,
Li, Zhonghua
and
Wang, Zhenlu
2023.
A note on the sum of finite multiple harmonic
q
-series on
r
-(
r
+ 1) indices
.
Quaestiones Mathematicae,
Vol. 46,
Issue. 11,
p.
2421.
Sakurada, Kosuke
2023.
Duality for finite/symmetric multiple zeta values of fixed weight, depth, and height.
International Journal of Number Theory,
Vol. 19,
Issue. 10,
p.
2299.
TAKEYAMA, Yoshihiro
and
TASAKA, Koji
2023.
SUPERCONGRUENCES OF MULTIPLE HARMONIC <i>q</i>-SUMS AND GENERALIZED FINITE/SYMMETRIC MULTIPLE ZETA VALUES.
Kyushu Journal of Mathematics,
Vol. 77,
Issue. 1,
p.
75.
Kawamura, Hanamichi
Maesaka, Takumi
and
Ono, Masataka
2024.
Weighted sum formula for variants of half multiple zeta values.
International Journal of Number Theory,
Vol. 20,
Issue. 09,
p.
2329.
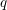 $q$-series at a primitive root of unity and show that these specialize to the finite multiple zeta value (FMZV) and the symmetric multiple zeta value (SMZV) through an algebraic and analytic operation, respectively. Further, we prove the duality formula for these values, as an example of linear relations, which induce those among FMZVs and SMZVs simultaneously. This gives evidence towards a conjecture of Kaneko and Zagier relating FMZVs and SMZVs. Motivated by the above results, we define cyclotomic analogues of FMZVs, which conjecturally generate a vector space of the same dimension as that spanned by the finite multiple harmonic
$q$-series at a primitive root of unity and show that these specialize to the finite multiple zeta value (FMZV) and the symmetric multiple zeta value (SMZV) through an algebraic and analytic operation, respectively. Further, we prove the duality formula for these values, as an example of linear relations, which induce those among FMZVs and SMZVs simultaneously. This gives evidence towards a conjecture of Kaneko and Zagier relating FMZVs and SMZVs. Motivated by the above results, we define cyclotomic analogues of FMZVs, which conjecturally generate a vector space of the same dimension as that spanned by the finite multiple harmonic 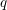 $q$-series at a primitive root of unity of sufficiently large degree.
$q$-series at a primitive root of unity of sufficiently large degree.

