Research Article
A Posteriori Error Estimates of Mixed Methods for Quadratic Optimal Control Problems Governed by Parabolic Equations
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 439-458
-
- Article
- Export citation
Convergence Estimates for Some Regularization Methods to Solve a Cauchy Problem of the Laplace Equation
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 459-477
-
- Article
- Export citation
Orthogonal Polynomials with Respect to Modified Jacobi Weight and Corresponding Quadrature Rules of Gaussian Type
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 478-488
-
- Article
- Export citation
Finite Element Approximation of Semilinear Parabolic Optimal Control Problems
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 489-504
-
- Article
- Export citation
Simulations of Shallow Water Equations by Finite Difference WENO Schemes with Multilevel Time Discretization
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 505-524
-
- Article
- Export citation
Cubic Spiral Transition Matching G2 Hermite End Conditions
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 525-536
-
- Article
- Export citation
Stability Analysis of Runge-Kutta Methods for Nonlinear Neutral Volterra Delay-Integro-Differential Equations
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 537-561
-
- Article
- Export citation
Numerical Analysis of a System of Singularly Perturbed Convection-Diffusion Equations Related to Optimal Control
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 562-575
-
- Article
- Export citation
High Order Scheme for Schrödinger Equation with Discontinuous Potential I: Immersed Interface Method
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 576-597
-
- Article
- Export citation

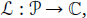 defined on the space of all algebraic polynomials
defined on the space of all algebraic polynomials 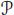 by
by