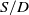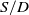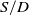Nomenclature
- A
-
area
- C
-
wing chord
-
 ${C_L}$
${C_L}$
-
lift coefficient, wing lift/engine thrust
-
 ${C_p}$
${C_p}$
-
pressure coefficient,
 ${C_p} = \left( {P - {P_\infty }} \right)/\left( {0.5{\rho _\infty }V_{ref}^2} \right)$
${C_p} = \left( {P - {P_\infty }} \right)/\left( {0.5{\rho _\infty }V_{ref}^2} \right)$
- CT
-
convection term
- D
-
diameter of the engine outlet
- h
-
height of the wing leading edge to the ground
- L
-
lift
-
 $\dot m$
$\dot m$
-
mass flow rate
- P
-
static pressure
- S
-
distance between engine axes
- T
-
engine thrust
- V
-
velocity magnitude
- V
-
velocity vector
-
 ${V_{ref}}$
${V_{ref}}$
-
reference velocity,
 ${V_{ref}} = \sqrt {T/{\rho _\infty }D} $
${V_{ref}} = \sqrt {T/{\rho _\infty }D} $
-
 ${V^{\rm{*}}}$
${V^{\rm{*}}}$
-
normalised velocity,
 ${V^{\rm{*}}} = V/{V_{ref}}$
${V^{\rm{*}}} = V/{V_{ref}}$
Greek Symbol
-
 $\rho $
$\rho $
-
density
-
 $\mu $
$\mu $
-
dynamic viscosity coefficient
-
 $\omega $
$\omega $
-
vorticity
-
 ${\omega ^{\rm{*}}}$
${\omega ^{\rm{*}}}$
-
normalised vorticity,
 ${\omega ^{\rm{*}}} = \omega \cdot C/{V_{ref}}$
${\omega ^{\rm{*}}} = \omega \cdot C/{V_{ref}}$
Subscript
-
 $\infty $
$\infty $
-
far field parameter
- e
-
engine
- in
-
inlet
- out
-
outlet
- x, y, z
-
coordinates
1.0 Introduction
For the eVTOL (electric vertical take-off and landing) industry, new designs with distributed propulsion systems are proposed as a key component of UAM (urban air mobility) [Reference Rajendran and Zack1–3], such as the Lilium illustrated in Fig. 1(a). A line of distributed engines is installed on the upper surface of the wing, close to the trailing edge. During vertical lifts, the engines generate downward jets, as demonstrated in Fig. 1(b). During cruise, the engines are angled to produce horizontal thrust, as shown in Fig. 1(c), with the wings primarily providing lift. However, the understanding of the aerodynamic performance of the major components, such as a wing with distributed engines, during takeoff is insufficient. Understanding the aerodynamic performance of the key components during takeoff are crucial for the development of advanced distributed propulsion eVTOL aircrafts.
Quite a few studies have been conducted on aircraft designs using distributed propulsion systems such as N3-X [5], which were not intended for vertical take-off. These designs can improve aerodynamic performance and propulsion efficiency [Reference Hyun, Aaron and Phillip6–Reference Wang and Zhou13]. Perry et al. examined the aerodynamic performance of a wing model with distributed engines under cruise conditions. The engines installed on the upper surface of the wing accelerated the suction surface boundary layer, thereby increasing wing lift (circulation) with thrust. Additionally, distributed propulsion demonstrates potential benefits in terms of noise and safety [Reference Perry, Phillip and Michael10, Reference Hall14, Reference Hall, Huang, Uranga, Greitzer, Drela and Sato15]. However, most studies on distributed propulsion have focused on performance during cruise conditions. For vectored-thrust eVTOL configurations (Fig. 1), the aerodynamic performance during vertical take-off is very different from that under cruise conditions, but has received little attention.
One of the most significant differences between cruise and take-off conditions for VTOL aircraft is the ground effect. Some research has been conducted on powered lift fixed-wing VTOL aircraft to examine the ground effect. Engine exit jets impinge on the ground, resulting in horizontal high-speed flow along the ground known as the ground jets. These jets induce various flow structures, such as the ground vortex, fountain flow and fountain vortices, which can negatively impact aircraft take-off performance. Poorly designed aircraft may experience significant downward forces [Reference Jorge, Andre and Diana16–Reference Peter, Richard and Richard18].
The ground vortex appears under the cockpit of the aircraft, when the ground jet rolls up due to the interaction with the freestream. As the freestream velocity increases, the ground vortex moves towards the engine exit jet. With self-similarity laws applicable to the ground vortex, the ground vortex position can be quantified by the positions of the ground vortex centre, the separation point or the maximum penetration point [Reference Knowles, Bray, Bailey and Curtis19, Reference Knowles and Bray20]. It is also found that the ground vortex can reduce the local pressure [Reference Barata, Durao and Mcguirk21, Reference Bray and Knowles22].

Figure 1. Distributed propulsion system under different operational conditions [4].
The fountain flow forms as the ground jets emanating from different engines collide in the middle and lift up [Reference Chuang and Nieh23–Reference Ozmen25]. Fountain vortices forms between the fountain flow and the engine exit jets. The size of the fountain vortices increases as the distance between the engine exit jets increases [Reference Ozmen25]. The fountain vortices can also reduce the local pressure [Reference Peter, Richard and Richard18, Reference Chuang and Nieh23, Reference Ozmen25].
The downward force is a challenging problem when developing fixed wing aircrafts capable of vertical take-off. A well-known example is the Yac-36 in the 1960s, which was unable to lift off due to the downward force induced by the ground effects [Reference Hirschberg17]. For similar aircraft, such as the Harrier [Reference Merritt, Kalpana and William26–Reference Chaderjian, Ahmad, Pandya and Murman29], Yac-141 [Reference Hirschberg17], and F-35 [Reference Buchholz30–Reference Parsons, Levin, Panteny, Wilson, Rask and Morris33], research into the ground effects has gained high priority. Vortex structures caused by the ground effects, including the ground vortex and fountain vortices, can create low pressure on the airframe and wing lower surface leading to downward forces on the aircraft. These forces not only reduce aircraft’s payload capacity but also affect the stability and controllability during take-off. For instance, the Harrier pilots struggle to maintain hovering below 10 meters due to poor performance associated with ground effects [Reference Pandya, Chaderjian, Ahmad and Murman28].
For eVTOL aircrafts with distributed propulsion, the coupling of distributed jets produced by the engines with the airframe creates a highly intertwined scenario. The interaction between vortices induced by the distributed jets is also significant. Bai and Zhou investigated the ground effect on the aerodynamics of a wing model coupled with slot type distributed propulsion [Reference Bai and Zhou34]. A low-pressure region was discovered on the wing lower surface, which is caused by the ground vortex, leading to a downward force equivalent to 14.2% of the thrust. Furthermore, the flow mechanism of the ground vortex was investigated, revealing that the pressure gradient near the ground vortex was primarily influenced by the convection term. Research into other distributed propulsion configurations such as distributed engines, which could lead to different flow structures and aerodynamic effects, can be hardly found in open publications.
The downward force induced by the vortices has a major effect on the payload and the safety of the VTOL aircrafts. Understanding the flow mechanism of the vortices is beneficial to improve the performance of the aircraft. The outcome of this research reveals the aero-dynamic effects of the jet induces vortices on a typical wing model coupled with distributed propulsion composed of a row of engines. A detailed analysis is performed on the flow field underneath the wing, with specific attention paid to the flow structures, including the spanwise vortex, chordwise vortex and their interaction. Cases with different ratios of the engine distance to the engine diameter (
![]() $S/D$
) are discussed.
$S/D$
) are discussed.
2.0 Experimental methods
2.1 Experimental model
Figure 2 shows the experimental setup consisting of a wing and a row of electrical fan engines, which is the same as the one used in Bai and Zhou [Reference Bai and Zhou34]. The aerofoil of the wing is NACA2418, and the aspect ratio of the wing is 3. To simulate realistic landing conditions for small-scale eVTOL aircraft, the wing is positioned at a height of 40% of the chord from the ground. This distance is both appropriate for accommodating the landing gear structures and operational convenience. Additional details of the geometric parameters can be found in Table 1. The diameter of the engine outlet is 13.5% of the chord.

Figure 2. Sketch of the experimental model.
A total of 14 engines were arranged in an array near the wing’s trailing edge to produce distributed jets. The model of the engines used in the experiment is POWERFUN DaBoFo. To replicate vertical take-off conditions, these jets were oriented perpendicular to the ground to generate an upward force. The exit jet velocity of each engine was set to 60 m/s and calibrated with a pitot tube. The exit Reynolds number of all the engines based on its outlet diameter and jet velocity was designed to be
![]() $2 \times {10^5}$
.
$2 \times {10^5}$
.
Engine spacing is defined by the ratio of the distance between engine axes (
![]() $S$
) to the outer diameter of the engine outlet (
$S$
) to the outer diameter of the engine outlet (
![]() $D$
), as shown in Fig. 3. Multiple engine spacing configurations were analysed in this study. Specifically, an
$D$
), as shown in Fig. 3. Multiple engine spacing configurations were analysed in this study. Specifically, an
![]() $S/D$
value of 1.59 was established when all engines were in operation, and an
$S/D$
value of 1.59 was established when all engines were in operation, and an
![]() $S/D$
value of 2.78 was studied when every other engine was deactivated.
$S/D$
value of 2.78 was studied when every other engine was deactivated.
2.2 Experimental facility
The experimental facility is shown in Fig. 4. An aerodynamic balance was connected to the wing to measure the lift force (
![]() ${L_{wing}}$
). The engines were mounted on poly methyl methacrylate brackets equipped with two strain gauges to measure the thrust (
${L_{wing}}$
). The engines were mounted on poly methyl methacrylate brackets equipped with two strain gauges to measure the thrust (
![]() $T$
) generated by the engines. As shown in Fig. 2(b), the wing and the engines were mounted on separate holders, with a 1mm gap between the wing and the engine brackets to allow for separate measurement of
$T$
) generated by the engines. As shown in Fig. 2(b), the wing and the engines were mounted on separate holders, with a 1mm gap between the wing and the engine brackets to allow for separate measurement of
![]() ${L_{wing}}$
and
${L_{wing}}$
and
![]() $T$
. Tapes were used to seal the gap, and their impact on the force measurements was deemed negligible. Data acquisition was performed using the NI PXIe-1078 chassis and NI TB-4339 terminal block. The accuracy of the aerodynamic balance was 0.38% at full scale, and the strain gauges exhibited a full-scale accuracy of 0.02%.
$T$
. Tapes were used to seal the gap, and their impact on the force measurements was deemed negligible. Data acquisition was performed using the NI PXIe-1078 chassis and NI TB-4339 terminal block. The accuracy of the aerodynamic balance was 0.38% at full scale, and the strain gauges exhibited a full-scale accuracy of 0.02%.
Table 1. Geometric parameters of the experimental model


Figure 3. Sketch of
![]() $S$
and
$S$
and
![]() $D$
.
$D$
.

Figure 4. Photos of the experimental facility.
Static pressure taps were positioned on the wing lower surface. The pressure scanner of Scanivalve MPS4000 is used and the full-scale accuracy of the pressure scanner is 0.06%. The sampling rate is 20Hz.
As the freestream velocity is often negligible during vertical take-off, the lift coefficient (
![]() ${C_L}$
) used in this study is different from the conventional one used in cruise conditions.
${C_L}$
) used in this study is different from the conventional one used in cruise conditions.
![]() ${C_L}$
of VTOL in the present investigation is defined as the ratio of lift force acting on the wing (
${C_L}$
of VTOL in the present investigation is defined as the ratio of lift force acting on the wing (
![]() ${L_{wing}}$
) to the total thrust produced by the engine array (
${L_{wing}}$
) to the total thrust produced by the engine array (
![]() $T$
).
$T$
).
The lift coefficient (
![]() ${C_L}$
) has an uncertainty of
${C_L}$
) has an uncertainty of
![]() $ \pm $
1.6%. For the wing surface pressure measurement, the uncertainty is
$ \pm $
1.6%. For the wing surface pressure measurement, the uncertainty is
![]() $ \pm $
1.5%. The engine outlet velocity has an uncertainty of
$ \pm $
1.5%. The engine outlet velocity has an uncertainty of
![]() $ \pm $
2.2%.
$ \pm $
2.2%.
3.0 Numerical methods
3.1 Numerical model setup
As shown in Fig. 5(a), a geometry model was developed for computational fluid dynamics (CFD) simulations based on the experimental setup. The CFD model was configured with main parameters, such as
![]() $h/C$
,
$h/C$
,
![]() $D/C$
, the aerofoil, and the wing aspect ratio, identical to those of the experiment model. In order to reduce computational costs, a half span model with a spanwise length of 1.5
$D/C$
, the aerofoil, and the wing aspect ratio, identical to those of the experiment model. In order to reduce computational costs, a half span model with a spanwise length of 1.5
![]() $C$
was employed. Figure 5(b) illustrates the cuboid-shaped computational domain of 3.5
$C$
was employed. Figure 5(b) illustrates the cuboid-shaped computational domain of 3.5
![]() $\; \times {\rm{\;}}$
8
$\; \times {\rm{\;}}$
8
![]() $ \times {\rm{\;}}$
15 chords.
$ \times {\rm{\;}}$
15 chords.

Figure 5. Geometry and boundary conditions of the CFD validation model.
The surface of the wing was defined as a no-slip wall. Velocity inlet boundary condition was applied at the engine outlet where the jets enter the computational domain. Conversely, a pressure outlet condition was utilised at the engine inlet where fluid exits the computational domain. The blades within the engines were not simulated. The outlet velocity of the engine (
![]() ${V_{e,out}}$
) was first set to match the Reynolds number of
${V_{e,out}}$
) was first set to match the Reynolds number of
![]() $2 \times {10^5}$
in the experiment, and then the pressure of the engine inlet was then adjusted to attain the same mass flow rate as the engine inlet. The boundary conditions for the outer boundaries of the computational domain are presented in Fig. 5(b). Symmetry condition was applied on the wing root surface, and the ground was modeled as a no-slip wall. Pressure outlet condition was used for the other four surfaces of the computational domain cuboid.
$2 \times {10^5}$
in the experiment, and then the pressure of the engine inlet was then adjusted to attain the same mass flow rate as the engine inlet. The boundary conditions for the outer boundaries of the computational domain are presented in Fig. 5(b). Symmetry condition was applied on the wing root surface, and the ground was modeled as a no-slip wall. Pressure outlet condition was used for the other four surfaces of the computational domain cuboid.
The engine motors and the holder in the experiment facility were simulated in the numerical validation model. Each engine was simulated separately, with a ring-shaped velocity distribution applied around each motor. The locations of the engines are the same in both the experiment and the CFD validation model.
The mesh used in this study was generated using ICEM CFD. The three-dimensional structured mesh is illustrated in Fig. 6, including the geometry and mesh details of the engine inlet duct. The averaged y+ of the wing and ground surfaces beneath the wing were both less than 1. The growing ratio of the mesh does not exceed 1.2. Mesh dependency studies were conducted, and the results are displayed in Fig. 7. For mesh sizes beyond 18.0 million, the lift coefficient (
![]() ${C_L}$
) variation was less than 0.7%. Therefore, the mesh with the size of 18.0 million was selected. For more flow field details, models with the wing aspect ratio of 6 were employed in the following CFD analyses.
${C_L}$
) variation was less than 0.7%. Therefore, the mesh with the size of 18.0 million was selected. For more flow field details, models with the wing aspect ratio of 6 were employed in the following CFD analyses.

Figure 6. Structured mesh details.

Figure 7. Mesh dependency results.
3.2 Turbulence model
The steady RANS equations were solved using ANSYS FLUENT with second-order spatial discretisation. The static pressure distribution on the wing lower surface from experiment (EXP) and CFD are presented at three span-wise locations (Fig. 8(a)). As illustrated in Fig. 8(b)–(d), low-pressure regions are observed, which are caused by the vortices induced beneath the wing. Following a comparison of several turbulent models, it was determined that the 4-equation Transition SST model exhibited the closest agreement with the experimental results and was therefore employed for subsequent analyses. It was revealed that both the S-A and
![]() $k - \omega $
models tended to overestimate the turbulent viscosity around engine exit jets, resulting in an excessive prediction of the strength of the vortices induced by viscous shear, and consequent overestimation of the pressure decrease caused by vortices.
$k - \omega $
models tended to overestimate the turbulent viscosity around engine exit jets, resulting in an excessive prediction of the strength of the vortices induced by viscous shear, and consequent overestimation of the pressure decrease caused by vortices.

Figure 8. Pressure distribtions on three span-wise locations on the wing lower surface, EXP and CFD.
The measured and predicted lift coefficient of the wing (
![]() ${C_L}$
) are also compared.
${C_L}$
) are also compared.
![]() $T$
obtained from CFD are calculated as:
$T$
obtained from CFD are calculated as:
where
![]() ${L_s}$
is the lift force of the engine shell. As shown in Table 2, The
${L_s}$
is the lift force of the engine shell. As shown in Table 2, The
![]() ${C_L}$
predicted by CFD utilising the Transition SST model was found to be 9.0% less than the experimental result, which was the closest match obtained among different turbulent models. The difference between CFD and experimental results may be partially attributed to factors such as the flow structures induced by the holder near the wing root or the secondary flow at the fan exit, which were not accounted for during the CFD simulations. Nonetheless, the CFD results demonstrated satisfactory agreement with the experimental data.
${C_L}$
predicted by CFD utilising the Transition SST model was found to be 9.0% less than the experimental result, which was the closest match obtained among different turbulent models. The difference between CFD and experimental results may be partially attributed to factors such as the flow structures induced by the holder near the wing root or the secondary flow at the fan exit, which were not accounted for during the CFD simulations. Nonetheless, the CFD results demonstrated satisfactory agreement with the experimental data.
4.0 Results and analysis
The distributed engine exit jets induce two main flow structures beneath the wing: chordwise vortices and spanwise vortices. In this section of the study, the flow mechanism of the chordwise vortices is analysed, specifically in the case of
![]() $S/D$
= 2.78, where chordwise vortices dominate. The analysis of spanwise vortices is based on the cases of
$S/D$
= 2.78, where chordwise vortices dominate. The analysis of spanwise vortices is based on the cases of
![]() $S/D$
= 1.10. Furthermore, the impact of
$S/D$
= 1.10. Furthermore, the impact of
![]() $S/D$
on the interaction between the vortices is also investigated.
$S/D$
on the interaction between the vortices is also investigated.
4.1 Chordwise vortices
In the case of
![]() $S/D$
= 2.78, where the spaces between engines are relatively larger, the flow beneath the wing is primarily dominated by the vortices that develop in the chordwise direction, which are referred to as chordwise vortices. Figure 9 illustrates the streamlines of the chordwise vortices, with their colours indicating normalised
$S/D$
= 2.78, where the spaces between engines are relatively larger, the flow beneath the wing is primarily dominated by the vortices that develop in the chordwise direction, which are referred to as chordwise vortices. Figure 9 illustrates the streamlines of the chordwise vortices, with their colours indicating normalised
![]() $x$
vorticity (
$x$
vorticity (
![]() $\omega _x^{\rm{*}}$
). The spanwise flow indicated by streamlines between the chordwise vortices and wing has a considerable impact on the pattern of the chordwise vortices. The wing tip vortex can also be observed in the vicinity of the wing tip region, which is driven by the pressure difference between the wing upper and lower surfaces.
$\omega _x^{\rm{*}}$
). The spanwise flow indicated by streamlines between the chordwise vortices and wing has a considerable impact on the pattern of the chordwise vortices. The wing tip vortex can also be observed in the vicinity of the wing tip region, which is driven by the pressure difference between the wing upper and lower surfaces.
4.1.1 The formation of the spanwise flow
As shown in Fig. 9, the spanwise flow originates from the wing tip region and travels in the spanwise direction towards the wing root, existing between the wing and the chordwise vortices. To investigate the formation mechanism of the spanwise flow, a control volume of the space between the wing and the ground is created, bounded by the ‘Front’, ‘Rear’ and ‘Side’ surfaces (as shown in Fig. 9). The high-velocity jets exiting the engine enter the control volume from the engine outlet surface and exit the control volume through the Front, Rear and Side surfaces. Due to shear stress, the high-velocity flow leaving the control volume entrains the low-velocity fluid nearby, increasing the mass flow rate leaving the control volume.
The mass flow rates entering and exiting the control volume through the Front, Rear and Side surfaces are investigated. Taking the Front surface for example, the mass flow rates are defined as:
where
![]() ${\dot m_{ex}}$
represents the mass flow rate exiting the control volume, and
${\dot m_{ex}}$
represents the mass flow rate exiting the control volume, and
![]() ${\dot m_{en}}$
represents the mass flow rate entering the control volume. It is found that the mass flow rate of the flow exiting the control volume is 44.7% higher than the engine exit mass flow rate. This implies that additional fluid is induced into the control volume via the Front, Rear and Side surfaces, where 39.4% of the mass flow rate flowing into the control volume transports via the Side’ surface and develops into the spanwise flow. Additionally, as shown in Fig. 9, the wing tip vortex forms when the spanwise flow separates near the wing tip region.
${\dot m_{en}}$
represents the mass flow rate entering the control volume. It is found that the mass flow rate of the flow exiting the control volume is 44.7% higher than the engine exit mass flow rate. This implies that additional fluid is induced into the control volume via the Front, Rear and Side surfaces, where 39.4% of the mass flow rate flowing into the control volume transports via the Side’ surface and develops into the spanwise flow. Additionally, as shown in Fig. 9, the wing tip vortex forms when the spanwise flow separates near the wing tip region.
Table 2.
![]() ${C_L}$
of experimental and numerical results
${C_L}$
of experimental and numerical results


Figure 9. Streamlines of the flow structures under the wing,
![]() $S/D$
= 2.78, CFD.
$S/D$
= 2.78, CFD.
4.1.2 The effect of the spanwise flow on chordwise vortices
To investigate the effect of the spanwise flow on the chordwise vortices, a confined case is studied, where the spanwise flow does not exist. In the confined case, symmetry boundary condition is applied on the side surface, as shown in Fig. 10. The flow pattern of the chordwise vortices, in the confined case, is different from that in the baseline case. Figure 11 explains the flow pattern of the chordwise vortices in the confined case. The engine outlet jets impinge on the ground and become ground jets flowing along the ground. Between two adjacent engines, the ground jets originating from different engines have opposite spanwise velocities. This results in wall jets from adjacent engines colliding and lifting, thereby forming the fountain flow. Chordwise vortices with different rotating directions are induced between the fountain flow. In the confined case (as shown in Figs. 10 and 11), the sizes of the negative rotating chordwise vortices and the positive ones are similar.

Figure 10. Streamlines of the flow structures under the wing,
![]() $S/D$
= 2.78, confined case, CFD.
$S/D$
= 2.78, confined case, CFD.

Figure 11. Illustration of the formation of the chordwise vortices,
![]() $y$
-
$y$
-
![]() $z$
plane, confined case.
$z$
plane, confined case.
In the baseline case (Fig. 9), where the wing tip region is an open space, the size of the negative rotating chordwise vortices is larger than the positive ones due to the effects of the spanwise flow. As shown in Fig. 12, the upper part of the negative rotating chordwise vortices exhibits negative
![]() $z$
-velocity that aligns with the spanwise flow. As a result, the negative vortices are enhanced, and on the other hand, the positive vortices become weakened. Moreover, the spanwise flow also tilts the fountain flow towards the wing root, which in turn influences the interaction of the vortices, and this will be discussed later.
$z$
-velocity that aligns with the spanwise flow. As a result, the negative vortices are enhanced, and on the other hand, the positive vortices become weakened. Moreover, the spanwise flow also tilts the fountain flow towards the wing root, which in turn influences the interaction of the vortices, and this will be discussed later.

Figure 12. Illustration of flow structures affected by the spanwise flow, y-z plane, baseline case.
4.1.3 The effect of the spanwise flow on the wing aerodynamic performance
The spanwise flow has a significant impact on the chordwise vortices. As a result, the characteristics of low-pressure region on the wing lower surface caused by the chordwise vortices is affected, which influences the wing aerodynamic performance. Table 3 shows the wing
![]() ${C_L}$
of the baseline case and the confined case. The
${C_L}$
of the baseline case and the confined case. The
![]() ${C_L}$
are negative, which means that the lift becomes lower due to the wing. The lift loss of the confined case is 18% higher than that of the baseline case, as shown in Table 3.
${C_L}$
are negative, which means that the lift becomes lower due to the wing. The lift loss of the confined case is 18% higher than that of the baseline case, as shown in Table 3.
The primary cause of the lift losses is the low-pressure region on the lower surface of the wing. This is evident from the
![]() ${C_p}$
distribution shown in Fig. 13, where strip shaped low-pressure regions can be seen, as highlighted in region ‘L’. In the confined case, each engine corresponds to two such low-pressure strips, as shown in region ‘A1’ in Fig. 13(a). However, in the baseline case, each engine corresponds to only one low-pressure strip (region ‘A2’ in Fig. 13(b)). Figure 14 shows the chordwise averaged
${C_p}$
distribution shown in Fig. 13, where strip shaped low-pressure regions can be seen, as highlighted in region ‘L’. In the confined case, each engine corresponds to two such low-pressure strips, as shown in region ‘A1’ in Fig. 13(a). However, in the baseline case, each engine corresponds to only one low-pressure strip (region ‘A2’ in Fig. 13(b)). Figure 14 shows the chordwise averaged
![]() ${C_p}$
distribution where the pressure of the single low-pressure strip in the baseline case (in region ‘B’) is higher than that of the twin low-pressure strips in the confined case.
${C_p}$
distribution where the pressure of the single low-pressure strip in the baseline case (in region ‘B’) is higher than that of the twin low-pressure strips in the confined case.
A cut plane of
![]() $x/C$
= 0.7 is used to investigate the flow structures under the wing, as shown in Fig. 15(a). The
$x/C$
= 0.7 is used to investigate the flow structures under the wing, as shown in Fig. 15(a). The
![]() ${C_p}$
distribution and local flow details on the plane are shown in Fig. 15(b) and (c). In the confined case (Fig. 15(b)), the low-pressure region is caused by the chordwise vortices shown as region L. The size of the positive rotating vortices is almost identical to that of the negative vortices, and every vortex corresponds to a low-pressure strip on the lower surface of the wing. In contrast, for the baseline case (Fig. 15(c)), the positive vortex is weakened, and the corresponding low-pressure area becomes narrower. The low-pressure region does not affect the wing’s lower surface, as a result, each engine corresponds only to one low-pressure strip (region A2 in Fig. 15(c)). Furthermore, due to the spanwise flow, the vortices move away from the lower surface of the wing, as shown in Fig. 15(c). Figure 16 shows the
${C_p}$
distribution and local flow details on the plane are shown in Fig. 15(b) and (c). In the confined case (Fig. 15(b)), the low-pressure region is caused by the chordwise vortices shown as region L. The size of the positive rotating vortices is almost identical to that of the negative vortices, and every vortex corresponds to a low-pressure strip on the lower surface of the wing. In contrast, for the baseline case (Fig. 15(c)), the positive vortex is weakened, and the corresponding low-pressure area becomes narrower. The low-pressure region does not affect the wing’s lower surface, as a result, each engine corresponds only to one low-pressure strip (region A2 in Fig. 15(c)). Furthermore, due to the spanwise flow, the vortices move away from the lower surface of the wing, as shown in Fig. 15(c). Figure 16 shows the
![]() $z$
-averaged
$z$
-averaged
![]() ${C_p}$
on the cut plane, indicating that the distance between the low-pressure region and the wing’s lower surface is larger in the baseline case, resulting in higher pressure on the lower surface and higher
${C_p}$
on the cut plane, indicating that the distance between the low-pressure region and the wing’s lower surface is larger in the baseline case, resulting in higher pressure on the lower surface and higher
![]() ${C_L}$
value.
${C_L}$
value.
4.1.4 The influence of engine space on chordwise vortices
The size of the chordwise vortices is affected by the engine space. Figure 17 shows the
![]() $\omega _x^{\rm{*}}$
distribution on the
$\omega _x^{\rm{*}}$
distribution on the
![]() $x/C$
= 0.7 plane (Fig. 15(a)) with different engine spaces (
$x/C$
= 0.7 plane (Fig. 15(a)) with different engine spaces (
![]() $S/D$
= 1.10, 1.59, 1.85 and 2.78). In the case with smaller engine apace, the large
$S/D$
= 1.10, 1.59, 1.85 and 2.78). In the case with smaller engine apace, the large
![]() $\omega _x^{\rm{*}}$
magnitude region covers a smaller area, which means that the size of the chordwise vortices is smaller. The variation of the chordwise vortices size is a critical factor for the vortices interaction mechanism, which will be discussed later.
$\omega _x^{\rm{*}}$
magnitude region covers a smaller area, which means that the size of the chordwise vortices is smaller. The variation of the chordwise vortices size is a critical factor for the vortices interaction mechanism, which will be discussed later.
4.2 Spanwise vortices
4.2.1 Overall flow structure
As
![]() $S/D$
decreases, the spanwise flow develops into spanwise vortices, as shown in Fig. 18 for case
$S/D$
decreases, the spanwise flow develops into spanwise vortices, as shown in Fig. 18 for case
![]() $S/D$
= 1.59 and
$S/D$
= 1.59 and
![]() $S/D$
= 1.85. The streamlines are coloured by
$S/D$
= 1.85. The streamlines are coloured by
![]() $\omega _x^{\rm{*}}$
, with the chordwise vortices located near the ground, represented by the blue and red streamlines. The spanwise vortices are located between the chordwise vortices and the wing, developing from the wing tip region to the wing root along the spanwise direction, as shown as the black arrows. The flow physics related to the spanwise vortex will be explained with the case of
$\omega _x^{\rm{*}}$
, with the chordwise vortices located near the ground, represented by the blue and red streamlines. The spanwise vortices are located between the chordwise vortices and the wing, developing from the wing tip region to the wing root along the spanwise direction, as shown as the black arrows. The flow physics related to the spanwise vortex will be explained with the case of
![]() $S/D$
= 1.10, as shown in Fig. 19, where the chordwise vortices are small and the spanwise vortex is the main flow structure under the wing. Later, the impact of engine space on the spanwise vortex will be discussed.
$S/D$
= 1.10, as shown in Fig. 19, where the chordwise vortices are small and the spanwise vortex is the main flow structure under the wing. Later, the impact of engine space on the spanwise vortex will be discussed.
Table 3.
![]() ${C_{L}}$
of the baseline case and the confined case,
${C_{L}}$
of the baseline case and the confined case,
![]() $S/D$
= 2.78, CFD
$S/D$
= 2.78, CFD


Figure 13.
![]() ${C_p}$
distribution on the wing lower surface, baseline and confined,
${C_p}$
distribution on the wing lower surface, baseline and confined,
![]() $S/D$
= 2.78, CFD.
$S/D$
= 2.78, CFD.

Figure 14. Chordwise averaged
![]() ${C_p}$
distribution, baseline and confined,
${C_p}$
distribution, baseline and confined,
![]() $S/D$
= 2.78, CFD.
$S/D$
= 2.78, CFD.

Figure 15.
![]() ${C_p}$
distribution and local flow details on
${C_p}$
distribution and local flow details on
![]() $x/C$
= 0.7 plane,
$x/C$
= 0.7 plane,
![]() $S/D$
= 2.78, CFD.
$S/D$
= 2.78, CFD.

Figure 16. Spanwise averaged
![]() ${C_p}$
distribution of
${C_p}$
distribution of
![]() $x/C$
= 0.7 plane,
$x/C$
= 0.7 plane,
![]() $S/D$
= 2.78, CFD.
$S/D$
= 2.78, CFD.

Figure 17.
![]() $\omega _x^{\rm{*}}$
distribution on plane
$\omega _x^{\rm{*}}$
distribution on plane
![]() $x/C$
= 0.7,
$x/C$
= 0.7,
![]() $S/D$
= 1.10, 1.59, 1.85 and 2.78, baseline, CFD.
$S/D$
= 1.10, 1.59, 1.85 and 2.78, baseline, CFD.

Figure 18. Streamlines of the main flow structures,
![]() $S/D$
= 1.59 and
$S/D$
= 1.59 and
![]() $S/D$
= 1.85, CFD.
$S/D$
= 1.85, CFD.

Figure 19. Streamlines of the main flow structures,
![]() $S/D$
= 1.10, CFD.
$S/D$
= 1.10, CFD.
With a lower
![]() $S/D$
of 1.10, the flow field under the wing is dominated by the spanwise vortex. Figure 19 displays the overall flow structures of case
$S/D$
of 1.10, the flow field under the wing is dominated by the spanwise vortex. Figure 19 displays the overall flow structures of case
![]() $S/D$
= 1.10. The 2D streamlines on the middle span cut plane, denoted as ‘M’, indicate that the engine outlet jets impinge vertically on the ground and turn into ground jets flowing horizontally along the ground. Additionally, the 3D streamlines are released from the low-pressure regions under the wing, with the colour of the 3D streamlines representing the pressure coefficient (
$S/D$
= 1.10. The 2D streamlines on the middle span cut plane, denoted as ‘M’, indicate that the engine outlet jets impinge vertically on the ground and turn into ground jets flowing horizontally along the ground. Additionally, the 3D streamlines are released from the low-pressure regions under the wing, with the colour of the 3D streamlines representing the pressure coefficient (
![]() ${C_p}$
) value. Region A in Fig. 19 shows the spanwise vortex, which covers a majority portion of the span. The low-pressure area resulting from the spanwise vortex has a significant effect on wing lift loss.
${C_p}$
) value. Region A in Fig. 19 shows the spanwise vortex, which covers a majority portion of the span. The low-pressure area resulting from the spanwise vortex has a significant effect on wing lift loss.
4.2.2 Flow mechanism of spanwise vortices
The spanwise vortices are induced by the high velocity jets. The formation mechanism of the spanwise vortex is illustrated in Fig. 20 based on the streamlines and normalised velocity (
![]() ${V^{\rm{*}}}$
) distribution on the mid-span plane M (Fig. 19). The red arrows labeled as A1 in Fig. 20 represent the vertical jets from the engine outlet that impinge on the ground, becoming ground jets along the ground. The velocity of the vertical and ground jets is higher than that of the area around them. Due to the viscous effect, the air around the jets is entrained, as shown by the blue arrows labeled as A2. A portion of the mass flow rate of A2 enters the underwing space from the wing leading edge area, as indicated by the green arrow labeled as ‘A3’. The flow directions of A2 and A3 are opposite, and the spanwise vortex is induced between them (the white streamline).
${V^{\rm{*}}}$
) distribution on the mid-span plane M (Fig. 19). The red arrows labeled as A1 in Fig. 20 represent the vertical jets from the engine outlet that impinge on the ground, becoming ground jets along the ground. The velocity of the vertical and ground jets is higher than that of the area around them. Due to the viscous effect, the air around the jets is entrained, as shown by the blue arrows labeled as A2. A portion of the mass flow rate of A2 enters the underwing space from the wing leading edge area, as indicated by the green arrow labeled as ‘A3’. The flow directions of A2 and A3 are opposite, and the spanwise vortex is induced between them (the white streamline).

Figure 20. Streamlines and
![]() ${V^{\rm{*}}}$
distribution on plane M,
${V^{\rm{*}}}$
distribution on plane M,
![]() $S/D$
= 1.10, CFD.
$S/D$
= 1.10, CFD.
4.2.3 The impact of the spanwise vortices on the wing aerodynamic performance
Low-pressure region caused by the spanwise vortex can be observed on the wing lower surface, which is the main reason of the wing lift loss. Figure 21 shows the
![]() ${C_p}$
distribution on the wing lower surface of case
${C_p}$
distribution on the wing lower surface of case
![]() $S/D$
= 1.10. The low pressure in region A is caused by the spanwise vortex, which covers most area of the wing lower surface. Region B is caused by the wing tip vortex, and the affect area is small. The
$S/D$
= 1.10. The low pressure in region A is caused by the spanwise vortex, which covers most area of the wing lower surface. Region B is caused by the wing tip vortex, and the affect area is small. The
![]() ${C_L}$
of this case is -0.304.
${C_L}$
of this case is -0.304.

Figure 21.
![]() ${C_p}$
distribution on wing lower surface,
${C_p}$
distribution on wing lower surface,
![]() $S/D$
= 1.10, CFD.
$S/D$
= 1.10, CFD.
4.3 The influence of engine spacing on vortices interaction
The wing lift loss is mainly attributed to the low-pressure region caused by the spanwise vortices. The covered range and the strength are two critical parameters of the spanwise vortices. These two parameters are affected by the vortices interaction with the chordwise vortices. The evaluation methods and the variation mechanism of the range and strength of the spanwise vortices are studied in this section.
4.3.1 Evaluation of the spanwise vortices range
One critical characteristic of the spanwise vortex is that positive velocity in
![]() $x$
direction (A3 in Fig. 20) is induced. Therefore,
$x$
direction (A3 in Fig. 20) is induced. Therefore,
![]() $x$
-axis positions without positive
$x$
-axis positions without positive
![]() $x$
-axis flow underneath the wing can be considered out of the range of the spanwise vortex. The spanwise averaged
$x$
-axis flow underneath the wing can be considered out of the range of the spanwise vortex. The spanwise averaged
![]() $x$
-axis velocity (
$x$
-axis velocity (
![]() ${\bar V_x}$
) is calculated to determine the range of the spanwise vortex. To exclude the influence of the wing tip vortex, the integral range is from the wing root to
${\bar V_x}$
) is calculated to determine the range of the spanwise vortex. To exclude the influence of the wing tip vortex, the integral range is from the wing root to
![]() $z$
= 2.5
$z$
= 2.5
![]() $C$
.
$C$
.
![]() ${\bar V_x}\left( {x,y} \right)$
is defined as below:
${\bar V_x}\left( {x,y} \right)$
is defined as below:
![]() ${y_0}$
is defined as the height where
${y_0}$
is defined as the height where
![]() ${\bar V_x}\left( {x,y} \right)$
equals to 0:
${\bar V_x}\left( {x,y} \right)$
equals to 0:
Figure 22 shows the
![]() ${y_0}/h$
of different
${y_0}/h$
of different
![]() $S/D$
cases. The regions where
$S/D$
cases. The regions where
![]() $y{y_0}$
denote the upper parts of the spanwise vortices, where
$y{y_0}$
denote the upper parts of the spanwise vortices, where
![]() ${\bar V_x}\left( {x,y} \right)0$
. As
${\bar V_x}\left( {x,y} \right)0$
. As
![]() $S/D$
increases from 1.10 to 1.59, the vertical range of the spanwise vortex decreases. As
$S/D$
increases from 1.10 to 1.59, the vertical range of the spanwise vortex decreases. As
![]() $S/D$
increases from 1.59 to 2.78, both the vertical and horizontal range of the spanwise vortex decrease and the spanwise vortex is confined around the wing trailing edge.
$S/D$
increases from 1.59 to 2.78, both the vertical and horizontal range of the spanwise vortex decrease and the spanwise vortex is confined around the wing trailing edge.

Figure 22.
![]() ${y_0}/h$
distributon,
${y_0}/h$
distributon,
![]() $S/D$
= 1.10, 1.59, 1.85 and 2.78, CFD.
$S/D$
= 1.10, 1.59, 1.85 and 2.78, CFD.
4.3.2 Mechanism of the spanwise vortices range variation
The
![]() $x$
-axis velocity under the wing is the key parameter determining the range of the spanwise vortices. Figure 23 shows the normalised
$x$
-axis velocity under the wing is the key parameter determining the range of the spanwise vortices. Figure 23 shows the normalised
![]() $x$
-axis velocity (
$x$
-axis velocity (
![]() $V_x^{\rm{*}}$
) distribution on the five cut planes of
$V_x^{\rm{*}}$
) distribution on the five cut planes of
![]() $x/C$
= 0.1, 0.3, 0.5, 0.7 and 0.9 in the cases of
$x/C$
= 0.1, 0.3, 0.5, 0.7 and 0.9 in the cases of
![]() $S/D$
= 1.59 and 1.85. The negative
$S/D$
= 1.59 and 1.85. The negative
![]() $V_x^{\rm{*}}$
areas correspond to the ground jet, the fountain flow and the chordwise vortices. Due to the viscous shear stress, these negative
$V_x^{\rm{*}}$
areas correspond to the ground jet, the fountain flow and the chordwise vortices. Due to the viscous shear stress, these negative
![]() $V_x^{\rm{*}}$
flow structures decelerate when transporting towards the wing leading edge (i.e.
$V_x^{\rm{*}}$
flow structures decelerate when transporting towards the wing leading edge (i.e.
![]() $x/C$
decreases), and the area of negative
$x/C$
decreases), and the area of negative
![]() $V_x^{\rm{*}}$
region increases, as shown in Fig. 23(a)–(e). Consequently,
$V_x^{\rm{*}}$
region increases, as shown in Fig. 23(a)–(e). Consequently,
![]() ${y_0}/h$
increase as
${y_0}/h$
increase as
![]() $x/C$
decreases, as shown in Fig. 22.
$x/C$
decreases, as shown in Fig. 22.

Figure 23.
![]() $V_x^{\rm{*}}$
distribution on different chordwise planes,
$V_x^{\rm{*}}$
distribution on different chordwise planes,
![]() $S/D$
= 1.59 and 1.85, CFD.
$S/D$
= 1.59 and 1.85, CFD.
The engine space also has a major impact on
![]() ${y_0}/h$
. As
${y_0}/h$
. As
![]() $S/D$
increases, the size of chordwise vortices expands, and the area of negative
$S/D$
increases, the size of chordwise vortices expands, and the area of negative
![]() $V_x^{\rm{*}}$
flow increases, which can be observed by comparing Fig. 23(a)–(e) with Fig. 23(f)–(j). Therefore, as shown in Fig. 22,
$V_x^{\rm{*}}$
flow increases, which can be observed by comparing Fig. 23(a)–(e) with Fig. 23(f)–(j). Therefore, as shown in Fig. 22,
![]() ${y_0}/h$
increases with
${y_0}/h$
increases with
![]() $S/D$
.
$S/D$
.
As shown in Fig. 23(i) and (j), where
![]() $S/D$
is high and
$S/D$
is high and
![]() $x/C$
is low, positive
$x/C$
is low, positive
![]() $V_x^{\rm{*}}$
area can hardly be found where
$V_x^{\rm{*}}$
area can hardly be found where
![]() $z/C2.5$
, which explains that
$z/C2.5$
, which explains that
![]() ${y_0}/h$
does not exist where
${y_0}/h$
does not exist where
![]() $x/C0.4$
for
$x/C0.4$
for
![]() $S/D$
= 1.85 case in Fig. 22. It is considered that the spanwise vortex hardly occurs at these
$S/D$
= 1.85 case in Fig. 22. It is considered that the spanwise vortex hardly occurs at these
![]() $x$
-axis positions. As engine space increases, the range of the spanwise vortices decreases.
$x$
-axis positions. As engine space increases, the range of the spanwise vortices decreases.
4.3.3 Evaluation of the spanwise vortices strength
The convective term in the Navier-Stokes (N-S) equation can be used to evaluate the strength of the spanwise vortices [Reference Bai and Zhou34]. To investigate the chordwise characteristics of the spanwise vortices, the
![]() $x$
component of the steady N-S equation is concerned (the body force is negligible):
$x$
component of the steady N-S equation is concerned (the body force is negligible):
where the first term on the right side is the convective term. At any
![]() $x$
-axis location, the normalised area averaged value of the convection term in the upper part of the spanwise vortex is defined as:
$x$
-axis location, the normalised area averaged value of the convection term in the upper part of the spanwise vortex is defined as:
where WLS means the wing lower surface.
Figure 24 shows the
![]() ${\overline {CT} ^{\rm{*}}}$
distribution of cases with different engine spaces. The points of
${\overline {CT} ^{\rm{*}}}$
distribution of cases with different engine spaces. The points of
![]() ${\overline {CT} ^{\rm{*}}}$
= 0 are considered to be the positions of vortex centres, which are identified as ‘P1’, ‘P2’, and ‘P3’ for
${\overline {CT} ^{\rm{*}}}$
= 0 are considered to be the positions of vortex centres, which are identified as ‘P1’, ‘P2’, and ‘P3’ for
![]() $S/D$
= 1.10, 1.59 and 1.85, respectively. The absolute magnitude of
$S/D$
= 1.10, 1.59 and 1.85, respectively. The absolute magnitude of
![]() ${\overline {CT} ^{\rm{*}}}$
represents the strength of the spanwise vortex. Higher
${\overline {CT} ^{\rm{*}}}$
represents the strength of the spanwise vortex. Higher
![]() $| {{{\overline {CT} }^{\rm{*}}}} |$
denotes a stronger vortex and larger absolute value of
$| {{{\overline {CT} }^{\rm{*}}}} |$
denotes a stronger vortex and larger absolute value of
![]() $\partial P/\partial x$
according to Equation (6). This indicates greater rate of pressure variation and lower pressure surrounding the spanwise vortices. As
$\partial P/\partial x$
according to Equation (6). This indicates greater rate of pressure variation and lower pressure surrounding the spanwise vortices. As
![]() $S/D$
increasing from 1.10 to 1.85, the vortex strength increases. As
$S/D$
increasing from 1.10 to 1.85, the vortex strength increases. As
![]() $S/D$
increasing to 2.78, the vortex strength decreases.
$S/D$
increasing to 2.78, the vortex strength decreases.

Figure 24.
![]() ${\overline {CT} ^{\rm{*}}}$
distribution,
${\overline {CT} ^{\rm{*}}}$
distribution,
![]() $S/D$
= 1.10, 1.59, 1.85 and 2.78, CFD.
$S/D$
= 1.10, 1.59, 1.85 and 2.78, CFD.
4.3.4 The influence of vortices interaction on spanwise vortex strength
The shear layer amid the spanwise vortex and the fountain flow affects the strength of the spanwise vortex. Figure 25 shows the normalised
![]() $z$
vorticity (
$z$
vorticity (
![]() $\omega _z^{\rm{*}}$
) distribution on
$\omega _z^{\rm{*}}$
) distribution on
![]() $x/C$
= 0.7 plane (Fig. 15(a)) in cases of different
$x/C$
= 0.7 plane (Fig. 15(a)) in cases of different
![]() $S/D$
. The low
$S/D$
. The low
![]() $\omega _z^{\rm{*}}$
region ‘SL’ in Fig. 25(b) represents a typical shear layer. The spanwise flow redirects the fountain flow towards the negative
$\omega _z^{\rm{*}}$
region ‘SL’ in Fig. 25(b) represents a typical shear layer. The spanwise flow redirects the fountain flow towards the negative
![]() $z$
-axis direction (Fig.12). Moreover, the
$z$
-axis direction (Fig.12). Moreover, the
![]() $x$
-velocity of the fountain flow is higher that of the spanwise flow occurring between the chordwise vortices and the wing. Consequently, an
$x$
-velocity of the fountain flow is higher that of the spanwise flow occurring between the chordwise vortices and the wing. Consequently, an
![]() $x$
-velocity gradient exists in the
$x$
-velocity gradient exists in the
![]() $y$
-direction, resulting in the development of a shear layer.
$y$
-direction, resulting in the development of a shear layer.

Figure 25.
![]() $\omega _z^{\rm{*}}$
distribution on
$\omega _z^{\rm{*}}$
distribution on
![]() $x/C$
= 0.7 plane, CFD.
$x/C$
= 0.7 plane, CFD.
Increasing
![]() $S/D$
triggers an increase in the chordwise vortex size and fountain flow height, consequently leading to a closer proximity of the shear layer to the wing’s surface. Figure 26 shows the spanwise averaged
$S/D$
triggers an increase in the chordwise vortex size and fountain flow height, consequently leading to a closer proximity of the shear layer to the wing’s surface. Figure 26 shows the spanwise averaged
![]() $\omega _z^{\rm{*}}$
of the planes illustrated in Fig. 25. The regions located around the valley points correspond to the shear layers, while the areas between the valley points and the top represent the spanwise vortex for cases with
$\omega _z^{\rm{*}}$
of the planes illustrated in Fig. 25. The regions located around the valley points correspond to the shear layers, while the areas between the valley points and the top represent the spanwise vortex for cases with
![]() $S/D$
values ranging from 1.10 to 1.85. As
$S/D$
values ranging from 1.10 to 1.85. As
![]() $S/D$
increases, the height of the valley point rises, leading to an increase in the magnitude of
$S/D$
increases, the height of the valley point rises, leading to an increase in the magnitude of
![]() $\omega _z^{\rm{*}}$
between the valley point and the top. This behaviour implies that the strength of the spanwise vortex augments. However, for the
$\omega _z^{\rm{*}}$
between the valley point and the top. This behaviour implies that the strength of the spanwise vortex augments. However, for the
![]() $S/D$
= 2.78 case, the shear layer is situated in very close proximity to the top, resulting in the almost non-existent observation of the spanwise vortex.
$S/D$
= 2.78 case, the shear layer is situated in very close proximity to the top, resulting in the almost non-existent observation of the spanwise vortex.

Figure 26. Spanwise averaged
![]() $\omega _z^{\rm{*}}$
distribution on
$\omega _z^{\rm{*}}$
distribution on
![]() $x/C$
= 0.7 plane, CFD.
$x/C$
= 0.7 plane, CFD.
4.4 The competition between the vortices interaction effects on range and strength
Figure 27 shows the variation of
![]() ${C_L}$
in relation to different
${C_L}$
in relation to different
![]() $S/D$
. The results reveal a non-linear trend, where
$S/D$
. The results reveal a non-linear trend, where
![]() ${C_L}$
reduces initially and then increases as the space between the engines widens. This trend is attributed mainly to the competition between vortices interaction effects on the range and strength of the spanwise vortices.
${C_L}$
reduces initially and then increases as the space between the engines widens. This trend is attributed mainly to the competition between vortices interaction effects on the range and strength of the spanwise vortices.

Figure 27.
![]() ${C_L}$
as a function of
${C_L}$
as a function of
![]() $S/D$
, CFD.
$S/D$
, CFD.
When
![]() $S/D$
increases from 1.10 to 1.59, the spanwise vortex is mainly influenced in the strength aspect, and the range is not obviously affected, as shown as phase 1 in Fig. 28. The spanwise averaged
$S/D$
increases from 1.10 to 1.59, the spanwise vortex is mainly influenced in the strength aspect, and the range is not obviously affected, as shown as phase 1 in Fig. 28. The spanwise averaged
![]() ${C_p}$
distribution on the wing lower surface is shown in Fig. 29. The low-pressure regions are mainly caused by the spanwise vortices. Compared with the case of
${C_p}$
distribution on the wing lower surface is shown in Fig. 29. The low-pressure regions are mainly caused by the spanwise vortices. Compared with the case of
![]() $S/D$
= 1.10, the spanwise vortex in the
$S/D$
= 1.10, the spanwise vortex in the
![]() $S/D$
= 1.59 case has higher strength, which causes lower
$S/D$
= 1.59 case has higher strength, which causes lower
![]() ${C_p}$
and
${C_p}$
and
![]() ${C_L}$
(Fig. 27).
${C_L}$
(Fig. 27).

Figure 28. Sketch of the competition mechanism.

Figure 29. Spanwise averaged
![]() ${C_p}$
distribution on wing lower surfaces, CFD.
${C_p}$
distribution on wing lower surfaces, CFD.

Figure 30. Pressure distribution on different spanwise locations on the wing lower surface, EXP and CFD.
As
![]() $S/D$
increases from 1.59 to 1.85, the vortices interaction effects on spanwise vortex strength and range both play important roles, which falls in the range of phase 2 in Fig. 28. As shown in Fig. 29, the
$S/D$
increases from 1.59 to 1.85, the vortices interaction effects on spanwise vortex strength and range both play important roles, which falls in the range of phase 2 in Fig. 28. As shown in Fig. 29, the
![]() ${C_p}$
gradient of
${C_p}$
gradient of
![]() $S/D$
= 1.85 near the low-pressure region is higher than that of
$S/D$
= 1.85 near the low-pressure region is higher than that of
![]() $S/D$
= 1.59, which is caused by higher spanwise vortex strength and resulting higher absolute value of
$S/D$
= 1.59, which is caused by higher spanwise vortex strength and resulting higher absolute value of
![]() $\partial P/\partial x$
. However, the position of the low
$\partial P/\partial x$
. However, the position of the low
![]() ${C_p}$
region moves to the trailing edge, and the range becomes smaller. This is caused by the range aspect of the vortices interaction influences. Combining the effects in vortex range and strength, the overall
${C_p}$
region moves to the trailing edge, and the range becomes smaller. This is caused by the range aspect of the vortices interaction influences. Combining the effects in vortex range and strength, the overall
![]() ${C_p}$
in the case of
${C_p}$
in the case of
![]() $S/D$
= 1.85 is higher than that of
$S/D$
= 1.85 is higher than that of
![]() $S/D$
= 1.59, and therefore, the
$S/D$
= 1.59, and therefore, the
![]() ${C_L}$
is higher.
${C_L}$
is higher.
As
![]() $S/D$
increases from 1.85 to 2.78, the spanwise vortex is mainly affected in the range aspect, and the strength enhancement effect almost disappears, as shown as phase 3 in Fig. 28. As shown in Fig. 29, in the case of
$S/D$
increases from 1.85 to 2.78, the spanwise vortex is mainly affected in the range aspect, and the strength enhancement effect almost disappears, as shown as phase 3 in Fig. 28. As shown in Fig. 29, in the case of
![]() $S/D$
= 2.78, the low-pressure region due to the spanwise vortex almost vanishes, and both
$S/D$
= 2.78, the low-pressure region due to the spanwise vortex almost vanishes, and both
![]() ${C_p}$
and
${C_p}$
and
![]() ${C_L}$
are higher.
${C_L}$
are higher.
In the CFD investigation, the minimum
![]() ${C_L}$
is achieved at
${C_L}$
is achieved at
![]() $S/D$
= 1.59, as shown in Fig. 27. In the experimental investigation, the pressure distribution on specified locations for
$S/D$
= 1.59, as shown in Fig. 27. In the experimental investigation, the pressure distribution on specified locations for
![]() $S/D$
= 1.59 and 2.78 was measured, with the locations shown in Fig. 8(a). As shown in Fig. 30, low-pressure regions can be observed in the case of
$S/D$
= 1.59 and 2.78 was measured, with the locations shown in Fig. 8(a). As shown in Fig. 30, low-pressure regions can be observed in the case of
![]() $S/D$
= 1.59, however, the low-pressure regions almost disappear in
$S/D$
= 1.59, however, the low-pressure regions almost disappear in
![]() $S/D$
= 2.78, which aligns with the conclusion from the CFD investigation.
$S/D$
= 2.78, which aligns with the conclusion from the CFD investigation.
When designing eVTOL distributed propulsion aircraft, designers should choose a proper engine space. In the configuration investigated in this paper,
![]() $S/D$
between 1.2 and 1.8 should be avoided.
$S/D$
between 1.2 and 1.8 should be avoided.
5.0 Conclusions
The lift loss caused by the ground effects can significantly reduce the payload and the controllability of distributed propulsion VTOL aircrafts. The coupling of the jets produced by distributed engines with the wing creates a highly intertwined scenario. This paper investigated a VTOL model with the distributed engines installed on the wing trailing edge. The effect of
![]() $S/D$
on the vortex structures is analysed. The following conclusions are drawn:
$S/D$
on the vortex structures is analysed. The following conclusions are drawn:
Chordwise vortices and spanwise vortices are observed underneath the wing. Chordwise vortices develop from the engine gap region, which is induced by the engine exit jets and the fountain flow. The spanwise vortices occurs between chordwise vortices and the wing lower surface, which are induced by the engine exit jets and the ground jets.
As
 $S/D$
increases, the size of the chordwise vortices increases. With a small
$S/D$
increases, the size of the chordwise vortices increases. With a small
 $S/D$
= 1.10, the size of chordwise vortices is smaller than the spanwise vortex, and the flow is dominated by the spanwise vortex. With a large
$S/D$
= 1.10, the size of chordwise vortices is smaller than the spanwise vortex, and the flow is dominated by the spanwise vortex. With a large
 $S/D$
= 2.78, the size of chordwise vortices is larger than the spanwise vortex, and the flow is dominated by the chordwise vortices.
$S/D$
= 2.78, the size of chordwise vortices is larger than the spanwise vortex, and the flow is dominated by the chordwise vortices.The range and strength of the spanwise vortices are affected by the vortices interaction. As the chordwise vortex size increases, more space below the wing is occupied by the chordwise vortices and range of the spanwise vortex is narrowed. Meanwhile, the shear layer around the fountain flow lifts, which makes the shear layer closer to the centre of the spanwise vortex. As a result, the vorticity magnitude within the spanwise vortex increases, and the strength of the spanwise vortex increases.
The range aspect influence of the vortices interaction tends to decrease the range of the spanwise vortex, and narrow the low-pressure region on the wing lower surface, which results in higher
 ${C_L}$
. The strength aspect tends to increase the strength of the spanwise vortex, and decrease the pressure on the wing lower surface, which results in lower
${C_L}$
. The strength aspect tends to increase the strength of the spanwise vortex, and decrease the pressure on the wing lower surface, which results in lower
 ${C_L}$
. The range aspect and the strength aspect compete with each other. As
${C_L}$
. The range aspect and the strength aspect compete with each other. As
 $S/D$
increases, the strength effects decrease, and the range effects increase. As an overall result,
$S/D$
increases, the strength effects decrease, and the range effects increase. As an overall result,
 ${C_L}$
first decreases and then increases.
${C_L}$
first decreases and then increases.
Acknowledgements
The authors would like to acknowledge the support of National Natural Science Foundation of China (NSFC), Grant No.52076001, No.91752106; National Science and Technology Major Project (2019-II-0011-0031); Advanced Jet Propulsion Innovation Center (AEAC), funding number HKCX2022-01-015; Key research and development program of Jiangxi Province (20223BBE51003).