Sir,

The modelling of heat and vapor flows through snow continues to be of interest in work on snow metamorphism and heat transfer. The effect of temperature on the vapor pressure of ice is of interest in several fields and it is worth reviewing how vapor pressure is approximated, and in examining some of the consequences of those approximations. While most are good approximations to the vapor pressure, they are not necessarily good approximations to its derivatives.

The flux of vapor (J) in the vertical direction (z) due to molecular diffusion depends on the density gradient, or

(1)

where D is the diffusion coefficient and vapor density (ρ) is given by the ideal gas law,

(2)

where ρ is vapor pressure, R is the gas constant for water vapor, and T is the absolute temperature. Given that the temperature gradient is conveniently measured, the flux is usually expressed with (dρ/dt)(dt/dz) where ρ is obtained from the ideal gas law and the Clausius-Clapeyron equation,

(3)

where L is the latent heat of sublimation, v is the specific volume of the gas, and V is the specific volume of the solid. When continuity is used to balance the rate of condensation with the gradient of flux, the second derivative is taken (i.e. Reference Palm and TveitereidPalm and Tveitereid, 1979). Given that the gradients of approximations are used, it is necessary to establish the accuracy of the gradients, apart from the accuracy of the approximations themselves.

Reference WashburnWashburn (1924) derived the dependence of vapor pressure on temperature by integrating the Clausius-Clapeyron equation using the latent heat at 0°C, the heat capacities of ice and water vapor at 0°C, and measured values of p at 0°, −50°, and −100°C. He rejected the measured values between 0° and −50°C, and stated that the following equation was more accurate

(4)

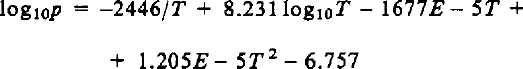
where p is in mm of mercury and T is in K. This formula was used by Reference DorseyDorsey (1940) and by the International critical tables (Reference WashburnWashburn, 1928) as the standard, and is accepted here as the basis for comparison. Only de Reference QuervainQuervain (1963) has used it in snow studies.

A common approximation to this formula can be derived (e.g. Reference ColbeckColbeck, 1980) by making the further assumption that the specific volume of water vapor (v) is much greater than the specific volume of ice, then

(5)

where p and 0 are usually taken as the triple point. Reference Giddings and LaChappelleGiddings and LaChapelle (1962) used the Clausius-Clapeyron equation and an approximation to Equation (5), while Reference ColbeckColbeck (1980) used Equation (5) as well as the analogous relationships between pressure and curvature, and temperature and curvature. Taking L as 2838 Jg⁻¹ (Reference Rossini, Wagman, Evans, Levine and JaffeRossini and others, 1952), R as 0.4619 Jg⁻¹ K⁻¹, and po as 610.5 Pa at 273.1 K, Washburn’s equation can be approximated by Equation (5) with great accuracy. Even the second derivative of this function is extremely close to Washburn’s as shown in Figure 1. Thus, Equation (5) is a very close approximation to Washburn’s formula for nearly all applications.

Fig. 1. Ratios of the derivatives versus temperature, (a) Second derivative: Yosida’s over Washburn’s equation, (b) First derivative: Yosida’s over Washburn’s equation, (c) and (d) First and second derivatives: Equation (5) over Washburn’s equation.

Reference YosidaYosida (1950) suggested and many have used an approximation to Equation (5). This is derived by setting T in the numerator of the exponential of Equation (5) equal to an average value in the temperature range of interest. The relationship is then simplified to

(6)

where c has generally been taken as 0.0857 K⁻¹ and p₀ as 611 or 642 Pa (Reference YenYen, 1962; de Reference QuervainQuervain, 1973; Reference PerlaPerla, 1978; Reference Palm and TveitereidPalm and Tveitereid, 1979; Reference SommerfeldSommerfeld, 1983; Reference Powers, O'Neill and ColbeckPowers and others, 1985). Reference YenYen (1962) has even reduced this to a linear approximation and used its derivative, which is in error by more than 200% in his range of temperatures. While the correlation coefficient between Yosida’s and Washburn’s expressions is very high, the derivatives are oí most interest and they are not so well correlated. As shown in Figure 1, the second derivative is off by 20% in this range of temperatures and would be further in error if a wider range of temperatures was of interest, in polar firn for example. The first derivative is used more frequently and incurs only a 5% error in this temperature range. Thus, for most problems in seasonal snow, Yosida’s approximation is adequate, whereas for studies using the second derivative the approximation is questionable. A considerable simplification in the mathematics would have to be achieved before Yosida’s approximation could be justified, whereas Yen’s linearization of the vapor-pressure-temperature relationship is highly suspect, even when it allows analytical solutions.

In summary, Equation (5) is a very good approximation to Washburn’s equation and can also be used to represent its derivatives. Yosida’s approximation continues to receive widespread use because it is also a good approximation, but its most common use is to represent the gradients, not the vapor-pressure-temperature relationship itself. In this regard, its use should be restricted to the first derivative over a narrow range of temperatures. Use of a linear approximation is always discouraged.

I acknowledge the financial support of Project 4A762730-AT42 at U.S. Army CRREL.