1 Introduction and statement of the main result
The p-adic Gross–Zagier formula of Perrin-Riou relates p-adic heights of Heegner points and derivatives of p-adic L-functions. In its original form [Reference Perrin-Riou26], it concerns (modular) elliptic curves over
![]() $\mathbf {Q}$
, and it is proved under two main assumptions: first, that the elliptic curve is p-ordinary; second, that p splits in the field E of complex multiplications of the Heegner points. The formula has applications to both the p-adic and the classical Birch and Swinnerton-Dyer conjecture.
$\mathbf {Q}$
, and it is proved under two main assumptions: first, that the elliptic curve is p-ordinary; second, that p splits in the field E of complex multiplications of the Heegner points. The formula has applications to both the p-adic and the classical Birch and Swinnerton-Dyer conjecture.
The first assumption was removed by Kobayashi [Reference Kobayashi19] (see also [Reference Büyükboduk, Pollack and Sasaki4]). The purpose of this work is to remove the second assumption.
We work in the context of our previous work [Reference Disegni9], which will enable us in [Reference Disegni13] to deduce, from the formula presented here, the analogous one for higher-weight (Hilbert-) modular motives, as well as a version in the universal ordinary family with some new applications. Nevertheless, the new idea we introduce is essentially orthogonal to previous innovations, including those of [Reference Disegni9] (and in fact it can be applied, at least in principle, to the nonordinary case as well). For this reason we start in §1.1 by informally discussing it in the simplest classical case of elliptic curves over
![]() $\mathbf {Q}$
. The general form of our results is presented in §1.2.
$\mathbf {Q}$
. The general form of our results is presented in §1.2.
1.1 The main ideas in a classical context
Classically, Heegner points on the elliptic curve
![]() $A_{/\mathbf {Q}}$
are images of CM points (or divisors) on a modular curve X, under a parametrization
$A_{/\mathbf {Q}}$
are images of CM points (or divisors) on a modular curve X, under a parametrization
![]() $f\colon X\to A$
. More precisely, choosing an imaginary quadratic field E, for each ring class character
$f\colon X\to A$
. More precisely, choosing an imaginary quadratic field E, for each ring class character
 $\chi \colon \mathrm {Gal}\left (\overline {E}/E\right )\to \overline {\mathbf {Q}}^{\times }$
one can construct a point
$\chi \colon \mathrm {Gal}\left (\overline {E}/E\right )\to \overline {\mathbf {Q}}^{\times }$
one can construct a point
![]() $P(f, \chi )\in A_{E}(\chi )$
, the
$P(f, \chi )\in A_{E}(\chi )$
, the
![]() $\chi $
-isotypic part of
$\chi $
-isotypic part of
 $A\left (\overline {E}\right )_{\overline {\mathbf {Q}}}$
. The landmark formula of Gross and Zagier [Reference Gross and Zagier17] relates the height of
$A\left (\overline {E}\right )_{\overline {\mathbf {Q}}}$
. The landmark formula of Gross and Zagier [Reference Gross and Zagier17] relates the height of
![]() $P(f,\chi )$
to the derivative
$P(f,\chi )$
to the derivative
![]() $L'(A_{E}\otimes \chi , 1)$
of the L-function of a twisted base change of A. The analogous formula in p-adic coefficients,Footnote
1
$L'(A_{E}\otimes \chi , 1)$
of the L-function of a twisted base change of A. The analogous formula in p-adic coefficients,Footnote
1
 $$ \begin{align}\begin{aligned} \left\langle P(f,\chi), P\left(f,{\chi}^{-1}\right)\right\rangle\doteq {d\over ds}_{\rvert s=0} L_{p}\left(A_{E}, \chi\cdot\chi_{\mathrm{cyc}}^{s}\right), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\langle P(f,\chi), P\left(f,{\chi}^{-1}\right)\right\rangle\doteq {d\over ds}_{\rvert s=0} L_{p}\left(A_{E}, \chi\cdot\chi_{\mathrm{cyc}}^{s}\right), \end{aligned}\end{align} $$
relates cyclotomic derivatives of p-adic L-functions to p-adic height pairings
![]() $\langle \ , \ \rangle $
. We outline its proof for p-ordinary elliptic curves.
$\langle \ , \ \rangle $
. We outline its proof for p-ordinary elliptic curves.
Review of Perrin-Riou’s proof
Our basic strategy is still Perrin-Riou’s variant of the one of Gross and Zagier; we briefly and informally review it, ignoring, for simplicity of exposition, the role of the character
![]() $\chi $
. Throughout the following discussion, we include pointers to corresponding statements in the main body of the paper, as guideposts meant to assist the reader’s navigation through the more technical framework used there.
$\chi $
. Throughout the following discussion, we include pointers to corresponding statements in the main body of the paper, as guideposts meant to assist the reader’s navigation through the more technical framework used there.
Denoting by
![]() $\varphi $
the ordinary eigenform attached to A, each side of formula (1.1.1) is expressed as the image under a functional ‘p-adic Petersson product with
$\varphi $
the ordinary eigenform attached to A, each side of formula (1.1.1) is expressed as the image under a functional ‘p-adic Petersson product with
![]() $\varphi $
’, denoted by
$\varphi $
’, denoted by
![]() $\ell _{\varphi } =formula~(3.1.6)$
, of a certain kernel function (a p-adic modular form).
$\ell _{\varphi } =formula~(3.1.6)$
, of a certain kernel function (a p-adic modular form).
For the left-hand side of formula (1.1.1), the form in question is the generating series (compare formula (3.3.4))
 $$ \begin{align}\begin{aligned} Z = \sum_{m\geq 1} \left\langle P^{0}, T_{m}P^{0}\right\rangle_{X} {\textbf{q}}^{m} =\sum_{v} Z_{v}, \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} Z = \sum_{m\geq 1} \left\langle P^{0}, T_{m}P^{0}\right\rangle_{X} {\textbf{q}}^{m} =\sum_{v} Z_{v}, \end{aligned} \end{align} $$
where
![]() $P^{0}\in \mathrm {Div}^{0}(X)$
is a degree
$P^{0}\in \mathrm {Div}^{0}(X)$
is a degree
![]() $0$
modification of the CM point
$0$
modification of the CM point
![]() $P\in X$
,
$P\in X$
,
![]() $\langle \ , \ \rangle _{X}$
is a p-adic height pairing on X compatible with the one on A, and the decomposition into a sum running over all the finite places of
$\langle \ , \ \rangle _{X}$
is a p-adic height pairing on X compatible with the one on A, and the decomposition into a sum running over all the finite places of
![]() $\mathbf {Q}$
(compare equation (3.6.1)) follows from a general decomposition of the global height pairing into a sum of local ones. More precisely, global height pairings are valued in the completed tensor product
$\mathbf {Q}$
(compare equation (3.6.1)) follows from a general decomposition of the global height pairing into a sum of local ones. More precisely, global height pairings are valued in the completed tensor product
![]() $H^{\times }\backslash {H}_{\mathbf {A}^{\infty }}^{\times }\hat {\otimes } L$
of the finite idèles of the Hilbert class field H of E, and of a suitable finite extension L of
$H^{\times }\backslash {H}_{\mathbf {A}^{\infty }}^{\times }\hat {\otimes } L$
of the finite idèles of the Hilbert class field H of E, and of a suitable finite extension L of
![]() $\mathbf {Q}_{p}$
. The series
$\mathbf {Q}_{p}$
. The series
![]() $Z_{v}$
collects the local pairings at
$Z_{v}$
collects the local pairings at
![]() $w\mid v$
, each valued in
$w\mid v$
, each valued in
![]() $H_{w}^{\times }\hat {\otimes }L$
.
$H_{w}^{\times }\hat {\otimes }L$
.
The analytic kernel
![]() $\mathscr {I}'$
giving the right-hand side of formula (1.1.1) is the derivative of a p-adic family of mixed theta-Eisenstein series (compare definition (3.2.5)). It also enjoys a decomposition
$\mathscr {I}'$
giving the right-hand side of formula (1.1.1) is the derivative of a p-adic family of mixed theta-Eisenstein series (compare definition (3.2.5)). It also enjoys a decomposition
 $$ \begin{align*} \mathscr{I}'= \sum_{v\neq p} \mathscr{I}^{\prime}_{v}, \end{align*} $$
$$ \begin{align*} \mathscr{I}'= \sum_{v\neq p} \mathscr{I}^{\prime}_{v}, \end{align*} $$
where, unlike in equation (1.1.2), the sum runs over the finite places of
![]() $\mathbf {Q}$
different from p (compare equation (3.5.2)). Once we have established that
$\mathbf {Q}$
different from p (compare equation (3.5.2)). Once we have established that
![]() $Z_{v}\doteq \mathscr {I}_{v}'$
for
$Z_{v}\doteq \mathscr {I}_{v}'$
for
![]() $v\neq p$
by computations similar to those of Gross and Zagier (compare Theorem 3.6.1), it remains to show that the p-adic modular form
$v\neq p$
by computations similar to those of Gross and Zagier (compare Theorem 3.6.1), it remains to show that the p-adic modular form
![]() $Z_{p}$
is annihilated by
$Z_{p}$
is annihilated by
![]() $\ell _{\varphi }$
(compare Proposition 3.6.2).
$\ell _{\varphi }$
(compare Proposition 3.6.2).
In order to achieve this, one aims at showing that after acting on
![]() $Z_{p}$
by a Hecke operator to replace
$Z_{p}$
by a Hecke operator to replace
![]() $P^{0}$
by
$P^{0}$
by
![]() $P^{\left [\varphi \right ]}$
(a lift of the component of its image in the
$P^{\left [\varphi \right ]}$
(a lift of the component of its image in the
![]() $\varphi $
-part of
$\varphi $
-part of
![]() ${\mathrm{Jac}}(X)$
), the resulting form
${\mathrm{Jac}}(X)$
), the resulting form
 $Z_{p}^{\left [\varphi \right ]}$
is p-critical (compare Proposition 3.6.3). That is, its coefficients
$Z_{p}^{\left [\varphi \right ]}$
is p-critical (compare Proposition 3.6.3). That is, its coefficients
 $$ \begin{align*} a_{mp^{s}}:=\left\langle P^{\left[\varphi\right]}, T_{mp^{s}}P^{0} \right\rangle_{X,p} \end{align*} $$
$$ \begin{align*} a_{mp^{s}}:=\left\langle P^{\left[\varphi\right]}, T_{mp^{s}}P^{0} \right\rangle_{X,p} \end{align*} $$
decay p-adically no more slowly than a constant multiple of
![]() $p^{s}$
. The p-shift of Fourier coefficients extends the action on modular forms of the operator
$p^{s}$
. The p-shift of Fourier coefficients extends the action on modular forms of the operator
![]() $\mathrm {U}_{p}$
– which, in contrast, acts by a p-adic unit on the ordinary form
$\mathrm {U}_{p}$
– which, in contrast, acts by a p-adic unit on the ordinary form
![]() $\varphi $
: this implies that p-critical forms are annihilated by
$\varphi $
: this implies that p-critical forms are annihilated by
![]() $\ell _{\varphi }$
.
$\ell _{\varphi }$
.
To study the terms
![]() $a_{mp^{s}}$
, one constructs a sequence of points
$a_{mp^{s}}$
, one constructs a sequence of points
![]() $P_{s}\in X_{H}$
whose fields of definitions are the layers
$P_{s}\in X_{H}$
whose fields of definitions are the layers
![]() $H_{s}$
of the anticyclotomic
$H_{s}$
of the anticyclotomic
![]() $p^{\infty }$
-extension of E. The relations they satisfy allow us to express
$p^{\infty }$
-extension of E. The relations they satisfy allow us to express
 $$ \begin{align*} a_{mp^{s}} = \left\langle P^{\left[\varphi\right]}, D_{m,s}\right\rangle_{X,p}, \end{align*} $$
$$ \begin{align*} a_{mp^{s}} = \left\langle P^{\left[\varphi\right]}, D_{m,s}\right\rangle_{X,p}, \end{align*} $$
where
![]() $D_{m,s}$
is a degree
$D_{m,s}$
is a degree
![]() $0$
divisor supported at Hecke-translates of
$0$
divisor supported at Hecke-translates of
![]() $P_{s}$
, which are all essentially CM points of conductor
$P_{s}$
, which are all essentially CM points of conductor
![]() $p^{s}$
defined over
$p^{s}$
defined over
![]() $H_{s}$
(compare Proposition 4.1.4). By a projection formula for
$H_{s}$
(compare Proposition 4.1.4). By a projection formula for
![]() $X_{H_{s}}\to X_{H}$
, the height
$X_{H_{s}}\to X_{H}$
, the height
![]() $a_{mp^{s}}$
is then a sum, over primes w of H above p, of the images
$a_{mp^{s}}$
is then a sum, over primes w of H above p, of the images
of heights
![]() $h_{m,s,w}$
computed on
$h_{m,s,w}$
computed on
![]() $X_{H_{s,w}}$
, under the norm map
$X_{H_{s,w}}$
, under the norm map
 $N_{s,w}\colon H_{s, w}^{\times }\hat {\otimes }L \to H_{w}^{\times } \hat {\otimes } L$
. Moreover, it can be shown that the L-denominators of
$N_{s,w}\colon H_{s, w}^{\times }\hat {\otimes }L \to H_{w}^{\times } \hat {\otimes } L$
. Moreover, it can be shown that the L-denominators of
 $h_{m,s,w}\in H_{s, w}^{\times }\hat {\otimes }L$
are uniformly bounded (compare Proposition 4.4.1), so that here we may ignore them and think of
$h_{m,s,w}\in H_{s, w}^{\times }\hat {\otimes }L$
are uniformly bounded (compare Proposition 4.4.1), so that here we may ignore them and think of
 $h_{m,s,w}\in H_{s, w}^{\times }\hat {\otimes }\mathscr {O}_{L}$
.
$h_{m,s,w}\in H_{s, w}^{\times }\hat {\otimes }\mathscr {O}_{L}$
.
A simple observation from [Reference Disegni9] is that the valuation
![]() $w\left (h_{m,s,w}\right )$
equals
$w\left (h_{m,s,w}\right )$
equals
 $$ \begin{align}\begin{aligned} m_{X_{H_{w}}}\left( P^{\left[\varphi\right]} ,D_{m,s}\right), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} m_{X_{H_{w}}}\left( P^{\left[\varphi\right]} ,D_{m,s}\right), \end{aligned}\end{align} $$
the intersection multiplicity of the flat extensions (§4.2) of those divisors to some regular integral model
![]() $\mathscr {X}$
of
$\mathscr {X}$
of
![]() $X_{H_{w}}$
. In the split case, it is almost immediate to see that this intersection multiplicity vanishes. This implies that
$X_{H_{w}}$
. In the split case, it is almost immediate to see that this intersection multiplicity vanishes. This implies that
 $$ \begin{align}\begin{aligned} N_{s,w}\left(h_{m,s} \right)\in N_{s,w}\left(\mathscr{O}_{H_{s,w}}^{\times}\right)\hat{\otimes}\mathscr{O}_{L}\subset H_{w}^{\times}\hat{\otimes}\mathscr{O}_{L}.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} N_{s,w}\left(h_{m,s} \right)\in N_{s,w}\left(\mathscr{O}_{H_{s,w}}^{\times}\right)\hat{\otimes}\mathscr{O}_{L}\subset H_{w}^{\times}\hat{\otimes}\mathscr{O}_{L}.\end{aligned}\end{align} $$
Since the extension
![]() $H_{s,w}/H_{w}$
is totally ramified of degree
$H_{s,w}/H_{w}$
is totally ramified of degree
![]() $p^{s}$
, the subset in formula (1.1.4) is
$p^{s}$
, the subset in formula (1.1.4) is
 $ p^{s} \left (\mathscr {O}_{H_{w}}^{\times }\hat {\otimes }\mathscr {O}_{L}\right )\subset p^{s} \left (H_{w}^{\times }\hat {\otimes }\mathscr {O}_{L}\right ) $
, as desired.
$ p^{s} \left (\mathscr {O}_{H_{w}}^{\times }\hat {\otimes }\mathscr {O}_{L}\right )\subset p^{s} \left (H_{w}^{\times }\hat {\otimes }\mathscr {O}_{L}\right ) $
, as desired.
The nonsplit case
In the nonsplit case, the p-adic intersection multiplicity has no reason to vanish. However, the foregoing argument will still go through if we more modestly show that expression (1.1.3) itself decays at least like a multiple of
![]() $p^{s}$
(compare Lemma 4.4.3). The idea to prove this is very simple: we show that if s is large, then for the purposes of computing intersection multiplicities with other divisors
$p^{s}$
(compare Lemma 4.4.3). The idea to prove this is very simple: we show that if s is large, then for the purposes of computing intersection multiplicities with other divisors
![]() $\mathscr {D}$
on
$\mathscr {D}$
on
![]() $\mathscr {X}$
, the Zariski closure of a CM point of conductor at least
$\mathscr {X}$
, the Zariski closure of a CM point of conductor at least
![]() $p^{s}$
can almost be approximated by some irreducible component V of the special fiber of
$p^{s}$
can almost be approximated by some irreducible component V of the special fiber of
![]() $\mathscr {X}$
; hence the multiplicity will be
$\mathscr {X}$
; hence the multiplicity will be
![]() $0$
if
$0$
if
![]() $\mathscr {D}$
arises as a flat extension of its generic fiber. The qualifier ‘almost’ means that the foregoing holds except if
$\mathscr {D}$
arises as a flat extension of its generic fiber. The qualifier ‘almost’ means that the foregoing holds except if
![]() $\lvert \mathscr {D}\rvert $
contains V itself, which will be responsible for a multiplicity error term equal to a constant multiple of
$\lvert \mathscr {D}\rvert $
contains V itself, which will be responsible for a multiplicity error term equal to a constant multiple of
![]() $ p^{s}$
.
$ p^{s}$
.
The approximation result (Proposition 4.3.3) is precisely formulated in an (ultra)metric space of irreducible divisors on the local ring of a regular arithmetic surface, which we introduce following a recent work of García Barroso, González Pérez, and Popescu-Pampu [Reference García Barroso, González Pérez and Popescu-Pampu15]. The proof of the result is also rather simple (albeit not effective), relying on Gross’s theory of quasicanonical liftings [Reference Gross18]. The problem of effectively identifying the approximating divisor V is treated in [Reference Disegni11].
Subtleties
This description ignores several difficulties of a relatively more technical nature, most of which we deal with by the representation-theoretic approach of [Reference Disegni9] (in turn adapted from Yuan, Zhang, and Zhang [Reference Yuan, Zhang and Zhang29]). Namely, we allow for arbitrary modular parametrizations f, resulting in an extra parameter
![]() $\phi $
in the kernels Z and
$\phi $
in the kernels Z and
![]() $\mathscr {I}'$
. By representation-theoretic results, one is free to some extent to choose the parameter
$\mathscr {I}'$
. By representation-theoretic results, one is free to some extent to choose the parameter
![]() $\phi $
to work with without losing generality. A fine choice (or rather a pair of choices) for its p-adic component is dictated by the goal of interpolation, while imposing suitable conditions on its other components allows us to circumvent many obstacles in the proof.
$\phi $
to work with without losing generality. A fine choice (or rather a pair of choices) for its p-adic component is dictated by the goal of interpolation, while imposing suitable conditions on its other components allows us to circumvent many obstacles in the proof.
1.2 Statement
We now describe our result in the general context in which we prove it – which is the same as that of [Reference Disegni9] (and [Reference Yuan, Zhang and Zhang29]), to which we refer for a less terse discussion of the background. (At some points, we find some slightly different formulations or normalizations from those of [Reference Disegni9], to be more natural: see §2.2 for the equivalence.)
Abelian varieties parametrized by Shimura curves
Let F be a totally real field and let
![]() $A_{/F}$
be a simple abelian variety of
$A_{/F}$
be a simple abelian variety of
![]() $\mathrm {GL}_{2}$
-type. Assume that
$\mathrm {GL}_{2}$
-type. Assume that
![]() $L(A,s)$
is modular (this is known in many cases if A is an elliptic curve). Let
$L(A,s)$
is modular (this is known in many cases if A is an elliptic curve). Let
![]() $\mathbf {B}$
be a quaternion algebra over the adèles
$\mathbf {B}$
be a quaternion algebra over the adèles
![]() $\mathbf {A}=\mathbf {A}_{F}$
of F, whose ramification set
$\mathbf {A}=\mathbf {A}_{F}$
of F, whose ramification set
![]() $\Sigma _{\mathbf {B}}$
has odd cardinality and contains all the infinite places. To
$\Sigma _{\mathbf {B}}$
has odd cardinality and contains all the infinite places. To
![]() $\mathbf {B}$
is attached a tower of Shimura curves
$\mathbf {B}$
is attached a tower of Shimura curves
 $\left (X_{U/F}\right )_{U\subset \mathbf {B}^{\infty \times }}$
, with respective Albanese varieties
$\left (X_{U/F}\right )_{U\subset \mathbf {B}^{\infty \times }}$
, with respective Albanese varieties
![]() $J_{U}$
. It carries a canonical system of divisor classes
$J_{U}$
. It carries a canonical system of divisor classes
![]() $\xi _{U}\in {\mathrm{Cl}}(X_{U})_{\mathbf {Q}}$
of degree
$\xi _{U}\in {\mathrm{Cl}}(X_{U})_{\mathbf {Q}}$
of degree
![]() $1$
, providing a system
$1$
, providing a system
![]() $\iota _{\xi }$
of maps
$\iota _{\xi }$
of maps
![]() $\iota _{\xi , U}\in \mathrm {Hom}\,_{F}(X_{U}, J_{U})_{\mathbf {Q}}$
defined by
$\iota _{\xi , U}\in \mathrm {Hom}\,_{F}(X_{U}, J_{U})_{\mathbf {Q}}$
defined by
![]() $P\mapsto P - \deg (P) \xi _{U}$
.
$P\mapsto P - \deg (P) \xi _{U}$
.
The space
 $$ \begin{align*} \pi=\pi_{A, \mathbf{B}}=\varinjlim_{U} \mathrm{Hom}\,^{0}(J_{U}, A) \end{align*} $$
$$ \begin{align*} \pi=\pi_{A, \mathbf{B}}=\varinjlim_{U} \mathrm{Hom}\,^{0}(J_{U}, A) \end{align*} $$
is either zero or a smooth irreducible representation of
![]() $\mathbf {B}^{\times }$
(trivial at the infinite places), with coefficients in the number field
$\mathbf {B}^{\times }$
(trivial at the infinite places), with coefficients in the number field
![]() $M:=\mathrm {End}\,^{0}(A)$
. We assume we are in the case
$M:=\mathrm {End}\,^{0}(A)$
. We assume we are in the case
![]() $\pi =\pi _{A , \mathbf {B}}\neq 0$
, which under the modularity assumption and condition (1.2.2) can be arranged by suitably choosing
$\pi =\pi _{A , \mathbf {B}}\neq 0$
, which under the modularity assumption and condition (1.2.2) can be arranged by suitably choosing
![]() $\mathbf {B}$
. Then for all places
$\mathbf {B}$
. Then for all places
![]() $v\nmid \infty $
, we have
$v\nmid \infty $
, we have
![]() $L_{v}(A, s)=L_{v}(s-1/2 , \pi )$
in
$L_{v}(A, s)=L_{v}(s-1/2 , \pi )$
in
![]() $M\otimes \mathbf {C}$
. We denote by
$M\otimes \mathbf {C}$
. We denote by
![]() $\omega \colon F^{\times }\backslash \mathbf {A}^{\times } \to M^{\times }$
the central character of
$\omega \colon F^{\times }\backslash \mathbf {A}^{\times } \to M^{\times }$
the central character of
![]() $\pi $
. We have a canonical isomorphism
$\pi $
. We have a canonical isomorphism
 $\pi _{A^{\vee }, \mathbf {B}}\cong \pi _{A,\mathbf {B}}^{\vee }$
[Reference Yuan, Zhang and Zhang29, §1.2.2], and we denote by
$\pi _{A^{\vee }, \mathbf {B}}\cong \pi _{A,\mathbf {B}}^{\vee }$
[Reference Yuan, Zhang and Zhang29, §1.2.2], and we denote by
![]() $( \ , \ )_{\pi }\colon \pi _{A, \mathbf {B}}\otimes \pi _{A^{\vee }, \mathbf {B}}\to M $
the duality pairing.
$( \ , \ )_{\pi }\colon \pi _{A, \mathbf {B}}\otimes \pi _{A^{\vee }, \mathbf {B}}\to M $
the duality pairing.
Heegner points
Let
![]() $E/F$
be a CM quadratic extension with associated quadratic character
$E/F$
be a CM quadratic extension with associated quadratic character
![]() $\eta $
, and assume that E admits an
$\eta $
, and assume that E admits an
![]() $\mathbf {A}$
-embedding
$\mathbf {A}$
-embedding
![]() $E_{\mathbf {A}^{}}\hookrightarrow \mathbf {B}^{}$
, which we fix. Then
$E_{\mathbf {A}^{}}\hookrightarrow \mathbf {B}^{}$
, which we fix. Then
![]() $E^{\times }$
acts on the right on
$E^{\times }$
acts on the right on
 $X=\varprojlim _{U}X_{U}$
. The fixed-points subscheme
$X=\varprojlim _{U}X_{U}$
. The fixed-points subscheme
![]() $X^{E^{\times }}\subset X$
is F-isomorphic to
$X^{E^{\times }}\subset X$
is F-isomorphic to
![]() $\mathrm {Spec}\, E^{\mathrm{ab}}$
, and we fix a point
$\mathrm {Spec}\, E^{\mathrm{ab}}$
, and we fix a point
 $P\in X^{E^{\times }}\left (E^{\mathrm{ab}}\right )$
. Let
$P\in X^{E^{\times }}\left (E^{\mathrm{ab}}\right )$
. Let
 $$ \begin{align*} \chi\colon E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times} \cong \mathrm{Gal}\left(E^{\mathrm{ab}}/E\right) \to L(\chi)^{\times} \end{align*} $$
$$ \begin{align*} \chi\colon E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times} \cong \mathrm{Gal}\left(E^{\mathrm{ab}}/E\right) \to L(\chi)^{\times} \end{align*} $$
be a character valued in a field extension of
![]() $L(\chi )\supset M$
, satisfying
$L(\chi )\supset M$
, satisfying
and define
 $$ \begin{align*} A_{E}(\chi):=\left(A\left(E^{\mathrm{ab}}\right)\otimes_{M}L(\chi)_{\chi}\right)^{\mathrm{Gal}\left(E^{\mathrm{ab}}/E\right)}, \end{align*} $$
$$ \begin{align*} A_{E}(\chi):=\left(A\left(E^{\mathrm{ab}}\right)\otimes_{M}L(\chi)_{\chi}\right)^{\mathrm{Gal}\left(E^{\mathrm{ab}}/E\right)}, \end{align*} $$
where
![]() $L(\chi )_{\chi }$
is an
$L(\chi )_{\chi }$
is an
![]() $L(\chi )$
-line with Galois action by
$L(\chi )$
-line with Galois action by
![]() $\chi $
.
$\chi $
.
Then we have a Heegner point functional

(integration for the Haar measure of volume
![]() $1$
) in the space of invariant linear functionals
$1$
) in the space of invariant linear functionals
 $$ \begin{align*} \mathrm{H}\left(\pi_{A, \mathbf{B}},\chi\right)\otimes_{L(\chi)}A_{E}(\chi) ,\qquad \mathrm{H}(\pi,\chi):= \mathrm{Hom}_{E_{\mathbf{A}^{}}^{\times}}(\pi\otimes\chi, L(\chi)), \end{align*} $$
$$ \begin{align*} \mathrm{H}\left(\pi_{A, \mathbf{B}},\chi\right)\otimes_{L(\chi)}A_{E}(\chi) ,\qquad \mathrm{H}(\pi,\chi):= \mathrm{Hom}_{E_{\mathbf{A}^{}}^{\times}}(\pi\otimes\chi, L(\chi)), \end{align*} $$
where
![]() $E_{\mathbf {A}^{}}^{\times }$
acts diagonally. There is a product decomposition
$E_{\mathbf {A}^{}}^{\times }$
acts diagonally. There is a product decomposition
![]() $\mathrm {H}(\pi , \chi )=\bigotimes _{v}\mathrm {H}(\pi _{v}, \chi _{v})$
, where similarly
$\mathrm {H}(\pi , \chi )=\bigotimes _{v}\mathrm {H}(\pi _{v}, \chi _{v})$
, where similarly
 $\mathrm {H}(\pi _{v}, \chi _{v}):=\mathrm {Hom}\,_{E_{v}^{\times }}(\pi _{v}\otimes \chi _{v}, L(\chi ))$
.
$\mathrm {H}(\pi _{v}, \chi _{v}):=\mathrm {Hom}\,_{E_{v}^{\times }}(\pi _{v}\otimes \chi _{v}, L(\chi ))$
.
A local unit of measure for invariant functionals
By foundational local results of Waldspurger, Tunnell, and Saito, the dimension of
![]() $\mathrm {H}(\pi ,\chi )$
(for any representation
$\mathrm {H}(\pi ,\chi )$
(for any representation
![]() $\pi $
of
$\pi $
of
![]() $\mathbf {B}^{\times }$
) is either
$\mathbf {B}^{\times }$
) is either
![]() $0$
or
$0$
or
![]() $1$
. If A is modular and the global root number
$1$
. If A is modular and the global root number
then the set of local root numbers determines a unique quaternion algebra
![]() $\mathbf {B}$
over
$\mathbf {B}$
over
![]() $\mathbf {A}$
, satisfying the conditions already required and containing
$\mathbf {A}$
, satisfying the conditions already required and containing
![]() $E_{\mathbf {A}}$
, such that
$E_{\mathbf {A}}$
, such that
![]() $\pi _{A, \mathbf {B}}\neq 0$
and
$\pi _{A, \mathbf {B}}\neq 0$
and
![]() $\dim _{L(\chi )} \mathrm {H}\left (\pi _{A, \mathbf {B}},\chi \right ) =1$
.Footnote
2
We place ourselves in this case; then there is a canonical factorizable generator
$\dim _{L(\chi )} \mathrm {H}\left (\pi _{A, \mathbf {B}},\chi \right ) =1$
.Footnote
2
We place ourselves in this case; then there is a canonical factorizable generator
 $$ \begin{align*} Q_{\left(, \right), dt} =\prod_{v}Q_{\left(, \right)_{v}, dt_{v}} \in \mathrm{H}(\pi,\chi) \otimes \mathrm{H}\left(\pi^{\vee},\chi^{-1}\right) \end{align*} $$
$$ \begin{align*} Q_{\left(, \right), dt} =\prod_{v}Q_{\left(, \right)_{v}, dt_{v}} \in \mathrm{H}(\pi,\chi) \otimes \mathrm{H}\left(\pi^{\vee},\chi^{-1}\right) \end{align*} $$
depending on the choice of a pairing
![]() $(,)=\prod _{v}(, )_{v}\colon \pi \otimes \pi ^{\vee }\to L(\chi )$
and a measure
$(,)=\prod _{v}(, )_{v}\colon \pi \otimes \pi ^{\vee }\to L(\chi )$
and a measure
![]() $dt=\prod _{v} dt_{v}$
on
$dt=\prod _{v} dt_{v}$
on
![]() $E_{\mathbf {A}^{}}^{\times }/\mathbf {A}^{\times }$
. It is defined locally as follows. Let us use symbols
$E_{\mathbf {A}^{}}^{\times }/\mathbf {A}^{\times }$
. It is defined locally as follows. Let us use symbols
![]() $V_{\left (A, \chi \right )}$
and
$V_{\left (A, \chi \right )}$
and
![]() $V_{\left (A, \chi \right ), v}$
, which we informally think of as denoting (up to abelian factors) the virtual motive over F with coefficients in
$V_{\left (A, \chi \right ), v}$
, which we informally think of as denoting (up to abelian factors) the virtual motive over F with coefficients in
![]() $L(\chi )$
$L(\chi )$
and its local components (the associated local Galois representation or, if v is Archimedean, Hodge structure). Then for each place v of F and any auxiliary
![]() $\iota \colon L(\chi )\hookrightarrow \mathbf {C}$
,Footnote
3
we define
$\iota \colon L(\chi )\hookrightarrow \mathbf {C}$
,Footnote
3
we define
 $$ \begin{align} \mathscr{L}\left(\iota V_{\left(A, \chi\right), v},s\right)&:= {\zeta_{F,v}(2) L\left(1/2+s,\iota \pi_{E,v}\otimes \iota\chi_{v}\right) \over {L(1, \eta_{v})L(1,\iota \pi_{v}, \mathrm{ad})}} \cdot \begin{cases} 1 \quad &\text{if}\ v\ \text{is finite},\\ \pi^{-1} &\text{if}\ v\mid \infty\end{cases} \quad \in \iota L(\chi), \end{align} $$
$$ \begin{align} \mathscr{L}\left(\iota V_{\left(A, \chi\right), v},s\right)&:= {\zeta_{F,v}(2) L\left(1/2+s,\iota \pi_{E,v}\otimes \iota\chi_{v}\right) \over {L(1, \eta_{v})L(1,\iota \pi_{v}, \mathrm{ad})}} \cdot \begin{cases} 1 \quad &\text{if}\ v\ \text{is finite},\\ \pi^{-1} &\text{if}\ v\mid \infty\end{cases} \quad \in \iota L(\chi), \end{align} $$
 $$ \begin{align} Q_{\left(, \right)_{v}, dt_{v}}\left(f_{1, v}, f_{2,v}, \chi_{v}\right)&:= \iota^{-1}\mathscr{L}\left(\iota V_{\left(A, \chi\right),v},0\right)^{-1} \int_{E_{v}^{\times}/F_{v}^{\times}}\chi(t_{v}) \left(\pi_{v}(t_{v})f_{1,v}, f_{2, v}\right)_{v} dt_{v}. \end{align} $$
$$ \begin{align} Q_{\left(, \right)_{v}, dt_{v}}\left(f_{1, v}, f_{2,v}, \chi_{v}\right)&:= \iota^{-1}\mathscr{L}\left(\iota V_{\left(A, \chi\right),v},0\right)^{-1} \int_{E_{v}^{\times}/F_{v}^{\times}}\chi(t_{v}) \left(\pi_{v}(t_{v})f_{1,v}, f_{2, v}\right)_{v} dt_{v}. \end{align} $$
We make the situation more canonical by choosing
![]() $dt=\prod _{v} dt_{v} $
to satisfy
$dt=\prod _{v} dt_{v} $
to satisfy
 $$ \begin{align*} \mathrm{vol}\left(E^{\times}\backslash E_{\mathbf{A}}^{\times}/\mathbf{A}^{\times}, dt\right)=1 \end{align*} $$
$$ \begin{align*} \mathrm{vol}\left(E^{\times}\backslash E_{\mathbf{A}}^{\times}/\mathbf{A}^{\times}, dt\right)=1 \end{align*} $$
and by defining, for any
![]() $f_{3}\in \pi , f_{4}\in \pi ^{\vee }$
such that
$f_{3}\in \pi , f_{4}\in \pi ^{\vee }$
such that
![]() $(f_{3}, f_{4})\neq 0$
,
$(f_{3}, f_{4})\neq 0$
,
 $$ \begin{align}\begin{aligned} Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}};\chi\right) := {Q_{\left( , \right), dt}(f_{1}, f_{2},\chi)\over ( f_{3}, f_{4})}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}};\chi\right) := {Q_{\left( , \right), dt}(f_{1}, f_{2},\chi)\over ( f_{3}, f_{4})}. \end{aligned}\end{align} $$
p-adic heights
Let us fix a prime
![]() $\mathfrak {p}$
of M and denote by p the underlying rational prime. Suppose from now on that for each
$\mathfrak {p}$
of M and denote by p the underlying rational prime. Suppose from now on that for each
![]() $v\mid p$
,
$v\mid p$
,
![]() $A_{F_{v}}$
has
$A_{F_{v}}$
has
![]() $\mathfrak {p}$
-ordinary (potentially good or semistable) reduction. That is, for a sufficiently large finite extension
$\mathfrak {p}$
-ordinary (potentially good or semistable) reduction. That is, for a sufficiently large finite extension
![]() $L\supset M_{\mathfrak {p}}$
, the rational
$L\supset M_{\mathfrak {p}}$
, the rational
![]() $\mathfrak {p}$
-Tate module
$\mathfrak {p}$
-Tate module
![]() $W_{v}:=V_{p}A\otimes _{M} L$
is a reducible
$W_{v}:=V_{p}A\otimes _{M} L$
is a reducible
![]() $2$
-dimensional representation of
$2$
-dimensional representation of
 $\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
:
$\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
:
Fix such a coefficient field L, and for each
![]() $v\mid p$
let
$v\mid p$
let
 $\alpha _{v}\colon F_{v}^{\times }\cong \mathrm {Gal}\left (F_{v}^{\mathrm{ab}}/F_{v}\right )\to L^{\times }$
be the character giving the action on the twist
$\alpha _{v}\colon F_{v}^{\times }\cong \mathrm {Gal}\left (F_{v}^{\mathrm{ab}}/F_{v}\right )\to L^{\times }$
be the character giving the action on the twist
![]() $W_{v}^{+}(-1) $
. The field
$W_{v}^{+}(-1) $
. The field
![]() $L(\chi )$
will from now on be assumed to be an extension of L. Under those conditions, there is a canonical p-adic height pairing
$L(\chi )$
will from now on be assumed to be an extension of L. Under those conditions, there is a canonical p-adic height pairing
 $$ \begin{align*} \langle \ , \ \rangle\colon A_{E}(\chi) \otimes A_{E}^{\vee}\left(\chi^{-1}\right) \to \Gamma_{F}\hat{\otimes}L(\chi), \end{align*} $$
$$ \begin{align*} \langle \ , \ \rangle\colon A_{E}(\chi) \otimes A_{E}^{\vee}\left(\chi^{-1}\right) \to \Gamma_{F}\hat{\otimes}L(\chi), \end{align*} $$
where
 $\Gamma _{F}:= \mathbf {A}^{\times }/\overline {F^{\times }\widehat {\mathscr {O}}^{p , \times }_{F}}$
(the bar denotes Zariski closure). It is normalized ‘over F’ as in [Reference Disegni9, §4.1].
$\Gamma _{F}:= \mathbf {A}^{\times }/\overline {F^{\times }\widehat {\mathscr {O}}^{p , \times }_{F}}$
(the bar denotes Zariski closure). It is normalized ‘over F’ as in [Reference Disegni9, §4.1].
For
![]() $f_{1}, f_{3}\in \pi $
,
$f_{1}, f_{3}\in \pi $
,
![]() $f_{2}, f_{4}\in \pi ^{\vee }$
, and
$f_{2}, f_{4}\in \pi ^{\vee }$
, and
 $P^{\vee } \colon \pi ^{\vee }\otimes \chi \to A_{E}^{\vee }\left (\chi ^{-1}\right )$
the Heegner point functional of the dual, our result will measure the ratio
$P^{\vee } \colon \pi ^{\vee }\otimes \chi \to A_{E}^{\vee }\left (\chi ^{-1}\right )$
the Heegner point functional of the dual, our result will measure the ratio
 $\left \langle P(f_{1}, \chi ), P^{\vee }\left (f_{2}, \chi ^{-1}\right )\right \rangle /( f_{3}, f_{4})_{\pi } $
against the value at the
$\left \langle P(f_{1}, \chi ), P^{\vee }\left (f_{2}, \chi ^{-1}\right )\right \rangle /( f_{3}, f_{4})_{\pi } $
against the value at the
![]() $f_{i}$
of the ‘unit’ Q. The size will be given by the derivative of the p-adic L-function that we now define.
$f_{i}$
of the ‘unit’ Q. The size will be given by the derivative of the p-adic L-function that we now define.
The p-adic L-function
We continue to assume that A is
![]() $\mathfrak {p}$
-ordinary, and review the definition of the p-adic L-function from [Reference Disegni9, Theorem A] (in an equivalent form). We start by defining the space on which it lives. Write
$\mathfrak {p}$
-ordinary, and review the definition of the p-adic L-function from [Reference Disegni9, Theorem A] (in an equivalent form). We start by defining the space on which it lives. Write
 $\Gamma _{F}=\varprojlim _{n}\Gamma _{F,n}$
as the limit of an inverse system of finite groups, and define
$\Gamma _{F}=\varprojlim _{n}\Gamma _{F,n}$
as the limit of an inverse system of finite groups, and define
 $$ \begin{align}\begin{aligned} \mathscr{Y}_{F}^{\mathrm{l.c.}} :=\bigcup_{n}\mathrm{Spec} L\left[\Gamma_{F,n}\right] \subset \mathscr{Y}_{F} := \mathrm{Spec} \mathscr{O}_{L}[\kern-1pt[ \Gamma_{F}]\kern-1pt]\otimes_{\mathscr{O}_{L}}L. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{Y}_{F}^{\mathrm{l.c.}} :=\bigcup_{n}\mathrm{Spec} L\left[\Gamma_{F,n}\right] \subset \mathscr{Y}_{F} := \mathrm{Spec} \mathscr{O}_{L}[\kern-1pt[ \Gamma_{F}]\kern-1pt]\otimes_{\mathscr{O}_{L}}L. \end{aligned} \end{align} $$
Then
![]() $\mathscr {Y}_{F}$
is a space of continuous characters on
$\mathscr {Y}_{F}$
is a space of continuous characters on
![]() $\Gamma _{F}$
, and the
$\Gamma _{F}$
, and the
![]() $0$
-dimensional ind-scheme
$0$
-dimensional ind-scheme
![]() $\mathscr {Y}_{F}^{\mathrm{l.c.}}$
is its subspace of locally constant (finite-order) characters.
$\mathscr {Y}_{F}^{\mathrm{l.c.}}$
is its subspace of locally constant (finite-order) characters.
For a character
 $\chi ' \colon \mathrm {Gal}\left (E^{\mathrm{ab}}/E\right )\to L^{\prime \times }$
together with an embedding
$\chi ' \colon \mathrm {Gal}\left (E^{\mathrm{ab}}/E\right )\to L^{\prime \times }$
together with an embedding
![]() $\iota \colon L'\to \mathbf {C}$
, we shall interpolate the ratio of complete L-functions
$\iota \colon L'\to \mathbf {C}$
, we shall interpolate the ratio of complete L-functions
 $$ \begin{align*} \mathscr{L}\left( \iota V_{\left(A, \chi'\right)}, s\right):= \prod_{v} \mathscr{L}\left( \iota V_{\left(A, \chi'\right),v}, s\right),\qquad \mathscr{L}\left(\iota V_{\left(A, \chi'\right),v}, s\right)=\text{formula~(1.2.3)}, \quad \Re(s)\gg0, \end{align*} $$
$$ \begin{align*} \mathscr{L}\left( \iota V_{\left(A, \chi'\right)}, s\right):= \prod_{v} \mathscr{L}\left( \iota V_{\left(A, \chi'\right),v}, s\right),\qquad \mathscr{L}\left(\iota V_{\left(A, \chi'\right),v}, s\right)=\text{formula~(1.2.3)}, \quad \Re(s)\gg0, \end{align*} $$
where the product runs over all places of F.
We now define the p-interpolation factors for the p-adic L-function. First, recall that the (inverse) Deligne–Langlands gamma factor of a Weil–Deligne representation
![]() $W'$
of
$W'$
of
 $\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
over a p-adic field
$\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
over a p-adic field
![]() $L'$
, with respect to a nontrivial character
$L'$
, with respect to a nontrivial character
![]() $\psi _{v}\colon F_{v}\to \mathbf {C}^{\times }$
and an embedding
$\psi _{v}\colon F_{v}\to \mathbf {C}^{\times }$
and an embedding
![]() $\iota \colon L'\hookrightarrow \mathbf {C}$
, is defined asFootnote
4
$\iota \colon L'\hookrightarrow \mathbf {C}$
, is defined asFootnote
4
 $$ \begin{align*} \gamma(W',\psi_{v})^{-1}:= {L(W')\over \varepsilon(W', \psi_{v}) L(W^{*}(1))}. \end{align*} $$
$$ \begin{align*} \gamma(W',\psi_{v})^{-1}:= {L(W')\over \varepsilon(W', \psi_{v}) L(W^{*}(1))}. \end{align*} $$
Let
![]() $\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A} \to \mathbf {C}^{\times }$
be the standard additive character such that
$\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A} \to \mathbf {C}^{\times }$
be the standard additive character such that
![]() $\psi _{\infty }(\cdot ) = e^{2\pi i \mathrm {Tr}_{F_{\infty }/\mathbf {R}}(\cdot )}$
; let
$\psi _{\infty }(\cdot ) = e^{2\pi i \mathrm {Tr}_{F_{\infty }/\mathbf {R}}(\cdot )}$
; let
![]() $\psi _{E}=\prod _{w}\psi _{E, w}=\psi \circ \mathrm {Tr}_{\mathbf {A}_{E}/\mathbf {A}}$
. For a place
$\psi _{E}=\prod _{w}\psi _{E, w}=\psi \circ \mathrm {Tr}_{\mathbf {A}_{E}/\mathbf {A}}$
. For a place
![]() $v\mid p $
of F, let
$v\mid p $
of F, let
![]() $d_{v}$
be a generator of the different ideal of
$d_{v}$
be a generator of the different ideal of
![]() $F_{v}$
. For a character
$F_{v}$
. For a character
 $\chi '\colon \mathrm {Gal}\left (\overline {E}/E\right )\to \mathbf {C}^{\times }$
, we define
$\chi '\colon \mathrm {Gal}\left (\overline {E}/E\right )\to \mathbf {C}^{\times }$
, we define
 $$ \begin{align}\begin{aligned} e_{v}\left(V_{\left(A, \chi'\right)}\right)= \lvert d_{v}\rvert^{-1/2} {\prod_{w\mid v}\gamma\left(\iota{\mathrm{WD}}\left(W^{+}_{v\mid\mathscr{G}_{E, w}} \otimes \chi^{\prime}_{w}\right), \psi_{E,w}\right)^{-1} \over \gamma(\iota{\mathrm{WD}}(\mathrm{ad}(W_{v})(1))^{++}, \psi_{v})^{-1}} \cdot \mathscr{L}\left( V_{\left(A, \chi'\right),v}\right)^{-1}, \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} e_{v}\left(V_{\left(A, \chi'\right)}\right)= \lvert d_{v}\rvert^{-1/2} {\prod_{w\mid v}\gamma\left(\iota{\mathrm{WD}}\left(W^{+}_{v\mid\mathscr{G}_{E, w}} \otimes \chi^{\prime}_{w}\right), \psi_{E,w}\right)^{-1} \over \gamma(\iota{\mathrm{WD}}(\mathrm{ad}(W_{v})(1))^{++}, \psi_{v})^{-1}} \cdot \mathscr{L}\left( V_{\left(A, \chi'\right),v}\right)^{-1}, \end{aligned} \end{align} $$
where
![]() $ \mathrm {ad}(W_{v})(1)^{++}:= \mathrm {Hom}\left (W^{-}_{v}, W^{+}_{ v}\right )(1)= \omega _{v}^{-1}\alpha _{v}^{2}\lvert \ \rvert _{v}^{2}$
and
$ \mathrm {ad}(W_{v})(1)^{++}:= \mathrm {Hom}\left (W^{-}_{v}, W^{+}_{ v}\right )(1)= \omega _{v}^{-1}\alpha _{v}^{2}\lvert \ \rvert _{v}^{2}$
and
![]() $\iota {\mathrm{WD}}$
is the functor from potentially semistable Galois representations to complex Weil–Deligne representations of [Reference Fontaine14].
$\iota {\mathrm{WD}}$
is the functor from potentially semistable Galois representations to complex Weil–Deligne representations of [Reference Fontaine14].
Theorem A. There is a function
 $$ \begin{align*} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}\right)\in \mathscr{O}(\mathscr{Y}_{F}) \end{align*} $$
$$ \begin{align*} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}\right)\in \mathscr{O}(\mathscr{Y}_{F}) \end{align*} $$
characterized by the following property. For each complex geometric point
![]() $s=\chi _{F}\in \mathscr {Y}_{F}^{\mathrm{l.c.}}(\mathbf {C}) $
, with underlying embedding
$s=\chi _{F}\in \mathscr {Y}_{F}^{\mathrm{l.c.}}(\mathbf {C}) $
, with underlying embedding
![]() $\iota \colon L(\chi _{F})\hookrightarrow \mathbf {C}$
,
$\iota \colon L(\chi _{F})\hookrightarrow \mathbf {C}$
,
 $$ \begin{align*} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)},s\right)= \iota {e}_{p}\left({ V}_{\left(A, \chi'\right)}\right) \cdot \mathscr{L}\left(\iota V_{\left(A, \chi'\right)}, 0\right), \quad\chi':= \chi\cdot \chi_{F\rvert\mathrm{Gal}\left(\overline{E}/E\right)}, \end{align*} $$
$$ \begin{align*} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)},s\right)= \iota {e}_{p}\left({ V}_{\left(A, \chi'\right)}\right) \cdot \mathscr{L}\left(\iota V_{\left(A, \chi'\right)}, 0\right), \quad\chi':= \chi\cdot \chi_{F\rvert\mathrm{Gal}\left(\overline{E}/E\right)}, \end{align*} $$
where
 $ {e}_{p}\left (V_{\left (A, \chi '\right )}\right ):= \prod _{v\mid p} e_{v}\left (V_{\left (A, \chi '\right )}\right )$
.
$ {e}_{p}\left (V_{\left (A, \chi '\right )}\right ):= \prod _{v\mid p} e_{v}\left (V_{\left (A, \chi '\right )}\right )$
.
The factor
 $ {e}_{p}\left (V_{\left (A, \chi '\right )}\right )$
coincides with the one predicted by Coates and Perrin-Riou [Reference Coates7] for
$ {e}_{p}\left (V_{\left (A, \chi '\right )}\right )$
coincides with the one predicted by Coates and Perrin-Riou [Reference Coates7] for
![]() $V_{\left (A, \chi '\right )}$
(their conjecture motivates the denominator terms in equation (1.2.8), which are constants), up to the removal of a trivial zero from their interpolation factor for
$V_{\left (A, \chi '\right )}$
(their conjecture motivates the denominator terms in equation (1.2.8), which are constants), up to the removal of a trivial zero from their interpolation factor for
![]() $\mathrm {ad}(W_{v})(1)$
.
$\mathrm {ad}(W_{v})(1)$
.
The p-adic Gross–Zagier formula
We are almost ready to state our main result. Denote by
![]() $0\in \mathscr {Y}_{F}$
the point corresponding to
$0\in \mathscr {Y}_{F}$
the point corresponding to
![]() $\chi _{F}=\mathbf {1}$
, and define
$\chi _{F}=\mathbf {1}$
, and define
 $$ \begin{align*} \mathscr{L}_{p}'\left(V_{\left(A, \chi\right)}, 0\right):= {\mathrm{d}} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}, 0\right)\in T_{0}\mathscr{Y}_{F}\cong \Gamma_{F}\hat{\otimes} L(\chi). \end{align*} $$
$$ \begin{align*} \mathscr{L}_{p}'\left(V_{\left(A, \chi\right)}, 0\right):= {\mathrm{d}} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}, 0\right)\in T_{0}\mathscr{Y}_{F}\cong \Gamma_{F}\hat{\otimes} L(\chi). \end{align*} $$
We say that
![]() $\chi _{p}$
is sufficiently ramified if it is nontrivial on a certain open subgroup of
$\chi _{p}$
is sufficiently ramified if it is nontrivial on a certain open subgroup of
 $\mathscr {O}_{E,p}^{\times }$
depending only on
$\mathscr {O}_{E,p}^{\times }$
depending only on
![]() $\omega _{p}$
(see Assumption 3.4.1 for the precise definition and a comment).
$\omega _{p}$
(see Assumption 3.4.1 for the precise definition and a comment).
Theorem B. Suppose that the abelian variety
![]() $A_{/F}$
is modular and that for all
$A_{/F}$
is modular and that for all
![]() $v\mid p$
, the
$v\mid p$
, the
 $\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
-representation
$\mathrm {Gal}\left (\overline {F}_{v}/F_{v}\right )$
-representation
![]() $V_{\mathfrak {p}}A$
is ordinary and potentially crystalline. Let
$V_{\mathfrak {p}}A$
is ordinary and potentially crystalline. Let
 $\chi \colon \mathrm {Gal}\left (E^{\mathrm{ab}}/E\right )\to L(\chi )^{\times }$
be a finite-order character satisfying
$\chi \colon \mathrm {Gal}\left (E^{\mathrm{ab}}/E\right )\to L(\chi )^{\times }$
be a finite-order character satisfying
and suppose that
![]() $\chi _{p}$
sufficiently ramified.
$\chi _{p}$
sufficiently ramified.
Then for any
![]() $f_{1},f_{3}\in \pi $
,
$f_{1},f_{3}\in \pi $
,
![]() $f_{2},f_{4}\in \pi ^{\vee }$
such that
$f_{2},f_{4}\in \pi ^{\vee }$
such that
![]() $(f_{3}, f_{4})_{\pi }\neq 0$
, we have
$(f_{3}, f_{4})_{\pi }\neq 0$
, we have
 $$ \begin{align*} {\left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle \over ( f_{3}, f_{4})_{\pi} } = {e}_{p}\left(V_{\left(A, \chi\right)}\right)^{-1}\cdot \mathscr{L}_{p}'\left(V_{\left(\mathbf{A} , \chi\right)}, 0\right) \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right) \end{align*} $$
$$ \begin{align*} {\left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle \over ( f_{3}, f_{4})_{\pi} } = {e}_{p}\left(V_{\left(A, \chi\right)}\right)^{-1}\cdot \mathscr{L}_{p}'\left(V_{\left(\mathbf{A} , \chi\right)}, 0\right) \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right) \end{align*} $$
in
![]() $ \Gamma _{F}\hat {\otimes } L(\chi )$
.
$ \Gamma _{F}\hat {\otimes } L(\chi )$
.
Remark 1.2.1. The technical assumptions that
![]() $\chi _{p}$
is sufficiently ramified and that
$\chi _{p}$
is sufficiently ramified and that
![]() $V_{\mathfrak {p}}A$
is potentially crystallineFootnote
5
are removed by p-adic analytic continuation in [Reference Disegni13, Theorem B], and replaced by the (necessary) assumption that
$V_{\mathfrak {p}}A$
is potentially crystallineFootnote
5
are removed by p-adic analytic continuation in [Reference Disegni13, Theorem B], and replaced by the (necessary) assumption that
![]() $\chi _{p}$
is not exceptional for A – that is,
$\chi _{p}$
is not exceptional for A – that is,
 ${e}_{p}\left (V_{\left (A, \chi \right )}\right )\neq 0$
(which in our case is implied by the potential crystallinity).
${e}_{p}\left (V_{\left (A, \chi \right )}\right )\neq 0$
(which in our case is implied by the potential crystallinity).
Note that for the removal of the first assumption, one only needs the anticyclotomic formula analogous to [Reference Disegni9, Theorem C.4], and not the full generality of the multivariable formula in [Reference Disegni13, Theorem D].
Remark 1.2.2. Concrete versions of the formula of Theorem B may be obtained by choosing explicit parametrizations
![]() $f_{i}$
and evaluating the term Q. This is a local problem, solved in [Reference Cai, Shu and Tian5]. In particular, by starting from Theorem B (as generalized to all characters following Remark 1.2.1) and applying the same steps as in the proofs of [Reference Disegni10, Theorems 4.3.1, 4.3.3], we obtain the simple p-adic Gross–Zagier formula in anticyclotomic families for elliptic curves
$f_{i}$
and evaluating the term Q. This is a local problem, solved in [Reference Cai, Shu and Tian5]. In particular, by starting from Theorem B (as generalized to all characters following Remark 1.2.1) and applying the same steps as in the proofs of [Reference Disegni10, Theorems 4.3.1, 4.3.3], we obtain the simple p-adic Gross–Zagier formula in anticyclotomic families for elliptic curves
![]() $A_{/\mathbf {Q}}$
proposed in [Reference Disegni10, Conjecture 4.3.2], and similarly the direct analogueFootnote
6
of Perrin-Riou’s original result in [Reference Perrin-Riou26].
$A_{/\mathbf {Q}}$
proposed in [Reference Disegni10, Conjecture 4.3.2], and similarly the direct analogueFootnote
6
of Perrin-Riou’s original result in [Reference Perrin-Riou26].
The theorem has familiar applications extending to the nonsplit case from [Reference Disegni9] (when the other ingredients are available); we leave their formulation to the interested reader, and highlight instead an application specific to this case pointed out in [Reference Disegni10], as well as a new application to the nonvanishing conjecture for p-adic heights.
A new proof of a result of Greenberg and Stevens
As noted in [Reference Disegni10, Remark 5.2.3], the anticylcotomic formula indicated in the previous remark, combined with a result of Bertolini and Darmon, gives yet another proof (quite likely the most complicated so far, but amenable to generalizations) of the following famous result of Greenberg and Stevens [Reference Greenberg and Stevens16]. If
![]() $A_{/\mathbf {Q}}$
is an elliptic curve of split multiplicative reduction at p, with Néron period
$A_{/\mathbf {Q}}$
is an elliptic curve of split multiplicative reduction at p, with Néron period
![]() $\Omega _{A}$
and p-adic L-function
$\Omega _{A}$
and p-adic L-function
![]() $L_{p}(A, -)$
on
$L_{p}(A, -)$
on
![]() $\mathscr {Y}_{\mathbf {Q}}$
, then
$\mathscr {Y}_{\mathbf {Q}}$
, then
![]() $L_{p}(A, \mathbf {1})=0$
and
$L_{p}(A, \mathbf {1})=0$
and
 $$ \begin{align}\begin{aligned} L_{p}'(A,\mathbf{1}) = \lambda_{p}(A) \cdot {L(A, 1)\over \Omega_{A}},\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} L_{p}'(A,\mathbf{1}) = \lambda_{p}(A) \cdot {L(A, 1)\over \Omega_{A}},\end{aligned}\end{align} $$
where
![]() $\lambda _{p}(A)$
is the
$\lambda _{p}(A)$
is the
![]() $\mathcal {L}$
-invariant of Mazur, Tate, and Teitelbaum [Reference Mazur, Tate and Teitelbaum21].
$\mathcal {L}$
-invariant of Mazur, Tate, and Teitelbaum [Reference Mazur, Tate and Teitelbaum21].
We recall a sketch of the argument, referring to [Reference Disegni10] for more details. One chooses an imaginary quadratic field E such that p is inert in E and that the twist
![]() $A^{(E)}$
satisfies
$A^{(E)}$
satisfies
 $L\left (A^{(E)}, 1\right )\neq 0$
. By the anticyclotomic p-adic Gross–Zagier formula,
$L\left (A^{(E)}, 1\right )\neq 0$
. By the anticyclotomic p-adic Gross–Zagier formula,
![]() $L_{p}'(A_{E},\mathbf {1})$
is the value at
$L_{p}'(A_{E},\mathbf {1})$
is the value at
![]() $\chi =\mathbf {1}$
of the height of an anticyclotomic family
$\chi =\mathbf {1}$
of the height of an anticyclotomic family
![]() $\mathscr {P}$
of Heegner points. It is shown in [Reference Bertolini and Darmon2, §5.2] that the value
$\mathscr {P}$
of Heegner points. It is shown in [Reference Bertolini and Darmon2, §5.2] that the value
![]() $\mathscr {P}(\mathbf {1})$
equals, in an extended Selmer group, the Tate parameter
$\mathscr {P}(\mathbf {1})$
equals, in an extended Selmer group, the Tate parameter
![]() $q_{A,p}$
of
$q_{A,p}$
of
![]() $A_{\mathbf {Q}_{p}}$
multiplied by a square root of
$A_{\mathbf {Q}_{p}}$
multiplied by a square root of
![]() $L(A_{E}, 1)/\Omega _{A_{E}}$
. The height of
$L(A_{E}, 1)/\Omega _{A_{E}}$
. The height of
![]() $q_{A,p}$
, in the ‘extended’ sense of [Reference Mazur, Tate and Teitelbaum21, Reference Nekovář25], essentially equals
$q_{A,p}$
, in the ‘extended’ sense of [Reference Mazur, Tate and Teitelbaum21, Reference Nekovář25], essentially equals
![]() $\lambda _{p}(A)$
. This shows that after harmless multiplication by
$\lambda _{p}(A)$
. This shows that after harmless multiplication by
 $L\left (A^{(E)},1 \right )/\Omega _{A^{(E)}}$
, the two sides of equation (1.2.9) are equal.
$L\left (A^{(E)},1 \right )/\Omega _{A^{(E)}}$
, the two sides of equation (1.2.9) are equal.
Exceptional cases and nonvanishing results
Suppose that
![]() $A_{/\mathbf {Q}}$
has multiplicative reduction at a prime p inert in E, and that
$A_{/\mathbf {Q}}$
has multiplicative reduction at a prime p inert in E, and that
![]() $ L(A_{E}, 1)\neq 0$
. Then for all but finitely many anticyclotomic characters
$ L(A_{E}, 1)\neq 0$
. Then for all but finitely many anticyclotomic characters
![]() $\chi $
of p-power conductor, a Heegner point in
$\chi $
of p-power conductor, a Heegner point in
![]() $A_{E}(\chi )$
is nonzero and the p-adic height pairing on
$A_{E}(\chi )$
is nonzero and the p-adic height pairing on
![]() $A_{E}(\chi )$
is nondegenerate. This follows from noting, similarly to before, that in the p-adic Gross–Zagier formula in anticyclotomic families for
$A_{E}(\chi )$
is nondegenerate. This follows from noting, similarly to before, that in the p-adic Gross–Zagier formula in anticyclotomic families for
![]() $A_{E}$
, both sides are nonzero since the height side specializes, at the character
$A_{E}$
, both sides are nonzero since the height side specializes, at the character
![]() $\chi =\mathbf {1}$
, to a nonzero multiple of
$\chi =\mathbf {1}$
, to a nonzero multiple of
![]() $\lambda _{p}(A)$
, which is in turn nonzero by [Reference Barré-Sirieix, Diaz, Gramain and Philibert1].
$\lambda _{p}(A)$
, which is in turn nonzero by [Reference Barré-Sirieix, Diaz, Gramain and Philibert1].
A similar argument, applied to the formula in Hida families of [Reference Disegni13], will yield the following result: if
![]() $A_{/\mathbf {Q}} $
is an elliptic curve with multiplicative reduction and
$A_{/\mathbf {Q}} $
is an elliptic curve with multiplicative reduction and
![]() $L(A,1)\neq 0$
, then the Selmer group of the self-dual Hida family
$L(A,1)\neq 0$
, then the Selmer group of the self-dual Hida family
![]() ${\mathbf {f}}$
through A has generic rank
${\mathbf {f}}$
through A has generic rank
![]() $1$
, and neither the height regulator nor the cyclotomic derivative of the p-adic L-function of
$1$
, and neither the height regulator nor the cyclotomic derivative of the p-adic L-function of
![]() ${\mathbf {f}}$
vanishes. The details will appear in [Reference Disegni13].
${\mathbf {f}}$
vanishes. The details will appear in [Reference Disegni13].
1.3 Organization of the paper
In §2, we restate our theorems in an equivalent form, a direct generalization of the statements from [Reference Disegni9] (up to a correction involving a factor of
![]() $2$
, discussed in Appendix B). In §3 we recall the proof strategy from [Reference Disegni9], with suitable modifications and corrections. The new argument to treat p-adic local heights in the nonsplit case is developed in §4.
$2$
, discussed in Appendix B). In §3 we recall the proof strategy from [Reference Disegni9], with suitable modifications and corrections. The new argument to treat p-adic local heights in the nonsplit case is developed in §4.
We conclude with two appendices, one dedicated to some local results and the other containing a list of errata to [Reference Disegni9].
2 Comparison with [Reference Disegni9]
We compare Theorems A and B with the corresponding results from [Reference Disegni9]. We continue with the setup and notation of §1.2.
2.1 The p-adic L-function
We deduce our Theorem A from [Reference Disegni9, Theorem A].
Let
![]() $\sigma ^{\infty }$
be the nearly
$\sigma ^{\infty }$
be the nearly
![]() $\mathfrak {p}$
-ordinary, M-rational [Reference Disegni9, Definition 1.2.1] representation of
$\mathfrak {p}$
-ordinary, M-rational [Reference Disegni9, Definition 1.2.1] representation of
![]() $\mathrm {GL}_{2}(\mathbf {A})$
attached to A as in [Reference Disegni9]. In [Reference Disegni9, Theorem A], we constructed a p-adic L-function
$\mathrm {GL}_{2}(\mathbf {A})$
attached to A as in [Reference Disegni9]. In [Reference Disegni9, Theorem A], we constructed a p-adic L-function
which is a bounded function on a rigid space
 $\mathscr {Y}^{\prime \rm rig}_{/L}$
(denoted by
$\mathscr {Y}^{\prime \rm rig}_{/L}$
(denoted by
![]() $\mathscr {Y}'$
in [Reference Disegni9]). In the construction of that theorem (and in all this paper), we use the same additive character
$\mathscr {Y}'$
in [Reference Disegni9]). In the construction of that theorem (and in all this paper), we use the same additive character
 $\psi _{p}=\prod _{v\mid p}\psi _{v}$
as in Theorem A (and see the correction in Appendix B for the exact ring of definition of
$\psi _{p}=\prod _{v\mid p}\psi _{v}$
as in Theorem A (and see the correction in Appendix B for the exact ring of definition of
![]() $L_{p, \alpha }(\sigma _{E})$
).
$L_{p, \alpha }(\sigma _{E})$
).
The space
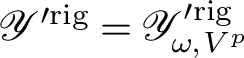 $\mathscr {Y}^{\prime \rm rig}=\mathscr {Y}^{\prime \rm rig}_{\omega , V^{p}}$
parametrizes certain continuous p-adic characters of
$\mathscr {Y}^{\prime \rm rig}=\mathscr {Y}^{\prime \rm rig}_{\omega , V^{p}}$
parametrizes certain continuous p-adic characters of
![]() $E^{\times }\backslash E_{\mathbf {A}}^{\times }$
invariant under an arbitrarily fixed compact open subgroup
$E^{\times }\backslash E_{\mathbf {A}}^{\times }$
invariant under an arbitrarily fixed compact open subgroup
![]() $V^{p}\subset E_{\mathbf {A}^{p\infty }}^{\times }$
. Boundedness means precisely that we may (and do) identify
$V^{p}\subset E_{\mathbf {A}^{p\infty }}^{\times }$
. Boundedness means precisely that we may (and do) identify
![]() $L_{p, \alpha }(\sigma _{E})$
with a function on a corresponding scheme
$L_{p, \alpha }(\sigma _{E})$
with a function on a corresponding scheme
 $$ \begin{align}\begin{aligned} \mathscr{Y}'\subset \mathrm{Spec} \mathscr{O}_{L}\left[\kern-1pt[ E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times}/V^{p} \right]\kern-1pt]\otimes {L} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{Y}'\subset \mathrm{Spec} \mathscr{O}_{L}\left[\kern-1pt[ E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times}/V^{p} \right]\kern-1pt]\otimes {L} \end{aligned}\end{align} $$
that, when also viewed as a space of characters
![]() $\chi '$
, is the subscheme cut out by the closed condition
$\chi '$
, is the subscheme cut out by the closed condition
 $\omega \cdot \chi ^{\prime }_{\rvert \widehat {\mathscr {O}}_{F}^{p,\times }}=\mathbf {1}$
. Similarly to
$\omega \cdot \chi ^{\prime }_{\rvert \widehat {\mathscr {O}}_{F}^{p,\times }}=\mathbf {1}$
. Similarly to
![]() $\mathscr {Y}_{F}$
, the scheme
$\mathscr {Y}_{F}$
, the scheme
![]() $\mathscr {Y}'$
contains a
$\mathscr {Y}'$
contains a
![]() $0$
-dimensional subscheme
$0$
-dimensional subscheme
![]() $\mathscr {Y}^{\prime \rm l.c.}$
parametrizing the locally constant characters in
$\mathscr {Y}^{\prime \rm l.c.}$
parametrizing the locally constant characters in
![]() $\mathscr {Y}'$
. The function
$\mathscr {Y}'$
. The function
![]() $L_{p, \alpha }(\sigma _{E})$
is characterized by the following property. Denote by
$L_{p, \alpha }(\sigma _{E})$
is characterized by the following property. Denote by
![]() $D_{K}$
the discriminant of a number field K. Then at all
$D_{K}$
the discriminant of a number field K. Then at all
![]() $\chi '\in \mathscr {Y}'$
with underlying embedding
$\chi '\in \mathscr {Y}'$
with underlying embedding
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, we have
$\iota \colon L\hookrightarrow \mathbf {C}$
, we have
 $$ \begin{align}\begin{aligned} L_{p,\alpha}(\sigma_{E})(\chi') =\prod_{v\mid p}Z_{v}^{\circ}\left(\chi^{\prime}_{v}, \psi_{v}\right)\cdot { \pi^{2\left[F:\mathbf{Q}\right]} \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot \mathscr{L}\left(\iota V_{\left(A, \chi'\right)}\right) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} L_{p,\alpha}(\sigma_{E})(\chi') =\prod_{v\mid p}Z_{v}^{\circ}\left(\chi^{\prime}_{v}, \psi_{v}\right)\cdot { \pi^{2\left[F:\mathbf{Q}\right]} \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot \mathscr{L}\left(\iota V_{\left(A, \chi'\right)}\right) \end{aligned}\end{align} $$
for certain local factors
![]() $Z_{v}^{\circ }$
.
$Z_{v}^{\circ }$
.
Fix a finite-order character
 $$ \begin{align*} \chi\colon E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times} \cong \mathrm{Gal}\left(E^{\mathrm{ab}}/E\right) \to L(\chi)^{\times} \end{align*} $$
$$ \begin{align*} \chi\colon E^{\times}\backslash E_{\mathbf{A}^{\infty}}^{\times} \cong \mathrm{Gal}\left(E^{\mathrm{ab}}/E\right) \to L(\chi)^{\times} \end{align*} $$
satisfying
![]() $\omega \cdot \chi _{\rvert \mathbf {A}^{\infty \times }}=\mathbf {1}, $
and consider the map
$\omega \cdot \chi _{\rvert \mathbf {A}^{\infty \times }}=\mathbf {1}, $
and consider the map
 $$ \begin{align*}\begin{aligned} j_{\chi} \colon \mathscr{Y}_{F} &\to \mathscr{Y}',\\ \chi_{F} &\mapsto \chi\cdot \chi_{F} \circ N_{E_{\mathbf{A}^{\infty\times}/\mathbf{A}^{\infty\times}}}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} j_{\chi} \colon \mathscr{Y}_{F} &\to \mathscr{Y}',\\ \chi_{F} &\mapsto \chi\cdot \chi_{F} \circ N_{E_{\mathbf{A}^{\infty\times}/\mathbf{A}^{\infty\times}}}. \end{aligned}\end{align*} $$
Proof of Theorem A
Define
 $$ \begin{align}\begin{aligned} C\left(\chi_{p}'\right):={ e_{p} \left(V_{\left(A, \chi'\right)}\right) \over \prod_{v\mid p }Z_{v}^{\circ}\left(\chi^{\prime}_{v}, \psi_{v}\right)}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} C\left(\chi_{p}'\right):={ e_{p} \left(V_{\left(A, \chi'\right)}\right) \over \prod_{v\mid p }Z_{v}^{\circ}\left(\chi^{\prime}_{v}, \psi_{v}\right)}. \end{aligned}\end{align} $$
We show in Proposition A.1.2 that this is a constant in
![]() $C\in L$
, independent of
$C\in L$
, independent of
![]() $\chi ^{\prime }_{p}$
.
$\chi ^{\prime }_{p}$
.
Define
 $$ \begin{align}\begin{aligned} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}\right):= {2 \zeta_{F}(2)\over \pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2}} \cdot C\cdot L(1, \sigma_{v}, \mathrm{ad}) \cdot j_{\chi}^{*}L_{p, \alpha}(\sigma_{E}), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{L}_{p}\left(V_{\left(A, \chi\right)}\right):= {2 \zeta_{F}(2)\over \pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2}} \cdot C\cdot L(1, \sigma_{v}, \mathrm{ad}) \cdot j_{\chi}^{*}L_{p, \alpha}(\sigma_{E}), \end{aligned}\end{align} $$
a function in
![]() $\mathscr {O}(\mathscr {Y}_{F})$
. It is clear from the definition and equation (2.1.2) that it satisfies the required interpolation property.
$\mathscr {O}(\mathscr {Y}_{F})$
. It is clear from the definition and equation (2.1.2) that it satisfies the required interpolation property.
2.2 Equivalence of statements
We now restate Theorem B in a form that directly generalizes [Reference Disegni9, Theorem B]. It is the form in which we will prove it, for convenience of reference.
We retain the setup of §1.2. Let
![]() ${\mathrm{d}}_{F}$
be the
${\mathrm{d}}_{F}$
be the
![]() $\Gamma _{F}$
-differential defined before [Reference Disegni9, Theorem B]. For all
$\Gamma _{F}$
-differential defined before [Reference Disegni9, Theorem B]. For all
![]() $v\nmid \infty $
, let
$v\nmid \infty $
, let
![]() $dt_{v}$
be the measure on
$dt_{v}$
be the measure on
![]() $E_{v}^{\times }/F_{v}^{\times }$
specified in [Reference Disegni9, paragraph after (1.1.2)] if
$E_{v}^{\times }/F_{v}^{\times }$
specified in [Reference Disegni9, paragraph after (1.1.2)] if
![]() $v\nmid \infty $
and the measure giving
$v\nmid \infty $
and the measure giving
![]() $\mathbf {C}^{\times }/\mathbf {R}^{\times }$
volume
$\mathbf {C}^{\times }/\mathbf {R}^{\times }$
volume
![]() $2$
if
$2$
if
![]() $v\mid \infty $
.
$v\mid \infty $
.
Theorem 2.2.1. Retain the assumptions of Theorem B, and fix a decomposition
![]() $(, )_{\pi }=\prod _{v}( ,)_{v}$
, with
$(, )_{\pi }=\prod _{v}( ,)_{v}$
, with
![]() $(1, 1)_{v}=1$
if
$(1, 1)_{v}=1$
if
![]() $v\mid \infty $
. Then for all
$v\mid \infty $
. Then for all
![]() $f_{1}\in \pi , f_{2}\in \pi ^{\vee }$
,
$f_{1}\in \pi , f_{2}\in \pi ^{\vee }$
,
 $$ \begin{align}\begin{aligned} \left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle = {c_{E}}\cdot \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1}\cdot {\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})(\chi)\cdot \prod_{v\nmid \infty} Q_{\left(, \right)_{v}, dt_{v}}(f_{1}, f_{2}, \chi)\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle = {c_{E}}\cdot \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1}\cdot {\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})(\chi)\cdot \prod_{v\nmid \infty} Q_{\left(, \right)_{v}, dt_{v}}(f_{1}, f_{2}, \chi)\end{aligned}\end{align} $$
in
![]() $ \Gamma _{F} \hat {\otimes } L(\chi )$
, where
$ \Gamma _{F} \hat {\otimes } L(\chi )$
, where
 $$ \begin{align*} c_{E}:={ \zeta_{F}(2)\over (\pi/2)^{\left[F:\mathbf{Q}\right]}\lvert D_{E}\rvert^{1/2} L(1, \eta) } \in\mathbf{Q}^{\times}. \end{align*} $$
$$ \begin{align*} c_{E}:={ \zeta_{F}(2)\over (\pi/2)^{\left[F:\mathbf{Q}\right]}\lvert D_{E}\rvert^{1/2} L(1, \eta) } \in\mathbf{Q}^{\times}. \end{align*} $$
Lemma 2.2.2. Theorem 2.2.1 is equivalent to Theorem B. When every prime
![]() $v\mid p$
splits in E, it specializes to [Reference Disegni9, Theorem B] as corrected in Appendix B.
$v\mid p$
splits in E, it specializes to [Reference Disegni9, Theorem B] as corrected in Appendix B.
Proof. The second assertion is immediate; we prove the first one. First, we note that equation (2.2.1) is equivalent to
 $$ \begin{align} &\left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle\over (f_{3},f_{4})_{\pi} \nonumber \\ &\quad = {c_{E}}\cdot \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1}\cdot {\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})(\chi) \cdot 2^{-\left[F:\mathbf{Q}\right]}\prod_{v} {Q_{\left(, \right)_{v}, dt_{v}}(f_{1}, f_{2}, \chi) \over \left(f_{3,v}, f_{4,v}\right)_{v}} \end{align} $$
$$ \begin{align} &\left\langle P(f_{1}, \chi), P^{\vee}\left(f_{2}, \chi^{-1}\right)\right\rangle\over (f_{3},f_{4})_{\pi} \nonumber \\ &\quad = {c_{E}}\cdot \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1}\cdot {\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})(\chi) \cdot 2^{-\left[F:\mathbf{Q}\right]}\prod_{v} {Q_{\left(, \right)_{v}, dt_{v}}(f_{1}, f_{2}, \chi) \over \left(f_{3,v}, f_{4,v}\right)_{v}} \end{align} $$
for any
![]() $f_{3}\in \pi , f_{4}\in \pi ^{\vee }$
with
$f_{3}\in \pi , f_{4}\in \pi ^{\vee }$
with
![]() $f_{3, \infty }=f_{4, \infty }=1$
and
$f_{3, \infty }=f_{4, \infty }=1$
and
![]() $(f_{3}, f_{4})_{\pi }\neq 0$
(the extra power of
$(f_{3}, f_{4})_{\pi }\neq 0$
(the extra power of
![]() $2$
comes from the Archimedean places). The left-hand side of equation (2.2.2) is the same as that of the formula of Theorem B, and the product of the terms after the L-derivative in the right-hand side equals
$2$
comes from the Archimedean places). The left-hand side of equation (2.2.2) is the same as that of the formula of Theorem B, and the product of the terms after the L-derivative in the right-hand side equals
 $$ \begin{align*} & 2^{-\left[F:\mathbf{Q}\right]} {\prod_{v} dt_{v}\over dt} \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right)\\ &\quad = 2^{1-\left[F:\mathbf{Q}\right]} \left\lvert D_{E/F}\right\rvert^{1/2}\lvert D_{F}\rvert^{1/2}\pi^{-\left[F:\mathbf{Q}\right]}L(1, \eta) \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right), \end{align*} $$
$$ \begin{align*} & 2^{-\left[F:\mathbf{Q}\right]} {\prod_{v} dt_{v}\over dt} \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right)\\ &\quad = 2^{1-\left[F:\mathbf{Q}\right]} \left\lvert D_{E/F}\right\rvert^{1/2}\lvert D_{F}\rvert^{1/2}\pi^{-\left[F:\mathbf{Q}\right]}L(1, \eta) \cdot Q\left( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi\right), \end{align*} $$
because the measure
![]() $\prod _{v} dt_{v}$
(resp.,
$\prod _{v} dt_{v}$
(resp.,
![]() $dt$
) gives
$dt$
) gives
![]() $E^{\times }\backslash \mathbf {A}_{E}^{\times }/\mathbf {A}^{\times }$
volume
$E^{\times }\backslash \mathbf {A}_{E}^{\times }/\mathbf {A}^{\times }$
volume
 $2 \left \lvert D_{E/F}\right \rvert ^{1/2} \lvert D_{F}\rvert ^{1/2} \pi ^{-\left [F:\mathbf {Q}\right ]}L(1, \eta )$
(resp.,
$2 \left \lvert D_{E/F}\right \rvert ^{1/2} \lvert D_{F}\rvert ^{1/2} \pi ^{-\left [F:\mathbf {Q}\right ]}L(1, \eta )$
(resp.,
![]() $1$
).
$1$
).
Next, we have
 ${\mathrm{d}}_{F}L_{p, \alpha }(\sigma _{E})(\chi )={1\over 2} {\mathrm{d}}\left ( j_{\chi }^{*} L_{p, \alpha }(\sigma _{E}) \right )(\mathbf {1})$
, and it is clear from comparing the interpolation properties that
${\mathrm{d}}_{F}L_{p, \alpha }(\sigma _{E})(\chi )={1\over 2} {\mathrm{d}}\left ( j_{\chi }^{*} L_{p, \alpha }(\sigma _{E}) \right )(\mathbf {1})$
, and it is clear from comparing the interpolation properties that
 $$ \begin{align*} \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1} \cdot {1\over 2} {\mathrm{d}} \left( j_{\chi}^{*} L_{p, \alpha}(\sigma_{E}) \right)(\mathbf{1})= {\pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot {e}_{p}\left(V_{\left(A, \chi\right)}\right)^{-1}\cdot \mathscr{L}_{p}'\left(V_{\left(A, \chi\right)}, 0\right). \end{align*} $$
$$ \begin{align*} \prod_{v\mid p}Z_{v}^{\circ}( \chi_{v})^{-1} \cdot {1\over 2} {\mathrm{d}} \left( j_{\chi}^{*} L_{p, \alpha}(\sigma_{E}) \right)(\mathbf{1})= {\pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot {e}_{p}\left(V_{\left(A, \chi\right)}\right)^{-1}\cdot \mathscr{L}_{p}'\left(V_{\left(A, \chi\right)}, 0\right). \end{align*} $$
It follows that the right-hand side of equation (2.2.1) equals
 $c \cdot {e}_{p}\left (V_{\left (A, \chi \right )}\right )^{-1}\cdot \mathscr {L}_{p}'\left (V_{\left (A, \chi \right )}, 0\right ) \cdot Q\left ( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi \right ),$
where
$c \cdot {e}_{p}\left (V_{\left (A, \chi \right )}\right )^{-1}\cdot \mathscr {L}_{p}'\left (V_{\left (A, \chi \right )}, 0\right ) \cdot Q\left ( { f_{1} \otimes f_{2}\over f_{3}\otimes f_{4}}; \chi \right ),$
where
 $$ \begin{align*} c= {c_{E}} \cdot {\pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot 2^{1-\left[F:\mathbf{Q}\right]} \left\lvert D_{E/F}\right\rvert^{1/2}\lvert D_{F}\rvert^{1/2} \pi^{-[F:\mathbf{Q}]}L(1, \eta)=1.\\[-47pt] \end{align*} $$
$$ \begin{align*} c= {c_{E}} \cdot {\pi^{2\left[F:\mathbf{Q}\right] } \lvert D_{F}\rvert^{1/2} \over 2\zeta_{F}(2)} \cdot 2^{1-\left[F:\mathbf{Q}\right]} \left\lvert D_{E/F}\right\rvert^{1/2}\lvert D_{F}\rvert^{1/2} \pi^{-[F:\mathbf{Q}]}L(1, \eta)=1.\\[-47pt] \end{align*} $$
3 Structure of the proof
We review the formal structure of the proof in [Reference Disegni9], dwelling only on those points where the arguments need to be modified or corrected. For an introductory description with some more details than are given in §1.1, see [Reference Disegni9, §1.7]. Readers interested in a detailed understanding of the present section are advised to keep a copy of [Reference Disegni9] handy.
3.1 Notation and setup
We very briefly review some notation and definitions from [Reference Disegni9], which will be used throughout the paper.
Galois groups
If K is a perfect field, we denote by
 $\mathscr {G}_{K}:=\mathrm {Gal}\left (\overline {K}/K\right )$
its absolute Galois group.
$\mathscr {G}_{K}:=\mathrm {Gal}\left (\overline {K}/K\right )$
its absolute Galois group.
Local fields
For v finite a place of F, we denote by
![]() $\varpi _{v}$
a fixed uniformizer and by
$\varpi _{v}$
a fixed uniformizer and by
![]() $q_{F, v}$
the cardinality of the residue field of
$q_{F, v}$
the cardinality of the residue field of
![]() $F_{v}$
. We denote by
$F_{v}$
. We denote by
![]() $d_{v}$
a generator of the absolute different of
$d_{v}$
a generator of the absolute different of
![]() $F_{v}$
, by
$F_{v}$
, by
![]() $D_{v}$
a generator of the relative discriminant of
$D_{v}$
a generator of the relative discriminant of
![]() $E_{v}/F_{v}$
(equal to
$E_{v}/F_{v}$
(equal to
![]() $1$
unless v ramifies in E), and by
$1$
unless v ramifies in E), and by
![]() $e_{v}$
the ramification degree of
$e_{v}$
the ramification degree of
![]() $E_{v}/F_{v}$
. If
$E_{v}/F_{v}$
. If
![]() $w\mid v$
is a place of E, we denote by
$w\mid v$
is a place of E, we denote by
![]() $q_{v}\colon E_{v}\to F_{v}$
and
$q_{v}\colon E_{v}\to F_{v}$
and
![]() $q_{w}\colon E_{w}\to F_{v}$
the relative norm maps.
$q_{w}\colon E_{w}\to F_{v}$
the relative norm maps.
We denote by
![]() $\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A} \to \mathbf {C}^{\times }$
the additive character fixed before Theorem A.
$\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A} \to \mathbf {C}^{\times }$
the additive character fixed before Theorem A.
Base change of rings and schemes
If R is a ring,
![]() $R'$
is an R-algebra, M is an R-module, and S is an R-scheme, we denote
$R'$
is an R-algebra, M is an R-module, and S is an R-scheme, we denote
![]() $M_{R'}=M\otimes _{R}R', S_{R'}= S\times _{\mathrm {Spec} R}\mathrm {Spec} R'$
.
$M_{R'}=M\otimes _{R}R', S_{R'}= S\times _{\mathrm {Spec} R}\mathrm {Spec} R'$
.
Groups, measures, integration
We adopt the same notation and choices of measures as in [Reference Disegni9, §1.9], including a regularized integration
![]() $\int ^{*}$
. In particular,
$\int ^{*}$
. In particular,
![]() $T:= {\mathrm{Res}}_{E/F}{\mathbf {G}}_{m, E}, Z={\mathbf {G}}_{m, F}$
, and on the adelic points of
$T:= {\mathrm{Res}}_{E/F}{\mathbf {G}}_{m, E}, Z={\mathbf {G}}_{m, F}$
, and on the adelic points of
![]() $T/Z$
we use two measures
$T/Z$
we use two measures
![]() $dt$
(the same as introduced before Theorem 2.2.1) and
$dt$
(the same as introduced before Theorem 2.2.1) and
![]() $d^{\circ }t$
. The measure denoted by
$d^{\circ }t$
. The measure denoted by
![]() $dt$
in the introduction will not be used.
$dt$
in the introduction will not be used.
Operators at p
Let
![]() $v\mid p$
be a place of F. We denote by
$v\mid p$
be a place of F. We denote by
![]() $\varpi _{v}$
a fixed uniformizer at v. For
$\varpi _{v}$
a fixed uniformizer at v. For
![]() $r\geq 1$
we let
$r\geq 1$
we let
![]() $K_{1}^{1}\left (\varpi _{v}^{r}\right ) \subset \mathrm {GL}_{2}\left (\mathscr {O}_{F, v}\right )$
be the subgroup of matrices which become upper unipotent upon reduction modulo
$K_{1}^{1}\left (\varpi _{v}^{r}\right ) \subset \mathrm {GL}_{2}\left (\mathscr {O}_{F, v}\right )$
be the subgroup of matrices which become upper unipotent upon reduction modulo
![]() $\varpi ^{r}$
. We denote by
$\varpi ^{r}$
. We denote by
 $$ \begin{align*} \mathrm{U}_{v,*}=K^{1}_{1}\left(\varpi_{v}^{r}\right) \left(\begin{array}{cc}1&\\&\varpi_{v}^{-1}\end{array}\right)K^{1}_{1}\left(\varpi_{v}^{r}\right), \qquad \mathrm{U}_{v}^{*}=K^{1}_{1}\left(\varpi_{v}^{r}\right) \left(\begin{array}{cc}\varpi^{r}&\\&1\end{array}\right)K^{1}_{1}\left(\varpi_{v}^{r}\right) \end{align*} $$
$$ \begin{align*} \mathrm{U}_{v,*}=K^{1}_{1}\left(\varpi_{v}^{r}\right) \left(\begin{array}{cc}1&\\&\varpi_{v}^{-1}\end{array}\right)K^{1}_{1}\left(\varpi_{v}^{r}\right), \qquad \mathrm{U}_{v}^{*}=K^{1}_{1}\left(\varpi_{v}^{r}\right) \left(\begin{array}{cc}\varpi^{r}&\\&1\end{array}\right)K^{1}_{1}\left(\varpi_{v}^{r}\right) \end{align*} $$
the usual double coset operators, and define
 $$ \begin{align*} w_{r,v}:= \left(\begin{array}{cc}&1\\-\varpi_{v}^{r}&\end{array}\right)\in \mathrm{GL}_{2}(F_{v}). \end{align*} $$
$$ \begin{align*} w_{r,v}:= \left(\begin{array}{cc}&1\\-\varpi_{v}^{r}&\end{array}\right)\in \mathrm{GL}_{2}(F_{v}). \end{align*} $$
We also define
 $w_{r}:=\prod _{v\mid p}w_{r,v}\in \mathrm {GL}_{2}(F_{p})$
, and if
$w_{r}:=\prod _{v\mid p}w_{r,v}\in \mathrm {GL}_{2}(F_{p})$
, and if
![]() $(\beta _{v})_{v\mid p}$
are characters of
$(\beta _{v})_{v\mid p}$
are characters of
![]() $F_{v}^{\times }$
, we denote
$F_{v}^{\times }$
, we denote
 $\beta _{p}(\varpi ):=\prod _{v\mid p}\beta _{v}(\varpi _{v})$
.
$\beta _{p}(\varpi ):=\prod _{v\mid p}\beta _{v}(\varpi _{v})$
.
Spaces of characters
We denote by
![]() $\mathscr {Y}_{F}, \mathscr {Y}', \mathscr {Y}$
, respectively, the schemes over L defined in formulas (1.2.7) and (2.1.1) and the subscheme of
$\mathscr {Y}_{F}, \mathscr {Y}', \mathscr {Y}$
, respectively, the schemes over L defined in formulas (1.2.7) and (2.1.1) and the subscheme of
![]() $\mathscr {Y}$
cut out by the condition
$\mathscr {Y}$
cut out by the condition
 $\chi _{\rvert \mathbf {A}^{\infty \times }}=\omega ^{-1}$
. We add to this notation a superscript ‘l.c.’ to denote the ind-subschemes of locally constant characters (which has a model over a finite extension of M in L).
$\chi _{\rvert \mathbf {A}^{\infty \times }}=\omega ^{-1}$
. We add to this notation a superscript ‘l.c.’ to denote the ind-subschemes of locally constant characters (which has a model over a finite extension of M in L).
Let
![]() $\mathscr {I}_{\mathscr {Y}/\mathscr {Y}'}$
be the ideal sheaf of
$\mathscr {I}_{\mathscr {Y}/\mathscr {Y}'}$
be the ideal sheaf of
![]() $\mathscr {Y}\subset \mathscr {Y}'$
. If
$\mathscr {Y}\subset \mathscr {Y}'$
. If
![]() $\mathscr {M}$
is a coherent
$\mathscr {M}$
is a coherent
![]() $\mathscr {O}_{\mathscr {Y}'}$
-module, we denote
$\mathscr {O}_{\mathscr {Y}'}$
-module, we denote
 $$ \begin{align*} {\mathrm{d}}_{F}\colon \mathscr{M}\otimes_{\mathscr{O}_{\mathscr{Y}'}} \mathscr{I}_{\mathscr{Y}/\mathscr{Y}'} \to \mathscr{M} \otimes_{\mathscr{O}_{\mathscr{Y}'}} \mathscr{I}_{\mathscr{Y}/\mathscr{Y}'}/\mathscr{I}_{\mathscr{Y}/\mathscr{Y}'}^{2} =\mathscr{M}_{\rvert\mathscr{Y}}\hat{\otimes}\Gamma_{F} \end{align*} $$
$$ \begin{align*} {\mathrm{d}}_{F}\colon \mathscr{M}\otimes_{\mathscr{O}_{\mathscr{Y}'}} \mathscr{I}_{\mathscr{Y}/\mathscr{Y}'} \to \mathscr{M} \otimes_{\mathscr{O}_{\mathscr{Y}'}} \mathscr{I}_{\mathscr{Y}/\mathscr{Y}'}/\mathscr{I}_{\mathscr{Y}/\mathscr{Y}'}^{2} =\mathscr{M}_{\rvert\mathscr{Y}}\hat{\otimes}\Gamma_{F} \end{align*} $$
the normal derivative (compare the definition before [Reference Disegni9, Theorem B]).
Kirillov models
Let
 $\sigma ^{\infty }=\bigotimes _{v\nmid \infty }\sigma _{v} $
be the M-rational automorphic representation of
$\sigma ^{\infty }=\bigotimes _{v\nmid \infty }\sigma _{v} $
be the M-rational automorphic representation of
![]() $\mathrm {GL}_{2}(\mathbf {A})$
attached to A, and denote abusively still by
$\mathrm {GL}_{2}(\mathbf {A})$
attached to A, and denote abusively still by
![]() $\sigma ^{\infty }$
its base change to L. For every place v the representations
$\sigma ^{\infty }$
its base change to L. For every place v the representations
![]() $\sigma _{v}$
of
$\sigma _{v}$
of
![]() $\mathbf {B}_{v}^{\times }$
and
$\mathbf {B}_{v}^{\times }$
and
![]() $\pi _{v}$
of
$\pi _{v}$
of
![]() $\mathrm {GL}_{2}(F_{v})$
are Jacquet–Langlands correspondents.
$\mathrm {GL}_{2}(F_{v})$
are Jacquet–Langlands correspondents.
For
![]() $v\mid p$
, we denote by
$v\mid p$
, we denote by
 $$ \begin{align*} \mathscr{K}_{\psi_{v}}\colon \sigma_{v} \to C^{\infty}\left(F_{v}^{\times}, L\right) \end{align*} $$
$$ \begin{align*} \mathscr{K}_{\psi_{v}}\colon \sigma_{v} \to C^{\infty}\left(F_{v}^{\times}, L\right) \end{align*} $$
a fixed rational Kirillov model.
Orthogonal spaces
We define
![]() ${\mathbf {V}}:=\mathbf {B}$
equipped with the reduced norm q, a quadratic form valued in
${\mathbf {V}}:=\mathbf {B}$
equipped with the reduced norm q, a quadratic form valued in
![]() $\mathbf {A}$
. The image of
$\mathbf {A}$
. The image of
![]() $E_{\mathbf {A}}$
is a subspace
$E_{\mathbf {A}}$
is a subspace
![]() ${\mathbf {V}}_{1}$
of the orthogonal space
${\mathbf {V}}_{1}$
of the orthogonal space
![]() ${\mathbf {V}}$
, and we let
${\mathbf {V}}$
, and we let
![]() ${\mathbf {V}}_{2}$
be its orthogonal complement. The restriction
${\mathbf {V}}_{2}$
be its orthogonal complement. The restriction
![]() $q_{\rvert {\mathbf {V}}_{1}}$
is the adelization of the norm of
$q_{\rvert {\mathbf {V}}_{1}}$
is the adelization of the norm of
![]() $E/F$
.
$E/F$
.
Schwartz spaces and Weil representation
If
![]() $\bf V'$
is any one of the spaces already discussed, we denote by
$\bf V'$
is any one of the spaces already discussed, we denote by
 ${\overline {\mathscr {S}}}({\mathbf {V}}'\times \mathbf {A}^{\times })=\bigotimes ^{\prime }_{v} {\overline {\mathscr {S}}}\left ({\mathbf {V}}^{\prime }_{v}\times F_{v}^{\times }\right )$
the Fock space of Schwartz functions considered in [Reference Disegni9]. (This differs from the usual Schwartz space only at infinity.) There is a Weil representation
${\overline {\mathscr {S}}}({\mathbf {V}}'\times \mathbf {A}^{\times })=\bigotimes ^{\prime }_{v} {\overline {\mathscr {S}}}\left ({\mathbf {V}}^{\prime }_{v}\times F_{v}^{\times }\right )$
the Fock space of Schwartz functions considered in [Reference Disegni9]. (This differs from the usual Schwartz space only at infinity.) There is a Weil representation
defined as in [Reference Disegni9, §3.1]. The orthogonal group of
![]() $\bf V$
naturally contains the product
$\bf V$
naturally contains the product
![]() $T(\mathbf {A})\times T(\mathbf {A})$
acting by left and right multiplication on
$T(\mathbf {A})\times T(\mathbf {A})$
acting by left and right multiplication on
![]() ${\mathbf {V}}$
. The Weil representation also depends on a choice of additive characters
${\mathbf {V}}$
. The Weil representation also depends on a choice of additive characters
![]() $\psi $
. The restriction
$\psi $
. The restriction
![]() $r_{\rvert T(\mathbf {A})\times T(\mathbf {A})}$
preserves the decomposition
$r_{\rvert T(\mathbf {A})\times T(\mathbf {A})}$
preserves the decomposition
![]() ${\mathbf {V}}_{1}\oplus { \bf V}_{2}$
, hence it accordingly decomposes as
${\mathbf {V}}_{1}\oplus { \bf V}_{2}$
, hence it accordingly decomposes as
![]() $r_{1}\oplus r_{2}$
.
$r_{1}\oplus r_{2}$
.
Special data at p
We list the functions at the places
![]() $v\mid p$
that we use.
$v\mid p$
that we use.
Define
the ordinary vector in the fixed Kirillov model
![]() $\mathscr {K}_{\psi _{v}}$
of
$\mathscr {K}_{\psi _{v}}$
of
![]() $\sigma _{A,v}$
. We consider
$\sigma _{A,v}$
. We consider
 $$ \begin{align}\begin{aligned} \varphi_{v}=\varphi_{v,r}:= \mathscr{K}_{\psi_{v}}^{-1} \left(\alpha_{v}(\varpi_{v})^{-r}w_{r} W_{v}\right) \in \sigma_{v}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \varphi_{v}=\varphi_{v,r}:= \mathscr{K}_{\psi_{v}}^{-1} \left(\alpha_{v}(\varpi_{v})^{-r}w_{r} W_{v}\right) \in \sigma_{v}. \end{aligned}\end{align} $$
Now we consider Schwartz functions. We let
be the indefinite quaternion algebra over
![]() $F_{v}$
; this choice is justified a posteriori by Corollary A.2.3. The following choices of functions correct and modify the ones fixed in [Reference Disegni9] (compare the errata in Appendix B); note in particular that we will use two different functions on
$F_{v}$
; this choice is justified a posteriori by Corollary A.2.3. The following choices of functions correct and modify the ones fixed in [Reference Disegni9] (compare the errata in Appendix B); note in particular that we will use two different functions on
![]() ${\mathbf {V}}_{2, v}$
.
${\mathbf {V}}_{2, v}$
.
Decompose orthogonally
![]() ${\mathbf {V}}_{v}={\mathbf {V}}_{1,v}\oplus {\mathbf {V}}_{2, v}$
, where
${\mathbf {V}}_{v}={\mathbf {V}}_{1,v}\oplus {\mathbf {V}}_{2, v}$
, where
![]() ${\mathbf {V}}_{1,v}=E_{v}$
under the fixed embedding
${\mathbf {V}}_{1,v}=E_{v}$
under the fixed embedding
![]() $E_{\mathbf {A}^{\infty }}\hookrightarrow \mathbf {B}^{\infty }$
. We define the following Schwartz functions on, respectively,
$E_{\mathbf {A}^{\infty }}\hookrightarrow \mathbf {B}^{\infty }$
. We define the following Schwartz functions on, respectively,
![]() $F_{v}^{\times }$
and its product with
$F_{v}^{\times }$
and its product with
![]() ${\mathbf {V}}_{1,v}$
,
${\mathbf {V}}_{1,v}$
,
![]() ${\mathbf {V}}_{2,v}$
,
${\mathbf {V}}_{2,v}$
,
![]() ${\mathbf {V}}_{v}$
:
${\mathbf {V}}_{v}$
:
 $$ \begin{align}\begin{aligned} \phi_{F,r}(u)&:=\delta_{1, U_{F, r}}(u),& \text{where } \delta_{1, U_{F, r}}(u)&:= {\mathrm{vol}\left(\mathscr{O}_{F,v}^{\times}\right)\over \mathrm{vol}\left(1+\varpi^{r}\mathscr{O}_{F,v}\right)}\mathbf{1}_{1+\varpi^{r}\mathscr{O}_{F,v}}(u),\\ \phi_{1, r}(x_{1}, u)& := \delta_{1, U_{T,r}}(x_{1}) \delta_{1, U_{F,r}}(u),& \text{where } \delta_{1, U_{T,r}}(x_{1}) &= {\mathrm{vol}\left(\mathscr{O}_{E,v}\right)\over \mathrm{vol}\left(1+\varpi^{r}\mathscr{O}_{E,v}\right)} \mathbf{1}_{1+\varpi^{r}\mathscr{O}_{E,v}}(x_{1}), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \phi_{F,r}(u)&:=\delta_{1, U_{F, r}}(u),& \text{where } \delta_{1, U_{F, r}}(u)&:= {\mathrm{vol}\left(\mathscr{O}_{F,v}^{\times}\right)\over \mathrm{vol}\left(1+\varpi^{r}\mathscr{O}_{F,v}\right)}\mathbf{1}_{1+\varpi^{r}\mathscr{O}_{F,v}}(u),\\ \phi_{1, r}(x_{1}, u)& := \delta_{1, U_{T,r}}(x_{1}) \delta_{1, U_{F,r}}(u),& \text{where } \delta_{1, U_{T,r}}(x_{1}) &= {\mathrm{vol}\left(\mathscr{O}_{E,v}\right)\over \mathrm{vol}\left(1+\varpi^{r}\mathscr{O}_{E,v}\right)} \mathbf{1}_{1+\varpi^{r}\mathscr{O}_{E,v}}(x_{1}), \end{aligned}\end{align} $$
and
 $$ \begin{align}\begin{aligned} \phi_{2}^{\circ}(x_{2}, u) & := \mathbf{1}_{\mathscr{O}_{{\textbf{V}}_{2,v}}}(x_{2}) \mathbf{1}_{\mathscr{O}_{F,v}^{\times}}(u),\\ \phi_{2, r}(x_{2}, u)& := e_{v}^{-1}\lvert d\rvert_{v}\cdot \mathbf{1}_{\mathscr{O}_{{\textbf{V}}_{2,v}}\cap q^{-1}\left(-1+\varpi^{r}\mathscr{O}_{F, v}\right)}(x_{2}) \mathbf{1}_{1+\varpi^{r}\mathscr{O}_{F,v}}(u), \\ \phi_{r}(x, u)&:= \phi_{1, r}(x_{1},u) \phi_{2, r}(x_{2}, u).&& \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \phi_{2}^{\circ}(x_{2}, u) & := \mathbf{1}_{\mathscr{O}_{{\textbf{V}}_{2,v}}}(x_{2}) \mathbf{1}_{\mathscr{O}_{F,v}^{\times}}(u),\\ \phi_{2, r}(x_{2}, u)& := e_{v}^{-1}\lvert d\rvert_{v}\cdot \mathbf{1}_{\mathscr{O}_{{\textbf{V}}_{2,v}}\cap q^{-1}\left(-1+\varpi^{r}\mathscr{O}_{F, v}\right)}(x_{2}) \mathbf{1}_{1+\varpi^{r}\mathscr{O}_{F,v}}(u), \\ \phi_{r}(x, u)&:= \phi_{1, r}(x_{1},u) \phi_{2, r}(x_{2}, u).&& \end{aligned}\end{align} $$
p-adic modular forms and q-expansions
In [Reference Disegni9, §2], we defined the notion of Hilbert automorphic forms and twisted Hilbert automorphic forms (the latter depend on an extra variable
![]() $u \in \mathbf {A}^{\times }$
). We also defined the associated space of q-expansions, and a less redundant space of reduced q-expansions. When the coefficient field is a finite extension L of
$u \in \mathbf {A}^{\times }$
). We also defined the associated space of q-expansions, and a less redundant space of reduced q-expansions. When the coefficient field is a finite extension L of
![]() $\mathbf {Q}_{p}$
, these spaces are endowed with a topology. We have an (injective) reduced-q-expansion map on modular forms, denoted by
$\mathbf {Q}_{p}$
, these spaces are endowed with a topology. We have an (injective) reduced-q-expansion map on modular forms, denoted by
The image of modular forms (resp., cusp forms) of level
![]() $K^{p}K^1_{1}(p^{\infty })\subset \mathrm {GL}_{2}(\mathbf {A}^{p\infty })$
, parallel weight
$K^{p}K^1_{1}(p^{\infty })\subset \mathrm {GL}_{2}(\mathbf {A}^{p\infty })$
, parallel weight
![]() $2$
, and central character
$2$
, and central character
![]() $\omega ^{-1}$
is denoted by
$\omega ^{-1}$
is denoted by
 ${\mathbf {M}}={\mathbf {M}}\left (K^{p}, \omega ^{-1}\right )$
(resp.,
${\mathbf {M}}={\mathbf {M}}\left (K^{p}, \omega ^{-1}\right )$
(resp.,
![]() ${\mathbf {S}}$
). The closure of
${\mathbf {S}}$
). The closure of
![]() ${\mathbf {M}}$
(resp.,
${\mathbf {M}}$
(resp.,
![]() ${\mathbf {S}}$
) in the space of q-expansions with coefficients in L is denoted
${\mathbf {S}}$
) in the space of q-expansions with coefficients in L is denoted
![]() ${\mathbf {M}}'$
(resp.,
${\mathbf {M}}'$
(resp.,
![]() ${\mathbf {S}}'$
) and its elements are called p-adic modular forms (resp., cusp forms).
${\mathbf {S}}'$
) and its elements are called p-adic modular forms (resp., cusp forms).
If
![]() $\mathscr {Y}^{?}=\mathscr {Y}_{F}, \mathscr {Y}'$
, we define the notion of a
$\mathscr {Y}^{?}=\mathscr {Y}_{F}, \mathscr {Y}'$
, we define the notion of a
![]() $\mathscr {Y}^{?}$
-family of modular forms by copying word for word [Reference Disegni9, Definition 2.1.3]; the resulting notion coincides with that of bounded families on the analogous rigid spaces considered there.
$\mathscr {Y}^{?}$
-family of modular forms by copying word for word [Reference Disegni9, Definition 2.1.3]; the resulting notion coincides with that of bounded families on the analogous rigid spaces considered there.
For a finite set of places S disjoint from those above p, we have also defined a certain quotient space
![]() $\overline {\mathbf {S}}^{\prime }_{S}$
of cuspidal reduced q-expansions modulo those whose coefficients of index
$\overline {\mathbf {S}}^{\prime }_{S}$
of cuspidal reduced q-expansions modulo those whose coefficients of index
![]() $a\in F^{\times }\mathbf {A}^{S\infty \times }$
all vanish. According to [Reference Disegni9, Lemma 2.1.2], for any S the reduced-q-expansion map induces an injection
$a\in F^{\times }\mathbf {A}^{S\infty \times }$
all vanish. According to [Reference Disegni9, Lemma 2.1.2], for any S the reduced-q-expansion map induces an injection
 $$ \begin{align}\begin{aligned} {\textbf{S}}\hookrightarrow \overline{\textbf{S}}_{S}'. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\textbf{S}}\hookrightarrow \overline{\textbf{S}}_{S}'. \end{aligned}\end{align} $$
p-adic Petersson product and p-critical forms
For
![]() $\varphi ^{p}\in \sigma $
, we defined in [Reference Disegni9, Proposition 2.4.4] a functional
$\varphi ^{p}\in \sigma $
, we defined in [Reference Disegni9, Proposition 2.4.4] a functional
 $$ \begin{align}\begin{aligned} \ell_{\varphi^{p},\alpha}\colon {\textbf{M}}\left(K^{p}, \omega^{-1}, L\right)\to L, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \ell_{\varphi^{p},\alpha}\colon {\textbf{M}}\left(K^{p}, \omega^{-1}, L\right)\to L, \end{aligned}\end{align} $$
whose restriction to classical modular forms equals, up to an adjoint L-value, the limit as
![]() $r\to \infty $
of Petersson products with antiholomorphic forms
$r\to \infty $
of Petersson products with antiholomorphic forms
![]() $\varphi ^{p}\varphi _{p,r}\in \sigma $
with component
$\varphi ^{p}\varphi _{p,r}\in \sigma $
with component
 $\varphi _{p, r}=\prod _{v\mid p}\varphi _{v, r}$
as in equation (3.1.2).
$\varphi _{p, r}=\prod _{v\mid p}\varphi _{v, r}$
as in equation (3.1.2).
Set
![]() $v\mid p$
. We say that a form or q-expansion over a finite-dimensional
$v\mid p$
. We say that a form or q-expansion over a finite-dimensional
![]() $\mathbf {Q}_{p}$
-vector space L is v-critical if its coefficients
$\mathbf {Q}_{p}$
-vector space L is v-critical if its coefficients
![]() $a_{*}$
(where
$a_{*}$
(where
![]() $*\in \mathbf {A}^{\infty \times }$
) satisfy
$*\in \mathbf {A}^{\infty \times }$
) satisfy
 $$ \begin{align}\begin{aligned} a_{m\varpi_{v}^{s}}= O\left(q_{F, v}^{s}\right) \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} a_{m\varpi_{v}^{s}}= O\left(q_{F, v}^{s}\right) \end{aligned} \end{align} $$
in L, uniformly in
![]() $m\in \mathbf {A}^{\infty \times }$
. Here for two functions
$m\in \mathbf {A}^{\infty \times }$
. Here for two functions
![]() $f, g\colon \mathbf {N}\to L$
, we write
$f, g\colon \mathbf {N}\to L$
, we write
The space of p-critical forms is the sum of the spaces of v-critical forms for
![]() $v\mid p$
. Any element in those spaces is annihilated by
$v\mid p$
. Any element in those spaces is annihilated by
![]() $\ell _{\varphi ^{p},\alpha }$
.
$\ell _{\varphi ^{p},\alpha }$
.
3.2 Analytic kernel
The analytic kernel is a p-adic family of theta-Eisenstein series, related to the p-adic L-function. We review its main properties.
Proposition 3.2.1. There exist p-adic families of q-expansions of modular forms
![]() $\mathscr {E}$
over
$\mathscr {E}$
over
![]() $\mathscr {Y}_{F}$
and
$\mathscr {Y}_{F}$
and
![]() $\mathscr {I}$
over
$\mathscr {I}$
over
![]() $\mathscr {Y}'$
, satisfying the following:
$\mathscr {Y}'$
, satisfying the following:
-
1. For any
 $\chi _{F}\in \mathscr {Y}_{F}^{\mathrm{l.c.}}(\mathbf {C})$
and any
$\chi _{F}\in \mathscr {Y}_{F}^{\mathrm{l.c.}}(\mathbf {C})$
and any
 $r=(r_{v})_{v\mid p}$
satisfying
$r=(r_{v})_{v\mid p}$
satisfying
 $c(\chi _{F})\mid p^{r}$
, we have the identity of q-expansions of twisted modular forms of weight 1: where
$c(\chi _{F})\mid p^{r}$
, we have the identity of q-expansions of twisted modular forms of weight 1: where $$ \begin{align*} \mathscr{E}\left(u,\phi_{2}^{p\infty};\chi_{F}\right)= \lvert D_{F}\rvert {L^{(p)}(1, \eta\chi_{F})\over L^{(p)}(1, \eta)} \, {}^{\mathbf{q}} E_{r}(u, \phi_{2} ,\chi_{F}), \end{align*} $$
(3.2.1)is the Eisenstein series defined in [Reference Disegni9, §3.2], with respect to
$$ \begin{align*} \mathscr{E}\left(u,\phi_{2}^{p\infty};\chi_{F}\right)= \lvert D_{F}\rvert {L^{(p)}(1, \eta\chi_{F})\over L^{(p)}(1, \eta)} \, {}^{\mathbf{q}} E_{r}(u, \phi_{2} ,\chi_{F}), \end{align*} $$
(3.2.1)is the Eisenstein series defined in [Reference Disegni9, §3.2], with respect to $$ \begin{align}\begin{aligned} E_{r}(g,u, \phi_{2} ,\chi_{F}):=\sum_{\gamma\in P^{1}(F)\backslash SL_{2}(F)} \delta_{\chi_{F}, r} (\gamma gw_{r}) r(\gamma g) \phi_{2}(0,u)\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} E_{r}(g,u, \phi_{2} ,\chi_{F}):=\sum_{\gamma\in P^{1}(F)\backslash SL_{2}(F)} \delta_{\chi_{F}, r} (\gamma gw_{r}) r(\gamma g) \phi_{2}(0,u)\end{aligned}\end{align} $$
 $\phi _{2}=\phi _{2}^{p\infty }(\chi _{F})\phi ^{\circ }_{2,p\infty }$
, with
$\phi _{2}=\phi _{2}^{p\infty }(\chi _{F})\phi ^{\circ }_{2,p\infty }$
, with
 $\phi _{2,v}^{\circ }$
as in formula (3.1.4) for
$\phi _{2,v}^{\circ }$
as in formula (3.1.4) for
 $v\mid p$
and
$v\mid p$
and
 $\phi _{2, v}(\chi _{v}) $
for
$\phi _{2, v}(\chi _{v}) $
for
 $v\nmid \infty $
and
$v\nmid \infty $
and
 $\phi _{2, v}^{\circ }$
for
$\phi _{2, v}^{\circ }$
for
 $v\mid \infty $
as defined in [Reference Disegni9, §3.2].
$v\mid \infty $
as defined in [Reference Disegni9, §3.2].
-
2. For
 $\phi _{1}\in \overline {\mathscr {S}}({\mathbf {V}}_{1}\times {\mathbf {A}}^{\times })$
and
$\phi _{1}\in \overline {\mathscr {S}}({\mathbf {V}}_{1}\times {\mathbf {A}}^{\times })$
and
 $\chi '\in \mathscr {Y}^{\prime \rm l.c.}$
, consider the twisted modular form of weight
$\chi '\in \mathscr {Y}^{\prime \rm l.c.}$
, consider the twisted modular form of weight
 $1$
with parameter
$1$
with parameter
 $t\in E_{\mathbf {A}}^{\times }$
: (3.2.2)For any
$t\in E_{\mathbf {A}}^{\times }$
: (3.2.2)For any $$ \begin{align}\begin{aligned} \theta(g,(t, 1) u, \phi_{1}):=\sum_{x_{1}\in E} r_{1}(g, (t, 1))\phi_{1}(x, u). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \theta(g,(t, 1) u, \phi_{1}):=\sum_{x_{1}\in E} r_{1}(g, (t, 1))\phi_{1}(x, u). \end{aligned}\end{align} $$
 $\chi ' \in \mathscr {Y}^{\prime \rm l.c.}$
, define
$\chi ' \in \mathscr {Y}^{\prime \rm l.c.}$
, define
 $\chi _{F} := \omega ^{-1}\chi ^{\prime }_{\rvert \mathbf {A}^{\times } }\in \mathscr {Y}_{F}^{\mathrm{l.c.}}$
. Then for any
$\chi _{F} := \omega ^{-1}\chi ^{\prime }_{\rvert \mathbf {A}^{\times } }\in \mathscr {Y}_{F}^{\mathrm{l.c.}}$
. Then for any
 $r=(r_{v})_{v\mid p}$
satisfying
$r=(r_{v})_{v\mid p}$
satisfying
 $r_{v}\geq 1$
and
$r_{v}\geq 1$
and
 $c(\chi _{F})\mid p^{r}$
, we have (3.2.3)where for
$c(\chi _{F})\mid p^{r}$
, we have (3.2.3)where for $$ \begin{align}\begin{aligned} \mathscr{I}(\phi^{p\infty}; \chi')= {c_{U^{p}} \lvert D_{E}\rvert^{1/2} \over \lvert D_{F}\rvert^{1/2}} \int_{[T]}^{*}\chi'(t) \sum_{u\in\mu_{U^{p}}^{2}\backslash F^{\times}} {}^{\mathbf{q}}\theta((t,1),u, \phi_{1}; \chi') \mathscr{E}\left(q(t)u,\phi_{2}^{p\infty};\chi_{F}\right) d^{\circ }t, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{I}(\phi^{p\infty}; \chi')= {c_{U^{p}} \lvert D_{E}\rvert^{1/2} \over \lvert D_{F}\rvert^{1/2}} \int_{[T]}^{*}\chi'(t) \sum_{u\in\mu_{U^{p}}^{2}\backslash F^{\times}} {}^{\mathbf{q}}\theta((t,1),u, \phi_{1}; \chi') \mathscr{E}\left(q(t)u,\phi_{2}^{p\infty};\chi_{F}\right) d^{\circ }t, \end{aligned}\end{align} $$
 $v\mid p$
, we have
$v\mid p$
, we have
 $\phi _{1,v}=\phi _{1, v,r}$
is as in formula (3.1.3).
$\phi _{1,v}=\phi _{1, v,r}$
is as in formula (3.1.3).
-
3. We have
(3.2.4)where the local terms $$ \begin{align} \ell_{\varphi^{p},\alpha}(\mathscr{I}(\phi^{p\infty}))= L_{p, \alpha}(\sigma_{E})\cdot \prod_{v\mid p} \lvert d\rvert^{2}_{v}\lvert D\rvert_{v} \prod_{v\nmid p \infty} \mathscr{R}_{v}^{\natural}\left(W_{v}, \phi_{v}, \chi_{v}'\right), \end{align} $$
$$ \begin{align} \ell_{\varphi^{p},\alpha}(\mathscr{I}(\phi^{p\infty}))= L_{p, \alpha}(\sigma_{E})\cdot \prod_{v\mid p} \lvert d\rvert^{2}_{v}\lvert D\rvert_{v} \prod_{v\nmid p \infty} \mathscr{R}_{v}^{\natural}\left(W_{v}, \phi_{v}, \chi_{v}'\right), \end{align} $$
 $\mathscr {R}_{v}^{\natural } $
are as in [Reference Disegni9, Propositions 3.5.1, 3.6.1].
$\mathscr {R}_{v}^{\natural } $
are as in [Reference Disegni9, Propositions 3.5.1, 3.6.1].
Proof. Part 1 is [Reference Disegni9, Proposition 3.3.2]. Part 2 summarizes [Reference Disegni9, §3.4]. Part 3 is [Reference Disegni9, (3.7.1)], with the correction of Appendix B.
Derivative of the analytic kernel
We denote
a p-adic modular form with coefficients in
![]() $\Gamma _{F}\hat {\otimes } L(\chi )$
.
$\Gamma _{F}\hat {\otimes } L(\chi )$
.
3.3 Geometric kernel
The geometric kernel function [Reference Disegni9, §§5.2, 5.3] is related to the heights of Heegner points. We recall its construction and modularity.
CM divisors
For any
![]() $x\in \mathbf {B}^{\infty \times }$
, we have a Hecke translation
$x\in \mathbf {B}^{\infty \times }$
, we have a Hecke translation
![]() ${\mathrm{T}}_{x}\colon X\to X$
, and a Hecke correspondence
${\mathrm{T}}_{x}\colon X\to X$
, and a Hecke correspondence
![]() $Z(x)_{U}$
on
$Z(x)_{U}$
on
![]() $X_{U }\times X_{U}$
. Fix any
$X_{U }\times X_{U}$
. Fix any
 $P\in X^{E^{\times }}\left (E^{\mathrm{ab}}\right )$
, and for
$P\in X^{E^{\times }}\left (E^{\mathrm{ab}}\right )$
, and for
![]() $x\in \mathbf {B}^{\infty \times }$
, let
$x\in \mathbf {B}^{\infty \times }$
, let
![]() $[x]:={\mathrm{T}}_{x}P$
be the Hecke-translate of P by x, and let
$[x]:={\mathrm{T}}_{x}P$
be the Hecke-translate of P by x, and let
![]() $[x]_{U}$
be its image in
$[x]_{U}$
be its image in
![]() $X_{U}$
. If
$X_{U}$
. If
![]() $H/E$
is any finite extension, the points in
$H/E$
is any finite extension, the points in
![]() $X_{U, H}$
corresponding to Galois orbits of points of the form
$X_{U, H}$
corresponding to Galois orbits of points of the form
![]() $[x]_{U}$
are called CM points (for the CM field E).
$[x]_{U}$
are called CM points (for the CM field E).
Let
 ${\mathrm{Cl}}(X_{U,{\overline {F}}})_{\mathbf {Q}}\supset {\mathrm{Cl}}^{0}(X_{U,{\overline {F}}} )_{\mathbf {Q}}$
be the space of divisor classes with
${\mathrm{Cl}}(X_{U,{\overline {F}}})_{\mathbf {Q}}\supset {\mathrm{Cl}}^{0}(X_{U,{\overline {F}}} )_{\mathbf {Q}}$
be the space of divisor classes with
![]() $\mathbf {Q}$
-coefficients and its subspace consisting of classes with degree
$\mathbf {Q}$
-coefficients and its subspace consisting of classes with degree
![]() $0$
on every connected component. Denote by
$0$
on every connected component. Denote by
 ${(\ )}^{0}\colon {\mathrm{Cl}}(X_{U,{\overline {F}}})_{\mathbf {Q}}\to {\mathrm{Cl}}^{0}(X_{U,{\overline {F}}})_{\mathbf {Q}}$
the linear section of the inclusion whose kernel is spanned by the push-forwards to
${(\ )}^{0}\colon {\mathrm{Cl}}(X_{U,{\overline {F}}})_{\mathbf {Q}}\to {\mathrm{Cl}}^{0}(X_{U,{\overline {F}}})_{\mathbf {Q}}$
the linear section of the inclusion whose kernel is spanned by the push-forwards to
![]() $X_{U, \overline {F}}$
of the classes of the canonical bundles of the connected components of
$X_{U, \overline {F}}$
of the classes of the canonical bundles of the connected components of
![]() $X_{U', \overline {F}} $
, for any sufficiently small
$X_{U', \overline {F}} $
, for any sufficiently small
![]() $U'$
.
$U'$
.
We define the
![]() $\chi $
-isotypic CM divisors
$\chi $
-isotypic CM divisors
 $$ \begin{align*}\begin{aligned} t_{\chi} &:=\int^{*}_{[T]}\chi(t) \left[t^{-1}\right]_{U}d^{\circ}t \in \mathrm{Div}\left(X_{U, \overline{F}}\right)_{L(\chi)}, \\ t_{\chi}^{0} &:=\int^{*}_{[T]}\chi(t) \left[t^{-1}\right]^{0}_{U}d^{\circ}t \in \mathrm{Div}^{0}\left(X_{U, \overline{F}}\right)_{L(\chi)}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} t_{\chi} &:=\int^{*}_{[T]}\chi(t) \left[t^{-1}\right]_{U}d^{\circ}t \in \mathrm{Div}\left(X_{U, \overline{F}}\right)_{L(\chi)}, \\ t_{\chi}^{0} &:=\int^{*}_{[T]}\chi(t) \left[t^{-1}\right]^{0}_{U}d^{\circ}t \in \mathrm{Div}^{0}\left(X_{U, \overline{F}}\right)_{L(\chi)}, \end{aligned}\end{align*} $$
where the integrations simply reduce to (normalized) finite sums.
Generating series
For
![]() $a\in \mathbf {A}^{\infty \times }$
,
$a\in \mathbf {A}^{\infty \times }$
,
![]() $\phi ^{\infty }\in \overline {\mathscr {S}}({\mathbf {V}}\times \mathbf {A}^{\times })$
, consider the correspondences
$\phi ^{\infty }\in \overline {\mathscr {S}}({\mathbf {V}}\times \mathbf {A}^{\times })$
, consider the correspondences
 $$ \begin{align} {\widetilde Z}_{a}(\phi^{\infty}):= c_{U^{p}}w_{U} \lvert a\rvert \sum_{x\in U \backslash \mathbf{B}^{\infty\times}/ U }\phi^{\infty}\left(x, aq(x)^{-1}\right) Z(x)_{U}, \end{align} $$
$$ \begin{align} {\widetilde Z}_{a}(\phi^{\infty}):= c_{U^{p}}w_{U} \lvert a\rvert \sum_{x\in U \backslash \mathbf{B}^{\infty\times}/ U }\phi^{\infty}\left(x, aq(x)^{-1}\right) Z(x)_{U}, \end{align} $$
where
![]() $w_{U}=\lvert \{\pm 1\}\cap U\rvert $
and
$w_{U}=\lvert \{\pm 1\}\cap U\rvert $
and
![]() $c_{U^{p}}$
is defined in [Reference Disegni9, (3.4.3)]. By [Reference Disegni9, Theorem 5.2.1] (due to Yuan, Zhang, and Zhang), there is an automorphic form
$c_{U^{p}}$
is defined in [Reference Disegni9, (3.4.3)]. By [Reference Disegni9, Theorem 5.2.1] (due to Yuan, Zhang, and Zhang), there is an automorphic form
 $$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty}) \in C^{\infty}(\mathrm{GL}_{2}(F)\backslash \mathrm{GL}_{2}(\mathbf{A}), \mathbf{C})\otimes_{\mathbf{Q}} {\mathrm{Pic}}(X_{U}\times X_{U})_{\mathbf{Q}}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty}) \in C^{\infty}(\mathrm{GL}_{2}(F)\backslash \mathrm{GL}_{2}(\mathbf{A}), \mathbf{C})\otimes_{\mathbf{Q}} {\mathrm{Pic}}(X_{U}\times X_{U})_{\mathbf{Q}}, \end{aligned}\end{align} $$
whose ath reduced coefficient is the image of
 ${\widetilde Z}_{a}(\phi ^{\infty })$
for each
${\widetilde Z}_{a}(\phi ^{\infty })$
for each
![]() $a\in \mathbf {A}^{\infty \times }$
.
$a\in \mathbf {A}^{\infty \times }$
.
Let
 $$ \begin{align}\begin{aligned} \langle\ , \ \rangle=\langle\ , \ \rangle_{X}\colon J^{\vee}\left(\overline{F}\right) \times J\left(\overline{F}\right) \to \Gamma_{F}\hat{\otimes} L \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \langle\ , \ \rangle=\langle\ , \ \rangle_{X}\colon J^{\vee}\left(\overline{F}\right) \times J\left(\overline{F}\right) \to \Gamma_{F}\hat{\otimes} L \end{aligned}\end{align} $$
be the p-adic height pairing defined as inFootnote
7
[Reference Disegni9, Lemma 5.3.1]. (We abusively omit the subscript X, as we will no longer need to use the pairing on
![]() $A_{E}(\chi )\otimes A_{E}^{\vee }(\chi )$
.)
$A_{E}(\chi )\otimes A_{E}^{\vee }(\chi )$
.)
We define the geometric kernel to be
 $$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty},\chi):= \sum_{a\in F^{\times}} \left\langle {\widetilde Z}_{a}(\phi^{\infty})[1]_{U}^{0}, t^{0}_{\chi} \right\rangle {\textbf{q}}^{a}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty},\chi):= \sum_{a\in F^{\times}} \left\langle {\widetilde Z}_{a}(\phi^{\infty})[1]_{U}^{0}, t^{0}_{\chi} \right\rangle {\textbf{q}}^{a}. \end{aligned}\end{align} $$
By [I, Proposition 5.3.2 and the formula after its proof], the series
 $ {\widetilde Z}(\phi ^{\infty },\chi )$
is (the q-expansion of) a weight
$ {\widetilde Z}(\phi ^{\infty },\chi )$
is (the q-expansion of) a weight
![]() $2$
cuspidal Hilbert modular form of central character
$2$
cuspidal Hilbert modular form of central character
![]() $\omega ^{-1}$
, with coefficients in
$\omega ^{-1}$
, with coefficients in
![]() $\Gamma _{F}\hat {\otimes } L(\chi )$
.
$\Gamma _{F}\hat {\otimes } L(\chi )$
.
Geometric kernel and Shimizu lifts
Let
 $$ \begin{align*} \theta_{\iota_{\mathfrak{p}}}\colon\left( \sigma^{\infty}\otimes \overline{\mathscr{S}}({\textbf{V}}^{\infty}\times \mathbf{A}^{\infty,\times})\right)\otimes_{M}L\to (\pi\otimes \pi^{\vee})\otimes_{M, \iota_{\mathfrak{p}}} L \end{align*} $$
$$ \begin{align*} \theta_{\iota_{\mathfrak{p}}}\colon\left( \sigma^{\infty}\otimes \overline{\mathscr{S}}({\textbf{V}}^{\infty}\times \mathbf{A}^{\infty,\times})\right)\otimes_{M}L\to (\pi\otimes \pi^{\vee})\otimes_{M, \iota_{\mathfrak{p}}} L \end{align*} $$
be Shimizu’s theta lifting defined in [Reference Disegni9, §5.1]. Let
be defined by
![]() ${\mathrm{T}}_{\mathrm{alg}}(f_{1}, f_{2}):= f_{2}^{\vee }\circ f_{1}$
.
${\mathrm{T}}_{\mathrm{alg}}(f_{1}, f_{2}):= f_{2}^{\vee }\circ f_{1}$
.
Proposition 3.3.1. If
![]() $\phi _{v}=\phi _{r,v}$
is as in formula (3.1.4) for all
$\phi _{v}=\phi _{r,v}$
is as in formula (3.1.4) for all
![]() $v\mid p$
, then for any sufficiently large
$v\mid p$
, then for any sufficiently large
![]() $r'$
, the geometric kernel
$r'$
, the geometric kernel
 $$ \begin{align*} {\widetilde Z}(\phi^{\infty},\chi) \end{align*} $$
$$ \begin{align*} {\widetilde Z}(\phi^{\infty},\chi) \end{align*} $$
is invariant under
 $\prod _{v\vert p}K_{1}^{1}(\varpi _{v}^{r'})$
, and it satisfies
$\prod _{v\vert p}K_{1}^{1}(\varpi _{v}^{r'})$
, and it satisfies
 $$ \begin{align} & \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right) \nonumber \\&\quad =2 \lvert D_{F}\rvert^{1/2} \lvert D_{E}\rvert^{1/2} L(1, \eta) \cdot \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}\left(\theta_{\iota_{\mathfrak{p}}}\left(\varphi,\alpha_{p} \lvert\cdot \rvert_{p}(\varpi)^{-r'}w_{r'}^{-1}\phi\right)\right) P_{\chi}, P_{\chi}^{-1}\right\rangle_{X}. \end{align} $$
$$ \begin{align} & \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right) \nonumber \\&\quad =2 \lvert D_{F}\rvert^{1/2} \lvert D_{E}\rvert^{1/2} L(1, \eta) \cdot \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}\left(\theta_{\iota_{\mathfrak{p}}}\left(\varphi,\alpha_{p} \lvert\cdot \rvert_{p}(\varpi)^{-r'}w_{r'}^{-1}\phi\right)\right) P_{\chi}, P_{\chi}^{-1}\right\rangle_{X}. \end{align} $$
Proof. The invariance under
 $\prod _{v\vert p}K_{1}^{1} (\varpi _{v}^{r'} )$
follows from the invariance of
$\prod _{v\vert p}K_{1}^{1} (\varpi _{v}^{r'} )$
follows from the invariance of
![]() $\phi _{r}$
under the action of
$\phi _{r}$
under the action of
 $(\begin {smallmatrix}1&\mathscr {O}_{F, p}\\&1\end {smallmatrix})$
and the continuity of the Weil representation. The proof of equation (3.3.5) is indicated in [Reference Disegni9, proof of Proposition 5.4.3] (with the correction of Appendix B).
$(\begin {smallmatrix}1&\mathscr {O}_{F, p}\\&1\end {smallmatrix})$
and the continuity of the Weil representation. The proof of equation (3.3.5) is indicated in [Reference Disegni9, proof of Proposition 5.4.3] (with the correction of Appendix B).
3.4 Kernel identity
We state our kernel identity and recall how it implies the main theorem.
Assumptions on the data
Consider the following local assumptions on the data at primes above
![]() $ p$
:
$ p$
:
Assumption 3.4.1. Let
![]() $U_{F,v}^{\circ }:=1+\varpi _{v}^{n}\mathscr {O}_{F,v}$
with
$U_{F,v}^{\circ }:=1+\varpi _{v}^{n}\mathscr {O}_{F,v}$
with
![]() $n\geq 1$
be such that
$n\geq 1$
be such that
![]() $\omega _{v}$
is invariant under
$\omega _{v}$
is invariant under
![]() $U_{F, v}^{\circ }$
. The character
$U_{F, v}^{\circ }$
. The character
![]() $\chi _{p}$
is sufficiently ramified in the sense that it is nontrivial on
$\chi _{p}$
is sufficiently ramified in the sense that it is nontrivial on
 $$ \begin{align*} V_{p}^{\circ}:=\prod_{v\mid p}q_{v\mid\mathscr{O}_{E,v}}^{-1}\left(U_{F,v}^{\circ}\right)\subset \mathscr{O}_{E,p}^{\times}. \end{align*} $$
$$ \begin{align*} V_{p}^{\circ}:=\prod_{v\mid p}q_{v\mid\mathscr{O}_{E,v}}^{-1}\left(U_{F,v}^{\circ}\right)\subset \mathscr{O}_{E,p}^{\times}. \end{align*} $$
(Recall from §3.1 that
![]() $q_{v}\colon E_{v}\to F_{v}$
is the norm map.)
$q_{v}\colon E_{v}\to F_{v}$
is the norm map.)
Under this assumption, we have
 $t_{\chi }=t_{\chi }^{0}$
; see [I, Proposition 8.1.1.3], where
$t_{\chi }=t_{\chi }^{0}$
; see [I, Proposition 8.1.1.3], where
![]() $\xi _{U}\in {\mathrm{Cl}}(X_{U})_{\mathbf {Q}}$
denotes the Hodge class defining the section
$\xi _{U}\in {\mathrm{Cl}}(X_{U})_{\mathbf {Q}}$
denotes the Hodge class defining the section
 ${\mathrm{Cl}}(X_{U})_{\mathbf {Q}}\to {\mathrm{Cl}}^{0}(X_{U})_{\mathbf {Q}}$
. The technical advantage gained, which is the same as in [I] and is implicitly reaped in Theorem 3.6.1, is that one may analyze the height-generating series purely in terms of pairs of CM divisors of degree
${\mathrm{Cl}}(X_{U})_{\mathbf {Q}}\to {\mathrm{Cl}}^{0}(X_{U})_{\mathbf {Q}}$
. The technical advantage gained, which is the same as in [I] and is implicitly reaped in Theorem 3.6.1, is that one may analyze the height-generating series purely in terms of pairs of CM divisors of degree
![]() $0$
, thus avoiding a study of
$0$
, thus avoiding a study of
![]() $\xi _{U}$
and the recourse to p-adic Arakelov theory made in [Reference Disegni8].
$\xi _{U}$
and the recourse to p-adic Arakelov theory made in [Reference Disegni8].
Assumption 3.4.2. For each
![]() $v \mid p$
, the open compact
$v \mid p$
, the open compact
![]() $U_{v}\subset \mathbf {B}_{v}^{\times }$
satisfies the following:
$U_{v}\subset \mathbf {B}_{v}^{\times }$
satisfies the following:
-
–
 $U_{v}= U_{v,r}=1+\varpi ^{r}M_{2}\left (\mathscr {O}_{F,{v}}\right )$
for some
$U_{v}= U_{v,r}=1+\varpi ^{r}M_{2}\left (\mathscr {O}_{F,{v}}\right )$
for some
 $r\geq 1$
.
$r\geq 1$
. -
– The integer
 $r\geq n$
is sufficiently large that the characters
$r\geq n$
is sufficiently large that the characters
 $\chi _{v}$
and
$\chi _{v}$
and
 $\alpha _{v}\circ q_{v}$
of
$\alpha _{v}\circ q_{v}$
of
 $E_{v}^{\times }$
are invariant under
$E_{v}^{\times }$
are invariant under
 $U_{v,r}\cap \mathscr {O}_{E,v}^{\times }$
.
$U_{v,r}\cap \mathscr {O}_{E,v}^{\times }$
.
Convention on citations from [Reference Disegni9]
In [Reference Disegni9], we denoted by
![]() $S_{\text {nonsplit}}$
the set of places of F nonsplit in E, and by
$S_{\text {nonsplit}}$
the set of places of F nonsplit in E, and by
![]() $S_{p}$
the set of places of F above p. When referring to results from [Reference Disegni9], we henceforth stipulate that one should read any assumption such as ‘set
$S_{p}$
the set of places of F above p. When referring to results from [Reference Disegni9], we henceforth stipulate that one should read any assumption such as ‘set
![]() $v\in S_{\text {nonsplit}}$
’ or ‘let v be a place in F nonsplit in E’ as ‘set
$v\in S_{\text {nonsplit}}$
’ or ‘let v be a place in F nonsplit in E’ as ‘set
![]() $v\in S_{\text {nonsplit}} -S_{p}$
’. Similarly, the set
$v\in S_{\text {nonsplit}} -S_{p}$
’. Similarly, the set
![]() $S_{1}$
fixed in [Reference Disegni9, §6.1] should be understood to consist only of places not above p.
$S_{1}$
fixed in [Reference Disegni9, §6.1] should be understood to consist only of places not above p.
Theorem 3.4.3 kernel identity
Assume the hypotheses of Theorem B, and that
![]() $U, \varphi ^{p}, \phi ^{p\infty }, \chi , r$
satisfy the assumptions of [Reference Disegni9, §6.1] as well as Assumptions 3.4.1 and 3.4.2. Define
$U, \varphi ^{p}, \phi ^{p\infty }, \chi , r$
satisfy the assumptions of [Reference Disegni9, §6.1] as well as Assumptions 3.4.1 and 3.4.2. Define
![]() $\phi _{p}:= \otimes _{v\mid p}\phi _{v, r}$
, with
$\phi _{p}:= \otimes _{v\mid p}\phi _{v, r}$
, with
![]() $\phi _{v,r}=$
formula (3.1.4). Then
$\phi _{v,r}=$
formula (3.1.4). Then
 $$ \begin{align*} \ell_{\varphi^{p},\alpha}({\mathrm{d}}_{F}\mathscr{I}(\phi^{p\infty}; \chi))= {2 \lvert D_{F}\rvert L_{(p)}(1, \eta)}\cdot \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right). \end{align*} $$
$$ \begin{align*} \ell_{\varphi^{p},\alpha}({\mathrm{d}}_{F}\mathscr{I}(\phi^{p\infty}; \chi))= {2 \lvert D_{F}\rvert L_{(p)}(1, \eta)}\cdot \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right). \end{align*} $$
The elements of the proof will be gathered in §3.6.
Proof. As in [Reference Disegni9, Proposition 5.4.3] as corrected in Appendix B, we consider the following equivalent (by [Reference Disegni9, Lemma 5.3.1]) form of the identity of Theorem 2.2.1:
 $$ \begin{align} & \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}(f_{1}\otimes f_{2}) P_{\chi}, P_{{\chi}^{-1}}\right\rangle_{J} \nonumber\\&\quad ={ \zeta_{F}^{\infty}(2)\over \left(\pi^{2}/2\right)^{\left[F:\mathbf{Q}\right]} \lvert D_{E}\rvert^{1/2} L(1, \eta)} \prod_{v\mid p}Z_{v}^{\circ}( \alpha_{v}, \chi_{v})^{-1} \cdot{\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})( \chi)\cdot Q(f_{1}, f_{2}, \chi), \end{align} $$
$$ \begin{align} & \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}(f_{1}\otimes f_{2}) P_{\chi}, P_{{\chi}^{-1}}\right\rangle_{J} \nonumber\\&\quad ={ \zeta_{F}^{\infty}(2)\over \left(\pi^{2}/2\right)^{\left[F:\mathbf{Q}\right]} \lvert D_{E}\rvert^{1/2} L(1, \eta)} \prod_{v\mid p}Z_{v}^{\circ}( \alpha_{v}, \chi_{v})^{-1} \cdot{\mathrm{d}}_{F} L_{p, \alpha}(\sigma_{A,E})( \chi)\cdot Q(f_{1}, f_{2}, \chi), \end{align} $$
where
![]() $\iota _{\mathfrak {p}}\colon M\hookrightarrow L(\chi )$
, and
$\iota _{\mathfrak {p}}\colon M\hookrightarrow L(\chi )$
, and
 . By linearity, equation (3.4.1) extends to an identity that makes sense for any element
. By linearity, equation (3.4.1) extends to an identity that makes sense for any element
![]() ${\mathbf {f}}\in \pi \otimes \pi ^{\vee }$
. By the multiplicity
${\mathbf {f}}\in \pi \otimes \pi ^{\vee }$
. By the multiplicity
![]() $1$
result for
$1$
result for
![]() $E_{\mathbf {A}^{\infty }}^{\times }$
-invariant linear functionals on each of
$E_{\mathbf {A}^{\infty }}^{\times }$
-invariant linear functionals on each of
![]() $\pi , \pi ^{\vee }$
, it suffices to prove equation (3.4.1) for one element
$\pi , \pi ^{\vee }$
, it suffices to prove equation (3.4.1) for one element
![]() ${\mathbf {f}}\in \pi \otimes \pi ^{\vee }$
such that
${\mathbf {f}}\in \pi \otimes \pi ^{\vee }$
such that
![]() $Q({\mathbf {f}} , \chi )\neq 0$
(compare [Reference Yuan, Zhang and Zhang29, Lemma 3.23]).
$Q({\mathbf {f}} , \chi )\neq 0$
(compare [Reference Yuan, Zhang and Zhang29, Lemma 3.23]).
We claim that Theorem 3.4.3 gives equation (3.4.1) for
![]() ${\mathbf {f}}=\theta (\varphi , \phi )$
, where:
${\mathbf {f}}=\theta (\varphi , \phi )$
, where:
-
–
 $\varphi _{\infty }$
is standard antiholomoprhic in the sense of [Reference Disegni9] and
$\varphi _{\infty }$
is standard antiholomoprhic in the sense of [Reference Disegni9] and
 $\phi _{\infty }$
is standard in the sense of [Reference Disegni9]; and
$\phi _{\infty }$
is standard in the sense of [Reference Disegni9]; and -
– for all
 $v\mid p$
, we have that
$v\mid p$
, we have that
 $\varphi _{v}=$
equation (3.1.2) and
$\varphi _{v}=$
equation (3.1.2) and
 $\phi _{v}=\phi _{v,r}=$
formula (3.1.4) for any sufficiently large r.
$\phi _{v}=\phi _{v,r}=$
formula (3.1.4) for any sufficiently large r.
The claim follows from equations (3.2.4) and (3.3.5), the local comparison between
![]() $\mathscr {R}_{v}^{\natural } $
and
$\mathscr {R}_{v}^{\natural } $
and
![]() $Q_{v}\circ \theta _{v}$
for
$Q_{v}\circ \theta _{v}$
for
![]() $v\nmid p$
of [Reference Disegni9, Lemma 5.1.1], and the local calculation at
$v\nmid p$
of [Reference Disegni9, Lemma 5.1.1], and the local calculation at
![]() $v\vert p$
of Proposition A.2.2.
$v\vert p$
of Proposition A.2.2.
Finally, the existence of
![]() $\varphi , \phi $
satisfying both the required assumptions and
$\varphi , \phi $
satisfying both the required assumptions and
![]() $Q(\theta (\varphi , \phi ))\neq 0$
follows from [Reference Disegni9, Lemma 6.1.6] away from p, and the explicit formula of Proposition A.2.2 at p.
$Q(\theta (\varphi , \phi ))\neq 0$
follows from [Reference Disegni9, Lemma 6.1.6] away from p, and the explicit formula of Proposition A.2.2 at p.
3.5 Derivative of the analytic kernel
We start by studying the incoherent Eisenstein series
![]() $\mathscr {E}\left (\phi _{2}^{p\infty }\right )$
. For
$\mathscr {E}\left (\phi _{2}^{p\infty }\right )$
. For
![]() $a\in F_{v}^{\times }$
, denote by
$a\in F_{v}^{\times }$
, denote by
the normalized local Whittaker function of
 $E_{r}\left (\phi _{2}^{p\infty }(\chi _{F}){\phi _{2,p}^{\circ }}, \chi _{F}\right )=\text {formula}~(3.2.1)$
, defined as in [Reference Disegni9, Proposition 3.2.1 and the paragraph after its proof].
$E_{r}\left (\phi _{2}^{p\infty }(\chi _{F}){\phi _{2,p}^{\circ }}, \chi _{F}\right )=\text {formula}~(3.2.1)$
, defined as in [Reference Disegni9, Proposition 3.2.1 and the paragraph after its proof].
The following reviews and corrects [Reference Disegni9, Proposition 7.1.1]:
Proposition 3.5.1. For each
![]() $v\mid p$
, let
$v\mid p$
, let
![]() $\phi _{2, v}=\phi _{2, r,v}$
be as in formula (3.1.4).
$\phi _{2, v}=\phi _{2, r,v}$
be as in formula (3.1.4).
-
1. Let v be a place of F and set
 $a\in F_{v}^{\times }$
.
$a\in F_{v}^{\times }$
.-
(a) If a is not represented by
 $({\mathbf {V}}_{2,v}, uq)$
, then
$({\mathbf {V}}_{2,v}, uq)$
, then
 $W_{a,v}^{\circ }(g,u, \mathbf {1})=0$
.
$W_{a,v}^{\circ }(g,u, \mathbf {1})=0$
. -
(b) (Local Siegel–Weil formula.) If
 $v\nmid p$
and there exists
$v\nmid p$
and there exists
 $x_{a}\in {\mathbf {V}}_{2,v}$
such that
$x_{a}\in {\mathbf {V}}_{2,v}$
such that
 $uq(x_{a})=a$
, then
$uq(x_{a})=a$
, then  $$ \begin{align*} W_{a,v}^{\circ}\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \mathbf{1}\right)= \int_{E_{v}^{1}}r\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right), h\right)\phi_{2,v}(x_{a},u) dh. \end{align*} $$
$$ \begin{align*} W_{a,v}^{\circ}\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \mathbf{1}\right)= \int_{E_{v}^{1}}r\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right), h\right)\phi_{2,v}(x_{a},u) dh. \end{align*} $$
-
(c) (Local Siegel–Weil formula at p.) If
 $v\mid p$
,
$v\mid p$
,
 $a\in -1+\varpi ^{r}\mathscr {O}_{F,v}$
, and
$a\in -1+\varpi ^{r}\mathscr {O}_{F,v}$
, and
 $u\in 1+\varpi ^{r}\mathscr {O}_{F,v} $
, let
$u\in 1+\varpi ^{r}\mathscr {O}_{F,v} $
, let
 $x_{a}\in {\mathbf {V}}_{2,v}$
be such that
$x_{a}\in {\mathbf {V}}_{2,v}$
be such that
 $uq(x_{a})=a$
. Then (3.5.1)
$uq(x_{a})=a$
. Then (3.5.1) $$ \begin{align}\begin{aligned} W_{a,v}^{\circ}\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \mathbf{1}\right)= \lvert d\rvert_{v}\int_{E_{v}^{1}}r\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right), h\right)\phi_{2,v}(x_{a},u) dh. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} W_{a,v}^{\circ}\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \mathbf{1}\right)= \lvert d\rvert_{v}\int_{E_{v}^{1}}r\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right), h\right)\phi_{2,v}(x_{a},u) dh. \end{aligned}\end{align} $$
-
-
2. For any
 $a\in F_{v}^{\times }\cap \prod _{v\mid p }\left ( -1+\varpi ^{r}\mathscr {O}_{F,v}\right )$
,
$a\in F_{v}^{\times }\cap \prod _{v\mid p }\left ( -1+\varpi ^{r}\mathscr {O}_{F,v}\right )$
,
 $u\in F^{\times }\cap \prod _{v\mid p} \left (1+\varpi ^{r}\mathscr {O}_{F,{v}}\right )$
, there is a place
$u\in F^{\times }\cap \prod _{v\mid p} \left (1+\varpi ^{r}\mathscr {O}_{F,{v}}\right )$
, there is a place
 $v\nmid p$
of F such that a is not represented by
$v\nmid p$
of F such that a is not represented by
 $({\mathbf {V}}_{2}, uq)$
.
$({\mathbf {V}}_{2}, uq)$
.
Proof. Parts 1(a) and (b) are as in [Reference Disegni9, Proposition 7.1.1]. Before continuing, observe that under our assumptions, a is always represented by
![]() $\left ({\mathbf {V}}_{2,v}, uq_{v}\right )$
for all
$\left ({\mathbf {V}}_{2,v}, uq_{v}\right )$
for all
![]() $v\mid p$
: this is clear if v splits in E, and up to possibly enlarging the integer r, it may be seen by the local constancy of
$v\mid p$
: this is clear if v splits in E, and up to possibly enlarging the integer r, it may be seen by the local constancy of
![]() $q_{v}$
and the explicit identity
$q_{v}$
and the explicit identity
![]() $q_{v}({\frak j}_{v})=-1$
, where
$q_{v}({\frak j}_{v})=-1$
, where
![]() ${\frak j}_{v}$
=formula (4.1.2) if v is nonsplit. Then part 1(c) follows by explicit computation of both sides (starting, for example, as in [Reference Yuan, Zhang and Zhang29, proof of Proposition 6.8] for the left-hand side). Explicitly, we have
${\frak j}_{v}$
=formula (4.1.2) if v is nonsplit. Then part 1(c) follows by explicit computation of both sides (starting, for example, as in [Reference Yuan, Zhang and Zhang29, proof of Proposition 6.8] for the left-hand side). Explicitly, we have
 $$ \begin{align*} &\text{equation~(3.5.1)}= \nonumber \\&\quad \begin{cases} e_{v}^{-1}\lvert d\rvert_{v}\mathrm{vol}\left(E^{1}_{v}\cap \mathscr{O}_{E,v}^{\times}, dh\right)\lvert y\rvert^{1/2} \mathbf{1}_{\mathscr{O}_{F,v}}(ay)\mathbf{1}_{\mathscr{O}_{F, v}^{\times}}\left(y^{-1}u\right) & \text{if } v(a)\geq 0 \text{ and } v(u)=0, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} &\text{equation~(3.5.1)}= \nonumber \\&\quad \begin{cases} e_{v}^{-1}\lvert d\rvert_{v}\mathrm{vol}\left(E^{1}_{v}\cap \mathscr{O}_{E,v}^{\times}, dh\right)\lvert y\rvert^{1/2} \mathbf{1}_{\mathscr{O}_{F,v}}(ay)\mathbf{1}_{\mathscr{O}_{F, v}^{\times}}\left(y^{-1}u\right) & \text{if } v(a)\geq 0 \text{ and } v(u)=0, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Finally, part 2 follows from the observation of the previous paragraph and [Reference Yuan, Zhang and Zhang29, Lemma 6.3].
Lemma 3.5.2. Suppose that for all
![]() $v\mid p$
, we have that
$v\mid p$
, we have that
![]() $\phi _{1,v}=\phi _{1,r,v}$
is as in formula (3.1.3). Then for any
$\phi _{1,v}=\phi _{1,r,v}$
is as in formula (3.1.3). Then for any
![]() $t\in T(\mathbf {A})$
, the ath q-expansion coefficient of the the theta series of formula (3.2.2) vanishes unless
$t\in T(\mathbf {A})$
, the ath q-expansion coefficient of the the theta series of formula (3.2.2) vanishes unless
 $$ \begin{align*} a\in \bigcap_{v\mid p} 1+\varpi^{r}\mathscr{O}_{F,v}. \end{align*} $$
$$ \begin{align*} a\in \bigcap_{v\mid p} 1+\varpi^{r}\mathscr{O}_{F,v}. \end{align*} $$
Proof. This is straightforward.
Denote
 $$ \begin{align*} \mathrm{U}_{p, *}^{r}:= \left(\prod_{v\vert p}\mathrm{U}_{v, *}\right)^{r}, \end{align*} $$
$$ \begin{align*} \mathrm{U}_{p, *}^{r}:= \left(\prod_{v\vert p}\mathrm{U}_{v, *}\right)^{r}, \end{align*} $$
an operator on modular forms that extends to an operator on all the spaces of p-adic q-expansions defined so far.
Corollary 3.5.3. Suppose that
![]() $\phi ^{p\infty } \in {\mathscr {S}}\left ({\mathbf {V}}_{2}^{p\infty }\times {\mathbf {A}^{p\infty , \times }}\right )$
satisfies the assumptions of [Reference Disegni9, §6.1]. Set
$\phi ^{p\infty } \in {\mathscr {S}}\left ({\mathbf {V}}_{2}^{p\infty }\times {\mathbf {A}^{p\infty , \times }}\right )$
satisfies the assumptions of [Reference Disegni9, §6.1]. Set
![]() $\chi \in \mathscr {Y}_{\omega }^{\mathrm{l.c.}}$
. For any sufficiently large r, we have
$\chi \in \mathscr {Y}_{\omega }^{\mathrm{l.c.}}$
. For any sufficiently large r, we have
Proof. For the first assertion, we need to show that the ath reduced q-expansion coefficient of
![]() $\mathscr {I}$
vanishes for all a satisfying
$\mathscr {I}$
vanishes for all a satisfying
![]() $v(a)\geq r$
for all
$v(a)\geq r$
for all
![]() $v\mid p$
. By the defining property (3.2.3) of
$v\mid p$
. By the defining property (3.2.3) of
![]() $\mathscr {I}(\chi ')$
and the choice of
$\mathscr {I}(\chi ')$
and the choice of
![]() $\phi _{p}$
, the group
$\phi _{p}$
, the group
![]() $T\left (F_{p}\right )\subset T(\mathbf {A})$
acts trivially on the q-expansion coefficients of
$T\left (F_{p}\right )\subset T(\mathbf {A})$
acts trivially on the q-expansion coefficients of
![]() $\mathscr {I}(\chi ')$
. The remaining integration on
$\mathscr {I}(\chi ')$
. The remaining integration on
![]() $T(F)Z(\mathbf {A})V^{p}\backslash T(\mathbf {A})/T\left (F_{p}\right ) $
is a finite sum, so the coefficients a are a sum of products of the coefficients of index
$T(F)Z(\mathbf {A})V^{p}\backslash T(\mathbf {A})/T\left (F_{p}\right ) $
is a finite sum, so the coefficients a are a sum of products of the coefficients of index
![]() $a_{1}$
of
$a_{1}$
of
![]() $\theta $
and of index
$\theta $
and of index
![]() $ a_{2}$
of
$ a_{2}$
of
![]() $\mathscr {E}(\mathbf {1})$
, for pairs
$\mathscr {E}(\mathbf {1})$
, for pairs
![]() $(a_{1}, a_{2}) $
with
$(a_{1}, a_{2}) $
with
![]() $a_{1}+a_{2}=a$
. When
$a_{1}+a_{2}=a$
. When
![]() $a=0$
, the vanishing follows from the vanishing of the constant term of
$a=0$
, the vanishing follows from the vanishing of the constant term of
![]() $\mathscr {E}$
, which is proved as in [Reference Yuan, Zhang and Zhang29, Proposition 6.7]. For
$\mathscr {E}$
, which is proved as in [Reference Yuan, Zhang and Zhang29, Proposition 6.7]. For
![]() $a\neq 0$
, by Lemma 3.5.2 only the pairs
$a\neq 0$
, by Lemma 3.5.2 only the pairs
![]() $(a_{1}, a_{2})$
with
$(a_{1}, a_{2})$
with
 $a_{1}\in \bigcap _{v\mid p}1+\varpi ^{r}\mathscr {O}_{F,v}$
contribute. If
$a_{1}\in \bigcap _{v\mid p}1+\varpi ^{r}\mathscr {O}_{F,v}$
contribute. If
![]() $v(a)\geq r$
for
$v(a)\geq r$
for
![]() $v\mid p$
, this forces
$v\mid p$
, this forces
 $a_{2}\in \bigcap _{v\mid p}-1+\varpi _{v}^{r}\mathscr {O}_{F,v}$
. Then the coefficient of index
$a_{2}\in \bigcap _{v\mid p}-1+\varpi _{v}^{r}\mathscr {O}_{F,v}$
. Then the coefficient of index
![]() $a_{2}$
of
$a_{2}$
of
![]() $\mathscr {E}(\mathbf {1})$
vanishes by Proposition 3.5.1.
$\mathscr {E}(\mathbf {1})$
vanishes by Proposition 3.5.1.
We can now proceed as in [Reference Disegni9, §7.2], except for the insertion of the operator
![]() $\mathrm {U}_{p, *}^{r}$
. (This will be innocuous for the purposes of Theorem 3.4.3, since the kernel of
$\mathrm {U}_{p, *}^{r}$
. (This will be innocuous for the purposes of Theorem 3.4.3, since the kernel of
![]() $\mathrm {U}_{p, *}^{r}$
is contained in the kernel of
$\mathrm {U}_{p, *}^{r}$
is contained in the kernel of
![]() $\ell _{\varphi ^{p},\alpha }$
.) We obtain, under the assumptions of [Reference Disegni9, §6.1], a decomposition of formula (3.2.5)
$\ell _{\varphi ^{p},\alpha }$
.) We obtain, under the assumptions of [Reference Disegni9, §6.1], a decomposition of formula (3.2.5)
 $$ \begin{align}\begin{aligned} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty};\chi)= \sum_{v\in S_{\text{nonsplit}}- S_{p}} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty};\chi)(v) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty};\chi)= \sum_{v\in S_{\text{nonsplit}}- S_{p}} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty};\chi)(v) \end{aligned}\end{align} $$
valid in the space
![]() ${\mathbf {S}}$
of p-adic q-expansions with coefficients in
${\mathbf {S}}$
of p-adic q-expansions with coefficients in
![]() $\Gamma _{F}\hat {\otimes } L(\chi )$
(see [Reference Disegni9, §6.1] for the definition of
$\Gamma _{F}\hat {\otimes } L(\chi )$
(see [Reference Disegni9, §6.1] for the definition of
![]() $\mathscr {I}'(\phi ^{p\infty };\chi )(v)$
).
$\mathscr {I}'(\phi ^{p\infty };\chi )(v)$
).
3.6 Decomposition of the geometric kernel and comparison
Suppose that Assumptions 3.4.1 and 3.4.2, as well as the assumptions of [Reference Disegni9, §6.1], are satisfied. Then we may decompose [Reference Disegni9, §8.2] the generating series (3.3.4) as
 $$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty},\chi) =\sum_{v}{\widetilde Z}(\phi^{\infty},\chi)(v), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {\widetilde Z}(\phi^{\infty},\chi) =\sum_{v}{\widetilde Z}(\phi^{\infty},\chi)(v), \end{aligned}\end{align} $$
according to the decomposition
![]() $\langle \ , \ \rangle _{X}=\sum _{v} \langle \ , \ \rangle _{X, v}$
of the height pairing. Here the sum runs over all finite places of F.
$\langle \ , \ \rangle _{X}=\sum _{v} \langle \ , \ \rangle _{X, v}$
of the height pairing. Here the sum runs over all finite places of F.
The following is the main result of [Reference Disegni9] on the local comparison away from p. Let
 $\overline {\mathbf {S}}{}'= \overline {\mathbf {S}}{}^{\prime }_{S_{1}}$
be the quotient of the space of p-adic q-expansions recalled before formula (3.1.5).
$\overline {\mathbf {S}}{}'= \overline {\mathbf {S}}{}^{\prime }_{S_{1}}$
be the quotient of the space of p-adic q-expansions recalled before formula (3.1.5).
Theorem 3.6.1 [Reference Disegni9, Theorem 8.3.2]
Let
![]() $\phi ^{\infty }=\phi ^{p\infty }\phi _{p}$
with
$\phi ^{\infty }=\phi ^{p\infty }\phi _{p}$
with
 $\phi _{p}=\prod _{v\mid p} \phi _{v}$
as in formula (3.1.4). Suppose that Assumptions 3.4.1 and 3.4.2, as well as the assumptions of [Reference Disegni9, §6.1], are satisfied. Then we have the following identities of reduced q-expansions in
$\phi _{p}=\prod _{v\mid p} \phi _{v}$
as in formula (3.1.4). Suppose that Assumptions 3.4.1 and 3.4.2, as well as the assumptions of [Reference Disegni9, §6.1], are satisfied. Then we have the following identities of reduced q-expansions in
![]() $\overline {\mathbf {S}}{}'$
:
$\overline {\mathbf {S}}{}'$
:
-
1. If
 $v\in S_{\mathrm{split}} - S_{p}$
, then
$v\in S_{\mathrm{split}} - S_{p}$
, then  $$ \begin{align*} \widetilde{Z}(\phi^{\infty}, \chi)(v)=0. \end{align*} $$
$$ \begin{align*} \widetilde{Z}(\phi^{\infty}, \chi)(v)=0. \end{align*} $$
-
2. If
 $v\in S_{\mathrm {nonsplit}}- S_{1}-S_{p}$
, then
$v\in S_{\mathrm {nonsplit}}- S_{1}-S_{p}$
, then  $$ \begin{align*} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty}; \chi)(v)=2 \lvert D_{F}\rvert L_{\left(p\right)}(1,\eta) \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(v). \end{align*} $$
$$ \begin{align*} \mathrm{U}_{p, *}^{r}\mathscr{I}'(\phi^{p\infty}; \chi)(v)=2 \lvert D_{F}\rvert L_{\left(p\right)}(1,\eta) \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(v). \end{align*} $$
-
3. If
 $v\in S_{1}$
, then are theta series attached to a quaternion algebra over F.
$v\in S_{1}$
, then are theta series attached to a quaternion algebra over F. $$ \begin{align*} \mathrm{U}_{p, *}^{r} \mathscr{I}'(\phi^{p\infty}; \chi)(v), \qquad \mathrm{U}_{p, *}^{r} \widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
$$ \begin{align*} \mathrm{U}_{p, *}^{r} \mathscr{I}'(\phi^{p\infty}; \chi)(v), \qquad \mathrm{U}_{p, *}^{r} \widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
-
4. The sum
belongs to the isomorphic image $$ \begin{align*} \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(p):=\sum_{v\in S_{p}} \mathrm{U}_{p, *}^{r} \widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
$$ \begin{align*} \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(p):=\sum_{v\in S_{p}} \mathrm{U}_{p, *}^{r} \widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
 $\overline {\mathbf {S}}\subset \overline {\mathbf {S}}{}'$
of the space of p-adic modular forms
$\overline {\mathbf {S}}\subset \overline {\mathbf {S}}{}'$
of the space of p-adic modular forms
 ${\mathbf {S}}$
.
${\mathbf {S}}$
.
By this theorem and the decompositions of
![]() $\mathscr {I}'$
and
$\mathscr {I}'$
and
![]() $\widetilde {Z}$
, the proof of the kernel identity of Theorem 3.4.3 (hence of the main theorem) is now reduced to showing the following proposition. (See [Reference Disegni9, §8.3, last paragraph] for the details of the deduction.)
$\widetilde {Z}$
, the proof of the kernel identity of Theorem 3.4.3 (hence of the main theorem) is now reduced to showing the following proposition. (See [Reference Disegni9, §8.3, last paragraph] for the details of the deduction.)
Proposition 3.6.2. Retain the assumptions of Theorem 3.6.1, and further assume that
![]() $V_{\mathfrak {p}}A $
is potentially crystalline at all
$V_{\mathfrak {p}}A $
is potentially crystalline at all
![]() $v\mid p$
. Then the p-adic modular form
$v\mid p$
. Then the p-adic modular form
 $$ \begin{align*} \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(p) \in \overline{\textbf{S}} \end{align*} $$
$$ \begin{align*} \mathrm{U}_{p, *}^{r}\widetilde{Z}(\phi^{\infty}, \chi)(p) \in \overline{\textbf{S}} \end{align*} $$
is annihilated by
![]() $\ell _{\varphi ^{p},\alpha }$
.
$\ell _{\varphi ^{p},\alpha }$
.
Let S be a finite set of non-Archimedean places of F such that for all
![]() $v\notin S$
, all the data are unramified,
$v\notin S$
, all the data are unramified,
![]() $U_{v}$
is maximal, and
$U_{v}$
is maximal, and
![]() $\phi _{v}$
is standard. Let
$\phi _{v}$
is standard. Let
![]() $K=K^{p}K_{p}$
be the level of the modular form
$K=K^{p}K_{p}$
be the level of the modular form
 $\widetilde {Z}(\phi ^{\infty })$
, and let
$\widetilde {Z}(\phi ^{\infty })$
, and let
 $$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\in \mathscr{H}^{S}({L})=\mathscr{H}^{S}({M})\otimes_{M, {\iota_{\mathfrak{p}}}} {L} \end{align*} $$
$$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\in \mathscr{H}^{S}({L})=\mathscr{H}^{S}({M})\otimes_{M, {\iota_{\mathfrak{p}}}} {L} \end{align*} $$
be any
![]() $\sigma ^{\vee }$
-idempotent in the Hecke algebra as in [Reference Disegni9, Proposition 2.4.4]. By that result, in order to establish Proposition 3.6.2 it suffices to prove that
$\sigma ^{\vee }$
-idempotent in the Hecke algebra as in [Reference Disegni9, Proposition 2.4.4]. By that result, in order to establish Proposition 3.6.2 it suffices to prove that
 $$ \begin{align} \ell_{\varphi^{p},\alpha}\left( \mathrm{U}_{p, *}^{r}T_{\iota_{\mathfrak{p}}}(\sigma^{\vee}) \widetilde{Z}(\phi^{\infty}, \chi)(p)\right)=0. \end{align} $$
$$ \begin{align} \ell_{\varphi^{p},\alpha}\left( \mathrm{U}_{p, *}^{r}T_{\iota_{\mathfrak{p}}}(\sigma^{\vee}) \widetilde{Z}(\phi^{\infty}, \chi)(p)\right)=0. \end{align} $$
As in [Reference Disegni9], we will in fact prove the following, which implies equation (3.6.2):
Proposition 3.6.3. Let
![]() $v\mid p$
. Under the assumptions of Proposition 3.6.2, for all
$v\mid p$
. Under the assumptions of Proposition 3.6.2, for all
![]() $v\mid p$
, the element
$v\mid p$
, the element
 $$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\widetilde{Z}(\phi^{\infty}, \chi)(v)\in \overline{\textbf{S}}{}' \end{align*} $$
$$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\widetilde{Z}(\phi^{\infty}, \chi)(v)\in \overline{\textbf{S}}{}' \end{align*} $$
is v-critical in the sense of equation (3.1.7).
The proof will occupy the following section.
4 Local heights at p
The goal of this section is to prove Proposition 3.6.3, whose assumptions we retain throughout except for an innocuous modification to the data at the places
![]() $v\mid p$
. Namely, let
$v\mid p$
. Namely, let
![]() $\widetilde {\phi }_{v}$
be the Schwartz function denoted by
$\widetilde {\phi }_{v}$
be the Schwartz function denoted by
![]() $\phi _{r}$
in formula (3.1.4), and let
$\phi _{r}$
in formula (3.1.4), and let
 $\widetilde {U}_{v}\subset \mathbf {B}_{v}^{\times }$
be the open compact subgroup denoted by
$\widetilde {U}_{v}\subset \mathbf {B}_{v}^{\times }$
be the open compact subgroup denoted by
![]() $U_{v, r}$
in Assumption 3.4.2. Then we define
$U_{v, r}$
in Assumption 3.4.2. Then we define

Since
 $\chi _{v|F_{v}^{\times }}=\omega _{v}^{-1}$
is by construction invariant under
$\chi _{v|F_{v}^{\times }}=\omega _{v}^{-1}$
is by construction invariant under
![]() $U_{F, v}^{\circ }$
, the geometric kernels
$U_{F, v}^{\circ }$
, the geometric kernels
 $\widetilde {Z}\left (\phi ^{p\infty }\widetilde {\phi }_{p}, \chi \right ) $
and
$\widetilde {Z}\left (\phi ^{p\infty }\widetilde {\phi }_{p}, \chi \right ) $
and
 $ \widetilde {Z}\left (\phi ^{p\infty }\phi _{p}, \chi \right )$
are equal. Therefore we may work on the curve
$ \widetilde {Z}\left (\phi ^{p\infty }\phi _{p}, \chi \right )$
are equal. Therefore we may work on the curve
![]() $X_{U}$
.
$X_{U}$
.
We fix a place
![]() $v\mid p$
. If v splits in E, then the desired result is proven in [Reference Disegni9, §9] with the correction in Appendix B. Therefore we may and do assume that v is nonsplit. We denote by w the place of E above v.
$v\mid p$
. If v splits in E, then the desired result is proven in [Reference Disegni9, §9] with the correction in Appendix B. Therefore we may and do assume that v is nonsplit. We denote by w the place of E above v.
We refer the reader to §1.1 for a general sketch of our argument. It is developed here as follows. In §4.1, we prove that after acting by a high power of
![]() $\mathrm {U}_{v,*}$
, the coefficients of the generating series are height pairings with CM points of high v-conductor (norm relation). After some general background in §4.2, we use the norm relation to prove the decay property of arithmetic intersection multiplicities in §4.3. Finally, in §4.4 we use again the norm relation and some p-adic Hodge theory to prove the decay property of local heights.
$\mathrm {U}_{v,*}$
, the coefficients of the generating series are height pairings with CM points of high v-conductor (norm relation). After some general background in §4.2, we use the norm relation to prove the decay property of arithmetic intersection multiplicities in §4.3. Finally, in §4.4 we use again the norm relation and some p-adic Hodge theory to prove the decay property of local heights.
4.1 Norm relation for the generating series
The goal of this subsection will be to show that for s large enough, each q-expansion coefficient of
 $\mathrm {U}_{p,*}^{s}\widetilde {Z}(\phi ^{\infty }, \chi )$
is a height pairing of CM divisors, one of which is supported on Galois orbits of CM points of the ‘pseudo-conductor’ s (as defined later).
$\mathrm {U}_{p,*}^{s}\widetilde {Z}(\phi ^{\infty }, \chi )$
is a height pairing of CM divisors, one of which is supported on Galois orbits of CM points of the ‘pseudo-conductor’ s (as defined later).
We start by considering the
![]() $\mathrm {U}_{v, *}$
-action on the generating series
$\mathrm {U}_{v, *}$
-action on the generating series
 $\widetilde {Z}(\phi ^{\infty })=\text {formula}~(3.3.2)$
. Recall that
$\widetilde {Z}(\phi ^{\infty })=\text {formula}~(3.3.2)$
. Recall that
![]() $d_{v}$
(§3.1) is a generator of the different ideal of
$d_{v}$
(§3.1) is a generator of the different ideal of
![]() $F_{v}$
.
$F_{v}$
.
Lemma 4.1.1. If
![]() $a\in \mathbf {A}^{\infty \times }$
satisfies
$a\in \mathbf {A}^{\infty \times }$
satisfies
![]() $v(a)\geq -v(d_{v})$
, the ath reduced q-expansion coefficient of
$v(a)\geq -v(d_{v})$
, the ath reduced q-expansion coefficient of
 $\mathrm {U}_{v,*}{\widetilde Z}(\phi ^{\infty })$
equals
$\mathrm {U}_{v,*}{\widetilde Z}(\phi ^{\infty })$
equals
 $$ \begin{align*} {\widetilde Z}_{a\varpi_{v}^{}}(\phi^{\infty}), \end{align*} $$
$$ \begin{align*} {\widetilde Z}_{a\varpi_{v}^{}}(\phi^{\infty}), \end{align*} $$
where
 $ {\widetilde Z}_{a'}(\phi ^{\infty })$
is defined in formula (3.3.1).
$ {\widetilde Z}_{a'}(\phi ^{\infty })$
is defined in formula (3.3.1).
Proof. After computing the Weil action of
![]() $\mathrm {U}_{v, *}$
on
$\mathrm {U}_{v, *}$
on
![]() $\phi $
, this is a simple change of variables.
$\phi $
, this is a simple change of variables.
We can factor
 $$ \begin{align*} {\widetilde Z}_{a}(\phi^{\infty}) = {\widetilde Z}_{a^{v}}(\phi^{v\infty}) Z_{a_{v}}(\phi_{v}) \end{align*} $$
$$ \begin{align*} {\widetilde Z}_{a}(\phi^{\infty}) = {\widetilde Z}_{a^{v}}(\phi^{v\infty}) Z_{a_{v}}(\phi_{v}) \end{align*} $$
as the composition of the commuting correspondences
 $$ \begin{align} \nonumber \widetilde{Z}_{a}^{v}(\phi^{v\infty}) &:=c_{U^{p}}\sum_{x^{v}\in U^{v}\backslash \mathbf{B}^{v\infty\times}/U^{v}}\phi^{v\infty}\left(x^{v}, aq(x^{v})^{-1}\right)Z(x^{v})_{{U}}, \\ Z_{a_{v}}(\phi_{v}) &:= \sum_{x_{v}\in U_{v}\backslash \mathbf{B}_{v}^{\times}/U_{v} } \phi_{v} \left(x_{v}, aq(x_{v})^{-1}\right)Z(x_{v})_{{U}}. \end{align} $$
$$ \begin{align} \nonumber \widetilde{Z}_{a}^{v}(\phi^{v\infty}) &:=c_{U^{p}}\sum_{x^{v}\in U^{v}\backslash \mathbf{B}^{v\infty\times}/U^{v}}\phi^{v\infty}\left(x^{v}, aq(x^{v})^{-1}\right)Z(x^{v})_{{U}}, \\ Z_{a_{v}}(\phi_{v}) &:= \sum_{x_{v}\in U_{v}\backslash \mathbf{B}_{v}^{\times}/U_{v} } \phi_{v} \left(x_{v}, aq(x_{v})^{-1}\right)Z(x_{v})_{{U}}. \end{align} $$
From here until after the proof of Lemma 4.1.2, we work in a local situation and drop v from the notation. Let
![]() $\theta \in \mathscr {O}_{E}$
be such that
$\theta \in \mathscr {O}_{E}$
be such that
![]() $\mathscr {O}_{E}= \mathscr {O}_{F}+\theta \mathscr {O}_{F}$
, and write
$\mathscr {O}_{E}= \mathscr {O}_{F}+\theta \mathscr {O}_{F}$
, and write
![]() $\mathrm {T}={\mathrm {Tr}_{E/F}}(\theta _{})$
,
$\mathrm {T}={\mathrm {Tr}_{E/F}}(\theta _{})$
,
![]() $\mathrm {N}_{} =\mathrm {N}_{E_{}/F_{}}(\theta _{})$
. Fix the embedding
$\mathrm {N}_{} =\mathrm {N}_{E_{}/F_{}}(\theta _{})$
. Fix the embedding
![]() $E_{}\to \mathbf {B}_{}=M_{2}(F_{})$
to be
$E_{}\to \mathbf {B}_{}=M_{2}(F_{})$
to be
 $$ \begin{align*}\begin{aligned} t=a+\theta b\mapsto \left(\begin{array}{cc}a+b\mathrm{T}& b {\mathrm{N}}\\ -b & a\end{array}\right). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} t=a+\theta b\mapsto \left(\begin{array}{cc}a+b\mathrm{T}& b {\mathrm{N}}\\ -b & a\end{array}\right). \end{aligned}\end{align*} $$
Set
 $$ \begin{align}\begin{aligned}\mathrm{j}:= \left(\begin{array}{cc} 1& \mathrm{T}\\ {} & {-1}\end{array}\right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned}\mathrm{j}:= \left(\begin{array}{cc} 1& \mathrm{T}\\ {} & {-1}\end{array}\right). \end{aligned}\end{align} $$
Then
![]() $\mathrm {j}^{2}=1$
,
$\mathrm {j}^{2}=1$
,
![]() $q({\mathrm {j}})=-1$
, and for all
$q({\mathrm {j}})=-1$
, and for all
![]() $t\in E$
,
$t\in E$
,
![]() $\mathrm {j} t =t^{c}\mathrm {j}$
; and in the orthogonal decomposition
$\mathrm {j} t =t^{c}\mathrm {j}$
; and in the orthogonal decomposition
![]() ${\mathbf {V}}={\mathbf {V}}_{1}\oplus {\mathbf {V}}_{2}$
, we have
${\mathbf {V}}={\mathbf {V}}_{1}\oplus {\mathbf {V}}_{2}$
, we have
Let
 $\Xi (\varpi ^{r}) =1+\varpi ^{r}\mathscr {O}_{E}+ \mathrm {j} \left (\mathscr {O}_{E}\cap q^{-1}(1+\varpi ^{r}\mathscr {O}_{F})\right )$
; then
$\Xi (\varpi ^{r}) =1+\varpi ^{r}\mathscr {O}_{E}+ \mathrm {j} \left (\mathscr {O}_{E}\cap q^{-1}(1+\varpi ^{r}\mathscr {O}_{F})\right )$
; then
![]() $\phi $
is a fixed multiple of the characteristic function of
$\phi $
is a fixed multiple of the characteristic function of
![]() $\Xi (\varpi ^{r}) \times (1+\varpi ^{r}\mathscr {O}_{F})\subset \mathbf {B} \times F^{\times }$
. For
$\Xi (\varpi ^{r}) \times (1+\varpi ^{r}\mathscr {O}_{F})\subset \mathbf {B} \times F^{\times }$
. For
![]() $a\in F^{\times }$
, let
$a\in F^{\times }$
, let
Then the local component (4.1.1) of the generating series equals
 $$ \begin{align*} Z_{a}(\phi) = \sum_{x \in U\backslash \Xi\left(\varpi^{r}\right)_{a} U_{F}^{\circ}/U } Z(x)_{{U}}, \end{align*} $$
$$ \begin{align*} Z_{a}(\phi) = \sum_{x \in U\backslash \Xi\left(\varpi^{r}\right)_{a} U_{F}^{\circ}/U } Z(x)_{{U}}, \end{align*} $$
up to a constant that is independent of a.
Lemma 4.1.2. Let
![]() $a\in F^{\times }$
satisfy
$a\in F^{\times }$
satisfy
![]() $v(a)=s\geq r$
. The natural map
$v(a)=s\geq r$
. The natural map
![]() $\Xi (\varpi ^{r})_{a} U_{F}^{\circ }/U \to U\backslash \Xi (\varpi ^{r})_{a} U_{F}^{\circ } /U$
is a bijection. For either quotient set, a complete set of representatives is given by the elements
$\Xi (\varpi ^{r})_{a} U_{F}^{\circ }/U \to U\backslash \Xi (\varpi ^{r})_{a} U_{F}^{\circ } /U$
is a bijection. For either quotient set, a complete set of representatives is given by the elements
as b ranges through a complete set of representatives for
Proof. It is equivalent to prove the same statement for the quotients of
![]() $\Xi (\varpi ^{r})_{a}$
by the group
$\Xi (\varpi ^{r})_{a}$
by the group
 $\widetilde {U}=1+\varpi ^{r} M_{2}(\mathscr {O}_{F})$
. By acting on the right with elements of
$\widetilde {U}=1+\varpi ^{r} M_{2}(\mathscr {O}_{F})$
. By acting on the right with elements of
![]() $\mathscr {O}_{E}\cap U$
, we can bring any element of
$\mathscr {O}_{E}\cap U$
, we can bring any element of
![]() $\Xi $
to one of the form
$\Xi $
to one of the form
![]() $x(b)$
. Write any
$x(b)$
. Write any
![]() $ \gamma \in \widetilde {U}$
as
$ \gamma \in \widetilde {U}$
as
![]() $\gamma =1+\varpi ^{r}u_{1} +{\mathrm{j}} \varpi ^{r}u_{2}$
with
$\gamma =1+\varpi ^{r}u_{1} +{\mathrm{j}} \varpi ^{r}u_{2}$
with
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{2}\in \mathscr {O}_{E}$
. Then
$u_{2}\in \mathscr {O}_{E}$
. Then
is another element of the form
![]() $x(b')$
if and only if
$x(b')$
if and only if
![]() $u_{1}=-b^{c}u_{2}$
. In this case,
$u_{1}=-b^{c}u_{2}$
. In this case,
Thus the class of b modulo
![]() $\varpi ^{r+s}$
is the only invariant of the quotient
$\varpi ^{r+s}$
is the only invariant of the quotient
 $\Xi /\widetilde {U}$
. The
$\Xi /\widetilde {U}$
. The
![]() $\widetilde {U}$
-action on the left similarly preserves this invariant.
$\widetilde {U}$
-action on the left similarly preserves this invariant.
We go back to a global setting and notation, restoring the subscripts v and w. Denote by
 ${\mathrm{rec}}_{E_{w}}\colon E_{w}^{\times }\to \mathscr {G}_{E,w}^{\mathrm{ab}}$
the reciprocity map of class field theory. Recall that for
${\mathrm{rec}}_{E_{w}}\colon E_{w}^{\times }\to \mathscr {G}_{E,w}^{\mathrm{ab}}$
the reciprocity map of class field theory. Recall that for
![]() $x\in \mathbf {B}^{\infty \times }$
, we have a point
$x\in \mathbf {B}^{\infty \times }$
, we have a point
![]() $[x]_{U}\in X_{U}$
; for a subset
$[x]_{U}\in X_{U}$
; for a subset
![]() $\Xi '\subset \mathbf {B}^{\infty \times }$
, we similarly denote
$\Xi '\subset \mathbf {B}^{\infty \times }$
, we similarly denote
![]() $[\Xi ']_{U}=\{[x]_{U} \mid x\in \Xi '\}$
.
$[\Xi ']_{U}=\{[x]_{U} \mid x\in \Xi '\}$
.
Lemma 4.1.3. Fix
![]() $a\in \mathscr {O}_{F,v}$
with
$a\in \mathscr {O}_{F,v}$
with
![]() $v(a)=s\geq r$
.
$v(a)=s\geq r$
.
-
1. Set
 $b\in \left ( \mathscr {O}_{E,w}/\varpi _{v}^{r+s}\mathscr {O}_{E,w}\right )^{\times }$
,
$b\in \left ( \mathscr {O}_{E,w}/\varpi _{v}^{r+s}\mathscr {O}_{E,w}\right )^{\times }$
,
 $t\in 1+\varpi _{v}^{r}\mathscr {O}_{E,w}$
. Then
$t\in 1+\varpi _{v}^{r}\mathscr {O}_{E,w}$
. Then  $$ \begin{align*} {\mathrm{rec}}_{E_{w}}(t)[x(b)]_{U}= [x(b t^{c}/t)]_{U}. \end{align*} $$
$$ \begin{align*} {\mathrm{rec}}_{E_{w}}(t)[x(b)]_{U}= [x(b t^{c}/t)]_{U}. \end{align*} $$
-
2. We have
where the Galois action is faithful, and $$ \begin{align*} \left[\Xi\left(\varpi_{v}^{r}\right)_{a}U_{F, v}^{\circ}\right]_{U}= \bigsqcup_{\overline{b}} {\mathrm{rec}}_{E_{w}}\left(\left(1+\varpi_{v}^{r}\mathscr{O}_{E,w}\right)/\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\right) \left[x\left(\overline{b}\right)\right]_{U}, \end{align*} $$
$$ \begin{align*} \left[\Xi\left(\varpi_{v}^{r}\right)_{a}U_{F, v}^{\circ}\right]_{U}= \bigsqcup_{\overline{b}} {\mathrm{rec}}_{E_{w}}\left(\left(1+\varpi_{v}^{r}\mathscr{O}_{E,w}\right)/\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\right) \left[x\left(\overline{b}\right)\right]_{U}, \end{align*} $$
 $\overline {b}$
ranges through a set of representatives for (4.1.3)The size of this set is bounded uniformly in a.
$\overline {b}$
ranges through a set of representatives for (4.1.3)The size of this set is bounded uniformly in a. $$ \begin{align}\begin{aligned} q_{v}^{-1}\left( 1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right) /\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\cdot \left(1+\varpi_{v}^{r+v\left(\theta-\theta^{c}\right) }\mathscr{O}_{E,w}\cap q_{v}^{-1}(1)\right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} q_{v}^{-1}\left( 1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right) /\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\cdot \left(1+\varpi_{v}^{r+v\left(\theta-\theta^{c}\right) }\mathscr{O}_{E,w}\cap q_{v}^{-1}(1)\right). \end{aligned}\end{align} $$
Proof. For part 1, we have
Part 2 follows Lemma 4.1.2 and part 1, noting that the group
 $\left (1+\varpi _{v}^{r+v\left (\theta -\theta ^{c}\right ) }\mathscr {O}_{E,{w}}\right )\cap q_{v}^{-1}(1)$
is the image of the map
$\left (1+\varpi _{v}^{r+v\left (\theta -\theta ^{c}\right ) }\mathscr {O}_{E,{w}}\right )\cap q_{v}^{-1}(1)$
is the image of the map
![]() $t\mapsto t^{c}/t$
on
$t\mapsto t^{c}/t$
on
![]() $1+\varpi _{v}^{r}\mathscr {O}_{E,w}$
. Finally, the map
$1+\varpi _{v}^{r}\mathscr {O}_{E,w}$
. Finally, the map
![]() $({\mathrm{projection}}, q_{v})$
gives an injection from
$({\mathrm{projection}}, q_{v})$
gives an injection from
 $$ \begin{align*} q_{v}^{-1}\left( 1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right) /\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\cdot \left(1+\varpi_{v}^{r+v\left(\theta-\theta^{c}\right) }\mathscr{O}_{E,w}\cap q_{v}^{-1}(1)\right) \end{align*} $$
$$ \begin{align*} q_{v}^{-1}\left( 1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right) /\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right)\cdot \left(1+\varpi_{v}^{r+v\left(\theta-\theta^{c}\right) }\mathscr{O}_{E,w}\cap q_{v}^{-1}(1)\right) \end{align*} $$
to
 $$ \begin{align*} \left(\mathscr{O}_{E,w}/\varpi_{v}^{r+v\left(\theta -\theta^{c}\right)}\mathscr{O}_{E,w}\right)^{\times} \times \left(1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right)/q\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right), \end{align*} $$
$$ \begin{align*} \left(\mathscr{O}_{E,w}/\varpi_{v}^{r+v\left(\theta -\theta^{c}\right)}\mathscr{O}_{E,w}\right)^{\times} \times \left(1-a\left(1+\varpi_{v}^{r}\mathscr{O}_{F,v}\right)\right)/q\left(1+\varpi_{v}^{r+s}\mathscr{O}_{E,w}\right), \end{align*} $$
whose size is bounded uniformly in a (more precisely, the second factor is isomorphic to
![]() $\mathscr {O}_{F,v}/{\mathrm{Tr}}\left (\mathscr {O}_{E,v}\right )$
via the map
$\mathscr {O}_{F,v}/{\mathrm{Tr}}\left (\mathscr {O}_{E,v}\right )$
via the map
![]() $1-a\left (1+\varpi _{v}^{r}x\right )\mapsto x$
).
$1-a\left (1+\varpi _{v}^{r}x\right )\mapsto x$
).
We denote by
![]() $\overline {w}$
an extension of the place w to
$\overline {w}$
an extension of the place w to
![]() $E^{\mathrm{ab}}$
. For
$E^{\mathrm{ab}}$
. For
![]() $s\geq 0$
, let
$s\geq 0$
, let
be the finite abelian extension of E with norm group
![]() $U_{F}^{\circ } U_{T}^{v}\left (1+ \varpi _{v}^{r_{v}+s}\mathscr {O}_{E,v}\right )$
, where
$U_{F}^{\circ } U_{T}^{v}\left (1+ \varpi _{v}^{r_{v}+s}\mathscr {O}_{E,v}\right )$
, where
![]() $U_{T}^{v}= U^{v} \cap E_{\mathbf {A}^{\infty }}^{\times }$
. Let
$U_{T}^{v}= U^{v} \cap E_{\mathbf {A}^{\infty }}^{\times }$
. Let
 $H_{\infty }= \bigcup _{s\geq 0} H_{s}$
. If
$H_{\infty }= \bigcup _{s\geq 0} H_{s}$
. If
![]() $r_{v}$
is sufficiently large, for all
$r_{v}$
is sufficiently large, for all
![]() $s\geq 0$
the extension
$s\geq 0$
the extension
![]() $H_{s}/H_{0}$
is totally ramified at
$H_{s}/H_{0}$
is totally ramified at
![]() $\overline {w}$
of degree
$\overline {w}$
of degree
![]() $q_{F, v}^{s}$
, and
$q_{F, v}^{s}$
, and
 $$ \begin{align*} \mathrm{Gal}(H_{s}/H_{0})\cong \mathrm{Gal}\left(H_{s, \overline{w}}/H_{0, \overline{w}}\right) \cong \left(1+{\varpi}_{v}^{r_{v}}\mathscr{O}_{E,v} \right)/\left(1+\varpi_{v}^{r_{v}}\mathscr{O}_{F,v}\right) \left(1+\varpi_{v}^{r_{v}+s}\mathscr{O}_{E, v}\right). \end{align*} $$
$$ \begin{align*} \mathrm{Gal}(H_{s}/H_{0})\cong \mathrm{Gal}\left(H_{s, \overline{w}}/H_{0, \overline{w}}\right) \cong \left(1+{\varpi}_{v}^{r_{v}}\mathscr{O}_{E,v} \right)/\left(1+\varpi_{v}^{r_{v}}\mathscr{O}_{F,v}\right) \left(1+\varpi_{v}^{r_{v}+s}\mathscr{O}_{E, v}\right). \end{align*} $$
In particular,
We will say that a CM point
![]() $z\in X_{H_{0}}$
has pseudo-conductor
$z\in X_{H_{0}}$
has pseudo-conductor
![]() $s\geq 0$
(at
$s\geq 0$
(at
![]() $\overline {w}$
) if
$\overline {w}$
) if
![]() $H_{0, \overline {w}}(z)=H_{s, \overline {w}}$
.
$H_{0, \overline {w}}(z)=H_{s, \overline {w}}$
.
Proposition 4.1.4. There exists an integer
![]() $d>0$
such that for all
$d>0$
such that for all
![]() $a\in \mathbf {A}^{\infty ,x}$
with
$a\in \mathbf {A}^{\infty ,x}$
with
![]() $v(a)=s\geq r_{v}$
, there exists a degree
$v(a)=s\geq r_{v}$
, there exists a degree
![]() $0$
divisor
$0$
divisor
 $D_{a}\in d^{-1} \mathrm {Div}^{0}\left (X_{U , H_{s}}\right )$
, supported on CM points, such that
$D_{a}\in d^{-1} \mathrm {Div}^{0}\left (X_{U , H_{s}}\right )$
, supported on CM points, such that
 $$ \begin{align*} \widetilde{Z}_{a}(\phi^{\infty})[1]_{U} = {\mathrm{Tr}}_{H_{s}/H_{0}} (D_{a}) \end{align*} $$
$$ \begin{align*} \widetilde{Z}_{a}(\phi^{\infty})[1]_{U} = {\mathrm{Tr}}_{H_{s}/H_{0}} (D_{a}) \end{align*} $$
in
 ${\mathrm{Div}}^{0}\left (X_{U, H_{0}}\right ).$
All prime divisor components of
${\mathrm{Div}}^{0}\left (X_{U, H_{0}}\right ).$
All prime divisor components of
![]() $D_{a}$
are CM points of pseudo-conductor s.
$D_{a}$
are CM points of pseudo-conductor s.
Proof. This follows from Lemma 4.1.3(2), by taking
![]() $D_{a}$
to be a fixed rational multiple (independent of a) of
$D_{a}$
to be a fixed rational multiple (independent of a) of
 $$ \begin{align*} \widetilde{Z}_{a}^{v}(\phi^{v\infty}) \sum_{\overline{b}\in \text{formula~(4.1.3)}} \left[x\left(\overline{b}\right)\right]_{U}. \end{align*} $$
$$ \begin{align*} \widetilde{Z}_{a}^{v}(\phi^{v\infty}) \sum_{\overline{b}\in \text{formula~(4.1.3)}} \left[x\left(\overline{b}\right)\right]_{U}. \end{align*} $$
The divisor is of degree
![]() $0$
by [Reference Disegni9, Proposition 8.1.1]. Its prime components are not defined over proper subfields
$0$
by [Reference Disegni9, Proposition 8.1.1]. Its prime components are not defined over proper subfields
![]() $H_{s'}\subset H_{s}$
, because of the faithfulness statement of Lemma 4.1.3(2).
$H_{s'}\subset H_{s}$
, because of the faithfulness statement of Lemma 4.1.3(2).
4.2 Intersection multiplicities on arithmetic surfaces
Before continuing, we gather some definitions and a key result.
Ultrametricity of intersections on surfaces
Let
![]() $\mathscr {X}$
be a
$\mathscr {X}$
be a
![]() $2$
-dimensional regular Noetherian scheme, finite flat over a field
$2$
-dimensional regular Noetherian scheme, finite flat over a field
![]() $\kappa $
or a discrete valuation ring
$\kappa $
or a discrete valuation ring
![]() $\mathscr {O}$
with residue field
$\mathscr {O}$
with residue field
![]() $\kappa $
. We denote by
$\kappa $
. We denote by
![]() $(\ \cdot \ )_{\mathscr {X}}$
the usual
$(\ \cdot \ )_{\mathscr {X}}$
the usual
![]() $\mathbf {Z}$
-bilinear intersection-multiplicity pairing of divisors intersecting properly on
$\mathbf {Z}$
-bilinear intersection-multiplicity pairing of divisors intersecting properly on
![]() $\mathscr {X}$
; for effective divisors
$\mathscr {X}$
; for effective divisors
![]() $D_{j}$
(
$D_{j}$
(
![]() $j=1, 2$
) with
$j=1, 2$
) with
![]() $\mathscr {O}_{D_{j}}=\mathscr {O}_{\mathscr {X}}/ \mathscr {I}_{j}$
, it is defined by
$\mathscr {O}_{D_{j}}=\mathscr {O}_{\mathscr {X}}/ \mathscr {I}_{j}$
, it is defined by
The subscript
![]() $\mathscr {X}$
will be omitted when it is clear from context.
$\mathscr {X}$
will be omitted when it is clear from context.
We will need the following result of García Barroso, González Pérez, and Popescu-Pampu:
Proposition 4.2.1. Let R be a Noetherian regular local ring of dimension
![]() $2$
, which is a flat module over a field or a discrete valuation ring. Let
$2$
, which is a flat module over a field or a discrete valuation ring. Let
![]() $\Delta $
be any irreducible curve in
$\Delta $
be any irreducible curve in
![]() $\mathrm {Spec}\, R$
. Then the function
$\mathrm {Spec}\, R$
. Then the function
 $$ \begin{align*}\begin{aligned} d_{\Delta}(D_{1}, D_{2}):= \begin{cases} (D_{1} \cdot \Delta) (D_{2} \cdot \Delta)/(D_{1}\cdot D_{2}) & \text{if}\ D_{1}\neq D_{2},\\ 0 & \text{if}\ D_{1}=D_{2} \end{cases} \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} d_{\Delta}(D_{1}, D_{2}):= \begin{cases} (D_{1} \cdot \Delta) (D_{2} \cdot \Delta)/(D_{1}\cdot D_{2}) & \text{if}\ D_{1}\neq D_{2},\\ 0 & \text{if}\ D_{1}=D_{2} \end{cases} \end{aligned}\end{align*} $$
is an ultrametric distance on the space of irreducible curves in
![]() $\mathrm {Spec} R$
different from
$\mathrm {Spec} R$
different from
![]() $\Delta $
.
$\Delta $
.
Proof. For those rings R that further satisfy the property of containing
![]() $\mathbf {C}$
, this is proved in [Reference García Barroso, González Pérez and Popescu-Pampu15]. The proof only relies on (i) the existence of embedded resolutions of divisors in the spectra of such rings and (ii) the negativity of the intersection matrix of the exceptional divisor of a projective birational morphism between spectra of such rings. Both results still hold under our weaker assumptions: see [Reference Liu20, Theorem 9.2.26] for (i) and [Reference Liu20, Theorem 9.1.27, Remark 9.1.28] for (ii).
$\mathbf {C}$
, this is proved in [Reference García Barroso, González Pérez and Popescu-Pampu15]. The proof only relies on (i) the existence of embedded resolutions of divisors in the spectra of such rings and (ii) the negativity of the intersection matrix of the exceptional divisor of a projective birational morphism between spectra of such rings. Both results still hold under our weaker assumptions: see [Reference Liu20, Theorem 9.2.26] for (i) and [Reference Liu20, Theorem 9.1.27, Remark 9.1.28] for (ii).
Arithmetic intersection multiplicities
Suppose now that
![]() $\mathscr {X}$
is a
$\mathscr {X}$
is a
![]() $2$
-dimensional regular Noetherian scheme, proper flat over a discrete valuation ring
$2$
-dimensional regular Noetherian scheme, proper flat over a discrete valuation ring
![]() $\mathscr {O}$
with residue field
$\mathscr {O}$
with residue field
![]() $\kappa $
. A divisor on
$\kappa $
. A divisor on
![]() $\mathscr {X}$
is called horizontal (resp., vertical) if each of the irreducible components of the support
$\mathscr {X}$
is called horizontal (resp., vertical) if each of the irreducible components of the support
![]() $\lvert D\rvert $
is flat over
$\lvert D\rvert $
is flat over
![]() $\mathscr {O}$
(resp., contained in the special fiber
$\mathscr {O}$
(resp., contained in the special fiber
![]() $\mathscr {X}_{\kappa }$
). We extend
$\mathscr {X}_{\kappa }$
). We extend
![]() $(\ \cdot \ ):=(\ \cdot \ )_{\mathscr {X}}$
to a bilinear form
$(\ \cdot \ ):=(\ \cdot \ )_{\mathscr {X}}$
to a bilinear form
![]() $(\ \bullet \ )$
on pairs of divisors on
$(\ \bullet \ )$
on pairs of divisors on
![]() $\mathscr {X}$
sharing no common horizontal irreducible component of the support by
$\mathscr {X}$
sharing no common horizontal irreducible component of the support by
if V is any vertical divisor.
Denote by X the generic fiber of
![]() $\mathscr {X}$
. If
$\mathscr {X}$
. If
![]() $D\in \mathrm {Div}^{0}(X)$
with Zariski closure
$D\in \mathrm {Div}^{0}(X)$
with Zariski closure
![]() $\overline {D}$
in
$\overline {D}$
in
![]() $\mathscr {X}$
, a flat extension of D is a divisor
$\mathscr {X}$
, a flat extension of D is a divisor
 $\widehat {D}\in \mathrm {Div}(\mathscr {X})_{\mathbf {Q}}$
such that
$\widehat {D}\in \mathrm {Div}(\mathscr {X})_{\mathbf {Q}}$
such that
![]() $\widehat {D}-\overline {D}$
is vertical and
$\widehat {D}-\overline {D}$
is vertical and
 $$ \begin{align*} \left(\widehat{D}\bullet V\right)=0 \end{align*} $$
$$ \begin{align*} \left(\widehat{D}\bullet V\right)=0 \end{align*} $$
for any vertical divisor V on
![]() $\mathscr {X}$
. A flat extension of D exists and is unique up to addition of rational linear combinations of the connected components of
$\mathscr {X}$
. A flat extension of D exists and is unique up to addition of rational linear combinations of the connected components of
![]() $\mathscr {X}_{\kappa }$
.
$\mathscr {X}_{\kappa }$
.
The arithmetic intersection multiplicity on divisors with disjoint supports in
![]() ${\mathrm{Div}}^{0}(X)$
is then defined by
${\mathrm{Div}}^{0}(X)$
is then defined by
 $$ \begin{align*} m_{X}(D_{1}, D_{2}):=\left(\overline{D}_{1}\bullet \widehat{D}_{2}\right) = \left(\widehat{D}_{1}\bullet \overline{D}_{2}\right) \in \mathbf{Q}. \end{align*} $$
$$ \begin{align*} m_{X}(D_{1}, D_{2}):=\left(\overline{D}_{1}\bullet \widehat{D}_{2}\right) = \left(\widehat{D}_{1}\bullet \overline{D}_{2}\right) \in \mathbf{Q}. \end{align*} $$
4.3 Decay of intersection multiplicities
We continue using the notation introduced in §4.1. Let
![]() $m_{\overline {w}}:= m_{X_{H_{0, \overline {w}}}}$
. Developing the approximation argument sketched in the introduction, we will show that for any degree-
$m_{\overline {w}}:= m_{X_{H_{0, \overline {w}}}}$
. Developing the approximation argument sketched in the introduction, we will show that for any degree-
![]() $0$
divisor D on
$0$
divisor D on
![]() $X_{H_{0}}$
, we have
$X_{H_{0}}$
, we have
 $$ \begin{align*} m_{\overline{w}}\left(\widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, D\right)= O\left(q_{F,v}^{s}\right) \end{align*} $$
$$ \begin{align*} m_{\overline{w}}\left(\widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, D\right)= O\left(q_{F,v}^{s}\right) \end{align*} $$
in L, uniformly in a.
Set
![]() $U_{0,v}:= \mathrm {GL}_{2}\left (\mathscr {O}_{F, v}\right )\subset \mathbf {B}_{v}^{\times }$
and
$U_{0,v}:= \mathrm {GL}_{2}\left (\mathscr {O}_{F, v}\right )\subset \mathbf {B}_{v}^{\times }$
and
![]() $X_{0}:= X_{U^{v}U_{0,v}}$
, let
$X_{0}:= X_{U^{v}U_{0,v}}$
, let
![]() $\mathscr {X}_{0}$
be the canonical model of
$\mathscr {X}_{0}$
be the canonical model of
![]() $X_{0, F_{v}}$
over
$X_{0, F_{v}}$
over
![]() $\mathscr {O}_{F, v}$
, which is smooth [Reference Carayol6], and let
$\mathscr {O}_{F, v}$
, which is smooth [Reference Carayol6], and let
![]() $\mathscr {X}_{0}'$
be its base change to
$\mathscr {X}_{0}'$
be its base change to
![]() $\mathscr {O}_{H_{0, \overline {w}}}$
. Let
$\mathscr {O}_{H_{0, \overline {w}}}$
. Let
![]() $\mathscr {X}$
be the integral closure of
$\mathscr {X}$
be the integral closure of
![]() $\mathscr {X}_{0}'$
in
$\mathscr {X}_{0}'$
in
![]() $X_{H_{0, \overline {w}}}$
, which is a regular model of
$X_{H_{0, \overline {w}}}$
, which is a regular model of
![]() $X_{H_{0, \overline {w}}} $
over
$X_{H_{0, \overline {w}}} $
over
![]() $\mathscr {O}_{H_{0, \overline {w}}}$
, and let
$\mathscr {O}_{H_{0, \overline {w}}}$
, and let
![]() ${\mathrm{p}}\colon \mathscr {X}\to \mathscr {X}_{0}'$
be the natural map. Thus we have a diagram
${\mathrm{p}}\colon \mathscr {X}\to \mathscr {X}_{0}'$
be the natural map. Thus we have a diagram

of curves and regular integral models. (The bottom row will be used in proving Lemma 4.3.2.)
Some intersection multiplicities
As a preliminary, we first compute the intersection multiplicities of Zariski closures of CM points with the special fiber of
![]() $\mathscr {X}$
, then bound their intersections with horizontal divisors.
$\mathscr {X}$
, then bound their intersections with horizontal divisors.
We denote by
![]() $\kappa $
the residue field of
$\kappa $
the residue field of
![]() $H_{0, \overline {w}}$
and by k the algebraic closure of
$H_{0, \overline {w}}$
and by k the algebraic closure of
![]() $\kappa $
. For a scheme
$\kappa $
. For a scheme
![]() $\mathscr {C}$
and a point
$\mathscr {C}$
and a point
![]() $y\in \mathscr {C}$
, we denote
$y\in \mathscr {C}$
, we denote
![]() $\mathscr {C}_{y}:=\mathrm {Spec}\, \mathscr {O}_{\mathscr {C}, y}$
.
$\mathscr {C}_{y}:=\mathrm {Spec}\, \mathscr {O}_{\mathscr {C}, y}$
.
Lemma 4.3.1. Let
![]() $z_{s}\in X_{H_{0}}$
be a CM point with pseudo-conductor s, let
$z_{s}\in X_{H_{0}}$
be a CM point with pseudo-conductor s, let
![]() $\overline {z}_{s}$
be its closure in
$\overline {z}_{s}$
be its closure in
![]() $\mathscr {X}$
, and let
$\mathscr {X}$
, and let
![]() $y\in \mathscr {X}_{\kappa }$
be its reduction modulo
$y\in \mathscr {X}_{\kappa }$
be its reduction modulo
![]() $\overline {w}$
. Then
$\overline {w}$
. Then
 $$ \begin{align*} \left(\overline{z}_{s} \cdot \left[\mathscr{X}_{y,\kappa}\right]\right)_{\mathscr{X}_{y}} =[\kappa(y):\kappa] q_{F,v}^{s}. \end{align*} $$
$$ \begin{align*} \left(\overline{z}_{s} \cdot \left[\mathscr{X}_{y,\kappa}\right]\right)_{\mathscr{X}_{y}} =[\kappa(y):\kappa] q_{F,v}^{s}. \end{align*} $$
(Recall that, following §3.1,
![]() $\mathscr {X}_{y, \kappa }$
denotes the special fiber of
$\mathscr {X}_{y, \kappa }$
denotes the special fiber of
![]() $\mathscr {X}_{y}$
.)
$\mathscr {X}_{y}$
.)
Proof. We will deduce this from Gross’s theory of quasicanonical liftings [Reference Gross18], which we recall. The situation is purely local, and we drop all subscripts v, w, and
![]() $\overline {w}$
. For a finite extension
$\overline {w}$
. For a finite extension
![]() $K\supset E$
contained in
$K\supset E$
contained in
![]() $E^{\mathrm{ab}}$
, let
$E^{\mathrm{ab}}$
, let
![]() $K^{\mathrm{un}}$
be the maximal unramified extension of K contained in
$K^{\mathrm{un}}$
be the maximal unramified extension of K contained in
![]() $E^{\mathrm{ab}}$
(thus the residue field of
$E^{\mathrm{ab}}$
(thus the residue field of
![]() $K^{\mathrm{un}}$
is identified with k).
$K^{\mathrm{un}}$
is identified with k).
By [Reference Carayol6, §7.4], for any supersingular point
![]() $y_{0} \in \mathscr {X}_{0,\mathscr {O}_{E}^{\mathrm{un}}}$
the completed local ring of
$y_{0} \in \mathscr {X}_{0,\mathscr {O}_{E}^{\mathrm{un}}}$
the completed local ring of
![]() $\mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
at
$\mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
at
![]() $ y_{0}$
is isomorphic to
$ y_{0}$
is isomorphic to
![]() $ \mathscr {O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] $
and is the deformation ring of formal modules studied by Gross. The main result of [Reference Gross18] is that for any CM point
$ \mathscr {O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] $
and is the deformation ring of formal modules studied by Gross. The main result of [Reference Gross18] is that for any CM point
![]() $z_{0}\in X_{0,{E}^{\mathrm{un}}}$
, there exists a unique integer t (the conductor of
$z_{0}\in X_{0,{E}^{\mathrm{un}}}$
, there exists a unique integer t (the conductor of
![]() $z_{0}$
) such that the following hold. First, the field
$z_{0}$
) such that the following hold. First, the field
![]() $E^{\mathrm{un }}(z_{0})$
is the abelian extension
$E^{\mathrm{un }}(z_{0})$
is the abelian extension
![]() $E^{(t)} $
of
$E^{(t)} $
of
![]() $E^{\mathrm{un}}$
with norm group
$E^{\mathrm{un}}$
with norm group
 $\left (\mathscr {O}_{F}+\varpi _{v}^{t}\mathscr {O}_{E}\right )^{\times }/\mathscr {O}_{F}^{\times }$
, which is totally ramified of some degree
$\left (\mathscr {O}_{F}+\varpi _{v}^{t}\mathscr {O}_{E}\right )^{\times }/\mathscr {O}_{F}^{\times }$
, which is totally ramified of some degree
![]() $d_{t}$
. Second, the inclusion of the Zariski closure
$d_{t}$
. Second, the inclusion of the Zariski closure
![]() $\overline {z}_{0}\hookrightarrow \mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
gives rise to a map of complete local rings
$\overline {z}_{0}\hookrightarrow \mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
gives rise to a map of complete local rings
which sends u to a uniformizer
![]() $\varpi ^{(t) }$
of
$\varpi ^{(t) }$
of
![]() $E^{(t)}$
. It follows that if
$E^{(t)}$
. It follows that if
![]() $\mu _{t}$
is the minimal polynomial of
$\mu _{t}$
is the minimal polynomial of
![]() $\varpi ^{(t)}$
,
$\varpi ^{(t)}$
,
 $$ \begin{align}\left(\overline{z_{0}} \cdot \mathscr{X}_{0, k}\right)_{\mathscr{X}_{0, \mathscr{O}_{E}^{\mathrm{un}}, y_{0}}} = \dim_{k} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] /(\varpi_{E}, \mu_{t}(u)) = \dim_{k}\mathscr{O}_{E^{(t)}}/ \varpi_{E}= d_{t}.\end{align} $$
$$ \begin{align}\left(\overline{z_{0}} \cdot \mathscr{X}_{0, k}\right)_{\mathscr{X}_{0, \mathscr{O}_{E}^{\mathrm{un}}, y_{0}}} = \dim_{k} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] /(\varpi_{E}, \mu_{t}(u)) = \dim_{k}\mathscr{O}_{E^{(t)}}/ \varpi_{E}= d_{t}.\end{align} $$
Consider now the situation of the lemma. By the projection formula,
 $$ \begin{align*} \left(\overline{z}_{s} \cdot \left[\mathscr{X}_{y, \kappa}\right] \right)_{\mathscr{X}_{y}} & =\left( \overline{z}_{s} \cdot {\mathrm{p}}^{*}\mathscr{X}_{0,\kappa_{0}} \right)_{\mathscr{X}_{y}} \\ &=\left( {\mathrm{p}}_{*}\overline{z}_{s} \cdot \mathscr{X}_{0,\kappa}\right)_{\mathscr{X}^{\prime}_{0,y'}} = \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left(\overline{z}_{0,s} \cdot \mathscr{X}_{0,\kappa }\right)_{\mathscr{X}^{\prime}_{0,y'}}, \end{align*} $$
$$ \begin{align*} \left(\overline{z}_{s} \cdot \left[\mathscr{X}_{y, \kappa}\right] \right)_{\mathscr{X}_{y}} & =\left( \overline{z}_{s} \cdot {\mathrm{p}}^{*}\mathscr{X}_{0,\kappa_{0}} \right)_{\mathscr{X}_{y}} \\ &=\left( {\mathrm{p}}_{*}\overline{z}_{s} \cdot \mathscr{X}_{0,\kappa}\right)_{\mathscr{X}^{\prime}_{0,y'}} = \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left(\overline{z}_{0,s} \cdot \mathscr{X}_{0,\kappa }\right)_{\mathscr{X}^{\prime}_{0,y'}}, \end{align*} $$
where
![]() $y'={\mathrm{p}}(y)$
and
$y'={\mathrm{p}}(y)$
and
![]() $z_{0, s}= {\mathrm{p}}(z_{s})\in X_{0, H_{0}}$
is a CM point. The last intersection multiplicity is
$z_{0, s}= {\mathrm{p}}(z_{s})\in X_{0, H_{0}}$
is a CM point. The last intersection multiplicity is
![]() $[\kappa (y):\kappa ]$
times the multiplicities of the base-changed divisors to the ring of integers of
$[\kappa (y):\kappa ]$
times the multiplicities of the base-changed divisors to the ring of integers of
![]() $H_{0}^{\mathrm{un}}$
, where
$H_{0}^{\mathrm{un}}$
, where
![]() $z_{0, s}$
remains an irreducible divisor since
$z_{0, s}$
remains an irreducible divisor since
![]() $H_{0}\left (z_{0, s}\right )\subset H_{0}(z_{s})$
is totally ramified over
$H_{0}\left (z_{0, s}\right )\subset H_{0}(z_{s})$
is totally ramified over
![]() $H_{0}$
. We perform such base change to
$H_{0}$
. We perform such base change to
![]() $\mathscr {O}_{H_{0}^{\mathrm{un}}}$
without altering the notation. Let z be the image of
$\mathscr {O}_{H_{0}^{\mathrm{un}}}$
without altering the notation. Let z be the image of
![]() $z_{0,s}\in X_{H_{0}^{\mathrm{un}}}$
in
$z_{0,s}\in X_{H_{0}^{\mathrm{un}}}$
in
![]() $X_{E^{\mathrm{un}}}$
, and let t be the conductor of z; so
$X_{E^{\mathrm{un}}}$
, and let t be the conductor of z; so
![]() $E^{(t)}\subset H_{0}^{\mathrm{un}}\left (z_{0,s}\right )$
. The fiber above
$E^{(t)}\subset H_{0}^{\mathrm{un}}\left (z_{0,s}\right )$
. The fiber above
![]() $z\cong \mathrm {Spec}\, E^{(t)}$
in
$z\cong \mathrm {Spec}\, E^{(t)}$
in
![]() $X_{H_{0}^{\mathrm{un}}}$
is
$X_{H_{0}^{\mathrm{un}}}$
is
 $$ \begin{align*} \mathrm{Spec} E^{(t)}\otimes_{E^{\mathrm{un}}} H_{0}^{\mathrm{un}}= \mathrm{Spec} H_{0}^{\mathrm{un}}\left(z_{0,s}\right)^{\oplus c} \end{align*} $$
$$ \begin{align*} \mathrm{Spec} E^{(t)}\otimes_{E^{\mathrm{un}}} H_{0}^{\mathrm{un}}= \mathrm{Spec} H_{0}^{\mathrm{un}}\left(z_{0,s}\right)^{\oplus c} \end{align*} $$
for
 $c=\left [E^{(t)}: E^{\mathrm{un}}\right ] \cdot \left [H_{0}^{\mathrm{un}}:E^{\mathrm{un}}\right ]/ \left [H_{0}^{\mathrm{}}\left (z_{0,s}\right ): H_{0}^{\mathrm{}}\right ] $
, and
$c=\left [E^{(t)}: E^{\mathrm{un}}\right ] \cdot \left [H_{0}^{\mathrm{un}}:E^{\mathrm{un}}\right ]/ \left [H_{0}^{\mathrm{}}\left (z_{0,s}\right ): H_{0}^{\mathrm{}}\right ] $
, and
![]() $z_{0,s}$
is one of the factors in the right-hand side. By the projection formula applied to
$z_{0,s}$
is one of the factors in the right-hand side. By the projection formula applied to
![]() $ \mathscr {X}_{0}\times \mathrm {Spec}\, \mathscr {O}_{H_{0}^{\mathrm{un }}} \to \mathscr {X}_{0}\times \mathrm {Spec}\, \mathscr {O}_{E^{\mathrm{un}}}$
and equation (4.3.1), we have
$ \mathscr {X}_{0}\times \mathrm {Spec}\, \mathscr {O}_{H_{0}^{\mathrm{un }}} \to \mathscr {X}_{0}\times \mathrm {Spec}\, \mathscr {O}_{E^{\mathrm{un}}}$
and equation (4.3.1), we have
 $$ \begin{align*}\begin{aligned} \ \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left(\overline{z}_{0,s} \cdot \mathscr{X}_{0,\kappa }\right)_{\mathscr{X}^{\prime}_{0,y'}} &=[\kappa(y):\kappa] c^{-1} \cdot \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left[H_{0}^{\mathrm{un}}:E^{\mathrm{un}}\right] \cdot d_{t} \\ &=[\kappa(y):\kappa] \cdot [H_{0}(z_{s}): H_{0}] \cdot d_{t}^{-1} \cdot d_{t}= [\kappa(y):\kappa] q_{F}^{s}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \ \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left(\overline{z}_{0,s} \cdot \mathscr{X}_{0,\kappa }\right)_{\mathscr{X}^{\prime}_{0,y'}} &=[\kappa(y):\kappa] c^{-1} \cdot \left[H_{0}(z_{s})\colon H_{0}\left(z_{0,s}\right)\right] \cdot \left[H_{0}^{\mathrm{un}}:E^{\mathrm{un}}\right] \cdot d_{t} \\ &=[\kappa(y):\kappa] \cdot [H_{0}(z_{s}): H_{0}] \cdot d_{t}^{-1} \cdot d_{t}= [\kappa(y):\kappa] q_{F}^{s}, \end{aligned}\end{align*} $$
as desired.
Lemma 4.3.2. Let
![]() $\Delta $
be an irreducible horizontal divisor in
$\Delta $
be an irreducible horizontal divisor in
![]() $\mathscr {X}$
. The intersection multiplicities
$\mathscr {X}$
. The intersection multiplicities
are bounded by an absolute constant as z ranges among CM points of sufficiently large pseudo-conductor reducing to y.
Proof. The intersection multiplicity
![]() $\left (\Delta \cdot \overline {z}\right )$
is bounded by the degree of the natural map
$\left (\Delta \cdot \overline {z}\right )$
is bounded by the degree of the natural map
![]() ${\mathrm{q}}\colon \mathscr {X}\to \mathscr {X}_{0, \mathscr {O}_{E,{v}}}$
near y, times the intersection multiplicities of the push-forward divisors to
${\mathrm{q}}\colon \mathscr {X}\to \mathscr {X}_{0, \mathscr {O}_{E,{v}}}$
near y, times the intersection multiplicities of the push-forward divisors to
![]() $\mathscr {X}_{0, \mathscr {O}_{E,v}}$
. Similar to the proof of Lemma 4.3.1, we may estimate this intersection in the base change of
$\mathscr {X}_{0, \mathscr {O}_{E,v}}$
. Similar to the proof of Lemma 4.3.1, we may estimate this intersection in the base change of
![]() $\mathscr {X}_{0}$
to
$\mathscr {X}_{0}$
to
![]() $\mathscr {O}_{E}^{\mathrm{un}}$
. The base change of the divisor
$\mathscr {O}_{E}^{\mathrm{un}}$
. The base change of the divisor
![]() ${\mathrm{q}}_{*}z_{}$
equals a sum of CM points of
${\mathrm{q}}_{*}z_{}$
equals a sum of CM points of
![]() $\mathscr {X}_{0, \mathscr {O}_{E^{\mathrm{un}}}}$
; because the extensions
$\mathscr {X}_{0, \mathscr {O}_{E^{\mathrm{un}}}}$
; because the extensions
![]() $H_{s}/H_{0}$
are totally ramified, the number of points in this divisor is bounded by an absolute constant, and the conductors of all those CM points go to infinity with the pseudo-conductor s of z. Thus it suffices to show that if
$H_{s}/H_{0}$
are totally ramified, the number of points in this divisor is bounded by an absolute constant, and the conductors of all those CM points go to infinity with the pseudo-conductor s of z. Thus it suffices to show that if
![]() $\Delta _{0}$
is a fixed horizontal divisor on
$\Delta _{0}$
is a fixed horizontal divisor on
![]() $\mathscr {X}_{0, E^{\mathrm{un}}}$
, its intersection multiplicity with CM points of conductor t is bounded as
$\mathscr {X}_{0, E^{\mathrm{un}}}$
, its intersection multiplicity with CM points of conductor t is bounded as
![]() $t\to \infty $
.
$t\to \infty $
.
Let
![]() $z\in \mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
be a CM point of conductor t, and let
$z\in \mathscr {X}_{0, \mathscr {O}_{E}^{\mathrm{un}}}$
be a CM point of conductor t, and let
![]() $y_{0}\in \mathscr {X}_{0, k}$
be the image of the reduction of t. Now write the image of
$y_{0}\in \mathscr {X}_{0, k}$
be the image of the reduction of t. Now write the image of
![]() $\Delta _{0}$
in the completion of
$\Delta _{0}$
in the completion of
![]() $\mathscr {X}_{0, \mathscr {O}_{E^{\mathrm{un}}}}$
at
$\mathscr {X}_{0, \mathscr {O}_{E^{\mathrm{un}}}}$
at
![]() $y_{0}$
as
$y_{0}$
as
 $$ \begin{align*} \widehat{\Delta}_{0}=\mathrm{Spec} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] /(f)\subset \mathrm{Spec} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt], \end{align*} $$
$$ \begin{align*} \widehat{\Delta}_{0}=\mathrm{Spec} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] /(f)\subset \mathrm{Spec} \mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt], \end{align*} $$
with
 $f=\sum _{i=1}^{d} a_{i}u^{i}$
an integral nonconstant monic polynomial. Let
$f=\sum _{i=1}^{d} a_{i}u^{i}$
an integral nonconstant monic polynomial. Let
 ${\widetilde f}\in k[u]$
be the reduction of f. Then
${\widetilde f}\in k[u]$
be the reduction of f. Then
 $$ \begin{align*} \left(\Delta_{0}\cdot \overline{z}\right) &= \dim_{k}\mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] / (f, \mu_{t}) \\&=\dim_{k} \mathscr{O}_{E^{(t)}}/\left(f\left(\varpi^{(t)}\right)\right) =\dim_{k} \mathscr{O}_{E^{(t)}}/\left(\left(\varpi^{(t)}\right)^{\deg \left(\tilde{f}\right)}\right)=\deg \left(\tilde{f}\right)\leq d \end{align*} $$
$$ \begin{align*} \left(\Delta_{0}\cdot \overline{z}\right) &= \dim_{k}\mathscr{O}_{E^{\mathrm{un}}}[\kern-1pt[ u]\kern-1pt] / (f, \mu_{t}) \\&=\dim_{k} \mathscr{O}_{E^{(t)}}/\left(f\left(\varpi^{(t)}\right)\right) =\dim_{k} \mathscr{O}_{E^{(t)}}/\left(\left(\varpi^{(t)}\right)^{\deg \left(\tilde{f}\right)}\right)=\deg \left(\tilde{f}\right)\leq d \end{align*} $$
if t is sufficiently large, since the normalized valuations of
![]() $\varpi ^{(t)}$
decrease to
$\varpi ^{(t)}$
decrease to
![]() $0$
as
$0$
as
![]() $t\to \infty $
. This completes the proof of the lemma.
$t\to \infty $
. This completes the proof of the lemma.
Approximation by vertical divisors
The following proposition contains the essential new ingredient of this work. We denote by
respectively the set of CM points of
![]() $X_{H_{0}}$
that have pseudo-conductor at least and equal to a given integer s. We denote by
$X_{H_{0}}$
that have pseudo-conductor at least and equal to a given integer s. We denote by
![]() $\mathscr {V}$
the set of irreducible components of
$\mathscr {V}$
the set of irreducible components of
![]() $\mathscr {X}_{\kappa }$
(henceforth: ‘vertical components’), and if
$\mathscr {X}_{\kappa }$
(henceforth: ‘vertical components’), and if
![]() $y\in \mathscr {X}_{\kappa }$
is a closed point, we denote by
$y\in \mathscr {X}_{\kappa }$
is a closed point, we denote by
![]() $\mathscr {V}_{y}\subset \mathscr {V}$
the set of vertical components of
$\mathscr {V}_{y}\subset \mathscr {V}$
the set of vertical components of
![]() $\mathscr {X}_{y, \kappa }$
. We still use a bar to denote Zariski closure.
$\mathscr {X}_{y, \kappa }$
. We still use a bar to denote Zariski closure.
Proposition 4.3.3. There exist an integer
![]() $s_{0}\geq 1$
, depending only on
$s_{0}\geq 1$
, depending only on
![]() $X_{H_{0}}$
, and a function
$X_{H_{0}}$
, and a function
 $$ \begin{align*} (V, \rho)\colon {\mathrm{CM}}\left(X_{H_{0}}\right)_{\geq s_{0}} \longrightarrow \mathscr{V}\times \mathbf{Q}^{\times} \end{align*} $$
$$ \begin{align*} (V, \rho)\colon {\mathrm{CM}}\left(X_{H_{0}}\right)_{\geq s_{0}} \longrightarrow \mathscr{V}\times \mathbf{Q}^{\times} \end{align*} $$
satisfying the following property:
For every divisor
![]() $D\in \mathrm {Div}(\mathscr {X})_{L}$
, there exists a constant
$D\in \mathrm {Div}(\mathscr {X})_{L}$
, there exists a constant
![]() $s_{D}\geq s_{0}$
depending only on the support of D, such that if
$s_{D}\geq s_{0}$
depending only on the support of D, such that if
![]() $z\in X_{H_{0}}$
is a CM point of conductor
$z\in X_{H_{0}}$
is a CM point of conductor
![]() $s\geq s_{D}$
, then
$s\geq s_{D}$
, then
![]() $\left (\overline {z}\cdot D\right ) $
may be computed as follows. Let
$\left (\overline {z}\cdot D\right ) $
may be computed as follows. Let
![]() $V=V(z)$
,
$V=V(z)$
,
![]() $\rho =\rho (z)$
, and write
$\rho =\rho (z)$
, and write
with
![]() $c\in L$
and
$c\in L$
and
![]() $D'\in \mathrm {Div}(\mathscr {X})_{L}$
a divisor whose support does not contain V. Then
$D'\in \mathrm {Div}(\mathscr {X})_{L}$
a divisor whose support does not contain V. Then
where
![]() $y\in \mathscr {X}_{\kappa }$
denotes the reduction of z modulo
$y\in \mathscr {X}_{\kappa }$
denotes the reduction of z modulo
![]() $\overline {w}$
.
$\overline {w}$
.
Remark 4.3.4. The vertical component
![]() $V(z)$
will be characterized as the one maximizing the intersection multiplicity with
$V(z)$
will be characterized as the one maximizing the intersection multiplicity with
![]() $\overline {z}$
. We refer the reader to [Reference Disegni11, §2, Figure 1 in §1] for an equivalent and possibly more vivid geometric descriptionFootnote
8
of the relation of V to
$\overline {z}$
. We refer the reader to [Reference Disegni11, §2, Figure 1 in §1] for an equivalent and possibly more vivid geometric descriptionFootnote
8
of the relation of V to
![]() $z_{s}$
: one can define pairwise disjoint open subsets (‘geometric basins’) of the Berkovich analytification of X, labelled by the irreducible components of the special fiber; then
$z_{s}$
: one can define pairwise disjoint open subsets (‘geometric basins’) of the Berkovich analytification of X, labelled by the irreducible components of the special fiber; then
![]() $z_{s}$
belongs to the basin corresponding to V.
$z_{s}$
belongs to the basin corresponding to V.
Proof. We will omit all subscripts
![]() $v, w, \overline {w}$
and use some of the notation introduced in the proof of Lemma 4.3.1.
$v, w, \overline {w}$
and use some of the notation introduced in the proof of Lemma 4.3.1.
Let
![]() $y\in \mathscr {X}_{\kappa }$
be a closed point, and write
$y\in \mathscr {X}_{\kappa }$
be a closed point, and write
 $\left [\mathscr {X}_{y, \kappa }\right ]= \sum _{V' \in \mathscr {V}_{y}} e_{V'}V'$
as divisors. By Lemma 4.3.1, the weighted sum
$\left [\mathscr {X}_{y, \kappa }\right ]= \sum _{V' \in \mathscr {V}_{y}} e_{V'}V'$
as divisors. By Lemma 4.3.1, the weighted sum
 $$ \begin{align}\begin{aligned} \sum_{V'} {e_{V'} } \left(\overline{z}_{s}\cdot V'\right)=\left(\overline{z}_{s}\cdot \left[\mathscr{X}_{y, \kappa}\right]\right)= [\kappa(y)\colon \kappa] q_{F}^{s}\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{V'} {e_{V'} } \left(\overline{z}_{s}\cdot V'\right)=\left(\overline{z}_{s}\cdot \left[\mathscr{X}_{y, \kappa}\right]\right)= [\kappa(y)\colon \kappa] q_{F}^{s}\end{aligned}\end{align} $$
is independent of the choice of a CM point
![]() $z_{s}\in X_{H_{0}}$
of pseudo-conductor s reducing to y. As equation (4.3.3) goes to infinity with s (and the coefficients
$z_{s}\in X_{H_{0}}$
of pseudo-conductor s reducing to y. As equation (4.3.3) goes to infinity with s (and the coefficients
![]() $e_{V'}$
are independent of s), the quantity
$e_{V'}$
are independent of s), the quantity
(more precisely, the minimum of those maxima as
![]() $z_{s}$
varies in
$z_{s}$
varies in
![]() ${\mathrm{CM}}(X_{H_{0}})_{s}$
) goes to infinity with s.
${\mathrm{CM}}(X_{H_{0}})_{s}$
) goes to infinity with s.
Fix now a CM point
![]() $z_{s}\in X_{H_{0}}$
of pseudo-conductor s, let
$z_{s}\in X_{H_{0}}$
of pseudo-conductor s, let
![]() $y\in \mathscr {X}_{\kappa }$
be its reduction, and let
$y\in \mathscr {X}_{\kappa }$
be its reduction, and let
![]() $V\in \mathscr {V}_{y}$
be a vertical component realizing the maximum in expression (4.3.4). Let
$V\in \mathscr {V}_{y}$
be a vertical component realizing the maximum in expression (4.3.4). Let
![]() $D\neq V$
be an irreducible divisor in
$D\neq V$
be an irreducible divisor in
![]() $\mathscr {X}_{y}$
. Pick any irreducible horizontal divisor
$\mathscr {X}_{y}$
. Pick any irreducible horizontal divisor
![]() $\Delta \neq D, \overline {z}_{s}$
in
$\Delta \neq D, \overline {z}_{s}$
in
![]() $\mathscr {X}_{y}$
, and consider the ultrametric distance
$\mathscr {X}_{y}$
, and consider the ultrametric distance
![]() $d_{\Delta }$
of Proposition 4.2.1 for
$d_{\Delta }$
of Proposition 4.2.1 for
![]() $ R=\mathscr {O}_{\mathscr {X}, y}$
. (Note that
$ R=\mathscr {O}_{\mathscr {X}, y}$
. (Note that
![]() $\Delta $
may be drawn from a finite set independent of
$\Delta $
may be drawn from a finite set independent of
![]() $z_{s}$
and D; in fact, we may fix any set
$z_{s}$
and D; in fact, we may fix any set
![]() $\underline {\Delta }$
of at least two irreducible horizontal divisors that are not Zariski closures of CM points, and for given D pick any
$\underline {\Delta }$
of at least two irreducible horizontal divisors that are not Zariski closures of CM points, and for given D pick any
![]() $\Delta \in \underline {\Delta }-\{D\}$
.)
$\Delta \in \underline {\Delta }-\{D\}$
.)
By the choice of V and Lemma 4.3.2, if s is sufficiently large (a condition depending on D), we have
 $$ \begin{align*} d_{\Delta}\left(\overline{z}_{s}, V\right) = {\left(\overline{z}_{s}\cdot \Delta\right) (V\cdot \Delta)\over \left(\overline{z}_{s}\cdot V\right)} < d_{\Delta}( V, D), \end{align*} $$
$$ \begin{align*} d_{\Delta}\left(\overline{z}_{s}, V\right) = {\left(\overline{z}_{s}\cdot \Delta\right) (V\cdot \Delta)\over \left(\overline{z}_{s}\cdot V\right)} < d_{\Delta}( V, D), \end{align*} $$
so that by Proposition 4.2.1,
Unwinding the definitions,
for
![]() $ \rho := {\left (\overline {z}_{s}\cdot \Delta \right )/ (V\cdot \Delta ) }$
. Applied to a vertical component
$ \rho := {\left (\overline {z}_{s}\cdot \Delta \right )/ (V\cdot \Delta ) }$
. Applied to a vertical component
![]() $D=V'\neq V$
, formula (4.3.5) together with Lemma 4.3.2 shows the uniqueness of the maximizing
$D=V'\neq V$
, formula (4.3.5) together with Lemma 4.3.2 shows the uniqueness of the maximizing
![]() $V =:V(z_{s})$
for large s; it is clear that
$V =:V(z_{s})$
for large s; it is clear that
![]() $\rho =:\rho (z_{s})$
is then uniquely determined as well. Now the intersection formula (4.3.2) follows by linearity from equation (4.3.5) and Lemma 4.3.1.
$\rho =:\rho (z_{s})$
is then uniquely determined as well. Now the intersection formula (4.3.2) follows by linearity from equation (4.3.5) and Lemma 4.3.1.
Corollary 4.3.5. If
 $D\in \mathrm {Div}^{0}\left (X_{H_{0}}\right )_{L}$
is any degree-
$D\in \mathrm {Div}^{0}\left (X_{H_{0}}\right )_{L}$
is any degree-
![]() $0$
divisor, then for all sufficiently large s and all a,
$0$
divisor, then for all sufficiently large s and all a,
 $$ \begin{align*} m_{\overline{w}}( \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, D)=O(q_{F,v}^{s}) \end{align*} $$
$$ \begin{align*} m_{\overline{w}}( \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, D)=O(q_{F,v}^{s}) \end{align*} $$
in L, where the implied constant can be fixed independently of a and s.
Proof. Let
![]() $\widehat {D}$
be a flat extension of D to a divisor on
$\widehat {D}$
be a flat extension of D to a divisor on
![]() $\mathscr {X}$
(with coefficients in L), and abbreviate
$\mathscr {X}$
(with coefficients in L), and abbreviate
 $Z_{a,s}:= \widetilde {Z}_{a\varpi ^{s}}(\phi ^{\infty }) [1]_{U}$
. Then by Propositions 4.1.4 and 4.3.3,
$Z_{a,s}:= \widetilde {Z}_{a\varpi ^{s}}(\phi ^{\infty }) [1]_{U}$
. Then by Propositions 4.1.4 and 4.3.3,
 $$ \begin{align*} m_{\overline{w}}( Z_{a,s}, D)= (\overline{Z}_{a,s}\cdot \widehat{D}) = A q_{F,v}^{s}+ \sum_{i} \lambda_{i}(V_{i} \bullet \widehat{D}) \end{align*} $$
$$ \begin{align*} m_{\overline{w}}( Z_{a,s}, D)= (\overline{Z}_{a,s}\cdot \widehat{D}) = A q_{F,v}^{s}+ \sum_{i} \lambda_{i}(V_{i} \bullet \widehat{D}) \end{align*} $$
for some vertical components
![]() $V_{i}\subset \mathscr {X} $
and some A,
$V_{i}\subset \mathscr {X} $
and some A,
![]() $\lambda _{i}\in L$
. By the definition of flat extension,
$\lambda _{i}\in L$
. By the definition of flat extension,
 $ (V_{i} \bullet \widehat {D} )=0$
for all i. The constant A is a linear combination of the constants c in equation (4.3.2) (which depend only on
$ (V_{i} \bullet \widehat {D} )=0$
for all i. The constant A is a linear combination of the constants c in equation (4.3.2) (which depend only on
![]() $\widehat {D}$
), with coefficients whose denominators are bounded by those of
$\widehat {D}$
), with coefficients whose denominators are bounded by those of
![]() $Z_{a,s}$
; by Proposition 4.1.4, the latter are bounded independently of a and s.
$Z_{a,s}$
; by Proposition 4.1.4, the latter are bounded independently of a and s.
4.4 Decay of local heights
Recall that we need to prove (Proposition 3.6.3) that
 $$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
$$ \begin{align*} T_{\iota_{\mathfrak{p}}}(\sigma^{\vee})\widetilde{Z}(\phi^{\infty}, \chi)(v) \end{align*} $$
is a v-critical element of
![]() $ \overline {\mathbf {S}}{}'$
.
$ \overline {\mathbf {S}}{}'$
.
As in [Reference Disegni9, §9.2, proof of Proposition 9.2.1], this is reduced to the following. For any
![]() $s\geq 0$
, denote by
$s\geq 0$
, denote by
![]() $\langle \ , \ \rangle _{s,\overline {w}}$
the local height pairing on
$\langle \ , \ \rangle _{s,\overline {w}}$
the local height pairing on
![]() $X_{H_{s, \overline {w}}}$
, which is valued in
$X_{H_{s, \overline {w}}}$
, which is valued in
 $H_{s, \overline {w}}^{\times }\hat {\otimes } L$
; and let
$H_{s, \overline {w}}^{\times }\hat {\otimes } L$
; and let
 $$ \begin{align*} \langle \ , \ \rangle_{\overline{w}}= \left[H_{s,\overline{w}}:F_{v}\right]^{-1} \cdot N_{H_{s,\overline{w}}/F_{v}} \left( \left\langle \ , \ \right\rangle_{s,\overline{w}}\right), \end{align*} $$
$$ \begin{align*} \langle \ , \ \rangle_{\overline{w}}= \left[H_{s,\overline{w}}:F_{v}\right]^{-1} \cdot N_{H_{s,\overline{w}}/F_{v}} \left( \left\langle \ , \ \right\rangle_{s,\overline{w}}\right), \end{align*} $$
which is valued in
![]() $F_{v}^{\times }\hat {\otimes } L\subset \Gamma _{F}\hat {\otimes }L$
and is compatible with varying s by [Reference Disegni9, (4.1.6)]. Then we will show that for all
$F_{v}^{\times }\hat {\otimes } L\subset \Gamma _{F}\hat {\otimes }L$
and is compatible with varying s by [Reference Disegni9, (4.1.6)]. Then we will show that for all
![]() $\overline {w}\mid v$
and all
$\overline {w}\mid v$
and all
![]() $a\in \mathbf {A}^{S_{1}\infty , \times }$
with
$a\in \mathbf {A}^{S_{1}\infty , \times }$
with
![]() $v(a)=r_{v}$
, we have
$v(a)=r_{v}$
, we have
 $$ \begin{align}\begin{aligned} \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})[1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{\overline{w}} &= O\left(q_{F,v}^{s}\right) & \text{in } {F}_{v}^{\times}\hat{\otimes}L(\chi),\\ \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})[1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} &= O\left(q_{F,v}^{s}\right) &\text{in } H_{0, \overline{w}}^{\times} \hat{\otimes}L(\chi),\\ \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})[1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{\overline{w}} &= O\left(q_{F,v}^{s}\right) & \text{in } {F}_{v}^{\times}\hat{\otimes}L(\chi),\\ \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})[1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} &= O\left(q_{F,v}^{s}\right) &\text{in } H_{0, \overline{w}}^{\times} \hat{\otimes}L(\chi),\\ \end{aligned}\end{align} $$
where the second statement implies the first one. Until Lemma 4.4.3, the argument follows the lines of previous works [Reference Disegni9, Reference Nekovář24, Reference Shnidman27].
The norm relation and heights
Denote by
![]() $N_{s}$
the norm from
$N_{s}$
the norm from
![]() $H_{s , \overline {w}}$
to
$H_{s , \overline {w}}$
to
![]() $H_{0, \overline {w}}$
, set
$H_{0, \overline {w}}$
, set
![]() $L':= L(\chi )$
, and let
$L':= L(\chi )$
, and let
![]() $\mathfrak {p}'\subset \mathscr {O}_{L'}$
be the maximal ideal. By the norm relation of Proposition 4.1.4, the aforementioned compatibility [Reference Disegni9, (4.1.6)], and the integrality result of [Reference Disegni9, Proposition 4.3.2],Footnote
9
$\mathfrak {p}'\subset \mathscr {O}_{L'}$
be the maximal ideal. By the norm relation of Proposition 4.1.4, the aforementioned compatibility [Reference Disegni9, (4.1.6)], and the integrality result of [Reference Disegni9, Proposition 4.3.2],Footnote
9
 $$ \begin{align}\begin{aligned} \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} &= \left\langle {\mathrm{Tr}}_{H_{s}/H_{0}} \left(D_{a\varpi^{s}}\right), {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} \\ &= N_{s}\left( \left\langle D_{a\varpi^{s}}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{s,\overline{w}}\right) \\ & \in \mathfrak{p}^{\prime-\left( d_{00}+ d_{0}+d_{1,s}+d_{2,s}\right)} N_{s}\left(H_{s, \overline{w}}^{\times}\hat{\otimes} \mathscr{O}_{L'}\right) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \left\langle \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty}) [1]_{U}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} &= \left\langle {\mathrm{Tr}}_{H_{s}/H_{0}} \left(D_{a\varpi^{s}}\right), {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{0, \overline{w}} \\ &= N_{s}\left( \left\langle D_{a\varpi^{s}}, {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right\rangle_{s,\overline{w}}\right) \\ & \in \mathfrak{p}^{\prime-\left( d_{00}+ d_{0}+d_{1,s}+d_{2,s}\right)} N_{s}\left(H_{s, \overline{w}}^{\times}\hat{\otimes} \mathscr{O}_{L'}\right) \end{aligned}\end{align} $$
for some integers
![]() $d_{i, (s)}\geq 0$
that we now define and study.
$d_{i, (s)}\geq 0$
that we now define and study.
Boundedness of denominators
Set
 $$ \begin{align*} V':=\pi_{A^{\vee}}^{U}\otimes_{M} V_{\mathfrak{p}}A^{\vee}(\chi^{-1}) \subset V:= V_{p}J_{U} \otimes_{\mathbf{Q}_{p}}L' \end{align*} $$
$$ \begin{align*} V':=\pi_{A^{\vee}}^{U}\otimes_{M} V_{\mathfrak{p}}A^{\vee}(\chi^{-1}) \subset V:= V_{p}J_{U} \otimes_{\mathbf{Q}_{p}}L' \end{align*} $$
considered as
![]() $\mathscr {G}_{E_{w}}$
-modules; let
$\mathscr {G}_{E_{w}}$
-modules; let
![]() $V''$
be its direct complement in the decomposition of V in [Reference Disegni9, (9.2.4)], and let
$V''$
be its direct complement in the decomposition of V in [Reference Disegni9, (9.2.4)], and let
![]() $0\to V^{\prime +}\to V'\to V^{\prime -}\to 0$
be the ordinary filtration analogous to formula (1.2.6). If
$0\to V^{\prime +}\to V'\to V^{\prime -}\to 0$
be the ordinary filtration analogous to formula (1.2.6). If
![]() $?\in \{ ', '', {}^{\prime +}\}$
, define
$?\in \{ ', '', {}^{\prime +}\}$
, define
 $T^{?}:= T_{p}J_{U}\otimes _{\mathbf {Z}_{p}}\mathscr {O}_{L'}\cap V^{?}$
, and let
$T^{?}:= T_{p}J_{U}\otimes _{\mathbf {Z}_{p}}\mathscr {O}_{L'}\cap V^{?}$
, and let
![]() $T^{\prime -}=T'/T^{\prime +}$
. Then the integers
$T^{\prime -}=T'/T^{\prime +}$
. Then the integers
![]() $d_{i, (s)}$
are defined as follows:
$d_{i, (s)}$
are defined as follows:
-
–
 $d_{00}$
accounts for the denominators of the divisors, and it can be taken to be independent of s by Proposition 4.1.4.
$d_{00}$
accounts for the denominators of the divisors, and it can be taken to be independent of s by Proposition 4.1.4. -
–
 $d_{0}$
is such that
$d_{0}$
is such that
 $\mathfrak {p}^{\prime d_{0}} T\subset T'\oplus T''$
.
$\mathfrak {p}^{\prime d_{0}} T\subset T'\oplus T''$
. -
–
 $d_{1,s}:={\mathrm{length}}_{\mathscr {O}_{L'}} H^{1}\left ({H}_{s,\overline {w}}, T^{\prime \prime *}(1)\right )_{\mathrm{tors}}$
.
$d_{1,s}:={\mathrm{length}}_{\mathscr {O}_{L'}} H^{1}\left ({H}_{s,\overline {w}}, T^{\prime \prime *}(1)\right )_{\mathrm{tors}}$
. -
–
 $d_{2, s}:= {\mathrm{length}}_{\mathscr {O}_{L'}} H^{1}_{f}\left (H_{s, \overline {w}}, T'\right )/{N}_{\infty } H^{1}_{f}\left (H_{s, \overline {w}}, T'\right )$
, where
$d_{2, s}:= {\mathrm{length}}_{\mathscr {O}_{L'}} H^{1}_{f}\left (H_{s, \overline {w}}, T'\right )/{N}_{\infty } H^{1}_{f}\left (H_{s, \overline {w}}, T'\right )$
, where
 $N_{\infty }$
denotes the universal norms ([Reference Nekovář23, §6], [Reference Disegni9, §4.3]) with respect to the infinite abelian extension of
$N_{\infty }$
denotes the universal norms ([Reference Nekovář23, §6], [Reference Disegni9, §4.3]) with respect to the infinite abelian extension of
 $H_{s, \overline {w}}$
cut out by the closure in
$H_{s, \overline {w}}$
cut out by the closure in
 $\mathscr {G}_{H_{s, \overline {w}}}^{\mathrm{ab}}\supset H_{s, \overline {w}}^{\times } $
of
$\mathscr {G}_{H_{s, \overline {w}}}^{\mathrm{ab}}\supset H_{s, \overline {w}}^{\times } $
of  $$ \begin{align*} \mathrm{Ker} \left[ H_{s, \overline{w}}^{\times} \stackrel{N_{H_{s, \overline{w}}/F_{v}}}{\longrightarrow} F_{v}^{\times} \to \Gamma_{F}\hat{\otimes} L\right]. \end{align*} $$
$$ \begin{align*} \mathrm{Ker} \left[ H_{s, \overline{w}}^{\times} \stackrel{N_{H_{s, \overline{w}}/F_{v}}}{\longrightarrow} F_{v}^{\times} \to \Gamma_{F}\hat{\otimes} L\right]. \end{align*} $$
Proposition 4.4.1. Suppose that
![]() $V_{\mathfrak {p}}A $
is potentially crystalline as a representation of
$V_{\mathfrak {p}}A $
is potentially crystalline as a representation of
![]() $\mathscr {G}_{F_{v}}$
; then the sequences of integers
$\mathscr {G}_{F_{v}}$
; then the sequences of integers
![]() $\left (d_{1,s}\right )$
and
$\left (d_{1,s}\right )$
and
![]() $\left (d_{2, s}\right )$
are bounded.
$\left (d_{2, s}\right )$
are bounded.
We will use the following vanishing result, in which
![]() $\overline {L}$
denotes an algebraic closure of
$\overline {L}$
denotes an algebraic closure of
![]() $L'$
:
$L'$
:
Lemma 4.4.2. Set
 $\Gamma _{\infty }:=\mathrm {Gal}\left (H_{\infty , \overline {w}}/E_{ {w}}\right )\cong E^{\times }\backslash E^{\times }_{\mathbf {A}^{\infty }}/ U^{v}U_{F,v}^{\circ }$
. For all Hodge–Tate characters
$\Gamma _{\infty }:=\mathrm {Gal}\left (H_{\infty , \overline {w}}/E_{ {w}}\right )\cong E^{\times }\backslash E^{\times }_{\mathbf {A}^{\infty }}/ U^{v}U_{F,v}^{\circ }$
. For all Hodge–Tate characters
 $\psi \colon \mathscr {G}_{E_{w}}\to \overline {L}^{\times }$
factoring through
$\psi \colon \mathscr {G}_{E_{w}}\to \overline {L}^{\times }$
factoring through
![]() $\Gamma _{\infty }$
, and for any
$\Gamma _{\infty }$
, and for any
 $$ \begin{align*} V^{?}\in \left\{V, V^{\prime\prime*}(1), V^{\prime+, *}(1), V^{\prime-}\right\}, \end{align*} $$
$$ \begin{align*} V^{?}\in \left\{V, V^{\prime\prime*}(1), V^{\prime+, *}(1), V^{\prime-}\right\}, \end{align*} $$
we have
 $$ \begin{align*} H^{0}\left(E_{w}, V^{?}(\psi)\right)= 0. \end{align*} $$
$$ \begin{align*} H^{0}\left(E_{w}, V^{?}(\psi)\right)= 0. \end{align*} $$
Proof. The proof is largely similar to that of [Reference Disegni9, Lemma 9.2.4], to which we refer for the background on the p-adic Hodge theory of characters.
We have
 $$ \begin{align*} H^{0}\left(E_{w}, V^{?}\right) = {\textbf{D}}_{\mathrm{crys}}\left(V^{?}(\psi)\right)^{\varphi=1}, \end{align*} $$
$$ \begin{align*} H^{0}\left(E_{w}, V^{?}\right) = {\textbf{D}}_{\mathrm{crys}}\left(V^{?}(\psi)\right)^{\varphi=1}, \end{align*} $$
where
![]() $\varphi $
is the crystalline Frobenius, and it suffices to prove that
$\varphi $
is the crystalline Frobenius, and it suffices to prove that
 $ {\mathbf {D}}_{\mathrm{crys}}\left (V^{?}(\psi )\right )^{\varphi ^{d}=1}=0$
for
$ {\mathbf {D}}_{\mathrm{crys}}\left (V^{?}(\psi )\right )^{\varphi ^{d}=1}=0$
for
![]() $d=\left [E_{w}:E_{w, 0}\right ]$
, where
$d=\left [E_{w}:E_{w, 0}\right ]$
, where
![]() $E_{w,0}$
is the maximal unramified extension of
$E_{w,0}$
is the maximal unramified extension of
![]() $\mathbf {Q}_{p}$
contained in
$\mathbf {Q}_{p}$
contained in
![]() $E_{w}$
. As
$E_{w}$
. As
![]() $V'$
has been assumed potentially crystalline, it is pure of weight
$V'$
has been assumed potentially crystalline, it is pure of weight
![]() $-1$
, hence so are all the subquotients of
$-1$
, hence so are all the subquotients of
![]() $V'$
and
$V'$
and
![]() $V^{\prime *}(1)$
. In particular,
$V^{\prime *}(1)$
. In particular,
![]() $\varphi ^{d}$
acts with negative weights on
$\varphi ^{d}$
acts with negative weights on
 ${\mathbf {D}}_{\mathrm{crys}}\left (V^{?}\right )$
for
${\mathbf {D}}_{\mathrm{crys}}\left (V^{?}\right )$
for
![]() $V^{?}=V^{\prime +, *}(1), V^{\prime -}$
; by [Reference Mokrane22, Theorem 5.3], this last assertion is also true of
$V^{?}=V^{\prime +, *}(1), V^{\prime -}$
; by [Reference Mokrane22, Theorem 5.3], this last assertion is also true of
![]() $V^{?}=V\cong V^{*}(1)$
and its subquotients such as
$V^{?}=V\cong V^{*}(1)$
and its subquotients such as
![]() $V^{?}=V^{\prime \prime *}(1)$
. Therefore, it suffices to show that
$V^{?}=V^{\prime \prime *}(1)$
. Therefore, it suffices to show that
![]() $\varphi ^{d}$
acts with weight
$\varphi ^{d}$
acts with weight
![]() $0$
on
$0$
on
![]() $ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
for m such that
$ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
for m such that
![]() $\psi ^{m}$
is crystalline.
$\psi ^{m}$
is crystalline.
Since
![]() $\psi $
is trivial on
$\psi $
is trivial on
![]() $U_{F}^{\circ }$
, the Hodge–Tate weights
$U_{F}^{\circ }$
, the Hodge–Tate weights
 $(n_{\tau })_{\tau \in \mathrm {Hom}\left (E_{w}, \overline {L}\right )}$
satisfy
$(n_{\tau })_{\tau \in \mathrm {Hom}\left (E_{w}, \overline {L}\right )}$
satisfy
![]() $n_{\tau }+n_{\tau c}=0$
, where c is the complex conjugation of
$n_{\tau }+n_{\tau c}=0$
, where c is the complex conjugation of
![]() $E_{w}/F_{v}$
. The action of
$E_{w}/F_{v}$
. The action of
![]() $\varphi ^{d}$
on
$\varphi ^{d}$
on
![]() $ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
is by
$ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
is by
 $$ \begin{align}\begin{aligned} \psi\circ {\mathrm{rec}}_{E, w}(\varpi_{w})^{-m}\cdot \prod_{\tau\in \mathrm{Hom}\left(E_{w}, \overline{L}\right)}\varpi_{w}^{mn_{\tau}},\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \psi\circ {\mathrm{rec}}_{E, w}(\varpi_{w})^{-m}\cdot \prod_{\tau\in \mathrm{Hom}\left(E_{w}, \overline{L}\right)}\varpi_{w}^{mn_{\tau}},\end{aligned}\end{align} $$
where
![]() $\varpi _{w}\in E_{w}$
is any uniformizer. Choose
$\varpi _{w}\in E_{w}$
is any uniformizer. Choose
![]() $\varpi _{w}$
so that
$\varpi _{w}$
so that
 $\varpi _{w}^{e\left (E_{w}/F_{v}\right )}=\varpi _{v}$
is a uniformizer in
$\varpi _{w}^{e\left (E_{w}/F_{v}\right )}=\varpi _{v}$
is a uniformizer in
![]() $F_{v}$
. Then
$F_{v}$
. Then
![]() $\varpi _{w}^{c}=\pm \varpi _{w}$
, so that the second factor in expression (4.4.3) is
$\varpi _{w}^{c}=\pm \varpi _{w}$
, so that the second factor in expression (4.4.3) is
![]() $\pm 1$
. On the other hand, the subgroup
$\pm 1$
. On the other hand, the subgroup
 $F^{\times }\backslash F_{\mathbf {A}^{\infty }}^{\times }/U_{F, v}^{\circ }\left (U^{v}\cap F_{\mathbf {A}^{\infty }}^{\times }\right )\subset \Gamma _{\infty }$
is finite, hence
$F^{\times }\backslash F_{\mathbf {A}^{\infty }}^{\times }/U_{F, v}^{\circ }\left (U^{v}\cap F_{\mathbf {A}^{\infty }}^{\times }\right )\subset \Gamma _{\infty }$
is finite, hence
![]() $\varpi _{v}$
and
$\varpi _{v}$
and
![]() $\varpi _{w}$
have finite order in
$\varpi _{w}$
have finite order in
![]() $\Gamma _{\infty }$
. It follows that the first factor in expression (4.4.3) is a root of unity too, hence
$\Gamma _{\infty }$
. It follows that the first factor in expression (4.4.3) is a root of unity too, hence
![]() $\varphi ^{d}$
acts with weight
$\varphi ^{d}$
acts with weight
![]() $0$
on
$0$
on
![]() $ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
.
$ {\mathbf {D}}_{\mathrm{crys}}(\psi ^{m})$
.
Proof Proof of Proposition 4.4.1
By the long exact sequence attached to
and the vanishing of
![]() $H^{0}\left ({H}_{s,\overline {w}}, V^{\prime *}(1)\right )$
(which follows from Lemma 4.4.2), we have
$H^{0}\left ({H}_{s,\overline {w}}, V^{\prime *}(1)\right )$
(which follows from Lemma 4.4.2), we have
 $$ \begin{align*}\begin{aligned} H^{1}\left({H}_{s,\overline{w}}, T^{\prime\prime*}(1)\right)_{\mathrm{tors}} &\cong H^{0}\left({H}_{s,\overline{w}}, T^{\prime\prime*}(1) \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) \\ &= H^{0}\left(E_{w}, T^{\prime\prime*}(1)\otimes_{\mathscr{O}_{L}} \mathscr{O}_{L}\left[\mathrm{Gal}\left({H}_{s,\overline{w}}/E_{w}\right)\right]\otimes_{\mathscr{O}_{L}} {L'/\mathscr{O}_{L'}} \right). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} H^{1}\left({H}_{s,\overline{w}}, T^{\prime\prime*}(1)\right)_{\mathrm{tors}} &\cong H^{0}\left({H}_{s,\overline{w}}, T^{\prime\prime*}(1) \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) \\ &= H^{0}\left(E_{w}, T^{\prime\prime*}(1)\otimes_{\mathscr{O}_{L}} \mathscr{O}_{L}\left[\mathrm{Gal}\left({H}_{s,\overline{w}}/E_{w}\right)\right]\otimes_{\mathscr{O}_{L}} {L'/\mathscr{O}_{L'}} \right). \end{aligned}\end{align*} $$
By [Reference Nekovář23, Theorems 6.6, 6.9] (or strictly speaking, a slightly generalized form thereof which still holds true by the arguments in [Reference Disegni9, proof of Proposition 4.3.2]) and the vanishing of
![]() $H^{0}\left ({H}_{s,\overline {w}}, V^{\prime +, *}(1)\oplus V^{\prime -}\right )$
(which follows from Lemma 4.4.2), we have
$H^{0}\left ({H}_{s,\overline {w}}, V^{\prime +, *}(1)\oplus V^{\prime -}\right )$
(which follows from Lemma 4.4.2), we have
 $$ \begin{align*}\begin{aligned} d_{2, s}&\leq {\mathrm{length}}_{\mathscr{O}_{L'}} H^{0} \left({H}_{s,\overline{w}}, T^{\prime+,*}(1) \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) + {\mathrm{length}}_{\mathscr{O}_{L'}} H^{0} \left({H}_{s,\overline{w}}, T^{\prime-} \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) \\ &={\mathrm{length}}_{\mathscr{O}_{L'}} H^{0}\left(E_{w},\left(T^{\prime+,*}(1) \oplus T^{\prime-}\right) \otimes_{\mathscr{O}_{L}} \mathscr{O}_{L}\left[\mathrm{Gal}\left({H}_{s,\overline{w}}/E_{w}\right)\right]\otimes_{\mathscr{O}_{L}} {L'/\mathscr{O}_{L'}} \right). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} d_{2, s}&\leq {\mathrm{length}}_{\mathscr{O}_{L'}} H^{0} \left({H}_{s,\overline{w}}, T^{\prime+,*}(1) \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) + {\mathrm{length}}_{\mathscr{O}_{L'}} H^{0} \left({H}_{s,\overline{w}}, T^{\prime-} \otimes_{\mathscr{O}_{L'}} L'/\mathscr{O}_{L'}\right) \\ &={\mathrm{length}}_{\mathscr{O}_{L'}} H^{0}\left(E_{w},\left(T^{\prime+,*}(1) \oplus T^{\prime-}\right) \otimes_{\mathscr{O}_{L}} \mathscr{O}_{L}\left[\mathrm{Gal}\left({H}_{s,\overline{w}}/E_{w}\right)\right]\otimes_{\mathscr{O}_{L}} {L'/\mathscr{O}_{L'}} \right). \end{aligned}\end{align*} $$
Then the boundedness of
![]() $d_{1,s}$
and
$d_{1,s}$
and
![]() $d_{2,s}$
follows as in [Reference Shnidman27, proof of Proposition 8.10] from the vanishing of
$d_{2,s}$
follows as in [Reference Shnidman27, proof of Proposition 8.10] from the vanishing of
 $$ \begin{align*} H^{0}\left(H_{\infty, \overline{w}}, V^{?}\right) \subset \bigoplus_{\psi\colon \Gamma_{\infty}\to \overline{L}^{\times} \text{ Hodge--Tate}} H^{0}\left(E_{w}, V^{?}(\psi)\right) \end{align*} $$
$$ \begin{align*} H^{0}\left(H_{\infty, \overline{w}}, V^{?}\right) \subset \bigoplus_{\psi\colon \Gamma_{\infty}\to \overline{L}^{\times} \text{ Hodge--Tate}} H^{0}\left(E_{w}, V^{?}(\psi)\right) \end{align*} $$
for
![]() $V^{?}\in \left \{ V^{\prime \prime *}(1),V^{\prime +,*}(1), V'\right \}$
, which is a consequence of Lemma 4.4.2.□
$V^{?}\in \left \{ V^{\prime \prime *}(1),V^{\prime +,*}(1), V'\right \}$
, which is a consequence of Lemma 4.4.2.□
Completion of the proofs
We are ready to reduce our decay statement for local heights to the decay statement for intersection multiplicities proved in §4.3.
Lemma 4.4.3. For all
![]() $s'\leq s$
, the restriction of the
$s'\leq s$
, the restriction of the
![]() $\overline {w}$
-adic valuation yields an isomorphism of
$\overline {w}$
-adic valuation yields an isomorphism of
![]() $\mathscr {O}_{L'}$
-modules
$\mathscr {O}_{L'}$
-modules
 $$ \begin{align*} \overline{w}\colon N_{s}\left(H_{s, \overline{w}}^{\times}\hat{\otimes}\mathscr{O}_{L'}\right) / q^{s'}\cdot\left( H_{0, \overline{w}}^{\times}\hat{\otimes}\mathscr{O}_{L'}\right) \to \mathscr{O}_{L'}/q^{s'}\mathscr{O}_{L'}. \end{align*} $$
$$ \begin{align*} \overline{w}\colon N_{s}\left(H_{s, \overline{w}}^{\times}\hat{\otimes}\mathscr{O}_{L'}\right) / q^{s'}\cdot\left( H_{0, \overline{w}}^{\times}\hat{\otimes}\mathscr{O}_{L'}\right) \to \mathscr{O}_{L'}/q^{s'}\mathscr{O}_{L'}. \end{align*} $$
Proof. We drop all subscripts
![]() $\overline {w}$
. Recall that the extension
$\overline {w}$
. Recall that the extension
![]() $H_{s}/H_{0}$
is totally ramified of degree
$H_{s}/H_{0}$
is totally ramified of degree
![]() $q^{s}$
. Let
$q^{s}$
. Let
![]() $\varpi _{s}\in \mathscr {O}_{H_{s}}$
be a uniformizer; then
$\varpi _{s}\in \mathscr {O}_{H_{s}}$
be a uniformizer; then
![]() $\omega _{0}:=N_{s}(\varpi _{s})$
is a uniformizer of
$\omega _{0}:=N_{s}(\varpi _{s})$
is a uniformizer of
![]() $H_{0} $
. For
$H_{0} $
. For
![]() $*=0,s$
we have the decompositions
$*=0,s$
we have the decompositions
 $$ \begin{align*} H_{*}^{\times}\hat{\otimes} \mathscr{O}_{L'} =\mathscr{O}_{H_{*}}^{\times}\hat{\otimes}\mathscr{O}_{L' }\oplus \varpi_{*}\otimes\mathscr{O}_{L'}. \end{align*} $$
$$ \begin{align*} H_{*}^{\times}\hat{\otimes} \mathscr{O}_{L'} =\mathscr{O}_{H_{*}}^{\times}\hat{\otimes}\mathscr{O}_{L' }\oplus \varpi_{*}\otimes\mathscr{O}_{L'}. \end{align*} $$
The map
![]() $N_{s}$
respects the decompositions and, by local class field theory, has image
$N_{s}$
respects the decompositions and, by local class field theory, has image
 $$ \begin{align*} q^{s}\cdot\left(\mathscr{O}_{H_{0}}^{\times}\hat{\otimes}\mathscr{O}_{ L'}\right) \oplus \varpi_{0}\otimes\mathscr{O}_{L'}. \end{align*} $$
$$ \begin{align*} q^{s}\cdot\left(\mathscr{O}_{H_{0}}^{\times}\hat{\otimes}\mathscr{O}_{ L'}\right) \oplus \varpi_{0}\otimes\mathscr{O}_{L'}. \end{align*} $$
The valuation map annihilates the first summand and sends the second one isomorphically to
![]() $\mathscr {O}_{L'}$
. The result follows.
$\mathscr {O}_{L'}$
. The result follows.
Proof Proof of Proposition 3.6.3
By the comparison of the valuation component of local heights with arithmetic intersections in [Reference Disegni9, Proposition 4.3.1], applied to the curve
![]() $X_{U,H_{0}}$
, the image of the left-hand side of equation (4.4.2) under
$X_{U,H_{0}}$
, the image of the left-hand side of equation (4.4.2) under
![]() $\overline {w}$
is
$\overline {w}$
is
 $$ \begin{align}\begin{aligned} m\left( \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})_{U}[1], {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} m\left( \widetilde{Z}_{a\varpi^{s}}(\phi^{\infty})_{U}[1], {\mathrm{T}}_{\iota_{\mathfrak{p}}}(\sigma^{\vee})_{U}^{\mathrm{t}} t_{\chi}\right). \end{aligned}\end{align} $$
By Corollary 4.3.4 applied to
![]() $D= {\mathrm{T}}_{\iota _{\mathfrak {p}}}(\sigma ^{\vee })_{U}^{\mathrm{t}} t_{\chi }$
, the right-hand side of expression (4.4.4) is
$D= {\mathrm{T}}_{\iota _{\mathfrak {p}}}(\sigma ^{\vee })_{U}^{\mathrm{t}} t_{\chi }$
, the right-hand side of expression (4.4.4) is
 $O\left (q_{F,v}^{s}\right )$
. By equation (4.4.2), Proposition 4.4.1, and Lemma 4.4.3, we deduce the desired decay statement (4.4.1).
$O\left (q_{F,v}^{s}\right )$
. By equation (4.4.2), Proposition 4.4.1, and Lemma 4.4.3, we deduce the desired decay statement (4.4.1).
Appendix A Local integrals
Throughout this appendix, v denotes a place of F above p unless specified otherwise. We use some of the notation introduced in §3.1, in particular the Weil representation r (see [Reference Disegni9, §3.1] or [Reference Yuan, Zhang and Zhang29] for the formulas defining it).
A.1 Interpolation factors
We relate the interpolation factors of the p-adic L-function of this paper with those from [Reference Disegni9].
Lemma A.1.1. Let
![]() $\xi \colon E_{w}^{\times }\to \mathbf {C}^{\times }$
and
$\xi \colon E_{w}^{\times }\to \mathbf {C}^{\times }$
and
![]() $\psi \colon E_{w} \to \mathbf {C}^{\times }$
be characters, with
$\psi \colon E_{w} \to \mathbf {C}^{\times }$
be characters, with
![]() $\psi \neq \mathbf {1}$
. Let
$\psi \neq \mathbf {1}$
. Let
![]() $dt$
be a Haar measure on
$dt$
be a Haar measure on
![]() $E_{w}^{\times }$
. Then
$E_{w}^{\times }$
. Then
 $$ \begin{align*} \int_{E_{w}^{\times}} \xi(t) \psi(t) dt={d^{}t \over d^{}_{\psi}t} \cdot \xi(-1)\cdot \gamma(\xi, \psi)^{-1}. \end{align*} $$
$$ \begin{align*} \int_{E_{w}^{\times}} \xi(t) \psi(t) dt={d^{}t \over d^{}_{\psi}t} \cdot \xi(-1)\cdot \gamma(\xi, \psi)^{-1}. \end{align*} $$
The left-hand side is to be understood in the sense of analytic continuation from characters
![]() $\xi \lvert \cdot \rvert ^{s}$
for
$\xi \lvert \cdot \rvert ^{s}$
for
![]() $\Re (s)\gg 0 $
.
$\Re (s)\gg 0 $
.
Proof. We may fix
![]() $d^{}t= d^{}_{\psi }t$
. Then the result follows from the functional equation for
$d^{}t= d^{}_{\psi }t$
. Then the result follows from the functional equation for
![]() $\mathrm {GL}_{1}$
[Reference Bushnell and Henniart3, (23.4.4)]:
$\mathrm {GL}_{1}$
[Reference Bushnell and Henniart3, (23.4.4)]:
 $$ \begin{align} Z(\phi, \xi) = \gamma(\xi, \psi)^{-1} Z\left(\hat{\phi}, \xi^{-1}\lvert\ \rvert\right), \end{align} $$
$$ \begin{align} Z(\phi, \xi) = \gamma(\xi, \psi)^{-1} Z\left(\hat{\phi}, \xi^{-1}\lvert\ \rvert\right), \end{align} $$
where for a Schwartz function
![]() $\phi $
on
$\phi $
on
![]() $E_{w}$
,
$E_{w}$
,
 $$ \begin{align*} Z( \phi, \xi) := \int_{E_{w}^{\times}} \phi(t) \xi(t) d_{\psi}^{}t , \qquad \hat{\phi}(t):= \int_{E_{w}}\phi(x) \psi(xt) d_{\psi}x. \end{align*} $$
$$ \begin{align*} Z( \phi, \xi) := \int_{E_{w}^{\times}} \phi(t) \xi(t) d_{\psi}^{}t , \qquad \hat{\phi}(t):= \int_{E_{w}}\phi(x) \psi(xt) d_{\psi}x. \end{align*} $$
Namely, we insert in equation (A.1.1) the function
 $$ \begin{align*} \hat{\phi}:=\delta_{-1+\varpi_{v}^{n}\mathscr{O}_{F}}:= \mathrm{vol}\left(1+{\varpi}_{v}^{n}\mathscr{O}_{F, v}, d_{\psi }t\right)^{-1}\mathbf{1}_{-1+{\varpi_{v}}^{n}\mathscr{O}_{F, v}}, \quad n\geq 1, \end{align*} $$
$$ \begin{align*} \hat{\phi}:=\delta_{-1+\varpi_{v}^{n}\mathscr{O}_{F}}:= \mathrm{vol}\left(1+{\varpi}_{v}^{n}\mathscr{O}_{F, v}, d_{\psi }t\right)^{-1}\mathbf{1}_{-1+{\varpi_{v}}^{n}\mathscr{O}_{F, v}}, \quad n\geq 1, \end{align*} $$
approximating a delta function at
![]() $t=-1$
. Then by Fourier inversion,
$t=-1$
. Then by Fourier inversion,
 $\phi (t)=\hat {\hat {\phi }}(-t) = \delta _{1+\varpi _{v}^{n}\mathscr {O}_{F}}*\psi (t) $
, which if n is sufficiently large (depending on the conductor of
$\phi (t)=\hat {\hat {\phi }}(-t) = \delta _{1+\varpi _{v}^{n}\mathscr {O}_{F}}*\psi (t) $
, which if n is sufficiently large (depending on the conductor of
![]() $\xi $
) has the same integral against
$\xi $
) has the same integral against
![]() $\xi $
as
$\xi $
as
![]() $\psi (t)$
.
$\psi (t)$
.
Proposition A.1.2. The ratio
 $C\left (\chi _{p}'\right ) $
defined in formula (2.1.3) is a constant
$C\left (\chi _{p}'\right ) $
defined in formula (2.1.3) is a constant
![]() $C\in L$
independent of
$C\in L$
independent of
![]() $\chi ^{\prime }_{p}$
.
$\chi ^{\prime }_{p}$
.
Proof. By the definition of
 $e_{p}\left (V_{\left (A,\chi '\right )}\right )$
and a comparison of [Reference Disegni9, Lemma A.1.1] with Lemma A.1.1 applied to
$e_{p}\left (V_{\left (A,\chi '\right )}\right )$
and a comparison of [Reference Disegni9, Lemma A.1.1] with Lemma A.1.1 applied to
 $\prod _{w\mid v}\chi ^{\prime }_{w}\alpha _{v}\lvert \cdot \rvert _{v}\circ q_{w}$
, we have
$\prod _{w\mid v}\chi ^{\prime }_{w}\alpha _{v}\lvert \cdot \rvert _{v}\circ q_{w}$
, we have
 $$ \begin{align*} C\left(\chi_{p}'\right)= \prod_{v\mid p } \gamma \left(\mathrm{ad}\left(W_{v}(1)^{++}\right), \psi_{v}\right)^{-1}\in L. \end{align*} $$
$$ \begin{align*} C\left(\chi_{p}'\right)= \prod_{v\mid p } \gamma \left(\mathrm{ad}\left(W_{v}(1)^{++}\right), \psi_{v}\right)^{-1}\in L. \end{align*} $$
A.2 Toric period at p
We compare the toric period at a p-adic place with the interpolation factor. Denote by
![]() $P_{v} \subset \mathrm {GL}_{2}(F_{v})$
the upper triangular Borel subgroup.
$P_{v} \subset \mathrm {GL}_{2}(F_{v})$
the upper triangular Borel subgroup.
Lemma A.2.1. The quotient space
 $K_{1}^{1}(\varpi ^{r'})\backslash \mathrm {GL}_{2}({F_{v}}) /P_{v}$
admits the set of representatives
$K_{1}^{1}(\varpi ^{r'})\backslash \mathrm {GL}_{2}({F_{v}}) /P_{v}$
admits the set of representatives
 $$ \begin{align*} n^{-}(c):=\begin{cases} \left(\begin{smallmatrix}1&\\c&1\end{smallmatrix}\right)& \text{if } c\neq \infty,\\ \left(\begin{smallmatrix}&1\\-1& \end{smallmatrix}\right){} & \text{if } c=\infty, \end{cases} \qquad c\in \mathscr{O}_{F, v}/\varpi^{r'}\mathscr{O}_{F,v}\cup \{\infty\}. \end{align*} $$
$$ \begin{align*} n^{-}(c):=\begin{cases} \left(\begin{smallmatrix}1&\\c&1\end{smallmatrix}\right)& \text{if } c\neq \infty,\\ \left(\begin{smallmatrix}&1\\-1& \end{smallmatrix}\right){} & \text{if } c=\infty, \end{cases} \qquad c\in \mathscr{O}_{F, v}/\varpi^{r'}\mathscr{O}_{F,v}\cup \{\infty\}. \end{align*} $$
Proposition A.2.2. Let
![]() $\chi \in \mathscr {Y}^{\mathrm{l.c.}}$
be a finite-order character, let r be sufficiently large (that is, satisfying the v-component of Assumption 3.4.2), let
$\chi \in \mathscr {Y}^{\mathrm{l.c.}}$
be a finite-order character, let r be sufficiently large (that is, satisfying the v-component of Assumption 3.4.2), let
![]() $W_{v}$
be as in formula (3.1.1), and let
$W_{v}$
be as in formula (3.1.1), and let
![]() $\phi _{v}=\phi _{v,r}$
be as in formula (3.1.4).
$\phi _{v}=\phi _{v,r}$
be as in formula (3.1.4).
Let
![]() $\pi _{v}=\sigma _{v}$
and let
$\pi _{v}=\sigma _{v}$
and let
![]() $(\ ,\ )_{v}\colon \pi _{v}\times \pi _{v}^{\vee }\to L$
be a duality pairing satisfying the compatibility of [Reference Disegni9, (5.1.2)] with the local Shimizu lift.Footnote
10
Finally, let
$(\ ,\ )_{v}\colon \pi _{v}\times \pi _{v}^{\vee }\to L$
be a duality pairing satisfying the compatibility of [Reference Disegni9, (5.1.2)] with the local Shimizu lift.Footnote
10
Finally, let
![]() $Z^{\circ }_{v}(\alpha _{v}, \chi _{v})$
be the interpolation factor of the p-adic L-function of [Reference Disegni9, Theorem A].
$Z^{\circ }_{v}(\alpha _{v}, \chi _{v})$
be the interpolation factor of the p-adic L-function of [Reference Disegni9, Theorem A].
Then for all sufficiently large
![]() $r'>r$
,
$r'>r$
,
 $$ \begin{align*} Q_{(, ), v, d^{\circ}t_{v}}\left(\theta_{v}\left(W_{v}, \alpha\lvert\cdot\rvert_{v}(\varpi_{v})^{-r^{\prime}_{v}} w_{r',v}^{-1}\phi_{v}\right),\chi_{v}\right) = \lvert d\rvert^{2}_{v}\lvert D\rvert_{v}\cdot L(1, \eta_{v})^{-1}\cdot Z^{\circ}_{v}(\alpha_{v}, \chi_{v}), \end{align*} $$
$$ \begin{align*} Q_{(, ), v, d^{\circ}t_{v}}\left(\theta_{v}\left(W_{v}, \alpha\lvert\cdot\rvert_{v}(\varpi_{v})^{-r^{\prime}_{v}} w_{r',v}^{-1}\phi_{v}\right),\chi_{v}\right) = \lvert d\rvert^{2}_{v}\lvert D\rvert_{v}\cdot L(1, \eta_{v})^{-1}\cdot Z^{\circ}_{v}(\alpha_{v}, \chi_{v}), \end{align*} $$
where
![]() $Q_{(, ), v, d^{\circ }t_{v}}$
uses the measure
$Q_{(, ), v, d^{\circ }t_{v}}$
uses the measure
 $d^{\circ }t_{v}= \lvert d\rvert ^{-1/2}_{v}\lvert D\rvert _{v}^{-1/2}dt$
.
$d^{\circ }t_{v}= \lvert d\rvert ^{-1/2}_{v}\lvert D\rvert _{v}^{-1/2}dt$
.
Proof. We drop all subscripts v, and assume as usual that
![]() $\psi $
is our fixed character of level
$\psi $
is our fixed character of level
![]() $d^{-1}$
. Let
$d^{-1}$
. Let
 $$ \begin{align} Q_{(, )}^{\sharp}(f_{1}, f_{2}, \chi_{v})= \int_{E^{\times}/F^{\times}} \chi(t) (\pi(t)f_{1}, f_{2})\, {dt}, \end{align} $$
$$ \begin{align} Q_{(, )}^{\sharp}(f_{1}, f_{2}, \chi_{v})= \int_{E^{\times}/F^{\times}} \chi(t) (\pi(t)f_{1}, f_{2})\, {dt}, \end{align} $$
where
![]() $dt$
is the usual Haar measure on
$dt$
is the usual Haar measure on
![]() $E^{\times }/F^{\times }$
, giving volume
$E^{\times }/F^{\times }$
, giving volume
![]() $\lvert d\rvert ^{1/2}\lvert D\rvert ^{1/2}$
to
$\lvert d\rvert ^{1/2}\lvert D\rvert ^{1/2}$
to
![]() $\mathscr {O}_{E}^{\times }/\mathscr {O}_{F}^{\times }$
.
$\mathscr {O}_{E}^{\times }/\mathscr {O}_{F}^{\times }$
.
By the definitions and [Reference Disegni9, Lemma A.1.1] (which expresses
![]() $Z^{\circ }$
as a normalized integral), it suffices to show that
$Z^{\circ }$
as a normalized integral), it suffices to show that
 $$ \begin{align*} Q^{\sharp}\left(\theta\left(W_{}, \alpha\lvert\cdot\rvert(\varpi)^{-r'} w_{r'}^{-1}\phi\right),\chi\right) = \lvert d\rvert^{3/2}\lvert D\rvert \cdot L(1, \eta_{})^{-1}\cdot \int_{E_{}^{\times}} \alpha|\cdot |\circ q(t) \chi(t)\psi_{E}(t) \, dt. \end{align*} $$
$$ \begin{align*} Q^{\sharp}\left(\theta\left(W_{}, \alpha\lvert\cdot\rvert(\varpi)^{-r'} w_{r'}^{-1}\phi\right),\chi\right) = \lvert d\rvert^{3/2}\lvert D\rvert \cdot L(1, \eta_{})^{-1}\cdot \int_{E_{}^{\times}} \alpha|\cdot |\circ q(t) \chi(t)\psi_{E}(t) \, dt. \end{align*} $$
By [Reference Disegni9, Lemma 5.1.1] (which spells out a consequence of the normalization of the local Shimizu lifting) and Lemma A.2.1, we can write
 $$ \begin{align*} Q^{\sharp}:= Q\left(\theta\left(W, \alpha\lvert\cdot\rvert(\varpi)^{-r'} w_{r'}^{-1}\phi_{r}\right),\chi_{v}\right)= \sum_{c\in{\textbf{P}}^{1}\left( \mathscr{O}_{F}/\varpi^{r'} \right)} Q^{\sharp (c)}, \end{align*} $$
$$ \begin{align*} Q^{\sharp}:= Q\left(\theta\left(W, \alpha\lvert\cdot\rvert(\varpi)^{-r'} w_{r'}^{-1}\phi_{r}\right),\chi_{v}\right)= \sum_{c\in{\textbf{P}}^{1}\left( \mathscr{O}_{F}/\varpi^{r'} \right)} Q^{\sharp (c)}, \end{align*} $$
where for each c,
 $$ \begin{align*} &Q^{\sharp (c)}:=\lvert d\rvert^{-3/2}\cdot\alpha\lvert\ \rvert(\varpi)^{-r}\int_{F^{\times}} W\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right) n^{-}(c)\right)\\ &\qquad\qquad\qquad\qquad \int_{T(F)}\chi(t) \int_{P\left(\varpi^{r'}\right)\backslash K_{1}^{1}\left(\varpi^{r'}\right)} \lvert y\rvert r\left( n^{-}(c) kw_{r}^{-1}\right)\phi\left(yt^{-1}, y^{-1}q(t)\right) dk dt {d^{\times }y\over \lvert y\rvert}. \end{align*} $$
$$ \begin{align*} &Q^{\sharp (c)}:=\lvert d\rvert^{-3/2}\cdot\alpha\lvert\ \rvert(\varpi)^{-r}\int_{F^{\times}} W\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right) n^{-}(c)\right)\\ &\qquad\qquad\qquad\qquad \int_{T(F)}\chi(t) \int_{P\left(\varpi^{r'}\right)\backslash K_{1}^{1}\left(\varpi^{r'}\right)} \lvert y\rvert r\left( n^{-}(c) kw_{r}^{-1}\right)\phi\left(yt^{-1}, y^{-1}q(t)\right) dk dt {d^{\times }y\over \lvert y\rvert}. \end{align*} $$
Here
 $P(\varpi ^{r'}) =P \cap K_{1}^{1}(\varpi ^{r'} )$
.
$P(\varpi ^{r'}) =P \cap K_{1}^{1}(\varpi ^{r'} )$
.
It is easy to see that
![]() $Q^{\sharp (\infty )}=0$
(observe that
$Q^{\sharp (\infty )}=0$
(observe that
![]() $\phi _{2,r}(0)=0$
). For
$\phi _{2,r}(0)=0$
). For
![]() $c\neq \infty $
, we have
$c\neq \infty $
, we have
 $$ \begin{align*} n^{-}(c) w_{r'}^{-1 } = w_{r'}^{-1} \left(\begin{array}{cc}1& -c\varpi^{-r'}\\ {}& {1} \end{array}\right), \end{align*} $$
$$ \begin{align*} n^{-}(c) w_{r'}^{-1 } = w_{r'}^{-1} \left(\begin{array}{cc}1& -c\varpi^{-r'}\\ {}& {1} \end{array}\right), \end{align*} $$
and when
![]() $x=(x_{1}, x_{2})$
with
$x=(x_{1}, x_{2})$
with
![]() $x_{2}=0$
,
$x_{2}=0$
,
 $$ \begin{align*} r\left(n^{-}(c )w_{r'}^{-1}\right)\phi(x,u)&= \int_{\textbf{V}} \psi_{E} (u x_{1}\xi_{1}) \psi(-uc q(\xi)) \phi_{r}\left(\xi, \varpi^{r'}u\right) d \xi. \end{align*} $$
$$ \begin{align*} r\left(n^{-}(c )w_{r'}^{-1}\right)\phi(x,u)&= \int_{\textbf{V}} \psi_{E} (u x_{1}\xi_{1}) \psi(-uc q(\xi)) \phi_{r}\left(\xi, \varpi^{r'}u\right) d \xi. \end{align*} $$
On the support of the integrand, we have
 $v(u)=\varpi ^{-r'}$
and
$v(u)=\varpi ^{-r'}$
and
![]() $v(q(\xi ))\geq r$
, by the definition of
$v(q(\xi ))\geq r$
, by the definition of
![]() $\phi _{r}$
. If
$\phi _{r}$
. If
![]() $v(c)< r'-r-v(d)$
, the integration in
$v(c)< r'-r-v(d)$
, the integration in
![]() $d\xi _{2}$
gives
$d\xi _{2}$
gives
![]() $0$
; hence
$0$
; hence
![]() $Q^{\sharp (c)}=0$
in that case.
$Q^{\sharp (c)}=0$
in that case.
Suppose from now on that
![]() $v(c)\geq r'-r-v(d)$
. Then
$v(c)\geq r'-r-v(d)$
. Then
![]() $\psi (-ucq(\xi ))=1$
and
$\psi (-ucq(\xi ))=1$
and
 $$ \begin{align*} r\left(n^{-}(c )w_{r'}^{-1}\right)\phi(x,u) = \lvert d\rvert^{3}\lvert D\rvert L(1, \eta)^{-1} \lvert\varpi\rvert^{r}\psi_{E, r}\left(\varpi^{-r'}x_{1}\right) \delta_{1,U_{F},r}(\varpi^{r}u), \end{align*} $$
$$ \begin{align*} r\left(n^{-}(c )w_{r'}^{-1}\right)\phi(x,u) = \lvert d\rvert^{3}\lvert D\rvert L(1, \eta)^{-1} \lvert\varpi\rvert^{r}\psi_{E, r}\left(\varpi^{-r'}x_{1}\right) \delta_{1,U_{F},r}(\varpi^{r}u), \end{align*} $$
where
![]() $\psi _{E,r}:=\mathrm {vol}(\mathscr {O}_{E})^{-1}\cdot \delta _{1,U_{T,r}}*\psi _{E}$
, and we have noted that
$\psi _{E,r}:=\mathrm {vol}(\mathscr {O}_{E})^{-1}\cdot \delta _{1,U_{T,r}}*\psi _{E}$
, and we have noted that
 $\hat \phi _{2, r}(0)= e^{-1}\lvert d\rvert \cdot \mathrm {vol}\left (q^{-1}(-1+ \varpi ^{r}\mathscr {O}_{F})\cap \mathscr {O}_{{\mathbf {V}}_{2}}\right )=\lvert \varpi \rvert ^{r} \lvert d\rvert ^{3}\lvert D\rvert ^{1/2} L(1, \eta )^{-1}$
.
$\hat \phi _{2, r}(0)= e^{-1}\lvert d\rvert \cdot \mathrm {vol}\left (q^{-1}(-1+ \varpi ^{r}\mathscr {O}_{F})\cap \mathscr {O}_{{\mathbf {V}}_{2}}\right )=\lvert \varpi \rvert ^{r} \lvert d\rvert ^{3}\lvert D\rvert ^{1/2} L(1, \eta )^{-1}$
.
If
![]() $r'$
is sufficiently large, the Whittaker function W is invariant under
$r'$
is sufficiently large, the Whittaker function W is invariant under
![]() $n^{-}(c)$
. Then
$n^{-}(c)$
. Then
 $$ \begin{align*} &Q^{\sharp (c)}= \lvert d\rvert^{3/2}\lvert D\rvert L(1, \eta)^{-1}\cdot \ lvert\varpi\rvert^{r-r'} \alpha(\varpi)^{-r'} \cdot \lvert d\rvert ^{1/2}\zeta_{F,v}(1)^{-1} \\ &\qquad\qquad\qquad\qquad\cdot \int_{F^{\times}} W\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right)\right) \int_{T(F)}\chi( t) \psi_{E, r}\left(\varpi^{-r'}x_{1}\right) \delta_{1,U_{F,r}}\left(\varpi^{r'}y^{-1}q(t)\right) dt d^{\times}y, \end{align*} $$
$$ \begin{align*} &Q^{\sharp (c)}= \lvert d\rvert^{3/2}\lvert D\rvert L(1, \eta)^{-1}\cdot \ lvert\varpi\rvert^{r-r'} \alpha(\varpi)^{-r'} \cdot \lvert d\rvert ^{1/2}\zeta_{F,v}(1)^{-1} \\ &\qquad\qquad\qquad\qquad\cdot \int_{F^{\times}} W\left(\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right)\right) \int_{T(F)}\chi( t) \psi_{E, r}\left(\varpi^{-r'}x_{1}\right) \delta_{1,U_{F,r}}\left(\varpi^{r'}y^{-1}q(t)\right) dt d^{\times}y, \end{align*} $$
where
 $\lvert \varpi \rvert ^{-r'}\lvert d\rvert ^{1/2}\zeta _{F,v}(1)^{-1}$
appears as
$\lvert \varpi \rvert ^{-r'}\lvert d\rvert ^{1/2}\zeta _{F,v}(1)^{-1}$
appears as
 $ \mathrm {vol}(P(\varpi ^{r'} )\backslash K_{1}^{1}(\varpi ^{r'} ))$
.
$ \mathrm {vol}(P(\varpi ^{r'} )\backslash K_{1}^{1}(\varpi ^{r'} ))$
.
Integrating in
![]() $d^{\times }y$
and summing the foregoing over the
$d^{\times }y$
and summing the foregoing over the
 $q_{F}^{r+v(d)}=\lvert d\rvert ^{-1}\lvert \varpi \rvert ^{-r}$
contributing values of c, we find
$q_{F}^{r+v(d)}=\lvert d\rvert ^{-1}\lvert \varpi \rvert ^{-r}$
contributing values of c, we find
 $$ \begin{align*} Q^{\sharp}= \lvert d\rvert^{3/2}\lvert D\rvert \cdot L(1, \eta)^{-1}\cdot \int_{E^{\times}}\chi(t)\alpha\lvert\ \rvert\circ q(t) \psi_{E}(t) dt, \end{align*} $$
$$ \begin{align*} Q^{\sharp}= \lvert d\rvert^{3/2}\lvert D\rvert \cdot L(1, \eta)^{-1}\cdot \int_{E^{\times}}\chi(t)\alpha\lvert\ \rvert\circ q(t) \psi_{E}(t) dt, \end{align*} $$
as desired.
Corollary A.2.3. If
![]() $\chi _{p}$
is not exceptional – that is,
$\chi _{p}$
is not exceptional – that is,
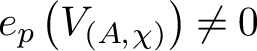 $e_{p}\left (V_{\left (A, \chi \right )}\right )\neq 0$
– then the quaternion algebra
$e_{p}\left (V_{\left (A, \chi \right )}\right )\neq 0$
– then the quaternion algebra
![]() ${\mathbf {B}}$
over
${\mathbf {B}}$
over
![]() $\mathbf {A}$
satisfying
$\mathbf {A}$
satisfying
![]() $ \mathrm {H}(\pi _{ \mathbf {B}},\chi )\neq 0$
is indefinite at all primes
$ \mathrm {H}(\pi _{ \mathbf {B}},\chi )\neq 0$
is indefinite at all primes
![]() $v\mid p$
.
$v\mid p$
.
Proof. By Propositions A.2.2 and A.1.2, if
![]() $\chi _{p}$
is not exceptional, then for all
$\chi _{p}$
is not exceptional, then for all
![]() $v\mid p$
the functional
$v\mid p$
the functional
 $Q_{v}\in \mathrm {H}\left (\pi _{M_{2}\left (F_{v}\right )}, \chi _{v}\right )\otimes \mathrm {H}\left (\pi _{M_{2}\left (F_{v}\right )}^{\vee }, \chi _{v}^{-1}\right )$
is not identically zero.
$Q_{v}\in \mathrm {H}\left (\pi _{M_{2}\left (F_{v}\right )}, \chi _{v}\right )\otimes \mathrm {H}\left (\pi _{M_{2}\left (F_{v}\right )}^{\vee }, \chi _{v}^{-1}\right )$
is not identically zero.
Appendix B Errata to [Reference Disegni9]
The salient mistakes are the following: the statement of the main theorem is off by a factor of
![]() $2$
; the proof given needs a further assumption, (no stronger than) that
$2$
; the proof given needs a further assumption, (no stronger than) that
![]() $V_{\mathfrak {p}}A$
is potentially crystalline at all
$V_{\mathfrak {p}}A$
is potentially crystalline at all
![]() $v\mid p$
(however, the theorem still holds true without the assumption; compare Remark 1.2.1); and the Schwartz function
$v\mid p$
(however, the theorem still holds true without the assumption; compare Remark 1.2.1); and the Schwartz function
![]() $\phi _{2, p} $
given by the local Siegel–Weil formula at p needs to be different from the Schwartz function used to construct the Eisenstein family.
$\phi _{2, p} $
given by the local Siegel–Weil formula at p needs to be different from the Schwartz function used to construct the Eisenstein family.
References in italics are directed to [Reference Disegni9], and references in roman letters to the present paper.
-
– Theorem A. It should be
 $L_{p, \alpha }(\sigma _{E})\in \mathscr {O}(\mathscr {Y}')^{\mathrm{b}}$
(with the interpolation property being correct for the choice of additive character
$L_{p, \alpha }(\sigma _{E})\in \mathscr {O}(\mathscr {Y}')^{\mathrm{b}}$
(with the interpolation property being correct for the choice of additive character
 $\psi _{p}$
as in Theorem A). For a correct discussion of the ring of rationality of
$\psi _{p}$
as in Theorem A). For a correct discussion of the ring of rationality of
 $L_{p, \alpha }(\sigma _{E})$
, within the context of a generalized construction, see [Reference Disegni12, Corollary 4.5.4].
$L_{p, \alpha }(\sigma _{E})$
, within the context of a generalized construction, see [Reference Disegni12, Corollary 4.5.4]. -
– Theorem B. The constant factor should be
 $c_{E}$
and not
$c_{E}$
and not
 $c_{E}/2$
(the latter is, according to (1.1.3), the constant factor of the Gross–Zagier formula in Archimedean coefficients).Footnote
11
The mistake is introduced in the proof of Proposition 5.4.3 (see later).
$c_{E}/2$
(the latter is, according to (1.1.3), the constant factor of the Gross–Zagier formula in Archimedean coefficients).Footnote
11
The mistake is introduced in the proof of Proposition 5.4.3 (see later).The proof works under the further assumption that
 $V_{\mathfrak {p}}A$
is potentially crystalline at all
$V_{\mathfrak {p}}A$
is potentially crystalline at all
 $v\mid p$
(see the correction to Proposition 9.2.1).
$v\mid p$
(see the correction to Proposition 9.2.1). -
– Theorem C. Similarly, the constant factor should be
 $c_{E}/2$
in part 3, and
$c_{E}/2$
in part 3, and
 $c_{E}$
in part 4.
$c_{E}$
in part 4. -
– §2.1. The space of p-adic modular forms is the closure of
 $M_{2}\left (K^{p}K_{1}^{1}(p^{\infty })_{p}\right )$
, not
$M_{2}\left (K^{p}K_{1}^{1}(p^{\infty })_{p}\right )$
, not
 $M_{2}\left (K^{p}K^{1}(p^{\infty })_{p}\right )$
.
$M_{2}\left (K^{p}K^{1}(p^{\infty })_{p}\right )$
. -
– Proposition 2.4.4.1. The multiplier in equation (2.4.3) should be
 $\alpha \lvert \cdot \rvert (\varpi ^{-r})=\prod _{v\mid p } \alpha _{v}\lvert \cdot \vert _{v}\left (\varpi _{v}^{-r}\right )$
, and the statement holds for forms in
$\alpha \lvert \cdot \rvert (\varpi ^{-r})=\prod _{v\mid p } \alpha _{v}\lvert \cdot \vert _{v}\left (\varpi _{v}^{-r}\right )$
, and the statement holds for forms in
 $M_{2}\left (K^{p}K_{1}^{1}(p^{r})_{p}\right )$
. Similarly, the definition of
$M_{2}\left (K^{p}K_{1}^{1}(p^{r})_{p}\right )$
. Similarly, the definition of
 $R_{r,v}^{\circ }$
in Proposition 3.5.1 should have an extra
$R_{r,v}^{\circ }$
in Proposition 3.5.1 should have an extra
 $\lvert \varpi _{v}\rvert ^{-r}$
. The result of Proposition A.2.2, as modified later, holds true for this definition of
$\lvert \varpi _{v}\rvert ^{-r}$
. The result of Proposition A.2.2, as modified later, holds true for this definition of
 $R_{r, v}^{\circ }$
(there, a complementary mistake appears between the third-last and second-last displayed equations in the proof).
$R_{r, v}^{\circ }$
(there, a complementary mistake appears between the third-last and second-last displayed equations in the proof). -
– Lemma 3.2.2. A factor
 $\eta (y)$
is missing in the right-hand side of the formula.
$\eta (y)$
is missing in the right-hand side of the formula. -
– Proposition 3.2.3.2. The proposition should be corrected as follows: Let
 $v\mid p$
and let
$v\mid p$
and let
 $\phi _{2,v}=\phi _{2,v}^{\circ }$
be as in formula (3.1.4) (of the present paper). Then
$\phi _{2,v}=\phi _{2,v}^{\circ }$
be as in formula (3.1.4) (of the present paper). Then  $$ \begin{align*} W_{a,r, v}^{\circ}(1, u, \chi_{F})= \begin{cases} \lvert d_{v}\rvert^{3/2}\lvert D_{v}\rvert^{1/2} \chi_{F,v}(-1) & \text{if } v(a)\geq 0 \text{ and } v(u)=0, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} W_{a,r, v}^{\circ}(1, u, \chi_{F})= \begin{cases} \lvert d_{v}\rvert^{3/2}\lvert D_{v}\rvert^{1/2} \chi_{F,v}(-1) & \text{if } v(a)\geq 0 \text{ and } v(u)=0, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
-
– Equation (3.7.1). The right-hand side should have an extra factor of
 $\prod _{v\mid p}\lvert d\vert ^{2}_{v}\lvert D\rvert _{v}$
owing to the correction to Proposition A.2.2.
$\prod _{v\mid p}\lvert d\vert ^{2}_{v}\lvert D\rvert _{v}$
owing to the correction to Proposition A.2.2. -
– Lemma 5.3.1. The left-hand side of the last equation in the statement should be
 $\left \langle f_{1}'(P_{1}), f_{2}'(P_{2})\right \rangle _{J, *}$
.
$\left \langle f_{1}'(P_{1}), f_{2}'(P_{2})\right \rangle _{J, *}$
. -
– Proof of Proposition 5.4.3. The second-last displayed equation should have the factor of
 $2$
on the right hand side, not the left hand side: Then the argument shows that first,
$2$
on the right hand side, not the left hand side: Then the argument shows that first, $$ \begin{align*} 2 \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right)= \lvert D_{F}\rvert^{1/2} \lvert D_{E}\rvert^{1/2} L(1, \eta)\left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}\left(\theta_{\iota_{\mathfrak{p}}}\left(\varphi,\alpha(\varpi)^{-r}w_{r}^{-1}\phi\right)\right) P_{\chi}, P_{\chi}^{-1}\right\rangle. \end{align*} $$
(without an incorrect factor of
$$ \begin{align*} 2 \ell_{\varphi^{p},\alpha}\left(\widetilde{Z}(\phi^{\infty}, \chi)\right)= \lvert D_{F}\rvert^{1/2} \lvert D_{E}\rvert^{1/2} L(1, \eta)\left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}\left(\theta_{\iota_{\mathfrak{p}}}\left(\varphi,\alpha(\varpi)^{-r}w_{r}^{-1}\phi\right)\right) P_{\chi}, P_{\chi}^{-1}\right\rangle. \end{align*} $$
(without an incorrect factor of $$ \begin{align*} & \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}(f_{1}\otimes f_{2}) P_{\chi}, P_{{\chi}^{-1}}\right\rangle_{J} \\&\quad ={ \zeta_{F}^{\infty}(2)\over \left(\pi^{2}/2\right)^{\left[F:\mathbf{Q}\right]} \lvert D_{E}\rvert^{1/2} L(1, \eta)} \prod_{v\mid p}Z_{v}^{\circ}( \alpha_{v}, \chi_{v})^{-1} \cdot{\mathrm{d}}_{F} L_{p, \alpha}\left(\sigma_{A,E}\right)( \chi)\cdot Q(f_{1}, f_{2}, \chi) \end{align*} $$
$$ \begin{align*} & \left\langle {\mathrm{T}}_{\mathrm{alg}}, \iota_{\mathfrak{p}}(f_{1}\otimes f_{2}) P_{\chi}, P_{{\chi}^{-1}}\right\rangle_{J} \\&\quad ={ \zeta_{F}^{\infty}(2)\over \left(\pi^{2}/2\right)^{\left[F:\mathbf{Q}\right]} \lvert D_{E}\rvert^{1/2} L(1, \eta)} \prod_{v\mid p}Z_{v}^{\circ}( \alpha_{v}, \chi_{v})^{-1} \cdot{\mathrm{d}}_{F} L_{p, \alpha}\left(\sigma_{A,E}\right)( \chi)\cdot Q(f_{1}, f_{2}, \chi) \end{align*} $$
 $2$
introduced in the denominator of the right-hand side of (5.4.1) there); and second, that this equation is equivalent to Theorem B as corrected.
$2$
introduced in the denominator of the right-hand side of (5.4.1) there); and second, that this equation is equivalent to Theorem B as corrected.
An extra factor
 $\prod _{v\mid p} \lvert d\rvert ^{2}_{v}\lvert D\rvert _{v}$
should be inserted in the right-hand sides of the last and fourth-last displayed equations; compare the corrections to (3.7.1) and Proposition A.3.1.
$\prod _{v\mid p} \lvert d\rvert ^{2}_{v}\lvert D\rvert _{v}$
should be inserted in the right-hand sides of the last and fourth-last displayed equations; compare the corrections to (3.7.1) and Proposition A.3.1. -
– Proposition 7.1.1(b). It should be replaced by Proposition 3.5.1(b) and (c).
-
– §7.2, third paragraph. The coefficient in the second displayed equation should have
 $\lvert D_{E}\rvert ^{1/2}$
, not
$\lvert D_{E}\rvert ^{1/2}$
, not
 $\lvert D_{E/F}\rvert ^{1/2}$
, in the denominator.
$\lvert D_{E/F}\rvert ^{1/2}$
, in the denominator. -
– Lemma 9.1.1. This is corrected by Lemma 4.1.1 (this does not significantly affect the rest).
-
– Lemma 9.1.5. The extension
 $H_{\infty }$
is contained in a relative Lubin–Tate extension. This is the only property used.
$H_{\infty }$
is contained in a relative Lubin–Tate extension. This is the only property used. -
– Proposition 9.2.1. The assumption that
 $V_{\mathfrak {p}}A$
is potentially crystalline at all
$V_{\mathfrak {p}}A$
is potentially crystalline at all
 $v\mid p$
should be added. The bounded dependence on s of the integer
$v\mid p$
should be added. The bounded dependence on s of the integer
 $d_{2}=d_{2,s}$
was not addressed; it holds true by the proofs of Proposition 4.4.1 and Lemma 4.4.2, which work verbatim in the split case (under the comparison given in footnote 8 of §4.4). The definition of
$d_{2}=d_{2,s}$
was not addressed; it holds true by the proofs of Proposition 4.4.1 and Lemma 4.4.2, which work verbatim in the split case (under the comparison given in footnote 8 of §4.4). The definition of
 $d_{1,s}$
contains an extra
$d_{1,s}$
contains an extra
 $\otimes _{\mathscr {O}_{L}} L/\mathscr {O}_{L}$
.
$\otimes _{\mathscr {O}_{L}} L/\mathscr {O}_{L}$
. -
– Lemma 9.2.4. The statement should be that
 $H^{0}\left (\widetilde {H}^{\prime }_{\infty ,\overline {w}}, V_{p}J_{U}^{*}(1)\right )$
vanishes, and it this group that should appear in the left-hand side of the first displayed equation in the proof.
$H^{0}\left (\widetilde {H}^{\prime }_{\infty ,\overline {w}}, V_{p}J_{U}^{*}(1)\right )$
vanishes, and it this group that should appear in the left-hand side of the first displayed equation in the proof. -
– Lemma A.2.1. The list of representatives is missing the element
 $n^{-}(\infty )=\left (\begin {smallmatrix}0&1\\-1&0\end {smallmatrix}\right )$
(compare Lemma A.2.1).
$n^{-}(\infty )=\left (\begin {smallmatrix}0&1\\-1&0\end {smallmatrix}\right )$
(compare Lemma A.2.1). -
– Proposition A.2.2. The statement should be
The factor $$ \begin{align*} R_{r,v}^{\natural}\left(W_{v}, \phi_{v}, \chi_{v}'{}^{\iota}\right) = \lvert d\rvert^{2}_{v}\lvert D\rvert_{v}\cdot Z_{v}^{\circ}\left( \chi^{\prime}_{v}\right):= \lvert d\vert^{2}_{v}\lvert D\rvert_{v}\cdot {\zeta_{F,v}(2)L(1, \eta_{v})^{2} \over L\left(1/2, \sigma_{E,v}^{\iota}, \chi^{\prime}_{v}\right)} {\prod_{w\mid v}Z_{w}\left( \chi_{w}' \right)}. \end{align*} $$
$$ \begin{align*} R_{r,v}^{\natural}\left(W_{v}, \phi_{v}, \chi_{v}'{}^{\iota}\right) = \lvert d\rvert^{2}_{v}\lvert D\rvert_{v}\cdot Z_{v}^{\circ}\left( \chi^{\prime}_{v}\right):= \lvert d\vert^{2}_{v}\lvert D\rvert_{v}\cdot {\zeta_{F,v}(2)L(1, \eta_{v})^{2} \over L\left(1/2, \sigma_{E,v}^{\iota}, \chi^{\prime}_{v}\right)} {\prod_{w\mid v}Z_{w}\left( \chi_{w}' \right)}. \end{align*} $$
 $\lvert d\rvert ^{2}_{v}\lvert D\rvert _{v}$
missing from [Reference Disegni9] should first appear in the right-hand side of the displayed formula for
$\lvert d\rvert ^{2}_{v}\lvert D\rvert _{v}$
missing from [Reference Disegni9] should first appear in the right-hand side of the displayed formula for
 $r\left (w_{r}^{-1}\right )\phi (x, u)$
in the middle of the proof.
$r\left (w_{r}^{-1}\right )\phi (x, u)$
in the middle of the proof.
-
– Proposition A.3.1. It should be replaced by Proposition A.2.2.
Acknowledgments
I would like to thank the referees for a sharp reading. This research was supported by ISF grant 1963/20.
Competing Interests
None













































