Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T13:16:26.956Z Has data issue: false hasContentIssue false
  • English
  • Français

Steiner Triple Systems Having a Prescribed Number of Triples in Common

Published online by Cambridge University Press:  20 November 2018

C. C. Lindner  and
A. Rosa
C. C. Lindner
Affiliation:
Auburn University, Auburn, Alabama
A. Rosa
Affiliation:
McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

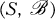A Steiner triple system (briefly STS) is a pair where S is a finite set and 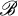is a collection of 3-subsets of S (called triples) such that every pair of distinct elements of S belongs to exactly one triple of 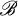. The number |S| is called the order of 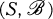. It is well-known that there is an STS of order if and only if 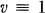or 3 (mod 6). Therefore in saying that a certain property concerning STS is true for all it is understood that 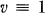or 3 (mod 6). An STS of order v will sometimes be denoted by .

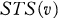Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 5 , 01 October 1975 , pp. 1166 - 1175
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Doyen, J., Constructions of disjoint Steiner triple systems, Proc. Amer. Math. Soc. 32 (1972), 409–416.Google Scholar
2. Doyen, J. and Wilson, R. M., Embeddings of Steiner triple systems, Discrete Math. 5 (1973), 229–239.Google Scholar
3. Hall, M. Jr., Combinatorial Theory (Ginn-Blaisdell, Waltham, Mass., 1967).Google Scholar
4. Harary, F., Graph Theory (Addison-Wesley, Reading, Mass., 1969).Google Scholar
5. Kramer, E. S. and Mesner, D. M., Intersections among Steiner systems, J. Combinatorial Theory, Ser. A 16 (1974), 273–285.Google Scholar
6. Lindner, C. C., Construction of Steiner triple systems having exactly one triple in common, Can. J. Math. 26 (1974), 225–232.Google Scholar
7. Lindner, C. C., Mendelsohn, E. and Rosa, A., On the number of 1-factorizations of the complete graph, to appear, J. Comb. Theory (B).Google Scholar
8. Lindner, C. C. and Rosa, A., On the existence of automorphism-free Steiner triple systems, J. Algebra, 34 (1975),430–443.Google Scholar
9. Rosa, A., Remark on cyclic Steiner triple systems (in Slovak), Mat.-fyz.casopis 16 (1966), 285–290.Google Scholar
10. Rosa, A., Steiner triple systems and their chromatic number, Acta Fac. Rerum Natur. Univ. Comenian. Math. 24 (1970), 159–174.Google Scholar
11. Roselle, D. P., Distributions of integers into s-tuples with given differences, Proc. Manitoba Conference on Numerical Mathematics, Winnipeg 1971, 31–42.Google Scholar