Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Finn, Justin R.
Li, Ming
and
Apte, Sourabh V.
2016.
Particle based modelling and simulation of natural sand dynamics in the wave bottom boundary layer.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
340.
M. Kuerten, J. G.
2016.
Point-Particle DNS and LES of Particle-Laden Turbulent flow - a state-of-the-art review.
Flow, Turbulence and Combustion,
Vol. 97,
Issue. 3,
p.
689.
Vreman, A. W.
2016.
Particle-resolved direct numerical simulation of homogeneous isotropic turbulence modified by small fixed spheres.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
40.
Fornari, W.
Formenti, A.
Picano, F.
and
Brandt, L.
2016.
The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions.
Physics of Fluids,
Vol. 28,
Issue. 3,
Costa, Pedro
Picano, Francesco
Brandt, Luca
and
Breugem, Wim-Paul
2016.
Universal Scaling Laws for Dense Particle Suspensions in Turbulent Wall-Bounded Flows.
Physical Review Letters,
Vol. 117,
Issue. 13,
Kumar, Manish
Roy, Somnath
and
Ali, Md Sujaat
2016.
An efficient immersed boundary algorithm for simulation of flows in curved and moving geometries.
Computers & Fluids,
Vol. 129,
Issue. ,
p.
159.
Fornari, Walter
Picano, Francesco
and
Brandt, Luca
2016.
Sedimentation of finite-size spheres in quiescent and turbulent environments.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
640.
Finn, Justin R.
and
Li, Ming
2016.
Regimes of sediment-turbulence interaction and guidelines for simulating the multiphase bottom boundary layer.
International Journal of Multiphase Flow,
Vol. 85,
Issue. ,
p.
278.
Spandan, Vamsi
Meschini, Valentina
Ostilla-Mónico, Rodolfo
Lohse, Detlef
Querzoli, Giorgio
de Tullio, Marco D.
and
Verzicco, Roberto
2017.
A parallel interaction potential approach coupled with the immersed boundary method for fully resolved simulations of deformable interfaces and membranes.
Journal of Computational Physics,
Vol. 348,
Issue. ,
p.
567.
Moradi Nour, Z.
Amberg, G.
and
Do-Quang, M.
2017.
Kinematics and dynamics of suspended gasifying particle.
Acta Mechanica,
Vol. 228,
Issue. 3,
p.
1135.
Lashgari, Iman
Picano, Francesco
Costa, Pedro
Breugem, Wim-Paul
and
Brandt, Luca
2017.
Turbulent channel flow of a dense binary mixture of rigid particles.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
623.
Niazi Ardekani, M.
Costa, P.
Breugem, W.-P.
Picano, F.
and
Brandt, L.
2017.
Drag reduction in turbulent channel flow laden with finite-size oblate spheroids.
Journal of Fluid Mechanics,
Vol. 816,
Issue. ,
p.
43.
Fornari, Walter
Picano, Francesco
and
Brandt, Luca
2018.
The effect of polydispersity in a turbulent channel flow laden with finite-size particles.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
54.
Spandan, Vamsi
Lohse, Detlef
de Tullio, Marco D.
and
Verzicco, Roberto
2018.
A fast moving least squares approximation with adaptive Lagrangian mesh refinement for large scale immersed boundary simulations.
Journal of Computational Physics,
Vol. 375,
Issue. ,
p.
228.
Alghalibi, Dhiya
Lashgari, Iman
Brandt, Luca
and
Hormozi, Sarah
2018.
Interface-resolved simulations of particle suspensions in Newtonian, shear thinning and shear thickening carrier fluids.
Journal of Fluid Mechanics,
Vol. 852,
Issue. ,
p.
329.
Costa, Pedro
Picano, Francesco
Brandt, Luca
and
Breugem, Wim-Paul
2018.
Effects of the finite particle size in turbulent wall-bounded flows of dense suspensions.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
450.
Jiang, Maoqiang
and
Liu, Zhaohui
2019.
A boundary thickening-based direct forcing immersed boundary method for fully resolved simulation of particle-laden flows.
Journal of Computational Physics,
Vol. 390,
Issue. ,
p.
203.
Roy, Somnath
2019.
Two-Phase Flow for Automotive and Power Generation Sectors.
p.
223.
Gruber, Andrea
2019.
Direct Numerical Simulations: Present and Future Role in Fundamental and Applied Combustion Research.
Peng, Cheng
and
Wang, Lian-Ping
2019.
Direct numerical simulations of turbulent pipe flow laden with finite-size neutrally buoyant particles at low flow Reynolds number.
Acta Mechanica,
Vol. 230,
Issue. 2,
p.
517.
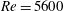 $\mathit{Re}=5600$. Their results give a tantalizing demonstration of the vastness of the vistas that this line of research is about to open.
$\mathit{Re}=5600$. Their results give a tantalizing demonstration of the vastness of the vistas that this line of research is about to open.
$\mathit{Re}=5600$ with different values of the particle volume fraction
${\it\Phi}$. The particles have been removed from half of the domain for clarity (adapted from Picano et al.2015).




1. Introduction
You are a computational fluid dynamicist and you are asked to simulate a turbulent flow in which thousands of solid particles are suspended in a fluid. The no-slip condition must be imposed on each and every one of the particles, the position and orientation of which evolves in time due to the action of the very forces exerted by the fluid. Why would anyone want, or need, to face such ‘death by boundary conditions’? Yet this is what Picano, Breugem & Brandt (Reference Picano, Breugem and Brandt2015) undertake in their recent paper, see figure 1. The subject must be important if an earlier paper on the same topic (Lucci, Ferrante & Elghobashi Reference Lucci, Ferrante and Elghobashi2010) was also the subject of a Focus on Fluids contribution by Tryggvason in 2010. And important it is: the remodelling of the ocean coast and of river beds, soil erosion and desertification, avalanches and many others are all natural phenomena in which particles are suspended in a fluid medium, affect its state of flow and are in their turn affected by it. About half of the world’s gasoline is produced by ‘cracking’ heavy-oil molecules in fluidized beds, large installations in which zeolite catalyst particles are suspended in a upward ‘wind’ of heavy oil vapour. Examples can be easily added: the production of synthetic fuels, the combustion of atomized sprays, drying operations and many others.
Much headway has been made by the drastic measure of simply killing the boundary: each particle is modelled as a point mass with zero volume, the force on it is parameterized on the basis of the local fluid velocity and acceleration, and an equal and opposite force is exerted by the particle on the fluid. For decades this point-particle model has been the most widely used tool to unlock the mysteries of particulate flows and its bibliography is by now quite extensive (see e.g. Balachandar & Eaton Reference Balachandar and Eaton2010). But it is also obvious that doing away with the particles as boundaries prevents the study of the interaction between the fluid and particle length scales, the simulation of wake effects, particle–particle interaction and many others.
Efforts to restore the finite size of the particles started in the 1980s with the use of finite-element methods. However, it was soon evident that the need for frequent re-gridding severely limited their effectiveness. Attention quickly shifted to fixed-grid methods but, here, the geometrical mismatch between the particle boundary and the grid posed a significant difficulty. The advent of immersed boundary methods, such as the one used in the paper under discussion by Picano et al. (Reference Picano, Breugem and Brandt2015), has provided a very effective way to solve the problem.
Figure 1. Snapshots of the streamwise velocity on several planes and instantaneous particle configurations in a turbulent pressure-driven channel flow with $\mathit{Re}=5600$
with different values of the particle volume fraction
$\mathit{Re}=5600$
with different values of the particle volume fraction
 ${\it\Phi}$
. The particles have been removed from half of the domain for clarity (adapted from Picano et al.
Reference Picano, Breugem and Brandt2015).
${\it\Phi}$
. The particles have been removed from half of the domain for clarity (adapted from Picano et al.
Reference Picano, Breugem and Brandt2015).
2. Overview
As applied to particulate flows, the basic idea of the immersed boundary method (originally invented in the 1970s for the simulation of blood flow in the heart, see Peskin Reference Peskin2002) is, once again, to disregard the particle boundary, but in a subtle way: the continuity and momentum equations are solved both outside and inside the particles but, in the latter domains, fictitious forces are imposed which cause the fluid to move like a solid so as to restore the no-slip boundary condition.
While the general idea is simple, its accurate and efficient implementation has proved far from straightforward and it is still a topic of current research. After some limited early work in the late 1990s, a major breakthrough was initiated by Uhlmann (Reference Uhlmann2008) who combined the direct-forcing method of Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) with the regularized ${\it\delta}$
-function approach of the original method of Peskin. In this way, he was able to simulate thousands of particles in a channel flow with a Reynolds number large enough for spontaneous turbulence to set in (Uhlmann Reference Uhlmann2008). The mismatch between the particle boundary and the underlying fixed grid required interpolation back and forth between one and the other. These steps make it difficult to satisfy the no-slip condition precisely on the particle surface, and this is one of several areas where recent work has focused (see e.g. Kempe & Frölich Reference Kempe and Frölich2012 and, in particular, earlier work by Breugem, one of the authors of the paper under discussion).
${\it\delta}$
-function approach of the original method of Peskin. In this way, he was able to simulate thousands of particles in a channel flow with a Reynolds number large enough for spontaneous turbulence to set in (Uhlmann Reference Uhlmann2008). The mismatch between the particle boundary and the underlying fixed grid required interpolation back and forth between one and the other. These steps make it difficult to satisfy the no-slip condition precisely on the particle surface, and this is one of several areas where recent work has focused (see e.g. Kempe & Frölich Reference Kempe and Frölich2012 and, in particular, earlier work by Breugem, one of the authors of the paper under discussion).
Picano et al. (Reference Picano, Breugem and Brandt2015) have carried out simulations of pressure-driven channel flow with a bulk Reynolds number of 5600 individually resolving up to 10 000 neutrally buoyant spherical particles for three values of the particle volume fraction ${\it\Phi}$
(i.e. the fraction of the total computational volume occupied by the particles). Even after the recent improvements of the immersed boundary method, simulations of this type still required a major effort, each one running for approximately
${\it\Phi}$
(i.e. the fraction of the total computational volume occupied by the particles). Even after the recent improvements of the immersed boundary method, simulations of this type still required a major effort, each one running for approximately
 $10^{6}$
CPU hours on a Cray XE6 with 2048 cores, i.e. of the order of a month of real time.
$10^{6}$
CPU hours on a Cray XE6 with 2048 cores, i.e. of the order of a month of real time.
The results give a striking sense of the profound and complex ways in which the addition of particles affects fluid flow. While a log layer can still be identified, the corresponding von Kármán constant decreases by nearly 50 % as ${\it\Phi}$
increases from 0 % to 20 %, suggesting a decrease of the turbulent drag, while the additive constant decreases from 5.5 to approximately
${\it\Phi}$
increases from 0 % to 20 %, suggesting a decrease of the turbulent drag, while the additive constant decreases from 5.5 to approximately
 $-6.3$
, which normally corresponds to an increased drag. The net result is still an increase in the overall drag, but not because turbulence intensity is increased. As a matter of fact, the authors stress the point that, at
$-6.3$
, which normally corresponds to an increased drag. The net result is still an increase in the overall drag, but not because turbulence intensity is increased. As a matter of fact, the authors stress the point that, at
 ${\it\Phi}=20\,\%$
, turbulent fluctuations are actually decreased by the presence of the particles. They attribute their drag increase to the counterbalancing and ultimately prevailing effect of the particle contribution to the mixture stress. In this connection they offer the interesting speculation that a neighbouring region of parameter space may exist in which the reduced turbulence intensity may be stronger than the particle stress effect, so much so that particles might even result in an overall drag reduction.
${\it\Phi}=20\,\%$
, turbulent fluctuations are actually decreased by the presence of the particles. They attribute their drag increase to the counterbalancing and ultimately prevailing effect of the particle contribution to the mixture stress. In this connection they offer the interesting speculation that a neighbouring region of parameter space may exist in which the reduced turbulence intensity may be stronger than the particle stress effect, so much so that particles might even result in an overall drag reduction.
Other interesting observations concern the wall region where, unlike the fluid, the particle velocity does not have to vanish. Thus, while the mean velocity of the particles is fairly close to that of the fluid over most of the channel, near the wall they are markedly different, and this is the only region of the flow where the particles are found to increase, rather than dampen, the fluid velocity fluctuations. The strong effect of the particles on the wall layer causes a considerable modification of the well-known low-velocity streaks of single-phase wall-bounded turbulence which can be clearly seen in figure 1. As ${\it\Phi}$
becomes larger there is a gradual increase of the separation between the streaks and a progressive fading of the low/high velocity contrast. The conclusion is that the structure of the wall turbulence is significantly altered by the particles with a much weaker organization into coherent structures.
${\it\Phi}$
becomes larger there is a gradual increase of the separation between the streaks and a progressive fading of the low/high velocity contrast. The conclusion is that the structure of the wall turbulence is significantly altered by the particles with a much weaker organization into coherent structures.
From the numerical point of view, a method stable enough to handle particles with the same density as the fluid is quite an achievement but, because of the peculiarities of this situation, the results of this paper cannot be easily extrapolated to other cases. A different particle inertia, for example, would promote a more developed relative motion with respect to the fluid, very likely resulting in an increase of the fluid velocity fluctuations, as Picano et al. (Reference Picano, Breugem and Brandt2015) have found in the only region of their flow where such a difference exists, namely near the wall. This was indeed the conclusion of the simulations of Lucci et al. (Reference Lucci, Ferrante and Elghobashi2010) who studied decaying homogeneous turbulence.
3. Future
The ability to perform direct numerical simulations of single-phase turbulent flows has had an enormous impact on the understanding of single-phase turbulence and the development of reduced descriptions such as large-eddy simulation. It may well be expected that the gradual emergence of a comparable possibility for particulate, or more general, multi-phase flows will prove equally beneficial. The addition of the particle parameters (size, number, density, shape, etc.) to those of the fluid generates a huge parameter space and so little work of this type has been carried out that this vast territory is still essentially virgin. We are really at the beginning of a golden age of science in this area. In addition to that of physicists, particulate flows must hold the interest of computational scientists. In spite of continuous progress, the available hardware will always fall short of what would be desirable. Thus, work on new algorithms and the further improvement of the existing ones is necessary. Adapting them to new computational platforms, such as massively parallel GPUs, may be expected to bring handsome rewards.
All this computing will of course shed light on the microphysics of the flow, but it will enable us to pursue an even more important practical objective. It is evident that the fully resolved simulation of systems large enough to approach the actual size of a fluidized bed, for example, will not be possible for a very long time, if ever. We must rely on some sort of averaged description. The impetus in this direction has been very strong over more than half a century, but the results have been somewhat meagre. Unlike single-phase turbulence, where even simple Reynolds closure models have proven of some usefulness, in the case of particulate flows simple closures by and large have failed. Restoring the necessary amount of information lost on averaging has proven a major obstacle, with adverse effects not only on the physical realism, but in some cases on the very mathematical structure of the equations. Basing closure relations on the results of fully resolved simulations requires the development of tools to interrogate and suitably average the simulation results. This is not a simple task as the amount of information is massive and convergence of averaging slow. Furthermore, while there is a general idea about the important quantities that need to be calculated, a large amount of work is still necessary to understand how to incorporate them in robust and physically relevant closure relations. With a few others, Picano and his colleagues belong to the vanguard of what can well be expected to represent a major component of fluid dynamics research for years to come.
Acknowledgement
This work has been supported by NSF under grant CBET 1335965.