1. Introduction
Two-phase flow, consisting of two immiscible fluids, is widely encountered in various engineering applications. The presence of a dispersed phase can significantly alter the flow characteristics, leading to either drag enhancement or drag reduction (Balachandar & Eaton Reference Balachandar and Eaton2010; Ceccio Reference Ceccio2010; Lohse Reference Lohse2018; Mathai, Lohse & Sun Reference Mathai, Lohse and Sun2020; Yi et al. Reference Yi, Wang, Huisman and Sun2023). A correct understanding of the mechanism of drag modulation is of great significance to relevant engineering applications; however, a comprehensive understanding of this mechanism is still missing.
A typical characteristic of liquid–liquid two-phase flow is the dynamics of the interface, which involves deformation (Rallison Reference Rallison1984; Rosti, De Vita & Brandt Reference Rosti, De Vita and Brandt2019; Hakansson et al. Reference Hakansson, Crialesi-Esposito, Nilsson and Brandt2022), coalescence (Stone Reference Stone1994; Kavehpour Reference Kavehpour2015) and breakup (Lemenand et al. Reference Lemenand, Della Valle, Dupont and Peerhossaini2017; Olad et al. Reference Olad, Innings, Crialesi-Esposito, Brandt and Hakansson2023; Ni Reference Ni2024). When coalescence is counterbalanced by breakup, the dispersed phase exhibits a specific size distribution which can be well described by a lognormal distribution (Yi, Toschi & Sun Reference Yi, Toschi and Sun2021). Under fixed Reynolds number, the dispersed phase has almost the same average size for different volume fractions (Yi et al. Reference Yi, Wang, van Vuren, Lohse, Risso, Toschi and Sun2022). It has been observed that the dispersed phase volume fraction is positively correlated with the global transport of a liquid–liquid two-phase turbulent flow (Yi et al. Reference Yi, Wang, van Vuren, Lohse, Risso, Toschi and Sun2022), indicating that increasing the interfacial area could contribute to the drag enhancement. The effect of dispersed phase coalescence in liquid–liquid two-phase flow has recently been studied using interface-resolved direct numerical simulations (De Vita et al. Reference De Vita, Rosti, Caserta and Brandt2019; Cannon et al. Reference Cannon, Izbassarov, Tammisola, Brandt and Rosti2021), and it is found that the coalescence effectively decreases the interfacial area, thus weakening the drag enhancement effect, and vice versa (De Vita et al. Reference De Vita, Rosti, Caserta and Brandt2019). Additionally, the interface deformation is also found to be important for the gas–liquid turbulent drag reduction (Van den Berg et al. Reference Van den Berg, Luther, Lathrop and Lohse2005; van Gils et al. Reference van Gils, Guzman, Sun and Lohse2013; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2017; Lohse Reference Lohse2018; Mathai et al. Reference Mathai, Lohse and Sun2020). The bubbles with large size or high deformability exhibit pronounced drag reduction effect (Lu, Fernández & Tryggvason Reference Lu, Fernández and Tryggvason2005; Verschoof et al. Reference Verschoof, Van Der Veen, Sun and Lohse2016), but the drag reduction effect is lost when the bubbles are reduced to small sizes after the addition of surfactants (Verschoof et al. Reference Verschoof, Van Der Veen, Sun and Lohse2016).
Existing studies show that interface dynamics induce very different drag modulation effects in liquid–liquid and gas–liquid two-phase flows (Lohse Reference Lohse2018; Mathai et al. Reference Mathai, Lohse and Sun2020; Yi et al. Reference Yi, Wang, Huisman and Sun2023). However, the role played by the fluid properties of the dispersed phase in these effects remains unclear. The interface dynamics, density and viscosity of the dispersed phase are intricately coupled, making it challenging to isolate the influence of the individual effects on drag modulation. In this study, we utilize interface-resolved three-dimensional direct numerical simulations to track interface dynamics in Taylor–Couette turbulence. Additionally, we employ momentum budget analysis to investigate the individual and coupling effects of the interface dynamics, density and viscosity of the dispersed phase. We aim to uncover how these factors operate and determine whether they cooperate or compete with each other in drag modulation.
2. Results and discussion
The interface-resolved three-dimensional direct numerical simulations of two-phase fluid–fluid flow in a Taylor–Couette (TC) system were carried out using a volume-of-fluid (VOF) method with the piecewise linear interface calculation (PLIC) based on the open-source OpenFOAM v8 (Rusche Reference Rusche2003; Chen, Zhao & Wan Reference Chen, Zhao and Wan2022). We consider two immiscible and incompressible fluids confined between two coaxial cylinders whose radii are ![]() $r_i$ (inner) and
$r_i$ (inner) and ![]() $r_o$ (outer). In this work, we have chosen to fix the outer cylinder while allowing the inner cylinder to rotate with a constant angular velocity
$r_o$ (outer). In this work, we have chosen to fix the outer cylinder while allowing the inner cylinder to rotate with a constant angular velocity ![]() $\omega _i$. The two-phase flow is governed by the Navier–Stokes equations
$\omega _i$. The two-phase flow is governed by the Navier–Stokes equations
where ![]() $\boldsymbol {u}$ is the velocity and
$\boldsymbol {u}$ is the velocity and ![]() $p$ is the pressure. The
$p$ is the pressure. The ![]() $\rho$ and
$\rho$ and ![]() $\mu$ are the variable density and viscosity, respectively. The continuous carrier phase is characterized by the density
$\mu$ are the variable density and viscosity, respectively. The continuous carrier phase is characterized by the density ![]() $\rho _f$ and viscosity
$\rho _f$ and viscosity ![]() $\mu _f$, whereas the dispersed phase is described by the density
$\mu _f$, whereas the dispersed phase is described by the density ![]() $\rho _d$ and viscosity
$\rho _d$ and viscosity ![]() $\mu _d$. The phase fraction
$\mu _d$. The phase fraction ![]() $\alpha$ is introduced to characterize the variable density and viscosity, i.e.
$\alpha$ is introduced to characterize the variable density and viscosity, i.e. ![]() $\rho =\alpha \rho _d+(1-\alpha )\rho _f$ and
$\rho =\alpha \rho _d+(1-\alpha )\rho _f$ and ![]() $\mu =\alpha \mu _d+(1-\alpha )\mu _f$. The continuum surface force method, as proposed by Brackbill, Kothe & Zemach (Reference Brackbill, Kothe and Zemach1992), is adopted in this study to describe the interfacial tension, i.e.
$\mu =\alpha \mu _d+(1-\alpha )\mu _f$. The continuum surface force method, as proposed by Brackbill, Kothe & Zemach (Reference Brackbill, Kothe and Zemach1992), is adopted in this study to describe the interfacial tension, i.e. ![]() $\boldsymbol {f}=-\sigma \kappa \boldsymbol {\nabla }\alpha$, where
$\boldsymbol {f}=-\sigma \kappa \boldsymbol {\nabla }\alpha$, where ![]() $\sigma$ denotes the surface tension coefficient and
$\sigma$ denotes the surface tension coefficient and ![]() $\kappa =\boldsymbol {\nabla }\boldsymbol {\cdot } (\boldsymbol {\nabla }\alpha /|\boldsymbol {\nabla }\alpha |)$ represents the interface curvature. The accuracy of the VOF method is often affected by interface sharpness (Gamet et al. Reference Gamet, Scala, Roenby, Scheufler and Pierson2020) and spurious currents (Vachaparambil & Einarsrud Reference Vachaparambil and Einarsrud2019; Fan & Anglart Reference Fan and Anglart2020). The detailed numerical methods and computational accuracy are presented in the supplementary material available at https://doi.org/10.1017/jfm.2024.206.
$\kappa =\boldsymbol {\nabla }\boldsymbol {\cdot } (\boldsymbol {\nabla }\alpha /|\boldsymbol {\nabla }\alpha |)$ represents the interface curvature. The accuracy of the VOF method is often affected by interface sharpness (Gamet et al. Reference Gamet, Scala, Roenby, Scheufler and Pierson2020) and spurious currents (Vachaparambil & Einarsrud Reference Vachaparambil and Einarsrud2019; Fan & Anglart Reference Fan and Anglart2020). The detailed numerical methods and computational accuracy are presented in the supplementary material available at https://doi.org/10.1017/jfm.2024.206.
In the simulated TC system, a rotational symmetry of six (i.e. the simulated azimuthal region is set as ![]() ${\rm \pi} /3$) is chosen to reduce computational costs without compromising the accuracy of our results. This choice has been validated for both single phase and multiphase TC turbulence (Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2018; Assen et al. Reference Assen, Ng, Will, Stevens, Lohse and Verzicco2022; Xu et al. Reference Xu, Zhao, Sun, He and Wang2022, Reference Xu, Su, Lan, Zhao, He, Sun and Wang2023). The curvature of a TC system is defined as
${\rm \pi} /3$) is chosen to reduce computational costs without compromising the accuracy of our results. This choice has been validated for both single phase and multiphase TC turbulence (Brauckmann & Eckhardt Reference Brauckmann and Eckhardt2013; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2018; Assen et al. Reference Assen, Ng, Will, Stevens, Lohse and Verzicco2022; Xu et al. Reference Xu, Zhao, Sun, He and Wang2022, Reference Xu, Su, Lan, Zhao, He, Sun and Wang2023). The curvature of a TC system is defined as ![]() $\eta =r_i/r_o=0.714$ and the aspect ratio is defined as
$\eta =r_i/r_o=0.714$ and the aspect ratio is defined as ![]() $\varGamma =L/d=2{\rm \pi} /3$, where
$\varGamma =L/d=2{\rm \pi} /3$, where ![]() $d = r_o-r_i$ is the gap width and
$d = r_o-r_i$ is the gap width and ![]() $L$ is the axial length. No-slip and impermeable boundary conditions are imposed in the radial direction, while periodicity is imposed in the axial and azimuthal directions. The inner and outer cylinders are subjected to a Neumann boundary condition for the phase fraction, resulting in a default contact angle of
$L$ is the axial length. No-slip and impermeable boundary conditions are imposed in the radial direction, while periodicity is imposed in the axial and azimuthal directions. The inner and outer cylinders are subjected to a Neumann boundary condition for the phase fraction, resulting in a default contact angle of ![]() $90^\circ$. The system is uniformly discretized by (
$90^\circ$. The system is uniformly discretized by (![]() $336\times 192\times 192$) grid points in the azimuthal, radial and axial directions, respectively. The grid spacing is measured in wall units
$336\times 192\times 192$) grid points in the azimuthal, radial and axial directions, respectively. The grid spacing is measured in wall units ![]() $y^+$ based on the shear stress at the inner cylinder for single-phase flow. In the radial direction, the uniform grid spacing is
$y^+$ based on the shear stress at the inner cylinder for single-phase flow. In the radial direction, the uniform grid spacing is ![]() $0.725y^+$. Alternatively, a total amount of six grids is embedded inside the viscous sublayer, whose thickness is
$0.725y^+$. Alternatively, a total amount of six grids is embedded inside the viscous sublayer, whose thickness is ![]() $0.0359d$. The uniform grid spacing in the axial direction is
$0.0359d$. The uniform grid spacing in the axial direction is ![]() $1.519y^+$. The grid spacing in the azimuthal direction ranges from
$1.519y^+$. The grid spacing in the azimuthal direction ranges from ![]() $1.085y^+$ near the inner wall to
$1.085y^+$ near the inner wall to ![]() $1.519y^+$ near the outer wall. The Reynolds number
$1.519y^+$ near the outer wall. The Reynolds number ![]() ${Re}={\rho _f}r_i \omega _i d/\mu _f$ and the Weber number
${Re}={\rho _f}r_i \omega _i d/\mu _f$ and the Weber number ![]() $We={\rho _f}r_i^2 \omega _i^2 d/\sigma$ are fixed at 2000 and 1260, respectively. The Taylor number is fixed as
$We={\rho _f}r_i^2 \omega _i^2 d/\sigma$ are fixed at 2000 and 1260, respectively. The Taylor number is fixed as ![]() ${Ta}=[Re(1+\eta )^3/(8\eta ^2)]^2=6.1\times 10^6$. Due to the increased computational resources required for resolving the two-phase interface and the smaller time step needed to capture capillary wave propagation (Brackbill et al. Reference Brackbill, Kothe and Zemach1992) in the two-phase flow compared with the single-phase case, we have chosen
${Ta}=[Re(1+\eta )^3/(8\eta ^2)]^2=6.1\times 10^6$. Due to the increased computational resources required for resolving the two-phase interface and the smaller time step needed to capture capillary wave propagation (Brackbill et al. Reference Brackbill, Kothe and Zemach1992) in the two-phase flow compared with the single-phase case, we have chosen ![]() $Ta=6.1\times 10^6$ to ensure compatibility with our available computational resources. When the Taylor number exceeds
$Ta=6.1\times 10^6$ to ensure compatibility with our available computational resources. When the Taylor number exceeds ![]() $3\times 10^6$, the flow field transitions into the classical regime of TC turbulence (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). Our chosen Taylor number falls within this regime, ensuring an adequate amount of turbulence information. The Weber number of 1260 is chosen to ensure that the spurious velocities remain within an acceptable range, as depicted in figure S2 in the supplementary material. The maximum Courant–Friedrichs–Lewy number is set to be 0.2. All the presented statistics are collected for at least 20 turns over time after reaching a statistically steady state.
$3\times 10^6$, the flow field transitions into the classical regime of TC turbulence (Grossmann, Lohse & Sun Reference Grossmann, Lohse and Sun2016). Our chosen Taylor number falls within this regime, ensuring an adequate amount of turbulence information. The Weber number of 1260 is chosen to ensure that the spurious velocities remain within an acceptable range, as depicted in figure S2 in the supplementary material. The maximum Courant–Friedrichs–Lewy number is set to be 0.2. All the presented statistics are collected for at least 20 turns over time after reaching a statistically steady state.
Due to the centrifugal effect in the TC system, the distribution of dispersed phase is affected by the density ratio ![]() $\xi _{\rho } = \rho _d/\rho _f$ as well as the viscosity ratio
$\xi _{\rho } = \rho _d/\rho _f$ as well as the viscosity ratio ![]() $\xi _{\mu } = \mu _d/\mu _f$ of the dispersed phase to the continuous phase. Figure 1 displays the instantaneous interface snapshots and phase distribution for the dispersed phase volume fraction of
$\xi _{\mu } = \mu _d/\mu _f$ of the dispersed phase to the continuous phase. Figure 1 displays the instantaneous interface snapshots and phase distribution for the dispersed phase volume fraction of ![]() $\varphi =20\,\%$, providing valuable insights into the spatial distribution and behaviour of the interface and phase components in the system. The averaged radial–axial velocity vectors are also displayed by green arrows to denote the structure and strength of the Taylor vortex. When
$\varphi =20\,\%$, providing valuable insights into the spatial distribution and behaviour of the interface and phase components in the system. The averaged radial–axial velocity vectors are also displayed by green arrows to denote the structure and strength of the Taylor vortex. When ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, the dispersed phase predominantly accumulates at the centre of the Taylor vortex, which is primarily attributed to the linear shear gradient present in the system (Hori et al. Reference Hori, Ng, Lohse and Verzicco2023). When
$\xi _{\mu } = 1$, the dispersed phase predominantly accumulates at the centre of the Taylor vortex, which is primarily attributed to the linear shear gradient present in the system (Hori et al. Reference Hori, Ng, Lohse and Verzicco2023). When ![]() $\xi _{\rho } = 1/4$ and
$\xi _{\rho } = 1/4$ and ![]() $\xi _{\mu } = 1$, the dispersed phase migrates towards the inner wall of the system due to the centrifugal force exerted by the rotating flow. Consequently, the dispersed phase gathers in the plume ejection region near the inner wall and weakens the Taylor vortex. Furthermore, when
$\xi _{\mu } = 1$, the dispersed phase migrates towards the inner wall of the system due to the centrifugal force exerted by the rotating flow. Consequently, the dispersed phase gathers in the plume ejection region near the inner wall and weakens the Taylor vortex. Furthermore, when ![]() $\xi _{\rho } = 1/4$ and
$\xi _{\rho } = 1/4$ and ![]() $\xi _{\mu } = 1/4$, the distribution of the dispersed phase becomes more concentrated near the inner wall and the Taylor vortex is again weakened. The results indicate that decreasing the density ratio
$\xi _{\mu } = 1/4$, the distribution of the dispersed phase becomes more concentrated near the inner wall and the Taylor vortex is again weakened. The results indicate that decreasing the density ratio ![]() $\xi _{\rho }$ and the viscosity ratio
$\xi _{\rho }$ and the viscosity ratio ![]() $\xi _{\mu }$ facilitates the gathering of the dispersed phase near the inner wall and the weakening of the Taylor vortex. Our objective is to analyse the specific effects of dispersed phase density and viscosity on the process of drag reduction.
$\xi _{\mu }$ facilitates the gathering of the dispersed phase near the inner wall and the weakening of the Taylor vortex. Our objective is to analyse the specific effects of dispersed phase density and viscosity on the process of drag reduction.

Figure 1. Instantaneous interface snapshots and corresponding azimuthally and time-averaged phase fraction ![]() $\langle \alpha \rangle _{\theta,t}$. The green arrows indicate the direction and magnitude of the averaged radial–axial velocity vectors
$\langle \alpha \rangle _{\theta,t}$. The green arrows indicate the direction and magnitude of the averaged radial–axial velocity vectors ![]() $\langle u_{rz} \rangle _{\theta,t}/u_i$, where
$\langle u_{rz} \rangle _{\theta,t}/u_i$, where ![]() $u_i=\omega _i r_i$ is the velocity of the inner cylinder and z denotes the axial position.
$u_i=\omega _i r_i$ is the velocity of the inner cylinder and z denotes the axial position.
Through sequential variations of the volume fraction ![]() $\varphi$, the density ratio
$\varphi$, the density ratio ![]() $\xi _{\rho }$ and the viscosity ratio
$\xi _{\rho }$ and the viscosity ratio ![]() $\xi _{\mu }$, we conducted a comprehensive study to investigate the influence of these parameters on the drag modulation (see table 1). The results reveal several important findings. Firstly, when
$\xi _{\mu }$, we conducted a comprehensive study to investigate the influence of these parameters on the drag modulation (see table 1). The results reveal several important findings. Firstly, when ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, it causes a minor increase in drag, indicating a slight drag enhancement effect. However, when we lower
$\xi _{\mu } = 1$, it causes a minor increase in drag, indicating a slight drag enhancement effect. However, when we lower ![]() $\xi _{\rho }$ to 1/4, a significant drag reduction is observed. Moreover, further reducing
$\xi _{\rho }$ to 1/4, a significant drag reduction is observed. Moreover, further reducing ![]() $\xi _{\mu }$ to 1/4 enhances the drag reduction effect even more. Furthermore, we found that the drag modulation shows similar trends for the dispersed phase volume fraction of
$\xi _{\mu }$ to 1/4 enhances the drag reduction effect even more. Furthermore, we found that the drag modulation shows similar trends for the dispersed phase volume fraction of ![]() $\varphi =10\,\%$ and
$\varphi =10\,\%$ and ![]() $\varphi =20\,\%$. Under fixed density ratio
$\varphi =20\,\%$. Under fixed density ratio ![]() $\xi _{\rho }$ and viscosity ratio
$\xi _{\rho }$ and viscosity ratio ![]() $\xi _{\mu }$, an increase in the volume fraction
$\xi _{\mu }$, an increase in the volume fraction ![]() $\varphi$ leads to a stronger drag enhancement or drag reduction effect. In other words, as the volume fraction of the dispersed phase increases, the influence on the drag becomes more pronounced. These results highlight the significant impact of the dispersed phase's density, viscosity and volume fraction on the flow dynamics, particularly in terms of drag enhancement and drag reduction effects.
$\varphi$ leads to a stronger drag enhancement or drag reduction effect. In other words, as the volume fraction of the dispersed phase increases, the influence on the drag becomes more pronounced. These results highlight the significant impact of the dispersed phase's density, viscosity and volume fraction on the flow dynamics, particularly in terms of drag enhancement and drag reduction effects.
Table 1. Drag modulation in two-phase flow. Here ![]() $T$ represents the torque exerted on the inner cylinder and
$T$ represents the torque exerted on the inner cylinder and ![]() $T_{\varphi =0}$ denotes the torque specifically associated with the single-phase flow condition.
$T_{\varphi =0}$ denotes the torque specifically associated with the single-phase flow condition.
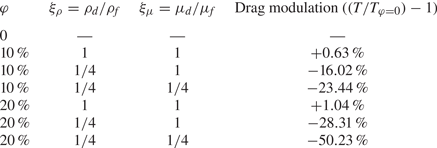
Given the similar trends in drag modulation for the dispersed phase volume fraction of ![]() $\varphi =10\,\%$ and
$\varphi =10\,\%$ and ![]() $\varphi =20\,\%$, we next focus on the case with
$\varphi =20\,\%$, we next focus on the case with ![]() $\varphi =20\,\%$. To investigate the impact of the dispersed phase on the flow field, figure 2 displays the radial profiles of the normalized azimuthal momentum and pressure calculated based on the phase distribution (see the inset figure) as a reference. When
$\varphi =20\,\%$. To investigate the impact of the dispersed phase on the flow field, figure 2 displays the radial profiles of the normalized azimuthal momentum and pressure calculated based on the phase distribution (see the inset figure) as a reference. When ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, the azimuthal momentum in the bulk region of the two-phase flow shows a slight decrease. The pressure is modulated in the region away from the inner cylinder and shows a decrease near the outer cylinder. Specifically, the modulation starts at a point where the phase fraction deviates from zero, but the modulation is insignificant overall. By reducing the density ratio
$\xi _{\mu } = 1$, the azimuthal momentum in the bulk region of the two-phase flow shows a slight decrease. The pressure is modulated in the region away from the inner cylinder and shows a decrease near the outer cylinder. Specifically, the modulation starts at a point where the phase fraction deviates from zero, but the modulation is insignificant overall. By reducing the density ratio ![]() $\xi _{\rho }$ or viscosity ratio
$\xi _{\rho }$ or viscosity ratio ![]() $\xi _{\mu }$, a notable decrease in the azimuthal momentum and pressure in the bulk region is observed, aligning with the observed drag modulation. It is revealed that the reduction in the density ratio and the viscosity ratio plays a vital role in causing this decrease. The density ratio and the viscosity ratio are identified as key factors influencing drag reduction.
$\xi _{\mu }$, a notable decrease in the azimuthal momentum and pressure in the bulk region is observed, aligning with the observed drag modulation. It is revealed that the reduction in the density ratio and the viscosity ratio plays a vital role in causing this decrease. The density ratio and the viscosity ratio are identified as key factors influencing drag reduction.

Figure 2. (a) The azimuthal momentum ![]() $\langle \rho u_\theta \rangle _{A, t}/(\rho _f u_i)$ and (b) pressure
$\langle \rho u_\theta \rangle _{A, t}/(\rho _f u_i)$ and (b) pressure ![]() $( \langle p \rangle _{A, t}- \langle p_i \rangle _{A, t})/ \langle p_{o,\varphi =0} \rangle _{A, t}$ as a function of the radial position, where
$( \langle p \rangle _{A, t}- \langle p_i \rangle _{A, t})/ \langle p_{o,\varphi =0} \rangle _{A, t}$ as a function of the radial position, where ![]() $u_\theta$ is the azimuthal velocity,
$u_\theta$ is the azimuthal velocity, ![]() $p_i$ is the pressure at the inner cylinder, and
$p_i$ is the pressure at the inner cylinder, and ![]() $p_{o,\varphi =0}$ is the pressure at the outer cylinder in single-phase flow. Correspondingly, the inset figure exhibits the radial profile of phase fraction
$p_{o,\varphi =0}$ is the pressure at the outer cylinder in single-phase flow. Correspondingly, the inset figure exhibits the radial profile of phase fraction ![]() $\langle \alpha \rangle _{A, t}$. The average operator
$\langle \alpha \rangle _{A, t}$. The average operator ![]() $\langle {\cdot } \rangle _{A, t}$ is to obtain the axially, azimuthally and time-averaged value of the quantity.
$\langle {\cdot } \rangle _{A, t}$ is to obtain the axially, azimuthally and time-averaged value of the quantity.
To investigate the effects of dispersed phase density and viscosity on the turbulent transport, we investigate the radial profile of total shear stress (figure 3a), viscous shear stress (figure 3b) and their difference (figure 3c). Due to the density difference between the dispersed and continuous phases, the Reynolds averaging is no longer applicable. We therefore adopt the Favre averaging (Favre Reference Favre1969), which applies a density-weighted average to the velocity. The difference between the total shear stress and viscous shear stress is thus written as ![]() $\tau -\tau _\mu =-{ \langle {\rho u_\theta ^{\prime \prime } u_r^{\prime \prime }} \rangle _{A, t}}$ (hereafter referred to as Favre shear stress), which could be used to characterize the turbulence term. For the two-phase flow with
$\tau -\tau _\mu =-{ \langle {\rho u_\theta ^{\prime \prime } u_r^{\prime \prime }} \rangle _{A, t}}$ (hereafter referred to as Favre shear stress), which could be used to characterize the turbulence term. For the two-phase flow with ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, the profiles of the shear stresses are nearly identical to those for the single-phase case. However, by reducing the density ratio
$\xi _{\mu } = 1$, the profiles of the shear stresses are nearly identical to those for the single-phase case. However, by reducing the density ratio ![]() $\xi _{\rho }$ or viscosity ratio
$\xi _{\rho }$ or viscosity ratio ![]() $\xi _{\mu }$, a significant decrease in the total shear stress is observed due to the decrease near the wall for the viscous shear stress and the decrease in the bulk region for the Favre shear stress, which is consistent with the observed drag reduction.
$\xi _{\mu }$, a significant decrease in the total shear stress is observed due to the decrease near the wall for the viscous shear stress and the decrease in the bulk region for the Favre shear stress, which is consistent with the observed drag reduction.
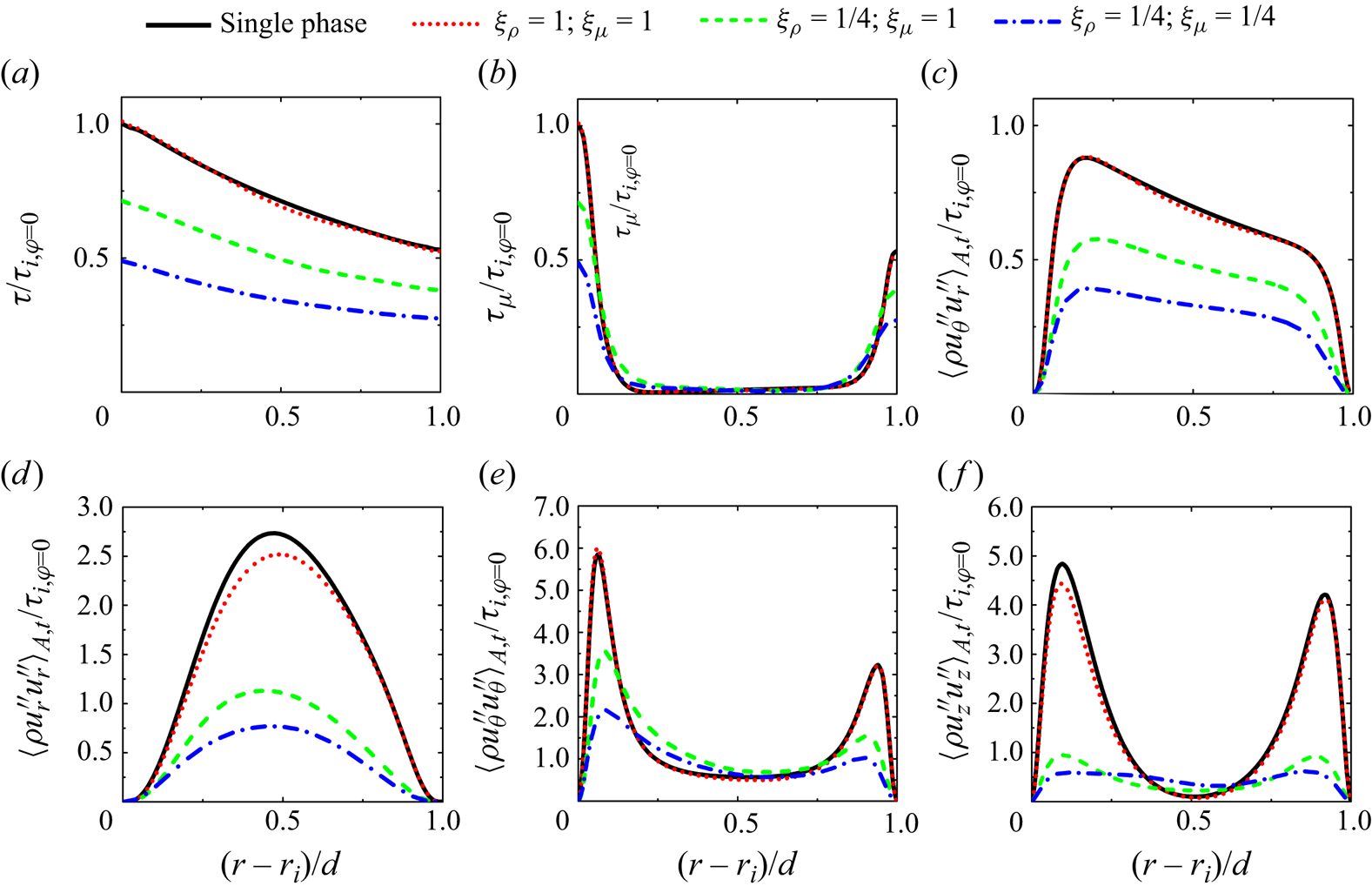
Figure 3. (a) The total shear stress ![]() $\tau /\tau _{i,\varphi =0}$, (b) viscous shear stress
$\tau /\tau _{i,\varphi =0}$, (b) viscous shear stress ![]() $\tau _\mu /\tau _{i,\varphi =0}$ and (c) Favre shear stress
$\tau _\mu /\tau _{i,\varphi =0}$ and (c) Favre shear stress ![]() $-{ \langle {\rho u_\theta ^{\prime \prime } u_r^{\prime \prime }} \rangle _{A, t}}/\tau _{i,\varphi =0}$ as a function of the radial position, where
$-{ \langle {\rho u_\theta ^{\prime \prime } u_r^{\prime \prime }} \rangle _{A, t}}/\tau _{i,\varphi =0}$ as a function of the radial position, where ![]() ${\tau }_{i,\varphi =0}$ is the total shear stress on the inner cylinder in single-phase flow. The Favre normal stresses (d)
${\tau }_{i,\varphi =0}$ is the total shear stress on the inner cylinder in single-phase flow. The Favre normal stresses (d) ![]() ${ \langle {\rho u_r^{\prime \prime } u_r^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$, (e)
${ \langle {\rho u_r^{\prime \prime } u_r^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$, (e) ![]() ${ \langle {\rho u_\theta ^{\prime \prime } u_\theta ^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$, and ( f)
${ \langle {\rho u_\theta ^{\prime \prime } u_\theta ^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$, and ( f) ![]() ${\langle {\rho u_z^{\prime \prime } u_z^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$ are also shown as a function of the radial position, where
${\langle {\rho u_z^{\prime \prime } u_z^{\prime \prime }} \rangle _{A,t}}/\tau _{i,\varphi =0}$ are also shown as a function of the radial position, where ![]() $u_r^{\prime\prime}=u_r-\langle\rho u_r\rangle_{A,t}/\langle\rho\rangle_{A,t}$,
$u_r^{\prime\prime}=u_r-\langle\rho u_r\rangle_{A,t}/\langle\rho\rangle_{A,t}$, ![]() $u_\theta^{\prime\prime}=u_\theta-\langle\rho u_\theta \rangle_{A,t}/\langle\rho\rangle_{A,t}$ and
$u_\theta^{\prime\prime}=u_\theta-\langle\rho u_\theta \rangle_{A,t}/\langle\rho\rangle_{A,t}$ and ![]() $u_z^{\prime\prime}=u_z-\langle\rho u_z\rangle_{A,t}/\langle\rho\rangle_{A,t}$ are the fluctuations of radial velocity
$u_z^{\prime\prime}=u_z-\langle\rho u_z\rangle_{A,t}/\langle\rho\rangle_{A,t}$ are the fluctuations of radial velocity ![]() $u_r$, azimuthal velocity
$u_r$, azimuthal velocity ![]() $u_\theta$ and azimuthal velocity
$u_\theta$ and azimuthal velocity ![]() $u_z$, respectively.
$u_z$, respectively.
To further study the influence of the dispersed phase on the turbulence fluctuations, we show the Favre normal stresses (figure 3d–f), which are generally investigated by the root mean square (r.m.s.) velocity fluctuations in the constant density flow system (Zhu et al. Reference Zhu, Ostilla-Mónico, Verzicco and Lohse2016; Wang et al. Reference Wang, Zhang, Wang, Li, Zhang and Li2023b). For the two-phase flow with ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, the normal stress modulation is not very significant and the profiles of the normal stresses almost coincide with those for the single-phase case. By reducing the density ratio
$\xi _{\mu } = 1$, the normal stress modulation is not very significant and the profiles of the normal stresses almost coincide with those for the single-phase case. By reducing the density ratio ![]() $\xi _{\rho }$ or viscosity ratio
$\xi _{\rho }$ or viscosity ratio ![]() $\xi _{\mu }$, there is an overall reduction in the normal stress
$\xi _{\mu }$, there is an overall reduction in the normal stress ![]() ${\langle {\rho u_r^{\prime \prime } u_r^{\prime \prime }} \rangle _{A,t}}$. The normal stress
${\langle {\rho u_r^{\prime \prime } u_r^{\prime \prime }} \rangle _{A,t}}$. The normal stress ![]() ${\langle {\rho u_\theta ^{\prime \prime } u_\theta ^{\prime \prime }} \rangle _{A,t}}$ shows a significant decrease near the inner and outer cylinders, while an increase is seen in the bulk region. A similar phenomenon has also been found in the study of the r.m.s. streamwise velocity fluctuations for polymer drag reduction systems, i.e. the r.m.s. streamwise velocity fluctuations decrease near the wall but increase away from the wall (Min et al. Reference Min, Yoo, Choi and Joseph2003; Wang et al. Reference Wang, Zhang, Wang, Li, Zhang and Li2023b). The normal stress
${\langle {\rho u_\theta ^{\prime \prime } u_\theta ^{\prime \prime }} \rangle _{A,t}}$ shows a significant decrease near the inner and outer cylinders, while an increase is seen in the bulk region. A similar phenomenon has also been found in the study of the r.m.s. streamwise velocity fluctuations for polymer drag reduction systems, i.e. the r.m.s. streamwise velocity fluctuations decrease near the wall but increase away from the wall (Min et al. Reference Min, Yoo, Choi and Joseph2003; Wang et al. Reference Wang, Zhang, Wang, Li, Zhang and Li2023b). The normal stress ![]() ${ \langle {\rho u_z^{\prime \prime } u_z^{\prime \prime }} \rangle _{A,t}}$ shows a stronger reduction, indicating that the Taylor vortex has been significantly weakened as indicated by the averaged radial–axial velocity vectors in figure 1. As a result, the drag reduction caused by decreasing the density or viscosity of the dispersed phase is accompanied by a significant decrease in turbulence fluctuations.
${ \langle {\rho u_z^{\prime \prime } u_z^{\prime \prime }} \rangle _{A,t}}$ shows a stronger reduction, indicating that the Taylor vortex has been significantly weakened as indicated by the averaged radial–axial velocity vectors in figure 1. As a result, the drag reduction caused by decreasing the density or viscosity of the dispersed phase is accompanied by a significant decrease in turbulence fluctuations.
To quantitatively characterize the effect of dispersed phase density and viscosity in drag modulation, we have derived a conserved quantity ![]() $J^\omega$ that characterizes the radial transport of azimuthal momentum in the two-phase TC turbulence,
$J^\omega$ that characterizes the radial transport of azimuthal momentum in the two-phase TC turbulence,
and provided the explicit expressions for the three terms on the right-hand side of (2.3), which are contributions from advection, diffusion and two-phase interface, respectively (see supplementary material for the detailed derivations):
These three terms are closely related to density, viscosity and interfacial tension, respectively. By normalizing (2.3) with the single-phase non-vortical laminar current ![]() $J_{lam}^\omega =2\mu _f r_i^2 r_o^2 \omega _i /(r_o^2 - r_i^2)$, we obtain the Nusselt number
$J_{lam}^\omega =2\mu _f r_i^2 r_o^2 \omega _i /(r_o^2 - r_i^2)$, we obtain the Nusselt number ![]() $Nu_{\omega } = J^\omega / J_{lam}^\omega$, which represents the overall transport of azimuthal momentum. Additionally, we can express the contributions of advection (
$Nu_{\omega } = J^\omega / J_{lam}^\omega$, which represents the overall transport of azimuthal momentum. Additionally, we can express the contributions of advection (![]() $Nu_{\omega,adv}(r)$), diffusion (
$Nu_{\omega,adv}(r)$), diffusion (![]() $Nu_{\omega,dif}(r)$) and two-phase interface (
$Nu_{\omega,dif}(r)$) and two-phase interface (![]() $Nu_{\omega,int}(r)$) as functions of the radial position
$Nu_{\omega,int}(r)$) as functions of the radial position ![]() $r$. It is well-established that the Nusselt number
$r$. It is well-established that the Nusselt number ![]() $Nu_{\omega }$ and torque
$Nu_{\omega }$ and torque ![]() $T$ in the TC system are related through the equation
$T$ in the TC system are related through the equation ![]() $T=2{\rm \pi} L J_{lam}^{\omega } Nu_\omega$ (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). This relationship offers a convenient way to effectively decouple the effects of density, viscosity and two-phase interface on drag reduction (see figure S3 in the supplementary material). Note that the advection contribution comprises both an average part and a turbulent part, with the average part being negligible compared with the turbulent part (see figure S4 in the supplementary material). Therefore, similar to that in plate flows (Picano, Breugem & Brandt Reference Picano, Breugem and Brandt2015; Wang, Jiang & Sun Reference Wang, Jiang and Sun2023a), the advection contribution may be equivalent to the turbulence contribution.
$T=2{\rm \pi} L J_{lam}^{\omega } Nu_\omega$ (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). This relationship offers a convenient way to effectively decouple the effects of density, viscosity and two-phase interface on drag reduction (see figure S3 in the supplementary material). Note that the advection contribution comprises both an average part and a turbulent part, with the average part being negligible compared with the turbulent part (see figure S4 in the supplementary material). Therefore, similar to that in plate flows (Picano, Breugem & Brandt Reference Picano, Breugem and Brandt2015; Wang, Jiang & Sun Reference Wang, Jiang and Sun2023a), the advection contribution may be equivalent to the turbulence contribution.
For the two-phase flow with ![]() $\xi _{\rho } = 1$ and
$\xi _{\rho } = 1$ and ![]() $\xi _{\mu } = 1$, the advection contribution is slightly reduced in regions where the interface contribution is relatively large (see figure 4a,c), suggesting that the two-phase interface has a subtle modulation effect on the advection processes, consistent with the conservation of azimuthal momentum transport.
$\xi _{\mu } = 1$, the advection contribution is slightly reduced in regions where the interface contribution is relatively large (see figure 4a,c), suggesting that the two-phase interface has a subtle modulation effect on the advection processes, consistent with the conservation of azimuthal momentum transport.
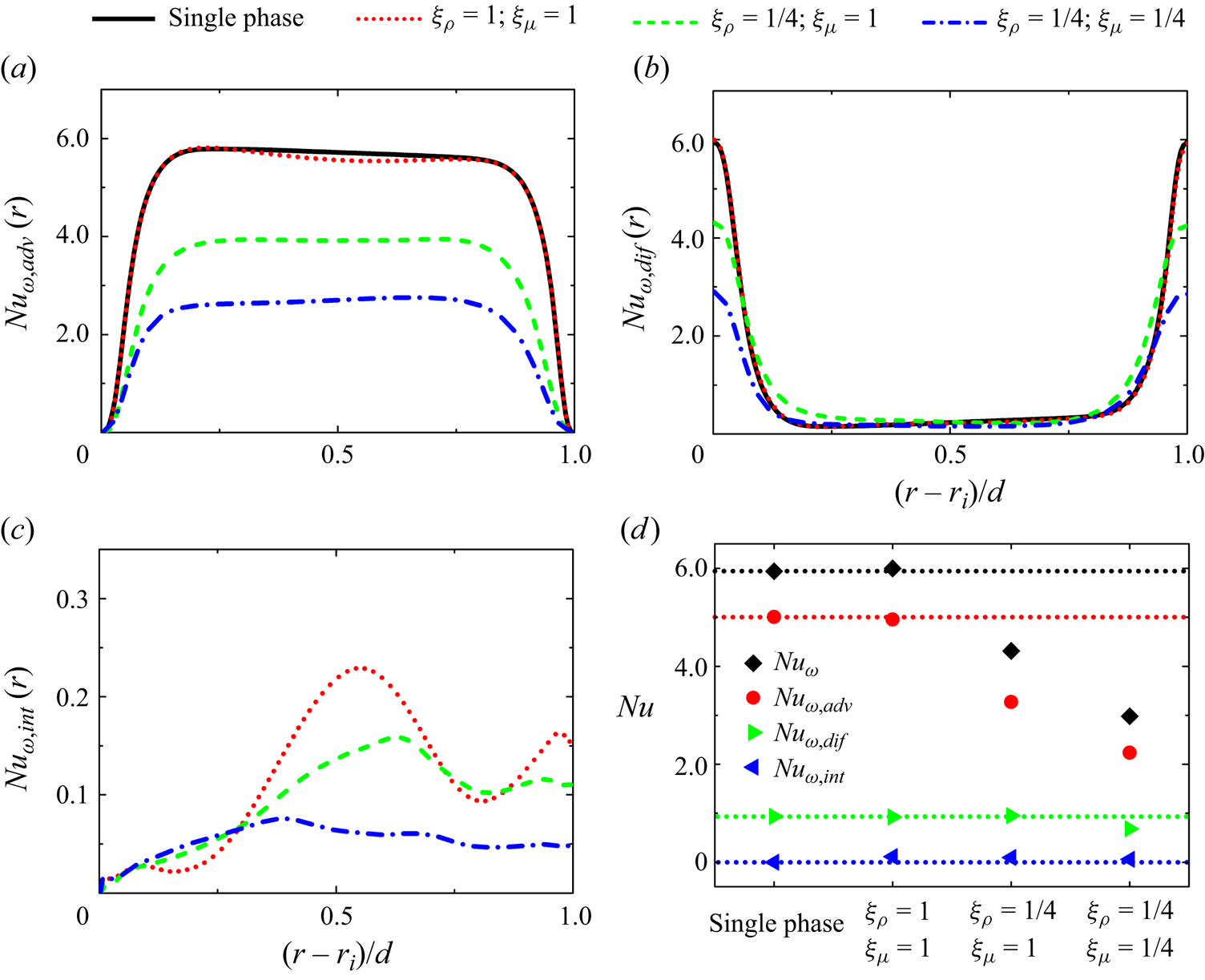
Figure 4. Momentum transport analysis. (a) The normalized advection contribution, (b) the normalized diffusion contribution and (c) the normalized interface contribution as a function of the radial position are shown. (d) The momentum transport and its three contributions are averaged in the radial direction to characterize the corresponding terms within the whole system. The dashed lines in (d) represent the averaged values for single-phase flow.
Considering the limited change in the diffusion contribution (see figure 4b), it is evident that the two-phase interface becomes the primary factor responsible for drag enhancement. In view of the insignificant effect of drag enhancement (see figure 4d), we additionally calculated a case where the Reynolds number and the surface tension coefficient are tripled, again showing the dominant role of interfacial tension in drag enhancement (see figure S5 in the supplementary material). It is important to note that the interface contribution, as shown in figures 4(c) and 4(d), is consistently positive, indicating that the two-phase interface does not contribute to drag reduction in the system. However, due to the small magnitude of the obtained interface contribution, which accounts for approximately ![]() $4\,\%$ of the conserved quantity, a more in-depth investigation specifically on this term should be conducted in future work.
$4\,\%$ of the conserved quantity, a more in-depth investigation specifically on this term should be conducted in future work.
Since the interface contribution (![]() $J_{int}^\omega (r)$) acts primarily to increase drag and is very small in our drag reduction cases (see figure 4d), we will focus on the advection (
$J_{int}^\omega (r)$) acts primarily to increase drag and is very small in our drag reduction cases (see figure 4d), we will focus on the advection (![]() $J_{adv}^\omega (r)$) and diffusion (
$J_{adv}^\omega (r)$) and diffusion (![]() $J_{dif}^\omega (r)$) contributions in the subsequent analysis. Lowering
$J_{dif}^\omega (r)$) contributions in the subsequent analysis. Lowering ![]() $\xi _{\rho }$ to 1/4 results in a reduction in the local advection contribution. The density ratio
$\xi _{\rho }$ to 1/4 results in a reduction in the local advection contribution. The density ratio ![]() $\xi _{\rho }=1/4$ promotes dispersed phase's gathering near the inner wall, which in turn leads to a significant decrease in the upstream advection contribution. This ultimately results in an overall reduction in the advection contribution (see figure 4a). Based on the conservation of momentum transport, the diffusion contribution is redistributed (see figure 4b) but the total diffusion contribution remains the same (see figure 4d). Further reducing
$\xi _{\rho }=1/4$ promotes dispersed phase's gathering near the inner wall, which in turn leads to a significant decrease in the upstream advection contribution. This ultimately results in an overall reduction in the advection contribution (see figure 4a). Based on the conservation of momentum transport, the diffusion contribution is redistributed (see figure 4b) but the total diffusion contribution remains the same (see figure 4d). Further reducing ![]() $\xi _{\mu }$ to 1/4 causes a decrease in the local diffusion contribution near the inner wall (see figure 4b), ultimately leading to a reduction in the total diffusion contribution (see figure 4d). Additionally, based on the conservation of momentum transport, the advection contribution is modulated and again overall reduced (see figure 4a). It is evident that the combination of decreasing density ratio
$\xi _{\mu }$ to 1/4 causes a decrease in the local diffusion contribution near the inner wall (see figure 4b), ultimately leading to a reduction in the total diffusion contribution (see figure 4d). Additionally, based on the conservation of momentum transport, the advection contribution is modulated and again overall reduced (see figure 4a). It is evident that the combination of decreasing density ratio ![]() $\xi _{\rho }$ and viscosity ratio
$\xi _{\rho }$ and viscosity ratio ![]() $\xi _{\mu }$ plays a dominant role in drag reduction. Therefore, the blocking effect of the dispersed phase on momentum transport is due to the decreased density and viscosity ratios. In our ongoing preliminary simulations on drag modulation in two-phase plane-Couette turbulence, we have observed similar drag modulation mechanisms. This is beyond the scope of the current work and will be systematically investigated and compared with the present study in our future work.
$\xi _{\mu }$ plays a dominant role in drag reduction. Therefore, the blocking effect of the dispersed phase on momentum transport is due to the decreased density and viscosity ratios. In our ongoing preliminary simulations on drag modulation in two-phase plane-Couette turbulence, we have observed similar drag modulation mechanisms. This is beyond the scope of the current work and will be systematically investigated and compared with the present study in our future work.
Given the generality of (2.3), our conclusion can be extended to analyse bubble drag reduction in turbulent flows (van Gils et al. Reference van Gils, Guzman, Sun and Lohse2013). Due to the extremely low density and viscosity ratios of the bubble to the continuous phase, the advection and diffusion contributions are significantly reduced, resulting in drag reduction. Meanwhile, it has been reported that bubbly drag reduction is effective when large bubbles are present, but the drag reduction effect is lost when the bubbles are reduced to small sizes after the addition of surfactants (Verschoof et al. Reference Verschoof, Van Der Veen, Sun and Lohse2016). We can provide a physical understanding of this observation. When surfactants are added to decrease the surface tension coefficient, it leads to a reduction in bubble size. However, this reduction in bubble size is accompanied by an increase in the interfacial area in the system. As a result, the interface contribution to drag, which is enhanced by the increased interfacial area, offsets the drag reduction caused by the low density and viscosity ratios. Furthermore, the decrease in bubble size also attenuates the effective centripetal Froude number exerted on the small bubbles (van Gils et al. Reference van Gils, Guzman, Sun and Lohse2013), leading to a reduced accumulation of gas near the inner wall. This can explain why the drag reduction is lost when the bubbles are shrunk to small sizes after the addition of surfactants.
3. Conclusions
In conclusion, we have derived a conserved quantity that characterizes the radial transport of azimuthal momentum in fluid–fluid two-phase TC turbulence. This conserved quantity consists of three terms: the density-related advection contribution, the viscosity-related diffusion contribution and the interface contribution. Our analysis highlights the significant roles played by two-phase interface, density and viscosity ratios in modulating drag. Specifically, decreasing the density ratio of the dispersed phase to the continuous phase reduces the local advection contribution, while decreasing the viscosity ratio reduces the local diffusion contribution. Through modulation and redistribution, these effects lead to an overall reduction in momentum transport. On the other hand, the two-phase interface consistently produces a positive contribution to drag enhancement. By considering the interplay between density ratio, viscosity ratio and two-phase interface, we conclude that drag modulation is achieved through the combined influence of these factors. The current findings contribute to a better understanding of the mechanisms underlying drag reduction in two-phase turbulent flows.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2024.206.
Funding
This work is financially supported by the National Natural Science Foundation of China under grant no. 11988102 and the New Cornerstone Science Foundation through the New Cornerstone Investigator Program and the XPLORER PRIZE.
Declaration of interests
The authors report no conflict of interest.


































