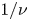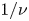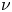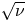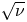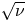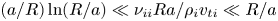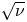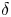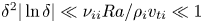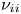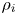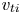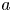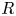1. Introduction
In stellarators, trapped particles can move a significant distance away from their initial flux surface even in the absence of collisions or turbulent fluctuations. Due to these large orbits, stellarator collisional transport at low collision frequencies (Kovrizhnykh Reference Kovrizhnykh1984) is of the order of or larger than the turbulent transport, dominating energy transport in the core (Dinklage et al. Reference Dinklage, Yokoyama, Tanaka, Velasco, López-Bruna, Beidler, Satake, Ascasíbar, Arévalo and Baldzuhn2013, Reference Dinklage, Beidler, Helander, Fuchert, Maaßberg, Rahbarnia, Pedersen, Turkin, Wolf and Alonso2018).
The width of the trapped-particle orbits is of the order of the size of the stellarator unless the stellarator is (i) optimized (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017), i.e. close to omnigeneous (Cary & Shasharina Reference Cary and Shasharina1997a,Reference Cary and Shasharinab; Parra et al. Reference Parra, Calvo, Helander and Landreman2015), or (ii) the stellarator has a small inverse aspect ratio $\epsilon := a/R \ll 1$![]() (Ho & Kulsrud Reference Ho and Kulsrud1987), where $R$
(Ho & Kulsrud Reference Ho and Kulsrud1987), where $R$![]() and $a$
and $a$![]() are the characteristic values of the major and minor radii of the stellarator, respectively.
are the characteristic values of the major and minor radii of the stellarator, respectively.
In the case of large aspect ratio stellarators, the ion orbit width is determined by the balance between the component of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift that is tangential to the flux surface, and the component of the ion curvature and $\boldsymbol {\nabla } B$
drift that is tangential to the flux surface, and the component of the ion curvature and $\boldsymbol {\nabla } B$![]() drifts that is perpendicular to the flux surface – the large $\boldsymbol {E} \times \boldsymbol {B}$
drifts that is perpendicular to the flux surface – the large $\boldsymbol {E} \times \boldsymbol {B}$![]() drift is mostly parallel to flux surfaces and its small radial component is comparable to or smaller than the average radial component of the curvature and $\boldsymbol {\nabla } B$
drift is mostly parallel to flux surfaces and its small radial component is comparable to or smaller than the average radial component of the curvature and $\boldsymbol {\nabla } B$![]() drifts (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017).
drifts (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017).
To estimate the width of the ion orbits, we assume that the electric field is the gradient of an electric potential, and that the potential has a variation of order $T_i/e$![]() across the minor radius $a$
across the minor radius $a$![]() , where $T_i$
, where $T_i$![]() is the ion temperature and $e$
is the ion temperature and $e$![]() is the proton charge. The lowest-order value of the radial electric field is set by the need to maintain ambipolarity. The $\boldsymbol {E} \times \boldsymbol {B}$
is the proton charge. The lowest-order value of the radial electric field is set by the need to maintain ambipolarity. The $\boldsymbol {E} \times \boldsymbol {B}$![]() drift is of order
drift is of order
whereas the curvature and $\boldsymbol {\nabla } B$![]() drifts are smaller by a factor of $\epsilon$
drifts are smaller by a factor of $\epsilon$![]() because they are proportional to the gradient of the magnetic field $\boldsymbol {B}$
because they are proportional to the gradient of the magnetic field $\boldsymbol {B}$![]() , $|\boldsymbol {\nabla } \boldsymbol {B}| \sim B/R$
, $|\boldsymbol {\nabla } \boldsymbol {B}| \sim B/R$![]() ,
,
Here
is the normalized ion gyroradius, $\rho _i := v_{ti}/\varOmega _i$![]() is the ion gyroradius, $v_{ti} := \sqrt {2T_i/m_i}$
is the ion gyroradius, $v_{ti} := \sqrt {2T_i/m_i}$![]() is the ion thermal speed, $\varOmega _i := Z_ieB / m_i c$
is the ion thermal speed, $\varOmega _i := Z_ieB / m_i c$![]() is the ion gyrofrequency, $B := |\boldsymbol {B}|$
is the ion gyrofrequency, $B := |\boldsymbol {B}|$![]() is the magnitude of the magnetic field, $Z_i e$
is the magnitude of the magnetic field, $Z_i e$![]() and $m_i$
and $m_i$![]() are the ion charge and mass, respectively, and $c$
are the ion charge and mass, respectively, and $c$![]() is the speed of light. The radial motion due to the drifts is not secular because it averages out once the $\boldsymbol {E} \times \boldsymbol {B}$
is the speed of light. The radial motion due to the drifts is not secular because it averages out once the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift has moved the particle several times around the stellarator. The typical length of the orbit parallel to the flux surfaces is of order $a$
drift has moved the particle several times around the stellarator. The typical length of the orbit parallel to the flux surfaces is of order $a$![]() , giving a characteristic orbital time of the order of
, giving a characteristic orbital time of the order of
During this time interval, the radial component of the curvature and $\boldsymbol {\nabla } B$![]() drifts (and, in some cases, the $\boldsymbol {E} \times \boldsymbol {B}$
drifts (and, in some cases, the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift) leads to an orbit width of order
drift) leads to an orbit width of order
that is, the width of these orbits is smaller than the characteristic size of the stellarator, although it is much larger than the typical width of orbits in tokamaks, of order $\rho _i$![]() .
.
For small collision frequencies (see (1.6) for a precise ordering for the collision frequency), the large width of the trapped-particle orbits has called into question the validity of local models for neoclassical transport. Here, ‘local’ refers to models that calculate neoclassical fluxes through a surface of interest using only the electric field, the magnetic field and certain radial gradients of the magnetic field at that flux surface, whereas ‘global’ codes need the electric and magnetic field of the flux surfaces neighbouring the flux surface of interest. The most naive way to obtain a local model is to zero out the radial component of the drifts in certain terms of the drift kinetic equation (Sugama et al. Reference Sugama, Matsuoka, Satake and Kanno2016; Paul et al. Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017), but it has been noted that there are different ways in which this could be done, none of them necessarily consistent (Paul et al. Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017). Moreover, global neoclassical codes (Satake et al. Reference Satake, Okamoto, Nakajima, Sugama and Yokoyama2006) have shown that neoclassical fluxes depend on parameters that do not appear in simplified drift kinetic models without radial drifts, such as the magnetic shear (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) used closeness to omnigeneity to derive local orbit-averaged equations without having to artificially zero out the radial magnetic drifts. In this article, we use another expansion parameter, the inverse aspect ratio, to derive a different set of self-consistent local orbit-averaged equations that is valid for a wide class of stellarators: large aspect ratio stellarators with a mirror ratio close to unity. In our derivation, we do not start by assuming that the distribution function is Maxwellian or that the problem can be solved using a local equation, but we derive these properties from the expansion. The equations presented in this article coincide with the low collisionality limit of the equations in the DKES code (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986) to lowest order in the small inverse aspect ratio expansion, but differ to higher order. The radial energy flux derived from the new equations in this paper, calculated using a modified version of the code KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra and García-Regaña2020, Reference Velasco, Calvo, Parra, d'Herbemont, Smith, Carralero and Estrada2021), has been shown to be close to the energy flux calculated by DKES in several experimentally relevant configurations (Velasco et al. Reference Velasco, Calvo, Parra, d'Herbemont, Smith, Carralero and Estrada2021).
There is a subtlety in the derivation of the orbit-averaged equations for large aspect ratio stellarators with mirror ratios close to unity. Given the smallness of the orbit width in $\epsilon$![]() , it is tempting to neglect the radial drifts when calculating the lowest-order particle motion. However, in large aspect ratio stellarators with mirror ratios close to unity, the radial displacement of the particles is sufficiently large to affect the trapped-particle motion to lowest order. Indeed, trapped particles in this type of large aspect ratio stellarators have very small parallel velocities of order $\sqrt {\epsilon } v_{ti}$
, it is tempting to neglect the radial drifts when calculating the lowest-order particle motion. However, in large aspect ratio stellarators with mirror ratios close to unity, the radial displacement of the particles is sufficiently large to affect the trapped-particle motion to lowest order. Indeed, trapped particles in this type of large aspect ratio stellarators have very small parallel velocities of order $\sqrt {\epsilon } v_{ti}$![]() , and small changes in energy of order $\epsilon T_i$
, and small changes in energy of order $\epsilon T_i$![]() affect their trajectories, causing trapped particles to become passing and vice versa. Radial displacements of order $\epsilon a$
affect their trajectories, causing trapped particles to become passing and vice versa. Radial displacements of order $\epsilon a$![]() are small compared with the size of the stellarator, but they lead to changes in energy of order $\epsilon T_i$
are small compared with the size of the stellarator, but they lead to changes in energy of order $\epsilon T_i$![]() due to the work done by the radial electric field. Our new equations keep the necessary finite orbit width effects by using the second adiabatic invariant as a velocity-space coordinate.
due to the work done by the radial electric field. Our new equations keep the necessary finite orbit width effects by using the second adiabatic invariant as a velocity-space coordinate.
Our derivation of a local model is valid for collisionalities as small as
where
is the collisionality,

is the ion–ion collision frequency (Braginskii Reference Braginskii1958), $n_i$![]() is the ion density and $\ln \varLambda$
is the ion density and $\ln \varLambda$![]() is the Coulomb logarithm. We analyse the behaviour of our new equations for large aspect ratio stellarators with mirror ratios close to unity in the limit $\nu _{i*} \gg \rho _{i*}$
is the Coulomb logarithm. We analyse the behaviour of our new equations for large aspect ratio stellarators with mirror ratios close to unity in the limit $\nu _{i*} \gg \rho _{i*}$![]() , in which we recover the $1/\nu$
, in which we recover the $1/\nu$![]() regime (Ho & Kulsrud Reference Ho and Kulsrud1987), and in the limit $\nu _{i*} \ll \rho _{i*}$
regime (Ho & Kulsrud Reference Ho and Kulsrud1987), and in the limit $\nu _{i*} \ll \rho _{i*}$![]() . Surprisingly, for $\nu _{i*} \ll \rho _{i*}$
. Surprisingly, for $\nu _{i*} \ll \rho _{i*}$![]() , a rigorous expansion of our equations does not lead to the $\sqrt {\nu }$
, a rigorous expansion of our equations does not lead to the $\sqrt {\nu }$![]() regime (Galeev et al. Reference Galeev, Sadgeev, Furth and Rosenbluth1969) for generic large aspect ratio stellarators with mirror ratio close to unity. Instead, the limit $\nu _{i*} \ll \rho _{i*}$
regime (Galeev et al. Reference Galeev, Sadgeev, Furth and Rosenbluth1969) for generic large aspect ratio stellarators with mirror ratio close to unity. Instead, the limit $\nu _{i*} \ll \rho _{i*}$![]() gives the $\nu$
gives the $\nu$![]() regime (Mynick Reference Mynick1983). In this regime, particles follow their collisionless orbits for long times, moving away from their initial flux surface a distance of order $\epsilon a$
regime (Mynick Reference Mynick1983). In this regime, particles follow their collisionless orbits for long times, moving away from their initial flux surface a distance of order $\epsilon a$![]() , as explained above. Particles can only move to a flux surface further away than $\epsilon a$
, as explained above. Particles can only move to a flux surface further away than $\epsilon a$![]() by having several collisions interrupt their orbits, thus leading to a radial flux that is proportional to the collision frequency. Importantly, trapped particles remain a distance of order $\epsilon a$
by having several collisions interrupt their orbits, thus leading to a radial flux that is proportional to the collision frequency. Importantly, trapped particles remain a distance of order $\epsilon a$![]() away from their initial flux surface even when they undergo transitions between different types of wells and these transitions make their motion stochastic (Beidler, Hitchon & Shohet Reference Beidler, Hitchon and Shohet1987). To treat these transitions between different types of wells, we do not need to introduce in the equations the transition probabilities calculated by Cary, Escande & Tennyson (Reference Cary, Escande and Tennyson1986).
away from their initial flux surface even when they undergo transitions between different types of wells and these transitions make their motion stochastic (Beidler, Hitchon & Shohet Reference Beidler, Hitchon and Shohet1987). To treat these transitions between different types of wells, we do not need to introduce in the equations the transition probabilities calculated by Cary, Escande & Tennyson (Reference Cary, Escande and Tennyson1986).
There is a class of stellarators for which the $\sqrt {\nu }$![]() regime exists for $\nu _{i*} \ll \rho _{i*}$
regime exists for $\nu _{i*} \ll \rho _{i*}$![]() : stellarators close to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). In stellarators far from omnigeneity, the transitions between different types of wells of certain trapped particles smear out the $\sqrt {\nu }$
: stellarators close to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). In stellarators far from omnigeneity, the transitions between different types of wells of certain trapped particles smear out the $\sqrt {\nu }$![]() velocity-space boundary layer (Mynick Reference Mynick1983). We show that large aspect ratio stellarators with large mirror ratios are close to omnigeneity and hence neoclassical transport in them can be calculated using the equations derived by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). We also consider large aspect ratio stellarators with mirror ratios close to unity that are close to omnigeneity, finding results that are consistent with our previous work on this area (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018).
velocity-space boundary layer (Mynick Reference Mynick1983). We show that large aspect ratio stellarators with large mirror ratios are close to omnigeneity and hence neoclassical transport in them can be calculated using the equations derived by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). We also consider large aspect ratio stellarators with mirror ratios close to unity that are close to omnigeneity, finding results that are consistent with our previous work on this area (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018).
Throughout the paper we focus on ion transport. In § 2 we remind the reader of the kinetic equations for a general stellarator in the limit $\nu _{i*} \sim \rho _{i*} \ll 1$![]() . In § 3 we discuss the MagnetoHydroDynamic (MHD) equilibrium equations for $\epsilon \ll 1$
. In § 3 we discuss the MagnetoHydroDynamic (MHD) equilibrium equations for $\epsilon \ll 1$![]() , making a distinction between large aspect ratio stellarators with mirror ratios close to unity and large aspect ratio stellarators with large mirror ratios. Most of the rest of the paper is dedicated to large aspect ratio stellarators with mirror ratios close to unity, with the only exception being § 8.1. In § 4 we propose a new set of velocity-space coordinates that are necessary to simplify the expansion in $\epsilon \ll 1$
, making a distinction between large aspect ratio stellarators with mirror ratios close to unity and large aspect ratio stellarators with large mirror ratios. Most of the rest of the paper is dedicated to large aspect ratio stellarators with mirror ratios close to unity, with the only exception being § 8.1. In § 4 we propose a new set of velocity-space coordinates that are necessary to simplify the expansion in $\epsilon \ll 1$![]() for large aspect ratio stellarators with mirror ratios close to unity, and in § 5 we finally perform the expansion in $\epsilon$
for large aspect ratio stellarators with mirror ratios close to unity, and in § 5 we finally perform the expansion in $\epsilon$![]() for the ion distribution function and the electric potential in this type of large aspect ratio stellarators. In §§ 6 and 7 we study the cases $\nu _{i*} \gg \rho _{i*}$
for the ion distribution function and the electric potential in this type of large aspect ratio stellarators. In §§ 6 and 7 we study the cases $\nu _{i*} \gg \rho _{i*}$![]() and $\nu _{i*} \ll \rho _{i*}$
and $\nu _{i*} \ll \rho _{i*}$![]() for large aspect ratio stellarators with mirror ratios close to unity. In § 8 we consider large aspect ratio stellarators close to omnigeneity. We divide our discussion of large aspect ratio stellarators close to omnigeneity into two parts: in one we show that large aspect ratio stellarators with large mirror ratios are close to omnigeneity, and in the other, we study optimized large aspect ratio stellarators with mirror ratios close to unity. We conclude in § 9.
for large aspect ratio stellarators with mirror ratios close to unity. In § 8 we consider large aspect ratio stellarators close to omnigeneity. We divide our discussion of large aspect ratio stellarators close to omnigeneity into two parts: in one we show that large aspect ratio stellarators with large mirror ratios are close to omnigeneity, and in the other, we study optimized large aspect ratio stellarators with mirror ratios close to unity. We conclude in § 9.
2. Drift kinetic equation for ions in a generic stellarator
We assume $a \sim R$![]() in this section, but we keep the distinction between $a$
in this section, but we keep the distinction between $a$![]() and $R$
and $R$![]() in our estimates in preparation for the expansion in small inverse aspect ratio in §§ 3, 4, 5 and 8.
in our estimates in preparation for the expansion in small inverse aspect ratio in §§ 3, 4, 5 and 8.
We assume that the magnetic field $\boldsymbol {B}$![]() is constant in time and hence the electric field $\boldsymbol {E}$
is constant in time and hence the electric field $\boldsymbol {E}$![]() satisfies $\boldsymbol {E}(\boldsymbol {x}, t) = - \boldsymbol {\nabla } \phi (\boldsymbol {x}, t)$
satisfies $\boldsymbol {E}(\boldsymbol {x}, t) = - \boldsymbol {\nabla } \phi (\boldsymbol {x}, t)$![]() . The electric potential $\phi$
. The electric potential $\phi$![]() is of order $T_i/e$
is of order $T_i/e$![]() , has a characteristic length scale of the order of the minor radius $a$
, has a characteristic length scale of the order of the minor radius $a$![]() , and is determined by the quasineutrality equation
, and is determined by the quasineutrality equation
where $f_i (\boldsymbol {x}, \boldsymbol {v}, t)$![]() and $f_e(\boldsymbol {x}, \boldsymbol {v}, t)$
and $f_e(\boldsymbol {x}, \boldsymbol {v}, t)$![]() are the distribution functions of ions and electrons, $\boldsymbol {x}$
are the distribution functions of ions and electrons, $\boldsymbol {x}$![]() and $\boldsymbol {v}$
and $\boldsymbol {v}$![]() are the particle's Cartesian position and velocity, and $t$
are the particle's Cartesian position and velocity, and $t$![]() is time. Throughout the paper, we assume that the electrons can be modelled with the modified Maxwell–Boltzmann response
is time. Throughout the paper, we assume that the electrons can be modelled with the modified Maxwell–Boltzmann response
where $T_e (r, t)$![]() is the temperature of the electrons and $\hat {n}_e(r, t)$
is the temperature of the electrons and $\hat {n}_e(r, t)$![]() is the density of electrons in the absence of $\phi$
is the density of electrons in the absence of $\phi$![]() . Note that $\hat {n}_e$
. Note that $\hat {n}_e$![]() and $T_e$
and $T_e$![]() are flux functions that only depend on the flux surface label $r(\boldsymbol {x})$
are flux functions that only depend on the flux surface label $r(\boldsymbol {x})$![]() . We define $r$
. We define $r$![]() more carefully below.
more carefully below.
We use the drift kinetic equation (Hazeltine Reference Hazeltine1973) to obtain the ion distribution function. To describe velocity space, we choose the coordinates $\{ \mathcal {E}, \mu, \sigma, \varphi \}$![]() , where $\mathcal {E} :=v^{2}/2 +Z_i e \phi /m_i$
, where $\mathcal {E} :=v^{2}/2 +Z_i e \phi /m_i$![]() is the total energy per unit mass, $\mu :=v_\perp ^{2} /2B$
is the total energy per unit mass, $\mu :=v_\perp ^{2} /2B$![]() is the magnetic moment, $\sigma$
is the magnetic moment, $\sigma$![]() is the sign of the parallel velocity and $\varphi$
is the sign of the parallel velocity and $\varphi$![]() is the gyrophase, defined such that
is the gyrophase, defined such that
Here, $\boldsymbol {v}_\perp$![]() is the component of $\boldsymbol {v}$
is the component of $\boldsymbol {v}$![]() perpendicular to the magnetic field, $v_\perp := |\boldsymbol {v}_\perp |$
perpendicular to the magnetic field, $v_\perp := |\boldsymbol {v}_\perp |$![]() and $\hat {\boldsymbol {e}}_1(\boldsymbol {x})$
and $\hat {\boldsymbol {e}}_1(\boldsymbol {x})$![]() and $\hat {\boldsymbol {e}}_2(\boldsymbol {x})$
and $\hat {\boldsymbol {e}}_2(\boldsymbol {x})$![]() are two unit vectors that form an orthonormal basis with the unit vector parallel to the magnetic field $\hat {\boldsymbol {b}}(\boldsymbol {x}) = \boldsymbol {B}/B$
are two unit vectors that form an orthonormal basis with the unit vector parallel to the magnetic field $\hat {\boldsymbol {b}}(\boldsymbol {x}) = \boldsymbol {B}/B$![]() and satisfy $\hat {\boldsymbol {e}}_1 \times \hat {\boldsymbol {e}}_2 = \hat {\boldsymbol {b}}$
and satisfy $\hat {\boldsymbol {e}}_1 \times \hat {\boldsymbol {e}}_2 = \hat {\boldsymbol {b}}$![]() . In the coordinates $\{ \mathcal {E}, \mu, \sigma, \varphi \}$
. In the coordinates $\{ \mathcal {E}, \mu, \sigma, \varphi \}$![]() , the velocity-space volume element is
, the velocity-space volume element is
where

is the parallel velocity.
The distribution function can be split into its gyroaverage, $\bar {f}_i := (2{\rm \pi} )^{-1} \int _0^{2{\rm \pi} } f_i\, \mathrm {d} \varphi$![]() , and the gyrophase-dependent piece $\tilde {f}_i := f_i - \bar {f}_i$
, and the gyrophase-dependent piece $\tilde {f}_i := f_i - \bar {f}_i$![]() . The gyrophase-dependent piece is of order $\rho _{i*} \bar {f}_i$
. The gyrophase-dependent piece is of order $\rho _{i*} \bar {f}_i$![]() and can be neglected in the limit $\rho _{i*} \sim \nu _{i*}$
and can be neglected in the limit $\rho _{i*} \sim \nu _{i*}$![]() because the fluxes of particles and energy depend to lowest order on the much larger gyroaveraged piece $\bar {f}_i$
because the fluxes of particles and energy depend to lowest order on the much larger gyroaveraged piece $\bar {f}_i$![]() , unlike the fluxes in the neoclassical regimes of moderate collisionality ($\nu _{i*} \sim 1$
, unlike the fluxes in the neoclassical regimes of moderate collisionality ($\nu _{i*} \sim 1$![]() ) in which the piece of the gyroaveraged distribution function that matters for transport is small in $\rho _{i*}$
) in which the piece of the gyroaveraged distribution function that matters for transport is small in $\rho _{i*}$![]() (see the discussion at the end of this section for more details). Since the ion–electron collisions can be neglected within an expansion in the electron-to-ion mass ratio, the equation for $\bar {f}_i$
(see the discussion at the end of this section for more details). Since the ion–electron collisions can be neglected within an expansion in the electron-to-ion mass ratio, the equation for $\bar {f}_i$![]() is
is
Here, $S_i$![]() is a source term representing fuelling and heating, and $\bar {S}_i$
is a source term representing fuelling and heating, and $\bar {S}_i$![]() is the gyroaverage of $S_i$
is the gyroaverage of $S_i$![]() . The particle motion can be split into parallel motion and perpendicular drifts,
. The particle motion can be split into parallel motion and perpendicular drifts,
where
are the curvature and $\boldsymbol {\nabla } B$![]() drifts, collectively known as magnetic drift, $\boldsymbol {\kappa } := \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } \hat {\boldsymbol {b}}$
drifts, collectively known as magnetic drift, $\boldsymbol {\kappa } := \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } \hat {\boldsymbol {b}}$![]() is the curvature of the magnetic field lines and
is the curvature of the magnetic field lines and
is the $\boldsymbol {E}\times \boldsymbol {B}$![]() drift. The time derivative of the total energy is
drift. The time derivative of the total energy is
The time derivative of the magnetic moment is
The ion–ion collision operator $C_{ii}$![]() is a Fokker–Planck collision operator,
is a Fokker–Planck collision operator,
where $\gamma _{ii} := 2{\rm \pi} Z_i^{4} e^{4} \ln \varLambda /m_i^{2}$![]() , and the Rosenbluth potentials $H$
, and the Rosenbluth potentials $H$![]() and $L$
and $L$![]() (Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957) are the functionals
(Rosenbluth, MacDonald & Judd Reference Rosenbluth, MacDonald and Judd1957) are the functionals
and
Note that, in our notation, the first argument of $C_{ii}$![]() refers to the distribution function that is evaluated at the velocity $\boldsymbol {v}$
refers to the distribution function that is evaluated at the velocity $\boldsymbol {v}$![]() of interest, whereas the second argument refers to the distribution function that is integrated to obtain the Rosenbluth potentials. In the coordinates $\{ \mathcal {E}, \mu, \sigma, \varphi \}$
of interest, whereas the second argument refers to the distribution function that is integrated to obtain the Rosenbluth potentials. In the coordinates $\{ \mathcal {E}, \mu, \sigma, \varphi \}$![]() , the Fokker–Planck collision operator is given by
, the Fokker–Planck collision operator is given by

where we have used the fact that $f_a$![]() does not depend on the gyrophase $\varphi$
does not depend on the gyrophase $\varphi$![]() , and we have defined $H_{pq} [f] := \boldsymbol {\nabla }_v p \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [f] \boldsymbol {\cdot } \boldsymbol {\nabla }_v q$
, and we have defined $H_{pq} [f] := \boldsymbol {\nabla }_v p \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [f] \boldsymbol {\cdot } \boldsymbol {\nabla }_v q$![]() and $L_p [ f] := \boldsymbol {\nabla }_v p \boldsymbol {\cdot } \boldsymbol {\nabla }_v L [f]$
and $L_p [ f] := \boldsymbol {\nabla }_v p \boldsymbol {\cdot } \boldsymbol {\nabla }_v L [f]$![]() , with $p = \mathcal {E}, \mu$
, with $p = \mathcal {E}, \mu$![]() and $q = \mathcal {E}, \mu$
and $q = \mathcal {E}, \mu$![]() . Note that, in (2.7), (2.10), (2.11) and on the right-hand side of (2.6), we have indicated the size of terms associated with the gyrophase-dependent piece of the distribution function $\tilde {f}_i \sim \rho _{i\ast } \bar {f}_i$
. Note that, in (2.7), (2.10), (2.11) and on the right-hand side of (2.6), we have indicated the size of terms associated with the gyrophase-dependent piece of the distribution function $\tilde {f}_i \sim \rho _{i\ast } \bar {f}_i$![]() that we have neglected – the errors in the collision operator $C_{ii}$
that we have neglected – the errors in the collision operator $C_{ii}$![]() are smaller than expected due to its gyrotropy.
are smaller than expected due to its gyrotropy.
Instead of the Cartesian coordinates $\boldsymbol {x}$![]() , it is convenient to use spatial coordinates that conform to the shape of the magnetic field. From here on, we use $\{ r, \alpha, l \}$
, it is convenient to use spatial coordinates that conform to the shape of the magnetic field. From here on, we use $\{ r, \alpha, l \}$![]() , where $r$
, where $r$![]() is a flux surface label with units of length and of the order of the minor radius $a$
is a flux surface label with units of length and of the order of the minor radius $a$![]() , $\alpha$
, $\alpha$![]() is a poloidal angle that labels magnetic field lines on a given flux surface and $l$
is a poloidal angle that labels magnetic field lines on a given flux surface and $l$![]() is the arc length of the magnetic field line and is used to determine the position along the field line. In these coordinates, the magnetic field can be written as
is the arc length of the magnetic field line and is used to determine the position along the field line. In these coordinates, the magnetic field can be written as
where $\varPsi _t(r)$![]() is the toroidal magnetic flux within the flux surface $r$
is the toroidal magnetic flux within the flux surface $r$![]() divided by $2{\rm \pi}$
divided by $2{\rm \pi}$![]() , and $\varPsi _t^{\prime } := \mathrm {d} \varPsi _t/\mathrm {d} r$
, and $\varPsi _t^{\prime } := \mathrm {d} \varPsi _t/\mathrm {d} r$![]() . In these coordinates, the unit vector $\hat {\boldsymbol {b}}$
. In these coordinates, the unit vector $\hat {\boldsymbol {b}}$![]() is given by
is given by
and the element of volume is
The equations for general stellarators with $\nu _{i*} \sim \rho _{i*}$![]() were derived in § 3.1 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Here, we generalize the work done in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), and change the presentation in places to make the derivation of the large aspect ratio stellarator equations easier. We remind the reader that in this section we assume $\epsilon \sim 1$
were derived in § 3.1 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). Here, we generalize the work done in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), and change the presentation in places to make the derivation of the large aspect ratio stellarator equations easier. We remind the reader that in this section we assume $\epsilon \sim 1$![]() , but that we will perform a subsidiary expansion in $\epsilon \ll 1$
, but that we will perform a subsidiary expansion in $\epsilon \ll 1$![]() in the rest of the paper. We expand the drift kinetic system of equations in $\rho _{i*}\ll 1$
in the rest of the paper. We expand the drift kinetic system of equations in $\rho _{i*}\ll 1$![]() assuming $\nu _{i*} \sim \rho _{i*}$
assuming $\nu _{i*} \sim \rho _{i*}$![]() and
and
Our assumption for the size of the time derivative and the source $S_i$![]() might be surprising, but it is justified by the fact that the final equation is consistent. Physically, these estimates are the result of the particle orbits being comparable to the size of the device. Thus, the time derivative and the source must compensate for both direct particle losses ($\partial _t \sim S_i/f_i \sim \rho _{i\ast } v_{ti}/R$
might be surprising, but it is justified by the fact that the final equation is consistent. Physically, these estimates are the result of the particle orbits being comparable to the size of the device. Thus, the time derivative and the source must compensate for both direct particle losses ($\partial _t \sim S_i/f_i \sim \rho _{i\ast } v_{ti}/R$![]() ) and, for particles in confined orbits, losses due to collisions ($\partial _t \sim S_i/f_i \sim \nu _{ii}$
) and, for particles in confined orbits, losses due to collisions ($\partial _t \sim S_i/f_i \sim \nu _{ii}$![]() ). With these assumptions, we can write $\bar {f}_i$
). With these assumptions, we can write $\bar {f}_i$![]() as
as
with $\bar {f}_{i}^{(n)}\sim \rho _{i*}^{n} \bar {f}_{i}^{(0)}$![]() . To lowest order in $\rho _{i*}$
. To lowest order in $\rho _{i*}$![]() , (2.6) gives
, (2.6) gives
To solve this equation, we need to distinguish between passing and trapped particles. The function
is an effective potential for the motion parallel to the magnetic field line. If $\mathcal {E}$![]() is larger than the maximum of $U$
is larger than the maximum of $U$![]() on a flux surface, $U_M (r, \mu, t)$
on a flux surface, $U_M (r, \mu, t)$![]() , the parallel velocity in (2.5) never vanishes and the particle is a passing particle. If $\mathcal {E}$
, the parallel velocity in (2.5) never vanishes and the particle is a passing particle. If $\mathcal {E}$![]() is smaller than $U_M (r, \mu, t)$
is smaller than $U_M (r, \mu, t)$![]() , the parallel velocity vanishes at least at two bounce points, $l_{bL,W} (r, \alpha, \mathcal {E}, \mu, t)$
, the parallel velocity vanishes at least at two bounce points, $l_{bL,W} (r, \alpha, \mathcal {E}, \mu, t)$![]() and $l_{bR,W}(r, \alpha, \mathcal {E}, \mu, t)$
and $l_{bR,W}(r, \alpha, \mathcal {E}, \mu, t)$![]() , defined by $\mathcal {E} - U(r, \alpha, l_{bL,W}, \mu, t) = 0 = \mathcal {E} - U(r, \alpha, l_{bR,W}, \mu, t)$
, defined by $\mathcal {E} - U(r, \alpha, l_{bL,W}, \mu, t) = 0 = \mathcal {E} - U(r, \alpha, l_{bR,W}, \mu, t)$![]() (the subscripts $L$
(the subscripts $L$![]() and $R$
and $R$![]() refer to ‘left’ and ‘right’, respectively; see figure 1). Note that, for given values of $\mathcal {E}$
refer to ‘left’ and ‘right’, respectively; see figure 1). Note that, for given values of $\mathcal {E}$![]() and $\mu$
and $\mu$![]() , a trapped particle can be located inside several different $U$
, a trapped particle can be located inside several different $U$![]() wells. We will use the discrete index $W$
wells. We will use the discrete index $W$![]() to distinguish between these wells, where $W$
to distinguish between these wells, where $W$![]() takes Roman numeral values (see figure 1).
takes Roman numeral values (see figure 1).

Figure 1. Sketch of the effective potential $U := \mu B + Z_i e \phi /m_i$![]() as a function of $l$
as a function of $l$![]() .
.
On an ergodic flux surface where a single field line connects any two points, (2.21) implies that $\bar {f}_{i}^{(0)}$![]() must be independent of $\alpha$
must be independent of $\alpha$![]() for passing particles. For trapped particles, due to continuity at the bounce points $l_{bL,W}$
for passing particles. For trapped particles, due to continuity at the bounce points $l_{bL,W}$![]() and $l_{bR,W}$
and $l_{bR,W}$![]() and (2.21), $\bar {f}_i^{(0)}$
and (2.21), $\bar {f}_i^{(0)}$![]() cannot depend on $\sigma$
cannot depend on $\sigma$![]() . Using these conditions, we write $\bar {f}_i^{(0)}$
. Using these conditions, we write $\bar {f}_i^{(0)}$![]() as
as
where $g_{i,W}$![]() is defined only in the trapped-particle region, $\mathcal {E} \leq U_M(r, \mu, t)$
is defined only in the trapped-particle region, $\mathcal {E} \leq U_M(r, \mu, t)$![]() , and $h_i$
, and $h_i$![]() is defined only in the passing-particle region, $\mathcal {E} > U_M(r, \mu, t)$
is defined only in the passing-particle region, $\mathcal {E} > U_M(r, \mu, t)$![]() . In most of this article, we will consider stellarators in which the effective potential $U$
. In most of this article, we will consider stellarators in which the effective potential $U$![]() only reaches the maximum value $U_M(r, \mu, t)$
only reaches the maximum value $U_M(r, \mu, t)$![]() at a finite number of points on the flux surface $r$
at a finite number of points on the flux surface $r$![]() (the exception is § 8, where we discuss a case with contours $U = U_M$
(the exception is § 8, where we discuss a case with contours $U = U_M$![]() that are lines that wrap around the flux surface: the omnigeneous stellarator). In an ergodic flux surface where the value $U_M$
that are lines that wrap around the flux surface: the omnigeneous stellarator). In an ergodic flux surface where the value $U_M$![]() is only reached at a finite number of points, there is one barely trapped particle orbit with $\mathcal {E} = U_M$
is only reached at a finite number of points, there is one barely trapped particle orbit with $\mathcal {E} = U_M$![]() that covers the entire flux surface between its two bounce points (except for possibly a subset of points that has no area, i.e. a segment of magnetic field line of finite length might connect two of the maxima of $U$
that covers the entire flux surface between its two bounce points (except for possibly a subset of points that has no area, i.e. a segment of magnetic field line of finite length might connect two of the maxima of $U$![]() , but not all of them). If a surface-covering barely-trapped-particle orbit did not exist, we would be able to join all the points with $U = U_M$
, but not all of them). If a surface-covering barely-trapped-particle orbit did not exist, we would be able to join all the points with $U = U_M$![]() with a single magnetic field line that closes on itself, contradicting the initial assumption that the surface is ergodic. We denote the well index of this surface-covering barely trapped particle as $W_\mathrm {bt}$
with a single magnetic field line that closes on itself, contradicting the initial assumption that the surface is ergodic. We denote the well index of this surface-covering barely trapped particle as $W_\mathrm {bt}$![]() . For $W = W_\mathrm {bt}$
. For $W = W_\mathrm {bt}$![]() and $\mathcal {E} = U_M$
and $\mathcal {E} = U_M$![]() , $g_{i,W}$
, $g_{i,W}$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() , and we can impose the boundary conditions
, and we can impose the boundary conditions
and
These conditions imply that $h_i$![]() cannot depend on $\sigma$
cannot depend on $\sigma$![]() at $\mathcal {E} = U_M$
at $\mathcal {E} = U_M$![]() .
.
To next order in $\rho _{i*}$![]() , (2.6) gives
, (2.6) gives

We proceed to eliminate $\bar {f}_i^{(1)}$![]() from the equation. For trapped particles, we divide equation (2.26) by $|v_\parallel |$
from the equation. For trapped particles, we divide equation (2.26) by $|v_\parallel |$![]() , sum over the two possible values of $\sigma$
, sum over the two possible values of $\sigma$![]() and integrate over $l$
and integrate over $l$![]() between bounce points to obtain
between bounce points to obtain

where we have used the transit average

and

is the period of a trapped-particle orbit. For passing particles, we divide equation (2.26) by $|v_\||$![]() and we integrate over $l$
and we integrate over $l$![]() and $\alpha$
and $\alpha$![]() to find
to find
where we have defined the flux surface average
Here, $L(r,\alpha )$![]() is the length along the magnetic field line between the two points where the magnetic field line crosses the curve defined by $l=0$
is the length along the magnetic field line between the two points where the magnetic field line crosses the curve defined by $l=0$![]() , and
, and
is the derivative with respect to $r$![]() of the volume $V(r)$
of the volume $V(r)$![]() contained within the flux surface $r$
contained within the flux surface $r$![]() . To obtain (2.30), we have written the radial component of the drifts as $(\boldsymbol {v}_E + \boldsymbol {v}_{Mi}) \boldsymbol {\cdot } \boldsymbol {\nabla } r = (v_\|/\varOmega _i) \boldsymbol {\nabla } \boldsymbol {\cdot } ( v_\| \hat {\boldsymbol {b}} \times \boldsymbol {\nabla } r)$
. To obtain (2.30), we have written the radial component of the drifts as $(\boldsymbol {v}_E + \boldsymbol {v}_{Mi}) \boldsymbol {\cdot } \boldsymbol {\nabla } r = (v_\|/\varOmega _i) \boldsymbol {\nabla } \boldsymbol {\cdot } ( v_\| \hat {\boldsymbol {b}} \times \boldsymbol {\nabla } r)$![]() to find
to find
Equation (2.27) cannot be used at values of $\mathcal {E}$![]() that are junctures of three or more types of wells. We show an example of such a value of $\mathcal {E}$
that are junctures of three or more types of wells. We show an example of such a value of $\mathcal {E}$![]() in figure 1. At these junctures, particles can and, in most cases, will transition from one type of well to another. In general, the value of $\mathcal {E}$
in figure 1. At these junctures, particles can and, in most cases, will transition from one type of well to another. In general, the value of $\mathcal {E}$![]() at which several types of well coincide, $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
at which several types of well coincide, $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() , depends on $r$
, depends on $r$![]() , $\alpha$
, $\alpha$![]() , $\mu$
, $\mu$![]() and $t$
and $t$![]() . Around these values of $\mathcal {E}$
. Around these values of $\mathcal {E}$![]() , there are boundary layers, thin in $\mathcal {E}$
, there are boundary layers, thin in $\mathcal {E}$![]() , where the dependence of $\bar {f}_i$
, where the dependence of $\bar {f}_i$![]() on $l$
on $l$![]() cannot be neglected (see, for example, Nemov et al. Reference Nemov, Kasilov, Kernbichler and Heyn1999; Calvo et al. Reference Calvo, Parra, Alonso and Velasco2014). These boundary layers impose continuity in $g_{i,W}$
cannot be neglected (see, for example, Nemov et al. Reference Nemov, Kasilov, Kernbichler and Heyn1999; Calvo et al. Reference Calvo, Parra, Alonso and Velasco2014). These boundary layers impose continuity in $g_{i,W}$![]() across these junctures. The derivatives of $g_{i,W}$
across these junctures. The derivatives of $g_{i,W}$![]() with respect $\mathcal {E}$
with respect $\mathcal {E}$![]() and $\mu$
and $\mu$![]() are not necessarily continuous. The derivatives of $g_{i, W}$
are not necessarily continuous. The derivatives of $g_{i, W}$![]() with respect to $\mathcal {E}$
with respect to $\mathcal {E}$![]() and $\mu$
and $\mu$![]() on the different wells of a juncture are related to each other by two conditions: the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$
on the different wells of a juncture are related to each other by two conditions: the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$![]() is continuous across a juncture, and the collisional flux in velocity space across a juncture must be conserved. The combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$
is continuous across a juncture, and the collisional flux in velocity space across a juncture must be conserved. The combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$![]() is continuous at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
is continuous at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() because $g_{i,W}$
because $g_{i,W}$![]() is continuous at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
is continuous at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() . In the example of figure 1, continuity of $g_{i, W}$
. In the example of figure 1, continuity of $g_{i, W}$![]() at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() imposes
imposes
for all $\mu$![]() . Differentiating this expression with respect to $\mu$
. Differentiating this expression with respect to $\mu$![]() , we find
, we find

that is, the combination $\partial _\mu \mathcal {E}_c\, \partial _\mathcal {E} g_{i, W} + \partial _\mu g_{i, W}$![]() is continuous. The other condition for the derivatives of $g_{i, W}$
is continuous. The other condition for the derivatives of $g_{i, W}$![]() at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
at $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() is conservation of particle number in phase space. For example, for the case represented in figure 1, one needs to calculate the particles that are leaving wells $I$
is conservation of particle number in phase space. For example, for the case represented in figure 1, one needs to calculate the particles that are leaving wells $I$![]() and $II$
and $II$![]() due to collisions, and then enforce that they enter well $III$
due to collisions, and then enforce that they enter well $III$![]() . This velocity-space flux continuity condition is manipulated in Appendix A to give the following relation between the derivatives of $g_{i, W}$
. This velocity-space flux continuity condition is manipulated in Appendix A to give the following relation between the derivatives of $g_{i, W}$![]() with respect of $\mathcal {E}$
with respect of $\mathcal {E}$![]() on different sides of the juncture:
on different sides of the juncture:

The relation between the derivatives $\partial _\mu g_{i,W}$![]() on each side of the juncture can be obtained from (2.36) by using the fact that the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$
on each side of the juncture can be obtained from (2.36) by using the fact that the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$![]() is continuous.
is continuous.
Equations (2.1), (2.2), (2.27), (2.30) and (2.36) are the same as (31), (33) and (37) of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) but for the inclusion of sources and time derivatives, and a different treatment of the split of $\bar {f}_i^{(0)}$![]() between trapped and passing particles. These equations are radially non-local and lead to very large transport and to a non-Maxwellian distribution function. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), closeness to omnigeneity was employed to derive radially local equations for a near-Maxwellian distribution function, but here we will use an expansion in the small inverse aspect ratio $\epsilon$
between trapped and passing particles. These equations are radially non-local and lead to very large transport and to a non-Maxwellian distribution function. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), closeness to omnigeneity was employed to derive radially local equations for a near-Maxwellian distribution function, but here we will use an expansion in the small inverse aspect ratio $\epsilon$![]() .
.
Equations (2.1), (2.2), (2.27), (2.30) and (2.36) are noticeably different from the usual neoclassical equations (Hinton & Hazeltine Reference Hinton and Hazeltine1976), derived assuming $\nu _{i*} \sim 1$![]() . In the limit $\nu _{i\ast } \sim 1$
. In the limit $\nu _{i\ast } \sim 1$![]() , to lowest order in $\rho _{i\ast }$
, to lowest order in $\rho _{i\ast }$![]() , the gyroaveraged ion distribution is a stationary Maxwellian with density $n_i$
, the gyroaveraged ion distribution is a stationary Maxwellian with density $n_i$![]() and temperature $T_i$
and temperature $T_i$![]() that only depend on the flux label $r$
that only depend on the flux label $r$![]() , $\bar {f}_i^{(0)} = f_{Mi}$
, $\bar {f}_i^{(0)} = f_{Mi}$![]() , and the electrostatic potential is a flux function to lowest order in $\rho _\ast$
, and the electrostatic potential is a flux function to lowest order in $\rho _\ast$![]() , $\phi (r, \alpha, l, t) = \phi ^{(0)}(r, t) + \phi ^{(1)} (r, \alpha, l, t) + \cdots$
, $\phi (r, \alpha, l, t) = \phi ^{(0)}(r, t) + \phi ^{(1)} (r, \alpha, l, t) + \cdots$![]() The next-order corrections in $\rho _{i*}$
The next-order corrections in $\rho _{i*}$![]() , $\bar {f}_i^{(1)}$
, $\bar {f}_i^{(1)}$![]() and $\phi ^{(1)}$
and $\phi ^{(1)}$![]() , are determined by
, are determined by
and the quasineutrality equation, respectively. Here, $C_{ii}^{\ell }$![]() is the linearized collision operator, discussed further in § 5.2. The density and temperature in the Maxwellian $f_{Mi}$
is the linearized collision operator, discussed further in § 5.2. The density and temperature in the Maxwellian $f_{Mi}$![]() are calculated using particle and energy conservation equations. The neoclassical fluxes in these conservation equations are integrals of $\bar {f}_i^{(1)}\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r$
are calculated using particle and energy conservation equations. The neoclassical fluxes in these conservation equations are integrals of $\bar {f}_i^{(1)}\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r$![]() , and hence scale as $\rho _{i\ast }^{2}$
, and hence scale as $\rho _{i\ast }^{2}$![]() . These neoclassical fluxes give a typical time scale for changes in density and temperature of $\partial _t \sim \rho _{i\ast }^{2} \nu _{ii}$
. These neoclassical fluxes give a typical time scale for changes in density and temperature of $\partial _t \sim \rho _{i\ast }^{2} \nu _{ii}$![]() . For comparison, in a generic stellarator with $\nu _{i\ast } \sim \rho _{i\ast }$
. For comparison, in a generic stellarator with $\nu _{i\ast } \sim \rho _{i\ast }$![]() , (2.1), (2.2), (2.27), (2.30) and (2.36) show that the distribution function need not be close to a Maxwellian, and the typical time scale for transport is $\partial _t \sim \nu _{ii} \sim \rho _{i\ast } v_{ti}/R$
, (2.1), (2.2), (2.27), (2.30) and (2.36) show that the distribution function need not be close to a Maxwellian, and the typical time scale for transport is $\partial _t \sim \nu _{ii} \sim \rho _{i\ast } v_{ti}/R$![]() . The difference between the orderings $\nu _{i\ast } \sim 1$
. The difference between the orderings $\nu _{i\ast } \sim 1$![]() and $\nu _{i\ast } \sim \rho _{i\ast }$
and $\nu _{i\ast } \sim \rho _{i\ast }$![]() is due to the typical radial separation between the position of a particle and the flux surface $r$
is due to the typical radial separation between the position of a particle and the flux surface $r$![]() that the particle started at. For $\nu _{i\ast } \sim 1$
that the particle started at. For $\nu _{i\ast } \sim 1$![]() , particles collide often, and hence the radial drift does not have time to act and move the particle away from its initial radial position more than a distance of the order of the ion gyroradius $\rho _i$
, particles collide often, and hence the radial drift does not have time to act and move the particle away from its initial radial position more than a distance of the order of the ion gyroradius $\rho _i$![]() between collisions. For smaller collision frequencies ($\rho _{i*} \ll \nu _{i*} \ll 1$
between collisions. For smaller collision frequencies ($\rho _{i*} \ll \nu _{i*} \ll 1$![]() ), particles in a stellarator drift out distances of order $\rho _i/\nu _{i\ast }$
), particles in a stellarator drift out distances of order $\rho _i/\nu _{i\ast }$![]() (Ho & Kulsrud Reference Ho and Kulsrud1987), giving higher and higher transport as the collision frequency decreases until eventually, for $\nu _{i\ast } \sim \rho _{i\ast }$
(Ho & Kulsrud Reference Ho and Kulsrud1987), giving higher and higher transport as the collision frequency decreases until eventually, for $\nu _{i\ast } \sim \rho _{i\ast }$![]() , the separation between the initial radial position of the particle and its typical position becomes of the order of the minor radius of the device, $a$
, the separation between the initial radial position of the particle and its typical position becomes of the order of the minor radius of the device, $a$![]() . In this regime, orbits are as large as the device, and transport occurs by either direct losses, giving the typical time scale $\partial _t \sim \rho _{i\ast } v_{ti}/R$
. In this regime, orbits are as large as the device, and transport occurs by either direct losses, giving the typical time scale $\partial _t \sim \rho _{i\ast } v_{ti}/R$![]() , or, for particles in confined orbits, by collisions, giving $\partial _t \sim \nu _{ii}$
, or, for particles in confined orbits, by collisions, giving $\partial _t \sim \nu _{ii}$![]() . By expanding in closeness to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017) or in the small inverse aspect ratio (this article), one can recover that the distribution function is close to a Maxwellian, and that the radial flux of particles and energy is determined by a higher-order correction to that Maxwellian. The equations for these higher corrections in general look similar to (2.37), but the parallel streaming term is replaced by the drift in the $\alpha$
. By expanding in closeness to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017) or in the small inverse aspect ratio (this article), one can recover that the distribution function is close to a Maxwellian, and that the radial flux of particles and energy is determined by a higher-order correction to that Maxwellian. The equations for these higher corrections in general look similar to (2.37), but the parallel streaming term is replaced by the drift in the $\alpha$![]() -direction. The correction to the Maxwellian in this case does not scale with $\rho _{i\ast }$
-direction. The correction to the Maxwellian in this case does not scale with $\rho _{i\ast }$![]() as the expansion parameter is not $\rho _{i\ast }$
as the expansion parameter is not $\rho _{i\ast }$![]() but closeness to omnigeneity or the inverse aspect ratio. One can devise equations for the correction to the Maxwellian that recover both orderings $\nu _{i\ast } \sim 1$
but closeness to omnigeneity or the inverse aspect ratio. One can devise equations for the correction to the Maxwellian that recover both orderings $\nu _{i\ast } \sim 1$![]() and $\nu _{i\ast } \sim \rho _{i\ast }$
and $\nu _{i\ast } \sim \rho _{i\ast }$![]() by including both parallel streaming and drifts in the $\alpha$
by including both parallel streaming and drifts in the $\alpha$![]() -direction – we show in Appendix G that the equations in DKES are an example of this, recovering both the $\nu _{i\ast } \sim 1$
-direction – we show in Appendix G that the equations in DKES are an example of this, recovering both the $\nu _{i\ast } \sim 1$![]() and $\nu _{i\ast } \sim \rho _{i\ast }$
and $\nu _{i\ast } \sim \rho _{i\ast }$![]() limits for large aspect ratio stellarators.
limits for large aspect ratio stellarators.
3. MHD equilibria in large aspect ratio stellarators
In the coordinates $\{ r, \alpha, l \}$![]() , a large aspect ratio stellarator shape is
, a large aspect ratio stellarator shape is
where $\boldsymbol {x}_0(l) \sim R$![]() is the magnetic axis, and $\boldsymbol {x}_n (r, \alpha, l) \sim \epsilon ^{n} R$
is the magnetic axis, and $\boldsymbol {x}_n (r, \alpha, l) \sim \epsilon ^{n} R$![]() . We assume that
. We assume that
Note that the expansion in (3.1) is not the Garren & Boozer (Reference Garren and Boozer1991) polynomial expansion because we are not assuming that $\boldsymbol {x}_n(r, \alpha, l)$![]() is proportional to $r^{n}$
is proportional to $r^{n}$![]() . The Garren & Boozer (Reference Garren and Boozer1991) expansion is a particular case of the expansion used here.
. The Garren & Boozer (Reference Garren and Boozer1991) expansion is a particular case of the expansion used here.
The values that $\boldsymbol {x}(r, \alpha, l)$![]() can take are constrained by the definition of arc length,
can take are constrained by the definition of arc length,
and by the MHD force balance equation,
where $\boldsymbol {\nabla }_\perp := \boldsymbol {\nabla } - \hat {\boldsymbol {b}} \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla }$![]() is the projection of the gradient in the plane perpendicular to the magnetic field, and $P(r)$
is the projection of the gradient in the plane perpendicular to the magnetic field, and $P(r)$![]() is the total plasma pressure, which is a flux function. We project equation (3.4) on $\partial _r \boldsymbol {x}$
is the total plasma pressure, which is a flux function. We project equation (3.4) on $\partial _r \boldsymbol {x}$![]() and $\partial _\alpha \boldsymbol {x}$
and $\partial _\alpha \boldsymbol {x}$![]() to obtain
to obtain
and
where $P^{\prime } := \mathrm {d} P/\mathrm {d} r$![]() . To solve these equations, we need to obtain the magnitude of the magnetic field $B$
. To solve these equations, we need to obtain the magnitude of the magnetic field $B$![]() from $\boldsymbol {x}(r, \alpha, l)$
from $\boldsymbol {x}(r, \alpha, l)$![]() . Using (2.18), we find that the magnitude of the magnetic field is given by
. Using (2.18), we find that the magnitude of the magnetic field is given by
We expand the MHD equilibrium equations in $\epsilon \ll 1$![]() by assuming that the plasma pressure is sufficiently small to satisfy
by assuming that the plasma pressure is sufficiently small to satisfy
We are particularly interested in the magnitude of the magnetic field, given by
where $B_n \sim \epsilon ^{n} B_0 \ll 1$![]() . To lowest order in $\epsilon$
. To lowest order in $\epsilon$![]() , (3.5) and (3.6) become $\partial _r ( B_0^{2}/8{\rm \pi} ) = 0$
, (3.5) and (3.6) become $\partial _r ( B_0^{2}/8{\rm \pi} ) = 0$![]() and $\partial _\alpha ( B_0^{2}/8{\rm \pi} ) = 0$
and $\partial _\alpha ( B_0^{2}/8{\rm \pi} ) = 0$![]() . The solution to these equations is that $B_0(l)$
. The solution to these equations is that $B_0(l)$![]() can only be a function of $l$
can only be a function of $l$![]() . As a result, the lowest-order version of (3.7),
. As a result, the lowest-order version of (3.7),
cannot depend on $\alpha$![]() . Here, $\hat {\boldsymbol {b}}_0 (l) := \mathrm {d} \boldsymbol {x}_0/\mathrm {d} l$
. Here, $\hat {\boldsymbol {b}}_0 (l) := \mathrm {d} \boldsymbol {x}_0/\mathrm {d} l$![]() is the unit vector parallel to the magnetic axis. Note that condition (3.10) implies that
is the unit vector parallel to the magnetic axis. Note that condition (3.10) implies that
Condition (3.10) limits the choice of $\boldsymbol {x}_1(r, \alpha, l)$![]() . The function $\boldsymbol {x}_1 (r, \alpha, l)$
. The function $\boldsymbol {x}_1 (r, \alpha, l)$![]() must satisfy two constraints in addition to satisfying (3.10): the first-order correction to (3.3) and the conservation of electric current. These two extra constraints will not be needed for rest of the article, but we give them in Appendix B for completeness. For the rest of this paper, we only need to know that the three scalar constraints discussed above can be satisfied by choosing the three components of $\boldsymbol {x}_1 (r, \alpha, l)$
must satisfy two constraints in addition to satisfying (3.10): the first-order correction to (3.3) and the conservation of electric current. These two extra constraints will not be needed for rest of the article, but we give them in Appendix B for completeness. For the rest of this paper, we only need to know that the three scalar constraints discussed above can be satisfied by choosing the three components of $\boldsymbol {x}_1 (r, \alpha, l)$![]() wisely, i.e. the large aspect ratio expansion is self-consistent.
wisely, i.e. the large aspect ratio expansion is self-consistent.
The first-order correction $B_1$![]() can be calculated using MHD force balance. Keeping only the first order terms in $\epsilon$
can be calculated using MHD force balance. Keeping only the first order terms in $\epsilon$![]() in (3.5) and (3.6), we find
in (3.5) and (3.6), we find
and
Equations (3.12) and (3.13) can be integrated to find
where $\boldsymbol {\kappa }_0 (l) := \mathrm {d}^{2} \boldsymbol {x}_0/\mathrm {d} l^{2}$![]() is the curvature of the magnetic axis.
is the curvature of the magnetic axis.
For a given $\boldsymbol {x}_1$![]() , we can calculate the components of the drifts that we need to solve (2.27). In a general stellarator, the radial and $\alpha$
, we can calculate the components of the drifts that we need to solve (2.27). In a general stellarator, the radial and $\alpha$![]() components of the magnetic drift are
components of the magnetic drift are
and
and the same components of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift are
drift are
and
To lowest order in $\epsilon \ll 1$![]() , the expressions for the magnetic drift become
, the expressions for the magnetic drift become

and

where we have used (3.14) to write the magnetic drift components as derivatives of $B_1$![]() . Similarly, the radial and $\alpha$
. Similarly, the radial and $\alpha$![]() components of the $\boldsymbol {E} \times \boldsymbol {B}$
components of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift are
drift are
and
to lowest order in $\epsilon \ll 1$![]() . For the $\boldsymbol {E} \times \boldsymbol {B}$
. For the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, we have emphasized that the size of the first-order corrections in $\epsilon$
drift, we have emphasized that the size of the first-order corrections in $\epsilon$![]() is proportional to the derivative of $\phi$
is proportional to the derivative of $\phi$![]() with respect to $l$
with respect to $l$![]() . The fact that the next-order corrections only depend on $\partial _l \phi$
. The fact that the next-order corrections only depend on $\partial _l \phi$![]() is important because we show in § 4 that the potential is a flux function to lowest order, making these corrections even smaller than first order in $\epsilon$
is important because we show in § 4 that the potential is a flux function to lowest order, making these corrections even smaller than first order in $\epsilon$![]() .
.
For most of this article (§§ 4–7 and § 8.2), we will focus on large aspect ratio stellarators with constant $B_0$![]() , that is, $\mathrm {d} B_0/\mathrm {d} l = 0$
, that is, $\mathrm {d} B_0/\mathrm {d} l = 0$![]() . According to (3.10), stellarators with constant $B_0$
. According to (3.10), stellarators with constant $B_0$![]() must have flux surfaces such that the area of a cut of a flux surface $r$
must have flux surfaces such that the area of a cut of a flux surface $r$![]() through a plane perpendicular to the magnetic axis cannot depend on the position along the magnetic axis. Indeed, this area is given by
through a plane perpendicular to the magnetic axis cannot depend on the position along the magnetic axis. Indeed, this area is given by
From here on, we refer to these large aspect ratio stellarators as stellarators with mirror ratios close to unity because the ratio between the maximum and the minimum of $B$![]() on a flux surface (mirror ratio) is $1 + O(\epsilon ) \simeq 1$
on a flux surface (mirror ratio) is $1 + O(\epsilon ) \simeq 1$![]() . We focus on large aspect ratio stellarators with mirror ratios close to unity for two reasons: (i) their description requires careful analysis and an unintuitive choice of velocity-space coordinates, and (ii) these stellarators with mirror ratio close to unity are extremely common – see, for example, the maps of magnetic field magnitude $B$
. We focus on large aspect ratio stellarators with mirror ratios close to unity for two reasons: (i) their description requires careful analysis and an unintuitive choice of velocity-space coordinates, and (ii) these stellarators with mirror ratio close to unity are extremely common – see, for example, the maps of magnetic field magnitude $B$![]() in Beidler et al. (Reference Beidler, Allmaier, Isaev, Kasilov, Kernblichler, Leitold, Maaßberg, Mikkelsen, Murakami and Schimdt2011) that show mirror ratios in the interval 1.05–1.2.
in Beidler et al. (Reference Beidler, Allmaier, Isaev, Kasilov, Kernblichler, Leitold, Maaßberg, Mikkelsen, Murakami and Schimdt2011) that show mirror ratios in the interval 1.05–1.2.
To have a mirror ratio significantly different from unity in a large aspect ratio stellarator, $B_0$![]() must depend on $l$
must depend on $l$![]() . In this case, the mirror ratio is $B_{0,M}/B_{0,m}$
. In this case, the mirror ratio is $B_{0,M}/B_{0,m}$![]() , where $B_{0, M}$
, where $B_{0, M}$![]() and $B_{0, m}$
and $B_{0, m}$![]() are the maximum and minimum of $B_0(l)$
are the maximum and minimum of $B_0(l)$![]() , respectively. We are not aware of any large aspect ratio stellarators with mirror ratios significantly different from unity that have been built. Despite this fact, we will study large aspect ratio stellarators with mirror ratios significantly different from unity (from here on, ‘with large mirror ratios’ for short) in § 8.1, where we will consider $B_0(l)$
, respectively. We are not aware of any large aspect ratio stellarators with mirror ratios significantly different from unity that have been built. Despite this fact, we will study large aspect ratio stellarators with mirror ratios significantly different from unity (from here on, ‘with large mirror ratios’ for short) in § 8.1, where we will consider $B_0(l)$![]() to be a general function of $l$
to be a general function of $l$![]() . This type of stellarator is always close to omnigeneous and hence one can use the formalism developed by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) to calculate neoclassical transport in them.
. This type of stellarator is always close to omnigeneous and hence one can use the formalism developed by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) to calculate neoclassical transport in them.
4. New velocity-space coordinates for large aspect ratio stellarators with mirror ratios close to unity
We first consider the possibility of the potential $\phi (\boldsymbol {x}, t)$![]() being very different from a flux function, that is, $\partial _\alpha \phi \neq 0$
being very different from a flux function, that is, $\partial _\alpha \phi \neq 0$![]() and $\partial _l \phi \neq 0$
and $\partial _l \phi \neq 0$![]() . We show that this is not possible in a large aspect ratio stellarator with mirror ratios close to unity, that is, large aspect ratio stellarators with constant $B_0$
. We show that this is not possible in a large aspect ratio stellarator with mirror ratios close to unity, that is, large aspect ratio stellarators with constant $B_0$![]() . If $\phi$
. If $\phi$![]() is not a flux function, the variation of $v_\|$
is not a flux function, the variation of $v_\|$![]() within a flux surface is dominated by the variation of $\phi$
within a flux surface is dominated by the variation of $\phi$![]() ,
,

Thus, for a general $\phi$![]() , trapped particles satisfy $\mathcal {E} \leq U_M \simeq \mu B_0 + Z_i e \phi _M(r, t)/m_i$
, trapped particles satisfy $\mathcal {E} \leq U_M \simeq \mu B_0 + Z_i e \phi _M(r, t)/m_i$![]() , where $\phi _M(r, t)$
, where $\phi _M(r, t)$![]() is the maximum of $\phi$
is the maximum of $\phi$![]() on the flux surface. The parallel velocity of trapped particles is of order $v_{ti}$
on the flux surface. The parallel velocity of trapped particles is of order $v_{ti}$![]() , and the fraction of trapped particles is of order unity. In this case, the quasineutrality equation (2.1) becomes
, and the fraction of trapped particles is of order unity. In this case, the quasineutrality equation (2.1) becomes

to lowest order in $\epsilon$![]() . The function $g_{i, W}$
. The function $g_{i, W}$![]() is defined for $\mathcal {E} \leq U_M$
is defined for $\mathcal {E} \leq U_M$![]() , but it is zero for the values of $\mathcal {E}$
, but it is zero for the values of $\mathcal {E}$![]() outside of well $W$
outside of well $W$![]() (in the example of figure 1, $g_{i, I}$
(in the example of figure 1, $g_{i, I}$![]() and $g_{i, II}$
and $g_{i, II}$![]() are zero for $\mathcal {E} > \mathcal {E}_c$
are zero for $\mathcal {E} > \mathcal {E}_c$![]() , and $g_{i, III}$
, and $g_{i, III}$![]() is zero for $\mathcal {E} < \mathcal {E}_c$
is zero for $\mathcal {E} < \mathcal {E}_c$![]() ). Then, the sum of $g_{i,W}$
). Then, the sum of $g_{i,W}$![]() over the well index $W$
over the well index $W$![]() gives a continuous function of $\mathcal {E}$
gives a continuous function of $\mathcal {E}$![]() . Note that the sum over $W$
. Note that the sum over $W$![]() is performed over a subset $\mathcal {W}$
is performed over a subset $\mathcal {W}$![]() of all possible wells. Set $\mathcal {W}$
of all possible wells. Set $\mathcal {W}$![]() depends on the location where the quasineutrality is being evaluated because any well $W$
depends on the location where the quasineutrality is being evaluated because any well $W$![]() has a limited range of values of $l$
has a limited range of values of $l$![]() . In the example in figure 1, $l$
. In the example in figure 1, $l$![]() in well $I$
in well $I$![]() is between $l_{bL, I}$
is between $l_{bL, I}$![]() and $l_{bR, I}$
and $l_{bR, I}$![]() , and $l$
, and $l$![]() in well $II$
in well $II$![]() is between $l_{bL, II}$
is between $l_{bL, II}$![]() and $l_{bR, II}$
and $l_{bR, II}$![]() . When the ion density is evaluated for $l \in [l_{bL, I}, l_{bR, I}]$
. When the ion density is evaluated for $l \in [l_{bL, I}, l_{bR, I}]$![]() , set $\mathcal {W}$
, set $\mathcal {W}$![]() should include wells $I$
should include wells $I$![]() and $III$
and $III$![]() , but exclude well $II$
, but exclude well $II$![]() . Note that set $\mathcal {W}$
. Note that set $\mathcal {W}$![]() is independent of $l$
is independent of $l$![]() in a finite region of $l$
in a finite region of $l$![]() around most points in the stellarator (e.g. in the case of figure 1, set $\mathcal {W}$
around most points in the stellarator (e.g. in the case of figure 1, set $\mathcal {W}$![]() includes wells $I$
includes wells $I$![]() and $III$
and $III$![]() for $l \in [l_{bL, I}, l_{bR, I}]$
for $l \in [l_{bL, I}, l_{bR, I}]$![]() ). Thus, the quasineutrality equation (4.2) only depends on $\phi$
). Thus, the quasineutrality equation (4.2) only depends on $\phi$![]() , $r$
, $r$![]() and $\alpha$
and $\alpha$![]() around most spatial points, giving a solution $\phi$
around most spatial points, giving a solution $\phi$![]() that can only depend on $r$
that can only depend on $r$![]() and $\alpha$
and $\alpha$![]() , that is, $\partial _l \phi = 0$
, that is, $\partial _l \phi = 0$![]() . As we are considering only ergodic flux surfaces, $\partial _l \phi = 0$
. As we are considering only ergodic flux surfaces, $\partial _l \phi = 0$![]() implies that $\partial _\alpha \phi = 0$
implies that $\partial _\alpha \phi = 0$![]() , and hence $\phi$
, and hence $\phi$![]() is a flux function, $\phi = \phi (r)$
is a flux function, $\phi = \phi (r)$![]() . Note that this is an arbitrary flux function because we can choose it at will using the free function $\hat {n}_e (r, t)$
. Note that this is an arbitrary flux function because we can choose it at will using the free function $\hat {n}_e (r, t)$![]() .
.
Since the electric potential is a flux function to lowest order in $\epsilon$![]() , we write it as
, we write it as
where $\phi _0(r, t) \sim T_i/e$![]() is a flux function, and $\phi _{3/2}(r, \alpha, l, t) \sim \epsilon ^{3/2} T_i/e$
is a flux function, and $\phi _{3/2}(r, \alpha, l, t) \sim \epsilon ^{3/2} T_i/e$![]() . We show that the correction to the lowest-order flux function is small in $\epsilon ^{3/2}$
. We show that the correction to the lowest-order flux function is small in $\epsilon ^{3/2}$![]() in § 5.2. Due to expansion (4.3), (4.1) is a bad approximation for trapped particles. Instead, we need to use
in § 5.2. Due to expansion (4.3), (4.1) is a bad approximation for trapped particles. Instead, we need to use

where the quantity $\mathcal {E}_1 := \mathcal {E} - \mu B_0 - Z_i e \phi _0(r, t)/m_i$![]() must be of order $\epsilon v_{ti}^{2}$
must be of order $\epsilon v_{ti}^{2}$![]() for trapped particles – otherwise, $v_\|$
for trapped particles – otherwise, $v_\|$![]() would not vanish. Thus, the characteristic size of the parallel velocity of trapped particles is $v_\| \sim \sqrt {\epsilon } v_{ti}$
would not vanish. Thus, the characteristic size of the parallel velocity of trapped particles is $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() , and the fraction of trapped particles is of order $\sqrt {\epsilon }$
, and the fraction of trapped particles is of order $\sqrt {\epsilon }$![]() .
.
Before expanding the ion distribution function in $\epsilon$![]() , we need new velocity-space coordinates for trapped and passing particles. We discuss the velocity-space coordinates for trapped and passing particles in §§ 4.1 and 4.2, respectively.
, we need new velocity-space coordinates for trapped and passing particles. We discuss the velocity-space coordinates for trapped and passing particles in §§ 4.1 and 4.2, respectively.
4.1. Velocity-space coordinates for trapped particles
Due to the smallness of $v_\|$![]() and to the expansion in (4.3), the magnetic and $\boldsymbol {E} \times \boldsymbol {B}$
and to the expansion in (4.3), the magnetic and $\boldsymbol {E} \times \boldsymbol {B}$![]() drifts in (3.19), (3.20), (3.21) and (3.22) simplify to
drifts in (3.19), (3.20), (3.21) and (3.22) simplify to
and
for trapped particles. Here $\phi _0^{\prime } := \partial _r \phi _0$![]() .
.
Since the radial component of the drifts is small in $\epsilon$![]() , it is tempting to neglect the term proportional to the radial drift in (2.27). Unfortunately, this term cannot be neglected because the radial derivative of $g_{i,W}$
, it is tempting to neglect the term proportional to the radial drift in (2.27). Unfortunately, this term cannot be neglected because the radial derivative of $g_{i,W}$![]() is very large,
is very large,
In order to understand estimate (4.7), one has to keep in mind that the potential changes significantly with radius. Indeed, the change in potential due to radial displacement $\Delta r \sim \epsilon a$![]() is $\Delta r\, \phi _0^{\prime } \sim \epsilon T_i/e$
is $\Delta r\, \phi _0^{\prime } \sim \epsilon T_i/e$![]() , and this change in potential energy means that $v_\parallel$
, and this change in potential energy means that $v_\parallel$![]() has to change by $\sqrt {Z_i e \Delta r\, \phi _0^{\prime } /m_i} \sim \sqrt {\epsilon } v_{ti}$
has to change by $\sqrt {Z_i e \Delta r\, \phi _0^{\prime } /m_i} \sim \sqrt {\epsilon } v_{ti}$![]() if we keep $\mathcal {E}$
if we keep $\mathcal {E}$![]() constant when varying $r$
constant when varying $r$![]() . Hence, surprisingly, trapped particles with the same value of $\mathcal {E}$
. Hence, surprisingly, trapped particles with the same value of $\mathcal {E}$![]() and separated only by $\Delta r \sim \epsilon a$
and separated only by $\Delta r \sim \epsilon a$![]() occupy very different heights with respect to the minimum of the $U$
occupy very different heights with respect to the minimum of the $U$![]() well. This situation is represented in figure 2. The difference in the height of the particle with respect to the minimum of the $U$
well. This situation is represented in figure 2. The difference in the height of the particle with respect to the minimum of the $U$![]() well leads to the large radial derivative in (4.7). Note that the characteristic length of $g_{i,W}$
well leads to the large radial derivative in (4.7). Note that the characteristic length of $g_{i,W}$![]() , $\Delta r \sim \epsilon a$
, $\Delta r \sim \epsilon a$![]() , is of the order of the width $w$
, is of the order of the width $w$![]() of the particle orbits in (1.5), indicating that we need to keep the radial drifts in (2.27).
of the particle orbits in (1.5), indicating that we need to keep the radial drifts in (2.27).

Figure 2. Trajectories of trapped particles in a given $U$![]() well in the $(\mathcal {E}, l)$
well in the $(\mathcal {E}, l)$![]() plane when one moves from a given flux surface to a neighbouring one keeping either $J$
plane when one moves from a given flux surface to a neighbouring one keeping either $J$![]() or $\mathcal {E}$
or $\mathcal {E}$![]() constant. The shape of the $U$
constant. The shape of the $U$![]() well does not change much whereas the whole well moves up and down due to the change in potential $\phi$
well does not change much whereas the whole well moves up and down due to the change in potential $\phi$![]() .
.
Importantly, the radial derivative of $g_{i,W}$![]() is very large because we are holding $\mathcal {E}$
is very large because we are holding $\mathcal {E}$![]() fixed and, as a result, the radial derivative of $g_{i,W}$
fixed and, as a result, the radial derivative of $g_{i,W}$![]() is related to the radial derivative of $\phi _0$
is related to the radial derivative of $\phi _0$![]() . In contrast with the electric potential, the magnitude of the magnetic field does not change much if $r$
. In contrast with the electric potential, the magnitude of the magnetic field does not change much if $r$![]() is changed by $\Delta r \sim \epsilon a$
is changed by $\Delta r \sim \epsilon a$![]() because its characteristic length of variation is $R$
because its characteristic length of variation is $R$![]() . Indeed, the change in $B$
. Indeed, the change in $B$![]() is $\Delta r\, \partial _r B \simeq \Delta r\, \partial _r B_1 \sim \epsilon ^{2} B_0$
is $\Delta r\, \partial _r B \simeq \Delta r\, \partial _r B_1 \sim \epsilon ^{2} B_0$![]() . The lack of rapid variation in $B$
. The lack of rapid variation in $B$![]() suggests using velocity-space coordinates that, when held constant, do not change the height of the trapped particle with respect to the minimum of the $B$
suggests using velocity-space coordinates that, when held constant, do not change the height of the trapped particle with respect to the minimum of the $B$![]() well. The coordinates $v$
well. The coordinates $v$![]() and
and
are often used because the variation of $v$![]() along a orbit is small in $\epsilon$
along a orbit is small in $\epsilon$![]() and $\lambda$
and $\lambda$![]() is equal to $1/B$
is equal to $1/B$![]() at the bounce points. To see that $v$
at the bounce points. To see that $v$![]() does not change much during an orbit, note that in a large aspect ratio stellarator, the parallel velocity of a trapped particle is very small, giving $v \simeq v_\perp \simeq \sqrt {2\mu B_0}$
does not change much during an orbit, note that in a large aspect ratio stellarator, the parallel velocity of a trapped particle is very small, giving $v \simeq v_\perp \simeq \sqrt {2\mu B_0}$![]() , where $B_0$
, where $B_0$![]() is constant. Conversely, $\lambda$
is constant. Conversely, $\lambda$![]() is not constant along trajectories. Writing $\lambda$
is not constant along trajectories. Writing $\lambda$![]() as
as
shows that $\lambda$![]() changes by an amount of order $\epsilon /B_0$
changes by an amount of order $\epsilon /B_0$![]() along the orbit because of the variation of $\phi _0$
along the orbit because of the variation of $\phi _0$![]() . Changes of order $\epsilon /B_0$
. Changes of order $\epsilon /B_0$![]() in $\lambda$
in $\lambda$![]() are important for trapped particles because the interval of $\lambda$
are important for trapped particles because the interval of $\lambda$![]() values where we find trapped particles, $\lambda \in [B_M^{-1}, B_m^{-1}]$
values where we find trapped particles, $\lambda \in [B_M^{-1}, B_m^{-1}]$![]() , has a length of order $\epsilon /B_0$
, has a length of order $\epsilon /B_0$![]() . Here $B_m(r)$
. Here $B_m(r)$![]() and $B_M(r)$
and $B_M(r)$![]() are the minimum and maximum of $B$
are the minimum and maximum of $B$![]() on flux surface $r$
on flux surface $r$![]() , respectively.
, respectively.
Instead of the usual coordinates $v$![]() and $\lambda$
and $\lambda$![]() , we propose two other coordinates. In § 5, we will discover that $v$
, we propose two other coordinates. In § 5, we will discover that $v$![]() is not constant to a sufficiently high order in $\epsilon$
is not constant to a sufficiently high order in $\epsilon$![]() for one of the calculations that we perform: $v = \sqrt {2 ( \mathcal {E} - Z_i e \phi /m_i )}$
for one of the calculations that we perform: $v = \sqrt {2 ( \mathcal {E} - Z_i e \phi /m_i )}$![]() causes problems because it introduces dependence on $l$
causes problems because it introduces dependence on $l$![]() through $\phi _{3/2}$
through $\phi _{3/2}$![]() . Due to this limitation, we choose
. Due to this limitation, we choose

to be one of our velocity-space coordinates. Regarding $\lambda$![]() , using it as a velocity-space coordinate is inconvenient because it is not constant in time. Fortunately, there is another quantity that gives the same information as $\lambda$
, using it as a velocity-space coordinate is inconvenient because it is not constant in time. Fortunately, there is another quantity that gives the same information as $\lambda$![]() and is constant in time: the second adiabatic invariant
and is constant in time: the second adiabatic invariant

We use the second adiabatic invariant as a velocity-space coordinate for trapped particles. Employing $\partial _\mathcal {E} J_W = \tau _W \sim \epsilon ^{-1/2} R/ v_{ti}$![]() and $\partial _\mu J_W = - \tau _W \langle B \rangle _{\tau, W} \sim \epsilon ^{-1/2} B_0 R/v_{ti}$
and $\partial _\mu J_W = - \tau _W \langle B \rangle _{\tau, W} \sim \epsilon ^{-1/2} B_0 R/v_{ti}$![]() to find
to find
we can calculate the velocity-space volume element,
Note that we use the symbol $J_W$![]() when the second adiabatic invariant is considered a function of $r$
when the second adiabatic invariant is considered a function of $r$![]() , $\alpha$
, $\alpha$![]() , $\mathcal {E}$
, $\mathcal {E}$![]() , $\mu$
, $\mu$![]() , $t$
, $t$![]() and the type of well $W$
and the type of well $W$![]() , whereas we employ the symbol $J$
, whereas we employ the symbol $J$![]() without the subscript $W$
without the subscript $W$![]() when the second adiabatic invariant is a coordinate.
when the second adiabatic invariant is a coordinate.
Previous work (Hazeltine & Catto Reference Hazeltine and Catto1981; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017) has used $J$![]() as a coordinate, but as a replacement for the radial coordinate $r$
as a coordinate, but as a replacement for the radial coordinate $r$![]() instead of as a replacement for the pitch-angle variable $\lambda$
instead of as a replacement for the pitch-angle variable $\lambda$![]() . Note that the three quantities $\mathcal {E}$
. Note that the three quantities $\mathcal {E}$![]() , $\mu$
, $\mu$![]() and $J$
and $J$![]() are all desirable coordinates because they are constant along particle trajectories. One of the three variables works as a proxy for the radial position of the particle, whereas the other two represent velocity space. In three-dimensional magnetic fields close to omnigeneity (Hazeltine & Catto Reference Hazeltine and Catto1981; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017), $J$
are all desirable coordinates because they are constant along particle trajectories. One of the three variables works as a proxy for the radial position of the particle, whereas the other two represent velocity space. In three-dimensional magnetic fields close to omnigeneity (Hazeltine & Catto Reference Hazeltine and Catto1981; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017), $J$![]() is a flux function to lowest order and hence it can be used to replace $r$
is a flux function to lowest order and hence it can be used to replace $r$![]() . For trapped particles in large aspect ratio stellarators with mirror ratios close to unity, the kinetic energy associated with the parallel velocity is negligible compared with the perpendicular kinetic energy $\mu B \simeq \mu B_0$
. For trapped particles in large aspect ratio stellarators with mirror ratios close to unity, the kinetic energy associated with the parallel velocity is negligible compared with the perpendicular kinetic energy $\mu B \simeq \mu B_0$![]() , giving $\mathcal {E} \simeq \mu B_0 + Z_i e\phi _0 (r, t)/m_i$
, giving $\mathcal {E} \simeq \mu B_0 + Z_i e\phi _0 (r, t)/m_i$![]() . As a result, the total energy determines the radial position $r$
. As a result, the total energy determines the radial position $r$![]() for a given $\mu$
for a given $\mu$![]() through the potential energy $Z_i e \phi _0(r, t)/m_i$
through the potential energy $Z_i e \phi _0(r, t)/m_i$![]() , and $\mu$
, and $\mu$![]() and $J$
and $J$![]() are the velocity-space coordinates – note that $\bar {v} \simeq \sqrt {2\mu B_0}$
are the velocity-space coordinates – note that $\bar {v} \simeq \sqrt {2\mu B_0}$![]() . We make the relation between the total energy and the radial position obvious in § 5.4, where we discuss the motion of the deeply trapped particles to demonstrate the advantages of our formulation.
. We make the relation between the total energy and the radial position obvious in § 5.4, where we discuss the motion of the deeply trapped particles to demonstrate the advantages of our formulation.
We remind the reader that we are changing from the coordinates $\mathcal {E}$![]() and $\mu$
and $\mu$![]() to the coordinates $\bar {v}$
to the coordinates $\bar {v}$![]() and $J$
and $J$![]() to reduce the size of the derivative $\partial _r \ln g_{i,W}$
to reduce the size of the derivative $\partial _r \ln g_{i,W}$![]() from $(\epsilon a)^{-1}$
from $(\epsilon a)^{-1}$![]() to $a^{-1}$
to $a^{-1}$![]() . We will not be able to show that the derivative of $g_{i,W}$
. We will not be able to show that the derivative of $g_{i,W}$![]() with respect to $r$
with respect to $r$![]() holding $\bar {v}$
holding $\bar {v}$![]() and $J$
and $J$![]() constant is small in $\epsilon$
constant is small in $\epsilon$![]() until § 5.2, but we can now show that if
until § 5.2, but we can now show that if
the derivative of $g_{i,W}$![]() with respect to $r$
with respect to $r$![]() holding $\mathcal {E}$
holding $\mathcal {E}$![]() and $\mu$
and $\mu$![]() fixed is as large as estimated in (4.7). Indeed, by using the chain rule, we find
fixed is as large as estimated in (4.7). Indeed, by using the chain rule, we find
Noting that

and
we obtain estimate (4.7).
4.2. Velocity-space coordinates for passing particles
For passing particles, the variable $J$![]() cannot be defined. For most passing particles, $v \simeq \bar {v} := \sqrt {2(\mathcal {E} - Z_i e \phi _0/m_i)}$
cannot be defined. For most passing particles, $v \simeq \bar {v} := \sqrt {2(\mathcal {E} - Z_i e \phi _0/m_i)}$![]() and $v_\| \simeq \sigma \sqrt {2(\mathcal {E} - \mu B_0 - Z_i e \phi _0/m_i)}$
and $v_\| \simeq \sigma \sqrt {2(\mathcal {E} - \mu B_0 - Z_i e \phi _0/m_i)}$![]() are approximate constants of the motion. For this reason, we use the coordinates $\bar {v}$
are approximate constants of the motion. For this reason, we use the coordinates $\bar {v}$![]() and $\xi := v_\|/v$
and $\xi := v_\|/v$![]() for passing particles. The velocity-space volume element in these variables is
for passing particles. The velocity-space volume element in these variables is
For the few passing particles with $|\xi | \sim \sqrt {\epsilon } \ll 1$![]() , $\xi$
, $\xi$![]() is not approximately constant, but we show in Appendix D that this region of phase space can be treated as a boundary condition for the passing-particle distribution function $h_i$
is not approximately constant, but we show in Appendix D that this region of phase space can be treated as a boundary condition for the passing-particle distribution function $h_i$![]() at $\xi = 0$
at $\xi = 0$![]() . Appendix D should be read after having gone through §§ 5.1 and 5.2 and Appendix C.
. Appendix D should be read after having gone through §§ 5.1 and 5.2 and Appendix C.
5. Ion distribution function and potential in low collisionality large aspect ratio stellarators with mirror ratios close to unity
We proceed to expand equations (2.27), (2.30) and (2.36) in the inverse aspect ratio $\epsilon \ll 1$![]() assuming that $B_0$
assuming that $B_0$![]() is independent of $l$
is independent of $l$![]() and that $\rho _{i*} \sim \nu _{i*}$
and that $\rho _{i*} \sim \nu _{i*}$![]() . Based on estimates (4.5) and (4.6) for the components of the $\boldsymbol {E} \times \boldsymbol {B}$
. Based on estimates (4.5) and (4.6) for the components of the $\boldsymbol {E} \times \boldsymbol {B}$![]() and magnetic drifts, we will show in § 5.3 that we need to order the time derivative and the source as
and magnetic drifts, we will show in § 5.3 that we need to order the time derivative and the source as
This estimate is the result of a subsidiary expansion in $\epsilon \ll 1$![]() of the radially global equations for generic stellarators in § 2. Note that it is consistent with assumption (2.19) in § 2 when $\epsilon \sim 1$
of the radially global equations for generic stellarators in § 2. Note that it is consistent with assumption (2.19) in § 2 when $\epsilon \sim 1$![]() .
.
We expand $g_{i,W}$![]() and $h_i$
and $h_i$![]() in $\epsilon \ll 1$
in $\epsilon \ll 1$![]() assuming that $\rho _{i*} \sim \nu _{i*}$
assuming that $\rho _{i*} \sim \nu _{i*}$![]() and using the estimates in (5.1). For $g_{i,W}$
and using the estimates in (5.1). For $g_{i,W}$![]() , we find
, we find
where $g_{i, n, W} \sim \epsilon ^{n} g_{i, 0, W}$![]() . For $h_i$
. For $h_i$![]() , the expansion gives
, the expansion gives
where $h_{i,n} \sim \epsilon ^{n} h_{i,0}$![]() . The corrections $g_{i, 3/2, W}$
. The corrections $g_{i, 3/2, W}$![]() , $g_{i, 2, W}$
, $g_{i, 2, W}$![]() and $h_{i.3/2}$
and $h_{i.3/2}$![]() are important because their size determines the boundary conditions for $g_{i, 1, W}$
are important because their size determines the boundary conditions for $g_{i, 1, W}$![]() , but in the end we do not need to calculate them.
, but in the end we do not need to calculate them.
We need to consider half-integer powers of $\epsilon$![]() in our expansion for two reasons: (i) the size of the trapped-particle region in velocity space is small by a factor of order $\sqrt {\epsilon }$
in our expansion for two reasons: (i) the size of the trapped-particle region in velocity space is small by a factor of order $\sqrt {\epsilon }$![]() , and (ii) boundary condition (2.25) introduces these half-integer powers naturally, as we will see shortly.
, and (ii) boundary condition (2.25) introduces these half-integer powers naturally, as we will see shortly.
We organize the calculation as follows. In § 5.1 we argue that the lowest-order solution is a Maxwellian. In § 5.2 we obtain the equation and boundary conditions for $g_{i, 1, W}$![]() . Finally, in § 5.3 we obtain the transport equations for the ion density and temperature. In § 5.4, we summarize the equations, we compared them with those implemented in DKES (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986) and we illustrate how they work by discussing the behaviour of deeply trapped particles.
. Finally, in § 5.3 we obtain the transport equations for the ion density and temperature. In § 5.4, we summarize the equations, we compared them with those implemented in DKES (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986) and we illustrate how they work by discussing the behaviour of deeply trapped particles.
5.1. Lowest-order ion distribution function
The proof that the distribution is a stationary Maxwellian to lowest order in $\epsilon$![]() does not follow the derivation used in standard neoclassical theory – for examples of the usual procedure, see § V.4 of Hinton & Hazeltine (Reference Hinton and Hazeltine1976) or § 3.1 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). In the typical derivation, the radial drifts are small and can be neglected in the lowest-order kinetic equation. By calculating a certain moment of this simplified lowest-order kinetic equation, one obtains an entropy equation for an infinitesimal volume between two flux surfaces close to each other. In this equation, the entropy production due to collisions within the infinitesimal volume cannot be compensated by any outward flow of entropy because the radial drifts are negligible. Consequently, in steady state, the average entropy production must vanish to lowest order, leading to a distribution function close to Maxwellian. In large aspect ratio stellarators with mirror ratios close to unity, we cannot follow this procedure because, for $\nu _{i*} \sim \rho _{i*}$
does not follow the derivation used in standard neoclassical theory – for examples of the usual procedure, see § V.4 of Hinton & Hazeltine (Reference Hinton and Hazeltine1976) or § 3.1 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). In the typical derivation, the radial drifts are small and can be neglected in the lowest-order kinetic equation. By calculating a certain moment of this simplified lowest-order kinetic equation, one obtains an entropy equation for an infinitesimal volume between two flux surfaces close to each other. In this equation, the entropy production due to collisions within the infinitesimal volume cannot be compensated by any outward flow of entropy because the radial drifts are negligible. Consequently, in steady state, the average entropy production must vanish to lowest order, leading to a distribution function close to Maxwellian. In large aspect ratio stellarators with mirror ratios close to unity, we cannot follow this procedure because, for $\nu _{i*} \sim \rho _{i*}$![]() , the typical frequency associated with the radial drift, $\langle (\boldsymbol {v}_E + \boldsymbol {v}_{Mi}) \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W}/a \sim \rho _{i*} v_{ti}/R$
, the typical frequency associated with the radial drift, $\langle (\boldsymbol {v}_E + \boldsymbol {v}_{Mi}) \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W}/a \sim \rho _{i*} v_{ti}/R$![]() , is comparable to the collision frequency $\nu _{ii}$
, is comparable to the collision frequency $\nu _{ii}$![]() . As a result, trapped particles move a significant radial distance in the time that the distribution function evolves towards a Maxwellian. This motion can, in principle, disrupt the natural evolution of the distribution function towards a Maxwellian.
. As a result, trapped particles move a significant radial distance in the time that the distribution function evolves towards a Maxwellian. This motion can, in principle, disrupt the natural evolution of the distribution function towards a Maxwellian.
We proceed to argue that the distribution function is close to a Maxwellian in large aspect ratio stellarator with mirror ratios close to unity even though the trapped-particle radial drifts are large. Collisions can drive the distribution function close to a Maxwellian because only trapped particles drift off flux surfaces. The number of trapped particles is small by $\sqrt {\epsilon }$![]() and, for this reason, despite the considerable radial displacements of trapped particles, the radial flux of entropy due to trapped particles is not sufficient to compensate for the large entropy production associated with a distribution function far from Maxwellian. Moreover, trapped particles themselves are close to Maxwellian despite their large displacements because they exchange momentum and energy with passing particles much faster than the ion–ion collision frequency $\nu _{ii}$
and, for this reason, despite the considerable radial displacements of trapped particles, the radial flux of entropy due to trapped particles is not sufficient to compensate for the large entropy production associated with a distribution function far from Maxwellian. Moreover, trapped particles themselves are close to Maxwellian despite their large displacements because they exchange momentum and energy with passing particles much faster than the ion–ion collision frequency $\nu _{ii}$![]() would suggest. Indeed, due to the small parallel velocity of trapped particles, $v_\| \sim \sqrt {\epsilon } v_{ti}$
would suggest. Indeed, due to the small parallel velocity of trapped particles, $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() , grazing collisions can detrap them, leading to an effective collision frequency $\nu _{ii}/\epsilon \gg \rho _{i*} v_{ti}/R$
, grazing collisions can detrap them, leading to an effective collision frequency $\nu _{ii}/\epsilon \gg \rho _{i*} v_{ti}/R$![]() .
.
Appendix C contains the calculations that show that the lowest-order distribution function is Maxwellian. In this appendix, we first argue that collisions force the lowest-order trapped-particle distribution function $g_{i,0,W} (r, \alpha, \bar {v}, J, t)$![]() to be independent of $\alpha$
to be independent of $\alpha$![]() and $J$
and $J$![]() . Continuity at the trapped–passing-particle boundary then imposes that the trapped-particle distribution function be the passing-particle distribution function $h_{i, 0} (r, \bar {v}, \xi, t)$
. Continuity at the trapped–passing-particle boundary then imposes that the trapped-particle distribution function be the passing-particle distribution function $h_{i, 0} (r, \bar {v}, \xi, t)$![]() at small pitch angles $\xi \sim \sqrt {\epsilon } \ll 1$
at small pitch angles $\xi \sim \sqrt {\epsilon } \ll 1$![]() ,
,
When we examine the barely-passing-particle region of velocity space, we find that, to the order of interest, the collisional flux from the trapped-particle region to the passing-particle region is negligible. Thus, passing particles collide with each other without exchanging significant momentum and energy with trapped particles and as a result their distribution function $h_{i, 0}$![]() becomes Maxwellian. The trapped particles, however, have a role to play. The lack of collisional flux imposes that the derivative of $h_{i, 0} (r, \bar {v}, \xi, t)$
becomes Maxwellian. The trapped particles, however, have a role to play. The lack of collisional flux imposes that the derivative of $h_{i, 0} (r, \bar {v}, \xi, t)$![]() with respect to $\xi$
with respect to $\xi$![]() at small values of $\xi \sim \sqrt {\epsilon } \ll 1$
at small values of $\xi \sim \sqrt {\epsilon } \ll 1$![]() must be close to zero. Thus, the Maxwellian must have zero average flow, that is, the friction between trapped and passing particles damps the average flow to subsonic levels. Finally, noting that the passing-particle distribution function $h_{i, 0}$
must be close to zero. Thus, the Maxwellian must have zero average flow, that is, the friction between trapped and passing particles damps the average flow to subsonic levels. Finally, noting that the passing-particle distribution function $h_{i, 0}$![]() cannot depend on $\alpha$
cannot depend on $\alpha$![]() or $l$
or $l$![]() , we find that $h_{i,0}$
, we find that $h_{i,0}$![]() is a Maxwellian with density $n_i$
is a Maxwellian with density $n_i$![]() and temperature $T_i$
and temperature $T_i$![]() that are flux functions,
that are flux functions,

The lowest-order trapped-particle distribution function $g_{i, 0, W}$![]() is also a Maxwellian because of (5.4),
is also a Maxwellian because of (5.4),
5.2. Corrections to the lowest-order solutions for the ion distribution function and the electric potential
Since the lowest-order distribution function is a Maxwellian, from here on we need to use the linearized collision operator $C_{ii}^{\ell }[f] :=C_{ii}[f, f_{Mi}] + C_{ii}[f_{Mi}, f]$![]() . The linearized Fokker–Planck collision operator is composed of two terms: a differential part $C_{ii, D}^{\ell }$
. The linearized Fokker–Planck collision operator is composed of two terms: a differential part $C_{ii, D}^{\ell }$![]() and an integral part $C_{ii, I}^{\ell }$
and an integral part $C_{ii, I}^{\ell }$![]() ,
,
The differential part of the linearized collision operator is
where $\boldsymbol{\mathsf{I}}$![]() is the unit matrix,
is the unit matrix,
is the pitch-angle scattering frequency and
is the energy diffusion frequency. Here, the function $H[f_{Mi}] (r, v, t)$![]() only depends on the velocity through its magnitude $v$
only depends on the velocity through its magnitude $v$![]() , $\mathrm {erf}(x) :=(2/\sqrt {{\rm \pi} })\int _0^{x} \exp (-s^{2})\,\mathrm {d}s$
, $\mathrm {erf}(x) :=(2/\sqrt {{\rm \pi} })\int _0^{x} \exp (-s^{2})\,\mathrm {d}s$![]() is the error function and
is the error function and
The integral part of the collision operator is
Using the linearized collision operator, we proceed to obtain an equation and boundary conditions for $g_{i, 1, W}$![]() , to discuss the equation for the passing-particle distribution function, and to show that the correction to the lowest-order potential $\phi _0(r)$
, to discuss the equation for the passing-particle distribution function, and to show that the correction to the lowest-order potential $\phi _0(r)$![]() is of order $\epsilon ^{3/2} T_i/e$
is of order $\epsilon ^{3/2} T_i/e$![]() .
.
5.2.1. Equation for $g_{i, 1, W}$
We first rewrite (2.27) using the coordinates $\bar {v}$![]() and $J$
and $J$![]() , and the fact that $g_{i, 0, W} = f_{Mi}$
, and the fact that $g_{i, 0, W} = f_{Mi}$![]() and $h_{i, 0} = f_{Mi}$
and $h_{i, 0} = f_{Mi}$![]() . We neglect the time derivatives and the source $S_i$
. We neglect the time derivatives and the source $S_i$![]() because of the estimates in (5.1). We also use the fact that the derivatives with respect to $J$
because of the estimates in (5.1). We also use the fact that the derivatives with respect to $J$![]() , $\partial _J \sim \epsilon ^{-1/2}/v_{ti} R$
, $\partial _J \sim \epsilon ^{-1/2}/v_{ti} R$![]() , are larger by $\epsilon ^{-1/2}$
, are larger by $\epsilon ^{-1/2}$![]() than the derivatives with respect to $\bar {v}$
than the derivatives with respect to $\bar {v}$![]() , $\partial _{\bar {v}} \sim v_{ti}^{-1}$
, $\partial _{\bar {v}} \sim v_{ti}^{-1}$![]() . This difference in size is particularly important for the linearized collision operator that can be approximated by
. This difference in size is particularly important for the linearized collision operator that can be approximated by
Finally, we take into account that, according to (4.5) and (4.6), the component of the drifts in the radial direction is much smaller than the component in the $\alpha$![]() direction. With all these considerations, to lowest order in $\epsilon$
direction. With all these considerations, to lowest order in $\epsilon$![]() , (2.27) becomes
, (2.27) becomes

where the derivatives of $g_{i,W}$![]() with respect to $r$
with respect to $r$![]() and $\alpha$
and $\alpha$![]() are performed holding $\bar {v}$
are performed holding $\bar {v}$![]() and $J$
and $J$![]() fixed, whereas the derivatives of $\bar {v}$
fixed, whereas the derivatives of $\bar {v}$![]() and $J_W$
and $J_W$![]() with respect to the same variables are performed holding $\mathcal {E}$
with respect to the same variables are performed holding $\mathcal {E}$![]() and $\mu$
and $\mu$![]() constant. To simplify (5.14), we need to use the fact that $J$
constant. To simplify (5.14), we need to use the fact that $J$![]() is an adiabatic invariant. Employing the exact expressions (3.15) and (3.17), we find
is an adiabatic invariant. Employing the exact expressions (3.15) and (3.17), we find
similarly, using (3.16) and (3.18), we obtain
Thus, the second adiabatic invariant satisfies
Employing the lowest-order expression (4.5), we find
With this result, (5.17) and employing the fact that $\boldsymbol {\nabla }_v J_W \simeq \tau _W v_\| \hat {\boldsymbol {b}}$![]() for trapped particles (see (4.12)), (5.14) can be rewritten as
for trapped particles (see (4.12)), (5.14) can be rewritten as
where
and the quantities $n_i^{\prime }$![]() and $T_i^{\prime }$
and $T_i^{\prime }$![]() are $\partial _r n_i$
are $\partial _r n_i$![]() and $\partial _r T_i$
and $\partial _r T_i$![]() , respectively. Importantly, note that $r$
, respectively. Importantly, note that $r$![]() only appears as a parameter in (5.14), and hence, the derivative of $g_{i, 1, W}$
only appears as a parameter in (5.14), and hence, the derivative of $g_{i, 1, W}$![]() with respect to $r$
with respect to $r$![]() is determined by the variation of the coefficients in (5.14), giving $\partial _r \ln g_{i, 1, W} \sim a^{-1}$
is determined by the variation of the coefficients in (5.14), giving $\partial _r \ln g_{i, 1, W} \sim a^{-1}$![]() , as announced in § 4.1.
, as announced in § 4.1.
We can rewrite (5.19) in a more convenient form. Using the variable
the coordinate $J$![]() can be expressed as
can be expressed as

to lowest order in $\epsilon$![]() . Here, $l_{bL,0,W} (r, \alpha, \bar {\lambda })$
. Here, $l_{bL,0,W} (r, \alpha, \bar {\lambda })$![]() and $l_{bR,0,W} (r, \alpha, \bar {\lambda })$
and $l_{bR,0,W} (r, \alpha, \bar {\lambda })$![]() are the approximate bounce points, determined by the equations $B_1(r, \alpha, l_{bL,0,W} ) /B_0 = 1 - \bar {\lambda } B_0 = B_1(r, \alpha, l_{bR,0,W} ) /B_0$
are the approximate bounce points, determined by the equations $B_1(r, \alpha, l_{bL,0,W} ) /B_0 = 1 - \bar {\lambda } B_0 = B_1(r, \alpha, l_{bR,0,W} ) /B_0$![]() . We can invert (5.22) to obtain $\bar {\lambda }_W (r, \alpha, \bar {v}, J, t)$
. We can invert (5.22) to obtain $\bar {\lambda }_W (r, \alpha, \bar {v}, J, t)$![]() as a function of $r$
as a function of $r$![]() , $\alpha$
, $\alpha$![]() , $\bar {v}$
, $\bar {v}$![]() , $J$
, $J$![]() and the well index $W$
and the well index $W$![]() . We can also calculate $\partial _\alpha \bar {\lambda }_W$
. We can also calculate $\partial _\alpha \bar {\lambda }_W$![]() by differentiating equation (5.22) with respect to $\alpha$
by differentiating equation (5.22) with respect to $\alpha$![]() holding $r$
holding $r$![]() , $\bar {v}$
, $\bar {v}$![]() and $J$
and $J$![]() constant,
constant,

This expression gives
We can use this result to rewrite (5.19) as
where
is the lowest-order radial displacement of the particle. We have defined $r_{i, 1, W}$![]() such that it goes to zero at $J \rightarrow \infty$
such that it goes to zero at $J \rightarrow \infty$![]() . This limit corresponds to the surface-filling barely trapped particle with $\mathcal {E} = U_M(r, \mu, t)$
. This limit corresponds to the surface-filling barely trapped particle with $\mathcal {E} = U_M(r, \mu, t)$![]() and $W = W_\mathrm {bt}$
and $W = W_\mathrm {bt}$![]() . Note that $\bar {\lambda }_W (r, \alpha, \bar {v}, J, t)$
. Note that $\bar {\lambda }_W (r, \alpha, \bar {v}, J, t)$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() for $J \rightarrow \infty$
for $J \rightarrow \infty$![]() .
.
In addition to (5.25), we need the conditions to be imposed in junctures of several types of wells. With the new variables $\bar {v}$![]() and $J$
and $J$![]() , these junctures of different types of wells happen at particular values of $J$
, these junctures of different types of wells happen at particular values of $J$![]() , $J = J_{c,W} (r, \alpha, \bar {v}, t)$
, $J = J_{c,W} (r, \alpha, \bar {v}, t)$![]() , which depend on $r$
, which depend on $r$![]() , $\alpha$
, $\alpha$![]() , $\bar {v}$
, $\bar {v}$![]() , $t$
, $t$![]() and the type of well $W$
and the type of well $W$![]() . Note, for example, the juncture in figure 1: the value of $J$
. Note, for example, the juncture in figure 1: the value of $J$![]() for the juncture is different for each type of well. These values of $J$
for the juncture is different for each type of well. These values of $J$![]() are related by
are related by
As we noted in § 2, the function $g_{i, W}$![]() is continuous across the juncture, but the derivatives $\partial _\mathcal {E} g_{i, W}$
is continuous across the juncture, but the derivatives $\partial _\mathcal {E} g_{i, W}$![]() and $\partial _\mu g_{i, W}$
and $\partial _\mu g_{i, W}$![]() are discontinuous. There are two conditions that we use to relate the discontinuous derivatives on different sides of the juncture. On the one hand, the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i, W} + \partial _\mu g_{i, W}$
are discontinuous. There are two conditions that we use to relate the discontinuous derivatives on different sides of the juncture. On the one hand, the combination $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i, W} + \partial _\mu g_{i, W}$![]() , which is the derivative along the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
, which is the derivative along the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() , is continuous. On the other hand, the discontinuous derivatives $\partial _\mathcal {E} g_{i, W}$
, is continuous. On the other hand, the discontinuous derivatives $\partial _\mathcal {E} g_{i, W}$![]() around the juncture are related to each other by (2.36). In the new variables $\bar {v}$
around the juncture are related to each other by (2.36). In the new variables $\bar {v}$![]() and $J$
and $J$![]() , the derivative along the boundary $J = J_{c, W} (r, \alpha, \bar {v}, t)$
, the derivative along the boundary $J = J_{c, W} (r, \alpha, \bar {v}, t)$![]() is $\partial _{\bar {v}} g_{i, 1, W} + \partial _{\bar {v}} J_{c, W}\, \partial _J g_{i, 1, W}$
is $\partial _{\bar {v}} g_{i, 1, W} + \partial _{\bar {v}} J_{c, W}\, \partial _J g_{i, 1, W}$![]() , and hence this combination of $\partial _{\bar {v}} g_{i, 1, W}$
, and hence this combination of $\partial _{\bar {v}} g_{i, 1, W}$![]() and $\partial _J g_{i, 1, W}$
and $\partial _J g_{i, 1, W}$![]() is continuous across the juncture. To finish our discussion of the junctures, we need to rewrite (2.36) in the new coordinates $\bar {v}$
is continuous across the juncture. To finish our discussion of the junctures, we need to rewrite (2.36) in the new coordinates $\bar {v}$![]() and $J$
and $J$![]() . We first note that expression (2.36) vanishes to lowest order in $\epsilon$
. We first note that expression (2.36) vanishes to lowest order in $\epsilon$![]() because $g_{i,0,W}$
because $g_{i,0,W}$![]() and $h_{i, 0}$
and $h_{i, 0}$![]() are Maxwellians. Thus, (2.36) becomes
are Maxwellians. Thus, (2.36) becomes

Note that the perturbations due to $H_{pq} [ h_{i,3/2} ]$![]() and $H_{pq} [ g_{i, 1, W} ]$
and $H_{pq} [ g_{i, 1, W} ]$![]() can be neglected because they are small in $\epsilon$
can be neglected because they are small in $\epsilon$![]() – in the case of $H_{pq} [ g_{i, 1, W} ]$
– in the case of $H_{pq} [ g_{i, 1, W} ]$![]() because the integral that gives $H_{pq} [ g_{i,1,W} ]$
because the integral that gives $H_{pq} [ g_{i,1,W} ]$![]() is over a region of velocity space small by $\sqrt {\epsilon }$
is over a region of velocity space small by $\sqrt {\epsilon }$![]() . Using the definitions (5.9) and (5.10), we find $H_{\mathcal {E}\mathcal {E}} = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mathcal {E} = v^{2}\, \partial _{vv}^{2} H [ f_{Mi}] = v^{4} \nu _{ii,\|}/2\gamma _{ii}$
. Using the definitions (5.9) and (5.10), we find $H_{\mathcal {E}\mathcal {E}} = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mathcal {E} = v^{2}\, \partial _{vv}^{2} H [ f_{Mi}] = v^{4} \nu _{ii,\|}/2\gamma _{ii}$![]() , $H_{\mathcal {E}\mu } = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = (v_\perp ^{2}/B)\, \partial _{vv}^{2} H [ f_{Mi}] = v^{2} v_\perp ^{2} \nu _{ii,\|}/2\gamma _{ii} B$
, $H_{\mathcal {E}\mu } = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = (v_\perp ^{2}/B)\, \partial _{vv}^{2} H [ f_{Mi}] = v^{2} v_\perp ^{2} \nu _{ii,\|}/2\gamma _{ii} B$![]() and $H_{\mu \mu } = \boldsymbol {\nabla }_v \mu \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = (v_\|^{2} v_\perp ^{2}/v^{3} B^{2}) \, \partial _v H [f_{Mi}] $
and $H_{\mu \mu } = \boldsymbol {\nabla }_v \mu \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [ f_{Mi} ] \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = (v_\|^{2} v_\perp ^{2}/v^{3} B^{2}) \, \partial _v H [f_{Mi}] $![]() $+ (v_\perp ^{4}/v^{2} B^{2}) \, \partial _{vv}^{2} H [ f_{Mi}] = v_\|^{2} v_\perp ^{2} \nu _{ii, \perp }/4\gamma _{ii} B^{2} + v_\perp ^{4} \nu _{ii,\|}/2\gamma _{ii} B^{2}$
$+ (v_\perp ^{4}/v^{2} B^{2}) \, \partial _{vv}^{2} H [ f_{Mi}] = v_\|^{2} v_\perp ^{2} \nu _{ii, \perp }/4\gamma _{ii} B^{2} + v_\perp ^{4} \nu _{ii,\|}/2\gamma _{ii} B^{2}$![]() . Moreover, $\mathcal {E}_c (r, \alpha, \mu, t)$
. Moreover, $\mathcal {E}_c (r, \alpha, \mu, t)$![]() for the example in figure 1 is given by
for the example in figure 1 is given by
to lowest order in $\epsilon$![]() . Here, $B_{lM} (r, \alpha )$
. Here, $B_{lM} (r, \alpha )$![]() is the local maximum of $B$
is the local maximum of $B$![]() on magnetic field line $(r, \alpha )$
on magnetic field line $(r, \alpha )$![]() on which the juncture occurs. Then, $\partial _\mu \mathcal {E}_c = B_{lM} + O(\epsilon ^{3/2} B_0)$
on which the juncture occurs. Then, $\partial _\mu \mathcal {E}_c = B_{lM} + O(\epsilon ^{3/2} B_0)$![]() . As a result of all these considerations, we find
. As a result of all these considerations, we find

Note that $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() and that $1 - B_{lM}/B \sim \epsilon$
and that $1 - B_{lM}/B \sim \epsilon$![]() . Then, expression (5.30) simplifies to
. Then, expression (5.30) simplifies to
With this result and the fact that $\tau _W \langle v_\|^{2} \rangle _{\tau, W} = J$![]() , we can simplify (5.28) to
, we can simplify (5.28) to
To obtain a final expression, we need to rewrite $\partial _\mathcal {E} g_{i, 1, W} (r, \alpha, \mathcal {E}, \mu, t)$![]() as a linear combination of the derivatives of $g_{i, 1, W} (r, \alpha, \bar {v}, J, t)$
as a linear combination of the derivatives of $g_{i, 1, W} (r, \alpha, \bar {v}, J, t)$![]() with respect to $\bar {v}$
with respect to $\bar {v}$![]() and $J$
and $J$![]() . Using $\partial _\mathcal {E} g_{i, 1, W} = \partial _\mathcal {E} \bar {v} \, \partial _{\bar {v}} g_{i, 1, W} + \partial _\mathcal {E} J_W\, \partial _J g_{i, 1, W}$
. Using $\partial _\mathcal {E} g_{i, 1, W} = \partial _\mathcal {E} \bar {v} \, \partial _{\bar {v}} g_{i, 1, W} + \partial _\mathcal {E} J_W\, \partial _J g_{i, 1, W}$![]() , $\partial _\mathcal {E} \bar {v} = \bar {v}^{-1} \sim v_{ti}^{-1}$
, $\partial _\mathcal {E} \bar {v} = \bar {v}^{-1} \sim v_{ti}^{-1}$![]() , $\partial _\mathcal {E} J_W = \tau _W \sim \epsilon ^{-1/2} R/v_{ti}$
, $\partial _\mathcal {E} J_W = \tau _W \sim \epsilon ^{-1/2} R/v_{ti}$![]() , $\partial _{\bar {v}} g_{i,1,W} \sim g_{i,1,W}/v_{ti}$
, $\partial _{\bar {v}} g_{i,1,W} \sim g_{i,1,W}/v_{ti}$![]() and $\partial _J g_{i,1,W} \sim \epsilon ^{-1/2} g_{i, 1, W}/v_{ti}R$
and $\partial _J g_{i,1,W} \sim \epsilon ^{-1/2} g_{i, 1, W}/v_{ti}R$![]() , we can approximate $\partial _\mathcal {E} g_{i, 1, W} \simeq \tau _W\, \partial _J g_{i,1,W}$
, we can approximate $\partial _\mathcal {E} g_{i, 1, W} \simeq \tau _W\, \partial _J g_{i,1,W}$![]() to lowest order in $\epsilon$
to lowest order in $\epsilon$![]() . This approximation might seem to be in contradiction with the fact that the two terms in the combination $\partial _{\bar {v}} g_{i,1,W} + \partial _{\bar {v}} J_{c, W}\, \partial _J g_{i, 1, W}$
. This approximation might seem to be in contradiction with the fact that the two terms in the combination $\partial _{\bar {v}} g_{i,1,W} + \partial _{\bar {v}} J_{c, W}\, \partial _J g_{i, 1, W}$![]() are of the same order, a property that we have used earlier in this paragraph. Note, however, that the function $J_{c, W} (r, \alpha, \bar {v}, t)$
are of the same order, a property that we have used earlier in this paragraph. Note, however, that the function $J_{c, W} (r, \alpha, \bar {v}, t)$![]() does not have a large derivative with respect to $\bar {v}$
does not have a large derivative with respect to $\bar {v}$![]() – indeed, when $\phi _{3/2}$
– indeed, when $\phi _{3/2}$![]() is neglected, $J_{c, W}$
is neglected, $J_{c, W}$![]() is simply proportional to $\bar {v}$
is simply proportional to $\bar {v}$![]() , giving $\partial _{\bar {v}} J_{c, W} \sim \epsilon ^{1/2} R$
, giving $\partial _{\bar {v}} J_{c, W} \sim \epsilon ^{1/2} R$![]() , which should be compared with the scaling with $\epsilon$
, which should be compared with the scaling with $\epsilon$![]() of $\partial _\mathcal {E} J_W = \tau _W \sim \epsilon ^{-1/2} R/v_{ti}$
of $\partial _\mathcal {E} J_W = \tau _W \sim \epsilon ^{-1/2} R/v_{ti}$![]() . Using $\partial _\mathcal {E} g_{i, 1, W} \simeq \tau _W\, \partial _J g_{i,1,W}$
. Using $\partial _\mathcal {E} g_{i, 1, W} \simeq \tau _W\, \partial _J g_{i,1,W}$![]() , (5.32) finally becomes
, (5.32) finally becomes
This equation gives the relationship among the derivatives $\partial _J g_{i, 1, W}$![]() on different sides of the juncture. The orbit periods $\tau _W$
on different sides of the juncture. The orbit periods $\tau _W$![]() diverge at junctures because particles spend a logarithmically large time at local maxima of $U$
diverge at junctures because particles spend a logarithmically large time at local maxima of $U$![]() , where the velocity $v_\|$
, where the velocity $v_\|$![]() vanishes. For this reason, we have to consider the discontinuities of the combination $\tau _W\, \partial _J g_{i, 1, W}$
vanishes. For this reason, we have to consider the discontinuities of the combination $\tau _W\, \partial _J g_{i, 1, W}$![]() instead of the discontinuities of $\partial _J g_{i, 1, W}$
instead of the discontinuities of $\partial _J g_{i, 1, W}$![]() .
.
Condition (2.24) determines the boundary condition for $g_{i, 1, W}$![]() at $J \rightarrow \infty$
at $J \rightarrow \infty$![]() . According to expansion (5.3), there is no correction to $h_{i,0}$
. According to expansion (5.3), there is no correction to $h_{i,0}$![]() of order $\epsilon f_{Mi}$
of order $\epsilon f_{Mi}$![]() , and as a result, the boundary condition for $g_{i, 1, W}$
, and as a result, the boundary condition for $g_{i, 1, W}$![]() is
is
We discuss this boundary condition in more detail in Appendix D.
5.2.2. Correction to the passing-particle distribution function
To obtain boundary condition (5.34), we had to use the fact that the first correction to $h_{i,0}$![]() is $h_{i,3/2}$
is $h_{i,3/2}$![]() . Indeed, had there been a correction to the passing-particle distribution function of order $\epsilon f_{Mi}$
. Indeed, had there been a correction to the passing-particle distribution function of order $\epsilon f_{Mi}$![]() , we could not have imposed condition (5.34).
, we could not have imposed condition (5.34).
We proceed to show that expansion (5.3) is consistent and that, indeed, the largest correction to $h_{i,0}$![]() is of order $\epsilon ^{3/2} h_{i,0}$
is of order $\epsilon ^{3/2} h_{i,0}$![]() . The correction to $h_{i,0}$
. The correction to $h_{i,0}$![]() can be driven by the integral contribution of the trapped-particle distribution function $g_{i, 1, W}$
can be driven by the integral contribution of the trapped-particle distribution function $g_{i, 1, W}$![]() to the linearized collision operator, by the time derivatives of $n_i$
to the linearized collision operator, by the time derivatives of $n_i$![]() and $T_i$
and $T_i$![]() , by the source $S_i$
, by the source $S_i$![]() and by boundary condition (2.25) that requires that the derivatives of $g_{i,W}$
and by boundary condition (2.25) that requires that the derivatives of $g_{i,W}$![]() and $h_i$
and $h_i$![]() with respect to $\boldsymbol {v}$
with respect to $\boldsymbol {v}$![]() are continuous at the trapped–passing boundary. The contribution of $g_{i, 1, W}$
are continuous at the trapped–passing boundary. The contribution of $g_{i, 1, W}$![]() to the integral piece of the linearized collision operator is $C_{ii, I}^{\ell } [ g_{i, 1, W} ] \sim \epsilon ^{3/2} \nu _{ii} f_{Mi}$
to the integral piece of the linearized collision operator is $C_{ii, I}^{\ell } [ g_{i, 1, W} ] \sim \epsilon ^{3/2} \nu _{ii} f_{Mi}$![]() because $g_{i, 1, W}$
because $g_{i, 1, W}$![]() is defined in a region of velocity space small by $\sqrt {\epsilon }$
is defined in a region of velocity space small by $\sqrt {\epsilon }$![]() . As a result, along with the time derivatives of $n_i$
. As a result, along with the time derivatives of $n_i$![]() and $T_i$
and $T_i$![]() and the source $S_i$
and the source $S_i$![]() , $C^{\ell }_{ii, I} [ g_{i, 1, W} ]$
, $C^{\ell }_{ii, I} [ g_{i, 1, W} ]$![]() drives a piece of $h_i$
drives a piece of $h_i$![]() that is of order $\epsilon ^{3/2} f_{Mi}$
that is of order $\epsilon ^{3/2} f_{Mi}$![]() , as demonstrated by the expansion of (2.30) in $\epsilon \ll 1$
, as demonstrated by the expansion of (2.30) in $\epsilon \ll 1$![]() ,
,
where we have used $B \simeq B_0$![]() and the fact that $v_\|$
and the fact that $v_\|$![]() is independent of $\alpha$
is independent of $\alpha$![]() and $l$
and $l$![]() for most passing particles. Recall that the time derivatives in (2.30) are performed holding $\mathcal {E}$
for most passing particles. Recall that the time derivatives in (2.30) are performed holding $\mathcal {E}$![]() and $\mu$
and $\mu$![]() fixed, and that $\bar {f}_i^{(0)}$
fixed, and that $\bar {f}_i^{(0)}$![]() in the term $\langle (B/|v_\| |) C_{ii} [h_i, \bar {f}_i^{(0)}] \rangle _\mathrm {fs}$
in the term $\langle (B/|v_\| |) C_{ii} [h_i, \bar {f}_i^{(0)}] \rangle _\mathrm {fs}$![]() in (2.30) includes both the passing- and trapped-particle distribution functions $h_i$
in (2.30) includes both the passing- and trapped-particle distribution functions $h_i$![]() and $g_{i, W}$
and $g_{i, W}$![]() . Thus, the integral collisional contribution $\langle C_{ii, I}^{\ell } [ g_{i, 1, W} ] \rangle _\mathrm {fs}$
. Thus, the integral collisional contribution $\langle C_{ii, I}^{\ell } [ g_{i, 1, W} ] \rangle _\mathrm {fs}$![]() is a result of the term $\langle (B/|v_\| |) C_{ii} [h_i, \bar {f}_i^{(0)}] \rangle _\mathrm {fs}$
is a result of the term $\langle (B/|v_\| |) C_{ii} [h_i, \bar {f}_i^{(0)}] \rangle _\mathrm {fs}$![]() in (2.30).
in (2.30).
To finish our discussion of the correction to the passing-particle distribution function, we need to consider the boundary condition (2.25). This condition establishes that the derivatives with respect to $\boldsymbol {v}$![]() of the trapped- and passing-particle distribution functions must be continuous across the trapped–passing boundary. It can also be viewed as a flux continuity condition: the collisional flux driven by the trapped-particle distribution function across the trapped–passing boundary must be the flux into the passing-particle region, driving a correction to the passing-particle distribution. The collisional flux across the trapped–passing boundary $J \rightarrow \infty$
of the trapped- and passing-particle distribution functions must be continuous across the trapped–passing boundary. It can also be viewed as a flux continuity condition: the collisional flux driven by the trapped-particle distribution function across the trapped–passing boundary must be the flux into the passing-particle region, driving a correction to the passing-particle distribution. The collisional flux across the trapped–passing boundary $J \rightarrow \infty$![]() driven by $g_{i, 1, W}$
driven by $g_{i, 1, W}$![]() is, according to the collision operator in (5.25), $- (\bar {v}^{2} \nu _{ii, \perp }/2)\, \tau _W J\, \partial _J g_{i, 1, W}$
is, according to the collision operator in (5.25), $- (\bar {v}^{2} \nu _{ii, \perp }/2)\, \tau _W J\, \partial _J g_{i, 1, W}$![]() for $J \rightarrow \infty$
for $J \rightarrow \infty$![]() . If this flux were different from zero, it would drive a correction to the passing-particle distribution function of order $\epsilon ^{1/2} f_{Mi}$
. If this flux were different from zero, it would drive a correction to the passing-particle distribution function of order $\epsilon ^{1/2} f_{Mi}$![]() . We can obtain this result by imposing continuity of derivatives across the trapped–passing boundary. Due to $v_\| \sim \sqrt {\epsilon } v_{ti}$
. We can obtain this result by imposing continuity of derivatives across the trapped–passing boundary. Due to $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() , $\boldsymbol {\nabla }_v g_{i,1,W} \sim \sqrt {\epsilon } f_{Mi}/v_{ti}$
, $\boldsymbol {\nabla }_v g_{i,1,W} \sim \sqrt {\epsilon } f_{Mi}/v_{ti}$![]() . This gradient must be equal to the gradient of the correction to the passing-particle distribution function, $\boldsymbol {\nabla }_v (h_i - f_{Mi}) \sim (h_i - f_{Mi})/v_{ti}$
. This gradient must be equal to the gradient of the correction to the passing-particle distribution function, $\boldsymbol {\nabla }_v (h_i - f_{Mi}) \sim (h_i - f_{Mi})/v_{ti}$![]() , giving the incorrect estimate $h_i - f_{Mi} \sim \sqrt {\epsilon } f_{Mi}$
, giving the incorrect estimate $h_i - f_{Mi} \sim \sqrt {\epsilon } f_{Mi}$![]() , as announced. This estimate is invalid because there is no net collisional flux across the trapped–passing boundary due to $g_{i, 1, W}$
, as announced. This estimate is invalid because there is no net collisional flux across the trapped–passing boundary due to $g_{i, 1, W}$![]() , a property that we prove below. Moreover, we will see that there is no flux due to $g_{i, 3/2, W}$
, a property that we prove below. Moreover, we will see that there is no flux due to $g_{i, 3/2, W}$![]() and hence the collisional flux across the trapped–passing boundary is due to the gradients in velocity space of $g_{i, 2, W}$
and hence the collisional flux across the trapped–passing boundary is due to the gradients in velocity space of $g_{i, 2, W}$![]() . Since $\boldsymbol {\nabla }_v g_{i, 2, W} \sim \epsilon ^{3/2} f_{Mi}/v_{ti}$
. Since $\boldsymbol {\nabla }_v g_{i, 2, W} \sim \epsilon ^{3/2} f_{Mi}/v_{ti}$![]() , the correction to the passing-particle distribution function is indeed $h_{i, 3/2}$
, the correction to the passing-particle distribution function is indeed $h_{i, 3/2}$![]() (see Appendix D for more detail on how the flux continuity condition across the barely-passing-particle region leads to this result). These arguments show that boundary condition (5.34) for $g_{i,1, W}$
(see Appendix D for more detail on how the flux continuity condition across the barely-passing-particle region leads to this result). These arguments show that boundary condition (5.34) for $g_{i,1, W}$![]() is justified because the largest correction to the passing-particle distribution function is indeed of order $\epsilon ^{3/2} f_{Mi}$
is justified because the largest correction to the passing-particle distribution function is indeed of order $\epsilon ^{3/2} f_{Mi}$![]() . We proceed to show that $\tau _W\, J\, \partial _J g_{i, 1, W}$
. We proceed to show that $\tau _W\, J\, \partial _J g_{i, 1, W}$![]() and $\tau _W\, J\, \partial _J g_{i, 3/2, W}$
and $\tau _W\, J\, \partial _J g_{i, 3/2, W}$![]() vanish at the trapped–passing boundary $J \rightarrow \infty$
vanish at the trapped–passing boundary $J \rightarrow \infty$![]() , that is, that neither $g_{i, 1, W}$
, that is, that neither $g_{i, 1, W}$![]() nor $g_{i, 3/2, W}$
nor $g_{i, 3/2, W}$![]() drive a collisional flux from the trapped-particle region into the passing-particle region.
drive a collisional flux from the trapped-particle region into the passing-particle region.
We start by showing
We first integrate equation (5.25) over the region in $J$![]() where orbits in well $W$
where orbits in well $W$![]() with given values of $\alpha$
with given values of $\alpha$![]() and $\bar {v}$
and $\bar {v}$![]() exist, $J \in [ J_{m, W} (r, \alpha, \bar {v}, t), J_{M, W} (r, \alpha, \bar {v}, t)]$
exist, $J \in [ J_{m, W} (r, \alpha, \bar {v}, t), J_{M, W} (r, \alpha, \bar {v}, t)]$![]() ,
,

The second and third terms in this equation are included to cancel the derivatives with respect to $\alpha$![]() of the limits of the integral in the first term. The values of $J_{m, W}$
of the limits of the integral in the first term. The values of $J_{m, W}$![]() and $J_{M, W}$
and $J_{M, W}$![]() are either $0$
are either $0$![]() , $\infty$
, $\infty$![]() or values at which there is a juncture between different wells. We proceed to integrate equation (5.37) for all the values of $\alpha$
or values at which there is a juncture between different wells. We proceed to integrate equation (5.37) for all the values of $\alpha$![]() allowed in well $W$
allowed in well $W$![]() for a given $\bar {v}$
for a given $\bar {v}$![]() . The interval $[ \alpha _{L, W}(r, \bar {v}, t), \alpha _{R, W}(r, \bar {v}, t) ]$
. The interval $[ \alpha _{L, W}(r, \bar {v}, t), \alpha _{R, W}(r, \bar {v}, t) ]$![]() is the region in $\alpha$
is the region in $\alpha$![]() where orbits in well $W$
where orbits in well $W$![]() with a given value of $\bar {v}$
with a given value of $\bar {v}$![]() exist. The limits $\alpha _{L, W}$
exist. The limits $\alpha _{L, W}$![]() and $\alpha _{R, W}$
and $\alpha _{R, W}$![]() exist for two different reasons:
exist for two different reasons:
(i) either well $W$
 closes at $\alpha _{L, W}$
closes at $\alpha _{L, W}$ and $\alpha _{R, W}$
and $\alpha _{R, W}$ because $J_{m, W} = J_{M, W}$
because $J_{m, W} = J_{M, W}$ ; or
; or(ii) well $W$
 extends to all values of $\alpha$
extends to all values of $\alpha$ and hence $\alpha _{L, W} = 0$
and hence $\alpha _{L, W} = 0$ and $\alpha _{R, W} = 2{\rm \pi}$
and $\alpha _{R, W} = 2{\rm \pi}$ .
.
In figure 3, we give an example in which one of the wells, well $IV$![]() , disappears ($J_{m, IV} = J_{M, IV}$
, disappears ($J_{m, IV} = J_{M, IV}$![]() at $\alpha = \alpha _{R, IV}$
at $\alpha = \alpha _{R, IV}$![]() ) and a new well, well $VI$
) and a new well, well $VI$![]() , appears ($J_{m, VI} \neq J_{M, VI}$
, appears ($J_{m, VI} \neq J_{M, VI}$![]() for $\alpha > \alpha _{R, IV}$
for $\alpha > \alpha _{R, IV}$![]() ). Not all cases in which a well disappears are as straightforward as the example in figure 3. We discuss a pathological example in Appendix E, where we also show that choices can be made such that either $J_{m, W} = J_{M, W}$
). Not all cases in which a well disappears are as straightforward as the example in figure 3. We discuss a pathological example in Appendix E, where we also show that choices can be made such that either $J_{m, W} = J_{M, W}$![]() or the distribution function is periodic at $\alpha _{L, W}$
or the distribution function is periodic at $\alpha _{L, W}$![]() and $\alpha _{R, W}$
and $\alpha _{R, W}$![]() . In either case, integrating equation (5.37) over $\alpha$
. In either case, integrating equation (5.37) over $\alpha$![]() , we find
, we find

Summing over all possible well indices $W$![]() , and using the fact that, at the juncture of several wells, $g_{i, 1, W}$
, and using the fact that, at the juncture of several wells, $g_{i, 1, W}$![]() is continuous and $\tau _W\, \partial _J g_{i, 1, W}$
is continuous and $\tau _W\, \partial _J g_{i, 1, W}$![]() satisfies (5.33), several terms cancel and we find the result in (5.36). To illustrate the different cancellations that lead to (5.36), we consider the juncture of wells $I$
satisfies (5.33), several terms cancel and we find the result in (5.36). To illustrate the different cancellations that lead to (5.36), we consider the juncture of wells $I$![]() , $II$
, $II$![]() and $IV$
and $IV$![]() in figure 3, characterized by $J_{c, I}$
in figure 3, characterized by $J_{c, I}$![]() , $J_{c, II}$
, $J_{c, II}$![]() and $J_{c, IV} = J_{c, I} + J_{c, II}$
and $J_{c, IV} = J_{c, I} + J_{c, II}$![]() . For well $I$
. For well $I$![]() , we find $J_{m, I} = 0$
, we find $J_{m, I} = 0$![]() and $J_{M, I} = J_{c, I}$
and $J_{M, I} = J_{c, I}$![]() . Similarly, for well $II$
. Similarly, for well $II$![]() , we have $J_{m, II} = 0$
, we have $J_{m, II} = 0$![]() and $J_{M, II} = J_{c, II}$
and $J_{M, II} = J_{c, II}$![]() . For well $IV$
. For well $IV$![]() we only know the minimum value $J_{m, IV} = J_{c, IV}$
we only know the minimum value $J_{m, IV} = J_{c, IV}$![]() . In the sum of (5.38) over all wells, the terms proportional to $J_{m, I}$
. In the sum of (5.38) over all wells, the terms proportional to $J_{m, I}$![]() , $J_{m, II}$
, $J_{m, II}$![]() and their derivatives with respect to $\alpha$
and their derivatives with respect to $\alpha$![]() vanish. The contributions from the juncture of wells $I$
vanish. The contributions from the juncture of wells $I$![]() , $II$
, $II$![]() and $IV$
and $IV$![]() in figure 3 are then
in figure 3 are then

The ellipsis points $\cdots$![]() here indicates that there are more terms corresponding to other junctures that we have not included in the equation. The first three lines of (5.39) cancel each other because of continuity of $g_{i, 1, W}$
here indicates that there are more terms corresponding to other junctures that we have not included in the equation. The first three lines of (5.39) cancel each other because of continuity of $g_{i, 1, W}$![]() and $r_{i, 1, W}$
and $r_{i, 1, W}$![]() across the juncture and the fact that $\partial _\alpha J_{c, I} + \partial _\alpha J_{c, II} = \partial _\alpha J_{c, IV}$
across the juncture and the fact that $\partial _\alpha J_{c, I} + \partial _\alpha J_{c, II} = \partial _\alpha J_{c, IV}$![]() . The displacement $r_{i, 1, W}$
. The displacement $r_{i, 1, W}$![]() is continuous across junctures because each juncture has a single value of $\bar {\lambda }$
is continuous across junctures because each juncture has a single value of $\bar {\lambda }$![]() , $\bar {\lambda } = \bar {\lambda }_c (r, \alpha, \bar {v})$
, $\bar {\lambda } = \bar {\lambda }_c (r, \alpha, \bar {v})$![]() . Lines four and five of (5.39) vanish because of condition (5.33).
. Lines four and five of (5.39) vanish because of condition (5.33).

Figure 3. Example of limits $\alpha _{L, W}$![]() and $\alpha _{R, W}$
and $\alpha _{R, W}$![]() . Well $IV$
. Well $IV$![]() disappears at $\alpha = \alpha _{R, IV}$
disappears at $\alpha = \alpha _{R, IV}$![]() , and at that same value of $\alpha$
, and at that same value of $\alpha$![]() , a new well $VI$
, a new well $VI$![]() appears, giving $\alpha _{L, VI} = \alpha _{R, IV}$
appears, giving $\alpha _{L, VI} = \alpha _{R, IV}$![]() .
.
The correction $g_{i, 3/2, W}$![]() to the trapped-particle distribution function is shown to be independent of $\alpha$
to the trapped-particle distribution function is shown to be independent of $\alpha$![]() and $J$
and $J$![]() in Appendix F. Using $\bar {v}$
in Appendix F. Using $\bar {v}$![]() instead of $v$
instead of $v$![]() is crucial to obtain this result (see Appendix F for more details on the role of $\bar {v}$
is crucial to obtain this result (see Appendix F for more details on the role of $\bar {v}$![]() in the derivation). By continuity across the trapped–passing boundary, we also find that
in the derivation). By continuity across the trapped–passing boundary, we also find that
Thus, $\tau _W\, J\, \partial _J g_{i, 3/2, W}$![]() is zero at the trapped–passing boundary.
is zero at the trapped–passing boundary.
5.2.3. Electric potential $\phi _{3/2}$
To determine the piece of the electric potential that is not a flux function, we use quasineutrality (2.1). To calculate the integral of $\bar {f}_i^{(0)}$![]() over velocity space, we employ $\bar {v} \simeq v + Z_i e \phi _{3/2}/m_i v$
over velocity space, we employ $\bar {v} \simeq v + Z_i e \phi _{3/2}/m_i v$![]() to perform a Taylor expansion around $v$
to perform a Taylor expansion around $v$![]() , finding
, finding
and
Then, the lowest-order quasineutrality equation (2.1) gives

showing that the next-order correction to the flux function $\phi _0$![]() is indeed small by $\epsilon ^{3/2}$
is indeed small by $\epsilon ^{3/2}$![]() , as predicted in § 4. Here, $n_e \simeq \hat {n}_e \exp ( e\phi _0/T_e)$
, as predicted in § 4. Here, $n_e \simeq \hat {n}_e \exp ( e\phi _0/T_e)$![]() , and $\int g_{i, 1, W} \, \mathrm {d}^{3} v \sim \epsilon ^{3/2} n_i$
, and $\int g_{i, 1, W} \, \mathrm {d}^{3} v \sim \epsilon ^{3/2} n_i$![]() because, again, the region of velocity space where $g_{i, 1, W}$
because, again, the region of velocity space where $g_{i, 1, W}$![]() is defined is small by $\sqrt {\epsilon }$
is defined is small by $\sqrt {\epsilon }$![]() . Note that we need not include $\int h_{i,3/2}\, \mathrm {d}^{3} v$
. Note that we need not include $\int h_{i,3/2}\, \mathrm {d}^{3} v$![]() in the quasineutrality equation because this integral does not depend on $\alpha$
in the quasineutrality equation because this integral does not depend on $\alpha$![]() or $l$
or $l$![]() to lowest order in $\epsilon$
to lowest order in $\epsilon$![]() , and hence can be absorbed into the definition of $n_i(r)$
, and hence can be absorbed into the definition of $n_i(r)$![]() .
.
5.3. Ion transport equations
We finish by integrating equations (2.27) and (2.30) to find equations for $n_i$![]() and $T_i$
and $T_i$![]() . Before we integrate, we rewrite the equations in a convenient form. Using (5.15) and (5.16) and employing $Z_i e \langle \partial _t \phi \rangle _{\tau, W}/m_i = - \tau _W^{-1} \partial _t ( \tau _W \langle v_\|^{2} \rangle _{\tau, W})$
. Before we integrate, we rewrite the equations in a convenient form. Using (5.15) and (5.16) and employing $Z_i e \langle \partial _t \phi \rangle _{\tau, W}/m_i = - \tau _W^{-1} \partial _t ( \tau _W \langle v_\|^{2} \rangle _{\tau, W})$![]() and $\partial _\mathcal {E} ( \tau _W \langle v_\|^{2} \rangle _{\tau, W}) = \tau _W$
and $\partial _\mathcal {E} ( \tau _W \langle v_\|^{2} \rangle _{\tau, W}) = \tau _W$![]() , (2.27) can be written as
, (2.27) can be written as

Using $Z_i e \langle (B/|v_\| |)\, \partial _t \phi \rangle _\mathrm {fs}/m_i = - \partial _t \langle B |v_\|| \rangle _\mathrm {fs}$![]() and $\partial _\mathcal {E} \langle B |v_\|| \rangle _\mathrm {fs} = \langle B/|v_\|| \rangle _\mathrm {fs}$
and $\partial _\mathcal {E} \langle B |v_\|| \rangle _\mathrm {fs} = \langle B/|v_\|| \rangle _\mathrm {fs}$![]() , (2.30) can be written as
, (2.30) can be written as

Multiplying (5.44) by $\tau _W$![]() and (5.45) by 1, integrating over $\alpha$
and (5.45) by 1, integrating over $\alpha$![]() , $\mathcal {E}$
, $\mathcal {E}$![]() , $\mu$
, $\mu$![]() and $\varphi$
and $\varphi$![]() , and summing over both signs of $\sigma$
, and summing over both signs of $\sigma$![]() and over the well index $W$
and over the well index $W$![]() , we find ion particle conservation equation
, we find ion particle conservation equation
where

is the particle flux. Note that the passing-particle piece $h_i$![]() does not contribute due to property (2.33). Using the expansion in (5.2), the integration variables $v \simeq \bar {v}$
does not contribute due to property (2.33). Using the expansion in (5.2), the integration variables $v \simeq \bar {v}$![]() and $J$
and $J$![]() and the lowest-order expression for the radial drifts in (4.5), and employing equation (5.24) to relate the drifts to $r_{i, 1, W}$
and the lowest-order expression for the radial drifts in (4.5), and employing equation (5.24) to relate the drifts to $r_{i, 1, W}$![]() , defined in (5.26), the particle flux becomes
, defined in (5.26), the particle flux becomes

To obtain the order of magnitude estimate, we have used $\phi _0^{\prime } \sim T_i/ea$![]() , $V^{\prime } \sim Ra$
, $V^{\prime } \sim Ra$![]() , $J \sim \sqrt {\epsilon } v_{ti} R$
, $J \sim \sqrt {\epsilon } v_{ti} R$![]() and $r_{i, 1, W} \sim \epsilon a$
and $r_{i, 1, W} \sim \epsilon a$![]() . The order of magnitude estimate in (5.48) justifies estimates (5.1).
. The order of magnitude estimate in (5.48) justifies estimates (5.1).
The estimate for the size of the particle flux in (5.48) can also be obtained from a random walk argument. In the introduction, in (1.5), we argued that trapped particle orbits had a radial width $w \sim \epsilon a$![]() due to the smallness of the magnetic drift compared with the $\boldsymbol {E} \times \boldsymbol {B}$
due to the smallness of the magnetic drift compared with the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, $|\boldsymbol {v}_M|/|\boldsymbol {v}_E| \sim \epsilon$
drift, $|\boldsymbol {v}_M|/|\boldsymbol {v}_E| \sim \epsilon$![]() . These orbits are interrupted by collisions that have an effective collision frequency $\nu _{ii}/\epsilon$
. These orbits are interrupted by collisions that have an effective collision frequency $\nu _{ii}/\epsilon$![]() , causing a radial random walk with steps of length $w$
, causing a radial random walk with steps of length $w$![]() every time $\epsilon /\nu _{ii}$
every time $\epsilon /\nu _{ii}$![]() . The effective collision frequency $\nu _{ii}/\epsilon$
. The effective collision frequency $\nu _{ii}/\epsilon$![]() is larger than $\nu _{ii}$
is larger than $\nu _{ii}$![]() because small angle collisions can easily detrap particles with $v_\| \sim \sqrt {\epsilon } v_{ti}$
because small angle collisions can easily detrap particles with $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() by providing a small amount of parallel momentum. Since we assume $\nu _{i*} \sim \rho _{i*}$
by providing a small amount of parallel momentum. Since we assume $\nu _{i*} \sim \rho _{i*}$![]() , $\nu _{ii}/\epsilon \sim \rho _{i*} v_{ti}/a$
, $\nu _{ii}/\epsilon \sim \rho _{i*} v_{ti}/a$![]() . Thus, the random walk diffusion coefficient associated with trapped-particle orbits is $D \sim \sqrt {\epsilon } w^{2} \rho _{i*} v_{ti}/a$
. Thus, the random walk diffusion coefficient associated with trapped-particle orbits is $D \sim \sqrt {\epsilon } w^{2} \rho _{i*} v_{ti}/a$![]() . The factor of $\sqrt {\epsilon }$
. The factor of $\sqrt {\epsilon }$![]() in the estimate of the diffusion coefficient is due to the fact that only trapped particles, which are a fraction of order $\sqrt {\epsilon } \ll 1$
in the estimate of the diffusion coefficient is due to the fact that only trapped particles, which are a fraction of order $\sqrt {\epsilon } \ll 1$![]() of the total number of particles, participate in the diffusion. Using $D \sim \epsilon ^{5/2} \rho _{i*} a v_{ti}$
of the total number of particles, participate in the diffusion. Using $D \sim \epsilon ^{5/2} \rho _{i*} a v_{ti}$![]() and $\varGamma _i \sim D |\boldsymbol {\nabla } n_i| \sim D n_i/a$
and $\varGamma _i \sim D |\boldsymbol {\nabla } n_i| \sim D n_i/a$![]() , we obtain the estimate in (5.48).
, we obtain the estimate in (5.48).
Multiplying (5.44) and (5.45) by $m_i \mathcal {E}$![]() and integrating over velocity space, we find the ion energy conservation equation
and integrating over velocity space, we find the ion energy conservation equation

where

is the ion energy flux. Note that, using (5.46), (5.49) can also be written as
The expressions for the particle and energy fluxes given in (5.48) and (5.50) would seem to suggest that both fluxes are proportional to the radial electric field $\phi _0^{\prime }$![]() . This is, however, not the case as $r_{i,1,W}$
. This is, however, not the case as $r_{i,1,W}$![]() , defined in (5.26), is inversely proportional to $\phi _0^{\prime }$
, defined in (5.26), is inversely proportional to $\phi _0^{\prime }$![]() . Thus, $\phi _0^{\prime }$
. Thus, $\phi _0^{\prime }$![]() only enters in the fluxes through its influence on the correction to the distribution function $g_{i, 1, W}$
only enters in the fluxes through its influence on the correction to the distribution function $g_{i, 1, W}$![]() .
.
5.4. Summary
To summarize, for $\rho _{i*} \sim \nu _{i*}$![]() , the ion distribution function is Maxwellian to lowest order. The density and temperature of this Maxwellian can be calculated using particle and energy conservation equations once the particle and energy fluxes in (5.48) and (5.50) are obtained. To calculate these fluxes, we must obtain the correction $g_{i, 1, W}$
, the ion distribution function is Maxwellian to lowest order. The density and temperature of this Maxwellian can be calculated using particle and energy conservation equations once the particle and energy fluxes in (5.48) and (5.50) are obtained. To calculate these fluxes, we must obtain the correction $g_{i, 1, W}$![]() that is only defined in the trapped-particle region. The equation for $g_{i, 1, W}$
that is only defined in the trapped-particle region. The equation for $g_{i, 1, W}$![]() is (5.25). This equation must be solved along with boundary condition (5.34) and relation (5.33) for the junctures of different types of wells.
is (5.25). This equation must be solved along with boundary condition (5.34) and relation (5.33) for the junctures of different types of wells.
Importantly, due to the presence of the small correction $\phi _{3/2}$![]() to the potential, we had to use the velocity-space coordinates $\bar {v}$
to the potential, we had to use the velocity-space coordinates $\bar {v}$![]() and $J$
and $J$![]() , defined in (4.10) and (4.11), and the approximate pitch-angle variable $\bar {\lambda }$
, defined in (4.10) and (4.11), and the approximate pitch-angle variable $\bar {\lambda }$![]() , defined in (5.21). These variables were crucial to show that boundary condition (5.34) applies, but once this is done, we can use the approximations $\bar {v} \simeq v$
, defined in (5.21). These variables were crucial to show that boundary condition (5.34) applies, but once this is done, we can use the approximations $\bar {v} \simeq v$![]() and $\bar {\lambda } \simeq \lambda$
and $\bar {\lambda } \simeq \lambda$![]() , where $\lambda$
, where $\lambda$![]() is defined in (4.8). From here on, we replace $\bar {v}$
is defined in (4.8). From here on, we replace $\bar {v}$![]() with $v$
with $v$![]() and $\bar {\lambda }$
and $\bar {\lambda }$![]() with $\lambda$
with $\lambda$![]() .
.
The same set of equations that we have obtained can be derived from the kinetic equation implemented in DKES (Hirshman et al. Reference Hirshman, Shaing, van Rij, Beasley and Crume1986) in the limit given by $\rho _{i*} \sim \nu _{i*} \ll 1$![]() and $\epsilon \ll 1$
and $\epsilon \ll 1$![]() . The procedure to derive (5.25), (5.33) and (5.34) from the DKES kinetic equation is similar to the method described in § 2 and in this section. We sketch the derivation in Appendix G. There are three differences with our derivation that are worth mentioning.
. The procedure to derive (5.25), (5.33) and (5.34) from the DKES kinetic equation is similar to the method described in § 2 and in this section. We sketch the derivation in Appendix G. There are three differences with our derivation that are worth mentioning.
(i) The DKES equations assume from the start that the lowest-order distribution is Maxwellian and that the potential is an exact flux function.
(ii) We use the second adiabatic invariant as a variable because it remains constant as the particle moves. However, the DKES kinetic equation does not ensure that the second adiabatic invariant remains constant. Instead, the DKES kinetic equation maintains the quantity
(5.52)\begin{equation} \hat{J}_W := 2 \int_{l_{bL,W}}^{l_{bR,W}} B |v_\| |\, \mathrm{d} l \end{equation}constant. In the expansion in $\epsilon \ll 1$
 , this quantity is approximately proportional to $J$
, this quantity is approximately proportional to $J$ , $\hat {J} \simeq B_0 J$
, $\hat {J} \simeq B_0 J$ .
.(iii) The perturbation to the passing-particle distribution function $h_i$
 calculated by DKES is of order $\epsilon ^{3/2} f_{Mi}$
calculated by DKES is of order $\epsilon ^{3/2} f_{Mi}$ , but unlike the physical correction $h_{i,3/2}$
, but unlike the physical correction $h_{i,3/2}$ , determined by (5.35), the DKES correction to the passing-particle distribution function is not driven by the time derivatives of density, potential and temperature, the heating and fuelling sources or the integral terms of the collision operator. In DKES, the perturbation to the passing-particle distribution function is only driven by the collisional flux from and to the trapped-particle region because DKES only evolves the perturbation to the Maxwellian and uses a simple pitch-angle scattering operator without integral contributions.
, determined by (5.35), the DKES correction to the passing-particle distribution function is not driven by the time derivatives of density, potential and temperature, the heating and fuelling sources or the integral terms of the collision operator. In DKES, the perturbation to the passing-particle distribution function is only driven by the collisional flux from and to the trapped-particle region because DKES only evolves the perturbation to the Maxwellian and uses a simple pitch-angle scattering operator without integral contributions.
The three previous differences mean that, even though the DKES kinetic equation leads to the same equations as the full kinetic equation to lowest order in $\rho _{i*} \sim \nu _{i*} \ll 1$![]() and $\epsilon \ll 1$
and $\epsilon \ll 1$![]() , the higher-order equations given by DKES will be very different from the physical ones. The higher-order equations merit further study because they might be important even for small values of $\epsilon$
, the higher-order equations given by DKES will be very different from the physical ones. The higher-order equations merit further study because they might be important even for small values of $\epsilon$![]() : for example, $g_{i, 1, W}$
: for example, $g_{i, 1, W}$![]() is not zero at the trapped–passing boundary, but of order $\sqrt {\epsilon } g_{i, 1, W}$
is not zero at the trapped–passing boundary, but of order $\sqrt {\epsilon } g_{i, 1, W}$![]() , and this boundary value is determined by the perturbation to the passing-particle distribution function, $h_i - f_{Mi}$
, and this boundary value is determined by the perturbation to the passing-particle distribution function, $h_i - f_{Mi}$![]() , that we have neglected. DKES cannot determine $h_i - f_{Mi}$
, that we have neglected. DKES cannot determine $h_i - f_{Mi}$![]() in the limit given by $\rho _{i*} \sim \nu _{i*} \ll 1$
in the limit given by $\rho _{i*} \sim \nu _{i*} \ll 1$![]() and $\epsilon \ll 1$
and $\epsilon \ll 1$![]() .
.
Finally, to demonstrate the advantages of (5.25), (5.33) and (5.34), we consider the deeply trapped particles. These particles were singled out as problematic for, for example, the first version of the local orbit-averaged code KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra and García-Regaña2020). The first version of KNOSOS was valid only for stellarators close to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017), and as a result, the radial displacement of particles is neglected to lowest order in the expansion in closeness to omnigeneity. This approximation is valid for most particles, but fails for deeply and barely trapped particles because these particles cannot move across magnetic field lines within the same flux surface if they do not move simultaneously along $\boldsymbol {\nabla } r$![]() (across flux surfaces).
(across flux surfaces).
We proceed to explain this problem in detail. First, we consider a particle deeply trapped in a given magnetic well $W$![]() on a given flux surface $r$
on a given flux surface $r$![]() . The deeply trapped particles have a small $J$
. The deeply trapped particles have a small $J$![]() and hence must have a parallel velocity close to zero to keep $J$
and hence must have a parallel velocity close to zero to keep $J$![]() constant. Their total energy per unit mass is, to lowest order in $\epsilon$
constant. Their total energy per unit mass is, to lowest order in $\epsilon$![]() ,
,
where $B_{lm, W}(r, \alpha )$![]() denotes the local minimum of $B$
denotes the local minimum of $B$![]() in well $W$
in well $W$![]() along the magnetic field line determined by $r$
along the magnetic field line determined by $r$![]() and $\alpha$
and $\alpha$![]() . Since the total energy $\mathcal {E}$
. Since the total energy $\mathcal {E}$![]() is a constant of the motion, a deeply trapped particle can move across magnetic field lines of the same flux surface $r$
is a constant of the motion, a deeply trapped particle can move across magnetic field lines of the same flux surface $r$![]() only if the value of $B_{lm, W}$
only if the value of $B_{lm, W}$![]() remains the same while it does so, as in the case represented in figure 4(a). In the case of omnigeneity, treated by Cary & Shasharina (Reference Cary and Shasharina1997a,Reference Cary and Shasharinab) and Parra et al. (Reference Parra, Calvo, Helander and Landreman2015), $B_{lm, W}$
remains the same while it does so, as in the case represented in figure 4(a). In the case of omnigeneity, treated by Cary & Shasharina (Reference Cary and Shasharina1997a,Reference Cary and Shasharinab) and Parra et al. (Reference Parra, Calvo, Helander and Landreman2015), $B_{lm, W}$![]() remains the same for different values of $\alpha$
remains the same for different values of $\alpha$![]() on a given flux surface. Thus, deeply trapped particles precess around the flux surface without moving radially.
on a given flux surface. Thus, deeply trapped particles precess around the flux surface without moving radially.
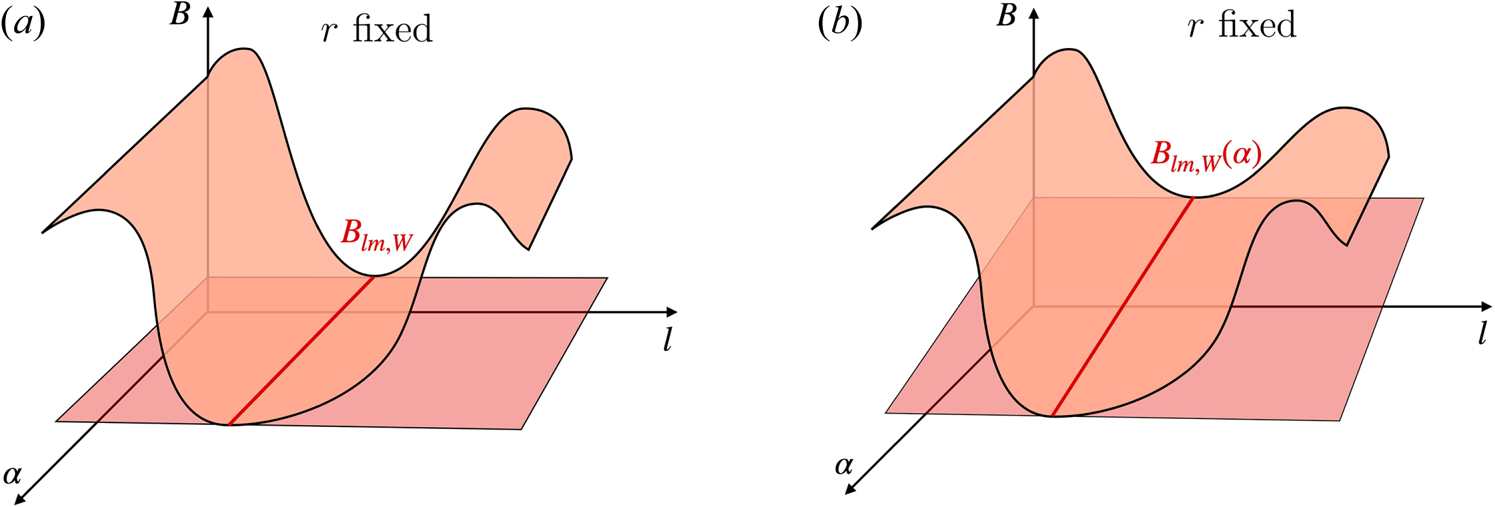
Figure 4. (a) A particle deeply trapped in well $W$![]() can move across field lines along the red line in the particular case in which the local minima of $B$
can move across field lines along the red line in the particular case in which the local minima of $B$![]() , $B_{lm, W} (r, \alpha )$
, $B_{lm, W} (r, \alpha )$![]() , are independent of $\alpha$
, are independent of $\alpha$![]() . The local minima of $B$
. The local minima of $B$![]() in omnigeneous magnetic fields behave in this manner. (b) In the more general case in which $B_{lm, W}$
in omnigeneous magnetic fields behave in this manner. (b) In the more general case in which $B_{lm, W}$![]() varies with $\alpha$
varies with $\alpha$![]() , deeply trapped particles cannot move along the red line to precess around the flux surface unless they are allowed to move radially as well.
, deeply trapped particles cannot move along the red line to precess around the flux surface unless they are allowed to move radially as well.
In a generic large aspect ratio stellarator with mirror ratio close to unity, the deeply trapped particles cannot move across magnetic field lines on a given flux surface, as shown on figure 4(b). However, since the electric potential $\phi _0$![]() varies with $r$
varies with $r$![]() , it is possible for $v_\parallel$
, it is possible for $v_\parallel$![]() to be approximately equal to zero after a displacement $\Delta \alpha$
to be approximately equal to zero after a displacement $\Delta \alpha$![]() if the particle moves across flux surfaces by a distance $\Delta r$
if the particle moves across flux surfaces by a distance $\Delta r$![]() . Using (5.53), we find that $\Delta \alpha$
. Using (5.53), we find that $\Delta \alpha$![]() and $\Delta r$
and $\Delta r$![]() must satisfy
must satisfy
where we have neglected the radial derivative of $B_{lm, W}(r, \alpha )$![]() because it is small by a factor of $\epsilon$
because it is small by a factor of $\epsilon$![]() compared with the radial derivative of $\phi _0$
compared with the radial derivative of $\phi _0$![]() . This is consistent with the velocities $\mathrm {d}\alpha /\mathrm {d}t$
. This is consistent with the velocities $\mathrm {d}\alpha /\mathrm {d}t$![]() and $\mathrm {d}r / \mathrm {d}t$
and $\mathrm {d}r / \mathrm {d}t$![]() obtained from the transit average drifts in (4.5) and (4.6),
obtained from the transit average drifts in (4.5) and (4.6),
and
where $B_{1,lm, W}(r, \alpha )$![]() is the local minimum of $B_1$
is the local minimum of $B_1$![]() in well $W$
in well $W$![]() along the magnetic field line determined by $r$
along the magnetic field line determined by $r$![]() and $\alpha$
and $\alpha$![]() . Moreover, (5.54) is also consistent with the definition of the radial displacement $r_{i, 1, W}$
. Moreover, (5.54) is also consistent with the definition of the radial displacement $r_{i, 1, W}$![]() given in (5.26). Indeed, to lowest order in $\epsilon$
given in (5.26). Indeed, to lowest order in $\epsilon$![]() , $\lambda = B_{lm, W}^{-1}$
, $\lambda = B_{lm, W}^{-1}$![]() for deeply trapped particles, and $\lambda \rightarrow B_M^{-1}$
for deeply trapped particles, and $\lambda \rightarrow B_M^{-1}$![]() for $J \rightarrow \infty$
for $J \rightarrow \infty$![]() , giving
, giving
This equation is a solution to (5.55) and (5.56), and it shows how the particle moves radially to increase and decrease its electric energy to keep its total energy constant.
We can draw the path followed by a deeply trapped particle with $J=0$![]() on an $(l,\alpha )$
on an $(l,\alpha )$![]() plane, sketched in figure 5 for $\phi _0^{\prime } > 0$
plane, sketched in figure 5 for $\phi _0^{\prime } > 0$![]() and $\varPsi _t^{\prime } > 0$
and $\varPsi _t^{\prime } > 0$![]() . The particle moves towards increasing $\alpha$
. The particle moves towards increasing $\alpha$![]() following the local minima $B_{lm, W}$
following the local minima $B_{lm, W}$![]() . Simultaneously, the particle moves back and forth across flux surfaces, increasing $r$
. Simultaneously, the particle moves back and forth across flux surfaces, increasing $r$![]() when $\partial _{\alpha }B < 0$
when $\partial _{\alpha }B < 0$![]() or decreasing $r$
or decreasing $r$![]() when $\partial _{\alpha }B > 0$
when $\partial _{\alpha }B > 0$![]() . It is interesting to note that
. It is interesting to note that
showing that the oscillating displacement across flux surfaces is much smaller that the precession around it. Equation (5.25) reproduces this motion for deeply trapped particles.

Figure 5. Map of the magnetic field magnitude $B$![]() in an $(l,\alpha )$
in an $(l,\alpha )$![]() plane. In black with arrows, we sketch the path followed by particles with $J=0$
plane. In black with arrows, we sketch the path followed by particles with $J=0$![]() in a stellarator with $\phi _0^{\prime } > 0$
in a stellarator with $\phi _0^{\prime } > 0$![]() and $\varPsi _t^{\prime } > 0$
and $\varPsi _t^{\prime } > 0$![]() . The coordinate $r$
. The coordinate $r$![]() is not constant, and its variation around its average value has the opposite sign to the value of $B_1 = B - B_0$
is not constant, and its variation around its average value has the opposite sign to the value of $B_1 = B - B_0$![]() , as shown in (5.57).
, as shown in (5.57).
6. The $1/\nu$ regime in large aspect ratio stellarators with mirror ratios close to unity
regime in large aspect ratio stellarators with mirror ratios close to unity
In this section, we briefly consider the limit $\nu _{i*} \gg \rho _{i*}$![]() . In this limit, we can neglect the term $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha g_{i, 1, W}$
. In this limit, we can neglect the term $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha g_{i, 1, W}$![]() in (5.25), giving to lowest order
in (5.25), giving to lowest order
This equation can be integrated using boundary condition (5.34) and relation (5.33) at the junctures of several types of wells. The final result is a trapped-particle distribution function of order $g_{i, 1, W} \sim \epsilon \rho _{i*} f_{Mi}/\nu _{i*}$![]() . Using this result in (5.48) and (5.50) for the particle and energy fluxes, we obtain
. Using this result in (5.48) and (5.50) for the particle and energy fluxes, we obtain
These are the typical $1/\nu$![]() regime order-of-magnitude estimates (Ho & Kulsrud Reference Ho and Kulsrud1987).
regime order-of-magnitude estimates (Ho & Kulsrud Reference Ho and Kulsrud1987).
Estimates (6.2a,b) can be obtained using a random walk argument. For $\nu _{i*} \gg \rho _{i*}$![]() , a typical trapped particle moves radially due to the radial magnetic drift $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \sim \epsilon \rho _{i*} v_{ti}$
, a typical trapped particle moves radially due to the radial magnetic drift $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \sim \epsilon \rho _{i*} v_{ti}$![]() until a collision detraps it. As a result, particles move a distance $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff}$
until a collision detraps it. As a result, particles move a distance $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff}$![]() between collisions, where $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$
between collisions, where $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$![]() is the effective collision frequency for trapped particles. After each detrapping collision, a trapped particle becomes passing and moves along the magnetic field line until another low angle collision reduces its parallel velocity sufficiently to trap it in a different well. The magnitude and sign of $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r$
is the effective collision frequency for trapped particles. After each detrapping collision, a trapped particle becomes passing and moves along the magnetic field line until another low angle collision reduces its parallel velocity sufficiently to trap it in a different well. The magnitude and sign of $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r$![]() in the new well will in general be different from the sign and magnitude of the radial drift in the original well because the particle has moved a significant distance along the magnetic field line while being a passing particle. For this reason, the radial displacement of a typical trapped particle is similar to a random walk with a characteristic step size $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff} \sim (\rho _{i*}/\nu _{i*}) \epsilon a \ll \epsilon a$
in the new well will in general be different from the sign and magnitude of the radial drift in the original well because the particle has moved a significant distance along the magnetic field line while being a passing particle. For this reason, the radial displacement of a typical trapped particle is similar to a random walk with a characteristic step size $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff} \sim (\rho _{i*}/\nu _{i*}) \epsilon a \ll \epsilon a$![]() and a characteristic time $1/\nu _\mathrm {eff} \sim \epsilon /\nu _{ii}$
and a characteristic time $1/\nu _\mathrm {eff} \sim \epsilon /\nu _{ii}$![]() . The corresponding diffusion coefficient is $D \sim \sqrt {\epsilon } (\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff})^{2} \nu _\mathrm {eff}$
. The corresponding diffusion coefficient is $D \sim \sqrt {\epsilon } (\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff})^{2} \nu _\mathrm {eff}$![]() , where $\sqrt {\epsilon }$
, where $\sqrt {\epsilon }$![]() is the estimate for the trapped-particle fraction. With $D \sim \epsilon ^{5/2} \rho _{i*}^{2} a v_{ti}/\nu _{i*}$
is the estimate for the trapped-particle fraction. With $D \sim \epsilon ^{5/2} \rho _{i*}^{2} a v_{ti}/\nu _{i*}$![]() and using $\varGamma _i \sim D|\boldsymbol {\nabla } n_i| \sim D n_i/a$
and using $\varGamma _i \sim D|\boldsymbol {\nabla } n_i| \sim D n_i/a$![]() and $Q_i \sim n_i D |\boldsymbol {\nabla } T_i| \sim D n_i T_i/a$
and $Q_i \sim n_i D |\boldsymbol {\nabla } T_i| \sim D n_i T_i/a$![]() , we recover estimates (6.2a,b).
, we recover estimates (6.2a,b).
7. The $\nu$ regime in large aspect ratio stellarators with mirror ratios close to unity
regime in large aspect ratio stellarators with mirror ratios close to unity
In this section, we study the limit $\nu _{i*} \ll \rho _{i*}$![]() . We expand $g_{i, 1, W}$
. We expand $g_{i, 1, W}$![]() in $\nu _{i*}/\rho _{i*} \ll 1$
in $\nu _{i*}/\rho _{i*} \ll 1$![]() ,
,
with $g_{i,1,W}^{\{n\}} \sim (\nu _{i*}/\rho _{i*})^{n} \epsilon f_{Mi}$![]() . We proceed to expand (5.25) in $\nu _{i*}/\rho _{i*} \ll 1$
. We proceed to expand (5.25) in $\nu _{i*}/\rho _{i*} \ll 1$![]() . In § 7.1, we solve the lowest-order version of (5.25) and we show that the lowest-order distribution function does not give rise to radial fluxes of particles or energy. In § 7.2, we go to next order in $\nu _{i*}/\rho _{i*} \ll 1$
. In § 7.1, we solve the lowest-order version of (5.25) and we show that the lowest-order distribution function does not give rise to radial fluxes of particles or energy. In § 7.2, we go to next order in $\nu _{i*}/\rho _{i*} \ll 1$![]() . Finally, in § 7.3, we calculate the particle and energy fluxes.
. Finally, in § 7.3, we calculate the particle and energy fluxes.
7.1. Lowest-order distribution function
Equation (5.25) becomes, to lowest order in $\nu _{i*}/\rho _{i*} \ll 1$![]() ,
,
Using the fact that $\varUpsilon _i f_{Mi}$![]() does not vary with $\alpha$
does not vary with $\alpha$![]() , we obtain the expression
, we obtain the expression
where the function $K_{i, W}$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() .
.
Due to the existence of junctures between different types of wells such as the one sketched in figure 1, the function $K_{i, W}$![]() can be independent of $J$
can be independent of $J$![]() in large regions of velocity space. Before we explain why, we need to consider what happens with well junctures in the limit $\nu _{i*}/\rho _{i*} \ll 1$
in large regions of velocity space. Before we explain why, we need to consider what happens with well junctures in the limit $\nu _{i*}/\rho _{i*} \ll 1$![]() . In this limit, it is in general impossible to impose continuity of $g_{i,1,W}$
. In this limit, it is in general impossible to impose continuity of $g_{i,1,W}$![]() across the juncture, or condition (5.33) that relates the derivatives $\partial _J g_{i, 1, W} \simeq \partial _J g_{i,1,W}^{\{0\} }$
across the juncture, or condition (5.33) that relates the derivatives $\partial _J g_{i, 1, W} \simeq \partial _J g_{i,1,W}^{\{0\} }$![]() on different sides of a juncture to each other. This is hardly surprising since continuity of $g_{i,1,W}$
on different sides of a juncture to each other. This is hardly surprising since continuity of $g_{i,1,W}$![]() and condition (5.33) are a result of collisions, and we have neglected collisions to lowest order. In reality, continuity and condition (5.33) are not satisfied in appearance only, because boundary layers where collisions become important can form around well junctures.
and condition (5.33) are a result of collisions, and we have neglected collisions to lowest order. In reality, continuity and condition (5.33) are not satisfied in appearance only, because boundary layers where collisions become important can form around well junctures.
The rest of this subsection is split into three parts. In the first one, we show that collisional boundary layers only form around certain junctures, and we find a condition that $K_{i, W}$![]() must satisfy when these boundary layers form. In the second part, we study an example that illustrates the shape of $K_{i, W}$
must satisfy when these boundary layers form. In the second part, we study an example that illustrates the shape of $K_{i, W}$![]() . We finish with a general discussion.
. We finish with a general discussion.
7.1.1. Junctures of different types of wells for very small collision frequencies
Not all well junctures are problematic and need a boundary layer. Whether a juncture has a boundary layer or not depends on the direction of the velocity in $\alpha$![]() , $c\phi _0^{\prime }/\varPsi _t^{\prime }$
, $c\phi _0^{\prime }/\varPsi _t^{\prime }$![]() , and the derivatives of the juncture coordinates $J_{c, W} (r, \alpha, v)$
, and the derivatives of the juncture coordinates $J_{c, W} (r, \alpha, v)$![]() with respect to $\alpha$
with respect to $\alpha$![]() . To explain this further, we consider the juncture in figure 1. Some particles in well $I$
. To explain this further, we consider the juncture in figure 1. Some particles in well $I$![]() leave this well if the time derivative of $J_{c, I} (r, \alpha, v)$
leave this well if the time derivative of $J_{c, I} (r, \alpha, v)$![]() is negative. Indeed, if a particle with $J = J_{c, I}(r(t), \alpha (t), v(t))$
is negative. Indeed, if a particle with $J = J_{c, I}(r(t), \alpha (t), v(t))$![]() at time $t$
at time $t$![]() were to stay in well $I$
were to stay in well $I$![]() , it would have to do so keeping its second adiabatic invariant constant. However, such a particle would find itself with $J > J_{c, I}(r(t+\Delta t), \alpha (t + \Delta t), v(t + \Delta t))$
, it would have to do so keeping its second adiabatic invariant constant. However, such a particle would find itself with $J > J_{c, I}(r(t+\Delta t), \alpha (t + \Delta t), v(t + \Delta t))$![]() at $t + \Delta t$
at $t + \Delta t$![]() . Since there are no possible orbits with $J > J_{c, I}$
. Since there are no possible orbits with $J > J_{c, I}$![]() in well $I$
in well $I$![]() , the particle must have moved into well $II$
, the particle must have moved into well $II$![]() or well $III$
or well $III$![]() , and in doing so, the value of $J$
, and in doing so, the value of $J$![]() of the particle has changed abruptly. This is consistent with $J$
of the particle has changed abruptly. This is consistent with $J$![]() being an adiabatic invariant: it is only constant when the motion is a slowly changing periodic orbit, a description that does not apply to a transition from one well to another. These transitions between different types of wells can be understood to be a result of the conservation of phase-space volume. The second adiabatic invariant is the phase-space volume inside a trapped orbit. When $J_{c, I}$
being an adiabatic invariant: it is only constant when the motion is a slowly changing periodic orbit, a description that does not apply to a transition from one well to another. These transitions between different types of wells can be understood to be a result of the conservation of phase-space volume. The second adiabatic invariant is the phase-space volume inside a trapped orbit. When $J_{c, I}$![]() becomes lower than the $J$
becomes lower than the $J$![]() of a particle, the phase-space volume of the particle orbit cannot be contained inside well $I$
of a particle, the phase-space volume of the particle orbit cannot be contained inside well $I$![]() and the particle ‘spills over’ into wells $II$
and the particle ‘spills over’ into wells $II$![]() and $III$
and $III$![]() (Dobrott & Greene Reference Dobrott and Greene1971; Cary et al. Reference Cary, Escande and Tennyson1986).
(Dobrott & Greene Reference Dobrott and Greene1971; Cary et al. Reference Cary, Escande and Tennyson1986).
Equivalently to particles moving out of well $I$![]() when the time derivative of $J_{c, I}$
when the time derivative of $J_{c, I}$![]() is negative, some particles move into well $I$
is negative, some particles move into well $I$![]() if the time derivative of $J_{c, I}$
if the time derivative of $J_{c, I}$![]() is positive. As we will see shortly, the fact that the time derivative of $J_{c, I}$
is positive. As we will see shortly, the fact that the time derivative of $J_{c, I}$![]() is positive implies that particles are leaving well $II$
is positive implies that particles are leaving well $II$![]() , well $III$
, well $III$![]() or both, and since these particles must move into another well, it is intuitive that conservation of phase-space volume will force these particles to move to a well where there is ‘space’. Well $I$
or both, and since these particles must move into another well, it is intuitive that conservation of phase-space volume will force these particles to move to a well where there is ‘space’. Well $I$![]() , with a positive time derivative of $J_{c, I}$
, with a positive time derivative of $J_{c, I}$![]() , is such a well because at time $t$
, is such a well because at time $t$![]() all particles in that well have $J \leq J_{c, I} (r(t), \alpha (t), v(t))$
all particles in that well have $J \leq J_{c, I} (r(t), \alpha (t), v(t))$![]() , and hence, if no particle were to move into well $I$
, and hence, if no particle were to move into well $I$![]() , at time $t + \Delta t$
, at time $t + \Delta t$![]() there would be no particles that have second adiabatic invariant between $J_{c, I} (r(t), \alpha (t), v(t))$
there would be no particles that have second adiabatic invariant between $J_{c, I} (r(t), \alpha (t), v(t))$![]() and $J_{c, I} (r(t + \Delta t), \alpha (t + \Delta t), v(t + \Delta t))$
and $J_{c, I} (r(t + \Delta t), \alpha (t + \Delta t), v(t + \Delta t))$![]() .
.
To summarize, some particles move out of well $I$![]() if the time derivative of $J_{c,I}$
if the time derivative of $J_{c,I}$![]() is negative and some particles move into well $I$
is negative and some particles move into well $I$![]() if the time derivative of $J_{c, I}$
if the time derivative of $J_{c, I}$![]() is positive. Similarly, some particles transition out of well $II$
is positive. Similarly, some particles transition out of well $II$![]() if the time derivative of $J_{c, II}$
if the time derivative of $J_{c, II}$![]() is negative, and some transition into it if the time derivative of $J_{c, II}$
is negative, and some transition into it if the time derivative of $J_{c, II}$![]() is positive. The signs reverse for well $III$
is positive. The signs reverse for well $III$![]() because the orbits in this well have $J$
because the orbits in this well have $J$![]() larger than $J_{c, III}$
larger than $J_{c, III}$![]() . Thus, particles move out of well $III$
. Thus, particles move out of well $III$![]() if the time derivative of $J_{c, III}$
if the time derivative of $J_{c, III}$![]() is positive, and transition into it if the time derivative of $J_{c, III}$
is positive, and transition into it if the time derivative of $J_{c, III}$![]() is negative.
is negative.
Since both $r$![]() and $v$
and $v$![]() have time derivatives that are small in $\epsilon$
have time derivatives that are small in $\epsilon$![]() , the time derivative of $J_{c, W} (r, \alpha, v)$
, the time derivative of $J_{c, W} (r, \alpha, v)$![]() is simply
is simply
Importantly, condition (5.27) imposes that $\partial _\alpha J_{c, I} + \partial _\alpha J_{c, II} = \partial _\alpha J_{c, III}$![]() . With this equality, it is easy to check that, if some particles are moving into well $I$
. With this equality, it is easy to check that, if some particles are moving into well $I$![]() , i.e. $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, I} > 0$
, i.e. $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, I} > 0$![]() , some particles must be leaving well $II$
, some particles must be leaving well $II$![]() , $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} < 0$
, $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} < 0$![]() , well $III$
, well $III$![]() , ${(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} > 0}$
, ${(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} > 0}$![]() , or both. It cannot be the case that particles are moving into all three wells, or leaving all three wells.
, or both. It cannot be the case that particles are moving into all three wells, or leaving all three wells.
Armed with the results above, we can start discussing the collisional boundary layers. There are two distinct cases to consider:
(i) the signs of $c\phi _0^{\prime }/\varPsi _t^{\prime }$
 and $\partial _\alpha J_{c, W}$
and $\partial _\alpha J_{c, W}$ are such that some particles leave one of the wells and move into the other two wells; in this case, there is no boundary layer around the juncture; or
are such that some particles leave one of the wells and move into the other two wells; in this case, there is no boundary layer around the juncture; or(ii) the signs of $c\phi _0^{\prime }/\varPsi _t^{\prime }$
 and $\partial _\alpha J_{c, W}$
and $\partial _\alpha J_{c, W}$ are such that some particles leave two of the wells and move into the third well; in this case, a thin boundary layer forms around the juncture.
are such that some particles leave two of the wells and move into the third well; in this case, a thin boundary layer forms around the juncture.
To illustrate what happens in the case that some particles leave one of the wells and enter the other two, we consider the following example. With the sign choices $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, I} < 0$![]() , $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} > 0$
, $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} > 0$![]() and $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} < 0$
and $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} < 0$![]() , some particles leave well $I$
, some particles leave well $I$![]() and enter well $II$
and enter well $II$![]() and $III$
and $III$![]() . For small collisionality, kinetic equation (7.2) imposes that the piece of the distribution function $K_{i, W}$
. For small collisionality, kinetic equation (7.2) imposes that the piece of the distribution function $K_{i, W}$![]() is continuous along particle trajectories. Since particles are leaving well $I$
is continuous along particle trajectories. Since particles are leaving well $I$![]() and moving into well $II$
and moving into well $II$![]() and well $III$
and well $III$![]() , the distribution function in wells $II$
, the distribution function in wells $II$![]() and $III$
and $III$![]() must be the same as in well $I$
must be the same as in well $I$![]() , that is, $K_{i,II} = K_{i,I}$
, that is, $K_{i,II} = K_{i,I}$![]() and $K_{i,III} = K_{i,I}$
and $K_{i,III} = K_{i,I}$![]() . Thus, there is no need for a boundary layer because the distribution is continuous. Note that this process is irreversible: if we reverse time, particles leave wells $II$
. Thus, there is no need for a boundary layer because the distribution is continuous. Note that this process is irreversible: if we reverse time, particles leave wells $II$![]() and $III$
and $III$![]() and move into well $I$
and move into well $I$![]() , and we will see shortly that this leads, in principle, to discontinuities in the distribution function. In our equations, collisions are the only element that introduces irreversibility, so it is surprising that they do not seem to play a role in the discussion. In reality, collisions have led to this solution indirectly. If one assumes that, due to some unknown mechanism, more particles move into well $II$
, and we will see shortly that this leads, in principle, to discontinuities in the distribution function. In our equations, collisions are the only element that introduces irreversibility, so it is surprising that they do not seem to play a role in the discussion. In reality, collisions have led to this solution indirectly. If one assumes that, due to some unknown mechanism, more particles move into well $II$![]() than into well $III$
than into well $III$![]() , giving $K_{i, II} > K_{i, III}$
, giving $K_{i, II} > K_{i, III}$![]() , the distribution function is discontinuous across the juncture. Fokker–Planck collisions impose continuity in the distribution function, and as a result we need a boundary layer around such a hypothetical juncture. Appendix H shows that it is impossible to construct such a boundary layer, a result that implies that the distribution function $K_{i, W}$
, the distribution function is discontinuous across the juncture. Fokker–Planck collisions impose continuity in the distribution function, and as a result we need a boundary layer around such a hypothetical juncture. Appendix H shows that it is impossible to construct such a boundary layer, a result that implies that the distribution function $K_{i, W}$![]() must be continuous across junctures where particles leave one well to move into the other two wells.
must be continuous across junctures where particles leave one well to move into the other two wells.
We proceed to consider a juncture in which particles leave two wells and enter into the third well. For example, consider the situation that arises if the signs of $\phi _0^{\prime }$![]() , $\varPsi _t^{\prime }$
, $\varPsi _t^{\prime }$![]() and the derivatives of $J_{c,I}$
and the derivatives of $J_{c,I}$![]() , $J_{c,II}$
, $J_{c,II}$![]() and $J_{c,III}$
and $J_{c,III}$![]() with respect to $\alpha$
with respect to $\alpha$![]() imply that particles leave wells $I$
imply that particles leave wells $I$![]() and $II$
and $II$![]() to enter well $III$
to enter well $III$![]() . In this case, in general, $K_{i,I}$
. In this case, in general, $K_{i,I}$![]() and $K_{i,II}$
and $K_{i,II}$![]() are different and we need to obtain a value for $K_{i,III}$
are different and we need to obtain a value for $K_{i,III}$![]() . One can think of this problem as particles flowing into the juncture from wells $I$
. One can think of this problem as particles flowing into the juncture from wells $I$![]() and $II$
and $II$![]() , mixing inside the juncture, and leaving through well $III$
, mixing inside the juncture, and leaving through well $III$![]() with a new distribution function $K_{i, III}$
with a new distribution function $K_{i, III}$![]() . A collisional boundary layer, described in Appendix H, forms around any juncture in which particles move out of two wells and into the third. The result of this boundary layer is simply a balance among the phase-space fluxes of particles across the juncture. The infinitesimal element of phase-space volume integrated over the gyrophase and $l$
. A collisional boundary layer, described in Appendix H, forms around any juncture in which particles move out of two wells and into the third. The result of this boundary layer is simply a balance among the phase-space fluxes of particles across the juncture. The infinitesimal element of phase-space volume integrated over the gyrophase and $l$![]() can be constructed from (2.18) and (4.13), and it is $(2{\rm \pi} \varPsi _t^{\prime } v/B_0)\, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v \, \mathrm {d} J$
can be constructed from (2.18) and (4.13), and it is $(2{\rm \pi} \varPsi _t^{\prime } v/B_0)\, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v \, \mathrm {d} J$![]() to lowest order in $\epsilon$
to lowest order in $\epsilon$![]() . With this phase-space volume element, we can calculate the number of particles crossing $J = J_{c,W}$
. With this phase-space volume element, we can calculate the number of particles crossing $J = J_{c,W}$![]() . One first replaces the variable $J$
. One first replaces the variable $J$![]() with $\Delta J_W := J - J_{c, W}$
with $\Delta J_W := J - J_{c, W}$![]() . With this new set of coordinates, the infinitesimal phase-space volume becomes $(2{\rm \pi} \varPsi _t^{\prime } v/B_0)\, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v \, \mathrm {d} \Delta J_W$
. With this new set of coordinates, the infinitesimal phase-space volume becomes $(2{\rm \pi} \varPsi _t^{\prime } v/B_0)\, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v \, \mathrm {d} \Delta J_W$![]() . Then, the rate at which phase-space volume crosses the boundary $J = J_{c, W}$
. Then, the rate at which phase-space volume crosses the boundary $J = J_{c, W}$![]() , equivalent to $\Delta J_W = 0$
, equivalent to $\Delta J_W = 0$![]() , is
, is
where we have used (7.4) and the fact that the time derivative of $J$![]() is zero to obtain $\mathrm {d} \Delta J_W/\mathrm {d} t \simeq - (c \phi _0^{\prime }/\varPsi _t^{\prime }) \, \partial _\alpha J_{c, W}$
is zero to obtain $\mathrm {d} \Delta J_W/\mathrm {d} t \simeq - (c \phi _0^{\prime }/\varPsi _t^{\prime }) \, \partial _\alpha J_{c, W}$![]() . Using (7.5), we find that the number of particles crossing the boundary is $- (2{\rm \pi} c \phi _0^{\prime } v g_{i,1,W}^{\{ 0 \} }/B_0)\, \partial _\alpha J_{c, W} \, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v$
. Using (7.5), we find that the number of particles crossing the boundary is $- (2{\rm \pi} c \phi _0^{\prime } v g_{i,1,W}^{\{ 0 \} }/B_0)\, \partial _\alpha J_{c, W} \, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v$![]() . Balance between the three fluxes leaving and entering the juncture in figure 1 gives
. Balance between the three fluxes leaving and entering the juncture in figure 1 gives

We can simplify this expression by dividing by $- (2{\rm \pi} c \phi _0^{\prime } v/B_0)\, \mathrm {d} r\, \mathrm {d} \alpha \, \mathrm {d} v$![]() . Furthermore, using (7.3), we find the relationship
. Furthermore, using (7.3), we find the relationship
The definition $r_{i, 1, W}$![]() in (5.26) implies that $r_{i, I} = r_{i, II} = r_{i, III}$
in (5.26) implies that $r_{i, I} = r_{i, II} = r_{i, III}$![]() at the juncture because all the particles on the juncture have the same value of $\bar {\lambda } \simeq \lambda$
at the juncture because all the particles on the juncture have the same value of $\bar {\lambda } \simeq \lambda$![]() . With this result and the fact that condition (5.27) gives $\partial _\alpha J_{c, I} + \partial _\alpha J_{c, II} = \partial _\alpha J_{c, III}$
. With this result and the fact that condition (5.27) gives $\partial _\alpha J_{c, I} + \partial _\alpha J_{c, II} = \partial _\alpha J_{c, III}$![]() , all the terms that contain $r_{i, 1, W}$
, all the terms that contain $r_{i, 1, W}$![]() cancel each other, leaving
cancel each other, leaving
Equation (7.8) can be used to calculate $K_{i,III}$![]() given $K_{i,I}$
given $K_{i,I}$![]() and $K_{i,II}$
and $K_{i,II}$![]() . Note that, due to condition (5.27), $K_{i,III}$
. Note that, due to condition (5.27), $K_{i,III}$![]() is equal to both $K_{i,I}$
is equal to both $K_{i,I}$![]() and $K_{i,II}$
and $K_{i,II}$![]() if $K_{i,I} = K_{i,II}$
if $K_{i,I} = K_{i,II}$![]() .
.
The discussion in this section is related to the probabilities of transition calculated by Cary et al. (Reference Cary, Escande and Tennyson1986). If instead of the particle distribution function, one considers individual particle motion across a juncture, the problem with junctures is reversed. When a particle leaves one well to move into two other wells, the particle cannot be split into two. The exact position of the trapped particle along its quasi-periodic motion (that is, its phase) when it reaches the juncture determines the well that it moves into. Orbit-averaged motion ignores this phase, but one can assume that particles are equally distributed along this phase and, using this assumption, obtain the probability of transitioning into one well or the other. Following Cary et al. (Reference Cary, Escande and Tennyson1986), if a particle leaves well $I$![]() , $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, I} < 0$
, $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, I} < 0$![]() , to move into either well $II$
, to move into either well $II$![]() , $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} > 0$
, $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, II} > 0$![]() , or well $III$
, or well $III$![]() , $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} < 0$
, $(c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, III} < 0$![]() , the probability that it moves into well $II$
, the probability that it moves into well $II$![]() is $- \partial _\alpha J_{c, II}/\partial _\alpha J_{c, I}$
is $- \partial _\alpha J_{c, II}/\partial _\alpha J_{c, I}$![]() , whereas the probability that it transitions to well $III$
, whereas the probability that it transitions to well $III$![]() is $\partial _\alpha J_{c, III}/\partial _\alpha J_{c, I}$
is $\partial _\alpha J_{c, III}/\partial _\alpha J_{c, I}$![]() . Thus, for single particle motion, the derivatives of $J_{c, W}$
. Thus, for single particle motion, the derivatives of $J_{c, W}$![]() with respect to $\alpha$
with respect to $\alpha$![]() enter in the problem, but they apply to the junctures in which the particle leaves one well to move into one of the other two wells, instead of applying to the case in which particles leave two wells to transition into the third well. In this latter type of juncture, a single particle leaving one of the wells does not have any other choice but to move into the well that is accepting particles. To summarize, our formulation does not require transition probabilities because it is based on the distribution function instead of single particle motion and because, by keeping collisions, it develops the collisional boundary layers described in Appendix H.
enter in the problem, but they apply to the junctures in which the particle leaves one well to move into one of the other two wells, instead of applying to the case in which particles leave two wells to transition into the third well. In this latter type of juncture, a single particle leaving one of the wells does not have any other choice but to move into the well that is accepting particles. To summarize, our formulation does not require transition probabilities because it is based on the distribution function instead of single particle motion and because, by keeping collisions, it develops the collisional boundary layers described in Appendix H.
7.1.2. Example
After explaining how the distribution function behaves around junctures of different types of wells, we proceed to argue that the function $K_{i, W}$![]() is independent of $J$
is independent of $J$![]() in large regions of velocity space. To illustrate the problem, we consider the simple situation sketched in figure 6. In this figure, we show the dependence of the effective potential $U \simeq \mu B + Z_i e \phi _0/m_i$
in large regions of velocity space. To illustrate the problem, we consider the simple situation sketched in figure 6. In this figure, we show the dependence of the effective potential $U \simeq \mu B + Z_i e \phi _0/m_i$![]() on $l$
on $l$![]() for several values of $\alpha$
for several values of $\alpha$![]() . We consider particle motion in this effective potential for a radial electric field that forces particles to move in the direction of increasing $\alpha$
. We consider particle motion in this effective potential for a radial electric field that forces particles to move in the direction of increasing $\alpha$![]() , that is, $c\phi _0^{\prime }/\varPsi _t^{\prime } > 0$
, that is, $c\phi _0^{\prime }/\varPsi _t^{\prime } > 0$![]() . Due to the changes in the $U$
. Due to the changes in the $U$![]() profile with $\alpha$
profile with $\alpha$![]() , we can divide the motion into four steps:
, we can divide the motion into four steps:
(i) Step (a) $\to$
 (b). The minimum of well $II$
(b). The minimum of well $II$ decreases with $\alpha$
decreases with $\alpha$ , while well $I$
, while well $I$ does not change. Thus, $\partial _\alpha J_{c, II} > 0$
does not change. Thus, $\partial _\alpha J_{c, II} > 0$ and $\partial _\alpha J_{c, III} > 0$
and $\partial _\alpha J_{c, III} > 0$ , but $\partial _\alpha J_{c, I} = 0$
, but $\partial _\alpha J_{c, I} = 0$ . Since $c\phi _0^{\prime }/\varPsi _t^{\prime } > 0$
. Since $c\phi _0^{\prime }/\varPsi _t^{\prime } > 0$ , the discussion of the previous section implies that particles in well $III$
, the discussion of the previous section implies that particles in well $III$ with low values of $J$
with low values of $J$ transition into well $II$
transition into well $II$ . Particles cannot transition into well $I$
. Particles cannot transition into well $I$ because $\partial _\alpha J_{c, I} = 0$
because $\partial _\alpha J_{c, I} = 0$ .
.(ii) Step (b) $\to$
 (c). The minimum of well $I$
(c). The minimum of well $I$ decreases, while well $II$
decreases, while well $II$ does not change. Hence, $\partial _\alpha J_{c, I} > 0$
does not change. Hence, $\partial _\alpha J_{c, I} > 0$ , $\partial _\alpha J_{c, II} = 0$
, $\partial _\alpha J_{c, II} = 0$ and $\partial _\alpha J_{c, III} > 0$
and $\partial _\alpha J_{c, III} > 0$ , and particles in well $III$
, and particles in well $III$ with low values of $J$
with low values of $J$ transition into well $I$
transition into well $I$ . Particles cannot transition into well $II$
. Particles cannot transition into well $II$ because $\partial _\alpha J_{c, II} = 0$
because $\partial _\alpha J_{c, II} = 0$ .
.(iii) Step (c) $\to$
 (d). The minimum of well $II$
(d). The minimum of well $II$ increases until it reaches the value it had in (a), while well $I$
increases until it reaches the value it had in (a), while well $I$ does not change. As a result, $\partial _\alpha J_{c, I} = 0$
does not change. As a result, $\partial _\alpha J_{c, I} = 0$ , $\partial _\alpha J_{c, II} < 0$
, $\partial _\alpha J_{c, II} < 0$ and $\partial _\alpha J_{c, III} < 0$
and $\partial _\alpha J_{c, III} < 0$ , and particles that had transitioned into well $II$
, and particles that had transitioned into well $II$ during step (i) go back into well $III$
during step (i) go back into well $III$ , but their value of $J$
, but their value of $J$ is greater than their initial one. Particles cannot transition into well $I$
is greater than their initial one. Particles cannot transition into well $I$ because $\partial _\alpha J_{c, I} = 0$
because $\partial _\alpha J_{c, I} = 0$ .
.(iv) Step (d) $\to$
 (e). The minimum of well $I$
(e). The minimum of well $I$ increases until it reaches the value it had in (a), while well $II$
increases until it reaches the value it had in (a), while well $II$ does not change. Then, $\partial _\alpha J_{c, I} < 0$
does not change. Then, $\partial _\alpha J_{c, I} < 0$ , $\partial _\alpha J_{c, II} = 0$
, $\partial _\alpha J_{c, II} = 0$ and $\partial _\alpha J_{c, III} < 0$
and $\partial _\alpha J_{c, III} < 0$ , and particles that had transitioned into well $I$
, and particles that had transitioned into well $I$ during step (ii) go back into well $III$
during step (ii) go back into well $III$ , but their value of $J$
, but their value of $J$ is lower than their initial one. Particles cannot transition into well $II$
is lower than their initial one. Particles cannot transition into well $II$ because $\partial _\alpha J_{c, II} = 0$
because $\partial _\alpha J_{c, II} = 0$ .
.

Figure 6. Example of effective potential $U(\alpha, l)$![]() . Each panel corresponds to a particular value of $\alpha$
. Each panel corresponds to a particular value of $\alpha$![]() .
.
In the configuration in figure 6, there is only one juncture between wells $I$![]() , $II$
, $II$![]() and $III$
and $III$![]() . This juncture is characterized by the functions $J_{c, I} (r, \alpha, v)$
. This juncture is characterized by the functions $J_{c, I} (r, \alpha, v)$![]() , $J_{c, II} (r, \alpha, v)$
, $J_{c, II} (r, \alpha, v)$![]() and $J_{c, III} (r, \alpha, v)$
and $J_{c, III} (r, \alpha, v)$![]() , sketched in figure 7(b). Each of these functions has a maximum and a minimum in $\alpha$
, sketched in figure 7(b). Each of these functions has a maximum and a minimum in $\alpha$![]() that we denote $J_{c, W, M} (r, v)$
that we denote $J_{c, W, M} (r, v)$![]() and $J_{c, W, m} (r, v)$
and $J_{c, W, m} (r, v)$![]() , respectively. Particles in well $I$
, respectively. Particles in well $I$![]() with values of $J$
with values of $J$![]() smaller than $J_{c, I, m} (r, v)$
smaller than $J_{c, I, m} (r, v)$![]() never transition to wells $II$
never transition to wells $II$![]() or $III$
or $III$![]() . Similarly, particles in well $II$
. Similarly, particles in well $II$![]() with $J$
with $J$![]() smaller than $J_{c, II, m}(r, v)$
smaller than $J_{c, II, m}(r, v)$![]() and particles in well $III$
and particles in well $III$![]() with $J$
with $J$![]() larger than $J_{c, III, M} (r, v)$
larger than $J_{c, III, M} (r, v)$![]() do not transition into the other two wells. In these regions of velocity space, the dependence of $K_{i, W}$
do not transition into the other two wells. In these regions of velocity space, the dependence of $K_{i, W}$![]() on $J$
on $J$![]() will be determined in § 7.2.
will be determined in § 7.2.

Figure 7. Evolution of the value of $J$![]() of a particle in the magnetic field sketched in figure 6. We start with a particle in well $III$
of a particle in the magnetic field sketched in figure 6. We start with a particle in well $III$![]() with initial value of the second adiabatic invariant $J = J_{\mathrm {in},0}$
with initial value of the second adiabatic invariant $J = J_{\mathrm {in},0}$![]() . Panel (a) shows the second adiabatic invariant of particles with $J = J_{III, \mathrm {in}}$
. Panel (a) shows the second adiabatic invariant of particles with $J = J_{III, \mathrm {in}}$![]() after these particles has transition into well $I$
after these particles has transition into well $I$![]() (dark pink straight line) or well $II$
(dark pink straight line) or well $II$![]() (light pink straight line), and then back to well $III$
(light pink straight line), and then back to well $III$![]() . The trajectory of the particle with initial second adiabatic invariant $J_{\mathrm {in}, 0}$
. The trajectory of the particle with initial second adiabatic invariant $J_{\mathrm {in}, 0}$![]() is represented by the black staircase-like line. Panel (b) shows the initial part of the same trajectory in the plane $(\alpha, J)$
is represented by the black staircase-like line. Panel (b) shows the initial part of the same trajectory in the plane $(\alpha, J)$![]() . The pink lines are $J_{c, I} (\alpha )$
. The pink lines are $J_{c, I} (\alpha )$![]() , $J_{c, II} (\alpha )$
, $J_{c, II} (\alpha )$![]() and $J_{c, III} (\alpha )$
and $J_{c, III} (\alpha )$![]() .
.
The situation is very different for particles in well $III$![]() that have $J_{c, III, m} (r, v) < J < J_{c, III, M} (r, v)$
that have $J_{c, III, m} (r, v) < J < J_{c, III, M} (r, v)$![]() . These particles transition into wells $I$
. These particles transition into wells $I$![]() and $II$
and $II$![]() and eventually transition back into well $III$
and eventually transition back into well $III$![]() . There is a value of $J$
. There is a value of $J$![]() , $J_{I, II} (r, v) := J_{c, I, m} (r, v) + J_{c, II, M}(r, v)$
, $J_{I, II} (r, v) := J_{c, I, m} (r, v) + J_{c, II, M}(r, v)$![]() , such that particles in well $III$
, such that particles in well $III$![]() with $J_{c, III, m} < J < J_{I, II}$
with $J_{c, III, m} < J < J_{I, II}$![]() transition into well $II$
transition into well $II$![]() , and particles with $J_{I, II} < J < J_{c, III, M}$
, and particles with $J_{I, II} < J < J_{c, III, M}$![]() transition into well $I$
transition into well $I$![]() .
.
To understand what happens for particles with $J_{c, III, m} < J < J_{c, III, M}$![]() , we define the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$
, we define the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$![]() . This function determines the value of the second adiabatic invariant of a particle in well $III$
. This function determines the value of the second adiabatic invariant of a particle in well $III$![]() after it has transitioned into well $I$
after it has transitioned into well $I$![]() or well $II$
or well $II$![]() and has then transitioned back to well $III$
and has then transitioned back to well $III$![]() . The value $J_{III, \mathrm {out}}$
. The value $J_{III, \mathrm {out}}$![]() of the adiabatic invariant after the particle has transition in and out of well $I$
of the adiabatic invariant after the particle has transition in and out of well $I$![]() or well $II$
or well $II$![]() depends only on the value that the adiabatic invariant had before the particle transitioned, $J_{III, \mathrm {in}}$
depends only on the value that the adiabatic invariant had before the particle transitioned, $J_{III, \mathrm {in}}$![]() . For the magnetic field configuration in figure 6, the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$
. For the magnetic field configuration in figure 6, the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$![]() is sketched in figure 7(a) as a light pink straight line for particles that transition into well $II$
is sketched in figure 7(a) as a light pink straight line for particles that transition into well $II$![]() ($J_{c, III, m} < J < J_{I, II}$
($J_{c, III, m} < J < J_{I, II}$![]() ), and as a dark pink straight line for particles that transition into well $I$
), and as a dark pink straight line for particles that transition into well $I$![]() ($J_{I, II} < J < J_{c, III, M}$
($J_{I, II} < J < J_{c, III, M}$![]() ). To sketch the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$
). To sketch the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$![]() , we have used the fact that
, we have used the fact that
Using the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$![]() , we can schematically describe particle motion for particles with $J_{c, III, m} < J < J_{c, III, M}$
, we can schematically describe particle motion for particles with $J_{c, III, m} < J < J_{c, III, M}$![]() . This motion is shown in figure 7(a) as a black staircase-like line with arrows. We start with a particle with initial second adiabatic invariant $J_{\mathrm {in, 0}} < J_{I, II}$
. This motion is shown in figure 7(a) as a black staircase-like line with arrows. We start with a particle with initial second adiabatic invariant $J_{\mathrm {in, 0}} < J_{I, II}$![]() . After its transitions in and out of well $II$
. After its transitions in and out of well $II$![]() , this particle has acquired the second adiabatic invariant $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$
, this particle has acquired the second adiabatic invariant $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$![]() , which is necessarily in the interval $[J_{c, III, m}, J_{c, III, M}]$
, which is necessarily in the interval $[J_{c, III, m}, J_{c, III, M}]$![]() . As a result, the particle will transition again into well $I$
. As a result, the particle will transition again into well $I$![]() or well $II$
or well $II$![]() . This fact is shown in figure 7(a) by noting that $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$
. This fact is shown in figure 7(a) by noting that $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$![]() becomes $J_{\mathrm {in}, 1}$
becomes $J_{\mathrm {in}, 1}$![]() , and this particle in turn will transition in and out of well $II$
, and this particle in turn will transition in and out of well $II$![]() to acquire the second adiabatic invariant $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1}) = J_{III, \mathrm {out}} (J_{III, \mathrm {out}} (J_{\mathrm {in}, 0}))$
to acquire the second adiabatic invariant $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1}) = J_{III, \mathrm {out}} (J_{III, \mathrm {out}} (J_{\mathrm {in}, 0}))$![]() . In figure 7(a), the fact that $J_{\mathrm {in}, 1} = J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$
. In figure 7(a), the fact that $J_{\mathrm {in}, 1} = J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$![]() is represented as a horizontal solid line that joins $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$
is represented as a horizontal solid line that joins $J_{III, \mathrm {out}} (J_{\mathrm {in}, 0})$![]() with the diagonal line $J_{III, \mathrm {out}} = J_{III, \mathrm {in}}$
with the diagonal line $J_{III, \mathrm {out}} = J_{III, \mathrm {in}}$![]() , shown as a dotted line, and the fact that $J_{\mathrm {in}, 1}$
, shown as a dotted line, and the fact that $J_{\mathrm {in}, 1}$![]() becomes $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1})$
becomes $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1})$![]() is represented as a vertical dashed line from the diagonal to $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1})$
is represented as a vertical dashed line from the diagonal to $J_{III, \mathrm {out}} (J_{\mathrm {in}, 1})$![]() . Thus, in the $J_{III, \mathrm {out}}$
. Thus, in the $J_{III, \mathrm {out}}$![]() vs $J_{III, \mathrm {in}}$
vs $J_{III, \mathrm {in}}$![]() graph, particle trajectories are the staircase-like lines sketched in figure 7(a). The initial part of the same trajectory is sketched in figure 7(b) in the $(\alpha, J)$
graph, particle trajectories are the staircase-like lines sketched in figure 7(a). The initial part of the same trajectory is sketched in figure 7(b) in the $(\alpha, J)$![]() plane.
plane.
Figure 7(a) shows that any particle that starts with $J_{c, III, m} < J < J_{c, III, M}$![]() ends up sampling all possible values of the second adiabatic invariant between $J_{c, III, m}$
ends up sampling all possible values of the second adiabatic invariant between $J_{c, III, m}$![]() and $J_{c, III, M}$
and $J_{c, III, M}$![]() unless the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$
unless the function $J_{III, \mathrm {out}} (J_{III, \mathrm {in}})$![]() is very specific – a possible special case of this kind is represented in figure 8, where particle trajectories close on themselves in a loop in the $(J, \alpha )$
is very specific – a possible special case of this kind is represented in figure 8, where particle trajectories close on themselves in a loop in the $(J, \alpha )$![]() plane. We expect magnetic field magnitude profiles to satisfy the necessary constraints that lead to configurations similar to the one in figure 8 only in a countable number of flux surfaces. Thus, in general, particles in well $III$
plane. We expect magnetic field magnitude profiles to satisfy the necessary constraints that lead to configurations similar to the one in figure 8 only in a countable number of flux surfaces. Thus, in general, particles in well $III$![]() with $J$
with $J$![]() values between $J_{c, III, m}$
values between $J_{c, III, m}$![]() and $J_{c, III, M}$
and $J_{c, III, M}$![]() sample all possible values of $J$
sample all possible values of $J$![]() between $J_{c, III, m}$
between $J_{c, III, m}$![]() and $J_{c, III, M}$
and $J_{c, III, M}$![]() . Since $K_{i, W}$
. Since $K_{i, W}$![]() is constant along particle trajectories (it is independent of $\alpha$
is constant along particle trajectories (it is independent of $\alpha$![]() and it is continuous at the junctures of several wells because both $g_{i, 1, W}$
and it is continuous at the junctures of several wells because both $g_{i, 1, W}$![]() and $r_{i, 1, W}$
and $r_{i, 1, W}$![]() are continuous there), we find that $K_{i, III}$
are continuous there), we find that $K_{i, III}$![]() does not depend on $J$
does not depend on $J$![]() for $J_{c, III, m} < J < J_{c, III, M}$
for $J_{c, III, m} < J < J_{c, III, M}$![]() . For the same reasons, $K_{i, I}$
. For the same reasons, $K_{i, I}$![]() in the interval $[J_{c, I, m}, J_{c, I, M}]$
in the interval $[J_{c, I, m}, J_{c, I, M}]$![]() and $K_{i, II}$
and $K_{i, II}$![]() in the interval $[J_{c, II, m}, J_{c, II, M}]$
in the interval $[J_{c, II, m}, J_{c, II, M}]$![]() are both independent of $J$
are both independent of $J$![]() and equal to the value of $K_{i, III}$
and equal to the value of $K_{i, III}$![]() in the interval $[J_{c, III, m}, J_{c, III, M}]$
in the interval $[J_{c, III, m}, J_{c, III, M}]$![]() . In figure 9, we sketch $K_{i, W}$
. In figure 9, we sketch $K_{i, W}$![]() for the configuration in figure 6.
for the configuration in figure 6.

Figure 8. Function $J_{III, \mathrm {out}}(J_{III, \mathrm {in}})$![]() for which particle trajectories describe a loop and do not sample a finite interval of $J$
for which particle trajectories describe a loop and do not sample a finite interval of $J$![]() .
.

Figure 9. Sketch of the function $K_{i, W}$![]() for the case in figure 6.
for the case in figure 6.
7.1.3. General considerations
We have used the example in figure 6 to illustrate the dependence of $K_{i, W}$![]() on $J$
on $J$![]() because of its simplicity. In this particular configuration, particles do not have the option to choose between two wells, and particles from two different wells are not forced to move into the same well at the same time (this last case requires using (7.8)). Despite the simplicity of the example, we believe that only very specific configurations allow for a $K_{i, W}$
because of its simplicity. In this particular configuration, particles do not have the option to choose between two wells, and particles from two different wells are not forced to move into the same well at the same time (this last case requires using (7.8)). Despite the simplicity of the example, we believe that only very specific configurations allow for a $K_{i, W}$![]() that is not constant in $J$
that is not constant in $J$![]() in regions with junctures of different types of wells. We note that (7.8) accepts a constant $K_{i, W}$
in regions with junctures of different types of wells. We note that (7.8) accepts a constant $K_{i, W}$![]() as a solution, and our believe is that in most cases this is the only solution. Interestingly, this $K_{i, W}$
as a solution, and our believe is that in most cases this is the only solution. Interestingly, this $K_{i, W}$![]() solution does not have discontinuities in $K_{i, W}$
solution does not have discontinuities in $K_{i, W}$![]() across junctures, and hence does not have the collisional boundary layers described in Appendix H. These layers disappear only to lowest order, as we will see that they are necessary for the next-order correction in the $\nu _{i*}/\rho _{i*} \ll 1$
across junctures, and hence does not have the collisional boundary layers described in Appendix H. These layers disappear only to lowest order, as we will see that they are necessary for the next-order correction in the $\nu _{i*}/\rho _{i*} \ll 1$![]() expansion.
expansion.
For large values of $J$![]() , there are always junctures of different types of wells (see figure 10 and the appendix of Boozer & Gardner Reference Boozer and Gardner1990), so we expect $K_{i, W}$
, there are always junctures of different types of wells (see figure 10 and the appendix of Boozer & Gardner Reference Boozer and Gardner1990), so we expect $K_{i, W}$![]() to be independent of $J$
to be independent of $J$![]() above certain value of $J$
above certain value of $J$![]() . Moreover, since $r_{i, 1, W} \rightarrow 0$
. Moreover, since $r_{i, 1, W} \rightarrow 0$![]() for $J \rightarrow \infty$
for $J \rightarrow \infty$![]() by definition (5.26), boundary condition (5.34) imposes that $K_{i, W} = 0$
by definition (5.26), boundary condition (5.34) imposes that $K_{i, W} = 0$![]() in this region. From here on, the value of $J$
in this region. From here on, the value of $J$![]() at which $K_{i, W}$
at which $K_{i, W}$![]() vanishes is denoted by $J_{K_{i, W} = 0}$
vanishes is denoted by $J_{K_{i, W} = 0}$![]() – see figure 9 for an example of $J_{K_{i, W} = 0}$
– see figure 9 for an example of $J_{K_{i, W} = 0}$![]() .
.

Figure 10. Sketch of trajectories with large $J$![]() in the $(l, \alpha )$
in the $(l, \alpha )$![]() plane. For large $J$
plane. For large $J$![]() , $\lambda$
, $\lambda$![]() must be close to $1/B_M$
must be close to $1/B_M$![]() , and hence it must have bounce points at a value of $B$
, and hence it must have bounce points at a value of $B$![]() close to $B_M$
close to $B_M$![]() . In the figure, we sketch the contour $B = 1/\lambda \approx B_M$
. In the figure, we sketch the contour $B = 1/\lambda \approx B_M$![]() as a thick red line (we have assumed that there is only one maximum of $B$
as a thick red line (we have assumed that there is only one maximum of $B$![]() ). The total trajectory of the particle is sketched in panel (a) as a thin red line. The best way to identify a trajectory with a given $\lambda$
). The total trajectory of the particle is sketched in panel (a) as a thin red line. The best way to identify a trajectory with a given $\lambda$![]() is to determine the location of the bounce points (note that the left bounce point $l_{bL,W}$
is to determine the location of the bounce points (note that the left bounce point $l_{bL,W}$![]() is on the right of the figure and the right bounce point $l_{bR,W}$
is on the right of the figure and the right bounce point $l_{bR,W}$![]() is on the left). Particles with the kind of trajectory shown in panel (a) are exposed to four junctures with other wells, as demonstrated by panels (b–e). In panel (b), if the particle moves towards negative $\alpha$
is on the left). Particles with the kind of trajectory shown in panel (a) are exposed to four junctures with other wells, as demonstrated by panels (b–e). In panel (b), if the particle moves towards negative $\alpha$![]() , it will transition to another type of well, similarly to panel (d). In panels (c,e), the particle transitions when it moves towards positive $\alpha$
, it will transition to another type of well, similarly to panel (d). In panels (c,e), the particle transitions when it moves towards positive $\alpha$![]() .
.
We finish by proving that the particle and energy fluxes due to $g_{i,1,W}^{\{0\}}$![]() vanish. From (5.48), we obtain that the flux of particles is
vanish. From (5.48), we obtain that the flux of particles is

The particle flux vanishes due to the integral over $\alpha$![]() and the fact that $r_{i, 1, W}$
and the fact that $r_{i, 1, W}$![]() and $K_{i, W}$
and $K_{i, W}$![]() are continuous across junctures between several wells. A similar proof shows that the ion heat flux vanishes to lowest order in $\nu _{i*}/\rho _{i*} \ll 1$
are continuous across junctures between several wells. A similar proof shows that the ion heat flux vanishes to lowest order in $\nu _{i*}/\rho _{i*} \ll 1$![]() .
.
7.2. Next-order distribution function
To next order in $\nu _{i*}/\rho _{i*} \ll 1$![]() , we would expect (5.25) to give
, we would expect (5.25) to give
We explain at the end of this section that, in the intervals of $J$![]() where there are junctures between different wells and hence $\partial _J K_{i, W} = 0$
where there are junctures between different wells and hence $\partial _J K_{i, W} = 0$![]() , (7.11) is not valid. Before discussing this case, we consider the intervals of $J$
, (7.11) is not valid. Before discussing this case, we consider the intervals of $J$![]() where particles never transition into other wells. Then, (7.11) gives
where particles never transition into other wells. Then, (7.11) gives
For these values of $J$![]() , $g_{i, 1, W}^{\{1\}}$
, $g_{i, 1, W}^{\{1\}}$![]() is defined for all $\alpha$
is defined for all $\alpha$![]() . For this reason, if we average equation (7.12) over $\alpha$
. For this reason, if we average equation (7.12) over $\alpha$![]() , the first term vanishes, leaving the equation for $K_{i, W}$
, the first term vanishes, leaving the equation for $K_{i, W}$![]()
where
Solving (7.13) for $K_{i,W}$![]() allows one to integrate equation (7.12) with periodic boundary conditions in $\alpha$
allows one to integrate equation (7.12) with periodic boundary conditions in $\alpha$![]() .
.
Equation (7.13) determines the dependence of $K_{i, W}$![]() on $J$
on $J$![]() within the intervals of $J$
within the intervals of $J$![]() where there are no junctures of different types of wells. If the interval of $J$
where there are no junctures of different types of wells. If the interval of $J$![]() considered includes $J = 0$
considered includes $J = 0$![]() , where $\tau _W = 0$
, where $\tau _W = 0$![]() , the integral of equation (7.13) is
, the integral of equation (7.13) is
In the example in figures 6 and 7, this solution is valid in well $I$![]() for $J < J_{c, I, m}$
for $J < J_{c, I, m}$![]() , and in well $II$
, and in well $II$![]() for $J < J_{c, II, m}$
for $J < J_{c, II, m}$![]() . Note that solution (7.15) leads to a discontinuity in $\partial _J K_{i, W}$
. Note that solution (7.15) leads to a discontinuity in $\partial _J K_{i, W}$![]() at $J_{c, I, m}$
at $J_{c, I, m}$![]() and $J_{c, II, m}$
and $J_{c, II, m}$![]() because intervals of $J$
because intervals of $J$![]() with $\partial _J K_{i, W} = 0$
with $\partial _J K_{i, W} = 0$![]() start at these values of $J$
start at these values of $J$![]() . These discontinuities in the derivatives of $K_{i, W}$
. These discontinuities in the derivatives of $K_{i, W}$![]() mean that there are boundary layers where the lowest-order equation (7.2) is not valid and one needs to keep the collision operator to lowest order (see Appendix I.1 for a discussion of these boundary layers). More importantly, the finite values of $\partial _J K_{i, W}$
mean that there are boundary layers where the lowest-order equation (7.2) is not valid and one needs to keep the collision operator to lowest order (see Appendix I.1 for a discussion of these boundary layers). More importantly, the finite values of $\partial _J K_{i, W}$![]() at $J = J_{c, I, m}$
at $J = J_{c, I, m}$![]() and $J_{c, II, m}$
and $J_{c, II, m}$![]() also mean that there is collisional flux into the region $J > J_{c,I,m}$
also mean that there is collisional flux into the region $J > J_{c,I,m}$![]() of well $I$
of well $I$![]() and the region $J > J_{c,II,m}$
and the region $J > J_{c,II,m}$![]() of well $II$
of well $II$![]() . These phase-space fluxes are rapidly transported into well $III$
. These phase-space fluxes are rapidly transported into well $III$![]() by the $\boldsymbol {E} \times \boldsymbol {B}$
by the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift in the direction $\alpha$
drift in the direction $\alpha$![]() and through jumps in $J$
and through jumps in $J$![]() due transitions to other wells. This phase-space flux must then leave at $J_{c, III, M}$
due transitions to other wells. This phase-space flux must then leave at $J_{c, III, M}$![]() , where the region with $\partial _J K_{i, W} = 0$
, where the region with $\partial _J K_{i, W} = 0$![]() ends. Conservation of collisional flux determines $\partial _J K_{i, III}$
ends. Conservation of collisional flux determines $\partial _J K_{i, III}$![]() at $J_{c, III, M}$
at $J_{c, III, M}$![]() ,
,

(See Appendix I.1 for a derivation of this condition using the equation for the higher-order correction $g_{i, 1, W}^{\{1\}}$![]() .) Since solution (7.15) is valid in wells $I$
.) Since solution (7.15) is valid in wells $I$![]() and $II$
and $II$![]() , condition (7.16) simply becomes
, condition (7.16) simply becomes
With this condition, we can integrate equation (7.13) to obtain
that is, solution (7.15) is valid in well $III$![]() even though this well does not have particles with $J = 0$
even though this well does not have particles with $J = 0$![]() . Following this procedure for higher and higher values $J$
. Following this procedure for higher and higher values $J$![]() , one can see that solution (7.15) is in fact valid in every well. With $\partial _J K_{i, W}$
, one can see that solution (7.15) is in fact valid in every well. With $\partial _J K_{i, W}$![]() calculated, we can integrate it to obtain $K_{i, W}$
calculated, we can integrate it to obtain $K_{i, W}$![]() imposing $K_{i, W} = 0$
imposing $K_{i, W} = 0$![]() at $J = J_{K_{i, W} = 0}$
at $J = J_{K_{i, W} = 0}$![]() .
.
The fact that $K_{i, W}$![]() vanishes for $J > J_{K_{i, W} = 0}$
vanishes for $J > J_{K_{i, W} = 0}$![]() implies that the solution for $g_{i, 1, W}^{\{ 0 \} }$
implies that the solution for $g_{i, 1, W}^{\{ 0 \} }$![]() for large values of $J$
for large values of $J$![]() is simply
is simply

where we have substituted the definition of $r_{i, 1, W}$![]() (see (5.26)) and we have used the approximation $\bar {\lambda }_W \simeq \lambda _W$
(see (5.26)) and we have used the approximation $\bar {\lambda }_W \simeq \lambda _W$![]() . Surprisingly, this solution does not satisfy property (5.36) (note that $\partial _J \lambda _W \simeq - 2/v^{2} \tau _W B_0$
. Surprisingly, this solution does not satisfy property (5.36) (note that $\partial _J \lambda _W \simeq - 2/v^{2} \tau _W B_0$![]() ) even though property (5.36) is a consequence of the equations for $g_{i, 1, W}$
) even though property (5.36) is a consequence of the equations for $g_{i, 1, W}$![]() . This apparent contradiction is resolved by a boundary layer where the lowest-order equation (7.2) is not valid because one needs to keep the collision operator to lowest order (see Appendix I.2 for a brief discussion of this boundary layer).
. This apparent contradiction is resolved by a boundary layer where the lowest-order equation (7.2) is not valid because one needs to keep the collision operator to lowest order (see Appendix I.2 for a brief discussion of this boundary layer).
We finish our discussion of the next-order correction $g_{i,1,W}^{\{1\}}$![]() by considering its value in the regions where $\partial _J K_{i, W} = 0$
by considering its value in the regions where $\partial _J K_{i, W} = 0$![]() . Naively, for this region of velocity space, (7.11) gives
. Naively, for this region of velocity space, (7.11) gives
This equation has to be solved in regions where there are junctures of different types of well, and as a result, there can be discontinuities in $g_{i,1,W}^{\{1\}}$![]() across the junctures. Following the same procedure that we developed in Appendix H, we find that there are boundary layers in the junctures where particles leave two of the wells to go into the third, and that the result of these boundary layers is that $g_{i,1,W}^{\{1\}}$
across the junctures. Following the same procedure that we developed in Appendix H, we find that there are boundary layers in the junctures where particles leave two of the wells to go into the third, and that the result of these boundary layers is that $g_{i,1,W}^{\{1\}}$![]() must satisfy an equation similar to (7.8),
must satisfy an equation similar to (7.8),
Despite their apparent validity, (7.20) and (7.21) cannot be solved. Using the definition of $r_{i,1, W}$![]() in (5.26) and $\partial _J \lambda _W \simeq - 2/v^{2} \tau _W B_0$
in (5.26) and $\partial _J \lambda _W \simeq - 2/v^{2} \tau _W B_0$![]() , we find that (7.20) is
, we find that (7.20) is
Then, $g_{i, 1, W}^{\{ 1 \}}$![]() increases with $\alpha$
increases with $\alpha$![]() , posing a problem of continuity: due to the ergodic nature of the trajectories in the regions of velocity space where $\partial _J K_{i, W} = 0$
, posing a problem of continuity: due to the ergodic nature of the trajectories in the regions of velocity space where $\partial _J K_{i, W} = 0$![]() , if we calculate $g_{i,1,W}^{\{ 1 \}}$
, if we calculate $g_{i,1,W}^{\{ 1 \}}$![]() using (7.22), the values of $g_{i,1,W}^{\{ 1 \}}$
using (7.22), the values of $g_{i,1,W}^{\{ 1 \}}$![]() at two contiguous values of $J$
at two contiguous values of $J$![]() would in general be very different because the lengths of the paths in $\alpha$
would in general be very different because the lengths of the paths in $\alpha$![]() needed to reach these similar values of $J$
needed to reach these similar values of $J$![]() starting from the same phase-space point are very different. Such large differences for contiguous values of $J$
starting from the same phase-space point are very different. Such large differences for contiguous values of $J$![]() mean that we cannot neglect the collision operator in the regions where $\partial _J K_{i, W} = 0$
mean that we cannot neglect the collision operator in the regions where $\partial _J K_{i, W} = 0$![]() , and instead of (7.22), we need to integrate
, and instead of (7.22), we need to integrate
For this equation to be valid, the characteristic size of $\partial _J$![]() must be at least $\partial _J \sim \sqrt {\rho _{i*}/\nu _{i*}}/\sqrt {\epsilon } v_{ti} R \gg 1/\sqrt {\epsilon } v_{ti} R$
must be at least $\partial _J \sim \sqrt {\rho _{i*}/\nu _{i*}}/\sqrt {\epsilon } v_{ti} R \gg 1/\sqrt {\epsilon } v_{ti} R$![]() , and hence we expect solution $g_{i, 1, W}^{\{ 1 \}}$
, and hence we expect solution $g_{i, 1, W}^{\{ 1 \}}$![]() to have oscillatory character in $J$
to have oscillatory character in $J$![]() . Due to the inclusion of collisions, the solutions to (7.23) contain the boundary layers that appear around junctures of different types of wells, described in Appendix H. At the junctures of different wells, we need to apply continuity of $g_{i, 1, W}^{\{ 1 \}}$
. Due to the inclusion of collisions, the solutions to (7.23) contain the boundary layers that appear around junctures of different types of wells, described in Appendix H. At the junctures of different wells, we need to apply continuity of $g_{i, 1, W}^{\{ 1 \}}$![]() and condition (5.33), which at this order is
and condition (5.33), which at this order is
We discuss the boundary conditions for $g_{i,1, W}^{\{ 1 \}}$![]() in regions with $\partial _J K_{i, W} = 0$
in regions with $\partial _J K_{i, W} = 0$![]() in Appendix I.1.
in Appendix I.1.
7.3. Radial fluxes
In § 7.1 we showed that substituting $g_{i,1,W}^{\{0\}}$![]() into (5.48) for the particle flux gives zero. Thus, the particle flux is determined by $g_{i,1,W}^{\{1\}}$
into (5.48) for the particle flux gives zero. Thus, the particle flux is determined by $g_{i,1,W}^{\{1\}}$![]() and the boundary layers that we have described in Appendices H and I. To account for these higher-order effects, we manipulate (5.48): we integrate by parts in $\alpha$
and the boundary layers that we have described in Appendices H and I. To account for these higher-order effects, we manipulate (5.48): we integrate by parts in $\alpha$![]() and we use (5.25) to rewrite $\partial _\alpha g_{i, 1, W}$
and we use (5.25) to rewrite $\partial _\alpha g_{i, 1, W}$![]() in terms of the collision operator and $r_{i, 1, W}$
in terms of the collision operator and $r_{i, 1, W}$![]() . We find
. We find

This expression is not useful because, inside the boundary layers described in Appendices H and I and in the regions of phase space where particles undergo transitions between different types of wells, the collision operator applied on $g_{i, 1, W}$![]() gives large contributions to the integrand that vanish upon integration. To avoid this delicate cancellation, we integrate by parts in $J$
gives large contributions to the integrand that vanish upon integration. To avoid this delicate cancellation, we integrate by parts in $J$![]() to find
to find

In this expression, we can neglect the higher-order corrections to $g_{i,1,W}^{\{ 0 \}}$![]() , and hence
, and hence

where we have used (7.3), and in the integral in $J$![]() , we have distinguished the region where $\partial _J K_{i, W}$
, we have distinguished the region where $\partial _J K_{i, W}$![]() vanishes from the region where it is equal to the value given in (7.15). Using $\partial _J \lambda _W \simeq - 2/v^{2} B_0 \tau _W$
vanishes from the region where it is equal to the value given in (7.15). Using $\partial _J \lambda _W \simeq - 2/v^{2} B_0 \tau _W$![]() to write $\partial _J r_{i, 1, W} \simeq - m_i/Z_i e \phi _0^{\prime } \tau _W$
to write $\partial _J r_{i, 1, W} \simeq - m_i/Z_i e \phi _0^{\prime } \tau _W$![]() , the particle flux simplifies to
, the particle flux simplifies to

Note that the contribution from the particles in phase-space regions where $\partial _J K_{i, W} \neq 0$![]() is reduced by a factor of $(1 - \tau _W/\langle \tau _W \rangle _\alpha )$
is reduced by a factor of $(1 - \tau _W/\langle \tau _W \rangle _\alpha )$![]() , that is, this expression shows that particles that suffer transitions between different types of wells cause higher fluxes.
, that is, this expression shows that particles that suffer transitions between different types of wells cause higher fluxes.
A similar procedure to the one that we have shown above gives the energy flux

The fluxes in (7.28) and (7.29) are inversely proportional to $\phi _0^{\prime 2}$![]() and hence diverge when $\phi _0^{\prime }$
and hence diverge when $\phi _0^{\prime }$![]() vanishes. The reason for this divergence is that the $\boldsymbol {E} \times \boldsymbol {B}$
vanishes. The reason for this divergence is that the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift was assumed to be much larger than the radial component of the drifts in (4.5). For $e a \phi _0^{\prime }/T_i \sim \epsilon$
drift was assumed to be much larger than the radial component of the drifts in (4.5). For $e a \phi _0^{\prime }/T_i \sim \epsilon$![]() , this assumption is not satisfied, and the first term in (7.3) becomes of the same order as the Maxwellian $f_{Mi}$
, this assumption is not satisfied, and the first term in (7.3) becomes of the same order as the Maxwellian $f_{Mi}$![]() , giving $g_{i, 1, W}^{\{ 0 \}} \sim f_{Mi}$
, giving $g_{i, 1, W}^{\{ 0 \}} \sim f_{Mi}$![]() , that is, the distribution function is not close to a Maxwellian. This is a manifestation of the fact that orbit widths become comparable to the minor radius of the stellarator. To summarize, formulas (7.28) and (7.29) are not valid for $e a \phi _0^{\prime }/T_e \lesssim \epsilon$
, that is, the distribution function is not close to a Maxwellian. This is a manifestation of the fact that orbit widths become comparable to the minor radius of the stellarator. To summarize, formulas (7.28) and (7.29) are not valid for $e a \phi _0^{\prime }/T_e \lesssim \epsilon$![]() . At these values of the electric field, the radially global equations (2.1), (2.2), (2.27), (2.30) and (2.36) must be used. Importantly, even for $e a \phi _0^{\prime }/T_e \sim 1$
. At these values of the electric field, the radially global equations (2.1), (2.2), (2.27), (2.30) and (2.36) must be used. Importantly, even for $e a \phi _0^{\prime }/T_e \sim 1$![]() , energetic particles with energies larger than $e R \phi _0^{\prime } \sim m_i v_{ti}^{2}/\epsilon$
, energetic particles with energies larger than $e R \phi _0^{\prime } \sim m_i v_{ti}^{2}/\epsilon$![]() have $\boldsymbol {\nabla } B$
have $\boldsymbol {\nabla } B$![]() and curvature drifts that are comparable to or larger than the $\boldsymbol {E} \times \boldsymbol {B}$
and curvature drifts that are comparable to or larger than the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. This means that, unless the stellarator is close to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017; Catto Reference Catto2019), energetic particles produced by fusion reactions, radiofrequency heating or neutral beams have to be modelled using the radially global equations (2.1), (2.2), (2.27), (2.30) and (2.36). These radially global orbit-averaged equations will be valid as long as the gyroradius and the banana orbit width of energetic particles are sufficiently small. In particular, the finite banana orbit width mechanism for energetic particle transport proposed by Goldston, White & Boozer (Reference Goldston, White and Boozer1981) is negligible in the limit in which the orbit-averaged equations (2.1), (2.2), (2.27), (2.30) and (2.36) are valid.
drift. This means that, unless the stellarator is close to omnigeneity (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017; Catto Reference Catto2019), energetic particles produced by fusion reactions, radiofrequency heating or neutral beams have to be modelled using the radially global equations (2.1), (2.2), (2.27), (2.30) and (2.36). These radially global orbit-averaged equations will be valid as long as the gyroradius and the banana orbit width of energetic particles are sufficiently small. In particular, the finite banana orbit width mechanism for energetic particle transport proposed by Goldston, White & Boozer (Reference Goldston, White and Boozer1981) is negligible in the limit in which the orbit-averaged equations (2.1), (2.2), (2.27), (2.30) and (2.36) are valid.
We finish by estimating the size of the particle and the energy flux. Using $\varPsi _t^{\prime } \sim a B_0$![]() , $\phi _0^{\prime } \sim T_i/ea$
, $\phi _0^{\prime } \sim T_i/ea$![]() , $V^{\prime } \sim Ra$
, $V^{\prime } \sim Ra$![]() , $J \sim \sqrt {\epsilon } v_{ti} R$
, $J \sim \sqrt {\epsilon } v_{ti} R$![]() , $\tau _W \sim R/\sqrt {\epsilon } v_{ti}$
, $\tau _W \sim R/\sqrt {\epsilon } v_{ti}$![]() and $\varUpsilon _i \sim 1/a$
and $\varUpsilon _i \sim 1/a$![]() , we find
, we find
These estimates can be obtained using a random walk estimate. As we explained in the introduction, in (1.5), the width of a typical trapped-particle orbit is $w \sim \epsilon a$![]() . Since the effective collision frequency for trapped particles is $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$
. Since the effective collision frequency for trapped particles is $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$![]() , trapped particles undergo a random walk with steps of length $w$
, trapped particles undergo a random walk with steps of length $w$![]() every time $\epsilon /\nu _{ii}$
every time $\epsilon /\nu _{ii}$![]() . The resulting diffusion coefficient is $D \sim \sqrt {\epsilon } w^{2} \nu _\mathrm {eff}$
. The resulting diffusion coefficient is $D \sim \sqrt {\epsilon } w^{2} \nu _\mathrm {eff}$![]() , where $\sqrt {\epsilon }$
, where $\sqrt {\epsilon }$![]() is an estimate for the trapped-particle fraction. The estimates for the fluxes are then obtained from $D \sim \epsilon ^{3/2} a^{2} \nu _{ii}$
is an estimate for the trapped-particle fraction. The estimates for the fluxes are then obtained from $D \sim \epsilon ^{3/2} a^{2} \nu _{ii}$![]() , $\varGamma _i \sim D|\boldsymbol {\nabla } n_i| \sim D n_i/a$
, $\varGamma _i \sim D|\boldsymbol {\nabla } n_i| \sim D n_i/a$![]() and $Q_i \sim n_i D |\boldsymbol {\nabla } T_i| \sim D n_i T_i/a$
and $Q_i \sim n_i D |\boldsymbol {\nabla } T_i| \sim D n_i T_i/a$![]() .
.
8. Large aspect ratio stellarators close to omnigeneity
In this section we study large aspect ratio stellarators close to omnigeneity. A magnetic field is omnigeneous when it satisfies $\partial _\alpha J_W = 0$![]() for all trapped particles, that is,
for all trapped particles, that is,

for all $\lambda$![]() . As explained by Cary & Shasharina (Reference Cary and Shasharina1997a,Reference Cary and Shasharinab) and Parra et al. (Reference Parra, Calvo, Helander and Landreman2015), this condition imposes stringent constraints on how the magnitude $B$
. As explained by Cary & Shasharina (Reference Cary and Shasharina1997a,Reference Cary and Shasharinab) and Parra et al. (Reference Parra, Calvo, Helander and Landreman2015), this condition imposes stringent constraints on how the magnitude $B$![]() depends on $\alpha$
depends on $\alpha$![]() and $l$
and $l$![]() . Of these constraints, two are particularly important for our discussion.
. Of these constraints, two are particularly important for our discussion.
(i) The maxima of $B$
 on a flux surface are not on isolated points, but on lines that close on themselves. Moreover, those lines where the maxima lie are separated from each other by such a distance that any particle that travels between these maxima has only one possible value of $J$
on a flux surface are not on isolated points, but on lines that close on themselves. Moreover, those lines where the maxima lie are separated from each other by such a distance that any particle that travels between these maxima has only one possible value of $J$ , which we denote by $J_{\mathrm {om}, M}$
, which we denote by $J_{\mathrm {om}, M}$ because it is also the maximum value that $J$
because it is also the maximum value that $J$ can take.
can take.(ii) In junctures of several types of wells like the one depicted in figure 1 (see Parra et al. (Reference Parra, Calvo, Helander and Landreman2015) for a discussion of the existence of omnigeneous magnetic fields with junctures of different types of wells), the values of the second adiabatic invariant at the juncture are independent of $\alpha$
 , that is, $\partial _\alpha J_{c, W} = 0$
, that is, $\partial _\alpha J_{c, W} = 0$ . This means that there are no transitions from one type of well to another.
. This means that there are no transitions from one type of well to another.
Collisional transport in omnigeneous stellarators is very small, and for this reason designing stellarators close to omnigeneity is of interest. We consider large aspect ratio stellarators that are close to omnigeneity. We find two distinct types. In § 8.1, we show that large aspect ratio stellarators with large mirror ratios are close to omnigeneity, and hence one can use the equations derived by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) to calculate neoclassical fluxes in these stellarators. In § 8.2, we study optimized large aspect ratio stellarators with mirror ratios close to unity.
8.1. Large aspect ratio stellarators with large mirror ratios
In previous sections, we have discussed in detail large aspect ratio stellarators with mirror ratios close to unity, an approximation that describes well many modern stellarators. However, it is possible that increasing the mirror ratio will be of interest in the future. For this reason, we consider large aspect ratio stellarators with $B_0(l)$![]() a general function of $l$
a general function of $l$![]() . Note that such stellarators satisfy (8.1) to lowest order because $B_0(l)$
. Note that such stellarators satisfy (8.1) to lowest order because $B_0(l)$![]() is independent of $\alpha$
is independent of $\alpha$![]() . This means that $B_1(r, \alpha, l)$
. This means that $B_1(r, \alpha, l)$![]() can be considered to be the deviation from omnigeneity. We can then use the formulation by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) by replacing the expansion parameter $\delta$
can be considered to be the deviation from omnigeneity. We can then use the formulation by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) by replacing the expansion parameter $\delta$![]() , which measures the size of the deviation from omnigeneity, with $\epsilon$
, which measures the size of the deviation from omnigeneity, with $\epsilon$![]() .
.
Using the same techniques as Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), it is possible to prove that the lowest-order solution for the ion distribution function is a stationary Maxwellian $f_{Mi}$![]() with density and temperature that are flux functions, and that the potential is a flux function to lowest order, $\phi (r, \alpha, l, t) \simeq \phi _0(r, t) \sim T_i/e$
with density and temperature that are flux functions, and that the potential is a flux function to lowest order, $\phi (r, \alpha, l, t) \simeq \phi _0(r, t) \sim T_i/e$![]() . The correction to the Maxwellian is only significantly different from zero for trapped particles, for which it satisfies $g_{i, 1, W} \sim \epsilon f_{Mi}$
. The correction to the Maxwellian is only significantly different from zero for trapped particles, for which it satisfies $g_{i, 1, W} \sim \epsilon f_{Mi}$![]() . As for large aspect ratio stellarators with mirror ratios close to unity, the typical radial width of a trapped-particle orbit is $\epsilon a$
. As for large aspect ratio stellarators with mirror ratios close to unity, the typical radial width of a trapped-particle orbit is $\epsilon a$![]() because the radial magnetic drift is small by $\epsilon$
because the radial magnetic drift is small by $\epsilon$![]() compared with the component of the $\boldsymbol {E} \times \boldsymbol {B}$
compared with the component of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift parallel to the flux surface. Apart from these similarities, the formulation by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) differs from the equations presented in previous sections of this paper in significant ways. For $B_{0, M}/B_{0, m} - 1 \sim 1$
drift parallel to the flux surface. Apart from these similarities, the formulation by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) differs from the equations presented in previous sections of this paper in significant ways. For $B_{0, M}/B_{0, m} - 1 \sim 1$![]() , the typical parallel velocity of trapped particles is not small compared with the thermal speed, and the fraction of trapped particles is of order unity. The energy gained or lost by work done by the radial electric field during a trapped particle's radial displacement is insufficient to affect trapped particles with $v_\| \sim v_{ti}$
, the typical parallel velocity of trapped particles is not small compared with the thermal speed, and the fraction of trapped particles is of order unity. The energy gained or lost by work done by the radial electric field during a trapped particle's radial displacement is insufficient to affect trapped particles with $v_\| \sim v_{ti}$![]() , unlike in large aspect ratio stellarators with mirror ratios close to unity, where trapped particles have $v_\| \sim \sqrt {\epsilon } v_{ti}$
, unlike in large aspect ratio stellarators with mirror ratios close to unity, where trapped particles have $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() . For this reason, the velocity coordinates $\mathcal {E}$
. For this reason, the velocity coordinates $\mathcal {E}$![]() and $\mu$
and $\mu$![]() are appropriate – in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), these coordinates are replaced by the equivalent coordinates $v$
are appropriate – in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), these coordinates are replaced by the equivalent coordinates $v$![]() and $\lambda := v_\perp ^{2}/v^{2} B$
and $\lambda := v_\perp ^{2}/v^{2} B$![]() for convenience. Another important difference with large aspect ratio stellarators with mirror ratios of order unity is that the correction to the lowest-order potential is $\phi _1 (r, \alpha, l, t) \sim \epsilon T_i/e$
for convenience. Another important difference with large aspect ratio stellarators with mirror ratios of order unity is that the correction to the lowest-order potential is $\phi _1 (r, \alpha, l, t) \sim \epsilon T_i/e$![]() instead of $\phi _{3/2} (r, \alpha, l, t) \sim \epsilon ^{3/2} T_i/e$
instead of $\phi _{3/2} (r, \alpha, l, t) \sim \epsilon ^{3/2} T_i/e$![]() , and as a result the radial component of the $\boldsymbol {E} \times \boldsymbol {B}$
, and as a result the radial component of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift contributes significantly to the radial displacement of trapped particles.
drift contributes significantly to the radial displacement of trapped particles.
We proceed to discuss the different transport regimes predicted by the formulation of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). For collision frequencies $\nu _{ii}$![]() larger than the characteristic frequency associated with the $\boldsymbol {E} \times \boldsymbol {B}$
larger than the characteristic frequency associated with the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, $|\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$
drift, $|\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$![]() , that is, for $\rho _{i*}/\epsilon \ll \nu _{i*} \ll \epsilon^{3/2}$
, that is, for $\rho _{i*}/\epsilon \ll \nu _{i*} \ll \epsilon^{3/2}$![]() , the equations derived by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) predict a $1/\nu$
, the equations derived by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) predict a $1/\nu$![]() regime. In this regime, the particle and energy fluxes are of order
regime. In this regime, the particle and energy fluxes are of order
Here, the characteristic length $L_0$![]() and the parameter $\delta$
and the parameter $\delta$![]() in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) have been replaced with $a$
in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) have been replaced with $a$![]() and $\epsilon$
and $\epsilon$![]() , and our definition of $\nu _{i*}$
, and our definition of $\nu _{i*}$![]() differs from the one used by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), $\nu _{i*}^{\mathrm{Ca}}$
differs from the one used by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), $\nu _{i*}^{\mathrm{Ca}}$![]() , by a factor of $\epsilon$
, by a factor of $\epsilon$![]() , $\nu _{i*} = \nu _{i*}^{\mathrm{Ca}}/\epsilon$
, $\nu _{i*} = \nu _{i*}^{\mathrm{Ca}}/\epsilon$![]() . Note that, for large aspect stellarators with large mirror ratios, the transition to the lower collisionality transport regime happens for $\nu _{i*} \sim \rho _{i*}/\epsilon$
. Note that, for large aspect stellarators with large mirror ratios, the transition to the lower collisionality transport regime happens for $\nu _{i*} \sim \rho _{i*}/\epsilon$![]() – in comparison, for large aspect ratio stellarators with mirror ratios close to unity, the transition happens for $\nu _{i*} \sim \rho _{i*}$
– in comparison, for large aspect ratio stellarators with mirror ratios close to unity, the transition happens for $\nu _{i*} \sim \rho _{i*}$![]() . The difference is due to the typical parallel velocity of the trapped particles: for large aspect ratio stellarators with mirror ratios close to unity, trapped particles have $v_\| \sim \sqrt {\epsilon } v_{ti}$
. The difference is due to the typical parallel velocity of the trapped particles: for large aspect ratio stellarators with mirror ratios close to unity, trapped particles have $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() and hence it is easy for collisions to detrap these particles, giving a large effective collision frequency $\nu _{ii}/\epsilon$
and hence it is easy for collisions to detrap these particles, giving a large effective collision frequency $\nu _{ii}/\epsilon$![]() for trapped particles.
for trapped particles.
The estimates for the fluxes in (8.2a,b) can also be obtained from a random walk argument similar to the one that gives the estimates in (6.2a,b). In large aspect ratio stellarators with large mirror ratios, the effective collision frequency for trapped particles is $\nu _{ii}$![]() and hence the random walk is composed of steps of length $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _{ii} \sim (\rho _{i*}/\nu _{i*}) a \ll \epsilon a$
and hence the random walk is composed of steps of length $\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _{ii} \sim (\rho _{i*}/\nu _{i*}) a \ll \epsilon a$![]() that happen with frequency $\nu _{ii}$
that happen with frequency $\nu _{ii}$![]() . The corresponding diffusion coefficient is $D \sim (\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _{ii})^{2} \nu _{ii} \sim \epsilon \rho _{i*}^{2} a v_{ti}/\nu _{i*}$
. The corresponding diffusion coefficient is $D \sim (\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _{ii})^{2} \nu _{ii} \sim \epsilon \rho _{i*}^{2} a v_{ti}/\nu _{i*}$![]() , where we have noted that the fraction of trapped particles is of order unity. This diffusion coefficient gives the estimates in (8.2a,b).
, where we have noted that the fraction of trapped particles is of order unity. This diffusion coefficient gives the estimates in (8.2a,b).
For $\nu _{i*} \ll \rho _{i*}/\epsilon$![]() , the derivation of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) does not assume that the component of the $\boldsymbol {\nabla } B$
, the derivation of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) does not assume that the component of the $\boldsymbol {\nabla } B$![]() and curvature drifts parallel to the flux surface is smaller than the same component of the $\boldsymbol {E} \times \boldsymbol {B}$
and curvature drifts parallel to the flux surface is smaller than the same component of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. For this reason, it allows for cancellation of the average drift parallel to the flux surface for certain particles. In large aspect ratio stellarators with large mirror ratios and an electric field $|\phi _0^{\prime }|$
drift. For this reason, it allows for cancellation of the average drift parallel to the flux surface for certain particles. In large aspect ratio stellarators with large mirror ratios and an electric field $|\phi _0^{\prime }|$![]() that is much larger than $T_i/eR$
that is much larger than $T_i/eR$![]() , the $\boldsymbol {E} \times \boldsymbol {B}$
, the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift is larger than the magnetic drifts by $e|\phi _0^{\prime }| R/T_i \gg 1$
drift is larger than the magnetic drifts by $e|\phi _0^{\prime }| R/T_i \gg 1$![]() , and hence only a exponentially small number of particles with energies above $e R \phi _0^{\prime } \gg m_i v_{ti}^{2}$
, and hence only a exponentially small number of particles with energies above $e R \phi _0^{\prime } \gg m_i v_{ti}^{2}$![]() can have vanishing drifts parallel to the flux surface. These particles can be neglected, and as a result the transport is dominated by boundary layers in velocity space of width $\Delta v_\| \ll v_{ti}$
can have vanishing drifts parallel to the flux surface. These particles can be neglected, and as a result the transport is dominated by boundary layers in velocity space of width $\Delta v_\| \ll v_{ti}$![]() that appear at the trapped–passing boundary or around junctures of different types of wells. In these layers, the effective collision frequency is
that appear at the trapped–passing boundary or around junctures of different types of wells. In these layers, the effective collision frequency is

The effective collision frequency becomes larger than $\nu _{ii}$![]() because very small angle collisions are sufficient to change the parallel velocity by a small amount $\Delta v_\| \ll v_{ti}$
because very small angle collisions are sufficient to change the parallel velocity by a small amount $\Delta v_\| \ll v_{ti}$![]() . The logarithmic reduction of the effective collision frequency is due to the fact that particles in these layers have bounce points that are very close to local maxima of $B$
. The logarithmic reduction of the effective collision frequency is due to the fact that particles in these layers have bounce points that are very close to local maxima of $B$![]() , where they spend logarithmically long times. Collisions near these maxima of $B$
, where they spend logarithmically long times. Collisions near these maxima of $B$![]() are ineffective because $v_\|$
are ineffective because $v_\|$![]() is very close to zero, $v_\| \ll v_{ti}$
is very close to zero, $v_\| \ll v_{ti}$![]() , and a collision that changes the parallel velocity of a particle by $\Delta v_\|$
, and a collision that changes the parallel velocity of a particle by $\Delta v_\|$![]() changes its parallel kinetic energy by $m_i v_\| \Delta v_\| \ll m_i v_{ti} \Delta v_\|$
changes its parallel kinetic energy by $m_i v_\| \Delta v_\| \ll m_i v_{ti} \Delta v_\|$![]() only. With such a small change in kinetic energy, the particle cannot leave the layer. The collisions that expel the particles from the boundary layer happen away from the bounce points, where $v_\| \sim v_{ti}$
only. With such a small change in kinetic energy, the particle cannot leave the layer. The collisions that expel the particles from the boundary layer happen away from the bounce points, where $v_\| \sim v_{ti}$![]() and particles spend only a fraction of its bounce period of order $1/\ln (v_{ti}/\Delta v_\|)$
and particles spend only a fraction of its bounce period of order $1/\ln (v_{ti}/\Delta v_\|)$![]() . The effective collision frequency $\nu _\mathrm {eff}$
. The effective collision frequency $\nu _\mathrm {eff}$![]() has to be comparable to the inverse of the time that it takes a particle to drift poloidally around the stellarator, $|\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$
has to be comparable to the inverse of the time that it takes a particle to drift poloidally around the stellarator, $|\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$![]() , giving
, giving

The transport due to these boundary layers is of order

The formulation by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) does not work for $\nu _{ii}a/|\boldsymbol {v}_E| \lesssim \epsilon ^{2} |\ln \epsilon |$![]() – this limit is derived in § 6 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) without the logarithmic correction (recall that $\delta$
– this limit is derived in § 6 of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) without the logarithmic correction (recall that $\delta$![]() must be replaced with $\epsilon$
must be replaced with $\epsilon$![]() ). This means that, in normalized quantities, the $\sqrt {\nu }$
). This means that, in normalized quantities, the $\sqrt {\nu }$![]() regime does not extend below $\nu _{i*} \sim \epsilon |\ln \epsilon | \rho _{i*}$
regime does not extend below $\nu _{i*} \sim \epsilon |\ln \epsilon | \rho _{i*}$![]() . We leave the study of what happens for collisionalities lower than this limit for another publication.
. We leave the study of what happens for collisionalities lower than this limit for another publication.
As other estimates given in previous sections, the estimates in (8.5a,b) can be obtained from a random walk argument. Only particles in velocity-space boundary layers with width $\Delta v_\|$![]() , given in (8.4), participate in the transport. These particles have an effective collision frequency $\nu _\mathrm {eff} \sim |\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$
, given in (8.4), participate in the transport. These particles have an effective collision frequency $\nu _\mathrm {eff} \sim |\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$![]() , and hence typical radial displacements ${\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff} \sim \epsilon a}$
, and hence typical radial displacements ${\boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r/\nu _\mathrm {eff} \sim \epsilon a}$![]() . Thus, the diffusion coefficient is
. Thus, the diffusion coefficient is

where the prefactor $(\Delta v_\|/v_{ti}) \ln (v_{ti}/\Delta v_\|)$![]() is due to the small fraction of particles that are in the boundary layers and cause transport. The logarithmic correction in $(\Delta v_\|/v_{ti}) \ln (v_{ti}/\Delta v_\|)$
is due to the small fraction of particles that are in the boundary layers and cause transport. The logarithmic correction in $(\Delta v_\|/v_{ti}) \ln (v_{ti}/\Delta v_\|)$![]() is due to the long bounce periods of the orbits of interest: the particles in the boundary layers spend logarithmically long times around local maxima of $B$
is due to the long bounce periods of the orbits of interest: the particles in the boundary layers spend logarithmically long times around local maxima of $B$![]() , where they accumulate, giving a density large by $\ln (v_{ti}/\Delta v_\|)$
, where they accumulate, giving a density large by $\ln (v_{ti}/\Delta v_\|)$![]() . The diffusion coefficient in (8.6) gives $D \sim \sqrt {(\epsilon \nu _{i*}/ \rho _{i*}) \ln (\rho _{i*}/\epsilon \nu _{i*})} \epsilon ^{2} \rho _{i*} a v_{ti}$
. The diffusion coefficient in (8.6) gives $D \sim \sqrt {(\epsilon \nu _{i*}/ \rho _{i*}) \ln (\rho _{i*}/\epsilon \nu _{i*})} \epsilon ^{2} \rho _{i*} a v_{ti}$![]() , and with it we can obtain the estimates in (8.5a,b).
, and with it we can obtain the estimates in (8.5a,b).
A comparison between expressions (8.2a,b) and (8.5a,b) and expressions (6.2a,b) and (7.30a,b), sketched in figure 11, reveals that neoclassical fluxes in large aspect ratio stellarators with large mirror ratios are larger than the fluxes in equivalent large aspect ratio stellarator with mirror ratios close to unity. This is perhaps part of the reason why no stellarators with large mirror ratios have been built.

Figure 11. Particle and energy fluxes as a function of $\nu _{i*}/\rho _{i*}$![]() for large aspect ratio stellarators with large mirror ratios (blue line) and mirror ratios close to unity (green line). Note that, for $\nu _{i*} \sim \rho _{i*}$
for large aspect ratio stellarators with large mirror ratios (blue line) and mirror ratios close to unity (green line). Note that, for $\nu _{i*} \sim \rho _{i*}$![]() , the difference between the fluxes of large aspect ratio stellarators with large mirror ratios and the fluxes of large aspect ratio stellarators with mirror ratios close to unity is only a factor of $\sqrt {|\ln \epsilon |}$
, the difference between the fluxes of large aspect ratio stellarators with large mirror ratios and the fluxes of large aspect ratio stellarators with mirror ratios close to unity is only a factor of $\sqrt {|\ln \epsilon |}$![]() .
.
8.2. Optimized large aspect ratio stellarators with mirror ratios close to unity
It is possible to optimize large aspect ratio stellarators with mirror ratios close to unity to achieve lower neoclassical transport. We treat such cases by using the expansion proposed by Calvo et al. (Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018), that is, we consider a magnetic field that can be written as
Here, $B_0 + B_1^{[0]}$![]() , with $B_1^{[0]} \sim \epsilon B_0$
, with $B_1^{[0]} \sim \epsilon B_0$![]() , is omnigeneous, that is,
, is omnigeneous, that is,

where we have used the large aspect ratio approximation to (8.1). Here, $l_{bL,0,W}^{[0]}(r, \alpha, \lambda )$![]() and $l_{bR,0,W}^{[0]}(r, \alpha, \lambda )$
and $l_{bR,0,W}^{[0]}(r, \alpha, \lambda )$![]() are the bounce points that correspond to the omnigeneous magnetic field, determined by the equations $B_1^{[0]} (r, \alpha, l_{bL,0,W}^{[0]})/B_0 = 1 - \lambda B_0 = B_1^{[0]} (r, \alpha, l_{bR,0,W}^{[0]})/B_0$
are the bounce points that correspond to the omnigeneous magnetic field, determined by the equations $B_1^{[0]} (r, \alpha, l_{bL,0,W}^{[0]})/B_0 = 1 - \lambda B_0 = B_1^{[0]} (r, \alpha, l_{bR,0,W}^{[0]})/B_0$![]() . The correction $B_1^{[1]} \sim \delta \epsilon B_0$
. The correction $B_1^{[1]} \sim \delta \epsilon B_0$![]() is the perturbation away from omnigeneity. We assume that $\delta \ll 1$
is the perturbation away from omnigeneity. We assume that $\delta \ll 1$![]() . Note that we are using the superscripts with square brackets $^{[n]}$
. Note that we are using the superscripts with square brackets $^{[n]}$![]() for the expansion in $\delta$
for the expansion in $\delta$![]() to distinguish it from the expansion in § 7.
to distinguish it from the expansion in § 7.
We proceed to expand (5.25) in $\delta \ll 1$![]() . We first obtain $r_{i, 1, W}$
. We first obtain $r_{i, 1, W}$![]() by writing
by writing
with

and

When we invert the relation $J_W (r, \alpha, v, \lambda )$![]() to obtain $\lambda _W(r, \alpha, v, J)$
to obtain $\lambda _W(r, \alpha, v, J)$![]() , we find that $\lambda _W$
, we find that $\lambda _W$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() to lowest order in the expansion in $\delta \ll 1$
to lowest order in the expansion in $\delta \ll 1$![]() . If we continue to next order in $\delta$
. If we continue to next order in $\delta$![]() , we obtain
, we obtain
where

Here,

is the lowest-order bounce time.
With the result in (8.12), (5.25) becomes
where $g_{i, 1, W}^{[1]} \sim \delta \epsilon f_{Mi}$![]() and
and

At the junctures of several wells, we need to impose condition (5.33), which in the expansion in $\delta$![]() becomes
becomes
Importantly, since the omnigeneous stellarator has a maximum value of $J$![]() , $J_{\mathrm {om}, M}$
, $J_{\mathrm {om}, M}$![]() , the boundary condition for $g_{i, 1, W}^{[1]}$
, the boundary condition for $g_{i, 1, W}^{[1]}$![]() is not imposed at $J \rightarrow \infty$
is not imposed at $J \rightarrow \infty$![]() , but at $J = J_{\mathrm {om}, M}^{[0]}$
, but at $J = J_{\mathrm {om}, M}^{[0]}$![]() ,
,
The particle and energy fluxes simplify to

and

Note that we have used the fact that there are no transitions between wells in an omnigeneous magnetic field to extend the integrals in $\alpha$![]() to the whole interval $[0, 2{\rm \pi} ]$
to the whole interval $[0, 2{\rm \pi} ]$![]() .
.
Comparing the estimates for the fluxes in (8.19) and (8.20) with the ones for a generic large aspect ratio stellarator with mirror ratio close to unity in (5.48) and (5.50), we see that a near-omnigeneous stellarator does indeed confine better than a generic one by a factor of $\delta ^{2} \ll 1$![]() . This factor, however, is not uniform for all values of $\nu _{i*}$
. This factor, however, is not uniform for all values of $\nu _{i*}$![]() . While in the $1/\nu$
. While in the $1/\nu$![]() regime, $\nu _{i*}/\rho _{i*} \gg 1$
regime, $\nu _{i*}/\rho _{i*} \gg 1$![]() , we can follow the arguments in § 6 to obtain
, we can follow the arguments in § 6 to obtain
for $\nu _{i*} \ll \rho _{i*}$![]() the scaling with $\delta$
the scaling with $\delta$![]() is not a simple $\delta ^{2}$
is not a simple $\delta ^{2}$![]() , as we explain below. Before considering the regime $\nu _{i*} \ll \rho _{i*}$
, as we explain below. Before considering the regime $\nu _{i*} \ll \rho _{i*}$![]() , we discuss how to obtain the estimates in (8.19), (8.20) and (8.21a,b) using a random walk argument. For $\nu _{i*} \gtrsim \rho _{i*}$
, we discuss how to obtain the estimates in (8.19), (8.20) and (8.21a,b) using a random walk argument. For $\nu _{i*} \gtrsim \rho _{i*}$![]() , in between collisions, trapped particles move a radial distance $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} /\nu _\mathrm {eff}$
, in between collisions, trapped particles move a radial distance $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} /\nu _\mathrm {eff}$![]() , where $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$
, where $\nu _\mathrm {eff} \sim \nu _{ii}/\epsilon$![]() is the effective collision frequency for trapped particles. Since $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} \sim \delta \epsilon \rho _{i*} v_{ti}$
is the effective collision frequency for trapped particles. Since $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} \sim \delta \epsilon \rho _{i*} v_{ti}$![]() , the typical radial displacement is $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} /\nu _\mathrm {eff} \sim (\rho _{i*}/\nu _{i*}) \delta \epsilon a \lesssim \delta \epsilon a$
, the typical radial displacement is $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} /\nu _\mathrm {eff} \sim (\rho _{i*}/\nu _{i*}) \delta \epsilon a \lesssim \delta \epsilon a$![]() . With this estimate, we obtain a random walk diffusion coefficient $D \sim \sqrt {\epsilon } ( \langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff})^{2} \nu _\mathrm {eff}$
. With this estimate, we obtain a random walk diffusion coefficient $D \sim \sqrt {\epsilon } ( \langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff})^{2} \nu _\mathrm {eff}$![]() , where the factor of $\sqrt {\epsilon }$
, where the factor of $\sqrt {\epsilon }$![]() is due to the trapped-particle fraction. This diffusion coefficient $D \sim \delta ^{2} \epsilon ^{5/2} \rho _{i*}^{2} a v_{ti}/\nu _{i*}$
is due to the trapped-particle fraction. This diffusion coefficient $D \sim \delta ^{2} \epsilon ^{5/2} \rho _{i*}^{2} a v_{ti}/\nu _{i*}$![]() gives the estimates (8.21a,b) for $\nu _{i*} \gg \rho _{i*}$
gives the estimates (8.21a,b) for $\nu _{i*} \gg \rho _{i*}$![]() , and the estimates in (8.19) and (8.20) for $\nu _{i*} \sim \rho _{i*}$
, and the estimates in (8.19) and (8.20) for $\nu _{i*} \sim \rho _{i*}$![]() .
.
If we try to solve (8.15) for $\nu _{i*} \ll \rho _{i*}$![]() following the procedure in § 7, we run into problems at the largest value of $J$
following the procedure in § 7, we run into problems at the largest value of $J$![]() , $J_{\mathrm {om}, M}^{[0]}$
, $J_{\mathrm {om}, M}^{[0]}$![]() , and at junctures of different types of wells. Indeed, if we neglect the collision operator in (8.15), the solution is
, and at junctures of different types of wells. Indeed, if we neglect the collision operator in (8.15), the solution is
where the function $K_{i, W}^{[1]} (r, v, J, t)$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() . Solution (8.22) cannot vanish at $J = J_{\mathrm {om}, M}^{[0]}$
. Solution (8.22) cannot vanish at $J = J_{\mathrm {om}, M}^{[0]}$![]() in general because $r_{i, 1, W}^{[1]}$
in general because $r_{i, 1, W}^{[1]}$![]() does not vanish there. The contribution proportional to $r_{i, 1, W}^{[1]}$
does not vanish there. The contribution proportional to $r_{i, 1, W}^{[1]}$![]() cannot be cancelled by a judicious choice of $K_{i, W}^{[1]}$
cannot be cancelled by a judicious choice of $K_{i, W}^{[1]}$![]() because $r_{i, 1, W}^{[1]}$
because $r_{i, 1, W}^{[1]}$![]() depends on $\alpha$
depends on $\alpha$![]() while $K_{i, W}^{[1]}$
while $K_{i, W}^{[1]}$![]() does not. Similarly, it is not possible to impose continuity of $g_{i,1,W}^{[1]}$
does not. Similarly, it is not possible to impose continuity of $g_{i,1,W}^{[1]}$![]() across junctures. The problem at $J = J_{\mathrm {om}, M}^{[0]}$
across junctures. The problem at $J = J_{\mathrm {om}, M}^{[0]}$![]() is a manifestation of the fact that there are orbits with second adiabatic invariants larger than $J_{\mathrm {om}, M}^{[0]}$
is a manifestation of the fact that there are orbits with second adiabatic invariants larger than $J_{\mathrm {om}, M}^{[0]}$![]() . The perturbation $B_1^{[1]}$
. The perturbation $B_1^{[1]}$![]() will in general introduce isolated local maxima in $B$
will in general introduce isolated local maxima in $B$![]() above those of the omnigeneous magnetic field, and these maxima will not be equal to each other. The fact that there are individual maxima means that we are back to the case that we have studied in §§ 5 and 7. Thus, one needs to include $J > J_{\mathrm {om}, M}^{[0]}$
above those of the omnigeneous magnetic field, and these maxima will not be equal to each other. The fact that there are individual maxima means that we are back to the case that we have studied in §§ 5 and 7. Thus, one needs to include $J > J_{\mathrm {om}, M}^{[0]}$![]() . The problem at junctures of different types of wells is due to the fact that approximation (8.15) does not allow transitions between different types of wells.
. The problem at junctures of different types of wells is due to the fact that approximation (8.15) does not allow transitions between different types of wells.
We proceed to study the distribution functions and fluxes for $\nu _{i*} \ll \rho _{i*}$![]() . There are two limits of interest that we consider: $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$
. There are two limits of interest that we consider: $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$![]() and $\nu _{i*}/\rho _{i*} \ll \delta ^{2} |\ln \delta |$
and $\nu _{i*}/\rho _{i*} \ll \delta ^{2} |\ln \delta |$![]() .
.
8.2.1. The $\sqrt {\nu }$ regime in optimized large aspect ratio stellarators with mirror ratios close to unity
regime in optimized large aspect ratio stellarators with mirror ratios close to unity
We start by considering the regime $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$![]() , where we will find the $\sqrt {\nu }$
, where we will find the $\sqrt {\nu }$![]() regime (Galeev et al. Reference Galeev, Sadgeev, Furth and Rosenbluth1969; Ho & Kulsrud Reference Ho and Kulsrud1987). In the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
regime (Galeev et al. Reference Galeev, Sadgeev, Furth and Rosenbluth1969; Ho & Kulsrud Reference Ho and Kulsrud1987). In the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , particles have bounce points at the new maxima introduced by the perturbation $B_1^{[1]}$
, particles have bounce points at the new maxima introduced by the perturbation $B_1^{[1]}$![]() above the maxima of the omnigeneous magnetic field. To understand estimate $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
above the maxima of the omnigeneous magnetic field. To understand estimate $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , note that the particles that bounce in the new maxima of $B$
, note that the particles that bounce in the new maxima of $B$![]() are in an interval of $\lambda$
are in an interval of $\lambda$![]() of order $\Delta \lambda \sim \delta \epsilon /B_0$
of order $\Delta \lambda \sim \delta \epsilon /B_0$![]() . This interval corresponds to an interval in $J$
. This interval corresponds to an interval in $J$![]() of order $\Delta \lambda \, \partial _\lambda J_W$
of order $\Delta \lambda \, \partial _\lambda J_W$![]() , where $\partial _\lambda J_W \sim \epsilon ^{-1/2} v_{ti} R B_0 |\ln \delta |$
, where $\partial _\lambda J_W \sim \epsilon ^{-1/2} v_{ti} R B_0 |\ln \delta |$![]() . The logarithm is due to the fact that the bounce points are always a small distance $\sqrt {\delta } R$
. The logarithm is due to the fact that the bounce points are always a small distance $\sqrt {\delta } R$![]() away from a local maximum of $B$
away from a local maximum of $B$![]() . Particles spend logarithmically long times near these local maxima, giving $\partial _\lambda J_W \simeq - v^{2} B_0 \tau _W/2 \sim \epsilon ^{-1/2} v_{ti} B_0 R |\ln \delta |$
. Particles spend logarithmically long times near these local maxima, giving $\partial _\lambda J_W \simeq - v^{2} B_0 \tau _W/2 \sim \epsilon ^{-1/2} v_{ti} B_0 R |\ln \delta |$![]() .
.
To determine whether the particles in the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() can make up for the difference between $g_{i, 1, W}^{[1]}$
can make up for the difference between $g_{i, 1, W}^{[1]}$![]() and the distribution function in the passing-particle region, we estimate the size of the change in the distribution function $\Delta g_{i, 1, \mathrm {om}}$
and the distribution function in the passing-particle region, we estimate the size of the change in the distribution function $\Delta g_{i, 1, \mathrm {om}}$![]() for $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
for $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() . For $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
. For $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , we find
, we find
Using this estimate in (5.25), we find that the dominant balance is between the collision operator and the term proportional to $\partial _\alpha r_{i, 1, W}$![]() , giving
, giving
Here, one of the logarithms $|\ln \delta |$![]() due to a derivative with respect to $J$
due to a derivative with respect to $J$![]() has cancelled with another logarithm $|\ln \delta |$
has cancelled with another logarithm $|\ln \delta |$![]() in $\tau _W$
in $\tau _W$![]() , which is of order $R |\ln \delta |/\sqrt {\epsilon } v_{ti}$
, which is of order $R |\ln \delta |/\sqrt {\epsilon } v_{ti}$![]() because the bounce points of the orbits are always a small distance $\sqrt {\delta } R$
because the bounce points of the orbits are always a small distance $\sqrt {\delta } R$![]() away from a local maximum of $B$
away from a local maximum of $B$![]() . In (8.24), $r_{i, 1, W}$
. In (8.24), $r_{i, 1, W}$![]() is proportional to $\lambda _W - 1/B_M \sim \delta \epsilon /B_0$
is proportional to $\lambda _W - 1/B_M \sim \delta \epsilon /B_0$![]() and hence of order $\delta \epsilon a$
and hence of order $\delta \epsilon a$![]() . As a result, we estimate $\Delta g_{i,1, \mathrm {om}}$
. As a result, we estimate $\Delta g_{i,1, \mathrm {om}}$![]() to be
to be
This means that the solution for $g_{i, 1, W}$![]() in the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
in the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() cannot match with $g_{i, 1, W}^{[1]}$
cannot match with $g_{i, 1, W}^{[1]}$![]() and we still have a discontinuity – see figure 12 for a sketch of the situation. A similar reasoning can be made for $g_{i,1,W}$
and we still have a discontinuity – see figure 12 for a sketch of the situation. A similar reasoning can be made for $g_{i,1,W}$![]() near a juncture.
near a juncture.

Figure 12. Sketch of the ion distribution function $g_{i, 1, W}$![]() in near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity for $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$
in near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity for $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$![]() (red line) and $\nu _{i*}/\rho _{i*} \ll \delta ^{2} |\ln \delta |$
(red line) and $\nu _{i*}/\rho _{i*} \ll \delta ^{2} |\ln \delta |$![]() (green line). The maximum value of the second adiabatic invariant in the omnigeneous magnetic field $J_{\mathrm {om}, M}^{[0]}$
(green line). The maximum value of the second adiabatic invariant in the omnigeneous magnetic field $J_{\mathrm {om}, M}^{[0]}$![]() is represented as a blue dashed line. We consider a case where there is a juncture in the region $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
is represented as a blue dashed line. We consider a case where there is a juncture in the region $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() (juncture A). Of all the junctures that appear for $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
(juncture A). Of all the junctures that appear for $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , we only sketch one (juncture B). The $\sqrt {\nu }$
, we only sketch one (juncture B). The $\sqrt {\nu }$![]() boundary layers that appear in the case $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$
boundary layers that appear in the case $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$![]() (red line) are highlighted as pink areas. Note that, outside of the $\sqrt {\nu }$
(red line) are highlighted as pink areas. Note that, outside of the $\sqrt {\nu }$![]() boundary layers and the junctures, the derivative of the distribution function $g_{i,1,W}$
boundary layers and the junctures, the derivative of the distribution function $g_{i,1,W}$![]() with respect to $J$
with respect to $J$![]() remains the same as $\nu _{i*}/\rho _{i*}$
remains the same as $\nu _{i*}/\rho _{i*}$![]() changes.
changes.
Collisional boundary layers appear at the discontinuity between $g_{i, 1, W}^{[1]}$![]() and the distribution function at $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
and the distribution function at $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , and at the discontinuities on junctures. In these boundary layers, $g_{i, 1, W}$
, and at the discontinuities on junctures. In these boundary layers, $g_{i, 1, W}$![]() changes significantly over a width $\Delta J_{\sqrt {\nu }} \ll \sqrt {\epsilon } v_{ti} R$
changes significantly over a width $\Delta J_{\sqrt {\nu }} \ll \sqrt {\epsilon } v_{ti} R$![]() , giving $\partial _J g_{i, 1, W} \sim g_{i, 1, W}/\Delta J_{\sqrt {\nu }} \gg g_{i, 1, W}/\sqrt {\epsilon } v_{ti} R$
, giving $\partial _J g_{i, 1, W} \sim g_{i, 1, W}/\Delta J_{\sqrt {\nu }} \gg g_{i, 1, W}/\sqrt {\epsilon } v_{ti} R$![]() . This large derivatives in $J$
. This large derivatives in $J$![]() make the collision operator large and comparable to the $\boldsymbol {E} \times \boldsymbol {B}$
make the collision operator large and comparable to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift (Ho & Kulsrud Reference Ho and Kulsrud1987; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017, Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018),
drift (Ho & Kulsrud Reference Ho and Kulsrud1987; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017, Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018),

The logarithm in this estimate comes from the fact that the bounce points of the particles in this layer are close to local maxima of the omnigeneous magnetic field. Solving (8.26) for $\Delta J_{\sqrt {\nu }}$![]() gives
gives

The distribution function in these boundary layers is not of the form in (8.22), and hence does not vanish under the integrals for the particle and energy fluxes, given in (8.19) and (8.20). Thus, the fluxes are mostly due to particles within the boundary layer, giving

These are the particle and energy fluxes of the $\sqrt {\nu }$![]() regime (Ho & Kulsrud Reference Ho and Kulsrud1987; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017, Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018). This regime only appears in large aspect ratio stellarators with mirror ratios close to unity when they are close to omnigeneity.
regime (Ho & Kulsrud Reference Ho and Kulsrud1987; Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017, Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018). This regime only appears in large aspect ratio stellarators with mirror ratios close to unity when they are close to omnigeneity.
The estimates in (8.28a,b) can be obtained from a random walk argument. The particles that contribute most to radial transport are the particles in velocity-space boundary layers of width $\Delta v_\| \ll \sqrt {\epsilon } v_{ti}$![]() . We start by estimating the width of the boundary layers. The effective collision frequency in these layers is
. We start by estimating the width of the boundary layers. The effective collision frequency in these layers is

We have obtained this effective collision frequency using the same arguments that we used to find (8.3). Note that the only difference between (8.3) and (8.29) is in the logarithm, where we find an extra factor of $\sqrt {\epsilon }$![]() in (8.29). In the layer, the effective collision frequency is of the same order as the inverse of the time that it takes for a particle to drift poloidally around the stellarator, $\nu _\mathrm {eff} \sim |\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$
in (8.29). In the layer, the effective collision frequency is of the same order as the inverse of the time that it takes for a particle to drift poloidally around the stellarator, $\nu _\mathrm {eff} \sim |\boldsymbol {v}_E|/a \sim \rho _{i*} v_{ti}/a$![]() . This balance gives a boundary layer width
. This balance gives a boundary layer width

Comparing this result with (8.27), we see that the width of the layer in $v_\|$![]() is smaller than in $J$
is smaller than in $J$![]() , $\Delta J_{\sqrt {\nu }}/\sqrt {\epsilon } v_{ti} R \sim \ln (\rho _{i*}/\nu _{i*}) (\Delta v_\|/\sqrt {\epsilon } v_{ti}) \gg \Delta v_\|/\sqrt {\epsilon } v_{ti}$
, $\Delta J_{\sqrt {\nu }}/\sqrt {\epsilon } v_{ti} R \sim \ln (\rho _{i*}/\nu _{i*}) (\Delta v_\|/\sqrt {\epsilon } v_{ti}) \gg \Delta v_\|/\sqrt {\epsilon } v_{ti}$![]() . This is consistent with the transformation between the velocity-space variables $\bar {v}$
. This is consistent with the transformation between the velocity-space variables $\bar {v}$![]() and $J$
and $J$![]() and the cartesian velocity $\boldsymbol {v}$
and the cartesian velocity $\boldsymbol {v}$![]() . Indeed, we can take $\Delta v_\|/\sqrt {\epsilon } v_{ti} \sim B_0 \Delta \lambda /\epsilon$
. Indeed, we can take $\Delta v_\|/\sqrt {\epsilon } v_{ti} \sim B_0 \Delta \lambda /\epsilon$![]() , with $\Delta \lambda$
, with $\Delta \lambda$![]() the size of the layer in $\lambda := v_\perp ^{2}/v^{2} B$
the size of the layer in $\lambda := v_\perp ^{2}/v^{2} B$![]() , and $\Delta J \sim \Delta \lambda \, \partial _\lambda J_W \sim \sqrt {\epsilon } v_{ti} R (B_0 \Delta \lambda /\epsilon ) \ln ( \epsilon / B_0 \Delta \lambda )$
, and $\Delta J \sim \Delta \lambda \, \partial _\lambda J_W \sim \sqrt {\epsilon } v_{ti} R (B_0 \Delta \lambda /\epsilon ) \ln ( \epsilon / B_0 \Delta \lambda )$![]() , where the logarithmic divergence is a result of particles spending a long time around the local maxima of $B$
, where the logarithmic divergence is a result of particles spending a long time around the local maxima of $B$![]() .
.
To obtain estimates for the fluxes, in addition to the layer width $\Delta v_\|$![]() and the effective collision frequency $\nu _\mathrm {eff}$
and the effective collision frequency $\nu _\mathrm {eff}$![]() , we need the typical radial displacement between collisions of particles in the boundary layers, given by $\langle \boldsymbol {v}_{Mi}\boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff}$
, we need the typical radial displacement between collisions of particles in the boundary layers, given by $\langle \boldsymbol {v}_{Mi}\boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff}$![]() . Since $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} \sim \delta \epsilon \rho _{i*} v_{ti}$
. Since $\langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} \sim \delta \epsilon \rho _{i*} v_{ti}$![]() and $\nu _\mathrm {eff} \sim \rho _{i*} v_{ti}/a$
and $\nu _\mathrm {eff} \sim \rho _{i*} v_{ti}/a$![]() , we find $\langle \boldsymbol {v}_{Mi}\boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff} \sim \delta \epsilon a$
, we find $\langle \boldsymbol {v}_{Mi}\boldsymbol {\cdot } \boldsymbol {\nabla } r\rangle _{\tau, W} /\nu _\mathrm {eff} \sim \delta \epsilon a$![]() . With all these results, we can write the random walk diffusion coefficient as
. With all these results, we can write the random walk diffusion coefficient as

where we have used that the fraction of particles in the boundary layers is of the order of $(\Delta v_\|/v_{ti}) \ln (\sqrt {\epsilon } v_{ti}/\Delta v_\|)$![]() . The logarithmic correction in the particle fraction is due to the accumulation of slow particles around the local maxima of $B$
. The logarithmic correction in the particle fraction is due to the accumulation of slow particles around the local maxima of $B$![]() . The diffusion coefficient in (8.31) gives $D \sim \delta ^{2} \sqrt {\nu _{i*} \rho _{i*} \ln (\rho _{i*}/\nu _{i*})} \epsilon ^{5/2} a v_{ti}$
. The diffusion coefficient in (8.31) gives $D \sim \delta ^{2} \sqrt {\nu _{i*} \rho _{i*} \ln (\rho _{i*}/\nu _{i*})} \epsilon ^{5/2} a v_{ti}$![]() , and with it we can obtain the estimates in (8.28a,b).
, and with it we can obtain the estimates in (8.28a,b).
8.2.2. The $\nu$ regime in optimized large aspect ratio stellarators with mirror ratios close to unity
regime in optimized large aspect ratio stellarators with mirror ratios close to unity
The $\sqrt {\nu }$![]() regime stops being valid for $\nu _{i*}/\rho _{i*} \sim \delta ^{2} |\ln \delta |$
regime stops being valid for $\nu _{i*}/\rho _{i*} \sim \delta ^{2} |\ln \delta |$![]() because the distribution function at $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
because the distribution function at $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() , given in (8.25), becomes comparable to $g_{i, 1, W}^{[1]}$
, given in (8.25), becomes comparable to $g_{i, 1, W}^{[1]}$![]() and there is no need for a boundary layer any longer – see figure 12 for a sketch. The same happens for the discontinuities on junctures of different types of wells.
and there is no need for a boundary layer any longer – see figure 12 for a sketch. The same happens for the discontinuities on junctures of different types of wells.
For $\nu _{i*}/\rho _{i*} \lesssim \delta ^{2} |\ln \delta |$![]() , we need to use the procedure laid out in § 7. The resulting fluxes are given in (7.28) and (7.29). Particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
, we need to use the procedure laid out in § 7. The resulting fluxes are given in (7.28) and (7.29). Particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() that are outside of the regions affected by junctures move without having to transition between different types of wells. Thus, particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
that are outside of the regions affected by junctures move without having to transition between different types of wells. Thus, particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() that are outside of regions affected by junctures are in the region of velocity space with $\partial _J K_{i, W} \neq 0$
that are outside of regions affected by junctures are in the region of velocity space with $\partial _J K_{i, W} \neq 0$![]() . The integral in this region has an integrand proportional to $1/\tau _W - 1/\langle \tau _W \rangle _\alpha$
. The integral in this region has an integrand proportional to $1/\tau _W - 1/\langle \tau _W \rangle _\alpha$![]() , and this difference is small because to lowest order, $\tau _W$
, and this difference is small because to lowest order, $\tau _W$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() , $1/\tau _W - 1/\langle \tau _W \rangle _\alpha \sim \delta \sqrt {\epsilon } v_{ti}/R$
, $1/\tau _W - 1/\langle \tau _W \rangle _\alpha \sim \delta \sqrt {\epsilon } v_{ti}/R$![]() . Moreover, $1/\tau _W - 1/\langle \tau _W \rangle _\alpha \sim \delta \sqrt {\epsilon } v_{ti}/R$
. Moreover, $1/\tau _W - 1/\langle \tau _W \rangle _\alpha \sim \delta \sqrt {\epsilon } v_{ti}/R$![]() is integrated over $\alpha$
is integrated over $\alpha$![]() , and the integral vanishes to lowest order, finally giving
, and the integral vanishes to lowest order, finally giving
Then, the contribution to $\varGamma _i$![]() and $Q_i$
and $Q_i$![]() from particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
from particles with $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() and outside of the regions affected by junctures are $\delta ^{2} \epsilon ^{5/2} \nu _{i*} n_i v_{ti}$
and outside of the regions affected by junctures are $\delta ^{2} \epsilon ^{5/2} \nu _{i*} n_i v_{ti}$![]() and $\delta ^{2} \epsilon ^{5/2} \nu _{i*} n_i T_i v_{ti}$
and $\delta ^{2} \epsilon ^{5/2} \nu _{i*} n_i T_i v_{ti}$![]() , respectively. Note that these are consistent with estimates that one can find using the approximate integrals (8.19) and (8.20) for the fluxes.
, respectively. Note that these are consistent with estimates that one can find using the approximate integrals (8.19) and (8.20) for the fluxes.
Conversely, in the region $J_{\mathrm {om}, M}^{[0]} - J \lesssim \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() or in the region where particles are affected by junctures, particles have multiple transitions, and hence $\partial _J K_{i, W} = 0$
or in the region where particles are affected by junctures, particles have multiple transitions, and hence $\partial _J K_{i, W} = 0$![]() . There is then no cancellation similar to the one in (8.32). Using that the typical size of the intervals of interest in $J$
. There is then no cancellation similar to the one in (8.32). Using that the typical size of the intervals of interest in $J$![]() is $\delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$
is $\delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() and that $\tau _W \sim R|\ln \delta |/\sqrt {\epsilon } v_{ti}$
and that $\tau _W \sim R|\ln \delta |/\sqrt {\epsilon } v_{ti}$![]() , the integrals in (7.28) and (7.29) give
, the integrals in (7.28) and (7.29) give
These contributions are larger than the ones from the particles that satisfy $J_{\mathrm {om}, M}^{[0]} - J \gg \delta |\ln \delta | \sqrt {\epsilon } v_{ti} R$![]() and are outside of the regions affected by junctures, and hence dominate the fluxes.
and are outside of the regions affected by junctures, and hence dominate the fluxes.
We proceed to obtain the estimates in (8.33a,b) using a random walk argument. For $\nu _{i*}/\rho _{i*} \ll \delta ^{2} |\ln \delta |$![]() , particles remain close to the flux surface in which they started because their radial drift averages out after several poloidal turns around the stellarator. The time for several poloidal turns is of the order of $a/|\boldsymbol {v}_E|$
, particles remain close to the flux surface in which they started because their radial drift averages out after several poloidal turns around the stellarator. The time for several poloidal turns is of the order of $a/|\boldsymbol {v}_E|$![]() and, in that time, particles drift radially a distance $w \sim \langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} a/|\boldsymbol {v}_E| \sim \delta \epsilon a$
and, in that time, particles drift radially a distance $w \sim \langle \boldsymbol {v}_{Mi} \boldsymbol {\cdot } \boldsymbol {\nabla } r \rangle _{\tau, W} a/|\boldsymbol {v}_E| \sim \delta \epsilon a$![]() . Transport is dominated by particles in thin velocity layers of width $\Delta v_\| /\sqrt {\epsilon } v_{ti} \sim \delta$
. Transport is dominated by particles in thin velocity layers of width $\Delta v_\| /\sqrt {\epsilon } v_{ti} \sim \delta$![]() located at the trapped–passing boundary or around junctures of several wells. For particles in these layers, we can apply the formula for the effective collision frequency in a thin layer in (8.29), finding $\nu _\mathrm {eff} \sim \nu _{ii}/\delta ^{2}|\ln \delta |$
located at the trapped–passing boundary or around junctures of several wells. For particles in these layers, we can apply the formula for the effective collision frequency in a thin layer in (8.29), finding $\nu _\mathrm {eff} \sim \nu _{ii}/\delta ^{2}|\ln \delta |$![]() . With these results, we find the diffusion coefficient $D \sim \delta |\ln \delta | \sqrt {\epsilon } w^{2} \nu _\mathrm {eff}$
. With these results, we find the diffusion coefficient $D \sim \delta |\ln \delta | \sqrt {\epsilon } w^{2} \nu _\mathrm {eff}$![]() , where the fraction of particles in the boundary layer is $\delta |\ln \delta | \sqrt {\epsilon }$
, where the fraction of particles in the boundary layer is $\delta |\ln \delta | \sqrt {\epsilon }$![]() . The logarithmic correction to the fraction of particles in the layer is due to the accumulation of particles around the local maxima of $B$
. The logarithmic correction to the fraction of particles in the layer is due to the accumulation of particles around the local maxima of $B$![]() . Using all our estimates, we finally obtain $D \sim \delta \epsilon ^{5/2} a v_{ti}$
. Using all our estimates, we finally obtain $D \sim \delta \epsilon ^{5/2} a v_{ti}$![]() , and this diffusion coefficient leads to the estimates in (8.33a,b).
, and this diffusion coefficient leads to the estimates in (8.33a,b).
In figure 13, we sketch the estimates in (8.21a,b), (8.28a,b) and (8.33a,b) for the fluxes in near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity. For comparison, we sketch the corresponding estimates (6.2a,b) and (7.30a,b) for generic large aspect ratio stellarators with mirror ratios close to unity. Note that the optimization towards omnigeneity is much more effective in the $1/\nu$![]() regime. The reduced effectiveness of the optimization in the $\sqrt {\nu }$
regime. The reduced effectiveness of the optimization in the $\sqrt {\nu }$![]() and $\nu$
and $\nu$![]() regimes is due to the barely trapped particles and the particles near junctures of different types of wells.
regimes is due to the barely trapped particles and the particles near junctures of different types of wells.

Figure 13. Particle and energy fluxes as a function of $\nu _{i*}/\rho _{i*}$![]() for generic large aspect ratio stellarators with mirror ratios close to unity (green line) and near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity (red line).
for generic large aspect ratio stellarators with mirror ratios close to unity (green line) and near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity (red line).
9. Conclusion
There are four results in this article that are worth emphasizing. The first one is the set of orbit-averaged equations for neoclassical transport at low collisionality in large aspect ratio stellarators with mirror ratios close to unity derived in § 5. It consists of a kinetic equation for trapped particles, given in (5.25), and the corresponding boundary conditions to be imposed around junctures of different types of wells (see (5.33)) and at the trapped–passing boundary (see (5.34)). The trapped-particle distribution function obtained from these equations can then be integrated to give the particle and energy fluxes (see (5.48) and (5.50)). To our knowledge, this is the most detailed derivation of a model for large aspect ratio stellarators with mirror ratios close to unity in the limit $\nu _{i*} \sim \rho _{i*}$![]() , and in conjunction with the model described in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) and Calvo et al. (Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018) for near-omnigeneous stellarators, is the only self-consistent local model for stellarator neoclassical transport at low collisionality that we are aware of. The set of equations has been implemented in KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra, d'Herbemont, Smith, Carralero and Estrada2021), and it produces fluxes close to those calculated by DKES but with much less computational effort. The fact that the model matches DKES neoclassical fluxes is unsurprising, as we have shown in Appendix G that the model and DKES kinetic equations are the same to lowest order in the inverse aspect ratio. Interestingly, the derivation in Appendix G also shows that there is an $O(\sqrt {\epsilon })$
, and in conjunction with the model described in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) and Calvo et al. (Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018) for near-omnigeneous stellarators, is the only self-consistent local model for stellarator neoclassical transport at low collisionality that we are aware of. The set of equations has been implemented in KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra, d'Herbemont, Smith, Carralero and Estrada2021), and it produces fluxes close to those calculated by DKES but with much less computational effort. The fact that the model matches DKES neoclassical fluxes is unsurprising, as we have shown in Appendix G that the model and DKES kinetic equations are the same to lowest order in the inverse aspect ratio. Interestingly, the derivation in Appendix G also shows that there is an $O(\sqrt {\epsilon })$![]() difference between our model and DKES equations, and DKES is not correct to that order. Thus, when the results from the equations in this paper differ from those of DKES, one cannot assume that DKES is correct by default. More theoretical and numerical work on these higher-order corrections to the aspect ratio expansion is needed as $\sqrt {\epsilon }$
difference between our model and DKES equations, and DKES is not correct to that order. Thus, when the results from the equations in this paper differ from those of DKES, one cannot assume that DKES is correct by default. More theoretical and numerical work on these higher-order corrections to the aspect ratio expansion is needed as $\sqrt {\epsilon }$![]() is not very small.
is not very small.
The second interesting result in this article is the limit $\nu _{i*} \ll \rho _{i*}$![]() for generic large aspect ratio stellarators with mirror ratios close to unity, described in § 7. We have been able to show that there is no $\sqrt {\nu }$
for generic large aspect ratio stellarators with mirror ratios close to unity, described in § 7. We have been able to show that there is no $\sqrt {\nu }$![]() regime when this type of stellarator is not close to omnigeneity. Instead, generic large aspect ratio stellarators with mirror ratios close to unity enter the $\nu$
regime when this type of stellarator is not close to omnigeneity. Instead, generic large aspect ratio stellarators with mirror ratios close to unity enter the $\nu$![]() regime directly for $\nu _{i*} \lesssim \rho _{i*}$
regime directly for $\nu _{i*} \lesssim \rho _{i*}$![]() . We have also examined the $\nu$
. We have also examined the $\nu$![]() regime in great detail, explaining how the distribution function behaves in this limit. The transitions from one type of well to another are a crucial aspect. While these transitions make the particle motion stochastic and diffuse particles in velocity space, there is no stochastic diffusion in real space and the neoclassical diffusion coefficient remains proportional to the collision frequency. We believe that transitions between different types of wells do not lead to stochastic real space diffusion independent of the collision frequency because ions in the regimes that we consider are confined by the electric field, and while transitions can cause jumps in the second adiabatic invariant $J$
regime in great detail, explaining how the distribution function behaves in this limit. The transitions from one type of well to another are a crucial aspect. While these transitions make the particle motion stochastic and diffuse particles in velocity space, there is no stochastic diffusion in real space and the neoclassical diffusion coefficient remains proportional to the collision frequency. We believe that transitions between different types of wells do not lead to stochastic real space diffusion independent of the collision frequency because ions in the regimes that we consider are confined by the electric field, and while transitions can cause jumps in the second adiabatic invariant $J$![]() , they do not change the total energy of the particle. When the total energy is conserved, particles cannot move long distances ($\gg \epsilon a$
, they do not change the total energy of the particle. When the total energy is conserved, particles cannot move long distances ($\gg \epsilon a$![]() ) radially because they cannot overcome the barrier set by the electric potential, that is, particles remain within a distance of order $\epsilon a$
) radially because they cannot overcome the barrier set by the electric potential, that is, particles remain within a distance of order $\epsilon a$![]() of the flux surface that they started at without collisions. Collisions are needed to break conservation of total energy for each particle. While collisions conserve energy overall, in each collision, individual trapped particles can gain or lose energy. In our calculation, they mostly exchange energy with a large population of passing particles. We should add that, even though transitions between different types of wells do not make the neoclassical diffusion independent of the collision frequency, they do enhance neoclassical diffusion, as we explain below (7.28).
of the flux surface that they started at without collisions. Collisions are needed to break conservation of total energy for each particle. While collisions conserve energy overall, in each collision, individual trapped particles can gain or lose energy. In our calculation, they mostly exchange energy with a large population of passing particles. We should add that, even though transitions between different types of wells do not make the neoclassical diffusion independent of the collision frequency, they do enhance neoclassical diffusion, as we explain below (7.28).
Part of the outcome of the $\nu$![]() regime calculation is the explicit formula for the fluxes in the $\nu$
regime calculation is the explicit formula for the fluxes in the $\nu$![]() regime, given in (7.28) and (7.29). With these formulas, the fluxes can be calculated from the magnetic field of the stellarator without solving a kinetic equation. These explicit formulas might be useful for optimization routines if they can be evaluated fast. We believe that this is possible using techniques similar to those developed to perform bounce averages for KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra and García-Regaña2020).
regime, given in (7.28) and (7.29). With these formulas, the fluxes can be calculated from the magnetic field of the stellarator without solving a kinetic equation. These explicit formulas might be useful for optimization routines if they can be evaluated fast. We believe that this is possible using techniques similar to those developed to perform bounce averages for KNOSOS (Velasco et al. Reference Velasco, Calvo, Parra and García-Regaña2020).
The third result that we want to emphasize is that large aspect ratio stellarators with large mirror ratios are close to omnigeneous and can be treated using the formulation developed by Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). These stellarators experience a $\sqrt {\nu }$![]() regime for $\epsilon |\ln \epsilon | \ll \nu _{i*}/\rho _{i*} \ll 1/\epsilon$
regime for $\epsilon |\ln \epsilon | \ll \nu _{i*}/\rho _{i*} \ll 1/\epsilon$![]() . The neoclassical fluxes in large aspect ratio stellarators with large mirror ratios are significantly larger than the ones that one would obtain in an equivalent large aspect ratio stellarator with mirror ratio close to unity.
. The neoclassical fluxes in large aspect ratio stellarators with large mirror ratios are significantly larger than the ones that one would obtain in an equivalent large aspect ratio stellarator with mirror ratio close to unity.
Finally, the fourth result of note is the limit of near omnigeneity for large aspect ratio stellarators with mirror ratios close to unity. When we consider this type of stellarator, we find the $\sqrt {\nu }$![]() regime for a range of collisionalities that depends on the deviation from omnigeneity $\delta$
regime for a range of collisionalities that depends on the deviation from omnigeneity $\delta$![]() : $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$
: $\delta ^{2} |\ln \delta | \ll \nu _{i*}/\rho _{i*} \ll 1$![]() . This interval of validity disappears when $\delta \sim 1$
. This interval of validity disappears when $\delta \sim 1$![]() , explaining why we could not find a $\sqrt {\nu }$
, explaining why we could not find a $\sqrt {\nu }$![]() regime in generic large aspect ratio stellarators with mirror ratios close to unity. The derivation for near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity gives another interesting result, namely, optimization is less effective for $\nu _{i*} \ll \rho _{i*}$
regime in generic large aspect ratio stellarators with mirror ratios close to unity. The derivation for near-omnigeneous large aspect ratio stellarators with mirror ratios close to unity gives another interesting result, namely, optimization is less effective for $\nu _{i*} \ll \rho _{i*}$![]() , and it is worse in the $\nu$
, and it is worse in the $\nu$![]() regime, where the fluxes are reduced only by a factor of $\delta$
regime, where the fluxes are reduced only by a factor of $\delta$![]() instead of by a factor of $\delta ^{2}$
instead of by a factor of $\delta ^{2}$![]() . For this reason, it is probably worth considering the use of the $\nu$
. For this reason, it is probably worth considering the use of the $\nu$![]() regime fluxes in (7.28) and (7.29) as optimization targets. If one can reduce effectively the fluxes in the regime that is less responsive to optimization, the fluxes in the other regimes will likely reduce even more. In particular, we expect that the optimization of the fluxes in (7.28) and (7.29) will target problematic particles at the trapped–passing boundary and in regions where there are transitions between different types of wells.
regime fluxes in (7.28) and (7.29) as optimization targets. If one can reduce effectively the fluxes in the regime that is less responsive to optimization, the fluxes in the other regimes will likely reduce even more. In particular, we expect that the optimization of the fluxes in (7.28) and (7.29) will target problematic particles at the trapped–passing boundary and in regions where there are transitions between different types of wells.
Acknowledgements
The authors would like to thank X. Liu, P.J. Catto and the two anonymous referees for their suggestions.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the U.S. Department of Energy under contract number DE-AC02-09CH11466. The United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. This research was supported in part by Grant PGC2018-095307-B-I00, Ministerio de Ciencia, Innovación y Universidades, Spain.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Discontinuities in the derivatives of the distribution function at junctures of different types of wells
In this appendix, we show how to obtain (2.36) by imposing, in the example juncture of figure 1, that the collisional flux of particles out of wells $I$![]() and $II$
and $II$![]() enters well $III$
enters well $III$![]() .
.
For trapped particles, the collision operator in (2.15) can be written as $C_{ii} [ g_{i, W}, \bar {f}_i^{(0)}] = - |v_\| | ( \partial _\mathcal {E} F_\mathcal {E} [ g_{i, W}, \bar {f}_i^{(0)}] + \partial _\mu F_\mu [ g_{i, W}, \bar {f}_i^{(0)}] )$![]() , where
, where
is the phase-space particle flux in the $\mathcal {E}$![]() direction and
direction and
is the phase-space particle flux in the $\mu$![]() direction. We need the particle flux perpendicular to the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
direction. We need the particle flux perpendicular to the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() . To obtain this flux, we use coordinates in which the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
. To obtain this flux, we use coordinates in which the boundary $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() becomes trivial: instead of using $r$
becomes trivial: instead of using $r$![]() , $\alpha$
, $\alpha$![]() , $\mathcal {E}$
, $\mathcal {E}$![]() , $\mu$
, $\mu$![]() and $\varphi$
and $\varphi$![]() , we replace the variable $\mathcal {E}$
, we replace the variable $\mathcal {E}$![]() by $\Delta \mathcal {E} := \mathcal {E} - \mathcal {E}_c (r, \alpha, \mu, t)$
by $\Delta \mathcal {E} := \mathcal {E} - \mathcal {E}_c (r, \alpha, \mu, t)$![]() such that $\Delta \mathcal {E} = 0$
such that $\Delta \mathcal {E} = 0$![]() gives the desired boundary. With these new variables, the collision operator in (2.15) becomes
gives the desired boundary. With these new variables, the collision operator in (2.15) becomes

where we have used the fact that $\partial _\mu \Delta \mathcal {E} = - \partial _\mu \mathcal {E}_c$![]() satisfies $\partial _{\Delta \mathcal {E}} ( \partial _\mu \Delta \mathcal {E} ) = 0$
satisfies $\partial _{\Delta \mathcal {E}} ( \partial _\mu \Delta \mathcal {E} ) = 0$![]() . Equation (A3) indicates that the flux of particles across the boundary $\Delta \mathcal {E} = 0$
. Equation (A3) indicates that the flux of particles across the boundary $\Delta \mathcal {E} = 0$![]() is given by $F_\mathcal {E} - \partial _\mu \mathcal {E}_c \, F_\mu$
is given by $F_\mathcal {E} - \partial _\mu \mathcal {E}_c \, F_\mu$![]() . Integrating this flux over the gyrophase $\varphi$
. Integrating this flux over the gyrophase $\varphi$![]() and along trapped orbits, we find that the phase-space flux across the boundary $\mathcal {E} = \mathcal {E}_c(r, \alpha, \mu, t)$
and along trapped orbits, we find that the phase-space flux across the boundary $\mathcal {E} = \mathcal {E}_c(r, \alpha, \mu, t)$![]() can finally be written as
can finally be written as

Using the definition of the transit average in (2.28), the balance between the three collisional fluxes in and out of wells $I$![]() , $II$
, $II$![]() and $III$
and $III$![]() in figure 1 is
in figure 1 is

This long expression can be simplified due to the continuity of $g_{i,W}$![]() and $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$
and $\partial _\mu \mathcal {E}_c \, \partial _\mathcal {E} g_{i,W} + \partial _\mu g_{i,W}$![]() across $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$
across $\mathcal {E} = \mathcal {E}_c (r, \alpha, \mu, t)$![]() . The continuity of $g_{i, W}$
. The continuity of $g_{i, W}$![]() implies that $\tau _I \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, I} + \tau _{II} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, II} = \tau _{III} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, III}$
implies that $\tau _I \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, I} + \tau _{II} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, II} = \tau _{III} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, III}$![]() and that $\tau _I \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, I} + \tau _{II} \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, II} = \tau _{III} \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, III}$
and that $\tau _I \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, I} + \tau _{II} \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, II} = \tau _{III} \langle L_p [ \bar {f}_i^{(0)} ] \rangle _{\tau, III}$![]() for $p = \mathcal {E}, \mu$
for $p = \mathcal {E}, \mu$![]() and $q = \mathcal {E}, \mu$
and $q = \mathcal {E}, \mu$![]() . Using these results and dividing by $-2{\rm \pi} \gamma _{ii}$
. Using these results and dividing by $-2{\rm \pi} \gamma _{ii}$![]() , expression (A5) simplifies to
, expression (A5) simplifies to

Using the continuity of the combination of $\partial _\mu \mathcal {E}_c\, \partial _\mathcal {E} g_{i, W} + \partial _\mu g_{i, W}$![]() , we can write $\partial _\mu g_{i,I} - \partial _\mu g_{i, III} = - \partial _\mu \mathcal {E}_c\, ( \partial _\mathcal {E} g_{i,I} - \partial _\mathcal {E} g_{i, III} )$
, we can write $\partial _\mu g_{i,I} - \partial _\mu g_{i, III} = - \partial _\mu \mathcal {E}_c\, ( \partial _\mathcal {E} g_{i,I} - \partial _\mathcal {E} g_{i, III} )$![]() and $\partial _\mu g_{i,II} - \partial _\mu g_{i, III} = - \partial _\mu \mathcal {E}_c\, ( \partial _\mathcal {E} g_{i,II} - \partial _\mathcal {E} g_{i, III} )$
and $\partial _\mu g_{i,II} - \partial _\mu g_{i, III} = - \partial _\mu \mathcal {E}_c\, ( \partial _\mathcal {E} g_{i,II} - \partial _\mathcal {E} g_{i, III} )$![]() . With these results, and employing the fact that $H_{\mathcal {E} \mu } = H_{\mu \mathcal {E}}$
. With these results, and employing the fact that $H_{\mathcal {E} \mu } = H_{\mu \mathcal {E}}$![]() , expression (A6) becomes
, expression (A6) becomes

Using the identities $\tau _I \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, I} + \tau _{II} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, II} = \tau _{III} \langle H_{pq} [ \bar {f}_i^{(0)} ] \rangle _{\tau, III}$![]() again, we obtain the compact expression in (2.36).
again, we obtain the compact expression in (2.36).
Appendix B. Conditions on the flux surface shape imposed by the MHD equilibrium equations
In this appendix, we give the constraints that $\boldsymbol {x}_1(r, \alpha, l)$![]() must satisfy. In addition to (3.10), $\boldsymbol {x}_1$
must satisfy. In addition to (3.10), $\boldsymbol {x}_1$![]() must satisfy the first-order version of (3.3),
must satisfy the first-order version of (3.3),
and a solvability constraint of the MHD force balance equations that we proceed to obtain. The second-order terms in the $\epsilon$![]() expansion of (3.5) and (3.6) are given by
expansion of (3.5) and (3.6) are given by

and

To eliminate $B_2$![]() and $\boldsymbol {x}_2$
and $\boldsymbol {x}_2$![]() from these equations, we differentiate (B2) with respect to $\alpha$
from these equations, we differentiate (B2) with respect to $\alpha$![]() and (B3) with respect to $r$
and (B3) with respect to $r$![]() , and we subtract these two derivatives from each other to obtain
, and we subtract these two derivatives from each other to obtain

where we have used (3.14) to write $B_1$![]() in terms of $\boldsymbol {x}_1$
in terms of $\boldsymbol {x}_1$![]() and (B1) to obtain $\hat {\boldsymbol {b}}_0 \boldsymbol {\cdot } \partial ^{2}_{lr} \boldsymbol {x}_1 = 0$
and (B1) to obtain $\hat {\boldsymbol {b}}_0 \boldsymbol {\cdot } \partial ^{2}_{lr} \boldsymbol {x}_1 = 0$![]() and $\hat {\boldsymbol {b}}_0 \boldsymbol {\cdot } \partial ^{2}_{l\alpha } \boldsymbol {x}_1 = 0$
and $\hat {\boldsymbol {b}}_0 \boldsymbol {\cdot } \partial ^{2}_{l\alpha } \boldsymbol {x}_1 = 0$![]() . Note that, if $\boldsymbol {x}_1$
. Note that, if $\boldsymbol {x}_1$![]() is a solution to (3.10), (B1) and (B4), the function $\boldsymbol {x}_1 (r, \alpha, l) + \lambda (r, \alpha ) \hat {\boldsymbol {b}}_0 (l)$
is a solution to (3.10), (B1) and (B4), the function $\boldsymbol {x}_1 (r, \alpha, l) + \lambda (r, \alpha ) \hat {\boldsymbol {b}}_0 (l)$![]() is also a solution. Here, $\lambda (r, \alpha )$
is also a solution. Here, $\lambda (r, \alpha )$![]() can be any function of r and $\alpha$
can be any function of r and $\alpha$![]() . This set of equivalent solutions arises from the fact that one is free to choose where $l$
. This set of equivalent solutions arises from the fact that one is free to choose where $l$![]() vanishes.
vanishes.
Appendix C. Lowest-order ion distribution function in large aspect ratio stellarators with mirror ratios close to unity
In this appendix, we first solve for the lowest-order trapped-particle distribution function $g_{i, 0, W}$![]() in Appendix C.1 and we then obtain the lowest-order passing-particle distribution function $h_{i,0}$
in Appendix C.1 and we then obtain the lowest-order passing-particle distribution function $h_{i,0}$![]() in Appendix C.2. We finish with a discussion of the distribution function in the barely-passing-particle region in Appendix C.3.
in Appendix C.2. We finish with a discussion of the distribution function in the barely-passing-particle region in Appendix C.3.
C.1. Lowest-order trapped-particle distribution function
We proceed to rewrite (2.27) using the coordinates $\bar {v}$![]() and $J$
and $J$![]() . We neglect the time derivatives and the source $S_i$
. We neglect the time derivatives and the source $S_i$![]() employing the estimates in (5.1). Thus, (2.27) becomes
employing the estimates in (5.1). Thus, (2.27) becomes

where the derivatives of $g_{i,W}$![]() with respect to $r$
with respect to $r$![]() and $\alpha$
and $\alpha$![]() are performed holding $\bar {v}$
are performed holding $\bar {v}$![]() and $J$
and $J$![]() fixed, whereas the derivatives of $\bar {v}$
fixed, whereas the derivatives of $\bar {v}$![]() and $J_W$
and $J_W$![]() with respect to the same variables are performed holding $\mathcal {E}$
with respect to the same variables are performed holding $\mathcal {E}$![]() and $\mu$
and $\mu$![]() constant. Employing (5.17) and (5.18), to lowest order in $\epsilon$
constant. Employing (5.17) and (5.18), to lowest order in $\epsilon$![]() , (C1) can be rewritten as
, (C1) can be rewritten as
The terms proportional to $\partial _{\bar {v}} g_{i, 0, W}$![]() and $\partial _r g_{i, 0, W}$
and $\partial _r g_{i, 0, W}$![]() have been neglected because we assume that the derivatives of $g_{i, 0, W}$
have been neglected because we assume that the derivatives of $g_{i, 0, W}$![]() with respect to $\bar {v}$
with respect to $\bar {v}$![]() and $r$
and $r$![]() satisfy $\partial _{\bar {v}} \ln g_{i, 0, W} \sim v_{ti}^{-1}$
satisfy $\partial _{\bar {v}} \ln g_{i, 0, W} \sim v_{ti}^{-1}$![]() and $\partial _r \ln g_{i, 0, W} \sim a^{-1}$
and $\partial _r \ln g_{i, 0, W} \sim a^{-1}$![]() . Recall that the estimate $\partial _r \ln g_{i, 0, W} \sim a^{-1} \ll (\epsilon a)^{-1}$
. Recall that the estimate $\partial _r \ln g_{i, 0, W} \sim a^{-1} \ll (\epsilon a)^{-1}$![]() is valid because the derivative is performed holding $\bar {v}$
is valid because the derivative is performed holding $\bar {v}$![]() and $J$
and $J$![]() constant.
constant.
The fact that the derivative of $g_{i, 0, W}$![]() with respect to $J$
with respect to $J$![]() is larger than its derivative with respect to $\bar {v}$
is larger than its derivative with respect to $\bar {v}$![]() (compare (4.18) and (4.19)) simplifies significantly the collision operator in (C2) because the term with two derivatives with respect to $J$
(compare (4.18) and (4.19)) simplifies significantly the collision operator in (C2) because the term with two derivatives with respect to $J$![]() becomes the largest,
becomes the largest,

Here, the Rosenbluth potential $H[h_{i,0}]$![]() is evaluated using only $h_{i,0}$
is evaluated using only $h_{i,0}$![]() because the contribution to the integral from $g_{i, 0, W}$
because the contribution to the integral from $g_{i, 0, W}$![]() is smaller by $\sqrt {\epsilon }$
is smaller by $\sqrt {\epsilon }$![]() due to the smallness of the region of velocity space where $g_{i, 0, W}$
due to the smallness of the region of velocity space where $g_{i, 0, W}$![]() is defined. Since $\boldsymbol {\nabla }_v J_W \simeq \tau _W v_\| \hat {\boldsymbol {b}}$
is defined. Since $\boldsymbol {\nabla }_v J_W \simeq \tau _W v_\| \hat {\boldsymbol {b}}$![]() for trapped particles (see (4.12)), we need the component $\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [h_{i,0}] \boldsymbol {\cdot } \hat {\boldsymbol {b}}$
for trapped particles (see (4.12)), we need the component $\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [h_{i,0}] \boldsymbol {\cdot } \hat {\boldsymbol {b}}$![]() of $\boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [h_{i,0}]$
of $\boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [h_{i,0}]$![]() for the lowest-order version of the collision operator. We find
for the lowest-order version of the collision operator. We find
Note that, for trapped particles, the parallel component of the velocity is small in $\epsilon$![]() , giving $\boldsymbol {v} \simeq \bar {v}\, \hat {\boldsymbol {e}}_\perp (\boldsymbol {x}, \varphi )$
, giving $\boldsymbol {v} \simeq \bar {v}\, \hat {\boldsymbol {e}}_\perp (\boldsymbol {x}, \varphi )$![]() , where $\hat {\boldsymbol {e}}_\perp$
, where $\hat {\boldsymbol {e}}_\perp$![]() is defined in (2.3). Using this result and writing $\boldsymbol {v}^{\prime } \simeq \bar {v}^{\prime } \xi ^{\prime } \hat {\boldsymbol {b}} + \bar {v}^{\prime } \sqrt {1 - \xi ^{\prime 2} } ( \cos \varphi ^{\prime }\, \hat {\boldsymbol {e}}_\perp + \sin \varphi ^{\prime }\, \hat {\boldsymbol {b}} \times \hat {\boldsymbol {e}}_\perp )$
is defined in (2.3). Using this result and writing $\boldsymbol {v}^{\prime } \simeq \bar {v}^{\prime } \xi ^{\prime } \hat {\boldsymbol {b}} + \bar {v}^{\prime } \sqrt {1 - \xi ^{\prime 2} } ( \cos \varphi ^{\prime }\, \hat {\boldsymbol {e}}_\perp + \sin \varphi ^{\prime }\, \hat {\boldsymbol {b}} \times \hat {\boldsymbol {e}}_\perp )$![]() , (C4) can be written as
, (C4) can be written as
where we have defined the new functional

This result demonstrates that $\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H [h_{i,0}] \boldsymbol {\cdot } \hat {\boldsymbol {b}}$![]() depends only on $\bar {v}$
depends only on $\bar {v}$![]() to lowest order in $\epsilon$
to lowest order in $\epsilon$![]() . With all these results, (C3) becomes
. With all these results, (C3) becomes
Transit averaging equation (C7), we obtain
At the junctures of several wells, we need to impose continuity of $g_{i, 0, W}$![]() and use condition (2.36) to relate the discontinuous derivatives on different sides of the well. We proceed to rewrite (2.36) in the new coordinates $\bar {v}$
and use condition (2.36) to relate the discontinuous derivatives on different sides of the well. We proceed to rewrite (2.36) in the new coordinates $\bar {v}$![]() and $J$
and $J$![]() . The derivative of $g_{i, 0, W}$
. The derivative of $g_{i, 0, W}$![]() with respect to $\mathcal {E}$
with respect to $\mathcal {E}$![]() is $\partial _\mathcal {E} g_{i, 0, W} = \partial _\mathcal {E} \bar {v}\, \partial _{\bar {v}} g_{i, 0, W} + \partial _\mathcal {E} J_W\, \partial _J g_{i, 0, W}$
is $\partial _\mathcal {E} g_{i, 0, W} = \partial _\mathcal {E} \bar {v}\, \partial _{\bar {v}} g_{i, 0, W} + \partial _\mathcal {E} J_W\, \partial _J g_{i, 0, W}$![]() . Noting that $\partial _\mathcal {E} \bar {v} = 1/\bar {v} \sim 1/v_{ti}$
. Noting that $\partial _\mathcal {E} \bar {v} = 1/\bar {v} \sim 1/v_{ti}$![]() , $\partial _\mathcal {E} J_W = \tau _W \simeq R/\sqrt {\epsilon } v_{ti}$
, $\partial _\mathcal {E} J_W = \tau _W \simeq R/\sqrt {\epsilon } v_{ti}$![]() , $\partial _{\bar {v}} g_{i, 0, W} \sim g_{i, 0, W}/v_{ti}$
, $\partial _{\bar {v}} g_{i, 0, W} \sim g_{i, 0, W}/v_{ti}$![]() and $\partial _J g_{i, 0, W} \sim g_{i, 0, W}/\sqrt {\epsilon } v_{ti} R$
and $\partial _J g_{i, 0, W} \sim g_{i, 0, W}/\sqrt {\epsilon } v_{ti} R$![]() , the derivative with respect to $\mathcal {E}$
, the derivative with respect to $\mathcal {E}$![]() simplifies to $\partial _\mathcal {E} g_{i, 0, W} \simeq \tau _W\, \partial _J g_{i, 0, W}$
simplifies to $\partial _\mathcal {E} g_{i, 0, W} \simeq \tau _W\, \partial _J g_{i, 0, W}$![]() . Equation (2.36) can be simplified further by noting that $\mathcal {E}_c (r, \alpha, \mu, t)$
. Equation (2.36) can be simplified further by noting that $\mathcal {E}_c (r, \alpha, \mu, t)$![]() is given by (5.29) and hence $\partial _\mu \mathcal {E}_c \simeq B_{lM}$
is given by (5.29) and hence $\partial _\mu \mathcal {E}_c \simeq B_{lM}$![]() . With these results, (2.36) becomes
. With these results, (2.36) becomes

Note that, $H_{\mathcal {E} \mathcal {E}} = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mathcal {E} = \boldsymbol {v} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {v}$![]() , $H_{\mathcal {E} \mu } = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = \boldsymbol {v} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {v}_\perp /B$
, $H_{\mathcal {E} \mu } = \boldsymbol {\nabla }_v \mathcal {E} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = \boldsymbol {v} \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {v}_\perp /B$![]() and $H_{\mu \mu } = \boldsymbol {\nabla }_v \mu \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = \boldsymbol {v}_\perp \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {v}_\perp /B^{2}$
and $H_{\mu \mu } = \boldsymbol {\nabla }_v \mu \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {\nabla }_v \mu = \boldsymbol {v}_\perp \boldsymbol {\cdot } \boldsymbol {\nabla }_v \boldsymbol {\nabla }_v H \boldsymbol {\cdot } \boldsymbol {v}_\perp /B^{2}$![]() . Thus,
. Thus,

Since $1 - B_{lM}/B \sim \epsilon$![]() but $v_\| \sim \sqrt {\epsilon } v_{ti}$
but $v_\| \sim \sqrt {\epsilon } v_{ti}$![]() , $H_{\mathcal {E} \mathcal {E}} [ h_{i, 0} ] - 2 B_{lM} H_{\mathcal {E} \mu }[ h_{i, 0} ] + B_{lM}^{2} H_{\mu \mu }[ h_{i, 0} ]$
, $H_{\mathcal {E} \mathcal {E}} [ h_{i, 0} ] - 2 B_{lM} H_{\mathcal {E} \mu }[ h_{i, 0} ] + B_{lM}^{2} H_{\mu \mu }[ h_{i, 0} ]$![]() = $v_\|^{2} H_{bb} [h_{i, 0}] ( 1 + O(\epsilon ^{1/2}) )$
= $v_\|^{2} H_{bb} [h_{i, 0}] ( 1 + O(\epsilon ^{1/2}) )$![]() . Then, by dividing (C9) by $H_{bb} [h_{i, 0}] (\bar {v})$
. Then, by dividing (C9) by $H_{bb} [h_{i, 0}] (\bar {v})$![]() , we find
, we find
Equation (C11) could have also been obtained by following a procedure similar to the one in Appendix A. Note that (C8) implies that the phase-space particle flux across the boundary $J = J_{c, W} (r, \alpha, \bar {v}, t)$![]() is $- 2{\rm \pi} \gamma _{ii} H_{bb} [h_{i,0}] (\bar {v})\, J_{c, W} \tau _W \partial _J g_{i, 0, W}$
is $- 2{\rm \pi} \gamma _{ii} H_{bb} [h_{i,0}] (\bar {v})\, J_{c, W} \tau _W \partial _J g_{i, 0, W}$![]() .
.
Using (C2) and (C8), we find that that the equation for $g_{i, 0, W}$![]() is
is
We need to impose the continuity condition (2.24) that implies that $g_{i, 0, W}$![]() for $J \rightarrow \infty$
for $J \rightarrow \infty$![]() must be equal to $h_{i,0}$
must be equal to $h_{i,0}$![]() at the trapped–passing boundary, where $\xi \sim \sqrt {\epsilon } \ll 1$
at the trapped–passing boundary, where $\xi \sim \sqrt {\epsilon } \ll 1$![]() . Then,
. Then,
Note that we have approximated the trapped–passing boundary by $\xi = 0$![]() . We discuss this approximation in detail in Appendix C.3.
. We discuss this approximation in detail in Appendix C.3.
To find the solution to (C12), we first need to show that
that is, there is no collisional flux from the trapped region into the passing region. Property (C14) can be shown to be true following the same procedure that we employed to find property (5.36). With property (C14), we can find the solution $g_{i, 0, W}$![]() given in (5.4). We multiply (C12) by $g_{i, 0, W}$
given in (5.4). We multiply (C12) by $g_{i, 0, W}$![]() to write
to write

We integrate this equation over $J$![]() and $\alpha$
and $\alpha$![]() and we sum over $W$
and we sum over $W$![]() . We use (C11) at the junctures of different wells, and we employ property (C14) to show that a boundary term at $J \rightarrow \infty$
. We use (C11) at the junctures of different wells, and we employ property (C14) to show that a boundary term at $J \rightarrow \infty$![]() vanishes. After all these calculations, we find
vanishes. After all these calculations, we find

This equation implies that $g_{i, 0, W}$![]() is independent of $J$
is independent of $J$![]() . Using this result in (C12), we also find that $g_{i, 0, W}$
. Using this result in (C12), we also find that $g_{i, 0, W}$![]() is independent of $\alpha$
is independent of $\alpha$![]() . We obtain solution (5.4) by applying the boundary condition (C13).
. We obtain solution (5.4) by applying the boundary condition (C13).
C.2. Lowest-order passing-particle distribution function
To lowest order in $\epsilon$![]() , according to (5.1), we can neglect the time derivatives and the source in (2.30), finding
, according to (5.1), we can neglect the time derivatives and the source in (2.30), finding
For most passing particles, $v_\| \simeq \sigma \sqrt {2( \mathcal {E} - \mu B_0 - Z_ie\phi _0 (r, t)/m_i)}$![]() is very close to being independent of $\alpha$
is very close to being independent of $\alpha$![]() and $l$
and $l$![]() . Thus, for most values of $\xi$
. Thus, for most values of $\xi$![]() , (C17) becomes
, (C17) becomes
We need to impose boundary condition (2.25) that requires that the derivatives of $g_{i,W}$![]() and $h_i$
and $h_i$![]() with respect to velocity are continuous across the trapped–passing boundary. The continuity of the derivatives imposes that the collisional flux across the trapped–passing boundary be continuous. This collisional flux is dominated by pitch-angle scattering events, and the pitch-angle scattering flux is controlled by the derivative of $g_{i,W}$
with respect to velocity are continuous across the trapped–passing boundary. The continuity of the derivatives imposes that the collisional flux across the trapped–passing boundary be continuous. This collisional flux is dominated by pitch-angle scattering events, and the pitch-angle scattering flux is controlled by the derivative of $g_{i,W}$![]() with respect to $J$
with respect to $J$![]() in the trapped region of velocity space. Since we have shown that $\partial _J g_{i, 0, W} = 0$
in the trapped region of velocity space. Since we have shown that $\partial _J g_{i, 0, W} = 0$![]() , only the derivatives of $g_{i, 1, W}$
, only the derivatives of $g_{i, 1, W}$![]() play a role in the collisional flux across the trapped–passing boundary. Due to the smallness of $|v_\| | \sim \sqrt {\epsilon } v_{ti}$
play a role in the collisional flux across the trapped–passing boundary. Due to the smallness of $|v_\| | \sim \sqrt {\epsilon } v_{ti}$![]() in the trapped region, $\boldsymbol {\nabla }_v g_{i, 1, W} \sim \epsilon ^{-1/2} g_{i, 1, W}/v_{ti} \sim \epsilon ^{1/2} h_{i,0}/v_{ti}$
in the trapped region, $\boldsymbol {\nabla }_v g_{i, 1, W} \sim \epsilon ^{-1/2} g_{i, 1, W}/v_{ti} \sim \epsilon ^{1/2} h_{i,0}/v_{ti}$![]() , where we have used $g_{i, 1, W} \sim \epsilon h_{i,0}$
, where we have used $g_{i, 1, W} \sim \epsilon h_{i,0}$![]() . Hence, the collisional flux across the trapped–passing boundary is small in $\epsilon$
. Hence, the collisional flux across the trapped–passing boundary is small in $\epsilon$![]() because $\boldsymbol {\nabla }_v g_{i, 1, W}$
because $\boldsymbol {\nabla }_v g_{i, 1, W}$![]() is small in $\epsilon$
is small in $\epsilon$![]() . The lack of collisional flux across the trapped–passing boundary gives the boundary condition
. The lack of collisional flux across the trapped–passing boundary gives the boundary condition
for $h_{i,0}$![]() . A more rigorous derivation of this boundary condition can be found in Appendix C.3.
. A more rigorous derivation of this boundary condition can be found in Appendix C.3.
To obtain boundary condition (C19), the fact that there is no piece of $g_{i,W}$![]() of order $\epsilon ^{1/2} g_{i, 0, W}$
of order $\epsilon ^{1/2} g_{i, 0, W}$![]() is important. Using (4.5), (4.6) and (5.18), we find that the next-order corrections to (C12) are
is important. Using (4.5), (4.6) and (5.18), we find that the next-order corrections to (C12) are

To obtain this result, we have used the fact that $\langle C_{ii} [ g_{i, 0, W}, h_{i,0} ] \rangle _{\tau, W}$![]() is of order $\nu _{ii} g_{i, 0, W}$
is of order $\nu _{ii} g_{i, 0, W}$![]() instead of $\nu _{ii} g_{i, 0, W}/\epsilon$
instead of $\nu _{ii} g_{i, 0, W}/\epsilon$![]() because $g_{i, 0, W}$
because $g_{i, 0, W}$![]() only depends on $\bar {v}$
only depends on $\bar {v}$![]() . Thus, there is no correction to $g_{i, 0, W}$
. Thus, there is no correction to $g_{i, 0, W}$![]() of order $\epsilon ^{1/2} g_{i, 0, W}$
of order $\epsilon ^{1/2} g_{i, 0, W}$![]() , and we can use boundary condition (C19).
, and we can use boundary condition (C19).
The only possible solution to (C18) with condition (C19) is a stationary Maxwellian with density and temperature that are flux functions, as shown in (5.5).
C.3. Lowest-order barely-passing-particle distribution function
The coordinate $\xi$![]() is not a constant of the motion for barely passing particles with $|\xi | \sim \sqrt {\epsilon } \ll 1$
is not a constant of the motion for barely passing particles with $|\xi | \sim \sqrt {\epsilon } \ll 1$![]() . In this small region of velocity space, it is more convenient to use as a coordinate the value of $\xi$
. In this small region of velocity space, it is more convenient to use as a coordinate the value of $\xi$![]() at the location of the maximum of $U$
at the location of the maximum of $U$![]() ,
,

where $\phi _{U_M}$![]() is the value of the potential at the location where $U$
is the value of the potential at the location where $U$![]() is maximum, and $B_M(r)$
is maximum, and $B_M(r)$![]() is the maximum of $B$
is the maximum of $B$![]() on flux surface $r$
on flux surface $r$![]() .
.
Using $\bar {v}$![]() and $\bar {\xi }$
and $\bar {\xi }$![]() as coordinates, the parallel velocity can be written as
as coordinates, the parallel velocity can be written as

where $B_{1,M} (r)$![]() is the maximum value of $B_1$
is the maximum value of $B_1$![]() on flux surface $r$
on flux surface $r$![]() . According to this approximation, $v_\|$
. According to this approximation, $v_\|$![]() and hence $\xi$
and hence $\xi$![]() are constant for $|\bar {\xi }| \gg \sqrt {\epsilon }$
are constant for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() . Moreover, $\bar {\xi } \simeq \xi$
. Moreover, $\bar {\xi } \simeq \xi$![]() for $|\bar {\xi }| \gg \sqrt {\epsilon }$
for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() . Unfortunately, we need to consider $|\bar {\xi }| \sim \sqrt {\epsilon }$
. Unfortunately, we need to consider $|\bar {\xi }| \sim \sqrt {\epsilon }$![]() because it is in this region that we find the trapped–passing boundary: at the trapped–passing boundary, $\bar {\xi } = 0$
because it is in this region that we find the trapped–passing boundary: at the trapped–passing boundary, $\bar {\xi } = 0$![]() .
.
In the barely-passing-particle region $|\bar {\xi }| \sim \sqrt {\epsilon }$![]() , we can write the distribution function as
, we can write the distribution function as
where $h_i (r, \bar {v}, \bar {\xi }, t)$![]() is the function $h_i (r, \bar {v}, \xi, t)$
is the function $h_i (r, \bar {v}, \xi, t)$![]() but with $\xi$
but with $\xi$![]() replaced by $\bar {\xi }$
replaced by $\bar {\xi }$![]() , and $h_i(r, \bar {v}, \xi, t) \simeq h_{i, 0} (r, \bar {v}, \xi, t)$
, and $h_i(r, \bar {v}, \xi, t) \simeq h_{i, 0} (r, \bar {v}, \xi, t)$![]() is the passing particle distribution function discussed in Appendix C.2. The passing-particle distribution function $h_i(r, \bar {v}, \xi, t) \simeq h_{i, 0} (r, \bar {v}, \xi, t)$
is the passing particle distribution function discussed in Appendix C.2. The passing-particle distribution function $h_i(r, \bar {v}, \xi, t) \simeq h_{i, 0} (r, \bar {v}, \xi, t)$![]() is determined by (C18) and satisfies
is determined by (C18) and satisfies
for $|\xi | \sim \sqrt {\epsilon }$![]() , as we will see at the end of this appendix. The piece $\Delta h_{i, \mathrm {bp}} (r, \bar {v}, \bar {\lambda }, t)$
, as we will see at the end of this appendix. The piece $\Delta h_{i, \mathrm {bp}} (r, \bar {v}, \bar {\lambda }, t)$![]() is small in $\epsilon$
is small in $\epsilon$![]() and vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$
and vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() , leaving the solution $h_i (r, \bar {v}, \xi, t)$
, leaving the solution $h_i (r, \bar {v}, \xi, t)$![]() for freely passing particles with $|\xi | \sim 1$
for freely passing particles with $|\xi | \sim 1$![]() . We proceed to show that $\Delta h_{i, \mathrm {bp}}$
. We proceed to show that $\Delta h_{i, \mathrm {bp}}$![]() simply ensures that there is continuity in the collisional fluxes across the barely-passing-particle region.
simply ensures that there is continuity in the collisional fluxes across the barely-passing-particle region.
In Appendix C.1, we show that $\partial _J g_{i, 0, W} = 0$![]() . With this result, we can give a bound for the size of $\partial _{\bar {\xi }} \Delta h_{i,\mathrm {bp}}$
. With this result, we can give a bound for the size of $\partial _{\bar {\xi }} \Delta h_{i,\mathrm {bp}}$![]() . Using the continuity condition (2.24) to write
. Using the continuity condition (2.24) to write
we can deduce that
Applying this result to (2.25), where $\partial _\mathcal {E} = \partial _\mathcal {E} \bar {v} \, \partial _{\bar {v}} + \partial _\mathcal {E} J_W \, \partial _J$![]() for trapped particles and $\partial _\mathcal {E} = \partial _\mathcal {E} \bar {v} \, \partial _{\bar {v}} + \partial _\mathcal {E} \bar {\xi } \, \partial _{\bar {\xi }}$
for trapped particles and $\partial _\mathcal {E} = \partial _\mathcal {E} \bar {v} \, \partial _{\bar {v}} + \partial _\mathcal {E} \bar {\xi } \, \partial _{\bar {\xi }}$![]() for passing particles, we find
for passing particles, we find
Using $\partial _\mathcal {E} J_W = \tau _W$![]() , $\partial _\mathcal {E} \bar {\xi } = (1 - \bar {\xi }^{2})/\bar {v}^{2} \bar {\xi }$
, $\partial _\mathcal {E} \bar {\xi } = (1 - \bar {\xi }^{2})/\bar {v}^{2} \bar {\xi }$![]() and $\partial _J g_{i, 0, W} = 0$
and $\partial _J g_{i, 0, W} = 0$![]() , this condition becomes
, this condition becomes
Using $|\bar {\xi }| \sim \sqrt {\epsilon }$![]() , $\tau _W \sim \epsilon ^{-1/2} R/v_{ti}$
, $\tau _W \sim \epsilon ^{-1/2} R/v_{ti}$![]() , $\partial _J \sim \epsilon ^{-1/2}/v_{ti} R$
, $\partial _J \sim \epsilon ^{-1/2}/v_{ti} R$![]() and (C24), we find the estimate
and (C24), we find the estimate
To calculate $\Delta h_{i, \mathrm {bp}}$![]() , we need to integrate $\partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}} \sim \sqrt {\epsilon } h_{i,0}$
, we need to integrate $\partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}} \sim \sqrt {\epsilon } h_{i,0}$![]() over $\bar {\xi }$
over $\bar {\xi }$![]() . Since the region of interest is $|\bar {\xi }| \sim \sqrt {\epsilon }$
. Since the region of interest is $|\bar {\xi }| \sim \sqrt {\epsilon }$![]() , the integral is over an interval of $\bar {\xi }$
, the integral is over an interval of $\bar {\xi }$![]() of order $\sqrt {\epsilon }$
of order $\sqrt {\epsilon }$![]() , and hence $\Delta h_{i, \mathrm {bp}} \sim \sqrt {\epsilon }\, \partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}} \sim \epsilon h_{i,0}$
, and hence $\Delta h_{i, \mathrm {bp}} \sim \sqrt {\epsilon }\, \partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}} \sim \epsilon h_{i,0}$![]() , justifying the neglect of $\Delta h_{i, \mathrm {bp}}$
, justifying the neglect of $\Delta h_{i, \mathrm {bp}}$![]() in (C25) to obtain (C13). In Appendix D we will see that $\Delta h_{i, \mathrm {bp}} \sim \epsilon h_{i,0}$
in (C25) to obtain (C13). In Appendix D we will see that $\Delta h_{i, \mathrm {bp}} \sim \epsilon h_{i,0}$![]() is in fact only a bound as $\Delta h_{i,\mathrm {bp}}$
is in fact only a bound as $\Delta h_{i,\mathrm {bp}}$![]() is smaller than $\epsilon h_{i,0}$
is smaller than $\epsilon h_{i,0}$![]() .
.
We proceed to solve (C17) in the barely-passing-particle region. Using $B \simeq B_0$![]() and (C18), we find that (C17) becomes, to lowest order in $\epsilon$
and (C18), we find that (C17) becomes, to lowest order in $\epsilon$![]() ,
,
where we have neglected the contributions of the difference $\bar {\xi } - \xi$![]() and of $\Delta h_{i,\mathrm {bp}}$
and of $\Delta h_{i,\mathrm {bp}}$![]() to the Rosenbluth potentials because they are small in $\epsilon$
to the Rosenbluth potentials because they are small in $\epsilon$![]() . The derivatives of $\bar {\xi } - \xi$
. The derivatives of $\bar {\xi } - \xi$![]() and $\Delta h_{i, \mathrm {bp}}$
and $\Delta h_{i, \mathrm {bp}}$![]() with respect to $\bar {\xi }$
with respect to $\bar {\xi }$![]() in the barely-passing-particle region are large, $\partial _{\bar {\xi }} \ln ( \bar {\xi } - \xi ) \sim \partial _{\bar {\xi }} \ln \Delta h_{i, \mathrm {bp}} \sim \epsilon ^{-1/2}$
in the barely-passing-particle region are large, $\partial _{\bar {\xi }} \ln ( \bar {\xi } - \xi ) \sim \partial _{\bar {\xi }} \ln \Delta h_{i, \mathrm {bp}} \sim \epsilon ^{-1/2}$![]() . Thus, in the collision operator applied to $\bar {\xi } - \xi$
. Thus, in the collision operator applied to $\bar {\xi } - \xi$![]() and $\Delta h_{i,\mathrm {bp}}$
and $\Delta h_{i,\mathrm {bp}}$![]() , the term that contains two derivatives with respect to $\bar {\xi }$
, the term that contains two derivatives with respect to $\bar {\xi }$![]() dominates,
dominates,

Using $\boldsymbol {\nabla }_v \bar {\xi } \simeq (\xi / \bar {\xi }) \hat {\boldsymbol {b}}$![]() , $\partial _{\bar {\xi }} \xi \simeq \bar {\xi }/\xi$
, $\partial _{\bar {\xi }} \xi \simeq \bar {\xi }/\xi$![]() and (C5), and employing the fact that the derivative of $\partial _\xi h_i (r, \bar {v}, \xi, t)$
and (C5), and employing the fact that the derivative of $\partial _\xi h_i (r, \bar {v}, \xi, t)$![]() with respect to $\overline{\xi}$
with respect to $\overline{\xi}$![]() is small compared with the derivatives of $\bar {\xi } - \xi$
is small compared with the derivatives of $\bar {\xi } - \xi$![]() and $\Delta h_{i, \mathrm {bp}}$
and $\Delta h_{i, \mathrm {bp}}$![]() with respect to $\bar {\xi }$
with respect to $\bar {\xi }$![]() , the collision operator simplifies to
, the collision operator simplifies to

Employing this result, (C30) becomes
We solve for $\partial _{\bar {\xi }} \Delta h_{i,\mathrm {bp}}$![]() by realizing that $\partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}}$
by realizing that $\partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}}$![]() is small for $|\bar {\xi }| \gg \sqrt {\epsilon }$
is small for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() because $\Delta h_{i, \mathrm {bp}}$
because $\Delta h_{i, \mathrm {bp}}$![]() vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$
vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() , finding
, finding

where we have used the lowest-order version of expression (C22) for the parallel velocity. We can integrate once more to obtain $\Delta h_{i, \mathrm {bp}}$![]() ,
,

where we have used that $\Delta h_{i, \mathrm {bp}}$![]() vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$
vanishes for $|\bar {\xi }| \gg \sqrt {\epsilon }$![]() .
.
Substituting (C34) into (C28), we obtain

Since the derivatives of $h_{i,0}$![]() with respect to $\xi$
with respect to $\xi$![]() at $\xi = 0$
at $\xi = 0$![]() are small in $\epsilon$
are small in $\epsilon$![]() , they have to be set to zero to lowest order, giving condition (C19).
, they have to be set to zero to lowest order, giving condition (C19).
Appendix D. Barely passing particles
In this appendix, we show that the correction to the distribution function due to the barely passing particles, $\Delta h_{i, \mathrm {bp}}$![]() , is of order $\epsilon ^{2} f_{Mi}$
, is of order $\epsilon ^{2} f_{Mi}$![]() and hence several boundary conditions that we have used in this article are valid. To discuss the barely passing particles, we use the formalism developed in Appendix C.3. In Appendix C.3, we state that $\Delta h_{i, \mathrm {bp}}$
and hence several boundary conditions that we have used in this article are valid. To discuss the barely passing particles, we use the formalism developed in Appendix C.3. In Appendix C.3, we state that $\Delta h_{i, \mathrm {bp}}$![]() is at most of order $\epsilon h_{i,0}$
is at most of order $\epsilon h_{i,0}$![]() , but in reality it is smaller. In § 5.2 and Appendix F, we show that $\tau _W \, \partial _J g_{i, 1, W}$
, but in reality it is smaller. In § 5.2 and Appendix F, we show that $\tau _W \, \partial _J g_{i, 1, W}$![]() and $\tau _W \, \partial _J g_{i, 3/2, W}$
and $\tau _W \, \partial _J g_{i, 3/2, W}$![]() vanish for $J \rightarrow \infty$
vanish for $J \rightarrow \infty$![]() . These results mean that (C28) must be modified to give
. These results mean that (C28) must be modified to give
This equation gives the estimate
By integrating $\partial _{\bar {\xi }} \Delta h_{i, \mathrm {bp}}$![]() over the barely-passing-particle region, of width $\Delta \bar {\xi } \sim \sqrt {\epsilon }$
over the barely-passing-particle region, of width $\Delta \bar {\xi } \sim \sqrt {\epsilon }$![]() , we obtain the size that we announced at the start of this appendix,
, we obtain the size that we announced at the start of this appendix,
The small size of this contribution justifies neglecting $\Delta h_{i, \mathrm {bp}}$![]() in the continuity condition (C25) to obtain the boundary conditions (5.34) and (F8).
in the continuity condition (C25) to obtain the boundary conditions (5.34) and (F8).
Solutions (C34) and (C35) are valid in the barely-passing-particle region even at the high order that we are considering. Following the same procedure that led to (C36) but using (D1) instead of (C28), we obtain the boundary condition

This is the boundary condition that connects $g_{i, 2, W}$![]() and $h_{i,3/2}$
and $h_{i,3/2}$![]() .
.
Appendix E. Example of a problematic well juncture
In § 5.2.2, we state that wells end at locations $\alpha _{L, W}$![]() and $\alpha _{R, W}$
and $\alpha _{R, W}$![]() where $J_{m, W} = J_{M, W}$
where $J_{m, W} = J_{M, W}$![]() . There are cases in which this property is not obvious. We show such an example in figure 14(a), in which well $I$
. There are cases in which this property is not obvious. We show such an example in figure 14(a), in which well $I$![]() disappears at $\alpha = \alpha _{R, I}$
disappears at $\alpha = \alpha _{R, I}$![]() because $J_{m, I} = J_{M, I} = 0$
because $J_{m, I} = J_{M, I} = 0$![]() at that value of $\alpha$
at that value of $\alpha$![]() . The problem with this configuration arises for $\alpha > \alpha _{R, I}$
. The problem with this configuration arises for $\alpha > \alpha _{R, I}$![]() , where well $II$
, where well $II$![]() and $III$
and $III$![]() merge into a new larger well. There are different ways to address this problem, and we comment on two: one could terminate wells $II$
merge into a new larger well. There are different ways to address this problem, and we comment on two: one could terminate wells $II$![]() and $III$
and $III$![]() at $\alpha = \alpha _{R, I}$
at $\alpha = \alpha _{R, I}$![]() and start a new well $IV$
and start a new well $IV$![]() at that value of $\alpha$
at that value of $\alpha$![]() , or one could terminate well $III$
, or one could terminate well $III$![]() and declare that the merged well beyond $\alpha _{R, I}$
and declare that the merged well beyond $\alpha _{R, I}$![]() is well $II$
is well $II$![]() . In either of these options, a well disappears without $J_{m, W}$
. In either of these options, a well disappears without $J_{m, W}$![]() being equal to $J_{M, W}$
being equal to $J_{M, W}$![]() . Moreover, if we were to choose the second option and declare that the merged well is well $II$
. Moreover, if we were to choose the second option and declare that the merged well is well $II$![]() , the function $J_{c, II}$
, the function $J_{c, II}$![]() that determines the location of the juncture in velocity space becomes discontinuous in $\alpha$
that determines the location of the juncture in velocity space becomes discontinuous in $\alpha$![]() . Both of these features are undesirable, and instead we choose to add a ‘false’ two-well juncture for $\alpha > \alpha _{R, I}$
. Both of these features are undesirable, and instead we choose to add a ‘false’ two-well juncture for $\alpha > \alpha _{R, I}$![]() , represented by a red dashed line in figure 14(a). We can locate the ‘false’ juncture $J_{c, II} = J_{c, III}$
, represented by a red dashed line in figure 14(a). We can locate the ‘false’ juncture $J_{c, II} = J_{c, III}$![]() that artificially separates particles into wells $II$
that artificially separates particles into wells $II$![]() and $III$
and $III$![]() wherever we wish. The only condition that we impose for convenience is that the extended functions $J_{c, II}$
wherever we wish. The only condition that we impose for convenience is that the extended functions $J_{c, II}$![]() and $J_{c, III}$
and $J_{c, III}$![]() be continuous, as shown in the example of figure 14(b). Note that such a ‘false’ juncture does not affect the final result because junctures impose continuity of the distribution function and continuity of the collisional velocity-space flux, and hence continuity of the distribution function derivatives. With these ‘false’ junctures, we ensure that wells end only at values of $\alpha$
be continuous, as shown in the example of figure 14(b). Note that such a ‘false’ juncture does not affect the final result because junctures impose continuity of the distribution function and continuity of the collisional velocity-space flux, and hence continuity of the distribution function derivatives. With these ‘false’ junctures, we ensure that wells end only at values of $\alpha$![]() where $J_{m, W} = J_{M, W}$
where $J_{m, W} = J_{M, W}$![]() .
.

Figure 14. (a) Example of limit $\alpha _{R, I}$![]() in which well $I$
in which well $I$![]() closes and well $II$
closes and well $II$![]() and $III$
and $III$![]() become indistinguishable. There are several ways to treat such a case. We choose to define a ‘false’ juncture $J_{c, II} = J_{c, III}$
become indistinguishable. There are several ways to treat such a case. We choose to define a ‘false’ juncture $J_{c, II} = J_{c, III}$![]() (represented by a dashed line) that splits particles into well $II$
(represented by a dashed line) that splits particles into well $II$![]() and well $III$
and well $III$![]() arbitrarily for $\alpha > \alpha _{R, I}$
arbitrarily for $\alpha > \alpha _{R, I}$![]() . (b) Sketch of the functions $J_{c, I}$
. (b) Sketch of the functions $J_{c, I}$![]() , $J_{c, II}$
, $J_{c, II}$![]() and $J_{c, III}$
and $J_{c, III}$![]() vs $\alpha$
vs $\alpha$![]() . The sketch is consistent with the $\alpha _{R, I}$
. The sketch is consistent with the $\alpha _{R, I}$![]() sketched in figure (a). The ‘false’ juncture $J_{c, II} = J_{c, III}$
sketched in figure (a). The ‘false’ juncture $J_{c, II} = J_{c, III}$![]() is represented by dashed lines. The shape of $J_{c,II} = J_{c, III}$
is represented by dashed lines. The shape of $J_{c,II} = J_{c, III}$![]() in the region where well $I$
in the region where well $I$![]() does not exist is arbitrary. We choose it such that $J_{c, II} (r, \alpha, \bar {v}, t)$
does not exist is arbitrary. We choose it such that $J_{c, II} (r, \alpha, \bar {v}, t)$![]() and $J_{c, III} (r, \alpha, \bar {v}, t)$
and $J_{c, III} (r, \alpha, \bar {v}, t)$![]() are continuous in $\alpha$
are continuous in $\alpha$![]() .
.
Appendix F. Correction $g_{i, 3/2, W}$ to the trapped-particle distribution function
to the trapped-particle distribution function
In this appendix, we show that $g_{i, 3/2, W}$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() or $J$
or $J$![]() and hence $\tau _W\, J\, \partial _J g_{i, 3/2, W} = 0$
and hence $\tau _W\, J\, \partial _J g_{i, 3/2, W} = 0$![]() for all $J$
for all $J$![]() and not only at the trapped–passing boundary.
and not only at the trapped–passing boundary.
We start by discussing the contributions to $g_{i, 3/2, W}$![]() due to the collision operator. One might think that the differential piece of the linearized collision operator applied on $g_{i, 1, W}$
due to the collision operator. One might think that the differential piece of the linearized collision operator applied on $g_{i, 1, W}$![]() has pieces of order $\epsilon ^{1/2} \nu _{ii} f_{Mi}$
has pieces of order $\epsilon ^{1/2} \nu _{ii} f_{Mi}$![]() that would have to be included in an equation for $g_{i, 3/2, W}$
that would have to be included in an equation for $g_{i, 3/2, W}$![]() , but after careful manipulations using $\boldsymbol {\nabla }_v \bar {v} = \boldsymbol {v}/\bar {v}$
, but after careful manipulations using $\boldsymbol {\nabla }_v \bar {v} = \boldsymbol {v}/\bar {v}$![]() and (4.12) for $\boldsymbol {\nabla }_v J_W$
and (4.12) for $\boldsymbol {\nabla }_v J_W$![]() , we find that this is not the case. Indeed, since $\boldsymbol {\nabla }_v = \boldsymbol {\nabla }_v \bar {v}\, \partial _{\bar {v}} + \boldsymbol {\nabla }_v J_W\, \partial _J$
, we find that this is not the case. Indeed, since $\boldsymbol {\nabla }_v = \boldsymbol {\nabla }_v \bar {v}\, \partial _{\bar {v}} + \boldsymbol {\nabla }_v J_W\, \partial _J$![]() and
and

we obtain

The contributions of the integral part of the linearized collision operator to the trapped particle equation can be neglected to the order that determines $g_{i, 3/2, W}$![]() because their size is given by $C_{ii, I}^{\ell } [h_{i,3/2}] \sim \nu _{ii} h_{i,3/2} \sim \epsilon ^{5/2} \rho _{i*} v_{ti} f_{Mi}/a$
because their size is given by $C_{ii, I}^{\ell } [h_{i,3/2}] \sim \nu _{ii} h_{i,3/2} \sim \epsilon ^{5/2} \rho _{i*} v_{ti} f_{Mi}/a$![]() and $C_{ii,I}^{\ell } [ g_{i, 1, W} ] \sim \epsilon ^{1/2} \nu _{ii} g_{i, 1, W} \sim \epsilon ^{5/2} \rho _{i*} v_{ti} f_{Mi}/a$
and $C_{ii,I}^{\ell } [ g_{i, 1, W} ] \sim \epsilon ^{1/2} \nu _{ii} g_{i, 1, W} \sim \epsilon ^{5/2} \rho _{i*} v_{ti} f_{Mi}/a$![]() . Here, the integral operator applied on $g_{i, 1, W}$
. Here, the integral operator applied on $g_{i, 1, W}$![]() has an extra factor of $\sqrt {\epsilon }$
has an extra factor of $\sqrt {\epsilon }$![]() because the region of velocity space where $g_{i, 1, W}$
because the region of velocity space where $g_{i, 1, W}$![]() is defined is small in $\sqrt {\epsilon }$
is defined is small in $\sqrt {\epsilon }$![]() .
.
We proceed to consider the contributions to the equation for $g_{i, 3/2, W}$![]() due to the $\boldsymbol {E} \times \boldsymbol {B}$
due to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift $(c/B)\, \hat {\boldsymbol {b}} \times \boldsymbol {\nabla } \phi _{3/2}$
drift $(c/B)\, \hat {\boldsymbol {b}} \times \boldsymbol {\nabla } \phi _{3/2}$![]() (see (4.5) and (5.18)). This $\boldsymbol {E} \times \boldsymbol {B}$
(see (4.5) and (5.18)). This $\boldsymbol {E} \times \boldsymbol {B}$![]() contribution has already been accounted for in (5.25) in the term proportional to $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha r_{i, 1, W}$
contribution has already been accounted for in (5.25) in the term proportional to $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha r_{i, 1, W}$![]() . Keeping higher-order corrections in (5.22), we find
. Keeping higher-order corrections in (5.22), we find

We calculate $\partial _\alpha \bar {\lambda }_W$![]() by differentiating equation (F3) with respect to $\alpha$
by differentiating equation (F3) with respect to $\alpha$![]() holding $r$
holding $r$![]() , $\bar {v}$
, $\bar {v}$![]() and $J$
and $J$![]() constant. We find
constant. We find
This result shows that the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift due to $\phi _{3/2}$
drift due to $\phi _{3/2}$![]() is included naturally in the term $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha r_{i, 1, W}$
is included naturally in the term $(c \phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha r_{i, 1, W}$![]() because, using (4.5), we can write the radial drifts as
because, using (4.5), we can write the radial drifts as

Due to all the considerations listed above, the equation for $g_{i, 3/2, W}$![]() is
is
At this order, the equation for the junctures of different wells is still the simple result
Equations (F6) and (F7) have to be solved in conjunction with the boundary condition
that we obtain from condition (2.24) (see Appendix D for more detail). Using the same methodology that led to solution (5.4), we can show that the solution to (F6), (F7) and (F8) is given by (5.40) and hence $g_{i, 3/2, W}$![]() does not depend on $\alpha$
does not depend on $\alpha$![]() or $J$
or $J$![]() .
.
Appendix G. Derivation of (5.25), (5.33) and (5.34) from the DKES kinetic equation
In this appendix, we derive (5.25), (5.33) and (5.34) from the DKES kinetic equation. The DKES kinetic equation assumes that the ion distribution function is the Maxwellian distribution function $f_{Mi}$![]() corrected by the small piece $\hat {f}_i$
corrected by the small piece $\hat {f}_i$![]() ,
,
The velocity-space coordinates are the magnitude of the velocity $v$![]() and the angle $\gamma$
and the angle $\gamma$![]() between the velocity $\boldsymbol {v}$
between the velocity $\boldsymbol {v}$![]() and the magnetic field, $\gamma := \arccos ( \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {v}/v)$
and the magnetic field, $\gamma := \arccos ( \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {v}/v)$![]() . The DKES kinetic equation in these variables is
. The DKES kinetic equation in these variables is

where
is a model pitch-angle scattering operator. This equation has to be solved with magnetic fields that satisfy the MHD constraint $(\boldsymbol {\nabla } \times \boldsymbol {B}) \boldsymbol {\cdot } \boldsymbol {\nabla } r = 0$![]() . In the $\{ r, \alpha, l \}$
. In the $\{ r, \alpha, l \}$![]() coordinates, this constraint is
coordinates, this constraint is
To obtain (5.25), (5.33) and (5.34) from (G2), we need to expand in $\rho _{i*} \sim \nu _{i*} \ll 1$![]() and in $\epsilon \ll 1$
and in $\epsilon \ll 1$![]() . We first expand in $\rho _{i*} \sim \nu _{i*} \ll 1$
. We first expand in $\rho _{i*} \sim \nu _{i*} \ll 1$![]() ,
,
where $\hat {f}_i^{(n)} \sim \rho _{i*}^{n} \hat {f}_i$![]() . For the expansion $\rho _{i*} \sim \nu _{i*} \ll 1$
. For the expansion $\rho _{i*} \sim \nu _{i*} \ll 1$![]() , we need to use the velocity-space coordinates $v$
, we need to use the velocity-space coordinates $v$![]() , $\lambda = \sin ^{2}\gamma /B$
, $\lambda = \sin ^{2}\gamma /B$![]() and $\sigma$
and $\sigma$![]() . In these coordinates, (G2) becomes
. In these coordinates, (G2) becomes

where $v_\| = v \cos \gamma = \sigma v \sqrt {1 - \lambda B}$![]() and
and
To lowest order in $\rho _{i*} \ll 1$![]() , (G6) simplifies to $v_\|\, \partial _l \hat {f}_i^{(0)} = 0$
, (G6) simplifies to $v_\|\, \partial _l \hat {f}_i^{(0)} = 0$![]() . Following the same procedure that we used in § 2, we split $\hat {f}_i^{(0)}$
. Following the same procedure that we used in § 2, we split $\hat {f}_i^{(0)}$![]() into a trapped-particle distribution function $\hat {g}_{i,W}(r, \alpha, v, \lambda, t)$
into a trapped-particle distribution function $\hat {g}_{i,W}(r, \alpha, v, \lambda, t)$![]() and a passing-particle distribution function $\hat {h}_i (r, v, \lambda, \sigma, t)$
and a passing-particle distribution function $\hat {h}_i (r, v, \lambda, \sigma, t)$![]() . To next order in $\rho _{i*} \ll 1$
. To next order in $\rho _{i*} \ll 1$![]() , (G6) becomes
, (G6) becomes

To eliminate the first term in this equation, we transit average in the trapped-particle region, and we multiply by $B/|v_\| |$![]() and flux surface average in the passing-particle region. To perform these operations, we use
and flux surface average in the passing-particle region. To perform these operations, we use
and (G4) to write
and
where $\hat {J}_W$![]() is defined in (5.52). With these results, the transit average of (G8) becomes
is defined in (5.52). With these results, the transit average of (G8) becomes

for trapped particles. The flux surface average of (G8) multiplied by $B/|v_\| |$![]() gives
gives
for passing particles.
Equation (G12) can be simplified even further for trapped particles by noting that
Using this expression, we can rewrite (G12) as

This form of the equation shows that $\hat {J}_W$![]() is a constant of the motion in DKES. Indeed, if instead of using $v$
is a constant of the motion in DKES. Indeed, if instead of using $v$![]() and $\lambda$
and $\lambda$![]() as velocity-space coordinates, we use $v$
as velocity-space coordinates, we use $v$![]() and $\hat {J}$
and $\hat {J}$![]() , (G15) can be written as
, (G15) can be written as
where

In the DKES kinetic equation, there will also be junctures of different wells such as the one shown in figure 1. These junctures are determined by values of $\hat {J}$![]() that depend on $r$
that depend on $r$![]() , $\alpha$
, $\alpha$![]() , $v$
, $v$![]() and the well index $W$
and the well index $W$![]() , $\hat {J} = \hat {J}_{c, W} (r, \alpha, v)$
, $\hat {J} = \hat {J}_{c, W} (r, \alpha, v)$![]() . These values of $\hat {J}$
. These values of $\hat {J}$![]() satisfy
satisfy
and imposing that the collisional flux across these junctures is continuous gives the condition

Equations (G13), (G16) and (G19) can be further simplified using the expansion in $\epsilon \ll 1$![]() . Using a procedure similar to the one we follow in § 5.2, we find
. Using a procedure similar to the one we follow in § 5.2, we find
and
where $\hat {g}_{i, n, W} \sim \epsilon ^{n} f_{Mi}$![]() and $\hat {h}_{i, n} \sim \epsilon ^{n} f_{Mi}$
and $\hat {h}_{i, n} \sim \epsilon ^{n} f_{Mi}$![]() . Using the fact that $B \simeq B_0$
. Using the fact that $B \simeq B_0$![]() to lowest order, we obtain that $\hat {J}$
to lowest order, we obtain that $\hat {J}$![]() and $J$
and $J$![]() are approximately the same coordinate, $\hat {J} \simeq B_0 J$
are approximately the same coordinate, $\hat {J} \simeq B_0 J$![]() . As a result, (G16) and (G19) become (5.25) and (5.33) to lowest order. As explained in § 5.2, the continuity of derivatives across the trapped–passing boundary implies that the size of $\hat {h}_i$
. As a result, (G16) and (G19) become (5.25) and (5.33) to lowest order. As explained in § 5.2, the continuity of derivatives across the trapped–passing boundary implies that the size of $\hat {h}_i$![]() is $\epsilon ^{3/2} f_{Mi}$
is $\epsilon ^{3/2} f_{Mi}$![]() , and as a result we obtain boundary condition (5.34) for $\hat {g}_{i,1,W}$
, and as a result we obtain boundary condition (5.34) for $\hat {g}_{i,1,W}$![]() .
.
Appendix H. Boundary layer at the juncture of several magnetic wells
In junctures where particles leave two of the wells and enter a third one, a collisional boundary layer appears in the region
(we justify this estimate below). The distribution function $g_{i, 1, W}$![]() in this boundary layer can be written as
in this boundary layer can be written as
where $\Delta J_\mathrm {junct} := J - J_{c, W} (r, \alpha, v)$![]() . The function $K_{i,\mathrm {junct}, W} (r, \alpha, v, \Delta J_\mathrm {junct}, t)$
. The function $K_{i,\mathrm {junct}, W} (r, \alpha, v, \Delta J_\mathrm {junct}, t)$![]() changes rapidly in $\Delta J_\mathrm {junct}$
changes rapidly in $\Delta J_\mathrm {junct}$![]() , and slowly in $\alpha$
, and slowly in $\alpha$![]() .
.
We can find the equation for $K_{i, \mathrm {junct}, W}$![]() by substituting (H2) into (5.25) and neglecting small terms
by substituting (H2) into (5.25) and neglecting small terms
where the logarithmically diverging function
is the asymptotic approximation for $\tau _W$![]() near $J = J_{c, W}$
near $J = J_{c, W}$![]() . We have neglected the derivative of $K_{i, \mathrm {junct}, W}$
. We have neglected the derivative of $K_{i, \mathrm {junct}, W}$![]() with respect to $\alpha$
with respect to $\alpha$![]() because it is small compared with the first term in (H3). We can obtain estimate (H1) by balancing the two terms in (H3),
because it is small compared with the first term in (H3). We can obtain estimate (H1) by balancing the two terms in (H3),
Indeed, this equation gives
For the order of magnitude estimate, we have used $\phi _0^{\prime } \sim T_i/ea$![]() , $\varPsi _t^{\prime } \sim a B_0$
, $\varPsi _t^{\prime } \sim a B_0$![]() , $J_{c, W} \sim \sqrt {\epsilon } v_{ti} R$
, $J_{c, W} \sim \sqrt {\epsilon } v_{ti} R$![]() and $\hat {\tau }_{c, W, \log } \sim R/\sqrt {\epsilon } v_{ti}$
and $\hat {\tau }_{c, W, \log } \sim R/\sqrt {\epsilon } v_{ti}$![]() . With (H6), we can simplify $\tau _{c, W}$
. With (H6), we can simplify $\tau _{c, W}$![]() to
to
From here on, we use this approximation that makes $\tau _{c, W}$![]() independent of $\Delta J_\mathrm {junct}$
independent of $\Delta J_\mathrm {junct}$![]() .
.
Equation (H3) has to be solved in conjunction with continuity of $K_{i,\mathrm {junct},W}$![]() across the juncture and along with condition (5.33), which in the layer becomes
across the juncture and along with condition (5.33), which in the layer becomes

For large $\Delta J_\mathrm {junct}$![]() , the function $K_{i,\mathrm {junct}, W} (r, \alpha, v, \Delta J_\mathrm {junct}, t)$
, the function $K_{i,\mathrm {junct}, W} (r, \alpha, v, \Delta J_\mathrm {junct}, t)$![]() must tend to the solutions outside of the layer,
must tend to the solutions outside of the layer,
With boundary conditions (H9), the solutions to (H3) are

where the function $A_W(r, \alpha, v, t)$![]() is a constant of integration.
is a constant of integration.
We proceed to discuss how to use solution (H10) to solve the problem. We consider a juncture like the one in figure 1 such that particles leave well $I$![]() and $II$
and $II$![]() to enter well $III$
to enter well $III$![]() , that is, $- (c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, W} > 0$
, that is, $- (c\phi _0^{\prime }/\varPsi _t^{\prime })\, \partial _\alpha J_{c, W} > 0$![]() for $W = I, II, III$
for $W = I, II, III$![]() . This means that the exponential in solution (H10) diverges for well $III$
. This means that the exponential in solution (H10) diverges for well $III$![]() , where $\Delta J_\mathrm {junct} > 0$
, where $\Delta J_\mathrm {junct} > 0$![]() , and thus the solution in well $III$
, and thus the solution in well $III$![]() can tend to $K_{i, III} (r, \alpha, v, J_{c, III}, t)$
can tend to $K_{i, III} (r, \alpha, v, J_{c, III}, t)$![]() only if $A_{III} (r, \alpha, v, t) = 0$
only if $A_{III} (r, \alpha, v, t) = 0$![]() . As a result, the derivative of $K_{i, \mathrm {junct}, III}$
. As a result, the derivative of $K_{i, \mathrm {junct}, III}$![]() with respect to $\Delta J_\mathrm {junct}$
with respect to $\Delta J_\mathrm {junct}$![]() vanishes, and condition (H8) simply gives
vanishes, and condition (H8) simply gives
Imposing this condition and the fact that $K_{i, \mathrm {junct}, I}$![]() and $K_{i, \mathrm {junct}, II}$
and $K_{i, \mathrm {junct}, II}$![]() have to be equal to each other at $\Delta J_\mathrm {junct} = 0$
have to be equal to each other at $\Delta J_\mathrm {junct} = 0$![]() to be continuous with $K_{i, \mathrm {junct}, III}$
to be continuous with $K_{i, \mathrm {junct}, III}$![]() , we find the functions $A_I$
, we find the functions $A_I$![]() and $A_{II}$
and $A_{II}$![]() . The final solutions are
. The final solutions are

and

With these solutions, we can find $K_{i, III} (r, \alpha, v, J_{c, III}, t) = K_{i, \mathrm {junct}, III} (r, \alpha, v, 0, t)$![]() because $K_{i, \mathrm {junct}, III} (r, \alpha, v, 0, t)$
because $K_{i, \mathrm {junct}, III} (r, \alpha, v, 0, t)$![]() has to be equal to the values $K_{i, \mathrm {junct}, I}$
has to be equal to the values $K_{i, \mathrm {junct}, I}$![]() and $K_{i, \mathrm {junct}, II}$
and $K_{i, \mathrm {junct}, II}$![]() at $\Delta J_\mathrm {junct} = 0$
at $\Delta J_\mathrm {junct} = 0$![]() . The solution for $K_{i, III} (r, \alpha, v, J_{c, III}, t)$
. The solution for $K_{i, III} (r, \alpha, v, J_{c, III}, t)$![]() is the same one that we found by applying conservation of particles, given in (7.8).
is the same one that we found by applying conservation of particles, given in (7.8).
It is worth noting that if we apply this method to a hypothetical boundary layer in a juncture where particles leave one well to enter two other wells, we find that the exponential in solution (H10) diverges in two of the wells (the two that the particles enter), and as a result, the functions $A_W$![]() have to vanish in those wells. One ends up finding that the solution is constant in all the wells, recovering the result that $K_{i, W}$
have to vanish in those wells. One ends up finding that the solution is constant in all the wells, recovering the result that $K_{i, W}$![]() is constant across this kind of juncture.
is constant across this kind of juncture.
Appendix I. Boundary layers around discontinuities in $\partial _J K_{i, W}$
There are two types of boundary layers that form around discontinuities in $\partial _J K_{i, W}$![]() : the layers on the boundaries of the regions where $K_{i, W}$
: the layers on the boundaries of the regions where $K_{i, W}$![]() is independent of $J$
is independent of $J$![]() , and the layer on the trapped–passing boundary. We describe both types of layers in this appendix.
, and the layer on the trapped–passing boundary. We describe both types of layers in this appendix.
I.1. Boundary layers on the boundaries of the regions where $\partial _J K_{i, W} = 0$
To discuss the boundary layers that appear on the boundaries of the regions where $K_{i, W}$![]() does not depend on $J$
does not depend on $J$![]() , we use the example of the layer that arises around $J = J_{c, III, M}$
, we use the example of the layer that arises around $J = J_{c, III, M}$![]() in the example discussed in § 7.1.2. We use the variable $\Delta J_\mathrm {bl} := J - J_{c, III, M}$
in the example discussed in § 7.1.2. We use the variable $\Delta J_\mathrm {bl} := J - J_{c, III, M}$![]() . The typical size of $\Delta J_\mathrm {bl}$
. The typical size of $\Delta J_\mathrm {bl}$![]() is
is
as we will show below.
Particles behave differently for $\Delta J_\mathrm {bl}$![]() positive or negative. For $\Delta J_\mathrm {bl} > 0$
positive or negative. For $\Delta J_\mathrm {bl} > 0$![]() , we can write the distribution function in the boundary layer region as
, we can write the distribution function in the boundary layer region as
where

Substituting (I2) into (5.25), we obtain the equation for the boundary layer for $\Delta J_\mathrm {bl} > 0$![]() ,
,
where $\tau _{III}$![]() is evaluated at $J = J_{c, III, M}$
is evaluated at $J = J_{c, III, M}$![]() . For $J > J_{c, III, M}$
. For $J > J_{c, III, M}$![]() , particles move uninterruptedly along $\alpha$
, particles move uninterruptedly along $\alpha$![]() . Thus, we impose periodic boundary conditions in $\alpha$
. Thus, we impose periodic boundary conditions in $\alpha$![]() for $g_{i, 1, III}^{\{\mathrm {bl}\}}$
for $g_{i, 1, III}^{\{\mathrm {bl}\}}$![]() . We also impose
. We also impose
and continuity and continuity of derivatives with $g_{i, 1, III}$![]() for $J < J_{c, III, M}$
for $J < J_{c, III, M}$![]() .
.
The distribution function in the region $J < J_{c, III, M}$![]() is simply $g_{i, 1, III} = K_{i, III} - r_{i, 1, III} \, \varUpsilon _i f_{Mi} + g_{i, 1, III}^{\{ 1 \}}$
is simply $g_{i, 1, III} = K_{i, III} - r_{i, 1, III} \, \varUpsilon _i f_{Mi} + g_{i, 1, III}^{\{ 1 \}}$![]() , where $g_{i,1,III}^{\{1\}}$
, where $g_{i,1,III}^{\{1\}}$![]() is determined by (7.23). In other words, unlike for $J > J_{c, III, M}$
is determined by (7.23). In other words, unlike for $J > J_{c, III, M}$![]() , we do not distinguish between $g_{i, 1, III}^{\{ 1 \}}$
, we do not distinguish between $g_{i, 1, III}^{\{ 1 \}}$![]() and the boundary layer piece of the distribution function because the equation for $g_{i, 1, III}^{\{ 1 \}}$
and the boundary layer piece of the distribution function because the equation for $g_{i, 1, III}^{\{ 1 \}}$![]() contains collisions. As a result, the continuity of $g_{i, 1, III}$
contains collisions. As a result, the continuity of $g_{i, 1, III}$![]() across $J = J_{c, III, M}$
across $J = J_{c, III, M}$![]() gives
gives
and the continuity of the derivative with respect to $J$![]() gives
gives
where $\partial _J K_{i, III} (r, v, J_{c, III, M}^{+}, t)$![]() is the derivative of $K_{i, III}$
is the derivative of $K_{i, III}$![]() with respect to $J$
with respect to $J$![]() evaluated at a value of $J$
evaluated at a value of $J$![]() slightly above $J = J_{c, III, M}$
slightly above $J = J_{c, III, M}$![]() . Recall that $\partial _J K_{i, III}$
. Recall that $\partial _J K_{i, III}$![]() vanishes for $J < J_{c, III, M}$
vanishes for $J < J_{c, III, M}$![]() .
.
By balancing the different terms in (I4), we obtain estimate (I1) for the boundary layer width. The estimate for the size of $g_{i, 1, III}^{\{\mathrm {bl}\}}$![]() in (I3) is obtained from the fact that $g_{i, 1, III}^{\{\mathrm {bl}\}}$
in (I3) is obtained from the fact that $g_{i, 1, III}^{\{\mathrm {bl}\}}$![]() is the integral of $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}}$
is the integral of $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}}$![]() over an interval of $\Delta J_\mathrm {bl}$
over an interval of $\Delta J_\mathrm {bl}$![]() of the size given in (I1). The size of $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}}$
of the size given in (I1). The size of $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}}$![]() , $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}} \sim \sqrt {\epsilon } f_{Mi}/v_{ti} R$
, $\partial _{\Delta J_\mathrm {bl}} g_{i, 1, III}^{\{\mathrm {bl}\}} \sim \sqrt {\epsilon } f_{Mi}/v_{ti} R$![]() , is determined by boundary condition (I7).
, is determined by boundary condition (I7).
Equations (I6) and (I7) are also the boundary conditions for $g_{i, 1, III}^{\{ 1 \}}$![]() in the region where $\partial _J K_{i, III}$
in the region where $\partial _J K_{i, III}$![]() vanishes. Note that this means that $g_{i, 1, III}^{\{1\}}$
vanishes. Note that this means that $g_{i, 1, III}^{\{1\}}$![]() is larger than expected by a factor of $\sqrt {\rho _{i*}/\nu _{i*}}$
is larger than expected by a factor of $\sqrt {\rho _{i*}/\nu _{i*}}$![]() near $J = J_{c, III, M}$
near $J = J_{c, III, M}$![]() , but it becomes of order $(\nu _{i*}/\rho _{i*}) \epsilon f_{Mi}$
, but it becomes of order $(\nu _{i*}/\rho _{i*}) \epsilon f_{Mi}$![]() for $(J_{c, III, M} - J)/\sqrt {\epsilon } v_{ti} R \gg \sqrt {\nu _{i*}/\rho _{i*}}$
for $(J_{c, III, M} - J)/\sqrt {\epsilon } v_{ti} R \gg \sqrt {\nu _{i*}/\rho _{i*}}$![]() , except for some regions of small phase-space volume that we proceed to discuss.
, except for some regions of small phase-space volume that we proceed to discuss.
In the example that we are considering (see figures 6 and 7), $g_{i, 1, III}^{\{1\}}$![]() at $J = J_{c, III, M}$
at $J = J_{c, III, M}$![]() for $\alpha$
for $\alpha$![]() slightly smaller than ${\rm \pi}$
slightly smaller than ${\rm \pi}$![]() ($\alpha = {\rm \pi}^{-}$
($\alpha = {\rm \pi}^{-}$![]() ) is different from $g_{i, 1, III}^{\{1\}}$
) is different from $g_{i, 1, III}^{\{1\}}$![]() at $J = J_{c, III, M}$
at $J = J_{c, III, M}$![]() for $\alpha$
for $\alpha$![]() slightly larger than ${\rm \pi}$
slightly larger than ${\rm \pi}$![]() ($\alpha = {\rm \pi}^{+}$
($\alpha = {\rm \pi}^{+}$![]() ). The particles with $J = J_{c, III, M}$
). The particles with $J = J_{c, III, M}$![]() at $\alpha = {\rm \pi}^{+}$
at $\alpha = {\rm \pi}^{+}$![]() are particles that used to have a second adiabatic invariant close to $J = J_{c, II, M}$
are particles that used to have a second adiabatic invariant close to $J = J_{c, II, M}$![]() and hence their number is determined by the value of $g_{i, 1, II}^{\{1\}}$
and hence their number is determined by the value of $g_{i, 1, II}^{\{1\}}$![]() around $J = J_{c, II, M}$
around $J = J_{c, II, M}$![]() and $\alpha = \pi^-$
and $\alpha = \pi^-$![]() . The particles with $J = J_{c, III, M}$
. The particles with $J = J_{c, III, M}$![]() at $\alpha = {\rm \pi}^{-}$
at $\alpha = {\rm \pi}^{-}$![]() transition into well $I$
transition into well $I$![]() where they have a second adiabatic invariant very similar to $J_{c, I, M}$
where they have a second adiabatic invariant very similar to $J_{c, I, M}$![]() . This means that $g_{i, 1, I}^{\{1\}}$
. This means that $g_{i, 1, I}^{\{1\}}$![]() around $J = J_{c, I, M}$
around $J = J_{c, I, M}$![]() and $\alpha = \pi^{+}$
and $\alpha = \pi^{+}$![]() is determined by $g_{i, 1, III}^{\{1\}}$
is determined by $g_{i, 1, III}^{\{1\}}$![]() at $J = J_{c, III, M}$
at $J = J_{c, III, M}$![]() and $\alpha = \pi^-$
and $\alpha = \pi^-$![]() , and hence is large by a factor of $\sqrt {\rho _{i*}/\nu _{i*}}$
, and hence is large by a factor of $\sqrt {\rho _{i*}/\nu _{i*}}$![]() in a region of width $\sqrt {\epsilon \nu _{i*}/\rho _{i*}} v_{ti} R$
in a region of width $\sqrt {\epsilon \nu _{i*}/\rho _{i*}} v_{ti} R$![]() around $J_{c, I, M}$
around $J_{c, I, M}$![]() . The particles in this region around $J_{c, I, M}$
. The particles in this region around $J_{c, I, M}$![]() , in turn, transition back into well $III$
, in turn, transition back into well $III$![]() at some value of $\alpha$
at some value of $\alpha$![]() between ${\rm \pi}$
between ${\rm \pi}$![]() and $2{\rm \pi}$
and $2{\rm \pi}$![]() . This means that there is another region around another value of $J$
. This means that there is another region around another value of $J$![]() that connects to $J_{c, I, M}$
that connects to $J_{c, I, M}$![]() where $g_{i, 1, III}^{\{1\}}$
where $g_{i, 1, III}^{\{1\}}$![]() is larger than expected. These regions of large $g_{i, 1, W}^{\{1\}}$
is larger than expected. These regions of large $g_{i, 1, W}^{\{1\}}$![]() go on until $g_{i, 1, W}^{\{1\}}$
go on until $g_{i, 1, W}^{\{1\}}$![]() becomes sufficiently small due to diffusion in $J$
becomes sufficiently small due to diffusion in $J$![]() .
.
Boundary condition (I7) gives the velocity-space flux conservation condition (7.16). Indeed, integrating (7.23) in $\alpha$![]() and in $J$
and in $J$![]() for the juncture sketched in figures 6 and 7, we find
for the juncture sketched in figures 6 and 7, we find

Using boundary condition (I7), the definition of $r_{i, 1, W}$![]() in (5.26) and $\partial _J \lambda _W \simeq - 2/v^{2} B_0 \tau _W$
in (5.26) and $\partial _J \lambda _W \simeq - 2/v^{2} B_0 \tau _W$![]() , (I8) becomes
, (I8) becomes

We obtain the velocity-space flux conservation condition (7.16) from this expression by employing the fact that (I4) and (I5) and the equivalent equations for the boundary layers at $J = J_{c, I, m}$![]() and $J_{c, II, m}$
and $J_{c, II, m}$![]() give
give
Incidentally, $\tau _{III}$![]() in (I4) diverges logarithmically at $\alpha = {\rm \pi}$
in (I4) diverges logarithmically at $\alpha = {\rm \pi}$![]() , where $J_{c, III} = J_{c, III, M}$
, where $J_{c, III} = J_{c, III, M}$![]() . This divergence is integrable and does not affect the previous discussion.
. This divergence is integrable and does not affect the previous discussion.
I.2. Boundary layer at the trapped–passing boundary
The collisional layer that appears at the trapped–passing boundary is a result of the lowest-order solution (7.19) not satisfying property (5.36) at the trapped–passing boundary. This layer is best described in the coordinate $\Delta \lambda := \lambda - 1/B_M \simeq \lambda - 1/B_0 + B_{1,M}/B_0^{2}$![]() , which is of order
, which is of order

(we will argue that this estimate is correct below). We consider $g_{i, 1, W}^{\{1\}}$![]() , determined by (7.23), as a function of $\Delta \lambda$
, determined by (7.23), as a function of $\Delta \lambda$![]() . We find below that in the region of velocity space that satisfies (I11), $g_{i, 1, W}^{\{1\}}$
. We find below that in the region of velocity space that satisfies (I11), $g_{i, 1, W}^{\{1\}}$![]() is not of order $(\nu _{i*}/\rho _{i*}) \epsilon f_{Mi}$
is not of order $(\nu _{i*}/\rho _{i*}) \epsilon f_{Mi}$![]() , but much larger,
, but much larger,

Using estimates (I11) and (I12) in (7.23), we find
Here, we can use $\partial _J \lambda _W \simeq - 2/v^{2} B_0 \tau _W$![]() and $\partial _\alpha \lambda _W \simeq - B_0^{-2} \langle \partial _\alpha B_1 \rangle _{\tau, W}$
and $\partial _\alpha \lambda _W \simeq - B_0^{-2} \langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() to simplify (I13) to
to simplify (I13) to
We need to evaluate the different coefficients in this equation for small $\Delta \lambda$![]() . We will use the property that, for $\Delta \lambda \rightarrow 0$
. We will use the property that, for $\Delta \lambda \rightarrow 0$![]() , the particle trajectory covers the whole flux surface in such a way that the average of any function over the length of the line is related to the flux surface average of the function by
, the particle trajectory covers the whole flux surface in such a way that the average of any function over the length of the line is related to the flux surface average of the function by

Then, we can write
where $v_{\|, \mathrm {tp}}$![]() is the parallel velocity of the particles at the trapped–passing boundary. Note that the average $\langle |v_{\|, \mathrm {tp}}|^{-1} \rangle _\mathrm {fs}$
is the parallel velocity of the particles at the trapped–passing boundary. Note that the average $\langle |v_{\|, \mathrm {tp}}|^{-1} \rangle _\mathrm {fs}$![]() does not diverge logarithmically despite $|v_{\|, \mathrm {tp}}|$
does not diverge logarithmically despite $|v_{\|, \mathrm {tp}}|$![]() depending linearly on $l$
depending linearly on $l$![]() near the maximum of $B_1$
near the maximum of $B_1$![]() because the integral over $\alpha$
because the integral over $\alpha$![]() eliminates de divergence. With this result, (I14) simplifies to
eliminates de divergence. With this result, (I14) simplifies to
To obtain an estimate for $\langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() , we need to consider the integral
, we need to consider the integral

We first note that, for $\Delta \lambda \rightarrow 0$![]() , this integral vanishes,
, this integral vanishes,

Here, we have used the fact that the length $L$![]() , defined below (2.31), is independent of $\alpha$
, defined below (2.31), is independent of $\alpha$![]() to lowest order in the aspect ratio expansion, $L (r, \alpha ) \simeq L_0 (r)$
to lowest order in the aspect ratio expansion, $L (r, \alpha ) \simeq L_0 (r)$![]() . We proceed to determine how integral (I18) goes to zero for small $\Delta \lambda$
. We proceed to determine how integral (I18) goes to zero for small $\Delta \lambda$![]() . A sketch of the integral path is shown in figure 15: the path of integration is composed of an almost surface-covering piece and a piece of short length in the region $\alpha _a < \alpha < \alpha _b$
. A sketch of the integral path is shown in figure 15: the path of integration is composed of an almost surface-covering piece and a piece of short length in the region $\alpha _a < \alpha < \alpha _b$![]() , where $\alpha _a$
, where $\alpha _a$![]() and $\alpha _b$
and $\alpha _b$![]() are the values of $\alpha$
are the values of $\alpha$![]() for which the maximum of $B$
for which the maximum of $B$![]() on the line $\alpha$
on the line $\alpha$![]() is equal to $1/\lambda$
is equal to $1/\lambda$![]() . For most values of $\alpha$
. For most values of $\alpha$![]() and $\Delta \lambda$
and $\Delta \lambda$![]() , the bulk of the integral is the almost surface-covering piece, and its size can be estimated by replacing the line integral by an integral over the surface that the line covers, shaded in figure 15,
, the bulk of the integral is the almost surface-covering piece, and its size can be estimated by replacing the line integral by an integral over the surface that the line covers, shaded in figure 15,

The value of this surface integral is dominated by the region near the maximum of $B_1$![]() because the rest of surface integral vanishes as shown by (I19). To avoid cluttering notation, we choose $\alpha$
because the rest of surface integral vanishes as shown by (I19). To avoid cluttering notation, we choose $\alpha$![]() and $l$
and $l$![]() such that $\alpha = 0$
such that $\alpha = 0$![]() and $l = 0$
and $l = 0$![]() at the maximum of $B_1$
at the maximum of $B_1$![]() , that is, $B_{1, M} = B_1(r, 0, 0)$
, that is, $B_{1, M} = B_1(r, 0, 0)$![]() . Then, around the maximum,
. Then, around the maximum,
with $\partial _{ll}^{2} B_1 (r, 0, 0) < 0$![]() , $\partial _{\alpha \alpha }^{2} B_1 (r, 0, 0) < 0$
, $\partial _{\alpha \alpha }^{2} B_1 (r, 0, 0) < 0$![]() and
and
This Taylor expansion around the maximum $l = 0$![]() and $\alpha = 0$
and $\alpha = 0$![]() implies that $\alpha _a \sim \alpha _b \sim \sqrt {\epsilon ^{-1}\Delta \lambda B_0}$
implies that $\alpha _a \sim \alpha _b \sim \sqrt {\epsilon ^{-1}\Delta \lambda B_0}$![]() , and that the integrals over $l$
, and that the integrals over $l$![]() in (I20) are of order
in (I20) are of order

for small $\alpha$![]() . Thus, we find
. Thus, we find
This is only an estimate. The real value and sign of $\langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() depends strongly on the particular orbit under consideration, determined by its $\alpha$
depends strongly on the particular orbit under consideration, determined by its $\alpha$![]() . Before we proceed, we point out that it is important not to confuse the $\alpha$
. Before we proceed, we point out that it is important not to confuse the $\alpha$![]() shown in figure 15, where a single orbit samples several values of $\alpha$
shown in figure 15, where a single orbit samples several values of $\alpha$![]() , with the value of $\alpha$
, with the value of $\alpha$![]() that we assign to the orbit (for example, we can assign to an orbit the value of $\alpha$
that we assign to the orbit (for example, we can assign to an orbit the value of $\alpha$![]() where it has its left bounce point). Going back to the dependence of $\langle \partial _\alpha B_1 \rangle _{\tau, W}$
where it has its left bounce point). Going back to the dependence of $\langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() on the particular orbit, consider what happens as the bounce points move from $\alpha _a$
on the particular orbit, consider what happens as the bounce points move from $\alpha _a$![]() to $\alpha _b$
to $\alpha _b$![]() . When a bounce point approaches $\alpha _a$
. When a bounce point approaches $\alpha _a$![]() , the part of the path near the bounce, which we ignored in our estimate (I24), becomes dominant due to a logarithmic divergence at the bounce point. As a result, $\langle \partial _\alpha B_1 \rangle _{\tau, W}$
, the part of the path near the bounce, which we ignored in our estimate (I24), becomes dominant due to a logarithmic divergence at the bounce point. As a result, $\langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() is the value of $\partial _\alpha B_1$
is the value of $\partial _\alpha B_1$![]() at the bounce point, which is of order $\alpha _a\, \partial _{\alpha \alpha }^{2} B_1(r, 0, 0) \sim \sqrt {\epsilon \Delta \lambda } B_0^{3/2}$
at the bounce point, which is of order $\alpha _a\, \partial _{\alpha \alpha }^{2} B_1(r, 0, 0) \sim \sqrt {\epsilon \Delta \lambda } B_0^{3/2}$![]() – importantly, note that the logarithmic divergence can only dominate when the bounce point is very close to $\alpha _b$
– importantly, note that the logarithmic divergence can only dominate when the bounce point is very close to $\alpha _b$![]() , that is, close by $\exp ( - R/(l_{bR,0,W} - l_{bL,0,W})) \ll 1$
, that is, close by $\exp ( - R/(l_{bR,0,W} - l_{bL,0,W})) \ll 1$![]() , and hence our estimate (I24) is valid for most orbits. The situation for a bounce point in $\alpha _b$
, and hence our estimate (I24) is valid for most orbits. The situation for a bounce point in $\alpha _b$![]() is similar, but in this case the sign of $\partial _\alpha B_1$
is similar, but in this case the sign of $\partial _\alpha B_1$![]() at the bounce point is the opposite to the one that we consider above, showing that $\langle \partial _\alpha B_1 \rangle _{\tau, W}$
at the bounce point is the opposite to the one that we consider above, showing that $\langle \partial _\alpha B_1 \rangle _{\tau, W}$![]() changes sign.
changes sign.

Figure 15. Path of integration of the integral in (I18) in the $(l, \alpha )$![]() plane (thin dark pink line), and area of integration for the integral in (I20) (shaded region). For large $J$
plane (thin dark pink line), and area of integration for the integral in (I20) (shaded region). For large $J$![]() , $\lambda$
, $\lambda$![]() must be close to $1/B_M$
must be close to $1/B_M$![]() , and hence it must have bounce points at a value of $B$
, and hence it must have bounce points at a value of $B$![]() close to $B_M$
close to $B_M$![]() . In the figure, we sketch the contour $B = 1/\lambda \approx B_M$
. In the figure, we sketch the contour $B = 1/\lambda \approx B_M$![]() as a red line (we have assumed that there is only one maximum of $B$
as a red line (we have assumed that there is only one maximum of $B$![]() ). The lines $\alpha _a$
). The lines $\alpha _a$![]() and $\alpha _b$
and $\alpha _b$![]() are marked in blue and green, respectively.
are marked in blue and green, respectively.
Using estimate (I24) in (I17), we find the estimate (I11) for the width of the layer. The estimate for the size of $g_{i, 1, W}^{\{1\}}$![]() in (I12) is obtained from the estimate for the width of the layer and the fact that the derivative of $g_{i, 1, W}^{\{1\}}$
in (I12) is obtained from the estimate for the width of the layer and the fact that the derivative of $g_{i, 1, W}^{\{1\}}$![]() with respect to $\Delta \lambda$
with respect to $\Delta \lambda$![]() must be such that property (5.36) is satisfied. Note, however, that property (5.36) is not imposed on the equation as a boundary condition. The boundary condition at $\Delta \lambda = 0$
must be such that property (5.36) is satisfied. Note, however, that property (5.36) is not imposed on the equation as a boundary condition. The boundary condition at $\Delta \lambda = 0$![]() is
is
The phase-space flows along $\alpha$![]() and across $J$
and across $J$![]() at large values of $\Delta \lambda$
at large values of $\Delta \lambda$![]() are the ones that ensure that property (5.36) is satisfied. These phase-space flows, determined by (7.23) and boundary conditions (I6) and (I7), are the boundary condition that we need to impose for large $\Delta \lambda$
are the ones that ensure that property (5.36) is satisfied. These phase-space flows, determined by (7.23) and boundary conditions (I6) and (I7), are the boundary condition that we need to impose for large $\Delta \lambda$![]() to solve (I17).
to solve (I17).