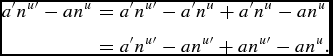1. INTRODUCTION
Empirical work plays a central role in economics. It is conducted in a variety of ways for various purposes. Some researchers collect stylized facts useful for economists. A famous example is Kuznets (Reference Kuznets1957), who documents the decline in agriculture associated with a rise in economic development. A more recent example is Aguiar and Hurst (Reference Aguiar and Hurst2007) who catalog the trends in the uses of time by American households. Other work uses nonstructural statistical models to measure things of interest to economists. Angrist and Krueger (Reference Angrist and Krueger1991) estimate the return to compulsory education using this approach. The impact of unemployment insurance benefits on the duration of unemployment is examined by Hagedorn et al. (Reference Hagedorn, Karahan, Manovskii and Mitman2015). Finally, some researchers estimate structural models. Classic examples are Keane and Wolpin’s (Reference Keane and Wolpin1997) study of the career decisions of young men and Berry, Levinsohn, and Pakes’ (Reference Berry, Levinsohn and Pakes1995) model of the automobile market. Sometimes, nonstructural statistical models are used to test economic theories. Here, care must be taken to ensure that the nonstructural model used provides an accurate representation of the theory to be tested. This is not always true. A case in point is the Bailey and Collins (Reference Bailey and Collins2011) test of the Greenwood, Seshadri, and Vandenbroucke (Reference Greenwood, Seshadri and Vandenbroucke2005) theory of the baby boom, to which the discussion now turns.
1.1. Greenwood, Seshadri, and Vandenbroucke (Reference Greenwood, Seshadri and Vandenbroucke2005)
Greenwood, Seshadri, and Vandenbroucke (Reference Greenwood, Seshadri and Vandenbroucke2005; henceforth GSV), hypothesize that the baby boom was partly due to a burst of productivity in the household sector. The idea is that the introduction of appliances (for example, clothes dryers, refrigerators, and washing machines) and new products (such as frozen and packaged foods and infant formula) reduced the cost of having children. Equally important was the home economics movement that introduced the principles of scientific management into the home. Albanesi and Olivetti (Reference Albanesi and Olivetti2014) argue that advances in obstetrics and pediatric medicine had much the same effect. By lowering the cost of having children, such forces promoted fertility.Footnote 1
1.2. Bailey and Collins (Reference Bailey and Collins2011)
Bailey and Collins (Reference Bailey and Collins2011; henceforth BC), argue that this hypothesis is not supported by evidence. BC’s empirical strategy is to regress fertility on household technology adoption rates, controlling for income and other variables. This is done for a set of U.S. counties. They assert that the GSV theory of the baby boom implies a positive coefficient of adoption on fertility, but a negative coefficient is found. This is interpreted as evidence against the theory. BC are, in fact, misinterpreting the theory. The negative correlation they find between the adoption rate for appliances and fertility is perfectly consistent with GSV’s model. The theory does suggest that households that adopt appliances should increase their fertility. To apply this theory at a more aggregated level, however, one needs to know which households will adopt appliances. BC ignore this factor. Suppose that technology adoption by households differed by income. In particular, postulate that richer households adopted electricity and appliances earlier than poorer ones. Richer families had lower levels of fertility than poorer ones. So, a regression may then associate low levels of fertility with the adoption of appliances, if the rich adopt new technology first.
BC also argue that the Amish, who limit the use of modern technology, had a baby boom. They conclude that the baby boom could not have been caused by technological progress, another point against GSV’s theory. The Amish may not have been as technology phobic as BC presume, as discussed later.
2. APPLYING THE GSV MODEL TO U.S. DATA
A simple version of the GSV model is fit to U.S. data using a minimum distance estimation procedure. The estimation incorporates an indirect inference strategy. It is shown that the regression coefficients estimated by BC are in fact consistent with the GSV model. Therefore, they do not constitute a challenge to the hypothesis that the baby boom resulted from a burst of time-saving technology adoption by households. Indirect inference is a simulation-based technique for estimating the parameters of a model. It was developed by Smith (Reference Smith1990, Reference Smith1993) and Gourieroux, Monfort, and Renault (Reference Gourieroux, Monfort and Renault1993). It is particularly useful here, since it implies that the regression coefficients estimated by BC can be used as moments to inform the estimation of the GSV model. In fact, the simulation exercise below results in a set of estimates for the GSV model consistent with (in fact, fitted using) the coefficients estimated by BC, even though BC interpret these coefficients as evidence rejecting the GSV model.
2.1. The Model
Start by specifying an economic model that is a static version of the GSV model, augmented with a technology adoption decision. The economy is composed of J counties indexed by j. In each county, there is a total of I households indexed by i. Let the wage rate of household i in county j be denoted by wij and assume that ln(wij ) ~ N(wj , σ A ), where ln(wj ) ~ N(0, σ B ). That is, the distribution of wages is lognormal in each county, with a county-specific mean, wj , and a common variance σ2 A . The distribution of county-specific mean wages is also lognormal with mean 0 and variance σ2 B .
The preferences of a household are represented by
\begin{equation*}
\mathbf {W}\left( c,n\right) =\phi U\left( c\right) +\left( 1-\phi \right) V\left( n\right) ,
\end{equation*}
where
\begin{equation*}
U\left( c\right) =\frac{c^{1-\eta }}{1-\eta }\text{ and }V\left( n\right) =n.
\end{equation*}
Two household technologies are available, old and new. The old technology is free and implies a time cost q for raising children. The new technology costs e units of the consumption good and implies a time cost z < q. Given a wage rate wij , the budget constraints for users and nonusers of the new technology are
\begin{equation*}
\begin{array}{ll}c+zw_{ij}n=w_{ij}-e, & \text{users (new technology),} \\
c+qw_{ij}n=w_{ij}, & \text{nonusers.} \end{array}
\end{equation*}
The first-order conditions for a maximum are
\begin{equation*}
\begin{array}{ll}\phi U^{\prime }\left( w-e-zw_{ij}n\right) zw_{ij}=\left( 1-\phi \right) V^{\prime }\left( n\right) , & \text{users (new technology),} \\
\phi U^{\prime }\left( w-qw_{ij}n\right) qw_{ij}=\left( 1-\phi \right) V^{\prime }\left( n\right) ,\text{ } & \text{nonusers.} \end{array}
\end{equation*}
Let Nu (wij ) denote the optimal fertility choice of a user and Nn (wij ) that of a nonuser. Similarly, let Cu (wij ) and Cn (wij ) denote the optimal consumption choices. The technology adoption decision for the new technology is
\begin{equation*}
a_{ij}= A(w_{ij})\left\lbrace
\begin{array}{l@{\hspace*{8pt}}l}
1,\text{ when }\mathbf {W}\left( C^{u}\left( w_{ij}\right) ,N^{u}\left( w_{ij}\right) \right) & \text{users (new technology);} \\
\quad >\mathbf {W}\left( C^{n}\left( w_{ij}\right) ,N^{n}\left( w_{ij}\right) \right) ,\\
0,\text{ otherwise,} & \text{nonusers.} \end{array} \right.
\end{equation*}
The income of household i in county j is yij = wij [1 − zNu (wij )] or yij = wij [1 − qNn (wij )], depending on whether or not the household is a user of the new technology. The fertility of the household is nij = Nu (wij ) or nij = Nn (wij ). The average income, fertility, and the proportion of users in county j are given by
\begin{equation}
y_{j}=I^{-1}\sum _{i=1}^{I}y_{ij}\text{, }n_{j}=I^{-1}\sum _{i=1}^{I}n_{ij}, \text{ and }a_{j}=I^{-1}\sum _{i=1}^{I}a_{ij}.
\end{equation}
2.2. Indirect Inference
The model described above is an economic, or structural, model. The model estimated by BC is not. Adopting the terminology used in the indirect inference literature, label BC’s model the “auxiliary model.” It consists of two equations:
\begin{equation}
n_{j}=\text{constant}+\tau _{1}a_{j}+\gamma _{1}y_{j}+\varepsilon _{j},
\end{equation}
and
\begin{equation}
\Delta n_{j}=\text{constant}+\tau _{2}\Delta a_{j}+\gamma _{2}\Delta y_{j}+\nu _{j},
\end{equation}
where Δ is the time-difference operator. A few points are worth mentioning at this stage. First, the representation of the BC model in equations (2) and (3) abstracts from all other controls, in addition to income, included in BC’s regression analysis. This is because the structural model does not feature heterogeneity with respect to the racial composition of counties, the sectorial allocation of workers, the urbanization rate, and so on. Second, BC’s model is misspecified. In general, adoption, fertility, and income are likely to be simultaneously determined as a function of the wage rates and technology prices facing the household. In the simple model presented, adoption and fertility determine the time spent raising children and therefore influence labor income.
The use of an auxiliary model as a tool to estimate a structural model is the novel idea underlying the indirect inference technique. The critical feature of the auxiliary model is that its parameters are estimated from observed data (as done by BC). The identical regression is estimated from the structural model using simulated data. Importantly, the auxiliary model does not need to be correctly specified for its moments to be useful in the estimation of the structural model—see Smith (Reference Smith, Blume and Durlauf2008).
Let τ ≡ (τ1, τ2) denote the vector of parameters of the auxiliary model and
$\widehat{\tau }$
denote the estimate obtained by BC using U.S. data. In particular, take
$\widehat{\tau } _{1}=-0.35$
and
$\widehat{\tau }_{2}=-0.15$
, which are based on the estimates presented in Tables 2 and 3 of Bailey and Collins (Reference Bailey and Collins2011).Footnote
2
Let θ ≡ (ϕ, η, e, q, σ
A
, σ
B
) denote the parameters to be estimated for the structural model and assume that the time-saving technology saves 20% of the time involved in child-rearing; that is,
\begin{equation*}
z=q\times 0.8.
\end{equation*}
Let
$\widehat{\tau }\left( \theta \right)$
denote an estimate of the auxiliary model based on data simulated from the structural model with parameters θ. To build
$\widehat{\tau }\left( \theta \right)$
, proceed as follows for a given θ.
-
1. Draw 500 realizations of wj using the distribution ln(wj ) ~ N(0, σ B ). For each realization of wj , draw 1,500 realizations of wij using the distribution ln(wij ) ~ N(wj , σ A ).
-
2. For each wij , compute the adoption and fertility decisions, aij and nij , respectively, as well as income yij . Compute the countywide averages described in equation (1).
-
3. Repeat step 2. Now, though, draw a new set of wages, and let w′ ij = wij × 1.0210 (i.e., a 2% annual increase in wages), and let e′ = e/1.0210 (i.e., a 2% annual decrease in the cost of the time-saving technology). Let the countywide averages so obtained be denoted by y′ j , n′ j , and a′ j . The term Δnj in equation (3) refers, therefore, to Δnj ≡ n′ j − nj , and, similarly, Δaj ≡ a′ j − aj and Δyj ≡ y′ j − yj .
-
4. Estimate the auxiliary model—that is, equations (2) and (3)—using the model-simulated data.
2.3. Minimum Distance Estimation
The parameters of the structural model are chosen using a minimum distance estimation procedure. Indirect inference is incorporated as part of this procedure. Specifically, the estimated parameters, θ, solve
\begin{equation*}
\min _{\theta }\lbrace \left[ \widehat{\tau }\left( \theta \right) -\widehat{\tau } \right] ^{2}+M\left( \theta \right) ^{\prime }M\left( \theta \right) \rbrace ,
\end{equation*}
where
\begin{equation*}
M( \theta ) \equiv \left[
\begin{array}{c}
var\left( \ln \left( y_{j}\right) \right) /0.17-1.0 \\[6pt]
var\left( \ln \left( y_{ij}\right) \right) /0.35-1.0 \\[6pt]
\left( IJ\right) ^{-1}\sum _{j=1}^{J}\sum _{i=1}^{I}a_{ij}/0.35-1.0 \\[6pt]
\left( IJ\right) ^{-1}\sum _{j=1}^{J}\sum _{i=1}^{I}n_{ij}/2.5-1.0 \end{array}\right].
\end{equation*}
The first part of the objective function is typical of the indirect inference approach: the distance between the estimate of the auxiliary model,
$\widehat{\tau }\left( \theta \right)$
, using model-generated data and the estimate obtained using actual data,
$\widehat{\tau }$
. The second part of the objective function ensures that the simulated data match a few key figures in the actual data: the variance of log income across counties, the variance of log-income across households in the U.S., the proportion of households equipped with the new technology, and the fertility rate of women in 1940. The variance of log-income across counties is obtained from the same source used by BC; i.e., Haines (Reference Haines2004). The earliest year in this dataset is 1950, and the figure for the variance of log-income across counties in that year is 0.17. The figure 0.35 for the variance of log-income across households is obtained from Census data. The proportion of households equipped with new technology varies from 23 to 55% in 1940 (see BC, Table 1). The average 0.35 is used. Finally, the total fertility rate of women between 15 and 44 years of age in 1940 is 2.2.
Table 1. Parameters of the structural model
2.4. Results
The estimated parameters are presented in Table 1.
Table 2 shows the model’s fit with respect to the targeted moments averaged over 200 simulations. The 95% confidence interval for
$\widehat{\tau } _{1}\left( \theta \right)$
is [ − 0.41, −0.17], and for
$\widehat{\tau }_{2}\left( \theta \right)$
, the 95% confidence interval is [ − 0.10, −0.004]. The estimate for e implies that the new technology costs 4% of the average income of households. The model, therefore, generates data consistent with BC’s significantly negative correlation between the rate of adoption and fertility, both in the cross-section and in a differenced regression. Yet, these findings are also consistent with a baby boom since the estimated structural model implies a 9% increase in average fertility over a 10-year period versus 32 (13)% between 1940 and 1950 (1950 and 1960) in the U.S. data (see BC, Table 1). Note that in the model the only cause for the baby boom is the endogenous adoption (from 30 to 97% of households) of the time-saving technology, prompted by the rise in wages and a decline in the price for technology.
Table 2. Targeted moments: Data and model
2.4.1. Decomposing the change in fertility
To better understand the results above, the following decomposition is useful. Fertility in county j can be expressed as
\begin{equation*}
n_{j}=a_{j}n_{j}^{u}+\left( 1-a_{j}\right) n_{j}^{n},
\end{equation*}
where aj is the proportion of adopters and nu j and nn j are the average fertility of users and nonusers, respectively:
\begin{eqnarray*}
n_{j}^{u} &=&\frac{\sum _{i=1}^{I}N^{u}\left( w_{ij}\right) }{\sum _{i=1}^{I} \mathbf {I}\left[ A\left( w_{ij}\right) =1\right] }, \\
n_{j}^{n} &=&\frac{\sum _{i=1}^{I}N^{n}\left( w_{ij}\right) }{\sum _{i=1}^{I} \mathbf {I}\left[ A\left( w_{ij}\right) =0\right] }.
\end{eqnarray*}
The change in fertility, n′ j − nj can then be written as (omitting the j-subscript for simplicity)
\begin{equation*}
\Delta n\equiv n^{\prime }-n=\left[ a^{\prime }n^{u\prime }-an^{u}\right] + \left[ \left( 1-a^{\prime }\right) n^{n\prime }-\left( 1-a\right) n^{n} \right] .
\end{equation*}
It can be shown that
\begin{equation*}
\Delta n=\underbrace{\kappa _{0}\Delta n^{u}}_{P_{1}}+\underbrace{\kappa _{1}\Delta n^{n}}_{P_{2}}+\underbrace{ \kappa _{2}\Delta a}_{P_{3}},
\end{equation*}
where
\begin{equation*}
\Delta n^{u}\equiv n^{u\prime }-n^{u},\Delta n^{n}\equiv n^{n\prime }-n^{n}, \text{ and }\Delta a\equiv a^{\prime }-a
\end{equation*}
are the changes in the fertility of users, nonusers, and the proportion of users, respectively, and where κ0 ≡ (a′ + a)/2, κ1 ≡ [(1 − a′) + (1 − a)]/2, and κ2 ≡ [(n u ′ − n n ′) + (nu − nn )]/2.Footnote 3
The first term, P 1, measures the contribution of the change in the fertility of users; the second term, P 2, measures the contribution of the fertility of nonusers; and the last term, P 3, measures the contribution of the change in the number of users. Table 3 reports the results of this decomposition. The first two terms reveal that the fertility of users and nonusers increase. The third (negative) term shows that the change in fertility is negatively related to the change in adoption. This term explains BC’s second (differenced) regression result; i.e., why the change in fertility is negatively related to the change in the fraction of adopters. The third term is negative because the fertility of users tends to be initially lower than that of nonusers (by 12% in model-generated data), because the first adopters have higher productivity and, therefore, lower fertility. The same is true in the U.S. data (using BC’s dataset). In 1940, for instance, the average general fertility rate in counties with above-average adoption is 69.6, while it is 86.47 for counties with below-average adoption— a 20% gap.
Table 3. Decomposition of the change in fertility (%)
2.5. Upshot
The exercise above shows that GSV’s model is not appropriately “tested” by regressions such as those used by BC. Such regressions are not implied by the model proposed by GSV on many grounds: They are linear, while the GSV model is not. They are based on static and incomplete theorizing about fertility alone, whereas in GSV’s model forward-looking people solve complicated dynamic optimization problems involving adoption, fertility, and time use, where current and future wages and prices will matter. Finally, they overlook the endogeneity of both adoption and income. A long time ago, Koopmans (Reference Koopmans1947, p. 161) railed against “measurement without theory:”
The various choices as to what to “look for,” what economic phenomena to observe, and what measure to define and compute, are made with a minimum of assistance from theoretical conceptions or hypothesis regarding the nature of the economic processes by which the variables studied are generated.
By dispensing with theoretical guidance it is easy to misinterpret the results from empirical measurement, in this case the observed correlation between fertility and adoption rates.
3. THE AMISH
According to BC, the Amish also experienced a baby boom. BC assert that the Amish do not use modern labor-saving technologies in their households. Taken at face value, this would seem to cast some doubt on GSV’s hypothesis. Certainly, the conventional wisdom is that the Amish are technology phobic. It is suspect, though.
As with many religious denominations, the Amish are not monolithic. All Amish orders live plain and simple lifestyles. Some are more welcoming of technology than others. The Swartzentuber and Andy Weaver Amish are more traditionalist than the Old Order and New Order Amish. As Table 4 shows, the Old Order and New Order Amish use a variety of appliances. Interestingly, all Amish households use washing machines to minimize the most burdensome household chore, washing clothes. An older washing machine used by the Amish is shown in Figure 1. An expert on Amish culture, D. B. Kraybill (Reference Kraybill1989, p. 235), relates the following on the Amish use of household technologies:
Figure 1. Old-fashioned Amish washer, Maytag (1920–1930). Source: Amish America (2015).
Table 4. Household technology adoption by affiliation
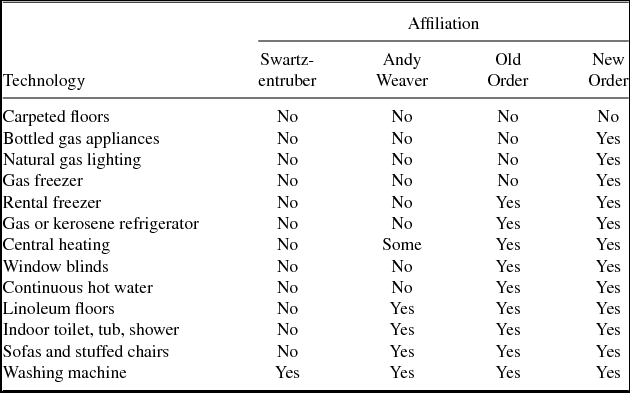
Source: Kraybill (Reference Kraybill, Kraybill and Olshan1994, Table 4.3).
Consider some of the household changes since 1940. Amish women no longer wash clothes in hand-operated machines. They use wringer washing machines powered by air, hydraulic, or gasoline engines. Gas refrigerators have replaced iceboxes, indoor flush toilets have replaced outdoor privies, hydraulic water pumps have replaced hand pumps, and gas water heaters have replaced the fire under iron kettles. Modern bathtubs have superseded old metal tubs. Kerosene lanterns have given way to gas lights. Wood-fired cookstoves have yielded to modern gas ranges. Hardwood floors and permanent-shine vinyl have replaced linoleum and rag carpets. Spray starch, detergents, paper towels, instant pudding, and instant coffee have eased household chores. Permanent-press fabrics have lifted the burden of incessant ironing. Although canning still predominates, some foods are preserved by freezing. Air-powered sewing machines are beginning to replace treadle machines.
In fact, today, in some areas the Amish are on the forefront of technology adoption. Holmes county, Ohio, hosts the largest Amish community in the world. About 80% of the Amish living there use solar power. Apparently, the Amish’s main concern regarding the use of electricity is its connection with a publicly shared grid, which reduces their independence from the outside world. This can be avoided through the use of diesel generators, windmills, and, in modern times, solar panels. To conclude, while there is some truth in the conventional wisdom that the Amish are technophobic, the true story is much more nuanced. To the extent that they adopted labor-saving practices in their homes, one would expect them to also experience a baby boom. Given their more limited use of appliances, their baby boom should have been more muted than that of the general population, which it was.
What else could have caused the Amish baby boom? The impact of World War II on the Amish population would have been more limited than on the rest of America, given their separation from the rest of society. Additionally, the Amish doctrine of nonresistance is central to their religion: “Resist not evil, but whoever shall smite thee on thy right cheek, turn to him the other also” (Matthew 5:39).Therefore, Amish men did not fight in World War II. It is interesting to note that according to conventional wisdom the Amish do not use any form of birth control, taking to heart the biblical injunction “be fruitful and multiply.” The presence of an Amish baby boom casts doubt on this (unless one believes that Amish women became more fertile during this period).
4. CONCLUSIONS
The baby boom that punctuated the secular decline in fertility in the United States and many countries in the mid-twentieth century is an active area of research in modern economics. Greenwood, Seshadri, and Vandenbroucke (Reference Greenwood, Seshadri and Vandenbroucke2005) propose that the baby boom was, in part, due to a burst of productivity in the household sector. Bailey and Collins (Reference Bailey and Collins2011), however, argue that this hypothesis is not supported by evidence. They use regression techniques to measure the correlation between technology adoption and fertility and find a negative correlation. Theoretically speaking, such a negative correlation is perfectly consistent with the theory proposed by GSV, however. It is likely that richer households adopted appliances and electricity before poorer ones did. Richer households had lower fertility levels than did poorer ones. Thus, simple regression analysis could associate the adoption of appliances and electricity with lower fertility levels. BC also argue that the Amish, who limit the use of modern technology, had a baby boom.
A twofold approach is taken to assess BC’s findings. First, a simplified version of the GSV model is fit to U.S. data using a minimum distance estimation procedure, which incorporates a modern indirect inference approach. Specifically, the BC regression results are added as a set of targets for the estimation exercise.Footnote 4 A negative correlation between adoption and fertility is found, just as in BC’s analysis, but also just as a simple version of GSV’s theory suggests could happen. Thus, the conclusion drawn by BC that this finding invalidates GSV’s model appears unfounded. This result should not be surprising to those familiar with Koopmans’ (Reference Koopmans1947) critique of measurement exercises performed without the guidance of economic theory. Second, evidence is presented that casts doubt on the presumed technology phobia of the Amish.
