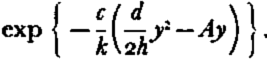Introduction
In this paper a new explanation is offered for the formation of a special kind of moraine which has been studied in great detail in the Thule area of GreenlandReference Bishop 1 , Reference Goldthwait 2 , Reference Nobles 3 and on Baffin Island.Reference Ward 4 , Reference Goldthwait 5 This type of moraine also occurs in the Antarctic.Reference Hollin and Cameron 6
The structure of the Thule-Baffin type of morainetFootnote † has been known for a long time and is discussed in detail by Chamberlin and Salisbury.Reference Chamberlin and Salisbury 7 They proposed the shear mechanism hypothesis to explain the origin of this phenomenon. Figure 1, which is taken from Bishop’s article (a similar picture is given in Ward’s paperReference Ward 4 ), serves to illustrate the mechanism as well as to describe the Thule-Baffin moraine. Figure 1 shows a cross-section of the edge of a cold ice sheet which contains a number of Thule-Baffin moraines. It is assumed that “active” ice from the interior of the ice sheet moves outward to the edge, where it is blocked by a zone of “dead” ice. The active ice rides over the dead ice by slippage over active shear planes. It is further assumed that these active shear planes extend to the bottom of the ice sheet and that debris from the bed can be scraped up, carried into the ice to form debris layers, and ultimately be transported to the upper surface along these planes. Of course, the edge of the ice sheet must be in an ablation zone if the debris is to be exposed at the upper surface. In time, a layer of dirt; rock, sand, etc. will accumulate at the upper surface. This layer then protects the ice underneath from further extensive ablation. A debris layer whose thickness is only of the order of 0. 5–1.0 m. will furnish such protection and can lead to the formation of ice hills approximately 15 m. in height. These debris-veneered ice hills are the Thule-Baffin moraines which are considered in this paper. They are often called shear moraines, because it has been taken for granted that the mechanism advanced in Figure 1 for their formation is the correct explanation.

Fig. 1. Diagram showing formation of successive moraines by the shear hypothesis. Figure is taken from Bishop’s paperReference Bishop 1
It is highly plausible to use the shear mechanism to explain the Thule-Baffin moraine. Yet there are serious difficulties associated with the theory which have not been pointed out in the literature and which will be discussed in the next section. Because of these difficulties, it is believed that another mechanism must be considered in order to give a satisfactory explanation of the phenomenon. In this paper it is proposed that the debris-carrying layers of ice are not formed by a scraping action of cold ice over the bed of an ice sheet, but rather are frozen into the ice by the freezing of water onto the bottom of the ice sheet.Footnote * The source of this water is ice which has been melted in the interior of the ice sheet (at the bottom surface) by geothermal heat and heat produced by the sliding of ice over the bed of the ice sheet. This water is forced by the pressure head to flow to the edges of the ice sheet, where it is refrozen to the bottom.
A third explanation for the formation of the Thule-Baffin moraine can be ruled out as highly unlikely. This hypothesis proposes that the debris-carrying ice layers originally were formed farther inland at the upper surface of the ice cap from rock, dirt, etc., which was derived from a protruding nunatak. This debris was buried later by snowfalls and eventually reappeared at the surface because of the ablation at the edge of the ice sheet. If this explanation were correct, one would not expect to find the Thule lobe of the Greenland Ice Sheet so completely fringed with Thule-Baffin type moraines. Instead one would see only an occasional moraine, each traceable to some local nunatak. It appears extremely probable that the debris which causes the Thule-Baffin moraines comes from the bottom of the ice sheet and not from the top surface. The fundamental question to be answered is: How does this debris become incorporated at the bottom surface into the ice mass?
Comments on the Shear Hypothesis
Appearance of the debris layers
There are a number of criticisms that can be made of the shear hypothesis. Perhaps the most serious of these is the appearance of the debris layers themselves. In the Thule area, tunnels have been dug into the ice sheet, through these layers. As a consequence, the layers are easily examined. Their appearance varies greatly. They can occur as solid layers of stone, sand, etc. up to about 0.5 m. in thickness. At the other extreme they may consist of a layer of slightly dirty ice containing a very fine dispersion of sand or dirt particles. These slightly dirty layers, which may be up to 1–2 m. in thickness, are quite common in occurrence.
Now it may be plausible that ice can scrape layers of solid debris into a shear plane. But it is highly unlikely that a meter-thick layer of very slightly dirty ice would be formed by such a scraping action. What would be the mechanism for dispersing the particles picked off the bed through such a thickness of ice? Yet, if the shear hypothesis is to be accepted, it must account for layers of ice containing a fine dispersion of particles. On the other hand, if water were being frozen to the bottom surface of an ice sheet, one would not be surprised to find that thick layers of this refrozen ice were sometimes slightly dirty.
The possibility of cold ice scraping up debris
A question that the shear hypothesis must answer satisfactorily is: Can debris be scraped from the bed? The present answer to this question is that it cannot if the bottom of the ice sheet is below the freezing point. Direct observation has shown that cold ice of an ice sheet does not slide over a boulder-strewn bed. GoldthwaitReference Goldthwait 2 has made this observation from the bottom of a vertical shaft dug from a horizontal tunnel which was excavated into the edge of the ice sheet in the Thule area. Although he found appreciable differential flow in the cold ice just above the ice sheet bed, there was no sliding over the bed. Even if an immeasurably small amount of sliding does occur, it is very ineffective in picking up debris. If sliding does occur, it is unable to remove even the moss covering the boulders at the bed. This moss was carbon dated as about 200 yr. old.Reference Goldthwait 2
If, in the interior of the ice sheet, the bottom is at the melting point, it could be possible for debris to be picked up. Direct observation by McCallReference McCall 8 has shown that sliding does occur at the bed of a temperate glacier. McCall’s study was made at the end of a tunnel dug to bedrock in a small Norwegian glacier. However, if one assumes that the debris is being scraped up in the interior of an ice sheet by temperate rather than cold ice, then one also must consider the mechanism that will be proposed for the formation of the debris layers.Footnote * This theory is based on the assumption that temperate ice does exist somewhere at the bottom of ice sheets which contain Thule-Baffin moraines. It might be mentioned that, from theoretical considerationsReference Wccrtman 9 as well as field observations, one expects that cold ice will not slide over a rock interface, but that ice at its melting point will.
Since direct observation has shown that cold ice does not slide over a rock when subjected to a stress which is sufficient to produce appreciable differential flow in the ice itself, it would appear highly unlikely that the shear hypothesis can work in an ice sheet which is cold everywhere. Against the field observation just mentioned, one might argue that cold ice will slide over a rock–ice interface if the shear stress in a particular area is sufficiently high. However, experiments of Raraty and TaborReference Raraty and Tabor 10 have shown that the shear strength of an ice-solid interface is usually of the order of 10 bars if the solid is stronger than cold ice and if the solid is wetable. This shear strength of the interface is an order of magnitude larger than the shear stresses which occur at the bottoms of glaciers and ice sheets (0.4 to 1.0 bar).
The shear across a debris layer
It is a requirement of the shear hypothesis (although not sufficient proof of the validity of this mechanism) that appreciable discrete shear displacements occur across the debris layers (or at least that a very large amount of differential flow occurs in a layer of finite thickness). The evidence for the existence of these shear displacements is conflicting. Butkovich and LandauerReference Butkovich and Landauer 11 observed no discrete shearing motion across a dirt layer exposed in a tunnel in the Thule area, although there was differential flow in the ice. HillyReference Hilty 12 made a similar observation in another tunnel in the Thule area. These measurements are evidence against the shear hypothesis. On the other hand, WardReference Ward 4 has published a photograph of the surface of the Barnes Ice Cap which shows a discrete shear across a dirt band. It can be argued, however, that Ward’s observation was made in the summer time and was only a surface observation. During the Summer the surface layer is at the melting point. According to the sliding mechanism here proposed,Reference Wccrtman 9 a discrete shear displacement of ice across a solid debris layer can occur when the ice is at the melting point. The shear seen by Ward may have occurred, therefore, only to those depths for which the ice is at the melting point.Footnote *
Even if further observations do show that appreciable shear does occur across debris layers, this result in itself would not be sufficient to prove the shear hypothesis. A condition necessary to the proof of the shear hypothesis would indeed have been met, but not a sufficient condition. Suppose that the debris layers were formed by a mechanism other than scraping. Then, let a layer be subjected to a stress which has a shear component such as is always found within a glacier or ice sheet. If the debris layer has the property that discrete shear takes place within it when such a stress is applied, this shear will occur regardless of how the debris layer was formed originally. A measurement of the shear across a debris layer thus yields information on a property of debris layers, but reveals nothing of their formation.
The geometry of the debris layers
Another criticism of the shear hypothesis is that it suffers from an “embarrassment of riches.” If one accepts the shear hypothesis, one can account for a few debris layers. But can one really explain the very large number of debris layers that actually are observed? For example, in the ice tunnel constructed in 1959 next to Camp TUTO in the Thule area, one can see countless numbers of distinct dirt and debris layers within a distance of about 20 m. These layers often are separated from each other by distances of the order of millimeters. How could such a fine spacing be achieved by the shear model of Figure 1? One way might be for one “active” shear plane to start operation and carry debris to the surface. It then becomes “inactive” and another plane very close to it becomes active and carries a load of debris to the surface. In turn, the second plane stops and another nearby plane becomes active. An explanation along these lines would be difficult to accept since one must explain why one shear plane is active and another inactive when the planes are separated by distances of the order of only 0.01 to 1.00 m.
On the other hand, one might propose that many closely spaced shear planes commence at about the same time to carry debris to the surface. But again one is in difficulties. The sequence that would be followed in this case is shown in Figure 2. Since it must be assumed that the spacing of the planes is close, one shear band will catch up with another, as shown in Figure 2. Thus, the slope of the shear planes will increase the farther one goes back into an ice sheet. In the tunnel dug near Camp TUTO the slope of the “shear” planes actually decreases the farther one goes into the tunnel, the opposite of the behavior predicted by this explanation.

Fig. 2. Sequence of events after the start of several closely spaced shear planes: (a) Planes just starting lo bring up debris from the bottom; (b) Intermediate stage, the shear layers have just caught up to each other by shearing over the bed; and (c) A late stage, in which the layers have joined each other and only a single layer can exist at the bottom
Although the shear hypothesis might account for debris planes which are separated by distances of the order of the thickness of an ice sheet (near the edge of the Thule ice lobe the separations would be of the order of 50 to 100 m.), it appears to be difficult to explainFootnote * with this mechanism the small scale separations which are actually observed. There really are too many “shear” planes present to be accounted for by the shear hypothesis.
The actual upward-curving form of an individual debris layer, which is approximately that shown in Figure 1, can be explained without the assumption that discrete shear occurs across a debris layer. It has been known for a long time from arguments based on the principle of conservation of mass that the flow lines of ice in an ablation area must go upwards. (The shape of flow lines in glaciers and ice sheets has been discussed recently by Nielsen and Stockton.Reference Nielsen and Stockton 13 ) Thus, even without the shear hypothesis, it is possible to understand the general shape of the debris layers.
Freezing Model
As an alternative to the shear hypothesis the mechanism illustrated in Figure 3 is proposed to explain the formation of Thule-Baffin moraines. Figure 3 shows a cross-section of an ice sheet whose edge is frozen to its bed, the actual situation existing at the Thule ice lobe and at Baffin Island. It is assumed that farther inland from the edge the bottom is at the melting point. This second region can be divided into two parts. In the furthermost inland part, the combination of geothermal heat and heat produced from sliding is greater than can be conducted down a temperature gradient in the ice. As a consequence ice is melted to water. This water is forced by the pressure gradient outward to the edge of the ice sheet. As it moves outward, it enters into a region where the temperature gradient in the ice can conduct away more heat than is produced by any sliding or comes from the geothermal heat. In this region the water refreezes to ice and rejoins the ice sheet. The bottom of the ice sheet will still be at the melting point in this region; the extra heat required to keep it at this temperature comes from the latent heat of freezing which is given up as the water freezes.

Fig. 3. The freezing model. a cross-section of an ice sheet is shown. The edge of the ice sheet is frozen to the bed and the 0° C. isotherm reaches the bottom of the ice sheet inland from the edge
The scheme presented in Figure 3 should always occur in any ice sheet whose edge is frozen to the bed and whose bottom surface at some positions in the interior is at the melting point. Thus, if direct measurements show that in the interior of a cold ice sheet the bottom surface is at the melting point, and that no water is escaping underneath the ice sheet, one can be sure that ice is being formed at certain places at the bottom surface.
Under steady-state conditions, the model of Figure 3 probably would not lead to the inclusion of solid dirt layers into the ice sheet, since ice would merely form at the ice surface. However, no glacier or ice sheet is ever in a completely steady-state condition. The thickness, among other things, varies as a function of time. A change in thickness changes the stress acting on the bed and, hence, affects the speed of sliding and, thus, the amount of heat available to melt ice or retard the freezing of water. This change will cause a shift in the position of the border between the region where the ice sheet is frozen to the bottom and where it is at the melting point. Figure 4 shows how a cyclic shift in the amount of heatFootnote * produced by sliding will lead to a freezing-in of debris. Since the border being considered is simply the point at which the 0° C. isotherm ceases to coincide with the bottom of the ice sheet, a shift of this border inland simply causes the zero point isotherm to descend into the material upon which the ice is resting. Debris can thus be frozen onto the bottom of the ice sheet. If the border shifts towards the edge of an ice sheet, the region in which water is being frozen to the bottom of the ice sheet is extended. If debris has already been frozen to the bottom, the new ice will have to start forming underneath this frozen-on debris, for it is here that the temperature is at the melting point. The debris will therefore be incorporated into the ice sheet with ice surrounding it, as shown in Figure 4. Through numerous repetitions of the cycle, a larger number of debris layers can be incorporated into the ice of an ice sheet lying on unconsolidated material. The thickness of these layers depends on the time frequency of the cyclic change and can have any value. The length of the debris layers depends on the magnitude of the change in slope or thickness of the ice sheet, as this change controls the distance the border in Figure 4 will shift.

Fig. 4. Illustrating how debris is incorporated into the ice sheet under non-steady state conditions: (a) The starting point. To the left of point x2, the 0° C. isotherm descends into the debris which makes up the bed. To the right of point x2, the bottom is at the melting point and water is being frozen to the bottom surface. Water flowing from the right permits the bottom to be kept at 0° C., but the water supply is exhausted at point x2; (b) Less water is flowing from the right and the point of descent of the 0° G. isotherm has shifted to the right; (c) A greater supply of water now flows from the right. Water now freezes to the 0° C. isotherm position given in (b) and pushes up into the ice the debris frozen on the bottom shown in (b). Point x2, which marks the limit of the flow of water, has moved to the left; and (d) The cycle repeated after many times with a number of debris layers fixed into the ice
Once horizontal layers of debris are incorporated into the ice, they flow with the ice. If the edge of an ice sheet is an ablation zone, as is the case in the Thule area and on Baffin Island, the flow lines of ice have to come up to the surface in this region. Hence the debris layers will become exposed in the ablation area and can form Thule-Baffin moraines.
Theory
In this section are set down some formulae which will indicate the conditions under which the freezing mechanism will operate. Of course, it would be desirable to be able to take known field data and prove conclusively that this mechanism has led to the formation of existing moraines. That hope, however, cannot be satisfied with the measurements at present available.
Consider an ice sheet whose thickness across a particular cross-section is given by h(x), where x is horizontal distance. Let a(x) be the accumulation or ablation at the position x; this function has a positive value for accumulation and a negative value when there is ablation.
Under steady-state conditions, the heat flowing down the temperature gradient at the bottom surface is exactly equal to the sum of the geothermal heat, Q g , the heat produced by any sliding, Q 8, and any heat given off or absorbed by the freezing of water or melting of ice at the bottom surface. Values of the geothermal heat vary between different places on the Earth.Reference Bullard and Kuiper 14 An average value listed by BullardReference Bullard and Kuiper 14 is 39 cal. cm.−2 yr.−1. The heat of sliding is given by the equation

where J is the mechanical equivalent of heat (J = 4.185 × 107 erg cal.−1), V is the velocity of sliding, and τ is the shear stress acting at the bottom surface which produces the sliding. To a good approximation, this shear stress is equal to ρgh α, where ρ is the average density of ice and α is the slope of the upper surface of the ice sheet. The velocity, V, itself also depends on shear stress. A theoretical expressionReference Wccrtman 9 for the velocity is
where m and B are constants. Reasonable values of these constantsReference Weertman 15 are m = 2 and B = 81 m. yr.−2 bar−2. Since typical valuesReference Orvig 16 , Reference Ward 17 of the shear stress on the bed of glaciers and ice sheets are in the range of 0.4 to 1.0 bar, equation (2) would give velocities of the order of 13 to 81 m. yr.−1. From equation (1), therefore, one would expect the heats of sliding to be of the order of 13 to 190 cal. cm.−2 yr.−1. These values are about the same order of magnitude as the geothermal heat.
Under steady-state conditions, the heat flowing through the bottom interface of an ice sheet must balance the heat from the geothermal heat flow, the heat produced by sliding, and the heat given up or absorbed by any melting or freezing at the bottom. If A(x) represents the thickness of ice being frozen to the bottom surface (it would be negative if the ice is melting) and γ(x) represents the vertical temperature gradient at the bottom surface, the condition for steady-state heat flow at the bottom interface is given by the following equation:
where S is the heat of fusion (S = 72 cal. cm.−3 ice) and k is the coefficient of heat conductivity of ice (k = 1.7 × 105 cal. cm.−1 yr.−1° C.−1).
The temperature gradient at the bottom surface can be calculated if the temperatures at the top and bottom surfaces are known. This calculation has been done by RobinReference Robin and de 18 for the case where heat flow in the horizontal direction (the x direction) can be neglected and where the longitudinal strain rate of the creep flow of ice is not a function of vertical distance. Since this longitudinal strain rate is approximately a/h, Robin was able to obtain the following equation for γ:

where ΔT is the temperature difference between the top and bottom surfaces and is considered to be positive if the bottom is warmer than the top, and h* is a “compensated” thickness given byFootnote †

where c is the specific heat of ice (c = 0.45 cal. cm.−3). When the longitudinal strain rate is zero (and there is no melting or freezing at the bottom surface) this “compensated” thickness is equal to the actual thickness of the ice sheet.
If equation (4) is substituted into equation (3) one obtains

If the bottom surface is below the freezing point, so that A = Q s = 0, this equation will determine the bottom temperature, if the values of the temperature at the upper surface and the geothermal heat are known. On the other hand, if the bottom surface is at the melting point, so that A ≠ 0, equation (6) will determine the amount of melting or freezing once the temperature of the top surface and the amount of sliding are fixed.
From equations (5) and (6) the conditions can be determined under which the bottom of an ice sheet can be at the melting point. As a very simple example, suppose that the accumulation rate is zero. It can be seen from equation (6) that the bottom surface will be at the melting point when the ice thickness is equal to h 0, where

and ΔT is taken to be the difference in temperature between the melting point of ice and the upper surface temperature. When equation (7) is valid, the heat conducted through the ice is exactly equal to the geothermal heat plus the heat of sliding. The ice at the bottom is at the melting point, but neither ice is melting nor is water freezing there. If the ice thickness is greater than h o, less heat can be conducted through the ice than is being supplied by the geothermal heat and the sliding heat. In this situation, ice melts off the bottom surface to make up the heat balance. If the ice thickness is less than h o, more heat is conducted away than is being supplied. The bottom can remain at the melting point only if water is being frozen onto the bottom surface. However, if no water is available to give up its latent heat by freezing, the bottom surface has to be at a temperature lower than the melting point of ice and the ice sheet is frozen onto its bed. Thus, when the accumulation is zero, the thickness h o separates the condition of freezing from that of melting.
Now consider the more general case when the accumulation or ablation is not zero. Corresponding to any particular set of values for ΔT, Q g, and Q s , there will be a curve on a plot of a versus h which divides freezing conditions from melting conditions. This curve is determined by setting A equal to zero in equation (6). One obtains the equation

where β = −ca/2kh and h 0 is given again by equation (7). This equation can be written as

For large values of h and a, equation (8) reduces to

Once h 0 has been found from equation (7), equations (9) and (10) determine a curve of a versus h. Figure 5 shows such curves for various values of h 0. Also indicated in Figure 5 are the temperature differences, ΔT, which correspond to these values of h 0 when Q g is the average geothermal heat of 39 cal. cm.−2 yr.−1 and Q s is taken to be equal to Q g . This value of the sliding heat corresponds to a shear stress of 0.58 bar and a sliding velocity of 27 m.yr.−1 (or any other combination of stress and sliding velocity whose product is the same)

Fig. 5. A plot showing freezing and melting conditions at the bottom of we sheets. Each curve is calculated for a different value of h0 = k ΔT/(Q + Qs), where k is the thermal conductivity of ice, ΔT the difference between the melting point of ice and the upper surface temperature of an ice sheet, and Qg, and Qs are the geothermal heat and the heat produced by the sliding of ice over the ice sheet bed. The region of the figure to the right of a particular curve corresponds to conditions where melting occurs, and the region to the left where freezing can take place
If the values of the ice thickness and accumulation or ablation in a region of an ice sheet are such that they correspond to a point lying to the right of the appropriate curve in Figure 5, the bottom of the ice sheet is melting away. If the thickness and accumulation are such that the point lies to the left the bottom is either frozen to the bed or water is freezing to the bottom. Hence, if the temperature at the upper surface and the geothermal heat and heat of sliding are known, it is possible to tell from the measurements of ice thickness and rate of accumulation or ablation whether or not it is possible for ice at the bottom to be melting or freezing.
The bottom surface of an ice sheet which is located in a region corresponding to a point in the freezing zone can remain at the melting point only if there is a water supply available. The melting zone can supply this water if a hydrostatic pressure head exists to push water from one region into the other. From Figure 5 it can be seen that, other things being equal, the thicker parts of an ice sheet are more likely to be in a melting zone, if a melting zone does exist. The greater weight of ice in the melting zone will supply the necessary pressure head to move water into the freezing zone.
The principle of the conservation of mass enables one to calculate the extent of the region in the freezing zone where the bottom of an ice sheet is at the melting point of ice. That is, all the water created in the melting zone must be turned back to ice in the freezing zone if no water is to escape from underneath a cold ice sheet. The amount of ice, A(x), which is either being melted from, or frozen to, the ice sheet in the regions where the ice is at the melting point is given by equation (6):

Consider how equation (11) can be applied to an actual problem. Suppose a two-dimensional ice sheet (center at x = 0 and edges at x = +L) has a melting zone extending over the distance from x 0 to x 1, where x 0 < x 1 < L. What would be the extent of the freezing zone in which the ice at the bottom of the sheet is at the melting point? In order to satisfy the principle of conservation of mass, when no water escapes from underneath the ice sheet, the following equation must be obeyed:

where the first integral covers the melting zone and the second the freezing zone. This equation fixes the value of x 2 (x 2 < L). Since ΔT (the difference between the melting point of ice and the surface temperature) and h* (determined from the thickness of ice and the rate of accumulation) can be determined as functions of distance, once the heat of sliding and the geothermal heat are known, equations (11) and (12) determine uniquely the extent of the freezing zone at the melting point. At distances greater than x 2 the bottom of an ice sheet is below the freezing point of ice and the sheet is frozen to its bed. In this region, there is no water available to freeze onto the bottom and hence raise the ice temperature to the melting point.
Discussion
In the previous section, it has been shown that under certain conditions a part of the bottom surface of a cold ice sheet may be at the melting temperature of ice and that, in this part, ice can be melting away from the bottom in some parts and water can be freezing onto the bottom in the other parts. Of course, one would like to know if the ice sheets which contain Thule-Baffin moraines meet the special conditions that lead to the ice at the bottom surface being melted in one place and refrozen in another. Since the edges of the Barnes Ice Cap on Baffin Island and of the Thule lobe of the Greenland Ice Sheet are known to be frozen to their beds, it is only necessary to show that in some inland regions the conditions are such that the bottom is at the melting point (or more exactly, was at the melting point during the time the debris which forms the moraines on the edges of these ice sheets was brought into the ice). Unfortunately, from the field evidence at hand, it is not possible to prove conclusively whether or not there exist regions on either of these ice sheets where the bottom surface is at the melting point of ice.
Consider first the Barnes Ice Cap on Baffin Island. The upper surface of the Barnes Ice Cap appears to be at −10.7° C. from one measurement made by Ward;Reference Ward 4 its thickness goes from 0 to about 450 m.;Reference Orvig 16 its accumulation ranges from −170 to +20 cm. of ice yr.−1, the value depending on the elevation of the upper surface. From these data, Figure 5 would predict that the bottom surface in the interior of the ice cap definitely is at the melting point. In order to arrive at this conclusion, consider the curve of Figure 5 marked ΔT = 10° C. This curve represents a temperature close to the actual temperature of −10.7° C. Any thickness greater than 280 m. corresponds to a point in the melting region, even for the maximum rate of accumulation of 20 cm. of ice yr.−1. One must remember, however, that the curves in Figure 5 were calculated on the assumption that the heat of sliding is equal to the geothermal heat, and it was assumed further that the geothermal heat is equal to 39 cal.cm.−2yr.−1. Suppose the estimate of the heat passing through the bottom is too great by a factor of 2. Then the curve to be considered is not the one marked 10° C., but rather the curve marked 20° C. In this case, it is open to question whether any part of the Barnes Ice Cap lies in the melting region and it may well be that the entire ice cap is frozen to the bottom. The only way one could really be sure is to sink bore holes to the bottom of the ice cap and actually measure the temperature.
The same uncertain situation occurs in the Thule ice lobe. The thickness of this ice has been only partially measured. RoethlisbergerReference Roethlisberger 19 found a thickness of 260 m. at a distance of 5 km. inland from the edge. (The ice sheet is about 33 km. wide and a somewhat greater thickness can be expected farther inland.) Accumulation and ablation ratesReference Schytt 20 , Reference Griffiths 21 depend on position and range from about −100 cm. of ice yr.−1 close to the edge to 70 cm.yr.−1 in the central region of the ice sheet. The temperature in the ablation zoneReference Schytt 20 near the edge of the ice sheet is about −12° C. Temperatures have been measuredReference Schytt 20 in the inland region at two points down to a depth of 9 m. The temperatures at 9 m. seem to be of the order of −3° to −6° C.Footnote * If these inland temperatures are representative values and if the curves of Figure 5 are valid, there is no question but that the bottom surface in the interior of the Thule ice lobe is at the melting point. On the other hand, if these temperatures are not reasonable and if other values of the heat of sliding and the geothermal heat are used, it is quite possible that the ice sheet is frozen everywhere to its bed.
Another problem connected with the determination of the temperature at the lower surface of a cold ice sheet concerns the question as to whether or not the ice is actually sliding over the bottom bed. If no sliding occurs, no heat will be produced by this mechanism. It is thus conceivable to have an ice sheet which would be frozen to its bottom surface, if the heat of sliding were not available, but whose lower surface would be at the melting point if this heat were present. Once the ice sheet started to slide, the heat produced would keep the bottom surface at the melting point and permit the sliding to continue. If the sliding were stopped, the ice sheet would refreeze to its bed and no further sliding would occur. In the absence of direct measurements, a knowledge of the past history of such an ice sheet would be necessary in order to determine whether or not the bottom is at the melting point.
Conclusion
It is concluded that there are a number of objections that can be raised against the shear hypothesis for the formation of a type of moraine found on Baffin Island and in Greenland. It is further concluded that in certain situations it is possible for ice to be formed at the bottom of an ice sheet and that this accretion of new ice can lead to a freezing-in of loose debris lying on the bed of the ice sheet. In turn, this frozen-in debris can result in the formation of moraines in the ablation areas of an ice sheet.
Although one can demonstrate the possibility that the moraines found on the Thule ice lobe in Greenland and on the Barnes Ice Cap of Baffin Island are formed by the mechanism proposed here, it is not possible from the field data at hand to prove conclusively that these moraines have been so formed.
Acknowledgements
I wish to thank Mr. James Bender for the opportunity of seeing at first hand the moraines near Thule, Greenland. I am indebted to him and to Dr. Hans Roethlisberger and Dr. George Swinzow for informative discussions and arguments on the formation of these moraines.
New Method of Citing References In Articles for the Journal of Glaciology
The current method of citing references in articles published in the Journal of Glaciology involves the use of numbered superscripts, which appear in numerical order throughout the text. Individual references in the list at the end of the article have been set out in corresponding order.
For a number of stylistic and technical reasons, the Editors of the Journal of Glaciology have decided to adopt a simpler system of referencing which will be introduced in the next issue of the Journal (Vol. 4, No. 31).
In the new system, reference in the text of an article to other papers would he made according to the author’s surname and date of publication of that paper. All references given in the list at the end of the article would be in alphabetical order and in each reference the full pagination of the paper would be given. By using this new method it is possible for an author to ease the already heavy burden of the serious reader by citing the individual page references of statements attributed to another author. This is especially important when the quoted paper is abnormally long or complex in layout. It also provides the author with the opportunity of either repeating the same page reference or making references to different pages in the same paper without further entries in the reference list.
References to personal communications have previously appeared in the reference list at the end of the article. These would now be set as footnotes following an asterisk or other indication in the text.
Correct referencing is of no mean importance, because it adds accuracy to the article and enables the reader to trace the cited reference easily. Since the correctness of references is the direct responsibility of the authors, the several examples given below should be of some assistance to intending authors.
In the following list a selection of examples is set out according to the type of reference cited giving (a) the correct reference in the text and (b) the correct form of reference in the list at the end of the article.
1. One author
-
a.
-
i. “… quoted by Smith (1960).”
-
ii. “Glaciological studies in South Georgia during the I.G.Y. (Smith, 1960) and in the South Orkney Islands …”
-
iii. (Smith, 1960, p. 711); (Smith, 1960, p. 711–13).
-
iv. (Smith, 1960, fig. 5).
-
v. (Smith, 1960[a]); (Smith, 1960 [a], [b]).
-
vi. Smith. J. 1960[a].Glacier problems in South Georgia., Journal of Glaciology, Vol. 3, No. 28, p. 705–4.
-
2. Two authors
-
a.
-
i. “…quoted by Wilson and Crary (1961).”
-
ii. (Wilson and Crary, 1961).
-
iii. Wilson, C. R., and Crary, A. P. 1961. Ice movement studies on the Skelton Glacier., Journal of Glaciology. Vol. 3, No. 29, p. 873–78.
-
3. More than two authors
-
a. (Scholander and others, 1961).
-
b. Scholander, P. F., and others. 1961. Composition of gas bubbles in Greenland icebergs, by P. F. Scholander, E. A. Hemmingsen, L. K. Coachman and D). C. Nutt. ,Journal of Glaciology. Vol. 3, No. 29, p. 813–22.
4. Papers in the press
-
a. (Glen, in press).
-
b. Glen, J. W. In press. Measurement of the strain of a glacier snout. Union Géodésique et Géophysique Internationale. Association Internationale d’Hydrologie Scientifique. Assemblée générale de Helsinki, 25–7–6–8 1960. Commission des .Neiges et Glaces.
5. Books of known publication date
-
a. (Zeuner, 1959)
-
b. Zeuner, F. E. 1959. The Pleistocene period. [Second edition.] London, Hutchinson.
In the case of books and monographs total pagination is not given.
6. Books of unknown or ambiguous publication date
In this case the “copyright date” should be used but failing that the date printed at the end of the preface could be taken as evidence of the publication date.
-
a. (Edwardes, [1961]).
-
b. Edwardes, M. [1961.] A history of India from the earliest times to the present day. London, Thames and Hudson.
7. Publication date differing from year of a conference volume
The publication date should be used in the reference.
-
a. (Meier, 1958).
-
b. Meier, M. F. 1958. The mechanics of crevasse formation. Union Géodésique et Géophysique Internationale. Association Internationale d’Hydrologie Scientifique. Assemblée générale de Toronto, 3–14 sept. 1957, Tom. 4, p. 500–08.
8. Journal with ambiguous publication date differing from stated year of volume
-
a. (Kosack, [1956]).
-
b. Kosack, H.-P. [1956.] Zur Frage des Wasserhaushalts in der Antarktis. Polarforschung, Bd. 3, 24 Jahrg., Ht. 1/2, 1954, p. 286–94.
9. A paper forming a chapter or part of a book
-
a. (Sorge, 1935, p. 259).
-
b. Sorge, E. 1935. Glaziologische Untersuchungen in Eismitte. (In Brockamp, B., and others. Glaziologie. Leipzig, F. A. Brockhaus, p. 62–270. (Wissenschaftliche Ergebnisse der deutschen Grönland-Expedition Alfred Wegener 1929 und 1930/1931,Bd 3.))