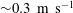1 Introduction
Impacting drops are present and important in many natural and industrial processes and have thus been a research topic of continued interest (Josserand & Thoroddsen Reference Josserand and Thoroddsen2016). A drop impacting a solid or liquid surface is deformed by the rise in pressure in the intervening gas prior to impact. As the drop deforms, the location of the maximum pressure in the gas layer moves from under the drop centre radially outwards, causing a small disc of air to be entrapped upon contact. In recent years, there have been many studies investigating the physics of the air-disc entrapment for drops impacting solid surfaces (see Thoroddsen et al. Reference Thoroddsen, Takehara, Etoh, Ootsuka and Hatsuki2005; Mandre, Mani & Brenner Reference Mandre, Mani and Brenner2009; Hicks & Purvis Reference Hicks and Purvis2010; Bouwhuis et al. Reference Bouwhuis, van der Veen, Tran, Keij, Winkels, Peters, van der Meer, Sun, Snoeijer and Lohse2012; de Ruiter et al. Reference de Ruiter, Oh, van den Ende and Mugele2012; van der Veen et al. Reference van der Veen, Tran, Lohse and Sun2012; Li & Thoroddsen Reference Li and Thoroddsen2015; Philippi, Lagrée & Antkowiak Reference Philippi, Lagrée and Antkowiak2016; Langley, Li & Thoroddsen Reference Langley, Li and Thoroddsen2017; Li et al. Reference Li, Langley, Tian, Hicks and Thoroddsen2017; Langley et al. Reference Langley, Li, Vakarelski and Thoroddsen2018).
For low impact velocities, Kolinski, Mahadevan & Rubinstein (Reference Kolinski, Mahadevan and Rubinstein2014a ) and de Ruiter, van den Ende & Mugele (Reference de Ruiter, van den Ende and Mugele2015) showed that a drop can rebound from even hydrophilic surfaces without contacting the solid surface. Mandre et al. (Reference Mandre, Mani and Brenner2009) postulated that the surface tension of the drop would stabilize the kink at the edge of the dimple, causing it to skate along the surface, avoiding contact even for high impact velocities, which was inconsistent with the observations of Thoroddsen et al. (Reference Thoroddsen, Takehara, Etoh, Ootsuka and Hatsuki2005). Kolinski et al. (Reference Kolinski, Rubinstein, Mandre, Brenner, Weitz and Mahadevan2012) used frustrated total internal reflection to further investigate the skating behaviour and found that the skating behaviour was fleeting, lasting only a few microseconds, and was difficult to observe for drops released from more than 4 cm height.
Taking into consideration the viscosity of the drop, Kolinski, Mahadevan & Rubinstein (Reference Kolinski, Mahadevan and Rubinstein2014b
) found that for impact velocities
![]() ${<}1~\text{m}~\text{s}^{-1}$
and viscosities between 1–100 cSt, the drop initially spreads on top of a thin layer of air. Langley et al. (Reference Langley, Li and Thoroddsen2017) explored a much larger range of viscosities (
${<}1~\text{m}~\text{s}^{-1}$
and viscosities between 1–100 cSt, the drop initially spreads on top of a thin layer of air. Langley et al. (Reference Langley, Li and Thoroddsen2017) explored a much larger range of viscosities (
![]() $10{-}2\times 10^{7}~\text{cSt}$
) and velocities (
$10{-}2\times 10^{7}~\text{cSt}$
) and velocities (
![]() $0.3{-}5.2~\text{m}~\text{s}^{-1}$
) impacting on smooth solid surfaces, and found that higher-viscosity drops glide over a thin layer of air even at high impact velocities of
$0.3{-}5.2~\text{m}~\text{s}^{-1}$
) impacting on smooth solid surfaces, and found that higher-viscosity drops glide over a thin layer of air even at high impact velocities of
![]() ${\sim}5~\text{m}~\text{s}^{-1}$
. The thin gliding layer was
${\sim}5~\text{m}~\text{s}^{-1}$
. The thin gliding layer was
![]() ${<}160~\text{nm}$
thick and the drop could glide for several radii of the initial air disc. During gliding, the air layer ruptured in numerous random locations. The localized contacts initially wet extremely rapidly, grow together, entrapping microbubbles and eventually fully entrapping the central air disc.
${<}160~\text{nm}$
thick and the drop could glide for several radii of the initial air disc. During gliding, the air layer ruptured in numerous random locations. The localized contacts initially wet extremely rapidly, grow together, entrapping microbubbles and eventually fully entrapping the central air disc.
Impacts onto liquid films and pools have long been investigated, with many studies focusing on splashing, bouncing, and bubble entrapment due to various mechanisms (see Thoroddsen Reference Thoroddsen2002; Josserand & Zaleski Reference Josserand and Zaleski2003; Thoroddsen, Takehara & Etoh Reference Thoroddsen, Takehara and Etoh2003; Howison et al. Reference Howison, Ockendon, Oliver, Purvis and Smith2005; Yarin Reference Yarin2006; Hicks & Purvis Reference Hicks and Purvis2011; Marston, Vakarelski & Thoroddsen Reference Marston, Vakarelski and Thoroddsen2011; Thoroddsen et al. Reference Thoroddsen, Thoraval, Takehara and Etoh2011, Reference Thoroddsen, Thoraval, Takehara and Etoh2012; Tang et al. Reference Tang, Saha, Law and Sun2018). Tran et al. (Reference Tran, De Maleprade, Sun and Lohse2013) and Hendrix et al. (Reference Hendrix, Bouwhuis, van der Meer, Lohse and Snoeijer2016) studied the initial impact dynamics and entrapment of air and found a unified scaling for the entrapped bubble volume for drop impacts onto solid or liquid surfaces, as well as for solid sphere impacts onto liquid pools, that incorporates the number of free interfaces involved in the impact.
The aim of this study is to further probe the gliding behaviour of large-viscosity drops during impacts onto liquid films of the same liquid. Using ultra-high-speed interferometry, we measure the thickness profile of the central air disc, as well as observe the extended gliding followed by the eventual rupture and contraction of the air layer. By impacting a liquid surface, we eliminate possible asperities from the surface, allowing further investigation into the transition between gliding and ring contact at the perimeter of the dimple.
2 Experimental setup
2.1 Interferometry setup

Figure 1. (a) Sketch of the experimental configuration. A small amount of liquid is deposited onto a microscope slide and allowed to coat uniformly. A small amount of liquid is expressed from an adjustable height syringe and allowed to pinch off under the force of gravity. A Phantom v710 views the impact from the side to measure the velocity of the impact (
![]() $V$
) and the bottom radius of curvature of the drop (
$V$
) and the bottom radius of curvature of the drop (
![]() $R_{b}$
). The Kirana camera simultaneously captures interference images from below through a beam splitter. The inset in the top left defines several geometric parameters. (b) Typical bottom-view interference image. Plots to the right show the averaged intensity profile along the red line in the image (top) and the resulting thickness profile of the air layer (bottom). (c) Side-view images showing the drop shapes just prior to impact over the large range of viscosities.
$R_{b}$
). The Kirana camera simultaneously captures interference images from below through a beam splitter. The inset in the top left defines several geometric parameters. (b) Typical bottom-view interference image. Plots to the right show the averaged intensity profile along the red line in the image (top) and the resulting thickness profile of the air layer (bottom). (c) Side-view images showing the drop shapes just prior to impact over the large range of viscosities.
The experimental configuration is shown in figure 1(a). A viscous drop is expressed from an adjustable height syringe and left to pinch off under the force of gravity. After pinch-off, the drop impacts a film of the same liquid that has been deposited onto a clean microscope slide. The camera views the impact through the bottom, using a long-distance microscope (Leica Z16 APO) with adjustable magnification and aperture. Magnifications as large as 29.2 were used, giving a corresponding pixel resolution of up to
![]() $1.04~\unicode[STIX]{x03BC}\text{m}~\text{px}^{-1}$
. The rapid initial decelerating motions were observed with a high-speed video camera (Kirana-05M, Specialized Imaging, Pitstone, UK) at frame rates up to 5 million f.p.s. (Crooks et al.
Reference Crooks, Marsh, Turchetta, Taylor, Chan, Lahav and Fenigstein2013). This camera takes 180 frames each with
$1.04~\unicode[STIX]{x03BC}\text{m}~\text{px}^{-1}$
. The rapid initial decelerating motions were observed with a high-speed video camera (Kirana-05M, Specialized Imaging, Pitstone, UK) at frame rates up to 5 million f.p.s. (Crooks et al.
Reference Crooks, Marsh, Turchetta, Taylor, Chan, Lahav and Fenigstein2013). This camera takes 180 frames each with
![]() $924\times 768~\text{px}$
. Video clips were acquired at between 20 and 100 k.f.p.s. to see the longer-term gliding behaviour and between 1 and 5 million f.p.s. to see the rapidly changing early dynamics. The illumination is provided by pulsed laser diodes (SI-LUX640, Specialized Imaging) with a wavelength
$924\times 768~\text{px}$
. Video clips were acquired at between 20 and 100 k.f.p.s. to see the longer-term gliding behaviour and between 1 and 5 million f.p.s. to see the rapidly changing early dynamics. The illumination is provided by pulsed laser diodes (SI-LUX640, Specialized Imaging) with a wavelength
![]() $\unicode[STIX]{x1D706}=640~\text{nm}$
and adjustable pulse duration set between 70 and 145 ns to minimize motion smearing and provide sufficiently bright illumination. In most cases we use reflective interferometry, with the light coming through the bottom, with a beam splitter, as shown in the sketch. Some imaging was also done with transmission interferometry, where the light comes from the top, to observed better the ruptures. An optical trigger (OT3, Specialized Imaging) intercepts the falling drop from the side and triggers the Kirana camera. The delay between the receipt of the trigger signal and the firing of the camera can be set within the camera software.
$\unicode[STIX]{x1D706}=640~\text{nm}$
and adjustable pulse duration set between 70 and 145 ns to minimize motion smearing and provide sufficiently bright illumination. In most cases we use reflective interferometry, with the light coming through the bottom, with a beam splitter, as shown in the sketch. Some imaging was also done with transmission interferometry, where the light comes from the top, to observed better the ruptures. An optical trigger (OT3, Specialized Imaging) intercepts the falling drop from the side and triggers the Kirana camera. The delay between the receipt of the trigger signal and the firing of the camera can be set within the camera software.
As the light emitted upwards from the laser encounters the free surface of the liquid film, some of the light is transmitted and some is reflected. The light transmitted through the first interface traverses the gas film and encounters the surface of the drop. At this interface, some of the light is again transmitted and some is reflected. The reflected light from the drop interface again traverses the gas film and encounters the free surface of the liquid film, where some is transmitted and some is reflected. The light that is then transmitted through the liquid film after being reflected by the drop surface can interfere with the light reflected initially from the liquid film surface based on the difference in the optical path lengths. Constructive interference is seen as bright fringes and destructive interference is seen as dark fringes with a
![]() $\unicode[STIX]{x1D706}/4$
difference in gas film thickness between adjacent bright and dark fringes. When the light is monochromatic and incident normal to the interface, the intensity in the image,
$\unicode[STIX]{x1D706}/4$
difference in gas film thickness between adjacent bright and dark fringes. When the light is monochromatic and incident normal to the interface, the intensity in the image,
![]() $I(r)$
, is given as
$I(r)$
, is given as
where
![]() $r$
is the radial location and
$r$
is the radial location and
![]() $\unicode[STIX]{x1D6FF}(r)$
is the air-film thickness, as a function of the radius
$\unicode[STIX]{x1D6FF}(r)$
is the air-film thickness, as a function of the radius
![]() $r$
from the axis of symmetry. Using the equipment outlined above, this technique can measure a maximum film thickness of
$r$
from the axis of symmetry. Using the equipment outlined above, this technique can measure a maximum film thickness of
![]() ${\sim}30~\unicode[STIX]{x03BC}\text{m}$
when the long-distance microscope is narrowly focused on the liquid free surface; therefore, only the interference due to the intervening air layer is seen in the images, but not the drop surface further from the centre. Figure 1(b) shows a typical bottom-view interference image with the extracted intensity profile and the resulting air-layer thickness profile. Typically, monochromatic interferometry can only yield relative measurements of film thicknesses. To overcome this, we use the rapid frame rates to track fringes in time to a point where a known reference height is seen. Herein, we take the point of contact between the drop and liquid film as our reference height of zero.
${\sim}30~\unicode[STIX]{x03BC}\text{m}$
when the long-distance microscope is narrowly focused on the liquid free surface; therefore, only the interference due to the intervening air layer is seen in the images, but not the drop surface further from the centre. Figure 1(b) shows a typical bottom-view interference image with the extracted intensity profile and the resulting air-layer thickness profile. Typically, monochromatic interferometry can only yield relative measurements of film thicknesses. To overcome this, we use the rapid frame rates to track fringes in time to a point where a known reference height is seen. Herein, we take the point of contact between the drop and liquid film as our reference height of zero.
2.2 Liquids and drop shapes
Table 1. Properties of the fluids used in the experiments. Properties for silicone oil (polydimethylsiloxane) are taken from the supplier’s data sheets (Clearco Products).

Our experiments focus on the influence of the liquid viscosity and we use silicone oils of viscosities spanning a wide range, between 10 to a million times that of water. Liquid properties are given in table 1. For drops with viscosity
![]() ${>}100~\text{cSt}$
, there was a viscous thread attached to the top of the drop, as shown in figure 1(c). For most cases, the viscous thread had separated from the nozzle prior to impact; however, in the few cases where the thread was still attached, the resulting effect was a significant reduction in the impact velocity from that expected based on the release height. A separate high-speed camera (Phantom v710) equipped with a
${>}100~\text{cSt}$
, there was a viscous thread attached to the top of the drop, as shown in figure 1(c). For most cases, the viscous thread had separated from the nozzle prior to impact; however, in the few cases where the thread was still attached, the resulting effect was a significant reduction in the impact velocity from that expected based on the release height. A separate high-speed camera (Phantom v710) equipped with a
![]() $1\times$
telecentric lens (Edmund Optics 55350) views the impact from the side to measure the impact velocity and bottom radius of curvature of the drop.
$1\times$
telecentric lens (Edmund Optics 55350) views the impact from the side to measure the impact velocity and bottom radius of curvature of the drop.
The impact is on a film of the same liquid
![]() ${\sim}400~\unicode[STIX]{x03BC}\text{m}$
thick. This is done by depositing a fixed amount of liquid (
${\sim}400~\unicode[STIX]{x03BC}\text{m}$
thick. This is done by depositing a fixed amount of liquid (
![]() $0.55\pm 0.05~\text{g}$
) on the microscope slide, which is then allowed to spread and become of uniform depth.
$0.55\pm 0.05~\text{g}$
) on the microscope slide, which is then allowed to spread and become of uniform depth.
The thickness of the liquid film was held at an approximately constant level of
![]() $T\sim 400~\unicode[STIX]{x03BC}\text{m}$
, except in § 3.4, where it is systematically varied. We did not systematically change the drop radius; however, there is significant variation between the different liquid viscosities, because of the drop oscillations during the free fall differ. This results in values of the bottom radius of curvature of the drop just prior to impact, showing a range of
$T\sim 400~\unicode[STIX]{x03BC}\text{m}$
, except in § 3.4, where it is systematically varied. We did not systematically change the drop radius; however, there is significant variation between the different liquid viscosities, because of the drop oscillations during the free fall differ. This results in values of the bottom radius of curvature of the drop just prior to impact, showing a range of
![]() $R_{b}=1.4{-}3.1~\text{mm}$
. By changing the release height we vary the impact velocity,
$R_{b}=1.4{-}3.1~\text{mm}$
. By changing the release height we vary the impact velocity,
![]() $V=0.3{-}4.7~\text{m}~\text{s}^{-1}$
. The liquid viscosities used are shown in table 1. We characterize the impact conditions by the following dimensionless quantities
$V=0.3{-}4.7~\text{m}~\text{s}^{-1}$
. The liquid viscosities used are shown in table 1. We characterize the impact conditions by the following dimensionless quantities
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}Re_{\ell }={\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }R_{b}V}{\unicode[STIX]{x1D707}_{\ell }}}=5.2\times 10^{-4}-661,\quad We={\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }R_{b}V^{2}}{\unicode[STIX]{x1D70E}}}=8-3120,\\ St={\displaystyle \frac{\unicode[STIX]{x1D707}_{g}}{\unicode[STIX]{x1D70C}_{\ell }R_{b}V}}=(0.13-3.6)\times 10^{-5},\quad Ca_{\ell }={\displaystyle \frac{\unicode[STIX]{x1D707}_{\ell }V}{\unicode[STIX]{x1D70E}}}=0.66-1.4\times 10^{5},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}Re_{\ell }={\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }R_{b}V}{\unicode[STIX]{x1D707}_{\ell }}}=5.2\times 10^{-4}-661,\quad We={\displaystyle \frac{\unicode[STIX]{x1D70C}_{\ell }R_{b}V^{2}}{\unicode[STIX]{x1D70E}}}=8-3120,\\ St={\displaystyle \frac{\unicode[STIX]{x1D707}_{g}}{\unicode[STIX]{x1D70C}_{\ell }R_{b}V}}=(0.13-3.6)\times 10^{-5},\quad Ca_{\ell }={\displaystyle \frac{\unicode[STIX]{x1D707}_{\ell }V}{\unicode[STIX]{x1D70E}}}=0.66-1.4\times 10^{5},\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{\ell }$
and
$\unicode[STIX]{x1D707}_{\ell }$
and
![]() $\unicode[STIX]{x1D70E}$
are the dynamic viscosity and surface tension of the liquid, while in the Stokes number
$\unicode[STIX]{x1D70E}$
are the dynamic viscosity and surface tension of the liquid, while in the Stokes number
![]() $St$
we use the density of the liquid,
$St$
we use the density of the liquid,
![]() $\unicode[STIX]{x1D70C}_{\ell }$
, balanced by the viscosity of the gas
$\unicode[STIX]{x1D70C}_{\ell }$
, balanced by the viscosity of the gas
![]() $\unicode[STIX]{x1D707}_{g}$
. The capillary number
$\unicode[STIX]{x1D707}_{g}$
. The capillary number
![]() $Ca_{\ell }$
compares the viscous stress in the liquid to the surface tension.
$Ca_{\ell }$
compares the viscous stress in the liquid to the surface tension.
3 Results and discussion
3.1 Gliding during impact onto a solid versus a liquid
Figure 2 compares the impact of a
![]() $10^{5}~\text{cSt}$
silicone oil drop on a dry, solid surface with an impact onto a liquid film of the same liquid. The impact velocity and drop size are similar in both cases. For the impact onto a solid surface, there are many localized, random ruptures of the air layer. The thickness of this layer is 160 nm or less, as reported by Langley et al. (Reference Langley, Li and Thoroddsen2017), who used two-colour interferometry to measure the absolute thickness. The local contacts rapidly wet the surface and merge together, sealing off the central air disc.
$10^{5}~\text{cSt}$
silicone oil drop on a dry, solid surface with an impact onto a liquid film of the same liquid. The impact velocity and drop size are similar in both cases. For the impact onto a solid surface, there are many localized, random ruptures of the air layer. The thickness of this layer is 160 nm or less, as reported by Langley et al. (Reference Langley, Li and Thoroddsen2017), who used two-colour interferometry to measure the absolute thickness. The local contacts rapidly wet the surface and merge together, sealing off the central air disc.

Figure 2. Comparison of bottom-view images for impacts of
![]() $10^{5}~\text{cSt}$
silicone oil on a solid versus a liquid surface. (a) Impact onto a clean, dry microscope slide at
$10^{5}~\text{cSt}$
silicone oil on a solid versus a liquid surface. (a) Impact onto a clean, dry microscope slide at
![]() $V=1.4~\text{m}~\text{s}^{-1}$
shown
$V=1.4~\text{m}~\text{s}^{-1}$
shown
![]() $120~\unicode[STIX]{x03BC}\text{s}$
after the dimple started to form. The gliding layer is ruptured in numerous random locations that wet extremely fast (Langley et al.
Reference Langley, Li and Thoroddsen2017). (b) Impact onto a film of the same
$120~\unicode[STIX]{x03BC}\text{s}$
after the dimple started to form. The gliding layer is ruptured in numerous random locations that wet extremely fast (Langley et al.
Reference Langley, Li and Thoroddsen2017). (b) Impact onto a film of the same
![]() $10^{5}~\text{cSt}$
silicone oil at
$10^{5}~\text{cSt}$
silicone oil at
![]() $V=1.6~\text{m}~\text{s}^{-1}$
shown
$V=1.6~\text{m}~\text{s}^{-1}$
shown
![]() $500~\unicode[STIX]{x03BC}\text{s}$
after the dimple is formed. In this case, the drop glides for an extended time, and there is only one localized contact (black arrow) during gliding prior to the simultaneous rupture of the air layer at a uniform radius (white arrow). The scale bar in each image is
$500~\unicode[STIX]{x03BC}\text{s}$
after the dimple is formed. In this case, the drop glides for an extended time, and there is only one localized contact (black arrow) during gliding prior to the simultaneous rupture of the air layer at a uniform radius (white arrow). The scale bar in each image is
![]() $200~\unicode[STIX]{x03BC}\text{m}$
long.
$200~\unicode[STIX]{x03BC}\text{m}$
long.
In contrast, for drops impacting onto liquid films, the drop still glides on an air layer, while the local contacts rarely occur. Instead the air layer ruptures uniformly at some radius,
![]() $L^{\ast }$
, measured from the centre of the dimple. The example shown in figure 2(b) has only a single local contact near the location of the final rupture. This difference is not solely an effect of the smoothness of the liquid versus the solid. Langley et al. (Reference Langley, Li and Thoroddsen2017) performed some impacts onto molecularly smooth mica and found the behaviour to be similar to that shown in figure 2(a). The other major difference is the deformability of the liquid surface. This compliance can result in a thicker initial gliding layer, thereby delaying its rupture. Further, as the liquid in the film is displaced by the drop, continuity dictates that the liquid must flow out of the region, resulting in a slightly different boundary condition than for impacts onto solid surfaces.
$L^{\ast }$
, measured from the centre of the dimple. The example shown in figure 2(b) has only a single local contact near the location of the final rupture. This difference is not solely an effect of the smoothness of the liquid versus the solid. Langley et al. (Reference Langley, Li and Thoroddsen2017) performed some impacts onto molecularly smooth mica and found the behaviour to be similar to that shown in figure 2(a). The other major difference is the deformability of the liquid surface. This compliance can result in a thicker initial gliding layer, thereby delaying its rupture. Further, as the liquid in the film is displaced by the drop, continuity dictates that the liquid must flow out of the region, resulting in a slightly different boundary condition than for impacts onto solid surfaces.
Aside from the absence of localized contacts in the gliding layer, the two cases also differ in both the time until rupture and the centreline height of the air layer. First, the time to rupture is drastically different. The impact onto a solid has nearly sealed off the air disc in
![]() $120~\unicode[STIX]{x03BC}\text{s}$
from the first deformation of the drop, whereas for the impact onto a liquid film, the rupture occurs after
$120~\unicode[STIX]{x03BC}\text{s}$
from the first deformation of the drop, whereas for the impact onto a liquid film, the rupture occurs after
![]() ${\sim}500~\unicode[STIX]{x03BC}\text{s}$
. The extended time for gliding results in a much larger radius at full rupture for impacts onto a liquid surface:
${\sim}500~\unicode[STIX]{x03BC}\text{s}$
. The extended time for gliding results in a much larger radius at full rupture for impacts onto a liquid surface:
![]() $L^{\ast }=650~\unicode[STIX]{x03BC}\text{m}$
for the liquid and
$L^{\ast }=650~\unicode[STIX]{x03BC}\text{m}$
for the liquid and
![]() $L^{\ast }=330~\unicode[STIX]{x03BC}\text{m}$
for the solid, taken as the innermost radius at which the local contacts merge together to fully entrap the air disc. Second, while the rupture of the air film occurs at approximately the same air-film thickness in both cases (
$L^{\ast }=330~\unicode[STIX]{x03BC}\text{m}$
for the solid, taken as the innermost radius at which the local contacts merge together to fully entrap the air disc. Second, while the rupture of the air film occurs at approximately the same air-film thickness in both cases (
![]() ${\lesssim}160~\text{nm}$
), the centreline heights of the air disc for these two comparable impact velocities are quite different. The impact onto the liquid film has a centreline height,
${\lesssim}160~\text{nm}$
), the centreline heights of the air disc for these two comparable impact velocities are quite different. The impact onto the liquid film has a centreline height,
![]() $H_{c}$
, nearly 50 % larger. This difference will be discussed in more detail in the following section.
$H_{c}$
, nearly 50 % larger. This difference will be discussed in more detail in the following section.
3.2 Centreline thickness of air layer
For impacts of an inviscid drop onto a solid surface, the centreline height of the air disc scales as
![]() $H_{c}\sim R_{b}St^{2/3}$
when compressibility of the gas is unimportant. For values of the compressibility factor
$H_{c}\sim R_{b}St^{2/3}$
when compressibility of the gas is unimportant. For values of the compressibility factor
![]() $\unicode[STIX]{x1D716}<1$
, compressibility becomes important and the initial height of the air layer decreases as a function of
$\unicode[STIX]{x1D716}<1$
, compressibility becomes important and the initial height of the air layer decreases as a function of
![]() $\unicode[STIX]{x1D716}$
(Mandre et al.
Reference Mandre, Mani and Brenner2009):
$\unicode[STIX]{x1D716}$
(Mandre et al.
Reference Mandre, Mani and Brenner2009):
where
![]() $P_{atm}$
is the atmosperic pressure. If the drop is formed instead from a highly viscous liquid,
$P_{atm}$
is the atmosperic pressure. If the drop is formed instead from a highly viscous liquid,
![]() $H_{c}$
can be much less than the value predicted for the inviscid liquid and the effects of gas compressibility are delayed. Langley et al. (Reference Langley, Li and Thoroddsen2017) found that
$H_{c}$
can be much less than the value predicted for the inviscid liquid and the effects of gas compressibility are delayed. Langley et al. (Reference Langley, Li and Thoroddsen2017) found that
![]() $H_{c}$
scales as a function of the impact parameter
$H_{c}$
scales as a function of the impact parameter
![]() $\unicode[STIX]{x1D6F7}$
that takes into account the drop viscosity and inertia and the dynamic pressure forces in the intervening air layer
$\unicode[STIX]{x1D6F7}$
that takes into account the drop viscosity and inertia and the dynamic pressure forces in the intervening air layer
In the problem at hand, the situation becomes further complicated by the presence of a second deformable interface at the impact surface. Tran et al. (Reference Tran, De Maleprade, Sun and Lohse2013) found that they could scale drop impacts onto solid and liquid interfaces alike by considering the penetration velocity
![]() $V_{p}$
of the gas film into the substrate instead of just the impact velocity of the drop or solid. They approached the problem from an energy balance, considering the energy before and after impact using the assumption of potential flow and a deep pool to determine the penetration velocity of the drop into the pool to be
$V_{p}$
of the gas film into the substrate instead of just the impact velocity of the drop or solid. They approached the problem from an energy balance, considering the energy before and after impact using the assumption of potential flow and a deep pool to determine the penetration velocity of the drop into the pool to be
![]() $V_{p}=V/2$
. This is consistent with other recent studies that consider the velocity of a cavity formed by multiple droplets or jets (Bouwhuis et al.
Reference Bouwhuis, Huang, Chan, Frommhold, Ohl, Lohse, Snoeijer and van der Meer2016; Speirs et al.
Reference Speirs, Pan, Belden and Truscott2018). Hendrix et al. (Reference Hendrix, Bouwhuis, van der Meer, Lohse and Snoeijer2016) furthered this argument and stated that if one of the interfaces is rigid then
$V_{p}=V/2$
. This is consistent with other recent studies that consider the velocity of a cavity formed by multiple droplets or jets (Bouwhuis et al.
Reference Bouwhuis, Huang, Chan, Frommhold, Ohl, Lohse, Snoeijer and van der Meer2016; Speirs et al.
Reference Speirs, Pan, Belden and Truscott2018). Hendrix et al. (Reference Hendrix, Bouwhuis, van der Meer, Lohse and Snoeijer2016) furthered this argument and stated that if one of the interfaces is rigid then
![]() $V_{p}=V$
, but for the case of a liquid drop impacting a liquid surface, both interfaces are deformable and
$V_{p}=V$
, but for the case of a liquid drop impacting a liquid surface, both interfaces are deformable and
![]() $V_{p}=V/2$
. In practice, we do not expect there to be a sharp transition from
$V_{p}=V/2$
. In practice, we do not expect there to be a sharp transition from
![]() $V_{p}=V\rightarrow V/2$
as soon as there exists any amount of liquid film beneath the drop, but that there will be a transition region until a deep enough pool is formed. We further discuss the effects of the film thickness in § 3.4.
$V_{p}=V\rightarrow V/2$
as soon as there exists any amount of liquid film beneath the drop, but that there will be a transition region until a deep enough pool is formed. We further discuss the effects of the film thickness in § 3.4.
Herein, we have to consider both the liquid viscosity and a film of finite thickness instead of a deep pool, so the same energy balance arguments used by Tran et al. (Reference Tran, De Maleprade, Sun and Lohse2013) may not apply here. For the film thickness, we are near the deep pool regime, which is discussed further in § 3.4. From our earlier work (Langley et al.
Reference Langley, Li and Thoroddsen2017), the liquid viscosity has a relatively weak influence on the size of the air disc, and so we persist with using
![]() $V_{p}=V/2$
to find an empirical scaling. However, simply substituting
$V_{p}=V/2$
to find an empirical scaling. However, simply substituting
![]() $V_{p}$
for
$V_{p}$
for
![]() $V$
in all of the non-dimensional parameters does not yield a consistent scaling for impacts onto both solid and liquid surfaces. We find that using
$V$
in all of the non-dimensional parameters does not yield a consistent scaling for impacts onto both solid and liquid surfaces. We find that using
![]() $V_{p}$
only in the parameters concerning the gas film, namely the Stokes number, which we denote as
$V_{p}$
only in the parameters concerning the gas film, namely the Stokes number, which we denote as
![]() $St_{p}$
, collapses the data for impacts onto solid and liquid surfaces. Using the penetration velocity in the Stokes number and the impact velocity elsewhere in the scaling is not without consequences; for example, what happens to the kinematic boundary condition? To fully understand these effects a more rigorous theoretical study is needed.
$St_{p}$
, collapses the data for impacts onto solid and liquid surfaces. Using the penetration velocity in the Stokes number and the impact velocity elsewhere in the scaling is not without consequences; for example, what happens to the kinematic boundary condition? To fully understand these effects a more rigorous theoretical study is needed.

Figure 3. (a) Plot of the normalized centreline height of the air disc.
![]() $H_{c}$
is measured at the first maximum during the impact, as shown in the inset in (b). The open symbols represent impacts onto liquid films and the filled symbols represent impacts onto solid surfaces from Langley et al. (Reference Langley, Li and Thoroddsen2017). Using the penetration velocity of the gas film in the Stokes number, the data for impacts onto liquid surfaces scale in accordance with the scaling for impacts onto solid surfaces. In both cases the centreline height is weakly dependent on the liquid viscosity to the
$H_{c}$
is measured at the first maximum during the impact, as shown in the inset in (b). The open symbols represent impacts onto liquid films and the filled symbols represent impacts onto solid surfaces from Langley et al. (Reference Langley, Li and Thoroddsen2017). Using the penetration velocity of the gas film in the Stokes number, the data for impacts onto liquid surfaces scale in accordance with the scaling for impacts onto solid surfaces. In both cases the centreline height is weakly dependent on the liquid viscosity to the
![]() $-1/9$
power. (b) Half-profiles of the air-layer thickness at several times for a
$-1/9$
power. (b) Half-profiles of the air-layer thickness at several times for a
![]() $10^{5}~\text{cSt}$
silicone oil drop impacting at
$10^{5}~\text{cSt}$
silicone oil drop impacting at
![]() $V=1.6~\text{m}~\text{s}^{-1}$
(
$V=1.6~\text{m}~\text{s}^{-1}$
(
![]() $\unicode[STIX]{x1D6F7}=7.8\times 10^{-3}$
). Time is measured from the first frame in which the dimple is visible. Inset: Centreline height of the air disc from the first appearance of the dimple until air film rupture for each viscosity used herein, for impact velocities of
$\unicode[STIX]{x1D6F7}=7.8\times 10^{-3}$
). Time is measured from the first frame in which the dimple is visible. Inset: Centreline height of the air disc from the first appearance of the dimple until air film rupture for each viscosity used herein, for impact velocities of
![]() $2.0~\text{m}~\text{s}^{-1}$
(10 cSt),
$2.0~\text{m}~\text{s}^{-1}$
(10 cSt),
![]() $1.9~\text{m}~\text{s}^{-1}$
(100 cSt,
$1.9~\text{m}~\text{s}^{-1}$
(100 cSt,
![]() $10^{6}~\text{cSt}$
),
$10^{6}~\text{cSt}$
),
![]() $1.8~\text{m}~\text{s}^{-1}$
(
$1.8~\text{m}~\text{s}^{-1}$
(
![]() $10^{3}~\text{cSt}$
),
$10^{3}~\text{cSt}$
),
![]() $1.6~\text{m}~\text{s}^{-1}$
(
$1.6~\text{m}~\text{s}^{-1}$
(
![]() $10^{4}~\text{cSt}$
,
$10^{4}~\text{cSt}$
,
![]() $10^{5}~\text{cSt}$
).
$10^{5}~\text{cSt}$
).
Figure 3(a) presents the centreline height of the air disc as a function of the impact parameter
![]() $\unicode[STIX]{x1D6F7}$
. Open markers are the data collected in this study for impacts onto liquid films. Filled markers represent the data from Langley et al. (Reference Langley, Li and Thoroddsen2017) for impacts onto solid surfaces. In prior studies,
$\unicode[STIX]{x1D6F7}$
. Open markers are the data collected in this study for impacts onto liquid films. Filled markers represent the data from Langley et al. (Reference Langley, Li and Thoroddsen2017) for impacts onto solid surfaces. In prior studies,
![]() $H_{c}$
was measured when the drop contacted the surface (Li & Thoroddsen Reference Li and Thoroddsen2015) or when the dimple became frozen in time (Langley et al.
Reference Langley, Li and Thoroddsen2017). In this study
$H_{c}$
was measured when the drop contacted the surface (Li & Thoroddsen Reference Li and Thoroddsen2015) or when the dimple became frozen in time (Langley et al.
Reference Langley, Li and Thoroddsen2017). In this study
![]() $H_{c}$
is more dynamic with time; therefore, the measured values in figure 3(a) are taken at the first maximum in the dimple height – see the inset in figure 3(b).
$H_{c}$
is more dynamic with time; therefore, the measured values in figure 3(a) are taken at the first maximum in the dimple height – see the inset in figure 3(b).
As mentioned above, the ordinate is scaled using
![]() $V_{p}$
; however, the abscissa is scaled using
$V_{p}$
; however, the abscissa is scaled using
![]() $V$
to fully account for the inertia of the drop. In this way, the data for both the impacts onto liquid surfaces and solid surface collapse to the same scaling and the centreline height scales as
$V$
to fully account for the inertia of the drop. In this way, the data for both the impacts onto liquid surfaces and solid surface collapse to the same scaling and the centreline height scales as
(See supplementary materials for alternate scalings, available at https://doi.org/10.1017/jfm.2019.682 using only
![]() $V$
or only
$V$
or only
![]() $V_{p}$
, which do not work as well.) Thus,
$V_{p}$
, which do not work as well.) Thus,
![]() $H_{c}$
is weakly dependent on the viscosity of the liquid drop to the
$H_{c}$
is weakly dependent on the viscosity of the liquid drop to the
![]() $-1/9$
power. As
$-1/9$
power. As
![]() $\unicode[STIX]{x1D6F7}$
approaches unity, the initial height of the air film approaches the incompressible, inviscid impact solution. For
$\unicode[STIX]{x1D6F7}$
approaches unity, the initial height of the air film approaches the incompressible, inviscid impact solution. For
![]() $\unicode[STIX]{x1D6F7}>1$
, viscosity becomes less important while the compressibility of the gas will become more important, resulting in a decrease in the scaled values of
$\unicode[STIX]{x1D6F7}>1$
, viscosity becomes less important while the compressibility of the gas will become more important, resulting in a decrease in the scaled values of
![]() $H_{c}$
again (see Langley et al.
Reference Langley, Li and Thoroddsen2017).
$H_{c}$
again (see Langley et al.
Reference Langley, Li and Thoroddsen2017).
Revisiting the example centreline heights from figure 2,
![]() $H_{c}$
for the impact onto the liquid film was nearly 50 % larger. Now, taking into account the penetration velocity for impacts of liquid drops onto liquid surfaces, this introduces a factor of
$H_{c}$
for the impact onto the liquid film was nearly 50 % larger. Now, taking into account the penetration velocity for impacts of liquid drops onto liquid surfaces, this introduces a factor of
![]() $2^{2/3}$
on the right-hand side of (3.3). Therefore, for a given impact velocity, we expect the centreline height of the air disc for impacts onto liquid surfaces to be 1.58 times the centreline height of impacts onto solid surfaces – which is in good agreement.
$2^{2/3}$
on the right-hand side of (3.3). Therefore, for a given impact velocity, we expect the centreline height of the air disc for impacts onto liquid surfaces to be 1.58 times the centreline height of impacts onto solid surfaces – which is in good agreement.
Figure 3(b) shows several air-layer profiles for a
![]() $10^{5}~\text{cSt}$
drop impacting a liquid film at
$10^{5}~\text{cSt}$
drop impacting a liquid film at
![]() $V=1.6~\text{m}~\text{s}^{-1}$
(
$V=1.6~\text{m}~\text{s}^{-1}$
(
![]() $\unicode[STIX]{x1D6F7}=7.8\times 10^{-3}$
). Time is relative to the first frame in which the deformation of the liquid interfaces was visible. As time progresses, the air layer becomes thinner and grows radially. At
$\unicode[STIX]{x1D6F7}=7.8\times 10^{-3}$
). Time is relative to the first frame in which the deformation of the liquid interfaces was visible. As time progresses, the air layer becomes thinner and grows radially. At
![]() $50~\unicode[STIX]{x03BC}\text{s}$
, the gliding layer is
$50~\unicode[STIX]{x03BC}\text{s}$
, the gliding layer is
![]() ${\sim}320~\text{nm}$
thick. At
${\sim}320~\text{nm}$
thick. At
![]() $100~\unicode[STIX]{x03BC}\text{s}$
, the centreline height has decreased and the drop is gliding on a layer
$100~\unicode[STIX]{x03BC}\text{s}$
, the centreline height has decreased and the drop is gliding on a layer
![]() ${<}160~\text{nm}$
thick. After
${<}160~\text{nm}$
thick. After
![]() $200~\unicode[STIX]{x03BC}\text{s}$
, the centreline height reaches a steady value and the gliding layer extends to nearly
$200~\unicode[STIX]{x03BC}\text{s}$
, the centreline height reaches a steady value and the gliding layer extends to nearly
![]() $1000~\unicode[STIX]{x03BC}\text{m}$
. The drop continues to glide for an additional
$1000~\unicode[STIX]{x03BC}\text{m}$
. The drop continues to glide for an additional
![]() ${\sim}300~\unicode[STIX]{x03BC}\text{s}$
before the air film ruptures. The gliding layer does not rupture at the farthest radial extent of the air layer, but at an intermediate location where the layer is close to the thinnest. For this case, the rupture occurs at
${\sim}300~\unicode[STIX]{x03BC}\text{s}$
before the air film ruptures. The gliding layer does not rupture at the farthest radial extent of the air layer, but at an intermediate location where the layer is close to the thinnest. For this case, the rupture occurs at
![]() $L^{\ast }=650~\unicode[STIX]{x03BC}\text{m}$
.
$L^{\ast }=650~\unicode[STIX]{x03BC}\text{m}$
.
The inset of figure 3(b) shows the centreline height for each viscosity for an impact velocity between 1.6 and
![]() $2~\text{m}~\text{s}^{-1}$
. At these velocities, each drop glides except the 10 cSt case, which makes ring contact at the kink when the dimple reaches its maximum height. For intermediate viscosities,
$2~\text{m}~\text{s}^{-1}$
. At these velocities, each drop glides except the 10 cSt case, which makes ring contact at the kink when the dimple reaches its maximum height. For intermediate viscosities,
![]() $10^{2}$
and
$10^{2}$
and
![]() $10^{3}~\text{cSt}$
, the dimple reaches its maximum height and then decreases as the drop glides. Rupture occurs much faster in the 100 cSt case. As the viscosity increases further, the centreline height of the dimple gradually decreases from its maximum to a steady value that is maintained until the air layer ruptures.
$10^{3}~\text{cSt}$
, the dimple reaches its maximum height and then decreases as the drop glides. Rupture occurs much faster in the 100 cSt case. As the viscosity increases further, the centreline height of the dimple gradually decreases from its maximum to a steady value that is maintained until the air layer ruptures.
3.3 Rupture of the air layer

Figure 4. (a) Plot of the location of the rupture of the air layer,
![]() $L^{\ast }$
, versus the impact parameter
$L^{\ast }$
, versus the impact parameter
![]() $\unicode[STIX]{x1D6F7}$
, where
$\unicode[STIX]{x1D6F7}$
, where
![]() $L^{\ast }$
is normalized by Stokes-number scaling. For impacts that glide above the liquid film, the normalized radial extent of the gliding layer increases as
$L^{\ast }$
is normalized by Stokes-number scaling. For impacts that glide above the liquid film, the normalized radial extent of the gliding layer increases as
![]() $\unicode[STIX]{x1D6F7}^{1/4}$
. At sufficiently high impact velocities, there is a transition from gliding to ring contact, seen in the plot as a sudden decrease in
$\unicode[STIX]{x1D6F7}^{1/4}$
. At sufficiently high impact velocities, there is a transition from gliding to ring contact, seen in the plot as a sudden decrease in
![]() $L^{\ast }$
with increasing
$L^{\ast }$
with increasing
![]() $\unicode[STIX]{x1D6F7}$
. For ring contact, the rupture location approaches the radial extent predicted by Hicks & Purvis (Reference Hicks and Purvis2010) for impacts onto a solid surface (horizontal line). (b) Plot of non-dimensional time when the air layer ruptures versus the Reynolds number
$\unicode[STIX]{x1D6F7}$
. For ring contact, the rupture location approaches the radial extent predicted by Hicks & Purvis (Reference Hicks and Purvis2010) for impacts onto a solid surface (horizontal line). (b) Plot of non-dimensional time when the air layer ruptures versus the Reynolds number
![]() $Re_{\ell }$
. Inset: dimensional rupture time versus Reynolds number.
$Re_{\ell }$
. Inset: dimensional rupture time versus Reynolds number.
The thin air layer on which the drops glide is inherently unstable and will eventually rupture when the film reaches a sufficient thinness. In our study, the air film ruptures when the film is
![]() ${<}160~\text{nm}$
thick. Figure 4(a) shows the radial location of rupture of the air film,
${<}160~\text{nm}$
thick. Figure 4(a) shows the radial location of rupture of the air film,
![]() $L^{\ast }$
, as a function of
$L^{\ast }$
, as a function of
![]() $\unicode[STIX]{x1D6F7}$
. Here we scale
$\unicode[STIX]{x1D6F7}$
. Here we scale
![]() $L^{\ast }$
with Stokes-number scaling, as is common for lower-viscosity drops (Smith, Li & Wu Reference Smith, Li and Wu2003; Korobkin, Ellis & Smith Reference Korobkin, Ellis and Smith2008; Mandre et al.
Reference Mandre, Mani and Brenner2009; Hicks & Purvis Reference Hicks and Purvis2011). In the gliding regime, the rupture location scales as
$L^{\ast }$
with Stokes-number scaling, as is common for lower-viscosity drops (Smith, Li & Wu Reference Smith, Li and Wu2003; Korobkin, Ellis & Smith Reference Korobkin, Ellis and Smith2008; Mandre et al.
Reference Mandre, Mani and Brenner2009; Hicks & Purvis Reference Hicks and Purvis2011). In the gliding regime, the rupture location scales as
![]() $L^{\ast }\sim \unicode[STIX]{x1D6F7}^{1/4}R_{b}St_{p}^{1/3}$
, meaning that as
$L^{\ast }\sim \unicode[STIX]{x1D6F7}^{1/4}R_{b}St_{p}^{1/3}$
, meaning that as
![]() $\unicode[STIX]{x1D6F7}$
increases the gliding layers become larger. For
$\unicode[STIX]{x1D6F7}$
increases the gliding layers become larger. For
![]() $\unicode[STIX]{x1D6F7}$
between
$\unicode[STIX]{x1D6F7}$
between
![]() $10^{-2}$
and
$10^{-2}$
and
![]() $10^{-1}$
, the transition between gliding and ring contact at the kink begins. Counterintuitively, a large liquid viscosity does not equate to a larger
$10^{-1}$
, the transition between gliding and ring contact at the kink begins. Counterintuitively, a large liquid viscosity does not equate to a larger
![]() $L^{\ast }$
. In fact, the highest-viscosity drops begin transitioning at lower values of
$L^{\ast }$
. In fact, the highest-viscosity drops begin transitioning at lower values of
![]() $\unicode[STIX]{x1D6F7}$
than intermediate viscosities. This is promoted in part by a slowed spreading rate and a smaller maximum spreading radius for the highest-viscosity cases (Langley et al.
Reference Langley, Li and Thoroddsen2017). In the plot, the transition is seen as a sharp decrease in
$\unicode[STIX]{x1D6F7}$
than intermediate viscosities. This is promoted in part by a slowed spreading rate and a smaller maximum spreading radius for the highest-viscosity cases (Langley et al.
Reference Langley, Li and Thoroddsen2017). In the plot, the transition is seen as a sharp decrease in
![]() $L^{\ast }$
. As in the analysis for the centreline height, the penetration velocity is used in the Stokes number for the scaling of the rupture location. As
$L^{\ast }$
. As in the analysis for the centreline height, the penetration velocity is used in the Stokes number for the scaling of the rupture location. As
![]() $\unicode[STIX]{x1D6F7}$
approaches unity, the rupture location approaches the normalized value predict by Hicks & Purvis (Reference Hicks and Purvis2010) for inviscid drop impacts onto solid surfaces (that is,
$\unicode[STIX]{x1D6F7}$
approaches unity, the rupture location approaches the normalized value predict by Hicks & Purvis (Reference Hicks and Purvis2010) for inviscid drop impacts onto solid surfaces (that is,
![]() $L_{0}=6.3R_{b}St_{p}^{1/3}$
). The behaviour of the rupture during the transition from gliding to ring contact at the kink is explored in more detail in § 3.5.
$L_{0}=6.3R_{b}St_{p}^{1/3}$
). The behaviour of the rupture during the transition from gliding to ring contact at the kink is explored in more detail in § 3.5.
Figure 4(b) shows the non-dimensional time of air film rupture,
![]() $\unicode[STIX]{x1D70F}=t_{r}V/R_{b}St_{p}^{2/3}$
, versus the Reynolds number
$\unicode[STIX]{x1D70F}=t_{r}V/R_{b}St_{p}^{2/3}$
, versus the Reynolds number
![]() $Re_{\ell }$
, while the inset shows the actual time. The time of rupture is measured relative to the first observed deformation of the drop. For the highest-viscosity cases
$Re_{\ell }$
, while the inset shows the actual time. The time of rupture is measured relative to the first observed deformation of the drop. For the highest-viscosity cases
![]() $10^{4}{-}10^{6}~\text{cSt}$
, the normalized time to rupture increases with increasing velocity until the drop transitions from gliding to ring contact at the kink, at which point there is a sudden decrease in the time to rupture. Although this transition decreases
$10^{4}{-}10^{6}~\text{cSt}$
, the normalized time to rupture increases with increasing velocity until the drop transitions from gliding to ring contact at the kink, at which point there is a sudden decrease in the time to rupture. Although this transition decreases
![]() $\unicode[STIX]{x1D70F}$
for these cases, the rupture time is still much larger than the rupture time for the low-viscosity cases, as shown in the inset of figure 4(b). The time to rupture reaches a maximum near
$\unicode[STIX]{x1D70F}$
for these cases, the rupture time is still much larger than the rupture time for the low-viscosity cases, as shown in the inset of figure 4(b). The time to rupture reaches a maximum near
![]() $Re_{\ell }=1$
, where the inertial and viscous stresses in the liquid balance. As
$Re_{\ell }=1$
, where the inertial and viscous stresses in the liquid balance. As
![]() $Re_{\ell }$
increases beyond unity, time until rupture decreases with increasing impact velocity. As the drop transitions from gliding to ring contact at the dimple edge, there is a much steeper decrease in
$Re_{\ell }$
increases beyond unity, time until rupture decreases with increasing impact velocity. As the drop transitions from gliding to ring contact at the dimple edge, there is a much steeper decrease in
![]() $\unicode[STIX]{x1D70F}$
with increasing
$\unicode[STIX]{x1D70F}$
with increasing
![]() $Re_{\ell }$
than for higher viscosities. In the lowest-viscosity case, 10 cSt, the time to rupture occurs at a near-constant value of
$Re_{\ell }$
than for higher viscosities. In the lowest-viscosity case, 10 cSt, the time to rupture occurs at a near-constant value of
![]() $\unicode[STIX]{x1D70F}\simeq 25$
or
$\unicode[STIX]{x1D70F}\simeq 25$
or
![]() $t_{r}\simeq 10~\unicode[STIX]{x03BC}\text{s}$
.
$t_{r}\simeq 10~\unicode[STIX]{x03BC}\text{s}$
.
3.4 Effects of liquid film thickness

Figure 5. Plot of the first maximum of the centreline height of the air disc
![]() $H^{\ast }$
versus the liquid film thickness,
$H^{\ast }$
versus the liquid film thickness,
![]() $T$
, for impacts of
$T$
, for impacts of
![]() $10^{4}~\text{cSt}$
silicone oil drops onto liquid films of the same liquid with
$10^{4}~\text{cSt}$
silicone oil drops onto liquid films of the same liquid with
![]() $R_{b}=1.4~\text{mm}$
and
$R_{b}=1.4~\text{mm}$
and
![]() $V=1.4~\text{m}~\text{s}^{-1}$
.
$V=1.4~\text{m}~\text{s}^{-1}$
.
Hicks & Purvis (Reference Hicks and Purvis2011) present a model for inviscid drop impacts onto an inviscid liquid film with air cushioning by the intervening viscous gas. When the ratio of the liquid layer depth to the horizontal interaction distance is much greater than 1, then the liquid film can be treated as a deep pool. In our study, the liquid layer is
![]() ${\sim}400~\unicode[STIX]{x03BC}\text{m}$
and the horizontal interaction length
${\sim}400~\unicode[STIX]{x03BC}\text{m}$
and the horizontal interaction length
![]() $L$
is
$L$
is
![]() ${\lesssim}300~\unicode[STIX]{x03BC}\text{m}$
when the dimple reaches its maximum height, which makes the ratio of order 1, suggesting there could be some effects from the closeness of the solid wall.
${\lesssim}300~\unicode[STIX]{x03BC}\text{m}$
when the dimple reaches its maximum height, which makes the ratio of order 1, suggesting there could be some effects from the closeness of the solid wall.
To assess the effects of the film thickness, we performed a series of experiments with
![]() $10^{4}~\text{cSt}$
silicone oil where all parameters were held constant except the film height,
$10^{4}~\text{cSt}$
silicone oil where all parameters were held constant except the film height,
![]() $T$
, which was varied from
$T$
, which was varied from
![]() $100~\unicode[STIX]{x03BC}\text{m}$
to 4 mm. Measurements of the centreline air-disc height
$100~\unicode[STIX]{x03BC}\text{m}$
to 4 mm. Measurements of the centreline air-disc height
![]() $H_{c}$
are plotted as a function of the film thickness in figure 5. As the film thickness increases to
$H_{c}$
are plotted as a function of the film thickness in figure 5. As the film thickness increases to
![]() $500~\unicode[STIX]{x03BC}\text{m}$
, the centreline height also increases, consistent with transitioning from an effectively solid to a compliant substrate. As the substrate film thickness continues to increase, there is a slight decrease in the height until it reaches a steady value of
$500~\unicode[STIX]{x03BC}\text{m}$
, the centreline height also increases, consistent with transitioning from an effectively solid to a compliant substrate. As the substrate film thickness continues to increase, there is a slight decrease in the height until it reaches a steady value of
![]() $1.28~\unicode[STIX]{x03BC}\text{m}$
. One caveat, for film thicknesses
$1.28~\unicode[STIX]{x03BC}\text{m}$
. One caveat, for film thicknesses
![]() ${\leqslant}1~\text{mm}$
, an absolute reference measurement is clearly visible in the videos; however, for the two thickest films there is ambiguity in the absolute thickness. If the films behave as in the lower thicknesses, the values of
${\leqslant}1~\text{mm}$
, an absolute reference measurement is clearly visible in the videos; however, for the two thickest films there is ambiguity in the absolute thickness. If the films behave as in the lower thicknesses, the values of
![]() $H_{c}$
may need to be adjusted by an additional 320 nm, as marked by the vertical bars. This must be addressed in future work using two-colour interferometry.
$H_{c}$
may need to be adjusted by an additional 320 nm, as marked by the vertical bars. This must be addressed in future work using two-colour interferometry.
Where then does our data fall on the shallow film to deep pool spectrum? For the initial formation of the dimple, the behaviour of our data suggests it is on the cusp of the deep pool behaviour. As the impact continues, the solid substrate forces the drop to spread radially outwards, resulting in a flatter air film instead of the hemispherical air film seen by Thoroddsen et al. (Reference Thoroddsen, Thoraval, Takehara and Etoh2012) and Tran et al. (Reference Tran, De Maleprade, Sun and Lohse2013). Therefore, the gliding behaviour and rupture dynamics presented in our study may only be applicable when the horizontal interaction distance and the liquid film depth are of similar magnitude.
3.5 Transition from gliding to ring contact at the kink

Figure 6. Bottom-view interferometry images showing the transition from gliding to ring contact at the kink. Image intensities have been inverted to better show the details at the rupture location. (a) A drop of
![]() $10^{5}~\text{cSt}$
silicone oil impacting in the gliding regime, shown at 0, 185 and
$10^{5}~\text{cSt}$
silicone oil impacting in the gliding regime, shown at 0, 185 and
![]() $375~\unicode[STIX]{x03BC}\text{s}$
relative to the first frame which shows the dimple. The right-facing arrows show the furthest that the drop has spread radially (that is, the extent of the region where a thin air layer separates the drop and substrate liquid film). In the last panel the drop has spread to
$375~\unicode[STIX]{x03BC}\text{s}$
relative to the first frame which shows the dimple. The right-facing arrows show the furthest that the drop has spread radially (that is, the extent of the region where a thin air layer separates the drop and substrate liquid film). In the last panel the drop has spread to
![]() ${\sim}75\,\%$
of
${\sim}75\,\%$
of
![]() $R_{b}$
. The drop has not yet contacted the liquid film in the middle panel. The left-facing arrow in the last panel shows the rupture location of the thin air layer. (b) The impact of a drop of
$R_{b}$
. The drop has not yet contacted the liquid film in the middle panel. The left-facing arrow in the last panel shows the rupture location of the thin air layer. (b) The impact of a drop of
![]() $10^{5}~\text{cSt}$
silicone oil under conditions at the transition between gliding and ring contact at the kink, shown at 0, 80 and
$10^{5}~\text{cSt}$
silicone oil under conditions at the transition between gliding and ring contact at the kink, shown at 0, 80 and
![]() $160~\unicode[STIX]{x03BC}\text{s}$
relative to the first frame showing the dimple. The right-facing arrows show the furthest extent of the drop spreading. The drop initially glides over a thin layer of air and has not yet contacted the liquid film in the middle panel. The air layer ruptures near the edge of the dimple in the drop (point 1). The outer edge of the rupture can be faintly seen at point 2, and point 3 shows a localized contact in the still present air layer. The outer rupture propagates towards the outer edge, leaving a myriad of microbubbles. (c) Bottom-view images for impacts of 100 cSt silicone oil onto a liquid film of the same liquid at different impact velocities. The arrows show the location of the rupture of the thin air film upon which the drop initially glides. For increasing
$160~\unicode[STIX]{x03BC}\text{s}$
relative to the first frame showing the dimple. The right-facing arrows show the furthest extent of the drop spreading. The drop initially glides over a thin layer of air and has not yet contacted the liquid film in the middle panel. The air layer ruptures near the edge of the dimple in the drop (point 1). The outer edge of the rupture can be faintly seen at point 2, and point 3 shows a localized contact in the still present air layer. The outer rupture propagates towards the outer edge, leaving a myriad of microbubbles. (c) Bottom-view images for impacts of 100 cSt silicone oil onto a liquid film of the same liquid at different impact velocities. The arrows show the location of the rupture of the thin air film upon which the drop initially glides. For increasing
![]() $\unicode[STIX]{x1D6F7}$
(increasing
$\unicode[STIX]{x1D6F7}$
(increasing
![]() $V$
) the rupture location moves closer to the initial kink at the edge of the drop dimple until the contact occurs at the kink as for impacts onto solid surfaces. Each
$V$
) the rupture location moves closer to the initial kink at the edge of the drop dimple until the contact occurs at the kink as for impacts onto solid surfaces. Each
![]() $\unicode[STIX]{x1D6F7}$
value corresponds with a blue triangle in figure 4. Each scale bar is
$\unicode[STIX]{x1D6F7}$
value corresponds with a blue triangle in figure 4. Each scale bar is
![]() $200~\unicode[STIX]{x03BC}\text{m}$
long.
$200~\unicode[STIX]{x03BC}\text{m}$
long.
Figures 6(a) and 6(b) show a drop of
![]() $10^{5}~\text{cSt}$
silicone oil impacting onto a liquid film before and after the transition from gliding to ring contact at the edge of the drop dimple. In the gliding regime just prior to transition, figure 6(a), the dimple forms and the drop glides for
$10^{5}~\text{cSt}$
silicone oil impacting onto a liquid film before and after the transition from gliding to ring contact at the edge of the drop dimple. In the gliding regime just prior to transition, figure 6(a), the dimple forms and the drop glides for
![]() ${\sim}350~\unicode[STIX]{x03BC}\text{s}$
before the air layer ruptures at a radial distance
${\sim}350~\unicode[STIX]{x03BC}\text{s}$
before the air layer ruptures at a radial distance
![]() $L^{\ast }=780~\unicode[STIX]{x03BC}\text{m}$
. As the impact transitions towards ring contact at larger
$L^{\ast }=780~\unicode[STIX]{x03BC}\text{m}$
. As the impact transitions towards ring contact at larger
![]() $\unicode[STIX]{x1D6F7}$
, figure 6(b) shows that the drop still glides prior to rupture of the air layer. The air layer now ruptures much faster in real time after only
$\unicode[STIX]{x1D6F7}$
, figure 6(b) shows that the drop still glides prior to rupture of the air layer. The air layer now ruptures much faster in real time after only
![]() $120~\unicode[STIX]{x03BC}\text{s}$
and ruptures near the edge of the dimple (point 1 in the last panel of figure 6
b). At the time of rupture, the drop does not make contact with the entire liquid film simultaneously. The contact begins near the dimple and then propagates outwards. Point 2 in the last panel, marks the faintly visible outer extent of the contacted area. Point 3 shows a local contact within the still present air layer between the drop and liquid film. Aside from point 3, there is no contact between the drop and liquid film between the outer extent of the contacted region (point 2) and the outer edge of the gliding layer, which is the furthest radially the drop has spread (right facing arrow). The outer edge of the contacted region will continue to spread outwards, entrapping microbubbles as it propagates. Li, Vakarelski & Throddsen (Reference Li, Vakarelski and Throddsen2015) showed similar film ruptures for water drops impacting a film of
$120~\unicode[STIX]{x03BC}\text{s}$
and ruptures near the edge of the dimple (point 1 in the last panel of figure 6
b). At the time of rupture, the drop does not make contact with the entire liquid film simultaneously. The contact begins near the dimple and then propagates outwards. Point 2 in the last panel, marks the faintly visible outer extent of the contacted area. Point 3 shows a local contact within the still present air layer between the drop and liquid film. Aside from point 3, there is no contact between the drop and liquid film between the outer extent of the contacted region (point 2) and the outer edge of the gliding layer, which is the furthest radially the drop has spread (right facing arrow). The outer edge of the contacted region will continue to spread outwards, entrapping microbubbles as it propagates. Li, Vakarelski & Throddsen (Reference Li, Vakarelski and Throddsen2015) showed similar film ruptures for water drops impacting a film of
![]() $2\times 10^{7}~\text{cSt}$
silicone oil.
$2\times 10^{7}~\text{cSt}$
silicone oil.
Figure 6(c) shows this transition for 100 cSt drops from gliding to contact at the kink. Each panel shows the rupture location for a different impact velocity, increasing from left to right. These frames also correspond to the light blue triangles that are trending downwards and to the right in figure 4. As the impact velocity increases, the rupture location moves progressively closer to the edge of the dimple until at a sufficiently high impact velocity,
![]() $V=3.8~\text{m}~\text{s}^{-1}$
, the drop makes contact at the kink. Unlike in the cases with higher viscosity, the lower-viscosity drop does not first glide for a large distance and then later rupture near the kink as in figure 6(b). The contact is made at the kink, before the drop begins to spread outwards.
$V=3.8~\text{m}~\text{s}^{-1}$
, the drop makes contact at the kink. Unlike in the cases with higher viscosity, the lower-viscosity drop does not first glide for a large distance and then later rupture near the kink as in figure 6(b). The contact is made at the kink, before the drop begins to spread outwards.
3.6 Contraction of the air film
When fluid films rupture within viscous outer fluids, the retraction velocity
![]() $V_{r}$
is typically dictated by balancing the capillary and viscous forces. Reyssat & Quéré (Reference Reyssat and Quéré2006) studied the bursting of thin films and proposed a logarithmic correction to a simple capillary–viscous balance,
$V_{r}$
is typically dictated by balancing the capillary and viscous forces. Reyssat & Quéré (Reference Reyssat and Quéré2006) studied the bursting of thin films and proposed a logarithmic correction to a simple capillary–viscous balance,
![]() $\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{\ell }$
, for the retraction velocity of the edge
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{\ell }$
, for the retraction velocity of the edge
where
![]() $r$
is the radius of the rim of the retracting fluid, which is on the order of the thickness of the film when it first bursts. Figure 7(a) shows the average measured retraction velocity of the extended air film versus liquid viscosity compared with (3.4). Here we have taken
$r$
is the radius of the rim of the retracting fluid, which is on the order of the thickness of the film when it first bursts. Figure 7(a) shows the average measured retraction velocity of the extended air film versus liquid viscosity compared with (3.4). Here we have taken
![]() $r=160~\text{nm}$
. For the low-viscosity cases,
$r=160~\text{nm}$
. For the low-viscosity cases,
![]() $V_{r}$
follows the expected behaviour; however, for
$V_{r}$
follows the expected behaviour; however, for
![]() $\unicode[STIX]{x1D707}_{\ell }>10^{2}~\text{cSt}$
the retraction velocity is nearly constant at
$\unicode[STIX]{x1D707}_{\ell }>10^{2}~\text{cSt}$
the retraction velocity is nearly constant at
![]() $0.28~\text{m}~\text{s}^{-1}$
. We suspect that the deviation is due to the thinness of the air film when rupture occurs being two orders of magnitude smaller than those studied by Reyssat & Quéré (Reference Reyssat and Quéré2006). For drop impacts onto solid surfaces where a similar thickness air layer exists, Langley et al. (Reference Langley, Li and Thoroddsen2017) measured contact line velocities to be independent of viscosity for the localized contacts within the gliding layer for
$0.28~\text{m}~\text{s}^{-1}$
. We suspect that the deviation is due to the thinness of the air film when rupture occurs being two orders of magnitude smaller than those studied by Reyssat & Quéré (Reference Reyssat and Quéré2006). For drop impacts onto solid surfaces where a similar thickness air layer exists, Langley et al. (Reference Langley, Li and Thoroddsen2017) measured contact line velocities to be independent of viscosity for the localized contacts within the gliding layer for
![]() $\unicode[STIX]{x1D707}_{\ell }$
as high as
$\unicode[STIX]{x1D707}_{\ell }$
as high as
![]() $2\times 10^{7}~\text{cSt}$
. At these thicknesses, perhaps the wetting behaviour is not solely due to a moving sharp edge and the liquid instead could be making contact by vertically draping over the surface or perhaps assisted by van der Waals forces when the thickness is on the order of 10 nm. The thickness of the air films is also of the same order as the mean free path of the air molecules, which may lead to possible rarefied gas effects that may enhance the wetting speed (see Li et al.
Reference Li, Langley, Tian, Hicks and Thoroddsen2017).
$2\times 10^{7}~\text{cSt}$
. At these thicknesses, perhaps the wetting behaviour is not solely due to a moving sharp edge and the liquid instead could be making contact by vertically draping over the surface or perhaps assisted by van der Waals forces when the thickness is on the order of 10 nm. The thickness of the air films is also of the same order as the mean free path of the air molecules, which may lead to possible rarefied gas effects that may enhance the wetting speed (see Li et al.
Reference Li, Langley, Tian, Hicks and Thoroddsen2017).
For contracting central air discs, the retraction velocity varies in time. The instantaneous initial retraction velocities can be much greater than the average velocity. Figure 7(b) shows the radius of a retracting air film within
![]() $10^{6}~\text{cSt}$
silicone oil versus time, with
$10^{6}~\text{cSt}$
silicone oil versus time, with
![]() $t=0$
corresponding to the time of rupture. The initial velocity is
$t=0$
corresponding to the time of rupture. The initial velocity is
![]() $0.7~\text{m}~\text{s}^{-1}$
, which slows to an average value of
$0.7~\text{m}~\text{s}^{-1}$
, which slows to an average value of
![]() $0.11~\text{m}~\text{s}^{-1}$
after
$0.11~\text{m}~\text{s}^{-1}$
after
![]() $200~\unicode[STIX]{x03BC}\text{s}$
. This drastic slow down corresponds with the edge of the retracting film reaching the outer edge of the much thicker central dimple.
$200~\unicode[STIX]{x03BC}\text{s}$
. This drastic slow down corresponds with the edge of the retracting film reaching the outer edge of the much thicker central dimple.

Figure 7. (a) Retraction velocity of the air film after rupture. The dotted line is the predicted velocity from Reyssat & Quéré (Reference Reyssat and Quéré2006) given in (3.4). (b) Radius versus time for a retracting air film in
![]() $10^{6}~\text{cSt}$
silicone oil. (c) Bottom-view image, with lighting from above, of a retracting air film entrapped in
$10^{6}~\text{cSt}$
silicone oil. (c) Bottom-view image, with lighting from above, of a retracting air film entrapped in
![]() $10^{6}~\text{cSt}$
silicone oil. White arrows mark microbubbles that were entrained as the film retracts. The drop initially impacted at
$10^{6}~\text{cSt}$
silicone oil. White arrows mark microbubbles that were entrained as the film retracts. The drop initially impacted at
![]() $V=1.7~\text{m}~\text{s}^{-1}$
. The scale bar is
$V=1.7~\text{m}~\text{s}^{-1}$
. The scale bar is
![]() $200~\unicode[STIX]{x03BC}\text{m}$
.
$200~\unicode[STIX]{x03BC}\text{m}$
.
Figure 7(c) shows a bottom-view image of an air film retracting in
![]() $10^{6}~\text{cSt}$
silicone oil. As the air film contracts, the rim of the film becomes unstable, forming a series of tips around the periphery. As the film continues to retract, the tips are pinched off, forming myriad microbubbles, as shown by the arrows in the figure. As the film radius decreases, the number of tips around the periphery also decreases.
$10^{6}~\text{cSt}$
silicone oil. As the air film contracts, the rim of the film becomes unstable, forming a series of tips around the periphery. As the film continues to retract, the tips are pinched off, forming myriad microbubbles, as shown by the arrows in the figure. As the film radius decreases, the number of tips around the periphery also decreases.
4 Conclusions
Herein, we have investigated the early impact dynamics of high-viscosity drops impacting onto films of the same liquid. As the drop approaches the liquid surface, the pressure in the intervening gas layer rises, deforming both the drop and film interfaces by the amount corresponding to an effective velocity equal to
![]() $1/2$
of the impact velocity. Using this approach velocity in the Stokes number,
$1/2$
of the impact velocity. Using this approach velocity in the Stokes number,
![]() $St_{p}$
, unifies the scaling for the centreline height of the air disc for highly viscous drop impacts onto solid and liquid surfaces. In both cases the normalized initial centreline height,
$St_{p}$
, unifies the scaling for the centreline height of the air disc for highly viscous drop impacts onto solid and liquid surfaces. In both cases the normalized initial centreline height,
![]() $H_{c}$
, scales with the impact parameter,
$H_{c}$
, scales with the impact parameter,
![]() $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D70C}_{\ell }V^{2}/P_{atm})Re_{\ell }^{1/3}$
, to the
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D70C}_{\ell }V^{2}/P_{atm})Re_{\ell }^{1/3}$
, to the
![]() $1/3$
power, revealing a weak dependence on liquid viscosity,
$1/3$
power, revealing a weak dependence on liquid viscosity,
![]() ${\sim}\unicode[STIX]{x1D707}_{\ell }^{-1/9}$
.
${\sim}\unicode[STIX]{x1D707}_{\ell }^{-1/9}$
.
For small
![]() $\unicode[STIX]{x1D6F7}$
, the drop does not initially make contact with the liquid film but instead glides on a thin layer of air. The normalized radial extent of the gliding layer increases as
$\unicode[STIX]{x1D6F7}$
, the drop does not initially make contact with the liquid film but instead glides on a thin layer of air. The normalized radial extent of the gliding layer increases as
![]() $\unicode[STIX]{x1D6F7}^{1/4}$
. For increasing
$\unicode[STIX]{x1D6F7}^{1/4}$
. For increasing
![]() $\unicode[STIX]{x1D6F7}$
, the drop transitions from gliding to ring contact at the kink on the edge of the central dimple. The transition is demarcated by a sudden decrease in the radial location of the rupture of the thin extended air layer. The time from dimple formation to air film rupture also decreases suddenly.
$\unicode[STIX]{x1D6F7}$
, the drop transitions from gliding to ring contact at the kink on the edge of the central dimple. The transition is demarcated by a sudden decrease in the radial location of the rupture of the thin extended air layer. The time from dimple formation to air film rupture also decreases suddenly.
Overall, the time at rupture behaves non-monotonically as a function of
![]() $Re_{\ell }$
. For liquid viscosities greater than
$Re_{\ell }$
. For liquid viscosities greater than
![]() $10^{3}~\text{cSt}$
, there is an increase in the time to rupture with increasing
$10^{3}~\text{cSt}$
, there is an increase in the time to rupture with increasing
![]() $Re_{\ell }$
, as
$Re_{\ell }$
, as
![]() $Re_{\ell }\rightarrow 1$
from below. For the smaller liquid viscosities, the time to rupture decreases with increasing
$Re_{\ell }\rightarrow 1$
from below. For the smaller liquid viscosities, the time to rupture decreases with increasing
![]() $Re_{\ell }$
.
$Re_{\ell }$
.
As
![]() $\unicode[STIX]{x1D6F7}\rightarrow 1$
, both the centreline height and rupture location approach the values expected for inviscid drop impacts onto solid surfaces. For lower-viscosity drops, the air film contracts after rupture according to established theory; however, for liquid viscosity
$\unicode[STIX]{x1D6F7}\rightarrow 1$
, both the centreline height and rupture location approach the values expected for inviscid drop impacts onto solid surfaces. For lower-viscosity drops, the air film contracts after rupture according to established theory; however, for liquid viscosity
![]() ${>}10^{2}~\text{cSt}$
the air film contracts with a near-constant velocity independent of viscosity.
${>}10^{2}~\text{cSt}$
the air film contracts with a near-constant velocity independent of viscosity.
It remains to study in more detail how the thickness of the liquid film influences the thickness of the entrapped air layer. Figure 5 shows this trend only for one viscosity of
![]() $10^{4}~\text{cSt}$
. Intuitively one may expect that the depth will be less important at higher viscosities, as the deformations become much smaller; however, a higher liquid viscosity could result in the presence of the wall being felt over larger distances.
$10^{4}~\text{cSt}$
. Intuitively one may expect that the depth will be less important at higher viscosities, as the deformations become much smaller; however, a higher liquid viscosity could result in the presence of the wall being felt over larger distances.
Acknowledgement
The work reported herein was funded by King Abdullah University of Science and Technology (KAUST) under grant URF/1/3727-01-01.
Supplementary materials
Supplementary materials are available at https://doi.org/10.1017/jfm.2019.682.