Introduction

The metamorphism of snow is of interest for a variety of reasons. The processes in snow can simulate those in high-temperature metal and ceramic powders, but at temperatures more convenient for experimental investigations. The metamorphism of snow causes large changes in snow properties, especially strength, permeability, reflectivity, and thermal conductivity. These properties affect every investigation of the snow cover including avalanche release, melt-water run-off, and radiant-energy penetration.

The metamorphism of snow at sub-freezing temperatures (where only the solid and vapor phases of water occur) has been described as either “temperature-gradient” or “equi-temperature metamorphism” (Reference Sonmierfild and LaChapdleSonmierfild and LaChapelle, 1970). In the former case a large temperature gradient is imposed on the snow cover; heat and vapor transfer arising from this temperature gradient dominate the exchange of heat and mass between snow particles and layers. Reference Giddings and LaChapelleGiddings and LaChapelle (1962) assumed the pore space to be saturated with water vapor and ignored radius of curvature effects, this allowed the temperature gradient to dominate the exchange processes. Their model, a significant first approximation in the presence of large temperature gradients, simulates the rate of formation of “depth hoar”, a cohesionless, cup-shaped crystal which forms at the base of those snow covers which experience strong cooling at the surface.

“Equi-temperature metamorphism” in sub-freezing snow, is poorly named since phase changes cannot occur without some heat flow and heat flow cannot occur without a temperature gradient. As shown later, the process is nearly isothermal since vapor-pressure gradients in isolated, dry snow are much larger than temperature gradients but a better term would be “radius-of-curvature metamorphism”.

Although a seasonal snow cover at a sub-freezing temperature can never be isothermal for an extended period, vapor migration due to differences in radius of curvature is thought to be important in the initial metamorphism of fresh snow when large temperature gradients are absent. This process is described here together with the metamorphic processes in liquid-saturated snow (i.e. pore spaces filled with liquid) and wet snow with a low liquid content.

Basic thermodynamics

A brief review of the basic concepts is made so that the limitations of the application of thermodynamics to snow metamorphism will be apparent. The basic approach is to assume that the phases of water (solid, liquid, and/or vapor) are in local equilibrium because they are finely divided (i.e. the specific surface area is very large). Although complete equilibrium is impossible in any system with a large surface area, local equilibrium between phases is a good approximation when the rate of mass exchange between the phases is very slow. We use the classical thermodynamic approach which assumes reversible processes although the basic Gibbs equation is also valid for a large class of irreversible processes (Reference prigoginePrigogine, 1949).

The chemical potential of the i th phase (μi) is given by (Reference Condon, Condon and OdishawCondon, 1958)

(1)

where F _i is the Gibbs free energy and m _i is the mass. The Gibbs free energy is a minimum at equilibrium and so the chemical potentials of the phases must be equal at equilibrium. This leads to a particularly useful relationship, the Gibbs-Duhem equation applied to the i th phase which is

(2)

where Ʋ_i is the specific volume, S_i is the specific entropy, p_i is pressure, and T is the temperature. This relationship could be applied to a multi-phase system as a whole or to an entire multicomponent system (e.g, water and air). However, for our purposes it is most convenient to apply Equation (2) to each phase separately. In fact it is not necessary to treat the inert component of snow (air) at all since its inclusion does not affect the calculation of the triple point of water except that the values of surface energy may be slightly different in the presence of air (Reference Defay and PrigogineDefay and Prigogine, 1951, p. 273). We assume that the liquid is saturated with dissolved air, which reduces the triple-point temperature by a constant value of 0.002 4 deg.

When other dissolved impurities (e.g. soluble salts) or chemically active impurities are present in snow it is necessary to take them into account as additional components. In general, when there are C components in a system of P phases, there are P(C+1) variables which must be specified at equilibrium (Reference Condon, Condon and OdishawCondon, 1958). However, since the value of the chemical potential of each component must be the same for all phases, there are C(P— 1) restrictions on the number of degrees of freedom. Also, since the temperature of all phases must be equal, there are (P— 1) additional restrictions. Thus for a system with curved interfaces, the variance or number of degrees of freedom is equal to C+1 since

(3)

This form of Gibb’s phase rule shows why we can ignore the air in the pore space; if we consider gaseous air and specify its pressure, the number of intensive variables which remain independent docs not change. In effect, snow is a one-component, two-or three-phase system with two degrees of freedom. Thus when two variables are specified, the remainder of the system is fixed at equilibrium. Reference LanghamLangham (1974) quoted the phase rule for a system with fiat surfaces (C —P+2). This form of the phase rule does not apply to a system with curved surfaces (e.g. snow or liquid veins in ice layers).

One other concept must be mentioned before snow metamorphism can be examined: curved interfaces are necessarily accompanied by a pressure difference between the adjacent phases. This balance of forces at an interface is expressed by Laplace’s equation (Reference Defay and PrigogineDefay and Prigogine, 1951)

(4)

where σ_ij is the interfacial energy between the i th and j th phases and r_ij is the “mean radius of curvature” of the interface. This mean curvature is related to the actual radii by

(5)

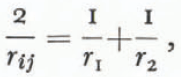
where r ₁, and r ₂ are the principal radii (or the radii of curvature measured in any two orthogonal planes) of the surface separating the two phases, r ₁, and r ₂ are positive when the i th side of the phase boundary is concave toward the point of measurement. It follows that r _ij =-r _ij. The solid, liquid, and vapor phases are indicated by the subscripts s, l, and g respectively. Gibbs (1928, equations 500 and 662) derived the same equation in a more general way for both fluid-fluid interfaces and fluid-solid interfaces. It is important to note that all derivations of Equation (4) are valid only for isotropic states of stress, hence analysis of metamorphism involving other states of stress (Reference YosidaYosida, 1963; Reference perlaPerla, 1978[a]) are not valid for curved surfaces. Furthermore, the effects of radius of curvature, elastic strains, and ionic impurities are not independent and cannot be simply added to correct the triple point for each effect (this is illustrated by Reference Dufour and DefayDufour and Defay (1963), equation 10.24); rather, it is necessary to account directly for effects like elastic strains in the first law of thermodynamics (Reference GibbsGibbs, 1928, equation 386).

Dry-snow metamorphism

Temperature usually varies within a snow cover on a time scale of hours to days and thus “equi-temperature metamorphism” or metamorphism driven by radius of curvature effects alone cannot dominate long-term changes occurring in a seasonal snow cover. Radius of curvature is important in firnification of cold ice sheets and could dominate the metamorphism of fresh snow during brief periods of isothermal conditions. Thus it is important to understand that metamorphism which is due to radius of curvature effects.

Reference Hobbs and MasonHobbs and Mason (1964) and Reference Hobbs and RadkeHobbs and Radke (1967), examined the sintering of ice spheres and found that mass transfer through the vapor is more important than transfer by surface or volume diffusion. Accordingly, it is most important to consider vapor transfer. We begin by deriving the basic equations, state the assumptions and limitations on the use of the equations, and analyze the relative size of vapor pressure and temperature gradients.

if we ignore the air phase (or fix its pressure), Gibb’s phase rule requires that the variance or number of degrees of freedom be two. Thus, we must specify two variables before the system is invariant at equilibrium. We consider three simple cases and then decide which is most applicable for dry snow:

(1) For a constant geometry r _sg is constant and Laplace’s equation requires that d(ps—pg) is zero. From Equation (2),

(6)

and

(7)

When the solid and vapor phases are in equilibrium, d( μ_g—μ_s) is zero so

(8)

Using the definition of entropy for a reversible process between states A and B,

(9)

and we find that

(10)

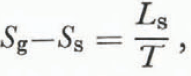
where L _s is the latent heat of sublimation at a temperature T. An expansion of the right-hand side of Equation (8) together with Equation (10) gives

(11)

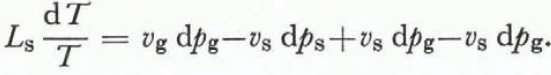
The approximation that the specific volume of air is much greater than the specific volume of ice (v_g v_s) and the knowledge that d(p_s—p_g) is zero yields

(12)

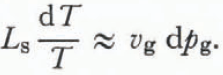
Using the ideal gas law,

(13)

then Equation (12) integrates to

(14)

where p ₀ and T ₀ are the reference pressure and temperature for the geometry specified (usually taken as the triple point of water). Note that this is only the ordinary triple point if we are working with a flat surface, otherwise p ₀ and T ₀ vary with the particular geometry considered. While this equation might be a useful approximation for “temperature-gradient meta-morphism” it cannot be used when metamorphism is dominated by radius of curvature effects.

(2) For a system at constant temperature, Equations (6) and (7) reduce to

(15)

One of Laplace’s equations is

(16)

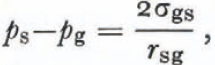
and this equation can be used with Equation (13) to obtain

(17)

which is the form of Kelvin’s equation for a small crystal. Reference Hobbs and MasonHobbs and Mason (1964) used this equation to describe the sintering of small ice spheres. As we will see later, it is the most nearly correct description of dry-snow metamorphism in the absence of imposed temperature gradients. Perla (1978[a]) used a similar equation but his equations (5) and (8) are not correct expressions of the first law or Kelvin’s equation.

(3) For a system with a constant vanor pressure. Equations (6) and (7) reduce to

(18)

With Equations (10) and (16), this integrates to

(19)

This can be converted to the Celsius temperature scale by

(20)

so that, with the approximation

(21)

we find

(22)

where the reference temperature T ₀ is the temperature at which the specified vapor pressure exists over a flat surface.

It is not obvious a priori that Equations (14), (17), or (22) are good approximations for “radius of curvature metamorphism”. The assumptions behind their derivations are very different and hence we must examine the temperature and pressure gradients closely to see which, if any, of these equations is close to the situation in the absence of imposed temperature gradients. Since large changes in radius of curvature occur, Equation (14) is of no value here although Reference Giddings and LaChapelleGiddings and LaChapelle (1962) and de Reference QuervainQuervain (1963) used this approach in their analyses of “temperature-gradient metamorphism”. In their case, radius of curvature was the least important effect whereas here we are concerned primarily with changes caused by variations in radius of curvature.

The group of ice grains (or branches of grains) with smaller mean radii of curvature are vapor sources and the group with larger radii of curvature are sinks. As metamorphism proceeds some grains (or branches of grains) move from one group to the other but, at any given instant, all ice surfaces fall into one category or the other. The vapor flux q is given by

(23)

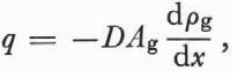
where D is the coefficient of diffusion of water vapor in air (it is weakly dependent on temperature (Reference DorseyDorsey, 1940, p. 772)) The area through which the vapor diffuses is A _g and the vapor- density gradient (dρ _g ⁄dx) drives the flux.

The heat flux Q is given by

(24)

where k is the thermal conductivity (a weak function of temperature and vapor pressure), A_h is the area through which the vapor moves, and dT⁄dx is the temperature gradient. Using average gradients between the source and sink, we find by conservation of energy and mass,

(25)

For the typical case of “destructive metamorphism” where the extremities of snow-flakes are disappearing (de Reference QuervainQuervain, 1963), the path length, and areas of heat and mass flow are about equal. Equation (25) then reduces to

(26)

It must be noted that this equation would be a poor approximation to the sintering of spherical grains as analyzed by Reference Hobbs and MasonHobbs and Mason (1964). It is only intended for application to the destruction of stellar snow-flakes, The more advanced stages of sintering require a more rigorous treatment of the geometry.

From Equation (13) we find that

(27)

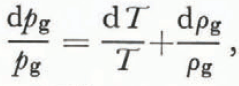
where dT and dρ _g have opposite signs. Using Equation (26),

(28)

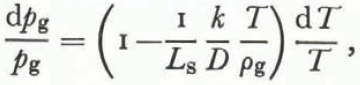
or

(29)

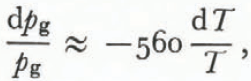
for characteristic values of k, D, T, ρ_g, and L_s.

Clearly the relative change in vapor pressure is much larger than the relative change in temperature and therefore the constant-temperature Kelvin’s equation (Equation (17)) is a good approximation for metamorphism dominated by radius of curvature effects (hence the term “equi-temperature metamorphism”).

The rate of mass transfer (dm⁄dt) between a source and sink is obtained from Equations (13),(17), and (23),

(30)

where (A _g⁄ Δl) is the ratio of the area to the path length between the source and sink, r_a and r _b are the mean radii of curvature of the source and sink, and T is the average temperature of the system. This equation depends on the particular geometry considered.

For one snow-flake undergoing destructive metamorphism in an isolated environment such as the case studied by de Quervain (1945, fig. 1), tens of days are required for the loss of the snow-flake’s characteristic shape. Estimates of the rate of mass loss from a particular arm of a dendrite made with Equation (30) account for the slow transfer observed by Reference Bader, Kuroiwa and HanoverBader and Kuroiwa (1962) and de Reference QuervainQuervain (1945). Perla (1978[a]) made similar estimates.

Since destructive metamorphism occurs mostly near the snow-pack surface where “equi- temperature metamorphism” for tens of days is essentially impossible, an accurate treatment of the geometry of this process would not be particularly useful. The correct principles are expressed in the development of Equation (30) and so a complete treatment of the geometry of a snow-flake undergoing metamorphism in the absence of imposed temperature gradients is possible. It is useful to define the conditions where either metamorphism due to variations in radius of curvature or metamorphism due to temperature gradients imposed by environmental conditions dominate. From Equations (13) and (28) we find that vapor pressure and temperature gradients arising from radius of curvature metamorphism are related by

(31)

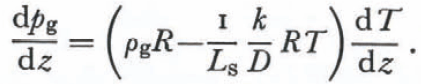
Using Equation (31) and Kelvin’s equation in the absence of an imposed temperature or vapor-pressure gradient (for mass exchanges on the scale of 1 mm from surfaces of mean radius of curvature equal 0. 1 mm), the local temperature gradient due to differences in radii of curvature is about 10^₋2 deg⁄m. It is very unlikely that such a small temperature gradient could prevail in a snow cover for tens of days and so it is very unlikely that radius of curvature effects alone could account for the metamorphism of snow grains with mean radius of curvature equal to or greater than 0.1 mm. Radius of curvature effects would be relatively more important in a layer of fresh snow with some dendrite branches of mean radius of curvature of less than 10^₋3 mm if the imposed temperature gradient were less than 1 deg⁄m (seeFig. 1). Thus it is possible that variations in radius of curvature initially control the metamorphism of fresh snow but, once the smaller parts of the dendrites disappear, the temperatures imposed on the bottom and top of the snow cover control the distributions of temperature and water vapor as well as the metamorphism.

Fig. 1. The temperature gradient arising from the sublimation of a branch of a snow-flake of given mean radius (the vapor sink is a fiat surface a distance of 1 mm from the sources)

Radius of curvature effects are of diminishing importance as metamorphism proceeds. The relative balance between the radius of curvature effects and the imposed temperature effects depends upon the relative sizes of the smallest dendrites and the magnitude of the imposed gradients. Figure 1 shows a rapid decrease of the temperature gradient arising from radius of curvature metamorphism with increasing radius of curvature. This suggests a rapid shift from radius of curvature to temperature-gradient metamorphism as the smaller parts of the dendrites disappear in a layer of fresh snow.

Liquid-saturated snow

In liquid-saturated snow, the pore space is filled with liquid so that only the solid and liquid phases are present. Saturated snow is characterized by grain-boundary melting, rapid grain rounding, and rapid grain growth. In the absence of an applied load, grain rounding takes only a few hours and grain growth requires only a few days in marked contrast to the case of dry snow where the same amount of grain growth take years (Gow, [1975]). Since both are two-phase systems at temperatures only a few degrees apart, we would not expect a priori such a radical difference.

In the case of dry snow we found that vapor diffusion was the rate-limiting process and that the temperature—radius-of-curvature relation (Equation (22)) greatly overestimated the actual temperature differences between grains. In liquid-saturated snow there is virtually no pressure gradient because the pore space is filled with the melt, and pressure disturbances propagate instantaneously between neighboring particles. Thus, heat flow is the rate- limiting process and the actual temperature distribution is closely approximated by a relation analogous to Equation (22),

(32)

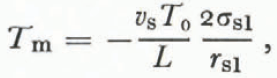
where the T _m is the melting temperature (°C), L is the specific latent heat of fusion, and T ₀ is 273.13 K. Experimental confirmation of this equation has been obtained for ice by Reference BerryBerry (1959) ard for metals by Reference Peppiatt and SamblesPeppiatt and Sambles (1975) and Reference Couchman and JesserCouchman and Jesser (1977). Although an equation relating liquid pressure and radius of curvature could also be derived, it would be meaningless in this case just as Equation (22) was meaningless in the case of dry snow undergoing “radius of curvature metamorphism”.

Since the grains round off quickly, the geometry is much simpler than that of snow-flakes and the grain-growth process can be modeled readily. Reference ColbeckColbeck (1973) constructed a simple model of heat flow between two grains which predicted accurately the life expectancy and accelerating rate of decay observed by Wakahama (1968, [1975]). Reference Raymond and TusimaRaymond and Tusima (1979) have recently analyzed and observed this process in more detail, including the effects of dissolved impurities.

Wet snow with a low liquid content

Snow covers are highly permeable and water drains readily through them with a characteristic liquid content of two to five per cent by volume. In most granular porous materials with a low liquid content, the liquid is held between spherical grains in individual liquid menisci. Spherical grains are inherently unstable in wet snow with low liquid contents (Reference ColbeckColbeck, 1979). The grains tend to regroup themselves into grain clusters around liquid- filled veins (Fig. 2) and “compressed”, two-grain contacts (Fig. 3). Perla (1978[b]) has incorrectly attributed these clusters to melt-freeze cycles alone. In fact they form just as rapidly where no freezing occurs (Reference ColbeckColbeck, 1979).

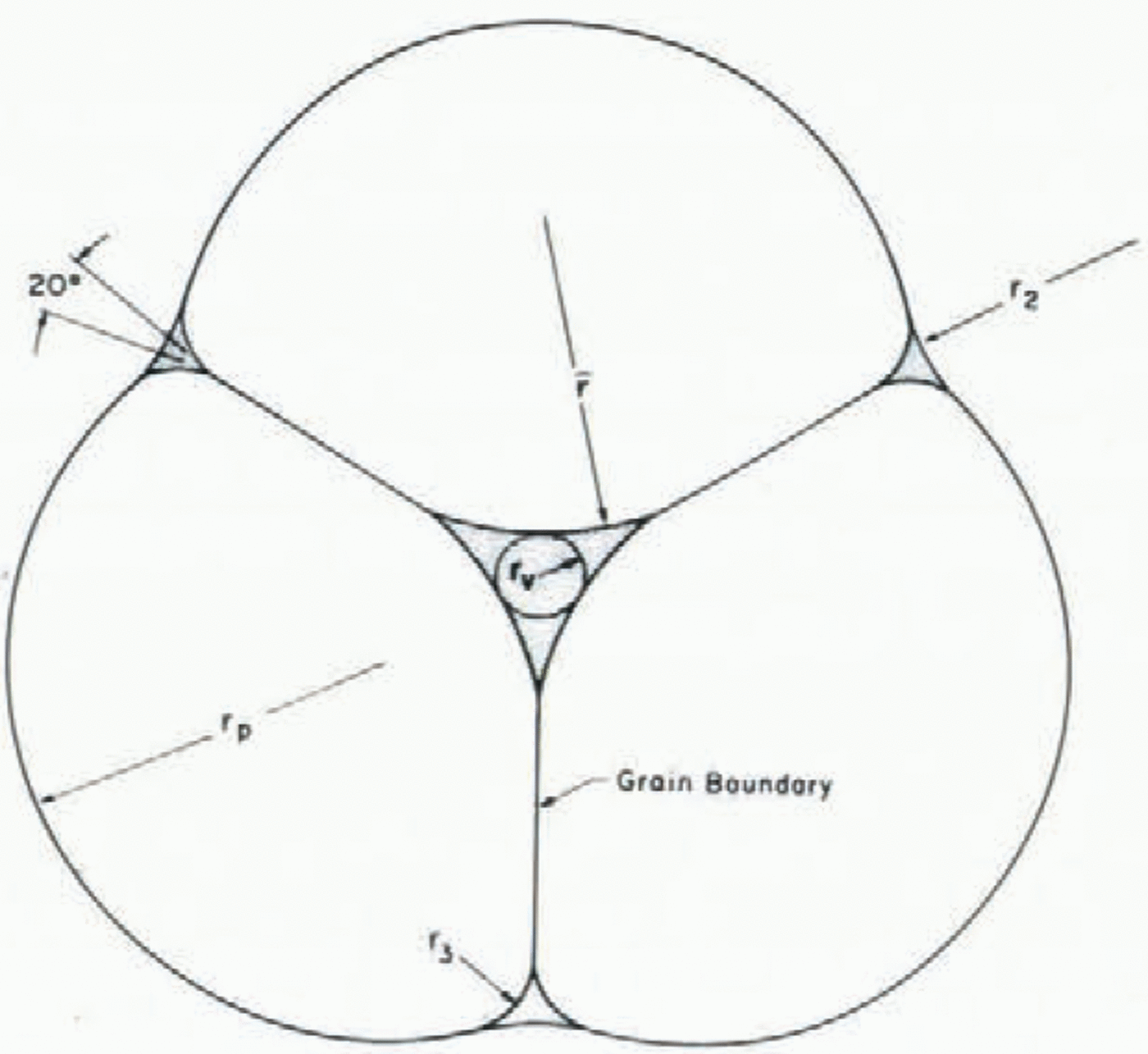
Fig. 2. The basic unit of a three-grain cluster. The size of the liquid vein is determined by the size of the particle r_p and the liquid-water content (after Reference ColbeckColbeck (1979)).

Fig. 3. The basic unit of a two-grain bond. The radius of curvature of the shoulder r₃ is about one-fifth that of the particle r_p (after Reference ColbeckColbeck (1979)).

As shown in Figures 2 and 3, each grain has solid-solid, solid-liquid, solid-vapor, and liquid-vapor interfaces. The radius of curvature of the solid-vapor interface controls the rate of grain growth while the radius of curvature of the liquid-vapor interface controls the liquid-water content. The presence of a stable grain boundary gives wet snow a considerable cohesive strength at low liquid contents (a low cohesive strength due to grain boundary melting is a distinguishing characteristic of wet snow at high liquid content).

The liquid content in a porous medium is generally related to the pressure deficiency in the liquid as dictated by Laplace’s equation. This is usually expressed as “liquid tension” or capillary pressure defined as (Reference ScheideggerScheidegger, 1974, p. 56)

(33)

In snow, capillary pressure increases during liquid withdrawal (Reference ColbeckColbeck, 1973) in a manner characteristic of large-grained porous media except that, after grain clusters form, changes in capillary pressure can be restricted by the geometry of the cluster (Reference ColbeckColbeck, 1979).

The temperature at which the three phases are in equilibrium T _m is the triple-point temperature for the particular geometry in question. Reference ColbeckColbeck (1973) derived this using Equations (2) and (4),

(34)

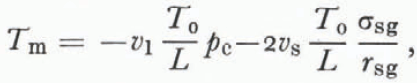
where r _sg is the radius of the solid-vapor interface shown on Figures 2 and 3. The mean radius of the liquid vein enters Equation (34) implicitly through the Laplace equations (4); its geometry is partly determined by the dihedral angle of a grain-boundary groove in ice.

Although Equation (34) is an accurate description of the triple-point temperature in unsaturated wet snow with a uniform grain size, it is unlikely that this relation is valid for each grain in an unsaturated snow of varying grain sizes. As in dry snow, the process of grain growth in unsaturated wet snow is dominated by mass exchange through vapor diffusion, and so the same arguments about the relative sizes of pressure and temperature gradients leading to Equation (29) are valid here (the difference between dp_g⁄p_g and dT⁄T is even larger for wet snow than for dry snow since we replace the latent heal of sublimation in Equation (28) with the smaller latent heat of fusion). Accordingly, a special case of Kelvin’s equation is a good approximation to the vapor pressure over the ice surface,

(35)

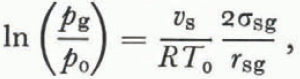
where p ₀ and T ₀ are the ordinary triple-point pressure and temperature for a flat surface and r _sg is the mean radius of the ice-vapor surface.

As shown by Equation (35), the vapor pressure is higher over small grains and grain growth is dominated by the same process as in dry snow. Grain growth dominated by vapor flux is much slower than grain growth dominated by heat flux which explains why Reference WakahamaWakahama (1968) observed much slower grain growth at low liquid contents than at high liquid contents. Since the air in the pore space is no longer interconnected at liquid saturations above about 14% of the pore volume (Reference ColbeckColbeck, 1973), this degree of liquid saturation should mark the transition from vapor-flux dominated to heat-flux dominated metamorphism in wet snow.

Conclusion

It has long been recognized that dry-snow metamorphism in the absence of imposed temperature gradients is a very slow process (e.g. de Reference QuervainQuervain, 1945). Vapor diffusion from surface to surface is the rate-limiting process and the necessary heat transfer occurs with a relatively small temperature gradient. The Kelvin equation relating the vapor pressure to the mean radius of curvature at a constant temperature is a good approximation and can be used to construct a model of metamorphism dominated by differences in radii of curvature. Calculations with our very simple model of the geometry and using direct observations (de Reference QuervainQuervain, 1945; Reference Bader, Kuroiwa and HanoverBader, 1962) show very slow rates of mass transfer by this process so it is unlikely that radius of curvature effects can contribute significantly to the metamorphism of a subfreezing, seasonal snow cover. When imposed temperature gradients are less than 1 deg⁄m, the smallest branches (radius less than 10^₋3 mm) will sublimate because of their high vapor pressure but the imposed temperature gradient in the snow cover generally dominates over differences in radius of curvature.

In contrast to vapor-saturated dry snow in the absence of imposed temperature gradients, liquid-saturated snow experiences very rapid grain growth due to relatively large temperature differences among the grains. Mass transfer between grains occurs instantaneously because the pore space is filled with the melt so the process is rate limited by heat flow at a constant liquid pressure. In dry snow the vapor pressure varies with the radius of curvature whereas in liquid-saturated snow the temperature varies with the radius of curvature.

In wet snow with liquid contents in the usual range of two to five per cent of the total volume the air is interconnected between the pores, and grain growth occurs predominantly by vapor diffusion. In this case grain growth is much slower than in liquid-saturated snow. It has often been suggested (e.g. Perla,[1978]) that melt-refreeze cycles are responsible for grain growth in wet snow because “as the temperature approaches 0°C, crystals with the smallest radii are the first to melt”. However, we show here that the triple-point temperature is not sensitive to radius of curvature in wet snow with a low liquid content and therefore this mechanism must be rejected. In fact grain growth in both dry snow and wet snow at a low liquid content is controlled by vapor diffusion between surfaces of different radii of curvature. Only wet snow with a high liquid content (where the air in the pore space is discontinuous) experiences large temperature differences among grains and rapid grain growth by heat flow.