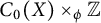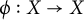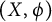1 Introduction and notation
Let
![]() $\mathcal A$
be a Banach algebra and
$\mathcal A$
be a Banach algebra and
![]() $a,b\in \mathcal A$
. The map
$a,b\in \mathcal A$
. The map
![]() $M_{a,b}:\mathcal A\rightarrow \mathcal A$
given by
$M_{a,b}:\mathcal A\rightarrow \mathcal A$
given by
![]() $M_{a,b}(x)=axb$
is called a multiplication operator. Vala [Reference Vala22] proved that if
$M_{a,b}(x)=axb$
is called a multiplication operator. Vala [Reference Vala22] proved that if
![]() $\mathcal {B(X)}$
is the algebra of all linear bounded operators on a Banach space
$\mathcal {B(X)}$
is the algebra of all linear bounded operators on a Banach space
![]() $\mathcal X$
and
$\mathcal X$
and
![]() $A,B\in \mathcal {B(X)}$
, then the multiplication operator
$A,B\in \mathcal {B(X)}$
, then the multiplication operator
![]() $M_{A, B}:\mathcal {B(X)}\rightarrow \mathcal {B(X)}$
, is compact if and only if A and B are compact operators. It follows that
$M_{A, B}:\mathcal {B(X)}\rightarrow \mathcal {B(X)}$
, is compact if and only if A and B are compact operators. It follows that
![]() $A\in \mathcal {B(X)}$
is a compact operator if and only if the multiplication operator
$A\in \mathcal {B(X)}$
is a compact operator if and only if the multiplication operator
![]() $M_{A,A}:\mathcal {B(X)}\rightarrow \mathcal {B(X)}$
is compact. Vala [Reference Vala23] defines an element a of a normed algebra
$M_{A,A}:\mathcal {B(X)}\rightarrow \mathcal {B(X)}$
is compact. Vala [Reference Vala23] defines an element a of a normed algebra
![]() $\mathcal A$
to be compact if the multiplication operator
$\mathcal A$
to be compact if the multiplication operator
![]() $M_{a,a}:\mathcal A\rightarrow \mathcal A$
is compact. He also proves that the set of compact elements of a Banach algebra is closed.
$M_{a,a}:\mathcal A\rightarrow \mathcal A$
is compact. He also proves that the set of compact elements of a Banach algebra is closed.
Ylinen [Reference Ylinen24] studied compact elements for abstract C*-algebras and showed that a is a compact element of a
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {A}$
if and only if there exists an isometric
$\mathcal {A}$
if and only if there exists an isometric
![]() $*$
-representation
$*$
-representation
![]() $\pi $
of
$\pi $
of
![]() $\mathcal {A}$
on a Hilbert space
$\mathcal {A}$
on a Hilbert space
![]() $\mathcal H$
such that the operator
$\mathcal H$
such that the operator
![]() $\pi (a)$
is compact.
$\pi (a)$
is compact.
Multiplication operators on algebras of operators have been studied, among others, by Akemann and Wright [Reference Akemann and Wright1], Saksman and Tylli [Reference Saksman and Tylli16, Reference Saksman and Tylli17], Johnson and Schechtman [Reference Johnson and Schechtman9], Lindström, Saksman and Tylli [Reference Lindström, Saksman and Tylli11], Mathieu and Tradacete [Reference Mathieu and Tradacete14] and also by Mathieu [Reference Mathieu12, Reference Mathieu13], Timoney [Reference Timoney20] in the more general framework of elementary operators.
Compactness properties of multiplication operators on nest algebras are studied by Andreolas and Anoussis [Reference Andreolas and Anoussis2]. Andreolas, Anoussis, and Magiatis obtain in [Reference Andreolas, Anoussis and Magiatis3] a characterization of the compact multiplication operators on semicrossed products.
If
![]() $\mathcal H$
is a separable Hilbert space, the set of compact elements coincides with the ideal
$\mathcal H$
is a separable Hilbert space, the set of compact elements coincides with the ideal
![]() $ \mathcal {K}(\mathcal H)$
of compact operators on
$ \mathcal {K}(\mathcal H)$
of compact operators on
![]() $\mathcal H$
, while the Calkin algebra
$\mathcal H$
, while the Calkin algebra
![]() $\mathcal {B}(\mathcal H)/\mathcal {K}(\mathcal H)$
does not have any nonzero compact element [Reference Fong and Sourour8, Section 5]. However, this is not a general phenomenon.
$\mathcal {B}(\mathcal H)/\mathcal {K}(\mathcal H)$
does not have any nonzero compact element [Reference Fong and Sourour8, Section 5]. However, this is not a general phenomenon.
Shulman and Turovskii observe in [Reference Shulman and Turovskii18, p. 298] that there exist Banach spaces
![]() $\mathcal X$
, such that the quotient
$\mathcal X$
, such that the quotient
![]() $\mathcal {B}(\mathcal X)/\mathcal {K}(\mathcal X)$
contains compact elements. A stronger instance of this phenomenon appears in the algebra of bounded linear operators on the Argyros–Haydon space [Reference Argyros and Haydon5]. This space is a Banach space
$\mathcal {B}(\mathcal X)/\mathcal {K}(\mathcal X)$
contains compact elements. A stronger instance of this phenomenon appears in the algebra of bounded linear operators on the Argyros–Haydon space [Reference Argyros and Haydon5]. This space is a Banach space
![]() $\mathcal X$
with the property that every operator in
$\mathcal X$
with the property that every operator in
![]() $\mathcal {B}(\mathcal X)$
is a scalar multiple of the identity plus a compact operator. It follows that
$\mathcal {B}(\mathcal X)$
is a scalar multiple of the identity plus a compact operator. It follows that
![]() $\mathcal {B}(\mathcal X)/\mathcal {K}(\mathcal X)$
is finite-dimensional and hence consists of compact elements.
$\mathcal {B}(\mathcal X)/\mathcal {K}(\mathcal X)$
is finite-dimensional and hence consists of compact elements.
Shulman and Turovskii prove in [Reference Shulman and Turovskii18] that if
![]() $\mathcal A$
is a Banach algebra, then there exists a closed ideal
$\mathcal A$
is a Banach algebra, then there exists a closed ideal
![]() $\mathcal I$
in
$\mathcal I$
in
![]() $\mathcal A$
such that if
$\mathcal A$
such that if
![]() $\mathcal J$
is a closed ideal in
$\mathcal J$
is a closed ideal in
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal A/\mathcal J$
does not have compact elements, then
$\mathcal A/\mathcal J$
does not have compact elements, then
![]() $\mathcal I$
is contained in
$\mathcal I$
is contained in
![]() $\mathcal J$
. This ideal is called the hypocompact radical of
$\mathcal J$
. This ideal is called the hypocompact radical of
![]() $\mathcal {A}$
and is denoted by
$\mathcal {A}$
and is denoted by
![]() $\mathcal {A}_{\mathrm {hc}} $
. This definition of the hypocompact radical is not the one given in [Reference Shulman and Turovskii18, Reference Turovskiĭ and Shuľman21], but it is equivalent to it as we show in Proposition 3.1.
$\mathcal {A}_{\mathrm {hc}} $
. This definition of the hypocompact radical is not the one given in [Reference Shulman and Turovskii18, Reference Turovskiĭ and Shuľman21], but it is equivalent to it as we show in Proposition 3.1.
A characterization of the hypocompact radical of nest algebras is proved in [Reference Andreolas and Anoussis2]. A characterization of the hypocompact radical of a semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
is proved in [Reference Andreolas, Anoussis and Magiatis4].
$C_0(X)\times _\phi \mathbb Z_+$
is proved in [Reference Andreolas, Anoussis and Magiatis4].
In this article, we characterize the compact elements and the hypocompact radical of a crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
, where X is a locally compact metrizable space and
$C_0(X)\times _\phi \mathbb Z$
, where X is a locally compact metrizable space and
![]() $\phi :X\rightarrow X$
is a homeomorphism, in terms of the corresponding dynamical system
$\phi :X\rightarrow X$
is a homeomorphism, in terms of the corresponding dynamical system
![]() $(X,\phi )$
.
$(X,\phi )$
.
Throughout this paper, X will be a locally compact metrizable space and
![]() $\phi :X\rightarrow X$
a homeomorphism. The pair
$\phi :X\rightarrow X$
a homeomorphism. The pair
![]() $(X,\phi )$
is called dynamical system. If
$(X,\phi )$
is called dynamical system. If
![]() $C_0(X)$
is the
$C_0(X)$
is the
![]() $C^*$
-algebra of continuous functions vanishing at infinity, an action of
$C^*$
-algebra of continuous functions vanishing at infinity, an action of
![]() $\mathbb Z$
on
$\mathbb Z$
on
![]() $C_0(X)$
by isometric
$C_0(X)$
by isometric
![]() $*$
-automorphisms
$*$
-automorphisms
![]() $\alpha _n$
,
$\alpha _n$
,
![]() $n\in \mathbb Z$
is obtained by defining
$n\in \mathbb Z$
is obtained by defining
![]() $\alpha _n(f)=f\circ \phi ^{-n}$
.
$\alpha _n(f)=f\circ \phi ^{-n}$
.
We follow the notation of [Reference Davidson7]. We will denote by
![]() $C_0(X)\times _\phi \mathbb Z$
the crossed product corresponding to the dynamical system
$C_0(X)\times _\phi \mathbb Z$
the crossed product corresponding to the dynamical system
![]() $(X,\phi )$
. If
$(X,\phi )$
. If
![]() $n\in \mathbb Z$
and
$n\in \mathbb Z$
and
![]() $A\in C_0(X)\times _\phi \mathbb Z$
, we write
$A\in C_0(X)\times _\phi \mathbb Z$
, we write
![]() $E_n(A)$
for the nth Fourier coefficient of A. Also, we denote an element
$E_n(A)$
for the nth Fourier coefficient of A. Also, we denote an element
![]() $A\in C_0(X)\times _\phi \mathbb Z$
as a formal series
$A\in C_0(X)\times _\phi \mathbb Z$
as a formal series
where
![]() $f_n\equiv E_n(A)$
,
$f_n\equiv E_n(A)$
,
![]() $n\in \mathbb Z$
. We recall that if
$n\in \mathbb Z$
. We recall that if
![]() $fU^m,gU^n\in C_0(X)\times _\phi \mathbb Z$
, the multiplication is defined by setting
$fU^m,gU^n\in C_0(X)\times _\phi \mathbb Z$
, the multiplication is defined by setting
and extending by linearity and continuity.
If
![]() $\mathcal X$
is a Banach space, we denote by
$\mathcal X$
is a Banach space, we denote by
![]() $\mathcal X_1$
the unit ball of
$\mathcal X_1$
the unit ball of
![]() $\mathcal X$
. If
$\mathcal X$
. If
![]() $\mathcal A$
is a Banach algebra, we will denote by
$\mathcal A$
is a Banach algebra, we will denote by
![]() $\mathcal C(\mathcal A)$
the set of compact elements of
$\mathcal C(\mathcal A)$
the set of compact elements of
![]() $\mathcal A$
.
$\mathcal A$
.
2 The compact elements of the crossed product
In this section, we characterize the compact elements of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
. We will denote by
$C_0(X)\times _\phi \mathbb Z$
. We will denote by
![]() $X_{\mathrm a}$
the set of accumulation points of X, by
$X_{\mathrm a}$
the set of accumulation points of X, by
![]() $X_{\mathrm i}$
the set of isolated points of X and by
$X_{\mathrm i}$
the set of isolated points of X and by
![]() $X_{\mathrm p}$
the set of periodic points of the dynamical system
$X_{\mathrm p}$
the set of periodic points of the dynamical system
![]() $(X,\phi )$
.
$(X,\phi )$
.
Proposition 2.1 If
![]() $f\in C_0(X)$
, the following are equivalent:
$f\in C_0(X)$
, the following are equivalent:
-
(1) The element f is a compact element of the Banach algebra
 $C_0(X)$
.
$C_0(X)$
. -
(2)
 $f(X_{\mathrm a})=\{0\}$
.
$f(X_{\mathrm a})=\{0\}$
.
Proof
![]() $1 \Rightarrow 2$
. Let
$1 \Rightarrow 2$
. Let
![]() $x_0\in X_{\mathrm a}$
such that
$x_0\in X_{\mathrm a}$
such that
![]() $f(x_0)\neq 0$
. Then there exists an open neighborhood U of
$f(x_0)\neq 0$
. Then there exists an open neighborhood U of
![]() $x_0$
such that
$x_0$
such that
![]() $|f(x)|>\frac {|f(x_0)|}{2}$
for all
$|f(x)|>\frac {|f(x_0)|}{2}$
for all
![]() $x\in U$
. We consider a sequence
$x\in U$
. We consider a sequence
![]() $\{x_i\}_{i=1}^\infty \subseteq U$
such that
$\{x_i\}_{i=1}^\infty \subseteq U$
such that
![]() $x_i\neq x_j$
for
$x_i\neq x_j$
for
![]() $i\neq j$
and a sequence of norm one functions
$i\neq j$
and a sequence of norm one functions
![]() $\{g_{i}\}_{i=1}^\infty \subseteq C_0(X)$
such that
$\{g_{i}\}_{i=1}^\infty \subseteq C_0(X)$
such that
![]() $g_{i}(x_i)=1$
and
$g_{i}(x_i)=1$
and
![]() $g_i(x_j)=0$
for
$g_i(x_j)=0$
for
![]() $i\neq j$
. Then, for
$i\neq j$
. Then, for
![]() $i\neq j$
we have
$i\neq j$
we have
 $$ \begin{align*} \|M_{f,f}(g_i)-M_{f,f}(g_j)\|&=\sup_{x\in X} |[f^2(g_i-g_j)](x)|\\ &\ge |[f^2(g_i-g_j)](x_i)|\\ &\ge \frac{|f^2(x_0)|}{4}, \end{align*} $$
$$ \begin{align*} \|M_{f,f}(g_i)-M_{f,f}(g_j)\|&=\sup_{x\in X} |[f^2(g_i-g_j)](x)|\\ &\ge |[f^2(g_i-g_j)](x_i)|\\ &\ge \frac{|f^2(x_0)|}{4}, \end{align*} $$
and thus the sequence
![]() $\{M_{f,f}(g_i)\}_{i=1}^{\infty }$
has no convergent subsequence.
$\{M_{f,f}(g_i)\}_{i=1}^{\infty }$
has no convergent subsequence.
![]() $2 \Rightarrow 1$
. Let
$2 \Rightarrow 1$
. Let
![]() $f\in C_0(X)$
be such that
$f\in C_0(X)$
be such that
![]() $f(X_{\mathrm a})=\{0\}$
.
$f(X_{\mathrm a})=\{0\}$
.
For
![]() $n\in \mathbb N$
, the set
$n\in \mathbb N$
, the set
is compact and hence finite. We denote by
![]() $f_n\in C_0(X)$
the function defined by
$f_n\in C_0(X)$
the function defined by
 $$ \begin{align*} f_n(x)=\left\{\begin{matrix} f(x), & x\in S_n, \\ 0, & x\in X\,{\backslash}\, S_n. \end{matrix}\right. \end{align*} $$
$$ \begin{align*} f_n(x)=\left\{\begin{matrix} f(x), & x\in S_n, \\ 0, & x\in X\,{\backslash}\, S_n. \end{matrix}\right. \end{align*} $$
We have that
![]() $\|f-f_n\|\leq \frac {1}{n}$
. Moreover, the operators
$\|f-f_n\|\leq \frac {1}{n}$
. Moreover, the operators
![]() $M_{f_n, f_n}$
are finite-rank operators, and
$M_{f_n, f_n}$
are finite-rank operators, and
![]() $M_{f, f}$
is the norm limit of the sequence
$M_{f, f}$
is the norm limit of the sequence
![]() $\{M_{f_n, f_n}\}_{n=1}^{\infty }$
.
$\{M_{f_n, f_n}\}_{n=1}^{\infty }$
.
Lemma 2.2 If
![]() $fU^0\in C_0(X)\times _\phi \mathbb Z$
is a compact element, then
$fU^0\in C_0(X)\times _\phi \mathbb Z$
is a compact element, then
![]() $f(X_{\mathrm a})=\{0\}$
.
$f(X_{\mathrm a})=\{0\}$
.
Proof If
![]() $S=\{gU^0\in C_0(X)\times _\phi \mathbb Z:\|gU^0\|\leq 1\}$
, then
$S=\{gU^0\in C_0(X)\times _\phi \mathbb Z:\|gU^0\|\leq 1\}$
, then
Therefore, if the multiplication operator
![]() $M_{fU^0,fU^0}$
is compact, f is a compact element of
$M_{fU^0,fU^0}$
is compact, f is a compact element of
![]() $C_0(X),$
which implies that
$C_0(X),$
which implies that
![]() $f(X_{\mathrm a})=\{0\}$
, by Proposition 2.1.
$f(X_{\mathrm a})=\{0\}$
, by Proposition 2.1.
Lemma 2.3 If
![]() $fU^0\in C_0(X)\times _\phi \mathbb Z$
is a compact element, then
$fU^0\in C_0(X)\times _\phi \mathbb Z$
is a compact element, then
![]() $f(X_{\mathrm p})=\{0\}$
.
$f(X_{\mathrm p})=\{0\}$
.
Proof If
![]() $fU^0$
is a compact element, then
$fU^0$
is a compact element, then
![]() $f(X_{\mathrm p}\cap X_{\mathrm a})=\{0\}$
, by Lemma 2.2. We assume that there exists
$f(X_{\mathrm p}\cap X_{\mathrm a})=\{0\}$
, by Lemma 2.2. We assume that there exists
![]() $x_0\in X_{\mathrm p}\cap X_{\mathrm i}$
such that
$x_0\in X_{\mathrm p}\cap X_{\mathrm i}$
such that
![]() $f(x_0)\neq 0$
, and we prove that the multiplication operator
$f(x_0)\neq 0$
, and we prove that the multiplication operator
![]() $M_{fU^0,fU^0}$
is not compact.
$M_{fU^0,fU^0}$
is not compact.
Since
![]() $x_0\in X_{\mathrm p}\cap X_{\mathrm i}$
, there exists
$x_0\in X_{\mathrm p}\cap X_{\mathrm i}$
, there exists
![]() $n_0\in \mathbb Z$
,
$n_0\in \mathbb Z$
,
![]() $n_0\neq 0$
, such that
$n_0\neq 0$
, such that
![]() $\phi ^{n_0}(x_0)=x_0$
. We consider the sequence
$\phi ^{n_0}(x_0)=x_0$
. We consider the sequence
![]() $\{\chi U^{in_0}\}_{i=1}^{\infty }$
, where
$\{\chi U^{in_0}\}_{i=1}^{\infty }$
, where
![]() $\chi $
is the characteristic function of the singleton
$\chi $
is the characteristic function of the singleton
![]() $\{x_0\}$
. For
$\{x_0\}$
. For
![]() $i,j\in \mathbb N$
,
$i,j\in \mathbb N$
,
![]() $i\neq j$
, we have
$i\neq j$
, we have
 $$ \begin{align*} \|M_{fU^0,fU^0}(\chi U^{in_0})-M_{fU^0,fU^0}(\chi U^{jn_0})\| &\ge \|E_{in_0}(M_{fU^0,fU^0}(\chi U^{in_0}-\chi U^{jn_0}))\|\\ & = \|E_{in_0}(M_{fU^0,fU^0}(\chi U^{in_0}))\|\\ & = |f^2(x_0)|. \end{align*} $$
$$ \begin{align*} \|M_{fU^0,fU^0}(\chi U^{in_0})-M_{fU^0,fU^0}(\chi U^{jn_0})\| &\ge \|E_{in_0}(M_{fU^0,fU^0}(\chi U^{in_0}-\chi U^{jn_0}))\|\\ & = \|E_{in_0}(M_{fU^0,fU^0}(\chi U^{in_0}))\|\\ & = |f^2(x_0)|. \end{align*} $$
Hence, the sequence
![]() $\{M_{fU^0,fU^0}(\chi U^{in_0})\}_{i=1}^{\infty }$
has no convergent subsequence.
$\{M_{fU^0,fU^0}(\chi U^{in_0})\}_{i=1}^{\infty }$
has no convergent subsequence.
Lemma 2.4 Let
![]() $m,n\in \mathbb Z$
,
$m,n\in \mathbb Z$
,
![]() $x,y\in X_{\mathrm i}\,{\backslash}\, X_{\mathrm p}$
and
$x,y\in X_{\mathrm i}\,{\backslash}\, X_{\mathrm p}$
and
![]() $\chi _x, \chi _y$
be the characteristic functions of the singletons
$\chi _x, \chi _y$
be the characteristic functions of the singletons
![]() $\{x\}$
and
$\{x\}$
and
![]() $\{y\}$
, respectively. Then, the multiplication operator
$\{y\}$
, respectively. Then, the multiplication operator
![]() $M_{\chi _xU^m,\chi _yU^n}:C_0(X)\times _\phi \mathbb Z\rightarrow C_0(X)\times _\phi \mathbb Z$
is compact.
$M_{\chi _xU^m,\chi _yU^n}:C_0(X)\times _\phi \mathbb Z\rightarrow C_0(X)\times _\phi \mathbb Z$
is compact.
Proof To prove that
![]() $M_{\chi _xU^m,\chi _yU^n}$
is compact, we distinguish two cases. If there is no
$M_{\chi _xU^m,\chi _yU^n}$
is compact, we distinguish two cases. If there is no
![]() $k\in \mathbb Z$
such that
$k\in \mathbb Z$
such that
![]() $\phi ^k(x)=y$
, then,
$\phi ^k(x)=y$
, then,
![]() $M_{\chi _xU^m,\chi _yU^n}\equiv 0$
. Indeed, for an element
$M_{\chi _xU^m,\chi _yU^n}\equiv 0$
. Indeed, for an element
![]() $C=\sum _l h_lU^l$
, we have
$C=\sum _l h_lU^l$
, we have
 $$ \begin{align*} M_{\chi_xU^m,\chi_yU^n}(C) & = \chi_xU^m\left(\sum_l h_lU^l\right)\chi_yU^n \\ & = \sum_l \chi_xh_l\circ\phi^{-m}\chi_y\circ\phi^{-m-l}U^{m+l+n}\\ & =0, \end{align*} $$
$$ \begin{align*} M_{\chi_xU^m,\chi_yU^n}(C) & = \chi_xU^m\left(\sum_l h_lU^l\right)\chi_yU^n \\ & = \sum_l \chi_xh_l\circ\phi^{-m}\chi_y\circ\phi^{-m-l}U^{m+l+n}\\ & =0, \end{align*} $$
since
![]() $\chi _x\chi _y\circ \phi ^{-m-l}=0$
.
$\chi _x\chi _y\circ \phi ^{-m-l}=0$
.
Now, assume that there exists
![]() $k\in \mathbb Z$
such that
$k\in \mathbb Z$
such that
![]() $\phi ^k(x)=y$
. Then k is unique, since
$\phi ^k(x)=y$
. Then k is unique, since
![]() $x,y\notin X_{\mathrm p}$
. It is easy to see that
$x,y\notin X_{\mathrm p}$
. It is easy to see that
hence
![]() $M_{\chi _xU^m,\chi _yU^n}$
is a rank-one operator.
$M_{\chi _xU^m,\chi _yU^n}$
is a rank-one operator.
Remark 2.5 The set of compact elements of a
![]() $C^*$
-algebra is an ideal [Reference Ylinen24]. Moreover, it is invariant under the
$C^*$
-algebra is an ideal [Reference Ylinen24]. Moreover, it is invariant under the
![]() $*$
-automorphisms of the algebra, and hence an element
$*$
-automorphisms of the algebra, and hence an element
![]() ${A=\sum _{n}f_nU^n }$
of the crossed product
${A=\sum _{n}f_nU^n }$
of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
is a compact element, if and only if
$C_0(X)\times _\phi \mathbb Z$
is a compact element, if and only if
![]() $f_nU^n$
is a compact element for all
$f_nU^n$
is a compact element for all
![]() $n \in \mathbb Z$
. Note also that if a is a compact element of a Banach algebra
$n \in \mathbb Z$
. Note also that if a is a compact element of a Banach algebra
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $b \in \mathcal A$
, then
$b \in \mathcal A$
, then
![]() $ab$
and
$ab$
and
![]() $ba$
are also compact elements. We shall use these facts in the sequel.
$ba$
are also compact elements. We shall use these facts in the sequel.
Recall that we denote by
![]() $\mathcal C(C_0(X)\times _\phi \mathbb Z)$
the set of compact elements of
$\mathcal C(C_0(X)\times _\phi \mathbb Z)$
the set of compact elements of
![]() ${C_0(X)\times _\phi \mathbb Z}$
.
${C_0(X)\times _\phi \mathbb Z}$
.
Theorem 2.6 The set of compact elements
![]() $\mathcal C(C_0(X)\times _\phi \mathbb Z)$
of the crossed product
$\mathcal C(C_0(X)\times _\phi \mathbb Z)$
of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
is the set
$C_0(X)\times _\phi \mathbb Z$
is the set
Proof If
![]() $A=\sum _{n}f_nU^n$
is a compact element, then
$A=\sum _{n}f_nU^n$
is a compact element, then
![]() $f_nU^n$
is a compact element for all
$f_nU^n$
is a compact element for all
![]() $n\in \mathbb Z$
and hence
$n\in \mathbb Z$
and hence
![]() $f_nU^0$
is a compact element for all
$f_nU^0$
is a compact element for all
![]() $n\in \mathbb Z$
. Therefore,
$n\in \mathbb Z$
. Therefore,
![]() $f_n(X_{\mathrm a}\cup X_{\mathrm p})=\{0\}$
for all
$f_n(X_{\mathrm a}\cup X_{\mathrm p})=\{0\}$
for all
![]() $n\in \mathbb Z$
, by Lemmas 2.2 and 2.3.
$n\in \mathbb Z$
, by Lemmas 2.2 and 2.3.
We will show the opposite direction. It is enough to prove that if
![]() $A=fU^0$
is such that
$A=fU^0$
is such that
![]() $f(X_{\mathrm a}\cup X_{\mathrm p})=\{0\}$
, then A is a compact element. To prove this, we will prove that the element A is the norm limit of a sequence of compact elements
$f(X_{\mathrm a}\cup X_{\mathrm p})=\{0\}$
, then A is a compact element. To prove this, we will prove that the element A is the norm limit of a sequence of compact elements
![]() $\{A_m\}_{m\in \mathbb N}$
of
$\{A_m\}_{m\in \mathbb N}$
of
![]() $C_0(X)\times _\phi \mathbb Z$
.
$C_0(X)\times _\phi \mathbb Z$
.
For
![]() $m\in \mathbb N$
, the set
$m\in \mathbb N$
, the set
is a finite subset of
![]() $X_{\mathrm i}\,{\backslash}\, X_{\mathrm p}$
. Let
$X_{\mathrm i}\,{\backslash}\, X_{\mathrm p}$
. Let
![]() $f_m\in C_0(X)$
be the function defined as follows:
$f_m\in C_0(X)$
be the function defined as follows:
 $$ \begin{align*} f_m(x)=\left\{\begin{matrix} f(x), & x\in S_m, \\ 0, & x\in X\,{\backslash}\, S_m. \end{matrix}\right. \end{align*} $$
$$ \begin{align*} f_m(x)=\left\{\begin{matrix} f(x), & x\in S_m, \\ 0, & x\in X\,{\backslash}\, S_m. \end{matrix}\right. \end{align*} $$
Then if
![]() $A_m=f_mU^0$
, it follows from Lemma 2.4 that
$A_m=f_mU^0$
, it follows from Lemma 2.4 that
![]() $A_m$
is a compact element of
$A_m$
is a compact element of
![]() $C_0(X)\times _\phi \mathbb Z$
. Moreover,
$C_0(X)\times _\phi \mathbb Z$
. Moreover,
![]() $\|A-A_m\|=\|f-f_m\|\leq \frac {1}{m}$
, which concludes the proof.
$\|A-A_m\|=\|f-f_m\|\leq \frac {1}{m}$
, which concludes the proof.
Remark 2.7 If X is a locally compact metrizable space and
![]() $\phi :X\rightarrow X$
is a homeomorphism, the semicrossed product
$\phi :X\rightarrow X$
is a homeomorphism, the semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
is isomorphic to a nonself-adjoint subalgebra of the crossed product
$C_0(X)\times _\phi \mathbb Z_+$
is isomorphic to a nonself-adjoint subalgebra of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
[Reference Peters15, Proposition II.4]. The compact elements of the semicrossed product
$C_0(X)\times _\phi \mathbb Z$
[Reference Peters15, Proposition II.4]. The compact elements of the semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
are characterized in [Reference Andreolas, Anoussis and Magiatis3]. Considering the semicrossed product
$C_0(X)\times _\phi \mathbb Z_+$
are characterized in [Reference Andreolas, Anoussis and Magiatis3]. Considering the semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
as a subalgebra of the crossed product
$C_0(X)\times _\phi \mathbb Z_+$
as a subalgebra of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
, we have that
$C_0(X)\times _\phi \mathbb Z$
, we have that
![]() $\mathcal C(C_0\times _\phi \mathbb Z)\cap (C_0\times _\phi \mathbb Z_+)\subseteq \mathcal C(C_0\times _\phi \mathbb Z_+)$
, but in general, this inclusion is strict and more compact elements appear in the semicrossed product.
$\mathcal C(C_0\times _\phi \mathbb Z)\cap (C_0\times _\phi \mathbb Z_+)\subseteq \mathcal C(C_0\times _\phi \mathbb Z_+)$
, but in general, this inclusion is strict and more compact elements appear in the semicrossed product.
Remark 2.8 An elementary operator on a Banach algebra is a finite sum of multiplication operators. R. M. Timoney proved in [Reference Timoney20, Theorem 3.1] that if
![]() $\mathcal A$
is a
$\mathcal A$
is a
![]() $C^*$
-algebra, then an elementary operator
$C^*$
-algebra, then an elementary operator
![]() $\Phi :\mathcal A\rightarrow \mathcal A$
is compact if and only if there exist compact elements
$\Phi :\mathcal A\rightarrow \mathcal A$
is compact if and only if there exist compact elements
![]() $a_i,b_i\in \mathcal A$
, for
$a_i,b_i\in \mathcal A$
, for
![]() $i=1,\dots ,n$
, such that
$i=1,\dots ,n$
, such that
![]() $\Phi =\sum _{i=1}^n M_{a_i,b_i}$
. It follows from the proof of this theorem that if
$\Phi =\sum _{i=1}^n M_{a_i,b_i}$
. It follows from the proof of this theorem that if
![]() $M_{a, b}$
is a compact multiplication operator on a
$M_{a, b}$
is a compact multiplication operator on a
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal A$
, then there exist compact elements
$\mathcal A$
, then there exist compact elements
![]() $c, d \in \mathcal A$
such that
$c, d \in \mathcal A$
such that
![]() $M_{a, b}=M_{c, d}$
. Hence, the knowledge of the compact elements implies the knowledge of the compact multiplication operators in this sense.
$M_{a, b}=M_{c, d}$
. Hence, the knowledge of the compact elements implies the knowledge of the compact multiplication operators in this sense.
3 The hypocompact radical of the crossed product
Shulman and Turovskii in [Reference Shulman and Turovskii18, Reference Turovskiĭ and Shuľman21] call a Banach algebra
![]() $\mathcal {A}$
hypocompact if any nonzero quotient
$\mathcal {A}$
hypocompact if any nonzero quotient
![]() $\mathcal {A}/\mathcal {I}$
by a closed ideal
$\mathcal {A}/\mathcal {I}$
by a closed ideal
![]() $\mathcal {I}$
contains a nonzero compact element. An ideal
$\mathcal {I}$
contains a nonzero compact element. An ideal
![]() $\mathcal I$
of a Banach algebra
$\mathcal I$
of a Banach algebra
![]() $\mathcal A$
is hypocompact if it is hypocompact as an algebra. Shulman and Turovskii have proved that any Banach algebra
$\mathcal A$
is hypocompact if it is hypocompact as an algebra. Shulman and Turovskii have proved that any Banach algebra
![]() $\mathcal {A}$
has a largest hypocompact ideal [Reference Shulman and Turovskii18, Corollary 3.10]. This ideal is closed, is called the hypocompact radical of
$\mathcal {A}$
has a largest hypocompact ideal [Reference Shulman and Turovskii18, Corollary 3.10]. This ideal is closed, is called the hypocompact radical of
![]() $\mathcal {A}$
, and is denoted by
$\mathcal {A}$
, and is denoted by
![]() $\mathcal {A}_{\mathrm {hc}} $
.
$\mathcal {A}_{\mathrm {hc}} $
.
If
![]() $\mathcal H$
is a separable Hilbert space, the ideal
$\mathcal H$
is a separable Hilbert space, the ideal
![]() $\mathcal {K}(\mathcal H)$
of compact operators on
$\mathcal {K}(\mathcal H)$
of compact operators on
![]() $\mathcal H$
is the only proper ideal of
$\mathcal H$
is the only proper ideal of
![]() $\mathcal {B}(\mathcal H)$
, while the Calkin algebra
$\mathcal {B}(\mathcal H)$
, while the Calkin algebra
![]() $\mathcal {B}(\mathcal H)/\mathcal {K}(\mathcal H)$
does not have any nonzero compact element [Reference Fong and Sourour8, Section 5]. It follows that the hypocompact radical of
$\mathcal {B}(\mathcal H)/\mathcal {K}(\mathcal H)$
does not have any nonzero compact element [Reference Fong and Sourour8, Section 5]. It follows that the hypocompact radical of
![]() $\mathcal {B}(\mathcal H)$
is
$\mathcal {B}(\mathcal H)$
is
![]() $\mathcal {K}(\mathcal H)$
.
$\mathcal {K}(\mathcal H)$
.
We already mentioned in the introduction that there are Banach spaces such that the hypocompact radical contains strictly the ideal of compact operators [Reference Shulman and Turovskii18, Lemma 3.12, p. 298]. Moreover, if
![]() $\mathcal X$
is the Argyros-Haydon space, it follows from [Reference Shulman and Turovskii18, Corollary 3.9] that the hypocompact radical of
$\mathcal X$
is the Argyros-Haydon space, it follows from [Reference Shulman and Turovskii18, Corollary 3.9] that the hypocompact radical of
![]() $\mathcal {B}(\mathcal X)$
coincides with
$\mathcal {B}(\mathcal X)$
coincides with
![]() $\mathcal {B}(\mathcal X)$
.
$\mathcal {B}(\mathcal X)$
.
The hypocompact radical of a nest algebra is characterized in [Reference Andreolas and Anoussis2] and the hypocompact radical of a semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
is characterized in [Reference Andreolas, Anoussis and Magiatis4]. In this section, we characterize the hypocompact radical of the crossed product
$C_0(X)\times _\phi \mathbb Z_+$
is characterized in [Reference Andreolas, Anoussis and Magiatis4]. In this section, we characterize the hypocompact radical of the crossed product
![]() $C_0(X)\times _\phi \mathbb Z$
.
$C_0(X)\times _\phi \mathbb Z$
.
We noted in the introduction that the hypocompact radical of a Banach algebra
![]() $\mathcal A$
is the smallest closed ideal
$\mathcal A$
is the smallest closed ideal
![]() $\mathcal I$
of
$\mathcal I$
of
![]() $\mathcal A$
, such that
$\mathcal A$
, such that
![]() $\mathcal A/\mathcal I$
does not contain compact elements. This follows from the results of [Reference Shulman and Turovskii18], though we could not find the exact statement in that paper. We state it as a proposition because it is important for our view.
$\mathcal A/\mathcal I$
does not contain compact elements. This follows from the results of [Reference Shulman and Turovskii18], though we could not find the exact statement in that paper. We state it as a proposition because it is important for our view.
Proposition 3.1 Let
![]() $\mathcal A$
be a Banach algebra and
$\mathcal A$
be a Banach algebra and
![]() $\mathcal J$
a closed ideal of
$\mathcal J$
a closed ideal of
![]() $\mathcal A$
such that
$\mathcal A$
such that
![]() $\mathcal A/\mathcal J$
has no compact elements. Then,
$\mathcal A/\mathcal J$
has no compact elements. Then,
![]() $ \mathcal J$
contains the hypocompact radical
$ \mathcal J$
contains the hypocompact radical
![]() $\mathcal A_{\mathrm hc}$
of
$\mathcal A_{\mathrm hc}$
of
![]() $\mathcal A$
.
$\mathcal A$
.
Proof It follows from [Reference Shulman and Turovskii18, Lemma 3.12] that
![]() $\mathcal A/\mathcal A_{\mathrm hc}$
does not have compact elements. Set
$\mathcal A/\mathcal A_{\mathrm hc}$
does not have compact elements. Set
![]() $\mathcal I=\mathcal A_{\mathrm hc}$
and let
$\mathcal I=\mathcal A_{\mathrm hc}$
and let
![]() $\mathcal J$
be a closed ideal of
$\mathcal J$
be a closed ideal of
![]() $\mathcal A$
. The hypocompact radical of
$\mathcal A$
. The hypocompact radical of
![]() $\overline {\mathcal I+\mathcal J}$
is
$\overline {\mathcal I+\mathcal J}$
is
![]() $\mathcal I$
by [Reference Shulman and Turovskii18, Lemma 3.11]. Let
$\mathcal I$
by [Reference Shulman and Turovskii18, Lemma 3.11]. Let
![]() $\pi : \overline {\mathcal {I+J}}\rightarrow \overline {\mathcal {I+J}}/\mathcal J$
be the natural quotient map. It follows from [Reference Shulman and Turovskii18, Proposition 3.8], that
$\pi : \overline {\mathcal {I+J}}\rightarrow \overline {\mathcal {I+J}}/\mathcal J$
be the natural quotient map. It follows from [Reference Shulman and Turovskii18, Proposition 3.8], that
![]() $\pi (\mathcal I)$
is
$\pi (\mathcal I)$
is
![]() $\{0\}$
or contains compact elements of
$\{0\}$
or contains compact elements of
![]() $\overline {\mathcal {I+J}}/\mathcal J$
. If
$\overline {\mathcal {I+J}}/\mathcal J$
. If
![]() $\overline {\mathcal {I+J}}/\mathcal J$
contains compact elements, it follows from [Reference Shulman and Turovskii18, Lemma 3.5] that
$\overline {\mathcal {I+J}}/\mathcal J$
contains compact elements, it follows from [Reference Shulman and Turovskii18, Lemma 3.5] that
![]() $\mathcal A/\mathcal J$
contains compact elements, which is contrary to our assumption. Hence,
$\mathcal A/\mathcal J$
contains compact elements, which is contrary to our assumption. Hence,
![]() $\pi (\mathcal I)=\{0\}$
and
$\pi (\mathcal I)=\{0\}$
and
![]() $\mathcal I \subseteq \mathcal J$
.
$\mathcal I \subseteq \mathcal J$
.
Let
![]() $X_1=X_{\mathrm a}\cup \overline {X_{\mathrm p}}$
and
$X_1=X_{\mathrm a}\cup \overline {X_{\mathrm p}}$
and
![]() $\phi _1=\phi |_{X_1}$
be the restriction of
$\phi _1=\phi |_{X_1}$
be the restriction of
![]() $\phi $
to
$\phi $
to
![]() $X_1$
. We thus obtain a dynamical system
$X_1$
. We thus obtain a dynamical system
![]() $(X_1,\phi _1)$
. Define by transfinite recursion a family
$(X_1,\phi _1)$
. Define by transfinite recursion a family
![]() $(X_\gamma ,\phi _\gamma )$
of dynamical systems. If
$(X_\gamma ,\phi _\gamma )$
of dynamical systems. If
![]() $(X_\gamma ,\phi _\gamma )$
is defined, then
$(X_\gamma ,\phi _\gamma )$
is defined, then
![]() $X_{\gamma +1}$
is the union of the set of accumulation points of
$X_{\gamma +1}$
is the union of the set of accumulation points of
![]() $X_{\gamma }$
and of
$X_{\gamma }$
and of
![]() $\overline {X_{\mathrm p}}$
and
$\overline {X_{\mathrm p}}$
and
![]() $\phi _{\gamma +1}=\phi |_{X_{\gamma +1}}$
, the restriction of
$\phi _{\gamma +1}=\phi |_{X_{\gamma +1}}$
, the restriction of
![]() $\phi $
to
$\phi $
to
![]() $X_{\gamma +1}$
. If
$X_{\gamma +1}$
. If
![]() $\gamma $
is a limit ordinal and the system
$\gamma $
is a limit ordinal and the system
![]() $(X_\beta ,\phi _\beta )$
have been defined for all
$(X_\beta ,\phi _\beta )$
have been defined for all
![]() $\beta <\gamma $
, set
$\beta <\gamma $
, set
![]() $X_{\gamma }=\cap _{\beta <\gamma } X_{\beta }$
and
$X_{\gamma }=\cap _{\beta <\gamma } X_{\beta }$
and
![]() $\phi _{\gamma }=\phi |_{X_{\gamma }}$
, the restriction of
$\phi _{\gamma }=\phi |_{X_{\gamma }}$
, the restriction of
![]() $\phi $
to
$\phi $
to
![]() $X_{\gamma }$
. This process must stop at some ordinal
$X_{\gamma }$
. This process must stop at some ordinal
![]() $\gamma _0$
since the cardinality of the family cannot exceed the cardinality of the power set of X. The set
$\gamma _0$
since the cardinality of the family cannot exceed the cardinality of the power set of X. The set
![]() $X_{\gamma }$
is a closed subset of X for all
$X_{\gamma }$
is a closed subset of X for all
![]() $\gamma \leq \gamma _0$
.
$\gamma \leq \gamma _0$
.
A subset Y of a topological space is said to be dense in itself, if it contains no isolated points. If Y is closed and dense in itself, it is called a perfect set. A set Y is called scattered, if it does not contain dense in themselves subsets. It is well known that every space is the disjoint union of a perfect set and a scattered one, and this decomposition is unique [Reference Kuratowski10, Theorem 3, p. 79]. If X is a locally compact metrizable space, we denote by
![]() $X_{\mathrm {pp}}$
the perfect set and by
$X_{\mathrm {pp}}$
the perfect set and by
![]() $X_{\mathrm s}$
the scattered set in this decomposition. We thus have
$X_{\mathrm s}$
the scattered set in this decomposition. We thus have
![]() $X = X_{\mathrm {pp}}\cup X_{\mathrm s}$
.
$X = X_{\mathrm {pp}}\cup X_{\mathrm s}$
.
Lemma 3.2
![]() $X_{\gamma _0}=\overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}$
.
$X_{\gamma _0}=\overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}$
.
Proof Clearly
![]() $X_{\mathrm {pp}}\subseteq X_{\beta }$
for all
$X_{\mathrm {pp}}\subseteq X_{\beta }$
for all
![]() $\beta <\gamma _0$
, and hence
$\beta <\gamma _0$
, and hence
![]() $\overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}\subseteq X_{\gamma _0}$
.
$\overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}\subseteq X_{\gamma _0}$
.
We prove that
![]() $X_{\gamma _0} \subseteq \overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}$
. Since
$X_{\gamma _0} \subseteq \overline {X_{\mathrm p}}\cup X_{\mathrm {pp}}$
. Since
![]() $\overline {X_{\mathrm p}}\subseteq X_{\gamma _0}$
, it is enough to prove that
$\overline {X_{\mathrm p}}\subseteq X_{\gamma _0}$
, it is enough to prove that
![]() ${X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}\subseteq X_{\mathrm {pp}}}$
.
${X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}\subseteq X_{\mathrm {pp}}}$
.
Let
![]() $x\in X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
. If x is an isolated point of
$x\in X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
. If x is an isolated point of
![]() $X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
, then x is an isolated point of
$X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
, then x is an isolated point of
![]() $X_{\gamma _0}$
, which is a contradiction since
$X_{\gamma _0}$
, which is a contradiction since
![]() $X_{\gamma _0}= X_{\gamma _0+1}$
. Therefore, the set
$X_{\gamma _0}= X_{\gamma _0+1}$
. Therefore, the set
![]() $X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
is dense in itself and hence
$X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}$
is dense in itself and hence
![]() $X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}\subseteq X_{\mathrm {pp}}$
.
$X_{\gamma _0}\,{\backslash}\, \overline {X_{\mathrm p}}\subseteq X_{\mathrm {pp}}$
.
If
![]() $\gamma \leq \gamma _0$
, we will denote by
$\gamma \leq \gamma _0$
, we will denote by
![]() $\mathcal I_\gamma $
the ideal
$\mathcal I_\gamma $
the ideal
The proof of the following lemma is straightforward and is omitted.
Lemma 3.3 If
![]() $\gamma $
is a limit ordinal, then
$\gamma $
is a limit ordinal, then
![]() $\mathcal I_{\mathrm {\gamma }}=\overline {\cup _{\beta <\gamma }\mathcal I_\beta }$
.
$\mathcal I_{\mathrm {\gamma }}=\overline {\cup _{\beta <\gamma }\mathcal I_\beta }$
.
Theorem 3.4
 $$ \begin{align*} (C_0(X)\times_\phi\mathbb Z)_{\mathrm{hc}}=\mathcal I_{\gamma_0}=\left\{A=\sum_{n}f_nU^n:f_n(\overline{X_{\mathrm p}}\cup X_{\mathrm{pp}})=\{0\}\right\}. \end{align*} $$
$$ \begin{align*} (C_0(X)\times_\phi\mathbb Z)_{\mathrm{hc}}=\mathcal I_{\gamma_0}=\left\{A=\sum_{n}f_nU^n:f_n(\overline{X_{\mathrm p}}\cup X_{\mathrm{pp}})=\{0\}\right\}. \end{align*} $$
Proof
1st step: First we shall prove that
![]() $\mathcal I_{\gamma _0}\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
. Assume the contrary.
$\mathcal I_{\gamma _0}\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
. Assume the contrary.
It follows from Theorem 2.6 that
![]() $\mathcal I_1=\mathcal C(C_0(X)\times _\phi \mathbb Z)$
. The hypocompact radical contains the ideal of compact elements [Reference Brešar and Turovskii6, Lemma 8.2], and hence
$\mathcal I_1=\mathcal C(C_0(X)\times _\phi \mathbb Z)$
. The hypocompact radical contains the ideal of compact elements [Reference Brešar and Turovskii6, Lemma 8.2], and hence
![]() ${\mathcal I_1\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}}$
.
${\mathcal I_1\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}}$
.
Let
![]() $\beta $
be the least ordinal
$\beta $
be the least ordinal
![]() $\beta \leq \gamma _0$
such that
$\beta \leq \gamma _0$
such that
![]() $\mathcal I_\beta $
is not contained in
$\mathcal I_\beta $
is not contained in
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
. We show that
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
. We show that
![]() $\beta $
is a successor. If not, since
$\beta $
is a successor. If not, since
![]() $\mathcal I_{\gamma }\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
for all
$\mathcal I_{\gamma }\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
for all
![]() $\gamma <\beta $
, we obtain from Lemma 3.3 that
$\gamma <\beta $
, we obtain from Lemma 3.3 that
![]() $\mathcal I_\beta =\overline {\cup _{\gamma <\beta }\mathcal I_\gamma }\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
, which is absurd.
$\mathcal I_\beta =\overline {\cup _{\gamma <\beta }\mathcal I_\gamma }\subseteq (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}$
, which is absurd.
We are going to prove that
![]() $\mathcal I_{\beta }$
is a hypocompact algebra. Consider the algebra
$\mathcal I_{\beta }$
is a hypocompact algebra. Consider the algebra
![]() $\mathcal I_{\beta }/\mathcal I_{\beta -1}$
. It suffices to show that
$\mathcal I_{\beta }/\mathcal I_{\beta -1}$
. It suffices to show that
![]() $\mathcal I_{\beta }/\mathcal I_{\beta -1}$
is a hypocompact algebra since the class of hypocompact algebras is closed under extensions and the ideal
$\mathcal I_{\beta }/\mathcal I_{\beta -1}$
is a hypocompact algebra since the class of hypocompact algebras is closed under extensions and the ideal
![]() $\mathcal I_{\beta -1}$
is hypocompact, [Reference Shulman and Turovskii18, Corollary 3.9].
$\mathcal I_{\beta -1}$
is hypocompact, [Reference Shulman and Turovskii18, Corollary 3.9].
We show that the algebra
![]() $\mathcal I_{\beta }/\mathcal I_{\beta -1}$
is generated by the compact elements it contains and hence is a hypocompact algebra by [Reference Brešar and Turovskii6, Lemma 8.2].
$\mathcal I_{\beta }/\mathcal I_{\beta -1}$
is generated by the compact elements it contains and hence is a hypocompact algebra by [Reference Brešar and Turovskii6, Lemma 8.2].
Let
![]() $A \in \mathcal I_{\beta }$
. It follows from the condition defining
$A \in \mathcal I_{\beta }$
. It follows from the condition defining
![]() $\mathcal I_{\beta }$
, that
$\mathcal I_{\beta }$
, that
![]() $E_n(A)U^n \in \mathcal I_{\beta }$
, for all
$E_n(A)U^n \in \mathcal I_{\beta }$
, for all
![]() $n\in \mathbb Z$
. Hence, it suffices to show that the image of
$n\in \mathbb Z$
. Hence, it suffices to show that the image of
![]() $E_n(A)U^n$
under the natural map
$E_n(A)U^n$
under the natural map
![]() $\pi : \mathcal I_{\beta }\rightarrow \mathcal I_{\beta }/\mathcal I_{\beta -1}$
is contained in the ideal generated by the compact elements of
$\pi : \mathcal I_{\beta }\rightarrow \mathcal I_{\beta }/\mathcal I_{\beta -1}$
is contained in the ideal generated by the compact elements of
![]() $\mathcal I_{\beta }/\mathcal I_{\beta -1}$
. It suffices to see this for an element of
$\mathcal I_{\beta }/\mathcal I_{\beta -1}$
. It suffices to see this for an element of
![]() $\mathcal I_{\beta }$
of the form
$\mathcal I_{\beta }$
of the form
![]() $fU^n$
with f compactly supported.
$fU^n$
with f compactly supported.
Let
![]() $fU^n\in \mathcal I_{\beta }$
with f compactly supported and
$fU^n\in \mathcal I_{\beta }$
with f compactly supported and
The set
![]() $S(f)$
is finite since f is compactly supported and vanishes
$S(f)$
is finite since f is compactly supported and vanishes
![]() $X_{\beta }$
. It follows that the multiplication operator
$X_{\beta }$
. It follows that the multiplication operator
![]() $M_{\pi (fU^n),\pi (fU^n)}$
is finite rank and hence it is compact.
$M_{\pi (fU^n),\pi (fU^n)}$
is finite rank and hence it is compact.
2nd step: Now we prove that
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\subseteq \left \{A=\sum _{n}f_nU^n:f_n(\overline {X_{\mathrm {p}}})=\{0\}\right \}$
. Let
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\subseteq \left \{A=\sum _{n}f_nU^n:f_n(\overline {X_{\mathrm {p}}})=\{0\}\right \}$
. Let
![]() $\mathcal P=\left \{A=\sum _{n}f_nU^n:f_n(\overline {X_{\mathrm {p}}})=\{0\}\right \}$
and
$\mathcal P=\left \{A=\sum _{n}f_nU^n:f_n(\overline {X_{\mathrm {p}}})=\{0\}\right \}$
and
![]() $\mathcal P_{\mathrm h}=(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\cap \mathcal P$
. We suppose that
$\mathcal P_{\mathrm h}=(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\cap \mathcal P$
. We suppose that
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\not \subseteq \mathcal P$
, and we will prove that the quotient algebra
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\not \subseteq \mathcal P$
, and we will prove that the quotient algebra
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
contains no nonzero compact elements.
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
contains no nonzero compact elements.
Let
![]() $\pi : (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
be the quotient map and
$\pi : (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
be the quotient map and
![]() ${A\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal P_{\mathrm h}}$
. We will prove that the multiplication operator
${A\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal P_{\mathrm h}}$
. We will prove that the multiplication operator
![]() $M_{\pi (A),\pi (A)}:(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
is not compact.
$M_{\pi (A),\pi (A)}:(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal P_{\mathrm h}$
is not compact.
It is enough to consider the case
![]() $A=fU^0$
. Then, there exists
$A=fU^0$
. Then, there exists
![]() $x_0\in X_{\mathrm p}$
such that
$x_0\in X_{\mathrm p}$
such that
![]() $f(x_{0})\neq 0$
. We denote
$f(x_{0})\neq 0$
. We denote
![]() $k_0=\min \{k\in \mathbb N:\phi ^{k}(x_0)=x_0\}$
.
$k_0=\min \{k\in \mathbb N:\phi ^{k}(x_0)=x_0\}$
.
We will prove that the sequence
![]() $\{M_{\pi (A),\pi (A)}(\pi (fU^{ik_0}))\}_{i=1}^\infty $
has no convergent subsequence.
$\{M_{\pi (A),\pi (A)}(\pi (fU^{ik_0}))\}_{i=1}^\infty $
has no convergent subsequence.
We estimate the quantity
for
![]() $i,j\in \mathbb {N}$
with
$i,j\in \mathbb {N}$
with
![]() $i\neq j$
. We have
$i\neq j$
. We have
 $$ \begin{align*} \left\|M_{\pi(A),\pi(A)}(\pi(fU^{ik_0}))-M_{\pi(A),\pi(A)}(\pi(fU^{jk_0}))\right\| &\\ = \inf_{B\in \mathcal P_{\mathrm h}}\left\|AfU^{ik_0}A-AfU^{jk_0}A+B\right\| &\\ = \inf_{B\in \mathcal P_{\mathrm h}}\left\|f^2(f\circ\phi^{-ik_0})U^{ik_0}-f^2(f\circ\phi^{-jk_0})U^{jk_0}+B\right\| & \\ \ge \inf_{B\in \mathcal P_{\mathrm h}}\|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}-f^2(f\circ\phi^{-jk_0})U^{jk_0}+B\right)\| & \\ = \inf_{B\in \mathcal P_{\mathrm h}}\|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}+B\right)\| & \\ \ge \inf_{B\in \mathcal P_{\mathrm h}}\left|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}+B\right)(x_0)\right| = |f^3(x_0)|, \end{align*} $$
$$ \begin{align*} \left\|M_{\pi(A),\pi(A)}(\pi(fU^{ik_0}))-M_{\pi(A),\pi(A)}(\pi(fU^{jk_0}))\right\| &\\ = \inf_{B\in \mathcal P_{\mathrm h}}\left\|AfU^{ik_0}A-AfU^{jk_0}A+B\right\| &\\ = \inf_{B\in \mathcal P_{\mathrm h}}\left\|f^2(f\circ\phi^{-ik_0})U^{ik_0}-f^2(f\circ\phi^{-jk_0})U^{jk_0}+B\right\| & \\ \ge \inf_{B\in \mathcal P_{\mathrm h}}\|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}-f^2(f\circ\phi^{-jk_0})U^{jk_0}+B\right)\| & \\ = \inf_{B\in \mathcal P_{\mathrm h}}\|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}+B\right)\| & \\ \ge \inf_{B\in \mathcal P_{\mathrm h}}\left|E_{ik_0}\left(f^2(f\circ\phi^{-ik_0})U^{ik_0}+B\right)(x_0)\right| = |f^3(x_0)|, \end{align*} $$
and the proof is complete.
3rd step: Now we prove
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\subseteq \left \{A=\sum _{n}f_nU^n:f_n(X_{\mathrm {pp}})=\{0\}\right \}$
. Let
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\subseteq \left \{A=\sum _{n}f_nU^n:f_n(X_{\mathrm {pp}})=\{0\}\right \}$
. Let
![]() $\mathcal R=\left \{A=\sum _{n}f_nU^n:f_n(X_{\mathrm {pp}})=\{0\}\right \}$
and
$\mathcal R=\left \{A=\sum _{n}f_nU^n:f_n(X_{\mathrm {pp}})=\{0\}\right \}$
and
![]() $\mathcal R_{\mathrm h}=(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\cap \mathcal R$
. We suppose that
$\mathcal R_{\mathrm h}=(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\cap \mathcal R$
. We suppose that
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\not \subseteq \mathcal R$
, and we will prove that the quotient algebra
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\not \subseteq \mathcal R$
, and we will prove that the quotient algebra
![]() $(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
contains no nonzero compact elements.
$(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
contains no nonzero compact elements.
Let
![]() $\pi : (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
be the quotient map and
$\pi : (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
be the quotient map and
![]() ${A\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal R_{\mathrm h}}$
. We shall prove that the multiplication operator
${A\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal R_{\mathrm h}}$
. We shall prove that the multiplication operator
![]() $M_{\pi (A),\pi (A)}:(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
is not compact.
$M_{\pi (A),\pi (A)}:(C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}\rightarrow (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}/ \mathcal R_{\mathrm h}$
is not compact.
It is enough to consider the case
![]() $A=fU^0$
. Then, there exists
$A=fU^0$
. Then, there exists
![]() $x_0\in X_{\mathrm {pp}}$
such that
$x_0\in X_{\mathrm {pp}}$
such that
![]() $f(x_{0})\neq 0$
. Let
$f(x_{0})\neq 0$
. Let
![]() $S_0$
be an open neighborhood of
$S_0$
be an open neighborhood of
![]() $x_0$
such that
$x_0$
such that
for all
![]() $x\in S_0$
. By the second step, the set
$x\in S_0$
. By the second step, the set
![]() $S_0$
contains no periodic points.
$S_0$
contains no periodic points.
Since
![]() $x_0\in S_0\cap X_{\mathrm {pp}}$
there exist a sequence of points
$x_0\in S_0\cap X_{\mathrm {pp}}$
there exist a sequence of points
![]() $\{x_i\}_{i=1}^\infty \subseteq S_0\cap X_{\mathrm {pp}}$
, a sequence of open subsets
$\{x_i\}_{i=1}^\infty \subseteq S_0\cap X_{\mathrm {pp}}$
, a sequence of open subsets
![]() $\{W_i\}_{i=1}^\infty \subseteq S_0$
with
$\{W_i\}_{i=1}^\infty \subseteq S_0$
with
![]() $x_i\in W_i$
and
$x_i\in W_i$
and
![]() $W_i\cap W_j$
, for
$W_i\cap W_j$
, for
![]() $i\neq j$
and a sequence of norm one functions
$i\neq j$
and a sequence of norm one functions
![]() $\{h_i\}_{i=1}^\infty \subseteq C_0(X)$
with
$\{h_i\}_{i=1}^\infty \subseteq C_0(X)$
with
![]() $h_i(x_i)=1$
and
$h_i(x_i)=1$
and
![]() $h_i(X\,{\backslash}\, W_i)=\{0\}$
, for all
$h_i(X\,{\backslash}\, W_i)=\{0\}$
, for all
![]() $i\in \mathbb N$
. Let
$i\in \mathbb N$
. Let
![]() $g_i=fh_i\in C_0(X)$
. It follows that
$g_i=fh_i\in C_0(X)$
. It follows that
![]() $g_iU^0\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal R_{\mathrm h}$
.
$g_iU^0\in (C_0(X)\times _\phi \mathbb Z)_{\mathrm {hc}}\,{\backslash}\, \mathcal R_{\mathrm h}$
.
We will prove that the sequence
![]() $\{M_{\pi (A),\pi (A)}(\pi (g_iU^{0}))\}_{i=1}^\infty $
has no convergent subsequence.
$\{M_{\pi (A),\pi (A)}(\pi (g_iU^{0}))\}_{i=1}^\infty $
has no convergent subsequence.
We estimate the quantity
for
![]() $i,j\in \mathbb {N}$
with
$i,j\in \mathbb {N}$
with
![]() $i< j$
. We have
$i< j$
. We have
 $$ \begin{align*} \left\|M_{\pi(A),\pi(A)}\left(\pi(g_iU^{0})\right)-M_{\pi(A),\pi(A)}\left(\pi(g_jU^{0})\right)\right\| & \\= \inf_{B\in \mathcal R_{\mathrm h}}\left\|M_{A,A}\left(g_iU^{0}\right)-M_{A,A}\left(g_jU^{0}\right)+B\right\| & \\= \inf_{B\in \mathcal R_{\mathrm h}}\left\|f^3h_iU^{0}-f^3h_jU^{0}+B\right\| & \\ \ge \inf_{B\in \mathcal R_{\mathrm h}}\|E_{0}\left(f^3h_iU^{0}-f^3h_jU^{0}+B\right)\| & \\ \ge \inf_{B\in \mathcal R_{\mathrm h}}\left|E_{0}\left(f^3h_iU^{0}-f^3h_jU^{0}+B\right)(x_i)\right|& \\= |f^3(x_i)|>|f^3(x_0)|, \end{align*} $$
$$ \begin{align*} \left\|M_{\pi(A),\pi(A)}\left(\pi(g_iU^{0})\right)-M_{\pi(A),\pi(A)}\left(\pi(g_jU^{0})\right)\right\| & \\= \inf_{B\in \mathcal R_{\mathrm h}}\left\|M_{A,A}\left(g_iU^{0}\right)-M_{A,A}\left(g_jU^{0}\right)+B\right\| & \\= \inf_{B\in \mathcal R_{\mathrm h}}\left\|f^3h_iU^{0}-f^3h_jU^{0}+B\right\| & \\ \ge \inf_{B\in \mathcal R_{\mathrm h}}\|E_{0}\left(f^3h_iU^{0}-f^3h_jU^{0}+B\right)\| & \\ \ge \inf_{B\in \mathcal R_{\mathrm h}}\left|E_{0}\left(f^3h_iU^{0}-f^3h_jU^{0}+B\right)(x_i)\right|& \\= |f^3(x_i)|>|f^3(x_0)|, \end{align*} $$
and the proof is complete.
Remark 3.5 The hypocompact radical of the semicrossed product
![]() $C_0(X)\times _\phi \mathbb Z_+$
is determined in [Reference Andreolas, Anoussis and Magiatis4].
$C_0(X)\times _\phi \mathbb Z_+$
is determined in [Reference Andreolas, Anoussis and Magiatis4].
Remark 3.6 Shulman and Turovskii call a Banach algebra scattered if the spectrum of every element
![]() $a\in \mathcal A$
is finite or countable [Reference Shulman and Turovskii19, Reference Turovskiĭ and Shuľman21]. They show that a Banach algebra
$a\in \mathcal A$
is finite or countable [Reference Shulman and Turovskii19, Reference Turovskiĭ and Shuľman21]. They show that a Banach algebra
![]() $\mathcal A$
has a largest scattered ideal denoted by
$\mathcal A$
has a largest scattered ideal denoted by
![]() $\mathcal A_{\mathrm s}$
[Reference Shulman and Turovskii19, Theorem 8.10]. This ideal is closed and is called the scattered radical of
$\mathcal A_{\mathrm s}$
[Reference Shulman and Turovskii19, Theorem 8.10]. This ideal is closed and is called the scattered radical of
![]() $\mathcal A$
. It follows from Theorem 3.4 and [Reference Shulman and Turovskii19, Theorem 8.22] that
$\mathcal A$
. It follows from Theorem 3.4 and [Reference Shulman and Turovskii19, Theorem 8.22] that