Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T12:37:48.527Z Has data issue: false hasContentIssue false
  • English
  • Français

Crown sealing and buckling instability during water entry of spheres

Published online by Cambridge University Press:  05 April 2016

J. O. Marston ,
T. T. Truscott Open the ORCID record for T. T. Truscott [Opens in a new window] ,
N. B. Speirs ,
M. M. Mansoor  and
S. T. Thoroddsen
J. O. Marston*
Affiliation:
Department of Chemical Engineering, Texas Tech University, Lubbock, TX 79409-3121, USA
T. T. Truscott
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322-4130, USA
N. B. Speirs
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322-4130, USA
M. M. Mansoor
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
S. T. Thoroddsen
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia Clean Combustion Research Centre, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present new observations from an experimental investigation of the classical problem of the crown splash and sealing phenomena observed during the impact of spheres onto quiescent liquid pools. In the experiments, a 6 m tall vacuum chamber was used to provide the required ambient conditions from atmospheric pressure down to 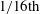$1/16\text{th}$ of an atmosphere, whilst high-speed videography was exploited to focus primarily on the above-surface crown formation and ensuing dynamics, paying particular attention to the moments just prior to the surface seal. In doing so, we have observed a buckling-type azimuthal instability of the crown. This instability is characterised by vertical striations along the crown, between which thin films form that are more susceptible to the air flow and thus are drawn into the closing cavity, where they atomize to form a fine spray within the cavity. To elucidate to the primary mechanisms and forces at play, we varied the sphere diameter, liquid properties and ambient pressure. Furthermore, a comparison between the entry of room-temperature spheres, where the contact line pins around the equator, and Leidenfrost spheres (i.e. an immersed superheated sphere encompassed by a vapour layer), where there is no contact line, indicates that the buckling instability appears in all crown sealing events, but is intensified by the presence of a pinned contact line.

JFM classification

Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Interfacial Flows (free surface) Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 506 - 529
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abelson, H. I. 1970 Pressure measurements in the water-entry cavity. J. Fluid Mech. 44, 129–144.Google Scholar
Aristoff, J. M. & Bush, J. W. M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Birkhoff, G. & Isaacs, R.1951 Transient cavities in air–water entry. NAVORD Report No. 1490.Google Scholar
Bischofberger, I., Mauser, K. W. & Nagel, S. R. 2013 Seeing the invisible – air vortices around a splashing drop. Phys. Fluids 25, 091110.Google Scholar
Darbois Texier, B., Piroird, K., Quere, D. & Clanet, C. 2013 Inertial collapse of liquid rings. J. Fluid Mech. 717, R3.CrossRefGoogle Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.Google Scholar
Enriquez, O. R., Peters, I. R., Gekle, S., Schmidt, L. E., Lohse, D. & van der Meer, D. 2012 Coolapse and pinch-off of a non-axisymmetric impact-created air cavity in water. J. Fluid Mech. 701, 40–58.Google Scholar
Enriquez, O. R., Peters, I. R., Gekle, S., Schmidt, L. E., van der Meer, D. & Lohse, D. 2011 Non-axisymmetric impact creates pineapple-shaped cavity. Phys. Fluids 23, 091106.Google Scholar
Gillbarg, D. & Anderson, R. 1948 Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water. J. Appl. Phys. 19, 127–139.CrossRefGoogle Scholar
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9, 540–550.Google Scholar
Lhuissier, H. & Villermaux, E. 2009 Destabilization of flapping sheets: the surprising analog of soap films. C. R. Mec. 337, 469–480.Google Scholar
Mansoor, M. M., Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.Google Scholar
Marston, J. O., Mansoor, M. M., Truscott, T. T. & Thoroddsen, S. T. 2015 Buckling instability of crown sealing. Phys. Fluids 27, 091112.Google Scholar
Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2012 Cavity formation by the impact of Leidenfrost spheres. J. Fluid Mech. 699, 465–488.Google Scholar
May, A. 1952 Vertical entry of missiles into water. J. Appl. Phys. 22, 1362–1372.CrossRefGoogle Scholar
McGraw, J. D., Li, J., Tran, D. L., Shi, A. C. & Dalnoki-Veress, K. 2010 Plateau–Rayleigh instability in a torus: formation and breakup of a polymer ring. Soft Matt. 6, 1258–1262.Google Scholar
Pairam, E. & Fernandez-Nieves, A. 2009 Generation and stability of toroidal droplets in a viscous liquid. Phys. Rev. Lett. 102, 234501.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Takano, Y. 2004 Impact jetting by a solid sphere. J. Fluid Mech. 499, 139–148.CrossRefGoogle Scholar
Thoroddsen, S. T., Thoraval, M.-J., Takehara, K. & Etoh, T. G. 2011 Droplet splashing by a slingshot mechanism. Phys. Rev. Lett. 106, 034501.CrossRefGoogle ScholarPubMed
Truscott, T. T., Epps, B. P. & Belden, J. 2013 Water entry of projectiles. Annu. Rev. Fluid Mech. 46, 355–378.Google Scholar
Villermaux, E. & Clanet, C. 2002 Life of a flapping liquid sheet. J. Fluid Mech. 462, 341–363.Google Scholar
Villermaux, E., Pistre, V. & Lhuissier, H. 2013 The viscous Savart sheet. J. Fluid Mech. 730, 607–625.Google Scholar
Worthington, A. M. 1908 A Study of Splashes. Longmans Green.Google Scholar
Worthington, A. M. & Cole, R. S. 1897 Impact with a liquid surface studied by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. A 189, 137–148.Google Scholar
Yakimov, Y. L. 1973 Effect of the atmosphere with the fall of bodies into water. Izv. Akad. Nauk. SSSR Mekh. Zhidk. Gaza 5, 3–6.Google Scholar
Zhang, V., Toole, J., Fezzaa, K. & Deegan, R. D. 2011 Evolution of the ejecta sheet from the impact of a drop with a deep pool. J. Fluid Mech. 690, 5–15.Google Scholar

Marston et al. supplementary movie

Video sequence showing a 10 mm-diameter steel sphere impacting onto a quiescent water surface at 10 m/s at atmospheric pressure. Re = 4.9 x 104, Fr = 2 x 103, We = 1.37 x 104.

Download Marston et al. supplementary movie(Video)
Video 1.5 MB

Marston et al. supplementary movie

Video sequence captured from above with a down-angle to focus on the rear wall of the crown splash created during the impact of a 10 mm-diameter sphere onto water at 10 m/s. Re = 5 x 104, Fr = 2 x 103, We = 6.9 x 103.

Download Marston et al. supplementary movie(Video)
Video 1 MB

Marston et al. supplementary movie

Close-up of the entry of a 20 mm-diameter sphere into water viewed from below the surface. The “sawtooth” contact line is pinned around the equator. Re = 8 x 104, Fr = 6.5 x 102, We = 8.8 x 103.

Download Marston et al. supplementary movie(Video)
Video 845.1 KB

Marston et al. supplementary movie

Video sequence of the entry of heated 15 mm-diameter steel sphere (T ≈ 200 oC) into perfluorohexane at 1.01 m/s. Re = 1.17 x 104, Fr = 13.8, We = 1.1 x 103.

Download Marston et al. supplementary movie(Video)
Video 717.1 KB