No CrossRef data available.
Published online by Cambridge University Press: 12 December 2022
Working toward showing the decidability of the 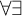 $\forall \exists $-theory of the
$\forall \exists $-theory of the 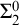 ${\Sigma ^0_2}$-enumeration degrees, we prove that no so-called Ahmad pair of
${\Sigma ^0_2}$-enumeration degrees, we prove that no so-called Ahmad pair of 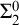 ${\Sigma ^0_2}$-enumeration degrees can join to
${\Sigma ^0_2}$-enumeration degrees can join to 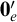 ${\mathbf 0}_e'$.
${\mathbf 0}_e'$.