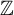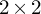1 Introduction
To a countable infinite group G and a standard measure space
![]() $(X_0,\mu _0)$
, called the base space, one associates the Bernoulli action
$(X_0,\mu _0)$
, called the base space, one associates the Bernoulli action
![]() $G\curvearrowright (X,\mu _0^{G})=\prod _{g\in G}(X_0,\mu _0)$
given by translating the coordinates by left multiplication. Bernoulli actions are at the heart of many classical, as well as recent, theorems in ergodic theory and operator algebras. Especially the role of Bernoulli actions in the theory of von Neumann algebras has been very prominent; see [Reference Popa42, Reference Popa43, Reference Chifan and Ioana12, Reference Ioana33, Reference Popa and Vaes44].
$G\curvearrowright (X,\mu _0^{G})=\prod _{g\in G}(X_0,\mu _0)$
given by translating the coordinates by left multiplication. Bernoulli actions are at the heart of many classical, as well as recent, theorems in ergodic theory and operator algebras. Especially the role of Bernoulli actions in the theory of von Neumann algebras has been very prominent; see [Reference Popa42, Reference Popa43, Reference Chifan and Ioana12, Reference Ioana33, Reference Popa and Vaes44].
By construction,
![]() $\mu _0^G$
is a probability measure, and it is preserved by the Bernoulli action of G. We rather equip
$\mu _0^G$
is a probability measure, and it is preserved by the Bernoulli action of G. We rather equip
![]() $X = X_0^G$
with a product of possibly distinct probability measures
$X = X_0^G$
with a product of possibly distinct probability measures
![]() $\mu _g$
on
$\mu _g$
on
![]() $X_0$
and thus consider the Bernoulli action
$X_0$
and thus consider the Bernoulli action
We require that the action (1.1) is nonsingular, i.e., preserves sets of measure zero. By Kakutani’s criterion for the equivalence of product measures, this is equivalent to all the measures
![]() $(\mu _g)_{g\in G}$
being equivalent and
$(\mu _g)_{g\in G}$
being equivalent and
where
![]() $H(\mu ,\nu )$
denotes the Hellinger distance; see equation (2.1).
$H(\mu ,\nu )$
denotes the Hellinger distance; see equation (2.1).
The key question that we address is the following: Given a countable infinite group G, what are the possible Krieger types of nonsingular Bernoulli actions
![]() $G \curvearrowright (X,\mu )$
? This question is particularly interesting in the classical case
$G \curvearrowright (X,\mu )$
? This question is particularly interesting in the classical case
![]() $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
.
Recall that an essentially free ergodic nonsingular action
![]() $G \curvearrowright (X,\mu )$
is said to be of type II
$G \curvearrowright (X,\mu )$
is said to be of type II
![]() $_1$
if it admits an equivalent G-invariant probability measure, of type II
$_1$
if it admits an equivalent G-invariant probability measure, of type II
![]() $_{\infty }$
if it admits an equivalent G-invariant infinite measure and of type III otherwise. Moreover, type III actions are further classified by Krieger’s associated flow [Reference Krieger38], an ergodic nonsingular action of
$_{\infty }$
if it admits an equivalent G-invariant infinite measure and of type III otherwise. Moreover, type III actions are further classified by Krieger’s associated flow [Reference Krieger38], an ergodic nonsingular action of
![]() $\mathbb {R}$
that is also equal to the Connes–Takesaki flow of weights [Reference Connes and Takesaki14] of the crossed product von Neumann algebra
$\mathbb {R}$
that is also equal to the Connes–Takesaki flow of weights [Reference Connes and Takesaki14] of the crossed product von Neumann algebra
![]() $L^{\infty }(X) \rtimes G$
. If the associated flow is trivial, the action is of type III
$L^{\infty }(X) \rtimes G$
. If the associated flow is trivial, the action is of type III
![]() $_1$
. If it is periodic with period
$_1$
. If it is periodic with period
![]() $|\log \lambda |$
and
$|\log \lambda |$
and
![]() $\lambda \in (0,1)$
, the action is of type III
$\lambda \in (0,1)$
, the action is of type III
![]() $_{\lambda }$
. If the associated flow is properly ergodic, the action is of type III
$_{\lambda }$
. If the associated flow is properly ergodic, the action is of type III
![]() $_0$
, and we are particularly interested in understanding which associated flows may arise from nonsingular Bernoulli actions.
$_0$
, and we are particularly interested in understanding which associated flows may arise from nonsingular Bernoulli actions.
The first example of an ergodic Bernoulli action of type III was given by Hamachi for the group of integers [Reference Hamachi30]. Much later in [Reference Kosloff35], Kosloff could give an example of a nonsingular Bernoulli action of
![]() $\mathbb {Z}$
that is of type III
$\mathbb {Z}$
that is of type III
![]() $_{1}$
.
$_{1}$
.
In the past few years, the study of nonsingular Bernoulli actions has gained momentum. The first systematic results for nonsingular Bernoulli actions of nonamenable groups G were obtained in [Reference Vaes and Wahl49]. In [Reference Björklund, Kosloff and Vaes7], very complete results on the ergodicity and type of nonsingular Bernoulli actions with base space
![]() $X_0=\{0,1\}$
were obtained, building on important earlier work in [Reference Kosloff36, Reference Danilenko and Lemańczyk22, Reference Kosloff37, Reference Danilenko18]. In particular, it was shown in [Reference Vaes and Wahl49] that the free groups
$X_0=\{0,1\}$
were obtained, building on important earlier work in [Reference Kosloff36, Reference Danilenko and Lemańczyk22, Reference Kosloff37, Reference Danilenko18]. In particular, it was shown in [Reference Vaes and Wahl49] that the free groups
![]() $\mathbb {F}_n$
,
$\mathbb {F}_n$
,
![]() $n \geq 2$
, admit Bernoulli actions of type III
$n \geq 2$
, admit Bernoulli actions of type III
![]() $_{\lambda }$
for all
$_{\lambda }$
for all
![]() $\lambda \in (0,1]$
. In [Reference Björklund, Kosloff and Vaes7], it was proven that locally finite groups admit Bernoulli actions of all possible types: II
$\lambda \in (0,1]$
. In [Reference Björklund, Kosloff and Vaes7], it was proven that locally finite groups admit Bernoulli actions of all possible types: II
![]() $_{1}$
, II
$_{1}$
, II
![]() $_{\infty }$
and III
$_{\infty }$
and III
![]() $_{\lambda }$
for
$_{\lambda }$
for
![]() $\lambda \in [0,1]$
. In [Reference Berendschot and Vaes8], we proved that the same holds for all infinite amenable groups if we allow the base space
$\lambda \in [0,1]$
. In [Reference Berendschot and Vaes8], we proved that the same holds for all infinite amenable groups if we allow the base space
![]() $X_0$
to be infinite. The latter is a necessary assumption since it was proven in [Reference Björklund, Kosloff and Vaes7] that Bernoulli actions of
$X_0$
to be infinite. The latter is a necessary assumption since it was proven in [Reference Björklund, Kosloff and Vaes7] that Bernoulli actions of
![]() $\mathbb {Z}$
with finite base space are never of type II
$\mathbb {Z}$
with finite base space are never of type II
![]() $_{\infty }$
. In [Reference Kosloff and Soo39], it was proven independently that infinite amenable groups admit Bernoulli actions of type III
$_{\infty }$
. In [Reference Kosloff and Soo39], it was proven independently that infinite amenable groups admit Bernoulli actions of type III
![]() $_{\lambda }$
for all
$_{\lambda }$
for all
![]() $\lambda \in (0,1]$
.
$\lambda \in (0,1]$
.
Ergodic, essentially free, nonsingular actions
![]() $G \curvearrowright (X,\mu )$
of amenable groups are completely classified, both up to orbit equivalence and up to isomorphism of their crossed product von Neumann algebras, by their type and associated flow; see [Reference Krieger38, Reference Connes13, Reference Connes and Takesaki14, Reference Connes, Feldman and Weiss11, Reference Haagerup29]. It is thus a very natural question to ask which ergodic flows arise as the associated flow of a nonsingular Bernoulli action, in particular of the group
$G \curvearrowright (X,\mu )$
of amenable groups are completely classified, both up to orbit equivalence and up to isomorphism of their crossed product von Neumann algebras, by their type and associated flow; see [Reference Krieger38, Reference Connes13, Reference Connes and Takesaki14, Reference Connes, Feldman and Weiss11, Reference Haagerup29]. It is thus a very natural question to ask which ergodic flows arise as the associated flow of a nonsingular Bernoulli action, in particular of the group
![]() $\mathbb {Z}$
. Put in an equivalent form, the question is which factors arise as crossed products
$\mathbb {Z}$
. Put in an equivalent form, the question is which factors arise as crossed products
![]() $L^{\infty }(X) \rtimes \mathbb {Z}$
by nonsingular Bernoulli shifts.
$L^{\infty }(X) \rtimes \mathbb {Z}$
by nonsingular Bernoulli shifts.
We prove in this paper the surprising result that not all injective factors can arise in this way. We also prove that many injective type III
![]() $_0$
factors do arise. In particular, we prove that all infinite tensor products of factors of type
$_0$
factors do arise. In particular, we prove that all infinite tensor products of factors of type
![]() $I_2$
(i.e.,
$I_2$
(i.e.,
![]() $2 \times 2$
matrices), the so-called ITPFI
$2 \times 2$
matrices), the so-called ITPFI
![]() $_2$
factors, arise as crossed products of nonsingular Bernoulli shifts.
$_2$
factors, arise as crossed products of nonsingular Bernoulli shifts.
In this paper, we call a flow any nonsingular action of
![]() $\mathbb {R}$
. We introduce below (see Definition 3.12) the concept of an infinitely divisible flow. By the classification of injective factors, the flow of weights of an injective factor M is infinitely divisible if and only if for every integer
$\mathbb {R}$
. We introduce below (see Definition 3.12) the concept of an infinitely divisible flow. By the classification of injective factors, the flow of weights of an injective factor M is infinitely divisible if and only if for every integer
![]() $n \geq 1$
, there exists an injective factor N such that
$n \geq 1$
, there exists an injective factor N such that
![]() $M \cong N^{\mathbin {\overline {\otimes }} n}$
. By [Reference Giordano, Skandalis and Woods28, Theorem 2.1], not every injective factor, and not even every ITPFI factor, is a tensor square. So not all ergodic flows are infinitely divisible.
$M \cong N^{\mathbin {\overline {\otimes }} n}$
. By [Reference Giordano, Skandalis and Woods28, Theorem 2.1], not every injective factor, and not even every ITPFI factor, is a tensor square. So not all ergodic flows are infinitely divisible.
Our first main result says that the associated flow of a nonsingular Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
must be infinitely divisible. We prove this result in complete generality, without making any other assumptions on the nature of the base space
$\mathbb {Z} \curvearrowright (X,\mu )$
must be infinitely divisible. We prove this result in complete generality, without making any other assumptions on the nature of the base space
![]() $X_0$
or the probability measures
$X_0$
or the probability measures
![]() $\mu _n$
, apart from the shift being nonsingular.
$\mu _n$
, apart from the shift being nonsingular.
We thus also need a completely general result on the ergodicity of nonsingular Bernoulli shifts. Ruling out the trivial cases where
![]() $\mu $
admits an atom or where the action
$\mu $
admits an atom or where the action
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
admits a fundamental domain (i.e., is dissipative), we prove the following result. We actually provide in Theorem 4.1 below a more precise description, also saying exactly what happens in the trivial cases with an atom or a fundamental domain.
$\mathbb {Z} \curvearrowright (X,\mu )$
admits a fundamental domain (i.e., is dissipative), we prove the following result. We actually provide in Theorem 4.1 below a more precise description, also saying exactly what happens in the trivial cases with an atom or a fundamental domain.
Theorem A. Let
![]() $\mathbb {Z} \curvearrowright (X,\mu ) = \prod _{n \in \mathbb {Z}} (X_0,\mu _n)$
be a nonsingular Bernoulli shift such that
$\mathbb {Z} \curvearrowright (X,\mu ) = \prod _{n \in \mathbb {Z}} (X_0,\mu _n)$
be a nonsingular Bernoulli shift such that
![]() $(X,\mu )$
is nonatomic and
$(X,\mu )$
is nonatomic and
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
is not dissipative.
$\mathbb {Z} \curvearrowright (X,\mu )$
is not dissipative.
There exists an essentially unique Borel set
![]() $C_0 \subset X_0$
such that
$C_0 \subset X_0$
such that
![]() $C_0^{\mathbb {Z}} \subset X$
has positive measure and the following holds.
$C_0^{\mathbb {Z}} \subset X$
has positive measure and the following holds.
-
• The nonsingular Bernoulli shift
 $\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
is weakly mixing, and its associated flow is infinitely divisible.
$\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
is weakly mixing, and its associated flow is infinitely divisible. -
• The action
 $\mathbb {Z} \curvearrowright X \setminus C_0^{\mathbb {Z}}$
is dissipative.
$\mathbb {Z} \curvearrowright X \setminus C_0^{\mathbb {Z}}$
is dissipative.
Note that it was proven in [Reference Björklund, Kosloff and Vaes7, Theorem A] that a Bernoulli shift of
![]() $\mathbb {Z}$
with base space
$\mathbb {Z}$
with base space
![]() $\{0,1\}$
is either weakly mixing, dissipative or atomic. This is compatible with Theorem A because a two-point base space is the only case in which a subset
$\{0,1\}$
is either weakly mixing, dissipative or atomic. This is compatible with Theorem A because a two-point base space is the only case in which a subset
![]() $C_0 \subset X_0$
is either empty, a single point or everything. Theorem A says in particular that, for every conservative nonsingular Bernoulli shift
$C_0 \subset X_0$
is either empty, a single point or everything. Theorem A says in particular that, for every conservative nonsingular Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
, the associated flow is infinitely divisible. The crossed product
$\mathbb {Z} \curvearrowright (X,\mu )$
, the associated flow is infinitely divisible. The crossed product
![]() $L^{\infty }(X) \rtimes \mathbb {Z}$
associated with a Bernoulli shift can only be a factor if
$L^{\infty }(X) \rtimes \mathbb {Z}$
associated with a Bernoulli shift can only be a factor if
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
is conservative and ergodic. As mentioned above, by [Reference Giordano, Skandalis and Woods28, Theorem 2.1], it thus follows that not every injective factor, and not even every ITPFI factor, is of the form
$\mathbb {Z} \curvearrowright (X,\mu )$
is conservative and ergodic. As mentioned above, by [Reference Giordano, Skandalis and Woods28, Theorem 2.1], it thus follows that not every injective factor, and not even every ITPFI factor, is of the form
![]() $L^{\infty }(X) \rtimes \mathbb {Z}$
where
$L^{\infty }(X) \rtimes \mathbb {Z}$
where
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
is a nonsingular Bernoulli shift.
$\mathbb {Z} \curvearrowright (X,\mu )$
is a nonsingular Bernoulli shift.
Complementing Theorem A, we determine in Theorem 4.3 in equally complete generality the type of an arbitrary nonsingular Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
.
$\mathbb {Z} \curvearrowright (X,\mu )$
.
In the converse direction, we prove that many ergodic flows do arise as associated flows of nonsingular Bernoulli actions. By [Reference Connes and Woods17], the possible flows of weights of ITPFI factors are precisely the tail boundary flows, i.e., the actions of
![]() $\mathbb {R}$
on the Poisson boundary of a time-dependent random walk on
$\mathbb {R}$
on the Poisson boundary of a time-dependent random walk on
![]() $\mathbb {R}$
given by a (nonconstant) sequence of transition probability measures
$\mathbb {R}$
given by a (nonconstant) sequence of transition probability measures
![]() $\mu _n$
on
$\mu _n$
on
![]() $\mathbb {R}$
. If the transition probabilities
$\mathbb {R}$
. If the transition probabilities
![]() $\mu _n$
can be chosen to be compound Poisson distributions, we call the tail boundary flow a Poisson flow
Footnote
1
, see Definition 3.7.
$\mu _n$
can be chosen to be compound Poisson distributions, we call the tail boundary flow a Poisson flow
Footnote
1
, see Definition 3.7.
We prove in Theorems 3.8 and 3.9 that the class of Poisson flows is large: It includes all almost periodic flows (i.e., flows with pure point spectrum), and it includes the flow of weights of any ITPFI
![]() $_2$
factor. By definition, Poisson flows are infinitely divisible, and therefore, not every ergodic flow is a Poisson flow. In Section 3, we obtain several results on the class of Poisson flows. They can be equivalently characterized as the tail boundary flows with transition probabilities
$_2$
factor. By definition, Poisson flows are infinitely divisible, and therefore, not every ergodic flow is a Poisson flow. In Section 3, we obtain several results on the class of Poisson flows. They can be equivalently characterized as the tail boundary flows with transition probabilities
![]() $\mu _n$
supported on two points and having uniformly bounded variance (see Proposition 3.11). Also, the flows of weights of ITPFI
$\mu _n$
supported on two points and having uniformly bounded variance (see Proposition 3.11). Also, the flows of weights of ITPFI
![]() $_2$
factors can be precisely characterized as the Poisson flows of positive type (see Definition 3.7 and Theorem 3.9).
$_2$
factors can be precisely characterized as the Poisson flows of positive type (see Definition 3.7 and Theorem 3.9).
We then prove that all these Poisson flows arise as the associated flow of a weakly mixing nonsingular Bernoulli action of any amenable group. As a corollary, it thus follows that every ITPFI
![]() $_2$
factor is of the form
$_2$
factor is of the form
![]() $L^{\infty }(X) \rtimes \mathbb {Z}$
for a nonsingular, weakly mixing Bernoulli shift
$L^{\infty }(X) \rtimes \mathbb {Z}$
for a nonsingular, weakly mixing Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
.
$\mathbb {Z} \curvearrowright (X,\mu )$
.
Theorem B. Let G be any countable infinite amenable group, and let
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
be any Poisson flow. There exists a family of equivalent probability measures
$\mathbb {R} \curvearrowright (Z,\eta )$
be any Poisson flow. There exists a family of equivalent probability measures
![]() $(\mu _g)_{g \in G}$
on a countable infinite base space
$(\mu _g)_{g \in G}$
on a countable infinite base space
![]() $X_0$
such that the Bernoulli action
$X_0$
such that the Bernoulli action
![]() $G \curvearrowright (X,\mu ) = \prod _{g \in G} (X_0,\mu _g)$
is nonsingular, weakly mixing and has associated flow
$G \curvearrowright (X,\mu ) = \prod _{g \in G} (X_0,\mu _g)$
is nonsingular, weakly mixing and has associated flow
![]() $\mathbb {R} \curvearrowright Z$
.
$\mathbb {R} \curvearrowright Z$
.
As a byproduct of our results on Poisson flows, it follows that every almost periodic flow is the flow of weights of an ITPFI
![]() $_2$
factor, answering a question that remained open since [Reference Hamachi and Osikawa32, Reference Giordano and Skandalis27].
$_2$
factor, answering a question that remained open since [Reference Hamachi and Osikawa32, Reference Giordano and Skandalis27].
Theorem C. Every injective factor with almost periodic flow of weights is an ITPFI
![]() $_2$
factor.
$_2$
factor.
To put Theorem C in a proper context, recall that an ergodic almost periodic flow is precisely given by the translation action
![]() $\mathbb {R} \curvearrowright \widehat {\Lambda }$
where
$\mathbb {R} \curvearrowright \widehat {\Lambda }$
where
![]() $\Lambda \subset \mathbb {R}$
is a countable subgroup. So, for every countable subgroup
$\Lambda \subset \mathbb {R}$
is a countable subgroup. So, for every countable subgroup
![]() $\Lambda \subset \mathbb {R}$
, there is a unique injective factor
$\Lambda \subset \mathbb {R}$
, there is a unique injective factor
![]() $M_{\Lambda }$
with flow of weights the translation action
$M_{\Lambda }$
with flow of weights the translation action
![]() $\mathbb {R} \curvearrowright \widehat {\Lambda }$
. Connes’ T-invariant of
$\mathbb {R} \curvearrowright \widehat {\Lambda }$
. Connes’ T-invariant of
![]() $M_{\Lambda }$
equals
$M_{\Lambda }$
equals
![]() $\Lambda $
. In [Reference Hamachi and Osikawa32, Theorem 2], it was proven that, for every
$\Lambda $
. In [Reference Hamachi and Osikawa32, Theorem 2], it was proven that, for every
![]() $\alpha \in \mathbb {R}\setminus \{0\}$
and every subgroup
$\alpha \in \mathbb {R}\setminus \{0\}$
and every subgroup
![]() $\Lambda \subset \alpha \mathbb {Q}$
, the factor
$\Lambda \subset \alpha \mathbb {Q}$
, the factor
![]() $M_{\Lambda }$
is ITPFI
$M_{\Lambda }$
is ITPFI
![]() $_2$
. In [Reference Giordano and Skandalis27, Proposition 1.1], it was proven that for every countable subgroup
$_2$
. In [Reference Giordano and Skandalis27, Proposition 1.1], it was proven that for every countable subgroup
![]() $\Lambda \subset \mathbb {R}$
, there exists an ITPFI
$\Lambda \subset \mathbb {R}$
, there exists an ITPFI
![]() $_2$
factor M with
$_2$
factor M with
![]() $T(M) = \Lambda $
, but it remained unclear if
$T(M) = \Lambda $
, but it remained unclear if
![]() $M \cong M_{\Lambda }$
. We now prove in Theorem C that all
$M \cong M_{\Lambda }$
. We now prove in Theorem C that all
![]() $M_{\Lambda }$
are ITPFI
$M_{\Lambda }$
are ITPFI
![]() $_2$
factors.
$_2$
factors.
Every ITPFI
![]() $_2$
factor is infinitely divisible. It is natural to speculate that also the converse holds. One may also speculate that the infinitely divisible ergodic flows are exactly the Poisson flows. If both of these speculations are true, it follows from Theorem A and Theorem B that the class of injective factors that can be realized as the crossed product
$_2$
factor is infinitely divisible. It is natural to speculate that also the converse holds. One may also speculate that the infinitely divisible ergodic flows are exactly the Poisson flows. If both of these speculations are true, it follows from Theorem A and Theorem B that the class of injective factors that can be realized as the crossed product
![]() $L^{\infty }(X)\rtimes \mathbb {Z}$
by a conservative nonsingular Bernoulli action
$L^{\infty }(X)\rtimes \mathbb {Z}$
by a conservative nonsingular Bernoulli action
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
equals the class of ITPFI
$\mathbb {Z}\curvearrowright (X,\mu )$
equals the class of ITPFI
![]() $_2$
. We refer to Remark 3.16 for a further discussion.
$_2$
. We refer to Remark 3.16 for a further discussion.
Poisson flows also appear naturally in the context of nonsingular Poisson suspensions (see Section 5 for terminology). Given an infinite,
![]() $\sigma $
-finite, standard measure space
$\sigma $
-finite, standard measure space
![]() $(X_0,\mu _0)$
with Poisson suspension
$(X_0,\mu _0)$
with Poisson suspension
![]() $(X,\mu )$
, under the appropriate assumptions, a nonsingular action
$(X,\mu )$
, under the appropriate assumptions, a nonsingular action
![]() $G \curvearrowright (X_0,\mu _0)$
has a canonical nonsingular suspension
$G \curvearrowright (X_0,\mu _0)$
has a canonical nonsingular suspension
![]() $G \curvearrowright (X,\mu )$
. To a certain extent, Poisson suspensions can be viewed as generalizations of Bernoulli actions, and many results were obtained recently (see [Reference Roy46, Reference Danilenko and Kosloff20, Reference Danilenko, Kosloff and Roy21, Reference Danilenko19]). In particular in [Reference Danilenko19], it was proven that any locally compact second countable group G that does not have property (T) admits nonsingular Poisson suspension actions of any possible type. We prove that in type III
$G \curvearrowright (X,\mu )$
. To a certain extent, Poisson suspensions can be viewed as generalizations of Bernoulli actions, and many results were obtained recently (see [Reference Roy46, Reference Danilenko and Kosloff20, Reference Danilenko, Kosloff and Roy21, Reference Danilenko19]). In particular in [Reference Danilenko19], it was proven that any locally compact second countable group G that does not have property (T) admits nonsingular Poisson suspension actions of any possible type. We prove that in type III
![]() $_0$
, any Poisson flow may arise as associated flow.
$_0$
, any Poisson flow may arise as associated flow.
Proposition D. Let G be any locally compact second countable group that does not have property (T). Let
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
be any Poisson flow. Then G admits a nonsingular action
$\mathbb {R} \curvearrowright (Z,\eta )$
be any Poisson flow. Then G admits a nonsingular action
![]() $G \curvearrowright (X_0,\mu _0)$
of which the Poisson suspension
$G \curvearrowright (X_0,\mu _0)$
of which the Poisson suspension
![]() $G \curvearrowright (X,\mu )$
is well-defined, weakly mixing, essentially free and has associated flow
$G \curvearrowright (X,\mu )$
is well-defined, weakly mixing, essentially free and has associated flow
![]() $\mathbb {R} \curvearrowright Z$
.
$\mathbb {R} \curvearrowright Z$
.
By [Reference Danilenko, Kosloff and Roy21, Theorem G], Proposition D is sharp: If G has property (T), then every nonsingular Poisson suspension action of G admits an equivalent G-invariant probability measure. We actually prove first Proposition D and then deduce Theorem B as a special case by taking
![]() $G \curvearrowright G \times \mathbb {N} : g \cdot (h,n) = (gh,n)$
and choosing the measure
$G \curvearrowright G \times \mathbb {N} : g \cdot (h,n) = (gh,n)$
and choosing the measure
![]() $\mu _0$
on
$\mu _0$
on
![]() $G \times \mathbb {N}$
appropriately.
$G \times \mathbb {N}$
appropriately.
2 Preliminaries
2.1 Nonsingular group actions
Suppose that
![]() $(X,\mu )$
is a standard measure space. The push forward of
$(X,\mu )$
is a standard measure space. The push forward of
![]() $\mu $
along a Borel map
$\mu $
along a Borel map
![]() $\varphi \colon X\rightarrow X$
, that we denote by
$\varphi \colon X\rightarrow X$
, that we denote by
![]() $\varphi \mu $
or
$\varphi \mu $
or
![]() $\varphi _*\mu $
, is the measure given by
$\varphi _*\mu $
, is the measure given by
![]() $(\varphi _*\mu )(\mathcal {U})=\mu (\varphi ^{-1}(\mathcal {U}))$
. We say that
$(\varphi _*\mu )(\mathcal {U})=\mu (\varphi ^{-1}(\mathcal {U}))$
. We say that
![]() $\varphi $
is nonsingular if the measures
$\varphi $
is nonsingular if the measures
![]() $\varphi _*\mu $
and
$\varphi _*\mu $
and
![]() $\mu $
are equivalent. If in addition
$\mu $
are equivalent. If in addition
![]() $\varphi $
is invertible, we say it is a nonsingular automorphism. In that case, we will also use the notation
$\varphi $
is invertible, we say it is a nonsingular automorphism. In that case, we will also use the notation
![]() $\mu \circ \varphi $
for the push forward measure
$\mu \circ \varphi $
for the push forward measure
![]() $\varphi ^{-1}\mu $
. The set
$\varphi ^{-1}\mu $
. The set
![]() $\operatorname {Aut}(X,\mu )$
is the group of all nonsingular automorphisms of
$\operatorname {Aut}(X,\mu )$
is the group of all nonsingular automorphisms of
![]() $(X,\mu )$
, where we identify two elements if they agree almost everywhere. It caries a canonical topology, making it into a Polish group. Both the set
$(X,\mu )$
, where we identify two elements if they agree almost everywhere. It caries a canonical topology, making it into a Polish group. Both the set
![]() $\operatorname {Aut}(X,\mu )$
and its topology only depend on the measure class of
$\operatorname {Aut}(X,\mu )$
and its topology only depend on the measure class of
![]() $\mu $
.
$\mu $
.
For a nonsingular automorphism
![]() $\varphi \colon X\rightarrow X$
the Radon–Nikodym derivative
$\varphi \colon X\rightarrow X$
the Radon–Nikodym derivative
is uniquely determined by the equality
A nonsingular action of a locally compact second countable group H on a standard measure space
![]() $(X,\mu )$
is a continuous homomorphism
$(X,\mu )$
is a continuous homomorphism
![]() $\alpha \colon H\rightarrow \operatorname {Aut}(X,\mu )$
, which we will also write as
$\alpha \colon H\rightarrow \operatorname {Aut}(X,\mu )$
, which we will also write as
![]() $H\overset {\alpha }{\curvearrowright } (X,\mu )$
. Such an action induces an action
$H\overset {\alpha }{\curvearrowright } (X,\mu )$
. Such an action induces an action
![]() $H\curvearrowright L^{\infty }(X,\mu )$
by
$H\curvearrowright L^{\infty }(X,\mu )$
by
![]() $(h\cdot F)(x)=F(h^{-1}\cdot x)$
. Conversely, if A is a separably represented abelian von Neumann algebra, and
$(h\cdot F)(x)=F(h^{-1}\cdot x)$
. Conversely, if A is a separably represented abelian von Neumann algebra, and
![]() $H\curvearrowright A$
acts by automorphisms, then there is a standard measure space
$H\curvearrowright A$
acts by automorphisms, then there is a standard measure space
![]() $(Y,\nu )$
, together with a nonsingular action
$(Y,\nu )$
, together with a nonsingular action
![]() $H\curvearrowright (Y,\nu )$
, such that the action
$H\curvearrowright (Y,\nu )$
, such that the action
![]() $H\curvearrowright A$
is the action induced by
$H\curvearrowright A$
is the action induced by
![]() $H\curvearrowright (Y,\nu )$
. We will frequently identify the actions
$H\curvearrowright (Y,\nu )$
. We will frequently identify the actions
![]() $H\curvearrowright A$
and
$H\curvearrowright A$
and
![]() $H\curvearrowright (Y,\nu )$
. Recall that a nonsingular group action
$H\curvearrowright (Y,\nu )$
. Recall that a nonsingular group action
![]() $H\curvearrowright (X,\mu )$
is called ergodic if there are no nontrivial H-invariant Borel sets (up to measure zero).
$H\curvearrowright (X,\mu )$
is called ergodic if there are no nontrivial H-invariant Borel sets (up to measure zero).
We call a flow any nonsingular action of
![]() $H = \mathbb {R}$
. We say that a flow
$H = \mathbb {R}$
. We say that a flow
![]() $\mathbb {R}\curvearrowright (X,\mu )$
is periodic if there exists a
$\mathbb {R}\curvearrowright (X,\mu )$
is periodic if there exists a
![]() $t\in \mathbb {R}\setminus \{0\}$
such that
$t\in \mathbb {R}\setminus \{0\}$
such that
![]() $t\cdot F=F$
for every
$t\cdot F=F$
for every
![]() $F\in L^{\infty }(X,\mu )$
.
$F\in L^{\infty }(X,\mu )$
.
A nonsingular action
![]() $G\curvearrowright (X,\mu )$
of a countable group G on a standard measure space
$G\curvearrowright (X,\mu )$
of a countable group G on a standard measure space
![]() $(X,\mu )$
is called essentially free if the set
$(X,\mu )$
is called essentially free if the set
![]() $\{x\in X:g\cdot x=x\}$
has measure zero for every
$\{x\in X:g\cdot x=x\}$
has measure zero for every
![]() $g\neq e$
. If
$g\neq e$
. If
![]() $G\curvearrowright (X,\mu )$
is essentially free and if there exists a fundamental domain, i.e., a Borel set
$G\curvearrowright (X,\mu )$
is essentially free and if there exists a fundamental domain, i.e., a Borel set
![]() $\mathcal {W} \subset X$
such that
$\mathcal {W} \subset X$
such that
![]() $(g \cdot \mathcal {W})_{g \in G}$
is a partition of X up to measure zero, then
$(g \cdot \mathcal {W})_{g \in G}$
is a partition of X up to measure zero, then
![]() $G \curvearrowright (X,\mu )$
is called dissipative. On the other hand, if for every nonnegligible Borel set
$G \curvearrowright (X,\mu )$
is called dissipative. On the other hand, if for every nonnegligible Borel set
![]() $\mathcal {U}\subset X$
there are infinitely many
$\mathcal {U}\subset X$
there are infinitely many
![]() $g\in G$
such that
$g\in G$
such that
![]() $\mu (g\mathcal {U}\cap \mathcal {U})>0$
, then we say the action
$\mu (g\mathcal {U}\cap \mathcal {U})>0$
, then we say the action
![]() $G\curvearrowright (X,\mu )$
is conservative.
$G\curvearrowright (X,\mu )$
is conservative.
If
![]() $G \curvearrowright (X,\mu )$
is an essentially free nonsingular action, there is a unique partition (up to measure zero)
$G \curvearrowright (X,\mu )$
is an essentially free nonsingular action, there is a unique partition (up to measure zero)
![]() $X = \mathcal {U} \sqcup \mathcal {W}$
of X into G-invariant Borel sets
$X = \mathcal {U} \sqcup \mathcal {W}$
of X into G-invariant Borel sets
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {W}$
such that the action
$\mathcal {W}$
such that the action
![]() $G \curvearrowright (\mathcal {U},\mu )$
is conservative and
$G \curvearrowright (\mathcal {U},\mu )$
is conservative and
![]() $G \curvearrowright (\mathcal {W},\mu )$
is dissipative. The actions
$G \curvearrowright (\mathcal {W},\mu )$
is dissipative. The actions
![]() $G \curvearrowright \mathcal {U}$
and
$G \curvearrowright \mathcal {U}$
and
![]() $G \curvearrowright \mathcal {W}$
are called the conservative, resp., dissipative parts of the action
$G \curvearrowright \mathcal {W}$
are called the conservative, resp., dissipative parts of the action
![]() $G \curvearrowright X$
. Finally, note that an essentially free ergodic action must be conservative, except when the action is transitive, i.e., when
$G \curvearrowright X$
. Finally, note that an essentially free ergodic action must be conservative, except when the action is transitive, i.e., when
![]() $\mu $
is atomic and supported on a single G-orbit, which means that the action is isomorphic with the translation action
$\mu $
is atomic and supported on a single G-orbit, which means that the action is isomorphic with the translation action
![]() $G \curvearrowright G$
.
$G \curvearrowright G$
.
2.2 Nonsingular Bernoulli actions
Suppose that
![]() $X_0$
is a standard measurable space and that G is a countable infinite group. For a family of equivalent probability measures
$X_0$
is a standard measurable space and that G is a countable infinite group. For a family of equivalent probability measures
![]() $(\mu _g)_{g\in G}$
on
$(\mu _g)_{g\in G}$
on
![]() $X_0$
, consider the product probability space
$X_0$
, consider the product probability space
The action
![]() $G\curvearrowright (X,\mu )$
given by
$G\curvearrowright (X,\mu )$
given by
![]() $(g\cdot x)_h = x_{g^{-1}h}$
, is called a Bernoulli action of G or Bernoulli shift if
$(g\cdot x)_h = x_{g^{-1}h}$
, is called a Bernoulli action of G or Bernoulli shift if
![]() $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
.
By Kakutani’s criterion for the equivalence of product measures [Reference Kakutani34], the Bernoulli action
![]() $G\curvearrowright (X,\mu )$
is nonsingular if and only if equation (1.2) holds, where
$G\curvearrowright (X,\mu )$
is nonsingular if and only if equation (1.2) holds, where
![]() $H(\mu ,\nu )$
denotes the Hellinger distance defined by
$H(\mu ,\nu )$
denotes the Hellinger distance defined by
 $$ \begin{align} H^2(\mu,\nu)=\frac{1}{2}\int_{X_0}\bigl(\sqrt{d\mu / d\zeta}-\sqrt{d\nu / d\zeta}\bigr)^2 \, d\zeta = 1 - \int_{X_0} \sqrt{\frac{d\mu}{d\zeta}} \, \sqrt{\frac{d\nu}{d\zeta}} \, d\zeta, \end{align} $$
$$ \begin{align} H^2(\mu,\nu)=\frac{1}{2}\int_{X_0}\bigl(\sqrt{d\mu / d\zeta}-\sqrt{d\nu / d\zeta}\bigr)^2 \, d\zeta = 1 - \int_{X_0} \sqrt{\frac{d\mu}{d\zeta}} \, \sqrt{\frac{d\nu}{d\zeta}} \, d\zeta, \end{align} $$
where
![]() $\zeta $
is any probability measure on X with
$\zeta $
is any probability measure on X with
![]() $\mu ,\nu \prec \zeta $
.
$\mu ,\nu \prec \zeta $
.
If
![]() $(X,\mu )=\prod _{g\in G}(X_0,\mu _g)$
is nonatomic and if the Bernoulli action
$(X,\mu )=\prod _{g\in G}(X_0,\mu _g)$
is nonatomic and if the Bernoulli action
![]() $G\curvearrowright (X,\mu )$
is nonsingular, then it is essentially free, by [Reference Björklund, Kosloff and Vaes7, Lemma 2.2].
$G\curvearrowright (X,\mu )$
is nonsingular, then it is essentially free, by [Reference Björklund, Kosloff and Vaes7, Lemma 2.2].
Recall that for any permutation
![]() $\rho $
of G (finite or infinite) such that the induced transformation
$\rho $
of G (finite or infinite) such that the induced transformation
is nonsingular we have that
 $$ \begin{align*} \frac{d(\mu\circ \alpha_{\rho})}{d\mu}(x)=\prod_{h\in G}\frac{d\mu_{\rho(h)}}{d\mu_h}(x_h), \;\;\text{with unconditional convergence a.e. on } X. \end{align*} $$
$$ \begin{align*} \frac{d(\mu\circ \alpha_{\rho})}{d\mu}(x)=\prod_{h\in G}\frac{d\mu_{\rho(h)}}{d\mu_h}(x_h), \;\;\text{with unconditional convergence a.e. on } X. \end{align*} $$
We then have that
2.3 Maharam extension and associated flow
Let
![]() $\lambda $
be the Lebesgue measure on
$\lambda $
be the Lebesgue measure on
![]() $\mathbb {R}$
. The Maharam extension of a nonsingular automorphism
$\mathbb {R}$
. The Maharam extension of a nonsingular automorphism
![]() $\varphi \in \operatorname {Aut}(X,\mu )$
is the nonsingular automorphism
$\varphi \in \operatorname {Aut}(X,\mu )$
is the nonsingular automorphism
![]() $\widetilde {\varphi }\in \operatorname {Aut}(X\times \mathbb {R},\mu \times \lambda )$
that is given by
$\widetilde {\varphi }\in \operatorname {Aut}(X\times \mathbb {R},\mu \times \lambda )$
that is given by
Note that
![]() $\widetilde {\varphi }$
preserves the infinite measure
$\widetilde {\varphi }$
preserves the infinite measure
![]() $d\mu (x) \times \exp (-t) d\lambda (t)$
. Also note that
$d\mu (x) \times \exp (-t) d\lambda (t)$
. Also note that
![]() $\varphi \mapsto \widetilde {\varphi }$
is a continuous group homomorphism between the Polish group
$\varphi \mapsto \widetilde {\varphi }$
is a continuous group homomorphism between the Polish group
![]() $\operatorname {Aut}(X,\mu )$
and the Polish group
$\operatorname {Aut}(X,\mu )$
and the Polish group
![]() $\operatorname {Aut}(X\times \mathbb {R},\mu \times \lambda )$
.
$\operatorname {Aut}(X\times \mathbb {R},\mu \times \lambda )$
.
The translation action
![]() $s \cdot (x,t) = (x, t+s)$
commutes with every
$s \cdot (x,t) = (x, t+s)$
commutes with every
![]() $\widetilde {\varphi }$
. For any nonsingular action
$\widetilde {\varphi }$
. For any nonsingular action
![]() $G \curvearrowright (X,\mu )$
Krieger’s associated flow (see [Reference Krieger38]) is defined as the action of
$G \curvearrowright (X,\mu )$
Krieger’s associated flow (see [Reference Krieger38]) is defined as the action of
![]() $\mathbb {R}$
on the ergodic decomposition of the Maharam extension
$\mathbb {R}$
on the ergodic decomposition of the Maharam extension
![]() $G \curvearrowright X \times \mathbb {R}$
, which amounts to the action of
$G \curvearrowright X \times \mathbb {R}$
, which amounts to the action of
![]() $\mathbb {R}$
on
$\mathbb {R}$
on
![]() $L^{\infty }(X \times \mathbb {R})^G$
.
$L^{\infty }(X \times \mathbb {R})^G$
.
Recall from the introduction how the type of a nonsingular group action
![]() $G \curvearrowright (X,\mu )$
is defined and that, for essentially free, ergodic actions of amenable groups, the type and associated flow form a complete invariant of the action, both up to orbit equivalence and up to isomorphism of the crossed product factors
$G \curvearrowright (X,\mu )$
is defined and that, for essentially free, ergodic actions of amenable groups, the type and associated flow form a complete invariant of the action, both up to orbit equivalence and up to isomorphism of the crossed product factors
![]() $L^{\infty }(X) \rtimes G$
.
$L^{\infty }(X) \rtimes G$
.
3 Poisson flows and infinite divisibility: proof of Theorem C
3.1 Tail boundary flows
Recall from [Reference Connes and Woods17] the construction of the tail boundary flow as the Poisson boundary of a time-dependent Markov random walk on
![]() $\mathbb {R}$
with transition probabilities
$\mathbb {R}$
with transition probabilities
![]() $(\mu _n)_{n \in \mathbb {N}}$
. Consider
$(\mu _n)_{n \in \mathbb {N}}$
. Consider
 $$ \begin{align} (\Omega, \mu)=\prod_{k=1}^{\infty}(\mathbb{R},\mu_k) \quad\text{and}\quad (\Omega_n, \widetilde{\mu}_n)=\prod_{k=n+1}^{\infty}(\mathbb{R},\mu_k) \;. \end{align} $$
$$ \begin{align} (\Omega, \mu)=\prod_{k=1}^{\infty}(\mathbb{R},\mu_k) \quad\text{and}\quad (\Omega_n, \widetilde{\mu}_n)=\prod_{k=n+1}^{\infty}(\mathbb{R},\mu_k) \;. \end{align} $$
Choose a probability measure
![]() $\mu _0$
on
$\mu _0$
on
![]() $\mathbb {R}$
that is equivalent with the Lebesgue measure, and define the nonsingular maps
$\mathbb {R}$
that is equivalent with the Lebesgue measure, and define the nonsingular maps
Define the von Neumann algebras
![]() $B = L^{\infty }(\mathbb {R} \times \Omega )$
and
$B = L^{\infty }(\mathbb {R} \times \Omega )$
and
![]() $A_n = (\pi _n)_*(L^{\infty }(\mathbb {R} \times \Omega _n))$
. Then the tail boundary is defined as
$A_n = (\pi _n)_*(L^{\infty }(\mathbb {R} \times \Omega _n))$
. Then the tail boundary is defined as
![]() $A=\bigcap _{n\geq 0} A_n$
. The translation action of
$A=\bigcap _{n\geq 0} A_n$
. The translation action of
![]() $\mathbb {R}$
in the first variable defines an ergodic action of
$\mathbb {R}$
in the first variable defines an ergodic action of
![]() $\mathbb {R}$
on A, which is called the tail boundary flow.
$\mathbb {R}$
on A, which is called the tail boundary flow.
We refer to [Reference Berendschot and Vaes8, Section 2.3] for several basic results on tail boundary flows.
Tail boundary flows play a key role in this paper. When working with elements x of a product space as in equation (3.1), we always denote by
![]() $x_k$
or
$x_k$
or
![]() $x_n$
the natural coordinates of x.
$x_n$
the natural coordinates of x.
Note that the tail boundary flow does not change if we permute the probability measures
![]() $\mu _n$
. More precisely, if
$\mu _n$
. More precisely, if
![]() $\sigma : \mathbb {N} \to \mathbb {N}$
is any bijection, then the tail boundary flows of
$\sigma : \mathbb {N} \to \mathbb {N}$
is any bijection, then the tail boundary flows of
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\mu _{\sigma (n)})_{n \in \mathbb {N}}$
are canonically isomorphic in the following way. Denoting by
$(\mu _{\sigma (n)})_{n \in \mathbb {N}}$
are canonically isomorphic in the following way. Denoting by
![]() $(\widetilde {\Omega },\widetilde {\mu })$
the path space for the family
$(\widetilde {\Omega },\widetilde {\mu })$
the path space for the family
![]() $(\mu _{\sigma (n)})_{n \in \mathbb {N}}$
, the map
$(\mu _{\sigma (n)})_{n \in \mathbb {N}}$
, the map
is a measure preserving bijection. We consider the von Neumann subalgebras
![]() $A_n \subset L^{\infty }(\mathbb {R} \times \Omega )$
and
$A_n \subset L^{\infty }(\mathbb {R} \times \Omega )$
and
![]() $\widetilde {A}_n \subset L^{\infty }(\mathbb {R} \times \widetilde {\Omega })$
, with intersections
$\widetilde {A}_n \subset L^{\infty }(\mathbb {R} \times \widetilde {\Omega })$
, with intersections
![]() $A = \bigcap _n A_n$
and
$A = \bigcap _n A_n$
and
![]() $\widetilde {A} = \bigcap _n \widetilde {A}_n$
realizing the respective tail boundaries. For every
$\widetilde {A} = \bigcap _n \widetilde {A}_n$
realizing the respective tail boundaries. For every
![]() $n \in \mathbb {N}$
, there exists an
$n \in \mathbb {N}$
, there exists an
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $\sigma (\{1,\ldots ,n\}) \subset \{1,\ldots ,m\}$
and
$\sigma (\{1,\ldots ,n\}) \subset \{1,\ldots ,m\}$
and
![]() $\sigma ^{-1}(\{1,\ldots ,n\}) \subset \{1,\ldots ,m\}$
. Then,
$\sigma ^{-1}(\{1,\ldots ,n\}) \subset \{1,\ldots ,m\}$
. Then,
![]() $\theta _*(A_m) \subset \widetilde {A}_n$
and
$\theta _*(A_m) \subset \widetilde {A}_n$
and
![]() $\widetilde {A}_m \subset \theta _*(A_n)$
. Therefore,
$\widetilde {A}_m \subset \theta _*(A_n)$
. Therefore,
![]() $\theta _*(A) = \widetilde {A}$
, implementing the isomorphism.
$\theta _*(A) = \widetilde {A}$
, implementing the isomorphism.
Note that tail boundary G-actions can be associated in a similar way to any family
![]() $(\mu _n)_{n \in \mathbb {N}}$
of Borel probability measures on a locally compact second countable abelian group G.
$(\mu _n)_{n \in \mathbb {N}}$
of Borel probability measures on a locally compact second countable abelian group G.
We prove in this section two results on tail boundary flows that are of independent interest. First recall for future reference the following well known and easy result. For completeness, we include the short proof. The Hellinger distance H was defined in equation (2.1). We also make use of the total variation distance between probability measures
![]() $\mu ,\nu $
on a standard Borel space X:
$\mu ,\nu $
on a standard Borel space X:
whenever
![]() $\zeta $
is a probability measure on X with
$\zeta $
is a probability measure on X with
![]() $\mu ,\nu \prec \zeta $
. Note that
$\mu ,\nu \prec \zeta $
. Note that
for all probability measures
![]() $\mu $
and
$\mu $
and
![]() $\nu $
on X.
$\nu $
on X.
Lemma 3.1 Cf. [Reference Connes and Woods17, Lemma 2.5]
If
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\nu _n)_{n \in \mathbb {N}}$
are sequences of probability measures on
$(\nu _n)_{n \in \mathbb {N}}$
are sequences of probability measures on
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
 $$ \begin{align} \sum_{n=1}^{\infty} H^2(\mu_n,\nu_n) < +\infty , \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} H^2(\mu_n,\nu_n) < +\infty , \end{align} $$
then the tail boundary flows of
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\nu _n)_{n \in \mathbb {N}}$
are isomorphic. This conclusion holds in particular if
$(\nu _n)_{n \in \mathbb {N}}$
are isomorphic. This conclusion holds in particular if
![]() $\sum _{n=1}^{\infty } d_{\operatorname {TV}}(\mu _n,\nu _n) < +\infty $
.
$\sum _{n=1}^{\infty } d_{\operatorname {TV}}(\mu _n,\nu _n) < +\infty $
.
Proof. Partition
![]() $\mathbb {R}$
into Borel sets
$\mathbb {R}$
into Borel sets
![]() $\mathbb {R} = U_n \sqcup V_n \sqcup W_n$
such that
$\mathbb {R} = U_n \sqcup V_n \sqcup W_n$
such that
![]() $\mu _n|_{U_n} \sim \nu _n|_{U_n}$
,
$\mu _n|_{U_n} \sim \nu _n|_{U_n}$
,
![]() $\nu _n(V_n) = 0$
and
$\nu _n(V_n) = 0$
and
![]() $\mu _n(W_n) = 0$
. From equation (3.2), it follows in particular that
$\mu _n(W_n) = 0$
. From equation (3.2), it follows in particular that
 $$ \begin{align} \sum_{n=1}^{\infty} \mu_n(V_n) < + \infty \quad\text{and}\quad \sum_{n =1}^{\infty} \nu_n(W_n) < + \infty \;. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \mu_n(V_n) < + \infty \quad\text{and}\quad \sum_{n =1}^{\infty} \nu_n(W_n) < + \infty \;. \end{align} $$
Define
![]() $(\Omega ,\mu )$
and
$(\Omega ,\mu )$
and
![]() $(\Omega _n,\widetilde {\mu }_n)$
as in equation (3.1) so that the tail boundary A of
$(\Omega _n,\widetilde {\mu }_n)$
as in equation (3.1) so that the tail boundary A of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is realized as the intersection of
$(\mu _n)_{n \in \mathbb {N}}$
is realized as the intersection of
![]() $A_n = (\pi _n)_*(L^{\infty }(\mathbb {R} \times \Omega _n))$
inside
$A_n = (\pi _n)_*(L^{\infty }(\mathbb {R} \times \Omega _n))$
inside
![]() $B = L^{\infty }(\mathbb {R} \times \Omega )$
. Similarly define
$B = L^{\infty }(\mathbb {R} \times \Omega )$
. Similarly define
![]() $(\Omega ',\nu )$
,
$(\Omega ',\nu )$
,
![]() $(\Omega ^{\prime }_n,\widetilde {\nu }_n)$
and
$(\Omega ^{\prime }_n,\widetilde {\nu }_n)$
and
![]() $\pi ^{\prime }_n$
so that the tail boundary C of
$\pi ^{\prime }_n$
so that the tail boundary C of
![]() $(\nu _n)_{n \in \mathbb {N}}$
is realized as the intersection of
$(\nu _n)_{n \in \mathbb {N}}$
is realized as the intersection of
![]() $C_n = (\pi ^{\prime }_n)_*(L^{\infty }(\mathbb {R} \times \Omega ^{\prime }_n))$
inside
$C_n = (\pi ^{\prime }_n)_*(L^{\infty }(\mathbb {R} \times \Omega ^{\prime }_n))$
inside
![]() $D = L^{\infty }(\mathbb {R} \times \Omega ')$
.
$D = L^{\infty }(\mathbb {R} \times \Omega ')$
.
Define
![]() $X_n \subset \mathbb {R} \times \Omega _n$
by
$X_n \subset \mathbb {R} \times \Omega _n$
by
![]() $(t,x) \in X_n$
iff
$(t,x) \in X_n$
iff
![]() $x_m \in U_m$
for all
$x_m \in U_m$
for all
![]() $m \geq n+1$
. Similarly, define
$m \geq n+1$
. Similarly, define
![]() $X^{\prime }_n \subset \mathbb {R} \times \Omega ^{\prime }_n$
. Denote
$X^{\prime }_n \subset \mathbb {R} \times \Omega ^{\prime }_n$
. Denote
![]() $p_n = (\pi _n)_*(1_{X_n})$
and
$p_n = (\pi _n)_*(1_{X_n})$
and
![]() $p^{\prime }_n = (\pi ^{\prime }_n)_*(1_{X^{\prime }_n})$
. The Kakutani criterion for the equivalence of product measures implies that the identity map
$p^{\prime }_n = (\pi ^{\prime }_n)_*(1_{X^{\prime }_n})$
. The Kakutani criterion for the equivalence of product measures implies that the identity map
![]() $X_n \to X^{\prime }_n$
is a nonsingular isomorphism, inducing a
$X_n \to X^{\prime }_n$
is a nonsingular isomorphism, inducing a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta _n : A_n p_n \to C_n p^{\prime }_n$
. By equation (3.3), the projections
$\theta _n : A_n p_n \to C_n p^{\prime }_n$
. By equation (3.3), the projections
![]() $p_n \in A$
and
$p_n \in A$
and
![]() $p^{\prime }_n \in D$
are increasing to
$p^{\prime }_n \in D$
are increasing to
![]() $1$
. The
$1$
. The
![]() $*$
-isomorphisms
$*$
-isomorphisms
![]() $\theta _n$
are compatible so that there is a unique
$\theta _n$
are compatible so that there is a unique
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta : A \to C$
satisfying
$\theta : A \to C$
satisfying
![]() $\theta (a)p^{\prime }_n = \theta _n(a p_n)$
for all
$\theta (a)p^{\prime }_n = \theta _n(a p_n)$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $n \in \mathbb {N}$
. By construction,
$n \in \mathbb {N}$
. By construction,
![]() $\theta $
conjugates the tail boundary flows of
$\theta $
conjugates the tail boundary flows of
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\nu _n)_{n \in \mathbb {N}}$
.
$(\nu _n)_{n \in \mathbb {N}}$
.
We start by proving that such an identification of tail boundary flows also holds under a different approximation assumption, replacing the Hellinger distance by the Wasserstein
![]() $2$
-metric. We can do even slightly better by taking the Wasserstein
$2$
-metric. We can do even slightly better by taking the Wasserstein
![]() $2$
-metric w.r.t. the metric on
$2$
-metric w.r.t. the metric on
![]() $\mathbb {R}$
given by
$\mathbb {R}$
given by
![]() $d(x,y) = |T_{\kappa }(x-y)|$
, where for
$d(x,y) = |T_{\kappa }(x-y)|$
, where for
![]() $\kappa> 0$
, we denote by
$\kappa> 0$
, we denote by
![]() $T_{\kappa }$
the cutoff function
$T_{\kappa }$
the cutoff function
 $$ \begin{align} T_{\kappa} : \mathbb{R} \to [-\kappa,\kappa] : T_{\kappa}(x)= \begin{cases} -\kappa &\;\;\text{if } x \leq -\kappa,\\ x &\;\;\text{if } -\kappa \leq x \leq \kappa,\\ \kappa &\;\;\text{if } x \geq \kappa.\end{cases} \end{align} $$
$$ \begin{align} T_{\kappa} : \mathbb{R} \to [-\kappa,\kappa] : T_{\kappa}(x)= \begin{cases} -\kappa &\;\;\text{if } x \leq -\kappa,\\ x &\;\;\text{if } -\kappa \leq x \leq \kappa,\\ \kappa &\;\;\text{if } x \geq \kappa.\end{cases} \end{align} $$
Recall that a coupling between probability measures
![]() $\mu $
,
$\mu $
,
![]() $\nu $
on
$\nu $
on
![]() $\mathbb {R}$
is a probability measure
$\mathbb {R}$
is a probability measure
![]() $\eta $
on
$\eta $
on
![]() $\mathbb {R}^2$
such that, writing
$\mathbb {R}^2$
such that, writing
![]() $\pi _1 : \mathbb {R}^2 \to \mathbb {R} : \pi _1(x,y) = x$
and
$\pi _1 : \mathbb {R}^2 \to \mathbb {R} : \pi _1(x,y) = x$
and
![]() $\pi _2 : \mathbb {R}^2 \to \mathbb {R} : \pi _2(x,y) = y$
, we have
$\pi _2 : \mathbb {R}^2 \to \mathbb {R} : \pi _2(x,y) = y$
, we have
![]() $(\pi _1)_*(\eta ) = \mu $
and
$(\pi _1)_*(\eta ) = \mu $
and
![]() $(\pi _2)_*(\eta ) = \nu $
. The set of all couplings between
$(\pi _2)_*(\eta ) = \nu $
. The set of all couplings between
![]() $\mu $
,
$\mu $
,
![]() $\nu $
is denoted as
$\nu $
is denoted as
![]() $\Gamma (\mu ,\nu )$
. For every
$\Gamma (\mu ,\nu )$
. For every
![]() $\kappa> 0$
, we then denote by
$\kappa> 0$
, we then denote by
the Wasserstein
![]() $2$
-metric between
$2$
-metric between
![]() $\mu $
and
$\mu $
and
![]() $\nu $
, w.r.t.
$\nu $
, w.r.t.
![]() $d(x,y) = |T_{\kappa }(x-y)|$
on
$d(x,y) = |T_{\kappa }(x-y)|$
on
![]() $\mathbb {R}$
. Note that the metrics
$\mathbb {R}$
. Note that the metrics
![]() $W_{2,\kappa }$
are equivalent for different values of
$W_{2,\kappa }$
are equivalent for different values of
![]() $\kappa> 0$
and are dominated by the usual Wasserstein
$\kappa> 0$
and are dominated by the usual Wasserstein
![]() $2$
-metric
$2$
-metric
![]() $W_2$
w.r.t. the metric
$W_2$
w.r.t. the metric
![]() $d(x,y) = |x-y|$
.
$d(x,y) = |x-y|$
.
Proposition 3.2. If
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\nu _n)_{n \in \mathbb {N}}$
are sequences of probability measures on
$(\nu _n)_{n \in \mathbb {N}}$
are sequences of probability measures on
![]() $\mathbb {R}$
such that for some
$\mathbb {R}$
such that for some
![]() $\kappa> 0$
,
$\kappa> 0$
,
 $$ \begin{align*}\sum_{n=1}^{\infty} W_{2,\kappa}(\mu_n,\nu_n)^2 < + \infty ,\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} W_{2,\kappa}(\mu_n,\nu_n)^2 < + \infty ,\end{align*} $$
then the tail boundary flows of
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\nu _n)_{n \in \mathbb {N}}$
are isomorphic.
$(\nu _n)_{n \in \mathbb {N}}$
are isomorphic.
Proof. Fix
![]() $\kappa> 0$
, and choose couplings
$\kappa> 0$
, and choose couplings
![]() $\zeta _n \in \Gamma (\mu _n,\nu _n)$
such that
$\zeta _n \in \Gamma (\mu _n,\nu _n)$
such that
So we get that
 $$ \begin{align*}\sum_{n=1}^{\infty} \int_{\mathbb{R}^2} T_{\kappa}(x-y)^2 \, d\zeta_n(x,y) < +\infty \; .\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} \int_{\mathbb{R}^2} T_{\kappa}(x-y)^2 \, d\zeta_n(x,y) < +\infty \; .\end{align*} $$
Define
![]() $\psi : \mathbb {R}^2 \to \mathbb {R}^2 : \psi (x,y) = (x-y,y)$
, and put
$\psi : \mathbb {R}^2 \to \mathbb {R}^2 : \psi (x,y) = (x-y,y)$
, and put
![]() $\eta _n = \psi _*(\zeta _n)$
. Fix a probability measure
$\eta _n = \psi _*(\zeta _n)$
. Fix a probability measure
![]() $\lambda $
on
$\lambda $
on
![]() $\mathbb {R}$
that is equivalent with the Lebesgue measure. Consider
$\mathbb {R}$
that is equivalent with the Lebesgue measure. Consider
 $$ \begin{align*}(X,\mu) = \prod_{n=1}^{\infty} (\mathbb{R},\mu_n), \quad (Y,\nu) = \prod_{n=1}^{\infty} (\mathbb{R},\nu_n) \quad\text{and}\quad (\Omega,\eta) = \prod_{n=1}^{\infty} (\mathbb{R}^2,\eta_n) \; .\end{align*} $$
$$ \begin{align*}(X,\mu) = \prod_{n=1}^{\infty} (\mathbb{R},\mu_n), \quad (Y,\nu) = \prod_{n=1}^{\infty} (\mathbb{R},\nu_n) \quad\text{and}\quad (\Omega,\eta) = \prod_{n=1}^{\infty} (\mathbb{R}^2,\eta_n) \; .\end{align*} $$
Whenever
![]() $x,y \in \mathbb {R}^{\mathbb {N}}$
, we denote by
$x,y \in \mathbb {R}^{\mathbb {N}}$
, we denote by
![]() $(x,y) \in \Omega $
the element
$(x,y) \in \Omega $
the element
![]() $(x_1,y_1,x_2,y_2,\ldots )$
. As in the definition of the tail boundary flow, define
$(x_1,y_1,x_2,y_2,\ldots )$
. As in the definition of the tail boundary flow, define
 $$ \begin{align*} & (\Omega_m,\widetilde{\eta}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R}^2,\eta_n) \quad\text{and}\\ & S_m : \mathbb{R} \times \Omega \to \mathbb{R} \times \Omega_m : S_m(t,x,y) = \left(t + \sum_{i=1}^m (x_i+y_i), x_{m+1},y_{m+1},x_{m+2},y_{m+2},\ldots\right) \;. \end{align*} $$
$$ \begin{align*} & (\Omega_m,\widetilde{\eta}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R}^2,\eta_n) \quad\text{and}\\ & S_m : \mathbb{R} \times \Omega \to \mathbb{R} \times \Omega_m : S_m(t,x,y) = \left(t + \sum_{i=1}^m (x_i+y_i), x_{m+1},y_{m+1},x_{m+2},y_{m+2},\ldots\right) \;. \end{align*} $$
Note that the maps
![]() $S_m$
are nonsingular factor maps. Denote
$S_m$
are nonsingular factor maps. Denote
![]() $B = L^{\infty }(\mathbb {R} \times \Omega ,\lambda \times \eta )$
, and define
$B = L^{\infty }(\mathbb {R} \times \Omega ,\lambda \times \eta )$
, and define
![]() $A_m \subset B$
by
$A_m \subset B$
by
![]() $A_m = (S_m)_*(L^{\infty }(\mathbb {R} \times \Omega _m))$
. Define
$A_m = (S_m)_*(L^{\infty }(\mathbb {R} \times \Omega _m))$
. Define
![]() $A = \bigcap _{m=1}^{\infty } A_m$
. We let
$A = \bigcap _{m=1}^{\infty } A_m$
. We let
![]() $\mathbb {R}$
act by translation in the first variable and obtain in this way an ergodic action
$\mathbb {R}$
act by translation in the first variable and obtain in this way an ergodic action
![]() $\mathbb {R} \curvearrowright A$
.
$\mathbb {R} \curvearrowright A$
.
We identify the ergodic action
![]() $\mathbb {R} \curvearrowright A$
with both the tail boundary flow of
$\mathbb {R} \curvearrowright A$
with both the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
and the tail boundary flow of
$(\mu _n)_{n \in \mathbb {N}}$
and the tail boundary flow of
![]() $(\nu _n)_{n \in \mathbb {N}}$
.
$(\nu _n)_{n \in \mathbb {N}}$
.
The first identification can be easily proved as follows and basically holds by definition. Writing
 $$ \begin{align*} & (X_m,\widetilde{\mu}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R},\mu_n) \quad\text{and}\\ & s_m : \mathbb{R} \times X \to \mathbb{R} \times X_m : s_m(t,x) = \left(t + \sum_{i=1}^m x_i, x_{m+1},x_{m+2},\ldots\right) , \end{align*} $$
$$ \begin{align*} & (X_m,\widetilde{\mu}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R},\mu_n) \quad\text{and}\\ & s_m : \mathbb{R} \times X \to \mathbb{R} \times X_m : s_m(t,x) = \left(t + \sum_{i=1}^m x_i, x_{m+1},x_{m+2},\ldots\right) , \end{align*} $$
the tail boundary of
![]() $(\mu _n)$
is defined by the intersection C of
$(\mu _n)$
is defined by the intersection C of
![]() $C_m = (s_m)_*(L^{\infty }(\mathbb {R} \times X_m))$
inside
$C_m = (s_m)_*(L^{\infty }(\mathbb {R} \times X_m))$
inside
![]() $D = L^{\infty }(\mathbb {R} \times X)$
. Write
$D = L^{\infty }(\mathbb {R} \times X)$
. Write
![]() $S : \mathbb {R}^2 \to \mathbb {R} : S(x,y) = x+y$
. By construction,
$S : \mathbb {R}^2 \to \mathbb {R} : S(x,y) = x+y$
. By construction,
![]() $S_*(\eta _n) = \mu _n$
, and we get the measure preserving factor map
$S_*(\eta _n) = \mu _n$
, and we get the measure preserving factor map
By independence, we have that
![]() $A \subset P_*(D)$
and
$A \subset P_*(D)$
and
![]() $A_m \cap P_*(D) = P_*(C_m)$
. Therefore,
$A_m \cap P_*(D) = P_*(C_m)$
. Therefore,
![]() $A = P_*(C)$
.
$A = P_*(C)$
.
The second identification requires more work. We disintegrate the probability measures
![]() $\eta _n$
w.r.t. the second variable. We thus find probability measures
$\eta _n$
w.r.t. the second variable. We thus find probability measures
![]() $\eta _{n,y}$
on
$\eta _{n,y}$
on
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
for all bounded Borel functions
![]() $F : \mathbb {R}^2 \to \mathbb {R}$
. Writing, for
$F : \mathbb {R}^2 \to \mathbb {R}$
. Writing, for
![]() $y \in Y$
,
$y \in Y$
,
 $$ \begin{align*}(\Omega_y,\eta_y) = \prod_{n=1}^{\infty} (\mathbb{R},\eta_{n,y_n}) ,\end{align*} $$
$$ \begin{align*}(\Omega_y,\eta_y) = \prod_{n=1}^{\infty} (\mathbb{R},\eta_{n,y_n}) ,\end{align*} $$
we can view
![]() $(\Omega _y,\eta _y)_{y \in Y}$
as the disintegration of
$(\Omega _y,\eta _y)_{y \in Y}$
as the disintegration of
![]() $(\Omega ,\eta )$
w.r.t. the measure preserving factor map
$(\Omega ,\eta )$
w.r.t. the measure preserving factor map
![]() $R : \Omega \to Y : R(x,y) = y$
.
$R : \Omega \to Y : R(x,y) = y$
.
Define the Borel functions
 $$ \begin{align*} & \varphi_n : \mathbb{R} \to [-\kappa,\kappa] : \varphi_n(z) = \int_{\mathbb{R}} T_{\kappa}(x) \, d\eta_{n,z}(x) \quad\text{and}\\ & F : Y \to [0,+\infty] : F(y) = \sum_{n=1}^{\infty} \int_{\mathbb{R}} T_{\kappa}(x)^2 \, d\eta_{n,y_n}(x) \;. \end{align*} $$
$$ \begin{align*} & \varphi_n : \mathbb{R} \to [-\kappa,\kappa] : \varphi_n(z) = \int_{\mathbb{R}} T_{\kappa}(x) \, d\eta_{n,z}(x) \quad\text{and}\\ & F : Y \to [0,+\infty] : F(y) = \sum_{n=1}^{\infty} \int_{\mathbb{R}} T_{\kappa}(x)^2 \, d\eta_{n,y_n}(x) \;. \end{align*} $$
Since
 $$ \begin{align*}\int_Y F(y) \, d\nu(y) = \sum_{n=1}^{\infty} \int_{\mathbb{R}^2} T_{\kappa}(x)^2 \, d\eta_n(x,y) < +\infty ,\end{align*} $$
$$ \begin{align*}\int_Y F(y) \, d\nu(y) = \sum_{n=1}^{\infty} \int_{\mathbb{R}^2} T_{\kappa}(x)^2 \, d\eta_n(x,y) < +\infty ,\end{align*} $$
we get that
![]() $F(y) < +\infty $
for
$F(y) < +\infty $
for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $y \in Y$
. Also note that
$y \in Y$
. Also note that
 $$ \begin{align*}\varphi_n(y)^2 \leq \int_{\mathbb{R}} T_{\kappa}(x)^2 \, d\eta_{n,y}(x) \quad\text{so that}\quad \sum_{n=1}^{\infty} \int_{\mathbb{R}} \varphi_n(y)^2 \, d\nu_n(y) < +\infty \; .\end{align*} $$
$$ \begin{align*}\varphi_n(y)^2 \leq \int_{\mathbb{R}} T_{\kappa}(x)^2 \, d\eta_{n,y}(x) \quad\text{so that}\quad \sum_{n=1}^{\infty} \int_{\mathbb{R}} \varphi_n(y)^2 \, d\nu_n(y) < +\infty \; .\end{align*} $$
Write
![]() $s_n = \int _{\mathbb {R}} \varphi _n(y) \, d\nu _n(y)$
. Define the Borel sets
$s_n = \int _{\mathbb {R}} \varphi _n(y) \, d\nu _n(y)$
. Define the Borel sets
![]() $\mathcal {U} \subset Y$
and
$\mathcal {U} \subset Y$
and
![]() $\mathcal {V}_y \subset \Omega _y$
by
$\mathcal {V}_y \subset \Omega _y$
by
 $$ \begin{align*} y \in \mathcal{U} &\quad\text{iff}\quad \varphi(y) = \lim_{n \to +\infty} \sum_{k=1}^n (\varphi_k(y_k) - s_k) \;\;\text{exists,}\\ x \in \mathcal{V}_y &\quad\text{iff}\quad \theta_y(x) = \lim_{n \to +\infty} \sum_{k=1}^n (x_k - \varphi_k(y_k)) \;\;\text{exists.} \end{align*} $$
$$ \begin{align*} y \in \mathcal{U} &\quad\text{iff}\quad \varphi(y) = \lim_{n \to +\infty} \sum_{k=1}^n (\varphi_k(y_k) - s_k) \;\;\text{exists,}\\ x \in \mathcal{V}_y &\quad\text{iff}\quad \theta_y(x) = \lim_{n \to +\infty} \sum_{k=1}^n (x_k - \varphi_k(y_k)) \;\;\text{exists.} \end{align*} $$
Also define the Borel set
We already proved that
![]() $F(y) <+\infty $
for
$F(y) <+\infty $
for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $y \in Y$
. By van Kampen’s version of Kolmogorov’s three series theorem (see, e.g., [Reference Shiryaev47, Theorem 3 in Section 4.2]), we have that
$y \in Y$
. By van Kampen’s version of Kolmogorov’s three series theorem (see, e.g., [Reference Shiryaev47, Theorem 3 in Section 4.2]), we have that
![]() $\nu (Y \setminus \mathcal {U}) = 0$
and that for all
$\nu (Y \setminus \mathcal {U}) = 0$
and that for all
![]() $y \in Y$
with
$y \in Y$
with
![]() $F(y) < +\infty $
, also
$F(y) < +\infty $
, also
![]() $\eta _y(\Omega _y \setminus \mathcal {V}_y) = 0$
. Since
$\eta _y(\Omega _y \setminus \mathcal {V}_y) = 0$
. Since
![]() $F(y) < +\infty $
for
$F(y) < +\infty $
for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $y \in Y$
, it follows that
$y \in Y$
, it follows that
![]() $\eta (\Omega \setminus \mathcal {V}) = 0$
. Write
$\eta (\Omega \setminus \mathcal {V}) = 0$
. Write
 $$ \begin{align} \pi : \mathcal{V} \to \mathbb{R} : \pi(x,y) = \theta_y(x) + \varphi(y) = \lim_{n \to +\infty} \sum_{k=1}^n (x_k - s_k), \end{align} $$
$$ \begin{align} \pi : \mathcal{V} \to \mathbb{R} : \pi(x,y) = \theta_y(x) + \varphi(y) = \lim_{n \to +\infty} \sum_{k=1}^n (x_k - s_k), \end{align} $$
and define the nonsingular factor map
![]() $Q : \mathbb {R} \times \Omega \to \mathbb {R} \times Y : Q(t,x,y) = (t+\pi (x,y),y)$
. We view the tail boundary of
$Q : \mathbb {R} \times \Omega \to \mathbb {R} \times Y : Q(t,x,y) = (t+\pi (x,y),y)$
. We view the tail boundary of
![]() $(\nu _n)_{n \in \mathbb {N}}$
as a von Neumann subalgebra
$(\nu _n)_{n \in \mathbb {N}}$
as a von Neumann subalgebra
![]() $N \subset L^{\infty }(\mathbb {R} \times Y)$
. We prove that
$N \subset L^{\infty }(\mathbb {R} \times Y)$
. We prove that
![]() $A = Q_*(N)$
.
$A = Q_*(N)$
.
More precisely, we write
 $$ \begin{align*} & (Y_m,\widetilde{\nu}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R},\nu_n) \quad\text{and}\\ & r_m : \mathbb{R} \times Y \to \mathbb{R} \times Y_m : r_m(t,y) = \left(t + \sum_{i=1}^m y_i, y_{m+1},y_{m+2},\ldots\right) \;. \end{align*} $$
$$ \begin{align*} & (Y_m,\widetilde{\nu}_m) = \prod_{n=m+1}^{\infty} (\mathbb{R},\nu_n) \quad\text{and}\\ & r_m : \mathbb{R} \times Y \to \mathbb{R} \times Y_m : r_m(t,y) = \left(t + \sum_{i=1}^m y_i, y_{m+1},y_{m+2},\ldots\right) \;. \end{align*} $$
Defining
![]() $N_m = (r_m)_*(L^{\infty }(\mathbb {R} \times Y_m))$
, we have
$N_m = (r_m)_*(L^{\infty }(\mathbb {R} \times Y_m))$
, we have
![]() $N = \bigcap _{m=1}^{\infty } N_m$
.
$N = \bigcap _{m=1}^{\infty } N_m$
.
It immediately follows from (3.5) that
![]() $Q_*(N_m) \subset A_m$
, so that
$Q_*(N_m) \subset A_m$
, so that
![]() $Q_*(N) \subset A$
. To prove the converse, fix
$Q_*(N) \subset A$
. To prove the converse, fix
![]() $F \in A$
. It follows that for
$F \in A$
. It follows that for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $y \in Y$
, we may view the function
$y \in Y$
, we may view the function
![]() $F(\cdot ,y)$
as an element of the tail boundary for the measures
$F(\cdot ,y)$
as an element of the tail boundary for the measures
![]() $(\eta _{n,y})_{n \in \mathbb {N}}$
. By e.g. [Reference Berendschot and Vaes8, Proposition 2.1], this tail boundary is given by the translation action
$(\eta _{n,y})_{n \in \mathbb {N}}$
. By e.g. [Reference Berendschot and Vaes8, Proposition 2.1], this tail boundary is given by the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
and we find a unique
$\mathbb {R} \curvearrowright \mathbb {R}$
and we find a unique
![]() $K_y \in L^{\infty }(\mathbb {R})$
such that
$K_y \in L^{\infty }(\mathbb {R})$
such that
![]() $F(t,x,y) = K_y(t+\theta _y(x))$
for a.e.
$F(t,x,y) = K_y(t+\theta _y(x))$
for a.e.
![]() $(t,x) \in \mathbb {R} \times \Omega _y$
. Defining
$(t,x) \in \mathbb {R} \times \Omega _y$
. Defining
![]() $G_y(t) = K_y(t-\varphi (y))$
, we get that
$G_y(t) = K_y(t-\varphi (y))$
, we get that
![]() $F(t,x,y) = G_y(t+\pi (x,y))$
for a.e.
$F(t,x,y) = G_y(t+\pi (x,y))$
for a.e.
![]() $(t,x) \in \mathbb {R} \times \Omega _y$
. Writing
$(t,x) \in \mathbb {R} \times \Omega _y$
. Writing
![]() $G(t,y) = G_y(t)$
, we have found
$G(t,y) = G_y(t)$
, we have found
![]() $G \in L^{\infty }(\mathbb {R} \times Y)$
such that
$G \in L^{\infty }(\mathbb {R} \times Y)$
such that
![]() $Q_*(G) = F$
.
$Q_*(G) = F$
.
It also follows from equation (3.5) that
![]() $Q_*(L^{\infty }(\mathbb {R} \times Y)) \cap A_m = Q_*(N_m)$
. Therefore,
$Q_*(L^{\infty }(\mathbb {R} \times Y)) \cap A_m = Q_*(N_m)$
. Therefore,
![]() $G \in N_m$
for all
$G \in N_m$
for all
![]() $m \in \mathbb {N}$
so that
$m \in \mathbb {N}$
so that
![]() $G \in N$
. This concludes the proof of the proposition.
$G \in N$
. This concludes the proof of the proposition.
In our applications of Proposition 3.2 in this paper, we will only need the following elementary estimate for the Wasserstein
![]() $2$
-distance. Assume that
$2$
-distance. Assume that
![]() $(\beta _n)_{n \in \mathbb {N}}$
are probability measures on
$(\beta _n)_{n \in \mathbb {N}}$
are probability measures on
![]() $\mathbb {R}$
, and assume that, for every
$\mathbb {R}$
, and assume that, for every
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
![]() $t_n \in \mathbb {R}$
and
$t_n \in \mathbb {R}$
and
![]() $p_n \in [0,1]$
with
$p_n \in [0,1]$
with
![]() $\sum _{n=1}^{\infty } p_n = 1$
. Define the probability measures
$\sum _{n=1}^{\infty } p_n = 1$
. Define the probability measures
![]() $\beta = \sum _{n=1}^{\infty } p_n \, \beta _n$
and
$\beta = \sum _{n=1}^{\infty } p_n \, \beta _n$
and
![]() $\nu = \sum _{n=1}^{\infty } p_n \, \delta _{t_n}$
. Then,
$\nu = \sum _{n=1}^{\infty } p_n \, \delta _{t_n}$
. Then,
 $$ \begin{align} W_2(\beta,\nu)^2 \leq \sum_{n=1}^{\infty} p_n \int_{\mathbb{R}} (x-t_n)^2 \, d\beta_n(x) , \end{align} $$
$$ \begin{align} W_2(\beta,\nu)^2 \leq \sum_{n=1}^{\infty} p_n \int_{\mathbb{R}} (x-t_n)^2 \, d\beta_n(x) , \end{align} $$
which follows immediately by using the coupling
![]() $\eta = \sum _{n=1}^{\infty } p_n \, (\beta _n \times \delta _{t_n})$
.
$\eta = \sum _{n=1}^{\infty } p_n \, (\beta _n \times \delta _{t_n})$
.
Secondly, we prove a generalization of Orey’s fundamental result in [Reference Orey40, Theorem 3.1]. He proved that, if
![]() $(\mu _n)_{n \in \mathbb {N}}$
is a sequence of probability measures on
$(\mu _n)_{n \in \mathbb {N}}$
is a sequence of probability measures on
![]() $\mathbb {R}$
with uniformly bounded support, i.e., for which there exists a
$\mathbb {R}$
with uniformly bounded support, i.e., for which there exists a
![]() $C> 0$
such that
$C> 0$
such that
![]() $\mu _n([-C,C]) = 1$
for all
$\mu _n([-C,C]) = 1$
for all
![]() $n \in \mathbb {N}$
, the tail boundary flow is never properly ergodic: if
$n \in \mathbb {N}$
, the tail boundary flow is never properly ergodic: if
![]() $\sum _{n=1}^{\infty } \operatorname {Var} \mu _n = +\infty $
, the tail boundary flow is periodic, and if
$\sum _{n=1}^{\infty } \operatorname {Var} \mu _n = +\infty $
, the tail boundary flow is periodic, and if
![]() $\sum _{n=1}^{\infty } \operatorname {Var} \mu _n < +\infty $
, the tail boundary flow is given by the translation action
$\sum _{n=1}^{\infty } \operatorname {Var} \mu _n < +\infty $
, the tail boundary flow is given by the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
.
$\mathbb {R} \curvearrowright \mathbb {R}$
.
The following result says that periodicity of the tail boundary flow already follows if we can find finite positive measures
![]() $\beta _n \leq \mu _n$
such that the sequence
$\beta _n \leq \mu _n$
such that the sequence
![]() $(\beta _n)_{n \in \mathbb {N}}$
has uniformly bounded width and such that the sum of the properly normalized variances of
$(\beta _n)_{n \in \mathbb {N}}$
has uniformly bounded width and such that the sum of the properly normalized variances of
![]() $\beta _n$
is infinite.
$\beta _n$
is infinite.
More precisely, we prove the following and, in particular, provide a functional analytic proof to [Reference Orey40, Theorem 3.1].
Proposition 3.3. Let
![]() $(\mu _n)_{n \in \mathbb {R}}$
be a sequence of probability measures on
$(\mu _n)_{n \in \mathbb {R}}$
be a sequence of probability measures on
![]() $\mathbb {R}$
. Assume that
$\mathbb {R}$
. Assume that
![]() $\beta _n$
are positive finite measures on
$\beta _n$
are positive finite measures on
![]() $\mathbb {R}$
satisfying
$\mathbb {R}$
satisfying
![]() $\beta _n \leq \mu _n$
. Assume that there exists a
$\beta _n \leq \mu _n$
. Assume that there exists a
![]() $C> 0$
such that
$C> 0$
such that
![]() $|x-y| \leq C$
for
$|x-y| \leq C$
for
![]() $\beta _n$
-a.e.
$\beta _n$
-a.e.
![]() $x,y \in \mathbb {R}$
. If
$x,y \in \mathbb {R}$
. If
 $$ \begin{align} \sum_{n=1}^{\infty} \beta_n(\mathbb{R}) \, \operatorname{Var}(\beta_n(\mathbb{R})^{-1} \beta_n) = +\infty , \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \beta_n(\mathbb{R}) \, \operatorname{Var}(\beta_n(\mathbb{R})^{-1} \beta_n) = +\infty , \end{align} $$
then the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {R}}$
is periodic.
$(\mu _n)_{n \in \mathbb {R}}$
is periodic.
Note that, by convention, if certain
![]() $\beta _n$
are zero, we interpret the corresponding term in equation (3.7) as zero. The assumptions of Proposition 3.3 say in particular that, for each fixed n, the measure
$\beta _n$
are zero, we interpret the corresponding term in equation (3.7) as zero. The assumptions of Proposition 3.3 say in particular that, for each fixed n, the measure
![]() $\beta _n$
has a bounded support so that its mean value and variance are well defined and finite.
$\beta _n$
has a bounded support so that its mean value and variance are well defined and finite.
Proof. Note that it suffices to prove the proposition assuming that all
![]() $\beta _n \neq 0$
. Indeed, it then follows that for
$\beta _n \neq 0$
. Indeed, it then follows that for
![]() $I = \{n \in \mathbb {N} \mid \beta _n \neq 0\}$
, the tail boundary flow of
$I = \{n \in \mathbb {N} \mid \beta _n \neq 0\}$
, the tail boundary flow of
![]() $(\mu _n)_{n \in I}$
is periodic, from which it follows that, a fortiori, the tail boundary flow of
$(\mu _n)_{n \in I}$
is periodic, from which it follows that, a fortiori, the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is periodic.
$(\mu _n)_{n \in \mathbb {N}}$
is periodic.
Assume that the sum in equation (3.7) is infinite. We prove that the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {R}}$
is periodic.
$(\mu _n)_{n \in \mathbb {R}}$
is periodic.
Define the finite positive measures
![]() $\alpha _n$
such that
$\alpha _n$
such that
![]() $\mu _n = \alpha _n + \beta _n$
. Define
$\mu _n = \alpha _n + \beta _n$
. Define
![]() $X_0 = \mathbb {R} \sqcup \mathbb {R}^2$
, and equip
$X_0 = \mathbb {R} \sqcup \mathbb {R}^2$
, and equip
![]() $X_0$
with the probability measures
$X_0$
with the probability measures
![]() $\zeta _n = \alpha _n \sqcup \beta _n(\mathbb {R})^{-1}(\beta _n \times \beta _n)$
. Define the map
$\zeta _n = \alpha _n \sqcup \beta _n(\mathbb {R})^{-1}(\beta _n \times \beta _n)$
. Define the map
![]() $T : X_0 \to \mathbb {R}$
by
$T : X_0 \to \mathbb {R}$
by
![]() $T(x) = 0$
if
$T(x) = 0$
if
![]() $x \in \mathbb {R}$
and
$x \in \mathbb {R}$
and
![]() $T(x,y) = x-y$
if
$T(x,y) = x-y$
if
![]() $(x,y) \in \mathbb {R}^2$
. Define
$(x,y) \in \mathbb {R}^2$
. Define
![]() $(X,\zeta ) = \prod _{n \in \mathbb {N}} (X_0,\zeta _n)$
and the independent random variables
$(X,\zeta ) = \prod _{n \in \mathbb {N}} (X_0,\zeta _n)$
and the independent random variables
![]() $T_n : X \to \mathbb {R} : T_n(z) = T(z_n)$
. Note that
$T_n : X \to \mathbb {R} : T_n(z) = T(z_n)$
. Note that
![]() $|T_n| \leq C$
for all n,
$|T_n| \leq C$
for all n,
![]() $E(T_n) = 0$
and
$E(T_n) = 0$
and
Since
![]() $\sum _{n=1}^{\infty } E(T_n^2) =+\infty $
and
$\sum _{n=1}^{\infty } E(T_n^2) =+\infty $
and
![]() $E(T_n^2) \leq C^2$
for every
$E(T_n^2) \leq C^2$
for every
![]() $n \in \mathbb {N}$
, we can choose
$n \in \mathbb {N}$
, we can choose
![]() $0 \leq n_1 < n_2 < \cdots $
such that
$0 \leq n_1 < n_2 < \cdots $
such that
 $$ \begin{align*}(40 C)^2 \leq \sum_{n=n_{k}+1}^{n_{k+1}} E(T_n^2) \leq (50 C)^2\end{align*} $$
$$ \begin{align*}(40 C)^2 \leq \sum_{n=n_{k}+1}^{n_{k+1}} E(T_n^2) \leq (50 C)^2\end{align*} $$
for all
![]() $k \in \mathbb {N}$
. Since
$k \in \mathbb {N}$
. Since
![]() $|T_n| \leq C$
for all n, we have that
$|T_n| \leq C$
for all n, we have that
![]() $E(|T_n|^3) \leq C \, E(T_n^2)$
for all
$E(|T_n|^3) \leq C \, E(T_n^2)$
for all
![]() $n \in \mathbb {N}$
. Define
$n \in \mathbb {N}$
. Define
![]() $\sigma _k \in [40 C,50 C]$
by
$\sigma _k \in [40 C,50 C]$
by
 $$ \begin{align*}\sigma_k^2 = \sum_{n=n_{k}+1}^{n_{k+1}} E(T_n^2) \; .\end{align*} $$
$$ \begin{align*}\sigma_k^2 = \sum_{n=n_{k}+1}^{n_{k+1}} E(T_n^2) \; .\end{align*} $$
Write
 $$ \begin{align*}S_k = \sum_{n=n_{k}+1}^{n_{k+1}} T_n \quad\text{and}\quad F_k(t) = \zeta\bigl(\{x \in X \mid S_k(x) \leq \sigma_k \, t \, \}\bigr) \; .\end{align*} $$
$$ \begin{align*}S_k = \sum_{n=n_{k}+1}^{n_{k+1}} T_n \quad\text{and}\quad F_k(t) = \zeta\bigl(\{x \in X \mid S_k(x) \leq \sigma_k \, t \, \}\bigr) \; .\end{align*} $$
Denote by G the distribution function of a standard Gaussian random variable. By the Berry–Esseen theorem (see, e.g., [Reference Stroock48, Theorem 2.2.17]), we get that
for all
![]() $k \in \mathbb {N}$
and all
$k \in \mathbb {N}$
and all
![]() $t \in \mathbb {R}$
. Take
$t \in \mathbb {R}$
. Take
![]() $\delta < 0$
such that
$\delta < 0$
such that
![]() $G(\delta ) = 1/3$
. Then,
$G(\delta ) = 1/3$
. Then,
![]() $F_k(\delta ) \geq 1/12$
. Since
$F_k(\delta ) \geq 1/12$
. Since
![]() $\sigma _k \geq 40 C$
and
$\sigma _k \geq 40 C$
and
![]() $\delta < 0$
, we conclude that
$\delta < 0$
, we conclude that
Define
![]() $(\Omega ,\mu ) = \prod _{n \in \mathbb {N}} (\mathbb {R},\mu _n)$
. Denote by
$(\Omega ,\mu ) = \prod _{n \in \mathbb {N}} (\mathbb {R},\mu _n)$
. Denote by
![]() $\mu _0$
the probability measure on
$\mu _0$
the probability measure on
![]() $\mathbb {R}$
given by
$\mathbb {R}$
given by
![]() $d\mu _0(t) = (\pi (1+t^2))^{-1} \, dt$
. Consider the Hilbert spaces
$d\mu _0(t) = (\pi (1+t^2))^{-1} \, dt$
. Consider the Hilbert spaces
and define the subspaces
![]() $H_N \subset H$
by
$H_N \subset H$
by
![]() $H_N = L^2((\mathbb {R},\mu ) \times \prod _{n=1}^N (\mathbb {R},\mu _n))$
.
$H_N = L^2((\mathbb {R},\mu ) \times \prod _{n=1}^N (\mathbb {R},\mu _n))$
.
Define the maps
 $$ \begin{align*} &\theta_1 : X_0 \to \mathbb{R} : \theta_1(x) = x \;\;\text{if } x \in \mathbb{R},\;\; \theta_1(x,y) = x \;\;\text{if } (x,y) \in \mathbb{R}^2,\\ &\theta_2 : X_0 \to \mathbb{R} : \theta_2(x) = x \;\;\text{if } x \in \mathbb{R},\;\; \theta_2(x,y) = y \;\;\text{if } (x,y) \in \mathbb{R}^2. \end{align*} $$
$$ \begin{align*} &\theta_1 : X_0 \to \mathbb{R} : \theta_1(x) = x \;\;\text{if } x \in \mathbb{R},\;\; \theta_1(x,y) = x \;\;\text{if } (x,y) \in \mathbb{R}^2,\\ &\theta_2 : X_0 \to \mathbb{R} : \theta_2(x) = x \;\;\text{if } x \in \mathbb{R},\;\; \theta_2(x,y) = y \;\;\text{if } (x,y) \in \mathbb{R}^2. \end{align*} $$
Note that
![]() $T(z) = \theta _1(z) - \theta _2(z)$
for all
$T(z) = \theta _1(z) - \theta _2(z)$
for all
![]() $z \in X_0$
. We consider the associated measure preserving factor maps
$z \in X_0$
. We consider the associated measure preserving factor maps
 $$ \begin{align*}\pi : X \to \Omega : (\pi(z))_n = \theta_1(z_n) \;\text{and}\; \rho_k : X \to \Omega : (\rho_k(z))_n = \begin{cases} \theta_2(z_n) &\text{if } n_k + 1 \leq n \leq n_{k+1},\\ \theta_1(z_n) &\text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}\pi : X \to \Omega : (\pi(z))_n = \theta_1(z_n) \;\text{and}\; \rho_k : X \to \Omega : (\rho_k(z))_n = \begin{cases} \theta_2(z_n) &\text{if } n_k + 1 \leq n \leq n_{k+1},\\ \theta_1(z_n) &\text{otherwise.}\end{cases}\end{align*} $$
Define the isometries
![]() $V : H \to K$
and
$V : H \to K$
and
![]() $W_k : H \to K$
by
$W_k : H \to K$
by
When
![]() $\xi \in H_N$
, we have
$\xi \in H_N$
, we have
![]() $W_k(\xi ) = V(\xi )$
for all k large enough. By density, we get that
$W_k(\xi ) = V(\xi )$
for all k large enough. By density, we get that
![]() $W_k \to V$
strongly.
$W_k \to V$
strongly.
Let
![]() $F \in L^{\infty }(\mathbb {R} \times \Omega )$
be a function that generates the tail boundary of
$F \in L^{\infty }(\mathbb {R} \times \Omega )$
be a function that generates the tail boundary of
![]() $(\mu _n)_{n \in \mathbb {N}}$
. Since F belongs to the tail boundary algebra, we have
$(\mu _n)_{n \in \mathbb {N}}$
. Since F belongs to the tail boundary algebra, we have
Since
and since each
![]() $S_k$
is a bounded function, we can define the bounded linear operators
$S_k$
is a bounded function, we can define the bounded linear operators
Write
![]() $D = \sqrt {2(1+(50C)^2)}$
. We claim that
$D = \sqrt {2(1+(50C)^2)}$
. We claim that
To prove this claim, note that the left-hand side can be estimated, using the Cauchy–Schwartz inequality and equation (3.10), by
 $$ \begin{align*} \frac{1}{\pi} \int_{X} d\zeta(z) \, &\int_{\mathbb{R}} dt \; \frac{1}{(1 + (t+S_k(z))^2)} \, |\xi(t,z)|^2 \\ & \leq \|\xi\|_{\infty} \, \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1}{\sqrt{\pi (1+ t^2)}} \, |\xi(t,z)| \, \frac{\sqrt{1+t^2}}{\sqrt{\pi} (1+(t+S_k(z))^2)} \\ & \leq \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1 + t^2}{\pi (1+(t+S_k(z))^2)^2}\Bigr)^{1/2} \\ & = \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1 + (t-S_k(z))^2}{\pi (1+t^2)^2}\Bigr)^{1/2} \\ & \leq \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} d\mu_0(t) \; 2 (1+S_k(z)^2)\Bigr)^{1/2} = D \, \|\xi\|_{\infty} \, \|\xi\|_2 \;. \end{align*} $$
$$ \begin{align*} \frac{1}{\pi} \int_{X} d\zeta(z) \, &\int_{\mathbb{R}} dt \; \frac{1}{(1 + (t+S_k(z))^2)} \, |\xi(t,z)|^2 \\ & \leq \|\xi\|_{\infty} \, \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1}{\sqrt{\pi (1+ t^2)}} \, |\xi(t,z)| \, \frac{\sqrt{1+t^2}}{\sqrt{\pi} (1+(t+S_k(z))^2)} \\ & \leq \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1 + t^2}{\pi (1+(t+S_k(z))^2)^2}\Bigr)^{1/2} \\ & = \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} dt \; \frac{1 + (t-S_k(z))^2}{\pi (1+t^2)^2}\Bigr)^{1/2} \\ & \leq \|\xi\|_{\infty} \, \|\xi\|_2 \, \Bigl( \int_{X} d\zeta(z) \, \int_{\mathbb{R}} d\mu_0(t) \; 2 (1+S_k(z)^2)\Bigr)^{1/2} = D \, \|\xi\|_{\infty} \, \|\xi\|_2 \;. \end{align*} $$
So, the claim is proven.
Define the probability measure
![]() $\eta _k = (S_k)_*(\zeta )$
. Then
$\eta _k = (S_k)_*(\zeta )$
. Then
so that
![]() $\eta _k$
is a tight family of probability measures. Choose a sequence
$\eta _k$
is a tight family of probability measures. Choose a sequence
![]() $k_j \to \infty $
such that
$k_j \to \infty $
such that
![]() $\eta _{k_j}$
converges weakly to a probability measure
$\eta _{k_j}$
converges weakly to a probability measure
![]() $\eta $
on
$\eta $
on
![]() $\mathbb {R}$
with
$\mathbb {R}$
with
![]() $\int _{\mathbb {R}} t^2 \, d\eta (t) \leq (50 C)^2 < +\infty $
. By equation (3.8), we have that
$\int _{\mathbb {R}} t^2 \, d\eta (t) \leq (50 C)^2 < +\infty $
. By equation (3.8), we have that
![]() $\eta _k((-\infty ,40 C \delta ]) \geq 1/12$
for all
$\eta _k((-\infty ,40 C \delta ]) \geq 1/12$
for all
![]() $k \in \mathbb {N}$
. Therefore,
$k \in \mathbb {N}$
. Therefore,
![]() $\eta \neq \delta _0$
.
$\eta \neq \delta _0$
.
We can then define the bounded convolution operator
Note that by the Cauchy–Schwarz inequality and equation (3.10),
 $$ \begin{align*} \|\eta * \xi\|_2^2 &\leq \int_X d\zeta(z) \, \int_{\mathbb{R}} d\eta(s) \, \int_{\mathbb{R}} d\mu_0(t) \, |\xi(t-s,z)|^2 \\ &\leq \int_X d\zeta(z) \, \int_{\mathbb{R}} d\eta(s) \, \int_{\mathbb{R}} d\mu_0(t) \, 2(1+s^2) \, |\xi(t,z)|^2 \; \end{align*} $$
$$ \begin{align*} \|\eta * \xi\|_2^2 &\leq \int_X d\zeta(z) \, \int_{\mathbb{R}} d\eta(s) \, \int_{\mathbb{R}} d\mu_0(t) \, |\xi(t-s,z)|^2 \\ &\leq \int_X d\zeta(z) \, \int_{\mathbb{R}} d\eta(s) \, \int_{\mathbb{R}} d\mu_0(t) \, 2(1+s^2) \, |\xi(t,z)|^2 \; \end{align*} $$
so that
![]() $\|\eta * \xi \|_2 \leq D \, \|\xi \|_2$
for all
$\|\eta * \xi \|_2 \leq D \, \|\xi \|_2$
for all
![]() $\xi \in K$
. We have a similar convolution operator
$\xi \in K$
. We have a similar convolution operator
![]() $\xi \mapsto \eta * \xi $
on H. Note that
$\xi \mapsto \eta * \xi $
on H. Note that
![]() $V(\eta * \xi ) = \eta * V(\xi )$
.
$V(\eta * \xi ) = \eta * V(\xi )$
.
We finally prove that, for every
![]() $\xi \in L^{\infty }(\mathbb {R} \times X) \subset K$
and every
$\xi \in L^{\infty }(\mathbb {R} \times X) \subset K$
and every
![]() $\xi ' \in K$
, we have that
$\xi ' \in K$
, we have that
Define the closed subspaces
![]() $K_N = L^2(\mathbb {R} \times \prod _{n=1}^N X_0)$
of K. Fix
$K_N = L^2(\mathbb {R} \times \prod _{n=1}^N X_0)$
of K. Fix
![]() $\xi \in L^{\infty }(\mathbb {R} \times X) \subset K$
and
$\xi \in L^{\infty }(\mathbb {R} \times X) \subset K$
and
![]() $\xi ' \in K$
. The orthogonal projection
$\xi ' \in K$
. The orthogonal projection
![]() $E_N : K \to K_N$
corresponds to the conditional expectation so that
$E_N : K \to K_N$
corresponds to the conditional expectation so that
![]() $\|E_N(\xi )\|_{\infty } \leq \|\xi \|_{\infty }$
for all
$\|E_N(\xi )\|_{\infty } \leq \|\xi \|_{\infty }$
for all
![]() $N \in \mathbb {N}$
. By equation (3.11), the sequence
$N \in \mathbb {N}$
. By equation (3.11), the sequence
![]() $\|R_{k_j}(\xi )\|_2$
is bounded. To prove equation (3.12), we may thus assume that
$\|R_{k_j}(\xi )\|_2$
is bounded. To prove equation (3.12), we may thus assume that
![]() $\xi ' \in K_N$
for some N. By (3.11), we also have that
$\xi ' \in K_N$
for some N. By (3.11), we also have that
 $$ \begin{align*} \|R_{k_j}(\xi) - R_{k_j}(E_N(\xi))\|_2^2 &= \|R_{k_j}(\xi - E_N(\xi))\|_2^2 \leq D \, \|\xi - E_N(\xi)\|_{\infty} \, \|\xi - E_N(\xi)\|_2 \\ & \leq 2 D \, \|\xi\|_{\infty} \, \|\xi - E_N(\xi)\|_2 , \end{align*} $$
$$ \begin{align*} \|R_{k_j}(\xi) - R_{k_j}(E_N(\xi))\|_2^2 &= \|R_{k_j}(\xi - E_N(\xi))\|_2^2 \leq D \, \|\xi - E_N(\xi)\|_{\infty} \, \|\xi - E_N(\xi)\|_2 \\ & \leq 2 D \, \|\xi\|_{\infty} \, \|\xi - E_N(\xi)\|_2 , \end{align*} $$
which tends to zero as
![]() $N \to \infty $
, uniformly in j. To prove (3.12), we may thus also assume that
$N \to \infty $
, uniformly in j. To prove (3.12), we may thus also assume that
![]() $\xi \in K_N$
. When
$\xi \in K_N$
. When
![]() $\xi ,\xi ' \in K_N$
and
$\xi ,\xi ' \in K_N$
and
![]() $n_{k_j}> N$
, we have
$n_{k_j}> N$
, we have
for all j so that equation (3.12) follows.
We now return to our element F generating the tail boundary. By equation (3.9), we get that
![]() $W_k(F) = R_k(V(F))$
. Since
$W_k(F) = R_k(V(F))$
. Since
![]() $W_k \to V$
strongly, we get that
$W_k \to V$
strongly, we get that
![]() $\|W_k(F) - V(F)\|_2 \to 0$
. By equation (3.12), we have that
$\|W_k(F) - V(F)\|_2 \to 0$
. By equation (3.12), we have that
![]() $R_k(V(F)) \to \eta * V(F) = V(\eta * F)$
weakly. We thus conclude that
$R_k(V(F)) \to \eta * V(F) = V(\eta * F)$
weakly. We thus conclude that
![]() $F = \eta * F$
. Since
$F = \eta * F$
. Since
![]() $\eta \neq \delta _0$
, it follows from the Choquet–Dény theorem (see [Reference Choquet and Deny9]) that F is periodic in the first variable. So, the tail boundary flow is periodic.
$\eta \neq \delta _0$
, it follows from the Choquet–Dény theorem (see [Reference Choquet and Deny9]) that F is periodic in the first variable. So, the tail boundary flow is periodic.
In our applications of Proposition 3.3, we will use a few times the following elementary equality and estimate
 $$ \begin{align} \begin{aligned} \operatorname{Var} \beta &= \frac{1}{2} \int_{\mathbb{R}^2} (x-y)^2 \, d\beta(x) \, d\beta(y) \\ &\geq \frac{1}{2} \int_{(\mathbb{R}^* \times \{0\})\cup (\{0\} \times \mathbb{R}^*)} (x-y)^2 \, d\beta(x) \, d\beta(y) = \beta(\{0\}) \, \int_{\mathbb{R}} x^2 \, d\beta(x) \; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{Var} \beta &= \frac{1}{2} \int_{\mathbb{R}^2} (x-y)^2 \, d\beta(x) \, d\beta(y) \\ &\geq \frac{1}{2} \int_{(\mathbb{R}^* \times \{0\})\cup (\{0\} \times \mathbb{R}^*)} (x-y)^2 \, d\beta(x) \, d\beta(y) = \beta(\{0\}) \, \int_{\mathbb{R}} x^2 \, d\beta(x) \; \end{aligned} \end{align} $$
for every probability measure
![]() $\beta $
on
$\beta $
on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proposition 3.3 already says that aperiodic tail boundary flows can only occur if the measures
![]() $(\mu _n)_{n \in \mathbb {N}}$
are sufficiently sparse: For each sequence of intervals
$(\mu _n)_{n \in \mathbb {N}}$
are sufficiently sparse: For each sequence of intervals
![]() $I_n \subset \mathbb {R}$
with uniformly bounded length
$I_n \subset \mathbb {R}$
with uniformly bounded length
![]() $|I_n|$
, there exist points
$|I_n|$
, there exist points
![]() $s_n \in I_n$
such that
$s_n \in I_n$
such that
 $$ \begin{align} \sum_{n=1}^{\infty} \int_{I_n} (x-s_n)^2 \, d\mu_n(x) < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \int_{I_n} (x-s_n)^2 \, d\mu_n(x) < +\infty \;. \end{align} $$
In the following proposition, we develop this further and prove that, under the appropriate assumptions, the resulting sequence
![]() $s_n$
must itself be sparse: Partitioning
$s_n$
must itself be sparse: Partitioning
![]() $\mathbb {R}$
into intervals
$\mathbb {R}$
into intervals
![]() $I_k$
of uniformly bounded length, we may assume that, within each
$I_k$
of uniformly bounded length, we may assume that, within each
![]() $I_k$
, the points
$I_k$
, the points
![]() $s_n$
lie close to a single element
$s_n$
lie close to a single element
![]() $t_k \in I_k$
.
$t_k \in I_k$
.
The proof of Proposition 3.4 is closely inspired by [Reference Giordano and Skandalis26, Proposition 1.1] and [Reference Araki and Woods3, Lemma 8.6]. Although this is not strictly needed for the rest of this paper, we use the opportunity to also deduce from Proposition 3.4 a more conceptual proof for the main result of [Reference Giordano and Skandalis26] saying that every ITPFI factor of bounded type is isomorphic with an ITPFI
![]() $_2$
factor; see Theorem 3.5. Recall that, by definition, an ITPFI factor of bounded type is an infinite tensor product of matrix algebras
$_2$
factor; see Theorem 3.5. Recall that, by definition, an ITPFI factor of bounded type is an infinite tensor product of matrix algebras
![]() $M_{n_k}(\mathbb {C})$
with
$M_{n_k}(\mathbb {C})$
with
![]() $\sup _k n_k < +\infty $
.
$\sup _k n_k < +\infty $
.
Proposition 3.4. Let
![]() $(\mu _n)_{n \in \mathbb {N}}$
be probability measures on
$(\mu _n)_{n \in \mathbb {N}}$
be probability measures on
![]() $\mathbb {R}$
. Let
$\mathbb {R}$
. Let
![]() $(J_k)_{k \in \mathbb {N}}$
be a family of disjoint subsets of
$(J_k)_{k \in \mathbb {N}}$
be a family of disjoint subsets of
![]() $\mathbb {N}$
. Assume that, for every
$\mathbb {N}$
. Assume that, for every
![]() $k \in \mathbb {N}$
, we are given
$k \in \mathbb {N}$
, we are given
![]() $p_k, q_k> 0$
and an interval
$p_k, q_k> 0$
and an interval
![]() $I_k \subset \mathbb {R} \setminus (-1,1)$
. Assume that
$I_k \subset \mathbb {R} \setminus (-1,1)$
. Assume that
![]() $|I_k| \leq C$
for all
$|I_k| \leq C$
for all
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
Assume that, for each
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $n \in J_k$
, we are given a probability measure
$n \in J_k$
, we are given a probability measure
![]() $\beta _n$
with
$\beta _n$
with
![]() $\beta _n(I_k) = 1$
and
$\beta _n(I_k) = 1$
and
![]() $p_k \delta _0 + q_k \beta _n \leq \mu _n$
.
$p_k \delta _0 + q_k \beta _n \leq \mu _n$
.
If the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is aperiodic, each
$(\mu _n)_{n \in \mathbb {N}}$
is aperiodic, each
![]() $J_k$
is a finite set and there exist
$J_k$
is a finite set and there exist
![]() $t_k \in I_k$
such that
$t_k \in I_k$
such that
 $$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in J_k} p_k q_k \int_{\mathbb{R}} (x-t_k)^2 \, d\beta_n(x) < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in J_k} p_k q_k \int_{\mathbb{R}} (x-t_k)^2 \, d\beta_n(x) < +\infty \;. \end{align} $$
Note that there is a twofold difference between equations (3.14) and (3.15). In equation (3.15), the concentration points
![]() $t_k$
only depend on the interval
$t_k$
only depend on the interval
![]() $I_k$
and are thus the same for each
$I_k$
and are thus the same for each
![]() $n \in J_k$
. On the other hand, the factor
$n \in J_k$
. On the other hand, the factor
![]() $p_k q_k$
appearing in equation (3.15) is strictly smaller than the factor
$p_k q_k$
appearing in equation (3.15) is strictly smaller than the factor
![]() $q_k = (q_k \beta _n)(I_k)$
that we would get in equation (3.14).
$q_k = (q_k \beta _n)(I_k)$
that we would get in equation (3.14).
Proof. For a fixed
![]() $k \in \mathbb {N}$
, we have that the measures
$k \in \mathbb {N}$
, we have that the measures
![]() $(p_k \delta _0 + q_k \beta _n)_{n \in J_k}$
have a uniformly bounded support in
$(p_k \delta _0 + q_k \beta _n)_{n \in J_k}$
have a uniformly bounded support in
![]() $\{0\} \cup I_k$
. It thus follows from Proposition 3.3 that
$\{0\} \cup I_k$
. It thus follows from Proposition 3.3 that
Since
![]() $I_k \subset \mathbb {R} \setminus (-1,1)$
and
$I_k \subset \mathbb {R} \setminus (-1,1)$
and
![]() $\beta _n$
is supported on
$\beta _n$
is supported on
![]() $I_k$
, by equation (3.13), the left-hand side is larger or equal than
$I_k$
, by equation (3.13), the left-hand side is larger or equal than
![]() $p_k q_k (p_k+q_k)^{-1} |J_k|$
so that
$p_k q_k (p_k+q_k)^{-1} |J_k|$
so that
![]() $J_k$
is a finite set.
$J_k$
is a finite set.
We can also apply Proposition 3.3 to all the finite measures
![]() $q_k \beta _n \leq \mu _n$
, with
$q_k \beta _n \leq \mu _n$
, with
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $n \in J_k$
, because they have uniformly bounded width C. Defining for any
$n \in J_k$
, because they have uniformly bounded width C. Defining for any
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $n \in J_k$
, the point
$n \in J_k$
, the point
![]() $s_n \in I_k$
by
$s_n \in I_k$
by
we get that
 $$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in J_k} q_k \int_{\mathbb{R}} (x-s_n)^2 \, d\beta_n(x) < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in J_k} q_k \int_{\mathbb{R}} (x-s_n)^2 \, d\beta_n(x) < +\infty \;. \end{align} $$
For every
![]() $k \in \mathbb {N}$
, we consider the finitely many points
$k \in \mathbb {N}$
, we consider the finitely many points
![]() $(s_n)_{n \in J_k}$
in the interval
$(s_n)_{n \in J_k}$
in the interval
![]() $I_k$
. We denote by
$I_k$
. We denote by
![]() $t_k$
a ‘middle point’. More precisely, if
$t_k$
a ‘middle point’. More precisely, if
![]() $|J_k|$
is odd, we write
$|J_k|$
is odd, we write
![]() $J_k = A_k \sqcup B_k \sqcup \{j_k\}$
with
$J_k = A_k \sqcup B_k \sqcup \{j_k\}$
with
![]() $|A_k| = |B_k|$
such that
$|A_k| = |B_k|$
such that
![]() $s_n \leq s_{j_k} \leq s_m$
for all
$s_n \leq s_{j_k} \leq s_m$
for all
![]() $n \in A_k$
and
$n \in A_k$
and
![]() $m \in B_k$
. We put
$m \in B_k$
. We put
![]() $t_k = s_{j_k}$
. If
$t_k = s_{j_k}$
. If
![]() $|J_k|$
is even, we write
$|J_k|$
is even, we write
![]() $J_k = A_k \sqcup B_k$
with
$J_k = A_k \sqcup B_k$
with
![]() $|A_k| = |B_k|$
such that for some
$|A_k| = |B_k|$
such that for some
![]() $t_k \in I_k$
, we again have that
$t_k \in I_k$
, we again have that
![]() $s_n \leq t_k \leq s_m$
for all
$s_n \leq t_k \leq s_m$
for all
![]() $n \in A_k$
and
$n \in A_k$
and
![]() $m \in B_k$
. We choose a bijection
$m \in B_k$
. We choose a bijection
![]() $\alpha _k : A_k \to B_k$
.
$\alpha _k : A_k \to B_k$
.
Since the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is aperiodic, also the measures
$(\mu _n)_{n \in \mathbb {N}}$
is aperiodic, also the measures
![]() $\mu _n * \mu _{\alpha _k(n)}$
with
$\mu _n * \mu _{\alpha _k(n)}$
with
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $n \in A_k$
have an aperiodic tail boundary. By construction,
$n \in A_k$
have an aperiodic tail boundary. By construction,
Moreover, the measures on the left have their support in
![]() $I_k$
, with
$I_k$
, with
![]() $|I_k| \leq C$
for all
$|I_k| \leq C$
for all
![]() $k \in \mathbb {N}$
. Again applying Proposition 3.3, we conclude that
$k \in \mathbb {N}$
. Again applying Proposition 3.3, we conclude that
 $$ \begin{align*}\sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \, \operatorname{Var}((\beta_n + \beta_{\alpha_k(n)})/2) < + \infty \; .\end{align*} $$
$$ \begin{align*}\sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \, \operatorname{Var}((\beta_n + \beta_{\alpha_k(n)})/2) < + \infty \; .\end{align*} $$
The mean value of
![]() $(\beta _n + \beta _{\alpha _k(n)})/2$
is
$(\beta _n + \beta _{\alpha _k(n)})/2$
is
![]() $(s_n + s_{\alpha _k(n)})/2$
, and we conclude that
$(s_n + s_{\alpha _k(n)})/2$
, and we conclude that
 $$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \int_{\mathbb{R}} \left(x - \frac{s_n + s_{\alpha_k(n)}}{2}\right)^2 \, d\beta_n(x) < + \infty \;. \end{align} $$
$$ \begin{align} \sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \int_{\mathbb{R}} \left(x - \frac{s_n + s_{\alpha_k(n)}}{2}\right)^2 \, d\beta_n(x) < + \infty \;. \end{align} $$
A direct computation gives that, for
![]() $n \in A_k$
,
$n \in A_k$
,
 $$ \begin{align*}\int_{\mathbb{R}} \left(x - \frac{s_n + s_{\alpha_k(n)}}{2}\right)^2 \, d\beta_n(x) &= \operatorname{Var}(\beta_n) + \frac{1}{4}(s_{\alpha_k(n)}-s_n)^2 \\ &\geq \frac{1}{4}\bigl((s_{\alpha_k(n)}-t_k)^2 + (t_k - s_n)^2\bigr)\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}} \left(x - \frac{s_n + s_{\alpha_k(n)}}{2}\right)^2 \, d\beta_n(x) &= \operatorname{Var}(\beta_n) + \frac{1}{4}(s_{\alpha_k(n)}-s_n)^2 \\ &\geq \frac{1}{4}\bigl((s_{\alpha_k(n)}-t_k)^2 + (t_k - s_n)^2\bigr)\end{align*} $$
because
![]() $s_n \leq t_k \leq s_{\alpha _k(n)}$
. It thus follows from equation (3.17) that
$s_n \leq t_k \leq s_{\alpha _k(n)}$
. It thus follows from equation (3.17) that
 $$ \begin{align*}\sum_{k = 1}^{\infty} \sum_{n \in J_k} p_k q_k \, (s_n - t_k)^2 = \sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \, \bigl((s_{\alpha_k(n)}-t_k)^2 + (t_k - s_n)^2\bigr) < +\infty \; .\end{align*} $$
$$ \begin{align*}\sum_{k = 1}^{\infty} \sum_{n \in J_k} p_k q_k \, (s_n - t_k)^2 = \sum_{k=1}^{\infty} \sum_{n \in A_k} p_k q_k \, \bigl((s_{\alpha_k(n)}-t_k)^2 + (t_k - s_n)^2\bigr) < +\infty \; .\end{align*} $$
Since
![]() $(x-t_k)^2 \leq 2(x-s_n)^2 + 2(s_n -t_k)^2$
and since
$(x-t_k)^2 \leq 2(x-s_n)^2 + 2(s_n -t_k)^2$
and since
![]() $p_k \leq 1$
, in combination with equation (3.16), we have proven that equation (3.15) holds.
$p_k \leq 1$
, in combination with equation (3.16), we have proven that equation (3.15) holds.
Theorem 3.5. Every ITPFI factor of bounded type is isomorphic with an ITPFI
![]() $_2$
factor.
$_2$
factor.
Proof. By induction, it suffices to prove that, for every integer
![]() $N \geq 2$
, every ITPFI
$N \geq 2$
, every ITPFI
![]() $_{N+1}$
factor of type III
$_{N+1}$
factor of type III
![]() $_0$
is isomorphic with the tensor product of an ITPFI
$_0$
is isomorphic with the tensor product of an ITPFI
![]() $_N$
factor and an ITPFI
$_N$
factor and an ITPFI
![]() $_2$
factor.
$_2$
factor.
We denote in this proof by
![]() $\delta (a)$
the Dirac measure in
$\delta (a)$
the Dirac measure in
![]() $a \in \mathbb {R}$
. For every
$a \in \mathbb {R}$
. For every
![]() $a \geq 0$
, we define the probability measure
$a \geq 0$
, we define the probability measure
For every
![]() $a \in \mathbb {R}_{\geq 0}^N$
, we define the probability measure
$a \in \mathbb {R}_{\geq 0}^N$
, we define the probability measure
 $$ \begin{align*}\rho(a) = \left(1 + \sum_{i=1}^N \exp(-a_i)\right)^{-1} \, \left(\delta(0) + \sum_{i=1}^N \exp(-a_i) \delta(a_i)\right)\end{align*} $$
$$ \begin{align*}\rho(a) = \left(1 + \sum_{i=1}^N \exp(-a_i)\right)^{-1} \, \left(\delta(0) + \sum_{i=1}^N \exp(-a_i) \delta(a_i)\right)\end{align*} $$
and the state
![]() $\psi _a$
on
$\psi _a$
on
![]() $M_{N+1}(\mathbb {C})$
by
$M_{N+1}(\mathbb {C})$
by
 $$ \begin{align*}\psi_a(A) = \left(1 + \sum_{i=1}^N \exp(-a_i)\right)^{-1} \, \left(A_{00} + \sum_{i=1}^N \exp(-a_i) A_{ii} \right) .\end{align*} $$
$$ \begin{align*}\psi_a(A) = \left(1 + \sum_{i=1}^N \exp(-a_i)\right)^{-1} \, \left(A_{00} + \sum_{i=1}^N \exp(-a_i) A_{ii} \right) .\end{align*} $$
By diagonalizing states, any ITPFI
![]() $_{N+1}$
factor can be written as the tensor product of a sequence
$_{N+1}$
factor can be written as the tensor product of a sequence
![]() $(M_{N+1}(\mathbb {C}),\psi _{a_n})$
with
$(M_{N+1}(\mathbb {C}),\psi _{a_n})$
with
![]() $a_n \in \mathbb {R}_{\geq 0}^N$
. By [Reference Connes and Woods17, Theorem 3.1], its flow of weights is precisely the tail boundary flow of the sequence
$a_n \in \mathbb {R}_{\geq 0}^N$
. By [Reference Connes and Woods17, Theorem 3.1], its flow of weights is precisely the tail boundary flow of the sequence
![]() $(\rho (a_n))_{n \in \mathbb {N}}$
.
$(\rho (a_n))_{n \in \mathbb {N}}$
.
We thus fix such a sequence
![]() $a_n \in \mathbb {R}_{\geq 0}^N$
, we assume that the tail boundary flow of
$a_n \in \mathbb {R}_{\geq 0}^N$
, we assume that the tail boundary flow of
is aperiodic and we prove that it is isomorphic with the tail boundary flow of a family of probability measures of the form
![]() $\rho (b)$
,
$\rho (b)$
,
![]() $b \in \mathbb {R}_{\geq 0}^{N-1}$
, and
$b \in \mathbb {R}_{\geq 0}^{N-1}$
, and
![]() $\gamma (c)$
,
$\gamma (c)$
,
![]() $c \geq 0$
.
$c \geq 0$
.
For every
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $1 \leq i \leq N$
, we denote
$1 \leq i \leq N$
, we denote
![]() $J_{k,i} = \{n \in \mathbb {N} \mid a_{n,i} \in [k-1,k)\}$
. We put
$J_{k,i} = \{n \in \mathbb {N} \mid a_{n,i} \in [k-1,k)\}$
. We put
![]() $p = (1+N)^{-1}$
and
$p = (1+N)^{-1}$
and
![]() $q_k = p \, \exp (-k)$
. Fix
$q_k = p \, \exp (-k)$
. Fix
![]() $i \in \{1,\ldots ,N\}$
.
$i \in \{1,\ldots ,N\}$
.
For every
![]() $n \in J_{1,i}$
, we have that
$n \in J_{1,i}$
, we have that
and that the measures
![]() $\delta (a_{n,i})$
are supported on the interval
$\delta (a_{n,i})$
are supported on the interval
![]() $[0,1]$
. It follows from Proposition 3.3 and equation (3.13) that
$[0,1]$
. It follows from Proposition 3.3 and equation (3.13) that
For every
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $n \in J_{k,i}$
, we have that
$n \in J_{k,i}$
, we have that
and that the measures at the left are supported on the interval
![]() $[k-1,k)$
. For
$[k-1,k)$
. For
![]() $n \in J_{k,i}$
, we have that
$n \in J_{k,i}$
, we have that
![]() $\exp (-a_{n,i}) \leq \exp (1) \, (N+1) \, q_k$
. By Proposition 3.4, we thus find
$\exp (-a_{n,i}) \leq \exp (1) \, (N+1) \, q_k$
. By Proposition 3.4, we thus find
![]() $b_{k,i} \in [k-1,k)$
such that
$b_{k,i} \in [k-1,k)$
such that
 $$ \begin{align} \sum_{k=2}^{\infty} \sum_{n \in J_{k,i}} \exp(-a_{n,i}) \, (b_{k,i} - a_{n,i})^2 < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{k=2}^{\infty} \sum_{n \in J_{k,i}} \exp(-a_{n,i}) \, (b_{k,i} - a_{n,i})^2 < +\infty \;. \end{align} $$
Defining
![]() $b_{1,i}=0$
for all
$b_{1,i}=0$
for all
![]() $i \in \{1,\ldots ,N\}$
and summing over
$i \in \{1,\ldots ,N\}$
and summing over
![]() $i \in \{1,\ldots ,N\}$
, it follows from equations (3.19) and (3.20) that
$i \in \{1,\ldots ,N\}$
, it follows from equations (3.19) and (3.20) that
 $$ \begin{align} \sum_{k=1}^{\infty} \sum_{i=1}^N \sum_{n \in J_{k,i}} \exp(-a_{n,i}) \, (b_{k,i} - a_{n,i})^2 < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{k=1}^{\infty} \sum_{i=1}^N \sum_{n \in J_{k,i}} \exp(-a_{n,i}) \, (b_{k,i} - a_{n,i})^2 < +\infty \;. \end{align} $$
Define the maps
![]() $\alpha _n : \{1,\ldots ,N\} \to \mathbb {N}$
by
$\alpha _n : \{1,\ldots ,N\} \to \mathbb {N}$
by
![]() $\alpha _n(i) = k$
if and only if
$\alpha _n(i) = k$
if and only if
![]() $n \in J_{k,i}$
. Define the probability measures
$n \in J_{k,i}$
. Define the probability measures
 $$ \begin{align*}\mu^{\prime}_n = \left(1 + \sum_{i=1}^N \exp(-a_{n,i})\right)^{-1} \, \left(\delta(0) + \sum_{i=1}^N \exp(-a_{n,i}) \delta(b_{\alpha_n(i),i})\right).\end{align*} $$
$$ \begin{align*}\mu^{\prime}_n = \left(1 + \sum_{i=1}^N \exp(-a_{n,i})\right)^{-1} \, \left(\delta(0) + \sum_{i=1}^N \exp(-a_{n,i}) \delta(b_{\alpha_n(i),i})\right).\end{align*} $$
Using the Wasserstein
![]() $2$
-distance, it follows from equations (3.21) and (3.6) that
$2$
-distance, it follows from equations (3.21) and (3.6) that
![]() $\sum _{n=1}^{\infty } W_2(\mu _n,\mu ^{\prime }_n)^2 < +\infty $
. It thus follows from Proposition 3.2 that
$\sum _{n=1}^{\infty } W_2(\mu _n,\mu ^{\prime }_n)^2 < +\infty $
. It thus follows from Proposition 3.2 that
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
have isomorphic tail boundary flows.
$(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
have isomorphic tail boundary flows.
When
![]() $s, t \in \mathbb {R}$
satisfy
$s, t \in \mathbb {R}$
satisfy
![]() $|s-t| \leq 1$
, we have that
$|s-t| \leq 1$
, we have that
It follows that for all
![]() $n \in J_{k,i}$
,
$n \in J_{k,i}$
,
Defining
![]() $\mu ^{\prime \prime }_n = \rho (b_{\alpha _n(1),1},\ldots ,b_{\alpha _n(N),N})$
, it thus follows from equations (3.21) and (3.22) that
$\mu ^{\prime \prime }_n = \rho (b_{\alpha _n(1),1},\ldots ,b_{\alpha _n(N),N})$
, it thus follows from equations (3.21) and (3.22) that
 $$ \begin{align*}\sum_{n=1}^{\infty} H^2(\mu^{\prime}_n,\mu^{\prime\prime}_n) < + \infty \; .\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} H^2(\mu^{\prime}_n,\mu^{\prime\prime}_n) < + \infty \; .\end{align*} $$
By Lemma 3.1, also
![]() $(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
and
$(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
and
![]() $(\mu ^{\prime \prime }_n)_{n \in \mathbb {N}}$
have isomorphic tail boundary flows.
$(\mu ^{\prime \prime }_n)_{n \in \mathbb {N}}$
have isomorphic tail boundary flows.
We order the elements
![]() $(b_{k,i})_{i = 1,\ldots ,N}$
in
$(b_{k,i})_{i = 1,\ldots ,N}$
in
![]() $[k-1,k)$
from smaller to larger, remove duplicates and relabel so as to find an increasing sequence
$[k-1,k)$
from smaller to larger, remove duplicates and relabel so as to find an increasing sequence
![]() $0 \leq b_1 < b_2 < \cdots $
with
$0 \leq b_1 < b_2 < \cdots $
with
![]() $b_m \geq m/N - 1$
for all
$b_m \geq m/N - 1$
for all
![]() $m \in \mathbb {N}$
and with all
$m \in \mathbb {N}$
and with all
![]() $b_{k,i}$
appearing in this sequence. Permuting elements
$b_{k,i}$
appearing in this sequence. Permuting elements
![]() $(d_1,\ldots ,d_N)$
does not change the probability measure
$(d_1,\ldots ,d_N)$
does not change the probability measure
![]() $\rho (d_1,\ldots ,d_N)$
. So every
$\rho (d_1,\ldots ,d_N)$
. So every
![]() $\mu ^{\prime \prime }_n$
is of the form
$\mu ^{\prime \prime }_n$
is of the form
for a nondecreasing function
![]() $\theta _n : \{1,\ldots ,N\} \to \mathbb {N}$
.
$\theta _n : \{1,\ldots ,N\} \to \mathbb {N}$
.
For every
![]() $1 \leq M \leq N$
, denote by
$1 \leq M \leq N$
, denote by
![]() $\mathcal {F}_M$
the set of nondecreasing functions from
$\mathcal {F}_M$
the set of nondecreasing functions from
![]() $\{1,\ldots ,M\}$
to
$\{1,\ldots ,M\}$
to
![]() $\mathbb {N}$
. For every
$\mathbb {N}$
. For every
![]() $\theta \in \mathcal {F}_M$
, denote
$\theta \in \mathcal {F}_M$
, denote
Define the subset
![]() $\mathcal {J} \subset \mathcal {F}_N$
as the set of all
$\mathcal {J} \subset \mathcal {F}_N$
as the set of all
![]() $\theta \in \mathcal {F}_N$
that are of the form
$\theta \in \mathcal {F}_N$
that are of the form
![]() $\theta _n$
for some
$\theta _n$
for some
![]() $n \in \mathbb {N}$
. Define
$n \in \mathbb {N}$
. Define
![]() $L_{\theta } \in \mathbb {N}$
as the cardinality of
$L_{\theta } \in \mathbb {N}$
as the cardinality of
![]() $\{ n \in \mathbb {N} \mid \theta _n = \theta \}$
. As explained in the beginning of Section 3.1, the tail boundary flow does not depend on the order of the transition probability measures. So, by construction, the tail boundary flow of the family
$\{ n \in \mathbb {N} \mid \theta _n = \theta \}$
. As explained in the beginning of Section 3.1, the tail boundary flow does not depend on the order of the transition probability measures. So, by construction, the tail boundary flow of the family
![]() $(\mu ^{\prime \prime }_n)_{n \in \mathbb {N}}$
, and hence also the tail boundary flow of
$(\mu ^{\prime \prime }_n)_{n \in \mathbb {N}}$
, and hence also the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
, is isomorphic with the tail boundary flow of the family of measures
$(\mu _n)_{n \in \mathbb {N}}$
, is isomorphic with the tail boundary flow of the family of measures
![]() $\zeta (\theta )^{* L_{\theta }}$
,
$\zeta (\theta )^{* L_{\theta }}$
,
![]() $\theta \in \mathcal {J}$
.
$\theta \in \mathcal {J}$
.
For every
![]() $\theta \in \mathcal {F}_N$
, we denote by
$\theta \in \mathcal {F}_N$
, we denote by
![]() $\widehat {\theta }$
the restriction of
$\widehat {\theta }$
the restriction of
![]() $\theta $
to
$\theta $
to
![]() $\{1,\ldots ,N-1\}$
. For every
$\{1,\ldots ,N-1\}$
. For every
![]() $\theta \in \mathcal {J}$
, we apply Lemma 3.6 below to
$\theta \in \mathcal {J}$
, we apply Lemma 3.6 below to
 $$ \begin{align*} & \alpha = \sum_{i=1}^{N-1} \exp(-b_{\theta(i)}) \geq \beta = \exp(-b_{\theta(N)}) \quad\text{and}\\ & P = \alpha^{-1} \sum_{i=1}^{N-1} \exp(-b_{\theta(i)}) \delta(b_{\theta(i)}) , \;\; Q = \delta(b_{\theta(N)}) \;. \end{align*} $$
$$ \begin{align*} & \alpha = \sum_{i=1}^{N-1} \exp(-b_{\theta(i)}) \geq \beta = \exp(-b_{\theta(N)}) \quad\text{and}\\ & P = \alpha^{-1} \sum_{i=1}^{N-1} \exp(-b_{\theta(i)}) \delta(b_{\theta(i)}) , \;\; Q = \delta(b_{\theta(N)}) \;. \end{align*} $$
By Lemma 3.6, we thus find
![]() $K_{\theta }, M_{\theta } \in \mathbb {N}$
such that with the notation of equation (3.18),
$K_{\theta }, M_{\theta } \in \mathbb {N}$
such that with the notation of equation (3.18),
Given
![]() $k \in \mathbb {N}$
, the number of elements
$k \in \mathbb {N}$
, the number of elements
![]() $\theta \in \mathcal {F}_N$
with
$\theta \in \mathcal {F}_N$
with
![]() $\theta (N) = k$
is smaller than
$\theta (N) = k$
is smaller than
![]() $k^{N-1}$
. Also recall that
$k^{N-1}$
. Also recall that
![]() $b_k \geq k/N - 1$
. Thus,
$b_k \geq k/N - 1$
. Thus,
 $$ \begin{align*}\sum_{\theta \in \mathcal{F}_N} \exp(-b_{\theta(N)}) \leq \sum_{k=1}^{\infty} k^{N-1} \exp(-b_k) \leq \sum_{k=1}^{\infty} k^{N-1} \, \exp(1) \, \exp(-k/N) < +\infty . \end{align*} $$
$$ \begin{align*}\sum_{\theta \in \mathcal{F}_N} \exp(-b_{\theta(N)}) \leq \sum_{k=1}^{\infty} k^{N-1} \exp(-b_k) \leq \sum_{k=1}^{\infty} k^{N-1} \, \exp(1) \, \exp(-k/N) < +\infty . \end{align*} $$
It then follows from equation (3.23) and Lemma 3.1 that the tail boundary flow of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is isomorphic with the tail boundary flow of the family of measures
$(\mu _n)_{n \in \mathbb {N}}$
is isomorphic with the tail boundary flow of the family of measures
This concludes the proof of the theorem.
Although the following lemma is an immediate consequence of [Reference Giordano and Skandalis26, Lemma 2.2], it has never been stated in this very general form.
Lemma 3.6. Let P and Q be probability measures on
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\alpha , \beta> 0$
. For every
$\alpha , \beta> 0$
. For every
![]() $L \in \mathbb {N}$
, we have that
$L \in \mathbb {N}$
, we have that
 $$ \begin{align*} d_{\operatorname{TV}}&\Big( \bigl((1+\alpha+\beta)^{-1}(\delta_0 + \alpha P + \beta Q)\bigr)^{*L} , \\ &\bigl((1+\alpha)^{-1}(\delta_0+\alpha P)\bigr)^{* K} \; * \; \bigl((1+\beta)^{-1} (\delta_0 + \beta Q)\bigr)^{* M}\Big) \leq 2 \sqrt{\beta} \end{align*} $$
$$ \begin{align*} d_{\operatorname{TV}}&\Big( \bigl((1+\alpha+\beta)^{-1}(\delta_0 + \alpha P + \beta Q)\bigr)^{*L} , \\ &\bigl((1+\alpha)^{-1}(\delta_0+\alpha P)\bigr)^{* K} \; * \; \bigl((1+\beta)^{-1} (\delta_0 + \beta Q)\bigr)^{* M}\Big) \leq 2 \sqrt{\beta} \end{align*} $$
for
![]() $K = L - \lfloor (1+\alpha +\beta )^{-1} \beta L \rfloor $
and
$K = L - \lfloor (1+\alpha +\beta )^{-1} \beta L \rfloor $
and
![]() $M = \lfloor (1+\alpha +\beta )^{-1} (1+\beta ) L \rfloor $
.
$M = \lfloor (1+\alpha +\beta )^{-1} (1+\beta ) L \rfloor $
.
Proof. For integers
![]() $k,\; m \geq 0$
with
$k,\; m \geq 0$
with
![]() $k+m \leq L$
, we write
$k+m \leq L$
, we write
 $$ \begin{align*}\mu(k,m) = \frac{L!}{(L-k-m)! \, k! \, m!} \, \frac{\alpha^k \, \beta^m}{(1+\alpha+\beta)^L} \; .\end{align*} $$
$$ \begin{align*}\mu(k,m) = \frac{L!}{(L-k-m)! \, k! \, m!} \, \frac{\alpha^k \, \beta^m}{(1+\alpha+\beta)^L} \; .\end{align*} $$
For all other integers
![]() $k,m \geq 0$
, we write
$k,m \geq 0$
, we write
![]() $\mu (k,m) = 0$
. Then,
$\mu (k,m) = 0$
. Then,
 $$ \begin{align*}\bigl((1+\alpha+\beta)^{-1}(\delta_0 + \alpha P + \beta Q)\bigr)^{*L} = \sum_{k,m \geq 0} \mu(k,m) \, P^{*k} \, Q^{*m} \; .\end{align*} $$
$$ \begin{align*}\bigl((1+\alpha+\beta)^{-1}(\delta_0 + \alpha P + \beta Q)\bigr)^{*L} = \sum_{k,m \geq 0} \mu(k,m) \, P^{*k} \, Q^{*m} \; .\end{align*} $$
We similarly write for all integers
![]() $0 \leq k \leq K$
and
$0 \leq k \leq K$
and
![]() $0 \leq m \leq M$
,
$0 \leq m \leq M$
,
 $$ \begin{align*}\mu'(k,m) = \frac{K!}{(K-k)! \, k!} \, \frac{\alpha^k}{(1+\alpha)^K} \, \frac{M!}{(M-m)! \, m!} \, \frac{\beta^m}{(1+\beta)^M}\end{align*} $$
$$ \begin{align*}\mu'(k,m) = \frac{K!}{(K-k)! \, k!} \, \frac{\alpha^k}{(1+\alpha)^K} \, \frac{M!}{(M-m)! \, m!} \, \frac{\beta^m}{(1+\beta)^M}\end{align*} $$
and
![]() $\mu '(k,m) = 0$
for all other integers
$\mu '(k,m) = 0$
for all other integers
![]() $k,m \geq 0$
so that
$k,m \geq 0$
so that
 $$ \begin{align*}\bigl((1+\alpha)^{-1}(\delta_0+\alpha P)\bigr)^{* K} \; * \; \bigl((1+\beta)^{-1} (\delta_0 + \beta Q)\bigr)^{* M} = \sum_{k,m \geq 0} \mu'(k,m) \, P^{*k} \, Q^{*m} \; .\end{align*} $$
$$ \begin{align*}\bigl((1+\alpha)^{-1}(\delta_0+\alpha P)\bigr)^{* K} \; * \; \bigl((1+\beta)^{-1} (\delta_0 + \beta Q)\bigr)^{* M} = \sum_{k,m \geq 0} \mu'(k,m) \, P^{*k} \, Q^{*m} \; .\end{align*} $$
Parts (a) and (b) of the proof of [Reference Giordano and Skandalis26, Lemma 2.2] are saying that
![]() $H^2(\mu ,\mu ') \leq 2 \beta $
. Then also
$H^2(\mu ,\mu ') \leq 2 \beta $
. Then also
![]() $d_{\operatorname {TV}}(\mu ,\mu ') \leq 2 \sqrt {\beta }$
.
$d_{\operatorname {TV}}(\mu ,\mu ') \leq 2 \sqrt {\beta }$
.
3.2 Poisson flows
Recall that to every finite positive measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {R}$
is associated the compound Poisson distribution on
$\mathbb {R}$
is associated the compound Poisson distribution on
![]() $\mathbb {R}$
, which is defined as the probability measure
$\mathbb {R}$
, which is defined as the probability measure
 $$ \begin{align*}\mathcal{E}(\mu) = \exp(-\|\mu\|) \, \exp(\mu) = \exp(-\mu(\mathbb{R})) \, \left( \delta_0 + \sum_{k=1}^{\infty} \frac{1}{k!} \mu^{*k} \right) \; .\end{align*} $$
$$ \begin{align*}\mathcal{E}(\mu) = \exp(-\|\mu\|) \, \exp(\mu) = \exp(-\mu(\mathbb{R})) \, \left( \delta_0 + \sum_{k=1}^{\infty} \frac{1}{k!} \mu^{*k} \right) \; .\end{align*} $$
Note that
![]() $\mathcal {E}(\mu )$
is supported on
$\mathcal {E}(\mu )$
is supported on
![]() $\mathbb {R}_{\geq 0} = [0,+\infty )$
iff
$\mathbb {R}_{\geq 0} = [0,+\infty )$
iff
![]() $\mu $
is supported on
$\mu $
is supported on
![]() $\mathbb {R}_{\geq 0}$
. If
$\mathbb {R}_{\geq 0}$
. If
![]() $x \mapsto x^2$
is
$x \mapsto x^2$
is
![]() $\mu $
-integrable, we have
$\mu $
-integrable, we have
Definition 3.7. We call a Poisson flow any ergodic flow
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
that arises as the tail boundary flow of a sequence of compound Poisson distributions on
$\mathbb {R} \curvearrowright (Z,\eta )$
that arises as the tail boundary flow of a sequence of compound Poisson distributions on
![]() $\mathbb {R}$
. If these compound Poisson distributions can be chosen with support in
$\mathbb {R}$
. If these compound Poisson distributions can be chosen with support in
![]() $\mathbb {R}_{\geq 0}$
, we call
$\mathbb {R}_{\geq 0}$
, we call
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
a Poisson flow of positive type.
$\mathbb {R} \curvearrowright (Z,\eta )$
a Poisson flow of positive type.
Note that compound Poisson distributions and tail boundary flows make sense on any locally compact second countable abelian group G, leading to the concept of a Poisson G-action, which we will use for
![]() $G = \mathbb {R}$
and
$G = \mathbb {R}$
and
![]() $G = \mathbb {Z}$
. In Remark 3.16, we discuss the relation between general Poisson flows and Poisson flows of positive type.
$G = \mathbb {Z}$
. In Remark 3.16, we discuss the relation between general Poisson flows and Poisson flows of positive type.
The two main results of this section are the following.
Theorem 3.8. Every ergodic almost periodic flow is a Poisson flow of positive type.
Theorem 3.9. The Poisson flows of positive type are precisely the flows of weights of ITPFI
![]() $_2$
factors.
$_2$
factors.
By [Reference Giordano and Skandalis26, Theorem 2.1], which we reproved as Theorem 3.5 above, every ITPFI factor of bounded type is isomorphic with an ITPFI
![]() $_2$
factor. So Poisson flows of positive type are also precisely the flows of weights of ITPFI factors of bounded type. Note that Theorem C is an immediate consequence of Theorems 3.8 and 3.9.
$_2$
factor. So Poisson flows of positive type are also precisely the flows of weights of ITPFI factors of bounded type. Note that Theorem C is an immediate consequence of Theorems 3.8 and 3.9.
For Poisson flows with a nontrivial eigenvalue group, Theorem 3.9 was proven in [Reference Giordano and Handelman25, Proposition 7.1]. It is easy to see that
![]() $2\pi / p$
is an eigenvalue of a Poisson flow
$2\pi / p$
is an eigenvalue of a Poisson flow
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
iff
$\mathbb {R} \curvearrowright (Z,\eta )$
iff
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
is the tail boundary flow of a sequence of compound Poisson distributions with support in
$\mathbb {R} \curvearrowright (Z,\eta )$
is the tail boundary flow of a sequence of compound Poisson distributions with support in
![]() $p \mathbb {Z}$
. The main step in the proof of Theorem 3.9 is to show that in general, if
$p \mathbb {Z}$
. The main step in the proof of Theorem 3.9 is to show that in general, if
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
is a Poisson flow that is aperiodic, then we may realize
$\mathbb {R} \curvearrowright (Z,\eta )$
is a Poisson flow that is aperiodic, then we may realize
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
as the tail boundary flow of a sequence of compound Poisson distributions with very sparse support: at most one atom in each length one interval.
$\mathbb {R} \curvearrowright (Z,\eta )$
as the tail boundary flow of a sequence of compound Poisson distributions with very sparse support: at most one atom in each length one interval.
Before proving Theorem 3.8, we recall the following definition from [Reference Hamachi, Oka and Osikawa31, Section 3], which we generalize in the natural way to multiple flows of locally compact abelian groups. We only use this concept for
![]() $G = \mathbb {R}$
and
$G = \mathbb {R}$
and
![]() $G = \mathbb {Z}$
.
$G = \mathbb {Z}$
.
Definition 3.10 [Reference Hamachi, Oka and Osikawa31, Section 3]
Let G be a locally compact second countable abelian group. For
![]() $i \in \{1,\ldots ,n\}$
, let
$i \in \{1,\ldots ,n\}$
, let
![]() $G \curvearrowright (Z_i,\eta _i)$
be a nonsingular action. Consider the direct sum
$G \curvearrowright (Z_i,\eta _i)$
be a nonsingular action. Consider the direct sum
![]() $G^{\oplus n}$
and its natural action
$G^{\oplus n}$
and its natural action
![]() $G^{\oplus n} \curvearrowright Z = Z_1 \times \cdots \times Z_n$
. Define the closed subgroup
$G^{\oplus n} \curvearrowright Z = Z_1 \times \cdots \times Z_n$
. Define the closed subgroup
![]() $G_0 = \{(g_1,\ldots ,g_n) \in G^{\oplus n} \mid g_1 + \cdots + g_n = 0\}$
and the ergodic decomposition
$G_0 = \{(g_1,\ldots ,g_n) \in G^{\oplus n} \mid g_1 + \cdots + g_n = 0\}$
and the ergodic decomposition
![]() $A = L^{\infty }(Z)^{G_0}$
for the action
$A = L^{\infty }(Z)^{G_0}$
for the action
![]() $G_0 \curvearrowright Z$
.
$G_0 \curvearrowright Z$
.
The action of G on A in the first variable (or, which is the same, in any of the other variables) is called the joint action of
![]() $G \curvearrowright (Z_i,\eta _i)$
. When
$G \curvearrowright (Z_i,\eta _i)$
. When
![]() $G = \mathbb {R}$
, we use the terminology joint flow, instead of joint action.
$G = \mathbb {R}$
, we use the terminology joint flow, instead of joint action.
By construction, the tail boundary flow of the disjoint union
![]() $(\mu _n)_{n \in I \sqcup J}$
of two countable infinite families of probability measures on
$(\mu _n)_{n \in I \sqcup J}$
of two countable infinite families of probability measures on
![]() $\mathbb {R}$
is the joint flow of the tail boundary flows of
$\mathbb {R}$
is the joint flow of the tail boundary flows of
![]() $(\mu _n)_{n \in I}$
and
$(\mu _n)_{n \in I}$
and
![]() $(\mu _n)_{n \in J}$
. Also by construction, the flow of weights of a tensor product factor
$(\mu _n)_{n \in J}$
. Also by construction, the flow of weights of a tensor product factor
![]() $M_1 \mathbin {\overline {\otimes }} M_2$
is the joint flow of the flows of weights of
$M_1 \mathbin {\overline {\otimes }} M_2$
is the joint flow of the flows of weights of
![]() $M_i$
.
$M_i$
.
As a final preparation to proving Theorem 3.8, we discuss the relation between tail boundary flows and induced actions. Assume that G is a locally compact second countable abelian group with closed subgroup H. Choose a probability measure
![]() $\nu $
on
$\nu $
on
![]() $G/H$
that is equivalent with the Haar measure. Recall that any nonsingular action
$G/H$
that is equivalent with the Haar measure. Recall that any nonsingular action
![]() $H \curvearrowright (Y,\eta )$
has an induced action
$H \curvearrowright (Y,\eta )$
has an induced action
![]() $G \curvearrowright (G/H \times Y,\nu \times \eta )$
, which is defined as follows. Choosing a Borel lift
$G \curvearrowright (G/H \times Y,\nu \times \eta )$
, which is defined as follows. Choosing a Borel lift
![]() $\psi : G/H \to G$
, one defines the
$\psi : G/H \to G$
, one defines the
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times G/H \to H : \Omega (g,x) = g + \psi (x) - \psi (g+x)$
and the induced action
$\Omega : G \times G/H \to H : \Omega (g,x) = g + \psi (x) - \psi (g+x)$
and the induced action
Another choice of lift
![]() $\psi $
gives a cohomologous
$\psi $
gives a cohomologous
![]() $1$
-cocycle and, thus, an isomorphic induced action.
$1$
-cocycle and, thus, an isomorphic induced action.
If
![]() $(\mu _n)_{n \in \mathbb {N}}$
is a family of probability measures on H, we have an associated tail boundary H-action. We can also view
$(\mu _n)_{n \in \mathbb {N}}$
is a family of probability measures on H, we have an associated tail boundary H-action. We can also view
![]() $(\mu _n)_{n \in \mathbb {N}}$
as a family of probability measures on G. Since the induction of the translation action
$(\mu _n)_{n \in \mathbb {N}}$
as a family of probability measures on G. Since the induction of the translation action
![]() $H \curvearrowright H$
is, by construction, the translation action
$H \curvearrowright H$
is, by construction, the translation action
![]() $G \curvearrowright G$
, we have by definition that the tail boundary G-action of
$G \curvearrowright G$
, we have by definition that the tail boundary G-action of
![]() $(\mu _n)_{n \in \mathbb {N}}$
is isomorphic with the induction to G of the tail boundary H-action of
$(\mu _n)_{n \in \mathbb {N}}$
is isomorphic with the induction to G of the tail boundary H-action of
![]() $(\mu _n)_{n \in \mathbb {N}}$
.
$(\mu _n)_{n \in \mathbb {N}}$
.
Proof of Theorem 3.8
The cases of a trivial flow or a periodic flow are straightforward. By, e.g., [Reference Berendschot and Vaes8, Proposition 2.1], taking
![]() $a> 0$
and
$a> 0$
and
![]() $\mu _n = \mathcal {E}(\delta _a)$
for all
$\mu _n = \mathcal {E}(\delta _a)$
for all
![]() $n \in \mathbb {N}$
, the tail boundary flow is the periodic flow
$n \in \mathbb {N}$
, the tail boundary flow is the periodic flow
![]() $\mathbb {R} \curvearrowright \mathbb {R}/a\mathbb {Z}$
. Similarly, taking
$\mathbb {R} \curvearrowright \mathbb {R}/a\mathbb {Z}$
. Similarly, taking
![]() $a> 0$
irrational and
$a> 0$
irrational and
![]() $\mu _n = \mathcal {E}(\delta _1 + \delta _a)$
for all
$\mu _n = \mathcal {E}(\delta _1 + \delta _a)$
for all
![]() $n \in \mathbb {N}$
, the tail boundary flow is trivial.
$n \in \mathbb {N}$
, the tail boundary flow is trivial.
So, it suffices to consider an almost periodic, aperiodic, ergodic flow. Such a flow is given by the translation action of
![]() $\mathbb {R}$
on a compact second countable abelian group L under a dense embedding
$\mathbb {R}$
on a compact second countable abelian group L under a dense embedding
![]() $\pi : \mathbb {R} \to L$
. We have to realize this flow as the tail boundary flow of a sequence of compound Poisson distributions
$\pi : \mathbb {R} \to L$
. We have to realize this flow as the tail boundary flow of a sequence of compound Poisson distributions
![]() $\mathcal {E}(\mu _n)$
with
$\mathcal {E}(\mu _n)$
with
![]() $\mu _n$
supported on
$\mu _n$
supported on
![]() $\mathbb {R}_{\geq 0}$
. We start by reducing this problem to a similar question for
$\mathbb {R}_{\geq 0}$
. We start by reducing this problem to a similar question for
![]() $\mathbb {Z}$
-actions.
$\mathbb {Z}$
-actions.
Fix a nontrivial character
![]() $\omega _0 \in \widehat {L}$
. Take
$\omega _0 \in \widehat {L}$
. Take
![]() $t_0 \in \mathbb {R} \setminus \{0\}$
such that
$t_0 \in \mathbb {R} \setminus \{0\}$
such that
![]() $\omega _0(\pi (t)) = \exp (2\pi i t / t_0)$
for all
$\omega _0(\pi (t)) = \exp (2\pi i t / t_0)$
for all
![]() $t \in \mathbb {R}$
. So,
$t \in \mathbb {R}$
. So,
![]() $\omega _0$
gives rise to a surjective, continuous group homomorphism
$\omega _0$
gives rise to a surjective, continuous group homomorphism
![]() $\theta : L \to \mathbb {R}/t_0 \mathbb {Z}$
such that
$\theta : L \to \mathbb {R}/t_0 \mathbb {Z}$
such that
![]() $\theta \circ \pi : \mathbb {R} \to \mathbb {R} / t_0 \mathbb {Z}$
is the natural quotient map. Define
$\theta \circ \pi : \mathbb {R} \to \mathbb {R} / t_0 \mathbb {Z}$
is the natural quotient map. Define
![]() $K = \operatorname {Ker} \theta $
as the kernel of
$K = \operatorname {Ker} \theta $
as the kernel of
![]() $\theta $
. Note that the restriction of
$\theta $
. Note that the restriction of
![]() $\pi $
to
$\pi $
to
![]() $t_0 \mathbb {Z}$
is a dense embedding of
$t_0 \mathbb {Z}$
is a dense embedding of
![]() $t_0 \mathbb {Z}$
into K. Note that the translation action
$t_0 \mathbb {Z}$
into K. Note that the translation action
![]() $\mathbb {R} \curvearrowright L$
is the induction to
$\mathbb {R} \curvearrowright L$
is the induction to
![]() $\mathbb {R}$
of the translation action
$\mathbb {R}$
of the translation action
![]() $t_0 \mathbb {Z} \curvearrowright K$
. By the discussion preceding this proof, it thus suffices to prove that this translation action
$t_0 \mathbb {Z} \curvearrowright K$
. By the discussion preceding this proof, it thus suffices to prove that this translation action
![]() $t_0 \mathbb {Z} \curvearrowright K$
can be realized as the tail boundary action of
$t_0 \mathbb {Z} \curvearrowright K$
can be realized as the tail boundary action of
![]() $t_0 \mathbb {Z}$
associated with a sequence of compound Poisson distributions
$t_0 \mathbb {Z}$
associated with a sequence of compound Poisson distributions
![]() $\mathcal {E}(\mu _n)$
, where
$\mathcal {E}(\mu _n)$
, where
![]() $\mu _n$
are finite positive measures on
$\mu _n$
are finite positive measures on
![]() $t_0 \mathbb {N} \subset t_0 \mathbb {Z}$
. Since we can rescale everything with
$t_0 \mathbb {N} \subset t_0 \mathbb {Z}$
. Since we can rescale everything with
![]() $t_0$
, we may assume that
$t_0$
, we may assume that
![]() $t_0 = 1$
.
$t_0 = 1$
.
Combining [Reference Connes and Woods16, Corollary 2.8] and [Reference Connes and Woods17, Theorem 3.4], we can take finitely supported probability measures
![]() $(\eta _n)_{n \in \mathbb {N}}$
on
$(\eta _n)_{n \in \mathbb {N}}$
on
![]() $\mathbb {Z}$
such that the associated tail boundary flow is given by the translation
$\mathbb {Z}$
such that the associated tail boundary flow is given by the translation
![]() $\mathbb {Z} \curvearrowright K$
. Denote by
$\mathbb {Z} \curvearrowright K$
. Denote by
![]() $\widetilde {\eta }_n$
the probability measure given by
$\widetilde {\eta }_n$
the probability measure given by
![]() $\widetilde {\eta }_n(\mathcal {U}) = \eta _n(-\mathcal {U})$
. The tail boundary flow of
$\widetilde {\eta }_n(\mathcal {U}) = \eta _n(-\mathcal {U})$
. The tail boundary flow of
![]() $(\widetilde {\eta }_n)_{n \in \mathbb {N}}$
is given by the action of
$(\widetilde {\eta }_n)_{n \in \mathbb {N}}$
is given by the action of
![]() $\mathbb {Z}$
on K by
$\mathbb {Z}$
on K by
![]() $n \cdot k = -n + k$
. Through the isomorphism
$n \cdot k = -n + k$
. Through the isomorphism
![]() $k \mapsto -k$
, this flow is isomorphic with the original translation action
$k \mapsto -k$
, this flow is isomorphic with the original translation action
![]() $\mathbb {Z} \curvearrowright K$
. Since the joint flow of
$\mathbb {Z} \curvearrowright K$
. Since the joint flow of
![]() $\mathbb {Z} \curvearrowright K$
with itself is again
$\mathbb {Z} \curvearrowright K$
with itself is again
![]() $\mathbb {Z} \curvearrowright K$
, the tail boundary flow of the measures
$\mathbb {Z} \curvearrowright K$
, the tail boundary flow of the measures
![]() $(\eta _n * \widetilde {\eta }_n)_{n \in \mathbb {N}}$
is still given by
$(\eta _n * \widetilde {\eta }_n)_{n \in \mathbb {N}}$
is still given by
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
For every
![]() $\mu \in \ell ^1(\mathbb {Z})$
, we consider the Fourier transform
$\mu \in \ell ^1(\mathbb {Z})$
, we consider the Fourier transform
We view
![]() $\widehat {K}$
as a dense countable subgroup of
$\widehat {K}$
as a dense countable subgroup of
![]() $\mathbb {T}$
. The Fourier transform of
$\mathbb {T}$
. The Fourier transform of
![]() $\eta _n * \widetilde {\eta }_n$
is a positive function. We replace
$\eta _n * \widetilde {\eta }_n$
is a positive function. We replace
![]() $\eta _n$
by
$\eta _n$
by
![]() $\eta _n * \widetilde {\eta }_n$
, and we may thus assume that the probability measures are finitely supported, with
$\eta _n * \widetilde {\eta }_n$
, and we may thus assume that the probability measures are finitely supported, with
![]() $\widehat {\eta }_n(\omega ) \geq 0$
for all
$\widehat {\eta }_n(\omega ) \geq 0$
for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\omega \in \widehat {K}$
, and with associated tail boundary flow
$\omega \in \widehat {K}$
, and with associated tail boundary flow
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
As each
![]() $\omega \in \widehat {K}$
is an eigenvalue of the translation action
$\omega \in \widehat {K}$
is an eigenvalue of the translation action
![]() $\mathbb {Z}\curvearrowright K$
, we know from [Reference Connes and Woods17, Theorem 4.2] that
$\mathbb {Z}\curvearrowright K$
, we know from [Reference Connes and Woods17, Theorem 4.2] that
 $$ \begin{align*} \lim_{n \to +\infty} \prod_{m=n}^{\infty}\widehat{\eta}_m(\omega) = 1 \;\;\text{for every } \omega\in \widehat{K}. \end{align*} $$
$$ \begin{align*} \lim_{n \to +\infty} \prod_{m=n}^{\infty}\widehat{\eta}_m(\omega) = 1 \;\;\text{for every } \omega\in \widehat{K}. \end{align*} $$
Choose an increasing sequence of finite subsets
![]() $\mathcal {F}_k \subset \widehat {K}$
such that
$\mathcal {F}_k \subset \widehat {K}$
such that
![]() $\widehat {K} = \bigcup _{k=1}^{\infty } \mathcal {F}_k$
. Then inductively choose
$\widehat {K} = \bigcup _{k=1}^{\infty } \mathcal {F}_k$
. Then inductively choose
![]() $1 \leq n_1 < n_2 < \cdots $
such that
$1 \leq n_1 < n_2 < \cdots $
such that
 $$ \begin{align*} \prod_{m=1+n_k}^{\infty} \widehat{\eta}_m(\omega)> 1 - (k+1)^{-3} \quad\text{for all } \omega \in \mathcal{F}_{k+1}. \end{align*} $$
$$ \begin{align*} \prod_{m=1+n_k}^{\infty} \widehat{\eta}_m(\omega)> 1 - (k+1)^{-3} \quad\text{for all } \omega \in \mathcal{F}_{k+1}. \end{align*} $$
Then define the probability measures
![]() $\alpha _k$
on
$\alpha _k$
on
![]() $\mathbb {Z}$
by
$\mathbb {Z}$
by
Since
![]() $0 \leq \widehat {\eta }_m(\omega ) \leq 1$
for all
$0 \leq \widehat {\eta }_m(\omega ) \leq 1$
for all
![]() $m \in \mathbb {N}$
,
$m \in \mathbb {N}$
,
![]() $\omega \in \widehat {K}$
, we thus have
$\omega \in \widehat {K}$
, we thus have
Also, the tail boundary flow of
![]() $(\alpha _k)_{k \in \mathbb {N}}$
is still given by
$(\alpha _k)_{k \in \mathbb {N}}$
is still given by
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
For every
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
is a neighborhood of
![]() $0 \in K$
. Since
$0 \in K$
. Since
![]() $\mathbb {Z} \subset K$
is dense, there are arbitrarily large positive integers
$\mathbb {Z} \subset K$
is dense, there are arbitrarily large positive integers
![]() $n \in \mathcal {U}_k$
. Since the measures
$n \in \mathcal {U}_k$
. Since the measures
![]() $\alpha _k$
have finite support, we can choose
$\alpha _k$
have finite support, we can choose
![]() $m_k \in \mathbb {N}$
large enough such that
$m_k \in \mathbb {N}$
large enough such that
![]() $m_k \in \mathcal {U}_k$
and such that the translated measures defined by
$m_k \in \mathcal {U}_k$
and such that the translated measures defined by
![]() $\gamma _k(\mathcal {V}) = \alpha _k(\mathcal {V}-m_k)$
have their support in
$\gamma _k(\mathcal {V}) = \alpha _k(\mathcal {V}-m_k)$
have their support in
![]() $\mathbb {N}$
. Since
$\mathbb {N}$
. Since
![]() $m_k \in \mathcal {U}_k$
, using equation (3.26), we get that
$m_k \in \mathcal {U}_k$
, using equation (3.26), we get that
The tail boundary flow of
![]() $(\gamma _k)_{k \in \mathbb {N}}$
is still given by
$(\gamma _k)_{k \in \mathbb {N}}$
is still given by
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
Define the compound Poisson distributions
![]() $\beta _k = \mathcal {E}(k \gamma _k)$
, and denote by
$\beta _k = \mathcal {E}(k \gamma _k)$
, and denote by
![]() $\mathbb {Z} \curvearrowright X$
the tail boundary flow of
$\mathbb {Z} \curvearrowright X$
the tail boundary flow of
![]() $(\beta _k)_{k \in \mathbb {N}}$
. We prove that
$(\beta _k)_{k \in \mathbb {N}}$
. We prove that
![]() $\mathbb {Z} \curvearrowright X$
is isomorphic with
$\mathbb {Z} \curvearrowright X$
is isomorphic with
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
Since
![]() $\widehat {\beta }_k(\omega ) = \exp (-k(1-\widehat {\gamma }_k(\omega )))$
, we get that
$\widehat {\beta }_k(\omega ) = \exp (-k(1-\widehat {\gamma }_k(\omega )))$
, we get that
![]() $|\widehat {\beta }_k(\omega )| = \exp (-k(1-\operatorname {Re} \widehat {\gamma }_k(\omega )))$
. From equation (3.27) and the assumption that
$|\widehat {\beta }_k(\omega )| = \exp (-k(1-\operatorname {Re} \widehat {\gamma }_k(\omega )))$
. From equation (3.27) and the assumption that
![]() $\widehat {K} = \bigcup _{k=1}^{\infty } \mathcal {F}_k$
, it follows that
$\widehat {K} = \bigcup _{k=1}^{\infty } \mathcal {F}_k$
, it follows that
 $$ \begin{align*}\prod_{k=1}^{\infty} |\widehat{\beta}_k(\omega)|> 0 \quad\text{for all } \omega \in \widehat{K}. \end{align*} $$
$$ \begin{align*}\prod_{k=1}^{\infty} |\widehat{\beta}_k(\omega)|> 0 \quad\text{for all } \omega \in \widehat{K}. \end{align*} $$
Again by [Reference Connes and Woods17, Theorem 4.2], it follows that each
![]() $\omega \in \widehat {K}$
is an eigenvalue of the tail boundary flow of
$\omega \in \widehat {K}$
is an eigenvalue of the tail boundary flow of
![]() $(\beta _k)_{k \in \mathbb {N}}$
.
$(\beta _k)_{k \in \mathbb {N}}$
.
Since
![]() $\exp (-k)$
is summable, by Lemma 3.1, the term
$\exp (-k)$
is summable, by Lemma 3.1, the term
![]() $\exp (-k)\delta _0$
in the definition of
$\exp (-k)\delta _0$
in the definition of
![]() $\beta _k = \mathcal {E}(k \gamma _k)$
is negligible so that
$\beta _k = \mathcal {E}(k \gamma _k)$
is negligible so that
![]() $\mathbb {Z} \curvearrowright X$
is isomorphic with the tail boundary flow of
$\mathbb {Z} \curvearrowright X$
is isomorphic with the tail boundary flow of
 $$ \begin{align*}\rho_k = \gamma_k * \zeta_k \quad\text{where}\quad \zeta_k = (\exp(k)-1)^{-1} \left(k \delta_0 + \sum_{j=1}^{\infty} \frac{k^{j+1}}{(j+1)!} \gamma_k^{*j}\right). \end{align*} $$
$$ \begin{align*}\rho_k = \gamma_k * \zeta_k \quad\text{where}\quad \zeta_k = (\exp(k)-1)^{-1} \left(k \delta_0 + \sum_{j=1}^{\infty} \frac{k^{j+1}}{(j+1)!} \gamma_k^{*j}\right). \end{align*} $$
Denoting by
![]() $\mathbb {Z} \curvearrowright Y$
the tail boundary flow of the sequence
$\mathbb {Z} \curvearrowright Y$
the tail boundary flow of the sequence
![]() $(\zeta _k)_{k \in \mathbb {N}}$
, we conclude that
$(\zeta _k)_{k \in \mathbb {N}}$
, we conclude that
![]() $\mathbb {Z} \curvearrowright X$
is the joint flow of
$\mathbb {Z} \curvearrowright X$
is the joint flow of
![]() $\mathbb {Z} \curvearrowright K$
and
$\mathbb {Z} \curvearrowright K$
and
![]() $\mathbb {Z} \curvearrowright Y$
. Realizing this joint flow inside
$\mathbb {Z} \curvearrowright Y$
. Realizing this joint flow inside
![]() $L^{\infty }(K \times Y)$
with
$L^{\infty }(K \times Y)$
with
![]() $\mathbb {Z}$
acting in the first variable, we conclude that the action
$\mathbb {Z}$
acting in the first variable, we conclude that the action
![]() $\mathbb {Z} \curvearrowright X$
can be continuously extended to an action of K. This means that
$\mathbb {Z} \curvearrowright X$
can be continuously extended to an action of K. This means that
![]() $\mathbb {Z} \curvearrowright X$
is isomorphic with a factor of
$\mathbb {Z} \curvearrowright X$
is isomorphic with a factor of
![]() $\mathbb {Z} \curvearrowright K$
. We have already seen that each
$\mathbb {Z} \curvearrowright K$
. We have already seen that each
![]() $\omega \in \widehat {K}$
is an eigenvalue of
$\omega \in \widehat {K}$
is an eigenvalue of
![]() $\mathbb {Z} \curvearrowright X$
. So,
$\mathbb {Z} \curvearrowright X$
. So,
![]() $\mathbb {Z} \curvearrowright X$
must be isomorphic with
$\mathbb {Z} \curvearrowright X$
must be isomorphic with
![]() $\mathbb {Z} \curvearrowright K$
.
$\mathbb {Z} \curvearrowright K$
.
We finally prove Theorem 3.9. Here and in the rest of this section, we often make use of Prokhorov’s theorem (see [Reference Prokhorov45]) estimating the total variation distance between a binomial distribution and a Poisson distribution. Given
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $p \in [0,1]$
and
$p \in [0,1]$
and
![]() $\lambda \geq 0$
, define the binomial distribution
$\lambda \geq 0$
, define the binomial distribution
![]() $\beta $
and Poisson distribution
$\beta $
and Poisson distribution
![]() $\pi $
by
$\pi $
by
 $$ \begin{align*} & \beta_{n,p}(k) = \left(\begin{smallmatrix} n \\ k\end{smallmatrix}\right) \, p^k (1-p)^{n-k} \quad\text{for } k \in \{0,1,\ldots,n\}, \text{ and}\\[4pt] & \pi_{\lambda}(k) = \exp(-\lambda) \frac{\lambda^k}{k!} \quad\text{for } k \in \{0,1,2,\ldots\}. \end{align*} $$
$$ \begin{align*} & \beta_{n,p}(k) = \left(\begin{smallmatrix} n \\ k\end{smallmatrix}\right) \, p^k (1-p)^{n-k} \quad\text{for } k \in \{0,1,\ldots,n\}, \text{ and}\\[4pt] & \pi_{\lambda}(k) = \exp(-\lambda) \frac{\lambda^k}{k!} \quad\text{for } k \in \{0,1,2,\ldots\}. \end{align*} $$
In the version of [Reference Barbour and Hall4, Theorem 1], Prokhorov’s theorem says that
Proof of Theorem 3.9
The trivial flow and every periodic flow arise as the flow of weights of an ITPFI
![]() $_2$
factor and also arise as a Poisson flow of positive type. We thus only consider the aperiodic case.
$_2$
factor and also arise as a Poisson flow of positive type. We thus only consider the aperiodic case.
First assume that
![]() $\mathbb {R} \curvearrowright X$
is the flow of weights of an ITPFI
$\mathbb {R} \curvearrowright X$
is the flow of weights of an ITPFI
![]() $_2$
factor and that
$_2$
factor and that
![]() $\mathbb {R} \curvearrowright X$
is aperiodic. As we have seen in the proof of Theorem 3.5, we find for all
$\mathbb {R} \curvearrowright X$
is aperiodic. As we have seen in the proof of Theorem 3.5, we find for all
![]() $k \in \mathbb {N}$
, elements
$k \in \mathbb {N}$
, elements
![]() $b_k \in [k-1,k)$
and integers
$b_k \in [k-1,k)$
and integers
![]() $L_k \geq 0$
such that
$L_k \geq 0$
such that
![]() $\mathbb {R} \curvearrowright X$
is isomorphic with the tail boundary flow of the sequence
$\mathbb {R} \curvearrowright X$
is isomorphic with the tail boundary flow of the sequence
![]() $\gamma (b_k)^{*L_k}$
, where
$\gamma (b_k)^{*L_k}$
, where
![]() $\gamma (b)$
is defined by equation (3.18). By equation (3.28), we get that
$\gamma (b)$
is defined by equation (3.18). By equation (3.28), we get that
 $$ \begin{align*}d_{\operatorname{TV}}\bigl(\gamma(b_k)^{*L_k} , \mathcal{E}(\lambda_k \delta_{b_k})\bigr) \leq \exp(-b_k) \quad\text{where}\;\; \lambda_k = \frac{L_k \exp(-b_k)}{1+\exp(-b_k)} \; .\end{align*} $$
$$ \begin{align*}d_{\operatorname{TV}}\bigl(\gamma(b_k)^{*L_k} , \mathcal{E}(\lambda_k \delta_{b_k})\bigr) \leq \exp(-b_k) \quad\text{where}\;\; \lambda_k = \frac{L_k \exp(-b_k)}{1+\exp(-b_k)} \; .\end{align*} $$
Since
![]() $\exp (-b_k) \leq \exp (-k+1)$
is summable, it follows from Lemma 3.1 that
$\exp (-b_k) \leq \exp (-k+1)$
is summable, it follows from Lemma 3.1 that
![]() $\mathbb {R} \curvearrowright X$
is a Poisson flow of positive type.
$\mathbb {R} \curvearrowright X$
is a Poisson flow of positive type.
Conversely, assume that
![]() $\mathbb {R} \curvearrowright X$
is the Poisson flow of positive type defined by the sequence of probability measures
$\mathbb {R} \curvearrowright X$
is the Poisson flow of positive type defined by the sequence of probability measures
![]() $\mu _n = \mathcal {E}(\eta _n)$
, where each
$\mu _n = \mathcal {E}(\eta _n)$
, where each
![]() $\eta _n$
is a finite positive measure supported on
$\eta _n$
is a finite positive measure supported on
![]() $(0,+\infty )$
. We may assume that
$(0,+\infty )$
. We may assume that
![]() $\mathbb {R} \curvearrowright X$
is aperiodic. Taking integers
$\mathbb {R} \curvearrowright X$
is aperiodic. Taking integers
![]() $L_n \geq \eta _n(\mathbb {R})$
, we can replace
$L_n \geq \eta _n(\mathbb {R})$
, we can replace
![]() $\mu _n$
by
$\mu _n$
by
![]() $\mathcal {E}(\eta _n / L_n)$
, each repeated
$\mathcal {E}(\eta _n / L_n)$
, each repeated
![]() $L_n$
times. We may thus assume that
$L_n$
times. We may thus assume that
![]() $\lambda _n := \eta _n(\mathbb {R}) \leq 1$
.
$\lambda _n := \eta _n(\mathbb {R}) \leq 1$
.
For every fixed
![]() $C> 0$
, we have that
$C> 0$
, we have that
for all
![]() $n \in \mathbb {N}$
and that all
$n \in \mathbb {N}$
and that all
![]() $\beta _n$
are supported on
$\beta _n$
are supported on
![]() $[0,C]$
. It follows from Proposition 3.3 that
$[0,C]$
. It follows from Proposition 3.3 that
 $$ \begin{align} \sum_{n=1}^{\infty} \beta_n(\mathbb{R}) \, \operatorname{Var}(\beta_n(\mathbb{R})^{-1} \, \beta_n) < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \beta_n(\mathbb{R}) \, \operatorname{Var}(\beta_n(\mathbb{R})^{-1} \, \beta_n) < +\infty \;. \end{align} $$
Since
![]() $\exp (-\lambda _n) \geq \exp (-1)$
and
$\exp (-\lambda _n) \geq \exp (-1)$
and
![]() $\eta _n((0,C]) \leq 1$
for all
$\eta _n((0,C]) \leq 1$
for all
![]() $n \in \mathbb {N}$
, it follows from equations (3.29) and (3.13) that for every
$n \in \mathbb {N}$
, it follows from equations (3.29) and (3.13) that for every
![]() $C> 0$
,
$C> 0$
,
 $$ \begin{align} \sum_{n=1}^{\infty} \int_{(0,C]} x^2 \, d\eta_n(x) < +\infty \;. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \int_{(0,C]} x^2 \, d\eta_n(x) < +\infty \;. \end{align} $$
Denote
![]() $\rho _n = \eta _n|_{(0,1]}$
and, for all
$\rho _n = \eta _n|_{(0,1]}$
and, for all
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $\eta _{n,k} = \eta _n|_{(k,k+1]}$
. Since
$\eta _{n,k} = \eta _n|_{(k,k+1]}$
. Since
![]() $\mathcal {E}(\eta _n)$
is the convolution of the measures
$\mathcal {E}(\eta _n)$
is the convolution of the measures
![]() $\mathcal {E}(\rho _n)$
and
$\mathcal {E}(\rho _n)$
and
![]() $\mathcal {E}(\eta _{n,k})$
,
$\mathcal {E}(\eta _{n,k})$
,
![]() $n,k \in \mathbb {N}$
, we conclude that
$n,k \in \mathbb {N}$
, we conclude that
![]() $\mathbb {R} \curvearrowright X$
also is the tail boundary flow of the union of the probability measures
$\mathbb {R} \curvearrowright X$
also is the tail boundary flow of the union of the probability measures
![]() $\mathcal {E}(\rho _n)$
,
$\mathcal {E}(\rho _n)$
,
![]() $n \in \mathbb {N}$
, and
$n \in \mathbb {N}$
, and
![]() $\mathcal {E}(\eta _{n,k})$
,
$\mathcal {E}(\eta _{n,k})$
,
![]() $n,k \in \mathbb {N}$
.
$n,k \in \mathbb {N}$
.
By equations (3.30) and (3.24), we have
![]() $\sum _{n=1}^{\infty } \operatorname {Var}(\mathcal {E}(\rho _n)) < +\infty $
. By, e.g., [Reference Berendschot and Vaes8, Proposition 2.1], the tail boundary flow of
$\sum _{n=1}^{\infty } \operatorname {Var}(\mathcal {E}(\rho _n)) < +\infty $
. By, e.g., [Reference Berendschot and Vaes8, Proposition 2.1], the tail boundary flow of
![]() $(\mathcal {E}(\rho _n))_{n \in \mathbb {N}}$
is given by the translation action
$(\mathcal {E}(\rho _n))_{n \in \mathbb {N}}$
is given by the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
, so that
$\mathbb {R} \curvearrowright \mathbb {R}$
, so that
![]() $\mathbb {R} \curvearrowright X$
is the tail boundary flow of the measures
$\mathbb {R} \curvearrowright X$
is the tail boundary flow of the measures
![]() $\mathcal {E}(\eta _{n,k})$
,
$\mathcal {E}(\eta _{n,k})$
,
![]() $n,k \in \mathbb {N}$
.
$n,k \in \mathbb {N}$
.
For every fixed
![]() $k \in \mathbb {N}$
, it follows from equation (3.30) that
$k \in \mathbb {N}$
, it follows from equation (3.30) that
![]() $\sum _{n =1}^{\infty } \eta _{n,k}(\mathbb {R}) < +\infty $
. We define
$\sum _{n =1}^{\infty } \eta _{n,k}(\mathbb {R}) < +\infty $
. We define
![]() $\zeta _k = \sum _{n=1}^{\infty } \eta _{n,k}$
and conclude that
$\zeta _k = \sum _{n=1}^{\infty } \eta _{n,k}$
and conclude that
![]() $\mathbb {R} \curvearrowright X$
is the tail boundary flow of
$\mathbb {R} \curvearrowright X$
is the tail boundary flow of
![]() $\mathcal {E}(\zeta _k)$
,
$\mathcal {E}(\zeta _k)$
,
![]() $k \in I$
, where
$k \in I$
, where
![]() $\zeta _k$
is a finite positive measure supported on
$\zeta _k$
is a finite positive measure supported on
![]() $(k,k+1]$
.
$(k,k+1]$
.
Write
![]() $\ell _k = \zeta _k(\mathbb {R})$
, and fix integers
$\ell _k = \zeta _k(\mathbb {R})$
, and fix integers
![]() $L_k \geq \ell _k$
. Since
$L_k \geq \ell _k$
. Since
![]() $\mathbb {R} \curvearrowright X$
also is the tail boundary flow of the measures
$\mathbb {R} \curvearrowright X$
also is the tail boundary flow of the measures
![]() $\mathcal {E}(\zeta _k/L_k)$
, each repeated
$\mathcal {E}(\zeta _k/L_k)$
, each repeated
![]() $L_k$
times, and since
$L_k$
times, and since
![]() $\exp (-1) L_k^{-1} \zeta _k \leq \mathcal {E}(\zeta _k/L_k)$
, it follows from Proposition 3.3 that the points
$\exp (-1) L_k^{-1} \zeta _k \leq \mathcal {E}(\zeta _k/L_k)$
, it follows from Proposition 3.3 that the points
 $$ \begin{align*}b_k = \ell_k^{-1} \int_{\mathbb{R}} x \, d\zeta_k(x) \in (k,k+1] \quad\text{satisfy}\quad \sum_{k=1}^{\infty} \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) < +\infty \; .\end{align*} $$
$$ \begin{align*}b_k = \ell_k^{-1} \int_{\mathbb{R}} x \, d\zeta_k(x) \in (k,k+1] \quad\text{satisfy}\quad \sum_{k=1}^{\infty} \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) < +\infty \; .\end{align*} $$
Denote by
![]() $W_2$
the Wasserstein
$W_2$
the Wasserstein
![]() $2$
-distance. By equation (3.6), we have that
$2$
-distance. By equation (3.6), we have that
 $$ \begin{align*}W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 \leq \exp(-\ell_k) \sum_{j=1}^{\infty} \frac{1}{j!} \int_{\mathbb{R}} (x - j b_k)^2 \, d\zeta_k^{* j}(x) \; .\end{align*} $$
$$ \begin{align*}W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 \leq \exp(-\ell_k) \sum_{j=1}^{\infty} \frac{1}{j!} \int_{\mathbb{R}} (x - j b_k)^2 \, d\zeta_k^{* j}(x) \; .\end{align*} $$
For every
![]() $j \geq 1$
, we have that
$j \geq 1$
, we have that
 $$ \begin{align*} \int_{\mathbb{R}} (x - j b_k)^2 \, d\zeta_k^{* j}(x) &= \int_{\mathbb{R}^j} \bigl( (x_1 - b_k) + \cdots + (x_j - b_k) \bigr)^2 \, d\zeta_k(x_1) \, \cdots \, d\zeta_k(x_j) \\ &= j \, \ell_k^{j-1} \, \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) \;. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}} (x - j b_k)^2 \, d\zeta_k^{* j}(x) &= \int_{\mathbb{R}^j} \bigl( (x_1 - b_k) + \cdots + (x_j - b_k) \bigr)^2 \, d\zeta_k(x_1) \, \cdots \, d\zeta_k(x_j) \\ &= j \, \ell_k^{j-1} \, \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) \;. \end{align*} $$
We conclude that
 $$ \begin{align*}W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 \leq \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) \quad\text{so that}\quad \sum_{k=1}^{\infty} W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 < + \infty \; .\end{align*} $$
$$ \begin{align*}W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 \leq \int_{\mathbb{R}} (x-b_k)^2 \, d\zeta_k(x) \quad\text{so that}\quad \sum_{k=1}^{\infty} W_2(\mathcal{E}(\zeta_k), \mathcal{E}(\ell_k \delta_{b_k}))^2 < + \infty \; .\end{align*} $$
By Proposition 3.2,
![]() $\mathbb {R} \curvearrowright X$
is also the tail boundary flow of the sequence
$\mathbb {R} \curvearrowright X$
is also the tail boundary flow of the sequence
![]() $\mathcal {E}(\ell _k \delta _{b_k})$
,
$\mathcal {E}(\ell _k \delta _{b_k})$
,
![]() $k \in \mathbb {N}$
. Write
$k \in \mathbb {N}$
. Write
![]() $\ell ^{\prime }_k = \exp (-b_k)(1+\exp (-b_k))^{-1}$
. Take integers
$\ell ^{\prime }_k = \exp (-b_k)(1+\exp (-b_k))^{-1}$
. Take integers
![]() $M_k \geq 1$
such that
$M_k \geq 1$
such that
![]() $|M_k \ell ^{\prime }_k - \ell _k| \leq \ell ^{\prime }_k$
. For all
$|M_k \ell ^{\prime }_k - \ell _k| \leq \ell ^{\prime }_k$
. For all
![]() $c,d> 0$
and
$c,d> 0$
and
![]() $k \in \mathbb {N}$
, one has
$k \in \mathbb {N}$
, one has
 $$ \begin{align*}|c^k - d^k| = |c-d| \, \bigl|\sum_{i=0}^{k-1} c^i d^{k-1-i}\bigr| \leq k \, |c-d| \, (\max\{c,d\})^{k-1} \; \end{align*} $$
$$ \begin{align*}|c^k - d^k| = |c-d| \, \bigl|\sum_{i=0}^{k-1} c^i d^{k-1-i}\bigr| \leq k \, |c-d| \, (\max\{c,d\})^{k-1} \; \end{align*} $$
so that
![]() $d_{\operatorname {TV}}(\mathcal {E}(c \delta _b) , \mathcal {E}(d \delta _b)) \leq |c-d|$
for all
$d_{\operatorname {TV}}(\mathcal {E}(c \delta _b) , \mathcal {E}(d \delta _b)) \leq |c-d|$
for all
![]() $c, d> 0$
. Therefore,
$c, d> 0$
. Therefore,
By equation (3.28), we have
Since
![]() $b_k> k$
, the sequence
$b_k> k$
, the sequence
![]() $\exp (-b_k)$
is summable. It then follows from Lemma 3.1 that
$\exp (-b_k)$
is summable. It then follows from Lemma 3.1 that
![]() $\mathbb {R} \curvearrowright X$
is the tail boundary flow of the measures
$\mathbb {R} \curvearrowright X$
is the tail boundary flow of the measures
![]() $(\gamma (b_k)^{* M_k})_{k \in \mathbb {N}}$
and, hence, is isomorphic with the flow of weights of an ITPFI
$(\gamma (b_k)^{* M_k})_{k \in \mathbb {N}}$
and, hence, is isomorphic with the flow of weights of an ITPFI
![]() $_2$
factor.
$_2$
factor.
The proof of Theorem 3.9 relied on Prokhorov’s (3.28). Using the full force of [Reference Barbour and Hall4, Theorem 1], we can also prove the following result.
Proposition 3.11. The Poisson flows are exactly the tail boundary flows of sequences
![]() $(\mu _n)_{n \in \mathbb {N}}$
where the support of all
$(\mu _n)_{n \in \mathbb {N}}$
where the support of all
![]() $\mu _n$
consists of two points and
$\mu _n$
consists of two points and
![]() $\sup _{n \in \mathbb {N}} \operatorname {Var} \mu _n < +\infty $
.
$\sup _{n \in \mathbb {N}} \operatorname {Var} \mu _n < +\infty $
.
The Poisson flows of positive type are exactly the tail boundary flows of such sequences
![]() $(\mu _n)_{n \in \mathbb {N}}$
with support
$(\mu _n)_{n \in \mathbb {N}}$
with support
![]() $a_n < b_n$
and
$a_n < b_n$
and
![]() $\mu _n(a_n) \geq \mu _n(b_n)$
, and
$\mu _n(a_n) \geq \mu _n(b_n)$
, and
![]() $\sup _{n \in \mathbb {N}} \operatorname {Var} \mu _n < +\infty $
.
$\sup _{n \in \mathbb {N}} \operatorname {Var} \mu _n < +\infty $
.
Some bound on the variances
![]() $\operatorname {Var} \mu _n$
must be imposed in order to get a Poisson flow. Combining [Reference Giordano, Skandalis and Woods28, Theorem 2.1] and Proposition 3.13 below, it follows that the tail boundary flow of the sequence of probability measures
$\operatorname {Var} \mu _n$
must be imposed in order to get a Poisson flow. Combining [Reference Giordano, Skandalis and Woods28, Theorem 2.1] and Proposition 3.13 below, it follows that the tail boundary flow of the sequence of probability measures
![]() $\bigl ((\delta _0 + \delta _{8^n})/2\bigr )_{n \in \mathbb {N}}$
is not a Poisson flow.
$\bigl ((\delta _0 + \delta _{8^n})/2\bigr )_{n \in \mathbb {N}}$
is not a Poisson flow.
Proof. First, assume that
![]() $\mathbb {R} \curvearrowright Z$
is a Poisson flow. In most of the proof of Theorem 3.9, we did not use that the measures are supported on the positive real line. Writing
$\mathbb {R} \curvearrowright Z$
is a Poisson flow. In most of the proof of Theorem 3.9, we did not use that the measures are supported on the positive real line. Writing
![]() $I = \mathbb {Z} \setminus \{-1,0\}$
, we find for every
$I = \mathbb {Z} \setminus \{-1,0\}$
, we find for every
![]() $k \in I$
, elements
$k \in I$
, elements
![]() $b_k \in (k,k+1]$
and constants
$b_k \in (k,k+1]$
and constants
![]() $\lambda _k> 0$
such that
$\lambda _k> 0$
such that
![]() $\mathbb {R} \curvearrowright Z$
is isomorphic with the tail boundary flow of the family
$\mathbb {R} \curvearrowright Z$
is isomorphic with the tail boundary flow of the family
![]() $(\mathcal {E}(\lambda _k \delta _{b_k}))_{k \in I}$
. Choose for every
$(\mathcal {E}(\lambda _k \delta _{b_k}))_{k \in I}$
. Choose for every
![]() $k \in I$
an integer
$k \in I$
an integer
![]() $M_k \geq 1$
such that
$M_k \geq 1$
such that
![]() $M_k^{-1} \lambda _k \leq 2^{-|k|}$
. Define for
$M_k^{-1} \lambda _k \leq 2^{-|k|}$
. Define for
![]() $k \in I$
, the probability measure
$k \in I$
, the probability measure
By equation (3.28), we have
![]() $d_{\operatorname {TV}}\bigl (\mathcal {E}(\lambda _k \delta _{b_k}) , \eta _k^{*M_k}\bigr ) \leq M_k^{-1} \lambda _k \leq 2^{-|k|}$
, which is summable. By Lemma 3.1,
$d_{\operatorname {TV}}\bigl (\mathcal {E}(\lambda _k \delta _{b_k}) , \eta _k^{*M_k}\bigr ) \leq M_k^{-1} \lambda _k \leq 2^{-|k|}$
, which is summable. By Lemma 3.1,
![]() $\mathbb {R} \curvearrowright Z$
is isomorphic with the tail boundary flow of the probability measures
$\mathbb {R} \curvearrowright Z$
is isomorphic with the tail boundary flow of the probability measures
![]() $\eta _k$
repeated
$\eta _k$
repeated
![]() $M_k$
times,
$M_k$
times,
![]() $k \in I$
. Since
$k \in I$
. Since
one implication of the proposition is proven.
Conversely, assume that
![]() $(\mu _n)_{n \in \mathbb {N}}$
is a sequence of probability measures whose support consists of two points and that satisfy
$(\mu _n)_{n \in \mathbb {N}}$
is a sequence of probability measures whose support consists of two points and that satisfy
![]() $\operatorname {Var} \mu _n \leq C$
for all
$\operatorname {Var} \mu _n \leq C$
for all
![]() $n \in \mathbb {N}$
. Denote by
$n \in \mathbb {N}$
. Denote by
![]() $\mathbb {R} \curvearrowright Z$
their tail boundary flow. We have to prove that
$\mathbb {R} \curvearrowright Z$
their tail boundary flow. We have to prove that
![]() $\mathbb {R} \curvearrowright Z$
is a Poisson flow. We may thus assume that
$\mathbb {R} \curvearrowright Z$
is a Poisson flow. We may thus assume that
![]() $\mathbb {R} \curvearrowright Z$
is aperiodic. Since translating the measures
$\mathbb {R} \curvearrowright Z$
is aperiodic. Since translating the measures
![]() $\mu _n$
does not change the tail boundary flow, we may assume that
$\mu _n$
does not change the tail boundary flow, we may assume that
![]() $\mu _n(0) \geq 1/2$
for all
$\mu _n(0) \geq 1/2$
for all
![]() $n \in \mathbb {N}$
, and we denote by
$n \in \mathbb {N}$
, and we denote by
![]() $d_n \in \mathbb {R}$
the other atom of
$d_n \in \mathbb {R}$
the other atom of
![]() $\mu _n$
. Write
$\mu _n$
. Write
![]() $p_n = \mu _n(d_n)$
Since
$p_n = \mu _n(d_n)$
Since
![]() $\operatorname {Var} \mu _n \leq C$
, we get that
$\operatorname {Var} \mu _n \leq C$
, we get that
![]() $p_n d_n^2 \leq 2 C$
for all
$p_n d_n^2 \leq 2 C$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
For every
![]() $k \in \mathbb {Z}$
, write
$k \in \mathbb {Z}$
, write
![]() $J_k = \{n \in \mathbb {N} \mid d_n \in [k,k+1)\}$
. Write
$J_k = \{n \in \mathbb {N} \mid d_n \in [k,k+1)\}$
. Write
![]() $I = \mathbb {Z} \setminus \{-1,0,1\}$
. Arguing as in the proof of Theorem 3.9, it follows from Proposition 3.3 that
$I = \mathbb {Z} \setminus \{-1,0,1\}$
. Arguing as in the proof of Theorem 3.9, it follows from Proposition 3.3 that
and it follows from Proposition 3.4 that we find for every
![]() $k \in I$
an element
$k \in I$
an element
![]() $b_k \in [k,k+1)$
such that
$b_k \in [k,k+1)$
such that
By equation (3.31), the tail boundary flow of the measures
![]() $(\mu _n)_{n \in J_{-1} \cup J_0 \cup J_1}$
is given by the translation action
$(\mu _n)_{n \in J_{-1} \cup J_0 \cup J_1}$
is given by the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
so that these measures may be ignored. Defining for every
$\mathbb {R} \curvearrowright \mathbb {R}$
so that these measures may be ignored. Defining for every
![]() $k \in I$
and
$k \in I$
and
![]() $n \in J_k$
the probability measure
$n \in J_k$
the probability measure
![]() $\eta _n = (1-p_n) \delta _0 + p_n \delta _{b_k}$
, note that equation (3.32) is saying that
$\eta _n = (1-p_n) \delta _0 + p_n \delta _{b_k}$
, note that equation (3.32) is saying that
It thus follows from Proposition 3.2 that
![]() $\mathbb {R} \curvearrowright Z$
is the tail boundary flow of the measures
$\mathbb {R} \curvearrowright Z$
is the tail boundary flow of the measures
![]() $\eta _n$
,
$\eta _n$
,
![]() $k \in I$
,
$k \in I$
,
![]() $n \in J_k$
. Write
$n \in J_k$
. Write
![]() $\lambda _k = \sum _{n \in J_k} p_n$
. By [Reference Barbour and Hall4, Theorem 1], we have for every
$\lambda _k = \sum _{n \in J_k} p_n$
. By [Reference Barbour and Hall4, Theorem 1], we have for every
![]() $k \in I$
that
$k \in I$
that
 $$ \begin{align*} d_{\operatorname{TV}}\Bigl( \operatorname*{{\Large {\ast}}}_{n \in J_k} \eta_n \, , \, \mathcal{E}(\lambda_k \delta_{b_k})\Bigr) \leq \lambda_k^{-1} \sum_{n \in J_k} p_n^2 \leq \max_{n \in J_k} p_n \leq \max_{n \in J_k} 2 C d_n^{-2} \leq \frac{2C}{(|k|-1)^2} , \end{align*} $$
$$ \begin{align*} d_{\operatorname{TV}}\Bigl( \operatorname*{{\Large {\ast}}}_{n \in J_k} \eta_n \, , \, \mathcal{E}(\lambda_k \delta_{b_k})\Bigr) \leq \lambda_k^{-1} \sum_{n \in J_k} p_n^2 \leq \max_{n \in J_k} p_n \leq \max_{n \in J_k} 2 C d_n^{-2} \leq \frac{2C}{(|k|-1)^2} , \end{align*} $$
where we used that
![]() $d_n \in [k,k+1)$
if
$d_n \in [k,k+1)$
if
![]() $n \in J_k$
. Since the right-hand side is summable, it follows from Lemma 3.1 that
$n \in J_k$
. Since the right-hand side is summable, it follows from Lemma 3.1 that
![]() $\mathbb {R} \curvearrowright Z$
is also the tail boundary flow of the Poisson distributions
$\mathbb {R} \curvearrowright Z$
is also the tail boundary flow of the Poisson distributions
![]() $(\mathcal {E}(\lambda _k \delta _{b_k}))_{k \in I}$
and thus is a Poisson flow.
$(\mathcal {E}(\lambda _k \delta _{b_k}))_{k \in I}$
and thus is a Poisson flow.
The positive case is proven entirely analogously.
3.3 Infinitely divisible flows
Definition 3.12. We say that a flow
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
is infinitely divisible if for every integer
$\mathbb {R} \curvearrowright (Z,\eta )$
is infinitely divisible if for every integer
![]() $L \geq 1$
, there exists a flow
$L \geq 1$
, there exists a flow
![]() $\mathbb {R} \curvearrowright (Z_1,\eta _1)$
such that
$\mathbb {R} \curvearrowright (Z_1,\eta _1)$
such that
![]() $\mathbb {R} \curvearrowright (Z,\eta )$
is isomorphic with the joint flow of L copies of
$\mathbb {R} \curvearrowright (Z,\eta )$
is isomorphic with the joint flow of L copies of
![]() $\mathbb {R} \curvearrowright (Z_1,\eta _1)$
.
$\mathbb {R} \curvearrowright (Z_1,\eta _1)$
.
Proposition 3.13. Every Poisson flow is infinitely divisible.
Every tail boundary flow of a sequence of infinitely divisible distributions is a Poisson flow.
Proof. If
![]() $\mathbb {R} \curvearrowright Z$
is the tail boundary flow of the sequence
$\mathbb {R} \curvearrowright Z$
is the tail boundary flow of the sequence
![]() $(\mathcal {E}(\mu _n))_{n \in \mathbb {N}}$
, where
$(\mathcal {E}(\mu _n))_{n \in \mathbb {N}}$
, where
![]() $\mu _n$
is a sequence of finite positive measures on
$\mu _n$
is a sequence of finite positive measures on
![]() $\mathbb {R}$
, and if
$\mathbb {R}$
, and if
![]() $L \geq 1$
is an integer, we can define
$L \geq 1$
is an integer, we can define
![]() $\mathbb {R} \curvearrowright Z_1$
as the tail boundary flow of the sequence
$\mathbb {R} \curvearrowright Z_1$
as the tail boundary flow of the sequence
![]() $(\mathcal {E}(L^{-1} \mu _n))_{n \in \mathbb {N}}$
. By construction,
$(\mathcal {E}(L^{-1} \mu _n))_{n \in \mathbb {N}}$
. By construction,
![]() $\mathbb {R} \curvearrowright Z$
is isomorphic with the joint flow of L copies of
$\mathbb {R} \curvearrowright Z$
is isomorphic with the joint flow of L copies of
![]() $\mathbb {R} \curvearrowright Z_1$
.
$\mathbb {R} \curvearrowright Z_1$
.
Since compound Poisson distributions
![]() $\mathcal {E}(\mu )$
are weakly dense in the set of infinitely divisible distributions (see, e.g., [Reference Stroock48, Theorem 3.2.7]), the second statement follows directly from Lemma 3.14 below.
$\mathcal {E}(\mu )$
are weakly dense in the set of infinitely divisible distributions (see, e.g., [Reference Stroock48, Theorem 3.2.7]), the second statement follows directly from Lemma 3.14 below.
Lemma 3.14. Let
![]() $\mathcal {F} \subset \operatorname {Prob}(\mathbb {R})$
with weak closure
$\mathcal {F} \subset \operatorname {Prob}(\mathbb {R})$
with weak closure
![]() $\overline {\mathcal {F}}$
. Every ergodic flow that can be obtained as the tail boundary flow of a sequence in
$\overline {\mathcal {F}}$
. Every ergodic flow that can be obtained as the tail boundary flow of a sequence in
![]() $\overline {\mathcal {F}}$
can also be obtained as the tail boundary flow of a sequence in
$\overline {\mathcal {F}}$
can also be obtained as the tail boundary flow of a sequence in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Proof. Let
![]() $(\mu _n)_{n \in \mathbb {N}}$
be a sequence in
$(\mu _n)_{n \in \mathbb {N}}$
be a sequence in
![]() $\overline {\mathcal {F}}$
. Denote by
$\overline {\mathcal {F}}$
. Denote by
![]() $\nu _n$
the uniform probability measure on the interval
$\nu _n$
the uniform probability measure on the interval
![]() $[-1/n,1/n]$
so that
$[-1/n,1/n]$
so that
![]() $\operatorname {Var} \nu _n = n^{-2}/2$
is summable. By, e.g., [Reference Berendschot and Vaes8, Proposition 2.1], the tail boundary flow of the sequence
$\operatorname {Var} \nu _n = n^{-2}/2$
is summable. By, e.g., [Reference Berendschot and Vaes8, Proposition 2.1], the tail boundary flow of the sequence
![]() $(\nu _n)_{n \in \mathbb {N}}$
is the translation action
$(\nu _n)_{n \in \mathbb {N}}$
is the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
. Therefore,
$\mathbb {R} \curvearrowright \mathbb {R}$
. Therefore,
![]() $(\mu _n)_{n \in \mathbb {N}}$
and
$(\mu _n)_{n \in \mathbb {N}}$
and
![]() $(\mu _n * \nu _n)_{n \in \mathbb {N}}$
give rise to isomorphic tail boundary flows.
$(\mu _n * \nu _n)_{n \in \mathbb {N}}$
give rise to isomorphic tail boundary flows.
Since
![]() $\mathcal {F}$
is weakly dense in
$\mathcal {F}$
is weakly dense in
![]() $\overline {\mathcal {F}}$
and since
$\overline {\mathcal {F}}$
and since
![]() $\nu _n$
is absolutely continuous, we can choose
$\nu _n$
is absolutely continuous, we can choose
![]() $\mu ^{\prime }_n \in \mathcal {F}$
such that
$\mu ^{\prime }_n \in \mathcal {F}$
such that
![]() $d_{\operatorname {TV}}\bigl (\mu ^{\prime }_n * \nu _n , \mu _n * \nu _n\bigr ) \leq n^{-2}$
. By Lemma 3.1, also
$d_{\operatorname {TV}}\bigl (\mu ^{\prime }_n * \nu _n , \mu _n * \nu _n\bigr ) \leq n^{-2}$
. By Lemma 3.1, also
![]() $(\mu _n * \nu _n)_{n \in \mathbb {N}}$
and
$(\mu _n * \nu _n)_{n \in \mathbb {N}}$
and
![]() $(\mu ^{\prime }_n * \nu _n)_{n \in \mathbb {N}}$
give rise to isomorphic tail boundary flows, with the latter being isomorphic to the tail boundary flow of
$(\mu ^{\prime }_n * \nu _n)_{n \in \mathbb {N}}$
give rise to isomorphic tail boundary flows, with the latter being isomorphic to the tail boundary flow of
![]() $(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
.
$(\mu ^{\prime }_n)_{n \in \mathbb {N}}$
.
Define for every
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $a \in \mathbb {R}$
the standard Poisson distribution with support
$a \in \mathbb {R}$
the standard Poisson distribution with support
![]() $\{k a \mid k=0,1,2,\ldots \}$
given by
$\{k a \mid k=0,1,2,\ldots \}$
given by
Proposition 3.15. Every Poisson flow is the tail boundary flow of a sequence
![]() $(\sigma _{\lambda _n,a_n})_{n \in \mathbb {N}}$
with
$(\sigma _{\lambda _n,a_n})_{n \in \mathbb {N}}$
with
![]() $\lambda _n> 0$
and
$\lambda _n> 0$
and
![]() $a_n \in \mathbb {R}$
.
$a_n \in \mathbb {R}$
.
Proof. The convolution products of measures of the form
![]() $\sigma _{\lambda ,a}$
are precisely the compound Poisson distributions
$\sigma _{\lambda ,a}$
are precisely the compound Poisson distributions
![]() $\mathcal {E}(\mu )$
where
$\mathcal {E}(\mu )$
where
![]() $\mu $
is a finite positive measure with finite support. These
$\mu $
is a finite positive measure with finite support. These
![]() $\mathcal {E}(\mu )$
are weakly dense in the set of all compound Poisson distributions. The conclusion thus immediately follows from Lemma 3.14.
$\mathcal {E}(\mu )$
are weakly dense in the set of all compound Poisson distributions. The conclusion thus immediately follows from Lemma 3.14.
Remark 3.16. Because of Proposition 3.13, it is tempting to speculate that every infinitely divisible flow is a Poisson flow, at least if the flow is assumed to be approximately transitive (and thus, the tail boundary flow of some sequence of probability measures, by [Reference Connes and Woods17, Theorem 3.2]). We have, however, no idea how to prove such a statement.
Going back to Theorem 3.9, it is also unclear whether every Poisson flow is automatically of positive type. Because of Theorem 3.9, this question is equivalent with the following seemingly innocent, but highly tantalizing, problem: If
![]() $\mathbb {R} \curvearrowright ^{\alpha } Z$
is the flow of weights of an ITPFI
$\mathbb {R} \curvearrowright ^{\alpha } Z$
is the flow of weights of an ITPFI
![]() $_2$
factor, does it follow that the reverse flow
$_2$
factor, does it follow that the reverse flow
![]() $\beta _t(z) = \alpha _{-t}(z)$
also is the flow of weights of an ITPFI
$\beta _t(z) = \alpha _{-t}(z)$
also is the flow of weights of an ITPFI
![]() $_2$
factor?
$_2$
factor?
Combining both open problems, it is tempting to speculate that the ITPFI
![]() $_2$
factors are precisely the injective factors M that are infinitely divisible, in the sense that for every integer
$_2$
factors are precisely the injective factors M that are infinitely divisible, in the sense that for every integer
![]() $L \geq 1$
, there exists a factor N such that
$L \geq 1$
, there exists a factor N such that
![]() $M \cong N^{\mathbin {\overline {\otimes }} L}$
, or to speculate that at least, infinite divisibility characterizes the ITPFI
$M \cong N^{\mathbin {\overline {\otimes }} L}$
, or to speculate that at least, infinite divisibility characterizes the ITPFI
![]() $_2$
factors among the ITPFI factors.
$_2$
factors among the ITPFI factors.
4 Nonsingular Bernoulli shifts: proof of Theorem A
The goal of this section is to prove the following more precise formulation of Theorem A. Since we want to describe absolutely general Bernoulli shifts, the formulation becomes a bit lengthy because we have to deal with the less interesting cases that may arise where the space has atoms or the action is dissipative.
We denote by
![]() $\mathcal {S}$
the group of finite permutations of the countable set
$\mathcal {S}$
the group of finite permutations of the countable set
![]() $\mathbb {Z}$
and let
$\mathbb {Z}$
and let
![]() $\mathcal {S}$
act on
$\mathcal {S}$
act on
![]() $(X,\mu ) = \prod _{n \in \mathbb {Z}} (X_n,\mu _n)$
by
$(X,\mu ) = \prod _{n \in \mathbb {Z}} (X_n,\mu _n)$
by
![]() $(\sigma \cdot x)_n = x_{\sigma ^{-1}(n)}$
.
$(\sigma \cdot x)_n = x_{\sigma ^{-1}(n)}$
.
Theorem 4.1. Let
![]() $X_0$
be any standard Borel space, and let
$X_0$
be any standard Borel space, and let
![]() $(\mu _n)_{n \in \mathbb {Z}}$
be any family of equivalent probability measures on
$(\mu _n)_{n \in \mathbb {Z}}$
be any family of equivalent probability measures on
![]() $X_0$
such that the Bernoulli shift
$X_0$
such that the Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu ) = \prod _{n \in \mathbb {Z}} (X_0,\mu _n)$
is nonsingular.
$\mathbb {Z} \curvearrowright (X,\mu ) = \prod _{n \in \mathbb {Z}} (X_0,\mu _n)$
is nonsingular.
Then precisely one of the following statements holds.
-
1. There exists an atom
 $b \in X_0$
with
$b \in X_0$
with
 $\sum _{n \in \mathbb {Z}} (1-\mu _n(\{b\})) < +\infty $
. Define
$\sum _{n \in \mathbb {Z}} (1-\mu _n(\{b\})) < +\infty $
. Define
 $a \in X$
by
$a \in X$
by
 $a_n = b$
for all
$a_n = b$
for all
 $n \in \mathbb {Z}$
. Then, a is an atom in X that is fixed by
$n \in \mathbb {Z}$
. Then, a is an atom in X that is fixed by
 $\mathbb {Z}$
. The action of
$\mathbb {Z}$
. The action of
 $\mathbb {Z}$
on
$\mathbb {Z}$
on
 $X \setminus \{a\}$
is essentially free and dissipative.
$X \setminus \{a\}$
is essentially free and dissipative. -
2. The action
 $\mathbb {Z} \curvearrowright (X,\mu )$
is essentially free and dissipative.
$\mathbb {Z} \curvearrowright (X,\mu )$
is essentially free and dissipative. -
3. The space
 $(X,\mu )$
is nonatomic, and there exists a Borel set
$(X,\mu )$
is nonatomic, and there exists a Borel set
 $C_0 \subset X_0$
of positive measure, unique up to a null set, such that
$C_0 \subset X_0$
of positive measure, unique up to a null set, such that
 $\sum _{n \in \mathbb {Z}} (1-\mu _n(C_0)) < + \infty $
and such that the following holds.
$\sum _{n \in \mathbb {Z}} (1-\mu _n(C_0)) < + \infty $
and such that the following holds.-
• The action
 $\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
is a weakly mixing Bernoulli shift, and its associated flow is infinitely divisible. Moreover, the permutation action
$\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
is a weakly mixing Bernoulli shift, and its associated flow is infinitely divisible. Moreover, the permutation action
 $\mathcal {S} \curvearrowright C_0^{\mathbb {Z}}$
is ergodic, and for every ergodic probability measure preserving (pmp) action
$\mathcal {S} \curvearrowright C_0^{\mathbb {Z}}$
is ergodic, and for every ergodic probability measure preserving (pmp) action
 $\mathbb {Z} \curvearrowright (Y,\nu )$
, the actions
$\mathbb {Z} \curvearrowright (Y,\nu )$
, the actions
 $\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
,
$\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}}$
,
 $\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}} \times Y$
and
$\mathbb {Z} \curvearrowright C_0^{\mathbb {Z}} \times Y$
and
 $\mathcal {S} \curvearrowright C_0^{\mathbb {Z}}$
have the same associated flow.
$\mathcal {S} \curvearrowright C_0^{\mathbb {Z}}$
have the same associated flow. -
• The action
 $\mathbb {Z} \curvearrowright X \setminus C_0^{\mathbb {Z}}$
is essentially free and dissipative.
$\mathbb {Z} \curvearrowright X \setminus C_0^{\mathbb {Z}}$
is essentially free and dissipative.
-
As already suggested by the formulation of Theorem 4.1, we again exploit the relation between a Bernoulli shift and the action
![]() $\mathcal {S} \curvearrowright (X,\mu )$
. This method was discovered in [Reference Kosloff37, Reference Danilenko18] and has been further developed in [Reference Björklund, Kosloff and Vaes7, Reference Berendschot and Vaes8].
$\mathcal {S} \curvearrowright (X,\mu )$
. This method was discovered in [Reference Kosloff37, Reference Danilenko18] and has been further developed in [Reference Björklund, Kosloff and Vaes7, Reference Berendschot and Vaes8].
Because of Theorem 4.1, to study nonsingular Bernoulli shifts in their full generality, it suffices to consider Bernoulli shifts that are conservative. Also, given any conservative Bernoulli action
![]() $G\curvearrowright \prod _{g\in G}(C_0,\eta _g)$
, we can add a standard Borel space
$G\curvearrowright \prod _{g\in G}(C_0,\eta _g)$
, we can add a standard Borel space
![]() $C_1$
to
$C_1$
to
![]() $C_0$
by putting
$C_0$
by putting
![]() $X_0=C_0\sqcup C_1$
and by choosing
$X_0=C_0\sqcup C_1$
and by choosing
![]() $\mu _g$
to be a family of equivalent measures on
$\mu _g$
to be a family of equivalent measures on
![]() $X_0$
such that
$X_0$
such that
![]() $\sum _{g\in G}\mu _g(C_1)<+\infty $
and such that
$\sum _{g\in G}\mu _g(C_1)<+\infty $
and such that
![]() $\mu _g|_{C_0}=\mu _g(C_0)\eta _g$
. The result is again a nonsingular Bernoulli action
$\mu _g|_{C_0}=\mu _g(C_0)\eta _g$
. The result is again a nonsingular Bernoulli action
![]() $G\curvearrowright (X,\mu )=\prod _{g\in G}(X_0,\mu _g)$
with dissipative part
$G\curvearrowright (X,\mu )=\prod _{g\in G}(X_0,\mu _g)$
with dissipative part
![]() $X\setminus C_0^{G}$
and conservative part
$X\setminus C_0^{G}$
and conservative part
![]() $C_0^{G}$
.
$C_0^{G}$
.
Note that if
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is a conservative ergodic nonsingular Bernoulli shift, it follows from Theorem 4.1 that it is has stable type in the strongest possible sense. Indeed, whenever
$\mathbb {Z}\curvearrowright (X,\mu )$
is a conservative ergodic nonsingular Bernoulli shift, it follows from Theorem 4.1 that it is has stable type in the strongest possible sense. Indeed, whenever
![]() $\mathbb {Z}\curvearrowright (Y,\nu )$
is an ergodic pmp action, the diagonal action
$\mathbb {Z}\curvearrowright (Y,\nu )$
is an ergodic pmp action, the diagonal action
![]() $\mathbb {Z}\curvearrowright X\times Y$
is ergodic of the same type, and with the same associated flow as
$\mathbb {Z}\curvearrowright X\times Y$
is ergodic of the same type, and with the same associated flow as
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
. This rigidity property for the group
$\mathbb {Z}\curvearrowright (X,\mu )$
. This rigidity property for the group
![]() $\mathbb {Z}$
is not shared by all countable infinite groups G, see [Reference Vaes and Wahl49, Proposition 7.3] and [Reference Björklund, Kosloff and Vaes7, Remark 6.4].
$\mathbb {Z}$
is not shared by all countable infinite groups G, see [Reference Vaes and Wahl49, Proposition 7.3] and [Reference Björklund, Kosloff and Vaes7, Remark 6.4].
When we rephrase Theorem 4.1 in terms of von Neumann algebras, we get the following result.
Corollary 4.2. Every crossed product
![]() $L^{\infty }(X)\rtimes \mathbb {Z}$
by a nonsingular Bernoulli shift
$L^{\infty }(X)\rtimes \mathbb {Z}$
by a nonsingular Bernoulli shift
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
, decomposes as
$\mathbb {Z}\curvearrowright (X,\mu )$
, decomposes as
where N is a type I von Neumann algebra, and M is an injective factor that is a p’th tensor power for every integer
![]() $p\geq 2$
.
$p\geq 2$
.
In addition to the structure result of Theorem 4.1, we are able to give a complete type classification for conservative nonsingular Bernoulli shifts, distinguishing between types II
![]() $_{1}$
, II
$_{1}$
, II
![]() $_{\infty }$
and III. The formulation of the result is similar to [Reference Berendschot and Vaes8, Theorem 4.1], but the important difference is that in our Theorem 4.3, we make no assumptions on the behavior of the Radon–Nikodym derivatives
$_{\infty }$
and III. The formulation of the result is similar to [Reference Berendschot and Vaes8, Theorem 4.1], but the important difference is that in our Theorem 4.3, we make no assumptions on the behavior of the Radon–Nikodym derivatives
![]() $d\mu _n/d\mu _0$
.
$d\mu _n/d\mu _0$
.
Theorem 4.3. Let
![]() $\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a conservative nonsingular Bernoulli shift. Then
$\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a conservative nonsingular Bernoulli shift. Then
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is weakly mixing and the following holds.
$\mathbb {Z}\curvearrowright (X,\mu )$
is weakly mixing and the following holds.
-
1.
 $\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
$\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
 $_{1}$
if and only if there exists a probability measure
$_{1}$
if and only if there exists a probability measure
 $\nu \sim \mu _0$
on
$\nu \sim \mu _0$
on
 $X_0$
such that
$X_0$
such that
 $\nu ^{\mathbb {Z}}\sim \mu $
.
$\nu ^{\mathbb {Z}}\sim \mu $
. -
2.
 $\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
$\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
 $_{\infty }$
if and only if there exists a
$_{\infty }$
if and only if there exists a
 $\sigma $
-finite measure
$\sigma $
-finite measure
 $\nu \sim \mu _0$
on
$\nu \sim \mu _0$
on
 $X_0$
and Borel sets
$X_0$
and Borel sets
 $\mathcal {U}_n\subset X_0$
such that
$\mathcal {U}_n\subset X_0$
such that
 $\nu (\mathcal {U}_n)<+\infty $
for all
$\nu (\mathcal {U}_n)<+\infty $
for all
 $n\in \mathbb {Z}$
and such that
$n\in \mathbb {Z}$
and such that  $$ \begin{align*} \sum_{n\in\mathbb{Z}}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty,\;\; \sum_{n\in \mathbb{Z}}H^{2}\left(\mu_n, \nu(\mathcal{U}_n)^{-1}\nu|_{\mathcal{U}_n}\right)<+\infty,\;\;\sum_{n\in \mathbb{Z}}\nu(X_0\setminus \mathcal{U}_n)=+\infty. \end{align*} $$
$$ \begin{align*} \sum_{n\in\mathbb{Z}}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty,\;\; \sum_{n\in \mathbb{Z}}H^{2}\left(\mu_n, \nu(\mathcal{U}_n)^{-1}\nu|_{\mathcal{U}_n}\right)<+\infty,\;\;\sum_{n\in \mathbb{Z}}\nu(X_0\setminus \mathcal{U}_n)=+\infty. \end{align*} $$
-
3.
 $\mathbb {Z}\curvearrowright (X,\mu )$
is of type III in all other cases.
$\mathbb {Z}\curvearrowright (X,\mu )$
is of type III in all other cases.
A key point in relating the Bernoulli shift
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
to the permutation action
$\mathbb {Z} \curvearrowright (X,\mu )$
to the permutation action
![]() $\mathcal {S} \curvearrowright (X,\mu )$
is the following lemma. The proof uses a key idea of [Reference Björklund, Kosloff and Vaes7, Theorem 3.3].
$\mathcal {S} \curvearrowright (X,\mu )$
is the following lemma. The proof uses a key idea of [Reference Björklund, Kosloff and Vaes7, Theorem 3.3].
Lemma 4.4. Let
![]() $\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a nonsingular Bernoulli shift that is essentially free and not dissipative. When viewing
$\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a nonsingular Bernoulli shift that is essentially free and not dissipative. When viewing
![]() $\mathbb {Z}$
and
$\mathbb {Z}$
and
![]() $\mathcal {S}$
as subgroups of
$\mathcal {S}$
as subgroups of
![]() $\operatorname {Aut}(X,\mu )$
, we have that
$\operatorname {Aut}(X,\mu )$
, we have that
![]() $\mathbb {Z}$
belongs to the closure of
$\mathbb {Z}$
belongs to the closure of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof. We start by proving the following claim.
Claim. There exist sequences
![]() $n_k\rightarrow -\infty , m_k\rightarrow +\infty $
such that
$n_k\rightarrow -\infty , m_k\rightarrow +\infty $
such that
We prove this claim using essentially the same argument as the one given in [Reference Björklund, Kosloff and Vaes7, Theorem 3.3]. Indeed, if such sequences do not exist, there are
![]() $\delta>0$
and
$\delta>0$
and
![]() $N\in \mathbb {N}$
such that for all
$N\in \mathbb {N}$
such that for all
![]() $n\leq -N, m\geq N$
we have that
$n\leq -N, m\geq N$
we have that
![]() $H(\mu _n,\mu _m)>\delta $
. Define the
$H(\mu _n,\mu _m)>\delta $
. Define the
![]() $1$
-cocycle
$1$
-cocycle
as introduced in [Reference Vaes and Wahl49, Theorem 3.1]. We have that
 $$ \begin{align*} \|c_k\|^2=\|c_{-k}\|^2=2 \sum_{m\in \mathbb{Z}}H^{2}(\mu_{m+k},\mu_m)\geq 2 \sum_{m=N-k}^{-N}H^{2}(\mu_{m+k},\mu_m)\geq 2(k-2N)\delta^2 \end{align*} $$
$$ \begin{align*} \|c_k\|^2=\|c_{-k}\|^2=2 \sum_{m\in \mathbb{Z}}H^{2}(\mu_{m+k},\mu_m)\geq 2 \sum_{m=N-k}^{-N}H^{2}(\mu_{m+k},\mu_m)\geq 2(k-2N)\delta^2 \end{align*} $$
for every
![]() $k\geq 2N$
. Therefore,
$k\geq 2N$
. Therefore,
![]() $\sum _{k\in \mathbb {Z}}\exp \left (-\|c_k\|^2/2\right )<+\infty $
, and it follows from [Reference Vaes and Wahl49, Theorem 4.1] that the action
$\sum _{k\in \mathbb {Z}}\exp \left (-\|c_k\|^2/2\right )<+\infty $
, and it follows from [Reference Vaes and Wahl49, Theorem 4.1] that the action
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is dissipative, which is in contradiction with our assumptions.
$\mathbb {Z}\curvearrowright (X,\mu )$
is dissipative, which is in contradiction with our assumptions.
Let
![]() $n_k\rightarrow -\infty $
and
$n_k\rightarrow -\infty $
and
![]() $m_k\rightarrow +\infty $
be sequences such that equation (4.1) holds. We may assume that
$m_k\rightarrow +\infty $
be sequences such that equation (4.1) holds. We may assume that
![]() $n_k<0<m_k$
for all
$n_k<0<m_k$
for all
![]() $k\in \mathbb {N}$
. Let
$k\in \mathbb {N}$
. Let
![]() $\alpha \in \operatorname {Aut}(X,\mu )$
denote the shift by one, i.e.,
$\alpha \in \operatorname {Aut}(X,\mu )$
denote the shift by one, i.e.,
![]() $(\alpha (x))_k=x_{k-1}$
. To prove the lemma, it suffices to show that
$(\alpha (x))_k=x_{k-1}$
. To prove the lemma, it suffices to show that
![]() $\alpha $
belongs to the closure of
$\alpha $
belongs to the closure of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
For each
![]() $k\in \mathbb {N}$
, we define the permutation
$k\in \mathbb {N}$
, we define the permutation
![]() $\sigma _k\in \mathcal {S}$
by
$\sigma _k\in \mathcal {S}$
by
 $$ \begin{align*} \sigma_k(n)=\begin{cases}n &\;\;\text{if}\;\; n\leq n_k \;\;\text{or}\;\; n\geq 1+m_k\\ n-1 &\;\;\text{if}\;\; 2+n_k\leq n\leq m_k\\ m_k &\;\;\text{if}\;\; n=1+n_k\end{cases} \end{align*} $$
$$ \begin{align*} \sigma_k(n)=\begin{cases}n &\;\;\text{if}\;\; n\leq n_k \;\;\text{or}\;\; n\geq 1+m_k\\ n-1 &\;\;\text{if}\;\; 2+n_k\leq n\leq m_k\\ m_k &\;\;\text{if}\;\; n=1+n_k\end{cases} \end{align*} $$
and write
![]() $\beta _k=\sigma _k\circ \alpha \in \operatorname {Aut}(X,\mu )$
. Define the unitary operators
$\beta _k=\sigma _k\circ \alpha \in \operatorname {Aut}(X,\mu )$
. Define the unitary operators
![]() $\theta _k\colon L^2(X,\mu )\rightarrow L^{2}(X,\mu )$
by
$\theta _k\colon L^2(X,\mu )\rightarrow L^{2}(X,\mu )$
by
 $$ \begin{align*} \theta_k(F)(x)=\sqrt{\frac{d(\mu\circ \beta_k)}{d\mu}(x)}F(\beta_k(x)). \end{align*} $$
$$ \begin{align*} \theta_k(F)(x)=\sqrt{\frac{d(\mu\circ \beta_k)}{d\mu}(x)}F(\beta_k(x)). \end{align*} $$
We will show that
![]() $\|\theta _k(F)-F\|_2\rightarrow 0$
for all F in a total subset of
$\|\theta _k(F)-F\|_2\rightarrow 0$
for all F in a total subset of
![]() $L^{2}(X,\mu )$
so that
$L^{2}(X,\mu )$
so that
![]() $\beta _k\rightarrow \mathord {\textrm{id}}$
as
$\beta _k\rightarrow \mathord {\textrm{id}}$
as
![]() $k\rightarrow +\infty $
. This then concludes the proof of the lemma.
$k\rightarrow +\infty $
. This then concludes the proof of the lemma.
Take
![]() $F\in L^{\infty }(X,\mu )$
depending only on the coordinates
$F\in L^{\infty }(X,\mu )$
depending only on the coordinates
![]() $x_n$
, for
$x_n$
, for
![]() $|n|\leq N$
, for some
$|n|\leq N$
, for some
![]() $N\in \mathbb {N}$
. With unconditional convergence almost everywhere, we have that
$N\in \mathbb {N}$
. With unconditional convergence almost everywhere, we have that
 $$ \begin{align*} \frac{d(\mu\circ \beta_k)}{d\mu}(x)=\prod_{n=-\infty}^{n_k-1}\frac{d\mu_{n+1}}{d\mu_n}(x_n)\cdot \frac{d\mu_{m_k}}{d\mu_{n_k}}(x_{n_k}) \cdot \prod_{n=m_k}^{\infty} \frac{d\mu_{n+1}}{d\mu_n}(x_n). \end{align*} $$
$$ \begin{align*} \frac{d(\mu\circ \beta_k)}{d\mu}(x)=\prod_{n=-\infty}^{n_k-1}\frac{d\mu_{n+1}}{d\mu_n}(x_n)\cdot \frac{d\mu_{m_k}}{d\mu_{n_k}}(x_{n_k}) \cdot \prod_{n=m_k}^{\infty} \frac{d\mu_{n+1}}{d\mu_n}(x_n). \end{align*} $$
Therefore,
 $$ \begin{align*} \int_{X}\sqrt{d(\mu\circ \beta_k) / d\mu} \, d\mu= \bigl(1-H^{2}(\mu_{n_k},\mu_{m_k})\bigr) \, \prod_{\substack{n\leq n_k \;\;\text{or}\;\; n\geq 1+m_k}}\left(1-H^2(\mu_{n-1},\mu_n)\right)\rightarrow 1 \end{align*} $$
$$ \begin{align*} \int_{X}\sqrt{d(\mu\circ \beta_k) / d\mu} \, d\mu= \bigl(1-H^{2}(\mu_{n_k},\mu_{m_k})\bigr) \, \prod_{\substack{n\leq n_k \;\;\text{or}\;\; n\geq 1+m_k}}\left(1-H^2(\mu_{n-1},\mu_n)\right)\rightarrow 1 \end{align*} $$
as
![]() $H^2(\mu _{n-1},\mu _n)$
is summable and by our choice of
$H^2(\mu _{n-1},\mu _n)$
is summable and by our choice of
![]() $n_k,m_k$
. We see that for
$n_k,m_k$
. We see that for
![]() $n_k<-N$
and
$n_k<-N$
and
![]() $m_k>N$
we have that
$m_k>N$
we have that
which converges to
![]() $0$
as k tends to infinity.
$0$
as k tends to infinity.
Lemma 4.5. Let
![]() $\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a nonsingular Bernoulli shift that is essentially free and not dissipative. Let
$\mathbb {Z}\curvearrowright (X,\mu )=\prod _{n\in \mathbb {Z}}(X_0,\mu _n)$
be a nonsingular Bernoulli shift that is essentially free and not dissipative. Let
![]() $C\subset X$
denote its conservative part. Let
$C\subset X$
denote its conservative part. Let
![]() $\mathbb {Z}\curvearrowright (Y,\nu )$
be any ergodic pmp action, and consider the diagonal product action
$\mathbb {Z}\curvearrowright (Y,\nu )$
be any ergodic pmp action, and consider the diagonal product action
![]() $\mathbb {Z}\curvearrowright X\times Y$
. Then the following holds.
$\mathbb {Z}\curvearrowright X\times Y$
. Then the following holds.
-
1. C is
 $\mathcal {S}$
-invariant.
$\mathcal {S}$
-invariant. -
2. The Maharam extensions satisfy
 $$ \begin{align*} L^{\infty}(C\times \mathbb{R}\times Y)^{\mathbb{Z}}= L^{\infty}(C\times \mathbb{R})^{\mathcal{S}}\mathbin{\overline{\otimes}} 1=L^{\infty}(C\times \mathbb{R})^{\mathbb{Z}}\mathbin{\overline{\otimes}} 1. \end{align*} $$
$$ \begin{align*} L^{\infty}(C\times \mathbb{R}\times Y)^{\mathbb{Z}}= L^{\infty}(C\times \mathbb{R})^{\mathcal{S}}\mathbin{\overline{\otimes}} 1=L^{\infty}(C\times \mathbb{R})^{\mathbb{Z}}\mathbin{\overline{\otimes}} 1. \end{align*} $$
Proof. Let
![]() $\alpha _k\in \operatorname {Aut}(X,\mu )$
denote the translation by k, i.e.,
$\alpha _k\in \operatorname {Aut}(X,\mu )$
denote the translation by k, i.e.,
![]() $(k\cdot x)_m=x_{m-k}$
. We proceed as in the proof of [Reference Björklund, Kosloff and Vaes7, Lemma 3.1] and show that the dissipative part
$(k\cdot x)_m=x_{m-k}$
. We proceed as in the proof of [Reference Björklund, Kosloff and Vaes7, Lemma 3.1] and show that the dissipative part
![]() $D\subset X$
given by
$D\subset X$
given by
 $$ \begin{align*} D=\left\{x\in X \Bigm| \sum_{k\in \mathbb{Z}}\frac{d(\mu\circ \alpha_k)}{d\mu}(x)<+\infty\right\} \end{align*} $$
$$ \begin{align*} D=\left\{x\in X \Bigm| \sum_{k\in \mathbb{Z}}\frac{d(\mu\circ \alpha_k)}{d\mu}(x)<+\infty\right\} \end{align*} $$
is
![]() $\mathcal {S}$
-invariant. It suffices to show that D is invariant under the permutation
$\mathcal {S}$
-invariant. It suffices to show that D is invariant under the permutation
![]() $\sigma _n\in \mathcal {S}$
that interchanges the coordinate
$\sigma _n\in \mathcal {S}$
that interchanges the coordinate
![]() $0$
and n. Fix
$0$
and n. Fix
![]() $n\in \mathbb {Z}\setminus \{0\}$
. For each
$n\in \mathbb {Z}\setminus \{0\}$
. For each
![]() $\eta>0$
and each
$\eta>0$
and each
![]() $k\in \mathbb {Z}$
, we define
$k\in \mathbb {Z}$
, we define
 $$ \begin{align} \begin{aligned} & A^{\eta}_k= \bigl\{x\in X_0 \bigm| \; \bigl|\sqrt{d\mu_{n+k}/d\mu_k}(x)-1\bigr| \geq \eta \bigr\} ,\\ & B^{\eta}_k= \bigl\{x\in X_0 \bigm| \; \bigl|\sqrt{d\mu_k / d\mu_{n+k}}(x)-1\bigr|\geq \eta \bigr\} \;. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & A^{\eta}_k= \bigl\{x\in X_0 \bigm| \; \bigl|\sqrt{d\mu_{n+k}/d\mu_k}(x)-1\bigr| \geq \eta \bigr\} ,\\ & B^{\eta}_k= \bigl\{x\in X_0 \bigm| \; \bigl|\sqrt{d\mu_k / d\mu_{n+k}}(x)-1\bigr|\geq \eta \bigr\} \;. \end{aligned} \end{align} $$
For every
![]() $\eta>0$
, we have that
$\eta>0$
, we have that
 $$ \begin{align*} \sum_{k\in \mathbb{Z}}\mu_k(A^{\eta}_k) &= \sum_{k\in \mathbb{Z}}\int_{A^{\eta}_k}\dfrac{d\mu_k}{d\mu_0}d\mu_0 \leq \eta^{-2}\sum_{k\in \mathbb{Z}}\int_{A^{\eta}_k}\dfrac{d\mu_k}{d\mu_0} \, \bigl|\sqrt{d\mu_{n+k}/d\mu_k}-1\bigr|^{2}d\mu_0\\ &\leq 2 \eta^{-2}\sum_{k\in \mathbb{Z}}H^{2}(\mu_{n+k},\mu_k)<+\infty. \end{align*} $$
$$ \begin{align*} \sum_{k\in \mathbb{Z}}\mu_k(A^{\eta}_k) &= \sum_{k\in \mathbb{Z}}\int_{A^{\eta}_k}\dfrac{d\mu_k}{d\mu_0}d\mu_0 \leq \eta^{-2}\sum_{k\in \mathbb{Z}}\int_{A^{\eta}_k}\dfrac{d\mu_k}{d\mu_0} \, \bigl|\sqrt{d\mu_{n+k}/d\mu_k}-1\bigr|^{2}d\mu_0\\ &\leq 2 \eta^{-2}\sum_{k\in \mathbb{Z}}H^{2}(\mu_{n+k},\mu_k)<+\infty. \end{align*} $$
This means that the set
has positive measure,
![]() $\mu (A_{\eta })> 0$
. From the nonsingularity of
$\mu (A_{\eta })> 0$
. From the nonsingularity of
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
, it follows that
$\mathbb {Z}\curvearrowright (X,\mu )$
, it follows that
![]() $\mu (\alpha _m(A_{\eta }))> 0$
for every
$\mu (\alpha _m(A_{\eta }))> 0$
for every
![]() $m \in \mathbb {Z}$
. Since
$m \in \mathbb {Z}$
. Since
![]() $x \in \alpha _m(A_{\eta })$
if and only if
$x \in \alpha _m(A_{\eta })$
if and only if
![]() $x_k \in X_0 \setminus A^{\eta }_{k-m}$
for all
$x_k \in X_0 \setminus A^{\eta }_{k-m}$
for all
![]() $k \in \mathbb {Z}$
, we conclude that
$k \in \mathbb {Z}$
, we conclude that
![]() $\sum _{k\in \mathbb {Z}}\mu _{k+m}(A^{\eta }_k)<+\infty $
for every
$\sum _{k\in \mathbb {Z}}\mu _{k+m}(A^{\eta }_k)<+\infty $
for every
![]() $m\in \mathbb {Z}$
.
$m\in \mathbb {Z}$
.
Similarly, we have that
![]() $\sum _{k\in \mathbb {Z}}\mu _{k+m}(B^{\eta }_k)<+\infty $
for every
$\sum _{k\in \mathbb {Z}}\mu _{k+m}(B^{\eta }_k)<+\infty $
for every
![]() $\eta>0$
and every
$\eta>0$
and every
![]() $m\in \mathbb {Z}$
. Write
$m\in \mathbb {Z}$
. Write
![]() $C^{\eta }_k=A^{\eta }_k\cup B^{\eta }_k$
. For
$C^{\eta }_k=A^{\eta }_k\cup B^{\eta }_k$
. For
![]() $x\in X_0$
, we define
$x\in X_0$
, we define
![]() $W_x^{\eta }=\{k\in \mathbb {Z} \mid x\in C_k^{\eta }\}$
. For
$W_x^{\eta }=\{k\in \mathbb {Z} \mid x\in C_k^{\eta }\}$
. For
![]() $m\in \mathbb {Z}$
, denote
$m\in \mathbb {Z}$
, denote
![]() $\pi _m\colon X\rightarrow X_0$
for the coordinate projection
$\pi _m\colon X\rightarrow X_0$
for the coordinate projection
![]() $\pi _m(x)=x_m$
. For any
$\pi _m(x)=x_m$
. For any
![]() $m\in \mathbb {Z}$
, we have that
$m\in \mathbb {Z}$
, we have that
 $$ \begin{align} \begin{aligned} \int_{X}\sum_{k\in W_{x_m}^{\eta}}\frac{d(\mu\circ \alpha_k)}{d\mu}d\mu&=\int_{X}\sum_{k\in \mathbb{Z}}1_{C_k^{\eta}}\circ \pi_m\frac{d(\mu\circ \alpha_k)}{d\mu}d\mu =\sum_{k\in \mathbb{Z}}\int_X 1_{C^{\eta}_k}\circ \pi_{m+k} d\mu\\ &=\sum_{k\in \mathbb{Z}}\mu_{k+m}\left(C_{k}^{\eta}\right)<+\infty. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{X}\sum_{k\in W_{x_m}^{\eta}}\frac{d(\mu\circ \alpha_k)}{d\mu}d\mu&=\int_{X}\sum_{k\in \mathbb{Z}}1_{C_k^{\eta}}\circ \pi_m\frac{d(\mu\circ \alpha_k)}{d\mu}d\mu =\sum_{k\in \mathbb{Z}}\int_X 1_{C^{\eta}_k}\circ \pi_{m+k} d\mu\\ &=\sum_{k\in \mathbb{Z}}\mu_{k+m}\left(C_{k}^{\eta}\right)<+\infty. \end{aligned} \end{align} $$
Therefore, we have that
 $$ \begin{align} \sum_{k\in W_{x_0}^1\cup W_{x_n}^1}\frac{d(\mu\circ\alpha_k)}{d\mu}(x)<+\infty \;\;\text{for a.e. } x\in X. \end{align} $$
$$ \begin{align} \sum_{k\in W_{x_0}^1\cup W_{x_n}^1}\frac{d(\mu\circ\alpha_k)}{d\mu}(x)<+\infty \;\;\text{for a.e. } x\in X. \end{align} $$
Borrowing some notation form [Reference Björklund, Kosloff and Vaes7], we write
Note that
By the definition of
![]() $W_{x_i}^{1}$
and the sets
$W_{x_i}^{1}$
and the sets
![]() $A_k^{\eta }$
and
$A_k^{\eta }$
and
![]() $B_k^{\eta }$
in equation (4.2), we have that
$B_k^{\eta }$
in equation (4.2), we have that
![]() $1/16\leq D_{k,k+n}(x_0,x_n)\leq 16$
whenever
$1/16\leq D_{k,k+n}(x_0,x_n)\leq 16$
whenever
![]() $k\notin W_{x_0}^1\cup W_{x_n}^1$
. So it follows from equations (4.4) and (4.5) that
$k\notin W_{x_0}^1\cup W_{x_n}^1$
. So it follows from equations (4.4) and (4.5) that
![]() $\mathcal {D}$
is invariant under
$\mathcal {D}$
is invariant under
![]() $\sigma _n$
.
$\sigma _n$
.
We now prove point 2. Let
![]() $G\curvearrowright (Y,\nu )$
be an ergodic pmp action. One can repeat the proof of [Reference Björklund, Kosloff and Vaes7, Lemma 3.1], making use of the ergodic theorem established in [Reference Danilenko18, Theorem A.1], to conclude that
$G\curvearrowright (Y,\nu )$
be an ergodic pmp action. One can repeat the proof of [Reference Björklund, Kosloff and Vaes7, Lemma 3.1], making use of the ergodic theorem established in [Reference Danilenko18, Theorem A.1], to conclude that
Write
![]() $\lambda $
for the Lebesgue measure on
$\lambda $
for the Lebesgue measure on
![]() $\mathbb {R}$
. As the Maharam extension map
$\mathbb {R}$
. As the Maharam extension map
is continuous, it follows from the
![]() $\mathcal {S}$
-invariance of C and Lemma 4.4 that
$\mathcal {S}$
-invariance of C and Lemma 4.4 that
In combination with equation (4.6), we get that
As
![]() $\mathbb {Z}\curvearrowright (Y,\nu )$
is ergodic, the
$\mathbb {Z}\curvearrowright (Y,\nu )$
is ergodic, the
![]() $\mathbb {Z}$
-invariant elements of
$\mathbb {Z}$
-invariant elements of
![]() $L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}} \mathbin {\overline {\otimes }} L^{\infty }(Y)$
are contained in
$L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}} \mathbin {\overline {\otimes }} L^{\infty }(Y)$
are contained in
![]() $L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1$
. The converse inclusion
$L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1$
. The converse inclusion
![]() $L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1\subset L^{\infty }(C\times \mathbb {R}\times Y)^{\mathbb {Z}}$
holds trivially, proving the second statement of the Lemma.
$L^{\infty }(C\times \mathbb {R})^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1\subset L^{\infty }(C\times \mathbb {R}\times Y)^{\mathbb {Z}}$
holds trivially, proving the second statement of the Lemma.
Remark 4.6. Except for the point where we invoke Lemma 4.4, the proof of Lemma 4.5 remains valid for a nonsingular Bernoulli action
![]() $G\curvearrowright \prod _{g\in G}(X_0,\mu _g)$
of any countable infinite amenable group G, as long as also the right Bernoulli action is nonsingular, e.g., when G is abelian. However, we were unable to prove an analogue of Lemma 4.4 for arbitrary abelian groups. That is the main reason why this section is restricted to the group of integers. Note that it is nevertheless straightforward to generalize our results from
$G\curvearrowright \prod _{g\in G}(X_0,\mu _g)$
of any countable infinite amenable group G, as long as also the right Bernoulli action is nonsingular, e.g., when G is abelian. However, we were unable to prove an analogue of Lemma 4.4 for arbitrary abelian groups. That is the main reason why this section is restricted to the group of integers. Note that it is nevertheless straightforward to generalize our results from
![]() $\mathbb {Z}$
to virtually cyclic abelian groups.
$\mathbb {Z}$
to virtually cyclic abelian groups.
Proof of Theorem 4.1
First, assume that
![]() $(X,\mu )$
admits an atom
$(X,\mu )$
admits an atom
![]() $d \in X$
. Then
$d \in X$
. Then
![]() $d_n \in X_0$
is an atom for every
$d_n \in X_0$
is an atom for every
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\sum _{n \in \mathbb {Z}} (1-\mu _n(\{d_n\})) < +\infty $
. Writing
$\sum _{n \in \mathbb {Z}} (1-\mu _n(\{d_n\})) < +\infty $
. Writing
it follows that
![]() $\mu (X \setminus \mathcal {U}) = 0$
. Since the shift is nonsingular, the set
$\mu (X \setminus \mathcal {U}) = 0$
. Since the shift is nonsingular, the set
![]() $1 \cdot \mathcal {U} \cap \mathcal {U}$
has measure
$1 \cdot \mathcal {U} \cap \mathcal {U}$
has measure
![]() $1$
. We thus find
$1$
. We thus find
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $d_{n-1} = d_n$
for all
$d_{n-1} = d_n$
for all
![]() $|n| \geq N$
.
$|n| \geq N$
.
There are now two possibilities. Either we find an atom
![]() $b \in X_0$
such that
$b \in X_0$
such that
![]() $d_n = b$
for all
$d_n = b$
for all
![]() $|n| \geq N$
, or we find two distinct atoms
$|n| \geq N$
, or we find two distinct atoms
![]() $b,c \in X_0$
such that
$b,c \in X_0$
such that
![]() $d_n = b$
for all
$d_n = b$
for all
![]() $n \geq N$
and
$n \geq N$
and
![]() $d_n = c$
for all
$d_n = c$
for all
![]() $n \leq -N$
.
$n \leq -N$
.
In the first case, we get that
![]() $\sum _{n \in \mathbb {Z}}(1-\mu _n(\{b\})) < + \infty $
, and we define the atom
$\sum _{n \in \mathbb {Z}}(1-\mu _n(\{b\})) < + \infty $
, and we define the atom
![]() $a \in X$
by
$a \in X$
by
![]() $a_n = b$
for all
$a_n = b$
for all
![]() $n \in \mathbb {Z}$
. Clearly,
$n \in \mathbb {Z}$
. Clearly,
![]() $g \cdot a = a$
for all
$g \cdot a = a$
for all
![]() $g \in \mathbb {Z}$
. We define for every
$g \in \mathbb {Z}$
. We define for every
![]() $k \in \mathbb {N}$
, the Borel set
$k \in \mathbb {N}$
, the Borel set
![]() $\mathcal {W}_k = \{x \in X \mid x_n = b \;\;\text {whenever } |n| \geq k\;\}$
. We have
$\mathcal {W}_k = \{x \in X \mid x_n = b \;\;\text {whenever } |n| \geq k\;\}$
. We have
![]() $\bigcup _{k \in \mathbb {N}} \mathcal {W}_k = \mathcal {U}$
so that this set has a complement of measure zero. Also,
$\bigcup _{k \in \mathbb {N}} \mathcal {W}_k = \mathcal {U}$
so that this set has a complement of measure zero. Also,
![]() $g \cdot (\mathcal {W}_k \setminus \{a\}) \cap \mathcal {W}_k = \emptyset $
whenever
$g \cdot (\mathcal {W}_k \setminus \{a\}) \cap \mathcal {W}_k = \emptyset $
whenever
![]() $g \in \mathbb {Z}$
and
$g \in \mathbb {Z}$
and
![]() $|g|> 2k$
. So, for every
$|g|> 2k$
. So, for every
![]() $k \in \mathbb {N}$
, the set
$k \in \mathbb {N}$
, the set
![]() $\mathcal {W}_k \setminus \{a\}$
belongs to the dissipative part of the essentially free action
$\mathcal {W}_k \setminus \{a\}$
belongs to the dissipative part of the essentially free action
![]() $\mathbb {Z} \curvearrowright X$
. Taking the union over k, we conclude that
$\mathbb {Z} \curvearrowright X$
. Taking the union over k, we conclude that
![]() $\mathbb {Z} \curvearrowright X \setminus \{a\}$
is essentially free and dissipative.
$\mathbb {Z} \curvearrowright X \setminus \{a\}$
is essentially free and dissipative.
In the second case, we define for every
![]() $k \in \mathbb {N}$
, the Borel set
$k \in \mathbb {N}$
, the Borel set
Again,
![]() $\bigcup _{k \in \mathbb {N}} \mathcal {V}_k = \mathcal {U}$
has a complement of measure zero and
$\bigcup _{k \in \mathbb {N}} \mathcal {V}_k = \mathcal {U}$
has a complement of measure zero and
![]() $g \cdot \mathcal {V}_k \cap \mathcal {V}_k = \emptyset $
whenever
$g \cdot \mathcal {V}_k \cap \mathcal {V}_k = \emptyset $
whenever
![]() $g \in \mathbb {Z}$
and
$g \in \mathbb {Z}$
and
![]() $|g|> 2k+1$
. So,
$|g|> 2k+1$
. So,
![]() $\mathbb {Z} \curvearrowright X$
is essentially free and dissipative.
$\mathbb {Z} \curvearrowright X$
is essentially free and dissipative.
For the rest of the proof, we may thus assume that
![]() $(X,\mu )$
is nonatomic. Then the Bernoulli shift
$(X,\mu )$
is nonatomic. Then the Bernoulli shift
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is essentially free by [Reference Björklund, Kosloff and Vaes7, Lemma 2.2]. If
$\mathbb {Z}\curvearrowright (X,\mu )$
is essentially free by [Reference Björklund, Kosloff and Vaes7, Lemma 2.2]. If
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
is dissipative, the conclusion of point 2 holds. It now remains to consider the case where the conservative part
$\mathbb {Z} \curvearrowright (X,\mu )$
is dissipative, the conclusion of point 2 holds. It now remains to consider the case where the conservative part
![]() $C \subset X$
of
$C \subset X$
of
![]() $\mathbb {Z} \curvearrowright (X,\mu )$
has positive measure. We have to prove the structural result in point 3 of the theorem.
$\mathbb {Z} \curvearrowright (X,\mu )$
has positive measure. We have to prove the structural result in point 3 of the theorem.
Note that C is
![]() $\mathbb {Z}$
-invariant. By Lemma 4.5, C is also
$\mathbb {Z}$
-invariant. By Lemma 4.5, C is also
![]() $\mathcal {S}$
-invariant. We claim that for any integer
$\mathcal {S}$
-invariant. We claim that for any integer
![]() $p\geq 2$
we have that
$p\geq 2$
we have that
To prove this claim, fix
![]() $p\geq 2$
and define
$p\geq 2$
and define
![]() $Y=\mathbb {Z}/p\mathbb {Z}$
, equipped with the normalized counting measure
$Y=\mathbb {Z}/p\mathbb {Z}$
, equipped with the normalized counting measure
![]() $\nu $
. We let
$\nu $
. We let
![]() $\mathbb {Z}$
act on Y by translation. From Lemma 4.5, we get the equality
$\mathbb {Z}$
act on Y by translation. From Lemma 4.5, we get the equality
![]() $L^{\infty }(C\times Y)^{\mathbb {Z}}=L^{\infty }(C)^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1$
, and this is exactly the statement (4.7).
$L^{\infty }(C\times Y)^{\mathbb {Z}}=L^{\infty }(C)^{\mathbb {Z}}\mathbin {\overline {\otimes }} 1$
, and this is exactly the statement (4.7).
For any integer
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $i\in \{0,1\dots , p-1\}$
, we write
$i\in \{0,1\dots , p-1\}$
, we write
![]() $(Z_{p,i},\nu _{p,i})=\prod _{n \in i+p\mathbb {Z}}(X_0,\mu _n)$
. We identify
$(Z_{p,i},\nu _{p,i})=\prod _{n \in i+p\mathbb {Z}}(X_0,\mu _n)$
. We identify
 $$ \begin{align} (X,\mu)=\prod_{i=0}^{p-1}(Z_{p,i},\nu_{p,i}), \end{align} $$
$$ \begin{align} (X,\mu)=\prod_{i=0}^{p-1}(Z_{p,i},\nu_{p,i}), \end{align} $$
and we obtain measure preserving factor maps
![]() $\pi _{p,i}\colon X\rightarrow Z_{p,i}$
. For each
$\pi _{p,i}\colon X\rightarrow Z_{p,i}$
. For each
![]() $i\in \{0,1,\dots ,p-1\}$
, we have a Bernoulli action
$i\in \{0,1,\dots ,p-1\}$
, we have a Bernoulli action
![]() $p\mathbb {Z}\curvearrowright Z_{p,i}$
, and the factor maps
$p\mathbb {Z}\curvearrowright Z_{p,i}$
, and the factor maps
![]() $\pi _{p,i}$
are
$\pi _{p,i}$
are
![]() $p\mathbb {Z}$
-equivariant. Let
$p\mathbb {Z}$
-equivariant. Let
![]() $\mathcal {S}_{p,i}$
denote the group of finite permutations of
$\mathcal {S}_{p,i}$
denote the group of finite permutations of
![]() $i+p\mathbb {Z}$
. We also have a nonsingular action
$i+p\mathbb {Z}$
. We also have a nonsingular action
![]() $\mathcal {S}_{p,i}\curvearrowright Z_{p,i}$
, and
$\mathcal {S}_{p,i}\curvearrowright Z_{p,i}$
, and
![]() $\pi _{p,i}$
is
$\pi _{p,i}$
is
![]() $\mathcal {S}_{p,i}$
-equivariant as well.
$\mathcal {S}_{p,i}$
-equivariant as well.
For
![]() $i\in \{0,1,\dots ,p-1\}$
, write
$i\in \{0,1,\dots ,p-1\}$
, write
![]() $\alpha _i\in \operatorname {Aut}(X,\mu )$
for the shift by i. There is a natural nonsingular isomorphism
$\alpha _i\in \operatorname {Aut}(X,\mu )$
for the shift by i. There is a natural nonsingular isomorphism
![]() $\theta _{p,i}\colon Z_{p,0}\rightarrow Z_{p,i}$
such that
$\theta _{p,i}\colon Z_{p,0}\rightarrow Z_{p,i}$
such that
![]() $\theta _{p,i}\circ \pi _{p,0}= \pi _{p,i}\circ \alpha _i$
.
$\theta _{p,i}\circ \pi _{p,0}= \pi _{p,i}\circ \alpha _i$
.
We start by using equation (4.7) for
![]() $p=2$
to show that
$p=2$
to show that
![]() $L^{\infty }(C)^{\mathbb {Z}}$
is discrete as a von Neumann algebra. To simplify the notation, we will drop the index p for this special case
$L^{\infty }(C)^{\mathbb {Z}}$
is discrete as a von Neumann algebra. To simplify the notation, we will drop the index p for this special case
![]() $p=2$
.
$p=2$
.
Let
![]() $E_0\subset Z_0$
be a Borel set such that
$E_0\subset Z_0$
be a Borel set such that
![]() $(\pi _0)_*\mu |_C\sim \nu _0|_{E_0}$
. Then
$(\pi _0)_*\mu |_C\sim \nu _0|_{E_0}$
. Then
![]() $E_0$
is uniquely determined up to a null set. As C is
$E_0$
is uniquely determined up to a null set. As C is
![]() $\mathbb {Z}$
-invariant and
$\mathbb {Z}$
-invariant and
![]() $\pi _0$
is a
$\pi _0$
is a
![]() $2\mathbb {Z}$
-equivariant factor map,
$2\mathbb {Z}$
-equivariant factor map,
![]() $E_0$
is
$E_0$
is
![]() $2\mathbb {Z}$
-invariant. Similarly,
$2\mathbb {Z}$
-invariant. Similarly,
![]() $E_0$
is
$E_0$
is
![]() $\mathcal {S}_0$
-invariant. Since
$\mathcal {S}_0$
-invariant. Since
![]() $2\mathbb {Z}\subset \mathbb {Z}$
has finite index, the action
$2\mathbb {Z}\subset \mathbb {Z}$
has finite index, the action
![]() $2\mathbb {Z}\curvearrowright C$
is conservative. Therefore, also
$2\mathbb {Z}\curvearrowright C$
is conservative. Therefore, also
![]() $2\mathbb {Z}\curvearrowright E_0$
is conservative, and it follows that
$2\mathbb {Z}\curvearrowright E_0$
is conservative, and it follows that
![]() $E_0$
is contained in the conservative part of the Bernoulli action
$E_0$
is contained in the conservative part of the Bernoulli action
![]() $2\mathbb {Z}\curvearrowright Z_0$
. By Lemma 4.5, we have that
$2\mathbb {Z}\curvearrowright Z_0$
. By Lemma 4.5, we have that
Put
![]() $E_1=\theta _1(E_0)\subset Z_1$
. As
$E_1=\theta _1(E_0)\subset Z_1$
. As
![]() $\theta _1\circ \pi _0 =\pi _1\circ \alpha _1$
, we have that
$\theta _1\circ \pi _0 =\pi _1\circ \alpha _1$
, we have that
![]() $(\pi _1)_*\mu |_C\sim \nu _1|_{E_1}$
. By the equivariance of
$(\pi _1)_*\mu |_C\sim \nu _1|_{E_1}$
. By the equivariance of
![]() $\theta _1$
, we also have that
$\theta _1$
, we also have that
![]() $E_1$
is
$E_1$
is
![]() $2\mathbb {Z}$
- and
$2\mathbb {Z}$
- and
![]() $\mathcal {S}_1$
-invariant and that
$\mathcal {S}_1$
-invariant and that
Let
![]() $F\in L^{\infty }(E_0)^{2\mathbb {Z}}$
be arbitrary. Then
$F\in L^{\infty }(E_0)^{2\mathbb {Z}}$
be arbitrary. Then
![]() $F\circ \pi _0\in L^{\infty }(C)^{2\mathbb {Z}}$
, and we apply equation (4.7) to conclude that
$F\circ \pi _0\in L^{\infty }(C)^{2\mathbb {Z}}$
, and we apply equation (4.7) to conclude that
![]() $F\circ \pi _0$
is
$F\circ \pi _0$
is
![]() $\mathbb {Z}$
-invariant. Using that
$\mathbb {Z}$
-invariant. Using that
![]() $\theta _1\circ \pi _0=\pi _1\circ \alpha _1$
and viewing
$\theta _1\circ \pi _0=\pi _1\circ \alpha _1$
and viewing
![]() $X=Z_0\times Z_1$
, we can also express this as
$X=Z_0\times Z_1$
, we can also express this as
The equality (4.9) holds for any
![]() $F\in L^{\infty }(E_0)^{2\mathbb {Z}}$
, forcing
$F\in L^{\infty }(E_0)^{2\mathbb {Z}}$
, forcing
![]() $L^{\infty }(E_0)^{2\mathbb {Z}}$
to be discrete. Similarly, we see that
$L^{\infty }(E_0)^{2\mathbb {Z}}$
to be discrete. Similarly, we see that
![]() $L^{\infty }(E_1)^{2\mathbb {Z}}$
is discrete as well.
$L^{\infty }(E_1)^{2\mathbb {Z}}$
is discrete as well.
Using once more the identification
![]() $X=Z_0\times Z_1$
, we have that
$X=Z_0\times Z_1$
, we have that
![]() $C\subset E_0\times E_1$
. Therefore, by Lemma 4.5, we have that
$C\subset E_0\times E_1$
. Therefore, by Lemma 4.5, we have that
 $$ \begin{align*} L^{\infty}(C)^{\mathbb{Z}} &=L^{\infty}(C)^{\mathcal{S}}\subset L^{\infty}(C)^{\mathcal{S}_0\times \mathcal{S}_1}\\ &=1_C\bigl(L^{\infty}(E_0)^{\mathcal{S}_0}\mathbin{\overline{\otimes}} L^{\infty}(E_1)^{\mathcal{S}_1} \bigr)=1_C\bigl(L^{\infty}(E_0)^{2\mathbb{Z}}\mathbin{\overline{\otimes}} L^{\infty}(E_1)^{2\mathbb{Z}} \bigr) \; \end{align*} $$
$$ \begin{align*} L^{\infty}(C)^{\mathbb{Z}} &=L^{\infty}(C)^{\mathcal{S}}\subset L^{\infty}(C)^{\mathcal{S}_0\times \mathcal{S}_1}\\ &=1_C\bigl(L^{\infty}(E_0)^{\mathcal{S}_0}\mathbin{\overline{\otimes}} L^{\infty}(E_1)^{\mathcal{S}_1} \bigr)=1_C\bigl(L^{\infty}(E_0)^{2\mathbb{Z}}\mathbin{\overline{\otimes}} L^{\infty}(E_1)^{2\mathbb{Z}} \bigr) \; \end{align*} $$
so that also
![]() $L^{\infty }(C)^{\mathbb {Z}}$
is discrete.
$L^{\infty }(C)^{\mathbb {Z}}$
is discrete.
Take a
![]() $\mathbb {Z}$
-invariant Borel set
$\mathbb {Z}$
-invariant Borel set
![]() $\mathcal {U}\subset X$
with
$\mathcal {U}\subset X$
with
![]() $\mu (\mathcal {U})>0$
such that
$\mu (\mathcal {U})>0$
such that
![]() $1_{\mathcal {U}}$
is a minimal projection in
$1_{\mathcal {U}}$
is a minimal projection in
![]() $L^{\infty }(C)^{\mathbb {Z}}$
. So,
$L^{\infty }(C)^{\mathbb {Z}}$
. So,
![]() $\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic. We prove that
$\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic. We prove that
![]() $\mathcal {U}$
is of the form
$\mathcal {U}$
is of the form
![]() $\mathcal {U}=C_0^{\mathbb {Z}}$
for some
$\mathcal {U}=C_0^{\mathbb {Z}}$
for some
![]() $C_0\subset X_0$
.
$C_0\subset X_0$
.
For any integer
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $i\in \{0,1,\dots , p-1\}$
, define the Borel set
$i\in \{0,1,\dots , p-1\}$
, define the Borel set
![]() $\mathcal {U}_{p,i}$
by
$\mathcal {U}_{p,i}$
by
![]() $(\pi _{p,i})_*\mu |_{\mathcal {U}}\sim (\nu _{p,i})|_{\mathcal {U}_{p,i}}$
. First of all, note that
$(\pi _{p,i})_*\mu |_{\mathcal {U}}\sim (\nu _{p,i})|_{\mathcal {U}_{p,i}}$
. First of all, note that
![]() $\mathcal {U}_{p,i}$
is
$\mathcal {U}_{p,i}$
is
![]() $p\mathbb {Z}$
-invariant and
$p\mathbb {Z}$
-invariant and
![]() $\mathcal {S}_{p,i}$
-invariant. By equation (4.7) the action
$\mathcal {S}_{p,i}$
-invariant. By equation (4.7) the action
![]() $p\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic so that also
$p\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic so that also
![]() $p\mathbb {Z}\curvearrowright \mathcal {U}_{p,i}$
is ergodic. Since we can view
$p\mathbb {Z}\curvearrowright \mathcal {U}_{p,i}$
is ergodic. Since we can view
![]() $p\mathbb {Z}\curvearrowright Z_{p,i}$
as a Bernoulli action, it follows from Lemma 4.5 that
$p\mathbb {Z}\curvearrowright Z_{p,i}$
as a Bernoulli action, it follows from Lemma 4.5 that
![]() $\mathcal {S}_{p,i}\curvearrowright \mathcal {U}_{p,i}$
is ergodic as well.
$\mathcal {S}_{p,i}\curvearrowright \mathcal {U}_{p,i}$
is ergodic as well.
Using the identification (4.8), we have that
![]() $\mathcal {U}\subset \mathcal {U}_{p,0}\times \mathcal {U}_{p,1}\times \dots \times \mathcal {U}_{p,p-1}$
for any
$\mathcal {U}\subset \mathcal {U}_{p,0}\times \mathcal {U}_{p,1}\times \dots \times \mathcal {U}_{p,p-1}$
for any
![]() $p\geq 2$
. As
$p\geq 2$
. As
![]() $\mathcal {U}$
is invariant under the subgroup
$\mathcal {U}$
is invariant under the subgroup
![]() $\mathcal {S}_{p,0}\times \mathcal {S}_{p,1}\times \dots \mathcal {S}_{p,p-1}$
and as
$\mathcal {S}_{p,0}\times \mathcal {S}_{p,1}\times \dots \mathcal {S}_{p,p-1}$
and as
![]() $\mathcal {S}_{p,i}\curvearrowright \mathcal {U}_{p,i}$
acts ergodically for each
$\mathcal {S}_{p,i}\curvearrowright \mathcal {U}_{p,i}$
acts ergodically for each
![]() $i\in \{0,1,\dots ,p-1\}$
, we have that
$i\in \{0,1,\dots ,p-1\}$
, we have that
Let
![]() $n\in \mathbb {N}$
, and let
$n\in \mathbb {N}$
, and let
![]() $A_n\subset L^{\infty }(X)$
denote the subalgebra of elements only depending on the variables
$A_n\subset L^{\infty }(X)$
denote the subalgebra of elements only depending on the variables
![]() $x_j$
, for
$x_j$
, for
![]() $-n\leq j\leq n$
, and let
$-n\leq j\leq n$
, and let
![]() $E_n\colon L^{\infty }(X)\rightarrow A_n$
be the unique conditional expectation preserving the measure
$E_n\colon L^{\infty }(X)\rightarrow A_n$
be the unique conditional expectation preserving the measure
![]() $\mu $
. For any
$\mu $
. For any
![]() $n\in \mathbb {N}$
, we apply the decomposition (4.10) to
$n\in \mathbb {N}$
, we apply the decomposition (4.10) to
![]() $p=2n+1$
. Since the numbers
$p=2n+1$
. Since the numbers
![]() $\{j \mid -n\leq j\leq n\}$
are distinct representatives of the elements of
$\{j \mid -n\leq j\leq n\}$
are distinct representatives of the elements of
![]() $\mathbb {Z}/(2n+1)\mathbb {Z}$
, there exist
$\mathbb {Z}/(2n+1)\mathbb {Z}$
, there exist
![]() $a_{n,j}\in L^{\infty }(X_0,\mu _j)$
such that
$a_{n,j}\in L^{\infty }(X_0,\mu _j)$
such that
Expressing that
![]() $E_n\circ E_m=E_n$
for
$E_n\circ E_m=E_n$
for
![]() $m\geq n$
yields
$m\geq n$
yields
 $$ \begin{align} E_n(1_{\mathcal{U}})=a_{n,-n}\otimes a_{n,-n+1}\otimes \dots\otimes a_{n,n}=a_{m,-n}\otimes a_{m,-n+1}\otimes \dots\otimes a_{m,n}\cdot \prod_{n<|j|\leq m}\mu_{j}(a_{m,j}) \;. \end{align} $$
$$ \begin{align} E_n(1_{\mathcal{U}})=a_{n,-n}\otimes a_{n,-n+1}\otimes \dots\otimes a_{n,n}=a_{m,-n}\otimes a_{m,-n+1}\otimes \dots\otimes a_{m,n}\cdot \prod_{n<|j|\leq m}\mu_{j}(a_{m,j}) \;. \end{align} $$
For each
![]() $j\in \mathbb {Z}$
, letting
$j\in \mathbb {Z}$
, letting
![]() $m\rightarrow +\infty $
, we have that
$m\rightarrow +\infty $
, we have that
![]() $a_{m,j}$
is a sequence in
$a_{m,j}$
is a sequence in
![]() $L^{\infty }(X_0,\mu _j)$
such that
$L^{\infty }(X_0,\mu _j)$
such that
![]() $0\leq a_{m,j}\leq 1$
for all m. Similarly, for a fixed
$0\leq a_{m,j}\leq 1$
for all m. Similarly, for a fixed
![]() $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
 $$ \begin{align*} \prod_{n<|j|\leq m}\mu_{j}(a_{m,j})\in [0,1] \;\;\text{for every } m\geq n. \end{align*} $$
$$ \begin{align*} \prod_{n<|j|\leq m}\mu_{j}(a_{m,j})\in [0,1] \;\;\text{for every } m\geq n. \end{align*} $$
Thus, we can choose a subsequence
![]() $m_k\rightarrow +\infty $
such that
$m_k\rightarrow +\infty $
such that
![]() $a_{m_k,j}\rightarrow b_j$
weakly for every
$a_{m_k,j}\rightarrow b_j$
weakly for every
![]() $j\in \mathbb {Z}$
and
$j\in \mathbb {Z}$
and
![]() $b_j\in L^{\infty }(X_0,\mu _j)$
satisfying
$b_j\in L^{\infty }(X_0,\mu _j)$
satisfying
![]() $0\leq b_j\leq 1$
and such that
$0\leq b_j\leq 1$
and such that
![]() $\prod _{n<|j|\leq m_k}\mu _{j}(a_{m_k,j})\rightarrow \lambda _n$
for every
$\prod _{n<|j|\leq m_k}\mu _{j}(a_{m_k,j})\rightarrow \lambda _n$
for every
![]() $n\in \mathbb {N}$
for some
$n\in \mathbb {N}$
for some
![]() $\lambda _n\in [0,1]$
. The equality (4.11) implies that
$\lambda _n\in [0,1]$
. The equality (4.11) implies that
As
![]() $E_n(1_{\mathcal {U}})$
is nonzero for every n, we see that
$E_n(1_{\mathcal {U}})$
is nonzero for every n, we see that
![]() $\lambda _n$
and
$\lambda _n$
and
![]() $b_j$
are nonzero for every
$b_j$
are nonzero for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $j\in \mathbb {Z}$
. Expressing once more that
$j\in \mathbb {Z}$
. Expressing once more that
![]() $E_n\circ E_m = E_n$
for
$E_n\circ E_m = E_n$
for
![]() $m\geq n$
, we obtain that
$m\geq n$
, we obtain that
 $$ \begin{align*} \lambda_n=\lambda_m \prod_{n<|j|\leq m}\mu_{j}(b_j)\leq \prod_{n<|j|\leq m}\mu_{j}(b_j), \end{align*} $$
$$ \begin{align*} \lambda_n=\lambda_m \prod_{n<|j|\leq m}\mu_{j}(b_j)\leq \prod_{n<|j|\leq m}\mu_{j}(b_j), \end{align*} $$
which shows that the infinite product
![]() $\prod _{|j|>n}\mu _{j}(b_j)$
converges to a nonzero limit for each
$\prod _{|j|>n}\mu _{j}(b_j)$
converges to a nonzero limit for each
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $\lambda \in [0,1]$
be any limit point of the sequence
$\lambda \in [0,1]$
be any limit point of the sequence
![]() $\lambda _n$
. Using that
$\lambda _n$
. Using that
![]() $E_n(1_{\mathcal {U}})\rightarrow 1_{\mathcal {U}}$
strongly as
$E_n(1_{\mathcal {U}})\rightarrow 1_{\mathcal {U}}$
strongly as
![]() $n\rightarrow +\infty $
, we see that the infinite product of the
$n\rightarrow +\infty $
, we see that the infinite product of the
![]() $b_j$
converges and that we have an equality
$b_j$
converges and that we have an equality
Together with the fact that
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $\mathbb {Z}$
-invariant, this implies that there is a Borel set
$\mathbb {Z}$
-invariant, this implies that there is a Borel set
![]() $C_0\subset X_0$
such that
$C_0\subset X_0$
such that
![]() $\mathcal {U}=C_0^{\mathbb {Z}}$
. Write
$\mathcal {U}=C_0^{\mathbb {Z}}$
. Write
![]() $C_1=X_0\setminus C_0$
. As
$C_1=X_0\setminus C_0$
. As
![]() $\mu (\mathcal {U})>0$
, we have that
$\mu (\mathcal {U})>0$
, we have that
By construction, the action
![]() $\mathbb {Z}\curvearrowright X\setminus C_0^{\mathbb {Z}}$
is dissipative. It follows that
$\mathbb {Z}\curvearrowright X\setminus C_0^{\mathbb {Z}}$
is dissipative. It follows that
![]() $C=C_0^{\mathbb {Z}}=\mathcal {U}$
. We have chosen
$C=C_0^{\mathbb {Z}}=\mathcal {U}$
. We have chosen
![]() $\mathcal {U}$
such that
$\mathcal {U}$
such that
![]() $\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic; thus, it follows from Lemma 4.5 that
$\mathbb {Z}\curvearrowright \mathcal {U}$
is ergodic; thus, it follows from Lemma 4.5 that
![]() $\mathcal {S}\curvearrowright C_0^{\mathbb {Z}}$
is ergodic, that
$\mathcal {S}\curvearrowright C_0^{\mathbb {Z}}$
is ergodic, that
![]() $\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}$
is weakly mixing and that for any ergodic pmp action
$\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}$
is weakly mixing and that for any ergodic pmp action
![]() $\mathbb {Z}\curvearrowright (Y,\nu )$
the nonsingular actions
$\mathbb {Z}\curvearrowright (Y,\nu )$
the nonsingular actions
![]() $\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}$
,
$\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}$
,
![]() $\mathcal {S}\curvearrowright C_0^{\mathbb {Z}}$
and
$\mathcal {S}\curvearrowright C_0^{\mathbb {Z}}$
and
![]() $\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}\times Y$
have the same associated flow. It remains to prove that this flow is infinitely divisible. For this remaining part of the proof, we may replace
$\mathbb {Z}\curvearrowright C_0^{\mathbb {Z}}\times Y$
have the same associated flow. It remains to prove that this flow is infinitely divisible. For this remaining part of the proof, we may replace
![]() $X_0$
by
$X_0$
by
![]() $C_0$
and thus assume that
$C_0$
and thus assume that
![]() $C_0 = X_0$
.
$C_0 = X_0$
.
To prove this, let
![]() $p\geq 1$
be an integer. We use the notation introduced in equation (4.8). Let
$p\geq 1$
be an integer. We use the notation introduced in equation (4.8). Let
![]() $\mathcal {S}_{p,i}\subset \mathcal {S}$
denote the subgroup of finite permutations of
$\mathcal {S}_{p,i}\subset \mathcal {S}$
denote the subgroup of finite permutations of
![]() $i+p\mathbb {Z}$
. We have that
$i+p\mathbb {Z}$
. We have that
For each
![]() $i\in \{0,1,\dots ,p-1\}$
, we write
$i\in \{0,1,\dots ,p-1\}$
, we write
![]() $\Gamma _{p,i}$
for the group
$\Gamma _{p,i}$
for the group
![]() $\Gamma _{p,i}=p\mathbb {Z}$
, acting naturally on
$\Gamma _{p,i}=p\mathbb {Z}$
, acting naturally on
![]() $Z_{p,i}$
. We can view the action
$Z_{p,i}$
. We can view the action
![]() $\Gamma _{p,i}\curvearrowright Z_{p,i}$
as a nonsingular Bernoulli action, which is a factor of the conservative nonsingular Bernoulli action
$\Gamma _{p,i}\curvearrowright Z_{p,i}$
as a nonsingular Bernoulli action, which is a factor of the conservative nonsingular Bernoulli action
![]() $p\mathbb {Z}\curvearrowright (X,\mu )$
. Therefore,
$p\mathbb {Z}\curvearrowright (X,\mu )$
. Therefore,
![]() $\Gamma _{p,i}\curvearrowright Z_{p,i}$
is conservative, and by Lemma 4.4, we have that
$\Gamma _{p,i}\curvearrowright Z_{p,i}$
is conservative, and by Lemma 4.4, we have that
![]() $L^{\infty }(Z_{p,i}\times \mathbb {R})^{\mathcal {S}_{p,i}}\subset L^{\infty }(Z_{p,i}\times \mathbb {R})^{\Gamma _{p,i}}$
, for each
$L^{\infty }(Z_{p,i}\times \mathbb {R})^{\mathcal {S}_{p,i}}\subset L^{\infty }(Z_{p,i}\times \mathbb {R})^{\Gamma _{p,i}}$
, for each
![]() $i\in \{0,1,\dots ,p-1\}$
so that
$i\in \{0,1,\dots ,p-1\}$
so that
Each
![]() $\Gamma _{p,i}$
is a copy of
$\Gamma _{p,i}$
is a copy of
![]() $p\mathbb {Z}$
, and the diagonal copy of
$p\mathbb {Z}$
, and the diagonal copy of
![]() $p\mathbb {Z}$
inside
$p\mathbb {Z}$
inside
![]() $\Gamma _{p,0}\times \dots \times \Gamma _{p,p-1}$
acts on X by the Bernoulli action
$\Gamma _{p,0}\times \dots \times \Gamma _{p,p-1}$
acts on X by the Bernoulli action
![]() $p\mathbb {Z}\curvearrowright X$
. Continuing the chain of inclusions (4.13), we obtain
$p\mathbb {Z}\curvearrowright X$
. Continuing the chain of inclusions (4.13), we obtain
where the last equality follows from point 2 of Lemma 4.5, applied to the ergodic pmp action
![]() $\mathbb {Z}\curvearrowright Y=\mathbb {Z}/p\mathbb {Z}$
. Combining equations (4.12), (4.13) and (4.14), we see that all inclusions must in fact be equalities.
$\mathbb {Z}\curvearrowright Y=\mathbb {Z}/p\mathbb {Z}$
. Combining equations (4.12), (4.13) and (4.14), we see that all inclusions must in fact be equalities.
Put
![]() $(D_p,\eta _p)=\prod _{n\in p\mathbb {Z}}(X_0,\mu _n)$
. For each
$(D_p,\eta _p)=\prod _{n\in p\mathbb {Z}}(X_0,\mu _n)$
. For each
![]() $i\in \{0,1,\dots ,p-1\}$
, the action
$i\in \{0,1,\dots ,p-1\}$
, the action
![]() $\Gamma _{p,i}\curvearrowright Z_{p,i}$
is conjugate with
$\Gamma _{p,i}\curvearrowright Z_{p,i}$
is conjugate with
![]() $p\mathbb {Z}\curvearrowright D_p$
. From the equality
$p\mathbb {Z}\curvearrowright D_p$
. From the equality
it then follows that the associated flow of
![]() $\mathbb {Z} \curvearrowright X$
is the joint flow of p copies of the associated flow of
$\mathbb {Z} \curvearrowright X$
is the joint flow of p copies of the associated flow of
![]() $p\mathbb {Z} \curvearrowright D_p$
. This concludes the proof of the theorem.
$p\mathbb {Z} \curvearrowright D_p$
. This concludes the proof of the theorem.
We end this section by proving Theorem 4.3. We first need the following lemma.
Lemma 4.7. Let
![]() $X_0$
be a standard Borel space equipped with a sequence of equivalent probability measures
$X_0$
be a standard Borel space equipped with a sequence of equivalent probability measures
![]() $\mu _n$
. Let
$\mu _n$
. Let
![]() $\mathcal {S}$
denote the group of finite permutations of
$\mathcal {S}$
denote the group of finite permutations of
![]() $\mathbb {N}$
, and let
$\mathbb {N}$
, and let
![]() $\mathcal {S}_1\subset \mathcal {S}$
be the subgroup fixing
$\mathcal {S}_1\subset \mathcal {S}$
be the subgroup fixing
![]() $1\in \mathbb {N}$
. Consider the nonsingular group actions
$1\in \mathbb {N}$
. Consider the nonsingular group actions
![]() $\mathcal {S}\curvearrowright (X,\mu )=\prod _{n=1}^{\infty }(X_0,\mu _n)$
and
$\mathcal {S}\curvearrowright (X,\mu )=\prod _{n=1}^{\infty }(X_0,\mu _n)$
and
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )= \prod _{n=2}^{\infty }(X_0,\mu _n)$
. Assume that the action
$\mathcal {S}_1\curvearrowright (Z,\eta )= \prod _{n=2}^{\infty }(X_0,\mu _n)$
. Assume that the action
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic.
$\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic.
Then
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is ergodic and the following holds.
$\mathcal {S}\curvearrowright (X,\mu )$
is ergodic and the following holds.
-
1.
 $\mathcal {S}\curvearrowright (X,\mu )$
is of type II
$\mathcal {S}\curvearrowright (X,\mu )$
is of type II
 $_{1}$
if and only if there exists a probability measure
$_{1}$
if and only if there exists a probability measure
 $\nu \sim \mu _1$
on
$\nu \sim \mu _1$
on
 $X_0$
such that
$X_0$
such that
 $\nu ^{\mathbb {N}}\sim \mu $
.
$\nu ^{\mathbb {N}}\sim \mu $
. -
2.
 $\mathcal {S}\curvearrowright (X,\mu )$
is of type II
$\mathcal {S}\curvearrowright (X,\mu )$
is of type II
 $_{\infty }$
if and only if there exists a
$_{\infty }$
if and only if there exists a
 $\sigma $
-finite measure
$\sigma $
-finite measure
 $\nu \sim \mu _1$
on
$\nu \sim \mu _1$
on
 $X_0$
and Borel sets
$X_0$
and Borel sets
 $\mathcal {U}_n\subset X_0$
such that
$\mathcal {U}_n\subset X_0$
such that
 $\nu (\mathcal {U}_n)<+\infty $
for all
$\nu (\mathcal {U}_n)<+\infty $
for all
 $n\in \mathbb {N}$
and such that
$n\in \mathbb {N}$
and such that  $$ \begin{align*} \sum_{n=1}^{\infty}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty,\;\; \sum_{n=1}^{\infty}H^{2}\bigl(\mu_n, \nu(\mathcal{U}_n)^{-1}\nu|_{\mathcal{U}_n}\bigr)<+\infty,\;\;\sum_{n=1}^{\infty}\nu(X_0\setminus \mathcal{U}_n)=+\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty,\;\; \sum_{n=1}^{\infty}H^{2}\bigl(\mu_n, \nu(\mathcal{U}_n)^{-1}\nu|_{\mathcal{U}_n}\bigr)<+\infty,\;\;\sum_{n=1}^{\infty}\nu(X_0\setminus \mathcal{U}_n)=+\infty. \end{align*} $$
Note that Lemma 4.7 strongly resembles [Reference Berendschot and Vaes8, Theorem 3.3]. There is, however, an important difference: In [Reference Berendschot and Vaes8, Theorem 3.3], it is part of the hypotheses that the Radon–Nikodym derivatives
![]() $d\mu _n / d\mu _0$
satisfy a certain boundedness condition. We do not make such an assumption because we will use Lemma 4.7 in the context of totally arbitrary Bernoulli shifts. As a compensation, we make an ergodicity assumption on the permutation action. Thanks to Theorem 4.1, this ergodicity assumption will hold automatically when the Bernoulli shift
$d\mu _n / d\mu _0$
satisfy a certain boundedness condition. We do not make such an assumption because we will use Lemma 4.7 in the context of totally arbitrary Bernoulli shifts. As a compensation, we make an ergodicity assumption on the permutation action. Thanks to Theorem 4.1, this ergodicity assumption will hold automatically when the Bernoulli shift
![]() $\mathbb {Z} \curvearrowright X$
is conservative.
$\mathbb {Z} \curvearrowright X$
is conservative.
When
![]() $X_0$
is a finite set and
$X_0$
is a finite set and
![]() $(\mu _n)_{n\geq 1}$
are equivalent probability measures on
$(\mu _n)_{n\geq 1}$
are equivalent probability measures on
![]() $X_0$
, there is a necessary and sufficient ergodicity criterion for the nonsingular permutation action
$X_0$
, there is a necessary and sufficient ergodicity criterion for the nonsingular permutation action
![]() $\mathcal {S}\curvearrowright (X,\mu )=\prod _{n=1}^{\infty }(X_0,\mu _n)$
in terms of the measures
$\mathcal {S}\curvearrowright (X,\mu )=\prod _{n=1}^{\infty }(X_0,\mu _n)$
in terms of the measures
![]() $\mu _n$
; see [Reference Aldous and Pitman2, Theorem 1.6]. However, when
$\mu _n$
; see [Reference Aldous and Pitman2, Theorem 1.6]. However, when
![]() $X_0$
is infinite, only sufficient conditions are known; see [Reference Aldous and Pitman2, Theorems 1.8 & 1.12].
$X_0$
is infinite, only sufficient conditions are known; see [Reference Aldous and Pitman2, Theorems 1.8 & 1.12].
The measure
![]() $\nu $
appearing in statement 2 of Lemma 4.7 is either finite or infinite. Of course, if
$\nu $
appearing in statement 2 of Lemma 4.7 is either finite or infinite. Of course, if
![]() $\nu $
is finite, the condition
$\nu $
is finite, the condition
![]() $\nu (\mathcal {U}_n)<+\infty $
is automatically fulfilled. Similarly, when
$\nu (\mathcal {U}_n)<+\infty $
is automatically fulfilled. Similarly, when
![]() $\nu $
is infinite, the conditions
$\nu $
is infinite, the conditions
![]() $\nu (\mathcal {U}_n)<+\infty $
trivially imply that
$\nu (\mathcal {U}_n)<+\infty $
trivially imply that
![]() $\sum _{n=1}^{\infty }\nu (X_0\setminus \mathcal {U}_n)=+\infty $
.
$\sum _{n=1}^{\infty }\nu (X_0\setminus \mathcal {U}_n)=+\infty $
.
Proof. Suppose that
![]() $F\in L^{\infty }(X)$
is
$F\in L^{\infty }(X)$
is
![]() $\mathcal {S}$
-invariant. As
$\mathcal {S}$
-invariant. As
![]() $\mathcal {S}_1$
acts ergodically on
$\mathcal {S}_1$
acts ergodically on
![]() $(Z,\eta )$
, we see that F essentially only depends on the coordinate
$(Z,\eta )$
, we see that F essentially only depends on the coordinate
![]() $x_1$
. But as F is
$x_1$
. But as F is
![]() $\mathcal {S}$
-invariant, it follows that F essentially only depends on the coordinate
$\mathcal {S}$
-invariant, it follows that F essentially only depends on the coordinate
![]() $x_2$
; thus, F must be essentially constant. So the action
$x_2$
; thus, F must be essentially constant. So the action
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is ergodic.
$\mathcal {S}\curvearrowright (X,\mu )$
is ergodic.
If
![]() $x,y\in X$
are elements that differ in only finitely many coordinates, we write
$x,y\in X$
are elements that differ in only finitely many coordinates, we write
 $$ \begin{align*} \alpha(x,y)=\sum_{n\in \mathbb{N}}\big(\alpha_n(x_n)-\alpha_n(y_n)\big) ,\;\; \text{where}\;\; \alpha_n=\log\frac{d\mu_n}{d\mu_1}. \end{align*} $$
$$ \begin{align*} \alpha(x,y)=\sum_{n\in \mathbb{N}}\big(\alpha_n(x_n)-\alpha_n(y_n)\big) ,\;\; \text{where}\;\; \alpha_n=\log\frac{d\mu_n}{d\mu_1}. \end{align*} $$
Assume that the action
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is semifinite. Then there exists a Borel map
$\mathcal {S}\curvearrowright (X,\mu )$
is semifinite. Then there exists a Borel map
![]() $F\colon X\rightarrow \mathbb {R}$
such that
$F\colon X\rightarrow \mathbb {R}$
such that
Define
![]() $(\widetilde {X},\widetilde {\mu })=(X_0\times X_0\times Z,\mu _1\times \mu _1\times \eta )$
, by doubling the first coordinate, and consider the map
$(\widetilde {X},\widetilde {\mu })=(X_0\times X_0\times Z,\mu _1\times \mu _1\times \eta )$
, by doubling the first coordinate, and consider the map
For each
![]() $\sigma \in \mathcal {S}_1$
, we have that
$\sigma \in \mathcal {S}_1$
, we have that
![]() $H(x,x',z)=H(x,x',\sigma (z))$
for a.e.
$H(x,x',z)=H(x,x',\sigma (z))$
for a.e.
![]() $(x,x',z)\in \widetilde {X}$
. As the action
$(x,x',z)\in \widetilde {X}$
. As the action
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic, H is essentially independent of the z-variable. Therefore, there exists a Borel map
$\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic, H is essentially independent of the z-variable. Therefore, there exists a Borel map
![]() $L\colon X_0\times X_0 \rightarrow \mathbb {R}$
such that
$L\colon X_0\times X_0 \rightarrow \mathbb {R}$
such that
![]() $H(x,x',z)=L(x,x')$
for a.e.
$H(x,x',z)=L(x,x')$
for a.e.
![]() $(x,x',z)\in \widetilde {X}$
. Let
$(x,x',z)\in \widetilde {X}$
. Let
![]() $z\in Z$
be an element that witnesses this equality a.e., and put
$z\in Z$
be an element that witnesses this equality a.e., and put
![]() $\beta (x)=F(x,z)$
. So we have found a Borel map
$\beta (x)=F(x,z)$
. So we have found a Borel map
![]() $\beta \colon X_0\rightarrow \mathbb {R}$
such that
$\beta \colon X_0\rightarrow \mathbb {R}$
such that
when x and y are unequal only in the first coordinate. For
![]() $n\geq 2$
, using equation (4.15) and the element
$n\geq 2$
, using equation (4.15) and the element
![]() $\sigma _n\in \mathcal {S}$
flipping the elements
$\sigma _n\in \mathcal {S}$
flipping the elements
![]() $1$
and n, we see that
$1$
and n, we see that
whenever
![]() $x,y\in X$
are unequal only in the n’th coordinate. When
$x,y\in X$
are unequal only in the n’th coordinate. When
![]() $x,y\in X$
are elements that differ in only finitely many coordinates, write
$x,y\in X$
are elements that differ in only finitely many coordinates, write
Let
![]() $\mathcal {R}_{\Omega }$
be the equivalence relation on
$\mathcal {R}_{\Omega }$
be the equivalence relation on
![]() $X\times \mathbb {R}$
that is given by
$X\times \mathbb {R}$
that is given by
![]() $(x,t)\sim (y,s)$
if and only if x and y differ only in finitely many coordinates and
$(x,t)\sim (y,s)$
if and only if x and y differ only in finitely many coordinates and
![]() $s-t=\Omega (x,y)$
. Then the flow
$s-t=\Omega (x,y)$
. Then the flow
![]() $\mathbb {R}\curvearrowright L^{\infty }(X\times \mathbb {R})^{\mathcal {R}_{\Omega }}$
is isomorphic with the tail boundary flow associated to the sequence of probability measures
$\mathbb {R}\curvearrowright L^{\infty }(X\times \mathbb {R})^{\mathcal {R}_{\Omega }}$
is isomorphic with the tail boundary flow associated to the sequence of probability measures
![]() $(\alpha _n+\beta )_*\mu _n$
. By equation (4.16), we have that
$(\alpha _n+\beta )_*\mu _n$
. By equation (4.16), we have that
![]() $\Omega (x,y)=F(x)-F(y)$
for
$\Omega (x,y)=F(x)-F(y)$
for
![]() $x,y\in X$
that differ only in finitely many coordinates. We conclude that the tail boundary flow associated to
$x,y\in X$
that differ only in finitely many coordinates. We conclude that the tail boundary flow associated to
![]() $(\alpha _n+\beta )_*\mu _n$
is isomorphic with the translation action
$(\alpha _n+\beta )_*\mu _n$
is isomorphic with the translation action
![]() $\mathbb {R}\curvearrowright \mathbb {R}$
.
$\mathbb {R}\curvearrowright \mathbb {R}$
.
We again use the cutoff function
![]() $T_{\kappa } : \mathbb {R} \to \mathbb {R}$
for
$T_{\kappa } : \mathbb {R} \to \mathbb {R}$
for
![]() $\kappa> 0$
, as defined in equation (3.4). By [Reference Berendschot and Vaes8, Proposition 2.1], there exists a sequence
$\kappa> 0$
, as defined in equation (3.4). By [Reference Berendschot and Vaes8, Proposition 2.1], there exists a sequence
![]() $t_n\in \mathbb {R}$
such that
$t_n\in \mathbb {R}$
such that
 $$ \begin{align} \sum_{n=1}^{\infty}\int_{X_0}T_{\kappa}(\alpha_n(x)+\beta(x)-t_n)^2d\mu_n(x)<+\infty, \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\int_{X_0}T_{\kappa}(\alpha_n(x)+\beta(x)-t_n)^2d\mu_n(x)<+\infty, \end{align} $$
for every
![]() $\kappa>0$
. Define the
$\kappa>0$
. Define the
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\nu \sim \mu _1$
by
$\nu \sim \mu _1$
by
![]() $d\nu /d\mu _1=\exp (-\beta )$
. If
$d\nu /d\mu _1=\exp (-\beta )$
. If
![]() $\nu $
is finite, then we can add a constant to
$\nu $
is finite, then we can add a constant to
![]() $\beta $
so that
$\beta $
so that
![]() $\nu $
becomes a probability measure. Then equation (4.17) still holds with a potentially different sequence
$\nu $
becomes a probability measure. Then equation (4.17) still holds with a potentially different sequence
![]() $t_n\in \mathbb {R}$
. Thus, we may assume that
$t_n\in \mathbb {R}$
. Thus, we may assume that
![]() $\nu $
is either infinite or a probability measure. Define the sets
$\nu $
is either infinite or a probability measure. Define the sets
By equation (4.17), we have that
![]() $\sum _{n=1}^{\infty }\mu _n(X_0\setminus \mathcal {U}_n)<+\infty $
. There exists a
$\sum _{n=1}^{\infty }\mu _n(X_0\setminus \mathcal {U}_n)<+\infty $
. There exists a
![]() $C>0$
such that
$C>0$
such that
![]() $|1-r|\leq C|\log (r)|$
for all
$|1-r|\leq C|\log (r)|$
for all
![]() $r\in [\exp (-1),\exp (1)]$
so that
$r\in [\exp (-1),\exp (1)]$
so that
Taking
![]() $\kappa =1$
, it follows from equation (4.17) that
$\kappa =1$
, it follows from equation (4.17) that
 $$ \begin{align*} \sum_{n=1}^{\infty}\int_{\mathcal{U}_n}|1-\exp(-(\alpha_n(x)+\beta(x)-t_n)/2)|^2d\mu_n(x)<+\infty \;. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}\int_{\mathcal{U}_n}|1-\exp(-(\alpha_n(x)+\beta(x)-t_n)/2)|^2d\mu_n(x)<+\infty \;. \end{align*} $$
The left-hand side equals
 $$ \begin{align*} \sum_{n=1}^{\infty}\int_{\mathcal{U}_n}\bigl(\sqrt{d\mu_n / d\mu_1}-\exp(t_n/2)\sqrt{d\nu / d\mu_1}\bigr)^{2} \, d\mu_1 \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}\int_{\mathcal{U}_n}\bigl(\sqrt{d\mu_n / d\mu_1}-\exp(t_n/2)\sqrt{d\nu / d\mu_1}\bigr)^{2} \, d\mu_1 \end{align*} $$
and since
 $$ \begin{align*} \sum_{n=1}^{\infty}\int_{X_0}\bigl(\sqrt{d\mu_n / d\mu_1}-1_{\mathcal{U}_n}\, \sqrt{d\mu_n/d\mu_1}\bigr)^{2} \, d\mu_1=\sum_{n=1}^{\infty}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty , \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}\int_{X_0}\bigl(\sqrt{d\mu_n / d\mu_1}-1_{\mathcal{U}_n}\, \sqrt{d\mu_n/d\mu_1}\bigr)^{2} \, d\mu_1=\sum_{n=1}^{\infty}\mu_n(X_0\setminus \mathcal{U}_n)<+\infty , \end{align*} $$
we conclude that also
 $$ \begin{align} \sum_{n=1}^{\infty}\int_{X_0}\bigl(\sqrt{d\mu_n / d\mu_1}-\exp(t_n/2) \, 1_{\mathcal{U}_n} \, \sqrt{d\nu / d\mu_1}\bigr)^{2} \, d\mu_1< +\infty \;. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\int_{X_0}\bigl(\sqrt{d\mu_n / d\mu_1}-\exp(t_n/2) \, 1_{\mathcal{U}_n} \, \sqrt{d\nu / d\mu_1}\bigr)^{2} \, d\mu_1< +\infty \;. \end{align} $$
On
![]() $\mathcal {U}_n$
we have that
$\mathcal {U}_n$
we have that
![]() $\exp (-\beta )\leq \exp (1+|t_n|)\exp (\alpha _n)$
. As
$\exp (-\beta )\leq \exp (1+|t_n|)\exp (\alpha _n)$
. As
![]() $\exp (\alpha _n)$
is
$\exp (\alpha _n)$
is
![]() $\mu _1$
-integrable, it follows that
$\mu _1$
-integrable, it follows that
![]() $\exp (-\beta )$
is
$\exp (-\beta )$
is
![]() $\mu _1|_{\mathcal {U}_n}$
-integrable, so
$\mu _1|_{\mathcal {U}_n}$
-integrable, so
![]() $\nu (\mathcal {U}_n)<+\infty $
. For each
$\nu (\mathcal {U}_n)<+\infty $
. For each
![]() $n\in \mathbb {N}$
define the probability measure
$n\in \mathbb {N}$
define the probability measure
![]() $\nu _n=\nu (\mathcal {U}_n)^{-1}\nu |_{\mathcal {U}_n}$
.
$\nu _n=\nu (\mathcal {U}_n)^{-1}\nu |_{\mathcal {U}_n}$
.
For any pair of nonzero vectors
![]() $\xi _1,\xi _2$
in a Hilbert space, with
$\xi _1,\xi _2$
in a Hilbert space, with
![]() $\|\xi _1\|=1$
, we have that
$\|\xi _1\|=1$
, we have that
![]() $\|\xi _1-\|\xi _2\|^{-1} \xi _2\|\leq 2\|\xi _1-\xi _2\|$
. Thus, it follows from equation (4.18) that
$\|\xi _1-\|\xi _2\|^{-1} \xi _2\|\leq 2\|\xi _1-\xi _2\|$
. Thus, it follows from equation (4.18) that
 $$ \begin{align*} \sum_{n=1}^{\infty}H^2(\mu_n,\nu_n)<+\infty \;. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}H^2(\mu_n,\nu_n)<+\infty \;. \end{align*} $$
Define the map
![]() $\gamma _n$
by
$\gamma _n$
by
Let
![]() $D>0$
be such that
$D>0$
be such that
![]() $T_{1}(r)\leq D|1-\exp (-r/2)|$
, for every
$T_{1}(r)\leq D|1-\exp (-r/2)|$
, for every
![]() $r\in \mathbb {R}$
. It follows that
$r\in \mathbb {R}$
. It follows that
Define an increasing sequence of subsets
![]() $Z_k\subset X$
by
$Z_k\subset X$
by
Note that
![]() $\mu (X\setminus Z_k)\rightarrow 0$
as
$\mu (X\setminus Z_k)\rightarrow 0$
as
![]() $\sum _{n=1}^{\infty }\mu _n(X\setminus \mathcal {U}_n)<+\infty $
. By equation (4.19) the function
$\sum _{n=1}^{\infty }\mu _n(X\setminus \mathcal {U}_n)<+\infty $
. By equation (4.19) the function
 $$ \begin{align} G(x)=\sum_{n=1}^{\infty}\bigl(\log\frac{d\mu_n}{d\nu}(x_n)+\log(\nu(\mathcal{U}_n))\bigr) \end{align} $$
$$ \begin{align} G(x)=\sum_{n=1}^{\infty}\bigl(\log\frac{d\mu_n}{d\nu}(x_n)+\log(\nu(\mathcal{U}_n))\bigr) \end{align} $$
converges unconditionally a.e. on
![]() $Z_k$
, for every
$Z_k$
, for every
![]() $k\in \mathbb {N}$
. Therefore, the sum converges unconditionally a.e. As in the proof of [Reference Berendschot and Vaes8, Theorem 3.3], the
$k\in \mathbb {N}$
. Therefore, the sum converges unconditionally a.e. As in the proof of [Reference Berendschot and Vaes8, Theorem 3.3], the
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\zeta \sim \mu $
defined by
$\zeta \sim \mu $
defined by
![]() $d\zeta /d\mu =\exp (-G)$
is
$d\zeta /d\mu =\exp (-G)$
is
![]() $\mathcal {S}$
-invariant and
$\mathcal {S}$
-invariant and
![]() $\zeta $
is a finite measure if and only if
$\zeta $
is a finite measure if and only if
![]() $\nu $
is finite and
$\nu $
is finite and
![]() $\sum _{n=1}^{\infty }\nu (X_0\setminus \mathcal {U}_n)<+\infty $
.
$\sum _{n=1}^{\infty }\nu (X_0\setminus \mathcal {U}_n)<+\infty $
.
If
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is of type II
$\mathcal {S}\curvearrowright (X,\mu )$
is of type II
![]() $_{1}$
, then
$_{1}$
, then
![]() $\zeta $
must be finite, and we have that
$\zeta $
must be finite, and we have that
![]() $\mu \sim \nu ^{\mathbb {N}}$
. Conversely, if there exists a probability measure
$\mu \sim \nu ^{\mathbb {N}}$
. Conversely, if there exists a probability measure
![]() $\nu \sim \mu _1$
such that
$\nu \sim \mu _1$
such that
![]() $\mu \sim \nu ^{\mathbb {N}}$
, it follows directly that
$\mu \sim \nu ^{\mathbb {N}}$
, it follows directly that
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is of type II
$\mathcal {S}\curvearrowright (X,\mu )$
is of type II
![]() $_{1}$
.
$_{1}$
.
If
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is of type II
$\mathcal {S}\curvearrowright (X,\mu )$
is of type II
![]() $_{\infty }$
, then
$_{\infty }$
, then
![]() $\zeta $
must be infinite. So we have shown that all conditions in point 2 of the lemma are true. Conversely, if there exist a
$\zeta $
must be infinite. So we have shown that all conditions in point 2 of the lemma are true. Conversely, if there exist a
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\nu $
and subsets
$\nu $
and subsets
![]() $\mathcal {U}_n\subset X_0$
satisfying the conditions of point 2, then the sum (4.20) converges a.e. and the
$\mathcal {U}_n\subset X_0$
satisfying the conditions of point 2, then the sum (4.20) converges a.e. and the
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\zeta \sim \mu $
defined by
$\zeta \sim \mu $
defined by
![]() $d\zeta /d\mu =\exp (-G)$
is infinite and
$d\zeta /d\mu =\exp (-G)$
is infinite and
![]() $\mathcal {S}$
-invariant.
$\mathcal {S}$
-invariant.
Proof of Theorem 4.3
First of all, by Theorem 4.1 the Bernoulli shift
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is weakly mixing and
$\mathbb {Z}\curvearrowright (X,\mu )$
is weakly mixing and
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is ergodic. Moreover the Maharam extensions of
$\mathcal {S}\curvearrowright (X,\mu )$
is ergodic. Moreover the Maharam extensions of
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
and
$\mathbb {Z}\curvearrowright (X,\mu )$
and
![]() $\mathcal {S}\curvearrowright (X,\mu )$
satisfy
$\mathcal {S}\curvearrowright (X,\mu )$
satisfy
Write
![]() $(Z,\eta )=\prod _{n\in \mathbb {Z}, n\neq 1}(X_0,\mu _n)$
. Let
$(Z,\eta )=\prod _{n\in \mathbb {Z}, n\neq 1}(X_0,\mu _n)$
. Let
![]() $\mathcal {S}_1\subset \mathcal {S}$
be the subgroup of finite permutations that fix
$\mathcal {S}_1\subset \mathcal {S}$
be the subgroup of finite permutations that fix
![]() $1\in \mathbb {Z}$
so that
$1\in \mathbb {Z}$
so that
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )$
. Let
$\mathcal {S}_1\curvearrowright (Z,\eta )$
. Let
![]() $\theta $
denote the partial shift
$\theta $
denote the partial shift
 $$ \begin{align*} \theta\colon (X,\mu)\rightarrow (Z,\eta):\;\; \theta(x)_n=\begin{cases}x_n &\;\;\text{if}\;\; n\leq 0\\ x_{n-1} &\;\;\text{if}\;\; n\geq 2 \end{cases}. \end{align*} $$
$$ \begin{align*} \theta\colon (X,\mu)\rightarrow (Z,\eta):\;\; \theta(x)_n=\begin{cases}x_n &\;\;\text{if}\;\; n\leq 0\\ x_{n-1} &\;\;\text{if}\;\; n\geq 2 \end{cases}. \end{align*} $$
It follows directly from the Kakutani criterion that
![]() $\theta $
is a nonsingular isomorphism. It intertwines the actions
$\theta $
is a nonsingular isomorphism. It intertwines the actions
![]() $\mathcal {S}\curvearrowright (X,\mu )$
and
$\mathcal {S}\curvearrowright (X,\mu )$
and
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )$
. So
$\mathcal {S}_1\curvearrowright (Z,\eta )$
. So
![]() $\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic, and Lemma 4.7 applies. If
$\mathcal {S}_1\curvearrowright (Z,\eta )$
is ergodic, and Lemma 4.7 applies. If
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is semifinite, then by equation (4.21) also
$\mathbb {Z}\curvearrowright (X,\mu )$
is semifinite, then by equation (4.21) also
![]() $\mathcal {S}\curvearrowright (X,\mu )$
is semifinite. To complete the proof of the theorem, it suffices to show that
$\mathcal {S}\curvearrowright (X,\mu )$
is semifinite. To complete the proof of the theorem, it suffices to show that
![]() $\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
$\mathbb {Z}\curvearrowright (X,\mu )$
is of type II
![]() $_{\infty }$
if there exist a
$_{\infty }$
if there exist a
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\nu $
and Borel sets
$\nu $
and Borel sets
![]() $\mathcal {U}_n\subset X_0$
satisfying the conditions of the second point of the theorem.
$\mathcal {U}_n\subset X_0$
satisfying the conditions of the second point of the theorem.
Assume we are given such
![]() $\nu $
and
$\nu $
and
![]() $\mathcal {U}_n$
. Then, as in equation (4.20), the sum
$\mathcal {U}_n$
. Then, as in equation (4.20), the sum
 $$ \begin{align*} G(x)=\sum_{n\in \mathbb{Z}}\left(\log\frac{d\mu_n}{d\nu}(x_n)+\log(\nu(\mathcal{U}_n))\right) \end{align*} $$
$$ \begin{align*} G(x)=\sum_{n\in \mathbb{Z}}\left(\log\frac{d\mu_n}{d\nu}(x_n)+\log(\nu(\mathcal{U}_n))\right) \end{align*} $$
is unconditionally convergent a.e. By equation (4.21), the map
![]() $(x,t)\mapsto t-G(x)$
is invariant under the Maharam extension of
$(x,t)\mapsto t-G(x)$
is invariant under the Maharam extension of
![]() $\mathbb {Z}$
. Also, it is
$\mathbb {Z}$
. Also, it is
![]() $\mathbb {R}$
-equivariant.
$\mathbb {R}$
-equivariant.
It follows that the
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\zeta \sim \mu $
defined by
$\zeta \sim \mu $
defined by
![]() $d\zeta /d\mu =\exp (-G)$
is an infinite
$d\zeta /d\mu =\exp (-G)$
is an infinite
![]() $\mathbb {Z}$
-invariant measure.
$\mathbb {Z}$
-invariant measure.
5 Nonsingular Poisson suspensions: proof of Proposition D
We start this section by recalling the construction of the Poisson suspension. For a detailed treatment, we refer to [Reference Roy46, Reference Danilenko, Kosloff and Roy21]. Let
![]() $(X_0,\mu _0)$
be a
$(X_0,\mu _0)$
be a
![]() $\sigma $
-finite standard measure space. We write
$\sigma $
-finite standard measure space. We write
![]() $\mathcal {B}_0=\{A\subset X_0 \mid A \;\;\text {is Borel and}\;\; \mu _0(A)<+\infty \}$
. To
$\mathcal {B}_0=\{A\subset X_0 \mid A \;\;\text {is Borel and}\;\; \mu _0(A)<+\infty \}$
. To
![]() $(X_0,\mu _0)$
, one associates a standard probability space
$(X_0,\mu _0)$
, one associates a standard probability space
![]() $(X,\mu )$
and random variables
$(X,\mu )$
and random variables
![]() $P_A\colon X\rightarrow \{0,1,2,\dots \}$
for every
$P_A\colon X\rightarrow \{0,1,2,\dots \}$
for every
![]() $A\in \mathcal {B}_0$
such that the following holds.
$A\in \mathcal {B}_0$
such that the following holds.
-
1. The random variable
 $P_A$
is Poisson distributed with intensity
$P_A$
is Poisson distributed with intensity
 $\mu _0(A)$
.
$\mu _0(A)$
. -
2. If
 $A,B\in \mathcal {B}_0$
are disjoint, then
$A,B\in \mathcal {B}_0$
are disjoint, then
 $P_A$
and
$P_A$
and
 $P_B$
are independent random variables and we have that
$P_B$
are independent random variables and we have that
 $P_{A\cup B}=P_A+P_B$
.
$P_{A\cup B}=P_A+P_B$
. -
3. The family
 $(P_A)_{A\in \mathcal {B}_0}$
separates the points of X.
$(P_A)_{A\in \mathcal {B}_0}$
separates the points of X.
These three properties uniquely characterize
![]() $(X,\mu )$
and the random variables
$(X,\mu )$
and the random variables
![]() $(P_A)_{A\in \mathcal {B}_0}$
. The probability space
$(P_A)_{A\in \mathcal {B}_0}$
. The probability space
![]() $(X,\mu )$
is called the Poisson suspension over the base space
$(X,\mu )$
is called the Poisson suspension over the base space
![]() $(X_0,\mu _0)$
.
$(X_0,\mu _0)$
.
By the functoriality of this construction, every measure preserving Borel automorphism
![]() $\theta : X_0 \to X_0$
gives rise to an essentially unique, measure preserving Borel automorphism
$\theta : X_0 \to X_0$
gives rise to an essentially unique, measure preserving Borel automorphism
![]() $\widehat {\theta } : X \to X$
such that for every
$\widehat {\theta } : X \to X$
such that for every
![]() $A \in \mathcal {B}_0$
, we have
$A \in \mathcal {B}_0$
, we have
In [Reference Danilenko, Kosloff and Roy21, Theorem 3.3], it was discovered that a nonsingular Borel automorphism
![]() $\theta : X_0 \to X_0$
gives rise to a nonsingular Borel automorphism
$\theta : X_0 \to X_0$
gives rise to a nonsingular Borel automorphism
![]() $\widehat {\theta } : X \to X$
satisfying equation (5.1) if and only if
$\widehat {\theta } : X \to X$
satisfying equation (5.1) if and only if
 $$ \begin{align} \sqrt{\frac{d(\theta_* \mu_0)}{d\mu_0}} - 1 \in L^2(X_0,\mu_0) \;. \end{align} $$
$$ \begin{align} \sqrt{\frac{d(\theta_* \mu_0)}{d\mu_0}} - 1 \in L^2(X_0,\mu_0) \;. \end{align} $$
For completeness, we include below a short proof of one implication, namely that every
![]() $\theta $
satisfying equation (5.2) has a suspension
$\theta $
satisfying equation (5.2) has a suspension
![]() $\widehat {\theta }$
. This proof is essentially taken from [Reference Danilenko, Kosloff and Roy21] but presented in a more direct way.
$\widehat {\theta }$
. This proof is essentially taken from [Reference Danilenko, Kosloff and Roy21] but presented in a more direct way.
So, whenever
![]() $G \curvearrowright (X_0,\mu _0)$
is a nonsingular action of a locally compact second countable (lcsc) group such that
$G \curvearrowright (X_0,\mu _0)$
is a nonsingular action of a locally compact second countable (lcsc) group such that
we have an essentially unique nonsingular action
![]() $G \curvearrowright (X,\mu )$
characterized by
$G \curvearrowright (X,\mu )$
characterized by
![]() $P_A(g \cdot x) = P_{g^{-1}\cdot A}(x)$
, which is called the Poisson suspension action.
$P_A(g \cdot x) = P_{g^{-1}\cdot A}(x)$
, which is called the Poisson suspension action.
The main goal of this section is to prove Proposition D. We actually prove the following stable version, that also considers the associated flow of the diagonal action
![]() $G\curvearrowright X\times Y$
for any ergodic pmp action
$G\curvearrowright X\times Y$
for any ergodic pmp action
![]() $G\curvearrowright (Y,\nu )$
.
$G\curvearrowright (Y,\nu )$
.
Proposition 5.1. Let G be any lcsc group that does not have property
![]() $(T)$
. Let
$(T)$
. Let
![]() $\mathbb {R}\curvearrowright (Z,\zeta )$
be any Poisson flow. Then G admits a nonsingular action
$\mathbb {R}\curvearrowright (Z,\zeta )$
be any Poisson flow. Then G admits a nonsingular action
![]() $G\curvearrowright (X_0,\mu _0)$
of which the Poisson suspension
$G\curvearrowright (X_0,\mu _0)$
of which the Poisson suspension
![]() $G\curvearrowright (X,\mu )$
is well-defined, weakly mixing, essentially free and such that for any ergodic pmp action
$G\curvearrowright (X,\mu )$
is well-defined, weakly mixing, essentially free and such that for any ergodic pmp action
![]() $G\curvearrowright (Y,\nu )$
the diagonal action
$G\curvearrowright (Y,\nu )$
the diagonal action
![]() $G\curvearrowright X\times Y$
has associated flow
$G\curvearrowright X\times Y$
has associated flow
![]() $\mathbb {R}\curvearrowright Z$
.
$\mathbb {R}\curvearrowright Z$
.
Proposition 5.1 is sharp in the following sense: By [Reference Danilenko, Kosloff and Roy21, Theorem G], if G has property (T), then every Poisson suspension action admits an equivalent invariant probability measure. This follows by applying the Delorme–Guichardet theorem (see, e.g., [Reference Bekka, De la Harpe and Valette5, Theorem 2.12.4]) to the
![]() $1$
-cocycle
$1$
-cocycle
![]() $g \mapsto \sqrt {d(g \mu _0)/d\mu _0} - 1$
with values in the Koopman representation of
$g \mapsto \sqrt {d(g \mu _0)/d\mu _0} - 1$
with values in the Koopman representation of
![]() $G \curvearrowright (X_0,\mu _0)$
.
$G \curvearrowright (X_0,\mu _0)$
.
Before proving Proposition 5.1, we introduce some further background, based on [Reference Danilenko, Kosloff and Roy21]. In particular, we give a short proof that every nonsingular automorphism
![]() $\theta : X_0 \to X_0$
satisfying equation (5.2) admits a Poisson suspension
$\theta : X_0 \to X_0$
satisfying equation (5.2) admits a Poisson suspension
![]() $\widehat {\theta }$
. This proof is essentially taken from [Reference Danilenko, Kosloff and Roy21], but since our approach is direct and short, we include it here for convenience of the reader.
$\widehat {\theta }$
. This proof is essentially taken from [Reference Danilenko, Kosloff and Roy21], but since our approach is direct and short, we include it here for convenience of the reader.
Write
![]() $\mathcal {H} = L^2_{\mathbb {R}}(X_0,\mu _0)$
, and denote by
$\mathcal {H} = L^2_{\mathbb {R}}(X_0,\mu _0)$
, and denote by
![]() $\mathcal {H}_n \subset \mathcal {H}^{\otimes n}$
the closed subspace of symmetric vectors (i.e., invariant under the action of the symmetric group
$\mathcal {H}_n \subset \mathcal {H}^{\otimes n}$
the closed subspace of symmetric vectors (i.e., invariant under the action of the symmetric group
![]() $S_n$
on
$S_n$
on
![]() $H^{\otimes n}$
). The key point is that there is a canonical isometric isomorphism
$H^{\otimes n}$
). The key point is that there is a canonical isometric isomorphism
between the symmetric Fock space
![]() $\mathcal {F}_s(\mathcal {H})$
of
$\mathcal {F}_s(\mathcal {H})$
of
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $L^2_{\mathbb {R}}(X,\mu )$
. This isomorphism U is defined as follows. For every
$L^2_{\mathbb {R}}(X,\mu )$
. This isomorphism U is defined as follows. For every
![]() $\xi \in \mathcal {H}$
, denote by
$\xi \in \mathcal {H}$
, denote by
![]() $\exp (\xi ) \in \mathcal {F}_s(\mathcal {H})$
the usual exponential given by
$\exp (\xi ) \in \mathcal {F}_s(\mathcal {H})$
the usual exponential given by
 $$ \begin{align*}\exp(\xi) = 1 \oplus \bigoplus_{n=1}^{\infty} \frac{1}{n!} \xi^{\otimes n} \; .\end{align*} $$
$$ \begin{align*}\exp(\xi) = 1 \oplus \bigoplus_{n=1}^{\infty} \frac{1}{n!} \xi^{\otimes n} \; .\end{align*} $$
For every
![]() $A\in \mathcal {B}_0$
and
$A\in \mathcal {B}_0$
and
![]() $\alpha \in \mathbb {R}$
, define
$\alpha \in \mathbb {R}$
, define
![]() $T_{\alpha ,A}\colon X\rightarrow \mathbb {R}$
by
$T_{\alpha ,A}\colon X\rightarrow \mathbb {R}$
by
If
![]() $\xi \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
takes only finitely many function values, i.e., is of the form
$\xi \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
takes only finitely many function values, i.e., is of the form
![]() $\xi =1_A +\sum _{i=1}^m\alpha _i1_{A_i}$
for
$\xi =1_A +\sum _{i=1}^m\alpha _i1_{A_i}$
for
![]() $\alpha _i\in \mathbb {R}$
, disjoint
$\alpha _i\in \mathbb {R}$
, disjoint
![]() $A_i\in \mathcal {B}_0$
and
$A_i\in \mathcal {B}_0$
and
![]() $A = \mathbb {R} \setminus \bigcup _{i=1}^m A_i$
, we define
$A = \mathbb {R} \setminus \bigcup _{i=1}^m A_i$
, we define
![]() $\mathcal {T}(\xi )\in L^2_{\mathbb {R}}(X,\mu )$
by
$\mathcal {T}(\xi )\in L^2_{\mathbb {R}}(X,\mu )$
by
 $$ \begin{align*} \mathcal{T}(\xi)=\prod_{i=1}^{m}T_{\alpha_i,A_i} \;. \end{align*} $$
$$ \begin{align*} \mathcal{T}(\xi)=\prod_{i=1}^{m}T_{\alpha_i,A_i} \;. \end{align*} $$
A direct computation shows that
for all
![]() $\xi ,\xi '$
of such a form. The vectors
$\xi ,\xi '$
of such a form. The vectors
![]() $\exp (\xi -1)$
are total in the symmetric Fock space
$\exp (\xi -1)$
are total in the symmetric Fock space
![]() $\mathcal {F}_s(\mathcal {H})$
, and the functions
$\mathcal {F}_s(\mathcal {H})$
, and the functions
![]() $\mathcal {T}(\xi )$
are total in
$\mathcal {T}(\xi )$
are total in
![]() $L^2_{\mathbb {R}}(X,\mu )$
. Therefore,
$L^2_{\mathbb {R}}(X,\mu )$
. Therefore,
![]() $\mathcal {T}$
uniquely extends to a continuous map
$\mathcal {T}$
uniquely extends to a continuous map
![]() $\mathcal {T} : 1+L^2_{\mathbb {R}}(X_0,\mu _0) \to L^{2}_{\mathbb {R}}(X,\mu )$
, and the isomorphism U in equation (5.4) is uniquely defined by
$\mathcal {T} : 1+L^2_{\mathbb {R}}(X_0,\mu _0) \to L^{2}_{\mathbb {R}}(X,\mu )$
, and the isomorphism U in equation (5.4) is uniquely defined by
![]() $U(\exp (\xi -1)) = \mathcal {T}(\xi )$
for all
$U(\exp (\xi -1)) = \mathcal {T}(\xi )$
for all
![]() $\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
.
$\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
.
When
![]() $\xi ,\xi ' \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
are such that their product
$\xi ,\xi ' \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
are such that their product
![]() $\xi \xi '$
still belongs to
$\xi \xi '$
still belongs to
![]() $1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
, we have
$1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
, we have
which is immediate when
![]() $\xi ,\xi '$
only take finitely many values and is then valid for all
$\xi ,\xi '$
only take finitely many values and is then valid for all
![]() $\xi ,\xi '$
by density and continuity.
$\xi ,\xi '$
by density and continuity.
When
![]() $\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
satisfies
$\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
satisfies
![]() $\xi (x) \geq 0$
for a.e.
$\xi (x) \geq 0$
for a.e.
![]() $x \in X_0$
, we have by construction that
$x \in X_0$
, we have by construction that
![]() $\mathcal {T}(\xi )(x) \geq 0$
for a.e.
$\mathcal {T}(\xi )(x) \geq 0$
for a.e.
![]() $x \in X$
. We next prove that if
$x \in X$
. We next prove that if
![]() $\xi (x)> 0$
for a.e.
$\xi (x)> 0$
for a.e.
![]() $x \in X_0$
, then
$x \in X_0$
, then
![]() $\mathcal {T}(\xi )(x)> 0$
for a.e.
$\mathcal {T}(\xi )(x)> 0$
for a.e.
![]() $x \in X$
. To see this, define
$x \in X$
. To see this, define
![]() $C_n = \{x \in X \mid n^{-1} \leq \xi (x) \leq n\}$
and define
$C_n = \{x \in X \mid n^{-1} \leq \xi (x) \leq n\}$
and define
![]() $\xi _n \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
by
$\xi _n \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
by
![]() $\xi _n(x) = \xi (x)^{-1}$
if
$\xi _n(x) = \xi (x)^{-1}$
if
![]() $x \in C_n$
and
$x \in C_n$
and
![]() $\xi _n(x) = 1$
if
$\xi _n(x) = 1$
if
![]() $x \not \in C_n$
. Define
$x \not \in C_n$
. Define
![]() $F_n \in L^2_{\mathbb {R}}(X,\mu )$
by
$F_n \in L^2_{\mathbb {R}}(X,\mu )$
by
![]() $F_n = \exp (-\langle \xi - 1, \xi _n - 1 \rangle ) \, \mathcal {T}(\xi _n)$
. By equation (5.6), we get that
$F_n = \exp (-\langle \xi - 1, \xi _n - 1 \rangle ) \, \mathcal {T}(\xi _n)$
. By equation (5.6), we get that
![]() $\mathcal {T}(\xi ) F_n \to 1$
in
$\mathcal {T}(\xi ) F_n \to 1$
in
![]() $L^2_{\mathbb {R}}(X,\mu )$
. Therefore,
$L^2_{\mathbb {R}}(X,\mu )$
. Therefore,
![]() $\mathcal {T}(\xi )(x) \neq 0$
for a.e.
$\mathcal {T}(\xi )(x) \neq 0$
for a.e.
![]() $x \in X$
.
$x \in X$
.
Note, for later use, that it follows in particular that if
![]() $\xi \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
is such that also
$\xi \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
is such that also
![]() $\xi ^{-1} \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
, then
$\xi ^{-1} \in 1+L^2_{\mathbb {R}}(X_0,\mu _0)$
, then
Now assume that
![]() $\nu _0$
is a
$\nu _0$
is a
![]() $\sigma $
-finite measure on
$\sigma $
-finite measure on
![]() $X_0$
such that
$X_0$
such that
![]() $\nu _0 \sim \mu _0$
. Write
$\nu _0 \sim \mu _0$
. Write
![]() $\xi = \sqrt {d\nu _0/d\mu _0}$
, and assume that
$\xi = \sqrt {d\nu _0/d\mu _0}$
, and assume that
![]() $\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
. Define
$\xi \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
. Define
![]() $F \in L^2(X,\mu )$
by
$F \in L^2(X,\mu )$
by
![]() $F = \exp (-\|\xi -1\|^2_2/2) \, \mathcal {T}(\xi )$
. By the discussion above,
$F = \exp (-\|\xi -1\|^2_2/2) \, \mathcal {T}(\xi )$
. By the discussion above,
![]() $F(x)>0$
for a.e.
$F(x)>0$
for a.e.
![]() $x \in X$
. Also,
$x \in X$
. Also,
We can thus define a unique probability measure
![]() $\nu \sim \mu $
such that
$\nu \sim \mu $
such that
We show that, for every
![]() $A \in \mathcal {B}_0$
, the variable
$A \in \mathcal {B}_0$
, the variable
![]() $P_A$
has, w.r.t.
$P_A$
has, w.r.t.
![]() $\nu $
, a Poisson distribution with intensity
$\nu $
, a Poisson distribution with intensity
![]() $\nu _0(A)$
. Let
$\nu _0(A)$
. Let
![]() $\alpha> 0$
be arbitrary. Still writing
$\alpha> 0$
be arbitrary. Still writing
![]() $\xi = \sqrt {d\nu _0/d\mu _0}$
, define
$\xi = \sqrt {d\nu _0/d\mu _0}$
, define
![]() $\xi _A \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
by
$\xi _A \in 1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
by
![]() $\xi _A(x) = \alpha \xi (x)$
if
$\xi _A(x) = \alpha \xi (x)$
if
![]() $x \in A$
and
$x \in A$
and
![]() $\xi _A(x) = \xi (x)$
if
$\xi _A(x) = \xi (x)$
if
![]() $x \not \in A$
. By equation (5.6), we get that
$x \not \in A$
. By equation (5.6), we get that
It follows that
Since this holds for every
![]() $\alpha> 0$
, the distribution of
$\alpha> 0$
, the distribution of
![]() $P_A$
w.r.t.
$P_A$
w.r.t.
![]() $\nu $
is Poisson with intensity
$\nu $
is Poisson with intensity
![]() $\nu _0(A)$
.
$\nu _0(A)$
.
Finally, given
![]() $A \in \mathcal {B}_0$
, the partition
$A \in \mathcal {B}_0$
, the partition
![]() $X_0 = A \sqcup (X_0 \setminus A)$
gives rise to a decomposition of X as the direct product of the Poisson suspension of
$X_0 = A \sqcup (X_0 \setminus A)$
gives rise to a decomposition of X as the direct product of the Poisson suspension of
![]() $(A,\mu _0)$
and the Poisson suspension of
$(A,\mu _0)$
and the Poisson suspension of
![]() $(X_0 \setminus A,\mu _0)$
. By equations (5.6) and (5.8), also
$(X_0 \setminus A,\mu _0)$
. By equations (5.6) and (5.8), also
![]() $\nu $
is a product measure in this decomposition. It follows that
$\nu $
is a product measure in this decomposition. It follows that
![]() $P_A$
is independent from
$P_A$
is independent from
![]() $P_B$
for every
$P_B$
for every
![]() $B \in \mathcal {B}_0$
that is disjoint from A.
$B \in \mathcal {B}_0$
that is disjoint from A.
Altogether, we have thus proven that
![]() $(X,\nu )$
is the Poisson suspension of
$(X,\nu )$
is the Poisson suspension of
![]() $(X_0,\nu _0)$
. This observation implies that, for every automorphisms
$(X_0,\nu _0)$
. This observation implies that, for every automorphisms
![]() $\theta $
satisfying equation (5.2), there is an essentially unique nonsingular Poisson suspension
$\theta $
satisfying equation (5.2), there is an essentially unique nonsingular Poisson suspension
![]() $\widehat {\theta }$
given by equation (5.1). So also, for every nonsingular action
$\widehat {\theta }$
given by equation (5.1). So also, for every nonsingular action
![]() $G \curvearrowright (X_0,\mu _0)$
satisfying equation (5.3), the Poisson suspension action
$G \curvearrowright (X_0,\mu _0)$
satisfying equation (5.3), the Poisson suspension action
![]() $G \curvearrowright (X,\mu )$
is well defined.
$G \curvearrowright (X,\mu )$
is well defined.
An important step in the proof of Proposition 5.1 is to ensure that the Poisson suspension action
![]() $G \curvearrowright (X,\mu )$
is conservative. If in the discussion above, both
$G \curvearrowright (X,\mu )$
is conservative. If in the discussion above, both
![]() $\xi = \sqrt {d\nu _0/d\mu _0}$
and
$\xi = \sqrt {d\nu _0/d\mu _0}$
and
![]() $\xi ^{-1}$
belong to
$\xi ^{-1}$
belong to
![]() $1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
, it follows from equation (5.7) that
$1 + L^2_{\mathbb {R}}(X_0,\mu _0)$
, it follows from equation (5.7) that
so that
So whenever
![]() $G \curvearrowright (X_0,\mu _0)$
is a nonsingular action, we denote
$G \curvearrowright (X_0,\mu _0)$
is a nonsingular action, we denote
The following result is then an immediate consequence of equation (5.9) and [Reference Berendschot and Vaes8, Lemma 2.6] (adapted to the locally compact setting) and is similar to [Reference Danilenko and Kosloff20, Lemma 1.3].
Proposition 5.2. Let
![]() $G\curvearrowright (X_0,\mu _0)$
be a nonsingular action of a locally compact second countable group G on an infinite,
$G\curvearrowright (X_0,\mu _0)$
be a nonsingular action of a locally compact second countable group G on an infinite,
![]() $\sigma $
-finite standard measure space
$\sigma $
-finite standard measure space
![]() $(X_0,\mu _0)$
such that equation (5.3) holds. Let
$(X_0,\mu _0)$
such that equation (5.3) holds. Let
![]() $\lambda $
denote a left invariant Haar measure on G. If
$\lambda $
denote a left invariant Haar measure on G. If
 $$ \begin{align*} \limsup_{s\rightarrow +\infty}\frac{\log\lambda(\{g\in G \mid \kappa(g^{\pm 1})\leq s\})}{s}>3 , \end{align*} $$
$$ \begin{align*} \limsup_{s\rightarrow +\infty}\frac{\log\lambda(\{g\in G \mid \kappa(g^{\pm 1})\leq s\})}{s}>3 , \end{align*} $$
then the nonsingular Poisson suspension
![]() $G\curvearrowright (X,\mu )$
is conservative.
$G\curvearrowright (X,\mu )$
is conservative.
For lcsc groups G with the Haagerup approximation property, one can give a very short proof of Proposition 5.1 by only using Proposition 5.2. For the general case, where G is only assumed to be non-(T), we have to make use of recurrence of
![]() $G \curvearrowright (X,\mu )$
along specific subsets
$G \curvearrowright (X,\mu )$
along specific subsets
![]() $\Lambda \subset G$
. We thus recall the following two definitions from [Reference Arano, Isono and Marrakchi1].
$\Lambda \subset G$
. We thus recall the following two definitions from [Reference Arano, Isono and Marrakchi1].
Definition 5.3 [Reference Arano, Isono and Marrakchi1, Definitions 7.12 and 7.13]
Let
![]() $\pi \colon G\curvearrowright \mathcal {H}$
be an orthogonal representation on a real Hilbert space
$\pi \colon G\curvearrowright \mathcal {H}$
be an orthogonal representation on a real Hilbert space
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\Lambda \subset G$
a countable subset. We say that
$\Lambda \subset G$
a countable subset. We say that
![]() $\pi $
is mixing along
$\pi $
is mixing along
![]() $\Lambda $
if
$\Lambda $
if
A pmp action
![]() $G \curvearrowright (X,\mu )$
is mixing along
$G \curvearrowright (X,\mu )$
is mixing along
![]() $\Lambda $
if the reduced Koopman representation
$\Lambda $
if the reduced Koopman representation
is mixing along
![]() $\Lambda $
.
$\Lambda $
.
A nonsingular action
![]() $G \curvearrowright (X,\mu )$
is said to be recurrent along
$G \curvearrowright (X,\mu )$
is said to be recurrent along
![]() $\Lambda $
if for every nonnegligible Borel set
$\Lambda $
if for every nonnegligible Borel set
![]() $A\subset X$
there exist infinitely many
$A\subset X$
there exist infinitely many
![]() $g\in \Lambda $
such that
$g\in \Lambda $
such that
![]() $\mu (g\cdot A\cap A)>0$
.
$\mu (g\cdot A\cap A)>0$
.
Similarly to Proposition 5.2, combining [Reference Arano, Isono and Marrakchi1, Lemma 7.15] and [Reference Berendschot and Vaes8, Lemma 2.6], we then get the following.
Proposition 5.4. Let
![]() $G\curvearrowright (X_0,\mu _0)$
be a nonsingular action of a locally compact second countable group G on an infinite,
$G\curvearrowright (X_0,\mu _0)$
be a nonsingular action of a locally compact second countable group G on an infinite,
![]() $\sigma $
-finite standard measure space
$\sigma $
-finite standard measure space
![]() $(X_0,\mu _0)$
such that equation (5.3) holds. Let
$(X_0,\mu _0)$
such that equation (5.3) holds. Let
![]() $\Lambda \subset G$
be a countable infinite subset. If
$\Lambda \subset G$
be a countable infinite subset. If
 $$ \begin{align*} \limsup_{s\rightarrow +\infty}\frac{\log |\{g\in \Lambda \mid \kappa(g^{\pm 1})\leq s\}|}{s}>3 , \end{align*} $$
$$ \begin{align*} \limsup_{s\rightarrow +\infty}\frac{\log |\{g\in \Lambda \mid \kappa(g^{\pm 1})\leq s\}|}{s}>3 , \end{align*} $$
then the nonsingular Poisson suspension
![]() $G\curvearrowright (X,\mu )$
, and for every pmp action
$G\curvearrowright (X,\mu )$
, and for every pmp action
![]() $G \curvearrowright (Y,\nu )$
, the Maharam extension of the diagonal action
$G \curvearrowright (Y,\nu )$
, the Maharam extension of the diagonal action
![]() $G \curvearrowright X \times Y$
are recurrent along
$G \curvearrowright X \times Y$
are recurrent along
![]() $\Lambda \Lambda ^{-1}$
.
$\Lambda \Lambda ^{-1}$
.
The first step in proving Proposition 5.1 is to translate the absence of property (T) to a dynamical property: There exists a measure preserving action
![]() $G \curvearrowright (W,\rho )$
on a standard, infinite,
$G \curvearrowright (W,\rho )$
on a standard, infinite,
![]() $\sigma $
-finite measure space such that the Koopman representation on
$\sigma $
-finite measure space such that the Koopman representation on
![]() $L^2(W,\rho )$
is weakly mixing and the action admits a Følner sequence, i.e., a sequence of Borel sets
$L^2(W,\rho )$
is weakly mixing and the action admits a Følner sequence, i.e., a sequence of Borel sets
![]() $A_n \subset W$
such that
$A_n \subset W$
such that
![]() $0<\rho (A_n)<+\infty $
for every
$0<\rho (A_n)<+\infty $
for every
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
 $$ \begin{align*} \lim_{n\rightarrow \infty}\frac{\rho(g \cdot A_n\vartriangle A_n)}{\rho(A_n)} = 0 \quad\text{uniformly on compact subsets } K\subset G. \end{align*} $$
$$ \begin{align*} \lim_{n\rightarrow \infty}\frac{\rho(g \cdot A_n\vartriangle A_n)}{\rho(A_n)} = 0 \quad\text{uniformly on compact subsets } K\subset G. \end{align*} $$
This characterization is proven in [Reference Danilenko19, Section 4] and is a consequence of the Connes–Weiss characterization of property (T) (see [Reference Connes and Weiss15] and [Reference Bekka, De la Harpe and Valette5, Theorem 6.3.4]): Taking a weakly mixing pmp action
![]() $G \curvearrowright (B,\beta )$
that admits a Følner sequence
$G \curvearrowright (B,\beta )$
that admits a Følner sequence
![]() $B_n \subset B$
with
$B_n \subset B$
with
![]() $\beta (B_n) = 1/2$
for all
$\beta (B_n) = 1/2$
for all
![]() $n \in \mathbb {N}$
, we can pass to a subsequence and assume that for every compact
$n \in \mathbb {N}$
, we can pass to a subsequence and assume that for every compact
![]() $K \subset G$
,
$K \subset G$
,
 $$ \begin{align*}\sum_{n=1}^{\infty} \sup_{g \in K} \beta(g \cdot B_n \vartriangle B_n) < +\infty \; .\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} \sup_{g \in K} \beta(g \cdot B_n \vartriangle B_n) < +\infty \; .\end{align*} $$
Then, the diagonal action of G on the restricted infinite product
 $$ \begin{align*} W = \prod_{n=1}^{\infty} (B,B_n) = \{x \in B^{\mathbb{N}} \mid x_n \in B_n \;\;\text{for all but finitely many } n \in \mathbb{N}\;\} \end{align*} $$
$$ \begin{align*} W = \prod_{n=1}^{\infty} (B,B_n) = \{x \in B^{\mathbb{N}} \mid x_n \in B_n \;\;\text{for all but finitely many } n \in \mathbb{N}\;\} \end{align*} $$
equipped with the product measure
![]() $\rho = (2\beta )^{\mathbb {N}}$
is well defined and satisfies all the requirements.
$\rho = (2\beta )^{\mathbb {N}}$
is well defined and satisfies all the requirements.
Lemma 5.5. Let G be an lcsc group and
![]() $G \curvearrowright (W,\rho )$
a measure preserving action on a standard, infinite,
$G \curvearrowright (W,\rho )$
a measure preserving action on a standard, infinite,
![]() $\sigma $
-finite measure space such that its Koopman representation is weakly mixing and the action admits a Følner sequence
$\sigma $
-finite measure space such that its Koopman representation is weakly mixing and the action admits a Følner sequence
![]() $A_n \subset W$
. Let
$A_n \subset W$
. Let
![]() $\lambda _n> 0$
and
$\lambda _n> 0$
and
![]() $a_n \in \mathbb {R} \setminus \{0\}$
. Define
$a_n \in \mathbb {R} \setminus \{0\}$
. Define
![]() $X_0 = W \times \mathbb {N}$
, and define the measure
$X_0 = W \times \mathbb {N}$
, and define the measure
![]() $\mu _0$
on
$\mu _0$
on
![]() $X_0$
by
$X_0$
by
Consider the nonsingular action
![]() $G \curvearrowright (X_0,\mu _0)$
defined by
$G \curvearrowright (X_0,\mu _0)$
defined by
![]() $g \cdot (x,n) = (g \cdot x , n)$
.
$g \cdot (x,n) = (g \cdot x , n)$
.
After replacing
![]() $A_n$
by a subsequence, we get that the Poisson suspension
$A_n$
by a subsequence, we get that the Poisson suspension
![]() $G \curvearrowright (X,\mu )$
of
$G \curvearrowright (X,\mu )$
of
![]() $G \curvearrowright (X_0,\mu _0)$
is well defined and weakly mixing and has the property that, for any ergodic pmp action
$G \curvearrowright (X_0,\mu _0)$
is well defined and weakly mixing and has the property that, for any ergodic pmp action
![]() $G\curvearrowright (Y,\nu )$
, the associated flow of the diagonal action
$G\curvearrowright (Y,\nu )$
, the associated flow of the diagonal action
![]() $G\curvearrowright X\times Y$
is given by the tail boundary flow of the sequence of Poisson distributions
$G\curvearrowright X\times Y$
is given by the tail boundary flow of the sequence of Poisson distributions
![]() $\sigma _{\lambda _n,a_n}$
defined by equation (3.33).
$\sigma _{\lambda _n,a_n}$
defined by equation (3.33).
Proof. Denote by
![]() $\pi : G \to \mathcal {U}(L^2(W,\rho )) : (\pi (g)\xi )(x) = \xi (g^{-1}\cdot x)$
the Koopman representation. By [Reference Arano, Isono and Marrakchi1, Lemma 7.17], we can fix an infinite subset
$\pi : G \to \mathcal {U}(L^2(W,\rho )) : (\pi (g)\xi )(x) = \xi (g^{-1}\cdot x)$
the Koopman representation. By [Reference Arano, Isono and Marrakchi1, Lemma 7.17], we can fix an infinite subset
![]() $\Lambda \subset G$
such that
$\Lambda \subset G$
such that
![]() $\pi $
is mixing along
$\pi $
is mixing along
![]() $\Lambda \Lambda ^{-1}$
. Define
$\Lambda \Lambda ^{-1}$
. Define
 $$ \begin{align*} & \kappa_n : G \to [0,+\infty) : \kappa_n(g) = \frac{1}{2} \, \lambda_n \, \frac{\rho(g \cdot A_n \vartriangle A_n)}{\rho(A_n)} \, (e^{a_n} - e^{-a_n})(e^{a_n} - 1) \quad\text{and}\\ & \kappa_0 : G \to [0,+\infty] : \kappa_0(g) = \sum_{n=1}^{\infty} \kappa_n(g) \;. \end{align*} $$
$$ \begin{align*} & \kappa_n : G \to [0,+\infty) : \kappa_n(g) = \frac{1}{2} \, \lambda_n \, \frac{\rho(g \cdot A_n \vartriangle A_n)}{\rho(A_n)} \, (e^{a_n} - e^{-a_n})(e^{a_n} - 1) \quad\text{and}\\ & \kappa_0 : G \to [0,+\infty] : \kappa_0(g) = \sum_{n=1}^{\infty} \kappa_n(g) \;. \end{align*} $$
Replacing
![]() $A_n$
by a subsequence, we may assume that
$A_n$
by a subsequence, we may assume that
 $$ \begin{align*} & \sup_{g \in K} \kappa_0(g) <+\infty \quad\text{for every compact subset } K \subset G, \text{ and}\\ & \limsup_{s\rightarrow +\infty}\frac{\log | \{g\in \Lambda \mid \kappa_0(g^{\pm 1})\leq s \}|}{s}>3 \;. \end{align*} $$
$$ \begin{align*} & \sup_{g \in K} \kappa_0(g) <+\infty \quad\text{for every compact subset } K \subset G, \text{ and}\\ & \limsup_{s\rightarrow +\infty}\frac{\log | \{g\in \Lambda \mid \kappa_0(g^{\pm 1})\leq s \}|}{s}>3 \;. \end{align*} $$
Define the measure
![]() $\mu _0$
as in the formulation of the lemma. A direct computation gives that
$\mu _0$
as in the formulation of the lemma. A direct computation gives that
Since
![]() $|a-1| \leq |a - a^{-1}|$
for all
$|a-1| \leq |a - a^{-1}|$
for all
![]() $a> 0$
, we also find that equation (5.3) holds. So, the Poisson suspension
$a> 0$
, we also find that equation (5.3) holds. So, the Poisson suspension
![]() $G\curvearrowright (X,\mu )$
of
$G\curvearrowright (X,\mu )$
of
![]() $G\curvearrowright (X_0,\mu _0)$
is well-defined. By Proposition 5.4, the action
$G\curvearrowright (X_0,\mu _0)$
is well-defined. By Proposition 5.4, the action
![]() $G \curvearrowright (X,\mu )$
is recurrent along
$G \curvearrowright (X,\mu )$
is recurrent along
![]() $\Lambda \Lambda ^{-1}$
.
$\Lambda \Lambda ^{-1}$
.
Let
![]() $\gamma : G\curvearrowright (Y,\nu )$
be any ergodic pmp action. We prove that the diagonal action
$\gamma : G\curvearrowright (Y,\nu )$
be any ergodic pmp action. We prove that the diagonal action
![]() $G \curvearrowright X \times Y$
is ergodic and that its associated flow is isomorphic with
$G \curvearrowright X \times Y$
is ergodic and that its associated flow is isomorphic with
![]() $\mathbb {R} \curvearrowright Z$
. Part of this argument is similar to the proof of [Reference Danilenko19, Proposition 1.17].
$\mathbb {R} \curvearrowright Z$
. Part of this argument is similar to the proof of [Reference Danilenko19, Proposition 1.17].
Denote by
![]() $\rho _n$
the measure on W given by
$\rho _n$
the measure on W given by
![]() $\rho _n(\mathcal {U}) = \mu _0(\mathcal {U} \times \{n\})$
. Viewing
$\rho _n(\mathcal {U}) = \mu _0(\mathcal {U} \times \{n\})$
. Viewing
![]() $X_0$
as the disjoint union of the G-invariant subsets
$X_0$
as the disjoint union of the G-invariant subsets
![]() $W\times \{n\}$
, we identify
$W\times \{n\}$
, we identify
![]() $(X,\mu )$
with
$(X,\mu )$
with
![]() $\prod _{n = 1}^{\infty } (X_n,\mu _n)$
, where
$\prod _{n = 1}^{\infty } (X_n,\mu _n)$
, where
![]() $(X_n,\mu _n)$
is the Poisson suspension of
$(X_n,\mu _n)$
is the Poisson suspension of
![]() $(W,\rho _n)$
. Then
$(W,\rho _n)$
. Then
![]() $\alpha : G \curvearrowright (X,\mu )$
is the diagonal product action of
$\alpha : G \curvearrowright (X,\mu )$
is the diagonal product action of
![]() $\alpha _n : G \curvearrowright (X_n,\mu _n)$
. Define the probability measures
$\alpha _n : G \curvearrowright (X_n,\mu _n)$
. Define the probability measures
![]() $\nu _n\sim \mu _n$
by
$\nu _n\sim \mu _n$
by
Then
![]() $G\curvearrowright (X_n,\nu _n)$
is the Poisson suspension of
$G\curvearrowright (X_n,\nu _n)$
is the Poisson suspension of
![]() $G\curvearrowright (W,\beta _n \rho )$
, with
$G\curvearrowright (W,\beta _n \rho )$
, with
![]() $\beta _n = \lambda _n e^{a_n} \rho (A_n)^{-1}$
. Since
$\beta _n = \lambda _n e^{a_n} \rho (A_n)^{-1}$
. Since
![]() $G\curvearrowright (W,\beta _n\rho )$
is measure preserving, the probability measure
$G\curvearrowright (W,\beta _n\rho )$
is measure preserving, the probability measure
![]() $\nu _n$
is G-invariant. Through equation (5.4), the Koopman representation of
$\nu _n$
is G-invariant. Through equation (5.4), the Koopman representation of
![]() $G \curvearrowright (X_n,\nu _n)$
is the natural representation of G on the symmetric Fock space
$G \curvearrowright (X_n,\nu _n)$
is the natural representation of G on the symmetric Fock space
![]() $\mathcal {F}_s(L^2_{\mathbb {R}}(W,\beta _n \rho ))$
associated with the Koopman representation of G on
$\mathcal {F}_s(L^2_{\mathbb {R}}(W,\beta _n \rho ))$
associated with the Koopman representation of G on
![]() $L^2_{\mathbb {R}}(W,\beta _n \rho )$
. Therefore,
$L^2_{\mathbb {R}}(W,\beta _n \rho )$
. Therefore,
![]() $G \curvearrowright (X_n,\nu _n)$
is weakly mixing along
$G \curvearrowright (X_n,\nu _n)$
is weakly mixing along
![]() $\Lambda \Lambda ^{-1}$
.
$\Lambda \Lambda ^{-1}$
.
Consider the Maharam extension
![]() $G \curvearrowright X \times Y \times \mathbb {R}$
of the diagonal action
$G \curvearrowright X \times Y \times \mathbb {R}$
of the diagonal action
![]() $G \curvearrowright X \times Y$
. Fix
$G \curvearrowright X \times Y$
. Fix
![]() $F \in L^{\infty }(X \times Y \times \mathbb {R})^G$
. Define
$F \in L^{\infty }(X \times Y \times \mathbb {R})^G$
. Define
![]() $\psi _n=-\log d\mu _n/d\nu _n$
. Fix
$\psi _n=-\log d\mu _n/d\nu _n$
. Fix
![]() $N \in \mathbb {N}$
, and write
$N \in \mathbb {N}$
, and write
 $$ \begin{align*}(X^{\prime}_N,\mu^{\prime}_N) = \prod_{n=1}^N (X_n,\mu_n) \quad\text{and}\quad (X^{\prime\prime}_N,\mu^{\prime\prime}_N) = \prod_{n=N+1}^{\infty} (X_n,\mu_n) \; .\end{align*} $$
$$ \begin{align*}(X^{\prime}_N,\mu^{\prime}_N) = \prod_{n=1}^N (X_n,\mu_n) \quad\text{and}\quad (X^{\prime\prime}_N,\mu^{\prime\prime}_N) = \prod_{n=N+1}^{\infty} (X_n,\mu_n) \; .\end{align*} $$
We identify
![]() $X = X^{\prime }_N \times X^{\prime \prime }_N$
and define
$X = X^{\prime }_N \times X^{\prime \prime }_N$
and define
 $$ \begin{align*} \mbox{}\hspace{1cm}\Psi_N : X^{\prime}_N \times X^{\prime\prime}_N \times Y \times \mathbb{R} \to X^{\prime}_N \times X^{\prime\prime}_N &\times Y \times \mathbb{R} : \\ &\Psi_N(x',x^{\prime\prime},y,t) = \Bigl(x',x^{\prime\prime},y,t+\sum_{n=1}^N \psi_n(x^{\prime}_n)\Bigr) \; .\hspace{1cm}\mbox{} \end{align*} $$
$$ \begin{align*} \mbox{}\hspace{1cm}\Psi_N : X^{\prime}_N \times X^{\prime\prime}_N \times Y \times \mathbb{R} \to X^{\prime}_N \times X^{\prime\prime}_N &\times Y \times \mathbb{R} : \\ &\Psi_N(x',x^{\prime\prime},y,t) = \Bigl(x',x^{\prime\prime},y,t+\sum_{n=1}^N \psi_n(x^{\prime}_n)\Bigr) \; .\hspace{1cm}\mbox{} \end{align*} $$
We denote by
![]() $\alpha ^{\prime }_N : G \curvearrowright X^{\prime }_N$
and
$\alpha ^{\prime }_N : G \curvearrowright X^{\prime }_N$
and
![]() $\alpha ^{\prime \prime }_N : G \curvearrowright X^{\prime \prime }_N$
the obvious diagonal product actions so that
$\alpha ^{\prime \prime }_N : G \curvearrowright X^{\prime \prime }_N$
the obvious diagonal product actions so that
![]() $\alpha $
is the diagonal product of
$\alpha $
is the diagonal product of
![]() $\alpha ^{\prime }_N$
and
$\alpha ^{\prime }_N$
and
![]() $\alpha ^{\prime \prime }_N$
.
$\alpha ^{\prime \prime }_N$
.
Since
![]() $\nu _n$
is G-invariant, the map
$\nu _n$
is G-invariant, the map
![]() $\Psi _N$
intertwines the Maharam extension of
$\Psi _N$
intertwines the Maharam extension of
![]() $\alpha \times \gamma $
with the diagonal product of
$\alpha \times \gamma $
with the diagonal product of
![]() $\alpha ^{\prime }_N$
and the Maharam extension of
$\alpha ^{\prime }_N$
and the Maharam extension of
![]() $\alpha ^{\prime \prime }_N \times \gamma $
. Since the pmp action
$\alpha ^{\prime \prime }_N \times \gamma $
. Since the pmp action
![]() $\alpha ^{\prime }_N$
of G on
$\alpha ^{\prime }_N$
of G on
![]() $(X^{\prime }_N,\nu _1 \times \cdots \times \nu _N)$
is mixing along
$(X^{\prime }_N,\nu _1 \times \cdots \times \nu _N)$
is mixing along
![]() $\Lambda \Lambda ^{-1}$
and since the Maharam extension of
$\Lambda \Lambda ^{-1}$
and since the Maharam extension of
![]() $\alpha ^{\prime \prime }_N \times \gamma $
is recurrent along
$\alpha ^{\prime \prime }_N \times \gamma $
is recurrent along
![]() $\Lambda \Lambda ^{-1}$
, it follows from [Reference Arano, Isono and Marrakchi1, Theorem 7.14] that the function
$\Lambda \Lambda ^{-1}$
, it follows from [Reference Arano, Isono and Marrakchi1, Theorem 7.14] that the function
![]() $F \circ \Psi _N^{-1}$
is essentially independent of the
$F \circ \Psi _N^{-1}$
is essentially independent of the
![]() $X^{\prime }_N$
-variable.
$X^{\prime }_N$
-variable.
So, for every
![]() $N \in \mathbb {N}$
, we find a unique
$N \in \mathbb {N}$
, we find a unique
![]() $F_N \in L^{\infty }(X^{\prime \prime }_N \times Y \times \mathbb {R})$
with
$F_N \in L^{\infty }(X^{\prime \prime }_N \times Y \times \mathbb {R})$
with
![]() $\|F_N\|_{\infty } = \|F\|_{\infty }$
and
$\|F_N\|_{\infty } = \|F\|_{\infty }$
and
![]() $F = F_N \circ \Psi _N$
a.e. Define the probability measures
$F = F_N \circ \Psi _N$
a.e. Define the probability measures
![]() $\zeta _n = (\psi _n)_*(\mu _n)$
on
$\zeta _n = (\psi _n)_*(\mu _n)$
on
![]() $\mathbb {R}$
. Denote
$\mathbb {R}$
. Denote
 $$ \begin{align*}(\Omega,\zeta) = \prod_{n =1}^{\infty} (\mathbb{R},\zeta_n),\end{align*} $$
$$ \begin{align*}(\Omega,\zeta) = \prod_{n =1}^{\infty} (\mathbb{R},\zeta_n),\end{align*} $$
and realize the tail boundary B of the sequence
![]() $(\zeta _n)_{n \in \mathbb {N}}$
inside
$(\zeta _n)_{n \in \mathbb {N}}$
inside
![]() $L^{\infty }(\mathbb {R} \times \Omega )$
. Consider the natural factor map
$L^{\infty }(\mathbb {R} \times \Omega )$
. Consider the natural factor map
We have thus proven that for every
![]() $F \in L^{\infty }(X \times Y \times \mathbb {R})^G$
, there exists a unique
$F \in L^{\infty }(X \times Y \times \mathbb {R})^G$
, there exists a unique
![]() $H \in B \mathbin {\overline {\otimes }} L^{\infty }(Y)$
such that
$H \in B \mathbin {\overline {\otimes }} L^{\infty }(Y)$
such that
![]() $F = H \circ \Phi $
a.e.
$F = H \circ \Phi $
a.e.
We also consider the diagonal action
![]() $\alpha ^{\prime }_N \times \mathord {\textrm{id}} \times \gamma $
of G on
$\alpha ^{\prime }_N \times \mathord {\textrm{id}} \times \gamma $
of G on
![]() $X \times Y$
, with its Maharam extension
$X \times Y$
, with its Maharam extension
![]() $M_N : G \curvearrowright X \times Y \times \mathbb {R}$
. Since
$M_N : G \curvearrowright X \times Y \times \mathbb {R}$
. Since
![]() $(\alpha ^{\prime }_N \times \mathord {\textrm{id}} \times \gamma )_g \to (\alpha \times \gamma )_g$
in
$(\alpha ^{\prime }_N \times \mathord {\textrm{id}} \times \gamma )_g \to (\alpha \times \gamma )_g$
in
![]() $\operatorname {Aut}(X \times Y)$
, we also have that
$\operatorname {Aut}(X \times Y)$
, we also have that
![]() $M_{N,g}(F) \to F$
weakly. For every
$M_{N,g}(F) \to F$
weakly. For every
![]() $K \in B \mathbin {\overline {\otimes }} L^{\infty }(Y)$
, we have that
$K \in B \mathbin {\overline {\otimes }} L^{\infty }(Y)$
, we have that
![]() $\Phi _*((\mathord {\textrm{id}} \otimes \gamma _g)(K)) = M_{N,g}(\Phi _*(K))$
for all
$\Phi _*((\mathord {\textrm{id}} \otimes \gamma _g)(K)) = M_{N,g}(\Phi _*(K))$
for all
![]() $N \in \mathbb {N}$
. Since
$N \in \mathbb {N}$
. Since
![]() $F = \Phi _*(H)$
, we conclude that
$F = \Phi _*(H)$
, we conclude that
![]() $\Phi _*((\mathord {\textrm{id}} \otimes \gamma _g)(H)) = \Phi _*(H)$
for all
$\Phi _*((\mathord {\textrm{id}} \otimes \gamma _g)(H)) = \Phi _*(H)$
for all
![]() $g \in G$
. Since the action
$g \in G$
. Since the action
![]() $\gamma $
is ergodic, we conclude that
$\gamma $
is ergodic, we conclude that
![]() $H \in B \otimes 1$
.
$H \in B \otimes 1$
.
Conversely, for every
![]() $H \in B$
, we find that
$H \in B$
, we find that
![]() $\Phi _*(H \otimes 1)$
is invariant under
$\Phi _*(H \otimes 1)$
is invariant under
![]() $M_{N,g}$
for all
$M_{N,g}$
for all
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $g \in G$
. Since
$g \in G$
. Since
![]() $M_{N,g}$
converges to the Maharam extension of
$M_{N,g}$
converges to the Maharam extension of
![]() $\alpha \times \gamma $
, it follows that
$\alpha \times \gamma $
, it follows that
![]() $\Phi _*(H \otimes 1)$
is invariant under the latter. We have thus identified the associated flow of
$\Phi _*(H \otimes 1)$
is invariant under the latter. We have thus identified the associated flow of
![]() $G \curvearrowright X \times Y$
with the tail boundary flow of the sequence
$G \curvearrowright X \times Y$
with the tail boundary flow of the sequence
![]() $(\zeta _n)_{n \in \mathbb {N}}$
.
$(\zeta _n)_{n \in \mathbb {N}}$
.
By equation (5.11) and using the notation (5.5),
Therefore,
![]() $\zeta _n$
is a translation of the Poisson distribution with support
$\zeta _n$
is a translation of the Poisson distribution with support
![]() $\{ka_n: k=0,1,2,\dots \}$
and intensity
$\{ka_n: k=0,1,2,\dots \}$
and intensity
![]() $\rho _n(A_n)=\lambda _n$
, i.e., a translation of
$\rho _n(A_n)=\lambda _n$
, i.e., a translation of
![]() $\sigma _{\lambda _n,a_n}$
. This concludes the proof of the lemma.
$\sigma _{\lambda _n,a_n}$
. This concludes the proof of the lemma.
Proof of Proposition 5.1
Take an lcsc group G that does not have property (T), and take a Poisson flow
![]() $\mathbb {R} \curvearrowright Z$
. By Proposition 3.15 and using the notation in equation (3.33), we write
$\mathbb {R} \curvearrowright Z$
. By Proposition 3.15 and using the notation in equation (3.33), we write
![]() $\mathbb {R} \curvearrowright Z$
as the tail boundary flow of a sequence
$\mathbb {R} \curvearrowright Z$
as the tail boundary flow of a sequence
![]() $\sigma _{\lambda _n,a_n}$
with
$\sigma _{\lambda _n,a_n}$
with
![]() $\lambda _n> 0$
and
$\lambda _n> 0$
and
![]() $a_n \in \mathbb {R} \setminus \{0\}$
. As explained above, we can take a measure preserving action
$a_n \in \mathbb {R} \setminus \{0\}$
. As explained above, we can take a measure preserving action
![]() $G \curvearrowright (W,\rho )$
on a standard, infinite,
$G \curvearrowright (W,\rho )$
on a standard, infinite,
![]() $\sigma $
-finite measure space such that the Koopman representation
$\sigma $
-finite measure space such that the Koopman representation
![]() $\pi $
of G on
$\pi $
of G on
![]() $L^2(W,\rho )$
is weakly mixing and the action admits a Følner sequence
$L^2(W,\rho )$
is weakly mixing and the action admits a Følner sequence
![]() $A_n \subset W$
.
$A_n \subset W$
.
Replace
![]() $A_n$
by a subsequence, and define
$A_n$
by a subsequence, and define
![]() $(X_0,\mu _0)$
so that the conclusions of Lemma 5.5 hold. Define
$(X_0,\mu _0)$
so that the conclusions of Lemma 5.5 hold. Define
![]() $V_0 = G \times \mathbb {N}$
, and denote by
$V_0 = G \times \mathbb {N}$
, and denote by
![]() $\eta _0$
the product of the Haar measure on G and the counting measure on
$\eta _0$
the product of the Haar measure on G and the counting measure on
![]() $\mathbb {N}$
. Let
$\mathbb {N}$
. Let
![]() $G \curvearrowright (V,\eta )$
be the Poisson suspension of
$G \curvearrowright (V,\eta )$
be the Poisson suspension of
![]() $G \curvearrowright (V_0,\eta _0)$
. Then,
$G \curvearrowright (V_0,\eta _0)$
. Then,
![]() $G \curvearrowright (V,\eta )$
is a mixing pmp action that can be written as the infinite product of a faithful pmp G-action. Hence,
$G \curvearrowright (V,\eta )$
is a mixing pmp action that can be written as the infinite product of a faithful pmp G-action. Hence,
![]() $G \curvearrowright (V,\eta )$
is essentially free. Taking the disjoint union of
$G \curvearrowright (V,\eta )$
is essentially free. Taking the disjoint union of
![]() $X_0$
and
$X_0$
and
![]() $V_0$
, we obtain the nonsingular action
$V_0$
, we obtain the nonsingular action
![]() $G \curvearrowright (X_0 \sqcup V_0,\mu _0 \sqcup \eta _0)$
that, by Lemma 5.5 satisfies all the conclusions of the proposition.
$G \curvearrowright (X_0 \sqcup V_0,\mu _0 \sqcup \eta _0)$
that, by Lemma 5.5 satisfies all the conclusions of the proposition.
6 Bernoulli actions of amenable groups: proof of Theorem B
In Theorem 6.1 below, as in the previous section, we prove a stable version of Theorem B.
Theorem 6.1. Let
![]() $\mathbb {R}\curvearrowright (Z,\zeta )$
be a Poisson flow, and let G be a countable infinite amenable group. Then there exists a countable set
$\mathbb {R}\curvearrowright (Z,\zeta )$
be a Poisson flow, and let G be a countable infinite amenable group. Then there exists a countable set
![]() $X_0$
and a family of equivalent probability measures
$X_0$
and a family of equivalent probability measures
![]() $(\mu _g)_{g\in G}$
on
$(\mu _g)_{g\in G}$
on
![]() $X_0$
such that the Bernoulli action
$X_0$
such that the Bernoulli action
is nonsingular, weakly mixing and such that for any ergodic pmp action
![]() $G\curvearrowright (Y,\eta )$
the associated flow of the diagonal action
$G\curvearrowright (Y,\eta )$
the associated flow of the diagonal action
![]() $G\curvearrowright X\times Y$
is isomorphic with
$G\curvearrowright X\times Y$
is isomorphic with
![]() $\mathbb {R}\curvearrowright Z$
.
$\mathbb {R}\curvearrowright Z$
.
For the periodic flows
![]() $\mathbb {R} \curvearrowright \mathbb {R} / \mathbb {Z} \log \lambda $
, i.e., the type III
$\mathbb {R} \curvearrowright \mathbb {R} / \mathbb {Z} \log \lambda $
, i.e., the type III
![]() $_{\lambda }$
case, Theorem 6.1 was proven independently in [Reference Berendschot and Vaes8] and [Reference Kosloff and Soo39]. For the trivial flow, which corresponds to the type III
$_{\lambda }$
case, Theorem 6.1 was proven independently in [Reference Berendschot and Vaes8] and [Reference Kosloff and Soo39]. For the trivial flow, which corresponds to the type III
![]() $_1$
case, the result was already proven in [Reference Björklund, Kosloff and Vaes7, Theorem 6.1]. The novelty lies in the type III
$_1$
case, the result was already proven in [Reference Björklund, Kosloff and Vaes7, Theorem 6.1]. The novelty lies in the type III
![]() $_0$
case, i.e., the properly ergodic flows.
$_0$
case, i.e., the properly ergodic flows.
As in the introduction, for any countable subgroup
![]() $\Lambda \subset \mathbb {R}$
, we denote by
$\Lambda \subset \mathbb {R}$
, we denote by
![]() $M_{\Lambda }$
the unique injective factor whose flow of weights is the almost periodic flow
$M_{\Lambda }$
the unique injective factor whose flow of weights is the almost periodic flow
![]() $\mathbb {R} \curvearrowright \widehat {\Lambda }$
. Combining Theorems 3.9 and 3.8 with Theorem 6.1, we obtain the following immediate corollary.
$\mathbb {R} \curvearrowright \widehat {\Lambda }$
. Combining Theorems 3.9 and 3.8 with Theorem 6.1, we obtain the following immediate corollary.
Corollary 6.2. Let G be a countable infinite amenable group. Any ITPFI
![]() $_2$
factor of type III, and in particular all the injective factors
$_2$
factor of type III, and in particular all the injective factors
![]() $M_{\Lambda }$
where
$M_{\Lambda }$
where
![]() $\Lambda \subset \mathbb {R}$
is a countable subgroup, are isomorphic to the crossed product
$\Lambda \subset \mathbb {R}$
is a countable subgroup, are isomorphic to the crossed product
![]() $L^{\infty }(X)\rtimes G$
of a nonsingular Bernoulli action
$L^{\infty }(X)\rtimes G$
of a nonsingular Bernoulli action
![]() $G\curvearrowright (X,\mu )$
of G.
$G\curvearrowright (X,\mu )$
of G.
If
![]() $\gamma _0$
is a measure on
$\gamma _0$
is a measure on
![]() $V_0 = G \times \mathbb {N}$
that is equivalent with the counting measure and if the nonsingular action
$V_0 = G \times \mathbb {N}$
that is equivalent with the counting measure and if the nonsingular action
![]() $G \curvearrowright (V_0,\gamma _0) : g \cdot (h,n) = (gh,n)$
has a well-defined Poisson suspension
$G \curvearrowright (V_0,\gamma _0) : g \cdot (h,n) = (gh,n)$
has a well-defined Poisson suspension
![]() $G \curvearrowright (V,\eta )$
, then
$G \curvearrowright (V,\eta )$
, then
![]() $G \curvearrowright (V,\eta )$
is canonically isomorphic with the nonsingular Bernoulli action
$G \curvearrowright (V,\eta )$
is canonically isomorphic with the nonsingular Bernoulli action
where
![]() $\mu _{n,g}$
is the Poisson distribution with intensity
$\mu _{n,g}$
is the Poisson distribution with intensity
![]() $\gamma _0(g,n)$
.
$\gamma _0(g,n)$
.
Therefore, Theorem 6.1 can be deduced as follows from Lemma 5.5.
Proof of Theorem 6.1
By Proposition 3.15 and using the notation in equation (3.33), we write
![]() $\mathbb {R} \curvearrowright Z$
as the tail boundary flow of a sequence
$\mathbb {R} \curvearrowright Z$
as the tail boundary flow of a sequence
![]() $\sigma _{\lambda _n,a_n}$
with
$\sigma _{\lambda _n,a_n}$
with
![]() $\lambda _n> 0$
and
$\lambda _n> 0$
and
![]() $a_n \in \mathbb {R} \setminus \{0\}$
.
$a_n \in \mathbb {R} \setminus \{0\}$
.
Denote by
![]() $\rho $
the counting measure on G. Since G is amenable, the translation action
$\rho $
the counting measure on G. Since G is amenable, the translation action
![]() $G \curvearrowright (G,\rho )$
admits a Følner sequence
$G \curvearrowright (G,\rho )$
admits a Følner sequence
![]() $A_n \subset G$
, which we may choose in such a way that
$A_n \subset G$
, which we may choose in such a way that
![]() $|A_n|$
is an increasing unbounded sequence. Replacing
$|A_n|$
is an increasing unbounded sequence. Replacing
![]() $A_n$
by a subsequence, we may further assume that
$A_n$
by a subsequence, we may further assume that
for all
![]() $n \in \mathbb {N}$
. Define
$n \in \mathbb {N}$
. Define
![]() $V_0 = G \times \mathbb {N}$
, and define the measure
$V_0 = G \times \mathbb {N}$
, and define the measure
![]() $\gamma _0$
on
$\gamma _0$
on
![]() $V_0$
by
$V_0$
by
 $$ \begin{align*} \gamma_0(g,n) = \begin{cases} \lambda_n \, |A_n|^{-1} &\;\;\text{if } g \in A_n,\\ \lambda_n \, |A_n|^{-1} \, e^{a_n} &\;\;\text{if } g \not\in A_n.\end{cases} \end{align*} $$
$$ \begin{align*} \gamma_0(g,n) = \begin{cases} \lambda_n \, |A_n|^{-1} &\;\;\text{if } g \in A_n,\\ \lambda_n \, |A_n|^{-1} \, e^{a_n} &\;\;\text{if } g \not\in A_n.\end{cases} \end{align*} $$
After replacing once more
![]() $A_n$
by a subsequence, it follows from Lemma 5.5 that the Poisson suspension
$A_n$
by a subsequence, it follows from Lemma 5.5 that the Poisson suspension
![]() $G \curvearrowright (X,\mu )$
of
$G \curvearrowright (X,\mu )$
of
![]() $G \curvearrowright (V_0,\gamma _0)$
is well defined, weakly mixing and has the property that for every ergodic pmp action
$G \curvearrowright (V_0,\gamma _0)$
is well defined, weakly mixing and has the property that for every ergodic pmp action
![]() $G \curvearrowright (Y,\eta )$
, the associated flow of the diagonal action
$G \curvearrowright (Y,\eta )$
, the associated flow of the diagonal action
![]() $G \curvearrowright X \times Y$
is isomorphic with
$G \curvearrowright X \times Y$
is isomorphic with
![]() $\mathbb {R} \curvearrowright Z$
. Note that equation (6.2) remains valid in this passage to a subsequence.
$\mathbb {R} \curvearrowright Z$
. Note that equation (6.2) remains valid in this passage to a subsequence.
By equation (6.1), we may view
![]() $G \curvearrowright (X,\mu )$
as a nonsingular Bernoulli action. Since by equation (6.2)
$G \curvearrowright (X,\mu )$
as a nonsingular Bernoulli action. Since by equation (6.2)
the base space
![]() $(X_0,\mu _e)$
of the nonsingular Bernoulli action
$(X_0,\mu _e)$
of the nonsingular Bernoulli action
![]() $G \curvearrowright (X,\mu )$
is atomic so that Theorem 6.1 is proven.
$G \curvearrowright (X,\mu )$
is atomic so that Theorem 6.1 is proven.
Remark 6.3. Note that, although our proof of Theorem 6.1 makes use of Lemma 5.5, the proof actually does not rely in an essential way on the theory of Poisson suspensions. It follows from equation (6.1) that the nonsingular Bernoulli action
![]() $G \curvearrowright (X,\mu )$
that we construct in the proof of Theorem 6.1 is an infinite product action
$G \curvearrowright (X,\mu )$
that we construct in the proof of Theorem 6.1 is an infinite product action
![]() $G \curvearrowright \prod _{n \in \mathbb {N}} (X_n,\mu _n)$
, where for each n, there is a natural G-invariant probability measure
$G \curvearrowright \prod _{n \in \mathbb {N}} (X_n,\mu _n)$
, where for each n, there is a natural G-invariant probability measure
![]() $\nu _n \sim \mu _n$
such that
$\nu _n \sim \mu _n$
such that
![]() $G \curvearrowright (X_n,\nu _n)$
is a pmp Bernoulli action. The argument in the proof of Lemma 5.5 then provides the identification of the associated flow as the correct tail boundary flow.
$G \curvearrowright (X_n,\nu _n)$
is a pmp Bernoulli action. The argument in the proof of Lemma 5.5 then provides the identification of the associated flow as the correct tail boundary flow.
Acknowledgement
T.B. and S.V. are supported by long term structural funding—Methusalem grant of the Flemish Government and Stefaan Vaes is supported by FWO research project G090420N of the Research Foundation Flanders.
We thank Alexandre Danilenko for his useful comments on the first draft of this paper.
Competing Interests
The authors declare none.