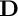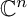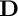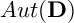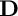1 Introduction
By the results of Gindikin, Pijatetcki-Shapiro, and Vinberg (see [Reference Gindikin, Pyatetskii-Shapiro and Vinberg4], [Reference Pyatetskii-Shapiro8]), every bounded homogeneous domain
![]() $\mathbf {D}$
in
$\mathbf {D}$
in
![]() ${\mathbb {C}}^n$
admits a realization as a Siegel domain. Such a realization relies on the existence of a simply transitive real split solvable group S of holomorphic automorphisms of
${\mathbb {C}}^n$
admits a realization as a Siegel domain. Such a realization relies on the existence of a simply transitive real split solvable group S of holomorphic automorphisms of
![]() $\mathbf {D}$
. In the symmetric case, the group
$\mathbf {D}$
. In the symmetric case, the group
![]() $G= Aut(\mathbf {D}) $
is semisimple and
$G= Aut(\mathbf {D}) $
is semisimple and
![]() $S=AN $
, where A and N are the abelian and the unipotent subgroups arising from an Iwasawa decomposition of G.
$S=AN $
, where A and N are the abelian and the unipotent subgroups arising from an Iwasawa decomposition of G.
In [Reference Geatti and Iannuzzi3], the N-invariant Stein domains in irreducible symmetric Siegel domains were characterized. The goal of this note is to prove a similar characterization for N-invariant Stein domains in arbitrary homogeneous Siegel domains, which form a much wider class of domains containing the symmetric ones as special cases.
As in the symmetric case, to an N-invariant domain D in
![]() $\mathbf {D}$
, we associate an r-dimensional tube domain in
$\mathbf {D}$
, we associate an r-dimensional tube domain in
![]() ${\mathbb {H}}^r$
, the product of r copies of the upper half plane
${\mathbb {H}}^r$
, the product of r copies of the upper half plane
![]() ${\mathbb {H}}$
in
${\mathbb {H}}$
in
![]() ${\mathbb {C}}$
(here r is the rank of
${\mathbb {C}}$
(here r is the rank of
![]() $\mathbf {D}$
). Then we prove that D is Stein if and only if the base of the associated tube is convex and satisfies an additional geometric condition (see Theorem 3.4). In the symmetric case, such condition only depends on whether
$\mathbf {D}$
). Then we prove that D is Stein if and only if the base of the associated tube is convex and satisfies an additional geometric condition (see Theorem 3.4). In the symmetric case, such condition only depends on whether
![]() $\mathbf {D}$
is of tube type or of non-tube type, while in the general case it depends on the specific root decomposition of the normal J-algebra
$\mathbf {D}$
is of tube type or of non-tube type, while in the general case it depends on the specific root decomposition of the normal J-algebra
![]() ${\mathfrak {s}}=Lie(S)$
of
${\mathfrak {s}}=Lie(S)$
of
![]() $\mathbf {D}$
.
$\mathbf {D}$
.
The univalence of holomorphically separable,
![]() $\,N$
-equivariant, Riemann domains over
$\,N$
-equivariant, Riemann domains over
![]() $\mathbf {D}$
continues to hold true in this more general context, yielding a precise description of the envelope of holomorphy (cf. Reference Rossi[9]) of an arbitrary N-invariant domain in
$\mathbf {D}$
continues to hold true in this more general context, yielding a precise description of the envelope of holomorphy (cf. Reference Rossi[9]) of an arbitrary N-invariant domain in
![]() $\mathbf {D}$
(see Corollary 3.5).
$\mathbf {D}$
(see Corollary 3.5).
Finally, we exhibit an N-invariant potential of the Bergman metric of
![]() $\mathbf {D}$
, expressed in a Lie theoretical fashion and obtained via an explicit N-moment map with respect to the Bergman Kähler structure of
$\mathbf {D}$
, expressed in a Lie theoretical fashion and obtained via an explicit N-moment map with respect to the Bergman Kähler structure of
![]() $\mathbf {D}$
(see Proposition 4.3).
$\mathbf {D}$
(see Proposition 4.3).
2 Preliminaries
Every bounded homogeneous domain
![]() $\mathbf {D}$
in
$\mathbf {D}$
in
![]() ${\mathbb {C}}^n$
admits a real split solvable group S of holomorphic automorphisms acting simply transitively on
${\mathbb {C}}^n$
admits a real split solvable group S of holomorphic automorphisms acting simply transitively on
![]() $\mathbf {D}$
. The Lie algebra
$\mathbf {D}$
. The Lie algebra
![]() ${\mathfrak {s}}$
of S has the structure of a normal J-algebra, with the complex structure J inherited from
${\mathfrak {s}}$
of S has the structure of a normal J-algebra, with the complex structure J inherited from
![]() $\mathbf {D}$
and the linear form
$\mathbf {D}$
and the linear form
![]() $-f_0\in {\mathfrak {s}}^{*}$
inducing the Bergman metric (cf. [Reference Koszul7]). This means in particular that
$-f_0\in {\mathfrak {s}}^{*}$
inducing the Bergman metric (cf. [Reference Koszul7]). This means in particular that
![]() ${\omega (X,Y):=-f_0([X,Y])}$
is a nondegenerate skew-symmetric J-invariant bilinear form on
${\omega (X,Y):=-f_0([X,Y])}$
is a nondegenerate skew-symmetric J-invariant bilinear form on
![]() ${\mathfrak {s}}$
and
${\mathfrak {s}}$
and
![]() ${ \langle X,Y\rangle :=-f_0([JX,Y])}$
is a J-invariant positive definite inner product on
${ \langle X,Y\rangle :=-f_0([JX,Y])}$
is a J-invariant positive definite inner product on
![]() ${\mathfrak {s}}$
.
${\mathfrak {s}}$
.
2.1 The normal J-algebra of a bounded domain
For the structure of normal J-algebras, we mainly refer to [Reference Rossi and Vergne10, §5A]. Further details and comments can be found in [Reference Geatti and Iannuzzi3]. Denote by
![]() ${\mathfrak {n}}:=[{\mathfrak {s}},{\mathfrak {s}}]$
the nilradical of
${\mathfrak {n}}:=[{\mathfrak {s}},{\mathfrak {s}}]$
the nilradical of
![]() ${\mathfrak {s}}$
, and let
${\mathfrak {s}}$
, and let
![]() ${\mathfrak {a}}$
be the orthogonal complement of
${\mathfrak {a}}$
be the orthogonal complement of
![]() ${\mathfrak {n}}$
in
${\mathfrak {n}}$
in
![]() ${\mathfrak {s}}$
, with respect to the inner product
${\mathfrak {s}}$
, with respect to the inner product
![]() $ \langle \cdot ,\cdot \rangle $
. Then
$ \langle \cdot ,\cdot \rangle $
. Then
![]() ${\mathfrak {a}}$
is an abelian subalgebra, whose dimension r is by definition the rank of D. The adjoint action of
${\mathfrak {a}}$
is an abelian subalgebra, whose dimension r is by definition the rank of D. The adjoint action of
![]() ${\mathfrak {a}}$
on
${\mathfrak {a}}$
on
![]() ${\mathfrak {s}}$
is symmetric with respect to
${\mathfrak {s}}$
is symmetric with respect to
![]() $ \langle \cdot ,\cdot \rangle $
and decomposes
$ \langle \cdot ,\cdot \rangle $
and decomposes
![]() ${\mathfrak {s}}$
into the orthogonal direct sum of root spaces
${\mathfrak {s}}$
into the orthogonal direct sum of root spaces
![]() ${\mathfrak {s}}^\alpha =\{X\in {\mathfrak {s}}~|~[H,X]=\alpha (H)X,~\forall H\in {\mathfrak {a}}\}$
. There exist
${\mathfrak {s}}^\alpha =\{X\in {\mathfrak {s}}~|~[H,X]=\alpha (H)X,~\forall H\in {\mathfrak {a}}\}$
. There exist
![]() $e_1,\ldots ,e_r\in {\mathfrak {s}}^{*}$
such that the roots
$e_1,\ldots ,e_r\in {\mathfrak {s}}^{*}$
such that the roots
![]() $\alpha $
are of the form
$\alpha $
are of the form
In the nonsymmetric case, not all possibilities need occur. Here, the roots are normalized so that, in the symmetric case, they coincide with the restricted roots. The complex structure J permutes the root spaces as follows:
 $$ \begin{align*}J{\mathfrak{a}}=\bigoplus_j{\mathfrak{s}}^{2e_j},\qquad J{\mathfrak{s}}^{e_j-e_l}={\mathfrak{s}}^{e_j+e_l},\qquad J{\mathfrak{s}}^{e_j}={\mathfrak{s}}^{e_j}.\end{align*} $$
$$ \begin{align*}J{\mathfrak{a}}=\bigoplus_j{\mathfrak{s}}^{2e_j},\qquad J{\mathfrak{s}}^{e_j-e_l}={\mathfrak{s}}^{e_j+e_l},\qquad J{\mathfrak{s}}^{e_j}={\mathfrak{s}}^{e_j}.\end{align*} $$
Let
![]() $H_1,\ldots ,H_r$
be the basis of
$H_1,\ldots ,H_r$
be the basis of
![]() ${\mathfrak {a}}$
dual to
${\mathfrak {a}}$
dual to
![]() $e_1,\ldots , e_r\in {\mathfrak {a}}^{*}$
. As
$e_1,\ldots , e_r\in {\mathfrak {a}}^{*}$
. As
![]() $\dim {\mathfrak {s}}^{2e_j}=1 $
, for
$\dim {\mathfrak {s}}^{2e_j}=1 $
, for
![]() $j=1,\ldots , r$
, one can fix generators
$j=1,\ldots , r$
, one can fix generators
![]() $E^j\in {\mathfrak {s}}^{2e_j}$
such that the pairs
$E^j\in {\mathfrak {s}}^{2e_j}$
such that the pairs
![]() $\{ H_j, \,E^j \}$
satisfy
$\{ H_j, \,E^j \}$
satisfy
For
![]() $j=1,\ldots , r$
, the real split solvable subalgebras generated by
$j=1,\ldots , r$
, the real split solvable subalgebras generated by
![]() $\{ H_j, \,E^j \}$
pairwise commute and are isomorphic to the
$\{ H_j, \,E^j \}$
pairwise commute and are isomorphic to the
![]() ${\mathfrak {a}} \oplus {\mathfrak {n}}$
-component of an Iwasawa decomposition of
${\mathfrak {a}} \oplus {\mathfrak {n}}$
-component of an Iwasawa decomposition of
![]() ${\mathfrak {s}}{\mathfrak {l}}(2,{\mathbb {R}})$
.
${\mathfrak {s}}{\mathfrak {l}}(2,{\mathbb {R}})$
.
Set
![]() $\,H_0:=\frac {1}{2}\sum _j H_j\in {\mathfrak {a}}\,$
. The adjoint action of
$\,H_0:=\frac {1}{2}\sum _j H_j\in {\mathfrak {a}}\,$
. The adjoint action of
![]() $H_0$
decomposes
$H_0$
decomposes
![]() ${\mathfrak {s}}$
and
${\mathfrak {s}}$
and
![]() ${\mathfrak {n}}$
as
${\mathfrak {n}}$
as
where
![]() $\,{\mathfrak {n}}_j={\mathfrak {n}}\cap {\mathfrak {s}}_j\,$
and
$\,{\mathfrak {n}}_j={\mathfrak {n}}\cap {\mathfrak {s}}_j\,$
and
 $$ \begin{align*}{\mathfrak{s}}_0={\mathfrak{a}}\oplus\bigoplus_{\scriptstyle1\le j<l\le r} {\mathfrak{s}}^{e_j-e_l},\quad {\mathfrak{s}}_{1/2}=\bigoplus_{\scriptstyle 1\le j\le r}{\mathfrak{s}}^{e_j}, \quad {\mathfrak{s}}_1=\bigoplus_{\scriptstyle 1\le j\le r}{\mathfrak{s}}^{2e_j}\oplus\bigoplus_{\scriptstyle 1\le j<l\le r}{\mathfrak{s}}^{e_j+e_l}. \end{align*} $$
$$ \begin{align*}{\mathfrak{s}}_0={\mathfrak{a}}\oplus\bigoplus_{\scriptstyle1\le j<l\le r} {\mathfrak{s}}^{e_j-e_l},\quad {\mathfrak{s}}_{1/2}=\bigoplus_{\scriptstyle 1\le j\le r}{\mathfrak{s}}^{e_j}, \quad {\mathfrak{s}}_1=\bigoplus_{\scriptstyle 1\le j\le r}{\mathfrak{s}}^{2e_j}\oplus\bigoplus_{\scriptstyle 1\le j<l\le r}{\mathfrak{s}}^{e_j+e_l}. \end{align*} $$
If
![]() ${\mathfrak {s}}_{1/2}=\{0\}$
, then the domain
${\mathfrak {s}}_{1/2}=\{0\}$
, then the domain
![]() $\mathbf {D}$
is of tube type, otherwise it is of non-tube type.
$\mathbf {D}$
is of tube type, otherwise it is of non-tube type.
Set
![]() $E_0:= \sum_j E^j$
. The complex structure on
$E_0:= \sum_j E^j$
. The complex structure on
![]() $ {\mathfrak {s}}_0$
is given by
$ {\mathfrak {s}}_0$
is given by
![]() $JX=[E_0,X]$
, for all
$JX=[E_0,X]$
, for all
![]() $X\in {\mathfrak {s}}_0$
. The orbit
$X\in {\mathfrak {s}}_0$
. The orbit
is a sharp convex cone in
![]() ${\mathfrak {s}}_1$
and
${\mathfrak {s}}_1$
and
is a
![]() $ V$
-valued Hermitian form, that is, it is sesquilinear and
$ V$
-valued Hermitian form, that is, it is sesquilinear and
![]() $F(W,W)\in \overline V$
(the topological closure of V), for all
$F(W,W)\in \overline V$
(the topological closure of V), for all
![]() $W \in {\mathfrak {s}}_{1/2} $
. The group S acts on
$W \in {\mathfrak {s}}_{1/2} $
. The group S acts on
![]() ${\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
by affine transformations, given by
${\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
by affine transformations, given by
where
![]() $\, s=\exp \zeta \exp \xi \, \exp \gamma $
, with
$\, s=\exp \zeta \exp \xi \, \exp \gamma $
, with
![]() $\, \zeta \in {\mathfrak {s}}_{1/2} $
,
$\, \zeta \in {\mathfrak {s}}_{1/2} $
,
![]() $\xi \in {\mathfrak {s}}_1$
,
$\xi \in {\mathfrak {s}}_1$
,
![]() $\,\gamma \in {\mathfrak {s}}_0$
. If we fix the base point
$\,\gamma \in {\mathfrak {s}}_0$
. If we fix the base point
![]() ${p_0:=(iE_0,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}}$
, then the map
${p_0:=(iE_0,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}}$
, then the map
defines a biholomorphism between
![]() $\mathbf {D}\cong S$
and the Siegel domain
$\mathbf {D}\cong S$
and the Siegel domain
(cf. [Reference Rossi and Vergne10, Lem. 5.2, p. 330]). Denote by
the elements in the dual
![]() ${\mathfrak {n}}^{*}$
of
${\mathfrak {n}}^{*}$
of
![]() ${\mathfrak {n}}$
, with the property that
${\mathfrak {n}}$
, with the property that
![]() $(E^j)^{*}(E^l)=\delta _{jl}$
and
$(E^j)^{*}(E^l)=\delta _{jl}$
and
![]() $(E^j)^{*}(X)=0$
, for all
$(E^j)^{*}(X)=0$
, for all
![]() $X \in {\mathfrak {s}}^\alpha $
, with
$X \in {\mathfrak {s}}^\alpha $
, with
![]() $\alpha \notin \{2e_1,\ldots ,2e_r\}$
.
$\alpha \notin \{2e_1,\ldots ,2e_r\}$
.
Lemma 2.1.
![]() $\mathrm{(a)}$
The form
$\mathrm{(a)}$
The form
![]() $\,-f_0\colon {\mathfrak {s}}\to {\mathbb {R}}\,$
is given by
$\,-f_0\colon {\mathfrak {s}}\to {\mathbb {R}}\,$
is given by
![]() $\,-f_0=\sum _kc_k(E^k)^{*} $
, for some
$\,-f_0=\sum _kc_k(E^k)^{*} $
, for some
![]() ${c_k\in {\mathbb {R}}^{>0}}$
.
${c_k\in {\mathbb {R}}^{>0}}$
.
![]() $\mathrm{(b)}$
Let
$\mathrm{(b)}$
Let
![]() $\,X \in {\mathfrak {s}}^{e_j-e_l}\setminus \{0\}\,$
. Then
$\,X \in {\mathfrak {s}}^{e_j-e_l}\setminus \{0\}\,$
. Then
![]() $\,[JX,X] =s E^j $
, for some
$\,[JX,X] =s E^j $
, for some
![]() $\,s\in {\mathbb {R}}^{>0}$
. Let
$\,s\in {\mathbb {R}}^{>0}$
. Let
![]() $X,Y\in {\mathfrak {s}}^{e_j-e_l}\setminus \{0\}\,$
, satisfying
$X,Y\in {\mathfrak {s}}^{e_j-e_l}\setminus \{0\}\,$
, satisfying
![]() $\langle X,Y\rangle =0$
. Then
$\langle X,Y\rangle =0$
. Then
![]() $[JX,Y]=0$
.
$[JX,Y]=0$
.
![]() $\mathrm{(c)}$
Let
$\mathrm{(c)}$
Let
![]() $\,X \in {\mathfrak {s}}^{e_j}\setminus \{0\}.$
Then
$\,X \in {\mathfrak {s}}^{e_j}\setminus \{0\}.$
Then
![]() $\,[JX,X] =tE^j$
, for some
$\,[JX,X] =tE^j$
, for some
![]() $\,t\in {\mathbb {R}}^{>0}$
. Let
$\,t\in {\mathbb {R}}^{>0}$
. Let
![]() $X,Y\in {\mathfrak {s}}^{e_j}\setminus \{0\}\,$
, satisfying
$X,Y\in {\mathfrak {s}}^{e_j}\setminus \{0\}\,$
, satisfying
![]() $\langle X,Y\rangle =0$
. Then
$\langle X,Y\rangle =0$
. Then
![]() $[JX,Y]=0$
.
$[JX,Y]=0$
.
Proof. The proof of statement (a) is contained in [Reference Rossi and Vergne10]. For the sake of completeness, we recall the main arguments. Let
![]() $f_0$
also denote the
$f_0$
also denote the
![]() $\,{\mathbb {C}}$
-linear extension of
$\,{\mathbb {C}}$
-linear extension of
![]() $\,f_0$
to
$\,f_0$
to
![]() ${\mathfrak {s}}^{\mathbb {C}}$
. From the integrability of J, one has that
${\mathfrak {s}}^{\mathbb {C}}$
. From the integrability of J, one has that
![]() $f_0([X+iJX,Y+iJY])=0$
, for all
$f_0([X+iJX,Y+iJY])=0$
, for all
![]() $X,Y\in {\mathfrak {s}}$
. This implies that
$X,Y\in {\mathfrak {s}}$
. This implies that
![]() $f_0([H,X])=f_0(J[H,X])=0$
, for all
$f_0([H,X])=f_0(J[H,X])=0$
, for all
![]() $H\in {\mathfrak {a}}$
and
$H\in {\mathfrak {a}}$
and
![]() $X\in {\mathfrak {q}}:={\mathfrak {s}}_{1/2}\oplus \bigoplus _{j<l}{\mathfrak {s}}^{e_j-e_l}$
. Since
$X\in {\mathfrak {q}}:={\mathfrak {s}}_{1/2}\oplus \bigoplus _{j<l}{\mathfrak {s}}^{e_j-e_l}$
. Since
![]() $[{\mathfrak {a}},{\mathfrak {q}}]={\mathfrak {q}}$
and
$[{\mathfrak {a}},{\mathfrak {q}}]={\mathfrak {q}}$
and
![]() $J{\mathfrak {q}}={\mathfrak {s}}_{1/2}\oplus \bigoplus _{j<l}{\mathfrak {s}}^{e_j+e_l}$
, the form
$J{\mathfrak {q}}={\mathfrak {s}}_{1/2}\oplus \bigoplus _{j<l}{\mathfrak {s}}^{e_j+e_l}$
, the form
![]() $f_0$
identically vanishes on
$f_0$
identically vanishes on
![]() ${\mathfrak {q}}$
and
${\mathfrak {q}}$
and
![]() $-f_0=\sum _jc_j (E^j)^{*}$
, for some
$-f_0=\sum _jc_j (E^j)^{*}$
, for some
![]() $c_j\in {\mathbb {R}}$
. The identity
$c_j\in {\mathbb {R}}$
. The identity
![]() $c_j=-f_0(E^j)=-\frac {1}{2}f_0([H_j,E^j])=-f_0([JE^j,E^j])= \langle E^j,E^j\rangle>0 $
concludes the proof.
$c_j=-f_0(E^j)=-\frac {1}{2}f_0([H_j,E^j])=-f_0([JE^j,E^j])= \langle E^j,E^j\rangle>0 $
concludes the proof.
(b) Let
![]() $X\in {\mathfrak {s}}^{e_j-e_l} \setminus \{0\}$
. Then
$X\in {\mathfrak {s}}^{e_j-e_l} \setminus \{0\}$
. Then
![]() $\,JX=[E^l,X]\in {\mathfrak {s}}^{e_j+e_l}$
. Since
$\,JX=[E^l,X]\in {\mathfrak {s}}^{e_j+e_l}$
. Since
![]() ${\mathfrak {s}}^{2e_j}$
is one-dimensional,
${\mathfrak {s}}^{2e_j}$
is one-dimensional,
![]() $ [JX,X]=sE^j$
, for some
$ [JX,X]=sE^j$
, for some
![]() $s\in {\mathbb {R}}$
. By applying
$s\in {\mathbb {R}}$
. By applying
![]() $-f_0$
to both terms, one obtains
$-f_0$
to both terms, one obtains
![]() $-f_0([JX,X])=\langle X,X\rangle =c_j s>0$
. Since
$-f_0([JX,X])=\langle X,X\rangle =c_j s>0$
. Since
![]() $c_j>0$
, also
$c_j>0$
, also
![]() $s>0$
. For the second part of the statement, write
$s>0$
. For the second part of the statement, write
![]() $[JX,Y]=s E^j$
, for some
$[JX,Y]=s E^j$
, for some
![]() $s\in {\mathbb {R}}$
. Then, from
$s\in {\mathbb {R}}$
. Then, from
 $$ \begin{align*} 0= \langle X,Y\rangle =-f_0([JX,Y])= -\sum_kc_k(E^k)^{*}( s E^j) = c_js , \end{align*} $$
$$ \begin{align*} 0= \langle X,Y\rangle =-f_0([JX,Y])= -\sum_kc_k(E^k)^{*}( s E^j) = c_js , \end{align*} $$
one obtains
![]() $s=0$
and therefore
$s=0$
and therefore
![]() $[JX,Y]=0$
, as desired.
$[JX,Y]=0$
, as desired.
As
![]() ${\mathfrak {s}}^{e_j}$
is J-invariant, statement (c) follows in a similar way.
${\mathfrak {s}}^{e_j}$
is J-invariant, statement (c) follows in a similar way.
Remark 2.2. The forms
![]() $\sum _jc_j(E^j)^{*}$
, where the
$\sum _jc_j(E^j)^{*}$
, where the
![]() $c_j$
’s vary in
$c_j$
’s vary in
![]() ${\mathbb {R}}^{>0}$
for
${\mathbb {R}}^{>0}$
for
![]() $j=1,\ldots ,r$
, determine all S-homogeneous Kähler metrics on
$j=1,\ldots ,r$
, determine all S-homogeneous Kähler metrics on
![]() $D(V,F)$
(cf. [Reference Dorfmeister2, Th. 1, p. 304]). By [Reference D’Atri1, Th. 4], one such metric is Kähler–Einstein if and only if the quantity
$D(V,F)$
(cf. [Reference Dorfmeister2, Th. 1, p. 304]). By [Reference D’Atri1, Th. 4], one such metric is Kähler–Einstein if and only if the quantity
![]() $\textstyle \frac {1}{c_j}(1+\frac {1}{4} \dim {\mathfrak {s}}^{e_j}+\frac {1}{2}\sum _{j<l}{\mathfrak {s}}^{e_j+e_l})$
is a constant independent of
$\textstyle \frac {1}{c_j}(1+\frac {1}{4} \dim {\mathfrak {s}}^{e_j}+\frac {1}{2}\sum _{j<l}{\mathfrak {s}}^{e_j+e_l})$
is a constant independent of
![]() $j=1,\ldots ,r$
.
$j=1,\ldots ,r$
.
2.2
N-invariant domains in
 $D(V,F)$
and tube domains in
$D(V,F)$
and tube domains in
 ${\mathbb {H}}^r$
${\mathbb {H}}^r$
In
![]() $S=NA$
, consider the unipotent abelian subgroup
$S=NA$
, consider the unipotent abelian subgroup
![]() $\,R:= \exp J{\mathfrak {a}}$
, isomorphic to
$\,R:= \exp J{\mathfrak {a}}$
, isomorphic to
![]() ${\mathbb {R}}^r$
. The
${\mathbb {R}}^r$
. The
![]() $\,R$
-invariant set
$\,R$
-invariant set
is an r-dimensional closed complex submanifold of
![]() $\,D(V,F),\,$
intersecting all N-orbits in
$\,D(V,F),\,$
intersecting all N-orbits in
![]() $D(V,F)$
. Define the positive octant in
$D(V,F)$
. Define the positive octant in
![]() $J{\mathfrak {a}}$
$J{\mathfrak {a}}$
Then the map
![]() $\mathcal L$
defined in (2.1) and (2.2) restricts to a biholomorphism
$\mathcal L$
defined in (2.1) and (2.2) restricts to a biholomorphism
given by
In particular,
![]() $\mathcal L|_{\exp ({\mathfrak {a}})}$
defines a diffeomorphism
$\mathcal L|_{\exp ({\mathfrak {a}})}$
defines a diffeomorphism
![]() $\ L\colon {\mathfrak {a}}\to J{\mathfrak {a}}^+ $
given by
$\ L\colon {\mathfrak {a}}\to J{\mathfrak {a}}^+ $
given by
 $$ \begin{align} \sum_kh_kH_k\mapsto Ad_{\exp(\sum_kh_kH_k)}E_0=\sum_je^{2h_j}E^j. \end{align} $$
$$ \begin{align} \sum_kh_kH_k\mapsto Ad_{\exp(\sum_kh_kH_k)}E_0=\sum_je^{2h_j}E^j. \end{align} $$
Write an N-invariant domain in a rank-r homogeneous Siegel domain
![]() $D(V,F)$
as
$D(V,F)$
as
![]() ${D=N\exp {\mathcal D}\cdot p_0}$
, for some domain
${D=N\exp {\mathcal D}\cdot p_0}$
, for some domain
![]() ${\mathcal D}\subset {\mathfrak {a}}$
. Then, as in the symmetric case (see [Reference Geatti and Iannuzzi3, §3]), one can associate with D an r-dimensional tube domain.
${\mathcal D}\subset {\mathfrak {a}}$
. Then, as in the symmetric case (see [Reference Geatti and Iannuzzi3, §3]), one can associate with D an r-dimensional tube domain.
Definition 2.3. The r-dimensional tube domain associated with an N-invariant domain D in
![]() $D(V,F)$
is the image of the set
$D(V,F)$
is the image of the set
![]() $\,R\exp (\mathcal D) \,$
under
$\,R\exp (\mathcal D) \,$
under
![]() $\mathcal L$
, namely,
$\mathcal L$
, namely,
3 N-invariant Stein domains in a homogeneous Siegel domain
Let
![]() $D(V,F)$
be a homogeneous bounded domain. In this section, we give a characterization of the N-invariant Stein domains D in
$D(V,F)$
be a homogeneous bounded domain. In this section, we give a characterization of the N-invariant Stein domains D in
![]() $D( V,F)$
in terms of the associated tube domain. If D is Stein, then such tube domain is Stein and its base
$D( V,F)$
in terms of the associated tube domain. If D is Stein, then such tube domain is Stein and its base
![]() $\Omega $
is an open convex set in
$\Omega $
is an open convex set in
![]() $J{\mathfrak {a}}^+$
. On the other hand, we will see that
$J{\mathfrak {a}}^+$
. On the other hand, we will see that
![]() $\Omega $
must satisfy some further geometric conditions which depend on the specific root decomposition of the normal J-algebra of
$\Omega $
must satisfy some further geometric conditions which depend on the specific root decomposition of the normal J-algebra of
![]() $D(V,F)$
.
$D(V,F)$
.
Let D be an N-invariant domain in
![]() $D(V,F)$
. Then
$D(V,F)$
. Then
where
![]() $ \boldsymbol {\Omega }$
is the
$ \boldsymbol {\Omega }$
is the
![]() $Ad_{\exp {\mathfrak {n}}_0}$
-invariant open subset in
$Ad_{\exp {\mathfrak {n}}_0}$
-invariant open subset in
![]() $ V$
determined by
$ V$
determined by
By (2.2)–(2.4), the base of the associated tube is
Note that, since
![]() $Ad_AE_0=J{\mathfrak {a}}^+$
, the set
$Ad_AE_0=J{\mathfrak {a}}^+$
, the set
![]() $i\Omega $
is a slice both for the
$i\Omega $
is a slice both for the
![]() $Ad_{\exp {\mathfrak {n}}_0}$
-action on
$Ad_{\exp {\mathfrak {n}}_0}$
-action on
![]() $i\boldsymbol {\Omega }$
and for the
$i\boldsymbol {\Omega }$
and for the
![]() $ N$
-action on D.
$ N$
-action on D.
For
![]() $D(V,F)$
irreducible, define a cone in
$D(V,F)$
irreducible, define a cone in
![]() $J{\mathfrak {a}}^+ $
as follows:
$J{\mathfrak {a}}^+ $
as follows:
 $$ \begin{align*} \textstyle C:=\begin{cases} {\mathcal C}_t, \text{in the tube case,}\\ {\mathcal C}_{nt}, \text{in the non-tube case,} \end{cases} \end{align*} $$
$$ \begin{align*} \textstyle C:=\begin{cases} {\mathcal C}_t, \text{in the tube case,}\\ {\mathcal C}_{nt}, \text{in the non-tube case,} \end{cases} \end{align*} $$
where
![]() $ {\mathcal C}_t:=cone\{E^j\}_j $
, with
$ {\mathcal C}_t:=cone\{E^j\}_j $
, with
![]() $j\in \{1,\ldots ,r-1\}$
such that
$j\in \{1,\ldots ,r-1\}$
such that
![]() ${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
for some
${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
for some
![]() $l>j$
, and
$l>j$
, and
![]() $ {\mathcal C}_{nt}=cone\{E^j\}_j$
, with
$ {\mathcal C}_{nt}=cone\{E^j\}_j$
, with
![]() $j\in \{1,\ldots ,r\}$
such that either
$j\in \{1,\ldots ,r\}$
such that either
![]() ${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
for some
${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
for some
![]() $l>j$
, or
$l>j$
, or
![]() ${\mathfrak {s}}^{e_j}\not =\{0\}$
. (Here, given nonzero vectors
${\mathfrak {s}}^{e_j}\not =\{0\}$
. (Here, given nonzero vectors
![]() $\mathbf {v}_1,\ldots ,\mathbf {v}_k $
, we set
$\mathbf {v}_1,\ldots ,\mathbf {v}_k $
, we set
![]() $cone\{\mathbf {v}_1,\ldots ,\mathbf {v}_k\}:=\{\sum _jt_j\mathbf {v}_j,~t_j> 0 \} $
.)
$cone\{\mathbf {v}_1,\ldots ,\mathbf {v}_k\}:=\{\sum _jt_j\mathbf {v}_j,~t_j> 0 \} $
.)
In the reducible case, if
![]() $D(V,F)$
decomposes in the product of irreducible domains as
$D(V,F)$
decomposes in the product of irreducible domains as
![]() $D(V^{(1)},F^{(1)})\times \cdots \times D(V^{(m)},F^{(m)})$
, then the normal J-algebra
$D(V^{(1)},F^{(1)})\times \cdots \times D(V^{(m)},F^{(m)})$
, then the normal J-algebra
![]() ${\mathfrak {s}}$
and all its related objects decompose accordingly. In particular, the cone decomposes as
${\mathfrak {s}}$
and all its related objects decompose accordingly. In particular, the cone decomposes as
![]() $C=C^{(1)}\times \cdots \times C^{(m)}$
, where
$C=C^{(1)}\times \cdots \times C^{(m)}$
, where
![]() $C^{(i)}$
is the cone associated with the i-th irreducible component of
$C^{(i)}$
is the cone associated with the i-th irreducible component of
![]() $D(V,F)$
.
$D(V,F)$
.
Example 3.1. (a) If
![]() $D(V,F)$
is irreducible symmetric, then
$D(V,F)$
is irreducible symmetric, then
![]() ${\mathcal C}_t=cone\{E^1,\ldots ,E^{r-1}\}$
and
${\mathcal C}_t=cone\{E^1,\ldots ,E^{r-1}\}$
and
![]() ${\mathcal C}_{nt}=cone\{E^1,\ldots ,E^{r}\}$
(see (9) in [Reference Geatti and Iannuzzi3]).
${\mathcal C}_{nt}=cone\{E^1,\ldots ,E^{r}\}$
(see (9) in [Reference Geatti and Iannuzzi3]).
(b) Let
![]() $D(V)$
be the tube domain over the five-dimensional Vinberg cone
$D(V)$
be the tube domain over the five-dimensional Vinberg cone
 $$ \begin{align*} D(V)=\left\{\begin{pmatrix}z_{11}&0&z_{13}\\ 0&z_{22}&z_{23}\\ z_{13}& z_{23}&z_{33}\end{pmatrix}~|~z_{ij}=x_{ij}+iy_{ij}\in{\mathbb{C}}, ~\begin{cases} y_{11} y_{33}-y_{13}^2>0 \\ y_{22} y_{33}-y_{23}^2>0\end{cases} \mathrm{and}\quad y_{33}>0\right\}. \end{align*} $$
$$ \begin{align*} D(V)=\left\{\begin{pmatrix}z_{11}&0&z_{13}\\ 0&z_{22}&z_{23}\\ z_{13}& z_{23}&z_{33}\end{pmatrix}~|~z_{ij}=x_{ij}+iy_{ij}\in{\mathbb{C}}, ~\begin{cases} y_{11} y_{33}-y_{13}^2>0 \\ y_{22} y_{33}-y_{23}^2>0\end{cases} \mathrm{and}\quad y_{33}>0\right\}. \end{align*} $$
Then
and
![]() ${\mathcal C}_t=cone\{E^1,E^2\}$
.
${\mathcal C}_t=cone\{E^1,E^2\}$
.
(b) Let
![]() $D(V,F)$
be the four-dimensional nonsymmetric domain
$D(V,F)$
be the four-dimensional nonsymmetric domain
 $$ \begin{align*}D(V,F)=\left\{\left(\begin{pmatrix}z_{11}&z_{12}\\ z_{12}&z_{22}\end{pmatrix},w\right)~|~z_{ij}=x_{ij}+iy_{ij},~w\in{\mathbb{C}}, ~\begin{cases} (y_{11}-|w|^2)y_{22}-y_{12}^2>0\\ y_{22} >0\end{cases}\!\!\!\!\!\!\!\!\!\right\}.\end{align*} $$
$$ \begin{align*}D(V,F)=\left\{\left(\begin{pmatrix}z_{11}&z_{12}\\ z_{12}&z_{22}\end{pmatrix},w\right)~|~z_{ij}=x_{ij}+iy_{ij},~w\in{\mathbb{C}}, ~\begin{cases} (y_{11}-|w|^2)y_{22}-y_{12}^2>0\\ y_{22} >0\end{cases}\!\!\!\!\!\!\!\!\!\right\}.\end{align*} $$
Then
and
![]() ${\mathcal C}_{nt}=cone\{E^1\}$
.
${\mathcal C}_{nt}=cone\{E^1\}$
.
Definition 3.2. A domain
![]() $\,\Omega \subset J{\mathfrak {a}}^+\,$
is C-invariant if
$\,\Omega \subset J{\mathfrak {a}}^+\,$
is C-invariant if
![]() $\,E\in \Omega \, $
implies
$\,E\in \Omega \, $
implies
![]() $\,E+C \subset \Omega $
or, equivalently, if
$\,E+C \subset \Omega $
or, equivalently, if
![]() $\,E\in \Omega \, $
implies
$\,E\in \Omega \, $
implies
![]() $\,E+\overline C \subset \Omega $
.
$\,E+\overline C \subset \Omega $
.
Denote by
the projection onto
![]() $iJ{\mathfrak {a}}$
, parallel to
$iJ{\mathfrak {a}}$
, parallel to
![]() $i( \oplus \, {\mathfrak {s}}^{e_j+e_l})$
and by
$i( \oplus \, {\mathfrak {s}}^{e_j+e_l})$
and by
the projection onto
![]() $\, iJ{\mathfrak {a}}$
parallel to
$\, iJ{\mathfrak {a}}$
parallel to
![]() ${\mathfrak {s}}_1\oplus i(\oplus \,{\mathfrak {s}}^{e_j+e_l})\oplus {\mathfrak {s}}_{1/2}$
.
${\mathfrak {s}}_1\oplus i(\oplus \,{\mathfrak {s}}^{e_j+e_l})\oplus {\mathfrak {s}}_{1/2}$
.
For simplicity, the next lemma is formulated in the irreducible case. In the reducible case, it applies to each irreducible component.
Lemma 3.3. The following statements hold true.
-
(i) Assume that
 ${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
, for some
${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
, for some
 $l>j$
, and let
$l>j$
, and let
 $X\in {\mathfrak {s}}^{e_j-e_l}$
be a nonzero element. Then
$X\in {\mathfrak {s}}^{e_j-e_l}$
be a nonzero element. Then
 $[[E^l,X],X]=s E^j$
, for some
$[[E^l,X],X]=s E^j$
, for some
 $s\in {\mathbb {R}}^{> 0}$
.
$s\in {\mathbb {R}}^{> 0}$
. -
(ii) Let
 $E=\sum y_kE^k \in J{\mathfrak {a}}^+$
. Then
$E=\sum y_kE^k \in J{\mathfrak {a}}^+$
. Then
 $\,p(iAd_{\exp {\mathfrak {n}}_0} E)=i(E+\overline {\mathcal C}_{t}).$
$\,p(iAd_{\exp {\mathfrak {n}}_0} E)=i(E+\overline {\mathcal C}_{t}).$
-
(iii) Let
 $E\in J{\mathfrak {a}}^+$
. Then
$E\in J{\mathfrak {a}}^+$
. Then
 $\widetilde p(N\cdot (iE,0))=i(E+ \overline {\mathcal C}_{nt})$
.
$\widetilde p(N\cdot (iE,0))=i(E+ \overline {\mathcal C}_{nt})$
.
Proof. (i) Since
![]() $[[E^l,X],X]=[JX,X]$
, then the statement follows from Lemma 2.1(b).
$[[E^l,X],X]=[JX,X]$
, then the statement follows from Lemma 2.1(b).
(ii) Fix
![]() $1\le j\le r-1$
and define
$1\le j\le r-1$
and define
![]() ${\mathcal L}_j:=\oplus _{l>j}{\mathfrak {s}}^{e_j-e_l}$
. In each root space
${\mathcal L}_j:=\oplus _{l>j}{\mathfrak {s}}^{e_j-e_l}$
. In each root space
![]() ${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
in
${\mathfrak {s}}^{e_j-e_l}\not =\{0\}$
in
![]() $ {\mathcal L}_j$
, there exists an orthogonal basis
$ {\mathcal L}_j$
, there exists an orthogonal basis
![]() $\{E^p_{jl}\}_p$
such that for
$\{E^p_{jl}\}_p$
such that for
![]() $X=\sum _{ l>j,\, p}x^p_{jl}E^p_{jl}\in {\mathcal L}_j$
, one has
$X=\sum _{ l>j,\, p}x^p_{jl}E^p_{jl}\in {\mathcal L}_j$
, one has
(cf. Lemma 2.1(b) and (c)). Moreover, from a discussion similar to the one in [Reference Rossi and Vergne10, p. 363], one obtains
[Reference Rossi and Vergne10, Th. 4.10 and (4.13)]. Hence,
![]() $p( iAd_{\exp {{\mathfrak {n}}_0}} E)= i(E+\overline {\mathcal C}_{t})$
, as claimed.
$p( iAd_{\exp {{\mathfrak {n}}_0}} E)= i(E+\overline {\mathcal C}_{t})$
, as claimed.
(iii) The N-orbit of the point
![]() $(iE,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
is given by
$(iE,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
is given by
By (3.1) and Lemma 3.3(ii), one has
If
![]() $ {\mathfrak {s}}^{e_j}\not =\{0\}$
and
$ {\mathfrak {s}}^{e_j}\not =\{0\}$
and
![]() $\zeta \not = 0$
in
$\zeta \not = 0$
in
![]() $ {\mathfrak {s}}^{e_j} $
, then by Lemma 2.1(c), the element
$ {\mathfrak {s}}^{e_j} $
, then by Lemma 2.1(c), the element
![]() $\,F(\zeta ,\zeta ) =\frac {1}{4} [J\zeta ,\zeta ] \,$
is a positive multiple of
$\,F(\zeta ,\zeta ) =\frac {1}{4} [J\zeta ,\zeta ] \,$
is a positive multiple of
![]() $E^j$
. Therefore,
$E^j$
. Therefore,
![]() $\tilde p(N\cdot (iE,0))=i(E+\overline {\mathcal C}_{nt})$
, as claimed.
$\tilde p(N\cdot (iE,0))=i(E+\overline {\mathcal C}_{nt})$
, as claimed.
Theorem 3.4. Let
![]() $\,D(V,F)\,$
be a homogeneous Siegel domain of rank r. Let D be an
$\,D(V,F)\,$
be a homogeneous Siegel domain of rank r. Let D be an
![]() $\,N$
-invariant domain in
$\,N$
-invariant domain in
![]() $\,D(V,F)\,$
, and let
$\,D(V,F)\,$
, and let
![]() $ \Omega $
be the base of the associated tube domain. Then
$ \Omega $
be the base of the associated tube domain. Then
![]() $\,D\,$
is Stein if and only if
$\,D\,$
is Stein if and only if
![]() $\,\Omega \,$
is convex and C-invariant.
$\,\Omega \,$
is convex and C-invariant.
Proof of Theorem 3.4
We first prove that D Stein implies
![]() $\Omega $
convex and C-invariant. Then we show that
$\Omega $
convex and C-invariant. Then we show that
![]() $\Omega $
convex and C-invariant implies D convex and therefore Stein (cf. [Reference Gunning5, Vol. 1, Th. 10, p. 67]). In particular, if
$\Omega $
convex and C-invariant implies D convex and therefore Stein (cf. [Reference Gunning5, Vol. 1, Th. 10, p. 67]). In particular, if
![]() $D $
is Stein, then it is necessarily convex. An essential fact is that the N-action on D is affine and every affine map commutes with taking convex hulls.
$D $
is Stein, then it is necessarily convex. An essential fact is that the N-action on D is affine and every affine map commutes with taking convex hulls.
3.1
We begin with the tube case. An N-invariant domain D in a homogeneous tube domain
![]() $D(V)$
is itself a tube domain with base the
$D(V)$
is itself a tube domain with base the
![]() $Ad_{\exp {\mathfrak {n}}_0}$
-invariant set
$Ad_{\exp {\mathfrak {n}}_0}$
-invariant set
![]() $ \boldsymbol {\Omega }$
. Since D is Stein if and only if its base is convex, all we have to show is that
$ \boldsymbol {\Omega }$
. Since D is Stein if and only if its base is convex, all we have to show is that
![]() $\Omega $
convex and
$\Omega $
convex and
![]() ${\mathcal C}_t$
-invariant is equivalent to
${\mathcal C}_t$
-invariant is equivalent to
![]() $ \boldsymbol {\Omega }$
being convex.
$ \boldsymbol {\Omega }$
being convex.
If
![]() $ \boldsymbol {\Omega }$
is convex, then
$ \boldsymbol {\Omega }$
is convex, then
![]() $\Omega $
is clearly convex. In order to prove that
$\Omega $
is clearly convex. In order to prove that
![]() $\Omega $
is
$\Omega $
is
![]() ${\mathcal C}_t$
-invariant, let
${\mathcal C}_t$
-invariant, let
![]() $E=\sum _ky_kE^k\in \Omega $
, with
$E=\sum _ky_kE^k\in \Omega $
, with
![]() $y_k>0$
, for
$y_k>0$
, for
![]() $k=1,\ldots ,r$
. If the root space
$k=1,\ldots ,r$
. If the root space
![]() ${\mathfrak {s}}^{e_j-e_l} \not =\{0\}$
, let
${\mathfrak {s}}^{e_j-e_l} \not =\{0\}$
, let
![]() $X $
be a nonzero element therein. Since
$X $
be a nonzero element therein. Since
![]() $ad_X$
is two-step nilpotent, for every
$ad_X$
is two-step nilpotent, for every
![]() $t\in {\mathbb {R}}$
,
$t\in {\mathbb {R}}$
,
is an element of
![]() $ \boldsymbol {\Omega }$
. As
$ \boldsymbol {\Omega }$
. As
![]() $ \boldsymbol {\Omega }$
is convex, by replacing t with
$ \boldsymbol {\Omega }$
is convex, by replacing t with
![]() $-t$
, one finds that also the midpoint
$-t$
, one finds that also the midpoint
![]() $E+ \frac {1}{2} t^2y_l [X,[X,E^l]]$
lies in
$E+ \frac {1}{2} t^2y_l [X,[X,E^l]]$
lies in
![]() $\boldsymbol {\Omega }$
. This says that
$\boldsymbol {\Omega }$
. This says that
![]() $E+\lambda E^j $
lies in
$E+\lambda E^j $
lies in
![]() $\boldsymbol {\Omega }$
, for all
$\boldsymbol {\Omega }$
, for all
![]() $\lambda \ge 0$
. The same argument applied to all
$\lambda \ge 0$
. The same argument applied to all
![]() $j\in \{1,\ldots ,r-1\}$
for which
$j\in \{1,\ldots ,r-1\}$
for which
![]() ${\mathfrak {s}}^{e_j-e_l} \not =\{0\}$
, for some
${\mathfrak {s}}^{e_j-e_l} \not =\{0\}$
, for some
![]() $l>j$
, and the convexity of
$l>j$
, and the convexity of
![]() $\Omega $
imply that
$\Omega $
imply that
![]() $\Omega +{\mathcal C}_{t}\subset \Omega $
, as desired.
$\Omega +{\mathcal C}_{t}\subset \Omega $
, as desired.
Conversely, assume that
![]() $\Omega $
is convex and
$\Omega $
is convex and
![]() ${\mathcal C}_t$
-invariant. We are going to prove that
${\mathcal C}_t$
-invariant. We are going to prove that
![]() $conv( \boldsymbol {\Omega })\subset \boldsymbol {\Omega }$
. Since
$conv( \boldsymbol {\Omega })\subset \boldsymbol {\Omega }$
. Since
![]() $\, \boldsymbol {\Omega } =Ad_{\exp {\mathfrak {n}}_0}\Omega $
, from Lemma 3.3(ii) and the
$\, \boldsymbol {\Omega } =Ad_{\exp {\mathfrak {n}}_0}\Omega $
, from Lemma 3.3(ii) and the
![]() ${\mathcal C}_t$
-invariance of
${\mathcal C}_t$
-invariance of
![]() $\Omega $
, one has
$\Omega $
, one has
From the above inclusion and the convexity of
![]() $\Omega $
, one has
$\Omega $
, one has
Finally, from the
![]() $Ad_{\exp {\mathfrak {n}}_0}$
-invariance of
$Ad_{\exp {\mathfrak {n}}_0}$
-invariance of
![]() $conv( i\boldsymbol {\Omega })$
, it follows that
$conv( i\boldsymbol {\Omega })$
, it follows that
This completes the proof of the theorem in the tube case.
3.2
Next we deal with the non-tube case. Let D be an N-invariant domain in a homogeneous Siegel domain
![]() $D( V,F)$
. Denote by
$D( V,F)$
. Denote by
![]() $conv(D)$
the convex hull of D in
$conv(D)$
the convex hull of D in
![]() ${\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
, which is N-invariant as well.
${\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}$
, which is N-invariant as well.
If D is Stein, then
![]() $D\cap ({\mathfrak {s}}_1^{\mathbb {C}}\times \{0\})=\{(Z,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}~| Im(Z)\in \boldsymbol {\Omega }\}$
is biholomorphic to a Stein tube domain in
$D\cap ({\mathfrak {s}}_1^{\mathbb {C}}\times \{0\})=\{(Z,0)\in {\mathfrak {s}}_1^{\mathbb {C}}\oplus {\mathfrak {s}}_{1/2}~| Im(Z)\in \boldsymbol {\Omega }\}$
is biholomorphic to a Stein tube domain in
![]() ${\mathfrak {s}}_1^{\mathbb {C}}$
, invariant under
${\mathfrak {s}}_1^{\mathbb {C}}$
, invariant under
![]() $\exp ({\mathfrak {n}}_0\oplus {\mathfrak {n}}_1)$
. Hence, by Theorem 3.4 in the tube case, the set
$\exp ({\mathfrak {n}}_0\oplus {\mathfrak {n}}_1)$
. Hence, by Theorem 3.4 in the tube case, the set
![]() $\Omega $
is convex and
$\Omega $
is convex and
![]() $\Omega +\overline {\mathcal C}_{t}\subset \Omega $
. The fact that
$\Omega +\overline {\mathcal C}_{t}\subset \Omega $
. The fact that
![]() $\Omega +\overline {\mathcal C}_{nt}\subset \Omega $
follows from (3.1) and the fact that
$\Omega +\overline {\mathcal C}_{nt}\subset \Omega $
follows from (3.1) and the fact that
![]() $F(\zeta ,\zeta )$
is an arbitrary positive multiple of
$F(\zeta ,\zeta )$
is an arbitrary positive multiple of
![]() $E^j$
, when
$E^j$
, when
![]() $\zeta $
varies in
$\zeta $
varies in
![]() ${\mathfrak {s}}^{e_j}\setminus \{0\}$
.
${\mathfrak {s}}^{e_j}\setminus \{0\}$
.
Conversely, assume that
![]() $\Omega $
is convex and
$\Omega $
is convex and
![]() ${\mathcal C}_{nt} $
-invariant. By Lemma 3.3(iii), one has
${\mathcal C}_{nt} $
-invariant. By Lemma 3.3(iii), one has
Moreover,
By the N-invariance of
![]() $conv(D)$
, one obtains
$conv(D)$
, one obtains
Hence, D is convex and therefore Stein (cf. [Reference Gunning5, Vol. 1, Th. 10, p. 67]). This concludes the proof of the theorem.
We conclude this section by observing that holomorphically separable,
![]() $\,N$
-equivariant, Riemann domains over a bounded homogeneous domain
$\,N$
-equivariant, Riemann domains over a bounded homogeneous domain
![]() $\mathbf {D}$
are univalent: the same proof as in the symmetric case works in this more general case (see [Reference Geatti and Iannuzzi3, Prop. 3.7]). As a consequence, one obtains the following corollary.
$\mathbf {D}$
are univalent: the same proof as in the symmetric case works in this more general case (see [Reference Geatti and Iannuzzi3, Prop. 3.7]). As a consequence, one obtains the following corollary.
Corollary 3.5. The envelope of holomorphy
![]() $\widehat D$
of an
$\widehat D$
of an
![]() $\,N$
-invariant domain
$\,N$
-invariant domain
![]() $\,D\,$
in
$\,D\,$
in
![]() $\,\mathbf {D}\,$
is the smallest Stein domain in
$\,\mathbf {D}\,$
is the smallest Stein domain in
![]() $\,\mathbf {D}\,$
containing D. Namely,
$\,\mathbf {D}\,$
containing D. Namely,
![]() $\widehat D$
is the N-invariant domain such that the base
$\widehat D$
is the N-invariant domain such that the base
![]() $\widehat \Omega $
of the associated tube is the convex C-invariant hull of
$\widehat \Omega $
of the associated tube is the convex C-invariant hull of
![]() $\,\Omega $
.
$\,\Omega $
.
4 An N-invariant potential of the Bergman metric
Let
![]() $D(V,F)$
be a homogeneous Siegel domain, and let
$D(V,F)$
be a homogeneous Siegel domain, and let
![]() $({\mathfrak {s}},J,-f_0)$
be the associated normal J-algebra, where
$({\mathfrak {s}},J,-f_0)$
be the associated normal J-algebra, where
![]() $-f_0\in {\mathfrak {s}}^{*}$
is the form inducing the Bergman metric g on
$-f_0\in {\mathfrak {s}}^{*}$
is the form inducing the Bergman metric g on
![]() $D(V,F)$
. In this section, we exhibit an N-invariant potential of g, expressed in a Lie theoretical fashion. In order to do this, we determine an explicit formula for the N-moment map associated with g.
$D(V,F)$
. In this section, we exhibit an N-invariant potential of g, expressed in a Lie theoretical fashion. In order to do this, we determine an explicit formula for the N-moment map associated with g.
For
![]() $X\in {\mathfrak {s}}$
, denote by
$X\in {\mathfrak {s}}$
, denote by
![]() $\widetilde X$
the vector field on
$\widetilde X$
the vector field on
![]() $D(V,F)$
induced by the left S-action. Its value at
$D(V,F)$
induced by the left S-action. Its value at
![]() $z=s\cdot p_0 $
is given by
$z=s\cdot p_0 $
is given by
![]() $\widetilde X_z=\frac {d}{dt}{\big |_{t=0}} \exp tX\cdot z$
. If
$\widetilde X_z=\frac {d}{dt}{\big |_{t=0}} \exp tX\cdot z$
. If
![]() $z=a\cdot p_0$
, with
$z=a\cdot p_0$
, with
![]() $a=\exp H$
and
$a=\exp H$
and
![]() $H\in {\mathfrak {a}}$
, and
$H\in {\mathfrak {a}}$
, and
![]() $X\in {\mathfrak {s}}^\alpha $
, then
$X\in {\mathfrak {s}}^\alpha $
, then
![]() $\widetilde X_z=e^{-\alpha (H)}a_* X$
.
$\widetilde X_z=e^{-\alpha (H)}a_* X$
.
Lemma 4.1.
(a) The map
![]() $\mu _S\colon D(V,F)\to {\mathfrak {s}}^{*},$
defined by
$\mu _S\colon D(V,F)\to {\mathfrak {s}}^{*},$
defined by
is an S-moment map with respect to g.
(b) The map
![]() $\mu _N\colon D(V,F)\to {\mathfrak {n}}^{*},$
defined by
$\mu _N\colon D(V,F)\to {\mathfrak {n}}^{*},$
defined by
is an N-moment map with respect to g.
Proof. (a) By definition, the map
![]() $\mu _S$
is S-equivariant and satisfies
$\mu _S$
is S-equivariant and satisfies
![]() $\mu _S(p_0)=-f_0$
.
$\mu _S(p_0)=-f_0$
.
We identify
![]() $D(V,F)$
with the group S by the map (2.1), and prove that
$D(V,F)$
with the group S by the map (2.1), and prove that
Let
![]() $W\in T_eS\cong {\mathfrak {s}}$
. Then
$W\in T_eS\cong {\mathfrak {s}}$
. Then
Now take
![]() $s\in S$
and let
$s\in S$
and let
![]() $s_*W\in T_{s}S\cong s_*{\mathfrak {s}}$
. On the left-hand side of (4.1), we find
$s_*W\in T_{s}S\cong s_*{\mathfrak {s}}$
. On the left-hand side of (4.1), we find
Since also the right-hand side of (4.1) is given by
 $$ \begin{align*} \omega_s\Bigg(\frac{d}{dt}{\big |_{t=0}} \exp tX\cdot s,s_*W\Bigg)=\omega_s(s_* Ad_{s^{-1}}X,s_*W)=\omega(Ad_{s^{-1}}X,W)=-f_0([ Ad_{s^{-1}} X,W]), \end{align*} $$
$$ \begin{align*} \omega_s\Bigg(\frac{d}{dt}{\big |_{t=0}} \exp tX\cdot s,s_*W\Bigg)=\omega_s(s_* Ad_{s^{-1}}X,s_*W)=\omega(Ad_{s^{-1}}X,W)=-f_0([ Ad_{s^{-1}} X,W]), \end{align*} $$
the proof of (a) is complete.
(b) The restriction of
![]() $\mu _S$
to
$\mu _S$
to
![]() ${\mathfrak {n}}$
defines an N-moment map
${\mathfrak {n}}$
defines an N-moment map
![]() $\mu _N$
on
$\mu _N$
on
![]() $D(V,F)$
. Since
$D(V,F)$
. Since
![]() $\mu _N$
is N-equivariant, it is uniquely determined by
$\mu _N$
is N-equivariant, it is uniquely determined by
![]() $\mu _N(a\cdot p_0)(X) =-Ad_a^{*}f_0( X)$
, for
$\mu _N(a\cdot p_0)(X) =-Ad_a^{*}f_0( X)$
, for
![]() $X\in {\mathfrak {n}}$
. It follows that
$X\in {\mathfrak {n}}$
. It follows that
![]() $\mu _N(z)(X)=-(Ad_a^{*}f_0)(Ad_{n^{-1}} X)$
, is an
$\mu _N(z)(X)=-(Ad_a^{*}f_0)(Ad_{n^{-1}} X)$
, is an
![]() $N$
-invariant moment map with respect to
$N$
-invariant moment map with respect to
![]() $g$
as claimed.
$g$
as claimed.
The moment map
![]() $\,\mu _S\,$
defined in Lemma 4.1 is an embedding of
$\,\mu _S\,$
defined in Lemma 4.1 is an embedding of
![]() $\,D(V,F)\,$
in
$\,D(V,F)\,$
in
![]() $\,{\mathfrak {s}}^{*}$
as the coadjoint orbit of
$\,{\mathfrak {s}}^{*}$
as the coadjoint orbit of
![]() $\,-f_0\,$
, with trivial isotropy subgroup. The image
$\,-f_0\,$
, with trivial isotropy subgroup. The image
![]() $\,\mu _S(D(V,F))\,$
is the convex domain
$\,\mu _S(D(V,F))\,$
is the convex domain
![]() $\,{\mathfrak {s}}_0^{*}+{\mathfrak {s}}_{1/2}^{*}+V^{*}\,$
in
$\,{\mathfrak {s}}_0^{*}+{\mathfrak {s}}_{1/2}^{*}+V^{*}\,$
in
![]() $\,{\mathfrak {s}}^{*}$
, where
$\,{\mathfrak {s}}^{*}$
, where
![]() $V^{*}:=\{\phi \in {\mathfrak {s}}_1^{*}~|~\phi (X)>0, ~\forall X\in \overline V\setminus \{0\}\} $
is the dual cone of V in
$V^{*}:=\{\phi \in {\mathfrak {s}}_1^{*}~|~\phi (X)>0, ~\forall X\in \overline V\setminus \{0\}\} $
is the dual cone of V in
![]() ${\mathfrak {s}}_1$
(cf. [Reference Rossi and Vergne10, Lem. 3.5, p. 350]). Similarly, the image
${\mathfrak {s}}_1$
(cf. [Reference Rossi and Vergne10, Lem. 3.5, p. 350]). Similarly, the image
![]() $\,\mu _N(D(V,F))\,$
is the convex domain
$\,\mu _N(D(V,F))\,$
is the convex domain
![]() $\,{\mathfrak {n}}_0^{*}+{\mathfrak {s}}_{1/2}^{*}+V^{*}\,$
in
$\,{\mathfrak {n}}_0^{*}+{\mathfrak {s}}_{1/2}^{*}+V^{*}\,$
in
![]() $\,{\mathfrak {n}}^{*}$
.
$\,{\mathfrak {n}}^{*}$
.
Convexity properties of the moment map have been studied in several settings (see [Reference Hilgert, Neeb and Plank6] and the references therein). Here, we show that the image under
![]() $\,\mu _N\,$
of a Stein
$\,\mu _N\,$
of a Stein
![]() $\,N$
-invariant domain in
$\,N$
-invariant domain in
![]() $D(V,F)$
is not necessarily convex.
$D(V,F)$
is not necessarily convex.
Let
![]() $D(V,F)$
be a homogeneous Siegel domain, and let
$D(V,F)$
be a homogeneous Siegel domain, and let
![]() $D=N\cdot i\Omega $
be an N-invariant Stein domain therein. One has
$D=N\cdot i\Omega $
be an N-invariant Stein domain therein. One has
and one can easily verify that
![]() $\mu _N$
maps
$\mu _N$
maps
![]() $A\cdot p_0=iJ{\mathfrak {a}}^+$
bijectively onto
$A\cdot p_0=iJ{\mathfrak {a}}^+$
bijectively onto
![]() $(J{\mathfrak {a}}^+)^{*}$
.
$(J{\mathfrak {a}}^+)^{*}$
.
Therefore,
![]() $\, \mu _N(i\Omega )=(J{\mathfrak {a}})^{*}\cap \mu _N(D)$
. Consequently, if
$\, \mu _N(i\Omega )=(J{\mathfrak {a}})^{*}\cap \mu _N(D)$
. Consequently, if
![]() $\mu _N(i\Omega )$
is not convex, then
$\mu _N(i\Omega )$
is not convex, then
![]() $\,\mu _N(D)$
is not convex either.
$\,\mu _N(D)$
is not convex either.
Example 4.2. Let
![]() ${\mathcal P}=\left \{ Z=X+iY~|~Z^t=Z,\, Y\gg 0\right \}$
be the Siegel upper half-plane of rank 2. Then
${\mathcal P}=\left \{ Z=X+iY~|~Z^t=Z,\, Y\gg 0\right \}$
be the Siegel upper half-plane of rank 2. Then
 $$ \begin{align*} A\cdot p_0=\left\{ i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix}~|~y_1,\,y_2>0\right\} \end{align*} $$
$$ \begin{align*} A\cdot p_0=\left\{ i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix}~|~y_1,\,y_2>0\right\} \end{align*} $$
and
 $$ \begin{align*} \textstyle \mu_{S}\Big ( i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix} \Big )=-3(\frac{1}{y_1}(E^1)^{*}+\frac{1}{y_2}(E^2)^{*}). \end{align*} $$
$$ \begin{align*} \textstyle \mu_{S}\Big ( i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix} \Big )=-3(\frac{1}{y_1}(E^1)^{*}+\frac{1}{y_2}(E^2)^{*}). \end{align*} $$
Let
![]() $\,D:= N\cdot i\Omega \,$
be the Stein N-invariant domain in
$\,D:= N\cdot i\Omega \,$
be the Stein N-invariant domain in
![]() $ {\mathcal P}$
associated with the convex,
$ {\mathcal P}$
associated with the convex,
![]() $C_t$
-invariant domain
$C_t$
-invariant domain
 $$ \begin{align*} \Omega : =\left\{ i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix}~|~y_1y_2>1\right\}. \end{align*} $$
$$ \begin{align*} \Omega : =\left\{ i\begin{pmatrix}y_1&0\\ 0&y_2\end{pmatrix}~|~y_1y_2>1\right\}. \end{align*} $$
The image
is clearly not convex. Therefore,
![]() $\mu _N(D)$
is not convex either.
$\mu _N(D)$
is not convex either.
As the domain
![]() $\,\Omega \subset J{\mathfrak {a}}^+\,$
is convex and also
$\,\Omega \subset J{\mathfrak {a}}^+\,$
is convex and also
![]() $\,{\mathcal C}_{nt}$
-invariant, a similar construction provides examples of N-invariant Stein domains with non-convex moment image in all rank-2 symmetric Siegel domains, both of tube type and of non-tube type.
$\,{\mathcal C}_{nt}$
-invariant, a similar construction provides examples of N-invariant Stein domains with non-convex moment image in all rank-2 symmetric Siegel domains, both of tube type and of non-tube type.
Proposition 4.3. The N-invariant function
![]() $\rho \colon D(V,F)\to {\mathbb {R}}$
, given by
$\rho \colon D(V,F)\to {\mathbb {R}}$
, given by
where
![]() $a=\exp H$
, for
$a=\exp H$
, for
![]() $H=\sum _k h_kH_k\in {\mathfrak {a}}\,$
, and
$H=\sum _k h_kH_k\in {\mathfrak {a}}\,$
, and
![]() $-f_0=\sum _kc_k(E^k)^{*}$
, is a potential for the Kähler metric induced by
$-f_0=\sum _kc_k(E^k)^{*}$
, is a potential for the Kähler metric induced by
![]() $-f_0$
.
$-f_0$
.
Proof. As in the previous lemma, we identify
![]() $\,D(V,F)\,$
with S. In order to check that
$\,D(V,F)\,$
with S. In order to check that
![]() $-dd^c\rho =\omega $
, we need to show that
$-dd^c\rho =\omega $
, we need to show that
![]() $\,d^c\rho (\widetilde X_s)= \,\mu _N^X(s)$
, for all
$\,d^c\rho (\widetilde X_s)= \,\mu _N^X(s)$
, for all
![]() $\,s \in S$
. By the
$\,s \in S$
. By the
![]() $\,N$
-invariance of
$\,N$
-invariance of
![]() $\,\rho \,$
and of
$\,\rho \,$
and of
![]() $\,J$
, one has
$\,J$
, one has
for every
![]() $\,na \in S$
. Then, as
$\,na \in S$
. Then, as
![]() $\,\mu _N\,$
is
$\,\mu _N\,$
is
![]() $\,N$
-equivariant, it is enough to show that
$\,N$
-equivariant, it is enough to show that
for all
![]() $\,a \in A\,$
and
$\,a \in A\,$
and
![]() $\,X\in {\mathfrak {n}}$
. If
$\,X\in {\mathfrak {n}}$
. If
![]() $X=E^j$
, then
$X=E^j$
, then
If
![]() $X\in {\mathfrak {s}}^\alpha $
, with
$X\in {\mathfrak {s}}^\alpha $
, with
![]() $0 \not = \alpha \notin \{2e_1,\dots ,2e_r\}$
, then
$0 \not = \alpha \notin \{2e_1,\dots ,2e_r\}$
, then
![]() $JX\in {\mathfrak {s}}^\beta $
, with
$JX\in {\mathfrak {s}}^\beta $
, with
![]() $0\not = \beta \notin \{2e_1,\dots ,2e_r\}$
. By the N-invariance of
$0\not = \beta \notin \{2e_1,\dots ,2e_r\}$
. By the N-invariance of
![]() $\,\rho $
, one obtains
$\,\rho $
, one obtains
Since
equation (4.2) holds true and the proposition follows.
Remark 4.4. The above computation produces an N-invariant potential and an associated N-moment map, for any S-invariant Kähler metric on
![]() $\mathbf {D}$
induced by an element
$\mathbf {D}$
induced by an element
![]() $\sum _jd_j(E^j)^{*}\in {\mathfrak {s}}^{*}$
, with
$\sum _jd_j(E^j)^{*}\in {\mathfrak {s}}^{*}$
, with
![]() $d_j\in {\mathbb {R}}^{>0}$
, for
$d_j\in {\mathbb {R}}^{>0}$
, for
![]() $j=1,\ldots ,r$
(cf. Remark 2.2).
$j=1,\ldots ,r$
(cf. Remark 2.2).
Acknowledgements
The authors acknowledge the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome “Tor Vergata,” CUP E83C23000330006. This research was partially supported by GNSAGA-INDAM.