Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-23T08:35:17.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model

Part of: Graph theory Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  09 October 2024

Ioana Dumitriu ,
Hai-Xiao Wang  and
Yizhe Zhu
Ioana Dumitriu
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla, CA, USA
Hai-Xiao Wang*
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla, CA, USA
Yizhe Zhu
Affiliation:
Department of Mathematics, University of California, Irvine, CA, USA
*
Corresponding author: Hai-Xiao Wang; Email: h9wang@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the community detection problem in sparse random hypergraphs under the non-uniform hypergraph stochastic block model (HSBM), a general model of random networks with community structure and higher-order interactions. When the random hypergraph has bounded expected degrees, we provide a spectral algorithm that outputs a partition with at least a $\gamma$ fraction of the vertices classified correctly, where 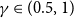$\gamma \in (0.5,1)$ depends on the signal-to-noise ratio (SNR) of the model. When the SNR grows slowly as the number of vertices goes to infinity, our algorithm achieves weak consistency, which improves the previous results in Ghoshdastidar and Dukkipati ((2017) Ann. Stat. 45(1) 289–315.) for non-uniform HSBMs.

Our spectral algorithm consists of three major steps: (1) Hyperedge selection: select hyperedges of certain sizes to provide the maximal signal-to-noise ratio for the induced sub-hypergraph; (2) Spectral partition: construct a regularised adjacency matrix and obtain an approximate partition based on singular vectors; (3) Correction and merging: incorporate the hyperedge information from adjacency tensors to upgrade the error rate guarantee. The theoretical analysis of our algorithm relies on the concentration and regularisation of the adjacency matrix for sparse non-uniform random hypergraphs, which can be of independent interest.

Keywords

Hypergraphcommunity detectionstochastic block model

MSC classification

Primary: 05C80: Random graphs
Secondary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 34 , Issue 1 , January 2025 , pp. 1 - 51
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abbe, E. (2018) Community detection and stochastic block models: Recent developments. J. Mach. Learn. Res. 18(177) 1–86.Google Scholar
Abbe, E., Bandeira, A. S. and Hall, G. (2016) Exact recovery in the stochastic block model. IEEE Trans. Inf. Theory 62(1) 471–487.CrossRefGoogle Scholar
Abbe, E., Fan, J., Wang, K. and Zhong, Y. (2020) Entrywise eigenvector analysis of random matrices with low expected rank. Ann. Stat. 48(3) 1452.CrossRefGoogle ScholarPubMed
Abbe, E. and Sandon, C. (2015) Community detection in general stochastic block models: Fundamental limits and efficient algorithms for recovery. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, IEEE, pp. 670–688.CrossRefGoogle Scholar
Abbe, E. and Sandon, C. (2018) Proof of the achievability conjectures for the general stochastic block model. Commun. Pure Appl. Math. 71(7) 1334–1406.CrossRefGoogle Scholar
Ahn, Kwangjun, Lee, Kangwook and Suh, Changho (2016) Community recovery in hypergraphs. In IEEE, pp. 657–663. 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton).CrossRefGoogle Scholar
Ahn, K., Lee, K. and Suh, C. (2018) Hypergraph spectral clustering in the weighted stochastic block model. Ieee J Sel. Top. Signal Process. 12(5) 959–974.CrossRefGoogle Scholar
Alaluusua, K., Avrachenkov, K. , Vinay Kumar, B. R. and Leskelä, L. (2023) Multilayer hypergraph clustering using the aggregate similarity matrix, pp. 83–98.CrossRefGoogle Scholar
Angelini, M. C., Caltagirone, F., Krzakala, F. and Zdeborová, L. (2015) Spectral detection on sparse hypergraphs. In IEEE, pp. 66–73, 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton).CrossRefGoogle Scholar
Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., Young, J.-G. and Petri, G. (2020) Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. 874 1–92.CrossRefGoogle Scholar
Benson, A. R., Gleich, D. F. and Leskovec, J. (2016) Higher-order organization of complex networks. Science 353(6295) 163–166.CrossRefGoogle ScholarPubMed
Bordenave, C., Lelarge, M. and Massoulié, L. (2018) Nonbacktracking spectrum of random graphs: Community detection and nonregular Ramanujan graphs. Ann. Probab. 46(1) 1–71.CrossRefGoogle Scholar
Bu, J., Tan, S., Chen, C., Wang, C., Wu, H., Zhang, L. and He, X. (2010) Music recommendation by unified hypergraph: Combining social media information and music content. In Proceedings of the 18th ACM International Conference on Multimedia, pp. 391–400.CrossRefGoogle Scholar
Cáceres, E., Misobuchi, A. and Pimentel, R. (2021) Sparse SYK and traversable wormholes. J. High Energy Phys. 2021(11) 1–32.CrossRefGoogle Scholar
Chen, Y., Chi, Y., Fan, J. and Ma, C. (2021) Spectral methods for data science: A statistical perspective. Found. Trends® Mach. Learn. 14(5) 566–806.CrossRefGoogle Scholar
Chien, I., Lin, Chung-Yi and Wang, I.-Hsiang (2018) Community detection in hypergraphs: Optimal statistical limit and efficient algorithms. In International Conference on Artificial Intelligence and Statistics, pp. 871–879.Google Scholar
Eli Chien, I., Lin, C.-Y. and Wang, I.-H. (2019) On the minimax misclassification ratio of hypergraph community detection. IEEE Trans. Inf. Theory 65(12) 8095–8118.CrossRefGoogle Scholar
Chin, B. and Sly, A. (2021) Optimal reconstruction of general sparse stochastic block models. arXiv preprint arXiv:2111.00697.Google Scholar
Chin, P., Rao, A. and Van, V. (2015) Stochastic block model and community detection in sparse graphs: A spectral algorithm with optimal rate of recovery. In Conference on Learning Theory, pp. 391–423.Google Scholar
Coja-Oghlan, A. (2010) Graph partitioning via adaptive spectral techniques. Comb. Probab. Comput. 19(2) 227–284.CrossRefGoogle Scholar
Cole, S. and Zhu, Y. (2020) Exact recovery in the hypergraph stochastic block model: A spectral algorithm. Linear Algebra Appl. 593 45–73.CrossRefGoogle Scholar
Cook, N., Goldstein, L. and Johnson, T. (2018) Size biased couplings and the spectral gap for random regular graphs. Ann. Probab. 46(1) 72–125.CrossRefGoogle Scholar
Cooper, J. (2020) Adjacency spectra of random and complete hypergraphs. Linear Algebra Appl. 596 184–202.CrossRefGoogle Scholar
Deng, C., Xu, X.-J. and Ying, S. (2024) Strong consistency of spectral clustering for the sparse degree-corrected hypergraph stochastic block model. IEEE Trans. Inf. Theory 70(3) 1962–1977.CrossRefGoogle Scholar
Dumitriu, I. and Wang, H. (2023) Optimal and exact recovery on general non-uniform hypergraph stochastic block model. arXiv preprint arXiv:2304.13139.Google Scholar
Dumitriu, I. and Zhu, Y. (2021) Spectra of random regular hypergraphs. Electron. J. Comb. 28(3) P3.36.CrossRefGoogle Scholar
Fei, Y. and Chen, Y. (2020) Achieving the bayes error rate in synchronization and block models by SDP, robustly. IEEE Trans. Inf. Theory 66(6) 3929–3953.CrossRefGoogle Scholar
Feige, Uriel and Ofek, Eran (2005) Spectral techniques applied to sparse random graphs. Random Struct Algor 27(2) 251–275.CrossRefGoogle Scholar
Friedman, Joel and Wigderson, Avi (1995) On the second eigenvalue of hypergraphs. Combinatorica 15(1) 43–65.CrossRefGoogle Scholar
Gaudio, Julia and Joshi, Nirmit (2023) Community detection in the hypergraph sbm: Optimal recovery given the similarity matrix. (Annual Conference Computational Learning TheoryGoogle Scholar
Ghoshdastidar, D. and Dukkipati, A. (2014) Consistency of spectral partitioning of uniform hypergraphs under planted partition model. In Advances in Neural Information Processing Systems, pp. 397–405.Google Scholar
Ghoshdastidar, D. and Dukkipati, A. (2017) Consistency of spectral hypergraph partitioning under planted partition model. Ann. Stat. 45(1) 289–315.CrossRefGoogle Scholar
Ghoshdastidar, D. and Dukkipati, A. (2017) Uniform hypergraph partitioning: Provable tensor methods and sampling techniques. J. Mach. Learn. Res. 18(1) 1638–1678.Google Scholar
Govindu, V. M. (2005) A tensor decomposition for geometric grouping and segmentation. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), IEEE, pp. 1150–1157, vol. 1.Google Scholar
Gu, Y. and Pandey, A. (2024) Community detection in the hypergraph stochastic block model and reconstruction on hypertrees. arXiv preprint arXiv:2402.06856.Google Scholar
Gu, Y. and Polyanskiy, Y. (2023) Weak recovery threshold for the hypergraph stochastic block model. In The Thirty Sixth Annual Conference on Learning Theory, PMLR, pp. 885–920.Google Scholar
Guédon, O. and Vershynin, R. (2016) Community detection in sparse networks via Grothendieck’s inequality. Probab. Theory Relat. 165(3-4) 1025–1049.CrossRefGoogle Scholar
Harris, K. D. and Zhu, Y. (2021) Deterministic tensor completion with hypergraph expanders. SIAM J. Math. Data Sci. 3(4) 1117–1140.CrossRefGoogle Scholar
Holland, P. W., Laskey, K. B. and Leinhardt, S. (1983) Stochastic blockmodels: First steps. Soc. Networks 5(2) 109–137.CrossRefGoogle Scholar
Jain, P. and Oh, S. (2014) Provable tensor factorization with missing data. In Advances in Neural Information Processing Systems, pp. 1431–1439.Google Scholar
Jin, J., Ke, T. and Liang, J. (2021) Sharp impossibility results for hyper-graph testing. In Advances in Neural Information Processing Systems, 34.Google Scholar
Ke, Z. T., Shi, F. and Xia, D. (2019) Community detection for hypergraph networks via regularized tensor power iteration. arXiv preprint arXiv:1909.06503.Google Scholar
Kim, C., Bandeira, A. S. and Goemans, M. X. (2018) Stochastic block model for hypergraphs: Statistical limits and a semidefinite programming approach. arXiv preprint arXiv:1807.02884.Google Scholar
Le, C. M. and Levina, E. (2022) Estimating the number of communities by spectral methods. Electron. J. Stat. 16(1) 3315–3342.CrossRefGoogle Scholar
Le, C. M., Levina, E. and Vershynin, R. (2017) Concentration and regularization of random graphs. Random Struct. Algorithms 51(3) 538–561.CrossRefGoogle Scholar
Lee, J., Kim, D. and Chung, H. W. (2020) Robust hypergraph clustering via convex relaxation of truncated mle. IEEE J. Selected Areas Inf. Theory 1(3) 613–631.CrossRefGoogle Scholar
Lei, J., Chen, K. and Lynch, B. (2020) Consistent community detection in multi-layer network data. Biometrika 107(1) 61–73.CrossRefGoogle Scholar
Lei, J. and Rinaldo, A. (2015) Consistency of spectral clustering in stochastic block models. Ann. Stat. 43(1) 215–237.CrossRefGoogle Scholar
Li, L. and Li, T. (2013) News recommendation via hypergraph learning: Encapsulation of user behavior and news content. In Proceedings of the Sixth ACM International Conference on Web Search and Data Mining, pp. 305–314.CrossRefGoogle Scholar
Lin, C.-Y. , Eli Chien, I. and Wang, I.-H. (2017) On the fundamental statistical limit of community detection in random hypergraphs. In 2017 IEEE International Symposium on Information Theory (ISIT), IEEE, pp. 2178–2182.CrossRefGoogle Scholar
Lung, R. I., Gaskó, N. and Suciu, M. A. (2018) A hypergraph model for representing scientific output. Scientometrics 117(3) 1361–1379.CrossRefGoogle Scholar
Massoulié, L. (2014) Community detection thresholds and the weak Ramanujan property. In Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing, ACM, pp. 694–703.CrossRefGoogle Scholar
Michoel, T. and Nachtergaele, B. (2012) Alignment and integration of complex networks by hypergraph-based spectral clustering. Phys. Rev. E 86(5) 056111.CrossRefGoogle ScholarPubMed
Montanari, A. and Sen, S. (2016) Semidefinite programs on sparse random graphs and their application to community detection. In Proceedings of the Forty-Eighth Annual ACM Symposium on Theory of Computing, pp. 814–827.CrossRefGoogle Scholar
Mossel, E., Neeman, J. and Sly, A. (2015) Reconstruction and estimation in the planted partition model. Probab. Theory Relat. 162(3-4) 431–461.CrossRefGoogle Scholar
Mossel, E., Neeman, J. and Sly, A. (2016) Belief propagation, robust reconstruction and optimal recovery of block models. Ann. Appl. Probab. 26(4) 2211–2256.CrossRefGoogle Scholar
Mossel, E., Neeman, J. and Sly, A. (2016) Consistency thresholds for the planted bisection model. Electron. J. Probab. 21(21) 1–24.CrossRefGoogle Scholar
Mossel, E., Neeman, J. and Sly, A. (2018) A proof of the block model threshold conjecture. Combinatorica 38(3) 665–708.CrossRefGoogle Scholar
Newman, M. E. J., Watts, D. J. and Strogatz, S. H. (2002) Random graph models of social networks. Proc. Natl. Acad. Sci. 99(suppl 1) 2566–2572.CrossRefGoogle ScholarPubMed
Ng, A. Y., Jordan, M. I. and Weiss, Y. (2002) On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems, pp. 849–856.Google Scholar
Nguyen, N. H., Drineas, P. and Tran, T. D. (2015) Tensor sparsification via a bound on the spectral norm of random tensors. Inf. Inference J. IMA 4(3) 195–229.Google Scholar
Pal, S. and Zhu, Y. (2021) Community detection in the sparse hypergraph stochastic block model. Random Struct. Algorithms 59(3) 407–463.CrossRefGoogle Scholar
Saade, A., Krzakala, F. and Zdeborová, L. (2014) Spectral clustering of graphs with the bethe hessian. In Advances in Neural Information Processing Systems, 27.Google Scholar
Sen, S. (2018) Optimization on sparse random hypergraphs and spin glasses. Random Struct. Algorithms 53(3) 504–536.CrossRefGoogle Scholar
Shi, J. and Malik, J. (2000) Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 22(8) 888–905.Google Scholar
Soma, T. and Yoshida, Y. (2019) Spectral sparsification of hypergraphs. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, pp. 2570–2581.CrossRefGoogle Scholar
Stephan, L. and Zhu, Y. (2024) Sparse random hypergraphs: Non-backtracking spectra and community detection. Inf. Inference J. IMA 13(1) iaae004.Google Scholar
Tian, Z., Hwang, T. and Kuang, R. (2009) A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge. Bioinformatics 25(21) 2831–2838.CrossRefGoogle ScholarPubMed
Vershynin, R. (2018) High-Dimensional Probability: An Introduction with Applications in Data Science, Cambridge University Press, Cambridge Series in Statistical and Probabilistic Mathematics.CrossRefGoogle Scholar
Van, V. (2018) A simple svd algorithm for finding hidden partitions. Comb. Probab. Comput. 27(1) 124–140.Google Scholar
Wang, H. (2023) Fundamental limits and strong consistency of binary non-uniform hypergraph stochastic block models.Google Scholar
Wang, J., Pun, Y.-M., Wang, X., Wang, P. and So, A. M.-C. (2023) Projected tensor power method for hypergraph community recovery. In International Conference on Machine Learning, PMLR, pp. 36285–36307.Google Scholar
Wen, L., Du, D., Li, S., Bian, X. and Lyu, S. (2019) Learning non-uniform hypergraph for multi-object tracking. In Proceedings of the AAAI Conference on Artificial Intelligence, pp. 8981–8988, vol. 33.CrossRefGoogle Scholar
Yuan, M., Liu, R., Feng, Y. and Shang, Z. (2022) Testing community structure for hypergraphs. Ann. Stat. 50(1) 147–169.CrossRefGoogle Scholar
Yuan, M., Zhao, B. and Zhao, X. (2021) Community detection in censored hypergraph. Statistica Sinica. arXiv preprint arXiv:2111.03179.Google Scholar
Zhang, A. Y. and Zhou, H. H. (2016) Minimax rates of community detection in stochastic block models. Ann. Stat. 44(5) 2252–2280.CrossRefGoogle Scholar
Zhang, Q. and Tan, V. Y. F. (2023) Exact recovery in the general hypergraph stochastic block model. IEEE Trans. Inf. Theory 69(1) 453–471.CrossRefGoogle Scholar
Zhen, Y. and Wang, J. (2022) Community detection in general hypergraph via graph embedding. J. Am. Stat. Assoc., 1–10.Google Scholar
Zhou, D., Huang, J. and Schölkopf, B. (2007) Learning with hypergraphs: Clustering, classification, and embedding. In Advances in Neural Information Processing Systems, pp. 1601–1608.Google Scholar
Zhou, Z. and Zhu, Y. (2021) Sparse random tensors: Concentration, regularization and applications. Electron. J. Stat. 15(1) 2483–2516.CrossRefGoogle Scholar