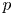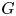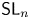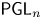1. Introduction
The local Langlands correspondence (LLC) predicts that the depth-zero irreducible smooth representations of a reductive 
$p$-adic group 
$G$ are controlled by the geometry of the Langlands dual group 
$G^\vee$. This idea is most well developed for the class of unipotent representations (or representations with unipotent reduction) of 
$G$ defined by Lusztig in [Reference LusztigLus95], which contains, in particular, all of the irreducible representations of 
$G$ with vectors fixed under an Iwahori subgroup [Reference Iwahori and MatsumotoIM65, Reference Kazhdan and LusztigKL87]. A correspondence for unipotent representations has now been defined that satisfies many of the desired properties of the LLC. These results have come from many years of developments, starting with the seminal papers of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] for Iwahori-spherical representations of split adjoint groups, Lusztig [Reference LusztigLus95, Reference LusztigLus02] for unipotent representations of adjoint groups, Reeder [Reference ReederRee02] for Iwahori-spherical representations of split groups of arbitrary isogeny and, finally, the recent papers of Solleveld [Reference SolleveldSol23a, Reference SolleveldSol23b] (building on [Reference Aubert, Moussaoui and SolleveldAMS18, Reference Aubert, Moussaoui and SolleveldAMS17, Reference Feng, Opdam and SolleveldFOS20]) for all reductive 
$p$-adic groups. Yet not all desired properties of the LLC have been verified in full generality, and one of the main outstanding questions is to understand stability in 
$L$-packets.
To be more precise, assume for simplicity that 
$G$ is the group of 
$F$-points of an absolutely simple, split connected reductive group over a non-Archimedean local field 
$F$ with finite residue field. In the correspondence mentioned above, the irreducible representations of 
$G$ (and of its inner forms) are partitioned into 
$L$-packets indexed by the conjugacy classes 
$G^\vee \cdot x$ for 
$x \in G^\vee$. From the perspective of abstract harmonic analysis, to understand these 
$L$-packets, the most basic case to consider is that of tempered 
$L$-packets, which correspond to the conjugacy classes 
$G^\vee \cdot x$ where the semisimple part of 
$x$ is compact. Many representation-theoretic questions can be reduced further to the case of elliptic tempered 
$L$-packets, as defined by Arthur: these consist of tempered representations that are not irreducibly parabolically induced from proper parabolic subgroups. As mentioned above, while most of the predicted properties of unipotent 
$L$-packets have now been verified, it is not yet known which linear combinations of Harish-Chandra distribution characters of the representations in a given (elliptic) tempered 
$L$-packet are stable, in the sense of being constant on geometric (compact) semisimple conjugacy classes.
To approach this question, a natural first step is to consider the restriction of unipotent representations to maximal compact open subgroups, as in Mœglin–Waldspurger's tour de force [Reference Mœglin and WaldspurgerMW03], which tackles the question of stability for elliptic tempered 
$L$-packets for the group 
${\mathsf {SO}}_{2n + 1}$. These maximal compact subgroups allow us to pass from representations of 
$p$-adic groups to unipotent representations of certain finite reductive groups, which have a rich structure (see, e.g., [Reference LusztigLuz84a]). In particular, while the characters of irreducible representations of a finite connected reductive group do not have good intrinsic stability properties, Lusztig's almost characters, certain class functions defined in terms of traces of character sheaves, do. The transition matrix between characters and almost characters is Lusztig's famous nonabelian Fourier transform [Reference LusztigLuz84a, Reference LusztigLus18]. If we can lift this Fourier transform to the setting of 
$p$-adic groups, we might be able to lift stability properties of combinations of almost characters of finite reductive groups, as in [Reference Mœglin and WaldspurgerMW03, Theorem 4.3].
With this idea in mind, in this paper, we formulate a conjecture that relates a nonabelian Fourier transform for pure inner twists of a (possibly disconnected) finite reductive group and an elliptic Fourier transform 
${\mathrm {FT}}^\vee _{{\mathrm {ell}}}$ (cf. [Reference Ciubotaru and OpdamCO17, Reference CiubotaruCiu20]) for pure inner twists of 
$G$. In addition to Mœglin and Waldspurger's work on the elliptic representations of the special orthogonal groups [Reference Mœglin and WaldspurgerMW03, Reference WaldspurgerWal18], our approach is also inspired by Lusztig's articles proposing a theory of almost characters for 
$p$-adic groups [Reference LusztigLus15, Reference LusztigLus14]. We are also influenced by Reeder's [Reference ReederRee01] and Waldspurger's [Reference WaldspurgerWal07] ideas relating the classification of elliptic tempered unipotent representations and the geometry of 
$G^\vee$.
We need two main innovations to formulate a precise conjecture. To understand the first, note that if we take a maximal compact open subgroup 
$K$ of 
$G$ with reductive quotient 
$\overline {K}$, then 
${\mathrm {FT}}^\vee _{{\mathrm {ell}}}$ does not necessarily induce a well-defined linear map on the unipotent representation space for 
$\overline {K}$. Instead we must look at maximal compact open subgroups in all pure inner twists of 
$G$ at the same time, and so we form the space 
${\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$ defined below. The reductive quotients 
$\overline {K}$ are not necessarily connected, and so the second innovation is to extend the definition of Lusztig's nonabelian Fourier transform to disconnected finite reductive groups. To do this, we must look at all pure inner twists of a disconnected finite reductive group, and the Fourier transform will mix the corresponding representation spaces. These two ideas are related: for every pure inner twist 
$H$ of 
$\overline {K}$, there is a pure inner twist 
$G'$ of 
$G$ and a maximal compact open subgroup 
$K'$ of 
$G'$ such that the reductive quotient 
$\overline {K}'$ is 
$H$.
1.1 Main results
We now describe our work in more detail. As above, let us assume that 
${\mathbf {G}}$ is a simple, split group over 
$F$ and 
$G = {\mathbf {G}}(F)$. Let 
${\mathrm {InnT}}^p(G)$ denote the set of equivalence classes of pure inner twists of 
$G$. Then the LLC (see § 4) states that the 
$L$-packets of irreducible tempered unipotent representations of the groups 
$G' \in {\mathrm {InnT}}^p(G)$ are in one-to-one correspondence with 
$G^\vee$-conjugacy classes of elements 
$x=su \in G^\vee$ (Jordan decomposition) such that 
$s$ is compact. The elements in the 
$L$-packet are parametrized by irreducible representations 
$\phi$ of the group of components 
$A_{G^\vee }(x)$ of the centralizer of 
$x$ in 
$G^\vee$. Hence, an 
$L$-packet is a collection 
$\{\pi (su,\phi )\mid \phi \in \widehat {A_{G^\vee }(su)}\}$. Let 
$\Gamma _u$ denote the reductive part of the centralizer of 
$u$ in 
$G^\vee$. In [Reference WaldspurgerWal18, Reference CiubotaruCiu20], one considered the set 
${\mathcal {Y}}(\Gamma _u)$ of pairs 
$(s,h)\in \Gamma _u^2$ of commuting semisimple elements and the subset 
${\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}$ of elliptic pairs (see § 8.3). These will play a role below in the Langlands parametrization.
Each group 
$G'\in {\mathrm {InnT}}^p(G)$ has a finite collection of conjugacy classes of maximal compact open subgroups 
$\max (G')$. These are classified in terms of the theory of [Reference Bruhat and TitsBT72, Reference Iwahori and MatsumotoIM65] (see § 7). A compact group 
$K'\in \max (G')$ has a finite quotient 
$\overline {K}'$ that is the group of 
$k$-points of a (possibly disconnected) reductive group over a finite field 
$k$. Write 
$R_{\mathrm {un}}(\overline {K}')$ for the 
$\mathbb {C}$-vector space spanned by the irreducible unipotent representations of 
$\overline {K}'$. As mentioned above, for connected finite reductive groups, Lusztig [Reference LusztigLuz84a] defined the nonabelian Fourier transform, which is the change-of-basis matrix between the basis of irreducible unipotent characters and the basis of unipotent almost characters. This is recalled in § 5. We need to define an extension of this map to disconnected finite groups in the spirit of [Reference LusztigLus86] and [Reference Digne and MichelDM90, § 5]. To fit with our picture, we define a nonabelian Fourier transform for the representations of the pure inner twists of the finite (possibly disconnected) reductive group 
$\overline {K}$, where 
$K \in \max (G)$. See § 6. The point is that this transform gives an involution
\begin{align} {\mathrm{FT}}_{{\mathrm{cpt}},{\mathrm{un}}}\colon{\mathcal{C}}(G)_{{\mathrm{cpt}},{\mathrm{un}}}\to {\mathcal{C}}(G)_{{\mathrm{cpt}},{\mathrm{un}}}, \end{align}on the space
\begin{align*} {\mathcal{C}}(G)_{{\mathrm{cpt}},{\mathrm{un}}}=\bigoplus_{G' \in {\mathrm{InnT}}^p(G)} \bigoplus_{K' \in \max (G')} R_{\mathrm{un}}(\overline{K}'), \end{align*}
which we can think of as the sum over 
$K\in \max (G)$ of the unipotent representation spaces of the pure inner twists of 
$\overline {K}$. See (7.2) and Definition 7.1. It is important to note that, in general, 
${\mathrm {FT}}_{{\mathrm {cpt}},{\mathrm {un}}}$ mixes the pure inner twists of a given 
$\overline {K}$.
Since parabolic induction of characters is generally well understood, of particular interest is the space of elliptic (unipotent) tempered representations for all pure inner twists
\[ {\mathcal{R}}^p_{{\mathrm{un}},{\mathrm{ell}}}(G)=\bigoplus_{G'\in{\mathrm{InnT}}^p(G)} \overline{R}_{\mathrm{un}}(G') \]
(see § 9.1). Generalizing [Reference ReederRee01], we prove the following theorem.
Theorem 1.1 (Theorem 11.1)
Suppose that 
$G$ is split and adjoint. The local Langlands correspondence induces an isometric isomorphism
\begin{equation} \overline{\mathsf{LLC}^p}_{{\mathrm{un}}}:\bigoplus_{u}{\mathbb{C}}[{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}]^{\Gamma_u}\longrightarrow {\mathcal{R}}^p_{{\mathrm{un}},{\mathrm{ell}}}(G),\ (s,h)\mapsto \Pi(u,s,h), \end{equation}
where the left-hand side has a natural elliptic inner product while the right-hand side is endowed with the Euler–Poincaré product. The element 
$u$ ranges over representatives of unipotent conjugacy classes in 
$G^\vee$ and 
$\Pi (u,s,h)$ is defined in (9.9).
We remark that 
$\Pi (u,s,1)$ is expected to be the stable combination of characters in the 
$L$-packet, while in general 
$\Pi (u,s,h)$ are expected to satisfy the endoscopic identities.
The proof of Theorem 11.1 in § 11 applies in more generality, for example for Iwahori-spherical representations of groups of arbitrary isogeny (see § 11.4). Since the left-hand side has an obvious involution given by the flip 
$(s,h)\to (h,s)$, this defines an involution, the dual elliptic nonabelian transform
\begin{equation} {\mathrm{FT}}^\vee_{\mathrm{ell}}\colon {\mathcal{R}}_{{\mathrm{un}},{\mathrm{ell}}}^p(G) \to{\mathcal{R}}_{{\mathrm{un}},{\mathrm{ell}}}^p(G). \end{equation}
We note that 
${\mathrm {FT}}^\vee _{\mathrm {ell}}$ mixes representations of the pure inner twists of 
$G$. We expect that there is a commutative diagram as follows.
Conjecture 1.2 (Conjecture 9.7)
Up to certain roots of unity (see Remark 9.8), the following diagram commutes.
Here the vertical arrows are defined by taking invariants by the pro-unipotent radicals of maximal compact subgroups.
It is also natural to expect that the images of irreducible elliptic tempered characters under 
${\mathrm {FT}}^\vee _{\mathrm {ell}}$ are the ‘almost characters’ (on elliptic elements) defined in [Reference LusztigLus15]: see, for comparison, [Reference LusztigLus14, Conjecture 2.2(c)].
Conjecture 1.2 is a generalization of [Reference CiubotaruCiu20, Conjecture 1.3] with an important difference: we remark that the role of maximal compact subgroups (rather than maximal parahoric subgroups) and, hence, of a Fourier transform for pure inner twists of disconnected finite reductive groups in the conjecture is essential for treating all pure inner twists of 
$G$. We verify the conjecture in some examples. In particular, we have the following theorem.
Theorem 1.3 If 
${\mathbf {G}}={\mathsf {SL}}_n$ or 
${\mathsf {PGL}}_n$, Conjecture 1.2 holds.
See §§ 13 and 14. We also verify the conjecture for 
${\mathbf {G}}= {\mathsf {Sp}}_4$ (§ 12). The results of Waldspurger [Reference WaldspurgerWal18] show that this conjecture holds when 
${\mathbf {G}}={\mathsf {SO}}_{2n+1}$.
In future work, we will consider a generalization of Conjecture 1.2 to the space of compact/rigid tempered representations defined in [Reference Ciubotaru and HeCH17, Reference Ciubotaru and HeCH21].
1.2 Structure of the paper
In §§ 2, 3, and 4, we review relevant background about inner twists of 
$p$-adic groups, the generalized Springer correspondence, and the LLC. In § 5, we recall Lusztig's parametrization of unipotent representations of a connected reductive group over a finite field and the definition of the nonabelian Fourier transform on the space spanned by these representations. We then extend Lusztig's parametrization: for the (possibly disconnected) groups 
$\overline {K}$ that arise as reductive quotients of subgroups 
$K \in \max (G)$ as defined above, we parametrize the union over all pure inner twists 
$\overline {K}'$ of 
$\overline {K}$ of the set of unipotent representations of 
$\overline {K}'$, and we then define a nonabelian Fourier transform on the space spanned by these representations (see § 6).
In § 7, we return to the setting of 
$p$-adic groups. We review the parametrization of maximal compact open subgroups of 
$G' \in {\mathrm {InnT}}^p(G)$, under the assumption 
$G$ is 
$F$-split. We define the space 
${\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$ in terms of these subgroups, and we use the Fourier transform of § 6 to define an involution 
${\mathrm {FT}}_{{\mathrm {cpt}}, {\mathrm {un}}}$ on 
${\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$. In § 8, we review the definition of 
${\mathcal {Y}}(\Gamma )_{{\mathrm {ell}}}$ for a complex reductive group 
$\Gamma$. We also review the definition of the elliptic pairing on the Grothendieck group of a finite group.
Section 9 contains the conjectures outlined above. We first review the Euler–Poincaré pairing and state Conjecture 9.1, which predicts that the LLC induces an isometric isomorphism at the level of elliptic spaces. We then define a restriction map 
$\operatorname {res}_{{\mathrm {cpt}}, {\mathrm {un}}}\colon {\mathcal {R}}^p_{{\mathrm {un}}, {\mathrm {ell}}}(G) \to {\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$ and state Conjecture 9.7, which predicts that the elliptic nonabelian Fourier transform 
${\mathrm {FT}}_{{\mathrm {ell}}}^\vee$ is compatible with 
${\mathrm {FT}}_{{\mathrm {cpt}}, {\mathrm {un}}}$ under 
$\operatorname {res}_{{\mathrm {cpt}}, {\mathrm {un}}}$. We give evidence for this conjecture in Proposition 9.10, which considers linear combinations of twists of Steinberg representations.
In § 10, we present an alternative definition of the elliptic nonabelian Fourier transform motivated by Lusztig's pairing [Reference LusztigLus14, § 1.3].
In § 11, we prove Conjecture 9.1 in the case when 
$G$ is simple, split, and adjoint. In § 11.4, we indicate how the proof can be extended to the non-adjoint case. In the final three sections, we verify the conjectures for explicit examples: in § 12, we consider the group 
${\mathsf {Sp}}_4(F)$; in § 13, we consider 
${\mathsf {SL}}_n(F)$; and in § 14, we consider 
${\mathsf {PGL}}_n(F)$.
1.3 Notation and conventions
Given a complex Lie group 
${\mathcal {G}}$, we write 
${\mathrm {Z}}_{{\mathcal {G}}}$ for the center of 
${\mathcal {G}}$. Given 
$x \in {\mathcal {G}}$, we write 
${\mathrm {Z}}_{{\mathcal {G}}}(x)$ for the centralizer of 
$x$ in 
${\mathcal {G}}$. Similarly, if 
$H$ is a subgroup of 
${\mathcal {G}}$, we write 
${\mathrm {Z}}_{{\mathcal {G}}}(H)$ for the centralizer of 
$H$ in 
${\mathcal {G}}$, and if 
$\varphi$ is a homomorphism with image in 
${\mathcal {G}}$, we write 
${\mathrm {Z}}_{{\mathcal {G}}}(\varphi )$ for 
${\mathrm {Z}}_{{\mathcal {G}}}(\text {im } \varphi )$. We write 
${\mathcal {G}}^\circ$ for the identity component of 
${\mathcal {G}}$. If 
$x \in {\mathcal {G}}$, we write 
$A_{{\mathcal {G}}}(x) = {\mathrm {Z}}_{{\mathcal {G}}}(x)/{\mathrm {Z}}_{{\mathcal {G}}}(x)^\circ$ for the component group of 
${\mathrm {Z}}_{{\mathcal {G}}}(x)$. If 
$u \in {\mathcal {G}}$ is unipotent, we write 
$\Gamma _u$ for the reductive part of 
${\mathrm {Z}}_{{\mathcal {G}}}(u)$. Given a torus 
$\mathcal {T}$, we write 
$X^*(\mathcal {T})$ for the character group of 
$\mathcal {T}$.
Given a finite group 
$A$, we write 
$\widehat {A}$ for the set of irreducible characters of 
$A$, and we write 
$R(A)$ for the 
$\mathbb {C}$-vector space with basis given by (isomorphism classes of) irreducible representations of 
$A$. Given a finite set 
$S$, we write 
$\mathbb {C}[S]$ for the 
$\mathbb {C}$-vector space of functions 
$S \to \mathbb {C}$.
2. Recollection on inner twists
2.1 Inner twists
Let 
$F$ be a non-Archimedean local field with finite residue field 
$k_F={\mathbb {F}_q}$. We denote by 
$\mathfrak {o}_F$ the ring of integers of 
$F$. Let 
$F_{\mathrm {s}}$ be a fixed separable closure of 
$F$, and let 
$\Gamma _F$ denote the Galois group of 
$F_{\mathrm {s}}/F$. Let 
$F_{\mathrm {un}}\subset F_{\mathrm {s}}$ be the maximal unramified extension of 
$F$. Let 
${\mathrm {Frob}}$ be the geometric Frobenius element of 
${\mathrm {Gal}}(F_{\mathrm {un}}/F)\simeq \widehat {{\mathbb {Z}}}$, i.e. the topological generator that induces the inverse of the automorphism 
$x\mapsto x^q$ of 
$k_F$. We denote by 
${\mathrm {Fr}}_{\mathbf {G}}$ the action of 
${\mathrm {Frob}}$ on a connected reductive 
$F$-group 
${\mathbf {G}}$. We now review definitions related to inner twists and pure inner twists of a 
$p$-adic group. For details see, e.g., [Reference VoganVog93, § 2], [Reference KalethaKal16, § 2] and [Reference Aubert, Baum, Plymen and SolleveldABPS17b, § 1.3]. (Note that [Reference VoganVog93] uses the term ‘pure rational form’ for what we call a pure inner twist.)
Let 
$G={\mathbf {G}}(F)$. Write 
$\operatorname {{\mathrm {Inn}}}({\mathbf {G}})$ for the group of inner automorphisms of 
${\mathbf {G}}$. Recall that given an algebraic group 
${\mathbf {H}}$ over 
$F$, an isomorphism 
$\alpha \colon {\mathbf {H}} \to {\mathbf {G}}$ defined over 
$F_s$ determines a 
$1$-cocycle
\begin{equation} \gamma_\alpha \colon \begin{array}{ccc} \Gamma_F & \to & {\mathrm{Aut}} ({\mathbf{G}}) \\ \sigma & \mapsto & \alpha \sigma \alpha^{-1} \sigma^{-1} . \end{array} \end{equation}
An inner twist of 
$G$ consists of a pair 
$(H,\alpha )$, where 
$H={\mathbf {H}}(F)$ for some connected reductive 
$F$-group 
${\mathbf {H}}$, and 
$\alpha \colon {\mathbf {H}}\xrightarrow {\;\sim \;}{\mathbf {G}}$ is an isomorphism of algebraic groups defined over 
$F_s$ such that 
$\text {im } (\gamma _\alpha ) \subset \operatorname {{\mathrm {Inn}}}({\mathbf {G}})$. Two inner twists 
$(H, \alpha ), (H', \alpha ')$ of 
$G$ are equivalent if there exists 
$f \in \operatorname {{\mathrm {Inn}}}({\mathbf {G}})$ such that
\begin{equation} \gamma_\alpha (\sigma) = f^{-1} \gamma_{\alpha'} (\sigma) \; \sigma f \sigma^{-1} \quad \text{for all } \sigma \in \Gamma_F . \end{equation}
Denote the set of equivalence classes of inner twists of 
$G$ by 
${\mathrm {InnT}}(G)$.
An inner twist of 
$G$ is the same thing as an inner twist of the unique quasi-split inner form 
$G^* = {\mathbf {G}}^* (F)$ of 
$G$. Thus the equivalence classes of inner twists of 
$G$ are parametrized by the Galois cohomology group 
$H^1(F,\operatorname {{\mathrm {Inn}}}({\mathbf {G}}^*))$:
\[ {\mathrm{InnT}}(G)\longleftrightarrow H^1(F,\operatorname{{\mathrm{Inn}}}({\mathbf{G}}^*)). \]
Example 2.1 For 
$G={\mathsf {SL}}_n(F)$, there is a one-to-one correspondence
\begin{equation} {\mathrm{InnT}}({\mathsf{SL}}_n(F))\longleftrightarrow\mathbb{Z}/n\mathbb{Z}. \end{equation}
This is given as follows. Let 
$r$ be an integer mod 
$n$ and let 
$m=\gcd (r,n)$. Then 
$n=dm$ and 
$r/m$ is coprime to 
$d$. Therefore, there exists a division algebra 
$D_{d,r/m}$, central over 
$F$ and of dimension 
$\dim _F D_{d,r/m}=d^2$. The corresponding inner twist is 
${\mathsf {SL}}_m(D_{d,r/m})$.
A pure inner twist of 
$G$ is a triple 
$(H,\alpha,z)$, where 
$(H,\alpha )$ is an inner twist and 
$z \in Z^1(F,G)$ such that 
$\alpha ^{-1}\circ \gamma (\alpha )={\mathrm {Ad}}(z(\gamma ))$ for any 
$\gamma \in \Gamma _F$ (see [Reference KalethaKal16, § 2.3]). When 
$G$ splits over an unramified extension of 
$F$ such a cocycle is determined by the image 
$u:= z({\mathrm {Frob}}) \in G$. The corresponding inner twist of 
${\mathbf {G}}$ is then defined by the functorial image 
$z_{\mathrm {ad}} \in Z^1(F,\operatorname {{\mathrm {Inn}}}({\mathbf {G}}^*))$ of 
$z$. This pure inner twist is defined by the twisted Frobenius action 
${\mathrm {Fr}}_u$ on 
${\mathbf {G}}$ given by 
${\mathrm {Fr}}_u={\mathrm {Ad}}(u)\circ {\mathrm {Fr}}_{\mathbf {G}}$.
In cohomological terms, the short exact sequence
\[ 1\longrightarrow {\mathrm{Z}}_{{\mathbf{G}}^*}\longrightarrow {\mathbf{G}}^*\longrightarrow \operatorname{{\mathrm{Inn}}}({\mathbf{G}}^*)\longrightarrow 1 \]
induces a map in cohomology 
${\mathrm {H}}^1(F,\operatorname {{\mathrm {Inn}}}({\mathbf {G}}^*))\to {\mathrm {H}}^2(F,{\mathrm {Z}}_{{\mathbf {G}}^*})$. An inner twist of 
${\mathbf {G}}^*$ has a corresponding pure inner twist if and only if the corresponding element of 
${\mathrm {H}}^2(F,{\mathrm {Z}}_{{\mathbf {G}}^*})$ is trivial [Reference VoganVog93, Lemma 2.10]. Denote by 
${\mathrm {InnT}}^p(G^*)$ the set of equivalence classes of pure inner twists of 
${\mathbf {G}}^*$. We have [Reference VoganVog93, Proposition 2.7]
\begin{equation} {\mathrm{InnT}}^p(G^*)\longleftrightarrow {\mathrm{H}}^1(F,{\mathbf{G}}^*). \end{equation}Example 2.2 If 
${\mathbf {G}}^*$ is semisimple adjoint, every inner twist corresponds to a unique pure inner twist: 
${\mathrm {InnT}}^p(G^*)={\mathrm {InnT}}(G^*)$. If 
${\mathbf {G}}^*$ is semisimple and simply connected, 
${\mathrm {H}}^1(F,\operatorname {{\mathrm {Inn}}}({\mathbf {G}}^*))\cong {\mathrm {H}}^2(F,{\mathrm {Z}}_{{\mathbf {G}}^*})$ and therefore there is only one class of pure inner twists, the quasi-split form, 
${\mathrm {InnT}}^p(G^*)= \{G^*\}$. When 
$G={\mathsf {SL}}_n(F)$, the only pure inner twist is 
$G$ itself (see [Reference VoganVog93, Example 2.12]).
2.2 The 
$L$-group
Let 
$G^\vee$ denote the 
${\mathbb {C}}$-points of the dual group of 
${\mathbf {G}}$. It is endowed with an action of 
$\Gamma _F$. Let 
$W_F$ be the Weil group of 
$F$ (relative to 
$F_{\mathrm {s}}/F$) and let 
${}^L G:= G^\vee \rtimes W_F$ denote the 
$L$-group of 
$G$.
Kottwitz proved in [Reference KottwitzKot84, Proposition 6.4] that there exists a natural isomorphism
\begin{equation} \kappa_G \colon {\mathrm{H}}^1 (F,{\mathbf{G}}) \xrightarrow{\;\sim\;} {\mathrm{Irr}}\Big(\pi_0 \big({\mathrm{Z}}_{G^\vee}^{W_F} \big) \Big). \end{equation} Let 
$G^\vee _{\mathrm {sc}}$ denote the simply connected cover of the derived group 
$G_{\mathrm {der}}^\vee$ of 
$G^\vee$. We have 
$G^\vee _{{\mathrm {sc}}}=(G_{{\mathrm {ad}}})^\vee$, and
\begin{equation} \kappa_{G^*_{{\mathrm{ad}}}} \colon {\mathrm{H}}^1 (F,\operatorname{{\mathrm{Inn}}}({\mathbf{G}}^*)) \xrightarrow{\;\sim\;} {\mathrm{Irr}} \big({\mathrm{Z}}_{G^\vee_{{\mathrm{sc}}}}^{W_F}\big). \end{equation}
All the inner twists of a given group 
$G$ share the same 
$L$-group, because the action of 
$W_F$ on 
$G^\vee$ is only uniquely defined up to inner automorphisms. This also works the other way around: from the Langlands dual group 
${}^L G$ one can recover the inner-form class of 
$G$.
Example 2.3 If 
$G={\mathsf {Sp}}_{2n}(F)$, then we have 
$G^\vee ={\mathsf {SO}}_{2n+1}({\mathbb {C}})$ and 
$G_{\mathrm {sc}}^\vee ={\mathsf {Spin}}_{2n+1}({\mathbb {C}})$, so 
${\mathrm {Z}}_{G^\vee _{{\mathrm {sc}}}}\simeq {\mathbb {Z}}/2{\mathbb {Z}}$. An inner twist of 
$G$ is determined by its Tits index [Reference TitsTit65]. The group 
$G^*=G$ is split and its nontrivial inner twist is the group 
${\mathsf {SU}}(n,h_r)$, where 
$h_r$ is a nondegenerate Hermitian form of index 
$r=\lfloor n/2\rfloor$ over the quaternion algebra 
$Q$ over 
$F$ (see for instance [Reference ArthurArt13, § 9]).
We will consider 
$G$ as an inner twist of 
$G^*$, so endowed with an isomorphism 
${\mathbf {G}}\to {\mathbf {G}}^*$ over 
$F_s$. Via (2.6), 
$G$ is labelled by a character 
$\zeta _G$ of 
${\mathrm {Z}}_{G_{\mathrm {sc}}^\vee }^{W_F}$. We choose an extension 
$\zeta$ of 
$\zeta _G$ to 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}$.
3. Generalized Springer correspondence for disconnected groups
Let 
${\mathcal {G}}$ be a possibly disconnected complex Lie group. We denote by 
${\mathcal {G}}^\circ$ the identity component of 
${\mathcal {G}}$. Let 
$u$ be a unipotent element in 
${\mathcal {G}}^\circ$, and let 
$A_{{\mathcal {G}}^\circ }(u)$ denote the group of components of 
${\mathrm {Z}}_{{\mathcal {G}}^\circ }(u)$.
Let 
$\phi ^\circ$ be an irreducible representation of 
$A_{{\mathcal {G}}^\circ }(u)$. The pair 
$(u,\phi ^\circ )$ is called cuspidal if it determines a 
${\mathcal {G}}^\circ$-equivariant cuspidal local system on the 
${\mathcal {G}}^\circ$-conjugacy class of 
$u$ as defined in [Reference LusztigLus84b]. In particular, if 
$(u,\phi ^\circ )$ is cuspidal, then 
$u$ is a distinguished unipotent element in 
${\mathcal {G}}^\circ$ (that is, 
$u$ does not meet the unipotent variety of any proper Levi subgroup of 
${\mathcal {G}}^\circ$), [Reference LusztigLus84b, Proposition 2.8]. However, in general not every distinguished unipotent element supports a cuspidal representation.
Example 3.1 For 
${\mathcal {G}}:={\mathsf {SL}}_n({\mathbb {C}})$, the unipotent classes in 
${\mathcal {G}}$ are in bijection with the partitions 
$\lambda =(\lambda _1,\lambda _2,\ldots,\lambda _r)$ of 
$n$: the corresponding 
${\mathcal {G}}$-conjugacy class 
$\mathcal {O}_\lambda$ consists of unipotent matrices with Jordan blocks of sizes 
$\lambda _1$, 
$\lambda _2, \ldots,\lambda _r$. We identify the center 
${\mathrm {Z}}_{{\mathcal {G}}}$ with the group 
$\mu _n$ of complex 
$n$th roots of unity. For 
$u\in \mathcal {O}_\lambda$, the natural homomorphism 
${\mathrm {Z}}_{\mathcal {G}}\to A_{\mathcal {G}}(u)$ is surjective with kernel 
$\mu _{n/\gcd (\lambda )}$, where 
$\gcd (\lambda ):=\gcd (\lambda _1,\lambda _2,\ldots,\lambda _r)$. Hence the irreducible 
${\mathcal {G}}$-equivariant local systems on 
$\mathcal {O}_\lambda$ all have rank one, and they are distinguished by their central characters, which range over those 
$\chi \in \widehat {\mu _n}$ such that 
$\gcd (\lambda )$ is a multiple of the order of 
$\chi$. We denote these local systems by 
${\mathcal {E}}_{\lambda,\chi }$. The unique distinguished unipotent class in 
${\mathcal {G}}$ is the regular unipotent class 
$\mathcal {O}_{(n)}$, consisting of unipotent matrices with a single Jordan block. The cuspidal irreducible 
${\mathcal {G}}$-equivariant local systems are supported on 
$\mathcal {O}_{(n)}$ and are of the form 
${\mathcal {E}}_{(n),\chi }$, with 
$\chi \in \widehat {\mu _n}$ of order 
$n$ (see [Reference LusztigLus84b, (10.3.2)]).
The group 
$A_{{\mathcal {G}}^\circ }(u)$ may be viewed as a subgroup of the group 
$A_u:=A_{{\mathcal {G}}}(u)$ of components of 
${\mathrm {Z}}_{{\mathcal {G}}}(u)$. Let 
$\phi$ be an irreducible representation of 
$A_{{\mathcal {G}}}(u)$. We say that 
$(u,\phi )$ is a cuspidal pair if the restriction of 
$\phi$ to 
$A_{{\mathcal {G}}^\circ }(u)$ is a direct sum of irreducible representations 
$\phi ^\circ$ such that one (or, equivalently, any) of the pairs 
$(u,\phi ^\circ )$ is cuspidal. Let
\begin{align*}
\mathbf{I}^{{\mathcal{G}}}\,{:=}\,\{(U,{\mathcal{E}})\kern0.7pt{\mid}\kern0.7ptU\text{
unipotent conjugacy class in }{\mathcal{G}},\
{\mathcal{E}}\text{ irreducible
${\mathcal{G}}$-equivariant local
system on }U\}. \end{align*}
This set can be identified with the set of 
${\mathcal {G}}$-orbits of pairs 
$(u,\phi )$, where 
$u\in {\mathcal {G}}$ is unipotent and 
$\phi \in \widehat {A}_u$. If 
$(\phi,V_\phi )$ is an irreducible 
$A_u$-representation, we can first regard it as an irreducible 
${\mathrm {Z}}_{\mathcal {G}}(u)$-representation, and then the corresponding local system is 
${\mathcal {E}}=({\mathcal {G}}\times _{{\mathrm {Z}}_{\mathcal {G}}(u)} V_\phi \to {\mathcal {G}}/{\mathrm {Z}}_{\mathcal {G}}(u)\cong U)$. We denote by 
$\mathbf {I}_{\mathrm {c}}^{\mathcal {G}}$ the subset of 
$\mathbf {I}^{\mathcal {G}}$ of cuspidal pairs. We write 
$\mathbf {I}:=\mathbf {I}^{{\mathcal {G}}^\circ }$ and 
$\mathbf {I}_{\mathrm {c}}:=\mathbf {I}_{\mathrm {c}}^{{\mathcal {G}}^\circ }$.
Let 
$\mathbf {J}^{{\mathcal {G}}}$ denote the set of 
${\mathcal {G}}$-orbits of triples 
$j=(\mathcal {M},U_{\mathrm {c}},{\mathcal {E}}_{\mathrm {c}})$ such that 
$\mathcal {M}^\circ$ is a Levi subgroup of 
${\mathcal {G}}^\circ$,
\begin{equation} \mathcal{M}:={\mathrm{Z}}_{{\mathcal{G}}}({\mathrm{Z}}_{\mathcal{M}^\circ}^\circ), \end{equation}
and 
$(U_{\mathrm {c}},{\mathcal {E}}_{\mathrm {c}})\in \mathbf {I}_{\mathrm {c}}^{\mathcal {M}^\circ }$. We observe that 
$\mathcal {M}$ has identity component 
$\mathcal {M}^\circ$ and that 
${\mathrm {Z}}_{\mathcal {M}}^\circ = {\mathrm {Z}}_{\mathcal {M}^\circ }^\circ$. We set 
$\mathbf {J}:=\mathbf {J}^{{\mathcal {G}}^\circ }$. We note that 
$\mathcal {M}=\mathcal {M}^\circ$ whenever 
${\mathcal {G}}={\mathcal {G}}^\circ$.
Let 
${\mathrm {Z}}^\circ _{\mathcal {M}^\circ,{\mathrm {reg}}}=\{z\in Z^\circ _{\mathcal {M}^\circ }\mid {\mathrm {Z}}_{\mathcal {G}}(z)=\mathcal {M}^\circ \}$ and 
$Y_j({\mathcal {G}})=\bigcup _{x\in {\mathcal {G}}} x ({\mathrm {Z}}^\circ _{\mathcal {M}^\circ,{\mathrm {reg}}} U_{\mathrm {c}}) x^{-1}$. Let 
$\overline {Y}_j({\mathcal {G}})$ be the closure of 
$Y_j({\mathcal {G}})$ in 
${\mathcal {G}}$. We set 
$Y_j=Y_j({\mathcal {G}}^\circ )$ and 
$\overline {Y}_j=\overline {Y}_j({\mathcal {G}}^\circ )$. For example, if 
$j_0=(T,1,{\mathrm {triv}})$ is the trivial cuspidal pair on the maximal torus 
$T$ in 
${\mathcal {G}}^\circ$, then 
$Y_{j_0}$ is the variety of regular semisimple elements in 
${\mathcal {G}}^\circ$, hence 
$\overline {Y}_{j_0}={\mathcal {G}}^\circ$.
Set 
$W_j^\circ :={\mathrm {N}}_{{\mathcal {G}}^\circ }(\mathcal {M}^\circ )/\mathcal {M}^\circ$. This is a Coxeter group due to the particular nature of the Levi subgroups in 
${\mathcal {G}}^\circ$ that support cuspidal local systems (see [Reference LusztigLus84b, Theorem 9.2]).
One constructs a 
${\mathcal {G}}^\circ$-equivariant semisimple perverse sheaf 
$K_j$ supported on 
$\overline {Y}_j$ that has a 
$W_j^\circ$-action and a decomposition [Reference LusztigLus84b, Theorem 6.5] and [Reference Aubert, Moussaoui and SolleveldAMS18, § 5]
\[ K_j=\bigoplus_{\rho^\circ\in \widehat{W}_j^\circ} V_{\rho^\circ}\otimes A_{j,\rho^\circ}, \]
where 
$(\rho ^\circ,V_{\rho ^\circ })$ ranges over the (equivalence classes of) irreducible 
$W_j^\circ$-representations and 
$A_{j,\rho ^\circ }$ is an irreducible 
${\mathcal {G}}^\circ$-equivariant perverse sheaf. The perverse sheaf 
$A_{j,\rho ^\circ }$ has the property that there exists a (unique) pair 
$(U,{\mathcal {E}}^\circ )\in \mathbf {I}$ such that its restriction to the variety 
${\mathcal {G}}^\circ _{\mathrm {un}}$ of unipotent elements in 
${\mathcal {G}}^\circ$ is
\begin{equation} (A_{j,\rho^\circ})|_{{\mathcal{G}}^\circ_{\mathrm{un}}}[-\dim({\mathrm{Z}}^\circ_{\mathcal{M}^\circ})]\cong {\mathrm{IC}}(\overline{U},{\mathcal{E}}^\circ)[\dim(U)]. \end{equation}
In particular, the hypercohomology of 
$A_{j^\circ,\rho ^\circ }$ on 
$U$ is concentrated in one degree, namely
\[ {\mathcal{H}}^{a_U}(A_{j,\rho^\circ})|_U\cong {\mathcal{E}}^\circ,\quad\text{where } a_U=-\dim(U)-\dim({\mathrm{Z}}^\circ_{\mathcal{M}^\circ}). \]
If we set 
$\widetilde {\mathbf {J}}=\widetilde {\mathbf {J}}^{{\mathcal {G}}^\circ }:=\{(j,\rho ^\circ ) : j\in \mathbf {J}^{{\mathcal {G}}^\circ },\ \rho ^\circ \in \widehat {{W_j^\circ }}\}$, the generalized Springer correspondence for 
${\mathcal {G}}^\circ$ is the bijection
\begin{equation} \nu^\circ\colon \mathbf{I}^{{\mathcal{G}}^\circ} \to \widetilde{\mathbf{J}}^{{\mathcal{G}}^\circ},\quad (U,{\mathcal{E}})\mapsto (j,\rho^\circ), \end{equation}
where the relation between 
$(j,\rho ^\circ )$ and 
$(U,{\mathcal {E}})$ is given by (3.2). Let 
$\nu ^\circ _{\mathrm {c}}\colon \mathbf {I}\to \mathbf {J}$ denote the composition of 
$\nu ^\circ$ with the projection from 
$\widetilde {\mathbf {J}}$ to 
$\mathbf {J}$.
We will now explain how, following [Reference Aubert, Moussaoui and SolleveldAMS18, § 4], one can extend the maps 
$\nu ^\circ$ and 
$\nu _{\mathrm {c}}^\circ$ to the case of disconnected groups. Let 
$j=(\mathcal {M},U_{\mathrm {c}},{\mathcal {E}}_{\mathrm {c}})\in \mathbf {J}^{{\mathcal {G}}}$. We set 
$W_j:={\mathrm {N}}_{{\mathcal {G}}}(j)/\mathcal {M}^\circ$. There exists a subgroup 
${\mathfrak {R}}_j$ of 
$W_j$ such that 
$W_j=W_j^\circ \rtimes {\mathfrak {R}}_j$ (see [Reference Aubert, Moussaoui and SolleveldAMS18, Lemma 4.2]). Suppose that 
$\sharp _j$ is a 
$2$-cocycle
\[ \sharp_j\colon {\mathfrak{R}}_j\times{\mathfrak{R}}_j\to \overline{{\mathbb{Q}}}_\ell^\times. \]
We view 
$\sharp _j$ as a 
$2$-cocycle on 
$W_j$ that is trivial on 
$W_j^\circ$. Then the 
$\sharp _j$-twisted group algebra of 
$W_j$, denoted by 
$\overline {{\mathbb {Q}}}_\ell [W_j,\sharp _j]$, is defined to be the 
$\overline {{\mathbb {Q}}}_\ell$-vector space 
$\overline {{\mathbb {Q}}}_\ell [W_j,\sharp _j]$ with basis 
$\big \{f_w : w\in W_j\big \}$ and multiplication rules
\[ f_wf_{w'}=\sharp_j(w,w')f_{ww'},\quad w,w'\in W_j. \]
One constructs a 
${\mathcal {G}}$-equivariant semisimple perverse sheaf 
$K_j$ supported on 
$\overline {Y}_j$ that has a 
$W_j$-action and a decomposition [Reference LusztigLus84b, Theorem 6.5]
\[ K_j=\bigoplus_{\rho\in {\mathrm{Irr}}(\overline{{\mathbb{Q}}}_\ell[W_j,\sharp_j])} V_\rho\otimes A_{j,\rho}, \]
where 
$(\rho,V_{\rho })$ ranges over the (equivalence classes of) simple modules of 
$\overline {{\mathbb {Q}}}_\ell [W_j,\sharp _j]$, and 
$A_{j,\rho }$ is an irreducible 
${\mathcal {G}}$-equivariant perverse sheaf.
We set
\begin{equation} \widetilde{\mathbf{J}}^{\mathcal{G}}:=\{(j,\rho) : j\in \mathbf{J}^{\mathcal{G}},\ \rho\in {\mathrm{Irr}}(\overline{{\mathbb{Q}}}_\ell[W_j,\sharp_j])\}. \end{equation}
The generalized Springer correspondence for 
${\mathcal {G}}$ is the bijection
\begin{equation} \nu\colon \mathbf{I}^{\mathcal{G}} \to \widetilde{\mathbf{J}}^{\mathcal{G}} \end{equation}defined in [Reference Aubert, Moussaoui and SolleveldAMS18, Theorem 5.5].
Definition 3.2 Let 
$\nu _{\mathrm {c}}=\nu _{\mathrm {c}}^{\mathcal {G}}\colon \mathbf {I}^{\mathcal {G}}\to \mathbf {J}^{\mathcal {G}}$ denote the composition of 
$\nu$ with the projection from 
$\widetilde {\mathbf {J}}^{\mathcal {G}}$ to 
$\mathbf {J}^{\mathcal {G}}$.
Suppose 
$(U, {\mathcal {E}}) \in \mathbf {I}^{\mathcal {G}}$, and suppose the 
${\mathcal {G}}$-class 
$U$ splits into 
${\mathcal {G}}^\circ$-classes 
$U^\circ _1, \ldots, U^\circ _\ell$, for some 
$\ell \geqslant 1$. If we regard 
${\mathcal {E}}$ as a 
${\mathcal {G}}^\circ$-equivariant local system, then it restricts as 
${\mathcal {E}} |_{U_i^\circ }=\bigoplus _{t=1}^{k_i}{\mathcal {E}}_{i,t}^\circ$, 
$1\leqslant i\leqslant \ell$, where 
$\nu ^\circ (U^\circ _i,{\mathcal {E}}_{i,t}^\circ )=(j^\circ,\rho _{i,t}^\circ )$, with 
$j^\circ =\nu ^\circ _{\mathrm {c}}(U^\circ _1,{\mathcal {E}}^\circ _{1,1})$ and 
$\rho |_{W_j^\circ }=\bigoplus _{i,t}\rho ^\circ _{i,t}$.
Example 3.3 Let 
${\mathcal {G}}=\mathsf {O}_{2n}({\mathbb {C}})$, so 
${\mathcal {G}}^\circ =\mathsf {SO}_{2n}({\mathbb {C}})$ and 
${\mathcal {G}}/{\mathcal {G}}^\circ \cong {\mathbb {Z}}/2{\mathbb {Z}}$. The unipotent classes in 
${\mathcal {G}}$ are parametrized by partitions 
$\lambda =(\lambda _1,\ldots,\lambda _m)$ of 
$2n$ such that each even part appears with even multiplicity. If 
$U_\lambda$ is the corresponding unipotent class, then 
$U_\lambda$ is a single 
${\mathcal {G}}^\circ$-class unless the partition 
$\lambda$ is ‘very even’ [Reference Springer and SteinbergSS70, Reference Collingwood and McGovernCM93], i.e. all parts 
$\lambda _i$ are even, in which case 
$U_\lambda$ splits into two 
${\mathcal {G}}^\circ$-classes, 
$U_\lambda ^+$ and 
$U_\lambda ^-$.
Let 
$j=j_0$ correspond to the trivial cuspidal local system on the torus of 
${\mathcal {G}}^\circ$. Then 
$W_{j_0}^\circ =W^\circ \cong W(D_n)$ and 
$W_j=W\cong W(B_n)$, hence 
$W/W^\circ \cong {\mathcal {G}}/{\mathcal {G}}^\circ ={\mathbb {Z}}/2{\mathbb {Z}}$. (Here 
$W(D_n)$ denotes a Weyl group of type 
$D_n$ and similarly for 
$W(B_n)$.) If 
$\lambda$ is not a very even partition and 
$u\in U_\lambda$, then 
$A_u/A_{{\mathcal {G}}^\circ }(u)={\mathbb {Z}}/2{\mathbb {Z}}$; if 
$(j_0,\rho ^\circ )=\nu ^\circ (U_\lambda ^\circ,\phi ^\circ )$, then there are two nonisomorphic ways 
$\phi,\phi '$ in which one can extend 
$\phi ^\circ$ to 
$A_u$, and two nonisomorphic ways 
$\rho,\rho '$ to extend 
$\rho ^\circ$ to 
$W$, which can be chosen such that 
$\rho$ corresponds to 
$\phi$ and 
$\rho '$ corresponds to 
$\phi '$ under the disconnected Springer correspondence.
If, on the other hand, 
$\lambda$ is a very even partition, 
$u=u^+$ is a representative of 
$U^+_\lambda$, and 
$u^-$ a representative of 
$U^-_\lambda$, then 
$A_u=A_{{\mathcal {G}}^\circ }(u^+)=A_{{\mathcal {G}}^\circ }(u^-)=\{1\}$. In this case, 
$\nu ^\circ (U^\pm,\mathbf {1})=\rho ^\pm$ (
$W(D_n)$-representations), where 
$\rho$ is parametrized by a bipartition of 
$n$ of the form 
$\lambda ' \times \lambda '$ (necessarily 
$n$ is even). Then 
$\nu (U,\mathbf {1})=\rho$ (
$W(B_n)$-representation), where 
$\rho |_{W(D_n)}=\rho ^+\oplus \rho ^-$.
4. The Langlands parametrization
We use the notation of § 2. In addition, we write 
$I_F$ for the inertia subgroup of 
$W_F$, and we set 
$W'_F:=W_F\times {\mathsf {SL}}_2({\mathbb {C}})$. We have natural projections from 
$p_1\colon W'_F\twoheadrightarrow W_F$ and 
$p_2\colon {}^LG\twoheadrightarrow W_F$.
4.1 Langlands parameters
A Langlands parameter (or 
$L$-parameter) for 
$G$ is a continuous morphism 
$\varphi \colon W'_F\to {}^LG$ such that 
$\varphi (w)$ is semisimple for each 
$w\in W_F$ (that is, 
$r (\varphi (w))$ is semisimple for every finite-dimensional representation 
$r$ of 
${}^L G$), the restriction of 
$\varphi$ to 
${\mathsf {SL}}_2({\mathbb {C}})$ is a morphism of complex algebraic groups, and the following diagram commutes.
Write 
$\Phi (G)$ for the set of 
$G^\vee$-conjugacy classes of Langlands parameters for 
$G$.
Let 
${\mathrm {Z}}_{G^\vee }(\varphi )$ denote the centralizer in 
$G^\vee$ of 
$\varphi (W'_F)$. We have
\begin{equation} {\mathrm{Z}}_{G^\vee}(\varphi)\cap{\mathrm{Z}}_{G^\vee}={\mathrm{Z}}_{G^\vee}^{W_F}, \end{equation}and, hence,
\[ {\mathrm{Z}}_{G^\vee}(\varphi)/{\mathrm{Z}}_{G^\vee}^{W_F}\simeq {\mathrm{Z}}_{G^\vee}(\varphi){\mathrm{Z}}_{G^\vee}/{\mathrm{Z}}_{G^\vee}. \]
The group 
${\mathrm {Z}}_{G^\vee }(\varphi ){\mathrm {Z}}_{G^\vee }/{\mathrm {Z}}_{G^\vee }$ can be considered as a subgroup of 
$G^\vee _{\mathrm {ad}}$ and we define 
${\mathrm {Z}}^1_{G^\vee _{\mathrm {sc}}}(\varphi )$ to be its inverse image under the canonical projection 
$p\colon G^\vee _{\mathrm {sc}} \to G^\vee _{\mathrm {ad}}$. The group 
${\mathrm {Z}}^1_{G^\vee _{\mathrm {sc}}}(\varphi )$ coincides with the group introduced by Arthur in [Reference ArthurArt06, (3.2)] (denoted there by 
$\widetilde {{\mathcal {S}}}_\varphi$). As observed in [Reference ArthurArt06], it is an extension of 
${\mathrm {Z}}_{G^\vee }(\varphi )/{\mathrm {Z}}_{G^\vee }^{W_F}$ by 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}$. Let 
$A^1_{\varphi }$ denote the component group of 
${\mathrm {Z}}^1_{G^\vee _{\mathrm {sc}}}(\varphi )$.
Remark 4.1 When 
$Z_{{\mathbf {G}}}^\circ$ is 
$F$-split, the group 
$A^1_{\varphi }$ also coincides with the group considered by Kaletha in [Reference KalethaKal18, § 4.6] in the parametrization of the 
$L$-packet of 
$\varphi$.
An enhancement of 
$\varphi$ is an irreducible representation 
$\phi$ of 
$A^1_\varphi$. We denote by 
$\widehat {A}^1_{\varphi }$ the set of irreducible characters of 
$A^1_{\varphi }$. The pairs 
$(\varphi,\phi )$ are called enhanced 
$L$-parameters. Let 
$\phi \in \widehat {A}^1_{\varphi }$. Then 
$\phi$ determines a character 
$\zeta _\phi$ of 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}$. An enhanced 
$L$-parameter 
$(\phi,\varphi )$ is said to be 
$G$-relevant if 
$\zeta _\phi =\zeta$, where 
$\zeta$ is as defined in § 2.2. The set 
$\Phi _{\mathrm {e}}(G)$ of 
$G^\vee$-conjugacy classes of 
$G$-relevant enhanced 
$L$-parameters is expected to parametrize the admissible dual of 
$G$.
The group 
$H^1(W_F,{\mathrm {Z}}_{G^\vee })$ acts on 
$\Phi (G)$ by
\begin{equation} (z\varphi)(w,x):=z'(w)\varphi(w,x),\quad\varphi\in\Phi(G),\ w\in W_F,\ x\in {\mathsf{SL}}_2({\mathbb{C}}), \end{equation}
where 
$z'\colon W_F\to {\mathrm {Z}}_{G^\vee }$ represents 
$z\in H^1(W_F,{\mathrm {Z}}_{G^\vee })$. This extends to an action of 
$H^1(W_F,{\mathrm {Z}}_{G^\vee })$ on 
$\Phi _{\mathrm {e}}(G)$ that does nothing to the enhancements.
A character of 
$G$ is called weakly unramified if it is trivial on the kernel of the Kottwitz homomorphism. Let 
$X_{\mathrm {wur}}(G)$ denote the group of weakly unramified characters of 
$G$. There is a natural isomorphism
\begin{equation} X_{\mathrm{wur}}(G)\simeq ({\mathrm{Z}}_{G^\vee}^{I_F})_{\mathrm{Frob}} \subset H^1(W_F,{\mathrm{Z}}_{G^\vee}) \end{equation}
(see [Reference HainesHai14, § 3.3.1]). Its identity component is the group 
$X_{\mathrm {un}}(G)$ of unramified characters of 
$G$. Via (4.2) and (4.3), the group 
$X_{\mathrm {wur}}(G)$ acts naturally on 
$\Phi _{\mathrm {e}}(G)$.
Let 
$\varphi \colon W_F\times {\mathsf {SL}}_2({\mathbb {C}}) \to {}^L G$ be an 
$L$-parameter. We consider the (possibly disconnected) complex reductive group
\begin{equation} {\mathcal{G}}_\varphi:={\mathrm{Z}}^1_{G^\vee_{\mathrm{sc}}}\big(\varphi|_{W_F}\big), \end{equation}
defined analogously to 
${\mathrm {Z}}^1_{G^\vee _{\mathrm {sc}}}(\varphi )$. Denote by 
${\mathcal {G}}_\varphi ^\circ$ its identity component.
We define elements 
$u_\varphi, s_\varphi \in G^\vee$ by
\begin{equation} (u_\varphi,1) =\varphi (1,\left(\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\right)) \quad\text{and}\quad (s_\varphi,{\mathrm{Frob}}) =\varphi({\mathrm{Frob}},{\mathrm{Id}}_{{\mathsf{SL}}_2({\mathbb{C}})}). \end{equation}
Then 
$u_\varphi \in {\mathcal {G}}_\varphi ^\circ$.
We recall that by the Jacobson–Morozov Theorem any unipotent element 
$u$ of 
${\mathcal {G}}_\varphi ^\circ$ determines (up to conjugation by 
${\mathrm {Z}}_{\mathcal {G}} (u)$) a homomorphism of algebraic groups 
${\mathsf {SL}}_2({\mathbb {C}})\to {\mathcal {G}}_\varphi ^\circ$ taking the value 
$u$ at 
$\left (\begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix}\right )$. Hence, any enhanced 
$L$-parameter 
$(\varphi,\phi )$ is completely determined, up to 
$G^\vee$-conjugacy, by 
$\varphi \vert _{W_F}$, 
$u_\varphi$ and 
$\phi$. More precisely, the map
\begin{equation} (\varphi,\phi)\mapsto (\varphi\vert_{W_F},u_\varphi,\phi) \end{equation}
provides a bijection between 
$\Phi _{\mathrm {e}}(G)$ and the set of 
$G^\vee$-conjugacy classes of triples 
$(\varphi \vert _{W_F},u_\varphi,\phi )$.
We define an action of 
$G^\vee _{\mathrm {sc}}$ on 
$G^\vee$ by setting
\[ h\cdot g:=h'gh^{\prime -1}\quad \text{for $h\in G^\vee_{\mathrm{sc}}$ and $g\in G^\vee$, where $p(h)=h'{\mathrm{Z}}_{G^\vee}$.} \]
It induces an action of 
$G^\vee _{\mathrm {sc}}$ on 
${}^LG$ and we denote by 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}(\varphi )$ the stabilizer in 
$G^\vee _{\mathrm {sc}}$ of 
$\varphi (W_F')$ for this action.
On the other hand, the inclusion 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}^1(\varphi )\hookrightarrow {\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}^1(\varphi \vert _{W_F})\cap {\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}(u_\varphi )$ induces a group isomorphism
\begin{equation}
A^1_\varphi\xrightarrow{\;\sim\;}
\pi_0({\mathrm{Z}}_{G^\vee_{\mathrm{sc}}}^1(\varphi\vert_{W_F})\cap
{\mathrm{Z}}_{G^\vee_{\mathrm{sc}}}(u_\varphi)).
\end{equation}
As observed in [Reference Aubert, Moussaoui and SolleveldAMS18, (92)], another way to formulate (4.7) is
\begin{equation} A^1_\varphi\simeq A_{{\mathcal{G}}_\varphi}(u_\varphi):={\mathrm{Z}}_{{\mathcal{G}}_\varphi}(u_\varphi)/{\mathrm{Z}}_{{\mathcal{G}}_\varphi}(u_\varphi)^\circ. \end{equation} The 
$L$-parameter 
$\varphi$ is called:
– discrete if there is no proper
$W_F$-stable Levi subgroup $L^\vee \subset G^\vee$ such that $\varphi (W_F') \subset L^\vee \rtimes W_F$;– bounded if
$s_\varphi$ belongs to a bounded subgroup of $G^\vee$.
We say that 
$(\varphi,\phi )\in \Phi _{\mathrm {e}}(G)$ is cuspidal if 
$\varphi$ is discrete and 
$(u_\varphi,\phi )$ is a cuspidal pair for 
${\mathcal {G}}_\varphi$ (as defined in § 3). The set of 
$G$-relevant cuspidal (respectively, discrete, bounded) enhanced 
$L$-parameters is expected to correspond to the set of supercuspidal (respectively, essentially square-integrable, tempered) irreducible smooth 
$G$-representations [Reference Aubert, Moussaoui and SolleveldAMS18, § 6].
4.2 Inertial classes
For 
$L$ a Levi subgroup of 
$G$ and 
$g\in G^\vee$, the group 
$g L^\vee g^{-1}$ is not necessarily 
$W_F$-stable, so the group 
$G^\vee$ need not act on pairs of the form 
$({}^LL,(\varphi _{\mathrm {c}},\phi _{\mathrm {c}}))$ with 
$(\varphi _{\mathrm {c}},\phi _{\mathrm {c}})$ a cuspidal enhanced 
$L$-parameter for 
$L$. In order to deal with this, as in [Reference Aubert, Moussaoui and SolleveldAMS18, Definition 7.1], we will have to consider all the pairs 
$({\mathrm {Z}}_{{}^LG}(\mathcal {T}),(\varphi _{\mathrm {c}},\phi _{\mathrm {c}}))$ of the following form.
–
$\mathcal {T}$ is a torus of $G^\vee$ such that the projection ${\mathrm {Z}}_{{}^LG}(\mathcal {T})\to W_F$ is surjective;–
$\varphi _{\mathrm {c}}\colon W'_F\to {\mathrm {Z}}_{{}^L G}(\mathcal {T})$ satisfies the requirements in the definition of an $L$-parameter;– let
${\mathcal {L}} =G^\vee \cap {\mathrm {Z}}_{{}^LG}(\mathcal {T})$, and let ${\mathcal {L}}_{\mathrm {sc}}$ be the simply connected cover of the derived group of ${\mathcal {L}}$. Then $\phi _{\mathrm {c}}$ is an irreducible representation of $\pi _0({\mathrm {Z}}_{{\mathcal {L}}_{\mathrm {sc}}}^1(\varphi ))$ such that $(u_{\varphi _{\mathrm {c}}},\phi )$ is a cuspidal pair for ${\mathrm {Z}}_{{\mathcal {L}}_{\mathrm {sc}}}^1(\varphi _{\mathrm {c}}\vert _{W_F}))$ and $\phi _{\mathrm {c}}$ is $G$-relevant as defined in [Reference Aubert, Moussaoui and SolleveldAMS18, Definition 7.2] (that is $\zeta _\phi =\zeta$ on ${\mathcal {L}}_{{\mathrm {sc}}}\cap {\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}^{W_F}$ and $\phi =1$ on ${\mathcal {L}}_{\mathrm {sc}}\cap {\mathrm {Z}}_{{\mathcal {L}}_c}^\circ$, where ${\mathcal {L}}_c$ denotes the preimage of ${\mathcal {L}}$ under $G^\vee _{\mathrm {sc}}\to G^\vee$).
Fix such a pair 
$({\mathrm {Z}}_{{}^LG}(\mathcal {T}),(\varphi _{\mathrm {c}},\phi _{\mathrm {c}}))$. The group
\begin{equation} X_{\mathrm{un}}({\mathrm{Z}}_{{}^LG}(\mathcal{T})) :=\Big({\mathrm{Z}}_{(G^\vee\rtimes I_F)\cap {\mathrm{Z}}_{{}^LG}(\mathcal{T})} \Big)_{{\mathrm{Frob}}}^\circ \end{equation}
plays the role of unramified characters for 
${\mathrm {Z}}_{{}^LG}(\mathcal {T})$. It acts on the enhanced 
$L$-parameters 
$(\varphi _{\mathrm {c}},\phi _{\mathrm {c}})$ (see [Reference Aubert, Moussaoui and SolleveldAMS18, (110) and (111)]) and we denote by 
$X_{\mathrm {un}}({\mathrm {Z}}_{{}^LG}(\mathcal {T}))\cdot (\varphi _{\mathrm {c}},\phi _{\mathrm {c}})$ the orbit of 
$(\varphi _{\mathrm {c}},\phi _{\mathrm {c}})$.
We denote by 
${\mathfrak {s}}^\vee$ the 
$G^\vee$-conjugacy class of 
$({\mathrm {Z}}_{{}^LG}(\mathcal {T}),X_{\mathrm {un}}({\mathrm {Z}}_{{}^LG}(\mathcal {T}))\cdot (\varphi _{\mathrm {c}},\phi _{\mathrm {c}}))$. We write
\[ {\mathfrak{s}}^\vee={\mathfrak{s}}^\vee_{G}=[{\mathrm{Z}}_{{}^LG}(\mathcal{T}),(\varphi_{\mathrm{c}},\phi_{\mathrm{c}})]_{G^\vee}, \]
and call 
${\mathfrak {s}}^\vee$ an inertial class for 
$\Phi _{\mathrm {e}}(G)$. We denote by 
${\mathfrak {B}}^\vee (G)$ the set of all such 
${\mathfrak {s}}^\vee$.
Note that there exists a 
$W_F$-stable Levi subgroup 
$L^\vee$ of 
$G^\vee$ such that 
${\mathrm {Z}}_{{}^LG}(\mathcal {T})$ is 
$G^\vee$-conjugate to 
$L^\vee \rtimes W_F$ and 
${\mathcal {L}} =G^\vee \cap {\mathrm {Z}}_{{}^LG}(\mathcal {T})$ is 
$G^\vee$-conjugate to 
$L^\vee$. Conversely, every 
$G^\vee$-conjugate of this 
$L^\vee \rtimes W_F$ is of the form 
${\mathrm {Z}}_{{}^LG}(\mathcal {T})$ for a torus 
$\mathcal {T}$ as above (see [Reference Aubert, Moussaoui and SolleveldAMS18, Lemma 6.2]).
We write
\begin{equation} {\mathfrak{s}}^\vee_L=({\mathrm{Z}}_{{}^LG}(\mathcal{T}),X_{\mathrm{un}}({\mathrm{Z}}_{{}^LG}(\mathcal{T}))\cdot(\varphi_{\mathrm{c}},\phi_{\mathrm{c}})). \end{equation}We will consider the groups
\begin{equation} W_{{\mathfrak{s}}^\vee}={\mathrm{N}}_{G^\vee} ({\mathfrak{s}}^\vee_L) / L^\vee\quad\text{and} \quad J_{\varphi_{\mathrm{c}}}:={\mathrm{Z}}_{G^\vee}(\varphi_{\mathrm{c}}(I_F)). \end{equation}
The group 
$J_{\varphi _{\mathrm {c}}}$ is a complex (possibly disconnected) reductive group. Define 
$R(J_{\varphi _{\mathrm {c}}}^\circ,\mathcal {T})$ as the set of 
$\alpha \in X^*(\mathcal {T}) \setminus \{0\}$ that appear in the adjoint action of 
$\mathcal {T}$ on the Lie algebra of 
$J_{\varphi _{\mathrm {c}}}^\circ$. It is a root system (see [Reference Aubert, Moussaoui and SolleveldAMS17, Proposition 3.9]).
We set 
$W_{{\mathfrak {s}}^\vee }^\circ :={\mathrm {N}}_{J_{\varphi _{\mathrm {c}}}^\circ } (\mathcal {T}) / {\mathrm {Z}}_{J^\circ _{\varphi _{\mathrm {c}}}} (\mathcal {T})$, where 
$W_{{\mathfrak {s}}^\vee }^\circ$ is the Weyl group of 
$R(J_{\varphi _{\mathrm {c}}}^\circ,\mathcal {T})$. Let 
$R^+(J^\circ _{\varphi _{\mathrm {c}}},\mathcal {T})$ be the positive system defined by a parabolic subgroup 
$P_{\varphi _{\mathrm {c}}}^\circ \subset J_{\varphi _{\mathrm {c}}}^\circ$ with Levi factor 
$(L_{\varphi _{\mathrm {c}}}^\vee )^\circ$. Two such parabolic subgroups 
$P_{\varphi _{\mathrm {c}}}^\circ$ are 
$J_{\varphi _{\mathrm {c}}}^\circ$-conjugate, so the choice is inessential.
Since 
$W_{{\mathfrak {s}}^\vee }^\circ$ acts simply transitively on the collection of positive systems for 
$R(J_{\varphi _{\mathrm {c}}}^\circ,\mathcal {T})$, we obtain a semi-direct factorization
\begin{align*}W_{{\mathfrak{s}}^\vee}
= W_{{\mathfrak{s}}^\vee}^\circ \rtimes
{\mathfrak{R}}_{{\mathfrak{s}}^\vee},\end{align*}
where 
${\mathfrak{R}}_{{\mathfrak{s}}^\vee} = \{ w \in W_{{\mathfrak{s}}^\vee} \mid w \cdot R^+ (J_{\varphi_{\mathrm{c}}}^\circ,\mathcal{T}) = R^+ (J_{\varphi_{\mathrm{c}}}^\circ,\mathcal{T}) \}$.
Definition 4.2 Let 
${\boldsymbol{\nu }}_{\mathrm {c}}\colon \Phi _{\mathrm {e}}(G)\to {\mathfrak {B}}^\vee (G)$ be the map defined by
\[ {\boldsymbol{\nu}}_{\mathrm{c}}(\varphi,\phi)=[{\mathrm{Z}}_{{}^LG}({\mathrm{Z}}_{\mathcal{M}_\varphi}^\circ),\varphi\vert_{W_F},u_{\mathrm{c}},\phi_{\mathrm{c}}]_{G^\vee}, \]
where 
$(\varphi \vert _{W_F},u,\phi )_{G^\vee }$ is the image of 
$(\varphi,\phi )_{G^\vee }$ via the bijection (4.6), 
$(u_{\mathrm {c}},\phi _{\mathrm {c}})$ corresponds to 
$(U_{\mathrm {c}},{\mathcal {E}}_{\mathrm {c}})\in \mathbf {I}^{\mathcal {M}_\varphi }_{\mathrm {c}}$ and 
$(\mathcal {M}_\varphi,U_{\mathrm {c}},{\mathcal {E}}_{\mathrm {c}}):=\nu _{\mathrm {c}}^{{\mathcal {G}}_\varphi }(U,{\mathcal {E}})$ is the image under the map 
$\nu _{\mathrm {c}}^{{\mathcal {G}}_\varphi }$ from Definition 3.2 of the pair 
$(U,{\mathcal {E}})\in \mathbf {I}^{{\mathcal {G}}_\varphi }$ associated with 
$(u,\phi )$.
We have the following decomposition (see [Reference Aubert, Moussaoui and SolleveldAMS18, (115)]):
\begin{equation} \Phi_{\mathrm{e}}(G)=\bigsqcup_{{\mathfrak{s}}^\vee\in{\mathfrak{B}}^\vee(G)}\Phi_{\mathrm{e}}(G)^{{\mathfrak{s}}^\vee},\quad\text{where}\ \Phi_{\mathrm{e}}(G)^{{\mathfrak{s}}^\vee}:={\boldsymbol{\nu}}^{-1}_{\mathrm{c}}({\mathfrak{s}}^\vee). \end{equation} Let 
${\mathrm {Irr}}(G)$ be the set of isomorphism classes of irreducible smooth 
$G$-representations. For 
$L$ a Levi subgroup of 
$G$, we denote by 
${\mathrm {Irr}}_{\mathrm {cusp}} (L)$ the set of isomorphism classes of supercuspidal irreducible smooth 
$L$-representations.
Let 
$\sigma \in {\mathrm {Irr}}_{\mathrm {cusp}} (L)$. We call 
$(L,\sigma )$ a supercuspidal pair, and we consider such pairs up to inertial equivalence. This is the equivalence relation generated by:
– unramified twists,
$(L,\sigma ) \sim (L,\sigma \otimes \chi )$ for $\chi \in X_{\mathrm {un}} (L)$;–
$G$-conjugation, $(L,\sigma ) \sim (g L g^{-1},g \cdot \sigma )$ for $g \in G$.
We denote the set of all inertial equivalence classes for 
$G$ by 
${\mathfrak {B}}(G)$ and a typical inertial equivalence class by 
${\mathfrak {s}}:= [L,\sigma ]_G$.
In [Reference Bernstein and DeligneBer84], Bernstein attached to every 
${\mathfrak {s}}\in {\mathfrak {B}}(G)$ a block 
${\mathfrak {R}}(G)^{\mathfrak {s}}$ in the category 
${\mathfrak {R}}(G)$ of smooth 
$G$-representations as follows. Denote by 
$I_P^G$ the normalized parabolic induction functor, where 
$P$ is a parabolic subgroup of 
$G$ with Levi subgroup 
$L$. If 
$\pi \in {\mathrm {Irr}}(G)$ is a constituent of 
$I_P^G (\tau )$ for some 
$\sigma \in {\mathrm {Irr}}(L)$ such that 
$[L,\sigma ]_G={\mathfrak {s}}$, then 
${\mathfrak {s}}$ is called the inertial supercuspidal support of 
$\pi$. We set
\begin{align*} & {\mathrm{Irr}}(G)^{\mathfrak{s}}: = \{ \pi \in {\mathrm{Irr}}(G) : \text{$\pi$ has inertial supercuspidal support ${\mathfrak{s}}$}\} , \\ & {\mathfrak{R}}(G)^{\mathfrak{s}}: = \{ \pi \in {\mathfrak{R}}(G) \;:\; \text{every irreducible constituent of } \pi \text{ belongs to } {\mathrm{Irr}}(G)^{\mathfrak{s}} \} . \end{align*}
4.3 Unipotent representations
An irreducible smooth representation 
$(\pi,V)$ of 
$G$ is called unipotent if there exists a parahoric subgroup 
$K$ of 
$G$ such that the subspace 
$V^{K^+}$ of the vectors in 
$V$ that are fixed by the pro-unipotent radical 
$K^+$ of 
$K$ contains an irreducible unipotent representation of the finite reductive group 
$\overline {K}:=K/K^+$. We denote by 
${\mathrm {Irr}}_{\mathrm {un}}(G)$ the set of isomorphism classes of irreducible unipotent 
$G$-representations.
For the rest of the section we will assume that the quasi-split inner form 
$G^*$ of 
$G$ is 
$F$-split.
Definition 4.3 An 
$L$-parameter 
$\varphi \colon W_F\times {\mathsf {SL}}_2({\mathbb {C}}) \to {}^L G$ is called unipotent if 
$\varphi (w,1)=(1,w)$ for any element 
$w$ of the inertia subgroup 
$I_F$ of 
$W_F$.
Denote by 
$\Phi _{{\mathrm {un}}}({}^LG)$ the set of 
$G^\vee$-conjugacy classes of unipotent 
$L$-parameters 
$\varphi$ and by 
$\Phi _{{\mathrm {e}},{\mathrm {un}}}(G)$ the set of unipotent enhanced 
$G$-relevant parameters, i.e. the subset of the 
$(\varphi,\phi )\in \Phi _{{\mathrm {e}}}(G)$ such that 
$\varphi$ is unipotent. We then set
\[ \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG) = G^\vee\backslash\{(\varphi,\phi)\mid \varphi\text{ unipotent}, \phi\in\widehat{A_\varphi^1}\}. \]
Given 
$\varphi \in \Phi _{{\mathrm {un}}}({}^LG)$, since 
$G^*$ is 
$F$-split, every 
$\phi \in \widehat {A_\varphi ^1}$ is 
$G'$-relevant for some 
$G' \in {\mathrm {InnT}}(G)$. We thus have
\[ \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG) = \bigsqcup_{G'\in{\mathrm{InnT}}(G)}\Phi_{{\mathrm{e}},{\mathrm{un}}}(G'). \]
Given 
$\varphi \in \Phi _{{\mathrm {un}}}({}^LG)$, let 
$A_\varphi$ be the component group of 
$Z_{G^\vee }(\varphi )$. We then set
\[ \Phi^p_{{\mathrm{e}},{\mathrm{un}}}({}^LG)=G^\vee\backslash\{(\varphi,\phi)\mid \varphi\text{ unipotent}, \phi\in\widehat{A_\varphi}\}. \]
The set 
$\Phi _{{\mathrm {e}},{\mathrm {un}}}(G)$ is known to parametrize 
${\mathrm {Irr}}_{\mathrm {un}}(G)$: such a parametrization was defined by Lusztig in [Reference LusztigLus95, Reference LusztigLus02] in the case when 
${\mathbf {G}}$ is simple adjoint, and extended by Solleveld in [Reference SolleveldSol23a, Reference SolleveldSol23b] to the case when 
$G$ is arbitrary. In the case when 
$G={\mathsf {GL}}_n(F)$ or 
${\mathsf {SL}}_n(F)$, it also follows from [Reference Hiraga and SaitoHS12, Reference Aubert, Baum, Plymen and SolleveldABPS16]. This parametrization induces a bijection:
\begin{equation} \mathsf{LLC}\colon \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG)\longleftrightarrow \bigsqcup_{G'\in {\mathrm{InnT}}(G)}{\mathrm{Irr}}_{\mathrm{un}}(G'). \end{equation}This correspondence sends cuspidal (respectively, discrete, bounded) parameters to supercuspidal (respectively, essentially square-integrable, tempered) irreducible unipotent representations.
Let 
$x\in G^\vee$ with Jordan decomposition 
$x=su$. There is an unipotent 
$L$-parameter 
$\varphi$ (unique up to 
$G^\vee$-conjugation) such that 
$u=u_\varphi$ and 
$s=s_\varphi$. We set
\begin{equation} {\mathcal{G}}_s={\mathrm{Z}}_{G^\vee_{\mathrm{sc}}}^1(\varphi|_{W_F}). \end{equation}
Note that 
$\varphi |_{W_F}$ depends only on 
$s$, which explains the notation. By (4.8),
\[ A^1_\varphi\cong A_{{\mathcal{G}}_s}(u). \]
We set
\[ \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG,s)=G^\vee\backslash\{(\varphi',\phi)\in \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG)\mid \varphi'({\mathrm{Frob}},1)=(s',{\mathrm{Frob}}),\ s'\in G^\vee\cdot s\}. \]
Then
\begin{align} \Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG,s)&={\mathrm{Z}}_{G^\vee}(\varphi|_{W_F})\text{-orbits in }\{(u',\phi)\mid u'\in {\mathcal{G}}_s^\circ\text{ unipotent},\ \phi\in \widehat{A_{{\mathcal{G}}_s}(u')}\}\nonumber\\ &={\mathcal{G}}_s\text{-orbits in }\{(u',\phi)\mid u'\in {\mathcal{G}}_s^\circ\text{ unipotent},\ \phi\in \widehat{A_{{\mathcal{G}}_s}(u')}\}. \end{align}
The second equality follows from the fact that conjugation of unipotent elements is insensitive to isogenies. This allows us to rephrase the unipotent LLC as follows. Let 
${\mathcal {C}}({\mathcal {G}})$, 
${\mathcal {C}}({\mathcal {G}})_{\mathsf {ss}}$, 
${\mathcal {C}}({\mathcal {G}})_{\mathrm {un}}$ denote the set of conjugacy classes, respectively semisimple, unipotent conjugacy classes in a complex group 
${\mathcal {G}}$. Let 
$R_{\mathrm {un}} (G')$ be the 
${\mathbb {C}}$-span of 
${\mathrm {Irr}}_{\mathrm {un}} (G')$. Then (4.13) can be written as the bijection
\[ \mathsf{LLC}_{{\mathrm{un}}}:\ \bigsqcup_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}} \bigsqcup_{u\in {\mathcal{C}}({\mathcal{G}}_s)_{\mathrm{un}}} \widehat{A_{{\mathcal{G}}_s}(u)}\longleftrightarrow \bigsqcup_{G'\in {\mathrm{InnT}}(G)}{\mathrm{Irr}}_{\mathrm{un}}(G'), \]
which induces a linear isomorphism
\begin{equation} \mathsf{LLC}_{{\mathrm{un}}}\colon R(\Phi_{{\mathrm{e}},{\mathrm{un}}}({}^LG)):=\bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\bigoplus_{u\in {\mathcal{C}}({\mathcal{G}}_s)_{\mathrm{un}}}R(A_{{\mathcal{G}}_s}(u)) \longrightarrow \bigoplus_{G'\in{\mathrm{InnT}}(G)} R_{\mathrm{un}}(G'). \end{equation}
If we instead consider pure inner twists, then we need to replace the group 
${\mathcal {G}}_s$ by the group
\begin{equation} {\mathcal{G}}_s^p={\mathrm{Z}}_{G^\vee}(\varphi|_{W_F}), \end{equation}and the correspondence becomes
\begin{equation} \mathsf{LLC}^p_{{\mathrm{un}}}\colon R(\Phi_{{\mathrm{e}},{\mathrm{un}}}^p({}^LG)):=\bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\bigoplus_{u\in {\mathcal{C}}({\mathcal{G}}_s^p)_{\mathrm{un}}}R(A_{{\mathcal{G}}_s^p}(u)) \longrightarrow \bigoplus_{G'\in{\mathrm{InnT}}^p(G)} R_{\mathrm{un}}(G'). \end{equation}
Given 
$\phi \in R(A_{{\mathcal {G}}_s^p}(u))$, write 
$\pi (s, u, \phi )$ for the image of 
$\phi$ under 
$\mathsf {LLC}^p_{{\mathrm {un}}}$.
Remark 4.4 Note that the existing LLC for unipotent representations is not entirely canonical (see the discussion in [Reference SolleveldSol23a, Introduction]) but for the rest of the paper, we fix a map 
$\mathsf {LLC}_{{\mathrm {un}}}^p$ as above satisfying the usual properties (described, for example, in [Reference SolleveldSol23a, Theorem 1]).
Example 4.5 For 
$G={\mathsf {SL}}_n(F)$, recall that there is a one-to-one correspondence between 
${\mathrm {InnT}}({\mathsf {SL}}_n(F))$ and 
$\mathbb {Z}/n\mathbb {Z}$, where the inner twists are 
${\mathsf {SL}}_m(D_{d,r/m})$, 
$m=\gcd (r,n)$, 
$r\in {\mathbb {Z}}/n{\mathbb {Z}}$.
The dual Langlands group is 
$G^\vee ={\mathsf {PGL}}_n(\mathbb {C})$. The correspondence (4.13) takes the form:
\begin{equation} \bigsqcup_{r\in \mathbb{Z}/n\mathbb{Z}} {\mathrm{Irr}}_{\mathrm{un}}({\mathsf{SL}}_m(D_{d,r/m}))\longleftrightarrow {\mathsf{PGL}}_n(\mathbb{C})\backslash\{(x,\phi)\,|\,x\in {\mathsf{PGL}}_n(\mathbb{C}), \phi\in\widehat{A^1_{x}}\}, \end{equation}in particular,
\begin{align*} {\mathrm{Irr}}_{\mathrm{un}}({\mathsf{SL}}_n(F))\longleftrightarrow {\mathsf{PGL}}_n(\mathbb{C})\backslash\{(x,\phi)\,|\,x\in {\mathsf{PGL}}_n(\mathbb{C}), \phi\in\widehat{A_{x}}\}. \end{align*}
In this case, 
$G^\vee _{\mathrm {sc}}={\mathsf {SL}}_n(\mathbb {C})$ and 
${\mathrm {Z}}_{G^\vee _{\mathrm {sc}}}=C_n$. The irreducible central characters are therefore 
$\widehat {{\mathrm {Z}}_{{\mathsf {SL}}_n(\mathbb {C})}}=\{\zeta _r\mid r\in \mathbb {Z}/n\mathbb {Z}\}$. A Langlands parameter 
$(x,\phi )$ parametrizes an irreducible unipotent representation of 
${\mathsf {SL}}_m(D_{d,r/m})$ if and only if 
$\zeta _\phi =\zeta _r$. In particular, the unipotent representations of 
${\mathsf {SL}}_n(F)$ correspond to central characters 
$\zeta _0=1$.
Moreover, for 
$x\in {\mathsf {PGL}}_n(\mathbb {C})$, 
$A^1_x$ is the group of components of 
${\mathrm {Z}}^1_{{\mathsf {SL}}_n({\mathbb {C}})}(x)=\{g\in {\mathsf {SL}}_n(\mathbb {C})\mid g x g^{-1}=x\}$.
Remark 4.6 Note the Langlands parameters we call unipotent here are also known as unramified Langlands parameters (cf. [Reference VoganVog93, Reference SolleveldSol23a]).
5. Lusztig's nonabelian Fourier transform for finite groups
We recall the definition of the nonabelian Fourier transform [Reference LusztigLuz84a]. For the background material, we follow [Reference LusztigLuz84a, Reference Geck and MalleGM20, Reference Digne and MichelDM90].
5.1 Fourier transforms
For a finite group 
$\Gamma$, define 
$\mathcal {M}(\Gamma )$ to be the set
\begin{equation} \{(x,\sigma)\mid x\in \Gamma,~\sigma\in \widehat{{\mathrm{Z}}_\Gamma(x)}\}, \end{equation}
modulo the equivalence relation given by conjugation by 
$\Gamma$: 
$g\cdot (x,\sigma )=(gxg^{-1},\sigma ^g)$, where 
$\sigma ^g(y)=\sigma (g^{-1}yg)$ for all 
$g\in \Gamma$, 
$y\in {\mathrm {Z}}_\Gamma (g x g^{-1})$. Define also
\begin{equation} {\mathcal{Y}}(\Gamma)= \{(y,z)\in \Gamma\times\Gamma\mid yz=zy\}. \end{equation}
Write 
$\Gamma \setminus {\mathcal {Y}}(\Gamma )$ for the set of 
$\Gamma$-orbits on 
${\mathcal {Y}}(\Gamma )$. Let 
$\mathsf {Sh}^\Gamma (\Gamma )$ be the category of 
$\Gamma$-equivariant coherent sheaves of 
$\Gamma$ (
$\Gamma$ acting on itself by conjugation). The irreducible objects in 
$\mathsf {Sh}^\Gamma (\Gamma )$ are parametrized by 
$\mathcal {M}(\Gamma )$: for every pair 
$(x,\sigma )\in \mathcal {M}(\Gamma )$, let 
${\mathcal {V}}({(x,\sigma )})=\Gamma \times _{{\mathrm {Z}}_\Gamma (x)}\sigma$ be the corresponding irreducible 
$\Gamma$-equivariant sheaf. This means that there is a natural isomorphism 
${\mathbb {C}}[\mathcal {M}(\Gamma )]\cong K(\mathsf {Sh}^\Gamma (\Gamma ))_{\mathbb {C}}$, where 
$K(\;)_{\mathbb {C}}$ is the complexification of the 
$K$-group. Moreover, there is an isomorphism
\[ \kappa\colon {\mathbb{C}}[\mathcal{M}(\Gamma)]\cong K(\mathsf{Sh}^\Gamma(\Gamma))_{\mathbb{C}}\to {\mathbb{C}}[\Gamma\setminus{\mathcal{Y}}(\Gamma)],\quad {\mathcal{V}}\mapsto ((y,z)\mapsto {\mathrm{tr}}(z,{\mathcal{V}}|_y)). \]
Lusztig [Reference LusztigLuz84a] defined a pairing on 
$\mathcal {M}(\Gamma )$:
\begin{equation} \{(x,\sigma),(y,\tau)\}=\frac 1{|{\mathrm{Z}}_\Gamma(x)| |{\mathrm{Z}}_\Gamma(y)|} \sum_{\substack{g\in \Gamma\\xgyg^{-1}=gyg^{-1}x}} \sigma(gyg^{-1})\tau(g^{-1}x^{-1}g), \end{equation}
which extends to a Hermitian pairing on 
$\mathbb {C}[\mathcal {M}(\Gamma )]$. He also defined a linear map, the Fourier transform for 
$\Gamma$,
\begin{equation} {\mathrm{FT}}_\Gamma\colon {\mathbb{C}}[\mathcal{M}(\Gamma)]\to {\mathbb{C}}[\mathcal{M}(\Gamma)],\quad {\mathrm{FT}}_\Gamma(f)(x,\sigma)=\sum_{(y,\tau)\in \mathcal{M}(\Gamma)}\{(x,\sigma),(y,\tau)\} f(y,\tau). \end{equation}
See Lemma 5.1 for the interpretation of 
${\mathrm {FT}}_\Gamma$ in terms of 
${\mathcal {Y}}(\Gamma )$.
Now consider the following generalization. Suppose 
$\widetilde {\Gamma }=\Gamma \rtimes \langle \alpha \rangle$, where 
$\alpha$ has order 
$c$. Set 
$\Gamma '=\Gamma \alpha \subset \widetilde {\Gamma }$. As in [Reference LusztigLuz84a, § 4.16], define two sets 
$\mathcal {M}=\mathcal {M}(\Gamma \unlhd \widetilde {\Gamma })$ and 
$\overline {\mathcal {M}}=\overline {\mathcal {M}}(\Gamma \unlhd \widetilde {\Gamma })$ as follows:
\begin{equation} \begin{aligned} \mathcal{M} & =\{(x,\sigma)\mid x\in\Gamma\text{ such that }{\mathrm{Z}}_{\widetilde{\Gamma}}(x)\cap \Gamma'\neq\emptyset,\ \sigma\in \widehat{{\mathrm{Z}}_{\widetilde{\Gamma}}(x)} \text{ with }\sigma|_{{\mathrm{Z}}_\Gamma(x)}\text{ irreducible}\},\\ \overline{\mathcal{M}} & =\{(x,\bar{\sigma})\mid x\in \Gamma',\ \bar{\sigma}\in \widehat{{\mathrm{Z}}_\Gamma(x)}\},\end{aligned} \end{equation}
in each case modulo the equivalence relation given by conjugation by 
$\widetilde{\Gamma}$.
In addition, the cyclic group 
$\langle \alpha \rangle$ acts on 
$\mathcal {M}$ by twists in the second entry of the pair 
$(x,\sigma )$. Denote by 
$\sim _c$ the corresponding equivalence relation.
The set 
$\mathcal {M}$ is a subset of 
$\mathcal {M}(\widetilde {\Gamma })$. Given 
$(x, \bar {\sigma }) \in \overline {\mathcal {M}}$, we have that 
$(x, \sigma ) \in \mathcal {M}(\widetilde {\Gamma })$ for any extension 
$\sigma$ of 
$\bar {\sigma }$ to 
${\mathrm {Z}}_{\widetilde {\Gamma }}(x)$. Thus, the pairing 
$\{~,~\}$ on 
$\mathcal {M}(\widetilde {\Gamma })$ induces a pairing
\begin{equation} \{~,~\}:\overline{\mathcal{M}}\times \mathcal{M}\to {\mathbb{C}},\quad \{(x,\bar{\sigma}),(y,\tau)\}:=c \{(x,\sigma),(y,\tau)\}, \end{equation}
for any fixed extension 
$\sigma$ of 
$\bar {\sigma }$ to 
${\mathrm {Z}}_{\widetilde {\Gamma }}(x)$.
Let 
$\mathcal {P}=\mathcal {P}(\Gamma \unlhd \widetilde {\Gamma })$ and 
$\overline {\mathcal {P}}=\overline {\mathcal {P}}(\Gamma \unlhd \widetilde {\Gamma })$ be the spaces of functions on 
$\mathcal {M}(\widetilde {\Gamma })$ with support in 
$\mathcal {M}$ and 
$\overline {\mathcal {M}}$, respectively. The operator [Reference LusztigLuz84a, (4.16.1)] (see also [Reference Geck and MalleGM20, § 4.2.14])
\begin{equation}
{\mathrm{FT}}_{\Gamma\unlhd\widetilde{\Gamma}}: \mathcal{P}\to \overline{\mathcal{P}},\
{\mathrm{FT}}_{\Gamma\unlhd\widetilde{\Gamma}}f(x,\bar{\sigma})=\sum_{(y,\tau)\in
\mathcal{M}/\sim_c}\{(x,\bar{\sigma}),(y,\tau)\} f(y,\tau)
\end{equation}
is an isomorphism with inverse 
${\mathrm {FT}}_{\Gamma \unlhd \widetilde {\Gamma }}^{-1}f(y,\tau )=\sum _{(x,\bar {\sigma })\in \overline {\mathcal {M}}}\{(x,\bar {\sigma }),(y,\tau )\} f(x,\bar {\sigma })$.
5.2 Families of Weyl group representations
Let 
$W$ be a finite Weyl group with the set of simple generators 
$S$. The partition of 
$\widehat {W}$ into families is defined in [Reference LusztigLuz84a, § 4.2] as follows. Let 
${\mathrm {sgn}}$ denote the sign character of 
$W$. If 
$W=\{1\}$, there is only one family consisting of the trivial representation. Otherwise, assume that the families have been defined for all proper parabolic subgroups of 
$W$. Then 
$\mu,\mu '\in \widehat {W}$ belong to the same family of 
$W$ if there exists a sequence 
$\mu =\mu _0,\mu _1,\ldots,\mu _m=\mu '$, 
$\mu _i\in \widehat {W}$, such that for each 
$i$ there exists a parabolic subgroup 
$W_i\subsetneq W$ and 
$\mu _i',\mu _i''\in \widehat {W}_i$ in the same family of 
$W_i$ such that either
\[ \langle \mu_i',\mu_{i-1}\rangle_{W_i}\neq 0,\ a_{\mu_i'}=a_{\mu_{i-1}},\quad \langle \mu_i'',\mu_{i}\rangle_{W_i}\neq 0,\ a_{\mu_i''}=a_{\mu_{i}} \]
or
\[ \langle \mu_i',\mu_{i-1}\otimes{\mathrm{sgn}}\rangle_{W_i}\neq 0,\ a_{\mu_i'}=a_{\mu_{i-1}\otimes{\mathrm{sgn}}},\quad \langle \mu_i'',\mu_{i}\otimes{\mathrm{sgn}}\rangle_{W_i}\neq 0,\ a_{\mu_i''}=a_{\mu_{i}\otimes{\mathrm{sgn}}}. \]
Here 
$a_\mu$ is the 
$a$-invariant of 
$\mu$ defined in [Reference LusztigLuz84a, § 4.1]. It follows from the definition that if 
${\mathcal {F}}\subset \widehat {W}$ is a family, then so is 
${\mathcal {F}}\otimes {\mathrm {sgn}}$ and the families for 
$W_1\times W_2$ are 
${\mathcal {F}}_1\boxtimes {\mathcal {F}}_2$, where 
${\mathcal {F}}_i$ is a family for 
$W_i$, 
$i=1,2$.
Suppose in addition that we have a Coxeter group automorphism 
$\sigma \colon W\to W$, i.e. 
$\sigma \in {\mathrm {Aut}}(W)$ such that 
$\sigma (S)=S$. Such an automorphism is called ordinary if, on each irreducible component of 
$W$, it is not the nontrivial graph automorphism of type 
$B_2$, 
$G_2$ or 
$F_4$. The automorphism 
$\sigma$ acts on 
$\widehat {W}$ and it permutes the families 
${\mathcal {F}}$. An important observation [Reference LusztigLuz84a, § 4.17] is that if 
$\sigma$ is ordinary and 
${\mathcal {F}}$ is 
$\sigma$-stable, then every element of 
${\mathcal {F}}$ is 
$\sigma$-stable.
5.3 Families of unipotent representations
Let 
${\mathbb {G}}$ be a connected reductive algebraic group over 
$\overline {\mathbb {F}}_q$ with a Frobenius map 
${\mathrm {Fr}} \colon {\mathbb {G}}\to {\mathbb {G}}$ such that there exists a maximal torus 
${\mathbb {T}}_0$ with the property 
${\mathrm {Fr}}(t)=t^q$, for all 
$t\in {\mathbb {T}}_0$. Let 
$W=N_{{\mathbb {G}}}({\mathbb {T}}_0)/{{\mathbb {T}}_0}$ be the Weyl group. Recall that an irreducible representation 
$\rho \in {\mathrm {Irr}}~{\mathbb {G}}^{\mathrm {Fr}}$ is called unipotent if 
$\langle \rho, R_{{\mathbb {T}}}^{{\mathbb {G}}}(1)\rangle _{{\mathbb {G}}^{\mathrm {Fr}}}\neq 0$ for some 
${\mathrm {Fr}}$-stable maximal torus 
${\mathbb {T}}$ of 
${\mathbb {G}}$. Here 
$R_{{\mathbb {T}}}^{{\mathbb {G}}}$ is Deligne–Lusztig induction [Reference Deligne and LusztigDL76, § 7.8]. Let 
${\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ denote the set of irreducible unipotent 
${\mathbb {G}}^{\mathrm {Fr}}$-representations. By the results of Lusztig, the classification of 
${\mathrm {Irr}}_{{\mathrm {un}}}{\mathbb {G}}^{\mathrm {Fr}}$ is reduced to the case when 
${\mathbb {G}}$ is adjoint simple (see, for example, the exposition in [Reference Geck and MalleGM20, Remark 4.2.1]). More precisely, if 
$\pi \colon {\mathbb {G}}\to {\mathbb {G}}_{{\mathrm {ad}}}$ is the surjective homomorphism with central kernel (
${\mathbb {G}}_{{\mathrm {ad}}}$ is the semisimple adjoint group isogeneous to 
${\mathbb {G}}/{\mathrm {Z}}_{{\mathbb {G}}}$), there exists a Frobenius map 
${\mathrm {Fr}}_{{\mathrm {ad}}}$ such that 
${\mathrm {Fr}}_{{\mathrm {ad}}}\circ \pi =\pi \circ {\mathrm {Fr}}$ such that the resulting group homomorphism 
$\pi \colon {\mathbb {G}}^{\mathrm {Fr}}\to {\mathbb {G}}_{{\mathrm {ad}}}^{{\mathrm {Fr}}_{{\mathrm {ad}}}}$ induces a bijection
\[ {\mathrm{Irr}}_{\mathrm{un}}{\mathbb{G}}^{\mathrm{Fr}}\leftrightarrow {\mathrm{Irr}}_{\mathrm{un}}{\mathbb{G}}^{{\mathrm{Fr}}_{{\mathrm{ad}}}}_{{\mathrm{ad}}}. \]
Furthermore, write 
${\mathbb {G}}_{{\mathrm {ad}}}={\mathbb {G}}_1\times \dots \times {\mathbb {G}}_r$ for the decomposition into factors such that each 
${\mathbb {G}}_i$ is semisimple adjoint, 
${\mathrm {Fr}}_{{\mathrm {ad}}}$-stable, and a direct product of simple algebraic groups that are cyclically permuted by 
${\mathrm {Fr}}_{{\mathrm {ad}}}$. Let 
${\mathbb {H}}_i$ be one of the simple factors in 
${\mathbb {G}}_i$: if 
$h_i$ is the number of copies of 
${\mathbb {H}}_i$, then 
${\mathrm {Fr}}^{h_i}_{{\mathrm {ad}}}$ preserves 
${\mathbb {H}}_i$. Denote by 
${\mathrm {Fr}}_i$ the restriction to 
${\mathbb {H}}_i$. Then
\[ {\mathrm{Irr}}_{\mathrm{un}}{\mathbb{G}}^{{\mathrm{Fr}}_{{\mathrm{ad}}}}_{{\mathrm{ad}}}\cong \prod_{i=1}^r {\mathrm{Irr}}_{\mathrm{un}} {\mathbb{H}}_i^{{\mathrm{Fr}}_i}. \]
The Frobenius map 
${\mathrm {Fr}}$ induces a Coxeter group automorphism 
$\sigma$ of 
$W$. Define a graph with vertices 
${\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ as follows: 
$\rho _1,\rho _2\in {\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ are joined by an edge if and only if there is 
$\sigma$-stable 
$\mu \in \widehat {W}$ such that 
$\langle \rho _i,R_{\widetilde \mu }\rangle _{{\mathbb {G}}^{\mathrm {Fr}}}\neq 0$ for 
$i=1,2$ where 
$R_{\widetilde \mu }$ is the almost character associated to a fixed extension 
$\widetilde \mu$ of 
$\mu$ to 
$\widetilde {W}=W\rtimes \langle \sigma \rangle$ as defined in [Reference LusztigLuz84a, (3.7.1)]. Each connected component of this graph is called a family in 
${\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$. One can define an equivalence relation on the set 
$\widehat {W}^\sigma$ of 
$\sigma$-stable irreducible 
$W$-representations: 
$\mu$ and 
$\mu '$ are equivalent if 
$R_{\widetilde \mu }$ and 
$R_{\widetilde \mu '}$ have unipotent constituents in the same family. By [Reference LusztigLuz84a] (see also [Reference Geck and MalleGM20, Proposition 4.2.3]), the equivalence classes are the same as the 
$\sigma$-stable families in 
$\widehat {W}$, when 
$\sigma$ is ordinary.
To each family 
$\mathcal {U}\subset {\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ corresponding to the 
$\sigma$-stable family 
${\mathcal {F}}\subset \widehat {W}^\sigma$, Lusztig [Reference LusztigLuz84a, § 4] attached finite groups 
$\Gamma _\mathcal {U}\unlhd \widetilde {\Gamma }_\mathcal {U}$ such that 
$\widetilde {\Gamma }_\mathcal {U}=\Gamma _\mathcal {U}\langle \sigma \rangle$, a bijection
\begin{equation} \mathcal{U}\longleftrightarrow \overline{\mathcal{M}}(\Gamma_\mathcal{U}\unlhd\widetilde{\Gamma}_\mathcal{U}),\quad \rho\mapsto \bar{x}_\rho, \end{equation}
scalars 
$\Delta (\bar {x}_\rho )\in \{\pm 1\}$ (see [Reference LusztigLuz84a, § 6.7]), and an injection
\begin{equation} {\mathcal{F}}\longrightarrow \mathcal{M}(\Gamma_\mathcal{U}\unlhd\widetilde{\Gamma}_\mathcal{U}),\quad \mu\mapsto x_\mu, \end{equation}
such that, when 
$\sigma$ is ordinary, [Reference LusztigLuz84a, Theorem 4.23] states that
\begin{equation} \langle \rho,R_{{\widetilde{ \mu}}}\rangle_{{\mathbb{G}}^{\mathrm{Fr}}}=\Delta(\bar{x}_\rho)\{\bar{x}_\rho,x_\mu\}. \end{equation}
Define the unipotent almost characters of 
${\mathbb {G}}^{\mathrm {Fr}}$ to be the set of orthonormal class functions
\begin{equation} R_x=\sum_{\rho\in \mathcal{U}}\Delta(\bar{x}_\rho)\{\bar{x}_\rho,x\}\rho,\quad x\in \mathcal{M}(\Gamma_\mathcal{U}\unlhd\widetilde{\Gamma}_\mathcal{U}). \end{equation}
Hence, the unipotent nonabelian Fourier transform of 
${\mathbb {G}}^{\mathrm {Fr}}$
\begin{equation} {\mathrm{FT}}_{{\mathbb{G}}^{\mathrm{Fr}}}:=\bigoplus_{\mathcal{U}\subset {\mathrm{Irr}}_{\mathrm{un}}{\mathbb{G}}^{\mathrm{Fr}}}{\mathrm{FT}}_{\Gamma_\mathcal{U}\unlhd\widetilde{\Gamma}_\mathcal{U}} \end{equation}
gives the change of bases matrix, up to the signs 
$\Delta (\bar {x}_\rho )$, between irreducible unipotent characters and almost characters.
Assume 
$\mathbb {G}$ is 
${\mathrm {Fr}}$-split, so that 
$\sigma$ is trivial and a family 
$\mathcal {U}$ is parametrized by 
$\mathcal {M}(\Gamma _\mathcal {U})$. Let 
$x\in \Gamma =\Gamma _\mathcal {U}$, and define the virtual combinations of unipotent characters
\begin{equation} \Pi_\mathcal{U}(x,y)=\sum_{\sigma\in \widehat{{\mathrm{Z}}_\Gamma(x)}}\sigma(y^{-1}) \rho_{(x,\sigma)},\quad\text{where }y\in {\mathrm{Z}}_\Gamma(x), \end{equation}
where 
$\rho _{(x,\sigma )}$ is the representation in 
$\mathcal {U}$ parametrized by 
$(x,\sigma )\in \mathcal {M}(\Gamma _\mathcal {U})$. If 
$\Gamma$ is abelian (which is often the case), we may also define
\begin{equation} \Pi_\mathcal{U}(\sigma,\tau)=\sum_{y\in \Gamma} \tau(y)\rho_{(y,\sigma)},\quad\text{if } \sigma,\tau\in \widehat{\Gamma}. \end{equation}Lemma 5.1 (Cf. [Reference Digne and MichelDM90])
With the notation of (5.13)–(5.14) and 
$\Gamma =\Gamma _\mathcal {U}$,
\[ {\mathrm{FT}}_{\Gamma}(\Pi_\mathcal{U}(x,y))=\Pi_\mathcal{U}(y,x),\quad {\mathrm{FT}}_{\Gamma}(\Pi_\mathcal{U}(\sigma,\tau))=\Pi_\mathcal{U}(\tau,\sigma), \]
the latter when 
$\Gamma$ is abelian.
Proof. We verify the first formula. The second is analogous (or it follows by change of bases). Denote by 
$C_y$ the conjugacy class of 
$y$ in 
${\mathrm {Z}}_\Gamma (x)$. Then,
\begin{align*} &{\mathrm{FT}}_{\Gamma_\mathcal{U}}(\Pi_\mathcal{U}(x,y))\\ &\quad=\sum_\sigma \sigma(y^{-1})\sum_{(z,\tau)}\{(x,\sigma),(z,\tau)\} \rho_{(z,\tau)}\\ &\quad=\sum_\sigma \sigma(y^{-1}) \sum_{(z,\tau)}\frac 1{|{\mathrm{Z}}_\Gamma(x)||{\mathrm{Z}}_\Gamma(z)|}\sum_{g\in\Gamma,~gzg^{-1}\in {\mathrm{Z}}_\Gamma(x)} \sigma(gzg^{-1})\tau(g^{-1}x^{-1}g)\rho_{(z,\tau)}\\ &\quad=\sum_{(z,\tau)}\frac 1{|{\mathrm{Z}}_\Gamma(z)|} \bigg(\sum_{g\in\Gamma,~gzg^{-1}\in {\mathrm{Z}}_\Gamma(x)}\frac 1{|{\mathrm{Z}}_\Gamma(x)|} \sum_\sigma \sigma(y^{-1})\sigma(gzg^{-1})\bigg) \tau(g^{-1}x^{-1}g) \rho_{(z,\tau)}\\ &\quad=\sum_{g,z\in \Gamma,~gzg^{-1}\in C_y} \frac 1{|C_y|} \frac 1{|{\mathrm{Z}}_\Gamma(z)|} \sum_{\tau\in \widehat{{\mathrm{Z}}_\Gamma(z)}} \tau(g^{-1}x^{-1} g)\rho_{(z,\tau)}\quad \text{(by character orthogonality)}\\ &\quad=\frac 1{|C_y|}\sum_{y'\in C_y}\sum_{\tau\in \widehat{{\mathrm{Z}}_\Gamma(g^{-1}y' g)}} \tau(g^{-1}x^{-1} g)\rho_{(g^{-1}y'g,\tau)}\quad\text{(setting $y'=gzg^{-1}$)}\\ &\quad=\frac 1{|C_y|}\sum_{y'\in C_y} \Pi_\mathcal{U}(g^{-1}y'g,g^{-1}xg)=\Pi_\mathcal{U}(y,x), \end{align*}
where we used column orthogonality of characters and that 
$(y,x)$ is 
$\Gamma$-conjugate to 
$(g^{-1}y'g,g^{-1}xg)$ when 
$y'\in C_y$.
6. Disconnected groups over finite fields
Suppose that 
${\mathbb {G}}$ is a disconnected reductive group over 
$\overline {\mathbb {F}}_p$ with Frobenius map 
${\mathrm {Fr}}\colon {\mathbb {G}}\to {\mathbb {G}}$ and identity component 
${\mathbb {G}}^\circ$ such that 
$A={\mathbb {G}}/{\mathbb {G}}^\circ$ is abelian. (In our applications, 
${\mathbb {G}}/{\mathbb {G}}^\circ$ will almost always be a cyclic group.) By definition, the irreducible unipotent 
${\mathbb {G}}^{\mathrm {Fr}}$-representations 
${\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ are the constituents of all induced representations 
${\mathrm {Ind}}_{{{\mathbb {G}}^\circ }^{\mathrm {Fr}}}^{{\mathbb {G}}^{\mathrm {Fr}}}\rho$, where 
$\rho \in {\mathrm {Irr}}_{\mathrm {un}}{{\mathbb {G}}^\circ }^{\mathrm {Fr}}$. See [Reference Geck and MalleGM20, Proposition 4.8.19] for the compatibility with the definition in terms of the appropriate version of 
$R_{{\mathbb {T}}}^{{\mathbb {G}}}(1)$. The parametrization of 
${\mathrm {Irr}}_{\mathrm {un}}{\mathbb {G}}^{\mathrm {Fr}}$ follows from that of 
${\mathrm {Irr}}_{\mathrm {un}}{{\mathbb {G}}^\circ }^{\mathrm {Fr}}$ via Mackey induction using the explicit results for simple groups, e.g. [Reference Geck and MalleGM20, Theorems 4.5.11 and 4.5.12].
We are interested in studying the irreducible unipotent representations for groups 
${\mathbb {G}}^{\mathrm {Fr}}$ that are related via the structure theory of 
$p$-adic groups.
Let 
${\mathbb {G}}$ be a reductive algebraic group over 
$\overline {\mathbb {F}}_p$ with identity component 
${\mathbb {G}}^\circ$ and such that 
${\mathbb {G}}/{\mathbb {G}}^\circ =A$ is a finite abelian group. Let 
${\mathrm {Fr}}_0$ be a Frobenius map on 
${\mathbb {G}}$ and assume that 
${{\mathbb {G}}}^{{\mathrm {Fr}}_0}$ is split. Given 
$a\in A$, conjugation by 
$a$ defines an outer automorphism of 
${\mathbb {G}}^\circ$, which induces an isomorphism, call it 
$\sigma _a$, of the based root datum of 
${\mathbb {G}}^\circ$. For every 
$a$, define the Frobenius automorphism 
${\mathrm {Fr}}_a={\mathrm {Fr}}_0\circ \sigma _a$. By analogy with § 2, we write
\[ {\mathrm{InnT}}^p{\mathbb{G}}=\{{\mathbb{G}}^{{\mathrm{Fr}}_a}\mid a\in A\} \]
and call this the set of pure inner twists of 
${\mathbb {G}}^{{\mathrm {Fr}}_0}$. Just as in the 
$p$-adic case, this set is in one-to-one correspondence with the first Galois cohomology group
\[ {\mathrm{InnT}}^p{\mathbb{G}}\leftrightarrow H^1(\mathbb{F}_q,{\mathbb{G}})\cong H^1(\mathbb{F}_q,{\mathbb{G}}/{\mathbb{G}}^\circ)=H^1(\mathbb{F}_q,A)\cong A, \]
using the fact that 
$H^1(\mathbb {F}_q,{\mathbb {G}}^\circ )=0$ by Lang's Theorem (see, for example, [Reference SerreSer02, III.§ 2, Corollary 3]), and the assumption that 
${\mathrm {Fr}}_0$ acts trivially on 
$A$.
By (5.8), every unipotent family 
$\mathcal {U}\subset {\mathrm {Irr}}_{\mathrm {un}}({{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0})$ has an associated finite group 
$\Gamma _\mathcal {U}=\widetilde {\Gamma }_\mathcal {U}$ (since 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$ is split). The group 
$A$ acts on the set of families 
$\mathcal {U}$. For every orbit 
$\mathcal {O}_A=A\cdot \mathcal {U}$ with representative 
$\mathcal {U}$, let 
${\mathrm {Z}}_A(\mathcal {U})$ be the corresponding isotropy group. Then 
${\mathrm {Z}}_A(\mathcal {U})$ permutes the elements of 
$\mathcal {U}$, hence the corresponding parameters 
$\mathcal {M}(\Gamma _\mathcal {U})$. If 
$\Gamma _\mathcal {U}$ is abelian, which turns out to be the case in all of the examples of interest to us when 
$A\neq \{1\}$, this automatically defines an action of 
${\mathrm {Z}}_A(\mathcal {U})$ on 
$\Gamma _\mathcal {U}$, hence a group
\begin{equation} \widetilde{\Gamma}_\mathcal{U}^A=\Gamma_\mathcal{U}\rtimes {\mathrm{Z}}_A(\mathcal{U}). \end{equation}See [Reference Digne and MichelDM90, § 5] and [Reference LusztigLus86, § 17] for more details.
Proposition 6.1 (Cf. [Reference Digne and MichelDM90, Proposition 5.2])
As above, assume 
${\mathbb {G}}$ is 
${\mathrm {Fr}}_0$-split. The parametrization (5.8) induces a bijection
\[ \bigsqcup_{a\in A}{\mathrm{Irr}}_{\mathrm{un}}({\mathbb{G}}^{F_a})\longleftrightarrow \bigsqcup_{\mathcal{U}\subset A\backslash{\mathrm{Irr}}_{\mathrm{un}}({{\mathbb{G}}^\circ}^{F_0})} \mathcal{M}(\widetilde{\Gamma}_\mathcal{U}^A), \]
where 
$\mathcal {U}$ in the right-hand side ranges over a set of representatives of the 
$A$-orbits of families in 
${\mathrm {Irr}}_{\mathrm {un}}({{\mathbb {G}}^\circ }^{F_0})$.
Proof. This can be viewed as a particular case of [Reference Digne and MichelDM90, Proposition 5.2]. There the right-hand side of the bijection involves the groups 
$\overline {\mathcal {M}}(\widetilde {\Gamma }_\mathcal {U}^A\subset \widetilde {\Gamma }_\mathcal {U}^A\rtimes \langle {\mathrm {Fr}}_0\rangle )$, but since we are assuming 
${\mathbb {G}}$ is 
${\mathrm {Fr}}_0$-split, 
$\overline {\mathcal {M}}(\widetilde {\Gamma }_\mathcal {U}^A\subset \widetilde {\Gamma }_\mathcal {U}^A\rtimes \langle {\mathrm {Fr}}_0\rangle )\cong \mathcal {M}(\widetilde {\Gamma }_\mathcal {U}^A)$.
Remark 6.2 The bijection in Proposition 6.1 is not unique. To account for this (and in order to be able to carry out computations later on), we will work out explicit parametrizations in Examples 6.3–6.8. These cases are relevant for the branching computations for the unipotent representations of reductive 
$p$-adic groups in the inner class of the split group.
Let 
$R_{{\mathrm {un}}}({\mathbb {G}}^{F_a})$ be the 
$\mathbb {C}$-span of 
${\mathrm {Irr}}_{\mathrm {un}}({\mathbb {G}}^{F_a})$. The bijection of Proposition 6.1 induces a linear isomorphism
\begin{equation} \bigoplus_{a \in A} R_{{\mathrm{un}}}({\mathbb{G}}^{{\mathrm{Fr}}_a}) \to \bigoplus_{\mathcal{U}\subset A\backslash{\mathrm{Irr}}_{\mathrm{un}}{{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_0}} {\mathbb{C}}[\mathcal{M}(\widetilde{\Gamma}_\mathcal{U}^A)]. \end{equation}The right-hand side of (6.2) has the involution given by (5.4). Define
\begin{equation} {\mathrm{FT}}_{{\mathbb{G}}}\colon \bigoplus_{a\in A}R_{{\mathrm{un}}}({\mathbb{G}}^{{\mathrm{Fr}}_a})\to \bigoplus_{a\in A}R_{{\mathrm{un}}}({\mathbb{G}}^{{\mathrm{Fr}}_a}), \end{equation}to be the corresponding involution on the left-hand side.
In the examples below, when 
$A$ is clear from the context, we may write 
$\widetilde {\Gamma }_\mathcal {U}$ in place of 
$\widetilde {\Gamma }_\mathcal {U}^A$ for simplicity of notation.
Example 6.3 Let 
${\mathbb {H}}$ be a connected almost simple 
$\mathbb {F}_q$-split group and 
${\mathbb {G}}=({\mathbb {H}}\times {\mathbb {H}})\rtimes {\mathbb {Z}}/2{\mathbb {Z}}$, where the nontrivial element 
$\delta$ of 
$A={\mathbb {Z}}/2{\mathbb {Z}}$ acts by flipping the two copies of 
${\mathbb {H}}$. There are two pure inner twists:
\[ {\mathrm{InnT}}^p {\mathbb{G}}=\{{\mathbb{H}}(\mathbb{F}_q)^2\rtimes {\mathbb{Z}}/2{\mathbb{Z}}, {\mathbb{H}}(\mathbb{F}_{q^2})\rtimes {\mathbb{Z}}/2{\mathbb{Z}}\}, \]
the second for the Frobenius map 
${\mathrm {Fr}}_1(h_1,h_2)=({\mathrm {Fr}}_0(h_2),{\mathrm {Fr}}_0(h_1))$, 
$h_1,h_2\in {\mathbb {H}}$. A family of 
${\mathbb {G}}^\circ (\mathbb {F}_q)={\mathbb {H}}(\mathbb {F}_q)^2$ is 
$\mathcal {U}_1\boxtimes \mathcal {U}_2$, where 
$\mathcal {U}_1$, 
$\mathcal {U}_2$ are unipotent families of 
${\mathbb {H}}$. The 
$A$-orbits are either 
$\{\mathcal {U}_1\boxtimes \mathcal {U}_2, \mathcal {U}_2\boxtimes \mathcal {U}_1\}$ for 
$\mathcal {U}_1\neq \mathcal {U}_2$ or 
$\{\mathcal {U}\boxtimes \mathcal {U}\}$. Assume that all 
$\Gamma _\mathcal {U}$ are abelian. Set
\[ \widetilde{\Gamma}_{\mathcal{U}_1\boxtimes\mathcal{U}_2}^{{\mathbb{Z}}/2{\mathbb{Z}}}=\Gamma_{\mathcal{U}_1}\times \Gamma_{\mathcal{U}_2},\ \mathcal{U}_1\neq \mathcal{U}_2,\quad \widetilde{\Gamma}_{\mathcal{U}\boxtimes\mathcal{U}}^{{\mathbb{Z}}/2{\mathbb{Z}}}=\Gamma_\mathcal{U}^2\rtimes {\mathbb{Z}}/2{\mathbb{Z}}, \]
with the flip action of 
$\delta$. There are 
${\ell (\ell +3)}/{2}$ conjugacy classes in 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}$, 
$\ell =|\Gamma _\mathcal {U}|$, and they are represented by:
–
$(x,x')\sim (x',x)$ if $x\neq x'\in \Gamma _\mathcal {U}$, ${\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}}((x,x'))=\Gamma _\mathcal {U}^2$;–
$(x,x)$, $x\in \Gamma _\mathcal {U}$, ${\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}}((x,x))=\Gamma _\mathcal {U}^2\rtimes {\mathbb {Z}}/2{\mathbb {Z}}$;–
$(x,1)\delta$, $x\in \Gamma _\mathcal {U}$, ${\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}}((x,1)\delta )=\langle \Gamma _\mathcal {U}^\Delta,(x,1)\delta \rangle$, where $\Gamma _{\mathcal {U}}^\Delta$ is the diagonal copy of $\Gamma _\mathcal {U}$.
When 
$\mathcal {U}_1\neq \mathcal {U}_2$, if 
$\rho _1\in \mathcal {U}_1$, 
$\rho _2\in \mathcal {U}_2$, then 
$\rho _1\times \rho _2:={\mathrm {Ind}}_{{\mathbb {G}}^\circ (\mathbb {F}_q)}^{{\mathbb {G}}(\mathbb {F}_q)}(\rho _1\boxtimes \rho _2)$ is parametrized by 
$(\bar {x}_{\rho _1},\bar {x}_{\rho _2})\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}_1\boxtimes \mathcal {U}_2})$.
In the second case, let 
$\rho,\rho '\in \mathcal {U}$. If 
$\rho \neq \rho '$, then 
$\rho \times \rho '\cong \rho '\times \rho$ is an irreducible representation of 
${\mathbb {G}}(\mathbb {F}_q)$. If 
$\bar {x}_\rho =(x,\sigma )$, 
$\bar {x}_{\rho '}=(x',\sigma ')$ are the corresponding parameters of 
$\rho$, 
$\rho '$ in 
$\mathcal {M}(\Gamma _u)$, then the parameter for 
$\rho \times \rho '$ in 
$\mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}})$ is 
$((x,x'), \sigma \boxtimes \sigma ')$, if 
$x\neq x'$, or 
$((x,x), \sigma \times \sigma ')$, where 
$\sigma \times \sigma '={\mathrm {Ind}}_{\Gamma _\mathcal {U}}^{\Gamma _\mathcal {U}^2\rtimes {\mathbb {Z}}/2{\mathbb {Z}}}(\sigma \boxtimes \sigma ')$, if 
$\sigma \neq \sigma '$.
If 
$\rho =\rho '$, then we can extend 
$\rho \boxtimes \rho$ in two different ways to 
${\mathbb {G}}(\mathbb {F}_q)$, denoted by 
$(\rho \times \rho )^\pm$ relative to the character of 
${\mathbb {Z}}/2{\mathbb {Z}}$. The corresponding parameters in 
$\mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}})$ are 
$((x,x), (\sigma \times \sigma )^\pm )$, with the obvious notation.
For the second pure inner twist, the irreducible unipotent representations of 
${\mathbb {H}}(\mathbb {F}_{q^2})$ are given by the same families 
$\mathcal {U}$ as for 
${\mathbb {H}}(\mathbb {F}_q)$ and 
$\delta$ fixes each unipotent representation 
$\rho$ of 
${\mathbb {H}}(\mathbb {F}_{q^2})$. Let 
$\rho$ be an irreducible 
${\mathbb {H}}(\mathbb {F}_{q^2})$-representation in 
$\mathcal {U}$ parametrized by 
$\bar {x}_\rho =(x,\sigma )$, 
$x\in \Gamma _\mathcal {U}$, 
$\sigma \in \widehat {\Gamma }_\mathcal {U}$. Then it can be extended in two different ways 
$\rho ^\pm$ to 
${\mathbb {H}}(\mathbb {F}_{q^2})\rtimes {\mathbb {Z}}/2{\mathbb {Z}}$. The centralizer 
${\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}}((x,1)\delta )=\langle \Gamma _\mathcal {U}^\Delta,(x,1)\delta \rangle$ is isomorphic to the direct product 
$C_x:=\langle (y,y)\mid y\neq x\in \Gamma _\mathcal {U}\rangle \times \langle (x,1)\delta \rangle$, since 
$\big ((x,1)\delta \big )^2=(x,x)$. Regard 
$\sigma$ as a representation of the subgroup 
$\Gamma _\mathcal {U}^\Delta$. There are two ways 
$\sigma ^\pm$ to extend it to 
$C_x$, coming from the short exact sequence 
$1\to \langle (x,x)\rangle \to \langle (x,1)\delta \rangle \to {\mathbb {Z}}/2{\mathbb {Z}}\to 1$. We attach 
$((x,1)\delta,\sigma ^\pm )\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}})$ to 
$\rho ^\pm$. To fix a choice of 
$\pm$, we fix a choice of primitive 
$\ell$th root of unity 
$\zeta _\ell$ for each 
$\ell$. Then, if 
$\sigma ((x,x))=\zeta _k^j$, for some 
$j$, where 
$k$ is the order of 
$x$, then 
$\sigma ^+((x,1)\delta )=\zeta _{2k}^j$. For our applications, 
${\mathbb {H}}$ will be a classical group and therefore, 
$\Gamma _\mathcal {U}$ a 
$2$-group, hence 
$x$ will have order 
$k\leqslant 2$.
Example 6.4 Let 
${\mathbb {G}}^\circ ={\mathsf {GL}}_k^m$, 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}={\mathsf {GL}}_k(\mathbb {F}_q)^m$ and 
$A={\mathbb {Z}}/m{\mathbb {Z}}$ acting by cyclic permutations on the factors of 
${\mathbb {G}}^\circ$. Then
\begin{align*} {\mathrm{InnT}}^p {\mathbb{G}}=\{{{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_r}\rtimes{\mathbb{Z}}/m{\mathbb{Z}}= {\mathsf{GL}}_k(\mathbb{F}_{q^{m/d}})^{d}\rtimes {\mathbb{Z}}/m{\mathbb{Z}} \mid r\in {\mathbb{Z}}/m{\mathbb{Z}},\ d=\gcd(r,m)\}. \end{align*}
Each unipotent family of 
${\mathsf {GL}}_k(\mathbb {F}_{q^{m/d}})^{d}$ is a singleton 
$\{\rho _1\boxtimes \cdots \boxtimes \rho _{d}\}$ where 
$\rho _i\in \widehat {S}_k$, 
$1\leqslant i\leqslant d$. Hence, we can ignore the difference between unipotent families and irreducible representations of symmetric groups. The irreducible representations of 
$S_k^{d}\rtimes {\mathbb {Z}}/m{\mathbb {Z}}$ are constructed by Mackey theory.
Start with a unipotent representation 
$\rho =\rho _1\boxtimes \cdots \boxtimes \rho _m$ of 
${\mathsf {GL}}_k(\mathbb {F}_{q})^{m}\rtimes {\mathbb {Z}}/m{\mathbb {Z}}$ with stabilizer 
${\mathbb {Z}}/c{\mathbb {Z}}$, 
$c|m$. This means that 
$\rho _i=\rho _{i+m/c}$ for all 
$i$ (viewed mod 
$m$) and that 
${\mathbb {Z}}/{(m/c)}{\mathbb {Z}}$ has no fixed points under the cyclic action on 
$\rho _1\boxtimes \cdots \boxtimes \rho _{m/c}$. The corresponding unipotent family 
$\widetilde {\mathcal {U}}$ that we construct for 
${\mathrm {InnT}}^p{\mathbb {G}}$ has
\[ \widetilde{\Gamma}_\mathcal{U}^{{\mathbb{Z}}/m{\mathbb{Z}}}={\mathbb{Z}}/c{\mathbb{Z}}. \]
The irreducible representations 
$\widetilde {\rho }$ of 
${{\mathbb {G}}}^{{\mathrm {Fr}}_0}$ whose restriction to 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$ contain 
$\rho$ are in one-to-one correspondence to the characters of 
${\mathbb {Z}}/c{\mathbb {Z}}$, hence they are parametrized in 
$\mathcal {M}(\widetilde {\Gamma }_\mathcal {U})$ by the pairs 
$(0,\sigma )$, 
$\sigma \in \widehat {{\mathbb {Z}}/c{\mathbb {Z}}}$.
For every 
$r\in {\mathbb {Z}}/m{\mathbb {Z}}$ such that 
$m/c$ divides 
$d=\gcd (r,m)$, consider the representation of 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_r}$ given by 
$\rho ^r=\rho _1\boxtimes \cdots \boxtimes \rho _{d}$. The stabilizer of this representation in 
${\mathbb {Z}}/m{\mathbb {Z}}$ is also 
${\mathbb {Z}}/c{\mathbb {Z}}$. The irreducible representations 
$\widetilde {\rho }^r$ of 
${{\mathbb {G}}}^{{\mathrm {Fr}}_r}$ whose restriction to 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_r}$ contain 
$\rho ^r$ are again in one-to-one correspondence to the characters of 
${\mathbb {Z}}/c{\mathbb {Z}}$, and we parametrize them in 
$\mathcal {M}(\widetilde {\Gamma }_\mathcal {U})$ by the pairs 
$({rc}m, / \sigma)$, 
$\sigma \in \widehat {{\mathbb {Z}}/c{\mathbb {Z}}}$. This completes the parametrization via 
$\mathcal {M}(\widetilde {\Gamma }_\mathcal {U}^{{\mathbb {Z}}/m{\mathbb {Z}}})$ of the unipotent representations for 
${\mathrm {InnT}}^p {\mathbb {G}}$ corresponding to the family 
$\mathcal {U}=\{\rho \}$ in 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$.
Example 6.5 Let 
${\mathbb {G}} = \mathrm {O}_{2n}, {\mathbb {G}}^\circ ={\mathsf {SO}}_{2n}$, 
$n\geqslant 2$, 
$A={\mathbb {Z}}/2{\mathbb {Z}} =\langle \delta \rangle$. There are two pure inner twists 
${\mathrm {InnT}}^p{\mathbb {G}}=\{\mathrm O^+_{2n}(\mathbb {F}_q),\mathrm O^-_{2n}(\mathbb {F}_q)\}$. In this case, we use the parametrizations of [Reference LusztigLuz84a, §§ 4.6, 4.18]. Recall that a symbol for type 
$D_n$ is an array 
$\Lambda =\big (\begin{smallmatrix}\lambda _1 & \lambda _2 & \dots & \lambda _b\\\mu _1 & \mu _2 & \dots & \mu _{b'}\end{smallmatrix}\big )$, 
$b+b'=2m$, 
$0\leqslant \lambda _1<\dots <\lambda _{b'}$, 
$0\leqslant \mu _1<\dots <\mu _{b'}$, which is considered the same as the array where the rows are flipped. A symbol where 
$b=b'=m$ and 
$\lambda _1\leqslant \mu _1\leqslant \lambda _2\leqslant \mu _2\leqslant \dots$, 
$\sum \lambda _i^2+\lambda \mu _i^2=n+m^2-m$ is called special.
Let 
$Z$ be a special symbol. In the case when 
$\lambda _i=\mu _i$ for all 
$1\leqslant i\leqslant m$, one attaches to 
$Z$ two unipotent 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$-families, 
$\mathcal {U}'=\{\rho \}$ and 
$\mathcal {U}''=\{\rho '\}$, each consisting of a single unipotent representation and with 
$\Gamma _{\mathcal {U}'}=\Gamma _{\mathcal {U}''}=\{1\}$. In this case, the action of 
$\delta$ flips the two families. Hence they give rise to a single family 
$\{\widetilde {\rho }\}$ for 
${\mathbb {G}}^{F_0}$, 
$\widetilde {\rho }|_{{{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}}=\rho \oplus \rho '$, and 
$\widetilde {\Gamma }_{\mathcal {U}'}=\{1\}$.
Assume now that the two rows of the symbol 
$Z$ are not identical, i.e. 
$Z$ is nondegenerate in the sense of [Reference LusztigLuz84a]. Then 
$Z$ defines one unipotent family for 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$ and one for 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_1}$. Each element of these families is stable under 
$\delta$ so it can be lifted to two different 
${\mathbb {G}}^{{\mathrm {Fr}}_0}$, respectively 
${\mathbb {G}}^{{\mathrm {Fr}}_1}$, representations.
The unipotent representations in the 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$-family 
$\mathcal {U}_Z$ corresponding to 
$Z$ are indexed by the set 
$\mathcal {M}_Z$ of symbols 
$\Lambda$ such that 
$b-b'\equiv 0$ mod 
$4$, 
$b+b'=2m$. The unipotent representations in the 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_1}$-family 
$\mathcal {U}^-_Z$ corresponding to 
$Z$ are indexed by the set 
$\mathcal {M}_Z^-$ of symbols 
$\Lambda$ such that 
$b-b'\equiv 2$ mod 
$4$, 
$b+b'=2m$. Let 
$Z_1$ be the set of elements that appear as entries of 
$Z$ only once. Let 
$2d=|Z_1|$. Define:
–
$V_{Z_1}$ as the set of subsets $X\subseteq Z_1$ of even cardinality, with the structure of an $\mathbb {F}_2$-vector space with the sum given by the symmetric difference;–
$V_{Z_1}'$ as the set of subsets $X\subseteq Z_1$ with the structure of an $\mathbb {F}_2$-vector space with the sum given by the symmetric difference, modulo the line spanned by $Z_1$ itself;–
$(V_{Z_1}')^+$ as the subspace of $V_{Z_1}'$ where the elements are the subsets $X$ of even cardinality;–
$(V_{Z_1}')^-$ as the subspace of $V_{Z_1}'$ where the elements are the subsets $X$ of odd cardinality.
Note that 
$(V_{Z_1}')^+$ is also the image of the projection of 
$V_{Z_1}$ to 
$V_{Z_1}'$. The dimensions of 
$V_{Z_1}'$ and 
$V_{Z_1}$ over 
$\mathbb {F}_2$ are 
$2d-1$, while the dimension of 
$(V_{Z_1}')$ is 
$2d-2$. There is a nonsingular pairing
\begin{equation} (\,{,}\,)\colon V_{Z_1}'\times V_{Z_1}\to \mathbb{F}_2,\quad (X_1,X_2)\mapsto |X_1\cap X_2| \text{ mod }2. \end{equation}
This pairing restricts to a nonsingular symplectic 
$\mathbb {F}_2$-form of 
$(V_{Z_1}')^+$. If 
$V_{Z_1}$ has the basis 
$e_1,e_2,\ldots,e_{2d-1}$ as in [Reference LusztigLuz84a], then 
$(V_{Z_1}')^+$ is spanned by the images 
$\bar {e}_1,\bar {e}_2,\ldots,\bar {e}_{2d-1}$ modulo the relation 
$\bar {e}_1+\bar {e}_3+\dots +\bar {e}_{2d-1}=0$. Let
\begin{align*} \bar{I}'&=\text{subspace of }(V_{Z_1}')^+\text{ spanned by } \bar{e}_1,\bar{e}_3,\ldots,\bar{e}_{2d-1},\\ \bar{I}''&=\text{subspace of }(V_{Z_1}')^+\text{ spanned by } \bar{e}_2,\bar{e}_4,\ldots,\bar{e}_{2d-2}; \end{align*}
they are maximal isotropic subspaces of 
$(V_{Z_1}')^+$ and 
$(V_{Z_1}')^+=\bar {I}'\oplus \bar {I}''$. Then
\[ \Gamma_{\mathcal{U}_Z}=\bar{I}''\cong ({\mathbb{Z}}/2{\mathbb{Z}})^{d-1}. \]
As shown in [Reference LusztigLuz84a, § 4.6], there is a natural bijection
\[ \mathcal{M}_Z\leftrightarrow \mathcal{M}(\Gamma_{\mathcal{U}_Z})\cong (V_{Z_1}')^+=\bar{I}'\oplus\bar{I}'' \]
(where 
$\bar {I}'$ is identified with the group of characters of 
$\Gamma _{\mathcal {U}_Z}$). Denote
\begin{equation} \widetilde{\Gamma}_{\mathcal{U}_Z}=\{v\in V_{Z_1}'\mid (v,e_{2i})=0,\ 1\leqslant i\leqslant d-1\}\cong ({\mathbb{Z}}/2{\mathbb{Z}})^d. \end{equation}
Clearly, 
$\Gamma _{\mathcal {U}_Z}\unlhd \widetilde {\Gamma }_{\mathcal {U}_Z}$. As shown in [Reference LusztigLuz84a, § 4.18], there is a natural bijection
\[ \mathcal{M}_Z^-\leftrightarrow \overline{\mathcal{M}}(\Gamma_{\mathcal{U}_Z}\unlhd\widetilde{\Gamma}_{\mathcal{U}_Z})\cong (V_{Z_1}')^-\cong (\widetilde{\Gamma}_{\mathcal{U}_Z}\setminus \Gamma_{\mathcal{U}_Z})\times \bar{I}'. \]
Let 
$\widetilde {\mathcal {U}}_Z$ be the set (family) of irreducible representations in 
${\mathrm {Irr}}_{\mathrm {un}} {\mathbb {G}}^{{\mathrm {Fr}}_0}\sqcup {\mathrm {Irr}}_{\mathrm {un}} {\mathbb {G}}^{{\mathrm {Fr}}_1}$ whose restrictions to 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$ (respectively, 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_1}$) are in 
$\mathcal {U}_Z$ (respectively, 
$\mathcal {U}_Z^-$). Since each unipotent representation in 
$\mathcal {U}_Z$ and 
$\mathcal {U}_Z^-$ extends in two different ways to the corresponding disconnected group, the parametrization above implies easily that there is natural bijection
\begin{equation} \widetilde{\mathcal{U}}_Z\longleftrightarrow \mathcal{M}(\widetilde{\Gamma}_{\mathcal{U}_Z}). \end{equation}
Explicitly, let 
$\{\bar {f}_1,\bar {f}_2,\ldots,\bar {f}_d\}$ be the spanning set of 
$V_{Z_1}'$ subject to 
$\sum _{i=1}^{2d} \bar {f}_i=0$, such that 
$\bar {e}_i=\bar {f}_i+\bar {f}_{i+1}$, 
$1\leqslant i \leqslant 2d-1$. Then an 
$\mathbb {F}_2$-basis of 
$\widetilde {\Gamma }_{\mathcal {U}_Z}$ is given by 
$\{\bar {f}_1,\bar {e}_2,\bar {e}_4,\ldots, \bar {e}_{2d}\}$. An irreducible character of 
$\Gamma _{\mathcal {U}_Z}=\langle \bar {e}_2,\bar {e}_4,\ldots, \bar {e}_{2d}\rangle$ can be extended in two different ways to 
$\widetilde {\Gamma }_{\mathcal {U}_Z}$ by setting the character value on 
$\bar {f}_1$ to 
$1$ or 
$-1$. The value 
$1$ corresponds to the representations of the identity components of 
${\mathbb {G}}^{{\mathrm {Fr}}_0}$, 
${\mathbb {G}}^{{\mathrm {Fr}}_1}$ extended by letting 
$\delta$ act trivially, while the 
$-1$ value corresponds to those where 
$\delta$ acts by 
$-1$.
Example 6.6 Let 
${\mathbb {G}}^\circ$ be of type 
$A_{k-1}$, 
$k\geqslant 3$ or 
$E_6$, and 
$A={\mathbb {Z}}/2{\mathbb {Z}}=\langle \delta \rangle$ acting by the nontrivial automorphism of the Dynkin diagram. The nonsplit pure inner twist has 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_1}$ of type 
$^2\!A_{k-1}$ or 
$^2\!E_6$, respectively. By [Reference LusztigLuz84a, § 4.19], every unipotent family 
$\mathcal {U}$ of 
${\mathbb {G}}^\circ$ is fixed pointwise by 
$A$. Hence,
\[ \widetilde{\Gamma}_\mathcal{U}^{{\mathbb{Z}}/2{\mathbb{Z}}}=\Gamma_U\times {\mathbb{Z}}/2{\mathbb{Z}},\quad\text{for all } \mathcal{U}. \]
Each irreducible representation 
$\rho$ of the split form 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$ can be extended to 
${\mathbb {G}}^{{\mathrm {Fr}}_0}$ in two different ways 
$\rho ^\pm$ corresponding to the two characters of 
$\mathbb {Z}/2{\mathbb {Z}}$. If the parameter for 
$\rho$ is 
$\bar {x}_\rho =(x,\sigma )\in \mathcal {M}(\Gamma _\mathcal {U})$, then the parameters for 
$\rho ^\pm$ are 
$((x,1), \sigma ^\pm )$ with the obvious notation.
Similarly, an irreducible representation 
$\rho '$ of the nonsplit pure inner twist 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_1}$ can be extended to 
${\mathbb {G}}^{{\mathrm {Fr}}_1}$ in two different ways 
${\rho '}^\pm$. If the parameter for 
$\rho '$ is 
$\bar {x}_\rho =(x',\sigma ')\in \mathcal {M}(\Gamma _\mathcal {U})$, then the parameters for 
${\rho '}^\pm$ are 
$((x',\delta ), {\sigma '}^\pm )$.
Example 6.7 Let 
${\mathbb {H}}$ be of type 
$D_k$, 
$k\geqslant 2$ and 
${\mathbb {G}}^\circ ={\mathbb {H}}\times {\mathbb {H}}$. Let 
$A=\langle \delta _1\rangle \times \langle \delta _2\rangle \cong {\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/2{\mathbb {Z}}$, where 
$\delta _1$ acts by the nontrivial outer automorphism of the Dynkin diagram of type 
$D_k$, and 
$\delta _2$ flips the 
${\mathbb {H}}$-factors. This case is therefore a combination of Examples 6.5 and 6.3 and the parametrization of families for the pure inner twists of 
${\mathbb {G}}$ follows from these examples, i.e. the same parametrizations as in Example 6.3 but constructed from the orthogonal families 
$\widetilde {U}_Z$ from Example 6.5.
Now for the same 
${\mathbb {H}}$ and 
${\mathbb {G}}^\circ$, suppose 
$A=\langle \delta \rangle ={\mathbb {Z}}/4{\mathbb {Z}}$. If 
$s'_1,s''_1$ are the two commuting extremal reflections of the first 
${\mathbb {H}}=D_k$ and 
$s'_2,s''_2$ are the similar reflections for the second 
${\mathbb {H}}=D_k$, then 
$\delta$ acts by the cyclic permutation:
\[ \delta\colon\quad s'_1\mapsto s'_2\mapsto s''_1\mapsto s''_2\mapsto s'_1. \]
On all the other simple reflections of the two components of type 
$D_k$, 
$\delta$ acts by the obvious diagram flip (of order 
$2$). To describe the pure inner twists, let 
${\mathrm {Fr}}$ denote the Frobenius map of 
${\mathbb {H}}$ whose fixed points is the nonsplit group of type 
$^2\!D_k$. Then
\[ {\mathrm{Fr}}_1\colon {\mathbb{H}}\times {\mathbb{H}}\to {\mathbb{H}}\times {\mathbb{H}}, \quad {\mathrm{Fr}}_1(h_1,h_2)=({\mathrm{Fr}}(h_2),h_1) \]
is a Frobenius automorphism and 
${\mathrm {Fr}}_r={\mathrm {Fr}}_1^r$, 
$r\in {\mathbb {Z}}/4{\mathbb {Z}}$ (see, e.g., [Reference Geck and MalleGM20, Example 1.4.23]). The identity components of the pure inner twists are the finite reductive groups of types:
\[ {{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_0}: ~D_k\times D_k,\quad {{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_1}: ~^2\!D_k,\quad {{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_2}: ~^2\!D_k\times ~^2\!D_k,\quad {{\mathbb{G}}^\circ}^{{\mathrm{Fr}}_3}: ~^2\!D_k. \]
If 
$\rho _1,\rho _2$ are two unipotent representations of 
$D_k$, the action of 
$\delta$ is
\[ \delta(\rho_1,\rho_2)=(\rho_2',\rho_1),\quad\text{where }\rho_2'=\begin{cases}\rho_2, & \text{ if the symbol of }\rho_2\text{ is nondegenerate},\\\rho_2^-, & \text{ otherwise},\end{cases} \]
where 
$\rho ^-_2$ is unipotent representation parametrized by the other degenerate symbol with the same rows. See Example 6.5.
We start with a family 
$\mathcal {U}_1\times \mathcal {U}_2$ of 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}=D_k\times D_k$. If 
$\mathcal {U}_2$ consists of a degenerate symbol, then the stabilizer in 
$A$ is always 
$1$, regardless of what 
$\mathcal {U}_1$ is. (Similarly if 
$\mathcal {U}_1$ is degenerate.) In this case,
\[ \widetilde{\Gamma}_{\mathcal{U}_1\times\mathcal{U}_2}^{{\mathbb{Z}}/4{\mathbb{Z}}}=\Gamma_{\mathcal{U}_1}. \]
(Recall that 
$\Gamma _{\mathcal {U}_2}=1$ necessarily.) Since the stabilizer in 
${\mathbb {Z}}/4{\mathbb {Z}}$ of each representation 
$\rho _1\boxtimes \rho _2$, 
$\rho _1\in \mathcal {U}_1$, 
$\rho _2\in \mathcal {U}_2$ is also trivial in this case, it follows that there is a one-to-one correspondence between the representations 
${\mathrm {Ind}}_{{{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}}^{{\mathbb {G}}^{{\mathrm {Fr}}_0}}(\rho _1\boxtimes \rho _2)$ and 
$\rho _1\in \mathcal {U}_1$, hence a parametrization by 
$\mathcal {M}(\Gamma _{\mathcal {U}_1})$ as expected.
For the rest of the example, assume that all families correspond to nondegenerate symbols. Let 
$Z_1$, 
$Z_2$ be two nondegenerate symbols of type 
$D_k$. Let 
$\mathcal {U}_1,\mathcal {U}_2$ be the corresponding families for 
$D_k$ and 
$\mathcal {U}_1^-$, 
$\mathcal {U}_2^-$ the families for 
$^2\!D_k$. Suppose first that 
$Z_1\neq Z_2$. Then the stabilizer in 
$A$ is 
${\mathbb {Z}}/2{\mathbb {Z}}=\langle \delta ^2\rangle$, hence the group for the pure inner twists is
\[ \widetilde{\Gamma}_{\mathcal{U}_1\boxtimes\mathcal{U}_2}^{{\mathbb{Z}}/4{\mathbb{Z}}}=\Gamma_{\mathcal{U}_1}\times\Gamma_{\mathcal{U}_2}\times {\mathbb{Z}}/2{\mathbb{Z}}. \]
If 
$\rho _1\in \mathcal {U}_1$ and 
$\rho _2\in \mathcal {U}_2$, the stabilizer in 
$A$ of 
$\rho _1\boxtimes \rho _2$ is also 
${\mathbb {Z}}/2{\mathbb {Z}}=\langle \delta ^2\rangle$. By Mackey theory, we get two irreducible representations of 
${\mathbb {G}}^{{\mathrm {Fr}}_0}$ by inducing 
$\rho _1\boxtimes \rho _2$ twisted by the trivial or the sign character of 
${\mathbb {Z}}/2{\mathbb {Z}}$. If 
$\bar {x}_{\rho _i}=(x_i,\sigma _i)\in \mathcal {M}(\Gamma _{\mathcal {U}_i})$, 
$i=1,2$, then the two induced representations are parametrized by 
$((x_1,x_2,1),\sigma _1\boxtimes \sigma _2\boxtimes \tau )\in \mathcal {M}(\Gamma _{\mathcal {U}_1}\times \Gamma _{\mathcal {U}_2}\times {\mathbb {Z}}/2{\mathbb {Z}})$, where 
$\tau$ is the trivial or the sign character of 
${\mathbb {Z}}/2{\mathbb {Z}}$.
If 
$\rho _1'\in \mathcal {U}_1^-$ and 
$\rho _2'\in \mathcal {U}_2^-$, the analysis is analogous. The difference is that 
$\bar {x}_{\rho _i'}=(x_i',\sigma _i')\in \overline {\mathcal {M}}(\Gamma _{\mathcal {U}_i}\unlhd \widetilde {\Gamma }_{\mathcal {U}_i})$, 
$i=1,2$, where 
$x_i'\in \widetilde {\Gamma }_{\mathcal {U}_i}\setminus \Gamma _{\mathcal {U}_i}$, 
$\sigma _i\in \widehat {\Gamma }_{\mathcal {U}_i}$. Write 
$x_i=y_i\alpha$, 
$i=1,2$, 
$y_i\in \Gamma _{\mathcal {U}_i}$, where 
$\alpha$ is the nontrivial automorphism of the 
$D_k$ diagram. Then the two unipotent representations of 
${\mathbb {G}}^{{\mathrm {Fr}}_2}$ whose restriction to 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_2}$ contain 
$\rho _1'\boxtimes \rho _2'$ are parametrized by 
$((y_1,y_2,\delta ^2),\sigma _1\boxtimes \sigma _2\boxtimes \tau )\in \mathcal {M}(\Gamma _{\mathcal {U}_1}\times \Gamma _{\mathcal {U}_2}\times {\mathbb {Z}}/2{\mathbb {Z}})$, where 
$\tau$ is the trivial or the sign character of 
${\mathbb {Z}}/2{\mathbb {Z}}$.
Finally, if 
$Z_1=Z_2=Z$ with the families 
$\mathcal {U}$ of 
$D_k$ and 
$\mathcal {U}^-$ of 
$^2\!D_k$, then the stabilizer of 
$\mathcal {U}\boxtimes \mathcal {U}$ is 
$A={\mathbb {Z}}/4{\mathbb {Z}}$. In this case, set
\begin{equation} \widetilde{\Gamma}_{\mathcal{U}\boxtimes\mathcal{U}}^{{\mathbb{Z}}/4{\mathbb{Z}}}=(\Gamma_{\mathcal{U}}\times\Gamma_{\mathcal{U}})\rtimes {\mathbb{Z}}/4{\mathbb{Z}}. \end{equation}
All four pure inner twists 
${\mathbb {G}}^{{\mathrm {Fr}}_r}$ contribute in this case. Each conjugacy class in 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}$ is represented by an element 
$(x,y,r)$ with 
$x,y\in \Gamma _\mathcal {U}$ and 
$r\in {\mathbb {Z}}/4{\mathbb {Z}}$. It will correspond to a unipotent representation of 
${\mathbb {G}}^{{\mathrm {Fr}}_r}$, for the same 
$r$.
If 
$r=0$, then the conjugacy classes are given by 
$(x,x',0)\sim (x',x,0)$ and its stabilizer in 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}$ is 
$\Gamma _\mathcal {U}^2 \times \langle \delta ^2\rangle$ if 
$x\neq x'$, or all of 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}$ if 
$x=x'$. If 
$\rho,\rho '\in \mathcal {U}$ with parameters 
$\bar {x}_\rho =(x,\sigma )$, 
$\bar {x}_{\rho '}=(x',\sigma ')$, it is clear that there is a perfect matching between the induced representation coming from the Mackey construction and the parameters 
$((x,x',\bar 0),\widetilde {\sigma })\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}})$, where 
$\widetilde {\sigma }\in \widehat {{\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}}((x,x',\bar 0))}$.
If 
$r=2$, the conjugacy classes are given by 
$(x,x',\delta ^2)\sim (x',x,\delta ^2)$ and its stabilizer in 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}$ is 
$\Gamma _\mathcal {U}^2 \times \langle \delta ^2\rangle$ if 
$x\neq x'$ or all 
$\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}$ if 
$x=x'$. If 
$\rho,\rho '\in \mathcal {U}^-$ with parameters 
$\bar {x}_\rho ^-=(x\alpha,\sigma )$, 
$\bar {x}_{\rho '}^-=(x'\alpha,\sigma ')$, again there is a perfect matching between the induced representations coming from the Mackey construction and the parameters 
$((x,x',\delta ^2),\widetilde {\sigma })\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}})$, where 
$\widetilde {\sigma }\in \widehat {{\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}}((x,x',\bar 2))}$.
If 
$r=1$ or 
$3$, the conjugacy classes are given by 
$(x,1,\delta ^r)$, cf. Example 6.3. The stabilizer in this case is 
$\langle \Gamma _\mathcal {U}^\Delta,\delta ^2,(x,1,\delta )\rangle$. Let 
$\rho$ be a representation in the unipotent family 
$\mathcal {U}^-$ with parameter 
$\bar {x}_\rho =(x\alpha,\sigma )$, 
$\sigma \in \widehat {\Gamma }_\mathcal {U}$. It can be extended in four different ways to 
$^2\!D_k\rtimes {\mathbb {Z}}/4{\mathbb {Z}}$ corresponding to the characters of 
${\mathbb {Z}}/4{\mathbb {Z}}$. Since 
$x$ has order 
$2$, the cyclic group
\[ \langle (x,1,\delta)\rangle=\langle (1,1,1), (x,1,\delta), (x,x,\delta^2), (1,x,\delta^3)\rangle\cong {\mathbb{Z}}/4{\mathbb{Z}}. \]
Note that there is a short exact sequence (that does not split)
\[ 1\longrightarrow \Gamma_\mathcal{U}^\Delta\longrightarrow {\mathrm{Z}}_{\widetilde{\Gamma}_{\mathcal{U}\boxtimes\mathcal{U}}^{{\mathbb{Z}}/4{\mathbb{Z}}}}((x,1,\delta^r))\longrightarrow {\mathbb{Z}}/4{\mathbb{Z}}\longrightarrow 1, \]
where the quotient 
${\mathbb {Z}}/4{\mathbb {Z}}$ is generated by the image of 
$(x,1,\delta )$. This means that 
$\sigma \in \widehat {\Gamma }_\mathcal {U}$, viewed as a representation of 
$\Gamma _\mathcal {U}^\Delta$ can be lifted in four different ways to 
${\mathrm {Z}}_{\widetilde {\Gamma }_{\mathcal {U}\boxtimes \mathcal {U}}^{{\mathbb {Z}}/4{\mathbb {Z}}}}((x,1,\delta ^r))$: the first can lift 
$\sigma$ in two different ways to 
$\sigma ^\pm$, representations of 
$\Gamma _\mathcal {U}^\Delta \times \langle \delta ^2\rangle$ corresponding to the trivial and the sign character of 
$\langle \delta ^2\rangle$. Then, fixing a square roots 
$\zeta ^\pm$ of 
$\sigma ^\pm (x,x,\delta ^2)$, one constructs lifts 
$\widetilde {\sigma }^i$ of 
$\sigma$, 
$0\leqslant i\leqslant 3$, by setting
\[ \widetilde{\sigma}^0((x,1,\delta))=\zeta^+,\quad \widetilde{\sigma}^1((x,1,\delta))=-\zeta^+,\quad \widetilde{\sigma}^2((x,1,\delta))=\zeta^-,\quad \widetilde{\sigma}^3((x,1,\delta))=-\zeta^-. \]
Note that 
$\{\pm \zeta ^\pm \}$ is the set of fourth roots of 
$1$, and this gives the desired parametrization.
Example 6.8 Let 
${\mathbb {G}}^\circ$ be of type 
$D_4$ and 
$A={\mathbb {Z}}/3{\mathbb {Z}}=\langle \delta \rangle$ acting on the Dynkin diagram by cyclically permuting the extremal nodes. The Weyl group 
$W(D_4)$ has 
$13$ irreducible representations which we denote by bipartitions of 
$4$, 
$\alpha \times \beta$ up to swapping 
$\alpha$ and 
$\beta$, except where 
$\alpha =\beta$, there are two nonisomorphic representations 
$\alpha \times \alpha ^\pm$. There is one cuspidal unipotent representation 
$\rho _c$, and in total 
$14$ unipotent representations of 
${{\mathbb {G}}^\circ }^{{\mathrm {Fr}}_0}$.
All families are singletons with associated finite group 
$\Gamma _\mathcal {U}=\{1\}$, except the family
\[ \{(12)\times(1), (22)\times\emptyset, (11)\times (2),\rho_c\} \]
for which the finite group is 
$\Gamma _\mathcal {U}={\mathbb {Z}}/2{\mathbb {Z}}$. This family and the following four singleton families:
\[ \{(4)\times\emptyset\},\quad \{(1111)\times\emptyset\},\quad \{(3)\times (1)\},\quad \{(111)\times (1)\} \]
are 
$A$-stable and, in fact, each element in the four-element family is 
$A$-stable. The remaining six unipotent (singleton) families form two 
$A$-orbits:
\[ \{(13)\times\emptyset, (2)\times (2)^+,(2)\times (2)^-\}\quad\text{and}\quad \{(112)\times\emptyset, (11)\times (11)^+,(11)\times (11)^-\}. \]
According to our recipe, the groups 
$\widetilde {\Gamma }_{\mathcal {U}}^{{\mathbb {Z}}/3{\mathbb {Z}}}$ are:
–
${\mathbb {Z}}/3{\mathbb {Z}}$ corresponding to each of the four $A$-stable singleton families $\mathcal {U}$;–
${\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}}$ for the unique family with four elements;–
$\{1\}$ for each one of the two nontrivial $A$-orbits.
Hence, the right-hand side of Proposition 6.1 is 
$\mathcal {M}({\mathbb {Z}}/3{\mathbb {Z}})^4\sqcup \mathcal {M}({\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/3{\mathbb {Z}})\sqcup \mathcal {M}(\{1\})^2$ which has 
$3^2\times 4+6^2+1^2\times 2=74$ elements.
The irreducible unipotent representations of the disconnected group 
$D_4\rtimes {\mathbb {Z}}/3{\mathbb {Z}}$ are parametrized, via Mackey theory, by the elements 
$(x,\sigma )\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}}^{{\mathbb {Z}}/3{\mathbb {Z}}})$, where 
$x\in \Gamma _{\mathcal {U}}$ and 
$\mathcal {U}$ ranges over a set of representatives of the 
$A$-orbits of families of 
$D_4$. There are 
$26$ such irreducible representations.
The other two 
$A$-forms corresponding to 
$\delta$ and 
$\delta ^{-1}$ are both isomorphic to the finite group of type 
$^3\!D_4$. There are eight irreducible unipotent representations of 
$^3\!D_4$ each coming from one of 
$\gamma$-stable irreducible unipotent representations of 
$D_4$. By induction, there are 
$8\times 3=24$ irreducible unipotent representations of 
$^3\!D_4\rtimes {\mathbb {Z}}/3{\mathbb {Z}}$. The irreducible representations of the 
$^3\!D_4$ corresponding to 
$\delta$ are parametrized by 
$(x\delta,\sigma )\in \mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}}^{{\mathbb {Z}}/3{\mathbb {Z}}})$, where 
$x\in \Gamma _{\mathcal {U}}$ and 
$\mathcal {U}$ ranges over the set of 
$A$-stable families. Similarly for 
$\delta ^{-1}$.
7. Maximal compact subgroups
We return to the setting of § 2, so 
${\mathbf {G}}$ is a connected reductive group over 
$F$ and 
$G = {\mathbf {G}}(F)$. In this section, we assume in addition that 
${\mathbf {G}}$ is simple and 
$F$-split with maximal 
$F$-split torus 
$\mathbf {S}$. Let 
$\Pi _G$ be a set of simple roots for 
${\mathbf {G}}$ with respect to 
$\mathbf {S}$, and extend 
$\Pi _G$ to a set of simple affine roots 
$\Pi ^a_G = \Pi _G \cup \{\alpha _0\}$. Let 
$I \subset {\mathbf {G}}({\mathfrak {o}}_F)$ be the corresponding Iwahori subgroup of 
$G$, with 
$\mathbf {S}(\mathfrak {o}_F)=\mathbf {S}(F)\cap I$. Let 
$\widetilde {W}_G={\mathrm {N}}_{G}(\mathbf {S}(F))/\mathbf {S}(\mathfrak {o}_F)$ be the Iwahori–Weyl group. We have
\[ G=\bigsqcup_{w\in \widetilde{W}_G} I \dot{w}I, \]
where 
$\dot {w}$ denotes a choice of a lift in 
$N_{G}(\mathbf {S}(F))$ of 
$w\in \widetilde {W}_G$. The finite Weyl group is 
$W_G = {\mathrm {N}}_{G}(\mathbf {S}(F))/\mathbf {S}(F)$. Let 
$W^a_G$ be the affine Weyl group generated by the simple reflections 
$\{s_i\mid i\in \Pi ^a_G\}$. Then
\[ \widetilde{W}_G=W^a_G\rtimes\Omega_G, \]
where 
$\Omega _G$ is a finite abelian group, the stabilizer in 
$\widetilde {W}_G$ of 
$I$.
Let 
$\max (G)$ denote the set of conjugacy classes of maximal compact open subgroups in 
$G$. To parametrize 
$\max (G)$, we define 
$S_{\rm max}(G)$ to be the set of 
$\Omega _G$-orbits of pairs 
$(A, \mathcal {O})$, where 
$A$ is a subgroup of 
$\Omega _G$ and 
$\mathcal {O}$ is an 
$A$-orbit in 
$\Pi ^a_G$ satisfying
\[ \mathrm{Stab}_{\Omega_G}(\mathcal{O})=A. \]
By [Reference Iwahori and MatsumotoIM65, Reference Bruhat and TitsBT72], 
$\max (G)$ is parametrized by 
$S_{\rm max}(G)$. Explicitly, given 
$(A, \mathcal {O}) \in S_{\rm max}(G)$, we construct an element 
$K_\mathcal {O} \in \max (G)$ as follows: let 
$\widetilde {W}_{\mathcal {O}}$ be the finite subgroup of 
$\widetilde {W}_G$ generated by 
$A$ and 
$\{s_i,\ i\in \Pi ^a_G\setminus \mathcal {O}\}$. Set
\[ K_{\mathcal{O}}=\bigsqcup_{w\in \widetilde{W}_{\mathcal{O}}} I\dot{w} I. \]
The map 
$(A, \mathcal {O}) \mapsto K_\mathcal {O}$ defines a bijection between 
$S_{\rm max}(G)$ and 
$\max (G)$. (Note that a pair 
$(A, \mathcal {O}) \in S_{\rm max}(G)$ is completely determined by 
$\mathcal {O}$, so the notation 
$K_\mathcal {O}$ is unambiguous.) In this notation, the maximal hyperspecial subgroup 
${\mathbf {G}}(\mathfrak {o}_F)$ is 
$K_{\{\alpha _0\}}$, where 
$\alpha _0$, as defined above, is the unique simple affine root in 
$\Pi ^a_G \setminus \Pi _G$.
Given 
$(A, \mathcal {O}) \in S_{\rm max}(G)$, let 
$\widetilde {W}_{\mathcal {O}}^\circ$ be the normal subgroup of 
$\widetilde {W}_{\mathcal {O}}$ generated by 
$\{s_i,\ i\in \Pi _G^a\setminus \mathcal {O}\}$. Then 
$K_{\mathcal {O}}^\circ :=\bigsqcup _{w\in \widetilde {W}_{\mathcal {O}}^\circ } I\dot {w} I$ is a parahoric subgroup of 
$G$, and we denote by 
$K_{\mathcal {O}}^+$ its pro-unipotent radical. There is a short exact sequence
\[ 1\longrightarrow K_{\mathcal{O}}^\circ\longrightarrow K_{\mathcal{O}}\longrightarrow A\longrightarrow 1. \]
Set 
$\overline {K}_{\mathcal {O}}^\circ =K_{\mathcal {O}}^\circ /K_{\mathcal {O}}^+$ and 
$\overline {K}_{\mathcal {O}}=K_{\mathcal {O}}/K_{\mathcal {O}}^+$. Then 
$\overline {K}_{\mathcal {O}}=M_{\mathcal {O}}(k_F)$, 
$\overline {K}_{\mathcal {O}}^\circ =M_{\mathcal {O}}^\circ (k_F)$, for a reductive 
$k_F$-split group 
$M_{\mathcal {O}}$ with identity component 
$M_{\mathcal {O}}^\circ$ and 
$M_{\mathcal {O}}/M_{\mathcal {O}}^\circ \cong A$. Let 
${\mathrm {InnT}}^p \overline {K}_{\mathcal {O}}\leftrightarrow A$ be the collection of pure inner twists of 
$M_\mathcal {O}$.
Now we consider pure inner twists of 
$G$. By § 2, 
${\mathrm {InnT}}^p G\cong {\mathrm {H}}^1(F,{\mathbf {G}})$. If 
${\mathbf {G}}_{\mathrm {sc}}$ is the simply connected cover of 
${\mathbf {G}}$ and identifying 
$\Omega _G$ with the kernel of the surjection 
${\mathbf {G}}_{\mathrm {sc}}\to {\mathbf {G}}$, then by [Reference KneserKne65, Satz 2], 
${\mathrm {H}}^1(F,{\mathbf {G}})\cong {\mathrm {H}}^2(F,\Omega _G)\cong \Omega _G$, with the last equivalence because 
${\mathbf {G}}$ is 
$F$-split. Given 
$x \in \Omega _G$, let 
$G_x \in {\mathrm {InnT}}^p G$ be the corresponding pure inner twist. If we denote the set of conjugacy classes of maximal compact open subgroups of 
$G_x$ by 
$\max (G_x)$, then there is a one-to-one correspondence
\begin{equation}
\{(A,\mathcal{O}) \in S_{\rm max}(G) \mid x \in A\} \longleftrightarrow \max(G_x), \end{equation}
which we write as 
$(A, \mathcal {O}) \mapsto K_{x, \mathcal {O}}$. More precisely, we can realize 
$K_{x, \mathcal {O}}$ in the following way. We realize 
$G_x$ as the subgroup of 
${\mathbf {G}}(F_{{\mathrm {un}}})$ fixed under the 
${\mathrm {Gal}}(F_{{\mathrm {un}}}/F)$-action corresponding to 
$x$. Then since 
$x \in A$, the parahoric of 
${\mathbf {G}}(F_{{\mathrm {un}}})$ corresponding to 
$(A, \mathcal {O})$ as above is 
${\mathrm {Gal}}(F_{{\mathrm {un}}}/F)$-stable. Let 
$K_{x, \mathcal {O}}^\circ \subset G_x$ be the Galois-fixed subgroup. By [Reference Bruhat and TitsBT72, 3.3.4 Proposition] (applied using [Reference Bruhat and TitsBT84, 5.2.12 Proposition]), the normalizer 
$K_{x, \mathcal {O}} := N_{G_x}(K_{x, \mathcal {O}}^\circ )$ is a maximal compact subgroup of 
$G_x$.
Note that 
$\overline {K}_{x,\mathcal {O}} \in {\mathrm {InnT}}^p\overline {K}_{\mathcal {O}}$ is the pure inner twist given by 
$x\in A\cong {\mathrm {H}}^1(k_F,M_\mathcal {O})\leftrightarrow {\mathrm {InnT}}^p\overline {K}_{\mathcal {O}}$ (see § 6). For fixed 
$(A, \mathcal {O}) \in S_{\rm max}(G)$, we have
\begin{equation} {\mathrm{InnT}}^p \overline{K}_\mathcal{O} = \{\overline{K}_{x, \mathcal{O}} \mid x \in A\}. \end{equation}
Given 
$G' \in {\mathrm {InnT}}^p(G)$, for every maximal compact open subgroup 
$K' \in \max (G')$, define 
$R_{\mathrm {un}}(\overline {K}')$ to be the 
$\mathbb {C}$-span of 
${\mathrm {Irr}}_{\mathrm {un}} \overline {K}'$, and let
\begin{equation}
{\mathcal{C}}(G)_{{\mathrm{cpt}},{\mathrm{un}}} =
\bigoplus_{G'\in {\mathrm{InnT}}^p G}\ \bigoplus_{K'\in \max(G')} R_{\mathrm{un}}
(\overline{K}'). \end{equation}
By the discussion above, we have
\begin{align}
\mathcal{C}(G)_{{\mathrm{cpt}, \mathrm{un}}} &= \bigoplus_{x \in \Omega}\ \bigoplus_{\substack{(A, \mathcal{O}) \in S_{\rm max}(G)\\ \text{ with } x \in A}} R_{\mathrm{un}}(\overline{K}_{x, \mathcal{O}}) \end{align}
\begin{align}
&=\bigoplus_{(A, \mathcal{O}) \in S_{\rm max}(G)}\ \bigoplus_{x \in A} R_{\mathrm{un}}(\overline{K}_{x, \mathcal{O}}). \end{align}
Note that for each 
$(A, \mathcal {O}) \in S_{\rm max}(G)$, by (7.2), 
$\bigoplus _{x \in A} R_{{\mathrm {un}}}(\overline {K}_{x, \mathcal {O}})$ has the involution 
${\mathrm {FT}}_{\overline {K}_\mathcal {O}}$ given by (6.3). Putting together these involutions for all choices of 
$(A, \mathcal {O})$ gives the following definition.
Definition 7.1 Let 
${\mathrm {FT}}_{{\mathrm {cpt}},{\mathrm {un}}}=\bigoplus _{(A, \mathcal {O}) \in S_{\rm max}(G)}{\mathrm {FT}}_{\overline {K}_\mathcal {O}}$ be the involution on 
${\mathcal {C}}(G)_{{\mathrm {cpt}},{\mathrm {un}}}$ defined by using (6.3) and (7.2).
Note that 
${\mathrm {FT}}_{{\mathrm {cpt}},{\mathrm {un}}}$ always preserves the space 
$R_{\mathrm {un}} (\overline {{\mathbf {G}}({\mathfrak {o}}_F)})$, since 
${\mathbf {G}}({\mathfrak {o}}_F)$ corresponds to the pair 
$(A, \{\alpha _0\})$ with 
$A$ trivial. In the case when 
${\mathbf {G}}$ is simply connected, we have 
$\Omega _G = 1$ and 
$K_{\mathcal {O}}=K^\circ _{\mathcal {O}}$ for all 
$\mathcal {O}$, so 
${\mathrm {FT}}_{{\mathrm {cpt}},{\mathrm {un}}}$ preserves the space 
$R_{\mathrm {un}} (\overline {K}_\mathcal {O})$ for all 
$K_\mathcal {O} \in \max (G)$. But, in general, it does not preserve 
$R_{\mathrm {un}} (\overline {K}_{x,\mathcal {O}})$ for every maximal compact open subgroup 
$K_{x, \mathcal {O}}$, which can be seen even in the case when 
${\mathbf {G}} = {\mathsf {PGL}}_2$ (see Example 14.3).
Example 7.2 We list the type of groups 
$\overline {K}_\mathcal {O}$ in the case when 
${\mathbf {G}}$ is adjoint. Since we are only interested in unipotent representations, only the Lie type of 
$\overline {K}_\mathcal {O}^\circ$ is important.
(i) If
${\mathbf {G}}$ is also simply connected, which is the case for types $G_2$, $F_4$ and $E_8$, the set $\max (G)$ is in one-to-one correspondence with the maximal subsets of $\Pi _a$ (equivalently, $\mathcal {O}$ is a single vertex in $\Pi ^a_G$).(ii) If
${\mathbf {G}}={\mathsf {PGL}}_n$, $\Omega _G={\mathbb {Z}}/n{\mathbb {Z}}$ acting by cyclically permuting $\Pi ^a_G$, then for every divisor $m$ of $n$, we have an orbit $\mathcal {O}_m$ in $\Pi ^a_G$ with stabilizer $A={\mathbb {Z}}/m{\mathbb {Z}}$ and
where the semidirect product is given by the permutation action. This case corresponds to Example 6.4.\[ \overline{K}_{\mathcal{O}_m}=P({\mathsf{GL}}_{n/m}^m)\rtimes {\mathbb{Z}}/m{\mathbb{Z}}, \]
(iii) If
${\mathbf {G}}={\mathsf {SO}}_{2n+1}$, $\Omega _G={\mathbb {Z}}/2{\mathbb {Z}}$, then $\overline {K}_\mathcal {O}$ is either ${\mathsf {SO}}_{2n+1}$ ($A=1$) or ${\mathsf {SO}}_{2m+1}\times {\mathrm {O}}_{2(n-m)}$ ($A={\mathbb {Z}}/2{\mathbb {Z}}$), for $0\leqslant m< n$. This case corresponds to Example 6.5.(iv) If
${\mathbf {G}}=\mathrm {PSp}_{2n}$, $\Omega ={\mathbb {Z}}/2{\mathbb {Z}}$, then $\overline {K}_\mathcal {O}$ is of type:
–
$C_k\times C_\ell$ ($A=1$) for $0\leqslant k<\ell$, $k+\ell =n$;–
$(C_k\times C_k)\rtimes {\mathbb {Z}}/2{\mathbb {Z}}$ ($A={\mathbb {Z}}/2{\mathbb {Z}}$), if $n=2k$; or–
$(C_i\times C_i\times A_{n-1-2i})\rtimes {\mathbb {Z}}/2$ ($A={\mathbb {Z}}/2{\mathbb {Z}}$), for $0\leqslant i < {{n}/{2}}$.
${\mathbb {Z}}/2{\mathbb {Z}}$ acts by flipping the two type $C$ factors and by the nontrivial diagram automorphism on the type $A$ factor. These cases are covered by Examples 6.3 and 6.6.(v) If
${\mathbf {G}}=\mathrm {PSO}_{4m}$, $m\geqslant 2$, $\Omega _G=\langle \delta _1\rangle \times \langle \delta _2\rangle \cong {\mathbb {Z}}/2{\mathbb {Z}}\times {\mathbb {Z}}/2{\mathbb {Z}}$, then $\delta _1$ acts by flipping $\Pi _a$ horizontally and $\delta _2$ by the vertical flip. For each subgroup $A\leqslant \Omega _G$, we give the possible $\overline {K}_\mathcal {O}^\circ$.
(a) If
$A=\Omega$, $\overline {K}_\mathcal {O}^\circ$ is of type $D_k\times D_k\times A_{2m-2k-1}$, $2\leqslant k< m$, $D_{m}\times D_{m}$ or $A_{2m-3}$, where $A$ acts on $D_\ell \times D_\ell$ as in Example 6.7, while on $A_{2m-2k-1}$ $\delta _1$ acts trivially and $\delta _2$ by the nontrivial diagram automorphism.(b) If
$A=\langle \delta _1\rangle$, $\overline {K}_\mathcal {O}^\circ$ is of type $D_k\times D_{2m-k}$, $2\leqslant k< m$ or $D_{2m-1}$, where $\delta _1$ acts by the nontrivial automorphism of type $D_\ell$. These cases are covered by Example 6.5.(c) If
$A=\langle \delta _2\rangle$ or $A=\langle \delta _1\delta _2\rangle$, $\overline {K}_\mathcal {O}^\circ$ is of type $A_{2m-1}$ with the diagram automorphism action as in Example 6.6.(d) If
$A=1$, then $\overline {K}_\mathcal {O}^\circ$ is the hyperspecial subgroup of type $D_{2m-1}$.
(vi) If
${\mathbf {G}}=\mathrm {PSO}_{4m+2}$, $m\geqslant 2$, then $\Omega _G=\langle \delta \rangle \cong {\mathbb {Z}}/4{\mathbb {Z}}$, and we have the following.
(a) If
$A=\Omega _G$, $\overline {K}_\mathcal {O}^\circ$ is of type $D_k\times D_k\times A_{2m-2k}$, $2\leqslant k\leqslant m$ or $A_{2m-2}$, where $\delta$ acts on $D_\ell \times D_\ell$ as in Example 6.7, while on $A_{2m-2k}$, $\delta$ acts by the nontrivial diagram automorphism.(b) If
$A=\langle \delta ^2\rangle$, $\overline {K}_\mathcal {O}^\circ$ is of type $D_{2m}$ or $D_k\times D_{2m-k+1}$, $2\leqslant k\leqslant m$, where $\delta ^2$ acts on each factor by the nontrivial automorphism of type $D_\ell$, as in Example 6.5.(c) If
$A=1$, then $\overline {K}_\mathcal {O}^\circ$ is the hyperspecial subgroup of type $D_{2m}$.
(vii) Let
${\mathbf {G}}$ be of type $E_6$ with $\Omega _G=\langle \delta \rangle \cong {\mathbb {Z}}/3{\mathbb {Z}}$.
(a) If
$A=1$, then $\overline {K}_\mathcal {O}^\circ$ is either of type $E_6$ or $A_5\times A_1$.(b) If
$A=\Omega _G$, then $\overline {K}_\mathcal {O}^\circ$ is of type: $A_2^3$ with $\delta$ acting by permutation, as in Example 6.4; $A_1^3\times A_1$, where $\delta$ permutes the first three factors and it fixes the last one; or $D_4$, where $\delta$ acts as in Example 6.8.
(viii) Let
${\mathbf {G}}$ be of type $E_7$ with $\Omega _G=\langle \delta \rangle \cong {\mathbb {Z}}/2{\mathbb {Z}}$.
(a) If
$A=1$, then $\overline {K}_\mathcal {O}^\circ$ is of type $E_7$, $D_6\times A_1$ or $A_5\times A_2$.(b) If
$A=\Omega _G$, then $\overline {K}_\mathcal {O}^\circ$ is of type: $E_6$ with $\delta$ acting by the nontrivial diagram automorphism as in Example 6.6; $D_4\times A_1^2$ with $\delta$ acting by an order-$2$ diagram automorphism of $D_4$ (Example 6.5) and by flipping the two $A_1$; $A_2^2\times A_2$, flipping the first $A_2$ and acting trivially on the third $A_2$; $A_3^2\times A_1$, with the flip on $A_3^2$ and trivial action on $A_1$; or $A_7$ with the nontrivial diagram automorphism (see Examples 6.3 and 6.6).
8. Elliptic pairs
8.1 Finite groups
Suppose 
$H$ is a finite group. Given a finite-dimensional 
$H$-representation 
$(\delta,V_\delta )$ over 
$\mathbb {C}$ and functions 
$f,f'\colon H\to \mathbb {C}$, define
\begin{equation} (f,f')^\delta_{{\mathrm{ell}}}=\frac 1{|H|} \sum_{h\in H}{\det}_{V_\delta}(1-\delta(h)) f(h^{-1}) f'(h). \end{equation}
For 
$\rho,\rho '\in R(H)$, set
\[ (\rho,\rho')^\delta_{{\mathrm{ell}}}=(\chi_\rho,\chi_{\rho'})^\delta_{{\mathrm{ell}}}, \]
where 
$\chi _\rho$, 
$\chi _{\rho '}$ denote the corresponding characters. The basic facts about 
$(\,{,}\,)^\delta _H$ can be found in [Reference ReederRee01, § 2]. An element 
$h\in H$ is called (
$\delta$-)elliptic if 
$V_{\delta }^{\delta (h)}=0$. The set 
$H_{\mathrm {ell}}$ of elliptic elements of 
$H$ is obviously closed under conjugation by 
$H$. Let 
$H\backslash H_{\mathrm {ell}}$ denote the set of elliptic conjugacy classes. Fix 
$(\delta, V_\delta )$, and let 
$\overline {R}(H)$ be the quotient of 
$R(H)$ by the radical of the form 
$(\,{,}\,)^\delta _{\mathrm {ell}}$. As in [Reference ReederRee01, § 2], there is a natural identification of 
$\overline {R}(H)$ with the space of class functions of 
$H$ supported on 
$H_{{\mathrm {ell}}}$.
For every 
$h\in H$, let 
$\mathbf {1}_h$ denote the characteristic function of the conjugacy class of 
$h$. Clearly, 
$\{\mathbf {1}_h\mid h\in H\backslash H_{\mathrm {ell}}\}$ is an orthogonal basis of 
$\overline {R}(H)$ with respect to the elliptic pairing 
$(\,{,}\,)^\delta _{\mathrm {ell}}$.
Suppose that, in addition, we are given an automorphism 
$\theta :H\to H$ . Let 
$\langle \theta \rangle$ denote the cyclic group generated by 
$\theta$ and 
$H'=H\rtimes \langle \theta \rangle$. Given a finite-dimensional complex 
$H'$-representation 
$(\delta,V_\delta )$ and functions 
$f,f': H'\to {\mathbb {C}}$, define
\begin{equation} (f,f')^\delta_{\theta-{\mathrm{ell}}}=\frac 1{|H|} \sum_{h\in H}{\det}_{V_\delta}(1-\delta(\theta h)) f((\theta h)^{-1}) f'(\theta h). \end{equation}
For 
$\rho,\rho '\in R(H')$, set
\[ (\rho,\rho')^\delta_{\theta-{\mathrm{ell}}}=(\chi_\rho,\chi_{\rho'})^\delta_{\theta-{\mathrm{ell}}}, \]
where 
$\chi _\rho$, 
$\chi _{\rho '}$ denote the corresponding characters. Note that if the representation 
$\delta$ is understood, we may write 
$(~, ~)_{\mathrm {ell}}^H$ for 
$(~, ~)_{\mathrm {ell}}^\delta$, and similarly for 
$(~, ~)_{\theta -{\mathrm {ell}}}^H$.
8.2 Complex reductive groups
Let 
${\mathcal {G}}$ be a possibly disconnected complex reductive group with identity component 
${\mathcal {G}}^\circ$. If 
$x\in {\mathcal {G}}$ is given, fix a Borel subgroup 
$B_x$ of 
${\mathrm {Z}}_{\mathcal {G}}(x)^\circ$ and a maximal torus 
$T_x$ in 
$B_x$. Let 
$\mathfrak {t}_x$ be the Lie algebra of 
$T_x$. As in [Reference WaldspurgerWal07, § 2] (see also [Reference ReederRee01, § 3.2]), we define a complex representation 
$(\delta _x,\mathfrak {t}_x)$ of 
$A_{{\mathcal {G}}}(x)$ as follows. Every 
$z\in {\mathrm {Z}}_{{\mathcal {G}}}(x)$ acts on 
${\mathrm {Z}}_{\mathcal {G}}(x)^\circ$ by the adjoint action, denote by 
$\alpha _z$ the resulting automorphism of 
${\mathrm {Z}}_{\mathcal {G}}(x)^\circ$. There exists 
$y\in {\mathrm {Z}}_{\mathcal {G}}(x)^\circ$ such that 
$\alpha _z\circ {\mathrm {Ad}}(y)$ preserves 
$B_x$ and 
$T_x$. This means that 
$\alpha _z\circ {\mathrm {Ad}}(y)$ defines an automorphism of the cocharacter lattice 
$X_*(T_x)$ in 
${\mathrm {Z}}_{\mathcal {G}}(x)^\circ$, and therefore a linear isomorphism of 
$\mathfrak {t}_x$ denoted 
$\delta _x(z)$. If 
$\bar z\in A_{{\mathcal {G}}}(x)$, let 
$z\in Z_{{\mathcal {G}}}(x)$ be a representative and set 
$\delta _x(\bar z):=\delta _x(z)$. This construction gives a representation of 
$A_{{\mathcal {G}}}(x)$. We consider the elliptic theory of the finite group 
$A_{{\mathcal {G}}}(x)$ with respect to the representation 
$\delta _x$.
An element 
$g\in {\mathcal {G}}$ is called elliptic if the centralizer 
${\mathrm {Z}}_{\mathcal {G}}(g)$ contains no nontrivial torus.
8.3 Definitions
Suppose 
$\Gamma$ is a (possibly disconnected) complex reductive group with identity component 
$\Gamma ^\circ$. Extending the definition in § 5.1, we define the sets (cf. [Reference CiubotaruCiu20, Definition 1.1])
\begin{equation} \begin{aligned} {\mathcal{Y}}(\Gamma) & =\{(s,h)\in \Gamma\times\Gamma\mid s,h \text{ semisimple}, \ sh=hs\},\\ {\mathcal{Y}}(\Gamma)_{\mathrm{ell}} & =\{(s,h)\in \Gamma\times\Gamma\mid s,h \text{ semisimple}, \ sh=hs, \ {\mathrm{Z}}_{\Gamma}(s,h)\text{ is finite}\}. \end{aligned} \end{equation}
Here 
${\mathrm {Z}}_{\Gamma }(s,h)={\mathrm {Z}}_\Gamma (s)\cap {\mathrm {Z}}_\Gamma (h)$ and the finiteness condition is equivalent to saying that no nontrivial torus in 
$\Gamma$ centralizes both 
$s$ and 
$h$. We refer to elements of 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$ as elliptic pairs. Note that the condition in 
${\mathcal {Y}}(\Gamma )_{{\mathrm {ell}}}$ is equivalent to saying that 
$h$ is elliptic in 
${\mathrm {Z}}_\Gamma (s)$ or equivalently 
$s$ is elliptic in 
${\mathrm {Z}}_\Gamma (h)$.
The sets 
${\mathcal {Y}}(\Gamma ), {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$ have 
$\Gamma$-actions via conjugation: 
$g\cdot (s,h)=(gsg^{-1},ghg^{-1})$. They also have a natural 
$\Gamma$-equivariant involution given by the flip
\[ (s,h)\mapsto (h,s). \]
Let 
$\Gamma \backslash {\mathcal {Y}}(\Gamma )$, 
$\Gamma \backslash {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$ be the sets of 
$\Gamma$-orbits, and given 
$(s, h) \in {\mathcal {Y}}(\Gamma )$, write 
$[(s, h)]$ for the corresponding orbit in 
$\Gamma \backslash {\mathcal {Y}}(\Gamma )$. Then we get an involution
\[ \mathsf{flip}\colon \Gamma\backslash {\mathcal{Y}}(\Gamma)\to \Gamma\backslash {\mathcal{Y}}(\Gamma), \mathsf{flip}([(s,h)])=[(h,s)], \]
which preserves 
$\Gamma \backslash {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$.
Lemma 8.1 The set 
$\Gamma \backslash {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$ is finite.
Proof. Suppose 
$(s,h)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$. The cyclic group 
$\langle s\rangle$ is in 
${\mathrm {Z}}_{\Gamma }(s,h)$, hence 
$s$ has finite order. Moreover, 
$s$ must be isolated in 
$\Gamma$ in the sense that 
${\mathrm {Z}}_\Gamma (s)$ does not contain a nontrivial central torus. The classification of isolated semisimple automorphisms of 
$\Gamma$ is well-known [Reference SteinbergSte68, Reference Digne and MichelDM18], in particular, there are finitely many automorphisms up to inner conjugation.
In the next lemma, we relate elliptic pairs in 
${\mathrm {Z}}_\Gamma (s)$ to elements of 
$A_\Gamma (s)$ that are elliptic with respect to the action described in § 8.2.
Lemma 8.2 Fix 
$s\in \Gamma$ semisimple. The projection map 
${\mathrm {Z}}_\Gamma (s)\to A_\Gamma (s)$, 
$h\mapsto \bar h$, induces a bijection between 
${\mathrm {Z}}_\Gamma (s)$-orbits of elliptic pairs 
$(s,h)$ and the elliptic conjugacy classes in 
$A_\Gamma (s)$.
Proof. We need a result from the theory of semisimple automorphisms of reductive groups, e.g. [Reference SommersSom98, Proposition 9]: if 
$x,y$ are semisimple elements in a reductive group 
${\mathcal {G}}$ such that their images in the group of components 
${\mathcal {G}}/{\mathcal {G}}^\circ$ are in the same conjugacy class, and 
$S$ is a maximal torus in 
${\mathrm {Z}}_{\mathcal {G}}(x)$, then there exist 
$g\in {\mathcal {G}}$ and 
$s\in S$ such that 
$g y g^{-1}=xs$.
We apply this to 
${\mathcal {G}}={\mathrm {Z}}_\Gamma (s)$ (a reductive group). Suppose 
$h,h'$ are semisimple elements such that 
$(s,h)$ and 
$(s,h')$ are elliptic pairs. The elliptic condition implies that the maximal torus in 
${\mathrm {Z}}_{\mathcal {G}}(h)$ is trivial, hence 
$s=1$ in the relation above, and 
$h$ and 
$h'$ are 
${\mathcal {G}}$-conjugate. This implies that if 
$\overline {h}=\overline {h'}$, then 
$[(s,h)]=[(s,h')]$.
It remains to show that 
$(s,h)$ is an elliptic pair if and only if 
$\bar h$ is elliptic in 
$A_\Gamma (s)$. This is just a matter of checking the definitions in the case 
${\mathcal {G}}={\mathrm {Z}}_\Gamma (s)$. Given the semisimple element 
$h\in {\mathcal {G}}$, choose a maximal torus 
$T_s$ in 
${\mathcal {G}}$ that is normalized by 
$h$. Then 
$h$ is not elliptic if and only if there exists a nontrivial torus 
$S\subset T_s$ that centralizes 
$h$, equivalently if and only if 
$\delta _s(\bar h)$ fixes a nonzero element of 
$\mathfrak {t}_s$, i.e. if 
$\overline {h}$ is not elliptic in 
$A_\Gamma (s)$.
For every 
$(s,h)\in {\mathcal {Y}}(\Gamma )$, define
\begin{equation} \Pi(s,h)=\sum_{\phi\in \widehat{A_\Gamma(s)}} \phi(h)\phi\in R(A_{\Gamma}(s)), \end{equation}
and let 
$\overline {\Pi }(s,h)$ denote the image in 
$\overline {R}(A_{\Gamma }(s))$. Here 
$\phi (h)$ is interpreted as 
$\phi (\bar {h})$ where 
$\bar {h}$ is the image of 
$h$ in 
$A_\Gamma (s)$. Let 
${\mathbb {C}}[{\mathcal {Y}}(\Gamma )_{\mathrm {ell}}]^\Gamma$ denote the 
$\Gamma$-invariant functions on 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$; this space can be identified with 
${\mathbb {C}}[\Gamma \backslash {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}]$. Let 
$\mathbf {1}_{[(s,h)]}$ denote the characteristic function of the 
$\Gamma$-orbit of 
$(s,h)$.
Proposition 8.3 The correspondence 
$\mathbf {1}_{[(s,h)]}\mapsto \overline {\Pi }(s,h)$ induces an isomorphism
\[ {\mathbb{C}}[{\mathcal{Y}}(\Gamma)_{\mathrm{ell}}]^\Gamma\cong \bigoplus_{s\in {\mathcal{C}}(\Gamma)_{\mathsf{ss}}} \overline{R}(A_\Gamma(s)). \]
Proof. In light of Lemma 8.2, the only thing left is to remark that the elements 
$\overline {\Pi }(s,h)$ form a basis of 
$\overline {R}(A_\Gamma (s))$ as 
$h$ ranges over a set of representatives of 
${\mathrm {Z}}_\Gamma (s)$-conjugacy classes such that 
$(s,h)$ is an elliptic pair. It is elementary that in 
$R(A_\Gamma (s))$,
\[ \overline{\Pi}(s,h)= |{\mathrm{Z}}_{A_\Gamma(s)}(\overline{h})|~\mathbf{1}_{\overline{h}^{-1}}, \]
and the claim follows.
We say that 
$\Gamma _M\subset \Gamma$ is a Levi subgroup if there exists a torus 
$S\subset \Gamma ^\circ$ such that 
$\Gamma _M={\mathrm {Z}}_\Gamma (S)$. If a pair 
$(s,h)$ is in 
${\mathcal {Y}}(\Gamma _M)$, denote by 
$\Pi ^{\Gamma _M}(s,h)$ the combination defined analogously to (8.4).
Lemma 8.4 Suppose 
$s\in \Gamma _M$ is semisimple.
(i) The inclusion
${\mathrm {Z}}_{\Gamma _M}(s)\to {\mathrm {Z}}_\Gamma (s)$ induces an inclusion $A_{\Gamma _M}(s)\to A_\Gamma (s)$.(ii) For every
$(s,h)\in {\mathcal {Y}}(\Gamma _M)$, ${\mathrm {Ind}}_{A_{\Gamma _M}(s)}^{A_\Gamma (s)}\Pi ^{\Gamma _M}(s,h)=\Pi (s,h)$.
Proof. (i) This is a well-known argument. We need to show that 
${\mathrm {Z}}_{\Gamma _M}(s)\cap {\mathrm {Z}}_{\Gamma }(s)^\circ$ is connected and, hence, in 
${\mathrm {Z}}_{\Gamma _M}(s)^\circ$. But 
${\mathrm {Z}}_{\Gamma _M}(s)\cap {\mathrm {Z}}_{\Gamma }(s)^\circ =\Gamma _M\cap {\mathrm {Z}}_{\Gamma }(s)^\circ ={\mathrm {Z}}_\Gamma (S)\cap {\mathrm {Z}}_{\Gamma }(s)^\circ ={\mathrm {Z}}_{{\mathrm {Z}}_{\Gamma }(s)^\circ }(S)$, which is connected since the centralizer of any torus in a connected reductive group is connected.
(ii) This is elementary using that 
$\phi (\overline {h})=\sum _{\psi \in \widehat {A_{\Gamma _M}(s)}} \langle \phi,\psi \rangle _{A_{\Gamma _M}(s)} \psi (\overline {h})$ for every 
$\phi \in \widehat {A_{\Gamma }(s)}$, by restriction of characters.
Lemma 8.5 Let 
$(s,h)\in {\mathcal {Y}}(\Gamma )$ be given and suppose 
$S$ is a maximal torus in 
${\mathrm {Z}}_\Gamma (s,h)^\circ$. Set 
$\Gamma _M={\mathrm {Z}}_\Gamma (S)$. Then 
${\mathrm {Z}}_{\Gamma _M}(s,h)^\circ ={\mathrm {Z}}_{\Gamma _M}^\circ$, i.e. 
$(s,h)$ is an elliptic pair in 
$\Gamma _M/{\mathrm {Z}}_{\Gamma _M}^\circ$.
Proof. Let 
$S_1$ be a torus in 
${\mathrm {Z}}_{\Gamma _M}(s,h)^\circ$. Then 
$S_1\subset {\mathrm {Z}}_\Gamma (s,h)^\circ$ and since it commutes with 
$S$ which is maximal in 
${\mathrm {Z}}_\Gamma (s,h)^\circ$, it follows that 
$S_1\subset S\subset {\mathrm {Z}}_{\Gamma _M}^\circ$.
Remark 8.6 Our main application will be to consider 
$\Gamma =\Gamma _u$, the reductive part of the centralizer of a unipotent element 
$u$ in the Langlands dual group 
$G^\vee$, while 
$\Gamma _M$ will be the centralizer of 
$u$ in a Levi subgroup 
$M^\vee$.
8.4 Elliptic pairs in $\Gamma ^\circ$
In applications, we will often encounter the situation where the group 
$\Gamma$ is connected. For this reason, it is useful to have a precise description of the elliptic pairs in 
$\Gamma ^\circ$. Suppose 
$s\in \Gamma ^\circ$ a semisimple element. Let 
$T$ be a maximal torus of 
$\Gamma$ containing 
$s$ and let 
$\Phi$ be the system of roots of 
$T$ in 
$\Gamma ^\circ$ and 
$W(\Gamma ^\circ )$ the Weyl group of 
$T$ in 
$\Gamma ^\circ$. If 
$\alpha \in \Phi$, let 
$X_\alpha$ be the corresponding one-parameter unipotent subgroup in 
$\Gamma ^\circ$. For each 
$w\in W(\Gamma ^\circ )$, we fix a representative 
$\dot {w}$ of 
$w$ in 
${\mathrm {N}}_{\Gamma ^\circ }(T)$. Recall [Reference CarterCar93, Theorem 3.5.3]
\begin{equation} \begin{aligned} Z_{\Gamma^\circ}(s)^\circ & =\langle T, X_\alpha\mid \alpha(s)=1,\ \alpha\in\Phi\rangle,\\ Z_{\Gamma^\circ}(s) & =\langle T, X_\alpha, \dot{w}\mid \alpha(s)=1,\ \alpha\in\Phi,\ wsw^{-1}=s,\ w\in W(\Gamma^\circ)\rangle. \end{aligned} \end{equation} We say that 
$w\in W(\Gamma ^\circ )$ is elliptic if 
$T^w$ is finite, equivalently if 
$\mathfrak {t}^w=0$, where 
$\mathfrak {t}$ is the Lie algebra of 
$T$.
Proposition 8.7 With the notation as above,
\[ \Gamma^\circ\backslash{\mathcal{Y}}(\Gamma^\circ)_{\mathrm{ell}}\leftrightarrow W(\Gamma^\circ)\backslash\{(s,w)\mid s\in T\text{ is regular},\ w\in W(\Gamma^\circ) \text{ is elliptic},\ s\in T^w\}. \]
Proof. Since we are considering 
$\Gamma ^\circ$-orbits of pairs 
$(s,h)\in {\mathcal {Y}}(\Gamma ^\circ )_{\mathrm {ell}}$, we may assume that 
$s\in T$ (in a fixed 
$W(\Gamma ^\circ )$-orbit in 
$T$) and 
$h$ is in a semisimple conjugacy class of 
$Z_{\Gamma ^\circ }(s)$. If 
$h\in Z_{\Gamma ^\circ }(s)^\circ$, since 
$Z_{\Gamma ^\circ }(s)^\circ$ is reductive [Reference CarterCar93, Theorem 3.5.4], 
$h$ is contained in a maximal torus of 
$Z_{\Gamma ^\circ }(s)^\circ$, hence 
$(s,h)$ is not an elliptic pair. This means that 
$h$ must be in 
$Z_{\Gamma ^\circ }(s)\setminus Z_{\Gamma ^\circ }(s)^\circ$. By (8.5), we can assume that 
$h=\dot {w}$ for some 
$w\in W(\Gamma ^\circ )$ such that 
$s\in T^w$. It is clear that 
$Z_{\Gamma ^\circ }(s,\dot {w})\supseteq T^w$, which means that 
$w$ is necessarily elliptic if 
$(s,\dot {w})$ is an elliptic pair. Suppose 
$s$ is not regular. Then there exists 
$\alpha \in \Phi$ such that 
$\alpha (s)=1$. Let 
$O_w=\{\alpha, w(\alpha ), w^2(\alpha ),\ldots, w^{n-1}(\alpha )\}$, where 
$n$ is the order of 
$w$. Then in the Lie algebra of 
$\Gamma$, there exists an appropriate sum of root vectors 
$e=\sum _{\beta \in O_w}e_\beta$ that is invariant under 
${\mathrm {Ad}}(\dot {w})$ and, therefore, 
$Z_{\Gamma ^\circ }(s,\dot {w})$ contains the one-parameter subgroup for 
$e$ and it is infinite.
Conversely, suppose 
$(s,\dot {w})$ is such that 
$s$ is regular and 
$w$ is elliptic. By (8.5), 
$Z_{\Gamma ^\circ }(s)= W({\Gamma ^\circ })_s T$, where 
$W({\Gamma ^\circ })_s=\{w_1\in W(\Gamma ^\circ )\mid w_1 s w_1^{-1}=s\}$. Then 
$Z_{\Gamma ^\circ }(s,\dot {w})$ is finite if and only if 
${\mathrm {Ad}}(\dot {w})$ has no nonzero fixed points on the Lie algebra 
$\mathfrak {z}_{\Gamma ^\circ }(s)$. But 
$\mathfrak {z}_{\Gamma ^\circ }(s)=\mathfrak {t}$, so this is equivalent to 
$w$ being elliptic.
Remark 8.8 If 
$\Gamma$ is connected and simply connected, then 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}=\emptyset$. This is because in that case, for every regular semisimple 
$s \in T$, 
$Z_\Gamma (s)=Z_\Gamma (s)^\circ =T$, a maximal torus.
9. The dual nonabelian Fourier transform
Let 
$\mathbf {G}$ be a connected semisimple algebraic 
$F$-group and 
$G=\mathbf {G}(F)$. Let 
${\mathfrak {R}}_{\mathrm {un}}(G)$ denote the category of smooth unipotent representations of 
$G$. If 
$V,V'\in {\mathrm {Irr}}_{\mathrm {un}} (G)$, let
\begin{equation} {\mathrm{EP}}_G(V,V')=\sum_{i\geqslant 0}(-1)^i\dim {\operatorname{Ext}}^i(V,V'), \end{equation}
where 
${\operatorname {Ext}}^i(V,V')$ are calculated in the category 
$\mathfrak {R}(G)$ of all smooth 
$G$-representations [Reference Schneider and StuhlerSS97] or, equivalently since 
${\mathfrak {R}}_{\mathrm {un}}(G)$ is a direct summand of 
$\mathfrak {R}(G)$, in the category 
${\mathfrak {R}}_{\mathrm {un}}(G)$. We remark that this is a finite sum by Bernstein's result on the finiteness of the cohomological dimension of 
$G$. Extend, as we may, 
${\mathrm {EP}}_G(\,{,}\,)$ as a Hermitian pairing on 
$R_{\mathrm {un}} (G)$ (as defined in § 4.3). Let 
$\overline {R}_{\mathrm {un}}(G)$ denote the quotient of 
$R_{\mathrm {un}}(G)$ by the radical of 
${\mathrm {EP}}_G$.
Let 
$R_{\mathrm {un}}^{\mathrm {temp}} (G)$ be the subspace spanned by the irreducible unipotent tempered representations and let 
$\overline {R}_{\mathrm {un}}^{\mathrm {temp}}(G)$ be the image of 
$R_{\mathrm {un}}^{\mathrm {temp}} (G)$ in 
$\overline {R}_{\mathrm {un}}(G)$. As is well-known [Reference Schneider and StuhlerSS97, Reference ReederRee02], as a consequence of the (parabolic induction) Langlands classification:
\begin{equation} \overline{R}_{\mathrm{un}}^{\mathrm{temp}} (G)=\overline{R}_{\mathrm{un}}(G). \end{equation} Let 
$\mathfrak {B}_{\mathrm {un}}(G)$ denote the unipotent Bernstein center so that 
$R_{\mathrm {un}} (G)=\bigoplus _{\mathfrak {s}\in \mathfrak {B}_{\mathrm {un}}(G)} R(G)^{\mathfrak {s}}$, where 
$R(G)^{\mathfrak {s}}$ is the 
${\mathbb {C}}$-span of irreducible objects in the subcategory 
$\mathfrak {R}(G)^{\mathfrak {s}}$ (defined in § 4.2). Since there are no nontrivial extensions between objects in different Bernstein components, we have an 
${\mathrm {EP}}$-orthogonal decomposition:
\[ \overline{R}_{\mathrm{un}} (G)=\bigoplus_{\mathfrak{s}\in \mathfrak{B}_{\mathrm{un}}(G)} \overline{R}(G)^{\mathfrak{s}}. \]
With the same notation for a pure inner twist 
$G'$ of 
$G$, we get
\begin{equation} \bigoplus_{G'\in{\mathrm{InnT}}^p(G)} \overline{R}_{\mathrm{un}}(G')=\bigoplus_{G'\in{{{\mathrm{InnT}}^p}}(G)}\bigoplus_{\mathfrak{s}\in \mathfrak{B}_{\mathrm{un}}(G')} \overline{R}(G')^{\mathfrak{s}}. \end{equation} Recall the unipotent Langlands correspondence in the form (4.18). Given a semisimple element 
$s \in G^\vee$ and a unipotent element 
$u \in {\mathcal {G}}_s^p$, apply the definitions of § 8.2 to 
$u\in {\mathcal {G}}_s^p$ to obtain a representation 
$\delta _u^s$ of 
$A_{{\mathcal {G}}^p_s}(u)$ on the Cartan subalgebra 
$\mathfrak {t}^s_u$ in the Lie algebra of 
${\mathrm {Z}}_{{\mathcal {G}}^p_s}(u)$. Let 
$(\,{,}\,)^{\delta _u^s}_{\mathrm {ell}}$ be the elliptic inner product on 
$R(A_{{\mathcal {G}}^p_s}(u))$ and let 
$\overline {R}(A_{{\mathcal {G}}^p_s}(u))$ be the elliptic quotient by the radical of the form. One expects the following correspondence to hold.
Conjecture 9.1 The unipotent Langlands correspondence (4.18) induces an isometric isomorphism
\begin{equation} \overline{\mathsf{LLC}^p}_{{\mathrm{un}}}:\bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\bigoplus_{u\in {\mathcal{C}}({\mathcal{G}}_s^p)_{\mathrm{un}}}\overline{R}(A_{{\mathcal{G}}_s^p}(u)) \longrightarrow \bigoplus_{G'\in{\mathrm{InnT}}^p(G)} \overline{R}_{\mathrm{un}}(G'), \end{equation}
where the spaces on the left are endowed with the elliptic inner products 
$(\,{,}\,)^{\delta _u^s}_{\mathrm {ell}}$, while the spaces on the right have the Euler–Poincaré pairings 
${\mathrm {EP}}_{G'}$.
Here 
${\mathcal {C}}(G^\vee )_{\mathsf {ss}}$ and 
${\mathcal {C}}({\mathcal {G}}_s)_{\mathrm {un}}$ refer to conjugacy classes of semisimple and unipotent elements, as defined in § 4.3.
Remark 9.2 In [Reference ReederRee02], Reeder proves that this elliptic correspondence holds in the case of irreducible representations with Iwahori-fixed vectors of a split adjoint group. In § 11, Theorem 11.1, we prove Conjecture 9.1 in the form (9.4) for a semisimple adjoint 
$F$-split group 
${\mathbf {G}}$. In § 11.4, we explain how this result could be extended to arbitrary isogenies and, in particular, in Corollary 11.13 we prove it in the Iwahori-fixed case for an arbitrary 
$F$-split group 
${\mathbf {G}}$. As a concrete example, in Proposition 13.6, we also illustrate the result with a direct proof for 
${\mathbf {G}}={\mathsf {SL}}_n$.
Remark 9.3 Given 
$s \in G^\vee$ as above and 
$u \in {\mathcal {G}}_s$, it also makes sense to define a representation of 
$A_{{\mathcal {G}}_s}(u)$ similarly to 
$\delta _u^s$. It would be natural to expect that the LLC for inner twists as described in (4.16) also induces an isometric isometry
\begin{equation} \overline{\mathsf{LLC}}_{{\mathrm{un}}}\colon \bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\,\bigoplus_{u\in {\mathcal{C}}({\mathcal{G}}_s)_{\mathrm{un}}}\overline{R}(A_{{\mathcal{G}}_s}(u)) \longrightarrow \bigoplus_{G'\in{\mathrm{InnT}}(G)} \overline{R}_{\mathrm{un}}(G'), \end{equation}though we will not consider a conjecture of this form in this paper.
Remark 9.4 One can formulate Conjecture 9.1 without restricting to the unipotent case. In general, the expected Langlands correspondence should induce an isometric isomorphism
\begin{equation} \overline{\mathsf{LLC}^p}\colon \bigoplus_{\varphi}\overline{R}(A_\varphi)\longrightarrow \bigoplus_{G'\in{\mathrm{InnT}}^p(G)} \overline{R}(G'), \end{equation}
where 
$\varphi$ ranges over the 
$G^\vee$-conjugacy classes of 
$L$-parameters 
$\varphi : W_F'\to {}^LG$ (equivalently, tempered 
$L$-parameters), and 
$A_\varphi = \pi _0({\mathrm {Z}}_{G^\vee }(\varphi ))$ (cf. § 4.3). The elliptic theory of the finite group 
$A_\varphi$ is taken with respect to the action on a Cartan subalgebra of 
${\mathrm {Z}}_{G^\vee }(\varphi )$ as before. This formulation is, of course, related to Arthur's ideas on elliptic representations: in [Reference ArthurArt93, Corollary 6.3], Arthur proved the equality of Kazhdan's elliptic pairing between irreducible tempered representations with the elliptic pairing of the corresponding irreducible characters of the Knapp–Stein 
$R$-groups. Later, Opdam and Solleveld [Reference Opdam and SolleveldOS13, Theorems 6.5 and 7.3] extended this work to all admissible representations using the homological Euler–Poincaré pairing. Moreover, Arthur [Reference ArthurArt89, § 7] expected an identification between the 
$R$-groups and the geometric 
$A$-groups and, in fact, Reeder [Reference ReederRee02, § 8], as part of his proof of the elliptic correspondence, proved this matching in the Iwahori case.
9.1 The elliptic Fourier transform: the split case
Suppose 
$G$ is the split 
$F$-form. In order to apply the ideas in § 8.3, we rephrase the left-hand side of (9.4). Since 
${\mathrm {Frob}}$ acts trivially on 
$G^\vee$, in this situation we have 
${\mathcal {G}}_s^p={\mathrm {Z}}_{G^\vee }(s)$ and, hence,
\begin{align*} \bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\ \bigoplus_{u\in
{\mathcal{C}}({\mathcal{G}}_s^p)_{\mathrm{un}}}\overline{R}(A_{{\mathcal{G}}_s^p}(u))
=\bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\ \bigoplus_{u\in
{\mathcal{C}}({\mathrm{Z}}_{G^\vee}(s))_{\mathrm{un}}}\overline{R}(A_{G^\vee}(su)), \end{align*}
which can be written as
\[ \bigoplus_{u\in
{\mathcal{C}}(G^\vee)_{\mathrm{un}}}\ \bigoplus_{s\in {\mathbb{C}}(\Gamma_u)_{\mathsf{ss}}} \overline{R}(A_{\Gamma_u}(s))=\bigoplus_{u\in
{\mathcal{C}}(G^\vee)_{\mathrm{un}}}{\mathbb{C}}[{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}]^{\Gamma_u},
\]
via Proposition 8.3, where 
$\Gamma _u$ is the reductive part of 
${\mathrm {Z}}_{G^\vee }(u)$, as before. For simplicity, we define
\begin{equation} {\mathcal{R}}_{{\mathrm{un}},{\mathrm{ell}}}^p(G)=\bigoplus_{G'\in{\mathrm{InnT}}^p(G)} \overline{R}_{\mathrm{un}}(G'), \end{equation}
endowed with the Euler–Poincaré pairing 
${\mathrm {EP}}=\bigoplus _{G'} {\mathrm {EP}}_{G'}$. Hence, the elliptic unipotent LLC for pure inner twists of a split group can be viewed as the isomorphism
\begin{equation} \overline{\mathsf{LLC}^p}_{{\mathrm{un}}}:\bigoplus_{u\in {\mathcal{C}}(G^\vee)_{\mathrm{un}}}{\mathbb{C}}[{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}]^{\Gamma_u}\longrightarrow {\mathcal{R}}_{{\mathrm{un}},{\mathrm{ell}}}^p(G). \end{equation}
For every class of elliptic pairs 
$[(s,h)]\in \Gamma _u\backslash {\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}$, define the virtual combination (cf. [Reference WaldspurgerWal18, Reference CiubotaruCiu20]):
\begin{equation} \Pi(u,s,h)=\sum_{\phi\in \widehat{A_{\Gamma_u}(s)}}{\phi(h)}\,\pi(s,u,\phi). \end{equation}
Regard 
$\Pi (u,s,h)$ (or rather its image) as an element in 
${\mathcal {R}}_{{\mathrm {un}},{\mathrm {ell}}}^p(G)$. As before 
$\phi (h)=\phi (\bar h)$, where 
$\bar h$ is the image of 
$h$ in 
$A_{\Gamma _u}(s)$.
Lemma 9.5 With notation as above and setting 
$A_x=A_{G^\vee }(x)$, we have:
(i)
${\mathrm {EP}}(\Pi (u,s,h),\Pi (u',s',h'))=0$ if $x=su$ and $x'=s'u'$ are not $G^\vee$-conjugate;(ii)
\begin{align*}{\mathrm{EP}}(\Pi(u,s,h),\Pi(u,s,h'))&=(|{\mathrm{Z}}_{A_x}(\bar{h})| \mathbf{1}_{\bar{h}^{-1}},|{\mathrm{Z}}_{A_x}(\bar{h}')| \mathbf{1}_{\bar{h'}^{-1}})_{\mathrm{ell}}^{A_x}\\ &=\begin{cases}|Z_{A_x}(\bar h)| {\det}_{\mathfrak{t}_x}(1-\bar h^{-1}), & \text{if }h,h'\text{ are conjugate,}\\0, & \text{otherwise.}\end{cases}\end{align*}
Hence, the combinations 
$\{\Pi (u,s,h)\}$ define an orthogonal basis of 
${\mathcal {R}}_{{\mathrm {un}},{\mathrm {ell}}}^p(G)$.
Proof. This is a straightforward consequence of Theorem 11.1 (and an elementary calculation for the last equality in part (ii)).
Definition 9.6 (Cf. [Reference CiubotaruCiu20, Reference WaldspurgerWal18])
The (dual) elliptic nonabelian Fourier transform is the involutive linear map 
${\mathrm {FT}}^\vee _{\mathrm {ell}}\colon {\mathcal {R}}_{{\mathrm {un}},{\mathrm {ell}}}^p(G) \to {\mathcal {R}}_{{\mathrm {un}},{\mathrm {ell}}}^p(G)$, defined by
\[ {\mathrm{FT}}^\vee_{\mathrm{ell}}(\Pi(u,s,h))=\Pi(u,h,s), \quad\text{$(s,h)\in \Gamma_u\backslash{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}$, $u\in G^\vee$ unipotent.} \]
Note that 
${\mathrm {FT}}^\vee _{\mathrm {ell}}$ is the just the image under 
$\overline {\mathsf {LLC}^p}_{\mathrm {un}}$ of the canonical involution of 
$\bigoplus _{s,u} \overline {R}(A_{su})$
\[ [u,s,h]\mapsto [u,h,s],\quad \text{where}\ [u,s,h]:= \sum_{\psi\in \widehat{A}_{su}} \psi(h)\psi. \]
For every 
$G'\in {\mathrm {InnT}}^p(G)$, and 
$K'_\mathcal {O}\in \max (G')$ consider the restriction map
\begin{equation} \operatorname{res}_{K'_\mathcal{O}}\colon {\mathrm{Irr}}_{\mathrm{un}} G'\to R_{\mathrm{un}}(\overline{K}_\mathcal{O}),\ V\mapsto V^{K'^+_\mathcal{O}}. \end{equation}
We define a linear map 
$\operatorname {res}_{{\mathrm {cpt}},{\mathrm {un}}}\colon \bigoplus _{G' \in {\mathrm {InnT}}^p(G)} R_{\mathrm {un}}(G') \to {\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$ by setting
\[ \operatorname{res}_{{\mathrm{cpt}}, {\mathrm{un}}}(V) = \sum_{K'_{\mathcal{O}} \in \max(G')} \operatorname{res}_{K'_\mathcal{O}}(V) \]
for all 
$G' \in {\mathrm {InnT}}^p(G)$ and 
$V \in {\mathrm {Irr}}_{\mathrm {un}}(G')$. With notation as in § 7, for each 
$(A,\mathcal {O}) \in S_{\rm max}(G)$, we let 
$\text {proj}_\mathcal {O}$ be the projection map 
${\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}} \to \bigoplus _{x \in A} R_{\mathrm {un}}(\overline {K}_{x, \mathcal {O}})$ with respect to the decomposition (7.5), and let 
$\operatorname {res}_\mathcal {O} = \text {proj}_\mathcal {O} \circ \operatorname {res}_{{\mathrm {cpt}}, {\mathrm {un}}}$. We have
\begin{equation}
\operatorname{res}_{{\mathrm{cpt}},{\mathrm{un}}}=\bigoplus_{(A, \mathcal{O}) \in S_{{\rm max}}(G)} \operatorname{res}_\mathcal{O}. \end{equation}We can now formulate the conjecture for elliptic representations.
Conjecture 9.7 Let 
$G$ be a simple 
$F$-split group. Consider the following diagram.
For every unipotent element 
$u\in G^\vee$, elliptic pair 
$(s,h) \in {\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}$ and maximal compact open subgroup 
$K_\mathcal {O}$ of 
$G$, there exists a root of unity 
$\zeta =\zeta (u,s,h,\mathcal {O})$ such that
\[ \operatorname{res}_\mathcal{O} (\Pi(u,h,s))=\zeta \cdot ({\mathrm{FT}}_{{\mathrm{cpt}},{\mathrm{un}}}\circ \operatorname{res}_\mathcal{O})(\Pi(u,s,h)). \]
Remark 9.8 If 
$K_\mathcal {O}$ is the maximal hyperspecial compact subgroup of 
$G$, so that in particular 
$\operatorname {res}_\mathcal {O}=\operatorname {res}_{K_\mathcal {O}}$, we expect that the only roots of unity 
$\zeta$ that appear are the well-known 
$\Delta (\bar {x}_\rho )\in \{\pm 1\}$ (see [Reference LusztigLuz84a, § 6.7]) for certain families of unipotent representations of the finite groups of types 
$E_7$ and 
$E_8$. But for other maximal compact subgroups, Proposition 13.9 shows that in 
${\mathsf {SL}}_n$ for example, new roots of unity can appear.
We remark that extra roots of unity already appear in relation with the nonabelian Fourier transform for finite reductive groups, although we do not know if this is a related issue. In that setting there are three bases of the Grothendieck group of unipotent characters:
(1) the irreducible characters;
(2) the ‘almost characters’ which, by definition, are the image of the basis of irreducible characters under Lusztig's nonabelian Fourier transform; and
(3) the traces of the Frobenius on unipotent character sheaves.
Lusztig's conjecture states that each element of the basis (2) equals an element of the basis (3) times a root of unity. Determining these roots of unity is a difficult question, see Shoji [Reference ShojiSho95] for classical groups, also Hetz's recent thesis [Reference HetzHe23] for progress on the exceptional groups.
Remark 9.9 Note that the definition of the linear combinations 
$\Pi (u, s, h)$ and, thus, the definition of 
${\mathrm {FT}}_{{\mathrm {ell}}}^\vee$, depends on the (in general, non-canonical) map 
$\mathsf {LLC}_{{\mathrm {un}}}^p$. It is an interesting question to understand how Conjecture 9.7 depends on 
$\mathsf {LLC}_{{\mathrm {un}}}^p$ and, more specifically, what choices one must make in constructing 
$\mathsf {LLC}_{{\mathrm {un}}}^p$ for the conjecture to be true. In the cases of the conjecture proved below, these subtleties do not arise.
9.2 Regular unipotent elements
In § 13, we will verify this conjecture completely when 
$G={\mathsf {SL}}_n$ and 
${\mathsf {PGL}}_n$, but here we illustrate it in the case when 
$u$ is a regular unipotent element.
Proposition 9.10 Let 
$u_r\in G^\vee$ be a regular unipotent element. Then
\[ \operatorname{res}_{{\mathrm{cpt}}, {\mathrm{un}}} (\Pi(u_r,h,s))= {\mathrm{FT}}_{{\mathrm{cpt}},{\mathrm{un}}}\circ \operatorname{res}_{{\mathrm{cpt}}, {\mathrm{un}}}(\Pi(u_r,s,h)) \]
for all 
$(s, h) \in {\mathcal {Y}}(\Gamma _{u_r})$. In particular, Conjecture 9.7 holds with trivial roots of unity.
Proof. In this case 
$\Gamma _{u_r}={\mathrm {Z}}_{G^\vee }$ and every pair 
$(s,h)$ in 
${\mathcal {Y}}({\mathrm {Z}}_{G^\vee })$ is elliptic. Write the natural identification
\[ \Omega_G \overset{\sim}\longrightarrow \widehat{{\mathrm{Z}}_{G^\vee}} \]
as 
$x \mapsto \phi _x$. Then for 
$(s, h) \in {\mathcal {Y}}(\Gamma _{u_r})$, we have 
$\Pi (u_r,s,h)=\sum _{x \in \Omega } \phi _x(h) \pi (s,u_r,\phi _x)$. Note that 
$\pi (1, u_r, \phi _x)$ is the Steinberg representation 
${\mathrm {St}}_{G_x}$ of 
$G_x$, so 
$\pi (s, u_r, \phi _x) \simeq {\mathrm {St}}_{G_x} \otimes \chi _s$, where 
$\chi _s$ is the weakly unramified character corresponding to 
$s$ under (4.3). This follows from the fact that 
$\mathsf {LLC}_{{\mathrm {un}}}$ is equivariant for the action of weakly unramified characters, cf. [Reference SolleveldSol23a, Theorem 1(b)].
For the rest of the proof, we fix 
$(A, \mathcal {O}) \in S_{\rm max}(G)$. Then given 
$s \in {\mathrm {Z}}_{G^\vee }$, the character 
$\chi _s$ is trivial on the parahoric 
$K_{x, \mathcal {O}}^\circ$ so defines a character, call it 
$\sigma _s$, of 
$K_{x, \mathcal {O}}/K_{x, \mathcal {O}}^\circ = \overline {K}_{x, \mathcal {O}}/\overline {K}_{x, \mathcal {O}}^\circ$. We have
\[ \operatorname{res}_{\mathcal{O}}\pi(s,u_r,\phi_x)=\begin{cases}0, & \text{if } x \notin A,\\ {\mathrm{St}}_{\overline{K}_{x, \mathcal{O}}^\circ}\rtimes \sigma_s, & \text{if } x \in A,\end{cases} \]
where 
${\mathrm {St}}_{\overline {K}_{x, \mathcal {O}}^\circ }$ is the Steinberg character of the finite group 
$\overline {K}_{\mathcal {O},x}^\circ$. Note that for every 
$x \in A$,
\[ \phi_x(h)=\sigma_h(x)\quad\text{for all }h\in {\mathrm{Z}}_{G^\vee}. \]
Thus,
\begin{equation} \operatorname{res}_\mathcal{O}\Pi(u_r,s,h)= \sum_{x\in A} \sigma_h(x) {\mathrm{St}}_{\overline{K}_{x, \mathcal{O}}^\circ}\rtimes \sigma_s. \end{equation}
With notation as in § 5, let 
$\mathcal {U}_{\mathcal {O},{\mathrm {St}}}=\{{\mathrm {St}}_{K_\mathcal {O}^\circ }\}$ be the Steinberg family in 
${\mathrm {Irr}}_{\mathrm {un}}(\overline {K}_\mathcal {O})$, and let 
$\widetilde {\mathcal {U}}_{\mathcal {O},{\mathrm {St}}} \subset \bigcup _{x \in A} {\mathrm {Irr}}_{\mathrm {un}}(\overline {K}_{x, \mathcal {O}})$ be the family parametrized by 
$\widetilde {\Gamma }_{\mathcal {U}_{\mathcal {O}, {\mathrm {St}}}}^A = A$ under the bijection of Proposition 6.1. Then by (9.12), 
$\operatorname {res}_\mathcal {O} \Pi (u_r, s, h)$ corresponds to 
$\Pi _{\widetilde {\mathcal {U}}_{\mathcal {O},{\mathrm {St}}}}(\sigma _s,\sigma _h)$ defined as in (5.13). The claim then follows from Lemma 5.1.
10. A definition of the elliptic Fourier transform à la Lusztig
We present an alternative definition of the elliptic nonabelian Fourier transform (cf. Definition 9.6) along the lines of Lusztig's pairing defined in [Reference LusztigLus14, § 1]. Retain the notation from § 8. In particular, 
$\Gamma$ is a complex reductive group, not necessarily connected, and 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$ is the set of elliptic semisimple pairs in 
$\Gamma$. Let 
$\Sigma$ be the set of semisimple elements of 
$\Gamma$. Extending the definition in § 5.1, we let
\[ \mathcal{M}(\Gamma)= \{(x,\sigma)\mid x\in \Sigma,~\sigma\in \widehat{A_\Gamma(x)}\}, \]
modulo the equivalence relation given by conjugation by 
$\Gamma$.
For any two semisimple elements 
$x,y\in \Gamma$, define the set
\begin{equation} {\mathcal{A}}_{x,y}=\{z\in \Gamma\mid zxz^{-1}\in Z_\Gamma(y)\} \end{equation}
with an action of 
$Z_\Gamma (x)^\circ \times Z_\Gamma (y)^\circ$ by 
$(\gamma,\gamma ')\cdot z=\gamma ' z \gamma ^{-1}$. Let 
$^0\!{\mathcal {A}}_{x,y}$ denote the set of orbits. By [Reference LusztigLus14, Lemma 1.2], this is a finite set. It is clear that 
${\mathcal {A}}_{y,x}={\mathcal {A}}_{x,y}^{-1}$.
Consider the subset
\begin{equation} {\mathcal{A}}_{x,y}^{\mathrm{ell}}=\{z\in \Gamma\mid (zxz^{-1},y)\in {\mathcal{Y}}(\Gamma)_{\mathrm{ell}}\}, \end{equation}
and let 
$^0\!{\mathcal {A}}_{x,y}^{\mathrm {ell}}$ be the corresponding finite set of 
$Z_\Gamma (x)^\circ \times Z_\Gamma (y)^\circ$-orbits. Following [Reference LusztigLus14, § 1.3], we suppose 
$\kappa : \Sigma \times \Sigma \to {\mathbb {R}}$ is a nonnegative function satisfying
\[ \kappa(x',y')=\kappa(y',x'),\quad \kappa(\gamma x'\gamma^{-1},\gamma' y'(\gamma')^{-1})=\kappa(x',y'),\quad \kappa(\zeta x',\zeta' y')=\kappa(x',y'), \]
for all 
$x', y' \in \Sigma, \gamma, \gamma ' \in \Gamma$, 
$\zeta,\zeta '\in {\mathrm {Z}}_\Gamma$. The following definition is an elliptic analogue of [Reference LusztigLus14, § 1.3 (a)].
Definition 10.1 For 
$(x,\sigma ),(y,\tau )\in \mathcal {M}(\Gamma )$, set
\[ \{(x,\sigma),(y,\tau)\}_{\mathrm{ell}}={\kappa(x,y)}\sum_{z\in ^0\!{\mathcal{A}}_{x,y}^{\mathrm{ell}}} \tau(zx^{-1} z^{-1}) \sigma(z^{-1} y z). \]
It is immediate that 
$\{(x,\sigma ),(y,\tau )\}_{\mathrm {ell}} = \overline {\{ (y, \tau ), (x, \sigma )\}}_{\mathrm {ell}}$ for all 
$(x, \sigma ), (y, \tau ) \in \mathcal {M}(\Gamma )$. Moreover, if 
$x\in \Sigma$ is such that 
$x$ does not belong to any elliptic pair, then it is clear that 
$(x,\sigma )$ is in the radical of 
$\{\,,\}_{\mathrm {ell}}$ for all 
$\sigma$.
Let 
$\mathbf {V} = {\mathbb {C}}[\mathcal {M}(\Gamma )]$ denote the 
${\mathbb {C}}$-span of 
$\mathcal {M}(\Gamma )$, and given 
$(x, \sigma ) \in \mathcal {M}(\Gamma )$, write 
$[(x, \sigma )]$ for its image in 
$\mathbf {V}$. Then 
$\{,\}_{\mathrm {ell}}$ extends to a Hermitian pairing on 
$\mathbf {V}$. Similarly to (5.13), for every pair of commuting elements 
$x,y\in \Sigma$, denote
\begin{equation} \Pi(x,y)=\sum_{\sigma\in \widehat{A_\Gamma(x)}} \sigma(y^{-1}) [(x,\sigma)]\in \mathbf{V}. \end{equation}
Let 
$\bar {y}$ denote the image of 
$y$ in 
$A_\Gamma (x)$. Let 
$C_{{\mathrm {Z}}(x)}(y)$ denote the conjugacy class of 
$y$ in 
${\mathrm {Z}}_\Gamma (x)$, and 
$C_{A(x)}(\bar {y})$ the conjugacy class of 
$\bar y$ in 
$A_\Gamma (x)$. Since 
$x$ and 
$y$ commute, we have that 
${\mathcal {A}}_{x, y}$ contains the set 
${\mathrm {Z}}_\Gamma (y){\mathrm {Z}}_\Gamma (x)$, and the action of 
${\mathrm {Z}}_\Gamma (x)^\circ \times {\mathrm {Z}}_\Gamma (y)^\circ$ on 
${\mathcal {A}}_{x, y}$ restricts to an action on 
${\mathrm {Z}}_\Gamma (y){\mathrm {Z}}_\Gamma (x)$. Let 
$^0\!\mathcal {B}_{x,y}$ denote a set of orbit representatives for this restricted action.
Lemma 10.2 For every 
$(t,\tau )\in \mathcal {M}(\Gamma )$,
\[ \{\Pi(x,y),(t,\tau)\}_{\mathrm{ell}}=\begin{cases} {\kappa(x,y)|}{|{\mathrm{Z}}_{A(x)}(\bar y)|} \sum_{z\in ^0\!\mathcal{B}_{x,y}} \tau(zx^{-1} z^{-1}), & \text{if } t=y\text{ and } (x,y)\in {\mathcal{Y}}(\Gamma)_{\mathrm{ell}},\\ 0, & \text{otherwise}. \end{cases} \]
Proof. This is similar to the calculation for the nonabelian Fourier transform in the case of finite reductive groups. We compute
\begin{align*} \{\Pi(x,y),(t,\tau)\}_{\mathrm{ell}}&= \sum_{\sigma\in \widehat{A_\Gamma(x)}} \sigma(y^{-1}) \{(x,\sigma),(t,\tau)\}_{\mathrm{ell}}\\ &={\kappa(x,t)}\sum_{z\in ^0\!{\mathcal{A}}_{x,t}^{\mathrm{ell}}} \tau(zx^{-1} z^{-1})\bigg(\sum_{\sigma\in \widehat{ A_\Gamma(x)}}\sigma(y^{-1}) \sigma(z^{-1} t z)\bigg). \end{align*}
Fix 
$z \in {}^0\!{\mathcal {A}}_{x, t}^{\mathrm {ell}}$. By the orthogonality relations for characters, 
$\sum _{\sigma \in \widehat {A_\Gamma (x)}}\sigma (y^{-1}) \sigma (z^{-1} t z)=0$ unless the image of 
$z^{-1}tz$ in 
$A_\Gamma (x)$ is conjugate to 
$\bar {y}$, in which case it equals 
${|{\mathrm {Z}}_{A(x)}(\bar {y})|}$. In addition, 
$(x,z^{-1}tz)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$, which implies by Lemma 8.2 that the image of 
$z^{-1}tz$ in 
$A_\Gamma (x)$ is in an elliptic class, so 
$\bar {y}$ is elliptic in 
$A_\Gamma (x)$, and so again by Lemma 8.2, 
$(x,y)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$. Moreover, by the same result, the image of 
$z^{-1}tz$ in 
$A_\Gamma (x)$ is conjugate to 
$\bar y$ if and only if 
$z^{-1}tz$ is conjugate to 
$y$ in 
${\mathrm {Z}}_\Gamma (x)$. In particular, this means that 
$t$ is conjugate to 
$y$ in 
$\Gamma$. This proves that 
$\{\Pi (x,y),(t,\tau )\}_{\mathrm {ell}} = 0$ unless 
$t = y$ and 
$(x,y)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$. (Since 
$\mathcal {M}(\Gamma )$ consists of 
$\Gamma$-orbits, we may identify 
$t=y$.)
To complete the proof, assume 
$(x, y) \in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$. We have
\[ \{\Pi(x,y),(y,\tau)\}_{\mathrm{ell}}={\kappa(x,y)}{|{\mathrm{Z}}_{A(x)}(\bar y)|} \sum_{\substack{z\in ^0\!{\mathcal{A}}_{x,y}^{\mathrm{ell}}\\z^{-1}yz\in C_{Z(x)}(y)}} \tau(zx^{-1} z^{-1}). \]
We analyze the index of summation. Note that 
$z^{-1}yz\in C_{{\mathrm {Z}}(x)}(y)$ is equivalent to 
$z\in {\mathrm {Z}}_\Gamma (y){\mathrm {Z}}_\Gamma (x)$. Since 
$(x,y)$ is an elliptic pair, it is also automatic that 
$(zxz^{-1}, y)$ is for any 
$z \in {\mathrm {Z}}_\Gamma (y){\mathrm {Z}}_\Gamma (x)$, hence 
$z$ ranges over representatives of 
${\mathrm {Z}}_\Gamma (x)^\circ \times {\mathrm {Z}}_\Gamma (y)^\circ$-orbits in 
${\mathrm {Z}}_\Gamma (y){\mathrm {Z}}_\Gamma (x)$.
Proposition 10.3 For 
$(x,y)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$:
(a)
$\displaystyle\sum_{\tau\in \widehat{A_\Gamma(y)}} \{\Pi(x,y),(y,\tau)\}_{\mathrm{ell}} [(y,\tau)]=\kappa(x,y) |{\mathrm{Z}}_{A(x)}(\bar{y})| |^0\!\mathcal{B}_{x,y}|\cdot \Pi(y,x)\text{ in }\mathbf{V};$(b)
$\displaystyle\sum_{h\in A_\Gamma(y)} \{\Pi(x,y),\Pi(y,h)\}_{\mathrm{ell}} \Pi(y,h) = \kappa(x,y) |A_\Gamma(y)| |{\mathrm{Z}}_{A(x)}(\bar{y})| |^0\!\mathcal{B}_{x,y}|\cdot \Pi(y,x).$
Proof. (a) Denote by 
$\tau ^{z^{-1}}\in \widehat {A_\Gamma (y)}$ the twist of 
$\tau$ by 
$z^{-1}$, so 
$\tau ^{z^{-1}}(a)=\tau (z a z^{-1})$. Applying the previous lemma, we get
\begin{align*} &\frac{1}{|\kappa(x,y)||{\mathrm{Z}}_{A(x)}(\bar{y})|}\sum_{\tau\in \widehat{A_\Gamma(y)}} \{\Pi(x,y),(y,\tau)\}_{\mathrm{ell}} [(y,\tau)]\\ &\quad=\sum_{z\in ^0\!\mathcal{B}_{x,y}} \sum_{\tau\in\widehat{A_\Gamma(y)}} \tau^{z^{-1}}(x^{-1})[(y,\tau)] =\sum_{z\in ^0\!\mathcal{B}_{x,y}} \sum_{\tau\in\widehat{A_\Gamma(y)}} \tau^{z^{-1}}(x^{-1})[(z^{-1}yz,\tau^{z^{-1}})]\\ &\quad=\sum_{z\in ^0\!\mathcal{B}_{x,y}}\sum_{\tau'\in \widehat{A_\Gamma(z^{-1}yz)}} \tau'(x^{-1}) [(z^{-1}yz,\tau')] =\sum_{z\in ^0\!\mathcal{B}_{x,y}}\Pi(z^{-1}yz,x)=|^0\!\mathcal{B}_{x,y}|~\Pi(y,x), \end{align*}
since 
$z^{-1}yz$ is conjugate to 
$y$ in 
${\mathrm {Z}}_\Gamma (x)$.
(b) This is immediate from part (a) using 
$\sum _{h\in A_\Gamma (y)} \tau (h^{-1}) \tau '(h)=|A_\Gamma (y)|\delta _{\tau,\tau '}$, 
$\tau,\tau '\in \widehat {A_\Gamma (y)}$.
Consider the set
\begin{equation} B_{\mathbf{V}}=\{|C_{A(y)}(\bar{h})|^{1/2} \Pi(y,h)\mid (y,h)\in \Gamma\backslash {\mathcal{Y}}(\Gamma)_{\mathrm{ell}}\}. \end{equation}
By Lemma 10.2, 
$B_{\mathbf {V}}$ spans 
$\bar {\mathbf {V}}_{\mathrm {ell}}:=\mathbf {V}/\ker \{\,,\,\}_{\mathrm {ell}}$, where 
$\ker \{\,,\,\}_{\mathrm {ell}}$ denotes the radical of the pairing. Define
\begin{equation} {\mathcal{F}}'_{\mathrm{ell}}: \mathbf{V}\to \mathbf{V},\quad {\mathcal{F}}'_{\mathrm{ell}}(v)=\sum_{b\in B_{\mathbf{V}}} \{v,b\} b. \end{equation}
Clearly, 
${\mathcal {F}}'_{\mathrm {ell}}$ descends to a linear map on 
$\bar {\mathbf {V}}_{\mathrm {ell}}$.
Corollary 10.4 For every 
$(x,y)\in {\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$,
\[ {\mathcal{F}}'_{\mathrm{ell}}(\Pi(x,y))=\kappa(x,y) |A_\Gamma(y)| |{\mathrm{Z}}_{A(x)}(\bar y)| |^0\!\mathcal{B}_{x,y}|\cdot \Pi(y,x). \]
Proof. From Lemma 10.2, we have 
${\mathcal {F}}'_{\mathrm {ell}}(\Pi (x,y))=\sum _h |C_{A(y)}(\bar {h})| \{\Pi (x,y),\Pi (y,h)\}_{\mathrm {ell}} [\Pi (y,h)]$, where the sum is over a set of representatives 
$h$ of the conjugacy classes of elliptic semisimple elements in 
${\mathrm {Z}}_\Gamma (y)$, equivalently, elliptic conjugacy classes in 
$A_\Gamma (y)$. Thus, we may rewrite
\[ {\mathcal{F}}'_{\mathrm{ell}}(\Pi(x,y))=\sum_{h\in A_\Gamma(y)_{\mathrm{ell}}} \{\Pi(x,y),\Pi(y,h)\}_{\mathrm{ell}} \Pi(y,h)=\sum_{h\in A_\Gamma(y)} \{\Pi(x,y),\Pi(y,h)\}_{\mathrm{ell}} \Pi(y,h), \]
using Lemma 10.2 again. Then the claim follows from Proposition 10.3.
In other words, 
${\mathcal {F}}'_{\mathrm {ell}}$ acts, up to a scalar multiple, by the flip on each 
$\Pi (x,y)$. If we set
\begin{equation} \kappa(x,y)=\frac{|C_{A(x)}(\bar y)|^{1/2} |C_{A(y)}(\bar{x})|^{1/2}}{|A_\Gamma(x)||A_\Gamma(y)| |^0\!\mathcal{B}_{x,y}|}, \end{equation}then
\begin{equation} {{\mathcal{F}}'_{\mathrm{ell}}}^2={\mathrm{Id}}. \end{equation}Remark 10.5 When we specialize to 
$\Gamma =\Gamma _u$ for a unipotent element 
$u \in \Gamma$, we see from Lemma 9.5 that 
$B_{\mathbf {V}}$ is in fact an orthogonal basis of 
$\bar {\mathbf {V}}_{\mathrm {ell}}$ with respect to the Euler–Poincaré pairing.
11. Elliptic unipotent representations
The main result of this section is as follows.
Theorem 11.1 Suppose 
$G$ is a semisimple split 
$F$-group of adjoint type. Then Conjecture 9.1 holds for all pure inner twists of 
$G$.
Remark 11.2 In § 11.4, we explain how Theorem 11.1 can be extended to other isogenies. See, in particular, Corollary 11.13.
The strategy of the proof is as follows. As explained in § 4, the set of unipotent enhanced Langlands parameters 
$\Phi _{{\mathrm {e}},{\mathrm {un}}}(G')$, where 
$G'$ is an inner twist of 
$G$, decomposes into a disjoint union 
$\Phi _{{\mathrm {e}},{\mathrm {un}}}(G')=\bigsqcup _{{\mathfrak {s}}^\vee \in \mathfrak {B}_{\mathrm {un}}^\vee (G')} \Phi _{{\mathrm {e}}}(G')^{\mathfrak {s}^\vee }$. Consequently, there is a decomposition
\[ R(\Phi_{{{{\mathrm{e}}}},{\mathrm{un}}}(G'))=\bigoplus_{{\mathfrak{s}}^\vee\in \mathfrak{B}_{\mathrm{un}}^\vee(G')} R(\Phi_{{{\mathrm{e}}}}(G')^{\mathfrak{s}^\vee}), \]
where 
$R(\Phi _{{{{\mathrm {e}}}},{\mathrm {un}}}(G'))$ and 
$\Phi _{{\mathrm {e}}}(G')^{\mathfrak {s}^\vee }$ are defined analogously to 
$R(\Phi _{{{{\mathrm {e}}}},{\mathrm {un}}}({}^LG))$ (see (4.16)). In [Reference LusztigLus95] (for adjoint simple groups) and later in [Reference Aubert, Moussaoui and SolleveldAMS17] (for arbitrary groups), an affine Hecke algebra with possibly unequal parameters 
${\mathcal {H}}(\mathfrak {s}^\vee )$ is constructed such that there is a bijection
\begin{equation} {\mathrm{Irr}} ~{\mathcal{H}}(\mathfrak{s}^\vee)\longleftrightarrow \Phi_{{{\mathrm{e}}}}(G')^{\mathfrak{s}^\vee}, \end{equation}which induces a linear isomorphism
\[ R({\mathcal{H}}(\mathfrak{s}^\vee))\cong R(\Phi_{{{\mathrm{e}}}}(G')^{\mathfrak{s}^\vee}). \]
We need to study the elliptic space 
$\overline {R}({\mathcal {H}}(\mathfrak {s}^\vee ))$. The important fact for the elliptic theory is that 
${\mathcal {H}}(\mathfrak {s}^\vee )$ is a deformation of an extended affine Weyl group 
${\widetilde {W}}_{\mathfrak {s}^\vee }=W_{\mathfrak {s}^\vee }\ltimes X^*(T_{\mathfrak {s}^\vee })$, where 
$T_{\mathfrak {s}^\vee }=\Phi _{{\mathrm {e}}}(L')^{{\mathfrak {s}}_{L'}^\vee }$ for 
$L'$ a Levi subgroup of 
$G'$ that corresponds to 
${\mathfrak {s}}^\vee$. This allows us to use the results of [Reference Opdam and SolleveldOS09] to further reduce to 
$\overline {R}({\mathcal {H}}(\mathfrak {s}^\vee ))\cong \overline {R}({\widetilde {W}}_{\mathfrak {s}^\vee })$. Moreover, the latter space is equivalent to a direct sum of elliptic spaces for certain finite groups
\[ \overline{R}({\widetilde{W}}_{\mathfrak{s}^\vee})\cong \bigoplus_{s\in W_{\mathfrak{s}^\vee}\backslash T_{\mathfrak{s}^\vee}} \overline{R}({\mathrm{Z}}_{W_{\mathfrak{s}^\vee}}(s)). \]
We then use results of [Reference WaldspurgerWal07] and the generalized Springer correspondence to relate the spaces 
$\overline {R}({\mathrm {Z}}_{W_{\mathfrak {s}^\vee }})(s)$ to the relevant spaces of Langlands parameters (for the various unipotent elements) in 
$\Phi _{{\mathrm {e}},{\mathrm {un}}}(G')^{\mathfrak {s}^\vee }$.
Finally, by [Reference LusztigLus95, Reference SolleveldSol23a] for each 
${\mathfrak {s}}^\vee \in {\mathfrak {B}}_{\mathrm {un}}^\vee (G')$, there exists 
$\mathfrak {s}\in {\mathfrak {B}}_{\mathrm {un}}(G')$ that is sent to 
${\mathfrak {s}}^\vee$ by the LLC, and then the Hecke algebra 
${\mathcal {H}}({\mathfrak {s}})$ for 
$\mathfrak {s}$ is isomorphic to 
${\mathcal {H}}(\mathfrak {s}^\vee )$. The fact that the elliptic space for the representations in the block 
${\mathfrak {R}}(G')^{\mathfrak {s}}$ is naturally isomorphic to 
$\overline {R}({\mathcal {H}}(\mathfrak {s}))$ is immediate by the exactness of the equivalence of categories between 
${\mathfrak {R}}(G')^{\mathfrak {s}}$ and 
${\mathcal {H}}(\mathfrak {s})$-modules.
11.1 Euler–Poincaré pairings for affine Hecke algebras
We begin by recalling several known facts about elliptic theory for affine Weyl groups and affine Hecke algebras. The main reference is [Reference Opdam and SolleveldOS09] (see also [Reference Ciubotaru and OpdamCO15]). The notation in this section is self contained and independent of the previous sections. For applications, the root datum in this section will be specialized to the root datum of the Langlands dual group 
$G^\vee$, as well as to the root data for the affine Hecke algebras 
${\mathcal {H}}(\mathfrak {s}^\vee )$ that occur on the dual side of the LLC.
Let 
${\mathcal {R}}=(X,R,X^\vee, R^\vee,\Pi )$ be a based root datum. Here 
$X,X^\vee$ are lattices in perfect duality 
$\langle ~,~\rangle \colon X\times X^\vee \to {\mathbb {Z}}$, 
$R\subset X\setminus \{0\}$ and 
$R^\vee \subset X^\vee \setminus \{0\}$ are the finite sets of roots and coroots, respectively, and 
$\Pi \subset R$ is a basis of simple roots. Let 
$W$ be the finite Weyl group with set of generators 
$S=\{s_\alpha :\alpha \in \Pi \}$. Set 
${\widetilde {W}}=W\ltimes X$, the (dual) extended affine Weyl group, and 
$W^a=W\ltimes Q$, the (dual) affine Weyl group, where 
$Q$ is the root lattice of 
$R$. Then 
$W^a$ is normal in 
${\widetilde {W}}$ and 
$\Omega :={\widetilde {W}}/W^a\cong X/Q$ is an abelian group. We assume that 
${\mathcal {R}}$ is semisimple, which means that 
$\Omega$ is a finite group.
The set 
$R^a=R^\vee \times {\mathbb {Z}}\subset X^\vee \times {\mathbb {Z}}$ is the set of affine roots. (Note that 
${\widetilde {W}}$ is the extended affine Weyl group of a split 
$p$-adic group 
$G$ with root datum dual to 
${\mathcal {R}}$, and 
$R^a$ is the set of affine roots for 
$G$.) A basis of simple affine roots is given by 
$\Pi ^a=(\Pi ^\vee \times \{0\})\cup \{(\gamma ^\vee,1): \gamma ^\vee \in R^\vee \text { minimal}\}$. For every affine root 
$\mathbf {a}=(\alpha ^\vee,n)$, let 
$s_{\mathbf {a}}\colon X\to X$ denote the reflection 
$s_{\mathbf {a}}(x)=x-((x,\alpha ^\vee )+n)\alpha$. The affine Weyl group 
$W^a$ has a set of generators 
$S^a=\{s_{\mathbf {a}} \mid \mathbf {a}\in \Pi ^a\}$. Given 
$J \subset S^a$, let 
$W_J$ be the subgroup of 
$W^a$ generated by 
$\{s_{\mathbf {a}} \mid \mathbf {a} \in J\}$. Let 
$l\colon {\widetilde {W}}\to {\mathbb {Z}}$ be the length function.
Set 
$E=X\otimes _{\mathbb {Z}} {\mathbb {C}}$, so the discussion regarding the elliptic theory of 
$W$ and 
$E$ from the previous sections applies. We denote a typical element of 
${\widetilde {W}}$ by 
$w t_x$, where 
$w\in W$ and 
$x\in X$. The extended affine Weyl group 
${\widetilde {W}}$ acts on 
$E$ via 
$(w t_x)\cdot v=w\cdot v+ x,$ 
$v\in E$.
An element 
$w t_x\in {\widetilde {W}}$ is called elliptic if 
$w\in W$ is elliptic (with respect to the action on 
$E$). For basic facts about elliptic theory for 
${\widetilde {W}}$, see [Reference Opdam and SolleveldOS09, §§ 3.1, 3.2]. There are finitely many elliptic conjugacy classes in 
${\widetilde {W}}$ (and in 
$W^a$). The following fact is well-known (see for example [Reference Ciubotaru and OpdamCO15, Lemma 5.4]).
Lemma 11.3 Suppose 
$C$ is an elliptic conjugacy class in 
$W^a$. Then there exists one and only one maximal 
$J\subsetneq S^a$ such that 
$C\cap W_J\neq \emptyset,$ and in this case 
$C\cap W_J$ forms a single elliptic 
$W_J$-conjugacy class.
Let 
$R({\widetilde {W}})$ be the Grothendieck group of 
${\widetilde {W}}$-mod (the category of finite-dimensional modules). Define the Euler–Poincaré pairing of 
${\widetilde {W}}$ by
\begin{equation} \langle V_1,V_2\rangle_{\mathrm{EP}}^{{\widetilde{W}}}=\sum_{i\geqslant 0}(-1)^i\dim {\operatorname{Ext}}^i_{{\widetilde{W}}}(V_1,V_2),\quad V_1,V_2 \text{ finite-dimensional } {\widetilde{W}}\text{-modules}. \end{equation}
Set 
$\overline {R}({\widetilde {W}})=R({\widetilde {W}})/\text {rad}\langle ~,~\rangle _{\mathrm {EP}}^{{\widetilde {W}}}$. By [Reference Opdam and SolleveldOS09, Theorem 3.3], the Euler–Poincaré pairing for 
${\widetilde {W}}$ can also be expressed as an elliptic integral. More precisely, define the conjugation-invariant elliptic measure 
$\mu _{\mathrm {ell}}$ on 
${\widetilde {W}}$ by setting 
$\mu _{\mathrm {ell}}=0$ on nonelliptic conjugacy classes, and for an elliptic conjugacy class 
$C$ such that 
$v\in E$ is an isolated fixed point for some element of 
$C$, set
\[ \mu_{\mathrm{ell}}(C)=\frac{|Z_{{\widetilde{W}}}(v)\cap C|}{|Z_{{\widetilde{W}}}(v)|}; \]
here 
$Z_{{\widetilde {W}}}(v)$ is the isotropy group of 
$v$ in 
${\widetilde {W}}$. Then
\begin{equation} \langle V_1, V_2\rangle_{\mathrm{EP}}^{{\widetilde{W}}}= (\chi_{V_1},\chi_{V_2})_{\mathrm{ell}}^{{\widetilde{W}}}:=\int_{{\widetilde{W}}}\chi_{V_1}\overline{\chi_{V_2}}~d\mu_{\mathrm{ell}},\quad V_1,V_2\in {\widetilde{W}}\text{-mod}, \end{equation}
where 
$\chi _{V_1},\chi _{V_2}$ are the characters of 
$V_1$ and 
$V_2$.
Set 
$T={\mathrm {Hom}}_{\mathbb {Z}}(X,{\mathbb {C}}^\times )$. Then 
$W$ acts on 
$T$. For every 
$s\in T,$ set 
$W_s=\{w\in W: w\cdot s=s\}$. One considers the elliptic theory of the finite group 
$W_s$ acting on the cotangent space 
$\mathfrak {t}_s^*$ of 
$T$ at 
$s$. By Clifford theory, the induction map
\[ {\mathrm{Ind}}_s\colon W_s\text{-mod}\to {\widetilde{W}}\text{-mod},\quad {\mathrm{Ind}}_s(V_1):={\mathrm{Ind}}_{W_s\ltimes X}^{{\widetilde{W}}}(V_1\otimes s) \]
maps irreducible modules to irreducible modules. By [Reference Opdam and SolleveldOS09, Theorem 3.2], the map
\begin{equation} \bigoplus_{s\in W\backslash T}{\mathrm{Ind}}_s\colon \bigoplus_{s\in W\backslash T}\overline{R}(W_s)_{\mathbb{C}}\to \overline{R}({\widetilde{W}})_{\mathbb{C}} \end{equation}is an isomorphism of metric spaces, in particular,
\begin{equation} \langle {\mathrm{Ind}}_s V_1,{\mathrm{Ind}}_s V_2\rangle_{\mathrm{EP}}^{{\widetilde{W}}}=(V_1,V_2)_{\mathrm{ell}}^{W_s},\quad V_1,V_2\in W_s\text{-mod}. \end{equation}
A space 
$\overline {R}(W_s)_{\mathbb {C}}$ in the left-hand side of (11.4) is nonzero if and only if 
$s$ is an isolated element of 
$T$, more precisely 
$s\in T_{\mathrm {iso}}$, where
\[ T_{\mathrm{iso}}=\{s\in T^\vee: w\cdot s=s\text{ for some elliptic }w\in W\}. \]
Example 11.4 Let 
${\mathcal {R}}$ be the root datum of 
${\mathsf {PGL}}_n({\mathbb {C}})$. We may take 
$T$ to be the maximal diagonal torus of 
${\mathsf {PGL}}_n({\mathbb {C}})$, with 
$X=X^*(T)$ the group of characters and 
$X^\vee =X_*(T)$ the group of cocharacters. In this case, 
$Q=X$ and
\[ {\widetilde{W}}=W^a=\langle s_i,~0\leqslant i\leqslant n-1\mid (s_is_j)^{m(i,j)}=1,\ 0\leqslant i,j\leqslant n-1\rangle, \]
where 
$m(i,i)=1$, 
$m(i,j)=2$ if 
$1<|i-j|< n-1$, and 
$m(i,j)=3$ if 
$|i-j|=1$ or 
$|i-j|=n-1$, when 
$n\geqslant 3$. This is the extended affine Weyl group associated to the 
$p$-adic group 
${\mathsf {SL}}_n$. If 
$n=2$, then 
${\widetilde {W}}=W^a=\langle s_0,s_1\mid s_0^2=s_1^2=1\rangle$.
With this notation, the finite Weyl group is 
$W=\langle s_1,\ldots,s_{n-1}\rangle \subset W^a$. For every 
$0\leqslant i\leqslant n-1$, let 
$W_i=\langle s_0,s_1,\ldots, s_{i-1},s_{i+1},\ldots, s_{n-1}\rangle \subset W^a$. These are the maximal (finite) parabolic subgroups of 
$W^a$. In particular, 
$W_0=W$ and 
$W_i\cong S_n$ for all 
$i$. The space 
$E=\mathfrak {t}^*\cong {\mathbb {C}}^{n-1}$ and each 
$W_i$ acts on 
$E$ by the reflection representation. Therefore, there exists a unique elliptic 
$W_i$-conjugacy class represented by the Coxeter element 
$w_i=s_0s_1\dotsb s_{i-1} s_{i+1}\dotsb s_{n-1}$. Thus, by Lemma 11.3, there are exactly 
$n$ elliptic conjugacy classes in 
$W^a$ each determined by the condition that it meets 
$W_i$ in the conjugacy class of 
$w_i$, 
$0\leqslant i\leqslant n-1$. In particular, 
$\dim \overline {R}({\widetilde {W}})_{\mathbb {C}}=n$ in this case.
On the other hand, by (11.4), we need to consider 
$W$-orbits in 
$T_{\mathrm {iso}}$. Since there is only one elliptic conjugacy class in 
$W$, every 
$W$-orbit in 
$T_{\mathrm {iso}}$ is represented by an element of
\[ T^{s_1s_2\dotsb s_{n-1}}=\{\Delta_n(z)\mid z\in\mu_n\},\quad \Delta_n(z)=\text{diag}(1,z,z^2,\ldots,z^{n-1}) \in T,\quad \mu_n=\{z\mid z^n=1\}, \]
as noted previously. Two elements 
$\Delta _n(z)$ and 
$\Delta _n(z')$ of 
$T^{s_1s_2\dotsb s_{n-1}}$ are 
$W$-conjugate if and only if 
$z$ and 
$z'$ have the same order. Fix a primitive 
$n$th root 
$\zeta$ of 
$1$. This means that (11.4) becomes, in this case,
\[ \bigoplus_{d | n} \overline{R}(W_{\Delta_n(\zeta^{n/d})})_{\mathbb{C}}\cong \overline{R}({\widetilde{W}})_{\mathbb{C}}. \]
If 
$z\,{=}\,\zeta ^m$, where 
$n\,{=}\,dm$, then 
$\Delta _n(z)$ is 
$W$-conjugate to 
$\text {diag}(\underbrace {1,\ldots,1}_m,\underbrace {z,\ldots,z}_m,\ldots,\underbrace {z^{d-1},\ldots,z^{d-1}}_m)$. Hence, one calculates
\begin{equation} W_{\Delta_n(z)}\cong S_m^d\rtimes C_d\quad\text{and}\quad \mathfrak{t}^*_{\Delta_n(z)}=\bigg\{(a_1,\ldots,a_n)\,\bigg|\, \sum_{i=1}^n a_i=0\bigg\}. \end{equation}
The action is the natural permutation action. There are 
$\varphi (d)$ elliptic conjugacy classes, represented by 
$(w_m,1,\ldots,1)\cdot x_d$, where 
$w_m$ is a fixed 
$m$-cycle (Coxeter element) of 
$S_m$ and 
$x_d$ is one of the 
$\varphi (d)$ generators of 
$C_d$ (see Lemma 13.5). Again 
$\sum _{d|n}\varphi (d)=n$.
Let 
$\vec {\mathbf {q}}=\{\mathbf {q}(s)\mid s\in S^a\}$ be a set of invertible, commuting indeterminates such that 
$\mathbf {q}(s)=\mathbf {q}(s')$ whenever 
$s,s'$ are 
$W^a$-conjugate. Let 
$\Lambda ={\mathbb {C}}[\mathbf {q}(s),\mathbf {q}(s)^{-1}\mid s\in S^a]$.
The generic affine Hecke algebra 
${\mathcal {H}}({\mathcal {R}},\vec {\mathbf {q}})$ associated to the root datum 
${\mathcal {R}}$ and the set of indeterminates 
$\vec {\mathbf {q}}$ is the unique associative, unital 
$\Lambda$-algebra with basis 
$\{T_w: w\in {\widetilde {W}}\}$ and relations:
(i)
$T_w T_{w'}=T_{ww'},$ for all $w,w'\in W$ such that $l(ww')=l(w)+l(w')$;(ii)
$(T_s-\mathbf {q}(s)^2)(T_s+1)=0$ for all $s\in S^a$.
Fix a real number 
$q>1$. Given a 
$W^a$-invariant function 
$m\colon S^a\to {\mathbb {R}}$, we may define a homomorphism 
$\lambda _{m}\colon \Lambda \to {\mathbb {C}}$, 
$\mathbf {q}(s)= q^{m(s)}$. Let 
${\mathbb {C}}_{\lambda _{m}}$ be the one-dimensional complex module on which 
$\Lambda$ acts by 
$\lambda _m$. Consider the specialized affine Hecke 
${\mathbb {C}}$-algebra
\begin{equation} {\mathcal{H}}({\mathcal{R}}, q, m)={\mathcal{H}}({\mathcal{R}},\vec{\mathbf{q}})\otimes_\Lambda {\mathbb{C}}_{\lambda_{m}}. \end{equation}Example 11.5 Let 
${\mathcal {R}}$ be the root datum of 
${\mathsf {PGL}}_n({\mathbb {C}})$. If 
$n=2$, the generic affine Hecke algebra has two indeterminates 
$\mathbf {q}(s_0)$ and 
$\mathbf {q}(s_1)$ and it is generated by 
$T_0=T_{s_0}$, 
$T_1=T_{s_1}$ subject only to the quadratic relations
\[ (T_{i}-\mathbf{q}(s_i)^2)(T_{i}+1)=0, \quad i=0,1. \]
If 
$n\geqslant 3$, all the simple reflections are 
$W^a$-conjugate. There is only one indeterminate 
$\mathbf {q}$ such that the affine Hecke algebra is generated by 
$\{T_i=T_{s_i}, 0\leqslant i\leqslant n-1\}$ subject to the relations:
(i)
$T_{i}T_{j}=T_{j}T_{i}$, $1<|i-j|< n-1$;(ii)
$T_{i}T_{i+1} T_{i}=T_{i+1}T_i T_{i+1}$, $0\leqslant i\leqslant n-1$; $T_0 T_{n-1} T_0=T_{n-1}T_0 T_{n-1}$;(iii)
$(T_i -\mathbf {q}^2)(T_i+1)=0$.
Let 
${\mathcal {H}}={\mathcal {H}}({\mathcal {R}}, q, m)$ for simplicity of notation. If 
$V_1,V_2$ are two finite-dimensional 
${\mathcal {H}}$-modules, define the Euler–Poincaré pairing [Reference Opdam and SolleveldOS09, § 3.4]:
\begin{equation} {\mathrm{EP}}_{\mathcal{H}}(V_1,V_2)=\sum_{i\geqslant 0} (-1)^i\dim {\operatorname{Ext}}^i_{\mathcal{H}}(V_1,V_2). \end{equation}
This is a finite sum since 
${\mathcal {H}}$ has finite cohomological dimension [Reference Opdam and SolleveldOS09, Proposition 2.4]. The pairing 
${\mathrm {EP}}_{\mathcal {H}}$ is symmetric and positive semidefinite. It extends to a Hermitian positive-semidefinite pairing on the complexified Grothendieck group 
$R({\mathcal {H}})_{\mathbb {C}}$ of finite-dimensional 
${\mathcal {H}}$-modules. We wish to compare the Euler–Poincaré pairings for 
${\mathcal {H}}({\mathcal {R}}, q, m)$ and 
${\mathcal {H}}({\mathcal {R}}, q^\epsilon, m)$, where 
$\epsilon \in [0,1]$. Suppose we have a family of maps
\begin{equation} \sigma_\epsilon\colon {\mathcal{H}}({\mathcal{R}},q,m)\text{-mod}\to {\mathcal{H}}({\mathcal{R}},q^\epsilon,m)\text{-mod},\quad \sigma_\epsilon(\pi,V)=(\pi_\epsilon,V), \end{equation}such that:
(a) for every
$w\in {\widetilde {W}}$ and every $(\pi,V)$, the assignment $\epsilon \mapsto \pi (\epsilon )(T_w)$ is a continuous map $[0,1]\to {\mathrm {End}}(V)$.
Then [Reference Opdam and SolleveldOS09, Theorem 3.5] shows that
\[ {\mathrm{EP}}_{{\mathcal{H}}({\mathcal{R}},q,m)}(V_1,V_2)={\mathrm{EP}}_{{\mathcal{H}}({\mathcal{R}},q^\epsilon,m)}(\sigma_\epsilon(V_1),\sigma_\epsilon(V_2)),\quad \text{for all }\epsilon\in[0,1]. \]
In particular, note that 
${\mathcal {H}}({\mathcal {R}},q^0,m)={\mathbb {C}}[{\widetilde {W}}]$, meaning that
\begin{equation} {\mathrm{EP}}_{{\mathcal{H}}({\mathcal{R}},q,m)}(V_1,V_2)=\langle\sigma_0(V_1),\sigma_0(V_2)\rangle_{\mathrm{EP}}^{{\widetilde{W}}}. \end{equation}
Using [Reference Opdam and SolleveldOS09, Theorem 1.7] or alternatively, for the affine Hecke algebras that occur for unipotent representations of 
$p$-adic groups, via the geometric constructions of [Reference Kazhdan and LusztigKL87, Reference LusztigLus95, Reference LusztigLus02], we know that scaling maps 
$\sigma _\epsilon$ as above exist and in addition, they also behave well with respect to harmonic analysis:
(b) for every
$\epsilon \in [0,1]$, $V$ is unitary (respectively, tempered) if and only if $\sigma _\epsilon (V)$ is unitary (respectively, tempered);(c) for every
$\epsilon \in (0,1]$, $V$ is discrete series if and only if $\sigma _\epsilon (V)$ is discrete series.
Denoting by 
$\overline {R}({\mathcal {H}})_{\mathbb {C}}$ the quotient of 
$R({\mathcal {H}})_{\mathbb {C}}$ by the radical of 
${\mathrm {EP}}_{\mathcal {H}}$, it follows [Reference Opdam and SolleveldOS09, Proposition 3.9] that the scaling map 
$\sigma _0$ induces an injective isometric map
\begin{equation} \sigma_0\colon \overline{R}({\mathcal{H}})_{\mathbb{C}}\to \overline{R}({\widetilde{W}})_{\mathbb{C}}\cong \bigoplus_{s\in T/W}\overline{R}(W_s)_{\mathbb{C}}. \end{equation}In fact, this map is also an isomorphism, for example via [Reference Ciubotaru and HeCH17, Theorem 8.1].
11.2 Elliptic inner products for Weyl groups (after Waldspurger [Wal07])
Let 
${\mathcal {G}}={\mathcal {G}}^\circ$ be a complex connected reductive group and 
$\theta \colon {\mathcal {G}}\to {\mathcal {G}}$ a quasi-semisimple automorphism of 
${\mathcal {G}}$ of finite order.
As in § 3, we let 
$\mathbf {I}$ be the set of pairs 
$(U, {\mathcal {E}})$ where 
$U$ is a unipotent conjugacy class in 
${\mathcal {G}}$ and 
${\mathcal {E}}$ is an irreducible 
${\mathcal {G}}$-equivariant local system on 
$U$. The automorphism 
$\theta$ acts on 
$\mathbf {I}$ via 
$(U,{\mathcal {E}})\mapsto (\theta (U),(\theta ^{-1})^*({\mathcal {E}}))$. Let 
$\mathbf {I}^\theta$ denote the fixed points of this action and suppose 
$(U,{\mathcal {E}})\in \mathbf {I}^\theta$. If we fix 
$u\in U$, there exists 
$x\in {\mathcal {G}}$ such that 
${\mathrm {Ad}}(x)\circ \theta (u)=u$, hence 
${\mathrm {Ad}}(x)\circ \theta$ preserves 
${\mathrm {Z}}_{\mathcal {G}}(u)$ and, hence, it defines an automorphism of 
$A_u$, denoted 
$\theta _u$. As explained in [Reference WaldspurgerWal07, p. 612], if 
$\phi \in \widehat {A}_u$ corresponds to the local system 
${\mathcal {E}}$, the fact that 
$(\theta ^{-1})^*({\mathcal {E}})\cong {\mathcal {E}}$ is equivalent to the condition that 
$\phi$ extends to a representation 
$\widetilde {\phi }$ of 
$A_u\rtimes \langle \theta _u\rangle$.
Fix a Borel subgroup 
$B_u$ of 
${\mathrm {Z}}_{\mathcal {G}}(u)^\circ$ and a maximal torus 
$T_u$ in 
$B_u$. Let 
$\mathfrak {t}_u$ be the complex Lie algebra of 
$T_u$. Define a complex representation 
$(\delta _u,{\mathfrak {t}}_u)$ of 
$A_u\rtimes \langle \theta _u\rangle$, extending the previous definition for the action of 
$A_u$. Similarly to § 8.2, since 
${\mathrm {Z}}_{\mathcal {G}}(u)$ acts on 
${\mathrm {Z}}_{\mathcal {G}}(u)^\circ$ by conjugation and 
$\theta _u$ acts on 
${\mathrm {Z}}_{\mathcal {G}}(u)^\circ$ as above, every element 
$z\in {\mathrm {Z}}_{\mathcal {G}}(u)\rtimes \langle \theta _u\rangle$ acts on 
${\mathrm {Z}}_{\mathcal {G}}(u)^\circ$ via an automorphism 
$\alpha _z$. There exists 
$y\in {\mathrm {Z}}_{\mathcal {G}}(u)^\circ$ such that 
$\alpha _z\circ {\mathrm {Ad}}(y)$ preserves 
$B_u$ and 
$T_u$. This means that 
$\alpha _z\circ {\mathrm {Ad}}(y)$ defines an automorphism of the cocharacter lattice 
$X_*(T_u)$ that also preserves the sublattice 
$X_*(Z_{\mathcal {G}}^\circ )$, and therefore a linear isomorphism 
$\delta _u(z)$ of 
${\mathfrak {t}}_u$. If 
$\bar {z}\in A_u\rtimes \langle \theta _u\rangle$, set 
$\delta _u(\bar {z}):=\delta _u(z)$, where 
$z$ is a lift of 
$\bar {z}$ in 
${\mathrm {Z}}_{\mathcal {G}}(u)\rtimes \langle \theta _u\rangle$. This defines a representation of 
$A_u\rtimes \langle \theta _u\rangle$.
Suppose 
$(U,{\mathcal {E}})$ and 
$(U',{\mathcal {E}}')$ are two elements of 
$\mathbf {I}^\theta$ represented by 
$(u,\phi )$ and 
$(u',\phi ')$, respectively. Define
\begin{equation} (\widetilde{\phi},\widetilde{\phi}')_{\theta-{\mathrm{ell}}}=\begin{cases} (\widetilde{\phi}, \widetilde{\phi}')^{\delta_u}_{\theta-{\mathrm{ell}}}, & \text{if }U=U',\\0, & \text{if }U\neq U'. \end{cases} \end{equation}
This is the 
$\theta$-elliptic pairing on 
$\bigoplus _{U} R(A_u\rtimes \langle \theta _u\rangle )$.
The relation between this elliptic pairing and the generalized Springer correspondence [Reference LusztigLus84b] is explained in [Reference WaldspurgerWal07, § 3]. The automorphism 
$\theta$ acts naturally on all of the objects involved in the definition of the Springer correspondence. As discussed in [Reference WaldspurgerWal07, § 3], this leads to an action of 
$W_j\rtimes \langle \theta \rangle$ on 
$\mathfrak {z}_{\mathcal {M}}$, the Lie algebra of 
${\mathrm {Z}}_{\mathcal {M}}$ (notation as in § 3), and to a 
$\theta$-generalized Springer correspondence 
$\nu \colon \mathbf {I}^\theta \to \mathbf {\widetilde {J}}^\theta$. For every 
$(j,\rho )\in \mathbf {\widetilde {J}}^\theta$, let 
$\widetilde {\rho }$ denote the extension of 
$\rho$ to a representation of 
$W_j\rtimes \langle \theta \rangle$ as in [Reference WaldspurgerWal07, § 3].
Let 
$i=(U,{\mathcal {E}})$, 
$i'=(U',{\mathcal {E}}')$ be two elements of 
$\mathbf {I}^\theta$, and 
$\nu (i)=(j,\rho )$, 
$\nu (i')=(j',\rho ')$. For every 
$m\in {\mathbb {Z}}$, the constructible sheaf 
${\mathcal {H}}^{2m+a_{U'}}(A_{j',\rho '})|_U$ decomposes as a direct sum of 
$G$-equivariant local systems on 
$U$. As in [Reference WaldspurgerWal07], setting
\[ H^m_{i,i'}={\mathrm{Hom}}({\mathcal{E}},{\mathcal{H}}^{2m+a_{U'}}(A_{j',\rho'})|_U), \]
the automorphism 
$\theta$ defines a linear map 
$\theta ^m_{i,i'}: H^m_{i,i'}\to H^m_{i,i'}$. In particular,
\[ H^m_{i,i}=0 \quad\text{if }m\neq 0\quad\text{and}\quad\dim H^\circ_{i,i}=1. \]
We may arrange the construction so that 
$\theta ^\circ _{i,i}$ is the identity map. Moreover, it is clear that 
$H^m_{i,i'}\neq 0$ for some 
$m$ only if 
$U\subset \overline {U'}$. (Recall that the restriction of 
$A_{j',\rho '}$ to the set of unipotent elements of 
${\mathcal {G}}$ is supported on 
$\overline {U'}$.)
Define the virtual representation of 
$W_j\rtimes \langle \theta \rangle$
\begin{equation} \boldsymbol{\widetilde{\rho}}=\sum_{\rho'\in \widehat{W}_j^\theta} P_{j,\rho,\rho'} \widetilde{\rho'},\quad\text{where } P_{j,\rho,\rho'}=\sum_{m\in{\mathbb{Z}}} {\mathrm{tr}} (\theta^m_{i,i'}). \end{equation}
In this virtual combination, 
$P_{j,\rho,\rho }=1$, and 
$P_{j,\rho,\rho '}\neq 0$ implies that 
$U\subset \overline {U'}$ if 
$(U,{\mathcal {E}})=\nu ^{-1}(j,\rho )$ and 
$(U',{\mathcal {E}}')=\nu ^{-1}(j,\rho ')$.
Example 11.6 When 
$\theta$ is the trivial automorphism of 
${\mathcal {G}}$ and 
$j=j_0$ (the case of the classical Springer correspondence), 
$\boldsymbol{\widetilde {\rho }}$ can be identified with the reducible 
$W$-representation on the 
$\phi$-isotypic component (
$\phi \in \widehat {A}_u$ corresponding to 
${\mathcal {E}}$) of the total cohomology of the Springer fiber of 
$u$.
Consider the 
$\theta$-elliptic pairing 
$(\,{,}\,)_{\theta -{\mathrm {ell}}}^{W_j}$ on 
$\bigoplus _{j\in \mathbf {J}^\theta } R(W_j\rtimes \langle \theta \rangle )$, defined on each summand via the action of 
$W_j\rtimes \langle \theta \rangle$ on 
${\mathfrak {z}}_{\mathcal {M}}$ and extended orthogonally to the direct sum.
Theorem 11.7 ([Reference WaldspurgerWal07, Théorème p. 616])
Let 
$i=(U,{\mathcal {E}})$, 
$i'=(U',{\mathcal {E}}')$ be two elements of 
$\mathbf {I}^\theta$, and 
$\nu (i)=(j,\rho )$, 
$\nu (i')=(j',\rho ')$. Let 
$(u,\phi )$, 
$(u',\phi ')$, 
$\phi \in \widehat {A}_u$ and 
$\phi '\in \widehat {A}_{u'}$ be representatives for 
$i,i'$, respectively. Then
\[ (\widetilde{\phi},\widetilde{\phi}')_{\theta-{\mathrm{ell}}}=(\boldsymbol{\widetilde{\rho}},\boldsymbol{\widetilde{\rho}}')_{\theta-{\mathrm{ell}}}^{W_j}. \]
The equality in the theorem does not depend on the choices involved in the construction.
11.3 The proof of Theorem 11.1: the case of adjoint groups
In this subsection, suppose that 
$G$ is a simple 
$F$-split group of adjoint type. This means that 
$G^\vee$ is simply connected, hence, for every 
$s\in T^\vee$, 
${\mathrm {Z}}_{G^\vee }(s)$ is connected. We may apply Theorem 11.7 to
\[ {\mathcal{G}}={\mathrm{Z}}_{G^\vee}(s)\quad \text{and} \quad \theta\text{ the trivial automorphism}. \]
Let 
$\mathbf {I}^s=\mathbf {I}^{{\mathrm {Z}}_{G^\vee }(s)}$, 
${\mathbf {J}}^s={\mathbf {J}}^{{\mathrm {Z}}_{G^\vee }(s)}$, and 
$\widetilde {\mathbf {J}}^s=\widetilde {\mathbf {J}}^{{\mathrm {Z}}_{G^\vee }(s)}$, so that the generalized Springer correspondence for 
${\mathrm {Z}}_{G^\vee }(s)$ is the map
\[ \nu_s\colon \mathbf{I}^s\to \widetilde{\mathbf{J}}^s,\quad (U,{\mathcal{E}})\mapsto (j,\rho), \]
and
\[ \boldsymbol{\widetilde{\rho}}=\sum_{\rho'\in \widehat{W}_j} P_{j,\rho,\rho'} \rho',\quad\text{where } P_{j,\rho,\rho'}=\sum_{m\in{\mathbb{Z}}}\dim {\mathrm{Hom}}({\mathcal{E}},{\mathcal{H}}^{2m+a_{U'}}(A_{j',\rho'})|_U). \]
For convenience, let us also define
\begin{equation} \widetilde{\nu}_s\colon \mathbf{I}^s\to \widetilde{\mathbf{J}}^s,\quad (U,{\mathcal{E}})\mapsto (j,\boldsymbol{\widetilde{\rho}}). \end{equation} Recall that for every semisimple element 
$s\in G^\vee$, 
${\mathcal {G}}_s^p={\mathrm {Z}}_{G^\vee }(s)$.
Proposition 11.8 Suppose 
$G$ is simple 
$F$-split group of adjoint type. The maps 
$\widetilde {\nu }_s$ from (11.14) induce an isometric isomorphism
\[ \bigoplus_{s\in
{\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\ \bigoplus_{u\in {\mathcal{C}}({\mathcal{G}}_s^p)_{\mathsf{un}}}\overline{R}(A_{{\mathcal{G}}_s^p}(u))\cong
\bigoplus_{s\in {\mathcal{C}}(G^\vee)_{\mathsf{ss}}}\ \bigoplus_{j\in {\mathbf{J}}^s} \overline{R}(W_j),\quad
(\phi,\phi')_{\mathrm{ell}}^{\delta_u^s}=(\widetilde{\nu}_s(\phi),\widetilde{\nu}_s(\phi'))_{\mathrm{ell}}^{W_j}.
\]
Proof. This is immediate from Theorem 11.7 applied to each 
${\mathcal {G}}_s^p$.
11.4 Extending Theorem 11.1
In order to extend the results to the case when 
$G$ is simple 
$F$-split but not adjoint, we first need some results about Mackey induction. We follow a construction from [Reference Ciubotaru and HeCH16, § 4.2]. Suppose 
$H'$ is a finite group, 
$H$ a normal subgroup of 
$H'$, and 
$H'/H={\mathfrak {R}}$ is abelian. The groups 
$H',{\mathfrak {R}}$ act on 
$\widehat {H}$. For every 
$H$-character 
$\chi$, and 
$\gamma \in {\mathfrak {R}}$, denote by 
${}^\gamma \chi$ the 
$H$-character 
${}^\gamma \chi (h)=\chi (\gamma ^{-1} h \gamma )$ (it does not depend on the choice of coset representative 
$\gamma$).
If 
$\sigma \in \widehat {H}$, let 
${\mathfrak {R}}_\sigma$ and 
$H'_\sigma$ denote the corresponding isotropy groups of 
$\sigma$. For each 
$\gamma \in {\mathfrak {R}}_\sigma$, fix an isomorphism 
$\phi _\gamma \colon {}^\gamma \sigma \to \sigma$ and define the twisted trace as 
${\mathrm {tr}}_\gamma (\sigma )(h)={\mathrm {tr}}(\sigma (h)\circ \phi _\gamma )$, 
$h\in H$. The choices of 
$\phi _\gamma$ (each unique up to scalar) define a factor set, or a 2-cocyle, 
$\beta _\sigma :{\mathfrak {R}}_\sigma \times {\mathfrak {R}}_\sigma \to {\mathbb {C}}^\times$.
Remark 11.9 We assume that the action of 
${\mathfrak {R}}$ can be normalized so that 
$\beta _\sigma$ is trivial. This is the case, for example, when 
${\mathfrak {R}}$ is cyclic.
If 
$\tau$ is a (virtual) 
${\mathfrak {R}}_\sigma$-representation, we may form the Mackey induced (virtual) 
$H'$-representation
\[ \sigma\rtimes \tau={\mathrm{Ind}}_{H'_\sigma}^{H'}(\sigma\otimes \tau). \]
If 
$\tau$ is an irreducible 
${\mathfrak {R}}_\sigma$-representation, then 
$\sigma \rtimes \tau$ is an irreducible 
$H'$-representation. In fact, 
$\widehat {H}'=\{\sigma \rtimes \tau \mid \sigma \in {\mathfrak {R}}\backslash \widehat {H},\ \tau \in \widehat {{\mathfrak {R}}}_\sigma \}$.
Given 
$\gamma \in {\mathfrak {R}}$, if 
$\gamma \in {\mathfrak {R}}_\sigma$, define 
$\tau _{\sigma,\gamma }$ to be the virtual 
${\mathfrak {R}}_\sigma$-representation whose character is the delta function on 
$\gamma$. Then 
$\{\sigma \rtimes \tau _{\sigma,\gamma }\mid \sigma \in {\mathfrak {R}}\backslash \widehat {H},\ \gamma \in {\mathfrak {R}}\}$ is a basis of 
$R(H')$. As in [Reference Ciubotaru and HeCH16, Lemma 4.2.2],
\begin{equation} \chi_{\sigma\rtimes \tau_{\sigma,\gamma}}(h)=\begin{cases} 0, & \text{if } h\notin H\gamma,\\ \sum_{\gamma'\in {\mathfrak{R}}/{\mathfrak{R}}_\sigma} {}^{\gamma'}\! ({\mathrm{tr}}_\gamma(\sigma))(h\gamma^{-1}), & \text{if } h\in H\gamma. \end{cases} \end{equation}Note that
\[ H'/H'_\sigma\cong {\mathfrak{R}}/{\mathfrak{R}}_\sigma \]
indexes the 
${\mathfrak {R}}$-orbit (equivalently, the 
$H'$-orbit) of 
$\sigma \in \widehat {H}$. Suppose 
$H'$ is endowed with a representation 
$\delta$ and we define the corresponding elliptic pairing 
$(\,{,}\,)^{H'}_{\mathrm {ell}} = (~, ~)^\delta _{\mathrm {ell}}$.
From now on, assume that 
$H'=H\rtimes {\mathfrak {R}}$, so that each 
$\gamma \in {\mathfrak {R}}$ acts on 
$H$ by automorphisms of 
$H$. (If 
$H$ is abelian, which is often the case for component groups, this assumption is not necessary.) Then we may define the twisted elliptic pairing 
$(\,{,}\,)^H_{\gamma -{\mathrm {ell}}}$ (for each 
$\gamma \in {\mathfrak {R}}$).
The existence of the intertwiner 
$\phi _\gamma$ (
$\gamma \in {\mathfrak {R}}_\sigma$) is equivalent to the existence of an extension of 
$\sigma$ to a representation of 
$H\rtimes \langle \gamma \rangle$, by setting 
$\sigma (h\gamma )=\sigma (h)\circ \phi _\gamma$, so 
${\mathrm {tr}}_\gamma (\sigma )(h)={\mathrm {tr}}\sigma (h\gamma )$, 
$h\in H$. This is implicit in the following lemma.
Lemma 11.10 For every 
$\gamma _1,\gamma _2\in {\mathfrak {R}}$ and every 
$\sigma _1,\sigma _2\in \widehat {H}$, the 
$H'$-elliptic pairing is given by
\[ (\sigma_1\rtimes\tau_{\sigma_1,\gamma_1},\sigma_2\rtimes\tau_{\sigma_2,\gamma_2})^{H'}_{\mathrm{ell}}=\begin{cases} \dfrac{1}{|{\mathfrak{R}}|}\sum_{\gamma'\in {\mathfrak{R}}/{\mathfrak{R}}_{\sigma_1},\gamma''\in {\mathfrak{R}}/{\mathfrak{R}}_{\sigma_2}} ({}^{\gamma'}\!\sigma_1,{}^{\gamma''} \!\sigma_2)^H_{\gamma_1-{\mathrm{ell}}}, & \text{if }\gamma_1=\gamma_2,\\[5pt] 0, & \text{if }\gamma_1\neq \gamma_2. \end{cases} \]
Proof. The orthogonality of the two characters when 
$\gamma _1\neq \gamma _2$ follows at once since the first is supported on 
$\gamma _1H$ and the second on 
$\gamma _2H$. The first formula follows from (11.15) by the definition of the elliptic pairing.
Lemma 11.10 allows us to extend the proof of Theorem 11.7 to the case when 
${\mathcal {G}}'$ is disconnected as long as the following holds.
(⋆) The cocycles
$\sharp _j$ that occur in the disconnected Springer correspondence (3.5) can be trivialized.
With the notation from § 3, set
\[ A_u(j)={\mathrm{Z}}_{{\mathfrak{R}}_j{\mathcal{G}}^\circ}(u)/{\mathrm{Z}}_{{\mathcal{G}}}(u)^\circ. \]
This is a normal subgroup of 
$A_u$ containing 
$A_{{\mathcal {G}}^\circ }(u)$.
In our case 
${\mathcal {G}}$ is not an arbitrary disconnected reductive group, but rather 
${\mathcal {G}}=Z_{G^\vee }(s)$, for some semisimple element 
$s\in T^\vee$. Let 
$W^\vee$ be the Weyl group of 
$T^\vee$ in 
$G^\vee$. If we fix 
$B(s)$ a Borel subgroup of 
${\mathcal {G}}^\circ$ with 
$T^\vee \subset B(s)$, and denote by 
$\Phi ^+({\mathcal {G}}^\circ )$ the positive roots of 
$T^\vee$ in 
${\mathcal {G}}^\circ$, then 
${\mathcal {A}}={\mathcal {G}}/{\mathcal {G}}^\circ$ can be identified with
\begin{equation} {\mathcal{A}}=\{w\in W^\vee\mid w(\Phi^+({\mathcal{G}}^\circ))=\Phi^+({\mathcal{G}}^\circ)\}, \end{equation}
see, for example, [Reference BonnaféBon05, § 1]. With this identification, 
${\mathcal {A}}$ acts on 
$T^\vee$ and 
$\Phi ^+({\mathcal {G}}^\circ )$, hence by automorphisms of the root datum of 
${\mathcal {G}}^\circ$. We will use this ‘global’ action on 
${\mathcal {G}}^\circ$ in the proof of the next result in order to construct the extensions to the appropriate semidirect products and apply Waldspurger's result to 
$\theta$-elliptic pairings.
Proposition 11.11 Retain the notation from § 3 and suppose that 
$(\star )$ holds. Let 
$\nu : \mathbf {I}^{{\mathcal {G}}}\to \widetilde {\mathbf {J}}^{{\mathcal {G}}}$ be the generalized Springer correspondence (3.5). Let 
$i=(U,\mathcal {E})$, 
$i'=(U',\mathcal {E}')$ be two elements of 
$\mathbf {I}^{{\mathcal {G}}}$, and 
$\nu (i)=(j,\rho )$, 
$\nu (i')=(j,\rho ')$. Let 
$(u,\phi )$, 
$(u',\phi ')$, 
$\phi \in \widehat {A}_u$, 
$\phi '\in \widehat {A}_{u'}$ be representatives for 
$i,i'$, respectively. Then:
(i) if
$U\neq U'$, $(\phi,\phi ')_{{\mathrm {ell}}}^{A_u}=0=(\boldsymbol{\rho},\boldsymbol{\rho} ')^{W_j}_{{\mathrm {ell}}}$;(ii) if
$U=U'$, $(\phi,\phi ')^{A_u(j)}_{{\mathrm {ell}}}=(\boldsymbol{\rho},\boldsymbol{\rho} ')^{W_j}_{{\mathrm {ell}}}$.
Proof. Suppose 
$j=j'$, otherwise the claim is true by definition. Let 
$\rho _1^\circ,\rho _2^\circ \in \widehat {W_j^\circ }$ and suppose that they have unipotent supports 
$U_1^\circ,U_2^\circ$, respectively, in the connected generalized Springer correspondence such that 
${\mathcal {G}}\cdot U_1^\circ \neq {\mathcal {G}}\cdot U_2^\circ$. Let 
$\boldsymbol{\rho}_i^{\circ}$, 
$i=1,2$ be the corresponding reducible Springer representations, as in § 11.2. We assume that they all have appropriate twisted extensions as in § 11.2 and drop 
$\widetilde{}$ from the notation. Using Lemma 11.10 applied to 
$H=W_j^\circ$, 
$H'=W_j$, 
${\mathfrak {R}}=\mathfrak {R}_j$, for every 
$\gamma \in (\mathfrak {R}_j)_{\rho _1^\circ }\cap (\mathfrak {R}_j)_{\rho _2^\circ }$,
\[
(\boldsymbol{\rho}_1^{\circ}\rtimes\tau_{\rho_1^\circ,\gamma},\boldsymbol{\rho}_2^{\circ}\rtimes\tau_{\rho_1^\circ,\gamma})^{W_j}_{\mathrm{ell}}=\frac
{1}{|\mathfrak{R}_j|}\sum_{\gamma',\gamma''}
({}^{\gamma'}\!\boldsymbol{\rho}_1^{\circ},{}^{\gamma''}\!\boldsymbol{\rho}_2^{\circ})^{W_j^\circ}_{\gamma-{\mathrm{ell}}}=0,
\]
by Theorem 11.7. We used implicitly here that the stabilizers in 
${\mathfrak {R}}_j$ of 
$\rho _i^\circ$ and 
$\boldsymbol{\rho}_i^{\circ}$ are the same. In conjunction with the second claim in Lemma 11.10, this implies that 
$(\boldsymbol{\rho}_1^{\circ}\rtimes \tau _1,\boldsymbol{\rho}_2^{\circ}\rtimes \tau _2)^{W_j}_{\mathrm {ell}}=0$ for all 
$\tau _i\in \widehat {(\mathfrak {R}_j)}_{\rho _i^\circ }$, 
$i=1,2$. Hence, 
$(\boldsymbol{\rho}_1,\boldsymbol{\rho}_2)^{W_j}_{\mathrm {ell}}=0$ whenever 
$\rho _1,\rho _2$ have distinct unipotent (disconnected) Springer support, which proves the first part of the claim.
Now assume that 
$u=u'$ and 
$\phi,\phi '\in \widehat {A}_u$. Suppose 
$\rho ^\circ _i$ occurs in the restriction of 
$\rho _i$ to 
$W_j^\circ$ and that 
$\phi _i^\circ \in \widehat {A}_{{\mathcal {G}}^\circ }(u)$ (which necessarily occurs in the restriction of 
$\phi _i$) corresponds to 
$\rho ^\circ _i$ in the connected generalized Springer correspondence. We observe that there is a natural injection
\begin{equation} {\mathfrak{R}}_j=W_j/W_j^\circ\simeq {\mathrm{N}}_{{\mathcal{G}}}(j)/{\mathrm{N}}_{{\mathcal{G}}^\circ}(\mathcal{M}^\circ)\hookrightarrow {\mathcal{G}}/{\mathcal{G}}^\circ={\mathcal{A}}. \end{equation}
Hence, every 
$\gamma \in {\mathfrak {R}}_j$ can be regarded as an automorphism of 
${\mathcal {G}}^\circ$ via (11.16) and, in particular, Theorem 11.7 can be applied with 
$\gamma$ in place of 
$\theta$. We wish to compare 
$(\boldsymbol{\rho}_1^{\circ}\rtimes \tau _{\rho _1^\circ,\gamma _1}, \boldsymbol{\rho}_2^{\circ}\rtimes \tau _{\rho _2^\circ,\gamma _2})^{W_j}_{\mathrm {ell}}$ and 
$(\phi _1^\circ \rtimes \tau _{\phi _1^\circ,\gamma _1}, \phi _2^\circ \rtimes \tau _{\phi _2^\circ,\gamma _2})^{A_u}_{\mathrm {ell}}$. By [Reference Aubert, Moussaoui and SolleveldAMS18, Lemma 4.4],
\[ ({\mathfrak{R}}_j)_{\rho_i^\circ}\cong (W_j)_{\rho_i^\circ}/W_j\cong (A_u)_{\phi_i^\circ}/A_{{\mathcal{G}}^\circ}(u),\quad i=1,2, \]
which implies that there is an identification between 
$\gamma _i$, 
$i=1,2$ for the 
$\rho ^\circ _i$ and for the 
$\phi ^\circ _i$ in the setting of Lemma 11.10. Hence, if 
$\gamma _1\neq \gamma _2$, both elliptic products are zero.
Suppose 
$\gamma _1=\gamma _2=\gamma \in ({\mathfrak {R}}_j)_{\rho _1^\circ }\cap ({\mathfrak {R}}_j)_{\rho _2^\circ }= ((A_u)_{\phi _1^\circ }\cap (A_u)_{\phi _2^\circ })/A_{{\mathcal {G}}^\circ }(u)$. To simplify the formulas, set 
$n_i=|({\mathfrak {R}}_j)_{\rho _i^\circ }|=|(A_u)_{\phi _i^\circ }/A_{{\mathcal {G}}^\circ }(u)|$, 
$i=1,2$. Then, first by Lemma 11.10 and second by Theorem 11.7,
\begin{align*} n_1 n_2|{\mathfrak{R}}_j|(\boldsymbol{\rho}_1^{\circ}\rtimes\tau_{\rho_1^\circ,\gamma},
\boldsymbol{\rho}_2^{\circ}\rtimes\tau_{\rho_2^\circ,\gamma})^{W_j}_{\mathrm{ell}}
&=\sum_{\gamma',\gamma''\in {\mathfrak{R}}_j} ({}^{\gamma'}\!\boldsymbol{\rho}_1^{\circ},{}^{\gamma''}\!\boldsymbol{\rho}_2^{\circ})^{W_j^\circ}_{\gamma-{\mathrm{ell}}}\\
&=\sum_{u_0\in {\mathfrak{R}}_j {\mathcal{G}}^\circ\cdot u/{\mathcal{G}}^\circ}\sum_{\substack{\gamma',\gamma''\in
{\mathfrak{R}}_j\\{\mathcal{G}}^\circ\cdot ({}^{\gamma'}\!u_0)= {\mathcal{G}}^\circ\cdot ({}^{\gamma''}\!u_0)={\mathcal{G}}^\circ\cdot u_0}}
({}^{\gamma'}\!\phi_1^\circ,{}^{\gamma''}\!\phi_2^\circ)^{A_{{\mathcal{G}}^\circ}(u_0)}_{\gamma-{\mathrm{ell}}}.
\end{align*}
The first sum is over the representatives of the 
${\mathcal {G}}^\circ$-orbits that are conjugate to 
${\mathcal {G}}^\circ \cdot u$ via 
${\mathfrak {R}}_j$. Since the corresponding summand for two different 
${\mathcal {G}}^\circ$-orbits 
$u_0,u_0'\in {\mathcal {G}}\cdot u$ are equal (as they are related by an outer automorphism of 
${\mathcal {G}}^\circ$), it follows that
\begin{equation} n_1n_2\frac{|{\mathfrak{R}}_j|}{N_u}(\boldsymbol{\rho}_1^{\circ}\rtimes\tau_{\rho_1^\circ,\gamma},\boldsymbol{\rho}_2^{\circ}\rtimes\tau_{\rho_2^\circ,\gamma})^{W_j}_{\mathrm{ell}}=\sum_{\substack{\gamma',\gamma''\in{\mathfrak{R}}_j\\{\mathcal{G}}^\circ\cdot
({}^{\gamma'}\!u)= {\mathcal{G}}^\circ\cdot ({}^{\gamma''}\!u)={\mathcal{G}}^\circ\cdot u}}
({}^{\gamma'}\!\phi_1^\circ,{}^{\gamma''}\!\phi_2^\circ)^{A_{{\mathcal{G}}^\circ}(u)}_{\gamma-{\mathrm{ell}}},
\end{equation}
where 
$N_u$ is the number of 
${\mathcal {G}}^\circ$-conjugacy classes in 
${\mathfrak {R}}_j{\mathcal {G}}^\circ \cdot u$. It is easy to see (using orbit-stabilizer counting) that 
$ {|{\mathfrak {R}}_j|}/{N_u}=|{\mathrm {Z}}_{{\mathfrak {R}}_j{\mathcal {G}}^\circ }(u)/{\mathrm {Z}}_{{\mathcal {G}}^\circ }(u)|$. Moreover, an element 
$\gamma \in {\mathfrak {R}}_j$ has the property that 
${\mathcal {G}}^\circ \cdot ({}^{\gamma }\!u)={\mathcal {G}}^\circ \cdot u$ if and only if 
$\gamma \in {\mathrm {Z}}_{\mathcal {G}}(u)$ mod 
${\mathcal {G}}^\circ$. Hence, (11.18) becomes
\begin{equation} n_1n_2{|{\mathrm{Z}}_{{\mathfrak{R}}_j{\mathcal{G}}^\circ}(u)/{\mathrm{Z}}_{{\mathcal{G}}^\circ}(u)|}(\boldsymbol{\rho}_1^{\circ}\rtimes\tau_{\rho_1^\circ,\gamma},\boldsymbol{ \rho_2^\circ}\rtimes\tau_{\rho_2^\circ,\gamma})^{W_j}_{\mathrm{ell}}=\sum_{\gamma',\gamma''\in{\mathrm{Z}}_{{\mathfrak{R}}_j{\mathcal{G}}^\circ}(u)/{\mathrm{Z}}_{{\mathcal{G}}^\circ}(u)} ({}^{\gamma'}\!\phi_1^\circ,{}^{\gamma''}\!\phi_2^\circ)^{A_{{\mathcal{G}}^\circ}(u)}_{\gamma-{\mathrm{ell}}}. \end{equation} On the other hand, applying Lemma 11.10 to 
$A_u(j)$, we get
\begin{equation} n_1n_2|A_u(j)/A_{{\mathcal{G}}^\circ}(u)|(\phi_1^\circ\rtimes\tau_{\phi_1^\circ,\gamma}, \phi_2^\circ\rtimes\tau_{\phi_2^\circ,\gamma})^{A_u(j)}_{\mathrm{ell}}=\sum_{r',r''\in A_u(j)/A_{{\mathcal{G}}^\circ}(u)}({}^{r'}\!\phi_1^\circ,{}^{r''}\!\phi_2^\circ)^{A_{{\mathcal{G}}^\circ}(u)}_{\gamma-{\mathrm{ell}}}. \end{equation}Note that
\[ A_u(j)/A_{{\mathcal{G}}^\circ}(u)\cong {\mathrm{Z}}_{{\mathfrak{R}}_j{\mathcal{G}}^\circ}(u)/{\mathrm{Z}}_{{\mathcal{G}}^\circ}(u)\hookrightarrow {\mathcal{G}}/{\mathcal{G}}^\circ. \]
Remark 11.12 (i) In our case, 
${\mathcal {G}}={\mathrm {Z}}_{G^\vee }(s)$ for a semisimple element 
$s$, and hence all of the groups 
$W_j^\circ$ that occur in our setting are finite Weyl groups. This means that 
$(\star )$ holds by [Reference Aubert, Baum, Plymen and SolleveldABPS17a, Proposition 4.3].
(ii) If 
${\mathrm {Z}}_{{\mathfrak {R}}_j{\mathcal {G}}^\circ }(u)/{\mathrm {Z}}_{{\mathcal {G}}^\circ }(u)={\mathrm {Z}}_{{\mathcal {G}}}(u)/{\mathrm {Z}}_{{\mathcal {G}}^\circ }(u)$, it follows from Proposition 11.11(ii) that, in fact, 
$(\phi,\phi ')^{A_u}_{{\mathrm {ell}}}=(\boldsymbol{\rho},\boldsymbol{\rho} ')^{W_j}_{{\mathrm {ell}}}$. For example, when 
$j=j_0$ is the cuspidal datum associated to the trivial local system on the maximal torus of 
${\mathcal {G}}^\circ$, the 
${\mathfrak {R}}_{j_0}={\mathcal {G}}/{\mathcal {G}}^\circ$, hence this condition holds automatically.
12. $\mathsf {Sp}_4(F)$
As a useful example, we present the case 
$G=\mathsf {Sp}_4(F)$. First, there are six unipotent representations of the finite group 
$\mathsf {Sp}_4(\mathbb {F}_q)$: five in bijection with irreducible representations of the finite Weyl group of type 
$C_2$ and one cuspidal representation 
$\theta$. Using Lusztig's notation for the irreducible representations of the Weyl group of type 
$B/C$, there are three families 
${\mathcal {F}}$ of unipotent representations with associated finite groups 
$\Gamma$ as follows:
–
$\Gamma =\{1\}$, ${\mathcal {F}}=\{2\times \emptyset \}$;–
$\Gamma =\{1\}$, ${\mathcal {F}}=\{0\times 11\}$;–
$\Gamma ={\mathbb {Z}}/2{\mathbb {Z}}$, ${\mathcal {F}}=\{1\times 1, 11\times \emptyset, \emptyset \times 2, \theta \}$ with associated parameters, in order, $M(\Gamma )=\{(1,\mathbf {1}),(-1,\mathbf {1}), (1,\epsilon ), (-1,\epsilon )\}$.
For the 
${\mathbb {Z}}/2{\mathbb {Z}}$-family, the stable combinations are
\begin{equation} \begin{aligned} \sigma(1,1)&=1\times 1+\emptyset\times 2,\quad\sigma(-1,1)=11\times\emptyset+\theta,\\ \sigma(1,-1)&=1\times 1-\emptyset\times 2, \quad\sigma(-1,-1)=11\times\emptyset-\theta, \end{aligned}
\end{equation}
and Lusztig's Fourier transform acts by the flip 
$\sigma (x,y)\mapsto \sigma (y,x)$. For the singleton families, the Fourier transform is the identity.
Next, we consider the 
$p$-adic group 
$\mathsf {Sp}_4(F)$: the unipotent representations are parameterized by data in the dual group 
$G^\vee =\mathsf {SO}_5({\mathbb {C}})$. In particular, the list of unipotent classes 
$u$ and their attached groups 
$\Gamma _u$ is as follows.
The interesting case is 
$u=(311)$. Write
\[ \Gamma_u=\langle z,\delta\mid z\in {\mathbb{C}}^\times,\ \delta^2=1,\ \delta z \delta^{-1}=z^{-1}\rangle. \]
Then 
${\mathrm {Z}}_{\Gamma _u}(\pm \delta )=A_{\Gamma _u}(\pm \delta )=\{\pm 1,\pm \delta \}\cong C_2\times C_2$ and 
$A_{\Gamma _u}(\pm 1)=\{1,\delta \}\cong C_2$. There are six conjugacy classes of elliptic pairs:
\begin{equation} [(\pm 1,\delta)],\quad [(\delta,\pm 1)],\quad [(\delta,\pm\delta)], \end{equation}and the flip acts as
\begin{equation} \mathsf{flip}([(\pm 1,\delta)])=[(\delta,\pm 1)],\quad \mathsf{flip}([(\delta,\pm\delta)])=[(\delta,\pm \delta)]. \end{equation}
There are three conjugacy classes of isolated semisimple elements in 
$T^\vee =\{(a,b)\mid a,b\in {\mathbb {C}}^\times \}$ in 
$\mathsf {SO}_5({\mathbb {C}})$. In this notation, the Weyl group 
$W(B_2)$ acts on 
$T$ by flips and inverses. The representatives of the three classes are:
–
$s_0=(1,1)$, ${\mathrm {Z}}_{G^\vee }(s_0)=\mathsf {SO}_5$;–
$s_1=(-1,1)$, ${\mathrm {Z}}_{G^\vee }(s_1)=\mathsf {S} (\mathsf {O}_2\times \mathsf {O}_3)$;–
$s_2=(-1,-1)$, ${\mathrm {Z}}_{G^\vee }(s_2)=\mathsf {S} (\mathsf {O}_1\times \mathsf {O}_4)\cong \mathsf {O}_4$.
All three 
$s_0,s_1,s_2$ occur in 
$\Gamma _u=\mathsf {O}_2$ and in the notation above for 
$\mathsf {O}_2=\langle z,\delta \rangle$, they are
\[ s_0\leftrightarrow 1\in \mathsf{O}_2,\quad s_1\leftrightarrow -1\in \mathsf{O}_2,\quad s_2\leftrightarrow \delta\in \mathsf{O}_2. \]
Consequently, there are eight elliptic tempered representations of the form 
$\pi (s_i,u,\phi )$, 
$i=0,1,2$, 
$u=(311)$: six are Iwahori-spherical and two are supercuspidal. Out of these, four are discrete series representations, all those for 
$s_2=\delta$. The parahoric restrictions are given in Table 1. We computed them using the same method as in [Reference ReederRee00, (6.2)], but since in our case 
$G^\vee$ is not simply connected, we also need to involve the Mackey induction for graded affine Hecke algebras attached to disconnected groups.
Table 1. Elliptic 
$\mathsf {Sp}_4(F)$-representations attached to 
$u=(311)\in \mathsf {SO}_5$.
The corresponding stable combinations are
\begin{align*} \Pi(u,1,\delta)&=\pi(u,s_0,\mathbf{1})-\pi(u,s_0,\epsilon),\\ \Pi(u,-1,\delta)&=\pi(u,s_1,\mathbf{1})-\pi(u,s_1,\epsilon),\\ \Pi(u,\delta,1)&=\pi(u,s_2,\mathbf{1}\boxtimes \mathbf{1})+\pi(u,s_2,\mathbf{1}\boxtimes \epsilon)+\pi(u,s_2,\epsilon\boxtimes \mathbf{1})+\pi(u,s_2,\epsilon\boxtimes \epsilon),\\ \Pi(u,\delta,-1)&=\pi(u,s_2,\mathbf{1}\boxtimes \mathbf{1})+\pi(u,s_2,\mathbf{1}\boxtimes \epsilon)-\pi(u,s_2,\epsilon\boxtimes \mathbf{1})-\pi(u,s_2,\epsilon\boxtimes \epsilon),\\ \Pi(u,\delta,\delta)&=\pi(u,s_2,\mathbf{1}\boxtimes \mathbf{1})-\pi(u,s_2,\mathbf{1}\boxtimes \epsilon)+\pi(u,s_2,\epsilon\boxtimes \mathbf{1})-\pi(u,s_2,\epsilon\boxtimes \epsilon),\\ \Pi(u,\delta,-\delta)&=\pi(u,s_2,\mathbf{1}\boxtimes \mathbf{1})-\pi(u,s_2,\mathbf{1}\boxtimes \epsilon)-\pi(u,s_2,\epsilon\boxtimes \mathbf{1})+\pi(u,s_2,\epsilon\boxtimes \epsilon). \end{align*}
The corresponding parahoric restrictions are in Table 2. Here the column labelled 
$K_i$ contains 
$\operatorname {res}_{K_i}(\Pi (u, s, h))$.
Table 2. Elliptic 
$\mathsf {Sp}_4(F)$ stable combinations attached to 
$u=(311)\in \mathsf {SO}_5$.
One can easily verify by inspection using Table 2 that the conjecture holds in this case.
13. ${\mathsf {SL}}_n(F)$
13.1 Elliptic pairs for $G^\vee ={\mathsf {PGL}}_n({\mathbb {C}})$
Consider the case 
$G^\vee ={\mathsf {PGL}}_n(\mathbb {C})$. Let 
$Z$ denote the centre of 
${\mathsf {GL}}_n(\mathbb {C})$. In the Weyl group of type 
$A_{n-1}$ (
$W=S_n$), denote by 
$\dot {w}_n$ the permutation matrix corresponding to the 
$n$-cycle 
$(1,2,3,\ldots,n)$. For every 
$n$th root 
$z$ of 
$1$, let
\[ \Delta_n(z)=\text{diag}(1,z,z^2,\ldots,z^{n-1}) Z\in {\mathsf{PGL}}_n(\mathbb{C}). \]
Fix 
$\zeta _n$ a primitive 
$n$th root of 
$1$ and set 
$s_n=\Delta _n(\zeta _n)$. Note that 
$\dot {w}_n$ and 
$s_n$ commute in 
${\mathsf {PGL}}_n({\mathbb {C}})$.
Lemma 13.1 Suppose 
$\Gamma ={\mathsf {PGL}}_n(\mathbb {C})$. Then
\[ {\mathcal{Y}}(\Gamma)_{\mathrm{ell}}=\bigsqcup_{k\in (\mathbb{Z}/n\mathbb{Z})^\times}\Gamma\cdot (s_n,\dot{w}_n^k). \]
In particular, there are 
$\varphi (n)$ 
$\Gamma$-orbits in 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$. The flip 
$(s,h)\to (h,s)$ induces the following map on 
$\Gamma$-orbits in 
${\mathcal {Y}}(\Gamma )_{\mathrm {ell}}$:
\[ \mathsf{flip}\colon ([(s_n,\dot{w}_n^k)])\to [(s_n, \dot{w}_n^{-k})],\quad k\in (\mathbb{Z}/n\mathbb{Z})^\times. \]
Proof. Let 
$T$ be the diagonal torus in 
$\Gamma$. By Proposition 8.7, the only possible elliptic pairs are conjugate to 
$(s,\dot {w})$ where 
$w$ is elliptic and 
$s$ is regular such that 
$s\in T^w$. If the group is semisimple of type 
$A_{n-1}$, then the only elliptic elements of the Weyl group are the 
$n$-cycles. We may assume that 
$\dot {w}=\dot {w}_n$. It is easy to see that
\[ T^{\dot{w}_n}=\{ \Delta_n(z)\mid z^n=1\}. \]
Since 
$s\in T^{\dot {w}_n}$ needs to be regular, it follows that the corresponding 
$z$ must be a primitive root of 
$1$.
Now fix 
$s=s_n$. Every other 
$\Delta (\zeta ')$ with 
$\zeta '$ a primitive 
$n$th root is conjugate in 
$\Gamma$ to 
$s_n$. The centralizer is 
${\mathrm {Z}}_\Gamma (s)=\langle T, \dot {w}_n^k\mid k\in \mathbb {Z}/n\mathbb {Z}\rangle \cong T\rtimes \mathbb {Z}/n\mathbb {Z}$. This means that 
$\dot {w}_n^i$ is conjugate to 
$\dot {w}_n^j$ in 
${\mathrm {Z}}_\Gamma (s)$ if and only if 
$i=j$. On the other hand, 
$\dot {w}_n^k$ is elliptic if and only if 
$k\in (\mathbb {Z}/n\mathbb {Z})^\times$, hence the claim follows.
For the claim about the Fourier transform, let 
$x\in {\mathsf {GL}}_n({\mathbb {C}})$ be such that 
$x^{-1} \dot {w}_n x=s_n$, where 
$x$ is the matrix corresponding to a basis of eigenvectors of 
$\dot {w}_n$. Then a calculation shows that
\[ x^{-1} s_n x=\dot{w}_n^{-1} \text{ in } {\mathsf{PGL}}_n({\mathbb{C}}). \]
From this,
\[ \mathsf{flip}([(s_n,\dot{w}_n^k)])=[(w_n^k, s_n)]=[(x s_n^k x^{-1},s_n)]=[(s_n^k, x^{-1} s_n x)]=[(s_n^k,\dot{w}_n^{-1})]. \]
Finally, let 
$p$ be a permutation matrix such that 
$p^{-1} s_n^k p=s_n$ (this exists since 
$k$ is coprime to 
$n$). This has the effect 
$p^{-1} \dot {w}_n p=\dot {w}_n^k$, hence 
$[(s_n^k,\dot {w}_n^{-1})]=[(s_n,\dot {w}_n^{-k})]$.
Now let 
$u$ be a unipotent element in 
${\mathsf {PGL}}_n(\mathbb {C})$. Via the Jordan canonical form, 
$u$ is parameterized by a partition 
$\lambda$ of 
$n$, where we write 
$\lambda =(\underbrace {1,\ldots,1}_{r_1},\underbrace {2,\ldots,2}_{r_2},\ldots,\underbrace {\ell,\ldots,\ell }_{r_\ell })$. As is well-known (see, for example, [Reference Collingwood and McGovernCM93, Theorem 6.1.3])
\begin{equation} \Gamma_u=\bigg(\prod_{i=1}^\ell {\mathsf{GL}}_{r_i}(\mathbb{C})^i_\Delta\bigg)\bigg/Z, \end{equation}
where 
$H^i_\Delta$ means 
$H$ embedded diagonally into the product of 
$i$ copies of 
$H$. In particular, 
$\Gamma _u$ is connected. Let 
$T_r$ denote the diagonal torus in 
${\mathsf {GL}}_r$, 
$Z_r$ the center of 
${\mathsf {GL}}_r$, 
$\bar T_r =T_r/Z_r$ and 
$W_r\cong S_r$ the Weyl group. A maximal torus in 
$\Gamma _u$ is 
$T_u=\prod _{i=1}^\ell (T_{r_i})_\Delta ^i/Z$ and the Weyl group is 
$W_u=\prod _{i=1}^\ell (W_{r_i})_\Delta ^i$.
Let 
$w=\prod _{i=1}^\ell (w_i)^i_\Delta \in W_u$, 
$w_i\in W_{r_i}$ be given. We need 
$T_u^w$ to be finite. The morphism
\[ \pi\colon T_u\twoheadrightarrow \prod_{i=1}^\ell (\bar{T}_{r_i})_\Delta^i,\ (t_i)_i\text{ mod }Z\mapsto (t_i\text{ mod }Z_i) \]
is surjective and 
$W_u$-equivariant. Since 
$(\bar 1,\ldots,\bar {1},(\bar {T}_{r_i}^{w_i})_\Delta ^i,\bar {1},\ldots,\bar {1})\subset T_u^w$ for each 
$i$, it follows that 
$w_i$ is elliptic for 
${\mathsf {PGL}}_{r_i}$, hence, each 
$w_i$ is an 
$r_i$-cycle.
Proposition 13.2 For 
$u\in {\mathsf {PGL}}_n(\mathbb {C})$, 
${\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}\neq \emptyset$ if and only if the partition 
$\lambda$ corresponding to 
$u$ is rectangular, i.e. 
$\lambda =(\underbrace {i,\ldots,i}_{r_i})$ for some 
$i$. In this case,
\[ \Gamma_u={\mathsf{GL}}_{r_i}(\mathbb{C})^i_\Delta/Z\cong {\mathsf{PGL}}_{r_i}(\mathbb{C}), \]
so 
${\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}$ is as in Lemma 13.1.
Proof. Let 
$w\in W_u$ be elliptic as above. We pass to the Lie algebra 
$\mathfrak {t}_u=\mathfrak {s} (\bigoplus (\mathfrak {t}_{r_i})^i_\Delta )$; here 
$\mathfrak {s}$ denotes the traceless matrices. Since 
$\mathfrak {t}_{r_i}^{w_i}=\mathbb {C} \cdot {\mathrm {Id}}_{r_i}$, we see that
\[ \mathfrak{t}_u^w=\bigg\{(a_1 {\mathrm{Id}}_{r_1}, a_2 {\mathrm{Id}}_{r_2},a_2{\mathrm{Id}}_{r_2}, \ldots, \underbrace{a_i{\mathrm{Id}}_{r_i},\ldots,a_i{\mathrm{Id}}_{r_i}}_{i},\dots)\,\bigg|\,\sum_{i=1}^\ell i a_i=0\bigg\}. \]
The element 
$w$ is elliptic if and only if 
$\mathfrak {t}_u^w=0$. From the condition 
$\sum _{i=1}^\ell i a_i=0$, we that this can only happen if there exists a unique 
$i$ such that 
$r_i\neq 0$.
Corollary 13.3 The number of orbits of elliptic pairs for 
${\mathsf {PGL}}_n(\mathbb {C})$ is
\[ \sum_{u \text{ unipotent class}} |\Gamma_u\backslash{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}|=n. \]
Proof. From Proposition 13.2, the only unipotent classes that contribute are the rectangular ones, which are in one-to-one correspondence with divisors 
$d$ of 
$n$. For the unipotent class 
$u=(\underbrace {n/d,\ldots,n/d}_d)$, Lemma 13.1 states that there are 
$\varphi (d)$ orbits of elliptic pairs. Hence, the total number is 
$\sum _{d|n}\varphi (d)=n$.
13.2 Elliptic unipotent representations of ${\mathsf {SL}}_n(F)$
It is instructive to make explicit the elliptic correspondence (Conjecture 9.1) for 
$G={\mathsf {SL}}_n(F)$. Let 
$K_0={\mathsf {SL}}_n({\mathfrak {o}}_F)$ and let 
$I\subset K_0$ be an Iwahori subgroup. Let 
${\mathcal {H}}(G,I)=\{f\in C^\infty _c(G)\mid f(i_1 g i_2)=f(g),\ \text {for all }i_1,i_2\in I\}$ be the Iwahori–Hecke algebra (under convolution with respect to a fixed Haar measure). The algebra 
${\mathcal {H}}(G,I)$ is naturally isomorphic to the affine Hecke algebra 
${\mathcal {H}}={\mathcal {H}}({\mathcal {R}},\sqrt q,1)$, where 
$q$ is the order of the residue field of 
$F$ and 
${\mathcal {R}}$ is the root datum for 
${\mathsf {PGL}}_n({\mathbb {C}})$.
Every irreducible unipotent 
$G$-representation has nonzero fixed vectors under 
$I$, in other words, 
${\mathfrak {R}}_{\mathrm {un}}(G)={\mathfrak {R}}_I(G)$, where 
${\mathfrak {R}}_I(G)$ is the category of smooth representations generated by their 
$I$-fixed vectors. The functor
\[ m_I\colon {\mathfrak{R}}_{\mathrm{un}}(G)={\mathfrak{R}}_I(G)\to {\mathcal{H}}(G,I)\text{-mod}, \quad V\mapsto V^I, \]
is an equivalence of categories. The Langlands parameterization in this case can be read off the Kazhdan–Lusztig classification of irreducible modules for 
${\mathcal {H}}(G,I)$ extended to this setting in [Reference ReederRee02]:
\begin{equation} {\mathrm{Irr}}_{\mathrm{un}} {\mathsf{SL}}_n(F)\leftrightarrow {\mathrm{Irr}}~{\mathcal{H}}(G,I)\leftrightarrow {\mathsf{PGL}}_n({\mathbb{C}})\backslash\{(x,\phi)\mid x\in{\mathsf{PGL}}_n({\mathbb{C}}),\phi\in\widehat{A}_x\}. \end{equation}
The exact functor 
$m_I$ induces an isomorphism
\[ {\operatorname{Ext}}^i_G(V,V')={\operatorname{Ext}}^i_{{\mathcal{H}}(G,I)}(V^I,V'^I),\quad \text{for all }i, \]
and therefore 
${\mathrm {EP}}_G(V,V')={\mathrm {EP}}_{{\mathcal {H}}(G,I)}(V^I,V'^I)$ for all 
$V,V'\in {\mathrm {Irr}}~{\mathfrak {R}}_I(G)$. Since 
${\mathrm {EP}}_G$ and 
${\mathrm {EP}}_{{\mathcal {H}}(G,I)}$ are additive, they extend to pairings on the Grothendieck groups of finite-length representations. Let 
$R_I(G)_{\mathbb {C}}$ be the 
${\mathbb {C}}$-span of 
${\mathrm {Irr}} ~{\mathfrak {R}}_I(G)$ and 
$\overline {R}_I(G)_{\mathbb {C}}$ the quotient by the radical of 
${\mathrm {EP}}_G$. Define 
$\overline {R}({\mathcal {H}}(G,I))_{\mathbb {C}}$ similarly. Thus, we have the following.
Lemma 13.4 The equivalence of categories 
$m_I$ gives an isomorphism 
$\overline {m}_I\colon \overline {R}_I(G)_{\mathbb {C}}\to \overline {R}({\mathcal {H}}(G,I))_{\mathbb {C}}$ which is isometric with respect to 
${\mathrm {EP}}_G$ and 
${\mathrm {EP}}_{{\mathcal {H}}(G,I)}$.
The elliptic theory of affine Hecke algebras is well understood [Reference Opdam and SolleveldOS09], and we reviewed the basic facts in § 11.1. In particular, via (11.10) and (11.4)), we get that
\begin{equation} \overline{R}_I(G)_{\mathbb{C}} \cong \overline{R}({\widetilde{W}})_{\mathbb{C}}\cong \bigoplus_{s\in W\backslash T_{{\mathrm{iso}}}^\vee} \overline{R}(W_s)_{\mathbb{C}}, \end{equation}
where 
${\widetilde {W}}=W^a$, 
$W$, 
$T^\vee$, 
$W_s$ are as in Example 11.4. If 
$n=dm$, we consider 
$s_{d\times m}:=\text {diag}(\underbrace {1,\ldots,1}_m,\underbrace {\zeta _d,\ldots,\zeta _d}_m,\ldots,\underbrace {\zeta _d^{d-1},\ldots,\zeta _d^{d-1}}_m)$, where 
$\zeta _d$ is a primitive 
$d$th root of 
$1$. This is 
$S_n$-conjugate to 
$\Delta _n(\zeta _d)$. In that case,
\[ {\mathrm{Z}}_{G^\vee}(s_{d\times m})=\mathrm{P}({\mathsf{GL}}_m({\mathbb{C}})^d)\rtimes {\mathbb{Z}}/d{\mathbb{Z}}, \]
which has component group 
$A_{G^\vee }(s_{d\times m})={\mathbb {Z}}/d{\mathbb {Z}}$. The Lie algebra of the maximal (diagonal) torus in 
${\mathrm {Z}}_{G^\vee }(s_{d\times m})$ is
\[ \mathfrak{t}^\vee_{d\times m}=\bigg\{\underline{x}=(x_1,\ldots,x_n)\,\bigg|\,\sum_i x_i=0\bigg\}, \]
on which 
$W_{s_{d\times m}}$ acts in the standard way: break 
$(x_1,\ldots,x_n)$ into 
$m$-tuples
\[ \underline{y}_i=(x_{(i-1)m+1},x_{(i-1)m+2},\ldots, x_{im}), \quad 1\leqslant i\leqslant d. \]
Then the 
$i$th 
$S_m$ acts by the natural permutation action on 
$\underline {y}_i$, whereas 
${\mathbb {Z}}/d{\mathbb {Z}}$ permutes cyclically 
$(\underline {y}_1,\ldots,\underline {y}_d)$. We consider the elliptic theory of 
$W_{s_{d\times m}}$ on 
$\mathfrak {t}^\vee _{d\times m}$ with respect to this action.
Lemma 13.5 There are 
$\varphi (d)$ elliptic conjugacy classes of 
$W_{s_{d\times m}}$ acting on 
$\mathfrak {t}^\vee _{d\times m}$ with representatives 
$g_\xi =(w_m,1,1,\ldots,1) \xi$, where 
$\xi$ ranges over the elements of order 
$d$ in 
${\mathbb {Z}}/d{\mathbb {Z}}$, and 
$w_m$ is a fixed 
$m$-cycle in 
$S_m$.
Proof. We first show that each such element is elliptic. Without loss of generality, suppose that 
$\xi$ acts as the standard cycle 
$(1,2,\ldots,d)$ and 
$w_m=(1,2,\ldots,m)$. Then 
$g_\xi \cdot \underline {x}=\underline {x}$ implies 
$x_1=x_{(d-1)m+1}=x_{(d-2)m+1}=\cdots =x_{m+1}$ which then is equal to 
$x_m$ (because of the effect of 
$w_m$), then with 
$x_{dm}=x_{(d-1)m}=\cdots =x_{2m}$, which then is equal to 
$x_{m-1}$, etc. It follows that all coordinates 
$x_i$ are the same and since the sum of the coordinates is 
$0$, we get that there are no nonzero fixed points.
Second, no two 
$g_{\xi }$ are conjugate. This is clear because if 
$\xi,\xi '$ are distinct in 
${\mathbb {Z}}/d{\mathbb {Z}}$, then 
$x\xi$ and 
$x'\xi '$ are in different conjugacy classes for all 
$x,x'$ in 
$S_m^d$.
It remains to show that these are all the elliptic conjugacy classes. Let 
$x\xi$ be an element with 
$x=(\sigma _1,\ldots,\sigma _d)\in S_m^d$ and 
$\xi \in {\mathbb {Z}}/d{\mathbb {Z}}$. If 
$\xi$ does not have order 
$d$, then there exists points 
$\underline {x}=(\underline {y}_1,\ldots,\underline {y}_d)\in \mathfrak {t}^\vee _{d\times m}$ (here, as above, each 
$\underline {y}_i$ is an 
$m$-tuple) fixed under the action of 
$\xi$ such that not all 
$y_i$ are equal. This means, in particular, that there exists 
$j$ such that 
$\underline {y}_j=(x_{(j-1)m+1},\ldots,x_{jm})$ is arbitrary and 
$\sum _{l=(j-1)m+1}^{jm} x_l\neq 0$. But then every 
$\sigma _j\in S_m$ has a nonzero fixed point 
$\underline {y}_j$, for example taking all of the entries of 
$\underline {y}_j$ to be equal, and therefore 
$x\xi$ is not elliptic.
This means that necessarily 
$\xi$ has order 
$d$. We claim that the conjugacy classes of 
$x\xi$ are in one-to-one correspondence with conjugacy classes of 
$S_m$ via the correspondence
\[ w\in S_m\mapsto (w,1,\ldots,1)\xi \in S_m^d\rtimes {\mathbb{Z}}/d{\mathbb{Z}}. \]
Without loss of generality, suppose 
$\xi$ acts by shifting the indices 
$i\to i+1$ mod 
$d$. We show that every element 
$x\xi$, 
$x=(\sigma _1,\ldots,\sigma _d)$, is conjugate to an element of the form 
$(w,1,\ldots,1)\xi$. This is equivalent to the existence of permutations 
$z_1,\ldots,z_d\in S_m$ such that
\[ \sigma_1=z_1 w z_2^{-1},\quad \sigma_2=z_2 z_3^{-1},\ldots,\sigma_{d-1}=z_{d-1} z_d^{-1},\quad \sigma_d=z_d z_1^{-1}. \]
This can be solved easily, by taking 
$z_1=1$, then 
$z_d=\sigma _d$, 
$z_{d-1}=\sigma _{d-1}\sigma _d,\ldots,$ 
$z_2=\sigma _2\sigma _3\dots \sigma _d$ and 
$w=\sigma _1\sigma _2\dots \sigma _d$.
A similar calculation shows that 
$(w,1,\ldots,1)\xi$ and 
$(w',1,\ldots,1)\xi$ are conjugate if and only if 
$w,w'$ are conjugate in 
$S_m$. (If 
$w'=zwz^{-1}$, then 
$(w',1,\ldots,1)\xi$ and 
$(w,1,\ldots,1)\xi$ are conjugate via 
$(z,z,\ldots,z)$.)
Finally, if an element 
$(w,1,\ldots,1)\xi$, 
$\xi$ of order 
$d$, is elliptic, then 
$w$ is elliptic in 
$S_m$, otherwise if 
$\underline {y}$ is a fixed point of 
$w$, 
$(\underline {y},\ldots,\underline {y})$ is a fixed point of 
$(w,1,\ldots,1)\xi$. This concludes the proof.
On the other hand, we have unipotent classes 
$u$ in 
$\mathrm {P}({\mathsf {GL}}_m({\mathbb {C}})^d)$ and we need to look at the elliptic theory of 
$A_{G^\vee }(s_{d\times m} u)$ on the Lie algebra of the maximal torus in 
${\mathrm {Z}}_{\mathrm {P}({\mathsf {GL}}_m({\mathbb {C}})^d)\rtimes {\mathbb {Z}}/d{\mathbb {Z}}}(u)$. Let 
$u=u_{d\times m}$ be the unipotent element given by the principal Jordan normal form on each of the 
${\mathsf {GL}}_m$-blocks. Then the reductive part of the centralizer is
\[ {\mathrm{Z}}_{G^\vee}(s_{d\times m} u_{d\times m})^{\mathrm{red}}=\mathrm{P}({\mathrm{Z}}_{{\mathsf{GL}}_m({\mathbb{C}})^d})\rtimes {\mathbb{Z}}/d{\mathbb{Z}}, \]
hence 
$A_{G^\vee }(s_{d\times m} u_{d\times m})={\mathbb {Z}}/d{\mathbb {Z}}$ and this acts on the Cartan subalgebra
\[ \mathfrak{t}^\vee(s_{d\times m} u_{d\times m})=\bigg\{(z_1 {\mathrm{Id}}_m,\ldots,z_d{\mathrm{Id}}_m)\,\bigg|\,\sum_i{z_i}=0\bigg\}. \]
In particular, 
$\overline {R}(A_{s_{d\times m} u_{d\times m}})_\mathbb {C}$ has dimension 
$\varphi (d)$ and can be identified with the class functions on the elements of order 
$d$ in 
${\mathbb {Z}}/d{\mathbb {Z}}$. Thus, in the case of 
$\mathsf {SL}_n(F)$, the elliptic correspondence for unipotent representations takes the following very concrete form.
Proposition 13.6 Let 
$G={\mathsf {SL}}_n(F)$. The local Langlands correspondence for unipotent representations induces an isometric isomorphism
\[ \overline{\mathsf{LLC}^p}_{\mathrm{un}}\colon \bigoplus_{d\mid n} \overline{R}(A_{x_{d\times m}}) \longrightarrow \overline{R}_{\mathrm{un}}({\mathsf{SL}}_n(F)),\quad \phi\mapsto \pi(x_{d\times m},\phi), \]
where 
$x_{d\times m}=s_{d\times m} u_{d\times m}\in {\mathsf {PGL}}_n({\mathbb {C}})$ is as above and 
$A_{x_{d\times m}}={\mathbb {Z}}/d{\mathbb {Z}}$.
The connection with the elliptic pairs for 
$G^\vee ={\mathsf {PGL}}_n({\mathbb {C}})$ from Proposition 13.2 is
\[ \bigoplus_{u\in {\mathcal{C}}({\mathsf{PGL}}_n({\mathbb{C}}))_{\mathrm{un}}} {\mathbb{C}}[{\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}]^{\Gamma_u}=\bigoplus_{d|n} {\mathbb{C}}[{\mathcal{Y}}(\Gamma_{u_{d\times m}})_{\mathrm{ell}}]^{\Gamma_{u_{d\times m}}} \cong \bigoplus_{d\mid n} \overline{R}(A_{x_{d\times m}}). \]
Remark 13.7 Note that by taking dimensions in Proposition 13.6, we recover the well-known formula 
$\sum _{d \mid n} \varphi (d) = n$, where, as above, 
$\varphi$ denotes the Euler phi function.
13.3 The elliptic Fourier transform for ${\mathsf {SL}}_n(F)$
The results so far imply that we have an equivalence
\[ \overline{R}_{\mathrm{un}}({\mathsf{SL}}_n(F))_\mathbb{C}\cong \overline{R}({\mathcal{H}})_\mathbb{C}\cong \overline{R}({\widetilde{W}})_\mathbb{C}\cong \bigoplus_{u\in {\mathcal{C}}({\mathsf{PGL}}_n({\mathbb{C}}))_{\mathrm{un}}} \Gamma_u\backslash {\mathcal{Y}}(\Gamma_u)_{\mathrm{ell}}. \]
The spaces involved are all 
$n$-dimensional and we describe the basis of 
$\overline {R}_{\mathrm {un}}(G)_\mathbb {C}$ given by the virtual characters 
$\Pi (u,s,h)$.
First, consider the two extremes. At one extreme, we have the regular unipotent class 
$u_{\mathrm {reg}}$. Then 
$\Gamma _{u_{\mathrm {reg}}}=\{1\}$ and 
$\pi (u_{\mathrm {reg}},1,1)={\mathrm {St}}$. At the other, end, 
$u=1$, 
$\Gamma _1={\mathsf {PGL}}_n({\mathbb {C}})$, and there are 
$\varphi (n)$ orbits of elliptic pairs 
$(s_n,\dot {w}_n^k)$, 
$k\in ({\mathbb {Z}}/n{\mathbb {Z}})^\times$, as in Lemma 13.1. The component group is 
$A_{s_n}=\langle \dot {w}_n\rangle \cong {\mathbb {Z}}/n{\mathbb {Z}}$. Let 
$\pi (1,s_n)$ denote the tempered unramified principal series of 
$G$ with Satake parameter 
$s_n\in W\backslash T^\vee$. Since 
$W_{s_n}=A_{s_n}={\mathbb {Z}}/n{\mathbb {Z}}$, the theory of (analytic) 
$R$-groups provides a well-known decomposition
\[ \pi(1,s_n)=\bigoplus_{\phi\in \widehat{A}_{s_n}} \pi(1,s_n,\phi), \]
where each 
$\pi (1,s_n,\phi )$ is an irreducible tempered 
$G$-representation. Identifying 
$\widehat {{\mathbb {Z}}/n{\mathbb {Z}}}$ with 
${\mathbb {Z}}/n{\mathbb {Z}}$ (via a choice 
$\zeta _n$ of primitive 
$n$th root of unity), we get
\begin{equation} \Pi(1,s_n,\dot{w}_n^k)=\sum_{\ell\in {\mathbb{Z}}/n{\mathbb{Z}}}\zeta_n^{\ell k} ~ \pi(1,s_n,\phi_\ell),\quad k\in ({\mathbb{Z}}/n{\mathbb{Z}})^\times, \end{equation}
where 
$\phi _\ell (\zeta _n)=\zeta _n^\ell$. Moreover, as an 
${\mathcal {H}}$-module, 
$\pi (1,s_n,\phi _\ell )^I$ is the (unique) irreducible tempered 
${\mathcal {H}}$-module with central character 
$W\cdot s_n$ such that
\[ \sigma_0(\pi(1,s_n,\phi_\ell)^I)={\mathrm{Ind}}_{{\mathbb{Z}}/n{\mathbb{Z}}\ltimes X}^{S_n\ltimes X} (\phi_\ell\otimes s_n). \]
Now, more generally, by Proposition 13.2, 
${\mathcal {Y}}(\Gamma _u)_{\mathrm {ell}}\neq \emptyset$ if and only if 
$u = u_{d\times m}$ is labelled by a rectangular partition 
$(\underbrace {m,\ldots,m}_d)$ of 
$n$. In this case 
$\Gamma _u={\mathsf {PGL}}_d(\mathbb {C})$. Recall 
$s_{d\times m}$ and 
$x_{d\times m}=s_{d\times m} u_{d\times m}$. Consider the parabolically induced tempered 
$G$-representation
\[ \pi(u_{d\times m},s_{d\times m})={\mathrm{Ind}}_{P_{d\times m}}^{{\mathsf{SL}}_n(F)}(({\mathrm{St}}_m\otimes{\mathbb{C}}_1)\boxtimes ({\mathrm{St}}_m\otimes {\mathbb{C}}_{\zeta_d})\boxtimes\cdots\boxtimes ({\mathrm{St}}_m\otimes {\mathbb{C}}_{\zeta_d^{d-1}})), \]
where 
$P_{d\times m}$ is the block-upper-triangular parabolic subgroup with Levi subgroup 
$M_{d\times m}=S({\mathsf {GL}}_m(F)^d)$, 
${\mathrm {St}}_m$ is the Steinberg representation of 
${\mathsf {GL}}_m(F)$, and 
${\mathbb {C}}_z$ is the unramified character of 
${\mathsf {GL}}_m(F)$ corresponding to the semisimple element 
$z{\mathrm {Id}}_m$ in the dual complex group 
${\mathsf {GL}}_m({\mathbb {C}})$. The R-group in this case is 
${\mathbb {Z}}/d{\mathbb {Z}}$ which coincides with 
$A_{x_{d\times m}}$. We have a decomposition into irreducible tempered 
$G$-representations:
\[ \pi(u_{d\times m},s_{d\times m})=\bigoplus_{\phi\in \widehat{A}_{x_{d\times m}}} \pi(u_{d\times m},s_{d\times m},\phi). \]
Taking 
$I$-fixed vectors and the deformation 
$\sigma _0$, we have
\[ \sigma_0((\pi_{d\times m},s_{d\times m},\phi_\ell)^I)={\mathrm{Ind}}_{W_{s_{d\times m}\ltimes X}}^{S_n\ltimes X}({\mathrm{sgn}}_{d\times m}\phi_\ell\otimes s_{d\times m}), \]
where recall that 
$W_{s_{d\times m}}=S_m^d\rtimes {\mathbb {Z}}/d{\mathbb {Z}}$ and 
${\mathrm {sgn}}_{d\times m}$ is the sign character of 
$S_m^d$.
Define
\begin{equation} \Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^k)=\sum_{\ell\in {\mathbb{Z}}/d{\mathbb{Z}}}\zeta_d^{\ell k} ~ \pi(u_{d\times m},s_{d\times m},\phi_\ell),\quad k\in ({\mathbb{Z}}/d{\mathbb{Z}})^\times. \end{equation}The elliptic Fourier transform in this case is
\begin{equation} {\mathrm{FT}}^\vee_{\mathrm{ell}}(\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^k))=\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^{-k}), \quad k\in ({\mathbb{Z}}/d{\mathbb{Z}})^\times. \end{equation}
The maximal compact open subgroups of 
${\mathsf {SL}}_n(F)$ are maximal parahoric subgroups 
$K_i$, one for each vertex 
$i$ of the affine Dynkin diagram. With this notation, 
$K_0={\mathsf {SL}}_n(\mathfrak {o}_F)$. Moreover, 
${\mathrm {InnT}}^p\overline {K}_i=\{\overline {K}_i\}$. All 
$K_i$ are isomorphic to 
$K_0$ (conjugate in 
${\mathsf {GL}}_n(F)$), hence for all 
$i$, the nonabelian Fourier transform of 
$\overline {K}_i$ is the identity. Let 
$W_i\cong S_n$ denote the finite parahoric subgroup of 
$W^a$ corresponding to 
$K_i$, so that 
$W_0=W$. The isomorphism 
$W_i\cong W$ is given by the map 
$s_j\mapsto s_{(j-i)\text { mod }n}$. By Mackey induction/restriction
\begin{equation} {\mathrm{Ind}}_{W_{s_{d\times m}\ltimes X}}^{S_n\ltimes X}({\mathrm{sgn}}_{d\times m}\phi_\ell\otimes s_{d\times m})|_{W_i}\cong {\mathrm{Ind}}_{(W_{s_{d\times m}})_i}^{W_i} ({\mathrm{sgn}}_{d\times m}\phi_\ell\otimes s_{d\times m}), \end{equation}
where 
$(W_{s_{d\times m}} )_i=(W_{s_{d\times m}}\ltimes X)\cap W_i$. Let 
$\gamma =\epsilon _1-\epsilon _n$ be the highest root of type 
$A_{n-1}$, in the standard coordinates, so that 
$s_0=s_\gamma t_\gamma$, denoting by 
$t_\gamma \in X\subset W^a$ the corresponding translation. Then one can see that 
$W_{s_{d\times m}} \cong (W_{s_{d\times m}} )_i$ is given by sending
\[ s_j\mapsto \begin{cases} s_j, & \text{if }j\neq i \\ s_i t_{\epsilon_i-\epsilon_{i+1}}, & \text{if }j=i, \end{cases}\quad 1\leqslant j< n. \]
Lemma 13.8 For every 
$0\leqslant i< n$,
\[ {\mathrm{Ind}}_{(W_{s_{d\times m}})_i}^{W_i} ({\mathrm{sgn}}_{d\times m}\phi_\ell\otimes s_{d\times m})\cong {\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell+\lfloor {i}/{m}\rfloor}). \]
Proof. In light of the observation before the statement of the lemma, we only need to trace how the inducing character changes on the generator corresponding to 
$i$. Denote by 
$(S_m^d)_i$ the image of 
$S_m^d$ inside 
$(W_{s_{d\times m}})_i$, and similarly for 
$({\mathbb {Z}}/d{\mathbb {Z}})_i$. If 
$s_i$ is a generator of 
$(S_m^d)_i$, then the value of the character 
$s_{d\times m}$ on 
$t_{\epsilon _i-\epsilon _{i+1}}$ is 
$1$. On the other hand, if 
$s_i$ is not a generator of 
$(S_m^d)_i$, then there is also no change. This means that the inducing character on the 
$(S_m^d)_i$ is still 
${\mathrm {sgn}}_{d\times m}$.
The generator 
$\xi$ of 
${\mathbb {Z}}/d{\mathbb {Z}}$ is, in cycle notation, a product of the disjoint cycles 
$(l,m+l,2m+l,\ldots,(d-1)m+l)$, where 
$l$ ranges from 
$0$ to 
$m-1$ (when 
$l=0$, we mean the cycle 
$(m,2m,\ldots,dm)$). Then the simple reflection 
$i$ contributes to the cycle 
$l$ for 
$i=jm+l$, 
$j=\lfloor {i}/{m}\rfloor$. In 
$({\mathbb {Z}}/d{\mathbb {Z}})_i$, we then get a 
$\theta _{\epsilon _i-\epsilon _{i+1}}$, which we need to move to the end of the product of cycles, and we get that the image 
$(\xi )_i$ in 
$({\mathbb {Z}}/d{\mathbb {Z}})_i$ is 
$(\xi )_i=\xi t_{\epsilon _i-\epsilon _{(d-1)m+l}}$. The character 
$s_{d\times m}$ acts on 
$t_{\epsilon _i-\epsilon _{(d-1)m+l}}$ by 
$\zeta _d^{j}$, which means that 
$\phi _\ell s_{d\times m}$ acts on 
$(\xi )_i$ by 
$\zeta _d^{\ell +j}$, which proves the claim.
Proposition 13.9 Conjecture 9.7 holds for 
$G={\mathsf {SL}}_n(F)$. More precisely, for each 
$0\leqslant i< n$,
\[ \operatorname{res}_{K_i}\circ {\mathrm{FT}}^\vee_{{\mathrm{ell}}}(\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^k))=\zeta_d^{2k\lfloor{i}/{m}\rfloor} {\mathrm{FT}}_{{\mathrm{cpt}},{\mathrm{un}}}\circ \operatorname{res}_{K_i} (\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^k)). \]
Proof. To verify Conjecture 9.7, given (13.6), it is sufficient to compare the restrictions to 
$W_i$ of 
$\sigma _0(\operatorname {res}_{K_i}(\Pi (u_{d\times m},s_{d\times m},\dot {w}_{d\times m}^k)^I))$ and 
$\sigma _0(\operatorname {res}_{K_i}(\Pi (u_{d\times m},s_{d\times m},\dot {w}_{d\times m}^{-k})^I)$ as virtual 
$W_i$-characters. For this, we apply (13.7) and Lemma 13.8 with 
$j=\lfloor {i}/{m}\rfloor$ and get
\begin{align*} \sigma_0(\operatorname{res}_{K_i}(\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^k)^I))&\cong\sum_{\ell\in {\mathbb{Z}}/d} \zeta_d^{k\ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell+j})\\ &=\zeta_d^{-kj} \sum_{\ell} \zeta_d^{k\ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell}). \end{align*}
On the other hand,
\begin{align*} \sigma_0(\operatorname{res}_{K_i}(\Pi(u_{d\times m},s_{d\times m},\dot{w}_{d\times m}^{-k})^I))&\cong \sum_{\ell\in {\mathbb{Z}}/d} \zeta_d^{-k\ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell+j})\\ &=\sum_{\ell\in {\mathbb{Z}}/d} \zeta_d^{k\ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{-\ell+j})\\ &=\sum_{\ell\in {\mathbb{Z}}/d} \zeta_d^{k\ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell-j})\\ &=\zeta_d^{kj} \sum_{\ell} \zeta_d^{k \ell}{\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell}). \end{align*}
Here we have used that
\[ {\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{\ell'})\cong {\mathrm{Ind}}_{W_{s_{d\times m}}}^{S_n}({\mathrm{sgn}}_{d\times m}\phi_{-\ell'}), \]
because 
$\phi _{-\ell '}$ is the 
${\mathbb {Z}}/d{\mathbb {Z}}$-representation contragredient to 
$\phi _{\ell '}$. This implies that the two sides are contragredient to each other, but all irreducible 
$S_n$-representations are self-contragredient.
14. ${\mathsf {PGL}}_n(F)$
Now suppose 
${\mathbf {G}} = {\mathsf {PGL}}_n$. The dual group 
$G^\vee$ is 
${\mathsf {SL}}_n(\mathbb {C})$. Each unipotent element 
$u \in G^\vee$ corresponds to a partition 
$\lambda _u$ of 
$n$, and if 
$\lambda _u = \lambda =(\underbrace {1,\ldots,1}_{r_1},\underbrace {2,\ldots,2}_{r_2},\ldots,\underbrace {\ell,\ldots,\ell }_{r_\ell })$, then
\begin{equation} \Gamma_u \simeq \bigg\{ (x_1, \dots, x_\ell) \in \prod_{i = 1}^\ell {\mathsf{GL}}_{r_i}( \mathbb{C}) \,\bigg|\,\prod_{i = 1}^\ell \det(x_i)^i = 1\bigg\}. \end{equation}Lemma 14.1 The group 
$\Gamma _u$ contains elliptic pairs if and only if 
$u$ is regular unipotent. In this case 
${\mathcal {Y}}(\Gamma _u) = {\mathcal {Y}}(\Gamma _u)_{{\mathrm {ell}}} = \{(s, h) \mid s, h \in {\mathrm {Z}}_{{\mathsf {SL}}_n(\mathbb {C})}\}$.
Proof. The proof is very similar to that of Proposition 13.2. Note that if 
$u$ is not rectangular, then 
$\Gamma _u$ has infinite center: for example, with notation as in (14.1), given 
$t \in \mathbb {C}^\times$, the element 
$(t{\mathrm {Id}}_{r_1}, t{\mathrm {Id}}_{r_2}, \dots, t{\mathrm {Id}}_{r_{\ell -1}}, t^{r_\ell - {n}/{\ell }}{\mathrm {Id}}_{r_\ell }) \in {\mathrm {Z}}_{\Gamma _u}$. Thus, if 
$\Gamma _u$ contains an elliptic pair, then 
$\lambda _u$ is of the form 
$(k, k, \dots, k)$ for some 
$k$ dividing 
$n$, and 
$\Gamma _u \simeq \{x \in {\mathsf {GL}}_{{n}/{k}}(\mathbb {C}) \mid \det (x)^k = 1\}$. Explicitly, we can think of 
$\Gamma _u$ as a split extension
\[ 1 \to {\mathsf{SL}}_{{n}/{k}}(\mathbb{C}) \to \Gamma_u \to \mu_{k} \to 1, \]
where the first inclusion is the natural one, and the map to 
$\mu _{k}$ is given by the determinant. Now, given semisimple elements 
$s, h \in \Gamma _u$ such that 
$sh = hs$, there exists 
$g \in {\mathsf {SL}}_{{n}/{k}}(\mathbb {C})$ such that 
$gsg^{-1}, ghg^{-1}$ are both diagonal in 
${\mathsf {GL}}_{{n}/{k}}(\mathbb {C})$. Thus, a maximal torus of 
${\mathsf {SL}}_{{n}/{k}}( \mathbb {C})$ centralizes both 
$s$ and 
$h$, and if 
$(s, h)$ is an elliptic pair, we must have 
$k = n$.
We can now easily prove Conjecture 9.7 in this case.
Theorem 14.2 Conjecture 9.7 holds when 
${\mathbf {G}} = {\mathsf {PGL}}_n$. More precisely, when 
${\mathbf {G}} = {\mathsf {PGL}}_n$, we have
\[ \operatorname{res}_{{\mathrm{cpt}}, {\mathrm{un}}} \circ {\mathrm{FT}}^\vee_{\mathrm{ell}} = {\mathrm{FT}}_{{\mathrm{cpt}}, {\mathrm{un}}} \circ \operatorname{res}_{{\mathrm{cpt}}, {\mathrm{un}}}. \]
To illustrate the theorem, we explicitly describe the case when 
${\mathbf {G}} = {\mathsf {PGL}}_2$. Note that even this low-rank example shows that certain choices were necessary in our setup: to relate 
${\mathrm {FT}}^\vee _{{\mathrm {ell}}}$ to a finite Fourier transform for the non-split inner twist of 
$G$, first, we must consider maximal compact subgroups instead of just parahorics (otherwise the restrictions of 
$\Pi (u, 1, 1)$ and 
$\Pi (u, -1, 1)$ would be the same, though 
${\mathrm {FT}}^\vee _{{\mathrm {ell}}}$ fixes the first but not the second); second, 
${\mathrm {FT}}_{{\mathrm {cpt}}, {\mathrm {un}}}$ must mix subspaces corresponding to distinct inner twists to give a well-defined linear map.
Example 14.3 Now let 
${\mathbf {G}} = {\mathsf {PGL}}_2$. Then 
$G$ has a unique non-split inner twist 
$G'$, which we can describe explicitly as follows: let
\[ D = \bigg\{ \begin{pmatrix} a & \varpi b\\\overline{b} & \overline{a} \end{pmatrix} \bigg|\, a, b \in F_{(2)} \bigg\}, \]
where 
$F_{(2)}$ is the degree-two unramified extension of 
$F$. Then 
$D$ is a four-dimensional division algebra over 
$F$, and we can take 
$G':= D^\times /F^\times$.
Let 
$\chi _0$ be the unramified character of 
$F^\times$ given by 
$\varpi \mapsto -1$. Then the nontrivial weakly unramified character of 
$G$ (respectively, 
$G'$) is given by 
$\chi := \chi _0 \circ \det$ (respectively, 
$\chi ' := \chi _0 \circ \det$). Let 
${\mathrm {St}}_G$ denote the Steinberg representation of 
$G$ (and similarly for 
${\mathrm {St}}_{G'}$, which is the trivial representation of 
$G'$), and let 
$u \in {\mathsf {SL}}_2(\mathbb {C})$ be regular unipotent. Then the virtual representations corresponding to our four elliptic pairs are
\begin{align*} \Pi(u, 1, 1) &= {\mathrm{St}}_G + {\mathrm{St}}_{G'},\\ \Pi(u, 1, -1) &= {\mathrm{St}}_G - {\mathrm{St}}_{G'},\\ \Pi(u, -1, 1) &= ({\mathrm{St}}_G \otimes \chi) + ({\mathrm{St}}_{G'}\otimes \chi'),\\ \Pi(u, -1, -1) &= ({\mathrm{St}}_{G} \otimes \chi) - ({\mathrm{St}}_{G'}\otimes \chi'). \end{align*}
The involution 
${\mathrm {FT}}^\vee _{{\mathrm {ell}}}$ switches 
$\Pi (u, 1, -1)$ and 
$\Pi (u, -1, 1)$, and fixes the other two sums.
Let 
$I$ be the Iwahori subgroup of 
$G$ given by
\[ I = \bigg\{ \begin{pmatrix} a & \varpi b\\c & d \end{pmatrix} \bigg|\, a, d \in \mathfrak{o}_F^\times, b, c \in \mathfrak{o}_F\bigg\}. \]
With notation as in § 7, we have 
$\Omega _G \simeq {\mathbb {Z}}/2{\mathbb {Z}}$. The set 
$S_{\rm max}(G)$ contains two elements 
$(A, \mathcal {O})$: one corresponding to 
$A = \Omega _G$ and one corresponding to 
$A$ trivial. Thus, the group 
$G$ has two conjugacy classes of maximal compact open subgroups: the maximal parahoric subgroup 
$K_0 := {\mathsf {PGL}}_2(\mathfrak {o}_F)$ (which corresponds to 
$A$ trivial) and 
$K_1 := {\mathrm {N}}_G(I)$ (which corresponds to 
$A = \Omega _G$). Note that 
$K_1$ contains 
$I$ with index 2: it is generated by 
$I$ and 
$\sigma := \big (\begin{smallmatrix} 0 & \varpi \\1 & 0\end{smallmatrix}\big )$. The reductive quotients are given by 
$\overline {K}_0 \simeq {\mathsf {PGL}}_2(\mathbb {F}_q)$ and 
$\overline {K}_1 \simeq \mathbb {F}_q^\times \rtimes {\mathbb {Z}}/2{\mathbb {Z}}$. Note that 
$\chi$ is trivial on 
$K_0$ and on 
$I$, but 
$\chi (\sigma ) = -1$, so 
$\chi$ induces the sign character on the component group of 
$\overline {K}_1$.
In the notation of § 7, we have 
$G' = G_x$, where 
$x$ is the nontrivial element of 
$\Omega _G$. Thus, 
$G'$ has a unique conjugacy class of maximal compact subgroups, corresponding to the element 
$(A, \mathcal {O})$ of 
$S_{\rm max}(G)$ with 
$A = \Omega _G$. Explicitly, 
$G'$ itself is compact. The only parahoric subgroup of 
$G'$ is 
$I' := \mathfrak {o}_D^\times /\mathfrak {o}_F^\times$, where 
$\mathfrak {o}_D$ is the ring of integers of 
$D$, and this parahoric is normal in 
$G'$. The group 
$G'$ is generated by 
$I'$ and 
$\sigma$ (defined as above), which again has order 2 in 
$G'$. The reductive quotient 
$\overline {G'} \simeq (\mathbb {F}_{q^2}^\times /\mathbb {F}_q^\times ) \rtimes {\mathbb {Z}}/2{\mathbb {Z}}$. Note that as above 
$\chi '$ is trivial on 
$I'$ but takes the value 
$-1$ on 
$\sigma$, so 
$\chi '$ factors through the sign character of the component group of 
$\overline {G'}$.
The space 
${\mathcal {C}}(G)_{{\mathrm {cpt}}, {\mathrm {un}}}$ is given by
\[ {\mathcal{C}}(G)_{{\mathrm{cpt}}, {\mathrm{un}}} = R_{{\mathrm{un}}}(\overline{K}_0) \oplus R_{{\mathrm{un}}}(\overline{K}_1) \oplus R_{{\mathrm{un}}}(\overline{G'}), \]
and the map 
$\operatorname {res}_{{\mathrm {cpt}}, {\mathrm {un}}}$ is defined on the virtual representations above by
\begin{align*} \Pi(u, 1, 1) &\mapsto {\mathrm{St}}_{K_0} + {\mathrm{St}}_{I} + {\mathrm{St}}_{I'},\\ \Pi(u, 1, -1) &\mapsto {\mathrm{St}}_{K_0} + {\mathrm{St}}_{I} - {\mathrm{St}}_{I'},\\ \Pi(u, -1, 1) &\mapsto {\mathrm{St}}_{K_0} + ({\mathrm{St}}_{I}\otimes {\mathrm{sgn}}) + ({\mathrm{St}}_{I'}\otimes {\mathrm{sgn}}),\\ \Pi(u, -1, -1) &\mapsto {\mathrm{St}}_{K_0} + ({\mathrm{St}}_{I} \otimes {\mathrm{sgn}}) - ({\mathrm{St}}_{I'}\otimes {\mathrm{sgn}}), \end{align*}
where, as in the proof of Proposition 9.10, 
${\mathrm {St}}_K$ denotes the Steinberg representation of 
$\overline {K}$, and 
${\mathrm {sgn}}$ denotes the sign representation of the relevant component group.
If 
$(A, \mathcal {O}) \in S_{\rm max}(G)$ with 
$A$ trivial, then 
$\operatorname {res}_{\mathcal {O}}(\Pi (u, s, h)) = {\mathrm {St}}_{K_0}$ for all elliptic pairs 
$(s, h)$. In this case, 
${\mathrm {FT}}_{{\mathrm {cpt}}, {\mathrm {un}}}$ restricts to the identity map on 
$R_{{\mathrm {un}}}(\overline {K}_0)$.
Now suppose 
$(A, \mathcal {O}) \in S_{\rm max}(G)$ with 
$A = \Omega _G$. Then 
$\operatorname {res}_{\mathcal {O}}$ is given by projection onto 
$R_{{\mathrm {un}}}(\overline {K}_1) \oplus R_{{\mathrm {un}}}(\overline {G'})$. In the notation of § 6, and with 
$\mathcal {U}$ the (one-element) family consisting of the Steinberg representation of 
$\overline {K}_1$, we have 
$\widetilde {\Gamma }_{\mathcal {U}}^A = A$, so 
$\mathcal {M}(\widetilde {\Gamma }_{\mathcal {U}}^A)$ consists of four elements: 
$(1, {\mathrm {triv}}), (1, {\mathrm {sign}}), (x, {\mathrm {triv}}), (x, {\mathrm {sgn}})$ (where, as above, 
$x$ is the nontrivial element of 
$\Omega _G$). These correspond to the following elements of 
$R_{\mathrm {un}} (\overline {K}_1) \oplus R_{\mathrm {un}} (\overline {G'})$:
\begin{align*} (1, {\mathrm{triv}}) &\longleftrightarrow {\mathrm{St}}_I,\\ (1, {\mathrm{sgn}}) &\longleftrightarrow {\mathrm{St}}_I \otimes {\mathrm{sgn}},\\ (x, {\mathrm{triv}}) &\longleftrightarrow {\mathrm{St}}_{I'},\\ (x, {\mathrm{sgn}}) &\longleftrightarrow {\mathrm{St}}_{I'} \otimes {\mathrm{sgn}}. \end{align*}
With notation as in (5.13), we have
\begin{align*} \operatorname{res}_\mathcal{O} (\Pi(u, 1, 1)) &= \Pi_{\widetilde{\mathcal{U}}}({\mathrm{triv}}, {\mathrm{triv}}),\\ \operatorname{res}_\mathcal{O} (\Pi(u, 1, -1)) &= \Pi_{\widetilde{\mathcal{U}}}({\mathrm{triv}}, {\mathrm{sgn}}),\\ \operatorname{res}_\mathcal{O} (\Pi(u, -1, 1)) &= \Pi_{\widetilde{\mathcal{U}}}({\mathrm{sgn}}, {\mathrm{triv}}),\\ \operatorname{res}_\mathcal{O} (\Pi(u, -1, -1)) &= \Pi_{\widetilde{\mathcal{U}}}({\mathrm{sgn}}, {\mathrm{sgn}}), \end{align*}
where 
$\widetilde {\mathcal {U}}$ is the family indexed by 
$\Gamma _{\mathcal {U}}^A$. Thus the proof of Proposition 9.10, and Conjecture 9.7, may be easily verified.
Acknowledgements
We thank M. Solleveld for his careful reading and many useful comments, particularly regarding § 11, and G. Lusztig and M. Reeder for their helpful suggestions. We also thank the referees for the thorough checking of the paper, for the corrections and suggestions for improvement. D.C. thanks Université Paris Cité and Sorbonne Université for their hospitality while part of this work was completed.
Conflicts of interest
None.
Financial support
This research was supported in part by the EPSRC grant EP/V046713/1 (2021).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.
Open access
