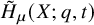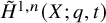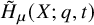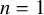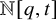1 Introduction
Tracing back to work of Young, raising operator formulas have been used as a powerful tool in classical symmetric function theory through modern Schubert calculus – see, for example, [Reference Anderson and Fulton1, Reference Blasiak, Morse, Pun and Summers8, Reference Blasiak, Morse and Seelinger10, Reference Skovsted Buch, Kresch and Tamvakis12, Reference Skovsted Buch, Kresch and Tamvakis13, Reference Garsia16, Reference Garsia and Remmel18, Reference Garsia and Remmel19, Reference Lascoux and Naruse27, Reference Pragacz33, Reference Pragacz34, Reference Tamvakis38, Reference Thomas39, Reference Young and Turnbull41]. Their applications in symmetric function theory include formulas for fundamental bases such as Schur functions and Schur Q-functions, as well as bases in the more contemporary framework involving a parameter t, such as the modified Hall-Littlewood polynomials [Reference Garsia20, Reference Milne31], given by the raising operator formula
 $$ \begin{align} H_\mu(X;t) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{{\mathbf z}^\mu}{\prod_{\alpha_{ij} \in R_+}(1 - t \hspace{.3mm} z_i/z_j)}\Big)\,. \end{align} $$
$$ \begin{align} H_\mu(X;t) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{{\mathbf z}^\mu}{\prod_{\alpha_{ij} \in R_+}(1 - t \hspace{.3mm} z_i/z_j)}\Big)\,. \end{align} $$
Many research directions have emerged from modifications to classical raising operator formulas. For example, other important families of symmetric functions, including the parabolic Hall-Littlewood polynomials of Shimozono-Weyman [Reference Shimozono and Weyman36], and k-Schur functions [Reference Blasiak, Morse, Pun and Summers8, Reference Chen15], can be defined by generalizing the formula (1).
The raising operator methodology lies at the foundation of Macdonald’s development in [Reference Macdonald and Zelevinsky29] of classical symmetric function theory and its one-parameter generalizations, including Hall-Littlewood polynomials. However, for the two-parameter generalization to Macdonald polynomials, no raising operator cornerstone similar to (1) has previously been known, forcing the theory of Macdonald polynomials to be developed in a more indirect way.
Here, we establish a raising operator formula for the modified Macdonald polynomials
![]() $\tilde {H}_{\mu }(X;q,t)$
, which reduces at
$\tilde {H}_{\mu }(X;q,t)$
, which reduces at
![]() $q=0$
to a previously known formula for Hall-Littlewood polynomials. Using notation defined in §3.1, our formula reads
$q=0$
to a previously known formula for Hall-Littlewood polynomials. Using notation defined in §3.1, our formula reads
 $$ \begin{align} &\tilde{H}_\mu (X;q,t) =\omega \operatorname{\mathrm{pol}} _{X} {\boldsymbol \sigma } \left( \frac{ z_1 \cdots z_l \prod\limits_{\alpha_{ij} \in R_{\mu^*} \setminus \widehat{R}_{\mu^*}} \!\!\!\big(1- q^{{\mathrm{arm}}({\boldsymbol {\mu^*}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\mu^*}[i]})} \dfrac{z_i}{z_j} \big) \prod\limits_{\alpha_{ij} \in \widehat{R}_{\mu^*}} \!\!\big(1-q\hspace{.3mm} t\, \dfrac{z_i}{z_j} \big)} {\prod\limits_{\alpha_{ij} \in R_+} \!\!\big(1-q \, \dfrac{z_i}{z_j}\big) \prod\limits_{\alpha_{ij} \in R_{\mu^*}} \!\!\big(1-t \, \dfrac{z_i}{z_j}\big)}\right). \end{align} $$
$$ \begin{align} &\tilde{H}_\mu (X;q,t) =\omega \operatorname{\mathrm{pol}} _{X} {\boldsymbol \sigma } \left( \frac{ z_1 \cdots z_l \prod\limits_{\alpha_{ij} \in R_{\mu^*} \setminus \widehat{R}_{\mu^*}} \!\!\!\big(1- q^{{\mathrm{arm}}({\boldsymbol {\mu^*}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\mu^*}[i]})} \dfrac{z_i}{z_j} \big) \prod\limits_{\alpha_{ij} \in \widehat{R}_{\mu^*}} \!\!\big(1-q\hspace{.3mm} t\, \dfrac{z_i}{z_j} \big)} {\prod\limits_{\alpha_{ij} \in R_+} \!\!\big(1-q \, \dfrac{z_i}{z_j}\big) \prod\limits_{\alpha_{ij} \in R_{\mu^*}} \!\!\big(1-t \, \dfrac{z_i}{z_j}\big)}\right). \end{align} $$
The proof begins with the Haglund-Haiman-Loehr formula [Reference Haglund, Haiman and Loehr21] for
![]() $\tilde {H}_{\mu }(X;q,t)$
as a weighted sum of LLT polynomials. We then apply the operator
$\tilde {H}_{\mu }(X;q,t)$
as a weighted sum of LLT polynomials. We then apply the operator
![]() $\nabla $
, which has
$\nabla $
, which has
![]() $\tilde {H}_{\mu }(X;q,t)$
as an eigenfunction, and use the formula for
$\tilde {H}_{\mu }(X;q,t)$
as an eigenfunction, and use the formula for
![]() $\nabla $
on an LLT polynomial established in our recent work [Reference Blasiak, Haiman, Morse, Pun and Seelinger7].
$\nabla $
on an LLT polynomial established in our recent work [Reference Blasiak, Haiman, Morse, Pun and Seelinger7].
A consequence of (2) is the emergence of an intriguing new family of higher Macdonald polynomials
![]() $\tilde {H}^{1,n}_\mu (X;q,t)$
, given by a formula similar to (2) with
$\tilde {H}^{1,n}_\mu (X;q,t)$
, given by a formula similar to (2) with
![]() $(z_1 \cdots z_l)^n$
in place of
$(z_1 \cdots z_l)^n$
in place of
![]() $z_1 \cdots z_l$
– see Theorem 5.2.1. We conjecture (Conjecture 5.2.2) that the coefficients of the resulting polynomials in terms of Schur functions belong to
$z_1 \cdots z_l$
– see Theorem 5.2.1. We conjecture (Conjecture 5.2.2) that the coefficients of the resulting polynomials in terms of Schur functions belong to
![]() ${\mathbb N}[q,t]$
, generalizing Macdonald positivity. As we will see, this conjecture can be formulated for all n simultaneously as the statement that the expression on the right-hand side of (2), before applying
${\mathbb N}[q,t]$
, generalizing Macdonald positivity. As we will see, this conjecture can be formulated for all n simultaneously as the statement that the expression on the right-hand side of (2), before applying
![]() $\omega \operatorname {\mathrm {pol}}_X $
, has coefficients in
$\omega \operatorname {\mathrm {pol}}_X $
, has coefficients in
![]() ${\mathbb N}[q,t]$
when regarded as an infinite series of
${\mathbb N}[q,t]$
when regarded as an infinite series of
![]() $\operatorname {\mathrm {GL}}_l$
characters.
$\operatorname {\mathrm {GL}}_l$
characters.
In §6, we also derive a new raising operator formula for the integral form Macdonald polynomials
![]() $J_\mu (X;q,t)$
.
$J_\mu (X;q,t)$
.
Other raising operator formulas for Macdonald polynomials have previously appeared in the literature. Lassalle-Schlosser [Reference Lassalle and Schlosser28] inverted the Pieri formula for Macdonald polynomials
![]() $Q_\mu (X;q,t)$
(which differ from
$Q_\mu (X;q,t)$
(which differ from
![]() $J_\mu (X;q,t)$
by a scalar factor) to obtain a formula for
$J_\mu (X;q,t)$
by a scalar factor) to obtain a formula for
![]() $Q_\mu (X;q,t)$
that can be interpreted as a raising operator formula. Shiraishi [Reference Shiraishi37] conjectured a similar raising operator formula for
$Q_\mu (X;q,t)$
that can be interpreted as a raising operator formula. Shiraishi [Reference Shiraishi37] conjectured a similar raising operator formula for
![]() $Q_\mu (X;q,t)$
, later proven by Noumi and Shiraishi in their work [Reference Noumi and Shiraishi32] on the bispectral problem of the Macdonald-Ruijnesaars q-difference operators. However, these formulas are quite different and more intricate than ours.
$Q_\mu (X;q,t)$
, later proven by Noumi and Shiraishi in their work [Reference Noumi and Shiraishi32] on the bispectral problem of the Macdonald-Ruijnesaars q-difference operators. However, these formulas are quite different and more intricate than ours.
2 Background
2.1 Partitions and symmetric functions
The (French style) diagram of a partition
![]() $\mu = (\mu _1 \ge \cdots \ge \mu _k> 0)$
is the set
$\mu = (\mu _1 \ge \cdots \ge \mu _k> 0)$
is the set
![]() $\{(i,j) \in {\mathbb Z}_{+}^2 : 1\leq j\leq k,\;1\leq i \leq \mu _{j}\}$
. We identify
$\{(i,j) \in {\mathbb Z}_{+}^2 : 1\leq j\leq k,\;1\leq i \leq \mu _{j}\}$
. We identify
![]() $(i,j)$
with the lattice square or box whose northeast corner has coordinates
$(i,j)$
with the lattice square or box whose northeast corner has coordinates
![]() $(x,y) = (i,j)$
and refer to this box as being in column i and row j. We set
$(x,y) = (i,j)$
and refer to this box as being in column i and row j. We set
![]() $|\mu | = \mu _{1}+\cdots +\mu _{k}$
and let
$|\mu | = \mu _{1}+\cdots +\mu _{k}$
and let
![]() $\ell (\mu )=k$
be the number of nonzero parts of
$\ell (\mu )=k$
be the number of nonzero parts of
![]() $\mu $
. We write
$\mu $
. We write
![]() $\mu ^*$
for the transpose of
$\mu ^*$
for the transpose of
![]() $\mu $
. The arm and leg of a box
$\mu $
. The arm and leg of a box
![]() $b\in \mu $
are the number of boxes in
$b\in \mu $
are the number of boxes in
![]() $\mu $
strictly east of b and strictly north of b, respectively.
$\mu $
strictly east of b and strictly north of b, respectively.
Let
![]() $\Lambda = \Lambda (X)$
be the algebra of symmetric functions in infinitely many variables
$\Lambda = \Lambda (X)$
be the algebra of symmetric functions in infinitely many variables
![]() $X = x_{1},x_{2},\ldots $
, with coefficients in the field
$X = x_{1},x_{2},\ldots $
, with coefficients in the field
![]() ${\mathbf k} = {\mathbb Q} (q,t)$
. We follow Macdonald’s notation [Reference Macdonald and Zelevinsky29] for the graded bases of
${\mathbf k} = {\mathbb Q} (q,t)$
. We follow Macdonald’s notation [Reference Macdonald and Zelevinsky29] for the graded bases of
![]() $\Lambda $
, and for the automorphism
$\Lambda $
, and for the automorphism
![]() $\omega \colon \Lambda \rightarrow \Lambda $
given on Schur functions by
$\omega \colon \Lambda \rightarrow \Lambda $
given on Schur functions by
![]() $\omega s_{\lambda } = s_{\lambda ^*}$
. We also work with series and symmetric functions in finitely many variables
$\omega s_{\lambda } = s_{\lambda ^*}$
. We also work with series and symmetric functions in finitely many variables
![]() ${\mathbf z} = z_1,\dots ,z_l$
. If
${\mathbf z} = z_1,\dots ,z_l$
. If
![]() $f(X)\in \Lambda $
is a formal symmetric function, then
$f(X)\in \Lambda $
is a formal symmetric function, then
![]() $f({\mathbf z} )$
or
$f({\mathbf z} )$
or
![]() $f(z_1, \ldots , z_l)$
denotes its specialization with
$f(z_1, \ldots , z_l)$
denotes its specialization with
![]() $X = z_1, \ldots , z_l,0,0,\ldots $
.
$X = z_1, \ldots , z_l,0,0,\ldots $
.
Given a symmetric function
![]() $f\in \Lambda $
and any expression A involving indeterminates, the plethystic evaluation
$f\in \Lambda $
and any expression A involving indeterminates, the plethystic evaluation
![]() $f[A]$
is defined by writing f as a polynomial in the power-sums
$f[A]$
is defined by writing f as a polynomial in the power-sums
![]() $p_{k}$
and evaluating with
$p_{k}$
and evaluating with
![]() $p_{k}\mapsto p_{k}[A]$
, where
$p_{k}\mapsto p_{k}[A]$
, where
![]() $p_{k}[A]$
is the result of substituting
$p_{k}[A]$
is the result of substituting
![]() $a^{k}$
for every indeterminate a occurring in A. The variables
$a^{k}$
for every indeterminate a occurring in A. The variables
![]() $q, t$
from our ground field
$q, t$
from our ground field
![]() ${\mathbf k} $
count as indeterminates.
${\mathbf k} $
count as indeterminates.
By convention, the name of an alphabet
![]() $X = x_{1},x_{2},\ldots $
stands for
$X = x_{1},x_{2},\ldots $
stands for
![]() $x_{1}+x_{2}+\cdots $
inside a plethystic evaluation. Then
$x_{1}+x_{2}+\cdots $
inside a plethystic evaluation. Then
![]() $f[X] = f[x_{1}+x_{2}+\cdots ] = f(x_{1},x_{2},\ldots ) = f(X)$
. For example, the evaluation
$f[X] = f[x_{1}+x_{2}+\cdots ] = f(x_{1},x_{2},\ldots ) = f(X)$
. For example, the evaluation
![]() $f[X/(1-t^{-1})]$
is the image of
$f[X/(1-t^{-1})]$
is the image of
![]() $f(X)$
under the
$f(X)$
under the
![]() ${\mathbf k} $
-algebra automorphism of
${\mathbf k} $
-algebra automorphism of
![]() $\Lambda $
that sends
$\Lambda $
that sends
![]() $p_{k}$
to
$p_{k}$
to
![]() $p_{k}/(1-t^{-k})$
.
$p_{k}/(1-t^{-k})$
.
The modified Macdonald polynomials
![]() $\tilde {H}_\mu = \tilde {H} _{\mu }(X;q,t)$
of [Reference Garsia and Haiman17] are defined in terms of the Macdonald polynomials
$\tilde {H}_\mu = \tilde {H} _{\mu }(X;q,t)$
of [Reference Garsia and Haiman17] are defined in terms of the Macdonald polynomials
![]() $Q_{\mu }(X;q,t)$
[Reference Macdonald and Zelevinsky29, VI (4.12)] or their integral forms
$Q_{\mu }(X;q,t)$
[Reference Macdonald and Zelevinsky29, VI (4.12)] or their integral forms
![]() $J_{\mu }(X;q,t)$
[Reference Macdonald and Zelevinsky29, VI (8.3)] by
$J_{\mu }(X;q,t)$
[Reference Macdonald and Zelevinsky29, VI (8.3)] by
 $$ \begin{align} \tilde{H} _{\mu }(X;q,t) = t^{\mathsf{n}(\mu )} J_{\mu}\Big[\frac{X}{1-t^{-1}};q,t^{-1} \Big] = t^{\mathsf{n}(\mu)} \Bigl( \prod_{b \in \mu}(1-q^{{\mathrm{arm}}(b)+1}t^{-{\mathrm{leg}}(b)}) \Bigr) Q_{\mu}\Big[\frac{X}{1-t^{-1}};q,t^{-1}\Big], \end{align} $$
$$ \begin{align} \tilde{H} _{\mu }(X;q,t) = t^{\mathsf{n}(\mu )} J_{\mu}\Big[\frac{X}{1-t^{-1}};q,t^{-1} \Big] = t^{\mathsf{n}(\mu)} \Bigl( \prod_{b \in \mu}(1-q^{{\mathrm{arm}}(b)+1}t^{-{\mathrm{leg}}(b)}) \Bigr) Q_{\mu}\Big[\frac{X}{1-t^{-1}};q,t^{-1}\Big], \end{align} $$
where
The
![]() $\tilde H_\mu (X;q,t)$
also have a direct combinatorial description [Reference Haglund, Haiman and Loehr21], which we will recall in Theorem 4.2.2.
$\tilde H_\mu (X;q,t)$
also have a direct combinatorial description [Reference Haglund, Haiman and Loehr21], which we will recall in Theorem 4.2.2.
When
![]() $q=0$
, the modified Macdonald polynomials reduce to the modified Hall-Littlewood polynomials
$q=0$
, the modified Macdonald polynomials reduce to the modified Hall-Littlewood polynomials
where the Hall-Littlewood polynomials
![]() $Q_{\mu }(X;t)$
are as defined in [Reference Macdonald and Zelevinsky29, III (2.11)]. At
$Q_{\mu }(X;t)$
are as defined in [Reference Macdonald and Zelevinsky29, III (2.11)]. At
![]() $t=1$
and
$t=1$
and
![]() $t = \infty $
, the
$t = \infty $
, the
![]() $\tilde {H}_\mu (X;0,t)$
specialize to the complete homogeneous symmetric functions
$\tilde {H}_\mu (X;0,t)$
specialize to the complete homogeneous symmetric functions
![]() $\tilde {H}_\mu (X;0,1) = h_\mu (X)$
and Schur functions
$\tilde {H}_\mu (X;0,1) = h_\mu (X)$
and Schur functions
![]() $t^{-\mathsf {n}(\mu )}\tilde {H}_\mu (X;0,t)|_{t=\infty }= s_\mu (X)$
. We will also work with the following variant of the modified Hall-Littlewood polynomials:
$t^{-\mathsf {n}(\mu )}\tilde {H}_\mu (X;0,t)|_{t=\infty }= s_\mu (X)$
. We will also work with the following variant of the modified Hall-Littlewood polynomials:
2.2 Weyl symmetrization and related operators
The Weyl symmetrization operator
![]() ${\boldsymbol \sigma }$
for
${\boldsymbol \sigma }$
for
![]() $\operatorname {\mathrm {GL}} _{l}$
is defined by
$\operatorname {\mathrm {GL}} _{l}$
is defined by
 $$ \begin{align} {\boldsymbol \sigma } (f(z_1,\dots,z_l)) = \sum _{w\in \mathcal{S}_{l}} w \bigg( \frac{f(z_1,\dots,z_l)}{\prod _{i < j} (1 - z_j/z_i)} \bigg) = \sum _{w\in \mathcal{S}_{l}} w \bigg( \frac{f(z_1,\dots,z_l)}{\prod _{\alpha_{ij} \in R_{+}} (1 - z_j/z_i)} \bigg) \,, \end{align} $$
$$ \begin{align} {\boldsymbol \sigma } (f(z_1,\dots,z_l)) = \sum _{w\in \mathcal{S}_{l}} w \bigg( \frac{f(z_1,\dots,z_l)}{\prod _{i < j} (1 - z_j/z_i)} \bigg) = \sum _{w\in \mathcal{S}_{l}} w \bigg( \frac{f(z_1,\dots,z_l)}{\prod _{\alpha_{ij} \in R_{+}} (1 - z_j/z_i)} \bigg) \,, \end{align} $$
where
![]() $f \in {\mathbf k}[z_1^{\pm 1},\dots , z_l^{\pm 1}]$
is a Laurent polynomial,
$f \in {\mathbf k}[z_1^{\pm 1},\dots , z_l^{\pm 1}]$
is a Laurent polynomial,
![]() $\mathcal {S}_l$
acts by permuting the variables
$\mathcal {S}_l$
acts by permuting the variables
![]() $z_1, \dots , z_l$
, and
$z_1, \dots , z_l$
, and
![]() $R_+= R_+(\operatorname {\mathrm {GL}}_l) = \{\alpha _{ij} : 1\leq i < j\leq l \}$
denotes the set of positive roots for
$R_+= R_+(\operatorname {\mathrm {GL}}_l) = \{\alpha _{ij} : 1\leq i < j\leq l \}$
denotes the set of positive roots for
![]() $\operatorname {\mathrm {GL}} _{l}$
, with
$\operatorname {\mathrm {GL}} _{l}$
, with
![]() $\alpha _{ij} = \epsilon _i -\epsilon _j \in {\mathbb Z}^l$
.
$\alpha _{ij} = \epsilon _i -\epsilon _j \in {\mathbb Z}^l$
.
When
![]() ${\mathbf z}^\nu = z_1^{\nu _1} \cdots z_l^{\nu _l}$
for a dominant weight
${\mathbf z}^\nu = z_1^{\nu _1} \cdots z_l^{\nu _l}$
for a dominant weight
![]() $\nu $
(a weight
$\nu $
(a weight
![]() $\nu \in {\mathbb Z}^l$
is dominant if
$\nu \in {\mathbb Z}^l$
is dominant if
![]() $\nu _1 \ge \cdots \ge \nu _l$
),
$\nu _1 \ge \cdots \ge \nu _l$
),
![]() ${\boldsymbol \sigma } ({\mathbf z} ^{\nu }) = \chi _{\nu }$
is an irreducible
${\boldsymbol \sigma } ({\mathbf z} ^{\nu }) = \chi _{\nu }$
is an irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
character. For an arbitrary weight
$\operatorname {\mathrm {GL}} _{l}$
character. For an arbitrary weight
![]() $\gamma \in {\mathbb Z} ^{l}$
, either
$\gamma \in {\mathbb Z} ^{l}$
, either
![]() ${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = \pm \chi _{\nu }$
for a suitable dominant weight
${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = \pm \chi _{\nu }$
for a suitable dominant weight
![]() $\nu $
, or
$\nu $
, or
![]() ${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = 0$
. We extend
${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = 0$
. We extend
![]() ${\boldsymbol \sigma }$
to an operator on formal
${\boldsymbol \sigma }$
to an operator on formal
![]() ${\mathbf k}$
-linear combinations
${\mathbf k}$
-linear combinations
![]() $\sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma $
by applying it term by term, giving an infinite formal linear combination of irreducible
$\sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma $
by applying it term by term, giving an infinite formal linear combination of irreducible
![]() $\operatorname {\mathrm {GL}}_l$
characters
$\operatorname {\mathrm {GL}}_l$
characters
![]() $\sum _{\nu } a_\nu \chi _\nu = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\boldsymbol \sigma }({\mathbf z}^\gamma ) $
. This makes sense because for each dominant weight
$\sum _{\nu } a_\nu \chi _\nu = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\boldsymbol \sigma }({\mathbf z}^\gamma ) $
. This makes sense because for each dominant weight
![]() $\nu $
, the set of monomials
$\nu $
, the set of monomials
![]() ${\mathbf z} ^{\gamma }$
such that
${\mathbf z} ^{\gamma }$
such that
![]() ${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = \pm \chi _{\nu }$
is finite.
${\boldsymbol \sigma } ({\mathbf z} ^{\gamma }) = \pm \chi _{\nu }$
is finite.
Recall that the polynomial characters of
![]() $\operatorname {\mathrm {GL}} _l$
are the irreducible characters
$\operatorname {\mathrm {GL}} _l$
are the irreducible characters
![]() $\chi _{\nu }$
for which
$\chi _{\nu }$
for which
![]() $\nu $
is a partition, that is,
$\nu $
is a partition, that is,
![]() $\nu _l\geq 0$
. Given any formal
$\nu _l\geq 0$
. Given any formal
![]() ${\mathbf k}$
-linear combination
${\mathbf k}$
-linear combination
![]() $\sum _{\nu } a_{\nu } \chi _{\nu }$
of irreducible
$\sum _{\nu } a_{\nu } \chi _{\nu }$
of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters, we define its polynomial truncation by
$\operatorname {\mathrm {GL}} _{l}$
characters, we define its polynomial truncation by
 $$ \begin{align} \operatorname{\mathrm{pol}}_X \! \Big(\sum _{\nu}a_{\nu }\hspace{.3mm} \chi _{\nu }\Big) = \sum _{ \nu_l \ge 0 }a_{\nu }\hspace{.3mm} s_{\nu }(X). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{pol}}_X \! \Big(\sum _{\nu}a_{\nu }\hspace{.3mm} \chi _{\nu }\Big) = \sum _{ \nu_l \ge 0 }a_{\nu }\hspace{.3mm} s_{\nu }(X). \end{align} $$
In principle, the right-hand side is an infinite formal sum of symmetric functions, but, for instance, if
![]() $\sum a_{\nu } \chi _{\nu }$
is homogeneous of degree d, then the right-hand side is an ordinary symmetric function, homogeneous of degree d.
$\sum a_{\nu } \chi _{\nu }$
is homogeneous of degree d, then the right-hand side is an ordinary symmetric function, homogeneous of degree d.
We define a related operator
![]() $\mathbf {h}_X$
on Laurent polynomials
$\mathbf {h}_X$
on Laurent polynomials
![]() $f({\mathbf z} )$
by
$f({\mathbf z} )$
by
 $$ \begin{align} \mathbf{h}_X(f({\mathbf z})) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg(\frac{f({\mathbf z})}{\prod_{\alpha_{ij} \in R_+} (1-z_i/z_j)} \bigg), \end{align} $$
$$ \begin{align} \mathbf{h}_X(f({\mathbf z})) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg(\frac{f({\mathbf z})}{\prod_{\alpha_{ij} \in R_+} (1-z_i/z_j)} \bigg), \end{align} $$
where the factors
![]() $(1- z_{i}/z_{j})^{-1}$
are expanded as geometric series in
$(1- z_{i}/z_{j})^{-1}$
are expanded as geometric series in
![]() $z_i/z_j$
before applying
$z_i/z_j$
before applying
![]() ${\boldsymbol \sigma }$
. When f is a monomial, it is well known [Reference Thomas39] that
${\boldsymbol \sigma }$
. When f is a monomial, it is well known [Reference Thomas39] that
where for any integer vector
![]() $\gamma \in {\mathbb Z}^l$
, we define
$\gamma \in {\mathbb Z}^l$
, we define
![]() $h_\gamma = h_{\gamma _1}\cdots h_{\gamma _l}$
to be the product of complete homogeneous symmetric functions, with
$h_\gamma = h_{\gamma _1}\cdots h_{\gamma _l}$
to be the product of complete homogeneous symmetric functions, with
![]() $h_d$
for
$h_d$
for
![]() $d\leq 0$
interpreted as
$d\leq 0$
interpreted as
![]() $h_0 =1$
, or
$h_0 =1$
, or
![]() $h_d = 0$
for
$h_d = 0$
for
![]() $d< 0$
.
$d< 0$
.
We again extend the definition to formal linear combinations of monomials, so that
![]() $\mathbf {h}_X(\sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma ) = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma h_\gamma (X)$
. With this interpretation, (9) still remains valid when f is a power series in
$\mathbf {h}_X(\sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma ) = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma h_\gamma (X)$
. With this interpretation, (9) still remains valid when f is a power series in
![]() $z_i/z_j$
for
$z_i/z_j$
for
![]() $i<j$
. As with
$i<j$
. As with
![]() $\operatorname {\mathrm {pol}}_X$
, in principle,
$\operatorname {\mathrm {pol}}_X$
, in principle,
![]() $\mathbf {h}_X(\sum _{\gamma } c_\gamma {\mathbf z}^\gamma )$
is an infinite formal sum of symmetric functions, but for instance, if
$\mathbf {h}_X(\sum _{\gamma } c_\gamma {\mathbf z}^\gamma )$
is an infinite formal sum of symmetric functions, but for instance, if
![]() $\sum _{\gamma } c_\gamma {\mathbf z}^\gamma $
is homogeneous of degree d, then
$\sum _{\gamma } c_\gamma {\mathbf z}^\gamma $
is homogeneous of degree d, then
![]() $\mathbf {h}_X(\sum _{\gamma } c_\gamma {\mathbf z}^\gamma )$
is an ordinary symmetric function, homogeneous of degree d.
$\mathbf {h}_X(\sum _{\gamma } c_\gamma {\mathbf z}^\gamma )$
is an ordinary symmetric function, homogeneous of degree d.
Remark 2.2.1. Below we will write other formulas involving
![]() ${\boldsymbol \sigma } $
applied to an expression with denominator factors resembling those in (9). Our convention is always to expand denominator factors of the form
${\boldsymbol \sigma } $
applied to an expression with denominator factors resembling those in (9). Our convention is always to expand denominator factors of the form
![]() $(1-c \hspace {.3mm} z_i/z_j)$
for
$(1-c \hspace {.3mm} z_i/z_j)$
for
![]() $c \in {\mathbf k}$
and
$c \in {\mathbf k}$
and
![]() $i < j$
as geometric series
$i < j$
as geometric series
![]() $(1 - c z_i/z_j)^{-1} = 1 + c z_i/z_j + \cdots $
before applying
$(1 - c z_i/z_j)^{-1} = 1 + c z_i/z_j + \cdots $
before applying
![]() ${\boldsymbol \sigma } $
.
${\boldsymbol \sigma } $
.
2.3 Raising operator formulas for modified Hall-Littlewood polynomials
To set the stage for our raising operator formula for modified Macdonald polynomials, we review two different raising operator formulas for the modified Hall-Littlewood polynomials. Both formulas naturally reflect the geometry of the flag variety
![]() $G/B$
; one realizes
$G/B$
; one realizes
![]() $\tilde {H}_\mu (X;0,t)$
as the graded Euler characteristic of the cotangent bundle of
$\tilde {H}_\mu (X;0,t)$
as the graded Euler characteristic of the cotangent bundle of
![]() $G/B$
twisted by a line bundle of weight
$G/B$
twisted by a line bundle of weight
![]() $-\mu $
, while the other is the graded Euler characteristic of the cotangent bundle of
$-\mu $
, while the other is the graded Euler characteristic of the cotangent bundle of
![]() $G/P_\mu $
, where
$G/P_\mu $
, where
![]() $P_\mu $
is the parabolic subgroup whose block sizes are the parts of
$P_\mu $
is the parabolic subgroup whose block sizes are the parts of
![]() $\mu $
. See [Reference Broer11] and [Reference Shimozono and Weyman36] for details.
$\mu $
. See [Reference Broer11] and [Reference Shimozono and Weyman36] for details.
The first raising operator formula for
![]() $\tilde {H}_\mu (X;0,t)$
is the one mentioned in the introduction, which we reproduce here (see [Reference Macdonald and Zelevinsky29, III (6.3)] or [Reference Milne31, (4.28) and §2]):
$\tilde {H}_\mu (X;0,t)$
is the one mentioned in the introduction, which we reproduce here (see [Reference Macdonald and Zelevinsky29, III (6.3)] or [Reference Milne31, (4.28) and §2]):
 $$ \begin{align} t^{\mathsf{n}(\mu)}\tilde{H}_\mu(X;0,t^{-1}) = H_\mu(X;t) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{{\mathbf z}^\mu}{\prod_{\alpha_{ij} \in R_+}(1 - t \hspace{.3mm} z_i/z_j)}\Big)\,, \end{align} $$
$$ \begin{align} t^{\mathsf{n}(\mu)}\tilde{H}_\mu(X;0,t^{-1}) = H_\mu(X;t) = \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{{\mathbf z}^\mu}{\prod_{\alpha_{ij} \in R_+}(1 - t \hspace{.3mm} z_i/z_j)}\Big)\,, \end{align} $$
where the denominator factors are expanded as geometric series in accordance with Remark 2.2.1.
A second raising operator formula follows from the work of Weyman and Shimozono-Weyman (see [Reference Weyman40, Theorem 6.10] and [Reference Shimozono and Weyman36, §2.3 (2) and (2.3)–(2.5)]). In this formula, the input partition
![]() $\mu $
appears in the set of roots, instead of in the weight
$\mu $
appears in the set of roots, instead of in the weight
![]() ${\mathbf z}^\mu $
, as it does in formula (11). Given a partition
${\mathbf z}^\mu $
, as it does in formula (11). Given a partition
![]() $\mu $
of l, consider the set partition of
$\mu $
of l, consider the set partition of
![]() $\{1,\ldots ,l \}$
into intervals of lengths
$\{1,\ldots ,l \}$
into intervals of lengths
![]() $\mu _{\ell (\mu )}, \dots , \mu _1$
, and let
$\mu _{\ell (\mu )}, \dots , \mu _1$
, and let
![]() $B_\mu $
denote the set of roots
$B_\mu $
denote the set of roots
![]() $\alpha _{ij}$
such that
$\alpha _{ij}$
such that
![]() $i < j$
appear in distinct blocks of this partition. Then
$i < j$
appear in distinct blocks of this partition. Then
Here, we chose to take the parts of
![]() $\mu $
in reverse order for compatibility with the formula (21) given later, but the order does not actually matter in (12).
$\mu $
in reverse order for compatibility with the formula (21) given later, but the order does not actually matter in (12).
Remark 2.3.1. Formulas such as (11) and (12) are traditionally written using an informal notation – as in [Reference Macdonald and Zelevinsky29], [Reference Milne31, (4.28)], or [Reference Tamvakis38, §2] – in which formula (11), for example, would be written as
 $$ \begin{align} t^{\mathsf{n}(\mu)}\tilde{H}_\mu(X;0,t^{-1}) = \frac{ 1 } { \prod_{\alpha_{i j} \in R_+} \big(1-t \hspace{.3mm} \mathbf{R}_{ij}\big)} \cdot s_{\mu}\,, \end{align} $$
$$ \begin{align} t^{\mathsf{n}(\mu)}\tilde{H}_\mu(X;0,t^{-1}) = \frac{ 1 } { \prod_{\alpha_{i j} \in R_+} \big(1-t \hspace{.3mm} \mathbf{R}_{ij}\big)} \cdot s_{\mu}\,, \end{align} $$
with raising ‘operators’
![]() $\mathbf {R}_{ij}$
which act on the subscript of a Schur function
$\mathbf {R}_{ij}$
which act on the subscript of a Schur function
![]() $s_\gamma $
by
$s_\gamma $
by
![]() $\mathbf {R}_{ij} \gamma = \gamma + \epsilon _i - \epsilon _j$
. Here, Schur functions indexed by non-partition weights are defined by
$\mathbf {R}_{ij} \gamma = \gamma + \epsilon _i - \epsilon _j$
. Here, Schur functions indexed by non-partition weights are defined by
![]() $s_\gamma (X) = \operatorname {\mathrm {pol}} _{X}{\boldsymbol \sigma }({\mathbf z}^\gamma )$
, which is equal to 0 or to
$s_\gamma (X) = \operatorname {\mathrm {pol}} _{X}{\boldsymbol \sigma }({\mathbf z}^\gamma )$
, which is equal to 0 or to
![]() $\pm 1$
times a Schur function of partition weight. Note that all the raising operators must be applied before converting Schur functions of non-partition weights to ones indexed by partition weights. The
$\pm 1$
times a Schur function of partition weight. Note that all the raising operators must be applied before converting Schur functions of non-partition weights to ones indexed by partition weights. The
![]() $\mathbf {R}_{ij}$
are not true operators (e.g.,
$\mathbf {R}_{ij}$
are not true operators (e.g.,
![]() $\mathbf {R}_{23}s_{(1,1,1)} = \operatorname {\mathrm {pol}} _{X}{\boldsymbol \sigma }(z_1z_2^2)= 0$
but
$\mathbf {R}_{23}s_{(1,1,1)} = \operatorname {\mathrm {pol}} _{X}{\boldsymbol \sigma }(z_1z_2^2)= 0$
but
![]() $\mathbf {R}_{12}\mathbf {R}_{23}s_{(1,1,1)} = s_{(2,1,0)}\not =0$
), so we think of (13) as a convenient but informal version of (11).
$\mathbf {R}_{12}\mathbf {R}_{23}s_{(1,1,1)} = s_{(2,1,0)}\not =0$
), so we think of (13) as a convenient but informal version of (11).
Remark 2.3.2. Raising operators as used here should not be confused with the creation or vertex operators of Bernstein (see, for example, [Reference Macdonald and Zelevinsky29, p. 96]) and Jing [Reference Jing25] for Schur functions and Hall-Littlewood polynomials.
3 Raising operator formula for modified Macdonald polynomials
3.1 The formula
We in fact give many different raising operator formulas for
![]() $ \tilde {H}_\mu (X;q,t)$
, one for each rearrangement
$ \tilde {H}_\mu (X;q,t)$
, one for each rearrangement
![]() $\beta $
of the parts of
$\beta $
of the parts of
![]() $\mu ^*$
.
$\mu ^*$
.
For
![]() $\beta = (\beta _1, \dots , \beta _k) \in {\mathbb Z}_{+}^k$
, we define the column diagram of
$\beta = (\beta _1, \dots , \beta _k) \in {\mathbb Z}_{+}^k$
, we define the column diagram of
![]() $\beta $
to be the set
$\beta $
to be the set
We identify
![]() $(i,j)$
with the box whose northeast corner has coordinates
$(i,j)$
with the box whose northeast corner has coordinates
![]() $(x,y) = (i,j)$
; we say that this box is in column i and row j. The reading order on
$(x,y) = (i,j)$
; we say that this box is in column i and row j. The reading order on
![]() $\boldsymbol {\beta }$
is the total order
$\boldsymbol {\beta }$
is the total order
![]() $\prec $
on the boxes of
$\prec $
on the boxes of
![]() $\boldsymbol {\beta }$
given by
$\boldsymbol {\beta }$
given by
![]() $(i,j) \prec (i',j')$
if
$(i,j) \prec (i',j')$
if
![]() $j> j'$
, or
$j> j'$
, or
![]() $j = j'$
and
$j = j'$
and
![]() $i < i'$
. We let
$i < i'$
. We let
![]() ${\boldsymbol {\beta }[1]},\dots , {\boldsymbol {\beta }[l]}$
denote the boxes of
${\boldsymbol {\beta }[1]},\dots , {\boldsymbol {\beta }[l]}$
denote the boxes of
![]() $\boldsymbol {\beta }$
listed in increasing reading order, which is the list of boxes of
$\boldsymbol {\beta }$
listed in increasing reading order, which is the list of boxes of
![]() $\boldsymbol {\beta }$
read by rows from left to right starting from the top row, as shown in Example 3.1.5. For a box
$\boldsymbol {\beta }$
read by rows from left to right starting from the top row, as shown in Example 3.1.5. For a box
![]() $b=(i,j)$
,
$b=(i,j)$
,
![]() ${\mathrm {south}}(b)=(i,j-1)$
denotes the box immediately south of b. Define subsets of
${\mathrm {south}}(b)=(i,j-1)$
denotes the box immediately south of b. Define subsets of
![]() $R_+ = R_+(\operatorname {\mathrm {GL}}_l)$
by
$R_+ = R_+(\operatorname {\mathrm {GL}}_l)$
by
For
![]() $\beta \in {\mathbb Z}_{+}^k$
and a box
$\beta \in {\mathbb Z}_{+}^k$
and a box
![]() $b = (i,j) \in \boldsymbol {\beta }$
with
$b = (i,j) \in \boldsymbol {\beta }$
with
![]() $j> 1$
, define the arm and leg of b by
$j> 1$
, define the arm and leg of b by
In words,
![]() ${\mathrm {arm}} (b)$
is the number of boxes strictly east of b in columns of height
${\mathrm {arm}} (b)$
is the number of boxes strictly east of b in columns of height
![]() $\beta _{i'}\leq \beta _{i}$
or strictly west of
$\beta _{i'}\leq \beta _{i}$
or strictly west of
![]() ${\mathrm {south}} (b)$
in columns of height
${\mathrm {south}} (b)$
in columns of height
![]() $\beta _{i'}<\beta _{i}$
.
$\beta _{i'}<\beta _{i}$
.
Example 3.1.1. For
![]() $\beta = (3,2,4,3,4,2,1,3)$
, the column diagram of
$\beta = (3,2,4,3,4,2,1,3)$
, the column diagram of
![]() $\beta $
is displayed below, along with the
$\beta $
is displayed below, along with the
![]() ${\mathrm {arm}}$
of box
${\mathrm {arm}}$
of box
![]() $\bullet =(4,2)$
where the a’s mark the boxes contributing to
$\bullet =(4,2)$
where the a’s mark the boxes contributing to
![]() ${\mathrm {arm}}(\bullet )$
.
${\mathrm {arm}}(\bullet )$
.

Remark 3.1.2. When
![]() $\beta $
is weakly decreasing (i.e.,
$\beta $
is weakly decreasing (i.e.,
![]() $\beta $
is a partition), the column diagram
$\beta $
is a partition), the column diagram
![]() $\boldsymbol {\beta }$
is the diagram of the transpose of the partition
$\boldsymbol {\beta }$
is the diagram of the transpose of the partition
![]() $\beta $
, and the arms and legs of the boxes of
$\beta $
, and the arms and legs of the boxes of
![]() $\boldsymbol {\beta }$
agree with the usual notions for partition diagrams mentioned in §2.1.
$\boldsymbol {\beta }$
agree with the usual notions for partition diagrams mentioned in §2.1.
Definition 3.1.3. For
![]() $\beta \in {\mathbb Z}_{+}^k$
, define the Macdonald series by
$\beta \in {\mathbb Z}_{+}^k$
, define the Macdonald series by
 $$ \begin{align} \mathbf{H}_{\beta}({\mathbf z};q,t) = {\boldsymbol \sigma } \Bigg( \frac{ \prod_{\alpha_{ij} \in R_{\beta} \setminus \widehat{R}_{\beta}} \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big) \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \big(1-t \, z_i/z_j\big)}\Bigg), \end{align} $$
$$ \begin{align} \mathbf{H}_{\beta}({\mathbf z};q,t) = {\boldsymbol \sigma } \Bigg( \frac{ \prod_{\alpha_{ij} \in R_{\beta} \setminus \widehat{R}_{\beta}} \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big) \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \big(1-t \, z_i/z_j\big)}\Bigg), \end{align} $$
which we interpret as an infinite formal linear combination of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters by expanding the denominator factors as geometric series, in accordance with Remark 2.2.1.
$\operatorname {\mathrm {GL}} _{l}$
characters by expanding the denominator factors as geometric series, in accordance with Remark 2.2.1.
We have the following raising operator formulas for the modified Macdonald polynomials
![]() $ \tilde {H}_{\mu }(X; q,t)$
. The proof will be given in §4.
$ \tilde {H}_{\mu }(X; q,t)$
. The proof will be given in §4.
Theorem 3.1.4. For any partition
![]() $\mu $
of l and any rearrangement
$\mu $
of l and any rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^*$
,
$\mu ^*$
,
where
![]() $\operatorname {\mathrm {pol}}_X$
is as defined in (8).
$\operatorname {\mathrm {pol}}_X$
is as defined in (8).
The case of Theorem 3.1.4 when
![]() $\beta = \mu ^*$
is the formula (2) previewed in the introduction.
$\beta = \mu ^*$
is the formula (2) previewed in the introduction.
Example 3.1.5. (i) For
![]() $\beta = (4,2)$
,
$\beta = (4,2)$
,
![]() $l = 6$
, we visualize the data for the series
$l = 6$
, we visualize the data for the series
![]() $\mathbf {H}_{\beta }$
below, with the subsets of roots
$\mathbf {H}_{\beta }$
below, with the subsets of roots
![]() $R_\beta $
and
$R_\beta $
and
![]() $\widehat {R}_\beta $
drawn in an
$\widehat {R}_\beta $
drawn in an
![]() $l \times l$
grid, labeled by matrix-style coordinates and specified by the legend, and with large circles marking the presence of the factors involving arm and leg, which are
$l \times l$
grid, labeled by matrix-style coordinates and specified by the legend, and with large circles marking the presence of the factors involving arm and leg, which are
![]() $(1-q \hspace {.3mm} z_1/z_2)$
,
$(1-q \hspace {.3mm} z_1/z_2)$
,
![]() $(1-qt^{-1}z_2/z_3)$
,
$(1-qt^{-1}z_2/z_3)$
,
![]() $(1-q^2t^{-2}z_3/z_5)$
,
$(1-q^2t^{-2}z_3/z_5)$
,
![]() $(1-q \hspace {.3mm} z_4/z_6)$
.
$(1-q \hspace {.3mm} z_4/z_6)$
.

(ii) For
![]() $\beta = (1,4,2,4)$
,
$\beta = (1,4,2,4)$
,
![]() $l = 11$
, we visualize the data for
$l = 11$
, we visualize the data for
![]() $\mathbf {H}_{\beta }$
with the same conventions; the factors involving arm and leg, marked by the large circles, are
$\mathbf {H}_{\beta }$
with the same conventions; the factors involving arm and leg, marked by the large circles, are
![]() $(1-q^2 \hspace {.3mm} z_1/z_3)$
,
$(1-q^2 \hspace {.3mm} z_1/z_3)$
,
![]() $(1-qz_2/z_4)$
,
$(1-qz_2/z_4)$
,
![]() $(1-q^2t^{-1}z_3/z_5)$
,
$(1-q^2t^{-1}z_3/z_5)$
,
![]() $(1-q^2t^{-1} \hspace {.3mm} z_4/z_7)$
,
$(1-q^2t^{-1} \hspace {.3mm} z_4/z_7)$
,
![]() $(1-q^4t^{-2} \hspace {.3mm} z_5/z_9)$
,
$(1-q^4t^{-2} \hspace {.3mm} z_5/z_9)$
,
![]() $(1-q^2 \hspace {.3mm} z_6/z_{10})$
,
$(1-q^2 \hspace {.3mm} z_6/z_{10})$
,
![]() $(1-q^3t^{-2} \hspace {.3mm} z_7/z_{11})$
.
$(1-q^3t^{-2} \hspace {.3mm} z_7/z_{11})$
.

3.2 Specializations
It is instructive to see how the well-known specializations of Macdonald polynomials,
![]() $\tilde {H} _{\mu }(X;1,1)=e_{1}^{|\mu |}(X)$
and the Hall-Littlewood specialization
$\tilde {H} _{\mu }(X;1,1)=e_{1}^{|\mu |}(X)$
and the Hall-Littlewood specialization
![]() $\tilde {H} _{\mu }(X;0,t)$
, can be recovered from formula (21). This can be done for general
$\tilde {H} _{\mu }(X;0,t)$
, can be recovered from formula (21). This can be done for general
![]() $\beta $
, but it is a little simpler when
$\beta $
, but it is a little simpler when
![]() $\beta $
is a partition. Accordingly, for this subsection, we now consider only the case
$\beta $
is a partition. Accordingly, for this subsection, we now consider only the case
![]() $\beta = \mu ^{*}$
.
$\beta = \mu ^{*}$
.
First, we consider the specialization
![]() $q=t=1$
. After specializing, the arm-leg and
$q=t=1$
. After specializing, the arm-leg and
![]() $(1-q\,t \,z_i/z_j)$
numerator factors in the definition (20) of
$(1-q\,t \,z_i/z_j)$
numerator factors in the definition (20) of
![]() $\mathbf {H}_\beta $
cancel with the
$\mathbf {H}_\beta $
cancel with the
![]() $(1-t\,z_i/z_j)$
factors in the denominator. Hence,
$(1-t\,z_i/z_j)$
factors in the denominator. Hence,
 $$ \begin{align} \mathbf{H}_\beta({\mathbf z};1,1) = {\boldsymbol \sigma }\Big(\frac{1}{\prod_{\alpha_{ij} \in R_+}(1 - z_i/z_j)}\Big). \end{align} $$
$$ \begin{align} \mathbf{H}_\beta({\mathbf z};1,1) = {\boldsymbol \sigma }\Big(\frac{1}{\prod_{\alpha_{ij} \in R_+}(1 - z_i/z_j)}\Big). \end{align} $$
Then, using (9) and (10), we recover the specialization
Now consider the specialization
![]() $q=0$
. After specializing (20), all numerator factors and the
$q=0$
. After specializing (20), all numerator factors and the
![]() $(1-q z_i/z_j)$
denominator factors reduce to 1. This gives
$(1-q z_i/z_j)$
denominator factors reduce to 1. This gives
Let
![]() $B_\mu $
be the set of roots defined before (12), which can also be described as the set of positive roots above a block diagonal matrix with block sizes
$B_\mu $
be the set of roots defined before (12), which can also be described as the set of positive roots above a block diagonal matrix with block sizes
![]() $\mu _{\ell (\mu )}, \dots , \mu _1$
. Now
$\mu _{\ell (\mu )}, \dots , \mu _1$
. Now
![]() $R_\beta $
is contained in
$R_\beta $
is contained in
![]() $B_\mu $
and
$B_\mu $
and
![]() $B_\mu \setminus R_\beta $
consists of triangular regions of roots between each pair of consecutive blocks. We reach the Hall-Littlewood raising operator formula using the identity
$B_\mu \setminus R_\beta $
consists of triangular regions of roots between each pair of consecutive blocks. We reach the Hall-Littlewood raising operator formula using the identity
This is proven by removing these triangular regions from
![]() $B_\mu $
one root at a time (starting with the bottommost region), and using the following simplified version of [Reference Blasiak, Morse, Pun and Summers9, Lemma 8.9] to show that the corresponding functions remain the same at each step.
$B_\mu $
one root at a time (starting with the bottommost region), and using the following simplified version of [Reference Blasiak, Morse, Pun and Summers9, Lemma 8.9] to show that the corresponding functions remain the same at each step.
Lemma 3.2.1. Let
![]() $k \in \{1,\dots , l-1\}$
and suppose that
$k \in \{1,\dots , l-1\}$
and suppose that
![]() $B \subseteq R_+(\operatorname {\mathrm {GL}}_l)$
is a set of roots such that
$B \subseteq R_+(\operatorname {\mathrm {GL}}_l)$
is a set of roots such that
![]() $\prod _{\alpha _{ij}\in B} (1-tz_i/z_j)$
is fixed by the simple reflection
$\prod _{\alpha _{ij}\in B} (1-tz_i/z_j)$
is fixed by the simple reflection
![]() $s_k$
. If B contains a root
$s_k$
. If B contains a root
![]() $\alpha = \alpha _{k+1,j}$
for some
$\alpha = \alpha _{k+1,j}$
for some
![]() $j> k+1$
, then
$j> k+1$
, then
Combining (24) and (25) now shows that the raising operator formula (21) for modified Macdonald polynomials reduces at
![]() $q=0$
to the raising operator formula (12) for Hall-Littlewood polynomials.
$q=0$
to the raising operator formula (12) for Hall-Littlewood polynomials.
4 Proof of Theorem 3.1.4
We prove Theorem 3.1.4 using two main ingredients: the Haglund-Haiman-Loehr formulas [Reference Haglund, Haiman and Loehr21, Reference Haglund, Haiman and Loehr22] and our recent formula for
![]() $\nabla $
on an LLT polynomial [Reference Blasiak, Haiman, Morse, Pun and Seelinger7]. We explain these two ingredients after a recap of LLT polynomials.
$\nabla $
on an LLT polynomial [Reference Blasiak, Haiman, Morse, Pun and Seelinger7]. We explain these two ingredients after a recap of LLT polynomials.
4.1 LLT polynomials
We recall the definition and basic properties of LLT polynomials [Reference Lascoux, Leclerc and Thibon26], using the ‘attacking inversions’ formulation from [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov23].
A skew diagram is a difference
![]() $\nu = \lambda / \mu $
of partition diagrams
$\nu = \lambda / \mu $
of partition diagrams
![]() $\mu \subseteq \lambda $
. The content of a box
$\mu \subseteq \lambda $
. The content of a box
![]() $b = (i,j)$
in row j, column i of a (skew) diagram is
$b = (i,j)$
in row j, column i of a (skew) diagram is
![]() $c(b) = i-j$
.
$c(b) = i-j$
.
Let
![]() ${\boldsymbol \nu } = (\nu _{(1)},\ldots ,\nu _{(k)})$
be a tuple of skew diagrams. We consider the set of boxes in
${\boldsymbol \nu } = (\nu _{(1)},\ldots ,\nu _{(k)})$
be a tuple of skew diagrams. We consider the set of boxes in
![]() ${\boldsymbol \nu } $
to be the disjoint union of the sets of boxes in the
${\boldsymbol \nu } $
to be the disjoint union of the sets of boxes in the
![]() $\nu _{(i)}$
, and define the adjusted content of a box
$\nu _{(i)}$
, and define the adjusted content of a box
![]() $a\in \nu _{(i)}$
to be
$a\in \nu _{(i)}$
to be
![]() $\tilde {c} (a) = c(a)+i\epsilon $
, where
$\tilde {c} (a) = c(a)+i\epsilon $
, where
![]() $\epsilon $
is a fixed positive number such that
$\epsilon $
is a fixed positive number such that
![]() $k \epsilon <1$
.
$k \epsilon <1$
.
A diagonal in
![]() ${\boldsymbol \nu } $
is the set of boxes of a fixed adjusted content – that is, a diagonal of fixed content in one of the
${\boldsymbol \nu } $
is the set of boxes of a fixed adjusted content – that is, a diagonal of fixed content in one of the
![]() $\nu _{(i)}$
.
$\nu _{(i)}$
.
The reading order on
![]() ${\boldsymbol \nu } $
is the total ordering
${\boldsymbol \nu } $
is the total ordering
![]() $<$
on the boxes of
$<$
on the boxes of
![]() ${\boldsymbol \nu } $
such that
${\boldsymbol \nu } $
such that
![]() $a<b \Rightarrow \tilde {c} (a)\leq \tilde {c}(b)$
and boxes on each diagonal increase from southwest to northeast. See Example 4.2.3. An attacking pair is an ordered pair of boxes
$a<b \Rightarrow \tilde {c} (a)\leq \tilde {c}(b)$
and boxes on each diagonal increase from southwest to northeast. See Example 4.2.3. An attacking pair is an ordered pair of boxes
![]() $(a,b)$
in
$(a,b)$
in
![]() $ {\boldsymbol \nu }$
such that
$ {\boldsymbol \nu }$
such that
![]() $a<b$
in reading order and
$a<b$
in reading order and
![]() $0<\tilde {c}(b)-\tilde {c}(a)<1$
.
$0<\tilde {c}(b)-\tilde {c}(a)<1$
.
A semistandard tableau on the tuple
![]() ${\boldsymbol \nu } $
is a map
${\boldsymbol \nu } $
is a map
![]() $T\colon {\boldsymbol \nu } \rightarrow {\mathbb Z} _{+}$
which restricts to a semistandard Young tableau on each component
$T\colon {\boldsymbol \nu } \rightarrow {\mathbb Z} _{+}$
which restricts to a semistandard Young tableau on each component
![]() $\nu _{(i)}$
. The set of these is denoted
$\nu _{(i)}$
. The set of these is denoted
![]() $\operatorname {\mathrm {SSYT}} ({\boldsymbol \nu } )$
. An attacking inversion in T is an attacking pair
$\operatorname {\mathrm {SSYT}} ({\boldsymbol \nu } )$
. An attacking inversion in T is an attacking pair
![]() $(a,b)$
such that
$(a,b)$
such that
![]() $T(a)>T(b)$
. The number of attacking inversions in T is denoted
$T(a)>T(b)$
. The number of attacking inversions in T is denoted
![]() $\operatorname {\mathrm {inv}} (T)$
.
$\operatorname {\mathrm {inv}} (T)$
.
Definition 4.1.1. The LLT polynomial indexed by a tuple of skew diagrams
![]() ${\boldsymbol \nu } $
is the generating function
${\boldsymbol \nu } $
is the generating function
where
![]() ${\mathbf x} ^{T} = \prod _{a\in {\boldsymbol \nu } } x_{T(a)}$
. By [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov23, Reference Lascoux, Leclerc and Thibon26],
${\mathbf x} ^{T} = \prod _{a\in {\boldsymbol \nu } } x_{T(a)}$
. By [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov23, Reference Lascoux, Leclerc and Thibon26],
![]() ${\mathcal G}_{{\boldsymbol \nu } }(X;q) $
is known to be symmetric.
${\mathcal G}_{{\boldsymbol \nu } }(X;q) $
is known to be symmetric.
4.2 The Haglund-Haiman-Loehr formula
Haglund-Haiman-Loehr [Reference Haglund, Haiman and Loehr21] gave a formula for the modified Macdonald polynomials
![]() $H_\mu (X;q,t)$
as a positive sum of LLT polynomials, and this was generalized in [Reference Haglund, Haiman and Loehr22] to give many different expressions for
$H_\mu (X;q,t)$
as a positive sum of LLT polynomials, and this was generalized in [Reference Haglund, Haiman and Loehr22] to give many different expressions for
![]() $H_\mu (X;q,t)$
as a positive sum of LLT polynomials, one for each rearrangement
$H_\mu (X;q,t)$
as a positive sum of LLT polynomials, one for each rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^*$
. We now recall this formula.
$\mu ^*$
. We now recall this formula.
A ribbon is a connected skew shape containing no
![]() $2 \times 2$
block of boxes.
$2 \times 2$
block of boxes.
For
![]() $\beta \in {\mathbb Z}_{+}^k$
, let
$\beta \in {\mathbb Z}_{+}^k$
, let
![]() $V_\beta = \{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) : {\boldsymbol {\beta }[j]} = {\mathrm {south}}({\boldsymbol {\beta }[i]}) \}$
be the set of ordered pairs of boxes that form vertical dominoes in
$V_\beta = \{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) : {\boldsymbol {\beta }[j]} = {\mathrm {south}}({\boldsymbol {\beta }[i]}) \}$
be the set of ordered pairs of boxes that form vertical dominoes in
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
Definition 4.2.1. For each
![]() $S \subseteq V_\beta $
, define
$S \subseteq V_\beta $
, define
![]() ${\boldsymbol \nu }(S) = (\nu _{(1)},\dots ,\nu _{(k)})$
to be the k-tuple of ribbons where the i-th ribbon
${\boldsymbol \nu }(S) = (\nu _{(1)},\dots ,\nu _{(k)})$
to be the k-tuple of ribbons where the i-th ribbon
![]() $\nu _{(i)}$
is determined by
$\nu _{(i)}$
is determined by
-
(i)
 $\nu _{(i)}$
has
$\nu _{(i)}$
has
 $\beta _i$
boxes, of contents
$\beta _i$
boxes, of contents
 $-1,-2,\dots , -\beta _i$
, and
$-1,-2,\dots , -\beta _i$
, and -
(ii) the boxes of contents
 $-j$
and
$-j$
and
 $-j+1$
in
$-j+1$
in
 $\nu _{(i)}$
form a vertical domino if and only if the domino
$\nu _{(i)}$
form a vertical domino if and only if the domino
 $((i,j),(i,j-1))$
in
$((i,j),(i,j-1))$
in
 $V_\beta $
belongs to S.
$V_\beta $
belongs to S.
Theorem 4.2.2 [Reference Haglund, Haiman and Loehr21, Reference Haglund, Haiman and Loehr22].
Let
![]() $\mu $
be a partition and let
$\mu $
be a partition and let
![]() $\beta $
be any rearrangement of
$\beta $
be any rearrangement of
![]() $\mu ^{*}$
. Then
$\mu ^{*}$
. Then
 $$ \begin{align} \tilde{H}_\mu(X;q,t) = \sum_{S \subseteq V_\beta} \Big( \prod_{({\boldsymbol {\beta}[i]},{\boldsymbol {\beta}[j]}) \in S} q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \Big) {\mathcal G}_{{\boldsymbol \nu }(S)}(X;q). \end{align} $$
$$ \begin{align} \tilde{H}_\mu(X;q,t) = \sum_{S \subseteq V_\beta} \Big( \prod_{({\boldsymbol {\beta}[i]},{\boldsymbol {\beta}[j]}) \in S} q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \Big) {\mathcal G}_{{\boldsymbol \nu }(S)}(X;q). \end{align} $$
Theorem 4.2.2 in the case that
![]() $\beta $
is a partition is immediate from [Reference Haglund, Haiman and Loehr21, Theorem 2.2, equation (23), and Proposition 3.4], while the generalization to any composition
$\beta $
is a partition is immediate from [Reference Haglund, Haiman and Loehr21, Theorem 2.2, equation (23), and Proposition 3.4], while the generalization to any composition
![]() $\beta $
is addressed in [Reference Haglund, Haiman and Loehr22, Theorem 5.1.1]. Note that our conventions for diagrams, arms, and legs are the same as those in [Reference Haglund, Haiman and Loehr22] except that we have reversed the order of the columns (which makes our notation consistent with that in [Reference Haglund, Haiman and Loehr21]); we have also used the symmetry property
$\beta $
is addressed in [Reference Haglund, Haiman and Loehr22, Theorem 5.1.1]. Note that our conventions for diagrams, arms, and legs are the same as those in [Reference Haglund, Haiman and Loehr22] except that we have reversed the order of the columns (which makes our notation consistent with that in [Reference Haglund, Haiman and Loehr21]); we have also used the symmetry property
![]() $H_\mu (X;q,t) = H_{\mu ^*}(X;t,q)$
to translate from the exact version stated in [Reference Haglund, Haiman and Loehr22, Theorem 5.1.1].
$H_\mu (X;q,t) = H_{\mu ^*}(X;t,q)$
to translate from the exact version stated in [Reference Haglund, Haiman and Loehr22, Theorem 5.1.1].
Example 4.2.3. For
![]() $\beta = (2,3)$
, the 8 summands appearing on the right-hand side of (28) are illustrated by drawing
$\beta = (2,3)$
, the 8 summands appearing on the right-hand side of (28) are illustrated by drawing
![]() ${\boldsymbol \nu }(S)$
with boxes labeled in reading order and with the corresponding coefficient
${\boldsymbol \nu }(S)$
with boxes labeled in reading order and with the corresponding coefficient
![]() $\prod _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in S} q^{-{\mathrm {arm}}({\boldsymbol {\beta }[i]})} \hspace {.3mm} t^{{\mathrm {leg}}({\boldsymbol {\beta }[i]})+1}$
beside it; the vertical dominoes of
β
are denoted v
1 = (
β
[1],
β
[3]), v
2 = (
β
[2],
β
[4]), v
3 = (
β
[3],
β
[5]). The arm and leg statistics for
$\prod _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in S} q^{-{\mathrm {arm}}({\boldsymbol {\beta }[i]})} \hspace {.3mm} t^{{\mathrm {leg}}({\boldsymbol {\beta }[i]})+1}$
beside it; the vertical dominoes of
β
are denoted v
1 = (
β
[1],
β
[3]), v
2 = (
β
[2],
β
[4]), v
3 = (
β
[3],
β
[5]). The arm and leg statistics for
![]() $\boldsymbol {\beta }$
are shown on the left.
$\boldsymbol {\beta }$
are shown on the left.

4.3 A formula for
 $\nabla $
on any LLT polynomial
$\nabla $
on any LLT polynomial
The operator
![]() $\nabla $
, introduced in [Reference Bergeron, Garsia, Haiman and Tesler2], is the linear operator on symmetric functions which acts diagonally on the basis of modified Macdonald polynomials
$\nabla $
, introduced in [Reference Bergeron, Garsia, Haiman and Tesler2], is the linear operator on symmetric functions which acts diagonally on the basis of modified Macdonald polynomials
![]() $\tilde {H}_{\mu }(X;q,t)$
by
$\tilde {H}_{\mu }(X;q,t)$
by
![]() $\nabla \tilde {H} _{\mu } = q^{\mathsf {n}(\mu ^{*})} t^{\mathsf {n}(\mu )}\tilde {H} _{\mu }$
.
$\nabla \tilde {H} _{\mu } = q^{\mathsf {n}(\mu ^{*})} t^{\mathsf {n}(\mu )}\tilde {H} _{\mu }$
.
In [Reference Blasiak, Haiman, Morse, Pun and Seelinger7], we give a raising operator formula for
![]() $\nabla $
on any LLT polynomial. The formula takes a simpler form in the case that the LLT polynomial is indexed by a tuple of ribbons. We state the result for the tuple
$\nabla $
on any LLT polynomial. The formula takes a simpler form in the case that the LLT polynomial is indexed by a tuple of ribbons. We state the result for the tuple
![]() ${\boldsymbol \nu }(S)$
in Definition 4.2.1, making use of the notation
${\boldsymbol \nu }(S)$
in Definition 4.2.1, making use of the notation
![]() $V_\beta , R_{\beta }, \widehat {R}_{\beta }$
defined in §4.2, (15), and (16). Also let
$V_\beta , R_{\beta }, \widehat {R}_{\beta }$
defined in §4.2, (15), and (16). Also let
![]() $A_\beta $
denote the number of attacking pairs in
$A_\beta $
denote the number of attacking pairs in
![]() ${\boldsymbol \nu }(S)$
, which depends only on
${\boldsymbol \nu }(S)$
, which depends only on
![]() $\beta $
and not on
$\beta $
and not on
![]() $S \subseteq V_\beta $
.
$S \subseteq V_\beta $
.
Theorem 4.3.1 [Reference Blasiak, Haiman, Morse, Pun and Seelinger7].
For
![]() $\beta \in {\mathbb Z}_{+}^k$
and
$\beta \in {\mathbb Z}_{+}^k$
and
![]() $S \subseteq V_\beta $
, consider the tuple of ribbons
$S \subseteq V_\beta $
, consider the tuple of ribbons
![]() ${\boldsymbol \nu }(S)$
. We have the following formula for the operator
${\boldsymbol \nu }(S)$
. We have the following formula for the operator
![]() $\nabla $
applied to the LLT polynomial
$\nabla $
applied to the LLT polynomial
![]() ${\mathcal G}_{{\boldsymbol \nu }(S)}(X;q)$
:
${\mathcal G}_{{\boldsymbol \nu }(S)}(X;q)$
:
 $$ \begin{align} &\nabla {\mathcal G}_{{\boldsymbol \nu }(S)}(X;q) = \omega\operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg( (-qt)^{|V_\beta\setminus S|} q^{A_\beta} \frac{z_1 \cdots z_l \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]}) \in V_\beta \setminus S} z_i/z_j \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \! \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_+} \! \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \! \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
$$ \begin{align} &\nabla {\mathcal G}_{{\boldsymbol \nu }(S)}(X;q) = \omega\operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg( (-qt)^{|V_\beta\setminus S|} q^{A_\beta} \frac{z_1 \cdots z_l \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]}) \in V_\beta \setminus S} z_i/z_j \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \! \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_+} \! \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \! \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
where
![]() $l= |\beta |$
and
$l= |\beta |$
and
![]() $R_+ = R_+(\operatorname {\mathrm {GL}} _l)$
.
$R_+ = R_+(\operatorname {\mathrm {GL}} _l)$
.
Proof. Our raising operator formula [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Corollary 9.4.1] for
![]() $\nabla $
on any LLT polynomial reduces to (29) using the following facts which hold when the LLT polynomial is indexed by a tuple of ribbons.
$\nabla $
on any LLT polynomial reduces to (29) using the following facts which hold when the LLT polynomial is indexed by a tuple of ribbons.
(1) The magic number
![]() $p({\boldsymbol \nu }(S))$
of
$p({\boldsymbol \nu }(S))$
of
![]() ${\boldsymbol \nu }(S)$
defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, §8.2] is equal to the number of boxes of
${\boldsymbol \nu }(S)$
defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, §8.2] is equal to the number of boxes of
![]() ${\boldsymbol \nu }(S)$
which are not the first box in a row, which is the same as
${\boldsymbol \nu }(S)$
which are not the first box in a row, which is the same as
![]() $|V_\beta \setminus S|$
.
$|V_\beta \setminus S|$
.
(2) The weight
![]() $\lambda $
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Corollary 9.4.1], defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 8.1.2], is obtained as follows in the case that the tuple of skew shapes consists of ribbons: fill the boxes of each row of
$\lambda $
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Corollary 9.4.1], defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 8.1.2], is obtained as follows in the case that the tuple of skew shapes consists of ribbons: fill the boxes of each row of
![]() ${\boldsymbol \nu }(S)$
with
${\boldsymbol \nu }(S)$
with
![]() $1,0,\dots , 0, -1$
or just
$1,0,\dots , 0, -1$
or just
![]() $0$
for a row of length 1, and then read this filling by increasing reading order. It is then easily seen that
$0$
for a row of length 1, and then read this filling by increasing reading order. It is then easily seen that
![]() $\mathbf {z}^\lambda = \prod _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]})\in V_\beta \setminus S} z_i/z_j$
.
$\mathbf {z}^\lambda = \prod _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]})\in V_\beta \setminus S} z_i/z_j$
.
(3) Under the bijection
![]() $f \colon \beta \to {\boldsymbol \nu }(S)$
which takes the i-th box
$f \colon \beta \to {\boldsymbol \nu }(S)$
which takes the i-th box
![]() ${\boldsymbol {\beta }[i]}$
of
${\boldsymbol {\beta }[i]}$
of
![]() $\boldsymbol {\beta }$
in reading order to the i-th box of
$\boldsymbol {\beta }$
in reading order to the i-th box of
![]() ${\boldsymbol \nu }(S)$
in reading order, the set
${\boldsymbol \nu }(S)$
in reading order, the set
![]() $\{(f({\boldsymbol {\beta }[i]}),f({\boldsymbol {\beta }[j]})) : \alpha _{ij} \in R_{\beta }\}$
is exactly the set of non-attacking pairs in
$\{(f({\boldsymbol {\beta }[i]}),f({\boldsymbol {\beta }[j]})) : \alpha _{ij} \in R_{\beta }\}$
is exactly the set of non-attacking pairs in
![]() ${\boldsymbol \nu }(S)$
. Thus,
${\boldsymbol \nu }(S)$
. Thus,
![]() $R_{\beta }$
agrees with the set of roots denoted
$R_{\beta }$
agrees with the set of roots denoted
![]() $R_t$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 8.1.2 and Remark 8.1.3 (i)].
$R_t$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 8.1.2 and Remark 8.1.3 (i)].
4.4 Proof of Theorem 3.1.4
Applying
![]() $\nabla $
to (28) and substituting (29) into this yields
$\nabla $
to (28) and substituting (29) into this yields
 $$ \begin{align} \nabla \tilde{H}_\mu(X;q,t) = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg(\frac{z_1 \cdots z_l \cdot \Upsilon \cdot \prod_{\alpha_{ij} \in \widehat{R}_{\beta} } \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
$$ \begin{align} \nabla \tilde{H}_\mu(X;q,t) = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg(\frac{z_1 \cdots z_l \cdot \Upsilon \cdot \prod_{\alpha_{ij} \in \widehat{R}_{\beta} } \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{\beta}} \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
where
 $$ \begin{align} \Upsilon = \sum_{S \subseteq V_\beta} (-qt)^{|V_\beta \setminus S|} q^{A_\beta} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta \setminus S} z_i/z_j. \end{align} $$
$$ \begin{align} \Upsilon = \sum_{S \subseteq V_\beta} (-qt)^{|V_\beta \setminus S|} q^{A_\beta} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta \setminus S} z_i/z_j. \end{align} $$
Defining
![]() $d = \! A_\beta - \mathsf {n}(\mu ^*) - \sum _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in V_\beta } {\mathrm {arm}}({\boldsymbol {\beta }[i]})$
and using
$d = \! A_\beta - \mathsf {n}(\mu ^*) - \sum _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in V_\beta } {\mathrm {arm}}({\boldsymbol {\beta }[i]})$
and using
![]() $\mathsf {n}(\mu ) = \! \sum _{({\boldsymbol {\beta }[i]}, {\boldsymbol {\beta }[j]})\in V_\beta } ({\mathrm {leg}}({\boldsymbol {\beta }[i]})+1)$
, the quantity
$\mathsf {n}(\mu ) = \! \sum _{({\boldsymbol {\beta }[i]}, {\boldsymbol {\beta }[j]})\in V_\beta } ({\mathrm {leg}}({\boldsymbol {\beta }[i]})+1)$
, the quantity
![]() $\Upsilon $
can be simplified as follows:
$\Upsilon $
can be simplified as follows:
 $$ \begin{align*} \Upsilon &= q^{\mathsf{n}(\mu^*)+d} \, t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta}\Big( (-qt)^{|V_\beta\setminus S|} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta} \!\!\!\! q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \, t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})-1} \\ & \hphantom{q^{\mathsf{n}(\mu^*)+d} \, t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta}\Big( (-qt)^{|V_\beta\setminus S|} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta}} \times \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} \!\!\!\! q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \, t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \!\!\! \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta \setminus S} \!\!\!\!\!\! z_i/z_j \Big) \\ &= q^{\mathsf{n}(\mu^*)+d} \hspace{.3mm} t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta\setminus S} \!\! \big(-q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1} \, t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big)\\ &= q^{\mathsf{n}(\mu^*)+d} \hspace{.3mm} t^{\mathsf{n}(\mu)} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]}) \in V_\beta} \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big). \end{align*} $$
$$ \begin{align*} \Upsilon &= q^{\mathsf{n}(\mu^*)+d} \, t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta}\Big( (-qt)^{|V_\beta\setminus S|} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta} \!\!\!\! q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \, t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})-1} \\ & \hphantom{q^{\mathsf{n}(\mu^*)+d} \, t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta}\Big( (-qt)^{|V_\beta\setminus S|} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta}} \times \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} \!\!\!\! q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \, t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \!\!\! \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta \setminus S} \!\!\!\!\!\! z_i/z_j \Big) \\ &= q^{\mathsf{n}(\mu^*)+d} \hspace{.3mm} t^{\mathsf{n}(\mu)} \sum_{S \subseteq V_\beta} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in V_\beta\setminus S} \!\! \big(-q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1} \, t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big)\\ &= q^{\mathsf{n}(\mu^*)+d} \hspace{.3mm} t^{\mathsf{n}(\mu)} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]}) \in V_\beta} \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{-{\mathrm{leg}}({\boldsymbol {\beta}[i]})} z_i/z_j \big). \end{align*} $$
Thus, plugging this back in for
![]() $\Upsilon $
in (30) and recalling the definition of
$\Upsilon $
in (30) and recalling the definition of
![]() $\mathbf {H}_{\beta }({\mathbf z};q, t)$
(Definition 3.1.3), we have
$\mathbf {H}_{\beta }({\mathbf z};q, t)$
(Definition 3.1.3), we have
By the definition of
![]() $\nabla $
, this implies
$\nabla $
, this implies
![]() $\tilde {H}_\mu (X;q,t) = q^{d} \omega \operatorname {\mathrm {pol}}_X \! \big (z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t) \big ).$
It remains to show that
$\tilde {H}_\mu (X;q,t) = q^{d} \omega \operatorname {\mathrm {pol}}_X \! \big (z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t) \big ).$
It remains to show that
![]() $d=0$
. This follows from the fact that the coefficient of
$d=0$
. This follows from the fact that the coefficient of
![]() $s_{1^l}(X) = \operatorname {\mathrm {pol}}_X(z_1\cdots z_l)$
in the Schur expansion of both
$s_{1^l}(X) = \operatorname {\mathrm {pol}}_X(z_1\cdots z_l)$
in the Schur expansion of both
![]() $\omega \tilde {H}_\mu (X;q,t)$
and
$\omega \tilde {H}_\mu (X;q,t)$
and
![]() $\operatorname {\mathrm {pol}}_X \! \big (z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t) \big )$
is 1; the former is well known, while the latter can be seen directly by expanding the series
$\operatorname {\mathrm {pol}}_X \! \big (z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t) \big )$
is 1; the former is well known, while the latter can be seen directly by expanding the series
![]() $z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t)$
to see that it is equal to
$z_1\cdots z_l \, \mathbf {H}_{\beta }({\mathbf z};q, t)$
to see that it is equal to
![]() ${\boldsymbol \sigma }(z_1\cdots z_l)= \chi _{1^l}$
plus terms of the form
${\boldsymbol \sigma }(z_1\cdots z_l)= \chi _{1^l}$
plus terms of the form
![]() $a_\nu \chi _\nu $
for
$a_\nu \chi _\nu $
for
![]() $\nu> 1^l$
in dominance order.
$\nu> 1^l$
in dominance order.
5 The
 $m,n$
-Macdonald polynomials
$m,n$
-Macdonald polynomials
For every pair of coprime positive integers
![]() $(m,n)$
, the action of the Burban-Schiffmann elliptic Hall algebra
$(m,n)$
, the action of the Burban-Schiffmann elliptic Hall algebra
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda (X)$
gives rise to a family of symmetric functions that we call
$\Lambda (X)$
gives rise to a family of symmetric functions that we call
![]() $m,n$
-Macdonald polynomials. The subfamily of
$m,n$
-Macdonald polynomials. The subfamily of
![]() $1,n$
-Macdonald polynomials is closely connected with the Macdonald series
$1,n$
-Macdonald polynomials is closely connected with the Macdonald series
![]() ${\mathbf H} _{\beta }$
from Definition 3.1.3. In this section, we will construct raising operator formulas for all
${\mathbf H} _{\beta }$
from Definition 3.1.3. In this section, we will construct raising operator formulas for all
![]() $m,n$
-Macdonald polynomials, reducing to Theorem 3.1.4 in the case
$m,n$
-Macdonald polynomials, reducing to Theorem 3.1.4 in the case
![]() $m=n=1$
.
$m=n=1$
.
To define
![]() $m,n$
-Macdonald polynomials we need to recall some facts about the algebra
$m,n$
-Macdonald polynomials we need to recall some facts about the algebra
![]() ${\mathcal E} $
, defined by Burban and Schiffmann [Reference Burban and Schiffmann14] in terms of Hall algebras of coherent sheaves on elliptic curves. For each pair of coprime integers
${\mathcal E} $
, defined by Burban and Schiffmann [Reference Burban and Schiffmann14] in terms of Hall algebras of coherent sheaves on elliptic curves. For each pair of coprime integers
![]() $(m,n)$
, the algebra
$(m,n)$
, the algebra
![]() ${\mathcal E} $
contains a distinguished subalgebra
${\mathcal E} $
contains a distinguished subalgebra
![]() $\Lambda (X^{m,n}) $
isomorphic to the algebra of symmetric functions over
$\Lambda (X^{m,n}) $
isomorphic to the algebra of symmetric functions over
![]() ${\mathbf k} $
; these subalgebras generate
${\mathbf k} $
; these subalgebras generate
![]() ${\mathcal E} $
, subject to relations given in [Reference Burban and Schiffmann14]. There is also an action of
${\mathcal E} $
, subject to relations given in [Reference Burban and Schiffmann14]. There is also an action of
![]() ${\mathcal E} $
on the space of symmetric functions
${\mathcal E} $
on the space of symmetric functions
![]() $\Lambda (X)$
, constructed by Schiffmann and Vasserot [Reference Schiffmann and Vasserot35]. Our notation here is the same as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger4, Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Reference Blasiak, Haiman, Morse, Pun and Seelinger5, Reference Blasiak, Haiman, Morse, Pun and Seelinger6] – in particular, we use the version of the action of
$\Lambda (X)$
, constructed by Schiffmann and Vasserot [Reference Schiffmann and Vasserot35]. Our notation here is the same as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger4, Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Reference Blasiak, Haiman, Morse, Pun and Seelinger5, Reference Blasiak, Haiman, Morse, Pun and Seelinger6] – in particular, we use the version of the action of
![]() ${\mathcal E}$
on
${\mathcal E}$
on
![]() $\Lambda (X)$
given by [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1]. The translation between our notation and that of [Reference Burban and Schiffmann14, Reference Schiffmann and Vasserot35] can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, §§3.2–3.3]; the defining relations of
$\Lambda (X)$
given by [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1]. The translation between our notation and that of [Reference Burban and Schiffmann14, Reference Schiffmann and Vasserot35] can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, §§3.2–3.3]; the defining relations of
![]() ${\mathcal E} $
written in our notation are given in [Reference Blasiak, Haiman, Morse, Pun and Seelinger5, §3.2].
${\mathcal E} $
written in our notation are given in [Reference Blasiak, Haiman, Morse, Pun and Seelinger5, §3.2].
Definition 5.1.1. Set
![]() $M = (1-q)(1-t) \in {\mathbf k}$
. For coprime positive integers
$M = (1-q)(1-t) \in {\mathbf k}$
. For coprime positive integers
![]() $m,n$
, define the
$m,n$
, define the
![]() $m,n$
-Macdonald polynomial
$m,n$
-Macdonald polynomial
![]() $\tilde {H}_{\mu }^{m,n} = \tilde {H}_{\mu }^{m,n}(X;q,t)$
by
$\tilde {H}_{\mu }^{m,n} = \tilde {H}_{\mu }^{m,n}(X;q,t)$
by
the symmetric function obtained by acting on
![]() $1 \in \Lambda (X)$
with (a plethystic transformation of) a modified Macdonald polynomial in the distinguished subalgebra
$1 \in \Lambda (X)$
with (a plethystic transformation of) a modified Macdonald polynomial in the distinguished subalgebra
![]() $\Lambda (X^{m,n}) \subseteq {\mathcal E}$
.
$\Lambda (X^{m,n}) \subseteq {\mathcal E}$
.
Remark 5.1.2. (i) For context, we note that
![]() $e_k[-M X^{m,n}] \cdot 1$
defines the symmetric function side of the
$e_k[-M X^{m,n}] \cdot 1$
defines the symmetric function side of the
![]() $(km,kn)$
-shuffle theorem of [Reference Bergeron, Garsia, Leven and Xin3, Reference Mellit30].
$(km,kn)$
-shuffle theorem of [Reference Bergeron, Garsia, Leven and Xin3, Reference Mellit30].
(ii)
![]() $\tilde {H}_{\mu }^{m,n}$
is a homogeneous symmetric function of degree
$\tilde {H}_{\mu }^{m,n}$
is a homogeneous symmetric function of degree
![]() $n|\mu |$
, as follows from the definition of the action of the Schiffmann algebra on symmetric functions [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1].
$n|\mu |$
, as follows from the definition of the action of the Schiffmann algebra on symmetric functions [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1].
5.2 The
 $1,n$
-Macdonald polynomials
$1,n$
-Macdonald polynomials
By [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Proposition 4.5.1],
![]() $\tilde {H}_\mu ^{m,1} = \tilde {H}_\mu [-M X^{m,1}] \cdot 1 = \nabla ^m \tilde {H}_\mu = q^{m \hspace {.3mm} \mathsf {n}(\mu ^*)}t^{m \hspace {.3mm} \mathsf {n}(\mu )} \tilde {H}_\mu $
, so this case is familiar. The
$\tilde {H}_\mu ^{m,1} = \tilde {H}_\mu [-M X^{m,1}] \cdot 1 = \nabla ^m \tilde {H}_\mu = q^{m \hspace {.3mm} \mathsf {n}(\mu ^*)}t^{m \hspace {.3mm} \mathsf {n}(\mu )} \tilde {H}_\mu $
, so this case is familiar. The
![]() $1,n$
-Macdonald polynomials, however, carry essentially the same data as the Macdonald series
$1,n$
-Macdonald polynomials, however, carry essentially the same data as the Macdonald series
![]() ${\mathbf H} _{\beta }$
by the following theorem, which will be proven in §5.3 as part of a more general result (see Remark 5.3.4 (ii)).
${\mathbf H} _{\beta }$
by the following theorem, which will be proven in §5.3 as part of a more general result (see Remark 5.3.4 (ii)).
Theorem 5.2.1. For any partition
![]() $\mu $
of l and any rearrangement
$\mu $
of l and any rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^{*}$
,
$\mu ^{*}$
,
Hence, also
![]() $\mathbf {H}_{\beta }({\mathbf z};q, t) = q^{-\mathsf {n}(\mu ^*)}t^{-\mathsf {n}(\mu )} \lim _{n \to \infty } (z_1\cdots z_l)^{-n}(\omega \tilde {H}_{\mu }^{1,n})(z_1,\dots , z_l).$
$\mathbf {H}_{\beta }({\mathbf z};q, t) = q^{-\mathsf {n}(\mu ^*)}t^{-\mathsf {n}(\mu )} \lim _{n \to \infty } (z_1\cdots z_l)^{-n}(\omega \tilde {H}_{\mu }^{1,n})(z_1,\dots , z_l).$
This also shows that
![]() $\mathbf {H}_{\beta }({\mathbf z};q, t)$
depends only on the partition rearrangement
$\mathbf {H}_{\beta }({\mathbf z};q, t)$
depends only on the partition rearrangement
![]() $\mu ^*$
of
$\mu ^*$
of
![]() $\beta $
.
$\beta $
.
The Macdonald polynomial
![]() $\tilde {H} _{\mu }(X;q,t)$
is known [Reference Haiman24] to be Schur positive (i.e., the coefficients
$\tilde {H} _{\mu }(X;q,t)$
is known [Reference Haiman24] to be Schur positive (i.e., the coefficients
![]() $\tilde {K} _{\lambda ,\mu }(q,t)$
in its Schur expansion are in
$\tilde {K} _{\lambda ,\mu }(q,t)$
in its Schur expansion are in
![]() ${\mathbb N} [q,t]$
). Based on extensive computations, we were led to the following positivity conjecture for the
${\mathbb N} [q,t]$
). Based on extensive computations, we were led to the following positivity conjecture for the
![]() $1,n$
-Macdonald polynomials, which generalizes the positivity theorem for Macdonald polynomials.
$1,n$
-Macdonald polynomials, which generalizes the positivity theorem for Macdonald polynomials.
Conjecture 5.2.2. The
![]() $1,n$
-Macdonald polynomials
$1,n$
-Macdonald polynomials
![]() $\tilde {H}_{\mu }^{1,n}(X;q,t)$
are Schur positive.
$\tilde {H}_{\mu }^{1,n}(X;q,t)$
are Schur positive.
Equivalently (by Theorem 5.2.1) for any partition
![]() $\mu $
of l and rearrangement
$\mu $
of l and rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^*$
, the series
$\mu ^*$
, the series
![]() ${\mathbf H}_\beta ({\mathbf z};q,t)$
is a positive sum of irreducible
${\mathbf H}_\beta ({\mathbf z};q,t)$
is a positive sum of irreducible
![]() $\operatorname {\mathrm {GL}}_l$
characters; that is, the coefficients in
$\operatorname {\mathrm {GL}}_l$
characters; that is, the coefficients in
are polynomials
![]() ${\mathbf K} _{\nu , \mu }(q,t)\in {\mathbb N}[q,t]$
with nonnegative integer coefficients.
${\mathbf K} _{\nu , \mu }(q,t)\in {\mathbb N}[q,t]$
with nonnegative integer coefficients.
Remark 5.2.3. For
![]() $m \ne 1$
and
$m \ne 1$
and
![]() $n \ne 1$
, the
$n \ne 1$
, the
![]() $m,n$
-Macdonald polynomials are typically not Schur positive.
$m,n$
-Macdonald polynomials are typically not Schur positive.
Example 5.2.4. The Schur expansions of the
![]() $1,n$
-Macdonald polynomials
$1,n$
-Macdonald polynomials
![]() $\tilde {H}^{1,n}_\mu (X;q,t)$
for
$\tilde {H}^{1,n}_\mu (X;q,t)$
for
![]() $n=2$
and
$n=2$
and
![]() $|\mu | = 2, 3$
, written as in (33), are
$|\mu | = 2, 3$
, written as in (33), are
 $$ \begin{align*} \tilde{H}^{1,2}_{2} \, &= \omega \, q \big( q^2s_{4} + q \hspace{.3mm} s_{31} + s_{22} \big)\\ \tilde{H}^{1,2}_{11} \, &= \omega \,t \big( t^2s_{4} + t \hspace{.3mm} s_{31} + s_{22} \big) \\ \tilde{H}^{1,2}_{3} \, &= \omega \,q^3 \big( q^6s_{6} + (q^5 + q^4)s_{51} + (q^4 + q^3 + q^2)s_{42} + q^3s_{33} + q^3s_{411} + (q^2 + q)s_{321} + s_{222}\big) \\ \tilde{H}^{1,2}_{21} \, &= \omega \, qt \big( q^2t^2s_{6} + (q^2t + qt^2)s_{51} + (q^2 + qt + t^2)s_{42} + qt \hspace{.3mm} s_{33} + qt \hspace{.3mm} s_{411} + (q + t)s_{321} + s_{222} \big) \\ \tilde{H}^{1,2}_{111} \, &= \omega\, t^3 \big( t^6s_{6} + (t^5 + t^4)s_{51} + (t^4 + t^3 + t^2)s_{42} + t^3s_{33} + t^3s_{411} + (t^2 + t)s_{321} + s_{222} \big). \end{align*} $$
$$ \begin{align*} \tilde{H}^{1,2}_{2} \, &= \omega \, q \big( q^2s_{4} + q \hspace{.3mm} s_{31} + s_{22} \big)\\ \tilde{H}^{1,2}_{11} \, &= \omega \,t \big( t^2s_{4} + t \hspace{.3mm} s_{31} + s_{22} \big) \\ \tilde{H}^{1,2}_{3} \, &= \omega \,q^3 \big( q^6s_{6} + (q^5 + q^4)s_{51} + (q^4 + q^3 + q^2)s_{42} + q^3s_{33} + q^3s_{411} + (q^2 + q)s_{321} + s_{222}\big) \\ \tilde{H}^{1,2}_{21} \, &= \omega \, qt \big( q^2t^2s_{6} + (q^2t + qt^2)s_{51} + (q^2 + qt + t^2)s_{42} + qt \hspace{.3mm} s_{33} + qt \hspace{.3mm} s_{411} + (q + t)s_{321} + s_{222} \big) \\ \tilde{H}^{1,2}_{111} \, &= \omega\, t^3 \big( t^6s_{6} + (t^5 + t^4)s_{51} + (t^4 + t^3 + t^2)s_{42} + t^3s_{33} + t^3s_{411} + (t^2 + t)s_{321} + s_{222} \big). \end{align*} $$
Proposition 5.2.5. The
![]() $m,n$
-Macdonald polynomials satisfy the same
$m,n$
-Macdonald polynomials satisfy the same
![]() $q,t$
symmetry property as ordinary modified Macdonald polynomials:
$q,t$
symmetry property as ordinary modified Macdonald polynomials:
![]() $\tilde {H}^{m,n}_\mu (X;q,t) = \tilde {H}^{m,n}_{\mu ^*}(X;t,q)$
.
$\tilde {H}^{m,n}_\mu (X;q,t) = \tilde {H}^{m,n}_{\mu ^*}(X;t,q)$
.
Proof. This follows from the symmetry property for Macdonald polynomials,
![]() $\tilde {H}_\mu (X;q,t) = \tilde {H}_{\mu ^*}(X;t,q)$
, and the fact that for any symmetric function f with coefficients in
$\tilde {H}_\mu (X;q,t) = \tilde {H}_{\mu ^*}(X;t,q)$
, and the fact that for any symmetric function f with coefficients in
![]() ${\mathbb Q}$
,
${\mathbb Q}$
,
![]() $f[-M X^{m,n}] \cdot 1$
is symmetric in q and t, which in turn follows from the description of the action of the Schiffmann algebra on symmetric functions in [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1].
$f[-M X^{m,n}] \cdot 1$
is symmetric in q and t, which in turn follows from the description of the action of the Schiffmann algebra on symmetric functions in [Reference Blasiak, Haiman, Morse, Pun and Seelinger6, Proposition 3.3.1].
We obtain several specializations of the
![]() $1,n$
-Macdonald polynomials easily from the raising operator formula in Theorem 5.2.1.
$1,n$
-Macdonald polynomials easily from the raising operator formula in Theorem 5.2.1.
Proposition 5.2.6. Let
![]() $\mu $
be a partition of l. The
$\mu $
be a partition of l. The
![]() $q=t=1$
,
$q=t=1$
,
![]() $q=1$
and
$q=1$
and
![]() $q=0$
specializations of the
$q=0$
specializations of the
![]() $1,n$
-Macdonald polynomials are given by
$1,n$
-Macdonald polynomials are given by
 $$ \begin{align} &\big(q^{-\mathsf{n}(\mu^*)} t^{-\mathsf{n}(\mu)}\tilde{H}^{1,n}_\mu(X;q,t) \big)|_{q=0} = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{(z_1\cdots z_l)^n}{\prod_{\alpha_{ij} \in B_\mu} (1 - t \hspace{.3mm} z_i/z_j)}\Big), \end{align} $$
$$ \begin{align} &\big(q^{-\mathsf{n}(\mu^*)} t^{-\mathsf{n}(\mu)}\tilde{H}^{1,n}_\mu(X;q,t) \big)|_{q=0} = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma }\Big(\frac{(z_1\cdots z_l)^n}{\prod_{\alpha_{ij} \in B_\mu} (1 - t \hspace{.3mm} z_i/z_j)}\Big), \end{align} $$
 $$ \begin{align} &\tilde{H}^{1,n}_\mu(X;1,t) = t^{\mathsf{n}(\mu)} \prod_{r = 1}^{\mu_1}\omega H_{(n^{\nu_r})}(X;t), \end{align} $$
$$ \begin{align} &\tilde{H}^{1,n}_\mu(X;1,t) = t^{\mathsf{n}(\mu)} \prod_{r = 1}^{\mu_1}\omega H_{(n^{\nu_r})}(X;t), \end{align} $$
where
![]() $\nu = \mu ^*$
,
$\nu = \mu ^*$
,
![]() $H_\mu (X;t) = t^{\mathsf {n}(\mu )}\tilde {H}_\mu (X;0,t^{-1})$
is as in (6), and
$H_\mu (X;t) = t^{\mathsf {n}(\mu )}\tilde {H}_\mu (X;0,t^{-1})$
is as in (6), and
![]() $B_\mu $
is as defined before (12).
$B_\mu $
is as defined before (12).
Remark 5.2.7. Like the familiar right-hand sides of (35) and (37), the right-hand side of (36) is also well studied. Its Schur expansion coefficients are instances of the generalized Kostka polynomials introduced by Shimozono-Weyman [Reference Shimozono and Weyman36] corresponding to the sequence of rectangle shapes
![]() $(n^{\mu _\ell }), \dots , (n^{\mu _2}), (n^{\mu _1})$
for
$(n^{\mu _\ell }), \dots , (n^{\mu _2}), (n^{\mu _1})$
for
![]() $\ell = \ell (\mu )$
.
$\ell = \ell (\mu )$
.
Proof. Throughout this proof, we only need the case
![]() $\beta = \mu ^* = \nu $
of Theorem 5.2.1.
$\beta = \mu ^* = \nu $
of Theorem 5.2.1.
By the same argument as in §3.2, the
![]() $q=t=1$
specialization of
$q=t=1$
specialization of
![]() $\operatorname {\mathrm {pol}}_X ((z_1\cdots z_l)^n\mathbf {H}_\nu )$
is the complete homogeneous symmetric function
$\operatorname {\mathrm {pol}}_X ((z_1\cdots z_l)^n\mathbf {H}_\nu )$
is the complete homogeneous symmetric function
![]() $h_{(n^l)}$
. Hence, (35) follows from Theorem 5.2.1. Similarly, (36) follows from Theorem 5.2.1 and from noting that
$h_{(n^l)}$
. Hence, (35) follows from Theorem 5.2.1. Similarly, (36) follows from Theorem 5.2.1 and from noting that
![]() $\operatorname {\mathrm {pol}}_X ((z_1\cdots z_l)^n\mathbf {H}_\nu ({\mathbf z}; 0,t))$
can be simplified just as
$\operatorname {\mathrm {pol}}_X ((z_1\cdots z_l)^n\mathbf {H}_\nu ({\mathbf z}; 0,t))$
can be simplified just as
![]() $\operatorname {\mathrm {pol}}_X (z_1\cdots z_l \, \mathbf {H}_\nu ({\mathbf z}; 0,t))$
was in §3.2.
$\operatorname {\mathrm {pol}}_X (z_1\cdots z_l \, \mathbf {H}_\nu ({\mathbf z}; 0,t))$
was in §3.2.
We now prove (37). By Theorem 5.2.1 and (9),
 $$ \begin{align} q^{-\mathsf{n}(\mu^*)}t^{-\mathsf{n}(\mu)} \omega\hspace{.3mm} \tilde{H}^{1,n}_{\mu }(X;q,t) = \mathbf{h}_X\Big( \hspace{.3mm} (z_1\cdots z_l)^n \prod_{\alpha_{ij} \in R_+}(1-z_i/z_j)\widehat{\mathbf{H}}_{\nu}\Big), \end{align} $$
$$ \begin{align} q^{-\mathsf{n}(\mu^*)}t^{-\mathsf{n}(\mu)} \omega\hspace{.3mm} \tilde{H}^{1,n}_{\mu }(X;q,t) = \mathbf{h}_X\Big( \hspace{.3mm} (z_1\cdots z_l)^n \prod_{\alpha_{ij} \in R_+}(1-z_i/z_j)\widehat{\mathbf{H}}_{\nu}\Big), \end{align} $$
where
![]() $\widehat {\mathbf {H}}_\nu ({\mathbf z};q,t)$
is the expression inside the
$\widehat {\mathbf {H}}_\nu ({\mathbf z};q,t)$
is the expression inside the
![]() ${\boldsymbol \sigma }(\cdot )$
on the right side of (20), with
${\boldsymbol \sigma }(\cdot )$
on the right side of (20), with
![]() $\beta $
equal to
$\beta $
equal to
![]() $\nu $
(so that
$\nu $
(so that
![]() $\mathbf {H}_\nu = {\boldsymbol \sigma }(\widehat {\mathbf {H}}_\nu )$
). Let
$\mathbf {H}_\nu = {\boldsymbol \sigma }(\widehat {\mathbf {H}}_\nu )$
). Let
![]() $C_1, \dots , C_{\mu _1}$
denote the columns of
$C_1, \dots , C_{\mu _1}$
denote the columns of
![]() $\boldsymbol {\nu }$
and note that
$\boldsymbol {\nu }$
and note that
![]() $R_\nu \setminus \widehat {R}_\nu $
is equal to
$R_\nu \setminus \widehat {R}_\nu $
is equal to
![]() $\bigsqcup _{r = 1}^{\mu _1} \{\alpha _{ij} : {\boldsymbol {\nu }[j]}={\mathrm {south}}({\boldsymbol {\nu }[i]}), \, {\boldsymbol {\nu }[i]} \in C_r \}$
. Hence, setting
$\bigsqcup _{r = 1}^{\mu _1} \{\alpha _{ij} : {\boldsymbol {\nu }[j]}={\mathrm {south}}({\boldsymbol {\nu }[i]}), \, {\boldsymbol {\nu }[i]} \in C_r \}$
. Hence, setting
![]() $q=1$
in (38) yields
$q=1$
in (38) yields
 $$ \begin{align} t^{-\mathsf{n}(\mu)} \omega \tilde{H}^{1,n}_{\mu }(X;1,t) & = \mathbf{h}_X\bigg( \prod_{r = 1}^{\mu_1} \frac{\big(\prod_{{\boldsymbol {\nu}[i]} \in C_r} z_i^n\big) \prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r } \big(1- t^{-{\mathrm{leg}}({\boldsymbol {\nu}[i]})} z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r}\big(1-t z_i/z_j \big)} \bigg) \end{align} $$
$$ \begin{align} t^{-\mathsf{n}(\mu)} \omega \tilde{H}^{1,n}_{\mu }(X;1,t) & = \mathbf{h}_X\bigg( \prod_{r = 1}^{\mu_1} \frac{\big(\prod_{{\boldsymbol {\nu}[i]} \in C_r} z_i^n\big) \prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r } \big(1- t^{-{\mathrm{leg}}({\boldsymbol {\nu}[i]})} z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r}\big(1-t z_i/z_j \big)} \bigg) \end{align} $$
 $$ \begin{align} &\qquad\qquad\qquad\qquad\,\, = \prod_{r = 1}^{\mu_1}\mathbf{h}_X\bigg( \frac{\big(\prod_{{\boldsymbol {\nu}[i]} \in C_r} z_i^n\big) \prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r } \big(1- t^{-{\mathrm{leg}}({\boldsymbol {\nu}[i]})} z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu\, {\boldsymbol {\nu}[i]} \in C_r}\big(1-t z_i/z_j \big)} \bigg), \end{align} $$
$$ \begin{align} &\qquad\qquad\qquad\qquad\,\, = \prod_{r = 1}^{\mu_1}\mathbf{h}_X\bigg( \frac{\big(\prod_{{\boldsymbol {\nu}[i]} \in C_r} z_i^n\big) \prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu, \, {\boldsymbol {\nu}[i]} \in C_r } \big(1- t^{-{\mathrm{leg}}({\boldsymbol {\nu}[i]})} z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_\nu \setminus \widehat{R}_\nu\, {\boldsymbol {\nu}[i]} \in C_r}\big(1-t z_i/z_j \big)} \bigg), \end{align} $$
where the second equality follows from (10) and the fact that
![]() $h_\gamma = h_\delta $
for
$h_\gamma = h_\delta $
for
![]() $\gamma , \delta \in {\mathbb Z}^l$
which are rearrangements of each other.
$\gamma , \delta \in {\mathbb Z}^l$
which are rearrangements of each other.
The factor
![]() $\mathbf {h}_X(\cdot )$
in (40) for a given index r is equal to
$\mathbf {h}_X(\cdot )$
in (40) for a given index r is equal to
![]() $t^{-\mathsf {n}(1^{\nu _r})} \omega \tilde {H}^{1,n}_{(1^{\nu _r})}(X;1,t)$
, by the computation we have just done, but with the partition
$t^{-\mathsf {n}(1^{\nu _r})} \omega \tilde {H}^{1,n}_{(1^{\nu _r})}(X;1,t)$
, by the computation we have just done, but with the partition
![]() $1^{\nu _r}$
in place of
$1^{\nu _r}$
in place of
![]() $\mu $
. It follows that
$\mu $
. It follows that
 $$ \begin{align} \tilde{H}^{1,n}_{\mu }(X;1,t) = \prod_{r = 1}^{\mu_1}\tilde{H}^{1,n}_{(1^{\nu_r})}(X;1,t). \end{align} $$
$$ \begin{align} \tilde{H}^{1,n}_{\mu }(X;1,t) = \prod_{r = 1}^{\mu_1}\tilde{H}^{1,n}_{(1^{\nu_r})}(X;1,t). \end{align} $$
Finally, we will show that each
![]() $\tilde {H}^{1,n}_{(1^{\nu _r})}(X;1,t)$
is essentially a Hall-Littlewood polynomial. Using the particularly simple form of the series
$\tilde {H}^{1,n}_{(1^{\nu _r})}(X;1,t)$
is essentially a Hall-Littlewood polynomial. Using the particularly simple form of the series
![]() $\mathbf {H}_{\nu }$
when
$\mathbf {H}_{\nu }$
when
![]() $\mu = (d)$
is a single row, Theorem 5.2.1 and (11) yield
$\mu = (d)$
is a single row, Theorem 5.2.1 and (11) yield
![]() $q^{-\binom {d}{2}}\omega \hspace {.3mm} \tilde {H}^{1,n}_{(d) }(X;q,t) = H_{(n^d)}(X;q)$
. By Proposition 5.2.5,
$q^{-\binom {d}{2}}\omega \hspace {.3mm} \tilde {H}^{1,n}_{(d) }(X;q,t) = H_{(n^d)}(X;q)$
. By Proposition 5.2.5,
![]() $\tilde {H}^{1,n}_{\mu }(X;q,t) = \tilde {H}^{1,n}_{\mu ^* }(X;t,q)$
, and thus,
$\tilde {H}^{1,n}_{\mu }(X;q,t) = \tilde {H}^{1,n}_{\mu ^* }(X;t,q)$
, and thus,
5.3 A raising operator formula for the
 $m,n$
-Macdonald polynomials
$m,n$
-Macdonald polynomials
We now give a raising operator formula for
![]() $\tilde {H}_\mu ^{m,n}$
which generalizes the raising operator formula for
$\tilde {H}_\mu ^{m,n}$
which generalizes the raising operator formula for
![]() $\tilde {H}_\mu $
in Theorem 3.1.4, and is derived in a similar way. Specifically, we combine the Haglund-Haiman-Loehr formula (Theorem 4.2.2) with an
$\tilde {H}_\mu $
in Theorem 3.1.4, and is derived in a similar way. Specifically, we combine the Haglund-Haiman-Loehr formula (Theorem 4.2.2) with an
![]() $m,n$
version of Theorem 4.3.1. This latter result requires some notation involving the dilation of a column diagram.
$m,n$
version of Theorem 4.3.1. This latter result requires some notation involving the dilation of a column diagram.
For
![]() $\beta \in {\mathbb Z}_{+}^k$
, let
$\beta \in {\mathbb Z}_{+}^k$
, let
![]() $m \beta = (m \beta _1,\dots , m \beta _k)$
. We think of the column diagram
$m \beta = (m \beta _1,\dots , m \beta _k)$
. We think of the column diagram
![]() $\boldsymbol {m\beta }$
of
$\boldsymbol {m\beta }$
of
![]() $m \beta $
as the result of dilating the column diagram
$m \beta $
as the result of dilating the column diagram
![]() $\boldsymbol {\beta }$
of
$\boldsymbol {\beta }$
of
![]() $\beta $
vertically by a factor of m, so that each box of
$\beta $
vertically by a factor of m, so that each box of
![]() $\boldsymbol {\beta }$
gives rise to m boxes of
$\boldsymbol {\beta }$
gives rise to m boxes of
![]() $\boldsymbol {m\beta }$
. To be more precise, define the map of boxes
$\boldsymbol {m\beta }$
. To be more precise, define the map of boxes
Thus, in the dilation process, each box b of
![]() $\boldsymbol {\beta }$
gives rise to a set
$\boldsymbol {\beta }$
gives rise to a set
![]() $\tau ^{-1}(b)$
of m boxes of
$\tau ^{-1}(b)$
of m boxes of
![]() $\boldsymbol {m\beta }$
, called a dilated box, which forms a contiguous subset of a column of
$\boldsymbol {m\beta }$
, called a dilated box, which forms a contiguous subset of a column of
![]() $\boldsymbol {m\beta }$
.
$\boldsymbol {m\beta }$
.
As in §3.1, we write
![]() ${\boldsymbol {\beta }[1]},\dots , {\boldsymbol {\beta }[d]}$
for the boxes of
${\boldsymbol {\beta }[1]},\dots , {\boldsymbol {\beta }[d]}$
for the boxes of
![]() $\boldsymbol {\beta }$
listed in increasing reading order and
$\boldsymbol {\beta }$
listed in increasing reading order and
![]() ${\boldsymbol {m\beta }[1]},\dots , {\boldsymbol {m\beta }[l]}$
for the boxes of
${\boldsymbol {m\beta }[1]},\dots , {\boldsymbol {m\beta }[l]}$
for the boxes of
![]() $\boldsymbol {m\beta }$
in increasing reading order, where
$\boldsymbol {m\beta }$
in increasing reading order, where
![]() $d = |\beta |$
and
$d = |\beta |$
and
![]() $l = dm$
. Define a map
$l = dm$
. Define a map
![]() ${\mathsf {s}} \colon V_\beta \to V_{m \beta }$
which takes a vertical domino
${\mathsf {s}} \colon V_\beta \to V_{m \beta }$
which takes a vertical domino
![]() $({\boldsymbol {\beta }[i]}, {\boldsymbol {\beta }[j]})$
of
$({\boldsymbol {\beta }[i]}, {\boldsymbol {\beta }[j]})$
of
![]() $\boldsymbol {\beta }$
to the vertical domino
$\boldsymbol {\beta }$
to the vertical domino
![]() $({\boldsymbol {m\beta }[i']}, {\boldsymbol {m\beta }[j']})$
of
$({\boldsymbol {m\beta }[i']}, {\boldsymbol {m\beta }[j']})$
of
![]() $\boldsymbol {m\beta }$
such that
$\boldsymbol {m\beta }$
such that
![]() $\tau ({\boldsymbol {m\beta }[i']}) = {\boldsymbol {\beta }[i]}$
and
$\tau ({\boldsymbol {m\beta }[i']}) = {\boldsymbol {\beta }[i]}$
and
![]() $\tau ({\boldsymbol {m\beta }[j']}) = {\boldsymbol {\beta }[j]}$
. Note that
$\tau ({\boldsymbol {m\beta }[j']}) = {\boldsymbol {\beta }[j]}$
. Note that
![]() ${\mathsf {s}}(V_\beta )$
is the set of vertical dominoes of the dilated diagram
${\mathsf {s}}(V_\beta )$
is the set of vertical dominoes of the dilated diagram
![]() $\boldsymbol {m\beta }$
which straddle two dilated boxes.
$\boldsymbol {m\beta }$
which straddle two dilated boxes.
Example 5.3.1. For m = 3 and β = (2, 1, 2), the dilated boxes of
![]() $\boldsymbol {m\beta }$
are shown below along with the labeling of the boxes of
$\boldsymbol {m\beta }$
are shown below along with the labeling of the boxes of
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {m\beta }$
by reading order. To clarify the definitions of
$\boldsymbol {m\beta }$
by reading order. To clarify the definitions of
![]() $\tau $
and
$\tau $
and
![]() ${\mathsf {s}}$
, note that τ
−1(
β
[3]) = {
mβ
[7],
mβ
[10],
mβ
[13]} and s(V
β
) = {(
mβ
[5],
mβ
[7]), (
mβ
[6],
mβ
[9])}.
${\mathsf {s}}$
, note that τ
−1(
β
[3]) = {
mβ
[7],
mβ
[10],
mβ
[13]} and s(V
β
) = {(
mβ
[5],
mβ
[7]), (
mβ
[6],
mβ
[9])}.

Given
![]() $(m,n)\in {\mathbb Z} _{+}\times {\mathbb Z}_+ $
, we define the sequence of m integers as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, (9.5)]
$(m,n)\in {\mathbb Z} _{+}\times {\mathbb Z}_+ $
, we define the sequence of m integers as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, (9.5)]
We then define, for any
![]() $\beta \in {\mathbb Z}_{+}^k$
of size
$\beta \in {\mathbb Z}_{+}^k$
of size
![]() $d= |\beta |$
, a weight
$d= |\beta |$
, a weight
![]() ${\mathbf b}(m,n,\beta ) \in {\mathbb Z}^{dm}$
as follows: fill each dilated box of
${\mathbf b}(m,n,\beta ) \in {\mathbb Z}^{dm}$
as follows: fill each dilated box of
![]() $\boldsymbol {m\beta }$
with the sequence
$\boldsymbol {m\beta }$
with the sequence
![]() ${\mathbf b}(m,n)$
from north to south, and then read this filling by the reading order on
${\mathbf b}(m,n)$
from north to south, and then read this filling by the reading order on
![]() $\boldsymbol {m\beta }$
. Equivalently,
$\boldsymbol {m\beta }$
. Equivalently,
![]() ${\mathbf b}(m,n,\beta )_r = {\mathbf b}(m,n)_a$
, where a is the integer
${\mathbf b}(m,n,\beta )_r = {\mathbf b}(m,n)_a$
, where a is the integer
![]() $a\in \{1,\dots ,m\}$
such that
$a\in \{1,\dots ,m\}$
such that
![]() $a\equiv -j+1 \pmod {m}$
for j the row index of the r-th box of
$a\equiv -j+1 \pmod {m}$
for j the row index of the r-th box of
![]() $\boldsymbol {m\beta }$
in reading order (i.e.,
$\boldsymbol {m\beta }$
in reading order (i.e.,
![]() ${\boldsymbol {m \beta }[\, r]} = (i,j)$
for some i).
${\boldsymbol {m \beta }[\, r]} = (i,j)$
for some i).
Theorem 5.3.2 [Reference Blasiak, Haiman, Morse, Pun and Seelinger7].
Let
![]() $m,n$
be coprime positive integers, let
$m,n$
be coprime positive integers, let
![]() $\beta \in {\mathbb Z}_{+}^k$
, and set
$\beta \in {\mathbb Z}_{+}^k$
, and set
![]() $d = |\beta |$
,
$d = |\beta |$
,
![]() $l = dm$
. For
$l = dm$
. For
![]() $S \subseteq V_\beta $
, let
$S \subseteq V_\beta $
, let
![]() ${\boldsymbol \nu }(S)$
be the k-tuple of ribbons in Definition 4.2.1. The action of the LLT polynomial
${\boldsymbol \nu }(S)$
be the k-tuple of ribbons in Definition 4.2.1. The action of the LLT polynomial
![]() ${\mathcal G}_{{\boldsymbol \nu }(S)}[-MX^{m,n}] \in \Lambda (X^{m,n})$
on 1 is given by
${\mathcal G}_{{\boldsymbol \nu }(S)}[-MX^{m,n}] \in \Lambda (X^{m,n})$
on 1 is given by
 $$ \begin{align} {\mathcal G}_{{\boldsymbol \nu }(S)}[-MX^{m,n}] \cdot 1 = \omega \operatorname{\mathrm{pol}}_X\, & {\boldsymbol \sigma } \bigg( (-qt)^{|V_\beta\setminus S|} q^{A_\beta+(m-1)\mathsf{n}(\beta^+)} \mathbf{z}^{{\mathbf b}(m,n,\beta)} \nonumber\\ &\times \frac{ \prod_{({\boldsymbol {m\beta }[i]}, {\boldsymbol {m\beta }[j]}) \in {\mathsf{s}}(V_\beta \setminus S)} z_i/z_j \prod_{\alpha_{ij} \in \widehat{R}_{m\beta}} \! \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_{+}(\operatorname{\mathrm{GL}}_{l})} \! \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{m\beta}} \! \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
$$ \begin{align} {\mathcal G}_{{\boldsymbol \nu }(S)}[-MX^{m,n}] \cdot 1 = \omega \operatorname{\mathrm{pol}}_X\, & {\boldsymbol \sigma } \bigg( (-qt)^{|V_\beta\setminus S|} q^{A_\beta+(m-1)\mathsf{n}(\beta^+)} \mathbf{z}^{{\mathbf b}(m,n,\beta)} \nonumber\\ &\times \frac{ \prod_{({\boldsymbol {m\beta }[i]}, {\boldsymbol {m\beta }[j]}) \in {\mathsf{s}}(V_\beta \setminus S)} z_i/z_j \prod_{\alpha_{ij} \in \widehat{R}_{m\beta}} \! \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} { \prod_{\alpha_{ij} \in R_{+}(\operatorname{\mathrm{GL}}_{l})} \! \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{m\beta}} \! \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
where
![]() $A_\beta $
is the number of attacking pairs of
$A_\beta $
is the number of attacking pairs of
![]() ${\boldsymbol \nu }(S)$
as in §4.3,
${\boldsymbol \nu }(S)$
as in §4.3,
![]() $\beta ^+$
is the partition rearrangement of
$\beta ^+$
is the partition rearrangement of
![]() $\beta $
, and
$\beta $
, and
![]() $R_{m\beta }, \hspace {.3mm} \widehat {R}_{m\beta } \subseteq R_+(\operatorname {\mathrm {GL}}_l)$
are as in (15, 16).
$R_{m\beta }, \hspace {.3mm} \widehat {R}_{m\beta } \subseteq R_+(\operatorname {\mathrm {GL}}_l)$
are as in (15, 16).
Proof. This is obtained by combining [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Theorem 9.3.1] and [Reference Blasiak, Haiman, Morse, Pun and Seelinger4, Proposition 2.3.2] and specializing to the case that the LLT polynomial is indexed by the tuple of ribbons
![]() ${\boldsymbol \nu }(S)$
. The notation here and that in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Theorem 9.3.1] are matched using the discussion in the proof of Theorem 4.3.1 and the following: the weight
${\boldsymbol \nu }(S)$
. The notation here and that in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Theorem 9.3.1] are matched using the discussion in the proof of Theorem 4.3.1 and the following: the weight
![]() ${\mathbf b}(m,n,\beta )$
is the same as
${\mathbf b}(m,n,\beta )$
is the same as
![]() $\tilde {{\mathbf b}}$
defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 9.2.1], and the weight
$\tilde {{\mathbf b}}$
defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Definition 9.2.1], and the weight
![]() $\lambda $
defined there satisfies
$\lambda $
defined there satisfies
![]() ${\mathbf z}^\lambda = \mathbf {z}^{{\mathbf b}(m,n,\beta )} \prod _{({\boldsymbol {m\beta }[i]}, {\boldsymbol {m\beta }[j]}) \in {\mathsf {s}}(V_\beta \setminus S)} z_i/z_j$
.
${\mathbf z}^\lambda = \mathbf {z}^{{\mathbf b}(m,n,\beta )} \prod _{({\boldsymbol {m\beta }[i]}, {\boldsymbol {m\beta }[j]}) \in {\mathsf {s}}(V_\beta \setminus S)} z_i/z_j$
.
We now give our raising operator formula for the
![]() $m,n$
-Macdonald polynomials
$m,n$
-Macdonald polynomials
![]() $\tilde {H}_{\mu }^{m,n}(X;q,t)$
.
$\tilde {H}_{\mu }^{m,n}(X;q,t)$
.
Theorem 5.3.3. Let
![]() $m,n$
be coprime positive integers. Given
$m,n$
be coprime positive integers. Given
![]() $\beta \in {\mathbb Z}_{+}^k$
and setting
$\beta \in {\mathbb Z}_{+}^k$
and setting
![]() $d = |\beta |$
and
$d = |\beta |$
and
![]() $l = dm$
, define the
$l = dm$
, define the
![]() $m,n$
-Macdonald series by
$m,n$
-Macdonald series by

which we regard as an infinite formal linear combination of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters using the convention of Remark 2.2.1. Then, for any partition
$\operatorname {\mathrm {GL}} _{l}$
characters using the convention of Remark 2.2.1. Then, for any partition
![]() $\mu $
and any rearrangement
$\mu $
and any rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^{*}$
,
$\mu ^{*}$
,
Remark 5.3.4. (i) In (46), the indices of
![]() $z_i$
correspond to the boxes of the dilated diagram
$z_i$
correspond to the boxes of the dilated diagram
![]() $\boldsymbol {m\beta }$
, while the arm and leg are taken with respect to the original diagram
$\boldsymbol {m\beta }$
, while the arm and leg are taken with respect to the original diagram
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
(ii) Since
![]() ${\mathbf b}(1,n,\beta ) = n^l$
,
${\mathbf b}(1,n,\beta ) = n^l$
,
![]() $\mathbf {H}^{1,n}_{\beta } = (z_1\cdots z_l)^n\mathbf {H}_{\beta }$
, where
$\mathbf {H}^{1,n}_{\beta } = (z_1\cdots z_l)^n\mathbf {H}_{\beta }$
, where
![]() $\mathbf {H}_{\beta }$
is the Macdonald series from Definition 3.1.3. Hence, Theorem 5.3.3 proves Theorem 5.2.1 by setting
$\mathbf {H}_{\beta }$
is the Macdonald series from Definition 3.1.3. Hence, Theorem 5.3.3 proves Theorem 5.2.1 by setting
![]() $m=1$
with n arbitrary. It also specializes to Theorem 3.1.4 when
$m=1$
with n arbitrary. It also specializes to Theorem 3.1.4 when
![]() $(m,n)= (1,1)$
.
$(m,n)= (1,1)$
.
(iii) Expanding on (ii), the series
![]() $\mathbf {H}^{m,n}_{\beta }$
simultaneously encodes the
$\mathbf {H}^{m,n}_{\beta }$
simultaneously encodes the
![]() $m,n$
-Macdonald polynomials
$m,n$
-Macdonald polynomials
![]() $\{H^{m,n'}_\mu : n' \in (n+m{\mathbb Z}) \cap {\mathbb Z}_+\}$
, in the following sense:
$\{H^{m,n'}_\mu : n' \in (n+m{\mathbb Z}) \cap {\mathbb Z}_+\}$
, in the following sense:
This follows from Theorem 5.3.3 using that
![]() ${\mathbf b}(m,n+a\hspace {.3mm} m,\beta ) = {\mathbf b}(m,n,\beta ) + a^l$
, which in turn holds by
${\mathbf b}(m,n+a\hspace {.3mm} m,\beta ) = {\mathbf b}(m,n,\beta ) + a^l$
, which in turn holds by
![]() ${\mathbf b}(m,n+a\hspace {.3mm} m) = {\mathbf b}(m,n)+a^m$
.
${\mathbf b}(m,n+a\hspace {.3mm} m) = {\mathbf b}(m,n)+a^m$
.
Theorem 5.3.3 and Remark 5.3.4 (iii) have the following corollary.
Corollary 5.3.5. The
![]() $m,n$
-Macdonald series
$m,n$
-Macdonald series
![]() $\mathbf {H}^{m,n}_{\beta }$
depends only on the multiset of parts of
$\mathbf {H}^{m,n}_{\beta }$
depends only on the multiset of parts of
![]() $\beta $
and not on their order:
$\beta $
and not on their order:
![]() $\mathbf {H}^{m,n}_{\beta } = \mathbf {H}^{m,n}_{\gamma }$
for any rearrangement
$\mathbf {H}^{m,n}_{\beta } = \mathbf {H}^{m,n}_{\gamma }$
for any rearrangement
![]() $\gamma $
of
$\gamma $
of
![]() $\beta $
.
$\beta $
.
Proof of Theorem 5.3.3.
By a plethystic transformation and change of variables we can replace X in (28) with
![]() $-MX^{m,n}$
. Letting both sides act on
$-MX^{m,n}$
. Letting both sides act on
![]() $1 \in \Lambda (X)$
and then substituting in (45) yields
$1 \in \Lambda (X)$
and then substituting in (45) yields
 $$ \begin{align} & \tilde{H}_\mu[-M X^{m,n}] \cdot 1 = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg( \frac{\mathbf{z}^{{\mathbf b}(m,n,\beta)} \cdot \Upsilon \cdot \prod_{\alpha_{ij} \in \widehat{R}_{m\beta} } \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{m\beta}} \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
$$ \begin{align} & \tilde{H}_\mu[-M X^{m,n}] \cdot 1 = \omega \operatorname{\mathrm{pol}}_X {\boldsymbol \sigma } \bigg( \frac{\mathbf{z}^{{\mathbf b}(m,n,\beta)} \cdot \Upsilon \cdot \prod_{\alpha_{ij} \in \widehat{R}_{m\beta} } \big(1-q\hspace{.3mm} t\, z_i/z_j \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, z_i/z_j\big) \prod_{\alpha_{ij} \in R_{m\beta}} \big(1-t \, z_i/z_j\big)}\bigg), \end{align} $$
where
 $$ \begin{align} \Upsilon = \sum_{S \subseteq V_\beta} (-qt)^{|V_\beta \setminus S|} q^{A_\beta+(m-1)\mathsf{n}(\mu^*)} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} \!\!\! q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \prod_{({\boldsymbol {m\beta}[i]}, {\boldsymbol {m\beta}[j]})\in {\mathsf{s}}(V_\beta \setminus S)} \!\!\!\!z_i/z_j. \end{align} $$
$$ \begin{align} \Upsilon = \sum_{S \subseteq V_\beta} (-qt)^{|V_\beta \setminus S|} q^{A_\beta+(m-1)\mathsf{n}(\mu^*)} \prod_{({\boldsymbol {\beta}[i]}, {\boldsymbol {\beta}[j]})\in S} \!\!\! q^{-{\mathrm{arm}}({\boldsymbol {\beta}[i]})} \hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})+1} \prod_{({\boldsymbol {m\beta}[i]}, {\boldsymbol {m\beta}[j]})\in {\mathsf{s}}(V_\beta \setminus S)} \!\!\!\!z_i/z_j. \end{align} $$
The proof of Theorem 3.1.4 establishes that
![]() $A_\beta = \mathsf {n}(\mu ^*)+ \sum _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in V_\beta } {\mathrm {arm}}({\boldsymbol {\beta }[i]})$
, as can also be checked combinatorially. Using this,
$A_\beta = \mathsf {n}(\mu ^*)+ \sum _{({\boldsymbol {\beta }[i]},{\boldsymbol {\beta }[j]}) \in V_\beta } {\mathrm {arm}}({\boldsymbol {\beta }[i]})$
, as can also be checked combinatorially. Using this,
![]() $\Upsilon $
simplifies essentially the same way it did in that proof:
$\Upsilon $
simplifies essentially the same way it did in that proof:
 $$ \begin{align} \Upsilon \ =\ q^{m \hspace{.3mm} \mathsf{n}(\mu^*)} \hspace{.3mm} t^{\mathsf{n}(\mu)} \prod_{({\boldsymbol {m\beta}[i]}, {\boldsymbol {m\beta}[j]}) \in {\mathsf{s}}(V_\beta)} \big(1- q^{{\mathrm{arm}}(\tau({\boldsymbol {m\beta}[i]}))+1}\hspace{.3mm} t^{-{\mathrm{leg}}(\tau({\boldsymbol {m\beta}[i]}))} z_i/z_j \big). \end{align} $$
$$ \begin{align} \Upsilon \ =\ q^{m \hspace{.3mm} \mathsf{n}(\mu^*)} \hspace{.3mm} t^{\mathsf{n}(\mu)} \prod_{({\boldsymbol {m\beta}[i]}, {\boldsymbol {m\beta}[j]}) \in {\mathsf{s}}(V_\beta)} \big(1- q^{{\mathrm{arm}}(\tau({\boldsymbol {m\beta}[i]}))+1}\hspace{.3mm} t^{-{\mathrm{leg}}(\tau({\boldsymbol {m\beta}[i]}))} z_i/z_j \big). \end{align} $$
Plugging this back into (49) completes the proof.
We obtain yet other expressions for the modified Macdonald polynomials from Theorem 5.3.3.
Corollary 5.3.6. Let
![]() $\mu $
be a partition of d and
$\mu $
be a partition of d and
![]() $\beta $
a rearrangement of
$\beta $
a rearrangement of
![]() $\mu ^*$
. The modified Macdonald polynomial
$\mu ^*$
. The modified Macdonald polynomial
![]() $\tilde {H}_{\mu }(X;q,t)$
can be expressed in terms of the
$\tilde {H}_{\mu }(X;q,t)$
can be expressed in terms of the
![]() $m,1$
-Macdonald series for any m as follows:
$m,1$
-Macdonald series for any m as follows:
Proof. By [Reference Blasiak, Haiman, Morse, Pun and Seelinger7, Proposition 4.5.1],
![]() $\tilde {H}_{\mu }[-MX^{m,1}] \cdot 1 = \nabla ^m \tilde {H}_\mu $
. Substitute this into the left side of (47).
$\tilde {H}_{\mu }[-MX^{m,1}] \cdot 1 = \nabla ^m \tilde {H}_\mu $
. Substitute this into the left side of (47).
6 A raising operator formula for the Macdonald polynomials
 $Q_\mu (X;q,t)$
and
$Q_\mu (X;q,t)$
and
 $J_\mu (X;q,t)$
$J_\mu (X;q,t)$
Our formulas for the modified Macdonald polynomials
![]() $\tilde {H}_\mu (X;q,t)$
can be converted into formulas for the integral form Macdonald polynomials
$\tilde {H}_\mu (X;q,t)$
can be converted into formulas for the integral form Macdonald polynomials
![]() $J_{\mu }(X;q,t)$
and for the
$J_{\mu }(X;q,t)$
and for the
![]() $Q_\mu (X;q,t)$
which differ from the
$Q_\mu (X;q,t)$
which differ from the
![]() $J_\mu $
by a scalar factor. Recall that
$J_\mu $
by a scalar factor. Recall that
![]() $\tilde {H}_{\mu }(X;q,t) = t^{\mathsf {n}(\mu )} J_{\mu }[\frac {X}{1-t^{-1}};q,t^{-1}]$
as in (3), hence
$\tilde {H}_{\mu }(X;q,t) = t^{\mathsf {n}(\mu )} J_{\mu }[\frac {X}{1-t^{-1}};q,t^{-1}]$
as in (3), hence
![]() $\tilde {H}_{\mu }[X(1-t^{-1});q,t] = t^{\mathsf {n}(\mu )} J_{\mu }(X;q,t^{-1})$
, or equivalently,
$\tilde {H}_{\mu }[X(1-t^{-1});q,t] = t^{\mathsf {n}(\mu )} J_{\mu }(X;q,t^{-1})$
, or equivalently,
Let
![]() $\mathbf {e}^{\prime }_X \colon {\mathbf k}[z_1^{\pm 1},\dots , z_l^{\pm 1}] \to \Lambda $
denote the linear operator determined by
$\mathbf {e}^{\prime }_X \colon {\mathbf k}[z_1^{\pm 1},\dots , z_l^{\pm 1}] \to \Lambda $
denote the linear operator determined by
 $$ \begin{align} \mathbf{e}^{\prime}_X({\mathbf z}^\gamma) &= e_\gamma[X(1-t)] = \prod_{i = 1}^l \sum_{j=0}^{\gamma _i} (-t)^{j} e_{\gamma _i -j}(X) h_{j}(X), \end{align} $$
$$ \begin{align} \mathbf{e}^{\prime}_X({\mathbf z}^\gamma) &= e_\gamma[X(1-t)] = \prod_{i = 1}^l \sum_{j=0}^{\gamma _i} (-t)^{j} e_{\gamma _i -j}(X) h_{j}(X), \end{align} $$
where for
![]() $\gamma \in {\mathbb Z}^l$
, we define
$\gamma \in {\mathbb Z}^l$
, we define
![]() $e_\gamma = e_{\gamma _1}\cdots e_{\gamma _l}$
to be the product of elementary symmetric functions, with
$e_\gamma = e_{\gamma _1}\cdots e_{\gamma _l}$
to be the product of elementary symmetric functions, with
![]() $e_d$
for
$e_d$
for
![]() $d\leq 0$
interpreted as
$d\leq 0$
interpreted as
![]() $e_0 =1$
, or
$e_0 =1$
, or
![]() $e_d = 0$
for
$e_d = 0$
for
![]() $d< 0$
. We extend
$d< 0$
. We extend
![]() $\mathbf {e}^{\prime }_X$
to an operator on formal linear combinations of monomials just as we did for
$\mathbf {e}^{\prime }_X$
to an operator on formal linear combinations of monomials just as we did for
![]() ${\boldsymbol \sigma }$
and
${\boldsymbol \sigma }$
and
![]() $\mathbf {h}_X$
in §2.2. The operators
$\mathbf {h}_X$
in §2.2. The operators
![]() $\mathbf {e}^{\prime }_X$
and
$\mathbf {e}^{\prime }_X$
and
![]() $\mathbf {h}_X$
are related as follows: for a formal linear combination
$\mathbf {h}_X$
are related as follows: for a formal linear combination
![]() $g = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma $
such that
$g = \sum _{\gamma \in {\mathbb Z}^l} c_\gamma {\mathbf z}^\gamma $
such that
![]() $\mathbf {h}_X(g)$
is a symmetric function and not just an infinite formal sum of symmetric functions,
$\mathbf {h}_X(g)$
is a symmetric function and not just an infinite formal sum of symmetric functions,
![]() $\mathbf {e}^{\prime }_X(g) = \theta \circ \omega \circ \mathbf {h}_X(g)$
, where
$\mathbf {e}^{\prime }_X(g) = \theta \circ \omega \circ \mathbf {h}_X(g)$
, where
![]() $\theta \colon \Lambda \to \Lambda $
is the automorphism sending
$\theta \colon \Lambda \to \Lambda $
is the automorphism sending
![]() $f(X)$
to
$f(X)$
to
![]() $f[X(1-t)]$
.
$f[X(1-t)]$
.
Theorem 6.1.1. For any partition
![]() $\mu $
of l and any rearrangement
$\mu $
of l and any rearrangement
![]() $\beta $
of
$\beta $
of
![]() $\mu ^*$
, the integral form Macdonald polynomial
$\mu ^*$
, the integral form Macdonald polynomial
![]() $J_{\mu }(X;q,t)$
is given by
$J_{\mu }(X;q,t)$
is given by
 $$ \begin{align} J_{\mu}(X;q,t) = t^{\mathsf{n}(\mu )} \mathbf{e}^{\prime}_X\Big(z_1\cdots z_l \prod_{\alpha_{ij} \in R_+} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}_{\beta}({\mathbf z};q,t^{-1})\Big), \end{align} $$
$$ \begin{align} J_{\mu}(X;q,t) = t^{\mathsf{n}(\mu )} \mathbf{e}^{\prime}_X\Big(z_1\cdots z_l \prod_{\alpha_{ij} \in R_+} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}_{\beta}({\mathbf z};q,t^{-1})\Big), \end{align} $$
where
![]() $\widehat {\mathbf {H}}_\beta ({\mathbf z};q,t)$
is the expression inside the
$\widehat {\mathbf {H}}_\beta ({\mathbf z};q,t)$
is the expression inside the
![]() ${\boldsymbol \sigma }(\cdot )$
on the right side of (20) (so that
${\boldsymbol \sigma }(\cdot )$
on the right side of (20) (so that
![]() $\mathbf {H}_\beta = {\boldsymbol \sigma }(\widehat {\mathbf {H}}_\beta )$
). Alternatively, using informal notation similar to Remark 2.3.1,
$\mathbf {H}_\beta = {\boldsymbol \sigma }(\widehat {\mathbf {H}}_\beta )$
). Alternatively, using informal notation similar to Remark 2.3.1,
 $$ \begin{align} J_{\mu}(X;q,t) &= t^{\mathsf{n}(\mu )} \Bigg( \frac{\prod_{\alpha_{ij} \in R_+}(1-\mathsf{R}_{ij}) \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \big(1-q\hspace{.3mm} t^{-1}\, \mathsf{R}_{ij} \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, \mathsf{R}_{ij}\big) \prod_{\alpha_{ij} \in R_\beta} \big(1-t^{-1} \, \mathsf{R}_{ij}\big)}\Bigg) \nonumber\\ &\quad \times \prod_{\alpha_{ij} \in R_\beta \setminus \widehat{R}_\beta } \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})} \mathsf{R}_{ij} \big) \cdot e_{1^l}[X(1-t)], \end{align} $$
$$ \begin{align} J_{\mu}(X;q,t) &= t^{\mathsf{n}(\mu )} \Bigg( \frac{\prod_{\alpha_{ij} \in R_+}(1-\mathsf{R}_{ij}) \prod_{\alpha_{ij} \in \widehat{R}_{\beta}} \big(1-q\hspace{.3mm} t^{-1}\, \mathsf{R}_{ij} \big)} {\prod_{\alpha_{ij} \in R_+} \big(1-q \, \mathsf{R}_{ij}\big) \prod_{\alpha_{ij} \in R_\beta} \big(1-t^{-1} \, \mathsf{R}_{ij}\big)}\Bigg) \nonumber\\ &\quad \times \prod_{\alpha_{ij} \in R_\beta \setminus \widehat{R}_\beta } \big(1- q^{{\mathrm{arm}}({\boldsymbol {\beta}[i]})+1}\hspace{.3mm} t^{{\mathrm{leg}}({\boldsymbol {\beta}[i]})} \mathsf{R}_{ij} \big) \cdot e_{1^l}[X(1-t)], \end{align} $$
where
![]() $\mathsf {R}_{ij}$
acts on subscripts of
$\mathsf {R}_{ij}$
acts on subscripts of
![]() $e_{\gamma }[X(1-t)]$
by
$e_{\gamma }[X(1-t)]$
by
![]() $\mathsf {R}_{ij} \gamma = \gamma + \epsilon _i - \epsilon _j$
.
$\mathsf {R}_{ij} \gamma = \gamma + \epsilon _i - \epsilon _j$
.
Proof. By Theorem 3.1.4 and (9),
 $$ \begin{align} \tilde{H} _{\mu }(X;q,t) = \omega \hspace{.3mm} \mathbf{h}_X\big(z_1\cdots z_l \prod_{\alpha_{ij} \in R_+} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}_{\beta}\big). \end{align} $$
$$ \begin{align} \tilde{H} _{\mu }(X;q,t) = \omega \hspace{.3mm} \mathbf{h}_X\big(z_1\cdots z_l \prod_{\alpha_{ij} \in R_+} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}_{\beta}\big). \end{align} $$
The result then follows from (53) and the definition of
![]() $\mathbf {e}^{\prime }_X$
.
$\mathbf {e}^{\prime }_X$
.
We also record the consequence of Corollary 5.3.6 for the integral form Macdonald polynomials.
Corollary 6.1.2. Let
![]() $\mu $
be a partition of d and
$\mu $
be a partition of d and
![]() $\beta $
a rearrangement of
$\beta $
a rearrangement of
![]() $\mu ^*$
. Then for any
$\mu ^*$
. Then for any
![]() $m \in {\mathbb Z}_{+}$
,
$m \in {\mathbb Z}_{+}$
,
 $$ \begin{align} J_{\mu}(X;q,t) = t^{m \hspace{.3mm} \mathsf{n}(\mu)} \mathbf{e}^{\prime}_X\Big(\prod_{\alpha_{ij} \in R_+(\operatorname{\mathrm{GL}}_l)} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}^{m,1}_{\beta}({\mathbf z};q,t^{-1})\Big), \end{align} $$
$$ \begin{align} J_{\mu}(X;q,t) = t^{m \hspace{.3mm} \mathsf{n}(\mu)} \mathbf{e}^{\prime}_X\Big(\prod_{\alpha_{ij} \in R_+(\operatorname{\mathrm{GL}}_l)} \!\! (1-z_i/z_j)\ \widehat{\mathbf{H}}^{m,1}_{\beta}({\mathbf z};q,t^{-1})\Big), \end{align} $$
where
![]() $l=dm$
and
$l=dm$
and
![]() $\widehat {\mathbf {H}}^{m,1}_{\beta }({\mathbf z};q,t)$
is the expression inside
$\widehat {\mathbf {H}}^{m,1}_{\beta }({\mathbf z};q,t)$
is the expression inside
![]() ${\boldsymbol \sigma }(\cdot )$
on the right side of (46), with n set to 1.
${\boldsymbol \sigma }(\cdot )$
on the right side of (46), with n set to 1.
Competing interest
The authors have no competing interest to declare.
Financial support
Authors were supported by NSF Grants DMS-1855784 (J. B.), DMS-1855804 (J. M., A. P. and G. S.), DMS-2303175 (G. S.) and Simons Foundation-821999 (J. M.).