I. INTRODUCTION
Single-image enhancement is one of the most important image processing techniques. The purpose of enhancing images is to show hidden details in unclear low-quality images. Early attempts at single-image enhancement such as histogram equalization (HE) [Reference Zuiderveld and Heckbert1–Reference Wu, Liu, Hiramatsu and Kashino5] focused on enhancing the contrast of grayscale images. Hence, these algorithms do not directly enhance color images. A way to handle color images with these algorithms is enhancing the luminance components of color images and then multiplying each RGB component by the ratio of enhanced and input luminance components. Although simple and efficient, algorithms for grayscale images have limited performance in terms of enhancing color images. Due to this, interest in color-image enhancement, such as 3-D histogram-, Retinex-, and fusion-based enhancement, has increased [Reference Trahanias and Venetsanopoulos6–Reference Kinoshita and Kiya12]. In addition, recent single-image-enhancement algorithms utilize deep neural networks trained to regress from unclear low-quality images to clear high-quality ones [Reference Gharbi, Chen, Barron, Hasinoff and Durand13–Reference Kinoshita and Kiya19]. These deep-learning-based approaches significantly improve the performance of image enhancement compared with conventional analytical approaches such as HE. However, these color-image-enhancement algorithms cause colors to be distorted.
To avoid color distortion, hue-preserving image-enhancement methods have also been studied [Reference Naik and Murthy20–Reference Azetsu and Suetake24]. These hue-preserving methods aim not only to enhance images, but also to preserve hue components of input images. In particular, by extending Naik's work, Kinoshita and Kiya made it possible to remove hue distortion caused by any image-enhancement algorithm by replacing the maximally saturated colors on the constant-hue planes of an enhanced image with those of an input image [Reference Kinoshita and Kiya23].
However, perceptual hue-distortion remains because the hue definition utilized in these hue-preserving methods does not sufficiently take into account human visual perception, although these methods can preserve hue components in the HSI color space. For this reason, Azetsu and Suetake [Reference Azetsu and Suetake24] proposed a hue-preserving image-enhancement method in the CIELAB color space. The CIELAB color space [25] is a high-precision model of human color perception, and it enables us to calculate accurate color differences including hue differences compared with conventional color spaces such as RGB and HSI color spaces. Azetsu's method enables us to remove perceptual hue-distortion based on CIEDE2000, but it uses a simple gamma-correction algorithm for enhancement. For this reason, the enhancement performance of Azetsu's method is lower than state-of-the-art image-enhancement algorithms.
Because of such a situation, in this paper, we propose a novel hue-correction scheme based on the recent color-difference formula ‘‘CIEDE2000” [26]. Similarly to Azetsu's method, in the proposed scheme, the hue difference between an enhanced image and the corresponding input image is perfectly removed. In contrast, any image-enhancement algorithm such as deep-learning-based ones can be used to enhance images in the proposed scheme. Furthermore, the use of a gamut-mapping method enables us to compress the color gamut of the CIELAB color space into an output RGB color gamut, without hue changes. For these reasons, the proposed scheme can perfectly correct hue distortion caused by any image-enhancement algorithm while maintaining the performance of the image processing method and ensuring the color gamut of output images.
We evaluated the proposed scheme in terms of the performance of hue correction and image enhancement. Experimental results show that the proposed scheme can completely correct hue distortion caused by image-enhancement algorithms, but conventional hue-preserving methods cannot. In addition, it is also confirmed that the proposed scheme can maintain the performance of image-enhancement algorithms in terms of two objective quality metrics: discrete entropy and NIQMC.
II. RELATED WORK
Here, we summarize typical single-image enhancement methods, including recent fusion-based ones and deep-learning-based ones, and problems with them.
A) Image enhancement
Various kinds of research on single-image enhancement have so far been reported [Reference Zuiderveld and Heckbert1–Reference Kinoshita and Kiya19, Reference Jobson, Rahman and Woodell27–Reference Cai, Xu, Guo, Jia, Hu and Tao29]. Classic enhancement methods such as HE focus on enhancing the contrast of grayscale images. For this reason, these methods do not directly handle color images. A way to handle color images with these methods is enhancing the luminance components of color images and then multiplying each RGB component by the ratio of enhanced and input luminance components. Although simple and efficient, the methods for grayscale images are limited in their ability to improve color-image quality. Due to this, interest in color-image enhancement, such as 3-D histogram-, Retinex-, and fusion-based enhancement, has increased. Today, many single-image enhancement methods utilize deep neural networks trained to regress from unclear low-quality images to clear high-quality ones.
Most classic enhancement methods were designed for grayscale images. Among these methods, HE has received the most attention because of its intuitive implementation quality and high efficiency. It aims to derive a mapping function such that the entropy of a distribution of output luminance values can be maximized. Since HE often causes over/under-enhancement problems, a huge number of HE-based methods have been developed to improve the performance of HE [Reference Zuiderveld and Heckbert1–Reference Wu, Liu, Hiramatsu and Kashino5]. However, these methods cannot directly handle color images. The most common way to handle color images with these methods is enhancing the luminance components of color images and then multiplying each RGB component by the ratio of enhanced and input luminance components. Otherwise, these simple and efficient methods for grayscale images are limited in their ability to improve color-image quality. As a result, enhancement methods that can directly work on color images have been developed.
A traditional approach for enhancing color images is 3-D HE, which is an extension of normal HE [Reference Trahanias and Venetsanopoulos6–Reference Han, Yang and Lee8]. In this approach, an image is enhanced so that a 3-dimensional histogram defined on RGB color space is uniformly distributed. Another way for enhancing color images is to use Retinex theory [Reference Land30]. In Retinex theory, the dominant assumption is that a (color) image can be decomposed into two factors, say reflectance and illumination. Early attempts based on Retinex, such as single-scale Retinex [Reference Jobson, Rahman and Woodell27] and multi-scale Retinex [Reference Jobson, Rahman and Woodell28], treat reflectance as the final result of enhancement, yet the image often looks unnatural and frequently appears to be over-enhanced. For this reason, recent Retinex-based methods [Reference Fu, Zeng, Huang, Zhang and Ding9, Reference Guo, Li and Ling10, Reference Cai, Xu, Guo, Jia, Hu and Tao29] decompose images into reflectance and illumination and then enhance images by manipulating illumination. Additionally, multi-exposure-fusion (MEF)-based single-image enhancement methods were recently proposed [Reference Ying, Li and Gao11, Reference Kinoshita and Kiya12, Reference Kinoshita and Kiya31]. One of them, a pseudo MEF scheme [Reference Kinoshita and Kiya12], makes any single image applicable to MEF methods by generating pseudo multi-exposure images from a single image. By using this scheme, images with improved quality are produced with the use of detailed local features. Furthermore, quality-optimized image enhancement algorithms [Reference Gu, Zhai, Yang, Zhang and Chen32–Reference Gu, Tao, Qiao and Lin34] enable us to automatically set parameters in these algorithms and enhance images, by finding optimal parameters in terms of a no-reference image quality metric. Recent work has demonstrated great progress by using data-driven approaches in preference to analytical approaches such as HE [Reference Gharbi, Chen, Barron, Hasinoff and Durand13–Reference Kinoshita and Kiya19]. These data-driven approaches utilize pairs of high- and low-quality images to train deep neural networks, and the trained networks can be used to enhance color images.
The approaches can directly enhance color images, but the resulting colors are distorted.
B) Hue-preserving image enhancement
Hue-preserving image-enhancement methods have also been studied to avoid color distortion [Reference Naik and Murthy20–Reference Ueda, Misawa, Koga, Suetake and Uchino22, Reference Azetsu and Suetake24].
Naik and Murthy showed conditions for preserving hue defined in the HSI color space without color gamut problems [Reference Naik and Murthy20]. On the basis of Naik's work, several hue-preserving methods have already been proposed [Reference Nikolova and Steidl21–Reference Kinoshita and Kiya23]. In particular, Kinoshita and Kiya made it possible to remove hue distortion caused by any image-enhancement algorithm by replacing the maximally saturated colors on the constant-hue planes of an enhanced image with those of an input image [Reference Kinoshita and Kiya23].
Although these hue-preserving methods can preserve hue components in the HSI color space, perceptual hue-distortion remains because the hue definition utilized in these methods does not sufficiently take into account human visual perception. For this reason, Azetsu and Suetake [Reference Azetsu and Suetake24] proposed a hue-preserving image-enhancement method in the CIELAB color space. The CIELAB color space [25] is a high-precision model of human color perception, and it enables us to calculate accurate color differences including hue differences compared with conventional color spaces such as RGB and HSI color spaces. However, Azetsu's method uses a simple gamma-correction algorithm for enhancement. Therefore, the enhancement performance of Azetsu's method is lower than state-of-the-art image-enhancement algorithms.
C) Problems in hue correction and our aim
In hue-preserving image-enhancement, there are two problems as follows:
(i) Kinoshita's method [Reference Kinoshita and Kiya23] cannot remove perceptual hue-distortion, although it can be applied to any image-enhancement algorithm.
(ii) Azetsu's method [Reference Azetsu and Suetake24] cannot be applied to state-of-the-art image-enhancement algorithms such as deep-learning-based ones, although it can remove perceptual hue-distortion.
For this reason, we propose a novel hue-preserving image-enhancement scheme that is applicable to any existing image-enhancement method including deep-learning-based ones and that perfectly removes perceptual hue-distortion on the basis of CIEDE2000.
III. COLOR SPACES
In this section, we briefly summarize RGB color spaces and the CIELAB color space. We use notations shown in Table 1 throughout this paper.
Table 1. Notation.

A) RGB color spaces
Digital color images are generally encoded by using an RGB color space such as the sRGB color space [35] and the Adobe RGB color space [36]. In those RGB color spaces, a color $\boldsymbol {C}$![]() can be written as a three-dimensional vector $\boldsymbol {C}_{RGB} = (R, G, B)^{\top }$
can be written as a three-dimensional vector $\boldsymbol {C}_{RGB} = (R, G, B)^{\top }$![]() , where $0 \le R, G, B \le 1$
, where $0 \le R, G, B \le 1$![]() , and the superscript $\top$
, and the superscript $\top$![]() denotes the transpose of a matrix or vector. RGB color spaces are defined on the basis of the CIE1931 XYZ color space [37] (hereinafter called ‘‘XYZ color space”). In the XYZ color space, a color $\boldsymbol {C}$
denotes the transpose of a matrix or vector. RGB color spaces are defined on the basis of the CIE1931 XYZ color space [37] (hereinafter called ‘‘XYZ color space”). In the XYZ color space, a color $\boldsymbol {C}$![]() can be written as $\boldsymbol {C}_{XYZ} = (X, Y, Z)^{\top }$
can be written as $\boldsymbol {C}_{XYZ} = (X, Y, Z)^{\top }$![]() , where $X, Y, Z \ge 0$
, where $X, Y, Z \ge 0$![]() . A map from the XYZ color space into an RGB color space is given as
. A map from the XYZ color space into an RGB color space is given as
where
Here, $\mathrm {\textit {M}}$![]() is a $3\times 3$
is a $3\times 3$![]() regular matrix, and $f(\cdot )$
regular matrix, and $f(\cdot )$![]() denotes an opto-electronic transfer function (usually called ‘‘gamma correction”). After applying equation (2), each component of $\boldsymbol {C}_{RGB}$
denotes an opto-electronic transfer function (usually called ‘‘gamma correction”). After applying equation (2), each component of $\boldsymbol {C}_{RGB}$![]() will be clipped so that $0 \le R, G, B \le 1$
will be clipped so that $0 \le R, G, B \le 1$![]() . In the case of the sRGB color space, matrix $\mathrm {\textit {M}}$
. In the case of the sRGB color space, matrix $\mathrm {\textit {M}}$![]() and transfer function $f(\cdot )$
and transfer function $f(\cdot )$![]() are defined as
are defined as
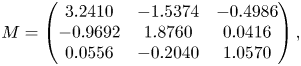
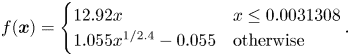
B) CIELAB color space
The CIELAB color space is designed to model human color perception, while many RGB color spaces are designed to encode digital images. Similarly to RGB color spaces, the CIELAB color space is defined on the basis of the XYZ color space.
A map from color $\boldsymbol {C}_{XYZ}$![]() in the XYZ color space into color $\boldsymbol {C} = (L^{*}, a^{*}, b^{*})^{\top }$
in the XYZ color space into color $\boldsymbol {C} = (L^{*}, a^{*}, b^{*})^{\top }$![]() in the CIELAB color space is given as
in the CIELAB color space is given as
where
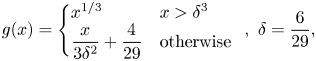
and $(X_w, Y_w, Z_w)$![]() indicates a white point in the XYZ color space.
indicates a white point in the XYZ color space.
By using the CIELAB color space, the perceptual color-difference between two colors $\boldsymbol {C}_1$![]() and $\boldsymbol {C}_2$
and $\boldsymbol {C}_2$![]() can objectively be calculated by using a color difference formula. CIEDE2000, which is one of the most recent color difference formulas, measures the color difference on the basis of lightness difference $\Delta L'$
can objectively be calculated by using a color difference formula. CIEDE2000, which is one of the most recent color difference formulas, measures the color difference on the basis of lightness difference $\Delta L'$![]() , chroma difference $\Delta C'$
, chroma difference $\Delta C'$![]() , and hue difference $\Delta H'$
, and hue difference $\Delta H'$![]() [26, Reference Sharma, Wu and Dalal38].
[26, Reference Sharma, Wu and Dalal38].
Given two colors $\boldsymbol {C}_i = (L^{*}_i, a^{*}_i, b^{*}_i)^{\top },~i = 1, 2$![]() , the lightness, chroma, and hue differences [$\Delta L' (\boldsymbol {C}_1, \boldsymbol {C}_2)$
, the lightness, chroma, and hue differences [$\Delta L' (\boldsymbol {C}_1, \boldsymbol {C}_2)$![]() , $\Delta C' (\boldsymbol {C}_1, \boldsymbol {C}_2)$
, $\Delta C' (\boldsymbol {C}_1, \boldsymbol {C}_2)$![]() , and $\Delta H' (\boldsymbol {C}_1, \boldsymbol {C}_2)$
, and $\Delta H' (\boldsymbol {C}_1, \boldsymbol {C}_2)$![]() ] in CIEDE2000 are calculated as follows (see also [Reference Sharma, Wu and Dalal38]).
] in CIEDE2000 are calculated as follows (see also [Reference Sharma, Wu and Dalal38]).
(i) Calculate $C'_i, h'_i$
 .
(9)\begin{align} C _ { i, a b } ^ { * } & = \sqrt { \left( a _ { i } ^ { * } \right) ^ { 2 } + \left( b _ { i } ^ { * } \right) ^ { 2 } } \end{align}
.
(9)\begin{align} C _ { i, a b } ^ { * } & = \sqrt { \left( a _ { i } ^ { * } \right) ^ { 2 } + \left( b _ { i } ^ { * } \right) ^ { 2 } } \end{align} (10)\begin{align} \overline { C } _ { a b } ^ { * } & = \frac { C _ { 1 , a b } ^ { * } + C _ { 2 , a b } ^ {*} } { 2 } \end{align}
(10)\begin{align} \overline { C } _ { a b } ^ { * } & = \frac { C _ { 1 , a b } ^ { * } + C _ { 2 , a b } ^ {*} } { 2 } \end{align} (11)\begin{align} G & = 0.5 \left( 1 - \sqrt { \frac {(\overline{C}_{ab}^{*})^{7}} {(\overline{C}_{ab}^{*})^{7}+25^{7}}} \right) \end{align}
(11)\begin{align} G & = 0.5 \left( 1 - \sqrt { \frac {(\overline{C}_{ab}^{*})^{7}} {(\overline{C}_{ab}^{*})^{7}+25^{7}}} \right) \end{align} (12)\begin{align} a _ { i } ^ { \prime } & = ( 1 + G ) a _ { i } ^ { * } \end{align}
(12)\begin{align} a _ { i } ^ { \prime } & = ( 1 + G ) a _ { i } ^ { * } \end{align} (13)\begin{align} C _ { i } ^ { \prime } & = \sqrt{\left(a_{i}^{\prime}\right)^{2}+\left(b_{i}^{*}\right)^{2}} \end{align}
(13)\begin{align} C _ { i } ^ { \prime } & = \sqrt{\left(a_{i}^{\prime}\right)^{2}+\left(b_{i}^{*}\right)^{2}} \end{align} (14)\begin{align} h_{i}^{\prime} & = \left\{ \begin{array}{@{}ll}{0} & {b_{i}^{*}=a_{i}^{\prime}=0}\\ {\tan^{-1}\left(b_{i}^{*}, a_{i}^{\prime}\right)} & { \text { otherwise } } \end{array} \right. \end{align}
(14)\begin{align} h_{i}^{\prime} & = \left\{ \begin{array}{@{}ll}{0} & {b_{i}^{*}=a_{i}^{\prime}=0}\\ {\tan^{-1}\left(b_{i}^{*}, a_{i}^{\prime}\right)} & { \text { otherwise } } \end{array} \right. \end{align}
(ii) Calculate $\Delta L'$
 , $\Delta C'$
, $\Delta C'$ , and $\Delta H'$
, and $\Delta H'$ .
(15)\begin{align} & \Delta L' (\boldsymbol{C}_1, \boldsymbol{C}_2) = L_2^{*} - L_1^{*} \end{align}
.
(15)\begin{align} & \Delta L' (\boldsymbol{C}_1, \boldsymbol{C}_2) = L_2^{*} - L_1^{*} \end{align} (16)\begin{align}& \Delta C' (\boldsymbol{C}_1, \boldsymbol{C}_2) = C'_2 - C'_1 \end{align}
(16)\begin{align}& \Delta C' (\boldsymbol{C}_1, \boldsymbol{C}_2) = C'_2 - C'_1 \end{align} (17)\begin{align}& \Delta h ^ { \prime } = \left\{ \begin{array}{@{}ll} {h_{2}^{\prime}-h_{1}^{\prime}} & \left| h_{2}^{\prime} - h_{1}^{\prime} \right| \leq 180^{\circ} \\ {\left( h_{2}^{\prime} - h_{1}^{\prime} \right) - 360^{\circ} } & \left( h_{2}^{\prime} - h_{1}^{\prime} \right) > 180^{\circ} \\ {\left( h_{2}^{\prime} - h_{1}^{\prime} \right) + 360^{\circ} } & \left( h_{2}^{\prime} - h_{1}^{\prime} \right) < -180^{\circ} \end{array} \right. \end{align}
(17)\begin{align}& \Delta h ^ { \prime } = \left\{ \begin{array}{@{}ll} {h_{2}^{\prime}-h_{1}^{\prime}} & \left| h_{2}^{\prime} - h_{1}^{\prime} \right| \leq 180^{\circ} \\ {\left( h_{2}^{\prime} - h_{1}^{\prime} \right) - 360^{\circ} } & \left( h_{2}^{\prime} - h_{1}^{\prime} \right) > 180^{\circ} \\ {\left( h_{2}^{\prime} - h_{1}^{\prime} \right) + 360^{\circ} } & \left( h_{2}^{\prime} - h_{1}^{\prime} \right) < -180^{\circ} \end{array} \right. \end{align} (18)\begin{align}& \Delta H^{\prime} (\boldsymbol{C}_1, \boldsymbol{C}_2) = 2 \sqrt{C_{1}^{\prime} C_{2}^{\prime}} \sin \left( \frac{\Delta h^{\prime}}{2} \right) \end{align}
(18)\begin{align}& \Delta H^{\prime} (\boldsymbol{C}_1, \boldsymbol{C}_2) = 2 \sqrt{C_{1}^{\prime} C_{2}^{\prime}} \sin \left( \frac{\Delta h^{\prime}}{2} \right) \end{align}
On the basis of CIEDE2000, we propose a novel hue-correction scheme for color-image enhancement.
IV. PROPOSED HUE-CORRECTION SCHEME
A) Overview
Figure 1(a) shows an overview of our hue-correction scheme. Our scheme consists of two steps: hue correction and gamut mapping.
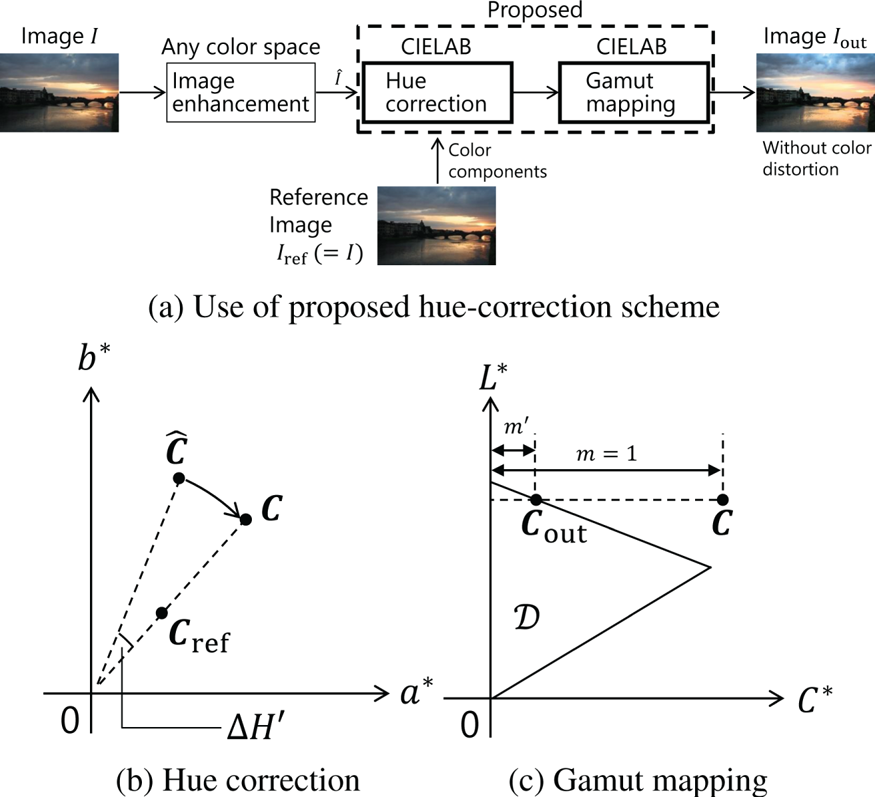
Fig. 1. Proposed hue-correction scheme. (a) Use of proposed hue-correction scheme. (b) Hue correction. (c) Gamut mapping.
The hue-correction step receives two images $\hat {I}$![]() and $I_{\mathrm {ref}}$
and $I_{\mathrm {ref}}$![]() , and it corrects the hue at each pixel of an enhanced image $\hat {I}$
, and it corrects the hue at each pixel of an enhanced image $\hat {I}$![]() so that the hue perfectly matches the hue at a corresponding pixel for $I_{\mathrm {ref}}$
so that the hue perfectly matches the hue at a corresponding pixel for $I_{\mathrm {ref}}$![]() , where the hue definition in the proposed scheme follows $\Delta H'$
, where the hue definition in the proposed scheme follows $\Delta H'$![]() in CIEDE2000. The reference image $I_{\mathrm {ref}}$
in CIEDE2000. The reference image $I_{\mathrm {ref}}$![]() can be any color image that has the same resolution as $\hat {I}$
can be any color image that has the same resolution as $\hat {I}$![]() . For removing hue distortion caused by image enhancement, we use an input image $I$
. For removing hue distortion caused by image enhancement, we use an input image $I$![]() and the corresponding enhanced image as $I_{\mathrm {ref}}$
and the corresponding enhanced image as $I_{\mathrm {ref}}$![]() and $\hat {I}$
and $\hat {I}$![]() , respectively. Any image-enhancement algorithm such as deep-learning-based ones can be used for obtaining $\hat {I}$
, respectively. Any image-enhancement algorithm such as deep-learning-based ones can be used for obtaining $\hat {I}$![]() . Since the hue-correction step is performed on the CIELAB color space, this step will produce images that have out-of-gamut colors of an output RGB color space. Therefore, we map the out-of-gamut colors into the output color space without hue changes by using an existing gamut-mapping method.
. Since the hue-correction step is performed on the CIELAB color space, this step will produce images that have out-of-gamut colors of an output RGB color space. Therefore, we map the out-of-gamut colors into the output color space without hue changes by using an existing gamut-mapping method.
B) Deriving proposed hue correction
As shown in Fig. 1(b), the goal of the proposed hue correction is to obtain a color $\boldsymbol {C} = (L^{*}, a^{*}, b^{*})^{\top }$![]() that satisfies the following conditions.
that satisfies the following conditions.
• $\Delta H'(\boldsymbol {C}, \boldsymbol {C}_{\mathrm {ref}}) = 0$
 ,
,• $\Delta L'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$
 ,
,• $\Delta C'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$
 ,
,
where $\hat {\boldsymbol {C}} = (\hat {L}^{*}, \hat {a}^{*}, \hat {b}^{*})^{\top }$![]() and $\boldsymbol {C}_{\mathrm {ref}} = (L^{*}_{\mathrm {ref}}, a^{*}_{\mathrm {ref}}, b^{*}_{\mathrm {ref}})^{\top }$
and $\boldsymbol {C}_{\mathrm {ref}} = (L^{*}_{\mathrm {ref}}, a^{*}_{\mathrm {ref}}, b^{*}_{\mathrm {ref}})^{\top }$![]() are colors at a pixel of enhanced image $\hat {I}$
are colors at a pixel of enhanced image $\hat {I}$![]() and reference image $I_{\mathrm {ref}}$
and reference image $I_{\mathrm {ref}}$![]() , respectively. Please note that any image enhancement algorithms can be used to obtain $\hat {\boldsymbol {C}}$
, respectively. Please note that any image enhancement algorithms can be used to obtain $\hat {\boldsymbol {C}}$![]() because there are no assumptions about $\hat {\boldsymbol {C}}$
because there are no assumptions about $\hat {\boldsymbol {C}}$![]() .
.
A sufficient condition for $\Delta H'(\boldsymbol {C}, \boldsymbol {C}_{\mathrm {ref}}) = 0$![]() is given from equations (9)–(18) as
is given from equations (9)–(18) as
where $k \ge 0$![]() . From equation (15), a necessary and sufficient condition for $\Delta L'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$
. From equation (15), a necessary and sufficient condition for $\Delta L'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$![]() is
is
In addition, when $\boldsymbol {C}$![]() satisfies equation (19), a necessary and sufficient condition for $\Delta C'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$
satisfies equation (19), a necessary and sufficient condition for $\Delta C'(\boldsymbol {C}, \hat {\boldsymbol {C}}) = 0$![]() is
is
from equations (9)–(13) and (16). Therefore, hue-corrected color $\boldsymbol {C}$![]() is calculated as
is calculated as
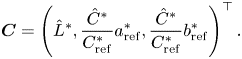
The CIELAB color space has a wider color gamut than RGB color spaces. The difference between color gamuts causes pixel values to be clipped, and the clipping causes output images to be color-distorted. In the next section, we introduce a gamut-mapping method in order to transform color $\boldsymbol {C}$![]() obtained by the hue correction into color in an RGB color space, without hue changes.
obtained by the hue correction into color in an RGB color space, without hue changes.
Algorithm 1 Gamut mapping using bisection method.

C) Deriving gamut-mapping method
Gamut-mapping methods map a color in a wide color space into a narrow color space $\mathcal {D}$![]() so that the color difference between colors before and after the mapping is minimized [Reference Morovič39]. In this paper, we calculate a gamut-mapped color $\boldsymbol {C}_{\mathrm {out}} \in \mathcal {D}$
so that the color difference between colors before and after the mapping is minimized [Reference Morovič39]. In this paper, we calculate a gamut-mapped color $\boldsymbol {C}_{\mathrm {out}} \in \mathcal {D}$![]() such that $\Delta H'(\boldsymbol {C}_{\mathrm {out}}, \boldsymbol {C}) = 0$
such that $\Delta H'(\boldsymbol {C}_{\mathrm {out}}, \boldsymbol {C}) = 0$![]() in order to preserve hue. Furthermore, we assume an additional condition, $\Delta L'(\boldsymbol {C}_{\mathrm {out}}, \boldsymbol {C}) = 0$
in order to preserve hue. Furthermore, we assume an additional condition, $\Delta L'(\boldsymbol {C}_{\mathrm {out}}, \boldsymbol {C}) = 0$![]() , for simplicity.
, for simplicity.
The solution $\boldsymbol {C}_{\mathrm {out}}$![]() is obtained by solving an optimizing problem:
is obtained by solving an optimizing problem:
From equations (19) and (20), equation (23) results in the problem asking for $m'$![]() [see Fig. 1(c)] as follows.
[see Fig. 1(c)] as follows.
In experiments, we utilized the bisection method to solve equation (24). This algorithm is shown in Algorithm 1, where we set $\mathrm {threshold}$![]() as $1/256$
as $1/256$![]() .
.
D) Proposed procedure
The procedure of our hue-correction scheme is shown as follows.
(i) Obtain image $\hat {I}$
 by applying an image-enhancement algorithm to input image $I$
by applying an image-enhancement algorithm to input image $I$ . Here, we can use state-of-the-art image-enhancement algorithms including deep-learning-based ones.
. Here, we can use state-of-the-art image-enhancement algorithms including deep-learning-based ones.(ii) Map RGB pixel values in $\hat {I}$
 and reference image $I_{\mathrm {ref}}$
and reference image $I_{\mathrm {ref}}$ into colors in CIELAB color space $\hat {\boldsymbol {C}} = (\hat {L}^{*}, \hat {a}^{*}, \hat {b}^{*})^{\top }$
into colors in CIELAB color space $\hat {\boldsymbol {C}} = (\hat {L}^{*}, \hat {a}^{*}, \hat {b}^{*})^{\top }$ and $\boldsymbol {C}_{\mathrm {ref}} = (L^{*}_{\mathrm {ref}}, a^{*}_{\mathrm {ref}}, b^{*}_{\mathrm {ref}})^{\top }$
and $\boldsymbol {C}_{\mathrm {ref}} = (L^{*}_{\mathrm {ref}}, a^{*}_{\mathrm {ref}}, b^{*}_{\mathrm {ref}})^{\top }$ in accordance with equations (1), (2), and (5)–(8).
in accordance with equations (1), (2), and (5)–(8).(iii) Obtain hue-corrected color $\boldsymbol {C}$
 by applying hue correction in equation (22) to $\hat {\boldsymbol {C}}$
by applying hue correction in equation (22) to $\hat {\boldsymbol {C}}$ .
.(iv) Obtain color $\boldsymbol {C}_{\mathrm {out}}$
 by applying gamut mapping to $\boldsymbol {C}$
by applying gamut mapping to $\boldsymbol {C}$ by
by
(a) Letting the color gamut of an output RGB color space be $\mathcal {D}$
 and calculating $m'$
and calculating $m'$ in accordance with equation (24).
in accordance with equation (24).(b) Calculating $\boldsymbol {C}_{\mathrm {out}}$
 as $\boldsymbol {C}_{\mathrm {out}} = (\hat {L}^{*}, m' a^{*}_{\mathrm {ref}}, m' b^{*}_{\mathrm {ref}})^{\top }$
as $\boldsymbol {C}_{\mathrm {out}} = (\hat {L}^{*}, m' a^{*}_{\mathrm {ref}}, m' b^{*}_{\mathrm {ref}})^{\top }$ .
.
(v) Map colors $\boldsymbol {C}_{\mathrm {out}}$
 into the output RGB color space, and obtain output image $I_{\mathrm {out}}$
into the output RGB color space, and obtain output image $I_{\mathrm {out}}$ .
.
E) Properties of proposed scheme
The proposed scheme has the following properties:
• The proposed scheme can be applied to any image-enhancement algorithms such as deep-learning-based ones (see Section IV.B).
• Perceptual hue-distortion, on the basis of CIEDE2000, between an enhanced image $\hat {I}$
 and the corresponding input image $I$
and the corresponding input image $I$ can perfectly be removed (see Section IV.B).
can perfectly be removed (see Section IV.B).• The resulting hue-corrected image $I_{\mathrm {out}}$
 has no out-of-gamut colors (see Section IV.C).
has no out-of-gamut colors (see Section IV.C).
In the next section, the three properties of the proposed scheme will be confirmed.
V. SIMULATION
We evaluated the effectiveness of the proposed scheme by using three objective quality metrics including a color difference formula.
A) Simulation conditions
Seven input images selected from a dataset [40] were used for a simulation. In this simulation, the proposed scheme was evaluated in terms of the hue-correction performance and the enhancement performance. To evaluate the hue-correction performance, the hue difference $\Delta H'$![]() defined in CIEDE2000 [26], between an input image and the corresponding enhanced image was calculated.
defined in CIEDE2000 [26], between an input image and the corresponding enhanced image was calculated.
Furthermore, the enhancement performance was also evaluated by using two objective image-quality metrics: discrete entropy and one of the no-reference image-quality metrics for contrast distortion (NIQMC) [Reference Gu, Lin, Zhai, Yang, Zhang and Chen41]. Discrete entropy represents the amount of information in an image. NIQMC assesses the quality of contrast-distorted images by considering both local and global information [Reference Gu, Lin, Zhai, Yang, Zhang and Chen41].
B) Applicability to enhancement algorithms
We first confirmed the applicability of the proposed scheme to image-enhancement algorithms including deep-learning-based ones. Three methods were used in the proposed scheme for enhancement (i.e. for generating $\hat {I}$![]() ): low-light image enhancement via illumination map estimation (LIME) [Reference Guo, Li and Ling10], iTM-Net [Reference Kinoshita and Kiya42], and deep underexposed photo enhancement (DeepUPE) [Reference Ruixing, Zhang, Fu, Shen, Zheng and Jia18], where LIME is a retinex-based algorithm, and the others are deep-learning-based ones. Table 2 shows the hue difference between the input and resulting images. Here, the hue difference was calculated as the absolute average of $\Delta H'$
): low-light image enhancement via illumination map estimation (LIME) [Reference Guo, Li and Ling10], iTM-Net [Reference Kinoshita and Kiya42], and deep underexposed photo enhancement (DeepUPE) [Reference Ruixing, Zhang, Fu, Shen, Zheng and Jia18], where LIME is a retinex-based algorithm, and the others are deep-learning-based ones. Table 2 shows the hue difference between the input and resulting images. Here, the hue difference was calculated as the absolute average of $\Delta H'$![]() for all pixels. The results indicate that the image-enhancement methods caused hue distortion. A comparison between the enhancement methods without any color correction and with the proposed scheme illustrates that the use of the proposed scheme completely removed the hue distortion for all cases.
for all pixels. The results indicate that the image-enhancement methods caused hue distortion. A comparison between the enhancement methods without any color correction and with the proposed scheme illustrates that the use of the proposed scheme completely removed the hue distortion for all cases.
Table 2. Hue difference scores $\Delta H'$![]() for image enhancement methods without any color correction (“w/o corr.’’) and with proposed scheme (“Prop.”).
for image enhancement methods without any color correction (“w/o corr.’’) and with proposed scheme (“Prop.”).
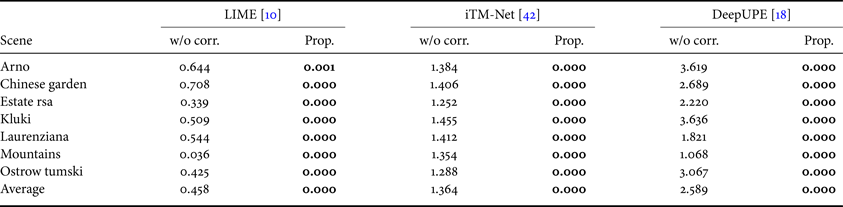
Boldface indicates better score.
Tables 3 and 4 illustrate discrete entropy and statistical naturalness scores, respectively. For each score, a larger value means higher quality. As shown in both tables, the proposed scheme can maintain the performance of image enhancement. This result is also confirmed by comparing Fig. 2(e) with Fig. 2(f).
Table 3. Discrete entropy scores for image-enhancement methods without any color correction (“w/o corr.’’) and with proposed scheme (“Prop.”).
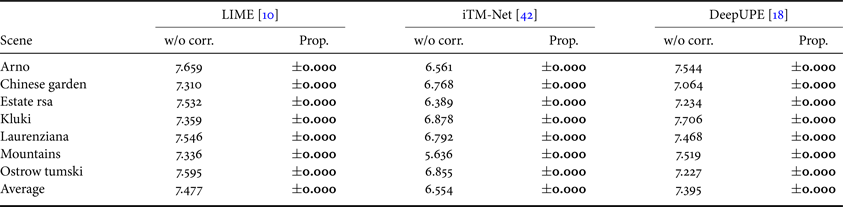
For proposed scheme, difference between scores for “w/o corr.” and “Prop.” are provided.
Boldface indicates difference whose absolute value is less than 0.01.
Table 4. NIQMC scores for image-enhancement methods without any color correction (“w/o corr.’’) and with proposed scheme (“Prop.”).
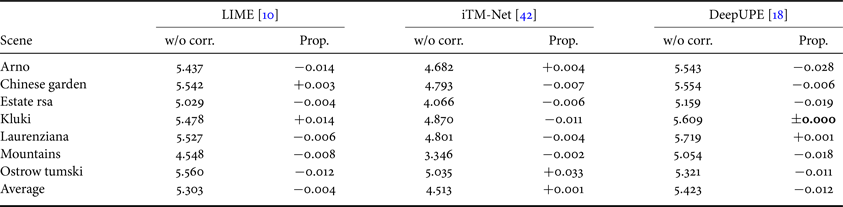
For proposed scheme, difference between scores for “w/o corr.” and “Prop.” are provided.
Boldface indicates difference whose absolute value is less than 0.01.

Fig. 2. Results of hue correction (for image “Arno”.) (a) Input. (b) Naik [Reference Naik and Murthy20]. (c) Ueda [Reference Ueda, Misawa, Koga, Suetake and Uchino22]. (d) Azetsu [Reference Azetsu and Suetake24]. (e) DeepUPE [Reference Ruixing, Zhang, Fu, Shen, Zheng and Jia18]. (f) Prop. w/ DeepUPE.
C) Comparison with hue-preserving enhancement methods
The proposed scheme was also compared with three conventional hue-preserving enhancement methods: Naik's method [Reference Naik and Murthy20], Ueda's method [Reference Ueda, Misawa, Koga, Suetake and Uchino22], and Azetsu's method [Reference Azetsu and Suetake24]. In this simulation, DeepUPE [Reference Ruixing, Zhang, Fu, Shen, Zheng and Jia18] was utilized for the proposed scheme. Table 5 illustrates the hue difference scores. From the table, it is confirmed that the proposed scheme and Azetsu's method could completely remove hue distortion. In contrast, Naik's and Ueda's method could not avoid hue distortion. This is because these methods use a hue definition that does not sufficiently take into account human visual perception. Although Azetsu's method completely avoided hue distortion, its enhancement performance was lower than the proposed scheme in terms of both entropy and NIQMC (see Tables 6 and 7). Entropy and NIQMC scores will be high when the luminance histogram of an image is uniform. These scores for Naik's and Ueda's methods tend to be high because these methods utilize HE-based enhancement algorithms. In contrast, Azetsu's method enhances images by a simple gamma correction that does not consider input images. Hence, the enhancement performance of Azetsu's method depends heavily on input images.
Table 5. Comparison with conventional hue-preserving image-enhancement methods (hue difference $\Delta H'$![]() ).
).
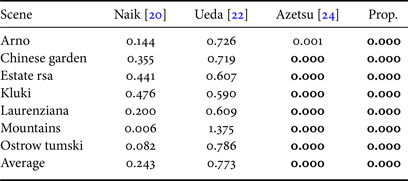
Table 6. Comparison with conventional hue-preserving image-enhancement methods (entropy).
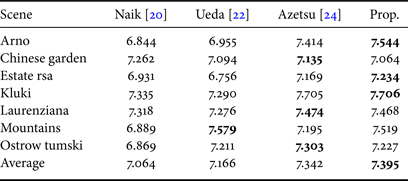
Table 7. Comparison with conventional hue-preserving image-enhancement methods (NIQMC).
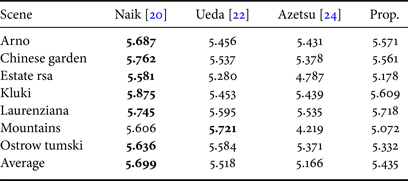
As shown in Tables 8 and 4, the entropy and NIQMC scores of the proposed scheme depended on the enhancement method used in the scheme. Please note that our aim is not to obtain the highest enhancement performance, but to remove hue distortion due to enhancement while maintaining the performance of enhancement algorithms.
Table 8. Hue difference $\Delta H'$![]() between input image and corresponding image enhanced with/without gamut mapping.
between input image and corresponding image enhanced with/without gamut mapping.

Figures 3–5 summarize quantitative evaluation results as box plots for the 500 images in the MIT-Adobe FiveK dataset [Reference Bychkovsky, Paris, Chan and Durand43] in terms of the hue-difference $\Delta H'$![]() , entropy, and NIQMC, respectively. The boxes span from the first to the third quartile, referred to as $Q_1$
, entropy, and NIQMC, respectively. The boxes span from the first to the third quartile, referred to as $Q_1$![]() and $Q_3$
and $Q_3$![]() , and the whiskers show the maximum and the minimum values in the range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$
, and the whiskers show the maximum and the minimum values in the range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$![]() . The band inside boxes indicates the median, i.e. the second quartile $Q_2$
. The band inside boxes indicates the median, i.e. the second quartile $Q_2$![]() , and the cross inside boxes denotes the average value. Figures 3–5 illustrates that the proposed scheme completely removed hue distortion and maintained the performance of the deep-learning-based image-enhancement method.
, and the cross inside boxes denotes the average value. Figures 3–5 illustrates that the proposed scheme completely removed hue distortion and maintained the performance of the deep-learning-based image-enhancement method.
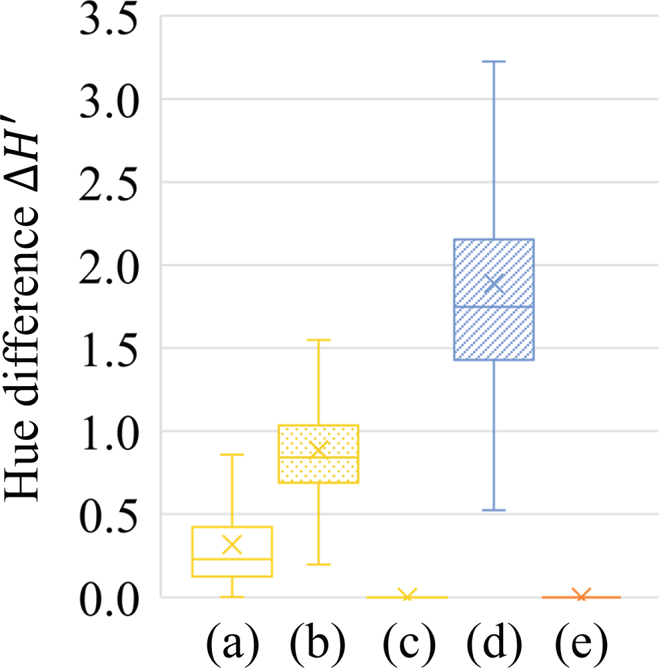
Fig. 3. Comparison with conventional hue-preserving image-enhancement methods using 500 images in MIT-Adobe FiveK dataset [Reference Bychkovsky, Paris, Chan and Durand43] (hue difference $\Delta H'$![]() ). (a) Naik's method, (b) Ueda's method, (c) Azetsu's method, (d) deepUPE, and (e) deepUPE with proposed scheme. Boxes span from first to third quartile, referred to as $Q_1$
). (a) Naik's method, (b) Ueda's method, (c) Azetsu's method, (d) deepUPE, and (e) deepUPE with proposed scheme. Boxes span from first to third quartile, referred to as $Q_1$![]() and $Q_3$
and $Q_3$![]() , and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$
, and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$![]() . Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to completely remove hue distortion caused by any of image-enhancement methods.
. Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to completely remove hue distortion caused by any of image-enhancement methods.
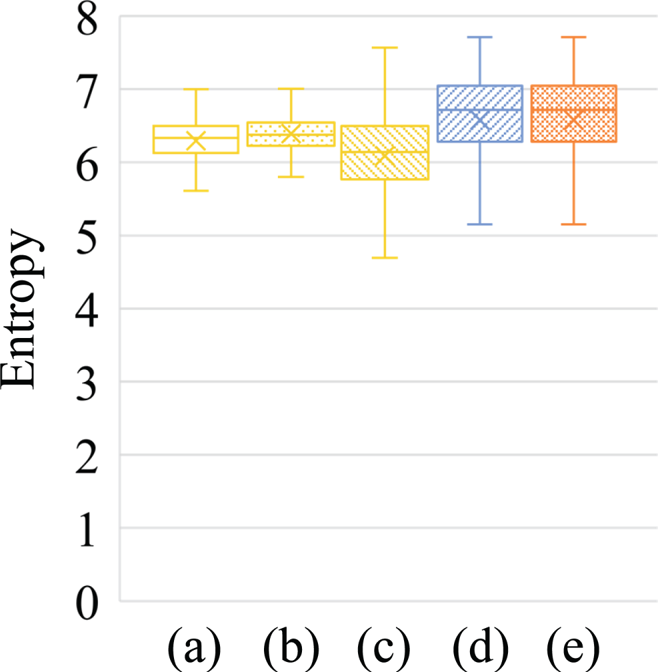
Fig. 4. Comparison with conventional hue-preserving image-enhancement methods using 500 images in MIT-Adobe FiveK dataset [Reference Bychkovsky, Paris, Chan and Durand43] (Entropy). (a) Naik's method, (b) Ueda's method, (c) Azetsu's method, (d) deepUPE, and (e) deepUPE with proposed scheme. Boxes span from first to third quartile, referred to as $Q_1$![]() and $Q_3$
and $Q_3$![]() , and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$
, and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$![]() . Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to maintain image enhancement performance.
. Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to maintain image enhancement performance.
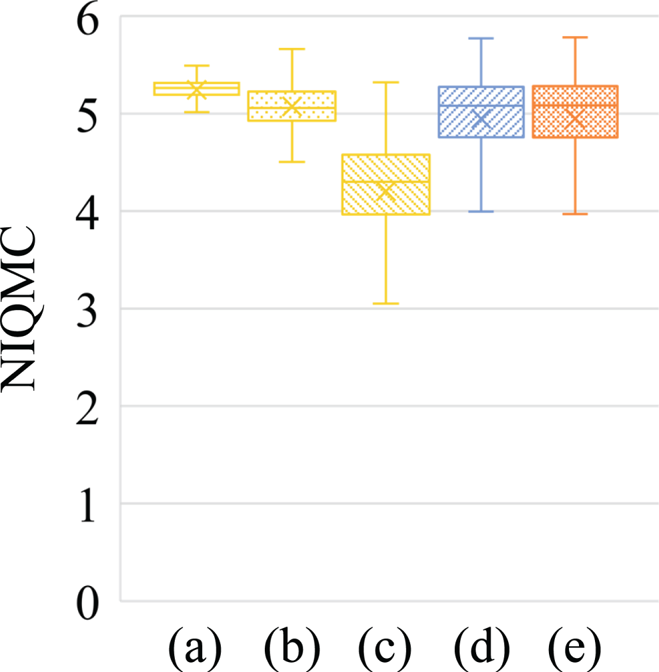
Fig. 5. Comparison with conventional hue-preserving image-enhancement methods using 500 images in MIT-Adobe FiveK dataset [Reference Bychkovsky, Paris, Chan and Durand43] (NIQMC). (a) Naik's method, (b) Ueda's method, (c) Azetsu's method, (d) deepUPE, and (e) deepUPE with proposed scheme. Boxes span from first to third quartile, referred to as $Q_1$![]() and $Q_3$
and $Q_3$![]() , and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$
, and whiskers show maximum and minimum values in range of $[Q_1 - 1.5(Q_3 - Q_1), Q_3 + 1.5(Q_3 - Q_1)]$![]() . Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to maintain image enhancement performance.
. Band and cross inside boxes indicate median and average value, respectively. Use of proposed scheme enabled us to maintain image enhancement performance.
For these reasons, it was confirmed that the proposed hue-correction scheme can completely remove hue distortion caused by image-enhancement algorithms while maintaining the performance of image enhancement. Furthermore, the proposed scheme is applicable to any image-enhancement algorithm including state-of-the-art deep-learning-based ones.
D) Effect of gamut mapping
Table 8 shows hue difference scores $\Delta H'$![]() between input images and the corresponding images enhanced by the proposed scheme with/without gamut mapping, where LIME [Reference Guo, Li and Ling10] was utilized as an image-enhancement algorithm. From the table, it is confirmed that the proposed scheme without the gamut mapping did not completely remove hue distortion but the proposed scheme with the gamut mapping did. This hue distortion is due to the clipping of out-of-gamut colors in the color space conversion process from the CIELAB color space to the sRGB color space. For this reason, it is showed that the gamut mapping in the proposed scheme is effective to avoid hue distortion due to color space conversion.
between input images and the corresponding images enhanced by the proposed scheme with/without gamut mapping, where LIME [Reference Guo, Li and Ling10] was utilized as an image-enhancement algorithm. From the table, it is confirmed that the proposed scheme without the gamut mapping did not completely remove hue distortion but the proposed scheme with the gamut mapping did. This hue distortion is due to the clipping of out-of-gamut colors in the color space conversion process from the CIELAB color space to the sRGB color space. For this reason, it is showed that the gamut mapping in the proposed scheme is effective to avoid hue distortion due to color space conversion.
VI. CONCLUSION
In this paper, we proposed a novel hue-correction scheme based on CIEDE2000. The proposed scheme removes hue distortion caused by image-enhancement algorithms so that the hue difference, which is defined in CIEDE2000, between an enhanced image and a reference image becomes zero. In addition, applying hue-preserving gamut-mapping enables us to compress the color gamut of the CIELAB color space into the color gamut of an output RGB color space. Experimental results showed that images corrected by the proposed scheme have completely the same hue as those of reference images (i.e. input images), but those with conventional hue-preserving methods do not. Furthermore, the proposed scheme can maintain the performance of image-enhancement algorithms in terms of discrete entropy and NIQMC. This result indicates that the use of the proposed scheme enables us to make all image-enhancement algorithms including deep-learning-based ones be hue-preserving ones.
FINANCIAL SUPPORT
This work was supported by JSPS KAKENHI Grant Number JP18J20326.
STATEMENT OF INTEREST
None.
Yuma Kinoshita received the B.Eng., M.Eng., and the Ph.D. degrees from Tokyo Metropolitan University, Japan, in 2016, 2018, and 2020 respectively. From April 2020, he worked as a Project Assistant Professor at Tokyo Metropolitan University. His research interest is in the area of signal processing, image processing, and machine learning. He is a Member of IEEE, APSIPA, and IEICE. He received the IEEE ISPACS Best Paper Award, in 2016, the IEEE Signal Processing Society Japan Student Conference Paper Award, in 2018, the IEEE Signal Processing Society Tokyo Joint Chapter Student Award, in 2018, the IEEE GCCE Excellent Paper Award (Gold Prize), in 2019, and the IWAIT Best Paper Award, in 2020.
Hitoshi Kiya received his B.E and M.E. degrees from Nagaoka University of Technology, in 1980 and 1982, respectively, and his Dr. Eng. degree from Tokyo Metropolitan University in 1987. In 1982, he joined Tokyo Metropolitan University, where he became Full Professor in 2000. From 1995 to 1996, he attended the University of Sydney, Australia as a Visiting Fellow. He is a Fellow of IEEE, IEICE, and ITE. He currently serves as President of APSIPA, and he served as Inaugural Vice President (Technical Activities) of APSIPA in 2009–2013, and as Regional Director-at-Large for Region 10 of the IEEE Signal Processing Society in 2016–2017. He was also President of IEICE Engineering Sciences Society in 2011–2012, and he served there as Vice President and Editor-in-Chief for IEICE Society Magazine and Society Publications. He was Editorial Board Member of eight journals, including IEEE Trans. on Signal Processing, Image Processing, and Information Forensics and Security, and Chair of two technical committees and Member of nine technical committees, including the APSIPA Image, Video, and Multimedia Technical Committee (TC) and IEEE Information Forensics and Security TC. He has organized a lot of international conferences in such roles as TPC Chair of IEEE ICASSP 2012 and as General Co-Chair of IEEE ISCAS 2019. Dr. Kiya has received numerous awards, including 10 best paper awards.































