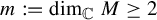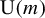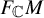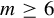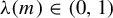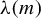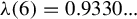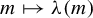1 Introduction
1.1 Ergodicity and mixing of unitary frame flows
Let
![]() $(M,g,J)$
be a smooth closed (compact, without boundary) Kähler manifold with negative sectional curvature and complex dimension
$(M,g,J)$
be a smooth closed (compact, without boundary) Kähler manifold with negative sectional curvature and complex dimension
![]() $m \geq 2$
. Let
$m \geq 2$
. Let
![]() $SM \to M$
be the unit tangent bundle and let
$SM \to M$
be the unit tangent bundle and let
![]() $F_{\mathbb {C}}M \to M$
be the principal
$F_{\mathbb {C}}M \to M$
be the principal
![]() $\mathrm {U}(m)$
-bundle of unitary bases over M. A point
$\mathrm {U}(m)$
-bundle of unitary bases over M. A point
![]() $w \in F_{\mathbb {C}}M$
over
$w \in F_{\mathbb {C}}M$
over
![]() $x \in M$
is the data of an orthonormal basis
$x \in M$
is the data of an orthonormal basis
![]() $(v, \operatorname {\mathrm {\mathbf {e}}}_2, \ldots , \operatorname {\mathrm {\mathbf {e}}}_{m})$
of
$(v, \operatorname {\mathrm {\mathbf {e}}}_2, \ldots , \operatorname {\mathrm {\mathbf {e}}}_{m})$
of
![]() $(T_xM, h_x)$
, where
$(T_xM, h_x)$
, where
![]() $h_x(\cdot , \cdot ) = g_x(\cdot , \cdot ) + ig_x(\cdot , J_x \cdot )$
is the canonical Hermitian inner product on the fibres of
$h_x(\cdot , \cdot ) = g_x(\cdot , \cdot ) + ig_x(\cdot , J_x \cdot )$
is the canonical Hermitian inner product on the fibres of
![]() $TM$
. Equivalently, we will see
$TM$
. Equivalently, we will see
![]() $F_{\mathbb {C}}M$
as a principal
$F_{\mathbb {C}}M$
as a principal
![]() $\mathrm {U}(m - 1)$
-bundle over
$\mathrm {U}(m - 1)$
-bundle over
![]() $SM$
by the projection map
$SM$
by the projection map
![]() $p : F_{\mathbb {C}}M \to SM$
defined as
$p : F_{\mathbb {C}}M \to SM$
defined as
![]() $p (v,\operatorname {\mathrm {\mathbf {e}}}_2,\ldots ,\operatorname {\mathrm {\mathbf {e}}}_{m}) = v$
.
$p (v,\operatorname {\mathrm {\mathbf {e}}}_2,\ldots ,\operatorname {\mathrm {\mathbf {e}}}_{m}) = v$
.
The geodesic flow
![]() $(\varphi _t)_{t \in \mathbb {R}}$
on
$(\varphi _t)_{t \in \mathbb {R}}$
on
![]() $SM$
is defined as
$SM$
is defined as
![]() $\varphi _t(v) :=\dot {\gamma }_{v}(t)$
, where
$\varphi _t(v) :=\dot {\gamma }_{v}(t)$
, where
![]() $t \mapsto \gamma _{v}(t) \in M$
is the geodesic generated by
$t \mapsto \gamma _{v}(t) \in M$
is the geodesic generated by
![]() $v\in SM$
. The unitary frame flow on
$v\in SM$
. The unitary frame flow on
![]() $F_{\mathbb {C}}M$
is then defined as
$F_{\mathbb {C}}M$
is then defined as
where
![]() $P_{\gamma _{v}(t)} : T_x M \to T_{\gamma _{v}(t)}M$
is the parallel transport along
$P_{\gamma _{v}(t)} : T_x M \to T_{\gamma _{v}(t)}M$
is the parallel transport along
![]() $\gamma _{v}$
with respect to the Levi-Civita connection.
$\gamma _{v}$
with respect to the Levi-Civita connection.
Recall that a flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
on a compact metric space
$(\Phi _t)_{t \in \mathbb {R}}$
on a compact metric space
![]() $\mathcal {M}$
is said to be ergodic with respect to an invariant probability measure
$\mathcal {M}$
is said to be ergodic with respect to an invariant probability measure
![]() $\mu $
if any flow-invariant function
$\mu $
if any flow-invariant function
![]() $f \in L^2(\mu )$
is constant. It is said to be mixing if for all
$f \in L^2(\mu )$
is constant. It is said to be mixing if for all
![]() $f_1, f_2 \in L^2(\mathcal {M},\mu )$
,
$f_1, f_2 \in L^2(\mathcal {M},\mu )$
,
The geodesic flow
![]() $(\varphi _t)_{t \in \mathbb {R}}$
of any negatively curved compact Riemannian manifold is well known to be ergodic [Reference AnosovAno67, Reference HopfHop36] with respect to the Liouville measure on
$(\varphi _t)_{t \in \mathbb {R}}$
of any negatively curved compact Riemannian manifold is well known to be ergodic [Reference AnosovAno67, Reference HopfHop36] with respect to the Liouville measure on
![]() $SM$
. However, for extensions of the geodesic flow to principal bundles, ergodicity is a more subtle question since these flows are only partially hyperbolic, not uniformly hyperbolic. The unitary frame flow
$SM$
. However, for extensions of the geodesic flow to principal bundles, ergodicity is a more subtle question since these flows are only partially hyperbolic, not uniformly hyperbolic. The unitary frame flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
defined above is such an extension of
$(\Phi _t)_{t \in \mathbb {R}}$
defined above is such an extension of
![]() $(\varphi _t)_{t \in \mathbb {R}}$
to
$(\varphi _t)_{t \in \mathbb {R}}$
to
![]() $F_{\mathbb {C}}M$
; it preserves a natural flow-invariant smooth measure
$F_{\mathbb {C}}M$
; it preserves a natural flow-invariant smooth measure
![]() $\omega $
induced by the Liouville measure and the Haar measure on the group
$\omega $
induced by the Liouville measure and the Haar measure on the group
![]() $\mathrm {U}(m-1)$
. The purpose of this paper is to investigate ergodicity of
$\mathrm {U}(m-1)$
. The purpose of this paper is to investigate ergodicity of
![]() $(\Phi _t)_{t \in \mathbb {R}}$
with respect to
$(\Phi _t)_{t \in \mathbb {R}}$
with respect to
![]() $\omega $
. It was proved by Brin and Gromov [Reference Brin and GromovBG80] that this flow is ergodic whenever
$\omega $
. It was proved by Brin and Gromov [Reference Brin and GromovBG80] that this flow is ergodic whenever
![]() $m:=\dim _{\mathbb {C}} M$
is odd or
$m:=\dim _{\mathbb {C}} M$
is odd or
![]() $m=2$
but the even-dimensional case when
$m=2$
but the even-dimensional case when
![]() $m\ge 4$
has remained open so far. Our aim is to bring a first positive answer when
$m\ge 4$
has remained open so far. Our aim is to bring a first positive answer when
![]() $m\ge 6$
is even and
$m\ge 6$
is even and
![]() $m \neq 28$
, under some pinching hypothesis for the sectional curvature.
$m \neq 28$
, under some pinching hypothesis for the sectional curvature.
Recall that the holomorphic sectional curvature of
![]() $(M,g,J)$
is defined as
$(M,g,J)$
is defined as
for all unit vectors
![]() $X \in TM$
, where R is the Riemann curvature tensor of
$X \in TM$
, where R is the Riemann curvature tensor of
![]() $(M,g)$
. The manifold is said to be holomorphically
$(M,g)$
. The manifold is said to be holomorphically
![]() $\unicode{x3bb} $
-pinched, for some
$\unicode{x3bb} $
-pinched, for some
![]() $\unicode{x3bb} \in (0, 1]$
, if there exists a constant
$\unicode{x3bb} \in (0, 1]$
, if there exists a constant
![]() $C> 0$
such that
$C> 0$
such that
for every unit vector X. The manifold is said to be strictly holomorphically
![]() $\unicode{x3bb} $
-pinched if the above inequalities are strict.
$\unicode{x3bb} $
-pinched if the above inequalities are strict.
To state our main result, we introduce the function
![]() $m \mapsto \unicode{x3bb} (m)$
, defined for even numbers
$m \mapsto \unicode{x3bb} (m)$
, defined for even numbers
![]() $m \geq 6$
by
$m \geq 6$
by
The function
![]() $m \mapsto \unicode{x3bb} (m)$
is decreasing,
$m \mapsto \unicode{x3bb} (m)$
is decreasing,
![]() $\unicode{x3bb} (6) = 0.9330...$
and
$\unicode{x3bb} (6) = 0.9330...$
and
![]() $\lim _{m \to +\infty } \unicode{x3bb} (m) = {11}/{12} = 0.9166...$
.
$\lim _{m \to +\infty } \unicode{x3bb} (m) = {11}/{12} = 0.9166...$
.
We will prove that the following theorem holds.
Theorem 1.1. Let
![]() $(M,g,J)$
be a closed connected Kähler manifold of complex dimension
$(M,g,J)$
be a closed connected Kähler manifold of complex dimension
![]() $m \geq 2$
, with negative sectional curvature. The unitary frame flow
$m \geq 2$
, with negative sectional curvature. The unitary frame flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
on
$(\Phi _t)_{t \in \mathbb {R}}$
on
![]() $F_{\mathbb {C}}M$
is ergodic and mixing with respect to the smooth measure
$F_{\mathbb {C}}M$
is ergodic and mixing with respect to the smooth measure
![]() $\omega $
if:
$\omega $
if:
-
(i) the complex dimension m is odd or
 $m=2$
[Reference Brin and GromovBG80];
$m=2$
[Reference Brin and GromovBG80]; -
(ii) the complex dimension
 $m\ge 6$
is even,
$m\ge 6$
is even,
 $m \neq 28$
, and the manifold is strictly holomorphically
$m \neq 28$
, and the manifold is strictly holomorphically
 $\unicode{x3bb} (m)$
-pinched.
$\unicode{x3bb} (m)$
-pinched.
We will actually show that the unitary frame flow is ergodic if and only if it is mixing. We believe that ergodicity should hold without any pinching condition but it is clear from the proofs that our method only works with a pinching condition close to
![]() $1$
. As a comparison, Brin conjectured that the real frame flow should be ergodic on negatively curved manifolds with
$1$
. As a comparison, Brin conjectured that the real frame flow should be ergodic on negatively curved manifolds with
![]() $0.25$
-pinched real sectional curvature (see [Reference Brin and KatokBri82, Conjecture 2.6]). (In the literature, the word ‘frame flow’ usually refers to what we call here the ‘real frame flow’, that is, the parallel transport of all bases regardless of any almost-complex structure. We added the word ‘unitary’ in the Kähler case and ‘real’ in the Riemannian case to make a distinction.)
$0.25$
-pinched real sectional curvature (see [Reference Brin and KatokBri82, Conjecture 2.6]). (In the literature, the word ‘frame flow’ usually refers to what we call here the ‘real frame flow’, that is, the parallel transport of all bases regardless of any almost-complex structure. We added the word ‘unitary’ in the Kähler case and ‘real’ in the Riemannian case to make a distinction.)
In the case of constant holomorphic curvature
![]() $H = -1$
(that is, on compact quotients
$H = -1$
(that is, on compact quotients
![]() $\Gamma \backslash \mathbb {C}\mathbb {H}^m$
of the complex hyperbolic space), the ergodicity of unitary frame flow was shown by Howe and Moore [Reference Howe and MooreHM79]. In non-constant holomorphic curvature, besides [Reference Brin and GromovBG80] in odd complex dimensions and
$\Gamma \backslash \mathbb {C}\mathbb {H}^m$
of the complex hyperbolic space), the ergodicity of unitary frame flow was shown by Howe and Moore [Reference Howe and MooreHM79]. In non-constant holomorphic curvature, besides [Reference Brin and GromovBG80] in odd complex dimensions and
![]() $m=2$
, Theorem 1.1 seems to be the first result proving ergodicity of unitary frame flows on negatively curved Kähler manifolds of even complex dimensions
$m=2$
, Theorem 1.1 seems to be the first result proving ergodicity of unitary frame flows on negatively curved Kähler manifolds of even complex dimensions
![]() $m\ge 6$
.
$m\ge 6$
.
As indicated in Theorem 1.1, it also seems that our technique does not apply in complex dimensions
![]() $m=4$
and
$m=4$
and
![]() $m=28$
. The former case is related to the fact that
$m=28$
. The former case is related to the fact that
![]() $S^7$
is parallelizable, whereas the latter case is connected to an open problem in algebraic topology which is to classify reductions of the structure group of the unitary frame bundle
$S^7$
is parallelizable, whereas the latter case is connected to an open problem in algebraic topology which is to classify reductions of the structure group of the unitary frame bundle
![]() $F_{\mathbb {C}}S^{55}$
over the sphere
$F_{\mathbb {C}}S^{55}$
over the sphere
![]() $S^{55}$
. More precisely, we are unable to rule out the possible existence of a special
$S^{55}$
. More precisely, we are unable to rule out the possible existence of a special
![]() $\mathrm {E}_6$
-structure on
$\mathrm {E}_6$
-structure on
![]() $S^{55}$
and this eventually turns out to be problematic to run our argument, see §3 where this is further discussed.
$S^{55}$
and this eventually turns out to be problematic to run our argument, see §3 where this is further discussed.
The structure of the argument, described in more detail in §1.2, is somewhat similar to our previous article [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21] proving ergodicity of real frame flows on negatively curved compact Riemannian manifolds of even real dimensions with nearly
![]() $0.25$
-pinched (real) sectional curvature, thus almost answering the long-standing [Reference Brin and KatokBri82, Conjecture 2.6] of Brin mentioned above. Nevertheless, the present article is not a mere adaptation of [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21] as we had to develop new techniques to take into account the specificities of the Kähler setting, see Theorem 3.1, §3.2 or §5.3 for instance. Although it is meant to be self-contained, we encourage the reader to consult [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS22, Reference LefeuvreLef23] as we build here on the framework developed in these articles.
$0.25$
-pinched (real) sectional curvature, thus almost answering the long-standing [Reference Brin and KatokBri82, Conjecture 2.6] of Brin mentioned above. Nevertheless, the present article is not a mere adaptation of [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21] as we had to develop new techniques to take into account the specificities of the Kähler setting, see Theorem 3.1, §3.2 or §5.3 for instance. Although it is meant to be self-contained, we encourage the reader to consult [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS22, Reference LefeuvreLef23] as we build here on the framework developed in these articles.
Prior to [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21], the real frame flow was known to be ergodic on negatively curved Riemannian manifolds of odd dimension
![]() $\neq 7$
by Brin and Gromov [Reference Brin and GromovBG80, Reference BrinBri75b], and in even dimensions (and in dimension
$\neq 7$
by Brin and Gromov [Reference Brin and GromovBG80, Reference BrinBri75b], and in even dimensions (and in dimension
![]() $7$
) for manifolds with a pinching close to
$7$
) for manifolds with a pinching close to
![]() $1$
by Brin and Karcher [Reference Brin and KarcherBK84] and Burns and Pollicott [Reference Burns and PollicottBP03].
$1$
by Brin and Karcher [Reference Brin and KarcherBK84] and Burns and Pollicott [Reference Burns and PollicottBP03].
The real frame flows are historically important examples of partially hyperbolic flows studied in the aftermath of Anosov’s seminal work on hyperbolic flows [Reference AnosovAno67] by Brin and Pesin [Reference Brin and PesinBP74, Reference BrinBri75b, Reference BrinBri75a]. The field of partially hyperbolic dynamical systems is now a well-established and active field of dynamical systems, see [Reference Hasselblatt, Pesin, Katok and HasselblattHP06] for instance for an introduction to this topic.
Finally, let us mention that, similarly to the real case where ergodicity of the real frame flow was shown to determine the high-energy behaviour of eigenfunctions of Dirac-type operators [Reference Jakobson and StrohmaierJS07], the ergodicity of the unitary frame flow on Kähler manifolds determines the high-energy behaviour of eigenfunctions of Dolbeault Laplacians and Spin
![]() ${}^c$
Dirac operators [Reference Jakobson, Strohmaier and ZelditchJSZ08].
${}^c$
Dirac operators [Reference Jakobson, Strohmaier and ZelditchJSZ08].
1.2 Proof ideas
Let us summarize the argument which, as mentioned above, is similar to that developed in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21] and consists of three steps.
-
(i) Hyperbolic dynamics. Following Brin’s ideas [Reference BrinBri75b] (see also [Reference LefeuvreLef23] for a more recent approach), the non-ergodicity of the unitary frame flow is described by means of a subgroup
 $H \lneqq \mathrm {U}(m-1)$
called the transitivity group, see §2.3. In particular, there exists a smooth flow-invariant principal H-subbundle
$H \lneqq \mathrm {U}(m-1)$
called the transitivity group, see §2.3. In particular, there exists a smooth flow-invariant principal H-subbundle
 $Q \subset F_{\mathbb {C}} M$
over
$Q \subset F_{\mathbb {C}} M$
over
 $SM$
, such that the restriction of
$SM$
, such that the restriction of
 $(\Phi _t)_{t \in \mathbb {R}}$
to Q is ergodic.
$(\Phi _t)_{t \in \mathbb {R}}$
to Q is ergodic. -
(ii) Algebraic topology. The group H thus provides a reduction of the structure group of
 $F_{\mathbb {C}}M$
from
$F_{\mathbb {C}}M$
from
 $\mathrm {U}(m-1)$
to H. In particular, restricting to a point
$\mathrm {U}(m-1)$
to H. In particular, restricting to a point
 $x_0 \in M$
and identifying
$x_0 \in M$
and identifying
 $S_{x_0}M \simeq S^{2m-1}$
, the unitary frame bundle
$S_{x_0}M \simeq S^{2m-1}$
, the unitary frame bundle
 $F_{\mathbb {C}}S^{2m-1} \to S^{2m-1}$
must admit a reduction of its structure group to H. In §3, we classify such reductions and show that for
$F_{\mathbb {C}}S^{2m-1} \to S^{2m-1}$
must admit a reduction of its structure group to H. In §3, we classify such reductions and show that for
 $m \neq 4,28$
, H must act reducibly on
$m \neq 4,28$
, H must act reducibly on
 $\mathbb {C}^{m-1}$
.
$\mathbb {C}^{m-1}$
. -
(iii) Riemannian geometry. Using the non-Abelian Livšic theorem of [Reference Cekić and LefeuvreCL22], we then deduce that there exists a smooth flow-invariant complex vector bundle
 $\mathcal {V} \to SM$
which is a subbundle
$\mathcal {V} \to SM$
which is a subbundle
 $\mathcal {V} \subset \pi ^*TM$
(where
$\mathcal {V} \subset \pi ^*TM$
(where
 $\pi : SM \to M$
is the projection) satisfying certain algebraic properties. In turn, using the twisted Pestov identity (see Lemma 2.1), we rule out the existence of such an object under a certain pinching condition
$\pi : SM \to M$
is the projection) satisfying certain algebraic properties. In turn, using the twisted Pestov identity (see Lemma 2.1), we rule out the existence of such an object under a certain pinching condition
 $\unicode{x3bb}> \unicode{x3bb} (m)$
in §§4 and 5.
$\unicode{x3bb}> \unicode{x3bb} (m)$
in §§4 and 5.
1.3 Structure of the article
In §2, we recall standard facts from Riemannian and complex geometry, and (partially) hyperbolic dynamical systems needed in the rest of the article. In §3, we study the possible reductions of the structure group of the unitary frame bundle over the sphere, and deduce the existence of non-zero flow-invariant projectors whenever the frame flow is not ergodic. In §4, we derive, using the twisted Pestov identity, an inequality that must be satisfied by such an invariant object. In §5, we complete the proof of Theorem 1.1.
2 Preliminaries
2.1 Riemannian geometry of the unit tangent bundle
Let
![]() $(M,g)$
be a closed connected Riemannian manifold of real dimension n. Denote by
$(M,g)$
be a closed connected Riemannian manifold of real dimension n. Denote by
the unit tangent bundle of
![]() $(M,g)$
and by
$(M,g)$
and by
![]() $\pi : SM \to M$
the projection map.
$\pi : SM \to M$
the projection map.
2.1.1 Tangent bundle of
 $SM$
$SM$
Let
![]() $(\varphi _t)_{t \in \mathbb {R}}$
be the geodesic flow on
$(\varphi _t)_{t \in \mathbb {R}}$
be the geodesic flow on
![]() $SM$
with generating vector field
$SM$
with generating vector field
![]() $X \in C^\infty (SM,T(SM))$
. The tangent bundle
$X \in C^\infty (SM,T(SM))$
. The tangent bundle
![]() $T(SM)$
splits as
$T(SM)$
splits as
where
![]() $\mathbb {V} := \ker \mathrm {d}\pi $
is the vertical bundle, and
$\mathbb {V} := \ker \mathrm {d}\pi $
is the vertical bundle, and
![]() $\mathbb {H}$
is the horizontal bundle defined by means of the Levi-Civita connection, see [Reference PaternainPat99, Ch. 1]. The metric g induces a canonical metric on
$\mathbb {H}$
is the horizontal bundle defined by means of the Levi-Civita connection, see [Reference PaternainPat99, Ch. 1]. The metric g induces a canonical metric on
![]() $T(SM)$
called the Sasaki metric such that the splitting equation (2.1) is orthogonal.
$T(SM)$
called the Sasaki metric such that the splitting equation (2.1) is orthogonal.
If
![]() $f \in C^\infty (SM)$
is a smooth function, its gradient
$f \in C^\infty (SM)$
is a smooth function, its gradient
![]() $\nabla f \in C^\infty (SM,T(SM))$
computed with respect to the Sasaki metric splits according to equation (2.1) as
$\nabla f \in C^\infty (SM,T(SM))$
computed with respect to the Sasaki metric splits according to equation (2.1) as
where
![]() $\nabla _{\mathbb {V}} f \in C^\infty (SM, \mathbb {V})$
is the vertical gradient and
$\nabla _{\mathbb {V}} f \in C^\infty (SM, \mathbb {V})$
is the vertical gradient and
![]() $\nabla _{\mathbb {H}}f \in C^\infty (SM,\mathbb {H})$
is the horizontal gradient. The
$\nabla _{\mathbb {H}}f \in C^\infty (SM,\mathbb {H})$
is the horizontal gradient. The
![]() $L^2$
-norm on
$L^2$
-norm on
![]() $SM$
is defined using the Liouville measure
$SM$
is defined using the Liouville measure
![]() $\mu $
on
$\mu $
on
![]() $SM$
which is the Riemannian measure induced by the Sasaki metric. Note that the Liouville measure is invariant by the geodesic flow.
$SM$
which is the Riemannian measure induced by the Sasaki metric. Note that the Liouville measure is invariant by the geodesic flow.
The vertical Laplacian
![]() $\Delta _{\mathbb {V}}$
is then defined as
$\Delta _{\mathbb {V}}$
is then defined as
![]() $\Delta _{\mathbb {V}} := \nabla _{\mathbb {V}}^* \nabla _{\mathbb {V}}$
, where
$\Delta _{\mathbb {V}} := \nabla _{\mathbb {V}}^* \nabla _{\mathbb {V}}$
, where
![]() $\nabla _{\mathbb {V}}^*$
denotes the
$\nabla _{\mathbb {V}}^*$
denotes the
![]() $L^2$
-adjoint. Equivalently, given
$L^2$
-adjoint. Equivalently, given
![]() $f \in C^\infty (SM)$
and
$f \in C^\infty (SM)$
and
![]() $x \in M$
, denoting the Laplacian of the restriction of
$x \in M$
, denoting the Laplacian of the restriction of
![]() $g_x$
to
$g_x$
to
![]() $S_xM$
by
$S_xM$
by
![]() $\Delta _{S_xM}$
,
$\Delta _{S_xM}$
,
2.1.2 Fourier decomposition in the fibres
Since
![]() $\pi : SM \to M$
is a sphere bundle, any smooth function
$\pi : SM \to M$
is a sphere bundle, any smooth function
![]() $f \in C^\infty (SM)$
can be decomposed into a sum of spherical harmonics on the sphere
$f \in C^\infty (SM)$
can be decomposed into a sum of spherical harmonics on the sphere
![]() $S_xM \simeq S^{n-1}$
above each point
$S_xM \simeq S^{n-1}$
above each point
![]() $x \in M$
. In other words, we can write
$x \in M$
. In other words, we can write
 $$ \begin{align*} f = \sum_{k=0}^{+\infty} f_k, \end{align*} $$
$$ \begin{align*} f = \sum_{k=0}^{+\infty} f_k, \end{align*} $$
where
![]() $f_k \in C^\infty (SM)$
is a spherical harmonic of degree
$f_k \in C^\infty (SM)$
is a spherical harmonic of degree
![]() $k \geq 0$
, that is, it satisfies the eigenvalue equation
$k \geq 0$
, that is, it satisfies the eigenvalue equation
where
![]() $\Delta _{\mathbb {V}}$
is the vertical Laplacian on each sphere
$\Delta _{\mathbb {V}}$
is the vertical Laplacian on each sphere
![]() $S_xM$
(for
$S_xM$
(for
![]() $x \in M$
) introduced in equation (2.2). The space of spherical harmonics of degree k over M defines a vector bundle
$x \in M$
) introduced in equation (2.2). The space of spherical harmonics of degree k over M defines a vector bundle
![]() $\Omega _k \to M$
which can be naturally identified with the vector bundle of trace-free symmetric k-tensors
$\Omega _k \to M$
which can be naturally identified with the vector bundle of trace-free symmetric k-tensors
![]() $S^k_0 TM \to M$
via the map (here we identify
$S^k_0 TM \to M$
via the map (here we identify
![]() $T^*M$
and
$T^*M$
and
![]() $TM$
by using the metric g)
$TM$
by using the metric g)
More generally, let
![]() $(E, h) \to M$
be a Hermitian (or Euclidean) vector bundle over M equipped with a unitary (or orthogonal) connection
$(E, h) \to M$
be a Hermitian (or Euclidean) vector bundle over M equipped with a unitary (or orthogonal) connection
![]() $\nabla ^E$
, by which we mean that
$\nabla ^E$
, by which we mean that
Denoting by
![]() $(\mathcal {E},\nabla ^{{\mathcal {E}}}) := (\pi ^* E,\pi ^*\nabla ^{E})$
the pullback of
$(\mathcal {E},\nabla ^{{\mathcal {E}}}) := (\pi ^* E,\pi ^*\nabla ^{E})$
the pullback of
![]() $(E,\nabla ^E)$
to
$(E,\nabla ^E)$
to
![]() $SM$
, any section
$SM$
, any section
![]() $f \in C^\infty (SM,\mathcal {E})$
can be uniquely decomposed into a sum of twisted spherical harmonics over each point
$f \in C^\infty (SM,\mathcal {E})$
can be uniquely decomposed into a sum of twisted spherical harmonics over each point
![]() $x \in M$
, that is,
$x \in M$
, that is,
 $$ \begin{align} f = \sum_{k=0}^{+\infty} f_k, \end{align} $$
$$ \begin{align} f = \sum_{k=0}^{+\infty} f_k, \end{align} $$
where
![]() $f_k \in C^\infty (SM,\mathcal {E})$
is a spherical harmonic of degree k (with values in
$f_k \in C^\infty (SM,\mathcal {E})$
is a spherical harmonic of degree k (with values in
![]() $\mathcal {E}$
). Note that, with respect to an orthonormal basis
$\mathcal {E}$
). Note that, with respect to an orthonormal basis
![]() $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
on E defined locally over
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
on E defined locally over
![]() $U \subset M$
, any section
$U \subset M$
, any section
![]() $f \in C^\infty (SM,\mathcal {E})$
can be written as
$f \in C^\infty (SM,\mathcal {E})$
can be written as
![]() $f|_{U} = \sum _{\alpha } f_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
, where
$f|_{U} = \sum _{\alpha } f_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
, where
![]() $f_\alpha \in C^\infty (SM|_U)$
. Then, the vertical Laplacian is defined as
$f_\alpha \in C^\infty (SM|_U)$
. Then, the vertical Laplacian is defined as
where
![]() $\Delta _{\mathbb {V}}$
was introduced in equation (2.2). The sections
$\Delta _{\mathbb {V}}$
was introduced in equation (2.2). The sections
![]() $f_k \in C^\infty (SM,\mathcal {E})$
then satisfy the eigenvalue equation
$f_k \in C^\infty (SM,\mathcal {E})$
then satisfy the eigenvalue equation
Equivalently,
![]() $f_k$
is a smooth section of the bundle
$f_k$
is a smooth section of the bundle
![]() $\Omega _k \otimes E$
over M and this can be identified via equation (2.3) to an element
$\Omega _k \otimes E$
over M and this can be identified via equation (2.3) to an element
![]() $S^k_0 TM \otimes E$
. We say that a section
$S^k_0 TM \otimes E$
. We say that a section
![]() $f \in C^\infty (SM,\mathcal {E})$
has even (respectively odd) Fourier degree if the decomposition of equation (2.4) only involves spherical harmonics of even (respectively odd) degree.
$f \in C^\infty (SM,\mathcal {E})$
has even (respectively odd) Fourier degree if the decomposition of equation (2.4) only involves spherical harmonics of even (respectively odd) degree.
We define the operator
![]() $\mathbf {X} := \nabla ^{{\mathcal {E}}}_X$
, where X is the geodesic vector field on
$\mathbf {X} := \nabla ^{{\mathcal {E}}}_X$
, where X is the geodesic vector field on
![]() $SM$
. This is the infinitesimal generator of the parallel transport of sections of E along geodesic flow-lines. It has the mapping property
$SM$
. This is the infinitesimal generator of the parallel transport of sections of E along geodesic flow-lines. It has the mapping property
and therefore splits as a sum
![]() $\mathbf {X} := \mathbf {X}_- + \mathbf {X}_+$
, where each term corresponds to the two summands in equation (2.5).
$\mathbf {X} := \mathbf {X}_- + \mathbf {X}_+$
, where each term corresponds to the two summands in equation (2.5).
There is a natural
![]() $L^2$
scalar product on sections
$L^2$
scalar product on sections
![]() $f,f' \in C^\infty (SM, {\mathcal {E}})$
given by
$f,f' \in C^\infty (SM, {\mathcal {E}})$
given by
where
![]() $\mu $
is the Liouville measure on
$\mu $
is the Liouville measure on
![]() $SM$
, and h is the Hermitian (or Euclidean) metric on E.
$SM$
, and h is the Hermitian (or Euclidean) metric on E.
2.1.3 Twisted Pestov identity
This identity will play a fundamental role in our proof of Theorem 1.1. In the non-twisted case, it was first discovered in some particular cases by Mukhometov [Reference MukhometovMuk75, Reference MukhometovMuk81] and Amirov [Reference AmirovAmi86], and then in its classical shape by Pestov and Sharafutdinov [Reference Pestov and SharafutdinovPS88, Reference SharafutdinovSha94]. Eventually, it was reformulated and described in a general coordinate-free way in [Reference Guillarmou, Paternain, Salo and UhlmannGPSU16, Reference Paternain, Salo and UhlmannPSU15]. It takes the following form.
Lemma 2.1. (Twisted Pestov identity)
Let
![]() $(M,g)$
be a closed n-dimensional Riemannian manifold and let
$(M,g)$
be a closed n-dimensional Riemannian manifold and let
![]() $(E,h)$
be a Hermitian (or Euclidean) vector bundle over M equipped with unitary (or orthogonal) connection
$(E,h)$
be a Hermitian (or Euclidean) vector bundle over M equipped with unitary (or orthogonal) connection
![]() $\nabla ^E$
. The following identity holds for all
$\nabla ^E$
. The following identity holds for all
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $u \in C^\infty (M,\Omega _k \otimes E)$
:
$u \in C^\infty (M,\Omega _k \otimes E)$
:
 $$ \begin{align} &\frac{(n+k-2)(n+2k-4)}{n+k-3} \|\mathbf{X}_-u\|^2_{L^2} - \frac{k(n+2k)}{k+1} \|\mathbf{X}_+u\|^2_{L^2} + \|Z(u)\|^2_{L^2} \nonumber\\&\quad= \langle R\nabla_{\mathbb{V}}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} + \langle \mathcal{F}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2}, \end{align} $$
$$ \begin{align} &\frac{(n+k-2)(n+2k-4)}{n+k-3} \|\mathbf{X}_-u\|^2_{L^2} - \frac{k(n+2k)}{k+1} \|\mathbf{X}_+u\|^2_{L^2} + \|Z(u)\|^2_{L^2} \nonumber\\&\quad= \langle R\nabla_{\mathbb{V}}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} + \langle \mathcal{F}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2}, \end{align} $$
where:
-
• Z is a first-order differential operator which we do not make explicit;
-
• the term involving R takes the form
where R is the Riemann curvature tensor, $$ \begin{align*} \langle R\nabla_{\mathbb{V}}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} = \int_{M} \int_{S_xM} \sum_\alpha R(v, \nabla_{\mathbb{V}}u_{\alpha},\nabla_{\mathbb{V}}u_{\alpha},v) ~|\mathrm{d} v| |\mathrm{d} x|, \end{align*} $$
$$ \begin{align*} \langle R\nabla_{\mathbb{V}}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} = \int_{M} \int_{S_xM} \sum_\alpha R(v, \nabla_{\mathbb{V}}u_{\alpha},\nabla_{\mathbb{V}}u_{\alpha},v) ~|\mathrm{d} v| |\mathrm{d} x|, \end{align*} $$
 $|dv|$
is the Lebesgue measure on the sphere
$|dv|$
is the Lebesgue measure on the sphere
 $S_xM$
(induced by
$S_xM$
(induced by
 $g_x$
) and
$g_x$
) and
 $|dx|$
is the Riemannian measure,
$|dx|$
is the Riemannian measure,
 $u = \sum _\alpha u_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
with
$u = \sum _\alpha u_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
with
 $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha \in I}$
an orthonormal frame at the point
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha \in I}$
an orthonormal frame at the point
 $x \in M$
of
$x \in M$
of
 $E_x$
;
$E_x$
;
-
• the term involving
 $\mathcal {F}^{E}$
takes the form (2.7)where
$\mathcal {F}^{E}$
takes the form (2.7)where $$ \begin{align} \langle \mathcal{F}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} = \int_M \int_{S_xM} \sum_{\alpha} R_E(v,\nabla_{\mathbb{V}} u_\alpha,u,\operatorname{\mathrm{\mathbf{e}}}_\alpha) ~ |\mathrm{d} v| |\mathrm{d} x|, \end{align} $$
$$ \begin{align} \langle \mathcal{F}^{E}u, \nabla_{\mathbb{V}}^{E}u \rangle_{L^2} = \int_M \int_{S_xM} \sum_{\alpha} R_E(v,\nabla_{\mathbb{V}} u_\alpha,u,\operatorname{\mathrm{\mathbf{e}}}_\alpha) ~ |\mathrm{d} v| |\mathrm{d} x|, \end{align} $$
 $R_E$
is the curvature tensor of E and we use the convention: and h is the Euclidean (or Hermitian) metric on the bundle E.
$R_E$
is the curvature tensor of E and we use the convention: and h is the Euclidean (or Hermitian) metric on the bundle E. $$ \begin{align*} R_E(X,Y,\omega,\eta) := h(R_E(X,Y)\omega,\eta) \quad \text{for all } X,Y \in TM\quad \text{for all } \omega, \eta \in E, \end{align*} $$
$$ \begin{align*} R_E(X,Y,\omega,\eta) := h(R_E(X,Y)\omega,\eta) \quad \text{for all } X,Y \in TM\quad \text{for all } \omega, \eta \in E, \end{align*} $$
The operator Z is not made explicit as we will only need to use
![]() $\|Z(u)\|^2_{L^2} \geq 0$
in equation (2.6). We refer to [Reference Guillarmou, Paternain, Salo and UhlmannGPSU16, Proposition 3.5] for a proof.
$\|Z(u)\|^2_{L^2} \geq 0$
in equation (2.6). We refer to [Reference Guillarmou, Paternain, Salo and UhlmannGPSU16, Proposition 3.5] for a proof.
2.2 Complex geometry
We use [Reference Kobayashi and NomizuKN96, Ch. IX] as basic reference for complex geometry.
2.2.1 Curvature tensors
Let
![]() $(V, g)$
be a Euclidean vector space of dimension n. We will usually identify V with its dual
$(V, g)$
be a Euclidean vector space of dimension n. We will usually identify V with its dual
![]() $V^*$
and
$V^*$
and
![]() $\Lambda ^2 V $
with the space of skew-symmetric endomorphisms of V using the metric g. We denote by
$\Lambda ^2 V $
with the space of skew-symmetric endomorphisms of V using the metric g. We denote by
![]() $S^p V$
the symmetric p-tensors on V,
$S^p V$
the symmetric p-tensors on V,
![]() $S^p_0 V$
the trace-free symmetric tensors and
$S^p_0 V$
the trace-free symmetric tensors and
![]() $\Lambda ^pV$
the pth exterior power. The space
$\Lambda ^pV$
the pth exterior power. The space
![]() $V^{\otimes 2}$
splits as
$V^{\otimes 2}$
splits as
where each summand is invariant under the
![]() $\mathrm {O}(n)$
-action, and
$\mathrm {O}(n)$
-action, and
![]() $S^2 V = \mathbb {R} g \oplus S^2_0 V$
. The space
$S^2 V = \mathbb {R} g \oplus S^2_0 V$
. The space
![]() $V^{\otimes 2} \simeq \operatorname {{\mathrm {End}}} V$
is equipped with the norm
$V^{\otimes 2} \simeq \operatorname {{\mathrm {End}}} V$
is equipped with the norm
where
![]() ${}^\top $
denotes the transpose operator and the decomposition given in equation (2.8) is orthogonal with respect to the metric defined in equation (2.9) so that
${}^\top $
denotes the transpose operator and the decomposition given in equation (2.8) is orthogonal with respect to the metric defined in equation (2.9) so that
![]() $S^2V$
and
$S^2V$
and
![]() $\Lambda^2V$
both inherit the metric from equation (2.9).
$\Lambda^2V$
both inherit the metric from equation (2.9).
A curvature tensor R is an element
![]() $R \in S^2(\Lambda ^2 V)$
satisfying the Bianchi identity
$R \in S^2(\Lambda ^2 V)$
satisfying the Bianchi identity
The sectional curvature associated to R is the quadratic map
![]() $\overline R:S^2V\to \mathbb {R}$
defined by
$\overline R:S^2V\to \mathbb {R}$
defined by
For every
![]() $X,Y \in V$
, we can see
$X,Y \in V$
, we can see
![]() $R(X,Y,\cdot ,\cdot )$
as a skew-symmetric endomorphism
$R(X,Y,\cdot ,\cdot )$
as a skew-symmetric endomorphism
![]() $R(X,Y)$
as follows:
$R(X,Y)$
as follows:
This skew-symmetric endomorphism extends as a derivation to skew-symmetric endomorphisms of the exterior, symmetric and tensor algebras of V, denoted respectively by
![]() $R_{\Lambda ^p}(X,Y)$
,
$R_{\Lambda ^p}(X,Y)$
,
![]() $R_{S^p}(X,Y)$
and
$R_{S^p}(X,Y)$
and
![]() $R_{V^{\otimes p}}(X,Y)$
. In particular, it can be easily checked that
$R_{V^{\otimes p}}(X,Y)$
. In particular, it can be easily checked that
for every
![]() $u \in V^{\otimes 2} =\operatorname {{\mathrm {End}}}(V)$
. The action equation (2.11) is diagonal with respect to the decomposition
$u \in V^{\otimes 2} =\operatorname {{\mathrm {End}}}(V)$
. The action equation (2.11) is diagonal with respect to the decomposition
![]() $V^{\otimes 2} = S^2 V \oplus \Lambda ^2 V$
. For
$V^{\otimes 2} = S^2 V \oplus \Lambda ^2 V$
. For
![]() $X,Y \in V$
and
$X,Y \in V$
and
![]() $\omega , \eta \in \Lambda ^p V$
, we set
$\omega , \eta \in \Lambda ^p V$
, we set
where
![]() $\Lambda ^p V$
is equipped with the canonical inner product. We use the analogous notation for
$\Lambda ^p V$
is equipped with the canonical inner product. We use the analogous notation for
![]() $S^pV$
.
$S^pV$
.
2.2.2 Curvature and pinching
If
![]() $(M,g)$
is a Riemannian manifold, we introduce the
$(M,g)$
is a Riemannian manifold, we introduce the
![]() $(4,0)$
-tensor
$(4,0)$
-tensor ![]() by
by
for all
![]() $X,Y,Z,W \in TM.$
This is precisely the curvature tensor when
$X,Y,Z,W \in TM.$
This is precisely the curvature tensor when
![]() $(M,g)$
is the real hyperbolic space
$(M,g)$
is the real hyperbolic space
![]() $\mathbb {H}^n$
, whereas if
$\mathbb {H}^n$
, whereas if
![]() $(M,g,J)$
is the complex hyperbolic space
$(M,g,J)$
is the complex hyperbolic space
![]() $\mathbb {C} \mathbb {H}^m$
, its curvature tensor G takes the form:
$\mathbb {C} \mathbb {H}^m$
, its curvature tensor G takes the form:

see [Reference Kobayashi and NomizuKN96, §7, Ch. IX]. Equivalently, equation (2.12) can be rewritten using equation (2.10) as
where
![]() $X \wedge Y$
is the skew-symmetric endomorphism of
$X \wedge Y$
is the skew-symmetric endomorphism of
![]() $TM$
defined by
$TM$
defined by
![]() $(X\wedge Y)(Z):=g(X,Z)Y-g(Y,Z)X$
for all
$(X\wedge Y)(Z):=g(X,Z)Y-g(Y,Z)X$
for all
![]() $Z\in TM$
.
$Z\in TM$
.
If
![]() $(M,g,J)$
is any Kähler manifold, the holomorphic sectional curvature is defined for a unit vector
$(M,g,J)$
is any Kähler manifold, the holomorphic sectional curvature is defined for a unit vector
![]() $X \in TM$
by
$X \in TM$
by
It can be easily checked that the holomorphic curvature of the complex hyperbolic space is
![]() $-1$
, that is,
$-1$
, that is,
for
![]() $|X|=1$
. By analogy with the real case, we introduce the notion of pinching of the holomorphic curvature (that we recall was also briefly introduced in the introduction).
$|X|=1$
. By analogy with the real case, we introduce the notion of pinching of the holomorphic curvature (that we recall was also briefly introduced in the introduction).
Definition 2.2. (Pinched holomorphic sectional curvature)
We say that a Kähler manifold
![]() $(M^{2m},g,J)$
is negatively holomorphically
$(M^{2m},g,J)$
is negatively holomorphically
![]() $\unicode{x3bb} $
-pinched (for some
$\unicode{x3bb} $
-pinched (for some
![]() $\unicode{x3bb} \in (0,1]$
) if there exists a constant
$\unicode{x3bb} \in (0,1]$
) if there exists a constant
![]() $C> 0$
such that for all unit vectors
$C> 0$
such that for all unit vectors
![]() $X \in TM$
,
$X \in TM$
,
The manifold is said to be strictly negatively holomorphically
![]() $\unicode{x3bb} $
-pinched if the above inequalities are strict.
$\unicode{x3bb} $
-pinched if the above inequalities are strict.
Similarly, one can talk about the real (or sectional)
![]() $\delta $
-pinching of the manifold
$\delta $
-pinching of the manifold
![]() $(M^{2m},g)$
by requiring the above inequalities to hold with
$(M^{2m},g)$
by requiring the above inequalities to hold with
![]() $\unicode{x3bb} $
being replaced by
$\unicode{x3bb} $
being replaced by
![]() $\delta $
, and
$\delta $
, and
![]() $H(X)$
being replaced by the sectional curvature
$H(X)$
being replaced by the sectional curvature
![]() $\overline {R}(X,Y)$
(for all pairs of orthogonal unit vectors
$\overline {R}(X,Y)$
(for all pairs of orthogonal unit vectors
![]() $X, Y \in TM$
). There exist relations between holomorphic and real pinchings, see [Reference BergerBer60a, Reference BergerBer60b, Reference Bishop and GoldbergBG63].
$X, Y \in TM$
). There exist relations between holomorphic and real pinchings, see [Reference BergerBer60a, Reference BergerBer60b, Reference Bishop and GoldbergBG63].
As in the real case, it is a well-known result that negative holomorphic
![]() $1$
-pinching implies that
$1$
-pinching implies that
![]() $(M^{2m},g,J)$
is holomorphically isometric to a compact quotient
$(M^{2m},g,J)$
is holomorphically isometric to a compact quotient
![]() $\Gamma \backslash \mathbb {C}\mathbb {H}^m$
, where
$\Gamma \backslash \mathbb {C}\mathbb {H}^m$
, where
![]() $\Gamma $
is a discrete subgroup of
$\Gamma $
is a discrete subgroup of
![]() $\mathrm {Isom}(\mathbb {C}\mathbb {H}^m)$
. In what follows, we will always assume that
$\mathrm {Isom}(\mathbb {C}\mathbb {H}^m)$
. In what follows, we will always assume that
![]() $(M^{2m},g,J)$
is negatively
$(M^{2m},g,J)$
is negatively
![]() $\unicode{x3bb} $
-holomorphically pinched and, without loss of generality, we rescale the metric such that
$\unicode{x3bb} $
-holomorphically pinched and, without loss of generality, we rescale the metric such that
![]() $C=1$
.
$C=1$
.
The following lemma proved in [Reference Bishop and GoldbergBG63, Proposition 4.2] will be useful.
Lemma 2.3. (Bishop and Goldberg 1963)
Assume
![]() $(M^{2m},g,J)$
is a closed Kähler manifold which is negatively holomorphically
$(M^{2m},g,J)$
is a closed Kähler manifold which is negatively holomorphically
![]() $\unicode{x3bb} $
-pinched. Consider unit vectors
$\unicode{x3bb} $
-pinched. Consider unit vectors
![]() $X,Y \in TM$
such that
$X,Y \in TM$
such that
![]() $g( X,Y) = 0$
and
$g( X,Y) = 0$
and
![]() $g( X, JY) = \cos \theta $
. Then,
$g( X, JY) = \cos \theta $
. Then,
In particular,
for all orthogonal unit vectors
![]() $X, Y \in TM$
. If
$X, Y \in TM$
. If
![]() $\unicode{x3bb} \geq 2/3$
, then
$\unicode{x3bb} \geq 2/3$
, then
![]() $(M^{2m},g)$
is negatively
$(M^{2m},g)$
is negatively
![]() $\delta $
-pinched for the sectional curvature with
$\delta $
-pinched for the sectional curvature with
![]() $\delta = ({3\unicode{x3bb} -2})/{4}$
.
$\delta = ({3\unicode{x3bb} -2})/{4}$
.
We now set
where G is the curvature tensor defined in equation (2.12). The following holds.
Lemma 2.4. Assume that
![]() $-1 \leq H(X) \leq -\unicode{x3bb} $
for all unit vectors
$-1 \leq H(X) \leq -\unicode{x3bb} $
for all unit vectors
![]() $X\in TM$
. Then, for all unit vectors
$X\in TM$
. Then, for all unit vectors
![]() $X,Y,Z,W \in TM$
,
$X,Y,Z,W \in TM$
,
More generally, for all unit vectors
![]() $X,Y \in TM$
, and for all unit
$X,Y \in TM$
, and for all unit
![]() $\omega ,\eta \in \Lambda ^p TM$
or
$\omega ,\eta \in \Lambda ^p TM$
or
![]() $S^p TM$
,
$S^p TM$
,
Proof. Let
![]() $X,Y$
be unit vectors such that
$X,Y$
be unit vectors such that
![]() $g( X,Y) = 0$
and
$g( X,Y) = 0$
and
![]() $g( X, JY) = \cos \theta $
. Then,
$g( X, JY) = \cos \theta $
. Then,
 $$ \begin{align*} \overline{R_0}(X,Y) = \overline{R}(X,Y)-\frac{1+\unicode{x3bb}}{2}\overline{G}(X,Y) = \overline{R}(X,Y)+\frac{1+\unicode{x3bb}}{2}\bigg(1-\frac{3}{4}\sin^2\theta\bigg). \end{align*} $$
$$ \begin{align*} \overline{R_0}(X,Y) = \overline{R}(X,Y)-\frac{1+\unicode{x3bb}}{2}\overline{G}(X,Y) = \overline{R}(X,Y)+\frac{1+\unicode{x3bb}}{2}\bigg(1-\frac{3}{4}\sin^2\theta\bigg). \end{align*} $$
Inserting equation (2.14) in the previous equation,
 $$ \begin{align*} -\frac{1-\unicode{x3bb}}{2}\bigg(1+\frac{3}{4} \sin^2\theta\bigg) \leq \overline{R_0}(X,Y) \leq \frac{1-\unicode{x3bb}}{2}\bigg(2 - \frac{3}{4}\sin^2\theta\bigg). \end{align*} $$
$$ \begin{align*} -\frac{1-\unicode{x3bb}}{2}\bigg(1+\frac{3}{4} \sin^2\theta\bigg) \leq \overline{R_0}(X,Y) \leq \frac{1-\unicode{x3bb}}{2}\bigg(2 - \frac{3}{4}\sin^2\theta\bigg). \end{align*} $$
In particular, the previous inequalities yield
Like in the proof of [Reference Bourguignon and KarcherBK78, Lemma 3.7], the previous inequality then implies equation (2.16) by writing
![]() $R_0(X,Y,Z,W)$
as a sum of terms only involving two vectors in the arguments. The general bound of equation (2.17) follows immediately from equation (2.16) by diagonalizing over
$R_0(X,Y,Z,W)$
as a sum of terms only involving two vectors in the arguments. The general bound of equation (2.17) follows immediately from equation (2.16) by diagonalizing over
![]() $\mathbb {C}$
the skew-symmetric endomorphism
$\mathbb {C}$
the skew-symmetric endomorphism
![]() $R_0(X,Y)$
.
$R_0(X,Y)$
.
2.3 Isometric extensions of the geodesic flow
The unitary frame bundle
![]() $\widehat {\pi } : F_{\mathbb {C}}M \to SM$
is a principal
$\widehat {\pi } : F_{\mathbb {C}}M \to SM$
is a principal
![]() $\mathrm {U}(m-1)$
-bundle over
$\mathrm {U}(m-1)$
-bundle over
![]() $SM$
. Given
$SM$
. Given
![]() $a \in \mathrm {U}(m-1)$
, we denote by
$a \in \mathrm {U}(m-1)$
, we denote by
![]() $R_a : F_{\mathbb {C}}M \to F_{\mathbb {C}}M$
the fibrewise right-action by a. The unitary frame flow
$R_a : F_{\mathbb {C}}M \to F_{\mathbb {C}}M$
the fibrewise right-action by a. The unitary frame flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
is an extension of the geodesic flow to a principal bundle in the sense that it satisfies
$(\Phi _t)_{t \in \mathbb {R}}$
is an extension of the geodesic flow to a principal bundle in the sense that it satisfies
for all
![]() $t \in \mathbb {R}, a \in \mathrm {U}(m-1)$
. We will denote by
$t \in \mathbb {R}, a \in \mathrm {U}(m-1)$
. We will denote by
![]() $X_{F_{\mathbb {C}}M}$
its infinitesimal generator.
$X_{F_{\mathbb {C}}M}$
its infinitesimal generator.
Initiated by the work of Brin [Reference BrinBri75b, Reference BrinBri75a], there is now an established theory describing the ergodic components of such an extension flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
. This is achieved via the introduction of a closed subgroup
$(\Phi _t)_{t \in \mathbb {R}}$
. This is achieved via the introduction of a closed subgroup
![]() $H \leqslant \mathrm {U}(m-1)$
, called the transitivity group, and defined by means of dynamical holonomies. We refer to [Reference LefeuvreLef23] for a modern construction of the transitivity group H. It has the following properties.
$H \leqslant \mathrm {U}(m-1)$
, called the transitivity group, and defined by means of dynamical holonomies. We refer to [Reference LefeuvreLef23] for a modern construction of the transitivity group H. It has the following properties.
Theorem 2.5. (Brin 1975, [Reference LefeuvreLef23])
The following hold:
-
(i) there exists a natural isomorphism
(2.18) $$ \begin{align} \mathrm{ev} : \ker_{L^2(\omega)} X_{F_{\mathbb{C}}M} \overset{\sim}{\longrightarrow} L^2(H\backslash \mathrm{U}(m-1)); \end{align} $$
$$ \begin{align} \mathrm{ev} : \ker_{L^2(\omega)} X_{F_{\mathbb{C}}M} \overset{\sim}{\longrightarrow} L^2(H\backslash \mathrm{U}(m-1)); \end{align} $$
-
(ii) there exists a principal H-subbundle
 $Q \subset F_{\mathbb {C}}M$
over
$Q \subset F_{\mathbb {C}}M$
over
 $SM$
which is invariant by
$SM$
which is invariant by
 $(\Phi _t)_{t \in \mathbb {R}}$
such that
$(\Phi _t)_{t \in \mathbb {R}}$
such that
 $(\Phi _t|_{Q})_{t \in \mathbb {R}}$
is ergodic (with respect to the induced measure on Q).
$(\Phi _t|_{Q})_{t \in \mathbb {R}}$
is ergodic (with respect to the induced measure on Q).In particular, the unitary frame flow is ergodic if and only if
 $H = \mathrm {U}(m-1)$
.
$H = \mathrm {U}(m-1)$
.
We refer to [Reference LefeuvreLef23, Corollary 3.10] for further details. Obviously, by the first item, the only possibility for
![]() $\ker _{L^2} X_{F_{\mathbb {C}}M}$
to be reduced to the constants is that
$\ker _{L^2} X_{F_{\mathbb {C}}M}$
to be reduced to the constants is that
![]() $H = \mathrm {U}(m-1)$
. The isomorphism in equation (2.18) is simply defined by taking an arbitrary point
$H = \mathrm {U}(m-1)$
. The isomorphism in equation (2.18) is simply defined by taking an arbitrary point
![]() $z_\star \in SM$
and setting for
$z_\star \in SM$
and setting for
![]() $f \in \ker _{L^2} X_{F_{\mathbb {C}}M}$
,
$f \in \ker _{L^2} X_{F_{\mathbb {C}}M}$
,
Such a function turns out to be in
![]() $L^2(F_{\mathbb {C}}M_{z_\star }) \simeq L^2(\mathrm {U}(m-1))$
(it is not clear a priori that such an evaluation map is well defined, so its definition is also part of Theorem 2.5) and is invariant by the action of H so it yields an element in
$L^2(F_{\mathbb {C}}M_{z_\star }) \simeq L^2(\mathrm {U}(m-1))$
(it is not clear a priori that such an evaluation map is well defined, so its definition is also part of Theorem 2.5) and is invariant by the action of H so it yields an element in
![]() $L^2(H\backslash \mathrm {U}(m-1))$
. The second item in Theorem 2.5 is already a strong topological constraint on the bundle
$L^2(H\backslash \mathrm {U}(m-1))$
. The second item in Theorem 2.5 is already a strong topological constraint on the bundle
![]() $F_{\mathbb {C}}M$
and is called a reduction of the structure group, see §3 where this is further discussed.
$F_{\mathbb {C}}M$
and is called a reduction of the structure group, see §3 where this is further discussed.
We introduce
![]() $\mathcal {N} \to SM$
, the normal bundle, to be the Euclidean bundle over
$\mathcal {N} \to SM$
, the normal bundle, to be the Euclidean bundle over
![]() $SM$
defined for
$SM$
defined for
![]() $v\in S_xM$
as
$v\in S_xM$
as
where
![]() $\perp $
denotes the orthogonal complement with respect to the Euclidean metric
$\perp $
denotes the orthogonal complement with respect to the Euclidean metric
![]() $g_x$
. Note that
$g_x$
. Note that
![]() $\mathcal {N}$
is equipped with the complex structure J. Observe that
$\mathcal {N}$
is equipped with the complex structure J. Observe that
so that
![]() $\mathcal {N}$
can be seen as a subbundle of the pullback bundle
$\mathcal {N}$
can be seen as a subbundle of the pullback bundle
![]() $\pi ^*TM$
. Parallel transport with respect to the Levi-Civita connection
$\pi ^*TM$
. Parallel transport with respect to the Levi-Civita connection
![]() $\nabla ^{\mathrm {LC}}$
of sections of
$\nabla ^{\mathrm {LC}}$
of sections of
![]() $\mathcal {N}$
along geodesic flow-lines is well defined and generated by a first-order differential operator
$\mathcal {N}$
along geodesic flow-lines is well defined and generated by a first-order differential operator
which is formally skew-adjoint and commutes with J.
Other than describing the ergodic components of the unitary frame flow, the group H allows to construct smooth flow-invariant objects. In what follows, we denote by
![]() $\mathrm {Vect}$
the category of finite-dimensional Euclidean vector spaces and call
$\mathrm {Vect}$
the category of finite-dimensional Euclidean vector spaces and call
![]() $\mathfrak {o} : \mathrm {Vect} \to \mathrm {Vect}$
an operation on this category if
$\mathfrak {o} : \mathrm {Vect} \to \mathrm {Vect}$
an operation on this category if
![]() $\mathfrak {o}$
is obtained as a finite composition of the following basic operations: tensor powers
$\mathfrak {o}$
is obtained as a finite composition of the following basic operations: tensor powers
![]() $V^{\otimes m}$
of a vector space V, symmetric powers
$V^{\otimes m}$
of a vector space V, symmetric powers
![]() $S^m V$
and exterior powers
$S^m V$
and exterior powers
![]() $\Lambda ^m V$
. Obviously, for any such operation
$\Lambda ^m V$
. Obviously, for any such operation
![]() $\mathfrak {o}$
,
$\mathfrak {o}$
,
![]() $\mathfrak {o}(\mathcal {N}) \to SM$
is a well-defined Euclidean bundle still equipped with an induced generator
$\mathfrak {o}(\mathcal {N}) \to SM$
is a well-defined Euclidean bundle still equipped with an induced generator
![]() $\mathbf {X}$
(for simplicity, we do not introduce any new notation for the generator on this bundle).
$\mathbf {X}$
(for simplicity, we do not introduce any new notation for the generator on this bundle).
The following theorem holds.
Theorem 2.6. (Non-Abelian Livšic theorem, [Reference Cekić and LefeuvreCL22, Theorem 3.5])
Let
be any operation on
![]() $\mathrm {Vect}$
. Then, there exists an isomorphism
$\mathrm {Vect}$
. Then, there exists an isomorphism
The isomorphism map is nothing but evaluation at an arbitrary point of
![]() $SM$
(similarly to Theorem 2.5(i)). In other words, flow-invariant smooth sections of tensor products of the normal bundle correspond exactly to algebraic H-invariant objects on
$SM$
(similarly to Theorem 2.5(i)). In other words, flow-invariant smooth sections of tensor products of the normal bundle correspond exactly to algebraic H-invariant objects on
![]() $\mathbb {R}^{2(m-1)}$
. Theorem 2.6 will allow us to generate smooth flow-invariant sections when the unitary frame flow is not ergodic. For instance, if one can show that
$\mathbb {R}^{2(m-1)}$
. Theorem 2.6 will allow us to generate smooth flow-invariant sections when the unitary frame flow is not ergodic. For instance, if one can show that
![]() $H \leqslant \mathrm {U}(m-1-p) \times \mathrm {U}(p) \lneqq \mathrm {U}(m-1)$
, that is, H acts reducibly on
$H \leqslant \mathrm {U}(m-1-p) \times \mathrm {U}(p) \lneqq \mathrm {U}(m-1)$
, that is, H acts reducibly on
![]() $\mathbb {R}^{2(m-1)} \simeq \mathbb {C}^{m-1}$
, then H fixes an orthogonal projector
$\mathbb {R}^{2(m-1)} \simeq \mathbb {C}^{m-1}$
, then H fixes an orthogonal projector
![]() $\pi \in S^2 \mathbb {R}^{2(m-1)}$
onto a complex (that is, J-invariant) space
$\pi \in S^2 \mathbb {R}^{2(m-1)}$
onto a complex (that is, J-invariant) space
![]() $V \subset \mathbb {R}^{2(m-1)}$
. In turn, Theorem 2.6 implies that there exists a flow-invariant complex vector bundle
$V \subset \mathbb {R}^{2(m-1)}$
. In turn, Theorem 2.6 implies that there exists a flow-invariant complex vector bundle
![]() $\mathcal {V} \subset \mathcal {N}$
which is the same as the existence of an orthogonal projector
$\mathcal {V} \subset \mathcal {N}$
which is the same as the existence of an orthogonal projector
![]() $\pi _{\mathcal {V}} \in C^\infty (SM, S^2 \mathcal {N}) \cap \ker \mathbf {X}$
commuting with J.
$\pi _{\mathcal {V}} \in C^\infty (SM, S^2 \mathcal {N}) \cap \ker \mathbf {X}$
commuting with J.
3 Topological reductions and flow-invariant sections
In what follows, we assume that the complex dimension of M is even and larger than
![]() $2$
, and we write it as
$2$
, and we write it as
![]() $\dim _{\mathbb {C}} M = m = :2p+2$
, with
$\dim _{\mathbb {C}} M = m = :2p+2$
, with
![]() $p \geq 1$
.
$p \geq 1$
.
3.1 Topological reductions
By Theorem 2.5, if the unitary frame flow on
![]() $F_{\mathbb {C}}M$
is not ergodic, its transitivity group is a strict subgroup
$F_{\mathbb {C}}M$
is not ergodic, its transitivity group is a strict subgroup
![]() $H \lneqq \mathrm {U}(2p+1)$
and there exists a strict principal H-subbundle
$H \lneqq \mathrm {U}(2p+1)$
and there exists a strict principal H-subbundle
![]() $Q \subset F_{\mathbb {C}}M$
. This is known as a reduction of the structure group of
$Q \subset F_{\mathbb {C}}M$
. This is known as a reduction of the structure group of
![]() $F_{\mathbb {C}}M$
to H. Since
$F_{\mathbb {C}}M$
to H. Since
![]() $F_{\mathbb {C}}M$
admits a reduction to H, the same holds true for the restriction of the unitary frame bundle to any sphere
$F_{\mathbb {C}}M$
admits a reduction to H, the same holds true for the restriction of the unitary frame bundle to any sphere
![]() $S_{x_0}M$
for
$S_{x_0}M$
for
![]() $x_0 \in M$
. In turn, as
$x_0 \in M$
. In turn, as
![]() $S_{x_0}M \simeq S^{4p+3}$
, this implies that the unitary frame bundle
$S_{x_0}M \simeq S^{4p+3}$
, this implies that the unitary frame bundle
![]() $F_{\mathbb {C}} S^{4p+3}$
admits a reduction of its structure group from
$F_{\mathbb {C}} S^{4p+3}$
admits a reduction of its structure group from
![]() $\mathrm {U}(2p+1)$
to H.
$\mathrm {U}(2p+1)$
to H.
Note that
![]() $\mathrm {U}(2p+2)$
and
$\mathrm {U}(2p+2)$
and
![]() $\mathrm {SU}(2p+2)$
act transitively on
$\mathrm {SU}(2p+2)$
act transitively on
![]() $S^{4p+3}$
with isotropy groups
$S^{4p+3}$
with isotropy groups
![]() $\mathrm {U}(2p+1)$
and
$\mathrm {U}(2p+1)$
and
![]() $\mathrm {SU}(2p+1)$
, respectively, so we can write
$\mathrm {SU}(2p+1)$
, respectively, so we can write
The unitary frame bundle
![]() $F_{\mathbb {C}}S^{4p+3}$
can be identified with
$F_{\mathbb {C}}S^{4p+3}$
can be identified with
![]() $\mathrm {U}(2p+2)$
. Thus, the subgroup
$\mathrm {U}(2p+2)$
. Thus, the subgroup
![]() $\mathrm {SU}(2p+2)$
of
$\mathrm {SU}(2p+2)$
of
![]() $ \mathrm {U}(2p+2)$
, seen as a principal
$ \mathrm {U}(2p+2)$
, seen as a principal
![]() $\mathrm {SU}(2p+1)$
-bundle
$\mathrm {SU}(2p+1)$
-bundle
![]() $F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
over
$F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
over
![]() $S^{4p+3}$
, is a reduction of
$S^{4p+3}$
, is a reduction of
![]() $F_{\mathbb {C}}S^{4p+3}$
to
$F_{\mathbb {C}}S^{4p+3}$
to
![]() $\mathrm {SU}(2p+1)$
.
$\mathrm {SU}(2p+1)$
.
The aim of this section is to examine the possible further reductions of
![]() $F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
. Note that as far as the spheres
$F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
. Note that as far as the spheres
![]() $S^{4p+1}$
are concerned (for
$S^{4p+1}$
are concerned (for
![]() $p \geq 1$
), it was proved in [Reference LeonardLeo71] that their special unitary frame bundle
$p \geq 1$
), it was proved in [Reference LeonardLeo71] that their special unitary frame bundle
![]() $F_{\mathbb {C},\mathrm {SU}} S^{4p+1} \to S^{4p+1}$
does not admit any reduction.
$F_{\mathbb {C},\mathrm {SU}} S^{4p+1} \to S^{4p+1}$
does not admit any reduction.
Theorem 3.1. Let
![]() $p \geq 1$
. Assume that the principal
$p \geq 1$
. Assume that the principal
![]() $\mathrm {SU}(2p+1)$
-bundle
$\mathrm {SU}(2p+1)$
-bundle
![]() $F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
over
$F_{\mathbb {C},\mathrm {SU}} S^{4p+3}$
over
![]() $S^{4p+3}$
admits a reduction of its structure group to a strict connected subgroup
$S^{4p+3}$
admits a reduction of its structure group to a strict connected subgroup
![]() $H_0 \lneqq \mathrm {SU}(2p+1)$
. Then one of the following holds:
$H_0 \lneqq \mathrm {SU}(2p+1)$
. Then one of the following holds:
-
(i) either the representation of
 $H_0$
on
$H_0$
on
 $\mathbb {C}^{2p+1}$
is reducible;
$\mathbb {C}^{2p+1}$
is reducible; -
(ii) or
 $p=1$
, and
$p=1$
, and
 $H_0$
is contained in
$H_0$
is contained in
 $\mathrm {SO}(3) \lneqq \mathrm {SU}(3)$
;
$\mathrm {SO}(3) \lneqq \mathrm {SU}(3)$
; -
(iii) or
 $p=13$
, and
$p=13$
, and
 $H_0$
is contained in
$H_0$
is contained in
 $\mathrm {E}_6 \lneqq \mathrm {SU}(27)$
.
$\mathrm {E}_6 \lneqq \mathrm {SU}(27)$
.
Proof. Let
![]() $\hat H_0$
be a maximal strict subgroup of
$\hat H_0$
be a maximal strict subgroup of
![]() $\mathrm {SU}(2p+1)$
containing
$\mathrm {SU}(2p+1)$
containing
![]() $H_0$
. Clearly the principal bundle
$H_0$
. Clearly the principal bundle
![]() $P_0=\mathrm {SU}(2p+2)\to S^{4p+3}$
also reduces to
$P_0=\mathrm {SU}(2p+2)\to S^{4p+3}$
also reduces to
![]() $\hat H_0$
. Then [Reference LeonardLeo71, Theorem 3] applied (with the notation of [Reference LeonardLeo71]) to
$\hat H_0$
. Then [Reference LeonardLeo71, Theorem 3] applied (with the notation of [Reference LeonardLeo71]) to
![]() $G_{2p + 1} := \mathrm {SU}(2p + 1)$
shows that
$G_{2p + 1} := \mathrm {SU}(2p + 1)$
shows that
![]() $\hat H_0$
is a simple Lie group.
$\hat H_0$
is a simple Lie group.
If
![]() $\hat H_0$
is a classical simple Lie group and
$\hat H_0$
is a classical simple Lie group and
![]() $p\ge 2$
, by [Reference Čadek and CrabbČC06, Theorem 2.1, (D) and (E)] applied to
$p\ge 2$
, by [Reference Čadek and CrabbČC06, Theorem 2.1, (D) and (E)] applied to
![]() $G=\hat H_0$
, we immediately obtain that the representation of
$G=\hat H_0$
, we immediately obtain that the representation of
![]() $\hat H_0$
(and thus also that of H) on
$\hat H_0$
(and thus also that of H) on
![]() $\mathbb {C}^{2p+1}$
is reducible. The above result does not hold for
$\mathbb {C}^{2p+1}$
is reducible. The above result does not hold for
![]() $p=1$
(when the corresponding sphere
$p=1$
(when the corresponding sphere
![]() $S^7$
is parallelizable), but it is easy to check that the only simple Lie group strictly contained in
$S^7$
is parallelizable), but it is easy to check that the only simple Lie group strictly contained in
![]() $\mathrm {SU}(3)$
whose representation on
$\mathrm {SU}(3)$
whose representation on
![]() $\mathbb {C}^3$
is irreducible is
$\mathbb {C}^3$
is irreducible is
![]() $\mathrm {SO}(3)$
, embedded in
$\mathrm {SO}(3)$
, embedded in
![]() $\mathrm {SU}(3)$
via the complexification of its standard representation on
$\mathrm {SU}(3)$
via the complexification of its standard representation on
![]() $\mathbb {R}^3$
. This corresponds to case (ii) of Theorem 3.1.
$\mathbb {R}^3$
. This corresponds to case (ii) of Theorem 3.1.
It remains to study the case where
![]() $\hat H_0$
is (a finite quotient of) one of the five exceptional simple compact Lie groups.
$\hat H_0$
is (a finite quotient of) one of the five exceptional simple compact Lie groups.
First of all, it suffices to look at complex irreducible representations of the exceptional Lie groups of odd dimension
![]() $2p+1$
. Moreover, by [Reference Čadek and CrabbČC06, Proposition 3.1], writing
$2p+1$
. Moreover, by [Reference Čadek and CrabbČC06, Proposition 3.1], writing
![]() $4p+3=\dim \hat H_0 + k + 1$
for some integer k, there must exist at least k vector fields on the sphere
$4p+3=\dim \hat H_0 + k + 1$
for some integer k, there must exist at least k vector fields on the sphere
![]() $S^{4p+3}$
, so the Radon–Hurwitz number
$S^{4p+3}$
, so the Radon–Hurwitz number
![]() $\rho (n)$
(defined by the fact that
$\rho (n)$
(defined by the fact that
![]() $\rho (n) - 1$
is the maximal number of linearly independent vector fields on
$\rho (n) - 1$
is the maximal number of linearly independent vector fields on
![]() $S^{n-1}$
) satisfies
$S^{n-1}$
) satisfies
For all
![]() $p\ge 3$
, we have
$p\ge 3$
, we have
![]() $\rho (4p+4)\leq 2p+3$
. Since no exceptional Lie group has an irreducible complex representation of dimension less than
$\rho (4p+4)\leq 2p+3$
. Since no exceptional Lie group has an irreducible complex representation of dimension less than
![]() $7$
, it follows that
$7$
, it follows that
![]() $2p+1$
has to be the dimension of an irreducible complex representation of an exceptional Lie group
$2p+1$
has to be the dimension of an irreducible complex representation of an exceptional Lie group
![]() $\hat H_0$
, with
$\hat H_0$
, with
Denoting by
![]() $\widehat {\mathfrak {h}}$
the Lie algebra of
$\widehat {\mathfrak {h}}$
the Lie algebra of
![]() $\hat H_0$
, it turns out that there is no complex odd-dimensional irreducible representation of an exceptional Lie group
$\hat H_0$
, it turns out that there is no complex odd-dimensional irreducible representation of an exceptional Lie group
![]() $\hat H_0$
satisfying equation (3.1) except in the following two cases.
$\hat H_0$
satisfying equation (3.1) except in the following two cases.
Case 1.
![]() $\widehat {\mathfrak {h}}=\mathfrak {e}_6$
,
$\widehat {\mathfrak {h}}=\mathfrak {e}_6$
,
![]() $\dim \widehat {\mathfrak {h}}=78$
. There are two 27-dimensional irreducible representations of
$\dim \widehat {\mathfrak {h}}=78$
. There are two 27-dimensional irreducible representations of
![]() $\mathfrak {e}_6$
satisfying equation (3.1). This case corresponds to a (theoretical) reduction of the structure group
$\mathfrak {e}_6$
satisfying equation (3.1). This case corresponds to a (theoretical) reduction of the structure group
![]() $\mathrm {SU}(27)$
of
$\mathrm {SU}(27)$
of
![]() $F_{\mathbb {C},\mathrm {SU}}S^{55}$
to a subgroup of
$F_{\mathbb {C},\mathrm {SU}}S^{55}$
to a subgroup of
![]() $\mathrm {E}_6$
(case (iii) of Theorem 3.1).
$\mathrm {E}_6$
(case (iii) of Theorem 3.1).
Case 2.
![]() $\widehat {\mathfrak {h}}=\mathfrak {g}_2$
,
$\widehat {\mathfrak {h}}=\mathfrak {g}_2$
,
![]() $\dim \widehat {\mathfrak {h}}=14$
. The only complex odd-dimensional irreducible representation of
$\dim \widehat {\mathfrak {h}}=14$
. The only complex odd-dimensional irreducible representation of
![]() $\mathfrak {g}_2$
satisfying equation (3.1) is the complexification of the real
$\mathfrak {g}_2$
satisfying equation (3.1) is the complexification of the real
![]() $7$
-dimensional representation
$7$
-dimensional representation
![]() $\rho _7:\mathrm {G}_2\to \mathrm {SO}(7)$
given by the embedding
$\rho _7:\mathrm {G}_2\to \mathrm {SO}(7)$
given by the embedding
![]() $\mathrm {G}_2\subset \mathrm {SO}(7)$
for
$\mathrm {G}_2\subset \mathrm {SO}(7)$
for
![]() $p=3$
. However, we will show that
$p=3$
. However, we will show that
![]() $F_{\mathbb {C},\mathrm {SU}}S^{15}$
does not admit any reduction to
$F_{\mathbb {C},\mathrm {SU}}S^{15}$
does not admit any reduction to
![]() $\mathrm {G}_2$
.
$\mathrm {G}_2$
.
Indeed, if such a reduction
![]() $P_{\mathrm {G}_2}$
exists, then the tangent bundle
$P_{\mathrm {G}_2}$
exists, then the tangent bundle
![]() $TS^{15}$
is isomorphic to the direct sum
$TS^{15}$
is isomorphic to the direct sum
![]() $\mathbb {R}\oplus (\mathbb {C}\otimes F_7)$
, where
$\mathbb {R}\oplus (\mathbb {C}\otimes F_7)$
, where
![]() $F_7:=P_{\mathrm {G}_2}\times _{\rho _7}\mathbb {R}^7$
is a real vector bundle of rank
$F_7:=P_{\mathrm {G}_2}\times _{\rho _7}\mathbb {R}^7$
is a real vector bundle of rank
![]() $7$
over
$7$
over
![]() $S^{15}$
.
$S^{15}$
.
Now, to each rank k real vector bundle E over
![]() $S^{15}$
, one can associate an element
$S^{15}$
, one can associate an element
![]() $\alpha (E)$
in the homotopy group
$\alpha (E)$
in the homotopy group
![]() $\pi _{14}(\mathrm {SO}(k))$
, namely, the homotopy class of its clutching function at the equator
$\pi _{14}(\mathrm {SO}(k))$
, namely, the homotopy class of its clutching function at the equator
![]() $S^{14} \hookrightarrow S^{15}$
. For
$S^{14} \hookrightarrow S^{15}$
. For
![]() $k<l$
, let
$k<l$
, let
![]() $f_{k,l}:\mathrm {SO}(k)\to \mathrm {SO}(l)$
be the standard embedding and denote by
$f_{k,l}:\mathrm {SO}(k)\to \mathrm {SO}(l)$
be the standard embedding and denote by
![]() $g_{k,l}:\pi _{14}(\mathrm {SO}(k))\to \pi _{14}(\mathrm {SO}(l))$
the group morphisms induced by
$g_{k,l}:\pi _{14}(\mathrm {SO}(k))\to \pi _{14}(\mathrm {SO}(l))$
the group morphisms induced by
![]() $f_{k,l}$
in homotopy. If E and F have ranks k and l, respectively, clearly
$f_{k,l}$
in homotopy. If E and F have ranks k and l, respectively, clearly
In our situation, since
![]() $\mathbb {C}\otimes F_7$
is topologically isomorphic to
$\mathbb {C}\otimes F_7$
is topologically isomorphic to
![]() $F_7\oplus F_7$
,
$F_7\oplus F_7$
,
![]() $T S^{15}$
is isomorphic to
$T S^{15}$
is isomorphic to
![]() $\mathbb {R}\oplus F_7\oplus F_7$
, so we can write
$\mathbb {R}\oplus F_7\oplus F_7$
, so we can write
 $$ \begin{align*} \alpha (T S^{15}) & =g_{14,15}(\alpha(F_7\oplus F_7)) \\ &=g_{14,15}(2g_{7,14}(\alpha(F_7)))=2g_{14,15}(g_{7,14}(\alpha(F_7)))=0, \end{align*} $$
$$ \begin{align*} \alpha (T S^{15}) & =g_{14,15}(\alpha(F_7\oplus F_7)) \\ &=g_{14,15}(2g_{7,14}(\alpha(F_7)))=2g_{14,15}(g_{7,14}(\alpha(F_7)))=0, \end{align*} $$
because
![]() $\pi _{14}(\mathrm {SO}(15))=\mathbb {Z}_2$
. This is a contradiction since the tangent bundle of
$\pi _{14}(\mathrm {SO}(15))=\mathbb {Z}_2$
. This is a contradiction since the tangent bundle of
![]() $S^{15}$
is non-trivial. Therefore, the case
$S^{15}$
is non-trivial. Therefore, the case
![]() $\widehat {\mathfrak {h}}=\mathfrak {g}_2$
is impossible, thus finishing the proof.
$\widehat {\mathfrak {h}}=\mathfrak {g}_2$
is impossible, thus finishing the proof.
Combined with Theorems 2.5 and 2.6, Theorem 3.1 yields the following corollary.
Corollary 3.2. Let
![]() $(M,g,J)$
be a closed connected Kähler manifold with even complex dimension m and non-ergodic unitary frame flow. Then, if
$(M,g,J)$
be a closed connected Kähler manifold with even complex dimension m and non-ergodic unitary frame flow. Then, if
![]() $m \neq 4, 28$
, there exists a finite cover
$m \neq 4, 28$
, there exists a finite cover
![]() $(\widehat {M},\widehat {g},\widehat {J})$
of
$(\widehat {M},\widehat {g},\widehat {J})$
of
![]() $(M,g,J)$
and a flow-invariant orthogonal projector
$(M,g,J)$
and a flow-invariant orthogonal projector
![]() $\pi _{\mathcal {V}} \in C^\infty (S\widehat {M},S^2 \mathcal {N})$
onto a complex subbundle
$\pi _{\mathcal {V}} \in C^\infty (S\widehat {M},S^2 \mathcal {N})$
onto a complex subbundle
![]() $\mathcal {V} \subset \mathcal {N}$
of rank
$\mathcal {V} \subset \mathcal {N}$
of rank
![]() $1 \leq r \leq m/2-1$
of even Fourier degree.
$1 \leq r \leq m/2-1$
of even Fourier degree.
Note that by equation (2.19),
![]() $\mathcal {N}$
is a subbundle of the pullback bundle
$\mathcal {N}$
is a subbundle of the pullback bundle
![]() $\pi ^*TM$
so it makes sense to talk about the decomposition of a section
$\pi ^*TM$
so it makes sense to talk about the decomposition of a section
![]() $f \in C^\infty (SM, S^2 \mathcal {N})$
as a sum of spherical harmonics as in equation (2.4). The fact that
$f \in C^\infty (SM, S^2 \mathcal {N})$
as a sum of spherical harmonics as in equation (2.4). The fact that
![]() $\mathcal {V}$
is complex is equivalent to the commutation relation
$\mathcal {V}$
is complex is equivalent to the commutation relation
![]() $[\pi _{\mathcal {V}},J]=0$
.
$[\pi _{\mathcal {V}},J]=0$
.
Proof of Corollary 3.2
Up to replacing M by a finite covering if necessary, we can assume that the transitivity group
![]() $H \leqslant \mathrm {U}(m-1)$
is connected, see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 3.3]. In what follows, to keep notation simple, we will still denote this finite cover by M.
$H \leqslant \mathrm {U}(m-1)$
is connected, see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 3.3]. In what follows, to keep notation simple, we will still denote this finite cover by M.
The representation
![]() $\rho : H \to \mathrm {U}(m-1)$
induces a representation
$\rho : H \to \mathrm {U}(m-1)$
induces a representation
![]() $\det \rho : H \to \mathrm {U}(1)$
whose image is either
$\det \rho : H \to \mathrm {U}(1)$
whose image is either
![]() $\mathrm {U}(1)$
or
$\mathrm {U}(1)$
or
![]() $\{1\}$
(by connectedness of H). Following an argument of Brin and Gromov [Reference Brin and GromovBG80], we first show that
$\{1\}$
(by connectedness of H). Following an argument of Brin and Gromov [Reference Brin and GromovBG80], we first show that
![]() $(\det \rho )(H)= \mathrm {U}(1)$
.
$(\det \rho )(H)= \mathrm {U}(1)$
.
Indeed, assume that
![]() $(\det \rho )(H) = \{1\}$
. As
$(\det \rho )(H) = \{1\}$
. As
![]() $(\det \rho )(H)$
is the transitivity group of the frame flow of the complex line bundle
$(\det \rho )(H)$
is the transitivity group of the frame flow of the complex line bundle
![]() $\Lambda ^{m-1,0} \mathcal {N}$
, we get by the non-Abelian Livšic Theorem 2.6 that
$\Lambda ^{m-1,0} \mathcal {N}$
, we get by the non-Abelian Livšic Theorem 2.6 that
![]() $\Lambda ^{m-1,0} \mathcal {N}$
is trivial. Now, using that
$\Lambda ^{m-1,0} \mathcal {N}$
is trivial. Now, using that
is an isomorphism, the triviality of
![]() $\Lambda ^{m-1,0} \mathcal {N}$
implies that
$\Lambda ^{m-1,0} \mathcal {N}$
implies that
However, it can be easily checked using the Gysin sequence [Reference Bott and TuBT82, Proposition 14.33] (and the fact that the dimension of M is
![]() $n \geq 4$
) that
$n \geq 4$
) that
is injective, so
![]() $c_1(\Lambda ^{m,0} TM) = 0 = -c_1(K_M)$
, where
$c_1(\Lambda ^{m,0} TM) = 0 = -c_1(K_M)$
, where
![]() $K_M = \Lambda ^{m,0} T^*M$
is the canonical line bundle. This is impossible since
$K_M = \Lambda ^{m,0} T^*M$
is the canonical line bundle. This is impossible since
![]() $(M,g)$
has negative sectional curvature. Hence,
$(M,g)$
has negative sectional curvature. Hence,
![]() $(\det \rho )(H)= \mathrm {U}(1)$
.
$(\det \rho )(H)= \mathrm {U}(1)$
.
We will now show that the H-representation
![]() $\rho $
on
$\rho $
on
![]() $\mathbb {C}^{m-1}$
is reducible. Assume for a contradiction that
$\mathbb {C}^{m-1}$
is reducible. Assume for a contradiction that
![]() $\rho $
is irreducible. By the Schur lemma, the center
$\rho $
is irreducible. By the Schur lemma, the center
![]() $C(H)$
of H is contained in the set
$C(H)$
of H is contained in the set
![]() $\mathrm {U}(1)$
of scalar matrices. However, the fact that
$\mathrm {U}(1)$
of scalar matrices. However, the fact that
![]() $(\det \rho )(H) = \mathrm {U}(1)$
shows that H is not semi-simple, so its centre is at least one-dimensional. We thus obtain the equality
$(\det \rho )(H) = \mathrm {U}(1)$
shows that H is not semi-simple, so its centre is at least one-dimensional. We thus obtain the equality
![]() $C(H)=\mathrm {U}(1)$
, that is, H contains the set of scalar matrices.
$C(H)=\mathrm {U}(1)$
, that is, H contains the set of scalar matrices.
We now fix an arbitrary point
![]() $x_0 \in M$
, restrict the unitary frame bundle
$x_0 \in M$
, restrict the unitary frame bundle
![]() $F_{\mathbb {C}}M$
to a bundle over
$F_{\mathbb {C}}M$
to a bundle over
![]() $S_{x_0}M$
and identify
$S_{x_0}M$
and identify
![]() $S_{x_0}M \simeq S^{4p+3}$
. As the structure group of
$S_{x_0}M \simeq S^{4p+3}$
. As the structure group of
![]() $F_{\mathbb {C}} M$
reduces to H by Theorem 2.5, we obtain by restriction to any fibre of
$F_{\mathbb {C}} M$
reduces to H by Theorem 2.5, we obtain by restriction to any fibre of
![]() $SM\to M$
that the structure group of
$SM\to M$
that the structure group of
![]() $F_{\mathbb {C}}S^{4p+3}$
also reduces to H, that is, there exists a principal H-bundle
$F_{\mathbb {C}}S^{4p+3}$
also reduces to H, that is, there exists a principal H-bundle
![]() $P_H \subset F_{\mathbb {C}}S^{4p+3}$
. We claim that
$P_H \subset F_{\mathbb {C}}S^{4p+3}$
. We claim that
![]() $F_{\mathbb {C}}S^{4p+3}$
admits a further reduction to
$F_{\mathbb {C}}S^{4p+3}$
admits a further reduction to
![]() $H_0:=H\cap \mathrm {SU}(2p+1)$
. Indeed, the principal
$H_0:=H\cap \mathrm {SU}(2p+1)$
. Indeed, the principal
![]() $\mathrm {SU}(2p+1)$
-bundle
$\mathrm {SU}(2p+1)$
-bundle
![]() $F_{\mathbb {C},\mathrm {SU}}S^{4p+3}$
is already a reduction of
$F_{\mathbb {C},\mathrm {SU}}S^{4p+3}$
is already a reduction of
![]() $F_{\mathbb {C}}S^{4p+3}$
to
$F_{\mathbb {C}}S^{4p+3}$
to
![]() $\mathrm {SU}(2p+1)$
and for every
$\mathrm {SU}(2p+1)$
and for every
![]() $v\in S^{4p+3}$
, the intersection of the fibres
$v\in S^{4p+3}$
, the intersection of the fibres
![]() $F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)\cap P_H(v)$
is non-empty: if
$F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)\cap P_H(v)$
is non-empty: if
![]() $u\in P_H(v)\subset F_{\mathbb {C}}S^{4p+3}(v)$
, there exists
$u\in P_H(v)\subset F_{\mathbb {C}}S^{4p+3}(v)$
, there exists
![]() $z\in \mathrm {U}(1)$
such that
$z\in \mathrm {U}(1)$
such that
![]() $uz\in F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)$
, and since
$uz\in F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)$
, and since
![]() $\mathrm {U}(1)\subset H$
(that is, H contains scalar matrices), we also have
$\mathrm {U}(1)\subset H$
(that is, H contains scalar matrices), we also have
![]() $uz\in P_H(v)$
, so
$uz\in P_H(v)$
, so
![]() $uz\in F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)\cap P_H(v)$
. It is then straightforward to check that
$uz\in F_{\mathbb {C},\mathrm {SU}}S^{4p+3}(v)\cap P_H(v)$
. It is then straightforward to check that
![]() $F_{\mathbb {C},\mathrm {SU}}S^{4p+3}\cap P_H$
is a principal bundle over
$F_{\mathbb {C},\mathrm {SU}}S^{4p+3}\cap P_H$
is a principal bundle over
![]() $ S^{4p+3}$
with group
$ S^{4p+3}$
with group
![]() $H_0$
.
$H_0$
.
As
![]() $m \neq 4, 28$
by assumption, we can apply case (i) of Theorem 3.1 to deduce that
$m \neq 4, 28$
by assumption, we can apply case (i) of Theorem 3.1 to deduce that
![]() $H_0 \lneqq \mathrm {SU}(m-1)$
acts reducibly on
$H_0 \lneqq \mathrm {SU}(m-1)$
acts reducibly on
![]() $\mathbb {C}^{m-1}$
. However, as H was assumed to act irreducibly on
$\mathbb {C}^{m-1}$
. However, as H was assumed to act irreducibly on
![]() $\mathbb {C}^{m-1}$
,
$\mathbb {C}^{m-1}$
,
![]() $H_0 = H \cap \mathrm {SU}(m-1)$
also acts irreducibly on
$H_0 = H \cap \mathrm {SU}(m-1)$
also acts irreducibly on
![]() $\mathbb {C}^{m-1}$
and this is a contradiction. Therefore, H acts reducibly on
$\mathbb {C}^{m-1}$
and this is a contradiction. Therefore, H acts reducibly on
![]() $\mathbb {C}^{m-1}$
.
$\mathbb {C}^{m-1}$
.
We can then conclude the following using the non-Abelian Livšic Theorem 2.6: by the remark after Theorem 2.6, there exists a smooth (non-zero) flow-invariant orthogonal projector
![]() $\pi _{\mathcal {V}'} \in C^\infty (SM,S^2 \mathcal {N})$
onto a flow-invariant smooth complex bundle
$\pi _{\mathcal {V}'} \in C^\infty (SM,S^2 \mathcal {N})$
onto a flow-invariant smooth complex bundle
![]() $\mathcal {V}' \subset \mathcal {N}$
. Following [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 3.10], one can find a (possibly different) smooth non-zero flow-invariant orthogonal projector
$\mathcal {V}' \subset \mathcal {N}$
. Following [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 3.10], one can find a (possibly different) smooth non-zero flow-invariant orthogonal projector
![]() $\pi _{\mathcal {V}} \in C^\infty (SM,S^2 \mathcal {N})$
of even Fourier degree onto a flow-invariant smooth complex bundle
$\pi _{\mathcal {V}} \in C^\infty (SM,S^2 \mathcal {N})$
of even Fourier degree onto a flow-invariant smooth complex bundle
![]() $\mathcal {V} \subset \mathcal {N}$
of complex rank
$\mathcal {V} \subset \mathcal {N}$
of complex rank
![]() $1 \leq r \leq m/2-1$
.
$1 \leq r \leq m/2-1$
.
3.2 Complex normal twisted conformal Killing tensors
If
![]() $m \neq 4,28$
and the unitary frame flow is not ergodic, we know by Corollary 3.2 that there exists a flow-invariant orthogonal projector
$m \neq 4,28$
and the unitary frame flow is not ergodic, we know by Corollary 3.2 that there exists a flow-invariant orthogonal projector
![]() $\pi _{\mathcal {V}} \in C^\infty (SM,S^2\mathcal {N})$
of even Fourier degree and commuting with J. The flow-invariance condition is equivalent to
$\pi _{\mathcal {V}} \in C^\infty (SM,S^2\mathcal {N})$
of even Fourier degree and commuting with J. The flow-invariance condition is equivalent to
![]() $\mathbf {X} \pi _{\mathcal {V}} = 0$
. A crucial step then is to show that such a flow-invariant section has finite Fourier degree, that is, the decomposition of equation (2.4) only involves a finite number of terms. This is the content of the following lemma.
$\mathbf {X} \pi _{\mathcal {V}} = 0$
. A crucial step then is to show that such a flow-invariant section has finite Fourier degree, that is, the decomposition of equation (2.4) only involves a finite number of terms. This is the content of the following lemma.
Lemma 3.3. For any operation
![]() $\mathfrak {o} : \mathrm {Vect} \to \mathrm {Vect}$
, a section
$\mathfrak {o} : \mathrm {Vect} \to \mathrm {Vect}$
, a section
![]() $f \in C^\infty (SM,\mathfrak {o}(\mathcal {N}))$
satisfying
$f \in C^\infty (SM,\mathfrak {o}(\mathcal {N}))$
satisfying
![]() $\mathbf {X} f = 0$
has finite Fourier degree.
$\mathbf {X} f = 0$
has finite Fourier degree.
The proof of Lemma 3.3 uses the fact that the sectional curvature of
![]() $(M,g)$
is negative and relies on the twisted Pestov identity in equation (2.6). Lemma 3.3 was first obtained in [Reference Guillarmou, Paternain, Salo and UhlmannGPSU16, Theorem 4.1], see also [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS22, Corollary 4.2] for a short self-contained proof. As a consequence, we can decompose
$(M,g)$
is negative and relies on the twisted Pestov identity in equation (2.6). Lemma 3.3 was first obtained in [Reference Guillarmou, Paternain, Salo and UhlmannGPSU16, Theorem 4.1], see also [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS22, Corollary 4.2] for a short self-contained proof. As a consequence, we can decompose
where
![]() $k \geq 0$
is even,
$k \geq 0$
is even,
![]() $u_i \in C^\infty (M,\Omega _i \otimes S^2 TM)$
and
$u_i \in C^\infty (M,\Omega _i \otimes S^2 TM)$
and
![]() $u_k \neq 0$
. Moreover, since J has degree
$u_k \neq 0$
. Moreover, since J has degree
![]() $0$
(that is, it does not depend on the velocity variable v), the commutation relation
$0$
(that is, it does not depend on the velocity variable v), the commutation relation
![]() $[\pi _{\mathcal {V}},J]=0$
yields
$[\pi _{\mathcal {V}},J]=0$
yields
![]() $[u_i,J] = 0$
for all
$[u_i,J] = 0$
for all
![]() $i \in \{0, \ldots , k\}$
.
$i \in \{0, \ldots , k\}$
.
We now set
the spherical harmonic of highest degree in the decomposition of equation (3.2) of
![]() $\pi _{\mathcal {V}}$
. Using the mapping property in equation (2.5) of
$\pi _{\mathcal {V}}$
. Using the mapping property in equation (2.5) of
![]() $\mathbf {X}$
, the equation
$\mathbf {X}$
, the equation
![]() $\mathbf {X} \pi _{\mathcal {V}} = 0$
then gives
$\mathbf {X} \pi _{\mathcal {V}} = 0$
then gives
![]() $\mathbf {X}_+ u = 0$
. Such a section u is called a twisted conformal Killing tensor in the literature. Moreover, since
$\mathbf {X}_+ u = 0$
. Such a section u is called a twisted conformal Killing tensor in the literature. Moreover, since
![]() $\iota _v \pi _{\mathcal {V}} := \pi _{\mathcal {V}} v = 0$
(because
$\iota _v \pi _{\mathcal {V}} := \pi _{\mathcal {V}} v = 0$
(because
![]() $\mathcal {V}$
is orthogonal to the span of v and
$\mathcal {V}$
is orthogonal to the span of v and
![]() $Jv$
) and
$Jv$
) and
![]() $\iota _v$
has the mapping properties
$\iota _v$
has the mapping properties
we obtain that
![]() $\iota _v u \in C^\infty (M,\Omega _{k-1} \otimes TM)$
is of degree
$\iota _v u \in C^\infty (M,\Omega _{k-1} \otimes TM)$
is of degree
![]() $k-1$
. The same argument also shows that
$k-1$
. The same argument also shows that
![]() $\iota _{Jv} u \in C^\infty (M,\Omega _{k-1} \otimes TM)$
.
$\iota _{Jv} u \in C^\infty (M,\Omega _{k-1} \otimes TM)$
.
Using similarly that
![]() $\iota _v \iota _v \pi _{\mathcal {V}} = \langle \pi _{\mathcal {V}} v, v \rangle = 0$
, a refined algebraic argument allows to show that
$\iota _v \iota _v \pi _{\mathcal {V}} = \langle \pi _{\mathcal {V}} v, v \rangle = 0$
, a refined algebraic argument allows to show that
![]() $\iota _v \iota _v u=\iota _{Jv} \iota _{Jv} u \in C^\infty (M,\Omega _{k-2})$
is of degree
$\iota _v \iota _v u=\iota _{Jv} \iota _{Jv} u \in C^\infty (M,\Omega _{k-2})$
is of degree
![]() $k-2$
, see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.2] for a proof. Furthermore, we have
$k-2$
, see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.2] for a proof. Furthermore, we have
![]() $\iota _v \iota _{Jv} u = \iota _{Jv} \iota _v u = 0$
, using that u is symmetric and J is skew-symmetric, and
$\iota _v \iota _{Jv} u = \iota _{Jv} \iota _v u = 0$
, using that u is symmetric and J is skew-symmetric, and
![]() $[u,J]=0$
.
$[u,J]=0$
.
A section
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
satisfying
$u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
satisfying
was called in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, §4.1] a normal twisted conformal Killing tensor. (The adjective normal refers to the conditions on
![]() $\iota _v u$
and
$\iota _v u$
and
![]() $\iota _v \iota _v u$
.) Here, the section u satisfies the extra condition
$\iota _v \iota _v u$
.) Here, the section u satisfies the extra condition
![]() $[u,J] = 0$
. It is thus worth introducing the following terminology.
$[u,J] = 0$
. It is thus worth introducing the following terminology.
Definition 3.4. A section
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
satisfying equation (3.3) and
$u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
satisfying equation (3.3) and
![]() $[u,J]=0$
is called a complex normal twisted conformal Killing tensor.
$[u,J]=0$
is called a complex normal twisted conformal Killing tensor.
By Corollary 3.2 and the discussion above, we obtain the following corollary.
Corollary 3.5. Let
![]() $(M,g,J)$
be a closed connected Kähler manifold with even complex dimension m and non-ergodic unitary frame flow. Then, if
$(M,g,J)$
be a closed connected Kähler manifold with even complex dimension m and non-ergodic unitary frame flow. Then, if
![]() $m \neq 4, 28$
, there exists a non-zero complex normal twisted conformal Killing tensor u of even degree
$m \neq 4, 28$
, there exists a non-zero complex normal twisted conformal Killing tensor u of even degree
![]() $k \geq 2$
.
$k \geq 2$
.
Proof. Corollary 3.5 follows immediately from Corollary 3.2 and the above discussion, except for the point that
![]() $k \geq 2$
which we now prove. If
$k \geq 2$
which we now prove. If
![]() $k = 0$
, then
$k = 0$
, then
![]() $\pi _{\mathcal {V}} = u =u_0$
is of degree
$\pi _{\mathcal {V}} = u =u_0$
is of degree
![]() $0$
and thus
$0$
and thus
![]() $\pi _{\mathcal {V}}$
can be identified with a section in
$\pi _{\mathcal {V}}$
can be identified with a section in
![]() $C^\infty (M,S^2 TM)$
. However, we must also have
$C^\infty (M,S^2 TM)$
. However, we must also have
![]() $\iota _v \pi _{\mathcal {V}} = 0$
for all
$\iota _v \pi _{\mathcal {V}} = 0$
for all
![]() $v \in TM$
by equation (3.3), so
$v \in TM$
by equation (3.3), so
![]() $\pi _{\mathcal {V}} = 0$
, which contradicts the non-vanishing of
$\pi _{\mathcal {V}} = 0$
, which contradicts the non-vanishing of
![]() $\pi _{\mathcal {V}}$
.
$\pi _{\mathcal {V}}$
.
The aim of the remaining sections is now to rule out the existence of such a non-zero complex twisted conformal Killing tensor of even degree
![]() $k \geq 2$
under a holomorphic pinching condition
$k \geq 2$
under a holomorphic pinching condition
![]() $\unicode{x3bb}> \unicode{x3bb} (m)$
.
$\unicode{x3bb}> \unicode{x3bb} (m)$
.
4 Bounding the terms in the twisted Pestov identity
Throughout this section,
![]() $(M,g,J)$
is a negatively curved compact Kähler manifold of real dimension
$(M,g,J)$
is a negatively curved compact Kähler manifold of real dimension
![]() $n=2m$
with
$n=2m$
with
![]() $\unicode{x3bb} $
-pinched holomorphic curvature, and
$\unicode{x3bb} $
-pinched holomorphic curvature, and
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
is a complex normal twisted conformal Killing tensor of even degree
$u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
is a complex normal twisted conformal Killing tensor of even degree
![]() $k \geq 2$
.
$k \geq 2$
.
Our aim is to bound from above the terms appearing on the right-hand side of the twisted Pestov identity in equation (2.6), namely, the first term
![]() $\langle R \nabla _{\mathbb {V}}^{S^2 TM} u, \nabla _{\mathbb {V}}^{S^2 TM} u \rangle _{L^2}$
and the second term
$\langle R \nabla _{\mathbb {V}}^{S^2 TM} u, \nabla _{\mathbb {V}}^{S^2 TM} u \rangle _{L^2}$
and the second term
![]() $\langle \mathcal {F}^{S^2 TM}u, \nabla _{\mathbb {V}}^{S^2 TM}u \rangle _{L^2}$
, and to bound from below the term
$\langle \mathcal {F}^{S^2 TM}u, \nabla _{\mathbb {V}}^{S^2 TM}u \rangle _{L^2}$
, and to bound from below the term
![]() $\|\mathbf {X}_-u\|^2_{L^2}$
on the left-hand side. Sometimes, it will be convenient to consider general vector bundles
$\|\mathbf {X}_-u\|^2_{L^2}$
on the left-hand side. Sometimes, it will be convenient to consider general vector bundles
![]() $E \to M$
rather than the specific bundle
$E \to M$
rather than the specific bundle
![]() $S^2 TM$
.
$S^2 TM$
.
To simplify notation, we will drop the volume forms in the integrands. The reader should keep in mind that integrals over spheres
![]() $S_xM$
(for
$S_xM$
(for
![]() $x \in M$
) are always computed with respect to the round measure
$x \in M$
) are always computed with respect to the round measure
![]() $|dv|$
on the sphere, while integrals over M are computed with respect to the Riemannian measure
$|dv|$
on the sphere, while integrals over M are computed with respect to the Riemannian measure
![]() $|dx|$
induced by the metric g. Moreover, we will often work with expressions involving a local orthonormal basis of a vector bundle E, usually denoted by
$|dx|$
induced by the metric g. Moreover, we will often work with expressions involving a local orthonormal basis of a vector bundle E, usually denoted by
![]() $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_\alpha $
; for the simplicity of notation, when we write sums over
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_\alpha $
; for the simplicity of notation, when we write sums over
![]() $\alpha $
, we will mean that the sums are pointwise (and the basis might change from point to point). We also introduce the following constants:
$\alpha $
, we will mean that the sums are pointwise (and the basis might change from point to point). We also introduce the following constants:
 $$ \begin{align*} \begin{array}{ll} \alpha_{n,k} := k(n+k-2), & \beta_{n,k} := (k(n+k-2)(n-1))^{1/2}, \\ \gamma_{n,k} := \dfrac{(n+k-2)(n+2k-4)k}{(n+k-3)(n+2k-2)(k-1)}, & \delta_{n,k} := n+2k-4. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \alpha_{n,k} := k(n+k-2), & \beta_{n,k} := (k(n+k-2)(n-1))^{1/2}, \\ \gamma_{n,k} := \dfrac{(n+k-2)(n+2k-4)k}{(n+k-3)(n+2k-2)(k-1)}, & \delta_{n,k} := n+2k-4. \end{array} \end{align*} $$
4.1 Bounding the first term in the right-hand side
Let
![]() $E \to M$
be a Euclidean vector bundle equipped with an orthogonal connection
$E \to M$
be a Euclidean vector bundle equipped with an orthogonal connection
![]() $\nabla ^E$
. Then, the following lemma holds.
$\nabla ^E$
. Then, the following lemma holds.
Lemma 4.1. For all
![]() $f \in C^\infty (M,\Omega _k \otimes E)$
,
$f \in C^\infty (M,\Omega _k \otimes E)$
,
 $$ \begin{align*} \langle R \nabla_{\mathbb{V}}^{E} f, \nabla_{\mathbb{V}}^{E} f \rangle_{L^2} \leq - \frac{3\unicode{x3bb}-2}{4} & \alpha_{n,k}\|f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2, \end{align*} $$
$$ \begin{align*} \langle R \nabla_{\mathbb{V}}^{E} f, \nabla_{\mathbb{V}}^{E} f \rangle_{L^2} \leq - \frac{3\unicode{x3bb}-2}{4} & \alpha_{n,k}\|f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2, \end{align*} $$
where we write locally
![]() $f = \sum _{\alpha } f_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
for
$f = \sum _{\alpha } f_\alpha \operatorname {\mathrm {\mathbf {e}}}_\alpha $
for
![]() $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha \in I}$
a local orthonormal basis of E.
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha \in I}$
a local orthonormal basis of E.
Proof. Using the upper bound in equation (2.14) on the sectional curvature from Lemma 2.3,
 $$ \begin{align*} \langle R \nabla_{\mathbb{V}}^{E} f, \nabla_{\mathbb{V}}^{E} f \rangle_{L^2} & = \int_{M} \int_{S_xM}\sum_\alpha R(v,\nabla_{\mathbb{V}}^{E} f_\alpha,\nabla_{\mathbb{V}}^{E} f_\alpha,v) \\ & \leq - \frac{3\unicode{x3bb}-2}{4} \|\nabla_{\mathbb{V}}^{E} f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2 \\ & = - \frac{3\unicode{x3bb}-2}{4} \langle \Delta_{\mathbb{V}}^{E} f, f \rangle_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM} \sum_{\alpha}\langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2 \\ & = - \frac{3\unicode{x3bb}-2}{4}k(n+k-2)\|f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4}\int_{M} \int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2. \end{align*} $$
$$ \begin{align*} \langle R \nabla_{\mathbb{V}}^{E} f, \nabla_{\mathbb{V}}^{E} f \rangle_{L^2} & = \int_{M} \int_{S_xM}\sum_\alpha R(v,\nabla_{\mathbb{V}}^{E} f_\alpha,\nabla_{\mathbb{V}}^{E} f_\alpha,v) \\ & \leq - \frac{3\unicode{x3bb}-2}{4} \|\nabla_{\mathbb{V}}^{E} f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2 \\ & = - \frac{3\unicode{x3bb}-2}{4} \langle \Delta_{\mathbb{V}}^{E} f, f \rangle_{L^2} - \frac{3\unicode{x3bb}}{4} \int_{M}\int_{S_xM} \sum_{\alpha}\langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2 \\ & = - \frac{3\unicode{x3bb}-2}{4}k(n+k-2)\|f\|^2_{L^2} - \frac{3\unicode{x3bb}}{4}\int_{M} \int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha \rangle^2. \end{align*} $$
Since
![]() $\alpha _{n,k} := k(n+k-2)$
, this completes the proof.
$\alpha _{n,k} := k(n+k-2)$
, this completes the proof.
4.2 Bounding the second term on the right-hand side
Assume now that
![]() $E = \Lambda ^p TM$
or
$E = \Lambda ^p TM$
or
![]() $E = S^p TM$
for some
$E = S^p TM$
for some
![]() $p \geq 1$
. Using the decomposition of the Riemannian curvature tensor
$p \geq 1$
. Using the decomposition of the Riemannian curvature tensor
![]() $R = R_0 + ({1+\unicode{x3bb} })/{2}G$
in equation (2.15), we can write the second term on the right-hand side of the Pestov identity in equation (2.6) as
$R = R_0 + ({1+\unicode{x3bb} })/{2}G$
in equation (2.15), we can write the second term on the right-hand side of the Pestov identity in equation (2.6) as
More precisely,
![]() $\mathcal {F}^{E}_0$
and
$\mathcal {F}^{E}_0$
and
![]() $\mathcal {G}^{E}$
are defined from
$\mathcal {G}^{E}$
are defined from
![]() $R_0$
and G, respectively, by extending the latter to E as in §2.2.1 and using equation (2.7). We now study separately the two terms in equation (4.1). We start with the following lemma.
$R_0$
and G, respectively, by extending the latter to E as in §2.2.1 and using equation (2.7). We now study separately the two terms in equation (4.1). We start with the following lemma.
Lemma 4.2. If
![]() $E=\Lambda ^pTM$
or
$E=\Lambda ^pTM$
or
![]() $E = S^pTM$
, then for all
$E = S^pTM$
, then for all
![]() $f \in C^\infty (M,\Omega _k \otimes E)$
,
$f \in C^\infty (M,\Omega _k \otimes E)$
,
Lemma 4.2 will be applied with
![]() $E=TM$
and
$E=TM$
and
![]() $E=S^2TM$
.
$E=S^2TM$
.
Proof. The proof is the same as [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.5] by inserting the bound in equation (2.17).
We now study the second term in equation (4.1).
Lemma 4.3. Let
![]() $f \in C^\infty (M,\Omega _k \otimes E)$
such that
$f \in C^\infty (M,\Omega _k \otimes E)$
such that
![]() $\iota _v f, \iota _{Jv} f$
are of degree
$\iota _v f, \iota _{Jv} f$
are of degree
![]() $k-1$
. Then, the following hold:
$k-1$
. Then, the following hold:
-
(i) if
 $E = TM$
,
$E = TM$
,  $$ \begin{align*} \langle \mathcal{G}^{TM}f, \nabla_{\mathbb{V}}^{TM}f \rangle_{L^2} & = \frac{1}{4}\delta_{n,k} ( \|\iota_v f\|^2_{L^2} + \|\iota_{Jv} f\|^2_{L^2} ) + \tfrac{1}{2}\|f\|^2_{L^2} \\ & \quad + \frac{1}{2}\int_M \int_{S_xM} \sum_\alpha\langle v,J\nabla_{\mathbb{V}} f_\alpha\rangle\langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle; \end{align*} $$
$$ \begin{align*} \langle \mathcal{G}^{TM}f, \nabla_{\mathbb{V}}^{TM}f \rangle_{L^2} & = \frac{1}{4}\delta_{n,k} ( \|\iota_v f\|^2_{L^2} + \|\iota_{Jv} f\|^2_{L^2} ) + \tfrac{1}{2}\|f\|^2_{L^2} \\ & \quad + \frac{1}{2}\int_M \int_{S_xM} \sum_\alpha\langle v,J\nabla_{\mathbb{V}} f_\alpha\rangle\langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle; \end{align*} $$
-
(ii) if
 $E = S^2 TM$
and
$E = S^2 TM$
and
 $[J,f] = 0$
,
$[J,f] = 0$
,  $$ \begin{align*} \langle \mathcal{G}^{S^2 TM}f, \nabla_{\mathbb{V}}^{S^2 TM}f \rangle_{L^2} = \delta_{n,k} \|\iota_v f\|^2_{L^2} + \|f\|^2_{L^2}. \end{align*} $$
$$ \begin{align*} \langle \mathcal{G}^{S^2 TM}f, \nabla_{\mathbb{V}}^{S^2 TM}f \rangle_{L^2} = \delta_{n,k} \|\iota_v f\|^2_{L^2} + \|f\|^2_{L^2}. \end{align*} $$
Proof. We start with the proof for
![]() $E = TM$
. Note that this equality is an integral equality over
$E = TM$
. Note that this equality is an integral equality over
![]() $SM$
. We will actually prove the integral equality over
$SM$
. We will actually prove the integral equality over
![]() $S_xM$
for every
$S_xM$
for every
![]() $x \in M$
, and then it suffices to integrate over
$x \in M$
, and then it suffices to integrate over
![]() $x \in M$
to obtain the result. Recall that G is defined in equation (2.12). Using the expressions in equations (2.7) and (2.13),
$x \in M$
to obtain the result. Recall that G is defined in equation (2.12). Using the expressions in equations (2.7) and (2.13),
 $$ \begin{align} 4 \sum_\alpha G(v, \nabla_{\mathbb{V}} f_\alpha, f, \operatorname{\mathrm{\mathbf{e}}}_\alpha) & = \sum_\alpha( \langle (v \wedge \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \nonumber\\ &\quad + \langle (Jv \wedge J \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle + 2\langle{v, J \nabla_{\mathbb{V}} f_\alpha}\rangle\langle{f, J \operatorname{\mathrm{\mathbf{e}}}_\alpha}\rangle). \end{align} $$
$$ \begin{align} 4 \sum_\alpha G(v, \nabla_{\mathbb{V}} f_\alpha, f, \operatorname{\mathrm{\mathbf{e}}}_\alpha) & = \sum_\alpha( \langle (v \wedge \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \nonumber\\ &\quad + \langle (Jv \wedge J \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle + 2\langle{v, J \nabla_{\mathbb{V}} f_\alpha}\rangle\langle{f, J \operatorname{\mathrm{\mathbf{e}}}_\alpha}\rangle). \end{align} $$
The integral over
![]() $S_xM$
of the first term on the right-hand side can be immediately computed using [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.6] (in the
$S_xM$
of the first term on the right-hand side can be immediately computed using [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.6] (in the
![]() $\Lambda ^p$
case with
$\Lambda ^p$
case with
![]() $p=1$
; we warn the reader that, in the notation of [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21], G denotes the curvature tensor of the real hyperbolic space, that is,
$p=1$
; we warn the reader that, in the notation of [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21], G denotes the curvature tensor of the real hyperbolic space, that is, ![]() . The term
. The term
![]() $\sum _\alpha \int _{S_xM} \langle v,f\rangle \langle \nabla _{\mathbb {V}} f_\alpha , \operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle - \langle v,\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle \langle \nabla _{\mathbb {V}} f_\alpha , f\rangle $
thus corresponds exactly to the term computed in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Equation after (4.14)] with
$\sum _\alpha \int _{S_xM} \langle v,f\rangle \langle \nabla _{\mathbb {V}} f_\alpha , \operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle - \langle v,\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle \langle \nabla _{\mathbb {V}} f_\alpha , f\rangle $
thus corresponds exactly to the term computed in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Equation after (4.14)] with
![]() $p=1$
) since
$p=1$
) since
![]() $\iota _v f$
is of degree
$\iota _v f$
is of degree
![]() $k-1$
and yields
$k-1$
and yields
 $$ \begin{align*} \int_{S_xM} \sum_\alpha \langle (v \wedge \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle& = \int_{S_xM} \bigg(\sum_\alpha \langle v,f\rangle \langle \nabla_{\mathbb{V}} f_\alpha, \operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle - \langle v,\operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle \langle \nabla_{\mathbb{V}} f_\alpha, f\rangle\bigg) \\ &= (n+2k-4)\|\iota_v f\|^2_{L^2(S_xM)} + \|f\|^2_{L^2(S_xM)}, \end{align*} $$
$$ \begin{align*} \int_{S_xM} \sum_\alpha \langle (v \wedge \nabla_{\mathbb{V}} f_\alpha) f, \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle& = \int_{S_xM} \bigg(\sum_\alpha \langle v,f\rangle \langle \nabla_{\mathbb{V}} f_\alpha, \operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle - \langle v,\operatorname{\mathrm{\mathbf{e}}}_\alpha\rangle \langle \nabla_{\mathbb{V}} f_\alpha, f\rangle\bigg) \\ &= (n+2k-4)\|\iota_v f\|^2_{L^2(S_xM)} + \|f\|^2_{L^2(S_xM)}, \end{align*} $$
where we use the notation
 $$ \begin{align*} \|f\|^2_{L^2(S_xM)} = \int_{S_xM} g_{x}(f(v),f(v)), \quad \|\iota_v f\|^2_{L^2(S_xM)} = \int_{S_xM} |(\iota_v f)(v)|^2. \end{align*} $$
$$ \begin{align*} \|f\|^2_{L^2(S_xM)} = \int_{S_xM} g_{x}(f(v),f(v)), \quad \|\iota_v f\|^2_{L^2(S_xM)} = \int_{S_xM} |(\iota_v f)(v)|^2. \end{align*} $$
We claim that the integral over
![]() $S_xM$
of the second term in equation (4.2) is equal to
$S_xM$
of the second term in equation (4.2) is equal to
![]() $(n+2k-4)\|\iota _{Jv} f\|^2_{L^2(S_xM)} + \|f\|^2_{L^2(S_xM)}$
. Indeed, observe first that for each
$(n+2k-4)\|\iota _{Jv} f\|^2_{L^2(S_xM)} + \|f\|^2_{L^2(S_xM)}$
. Indeed, observe first that for each
![]() $\alpha $
,
$\alpha $
,
Now, since
![]() $f_\alpha = \langle f,\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle = \langle Jf,J\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle $
, changing the basis
$f_\alpha = \langle f,\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle = \langle Jf,J\operatorname {\mathrm {\mathbf {e}}}_\alpha \rangle $
, changing the basis
![]() $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
by
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
by
![]() $(J\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
, we see that the second term in equation (4.2) is the same as the first term with f replaced by
$(J\operatorname {\mathrm {\mathbf {e}}}_\alpha )$
, we see that the second term in equation (4.2) is the same as the first term with f replaced by
![]() $Jf$
. Using
$Jf$
. Using
![]() $\iota _v Jf = -\iota _{Jv} f$
, the result now follows from the previous computation. Inserting the previous equality in equation (4.2) gives the desired result (after integration over M) since
$\iota _v Jf = -\iota _{Jv} f$
, the result now follows from the previous computation. Inserting the previous equality in equation (4.2) gives the desired result (after integration over M) since
![]() $\delta _{n,k} = n+2k-4$
.
$\delta _{n,k} = n+2k-4$
.
We now deal with the case
![]() $E = S^2TM$
. As before, using the expressions in equations (2.7), (2.11) and (2.13),
$E = S^2TM$
. As before, using the expressions in equations (2.7), (2.11) and (2.13),
 $$ \begin{align} 4\! \sum_\alpha G_{S^2 TM}(v, \nabla_{\mathbb{V}} f_\alpha, f, \operatorname{\mathrm{\mathbf{e}}}_\alpha) &= {\kern-1pt}\sum_\alpha ( \langle [(v \wedge \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \nonumber \\&\quad + \langle [(J v {\kern-1pt}\wedge{\kern-1pt} J \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle - 2 \langle{v, J \nabla_{\mathbb{V}} f_\alpha}\rangle.\langle{[J,{\kern-1pt}f], \operatorname{\mathrm{\mathbf{e}}}_\alpha}\rangle), \end{align} $$
$$ \begin{align} 4\! \sum_\alpha G_{S^2 TM}(v, \nabla_{\mathbb{V}} f_\alpha, f, \operatorname{\mathrm{\mathbf{e}}}_\alpha) &= {\kern-1pt}\sum_\alpha ( \langle [(v \wedge \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \nonumber \\&\quad + \langle [(J v {\kern-1pt}\wedge{\kern-1pt} J \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle - 2 \langle{v, J \nabla_{\mathbb{V}} f_\alpha}\rangle.\langle{[J,{\kern-1pt}f], \operatorname{\mathrm{\mathbf{e}}}_\alpha}\rangle), \end{align} $$
where
![]() $(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha }$
is a local orthonormal basis of
$(\operatorname {\mathrm {\mathbf {e}}}_\alpha )_{\alpha }$
is a local orthonormal basis of
![]() $S^2TM$
. The integral over
$S^2TM$
. The integral over
![]() $S_xM$
of the first term can be computed using [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.6] (case of symmetric
$S_xM$
of the first term can be computed using [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.6] (case of symmetric
![]() $2$
-tensors) since
$2$
-tensors) since
![]() $\iota _v f$
is of degree
$\iota _v f$
is of degree
![]() $k-1$
and yields
$k-1$
and yields
 $$ \begin{align} \int_{S_xM} \sum_\alpha\langle [(v \wedge \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle = 2(n+2k-4)\|\iota_v f\|^2_{L^2(S_xM)} + 2\|f\|^2_{L^2(S_xM)}. \end{align} $$
$$ \begin{align} \int_{S_xM} \sum_\alpha\langle [(v \wedge \nabla_{\mathbb{V}} f_\alpha), f], \operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle = 2(n+2k-4)\|\iota_v f\|^2_{L^2(S_xM)} + 2\|f\|^2_{L^2(S_xM)}. \end{align} $$
The third term vanishes in equation (4.3) since
![]() $[J,f]=0$
by assumption.
$[J,f]=0$
by assumption.
We now claim that the integral over
![]() $S_xM$
of the second term in equation (4.3) is also equal to
$S_xM$
of the second term in equation (4.3) is also equal to
![]() $2(n+2k-4)\|\iota _v f\|^2_{L^2(S_xM)} + 2\|f\|^2_{L^2(S_xM)}$
, which will finish the proof. Indeed, observe that
$2(n+2k-4)\|\iota _v f\|^2_{L^2(S_xM)} + 2\|f\|^2_{L^2(S_xM)}$
, which will finish the proof. Indeed, observe that
![]() $JX \wedge JY = -J \circ (X \wedge Y) \circ J$
for any
$JX \wedge JY = -J \circ (X \wedge Y) \circ J$
for any
![]() $X, Y \in TM$
, and therefore using also
$X, Y \in TM$
, and therefore using also
![]() $[J, f] = 0$
, we get for each
$[J, f] = 0$
, we get for each
![]() $\alpha $
,
$\alpha $
,
Consequently, we can rewrite
Note that
![]() $(-J \circ \operatorname {\mathrm {\mathbf {e}}}_\alpha \circ J)_\alpha $
is also an orthonormal basis of
$(-J \circ \operatorname {\mathrm {\mathbf {e}}}_\alpha \circ J)_\alpha $
is also an orthonormal basis of
![]() $S^2TM$
, and since
$S^2TM$
, and since
![]() $f=-J \circ f \circ J =- \sum _\alpha f_\alpha J \circ \operatorname {\mathrm {\mathbf {e}}}_\alpha \circ J$
,
$f=-J \circ f \circ J =- \sum _\alpha f_\alpha J \circ \operatorname {\mathrm {\mathbf {e}}}_\alpha \circ J$
,
The claim thus follows from equation (4.4).
4.3 Bounding from below the left-hand side
Going back to the case
![]() $E = S^2TM$
, we now bound from below the term
$E = S^2TM$
, we now bound from below the term
![]() $\|\mathbf {X}_-u\|^2_{L^2}$
appearing on the left-hand side of the twisted Pestov identity in equation (2.6).
$\|\mathbf {X}_-u\|^2_{L^2}$
appearing on the left-hand side of the twisted Pestov identity in equation (2.6).
Lemma 4.4. Let
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
be a complex normal twisted conformal Killing tensor in the sense of Definition 3.4. Then, for
$u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
be a complex normal twisted conformal Killing tensor in the sense of Definition 3.4. Then, for
![]() $k> 0$
, the following inequality holds:
$k> 0$
, the following inequality holds:
 $$ \begin{align*} &\frac{(k-1)(n+2k-2)}{k} \|\mathbf{X}_-u\|^2_{L^2}\\ &\quad\geq \bigg(\frac{3\unicode{x3bb}-2}{2}\alpha_{n,k-1}-\frac{8(1-\unicode{x3bb})}{3}\beta_{n,k-1}- \frac{29(1+\unicode{x3bb})}{48} - \frac{1+\unicode{x3bb}}{4} \delta_{n,k-1}\bigg) \|\iota_v u\|^2_{L^2}. \end{align*} $$
$$ \begin{align*} &\frac{(k-1)(n+2k-2)}{k} \|\mathbf{X}_-u\|^2_{L^2}\\ &\quad\geq \bigg(\frac{3\unicode{x3bb}-2}{2}\alpha_{n,k-1}-\frac{8(1-\unicode{x3bb})}{3}\beta_{n,k-1}- \frac{29(1+\unicode{x3bb})}{48} - \frac{1+\unicode{x3bb}}{4} \delta_{n,k-1}\bigg) \|\iota_v u\|^2_{L^2}. \end{align*} $$
The proof of Lemma 4.4 requires an additional step and is postponed to the end of this paragraph.
Lemma 4.5. Let
![]() $f \in C^\infty (M, \Omega _k \otimes TM)$
such that
$f \in C^\infty (M, \Omega _k \otimes TM)$
such that
![]() $\iota _v f, \iota _{Jv} f$
are of degree
$\iota _v f, \iota _{Jv} f$
are of degree
![]() $k-1$
, and assume
$k-1$
, and assume
![]() $\unicode{x3bb} \in [{2}/{3}, 1]$
. Then, the following holds:
$\unicode{x3bb} \in [{2}/{3}, 1]$
. Then, the following holds:
 $$ \begin{align*} \frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2} \geq &\bigg( \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k} - \frac{4(1-\unicode{x3bb})}{3} \beta_{n,k} - \frac{29(1+\unicode{x3bb}) }{96}\bigg) \|f\|^2_{L^2} \\ & - \frac{1+\unicode{x3bb}}{8}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}). \end{align*} $$
$$ \begin{align*} \frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2} \geq &\bigg( \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k} - \frac{4(1-\unicode{x3bb})}{3} \beta_{n,k} - \frac{29(1+\unicode{x3bb}) }{96}\bigg) \|f\|^2_{L^2} \\ & - \frac{1+\unicode{x3bb}}{8}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}). \end{align*} $$
Proof. Using the twisted Pestov identity in equation (2.6) with
![]() $E =TM$
, and applying the bounds provided by Lemmas 4.1, 4.2 and 4.3,
$E =TM$
, and applying the bounds provided by Lemmas 4.1, 4.2 and 4.3,
 $$ \begin{align*} &\frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2}\\ &\quad\geq - \langle R \nabla_{\mathbb{V}}^{TM} f, \nabla_{\mathbb{V}}^{TM}f \rangle_{L^2} - \langle \mathcal{F}^{TM}f,\nabla_{\mathbb{V}}^{TM} f\rangle_{L^2} \\ &\quad\geq \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k}\|f\|^2_{L^2} + \frac{3\unicode{x3bb}}{4} \int_M\int_{S_xM} \sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2 -\frac{4(1-\unicode{x3bb})}{3}\beta_{n,k}\|f\|^2_{L^2} \\ & \qquad- \frac{1+\unicode{x3bb}}{2}\bigg( \dfrac{1}{4}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}) + \frac{1}{2}\|f\|^2_{L^2}\\ &\qquad+ \frac{1}{2}\int_M \int_{S_xM} \sum_{\alpha} |\langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle| |\langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle| \bigg). \end{align*} $$
$$ \begin{align*} &\frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2}\\ &\quad\geq - \langle R \nabla_{\mathbb{V}}^{TM} f, \nabla_{\mathbb{V}}^{TM}f \rangle_{L^2} - \langle \mathcal{F}^{TM}f,\nabla_{\mathbb{V}}^{TM} f\rangle_{L^2} \\ &\quad\geq \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k}\|f\|^2_{L^2} + \frac{3\unicode{x3bb}}{4} \int_M\int_{S_xM} \sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2 -\frac{4(1-\unicode{x3bb})}{3}\beta_{n,k}\|f\|^2_{L^2} \\ & \qquad- \frac{1+\unicode{x3bb}}{2}\bigg( \dfrac{1}{4}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}) + \frac{1}{2}\|f\|^2_{L^2}\\ &\qquad+ \frac{1}{2}\int_M \int_{S_xM} \sum_{\alpha} |\langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle| |\langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle| \bigg). \end{align*} $$
We now use the estimate
 $$ \begin{align*} \frac{1}{2} \int_M \int_{S_xM} \sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle \langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \leq \frac{1}{4\varepsilon} \|f\|^2_{L^2} + \frac{\varepsilon}{4}\int_M \int_{S_xM} \sum_\alpha \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2, \end{align*} $$
$$ \begin{align*} \frac{1}{2} \int_M \int_{S_xM} \sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle \langle f,J\operatorname{\mathrm{\mathbf{e}}}_\alpha \rangle \leq \frac{1}{4\varepsilon} \|f\|^2_{L^2} + \frac{\varepsilon}{4}\int_M \int_{S_xM} \sum_\alpha \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2, \end{align*} $$
which holds for all
![]() $\varepsilon> 0$
, to deduce that
$\varepsilon> 0$
, to deduce that
 $$ \begin{align*} \frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2} &\geq \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k}\|f\|^2_{L^2} + \frac{3\unicode{x3bb}}{4}\int_M\int_{S_xM} \sum_{\alpha}\langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2\\&\quad-\frac{4(1-\unicode{x3bb})}{3}\beta_{n,k}\|f\|^2_{L^2} \\&\quad - \frac{1+\unicode{x3bb}}{2}\bigg( \frac{1}{4}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}) + \bigg(\frac{1}{2} +\frac{1}{4\varepsilon}\bigg)\|f\|^2_{L^2}\\&\quad+ \frac{\varepsilon}{4} \int_M \int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2 \bigg). \end{align*} $$
$$ \begin{align*} \frac{k(n+2k)}{k+1}\|\mathbf{X}_+f\|^2_{L^2} &\geq \frac{3\unicode{x3bb}-2}{4} \alpha_{n,k}\|f\|^2_{L^2} + \frac{3\unicode{x3bb}}{4}\int_M\int_{S_xM} \sum_{\alpha}\langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2\\&\quad-\frac{4(1-\unicode{x3bb})}{3}\beta_{n,k}\|f\|^2_{L^2} \\&\quad - \frac{1+\unicode{x3bb}}{2}\bigg( \frac{1}{4}\delta_{n,k}(\|\iota_v f\|^2_{L^2} + \|\iota_{Jv}f\|^2_{L^2}) + \bigg(\frac{1}{2} +\frac{1}{4\varepsilon}\bigg)\|f\|^2_{L^2}\\&\quad+ \frac{\varepsilon}{4} \int_M \int_{S_xM}\sum_{\alpha} \langle v,J\nabla_{\mathbb{V}}f_\alpha\rangle^2 \bigg). \end{align*} $$
Taking the specific value
![]() $\varepsilon := 6\unicode{x3bb} /(1+\unicode{x3bb} )$
, we see that the coefficients in front of the term
$\varepsilon := 6\unicode{x3bb} /(1+\unicode{x3bb} )$
, we see that the coefficients in front of the term
![]() $\int _M \sum _{\alpha } \int _{S_xM} \langle v,J\nabla _{\mathbb {V}}f_\alpha \rangle ^2$
cancel out. Moreover, since by assumption
$\int _M \sum _{\alpha } \int _{S_xM} \langle v,J\nabla _{\mathbb {V}}f_\alpha \rangle ^2$
cancel out. Moreover, since by assumption
![]() $\unicode{x3bb} \in [2/3,1]$
, we have the lower bound
$\unicode{x3bb} \in [2/3,1]$
, we have the lower bound
![]() $\varepsilon ={6\unicode{x3bb} }/({1 + \unicode{x3bb} }) \geq {12}/5$
and this eventually yields the result.
$\varepsilon ={6\unicode{x3bb} }/({1 + \unicode{x3bb} }) \geq {12}/5$
and this eventually yields the result.
Remark 4.6. In the last paragraph of the proof of Lemma 4.5, one could decide to keep using the exact value
![]() $\varepsilon = {6\unicode{x3bb} }/({1 + \unicode{x3bb} })$
in the estimate. However, the benefit of doing so would be minor in the final result so, for simplicity, we decided to use the trivial lower bound
$\varepsilon = {6\unicode{x3bb} }/({1 + \unicode{x3bb} })$
in the estimate. However, the benefit of doing so would be minor in the final result so, for simplicity, we decided to use the trivial lower bound
![]() $\varepsilon \geq {12}/5$
.
$\varepsilon \geq {12}/5$
.
We can now prove Lemma 4.4.
Proof of Lemma 4.4
Using the equality
![]() $\mathbf {X}(\iota _v u) = \iota _v \mathbf {X} u = \iota _v \mathbf {X}_- u$
and the fact that
$\mathbf {X}(\iota _v u) = \iota _v \mathbf {X} u = \iota _v \mathbf {X}_- u$
and the fact that
![]() $\iota _{Jv}\mathbf {X}_-u=J(\iota _{v}\mathbf {X}_-u)$
,
$\iota _{Jv}\mathbf {X}_-u=J(\iota _{v}\mathbf {X}_-u)$
,
 $$ \begin{align*} \|\mathbf{X}_-u\|^2_{L^2} & \geq \|\iota_v \mathbf{X}_- u\|^2_{L^2} + \|\iota_{Jv}\mathbf{X}_-u\|^2_{L^2} =2\|\iota_v \mathbf{X}_- u\|^2_{L^2} \\ & =2 \|\mathbf{X}(\iota_vu)\|^2_{L^2} =2 \|\mathbf{X}_+(\iota_v u)\|^2_{L^2} +2 \|\mathbf{X}_-(\iota_v u)\|^2_{L^2} \\ & \geq 2\|\mathbf{X}_+(\iota_v u)\|^2_{L^2} , \end{align*} $$
$$ \begin{align*} \|\mathbf{X}_-u\|^2_{L^2} & \geq \|\iota_v \mathbf{X}_- u\|^2_{L^2} + \|\iota_{Jv}\mathbf{X}_-u\|^2_{L^2} =2\|\iota_v \mathbf{X}_- u\|^2_{L^2} \\ & =2 \|\mathbf{X}(\iota_vu)\|^2_{L^2} =2 \|\mathbf{X}_+(\iota_v u)\|^2_{L^2} +2 \|\mathbf{X}_-(\iota_v u)\|^2_{L^2} \\ & \geq 2\|\mathbf{X}_+(\iota_v u)\|^2_{L^2} , \end{align*} $$
where in the second line, we used that
![]() $\iota _v u$
and
$\iota _v u$
and
![]() $\iota _{Jv} u$
are of degree
$\iota _{Jv} u$
are of degree
![]() $k - 1$
and the mapping property in equation (2.5). By assumption, u is a complex normal twisted conformal Killing tensor, so this implies that
$k - 1$
and the mapping property in equation (2.5). By assumption, u is a complex normal twisted conformal Killing tensor, so this implies that
![]() $\iota _v \iota _{Jv} u = \iota _{Jv} \iota _v u = 0$
and
$\iota _v \iota _{Jv} u = \iota _{Jv} \iota _v u = 0$
and
![]() $\iota _v \iota _v u= \iota _{Jv}\iota _{Jv}u$
is of degree
$\iota _v \iota _v u= \iota _{Jv}\iota _{Jv}u$
is of degree
![]() $k-2$
. As a consequence, we can apply Lemma 4.5 with
$k-2$
. As a consequence, we can apply Lemma 4.5 with
![]() $f:=\iota _v u$
(which is of degree
$f:=\iota _v u$
(which is of degree
![]() $k-1$
). Using the fact that
$k-1$
). Using the fact that
![]() $\iota _{Jv} f=0$
, together with the fact that
$\iota _{Jv} f=0$
, together with the fact that
we obtain the announced result.
5 Pinching estimates
In this section, we prove our main result, Theorem 1.1.
5.1 Computations
We start with the following lemma.
Lemma 5.1. If
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
is a complex normal twisted conformal Killing tensor, the following inequality holds:
$u \in C^\infty (M,\Omega _k \otimes S^2 TM)$
is a complex normal twisted conformal Killing tensor, the following inequality holds:
where
and
 $$ \begin{align} C_{n,k}(\unicode{x3bb}) :&= \gamma_{n,k}\bigg( \frac{3\unicode{x3bb}-2}{2}\alpha_{n,k-1}-\frac{8(1-\unicode{x3bb})}{3}\beta_{n,k-1}-\frac{29(1+\unicode{x3bb})}{48} - \frac{1+\unicode{x3bb}}{4}\delta_{n,k-1}\bigg)\nonumber\\ &\quad- \frac{1+\unicode{x3bb}}{2}\delta_{n,k}. \end{align} $$
$$ \begin{align} C_{n,k}(\unicode{x3bb}) :&= \gamma_{n,k}\bigg( \frac{3\unicode{x3bb}-2}{2}\alpha_{n,k-1}-\frac{8(1-\unicode{x3bb})}{3}\beta_{n,k-1}-\frac{29(1+\unicode{x3bb})}{48} - \frac{1+\unicode{x3bb}}{4}\delta_{n,k-1}\bigg)\nonumber\\ &\quad- \frac{1+\unicode{x3bb}}{2}\delta_{n,k}. \end{align} $$
Proof. Straightforward computation, inserting in the twisted Pestov identity in equation (2.6) the lower bound for
![]() $\|\mathbf {X}_-u\|^2$
(Lemma 4.4), the upper bounds for the terms on the right-hand side (Lemmas 4.1 and 4.2 applied to
$\|\mathbf {X}_-u\|^2$
(Lemma 4.4), the upper bounds for the terms on the right-hand side (Lemmas 4.1 and 4.2 applied to
![]() $f=u$
, and Lemma 4.3(ii)), as well as using the facts that
$f=u$
, and Lemma 4.3(ii)), as well as using the facts that
![]() $\mathbf {X}_+ u = 0$
(by the definition in equation (3.3)) and
$\mathbf {X}_+ u = 0$
(by the definition in equation (3.3)) and
![]() $\|Z(u)\|_{L^2}^2 \geq 0$
.
$\|Z(u)\|_{L^2}^2 \geq 0$
.
Recall that
![]() $n=2m$
is the real dimension of M. The end of the proof of Theorem 1.1 then consists in finding a pinching condition
$n=2m$
is the real dimension of M. The end of the proof of Theorem 1.1 then consists in finding a pinching condition
![]() $\unicode{x3bb}> \unicode{x3bb} (m)$
for which the left-hand side of equation (5.1) is non-negative, thus forcing the complex normal twisted conformal Killing tensor u to be zero, which then contradicts Corollary 3.2. More precisely, we have the following lemma.
$\unicode{x3bb}> \unicode{x3bb} (m)$
for which the left-hand side of equation (5.1) is non-negative, thus forcing the complex normal twisted conformal Killing tensor u to be zero, which then contradicts Corollary 3.2. More precisely, we have the following lemma.
Lemma 5.2. If the inequalities
hold, then equation (5.1) implies
![]() $u \equiv 0$
.
$u \equiv 0$
.
Proof. If
![]() ${C}_{n,k}(\unicode{x3bb} ) \geq 0$
, this is immediate from the first part of equation (5.4). If
${C}_{n,k}(\unicode{x3bb} ) \geq 0$
, this is immediate from the first part of equation (5.4). If
![]() ${C}_{n,k}(\unicode{x3bb} ) <0$
, using that
${C}_{n,k}(\unicode{x3bb} ) <0$
, using that
![]() $ \|u\|^2_{L^2}\geq \|\iota _vu\|^2_{L^2}+\|\iota _{Jv}u\|^2_{L^2}=2\|\iota _vu\|^2_{L^2}$
, we get by equation (5.1):
$ \|u\|^2_{L^2}\geq \|\iota _vu\|^2_{L^2}+\|\iota _{Jv}u\|^2_{L^2}=2\|\iota _vu\|^2_{L^2}$
, we get by equation (5.1):
so
![]() $u \equiv 0$
by the second part of equation (5.4).
$u \equiv 0$
by the second part of equation (5.4).
Moreover, the following lemma holds.
Lemma 5.3. Assume
![]() $n \geq 4$
and
$n \geq 4$
and
![]() $k \geq 2$
. One has
$k \geq 2$
. One has
![]() $B_{n,k}> 0 \iff \unicode{x3bb} > \unicode{x3bb} _1(n,k)$
, where
$B_{n,k}> 0 \iff \unicode{x3bb} > \unicode{x3bb} _1(n,k)$
, where

and
![]() $B_{n,k} +\tfrac 12 C_{n,k}> 0 \iff \unicode{x3bb} > \unicode{x3bb} _2(n,k)$
, where
$B_{n,k} +\tfrac 12 C_{n,k}> 0 \iff \unicode{x3bb} > \unicode{x3bb} _2(n,k)$
, where

Proof. Follows immediately from equations (5.2) and (5.3), as the expressions of
![]() $B_{n,k}$
and
$B_{n,k}$
and
![]() $C_{n,k}$
are affine functions in
$C_{n,k}$
are affine functions in
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
Before proving Theorem 1.1, we need to study the variations of the sequences
![]() $k \mapsto \unicode{x3bb} _{1}(n,k)$
and
$k \mapsto \unicode{x3bb} _{1}(n,k)$
and
![]() $k \mapsto \unicode{x3bb} _{2}(n,k)$
.
$k \mapsto \unicode{x3bb} _{2}(n,k)$
.
Lemma 5.4. For
![]() $n \geq 4$
, the sequences
$n \geq 4$
, the sequences
![]() $k \mapsto \unicode{x3bb} _{1}(n,k)$
and
$k \mapsto \unicode{x3bb} _{1}(n,k)$
and
![]() $k \mapsto \unicode{x3bb} _{2}(n,k)$
are decreasing for
$k \mapsto \unicode{x3bb} _{2}(n,k)$
are decreasing for
![]() $k \geq 2$
.
$k \geq 2$
.
Proof. It is straightforward to check that both sequences are positive for
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $n\ge 4$
. Using that
$n\ge 4$
. Using that
![]() $\alpha _{n,k}={\beta _{n,k}^2}/({n-1})$
, we can write
$\alpha _{n,k}={\beta _{n,k}^2}/({n-1})$
, we can write

Since
![]() $\alpha _{n,k}$
and
$\alpha _{n,k}$
and
![]() $\beta _{n,k}$
are positive and increasing in k, the numerator in the right-hand term is increasing in k, whereas the denominator is positive and decreasing in k. Thus,
$\beta _{n,k}$
are positive and increasing in k, the numerator in the right-hand term is increasing in k, whereas the denominator is positive and decreasing in k. Thus,
![]() $k \mapsto \unicode{x3bb} _{1}(n,k)$
is decreasing.
$k \mapsto \unicode{x3bb} _{1}(n,k)$
is decreasing.
Consider now the expression
![]() $\unicode{x3bb} _{2}(n,k)$
. Again it is easy to check that
$\unicode{x3bb} _{2}(n,k)$
. Again it is easy to check that
![]() $\unicode{x3bb} _{2}(n,k)>0$
for
$\unicode{x3bb} _{2}(n,k)>0$
for
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $n\ge 4$
, and
$n\ge 4$
, and

Let us denote this last expression by
![]() ${E_{n,k}}/{F_{n,k}}$
. We claim that
${E_{n,k}}/{F_{n,k}}$
. We claim that
![]() $E_{n,k}$
is increasing in k and
$E_{n,k}$
is increasing in k and
![]() $F_{n,k}$
is decreasing in k.
$F_{n,k}$
is decreasing in k.
Using the fact that
![]() ${\gamma _{n,k}}/{\alpha _{n,k}}=({n+2k-4})/({(n+2k-2)\alpha _{n,k-1}})$
,
${\gamma _{n,k}}/{\alpha _{n,k}}=({n+2k-4})/({(n+2k-2)\alpha _{n,k-1}})$
,
 $$ \begin{align*}E_{n,k}&=3+3\frac{\gamma_{n,k}}{\alpha_{n,k}}\alpha_{n,k-1}-\frac{12+6\delta_{n,k}}{\alpha_{n,k}}-\frac{29}{4}\frac{\gamma_{n,k}}{\alpha_{n,k}}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\delta_{n,k-1}\\ &=6\frac{n+2k-3}{n+2k-2}-6\frac{n+2k-2}{\alpha_{n,k}}-\frac{29}{4}\frac{\gamma_{n,k}}{\alpha_{n,k}}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\delta_{n,k-1}\\ &=6-\frac6{n+2k-2}-\frac6k-\frac6{n+k-2}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\bigg((n+2k-4)+\frac5{12}\bigg). \end{align*} $$
$$ \begin{align*}E_{n,k}&=3+3\frac{\gamma_{n,k}}{\alpha_{n,k}}\alpha_{n,k-1}-\frac{12+6\delta_{n,k}}{\alpha_{n,k}}-\frac{29}{4}\frac{\gamma_{n,k}}{\alpha_{n,k}}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\delta_{n,k-1}\\ &=6\frac{n+2k-3}{n+2k-2}-6\frac{n+2k-2}{\alpha_{n,k}}-\frac{29}{4}\frac{\gamma_{n,k}}{\alpha_{n,k}}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\delta_{n,k-1}\\ &=6-\frac6{n+2k-2}-\frac6k-\frac6{n+k-2}-3\frac{\gamma_{n,k}}{\alpha_{n,k}}\bigg((n+2k-4)+\frac5{12}\bigg). \end{align*} $$
To express
![]() $F_{n,k}$
, we remark that
$F_{n,k}$
, we remark that
 $$ \begin{align*}\frac{\gamma_{n,k}}{\alpha_{n,k}}\beta_{n,k-1}=\frac{n+2k-4}{n+2k-2}\frac{\beta_{n,k-1}}{\alpha_{n,k-1}}=\frac{s_{n,k-1}}{n+2k-2},\end{align*} $$
$$ \begin{align*}\frac{\gamma_{n,k}}{\alpha_{n,k}}\beta_{n,k-1}=\frac{n+2k-4}{n+2k-2}\frac{\beta_{n,k-1}}{\alpha_{n,k-1}}=\frac{s_{n,k-1}}{n+2k-2},\end{align*} $$
where we denote
![]() $s_{n,k}:={(n+2k-2)\beta _{n,k}}/{\alpha _{n,k}}.$
A straightforward computation similar to that for
$s_{n,k}:={(n+2k-2)\beta _{n,k}}/{\alpha _{n,k}}.$
A straightforward computation similar to that for
![]() $E_{n,k}$
shows that
$E_{n,k}$
shows that
 $$ \begin{align*}F_{n,k}&=6+3\frac{n+2k-2}{\alpha_{n,k}}+6\frac{n+2k-4}{n+2k-2}+\frac{3}{2}\frac{\gamma_{n,k}}{\alpha_{n,k}}\bigg((n+2k-4)+\frac5{12}\bigg)\\ &\quad+32\frac{s_{n,k}}{n+2k-2}+16\frac{s_{n,k-1}}{n+2k-2}.\end{align*} $$
$$ \begin{align*}F_{n,k}&=6+3\frac{n+2k-2}{\alpha_{n,k}}+6\frac{n+2k-4}{n+2k-2}+\frac{3}{2}\frac{\gamma_{n,k}}{\alpha_{n,k}}\bigg((n+2k-4)+\frac5{12}\bigg)\\ &\quad+32\frac{s_{n,k}}{n+2k-2}+16\frac{s_{n,k-1}}{n+2k-2}.\end{align*} $$
To prove our claim, it is thus enough to remark that
 $$ \begin{align*}(n+2k-4)\frac{\gamma_{n,k}}{\alpha_{n,k}}&=\frac{(n+2k-4)^2}{(k-1)(n+k-3)(n+2k-2)}\\ &=\frac{n-4}{n-2}\cdot\frac1{k-1}+\frac{n}{n-2}\cdot\frac1{n+k-3}+\frac{4}{(k-1)(n+k-3)(n+2k-2)}\end{align*} $$
$$ \begin{align*}(n+2k-4)\frac{\gamma_{n,k}}{\alpha_{n,k}}&=\frac{(n+2k-4)^2}{(k-1)(n+k-3)(n+2k-2)}\\ &=\frac{n-4}{n-2}\cdot\frac1{k-1}+\frac{n}{n-2}\cdot\frac1{n+k-3}+\frac{4}{(k-1)(n+k-3)(n+2k-2)}\end{align*} $$
is decreasing in k (and thus
![]() ${\gamma _{n,k}}/{\alpha _{n,k}}$
is decreasing in k too);
${\gamma _{n,k}}/{\alpha _{n,k}}$
is decreasing in k too);
 $$ \begin{align*}s_{n,k}=(n+2k-2)\frac{\sqrt{(n-1)k(n+k-2)}}{k(n+k-2)}=\sqrt{(n-1)\bigg(4+\frac{(n-2)^2}{k(n+k-2)}\bigg)}\end{align*} $$
$$ \begin{align*}s_{n,k}=(n+2k-2)\frac{\sqrt{(n-1)k(n+k-2)}}{k(n+k-2)}=\sqrt{(n-1)\bigg(4+\frac{(n-2)^2}{k(n+k-2)}\bigg)}\end{align*} $$
is decreasing in k, and
 $$ \begin{align*}\frac{n+2k-2}{\alpha_{n,k}}+2\frac{n+2k-4}{n+2k-2}&=2+\frac{n+2k-2}{k(n+k-2)}-\frac4{n+2k-2}\\&=2+\frac{(n-2)^2}{k(n+k-2)(n+2k-2)}\end{align*} $$
$$ \begin{align*}\frac{n+2k-2}{\alpha_{n,k}}+2\frac{n+2k-4}{n+2k-2}&=2+\frac{n+2k-2}{k(n+k-2)}-\frac4{n+2k-2}\\&=2+\frac{(n-2)^2}{k(n+k-2)(n+2k-2)}\end{align*} $$
is decreasing in k.
5.2 Proof of ergodicity
We can now conclude the proof of the ergodicity statement in Theorem 1.1.
Proof of ergodicity in Theorem 1.1
We need to show that under the pinching condition
![]() $\unicode{x3bb}> \unicode{x3bb} (m)$
of Theorem 1.1, the unitary frame flow is ergodic. If the frame flow is not ergodic, and
$\unicode{x3bb}> \unicode{x3bb} (m)$
of Theorem 1.1, the unitary frame flow is ergodic. If the frame flow is not ergodic, and
![]() $m \neq 4,28$
, we know by Corollary 3.2 that there exists a flow-invariant orthogonal projector
$m \neq 4,28$
, we know by Corollary 3.2 that there exists a flow-invariant orthogonal projector
![]() $\pi _{\mathcal {V}} \in C^\infty (SM,S^2 \mathcal {N})$
of even Fourier degree onto a complex vector bundle
$\pi _{\mathcal {V}} \in C^\infty (SM,S^2 \mathcal {N})$
of even Fourier degree onto a complex vector bundle
![]() $\mathcal {V} \subset \mathcal {N}$
of rank
$\mathcal {V} \subset \mathcal {N}$
of rank
![]() $1 \leq r \leq m/2-1$
.
$1 \leq r \leq m/2-1$
.
By Corollary 3.5 and Lemma 5.1, this yields the existence of a non-zero complex normal twisted conformal Killing tensor
![]() $u \in C^\infty (M,\Omega _k \otimes S^2 T^*M)$
of even degree
$u \in C^\infty (M,\Omega _k \otimes S^2 T^*M)$
of even degree
![]() $k \geq 2$
which satisfies the inequality in equation (5.1). We distinguish two cases.
$k \geq 2$
which satisfies the inequality in equation (5.1). We distinguish two cases.
Case 1. If
![]() $k \geq 4$
, Lemmas 5.3 and 5.4 show that if the holomorphic pinching
$k \geq 4$
, Lemmas 5.3 and 5.4 show that if the holomorphic pinching
![]() $\unicode{x3bb} $
satisfies
$\unicode{x3bb} $
satisfies
![]() $\unicode{x3bb}> \max (\unicode{x3bb} _1(n,4),\unicode{x3bb} _2(n,4))$
, we then have
$\unicode{x3bb}> \max (\unicode{x3bb} _1(n,4),\unicode{x3bb} _2(n,4))$
, we then have
![]() $B_{n,k}> 0$
and
$B_{n,k}> 0$
and
![]() $B_{n,k}+\frac 12C_{n,k}> 0$
which by Lemma 5.2 implies that
$B_{n,k}+\frac 12C_{n,k}> 0$
which by Lemma 5.2 implies that
![]() $u \equiv 0$
.
$u \equiv 0$
.
Case 2. If
![]() $k=2$
, let
$k=2$
, let
![]() $\pi _{\mathcal {V}}$
be the projector given by Corollary 3.2, whose complex rank r satisfies
$\pi _{\mathcal {V}}$
be the projector given by Corollary 3.2, whose complex rank r satisfies
![]() $1\le r\le m/2-1$
. By [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.2], one can then show that
$1\le r\le m/2-1$
. By [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Lemma 4.2], one can then show that
![]() $\pi _{\mathcal {V}}$
must be of the form
$\pi _{\mathcal {V}}$
must be of the form
with
![]() $u \in C^\infty (M,\Omega _2 \otimes S^2 T^*M)$
as above. In particular, since
$u \in C^\infty (M,\Omega _2 \otimes S^2 T^*M)$
as above. In particular, since ![]() is parallel, this implies
is parallel, this implies
![]() $\mathbf {X} u = 0$
, that is,
$\mathbf {X} u = 0$
, that is,
![]() $\mathbf {X}_\pm u = 0$
. Moreover, a quick algebraic computation (see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, p. 38]) gives
$\mathbf {X}_\pm u = 0$
. Moreover, a quick algebraic computation (see [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, p. 38]) gives
and since
![]() $2r\le m-2=n/2-2$
,
$2r\le m-2=n/2-2$
,
Applying the twisted Pestov identity in equation (2.6) to u for
![]() $k=2$
, using that
$k=2$
, using that
![]() $\mathbf {X}_\pm u = 0$
(the bound of Lemma 4.4 is therefore useless), and the upper bounds of Lemmas 4.1, 4.2 and 4.3, we find that
$\mathbf {X}_\pm u = 0$
(the bound of Lemma 4.4 is therefore useless), and the upper bounds of Lemmas 4.1, 4.2 and 4.3, we find that
 $$ \begin{align*} \bigg(\frac{3\unicode{x3bb}-2}{2}n-\frac{8(1-\unicode{x3bb})}{3}(2n(n-1))^{1/2}-\frac{1+\unicode{x3bb}}{2}\bigg)\|u\|^2_{L^2} - \frac{1+\unicode{x3bb}}{2} n \|\iota_vu\|^2_{L^2} \leq 0. \end{align*} $$
$$ \begin{align*} \bigg(\frac{3\unicode{x3bb}-2}{2}n-\frac{8(1-\unicode{x3bb})}{3}(2n(n-1))^{1/2}-\frac{1+\unicode{x3bb}}{2}\bigg)\|u\|^2_{L^2} - \frac{1+\unicode{x3bb}}{2} n \|\iota_vu\|^2_{L^2} \leq 0. \end{align*} $$
Inserting equation (5.5) in the previous inequality, then
 $$ \begin{align*} \bigg(\frac{3\unicode{x3bb}-2}{2}n-\frac{8(1-\unicode{x3bb})}{3}(2n(n-1))^{1/2}-\frac{1+\unicode{x3bb}}{2} \frac{2n}{n+4} \bigg)\|u\|^2_{L^2} \leq 0. \end{align*} $$
$$ \begin{align*} \bigg(\frac{3\unicode{x3bb}-2}{2}n-\frac{8(1-\unicode{x3bb})}{3}(2n(n-1))^{1/2}-\frac{1+\unicode{x3bb}}{2} \frac{2n}{n+4} \bigg)\|u\|^2_{L^2} \leq 0. \end{align*} $$
This shows that
![]() $u \equiv 0$
when
$u \equiv 0$
when
![]() $k=2$
, as soon as the holomorphic pinching
$k=2$
, as soon as the holomorphic pinching
![]() $\unicode{x3bb} $
satisfies
$\unicode{x3bb} $
satisfies

Summarizing the two cases
![]() $k\ge 4$
and
$k\ge 4$
and
![]() $k=2$
, we have obtained that the the unitary frame flow is ergodic as soon as the holomorphic pinching
$k=2$
, we have obtained that the the unitary frame flow is ergodic as soon as the holomorphic pinching
![]() $\unicode{x3bb} $
satisfies
$\unicode{x3bb} $
satisfies
Using a formal computing tool, it can be easily checked that
![]() $ \unicode{x3bb} _0(m)=\unicode{x3bb} _2(2m)$
for
$ \unicode{x3bb} _0(m)=\unicode{x3bb} _2(2m)$
for
![]() $m \geq 6$
. However, for practical reasons, we will give a bound which is slightly less accurate, but much easier to compute.
$m \geq 6$
. However, for practical reasons, we will give a bound which is slightly less accurate, but much easier to compute.
Namely, using the obvious inequality
![]() $((n+2)(n-1))^{1/2}<n+1/2$
, we can write
$((n+2)(n-1))^{1/2}<n+1/2$
, we can write

Similarly, since
![]() $16\sqrt 2<68/3$
,
$16\sqrt 2<68/3$
,

Finally, using the calculation in the proof of Lemma 5.4 together with the obvious inequalities
![]() $64/\sqrt 3<37$
and
$64/\sqrt 3<37$
and
we obtain

It is straightforward to check that
which implies
![]() $1/{\unicode{x3bb} _0(m)}-1>({14n-26})/({154n+131})$
, so eventually
$1/{\unicode{x3bb} _0(m)}-1>({14n-26})/({154n+131})$
, so eventually
thus proving the ergodicity statement of Theorem 1.1.
We conclude this paragraph by a remark on the remaining cases
![]() $m=4,28$
.
$m=4,28$
.
Remark 5.5. In the case
![]() $m=28$
, one can check (using the LiE program for instance) that
$m=28$
, one can check (using the LiE program for instance) that
![]() $\mathrm {E}_6$
fixes an element of
$\mathrm {E}_6$
fixes an element of
![]() $S^3 \mathbb {C}^{27}$
. As we saw in the proof of Corollary 3.2, the transitivity group is never semi-simple as it always contains the scalar matrices: Theorem 3.1 therefore does not exclude that subgroups of
$S^3 \mathbb {C}^{27}$
. As we saw in the proof of Corollary 3.2, the transitivity group is never semi-simple as it always contains the scalar matrices: Theorem 3.1 therefore does not exclude that subgroups of
![]() $\mathrm {E}_6 \times \mathrm {U}(1) \lneqq \mathrm {U}(27)$
occur as transitivity groups in complex dimension
$\mathrm {E}_6 \times \mathrm {U}(1) \lneqq \mathrm {U}(27)$
occur as transitivity groups in complex dimension
![]() $m=28$
. In this case, the transitivity group would fix an orthogonal projector of
$m=28$
. In this case, the transitivity group would fix an orthogonal projector of
![]() $\mathrm {End}(S^3 \mathbb {C}^{27})$
. Nevertheless, the argument given below involving the twisted Pestov identity does not carry over to
$\mathrm {End}(S^3 \mathbb {C}^{27})$
. Nevertheless, the argument given below involving the twisted Pestov identity does not carry over to
![]() $\mathrm {End}(S^3 \mathbb {C}^{27})$
because this vector space involves tensorial powers of too high degree. In other words, the argument would result in a pinching condition
$\mathrm {End}(S^3 \mathbb {C}^{27})$
because this vector space involves tensorial powers of too high degree. In other words, the argument would result in a pinching condition
![]() $\unicode{x3bb}> \unicode{x3bb} (28)$
for some
$\unicode{x3bb}> \unicode{x3bb} (28)$
for some
![]() $\unicode{x3bb} (28)> 1$
so the statement would be empty. A similar remark holds for the case
$\unicode{x3bb} (28)> 1$
so the statement would be empty. A similar remark holds for the case
![]() $m=4$
. This should be compared with [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Theorem 3.8] where we only deal with elements of
$m=4$
. This should be compared with [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Theorem 3.8] where we only deal with elements of
![]() $\mathfrak {o}(\mathcal {N})$
with
$\mathfrak {o}(\mathcal {N})$
with
![]() $\mathfrak {o} \in \{\mathrm {id},S^2,\Lambda ^2,\Lambda ^3\}$
. The worse pinching estimate in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Theorem 1.2] comes from the exterior power
$\mathfrak {o} \in \{\mathrm {id},S^2,\Lambda ^2,\Lambda ^3\}$
. The worse pinching estimate in [Reference Cekić, Lefeuvre, Moroianu and SemmelmannCLMS21, Theorem 1.2] comes from the exterior power
![]() $\Lambda ^3 \mathcal {N}$
.
$\Lambda ^3 \mathcal {N}$
.
5.3 Proof of mixing
It now remains to show the mixing property of Theorem 1.1, which is implied by the following result.
Proposition 5.6. The unitary frame flow on a negatively curved Kähler manifold
![]() $(M,g)$
is ergodic if and only if it is mixing.
$(M,g)$
is ergodic if and only if it is mixing.
Proof. Mixing implies ergodicity so it remains to show that ergodicity implies mixing in this setting. By [Reference LefeuvreLef23, Proof of Lemma 3.7], it suffices to show that the equation
implies that
![]() $u \equiv 0$
. Let
$u \equiv 0$
. Let
![]() $u \in L^2(F_{\mathbb {C}}M)$
be a solution to equation (5.7). Since
$u \in L^2(F_{\mathbb {C}}M)$
be a solution to equation (5.7). Since
![]() $F_{\mathbb {C}}M \to SM$
is a principal
$F_{\mathbb {C}}M \to SM$
is a principal
![]() $\mathrm {U}(m-1)$
-bundle over
$\mathrm {U}(m-1)$
-bundle over
![]() $SM$
, the space
$SM$
, the space
![]() $L^2(F_{\mathbb {C}}M)$
splits as
$L^2(F_{\mathbb {C}}M)$
splits as
 $$ \begin{align} L^2(F_{\mathbb{C}}M) = \bigoplus_{k=0}^{+\infty} L^2(SM, \Theta_k), \end{align} $$
$$ \begin{align} L^2(F_{\mathbb{C}}M) = \bigoplus_{k=0}^{+\infty} L^2(SM, \Theta_k), \end{align} $$
where
![]() $\Theta _k$
is the vector bundle over
$\Theta _k$
is the vector bundle over
![]() $SM$
whose fibre over
$SM$
whose fibre over
![]() $v\in SM$
is the eigenspace of the Casimir operator of
$v\in SM$
is the eigenspace of the Casimir operator of
![]() $\mathrm {U}(m-1)$
acting on functions of the fibre
$\mathrm {U}(m-1)$
acting on functions of the fibre
![]() $(F_{\mathbb {C}}M)_v$
, associated to the eigenvalue
$(F_{\mathbb {C}}M)_v$
, associated to the eigenvalue
![]() $\mu _k \geq 0$
(and
$\mu _k \geq 0$
(and
![]() $\mu _k \neq \mu _j$
for
$\mu _k \neq \mu _j$
for
![]() $k \neq j$
). Since
$k \neq j$
). Since
![]() $X_{F_{\mathbb {C}}M}$
preserves the splitting equation (5.8) (because the frame flow
$X_{F_{\mathbb {C}}M}$
preserves the splitting equation (5.8) (because the frame flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
commutes with the right-action of
$(\Phi _t)_{t \in \mathbb {R}}$
commutes with the right-action of
![]() $\mathrm {U}(m-1)$
), we deduce that for each
$\mathrm {U}(m-1)$
), we deduce that for each
![]() $k\ge 0$
, the component
$k\ge 0$
, the component
![]() $u_k\in L^2(SM,\Theta _k)$
of some function
$u_k\in L^2(SM,\Theta _k)$
of some function
![]() $u = \sum _{k} u_k \in \oplus _{k=0}^{+\infty }L^2(SM,\Theta _k)$
satisfying equation (5.7) must satisfy
$u = \sum _{k} u_k \in \oplus _{k=0}^{+\infty }L^2(SM,\Theta _k)$
satisfying equation (5.7) must satisfy
Since
![]() $\Theta _0 = \mathbb {C}$
is trivial over
$\Theta _0 = \mathbb {C}$
is trivial over
![]() $SM$
, the equation
$SM$
, the equation
![]() $X_{F_{\mathbb {C}}M} u_0 = i\unicode{x3bb} u_0$
reads
$X_{F_{\mathbb {C}}M} u_0 = i\unicode{x3bb} u_0$
reads
![]() $X u_0 = i \unicode{x3bb} u_0$
, where
$X u_0 = i \unicode{x3bb} u_0$
, where
![]() $u_0 \in L^2(SM)$
and X is the geodesic vector field. However, the geodesic flow is mixing as
$u_0 \in L^2(SM)$
and X is the geodesic vector field. However, the geodesic flow is mixing as
![]() $(M,g)$
has negative curvature, so we deduce that
$(M,g)$
has negative curvature, so we deduce that
![]() $u_0 = 0$
.
$u_0 = 0$
.
For
![]() $k \neq 0$
, [Reference LefeuvreLef23, Proposition 2.7] based on microlocal analysis shows that
$k \neq 0$
, [Reference LefeuvreLef23, Proposition 2.7] based on microlocal analysis shows that
![]() $u_k \in ~L^2 (SM,\Theta _k)$
is actually smooth, that is,
$u_k \in ~L^2 (SM,\Theta _k)$
is actually smooth, that is,
![]() $u_k \in C^\infty (SM,\Theta _k)$
. Moreover,
$u_k \in C^\infty (SM,\Theta _k)$
. Moreover,
![]() $X_{F_{\mathbb {C}}M}|u_k|^2 = 0$
, so using the ergodicity assumption on the frame flow
$X_{F_{\mathbb {C}}M}|u_k|^2 = 0$
, so using the ergodicity assumption on the frame flow
![]() $(\Phi _t)_{t \in \mathbb {R}}$
, we get that
$(\Phi _t)_{t \in \mathbb {R}}$
, we get that
![]() $|u_k|$
is constant on
$|u_k|$
is constant on
![]() $F_{\mathbb {C}}M$
. If
$F_{\mathbb {C}}M$
. If
![]() $u_k \neq 0$
, then up to rescaling, we obtain that
$u_k \neq 0$
, then up to rescaling, we obtain that
![]() $u_k : F_{\mathbb {C}} M \to \mathrm {U}(1)$
is a well-defined smooth map. To simplify the notation, we will drop the index k from now on and simply write u instead of
$u_k : F_{\mathbb {C}} M \to \mathrm {U}(1)$
is a well-defined smooth map. To simplify the notation, we will drop the index k from now on and simply write u instead of
![]() $u_k$
, and
$u_k$
, and
![]() $\mu $
instead of
$\mu $
instead of
![]() $\mu _k$
.
$\mu _k$
.
Denote by P the unit circle bundle of the complex line bundle
![]() $\Lambda ^{m-1,0}\mathcal {N} \to SM$
. Now, observe that there is a natural surjective bundle map
$\Lambda ^{m-1,0}\mathcal {N} \to SM$
. Now, observe that there is a natural surjective bundle map
![]() $\psi : F_{\mathbb {C}}M \to P$
given by
$\psi : F_{\mathbb {C}}M \to P$
given by
 $$ \begin{align*} \psi : (v, \operatorname{\mathrm{\mathbf{e}}}_2, \ldots,\operatorname{\mathrm{\mathbf{e}}}_m) \mapsto \bigg(v,\frac{1}{\sqrt{2}} (\operatorname{\mathrm{\mathbf{e}}}_2-i J\operatorname{\mathrm{\mathbf{e}}}_2) \wedge \ldots\wedge \frac{1}{\sqrt{2}} (\operatorname{\mathrm{\mathbf{e}}}_m-iJ\operatorname{\mathrm{\mathbf{e}}}_m)\bigg). \end{align*} $$
$$ \begin{align*} \psi : (v, \operatorname{\mathrm{\mathbf{e}}}_2, \ldots,\operatorname{\mathrm{\mathbf{e}}}_m) \mapsto \bigg(v,\frac{1}{\sqrt{2}} (\operatorname{\mathrm{\mathbf{e}}}_2-i J\operatorname{\mathrm{\mathbf{e}}}_2) \wedge \ldots\wedge \frac{1}{\sqrt{2}} (\operatorname{\mathrm{\mathbf{e}}}_m-iJ\operatorname{\mathrm{\mathbf{e}}}_m)\bigg). \end{align*} $$
There is a natural unitary parallel transport along geodesic flow-lines of sections of
![]() $\Lambda ^{m-1,0}\mathcal {N}$
, so there is a flow
$\Lambda ^{m-1,0}\mathcal {N}$
, so there is a flow
![]() $(\Phi _t^P)_{t \in \mathbb {R}}$
on P with generator
$(\Phi _t^P)_{t \in \mathbb {R}}$
on P with generator
![]() $X_P$
extending the geodesic flow
$X_P$
extending the geodesic flow
![]() $(\varphi _t)_{t\in \mathbb {R}}$
as in §2.3, that is, writing
$(\varphi _t)_{t\in \mathbb {R}}$
as in §2.3, that is, writing
![]() $\pi : P \to SM$
for the projection map, one has
$\pi : P \to SM$
for the projection map, one has
![]() $\pi \circ \Phi _t^P = \varphi _t \circ \pi $
for all
$\pi \circ \Phi _t^P = \varphi _t \circ \pi $
for all
![]() $t \in \mathbb {R}$
. Moreover,
$t \in \mathbb {R}$
. Moreover,
![]() $\psi $
intertwines the frame flow on
$\psi $
intertwines the frame flow on
![]() $F_{\mathbb {C}}M$
and the flow on P, that is
$F_{\mathbb {C}}M$
and the flow on P, that is
We claim that the following holds.
Claim 5.7. There exists a smooth function
![]() $w \in C^\infty (P)$
such that
$w \in C^\infty (P)$
such that
![]() $u = \psi ^* w$
and
$u = \psi ^* w$
and
![]() $X_P w = i \unicode{x3bb} w$
.
$X_P w = i \unicode{x3bb} w$
.
Note that, once we know that
![]() $u = \psi ^*w$
for some function w, the relation
$u = \psi ^*w$
for some function w, the relation
![]() $X_P w = i \unicode{x3bb} w$
is immediate using equation (5.9) and
$X_P w = i \unicode{x3bb} w$
is immediate using equation (5.9) and
![]() $X_{F_{\mathbb {C}}M} u = i \unicode{x3bb} u$
.
$X_{F_{\mathbb {C}}M} u = i \unicode{x3bb} u$
.
Proof. We show that
![]() $u = \psi ^*w$
for some
$u = \psi ^*w$
for some
![]() $w \in C^\infty (P)$
. We fix an arbitrary point
$w \in C^\infty (P)$
. We fix an arbitrary point
![]() $v_0 \in SM$
and
$v_0 \in SM$
and
![]() $w_0 \in (F_{\mathbb {C}}M)_{v_0}$
. There is then a commutative diagram
$w_0 \in (F_{\mathbb {C}}M)_{v_0}$
. There is then a commutative diagram

where the downward arrows are isometries. Hence, by restricting u to the fibre
![]() $(F_{\mathbb {C}}M)_{v_0}$
and identifying isometrically
$(F_{\mathbb {C}}M)_{v_0}$
and identifying isometrically
![]() $(F_{\mathbb {C}}M)_{v_0} \simeq \mathrm {U}(m-1)$
, we get a map
$(F_{\mathbb {C}}M)_{v_0} \simeq \mathrm {U}(m-1)$
, we get a map
![]() $F := u(v_0)$
such that
$F := u(v_0)$
such that
and
![]() $\Delta _{\mathrm {U}(m-1)}F = \mu F$
with
$\Delta _{\mathrm {U}(m-1)}F = \mu F$
with
![]() $\mu \neq 0$
since u takes values in
$\mu \neq 0$
since u takes values in
![]() $\Theta _k$
for
$\Theta _k$
for
![]() $k \neq 0$
. In other words, F is an eigenfunction of the Casimir operator on
$k \neq 0$
. In other words, F is an eigenfunction of the Casimir operator on
![]() $\mathrm {U}(m-1)$
associated to the eigenvalue
$\mathrm {U}(m-1)$
associated to the eigenvalue
![]() $\mu \neq 0$
and of constant modulus.
$\mu \neq 0$
and of constant modulus.
Now, recall that
![]() $\mathrm {U}(m-1)$
is a split group extension of the circle group
$\mathrm {U}(m-1)$
is a split group extension of the circle group
![]() $\mathrm {U}(1)$
by the special unitary group
$\mathrm {U}(1)$
by the special unitary group
![]() $\mathrm {SU}(m-1)$
, that is,
$\mathrm {SU}(m-1)$
, that is,
![]() $\mathrm {det} : \mathrm {U}(m-1) \to \mathrm {U}(1)$
is a fibre bundle with fibres isometric to
$\mathrm {det} : \mathrm {U}(m-1) \to \mathrm {U}(1)$
is a fibre bundle with fibres isometric to
![]() $\mathrm {SU}(m-1)$
. We claim that such a function F must then necessarily be constant on the
$\mathrm {SU}(m-1)$
. We claim that such a function F must then necessarily be constant on the
![]() $\mathrm {SU}(m-1)$
-fibres of the bundle
$\mathrm {SU}(m-1)$
-fibres of the bundle
![]() $\mathrm {U}(m-1)$
, that is,
$\mathrm {U}(m-1)$
, that is,
![]() $F = \mathrm {det}^* f$
for some
$F = \mathrm {det}^* f$
for some
![]() $f \in C^\infty (\mathrm {U}(1))$
,
$f \in C^\infty (\mathrm {U}(1))$
,
![]() $\mu = j^2$
for some integer
$\mu = j^2$
for some integer
![]() $j \geq 0$
and f is an eigenfunction of
$j \geq 0$
and f is an eigenfunction of
![]() $\Delta _{\mathrm {U}(1)}$
with eigenvalue
$\Delta _{\mathrm {U}(1)}$
with eigenvalue
![]() $j^2$
.
$j^2$
.
Indeed, since
![]() $\mathrm {U}(m-1) = \mathrm {SU}(m-1) \times _{\mathbb {Z}_{m-1}} \mathrm {U}(1)$
, there is a
$\mathrm {U}(m-1) = \mathrm {SU}(m-1) \times _{\mathbb {Z}_{m-1}} \mathrm {U}(1)$
, there is a
![]() $\mathbb {Z}_{m-1}$
-bundle map
$\mathbb {Z}_{m-1}$
-bundle map
![]() $p : \mathrm {SU}(m-1) \times \mathrm {U}(1) \to \mathrm {U}(m-1)$
,
$p : \mathrm {SU}(m-1) \times \mathrm {U}(1) \to \mathrm {U}(m-1)$
,
![]() $p(w, z) = wz$
, and this map is locally a Riemannian isometry. (The
$p(w, z) = wz$
, and this map is locally a Riemannian isometry. (The
![]() $\mathbb {Z}_{m-1}$
-action on
$\mathbb {Z}_{m-1}$
-action on
![]() $\mathrm {SU}(m-1) \times \mathrm {U}(1)$
is simply given by
$\mathrm {SU}(m-1) \times \mathrm {U}(1)$
is simply given by
![]() $(w,z) \mapsto (w \omega ^{-k}, \omega ^k z)$
for
$(w,z) \mapsto (w \omega ^{-k}, \omega ^k z)$
for
![]() $(w,z) \in \mathrm {SU}(m-1) \times \mathrm {U}(1)$
,
$(w,z) \in \mathrm {SU}(m-1) \times \mathrm {U}(1)$
,
![]() $k \in \{0,\ldots ,m-2\}$
and
$k \in \{0,\ldots ,m-2\}$
and
![]() $\omega := e^{2i\pi /{(m-1)}}$
.) As a consequence, we get that
$\omega := e^{2i\pi /{(m-1)}}$
.) As a consequence, we get that
![]() $\Delta _{\mathrm {SU}(m-1) \times \mathrm {U}(1)} p^*F = \mu ~ p^* F$
. As
$\Delta _{\mathrm {SU}(m-1) \times \mathrm {U}(1)} p^*F = \mu ~ p^* F$
. As
![]() $\mathrm {SU}(m-1) \times \mathrm {U}(1)$
is a Riemannian product, its eigenfunctions are obtained as sums of products of eigenfunctions on each factor and the eigenvalues are sums of the eigenvalues on each factor. Hence, we can write
$\mathrm {SU}(m-1) \times \mathrm {U}(1)$
is a Riemannian product, its eigenfunctions are obtained as sums of products of eigenfunctions on each factor and the eigenvalues are sums of the eigenvalues on each factor. Hence, we can write
 $$ \begin{align*} p^*F(w,z) = \sum_{j=1}^N a_j(w) b_j(z) = \sum_{j=1}^N a_j(w) z^{k_j} \end{align*} $$
$$ \begin{align*} p^*F(w,z) = \sum_{j=1}^N a_j(w) b_j(z) = \sum_{j=1}^N a_j(w) z^{k_j} \end{align*} $$
for some finite number
![]() $N> 0$
, where
$N> 0$
, where
![]() $(w,z) \in \mathrm {SU}(m-1) \times \mathrm {U}(1)$
,
$(w,z) \in \mathrm {SU}(m-1) \times \mathrm {U}(1)$
,
![]() $k_j \in \mathbb {Z}$
and
$k_j \in \mathbb {Z}$
and
![]() $k_{j_1} \neq k_{j_2}$
for
$k_{j_1} \neq k_{j_2}$
for
![]() $j_1 \neq j_2$
,
$j_1 \neq j_2$
,
![]() $a_j \neq 0$
is an eigenfunction of
$a_j \neq 0$
is an eigenfunction of
![]() $\Delta _{\mathrm {SU}(m-1)}$
associated to the eigenvalue
$\Delta _{\mathrm {SU}(m-1)}$
associated to the eigenvalue
![]() $\unicode{x3bb} _j$
and
$\unicode{x3bb} _j$
and
![]() $\unicode{x3bb} _j + k^2_j = \mu> 0$
. However, we also know that
$\unicode{x3bb} _j + k^2_j = \mu> 0$
. However, we also know that
![]() $p^*F$
has constant modulus (equal to
$p^*F$
has constant modulus (equal to
![]() $1$
). Freezing an arbitrary point
$1$
). Freezing an arbitrary point
![]() $w \in \mathrm {SU}(m - 1)$
and looking at
$w \in \mathrm {SU}(m - 1)$
and looking at
![]() $|p^*F|^2(w, z)$
as a function of
$|p^*F|^2(w, z)$
as a function of
![]() $z \in \mathbb {S}^1$
, we easily get that N must be equal to
$z \in \mathbb {S}^1$
, we easily get that N must be equal to
![]() $1$
, that is,
$1$
, that is,
![]() $p^*F(w,z) = a(w) z^{k}$
for some
$p^*F(w,z) = a(w) z^{k}$
for some
![]() $k\in \mathbb {Z}$
. Hence,
$k\in \mathbb {Z}$
. Hence,
![]() $a \in C^\infty (\mathrm {SU}(m-1))$
satisfies
$a \in C^\infty (\mathrm {SU}(m-1))$
satisfies
![]() $|a|=1$
and
$|a|=1$
and
![]() $\Delta _{\mathrm {SU}(m-1)} a = \unicode{x3bb} a$
for some
$\Delta _{\mathrm {SU}(m-1)} a = \unicode{x3bb} a$
for some
![]() $\unicode{x3bb} \geq 0$
(with
$\unicode{x3bb} \geq 0$
(with
![]() $k^2+\unicode{x3bb} =\mu $
).
$k^2+\unicode{x3bb} =\mu $
).
We claim that
![]() $\unicode{x3bb} = 0$
, that is, a is constant, and F is thus constant along the
$\unicode{x3bb} = 0$
, that is, a is constant, and F is thus constant along the
![]() $\mathrm {SU}(m-1)$
-fibres. Indeed, if
$\mathrm {SU}(m-1)$
-fibres. Indeed, if
![]() $\unicode{x3bb} \neq 0$
, using
$\unicode{x3bb} \neq 0$
, using
 $$ \begin{align*} 0&=\Delta_{\mathrm{SU}(m-1)} |a|^2 = (\Delta_{\mathrm{SU}(m-1)} a) \overline{a} + a (\Delta_{\mathrm{SU}(m-1)} \overline{a}) - 2 \nabla a \cdot \nabla \overline{a} \\ & = 2 \unicode{x3bb} - 2 |\nabla a|^2, \end{align*} $$
$$ \begin{align*} 0&=\Delta_{\mathrm{SU}(m-1)} |a|^2 = (\Delta_{\mathrm{SU}(m-1)} a) \overline{a} + a (\Delta_{\mathrm{SU}(m-1)} \overline{a}) - 2 \nabla a \cdot \nabla \overline{a} \\ & = 2 \unicode{x3bb} - 2 |\nabla a|^2, \end{align*} $$
we get that
![]() $|\nabla a|$
is a non-zero constant. Since
$|\nabla a|$
is a non-zero constant. Since
![]() $\mathrm {SU}(m-1)$
is simply connected, the map a lifts to the universal cover of
$\mathrm {SU}(m-1)$
is simply connected, the map a lifts to the universal cover of
![]() $\mathrm {U}(1)$
, so there exists a map
$\mathrm {U}(1)$
, so there exists a map
![]() $\theta :\mathrm {SU}(m-1)\to \mathbb {R}$
such that
$\theta :\mathrm {SU}(m-1)\to \mathbb {R}$
such that
![]() $a=e^{i\theta }$
. At a critical point of
$a=e^{i\theta }$
. At a critical point of
![]() $\theta $
, we thus get
$\theta $
, we thus get
![]() $\nabla a=0$
, which is absurd.
$\nabla a=0$
, which is absurd.
As a consequence,
![]() $\unicode{x3bb} = 0$
and this shows that F is constant along
$\unicode{x3bb} = 0$
and this shows that F is constant along
![]() $\mathrm {SU}(m-1)$
-fibres of the bundle map
$\mathrm {SU}(m-1)$
-fibres of the bundle map
![]() $\mathrm {det} : \mathrm {U}(m-1) \to \mathrm {U}(1)$
. In turn, as equation (5.10) commutes, we get that u is constant on the preimages of the map
$\mathrm {det} : \mathrm {U}(m-1) \to \mathrm {U}(1)$
. In turn, as equation (5.10) commutes, we get that u is constant on the preimages of the map
![]() $\psi : F_{\mathbb {C}} M \to P$
so
$\psi : F_{\mathbb {C}} M \to P$
so
![]() $u = \psi ^* w$
for some smooth
$u = \psi ^* w$
for some smooth
![]() $w \in C^\infty (P)$
.
$w \in C^\infty (P)$
.
We thus have just shown that if there is a non-zero solution to equation (5.7), then there is also a non-zero solution to
Hence, it remains to show that equation (5.11) has no non-zero solutions, and we will actually show it for
![]() $w \in L^2(P)$
.
$w \in L^2(P)$
.
Assume that
![]() $w \in L^2(P)$
is a solution to equation (5.11). As above, using that P is a principal
$w \in L^2(P)$
is a solution to equation (5.11). As above, using that P is a principal
![]() $\mathrm {U}(1)$
-bundle, we can decompose
$\mathrm {U}(1)$
-bundle, we can decompose
where the sections of
![]() $L_k$
are given by functions
$L_k$
are given by functions
![]() $f \in L^2(P)$
satisfying
$f \in L^2(P)$
satisfying
![]() $V f = ik f$
, where V is the infinitesimal generator of the
$V f = ik f$
, where V is the infinitesimal generator of the
![]() $\mathrm {U}(1)$
-action on the fibres of P. Observe that
$\mathrm {U}(1)$
-action on the fibres of P. Observe that
![]() $L_k = L^{\otimes k}$
for
$L_k = L^{\otimes k}$
for
![]() $k \in \mathbb {Z}$
where
$k \in \mathbb {Z}$
where
![]() $L := L_1$
and
$L := L_1$
and
![]() $L_1 \simeq \Lambda ^{m-1,0} \mathcal {N}$
. Now, using the splitting equation (5.12), the equation
$L_1 \simeq \Lambda ^{m-1,0} \mathcal {N}$
. Now, using the splitting equation (5.12), the equation
![]() $X_P w = i \unicode{x3bb} w$
reads
$X_P w = i \unicode{x3bb} w$
reads
![]() $X_P w_k = i \unicode{x3bb} w_k$
for all
$X_P w_k = i \unicode{x3bb} w_k$
for all
![]() $k \in \mathbb {Z}$
, where
$k \in \mathbb {Z}$
, where
![]() $w_k \in L^2(SM,L_k)$
(similarly to equation (5.8) and the subsequent argument). By [Reference LefeuvreLef23, Proposition 2.7], we also have that
$w_k \in L^2(SM,L_k)$
(similarly to equation (5.8) and the subsequent argument). By [Reference LefeuvreLef23, Proposition 2.7], we also have that
![]() $w_k$
is smooth, that is,
$w_k$
is smooth, that is,
![]() $w_k \in C^\infty (SM,L_k)$
. Moreover,
$w_k \in C^\infty (SM,L_k)$
. Moreover,
![]() $X|w_k|^2 = 0$
, where
$X|w_k|^2 = 0$
, where
![]() $|w_k|^2(v) := \int _{P_v} |w_k(v, u)|^2\, du$
and
$|w_k|^2(v) := \int _{P_v} |w_k(v, u)|^2\, du$
and
![]() $u \in P_v$
is the variable in the
$u \in P_v$
is the variable in the
![]() $\mathrm {U}(1)$
-fibre, so
$\mathrm {U}(1)$
-fibre, so
![]() $|w_k|$
is constant by ergodicity of the flow
$|w_k|$
is constant by ergodicity of the flow
![]() $(\varphi _t)_{t \in \mathbb {R}}$
. If
$(\varphi _t)_{t \in \mathbb {R}}$
. If
![]() $k=0$
,
$k=0$
,
![]() $L_0 = \mathbb {C}$
is trivial over
$L_0 = \mathbb {C}$
is trivial over
![]() $SM$
so the mixing of the geodesic flow
$SM$
so the mixing of the geodesic flow
![]() $(\varphi _t)_{t \in \mathbb {R}}$
then implies that
$(\varphi _t)_{t \in \mathbb {R}}$
then implies that
![]() $w_0 \equiv 0$
. If
$w_0 \equiv 0$
. If
![]() $k \neq 0$
and
$k \neq 0$
and
![]() $w_k \neq 0$
, then we obtain a smooth nowhere vanishing section
$w_k \neq 0$
, then we obtain a smooth nowhere vanishing section
![]() $w_k \in C^\infty (SM,L_k)$
, so
$w_k \in C^\infty (SM,L_k)$
, so
![]() $L_k$
is trivial. However, in turn, this implies that the first Chern class of
$L_k$
is trivial. However, in turn, this implies that the first Chern class of
![]() $L_1 = \Lambda ^{m-1,0}\mathcal {N}$
is torsion. From the proof of Corollary 3.2, we obtain that the canonical bundle
$L_1 = \Lambda ^{m-1,0}\mathcal {N}$
is torsion. From the proof of Corollary 3.2, we obtain that the canonical bundle
![]() $K_M$
of M has torsion first Chern class so the image of
$K_M$
of M has torsion first Chern class so the image of
![]() $c_1(K_M)$
in
$c_1(K_M)$
in
![]() $H^2(M,\mathbb {R})$
vanishes. This is a contradiction since this image is equal to
$H^2(M,\mathbb {R})$
vanishes. This is a contradiction since this image is equal to
![]() $[-1/({2\pi })\rho ]$
where
$[-1/({2\pi })\rho ]$
where
![]() $\rho $
is the Ricci form of M, which is not exact since M has negative definite Ricci tensor. Hence, any solution to equation (5.11) is trivial, and thus, so is any solution to equation (5.7). This finishes the proof of Proposition 5.6.
$\rho $
is the Ricci form of M, which is not exact since M has negative definite Ricci tensor. Hence, any solution to equation (5.11) is trivial, and thus, so is any solution to equation (5.7). This finishes the proof of Proposition 5.6.
Acknowledgements
We thank Maxime Zavidovique, one of the participants of the Geometry and Topology seminar in Jussieu, for pointing out that it could be worth studying this problem (although we first mistakenly thought that it had already been solved a long time ago). We also thank the anonymous referee for the comments. M.C. has received funding from an Ambizione grant (project number 201806) from the Swiss National Science Foundation.