1. Introduction
Goat meat is the most heavily consumed red meat in the world (Barkley et al., 2014), and much of the rural population in developing countries depends on meat goat production as an important income source and food. Though developing countries produced approximately 97% of the world's total goat meat in 2008 (FAOSTAT, 2014), the industry has rapidly expanded in the United States in recent years. Expansion of the industry has occurred alongside (1) the formation of the American Meat Goat Association in 1992 and the American Boer Goat Association in 1993, with Boer goats displacing a significant portion of the Spanish goats that were previously the bulk of the meat goat population; (2) the repeal of the Wool Act of 1954 in 1993, which caused Angora goat producers to switch to meat goat production; and (3) the financial settlements of the U.S. tobacco industry, which caused former tobacco farmers to search for alternative farm enterprises (Spencer, Reference Spencer2008). Furthermore, diversification of U.S. population demographics with immigration from goat meat–consuming countries has led to increased demand for goat meat. The number of meat goats produced in the United States increased from 1.23 million to 2.05 million over the period 1997 to 2012 (U.S. Department of Agriculture, National Agricultural Statistics Service [USDA-NASS], 2014).
The majority of U.S. meat goat production is scattered throughout the southeastern United States, with Texas dominating the production of meat goats among all U.S. states. The strong interest of Texas in meat goat production has been largely due to its dry climate and suitable forage species (Shurley and Craddock, Reference Shurley and Craddock2014). The Southeast region is well suited to producing meat goats because of ample acreage suitable for grazing and extended grazing periods for goat production. Southeastern meat goat producers have the opportunity to pasture goats year-round, decreasing their dependence on concentrated feedstuffs and adding value to goats with less expensive inputs compared with other regions. Other regions must depend on the use of conserved or stockpiled forages during a few months of the year. The advantage of southeastern U.S. meat goat production is the region's more amenable weather, considerably longer grazing season, lower need for supplemental feed, and simpler and cheaper goat housing (Singh-Knights and Knights, Reference Singh-Knights and Knights2005).
As a relatively new livestock industry in the United States, the meat goat industry has not been studied extensively compared with other livestock industries such as beef cattle or swine. Therefore, comparatively little information exists regarding U.S. meat goat production, specifically the factors that can positively impact meat goat production efficiency. Much of the meat goat economics research in the United States has focused on goat meat marketing and consumer preferences for goat meat (Ibrahim, Reference Ibrahim2011; Knight et al., Reference Knight, House, Nelson and Degner2006; Worley et al., Reference Worley, Ellerman, Mangione, West and Yang2004). Studies on goat farm production efficiency, productivity, and profitability are limited; those that have focused on production efficiency have addressed the industry in other countries (Alex, Cheemani, and Thomas, Reference Alex, Cheemani and Thomas2013; Ogunniyi, Reference Ogunniyi2010; Zaibet et al., Reference Zaibet, Dharmapala, Boughanmi, Mahgoub and Al-Marshudi2004). The 2012 Census of Agriculture (USDA-NASS, 2014) estimated that approximately 77% and 78% of all goats in the United States were raised for meat in 2002 and 2012, respectively. Meat goat farm numbers and operation sizes increased, respectively, by 34.6% and 5.9% from 2002 to 2012, showing increased meat goat production.
The objectives of this study are to determine the factors influencing meat goat production technical efficiency (TE) and to quantify scale and scope economies for meat goat production in the southeastern United States. An input distance function (IDF) using stochastic production frontier (SPF) techniques is estimated for southeastern U.S. meat goat production. The costs of production for different sizes of operations for southeastern U.S. meat goat production are estimated, and results are compared with the IDF analysis. Empirical Monte Carlo (MC) simulation techniques are employed to show the consistency of small-sample properties for the IDF analysis.
2. Estimating an Input Distance Function for Southeastern Meat Goat Farms
To estimate the efficiency of southeastern U.S. meat goat production, a parametric SPF technique is used, which reveals the nature of the production technology, allows for statistical inferences, and measures the firm-specific efficiency characteristics. In general, the SPF model is specified as follows:
$$\begin{equation}
{\rm ln} y = f\left( {\rm ln} x\right) + v - u,
\end{equation}$$where y is the production level, x is a vector of input quantities, v is a vector of unobserved farmer heterogeneity, and u is the vector representing technical inefficiency. The random error v is independently and identically distributed as N(0, σ2v) and is independent of u; error u ⩾ 0 is independently and identically distributed as half-normal, u|N(0, σ2u)|. Using the SPF, we estimate an IDF to determine the economic performance of southeastern U.S. meat goat farms. The IDF is specified as DI(X, Y) for this study, where X and Y denote vectors of inputs and outputs, respectively.
A translog functional form is used to approximate the IDF for empirical implementation to limit a priori restrictions on the relationship among inputs. Applying homogeneity of degree 1 in inputs and symmetry restrictions of the parameters, the IDF can be specified as follows:
$$\begin{eqnarray}
\ln \left( {\frac{{D_i^I\left( {X,Y} \right)}}{{{X_{1,i}}}}} \right) &\hspace*{-1pt}=\hspace*{-1pt}& {\alpha _0} \hspace*{-1pt}+\hspace*{-1pt} \mathop \sum \limits_m {\alpha _m}{\rm{ln}}X_{mi}^{\rm{*}} \hspace*{-1pt}+\hspace*{-1pt} \frac{1}{2}\mathop \sum \limits_m \mathop \sum \limits_n {\alpha _{mn}}{\rm{ln\ }}X_{mi}^{\rm{*}}\ln X_{ni}^{\rm{*}} + \mathop \sum \limits_k {\beta _k}\ln {Y_{ki}} \nonumber\\
&&+\,\frac{1}{2}\mathop \sum \limits_k \mathop \sum \limits_l {\beta _{kl}}{\rm{ln}}{Y_{ki}}{\rm{ln}}\ {Y_{li}} + \ \mathop \sum \limits_k \mathop \sum \limits_m {\theta _{km}}{\rm{ln\ }}{Y_{ki}}{\rm{ln\ }}X_{mi}^*\ + \ {\nu _i}\nonumber\\
& = & TL\left( {{X^*},\ Y} \right) + {\nu _i},
\end{eqnarray}$$
where i denotes farms; k and l denote the outputs; m and n denote the inputs; and 
${X^*} = \frac{X}{{{X_1}}}$ with X 1 specified as a normalization factor in inputs. The term ln DIi(X, Y) is the distance from the frontier, and it characterizes the technical inefficiency error, − ui. Technical inefficiency is a function of farm- and farmer-specific characteristics.
Dividing all inputs and the distance term, DIi(X, Y), by an input, quality-adjusted land, specified as X 1 = XLAND to be consistent with much of the literature on farm production, is the same as imposing the homogeneity restrictions. The IDF is specified on a per acre basis.
Equation (2) can be rewritten as follows:
$$\begin{equation}- {\rm{ln}}\ {X_{1,i}} = \ TL\left( {{X^*},\ Y} \right) + \ {\nu _i} - {\rm{ln}}\ D_i^I\left( {X,Y} \right) = \ TL\left( {{X^*},\ Y} \right) + \ {\nu _i} - \ {u_i}.
\end{equation}$$TE is obtained as the expectation of the term − ui conditional on the composed error term εi = νi − ui and is measured as TE = exp−ui.
The following specific IDF is estimated using an SPF for southeastern U.S. meat goat production enterprises:
$$\begin{eqnarray}
&& - \ln {X_{Land,i}} = {\alpha _1} + {\varphi _1}Y_{Mgoat,i}^d + {\varphi _2}Y_{Gbstock,i}^d + {\varphi _3}X_{Fixed,i}^d + {\alpha _1}{\rm{ln\ }}X_{Var,i}^{\rm{*}} \nonumber\\
&&+ \hspace*{-1pt} {\alpha _2}{\rm{ln\ }}X_{Fixed,i}^{\rm{*}} \hspace*{-1pt}+\hspace*{-1pt} 0.5{\alpha _3}\ln X_{Varsq,i}^{\rm{*}} \hspace*{-1pt}+\hspace*{-1pt} 0.5{\alpha _4}\ln X_{Fixedsq,i}^{\rm{*}} \hspace*{-1pt}+\hspace*{-1pt} 0.5{\alpha _5}{\rm{ln\ }}X_{Var,i}^{\rm{*}}{\rm{ln\ }}X_{Fixed,i}^{\rm{*}} \nonumber\\
&& + {\beta _1}{\rm{ln\ }}{Y_{Mgoat,i}} + {\beta _2}{\rm{ln\ }}{Y_{Gbstock,i}} + 0.5{\beta _3}{\rm{ln\ }}{Y_{Mgoatsq,i}} + 0.5{\beta _4}\ln {Y_{Gbstocksq,i}} \nonumber\\
&& + 0.5{\beta _5}{\rm{ln\ }}{Y_{Mgoat,i}}\ln {Y_{Gbstock,i}} + {\theta _1}{\rm{ln\ }}{Y_{Mgoat,i}}{\rm{ln\ }}X_{Var,i}^{\rm{*}} +{\theta _2}{\rm{ln}}\ {Y_{Gbstock,i}}{\rm{ln}}\ X_{Var,i}^* \nonumber\\
&& + \, {\theta _3}{\rm{ln}}\ {Y_{Mgoat,i}}{\rm{ln}}\ X_{Fixed,i}^* + \ {\theta _4}{\rm{ln}}\ {Y_{Gbstock,i}}{\rm{ln}}\ X_{Fixed,i}^* + \ {\nu _i} - \ {u_i}.
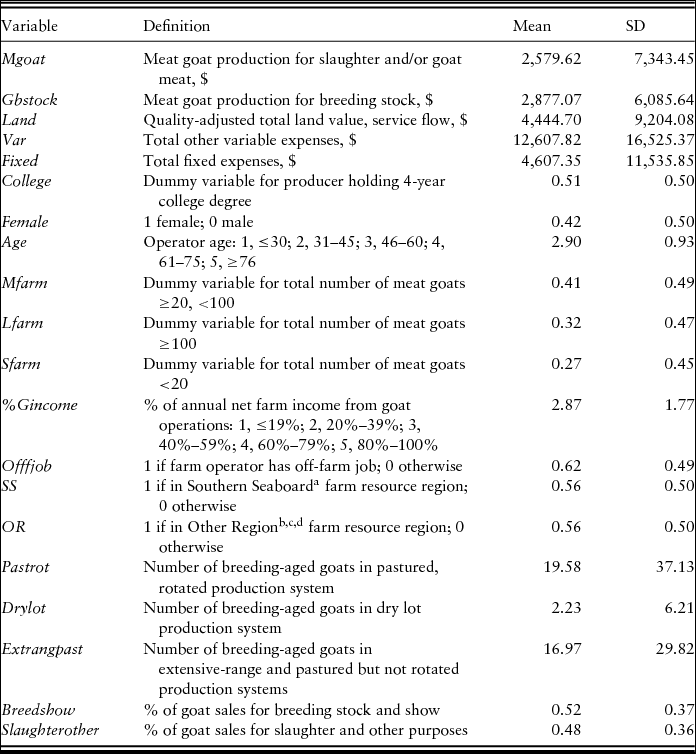
\end{eqnarray}$$The output variables are defined (Table 1) as follows: YMgoat is the value of meat goat production for slaughter and/or goat meat, and YGbstock is the value of meat goat production for breeding stock. This study specifically analyzes the meat goat enterprise rather than the whole farm; however, we did not request enterprise-specific expenses for the following input variables in the survey questionnaire: Seeds/Plants, Fertilizer, Chemicals, Utilities, Supplies, Repairs on Equipment, Custom Machine and Hired Labor, Insurance, Interest/Fees, Vehicle/Licensing Fees, Taxes, and Equipment Rental. In order to obtain enterprise-specific expenses for these input variables, first, the percentage or portion of the meat goat enterprise total return was calculated as the total meat goat enterprise return (MER) divided by the total whole farm return (WFR) to result in MER/WFR. To estimate the meat goat enterprise-specific expenses for variables, where farmers were not specifically asked to allocate them to the meat goat enterprise, the whole farm expense values were multiplied by MER/WFR. Inputs are the following: XLand is the quality-adjusted land price,Footnote 1XVar represents the total variable expenses,Footnote 2 and XFixed represents total fixed expenses.Footnote 3
Table 1. Summary Statistics and Variable Definitions for Southeastern U.S. Meat Goat Enterprises
a Goat farms in eastern halves of Texas are included into Southern Seaboard farm resource region.
b Goat farms in Eastern Upland, Fruitful Rim, and Mississippi Portal farm resource regions are combined as Other Region.
c Goat farms in southernmost counties of Missouri are included into Other Region.
d Goat farms in eastern halves of Oklahoma are included into Other Region.
Note: SD, standard deviation.
The random error νi is independently and identically distributed asN(0, σ2v), and independent of ui. ui ⩾ 0 is a one-sided error term independently distributed with truncation at zero of theN(μi, σ2u) distribution, where
$ {\mu _i} = \ \mathop \sum_g {F_g}\zeta $, Fg is a vector of farm efficiency determinants, and ζ represents parameters to be estimated. The term μi is defined as the conditional mean of ui:
$$\begin{eqnarray}
{\mu _i} &=& {\tau _0} + {\tau _1}{F_{College}} + {\tau _2}{F_{Female}} + {\tau _3}{F_{Age}} + {\tau _4}{F_{Mfarm}} + {\tau _5}{F_{Lfarm}} + {\tau _6}{F_{{\rm{\% }}Gincome}} \nonumber\\
&&+\, {\tau _7}{F_{Offfjob}} + {\tau _8}{F_{SS}} + \ {\tau _9}{F_{Extrangpast}} + \ {\tau _{10}}{F_{Drylot}} + {\tau _{11}}{F_{Breedshow}} + {\epsilon _i},\nonumber\\
\end{eqnarray}$$where εi represents unobservable independently distributed random variables. The southeastern U.S. meat goat enterprise efficiency variables (Table 1) include the following: FCollege is a dummy variable indicating the farmer held a bachelor's degree or higher (the base category is a less than a college degree). FFemale is a dummy variable indicating the meat goat operator was a female (the base category is a male operator). FAge is a categorical variable in years (15-year increments) indicating the age of the farmer. FMfarm and FLfarm are dummy variables for operation sizes with 20 to 100 and >100 meat goats, respectively (a small operation with <20 meat goats is the base). F %Gincome is the percentage of annual net farm income from the meat goat enterprise, a measure of farm specialization. FOfffjob is a dummy variable for the operator holding an off-farm job. FSS is subregional dummy variable for the Southern Seaboard farm resource region, as defined by USDA Economic Research Service (ERS) (FOR is the Other Region, which includes Eastern Uplands, Mississippi Portal, and Fruitful Rim farm resource regions and is considered as the base level).
FPastrot is the number of breeding-aged goats in a pastured and rotated production system. FDrylot is the number of breeding-aged goats in a dry lot production system (FExtrangpast is the number of breeding-aged goats in extensive-range or pasture/woods and pastured but not rotated production systems, serving as the base). The variable FBreedshow refers to the percentage of meat goat sales for breeding stock or show, with the percentage of meat goat sales for slaughter/other purposes being the base.
Output and input variables may have zero values in the data. The zero value observations lead to biased estimation of the parameters of the translog function. Therefore, it is problematic for the production function (Battese, Reference Battese1997). However, the coefficients of the variables with zero values can be estimated using dummy variables to avoid biased estimation (Battese, Reference Battese1997):
$$\begin{eqnarray}
\mathop \sum \limits_{k = 1,2} Y_{k,i}^d &=& 1\; {\rm{if}}\mathop \sum \limits_{k = 1,2} {Y_{k,i}} = 0, \mathop \sum \limits_{k = 1,2} Y_{k,i}^d = 0{\rm{\ if}}\mathop \sum \limits_{k = 1,2} {Y_{k,i}} >0,{\rm{\ and}}\nonumber\\
\mathop \sum \limits_{k = 1,2} {Y_{k,i}} &=& \max \left( {{Y_{k,i}}, Y_{k,i}^d} \right)
\mathop \sum \limits_{m = 3} X_{m,i}^d = 1\; {\rm{if}}\mathop \sum \limits_{m = 3} {X_{m,i}} = 0, \nonumber\\
\mathop \sum \limits_{m = 3} X_{m,i}^d &=& 0{\rm{\ if}}\mathop \sum \limits_{m = 3} {X_{m,i}} >0,{\rm{and}}\nonumber\\
\mathop \sum \limits_{m = 3} X_{m,i}^{\rm{*}} &=& \max \left( {{X_{m,i}}, X_{m,i}^d} \right),
\end{eqnarray}$$where i denotes the number of observations, k = 1 is YMgoat, k = 2 is YGbstock, m = 3 is XFixed; and Yd k, i and Xd m, i are dummies accounting for the intercept change.
Past studies have used two-step estimation of stochastic frontier models and TE measures (Alex, Cheemani, and Thomas, Reference Alex, Cheemani and Thomas2013; Featherstone, Langemeier, and Ismet, Reference Featherstone, Langemeier and Ismet1997; Rakipova, Gillespie, and Franke, Reference Rakipova, Gillespie and Franke2003). We also use the two-step maximum likelihood method to estimate the parameters of the IDF using SPF techniques and a Tobit model to determine the relationship between the efficiency measures and farm/farmer characteristics due to relatively small sample size in this study. However, a single-step maximum likelihood method estimation procedure is recommended (Schmidt, Reference Schmidt2011; Wang and Schmidt, Reference Wang and Schmidt2002). For comparison analysis, we use a single-step maximum likelihood methodFootnote 4 to estimate the parameters of the IDF and the technical inefficiency jointly using SPF techniques. The results of the single-step maximum likelihood method were very close to the two-step maximum likelihood method and confirmed consistency of estimations.
2.1. Data
We conducted a nationwide mail survey of U.S. commercial meat goat producers during January 2013, collecting cost and returns data from those farms for 2011. The cost and returns survey was a follow-up to an earlier mail survey of late summer 2012, which addressed U.S. commercial meat goat production technology, marketing, farmer attitudes, and farm and farmer characteristics. Dillman's (Reference Dillman2007) tailored design method was used to design the survey. At the end of the first survey, meat goat producers were asked whether they would be willing to complete a follow-up survey on costs and returns of meat goat production. A total of 435 meat goat producers indicated their willingness to complete the follow-up questionnaire. Two contacts were made, both with copies of the questionnaire on cost and returns of meat goat production. For the follow-up questionnaire, we received a total of 124 completed responses. After adjusting for undeliverable surveys, producers who did not produce meat goats, and incomplete surveys, the effective return rate was 30%.
In this study, we use 69 farms as a subsample population for southeastern U.S. meat goat production efficiency. The Southeast includes parts of the following farm resource regions as designated by USDA-ERS (2000): Eastern Uplands, Fruitful Rim, Mississippi Portal, and Southern Seaboard. The southeastern states include Alabama, Arkansas, Florida, Georgia, Kentucky, Louisiana, Mississippi, Missouri, North Carolina, Oklahoma, South Carolina, Tennessee, Texas, Virginia, and West Virginia. Parts of Oklahoma and Texas are included, divided on a line corresponding to north–south Interstate 35, with the eastern halves of these states being included in the Southeast region. The southernmost counties of Missouri were also included in the Southeast region.
Missing information is a common issue for survey data; missing data may result in biased estimates and reduce regression estimate efficiency (Rubin, Reference Rubin1987). Various methods exist to handle missing data issues. The multiple imputation method (Rubin, Reference Rubin1987) was used to handle missing data in this study. We employed the truncated regression imputation method to estimate missing values of continuous variables.
2.2. Monte Carlo Simulation
There is often the concern that a small sample size may result in a lack of statistical representation of the population causing a concern over consistency of estimates. MC simulation is used in this study to investigate small-sample properties of the data given that our sample size is not large. Hypothetical (based on artificial data) and empirical (based on our data) MC simulations were conducted to determine consistency: that the sampling distributions of the estimators approach very closely their true parameter values as the sample size increases. The idea behind the MC simulation experiment is to model the data generation process (DGP). The MC simulation technique is designed to elucidate the finite-sample properties of competing estimators for a given estimation problem (Kennedy, Reference Kennedy2003). The MC simulation method provides valid statistical inferences of small-sample distributions through the repeated sample. The reader is referred to Davidson and MacKinnon (Reference Davidson and MacKinnon1992, Reference Davidson and MacKinnon2004), Reference KivietKiviet (2012), Kennedy (Reference Kennedy2003), and Cameron and Trivedi (Reference Cameron and Trivedi2009) for greater detail on the MC procedure.
Our hypothetical MC simulation and the estimation resultsFootnote 5 showed that there was no significant bias and the asymptotic distribution approximated the small-sample distribution well for the DGP with samples of sizes 250, 500, and 1,000. For the empirical MC simulation, the SPF was specified as a normal-exponential model, and the following DGP was considered:
$$\begin{eqnarray}
- {x_{1,i}} &\hspace*{-1pt}=\hspace*{-1pt}& {\alpha _0} \hspace*{-1pt}+\hspace*{-1pt} 2y_{1,i}^d \hspace*{-1pt}+\hspace*{-1pt} y_{2,i}^d \hspace*{-1pt}+\hspace*{-1pt} x_{3,i}^d \hspace*{-1pt}+\hspace*{-1pt} 2x_{2,i}^{\rm{*}} + 3x_{3,i}^{\rm{*}} + x_{2sq,i}^{\rm{*}} + 2x_{3sq,i}^{\rm{*}} + 2x_{2,i}^{\rm{*}}x_{3,i}^{\rm{*}} + 2{y_{1,i}} \nonumber \\
&&+\,3{y_{2,i}} + \ {y_{1sq,i}} + \ 2{y_{2sq,i}} + \ 3{y_{1,i}}{y_{2,i}} + \ 4{y_{1,i}}x_{2,i}^* + \ 3{y_{2,i}}x_{2,i}^* + \ {y_{1,i}}x_{3,i}^* \nonumber \\
&&+\, 2{y_{2,i}}x_{3,i}^* + \ {\nu _i}\ - \ {u_i},
\end{eqnarray}$$
where vi ~ N(0, σvi), ui ~ rgamma(1, σui), 
${\sigma _{vi}} {=} {\rm{exp}}( {\frac{1}{2}z{v_i}} )$, 
${\sigma _{ui}} {=} {\rm{exp}}[ {\frac{1}{2}( {1 {+} \frac{1}{2}z{u_i}} )}]$.Footnote 6
Both idiosyncratic and inefficiency error scale parameters were a function of a constant term and of an exogenous covariate (zvi and zui) drawn from a standard normal random variable of [rnormal (0, 1)]. The y and x variables are outputs and inputs, respectively, in the DGP equation (equation 7). In other words, equation (7) is the same as equation (4). The difference is that we assigned arbitrary numerical values for each of the variables in the DGP equation (equation 7) as “true” values (or population values) to see how closely our parameter estimates approach those “true” values with increasing sample size (or with increasing numbers of replications in the MC simulation). We used the DGP equation (equation 7) to conduct MC simulations for the SPF model.
We performed 250, 500, and 1,000 simulations and for each simulation, and we obtained parameter estimates, standard errors, and test sizes. The average of 
$\widehat {{\beta _j}}$ over the N estimates, 
$\overline {\widehat {{\beta _j}}} = ( {1/N} )\ \mathop \sum _{n = 1}^N \widehat {{\beta _n}}$, represents the simulation estimates of 
$E( {\widehat {{\beta _j}}} )$, where N is the number of simulations and j is the number of parameters. The variance of 
$\widehat {{\beta _j}}$ over the N estimates, 
$s_{\widehat {{\beta _j}}}^2\ = [ {1/( {N - 1} )}]\ \mathop \sum _{n = 1}^N {( {\widehat {{\beta _n}} - \ \overline {\widehat {{\beta _j}}} } )^2}$, represents the simulation estimates of 
$\sigma _{\widehat {{\beta _j}}}^2 = Var( {\widehat {{\beta _j}}} )$, the variance of 
$\widehat {{\beta _j}}$. The test size is the probability of rejecting the null hypothesis when it is true. Because the DGP sets βj as the “true” value, we consider a two-sided test of the null hypothesis (H0: βj = the “true” value) against the alternative hypothesis (H1: βj ≠ the “true” value). “True” values are the DGP values of equation (7). The nominal size of the test α = 0.05, and we use the t-test. The proportion of simulations that lead to a rejection of H0 is known as the rejection rate, and this proportion is the simulation estimate of the true test size.
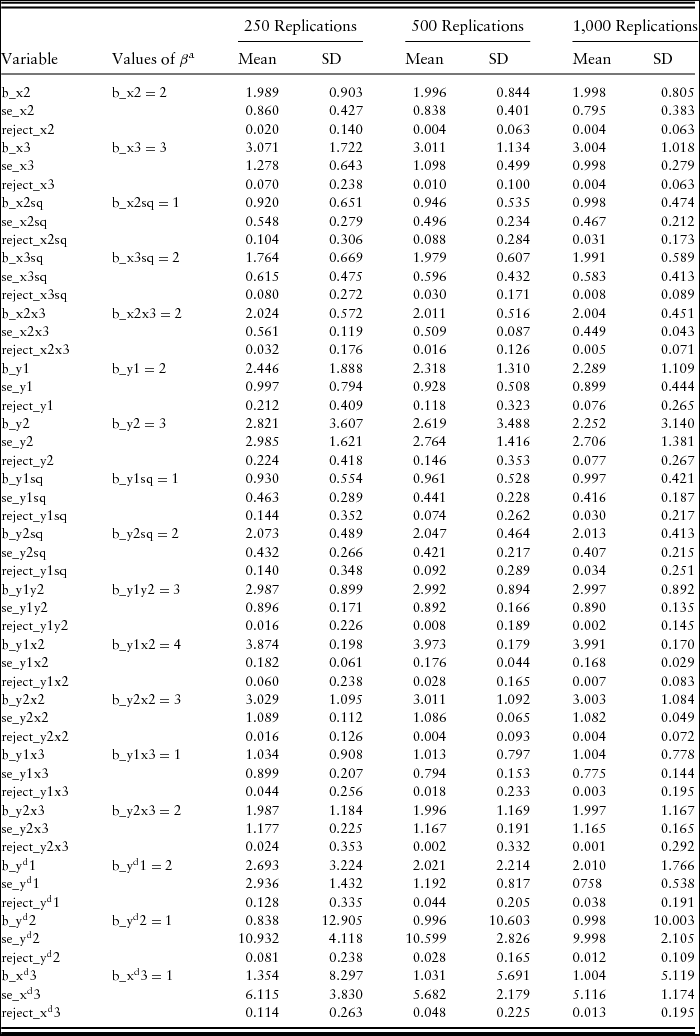
Empirical MC simulation results for the southeastern U.S. meat goat enterprise are presented in Appendix A. Results indicate that the means of the parameter estimates approach very closely the true values of the DGP, and the standard deviations (SDs) of the parameter estimates become close to the means of the standard errors with increasing numbers of simulations. The rejection rates of the parameters become less than the nominal size of 0.05 or 5% with increasing numbers of simulations. We estimated 95% confidence intervals for the MC simulation averages.Footnote 7 The results for the parameter estimates and the rejection rates indicate that there are no significant biases and that the asymptotic distribution approximated the finite-sample distribution well for the DGP with samples of sizes 250, 500, and 1,000 (number of replications). The confidence intervals for the standard errors include the sample SDs for the parameter estimates, another indication that large-sample theory provides a good approximation to the finite-sample distribution.
3. Results
Data from first and follow-up surveys were used for this study; therefore, there was concern as to whether there were differences between the survey sample means. We conducted t-tests were conducted to determine statistically significant differences between the survey subsample means for southeastern U.S. meat goat production (Table 2). The null hypothesis is defined as 
${\hbox{H}_0}{:} \ {\bar x_{fs}} = \ {\bar x_{ss}}$, and the alternative hypothesis as 
${\hbox{H}_{{1}}}{:} \ {\bar x_{fs}} \ne \ {\bar x_{ss}}$, where 
${\bar x_{fs}}$ is the mean for the first survey subsample variables and 
${\bar x_{ss}}$ is the mean for the follow-up survey subsample variables. The t-test results failed to reject the null hypothesis, concluding that there is not sufficient evidence to suggest the subsample means differ at P ⩽ 0.10 levels (Table 2).
Table 2. The t-Test Results for the First and Follow-Up Survey Variable Means
We conducted a number of tests on the structural form of the translog model by incorporating restrictions on the parameters. The likelihood ratio test was used to test the restrictions on the parameters. Test results showed that the explanatory variables in the model for inefficiency effects contributed significantly to the explanation of technical inefficiency effects. Test resultsFootnote 8 showed that the translog functional form described better the underlining production technology of southeastern U.S. meat goat enterprises relative to the alternative Cobb-Douglas production functional form.
3.1. Comparing Meat Goat Cost of Production by Operation Size
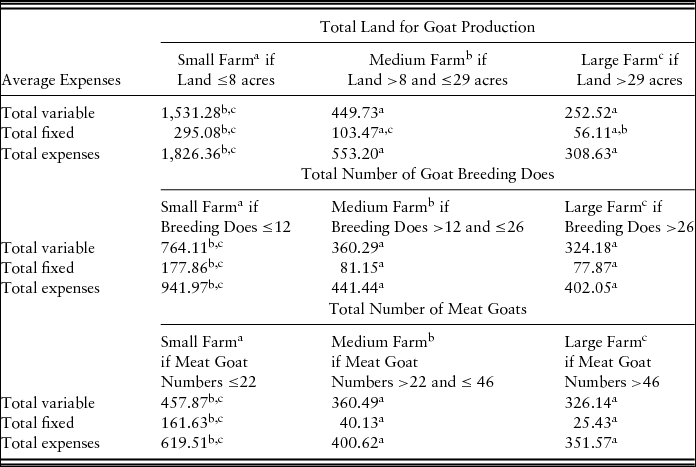
We compared costs for three different tertiles of southeastern U.S. meat goat farms. The sample population of this study, 69 southeastern U.S. farms, was divided into three equal operation sizes (23 farms each) based on goat production land, number of goat breeding does, and number of meat goats. A comparison of southeastern U.S. meat goat enterprise expenses per acre of goat production land by operation size (small, medium, and large) is shown in Table 3. The meat goat enterprise total and variable expenses per acre for medium- and large-sized farms were lower than for small-sized farms. The fixed expense per acre for medium-sized farms was lower than for small-sized farms. The fixed expense per acre for large-sized farms was lower than for small- and medium-sized farms.
Table 3. Southeastern U.S. Meat Goat Enterprise Expenses per Goat Production Acre, per Breeding Doe, and per Meat Goat Produced
Note: Superscripts (a, b, c) indicate significant differences (P < 0.10) in means across columns with a = small farms, b = medium farms, and c = large farms.
The comparison of southeastern U.S. meat goat enterprise expenses per breeding doe based on three different sizes of operations (small, medium, and large) is shown in Table 3. The meat goat enterprise total, variable, and fixed expenses per breeding doe for medium- and large-sized farms were lower than for small-sized farms.
The comparison of southeastern U.S. meat goat enterprise expenses per meat goat produced based on three operation sizes (small, medium, and large farms) is also shown in Table 3. The meat goat enterprise total, variable, and fixed expenses per meat goat in medium- and large-sized farms were lower than for small-sized farms. All three of the meat goat enterprise cost analyses show that scale of operation is important: with increasing meat goat enterprise scale, input expenses (variable, fixed, and total expenses) decrease significantly.
3.2. Input Distance Function Analysis Results
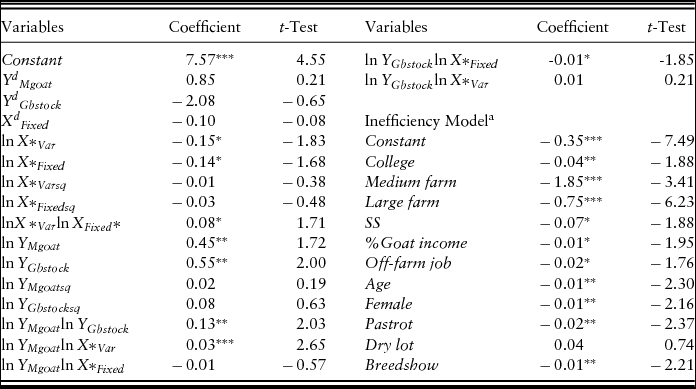
The maximum likelihood parameter estimates for the IDF are presented in Table 4. The main effect parameter estimates for both outputs and two inputs are statistically significant. The cross-input variable parameter for total variable and fixed expenses is significant and positive, suggesting that these inputs are complementary.
Table 4. The Input Distance Function Estimates for Southeastern U.S. Meat Goat Enterprises
a The inefficiency model parameters for southeastern U.S. meat goat enterprises are estimated separately using Tobit regression.
Note: Asterisks (*, **, and ***) indicate significance at the 10%, 5%, and 1% level, respectively.
The output variable parameters have the expected signs and are statistically significant. The statistically significant meat goat production for slaughter/goat meat and meat goat breeding stock production variables suggest that increases in slaughter meat goat and meat goat breeding stock production increase the productive contribution of the land. The output interaction of slaughter meat goat production and meat goat breeding stock production is positive and statistically significant, implying their complementarity in production. This also suggests that an increase in meat goat breeding stock production enhanced the contribution of meat goat production in the goat enterprise. Interaction between outputs and inputs, 
${\varepsilon _{X{Y_k}{X_m}}} = \frac{{\partial {\varepsilon _{X,{Y_k}}}}}{{\partial ln{X_m}}} <0$, indicates the increase in Yk from an increase in Xm or output-input jointness (complementarity). The parameter estimates for the interactions between the value of meat goat production for slaughter/goat meat and total variable expenses and the value of meat goat breeding stock production and total fixed expenses are also statistically significant.
Estimated inefficiency model parameter estimates are also presented in Table 4. We find that operation size, college education, percentage of annual net farm income from the goat operation, Southern Seaboard farm resource region, female operator, operator age, a pastured and rotated production system, percentage of goat sales for breeding stock or show, and operator off-farm job are positive efficiency drivers for southeastern U.S. meat goat production. These meat goat farm and farmer characteristics are statistically significant and increase meat goat production TE.
Farmers with college degrees have generally been more technically efficient as a result of superior managerial ability. Pruitt et al. (Reference Pruitt, Gillespie, Nehring and Qushim2012) found that farmers with college degrees were more likely to adopt new technologies in U.S. cow-calf production. Rakipova, Gillespie, and Franke (Reference Rakipova, Gillespie and Franke2003) found that Louisiana beef cattle producers with college degrees were more technically efficient. We have also found that meat goat farmers with college degrees were more technically efficient than those without college degrees. Large-sized farms have generally been more efficient than small-sized farms. Paul et al. (Reference Paul, Nehring, Banker and Somwaru2004) found that small family farm corn producers in the United States were generally less efficient in terms of both their scale of operations and technical aspects of production than large farms. Our study results show that large-sized and medium-sized meat goat operations were more technically efficient than small-sized operations. The U.S. regions have different forage availability, grazing periods, and weather conditions such as heat and humidity and require different housing for goat production. Therefore, the U.S. regions may have different impacts on meat goat production efficiency. We found that Southern Seaboard meat goat farmers were more technically efficient than those in the other regions of the southeastern United States. Higher percentages of income from meat goat production (degree of specialization) increased TE.
For the impact of off-farm jobs on production efficiency, studies have found mixed results. On the one hand, farmers holding off-farm employment generally spend less time on the farm with their animals, potentially resulting in lower output. On the other hand, off-farm employment allows farmers to use off-farm income to invest in farm production. Nehring, Peel, and Nulph (Reference Nehring, Peel and Nulph2009) found that for U.S. corn and cow-calf producers, off-farm employment or off-farm income boosted small operations’ scale and TE. In this study, meat goat farmers holding off-farm jobs were more technically efficient than farmers who did not hold off-farm jobs. The TE of production for older farmers might be different from that of younger farmers as a result of experience. Studies have found mixed results for the impact of farmer age on production efficiency (Amara et al., Reference Amara, Traoré, Landry and Remain1999; Featherstone, Langemeier, and Ismet, Reference Featherstone, Langemeier and Ismet1997; Nehring et al., Reference Nehring, Barnard, Banker and Breneman2006). Meat goat farms operated by older farmers were more technically efficient than farms run by younger operators. Female farmers operated more technically efficient farms than male farmers.
Producers in the pastured and rotated production system are generally more heavily involved with their goats on a daily basis. This system requires more inputs of labor and capital but less usage of land. As an intensive production system, producers have the potential to more extensively incorporate new technologies and management practices to improve meat goat efficiency. Extensive-range or pasture/woods and pastured but not rotated systems allow goats to browse freely on pasture or rangeland and generally use less labor, fertilizer, and capital inputs. These production systems also require less producer participation in farm production on a daily basis, and few capital and other inputs are required compared with intensive production systems. Meat goat farms using pastured and rotated production systems were more technically efficient than those using extensive-range or pasture/woods and pastured but not rotated systems. Raising goats for breeding stock or for show is likely to result in higher cost, but also higher revenue. Goat farms selling higher percentages of meat goats for breeding stock or show were more technically efficient than those selling goats for slaughter/other purposes.
The distribution of the estimated input-oriented TE scores is presented in Table 5. Past studies have found different average TE measures for agricultural farms. Featherstone, Langemeier, and Ismet (Reference Featherstone, Langemeier and Ismet1997) found an average TE of 0.78 for Kansas beef cow farms. However, other studies have found relatively higher levels of TE. Louisiana beef cattle producers had an average TE of 0.92 (Rakipova, Gillespie, and Franke, Reference Rakipova, Gillespie and Franke2003). U.S. agricultural farms with corn as a major component of their output had an average TE of 0.89 (Paul et al., Reference Paul, Nehring, Banker and Somwaru2004). Surprisingly, goat producers in developing countries also had relatively higher average TE. Alex, Cheemani, and Thomas (Reference Alex, Cheemani and Thomas2013) found an average TE of 0.88 for goat producers in India. This study found an average TE of 0.81, which implies that the average southeastern U.S. meat goat farm could reduce approximately 19% in inputs to produce the same output as an efficient farm on the production frontier. Differences in average TE by study can generally be attributed to method of estimation (i.e., parametric or nonparametric; Paul et al., Reference Paul, Nehring, Banker and Somwaru2004), specification of inputs and outputs, and stage of industry development. For example, Gillespie, Schupp, and Taylor (Reference Gillespie, Schupp and Taylor1997) found relatively low TE scores in a new alternative enterprise, ratites. The table also shows that approximately 78% of the farmers achieved TE levels of 70% or higher.
Table 5. Distribution of Technical Efficiency (TE) Estimates for Southeastern U.S. Meat Goat Enterprises
Note: SD, standard deviation.
The marginal productive contributions (MPCs) of outputs and inputs can be estimated from the IDF, respectively, as MPCk = − εDIYk = − ∂ln DI(X, Y)/∂ln Yk = εX 1Yk, and MPCm = − εDIX*m = −∂ln DI(X, Y)/∂ln X*m = εX 1X*m. All MPCs have the hypothesized signs, negative for inputs and positive for outputs, as shown in Table 6, and are significant. MPCs for outputs, ln YMgoat and ln YGbstock, indicate that an increase in all inputs results in an increase in output and are positive, like an output elasticity or marginal cost. MPCs for inputs indicate the shadow values of inputs, ln X*Feed, ln X*Fixed, and ln X*Var, relative to land, XLand, and are negative, like the slope of a isoquant. The largest MPC in absolute value for inputs is land expense, followed by feed expense, total fixed expenses, and total other variable expenses. The MPC for meat goat breeding stock production output has the largest input share—approximately 47% on average.
Table 6. Marginal Productive Contributions for Inputs and Outputs and Returns to Scale, Scope Economies, and Scale Efficiency Measures for Southeastern U.S. Meat Goat Enterprises
Note: Asterisks (*, **, and ***) indicate significance at the 10%, 5%, and 1% level, respectively.
Overall economic performance indicators for southeastern U.S. meat goat enterprises are presented in Table 6. The estimated returns to scale (RTS) parameter for the southeastern U.S. meat goat enterprises shows that a 1% increase in all outputs increased overall input use by 0.79%. This means an increasing RTS economy exists in southeastern U.S. meat goat production. A measure of scope economies was estimated from the IDF by taking the second cross partial output derivative, ∂2ln DI(X, Y)/∂ln Yk∂ln Yl > 0. Denny and Pinto (Reference Denny, Pinto, Fuss and McFadden1978) also show that scope economies exist in the translog function if − βkβl < βkl and can be determined by testing the − βkβl = βkl constraint. It was statistically significant, implying that scope economies exist in southeastern U.S. meat goat production. A coefficient of 0.11 suggests that joint production of meat goat breeding stock and meat goat for slaughter and/or goat meat decreased average total cost by 11% relative to the separate production of these two outputs on southeastern U.S. meat goat farms.
Scale efficiency is the potential productivity gain from moving to the optimal farm size (Table 6). The method for estimating scale efficiency was introduced Ray (Reference Ray1998) for a frontier production function, and Balk (Reference Balk2001), Ray (Reference Ray2003), and Nahn and Vu (Reference Nahm and Vu2013) extended the scale efficiency measure for multiple-output multiple-input and multiple-input multiple-output distance functions.Footnote 9 Following Ray (Reference Ray2003), a scale efficiency measure can be estimated from the IDF.Footnote 10 The scale efficiency is an economic performance indicator representing the improvement in average productivity of southeastern U.S. meat goat production through a change in scale. We found that southeastern U.S. meat goat enterprises are on average scale efficient if the enterprise's scale of production is >60 goats or >40 breeding does per operation.
The estimation results for hypotheticalFootnote 11 or empirical MC simulation show that there was no significant bias, and the asymptotic distribution approximated the small-sample distribution well for the DGP with samples of sizes 250, 500, and 1,000. Empirical MC simulation results for the southeastern U.S. meat goat enterprises indicate that the means of the parameter estimates approach very closely the true values of the DGP, and the SDs of the parameter estimates get close to the means of the standard errors with increasing numbers of simulations (Appendix A). The rejection rates of the parameters become less than the nominal size of 0.05 or 5% with increasing numbers of simulations. We estimated 95% confidence intervals for the MC simulation averages.Footnote 12 The results for the parameter estimates and the rejection rates indicate that there are no significant biases and that the asymptotic distribution approximated the finite-sample distribution well for the DGP with samples of sizes 250, 500, and 1,000 (number of replications). The confidence intervals for the standard errors include the sample SDs for the parameter estimates, another indication that large-sample theory provides a good approximation to the finite-sample distribution.
4. Discussion and Conclusions
Our study reveals that the efficiency of southeastern U.S. meat goat production is impacted by factors such as farm size, diversification, production system, farmer demographics, percentage of goat sales for breeding stock or show, and region (location of farms). We found increasing RTS, scale efficiency, and scope economies, exposing insights into the growth potential for the southeastern U.S. meat goat industry. For meat goat enterprise productivity growth, specialization and scope economies within the meat goat enterprise were found to be potential factors for increasing efficiency.
The effect of operation size on the efficiency and productivity of U.S. meat goat farms is significant. Large-sized and medium-sized meat goat enterprises were more technically efficient than small-sized operations. Small farms have the potential to enhance their competitiveness by increasing the scale of their operations. Cost analyses show that increased farm size in southeastern U.S. meat goat production substantially decreased total, variable, and fixed expenses. This indicates along with IDF estimates that there are economies of size in southeastern U.S. meat goat production. In addition to cost analysis, increasing RTS for the southeastern U.S. meat goat enterprise suggests that producers can increase the size of their operations, resulting in less overall input usage per unit produced. Note, however, that the operation size for which economies of size are realized is still relatively small, suggesting the possibility of efficient production on rather small landholdings. Our results suggest that southeastern U.S. meat goat enterprises can be scale efficient if their operation size is >60 goats or >40 breeding does. The 2012 Census of Agriculture (USDA-NASS, 2014) results suggest the average meat goat farm includes 20 goats, which is not a scale-efficient production size based on findings of this study. In our study, the average farm producing 60 goats farmed approximately 41 acres in goats, which is a relatively small-sized farm.
Results suggest that extension educational efforts will lead to greater increases in farm efficiency if directed to small-scale producers who are full-time farmers, those who are less specialized in meat goat production, and those who have lower education levels. Extension education could be used by the industry to educate and encourage small-scale meat goat farmers with low TE levels to utilize information on new technologies and better farming practices to improve their farming efficiency and productivity.
Table A1. Empirical MC Simulation Results for SPF Analysis
Open access
