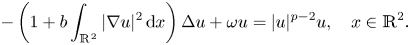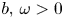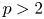1. Introduction and main results
The stability of bound states of nonlinear Schrödinger equations in the attractive case has been studied since 1983. In particular, the ground state was described by minimizing the corresponding energy functionals in several manifolds with constrained conditions. In this paper, we study the bound states for the following Kirchhoff type equation

where $b,\, \omega >0$![]() are constants, $p\in (2,\,+\infty )$
are constants, $p\in (2,\,+\infty )$![]() . It is known that every solution to Eq. (1.1) is a critical point of the energy functional $S: H^1(\mathbb {R}^2)\rightarrow \mathbb {R}$
. It is known that every solution to Eq. (1.1) is a critical point of the energy functional $S: H^1(\mathbb {R}^2)\rightarrow \mathbb {R}$![]() , given by
, given by
Equation (1.1) is related to the stationary form of the classical Kirchhoff equation

where $\Omega \subset \mathbb {R}^N$![]() ($N\geq 1$
($N\geq 1$![]() ) and $h\in C(\Omega \times \mathbb {R},\,\mathbb {R})$
) and $h\in C(\Omega \times \mathbb {R},\,\mathbb {R})$![]() . Problem (1.2) was proposed by Kirchhoff [Reference Kirchhoff17] as an extensional the classical D'Alember's wave equation for free vibrations of elastic strings which corresponds to the case $b=0$
. Problem (1.2) was proposed by Kirchhoff [Reference Kirchhoff17] as an extensional the classical D'Alember's wave equation for free vibrations of elastic strings which corresponds to the case $b=0$![]() in (1.2). As we know, Kirchhoff's model takes into account modifications in length of the string produced by transversal vibrations. After the pioneering work of Lions [Reference Lions22], where an abstract framework was introduced, the stationary elliptic version of problem (1.2) has been widely studied in the literature, for example, we refer to the papers [Reference Autuori, Fiscella and Pucci1, Reference Chen, Kuo and Wu5, Reference Deng, Peng and Shuai7, Reference Huang, Liu and Wu13–Reference Jünior and Siciliano15, Reference Li, Li and Shi21, Reference Liu, Hou and Liao23–Reference Perera and Zhang25, Reference Wang, Xie and Zhang28].
in (1.2). As we know, Kirchhoff's model takes into account modifications in length of the string produced by transversal vibrations. After the pioneering work of Lions [Reference Lions22], where an abstract framework was introduced, the stationary elliptic version of problem (1.2) has been widely studied in the literature, for example, we refer to the papers [Reference Autuori, Fiscella and Pucci1, Reference Chen, Kuo and Wu5, Reference Deng, Peng and Shuai7, Reference Huang, Liu and Wu13–Reference Jünior and Siciliano15, Reference Li, Li and Shi21, Reference Liu, Hou and Liao23–Reference Perera and Zhang25, Reference Wang, Xie and Zhang28].
The existence and qualitative properties of positive solutions for the following Kirchhoff-type equation

have been extensively in the past several decades where $f\in C(\mathbb {R}^N\times \mathbb {R},\,\mathbb {R})$![]() , $a,\,b>0$
, $a,\,b>0$![]() are constants. It is well known that Eq. (1.3) is the Euler–Lagrange equation of the energy functional $I: H^1(\mathbb {R}^N)\rightarrow \mathbb {R}$
are constants. It is well known that Eq. (1.3) is the Euler–Lagrange equation of the energy functional $I: H^1(\mathbb {R}^N)\rightarrow \mathbb {R}$![]() defined as
defined as
where $F(x,\,u)=\int _0^uf(x,\,s)\,{\rm d}s$![]() . Define
. Define
A nontrivial solution $u$![]() to problem (1.3) is called a ground state if $I(u)=m$
to problem (1.3) is called a ground state if $I(u)=m$![]() .
.
For $N=2$![]() or 3, by using the fountain theorem, Jin and Wu [Reference Jin and Wu16] proved that problem (1.3) has infinitely many radial solutions when $f$
or 3, by using the fountain theorem, Jin and Wu [Reference Jin and Wu16] proved that problem (1.3) has infinitely many radial solutions when $f$![]() satisfies some suitable assumptions. Later, on $\mathbb {R}^3$
satisfies some suitable assumptions. Later, on $\mathbb {R}^3$![]() , He and Zou [Reference He and Zou11] studied (1.3) under the conditions that $f(x,\,u):=f(u)$
, He and Zou [Reference He and Zou11] studied (1.3) under the conditions that $f(x,\,u):=f(u)$![]() satisfies $\lim _{|u|\rightarrow 0}f(u)/|u|^3=0$
satisfies $\lim _{|u|\rightarrow 0}f(u)/|u|^3=0$![]() , $\lim _{|u|\rightarrow \infty }f(u)/|u|^q=0$
, $\lim _{|u|\rightarrow \infty }f(u)/|u|^q=0$![]() for some $3< q<5$
for some $3< q<5$![]() , $f(t)/t^3$
, $f(t)/t^3$![]() is strictly increasing for $t>0$
is strictly increasing for $t>0$![]() and
and
The authors obtained existence and concentration behavior of positive solutions and ground state solutions to (1.3) via using the mountain pass theorem and the Nehari manifold, respectively. When $f(x,\,u):=\lambda f(u)+|u|^4u$![]() , where $f(u)$
, where $f(u)$![]() satisfies some appropriate assumptions, Wang et al. [Reference Wang, Tian, Xu and Zhang27], He et al. [Reference He, Li and Peng12], Li and Ye [Reference Li and Ye20] used the same arguments as in [Reference He and Zou11] to prove the existence of ground state solutions and concentration behavior of positive solutions. There are also some studies on ground state solutions and concentration behavior of positive solutions results, we refer to [Reference Figueiredo, Ikoma and Júnior8, Reference Figueiredo and Jünior9, Reference Ikoma14].
satisfies some appropriate assumptions, Wang et al. [Reference Wang, Tian, Xu and Zhang27], He et al. [Reference He, Li and Peng12], Li and Ye [Reference Li and Ye20] used the same arguments as in [Reference He and Zou11] to prove the existence of ground state solutions and concentration behavior of positive solutions. There are also some studies on ground state solutions and concentration behavior of positive solutions results, we refer to [Reference Figueiredo, Ikoma and Júnior8, Reference Figueiredo and Jünior9, Reference Ikoma14].
Recently, Li et al. [Reference Li, Luo, Peng, Wang and Xiang19] considered the existence of positive ground state solutions of (1.3) when $f(x,\,u):=u^p$![]() with $1< p<5$
with $1< p<5$![]() on $\mathbb {R}^3$
on $\mathbb {R}^3$![]() . Furthermore, they exploited the smoothness, symmetry and asymptotic behavior of positive solutions. Qi and Zou [Reference Qi and Zou26] studied the exact number and expressions of the positive solutions for problem (1.1) with the prescribed $L^2$
. Furthermore, they exploited the smoothness, symmetry and asymptotic behavior of positive solutions. Qi and Zou [Reference Qi and Zou26] studied the exact number and expressions of the positive solutions for problem (1.1) with the prescribed $L^2$![]() -norm and the unknown frequency. Wei et al. [Reference Wei, Tang and Zhang29] established the existence of ground state solution for problem (1.1) with critical exponential and periodic nonlinearity, see also [Reference Chen and Yu6] for some existence results for a Kirchhoff-type problem in $\mathbb {R}^2$
-norm and the unknown frequency. Wei et al. [Reference Wei, Tang and Zhang29] established the existence of ground state solution for problem (1.1) with critical exponential and periodic nonlinearity, see also [Reference Chen and Yu6] for some existence results for a Kirchhoff-type problem in $\mathbb {R}^2$![]() with critical exponential.
with critical exponential.
Inspired by the above work, we are interested in necessary and sufficient conditions for ground state solutions for Kirchhoff-type problems in the whole space $\mathbb {R}^2$![]() , which have not been investigated in the literature until now. However, the main difficulty faced is that we have to consider the nonlocal term $b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x$
, which have not been investigated in the literature until now. However, the main difficulty faced is that we have to consider the nonlocal term $b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x$![]() in the whole space. For this, we introduce a new scale technique to deal with this problem.
in the whole space. For this, we introduce a new scale technique to deal with this problem.
Before stating our main results, we introduce the following functionals and sets, respectively.

Now our main results are listed as follows.
Theorem 1.1 Assume $b,\,\omega >0$![]() and $p>2$
and $p>2$![]() . Then
. Then
(i) $A$
 and $G$
and $G$ are nonempty.
are nonempty.(ii) $u\in G$
 if and only if $u$
if and only if $u$ solves the minimization problem
(1.7)\begin{equation} \begin{cases} u\in N \ \text{and} \ \int_{\mathbb{R}^2}|u|^2\,{\rm d}x=\frac{2(4bd_N+1)-2\sqrt{4bd_N+1}}{\omega b(p-2)},\\ S(u)=d_N:=\min\{S(w): w\in N\}. \end{cases} \end{equation}
solves the minimization problem
(1.7)\begin{equation} \begin{cases} u\in N \ \text{and} \ \int_{\mathbb{R}^2}|u|^2\,{\rm d}x=\frac{2(4bd_N+1)-2\sqrt{4bd_N+1}}{\omega b(p-2)},\\ S(u)=d_N:=\min\{S(w): w\in N\}. \end{cases} \end{equation}
(iii) There exists a real-valued, positive, spherically symmetric, and decreasing function $\varphi \in G$
 such that
\[ G=\bigcup\{\varphi({\cdot}{-}y): y\in\mathbb{R}^2\}. \]
such that
\[ G=\bigcup\{\varphi({\cdot}{-}y): y\in\mathbb{R}^2\}. \]
Theorem 1.2 Assume $b,\,\omega >0$![]() and $p>6$
and $p>6$![]() . If $u\in H^1(\mathbb {R}^2)$
. If $u\in H^1(\mathbb {R}^2)$![]() , then $u\in G$
, then $u\in G$![]() if and only if $u$
if and only if $u$![]() solves the minimization problem
solves the minimization problem

Remark 1.3 Note that our results are new even in the available literature concerning the case of $\mathbb {R}^N$![]() ($N\geq 3$
($N\geq 3$![]() ). As a matter of fact, our scale technique seems difficult to be employed in $\mathbb {R}^N$
). As a matter of fact, our scale technique seems difficult to be employed in $\mathbb {R}^N$![]() ($N\geq 3$
($N\geq 3$![]() ). Of course, it would be interesting to extend our results to $\mathbb {R}^N$
). Of course, it would be interesting to extend our results to $\mathbb {R}^N$![]() ($N\geq 3$
($N\geq 3$![]() ). In addition, our results could not be deduced if the nonlinearity $|u|^{p-2}u$
). In addition, our results could not be deduced if the nonlinearity $|u|^{p-2}u$![]() is replaced by the one with subcritical or critical exponential growth.
is replaced by the one with subcritical or critical exponential growth.
The paper is organized as follows. In § 2, we establish a regularity result and give the proof of theorem 1.1. In § 3, we deal with the proof of theorem 1.2.
2. Proof of theorem 1.1
If $u$![]() is a solution of problem (1.1), then
is a solution of problem (1.1), then
Now, $u$![]() is also the critical point of $S(u)$
is also the critical point of $S(u)$![]() in $H^1(\mathbb {R}^2)$
in $H^1(\mathbb {R}^2)$![]() . So we have the Pohozaev's identity $\frac {d}{d\lambda }|_{\lambda =1}S(u(\lambda ^{-1}x))=0$
. So we have the Pohozaev's identity $\frac {d}{d\lambda }|_{\lambda =1}S(u(\lambda ^{-1}x))=0$![]() . This implies $V(u)=0$
. This implies $V(u)=0$![]() , that is,
, that is,
and hence
Consequently

which leads to

Lemma 2.1 Assume $2< p<\infty$![]() , $\omega >0$
, $\omega >0$![]() . If $u$
. If $u$![]() is a solution of (1.1). Then the following properties hold:
is a solution of (1.1). Then the following properties hold:
(i) $u\in W^{3,q}(\mathbb {R}^2)$
 for every $2\leq q<+\infty$
for every $2\leq q<+\infty$ . In particular, $u\in C^2(\mathbb {R}^2)$
. In particular, $u\in C^2(\mathbb {R}^2)$ and $|D^\beta u(x)|\rightarrow 0$
and $|D^\beta u(x)|\rightarrow 0$ as $|x|\rightarrow \infty$
as $|x|\rightarrow \infty$ for all $|\beta |\leq 2$
for all $|\beta |\leq 2$ .
.(ii) There exists $\varepsilon >0$
 such that $e^{\varepsilon |x|}(|u(x)|+|\nabla u(x)|)\in L^\infty (\mathbb {R}^2)$
such that $e^{\varepsilon |x|}(|u(x)|+|\nabla u(x)|)\in L^\infty (\mathbb {R}^2)$ .
.
Proof. $(i)$![]() We borrow the idea from [Reference Cazenave4]. Let $u$
We borrow the idea from [Reference Cazenave4]. Let $u$![]() be a solution of problem (1.1). Thus,
be a solution of problem (1.1). Thus,
Let $A=1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x$![]() ($A<\infty$
($A<\infty$![]() ), $B=\frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{\omega ^2}$
), $B=\frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{\omega ^2}$![]() . Changing $u(x)$
. Changing $u(x)$![]() to
to
we may assume that $v$![]() satisfies
satisfies
Note that (2.3) can be written in the form
where $\mathcal {F}$![]() is the Fourier transform. For $K>0$
is the Fourier transform. For $K>0$![]() , set
, set
Observing that, for $\beta \geq 1$![]() ,
,
we get

Taking the test function $\varphi =|v_K|^{2\beta -2}v$![]() in (2.3), we have
in (2.3), we have

It follows from (2.5) and (2.6) that
On one hand, by the Sobolev inequality, we have

where

On the other hand, by the Hölder inequality, we deduce that

The symbol $\|\cdot \|$![]() is used only for the norm in $H^1(\mathbb {R}^2)$
is used only for the norm in $H^1(\mathbb {R}^2)$![]() . Applying (2.7) and letting $K\rightarrow \infty$
. Applying (2.7) and letting $K\rightarrow \infty$![]() , we obtain
, we obtain
where $|\cdot |_{L^q}$![]() denotes the standard norm in $L^q(\mathbb {R}^2)$
denotes the standard norm in $L^q(\mathbb {R}^2)$![]() . It follows from the above inequality that
. It follows from the above inequality that
Set
so that
Consequently, $\beta _n\rightarrow \infty$![]() as $n\rightarrow \infty$
as $n\rightarrow \infty$![]() . Therefore,
. Therefore,
Doing iteration by (2.8), we obtain $v\in L^\infty (\mathbb {R}^2)$![]() . Thus $|v|^{p-2}v\in L^2(\mathbb {R}^2)\cap L^\infty (\mathbb {R}^2)$
. Thus $|v|^{p-2}v\in L^2(\mathbb {R}^2)\cap L^\infty (\mathbb {R}^2)$![]() , so that $v\in W^{2,q}(\mathbb {R}^2)$
, so that $v\in W^{2,q}(\mathbb {R}^2)$![]() and $|v|^{p-2}v\in W^{1,q}(\mathbb {R}^2)$
and $|v|^{p-2}v\in W^{1,q}(\mathbb {R}^2)$![]() for all $2\leq q<\infty$
for all $2\leq q<\infty$![]() . Therefore, it follows from (2.4) that $(-\Delta +I)\partial _jv\in L^q(\mathbb {R}^2)$
. Therefore, it follows from (2.4) that $(-\Delta +I)\partial _jv\in L^q(\mathbb {R}^2)$![]() , i.e., $\mathcal {F}^{-1}((1+4\pi ^2|\xi |^2)\mathcal {F}\partial _jv)\in L^q(\mathbb {R}^2)$
, i.e., $\mathcal {F}^{-1}((1+4\pi ^2|\xi |^2)\mathcal {F}\partial _jv)\in L^q(\mathbb {R}^2)$![]() . Thus $\partial _jv\in H^{2,q}(\mathbb {R}^2)=W^{2,q}(\mathbb {R}^2)$
. Thus $\partial _jv\in H^{2,q}(\mathbb {R}^2)=W^{2,q}(\mathbb {R}^2)$![]() , and so $v\in W^{3,q}(\mathbb {R}^2)$
, and so $v\in W^{3,q}(\mathbb {R}^2)$![]() . By the Sobolev's embedding theorem, $v\in C^{2,\delta }(\mathbb {R}^2)$
. By the Sobolev's embedding theorem, $v\in C^{2,\delta }(\mathbb {R}^2)$![]() for $0<\delta <1$
for $0<\delta <1$![]() . Therefore, $|D^\beta v(x)|\rightarrow 0$
. Therefore, $|D^\beta v(x)|\rightarrow 0$![]() as $|x|\rightarrow \infty$
as $|x|\rightarrow \infty$![]() for all $|\beta |\leq 2$
for all $|\beta |\leq 2$![]() , so that $|D^\beta u(x)|\rightarrow 0$
, so that $|D^\beta u(x)|\rightarrow 0$![]() as $|x|\rightarrow \infty$
as $|x|\rightarrow \infty$![]() .
.
$(ii)$![]() Let $\varepsilon >0$
Let $\varepsilon >0$![]() and $\theta _\varepsilon (x)=e^{\frac {|x|}{1+\varepsilon |x|}}$
and $\theta _\varepsilon (x)=e^{\frac {|x|}{1+\varepsilon |x|}}$![]() . $\theta _\varepsilon$
. $\theta _\varepsilon$![]() is bounded, Lipschitz continuous, and $|\nabla \theta _\varepsilon |\leq \theta _\varepsilon$
is bounded, Lipschitz continuous, and $|\nabla \theta _\varepsilon |\leq \theta _\varepsilon$![]() a.e. Taking the test function $\theta _\varepsilon v\in H^1(\mathbb {R}^2)$
a.e. Taking the test function $\theta _\varepsilon v\in H^1(\mathbb {R}^2)$![]() in (2.3), we get
in (2.3), we get
Noting that

we obtain

Since $u\in H^1(\mathbb {R}^2)$![]() , there exists $R>0$
, there exists $R>0$![]() such that $|v(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$
such that $|v(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$![]() for $|x|\geq R$
for $|x|\geq R$![]() . Thus
. Thus

It follows from (2.10) that

Letting $\varepsilon \downarrow 0$![]() , we deduce that
, we deduce that
Since $v$![]() is globally Lipschitz continuous by $(i)$
is globally Lipschitz continuous by $(i)$![]() , $|v(x)|^{4}e^{|x|}$
, $|v(x)|^{4}e^{|x|}$![]() is bounded. Similarly, applying $\partial _j$
is bounded. Similarly, applying $\partial _j$![]() to equation (2.3) and multiplying the resulting equation by $\theta _\varepsilon \partial _j u$
to equation (2.3) and multiplying the resulting equation by $\theta _\varepsilon \partial _j u$![]() for $j=1,\,2$
for $j=1,\,2$![]() , we have
, we have
Applying the fact

we have

Consequently
By $(i)$![]() , there exists $R>0$
, there exists $R>0$![]() such that $|\partial _jv(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$
such that $|\partial _jv(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$![]() for $|x|\geq R$
for $|x|\geq R$![]() . Thus
. Thus

It follows from (2.12) that

Letting $\varepsilon \downarrow 0$![]() , we deduce that
, we deduce that
Since $\nabla v$![]() is globally Lipschitz continuous, similarly, we deduce that $|\nabla v(x)|^{4}e^{|x|}$
is globally Lipschitz continuous, similarly, we deduce that $|\nabla v(x)|^{4}e^{|x|}$![]() is bounded. The proof is now finished.
is bounded. The proof is now finished.
Lemma 2.2 Assume that $2< p<\infty$![]() and $b,\,\omega >0$
and $b,\,\omega >0$![]() . It follows that the minimization problem
. It follows that the minimization problem
has a positive solution, where $N$![]() is defined in (1.5). Moreover, every solution of (2.13) is the solution of equation (1.1).
is defined in (1.5). Moreover, every solution of (2.13) is the solution of equation (1.1).
Proof. A similar argument to the proof of Theorem 8.1.5 in [Reference Cazenave4], we observe that $d_N>0$![]() . Indeed, consider $u\in N$
. Indeed, consider $u\in N$![]() , it implies that $V(u)=0$
, it implies that $V(u)=0$![]() , namely
, namely
It follows from the Gagliardo–Nirenberg inequality that there exists $C$![]() independent of $u$
independent of $u$![]() such that
such that

From the above information, there exists $c>0$![]() such that $\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x\geq c$
such that $\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x\geq c$![]() , and so
, and so

for all $u\in N$![]() , which implies that $d_N>0$
, which implies that $d_N>0$![]() .
.
We recall the definition of the Schwarz symmetrization [Reference Berestycki and Lions3]. If $u\in L^2(\mathbb {R}^2)$![]() is a nonnegative function, we denote by $u^*$
is a nonnegative function, we denote by $u^*$![]() the unique spherically symmetric, nonnegative, non-increasing function such that
the unique spherically symmetric, nonnegative, non-increasing function such that
In particular,

The proof of lemma 2.2 is divided into three steps.
Step 1. we claim that the minimization problem (2.13) has a solution.
Similar to the proof of [Reference Berestycki, Gallouët and Kavian2], it is clear that $N\neq \emptyset$![]() . Let $\{v_n\}\subset N$
. Let $\{v_n\}\subset N$![]() be a minimizing sequence of $S$
be a minimizing sequence of $S$![]() , that is, $V(v_n)=0$
, that is, $V(v_n)=0$![]() , and $S(v_n)\rightarrow d_N$
, and $S(v_n)\rightarrow d_N$![]() . Let $w_n=|v_n|^*$
. Let $w_n=|v_n|^*$![]() . It follows from (2.14) that $V(w_n)=V(v_n)$
. It follows from (2.14) that $V(w_n)=V(v_n)$![]() , and hence $\{w_n\}$
, and hence $\{w_n\}$![]() is also a minimizing sequence of $S$
is also a minimizing sequence of $S$![]() . Define now $u_n$
. Define now $u_n$![]() by $u_n(x)=w_n(\lambda ^{1/2}_nx)$
by $u_n(x)=w_n(\lambda ^{1/2}_nx)$![]() , where
, where
where
We deduce that

and

These results imply
We obtain that $\{u_n\}$![]() is also a minimizing sequence of $S$
is also a minimizing sequence of $S$![]() . It follows from (2.15) that $\{u_n\}$
. It follows from (2.15) that $\{u_n\}$![]() is bounded in $H^1(\mathbb {R}^2)$
is bounded in $H^1(\mathbb {R}^2)$![]() . Therefore, there exist a subsequence of $u_n$
. Therefore, there exist a subsequence of $u_n$![]() (denoted by itself) and $u\in H^1(\mathbb {R}^2)$
(denoted by itself) and $u\in H^1(\mathbb {R}^2)$![]() such that $u_n\rightharpoonup u$
such that $u_n\rightharpoonup u$![]() weakly in $H^1(\mathbb {R}^2)$
weakly in $H^1(\mathbb {R}^2)$![]() and $u_n\rightarrow u$
and $u_n\rightarrow u$![]() strongly in $L^{p}(\mathbb {R}^2)$
strongly in $L^{p}(\mathbb {R}^2)$![]() . By the Fatou's lemma,
. By the Fatou's lemma,

By the weak lower semicontinuity of the $L^2$![]() norm,
norm,
Therefore,
We claim that $V(u)=0$![]() . Indeed, if $V(u)>0$
. Indeed, if $V(u)>0$![]() , then $u\neq 0$
, then $u\neq 0$![]() . So there exists $\lambda \in (0,\,1)$
. So there exists $\lambda \in (0,\,1)$![]() such that $v=\lambda u$
such that $v=\lambda u$![]() satisfies $V(v)=0$
satisfies $V(v)=0$![]() . Thus $v\in N$
. Thus $v\in N$![]() . Furthermore,
. Furthermore,

Noting that $d_N=\lim _{n\to \infty }S(u_n)$![]() and $V(u_n)=0$
and $V(u_n)=0$![]() , then we have
, then we have

From the above information, we get

This implies that $S(v)< d_N$![]() . This contradicts (2.13) since $S(v)\geq d_N$
. This contradicts (2.13) since $S(v)\geq d_N$![]() . Therefore, $V(u)=0$
. Therefore, $V(u)=0$![]() . This implies that
. This implies that
Consequently,
and so $u$![]() satisfies (2.13).
satisfies (2.13).
Step 2. We claim that every solutions of (2.13) belongs to $A$![]() .
.
Indeed, consider a solution $u$![]() of (2.13). There exists a Lagrange multiplier $\lambda$
of (2.13). There exists a Lagrange multiplier $\lambda$![]() such that
such that
For any $\varphi \in H^1(\mathbb {R}^2)$![]() , it follows from (2.16) that
, it follows from (2.16) that
Taking the test function $\varphi =u$![]() , we obtain
, we obtain
Noting that

we deduce that
so that
It follows from $V(u)=0$![]() and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma$
and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma$![]() that
that
Together with (2.17), there holds
and so $\lambda =1$![]() . Therefore, $u$
. Therefore, $u$![]() satisfies problem (1.1). So $A\neq \emptyset$
satisfies problem (1.1). So $A\neq \emptyset$![]() .
.
Step 3. We claim that $u$![]() satisfies problem (2.13) if and only if $u\in G$
satisfies problem (2.13) if and only if $u\in G$![]() .
.
Consider any solution $u$![]() of (2.13) and any $v\in A$
of (2.13) and any $v\in A$![]() . That is,
. That is,
By Pohozaev's identity, we get $V(v)=0$![]() . This means $v\in N$
. This means $v\in N$![]() , and
, and

From (2.2), there holds

Since $v\in N$![]() , by the definition of $d_N$
, by the definition of $d_N$![]() , we have
, we have
which implies that $u\in G\neq \emptyset$![]() .
.
Assume further that $v\in G$![]() . Since $u\in G$
. Since $u\in G$![]() also, we have $S(u)=S(v)$
also, we have $S(u)=S(v)$![]() . Noting that $S(u)=d_N$
. Noting that $S(u)=d_N$![]() and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma =\frac {2(4bd_N+1)-2\sqrt {4bd_N+1}}{\omega b(p-2)}$
and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma =\frac {2(4bd_N+1)-2\sqrt {4bd_N+1}}{\omega b(p-2)}$![]() , we obtain
, we obtain
Applying (2.18), we have

which implies that $\gamma =\int _{\mathbb {R}^2}|v|^2\,{\rm d}x,$![]() which means that $v$
which means that $v$![]() satisfies (2.13). Hence, the proof is complete.
satisfies (2.13). Hence, the proof is complete.
Proof. Proof of theorem 1.1
Consider $u\in G$![]() , it follows that
, it follows that
and so
where
According to lemma 2.1, $u\in C^2(\mathbb {R}^2)$![]() and $a(x)\rightarrow 0$
and $a(x)\rightarrow 0$![]() as $|x|\rightarrow \infty$
as $|x|\rightarrow \infty$![]() . Applying Theorem 2 in [Reference Gidas, Ni and Nirenberg10], we obtain that there exists a positive, spherically symmetric solution $\varphi$
. Applying Theorem 2 in [Reference Gidas, Ni and Nirenberg10], we obtain that there exists a positive, spherically symmetric solution $\varphi$![]() of Eq. (2.19) and $y\in \mathbb {R}^2$
of Eq. (2.19) and $y\in \mathbb {R}^2$![]() such that $u(\cdot )=\varphi (\cdot -y)$
such that $u(\cdot )=\varphi (\cdot -y)$![]() . Note that $\varphi$
. Note that $\varphi$![]() , being radially symmetric, satisfies the ordinary differential equation
, being radially symmetric, satisfies the ordinary differential equation
Since $\int _0^\infty 4\pi r^2u_r^2dr$![]() is independent of choice of $u$
is independent of choice of $u$![]() , we deduce that $1+b\int _0^\infty 4\pi r^2u_r^2dr$
, we deduce that $1+b\int _0^\infty 4\pi r^2u_r^2dr$![]() is a positive constant. As a result, we obtain that $\varphi$
is a positive constant. As a result, we obtain that $\varphi$![]() is unique by applying the uniqueness results in [Reference Kwong18] and [Reference Li, Luo, Peng, Wang and Xiang19]. The proof is now complete.
is unique by applying the uniqueness results in [Reference Kwong18] and [Reference Li, Luo, Peng, Wang and Xiang19]. The proof is now complete.
3. Proof of theorem 1.2
For the proof of theorem 1.2, we will use the following lemma.
Lemma 3.1 Given $u\in H^1(\mathbb {R}^2),\, u\neq 0$![]() , and $\lambda >0$
, and $\lambda >0$![]() , set $\mathcal {P}(\lambda,\,u)(x)=\lambda u(\lambda x)$
, set $\mathcal {P}(\lambda,\,u)(x)=\lambda u(\lambda x)$![]() . Then following properties hold:
. Then following properties hold:
(i) There exists a unique $\lambda ^*(u)>0$
 such that $\mathcal {P}(\lambda ^*(u),\,u)\in M$
such that $\mathcal {P}(\lambda ^*(u),\,u)\in M$ .
.(ii) The function $\lambda \mapsto S(\mathcal {P}(\lambda,\,u))$
 is convex on $(\lambda ^*(u),\,+\infty )$
is convex on $(\lambda ^*(u),\,+\infty )$ .
.(iii) $\lambda ^*(u)<1$
 if and only if $Q(u)<0$
if and only if $Q(u)<0$ .
.(iv) $\lambda ^*(u)=1$
 if and only if $u\in M$
if and only if $u\in M$ .
.(v) $S(\mathcal {P}(\lambda,\,u))< S(\mathcal {P}(\lambda ^*(u),\,u))$
 for each $\lambda >0$
for each $\lambda >0$ , $\lambda \neq \lambda ^*(u)$
, $\lambda \neq \lambda ^*(u)$ .
.(vi) $\frac {d}{d\lambda }S(\mathcal {P}(\lambda,\,u))=\frac {1}{\lambda }Q(\mathcal {P}(\lambda,\,u))$
 for each $\lambda >0$
for each $\lambda >0$ .
.(vii) $|\mathcal {P}(\lambda,\,u)|^*=\mathcal {P}(\lambda,\,|u|^*)$
 for each $\lambda >0$
for each $\lambda >0$ , where $*$
, where $*$ is the Schwarz symmetrization.
is the Schwarz symmetrization.(viii) If $u_m\rightharpoonup u$
 in $H^1(\mathbb {R}^2)$
in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$
weakly and in $L^{p}(\mathbb {R}^2)$ strongly, then $\mathcal {P}(\lambda,\,u_m)\rightarrow \mathcal {P}(\lambda,\,u)$
strongly, then $\mathcal {P}(\lambda,\,u_m)\rightarrow \mathcal {P}(\lambda,\,u)$ in $H^1(\mathbb {R}^2)$
in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$
weakly and in $L^{p}(\mathbb {R}^2)$ strongly for each $\lambda >0$
strongly for each $\lambda >0$ .
.
Proof. Let $u\in H^1(\mathbb {R}^2)$![]() , $u\neq 0$
, $u\neq 0$![]() , and let $u_\lambda =\mathcal {P}(\lambda,\,u)$
, and let $u_\lambda =\mathcal {P}(\lambda,\,u)$![]() . We have
. We have

Then
so that
Consequently, property (vi) holds. It follows from $f'(\lambda )=0$![]() that
that
Thus

which implies that (3.1) has a unique positive solution $\lambda ^*(u)$![]() (by Rello's theorem). In particular, $f$
(by Rello's theorem). In particular, $f$![]() achieves its maximum at $\lambda ^*(u)$
achieves its maximum at $\lambda ^*(u)$![]() . Therefore, properties (i), (ii) and (v) follow.
. Therefore, properties (i), (ii) and (v) follow.
(iii) Let $\lambda ^*(u)$![]() be the solution of (3.1), namely
be the solution of (3.1), namely
If $Q(u)<0$![]() . Then
. Then
which implies that
If $\lambda ^*(u)\geq 1$![]() . By (3.2), we deduce that
. By (3.2), we deduce that

which is impossible. This implies that if $Q(u)<0$![]() then $\lambda ^*(u)<1$
then $\lambda ^*(u)<1$![]() . Now we claim that $Q(u)<0$
. Now we claim that $Q(u)<0$![]() when $\lambda ^*(u)<1$
when $\lambda ^*(u)<1$![]() . Indeed, $\lambda ^*(u)<1$
. Indeed, $\lambda ^*(u)<1$![]() leads to
leads to
Therefore,

Thus, property (iii) follows.
(iv) If $\lambda ^*(u)=1$![]() , it follows from (3.2) that $u\in M$
, it follows from (3.2) that $u\in M$![]() . On the other hand, assume $u\in M$
. On the other hand, assume $u\in M$![]() , then
, then

so that
If $\lambda ^*(u)>1$![]() , using (3.3), we have
, using (3.3), we have

Consequently, $\lambda ^*(u)\leq 1$![]() . Similarly, we can reach a contradiction for the case of $\lambda ^*(u)<1$
. Similarly, we can reach a contradiction for the case of $\lambda ^*(u)<1$![]() . As a result, $\lambda ^*(u)=1$
. As a result, $\lambda ^*(u)=1$![]() .
.
Finally, property (vii) follows easily from the definition of Schwarz's symmetrization. For (viii), given $\lambda >0$![]() , the operator $u\mapsto \mathcal {P}(\lambda,\,u)$
, the operator $u\mapsto \mathcal {P}(\lambda,\,u)$![]() is linear and strongly continuous $H^1(\mathbb {R}^2)\rightarrow H^1(\mathbb {R}^2)$
is linear and strongly continuous $H^1(\mathbb {R}^2)\rightarrow H^1(\mathbb {R}^2)$![]() . Therefore, it is also weakly continuous. The $L^{p}(\mathbb {R}^2)$
. Therefore, it is also weakly continuous. The $L^{p}(\mathbb {R}^2)$![]() continuity is immediate. Thus (viii) follows. This ends the proof.
continuity is immediate. Thus (viii) follows. This ends the proof.
Lemma 3.2 The set $M$![]() is nonempty. If we set
is nonempty. If we set
then $Q(u)\leq S(u)-m$![]() for every $u\in H^1(\mathbb {R}^2)$
for every $u\in H^1(\mathbb {R}^2)$![]() such that $Q(u)<0$
such that $Q(u)<0$![]() .
.
Proof. The set $M$![]() is nonempty from lemma 3.1 (i). Let $u\in H^1(\mathbb {R}^2)$
is nonempty from lemma 3.1 (i). Let $u\in H^1(\mathbb {R}^2)$![]() such that $Q(u)<0$
such that $Q(u)<0$![]() . By lemma 3.1 (ii) (iii), $f''(x)\leq 0$
. By lemma 3.1 (ii) (iii), $f''(x)\leq 0$![]() on $(\lambda ^*(u),\, 1)$
on $(\lambda ^*(u),\, 1)$![]() . Therefore,
. Therefore,
which means
Applying lemma 3.1 (vi), we obtain
Noting that $\lambda ^*(u)\in M$![]() , we have $f(\lambda ^*(u))=S(\lambda ^*(u))\geq m$
, we have $f(\lambda ^*(u))=S(\lambda ^*(u))\geq m$![]() , and so
, and so
which completes the proof.
Proof. Proof of theorem 1.2
We proceed in three steps.
Step 1. We claim that the minimization problem (3.4) has a solution.
Since $M\neq \emptyset$![]() , $S$
, $S$![]() has a minimizing sequence $\{v_n\}$
has a minimizing sequence $\{v_n\}$![]() . In particular, $Q(v_n)=0$
. In particular, $Q(v_n)=0$![]() and $S(v_n)\rightarrow m$
and $S(v_n)\rightarrow m$![]() . Let $w_n=|v_n|^*$
. Let $w_n=|v_n|^*$![]() , and $u_n=\mathcal {P}(\lambda ^*(w_n),\,w_n)$
, and $u_n=\mathcal {P}(\lambda ^*(w_n),\,w_n)$![]() . It follows from lemma 3.1 (i) that $u_n\in M$
. It follows from lemma 3.1 (i) that $u_n\in M$![]() . Furthermore, it follows from lemma 3.1 (vii) that $u_n=|\mathcal {P}(\lambda ^*(w_n),\,v_n)|^*$
. Furthermore, it follows from lemma 3.1 (vii) that $u_n=|\mathcal {P}(\lambda ^*(w_n),\,v_n)|^*$![]() . Therefore,
. Therefore,
In particular, $\{u_n\}$![]() is a nonnegative, spherically symmetric, nonincreasing minimizing sequence of $S$
is a nonnegative, spherically symmetric, nonincreasing minimizing sequence of $S$![]() . Furthermore, note that as $n\rightarrow \infty$
. Furthermore, note that as $n\rightarrow \infty$![]()

which implies that $\{u_n\}$![]() is bounded in $H^1(\mathbb {R}^2)$
is bounded in $H^1(\mathbb {R}^2)$![]() . Since $Q(u_n)=0$
. Since $Q(u_n)=0$![]() , then
, then
Therefore, by the Gagliardo–Nirenberg inequality and the boundedness of $\{u_n\}$![]() in $L^2(\mathbb {R}^2)$
in $L^2(\mathbb {R}^2)$![]() , there exists a constant $C>0$
, there exists a constant $C>0$![]() such that
such that

We obtain that $|\nabla u_n|_{L^2}$![]() is bounded from below, and so it follows from (3.5) that
is bounded from below, and so it follows from (3.5) that
Therefore, there exist $v\in H^1(\mathbb {R}^2)$![]() and a subsequence, which we still denoted by $\{u_n\}$
and a subsequence, which we still denoted by $\{u_n\}$![]() , such that $u_n\rightharpoonup v$
, such that $u_n\rightharpoonup v$![]() in $H^1(\mathbb {R}^2)$
in $H^1(\mathbb {R}^2)$![]() weakly and in $L^{p}(\mathbb {R}^2)$
weakly and in $L^{p}(\mathbb {R}^2)$![]() strongly ($v\neq 0$
strongly ($v\neq 0$![]() , by (3.6)). Therefore, we may define $\zeta =\mathcal {P}(\lambda ^*(v),\,v)=\lambda ^*(v)v(\lambda ^*(v)x)$
, by (3.6)). Therefore, we may define $\zeta =\mathcal {P}(\lambda ^*(v),\,v)=\lambda ^*(v)v(\lambda ^*(v)x)$![]() . By lemma 3.1 (i), it follows directly that $\zeta \in M$
. By lemma 3.1 (i), it follows directly that $\zeta \in M$![]() , and hence
, and hence
On the other hand, according to lemma 3.1 (viii), we know that $\mathcal {P}(\lambda ^*(v),\,u_n)\rightharpoonup \zeta$![]() in $H^1(\mathbb {R}^2)$
in $H^1(\mathbb {R}^2)$![]() weakly and in $L^{p}(\mathbb {R}^2)$
weakly and in $L^{p}(\mathbb {R}^2)$![]() strongly. Therefore,
strongly. Therefore,

Consequently, we obtain $S(\zeta )=m$![]() . Thus, $\zeta$
. Thus, $\zeta$![]() is the solution of (3.4).
is the solution of (3.4).
Step 2. We claim that every solution of (3.4) satisfies equation (1.1).
Consider any solution $u$![]() of (3.4). We have
of (3.4). We have
Then $\langle S'(u),\,u\rangle _{H^{-1},\,H^1}=0$![]() , where $S'$
, where $S'$![]() is the gradient of the $C^1$
is the gradient of the $C^1$![]() functional $S$
functional $S$![]() , i.e.,
, i.e.,
Notice that
It follows from $u\in M$![]() that
that

Finally, since $u$![]() solves (3.4), there exists a Lagrange multiplier $\lambda$
solves (3.4), there exists a Lagrange multiplier $\lambda$![]() such that
such that
Thus,
Noting that $\langle Q'(u),\,u\rangle _{H^{-1},\,H^1}<0$![]() , we obtain $\lambda =0$
, we obtain $\lambda =0$![]() . Consequently, $S'(u)=0$
. Consequently, $S'(u)=0$![]() , which means that $u$
, which means that $u$![]() solves problem (1.1).
solves problem (1.1).
Step 3. Conclusion.
Consider
Let $u\in G$![]() be such that $S(u)=l$
be such that $S(u)=l$![]() . Now we claim that $u\in M$
. Now we claim that $u\in M$![]() . Indeed, since $u$
. Indeed, since $u$![]() is a solution of equation (1.1), we have $V(u)=0$
is a solution of equation (1.1), we have $V(u)=0$![]() and
and
Thus

Therefore, $u\in M$![]() , which implies that $S(u)\geq m$
, which implies that $S(u)\geq m$![]() . In particular
. In particular
Consider now a solution $v$![]() of (3.4). Since $S(v)=m$
of (3.4). Since $S(v)=m$![]() and $v\in A$
and $v\in A$![]() (by Step 2), it follows from (3.7) that $m\geq l$
(by Step 2), it follows from (3.7) that $m\geq l$![]() . Combining with (3.8), we obtain $m=l$
. Combining with (3.8), we obtain $m=l$![]() . The equivalence of the two problems follows easily. The proof is complete.
. The equivalence of the two problems follows easily. The proof is complete.
Acknowledgements
The authors would like to thank the anonymous referees and the editors for value comments.
The research of Chunyu Lei is supported by Science and Technology Foundation of Guizhou Province (No. ZK[2022]199), The Natural Science Research Project of Department of Education of Guizhou Province (Grant Nos. QJJ2022015,QJJ2023012,QJJ2023061,QJJ2023062) and the High-Level Innovative Talent Project of Guizhou Province (Grant no. QKHPTRC-GCC2023027). The research of Binlin Zhang was supported by National Natural Science Foundation of China (No. 1187 1199 and No. 12171152) and Cultivation Project of Young and Innovative Talents in Universities of Shandong Province.