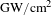1 Introduction
Laser pulses with high peak power have made significant breakthroughs in the fields of high-field physics[Reference Schwoerer, Pfotenhauer, Jäckel, Amthor, Liesfeld, Ziegler, Sauerbrey, Ledingham and Esirkepov1, Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer2], inertial confinement fusion (ICF)[Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington and Salmonson3], and particle beams[Reference Barberio, Sciscio, Vallieres, Cardelli, Chen, Famulari, Gangolf, Revet, Schiavi, Senzacqua and Antici4, Reference Vranic, Klimo, Korn and Weber5]. To successfully explore physical phenomena in extreme conditions, investigations of laser pulses have focused on achieving higher power and energy. Existing amplification methods have been developed to produce nanosecond-long pulse amplification, via master oscillator power amplification (MOPA) techniques, and femtosecond ultrashort pulse amplification, using chirped-pulse amplification (CPA) and optical parametric chirped-pulse amplification (OPCPA) techniques. Research on MOPA technology has motivated the development of large-aperture high-power laser systems, such as those of the National Ignition Facility (NIF)[Reference Miller, Moses and Wuest6, Reference Haynam, Wegner, Auerbach, Bowers, Dixit, Erbert, Heestand, Henesian, Hermann, Jancaitis, Manes, Marshall, Mehta, Menapace, Moses, Murray, Nostrand, Orth, Patterson, Sacks, Shaw, Spaeth, Sutton, Williams, Widmayer, White, Yang and Van Wonterghem7] at the Lawrence Livermore National Laboratory (LLNL) in the USA, Laser Megajoule[Reference Fleurot, Cavailler and Bourgade8, Reference Miquel, Lion and Vivini9] in France, and the SG-III laser facility[Reference Yu, Jing, Wei, Zheng, Zhang, Sui, Li, Hu, He and Peng10] in China. To date, using CPA[Reference Strickland and Mourou11] or OPCPA[Reference Piskarskas, Stabinis and Yankauskas12], femtosecond lasers with peak powers from hundreds of terawatts to petawatts have been achieved[Reference Bulanov, Miyanaga, Kiriyama, Shimomura, Sasao, Nakai, Tanoue, Kondo, Kanazawa, Pirozhkov, Mori, Fukuda, Nishiuchi, Kando, Bulanov, Nagashima, Yamagiwa, Kondo, Sugiyama, Bolton, Tajima and Miyanaga13–Reference Sistrunk, Spinka, Bayramian, Betts, Bopp, Buck, Charron, Cupal, Deri, Drouin, Erlandson, Fulkerson, Horner, Horacek, Jarboe, Kasl, Kim, Koh, Koubikova, Lanning, Maranville, Marshall, Mason, Menapace, Miller, Mazurek, Naylon, Novak, Peceli, Rosso, Schaffers, Smith, Stanley, Steele, Telford, Thoma, VanBlarcom, Weiss, Wegner, Rus and Haefner16].
Laser pulses with durations of several hundreds of picoseconds, much shorter than nanosecond pulses and much longer than femtosecond pulses, have attracted the attention of fewer researchers. Furthermore, amplifying pulses with widths of several hundreds of picoseconds to generate pulses of high energy and power is difficult, and suffers from the limitations of both MOPA and CPA approaches. For MOPA, because of the damage threshold fluence of the laser system, shorter pulses require larger-aperture components, and thus a larger scale of the entire system, which means the output laser intensity is limited. Moreover, the output intensity must be modulated to avoid exceeding the B integral limit, to avoid self-focusing damage and the loss of beam quality. It must also be noted that the laser energy extraction efficiency is very low for short pulses. CPA and OPCPA are limited by the Fourier spectral widths in 100-ps laser-pulse amplification. A 200-ps laser pulse can only be expanded to 280 ps by a
$1740~\text{mm}^{-1}$
grating at the Fourier transform limit. Meanwhile, the damage threshold of gratings limits their use to fluences below values of the order of
$100~\text{mJ}/\text{cm}^{2}$
[Reference Stuart, Feit, Rubenchik, Shore and Perry17].
Recently, 200-ps laser pulses have attracted interest in the field of ICF. Shock ignition[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov18–Reference Theobald, Nora, Seka, Lafon, Anderson, Hohenberger, Marshall, Michel, Solodov, Stoeckl, Edgell, Yaakobi, Casner, Reverdin, Ribeyre, Shvydky, Vallet, Peebles, Beg, Wei and Betti21] is an advanced concept for achieving ICF ignition that promises to provide four times greater neutron yield than conventional ignition[Reference Theobald, McCrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Betti, Frenje, Li, Séguin, Petrasso, Perkins, Stoeckl, Anderson, Delettrez, Glebov, Goncharov, Marshall and Maywar22]. Shock ignition proceeds via a two-step process in which the compression and the ignition parts are separated. Ignition requires 200-ps laser pulses of high intensity to launch a strong convergent shock[Reference Theobald, McCrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Betti, Frenje, Li, Séguin, Petrasso, Perkins, Stoeckl, Anderson, Delettrez, Glebov, Goncharov, Marshall and Maywar22, Reference Bates, Schmitt, Fyfe, Obenschain and Zalesak23]. Theoretical analysis shows that the required ignition energy is 425 kJ, of which 275 kJ is compression energy with a pulse width of 5 ns, and 150 kJ is shock energy with a pulse width of 170–230 ps. Raman amplification in warm plasma has the capacity to generate 200-ps laser-pulse amplification. However, the output pulse energy is on the order of millijoules[Reference Chiaramello, Amiranoff, Riconda and Weber24–Reference Yang, Vieux, Brunetti, Ersfeld, Farmer, Hur, Issac, Raj, Wiggins, Welsh, Yoffe and Jaroszynski26]. Few facilities have the ability to provide high-energy laser pulses of widths around 200 ps. According to the NIF[Reference Haynam, Wegner, Auerbach, Bowers, Dixit, Erbert, Heestand, Henesian, Hermann, Jancaitis, Manes, Marshall, Mehta, Menapace, Moses, Murray, Nostrand, Orth, Patterson, Sacks, Shaw, Spaeth, Sutton, Williams, Widmayer, White, Yang and Van Wonterghem7], their output 200-ps laser pulses can have energies of 100 kJ by direct amplification in a total of 192 beams. In order to achieve shock ignition, the beam size needs to be expanded by 50%.
In this study, we report a novel frequency-matching scheme for SBS (stimulated Brillouin scattering) amplification to achieve high-power 200-ps laser pulses in existing ICF laser drivers that already achieve higher energies for longer pulses. However, it is difficult to efficiently produce strong amplification for a 200-ps pulse. We have adopted a method to realize high energies for such pulses, transferring energy from nanosecond pulses to 200-ps pulses through Brillouin power amplification (BPA). In this process, the high energy of a long-pulse-width pump is transferred to the 200-ps Stokes pulse. Distinguishing it from traditional SBS amplification, BPA Stokes pulses are downshifted and modulated in the fiber front end of the laser driver, rather than generated from the noise.
Experiments have been carried out in an SG-III prototype system. Our results show that the method can overcome the temporal instabilities of the Stokes beam, provide high gain, and thus make it possible to obtain high-efficiency 200-ps laser-pulse amplification in a high-power solid-state laser system.
2 Methods
The pulse train is amplified first by MOPA, and subsequently the energy of the nanosecond pulse is transferred to 200-ps pulses by BPA. This technique has the potential to significantly reduce the size and cost of laser systems while effectively amplifying the laser pulse to the desired intensity. To ensure that requirements for precision of synchronization are met, the Stokes pulse in our SBS amplifier undergoes injection seeding. The 200-ps laser pulse is generated at the front end. As SBS produces a frequency shift in the scattered wave spectra, it is necessary for the seed laser to be downshifted so that coupling between the laser beams is realized. Thus, the acoustic wave is driven by the coherence of the Stokes and pump light. Previous reports presented phase detuning leading to gain reduction in Brillouin amplification[Reference Chen, Lu, Wang and He27]. Thus, the modulated frequency shift between the Stokes and pump light should obey its own acoustic frequency in the SBS medium. A schematic diagram of the experiment is shown in Figure 1(c).
The shaping of 200-ps and 5-ns square pulses is achieved by driving an amplitude (Mach–Zehnder) modulator controlled by an arbitrary waveform generator (AWG). These two pulses are separated into two fibers by a splitter (Figure 1(a)). The 200-ps laser pulse is modulated with a down-frequency shift (Figure 1(b)), which is generated using an acoustic optical modulator (AOM).
In the experiments, the Brillouin amplification system is based on a noncollinear structure[Reference Wang, Lu, Wang, Zheng, He and Lin28], because collinear arrangements introduce complexity to optical systems due to the need for polarizers and wave plates for beam separation or coupling. Collinear structures are optimal for amplification of the Stokes seed with low power and small size, for maximum gain, under the condition that the pump propagates in the opposite direction to the Stokes seed. However, such an arrangement is not applicable for large-sized high-power lasers. Many optical polarization components are necessary to separate and couple the beams (pump, Stokes seed, nondepleted pump, amplified Stokes), resulting in a high degree of complexity. The requirements of high damage threshold and efficient isolation for large polarizers and wave plates are difficult to achieve technically. A noncollinear Brillouin amplifier is therefore a promising candidate for high-energy SBS amplification applications, owing to its simple structure[Reference Yuan, Wang, Lu and Zheng29].
The noncollinear structure not only affects the frequency shift between the Stokes and pump beams, but also has an effect on the interaction volume of the two beams, which plays a more important role in energy extraction. Thus, we designed our noncollinear Brillouin amplification experiment with a
$4^{\circ }$
crossing angle, minimizing the interaction volume effects with the small crossing angle. One of the problems of noncollinear amplification is the decrease of the Brillouin gain coefficient, which can be solved by frequency-shift modulation. Another problem is the decrease of the interaction region between the Stokes beam and the pump beam. This can be controlled, as already mentioned, by optimization of the crossing angle.
Figure 1. Experimental setup. (a) The 200-ps Stokes pulse and 5-ns pump pulse are generated at the front end. (b) The Stokes pulse is frequency-shifted by an amount determined by the chosen SBS medium. (c) Block diagram of the experimental setup. (d) Energy is transferred from the pump pulse to the Stokes pulse in an SBS cell.
The laser beam is narrowed by a factor of
$1/3$
by two lenses to increase its intensity. Then, it passes through two color-separation mirrors to isolate the 1053-nm laser. Before and after SBS amplification, the energy, near-field and waveform of the laser are sampled via measurements using a wedge plate. The cell used in this experiment is 600 mm in length with a cross-section of
$100~\text{mm}\times 80$
mm. The length of the cell is calculated according to
$L=c\unicode[STIX]{x1D70F}_{\text{pump}}/2n$
, where
$L$
is the length of the cell,
$c$
is the speed of light in vacuum,
$\unicode[STIX]{x1D70F}_{\text{pump}}$
is the pulse width of the pump, and
$n$
is the refractive index of the SBS medium. After passing through the cell, the laser re-enters it via reflection from two mirrors, so that the 200-ps pulse can extract energy from the 5-ns pulse. The crossing angle between the Stokes and pump light is
$4^{\circ }$
(
$\unicode[STIX]{x1D703}=4^{\circ }$
), and the spot size is
$50~\text{mm}\times 50$
mm. The SBS energy transformation is shown in Figure 1(d); the acoustic field is produced by Stokes and pump beams that have been modulation frequency-shifted. Then energy is transferred from the pump pulse to the Stokes pulse through the acoustic field.
The medium selected for SBS amplification in this experiment is FC-43, a hydrocarbon fluid with stoichiometric formula
$(\text{C}_{3}\text{F}_{7})_{3}\text{N}$
. Its refractive index is 1.29. Considering the medium and the crossing angle between the Stokes and pump light, the frequency shift between them is 3.1 GHz at 527 nm, with a gain coefficient of
$1.3~\text{cm}/\text{GW}$
and a phonon lifetime of 0.2 ns. Thus, the frequency shift modulated at the front end should be 1.55 GHz at 1053 nm.
Frequency-mismatch conditions will result in a decrease in the gain. In this case, the frequency of the acoustic wave changes. The Brillouin gain decreases by half when the frequency shift is inaccurate by 500 MHz, and the accuracy of the frequency shift of the Stokes pulse requires strict modulation. According to the theoretical modulation, the accuracy of the frequency shift should be controlled to within 100 MHz.
In our case, the pump and Stokes pulses are coupled with pulse stacking, so the frequency shift between the Stokes and pump light should be modulated carefully. The Stokes pulse is a 200-ps Gaussian pulse and the pump pulse is a 5-ns eighth-order super-Gaussian pulse. The measured frequency shift is 1.55 GHz, which is suitable for amplification experiments.
The pre-shaped pulse should be considered carefully to compensate the spatial and temporal distortion caused by the amplification and transmission in the laser system. For convenient experimental analysis, as well as to reduce the risk of damaging the optical elements, the power for the 200-ps pulse is set to the same value as that of the 5-ns pulse.
Figure 2. Experimental results. (a) Output Stokes intensity varies with the input intensity; input Stokes and pump intensities are the same. (b) Probability distribution of the output pulse width when the output Stokes pulse widths are in the range 150–200 ps. (c) Temporal intensities of the Stokes and pump pulses for input pump intensity of
$150~\text{MW}/\text{cm}^{2}$
. The output Stokes pulse width is 165 ps. The pump is not exhausted. (d) Temporal intensities of SBS amplification results for an input pump intensity of
$398~\text{MW}/\text{cm}^{2}$
. The output Stokes pulse width is 170 ps. Energy is efficiently transferred from the pump pulse to the Stokes pulse.
In the experiments reported here, the waveform was measured by photodiodes (Ultrafast UPD-50-UP) and displayed on an oscilloscope (Tektronix DPO71604B). The energy was measured by an energy meter (Ophir PE100BF-DIF ROHS). As the Stokes and pump pulses are coupled by pulse stacking, the measured energy is the sum of the Stokes and the pump pulses. In order to obtain the exact energy of the Stokes and pump pulses in Brillouin amplification, we need to record the integrated area of the pulse. According to this, the Stokes or the pump energy can be calculated.
3 Experimental results
In order to improve the energy extraction efficiency, the position at which the pump encounters the Stokes seed needs to be strictly controlled. By modulating the delay time between the 200-ps and 5-ns pulses and regulating the re-entering optical path length, this position should be controlled at the entrance of the cell. Under this circumstance, as soon as the Stokes light enters into the cell, it can be amplified by the pump light.
The output Stokes intensity and waveform are plotted in Figure 2 as a function of pump intensity, which was varied from
$100~\text{MW}/\text{cm}^{2}$
to
$450~\text{MW}/\text{cm}^{2}$
. With higher input pump intensity, the output Stokes intensity rises continuously, reaching values as high as
$7~\text{GW}/\text{cm}^{2}$
. However, when the input pump intensity is higher than
$450~\text{MW}/\text{cm}^{2}$
(Figure 2(a)), the output Stokes intensity rises very little. Under these circumstances, there are significant energy losses after the SBS interaction. This is because, at high Stokes intensity, stimulated Raman scattering (SRS) and nonlinear absorption will occur in this type of medium, limiting the output intensity of the Stokes light.
According to our measurements, pulse compression occurs in SBS amplification (Figure 2(b)). Compared to the input 200-ps Stokes pulse, the output Stokes pulse width mainly lies in the range 170–180 ps. This pulse compression occurs during amplification mainly because the early part of the Stokes pulse gets amplified earlier and extracts more energy, causing the pulse front to steepen, resulting in pulse compression.
The temporal structure of the pulse for an input pump intensity of
$150~\text{MW}/\text{cm}^{2}$
is shown in Figure 2(c). At this low pump intensity, the pump is not exhausted. Some energy remains in the pump after amplification. When the pump intensity was increased to
$320~\text{MW}/\text{cm}^{2}$
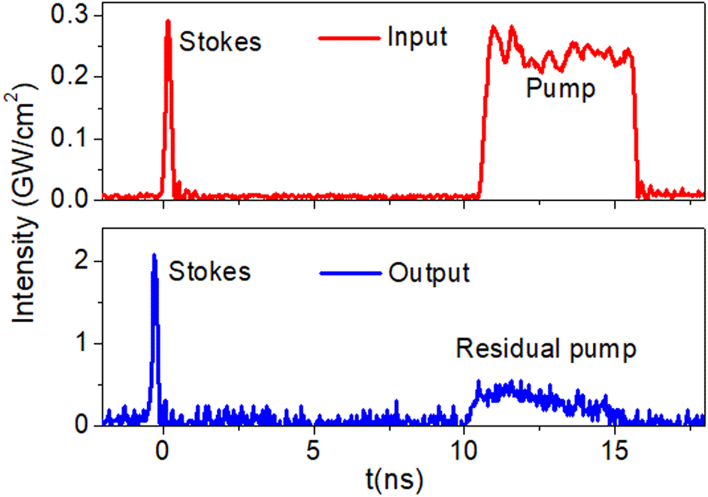
(Figure 2(d)), the pump was exhausted so that after amplification, no pump residual was detected. This indicates that almost all the pump energy was converted to the short Stokes pulse at high pump intensity, demonstrating that energy is transferred from the nanosecond pulse to the 100-ps pulse through the SBS interaction with a high conversion efficiency.
Our work demonstrated the feasibility of this novel frequency-matching stimulated Brillouin scattering to achieve high-intensity 200-ps laser pulses in a large-scale solid-state laser system. In our experiments, via the active frequency-matching method, the acoustic wave is locked in the SBS interaction. In this way, energy can be effectively transferred from the pump pulse to the Stokes pulse.
4 Discussion
4.1 Theoretical analysis and nonlinear absorption
Our method depends on energy transmission between the pump light and the Stokes light through an acoustic field. Compared to direct MOPA in Nd:glass, this method has a higher extraction rate of the stored energy in the amplifier. However, if the 200-ps laser pulse is directly amplified in Nd:glass, small-scale self-focusing must be taken into consideration as the output intensity is limited by the B integral. For this SBS energy transmission method, because the medium used is liquid, if the chemical bonds in the medium remain stable, the entire system can be restored.
However, this experiment also exposes some technical problems. As the pump intensity varies from
$150~\text{MW}/\text{cm}^{2}$
to
$250~\text{MW}/\text{cm}^{2}$
, the energy extraction efficiency of the Stokes pulse is relatively stable. The output Stokes intensity increases steadily with the pump intensity. However, with an increase of the pump intensity up to
$300~\text{MW}/\text{cm}^{2}$
, the energy extraction efficiency has a downward trend, which restricts a further increase of the output intensity. There are significant energy losses after the SBS interaction. These energy losses make it difficult to achieve higher intensities. In an analysis of the lost energy, we transmit a
$320~\text{MW}/\text{cm}^{2}$
pump pulse in the medium without seed injection. No energy loss was observed. At this pump intensity, the Stokes intensity gets amplified by more than 15 times, and the pump pulse is exhausted. Considering that the nonlinear absorption is proportional to the square of the light intensity, we propose that the energy loss comes from nonlinear absorption of the amplified Stokes pulse.
The equations describing the pump and Stokes optical fields are derived from Maxwell’s equations. Moreover, the acoustic field in the medium is due to the Navier–Stokes equation. The slowly varying approximation is applied in solving the equations. As the bandwidth of the acoustic field is similar to its frequency, the second-order term in the acoustic field equation cannot be ignored. Thus, the wave equations can be described as[Reference Boyd30]
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}t}=\frac{i\unicode[STIX]{x1D714}_{\text{L}}\unicode[STIX]{x1D6FE}}{2nc\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70C}E_{\text{S}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}t}=\frac{i\unicode[STIX]{x1D714}_{\text{S}}\unicode[STIX]{x1D6FE}}{2nc\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70C}^{\ast }E_{\text{L}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t^{2}}-(2i\unicode[STIX]{x1D714}-\unicode[STIX]{x1D6E4}_{\text{B}})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}-(i\unicode[STIX]{x1D714}\unicode[STIX]{x1D6E4}_{\text{B}})\unicode[STIX]{x1D70C}=\frac{\unicode[STIX]{x1D6FE}}{4\unicode[STIX]{x03C0}}q_{\text{B}}^{2}E_{\text{L}}E_{\text{S}}^{\ast }. & \displaystyle\end{eqnarray}$$
$E_{\text{L}}$
and
$E_{\text{S}}$
are the amplitudes of pumping light and Stokes light, respectively,
$\unicode[STIX]{x1D70C}$
is the density amplitude in the medium,
$n$
is the refractive index of the medium,
$c$
is the speed of light,
$\unicode[STIX]{x1D6FE}$
is the electrostrictive coefficient, and
$\unicode[STIX]{x1D6E4}_{\text{B}}$
is the Brillouin line width.
Equation (3) can be solved by Fourier transformation; thus, the wave equations can be expressed as[Reference Velchev, Neshev, Hogervorst and Ubachs31]
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(z,t) & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}q_{\text{B}}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FA}_{\text{B}}}\frac{1}{\sqrt{2\unicode[STIX]{x03C0}}}\int _{-\infty }^{t}f(t-\unicode[STIX]{x1D70F})E_{\text{L}}(z,\unicode[STIX]{x1D70F})E_{\text{S}}^{\ast }(z,\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f(t) & = & \displaystyle \frac{-\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6FA}_{\text{B}}\exp [-(\unicode[STIX]{x1D6E4}_{\text{B}}/2)t]}{\sqrt{\unicode[STIX]{x1D6FA}_{\text{B}}-\frac{\unicode[STIX]{x1D6E4}_{\text{B}}^{2}}{4}t}}\exp (i\unicode[STIX]{x1D6FA}_{\text{B}}t)\nonumber\\ \displaystyle & & \displaystyle \times \,\sin \left(\sqrt{\unicode[STIX]{x1D6FA}_{\text{B}}-\frac{\unicode[STIX]{x1D6E4}_{\text{B}}^{2}}{4}}t\right),\quad t\geqslant 0.\end{eqnarray}$$
From above, the coupled wave equation can be expressed as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}t}=-ig\unicode[STIX]{x1D710}E_{\text{S}},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}t}=-ig\unicode[STIX]{x1D710}^{\ast }E_{\text{L}},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D710}(z,t)=\frac{1}{\sqrt{2\unicode[STIX]{x03C0}}}\int _{-\infty }^{t}f(t-\unicode[STIX]{x1D70F})E_{\text{L}}(z,\unicode[STIX]{x1D70F})E_{\text{S}}^{\ast }(z,\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}.\quad & \displaystyle\end{eqnarray}$$
Here,
$g=\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}/2nc^{3}\unicode[STIX]{x1D710}\unicode[STIX]{x1D70C}_{0}$
is the gain coefficient,
$\unicode[STIX]{x1D70F}_{\text{B}}=1/\unicode[STIX]{x1D6E4}_{\text{B}}$
is the phonon lifetime,
$\unicode[STIX]{x1D6FA}_{\text{B}}$
is the Brillouin shift,
$t$
represents the time axis, and
$z$
is the pump propagation coordinates. The Stokes signal is generated from spontaneous noise in the medium. Under the influence of the acoustic field, energy transfers from the pump to the oppositely-propagating Stokes signal.
Considering both linear absorption and nonlinear absorption in the medium, the equations can be expressed as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{L}}}{\unicode[STIX]{x2202}t}=-ig\unicode[STIX]{x1D710}E_{\text{S}}-\frac{\unicode[STIX]{x1D6FC}}{2}E_{\text{L}}-\frac{\unicode[STIX]{x1D6FD}}{4}E_{\text{L}}^{2},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}z}+\frac{n}{c}\frac{\unicode[STIX]{x2202}E_{\text{S}}}{\unicode[STIX]{x2202}t}=-ig\unicode[STIX]{x1D710}^{\ast }E_{\text{L}}-\frac{\unicode[STIX]{x1D6FC}}{2}E_{\text{S}}-\frac{\unicode[STIX]{x1D6FD}}{4}E_{\text{S}}^{2},\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D710}(z,t)=\frac{1}{\sqrt{2\unicode[STIX]{x03C0}}}\int _{-\infty }^{t}f(t-\unicode[STIX]{x1D70F})E_{\text{L}}(z,\unicode[STIX]{x1D70F})E_{\text{S}}^{\ast }(z,\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}.\quad & \displaystyle\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D6FC}$
represents the linear absorption coefficient and
$\unicode[STIX]{x1D6FD}$
represents the nonlinear absorption coefficient.
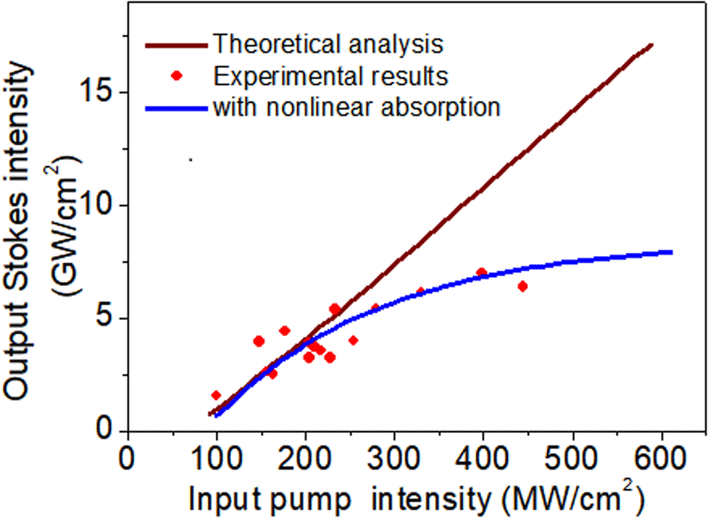
Figure 3. Theoretical analysis of Brillouin amplification within nonlinear absorption: comparison between Brillouin amplification with and without considering nonlinear absorption.
Compared to the theoretical simulation results shown in Figure 3 (the brown line), by introducing a nonlinear absorption coefficient of
$0.01~\text{cm}/\text{GW}$
(measured by a high-power mode-locking laser system) in the Brillouin amplification process, the experimental results fit the theoretical simulation at low intensity. But as the injected pump intensity increases, the agreement between experiment and theory is lost. Because the nonlinear absorption is proportional to the square of the laser intensity, at low pump intensity, the output Stokes intensity is low and the nonlinear absorption effect is weak. With an increase in the Stokes intensity, nonlinear absorption increases, resulting in greater energy loss. Thus, the output Stokes intensity cannot be further improved.
Simulation results obtained by introducing nonlinear absorption into the theoretical analysis are shown in Figure 3. This result fits well with the experimental data points. Consequently, we observe that nonlinear absorption prevents Brillouin amplification from achieving higher Stokes intensities. In the future, we will use another type of SBS medium with lower nonlinear absorption.
4.2 Phase-modulated light SBS amplification
In high-power solid-state laser systems, to avoid SBS optical damage in large components, the spectrum is always modulated into a small bandwidth by phase modulation. For high modulation frequencies,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}\gg \unicode[STIX]{x1D6E4}_{\text{B}}$
, the Stokes spectrum modes resulting from the phase modulation are separated and act independently. The SBS threshold is determined by the sideband with the highest spectral power. To that end, the SBS threshold enhancement factor as compared to an unmodulated wave is given by[Reference Zeringue, Dajani, Naderi, Moore and Robin32]
$$\begin{eqnarray}\displaystyle \frac{P_{\text{th}}}{P_{0}}=\frac{1}{\max [J_{n}^{2}(\unicode[STIX]{x1D6FE})]}, & & \displaystyle\end{eqnarray}$$
where
$P_{\text{th}}$
is the SBS modulated threshold,
$P_{0}$
is the SBS threshold for the case of an unmodulated field, and
$J_{n}(\unicode[STIX]{x1D6FE})$
is the Bessel function of the first kind corresponding to the sideband with the maximum value.
When considering a phase-modulated laser in SBS amplification, the pulse should be modulated with a large frequency shift to ensure that each spectral line acts independently. Thus, the spectral line of the Stokes seed light should be frequency matched to that of the pump light, so SBS amplification can be used for phase-modulated lasers. This has been experimentally tested on a laser system[Reference Li, Wang, Lu, Ding, Du, Chen, Zheng, Ba, Dong, Yuan, Bai, Liu and Cui33].
Figure 4. Phase-modulated pump spectrum.
The experimental pump spectrum is shown in Figure 4.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}$
is 14.25 GHz (0.13 nm), which is much wider than the Brillouin gain bandwidth. After frequency-shift modulation, the Stokes seed will match its spectral lines independently.
Figure 5. Temporal intensities of the Stokes and pump pulses of the phase-modulated laser.
The temporal structures of the pulse for an input pump intensity of
$303~\text{MW}/\text{cm}^{2}$
are shown in Figure 5. Compared with the experimental results of the single longitudinal mode shown in Figure 2(d), phase modulation results in a decrease in Brillouin gain due to spectral separation. The power amplification is lower than that of the unmodulated case. Some energy remained in the pump after amplification. For the experimental results of this shot, the amplified output of the Stokes pulse has an intensity of
$2170~\text{MW}/\text{cm}^{2}$
and a power amplification of 7.3 times. Therefore, Brillouin amplification can still be achieved for phase-modulated laser pulses with high modulation frequencies.
4.3 Noncollinear SBS amplification with large beams
For noncollinear SBS amplification, the interaction volume between the Stokes and the pump light decreases with an increase in the crossing angle. Generally, we would calculate the interaction length in noncollinear SBS amplification[Reference Wang, Lü, Lin, Ding and Jiang34]. Taking a square beam as an example, assume that the Stokes and pump beams have the same diameter
$d$
. The equivalent interaction length in the noncollinear SBS process is denoted as
$l_{\text{eff}}$
, and is expressed as
$$\begin{eqnarray}\displaystyle l_{\text{eff}}=\left\{\begin{array}{@{}ll@{}}\frac{d}{2\sin \big(\frac{\unicode[STIX]{x1D703}}{2}\big)}, & l_{m}\leqslant l,\\ \frac{d-d\Big[1-\frac{l\sin \big(\frac{\unicode[STIX]{x1D703}}{2}\big)}{d}\Big]^{2}}{2\sin \big(\frac{\unicode[STIX]{x1D703}}{2}\big)}, & l_{m}>l,\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
$l$
is the cell length and
$l_{m}$
is the length of the intersection between the Stokes and the pump beams.
The variation of the equivalent interaction length with crossing angle can be calculated. For an 8th-order super-Gaussian pulse with a
$20~\text{mm}\times 20$
mm beam size, the calculated results are shown in Figure 6(a). For a noncollinear SBS interaction with a small beam size, the equivalent interaction length decreases rapidly with increasing crossing angle. We compared this with the case when we expand the beam diameter to
$370~\text{mm}\times 370$
mm (shown in Figure 6(b)). Due to the large beam size, the decrease of the interaction length caused by noncollinearity is clearly slowed down. This means that when Brillouin amplification is applied with a large beam, it is possible to increase the crossing angle to save optical path space.
Figure 6. (a) Variation of the interaction length with the crossing angle at
$20~\text{mm}\times 20$
mm. (b) Variation of the interaction length with the crossing angle at
$370~\text{mm}\times 370$
mm.
In shock ignition, it is necessary to use a three-step pulse that can first achieve compression and then a shock pulse to achieve ignition. SBS technology does not have the capability of arbitrary waveform modulation. Therefore, the spatial domain composite technique can be used to separate the compression pulse from the ignition pulse, amplified in a different path, and coupled at the target for ignition.
5 Conclusions
In summary, we have described an amplification method and demonstrated its ability to obtain 7-
$\text{GW}/\text{cm}^{2}$
200-ps laser pulses. We showed experimentally that significant energy can be transferred from long 5-ns pulses to short 200-ps pulses by accurate frequency modulation. By modulating stacked pulses and frequency shifting at the front end, this technology can be applied directly to ICF drivers while adding the SBS amplifier before target. Moreover, this SBS amplification can be applied to phase-modulated lasers. In light of these experimental results, it is suggested that if the beam size was expanded to
$370~\text{mm}\times 370$
mm at the same intensity, sub-nanosecond laser pulses with energies greater than 1340 J should be obtained. In future research, we will attempt to find a more suitable medium for high-power high-energy SBS amplification, which would optimize the present amplification scheme.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (NSFC) (No. 61622501) and the China Postdoctoral Science Foundation (No. BX20180085). We also thank the operation group of the SG-III prototype system for their help with the experiments.
Open access
