2. Governing equations

By introducing the concept of radiation stress to represent the phase-averaged residual momentum flux due to the presence of waves, Reference Longuet-Higgins and StewartLHS62 proposed the theory of low-frequency subharmonic induced by the nonlinear group forcing of radiation stress. For regular waves under non-breaking conditions, the radiation stress $S$ accurate to second order in wave steepness is expressed as (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1960)

(2.1)\begin{equation} S=E\left( \frac{2{{c}_{g}}}{c}-\frac{1}{2} \right), \end{equation}

where $E$ denotes the wave energy, $c_g$ is the wave group velocity and $c$ is the wave phase speed.

Consider a unidirectional bichromatic wave group propagating in the positive direction of $x$ with the surface elevation

(2.2) \begin{equation} \eta \left( x,t \right)=\tfrac{1}{2}A\left( x,t \right)\ {\rm e}^{\text{i}\left(\int^{x}k\,\text{d}\kern0.7pt{x}'-\omega t \right)}+\text{c.c.}, \end{equation}

where

(2.3) \begin{align} A\left( x,t \right)={{A}_{1}}\left( x \right)\ {\rm e}^{\frac{\text{i}}{2}\left(\int^{x}{{k}_{g}}\,\text{d}\kern0.7pt{x}'-{{\omega }_{g}}t \right)}+{{A}_{2}}\left( x \right)\ {\rm e}^{-\frac{\text{i}}{2}\left(\int^{x}{{k}_{g}}\,\text{d}\kern0.7pt{x}'-{{\omega }_{g}}t \right)}, \end{align}

$A_1$ and $A_2$ are the real amplitudes of the two wave components; $A( x,t )$ is the slowly varying modulated complex amplitude; $k$ and $\omega$ are the wavenumber and radian frequency of the short wave; $k_g$ and $\omega _g$ are the wavenumber and radian frequency of the wave group; and c.c. denotes the complex conjugate and will be omitted hereinafter. Assuming that the two wave frequencies are close to each other, substituting (2.3) into the equation of wave energy

(2.4)\begin{equation} E(x,t)=\tfrac{1}{2}\rho g\left| A(x,t) \right|^2, \end{equation}

where $g$ is the gravitational acceleration and $\rho$ is the water density, gives

(2.5)\begin{equation} E(x,t)=\tfrac{1}{2}\rho g\left[A_1^2(x) + A_2^2(x) + 2A_1(x)A_2(x) \cos \left(\int^{x}{{k}_{g}}\,\mathrm{d}\,{x}'-{{\omega }_{g}}t\right)\right]. \end{equation}

Equation (2.5) can be decomposed into a steady component and an unsteady oscillatory component. With the $\cos$ function expressed in complex form, the oscillatory wave energy is given by

(2.6)\begin{equation} \tilde{E}\left( x,t \right)=\tfrac{1}{2}\rho g{{A}_{1}}\left( x \right){{A}_{2}}\left( x \right){\exp\left({\text{i}\left( \int^{x}{{{k}_{g}}\,\mathrm{d}\,{x}'-{{\omega }_{g}}t} \right)}\right)}. \end{equation}

Assuming negligible breaking and bottom-friction-induced dissipation which may have a significant effect on wave radiation stress (Zou, Bowen & Hay Reference Zou, Bowen and Hay2006), the evolution of wave energy is governed by (see (2.6) in Mei & Benmoussa (Reference Mei and Benmoussa1984) and (2.4a) in Zou (Reference Zou2011))

(2.7)\begin{equation} \frac{\partial }{\partial t}E + \frac{\partial }{\partial x}\left(c_g E\right) = 0, \end{equation}

and substituting (2.5) into (2.7), we have

(2.8a,b) \begin{equation} A_1^2 + A_2^2 = \frac{[(A_1^2 + A_2^2)c_g]_0}{c_g}, \quad A_1A_2 = \frac{(A_1A_2c_g)_0}{c_g}, \end{equation}

where the subscript 0 denotes quantities at the incoming boundary of waves.

Substituting (2.6) into to (2.1) yields the oscillating component of the radiation stress:

(2.9)\begin{equation} \tilde{S}\left(x,t \right) = \tfrac{1}{2}\hat{S}\left( x \right){\rm e}^{-\text{i}{{\omega }_{g}}t}, \end{equation}

where

(2.10)\begin{equation} \hat{S}\left( x \right) = \rho g{{A}_{1}}{{A}_{2}}\left( \frac{2{{c}_{g}}}{c}-\frac{1}{2} \right){\exp\left({\text{i}\int^{x}{{{k}_{g}}\,{\rm d}\,{x}'}}\right)} = \left|\hat{S}\left( x \right)\right|{\exp\left({\text{i}\int^{x}{{{k}_{g}}\,{\rm d}\,{x}'}}\right)}. \end{equation}

Substituting (2.8b) into (2.10), we obtain

(2.11)\begin{equation} \left|\hat{S}\left( x \right)\right| = \rho g \left(A_1A_2c_g\right)_0 \left(\frac{2}{c} - \frac{1}{2c_g}\right). \end{equation}

Following Reference Longuet-Higgins and StewartLHS62 (equations (3.33) and (3.34) therein), the 1-D linearised mass and momentum conservation equations for the subharmonic under the forcing of radiation stress are

(2.12)\begin{gather} \rho \frac{\partial \tilde{\xi }}{\partial t}+\frac{\partial \tilde{M}}{\partial x}=0, \end{gather}

(2.13)\begin{gather} \frac{\partial \tilde{M}}{\partial t}+\rho gh\frac{\partial \tilde{\xi }}{\partial x}={-}\frac{\partial \tilde{S}}{\partial x}, \end{gather}

where $\tilde {\xi }(x,t )$ and $\tilde {M}( x,t )$ are the surface elevation and mass flux of the subharmonic, respectively, and $h$ is the still water depth (see figure 1 for the definition of variables). Equations (2.12) and (2.13) are equivalent to the linearised equations (2.1) and (2.2) in Schäffer (Reference Schäffer1993). Eliminating $\tilde {M}$ in (2.12)–(2.13) yields

(2.14)\begin{equation} \frac{{{\partial }^{2}}\tilde{\xi }}{\partial {{t}^{2}}}-g\frac{\partial }{\partial x}\left( h\frac{\partial \tilde{\xi }}{\partial x} \right)=\frac{1}{\rho }\frac{{{\partial }^{2}}\tilde{S}}{\partial {{x}^{2}}}. \end{equation}

Equation (2.14) is the governing equation of the surface elevation of group-induced subharmonics for 1-D wave groups propagating over a depth small compared with the wave group length (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962). For non-breaking waves outside the surf zone, (2.9)–(2.11) are adopted, and (2.14) is consistent with the governing equation (2.11) in Mei & Benmoussa (Reference Mei and Benmoussa1984), equation (7) in Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and equation (2.7) in Zou (Reference Zou2011). For breaking waves in the surf zone, Symonds et al. (Reference Symonds, Huntley and Bowen1982) and Schäffer (Reference Schäffer1993) adopted the saturated breaking model assuming the wave height is proportional to local depth to model the forcing term and then solved equation (2.14), but no satisfactory verification against experiment has been reported. Using numerically modelled flow field to calculate the radiation stress, Rijnsdorp, Smit & Guza (Reference Rijnsdorp, Smit and Guza2022) showed that the linearised equation (2.14) remains adequate in the outer surf zone. Furthermore, Rijnsdorp et al. (Reference Rijnsdorp, Smit and Guza2022) demonstrated that the nonlinearity of infragravity wave itself starts to become important only in the inner surf zone over a mildly sloping beach of bottom slope 1/100. Liu et al. (Reference Liu, Yao, Liao, Li, Zhang and Zou2023) showed that fully nonlinear analysis of the infragravity wave energy budget is required for reef topography where the depth sharply reduces when offshore waves propagate over the foreslope into the reef flat.

Figure 1. Definition sketch of variables for wave groups propagating over variable bottom.

The group-induced subharmonic surface elevation $\tilde {\xi }( x,t )$ oscillates in time with the same frequency $\omega _g$ as the wave radiation stress $\tilde {S}$ in (2.9), i.e.

(2.15)\begin{equation} \tilde{\xi }\left( x,t \right)=\tfrac{1}{2}\hat{\xi }\left( x \right){{{\rm e}}^{-\mathrm{i}{{\omega }_{g}}t}}, \end{equation}

where $\hat {\xi }$ is the complex amplitude of $\tilde {\xi }( x,t )$. Substituting (2.9) and (2.15) into (2.14), we obtain the governing equation for the subharmonic complex amplitude $\hat {\xi }(x)$:

(2.16)\begin{equation} \frac{1}{h}\frac{\rm d}{{\rm d}\,x}\left( h\frac{{\rm d}\hat{\xi }}{{\rm d}\,x} \right)+k_{f}^{2}\hat{\xi }={-}\frac{1}{\rho gh}\frac{{{\rm d}^{2}}\hat{S}}{{\rm d}\,{{x}^{2}}}, \end{equation}

where $k_f=\omega _g / \sqrt {gh}$ is the wavenumber of free subharmonics propagating at the speed of shallow-water wave. Equation (2.16) is consistent with the governing equation (4.9) in Schäffer (Reference Schäffer1993), equation (10) in Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and equation (3.4) in Zou (Reference Zou2011). A novel unified solution to (2.16) is developed based on Green's function in the present study.

3. Unified solution based on Green's function

3.1. General form of solution

The Green's function $G(x,y)$ of a 1-D linear differential equation describes the response at $x$ to a unit forcing at $y$, where $x$ and $y$ denote two spatial coordinates in 1-D space. Assuming a continuously varying water depth $h(x)$, the governing equation (2.16) becomes a Sturm–Liouville type equation. The corresponding Green's function satisfies (see equations (3.3.6), (3.3.9) and (3.3.10) in Duffy Reference Duffy2015) the following equations:

(3.1a)$$\begin{gather} \frac{1}{h}\frac{{\rm d}}{{\rm d}\,x}\left[ h\frac{\rm d}{{\rm d}\,x}G\left( x,y \right) \right]+k_{f}^{2}G\left( x,y \right)={{\delta }_{{Dirac}}}\left( x-y \right), \end{gather}$$

(3.1b)$$\begin{gather}\underset{x\to {{y}^{-}}}{\lim}\,G\left( x,y \right)=\underset{x\to {{y}^{+}}}{\lim}\,G\left( x,y \right), \end{gather}$$

(3.1c)$$\begin{gather}\underset{x\to {{y}^{+}}}{\lim}\,\frac{\partial G\left( x,y \right)}{\partial x}-\underset{x\to {{y}^{-}}}{\lim}\,\frac{\partial G\left( x,y \right)}{\partial x}=1, \end{gather}$$

where $\delta _{Dirac}(x-y )$ is the Dirac Delta function that physically describes the unit point forcing oscillating at the wave group frequency at $x'=x-y=0$ and satisfies $\delta _{Dirac}(x') = 0$ for $x'\neq 0$ and $\int _{-\infty }^{+\infty }\delta _{Dirac}(x')\,\mathrm {d}\,x'=1$. An example of $G(x,y)$ over a flat bottom is later shown in figure 3.

Let $\hat {f}(x )$ be the complex amplitude of the forcing term of (2.16), i.e.

(3.2)\begin{equation} \hat{f}\left( x \right)={-}\frac{1}{\rho gh}\frac{{{\rm d}^{2}}\hat{S}}{{\rm d}\,{{x}^{2}}}. \end{equation}

For any given response position $x$, we can always find a subdomain $a < x < b$ where the equality

(3.3)\begin{equation} \hat{f}\left( x \right)=\int_{a}^{b}{\hat{f}\left(\kern0.7pt y \right){{\delta }_{{Dirac}}}\left( x-y \right)\,\mathrm{d} y} \end{equation}

is valid.

Applying the multiplication and then integration on the right-hand side of (3.3) to both sides of (3.1a) and comparing with the governing equation of subharmonic complex amplitude (2.16), the inhomogeneous solution $\hat \xi _g(x)$ to (2.16) is found in the form of

(3.4)\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^b {\hat f\left(\kern0.7pt y \right)G\left( {x,y} \right)\,\mathrm{d} y}, \end{equation}

which physically describes the group-induced subharmonic at $x$ as the linear superposition of the responses at $x$ induced by all the wave group forcing $\hat f(\kern0.7pt y )$ distributed in the domain $a< y< b$. The generalised solution to (2.16) can be constructed as the sum of homogeneous and inhomogeneous components (cf. Ince Reference Ince1956, § XI):

(3.5)\begin{equation} \hat \xi \left( x \right) = {\hat \xi _g}\left( x \right) + {\hat \xi _f}\left( x \right), \end{equation}

where the homogeneous solution ${\hat \xi _f}( x )$ denotes the free infragravity wave that satisfies the homogeneous counterpart of governing equation (2.16). Physically, the response to each point forcing $\hat f(\kern0.7pt y )$ over $a< y< b$ propagates away from the source point $x = y$ as free subharmonics (figure 2), because (3.1a) indicates that $G( {x,y} )$ is the homogeneous solution to (2.16) at all $x$ in the domain except for $x = y$. Therefore, (3.4) shows that the group-induced subharmonic at an observation point $x$ is the linear superposition of free subharmonics generated from all source points $x = y$ in the wave field due to local group forcing. Note that, at the observation position $x$ within this domain, the response to group forcing outside this domain appears as ambient free subharmonic ${\hat \xi _f}$ in solution (3.5).

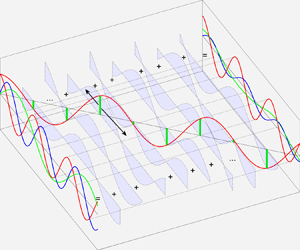
Figure 2. Diagram of two downwave-propagating (red) and upwave-propagating (blue) free subharmonics emitted from an arbitrary spatial point $x=y$ in the source field $\hat \sigma (\kern0.7pt y )$ (3.7) due to group forcing. The source field $\hat \sigma (\kern0.7pt y )$ due to the forcing of radiation stress varies at the spatial scale of wave group length (see (3.22) for an example). The superposition of all the free subharmonics emitted everywhere yields the group-induced subharmonic.

Equation (3.4) may be rewritten as

(3.6)\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^b {\hat f\left(\kern0.7pt y \right)G\left(\kern0.7pt {y,y} \right)\left[ {\frac{{G\left( {x,y} \right)}}{{G\left(\kern0.7pt {y,y} \right)}}} \right]\,{\rm d} y}. \end{equation}

The initial complex amplitude of each emitted subharmonic generated per unit distance is $\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, whose spatial variation from $y$ to $x$ is described by $G( {x,y} ) / G(\kern0.7pt {y,y} )$ (figure 2). Accordingly, $\hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$ is defined as the source field of the group-induced subharmonic $\hat \sigma (\kern0.7pt y )$, i.e.

(3.7)\begin{equation} \hat \sigma \left(\kern0.7pt y \right) = \hat f \left(\kern0.7pt y \right)G\left(\kern0.7pt {y,y} \right). \end{equation}

Let $\hat \xi _h^+ ( x )$ and $\hat \xi _h^- ( x )$ be the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively. The Green's function that satisfies (3.1) can be constructed using two distinct linear combinations of $\hat \xi _h^+ ( x )$ and $\hat \xi _h^- ( x )$ (see Ince Reference Ince1956, p. 257). Assuming open boundaries at both $x=a$ and $x=b$, we seek a solution of $G(x,y)$ that satisfies the following boundary condition:

(3.8a,b)\begin{equation} \frac{G(b,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^+ \left( b \right)}{\hat \xi _h^+ \left(\kern0.7pt y \right)},\quad \frac{G(a,y)}{G(\kern0.7pt y,y)} = \frac{\hat \xi _h^- \left( a \right)}{\hat \xi _h^- \left(\kern0.7pt y \right)}, \end{equation}

which physically indicates that the local response generated at source location $y$ arrives at boundary $x=a$ and $x=b$ as an upwave- and downwave-propagating free wave so that the spatial evolution of its complex amplitude is described by $\hat \xi _h^+$ or $\hat \xi _h^-$.

The solution for the governing equation (3.1) and the boundary condition (3.8a,b) is given by

(3.9)\begin{equation} G\left(x,y\right) = \left\{ \begin{array}{@{}ll@{}} G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{+}\left( x \right)}{\hat{\xi }_{h}^{+}\left(\kern0.7pt y \right)}, & \text{ for }x>y,\\ G\left(\kern0.7pt y,y \right)\dfrac{\hat{\xi }_{h}^{-}\left( x \right)}{\hat{\xi }_{h}^{-}\left(\kern0.7pt y \right)}, & \text{ for }x< y, \end{array} \right. \end{equation}

with

(3.10)\begin{equation} G\left(\kern0.7pt {y,y} \right) = {\left. {\dfrac{{\hat \xi _h^+ \hat \xi _h^- }}{{\hat \xi _h^- \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+{-} \hat \xi _h^+ \dfrac{\rm d}{{{\rm d}\,x}}\hat \xi _h^- }}} \right|_{x = y}}, \end{equation}

where the denominator of (3.10) is the Wronskian of $\hat \xi _h^-$ and $\hat \xi _h^+$, and it is non-zero owing to the linear independence between $\hat \xi _h^+$ and $\hat \xi _h^-$.

In (3.9), the Green's function at the source point $x = y$, $G(\kern0.7pt {y,y} )$, represents the initial complex amplitude of the subharmonic generated by the local unit point forcing, while the factor $\hat \xi _h^ \pm (x)/\hat \xi _h^ \pm (\kern0.7pt y ) = G(x,y)/G(\kern0.7pt y,y)$ describes the relative changes in amplitude and phase of $G(x,y)$ from $x=y$ to $x=x$.

Substituting (3.9) into (3.6), and recalling the definition of the source field $\hat \sigma (\kern0.7pt y )$ (3.7), yields

(3.11)\begin{equation} {\hat \xi _g}\left( x \right) = \hat \xi _g^+ \left( x \right) + \hat \xi _g^- \left( x \right), \end{equation}

where

(3.12a,b)\begin{equation} \hat \xi _g^+ \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} ,\quad \hat \xi _g^- \left( x \right) = \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y}. \end{equation}

The superscripts $+$ and $-$ denote the two components that form due to the downwave- and upwave-propagating free subharmonics being generated on the upwave and downwave sides of $x$, respectively.

Given the complex amplitudes of the ambient downwave- and upwave-propagating subharmonics at the boundary, i.e. $\hat \xi _f^+ ( a )$ and $\hat \xi _f^- ( b )$, the ambient free subharmonic in the domain $a< x< b$ can be expressed as

(3.13)\begin{equation} \hat \xi _f(x) = \hat \xi _f^+(x) + \hat \xi _f^-(x), \end{equation}

where

(3.14a,b)\begin{equation} \hat \xi _f^+ \left( x \right) = \hat \xi _f^+ \left( a \right)\dfrac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}},\quad \hat \xi _f^- \left( x \right) = \hat \xi _f^- \left( b \right)\dfrac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}} \end{equation}

describe the downwave- and upwave-propagating components, respectively. Note that $\hat \xi _f^ \pm (x)$ differs from $\hat \xi _h^ \pm (x)$ in that the former's boundary values vary with the boundary locations in the manner of a group-induced subharmonic instead of a free subharmonic, in order to incorporate the contribution of the source field in the incremental domain due to changing boundary locations. This is later demonstrated by the relationship between $\hat \xi _f^-(a)$ and $\hat \xi _f^-(b)$ in (3.17).

Substituting (3.11)–(3.14a,b) into (3.5) yields

(3.15)\begin{align} \hat \xi \left( x \right) = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}} + \int_x^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}}. \end{align}

Equation (3.15) is the general form of the solution to (2.16), and its exact form depends on the expression of the wave radiation stress field and homogeneous solution. However, the solution in the form of (3.15) requires the information at two boundaries on both sides of $x$. To facilitate its practical applications, (3.15) can be rewritten as a solution with only one boundary for integration retained:

(3.16)\begin{align} \hat \xi \left( x \right) & = \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}} \nonumber\\ &\quad+ \int_x^a {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} + \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( b \right)}} \nonumber\\ & = \hat \xi _f^+ \left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}} + \hat \xi _f^- \left( a \right)\frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left( a \right)}} + \int_a^x {\hat \sigma \left(\kern0.7pt y \right)\left[\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}} - \frac{{\hat \xi _h^- \left( x \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\right]\,\mathrm{d} y}, \end{align}

where

(3.17)\begin{equation} \hat \xi _f^- \left( a \right) = \hat \xi _f^- \left( b \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left( b \right)}} + \int_a^b {\hat \sigma \left(\kern0.7pt y \right)\frac{{\hat \xi _h^- \left( a \right)}}{{\hat \xi _h^- \left(\kern0.7pt y \right)}}\,\mathrm{d} y} \end{equation}

is the complex amplitude of upwave-propagating free wave at $x=a$, which includes the contributions of free waves entering the region through the right-hand boundary $x=b$ and those generated due to the group forcing in the region $a< x< b$. The solution in the form of (3.16) is more computationally feasible than (3.15) and is used for the calculation in figure 6, but the former is physically not as intuitive as the latter because the effect of group forcing on the upwave-propagating components is manifested by deducting the contribution of sources along integral path from the overall contributions of sources.

3.2. Flat bottom

Over a flat bottom, the governing equation (2.16) reduces to

(3.18)\begin{equation} \frac{{{\mathrm{d}^2}\hat \xi }}{{\mathrm{d}\,{x^2}}} + k_f^2\hat \xi = \hat f, \end{equation}

where the forcing term $\hat f$ is given by (3.2). According to (2.10)–(2.11), over a flat bottom $\hat f$ may be rewritten as

(3.19)\begin{equation} \hat{f}\left( x \right)=\frac{k_{g}^{2}\hat{S}\left( x \right)}{\rho gh}=\frac{k_{g}^{2}\hat{S}\left( a \right)}{\rho gh}{\rm e}^{\mathrm{i}k_g(x - a)} = \hat{f}\left( 0 \right){\rm e}^{\mathrm{i}k_g x}, \end{equation}

which is in phase with the wave group. In addition, over a flat bottom, the homogeneous solutions to the governing equation (2.16) and thus the local response to unit point forcing described in equation (3.10) are given by

(3.20a,b)\begin{equation} \hat{\xi }_{h}^{{\pm} }\left( x \right) = C^{{\pm}}{{{\rm e}}^{{\pm} \mathrm{i}{{k}_{f}}x}}, \quad G\left(\kern0.7pt y,y \right)=\frac{1}{2\mathrm{i}{{k}_{f}}}, \end{equation}

where $C^{\pm }$ is a non-zero constant.

Substituting (3.20a,b) into (3.9), we derive the Green's function for a flat bottom:

(3.21)\begin{equation} G(x,y) = \frac{1}{2\mathrm{i} k_f}{\rm e}^{\mathrm{i}k_f|x-y|}, \end{equation}

where the variation of $G(x,y)$ with source location $y$ and response location $x$ is shown in figure 3. For a point unit forcing at $x=y$ described by $\delta _{Dirac}(x-y) {\rm e}^{-\mathrm {i}\omega _g t}$, the modulus and phase angle of $G(x,y)$ are the amplitude and phase lag with respect to the forcing of the subharmonic at $x$. The gradient of the real part of $G(x,y)$ is not continuous as the right-hand side of (3.1c) is real.

Figure 3. (a) Real and (b) imaginary parts of the normalised Green's function for a flat bottom (3.21).

Substituting (3.19) and (3.20b) into the source field $\hat \sigma (\kern0.7pt y )= \hat f(\kern0.7pt y )G(\kern0.7pt {y,y} )$, we have

(3.22)\begin{equation} \hat \sigma \left(\kern0.7pt y \right) = \frac{\hat{f}(0)}{2\mathrm{i}k_f}{\rm e}^{\mathrm{i}k_g y} = \frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat S\left( a \right)}}{{\rho gh}}{\rm e}^{\mathrm{i}k_g(\kern0.7pt y - a)}, \end{equation}

which is spatially uniform in amplitude and leads the wave group by ${\rm \pi} /2$ in phase as $\hat S(a){\rm e}^{\mathrm {i}k_g(\kern0.7pt y - a)}$ is in phase with the wave group according to (2.10) and the phase of the complex factor $\mathrm {i}^{-1}$ is $-{\rm \pi} /2$. Equation (3.22) indicates that each free subharmonic emitted from the source field has the same amplitude and is initially in quadrature with the wave group.

Substituting (3.20a) into (3.11)–(3.12a,b) yields the solution for $\hat \xi _g$:

(3.23a) \begin{equation} \hat \xi_g(x) = \int_{a}^{b} \hat{\sigma}(\kern0.7pt y ) {\rm e}^{\mathrm{i}{k_f|x-y|}} \,\mathrm{d} y. \end{equation}

Invoking (3.22) further yields the expressions

(3.23b) \begin{align} \hat \xi_g(x) &= \frac{\hat{f}(0)}{2 \mathrm{i} k_f} \int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\, \mathrm{d} y \nonumber\\ & = \frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat S\left( a \right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}} \int_{a}^{b}\ {\rm e}^{\mathrm{i}{(k_g y + k_f|x-y|)}}\, \mathrm{d} y. \end{align}

Taking the integral in (3.23b) over the upwave side of $x$ ($a< y< x$) yields the solution for $\hat \xi _g^+$ as defined in (3.12a):

(3.24) \begin{align} \hat \xi _g^+ \left( x \right) & = \frac{{k_g^2}}{{2\mathrm{i}{k_f}}}\frac{{\hat S\left( a \right)}}{{\rho gh}} {\rm e}^{-\mathrm{i}{k_g a}} \int_{a}^{x}\ {\rm e}^{\mathrm{i}{[k_g y + k_f(x-y)]}} \,\mathrm{d} y\nonumber\\ & = \frac{k_g^2}{2\mathrm{i}k_f}\frac{\hat{S}(a)}{\rho g h} {\rm e}^{\mathrm{i}(k_f x-k_g a)} \int_a^x {\rm e}^{\mathrm{i}(k_g -k_f)y}\,\mathrm{d} y\nonumber\\ & ={-} \frac{k_g^2}{2k_f} \frac{\hat{S}(x) - \hat{S}(a){\rm e}^{\mathrm{i}k_f(x-a)}}{{\rho g h}(k_g - k_f)}, \end{align}

where the relationship $\hat {S}(x) = \hat {S}(a){\rm e}^{\mathrm {i}k_g(x-a)}$ is used. Similarly, the solution for $\hat \xi _g^-$ is derived by integrating over the downwave side $x< y< b$ as

(3.25)\begin{equation} \hat \xi _g^- \left( x \right) = \frac{k_g^2}{2k_f} \frac{\hat{S}(x) - \hat{S}(b) {\rm e}^{-\mathrm{i}k_f(x-b)}}{{\rho g h}(k_g + k_f)}, \end{equation}

where the relationship $\hat {S}(x) = \hat {S}(b){\rm e}^{\mathrm {i}k_g(x-b)}$ is used. Let $\hat \xi _b^+$ and $\hat \xi _b^-$ be the corresponding components bound to $\hat S(x)$ and therefore wave group in (3.24) and (3.25), i.e.

(3.26)\begin{equation} \hat \xi _b^ \pm \left( x \right) ={\mp} \frac{{k_g^2}}{{2{k_f}( {{k_g} \mp {k_f}})}}\frac{{\hat S(x)}}{{\rho gh}}. \end{equation}

Equations (3.24) and (3.25) can be rewritten as

(3.27)\begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \hat \xi _b^+ \left( x \right) - \hat \xi _b^+ \left( a \right) {{\rm e}^{\mathrm{i}{k_f}\left( {x - a} \right)}},\\ \hat \xi _g^- \left( x \right) & = \hat \xi _b^- \left( x \right) - \hat \xi _b^- \left( b \right){{\rm e}^{ - \mathrm{i}{k_f}\left( {x - b} \right)}}. \end{aligned} \right\} \end{equation}

3.2.1. Intermediate water

In intermediate water, ${c_g} < \sqrt {gh}$ and ${k_g} > {k_f}$. Figure 4(a) shows the spatial variation of the phase of all subharmonics emitted for the source location $y$ and the observation position $x$, as described by $\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ (the integrand in (3.23b)). On the one hand, at each given $y$, the horizontal slice of figure 4(a) describes the phase change of the upwave- and downwave-propagating subharmonics emitted from $x=y$, resembling the picture shown in figure 2. On the other hand, at each given $x$, the vertical slice of figure 4(a) describes the phase variation with the source location $y$ of all subharmonics arriving at $x$. Figure 4(b,c) shows that the superposition of all free subharmonics can be further decomposed into a subharmonic bound to the wave group and a free subharmonic which are respectively described by the first and second terms on the right-hand side of (3.27).

Figure 4. Diagram of the emission, propagation and interference of subharmonics generated from the source field $\hat \sigma (\kern0.7pt y ) = \hat f (\kern0.7pt y )G(\kern0.7pt {y,y} )$ due to group forcing of bichromatic waves over a flat bottom in intermediate depth (${k_g} > {k_f}$, where $k_g=\omega _g/c_g$ and $k_f= \omega _g / \sqrt {gh}$ are the wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively). Here $\hat {f}$ is the forcing term and $G(\kern0.7pt y,y)$ is the Green's function at $x=y$. (a) Term $\exp [\mathrm {i}(k_g y + k_f | x - y |) ]$ gives the spatial variation of product of source field and Green's function as shown in (3.23), which in turn describe the spatial variation of the free subharmonic with its source position $y$ and observation position $x$. The vertical and horizontal white arrows denote the wavenumber of each emitted subharmonic component on the source and observation position, respectively. (b) The $y$ axis denotes the real part of the superposed downwave-propagating subharmonic ($\hat \xi _g^+$, (3.24)), showing the surface elevation snapshot for $t = 0$. (c) Similar to (b) but for the upwave component ($\hat \xi _g^-$, (3.25)).

The emergence of a bound subharmonic from the superposition of all free subharmonics is essentially the consequence of wave-group-modulated emission of each free subharmonic through the source field bound to the wave group, which does not conflict with the interpretation of the group-induced subharmonic as the superposition of free subharmonics. More specifically, the modulated emission means the phase of the source field by (3.22) varies with space as $k_g y$ due to direct modulation of group forcing, indicating that free subharmonics with the same initial phase are generated at equidistant locations separated by $2{\rm \pi} /k_g$, i.e. one wave-group length. Consequently, a de facto waveform with the same wavelength as the wave group forms and appears phase locked to the wave group, i.e. so-called bound subharmonic in previous studies. Similarly, in (3.27), the superposition of all the upwave-propagating free subharmonics leads to a downwave-propagating bound subharmonic. However, for an observer at a fixed observation position, the bound subharmonic does not exist because there is no space for the aforementioned superposition of the emitted free subharmonics to occur, which mathematically corresponds to an integral interval of zero length in (3.4), and only the free subharmonics arriving from elsewhere will be observed.

Interestingly, (3.26) shows that $\hat \xi _b^+ ( x )$ and $\hat \xi _b^- ( x )$ are respectively in antiphase and phase with the wave groups, and $| {\hat \xi _b^+ } |$ is $( k_g + k_f ) / ( k_g - k_f )$ times larger than $| {\hat \xi _b^- } |$. Thus, the expression for the total bound subharmonics ${\hat \xi _b} = \hat \xi _b^+ + \hat \xi _b^-$ is given by

(3.28) \begin{equation} {\hat \xi _b}\left(x \right) = \left[ {\frac{1}{{( {{k_g} + {k_f}} )}} - \frac{1}{{( {{k_g} - {k_f}} )}}} \right]\frac{{k_g^2}}{{2{k_f}}}\frac{{\hat S\left( x \right)}}{{\rho gh}} ={-} \frac{{k_g^2}}{{k_g^2 - k_f^2}}\frac{{\hat S\left( x \right)}}{{\rho gh}}, \end{equation}

which is in antiphase with the group forcing. Equation (3.28) is the same as the Reference Longuet-Higgins and StewartLHS62 solution:

(3.29)\begin{equation} {\hat \xi_{{{LHS62}}}}\left( x \right) ={-} \frac{{\hat S\left( x \right)}}{{\rho ( {gh - c_g^2})}}. \end{equation}

3.2.2. Shallow water

In shallow water, $c_g \to \sqrt {gh}$ and $k_g \to k_f$, the diagram in figure 4 changes to that in figure 5 and the emitted downwave-propagating subharmonics are now in phase with each other. This is because according to (3.12a) the phase of the downwave-propagating subharmonic emitted from $y$ is $\arg [\hat {\sigma }(\kern0.7pt y )\hat {\xi }_h^+(x)/\hat {\xi }_h^+(\kern0.7pt y )] \propto (k_g-k_f)y+k_fx$, which becomes independent of its source position $y$ as $k_g \to k_f$, indicating that all downwave-propagating subharmonics interfere with each other constructively. In addition, because the initial amplitudes of all the downwave subharmonics are the same, the superposed amplitude of $| {\hat \xi _g^+ } |$ increases proportionally with the number of forcing pulses, which in turn increases linearly with travel distance $k_g x$.

Figure 5. Same as figure 4, but for shallow water where $c_g=\sqrt {gh}$ and $k_g = k_f$, where $k_g=\omega _g/c_g$ and $k_f= \omega _g / \sqrt {gh}$ are wavenumbers of wave group and free subharmonic propagating as shallow-water wave, respectively. The vertical and horizontal white arrows denote the wavenumber of the emitted subharmonic component on the source and observation position, respectively. Values of the group-forcing lines in (b,c) are the same for reference.

Figure 6. Amplitude (a,b) and phase (c,d) of the complex amplitude $\hat \xi (x)$ of the subharmonic surface elevation $\tilde {\xi }(x,t)$ forced by bichromatic wave groups normally incident over a plane sloping bottom. Wave conditions and topography of tests A-4 (a,c) and B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the off-resonant solution of Zou (Reference Zou2011) ((B5), black dash-dotted lines), the near-resonance solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) ((B7), black dashed lines), Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) ((B8), black dotted lines), the present solution $\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where $\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components, $\hat \xi _g^+$ (blue lines) and $\hat \xi _g^-$ (red lines) in (B12). Phase is the phase lag with respect to wave groups plus ${\rm \pi}$. Note that in (b), the phase of the upwave component $\hat {\xi }_g^-$ was manually shifted by ${\rm \pi}$ for plotting purposes.

This result can also be derived by taking the limit $k_g \to k_f$ for $\hat \xi _g^+$ in (3.27). From (2.10)–(2.11) we have $\hat {S}( x )=\hat {S}( a ) {\rm e}^{\text {i}{{k_g(x-a)}}}$ over a flat bottom. Substituting this for $\hat {S}( x )$ in (3.26) and subsequently (3.26) into (3.27) for $\hat {\xi }_g^+$ and then taking the limit $k_g \to k_f$, we have

(3.30)\begin{equation} \lim_{{k_g} \to {k_f}} \hat \xi _g^+ \left( x \right) = \lim_{{k_g} \to {k_f}} - \frac{{k_g^2}}{{2{k_f}}}\frac{{\hat S\left( a \right)}}{{\rho gh}}\frac{{\rm e}^{\text{i}{{k_g(x-a)}}} - {\rm e}^{\text{i}{{k_f(x-a)}}}}{{{k_g} - {k_f}}} = \frac{{{k_f}\left( {x - a} \right)\hat S\left( x \right)}}{{2{\text{i}}\rho gh}}. \end{equation}

Thus, $| {\hat \xi _g^+ } |$ is proportional to the travel distance ${k_g}( {x - a} )$. Equation (3.30) also shows that the downwave group-induced subharmonic leads the group forcing by ${\rm \pi} /2$ because of the complex factor $\mathrm {i}^{-1}$, since each emitted downwave-propagating subharmonic is initially ahead of the group forcing by ${\rm \pi} /2$ according to (3.22).

Remarkably, in (3.30), the bound subharmonic cannot be distinguished from the free mode as in (3.27); hence, it is only meaningful to describe the superposed downwave-propagating group-induced subharmonic as a whole. This phenomenon indicates that $\hat \xi _b^+$ is released when the system is in full resonance. To some extent, it is consistent with the viewpoint of Baldock (Reference Baldock2012) that the bound subharmonic is released in shallow water with and without wave breaking. Nevertheless, the resonance only occurs in the propagating direction of group forcing, not in the upwave-propagating direction. Thereby, the present result partially differs from that of Baldock (Reference Baldock2012) in that the bound subharmonic component $\hat \xi _b^-$ still exists in shallow water. This can be found by taking the limit $k_g \to k_f$ for $\hat \xi _b^-$ in (3.26):

(3.31)\begin{equation} \lim_{{k_g} \to {k_f}} \hat \xi _b^- \left( x \right) = \lim_{{k_g} \to {k_f}} \frac{{k_g^2}}{{2{k_f}\left( {{k_g} + {k_f}} \right)}}\frac{{\hat S\left( x \right)}}{{\rho gh}} = \frac{{\hat S\left( x \right)}}{{4\rho gh}}. \end{equation}

When the resonance occurs, $| {\hat \xi _g^+ } |$ far exceeds $| {\hat \xi _b^- } |$ after a certain distance (figure 5b,c), hence dominating $\hat \xi _g$.

3.3. Uneven bottom

Over an uneven bottom, assuming a mild bottom slope, i.e. $\vert \beta \vert = \vert h_x /(k_gh)\vert < \vert h_x/(k_fh)\vert \ll 1$ and $h_{xx} /(k_gh)=O(\beta ^2)$, substituting (2.10) into the forcing field (3.2) yields

(3.32)\begin{equation} \hat f(x) = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { - \frac{1}{{k_g^2\left| {\hat S} \right|}}\frac{{{\mathrm{d}^2}\left| {\hat S} \right|}}{{\mathrm{d}\,{x^2}}} - \frac{{\rm 2i}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}} + 1} \right) {\rm e}^{\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}. \end{equation}

Following Zou (Reference Zou2011), (3.32) can be decomposed into ${\hat f_{{M}}}$ at leading order, which is the forcing field for a flat bottom in (3.19), $\hat f_{{S}}$ induced by bottom slope and ${\hat f_{r}}$ due to higher-order bottom gradient $h_x^2$ and ${h_{xx}}$, i.e.

(3.33)\begin{equation} \hat{f} = \hat{f}_{{M}} + \hat{f}_{{S}} + \hat{f}_{{r}}, \end{equation}

where

(3.34)\begin{equation} \left. \begin{aligned} {{\hat f}_{{M}}} & = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}} \exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right),\\ {{\hat f}_{{S}}} & = {{\hat f}_{{M}}}\left( { - \frac{{\text{2i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\text{i}}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) = {{\hat f}_{{M}}}O\left( \beta \right),\\ {{\hat f}_{{r}}} & = {{\hat f}_{{M}}}\left( { - \frac{1}{{k_g^2\left| {\hat S} \right|}}\frac{{{\mathrm{d}^2}\left| {\hat S} \right|}}{{\mathrm{d}\,{x^2}}}} \right) = {{\hat f}_{{M}}}O\left( {{\beta ^2}} \right), \end{aligned} \right\} \end{equation}

which is the same as the forcing field in Zou (Reference Zou2011).

The homogeneous solution in this case can be obtained by the perturbation method utilising the small parameter of $h_x/(k_fh)$. At leading order of $O( 1 )$, the homogeneous solution is given by (cf. Zou Reference Zou2011, equation (3.9c))

(3.35)\begin{equation} \hat \xi _h^ \pm \left( x \right) = C^{{\pm}} {h^{ - 0.25}}\left( x \right) {\exp\left({\mathrm{i}\int^x { \pm {k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right], \end{equation}

which is substituted into (3.10) to yield

(3.36)\begin{equation} G\left(\kern0.7pt {y,y} \right) = \frac{1}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]. \end{equation}

Linearised to the first order of bottom slope, the forcing field (3.33) becomes

(3.37)\begin{equation} \hat{f}_{{L}} = \hat{f}_{{M}} + \hat{f}_{{S}} = \frac{{k_g^2 \left| \hat S \right|}}{{\rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{x}k_g \,\mathrm{d}\,x'}\right), \end{equation}

which together with (3.36) are substituted into (3.7) to yield the expression for the source field $\hat \sigma (\kern0.7pt y )$:

(3.38)\begin{align} \hat \sigma(\kern0.7pt y ) = \frac{{k_g^2 \left| \hat S \right|}}{{2 \mathrm{i} k_f \rho gh}}\left( { 1 - \frac{{2{\rm i}}}{{{k_g}\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}\,x}} - \frac{\rm i}{{k_g^2}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}\,x}}} \right) \exp\left({\mathrm{i}\int^{y}k_g \,\mathrm{d}\,x'}\right) \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]. \end{align}

Substituting (3.38) and (3.35) into (3.12a,b) yields

(3.39)\begin{equation} \left. \begin{aligned} \hat \xi _g^+ \left( x \right) & = \int_a^x {\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[ {\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}} \right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x {{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d} y}, \\ \hat \xi _g^- \left( x \right) & = \int_x^b {\frac{{{{\hat f}_{{L}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}{{\left[ {\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}} \right]}^{ - 0.25}} {\exp\left({ - \mathrm{i}\int_y^x {{k_f}\,\mathrm{d}\,x'} }\right)} \left[ {1 + O\left( \beta{\frac{{{k_g}}}{{{k_f}}}} \right)} \right]\,\mathrm{d} y}. \end{aligned} \right\} \end{equation}

The phase dependence of the integrand in (3.39) on source location $y$ determines the interference among all free components generated from different sources arriving at observation point $x$. At leading order, $\hat f_{{L}}(\kern0.7pt y )$ in (3.37) is in phase with the wave group and hence its phase varies with $y$ as $\int ^y{k_g}\,\mathrm {d}\,x'$. Therefore, in (3.39) the phase of each component of $\hat \xi ^\pm _g$ mainly varies with $y$ as $\int ^y{k_g\pm k_f}\,\mathrm {d}\,x'$, which largely determines the relative magnitude between $\hat \xi _g^+$ and $\hat \xi _g^-$ as discussed in detail in Appendix C.

3.3.1. Shallow water

In shallow water, according to (3.26)–(3.27), as ${k_g} \to {k_f}$ and the resonance is intensified, $\hat \xi _g^+$ becomes the predominant part of the group-induced subharmonic, i.e. ${\hat \xi _g} \approx \hat \xi _g^+$.

Without wave breaking, given the shallow-water approximations of $c_g\approx c \approx \sqrt {gh}$ and $k_g=\omega _g/c_g\approx \omega _g/\sqrt {gh}$, (2.11) indicates $| {\hat S(x)} | = | {\hat S(a)} |\sqrt {h(a)/h(x)}$. Hence the spatial evolution of $\hat S$ described by the energy conservation (2.10)–(2.11) becomes

(3.40)\begin{equation} \hat S(x) = \hat S(a) \left[\frac{h(x)}{h(a)}\right]^{{-}0.5} \exp\left({\mathrm{i}\int_a^x \frac{\omega_g}{\sqrt{gh}}\,\mathrm{d}\,x'}\right). \end{equation}

Substituting (3.40) into the forcing term (3.32) yields

(3.41)\begin{equation} \hat f\left( x \right) = \frac{{\omega _g^2}}{{gh\left( x \right)}}\frac{{\hat S\left( a \right)}}{{\rho gh\left( x \right)}}{\left[ {\frac{{h\left( x \right)}}{{h\left( a \right)}}} \right]^{ - 0.5}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\,x'} }\right)}\left[ {1 + O\left( \beta \right)} \right] \end{equation}

at leading order.

Substituting (3.41) into the solution for $\hat \xi _g^+$ in (3.39) yields

(3.42)\begin{equation} \hat \xi _g^+ \left( x \right) = \frac{{{\omega _g}\hat S\left( a \right)}}{{2\mathrm{i}\rho {g^{1.5}}}}{\left[ {\frac{{h\left( x \right)}}{{h\left( a \right)}}} \right]^{ - 0.5}}\left[ {{h^{0.25}}\left( x \right)\int_a^x {h{{\left(\kern0.7pt y \right)}^{ - 1.75}}\,\mathrm{d} y} } \right] {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\,x'} }\right)} \end{equation}

at leading order, which is dependent on the bottom profile. The amplitude of $\hat \xi _g^+$ in (3.42) is proportional to $\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$, which in turn is proportional to the horizontal length of the bottom profile between $a$ and $x$. More specifically, suppose that the topography is horizontally stretched by a factor; considering the integrand in $\int _a^x {h{{(\kern0.7pt y )}^{ - 1.75}}\,\mathrm {d} y}$ is only a function of depth, the integral covering the same bottom profile would also be enlarged by the same factor, and so is the amplitude of $\hat \xi _g^+$. This is essentially ascribed to the same accumulative constructive interference process of the downwave-propagating subharmonics demonstrated in figure 5, which causes the subharmonic amplitude to increase linearly with travel distance. This finding is consistent with the semi-analytical result of Liao et al. (Reference Liao, Li, Liu and Zou2021) that the amplitude of a group-induced subharmonic over the front slope of a shoal increases with the travel distance.

Over a uniform slope (${h_x} = {\textrm {const.}}$), (3.42) reduces to

(3.43)\begin{equation} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \left[\frac{h(a)}{h(x)} - \left(\frac{h(a)}{h(x)}\right)^{0.25}\right]\frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\kern0.7pt x'} }\right)}. \end{equation}

Invoking (3.40) reduces (3.43) further to

(3.44)\begin{align} \hat \xi _g^+ \left( x \right) = \frac{2\mathrm{i}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( x \right)}}{g}} \frac{{\hat S\left( x \right)}}{{\rho gh\left( x \right)}} - \frac{{2\mathrm{i}}}{3}\frac{{{\omega _g}}}{{{h_x}}}\sqrt {\frac{{h\left( a \right)}}{g}} \frac{{\hat S\left( a \right)}}{{\rho gh\left( a \right)}}{\left[ {\frac{{h\left( x \right)}}{{h\left( a \right)}}} \right]^{ - 0.25}} {\exp\left({\mathrm{i}\int_a^x {\frac{{{\omega _g}}}{{\sqrt {gh} }}\,\mathrm{d}\,x'} }\right)}, \end{align}

where the first term is consistent with the shallow-water limit of the near-resonant solution by equation (20) of Liao et al. (Reference Liao, Li, Liu and Zou2021) and the second term represents a free subharmonic. The second term appears because only the forcing inside the finite region $a$ to $x$ is considered; therefore, $\hat \xi _g^+(a)=0$ has to be satisfied at the boundary $x=a$. Equation (3.44) indicates that the amplitude of group-induced subharmonic is inversely proportional to the bottom slope in shallow water, which is due to the increase of group-induced subharmonic amplitude linearly with travel distance. This result provides a theoretical explanation for the well-known decrease of shoaling rate of group-induced subharmonic with the relative bottom slope (e.g. Battjes et al. Reference Battjes, Bakkenes, Janssen and van Dongeren2004; Van Dongeren et al. Reference Van Dongeren, Battjes, Janssen, Van Noorloos, Steenhauer, Steenbergen and Reniers2007; De Bakker, Tissier & Ruessink Reference De Bakker, Tissier and Ruessink2016; Zhang, Toorman & Monbaliu Reference Zhang, Toorman and Monbaliu2020). The dependence of subharmonic amplitude on the travel distance of wave groups corroborates the historical effect of spatial evolution of wave groups in the region of shallow water on the subharmonic amplitude in the subsequent region as previously studied by Li et al. (Reference Li, Liao, Liu and Zou2020) and Liao et al. (Reference Liao, Li, Liu and Zou2021). Apart from that, the present model indicates that the group-forcing field also affects the subharmonic on the upwave side because of the generation of those upwave-propagating subharmonics. The topographic effect on the group-induced subharmonics is examined in detail in Appendix D.

4. Comparisons of present and previous solutions

The present unified solution is shown to reduce to the existing solutions (Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993; Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Zou Reference Zou2011; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021) in this section.

4.1. Solution over a plane sloping beach

The solution of the group-induced subharmonic over a plane sloping beach was obtained by Van Leeuwen (Reference Van Leeuwen1992) and Schäffer (Reference Schäffer1993). For a plane sloping beach with $x=0$ at the shoreline, $h = h_x x$, where $h_x < 0$ is a constant, the governing equation (2.16) can be rewritten with the new dependent variable

(4.1)\begin{equation} u = \frac{2\omega_g}{g h_x}\sqrt{gh} \end{equation}

as

(4.2)\begin{equation} u^2\frac{\mathrm{d}^2\hat \xi}{\mathrm{d}u^2} + u\frac{\mathrm{d}\hat \xi}{\mathrm{d}u} + u^2 \hat \xi ={-}\frac{4h}{\rho gh_x^2}\frac{{{\rm d}^{2}}\hat{S}}{{\rm d}\,{{x}^{2}}}, \end{equation}

whose homogeneous solutions are given by

(4.3)\begin{equation} \left. \begin{aligned} \hat \xi_h^+(x) & = {\rm H}_0^{(2)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] - \mathrm{i}{\rm Y}_0\left[ u(x) \right],\\ \hat \xi_h^-(x) & = {\rm H}_0^{(1)}\left[ u(x) \right] = {\rm J}_0\left[ u(x) \right] + \mathrm{i}{\rm Y}_0\left[ u(x) \right], \end{aligned} \right\} \end{equation}

where $\textrm {H}_0^{(1)}$ and $\textrm {H}_0^{(2)}$ are the first- and second-kind Hankel function of order zero and $\textrm {J}_0$ and $\textrm {Y}_0$ are the zeroth-order Bessel function of the first and second kind. Note that $\textrm {H}_0^{(2)}$ instead of $\textrm {H}_0^{(1)}$ becomes $\hat \xi _h^+(x)$ because as $x$ increases the phase of $\hat \xi _h^+(x)$ must increase. The Wronskian of $\hat \xi _h^-$ and $\hat \xi _h^+$ in the denominator of (3.10) now becomes

(4.4)\begin{align} & {\hat \xi _h^-(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^+(x) - \hat \xi _h^+(x) \frac{\rm d}{{{\rm d}\,x}}\hat \xi _h^-(x) }\nonumber\\ &\quad = \left[{\rm H}_0^{(1)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm H}_0^{(2)}(u) - {\rm H}_0^{(2)}(u)\frac{\mathrm{d}}{\mathrm{d}u}{\rm H}_0^{(1)}(u)\right] \frac{\mathrm{d}u}{\mathrm{d}\,x}\nonumber\\ &\quad ={-}\frac{4 \mathrm{i}}{{\rm \pi} u}\frac{\omega_g}{\sqrt{gh}} ={-} \frac{2\mathrm{i}}{\rm \pi}\frac{h_x}{h}. \end{align}

Substituting (3.2), (4.3) and (4.4) into (3.7) yields

(4.5) \begin{equation} \hat \sigma(\kern0.7pt y ) ={-} \frac{\mathrm{i}{\rm \pi} h}{2h_x} \frac{{\rm H}_0^{(1)}[u(\kern0.7pt y )]{\rm H}_0^{(2)}[u(\kern0.7pt y )]}{\rho g h} \frac{\mathrm{d}^2 \hat S}{\mathrm{d}\,x^2}. \end{equation}

Substituting (4.3) and (4.5) into the solution (3.16) yields

(4.6)$$\begin{align} \hat \xi(x) &= {\rm H}_0^{(1)}\left[u(x)\right] \left[\frac{\hat \xi_f^-(a)}{{\rm H}_0^{(1)}\left[u(a)\right]} + \frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm H}_0^{(2)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right]\nonumber\\ &\quad + {\rm H}_0^{(2)}\left[u(x)\right] \left[\frac{\hat \xi_f^+(a)}{{\rm H}_0^{(2)}\left[u(a)\right]} - \frac{\mathrm{i} {\rm \pi}}{2\rho g h_x} \int_{a}^{x} {\rm H}_0^{(1)}[u(\kern0.7pt y )] \frac{\mathrm{d}^2 \hat S}{\mathrm{d}\,x^2}\,\mathrm{d} y \right], \end{align}$$

which is equivalent to the solution given by equation (4.16) in Schäffer (Reference Schäffer1993). Moreover, the non-homogeneous part of (4.6) can be easily converted to the solution given by equation (3.1.62) in Van Leeuwen (Reference Van Leeuwen1992) using the definition of Hankel function in (4.3).

4.2. Off-resonant solution for intermediate water

Let $\mu = 1 - k_f^2/k_g^2$ measure the departure of the system from resonance (Janssen et al. Reference Janssen, Battjes and van Dongeren2003), which decreases from $O(1)$ in intermediate water to zero in shallow water, and let $\beta /\mu$ measure the resonance intensity of the system. The parameter regime of $\beta {\mu ^{ - 1}} = O( \beta )$ in intermediate water and $\beta {\mu ^{ - 1}} = O( 1 )$ are referred to as off- and near-resonance conditions, respectively, as per Janssen et al. (Reference Janssen, Battjes and van Dongeren2003). Under off-resonant condition, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003), Zou (Reference Zou2011) and Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the analytical solution of subharmonic for uneven bottom using perturbation expansion with small parameter $\beta$. Accurate to order $O(\beta )$, their group-bounded subharmonic solutions are equivalent to each other:

(4.7)\begin{align} {\hat \xi _b} ={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 + \frac{{\mathrm{i}\beta }}{\mu }\left[ {\left( {\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{{\rm d}\left| {\hat S} \right|}}{\mathrm{d}h} + \frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}} \right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu }\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O({{\beta ^2}})} \right\}. \end{align}

For an uneven bottom in intermediate water, the solution (3.11) can be first transformed into (3.39). The phase factor of the integrand in (3.39) is ${\exp ({\textrm {i}\int ^y {{k_g} \pm {k_f}\,\mathrm {d}\,x'} })}$ for $\hat \xi _g^ \pm ( x )$, and applying the integration by parts technique to (3.39) using this phase factor twice, and retaining the variable upper bound of the integral, yields

(4.8)$$\begin{align} \hat \xi _b^ \pm &= \pm \frac{{{{\hat f}_{{L}}}}}{{2\mathrm{i}{k_f}}}\left\{ {\frac{1}{{\mathrm{i}\left( {{k_g} \mp {k_f}} \right)}} + \frac{1}{{{{\left( {{k_g} \mp {k_f}} \right)}^2}}}{{\left[ {\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp {k_f}} \right)}}} \right]}^{ - 1}}\frac{\mathrm{d}}{{\mathrm{d}\,x}}\left[ {\frac{{{h^{0.25}}{f_{{L}}}}}{{{k_f}\left( {{k_g} \mp {k_f}} \right)}}} \right]} \right\}\nonumber\\ &\quad \times \left[ {1 + O\left( {\beta\frac{{{k_g}}}{{{k_f}}}} \right)} \right], \end{align}$$

where ${f_{{L}}} = {\hat f_{{L}}}| {\hat S} |{\hat S^{ - 1}} = (\kern0.7pt {{{\hat f}_{{M}}} + {{\hat f}_{{S}}}} )| {\hat S} |{\hat S^{ - 1}}$ is the linearised forcing term excluding the phase factor of wave group.

Substituting (3.37) and $\mu = 1 - k_f^2/k_g^2$ into (4.8), we have

(4.9)\begin{align} \hat{\xi}_{b}^{{\pm}}(x)={\mp} \frac{\hat{S}}{\rho g h \mu} \frac{k_{g} \pm k_{f}}{2 k_{f}}\left[\begin{array}{@{}l@{}} \left(1-\dfrac{2 \mathrm{i}}{k_{g}|\hat{S}|} \dfrac{\mathrm{d}|\hat{S}|}{\mathrm{d}\,x}-\dfrac{\mathrm{i}}{k_{g}^{2}} \dfrac{\mathrm{d} k_{g}}{\mathrm{d}\,x}\right)-\dfrac{k_{g} \pm k_{f}}{\mathrm{i} k_{g}^{2} \mu}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right)^{{-}1} \\ \quad \times \dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(\dfrac{|\hat{S}|}{h^{0.25} \mu}\right) -\dfrac{1}{\mathrm{i} k_{g}^{2} \mu} \dfrac{\mathrm{d}}{\mathrm{d}\,x}\left(k_{g} \pm k_{f}\right)+O\left(\beta\dfrac{k_{g}}{k_{f}}\right) \end{array}\right]. \end{align}

Adding $\hat \xi _b^+$ and $\hat \xi _b^-$ in (4.9) yields

(4.10)\begin{align} {\hat \xi _b} &= \hat \xi _b^+ + \hat \xi _b^- \nonumber\\ &={-} \frac{{\hat S}}{{\rho gh\mu }}\left\{ {1 + \frac{{\mathrm{i}\beta }}{\mu }\left[ {\left( {\frac{{2h}}{{\left| {\hat S} \right|}}\frac{{\mathrm{d}\left| {\hat S} \right|}}{{\mathrm{d}h}} + \frac{h}{{{k_g}}}\frac{{\mathrm{d}{k_g}}}{{\mathrm{d}h}}} \right)\left( {1 - \mu } \right) - 1 - \frac{{2h}}{\mu }\frac{{\mathrm{d}\mu }}{{\mathrm{d}h}}} \right] + O\left( {{\beta ^2}} \right)} \right\}, \end{align}

which is the same as solution (4.7). Note that the relative error for $\hat \xi _b^ \pm$ in (4.9) is of $O[ h_x/ (k_fh)]$, but the error for ${\hat \xi _b}$ in (4.10) is of $O( \beta ^2 )$ (see Appendix A for more details).

4.3. Near-resonant solution for shallow water

4.3.1. Liao et al. (2021) solution

In the case of near resonance in shallow water $(\beta \mu ^{ - 1} = O(1) )$, Liao et al. (Reference Liao, Li, Liu and Zou2021) derived the following solution of group-induced subharmonic (cf. equation (19) therein):

(4.11)\begin{align} {\hat \xi _g}\left( x \right) ={-} \frac{{\mathrm{i}\hat S\left( x \right)}}{{2\rho gh\left( x \right)}}\int_a^x {\left| {\frac{{\hat S\left(\kern0.7pt y \right)}}{{\hat S\left( x \right)}}} \right|\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left( x \right)}}{{{k_g}\left( x \right)h\left(\kern0.7pt y \right)}}} {k_g}\left(\kern0.7pt y \right) {\exp\left({ - \mathrm{i}\int_y^x {\frac{\mu }{2}{k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \left[ {1 + O\left( \beta \right)} \right]. \end{align}

The relationship $\hat {S}(x) /|\hat {S}(x)|=\hat {S}(\kern0.7pt y ) /|\hat {S}(\kern0.7pt y )| \exp (\mathrm {i} \int _{y}^{x} k_{g}\, {\textrm {d}\kern0.7pt x}^{\prime })$ could be derived from (2.10) and then substituted together with ${\hat f_{{M}}}$ in (3.34) into (4.11) to obtain

(4.12)\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\left({\mathrm{i}\int_y^x {\left( {1 - \frac{\mu }{2}} \right){k_g}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} . \end{equation}

In this condition, (3.26)–(3.27) indicate that $| {\hat \xi _g^+ } |$ is greater than $| {\hat \xi _g^- } |$ by an order of factor $(k_{g}+k_{f}) /(k_{g}-k_{f})=(1+\sqrt {1-\mu }) /(1-\sqrt {1-\mu })$, which is of $O( \mu ^{ - 1} ) = O( \beta ^{ - 1} )$ for $\mu = O( \beta ) \ll 1$ in shallow water. Besides, as shown in Appendix A, the error of (3.39) is now of $O(\beta )$ relative to leading order, and hence we aim to prove that the solution for $\hat \xi _g^+$ in (3.39) at leading order

(4.13)\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_f}\left(\kern0.7pt y \right)}}\left[ {1 + O\left( \beta \right)} \right]{{\left[ {\frac{{h\left( x \right)}}{{h\left(\kern0.7pt y \right)}}} \right]}^{ - 0.25}} {\exp\left({\mathrm{i}\int_y^x {{k_f}\,\mathrm{d}\,x'} }\right)}\,\mathrm{d} y} \end{equation}

is consistent with (4.12).

Because $k_{f} / k_{g}=\sqrt {1-\mu }=1+O(\beta )$ and $k_{g}-k_{f}=k_{g}(1-\sqrt {1-\mu })=k_{g}[\mu / 2+O(\beta ^{2})]$, hence $[1-\mu /2+O(\beta ^2)]k_g=k_f$ and at leading order the integrands of (4.12) and (4.13) are consistent with each other and so are the two solutions.

4.3.2. Janssen et al. (2003) solution

For the near-resonance condition $(\beta \mu ^{-1} = O(1) )$, Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) derived the following governing equation for the complex amplitude of subharmonic $\hat \xi$ (equation (23) therein). Using the notations of the present study, it reads as

(4.14)\begin{align} \frac{\mathrm{d} \hat{\xi}}{\mathrm{d}\,x} + \hat{\xi}\left[\frac{h_x}{2h} + \frac{(k_g)_x}{2k_g} + \mathrm{i} k_g (\frac{\mu}{2} - 1)\right] ={-} \frac{\mathrm{i}k_g \hat{S}}{2 \rho gh}\left(1 - \frac{2\mathrm{i}k_g \left|\hat{S}\right|_x}{k_g \left|\hat{S}\right|} - \frac{\mathrm{i} (k_g)_x}{k_g^2}\right) + O(\beta^2). \end{align}

Recalling the expressions for the leading- and first-order forcing terms ( $\hat {f}_{M}$ and $\hat {f}_S$; equation (3.34)), (4.14) reduces to

(4.15) \begin{equation} \frac{\mathrm{d} \hat{\xi}}{\mathrm{d}\,x} + \hat{\xi}\Biggl[\frac{h_x}{2h} + \frac{(k_g)_x}{2k_g} + \mathrm{i} k_g \Biggl(\frac{\mu}{2} - 1\Biggr)\Biggr] = \frac{1}{2\mathrm{i}k_g}(\hat{f}_{M} + \hat{f}_S) + O(\beta^2), \end{equation}

which has the solution

(4.16)\begin{equation} {\hat \xi _g}\left( x \right) = \int_a^x {\frac{{{{\hat f}_{{M}}(\kern0.7pt y ) + {\hat f}_{{S}}}\left(\kern0.7pt y \right)}}{{2\mathrm{i}{k_g}\left(\kern0.7pt y \right)}}\sqrt {\frac{{{k_g}\left(\kern0.7pt y \right)h\left(\kern0.7pt y \right)}}{{{k_g}\left( x \right)h\left( x \right)}}} {\exp\Biggl({\mathrm{i}\int_y^x {\Biggl( {1 - \frac{\mu }{2}} \Biggr){k_g}\,\mathrm{d}\,x'} }\Biggr)}\,\mathrm{d} y} . \end{equation}

At leading order, (4.16) is equivalent to the solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) (equation (4.12) therein), which has been demonstrated above to be equivalent to the present solution (4.13).

Figure 6 shows the theoretical predictions of the amplitude and phase of group-induced subharmonic on a plane sloping bottom under the conditions of the A-4 and B-5 series in the bichromatic wave experiment of Van Noorloos (Reference Van Noorloos2003) using the off-resonant solution of Zou (Reference Zou2011), the near-resonant solutions of Liao et al. (Reference Liao, Li, Liu and Zou2021) and Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) and the present solution. To compare with laboratory measurements, the free subharmonic generated due to scattering at the toe of the slope was also calculated and added to the group-induced subharmonic in figure 6 (see Appendix B for details of calculation). Note that although the component $\hat \xi _g^-$ is induced by upwave-propagating free subharmonics, its waveform actually propagates in the downwave direction as indicated by $\hat \xi _b^-$ in (3.27) and (4.9) as well as the slowly varying phase difference between $\hat \xi _g^-$ and the wave group (red lines in figure 6c,d). For this reason, and also because the incoming and outgoing subharmonics were separated in Van Noorloos (Reference Van Noorloos2003) by detecting the propagation of waveform, the component $\hat \xi _g^-$ should be included in the total solution $\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ to compare with the incoming subharmonic in Van Noorloos (Reference Van Noorloos2003) (circles in figure 6).

As the water depth diminishes, the amplitude predicted by the off-resonant solution of Zou (Reference Zou2011) diverges as expected; the near-resonant solution of Janssen et al. (Reference Janssen, Battjes and van Dongeren2003) slightly overestimated the subharmonic amplitude but underestimated the subharmonic phase lag behind the wave group. The near-resonant solution of Liao et al. (Reference Liao, Li, Liu and Zou2021) predicts the amplitude similar to the present solution but with lower phase lag. Among the three near-resonant solutions included, the present solution agrees with laboratory measurements the best. In addition, figure 6 also indicates that in shallow water, the downwave-propagating group-induced subharmonic $\hat \xi _g^+$ eventually dominates the group-induced subharmonic, thus becoming the major contributor to both its amplitude and phase. Despite the dominance of $\hat \xi _g^+$, however, discernible discrepancy between the total solution $\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ (black solid lines) and the downwave-propagating component $\hat \xi _g^+$ remains over the full depth range. The disagreement between experiment and theory becomes more evident at deeper water for scenario of test B-5 than A-4, due to the larger primary wave amplitude $A_1+A_2$ and therefore the onset of wave breaking at deeper water. This is discussed further in figure 10.

4.3.3. Contardo et al. (2021) solution

Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021) discretised a 1-D topography into a succession of small steps. By applying the Reference Longuet-Higgins and StewartLHS62 solution for the flat bottom on both sides of the step and applying the mass and momentum matching conditions across the step, the scattered free subharmonics induced by the wave group propagating across each single depth discontinuity were calculated. Assuming an in-phase relationship with the wave radiation stress, the initial complex amplitude of the transmitted free subharmonic is given by

(4.17) \begin{equation} {\hat \sigma _{{{CLHRDS21}}}}\left( x \right) = \frac{{\left. {\left({\left| {{{\hat \xi }_{{{LHS62}}}}} \right|{k_g}h}\right)} \right|_{{x-\Delta x}}^x + {{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}}\left. {\left( {\left| {{{\hat \xi }_{{{LHS62}}}}} \right|} \right)} \right|_{{x-\Delta x}}^x}}{{{{\left. {( {{k_f}h})} \right|}_{{x-\Delta x}}} + {{\left. {( {{k_f}h} )} \right|}_{{x}}}}}\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}

where ${{ {} |}_{x-\Delta x}}$ and ${{ {} |}_{x}}$ denote the quantities at the locations immediately before ($x-\Delta x$) and after ($x$) the step respectively, corresponding to the subscripts ‘sea’ and ‘shore’ adopted by Contardo et al. (Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021), and ${} |_{x-\Delta x}^{x}$ denotes the difference between the variables at $x$ and $x-\Delta x$. The total downwave subharmonic is the superposition of the bound subharmonic as described by Reference Longuet-Higgins and StewartLHS62 and all the transmitted free subharmonics generated over the steps through which the wave groups have passed. In the case of continuous depth change, consider that the depth changes from $h( x-\Delta x )$ to $h( x )$ within a small distance $\Delta x$ and then taking the limit $\Delta x \to 0$ yields

(4.18)\begin{equation} {\hat \sigma _{{{CLHRDS21}}}}\left( x \right) = \left[ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}({{k_g}h})}}{{\mathrm{d}\,x}}} \right]\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}

which, as shown below, is consistent with the present solution after subtracting the Reference Longuet-Higgins and StewartLHS62 solution from $\hat \xi _g^+$ in (4.13) at leading order.

With the phase factor ${\exp ({\mathrm {i}\int ^y {{k_g}\,\mathrm {d}\,x'} })}$ in ${\hat f_{{M}}}(\kern0.7pt y )$, the phase factor of the integrand for $\hat \xi _g^+$ in (4.13) is ${\exp ({\mathrm {i}\int ^y {({k_g} - {k_f})\,\mathrm {d}\,x'} })}$. Applying integration by parts utilising this phase factor once and combining with the Reference Longuet-Higgins and StewartLHS62 solution (3.29) reduces $\hat \xi _g^+$ in (4.13) to

(4.19)\begin{equation} \hat \xi _g^+ \left( x \right) = \left[ {{{\hat \xi }_{{{LHS62}}}}\left( x \right) - {{\hat \xi }_{{{LHS62}}}}\left( a \right)\frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left( a \right)}}} \right]\left[ {1 + O\left( \beta \right)} \right] + \int_a^x {{{\hat \sigma }_{{r}}}\left(\kern0.7pt y \right)} \frac{{\hat \xi _h^+ \left( x \right)}}{{\hat \xi _h^+ \left(\kern0.7pt y \right)}}\,\mathrm{d} y, \end{equation}

where the term in the first square brackets $\hat {\xi }_{{LHS62}}(a) \hat {\xi }_{h}^{+}(x) / \hat {\xi }_{h}^{+}(a)$ appears due to boundary condition $\hat \xi _g^+ ( a ) = 0$ and the residual source field $\hat \sigma _{{r}}$ due to the subtraction of the Reference Longuet-Higgins and StewartLHS62 solution is

(4.20)\begin{equation} {\hat \sigma _{{r}}} = \left\{ {\frac{{{k_g} + {k_f}}}{{2{k_f}}}\frac{{\mathrm{d}\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{\mathrm{d}\,x}} + \frac{{\left| {{{\hat \xi }_{{{LHS62}}}}} \right|}}{{2{k_f}h}}\frac{{\mathrm{d}( {{k_g}h} )}}{{\mathrm{d}\,x}}\left[ {1 + O\left( \beta \right)} \right]} \right\}\frac{{\hat S}}{{\left| {\hat S} \right|}}, \end{equation}

which is the same as $\hat \sigma _{{{CLHRDS21}}}$ in (4.18) at leading order.

The present unified solution of group-induced subharmonic (3.11) reduces to the existing solutions as summarised in figure 7.

Figure 7. The present generalised solution based on Green's function (3.15) of group-induced subharmonic reduces to the solution over a flat bottom (Longuet-Higgins & Stewart Reference Longuet-Higgins and Stewart1962), a variable bottom (Zou Reference Zou2011) at off-resonant condition of intermediate water, a variable bottom at near-resonant condition of shallow water (Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Contardo et al. Reference Contardo, Lowe, Hansen, Rijnsdorp, Dufois and Symonds2021; Liao et al. Reference Liao, Li, Liu and Zou2021) and over a plane beach (Van Leeuwen Reference Van Leeuwen1992; Schäffer Reference Schäffer1993). Here $k_g=\omega _g/c_g$ and $k_f= \omega _g / \sqrt {gh}$ are the wavenumber of the wave group and free subharmonic propagating at the speed of shallow-water wave; $\mu = 1 - k_f^2/k_g^2$ is the degree of departure from resonance; and $\hat \xi _h^+ ( x )$ and $\hat \xi _h^- ( x )$ are the linearly independent homogeneous solutions of (2.16) that describe the downwave- and upwave-propagating free subharmonics, respectively.

5. Effect of moving-breakpoint forcing

As long as the forcing term $\hat f$ for breaking waves can be theoretically pre-described, the present solution of group-induced subharmonic (3.11) can, in principle, be applied to the surf zone, assuming negligible nonlinearity of the subharmonic so that the linearised shallow-water equation is valid. As the first step, the present solution is combined with the seminal moving-breakpoint forcing model (Symonds et al. Reference Symonds, Huntley and Bowen1982; Schäffer Reference Schäffer1993; Contardo & Symonds Reference Contardo and Symonds2016). The sum of downwave and upwave components instead of individual components was solved in previous moving-breakpoint models. In contrast, these two components are independently described in the present model; therefore, the spatial evolution of the downwave component in the excursion region of moving breakpoint can be examined.

In the surf zone , the energy conservation equation (2.7) and the corresponding radiation stress solution (2.10)–(2.11) are no longer valid due to significant breaking-induced dissipation. Following Schäffer (Reference Schäffer1993), we consider weakly modulated bichromatic wave groups (modulation rate $\delta =A_2/A_1\ll 1$ is the ratio of amplitudes of two components of bichromatic waves) normally incident onto a plane sloping bottom (figure 8). Let ${x_a}$ and ${x_c}$ be the horizontal coordinates of the boundaries of the moving-breakpoint region B in figure 8, and the groupiness is assumed to vanish shoreward of region B. At $x_c$, waves with the maximum amplitude $A_1( {1 + \delta } )$ start to break, i.e.

(5.1)\begin{equation} h\left(x_{c}\right)=2\sqrt{2}A_{1}\left(x_{c}\right)(1+\delta) / \gamma , \end{equation}

where $\gamma =\textrm {significant wave height/depth}$ at breakpoint is the breaker index that ranges between 0.5 and 1 (Goda Reference Goda2010). Similarly, at $x_a$, waves with the minimum amplitude $A_1( 1 - \delta )$ start to break, i.e.

(5.2)\begin{equation} h\left(x_{a}\right)=2\sqrt{2}A_{1}\left(x_{a}\right)(1-\delta) / \gamma . \end{equation}

Figure 8. Sketch of bottom topography and spatial variation of the amplitude of bichromatic waves normally incident on a plane sloping bottom. Positions $x_a$, $x_m$ and $x_c$ are where waves with the minimum, mean and maximum amplitude break. Reproduced from figure 3 in Schäffer (Reference Schäffer1993).

The steady components of radiation stress in the surf zone and shoaling zone indicated by regions I and II in figure 8 are

(5.3a,b)\begin{equation} {\bar S^{\left( {{I}} \right)}} = \frac{1}{16}\rho g{\gamma ^2}{h^2}\left( {\frac{{2{c_g}}}{c} - \frac{1}{2}} \right),\quad {\bar S^{\left( {{{II}}} \right)}} = \frac{1}{2}\rho gA_1^2( {1 + {\delta ^2}})\left( {\frac{{2{c_g}}}{c} - \frac{1}{2}} \right). \end{equation}

To leading order of $O( \delta )$, Schäffer (Reference Schäffer1993) derived the complex amplitude of the radiation stress gradient oscillating with group frequency in the moving-breakpoint region B:

(5.4)\begin{equation} \frac{{\mathrm{d}{{\hat S}^{\left( {{B}} \right)}}}}{{\mathrm{d}\,x}} = \frac{2}{{\rm \pi} }\left( {\frac{{\mathrm{d}{{\bar S}^{\left( {{I}} \right)}}}}{{\mathrm{d}\,x}} - \frac{{\mathrm{d}{{\bar S}^{\left( {{{II}}} \right)}}}}{{\mathrm{d}\,x}}} \right)\sin \tau + O(\delta ), \end{equation}

where $0 \leq \tau ( x ) \leq {\rm \pi}$ denotes the group phase when wave breaking ceases and is given by

(5.5) \begin{equation} 2\sqrt{2}{A_1}(x)\{ {1 + \delta \cos [ {\tau (x)} ] + O( {{\delta ^2}})} \} = \gamma h\left( x \right). \end{equation}

The spatial evolution of $A_1$ and $A_2$ during energy conservative shoaling can be solved from (2.8a,b) as

(5.6)\begin{equation} \frac{A_1(x)}{A_1(x_a)} = \frac{A_2(x)}{A_2(x_a)} = \sqrt{\frac{c_g(x_a)}{c_g(x)}}, \end{equation}

and therefore $\delta =A_2/A_1$ remains spatially invariant.

Substituting (5.1) and (5.2) into (5.5) yields $\tau ( {{x_a}} ) = {\rm \pi}$ and $\tau ( {{x_c}} ) = 0$. In addition, at $x = {x_m}$ where the primary component of the bichromatic wave breaks, we have $2\sqrt {2}{A_1}( {{x_m}} ) = \gamma h( {{x_m}} )$ and $\tau (x_{m})={\rm \pi} / 2$ according to (5.5).

The derivative of (5.4) gives the forcing term for governing equation of the subharmonic:

(5.7)\begin{equation} \frac{{{\mathrm{d}^2}{{\hat S}^{\left( {{B}} \right)}}}}{{\mathrm{d}\,{x^2}}} = \frac{2}{{\rm \pi} }\left( {\frac{{{\mathrm{d}^2}{{\bar S}^{\left( {{I}} \right)}}}}{{d{x^2}}} - \frac{{{\mathrm{d}^2}{{\bar S}^{\left( {{{II}}} \right)}}}}{{d{x^2}}}} \right)\sin \tau + \frac{2}{{\rm \pi} }\left( {\frac{{\mathrm{d}{{\bar S}^{\left( {{I}} \right)}}}}{{\mathrm{d}\,x}} - \frac{{\mathrm{d}{{\bar S}^{\left( {{{II}}} \right)}}}}{{\mathrm{d}\,x}}} \right)\cos \tau \frac{{{\rm d}\tau }}{{\mathrm{d}\,x}}, \end{equation}

where $\mathrm {d}\tau /\mathrm {d}\,x$ can be obtained from the derivatives of (5.5) and (5.6):

(5.8)\begin{equation} \frac{{\mathrm{d}\tau }}{{\mathrm{d}\,x}} ={-} \frac{{\gamma {h_x}}}{2\sqrt{2}{{A_1}\delta \sin \tau }}\left( {\frac{h}{{2{c_g}}}\frac{{{\rm d}{c_g}}}{{{\rm d}h}} + 1} \right) + O\left( \delta \right). \end{equation}

Positive and negative $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ indicate the forcing term is in phase or antiphase with the wave group at ${x_c}$, because the excursion of region B was small, and the group phase variation was neglected.

Substituting the shallow-water approximation $c_g\approx c\approx \sqrt {gh}$ and (5.8) into (5.7) yields

(5.9) \begin{equation} \frac{8{\rm \pi} }{{3\rho g{\gamma ^2}h_x^2}}\frac{{{\mathrm{d}^2}\hat S_1^{({{B}})}}}{{\mathrm{d}\,{x^2}}} = \Biggl[ {1 - 3{{\left( {\frac{{{A_1}}}{{\gamma h}}} \right)}^2}} \Biggr]\sin \tau + \frac{5\sqrt{2}}{16}\frac{{\gamma h}}{{{A_1}\delta }}\Biggl[ {1 + 2{{\left( {\frac{{{A_1}}}{{\gamma h}}} \right)}^2}} \Biggr]\left( { - \cot \tau } \right). \end{equation}

The second term on the right-hand side in (5.9) is of leading order $O({\delta ^{ - 1}})$, thus determining the sign of $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$. In the outer half of region B (${x_m} < x < {x_c}$), $0 < \tau <{\rm \pi} /2$ and $- \cot \tau < 0$, hence $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2} < 0$; in the inner half (${x_a} < x < {x_m}$), ${\rm \pi} /2<\tau <{\rm \pi}$ and $- \cot \tau > 0$, hence $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}> 0$. According to (3.34), at leading order, $\mathrm {d}^2\hat S/\mathrm {d}\,x^2$ prior to breaking is in antiphase with the wave group, and the above result indicates that the opposite is true once wave groups pass ${x_m}$. Therefore, the subharmonic locally generated in region B ($\hat \xi _{( {{B}} )}^+$) interferes with the subharmonic entering region B constructively seaward of ${x_m}$, but destructively shoreward of ${x_m}$ (figure 9).

Figure 9. Diagram of phase difference between the downwave-propagating subharmonic ($\hat \xi _g^+$) entering the moving-breakpoint region B in figure 8 at $x=x_c$ and the downwave component generated in region B ($\hat \xi _{( {{B}} )}^+$). Here $\Delta \varphi \leq {\rm \pi}/ 2$ denotes a certain phase lag between $\hat \xi _g^+ ( {{x_c}} )$ and radiation stress in addition to ${\rm \pi}$, which is developed during shoaling prior to breaking.

The overall effect of group forcing in region B depends on the spatial variation of the source field magnitude. Substituting (5.9) into (3.2), (3.36) and (3.7), the source field in region B, $\hat \sigma ^{({\rm B})}$, is given by

(5.10)\begin{equation} \frac{{64{\rm \pi} }}{{15\mathrm{i}h_x^2}}{\hat \sigma ^{({{B}})}} = \frac{{{\gamma ^2}}}{\delta }\frac{1}{{{k_f}h}}\left( {\frac{{\gamma h}}{{2\sqrt{2}{A_1}}} + \frac{1}{4}\frac{{2\sqrt{2}{A_1}}}{{\gamma h}}} \right)\left( { - \cot \tau } \right) + O\left( 1 \right). \end{equation}

Given that $A_1 \propto c_g^{-0.5} \propto h^{ - 1/4}$ (5.6) and $2\sqrt {2}A_1( x_m ) = \gamma h( {{x_m}} )$, the coefficient of $- \cot \tau$ in the above equation reduces to

(5.11)\begin{equation} \frac{1}{k_{f} h}\left(\frac{\gamma h}{2\sqrt{2}A_{1}}+\frac{1}{4} \frac{2\sqrt{2}A_{1}}{\gamma h}\right)=\frac{1}{\omega_{g}} \sqrt{\frac{g}{h\left(x_{m}\right)}}\left\{\left[\frac{h}{h\left(x_{m}\right)}\right]^{3 / 4}+\frac{1}{4}\left[\frac{h}{h\left(x_{m}\right)}\right]^{{-}7 / 4}\right\} . \end{equation}

Because $\gamma h / (2\sqrt {2}A_{1})=[A_{1}(x_{m}) / h(x_{m})] /(A_{1} / h)=[h / h(x_{m})]^{5 / 4}$ and $\gamma h \geqslant 2\sqrt {2}{A_1} ( {1 - \delta } )$, for $\delta < 0.23$, we have $h / h(x_{m}) =(\gamma h / 2\sqrt {2}A_{1})^{4 / 5} \geq (1-\delta )^{4 / 5}>0.81$ and (5.11) decreases with decreasing depth. Thus the source field $\hat \sigma ^{({\rm B})}$ is stronger in the outer than in the inner half of region B; therefore, the downwave subharmonic is slightly enhanced over region B.

As an example of applying the present solution to the moving-breakpoint forcing model, the present solution shown in figure 6 is re-calculated here with the forcing term in region B replaced by $\mathrm {d}^{2} \hat {S}^{({B})} / \mathrm {d}\,x^{2}$ in (5.7) and the results are shown as dashed lines in figure 10 (see Appendix B for details of calculation). Note that $\hat \xi _g^-(x)$ in region shoreward of $x_a$ is set to zero because the present model assumes zero groupiness and hence zero group forcing in this region; therefore theoretically no upwave-propagating component of group-induced subharmonic exists. For the same reason, no phase lag was calculated shoreward of $x_a$ where there is no wave group.

Figure 10. Amplitude (a,b) and phase (c,d) of the complex amplitude $\hat \xi (x)$ of the subharmonic surface elevation $\tilde {\xi }(x,t)$ induced by bichromatic wave groups normally incident over a plane sloping bottom. Weakly modulated test case A-4 (a,c) and strongly modulated test case B-5 (b,d) of the flume experiment of Van Noorloos (Reference Van Noorloos2003). Laboratory measurements (circles), the present solution for non-breaking wave $\hat \xi =\hat \xi _g^+ + \hat \xi _{sc} + \hat \xi _g^-$ where $\hat \xi _{sc}$ denotes the downwave free subharmonic generated due to scattering at the slope toe ((B11), black solid lines) and its downwave- and upwave-propagating group-induced subharmonic components, $\hat \xi _g^+$ (blue solid lines) and $\hat \xi _g^-$ (red solid lines) in (B13). The counterpart solution combined with moving-breakpoint forcing model for breaking waves is shown as dashed lines. The yellow shaded area denotes the moving breakpoint within $[x_a,x_c]$. Phase is the phase lag behind wave groups plus ${\rm \pi}$. Note that in (b), the phase of the upwave component $\hat {\xi }_g^-$ was manually shifted by ${\rm \pi}$ for plotting purposes.

In both the weakly and strongly modulated test cases, the present solution predicts the spatial variation of the subharmonic amplitude to be in good agreement with observation, despite that the model was developed for weak modulation initially. As the water depth decreases, the predicted amplitude of the downwave-propagating subharmonic in test A-4 first increases in the outer half of the moving-breakpoint region and then decreases in the inner half by almost the same amount. The trend of the spatial evolution of amplitude is consistent with the analysis above for (5.9) in the case of the weak modulation in test A-4. For the strong modulation case of test B-5, the amplitude of the downwave-propagating component keeps increasing in the moving-breakpoint region. The predicted phase lag between the subharmonic and group deviates from observation in the moving-breakpoint region, possibly due to growing discrepancy between theoretical predictions of the wave group and observations in the surf zone. It is well known that wave groupiness is subject to drastic change after wave breaking, possibly due to greater decay of higher waves (Svendsen & Veeramony Reference Svendsen and Veeramony2001) or the modulation of breaking water depth by group-induced subharmonics (Janssen et al. Reference Janssen, Battjes and van Dongeren2003; Liu & Li Reference Liu and Li2018). Accurate estimation of the wave group phase from observations inside the surf zone would improve the prediction of phase lag. Albeit minor compared to the breaking effect, partial reflections of downwave-propagating components may also be included to further improve the accuracy of theoretical predictions (Contardo et al. Reference Contardo, Lowe, Dufois, Hansen, Buckley and Symonds2023).

6. Future work

The exact form of the solution (3.11) directly relies on the spectral expression for the radiation stress, which is not well established for irregular waves in the surf zone. For bichromatic waves, (2.1) combined with the concept of breaker index results in the steady component of radiation stress solution in the surf zone ${\bar S^{( {{I}} )}}$ in (5.3a) used in the moving-breakpoint forcing model. This approach does not account for the effect of surface rollers, and therefore can be erroneous. For instance, for plunging-type wave breaking, there is little change in the radiation stress between the breakpoint and the plunge point (Bowen, Inman & Simmons Reference Bowen, Inman and Simmons1968), indicating that the radiation stress in the outer surf zone does not decrease with depth as quickly as what is predicted by $\bar S^{( {I} )} \propto h^2$ in (5.3a,b). Accordingly, $\mathrm {d}\bar S^{(I)}/\mathrm {d}\,x$ in (5.7) can be overestimated, as can the growth of downwave-propagating subharmonic in the outer half of the moving-breakpoint region. Similarly, Rijnsdorp, Smit & Zijlema (Reference Rijnsdorp, Smit and Zijlema2014) found that a non-hydrostatic model incapable of reproducing surface rollers tends to over-predict the amplitude of the subharmonic in the moving-breakpoint region. Zou et al. (Reference Zou, Bowen and Hay2006) derived a generalised analytical solution for the vertical distribution of wave radiation stress in the presence of bottom slope, bottom friction and depth-induced wave breaking in the shoaling region and surf zone and conducted field observations to verify the theory. The cross-shore evolution of wave energy is described by the wave energy flux conservation equation including dissipation due to bottom friction and breaking in analogy with a travelling bore as in Thornton & Guza (Reference Thornton and Guza1983). Existing models that account for the surface roller effect, such as those of Svendsen (Reference Svendsen1984) and Dally & Brown (Reference Dally and Brown1995), only consider the steady component of radiation stress that is not responsible for driving the subharmonic. Moreover, despite some efforts (e.g. Reniers et al. Reference Reniers, van Dongeren, Battjes and Thornton2002; Contardo & Symonds Reference Contardo and Symonds2016), the extension of the spectral expression of radiation stress from bichromatic to irregular wave groups in the surf zone is not as straightforward as it is for non-breaking waves. Future work of spectral expression of radiation stress for realistic irregular waves in the surf zone is needed, based on high-resolution datasets of velocity profiles from numerical or physical experiments, as per Ting & Kirby (Reference Ting and Kirby1994), Chang & Liu (Reference Chang and Liu1999), Lin & Liu (Reference Lin and Liu1998), Wang, Zou & Reeve (Reference Wang, Zou and Reeve2009), Kimmoun & Branger (Reference Kimmoun and Branger2007), Bakhtyar et al. (Reference Bakhtyar, Razmi, Barry, Yeganeh-Bakhtiary and Zou2010), Pedrozo-Acuña et al. (Reference Pedrozo-Acuña, Torres-Freyermuth, Zou, Hsu and Reeve2010), Ruju, Lara & Losada (Reference Ruju, Lara and Losada2012), Na, Chang & Lim (Reference Na, Chang and Lim2020) and Xie & Lin (Reference Xie and Lin2022).

In the present theoretical study, the linearised shallow-water equation is used in combination with the moving-breakpoint forcing model for the surf zone. It is necessary to adopt the fully nonlinear shallow-water equation in the nearshore region near the shoreline, where the self-interaction of the subharmonic may lead to energy dissipation in the infragravity band by transferring energy back to the short-wave band (De Bakker et al. Reference De Bakker, Herbers, Smit, Tissier and Ruessink2015, Reference De Bakker, Tissier and Ruessink2016) or even by breaking (Van Dongeren et al. Reference Van Dongeren, Battjes, Janssen, Van Noorloos, Steenhauer, Steenbergen and Reniers2007). Moreover, subharmonics may also gain energy in the inner surf zone through bore merging by modulating the celerity of individual bores (Bonneton & Dupuis Reference Bonneton and Dupuis2001; Sénéchal et al. Reference Sénéchal, Dupuis, Bonneton, Howa and Pedreros2001; Tissier et al. Reference Tissier, Bonneton, Michallet and Ruessink2015), which is highly nonlinear.

The present Green's function-based solution has the potential advantage for practical application in that the Green's function for a certain area is only a function of the whole topography within that area regardless of wave conditions. The local Green's function can be extracted from in situ datasets through data-driven deep learning (Gin et al. Reference Gin, Shea, Brunton and Kutz2021; Boullé, Earls & Townsend Reference Boullé, Earls and Townsend2022) and then used for fast forecasts for any incident wave conditions and group forcing. Furthermore, the forcing term (3.2) can be extended to account for forcing factors other than radiation stress in governing equation (2.16) and then substituted into (3.4).

The present 1-D solution can be extended to two-dimensional wave fields by incorporating two-dimensional radiation stress and replacing the present Green's function for the 1-D shallow-water equation with the two-dimensional counterpart.