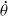Nomenclature
-
 $\alpha $
$\alpha $
-
Angle-of-attack
- c
-
body length
- Cp
-
pressure coefficient
 $\dfrac{2}{{\gamma M_\infty ^2}}\left\{ {\dfrac{p}{{{p_\infty }}} - 1} \right\}$
$\dfrac{2}{{\gamma M_\infty ^2}}\left\{ {\dfrac{p}{{{p_\infty }}} - 1} \right\}$
-
 $C{m_{q\;}}$
$C{m_{q\;}}$
-
 $\dfrac{{2{V_\infty }}}{c}\dfrac{{\partial Cm}}{{\partial q}}$
$\dfrac{{2{V_\infty }}}{c}\dfrac{{\partial Cm}}{{\partial q}}$
-
 $C{m_{\alpha \;}}$
$C{m_{\alpha \;}}$
-
 $\;\dfrac{{{V_\infty }}}{c}\dfrac{{\partial Cm}}{{\partial \alpha }}$
$\;\dfrac{{{V_\infty }}}{c}\dfrac{{\partial Cm}}{{\partial \alpha }}$
- h(x,t)
-
instantaneous height of a point on the body
- l
-
Moment arm
-
 $\rho $
$\rho $
-
Fluid density
-
 $p$
$p$
-
Pressure
-
 ${P_{b,s}}$
${P_{b,s}}$
-
Pressure with blowing or on solid surface
-
 $p_{b,s}^{\prime}$
$p_{b,s}^{\prime}$
-
Pressure perturbation due to unsteadiness
-
 ${P_{ref}}$
${P_{ref}}$
-
Pressure at the reference location
-
 ${P_\infty }$
${P_\infty }$
-
Free stream pressure
- R B
-
Base radius
- R N
-
Nose radius
- S
-
Reference area
-
 $T$
$T$
-
Temperature
- X
-
Axial distance
- V
-
Velocity magnitude
- R(x)
-
Local radius
- Re
-
Reynolds number
-
 $M$
$M$
-
Mach number
- M x
-
Local Mach number
- q
-
pitch rate
- t
-
time for particle to move from apex to station x
-
 $\Delta {\varepsilon _{p\;}}\left( x \right)\;$
$\Delta {\varepsilon _{p\;}}\left( x \right)\;$
-
change in angle of inclination of tangent to (projected) streamline (path line) of a particular fluid element between vertex and point (x, R(x),
 $\varphi$
) on body surface, measured in osculating plane of reference
$\varphi$
) on body surface, measured in osculating plane of reference - θ b (x)
-
local angle of inclination of body surface to axis of symmetry
- θ0
-
slope of the body at the designated apex
- ϑ
-
pitch angle
-
 $\varphi$
$\varphi$
-
azimuthal direction (360-θ) measured clockwise from the starboard radius on the horizontal diameter plane through the vertex
1.0 Introduction
Dynamic stability for vehicles pitching or plunging in hypersonic flow has been studied at length both experimentally and analytically. Dynamic sability at hypersonic Mach numbers is difficult to resolve as the disturbances that influence unsteady aerodynamic loads promoting high-frequency model oscillations are difficult to model. Accounting for the effect of these small-scale disturbances in experiments or through numerical resolution is difficult and times consuming, respectively. In wind tunnel experiments, the model mounted on a cross flexure or held about a typical CG location in a magnetic field is subjected to oscillations under wind-off and wind on hypersonic flow conditions. In more sophisticated free range facilities, the model is literally fired in between two stations up to 100 m apart. The frequency of oscillations trace and the decay in oscillation amplitude trace under wind-on and wind off conditions along with the spring constant readily provides the static (
![]() ${C_{{m_\alpha }}}$
) and dynamic moment coefficients (
${C_{{m_\alpha }}}$
) and dynamic moment coefficients (
![]() ${C_{{m_{\dot \theta }}}}$
). The challenge in the experimental method using short duration facilities is being able to maintain uniform hypersonic flow to obtain at least 10–15 complete oscillation cycles to ascertain accurate and adequate amplitude decay and frequency determination. On the other hand, larger industrial level hypersonic facilities can readily provide the uniform flow for sufficiently long run times to comfortably recover dynamic stability characteristics.
${C_{{m_{\dot \theta }}}}$
). The challenge in the experimental method using short duration facilities is being able to maintain uniform hypersonic flow to obtain at least 10–15 complete oscillation cycles to ascertain accurate and adequate amplitude decay and frequency determination. On the other hand, larger industrial level hypersonic facilities can readily provide the uniform flow for sufficiently long run times to comfortably recover dynamic stability characteristics.
For numerical simulation using CFD techniques, the unsteady flow field past a blunt model executing high-frequency oscillation would be extremely difficult and expensive to resolve. The viscous flow field near the blunt nose would be even more difficult to resolve for an unsteady oscillating model. The use of LES or DNS would put it beyond the reach of most universities as the mesh requirements and other costs related to extensive computational times would be absolutely prohibitive. The iterative computational time step would have to be a very small, as the high-frequency motion would dictate a very small periodic time for a complete cycle necessitating an enormous number of individual time steps at which the required level of density or other lux residual levels are adequately satisfied. One of the first numerical modeling was carried out by Rie et al. [Reference Rie, Linkiewicz and Bosworth1].
Tracking the progress in this discipline, there were important AGARD Refs [Reference Shueler, Ward and Hodapp2, 3], which took a comprehensive stock of the dynamic stability parametres from all experimental and numerical sources. Other important individual contributions have been itemised by Khalid [Reference Khalid and Juhany4, Reference Khalid and Juhany5] in some earlier publications. Beyond solid body dynamic stability investigation for sharp- or blunt-nosed configurations, there have been little effort in recovering static or dynamic moment derivatives when the blowing is turned on at the nose to alleviate any heating effects. For experimental studies, such mechanisms would be difficult to install around the blunt nose, where the flow ejection rates from the solid surface in the local region would have to be higher than the on-coming flow velocities in order to make a noticeable difference to the heating flux. For the numerical studies, even under steady flow conditions it was found that the interaction between the on-coming flow and the strong efflux from the nose leads to complex flow instabilities known as the carbuncle flow phenomenon The flow field continues to show signs of convergence followed by instantaneous breakdown of flow convergence before it begins to converge again. This complexity is only a small part of the problems experienced when simulating unsteady viscous hypersonic flows.
The present work makes use of the more exactly flow field past the blunt models equipped with the blowing near the nose switched on to minimise the heating effects. Dynamic stability for blunt hypersonic vehicles with blowing has not been investigated in any depth in the past. Computation of flow field past blunt axi-symmetric bodies is difficult owing to strong shock effects and complexity of flow in the blunt-nose region where the flow passes through subsonic to sonic to hypersonic flow regimes in a very small region of the flow. When the flow is equipped with surface blowing out of the blunt surface it exacerbates the flow further as the efflux boundary condition is difficult to apply invariably leading to solution breakdown as the solution becomes instable as the physics transforms instantly. It is a non-trivial exercise to successfully recover the steady pressure flow field on a body with efflux and pitching in hypersonic flow field. The resulting steady pressure field is then perturbed using the shock expansion to account for the unsteady effects instead of actually computing the complex and costly unsteady flow field. The effects of immediate angle–of-attack is duly built into the analytic expression before obtaining the appropriate static and dynamic moment coefficients, which are in turn integrated over the surface of the complete model to obtain the dynamic stability characteristics.
In all, four blunt models were investigated, which included two blunt cones of bluntness (R N /R B ) 0.34 and 0.12 with a half-angle of 12.5o, as well as a truncated model flat sharp nosed model having a circular front nose to base diameter ratio of 0.11. In order to assess the effects of tangential blowing as separate from the previous frontal blowing, a round-nosed model of bluntness 0.34 was also investigated. In each case, the results from a corresponding solid model were also computed to identify the isolate the effects of blowing. The steady state results obtained from the computational study were duly compared to the experiment as reported by Nowak [Reference Nowak6]. The results reported by Nowak were directly related to the pure cones studies in this paper. Elsewhere, there have been other more recent flow field studies on non-pure cones carried out by Tissera et al. [Reference Tissera, Drikakis and Birch7] to obtain pressure distribution and heat transfer rates on HB-2 configurations. This study made successful use of the Harten-Lax van Leer contact Riemann solver in conjunction with fifth and nineth order WENO-M schemes as well as the second order MUSCLE scheme. Paranas and Drikakis [Reference Panaras and Drikakis8] have also numerically simulated unsteady flows at high Mach numbers around spiked blunt bodies. The experimental studies as reported by Paranas and Drikakis were also carried out to know the effect of variations to the spike diameter to blunt body. Along similar vein the work by Narayan et al. [Reference Narayan, Suramanian, Kumar and Singh9] numerically and experimentally investigates the flow at M = 5.8 flow past varying nose cone configurations such as taper/stepped taper spiked, spherically blunted, and parabolic nose cones at a fineness ratio of 3.6 and α = 0, in order to determine the best passively modified geometry that provides the control of both the aerodynamic drag coefficient and surface heat flux. Another important by Wantabe et al. [Reference Watanabe10] study involves investigating the flow field by allowing the air at M = 7 to enter the stagnation region at the blunt nose and ejected at the base. The alleviation of pressure at the nose and suction at the nose should allegedly lead to at least 5% drag reduction.
Other than the Newak [Reference Nowak6] work dealing with simple conical shapes, most of the above cases deal with spiked models or the HP-2 configurations. Steady pressure distributions were suitably perturbed using the shock expansion technique and the deflection of the surface streamlines as the underlying body oscillates. It was learnt in all cases that blowing leads to deterioration in dynamic stability performance. A parallel observation for dynamic stability of blunt cones was that using classic universal curve for steady pressure field indiscriminately for blunt cones of any bluntness may lead to erroneous result.
2.0 Computational approach to steady flow field with and without frontal blowing
The conservative form of the compressible Reynolds-Averaged Navier-Stokes equations as used in the algorithm is as follows:
ρ in these equations refers to the density, p the pressure and T is the temperature. E is the total energy and u is the velocity vector in tensor format. τ ij is the viscous stress tensor which may be written as:
The above Navier Stokes equations, formulated in strong conservation form to be used in the structured meshes of the present study, are first cast into curvilinear coordinate scheme following Vinokur [Reference Vinokur11] transformation method. The numerical algorithm used to solve the Navier Stokes equations is an implicit factorisation finite centre difference scheme about a regular rectangular prism, which is described at length by Beam and Warming [Reference Beam and Warming12]. Local time linearisation is applied to the non-linear terms following Pulliam and Chausee [Reference Pulliam and Chaussee13]. Approximate factorisation scheme is applied to the resulting matrices, which factorises the operator itself resulting in efficient matrix equations with narrow bandwidth. This results in block tridiagonal matrices, which are easy to solve. The spatial derivatives can thus be approximated using second order central differences. Explicit and implicit artificial dissipation terms are added to achieve nonlinear stability. A spatially variable time step is used to accelerate convergence to steady state solutions. The algorithm can be used to solve time accurate or steady state flow problems.
The fact that the Navier Stokes equations are formulated in a strong conservation form as well as the implicit treatment of the artificial dissipation and the inclusion of a second order dissipation terms helps in the shock capturing at high Mach numbers.
We selected k-
![]() $\varepsilon $
and the Wilcox k-
$\varepsilon $
and the Wilcox k-
![]() $\omega $
turbulence models for this investigation. For the two equations turbulence models, the convection and diffusion terms of their transport equations are negligible in the inertial sublayer so that local equilibrium prevails, which implies that the production of the turbulent kinetic energy k is equal to the dissipation rate. The local equilibrium condition leads to two simple relations that can be used as boundary conditions for k and the dissipation terms for both incompressible and compressible flows. The compressible wall functions have been successfully applied to both attached and separated flows under Mach number ranging from 0.1 to 10.
$\omega $
turbulence models for this investigation. For the two equations turbulence models, the convection and diffusion terms of their transport equations are negligible in the inertial sublayer so that local equilibrium prevails, which implies that the production of the turbulent kinetic energy k is equal to the dissipation rate. The local equilibrium condition leads to two simple relations that can be used as boundary conditions for k and the dissipation terms for both incompressible and compressible flows. The compressible wall functions have been successfully applied to both attached and separated flows under Mach number ranging from 0.1 to 10.
While the purpose in this study was not to scrutinise the capabilities of the turbulence models, nevertheless for these simple bodies, very little difference in results was observed from the two turbulence models. The Sutherland law is implemented to compute the laminar viscosity coefficient (
![]() $\mu $
). Since the flows computed involve hypersonic Mach number the choice of the Prandtl number is selected to suite the Mach number whereas the use of specific heat and the specific heat ratio c
p
/c
v
(γ) in the algorithm for one species gas must also respect the high Mach number flow conditions subject to the relations by Grundmann [Reference Grundmann14] and Gordon and McBride [Reference Gordon and McBride15]:
$\mu $
). Since the flows computed involve hypersonic Mach number the choice of the Prandtl number is selected to suite the Mach number whereas the use of specific heat and the specific heat ratio c
p
/c
v
(γ) in the algorithm for one species gas must also respect the high Mach number flow conditions subject to the relations by Grundmann [Reference Grundmann14] and Gordon and McBride [Reference Gordon and McBride15]:
 \begin{equation*}{c_v}\!\left( T \right) = R\left( {\dfrac{5}{2} + \;\dfrac{{\left( {{{\dfrac{{hv}}{{kT}}}^2}} \right){e^{{\raise0.7ex\hbox{${hv}$} \!\mathord{\big/ }\!\lower0.7ex\hbox{${kT}$}}}}}}{{{{\left( {{e^{\dfrac{{hv}}{{kT}}}} - 1} \right)}^2}}}} \right),\;\;\;\;\;\;{c_p}\!\left( T \right) - {c_v}\!\left( T \right) = R\end{equation*}
\begin{equation*}{c_v}\!\left( T \right) = R\left( {\dfrac{5}{2} + \;\dfrac{{\left( {{{\dfrac{{hv}}{{kT}}}^2}} \right){e^{{\raise0.7ex\hbox{${hv}$} \!\mathord{\big/ }\!\lower0.7ex\hbox{${kT}$}}}}}}{{{{\left( {{e^{\dfrac{{hv}}{{kT}}}} - 1} \right)}^2}}}} \right),\;\;\;\;\;\;{c_p}\!\left( T \right) - {c_v}\!\left( T \right) = R\end{equation*}
Where T is temperature, R is the real gas constant, h is Planck’s constant, v is the fundamental vibrational frequency and k is Boltzman’s constant, and where
![]() ${a_n}$
are curve-fit constants. As explained in Khalid and Juhany [Reference Khalid and Juhany16] the input flow conditions (ρ, ρu
i
, E) for the outflow surface are treated like a new ‘slip’ condition, which remains fixed during the flow applied run. The algorithm iterates between the successive grid planes near the exit control boundary until the desired flow conditions are matched at the exit boundary as the convergence criterion is reached. For the corresponding solid surface run this surface would understandably carry a no-slip boundary condition. Since the present applications of the code deals with axi-symmetric flow fields produced when a simple two-dimensional mesh is rotated about the body axis through a 45° azimuthal angle. The flow has to be carefully treated near the polar stations. In such cases a computational coordinate surface may represent a physical 3D line. For example, with an “O” grid the circles (2D) or cylinders (3D) collapse to points and lines, respectively. The flow variables at the singular boundary are the average of the points surrounding the singular point.
${a_n}$
are curve-fit constants. As explained in Khalid and Juhany [Reference Khalid and Juhany16] the input flow conditions (ρ, ρu
i
, E) for the outflow surface are treated like a new ‘slip’ condition, which remains fixed during the flow applied run. The algorithm iterates between the successive grid planes near the exit control boundary until the desired flow conditions are matched at the exit boundary as the convergence criterion is reached. For the corresponding solid surface run this surface would understandably carry a no-slip boundary condition. Since the present applications of the code deals with axi-symmetric flow fields produced when a simple two-dimensional mesh is rotated about the body axis through a 45° azimuthal angle. The flow has to be carefully treated near the polar stations. In such cases a computational coordinate surface may represent a physical 3D line. For example, with an “O” grid the circles (2D) or cylinders (3D) collapse to points and lines, respectively. The flow variables at the singular boundary are the average of the points surrounding the singular point.
The flow field as recovered from using above CFD method on a solid blunt cone of bluntness 0.34 and the same body with frontal blowing rate of
![]() $\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.576\;$
are shown in Fig. 1. The outflow at the leading edge was only implemented around the front blunt nose. Following the hypersonic heat alleviation experiment [Reference Nowak6], the efflux rate here corresponds to mass rate of 2.09 kg/s. A similar study was conducted on a blunt cone of bluntness 0.12.
$\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.576\;$
are shown in Fig. 1. The outflow at the leading edge was only implemented around the front blunt nose. Following the hypersonic heat alleviation experiment [Reference Nowak6], the efflux rate here corresponds to mass rate of 2.09 kg/s. A similar study was conducted on a blunt cone of bluntness 0.12.

Figure 1. Mach number (solid surface) and velocity vectors (with frontal blowing) past a blunt cone of bluntness 0.32.
Another blunt Gasjet configuration with a flat frontal surface of the same circular cross section as the 0.12 blunt cone was computed at a Mach number of M = 6.8. The Mach number distribution and velocity vectors for the truncated blunt frontal nose are shown in Fig. 2.

Figure 2. Mach number distribution past a solid blunt cone of (left) and with blowing (right).
A feature of particular bearing on flow stability is the inherent unsteady flow field (Fig. 3, right), which evolves as a result of the high Mach number flow field being confronted by the outflow immediately in front of the flat front surface. As discussed by Khalid and Juhany [Reference Khalid and Juhany17], the flow seems to be numerically instable as the solution seems to converge followed by a breakdown of the flow field uniformity and deterioration of convergence. This behaviour seems to repeat near the convergence. This type of flow behaviour as discussed in reference [Reference Garicano-Mena, Lani and Deconinck18, Reference Ismail and Roe19] is due to the carbuncle instability phenomenon.

Figure 3. Gasjet experiment by Nowak (Ref. Reference Panaras and Drikakis8) M = 6.8, with a frontal blowing rate of,
![]() $\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
(left). Note the unsteady flow near the leading edge (right).
$\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
(left). Note the unsteady flow near the leading edge (right).
It was observed in both computations and the shadowgraph that the outflow at the nose causes the stagnation region to be blown outwards in a spherical bubble shape pushing against the frontal shock. Note the presence of the supersonic bubble inside of the main shock. The flow region in between the main jet interface and the nozzle shock contains the slower expanded flow in both simulation and the experiment.
The final set of results deal with a 0.32 bluntness cone with shoulder peripheral blowing just past the spherical nose. The flow field with and without the blowing from the shoulder jet of the Slatjet is shown in Fig. 4. It is clear from the viewgraph with shoulder blowing that the boundary layer is blown off from the surface with the strong peripheral jet from the shoulder.

Figure 4. Slatjet solid model (top) and with shoulder blowing (bottom), blowing rate =
![]() $\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
.
$\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
.
The most important aspect of the present study was to be able to recover the steady pressure fields from above cases which are then in turn used in the following analysis to recover dynamic stability characteristics of blunt bodies. The pressure fields for the above blunt-nosed case bodies are shown in the following Fig. 5. While grid sensitivity study and the numerical error has been discussed in Khalid and Juhany [Reference Khalid and Juhany16, Reference Khalid and Juhany17], it can be seen that the prediction especially on the straight portion of the model lies within 1–2% of the experiment.

Figure 5. Pressure distributions on blunt-nosed bodies: R3 (a), R1 (b), Gasjet (c) and Slat-jet (d).
The pressure distributions as computed on the blunt models showed satisfactory agreement with the measurements on the straight potion away from the blunt nose. The comparison for the blunt region was difficult, as no measurements had been recorded for this region.
3.0 Analytic approach to dynamic stability from steady flow field
The analytic approach relies on being able to obtain of a reliable pressure flow field and then using the classic shock expansion approach to perturb this solution. The angular displacement of a typical streamline near the surface of the body can be evaluated in terms of the pitch rate, the body half-angle and the flow velocity. The steady pressure distribution in all cases as discussed in previous discussion was used from existing results on heat alleviation study [Reference Khalid and Juhany16, Reference Khalid and Juhany17] on blunt conical bodies in hypersonic flow. The unsteady pressure at small angles of attack on an oscillating blunt body with or without blowing may be expressed in terms of the steady and unsteady component:
Where, the subscripts b and s refer to either solid or frontal blowing condition and
![]() $p_{b,s}^{\prime}$
refer to the instantaneous perturbation value as results of the body oscillations.
$p_{b,s}^{\prime}$
refer to the instantaneous perturbation value as results of the body oscillations.
The unsteady pressure perturbation
![]() $p_{b,s}^{\prime}$
may be evaluated from the shock expansion expression as developed by Eggers [Reference Eggers20]. The shock expansion as used here will be drawn from Refs [Reference Khalid and East21, Reference Khalid and East22] without entering too much detail. Hence:
$p_{b,s}^{\prime}$
may be evaluated from the shock expansion expression as developed by Eggers [Reference Eggers20]. The shock expansion as used here will be drawn from Refs [Reference Khalid and East21, Reference Khalid and East22] without entering too much detail. Hence:
which gives,
 \begin{equation}\frac{{{P_{b,s}}\!\left( {x,\alpha ,t} \right)}}{{{P_{b,s}}\!\left( {x,\alpha } \right)}} = 1 + \;\;\frac{{\gamma M_x^2}}{{\sqrt {(M_x^2} - 1)}}\Delta {\varepsilon _p}\!\left( x \right)\end{equation}
\begin{equation}\frac{{{P_{b,s}}\!\left( {x,\alpha ,t} \right)}}{{{P_{b,s}}\!\left( {x,\alpha } \right)}} = 1 + \;\;\frac{{\gamma M_x^2}}{{\sqrt {(M_x^2} - 1)}}\Delta {\varepsilon _p}\!\left( x \right)\end{equation}
Where
![]() $\Delta {\varepsilon _p}$
is the angular change of a particle from the body vertex to a station x along the body subject to a motion schedule involving plunging and or pitching motion. This angular change may be written in terms of the instantaneous height of the particle h(x,t) and the expansion of the streamline along which it traverses. Thus following Scott [Reference Scott23],
$\Delta {\varepsilon _p}$
is the angular change of a particle from the body vertex to a station x along the body subject to a motion schedule involving plunging and or pitching motion. This angular change may be written in terms of the instantaneous height of the particle h(x,t) and the expansion of the streamline along which it traverses. Thus following Scott [Reference Scott23],
This inclination angle
![]() $\Delta {\varepsilon _{p\;}}\left( x \right)$
of a path line projected on the surface of the body in purely pitching motion can be shown [Reference Khalid and Juhany16] as:
$\Delta {\varepsilon _{p\;}}\left( x \right)$
of a path line projected on the surface of the body in purely pitching motion can be shown [Reference Khalid and Juhany16] as:
 \begin{align}&\Bigg\{ 2x + \;\tan {\theta _{0\;}}.\left[ {\mathop \smallint \nolimits_0^x \left( {{\theta _b}\!\left( x \right) - \;{\theta _0}} \right)dx - \left( {x - \;{x_0}} \right).\left( {{\theta _b}\!\left( x \right) - {\theta _0}} \right)} \right] \nonumber\\ & + \frac{1}{{\sqrt {M_\infty ^2 - 1} }}.\;\;\left[ {\mathop \smallint \nolimits_0^x \left( {{\theta _b}\!\left( x \right) - \;{\theta _0}} \right)dx - \left( {x - \;{x_0}} \right).\left( {{\theta _b}\!\left( x \right) - {\theta _0}} \right)} \right] \Bigg\}\end{align}
\begin{align}&\Bigg\{ 2x + \;\tan {\theta _{0\;}}.\left[ {\mathop \smallint \nolimits_0^x \left( {{\theta _b}\!\left( x \right) - \;{\theta _0}} \right)dx - \left( {x - \;{x_0}} \right).\left( {{\theta _b}\!\left( x \right) - {\theta _0}} \right)} \right] \nonumber\\ & + \frac{1}{{\sqrt {M_\infty ^2 - 1} }}.\;\;\left[ {\mathop \smallint \nolimits_0^x \left( {{\theta _b}\!\left( x \right) - \;{\theta _0}} \right)dx - \left( {x - \;{x_0}} \right).\left( {{\theta _b}\!\left( x \right) - {\theta _0}} \right)} \right] \Bigg\}\end{align}
where,
![]() ${\theta _0}$
is the angle at the vertex and
${\theta _0}$
is the angle at the vertex and
![]() ${\theta _b}\!\left( x \right)$
is the inclination of the surface at the stations x.
${\theta _b}\!\left( x \right)$
is the inclination of the surface at the stations x.
![]() $\;q$
is the body pitch rate, is the magnitude of the free stream velocity at the nose and
$\;q$
is the body pitch rate, is the magnitude of the free stream velocity at the nose and
![]() ${M_\infty }$
is the Mach number, which corresponds to the free stream velocity at the nose. For a conical body with constant surface slope (
${M_\infty }$
is the Mach number, which corresponds to the free stream velocity at the nose. For a conical body with constant surface slope (
![]() ${\theta _b}\!\left( x \right) = {\theta _0}),$
the above expression simplifies to:
${\theta _b}\!\left( x \right) = {\theta _0}),$
the above expression simplifies to:
and the effective angle-of-attack of the body pitching at q and instantaneous pitch angle
![]() $\vartheta $
is given by:
$\vartheta $
is given by:
The unsteady pressure can thus be written in terms of the instantaneous pressure perturbation and the effects from pitch rate and the effective angle-of-attack.
The pressure distribution of a body at angle–of-attack with respect to the pressure at zero angle-of-attack is given by [Reference Krasnov24]
and where
![]() $\dfrac{{{P_{x,ref}}}}{{{P_\infty }}}$
represents the location on the spherical nose where the supersonic condition are first reached. This leads us to write the unsteady pressure coefficient as:
$\dfrac{{{P_{x,ref}}}}{{{P_\infty }}}$
represents the location on the spherical nose where the supersonic condition are first reached. This leads us to write the unsteady pressure coefficient as:
Static and pitching moment derivatives can now be obtained by obtaining
![]() $\dfrac{{\partial {C_{p\left( {b,s} \right)}}}}{{\partial \alpha }}$
and
$\dfrac{{\partial {C_{p\left( {b,s} \right)}}}}{{\partial \alpha }}$
and
![]() $\dfrac{{\partial {C_{p\left( {b,s} \right)}}}}{{\partial q}}$
and integrating the expression over the complete surface of the blunt body under solid and frontal blowing conditions, i.e.
$\dfrac{{\partial {C_{p\left( {b,s} \right)}}}}{{\partial q}}$
and integrating the expression over the complete surface of the blunt body under solid and frontal blowing conditions, i.e.
![]() $l\!\left( x \right)$
is the moment ars
$l\!\left( x \right)$
is the moment ars
![]() $l = x\;Se{c^2}{\theta _0} - \;{x_0}$
and
$l = x\;Se{c^2}{\theta _0} - \;{x_0}$
and
![]() $R\!\left( x \right)$
is the local radius at station x. Pressure distribution for the blunt body under solid and blowing condition were successively introduced in the expression for the static and dynamic stability derivatives to obtain the stability characteristics. The above expression for
$R\!\left( x \right)$
is the local radius at station x. Pressure distribution for the blunt body under solid and blowing condition were successively introduced in the expression for the static and dynamic stability derivatives to obtain the stability characteristics. The above expression for
![]() $C{m_{q\;}}$
assumes that the
$C{m_{q\;}}$
assumes that the
![]() $\dot \alpha $
effects in the expression
$\dot \alpha $
effects in the expression
![]() $C{m_{\dot \theta }}$
are very small and, in fact,
$C{m_{\dot \theta }}$
are very small and, in fact,
![]() $C{m_{\dot \theta }}$
=
$C{m_{\dot \theta }}$
=
![]() $C{m_{q\;}}$
.
$C{m_{q\;}}$
.
4.0 Results
Static and dynamic derivatives were computed for the blunt configurations discussed above. For consistency, and also due to absence of measured date in the nose region, only the computed pressure fields were introduced into the expressions for static and dynamic derivatives. The static derivative
![]() $C{m_{\alpha \;}}$
for the blunt cones is shown on the left side of Fig. 6.
$C{m_{\alpha \;}}$
for the blunt cones is shown on the left side of Fig. 6.

Figure 6. Static stability derivative (left) and dynamic stability derivative versus X0/C.

Figure 7. Staic stability (left) and dynamic stability derivatives for the Gasjet and Slatjet versus X0/C.
The sharp cone result for the 12.5 deg half-angle (θo) is only introduced as a reference. The constant surface pressure from the conical relationships was Pc/P∞ = 3.94, and the surface Mach number used was M = 5.12. It is clear that for axis position ahead of X0 = 0.66, the static stability deceases with increasing bluntness for the two blunt cones when compared to a corresponding sharp cone. The trend reverses after X0 = 0.66. It was learnt that the frontal blowing has no noticeable effect on the static stability. The blunt cones do, however, show that bluntness causes a consistent decrease in dynamic stability for all axis positions. It is also noted that, for cones of large bluntness, the blowing leads to deterioration in dynamic stability. For cones of smaller bluntness, the frontal blowing only has a relatively smaller surface area through which the outflow can be pumped, whereas the cones of larger bluntness will have a larger region through which the outflow can be effectuated, which leads to a relative larger interplay against the oncoming flow.
Examining the flow field physically, it appears that the flow impacting on the nose is opposed by the flow emerging from the blunt nose, which comprises the existing dynamic instability
![]() $C{m_q}$
between the flow and pitching cone. Increasing the bluntness leads to increasing interference between the flow and the underlying oscillating flow. This is certainly borne out by the fact that cones with larger bluntness experience incrementally more deterioration in dynamic stability. Since the effective angle-of-attack,
$C{m_q}$
between the flow and pitching cone. Increasing the bluntness leads to increasing interference between the flow and the underlying oscillating flow. This is certainly borne out by the fact that cones with larger bluntness experience incrementally more deterioration in dynamic stability. Since the effective angle-of-attack,
![]() ${\alpha _e} = \;\vartheta - \dfrac{{q\left( {x\sec {\theta _0} + {\theta _0}} \right)}}{{{V_\infty }}}$
is not too adversely affected by the efflux from the blunt nose, the static stability
${\alpha _e} = \;\vartheta - \dfrac{{q\left( {x\sec {\theta _0} + {\theta _0}} \right)}}{{{V_\infty }}}$
is not too adversely affected by the efflux from the blunt nose, the static stability
![]() $C{m_\alpha }$
remains unaffected by blowing.
$C{m_\alpha }$
remains unaffected by blowing.
The static and dynamic derivative response against axis of oscillation position X/0/C for the Gasjet and the Slatjet are shown in Fig. 7. Once again the static stability derivative
![]() $C{m_{\alpha \;}}$
, although shows a loss in stability with increased level of bluntness whether for the Gasjet or the Slatjet, yet the blowing does not cause any noticeable difference to the staic stability. The dynamic stability derivate
$C{m_{\alpha \;}}$
, although shows a loss in stability with increased level of bluntness whether for the Gasjet or the Slatjet, yet the blowing does not cause any noticeable difference to the staic stability. The dynamic stability derivate
![]() $C{m_q}$
, however, is affected by the bluntness as well as by the blowing. The Gasjet, which is equipped with a flat surface to incorprate appropriate blowing, is most effective for creating a cooling bubble in front of the blunt nose. This cooling bubble produces a virtual bluntness which causes a depreciation of dynamic stability. Thus cooling in front leads to a decrease in dynamic stability derivative
$C{m_q}$
, however, is affected by the bluntness as well as by the blowing. The Gasjet, which is equipped with a flat surface to incorprate appropriate blowing, is most effective for creating a cooling bubble in front of the blunt nose. This cooling bubble produces a virtual bluntness which causes a depreciation of dynamic stability. Thus cooling in front leads to a decrease in dynamic stability derivative
![]() $C{m_q}$
when compared to the solid Gasjet body. The Slatjet experment had used a small value of blowing
$C{m_q}$
when compared to the solid Gasjet body. The Slatjet experment had used a small value of blowing
![]() $\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
from the peripheral shoulder, which when applied at the aft conical surface of the Slatjet, may make a difference to the underlying heating rate, but it makes little difference to the dynamic stability derivative.
$\dfrac{{\rho {u_{\;local}}}}{{{\rho _\infty }{u_\infty }}} = 0.15$
from the peripheral shoulder, which when applied at the aft conical surface of the Slatjet, may make a difference to the underlying heating rate, but it makes little difference to the dynamic stability derivative.
Once again, interpreting the flow physically, the model with larger efflux against the on-coming flow experiences larger adverse effect from blowing. The Gasjet model with a notably large blowing frontal area opposing the incoming flow and supporting a spherical flow bubble experiences the largest drop in dynamic stability for almost all axis locations upstream of X0/C = 0.8. Beyond X0/C the bluntness and blowing effects are reduced as additional mass flow gives rise to body thickness effects showing some increase in dynamic stability. The slatjet, introduced tangentially into the flow field past the blunt surface region does not interfere as much with the incoming flow and the underlying blunt body. The slatjet may help with heat alleviation but does not adversely affect the dynamic stability. The static stability as alluded to earlier, depends directly upon the instantaneous angle-of-attack and is not affected by the pitching conditions q or
![]() $\dot \vartheta $
.
$\dot \vartheta $
.
5.0 Conclusion
The present analytic modeling shows that the static stability derivative is not too adversely by blowing as the expression for
![]() $C{m_{\alpha \;}}$
is driven largely by the steady pressure distribution and not by the pitching conditions q or
$C{m_{\alpha \;}}$
is driven largely by the steady pressure distribution and not by the pitching conditions q or
![]() $\;\dot \vartheta $
. The dynamic stability appears to depreciate with both bluntness and blowing rate. Cones of smaller bluntness cannot be equipped to force excessive outflow from small blunt regions and thus their stability is not affected by blowing.
$\;\dot \vartheta $
. The dynamic stability appears to depreciate with both bluntness and blowing rate. Cones of smaller bluntness cannot be equipped to force excessive outflow from small blunt regions and thus their stability is not affected by blowing.
Dynamic stability of cones with sharp square-edged frontal bluntness equipped with blowing suffer more than the cones with tangential shoulder blowing. This is because the sharp edge in front traps a larger region of slower air bubble than simple rounded nose, which smoothly diverts the air downstream. The incoming flow is disturbed with larger bluntness and blowing leading to depreciation of
![]() $\;C{m_q}$
.
$\;C{m_q}$
.
Competing interests
The authors declare none.