Hostname: page-component-6bf8c574d5-86b6f Total loading time: 0 Render date: 2025-03-07T03:38:27.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolving an open problem on the hazard rate ordering of p-spacings

Published online by Cambridge University Press:  11 November 2022

Mahdi Alimohammadi Open the ORCID record for Mahdi Alimohammadi [Opens in a new window]
Mahdi Alimohammadi*
Affiliation:
Department of Statistics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

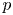Let $V_{(r,n,\tilde {m}_n,k)}^{(p)}$ and $W_{(r,n,\tilde {m}_n,k)}^{(p)}$ be the $p$-spacings of generalized order statistics based on absolutely continuous distribution functions 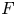$F$ and 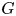$G$, respectively. Imposing some conditions on $F$ and 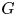$G$ and assuming that 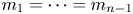$m_1=\cdots =m_{n-1}$, Hu and Zhuang (2006. Stochastic orderings between p-spacings of generalized order statistics from two samples. Probability in the Engineering and Informational Sciences 20: 475) established 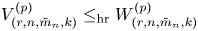$V_{(r,n,\tilde {m}_n,k)}^{(p)} \leq _{{\rm hr}} W_{(r,n,\tilde {m}_n,k)}^{(p)}$ for 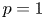$p=1$ and left the case 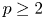$p\geq 2$ as an open problem. In this article, we not only resolve it but also give the result for unequal 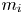$m_i$'s. It is worth mentioning that this problem has not been proved even for ordinary order statistics so far.

Keywords

LogconvexityStochastic comparisonsTotal positivity
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 37 , Issue 4 , October 2023 , pp. 1020 - 1028
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alimohammadi, M. & Alamatsaz, M.H. (2011). Some new results on unimodality of generalized order statistics and their spacings. Statistics and Probability Letters 81(11): 1677–1682.CrossRefGoogle Scholar
Alimohammadi, M., Alamatsaz, M.H., & Cramer, E. (2014). Some convexity properties of the distribution of lower k-record values with extensions. Probability in the Engineering and Informational Sciences 28(3): 389–399.CrossRefGoogle Scholar
Alimohammadi, M., Alamatsaz, M.H., & Cramer, E. (2016). Convolutions and generalization of logconcavity: Implications and applications. Naval Research Logistics 63(2): 109–123.CrossRefGoogle Scholar
Alimohammadi, M., Esna-Ashari, M., & Navarro, J. (2021). Likelihood ratio comparisons and logconvexity properties of $p$-spacings from generalized order statistics. Probability in the Engineering and Informational Sciences 1–20. doi:10.1017/S0269964821000498Google Scholar
Balakrishnan, N. & Cramer, E. (2014). The art of progressive censoring. Applications to reliability and quality. New York: Birkhäuser.CrossRefGoogle Scholar
Belzunce, F., Lillo, R.E., Ruiz, J.M., & Shaked, M. (2001). Stochastic comparisons of nonhomogeneous processes. Probability in the Engineering and Informational Sciences 15(2): 199–224.CrossRefGoogle Scholar
Belzunce, F., Mercader, J.A., & Ruiz, J.M. (2005). Stochastic comparisons of generalized order statistics. Probability in the Engineering and Informational Sciences 19(1): 99–120.CrossRefGoogle Scholar
Block, H.W., Savits, T.H., & Singh, H. (1998). The reversed hazard rate function. Probability in the Engineering and informational Sciences 12(1): 69–90.CrossRefGoogle Scholar
Cramer, E. & Kamps, U. (1996). Sequential order statistics and $k$-out-of-$n$ systems with sequentially adjusted failure rates. Annals of the Institute of Statistical Mathematics 48(3): 535–549.CrossRefGoogle Scholar
Cramer, E. & Kamps, U. (2003). Marginal distributions of sequential and generalized order statistics. Metrika 58(3): 293–310.CrossRefGoogle Scholar
Cramer, E., Kamps, U., & Rychlik, T. (2004). Unimodality of uniform generalized order statistics, with applications to mean bounds. Annals of the Institute of Statistical Mathematics 56(1): 183–192.CrossRefGoogle Scholar
Franco, M., Ruiz, J.M., & Ruiz, M.C. (2002). Stochastic orderings between spacings of generalized order statistics. Probability in the Engineering and Informational Science 16(4): 471–484.CrossRefGoogle Scholar
Hu, T. & Zhuang, W. (2005). Stochastic properties of $p$-spacings of generalized order statistics. Probability in the Engineering and Informational Sciences 19(2): 257–276.CrossRefGoogle Scholar
Hu, T. & Zhuang, W. (2006). Stochastic comparisons of $m$-spacings. Journal of Statistical Planning and Inference 136(1): 33–42.CrossRefGoogle Scholar
Hu, T. & Zhuang, W. (2006). Stochastic orderings between $p$-spacings of generalized order statistics from two samples. Probability in the Engineering and Informational Sciences 20(3): 465–479.CrossRefGoogle Scholar
Kamps, U. (1995). A concept of generalized order statistics. Journal of Statistical Planning and Inference 48(1): 1–23.CrossRefGoogle Scholar
Kamps, U. (1995). A concept of generalized order statistics. Stuttgart: Teubner.CrossRefGoogle Scholar
Kamps, U. & Cramer, E. (2001). On distributions of generalized order statistics. Statistics 35(3): 269–280.CrossRefGoogle Scholar
Karlin, S. (1968). Total positivity. Stanford, CA: Stanford University Press.Google Scholar
Kochar, S.C. (1999). On stochastic orderings between distributions and their sample spacings. Statistics and Probability Letters 42(4): 345–352.CrossRefGoogle Scholar
Misra, N. & van der Meulen, E.C. (2003). On stochastic properties of $m$-spacings. Journal of Statistical Planning and Inference 115(2): 683–697, 353–373.CrossRefGoogle Scholar
Pellerey, F., Shaked, M., & Zinn, J. (2000). Nonhomogeneous Poisson processes and logconcavity. Probability in the Engineering and Informational Sciences 14(3): 353–373.CrossRefGoogle Scholar
Shaked, M. & Shanthikumar, J.G. (2007). Stochastic orders. New York: Springer.CrossRefGoogle Scholar
Tavangar, M & Asadi, M (2012). Some unified characterization results on the generalized Pareto distributions based on generalized order statistics. Metrika 75: 997–1007.CrossRefGoogle Scholar
Xie, H. & Hu, T. (2009). Ordering $p$-spacings of generalized order statistics revisited. Probability in the Engineering and Informational Sciences 23(1): 1–16.CrossRefGoogle Scholar