Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T07:35:51.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Splash wave and crown breakup after disc impact on a liquid surface

Published online by Cambridge University Press:  29 April 2013

Ivo R. Peters ,
Devaraj van der Meer  and
J. M. Gordillo
Ivo R. Peters
Affiliation:
Department of Applied Physics and J. M. Burgers Centre for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands James Franck Institute, The University of Chicago, Chicago, IL 60637, USA
Devaraj van der Meer
Affiliation:
Department of Applied Physics and J. M. Burgers Centre for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
J. M. Gordillo*
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingenería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we analyse the impact of a circular disc on a free surface using experiments, potential flow numerical simulations and theory. We focus our attention both on the study of the generation and possible breakup of the splash wave created after the impact and on the calculation of the force on the disc. We have experimentally found that drops are only ejected from the rim located at the top part of the splash – giving rise to what is known as the crown splash – if the impact Weber number exceeds a threshold value 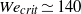${\mathit{We}}_{crit} \simeq 140$. We explain this threshold by defining a local Bond number 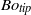$B{o}_{\mathit{tip}} $ based on the rim deceleration and its radius of curvature, with which we show using both numerical simulations and experiments that a crown splash only occurs when 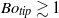$B{o}_{\mathit{tip}} \gtrsim 1$, revealing that the rim disrupts due to a Rayleigh–Taylor instability. Neglecting the effect of air, we show that the flow in the region close to the disc edge possesses a Weber-number-dependent self-similar structure for every Weber number. From this we demonstrate that 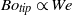${\mathit{Bo}}_{\mathit{tip}} \propto \mathit{We}$, explaining both why the transition to crown splash can be characterized in terms of the impact Weber number and why this transition occurs for 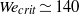$W{e}_{crit} \simeq 140$. Next, including the effect of air, we have developed a theory which predicts the time-varying thickness of the very thin air cushion that is entrapped between the impacting solid and the liquid. Our analysis reveals that gas critically affects the velocity of propagation of the splash wave as well as the time-varying force on the disc, 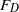${F}_{D} $. The existence of the air layer also limits the range of times in which the self-similar solution is valid and, accordingly, the maximum deceleration experienced by the liquid rim, that sets the length scale of the splash drops ejected when 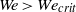$We\gt {\mathit{We}}_{crit} $.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 553 - 580
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergmann, R., van der Meer, D., Gekle, S., van der Bos, A. & Lohse, D. 2009 Controlled impact of a disk on a water surface: cavity dynamics. J. Fluid Mech. 633, 381–409.CrossRefGoogle Scholar
Bergmann, R., van der Meer, D., Stijnman, M., Sandtke, M., Prosperetti, A. & Lohse, D. 2006 Giant bubble pinch-off. Phys. Rev. Lett. 96 (15), 154505.CrossRefGoogle ScholarPubMed
Deegan, R. D., Brunet, P. & Eggers, J. 2008 Complexities of splashing. Nonlinearity 21 (1), C1–C11.CrossRefGoogle Scholar
Duchemin, L. & Josserand, C. 2011 Curvature singularity and film-skating during drop impact. Phys. Fluids 23, 091701.CrossRefGoogle Scholar
Duchemin, L., Popinet, S., Josserand, C. & Zaleski, S. 2002 Jet formation in bubbles bursting at a free surface. Phys. Fluids 14 (9), 3000–3008.CrossRefGoogle Scholar
Ducleaux, V., Caillé, F., Duez, C., Ybert, C., Bocquet, L. & Clanet, C. 2007 Dynamics of transient cavities. J. Fluid Mech. 591, 1–19.CrossRefGoogle Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3 (3), 180–183.CrossRefGoogle Scholar
Gaudet, S. 1998 Numerical simulation of circular disks entering the free surface of a fluid. Phys. Fluids 10 (10), 2489–2499.CrossRefGoogle Scholar
Gekle, S., van der Bos, A., Bergmann, R., van der Meer, D. & Lohse, D. 2008 Noncontinuous Froude number scaling for the closure depth of a cylindrical cavity. Phys. Rev. Lett. 100 (8), 084502.CrossRefGoogle ScholarPubMed
Gekle, S. & Gordillo, J. M. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 1. Jet formation. J. Fluid Mech. 663, 293–330.CrossRefGoogle Scholar
Gekle, S. & Gordillo, J. M. 2011 Compressible air flow through a collapsing liquid cavity. Intl J. Numer. Meth. Fluids 67, 1456–1469.CrossRefGoogle Scholar
Gekle, S., Gordillo, J. M., van der Meer, D. & Lohse, D. 2009 High-speed jet formation after solid object impact. Phys. Rev. Lett. 102 (3), 034502.CrossRefGoogle ScholarPubMed
Gordillo, J. M. 2008 Axisymmetric bubble collapse in a quiescent liquid pool. I. Theory and numerical simulations. Phys. Fluids 20, 112103.CrossRefGoogle Scholar
Gordillo, J. M. & Fontelos, M. A. 2007 Satellites in the inviscid breakup of bubbles. Phys. Rev. Lett. 98, 144503.CrossRefGoogle ScholarPubMed
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 331–346.CrossRefGoogle Scholar
Gordillo, J. M., Sevilla, A. & Martínez-Bazán, C. 2007 Bubbling in a co-flow at high reynolds numbers. Phys. Fluids 19, 077102.CrossRefGoogle Scholar
Hogrefe, J. E., Peffley, N. L., Goodridge, C. L., Shi, W. T., Hentschel, H. G. E. & Lathrop, D. P. 1998 Power-law singularities in gravity-capillary waves. Physica D 123 (1–4), 183–205.CrossRefGoogle Scholar
Howison, S. D., Ockendon, J. R. & Wilson, S. K. 1991 Incompressible water-entry problems at small deadrise angles. J . Fluid Mech. 222, 215–230.CrossRefGoogle Scholar
Iafrati, A. & Korobkin, A. A. 2004 Initial stage of flat plate impact onto liquid free surface. Phys. Fluids 16 (7), 2214–2227.CrossRefGoogle Scholar
Iafrati, A. & Korobkin, A. A. 2008 Hydrodynamic loads during early stage of flat plate impact onto water surface. Phys. Fluids 20 (8), 082104.CrossRefGoogle Scholar
Iafrati, A. & Korobkin, A. A. 2011 Asymptotic estimates of hydrodynamic loads in the early stage of water entry of a circular disk. J. Engng Maths 69, 199–224.CrossRefGoogle Scholar
Krechetnikov, R. 2009 Rayleigh–Taylor and Richtmyer–Meshkov instabilities of flat and curved interfaces. J. Fluid Mech. 625, 387–410.CrossRefGoogle Scholar
Krechetnikov, R. 2010 Stability of liquid sheet edges. Phys. Fluids 22 (9), 092101.CrossRefGoogle Scholar
Krechetnikov, R. & Homsy, G. M. 2009 Crown-forming instability phenomena in the drop splash problem. J. Colloid Interface Sci. 331 (2), 555–559.CrossRefGoogle ScholarPubMed
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9 (3), 540–550.CrossRefGoogle Scholar
Lhuissier, H. & Villermaux, E. 2012 Bursting bubble aerosols. J. Fluid Mech. 696, 5–44.CrossRefGoogle Scholar
Lister, J. R., Kerr, R. C., Russell, N. J. & Crosby, A. 2011 Rayleigh–Taylor instability of an inclined buoyant viscous cylinder. J. Fluid Mech. 671, 1–26.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1983 Bubbles, breaking waves and hyperbolic jets at a free surface. J. Fluid Mech. 127, 103–121.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Oguz, H. 1995 Critical microjets in collapsing cavities. J. Fluid Mech. 290, 183–201.CrossRefGoogle Scholar
Mandre, S., Mani, M. & Brenner, M. P. 2009 Precursors to splashing of liquid droplets on a solid surface. Phys. Rev. Lett. 102, 134502.CrossRefGoogle ScholarPubMed
May, A. 1951 The effect of surface conditions of a sphere on its water-entry cavity. Intl J. Numer. Meth. Fluids 22, 1219–1222.Google Scholar
Oguz, H. N. & Prosperetti, A. 1993 Dynamics of bubble growth and detachment from a needle. J. Fluid Mech. 257, 111–145.CrossRefGoogle Scholar
Richardson, E. G. 1948 The impact of a solid on a liquid surface. Proc. Phys. Soc. 61 (4), 352–367.CrossRefGoogle Scholar
Scolan, Y.-M. & Korobkin, A. A. 2001 Three-dimensional theory of water impact. Part 1. Inverse Wagner problem. J. Fluid Mech. 440, 293–326.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2003 Air entrapment under an impacting drop. J. Fluid Mech. 478, 125–134.CrossRefGoogle Scholar
Villermaux, E. & Bossa, B. 2011 Drop fragmentation on impact. J. Fluid Mech. 668, 412–435.CrossRefGoogle Scholar
Wagner, H. 1932 Über Stoß- und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Z. Angew. Math. Mech. 12 (4), 193–215.CrossRefGoogle Scholar
Wilson, S. K. 1991 A mathematical model for the initial stages of fluid impact in the presence of a cushioning fluid layer. J. Engng Maths 25, 265–285.CrossRefGoogle Scholar
Worthington, A. M. 1908 A Study of Splashes. Longman and Green.Google Scholar
Worthington, A. M. & Cole, R. S. 1896 Impact with a liquid surface, studies by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. A 189, 137–148.Google Scholar
Worthington, A. M. & Cole, R. S. 1900 Impact with a liquid surface studied by the aid of instantaneous photography. Paper II. Phil. Trans. R. Soc. Lond. A 194, 175–199.Google Scholar
Yakimov, Yu. L. 1973 Effect of the atmosphere with the fall of bodies into water. Fluid Dyn. 8 (5), 679–682.CrossRefGoogle Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing…. Annu. Rev. Fluid. Mech. 38, 159–192.CrossRefGoogle Scholar
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403 (6768), 401–404.CrossRefGoogle ScholarPubMed
Zhang, L. V., Brunet, P., Eggers, J. & Deegan, R. D. 2010 Wavelength selection in the crown splash. Phys. Fluids 22, 122105.CrossRefGoogle Scholar