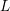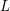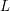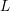1 Introduction
In the early 1970s, Montgomery [Reference Montgomery11] published his famous paper titled “The pair correlation of zeros of the zeta function”. In this paper, assuming the Riemann hypothesis (RH), he investigated the function
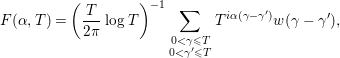 $$\begin{eqnarray}F({\it\alpha},T)=\left(\frac{T}{2{\it\pi}}\log T\right)^{-1}\mathop{\sum }_{\substack{ 0<{\it\gamma}\leqslant T \\ 0<{\it\gamma}^{\prime }\leqslant T}}T^{i{\it\alpha}({\it\gamma}-{\it\gamma}^{\prime })}w({\it\gamma}-{\it\gamma}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}F({\it\alpha},T)=\left(\frac{T}{2{\it\pi}}\log T\right)^{-1}\mathop{\sum }_{\substack{ 0<{\it\gamma}\leqslant T \\ 0<{\it\gamma}^{\prime }\leqslant T}}T^{i{\it\alpha}({\it\gamma}-{\it\gamma}^{\prime })}w({\it\gamma}-{\it\gamma}^{\prime }),\end{eqnarray}$$
where
![]() $w(u)=4/(4+u^{2})$
and
$w(u)=4/(4+u^{2})$
and
![]() ${\it\gamma}$
,
${\it\gamma}$
,
![]() ${\it\gamma}^{\prime }$
run over the set of the imaginary parts of the nontrivial zeros of the Riemann zeta-function
${\it\gamma}^{\prime }$
run over the set of the imaginary parts of the nontrivial zeros of the Riemann zeta-function
![]() ${\it\zeta}(s)$
in
${\it\zeta}(s)$
in
![]() $0<\text{Im}(s)\leqslant T$
. He obtained an asymptotic formula for
$0<\text{Im}(s)\leqslant T$
. He obtained an asymptotic formula for
![]() $F({\it\alpha},T)$
$F({\it\alpha},T)$
![]() $(0<{\it\alpha}\leqslant 1-{\it\epsilon})$
, and using this formula, he obtained several results on the distances of the nontrivial zeros. For example, under the assumption of the RH, he proved that at least
$(0<{\it\alpha}\leqslant 1-{\it\epsilon})$
, and using this formula, he obtained several results on the distances of the nontrivial zeros. For example, under the assumption of the RH, he proved that at least
![]() $2/3-{\it\epsilon}$
of the nontrivial zeros are simple, and that
$2/3-{\it\epsilon}$
of the nontrivial zeros are simple, and that
holds for specific
![]() ${\it\lambda}$
, where
${\it\lambda}$
, where
![]() ${\it\gamma}_{n}$
denotes the imaginary part of the
${\it\gamma}_{n}$
denotes the imaginary part of the
![]() $n$
th nontrivial zero of
$n$
th nontrivial zero of
![]() ${\it\zeta}(s)$
in the upper half-plane.
${\it\zeta}(s)$
in the upper half-plane.
Later, Montgomery’s idea, combined with new conceptions or improvements, was extended to many types of
![]() $L$
-functions or other situations. For example, Özlük [Reference Özlük12] investigated the nontrivial zeros of the Dirichlet
$L$
-functions or other situations. For example, Özlük [Reference Özlük12] investigated the nontrivial zeros of the Dirichlet
![]() $L$
-functions near the real axis. Assuming the generalized Riemann hypothesis (GRH), he proved that at least
$L$
-functions near the real axis. Assuming the generalized Riemann hypothesis (GRH), he proved that at least
![]() $11/12$
of such zeros are simple in some sense. One of the other interesting generalizations is the work of Hejhal [Reference Hejhal7]. From the explicit formula of the Riemann zeta-function introduced in another of his papers [Reference Hejhal6], he constructed a certain asymptotic formula for the function involving the pairs of three distinct zeros of
$11/12$
of such zeros are simple in some sense. One of the other interesting generalizations is the work of Hejhal [Reference Hejhal7]. From the explicit formula of the Riemann zeta-function introduced in another of his papers [Reference Hejhal6], he constructed a certain asymptotic formula for the function involving the pairs of three distinct zeros of
![]() ${\it\zeta}(s)$
. Further, the result of Hejhal was generalized by Rudnick and Sarnak [Reference Rudnick and Sarnak16], and the
${\it\zeta}(s)$
. Further, the result of Hejhal was generalized by Rudnick and Sarnak [Reference Rudnick and Sarnak16], and the
![]() $n$
-level correlation of the zeros of principal
$n$
-level correlation of the zeros of principal
![]() $L$
-functions was obtained. In particular, their results agree with the prediction for the Gaussian unitary ensemble of random matrix theory.
$L$
-functions was obtained. In particular, their results agree with the prediction for the Gaussian unitary ensemble of random matrix theory.
Our aim in this paper is to investigate the pair correlation of the zeros of the quadratic
![]() $L$
-functions near the real axis. As prior research, Özlük and Snyder [Reference Özlük and Snyder13] investigated such zeros. Under the assumption of the GRH, they studied the asymptotic behavior of the function
$L$
-functions near the real axis. As prior research, Özlük and Snyder [Reference Özlük and Snyder13] investigated such zeros. Under the assumption of the GRH, they studied the asymptotic behavior of the function
as
![]() $D\rightarrow \infty$
for
$D\rightarrow \infty$
for
![]() $|{\it\alpha}|<2$
, where
$|{\it\alpha}|<2$
, where
![]() ${\it\rho}=1/2+i{\it\gamma}$
runs over the set of all nontrivial zeros of
${\it\rho}=1/2+i{\it\gamma}$
runs over the set of all nontrivial zeros of
![]() $L(s,{\it\chi}_{d})$
, the quadratic
$L(s,{\it\chi}_{d})$
, the quadratic
![]() $L$
-function associated to the Kronecker symbol
$L$
-function associated to the Kronecker symbol
![]() ${\it\chi}_{d}=(d/\cdot )$
, and
${\it\chi}_{d}=(d/\cdot )$
, and
![]() $K(s)$
is some weight function. From their asymptotic formula, they proved that assuming the GRH, not more than
$K(s)$
is some weight function. From their asymptotic formula, they proved that assuming the GRH, not more than
![]() $6.25\%$
of all integers
$6.25\%$
of all integers
![]() $d$
have the property that
$d$
have the property that
![]() $s=1/2$
is a zero of
$s=1/2$
is a zero of
![]() $L(s,{\it\chi}_{d})$
. Slightly later, by a completely different method, Soundararajan [Reference Soundararajan18] unconditionally proved that
$L(s,{\it\chi}_{d})$
. Slightly later, by a completely different method, Soundararajan [Reference Soundararajan18] unconditionally proved that
![]() $L(1/2,{\it\chi}_{d})\neq 0$
for at least
$L(1/2,{\it\chi}_{d})\neq 0$
for at least
![]() $87.5\%$
of all fundamental discriminants
$87.5\%$
of all fundamental discriminants
![]() $d$
. On the other hand, there are several researches on the ‘
$d$
. On the other hand, there are several researches on the ‘
![]() $n$
-level density’ of the low-lying zeros of quadratic
$n$
-level density’ of the low-lying zeros of quadratic
![]() $L$
-functions. For an odd, square-free integer
$L$
-functions. For an odd, square-free integer
![]() $d>0$
,
$d>0$
,
![]() ${\it\chi}_{8d}=\left(\frac{8d}{\cdot }\right)$
becomes a primitive character. Assuming the GRH, we denote the nontrivial zeros of
${\it\chi}_{8d}=\left(\frac{8d}{\cdot }\right)$
becomes a primitive character. Assuming the GRH, we denote the nontrivial zeros of
![]() $L(s,{\it\chi}_{8d})$
by
$L(s,{\it\chi}_{8d})$
by
where
![]() $0\leqslant {\it\gamma}_{8d,1}\leqslant {\it\gamma}_{8d,2}\leqslant \cdots \,$
and
$0\leqslant {\it\gamma}_{8d,1}\leqslant {\it\gamma}_{8d,2}\leqslant \cdots \,$
and
![]() ${\it\gamma}_{8d,-j}=-{\it\gamma}_{8d,j}$
. For
${\it\gamma}_{8d,-j}=-{\it\gamma}_{8d,j}$
. For
![]() $X>0$
, we put
$X>0$
, we put
and for a Schwartz function
![]() $f\in {\mathcal{S}}(\mathbf{R}^{n})$
, we put
$f\in {\mathcal{S}}(\mathbf{R}^{n})$
, we put
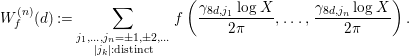 $$\begin{eqnarray}W_{f}^{(n)}(d):=\mathop{\sum }_{\substack{ j_{1},\ldots ,j_{n}=\pm 1,\pm 2,\ldots \\ |j_{k}|:\text{distinct}}}f\left(\frac{{\it\gamma}_{8d,j_{1}}\log X}{2{\it\pi}},\ldots ,\frac{{\it\gamma}_{8d,j_{n}}\log X}{2{\it\pi}}\right).\end{eqnarray}$$
$$\begin{eqnarray}W_{f}^{(n)}(d):=\mathop{\sum }_{\substack{ j_{1},\ldots ,j_{n}=\pm 1,\pm 2,\ldots \\ |j_{k}|:\text{distinct}}}f\left(\frac{{\it\gamma}_{8d,j_{1}}\log X}{2{\it\pi}},\ldots ,\frac{{\it\gamma}_{8d,j_{n}}\log X}{2{\it\pi}}\right).\end{eqnarray}$$
Then, the Katz–Sarnak density conjecture [Reference Katz and Sarnak9] asserts that
as
![]() $X\rightarrow \infty$
, where
$X\rightarrow \infty$
, where
![]() ${\rm\Phi}$
is a nonnegative smooth function supported in
${\rm\Phi}$
is a nonnegative smooth function supported in
![]() $(1,2)$
satisfying
$(1,2)$
satisfying
![]() $\int {\rm\Phi}(x)\,dx=1$
, and
$\int {\rm\Phi}(x)\,dx=1$
, and
with
Katz and Sarnak [Reference Katz and Sarnak9], assuming the GRH, proved that (1.1) holds if
![]() $n=1$
and
$n=1$
and
![]() $\hat{f}(u)=\int _{\mathbf{R}}f(x)e^{-2{\it\pi}iux}\,dx$
has a support in
$\hat{f}(u)=\int _{\mathbf{R}}f(x)e^{-2{\it\pi}iux}\,dx$
has a support in
![]() $|u|<2$
. Rubinstein [Reference Rubinstein14], [Reference Rubinstein15], assuming the GRH, established (1.1) under the condition that
$|u|<2$
. Rubinstein [Reference Rubinstein14], [Reference Rubinstein15], assuming the GRH, established (1.1) under the condition that
![]() $\hat{f}(u)=\int _{\mathbf{R}^{n}}f(u)e^{-2{\it\pi}iu\cdot x}\,dx$
has a support in
$\hat{f}(u)=\int _{\mathbf{R}^{n}}f(u)e^{-2{\it\pi}iu\cdot x}\,dx$
has a support in
![]() $\sum _{j=1}^{n}|u_{j}|<1$
, and later Gao [Reference Gao3], [Reference Gao4], under the GRH, proved that if
$\sum _{j=1}^{n}|u_{j}|<1$
, and later Gao [Reference Gao3], [Reference Gao4], under the GRH, proved that if
![]() $f$
is of the form
$f$
is of the form
![]() $f(x_{1},\ldots ,x_{n})=\prod _{j=1}^{n}f_{j}(x_{j})$
and each
$f(x_{1},\ldots ,x_{n})=\prod _{j=1}^{n}f_{j}(x_{j})$
and each
![]() $\hat{f}_{j}$
is supported in
$\hat{f}_{j}$
is supported in
![]() $|u_{j}|<s_{j}$
with
$|u_{j}|<s_{j}$
with
![]() $\sum s_{j}<2$
, then
$\sum s_{j}<2$
, then
where
![]() $A(f)$
is some complicated expression involving
$A(f)$
is some complicated expression involving
![]() $f_{1},\ldots ,f_{n}$
. Moreover, he confirmed that
$f_{1},\ldots ,f_{n}$
. Moreover, he confirmed that
![]() $A(f)$
is equal to the right-hand side of (1.1) if
$A(f)$
is equal to the right-hand side of (1.1) if
![]() $n=2,3$
. More recently, Levinson and Miller [Reference Levinson and Miller10] proved that this fact is also valid for
$n=2,3$
. More recently, Levinson and Miller [Reference Levinson and Miller10] proved that this fact is also valid for
![]() $4\leqslant n\leqslant 7$
. Finally, Entin, Roditty-Gershon and Rudnick [Reference Entin, Roditty-Gershon and Rudnick2] proved that assuming the GRH, (1.1) is valid for all
$4\leqslant n\leqslant 7$
. Finally, Entin, Roditty-Gershon and Rudnick [Reference Entin, Roditty-Gershon and Rudnick2] proved that assuming the GRH, (1.1) is valid for all
![]() $n$
if
$n$
if
![]() $\hat{f}$
is supported in
$\hat{f}$
is supported in
![]() $\sum _{j=1}^{n}|u_{j}|<2$
.
$\sum _{j=1}^{n}|u_{j}|<2$
.
If anything, our approach to investigate the pair correlation of low-lying zeros is similar to that of Özlük and Snyder [Reference Özlük and Snyder13], in which they investigated the 1-level density of these zeros. In this paper, assuming the GRH (including the RH), we investigate the function
![]() $F_{K}({\it\alpha},D)$
, defined as follows. Let
$F_{K}({\it\alpha},D)$
, defined as follows. Let
![]() $K(s)$
be analytic in
$K(s)$
be analytic in
![]() $-1<\text{Re}(s)<2$
and satisfy
$-1<\text{Re}(s)<2$
and satisfy
![]() $K(1/2-it)=K(1/2+it)$
for any
$K(1/2-it)=K(1/2+it)$
for any
![]() $t\in \mathbf{R}$
. Moreover, we assume that its Mellin inverse transform
$t\in \mathbf{R}$
. Moreover, we assume that its Mellin inverse transform
converges absolutely for any
![]() $-1<c<2$
,
$-1<c<2$
,
![]() $x>0$
, and that
$x>0$
, and that
![]() $a(x)$
is real, nonnegative, belongs to the
$a(x)$
is real, nonnegative, belongs to the
![]() $C^{1}$
-class, and has a support in
$C^{1}$
-class, and has a support in
![]() $[A,B]$
for some
$[A,B]$
for some
![]() $0<A<B<\infty$
. Then,
$0<A<B<\infty$
. Then,
![]() $K(s)$
is given by
$K(s)$
is given by
For
![]() $d\in \mathbf{Z}$
, let
$d\in \mathbf{Z}$
, let
![]() ${\it\chi}_{d}=(d/\cdot )$
be the Kronecker symbol, and let
${\it\chi}_{d}=(d/\cdot )$
be the Kronecker symbol, and let
![]() $L(s,{\it\chi}_{d})$
be the
$L(s,{\it\chi}_{d})$
be the
![]() $L$
-function associated to
$L$
-function associated to
![]() ${\it\chi}_{d}$
. We denote the set of nontrivial zeros of
${\it\chi}_{d}$
. We denote the set of nontrivial zeros of
![]() $L(s,{\it\chi}_{d})$
by
$L(s,{\it\chi}_{d})$
by
![]() $Z_{d}$
. For
$Z_{d}$
. For
![]() $x>0$
,
$x>0$
,
![]() $D>0$
, we put
$D>0$
, we put
and for
![]() ${\it\alpha}\in \mathbf{R}$
, we put
${\it\alpha}\in \mathbf{R}$
, we put
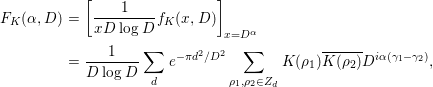 $$\begin{eqnarray}\displaystyle F_{K}({\it\alpha},D) & = & \displaystyle \left[\frac{1}{xD\log D}f_{K}(x,D)\right]_{x=D^{{\it\alpha}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}D^{i{\it\alpha}({\it\gamma}_{1}-{\it\gamma}_{2})},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{K}({\it\alpha},D) & = & \displaystyle \left[\frac{1}{xD\log D}f_{K}(x,D)\right]_{x=D^{{\it\alpha}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}D^{i{\it\alpha}({\it\gamma}_{1}-{\it\gamma}_{2})},\end{eqnarray}$$
where
![]() ${\it\rho}_{j}=1/2+i{\it\gamma}_{j}$
for
${\it\rho}_{j}=1/2+i{\it\gamma}_{j}$
for
![]() $j=1,2$
. Then, the main theorem is stated as follows.
$j=1,2$
. Then, the main theorem is stated as follows.
Theorem 1.1. Assuming the GRH, for any small
![]() ${\it\delta}>0$
, we have
${\it\delta}>0$
, we have
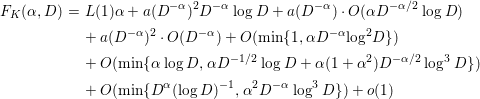 $$\begin{eqnarray}\displaystyle F_{K}({\it\alpha},D) & = & \displaystyle L(1){\it\alpha}+a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\log D+a(D^{-{\it\alpha}})\cdot O({\it\alpha}D^{-{\it\alpha}/2}\log D)\nonumber\\ \displaystyle & & \displaystyle +\,a(D^{-{\it\alpha}})^{2}\cdot O(D^{-{\it\alpha}})+O(\text{min}\{1,{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle +\,O(\min \{{\it\alpha}\log D,{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\})\nonumber\\ \displaystyle & & \displaystyle +\,O(\text{min}\{D^{{\it\alpha}}(\log D)^{-1},{\it\alpha}^{2}D^{-{\it\alpha}}\log ^{3}D\})+o(1)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{K}({\it\alpha},D) & = & \displaystyle L(1){\it\alpha}+a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\log D+a(D^{-{\it\alpha}})\cdot O({\it\alpha}D^{-{\it\alpha}/2}\log D)\nonumber\\ \displaystyle & & \displaystyle +\,a(D^{-{\it\alpha}})^{2}\cdot O(D^{-{\it\alpha}})+O(\text{min}\{1,{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle +\,O(\min \{{\it\alpha}\log D,{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\})\nonumber\\ \displaystyle & & \displaystyle +\,O(\text{min}\{D^{{\it\alpha}}(\log D)^{-1},{\it\alpha}^{2}D^{-{\it\alpha}}\log ^{3}D\})+o(1)\end{eqnarray}$$
uniformly for
![]() $0<{\it\alpha}<1-{\it\delta}$
as
$0<{\it\alpha}<1-{\it\delta}$
as
![]() $D\rightarrow \infty$
, where
$D\rightarrow \infty$
, where
The implied constants depend only on
![]() $K(s)$
and
$K(s)$
and
![]() ${\it\delta}>0$
.
${\it\delta}>0$
.
It should be noticed that the result on the
![]() $1$
-level density by Katz and Sarnak [Reference Katz and Sarnak9] is stronger than that of Özlük and Snyder [Reference Özlük and Snyder13] in some sense. However, the author believes that the asymptotic formula of Theorem 1.1 is more useful than the limit formula (1.1) (
$1$
-level density by Katz and Sarnak [Reference Katz and Sarnak9] is stronger than that of Özlük and Snyder [Reference Özlük and Snyder13] in some sense. However, the author believes that the asymptotic formula of Theorem 1.1 is more useful than the limit formula (1.1) (
![]() $n=2$
) if we restrict the target only to the study of the pair correlation of low-lying zeros of
$n=2$
) if we restrict the target only to the study of the pair correlation of low-lying zeros of
![]() $L(s,{\it\chi}_{d})$
, since the factor
$L(s,{\it\chi}_{d})$
, since the factor
![]() ${\it\gamma}_{1}-{\it\gamma}_{2}$
is contained in the definition of
${\it\gamma}_{1}-{\it\gamma}_{2}$
is contained in the definition of
![]() $F_{K}({\it\alpha},D)$
, and both the left-hand side and the main terms of the right-hand side of (1.5) are very simple; hence, we can easily compute the integrals involving these terms. In fact, several concrete results on the average gaps of the nontrivial zeros are obtained. Section 4 of this paper is devoted to their study. In Corollary 4.2, we give a certain upper bound for the number of pairs of ‘close zeros’ near the real axis. In Corollary 4.3, we give a lower bound for the weighted sum involving simple zeros of
$F_{K}({\it\alpha},D)$
, and both the left-hand side and the main terms of the right-hand side of (1.5) are very simple; hence, we can easily compute the integrals involving these terms. In fact, several concrete results on the average gaps of the nontrivial zeros are obtained. Section 4 of this paper is devoted to their study. In Corollary 4.2, we give a certain upper bound for the number of pairs of ‘close zeros’ near the real axis. In Corollary 4.3, we give a lower bound for the weighted sum involving simple zeros of
![]() $L(s,{\it\chi}_{d})$
. Finally, in Corollary 4.4, we prove that there are quite a few pairs of zeros
$L(s,{\it\chi}_{d})$
. Finally, in Corollary 4.4, we prove that there are quite a few pairs of zeros
![]() $(1/2+i{\it\gamma}_{1},1/2+i{\it\gamma}_{2})$
of
$(1/2+i{\it\gamma}_{1},1/2+i{\it\gamma}_{2})$
of
![]() $L(s,{\it\chi}_{d})$
$L(s,{\it\chi}_{d})$
![]() $(d\in \mathbf{Z}\setminus \{0\})$
satisfying
$(d\in \mathbf{Z}\setminus \{0\})$
satisfying
![]() $0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant (2{\it\pi}{\it\lambda})/\log D$
, if
$0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant (2{\it\pi}{\it\lambda})/\log D$
, if
![]() ${\it\lambda}$
is large to a certain extent.
${\it\lambda}$
is large to a certain extent.
2 Preliminaries
To prove the main theorem, we prepare several lemmas. The following nine lemmas (Lemmas 2.1–2.9) are all found in [Reference Özlük and Snyder13].
Lemma 2.1. We have
Here,
![]() $\sum _{d}$
denotes the sum over all nonzero integers
$\sum _{d}$
denotes the sum over all nonzero integers
![]() $d$
.
$d$
.
Lemma 2.2.
Lemma 2.3. We have
as
![]() $y\rightarrow \infty$
. Here,
$y\rightarrow \infty$
. Here,
![]() $I=(1/4){\it\pi}^{-1/4}{\rm\Gamma}(1/4)$
, and
$I=(1/4){\it\pi}^{-1/4}{\rm\Gamma}(1/4)$
, and
![]() $\sum _{d=\Box }$
denotes the sum over all positive square integers.
$\sum _{d=\Box }$
denotes the sum over all positive square integers.
Instead of (2.3), sometimes we use
or
Lemma 2.4. Assuming the RH, we have
Here,
![]() $\sum _{p}$
denotes the sum over all primes
$\sum _{p}$
denotes the sum over all primes
![]() $p$
.
$p$
.
It should be noticed that the implied constant in (2.6) is dependent on
![]() $a(x)$
(and hence on
$a(x)$
(and hence on
![]() $K(s)$
). Hereafter, this fact will be valid for almost all asymptotic formulas, although we will not comment again.
$K(s)$
). Hereafter, this fact will be valid for almost all asymptotic formulas, although we will not comment again.
Lemma 2.5. Assuming the RH, we have
Lemma 2.6. Assuming the RH, we have
Lemma 2.7. Assuming the RH, we have
Lemma 2.8. Assuming the RH, we have
Lemma 2.9. We have
In addition to these nine lemmas quoted from [Reference Özlük and Snyder13], we need several asymptotic formulas.
Lemma 2.10. We have
Proof. The left-hand side is
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}d & = & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}\left(\frac{d}{y}\right)+2(\log y)\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log d\nonumber\\ \displaystyle & & \displaystyle -\,(\log y)^{2}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}d & = & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}\left(\frac{d}{y}\right)+2(\log y)\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log d\nonumber\\ \displaystyle & & \displaystyle -\,(\log y)^{2}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}.\end{eqnarray}$$
The first term on the right-hand side of (2.13) is
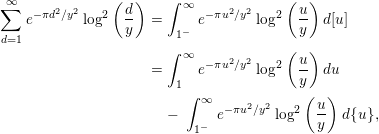 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}\left(\frac{d}{y}\right) & = & \displaystyle \int _{1^{-}}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)d[u]\nonumber\\ \displaystyle & = & \displaystyle \int _{1}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)du\nonumber\\ \displaystyle & & \displaystyle -\,\int _{1^{-}}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)d\{u\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/y^{2}}\log ^{2}\left(\frac{d}{y}\right) & = & \displaystyle \int _{1^{-}}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)d[u]\nonumber\\ \displaystyle & = & \displaystyle \int _{1}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)du\nonumber\\ \displaystyle & & \displaystyle -\,\int _{1^{-}}^{\infty }e^{-{\it\pi}u^{2}/y^{2}}\log ^{2}\left(\frac{u}{y}\right)d\{u\},\end{eqnarray}$$
where
![]() $[u]$
denotes the integer part of
$[u]$
denotes the integer part of
![]() $u$
, and
$u$
, and
![]() $\{u\}:=u-[u]$
. By the change of parameters
$\{u\}:=u-[u]$
. By the change of parameters
![]() $u/y=v$
, we can easily see that
$u/y=v$
, we can easily see that
and by partial integration, we have
Hence, the first term on the right-hand side of (2.13) is
![]() $O(y)$
. Moreover, by Lemma 2.1, we have
$O(y)$
. Moreover, by Lemma 2.1, we have
and by Lemma 2.2, we have
By inserting these into (2.13), we obtain the result.◻
Lemma 2.11. We have
Proof. It should be recalled that the function
![]() $a(u)$
is bounded and has a support in
$a(u)$
is bounded and has a support in
![]() $[A,B]$
. By the prime number theorem (PNT), the number of primes
$[A,B]$
. By the prime number theorem (PNT), the number of primes
![]() $p$
satisfying the condition
$p$
satisfying the condition
![]() $p/x\leqslant B$
is
$p/x\leqslant B$
is
![]() $O(x/\log x)$
. Therefore,
$O(x/\log x)$
. Therefore,
By a similar argument, we obtain the following.
Lemma 2.12. We have
Hereafter, we put
Lemma 2.13. Assuming the RH, we have
Proof. We write
Then, it is well known that
![]() $E(u)$
is evaluated by
$E(u)$
is evaluated by
![]() $O(u^{1/2}\log ^{2}u)$
under the assumption of the RH. Now, we have
$O(u^{1/2}\log ^{2}u)$
under the assumption of the RH. Now, we have
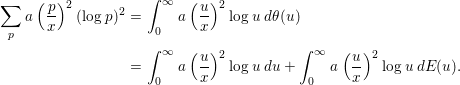 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2} & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,d{\it\theta}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,du+\int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,dE(u).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2} & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,d{\it\theta}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,du+\int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,dE(u).\end{eqnarray}$$
By the change of parameters
![]() $u/x=v$
, we have
$u/x=v$
, we have
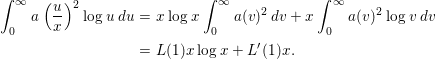 $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,du & = & \displaystyle x\log x\int _{0}^{\infty }a(v)^{2}\,dv+x\int _{0}^{\infty }a(v)^{2}\log v\,dv\nonumber\\ \displaystyle & = & \displaystyle L(1)x\log x+L^{\prime }(1)x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,du & = & \displaystyle x\log x\int _{0}^{\infty }a(v)^{2}\,dv+x\int _{0}^{\infty }a(v)^{2}\log v\,dv\nonumber\\ \displaystyle & = & \displaystyle L(1)x\log x+L^{\prime }(1)x.\end{eqnarray}$$
On the other hand, by partial integration, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,dE(u)\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{0}^{\infty }E(u)\left\{\frac{2a\left(\frac{u}{x}\right)a^{\prime }\left(\frac{u}{x}\right)\log u}{x}+\frac{a\left(\frac{u}{x}\right)^{2}}{u}\right\}\,du,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)^{2}\log u\,dE(u)\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{0}^{\infty }E(u)\left\{\frac{2a\left(\frac{u}{x}\right)a^{\prime }\left(\frac{u}{x}\right)\log u}{x}+\frac{a\left(\frac{u}{x}\right)^{2}}{u}\right\}\,du,\nonumber\end{eqnarray}$$
and by the change of parameters
![]() $u/x=v$
, combining with the estimate
$u/x=v$
, combining with the estimate
![]() $E(u)\ll \sqrt{u}\log ^{2}u$
, we easily find that
$E(u)\ll \sqrt{u}\log ^{2}u$
, we easily find that
 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{\infty }E(u)\frac{a\left(\frac{u}{x}\right)a^{\prime }\left(\frac{u}{x}\right)\log u}{x}\,du\ll \sqrt{x}\log ^{3}x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{0}^{\infty }E(u)\frac{a\left(\frac{u}{x}\right)^{2}}{u}\,du\ll \sqrt{x}\log ^{2}x. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{\infty }E(u)\frac{a\left(\frac{u}{x}\right)a^{\prime }\left(\frac{u}{x}\right)\log u}{x}\,du\ll \sqrt{x}\log ^{3}x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{0}^{\infty }E(u)\frac{a\left(\frac{u}{x}\right)^{2}}{u}\,du\ll \sqrt{x}\log ^{2}x. & \displaystyle \nonumber\end{eqnarray}$$
Hence, we get
Lemma 2.14. Assuming the RH, we have
The proof of Lemma 2.14 is almost the same as that of Lemma 2.13; hence, we omit it.
Lemma 2.15. We assume the RH. Then, when
![]() $x^{\frac{1}{l}}\gg 1$
, we have
$x^{\frac{1}{l}}\gg 1$
, we have
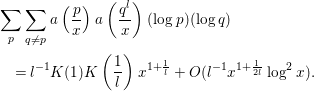 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad =l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}+O(l^{-1}x^{1+\frac{1}{2l}}\log ^{2}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad =l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}+O(l^{-1}x^{1+\frac{1}{2l}}\log ^{2}x).\end{eqnarray}$$
The implied constant is independent of
![]() $l$
.
$l$
.
Proof. The left-hand side is
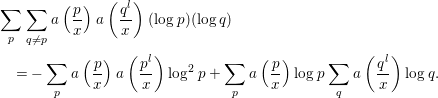 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad =-\mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p+\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad =-\mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p+\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q.\end{eqnarray}$$
By the PNT, the number of primes
![]() $p$
satisfying
$p$
satisfying
![]() $p^{l}/x\leqslant B$
is
$p^{l}/x\leqslant B$
is
![]() $O(lx^{1/l}/\log x)$
. Therefore,
$O(lx^{1/l}/\log x)$
. Therefore,
By Lemma 2.5,
Further,
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)d{\it\theta}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)du+\int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)dE(u).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)d{\it\theta}(u)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)du+\int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)dE(u).\nonumber\end{eqnarray}$$
By the change of parameters
![]() $u^{l}/x=v$
, the first term on the right-hand side becomes
$u^{l}/x=v$
, the first term on the right-hand side becomes
Since
![]() $E(u)\ll u^{1/2}\log ^{2}u$
, and since
$E(u)\ll u^{1/2}\log ^{2}u$
, and since
![]() $a^{\prime }(v)$
is bounded and has a support in
$a^{\prime }(v)$
is bounded and has a support in
![]() $[A,B]$
, the second integral is
$[A,B]$
, the second integral is
 $$\begin{eqnarray}\displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)dE(u) & = & \displaystyle -\int _{0}^{\infty }E(u)\frac{lu^{l-1}}{x}a^{\prime }\left(\frac{u^{l}}{x}\right)du\nonumber\\ \displaystyle & \ll & \displaystyle lx^{-1}\int _{0}^{\infty }u^{l-\frac{1}{2}}\left|a^{\prime }\left(\frac{u^{l}}{x}\right)\right|\log ^{2}u\,du\nonumber\\ \displaystyle & \ll & \displaystyle lx^{-1}(x^{\frac{1}{l}})^{l-\frac{1}{2}}\log ^{2}(x^{\frac{1}{l}})\cdot x^{\frac{1}{l}}\nonumber\\ \displaystyle & \ll & \displaystyle l^{-1}x^{\frac{1}{2l}}\log ^{2}x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)dE(u) & = & \displaystyle -\int _{0}^{\infty }E(u)\frac{lu^{l-1}}{x}a^{\prime }\left(\frac{u^{l}}{x}\right)du\nonumber\\ \displaystyle & \ll & \displaystyle lx^{-1}\int _{0}^{\infty }u^{l-\frac{1}{2}}\left|a^{\prime }\left(\frac{u^{l}}{x}\right)\right|\log ^{2}u\,du\nonumber\\ \displaystyle & \ll & \displaystyle lx^{-1}(x^{\frac{1}{l}})^{l-\frac{1}{2}}\log ^{2}(x^{\frac{1}{l}})\cdot x^{\frac{1}{l}}\nonumber\\ \displaystyle & \ll & \displaystyle l^{-1}x^{\frac{1}{2l}}\log ^{2}x.\nonumber\end{eqnarray}$$
Combining these, we have
By inserting (2.25)–(2.27) into (2.24), we obtain the result.◻
Lemma 2.16. We assume the RH. Then, when
![]() $x^{\frac{1}{l}}\gg 1$
, we have
$x^{\frac{1}{l}}\gg 1$
, we have
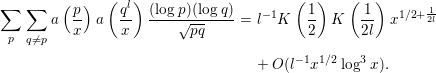 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}} & = & \displaystyle l^{-1}K\left(\frac{1}{2}\right)K\left(\frac{1}{2l}\right)x^{1/2+\frac{1}{2l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}x^{1/2}\log ^{3}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}\mathop{\sum }_{q\neq p}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}} & = & \displaystyle l^{-1}K\left(\frac{1}{2}\right)K\left(\frac{1}{2l}\right)x^{1/2+\frac{1}{2l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}x^{1/2}\log ^{3}x).\end{eqnarray}$$
The implied constant is independent of
![]() $l$
.
$l$
.
The proof of Lemma 2.16 is almost the same as that of Lemma 2.15; hence, we omit it. It should be noticed that the asymptotic formulas of Lemmas 2.15, 2.16 are still valid if we replace the sum with
![]() $p,q\geqslant 3$
,
$p,q\geqslant 3$
,
![]() $p\neq q$
.
$p\neq q$
.
To obtain the asymptotic formula of the main theorem, we need the following translation formula for the theta function.
Lemma 2.17. Let
![]() $p,q\geqslant 3$
be distinct primes, and let
$p,q\geqslant 3$
be distinct primes, and let
![]() $D>0$
. Then,
$D>0$
. Then,
Here,
![]() $d$
and
$d$
and
![]() $m$
above run over the set of all nonzero integers.
$m$
above run over the set of all nonzero integers.
Proof. If
![]() $(-1/pq)=-1$
, the identity (2.29) clearly holds, since both sides become 0. We assume
$(-1/pq)=-1$
, the identity (2.29) clearly holds, since both sides become 0. We assume
![]() $(-1/pq)=1$
, and put
$(-1/pq)=1$
, and put
Then,
![]() ${\it\chi}_{pq}$
becomes a primitive character of modulo
${\it\chi}_{pq}$
becomes a primitive character of modulo
![]() $pq$
. We define the theta function
$pq$
. We define the theta function
![]() ${\it\psi}(x,{\it\chi}_{pq})$
by
${\it\psi}(x,{\it\chi}_{pq})$
by
for
![]() $x>0$
. Then,
$x>0$
. Then,
![]() ${\it\psi}(x,{\it\chi}_{pq})$
satisfies
${\it\psi}(x,{\it\chi}_{pq})$
satisfies
where
![]() ${\it\tau}({\it\chi}_{pq})$
is the Gaussian sum associated to
${\it\tau}({\it\chi}_{pq})$
is the Gaussian sum associated to
![]() ${\it\chi}_{pq}$
(for example, see [Reference Davenport1, p. 67]). Moreover, we have
${\it\chi}_{pq}$
(for example, see [Reference Davenport1, p. 67]). Moreover, we have
![]() ${\it\tau}({\it\chi}_{pq})=\sqrt{pq}$
. Hence, we get
${\it\tau}({\it\chi}_{pq})=\sqrt{pq}$
. Hence, we get
By putting
![]() $x=pq/D^{2}$
, we obtain (2.29).◻
$x=pq/D^{2}$
, we obtain (2.29).◻
3 The proof of Theorem 1.1
We start from the explicit formula
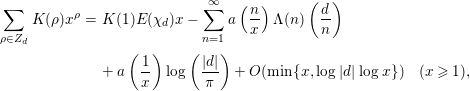 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})x^{{\it\rho}} & = & \displaystyle K(1)E({\it\chi}_{d})x-\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)+O(\text{min}\{x,\log |d|\log x\})\quad (x\geqslant 1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})x^{{\it\rho}} & = & \displaystyle K(1)E({\it\chi}_{d})x-\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)+O(\text{min}\{x,\log |d|\log x\})\quad (x\geqslant 1),\nonumber\end{eqnarray}$$
introduced in [Reference Özlük and Snyder13]. Here,
![]() $E({\it\chi})=1$
if
$E({\it\chi})=1$
if
![]() ${\it\chi}$
is a principal character, and otherwise
${\it\chi}$
is a principal character, and otherwise
![]() $E({\it\chi})=0$
. The error term is interpreted as
$E({\it\chi})=0$
. The error term is interpreted as
![]() $O(1)$
if
$O(1)$
if
![]() $x=1$
. Since the main terms on the right-hand side are real, we have
$x=1$
. Since the main terms on the right-hand side are real, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}x^{{\it\rho}_{1}+\overline{{\it\rho}_{2}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{K(1)E({\it\chi}_{d})x-\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad \quad \quad \quad \quad \quad \quad \quad +\,a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)+O(\text{min}\{x,\log |d|\log x\})\right\}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =K(1)^{2}E({\it\chi}_{d})^{2}x^{2}+\mathop{\sum }_{n,m=1}^{\infty }a\left(\frac{n}{x}\right)a\left(\frac{m}{x}\right){\rm\Lambda}(n){\rm\Lambda}(m)\left(\frac{d}{n}\right)\left(\frac{d}{m}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,a\left(\frac{1}{x}\right)^{2}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right)-2K(1)E({\it\chi}_{d})x\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2K(1)E({\it\chi}_{d})xa\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\max \left\{K(1)E({\it\chi}_{d})x,\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right),a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,O\left(\text{min}\{x,\log |d|\log x\}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\text{min}\{x^{2},\log ^{2}|d|\log ^{2}x\}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}x^{{\it\rho}_{1}+\overline{{\it\rho}_{2}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{K(1)E({\it\chi}_{d})x-\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad \quad \quad \quad \quad \quad \quad \quad +\,a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)+O(\text{min}\{x,\log |d|\log x\})\right\}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =K(1)^{2}E({\it\chi}_{d})^{2}x^{2}+\mathop{\sum }_{n,m=1}^{\infty }a\left(\frac{n}{x}\right)a\left(\frac{m}{x}\right){\rm\Lambda}(n){\rm\Lambda}(m)\left(\frac{d}{n}\right)\left(\frac{d}{m}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,a\left(\frac{1}{x}\right)^{2}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right)-2K(1)E({\it\chi}_{d})x\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2K(1)E({\it\chi}_{d})xa\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\max \left\{K(1)E({\it\chi}_{d})x,\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right),a\left(\frac{1}{x}\right)\log \left(\frac{|d|}{{\it\pi}}\right)\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,O\left(\text{min}\{x,\log |d|\log x\}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\text{min}\{x^{2},\log ^{2}|d|\log ^{2}x\}\right).\nonumber\end{eqnarray}$$
By multiplying both sides by
![]() $e^{-{\it\pi}d^{2}/D^{2}}$
and taking the sum over
$e^{-{\it\pi}d^{2}/D^{2}}$
and taking the sum over
![]() $d$
, we have
$d$
, we have
where
 $$\begin{eqnarray}\displaystyle & \displaystyle M_{1}=K(1)^{2}x^{2}\mathop{\sum }_{d}E({\it\chi}_{d})^{2}e^{-{\it\pi}d^{2}/D^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{2}=\mathop{\sum }_{n,m=1}^{\infty }a\left(\frac{n}{x}\right)a\left(\frac{m}{x}\right){\rm\Lambda}(n){\rm\Lambda}(m)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\left(\frac{d}{m}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{3}=a\left(\frac{1}{x}\right)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{4}=-2K(1)x\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\left(\frac{d}{n}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{5}=2K(1)xa\left(\frac{1}{x}\right)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log \left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{6}=-2a\left(\frac{1}{x}\right)\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\log \left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{1}=O\left(\text{min}\left\{O_{11},O_{12}\right\}\right),\qquad O_{2}=O\left(\text{min}\left\{O_{21},O_{22}\right\}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{3}=O\left(\text{min}\left\{O_{31},O_{32}\right\}\right),\qquad O_{4}=\left(\text{min}\left\{O_{41},O_{42}\right\}\right), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{1}=K(1)^{2}x^{2}\mathop{\sum }_{d}E({\it\chi}_{d})^{2}e^{-{\it\pi}d^{2}/D^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{2}=\mathop{\sum }_{n,m=1}^{\infty }a\left(\frac{n}{x}\right)a\left(\frac{m}{x}\right){\rm\Lambda}(n){\rm\Lambda}(m)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\left(\frac{d}{m}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{3}=a\left(\frac{1}{x}\right)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{4}=-2K(1)x\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\left(\frac{d}{n}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{5}=2K(1)xa\left(\frac{1}{x}\right)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log \left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M_{6}=-2a\left(\frac{1}{x}\right)\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\log \left(\frac{|d|}{{\it\pi}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{1}=O\left(\text{min}\left\{O_{11},O_{12}\right\}\right),\qquad O_{2}=O\left(\text{min}\left\{O_{21},O_{22}\right\}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{3}=O\left(\text{min}\left\{O_{31},O_{32}\right\}\right),\qquad O_{4}=\left(\text{min}\left\{O_{41},O_{42}\right\}\right), & \displaystyle \nonumber\end{eqnarray}$$
with
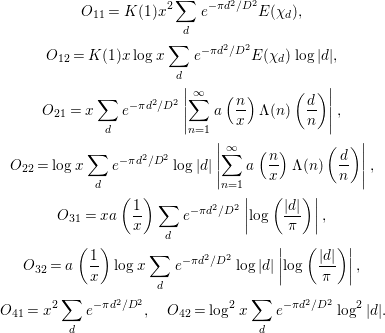 $$\begin{eqnarray}\displaystyle & \displaystyle O_{11}=K(1)x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{12}=K(1)x\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log |d|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{21}=x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{22}=\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{31}=xa\left(\frac{1}{x}\right)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{32}=a\left(\frac{1}{x}\right)\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{41}=x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}},\quad O_{42}=\log ^{2}x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}|d|. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle O_{11}=K(1)x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{12}=K(1)x\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log |d|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{21}=x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{22}=\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{31}=xa\left(\frac{1}{x}\right)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{32}=a\left(\frac{1}{x}\right)\log x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|, & \displaystyle \nonumber\\ \displaystyle & \displaystyle O_{41}=x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}},\quad O_{42}=\log ^{2}x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}|d|. & \displaystyle \nonumber\end{eqnarray}$$
3.1 Evaluations of
 $O_{1}$
,
$O_{1}$
,
 $O_{2}$
,
$O_{2}$
,
 $O_{3}$
,
$O_{3}$
,
 $O_{4}$
$O_{4}$
First, we evaluate the error terms
![]() $O_{i}$
$O_{i}$
![]() $(i=1,2,3,4)$
. By Lemma 2.3,
$(i=1,2,3,4)$
. By Lemma 2.3,
Combining this with abelian summation, we find that
Therefore, we have
By Lemmas 2.2 and 2.10, we have
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|\ll D\log D, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|\ll D\log ^{2}D. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|\ll D\log D, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\log \left(\frac{|d|}{{\it\pi}}\right)\right|\ll D\log ^{2}D. & \displaystyle \nonumber\end{eqnarray}$$
Hence, we obtain
Next, we evaluate
![]() $O_{2}$
. In particular, we evaluate
$O_{2}$
. In particular, we evaluate
![]() $O_{22}$
in two ways. First, since
$O_{22}$
in two ways. First, since
by Lemma 2.2, we have
On the other hand, we decompose
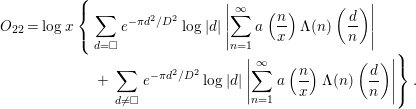 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle O_{22}=\log x\left\{\vphantom{+\,\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|}\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\right.\\ \displaystyle \qquad \qquad \qquad \quad \qquad \left.+\,\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\right\}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle O_{22}=\log x\left\{\vphantom{+\,\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|}\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\right.\\ \displaystyle \qquad \qquad \qquad \quad \qquad \left.+\,\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\right\}.\end{array}\end{eqnarray}$$
Then, the first term is evaluated by
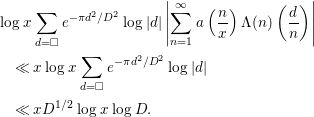 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \log x\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \ll x\log x\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \ll xD^{1/2}\log x\log D.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \log x\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \ll x\log x\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \ll xD^{1/2}\log x\log D.\end{eqnarray}$$
We evaluate the second term on the right-hand side of (3.5). It is known that, assuming the GRH, for
![]() $d\neq \Box$
, the estimate
$d\neq \Box$
, the estimate
holds (see [Reference Özlük and Snyder13, p. 221]). We decompose
Using the estimate above, the first term is evaluated by
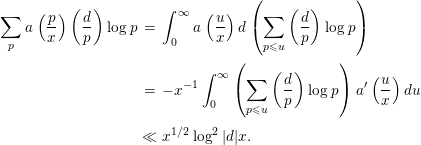 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\left(\frac{d}{p}\right)\log p & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)d\left(\mathop{\sum }_{p\leqslant u}\left(\frac{d}{p}\right)\log p\right)\nonumber\\ \displaystyle & = & \displaystyle -x^{-1}\int _{0}^{\infty }\left(\mathop{\sum }_{p\leqslant u}\left(\frac{d}{p}\right)\log p\right)a^{\prime }\left(\frac{u}{x}\right)du\nonumber\\ \displaystyle & \ll & \displaystyle x^{1/2}\log ^{2}|d|x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\left(\frac{d}{p}\right)\log p & = & \displaystyle \int _{0}^{\infty }a\left(\frac{u}{x}\right)d\left(\mathop{\sum }_{p\leqslant u}\left(\frac{d}{p}\right)\log p\right)\nonumber\\ \displaystyle & = & \displaystyle -x^{-1}\int _{0}^{\infty }\left(\mathop{\sum }_{p\leqslant u}\left(\frac{d}{p}\right)\log p\right)a^{\prime }\left(\frac{u}{x}\right)du\nonumber\\ \displaystyle & \ll & \displaystyle x^{1/2}\log ^{2}|d|x.\end{eqnarray}$$
Next, we evaluate the second term on the right-hand side of (3.7). Since
![]() $a(x)$
has a support in
$a(x)$
has a support in
![]() $[A,B]$
for some
$[A,B]$
for some
![]() $0<A<B<\infty$
, we may assume that the range of
$0<A<B<\infty$
, we may assume that the range of
![]() $l$
is restricted to
$l$
is restricted to
![]() $2\leqslant l\ll \log x$
. Therefore,
$2\leqslant l\ll \log x$
. Therefore,
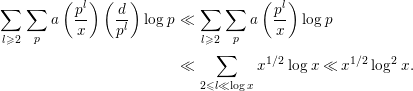 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{p}a\left(\frac{p^{l}}{x}\right)\left(\frac{d}{p^{l}}\right)\log p & \ll & \displaystyle \mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{p}a\left(\frac{p^{l}}{x}\right)\log p\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{2\leqslant l\ll \log x}x^{1/2}\log x\ll x^{1/2}\log ^{2}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{p}a\left(\frac{p^{l}}{x}\right)\left(\frac{d}{p^{l}}\right)\log p & \ll & \displaystyle \mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{p}a\left(\frac{p^{l}}{x}\right)\log p\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{2\leqslant l\ll \log x}x^{1/2}\log x\ll x^{1/2}\log ^{2}x.\end{eqnarray}$$
Combining (3.7)–(3.9), we obtain
for
![]() $d\neq \Box$
, assuming the GRH. Therefore, the second term on the right-hand side of (3.5) is
$d\neq \Box$
, assuming the GRH. Therefore, the second term on the right-hand side of (3.5) is
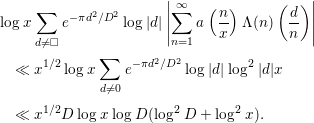 $$\begin{eqnarray}\displaystyle & & \displaystyle \log x\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{1/2}\log x\mathop{\sum }_{d\neq 0}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\log ^{2}|d|x\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \log x\mathop{\sum }_{d\neq \Box }e^{-{\it\pi}d^{2}/D^{2}}\log |d|\left|\mathop{\sum }_{n=1}^{\infty }a\left(\frac{n}{x}\right){\rm\Lambda}(n)\left(\frac{d}{n}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{1/2}\log x\mathop{\sum }_{d\neq 0}e^{-{\it\pi}d^{2}/D^{2}}\log |d|\log ^{2}|d|x\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x).\end{eqnarray}$$
Combining (3.6) and (3.11), we obtain
By combining (3.4), (3.12), and the evaluation
![]() $O_{2}\ll O_{22}$
, we obtain
$O_{2}\ll O_{22}$
, we obtain
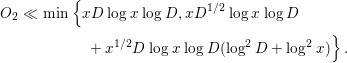 $$\begin{eqnarray}\displaystyle O_{2} & \ll & \displaystyle \min \left\{xD\log x\log D,xD^{1/2}\log x\log D\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle O_{2} & \ll & \displaystyle \min \left\{xD\log x\log D,xD^{1/2}\log x\log D\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \left.+\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\right\}.\end{eqnarray}$$
Finally, since
 $$\begin{eqnarray}\displaystyle & \displaystyle x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\ll x^{2}D, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \log ^{2}x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}|d|\ll D\log ^{2}x\log ^{2}D, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle x^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\ll x^{2}D, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \log ^{2}x\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}|d|\ll D\log ^{2}x\log ^{2}D, & \displaystyle \nonumber\end{eqnarray}$$
we have
3.2 The computations of
 $M_{1}$
,
$M_{1}$
,
 $M_{3}$
and the evaluation of
$M_{3}$
and the evaluation of
 $M_{5}$
$M_{5}$
Next, we compute
![]() $M_{1}$
,
$M_{1}$
,
![]() $M_{3}$
,
$M_{3}$
,
![]() $M_{5}$
. These terms do not involve Kronecker symbols. First, by Lemma 2.3,
$M_{5}$
. These terms do not involve Kronecker symbols. First, by Lemma 2.3,
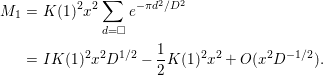 $$\begin{eqnarray}\displaystyle M_{1} & = & \displaystyle K(1)^{2}x^{2}\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & = & \displaystyle IK(1)^{2}x^{2}D^{1/2}-\frac{1}{2}K(1)^{2}x^{2}+O(x^{2}D^{-1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{1} & = & \displaystyle K(1)^{2}x^{2}\mathop{\sum }_{d=\Box }e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & = & \displaystyle IK(1)^{2}x^{2}D^{1/2}-\frac{1}{2}K(1)^{2}x^{2}+O(x^{2}D^{-1/2}).\end{eqnarray}$$
Next, we compute
![]() $M_{3}$
. The sum with respect to
$M_{3}$
. The sum with respect to
![]() $d$
is
$d$
is
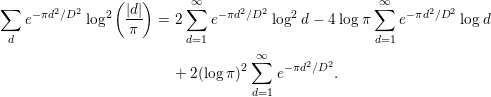 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right) & = & \displaystyle 2\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}d-4\log {\it\pi}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log d\nonumber\\ \displaystyle & & \displaystyle +\,2(\log {\it\pi})^{2}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}\left(\frac{|d|}{{\it\pi}}\right) & = & \displaystyle 2\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}d-4\log {\it\pi}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log d\nonumber\\ \displaystyle & & \displaystyle +\,2(\log {\it\pi})^{2}\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
By Lemmas 2.1, 2.2, 2.10, we have
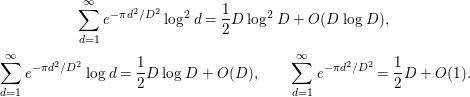 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}d=\frac{1}{2}D\log ^{2}D+O(D\log D), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log d=\frac{1}{2}D\log D+O(D),\qquad \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}=\frac{1}{2}D+O(1). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log ^{2}d=\frac{1}{2}D\log ^{2}D+O(D\log D), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}\log d=\frac{1}{2}D\log D+O(D),\qquad \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{2}/D^{2}}=\frac{1}{2}D+O(1). & \displaystyle \nonumber\end{eqnarray}$$
By inserting these into (3.16), we obtain
Hence,
Finally, we evaluate
![]() $M_{5}$
. Since
$M_{5}$
. Since
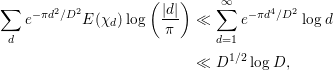 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log \left(\frac{|d|}{{\it\pi}}\right) & \ll & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\log d\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\log D,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\log \left(\frac{|d|}{{\it\pi}}\right) & \ll & \displaystyle \mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\log d\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\log D,\nonumber\end{eqnarray}$$
we obtain
3.3 The computation of
 $M_{4}$
and the evaluation of
$M_{4}$
and the evaluation of
 $M_{6}$
$M_{6}$
Next, we compute
![]() $M_{4}$
. We decompose this by
$M_{4}$
. We decompose this by
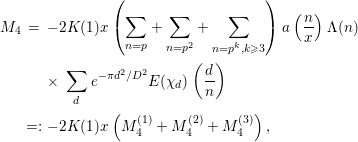 $$\begin{eqnarray}\displaystyle M_{4} & = & \displaystyle -2K(1)x\left(\mathop{\sum }_{n=p}+\mathop{\sum }_{n=p^{2}}+\mathop{\sum }_{n=p^{k},k\geqslant 3}\right)a\left(\frac{n}{x}\right){\rm\Lambda}(n)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & =: & \displaystyle -2K(1)x\left(M_{4}^{(1)}+M_{4}^{(2)}+M_{4}^{(3)}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{4} & = & \displaystyle -2K(1)x\left(\mathop{\sum }_{n=p}+\mathop{\sum }_{n=p^{2}}+\mathop{\sum }_{n=p^{k},k\geqslant 3}\right)a\left(\frac{n}{x}\right){\rm\Lambda}(n)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}E({\it\chi}_{d})\left(\frac{d}{n}\right)\nonumber\\ \displaystyle & =: & \displaystyle -2K(1)x\left(M_{4}^{(1)}+M_{4}^{(2)}+M_{4}^{(3)}\right),\end{eqnarray}$$
say. First,
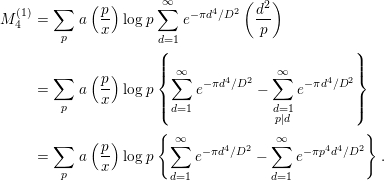 $$\begin{eqnarray}\displaystyle M_{4}^{(1)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\left(\frac{d^{2}}{p}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\right\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{4}^{(1)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\left(\frac{d^{2}}{p}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\right\}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\right\}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(K(1)x+O(x^{1/2}\log ^{2}x)\right)\left(ID^{1/2}-\frac{1}{2}+O(D^{-1/2})\right)\nonumber\\ \displaystyle & & \displaystyle \quad =IK(1)xD^{1/2}-\frac{1}{2}K(1)x+O((Dx)^{1/2}\log ^{2}x)+O(xD^{-1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(K(1)x+O(x^{1/2}\log ^{2}x)\right)\left(ID^{1/2}-\frac{1}{2}+O(D^{-1/2})\right)\nonumber\\ \displaystyle & & \displaystyle \quad =IK(1)xD^{1/2}-\frac{1}{2}K(1)x+O((Dx)^{1/2}\log ^{2}x)+O(xD^{-1/2}).\end{eqnarray}$$
By Lemma 2.3,
Therefore, by Lemmas 2.5 and 2.7, we have
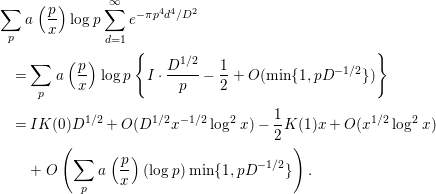 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =IK(0)D^{1/2}+O(D^{1/2}x^{-1/2}\log ^{2}x)-\frac{1}{2}K(1)x+O(x^{1/2}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\;\text{min}\{1,pD^{-1/2}\}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\left\{I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =IK(0)D^{1/2}+O(D^{1/2}x^{-1/2}\log ^{2}x)-\frac{1}{2}K(1)x+O(x^{1/2}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O\left(\mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\;\text{min}\{1,pD^{-1/2}\}\right).\end{eqnarray}$$
By Lemmas 2.5 and 2.11, we have
Therefore, the last line of (3.22) is evaluated by
![]() $O(\text{min}\{x,x^{2}D^{-1/2}\})$
. Hence, we have
$O(\text{min}\{x,x^{2}D^{-1/2}\})$
. Hence, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =IK(0)D^{1/2}-\frac{1}{2}K(1)x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{-1/2}\log ^{2}x+x^{1/2}\log ^{2}x+\text{min}\{x,x^{2}D^{-1/2}\}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}p^{4}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =IK(0)D^{1/2}-\frac{1}{2}K(1)x\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{-1/2}\log ^{2}x+x^{1/2}\log ^{2}x+\text{min}\{x,x^{2}D^{-1/2}\}).\end{eqnarray}$$
By inserting (3.21), (3.23) into (3.20), we obtain
Next,
 $$\begin{eqnarray}\displaystyle M_{4}^{(2)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\left(\frac{d^{2}}{p^{2}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{4}^{(2)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\left(\frac{d^{2}}{p^{2}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\left\{\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}-\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\right\}.\end{eqnarray}$$
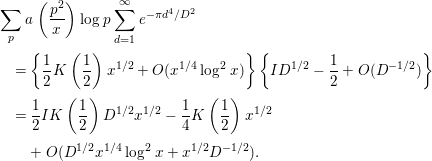 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\frac{1}{2}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{1/4}\log ^{2}x)\right\}\left\{ID^{1/2}-\frac{1}{2}+O(D^{-1/2})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}IK\left(\frac{1}{2}\right)D^{1/2}x^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{1/4}\log ^{2}x+x^{1/2}D^{-1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{d=1}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\frac{1}{2}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{1/4}\log ^{2}x)\right\}\left\{ID^{1/2}-\frac{1}{2}+O(D^{-1/2})\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}IK\left(\frac{1}{2}\right)D^{1/2}x^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{1/4}\log ^{2}x+x^{1/2}D^{-1/2}).\end{eqnarray}$$
On the other hand, since
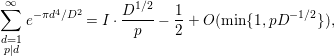 $$\begin{eqnarray}\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}=I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}=I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\}),\end{eqnarray}$$
by Lemmas 2.4 and 2.8, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\left\{I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\})\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =ID^{1/2}\left\{\frac{1}{2}K(0)+O(x^{-1/4}\log ^{2}x)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\left\{\frac{1}{2}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{1/4}\log ^{2}x)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,O\left(\text{min}\left\{\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p,D^{-1/2}\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)p\log p\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{1}{2}IK(0)D^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{-1/4}D^{1/2}\log ^{2}x)+O(x^{1/4}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,O\left(\text{min}\left\{\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p,D^{-1/2}\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)p\log p\right\}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\left\{I\cdot \frac{D^{1/2}}{p}-\frac{1}{2}+O(\text{min}\{1,pD^{-1/2}\})\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =ID^{1/2}\left\{\frac{1}{2}K(0)+O(x^{-1/4}\log ^{2}x)\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2}\left\{\frac{1}{2}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{1/4}\log ^{2}x)\right\}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,O\left(\text{min}\left\{\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p,D^{-1/2}\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)p\log p\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{1}{2}IK(0)D^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{-1/4}D^{1/2}\log ^{2}x)+O(x^{1/4}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,O\left(\text{min}\left\{\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p,D^{-1/2}\mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)p\log p\right\}\right).\end{eqnarray}$$
By Lemmas 2.4 and 2.12, we have
Hence, the last line of (3.27) becomes
![]() $O(\text{min}\{x^{1/2},xD^{-1/2}\})$
. Therefore,
$O(\text{min}\{x^{1/2},xD^{-1/2}\})$
. Therefore,
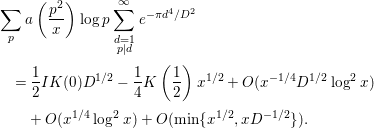 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}IK(0)D^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{-1/4}D^{1/2}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{1/4}\log ^{2}x)+O(\text{min}\{x^{1/2},xD^{-1/2}\}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p^{2}}{x}\right)\log p\mathop{\sum }_{\substack{ d=1 \\ p|d}}^{\infty }e^{-{\it\pi}d^{4}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}IK(0)D^{1/2}-\frac{1}{4}K\left(\frac{1}{2}\right)x^{1/2}+O(x^{-1/4}D^{1/2}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{1/4}\log ^{2}x)+O(\text{min}\{x^{1/2},xD^{-1/2}\}).\end{eqnarray}$$
By inserting (3.26), (3.28) into (3.25), we obtain
Next, we evaluate
Since
![]() $a(u)=0$
for
$a(u)=0$
for
![]() $u>B$
, we only have to compute the part
$u>B$
, we only have to compute the part
![]() $p^{k}/x\leqslant B$
. The number of such
$p^{k}/x\leqslant B$
. The number of such
![]() $k$
is
$k$
is
![]() $O(\log x)$
. Since
$O(\log x)$
. Since
![]() $p$
must satisfy
$p$
must satisfy
![]() $p\leqslant (Bx)^{1/k}\leqslant (Bx)^{1/3}$
, and
$p\leqslant (Bx)^{1/k}\leqslant (Bx)^{1/3}$
, and
using the PNT, we find that
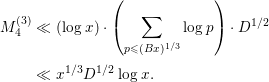 $$\begin{eqnarray}\displaystyle M_{4}^{(3)} & \ll & \displaystyle (\log x)\cdot \left(\mathop{\sum }_{p\leqslant (Bx)^{1/3}}\log p\right)\cdot D^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle x^{1/3}D^{1/2}\log x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{4}^{(3)} & \ll & \displaystyle (\log x)\cdot \left(\mathop{\sum }_{p\leqslant (Bx)^{1/3}}\log p\right)\cdot D^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle x^{1/3}D^{1/2}\log x.\end{eqnarray}$$
By inserting (3.24), (3.29), (3.30) into (3.19), we obtain
Next, we evaluate
![]() $M_{6}$
. We decompose this by
$M_{6}$
. We decompose this by
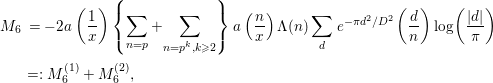 $$\begin{eqnarray}\displaystyle M_{6} & = & \displaystyle \!-2a\left(\frac{1}{x}\right)\left\{\mathop{\sum }_{n=p}+\!\mathop{\sum }_{n=p^{k},k\geqslant 2}\right\}a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\text{log}\left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & =: & \displaystyle M_{6}^{(1)}+M_{6}^{(2)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{6} & = & \displaystyle \!-2a\left(\frac{1}{x}\right)\left\{\mathop{\sum }_{n=p}+\!\mathop{\sum }_{n=p^{k},k\geqslant 2}\right\}a\left(\frac{n}{x}\right){\rm\Lambda}(n)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{n}\right)\text{log}\left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & =: & \displaystyle M_{6}^{(1)}+M_{6}^{(2)},\nonumber\end{eqnarray}$$
say. By the Pólya–Vinogradov inequality, we find that
Hence, by Lemma 2.9,
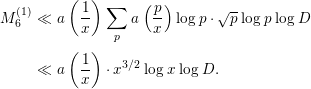 $$\begin{eqnarray}\displaystyle M_{6}^{(1)} & \ll & \displaystyle a\left(\frac{1}{x}\right)\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\cdot \sqrt{p}\log p\log D\nonumber\\ \displaystyle & \ll & \displaystyle a\left(\frac{1}{x}\right)\cdot x^{3/2}\log x\log D.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{6}^{(1)} & \ll & \displaystyle a\left(\frac{1}{x}\right)\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\cdot \sqrt{p}\log p\log D\nonumber\\ \displaystyle & \ll & \displaystyle a\left(\frac{1}{x}\right)\cdot x^{3/2}\log x\log D.\end{eqnarray}$$
Next, we evaluate
![]() $M_{6}^{(2)}$
. By Lemmas 2.1, 2.2 and the conditions
$M_{6}^{(2)}$
. By Lemmas 2.1, 2.2 and the conditions
![]() $k\ll \log x$
,
$k\ll \log x$
,
![]() $p\leqslant \sqrt{Bx}$
, we have
$p\leqslant \sqrt{Bx}$
, we have
 $$\begin{eqnarray}\displaystyle M_{6}^{(2)} & \ll & \displaystyle a\left(\frac{1}{x}\right)\log x\mathop{\sum }_{p\leqslant \sqrt{Bx}}\log p\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log \left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & \ll & \displaystyle a\left(\frac{1}{x}\right)Dx^{1/2}\log x\log D.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{6}^{(2)} & \ll & \displaystyle a\left(\frac{1}{x}\right)\log x\mathop{\sum }_{p\leqslant \sqrt{Bx}}\log p\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log \left(\frac{|d|}{{\it\pi}}\right)\nonumber\\ \displaystyle & \ll & \displaystyle a\left(\frac{1}{x}\right)Dx^{1/2}\log x\log D.\end{eqnarray}$$
Combining (3.32), (3.33), we obtain
3.4 The computation of
 $M_{2}$
$M_{2}$
Finally, we compute
where
![]() $P$
denotes the set of all prime numbers. It will be convenient to keep in mind that only
$P$
denotes the set of all prime numbers. It will be convenient to keep in mind that only
![]() $k,l$
satisfying
$k,l$
satisfying
![]() $k,l\ll \log x$
contribute to the sum above. First, we evaluate the contribution of the part
$k,l\ll \log x$
contribute to the sum above. First, we evaluate the contribution of the part
![]() $p=2$
to
$p=2$
to
![]() $M_{2}$
. The contribution of the part
$M_{2}$
. The contribution of the part
![]() $p=q=2$
is
$p=q=2$
is
The contribution of the part
![]() $p=2$
,
$p=2$
,
![]() $q\geqslant 3$
,
$q\geqslant 3$
,
![]() $l\geqslant 2$
is
$l\geqslant 2$
is
 $$\begin{eqnarray}\displaystyle & \ll & \displaystyle \mathop{\sum }_{k}\mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{q\in P}a\left(\frac{2^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle Dx^{1/2}\log ^{2}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \ll & \displaystyle \mathop{\sum }_{k}\mathop{\sum }_{l\geqslant 2}\mathop{\sum }_{q\in P}a\left(\frac{2^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle Dx^{1/2}\log ^{2}x.\end{eqnarray}$$
Since
![]() $(\cdot /2^{k}q)$
is a nonprincipal character whose conductor is at most
$(\cdot /2^{k}q)$
is a nonprincipal character whose conductor is at most
![]() $2q$
, by the Pólya–Vinogradov inequality, we have
$2q$
, by the Pólya–Vinogradov inequality, we have
for primes
![]() $q\geqslant 3$
. Therefore, the contribution of the part
$q\geqslant 3$
. Therefore, the contribution of the part
![]() $p=2$
,
$p=2$
,
![]() $q\geqslant 3$
,
$q\geqslant 3$
,
![]() $l=1$
is
$l=1$
is
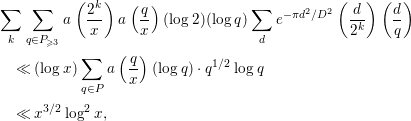 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{k}\mathop{\sum }_{q\in P_{{\geqslant}3}}a\left(\frac{2^{k}}{x}\right)a\left(\frac{q}{x}\right)(\log 2)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{2^{k}}\right)\left(\frac{d}{q}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \ll (\log x)\mathop{\sum }_{q\in P}a\left(\frac{q}{x}\right)(\log q)\cdot q^{1/2}\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{3/2}\log ^{2}x,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{k}\mathop{\sum }_{q\in P_{{\geqslant}3}}a\left(\frac{2^{k}}{x}\right)a\left(\frac{q}{x}\right)(\log 2)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{2^{k}}\right)\left(\frac{d}{q}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \ll (\log x)\mathop{\sum }_{q\in P}a\left(\frac{q}{x}\right)(\log q)\cdot q^{1/2}\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{3/2}\log ^{2}x,\end{eqnarray}$$
where
![]() $P_{{\geqslant}3}$
denotes the set of all prime numbers greater than 2. By (3.35), (3.36) and (3.37), the contribution of the part
$P_{{\geqslant}3}$
denotes the set of all prime numbers greater than 2. By (3.35), (3.36) and (3.37), the contribution of the part
![]() $p=2$
to
$p=2$
to
![]() $M_{2}$
is at most
$M_{2}$
is at most
![]() $O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x)$
. The contribution of the part
$O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x)$
. The contribution of the part
![]() $q=2$
is the same. Therefore, we conclude that
$q=2$
is the same. Therefore, we conclude that
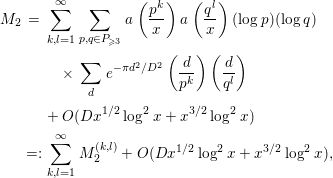 $$\begin{eqnarray}\displaystyle M_{2} & = & \displaystyle \mathop{\sum }_{k,l=1}^{\infty }\mathop{\sum }_{p,q\in P_{{\geqslant}3}}a\left(\frac{p^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{p^{k}}\right)\left(\frac{d}{q^{l}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x)\nonumber\\ \displaystyle & =: & \displaystyle \mathop{\sum }_{k,l=1}^{\infty }M_{2}^{(k,l)}+O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2} & = & \displaystyle \mathop{\sum }_{k,l=1}^{\infty }\mathop{\sum }_{p,q\in P_{{\geqslant}3}}a\left(\frac{p^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{p^{k}}\right)\left(\frac{d}{q^{l}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x)\nonumber\\ \displaystyle & =: & \displaystyle \mathop{\sum }_{k,l=1}^{\infty }M_{2}^{(k,l)}+O(Dx^{1/2}\log ^{2}x+x^{3/2}\log ^{2}x),\end{eqnarray}$$
say. Moreover, by the PNT and Lemma 2.1, we have
 $$\begin{eqnarray}\displaystyle M_{2}^{(k,l)} & \ll & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle klDx^{1/k+\frac{1}{l}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2}^{(k,l)} & \ll & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p^{k}}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle klDx^{1/k+\frac{1}{l}}\nonumber\end{eqnarray}$$
for each
![]() $k,l$
. Hence, the total contribution of the part
$k,l$
. Hence, the total contribution of the part
![]() $k\geqslant 3,l\geqslant 2$
or
$k\geqslant 3,l\geqslant 2$
or
![]() $k\geqslant 2,l\geqslant 3$
is at most
$k\geqslant 2,l\geqslant 3$
is at most
![]() $O(Dx^{5/6}\log ^{4}x)$
. Therefore,
$O(Dx^{5/6}\log ^{4}x)$
. Therefore,
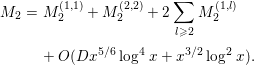 $$\begin{eqnarray}\displaystyle M_{2} & = & \displaystyle M_{2}^{(1,1)}+M_{2}^{(2,2)}+2\mathop{\sum }_{l\geqslant 2}M_{2}^{(1,l)}\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{5/6}\log ^{4}x+x^{3/2}\log ^{2}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2} & = & \displaystyle M_{2}^{(1,1)}+M_{2}^{(2,2)}+2\mathop{\sum }_{l\geqslant 2}M_{2}^{(1,l)}\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{5/6}\log ^{4}x+x^{3/2}\log ^{2}x).\end{eqnarray}$$
By the computation above,
![]() $M_{2}^{(2,2)}$
is evaluated by
$M_{2}^{(2,2)}$
is evaluated by
Next, we compute
![]() $M_{2}^{(1,l)}$
for
$M_{2}^{(1,l)}$
for
![]() $l\geqslant 1$
,
$l\geqslant 1$
,
![]() $1\ll x\ll D^{1-{\it\delta}}$
.
$1\ll x\ll D^{1-{\it\delta}}$
.
(A) First, we consider the case that
![]() $l$
is odd. In this case, we decompose
$l$
is odd. In this case, we decompose
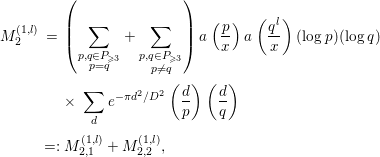 $$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle \left(\mathop{\sum }_{\substack{ p,q\in P_{{\geqslant}3} \\ p=q}}+\mathop{\sum }_{\substack{ p,q\in P_{{\geqslant}3} \\ p\neq q}}\right)a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{p}\right)\left(\frac{d}{q}\right)\nonumber\\ \displaystyle & =: & \displaystyle M_{2,1}^{(1,l)}+M_{2,2}^{(1,l)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle \left(\mathop{\sum }_{\substack{ p,q\in P_{{\geqslant}3} \\ p=q}}+\mathop{\sum }_{\substack{ p,q\in P_{{\geqslant}3} \\ p\neq q}}\right)a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\left(\frac{d}{p}\right)\left(\frac{d}{q}\right)\nonumber\\ \displaystyle & =: & \displaystyle M_{2,1}^{(1,l)}+M_{2,2}^{(1,l)},\end{eqnarray}$$
say. First, we compute
![]() $M_{2,1}^{(1,1)}$
. This term is given by
$M_{2,1}^{(1,1)}$
. This term is given by
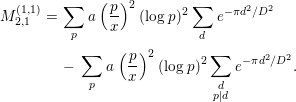 $$\begin{eqnarray}\displaystyle M_{2,1}^{(1,1)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{\substack{ d \\ p|d}}e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2,1}^{(1,1)} & = & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{\substack{ d \\ p|d}}e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
By Lemmas 2.1, 2.13, the first term on the right-hand side of (3.42) is
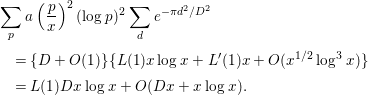 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\{D+O(1)\}\{L(1)x\log x+L^{\prime }(1)x+O(x^{1/2}\log ^{3}x)\}\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x+O(Dx+x\log x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\{D+O(1)\}\{L(1)x\log x+L^{\prime }(1)x+O(x^{1/2}\log ^{3}x)\}\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x+O(Dx+x\log x).\end{eqnarray}$$
By Lemmas 2.1, 2.13, 2.14, the second term on the right-hand side of (3.42) is
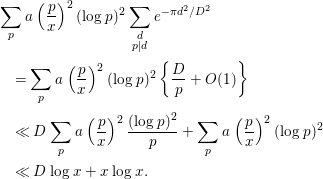 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{\substack{ d \\ p|d}}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\left\{\frac{D}{p}+O(1)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}\frac{(\log p)^{2}}{p}+\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\log x+x\log x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\mathop{\sum }_{\substack{ d \\ p|d}}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\left\{\frac{D}{p}+O(1)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}\frac{(\log p)^{2}}{p}+\mathop{\sum }_{p}a\left(\frac{p}{x}\right)^{2}(\log p)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\log x+x\log x.\end{eqnarray}$$
By inserting (3.43), (3.44) into (3.42), we obtain
If
![]() $l\geqslant 2$
(including the case that
$l\geqslant 2$
(including the case that
![]() $l$
is even), by the PNT and Lemma 2.1,
$l$
is even), by the PNT and Lemma 2.1,
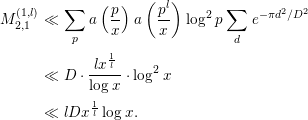 $$\begin{eqnarray}\displaystyle M_{2,1}^{(1,l)} & \ll & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\cdot \frac{lx^{\frac{1}{l}}}{\log x}\cdot \log ^{2}x\nonumber\\ \displaystyle & \ll & \displaystyle lDx^{\frac{1}{l}}\log x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2,1}^{(1,l)} & \ll & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\cdot \frac{lx^{\frac{1}{l}}}{\log x}\cdot \log ^{2}x\nonumber\\ \displaystyle & \ll & \displaystyle lDx^{\frac{1}{l}}\log x.\end{eqnarray}$$
Next, we compute
![]() $M_{2,2}^{(1,l)}$
.
$M_{2,2}^{(1,l)}$
.
(a) Let
![]() $x=o(D^{1/2})$
. By the Pólya–Vinogradov inequality, we obtain
$x=o(D^{1/2})$
. By the Pólya–Vinogradov inequality, we obtain
Hence, by the PNT, we have
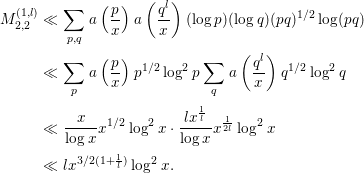 $$\begin{eqnarray}\displaystyle M_{2,2}^{(1,l)} & \ll & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)(pq)^{1/2}\log (pq)\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)p^{1/2}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)q^{1/2}\log ^{2}q\nonumber\\ \displaystyle & \ll & \displaystyle \frac{x}{\log x}x^{1/2}\log ^{2}x\cdot \frac{lx^{\frac{1}{l}}}{\log x}x^{\frac{1}{2l}}\log ^{2}x\nonumber\\ \displaystyle & \ll & \displaystyle lx^{3/2(1+\frac{1}{l})}\log ^{2}x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2,2}^{(1,l)} & \ll & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)(pq)^{1/2}\log (pq)\nonumber\\ \displaystyle & \ll & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)p^{1/2}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)q^{1/2}\log ^{2}q\nonumber\\ \displaystyle & \ll & \displaystyle \frac{x}{\log x}x^{1/2}\log ^{2}x\cdot \frac{lx^{\frac{1}{l}}}{\log x}x^{\frac{1}{2l}}\log ^{2}x\nonumber\\ \displaystyle & \ll & \displaystyle lx^{3/2(1+\frac{1}{l})}\log ^{2}x.\end{eqnarray}$$
(b) If
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by the translation formula of the theta function (Lemma 2.17), we have
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by the translation formula of the theta function (Lemma 2.17), we have
 $$\begin{eqnarray}M_{2,2}^{(1,l)}=D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m}\left(\frac{m}{pq}\right)e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}M_{2,2}^{(1,l)}=D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m}\left(\frac{m}{pq}\right)e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}}.\end{eqnarray}$$
We decompose this by
where
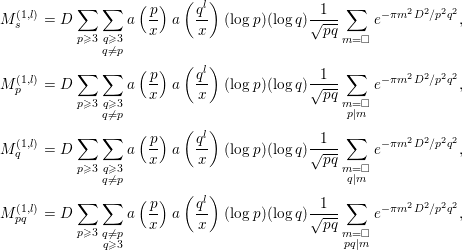 $$\begin{eqnarray}\displaystyle M_{s}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=\Box }e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{p}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ p|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{q}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ q|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{pq}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\neq p \\ q\geqslant 3}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ pq|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{s}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=\Box }e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{p}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ p|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{q}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ q|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\\ \displaystyle M_{pq}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\neq p \\ q\geqslant 3}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{\substack{ m=\Box \\ pq|m}}e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}},\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}E=D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}E=D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }e^{-{\it\pi}m^{2}D^{2}/p^{2}q^{2}}.\end{eqnarray}$$
First, by Lemma 2.3,
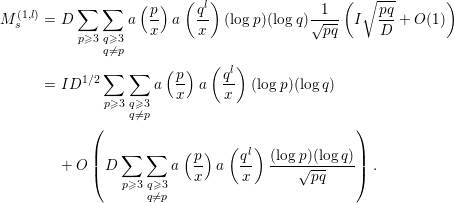 $$\begin{eqnarray}\displaystyle M_{s}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\left(I\sqrt{\frac{pq}{D}}+O(1)\right)\nonumber\\ \displaystyle & = & \displaystyle ID^{1/2}\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle +\,O\left(D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{s}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\left(I\sqrt{\frac{pq}{D}}+O(1)\right)\nonumber\\ \displaystyle & = & \displaystyle ID^{1/2}\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\nonumber\\ \displaystyle & & \displaystyle +\,O\left(D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\right).\end{eqnarray}$$
By applying Lemmas 2.15, 2.16 to (3.49), we obtain
In the computation above, we used
![]() $\left|K\left(1/2l\right)\right|\ll \int _{A}^{B}t^{1/2l}\,dt/t\ll l$
. Next, by Lemma 2.3,
$\left|K\left(1/2l\right)\right|\ll \int _{A}^{B}t^{1/2l}\,dt/t\ll l$
. Next, by Lemma 2.3,
 $$\begin{eqnarray}\displaystyle M_{p}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}p^{2}D^{2}m^{4}/q^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}\mathop{\sum }_{q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\left(\sqrt{\frac{q}{pD}}+O(1)\right)\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{p}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)(\log q)\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{p}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}p^{2}D^{2}m^{4}/q^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}\mathop{\sum }_{q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\left(\sqrt{\frac{q}{pD}}+O(1)\right)\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{p}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)(\log q)\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}.\nonumber\end{eqnarray}$$
By Lemma 2.7,
By the PNT,
By Lemma 2.6,
By the PNT and the Stieltjes integral,
 $$\begin{eqnarray}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\ll \int _{1}^{\infty }a\left(\frac{u^{l}}{x}\right)\,\frac{du}{\sqrt{u}}\ll \int _{1}^{(Bx)^{\frac{1}{l}}}\,\frac{du}{\sqrt{u}}\ll x^{\frac{1}{2l}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\ll \int _{1}^{\infty }a\left(\frac{u^{l}}{x}\right)\,\frac{du}{\sqrt{u}}\ll \int _{1}^{(Bx)^{\frac{1}{l}}}\,\frac{du}{\sqrt{u}}\ll x^{\frac{1}{2l}}.\end{eqnarray}$$
Combining these, we obtain
Next, by Lemma 2.3,
 $$\begin{eqnarray}\displaystyle M_{q}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}q^{2}D^{2}m^{4}/p^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}\mathop{\sum }_{q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\left(\sqrt{\frac{p}{qD}}+O(1)\right)\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{q}\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{q}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}q^{2}D^{2}m^{4}/p^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}\mathop{\sum }_{q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)\frac{(\log p)(\log q)}{\sqrt{pq}}\left(\sqrt{\frac{p}{qD}}+O(1)\right)\nonumber\\ \displaystyle & \ll & \displaystyle D^{1/2}\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{q}\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}.\end{eqnarray}$$
By the PNT and the Stieltjes integral,
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\ll x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{q}\ll \int _{1}^{\infty }a\left(\frac{u^{l}}{x}\right)\,\frac{du}{u}\ll \int _{1}^{(Bx)^{\frac{1}{l}}}\,\frac{du}{u}\ll l^{-1}\log x. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\log p\ll x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{q}\ll \int _{1}^{\infty }a\left(\frac{u^{l}}{x}\right)\,\frac{du}{u}\ll \int _{1}^{(Bx)^{\frac{1}{l}}}\,\frac{du}{u}\ll l^{-1}\log x. & \displaystyle \nonumber\end{eqnarray}$$
The last line of (3.52) is
![]() $O(Dx^{1/2+1/2l})$
, as we computed in the evaluation of
$O(Dx^{1/2+1/2l})$
, as we computed in the evaluation of
![]() $M_{p}^{(1,l)}$
. Combining these, we obtain
$M_{p}^{(1,l)}$
. Combining these, we obtain
The term
![]() $M_{pq}^{(1,l)}$
is evaluated by
$M_{pq}^{(1,l)}$
is evaluated by
 $$\begin{eqnarray}\displaystyle M_{pq}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}p^{2}q^{2}D^{2}m^{4}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\nonumber\\ \displaystyle & \ll & \displaystyle Dx^{1/2+\frac{1}{2l}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{pq}^{(1,l)} & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}p^{2}q^{2}D^{2}m^{4}}\nonumber\\ \displaystyle & \ll & \displaystyle D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\nonumber\\ \displaystyle & \ll & \displaystyle Dx^{1/2+\frac{1}{2l}}.\end{eqnarray}$$
Finally, we evaluate
![]() $E$
. First,
$E$
. First,
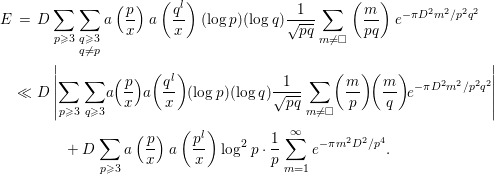 $$\begin{eqnarray}\displaystyle E & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{pq}\right)e^{-{\it\pi}D^{2}m^{2}/p^{2}q^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\left|\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{q\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{p}\right)\left(\frac{m}{q}\right)e^{-{\it\pi}D^{2}m^{2}/p^{2}q^{2}}\right|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,D\mathop{\sum }_{p\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\cdot \frac{1}{p}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}m^{2}D^{2}/p^{4}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E & = & \displaystyle D\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{\substack{ q\geqslant 3 \\ q\neq p}}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{pq}\right)e^{-{\it\pi}D^{2}m^{2}/p^{2}q^{2}}\nonumber\\ \displaystyle & \ll & \displaystyle D\left|\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{q\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{p}\right)\left(\frac{m}{q}\right)e^{-{\it\pi}D^{2}m^{2}/p^{2}q^{2}}\right|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,D\mathop{\sum }_{p\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\cdot \frac{1}{p}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}m^{2}D^{2}/p^{4}}.\end{eqnarray}$$
By the PNT and Lemma 2.1, the second term on the right-hand side of (3.55) is
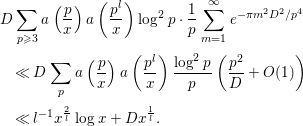 $$\begin{eqnarray}\displaystyle & & \displaystyle D\mathop{\sum }_{p\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\cdot \frac{1}{p}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}m^{2}D^{2}/p^{4}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\frac{\log ^{2}p}{p}\left(\frac{p^{2}}{D}+O(1)\right)\nonumber\\ \displaystyle & & \displaystyle \quad \ll l^{-1}x^{\frac{2}{l}}\log x+Dx^{\frac{1}{l}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D\mathop{\sum }_{p\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\log ^{2}p\cdot \frac{1}{p}\mathop{\sum }_{m=1}^{\infty }e^{-{\it\pi}m^{2}D^{2}/p^{4}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll D\mathop{\sum }_{p}a\left(\frac{p}{x}\right)a\left(\frac{p^{l}}{x}\right)\frac{\log ^{2}p}{p}\left(\frac{p^{2}}{D}+O(1)\right)\nonumber\\ \displaystyle & & \displaystyle \quad \ll l^{-1}x^{\frac{2}{l}}\log x+Dx^{\frac{1}{l}}.\end{eqnarray}$$
Next, since
holds for
![]() $p\leqslant Bx$
,
$p\leqslant Bx$
,
![]() $q\leqslant (Bx)^{1/l}$
, the first term on the right-hand side of (3.55) is evaluated by
$q\leqslant (Bx)^{1/l}$
, the first term on the right-hand side of (3.55) is evaluated by
 $$\begin{eqnarray}\displaystyle & & \displaystyle D\left|\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{q\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{p}\right)\left(\frac{m}{q}\right)e^{-{\it\pi}D^{2}m^{4}/p^{2}q^{2}}\right|\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \ll D\mathop{\sum }_{m\neq \Box }e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}\left|\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\left(\frac{m}{p}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \times \left|\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\left(\frac{m}{q}\right)\right|.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D\left|\mathop{\sum }_{p\geqslant 3}\mathop{\sum }_{q\geqslant 3}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\frac{1}{\sqrt{pq}}\mathop{\sum }_{m\neq \Box }\left(\frac{m}{p}\right)\left(\frac{m}{q}\right)e^{-{\it\pi}D^{2}m^{4}/p^{2}q^{2}}\right|\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \ll D\mathop{\sum }_{m\neq \Box }e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}\left|\mathop{\sum }_{p}a\left(\frac{p}{x}\right)\frac{\log p}{\sqrt{p}}\left(\frac{m}{p}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \times \left|\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\left(\frac{m}{q}\right)\right|.\end{eqnarray}$$
According to [Reference Özlük and Snyder13, p. 221], under the assumption of the GRH,
holds uniformly for
![]() $m\ll x~m\neq \Box$
. Moreover, since the GRH implies
$m\ll x~m\neq \Box$
. Moreover, since the GRH implies
uniformly for
![]() $m\ll x^{1/l}$
$m\ll x^{1/l}$
![]() $m\neq \Box$
, we have
$m\neq \Box$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\left(\frac{m}{q}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)\frac{1}{\sqrt{u}}\,d\left(\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right\}a\left(\frac{u^{l}}{x}\right)u^{-3/2}\,du\nonumber\\ \displaystyle & & \displaystyle \quad \quad -\,\frac{l}{x}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right\}a^{\prime }\left(\frac{u^{l}}{x}\right)u^{l-\frac{3}{2}}\,du\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant (xv)^{\frac{1}{l}}}\left(\frac{m}{q}\right)\log q\right\}a(v)(xv)^{-\frac{3}{2l}}\cdot x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \quad -\,\frac{l}{x}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant (xv)^{\frac{1}{l}}}\left(\frac{m}{q}\right)\log q\right\}a^{\prime }(v)(xv)^{\frac{1}{l}(l-\frac{3}{2})}\cdot x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{1}{2}\int _{A}^{B}(xv)^{\frac{1}{2l}}\log ^{2}(m(xv)^{\frac{1}{l}})a(v)(xv)^{-\frac{3}{2l}}x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,lx^{-1}\int _{A}^{B}(xv)^{\frac{1}{2l}}\log ^{2}(m(xv)^{\frac{1}{l}})a^{\prime }(v)(xv)^{\frac{1}{l}(l-\frac{3}{2})}x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \ll \log ^{2}mx\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\frac{\log q}{\sqrt{q}}\left(\frac{m}{q}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }a\left(\frac{u^{l}}{x}\right)\frac{1}{\sqrt{u}}\,d\left(\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right\}a\left(\frac{u^{l}}{x}\right)u^{-3/2}\,du\nonumber\\ \displaystyle & & \displaystyle \quad \quad -\,\frac{l}{x}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant u}\left(\frac{m}{q}\right)\log q\right\}a^{\prime }\left(\frac{u^{l}}{x}\right)u^{l-\frac{3}{2}}\,du\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant (xv)^{\frac{1}{l}}}\left(\frac{m}{q}\right)\log q\right\}a(v)(xv)^{-\frac{3}{2l}}\cdot x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \quad -\,\frac{l}{x}\int _{0}^{\infty }\left\{\mathop{\sum }_{q\leqslant (xv)^{\frac{1}{l}}}\left(\frac{m}{q}\right)\log q\right\}a^{\prime }(v)(xv)^{\frac{1}{l}(l-\frac{3}{2})}\cdot x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{1}{2}\int _{A}^{B}(xv)^{\frac{1}{2l}}\log ^{2}(m(xv)^{\frac{1}{l}})a(v)(xv)^{-\frac{3}{2l}}x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,lx^{-1}\int _{A}^{B}(xv)^{\frac{1}{2l}}\log ^{2}(m(xv)^{\frac{1}{l}})a^{\prime }(v)(xv)^{\frac{1}{l}(l-\frac{3}{2})}x^{\frac{1}{l}}l^{-1}v^{\frac{1}{l}-1}\,dv\nonumber\\ \displaystyle & & \displaystyle \quad \ll \log ^{2}mx\nonumber\end{eqnarray}$$
uniformly for
![]() $m\ll x^{1/l}$
. On the other hand, by forgetting the Kronecker symbols, we have
$m\ll x^{1/l}$
. On the other hand, by forgetting the Kronecker symbols, we have
Hence, the first term on the right-hand side of (3.55) is
 $$\begin{eqnarray}\displaystyle & \ll & \displaystyle D\mathop{\sum }_{m\leqslant x^{\frac{1}{l}}}e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}\log ^{4}mx\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{m\geqslant x^{\frac{1}{l}}}e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}x^{1/2+\frac{1}{2l}}\nonumber\\ \displaystyle & \ll & \displaystyle x^{1+\frac{1}{l}}\log ^{4}x+D\log ^{4}x\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \ll & \displaystyle D\mathop{\sum }_{m\leqslant x^{\frac{1}{l}}}e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}\log ^{4}mx\nonumber\\ \displaystyle & & \displaystyle +\,D\mathop{\sum }_{m\geqslant x^{\frac{1}{l}}}e^{-{\it\pi}m^{2}D^{2}/(Bx)^{2+\frac{2}{l}}}x^{1/2+\frac{1}{2l}}\nonumber\\ \displaystyle & \ll & \displaystyle x^{1+\frac{1}{l}}\log ^{4}x+D\log ^{4}x\end{eqnarray}$$
for
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
. By inserting (3.56), (3.58) into (3.55), we obtain
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
. By inserting (3.56), (3.58) into (3.55), we obtain
By combining (3.50), (3.51), (3.53), (3.54) and (3.59), for odd
![]() $l$
and
$l$
and
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, we have
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, we have
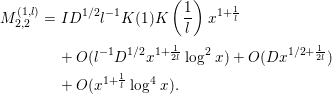 $$\begin{eqnarray}\displaystyle M_{2,2}^{(1,l)} & = & \displaystyle ID^{1/2}l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}D^{1/2}x^{1+\frac{1}{2l}}\log ^{2}x)+O(Dx^{1/2+\frac{1}{2l}})\nonumber\\ \displaystyle & & \displaystyle +\,O(x^{1+\frac{1}{l}}\log ^{4}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2,2}^{(1,l)} & = & \displaystyle ID^{1/2}l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}D^{1/2}x^{1+\frac{1}{2l}}\log ^{2}x)+O(Dx^{1/2+\frac{1}{2l}})\nonumber\\ \displaystyle & & \displaystyle +\,O(x^{1+\frac{1}{l}}\log ^{4}x).\end{eqnarray}$$
By combining this and (3.46), for odd
![]() $l\geqslant 3$
and
$l\geqslant 3$
and
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, we have
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, we have
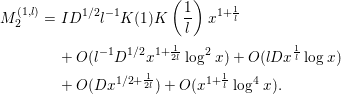 $$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle ID^{1/2}l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}D^{1/2}x^{1+\frac{1}{2l}}\log ^{2}x)+O(lDx^{\frac{1}{l}}\log x)\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{1/2+\frac{1}{2l}})+O(x^{1+\frac{1}{l}}\log ^{4}x).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle ID^{1/2}l^{-1}K(1)K\left(\frac{1}{l}\right)x^{1+\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle +\,O(l^{-1}D^{1/2}x^{1+\frac{1}{2l}}\log ^{2}x)+O(lDx^{\frac{1}{l}}\log x)\nonumber\\ \displaystyle & & \displaystyle +\,O(Dx^{1/2+\frac{1}{2l}})+O(x^{1+\frac{1}{l}}\log ^{4}x).\end{eqnarray}$$
If
![]() $l=1$
,
$l=1$
,
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by (3.45) and (3.60), we have
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by (3.45) and (3.60), we have
On the other hand, for odd
![]() $l\geqslant 3$
and
$l\geqslant 3$
and
![]() $x=o(D^{1/2})$
, by (3.46) and (3.47), we have
$x=o(D^{1/2})$
, by (3.46) and (3.47), we have
and for
![]() $l=1$
,
$l=1$
,
![]() $x=o(D^{1/2})$
, by (3.45) and (3.47), we have
$x=o(D^{1/2})$
, by (3.45) and (3.47), we have
(B) Next, we consider the case that
![]() $l$
is even. In this case, we have
$l$
is even. In this case, we have
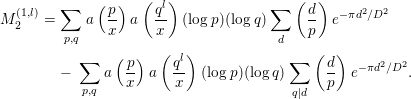 $$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{2}^{(1,l)} & = & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}.\end{eqnarray}$$
Since
the first term on the right-hand side of (3.65) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\sqrt{p}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{3/2}\log x\cdot lx^{\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll lx^{3/2+\frac{1}{l}}\log x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\sqrt{p}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll x^{3/2}\log x\cdot lx^{\frac{1}{l}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll lx^{3/2+\frac{1}{l}}\log x.\end{eqnarray}$$
The second term on the right-hand side of (3.65) is
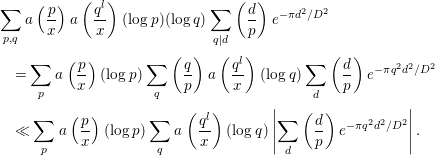 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\mathop{\sum }_{q}\left(\frac{q}{p}\right)a\left(\frac{q^{l}}{x}\right)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}q^{2}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)(\log q)\left|\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}q^{2}d^{2}/D^{2}}\right|.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\mathop{\sum }_{q}\left(\frac{q}{p}\right)a\left(\frac{q^{l}}{x}\right)(\log q)\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}q^{2}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)(\log p)\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)(\log q)\left|\mathop{\sum }_{d}\left(\frac{d}{p}\right)e^{-{\it\pi}q^{2}d^{2}/D^{2}}\right|.\end{eqnarray}$$
Now, since
![]() $q$
satisfies
$q$
satisfies
![]() $q\leqslant (Bx)^{1/l}\ll D^{1-{\it\delta}}\ll D$
,
$q\leqslant (Bx)^{1/l}\ll D^{1-{\it\delta}}\ll D$
,
![]() $D/q\gg 1$
holds. Therefore, by the Pólya–Vinogradov inequality, we have
$D/q\gg 1$
holds. Therefore, by the Pólya–Vinogradov inequality, we have
Therefore,
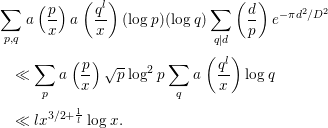 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\sqrt{p}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll lx^{3/2+\frac{1}{l}}\log x.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{p,q}a\left(\frac{p}{x}\right)a\left(\frac{q^{l}}{x}\right)(\log p)(\log q)\mathop{\sum }_{q|d}\left(\frac{d}{p}\right)e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \mathop{\sum }_{p}a\left(\frac{p}{x}\right)\sqrt{p}\log ^{2}p\mathop{\sum }_{q}a\left(\frac{q^{l}}{x}\right)\log q\nonumber\\ \displaystyle & & \displaystyle \quad \ll lx^{3/2+\frac{1}{l}}\log x.\end{eqnarray}$$
By combining (3.66) and (3.69), we obtain
for even
![]() $l$
.
$l$
.
Now, we have computed or evaluated
![]() $M_{2}^{(1,l)}$
for all
$M_{2}^{(1,l)}$
for all
![]() $l$
. If
$l$
. If
![]() $x=o(D^{1/2})$
, by (3.63) and (3.70), we have
$x=o(D^{1/2})$
, by (3.63) and (3.70), we have
By inserting (3.40), (3.64), (3.71) into (3.39), we obtain
If
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by (3.61),
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, by (3.61),
(It should be noticed that
![]() $K(1/l)\ll l$
.) On the other hand, by (3.70),
$K(1/l)\ll l$
.) On the other hand, by (3.70),
By inserting (3.40), (3.62), (3.73), (3.74) into (3.39), we obtain
for
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
.
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
.
3.5 Conclusion
Now, we have computed or evaluated all terms appearing on the right-hand side of (3.1). We fix
![]() ${\it\delta}>0$
sufficiently small. Then, we have the following.
${\it\delta}>0$
sufficiently small. Then, we have the following.
(1) If
![]() $1<x\ll D^{1/2-{\it\delta}}$
, by inserting (3.2), (3.3), (3.13), (3.14), (3.15), (3.17), (3.18), (3.31), (3.34) and (3.72) into (3.1), we obtain
$1<x\ll D^{1/2-{\it\delta}}$
, by inserting (3.2), (3.3), (3.13), (3.14), (3.15), (3.17), (3.18), (3.31), (3.34) and (3.72) into (3.1), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle f_{K}(x,D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x-IK(1)^{2}D^{1/2}x^{2}-\frac{1}{2}K(1)^{2}x^{2}+a\left(\frac{1}{x}\right)^{2}D\log ^{2}D\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,a\left(\frac{1}{x}\right)O(xD^{1/2}\log D+x^{3/2}\log x\log D+Dx^{1/2}\log x\log D)\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,a\left(\frac{1}{x}\right)^{2}O(D\log D)+O(x^{2}D^{-1/2})+O(Dx+x^{3}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(D^{1/2}x^{3/2}\log ^{2}x)+O(\text{min}\{x^{2},x^{3}D^{-1/2}\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{x^{2}D^{1/2},xD^{1/2}\log x\log D\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\min \{xD\log x\log D,xD^{1/2}\log x\log D\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{xD\log D,D\log x\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{x^{2}D,D\log ^{2}x\log ^{2}D\}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{K}(x,D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x-IK(1)^{2}D^{1/2}x^{2}-\frac{1}{2}K(1)^{2}x^{2}+a\left(\frac{1}{x}\right)^{2}D\log ^{2}D\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,a\left(\frac{1}{x}\right)O(xD^{1/2}\log D+x^{3/2}\log x\log D+Dx^{1/2}\log x\log D)\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,a\left(\frac{1}{x}\right)^{2}O(D\log D)+O(x^{2}D^{-1/2})+O(Dx+x^{3}\log ^{2}x)\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(D^{1/2}x^{3/2}\log ^{2}x)+O(\text{min}\{x^{2},x^{3}D^{-1/2}\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{x^{2}D^{1/2},xD^{1/2}\log x\log D\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\min \{xD\log x\log D,xD^{1/2}\log x\log D\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{xD\log D,D\log x\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \quad \quad +\,O(\text{min}\{x^{2}D,D\log ^{2}x\log ^{2}D\}).\nonumber\end{eqnarray}$$
(2) If
![]() $D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, since
$D^{1/2-{\it\delta}}\ll x\ll D^{1-{\it\delta}}$
, since
![]() $a(1/x)=0$
, by inserting (3.2), (3.3), (3.13), (3.14), (3.15), (3.17), (3.18), (3.31), (3.34) and (3.75) into (3.1), we obtain
$a(1/x)=0$
, by inserting (3.2), (3.3), (3.13), (3.14), (3.15), (3.17), (3.18), (3.31), (3.34) and (3.75) into (3.1), we obtain
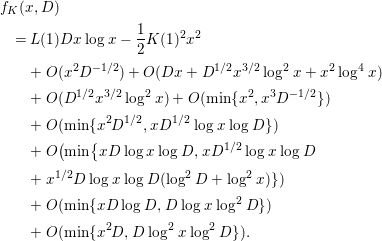 $$\begin{eqnarray}\displaystyle & & \displaystyle f_{K}(x,D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x-\frac{1}{2}K(1)^{2}x^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{2}D^{-1/2})+O(Dx+D^{1/2}x^{3/2}\log ^{2}x+x^{2}\log ^{4}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{3/2}\log ^{2}x)+O(\text{min}\{x^{2},x^{3}D^{-1/2}\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{x^{2}D^{1/2},xD^{1/2}\log x\log D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\min \{xD\log x\log D,xD^{1/2}\log x\log D\nonumber\\ \displaystyle & & \displaystyle \qquad +\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{xD\log D,D\log x\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{x^{2}D,D\log ^{2}x\log ^{2}D\}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{K}(x,D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1)Dx\log x-\frac{1}{2}K(1)^{2}x^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(x^{2}D^{-1/2})+O(Dx+D^{1/2}x^{3/2}\log ^{2}x+x^{2}\log ^{4}x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(D^{1/2}x^{3/2}\log ^{2}x)+O(\text{min}\{x^{2},x^{3}D^{-1/2}\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{x^{2}D^{1/2},xD^{1/2}\log x\log D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\min \{xD\log x\log D,xD^{1/2}\log x\log D\nonumber\\ \displaystyle & & \displaystyle \qquad +\,x^{1/2}D\log x\log D(\log ^{2}D+\log ^{2}x)\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{xD\log D,D\log x\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{x^{2}D,D\log ^{2}x\log ^{2}D\}).\nonumber\end{eqnarray}$$
By dividing both sides by
![]() $xD\log D$
and putting
$xD\log D$
and putting
![]() $x=D^{{\it\alpha}}$
(
$x=D^{{\it\alpha}}$
(
![]() ${\it\alpha}>0$
), we obtain the following formulas.
${\it\alpha}>0$
), we obtain the following formulas.
(1) If
![]() $0<{\it\alpha}\leqslant 1/2-{\it\delta}$
, we have
$0<{\it\alpha}\leqslant 1/2-{\it\delta}$
, we have
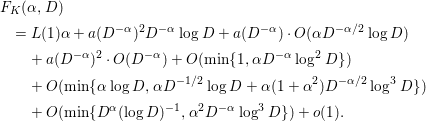 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{K}({\it\alpha},D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1){\it\alpha}+a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\log D+a(D^{-{\it\alpha}})\cdot O({\it\alpha}D^{-{\it\alpha}/2}\log D)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,a(D^{-{\it\alpha}})^{2}\cdot O(D^{-{\it\alpha}})+O(\text{min}\{1,{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\min \{{\it\alpha}\log D,{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{D^{{\it\alpha}}(\log D)^{-1},{\it\alpha}^{2}D^{-{\it\alpha}}\log ^{3}D\})+o(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{K}({\it\alpha},D)\nonumber\\ \displaystyle & & \displaystyle \quad =L(1){\it\alpha}+a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\log D+a(D^{-{\it\alpha}})\cdot O({\it\alpha}D^{-{\it\alpha}/2}\log D)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,a(D^{-{\it\alpha}})^{2}\cdot O(D^{-{\it\alpha}})+O(\text{min}\{1,{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\min \{{\it\alpha}\log D,{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\text{min}\{D^{{\it\alpha}}(\log D)^{-1},{\it\alpha}^{2}D^{-{\it\alpha}}\log ^{3}D\})+o(1).\end{eqnarray}$$
(2) If
![]() $1/2-{\it\delta}<{\it\alpha}\leqslant 1-{\it\delta}$
, we have
$1/2-{\it\delta}<{\it\alpha}\leqslant 1-{\it\delta}$
, we have
Here, the implied constants depend only on
![]() $K(s)$
and
$K(s)$
and
![]() ${\it\delta}>0$
. However, the identity (3.76) is still valid for
${\it\delta}>0$
. However, the identity (3.76) is still valid for
![]() $1/2-{\it\delta}<{\it\alpha}\leqslant 1-{\it\delta}$
, since the terms except for the first term on the right-hand side of (3.76) are all
$1/2-{\it\delta}<{\it\alpha}\leqslant 1-{\it\delta}$
, since the terms except for the first term on the right-hand side of (3.76) are all
![]() $o(1)$
if
$o(1)$
if
![]() ${\it\alpha}$
is large. Hence, we obtain (1.5).◻
${\it\alpha}$
is large. Hence, we obtain (1.5).◻
4 Applications of Theorem 1.1
We extend
![]() $F_{K}({\it\alpha},D)$
to the whole of
$F_{K}({\it\alpha},D)$
to the whole of
![]() ${\it\alpha}\in \mathbf{R}$
by
${\it\alpha}\in \mathbf{R}$
by
![]() $F_{K}({\it\alpha},D):=F_{K}(-{\it\alpha},D)$
for
$F_{K}({\it\alpha},D):=F_{K}(-{\it\alpha},D)$
for
![]() ${\it\alpha}<0$
. Then, the identity (1.5) holds for
${\it\alpha}<0$
. Then, the identity (1.5) holds for
![]() $0<|{\it\alpha}|\leqslant 1-{\it\delta}$
, by replacing
$0<|{\it\alpha}|\leqslant 1-{\it\delta}$
, by replacing
![]() ${\it\alpha}$
on the right-hand side with
${\it\alpha}$
on the right-hand side with
![]() $|{\it\alpha}|$
. To investigate the low-lying zeros of quadratic
$|{\it\alpha}|$
. To investigate the low-lying zeros of quadratic
![]() $L$
-functions, we consider the integral of
$L$
-functions, we consider the integral of
![]() $F_{K}({\it\alpha},D)$
multiplied by some bounded function. First, we prove that in this integral, the contribution of the error terms in (1.5) is small.
$F_{K}({\it\alpha},D)$
multiplied by some bounded function. First, we prove that in this integral, the contribution of the error terms in (1.5) is small.
Lemma 4.1. We have
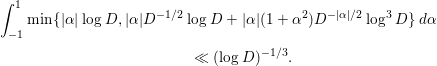 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{-1}^{1}\min \{|{\it\alpha}|\log D,|{\it\alpha}|D^{-1/2}\log D+|{\it\alpha}|(1+{\it\alpha}^{2})D^{-|{\it\alpha}|/2}\log ^{3}D\}\,d{\it\alpha} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hspace{36.0pt}\ll (\log D)^{-1/3}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{-1}^{1}\min \{|{\it\alpha}|\log D,|{\it\alpha}|D^{-1/2}\log D+|{\it\alpha}|(1+{\it\alpha}^{2})D^{-|{\it\alpha}|/2}\log ^{3}D\}\,d{\it\alpha} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hspace{36.0pt}\ll (\log D)^{-1/3}. & \displaystyle\end{eqnarray}$$
Proof. The estimates (4.1), (4.2) follow from direct computations of integrals. The estimate (4.3) follows from
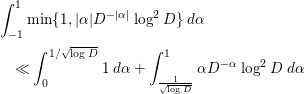 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}\text{min}\{1,|{\it\alpha}|D^{-|{\it\alpha}|}\log ^{2}D\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{0}^{1/\sqrt{\log D}}1\,d{\it\alpha}+\int _{\frac{1}{\sqrt{\log D}}}^{1}{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\,d{\it\alpha}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}\text{min}\{1,|{\it\alpha}|D^{-|{\it\alpha}|}\log ^{2}D\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{0}^{1/\sqrt{\log D}}1\,d{\it\alpha}+\int _{\frac{1}{\sqrt{\log D}}}^{1}{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\,d{\it\alpha}\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{1/\sqrt{\log D}}1\,d{\it\alpha}\ll \frac{1}{\sqrt{\log D}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\frac{1}{\sqrt{\log D}}}^{1}{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\,d{\it\alpha}\ll D^{-1/\sqrt{\log D}}\log ^{1/2}D. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{1/\sqrt{\log D}}1\,d{\it\alpha}\ll \frac{1}{\sqrt{\log D}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{\frac{1}{\sqrt{\log D}}}^{1}{\it\alpha}D^{-{\it\alpha}}\log ^{2}D\,d{\it\alpha}\ll D^{-1/\sqrt{\log D}}\log ^{1/2}D. & \displaystyle \nonumber\end{eqnarray}$$
The estimate (4.4) follows from
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}\text{min}\{D^{|{\it\alpha}|}(\log D)^{-1},{\it\alpha}^{2}D^{-|{\it\alpha}|}\log ^{3}D\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{0}^{\log \log D/\log D}D^{{\it\alpha}}(\log D)^{-1}\,d{\it\alpha}+(\log ^{3}D)\int _{\frac{\log \log D}{\log D}}^{1}{\it\alpha}^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-1}^{1}\text{min}\{D^{|{\it\alpha}|}(\log D)^{-1},{\it\alpha}^{2}D^{-|{\it\alpha}|}\log ^{3}D\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \int _{0}^{\log \log D/\log D}D^{{\it\alpha}}(\log D)^{-1}\,d{\it\alpha}+(\log ^{3}D)\int _{\frac{\log \log D}{\log D}}^{1}{\it\alpha}^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\end{eqnarray}$$
and
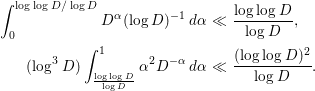 $$\begin{eqnarray}\displaystyle \int _{0}^{\log \log D/\log D}D^{{\it\alpha}}(\log D)^{-1}\,d{\it\alpha} & \ll & \displaystyle \frac{\log \log D}{\log D},\nonumber\\ \displaystyle (\log ^{3}D)\int _{\frac{\log \log D}{\log D}}^{1}{\it\alpha}^{2}D^{-{\it\alpha}}\,d{\it\alpha} & \ll & \displaystyle \frac{(\log \log D)^{2}}{\log D}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{\log \log D/\log D}D^{{\it\alpha}}(\log D)^{-1}\,d{\it\alpha} & \ll & \displaystyle \frac{\log \log D}{\log D},\nonumber\\ \displaystyle (\log ^{3}D)\int _{\frac{\log \log D}{\log D}}^{1}{\it\alpha}^{2}D^{-{\it\alpha}}\,d{\it\alpha} & \ll & \displaystyle \frac{(\log \log D)^{2}}{\log D}.\nonumber\end{eqnarray}$$
Finally, the left-hand side of (4.5) is at most
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\int _{0}^{(\log D)^{-2/3}}{\it\alpha}\log D\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad +\,2\int _{(\log D)^{-2/3}}^{1}\{{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\}\,d{\it\alpha},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\int _{0}^{(\log D)^{-2/3}}{\it\alpha}\log D\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad +\,2\int _{(\log D)^{-2/3}}^{1}\{{\it\alpha}D^{-1/2}\log D+{\it\alpha}(1+{\it\alpha}^{2})D^{-{\it\alpha}/2}\log ^{3}D\}\,d{\it\alpha},\nonumber\end{eqnarray}$$
and by direct computations, we easily find that these integrals are at most
![]() $O((\log D)^{-1/3})$
.◻
$O((\log D)^{-1/3})$
.◻
Next, we mention the
![]() $L$
-functions associated to Kronecker symbols. If
$L$
-functions associated to Kronecker symbols. If
![]() $d\not \equiv 3$
$d\not \equiv 3$
![]() $(\text{mod}\;4)$
,
$(\text{mod}\;4)$
,
![]() ${\it\chi}_{d}=(d/\cdot )$
becomes a Dirichlet character modulo
${\it\chi}_{d}=(d/\cdot )$
becomes a Dirichlet character modulo
![]() $4|d|$
or
$4|d|$
or
![]() $|d|$
. In this case, we denote the conductor of
$|d|$
. In this case, we denote the conductor of
![]() ${\it\chi}_{d}$
by
${\it\chi}_{d}$
by
![]() $d^{\ast }$
. If
$d^{\ast }$
. If
![]() $d\equiv 3$
(
$d\equiv 3$
(
![]() $\text{mod}\;4$
), by the reciprocity law of Kronecker symbols, we find that
$\text{mod}\;4$
), by the reciprocity law of Kronecker symbols, we find that
 $$\begin{eqnarray}{\it\chi}_{d}(p^{k})=\left\{\begin{array}{@{}ll@{}}\displaystyle \left(\frac{p}{d}\right)^{k}\quad & (p\equiv 1\;(\text{mod}\;4)\;\text{or}\;p=2)\\ \displaystyle (-1)^{k}\left(\frac{p}{d}\right)^{k}\quad & (p\equiv 3\;(\text{mod}\;4))\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\chi}_{d}(p^{k})=\left\{\begin{array}{@{}ll@{}}\displaystyle \left(\frac{p}{d}\right)^{k}\quad & (p\equiv 1\;(\text{mod}\;4)\;\text{or}\;p=2)\\ \displaystyle (-1)^{k}\left(\frac{p}{d}\right)^{k}\quad & (p\equiv 3\;(\text{mod}\;4))\end{array}\right.\end{eqnarray}$$
for primes
![]() $p$
. Hence, the
$p$
. Hence, the
![]() $L$
-function associated to
$L$
-function associated to
![]() ${\it\chi}_{d}$
is expressed by
${\it\chi}_{d}$
is expressed by
where
![]() ${\it\eta}_{4}$
is the nonprincipal character of modulo 4. In this case, we denote the conductor of
${\it\eta}_{4}$
is the nonprincipal character of modulo 4. In this case, we denote the conductor of
![]() ${\it\eta}_{4}(\cdot )(\cdot /d)$
by
${\it\eta}_{4}(\cdot )(\cdot /d)$
by
![]() $d^{\ast }$
. Let
$d^{\ast }$
. Let
![]() $N({\it\chi}_{d},T)$
denote the number of zeros of
$N({\it\chi}_{d},T)$
denote the number of zeros of
![]() $L(s,{\it\chi}_{d})$
in the rectangle
$L(s,{\it\chi}_{d})$
in the rectangle
![]() $0<{\it\sigma}<1$
,
$0<{\it\sigma}<1$
,
![]() $-T\leqslant t\leqslant T$
. Then, it is well known that
$-T\leqslant t\leqslant T$
. Then, it is well known that
holds uniformly for
![]() $d^{\ast }T>1$
(for example, see [Reference Selberg17]). Then, by partial integration, we have
$d^{\ast }T>1$
(for example, see [Reference Selberg17]). Then, by partial integration, we have
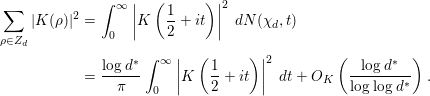 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2} & = & \displaystyle \int _{0}^{\infty }\left|K\left(\frac{1}{2}+it\right)\right|^{2}\,dN({\it\chi}_{d},t)\nonumber\\ \displaystyle & = & \displaystyle \frac{\log d^{\ast }}{{\it\pi}}\int _{0}^{\infty }\left|K\left(\frac{1}{2}+it\right)\right|^{2}\,dt+O_{K}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2} & = & \displaystyle \int _{0}^{\infty }\left|K\left(\frac{1}{2}+it\right)\right|^{2}\,dN({\it\chi}_{d},t)\nonumber\\ \displaystyle & = & \displaystyle \frac{\log d^{\ast }}{{\it\pi}}\int _{0}^{\infty }\left|K\left(\frac{1}{2}+it\right)\right|^{2}\,dt+O_{K}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right).\end{eqnarray}$$
We define the constants
![]() $A_{+}^{\ast }$
,
$A_{+}^{\ast }$
,
![]() $A_{-}^{\ast }$
by
$A_{-}^{\ast }$
by
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle A_{-}^{\ast }=\liminf _{D\rightarrow \infty }\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast },\\ \displaystyle A_{+}^{\ast }=\limsup _{D\rightarrow \infty }\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle A_{-}^{\ast }=\liminf _{D\rightarrow \infty }\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast },\\ \displaystyle A_{+}^{\ast }=\limsup _{D\rightarrow \infty }\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }.\end{array}\end{eqnarray}$$
It should be noticed that since
![]() $\log d^{\ast }\leqslant \log d+O(1)$
, we have
$\log d^{\ast }\leqslant \log d+O(1)$
, we have
![]() $A_{+}^{\ast }\leqslant 1$
.
$A_{+}^{\ast }\leqslant 1$
.
Corollary 4.2. Assuming the GRH, for any
![]() $C>0$
,
$C>0$
,
![]() $0\leqslant {\it\mu}<2{\it\pi}$
,
$0\leqslant {\it\mu}<2{\it\pi}$
,
![]() ${\it\epsilon}>0$
, we have
${\it\epsilon}>0$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{175.20007pt}\left.0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{\sin ^{4}1}\left\{\left(\frac{4}{9}C+{\it\epsilon}\right)g({\it\mu})-B_{-}^{\ast }C+{\it\epsilon}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{175.20007pt}\left.0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{\sin ^{4}1}\left\{\left(\frac{4}{9}C+{\it\epsilon}\right)g({\it\mu})-B_{-}^{\ast }C+{\it\epsilon}\right\}.\end{eqnarray}$$
Here,
and
![]() $A_{-}^{\ast }$
is the constant given by (4.7).
$A_{-}^{\ast }$
is the constant given by (4.7).
Proof. We fix
![]() ${\it\lambda}$
such that
${\it\lambda}$
such that
![]() $1/2<{\it\lambda}\leqslant 1-{\it\delta}$
, and put
$1/2<{\it\lambda}\leqslant 1-{\it\delta}$
, and put
Then, its Fourier transform is given by
In particular,
![]() $\hat{r}({\it\alpha})$
is bounded and has a support in
$\hat{r}({\it\alpha})$
is bounded and has a support in
![]() $[-1+{\it\delta},1-{\it\delta}]$
. Therefore, by (1.5) and Lemma 4.1, we have
$[-1+{\it\delta},1-{\it\delta}]$
. Therefore, by (1.5) and Lemma 4.1, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-5.0pt}\int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \hspace{25.20007pt}=L(1)\int _{-\infty }^{\infty }|{\it\alpha}|\hat{r}({\it\alpha})\,d{\it\alpha}+(\log D)\int _{-\infty }^{\infty }a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\hat{r}({\it\alpha})\,d{\it\alpha}+o(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-5.0pt}\int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \hspace{25.20007pt}=L(1)\int _{-\infty }^{\infty }|{\it\alpha}|\hat{r}({\it\alpha})\,d{\it\alpha}+(\log D)\int _{-\infty }^{\infty }a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\hat{r}({\it\alpha})\,d{\it\alpha}+o(1).\end{eqnarray}$$
The implied constant is dependent only on
![]() $K(s)$
and
$K(s)$
and
![]() ${\it\lambda}$
. By a direct computation, the first integral on the right-hand side of (4.9) is
${\it\lambda}$
. By a direct computation, the first integral on the right-hand side of (4.9) is
On the other hand, the second integral of the right hand side of (4.9) is
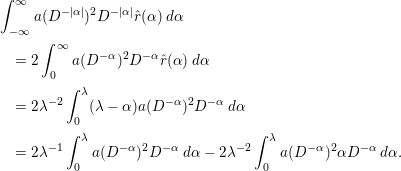 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2\int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}^{-2}\int _{0}^{{\it\lambda}}({\it\lambda}-{\it\alpha})a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}^{-1}\int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}-2{\it\lambda}^{-2}\int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}{\it\alpha}D^{-{\it\alpha}}\,d{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2\int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}^{-2}\int _{0}^{{\it\lambda}}({\it\lambda}-{\it\alpha})a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}^{-1}\int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}-2{\it\lambda}^{-2}\int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}{\it\alpha}D^{-{\it\alpha}}\,d{\it\alpha}.\end{eqnarray}$$
By the change of parameters
![]() $t=D^{-{\it\alpha}}$
, the first integral on the right-hand side of (4.11) is
$t=D^{-{\it\alpha}}$
, the first integral on the right-hand side of (4.11) is
 $$\begin{eqnarray}\displaystyle \int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha} & = & \displaystyle \int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\log D}\int _{0}^{1}a(t)^{2}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{M}{\log D},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{{\it\lambda}}a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha} & = & \displaystyle \int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\,d{\it\alpha}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\log D}\int _{0}^{1}a(t)^{2}\,dt\nonumber\\ \displaystyle & = & \displaystyle \frac{M}{\log D},\end{eqnarray}$$
where
On the other hand, since
![]() $a(D^{-{\it\alpha}})^{2}$
is bounded, we have
$a(D^{-{\it\alpha}})^{2}$
is bounded, we have
By inserting (4.12), (4.14) into (4.11), we have
By inserting (4.10), (4.15) into (4.9), we obtain
For
![]() $C>0$
, we take
$C>0$
, we take
Then, since
![]() $K(1/2+it)=C^{2}(t^{-1}\sin (t/C))^{2}$
,
$K(1/2+it)=C^{2}(t^{-1}\sin (t/C))^{2}$
,
![]() $K(s)$
is real on the line
$K(s)$
is real on the line
![]() $\text{Re}(s)=1/2$
and satisfies
$\text{Re}(s)=1/2$
and satisfies
![]() $K(1/2+it_{1})\overline{K(1/2+it_{2})}\geqslant 0$
for all
$K(1/2+it_{1})\overline{K(1/2+it_{2})}\geqslant 0$
for all
![]() $t_{1},t_{2}\in \mathbf{R}$
. Moreover, by an easy computation, its Mellin inverse transform
$t_{1},t_{2}\in \mathbf{R}$
. Moreover, by an easy computation, its Mellin inverse transform
![]() $a(x)=a_{C}(x)$
, defined in (1.2), is given by
$a(x)=a_{C}(x)$
, defined in (1.2), is given by
 $$\begin{eqnarray}a(x)=\left\{\begin{array}{@{}ll@{}}0\quad & \displaystyle (x<e^{-2/C}\;\text{or}\;x\geqslant e^{2/C})\\ \displaystyle \frac{C^{2}}{2}x^{-1/2}\left(\frac{1}{C}+\frac{1}{2}\log x\right)\quad & (e^{-2/C}\leqslant x<1)\\ \displaystyle \frac{C^{2}}{2}x^{-1/2}\left(\frac{1}{C}-\frac{1}{2}\log x\right)\quad & (1\leqslant x<e^{2/C}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}a(x)=\left\{\begin{array}{@{}ll@{}}0\quad & \displaystyle (x<e^{-2/C}\;\text{or}\;x\geqslant e^{2/C})\\ \displaystyle \frac{C^{2}}{2}x^{-1/2}\left(\frac{1}{C}+\frac{1}{2}\log x\right)\quad & (e^{-2/C}\leqslant x<1)\\ \displaystyle \frac{C^{2}}{2}x^{-1/2}\left(\frac{1}{C}-\frac{1}{2}\log x\right)\quad & (1\leqslant x<e^{2/C}).\end{array}\right.\end{eqnarray}$$
This function surely satisfies the conditions given in Section 1. By the definition of
![]() $F_{K}({\it\alpha},D)$
, we have
$F_{K}({\it\alpha},D)$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\int _{-\infty }^{\infty }D^{i{\it\alpha}({\it\gamma}_{1}-{\it\gamma}_{2})}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}r\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\int _{-\infty }^{\infty }D^{i{\it\alpha}({\it\gamma}_{1}-{\it\gamma}_{2})}\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}r\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
We fix a real number
![]() ${\it\mu}$
satisfying
${\it\mu}$
satisfying
![]() $0\leqslant {\it\mu}<2{\it\pi}$
. Since the function
$0\leqslant {\it\mu}<2{\it\pi}$
. Since the function
![]() $f(x):=((\sin x)/x)^{2}$
is even and decreasing in
$f(x):=((\sin x)/x)^{2}$
is even and decreasing in
![]() $[0,{\it\pi}]$
, the inequality
$[0,{\it\pi}]$
, the inequality
holds if
![]() ${\it\gamma}_{1}$
,
${\it\gamma}_{1}$
,
![]() ${\it\gamma}_{2}$
satisfy
${\it\gamma}_{2}$
satisfy
![]() $|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant {\it\mu}/({\it\lambda}\log D)$
. Therefore, by (4.17), we have
$|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant {\it\mu}/({\it\lambda}\log D)$
. Therefore, by (4.17), we have
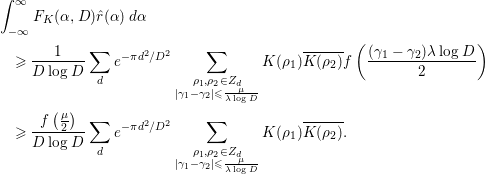 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}f\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}f\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Now, we have
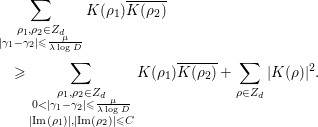 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D} \\ |\text{Im}({\it\rho}_{1})|,|\text{Im}({\it\rho}_{2})|\leqslant C}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}+\mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D} \\ |\text{Im}({\it\rho}_{1})|,|\text{Im}({\it\rho}_{2})|\leqslant C}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}+\mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2}.\end{eqnarray}$$
By (4.6), the second term on the right-hand side of (4.19) is given by
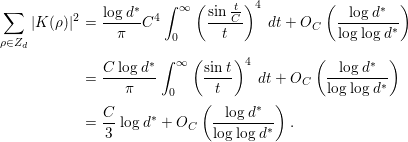 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2} & = & \displaystyle \frac{\log d^{\ast }}{{\it\pi}}C^{4}\int _{0}^{\infty }\left(\frac{\sin \frac{t}{C}}{t}\right)^{4}\,dt+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{C\log d^{\ast }}{{\it\pi}}\int _{0}^{\infty }\left(\frac{\sin t}{t}\right)^{4}\,dt+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{C}{3}\log d^{\ast }+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}|K({\it\rho})|^{2} & = & \displaystyle \frac{\log d^{\ast }}{{\it\pi}}C^{4}\int _{0}^{\infty }\left(\frac{\sin \frac{t}{C}}{t}\right)^{4}\,dt+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{C\log d^{\ast }}{{\it\pi}}\int _{0}^{\infty }\left(\frac{\sin t}{t}\right)^{4}\,dt+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{C}{3}\log d^{\ast }+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right).\end{eqnarray}$$
On the other hand, since
the first term on the right-hand side of (4.19) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D} \\ |\text{Im}({\it\rho}_{1})|,|\text{Im}({\it\rho}_{2})|\leqslant C}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant (\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant (\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D} \\ |\text{Im}({\it\rho}_{1})|,|\text{Im}({\it\rho}_{2})|\leqslant C}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant (\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{{\it\lambda}\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant (\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}.\nonumber\end{eqnarray}$$
Hence, by (4.18), we obtain
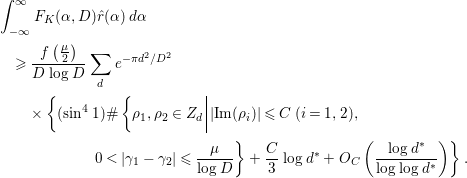 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{(\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\quad \quad \quad \quad \quad \quad 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}+\frac{C}{3}\log d^{\ast }+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left\{(\sin ^{4}1)\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\quad \quad \quad \quad \quad \quad 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}+\frac{C}{3}\log d^{\ast }+O_{C}\left(\frac{\log d^{\ast }}{\log \log d^{\ast }}\right)\right\}.\end{eqnarray}$$
Combining (4.16) and (4.21), we obtain
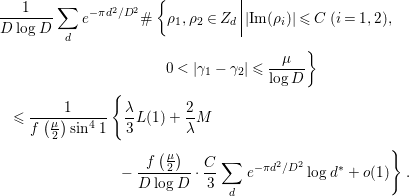 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \qquad \qquad \qquad \qquad \quad 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{f\left(\frac{{\it\mu}}{2}\right)\sin ^{4}1}\left\{\vphantom{-\,\frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\cdot \frac{C}{3}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)}\frac{{\it\lambda}}{3}L(1)+\frac{2}{{\it\lambda}}M\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \qquad \qquad \quad \quad -\,\frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\cdot \frac{C}{3}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\#\left\{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}\;\;|\text{Im}({\it\rho}_{i})|\leqslant C\;(i=1,2),\vphantom{\frac{{\it\mu}}{\log D}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \qquad \qquad \qquad \qquad \quad 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{{\it\mu}}{\log D}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{f\left(\frac{{\it\mu}}{2}\right)\sin ^{4}1}\left\{\vphantom{-\,\frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\cdot \frac{C}{3}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)}\frac{{\it\lambda}}{3}L(1)+\frac{2}{{\it\lambda}}M\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \qquad \qquad \quad \quad -\,\frac{f\left(\frac{{\it\mu}}{2}\right)}{D\log D}\cdot \frac{C}{3}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)\right\}.\end{eqnarray}$$
By direct computation, we find that
Moreover, by our assumption,
By inserting these results into (4.22) and putting
![]() ${\it\lambda}=1-{\it\delta}$
with sufficiently small
${\it\lambda}=1-{\it\delta}$
with sufficiently small
![]() ${\it\delta}>0$
, we obtain (4.8).◻
${\it\delta}>0$
, we obtain (4.8).◻
Next, we give a certain lower bound for the rate of simple zeros of quadratic
![]() $L$
-functions.
$L$
-functions.
Corollary 4.3. We assume the GRH. For any
![]() ${\it\epsilon}>0$
, we have
${\it\epsilon}>0$
, we have
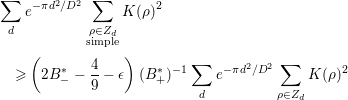 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \left(2B_{-}^{\ast }-\frac{4}{9}-{\it\epsilon}\right)(B_{+}^{\ast })^{-1}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \left(2B_{-}^{\ast }-\frac{4}{9}-{\it\epsilon}\right)(B_{+}^{\ast })^{-1}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\end{eqnarray}$$
when
![]() $D>1$
is sufficiently large. Here,
$D>1$
is sufficiently large. Here,
and
![]() $A_{\pm }^{\ast }$
are the constants defined by (4.7).
$A_{\pm }^{\ast }$
are the constants defined by (4.7).
Proof. In the proof of Corollary 4.2, we showed that
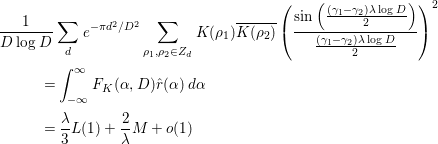 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{{\it\lambda}}{3}L(1)+\frac{2}{{\it\lambda}}M+o(1)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\hat{r}({\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{{\it\lambda}}{3}L(1)+\frac{2}{{\it\lambda}}M+o(1)\end{eqnarray}$$
holds for
![]() ${\it\lambda}=1-{\it\delta}$
. Moreover, in this case, we have
${\it\lambda}=1-{\it\delta}$
. Moreover, in this case, we have
since
![]() $C=1$
. Therefore,
$C=1$
. Therefore,
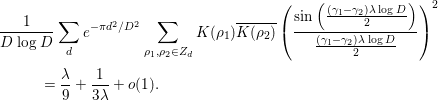 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{{\it\lambda}}{9}+\frac{1}{3{\it\lambda}}+o(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})\overline{K({\it\rho}_{2})}\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{{\it\lambda}}{9}+\frac{1}{3{\it\lambda}}+o(1).\end{eqnarray}$$
Let
![]() $m_{{\it\rho},d}$
be the multiplicity of the zero of
$m_{{\it\rho},d}$
be the multiplicity of the zero of
![]() $L(s,{\it\chi}_{d})$
at
$L(s,{\it\chi}_{d})$
at
![]() ${\it\rho}=1/2+i{\it\gamma}$
. Then,
${\it\rho}=1/2+i{\it\gamma}$
. Then,
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2} & {\geqslant} & \displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}(2-m_{{\it\rho},d})K({\it\rho})^{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}-\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2} & {\geqslant} & \displaystyle \mathop{\sum }_{{\it\rho}\in Z_{d}}(2-m_{{\it\rho},d})K({\it\rho})^{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}-\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\nonumber\end{eqnarray}$$
Hence, we obtain
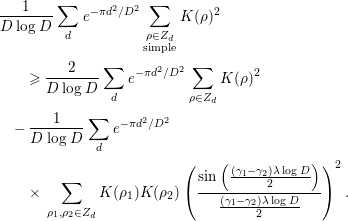 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \geqslant \frac{2}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \geqslant \frac{2}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})\left(\frac{\sin \left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}\right)}{\frac{({\it\gamma}_{1}-{\it\gamma}_{2}){\it\lambda}\log D}{2}}\right)^{2}.\end{eqnarray}$$
The second term on the right-hand side is given by (4.25), since
![]() $K({\it\rho}_{2})$
is real. On the other hand, the first term is
$K({\it\rho}_{2})$
is real. On the other hand, the first term is
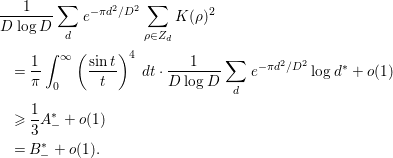 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{{\it\pi}}\int _{0}^{\infty }\left(\frac{\sin t}{t}\right)^{4}\,dt\cdot \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{3}A_{-}^{\ast }+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad =B_{-}^{\ast }+o(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{{\it\pi}}\int _{0}^{\infty }\left(\frac{\sin t}{t}\right)^{4}\,dt\cdot \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\log d^{\ast }+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{1}{3}A_{-}^{\ast }+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad =B_{-}^{\ast }+o(1).\end{eqnarray}$$
Therefore, by inserting (4.25), (4.27) into (4.26) and taking
![]() ${\it\delta}>0$
sufficiently small, we obtain
${\it\delta}>0$
sufficiently small, we obtain
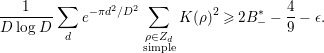 $$\begin{eqnarray}\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\geqslant 2B_{-}^{\ast }-\frac{4}{9}-{\it\epsilon}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}\in Z_{d} \\ \text{simple}}}K({\it\rho})^{2}\geqslant 2B_{-}^{\ast }-\frac{4}{9}-{\it\epsilon}.\end{eqnarray}$$
By combining this and
we obtain (4.23).◻
Corollary 4.4. We assume the GRH, and that all zeros of
![]() $L(s,{\it\chi}_{d})$
are simple. For
$L(s,{\it\chi}_{d})$
are simple. For
![]() $0<{\it\lambda}<1$
, we have
$0<{\it\lambda}<1$
, we have
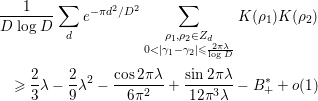 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{2}{3}{\it\lambda}-\frac{2}{9}{\it\lambda}^{2}-\frac{\cos 2{\it\pi}{\it\lambda}}{6{\it\pi}^{2}}+\frac{\sin 2{\it\pi}{\it\lambda}}{12{\it\pi}^{3}{\it\lambda}}-B_{+}^{\ast }+o(1)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \frac{2}{3}{\it\lambda}-\frac{2}{9}{\it\lambda}^{2}-\frac{\cos 2{\it\pi}{\it\lambda}}{6{\it\pi}^{2}}+\frac{\sin 2{\it\pi}{\it\lambda}}{12{\it\pi}^{3}{\it\lambda}}-B_{+}^{\ast }+o(1)\end{eqnarray}$$
as
![]() $D\rightarrow \infty$
, where
$D\rightarrow \infty$
, where
![]() $B_{+}^{\ast }=A_{+}^{\ast }/3$
and
$B_{+}^{\ast }=A_{+}^{\ast }/3$
and
In particular, if
![]() ${\it\lambda}>{\it\lambda}_{0}=0.6073$
, we have
${\it\lambda}>{\it\lambda}_{0}=0.6073$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})\gg D\log D\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})\gg D\log D\end{eqnarray}$$
as
![]() $D\rightarrow \infty$
.
$D\rightarrow \infty$
.
Proof. Instead of the function
![]() $r(u)$
used in the proof of Corollary 4.2, we use the Selberg minorant
$r(u)$
used in the proof of Corollary 4.2, we use the Selberg minorant
This function is bounded and satisfies
![]() $h(u)\leqslant 1$
,
$h(u)\leqslant 1$
,
![]() $h(u)<0$
if
$h(u)<0$
if
![]() $|u|>1$
. The Fourier transform of
$|u|>1$
. The Fourier transform of
![]() $h(u)$
is given by
$h(u)$
is given by
 $$\begin{eqnarray}{\hat{h}}({\it\alpha})=\left\{\begin{array}{@{}ll@{}}\displaystyle 1-|{\it\alpha}|+\frac{\sin 2{\it\pi}|{\it\alpha}|}{2{\it\pi}}\quad & (|{\it\alpha}|\leqslant 1)\\ 0\quad & (|{\it\alpha}|>1)\\ \quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{h}}({\it\alpha})=\left\{\begin{array}{@{}ll@{}}\displaystyle 1-|{\it\alpha}|+\frac{\sin 2{\it\pi}|{\it\alpha}|}{2{\it\pi}}\quad & (|{\it\alpha}|\leqslant 1)\\ 0\quad & (|{\it\alpha}|>1)\\ \quad \end{array}\right.\end{eqnarray}$$
(for example, see [Reference Goldston, Gonek, Özlük and Snyder5]). For
![]() $0<{\it\lambda}<1$
, we give lower and upper bounds for the integral
$0<{\it\lambda}<1$
, we give lower and upper bounds for the integral
First, since the integrant is nonnegative and
![]() $1/{\it\lambda}>1$
, by (1.5), we have
$1/{\it\lambda}>1$
, by (1.5), we have
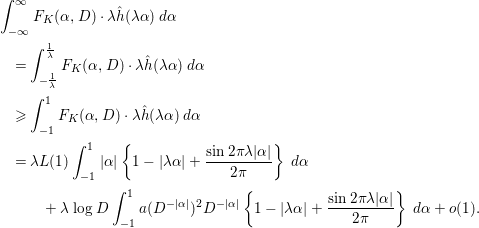 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\frac{1}{{\it\lambda}}}^{\frac{1}{{\it\lambda}}}F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \int _{-1}^{1}F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}L(1)\int _{-1}^{1}|{\it\alpha}|\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,{\it\lambda}\log D\int _{-1}^{1}a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}+o(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{-\frac{1}{{\it\lambda}}}^{\frac{1}{{\it\lambda}}}F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \int _{-1}^{1}F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad ={\it\lambda}L(1)\int _{-1}^{1}|{\it\alpha}|\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,{\it\lambda}\log D\int _{-1}^{1}a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}+o(1).\end{eqnarray}$$
The first term on the right-hand side of (4.30) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\lambda}L(1)\int _{-1}^{1}|{\it\alpha}|\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}L(1)\int _{0}^{1}\left({\it\alpha}-{\it\lambda}{\it\alpha}^{2}+\frac{{\it\alpha}\sin 2{\it\pi}{\it\lambda}{\it\alpha}}{2{\it\pi}}\right)d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}L(1)\left\{\frac{1}{2}-\frac{{\it\lambda}}{3}-\frac{\cos 2{\it\pi}{\it\lambda}}{4{\it\pi}^{2}{\it\lambda}}+\frac{\sin 2{\it\pi}{\it\lambda}}{8{\it\pi}^{3}{\it\lambda}^{2}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\lambda}L(1)\int _{-1}^{1}|{\it\alpha}|\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}L(1)\int _{0}^{1}\left({\it\alpha}-{\it\lambda}{\it\alpha}^{2}+\frac{{\it\alpha}\sin 2{\it\pi}{\it\lambda}{\it\alpha}}{2{\it\pi}}\right)d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}L(1)\left\{\frac{1}{2}-\frac{{\it\lambda}}{3}-\frac{\cos 2{\it\pi}{\it\lambda}}{4{\it\pi}^{2}{\it\lambda}}+\frac{\sin 2{\it\pi}{\it\lambda}}{8{\it\pi}^{3}{\it\lambda}^{2}}\right\}.\end{eqnarray}$$
Next, we compute the second term on the right-hand side of (4.30). Since
for
![]() $|{\it\alpha}|\ll 1/(\log D)$
, we have
$|{\it\alpha}|\ll 1/(\log D)$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\lambda}\log D\int _{-1}^{1}a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}\log D\int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\left\{1+O\left(\frac{1}{\log ^{3}D}\right)\right\}\,d{\it\alpha}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\lambda}\log D\int _{-1}^{1}a(D^{-|{\it\alpha}|})^{2}D^{-|{\it\alpha}|}\left\{1-|{\it\lambda}{\it\alpha}|+\frac{\sin 2{\it\pi}{\it\lambda}|{\it\alpha}|}{2{\it\pi}}\right\}\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad =2{\it\lambda}\log D\int _{0}^{\infty }a(D^{-{\it\alpha}})^{2}D^{-{\it\alpha}}\left\{1+O\left(\frac{1}{\log ^{3}D}\right)\right\}\,d{\it\alpha}.\nonumber\end{eqnarray}$$
By the change of parameters
![]() $D^{-{\it\alpha}}=v$
, we have
$D^{-{\it\alpha}}=v$
, we have
where
![]() $M=\int _{0}^{1}a(v)^{2}\,dv$
. Therefore,
$M=\int _{0}^{1}a(v)^{2}\,dv$
. Therefore,
By inserting (4.31), (4.32) into (4.30), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 2{\it\lambda}L(1)\left\{\frac{1}{2}-\frac{{\it\lambda}}{3}-\frac{\cos 2{\it\pi}{\it\lambda}}{4{\it\pi}^{2}{\it\lambda}}+\frac{\sin 2{\it\pi}{\it\lambda}}{8{\it\pi}^{3}{\it\lambda}^{2}}\right\}+2M{\it\lambda}+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2}{3}{\it\lambda}-\frac{2}{9}{\it\lambda}^{2}-\frac{\cos 2{\it\pi}{\it\lambda}}{6{\it\pi}^{2}}+\frac{\sin 2{\it\pi}{\it\lambda}}{12{\it\pi}^{3}{\it\lambda}}+o(1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 2{\it\lambda}L(1)\left\{\frac{1}{2}-\frac{{\it\lambda}}{3}-\frac{\cos 2{\it\pi}{\it\lambda}}{4{\it\pi}^{2}{\it\lambda}}+\frac{\sin 2{\it\pi}{\it\lambda}}{8{\it\pi}^{3}{\it\lambda}^{2}}\right\}+2M{\it\lambda}+o(1)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2}{3}{\it\lambda}-\frac{2}{9}{\it\lambda}^{2}-\frac{\cos 2{\it\pi}{\it\lambda}}{6{\it\pi}^{2}}+\frac{\sin 2{\it\pi}{\it\lambda}}{12{\it\pi}^{3}{\it\lambda}}+o(1),\end{eqnarray}$$
since
![]() $L(1)=1/3$
,
$L(1)=1/3$
,
![]() $M=1/6$
. On the other hand, we have
$M=1/6$
. On the other hand, we have
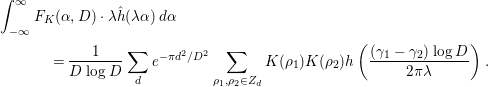 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \qquad \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}_{1},{\it\rho}_{2}\in Z_{d}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right).\end{eqnarray}$$
Now, since
![]() $h(({\it\gamma}_{1}-{\it\gamma}_{2})\log D/(2{\it\pi}{\it\lambda}))$
is negative if
$h(({\it\gamma}_{1}-{\it\gamma}_{2})\log D/(2{\it\pi}{\it\lambda}))$
is negative if
![]() $|{\it\gamma}_{1}-{\it\gamma}_{2}|>(2{\it\pi}{\it\lambda})/\log D$
, by (4.34), we have
$|{\it\gamma}_{1}-{\it\gamma}_{2}|>(2{\it\pi}{\it\lambda})/\log D$
, by (4.34), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant B_{+}^{\ast }+\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})+o(1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{-\infty }^{\infty }F_{K}({\it\alpha},D)\cdot {\it\lambda}{\hat{h}}({\it\lambda}{\it\alpha})\,d{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ |{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{{\it\rho}\in Z_{d}}K({\it\rho})^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})h\left(\frac{({\it\gamma}_{1}-{\it\gamma}_{2})\log D}{2{\it\pi}{\it\lambda}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant B_{+}^{\ast }+\frac{1}{D\log D}\mathop{\sum }_{d}e^{-{\it\pi}d^{2}/D^{2}}\mathop{\sum }_{\substack{ {\it\rho}_{1},{\it\rho}_{2}\in Z_{d} \\ 0<|{\it\gamma}_{1}-{\it\gamma}_{2}|\leqslant \frac{2{\it\pi}{\it\lambda}}{\log D}}}K({\it\rho}_{1})K({\it\rho}_{2})+o(1).\nonumber\end{eqnarray}$$
By combining (4.33) and the above, we obtain (4.28). Since
![]() $B_{+}^{\ast }=A_{+}^{\ast }/3\leqslant 1/3$
, the right-hand side of (4.28) becomes positive if
$B_{+}^{\ast }=A_{+}^{\ast }/3\leqslant 1/3$
, the right-hand side of (4.28) becomes positive if
![]() ${\it\lambda}>{\it\lambda}_{0}=0.6073$
. Therefore, we obtain (4.29).◻
${\it\lambda}>{\it\lambda}_{0}=0.6073$
. Therefore, we obtain (4.29).◻
Acknowledgments
The author would like to express his gratitude to the referees for giving him valuable comments and suggestions.