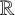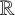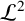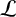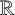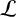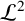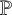1 Proofs from the book
The Preface of the book ‘Proofs from The Book’ [Reference Aigner and Ziegler1] begins ‘Paul Erdős liked to talk about The Book, in which God maintains the perfect proofs for mathematical theorems
![]() $\dots $
you need not believe in God but, as a mathematician, you should believe in The Book.’ Erdős was very enthusiastic about Aigner and Ziegler writing [Reference Aigner and Ziegler1], which they dedicated to Erdős and to which Erdős made many suggestions. The aim in this paper is to give an elegant proof that a thin set can be continuously mapped onto a fat set.
$\dots $
you need not believe in God but, as a mathematician, you should believe in The Book.’ Erdős was very enthusiastic about Aigner and Ziegler writing [Reference Aigner and Ziegler1], which they dedicated to Erdős and to which Erdős made many suggestions. The aim in this paper is to give an elegant proof that a thin set can be continuously mapped onto a fat set.
2 Thin sets and fat sets
There are many measures of the thinness of a set. When considering subsets of Euclidean space, Lebesgue measure zero is one measure of thinness. Another measure of thinness is that the set is zero-dimensional [Reference Morris9], that is, its topology has a basis of open and closed sets. If C denotes the usual middle-third set in
![]() $\mathbb {R}$
, then it is easily seen that C is measure zero and is zero-dimensional. Further, by [Reference van Mill11, Theorem 1.5.10], every compact separable metrisable space is a continuous image of C. In particular, the unit interval
$\mathbb {R}$
, then it is easily seen that C is measure zero and is zero-dimensional. Further, by [Reference van Mill11, Theorem 1.5.10], every compact separable metrisable space is a continuous image of C. In particular, the unit interval
![]() $[0,1]$
, which has Lebesgue measure
$[0,1]$
, which has Lebesgue measure
![]() $1$
in
$1$
in
![]() $\mathbb {R}$
and is path-connected, is a continuous image of C.
$\mathbb {R}$
and is path-connected, is a continuous image of C.
Another measure of thinness is Hausdorff measure
![]() $0$
. The related Hausdorff dimension and Hausdorff measure are discussed in [Reference Falconer7, Reference Morris9]. The Hausdorff dimension of a countable set is zero, of Euclidean space
$0$
. The related Hausdorff dimension and Hausdorff measure are discussed in [Reference Falconer7, Reference Morris9]. The Hausdorff dimension of a countable set is zero, of Euclidean space
![]() $\mathbb {R}^{n}$
is n and of the Cantor set C is
$\mathbb {R}^{n}$
is n and of the Cantor set C is
![]() ${\log 2}/{\log 3}$
. So in this sense, the Cantor set is not thin.
${\log 2}/{\log 3}$
. So in this sense, the Cantor set is not thin.
We now define our notion of thinness. A subset of Euclidean space is said to be thin if it is an uncountable dense zero-dimensional set of measure zero and Hausdorff measure zero. An uncountable dense path-connected subspace of Euclidean space is said to be fat if it is a subspace of full measure, that is, its complement has Lebesgue measure zero.
3 Spaces homeomorphic to the space of irrational numbers
Recall that a topological space X is said to be topologically complete (or completely metrisable) if the topology of X is the same as the topology induced by a complete metric on X. Of course, every complete metric space is topologically complete.
We denote by
![]() $\mathbb {P}$
the set of all irrational real numbers with the topology it inherits as a subspace of the Euclidean space
$\mathbb {P}$
the set of all irrational real numbers with the topology it inherits as a subspace of the Euclidean space
![]() $\mathbb {R}$
. Theorem 3.1 from [Reference van Mill11, Theorem 1.9.8] is a beautiful characterisation of the topological space
$\mathbb {R}$
. Theorem 3.1 from [Reference van Mill11, Theorem 1.9.8] is a beautiful characterisation of the topological space
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Theorem 3.1. The space of all irrational real numbers
![]() $\mathbb {P}$
is topologically the unique nonempty, separable metrisable, topologically complete, nowhere locally compact and zero-dimensional space.
$\mathbb {P}$
is topologically the unique nonempty, separable metrisable, topologically complete, nowhere locally compact and zero-dimensional space.
This has a corollary, [Reference van Mill11, Corollary 1.9.9], which is usually proved using continued fractions.
Corollary 3.2. The space
![]() $\mathbb {P}$
is homeomorphic to the Tychonoff product
$\mathbb {P}$
is homeomorphic to the Tychonoff product
![]() $\mathbb {N}^{\aleph _{0}}$
of a countably infinite number of homeomorphic copies of the discrete space
$\mathbb {N}^{\aleph _{0}}$
of a countably infinite number of homeomorphic copies of the discrete space
![]() $\mathbb {N}$
of positive integers. Hence,
$\mathbb {N}$
of positive integers. Hence,
![]() $\mathbb {P}\times \mathbb {P}$
is homeomorphic to
$\mathbb {P}\times \mathbb {P}$
is homeomorphic to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
These results and a similar one [Reference van Mill11, Theorem 1.9.6] characterising the space
![]() $\mathbb {Q}$
of all rational numbers with its Euclidean topology are used in [Reference Chalebgwa and Morris5, Reference Morris8] to describe the transcendental groups and the topological transcendental fields.
$\mathbb {Q}$
of all rational numbers with its Euclidean topology are used in [Reference Chalebgwa and Morris5, Reference Morris8] to describe the transcendental groups and the topological transcendental fields.
Recall that a subset X of a topological space Y is said to be a
![]() $G_{\delta }$
-set if it is a countable intersection of open sets in Y. A subset X of a topological space Y is said to be an
$G_{\delta }$
-set if it is a countable intersection of open sets in Y. A subset X of a topological space Y is said to be an
![]() $F_{\sigma }$
-set if it is a countable union of closed sets. A subset X of a topological space Y is a
$F_{\sigma }$
-set if it is a countable union of closed sets. A subset X of a topological space Y is a
![]() $G_{\delta }$
-set if and only if its complement is an
$G_{\delta }$
-set if and only if its complement is an
![]() $F_{\sigma }$
-set. We see immediately that in a metric space such as
$F_{\sigma }$
-set. We see immediately that in a metric space such as
![]() $\mathbb {R}$
, the set
$\mathbb {R}$
, the set
![]() $\mathcal {T}$
of all transcendental real numbers is a
$\mathcal {T}$
of all transcendental real numbers is a
![]() $G_{\delta }$
-set as its complement is the countably infinite set
$G_{\delta }$
-set as its complement is the countably infinite set
![]() $\mathbb {A}$
of all real algebraic numbers.
$\mathbb {A}$
of all real algebraic numbers.
Now we connect the notions of
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
and the property of being topologically complete. The next theorem is [Reference van Mill11, Theorem A.63].
$\mathbb {R}$
and the property of being topologically complete. The next theorem is [Reference van Mill11, Theorem A.63].
Theorem 3.3. A subset of a separable metric topologically complete space is a
![]() $G_{\delta }$
-set in that space if and only if it is topologically complete.
$G_{\delta }$
-set in that space if and only if it is topologically complete.
Corollary 3.4. The space
![]() $\mathcal {T}$
of all real transcendental numbers is homeomorphic to
$\mathcal {T}$
of all real transcendental numbers is homeomorphic to
![]() $\mathbb {P}$
and to
$\mathbb {P}$
and to
![]() $\mathbb {N}^{\aleph _{0}}$
.
$\mathbb {N}^{\aleph _{0}}$
.
Remark 3.5. We mention in passing that the above corollary remains true if the space
![]() $\mathcal {T}$
of all real transcendental numbers is replaced by the space of all transcendental complex numbers. We also mention that the space of all algebraic real numbers and the space of all algebraic complex numbers are both homeomorphic to the space
$\mathcal {T}$
of all real transcendental numbers is replaced by the space of all transcendental complex numbers. We also mention that the space of all algebraic real numbers and the space of all algebraic complex numbers are both homeomorphic to the space
![]() $\mathbb {Q}$
of all rational (real) numbers.
$\mathbb {Q}$
of all rational (real) numbers.
4 The set
 $\mathcal {L}$
of all Liouville numbers
$\mathcal {L}$
of all Liouville numbers
In 1844, Joseph Liouville proved the existence of transcendental numbers [Reference Angell2, Reference Baker3]. He introduced the set
![]() $\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
$\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
![]() $(p,q)$
with
$(p,q)$
with
![]() $q>1$
such that
$q>1$
such that
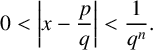 $$ \begin{align*}0< \bigg|x-\frac{p}{q}\bigg|<\frac{1}{q^{n}}.\end{align*} $$
$$ \begin{align*}0< \bigg|x-\frac{p}{q}\bigg|<\frac{1}{q^{n}}.\end{align*} $$
It is known [Reference Baker3, Reference Erdős6] that the set
![]() $\mathcal L$
has cardinality
$\mathcal L$
has cardinality
![]() $\mathfrak {c}$
, the cardinality of the continuum, and is a dense
$\mathfrak {c}$
, the cardinality of the continuum, and is a dense
![]() $G_{\delta }$
-set in the space
$G_{\delta }$
-set in the space
![]() $\mathbb {R}$
of all real numbers. Clearly, the space
$\mathbb {R}$
of all real numbers. Clearly, the space
![]() $\mathcal {L}$
is zero-dimensional and thus the product space
$\mathcal {L}$
is zero-dimensional and thus the product space
![]() $\mathcal {L}^{2}$
is also zero-dimensional.
$\mathcal {L}^{2}$
is also zero-dimensional.
The following Theorem 4.1 follows by combining Theorems 3.3 and 3.1 and Corollary 3.2.
Theorem 4.1. The spaces
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}^{2}$
are both homeomorphic to
$\mathcal {L}^{2}$
are both homeomorphic to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Remark 4.2. As pointed out in [Reference Bluhm4], the Jarnik–Besicovitch theorem says that the set
![]() $\mathcal {L}$
of Liouville numbers has Hausdorff 1-dimensional measure
$\mathcal {L}$
of Liouville numbers has Hausdorff 1-dimensional measure
![]() $0$
. This implies that
$0$
. This implies that
![]() $\mathcal {L}^{2}$
has Hausdorff 2-dimensional measure
$\mathcal {L}^{2}$
has Hausdorff 2-dimensional measure
![]() $0$
, since if d is a positive integer, the d-dimensional Hausdorff measure on
$0$
, since if d is a positive integer, the d-dimensional Hausdorff measure on
![]() $\mathbb {R}^{n}$
is simply a rescaling of the n-dimensional Lebesgue measure. See also [Reference Schleischitz10, Theorem 2.1].
$\mathbb {R}^{n}$
is simply a rescaling of the n-dimensional Lebesgue measure. See also [Reference Schleischitz10, Theorem 2.1].
Remark 4.3. The spaces
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}^{2}$
are thin sets.
$\mathcal {L}^{2}$
are thin sets.
5 Mapping a thin set onto a fat set
Finally, in this section, we give the elegant proof that a thin set can be mapped continuously onto a fat set.
In 1962, Paul Erdős proved Theorem 5.1 in [Reference Erdős6].
Theorem 5.1. Every real number is the sum of two Liouville numbers and is also the product of two Liouville numbers.
The desired Theorem 5.2 follows immediately from Theorem 5.1 and Remark 4.3.
Theorem 5.2. Let
![]() $f:\mathbb {R}^{2}\to \mathbb {R}$
be the addition map
$f:\mathbb {R}^{2}\to \mathbb {R}$
be the addition map
![]() $f(x,y)= x+y$
. Then f is a continuous homomorphism which maps the thin set
$f(x,y)= x+y$
. Then f is a continuous homomorphism which maps the thin set
![]() $\mathcal {L}^{2}$
onto the fat set
$\mathcal {L}^{2}$
onto the fat set
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Remark 5.3. The referee has pointed out that Theorem 5.2 can be easily generalised using the method of [Reference Schleischitz10, Theorem 2.1] to obtain a continuous homomorphism from
![]() $\mathbb {R}^{n+1}$
to
$\mathbb {R}^{n+1}$
to
![]() $ \mathbb {R}^{n}$
which surjects
$ \mathbb {R}^{n}$
which surjects
![]() $\mathcal {L}^{n+1}$
onto
$\mathcal {L}^{n+1}$
onto
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
Acknowledgement
The authors thank the referee for their careful review and helpful comments.