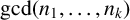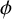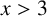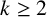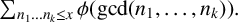1 Introduction and main results
Let
![]() $s=\sigma +it$
be the complex variable and let
$s=\sigma +it$
be the complex variable and let
![]() $\zeta (s)$
denote the Riemann zeta-function. For any positive integer
$\zeta (s)$
denote the Riemann zeta-function. For any positive integer
![]() $k\geq 2$
, let
$k\geq 2$
, let
![]() $\tau _{k}$
denote the k-factors divisor function defined by
$\tau _{k}$
denote the k-factors divisor function defined by
![]() ${\textbf {1}*\textbf {1}*\cdots *\textbf {1}}_{}$
and
${\textbf {1}*\textbf {1}*\cdots *\textbf {1}}_{}$
and
![]() $\tau =\tau _{2}$
. Here
$\tau =\tau _{2}$
. Here
![]() $*$
denotes the Dirichlet convolution of arithmetic functions and
$*$
denotes the Dirichlet convolution of arithmetic functions and
![]() $\textbf {1}$
is given by
$\textbf {1}$
is given by
![]() $\textbf {1}(n)=1$
for any positive integer n. We define the error term
$\textbf {1}(n)=1$
for any positive integer n. We define the error term
![]() $\Delta _{k}(x)$
in the generalised divisor problem by
$\Delta _{k}(x)$
in the generalised divisor problem by
where
![]() $Q_{k}(\log x)={\mathrm {Res}}_{s=1}\,\zeta ^{k}(s){x^{s-1}}/{s}$
is a polynomial in
$Q_{k}(\log x)={\mathrm {Res}}_{s=1}\,\zeta ^{k}(s){x^{s-1}}/{s}$
is a polynomial in
![]() $\log x$
of degree
$\log x$
of degree
![]() $k-1$
. The order of magnitude of
$k-1$
. The order of magnitude of
![]() $\Delta _{k}(x)$
as
$\Delta _{k}(x)$
as
![]() $x\to \infty $
is an open problem called the Piltz divisor problem and it has attracted much interest in analytic number theory. It has been conjectured that
$x\to \infty $
is an open problem called the Piltz divisor problem and it has attracted much interest in analytic number theory. It has been conjectured that
for any integer
![]() $k\geq 2$
and any
$k\geq 2$
and any
![]() $\varepsilon>0$
(see Ivić [Reference Ivić7, Chapter 13] or Titchmarsh [Reference Titchmarsh14]). Let
$\varepsilon>0$
(see Ivić [Reference Ivić7, Chapter 13] or Titchmarsh [Reference Titchmarsh14]). Let
![]() $\mu $
denote the Möbius function defined by
$\mu $
denote the Möbius function defined by
 $$ \begin{align*} \mu(n)=\left\{\begin{array}{ll} \displaystyle 1 &\ \ \ \mathrm{if} \ n=1, \ \ \mbox{} \\ \displaystyle (-1)^k &\ \ \ \mathrm{if} \ n\ \mathrm{is\ squarefree\ and}\ n=p_1p_2\ldots p_k, \ \ \mbox{} \\ \displaystyle 0 &\ \ \ \mathrm{if} \ n\ \mathrm{is\ not\ squarefree}, \\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \mu(n)=\left\{\begin{array}{ll} \displaystyle 1 &\ \ \ \mathrm{if} \ n=1, \ \ \mbox{} \\ \displaystyle (-1)^k &\ \ \ \mathrm{if} \ n\ \mathrm{is\ squarefree\ and}\ n=p_1p_2\ldots p_k, \ \ \mbox{} \\ \displaystyle 0 &\ \ \ \mathrm{if} \ n\ \mathrm{is\ not\ squarefree}, \\ \end{array} \right. \end{align*} $$
and let
![]() $\gcd (n_{1},\ldots ,n_{k})$
denote the greatest common divisor of the positive integers
$\gcd (n_{1},\ldots ,n_{k})$
denote the greatest common divisor of the positive integers
![]() $n_{1},\ldots ,n_{k}$
for any integer
$n_{1},\ldots ,n_{k}$
for any integer
![]() $k\geq 2$
. For a real number
$k\geq 2$
. For a real number
![]() $x>3$
, let
$x>3$
, let
![]() $S_{f,k}(x)$
denote the summatory function
$S_{f,k}(x)$
denote the summatory function
where f is any arithmetic function, by summing over the hyperbolic region
![]() $\{(n_{1},\ldots ,n_{k}) \in {\mathbb N}^{k}:\ n_{1}\ldots n_{k}\leq x \}$
. In 2012, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] showed that
$\{(n_{1},\ldots ,n_{k}) \in {\mathbb N}^{k}:\ n_{1}\ldots n_{k}\leq x \}$
. In 2012, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] showed that
where
 $$ \begin{align} g_{f,k}(n) = \sum_{n=m^{k}l}(\mu*f)(m)\tau_{k}(l) \end{align} $$
$$ \begin{align} g_{f,k}(n) = \sum_{n=m^{k}l}(\mu*f)(m)\tau_{k}(l) \end{align} $$
(see also Heyman and Tóth [Reference Heyman and Tóth3], Kiuchi and Saad Eddin [Reference Kiuchi and Saad Eddin8]). If f is multiplicative, then (1.4) is multiplicative. We use (1.4) to get the formal Dirichlet series
 $$ \begin{align} \sum_{n=1}^{\infty}\frac{g_{f,k}(n) }{n^s} = \frac{\zeta^{k}(s)}{\zeta(ks)}\sum_{n=1}^{\infty}\frac{f(n)}{n^{ks}}, \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\frac{g_{f,k}(n) }{n^s} = \frac{\zeta^{k}(s)}{\zeta(ks)}\sum_{n=1}^{\infty}\frac{f(n)}{n^{ks}}, \end{align} $$
which converges absolutely in the half-plane
![]() $\sigma>\sigma _{0}$
, where
$\sigma>\sigma _{0}$
, where
![]() $\sigma _{0}$
depends on f and k.
$\sigma _{0}$
depends on f and k.
When
![]() $f={\mathrm {id}}$
, it follows from (1.5) that
$f={\mathrm {id}}$
, it follows from (1.5) that
 $$ \begin{align*}\sum_{n=1}^{\infty}\frac{g_{{\mathrm{id}},k}(n) }{n^s} = \frac{\zeta^{k}(s)\zeta(ks-1)}{\zeta(ks)} \quad\mbox{for Re } s>1. \end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}\frac{g_{{\mathrm{id}},k}(n) }{n^s} = \frac{\zeta^{k}(s)\zeta(ks-1)}{\zeta(ks)} \quad\mbox{for Re } s>1. \end{align*} $$
Here the symbol
![]() $\mathrm {id}$
is given by
$\mathrm {id}$
is given by
![]() $\mathrm {id}(n)=n$
for any positive integer n. For
$\mathrm {id}(n)=n$
for any positive integer n. For
![]() $k=2$
, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] used the following three methods:
$k=2$
, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] used the following three methods:
-
(1) the complex integration approach (see [Reference Ivić7, Reference Titchmarsh14]);
-
(2) a combination of fractional part sums and the theory of exponent pairs (see [Reference Graham and Kolesnik2, Reference Krätzel9]); and
-
(3) Huxley’s method (see [Reference Huxley4–Reference Huxley and Watt6]),
to prove
Here
![]() $\theta $
satisfies
$\theta $
satisfies
![]() $\tfrac 12 < \theta <1$
,
$\tfrac 12 < \theta <1$
,
![]() $\theta '$
is some real number and
$\theta '$
is some real number and
![]() $P_{2}$
is a certain quadratic polynomial with
$P_{2}$
is a certain quadratic polynomial with
 $$ \begin{align*} P_{2}(\log{x})= \underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta(2s)}\frac{x^{s-1}}{s}. \end{align*} $$
$$ \begin{align*} P_{2}(\log{x})= \underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta(2s)}\frac{x^{s-1}}{s}. \end{align*} $$
They showed that methods (1), (2) and (3) imply the results
![]() $\theta =\tfrac 23$
and
$\theta =\tfrac 23$
and
![]() $\theta '={16}/{9}$
,
$\theta '={16}/{9}$
,
![]() $\theta ={925}/{1392}$
and
$\theta ={925}/{1392}$
and
![]() $\theta '=0$
, and
$\theta '=0$
, and
![]() $\theta ={547}/{832}$
and
$\theta ={547}/{832}$
and
![]() $\theta '={26947}/{8320}$
, respectively. Let
$\theta '={26947}/{8320}$
, respectively. Let
![]() $\phi $
denote the Euler totient function defined by
$\phi $
denote the Euler totient function defined by
![]() $ \phi ={\mathrm {id}}*\mu. $
The Dirichlet series (1.5) with
$ \phi ={\mathrm {id}}*\mu. $
The Dirichlet series (1.5) with
![]() $f=\phi $
implies that
$f=\phi $
implies that
 $$ \begin{align} \sum_{n=1}^{\infty}\frac{g_{\phi,k}(n)}{n^{s}} = \frac{\zeta^{k}(s) \zeta(ks-1)}{\zeta^{2}(ks)} \quad\mbox{for Re } s>1. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\frac{g_{\phi,k}(n)}{n^{s}} = \frac{\zeta^{k}(s) \zeta(ks-1)}{\zeta^{2}(ks)} \quad\mbox{for Re } s>1. \end{align} $$
We consider some properties of the hyperbolic summation for the Euler totient function involving the gcd. The first purpose of this paper is to investigate the asymptotic behaviour of (1.3) with
![]() $f=\phi $
for
$f=\phi $
for
![]() $k=2$
. Applying fractional part sums and the theory of exponent pairs, we obtain the following result.
$k=2$
. Applying fractional part sums and the theory of exponent pairs, we obtain the following result.
Theorem 1.1. For any real number
![]() $x>3$
,
$x>3$
,
 $$ \begin{align} &\sum_{ab\leq x}\phi(\gcd(a,b)) = \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \nonumber\\ &\quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x\nonumber \\ &\quad + O(x^{{55}/{84}+\varepsilon}), \end{align} $$
$$ \begin{align} &\sum_{ab\leq x}\phi(\gcd(a,b)) = \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \nonumber\\ &\quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x\nonumber \\ &\quad + O(x^{{55}/{84}+\varepsilon}), \end{align} $$
where
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma _{1}$
are the Euler constant and the first Stieltjes constant, respectively.
$\gamma _{1}$
are the Euler constant and the first Stieltjes constant, respectively.
We note that the main term of (1.8) is given by (7.2) below.
Remark 1.2. Note that
![]() $\tfrac 12 < {55}/{84}=\tfrac 12+ {13}/{84}<{547}/{832}= \tfrac 12 +{131}/{832}$
.
$\tfrac 12 < {55}/{84}=\tfrac 12+ {13}/{84}<{547}/{832}= \tfrac 12 +{131}/{832}$
.
The summation for the arithmetic functions
![]() $h(n)$
in the Dirichlet series
$h(n)$
in the Dirichlet series
 $$ \begin{align*} F_{h}(s)= \sum_{n=1}^{\infty}\frac{h_{}(n)}{n^s} = \zeta^{2}(s)\zeta(2s-1)\zeta^{M}(2s) \end{align*} $$
$$ \begin{align*} F_{h}(s)= \sum_{n=1}^{\infty}\frac{h_{}(n)}{n^s} = \zeta^{2}(s)\zeta(2s-1)\zeta^{M}(2s) \end{align*} $$
for
![]() $\mathrm {Re}~s>1$
and any fixed integer M was considered by Kühleitner and Nowak [Reference Kühleitner and Nowak11] in 2013. We use their results to show that the error term on the right-hand side of (1.8) is
$\mathrm {Re}~s>1$
and any fixed integer M was considered by Kühleitner and Nowak [Reference Kühleitner and Nowak11] in 2013. We use their results to show that the error term on the right-hand side of (1.8) is
![]() $\Omega (x^{1/2}{\log ^{2}x}/{\log \log x})$
as
$\Omega (x^{1/2}{\log ^{2}x}/{\log \log x})$
as
![]() $x\to \infty $
. This suggests the following conjecture.
$x\to \infty $
. This suggests the following conjecture.
Conjecture 1.3. The order of magnitude of the error term on the right-hand side of (1.8) is
![]() $ O(x^{1/2}(\log x)^{A}) $
with
$ O(x^{1/2}(\log x)^{A}) $
with
![]() $A>2$
.
$A>2$
.
When
![]() $k=3$
, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] also derived the formula
$k=3$
, Krätzel et al. [Reference Krätzel, Nowak and Tóth10] also derived the formula
where
 $$ \begin{align*} M_{3}(x) & = \sum_{s_{0}=1,2/3} \underset{s=s_{0}}{\mathrm{Res}} \bigg(\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta(3s)}\frac{x^s}{s}\bigg) \\ &= x(0.6842 \ldots \log^{2}x - 0.6620\ldots \log x + 4.845\ldots) - 4.4569\ldots x^{2/3}. \end{align*} $$
$$ \begin{align*} M_{3}(x) & = \sum_{s_{0}=1,2/3} \underset{s=s_{0}}{\mathrm{Res}} \bigg(\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta(3s)}\frac{x^s}{s}\bigg) \\ &= x(0.6842 \ldots \log^{2}x - 0.6620\ldots \log x + 4.845\ldots) - 4.4569\ldots x^{2/3}. \end{align*} $$
For
![]() $k=3$
, we derive an asymptotic formula for (1.3) with
$k=3$
, we derive an asymptotic formula for (1.3) with
![]() $f=\phi $
by using the complex integration approach.
$f=\phi $
by using the complex integration approach.
Theorem 1.4. For any real number
![]() $x>3$
,
$x>3$
,
 $$ \begin{align} \sum_{abc\leq x} & \phi(\gcd(a,b,c)) \nonumber \\ &= \frac{\zeta(2)}{2\zeta^{2}(3)} x \log^{2} x + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma - 1 + 3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)} \bigg) x \log x \nonumber \\ &\quad + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma^{2}+3\gamma_{1}-3\gamma + 1 +3(3\gamma -1)\frac{\zeta'(2)}{\zeta(2)} -6(3\gamma -1) \frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^{2} +\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)}-18\frac{\zeta'(2)}{\zeta(2)}\frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad + \frac{\zeta^{3}(\frac{2}{3})}{2\zeta^{2}(2)}x^{{2}/{3}} + O(x^{{1}/{2}}\log^{5}x), \end{align} $$
$$ \begin{align} \sum_{abc\leq x} & \phi(\gcd(a,b,c)) \nonumber \\ &= \frac{\zeta(2)}{2\zeta^{2}(3)} x \log^{2} x + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma - 1 + 3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)} \bigg) x \log x \nonumber \\ &\quad + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma^{2}+3\gamma_{1}-3\gamma + 1 +3(3\gamma -1)\frac{\zeta'(2)}{\zeta(2)} -6(3\gamma -1) \frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^{2} +\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)}-18\frac{\zeta'(2)}{\zeta(2)}\frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad + \frac{\zeta^{3}(\frac{2}{3})}{2\zeta^{2}(2)}x^{{2}/{3}} + O(x^{{1}/{2}}\log^{5}x), \end{align} $$
where
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma _{1}$
are the Euler constant and the first Stieltjes constant, respectively.
$\gamma _{1}$
are the Euler constant and the first Stieltjes constant, respectively.
We note that the main term of (1.9) is given by (7.3) below.
For
![]() $k=4$
, we use the complex integration approach to calculate the asymptotic formula for (1.3) with
$k=4$
, we use the complex integration approach to calculate the asymptotic formula for (1.3) with
![]() $f=\phi $
.
$f=\phi $
.
Theorem 1.5. For any real number
![]() $x>3$
,
$x>3$
,
where
![]() ${P}_{\phi ,4}(u)$
is a polynomial in u of degree three depending on
${P}_{\phi ,4}(u)$
is a polynomial in u of degree three depending on
![]() $\phi $
.
$\phi $
.
For
![]() $k=5$
, from Ivić [Reference Ivić7, Theorem 13.2], the error term
$k=5$
, from Ivić [Reference Ivić7, Theorem 13.2], the error term
![]() $\Delta _{5}(x)$
is estimated by
$\Delta _{5}(x)$
is estimated by
for any
![]() $\varepsilon>0$
. We use an elementary method and (1.1) to obtain the following result.
$\varepsilon>0$
. We use an elementary method and (1.1) to obtain the following result.
Theorem 1.6. For any real number
![]() $x>3$
,
$x>3$
,
 $$ \begin{align} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) &= x {P}_{\phi,5}(\log x) + \sum_{n\leq x^{1/5}}(\mu*\mu)(n)\sum_{m\leq x^{1/5}/n}m\Delta_{5}\bigg(\frac{x}{m^{5}n^{5}}\bigg), \end{align} $$
$$ \begin{align} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) &= x {P}_{\phi,5}(\log x) + \sum_{n\leq x^{1/5}}(\mu*\mu)(n)\sum_{m\leq x^{1/5}/n}m\Delta_{5}\bigg(\frac{x}{m^{5}n^{5}}\bigg), \end{align} $$
where
![]() ${P}_{\phi ,5}(u)$
is a polynomial in u of degree four depending on
${P}_{\phi ,5}(u)$
is a polynomial in u of degree four depending on
![]() $\phi $
. In particular, it follows from (1.11) that the error term on the right-hand side of (1.12) is
$\phi $
. In particular, it follows from (1.11) that the error term on the right-hand side of (1.12) is
![]() $O(x^{{11}/{20}+\varepsilon }).$
$O(x^{{11}/{20}+\varepsilon }).$
Remark 1.7. If we can use Conjecture (1.2) with
![]() $k=5$
, then the error term on the right-hand side of (1.12) becomes
$k=5$
, then the error term on the right-hand side of (1.12) becomes
![]() $O(x^{{2}/{5}+\varepsilon })$
.
$O(x^{{2}/{5}+\varepsilon })$
.
Assuming Conjecture (1.2), it is easy to obtain an asymptotic formula for
![]() $S_{\phi ,k}(x)$
for any integer
$S_{\phi ,k}(x)$
for any integer
![]() $k \geq 5$
.
$k \geq 5$
.
Proposition 1.8. Assume Conjecture (1.2). With the previous notation,
for any real number
![]() $x>3$
, where
$x>3$
, where
![]() ${P}_{\phi ,k}(u)\ (k \geq 5)$
is a polynomial in u of degree
${P}_{\phi ,k}(u)\ (k \geq 5)$
is a polynomial in u of degree
![]() $k-1$
depending on
$k-1$
depending on
![]() $\phi $
.
$\phi $
.
Notation
We denote by
![]() $\varepsilon $
an arbitrary small positive number which may be different at each occurrence.
$\varepsilon $
an arbitrary small positive number which may be different at each occurrence.
2 Auxiliary results
We will need the following lemma.
Lemma 2.1. For
![]() $t\geq t_{0}>0$
, uniformly in
$t\geq t_{0}>0$
, uniformly in
![]() $\sigma $
,
$\sigma $
,
 $$ \begin{align*} \zeta(\sigma+it) &\ll \left\{\begin{array}{ll} t^{(3-4\sigma)/6}\log t & \text{if } 0\leq \sigma \leq 1/2, \\ t^{(1-\sigma)/3} \log t & \text{if } 1/2 \leq \sigma \leq 1, \\ \log t & \text{if } 1\leq \sigma < 2, \\ 1 & \text{if } \sigma \geq 2. \end{array} \right. \end{align*} $$
$$ \begin{align*} \zeta(\sigma+it) &\ll \left\{\begin{array}{ll} t^{(3-4\sigma)/6}\log t & \text{if } 0\leq \sigma \leq 1/2, \\ t^{(1-\sigma)/3} \log t & \text{if } 1/2 \leq \sigma \leq 1, \\ \log t & \text{if } 1\leq \sigma < 2, \\ 1 & \text{if } \sigma \geq 2. \end{array} \right. \end{align*} $$
Proof. The lemma follows from Tenenbaum [Reference Tenenbaum13, Theorem II.3.8]; see also Ivić [Reference Ivić7] or Titchmarsh [Reference Titchmarsh14].
3 Proof of Theorem 1.1
Our main work is to evaluate the sum
![]() $ A(x)=\sum _{mnl^{2}\leq x,\, m,n,l>0}l $
. We utilise [Reference Krätzel, Nowak and Tóth10, Section 3.2] to derive the formula
$ A(x)=\sum _{mnl^{2}\leq x,\, m,n,l>0}l $
. We utilise [Reference Krätzel, Nowak and Tóth10, Section 3.2] to derive the formula
where the error term
![]() $\Delta (x)$
is estimated by
$\Delta (x)$
is estimated by
![]() $O(x^{1/4+(\alpha+\beta)/2})$
. Here
$O(x^{1/4+(\alpha+\beta)/2})$
. Here
![]() $(\alpha ,\beta )$
is an exponent pair (see [Reference Graham and Kolesnik2, Reference Ivić7]) and
$(\alpha ,\beta )$
is an exponent pair (see [Reference Graham and Kolesnik2, Reference Ivić7]) and
![]() $M_{1}(x)$
is the main term given by
$M_{1}(x)$
is the main term given by
From (1.7), this gives
 $$ \begin{align} \sum_{ab\leq x}\phi(\gcd(a,b)) = \sum_{l\leq \sqrt{x}}(\mu*\mu)(l)A\bigg(\frac{x}{l^2}\bigg) = M_{2}(x) + O(x^{1/4+(\alpha+\beta)/2+\varepsilon}), \end{align} $$
$$ \begin{align} \sum_{ab\leq x}\phi(\gcd(a,b)) = \sum_{l\leq \sqrt{x}}(\mu*\mu)(l)A\bigg(\frac{x}{l^2}\bigg) = M_{2}(x) + O(x^{1/4+(\alpha+\beta)/2+\varepsilon}), \end{align} $$
where the main term
![]() $M_{2}(x)$
is given by
$M_{2}(x)$
is given by
 $$ \begin{align*} M_{2}(x) & =\underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta^{2}(2s)}\frac{x^{s}}{s} \\ &= \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \\ & \quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x \end{align*} $$
$$ \begin{align*} M_{2}(x) & =\underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta^{2}(2s)}\frac{x^{s}}{s} \\ &= \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \\ & \quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x \end{align*} $$
by (7.2) below. Choosing, in particular, the exponent pair
discovered by Bourgain [Reference Bourgain1, Theorem 6], we obtain the order of magnitude
![]() $ O(x^{{55}/{84}+\varepsilon }) $
of the error term on the right-hand side of (3.1). This completes the proof of Theorem 1.1.
$ O(x^{{55}/{84}+\varepsilon }) $
of the error term on the right-hand side of (3.1). This completes the proof of Theorem 1.1.
4 Preparations for the proof of Theorems 1.4 and 1.5
In order to derive the formulas (1.9) and (1.10), we use the following notation. Let k be any integer such that
![]() $k \geq 3$
and let
$k \geq 3$
and let
![]() $ \sigma _{0} =1+{1}/{k}+\varepsilon. $
Consider the estimation of the error terms of Perron’s formula (see [Reference Montgomery and Vaughan12, Theorem 5.2 and Corollary 5.3]) for (1.4) with
$ \sigma _{0} =1+{1}/{k}+\varepsilon. $
Consider the estimation of the error terms of Perron’s formula (see [Reference Montgomery and Vaughan12, Theorem 5.2 and Corollary 5.3]) for (1.4) with
![]() $f=\phi $
. The estimation of
$f=\phi $
. The estimation of
![]() $g_{\phi ,k}(n)$
is given by
$g_{\phi ,k}(n)$
is given by
 $$ \begin{align*} g_{\phi,k}(n) = \sum_{n=m^{k}l}({\mathrm{id}} *\mu*\mu)(m) \tau_{k}(l) & = \sum_{n=d^{k}m^{k}l}d (\mu*\mu)(m) \tau_{k}(l) \\ & \ll n^{1/k} \sum_{n=d^{k}m^{k}l} \tau_{}(m)\tau_{k}(l) \ll n^{{1}/{k}+\varepsilon}. \end{align*} $$
$$ \begin{align*} g_{\phi,k}(n) = \sum_{n=m^{k}l}({\mathrm{id}} *\mu*\mu)(m) \tau_{k}(l) & = \sum_{n=d^{k}m^{k}l}d (\mu*\mu)(m) \tau_{k}(l) \\ & \ll n^{1/k} \sum_{n=d^{k}m^{k}l} \tau_{}(m)\tau_{k}(l) \ll n^{{1}/{k}+\varepsilon}. \end{align*} $$
In Perron’s formula,
 $$ \begin{align*} R \ll x^{{1}/{k} +\varepsilon} \bigg(1+\frac{x}{T}\sum_{1\leq k \leq x}\frac{1}{k}\bigg) + \frac{(4x)^{\sigma_0}}{T} \bigg|\frac{\zeta^{k}(\sigma_{0})\zeta(k\sigma_{0}-1)}{\zeta^{2}(k\sigma_{0})}\bigg| \ll \frac{x^{\sigma_0}}{T} \end{align*} $$
$$ \begin{align*} R \ll x^{{1}/{k} +\varepsilon} \bigg(1+\frac{x}{T}\sum_{1\leq k \leq x}\frac{1}{k}\bigg) + \frac{(4x)^{\sigma_0}}{T} \bigg|\frac{\zeta^{k}(\sigma_{0})\zeta(k\sigma_{0}-1)}{\zeta^{2}(k\sigma_{0})}\bigg| \ll \frac{x^{\sigma_0}}{T} \end{align*} $$
for
![]() $T\leq x$
. Hence, from Perron’s formula and (1.7),
$T\leq x$
. Hence, from Perron’s formula and (1.7),
 $$ \begin{align*}S_{\phi,k}(x) = \frac{1}{2\pi i}\int_{\sigma_0-iT}^{\sigma_0+iT}\frac{\zeta^{k}(s)\zeta(ks-1)}{\zeta^{2}(ks)} \frac{x^s}{s} \,ds + O\bigg(\frac{x^{\sigma_0}}{T}\bigg) \end{align*} $$
$$ \begin{align*}S_{\phi,k}(x) = \frac{1}{2\pi i}\int_{\sigma_0-iT}^{\sigma_0+iT}\frac{\zeta^{k}(s)\zeta(ks-1)}{\zeta^{2}(ks)} \frac{x^s}{s} \,ds + O\bigg(\frac{x^{\sigma_0}}{T}\bigg) \end{align*} $$
for any real number
![]() $x>3$
. When
$x>3$
. When
![]() $k=3$
, we move the line of integration to
$k=3$
, we move the line of integration to
![]() $\mathrm {Re}~s=\tfrac 12$
and consider the rectangular contour formed by the line segments joining the points
$\mathrm {Re}~s=\tfrac 12$
and consider the rectangular contour formed by the line segments joining the points
![]() $c_{0}-iT$
,
$c_{0}-iT$
,
![]() $c_{0}+iT$
,
$c_{0}+iT$
,
![]() $\tfrac 12+iT$
,
$\tfrac 12+iT$
,
![]() $\tfrac 12-iT$
and
$\tfrac 12-iT$
and
![]() $c_{0}-iT$
in the anticlockwise sense. We observe that the integrand has a triple pole at
$c_{0}-iT$
in the anticlockwise sense. We observe that the integrand has a triple pole at
![]() $s=1$
and a simple pole at
$s=1$
and a simple pole at
![]() $s=\tfrac 23$
. Thus, we obtain the main term from the sum of the residues coming from the poles at
$s=\tfrac 23$
. Thus, we obtain the main term from the sum of the residues coming from the poles at
![]() $s=1$
and
$s=1$
and
![]() $\tfrac 23$
. Hence, using the Cauchy residue theorem,
$\tfrac 23$
. Hence, using the Cauchy residue theorem,
where
 $$ \begin{align} J_{3}(x,T) &= \Big(\underset{s=1}{\mathrm{Res}} + \underset{s=\frac23}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s}. \end{align} $$
$$ \begin{align} J_{3}(x,T) &= \Big(\underset{s=1}{\mathrm{Res}} + \underset{s=\frac23}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s}. \end{align} $$
Here the integrals are given by
 $$ \begin{align} I_{3,1}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+iT}^{4/3+\varepsilon +iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \,ds, \end{align} $$
$$ \begin{align} I_{3,1}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+iT}^{4/3+\varepsilon +iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \,ds, \end{align} $$
 $$ \begin{align} I_{3,2}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}-iT}^{{1}/{2}+iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s}\,ds, \end{align} $$
$$ \begin{align} I_{3,2}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}-iT}^{{1}/{2}+iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s}\,ds, \end{align} $$
 $$ \begin{align*} I_{3,3}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}-iT}^{4/3+\varepsilon -iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \,ds. \end{align*} $$
$$ \begin{align*} I_{3,3}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}-iT}^{4/3+\varepsilon -iT} \frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \,ds. \end{align*} $$
Similarly,
where
 $$ \begin{align} J_{4}(x,T) &= \underset{s=1}{\mathrm{Res}}~\frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s}, \end{align} $$
$$ \begin{align} J_{4}(x,T) &= \underset{s=1}{\mathrm{Res}}~\frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s}, \end{align} $$
 $$ \begin{align} I_{4,1}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+a+iT}^{5/4+\varepsilon +iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s} \,ds, \end{align} $$
$$ \begin{align} I_{4,1}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+a+iT}^{5/4+\varepsilon +iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s} \,ds, \end{align} $$
 $$ \begin{align*} I_{4,2}(x,T) &= \frac{1}{2\pi i} \int_{{1}/{2}+a-iT}^{{1}/{2}+a+iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s}\,ds, \end{align*} $$
$$ \begin{align*} I_{4,2}(x,T) &= \frac{1}{2\pi i} \int_{{1}/{2}+a-iT}^{{1}/{2}+a+iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s}\,ds, \end{align*} $$
 $$ \begin{align*} I_{4,3}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+a-iT}^{5/4+\varepsilon -iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s} \,ds \end{align*} $$
$$ \begin{align*} I_{4,3}(x,T) &= \frac{1}{2\pi i}\int_{{1}/{2}+a-iT}^{5/4+\varepsilon -iT} \frac{\zeta^{4}(s)\zeta(4s-1)}{\zeta^{2}(4s)}\frac{x^{s}}{s} \,ds \end{align*} $$
with
![]() $ a={1}/{\log T}$
for any large number
$ a={1}/{\log T}$
for any large number
![]() $T(>5)$
.
$T(>5)$
.
5 Proofs of Theorems 1.4 and 1.5
5.1 Proof of the formula (1.9)
Consider the estimate
![]() $I_{3,1}(x,T)$
. We use Lemma 2.1 and (4.3) to deduce the estimation
$I_{3,1}(x,T)$
. We use Lemma 2.1 and (4.3) to deduce the estimation
 $$ \begin{align*} I_{3,1}(x;T) &= \frac{1}{2\pi i} \int_{1/2}^{4/3+\varepsilon} \frac{\zeta^{}(\sigma+iT)^3 \zeta(3\sigma-1+3iT)}{\zeta^{}(3\sigma+3iT)^2 (\sigma+iT)} x^{\sigma+iT} \,d\sigma \\ &\ll \frac{1}{T} \bigg(\int_{1/2}^{2/3}+\int_{2/3}^{1} + \int_{1}^{4/3 +\varepsilon}\bigg) |\zeta^{}(\sigma+iT)|^3 |\zeta(3\sigma-1+3iT)| x^{\sigma} \,d\sigma \\ &\ll T^{2/3} \log^{4}T \int_{1/2}^{2/3} \bigg(\frac{x}{T^{2}}\bigg)^{\sigma}\,d\sigma + \log^{4}T \int_{2/3}^{1} \bigg(\frac{x}{T^{}}\bigg)^{\sigma} \,d\sigma + \frac{\log^{4}T}{T} \int_{1}^{4/3+\varepsilon} {x}^{\sigma}\,d\sigma \\ &\ll \frac{x^{{4}/{3}+\varepsilon}}{T^{}}\log^{4}T. \end{align*} $$
$$ \begin{align*} I_{3,1}(x;T) &= \frac{1}{2\pi i} \int_{1/2}^{4/3+\varepsilon} \frac{\zeta^{}(\sigma+iT)^3 \zeta(3\sigma-1+3iT)}{\zeta^{}(3\sigma+3iT)^2 (\sigma+iT)} x^{\sigma+iT} \,d\sigma \\ &\ll \frac{1}{T} \bigg(\int_{1/2}^{2/3}+\int_{2/3}^{1} + \int_{1}^{4/3 +\varepsilon}\bigg) |\zeta^{}(\sigma+iT)|^3 |\zeta(3\sigma-1+3iT)| x^{\sigma} \,d\sigma \\ &\ll T^{2/3} \log^{4}T \int_{1/2}^{2/3} \bigg(\frac{x}{T^{2}}\bigg)^{\sigma}\,d\sigma + \log^{4}T \int_{2/3}^{1} \bigg(\frac{x}{T^{}}\bigg)^{\sigma} \,d\sigma + \frac{\log^{4}T}{T} \int_{1}^{4/3+\varepsilon} {x}^{\sigma}\,d\sigma \\ &\ll \frac{x^{{4}/{3}+\varepsilon}}{T^{}}\log^{4}T. \end{align*} $$
Similarly, the estimation of
![]() $ I_{3,3}(x,T) $
is of the same order. Hence, taking
$ I_{3,3}(x,T) $
is of the same order. Hence, taking
![]() $T=x^{}$
in the estimations of
$T=x^{}$
in the estimations of
![]() $I_{3,1}(x,T)$
and
$I_{3,1}(x,T)$
and
![]() $I_{3,3}(x,T)$
, we find that the total contribution of the horizontal lines in absolute value is
$I_{3,3}(x,T)$
, we find that the total contribution of the horizontal lines in absolute value is
Now we estimate
![]() $I_{3,2}(x,T)$
. We use (4.4), the estimate
$I_{3,2}(x,T)$
. We use (4.4), the estimate
![]() $ \zeta (\tfrac 32+it) \asymp 1 $
for
$ \zeta (\tfrac 32+it) \asymp 1 $
for
![]() $t\geq 1$
, the well-known estimate
$t\geq 1$
, the well-known estimate
 $$ \begin{align} \int_{1}^{T}\frac{|\zeta(\frac12 +iu)|^{4}}{u}\,du \ll \log^{5}T \end{align} $$
$$ \begin{align} \int_{1}^{T}\frac{|\zeta(\frac12 +iu)|^{4}}{u}\,du \ll \log^{5}T \end{align} $$
for any large T and the Hölder inequality to obtain the estimate
 $$ \begin{align} I_{3,2}(x,T) & = \frac{1}{2\pi}\int_{-T}^{T}\frac{\zeta^{3}(\frac{1}{2}+it)\zeta(\frac{1}{2}+3it)}{\zeta^{2}(\frac32+3it)} \frac{x^{1/2 +it}}{\frac12 +it} \,dt \nonumber \\ &\ll x^{1/2} + x^{1/2} \int_{1}^{T} \frac{|\zeta(\frac12 +it)|^3}{|\zeta(\frac32 +3it)|^2}\cdot \frac{|\zeta(\frac12+3it)|}{t}\,dt \nonumber \\ &\ll x^{1/2} \bigg(\int_{1}^{T} \frac{|\zeta(\frac12 +it)|^4}{t} \,dt\bigg)^{3/4} \bigg(\int_{1}^{T} \frac{|\zeta(\frac12 +3it)|^4}{3t} \,dt\bigg)^{1/4} \nonumber \\ &\ll x^{1/2} \log^{5}T. \end{align} $$
$$ \begin{align} I_{3,2}(x,T) & = \frac{1}{2\pi}\int_{-T}^{T}\frac{\zeta^{3}(\frac{1}{2}+it)\zeta(\frac{1}{2}+3it)}{\zeta^{2}(\frac32+3it)} \frac{x^{1/2 +it}}{\frac12 +it} \,dt \nonumber \\ &\ll x^{1/2} + x^{1/2} \int_{1}^{T} \frac{|\zeta(\frac12 +it)|^3}{|\zeta(\frac32 +3it)|^2}\cdot \frac{|\zeta(\frac12+3it)|}{t}\,dt \nonumber \\ &\ll x^{1/2} \bigg(\int_{1}^{T} \frac{|\zeta(\frac12 +it)|^4}{t} \,dt\bigg)^{3/4} \bigg(\int_{1}^{T} \frac{|\zeta(\frac12 +3it)|^4}{3t} \,dt\bigg)^{1/4} \nonumber \\ &\ll x^{1/2} \log^{5}T. \end{align} $$
Taking
![]() $T=x^{}$
in (5.1), (5.3) and (4.1) with
$T=x^{}$
in (5.1), (5.3) and (4.1) with
![]() $k=3$
, and substituting the above and the residue (4.2) into (4.1) with
$k=3$
, and substituting the above and the residue (4.2) into (4.1) with
![]() $k=3$
, we obtain the formula (1.9).
$k=3$
, we obtain the formula (1.9).
5.2 Proof of the formula (1.10)
Let
![]() $a={1}/{\log T}\ (T\geq 5)$
. From (4.5) with
$a={1}/{\log T}\ (T\geq 5)$
. From (4.5) with
![]() $k=4$
,
$k=4$
,
since
![]() $s=1$
is a pole of
$s=1$
is a pole of
![]() $\zeta ^{4}(s)$
of order four, where
$\zeta ^{4}(s)$
of order four, where
![]() $ {P}_{\phi ,4}(u)$
is a polynomial in u of degree three depending on
$ {P}_{\phi ,4}(u)$
is a polynomial in u of degree three depending on
![]() $\phi $
. Consider the estimate
$\phi $
. Consider the estimate
![]() $I_{4,1}(x,T)$
. From (4.6) and Lemma 2.1,
$I_{4,1}(x,T)$
. From (4.6) and Lemma 2.1,
 $$ \begin{align*} I_{4,1}(x,T) &\ll \frac{1}{T} \bigg(\int_{1/2+a}^{1}+\int_{1}^{5/4 +\varepsilon}\bigg) |\zeta^{}(\sigma+iT)|^4 |\zeta(4\sigma-1+4iT)| x^{\sigma} \,d\sigma \\ &\ll T^{1/3}\log^{5}T \int_{1/2+a}^{1} \bigg(\frac{x}{T^{4/3}}\bigg)^{\sigma}\,d\sigma + \frac{\log^{5}T}{T} \int_{1}^{5/4 +\varepsilon} {x}^{\sigma} \,d\sigma \\ &\ll x^{1/2+a}\frac{\log^{5}T}{T^{1/3}} + x^{5/4 +\varepsilon} \frac{\log^{5}T}{T}. \end{align*} $$
$$ \begin{align*} I_{4,1}(x,T) &\ll \frac{1}{T} \bigg(\int_{1/2+a}^{1}+\int_{1}^{5/4 +\varepsilon}\bigg) |\zeta^{}(\sigma+iT)|^4 |\zeta(4\sigma-1+4iT)| x^{\sigma} \,d\sigma \\ &\ll T^{1/3}\log^{5}T \int_{1/2+a}^{1} \bigg(\frac{x}{T^{4/3}}\bigg)^{\sigma}\,d\sigma + \frac{\log^{5}T}{T} \int_{1}^{5/4 +\varepsilon} {x}^{\sigma} \,d\sigma \\ &\ll x^{1/2+a}\frac{\log^{5}T}{T^{1/3}} + x^{5/4 +\varepsilon} \frac{\log^{5}T}{T}. \end{align*} $$
Similarly, the estimation of
![]() $ I_{4,3}(x,T) $
is of the same order. Hence, taking
$ I_{4,3}(x,T) $
is of the same order. Hence, taking
![]() $T=x^{}$
in the estimations
$T=x^{}$
in the estimations
![]() $I_{4,1}(x,T)$
and
$I_{4,1}(x,T)$
and
![]() $I_{4,3}(x,T)$
, we find that the total contribution of the horizontal lines in absolute value is
$I_{4,3}(x,T)$
, we find that the total contribution of the horizontal lines in absolute value is
We use (5.2) and the estimation
![]() $ \zeta (1+it) \ll {\log ^{2/3} t} $
for
$ \zeta (1+it) \ll {\log ^{2/3} t} $
for
![]() $t\geq t_{0}$
(see [Reference Ivić7, Theorem 6.3]) to obtain the estimation
$t\geq t_{0}$
(see [Reference Ivić7, Theorem 6.3]) to obtain the estimation
 $$ \begin{align} I_{4,2}(x,T) \ll x^{1/2+a} + x^{1/2+a}\log^{2/3}T \int_{1}^{T} \frac{|\zeta(\frac12 +it)|^4}{t} \,dt \ll x^{1/2} \log^{{17}/{3}}T. \end{align} $$
$$ \begin{align} I_{4,2}(x,T) \ll x^{1/2+a} + x^{1/2+a}\log^{2/3}T \int_{1}^{T} \frac{|\zeta(\frac12 +it)|^4}{t} \,dt \ll x^{1/2} \log^{{17}/{3}}T. \end{align} $$
We take
![]() $T=x^{}$
in (5.4), (5.5), (5.6) and (4.1) with
$T=x^{}$
in (5.4), (5.5), (5.6) and (4.1) with
![]() $k=4$
to complete the proof of the formula (1.10).
$k=4$
to complete the proof of the formula (1.10).
6 Proof of Theorem 1.6
We use (1.4) with
![]() $k=5$
to deduce that
$k=5$
to deduce that
 $$ \begin{align} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) =\sum_{lm^{5}n^{5}\leq x}(\mu*\mu)(n)m\tau_{5}(l) =\sum_{n\leq x^{1/5}}(\mu*\mu)(n)B\bigg(\frac{x}{n^5}\bigg), \end{align} $$
$$ \begin{align} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) =\sum_{lm^{5}n^{5}\leq x}(\mu*\mu)(n)m\tau_{5}(l) =\sum_{n\leq x^{1/5}}(\mu*\mu)(n)B\bigg(\frac{x}{n^5}\bigg), \end{align} $$
where
![]() $ B(x):=\sum _{lm^{5}\leq x}m\tau _{5}(l). $
From (1.1),
$ B(x):=\sum _{lm^{5}\leq x}m\tau _{5}(l). $
From (1.1),
 $$ \begin{align} B(x) &= \sum_{m\leq x^{1/5}}m\sum_{n\leq {x}/{m^5}} \tau_{5}(n) \nonumber \\ &= \sum_{m\leq x^{1/5}}m\bigg(A_{1}\frac{x}{m^5}\log^{4}\frac{x}{m^5} + \cdots + A_{5}\frac{x}{m^5} + \Delta_{5}\bigg(\frac{x}{m^5}\bigg) \bigg) \nonumber \\ &= \widetilde{Q_{4}}(\log x) x + \sum_{m\leq x^{1/5}}m\Delta_{5}\bigg(\frac{x}{m^5}\bigg), \end{align} $$
$$ \begin{align} B(x) &= \sum_{m\leq x^{1/5}}m\sum_{n\leq {x}/{m^5}} \tau_{5}(n) \nonumber \\ &= \sum_{m\leq x^{1/5}}m\bigg(A_{1}\frac{x}{m^5}\log^{4}\frac{x}{m^5} + \cdots + A_{5}\frac{x}{m^5} + \Delta_{5}\bigg(\frac{x}{m^5}\bigg) \bigg) \nonumber \\ &= \widetilde{Q_{4}}(\log x) x + \sum_{m\leq x^{1/5}}m\Delta_{5}\bigg(\frac{x}{m^5}\bigg), \end{align} $$
where
![]() $\widetilde {{Q}_{4}}(u)$
is a polynomial in u of degree four and
$\widetilde {{Q}_{4}}(u)$
is a polynomial in u of degree four and
![]() $A_{1},A_{2},\ldots , A_{5}$
are computable constants. Inserting (6.2) into (6.1),
$A_{1},A_{2},\ldots , A_{5}$
are computable constants. Inserting (6.2) into (6.1),
 $$ \begin{align*} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) = x {P}_{\phi,5}(\log x) + \sum_{n\leq x^{1/5}}(\mu*\mu)(n)\sum_{m\leq x^{1/5}/n}m\Delta_{5}\bigg(\frac{x}{m^{5}n^{5}}\bigg). \end{align*} $$
$$ \begin{align*} \sum_{abcde\leq x}\phi(\gcd(a,b,c,d,e)) = x {P}_{\phi,5}(\log x) + \sum_{n\leq x^{1/5}}(\mu*\mu)(n)\sum_{m\leq x^{1/5}/n}m\Delta_{5}\bigg(\frac{x}{m^{5}n^{5}}\bigg). \end{align*} $$
Hence, we obtain the formula (1.12).□
7 Appendix
To calculate the main terms of Theorems 1.1 and 1.4, we use the Laurent expansion of the Riemann zeta-function at
![]() $s=1$
: that is,
$s=1$
: that is,
as
![]() $s\to \infty $
, where
$s\to \infty $
, where
![]() $\gamma $
is the Euler constant and
$\gamma $
is the Euler constant and
![]() $\gamma _{k}\ (k=1,2,3,\ldots )$
are the Stieltjes constants,
$\gamma _{k}\ (k=1,2,3,\ldots )$
are the Stieltjes constants,
 $$ \begin{align*}\gamma_{k}:=\frac{(-1)^k}{k!}\lim_{N\to \infty}\bigg(\sum_{m\leq N}\frac{\log^{k}m}{m}-\frac{\log^{k+1}N}{k+1}\bigg). \end{align*} $$
$$ \begin{align*}\gamma_{k}:=\frac{(-1)^k}{k!}\lim_{N\to \infty}\bigg(\sum_{m\leq N}\frac{\log^{k}m}{m}-\frac{\log^{k+1}N}{k+1}\bigg). \end{align*} $$
We need the following residues.
 $$ \begin{align} M_{2}(x) &:=\underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta^{2}(2s)}\frac{x^{s}}{s} \nonumber\\ &= \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \nonumber\\ &\quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x, \end{align} $$
$$ \begin{align} M_{2}(x) &:=\underset{s=1}{\mathrm{Res}}~\frac{\zeta^{2}(s)\zeta(2s-1)}{\zeta^{2}(2s)}\frac{x^{s}}{s} \nonumber\\ &= \frac{1}{4\zeta^{2}(2)} x \log^{2} x + \frac{1}{\zeta^{2}(2)}\bigg(2\gamma - \frac12 - 2\frac{\zeta'(2)}{\zeta(2)}\bigg) x \log x \nonumber\\ &\quad + \frac{1}{2\zeta^{2}(2)}\bigg({5}\gamma^{2}+6\gamma_{1}-4\gamma + 1 -4(4\gamma -1)\frac{\zeta'(2)}{\zeta(2)} - 4\frac{\zeta"(2)}{\zeta(2)} +12\bigg(\frac{\zeta'(2)}{\zeta(2)}\bigg)^{2}\bigg) x, \end{align} $$
and
 $$ \begin{align} J_{3}(x,T) &:= \Big(\underset{s=1}{\mathrm{Res}} + \underset{s=2/3}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \nonumber\\ & = \frac{\zeta(2)}{2\zeta^{2}(3)} x \log^{2} x + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma - 1 + 3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)} \bigg) x \log x \nonumber \\ &\quad+ \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma^{2}+3\gamma_{1}-3\gamma + 1 +3(3\gamma -1)\frac{\zeta'(2)}{\zeta(2)} -6(3\gamma -1) \frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad+ \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^{2} +\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)}-18\frac{\zeta'(2)}{\zeta(2)}\frac{\zeta'(3)}{\zeta(3)} \bigg) x +\frac{\zeta(\frac{2}{3})^3}{2\zeta^{2}(2)}x^{{2}/{3}}. \end{align} $$
$$ \begin{align} J_{3}(x,T) &:= \Big(\underset{s=1}{\mathrm{Res}} + \underset{s=2/3}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \nonumber\\ & = \frac{\zeta(2)}{2\zeta^{2}(3)} x \log^{2} x + \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma - 1 + 3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)} \bigg) x \log x \nonumber \\ &\quad+ \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(3\gamma^{2}+3\gamma_{1}-3\gamma + 1 +3(3\gamma -1)\frac{\zeta'(2)}{\zeta(2)} -6(3\gamma -1) \frac{\zeta'(3)}{\zeta(3)} \bigg) x \nonumber \\ &\quad+ \frac{\zeta(2)}{\zeta^{2}(3)}\bigg(27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^{2} +\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)}-18\frac{\zeta'(2)}{\zeta(2)}\frac{\zeta'(3)}{\zeta(3)} \bigg) x +\frac{\zeta(\frac{2}{3})^3}{2\zeta^{2}(2)}x^{{2}/{3}}. \end{align} $$
Proof. Suppose that
![]() $g(s)$
is regular in the neighbourhood of
$g(s)$
is regular in the neighbourhood of
![]() $s=1$
and
$s=1$
and
![]() $f(s)$
has only a triple pole at
$f(s)$
has only a triple pole at
![]() $s=1$
. Then the Laurent expansion of
$s=1$
. Then the Laurent expansion of
![]() $f(s)$
implies that
$f(s)$
implies that
where
![]() $h(s)$
is regular in the neighbourhood of
$h(s)$
is regular in the neighbourhood of
![]() $s=1$
and
$s=1$
and
![]() $a,b,c$
are computable constants. We use the residue calculation to deduce that
$a,b,c$
are computable constants. We use the residue calculation to deduce that
To prove (7.3), we use (7.1) to deduce that
 $$ \begin{align*} \zeta^{3}(s)&= \frac{1}{(s-1)^3} + \frac{3\gamma}{(s-1)^2} + \frac{3\gamma^{2}+3\gamma_{1}}{s-1} + O(1) \quad\mbox{as } s\to 1. \end{align*} $$
$$ \begin{align*} \zeta^{3}(s)&= \frac{1}{(s-1)^3} + \frac{3\gamma}{(s-1)^2} + \frac{3\gamma^{2}+3\gamma_{1}}{s-1} + O(1) \quad\mbox{as } s\to 1. \end{align*} $$
Setting
 $$ \begin{align*}g(s):=\frac{\zeta(3s-1)}{\zeta^{2}(3s)}\cdot \frac{x^s}{s}, \end{align*} $$
$$ \begin{align*}g(s):=\frac{\zeta(3s-1)}{\zeta^{2}(3s)}\cdot \frac{x^s}{s}, \end{align*} $$
we have
 $$ \begin{align*}g(1) =\frac{\zeta(2)}{\zeta^{2}(3)}x, \quad g'(1) =\frac{\zeta(2)}{\zeta^{2}(3)}\bigg(\log x + 3\frac{\zeta'(2)}{\zeta(2)} -6\frac{\zeta'(3)}{\zeta(3)}-1\bigg)x, \end{align*} $$
$$ \begin{align*}g(1) =\frac{\zeta(2)}{\zeta^{2}(3)}x, \quad g'(1) =\frac{\zeta(2)}{\zeta^{2}(3)}\bigg(\log x + 3\frac{\zeta'(2)}{\zeta(2)} -6\frac{\zeta'(3)}{\zeta(3)}-1\bigg)x, \end{align*} $$
 $$ \begin{align*} g"(1)&= \frac{\zeta(2)}{\zeta^{2}(3)}x \log^{2} x + \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)}-1 \bigg)x\log x \\ &\quad+ \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(1+6\frac{\zeta'(3)}{\zeta(3)} - 3\frac{\zeta'(2)}{\zeta(2)} + 27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^2 \bigg)x \\ &\quad+ \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)} - 18\frac{\zeta'(2)}{\zeta(2)} \frac{\zeta'(3)}{\zeta(3)} \bigg)x. \end{align*} $$
$$ \begin{align*} g"(1)&= \frac{\zeta(2)}{\zeta^{2}(3)}x \log^{2} x + \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(3\frac{\zeta'(2)}{\zeta(2)} - 6\frac{\zeta'(3)}{\zeta(3)}-1 \bigg)x\log x \\ &\quad+ \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(1+6\frac{\zeta'(3)}{\zeta(3)} - 3\frac{\zeta'(2)}{\zeta(2)} + 27\bigg(\frac{\zeta'(3)}{\zeta(3)}\bigg)^2 \bigg)x \\ &\quad+ \frac{2\zeta(2)}{\zeta^{2}(3)}\bigg(\frac{9}{2}\frac{\zeta"(2)}{\zeta(2)} -9\frac{\zeta"(3)}{\zeta(3)} - 18\frac{\zeta'(2)}{\zeta(2)} \frac{\zeta'(3)}{\zeta(3)} \bigg)x. \end{align*} $$
Hence,
 $$ \begin{align*} &\Big(\underset{s=1}{\mathrm{Res}} + \underset{s=2/3}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \\ &\quad=\frac{1}{2}g"(1) +3\gamma g'(1) + 3(\gamma_{1}+\gamma^2)g(1) + \frac{\zeta^{3}(\frac{2}{3})}{2\zeta^{2}(2)}x^{2/3}. \end{align*} $$
$$ \begin{align*} &\Big(\underset{s=1}{\mathrm{Res}} + \underset{s=2/3}{\mathrm{Res}}\Big)~\frac{\zeta^{3}(s)\zeta(3s-1)}{\zeta^{2}(3s)}\frac{x^{s}}{s} \\ &\quad=\frac{1}{2}g"(1) +3\gamma g'(1) + 3(\gamma_{1}+\gamma^2)g(1) + \frac{\zeta^{3}(\frac{2}{3})}{2\zeta^{2}(2)}x^{2/3}. \end{align*} $$
Hence, we obtain the stated identity. To prove (7.2), we use
 $$ \begin{align*} \zeta^{2}(s)\zeta(2s-1)&= \frac{\frac12}{(s-1)^3} + \frac{2\gamma}{(s-1)^2} + \frac{\frac52 \gamma^{2}+3\gamma_{1}}{s-1} + O(1) \quad\mbox{as } s\to 1. \end{align*} $$
$$ \begin{align*} \zeta^{2}(s)\zeta(2s-1)&= \frac{\frac12}{(s-1)^3} + \frac{2\gamma}{(s-1)^2} + \frac{\frac52 \gamma^{2}+3\gamma_{1}}{s-1} + O(1) \quad\mbox{as } s\to 1. \end{align*} $$
Acknowledgement
The authors would like to thank the referee for many valuable suggestions and remarks.