1 Introduction
Electronic and nuclear dynamics play essential roles in the properties and functions of matter[ Reference Stolow, Bragg and Neumark 1 ]. Such dynamics span timescales from picoseconds down to attoseconds[ Reference Yamanouchi 2 – Reference Xie, Roither, Kartashov, Persson, Arbó, Zhang, Gräfe, Schöffler, Burgdörfer, Baltuška and Kitzler 7 ]. In many cases, ultrashort pulses are required to initiate and probe the selected dynamics. Such pulses can be provided by both optical-frequency lasers and free-electron lasers (FELs)[ Reference Fermann, Galvanauskas and Sucha 8 – Reference Seddon, Clarke, Dunning, Masciovecchio, Milne, Parmigiani, Rugg, Spence, Thompson, Ueda, Vinko, Wark and Wurth 10 ]. Optical-wavelength pulses can reach pulse durations down to a few femtoseconds and, high-order harmonic generation, can in turn be used to produce pulses in the extreme ultraviolet/soft X-ray spectral regime with pulse durations below 100 attoseconds[ Reference Krausz and Ivanov 3 ]. In the past decades, these pulses have been successfully applied to many studies of ultrafast dynamics in gases and solids (see Chang[ Reference Chang 11 ] and Nisoli et al.[ Reference Nisoli, Decleva, Calegari, Palacios and Martín 12 ] and references therein). One of the major limitations of these high-harmonic sources is low photon flux at photon energies above 200 eV.
Recently, X-ray FELs have achieved significantly higher photon fluxes at such photon energies, with pulse durations down to a few femtoseconds and, in some cases, a few hundreds of attoseconds[ Reference Helml, Maier, Schweinberger, Grguraš, Radcliffe, Doumy, Roedig, Gagnon, Messerschmidt, Schorb, Bostedt, Grüner, DiMauro, Cubaynes, Bozek, Tschentscher, Costello, Meyer, Coffee, Düsterer, Cavalieri and Kienberger 13 – Reference Duris, Li, Driver, Champenois, MacArthur, Lutman, Zhang, Rosenberger, Aldrich, Coffee, Coslovich, Decker, Glownia, Hartmann, Helml, Kamalov, Knurr, Krzywinski, Lin, Nantel, Natan, O'Neal, Shivaram, Walter, Wang, Welch, Wolf, Xu, Kling, Bucksbaum, Zholents, Huang, Cryan and Marinelli 15 ]. The Linac Coherent Light Source (LCLS) has already demonstrated tunable free-electron X-ray pulses with pulse durations of a few hundreds of attoseconds and pulse energies of a few tens of microjoules, and a photon flux of more than one million times higher than that is currently possible from laser-driven high-harmonic sources[ Reference Duris, Li, Driver, Champenois, MacArthur, Lutman, Zhang, Rosenberger, Aldrich, Coffee, Coslovich, Decker, Glownia, Hartmann, Helml, Kamalov, Knurr, Krzywinski, Lin, Nantel, Natan, O'Neal, Shivaram, Walter, Wang, Welch, Wolf, Xu, Kling, Bucksbaum, Zholents, Huang, Cryan and Marinelli 15 ]. The SwissFEL also aims to generate bright ultrashort X-ray pulses in both hard and soft X-ray spectral regimes, with properties ideal for time-resolved studies of ultrafast electron and nuclear dynamics in atoms, molecules, and condensed matter[ Reference Milne, Schietinger, Aiba, Alarcon, Alex, Anghel, Arsov, Beard, Beaud, Bettoni, Bopp, Brands, Brönnimann, Brunnenkant, Calvi, Citterio, Craievich, Divall, Dällenbach, D’Amico, Dax, Deng, Dietrich, Dinapoli, Divall, Dordevic, Ebner, Erny, Fitze, Flechsig, Follath, Frei, Gärtner, Ganter, Garvey, Geng, Gorgisyan, Gough, Hauff, Hauri, Hiller, Humar, Hunziker, Ingold, Ischebeck, Janousch, Juranić, Jurcevic, Kaiser, Kalantari, Kalt, Keil, Kittel, Knopp, Koprek, Lemke, Lippuner, Sancho, Löhl, Lopez-Cuenca, Märki, Marcellini, Marinkovic, Martiel, Menzel, Mozzanica, Nass, Orlandi, Loch, Panepucci, Paraliev, Patterson, Pedrini, Pedrozzi, Pollet, Pradervand, Prat, Radi, Raguin, Redford, Rehanek, Réhault, Reiche, Ringele, Rittmann, Rivkin, Romann, Ruat, Ruder, Sala, Schebacher, Schilcher, Schlott, Schmidt, Schmitt, Shi, Stadler, Stingelin, Sturzenegger, Szlachetko, Thattil, Treyer, Trisorio, Tron, Vetter, Vicario, Voulot, Wang, Zamofing, Zellweger, Zennaro, Zimoch, Abela, Patthey and Braun 16 , Reference Prat, Abela, Aiba, Alarcon, Alex, Arbelo, Arrell, Arsov, Bacellar, Beard, Beaud, Bettoni, Biffiger, Bopp, Braun, Calvi, Cassar, Celcer, Chergui, Chevtsov, Cirelli, Citterio, Craievich, Divall, Dax, Dehler, Deng, Dietrich, Dijkstal, Dinapoli, Dordevic, Ebner, Engeler, Erny, Esposito, Ferrari, Flechsig, Follath, Frei, Ganter, Garvey, Geng, Gobbo, Gough, Hauff, Hauri, Hiller, Hunziker, Huppert, Ingold, Ischebeck, Janousch, Johnson, Johnson, Juranić, Jurcevic, Kaiser, Kalt, Keil, Kiselev, Kittel, Knopp, Koprek, Laznovsky, Lemke, Sancho, Löhl, Malyzhenkov, Mancini, Mankowsky, Marcellini, Marinkovic, Martiel, Märki, Milne, Mozzanica, Nass, Orlandi, Loch, Paraliev, Patterson, Patthey, Pedrini, Pedrozzi, Pradervand, Radi, Raguin, Redford, Rehanek, Reiche, Rivkin, Romann, Sala, Sander, Schietinger, Schilcher, Schlott, Schmidt, Seidel, Stadler, Stingelin, Svetina, Treyer, Trisorio, Vicario, Voulot, Wrulich, Zerdane and Zimoch 17 ]. Currently, SwissFEL has two beamlines for X-ray generation with complementary wavelength ranges. The ARAMIS beamline produces X-ray pulses with photon energies ranging from 1.77 to 12.4 keV. The recently constructed ATHOS beamline delivers soft X-rays with photon energy between 250 eV and 1.8 keV and pulse durations below 100 fs. In special running modes, these pulses can be reduced in duration to sub-10-fs or even sub-femtosecond levels[ Reference Abela, Alarcon, Alex, Arrell, Arsov, Bettoni, Bopp, Bostedt, Braun, Calvi, Celcer, Craievich, Dax, Dijkstal, Dordevic, Ferrari, Flechsig, Follath, Frei, Gaiffi, Geng, Gough, Hiller, Hunziker, Huppert, Ischebeck, Jöhri, Juranic, Kalt, Kaiser, Keil, Kittel, Künzi, Lippuner, Löhl, Marcellini, Marinkovic, Loch, Orlandi, Patterson, Pradervand, Paraliev, Pedrozzi, Prat, Ranitovic, Reiche, Rosenberg, Sanfilippo, Schietinger, Schmidt, Schnorr, Svetina, Trisorio, Vicario, Voulot, Wagner, Wörner, Zandonella, Patthey and Ganter 18 ].
Fully exploiting the potential for high time resolution for pump-probe experiments requires synchronization of the FEL output with another laser of comparable pulse duration operating in the near-optical wavelength range. The amplified Ti:sapphire laser system used for pump-probe experiments at the ATHOS beamline delivers pulses with two Fourier-transform-limited pulse duration modes: 30 and 100 fs. To obtain a laser pulse with a pulse duration of sub-10 fs, post-compression of the pulses from the laser amplifier is required. Owing to the tight time constraints imposed by user facility operation, such a short-pulse compressor must be exceedingly stable and robust.
An additional requirement for high-time-resolution experiments at X-ray FELs is the need for precise and accurate measurements of the relative timing between the pump and probe pulses. The timing between these pulses typically changes from pulse to pulse by an amount dependent on the methods used to synchronize the different sources, but is typically of the order of 30–100 fs. So-called laser timing arrival measurements use a variety of methods to encode the relative timing information between the X-ray pulses and a short pulse derived from the optical-wavelength laser[ Reference Frühling, Wieland, Gensch, Gebert, Schütte, Krikunova, Kalms, Budzyn, Grimm, Rossbach, Plönjes and Drescher 19 – Reference Sato, Togashi, Ogawa, Katayama, Inubushi, Tono and Yabashi 27 ]. Many such methods rely on ultrafast X-ray-induced changes to the optical properties of a condensed phase material. One common implementation of a laser arrival time measurement requires that the X-ray and optical pulses intersect with a large relative angle on a thin slab of a material that absorbs a fraction of the X-ray pulse. As the relative arrival time of the two pulses varies with position on the slab, an image of the reflected or transmitted optical light pulse from the slab can encode the relative timing of the two pulses. The temporal resolution of such a timing tool is typically limited by the pulse durations of both the optical laser and the X-ray pulses. This means that for very high-time-resolution experiments, not only are sub-10-fs optical laser pulses often needed for the experiment itself, but also are potentially vital for the arrival time tool.
An alternative implementation of the arrival time tool is spectral encoding, where the X-ray and optical pulses are collinear, but the optical pulses are chirped by a small amount so that different wavelength components overlap at different times. By measuring the changes to the transmitted spectrum of the optical pulse through a thin plate with optical properties that are modified by the X-ray pulse on fast time scales, it is possible to infer the relative timing of the two pulses. Here the chirp of the laser pulse sets the relationship between the wavelength and relative arrival time. The spectral resolution of the optical spectrometer and the magnitude of the chirp of the pulse set the time resolution, with high spectral resolution and small chirp values leading to more precise timing measurements. These parameters, however, must be balanced against the need for an adequate measurement range to cover the synchronization jitter or small timing drifts, which favor a larger value for the chirp. A large bandwidth of the laser pulse is therefore highly desirable because it allows for both high time resolution (small chirp) and a large timing range. This also indicates a need for generating ultrabroadband optical pulses for optimal arrival time measurement performance.
The very large bandwidths needed for these applications can in principle be generated from femtosecond or picosecond pulses via supercontinuum generation in bulk solids such as sapphire, CaF2, or YAG[ Reference Dubietis, Tamošauskas, Šuminas, Jukna and Couairon 28 ]. The generated supercontinuum typically covers a broad range with extended plateaus to the red and blue sides of the fundamental wavelength. Most of the pulse energy, however, remains at the fundamental wavelength which limits the energy of the supercontinuum to the nanojoule level. In addition, the beam quality is hard to maintain due to conical diffraction from the filamentation in the solids[ Reference Dubietis, Tamošauskas, Šuminas, Jukna and Couairon 28 ]. Both the pulse energy and the beam quality of the supercontinuum are critical to obtain sufficient spectral intensity for the spectral encoding to achieve a decent signal-to-noise ratio. Therefore, new supercontinuum sources with higher pulse energies and better beam quality are highly desirable.
The most frequently used mechanism to broaden the spectrum of an ultrashort pulse is self-phase modulation (SPM)[
Reference Boyd
29
]. The third-order nonlinear susceptibility of a medium results in an effective index of refraction
![]() ${n}_{\mathrm{eff}}$
that depends on the pulse intensity
${n}_{\mathrm{eff}}$
that depends on the pulse intensity
![]() $I$
as
$I$
as
![]() ${n}_{\mathrm{eff}}=n+{n}_2I$
, where
${n}_{\mathrm{eff}}=n+{n}_2I$
, where
![]() $n$
is the linear index of refraction. In most materials
$n$
is the linear index of refraction. In most materials
![]() ${n}_2>0$
, so
${n}_2>0$
, so
![]() ${n}_{\mathrm{eff}}$
increases with intensity. As a consequence, for an ultrashort pulse the center of the pulse has a lower phase velocity than either edge. This leads to the generation of new frequencies over the pulse after propagation: a red shift on the leading edge and blue shift on the falling edge. With further dispersion compensation, the spectrally broadened pulses can be compressed to a shorter pulse duration that is, in principle, limited by the Fourier transform of the spectrum.
${n}_{\mathrm{eff}}$
increases with intensity. As a consequence, for an ultrashort pulse the center of the pulse has a lower phase velocity than either edge. This leads to the generation of new frequencies over the pulse after propagation: a red shift on the leading edge and blue shift on the falling edge. With further dispersion compensation, the spectrally broadened pulses can be compressed to a shorter pulse duration that is, in principle, limited by the Fourier transform of the spectrum.
To obtain sub-10-fs laser pulses, the most commonly used techniques are based on SPM in gas-filled hollow-core capillaries and photonic crystal fibers[
Reference Nisoli, De Silvestri and Svelto
30
–
Reference Travers, Grigorova, Brahms and Belli
33
]. Pulses with durations below 5 fs can be achieved[
Reference Nisoli, De Silvestri, Svelto, Szipöcs, Ferencz, Spielmann, Sartania and Krausz
31
]. There are, however, some disadvantages of these techniques that become especially problematic for applications at X-ray FEL facilities. One issue is timing stability: successfully using arrival time monitors to correct for both fast jitter and slow drifts in the relative timing of the optical laser relative to the X-ray pulses requires that the timing of the pulses used for the timing tool be exactly stable with respect to the timing of the pulse used for the experiment. For pulse compression techniques based on gas-filled waveguides, the fluctuation and long-term changes of the gas pressure inside a waveguide can introduce a significant timing fluctuation and drift to the laser arrival time. Moreover, the inner diameter of the fiber is on the order of
![]() $10-100\kern0.22em \unicode{x3bc} \mathrm{m}$
which makes the performance very sensitive to the beam pointing of the input laser beam. In addition, the gas-filled waveguide is in general implemented in a vacuum system which adds bulk and complexity to the setup. To overcome these disadvantages, we propose to use the newly developed technique based on multi-plate spectral broadening[
Reference Lu, Tsou, Chen, Chen, Cheng, Yang, Chen, Hsu and Kung
34
–
Reference Cao, Nagymihaly, Khodakovskiy, Lopez-Martens, Pajer, Bohus, Bussiere, Falcoz, Borzsonyi and Kalashnikov
42
]. This technique uses several pieces of thin fused silica plates, each with a thickness of a few hundred micrometers, placed after the focus of the fundamental laser beam to broaden the spectra of the input pulse through SPM while avoiding the breakdown and the spatial distortion in the medium due to self-focusing and conical diffraction[
Reference Couairon and Mysyrowicz
43
,
Reference Cheng, Lu, Lin and Kung
44
]. The setup is simple, compact, and timing stable due to the use of solid-state materials for the nonlinear interactions. Using 4 pieces of 100-μm fused silica plates, we demonstrate compression of 30 fs pulse duration down to 9.6 fs using chirped mirrors to compensate for the group delay dispersion (GDD). For input pulse energies in the range of 50 μJ up to 500 μJ we measure a conversion efficiency of more than 80% for this one-stage setup. With a sequence of two such stages, we observe a supercontinuum covering the wavelength from about 500 to 1100 nm. These super broadband pulses are compressed to a pulse duration of 4.4 fs with a conversion efficiency of more than 60%.
$10-100\kern0.22em \unicode{x3bc} \mathrm{m}$
which makes the performance very sensitive to the beam pointing of the input laser beam. In addition, the gas-filled waveguide is in general implemented in a vacuum system which adds bulk and complexity to the setup. To overcome these disadvantages, we propose to use the newly developed technique based on multi-plate spectral broadening[
Reference Lu, Tsou, Chen, Chen, Cheng, Yang, Chen, Hsu and Kung
34
–
Reference Cao, Nagymihaly, Khodakovskiy, Lopez-Martens, Pajer, Bohus, Bussiere, Falcoz, Borzsonyi and Kalashnikov
42
]. This technique uses several pieces of thin fused silica plates, each with a thickness of a few hundred micrometers, placed after the focus of the fundamental laser beam to broaden the spectra of the input pulse through SPM while avoiding the breakdown and the spatial distortion in the medium due to self-focusing and conical diffraction[
Reference Couairon and Mysyrowicz
43
,
Reference Cheng, Lu, Lin and Kung
44
]. The setup is simple, compact, and timing stable due to the use of solid-state materials for the nonlinear interactions. Using 4 pieces of 100-μm fused silica plates, we demonstrate compression of 30 fs pulse duration down to 9.6 fs using chirped mirrors to compensate for the group delay dispersion (GDD). For input pulse energies in the range of 50 μJ up to 500 μJ we measure a conversion efficiency of more than 80% for this one-stage setup. With a sequence of two such stages, we observe a supercontinuum covering the wavelength from about 500 to 1100 nm. These super broadband pulses are compressed to a pulse duration of 4.4 fs with a conversion efficiency of more than 60%.
2 Experiments
A schematic view of the experimental setup is shown in Figure 1. The entire setup fits onto an aluminum breadboard with a size of 200 mm
![]() $\times$
900 mm. The input pulses are from a Ti:sapphire laser amplifier with a center wavelength of 800 nm, a pulse energy of 20 mJ, and a pulse duration of 30 fs. After a beam splitter, a portion of the laser beam is sent through an aperture, which reduces the beam size from 18 mm to a diameter of 5 mm to achieve a large focus size while keeping the setup compact by avoiding the use of a telescope. The pulse energy after the aperture is 100 μJ. The beam is then focused by a lens (focal length 300 mm) to a waist diameter of about 150 μm (1/e). The peak intensity at the focus is about
$\times$
900 mm. The input pulses are from a Ti:sapphire laser amplifier with a center wavelength of 800 nm, a pulse energy of 20 mJ, and a pulse duration of 30 fs. After a beam splitter, a portion of the laser beam is sent through an aperture, which reduces the beam size from 18 mm to a diameter of 5 mm to achieve a large focus size while keeping the setup compact by avoiding the use of a telescope. The pulse energy after the aperture is 100 μJ. The beam is then focused by a lens (focal length 300 mm) to a waist diameter of about 150 μm (1/e). The peak intensity at the focus is about
![]() $2\times {10}^{13}$
W/cm
$2\times {10}^{13}$
W/cm
![]() ${}^2$
. A set of fused silica thin plates with a thickness of a few hundreds of micrometers are placed with the Brewster’s angle after the laser focus, with the exact number and position of the plates varied for optimization. Owing to SPM, the spectrum of the beam is broadened as it propagates through the plates. After that, the beam is recollimated by a silver concave mirror (FM1, focal length 500 mm) and bounced several times between a pair of chirped mirrors (CM1, Ultrafast Innovations PC70; bandwidth 500–1050 nm; nominal GDD per bounce –40 fs
${}^2$
. A set of fused silica thin plates with a thickness of a few hundreds of micrometers are placed with the Brewster’s angle after the laser focus, with the exact number and position of the plates varied for optimization. Owing to SPM, the spectrum of the beam is broadened as it propagates through the plates. After that, the beam is recollimated by a silver concave mirror (FM1, focal length 500 mm) and bounced several times between a pair of chirped mirrors (CM1, Ultrafast Innovations PC70; bandwidth 500–1050 nm; nominal GDD per bounce –40 fs
![]() ${}^2$
)and passes through a pair of fused silica wedges to compensate for the GDD. This completes one stage of compression. To achieve even shorter pulses and broader bandwidths, we can optionally send the beam through an additional compression stage. Here, the compressed pulses from the first stage are refocused with a silver concave mirror (focal length 500 mm) to another set of fused silica thin plates to further broaden the spectrum of the beam, recollimated with a 250-mm focal length concave silver mirror, and recompressed with another identical chirped-mirror pair and a pair of fused silica wedges. The optical path length of the beam through the wedges is adjusted to fine-tune the dispersion compensation. An aperture is used in each multi-plate stage before beam recollimation to block outer diffraction rings.
${}^2$
)and passes through a pair of fused silica wedges to compensate for the GDD. This completes one stage of compression. To achieve even shorter pulses and broader bandwidths, we can optionally send the beam through an additional compression stage. Here, the compressed pulses from the first stage are refocused with a silver concave mirror (focal length 500 mm) to another set of fused silica thin plates to further broaden the spectrum of the beam, recollimated with a 250-mm focal length concave silver mirror, and recompressed with another identical chirped-mirror pair and a pair of fused silica wedges. The optical path length of the beam through the wedges is adjusted to fine-tune the dispersion compensation. An aperture is used in each multi-plate stage before beam recollimation to block outer diffraction rings.

Figure 1 Schematic view of the multi-plate (MP) setup with two compression stages (FM, focusing mirror; CM, chirped mirror). For single-stage operation, the beam parameters are measured after the first pair of chirped mirrors CM1 and before the refocusing mirror FM2.
We operated the setup with slightly different sets and configurations of thin plates, depending on whether we tried to optimize performance after only one stage or after both stages. For the one-stage configuration, we used four fused silica plates each with a thickness of 100 μm. The plates are positioned after the focus of the lens at distances of 5, 25, 35, and 45 mm with respect to the waist position. The recollimated beam had a diameter of 5 mm. After 8 reflections from the chirped mirrors (dispersion compensation of –320 fs2), the beam passes through a pair of fused silica wedges to fine tune the group velocity dispersion and achieve optimal compression. The output pulses have a pulse energy of 81 μJ, indicating a conversion efficiency of 81%.
In the case of the two-stage configuration, we used one 200 μm fused silica plate in the first stage and four plates in the second stage. After one 200 μm fused silica plate placed 10 mm after the focus, the spectrum of the beam is only slightly broadened but maintains a high-quality beam profile. The beam is then compressed through bouncing twice through the chirped-mirror pair (dispersion compensation of –160 fs2) before being sent to the second stage. In the second stage the beam is focused to a diameter of about 150 μm with a peak intensity of about
![]() $2\times {10}^{13}$
W/cm2. Four plates with thickness of 100 μm were placed after the laser focus at distances of 5, 15, 35, and 55 mm. The laser intensities at the positions of the plates are below the damage threshold such that the beam quality can be maintained with the spectrum of the beam effectively broadened. After this the beam is reflected 8 times from the chirped mirrors (dispersion compensation of –320 fs2) and transmitted through the pair of fused silica wedges that are adjusted to optimize compression. The output energy from the second stage is about 65 μJ, corresponding to a conversion efficiency of about 65%.
$2\times {10}^{13}$
W/cm2. Four plates with thickness of 100 μm were placed after the laser focus at distances of 5, 15, 35, and 55 mm. The laser intensities at the positions of the plates are below the damage threshold such that the beam quality can be maintained with the spectrum of the beam effectively broadened. After this the beam is reflected 8 times from the chirped mirrors (dispersion compensation of –320 fs2) and transmitted through the pair of fused silica wedges that are adjusted to optimize compression. The output energy from the second stage is about 65 μJ, corresponding to a conversion efficiency of about 65%.
The output spectra are measured using a commercial grating spectrometer (Ocean Optics Flame). The compressed pulse temporal properties are characterized via second-order harmonic generation frequency-resolved optical gating (SHG-FROG). From the measured FROG traces, we reconstruct the temporal shape of the measured pulses using an iterative phase retrieval algorithm[ Reference Kane and Trebino 45 ].
3 Results and discussion
3.1 Supercontinuum generation
The measured spectra both before and after the one-stage and two-stage configurations are shown in Figure 2. The spectrum of the 30-fs incoming pulse from the laser amplifier centers at 800 nm with a spectral range from 750 to 850 nm (–20 dB from the peak). After passing through the one-stage configuration, the spectrum broadens to span a spectral range from 593 to 944 nm (–20 dB from the peak) with strong peaks developing at 750 and 850 nm. The two-stage configuration results in a dramatically broader spectrum with a supercontinuum extending down to below 500 nm and up to 1100 nm, with total pulse energy of 70 μJ before compression. Such broad and bright supercontinuum can be further chirped and directly applied for spectral timing tool applications without filtering the fundamental frequency.
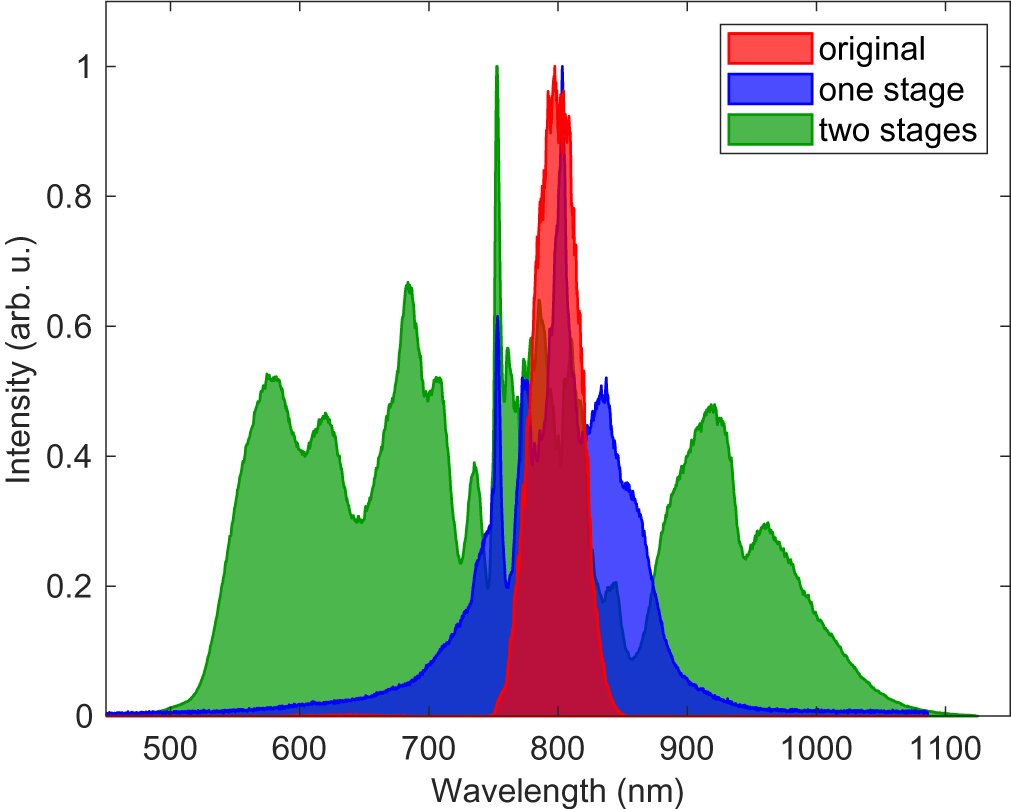
Figure 2 Measured spectra of the pulse before the broadening, after the one-stage configuration and after the two-stage configuration.
3.2 Compression
The measured and reconstructed FROG traces for the one-stage configuration after compression are illustrated in Figures 3(a) and 3(b). The reconstructed pulse intensity envelope is plotted in Figure 3(c), which yields a pulse duration of 9.6 fs in FWHM with the intensity of the pedestal below 5% of the main pulse. Figure 3(c) also shows the calculated Fourier-transform-limited pulse, which has a pulse duration of 6.8 fs. This indicates that there are some higher-order contributions to the dispersion that are not at present possible to compensate for in our setup.

Figure 3 (a), (d) Measured and (b), (e) retrieved SHG-FROG traces for the output from the one-stage setup (upper panels) and the two-stage setup (lower panels); (c), (f) the reconstructed pulse from the FROG retrieval and the Fourier-transform-limited (FTL) pulse from the measured spectra.
For the two-stage configuration, the spectrum covers more than one octave from about 495 to 1080 nm (–20 dB range), as shown in Figure 2, which supports a Fourier-transform-limited pulse duration of 3.2 fs, as shown in Figure 3(f). The measured and reconstructed FROG traces of the compressed pulses are shown in Figures 3(d) and 3(e). The reconstructed pulse envelope in Figure 3(f) has a pulse duration of 4.4 fs in FWHM, with a pedestal of about 10 fs duration. The pulse duration is limited by higher-order dispersion on the red side that is not well compensated.
3.3 Beam profile and stability
A smooth beam profile is often critical for many applications of short pulses at X-ray FELs, both for arrival time tools and experiments. Owing to the diffraction effect in the plates, the distribution of the beam profile represents as a Bessel function[ Reference Couairon and Mysyrowicz 43 ], shown in Figure 4 for the beam in the two-stage configuration after the second set of plates. More than 90% of the pulse energy is within the zero-order peak. We placed an aperture to block the outer diffraction rings before sending the beam for further compression.

Figure 4 The beam profile of the compressed pulses after the two-stage configuration, just before final compression. The profile is collected by imaging a flat piece of paper in the beam, imaged onto a camera.
In addition, the stability of the supercontinuum and compressed pulse is also very important for applications. We carried out single-shot measurements every 2 s of the pulse energy and beam pointing of the two-stage configuration over a period of 4 h. The beam-pointing measurement was carried out with a lens with a focal length of 500 mm and a CCD camera at the focus to capture the beam profile. The position of the beam along horizontal and vertical directions at the focus is obtained by fitting the measured beam profile to a two-dimensional Gaussian function, and the angular pointing deviations are calculated by dividing the changes in the peak position by the focal length of the lens. Over the same period the angular pointing deviations from the laser amplifier were 3.5 and 4.2 μrad (rms) along the horizontal and vertical directions, respectively, measured with the leakage beam from the first highly reflective mirror after the laser amplifier. The measured beam pointing stabilities of the two-stage post-compressed pulses along horizontal and vertical directions were 11.9 and 11.7 μrad (rms) as shown in Figures 5(a) and 5(b), respectively. The worse beam pointing stability is mainly due to the optical magnification of focusing optics used in the setup with additional vibrations picked up by all optics in the beam path after the laser amplifier. In the measurement, we observed slight drifts of the beam that contributed to the above estimates for the stability. These drifts could be compensated for with a beam stabilization system with motorized mirrors before the multi-plate setup to improve further the beam pointing stability of the compressed pulses. The energy stability of the laser amplifier is about 0.15% rms and 1% peak-to-peak over 24 h, measured at a location directly after the laser amplifier. The measured pulse energy of the two-stage compressed pulse over a 4-h time interval is depicted in Figure 5(c), with an rms of 0.37% and a peak-to-peak value of 3%.

Figure 5 (a), (b) Single-shot measurements of beam pointing along the horizontal (
![]() ${\theta}_x$
) and vertical (
${\theta}_x$
) and vertical (
![]() ${\theta}_y$
) directions and (c) pulse energy stability over 4 h for the compressed pulses after the two-stage configuration. The histograms of the stability distributions are plotted on the corresponding right-hand side panels.
${\theta}_y$
) directions and (c) pulse energy stability over 4 h for the compressed pulses after the two-stage configuration. The histograms of the stability distributions are plotted on the corresponding right-hand side panels.
4 Conclusion
Using spectral broadening from multiple thin fused silica plates, we have built a compact pulse post-compression and supercontinuum generation setup which is ready for applications to X-ray FEL pump-probe experiments and precise measurements of X-ray/laser arrival time. From a single-stage configuration, we have achieved sub-10-fs pulses with a compression efficiency of more than 80%. The supercontinuum generated from a two-stage configuration covers the spectral range from about 500 to 1100 nm, which can be directly used for spectral encoding timing tools. This supercontinuum spectrum can be compressed down to 4.4 fs with energy and beam pointing stability sufficient for most applications. We anticipate that this method is widely applicable to similar facilities and will enable robust implementations of pump-probe measurements with significantly improved time resolution compared with what has to date been possible.
Acknowledgement
Steven L. Johnson acknowledges NCCR Molecular Ultrafast Science and Technology (NCCR MUST), a research instrument of the Swiss National Science Foundation (SNSF).










