Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-20T10:50:53.474Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS

Part of: Classical measure theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms Real functions

Published online by Cambridge University Press:  18 April 2024

XIAO CHEN Open the ORCID record for XIAO CHEN [Opens in a new window] ,
LULU FANG Open the ORCID record for LULU FANG [Opens in a new window] ,
JUNJIE LI Open the ORCID record for JUNJIE LI [Opens in a new window] ,
LEI SHANG Open the ORCID record for LEI SHANG [Opens in a new window]  and
XIN ZENG Open the ORCID record for XIN ZENG [Opens in a new window]
XIAO CHEN
Affiliation:
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, China e-mail: [email protected]
LULU FANG
Affiliation:
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, China e-mail: [email protected]
JUNJIE LI
Affiliation:
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, China e-mail: [email protected]
LEI SHANG*
Affiliation:
College of Sciences, Nanjing Agricultural University, Nanjing 210095, China
XIN ZENG
Affiliation:
School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $[a_1(x),a_2(x),a_3(x),\ldots ]$ be the continued fraction expansion of an irrational number 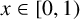$x\in [0,1)$. We are concerned with the asymptotic behaviour of the product of consecutive partial quotients of x. We prove that, for Lebesgue almost all $x\in [0,1)$,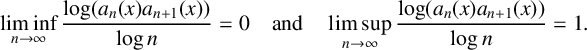

$$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0\quad \text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align*} $$

We also study the Baire category and the Hausdorff dimension of the set of points for which the above liminf and limsup have other different values and similarly analyse the weighted product of consecutive partial quotients.

Keywords

continued fractionsproduct of consecutive partial quotientsresidual setsHausdorff dimension

MSC classification

Primary: 11K50: Metric theory of continued fractions
Secondary: 26A21: Classification of real functions; Baire classification of sets and functions 28A80: Fractals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 3 , December 2024 , pp. 448 - 459
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research is supported by the National Natural Science Foundation of China (No. 11801591), the Natural Science Foundation of Jiangsu Province (No. BK20231452), the Fundamental Research Funds for the Central Universities (No. 30922010809) and the China Postdoctoral Science Foundation (No. 2023M731697).

References

Bakhtawar, A., ‘Hausdorff dimension for the set of points connected with the generalized Jarník–Besicovitch set’, J. Aust. Math. Soc. 112 (2022), 1–29.CrossRefGoogle Scholar
Bakhtawar, A., Bos, P. and Hussain, M., ‘Hausdorff dimension of an exceptional set in the theory of continued fractions’, Nonlinearity 33 (2020), 2615–2639.CrossRefGoogle Scholar
Bakhtawar, A., Bos, P. and Hussain, M., ‘The sets of Dirichlet non-improvable numbers versus well-approximable numbers’, Ergodic Theory Dynam. Systems 40 (2020), 3217–3235.CrossRefGoogle Scholar
Bakhtawar, A., Hussain, M., Kleinbock, D. and Wang, B., ‘Metrical properties for the weighted products of multiple partial quotients in continued fractions’, Houston J. Math. 49 (2023), 159–194.Google Scholar
Bos, P., Hussain, M. and Simmons, D., ‘The generalised Hausdorff measure of sets of Dirichlet non-improvable numbers’, Proc. Amer. Math. Soc. 151 (2023), 1823–1838.Google Scholar
Brown-Sarre, A. and Hussain, M., ‘A note on the relative growth of products of multiple partial quotients in the plane’, Canad. Math. Bull. 66 (2023), 544–552.CrossRefGoogle Scholar
Cassels, J. W. S., An Introduction to Diophantine Approximation (Cambridge University Press, New York, 1957).Google Scholar
Chang, X., Dong, Y., Liu, M. and Shang, L., ‘Baire category and the relative growth rate for partial quotients in continued fractions’, Arch. Math. (Basel) 122 (2024), 41–46.CrossRefGoogle Scholar
Falconer, K., Fractal Geometry: Mathematical Foundations and Applications (John Wiley and Sons, Chichester, 1990).Google Scholar
Fang, L., Ma, J., Song, K. and Yang, X., ‘Multifractal analysis of convergence exponents for products of consecutive partial quotients in continued fractions’, Acta Math. Sci. (to appear). Published online (21 March 2024).CrossRefGoogle Scholar
Feng, J. and Xu, J., ‘Sets of Dirichlet non-improvable numbers with certain order in the theory of continued fractions’, Nonlinearity 34 (2021), 1598–1611.CrossRefGoogle Scholar
Huang, L. and Wu, J., ‘Uniformly non-improvable Dirichlet set via continued fractions’, Proc. Amer. Math. Soc. 147 (2019), 4617–4624.CrossRefGoogle Scholar
Huang, L., Wu, J. and Xu, J., ‘Metric properties of the product of consecutive partial quotients in continued fractions’, Israel J. Math. 238 (2020), 901–943.CrossRefGoogle Scholar
Hussain, M., Kleinbock, D., Wadleigh, N. and Wang, B., ‘Hausdorff measure of sets of Dirichlet non-improvable numbers’, Mathematika 64 (2018), 502–518.CrossRefGoogle Scholar
Hussain, M., Li, B. and Shulga, N., ‘Hausdorff dimension analysis of sets with the product of consecutive vs single partial quotients in continued fractions’, Discrete Contin. Dyn. Syst. 44 (2024), 154–181.CrossRefGoogle Scholar
Iosifescu, M. and Kraaikamp, C., Metrical Theory of Continued Fractions (Kluwer Academic Publishers, Dordrecht, 2002).CrossRefGoogle Scholar
Kleinbock, D. and Wadleigh, N., ‘A zero-one law for improvements to Dirichlet’s Theorem’, Proc. Amer. Math. Soc. 146 (2018), 1833–1844.CrossRefGoogle Scholar
Li, B., Wang, B. and Xu, J., ‘Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set’, Ergodic Theory Dynam. Systems 43 (2023), 2707–2731.CrossRefGoogle Scholar
Liao, L. and Rams, M., ‘Big Birkhoff sums in $d$ -decaying Gauss like iterated function systems’, Studia Math. 264 (2022), 1–25.CrossRefGoogle Scholar
Olsen, L., ‘Extremely non-normal continued fractions’, Acta Arith. 108 (2003), 191–202.CrossRefGoogle Scholar
Oxtoby, J., Measure and Category (Springer, New York, 1980).CrossRefGoogle Scholar
Schmidt, W. M., Diophantine Approximation (Springer, Berlin, 1980).Google Scholar
Shang, L. and Wu, M., ‘On the growth behavior of partial quotients in continued fractions’, Arch. Math. (Basel) 120 (2023), 297–305.CrossRefGoogle Scholar
Zhang, L., ‘Set of extremely Dirichlet non-improvable points’, Fractals 28 (2020), Article no. 2050034.CrossRefGoogle Scholar