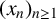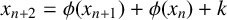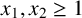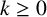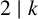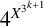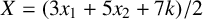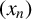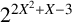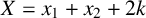1 Introduction
In a recent study of integer sequences generated by Euler’s totient function, Leonetti and Luca [Reference Leonetti and Luca3] proved the following theorem.
Theorem 1.1. Fix an even integer
![]() $k\geq 0$
. The integer sequence
$k\geq 0$
. The integer sequence
![]() $(x_n)_{n\geq 1}$
defined by
$(x_n)_{n\geq 1}$
defined by
![]() $x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$
, where
$x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$
, where
![]() ${x_1,x_2\geq 1}$
, is bounded by
${x_1,x_2\geq 1}$
, is bounded by
![]() $4^{X^{3^{k+1}}}$
, where
$4^{X^{3^{k+1}}}$
, where
![]() ${X=(3x_1+5x_2+7k)/2}$
.
${X=(3x_1+5x_2+7k)/2}$
.
It is natural to ask whether the size of the upper bound for the sequence
![]() $(x_n)$
in Theorem 1.1 could be reduced. In this paper, we will provide such an improvement. The main result of this paper is the following theorem.
$(x_n)$
in Theorem 1.1 could be reduced. In this paper, we will provide such an improvement. The main result of this paper is the following theorem.
Theorem 1.2. Fix an even integer
![]() $k\geq 0$
. The integer sequence
$k\geq 0$
. The integer sequence
![]() $(x_n)_{n\geq 1}$
defined by
$(x_n)_{n\geq 1}$
defined by
![]() $x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$
, where
$x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$
, where
![]() $x_1,x_2\geq 1$
, is bounded by
$x_1,x_2\geq 1$
, is bounded by
![]() $2^{2X^2+X-3}$
, where
$2^{2X^2+X-3}$
, where
![]() ${X=x_1+x_2+2k}$
.
${X=x_1+x_2+2k}$
.
Note that the bound in Theorem 1.2 is exponentially smaller than the bound in Theorem 1.1. To prove Theorem 1.2, we will use the Chinese remainder theorem in combination with some estimates on prime numbers due to Erdős (Lemma 2.4) and Rosser (Lemma 2.3).
2 Proof of Theorem 1.2
Case 1:
![]() $x_3=2$
. Since
$x_3=2$
. Since
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $2 \mid k$
and
$2 \mid k$
and
![]() $\phi (x_1)+\phi (x_2)+k=x_3=2$
, we must have
$\phi (x_1)+\phi (x_2)+k=x_3=2$
, we must have
![]() $k=0$
and
$k=0$
and
![]() $\phi (x_1)=\phi (x_2)=1$
. Hence,
$\phi (x_1)=\phi (x_2)=1$
. Hence,
![]() $x_1,x_2\in \{1,2\}$
. Note that if
$x_1,x_2\in \{1,2\}$
. Note that if
![]() ${\phi (x_n)=\phi (x_{n-1})=1}$
, then
${\phi (x_n)=\phi (x_{n-1})=1}$
, then
![]() $x_{n+1}=\phi (x_n)+\phi (x_{n-1})=2$
. By induction,
$x_{n+1}=\phi (x_n)+\phi (x_{n-1})=2$
. By induction,
![]() $x_n=2$
for all
$x_n=2$
for all
![]() $n\geq 3$
. Since
$n\geq 3$
. Since
![]() $X=x_1+x_2+ 2k\geq 2$
, we have
$X=x_1+x_2+ 2k\geq 2$
, we have
![]() $2^{2X^2+X-3}>2$
. Hence,
$2^{2X^2+X-3}>2$
. Hence,
![]() ${x_n< 2^{2X^2+X-3}}$
for all
${x_n< 2^{2X^2+X-3}}$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Case 2:
![]() $x_3\geq 3$
. Then
$x_3\geq 3$
. Then
![]() $x_{4}=\phi (x_3)+\phi (x_2)+k\geq 3$
. Note that if
$x_{4}=\phi (x_3)+\phi (x_2)+k\geq 3$
. Note that if
![]() $x_n\geq 3$
with
$x_n\geq 3$
with
![]() $n\geq 3$
, then
$n\geq 3$
, then
By induction,
![]() $x_n\geq 3$
for all
$x_n\geq 3$
for all
![]() $n\geq 3$
, so that
$n\geq 3$
, so that
![]() $2 \mid \phi (x_n)$
for all
$2 \mid \phi (x_n)$
for all
![]() $n\geq 3$
. Therefore,
$n\geq 3$
. Therefore,
![]() ${2 \mid \phi (x_{n-1})+\phi (x_{n-2})+k=x_n}$
for all
${2 \mid \phi (x_{n-1})+\phi (x_{n-2})+k=x_n}$
for all
![]() $n\geq 5$
and so
$n\geq 5$
and so
Lemma 2.1. For
![]() $n=1,2,\ldots ,6$
,
$n=1,2,\ldots ,6$
,
Proof. We consider each value of n in turn.
![]() $n=1$
or
$n=1$
or
![]() $n=2$
. Then (2.2) holds because
$n=2$
. Then (2.2) holds because
![]() $\max \{x_1,x_2\}<x_1+x_2\leq X<2^{X}$
.
$\max \{x_1,x_2\}<x_1+x_2\leq X<2^{X}$
.
![]() $n=3$
. Then (2.2) holds because
$n=3$
. Then (2.2) holds because
![]() $3\leq x_3=\phi (x_1)+\phi (x_2)+k\leq x_1+x_2+k\leq X<2^{X}$
.
$3\leq x_3=\phi (x_1)+\phi (x_2)+k\leq x_1+x_2+k\leq X<2^{X}$
.
![]() $n=4$
. Since
$n=4$
. Since
![]() $\phi (x_3)\leq x_3-1\leq x_1+x_2+k-1$
and
$\phi (x_3)\leq x_3-1\leq x_1+x_2+k-1$
and
![]() $\phi (x_2)\leq x_2$
,
$\phi (x_2)\leq x_2$
,
![]() $n=5$
. Since
$n=5$
. Since
![]() $\phi (x_4)\leq x_4-1\leq x_1+2x_2+2k-2$
and
$\phi (x_4)\leq x_4-1\leq x_1+2x_2+2k-2$
and
![]() $\phi (x_3)\leq x_1+x_2+k-1$
,
$\phi (x_3)\leq x_1+x_2+k-1$
,
 $$ \begin{align} x_5=\phi(x_4)+\phi(x_3)+k &\leq 2x_1+3x_2+4k-3\nonumber\\[2pt]&=3(x_1+x_2+2k)-x_1-2k-3\nonumber\\[2pt]&\leq 3X-4\quad (\text{since}\ x_1+2k+3\geq 4)\nonumber\\[2pt]&<2^X \quad(\text{since}\ 2^X>3X-4\ \mathrm{for}\ X\geq 2). \end{align} $$
$$ \begin{align} x_5=\phi(x_4)+\phi(x_3)+k &\leq 2x_1+3x_2+4k-3\nonumber\\[2pt]&=3(x_1+x_2+2k)-x_1-2k-3\nonumber\\[2pt]&\leq 3X-4\quad (\text{since}\ x_1+2k+3\geq 4)\nonumber\\[2pt]&<2^X \quad(\text{since}\ 2^X>3X-4\ \mathrm{for}\ X\geq 2). \end{align} $$
![]() $n=6$
. By (2.1) and (2.3),
$n=6$
. By (2.1) and (2.3),
![]() $\phi (x_5)\leq x_5/2\leq (2x_1+3x_2+4k-3)/2$
. Combining this with the estimate
$\phi (x_5)\leq x_5/2\leq (2x_1+3x_2+4k-3)/2$
. Combining this with the estimate
![]() $\phi (x_4)\leq x_1+2x_2+2k-2$
gives
$\phi (x_4)\leq x_1+2x_2+2k-2$
gives
 $$ \begin{align*} x_6=\phi(x_5)+\phi(x_4)+k &\leq \dfrac{2x_1+3x_2+4k-3}{2}+(x_1+2x_2+2k-2)+k\\[4pt]&=\dfrac{4x_1+7x_2+10k-7}{2} =\dfrac{7(x_1+x_2+2k)}{2}-\dfrac{3x_1+4k+7}{2}\\&\leq \dfrac{7}{2}X-5\quad(\text{since}\ (3x_1+4k+7)/2\geq 5\\&<2^X\quad(\text{since}\ 2^X>7X/2-5\ \text{for}\ X\geq 2).\\[-35pt] \end{align*} $$
$$ \begin{align*} x_6=\phi(x_5)+\phi(x_4)+k &\leq \dfrac{2x_1+3x_2+4k-3}{2}+(x_1+2x_2+2k-2)+k\\[4pt]&=\dfrac{4x_1+7x_2+10k-7}{2} =\dfrac{7(x_1+x_2+2k)}{2}-\dfrac{3x_1+4k+7}{2}\\&\leq \dfrac{7}{2}X-5\quad(\text{since}\ (3x_1+4k+7)/2\geq 5\\&<2^X\quad(\text{since}\ 2^X>7X/2-5\ \text{for}\ X\geq 2).\\[-35pt] \end{align*} $$
We now return to the proof of Theorem 1.2 when
![]() $x_3\ge 3$
(Case 2).
$x_3\ge 3$
(Case 2).
Case 2.1:
![]() $k=0$
. Then
$k=0$
. Then
![]() $x_n=\phi (x_{n-1})+\phi (x_{n-2})$
for all
$x_n=\phi (x_{n-1})+\phi (x_{n-2})$
for all
![]() $n\geq 3$
. By (2.1),
$n\geq 3$
. By (2.1),
An induction, using Lemma 2.1 and (2.4), shows that
![]() $x_n< 2^X$
for all
$x_n< 2^X$
for all
![]() $n\geq 1$
. Hence,
$n\geq 1$
. Hence,
![]() $x_n<2^X<2^{2X^2+X-3}$
for all
$x_n<2^X<2^{2X^2+X-3}$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Case 2.2:
![]() $k\geq 1$
. Let
$k\geq 1$
. Let
![]() $p_1<p_2<\cdots <p_{2k+2}$
be the first
$p_1<p_2<\cdots <p_{2k+2}$
be the first
![]() $2k+2$
primes. By the Chinese remainder theorem, there exist infinitely many positive integers x such that
$2k+2$
primes. By the Chinese remainder theorem, there exist infinitely many positive integers x such that
Lemma 2.2. Let M be a positive integer satisfying the congruences (2.5) and such that
![]() $M\geq \max \{2^{X}-2k-2,kp_{2k+2}-k-2\}$
. Then, for all positive integers n,
$M\geq \max \{2^{X}-2k-2,kp_{2k+2}-k-2\}$
. Then, for all positive integers n,
Proof. Since
![]() $M+2k+2\geq 2^{X}$
, by Lemma 2.1, (2.6) holds for
$M+2k+2\geq 2^{X}$
, by Lemma 2.1, (2.6) holds for
![]() $n=1,2,\ldots ,6$
. Suppose
$n=1,2,\ldots ,6$
. Suppose
![]() $n\geq 7$
and assume that Lemma 2.2 is not true. Let m be the smallest positive integer such that
$n\geq 7$
and assume that Lemma 2.2 is not true. Let m be the smallest positive integer such that
![]() $x_m>M+2k+2$
. Then
$x_m>M+2k+2$
. Then
![]() $x_{m-1},x_{m-2}\leq M+2k+2$
and
$x_{m-1},x_{m-2}\leq M+2k+2$
and
![]() $m\geq 7$
. Thus,
$m\geq 7$
. Thus,
![]() $2 \mid x_{m-1}, x_{m-2}$
. Therefore,
$2 \mid x_{m-1}, x_{m-2}$
. Therefore,
and so
![]() $x_{m-1}+x_{m-2}>2M+2k+4$
. It follows that
$x_{m-1}+x_{m-2}>2M+2k+4$
. It follows that
![]() $x_{m-1},x_{m-2}>M+2$
since
$x_{m-1},x_{m-2}>M+2$
since
![]() $x_{m-1},x_{m-2}\leq M+2k+2$
. Let
$x_{m-1},x_{m-2}\leq M+2k+2$
. Let
![]() $x_{m-1}=M+2+r$
and
$x_{m-1}=M+2+r$
and
![]() $x_{m-2}=M+2+s$
, where
$x_{m-2}=M+2+s$
, where
![]() $r,s\in {\mathbb{Z}} $
and
$r,s\in {\mathbb{Z}} $
and
![]() $0< r,s\leq 2k$
. Since M satisfies (2.5), there exist odd primes
$0< r,s\leq 2k$
. Since M satisfies (2.5), there exist odd primes
![]() $p,q\leq p_{2k+2}$
such that
$p,q\leq p_{2k+2}$
such that
![]() $p \mid M+2+r=x_{m-1}$
and
$p \mid M+2+r=x_{m-1}$
and
![]() $q \mid M+2+s=x_{m-2}$
. Therefore,
$q \mid M+2+s=x_{m-2}$
. Therefore,
![]() $2p \mid x_{m-1}$
and
$2p \mid x_{m-1}$
and
![]() $2q \mid x_{m-2}$
. Recalling that
$2q \mid x_{m-2}$
. Recalling that
![]() $x_{m-1},x_{m-2}\leq M+2k+2$
and
$x_{m-1},x_{m-2}\leq M+2k+2$
and
![]() $p,q\leq p_{2k+2}$
,
$p,q\leq p_{2k+2}$
,
 $$ \begin{align*} x_{m}=\phi(x_{m-1})+\phi(x_{m-2})+k &\leq \dfrac{x_{m-1}}{2}\bigg(1-\dfrac{1}{p}\bigg)+\dfrac{x_{m-2}}{2}\bigg(1-\dfrac{1}{q}\bigg)+k\\ &\leq 2\cdot \dfrac{M+2k+2}{2}\bigg(1-\dfrac{1}{p_{2k+2}}\bigg)+k \\ &= (M+2k+2)\bigg(1-\dfrac{1}{p_{2k+2}}\bigg)+k\\ &\leq M+2k+2\quad (\text{since}\ M+2k+2\geq p_{2k+2}k), \end{align*} $$
$$ \begin{align*} x_{m}=\phi(x_{m-1})+\phi(x_{m-2})+k &\leq \dfrac{x_{m-1}}{2}\bigg(1-\dfrac{1}{p}\bigg)+\dfrac{x_{m-2}}{2}\bigg(1-\dfrac{1}{q}\bigg)+k\\ &\leq 2\cdot \dfrac{M+2k+2}{2}\bigg(1-\dfrac{1}{p_{2k+2}}\bigg)+k \\ &= (M+2k+2)\bigg(1-\dfrac{1}{p_{2k+2}}\bigg)+k\\ &\leq M+2k+2\quad (\text{since}\ M+2k+2\geq p_{2k+2}k), \end{align*} $$
which contradicts the assumption that
![]() $x_m>M+2k+2$
. Therefore, (2.6) holds for all positive integers n. Lemma 2.2 is proved.
$x_m>M+2k+2$
. Therefore, (2.6) holds for all positive integers n. Lemma 2.2 is proved.
Lemma 2.3 (Rosser [Reference Rosser4, Theorem 2])
For all positive integers
![]() $n\geq 4$
,
$n\geq 4$
,
where
![]() $p_n$
is the nth prime and
$p_n$
is the nth prime and
![]() $\log $
denotes the natural logarithm.
$\log $
denotes the natural logarithm.
Lemma 2.4 (Erdős [Reference Erdős2]; see Aigner and Ziegler [Reference Aigner and Ziegler1, Ch. 2, page 10])
For all positive integers
![]() $n\geq 2$
,
$n\geq 2$
,
where the product is taken over all primes
![]() $p\leq n$
.
$p\leq n$
.
Lemma 2.5. For all positive integers
![]() $n\geq 4$
,
$n\geq 4$
,
Proof. It is a routine verification that
![]() $\log {x}+2\log {\log {x}}<x$
for all
$\log {x}+2\log {\log {x}}<x$
for all
![]() $x>1$
. Hence,
$x>1$
. Hence,
Then (2.7) follows from Lemma 2.3 and inequality (2.9).
Inequality (2.8) is a consequence of Lemma 2.4 and (2.7). Indeed,
We return to the proof of Theorem 1.2. Let
![]() $\alpha $
be the smallest positive integer satisfying (2.5). Then
$\alpha $
be the smallest positive integer satisfying (2.5). Then
![]() $\alpha \leq p_1p_2\cdots p_{2k+2}$
. Note that
$\alpha \leq p_1p_2\cdots p_{2k+2}$
. Note that
![]() $4\leq 2k+2\leq 2k+x_1+x_2=X$
. It follows from (2.8) that
$4\leq 2k+2\leq 2k+x_1+x_2=X$
. It follows from (2.8) that
Let
![]() $M=\alpha +2^{x_1+x_2}p_1p_2\cdots p_{2k+2}$
. Then M satisfies (2.5). Since
$M=\alpha +2^{x_1+x_2}p_1p_2\cdots p_{2k+2}$
. Then M satisfies (2.5). Since
![]() $p_1p_2\cdots p_{2k+2}>2^{2k}$
and
$p_1p_2\cdots p_{2k+2}>2^{2k}$
and
![]() $p_1p_2\cdots p_{2k+2}>p_kp_{2k+2}>kp_{2k+2}$
,
$p_1p_2\cdots p_{2k+2}>p_kp_{2k+2}>kp_{2k+2}$
,
and
Thus, M satisfies all the conditions in Lemma 2.2. Hence,
Since
![]() $x_1+x_2=X-2k\leq X-2$
, by (2.10),
$x_1+x_2=X-2k\leq X-2$
, by (2.10),
Note that
![]() $X\leq 2^{X-2}$
since
$X\leq 2^{X-2}$
since
![]() $X\geq 4$
. Thus,
$X\geq 4$
. Thus,
Combining (2.12) and (2.13) gives
 $$ \begin{align} M+2k+2\leq M+2^{X-2}&< (1+2^{X-2})\cdot 4^{X^2-1}+2^{X-2}\nonumber\\ & <2^{X-2}\cdot 4^{X^2-1}+2^{X-2}\cdot 4^{X^2-1}=2^{2X^2+X-3}.\end{align} $$
$$ \begin{align} M+2k+2\leq M+2^{X-2}&< (1+2^{X-2})\cdot 4^{X^2-1}+2^{X-2}\nonumber\\ & <2^{X-2}\cdot 4^{X^2-1}+2^{X-2}\cdot 4^{X^2-1}=2^{2X^2+X-3}.\end{align} $$
It follows from (2.11) and (2.14) that
![]() $x_n<2^{2X^2+X-3}$
for all
$x_n<2^{2X^2+X-3}$
for all
![]() $n\geq 1$
. This completes the proof of Theorem 1.2.
$n\geq 1$
. This completes the proof of Theorem 1.2.
Remark 2.6. Leonetti and Luca [Reference Leonetti and Luca3] also proved that the integer sequence
![]() $(x_n)_{n\geq 1}$
defined by
$(x_n)_{n\geq 1}$
defined by
![]() $x_{n+1}=\phi (x_n)+k$
, where
$x_{n+1}=\phi (x_n)+k$
, where
![]() $x_1\geq 1$
and
$x_1\geq 1$
and
![]() $k\geq 0$
, is bounded by
$k\geq 0$
, is bounded by
![]() ${\max \{x_1,k^4\}+(k+1)^2}$
. A similar argument to that in the proof of Theorem 1.2 shows that the sequence
${\max \{x_1,k^4\}+(k+1)^2}$
. A similar argument to that in the proof of Theorem 1.2 shows that the sequence
![]() $(x_n)$
is bounded but with a worse upper bound.
$(x_n)$
is bounded but with a worse upper bound.
Acknowledgements
This project started during a training session of the Vietnam team preparing for the 2023 International Mathematical Olympiad (IMO). The first six authors are the members of the Vietnam 2023 IMO team. The idea of using the Chinese remainder theorem is due to Dung and Hung. Dung won a silver medal in IMO 2023 and Hung won gold medals in both IMO 2022 and IMO 2023.
We would like to thank the Vietnam Institute for Advanced Study in Mathematics (VIASM) for their support. We would like to thank Professor Le Anh Vinh (the IMO team leader), Doctor Pham Duc Hiep and Master Tran Quang Hung for giving us the opportunity to work together.