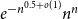1. Introduction
A family
![]() $\mathcal{F}$
of finite sets is called intersecting if any two sets from
$\mathcal{F}$
of finite sets is called intersecting if any two sets from
![]() $\mathcal{F}$
have a non-empty intersection. A family
$\mathcal{F}$
have a non-empty intersection. A family
![]() $\mathcal{F}$
is called
$\mathcal{F}$
is called
![]() $n$
-uniform if every member of
$n$
-uniform if every member of
![]() $\mathcal{F}$
has cardinality
$\mathcal{F}$
has cardinality
![]() $n$
. Suppose that
$n$
. Suppose that
![]() $\mathcal{F}$
is an
$\mathcal{F}$
is an
![]() $n$
-uniform intersecting family which is maximal, i.e. for any
$n$
-uniform intersecting family which is maximal, i.e. for any
![]() $n$
-element set
$n$
-element set
![]() $F \not \in{\mathcal{F}}$
the family
$F \not \in{\mathcal{F}}$
the family
![]() ${\mathcal{F}} \cup \{F\}$
is not intersecting. Note that the ground set of
${\mathcal{F}} \cup \{F\}$
is not intersecting. Note that the ground set of
![]() $\mathcal{F}$
is not fixed here, so we allow
$\mathcal{F}$
is not fixed here, so we allow
![]() $F$
to have some elements which do not belong to the support of
$F$
to have some elements which do not belong to the support of
![]() $\mathcal{F}$
. In 1973, Erdős and Lovász [Reference Erdős and Lovász4] asked how large such a family
$\mathcal{F}$
. In 1973, Erdős and Lovász [Reference Erdős and Lovász4] asked how large such a family
![]() $\mathcal{F}$
can be. Another way to phrase this question is to ask for the largest size of an
$\mathcal{F}$
can be. Another way to phrase this question is to ask for the largest size of an
![]() $n$
-uniform intersecting family
$n$
-uniform intersecting family
![]() $\mathcal{F}$
such that
$\mathcal{F}$
such that
![]() $\tau ({\mathcal{F}}) = n$
. Here,
$\tau ({\mathcal{F}}) = n$
. Here,
![]() $\tau ({\mathcal{F}})$
denotes the covering number of the family
$\tau ({\mathcal{F}})$
denotes the covering number of the family
![]() $\mathcal{F}$
, that is, the minimum size of a set
$\mathcal{F}$
, that is, the minimum size of a set
![]() $T$
which intersects any member of
$T$
which intersects any member of
![]() $\mathcal{F}$
. It is easy to see that any such family
$\mathcal{F}$
. It is easy to see that any such family
![]() $\mathcal{F}$
is contained in a maximal intersecting family and any maximal intersecting family
$\mathcal{F}$
is contained in a maximal intersecting family and any maximal intersecting family
![]() $\mathcal{F}$
satisfies
$\mathcal{F}$
satisfies
![]() $\tau ({\mathcal{F}}) = n$
. A related question about the minimal size of an
$\tau ({\mathcal{F}}) = n$
. A related question about the minimal size of an
![]() $n$
-uniform intersecting family
$n$
-uniform intersecting family
![]() $\mathcal{F}$
with
$\mathcal{F}$
with
![]() $\tau ({\mathcal{F}})=n$
was famously solved by Kahn [Reference Kahn10].
$\tau ({\mathcal{F}})=n$
was famously solved by Kahn [Reference Kahn10].
In [Reference Erdős and Lovász4], Erdős and Lovász proved the first non-trivial upper bound
![]() $n^n$
on the size of a maximal
$n^n$
on the size of a maximal
![]() $n$
-uniform intersecting family, and they also constructed such a family of size
$n$
-uniform intersecting family, and they also constructed such a family of size
![]() $[(e -1)n!]$
and conjectured this to be best possible (see also Section 4 for the construction). However, 20 years later, Frankl et al. [Reference Frankl, Ota and Tokushige7] gave a new construction of size roughly
$[(e -1)n!]$
and conjectured this to be best possible (see also Section 4 for the construction). However, 20 years later, Frankl et al. [Reference Frankl, Ota and Tokushige7] gave a new construction of size roughly
![]() $(n/2)^n$
. The upper bound
$(n/2)^n$
. The upper bound
![]() $n^n$
was improved to
$n^n$
was improved to
![]() $(1 - 1/e +o(1))n^n$
in 1994 by Tuza [Reference Tuza14]. In 2011, Cherkashin [Reference Cherkashin3] obtained a bound
$(1 - 1/e +o(1))n^n$
in 1994 by Tuza [Reference Tuza14]. In 2011, Cherkashin [Reference Cherkashin3] obtained a bound
![]() $|{\mathcal{F}}| = O(n^{n-1/2})$
and then in 2017 Arman and Retter [Reference Arman and Retter2] improved this further to
$|{\mathcal{F}}| = O(n^{n-1/2})$
and then in 2017 Arman and Retter [Reference Arman and Retter2] improved this further to
![]() $(1+o(1))n^{n-1}$
. The best currently known upper bound was obtained in 2019 by Frankl [Reference Frankl6]:
$(1+o(1))n^{n-1}$
. The best currently known upper bound was obtained in 2019 by Frankl [Reference Frankl6]:
Frankl [Reference Frankl6] also stated that it is possible to modify the argument and improve the exponent in (1) from
![]() $1/4$
to
$1/4$
to
![]() $1/3$
. In this paper, we provide an even stronger improvement of (1):
$1/3$
. In this paper, we provide an even stronger improvement of (1):
Theorem 1.1.
Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $n$
-uniform maximal intersecting family. Then
$n$
-uniform maximal intersecting family. Then
Frankl et al. conjecture in [Reference Frankl, Ota and Tokushige7] that
![]() $|{\mathcal{F}}| \leqslant (\alpha n)^n$
should hold for any maximal intersecting family and some absolute constant
$|{\mathcal{F}}| \leqslant (\alpha n)^n$
should hold for any maximal intersecting family and some absolute constant
![]() $\alpha \lt 1$
. The methods of the present paper do not seem to be sufficient to prove this conjecture.
$\alpha \lt 1$
. The methods of the present paper do not seem to be sufficient to prove this conjecture.
To prove Theorem 1.1, we consider a more general problem of estimating the number of minimal coverings of an arbitrary intersecting family. Given a family
![]() $\mathcal{F}$
, a set
$\mathcal{F}$
, a set
![]() $T$
is called a minimal covering of
$T$
is called a minimal covering of
![]() $\mathcal{F}$
if
$\mathcal{F}$
if
![]() $T \cap F \neq \emptyset$
holds for any
$T \cap F \neq \emptyset$
holds for any
![]() $F \in{\mathcal{F}}$
(
$F \in{\mathcal{F}}$
(
![]() $T$
covers
$T$
covers
![]() $\mathcal{F}$
) but this condition does not hold for any proper subset
$\mathcal{F}$
) but this condition does not hold for any proper subset
![]() $T^{\prime} \subset T$
(
$T^{\prime} \subset T$
(
![]() $T$
is minimal). The minimum size of a covering of
$T$
is minimal). The minimum size of a covering of
![]() $\mathcal{F}$
is called the covering number and denoted
$\mathcal{F}$
is called the covering number and denoted
![]() $\tau ({\mathcal{F}})$
. Let
$\tau ({\mathcal{F}})$
. Let
![]() ${\mathcal{T}}({\mathcal{F}})$
denote the family of all minimal coverings
${\mathcal{T}}({\mathcal{F}})$
denote the family of all minimal coverings
![]() $T$
of a family
$T$
of a family
![]() $\mathcal{F}$
. For technical reasons, it is convenient to restrict attention to the subfamily
$\mathcal{F}$
. For technical reasons, it is convenient to restrict attention to the subfamily
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{F}}) \subset{\mathcal{T}}({\mathcal{F}})$
of all minimal coverings of
${\mathcal{T}}_{\leqslant n}({\mathcal{F}}) \subset{\mathcal{T}}({\mathcal{F}})$
of all minimal coverings of
![]() $\mathcal{F}$
of size at most
$\mathcal{F}$
of size at most
![]() $n$
(where
$n$
(where
![]() $n$
will be taken equal to the uniformity of
$n$
will be taken equal to the uniformity of
![]() $\mathcal{F}$
). For a not necessarily uniform family
$\mathcal{F}$
). For a not necessarily uniform family
![]() $\mathcal G$
and
$\mathcal G$
and
![]() $\lambda \gt 0$
we define its weight
$\lambda \gt 0$
we define its weight
![]() $w_\lambda ({\mathcal{G}})$
as follows:
$w_\lambda ({\mathcal{G}})$
as follows:
If
![]() $\mathcal{F}$
is an
$\mathcal{F}$
is an
![]() $n$
-uniform maximal intersecting family, then
$n$
-uniform maximal intersecting family, then
![]() $\tau ({\mathcal{F}}) = n$
and so any element
$\tau ({\mathcal{F}}) = n$
and so any element
![]() $F \in{\mathcal{F}}$
is a minimal covering of
$F \in{\mathcal{F}}$
is a minimal covering of
![]() $\mathcal{F}$
. That is,
$\mathcal{F}$
. That is,
![]() ${\mathcal{F}} \subset{\mathcal{T}}({\mathcal{F}})$
and so
${\mathcal{F}} \subset{\mathcal{T}}({\mathcal{F}})$
and so
holds for any
![]() $\lambda \gt 0$
. On the other hand, the classical encoding procedure of Erdős and Lovász [Reference Erdős and Lovász4] actually shows that any
$\lambda \gt 0$
. On the other hand, the classical encoding procedure of Erdős and Lovász [Reference Erdős and Lovász4] actually shows that any
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{F}$
satisfies
$\mathcal{F}$
satisfies
By putting (3) and (4) together, we recover the upper bound
![]() $|{\mathcal{F}}| \leqslant n^n$
. Note that the inequality (4) is actually tight for arbitrary
$|{\mathcal{F}}| \leqslant n^n$
. Note that the inequality (4) is actually tight for arbitrary
![]() $n$
-uniform families:
$n$
-uniform families:
Example 1.2. Let
![]() ${\mathcal{F}} = \{F_1, \ldots, F_k\}$
be a collection of
${\mathcal{F}} = \{F_1, \ldots, F_k\}$
be a collection of
![]() $k$
pairwise disjoint
$k$
pairwise disjoint
![]() $n$
-element sets
$n$
-element sets
![]() $F_1, \ldots, F_k$
; then clearly
$F_1, \ldots, F_k$
; then clearly
and so
![]() $w_n({\mathcal{T}}({\mathcal{F}})) = |{\mathcal{T}}({\mathcal{F}})| n^{-k} = 1$
.
$w_n({\mathcal{T}}({\mathcal{F}})) = |{\mathcal{T}}({\mathcal{F}})| n^{-k} = 1$
.
However, the family
![]() $\mathcal{F}$
in this example is very far from being intersecting. This suggests that perhaps one can improve (4) provided that
$\mathcal{F}$
in this example is very far from being intersecting. This suggests that perhaps one can improve (4) provided that
![]() $\mathcal{F}$
is an intersecting family. Another obstruction comes from the case when
$\mathcal{F}$
is an intersecting family. Another obstruction comes from the case when
![]() $\mathcal{F}$
has small covering number:
$\mathcal{F}$
has small covering number:
Example 1.3. Let
![]() $K_1, \ldots, K_k$
be pairwise disjoint
$K_1, \ldots, K_k$
be pairwise disjoint
![]() $(n-k+1)$
-element sets and let
$(n-k+1)$
-element sets and let
![]() $\mathcal{F}$
be the family of sets of the form
$\mathcal{F}$
be the family of sets of the form
![]() $F = K_i \cup T$
where
$F = K_i \cup T$
where
![]() $|T \cap K_j| = 1$
for all
$|T \cap K_j| = 1$
for all
![]() $j = 1, \ldots, k$
. Then
$j = 1, \ldots, k$
. Then
![]() $\mathcal{F}$
is intersecting,
$\mathcal{F}$
is intersecting,
![]() $\tau ({\mathcal{F}}) = \min \{k, n-k+1\}$
and
$\tau ({\mathcal{F}}) = \min \{k, n-k+1\}$
and
![]() $w_n({\mathcal{T}}({\mathcal{F}})) \geqslant \frac{(n-k+1)^{k}}{n^k} \gtrsim e^{- \frac{k^2}{n} }$
.
$w_n({\mathcal{T}}({\mathcal{F}})) \geqslant \frac{(n-k+1)^{k}}{n^k} \gtrsim e^{- \frac{k^2}{n} }$
.
So the bound in (4) is essentially tight for
![]() $n$
-uniform intersecting families
$n$
-uniform intersecting families
![]() $\mathcal{F}$
with covering number
$\mathcal{F}$
with covering number
![]() $\tau ({\mathcal{F}}) \lesssim n^{1/2}$
. Our main result states that if
$\tau ({\mathcal{F}}) \lesssim n^{1/2}$
. Our main result states that if
![]() $\mathcal{F}$
is intersecting and the covering number
$\mathcal{F}$
is intersecting and the covering number
![]() $\tau ({\mathcal{F}})$
is large enough, then we indeed can win over (4) by a significant amount:
$\tau ({\mathcal{F}})$
is large enough, then we indeed can win over (4) by a significant amount:
Theorem 1.4.
For all
![]() $\varepsilon \gt 0$
and sufficiently large
$\varepsilon \gt 0$
and sufficiently large
![]() $n \gt n_0(\varepsilon )$
we have the following. Let
$n \gt n_0(\varepsilon )$
we have the following. Let
![]() $\mathcal{A}$
be an intersecting
$\mathcal{A}$
be an intersecting
![]() $n$
-uniform family. Then
$n$
-uniform family. Then
Note that this gives a substantial improvement over (4) provided that
![]() $\tau ({\mathcal{A}}) \gt n^{2/3+\varepsilon }$
. By applying Theorem 1.4 to a maximal intersecting family
$\tau ({\mathcal{A}}) \gt n^{2/3+\varepsilon }$
. By applying Theorem 1.4 to a maximal intersecting family
![]() $\mathcal{F}$
and using (3), Theorem 1.1 follows.
$\mathcal{F}$
and using (3), Theorem 1.1 follows.
We now turn to explain the main ideas of the proof of Theorem 1.4. In what follows, we use the notation
![]() $c_\lambda ({\mathcal{A}}) = w_\lambda ({\mathcal{T}}_{\leqslant n}({\mathcal{A}}))$
for an
$c_\lambda ({\mathcal{A}}) = w_\lambda ({\mathcal{T}}_{\leqslant n}({\mathcal{A}}))$
for an
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\lambda \gt 0$
.
$\lambda \gt 0$
.
Fix
![]() $\varepsilon \gt 0$
. Using induction, we are going to show that for any
$\varepsilon \gt 0$
. Using induction, we are going to show that for any
![]() $n \gt n_0(\varepsilon )$
and any
$n \gt n_0(\varepsilon )$
and any
![]() $n$
-uniform intersecting family
$n$
-uniform intersecting family
![]() $\mathcal{A}$
we have
$\mathcal{A}$
we have
where
![]() $\lambda = e^{-\frac{1}{n^{0.5+\varepsilon }}}$
. This is much weaker than what is claimed in (5) for
$\lambda = e^{-\frac{1}{n^{0.5+\varepsilon }}}$
. This is much weaker than what is claimed in (5) for
![]() $n^{2/3} \leqslant \tau ({\mathcal{A}}) \leqslant n/2$
but gives the same result when
$n^{2/3} \leqslant \tau ({\mathcal{A}}) \leqslant n/2$
but gives the same result when
![]() $\tau ({\mathcal{A}})$
is close to
$\tau ({\mathcal{A}})$
is close to
![]() $n$
. By writing down the inductive statement (6) more carefully, one can recover (5) in the full range of parameters, see Section 3 for details.
$n$
. By writing down the inductive statement (6) more carefully, one can recover (5) in the full range of parameters, see Section 3 for details.
If
![]() $\tau ({\mathcal{A}}) \leqslant n/2$
then (6) follows from (4) (which we will prove later) so we may assume that
$\tau ({\mathcal{A}}) \leqslant n/2$
then (6) follows from (4) (which we will prove later) so we may assume that
![]() $\tau ({\mathcal{A}}) \geqslant n/2$
. For the purpose of induction, we may assume that (6) holds for all
$\tau ({\mathcal{A}}) \geqslant n/2$
. For the purpose of induction, we may assume that (6) holds for all
![]() $n$
-uniform intersecting families of size strictly smaller than
$n$
-uniform intersecting families of size strictly smaller than
![]() $\mathcal{A}$
. The following proposition is at the core of our inductive approach:
$\mathcal{A}$
. The following proposition is at the core of our inductive approach:
Proposition 1.5.
Let
![]() $\lambda = e^{-\frac{1}{n^{0.5+\varepsilon }}}$
. If there exists a subfamily
$\lambda = e^{-\frac{1}{n^{0.5+\varepsilon }}}$
. If there exists a subfamily
![]() ${\mathcal{G}} \subset{\mathcal{A}}$
such that
${\mathcal{G}} \subset{\mathcal{A}}$
such that
![]() $c_{\lambda n}({\mathcal{G}}) \leqslant 1$
then
$c_{\lambda n}({\mathcal{G}}) \leqslant 1$
then
![]() $c_{n}({\mathcal{A}}) \leqslant \lambda ^{\tau ({\mathcal{A}})-n/2}$
.
$c_{n}({\mathcal{A}}) \leqslant \lambda ^{\tau ({\mathcal{A}})-n/2}$
.
Roughly speaking, Proposition 1.5 tells us that if we can find a subfamily
![]() ${\mathcal{G}} \subset{\mathcal{A}}$
which is ‘difficult’ to cover then we can use it for the induction step and get a bound on
${\mathcal{G}} \subset{\mathcal{A}}$
which is ‘difficult’ to cover then we can use it for the induction step and get a bound on
![]() $c_n({\mathcal{A}})$
in terms of
$c_n({\mathcal{A}})$
in terms of
![]() $c_n({\mathcal{A}}^{\prime})$
for some proper subfamilies
$c_n({\mathcal{A}}^{\prime})$
for some proper subfamilies
![]() ${\mathcal{A}}^{\prime}\subset{\mathcal{A}}$
. The idea of finding a special subfamilies in
${\mathcal{A}}^{\prime}\subset{\mathcal{A}}$
. The idea of finding a special subfamilies in
![]() $\mathcal{A}$
to bound the number of minimal covers also appears in a somewhat different form in [Reference Frankl6].
$\mathcal{A}$
to bound the number of minimal covers also appears in a somewhat different form in [Reference Frankl6].
Proposition 1.5 puts rather strict limitations on how a potential minimal family
![]() $\mathcal{A}$
contradicting (6) might look like. The first key observation (also originating from [Reference Frankl6]) is that all pairwise intersections of sets in
$\mathcal{A}$
contradicting (6) might look like. The first key observation (also originating from [Reference Frankl6]) is that all pairwise intersections of sets in
![]() $\mathcal{A}$
are either very small or very large.
$\mathcal{A}$
are either very small or very large.
Indeed, let
![]() $A_1, A_2 \in{\mathcal{A}}$
be a pair of sets such that
$A_1, A_2 \in{\mathcal{A}}$
be a pair of sets such that
![]() $ |A_1 \cap A_2| = k$
for some
$ |A_1 \cap A_2| = k$
for some
![]() $k$
. Observe that
$k$
. Observe that
and so we have
![]() $c_{\lambda n}(\{A_1, A_2\}) \leqslant 1$
for any
$c_{\lambda n}(\{A_1, A_2\}) \leqslant 1$
for any
![]() $k \in [\sqrt{n}, n-\sqrt{n}]$
. So by Proposition 1.5, unless
$k \in [\sqrt{n}, n-\sqrt{n}]$
. So by Proposition 1.5, unless
![]() $\mathcal{A}$
satisfies (6), for any pair
$\mathcal{A}$
satisfies (6), for any pair
![]() $A_1, A_2 \in{\mathcal{A}}$
we either have
$A_1, A_2 \in{\mathcal{A}}$
we either have
![]() $|A_1 \cap A_2| \leqslant \sqrt{n}$
or
$|A_1 \cap A_2| \leqslant \sqrt{n}$
or
![]() $|A_1 \cap A_2| \geqslant n-\sqrt{n}$
.
$|A_1 \cap A_2| \geqslant n-\sqrt{n}$
.
Let
![]() $k = \sqrt{n}$
. The above property allows us to write
$k = \sqrt{n}$
. The above property allows us to write
![]() $\mathcal{A}$
as a union
$\mathcal{A}$
as a union
where for any
![]() $i, j = 1, \ldots, N$
and
$i, j = 1, \ldots, N$
and
![]() $K_i \in{\mathcal{K}}_i$
and
$K_i \in{\mathcal{K}}_i$
and
![]() $K_j \in{\mathcal{K}}_j$
we have
$K_j \in{\mathcal{K}}_j$
we have
![]() $|K_i \cap K_j| \geqslant n-k$
if
$|K_i \cap K_j| \geqslant n-k$
if
![]() $i= j$
and
$i= j$
and
![]() $|K_i \cap K_j| \leqslant k$
otherwise. This decomposition step is actually quite robust and works for any
$|K_i \cap K_j| \leqslant k$
otherwise. This decomposition step is actually quite robust and works for any
![]() $k \lt n/3$
; so if one were to prove (6) with
$k \lt n/3$
; so if one were to prove (6) with
![]() $\lambda \lt 1-c$
for a small constant
$\lambda \lt 1-c$
for a small constant
![]() $c$
, then one may still assume that, say,
$c$
, then one may still assume that, say,
![]() $|A_1 \cap A_2| \not \in [0.1 n, 0.9 n]$
holds for all
$|A_1 \cap A_2| \not \in [0.1 n, 0.9 n]$
holds for all
![]() $A_1, A_2 \in{\mathcal{A}}$
, and so we have (7) with
$A_1, A_2 \in{\mathcal{A}}$
, and so we have (7) with
![]() $k = 0.1n$
.
$k = 0.1n$
.
The decomposition (7) has the following properties:
Each family
![]() ${\mathcal{K}}_i$
has a core of size
${\mathcal{K}}_i$
has a core of size
![]() $n-5k$
. That is, there exists a set
$n-5k$
. That is, there exists a set
![]() $K_i$
of size
$K_i$
of size
![]() $n-5k$
such that
$n-5k$
such that
![]() $K_i \subset A$
for any
$K_i \subset A$
for any
![]() $A \in{\mathcal{K}}_i$
. Note that we only know that
$A \in{\mathcal{K}}_i$
. Note that we only know that
![]() $|A_1\cap A_2| \geqslant n-k$
for any
$|A_1\cap A_2| \geqslant n-k$
for any
![]() $A_1, A_2 \in{\mathcal{K}}_i$
and so a priori the sets in
$A_1, A_2 \in{\mathcal{K}}_i$
and so a priori the sets in
![]() ${\mathcal{K}}_i$
do not have to have a large common intersection. However, if
${\mathcal{K}}_i$
do not have to have a large common intersection. However, if
![]() $|\bigcap{\mathcal{K}}_i|\leqslant n-5k$
then we can take
$|\bigcap{\mathcal{K}}_i|\leqslant n-5k$
then we can take
![]() ${\mathcal{G}} ={\mathcal{K}}_i$
in Proposition 1.5:
${\mathcal{G}} ={\mathcal{K}}_i$
in Proposition 1.5:
Lemma 1.6.
Let
![]() $k \leqslant n/10$
. Let
$k \leqslant n/10$
. Let
![]() $\mathcal{K}$
be an
$\mathcal{K}$
be an
![]() $n$
-uniform family. Suppose that there is an
$n$
-uniform family. Suppose that there is an
![]() $(n-k)$
-element set
$(n-k)$
-element set
![]() $K$
such that we have
$K$
such that we have
![]() $|F \cap K| \geqslant n-2k$
for every
$|F \cap K| \geqslant n-2k$
for every
![]() $F \in{\mathcal{K}}$
. Then we either have
$F \in{\mathcal{K}}$
. Then we either have
![]() $c_{n-k}({\mathcal{K}}) \leqslant 1$
or
$c_{n-k}({\mathcal{K}}) \leqslant 1$
or
![]() $|\bigcap{\mathcal{K}}| \geqslant n-5k$
.
$|\bigcap{\mathcal{K}}| \geqslant n-5k$
.
The idea is use the Lubell–Yamamoto–Meshalkin inequality to control possible intersections of a minimal cover of
![]() $\mathcal{K}$
with the set
$\mathcal{K}$
with the set
![]() $K$
above. This step is also quite flexible and can be employed if one were to prove (6) with
$K$
above. This step is also quite flexible and can be employed if one were to prove (6) with
![]() $\lambda =1-c$
(and
$\lambda =1-c$
(and
![]() $k \approx c n$
).
$k \approx c n$
).
Each family
![]() ${\mathcal{K}}_i$
is small. Namely, we have
${\mathcal{K}}_i$
is small. Namely, we have
![]() $|{\mathcal{K}}_i| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + 2k\\[-3pt]2k\end{array}\bigg)$
for all
$|{\mathcal{K}}_i| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + 2k\\[-3pt]2k\end{array}\bigg)$
for all
![]() $i$
. We say that a family
$i$
. We say that a family
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $\tau$
-critical if removing any set from
$\tau$
-critical if removing any set from
![]() $\mathcal{F}$
reduces
$\mathcal{F}$
reduces
![]() $\tau ({\mathcal{F}})$
. The family
$\tau ({\mathcal{F}})$
. The family
![]() $\mathcal{A}$
in question is
$\mathcal{A}$
in question is
![]() $\tau$
-critical: if not, then for some proper
$\tau$
-critical: if not, then for some proper
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
we have
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
we have
![]() $\tau ({\mathcal{A}}^{\prime}) = \tau ({\mathcal{A}})$
. But then by the induction assumption we get
$\tau ({\mathcal{A}}^{\prime}) = \tau ({\mathcal{A}})$
. But then by the induction assumption we get
Here we also use a simple monotonicity property
![]() $c_n({\mathcal{A}}) \leqslant c_n({\mathcal{A}}^{\prime})$
which we prove in the next section.
$c_n({\mathcal{A}}) \leqslant c_n({\mathcal{A}}^{\prime})$
which we prove in the next section.
So we can apply the following simple lemma:
Lemma 1.7.
Let
![]() $\mathcal{A}$
be a
$\mathcal{A}$
be a
![]() $\tau$
-critical
$\tau$
-critical
![]() $n$
-uniform family (that is, removing any element from
$n$
-uniform family (that is, removing any element from
![]() $\mathcal{A}$
reduces
$\mathcal{A}$
reduces
![]() $\tau ({\mathcal{A}})$
) and let
$\tau ({\mathcal{A}})$
) and let
![]() ${\mathcal{K}} \subset{\mathcal{A}}$
be a subfamily such that
${\mathcal{K}} \subset{\mathcal{A}}$
be a subfamily such that
![]() $|\bigcap{\mathcal{K}}| \geqslant n-k$
for some
$|\bigcap{\mathcal{K}}| \geqslant n-k$
for some
![]() $k \geqslant 0$
. Then
$k \geqslant 0$
. Then
![]() $|{\mathcal{K}}| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + k\\[-3pt]k\end{array}\bigg)$
.
$|{\mathcal{K}}| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + k\\[-3pt]k\end{array}\bigg)$
.
Proof. Denote
![]() $K = \bigcap{\mathcal{K}}$
. By
$K = \bigcap{\mathcal{K}}$
. By
![]() $\tau$
-criticality of
$\tau$
-criticality of
![]() $\mathcal{A}$
, for any set
$\mathcal{A}$
, for any set
![]() $A \in{\mathcal{K}}$
there is a covering
$A \in{\mathcal{K}}$
there is a covering
![]() $T_A$
of
$T_A$
of
![]() ${\mathcal{A}} \setminus \{A\}$
of size less than
${\mathcal{A}} \setminus \{A\}$
of size less than
![]() $\tau ({\mathcal{A}})$
which does not intersect
$\tau ({\mathcal{A}})$
which does not intersect
![]() $A$
. Note that
$A$
. Note that
![]() $T_A$
does not intersect
$T_A$
does not intersect
![]() $K$
and so it is a covering of the family
$K$
and so it is a covering of the family
![]() $({\mathcal{K}} \setminus \{A\}) \setminus K$
. Thus, the system of pairs of sets
$({\mathcal{K}} \setminus \{A\}) \setminus K$
. Thus, the system of pairs of sets
![]() $(A\setminus K, T_A)_{A \in{\mathcal{K}}}$
satisfies the Bollobás’s Two Families theorem [Reference Jukna9, p. 113, Theorem 8.8] and so
$(A\setminus K, T_A)_{A \in{\mathcal{K}}}$
satisfies the Bollobás’s Two Families theorem [Reference Jukna9, p. 113, Theorem 8.8] and so
![]() $|{\mathcal{K}}| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + k\\[-3pt]k\end{array}\bigg)$
.
$|{\mathcal{K}}| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}}) + k\\[-3pt]k\end{array}\bigg)$
.
The number of families
![]() $N$
is small. Namely, we may assume that
$N$
is small. Namely, we may assume that
![]() $N \leqslant n^{C}$
holds for some constant
$N \leqslant n^{C}$
holds for some constant
![]() $C$
. This is the part of the proof where we rely on the Spread Lemma of Alweiss–Lovett–Wu–Zhang [Reference Alweiss, Lovett, Wu and Zhang1]. Namely, we have the following:
$C$
. This is the part of the proof where we rely on the Spread Lemma of Alweiss–Lovett–Wu–Zhang [Reference Alweiss, Lovett, Wu and Zhang1]. Namely, we have the following:
Lemma 1.8.
Let
![]() $\mathcal{A}$
be an
$\mathcal{A}$
be an
![]() $n$
-uniform family where
$n$
-uniform family where
![]() $n$
is sufficiently large. Let
$n$
is sufficiently large. Let
![]() ${\mathcal{B}} \subset{\mathcal{A}}$
be a subfamily such that
${\mathcal{B}} \subset{\mathcal{A}}$
be a subfamily such that
![]() $|B_1 \cap B_2| \leqslant k$
for all distinct
$|B_1 \cap B_2| \leqslant k$
for all distinct
![]() $B_1, B_2 \in{\mathcal{B}}$
. If
$B_1, B_2 \in{\mathcal{B}}$
. If
![]() $k \leqslant \frac{n}{10^4\log n}$
then one of the following 2 possibilities holds:
$k \leqslant \frac{n}{10^4\log n}$
then one of the following 2 possibilities holds:
-
1. We have
 $|{\mathcal{B}}| \leqslant n^{C}$
for some absolute constant
$|{\mathcal{B}}| \leqslant n^{C}$
for some absolute constant
 $C$
.
$C$
. -
2. There is a proper subfamily
 ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
 \begin{equation*} 2^{\tau ({\mathcal {A}})}c_n({\mathcal {A}}) \leqslant 2^{\tau ({\mathcal {A}}^{\prime})} c_n({\mathcal {A}}^{\prime}). \end{equation*}
\begin{equation*} 2^{\tau ({\mathcal {A}})}c_n({\mathcal {A}}) \leqslant 2^{\tau ({\mathcal {A}}^{\prime})} c_n({\mathcal {A}}^{\prime}). \end{equation*}
Note that this lemma has a mild restriction
![]() $k \lesssim \frac{n}{\log n}$
. This means that the best possible bound in (6) using Lemma 1.8 has
$k \lesssim \frac{n}{\log n}$
. This means that the best possible bound in (6) using Lemma 1.8 has
![]() $\lambda = 1- \frac{c}{\log n}$
(corresponding to a bound of the form
$\lambda = 1- \frac{c}{\log n}$
(corresponding to a bound of the form
![]() $|{\mathcal{F}}| \leqslant e^{-\frac{cn}{\log n}} n^n$
for maximal intersecting families). So even though this is not enough to prove an exponential bound in the Erdős–Lovász problem, this is by far not the main bottleneck of the argument.
$|{\mathcal{F}}| \leqslant e^{-\frac{cn}{\log n}} n^n$
for maximal intersecting families). So even though this is not enough to prove an exponential bound in the Erdős–Lovász problem, this is by far not the main bottleneck of the argument.
The proof of Lemma 1.8 is based on the following idea. Let
![]() $p = \frac{C \log n}{n}$
and consider a random set
$p = \frac{C \log n}{n}$
and consider a random set
![]() $\bf U$
where each element of the ground set is included in
$\bf U$
where each element of the ground set is included in
![]() $\bf U$
independently with probability
$\bf U$
independently with probability
![]() $p$
. If the family
$p$
. If the family
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
is not
${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
is not
![]() $\frac{n}{2}$
-spread the one can check that the second option of the lemma holds. Otherwise, by the Spread Lemma (see Lemma 2.8 below), with probability at least
$\frac{n}{2}$
-spread the one can check that the second option of the lemma holds. Otherwise, by the Spread Lemma (see Lemma 2.8 below), with probability at least
![]() $0.9$
there exists an element
$0.9$
there exists an element
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
such that
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
such that
![]() $T \subset{\bf U}$
. On the other hand, a routine second moment computation shows that if
$T \subset{\bf U}$
. On the other hand, a routine second moment computation shows that if
![]() $N$
is large enough and sets
$N$
is large enough and sets
![]() $B_1, \ldots, B_N$
have small pairwise intersections, then with probability at least
$B_1, \ldots, B_N$
have small pairwise intersections, then with probability at least
![]() $0.9$
there exists
$0.9$
there exists
![]() $i \in [N]$
so that
$i \in [N]$
so that
![]() $B_i$
is disjoint from
$B_i$
is disjoint from
![]() $\bf U$
. So with probability at least
$\bf U$
. So with probability at least
![]() $0.8$
there is a covering
$0.8$
there is a covering
![]() $T \subset{\bf U}$
of
$T \subset{\bf U}$
of
![]() $\mathcal{A}$
and a set
$\mathcal{A}$
and a set
![]() $B_i \in{\mathcal{A}}$
disjoint from
$B_i \in{\mathcal{A}}$
disjoint from
![]() $\bf U$
. In particular,
$\bf U$
. In particular,
![]() $T \cap B_i = \emptyset$
with positive probability which contradicts the definition of a covering.
$T \cap B_i = \emptyset$
with positive probability which contradicts the definition of a covering.
Conclusion:
![]() $\mathcal{A}$
is small. We conclude from the above observations that the family
$\mathcal{A}$
is small. We conclude from the above observations that the family
![]() $\mathcal{A}$
itself must be small:
$\mathcal{A}$
itself must be small:
Once we know that the family
![]() $\mathcal{A}$
is small, we can start exploiting the fact that
$\mathcal{A}$
is small, we can start exploiting the fact that
![]() $\tau ({\mathcal{A}})$
is large. In fact, we show that
$\tau ({\mathcal{A}})$
is large. In fact, we show that
![]() $\mathcal{A}$
cannot be too ‘clustered’ around a few elements of the ground set since otherwise we can find a covering of
$\mathcal{A}$
cannot be too ‘clustered’ around a few elements of the ground set since otherwise we can find a covering of
![]() $\mathcal{A}$
of size less than
$\mathcal{A}$
of size less than
![]() $\tau ({\mathcal{A}})$
by sampling a random set according to the degree distribution of
$\tau ({\mathcal{A}})$
by sampling a random set according to the degree distribution of
![]() $\mathcal{A}$
. A careful execution of this idea results in the following lemma:
$\mathcal{A}$
. A careful execution of this idea results in the following lemma:
Lemma 1.9.
Let
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $m, t \geqslant 1$
. Let
$m, t \geqslant 1$
. Let
![]() $\mathcal{A}$
be an
$\mathcal{A}$
be an
![]() $n$
-uniform family of size at most
$n$
-uniform family of size at most
![]() $e^{m}$
and
$e^{m}$
and
![]() $\tau ({\mathcal{A}}) \geqslant t$
. Then, for every
$\tau ({\mathcal{A}}) \geqslant t$
. Then, for every
![]() $l \geqslant 1$
, there is a subfamily
$l \geqslant 1$
, there is a subfamily
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
![]() $\tau ({\mathcal{A}} \setminus{\mathcal{A}}^{\prime}) \leqslant t/2$
and for every
$\tau ({\mathcal{A}} \setminus{\mathcal{A}}^{\prime}) \leqslant t/2$
and for every
![]() $i = 1, \ldots, l$
we have
$i = 1, \ldots, l$
we have
where
![]() $C_l \ll 2^{l^2}$
depends only on
$C_l \ll 2^{l^2}$
depends only on
![]() $l$
and the average is taken over all
$l$
and the average is taken over all
![]() $A_1, \ldots, A_l \in{\mathcal{A}}$
chosen uniformly and independently.
$A_1, \ldots, A_l \in{\mathcal{A}}$
chosen uniformly and independently.
That is, we can remove a few sets from
![]() $\mathcal{A}$
and obtain the property that the
$\mathcal{A}$
and obtain the property that the
![]() $l$
-wise intersections of sets in
$l$
-wise intersections of sets in
![]() $\mathcal{A}$
are very small on average. Note that in our case
$\mathcal{A}$
are very small on average. Note that in our case
![]() $m \sim k \log n \sim \sqrt{n} \log n$
and
$m \sim k \log n \sim \sqrt{n} \log n$
and
![]() $t = \tau ({\mathcal{A}}) \geqslant n/2$
, so that
$t = \tau ({\mathcal{A}}) \geqslant n/2$
, so that
that is, almost all
![]() $l$
-wise intersections of sets from
$l$
-wise intersections of sets from
![]() $\mathcal{A}$
are empty for constant
$\mathcal{A}$
are empty for constant
![]() $l$
. Let
$l$
. Let
![]() $r = n^{0.5-\varepsilon/2}$
and
$r = n^{0.5-\varepsilon/2}$
and
![]() $l = 10\varepsilon ^{-1}$
and sample a uniformly random subfamily
$l = 10\varepsilon ^{-1}$
and sample a uniformly random subfamily
![]() ${\mathcal{B}} = \{B_1, \ldots, B_r\} \subset{\mathcal{A}}^{\prime}$
, where
${\mathcal{B}} = \{B_1, \ldots, B_r\} \subset{\mathcal{A}}^{\prime}$
, where
![]() ${\mathcal{A}}^{\prime}$
is given by Lemma 1.9. Then by (9) and the union bound, with positive probability all
${\mathcal{A}}^{\prime}$
is given by Lemma 1.9. Then by (9) and the union bound, with positive probability all
![]() $l$
-wise intersections of sets in
$l$
-wise intersections of sets in
![]() $\mathcal{B}$
are empty. We remark that the family
$\mathcal{B}$
are empty. We remark that the family
![]() $\mathcal{B}$
is a natural generalization of ‘brooms’ used by Frankl in [Reference Frankl6]; the advantage of our approach is that we can find (generalized) brooms of size
$\mathcal{B}$
is a natural generalization of ‘brooms’ used by Frankl in [Reference Frankl6]; the advantage of our approach is that we can find (generalized) brooms of size
![]() $\sim n^{1/2}$
whereas Frankl could only construct brooms of size
$\sim n^{1/2}$
whereas Frankl could only construct brooms of size
![]() $\sim n^{1/4}$
.
$\sim n^{1/4}$
.
The final step of the proof is to show that one can take
![]() ${\mathcal{G}} ={\mathcal{B}}$
in Proposition 1.5:
${\mathcal{G}} ={\mathcal{B}}$
in Proposition 1.5:
Lemma 1.10.
Let
![]() $n \geqslant 1$
and
$n \geqslant 1$
and
![]() $r \geqslant 2l$
be such that
$r \geqslant 2l$
be such that
![]() $r^2 \leqslant l^3 n$
. Let
$r^2 \leqslant l^3 n$
. Let
![]() $\mathcal{B}$
be an
$\mathcal{B}$
be an
![]() $n$
-uniform intersecting family of size
$n$
-uniform intersecting family of size
![]() $r$
such that every
$r$
such that every
![]() $l$
distinct sets from
$l$
distinct sets from
![]() $\mathcal{B}$
have an empty intersection. Then for
$\mathcal{B}$
have an empty intersection. Then for
![]() $k \leqslant \frac{r}{20 l^3}$
we have
$k \leqslant \frac{r}{20 l^3}$
we have
The proof of this lemma crucially uses the intersecting property of the family
![]() $\mathcal{B}$
. In fact, this is the only place in the argument where we really use the fact that the initial family is intersecting. The construction of a large bounded degree family
$\mathcal{B}$
. In fact, this is the only place in the argument where we really use the fact that the initial family is intersecting. The construction of a large bounded degree family
![]() $\mathcal{B}$
and Lemma 1.10 appear to be the main bottlenecks of the argument and are the reason for the resulting bound of
$\mathcal{B}$
and Lemma 1.10 appear to be the main bottlenecks of the argument and are the reason for the resulting bound of
![]() $e^{-n^{0.5+\varepsilon }}n^n$
for maximal intersecting families.
$e^{-n^{0.5+\varepsilon }}n^n$
for maximal intersecting families.
The proof of Lemma 1.10 is based on a more careful analysis of the classical Erdős–Lovász encoding procedure: the intersecting property and bounded degree of
![]() $\mathcal{B}$
ensure that there is enough ‘overlap’ between sets
$\mathcal{B}$
ensure that there is enough ‘overlap’ between sets
![]() $B_i$
which makes the encoding more efficient. This completes the proof of Theorem 1.4. The next section contains all the proofs of the lemmas which appeared in this outline and in Section 3 we formally deduce Theorem 1.4. Section 4 contains some final remarks and questions.
$B_i$
which makes the encoding more efficient. This completes the proof of Theorem 1.4. The next section contains all the proofs of the lemmas which appeared in this outline and in Section 3 we formally deduce Theorem 1.4. Section 4 contains some final remarks and questions.
2. Proving auxiliary results
2.1 Minimal covers
Fix
![]() $n \in{\mathbb{N}}$
and let
$n \in{\mathbb{N}}$
and let
![]() $\mathcal{A}$
be a finite family of sets of size at most
$\mathcal{A}$
be a finite family of sets of size at most
![]() $n$
. For
$n$
. For
![]() $\lambda \gt 0$
, we define the weight
$\lambda \gt 0$
, we define the weight
![]() $w_\lambda ({\mathcal{A}})$
of
$w_\lambda ({\mathcal{A}})$
of
![]() $\mathcal{A}$
by the following expression:
$\mathcal{A}$
by the following expression:
The parameter
![]() $\lambda$
will be usually taken to be
$\lambda$
will be usually taken to be
![]() $\lambda = n$
or
$\lambda = n$
or
![]() $\lambda = n - k$
for a relatively small number
$\lambda = n - k$
for a relatively small number
![]() $k$
. The following characteristic of a family will be crucial for our arguments. Recall that a covering of
$k$
. The following characteristic of a family will be crucial for our arguments. Recall that a covering of
![]() $\mathcal{A}$
is a set
$\mathcal{A}$
is a set
![]() $T$
intersecting all members of
$T$
intersecting all members of
![]() $\mathcal{A}$
and a covering
$\mathcal{A}$
and a covering
![]() $T$
is minimal if any proper subset
$T$
is minimal if any proper subset
![]() $T^{\prime} \subset T$
does not cover
$T^{\prime} \subset T$
does not cover
![]() $\mathcal{A}$
. We denote
$\mathcal{A}$
. We denote
![]() $\tau ({\mathcal{A}})$
the minimum size of a covering of
$\tau ({\mathcal{A}})$
the minimum size of a covering of
![]() $\mathcal{A}$
. We denote
$\mathcal{A}$
. We denote
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
the family of all minimal covers of
${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
the family of all minimal covers of
![]() $\mathcal{A}$
of size at most
$\mathcal{A}$
of size at most
![]() $n$
. For
$n$
. For
![]() $\lambda \gt 0$
, put
$\lambda \gt 0$
, put
We remark that the family
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{F}})$
was also introduced in [Reference Tuza14] to prove the bound
${\mathcal{T}}_{\leqslant n}({\mathcal{F}})$
was also introduced in [Reference Tuza14] to prove the bound
![]() $|{\mathcal{F}}| \leqslant (1 - e^{-1} + o(1))n^n$
. We have the following basic monotonicity result:
$|{\mathcal{F}}| \leqslant (1 - e^{-1} + o(1))n^n$
. We have the following basic monotonicity result:
Observation 2.1.
For any family
![]() $\mathcal{F}$
and all
$\mathcal{F}$
and all
![]() $\lambda \leqslant \mu$
we have
$\lambda \leqslant \mu$
we have
Proof. Indeed, since every minimal covering
![]() $T$
of
$T$
of
![]() $\mathcal{F}$
has size at least
$\mathcal{F}$
has size at least
![]() $\tau ({\mathcal{F}})$
we have
$\tau ({\mathcal{F}})$
we have
Summing over all
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{F}})$
gives the desired inequality.
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{F}})$
gives the desired inequality.
Let
![]() $X$
be the ground set of
$X$
be the ground set of
![]() $\mathcal{A}$
. For
$\mathcal{A}$
. For
![]() $S \subset X$
we denote by
$S \subset X$
we denote by
![]() ${\mathcal{A}}(\bar S)$
the set of elements of
${\mathcal{A}}(\bar S)$
the set of elements of
![]() $\mathcal{A}$
which do not intersect
$\mathcal{A}$
which do not intersect
![]() $S$
. The following lemma lies at the foundation of our arguments.
$S$
. The following lemma lies at the foundation of our arguments.
Lemma 2.2.
For any subfamily
![]() ${\mathcal{A}}^{\prime}\subset{\mathcal{A}}$
of any family
${\mathcal{A}}^{\prime}\subset{\mathcal{A}}$
of any family
![]() $\mathcal{A}$
and for any
$\mathcal{A}$
and for any
![]() $\lambda \gt 1$
we have
$\lambda \gt 1$
we have
In particular, we have
Proof. Each minimal covering
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
contains a minimal covering
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
contains a minimal covering
![]() $T^{\prime} \subset T$
of
$T^{\prime} \subset T$
of
![]() ${\mathcal{A}}^{\prime}$
. Moreover, by the minimality of
${\mathcal{A}}^{\prime}$
. Moreover, by the minimality of
![]() $T$
, the set
$T$
, the set
![]() $T\setminus T^{\prime}$
is a minimal covering of the family
$T\setminus T^{\prime}$
is a minimal covering of the family
![]() ${\mathcal{A}}(\bar T^{\prime})$
. So each term
${\mathcal{A}}(\bar T^{\prime})$
. So each term
![]() $\lambda ^{-|T|}$
on the left-hand side of (10) corresponds to at least one term
$\lambda ^{-|T|}$
on the left-hand side of (10) corresponds to at least one term
![]() $\lambda ^{-|T^{\prime}|} \lambda ^{-|T\setminus T^{\prime}|}$
on the right-hand side of (10) (there could be more than one way to choose
$\lambda ^{-|T^{\prime}|} \lambda ^{-|T\setminus T^{\prime}|}$
on the right-hand side of (10) (there could be more than one way to choose
![]() $T^{\prime}$
). This proves (10).
$T^{\prime}$
). This proves (10).
In particular, we have:
Corollary 2.3 (Tuza, [Reference Tuza14]). For any
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{F}$
we have
$\mathcal{F}$
we have
![]() $c_n({\mathcal{F}}) \leqslant 1$
.
$c_n({\mathcal{F}}) \leqslant 1$
.
This bound was also proved in [Reference Tuza14], similar ideas appear in [Reference Gyárfás8].
Proof. Note that if
![]() $|{\mathcal{F}}| \leqslant 1$
then the proposition holds. If
$|{\mathcal{F}}| \leqslant 1$
then the proposition holds. If
![]() $|{\mathcal{F}}| \geqslant 2$
then choose a proper non-empty subfamily
$|{\mathcal{F}}| \geqslant 2$
then choose a proper non-empty subfamily
![]() ${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
and apply the second part of Lemma 2.2. The statement now follows by induction.
${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
and apply the second part of Lemma 2.2. The statement now follows by induction.
The basic idea behind the proof of Theorem 1.1 is to use apply Lemma 2.2 to various subfamilies
![]() ${\mathcal{F}}^{\prime}$
with small
${\mathcal{F}}^{\prime}$
with small
![]() $c_n({\mathcal{F}}^{\prime})$
and use induction to estimate the terms
$c_n({\mathcal{F}}^{\prime})$
and use induction to estimate the terms
![]() $c_n({\mathcal{F}}(\bar T^{\prime}))$
. More precisely, we will use the following consequence of Lemma 2.2.
$c_n({\mathcal{F}}(\bar T^{\prime}))$
. More precisely, we will use the following consequence of Lemma 2.2.
Lemma 2.4.
Let
![]() $f\,:\,{\mathbb{R}}\rightarrow{\mathbb{R}}$
be a differentiable convex function. Let
$f\,:\,{\mathbb{R}}\rightarrow{\mathbb{R}}$
be a differentiable convex function. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $n$
-uniform family such that for any proper subfamily
$n$
-uniform family such that for any proper subfamily
![]() ${\mathcal{A}} \subset{\mathcal{F}}$
we have
${\mathcal{A}} \subset{\mathcal{F}}$
we have
![]() $c_n({\mathcal{A}}) \leqslant e^{- f(\tau ({\mathcal{A}}))}$
. Let
$c_n({\mathcal{A}}) \leqslant e^{- f(\tau ({\mathcal{A}}))}$
. Let
![]() $\lambda = e^{-f^{\prime}(\tau ({\mathcal{F}}))}$
and suppose that there exists a non-empty family
$\lambda = e^{-f^{\prime}(\tau ({\mathcal{F}}))}$
and suppose that there exists a non-empty family
![]() ${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
such that
${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
such that
![]() $c_{\lambda n}({\mathcal{F}}^{\prime}) \leqslant 1$
. Then
$c_{\lambda n}({\mathcal{F}}^{\prime}) \leqslant 1$
. Then
![]() $c_n({\mathcal{F}}) \leqslant e^{-f(\tau ({\mathcal{F}}))}$
.
$c_n({\mathcal{F}}) \leqslant e^{-f(\tau ({\mathcal{F}}))}$
.
Proof. By Lemma 2.2 applied to
![]() ${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
we have
${\mathcal{F}}^{\prime} \subset{\mathcal{F}}$
we have
We have
![]() $\tau ({\mathcal{F}}(\bar T)) \geqslant \tau ({\mathcal{F}}) - |T|$
and so by convexity
$\tau ({\mathcal{F}}(\bar T)) \geqslant \tau ({\mathcal{F}}) - |T|$
and so by convexity
![]() $f(\tau ({\mathcal{F}}(\bar T))) \geqslant f(\tau ({\mathcal{F}})) - |T| f^{\prime}(\tau ({\mathcal{F}}))$
, which leads to
$f(\tau ({\mathcal{F}}(\bar T))) \geqslant f(\tau ({\mathcal{F}})) - |T| f^{\prime}(\tau ({\mathcal{F}}))$
, which leads to
completing the proof.
Note that Proposition 1.5 from the proof outline above follows from this lemma with
![]() $f(t) = - (t-n/2) \log \lambda$
.
$f(t) = - (t-n/2) \log \lambda$
.
2.2 Large intersections
In this section we study families
![]() $\mathcal{K}$
in which every pair of sets has ‘large’ intersection.
$\mathcal{K}$
in which every pair of sets has ‘large’ intersection.
Lemma 2.5.
Let
![]() $k \leqslant n/10$
. Let
$k \leqslant n/10$
. Let
![]() $\mathcal{K}$
be an
$\mathcal{K}$
be an
![]() $n$
-uniform family. Suppose that there is an
$n$
-uniform family. Suppose that there is an
![]() $(n-k)$
-element set
$(n-k)$
-element set
![]() $K$
such that we have
$K$
such that we have
![]() $|F \cap K| \geqslant n-2k$
for every
$|F \cap K| \geqslant n-2k$
for every
![]() $F \in{\mathcal{K}}$
. Then we either have
$F \in{\mathcal{K}}$
. Then we either have
![]() $c_{n-k}({\mathcal{K}}) \leqslant 1$
or
$c_{n-k}({\mathcal{K}}) \leqslant 1$
or
![]() $|\bigcap{\mathcal{K}}| \geqslant n-5k$
.
$|\bigcap{\mathcal{K}}| \geqslant n-5k$
.
Proof. Let
![]() $K^{\prime} = \bigcap{\mathcal{K}}$
and
$K^{\prime} = \bigcap{\mathcal{K}}$
and
![]() $R = K \setminus K^{\prime}$
and let
$R = K \setminus K^{\prime}$
and let
![]() $u = |K^{\prime} \setminus K|$
. Note that
$u = |K^{\prime} \setminus K|$
. Note that
![]() $u \in [0, k]$
since
$u \in [0, k]$
since
![]() $|F \setminus K| \leqslant k$
for all
$|F \setminus K| \leqslant k$
for all
![]() $F \in{\mathcal{K}}$
. Denote by
$F \in{\mathcal{K}}$
. Denote by
![]() $\mathcal{A}$
the family of all sets
$\mathcal{A}$
the family of all sets
![]() $F \setminus K^{\prime}$
for
$F \setminus K^{\prime}$
for
![]() $F \in{\mathcal{K}}$
. By the definition of
$F \in{\mathcal{K}}$
. By the definition of
![]() $\mathcal{A}$
we have
$\mathcal{A}$
we have
![]() $\tau ({\mathcal{A}}) \geqslant 2$
. Note also that for any
$\tau ({\mathcal{A}}) \geqslant 2$
. Note also that for any
![]() $A \in{\mathcal{A}}$
we have
$A \in{\mathcal{A}}$
we have
![]() $|A \setminus R| \leqslant k-u$
(since
$|A \setminus R| \leqslant k-u$
(since
![]() $A$
has size at most
$A$
has size at most
![]() $k$
and contains the
$k$
and contains the
![]() $u$
-element set
$u$
-element set
![]() $K^{\prime}\setminus K$
).
$K^{\prime}\setminus K$
).
Note that a minimal covering
![]() $T$
of the family
$T$
of the family
![]() $\mathcal{K}$
is either contained in
$\mathcal{K}$
is either contained in
![]() $K^{\prime}$
and
$K^{\prime}$
and
![]() $|T| = 1$
or
$|T| = 1$
or
![]() $T \cap K^{\prime} = \emptyset$
. In the latter case
$T \cap K^{\prime} = \emptyset$
. In the latter case
![]() $T$
is obviously a minimal covering of
$T$
is obviously a minimal covering of
![]() $\mathcal{A}$
. Thus, we have
$\mathcal{A}$
. Thus, we have
Let
![]() ${\mathcal{T}}_1 \subset{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
be the family of minimal coverings
${\mathcal{T}}_1 \subset{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
be the family of minimal coverings
![]() $T$
of
$T$
of
![]() $\mathcal{A}$
which are subsets of
$\mathcal{A}$
which are subsets of
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{T}}_2 ={\mathcal{T}}_{\leqslant n}({\mathcal{A}}) \setminus{\mathcal{T}}_1$
. We will estimate weights of
${\mathcal{T}}_2 ={\mathcal{T}}_{\leqslant n}({\mathcal{A}}) \setminus{\mathcal{T}}_1$
. We will estimate weights of
![]() ${\mathcal{T}}_1$
and
${\mathcal{T}}_1$
and
![]() ${\mathcal{T}}_2$
separately.
${\mathcal{T}}_2$
separately.
Note that
![]() ${\mathcal{T}}_1 \subset 2^R$
and observe that
${\mathcal{T}}_1 \subset 2^R$
and observe that
![]() $T^{\prime} \not \subset T$
for any distinct
$T^{\prime} \not \subset T$
for any distinct
![]() $T, T^{\prime} \in{\mathcal{T}}_1$
(i.e.
$T, T^{\prime} \in{\mathcal{T}}_1$
(i.e.
![]() ${\mathcal{T}}_1$
is an antichain in
${\mathcal{T}}_1$
is an antichain in
![]() $2^R$
).
$2^R$
).
Proposition 2.6.
Suppose that
![]() ${\mathcal{T}} \subset 2^R$
is an antichain such that every element of
${\mathcal{T}} \subset 2^R$
is an antichain such that every element of
![]() $\mathcal{T}$
has size at least
$\mathcal{T}$
has size at least
![]() $t$
. If
$t$
. If
![]() $\lambda \geqslant |R|$
then
$\lambda \geqslant |R|$
then
 \begin{equation*} \sum _{T \in {\mathcal {T}}} \lambda ^{-|T|} \leqslant \lambda ^{-t} \bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg). \end{equation*}
\begin{equation*} \sum _{T \in {\mathcal {T}}} \lambda ^{-|T|} \leqslant \lambda ^{-t} \bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg). \end{equation*}
This statement also appears in [Reference Frankl5].
Proof. Note that for any
![]() $s \geqslant t$
we have
$s \geqslant t$
we have
![]() $\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg) \leqslant\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg) \lambda ^{s-t}$
and so by the Lubell–Yamamoto–Meshalkin inequality [Reference Jukna9, p. 112, Theorem 8.6]:
$\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg) \leqslant\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg) \lambda ^{s-t}$
and so by the Lubell–Yamamoto–Meshalkin inequality [Reference Jukna9, p. 112, Theorem 8.6]:
 \begin{equation*} \sum _{T \in {\mathcal {T}}} \lambda ^{-|T|} \leqslant \sum _{T \in {\mathcal {T}}} \lambda ^{-t}\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg)/ \bigg(\begin{array}{c}|R|\\[-3pt]|T|\end{array}\bigg) = \lambda ^{-t}\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg) \sum _{T \in {\mathcal {T}}} \frac {1}{\bigg(\begin{array}{c}|R|\\[-3pt]|T|\end{array}\bigg)} \leqslant \lambda ^{-t} \bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg). \end{equation*}
\begin{equation*} \sum _{T \in {\mathcal {T}}} \lambda ^{-|T|} \leqslant \sum _{T \in {\mathcal {T}}} \lambda ^{-t}\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg)/ \bigg(\begin{array}{c}|R|\\[-3pt]|T|\end{array}\bigg) = \lambda ^{-t}\bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg) \sum _{T \in {\mathcal {T}}} \frac {1}{\bigg(\begin{array}{c}|R|\\[-3pt]|T|\end{array}\bigg)} \leqslant \lambda ^{-t} \bigg(\begin{array}{c}|R|\\[-3pt]t\end{array}\bigg). \end{equation*}
By Lemma 2.6 for every
![]() $\lambda \geqslant |R|$
the
$\lambda \geqslant |R|$
the
![]() $\lambda$
-weight of
$\lambda$
-weight of
![]() ${\mathcal{T}}_1$
is at most
${\mathcal{T}}_1$
is at most
Now we estimate the weight of
![]() ${\mathcal{T}}_2$
. Let
${\mathcal{T}}_2$
. Let
![]() ${\mathcal{S}} \subset 2^R$
be the family of all sets
${\mathcal{S}} \subset 2^R$
be the family of all sets
![]() $S \subset R$
such that
$S \subset R$
such that
![]() $S$
does not cover
$S$
does not cover
![]() $\mathcal{A}$
. Then the weight of
$\mathcal{A}$
. Then the weight of
![]() ${\mathcal{T}}_2$
is bounded by the following expression:
${\mathcal{T}}_2$
is bounded by the following expression:
Indeed, the contribution of an element
![]() $T \in{\mathcal{T}}_2$
on the left-hand side is accounted by the term corresponding to
$T \in{\mathcal{T}}_2$
on the left-hand side is accounted by the term corresponding to
![]() $S = T\cap R \in{\mathcal{S}}$
on the right-hand side (since
$S = T\cap R \in{\mathcal{S}}$
on the right-hand side (since
![]() $T\setminus R$
is a minimal covering of the family
$T\setminus R$
is a minimal covering of the family
![]() ${\mathcal{A}}(\bar S)\setminus R$
). Here the family
${\mathcal{A}}(\bar S)\setminus R$
). Here the family
![]() ${\mathcal{A}}(\bar S) \setminus R$
consists of all sets of the form
${\mathcal{A}}(\bar S) \setminus R$
consists of all sets of the form
![]() $A \setminus R$
where
$A \setminus R$
where
![]() $A \in{\mathcal{A}}$
does not intersect
$A \in{\mathcal{A}}$
does not intersect
![]() $S$
. Every element in
$S$
. Every element in
![]() ${\mathcal{A}}(\bar S)\setminus R$
has cardinality at most
${\mathcal{A}}(\bar S)\setminus R$
has cardinality at most
![]() $k-u$
and so by Observation 2.1 and Corollary 2.3 applied to
$k-u$
and so by Observation 2.1 and Corollary 2.3 applied to
![]() ${\mathcal{A}}(\bar S)\setminus R$
for every
${\mathcal{A}}(\bar S)\setminus R$
for every
![]() $\lambda \geqslant k-u$
we have
$\lambda \geqslant k-u$
we have
Let
![]() $S \in{\mathcal{S}}$
. Note that we have the following lower bound on
$S \in{\mathcal{S}}$
. Note that we have the following lower bound on
![]() $\tau ({\mathcal{A}}(\bar S)\setminus R)$
:
$\tau ({\mathcal{A}}(\bar S)\setminus R)$
:
Using this lower bound, (13) and (14) we obtain an upper bound on the weight of
![]() ${\mathcal{T}}_2$
for
${\mathcal{T}}_2$
for
![]() $\lambda \geqslant k$
:
$\lambda \geqslant k$
:
 \begin{align} w_\lambda ({\mathcal{T}}_2) \leqslant \sum _{s = 0}^{\tau ({\mathcal{A}})-1} \lambda ^{-s}\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg) \left (\frac{k-u}{\lambda }\right )^{\tau ({\mathcal{A}}) - s} + \sum _{s = \tau ({\mathcal{A}})}^{|R|} \lambda ^{-s}\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg)\left (\frac{k-u}{\lambda }\right ). \end{align}
\begin{align} w_\lambda ({\mathcal{T}}_2) \leqslant \sum _{s = 0}^{\tau ({\mathcal{A}})-1} \lambda ^{-s}\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg) \left (\frac{k-u}{\lambda }\right )^{\tau ({\mathcal{A}}) - s} + \sum _{s = \tau ({\mathcal{A}})}^{|R|} \lambda ^{-s}\bigg(\begin{array}{c}|R|\\[-3pt]s\end{array}\bigg)\left (\frac{k-u}{\lambda }\right ). \end{align}
Now we combine all obtained inequalities to prove Lemma 1.6. Suppose that
![]() $|K^{\prime}| = |\bigcap{\mathcal{K}}| \lt n-5k$
, we need to show that
$|K^{\prime}| = |\bigcap{\mathcal{K}}| \lt n-5k$
, we need to show that
![]() $c_{n-k}({\mathcal{K}}) \leqslant 1$
holds. We have
$c_{n-k}({\mathcal{K}}) \leqslant 1$
holds. We have
so that
![]() $|K^{\prime}| = n-k + u - r$
holds. In particular, by the assumption
$|K^{\prime}| = n-k + u - r$
holds. In particular, by the assumption
![]() $|K^{\prime}|\lt n-5k$
we have
$|K^{\prime}|\lt n-5k$
we have
![]() $n-k \geqslant r \gt u+4k$
.
$n-k \geqslant r \gt u+4k$
.
Denote
![]() $t = \tau ({\mathcal{A}}) \geqslant 2$
,
$t = \tau ({\mathcal{A}}) \geqslant 2$
,
![]() $r = |R|$
,
$r = |R|$
,
![]() $\rho = \frac{r}{n-k}$
and
$\rho = \frac{r}{n-k}$
and
![]() $\delta = \frac{k-u}{n-k}$
. We can use (12) and (15) with
$\delta = \frac{k-u}{n-k}$
. We can use (12) and (15) with
![]() $\lambda = n-k$
and get:
$\lambda = n-k$
and get:
 \begin{align*} w_{n-k}({\mathcal{T}}_1) &\leqslant \frac{\rho ^{t}}{t!},\\ w_{n-k}({\mathcal{T}}_2) &\leqslant \sum _{s=0}^{t-1} \frac{\rho ^s \delta ^{t-s}}{s!} + \sum _{s=t}^{r} \frac{\rho ^s \delta }{s!}. \end{align*}
\begin{align*} w_{n-k}({\mathcal{T}}_1) &\leqslant \frac{\rho ^{t}}{t!},\\ w_{n-k}({\mathcal{T}}_2) &\leqslant \sum _{s=0}^{t-1} \frac{\rho ^s \delta ^{t-s}}{s!} + \sum _{s=t}^{r} \frac{\rho ^s \delta }{s!}. \end{align*}
By (11), formula
![]() $|K^{\prime}| = n-k+u-r$
and decomposition
$|K^{\prime}| = n-k+u-r$
and decomposition
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{K}}) ={\mathcal{T}}_1\cup{\mathcal{T}}_2$
:
${\mathcal{T}}_{\leqslant n}({\mathcal{K}}) ={\mathcal{T}}_1\cup{\mathcal{T}}_2$
:
 \begin{align*} c_{n-k}({\mathcal{K}}) &\leqslant \frac{n-k+u-r}{n-k} + w_{n-k}({\mathcal{T}}_1) + w_{n-k}({\mathcal{T}}_2) \le \\ & \leqslant \frac{n-k+u-r}{n-k} + \frac{\rho ^t}{t!} + \sum _{s=0}^{t-1} \frac{\rho ^s \delta ^{t-s}}{s!} + \sum _{s=t}^{r} \frac{\rho ^s \delta }{s!}. \end{align*}
\begin{align*} c_{n-k}({\mathcal{K}}) &\leqslant \frac{n-k+u-r}{n-k} + w_{n-k}({\mathcal{T}}_1) + w_{n-k}({\mathcal{T}}_2) \le \\ & \leqslant \frac{n-k+u-r}{n-k} + \frac{\rho ^t}{t!} + \sum _{s=0}^{t-1} \frac{\rho ^s \delta ^{t-s}}{s!} + \sum _{s=t}^{r} \frac{\rho ^s \delta }{s!}. \end{align*}
Both
![]() $\rho$
and
$\rho$
and
![]() $\delta$
are between 0 and 1 so it is easy to see that the second line is the largest when
$\delta$
are between 0 and 1 so it is easy to see that the second line is the largest when
![]() $t=2$
, i.e.
$t=2$
, i.e.
where in the last transition we used
![]() $0\leqslant \delta, \rho \leqslant 1$
to group the last 3 terms together and replace
$0\leqslant \delta, \rho \leqslant 1$
to group the last 3 terms together and replace
![]() $\rho ^2$
by
$\rho ^2$
by
![]() $\rho$
. Recalling
$\rho$
. Recalling
![]() $\rho = \frac{r}{n-k}$
and
$\rho = \frac{r}{n-k}$
and
![]() $\delta = \frac{k-u}{n-k}$
we get
$\delta = \frac{k-u}{n-k}$
we get
since
![]() $r \geqslant 4k$
and
$r \geqslant 4k$
and
![]() $u \geqslant 0$
.
$u \geqslant 0$
.
2.3 Small intersections
In this section, we show that in some cases it is possible to estimate the size of a subfamily
![]() ${\mathcal{B}} \subset{\mathcal{A}}$
provided that elements of
${\mathcal{B}} \subset{\mathcal{A}}$
provided that elements of
![]() $\mathcal{B}$
have very small pairwise intersections.
$\mathcal{B}$
have very small pairwise intersections.
Lemma 2.7.
Let
![]() $\mathcal{A}$
be an
$\mathcal{A}$
be an
![]() $n$
-uniform family where
$n$
-uniform family where
![]() $n$
is sufficiently large. Let
$n$
is sufficiently large. Let
![]() ${\mathcal{B}} \subset{\mathcal{A}}$
be a subfamily such that
${\mathcal{B}} \subset{\mathcal{A}}$
be a subfamily such that
![]() $|B_1 \cap B_2| \leqslant k$
for all distinct
$|B_1 \cap B_2| \leqslant k$
for all distinct
![]() $B_1, B_2 \in{\mathcal{B}}$
. If
$B_1, B_2 \in{\mathcal{B}}$
. If
![]() $k \leqslant \frac{n}{10^4\ln n}$
then one of the following 2 possibilities holds:
$k \leqslant \frac{n}{10^4\ln n}$
then one of the following 2 possibilities holds:
-
1. We have
 $|{\mathcal{B}}| \leqslant n^{C}$
for some absolute constant
$|{\mathcal{B}}| \leqslant n^{C}$
for some absolute constant
 $C$
.
$C$
. -
2. There is a proper subfamily
 ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
 \begin{equation*} 2^{\tau ({\mathcal {A}})}c_n({\mathcal {A}}) \leqslant 2^{\tau ({\mathcal {A}}^{\prime})} c_n({\mathcal {A}}^{\prime}). \end{equation*}
\begin{equation*} 2^{\tau ({\mathcal {A}})}c_n({\mathcal {A}}) \leqslant 2^{\tau ({\mathcal {A}}^{\prime})} c_n({\mathcal {A}}^{\prime}). \end{equation*}
To prove this lemma we will need a result on
![]() $R$
-spread families which was recently used to substantially improve the upper bound in the Erdős-Rado Sunflower problem [Reference Alweiss, Lovett, Wu and Zhang1,Reference Rao12]. We will use a variant of this result proved in [Reference Tao13, Corollary 7]. Let
$R$
-spread families which was recently used to substantially improve the upper bound in the Erdős-Rado Sunflower problem [Reference Alweiss, Lovett, Wu and Zhang1,Reference Rao12]. We will use a variant of this result proved in [Reference Tao13, Corollary 7]. Let
![]() $\bf C$
be a random set, that is a probability distribution on
$\bf C$
be a random set, that is a probability distribution on
![]() $2^X$
for some finite ground set
$2^X$
for some finite ground set
![]() $X$
. For
$X$
. For
![]() $R \geqslant 1$
we say that
$R \geqslant 1$
we say that
![]() $\bf C$
is an
$\bf C$
is an
![]() $R$
-spread random set if for every set
$R$
-spread random set if for every set
![]() $S \subset X$
the probability that
$S \subset X$
the probability that
![]() $\bf C$
contains
$\bf C$
contains
![]() $S$
is at most
$S$
is at most
![]() $R^{-|S|}$
.
$R^{-|S|}$
.
Lemma 2.8 ([Reference Tao13]). Let
![]() $R \gt 1$
,
$R \gt 1$
,
![]() $\delta \in (0, 1)$
and
$\delta \in (0, 1)$
and
![]() $m \geqslant 1$
. Let
$m \geqslant 1$
. Let
![]() $\bf C$
be an
$\bf C$
be an
![]() $R$
-spread random subset of a finite set
$R$
-spread random subset of a finite set
![]() $X$
. Let
$X$
. Let
![]() ${\bf W} \subset X$
be a random set independent from
${\bf W} \subset X$
be a random set independent from
![]() $\bf C$
and such that each
$\bf C$
and such that each
![]() $x \in X$
belongs to
$x \in X$
belongs to
![]() $\bf W$
with independent probability
$\bf W$
with independent probability
![]() $1 - (1-\delta )^m$
. Then there exists a random set
$1 - (1-\delta )^m$
. Then there exists a random set
![]() $\bf C^{\prime}$
with the same distribution as
$\bf C^{\prime}$
with the same distribution as
![]() $\bf C$
and such that
$\bf C$
and such that
We will in fact only need the following corollary of this result.
Corollary 2.9.
In the notations of Lemma 2.8, let
![]() ${\mathcal{C}} \subset 2^X$
be the support of the random set
${\mathcal{C}} \subset 2^X$
be the support of the random set
![]() $\bf C$
. Then the probability that a random set
$\bf C$
. Then the probability that a random set
![]() $\bf W$
of density
$\bf W$
of density
![]() $1 - (1-\delta )^m$
contains an element of
$1 - (1-\delta )^m$
contains an element of
![]() $\mathcal{C}$
is at least
$\mathcal{C}$
is at least
Proof of Lemma
1.8. Denote by
![]() $X$
the ground set of
$X$
the ground set of
![]() $\mathcal{A}$
. Put
$\mathcal{A}$
. Put
![]() $C = 2048$
,
$C = 2048$
,
![]() $R=\frac{n}{2}$
and
$R=\frac{n}{2}$
and
![]() $m = \lceil \log _2{n}+10\rceil$
. Let
$m = \lceil \log _2{n}+10\rceil$
. Let
![]() $\delta = \frac{C}{n}$
and let
$\delta = \frac{C}{n}$
and let
![]() ${\bf U} \subset X$
be a subset of
${\bf U} \subset X$
be a subset of
![]() $X$
of density
$X$
of density
![]() $(1-\delta )^m$
. Let
$(1-\delta )^m$
. Let
![]() ${\bf T} \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
be a random set with distribution
${\bf T} \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
be a random set with distribution
where
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
and such that
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
and such that
![]() $\bf T$
is independent from
$\bf T$
is independent from
![]() $\bf U$
.
$\bf U$
.
Let us suppose that the random set
![]() $\bf T$
is not
$\bf T$
is not
![]() $R$
-spread. By definition, this means that there is a non-empty set
$R$
-spread. By definition, this means that there is a non-empty set
![]() $S \subset X$
such that
$S \subset X$
such that
Let
![]() ${\mathcal{A}}^{\prime} ={\mathcal{A}}(\bar S)$
be the family of
${\mathcal{A}}^{\prime} ={\mathcal{A}}(\bar S)$
be the family of
![]() $A \in{\mathcal{A}}$
such that
$A \in{\mathcal{A}}$
such that
![]() $A \cap S = \emptyset$
. Note that
$A \cap S = \emptyset$
. Note that
![]() $\tau ({\mathcal{A}}^{\prime})\geqslant \tau ({\mathcal{A}}) - |S|$
. Note that if a covering
$\tau ({\mathcal{A}}^{\prime})\geqslant \tau ({\mathcal{A}}) - |S|$
. Note that if a covering
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
satisfies
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
satisfies
![]() $S \subset T$
then
$S \subset T$
then
![]() $T\setminus S$
is a minimal covering of the family
$T\setminus S$
is a minimal covering of the family
![]() ${\mathcal{A}}^{\prime}$
. Thus,
${\mathcal{A}}^{\prime}$
. Thus,
By (16), the left-hand side of this inequality equals to
![]() $c_n({\mathcal{A}}){\mathbb{P}}(S \subset{\bf T})$
. We conclude
$c_n({\mathcal{A}}){\mathbb{P}}(S \subset{\bf T})$
. We conclude
This implies the second alternative of Lemma 2.7. So we may assume that
![]() $\bf T$
is
$\bf T$
is
![]() $R$
-spread.
$R$
-spread.
By Corollary 2.9 (applied to
![]() ${\bf W} = X\setminus{\bf U}$
), we have the following estimate on the probability that there is a covering
${\bf W} = X\setminus{\bf U}$
), we have the following estimate on the probability that there is a covering
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
which does not intersect
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
which does not intersect
![]() $\bf U$
:
$\bf U$
:
here we used the fact that
![]() $R\delta = 1024$
,
$R\delta = 1024$
,
![]() $m \gt \log _2 n + 9$
and that every element of
$m \gt \log _2 n + 9$
and that every element of
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
has size at most
${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
has size at most
![]() $n$
.Footnote
1
We conclude that if we take a random set
$n$
.Footnote
1
We conclude that if we take a random set
![]() $\bf U$
of density
$\bf U$
of density
![]() $(1-\delta )^m$
then with probability at least
$(1-\delta )^m$
then with probability at least
![]() $0.9$
there is a
$0.9$
there is a
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
which does not intersect
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
which does not intersect
![]() $\bf U$
. Let us now show that with probability at least
$\bf U$
. Let us now show that with probability at least
![]() $0.5$
the set
$0.5$
the set
![]() $\bf U$
contains an element of
$\bf U$
contains an element of
![]() $\mathcal{B}$
, provided that
$\mathcal{B}$
, provided that
![]() $\mathcal{B}$
is large enough. Since by definition of
$\mathcal{B}$
is large enough. Since by definition of
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
every
${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
every
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
intersects every set from
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
intersects every set from
![]() $\mathcal{B}$
, this will lead to a contradiction if
$\mathcal{B}$
, this will lead to a contradiction if
![]() $|{\mathcal{B}}|$
is large enough.
$|{\mathcal{B}}|$
is large enough.
Note that an element
![]() $A$
of
$A$
of
![]() $\mathcal{B}$
is contained in
$\mathcal{B}$
is contained in
![]() $\bf U$
with probability
$\bf U$
with probability
provided that
![]() $n$
is sufficiently large. Denote
$n$
is sufficiently large. Denote
![]() $\rho = (1-\delta )^{n m}$
. For
$\rho = (1-\delta )^{n m}$
. For
![]() $A \in{\mathcal{B}}$
denote by
$A \in{\mathcal{B}}$
denote by
![]() $\xi _A$
the indicator of the event that
$\xi _A$
the indicator of the event that
![]() $A \subset \bf U$
and by
$A \subset \bf U$
and by
![]() $\xi$
the sum of
$\xi$
the sum of
![]() $\xi _A$
over
$\xi _A$
over
![]() $\mathcal{B}$
. Hence, we have
$\mathcal{B}$
. Hence, we have
![]() ${\mathbb{E}} \xi _A = \rho$
for every
${\mathbb{E}} \xi _A = \rho$
for every
![]() $A \in{\mathcal{B}}$
and
$A \in{\mathcal{B}}$
and
By Chebyshev’s inequality (see, for instance, [Reference Jukna9, p. 303, (21.2)]), it is enough to show that
![]() $\textrm{Var}\, \xi \lt ({\mathbb{E}} \xi )^2/ 2$
, where
$\textrm{Var}\, \xi \lt ({\mathbb{E}} \xi )^2/ 2$
, where
![]() $\textrm{Var}\, \xi$
denotes the variance of the random variable
$\textrm{Var}\, \xi$
denotes the variance of the random variable
![]() $\xi$
. Let us estimate the correlations
$\xi$
. Let us estimate the correlations
![]() $({\mathbb{E}} \xi _A \xi _{A^{\prime}} - \rho ^2)$
for
$({\mathbb{E}} \xi _A \xi _{A^{\prime}} - \rho ^2)$
for
![]() $A \neq A^{\prime}$
. It is clear that
$A \neq A^{\prime}$
. It is clear that
By (17), we have
provided that
![]() $n$
is large enough. We conclude that the variance of
$n$
is large enough. We conclude that the variance of
![]() $\xi$
is at most
$\xi$
is at most
which is less than
![]() $({\mathbb{E}}\xi )^2/2$
if
$({\mathbb{E}}\xi )^2/2$
if
![]() $|{\mathcal{B}}| \gt 10/\rho$
. Therefore, provided, that
$|{\mathcal{B}}| \gt 10/\rho$
. Therefore, provided, that
![]() $|{\mathcal{B}}| \geqslant n^{3000} \gt 10/\rho$
, with probability at least
$|{\mathcal{B}}| \geqslant n^{3000} \gt 10/\rho$
, with probability at least
![]() $0.5$
the random set
$0.5$
the random set
![]() $\bf U$
contains an element of
$\bf U$
contains an element of
![]() $\mathcal{B}$
and with probability at least
$\mathcal{B}$
and with probability at least
![]() $0.9$
it does not intersect an element of
$0.9$
it does not intersect an element of
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
. But these two events cannot happen simultaneously. This is a contradiction and Lemma 2.7 is proved.
${\mathcal{T}}_{\leqslant n}({\mathcal{A}})$
. But these two events cannot happen simultaneously. This is a contradiction and Lemma 2.7 is proved.
2.4 Moments of the degree function
In this section, we show that if we have an
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{A}$
such that
$\mathcal{A}$
such that
![]() $\tau ({\mathcal{A}})$
is ‘large’ but
$\tau ({\mathcal{A}})$
is ‘large’ but
![]() $|{\mathcal{A}}|$
is ‘small’ then the
$|{\mathcal{A}}|$
is ‘small’ then the
![]() $l$
-wise intersections of sets from
$l$
-wise intersections of sets from
![]() $\mathcal{A}$
are very small on average. More precisely, we will prove the following:
$\mathcal{A}$
are very small on average. More precisely, we will prove the following:
Lemma 2.10.
Let
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $m, t \geqslant 1$
. Let
$m, t \geqslant 1$
. Let
![]() $\mathcal{A}$
be an
$\mathcal{A}$
be an
![]() $n$
-uniform family of size at most
$n$
-uniform family of size at most
![]() $e^{m}$
and
$e^{m}$
and
![]() $\tau ({\mathcal{A}}) \geqslant t$
. Then, for every
$\tau ({\mathcal{A}}) \geqslant t$
. Then, for every
![]() $l \geqslant 1$
, there is a subfamily
$l \geqslant 1$
, there is a subfamily
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
![]() $\tau ({\mathcal{A}} \setminus{\mathcal{A}}^{\prime}) \leqslant t/2$
and for every
$\tau ({\mathcal{A}} \setminus{\mathcal{A}}^{\prime}) \leqslant t/2$
and for every
![]() $i = 1, \ldots, l$
we have
$i = 1, \ldots, l$
we have
where
![]() $C_l \ll 2^{l^2}$
depends only on
$C_l \ll 2^{l^2}$
depends only on
![]() $l$
and the average is taken over all
$l$
and the average is taken over all
![]() $A_1, \ldots, A_l \in{\mathcal{A}}$
chosen uniformly and independently.
$A_1, \ldots, A_l \in{\mathcal{A}}$
chosen uniformly and independently.
Let
![]() $X$
denote the ground set of an
$X$
denote the ground set of an
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{F}$
. For a function
$\mathcal{F}$
. For a function
![]() $f\,:\, X \rightarrow{\mathbb{R}}_+$
and
$f\,:\, X \rightarrow{\mathbb{R}}_+$
and
![]() $S \subset X$
we denote by
$S \subset X$
we denote by
![]() $f(S)$
the sum
$f(S)$
the sum
![]() $\sum _{x\in S}f(x)$
.
$\sum _{x\in S}f(x)$
.
Observation 2.11.
For any non-zero function
![]() $f\,:\, X \rightarrow{\mathbb{R}}_+$
and any family
$f\,:\, X \rightarrow{\mathbb{R}}_+$
and any family
![]() $\mathcal{F}$
on
$\mathcal{F}$
on
![]() $X$
we have
$X$
we have
 \begin{equation} \sum _{F \in{\mathcal{F}}} \left (1 - \frac{f(F)}{f(X)} \right )^{\tau ({\mathcal{F}})-1} \geqslant 1. \end{equation}
\begin{equation} \sum _{F \in{\mathcal{F}}} \left (1 - \frac{f(F)}{f(X)} \right )^{\tau ({\mathcal{F}})-1} \geqslant 1. \end{equation}
In particular, for any
![]() $f\,:\, X \rightarrow{\mathbb{R}}_+$
there always exists
$f\,:\, X \rightarrow{\mathbb{R}}_+$
there always exists
![]() $F \in{\mathcal{F}}$
such that
$F \in{\mathcal{F}}$
such that
Proof. Put
![]() $t = \tau ({\mathcal{F}}) - 1$
and let
$t = \tau ({\mathcal{F}}) - 1$
and let
![]() $x_1, \ldots, x_t \in X$
be a sequence of random independent elements of
$x_1, \ldots, x_t \in X$
be a sequence of random independent elements of
![]() $X$
sampled according to distribution
$X$
sampled according to distribution
![]() $f$
. Then the left-hand side of (18) is the expectation of the number of sets
$f$
. Then the left-hand side of (18) is the expectation of the number of sets
![]() $F \in{\mathcal{F}}$
which are not covered by the set
$F \in{\mathcal{F}}$
which are not covered by the set
![]() $\{x_1, \ldots, x_t\}$
. Since
$\{x_1, \ldots, x_t\}$
. Since
![]() $\tau ({\mathcal{F}}) \gt t$
, this number is always positive and (18) follows.
$\tau ({\mathcal{F}}) \gt t$
, this number is always positive and (18) follows.
The following variant of this observation will be slightly more convenient to use.
Corollary 2.12.
Let
![]() $f_1, \ldots, f_l\,:\, X \rightarrow{\mathbb{R}}_+$
be arbitrary non-zero functions and
$f_1, \ldots, f_l\,:\, X \rightarrow{\mathbb{R}}_+$
be arbitrary non-zero functions and
![]() $\mathcal{F}$
be an arbitrary family on
$\mathcal{F}$
be an arbitrary family on
![]() $X$
. Then there exists
$X$
. Then there exists
![]() $F \in{\mathcal{F}}$
such that
$F \in{\mathcal{F}}$
such that
![]() $f_i(F) \leqslant f_i(X) l (1 - |{\mathcal{F}}|^{-1/(\tau ({\mathcal{F}})-1)})$
for any
$f_i(F) \leqslant f_i(X) l (1 - |{\mathcal{F}}|^{-1/(\tau ({\mathcal{F}})-1)})$
for any
![]() $i = 1, \ldots, l$
.
$i = 1, \ldots, l$
.
Proof. Apply Observation 2.11 to
![]() $f(x) = \sum _{i = 1}^l \frac{f_i(x)}{f_i(X)}$
.
$f(x) = \sum _{i = 1}^l \frac{f_i(x)}{f_i(X)}$
.
For a family
![]() $\mathcal{F}$
on the ground set
$\mathcal{F}$
on the ground set
![]() $X$
let
$X$
let
![]() $d_{\mathcal{F}}\,:\, X \rightarrow{\mathbb{R}}_+$
be the degree function of the family
$d_{\mathcal{F}}\,:\, X \rightarrow{\mathbb{R}}_+$
be the degree function of the family
![]() $\mathcal{F}$
, that is, if
$\mathcal{F}$
, that is, if
![]() $x \in X$
then
$x \in X$
then
![]() $d_{\mathcal{F}}(x)$
equals to the number of sets
$d_{\mathcal{F}}(x)$
equals to the number of sets
![]() $F \in{\mathcal{F}}$
which contain
$F \in{\mathcal{F}}$
which contain
![]() $x$
. Let
$x$
. Let
![]() $d_{\mathcal{F}}^l\,:\, X \rightarrow{\mathbb{R}}_+$
denote the
$d_{\mathcal{F}}^l\,:\, X \rightarrow{\mathbb{R}}_+$
denote the
![]() $l$
th power of
$l$
th power of
![]() $d_{\mathcal{F}}$
, i.e.
$d_{\mathcal{F}}$
, i.e.
![]() $d_{\mathcal{F}}^l(x) = (d_{\mathcal{F}}(x))^l$
. By abusing notation, we also denote by
$d_{\mathcal{F}}^l(x) = (d_{\mathcal{F}}(x))^l$
. By abusing notation, we also denote by
![]() $d^l_{\mathcal{F}}$
the number
$d^l_{\mathcal{F}}$
the number
![]() $d^l_{\mathcal{F}}(X)$
.
$d^l_{\mathcal{F}}(X)$
.
Observation 2.13.
For any family
![]() $\mathcal{F}$
and any
$\mathcal{F}$
and any
![]() $l \geqslant 1$
we have the following identity
$l \geqslant 1$
we have the following identity
where
![]() $F_1, \ldots, F_l$
are taken from
$F_1, \ldots, F_l$
are taken from
![]() $\mathcal{F}$
uniformly and independently.
$\mathcal{F}$
uniformly and independently.
Applying Corollary 2.12 to functions
![]() $d_{\mathcal{F}}^1, \ldots, d_{\mathcal{F}}^l$
we obtain the following result.
$d_{\mathcal{F}}^1, \ldots, d_{\mathcal{F}}^l$
we obtain the following result.
Lemma 2.14.
Let
![]() $l, t \geqslant 1$
, let
$l, t \geqslant 1$
, let
![]() ${\mathcal{F}} \subset{\mathcal{A}}$
be a subfamily of a family
${\mathcal{F}} \subset{\mathcal{A}}$
be a subfamily of a family
![]() $\mathcal{A}$
such that
$\mathcal{A}$
such that
![]() $\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \geqslant t+1$
. Then there exists
$\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \geqslant t+1$
. Then there exists
![]() $A \in{\mathcal{A}} \setminus{\mathcal{F}}$
such that the following holds. Denote
$A \in{\mathcal{A}} \setminus{\mathcal{F}}$
such that the following holds. Denote
![]() ${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{A\}$
, then for any
${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{A\}$
, then for any
![]() $i = 1, \ldots, l$
we have:
$i = 1, \ldots, l$
we have:
Proof. For
![]() $i = 1, \ldots, l$
let
$i = 1, \ldots, l$
let
 \begin{equation} f_i(x) = \sum _{j = 1}^{i-1}\bigg(\begin{array}{c}i\\[-3pt]j\end{array}\bigg) d_{\mathcal{F}}^j(x). \end{equation}
\begin{equation} f_i(x) = \sum _{j = 1}^{i-1}\bigg(\begin{array}{c}i\\[-3pt]j\end{array}\bigg) d_{\mathcal{F}}^j(x). \end{equation}
Apply Corollary 2.12 to functions
![]() $f_1, \ldots, f_l$
and the family
$f_1, \ldots, f_l$
and the family
![]() ${\mathcal{A}} \setminus{\mathcal{F}}$
. Then there exists
${\mathcal{A}} \setminus{\mathcal{F}}$
. Then there exists
![]() $A \in{\mathcal{A}}\setminus{\mathcal{F}}$
such that for every
$A \in{\mathcal{A}}\setminus{\mathcal{F}}$
such that for every
![]() $i = 1, \ldots, l$
we have
$i = 1, \ldots, l$
we have
by the standard inequality
![]() $1-e^{-x} \leqslant x$
. But note that for
$1-e^{-x} \leqslant x$
. But note that for
![]() ${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{A\}$
by (20) we have
${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{A\}$
by (20) we have
Note that
![]() $d_{\mathcal{F}}^i$
is monotone increasing in
$d_{\mathcal{F}}^i$
is monotone increasing in
![]() $i$
and so
$i$
and so
 \begin{equation*} f_i(X) = \sum _{j = 1}^{i-1} \bigg(\begin{array}{c}i\\[-3pt]j\end{array}\bigg) d_{\mathcal {F}}^j \leqslant 2^i d_{\mathcal {F}}^{i-1}. \end{equation*}
\begin{equation*} f_i(X) = \sum _{j = 1}^{i-1} \bigg(\begin{array}{c}i\\[-3pt]j\end{array}\bigg) d_{\mathcal {F}}^j \leqslant 2^i d_{\mathcal {F}}^{i-1}. \end{equation*}
Now we are ready to prove Lemma 2.10.
Proof of Lemma
2.10. Let
![]() $X$
denote the ground set of
$X$
denote the ground set of
![]() $\mathcal{A}$
and put
$\mathcal{A}$
and put
![]() $\gamma = 2l m/t$
.
$\gamma = 2l m/t$
.
Let
![]() ${\mathcal{F}} \subset{\mathcal{A}}$
be a maximal subfamily in
${\mathcal{F}} \subset{\mathcal{A}}$
be a maximal subfamily in
![]() $\mathcal{A}$
such that for every
$\mathcal{A}$
such that for every
![]() $i = 1, \ldots, l$
we have
$i = 1, \ldots, l$
we have
Note that if
![]() $|{\mathcal{F}}| = 1$
then (23) clearly holds and so
$|{\mathcal{F}}| = 1$
then (23) clearly holds and so
![]() $\mathcal{F}$
is well-defined. To prove Lemma 1.9 it is clearly enough to show that any such
$\mathcal{F}$
is well-defined. To prove Lemma 1.9 it is clearly enough to show that any such
![]() $\mathcal{F}$
satisfies
$\mathcal{F}$
satisfies
![]() $\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \leqslant t/ 2$
. Indeed, in this case we have
$\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \leqslant t/ 2$
. Indeed, in this case we have
![]() $\tau ({\mathcal{F}}) \geqslant t/2$
and, in particular,
$\tau ({\mathcal{F}}) \geqslant t/2$
and, in particular,
![]() $|{\mathcal{F}}| \geqslant t/2$
. Then
$|{\mathcal{F}}| \geqslant t/2$
. Then
![]() $\gamma |{\mathcal{F}}| \geqslant m \geqslant 1$
and, therefore, the first term in (23) dominates the second one.
$\gamma |{\mathcal{F}}| \geqslant m \geqslant 1$
and, therefore, the first term in (23) dominates the second one.
Now we show that it is impossible to have
![]() $\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \geqslant t/2 + 1$
. Indeed, in this case we can apply Lemma 2.14 to the pair
$\tau ({\mathcal{A}} \setminus{\mathcal{F}}) \geqslant t/2 + 1$
. Indeed, in this case we can apply Lemma 2.14 to the pair
![]() ${\mathcal{F}} \subset{\mathcal{A}}$
and obtain a family
${\mathcal{F}} \subset{\mathcal{A}}$
and obtain a family
![]() ${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{ A \}$
such that (19) holds for
${\mathcal{F}}^{\prime} ={\mathcal{F}} \cup \{ A \}$
such that (19) holds for
![]() $i = 1, \ldots, l$
and with
$i = 1, \ldots, l$
and with
![]() $t/2$
instead of
$t/2$
instead of
![]() $t$
. Note that
$t$
. Note that
![]() $l \log |{\mathcal{A}}|/(t/2) \leqslant \gamma$
. On the other hand, the maximality of
$l \log |{\mathcal{A}}|/(t/2) \leqslant \gamma$
. On the other hand, the maximality of
![]() $\mathcal{F}$
implies that there is some
$\mathcal{F}$
implies that there is some
![]() $i \in \{2, \ldots, l\}$
(
$i \in \{2, \ldots, l\}$
(
![]() $i \neq 1$
because otherwise (23) holds automatically) such that
$i \neq 1$
because otherwise (23) holds automatically) such that
On the other hand, from (19) we get
Combining these two inequalities and cancelling same terms we get
So if we let
![]() $x = \gamma |{\mathcal{F}}|$
then, after dividing by
$x = \gamma |{\mathcal{F}}|$
then, after dividing by
![]() $2^{i^2}n$
, we obtain
$2^{i^2}n$
, we obtain
Recall that
![]() $i \geqslant 2$
. So if
$i \geqslant 2$
. So if
![]() $x \geqslant 1$
then the first term on the right-hand side (24) is greater than
$x \geqslant 1$
then the first term on the right-hand side (24) is greater than
![]() $2^{-i+1}x$
. If
$2^{-i+1}x$
. If
![]() $x \lt 1$
then the second term is greater than
$x \lt 1$
then the second term is greater than
![]() $2^{-i+1}x$
. In both cases, we arrive at a contradiction. Lemma 1.9 is proved.
$2^{-i+1}x$
. In both cases, we arrive at a contradiction. Lemma 1.9 is proved.
2.5 Bounded degree families
In this section, we consider intersecting families of bounded degree. In fact, this is essentially the only place in the paper where we use the fact that the family is intersecting. The idea to consider low-degree families in the Erdős–Lovász problem also appears in [Reference Frankl6, Section 2].
Lemma 2.15.
Let
![]() $n \geqslant 1$
and
$n \geqslant 1$
and
![]() $r \geqslant 2l$
be such that
$r \geqslant 2l$
be such that
![]() $r^2 \leqslant l^3 n$
. Let
$r^2 \leqslant l^3 n$
. Let
![]() $\mathcal{B}$
be an
$\mathcal{B}$
be an
![]() $n$
-uniform intersecting family of size
$n$
-uniform intersecting family of size
![]() $r$
such that every
$r$
such that every
![]() $l$
distinct sets from
$l$
distinct sets from
![]() $\mathcal{B}$
have an empty intersection. Then
$\mathcal{B}$
have an empty intersection. Then
Proof of Lemma
2.15. In order to prove this lemma, we need to recall the classical Erős–Lovász encoding procedure which they used to obtain the bound
![]() $|{\mathcal{F}}| \leqslant n^n$
for the size of an
$|{\mathcal{F}}| \leqslant n^n$
for the size of an
![]() $n$
-uniform maximal intersecting family. Denote
$n$
-uniform maximal intersecting family. Denote
![]() ${\mathcal{B}} = \{F_1, \ldots, F_r\}$
.
${\mathcal{B}} = \{F_1, \ldots, F_r\}$
.
Procedure.
Let
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
![]() $S \subset T$
be a proper subset. From the pair
$S \subset T$
be a proper subset. From the pair
![]() $(T, S)$
we construct a new pair
$(T, S)$
we construct a new pair
![]() $(T, S^{\prime})$
as follows. Let
$(T, S^{\prime})$
as follows. Let
![]() $i \in [r]$
be the minimum number so that
$i \in [r]$
be the minimum number so that
![]() $F_i \cap S = \emptyset$
. Pick arbitrary
$F_i \cap S = \emptyset$
. Pick arbitrary
![]() $x \in F_i \cap T$
and let
$x \in F_i \cap T$
and let
![]() $S^{\prime} = S \cup \{x\}$
.
$S^{\prime} = S \cup \{x\}$
.
So if we apply this procedure to any
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
![]() $S = \emptyset$
, then we will obtain a sequence of sets of the form:
$S = \emptyset$
, then we will obtain a sequence of sets of the form:
Note that the sequence
![]() $(S_0, \ldots, S_{|T|})$
is not determined uniquely by
$(S_0, \ldots, S_{|T|})$
is not determined uniquely by
![]() $T$
since there may be an ambiguity in the choice of
$T$
since there may be an ambiguity in the choice of
![]() $x \in F_i \cap T$
during the procedure. Let
$x \in F_i \cap T$
during the procedure. Let
![]() ${\mathcal{T}}_1 \subset{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
the the family of sets
${\mathcal{T}}_1 \subset{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
the the family of sets
![]() $T$
such that the sequence
$T$
such that the sequence
![]() $(S_0, \ldots, S_{|T|})$
is determined uniquely by
$(S_0, \ldots, S_{|T|})$
is determined uniquely by
![]() $T$
. In other words, at each step we have an equality
$T$
. In other words, at each step we have an equality
![]() $|F_i \cap T| = 1$
. Let
$|F_i \cap T| = 1$
. Let
![]() ${\mathcal{T}}_2 ={\mathcal{T}}_{\leqslant n}({\mathcal{B}}) \setminus{\mathcal{T}}_1$
.
${\mathcal{T}}_2 ={\mathcal{T}}_{\leqslant n}({\mathcal{B}}) \setminus{\mathcal{T}}_1$
.
Now we denote by
![]() $\mathcal J$
the set of all sequences
$\mathcal J$
the set of all sequences
![]() $(S_0, S_1, \ldots, S_k)$
which may occur during the procedure starting from some
$(S_0, S_1, \ldots, S_k)$
which may occur during the procedure starting from some
![]() $T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
$T \in{\mathcal{T}}_{\leqslant n}({\mathcal{B}})$
and
![]() $S = \emptyset$
. Let
$S = \emptyset$
. Let
![]() ${\mathcal{J}} ={\mathcal{J}}_1 \cup{\mathcal{J}}_2$
be the decomposition arising from the decomposition
${\mathcal{J}} ={\mathcal{J}}_1 \cup{\mathcal{J}}_2$
be the decomposition arising from the decomposition
![]() ${\mathcal{T}}_{\leqslant n}({\mathcal{B}}) ={\mathcal{T}}_1 \cup{\mathcal{T}}_2$
. The weight
${\mathcal{T}}_{\leqslant n}({\mathcal{B}}) ={\mathcal{T}}_1 \cup{\mathcal{T}}_2$
. The weight
![]() $w(\bar S)$
of a sequence
$w(\bar S)$
of a sequence
![]() $\bar S = (S_0, \ldots, S_k)$
is defined to be
$\bar S = (S_0, \ldots, S_k)$
is defined to be
![]() $n^{-|S_k|}$
. The standard Erdős–Lovász [Reference Erdős and Lovász4] argument shows that the weight
$n^{-|S_k|}$
. The standard Erdős–Lovász [Reference Erdős and Lovász4] argument shows that the weight
![]() $w({\mathcal{J}})$
of the family
$w({\mathcal{J}})$
of the family
![]() $\mathcal{J}$
is always at most
$\mathcal{J}$
is always at most
![]() $1$
. We omit the proof since it is very similar in spirit to the proof of Lemma 2.2 and Corollary 2.3.
$1$
. We omit the proof since it is very similar in spirit to the proof of Lemma 2.2 and Corollary 2.3.
On the other hand, we can bound weights of families
![]() ${\mathcal{T}}_1$
and
${\mathcal{T}}_1$
and
![]() ${\mathcal{T}}_2$
in terms of weights of
${\mathcal{T}}_2$
in terms of weights of
![]() ${\mathcal{J}}_1$
and
${\mathcal{J}}_1$
and
![]() ${\mathcal{J}}_2$
as follows:
${\mathcal{J}}_2$
as follows:
So it is enough to obtain a good upper bound on
![]() $w({\mathcal{J}}_1)$
. For
$w({\mathcal{J}}_1)$
. For
![]() $T \in{\mathcal{T}}_1$
we denote by
$T \in{\mathcal{T}}_1$
we denote by
![]() $S_i(T)$
the
$S_i(T)$
the
![]() $i$
-th element of the sequence of
$i$
-th element of the sequence of
![]() $T$
in the process (which is defined uniquely for elements of
$T$
in the process (which is defined uniquely for elements of
![]() ${\mathcal{T}}_1$
). We denote by
${\mathcal{T}}_1$
). We denote by
![]() $A_i(T) \in{\mathcal{B}}$
the element of
$A_i(T) \in{\mathcal{B}}$
the element of
![]() $\mathcal{B}$
which was picked at step
$\mathcal{B}$
which was picked at step
![]() $i-1$
of the process. In particular,
$i-1$
of the process. In particular,
![]() $S_{i-1}(T) \cap A_i(T) = \emptyset$
and
$S_{i-1}(T) \cap A_i(T) = \emptyset$
and
![]() $|S_{i}(T) \cap A_i(T)| = 1$
. We denote by
$|S_{i}(T) \cap A_i(T)| = 1$
. We denote by
![]() $x_i(T)$
the unique element in the intersection
$x_i(T)$
the unique element in the intersection
![]() $S_{i}(T) \cap A_i(T)$
.
$S_{i}(T) \cap A_i(T)$
.
The uniqueness of the sequence
![]() $\bar S(T)$
implies that for any
$\bar S(T)$
implies that for any
![]() $j \lt i$
we have
$j \lt i$
we have
Indeed, otherwise at step
![]() $j$
we may have picked the element
$j$
we may have picked the element
![]() $x_i(T)$
instead of
$x_i(T)$
instead of
![]() $x_j(T)$
and thus form a different sequence
$x_j(T)$
and thus form a different sequence
![]() $(S^{\prime}_0, \ldots, S^{\prime}_{|T|})$
which corresponds to the covering
$(S^{\prime}_0, \ldots, S^{\prime}_{|T|})$
which corresponds to the covering
![]() $T$
. We conclude that
$T$
. We conclude that
Since the family
![]() $\mathcal{B}$
is intersecting and does not contain
$\mathcal{B}$
is intersecting and does not contain
![]() $l$
-wise intersections we have the following upper bound on the size of
$l$
-wise intersections we have the following upper bound on the size of
![]() $Y_i(T)$
:
$Y_i(T)$
:
For
![]() $q \geqslant 0$
and a given sequence
$q \geqslant 0$
and a given sequence
![]() $\bar S = (S_0 \subset S_1 \subset \ldots \subset S_q)$
we denote by
$\bar S = (S_0 \subset S_1 \subset \ldots \subset S_q)$
we denote by
![]() ${\mathcal{J}}_1(\bar S)$
the family of sequences from
${\mathcal{J}}_1(\bar S)$
the family of sequences from
![]() ${\mathcal{J}}_1$
which start from
${\mathcal{J}}_1$
which start from
![]() $\bar S$
.
$\bar S$
.
Observation 2.16.
For any sequence
![]() $\bar S = (S_0, S_1, \ldots, S_{i-1})$
which is a part of the sequence of some
$\bar S = (S_0, S_1, \ldots, S_{i-1})$
which is a part of the sequence of some
![]() $T\in{\mathcal{T}}_1$
such that
$T\in{\mathcal{T}}_1$
such that
![]() $|T| \gt i$
we have
$|T| \gt i$
we have
Proof. Indeed, the observation says that a sequence
![]() $\bar S$
can be extended only by the elements of the set
$\bar S$
can be extended only by the elements of the set
![]() $Y_i(T)$
and, therefore, its weight is bounded by the sum of the weights of all possible extensions.
$Y_i(T)$
and, therefore, its weight is bounded by the sum of the weights of all possible extensions.
For
![]() $q \geqslant 0$
let
$q \geqslant 0$
let
The following proposition will finish the proof. Note that
![]() $\tau ({\mathcal{B}}) \geqslant r/l$
because any element
$\tau ({\mathcal{B}}) \geqslant r/l$
because any element
![]() $x \in X$
covers at most
$x \in X$
covers at most
![]() $l$
sets from
$l$
sets from
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Proposition 2.17.
For any
![]() $q \in [0, r/l]$
we have
$q \in [0, r/l]$
we have
 \begin{equation*} f(q) \leqslant \prod _{i = q}^{[r/l]-1} \left (1 - \frac {i-1}{n l}\right ). \end{equation*}
\begin{equation*} f(q) \leqslant \prod _{i = q}^{[r/l]-1} \left (1 - \frac {i-1}{n l}\right ). \end{equation*}
Proof. The proof is by induction. The base case
![]() $q = [r/l]$
states that
$q = [r/l]$
states that
![]() $f([r/l]) \leqslant 1$
which we already know by the Erdős–Lovász argument.
$f([r/l]) \leqslant 1$
which we already know by the Erdős–Lovász argument.
For the induction step, let
![]() $T \in{\mathcal{T}}_1$
be a covering on which the maximum in (28) is attained. Now apply Observation 2.16 and the induction hypothesis to conclude that
$T \in{\mathcal{T}}_1$
be a covering on which the maximum in (28) is attained. Now apply Observation 2.16 and the induction hypothesis to conclude that
where
![]() $T$
corresponds to a maximizer of the supremum on the left-hand side.
$T$
corresponds to a maximizer of the supremum on the left-hand side.
Substituting
![]() $q = 0$
in Proposition 2.17 we get
$q = 0$
in Proposition 2.17 we get
 \begin{equation*} w({\mathcal {J}}_1) = f(0) \leqslant \prod _{i = 1}^{[r/l]-1} \left(1 - \frac {i-1}{n l}\right) \leqslant \left ( 1 - \frac {r}{2n l^2} \right )^{r/2l} \leqslant e^{ - \frac {r^2}{4l^3 n}}. \end{equation*}
\begin{equation*} w({\mathcal {J}}_1) = f(0) \leqslant \prod _{i = 1}^{[r/l]-1} \left(1 - \frac {i-1}{n l}\right) \leqslant \left ( 1 - \frac {r}{2n l^2} \right )^{r/2l} \leqslant e^{ - \frac {r^2}{4l^3 n}}. \end{equation*}
Let
![]() $y = \frac{r^2}{l^3 n}$
. By assumption we have
$y = \frac{r^2}{l^3 n}$
. By assumption we have
![]() $y \leqslant 1$
and so we have the following elementary inequality:
$y \leqslant 1$
and so we have the following elementary inequality:
![]() $e^{-y/4}+1 \leqslant 2 e^{-y/10}$
. By (27), the desired inequality (25) follows.
$e^{-y/4}+1 \leqslant 2 e^{-y/10}$
. By (27), the desired inequality (25) follows.
The following simple corollary will be more convenient to combine with Lemma 2.4 in the proof of Theorem 1.1.
Corollary 2.18.
Let
![]() $n \geqslant 1$
and
$n \geqslant 1$
and
![]() $r \geqslant 2l$
be such that
$r \geqslant 2l$
be such that
![]() $r^2 \leqslant l^3 n$
. Let
$r^2 \leqslant l^3 n$
. Let
![]() $\mathcal{B}$
be an
$\mathcal{B}$
be an
![]() $n$
-uniform intersecting family of size
$n$
-uniform intersecting family of size
![]() $r$
such that every
$r$
such that every
![]() $l$
distinct sets from
$l$
distinct sets from
![]() $\mathcal{B}$
have an empty intersection. Then for
$\mathcal{B}$
have an empty intersection. Then for
![]() $k \leqslant \frac{r}{20 l^3}$
we have
$k \leqslant \frac{r}{20 l^3}$
we have
Proof. Note that any minimal covering of
![]() $\mathcal{B}$
has size at most
$\mathcal{B}$
has size at most
![]() $|{\mathcal{B}}| = r$
. So for any
$|{\mathcal{B}}| = r$
. So for any
![]() $\lambda \leqslant 1$
we have
$\lambda \leqslant 1$
we have
By Lemma 2.15, if we let
![]() $\lambda = e^{- \frac{r}{10 l^3 n}}$
then
$\lambda = e^{- \frac{r}{10 l^3 n}}$
then
![]() $c_{\lambda n}({\mathcal{B}}) \leqslant 1$
. Now if
$c_{\lambda n}({\mathcal{B}}) \leqslant 1$
. Now if
![]() $k \leqslant \frac{r}{20 l^3}$
then
$k \leqslant \frac{r}{20 l^3}$
then
which implies that
![]() $c_{n-k}({\mathcal{B}}) \leqslant 1$
.
$c_{n-k}({\mathcal{B}}) \leqslant 1$
.
3. Proof of Theorem 1.4
In this section, we put all developed machinery together to prove Theorem 1.4. We restate the theorem below for convenience.
Theorem 3.1.
For all
![]() $\varepsilon \gt 0$
and sufficiently large
$\varepsilon \gt 0$
and sufficiently large
![]() $n \gt n_0(\varepsilon )$
, we have the following. Let
$n \gt n_0(\varepsilon )$
, we have the following. Let
![]() $\mathcal{A}$
be an intersecting
$\mathcal{A}$
be an intersecting
![]() $n$
-uniform family. Then
$n$
-uniform family. Then
Now we begin the proof of Theorem 1.4. Fix
![]() $n \gt n_0(\varepsilon )$
and suppose that there exists an intersecting family
$n \gt n_0(\varepsilon )$
and suppose that there exists an intersecting family
![]() $\mathcal{A}$
which violates (5). Let
$\mathcal{A}$
which violates (5). Let
![]() $\mathcal{A}$
be any such family of minimal possible size. In particular,
$\mathcal{A}$
be any such family of minimal possible size. In particular,
![]() $\mathcal{A}$
is a
$\mathcal{A}$
is a
![]() $\tau$
-critical family and
$\tau$
-critical family and
![]() $\tau ({\mathcal{A}}) \gt n^{2/3}$
because otherwise the right-hand side of (29) is greater than 1 and so we done by Corollary 2.3.
$\tau ({\mathcal{A}}) \gt n^{2/3}$
because otherwise the right-hand side of (29) is greater than 1 and so we done by Corollary 2.3.
By the minimality of
![]() $\mathcal{A}$
, for any proper subfamily
$\mathcal{A}$
, for any proper subfamily
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
we have
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
we have
We are going to apply Lemma 2.4 to various subfamilies of
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $f(t) = t^{1.5-\varepsilon } - 1$
. Let
$f(t) = t^{1.5-\varepsilon } - 1$
. Let
![]() $\lambda = e^{-f^{\prime}(\tau ({\mathcal{A}}))} = e^{-(1.5-\varepsilon ) \frac{\tau ({\mathcal{A}})^{0.5-\varepsilon }}{n}}$
and
$\lambda = e^{-f^{\prime}(\tau ({\mathcal{A}}))} = e^{-(1.5-\varepsilon ) \frac{\tau ({\mathcal{A}})^{0.5-\varepsilon }}{n}}$
and
![]() $k =\sqrt{\tau ({\mathcal{A}})}$
.
$k =\sqrt{\tau ({\mathcal{A}})}$
.
Proposition 3.2.
For any
![]() $A_1, A_2 \in{\mathcal{A}}$
we have
$A_1, A_2 \in{\mathcal{A}}$
we have
Proof. Suppose that there are some
![]() $A_1, A_2 \in{\mathcal{A}}$
such that
$A_1, A_2 \in{\mathcal{A}}$
such that
![]() $|A_1 \cap A_2| = x \in [k, n-k]$
. Denote
$|A_1 \cap A_2| = x \in [k, n-k]$
. Denote
![]() ${\mathcal{A}}^{\prime} = \{A_1, A_2\}$
and note that
${\mathcal{A}}^{\prime} = \{A_1, A_2\}$
and note that
where the latter inequality holds for every
![]() $x \in [k, n-k]$
and any
$x \in [k, n-k]$
and any
![]() $k \leqslant 0.1 n$
.
$k \leqslant 0.1 n$
.
Since
![]() $\frac{n-k/3}{n} \leqslant \lambda$
for sufficiently large
$\frac{n-k/3}{n} \leqslant \lambda$
for sufficiently large
![]() $n$
, by Lemma 2.4 applied to
$n$
, by Lemma 2.4 applied to
![]() ${\mathcal{A}}^{\prime}$
we deduce that (30) holds for
${\mathcal{A}}^{\prime}$
we deduce that (30) holds for
![]() $\mathcal{A}$
as well. This is, however, a contradiction to our initial assumption that
$\mathcal{A}$
as well. This is, however, a contradiction to our initial assumption that
![]() $\mathcal{A}$
does not satisfy (29).
$\mathcal{A}$
does not satisfy (29).
Now we define a relation
![]() $\sim$
on
$\sim$
on
![]() $\mathcal{A}$
as follows: two sets
$\mathcal{A}$
as follows: two sets
![]() $A_1$
,
$A_1$
,
![]() $A_2 \in{\mathcal{A}}$
are equivalent if
$A_2 \in{\mathcal{A}}$
are equivalent if
![]() $|A_1 \cap A_2| \geqslant n/2$
. Then Proposition 3.2 implies that
$|A_1 \cap A_2| \geqslant n/2$
. Then Proposition 3.2 implies that
![]() $\sim$
is an equivalence relation on
$\sim$
is an equivalence relation on
![]() $\mathcal{A}$
. Let
$\mathcal{A}$
. Let
be the equivalence class decomposition on
![]() $\mathcal{A}$
corresponding to
$\mathcal{A}$
corresponding to
![]() $\sim$
. This means that for every
$\sim$
. This means that for every
![]() $i = 1, \ldots, N$
and any
$i = 1, \ldots, N$
and any
![]() $F_1, F_2 \in{\mathcal{K}}_i$
we have
$F_1, F_2 \in{\mathcal{K}}_i$
we have
![]() $|F_1 \cap F_2| \geqslant n-k$
and for any
$|F_1 \cap F_2| \geqslant n-k$
and for any
![]() $i \neq j$
and
$i \neq j$
and
![]() $F_1 \in{\mathcal{K}}_i$
and
$F_1 \in{\mathcal{K}}_i$
and
![]() $F_2 \in{\mathcal{K}}_j$
we have
$F_2 \in{\mathcal{K}}_j$
we have
![]() $|F_1 \cap F_2| \leqslant k$
.
$|F_1 \cap F_2| \leqslant k$
.
Proposition 3.3.
For every
![]() $i = 1, \ldots, N$
we have
$i = 1, \ldots, N$
we have
![]() $|\bigcap{\mathcal{K}}_i| \geqslant n-5k$
.
$|\bigcap{\mathcal{K}}_i| \geqslant n-5k$
.
Proof. Suppose that
![]() $|\bigcap{\mathcal{K}}_i| \lt n-5k$
for some
$|\bigcap{\mathcal{K}}_i| \lt n-5k$
for some
![]() $i$
. Let
$i$
. Let
![]() $F \in{\mathcal{K}}_i$
be an arbitrary set from
$F \in{\mathcal{K}}_i$
be an arbitrary set from
![]() ${\mathcal{K}}_i$
and let
${\mathcal{K}}_i$
and let
![]() $K \subset F$
be any subset of size
$K \subset F$
be any subset of size
![]() $(n-k)$
. Lemma 2.5 applied to the family
$(n-k)$
. Lemma 2.5 applied to the family
![]() ${\mathcal{K}}_i$
and the set
${\mathcal{K}}_i$
and the set
![]() $K$
implies that
$K$
implies that
![]() $c_{n-k}({\mathcal{K}}_i) \leqslant 1$
. So Lemma 2.4 applied to
$c_{n-k}({\mathcal{K}}_i) \leqslant 1$
. So Lemma 2.4 applied to
![]() ${\mathcal{K}}_i$
implies that
${\mathcal{K}}_i$
implies that
![]() $\mathcal{A}$
satisfies (30), a contradiction.
$\mathcal{A}$
satisfies (30), a contradiction.
Proposition 3.4.
We have
![]() $|{\mathcal{A}}| \leqslant n^{6k}$
.
$|{\mathcal{A}}| \leqslant n^{6k}$
.
Proof. Indeed, by Lemma 1.7, Proposition 3.3 and
![]() $\tau$
-criticality of
$\tau$
-criticality of
![]() $\mathcal{A}$
we have
$\mathcal{A}$
we have
![]() $|{\mathcal{K}}_i| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}})+5k\\[-3pt]5k\end{array}\bigg)$
for any
$|{\mathcal{K}}_i| \leqslant\bigg(\begin{array}{c}\tau ({\mathcal{A}})+5k\\[-3pt]5k\end{array}\bigg)$
for any
![]() $i = 1, \ldots, N$
.
$i = 1, \ldots, N$
.
Now let
![]() $A_i \in{\mathcal{K}}_i$
be arbitrary representatives. Note that
$A_i \in{\mathcal{K}}_i$
be arbitrary representatives. Note that
![]() $|A_i \cap A_j| \leqslant k$
for any
$|A_i \cap A_j| \leqslant k$
for any
![]() $i \neq j$
. Obviously
$i \neq j$
. Obviously
![]() $k \ll \frac{n}{\log n}$
, so by Lemma 2.7 we either have
$k \ll \frac{n}{\log n}$
, so by Lemma 2.7 we either have
![]() $N \leqslant n^{C^{\prime}}$
or there is a proper subfamily
$N \leqslant n^{C^{\prime}}$
or there is a proper subfamily
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
which immediately implies (5). This implies that we in fact have
![]() $N \leqslant n^{C^{\prime}}$
and so
$N \leqslant n^{C^{\prime}}$
and so
provided that
![]() $n$
is large enough.
$n$
is large enough.
Denote
![]() $m = \log n^{6k} = 6k \log n$
and let
$m = \log n^{6k} = 6k \log n$
and let
![]() $l = 10\varepsilon ^{-1}$
. By Lemma 2.10, there is a subfamily
$l = 10\varepsilon ^{-1}$
. By Lemma 2.10, there is a subfamily
![]() ${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
${\mathcal{A}}^{\prime} \subset{\mathcal{A}}$
such that
![]() $\tau ({\mathcal{A}}\setminus{\mathcal{A}}^{\prime}) \leqslant \tau ({\mathcal{A}})/2$
such that for every
$\tau ({\mathcal{A}}\setminus{\mathcal{A}}^{\prime}) \leqslant \tau ({\mathcal{A}})/2$
such that for every
![]() $i = 2, \ldots, l$
we have
$i = 2, \ldots, l$
we have
for some new constant
![]() $C_l \ll 2^{l^2}$
. Let
$C_l \ll 2^{l^2}$
. Let
![]() $r = n^{-\varepsilon } \frac{\tau ({\mathcal{A}})}{m}$
(note that
$r = n^{-\varepsilon } \frac{\tau ({\mathcal{A}})}{m}$
(note that
![]() $r \gg 1$
since
$r \gg 1$
since
![]() $\tau ({\mathcal{A}}) \geqslant n^{2/3}$
by assumption).
$\tau ({\mathcal{A}}) \geqslant n^{2/3}$
by assumption).
Sample uniformly and independently sets
![]() $B_1, \ldots, B_r \in{\mathcal{A}}^{\prime}$
and form a random family
$B_1, \ldots, B_r \in{\mathcal{A}}^{\prime}$
and form a random family
![]() ${\mathcal{B}} = \{B_1, \ldots, B_r\}$
. Applying (34) to all
${\mathcal{B}} = \{B_1, \ldots, B_r\}$
. Applying (34) to all
![]() $l$
-element intersections in
$l$
-element intersections in
![]() $\mathcal{B}$
, we get
$\mathcal{B}$
, we get
 \begin{equation*} {\mathbb {E}} \sum _{S \in \bigg(\begin{array}{c}[r]\\[-3pt]l\end{array}\bigg)} \left |\bigcap _{i \in S} B_i\right | \leqslant C_l \bigg(\begin{array}{c}r\\[-3pt]l\end{array}\bigg) \left ( \frac {m}{\tau ({\mathcal {A}})}\right )^{l-1}n \leqslant C_l n^{1- \varepsilon l} \frac {\tau ({\mathcal {A}})}{m} \leqslant n^{2-\varepsilon l} \lt 1 \end{equation*}
\begin{equation*} {\mathbb {E}} \sum _{S \in \bigg(\begin{array}{c}[r]\\[-3pt]l\end{array}\bigg)} \left |\bigcap _{i \in S} B_i\right | \leqslant C_l \bigg(\begin{array}{c}r\\[-3pt]l\end{array}\bigg) \left ( \frac {m}{\tau ({\mathcal {A}})}\right )^{l-1}n \leqslant C_l n^{1- \varepsilon l} \frac {\tau ({\mathcal {A}})}{m} \leqslant n^{2-\varepsilon l} \lt 1 \end{equation*}
for sufficiently large
![]() $n$
.
$n$
.
So there exists an
![]() $r$
-element family
$r$
-element family
![]() ${\mathcal{B}} \subset{\mathcal{A}}^{\prime}$
such that all
${\mathcal{B}} \subset{\mathcal{A}}^{\prime}$
such that all
![]() $l$
-wise intersections of sets from
$l$
-wise intersections of sets from
![]() $\mathcal{B}$
are empty. By Corollary 2.18, for
$\mathcal{B}$
are empty. By Corollary 2.18, for
![]() $h = \frac{r}{20l^3}$
, we have
$h = \frac{r}{20l^3}$
, we have
![]() $c_{n-h}({\mathcal{B}}) \leqslant 1$
. But
$c_{n-h}({\mathcal{B}}) \leqslant 1$
. But
by the choice of
![]() $k = \sqrt{\tau ({\mathcal{A}})}$
and
$k = \sqrt{\tau ({\mathcal{A}})}$
and
![]() $\lambda = e^{-(1.5-\varepsilon ) \frac{\tau ({\mathcal{A}})^{0.5-\varepsilon }}{n}}$
and sufficiently large
$\lambda = e^{-(1.5-\varepsilon ) \frac{\tau ({\mathcal{A}})^{0.5-\varepsilon }}{n}}$
and sufficiently large
![]() $n$
. So by Lemma 2.4 applied to
$n$
. So by Lemma 2.4 applied to
![]() ${\mathcal{F}}^{\prime} ={\mathcal{B}}$
we have (29). Theorem 1.4 is proved.
${\mathcal{F}}^{\prime} ={\mathcal{B}}$
we have (29). Theorem 1.4 is proved.
4. Remarks
Let us describe a construction of a maximal intersecting family which generalizes examples from [Reference Erdős and Lovász4] and [Reference Frankl, Ota and Tokushige7]. Let
![]() $G$
be a tournament on the vertex set
$G$
be a tournament on the vertex set
![]() $\{1, \ldots, m\}$
and let
$\{1, \ldots, m\}$
and let
![]() $K_1, \ldots, K_m$
be a sequence of disjoint non-empty sets. Let
$K_1, \ldots, K_m$
be a sequence of disjoint non-empty sets. Let
![]() ${\mathcal{K}}_i$
be the family of all sets
${\mathcal{K}}_i$
be the family of all sets
![]() $F$
such that
$F$
such that
![]() $K_i \subset F$
and for
$K_i \subset F$
and for
![]() $i \neq j$
:
$i \neq j$
:
 \begin{align*} |F \cap K_j| = \begin{cases} 1,\text{ if $(i, j) \in G$,}\\[5pt] 0, \text{ if $(i, j) \not \in G$.} \end{cases} \end{align*}
\begin{align*} |F \cap K_j| = \begin{cases} 1,\text{ if $(i, j) \in G$,}\\[5pt] 0, \text{ if $(i, j) \not \in G$.} \end{cases} \end{align*}
It is clear from this definition that the family
![]() ${\mathcal{F}} ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_m$
is intersecting. Let
${\mathcal{F}} ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_m$
is intersecting. Let
![]() $d_i$
be the outdegree of the vertex
$d_i$
be the outdegree of the vertex
![]() $i$
and let
$i$
and let
![]() $n \gt \max d_i$
. If we let
$n \gt \max d_i$
. If we let
![]() $|K_i| = n-d_i$
, then the family
$|K_i| = n-d_i$
, then the family
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $n$
-uniform and intersecting.
$n$
-uniform and intersecting.
It is not difficult to characterize all minimal coverings of
![]() $\mathcal{F}$
. First, observe that if
$\mathcal{F}$
. First, observe that if
![]() $T$
is a minimal covering of
$T$
is a minimal covering of
![]() $\mathcal{F}$
then
$\mathcal{F}$
then
![]() $|T \cap K_i| \in \{0, 1, |K_i|\}$
. Then for every minimal covering
$|T \cap K_i| \in \{0, 1, |K_i|\}$
. Then for every minimal covering
![]() $T$
, we can define two sets
$T$
, we can define two sets
![]() $A, B \subset [m]$
, namely,
$A, B \subset [m]$
, namely,
![]() $A$
is the set of all
$A$
is the set of all
![]() $i$
such that
$i$
such that
![]() $|C \cap K_i| = 1$
and
$|C \cap K_i| = 1$
and
![]() $B$
is the set of all
$B$
is the set of all
![]() $i$
such that
$i$
such that
![]() $K_i \subset T$
. Now the fact that
$K_i \subset T$
. Now the fact that
![]() $T$
is a covering is equivalent to the assertion that
$T$
is a covering is equivalent to the assertion that
![]() $A \cup B \cup N_{in}(B) = [m]$
, where
$A \cup B \cup N_{in}(B) = [m]$
, where
![]() $N_{in}(B)$
denotes the set of all vertices of
$N_{in}(B)$
denotes the set of all vertices of
![]() $G$
from which there is an edge to
$G$
from which there is an edge to
![]() $B$
.
$B$
.
Example 1. If we let
![]() $G$
to be the linearly ordered complete directed graph, then
$G$
to be the linearly ordered complete directed graph, then
![]() $\mathcal{F}$
coincides with the family constructed by Erdős–Lovász [Reference Erdős and Lovász4]. In this case,
$\mathcal{F}$
coincides with the family constructed by Erdős–Lovász [Reference Erdős and Lovász4]. In this case,
![]() $\tau ({\mathcal{F}}) = n$
and
$\tau ({\mathcal{F}}) = n$
and
![]() $|{\mathcal{F}}|$
is approximately
$|{\mathcal{F}}|$
is approximately
![]() $n!$
.
$n!$
.
Example 2. Let
![]() $G$
be graph on the vertex set
$G$
be graph on the vertex set
![]() ${\mathbb{Z}}_{2t-1} \cup \{v\}$
, where the vertices
${\mathbb{Z}}_{2t-1} \cup \{v\}$
, where the vertices
![]() $i, j \in{\mathbb{Z}}_{2t-1}$
from the cyclic group are connected if
$i, j \in{\mathbb{Z}}_{2t-1}$
from the cyclic group are connected if
![]() $j-i \in [1, t-1]$
and the vertex
$j-i \in [1, t-1]$
and the vertex
![]() $v$
has outdegree
$v$
has outdegree
![]() $2t-1$
. In this case, we have
$2t-1$
. In this case, we have
![]() $n = 2t$
,
$n = 2t$
,
![]() $\tau ({\mathcal{F}}) = n$
and
$\tau ({\mathcal{F}}) = n$
and
![]() $|{\mathcal{F}}|$
is approximately
$|{\mathcal{F}}|$
is approximately
![]() $\left (\frac{n}{2} \right )^{n}$
. Note that the main contribution to the size of
$\left (\frac{n}{2} \right )^{n}$
. Note that the main contribution to the size of
![]() $\mathcal{F}$
comes from the family
$\mathcal{F}$
comes from the family
![]() ${\mathcal{K}}_v$
corresponding to the vertex
${\mathcal{K}}_v$
corresponding to the vertex
![]() $v$
.Footnote 2
$v$
.Footnote 2
It is not hard to see that the construction in the second example gives the maximum size of
![]() $\mathcal{F}$
among all constructions of this type.
$\mathcal{F}$
among all constructions of this type.
The construction above and the decomposition (33) which we used in the proof of Theorem 1.1 suggest to consider the following special class of families. Let
![]() $K_1, \ldots, K_n$
be disjoint sets such that
$K_1, \ldots, K_n$
be disjoint sets such that
![]() $|K_i| = n-a_i$
. Let
$|K_i| = n-a_i$
. Let
![]() ${\mathcal{K}}_i$
be an
${\mathcal{K}}_i$
be an
![]() $n$
-uniform family of sets containing
$n$
-uniform family of sets containing
![]() $K_i$
. Let
$K_i$
. Let
![]() ${\mathcal{F}} ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_n$
and suppose that
${\mathcal{F}} ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_n$
and suppose that
![]() $\tau ({\mathcal{F}}) = n$
and
$\tau ({\mathcal{F}}) = n$
and
![]() $\mathcal{F}$
is intersecting.
$\mathcal{F}$
is intersecting.
Conjecture 1 ([Reference Kupavskii11]). In the situation described above we have
![]() $\sum _{i = 1}^n a_i \geqslant\bigg(\begin{array}{c}n\\[-3pt]2\end{array}\bigg)$
. Moreover, the condition that
$\sum _{i = 1}^n a_i \geqslant\bigg(\begin{array}{c}n\\[-3pt]2\end{array}\bigg)$
. Moreover, the condition that
![]() $|K_i| = n-a_i$
can be replaced by the condition that
$|K_i| = n-a_i$
can be replaced by the condition that
![]() ${\mathcal{K}}_i$
is
${\mathcal{K}}_i$
is
![]() $(|K_i|+a_i)$
-uniform.
$(|K_i|+a_i)$
-uniform.
Note that, if true, Conjecture 1 is best possible: we can take
![]() $G$
to be a graph whose outdegrees are precisely
$G$
to be a graph whose outdegrees are precisely
![]() $a_1, \ldots, a_n$
and then use the construction of an
$a_1, \ldots, a_n$
and then use the construction of an
![]() $n$
-uniform family
$n$
-uniform family
![]() $\mathcal{F}$
described above. One can easily produce sequences of degrees
$\mathcal{F}$
described above. One can easily produce sequences of degrees
![]() $a_1, \ldots, a_n$
such that the corresponding graph exists and
$a_1, \ldots, a_n$
such that the corresponding graph exists and
![]() $\tau ({\mathcal{F}}) = n$
.
$\tau ({\mathcal{F}}) = n$
.
Note that if there is a counterexample to Conjecture 1 such that, say,
![]() $a_i \sim n^{1-\varepsilon }$
for some
$a_i \sim n^{1-\varepsilon }$
for some
![]() $\varepsilon \gt 0$
and every
$\varepsilon \gt 0$
and every
![]() $i = 1, \ldots, n$
, then one can construct a very large maximal intersecting family as follows.
$i = 1, \ldots, n$
, then one can construct a very large maximal intersecting family as follows.
Let
![]() ${\mathcal{F}}_0 ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_n$
be an
${\mathcal{F}}_0 ={\mathcal{K}}_1 \cup \ldots \cup{\mathcal{K}}_n$
be an
![]() $n$
-uniform family such that
$n$
-uniform family such that
![]() $\tau ({\mathcal{F}}_0) = n$
. Then any set
$\tau ({\mathcal{F}}_0) = n$
. Then any set
![]() $F$
such that
$F$
such that
![]() $|F \cap K_i| = 1$
, for every
$|F \cap K_i| = 1$
, for every
![]() $i$
, is a minimal covering of
$i$
, is a minimal covering of
![]() ${\mathcal{F}}_0$
. Denote the family of all such sets by
${\mathcal{F}}_0$
. Denote the family of all such sets by
![]() ${\mathcal{F}}^{\prime}_1$
. We have
${\mathcal{F}}^{\prime}_1$
. We have
Moreover, if we let
![]() ${\mathcal{F}}_1$
be an
${\mathcal{F}}_1$
be an
![]() $(n+1)$
-uniform family of sets
$(n+1)$
-uniform family of sets
![]() $F \cup \{x_0\}$
, where
$F \cup \{x_0\}$
, where
![]() $F \in{\mathcal{F}}^{\prime}_1$
and
$F \in{\mathcal{F}}^{\prime}_1$
and
![]() $x_0$
is a ‘new’ element of the ground set, then
$x_0$
is a ‘new’ element of the ground set, then
![]() ${\mathcal{F}} ={\mathcal{F}}_0 \cup{\mathcal{F}}_1$
is an intersecting family of
${\mathcal{F}} ={\mathcal{F}}_0 \cup{\mathcal{F}}_1$
is an intersecting family of
![]() $n$
and
$n$
and
![]() $n+1$
element sets such that
$n+1$
element sets such that
![]() $\tau ({\mathcal{F}}) = n$
and each member of
$\tau ({\mathcal{F}}) = n$
and each member of
![]() $\mathcal{F}$
is a minimal covering of
$\mathcal{F}$
is a minimal covering of
![]() $\mathcal{F}$
. The family
$\mathcal{F}$
. The family
![]() $\mathcal{F}$
has size at least
$\mathcal{F}$
has size at least
![]() $e^{-n^{1-\varepsilon }} n^n$
and so it essentially contradicts the conjecture of Frankl–Ota–Tokushige [Reference Frankl, Ota and Tokushige7].
$e^{-n^{1-\varepsilon }} n^n$
and so it essentially contradicts the conjecture of Frankl–Ota–Tokushige [Reference Frankl, Ota and Tokushige7].
In the setting of Conjecture 1, we were only able to prove the lower bound
![]() $\sum _{i=1}^n a_i \gg n^{3/2}$
but any improvement seems to require new ideas.
$\sum _{i=1}^n a_i \gg n^{3/2}$
but any improvement seems to require new ideas.
Acknowledgements
I thank Andrey Kupavskii for valuable discussions and for telling me about Conjecture 1. I thank Péter Frankl, Stijn Cambie, and the anonymous referee for useful comments on an earlier version of this paper.