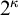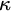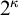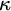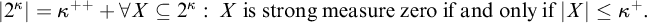1 Introduction
In searching for a useful notion related to being a Lebesgue measure zero set, Borel [Reference Borel3] introduced strong measure zero sets.
Definition 1.1. A subset X of the real line is strong measure zero iff for any sequence
![]() $(\varepsilon _n)_{n \in \omega }$
of positive real numbers there exists a sequence of intervals
$(\varepsilon _n)_{n \in \omega }$
of positive real numbers there exists a sequence of intervals
![]() $(I_n)_{n \in \omega }$
with
$(I_n)_{n \in \omega }$
with
![]() $\lambda (I_n) \leq \varepsilon _n$
and
$\lambda (I_n) \leq \varepsilon _n$
and
![]() $X \subseteq \bigcup _{n \in \omega } I_n$
.
$X \subseteq \bigcup _{n \in \omega } I_n$
.
Clearly, strong measure zero sets are measure zero and every countable set is strong measure zero. Moreover, it is also easy to see that perfect sets cannot be strong measure zero. It was conjectured by Borel that countability is perhaps the only constraint on strong measure zero sets, giving rise to the Borel Conjecture (BC): “A set X is strong measure zero if and only if X is countable.”
In 1928, Sierpiński [Reference Sierpiński24] showed that CH implies the existence of uncountable strong measure zero sets (specifically, he showed that any Luzin set is strong measure zero). It was not until after the advent of Cohen’s revolutionary technique of forcing that Laver [Reference Laver18] established the relative consistency (and thus independence from ZFC) of BC.
Over the years, investigations into matters related to strong measure zero sets (such as the interplay between BC and the size of the continuum [Reference Judah, Shelah and Woodin14], the dual notion of strongly meager sets [Reference Goldstern, Kellner, Shelah and Wohofsky9] and others) became testament to the fact that Borel’s notion was indeed worthy of interest.
For our purposes the most interesting of these is Corazza’s proof of the consistency of “a set is strong measure zero iff it has size less than continuum” (see [Reference Corazza4]) in which he employs an
![]() $\omega _2$
-length iteration of strongly proper forcings (a notion stronger than “proper +
$\omega _2$
-length iteration of strongly proper forcings (a notion stronger than “proper +
![]() $\omega ^\omega $
-bounding” that includes well-known forcings such as Sacks and Silver), together with a previous result of Miller [Reference Miller20] to construct a model with
$\omega ^\omega $
-bounding” that includes well-known forcings such as Sacks and Silver), together with a previous result of Miller [Reference Miller20] to construct a model with
“Every set of reals of size continuum can be mapped uniformly continuously onto
![]() $[0,1]$
”.
$[0,1]$
”.
We are interested in a version of Borel’s Conjecture on higher cardinals
![]() $\kappa $
. The higher Cantor space
$\kappa $
. The higher Cantor space
![]() $2^\kappa $
and the higher Baire space
$2^\kappa $
and the higher Baire space
![]() $\kappa ^\kappa $
come equipped with the standard
$\kappa ^\kappa $
come equipped with the standard
![]() ${<}\kappa $
-box topology (see [Reference Friedman, Khomskii and Kulikov7] for basic properties of these spaces). Their elements are called
${<}\kappa $
-box topology (see [Reference Friedman, Khomskii and Kulikov7] for basic properties of these spaces). Their elements are called
![]() $\kappa $
-reals, or simply reals. Note that near universally, the assumption
$\kappa $
-reals, or simply reals. Note that near universally, the assumption
![]() $\kappa ^{<\kappa } = \kappa $
is made in discussions on the higher Baire space, without which the space exhibits some undesirable topological properties (see [Reference Friedman, Hyttinen and Kulikov6, Section 2.1.]). Especially in recent years, renewed interest has sparked among set theorists in studying these spaces; a compendium of open questions can be found in [Reference Khomskii, Laguzzi, Löwe and Sharankou17].
$\kappa ^{<\kappa } = \kappa $
is made in discussions on the higher Baire space, without which the space exhibits some undesirable topological properties (see [Reference Friedman, Hyttinen and Kulikov6, Section 2.1.]). Especially in recent years, renewed interest has sparked among set theorists in studying these spaces; a compendium of open questions can be found in [Reference Khomskii, Laguzzi, Löwe and Sharankou17].
The following definition is due to Halko [Reference Halko10]:
Definition 1.2. Let
![]() $X \subseteq 2^\kappa $
. We call X strong measure zero iff
$X \subseteq 2^\kappa $
. We call X strong measure zero iff
This is a straightforward combinatorial reformulation (here
![]() $[\eta ]$
is a basic clopen set as defined in the next section) of Borel’s definition that is agnostic towards the existence of a measure on
$[\eta ]$
is a basic clopen set as defined in the next section) of Borel’s definition that is agnostic towards the existence of a measure on
![]() $2^\kappa $
. Let
$2^\kappa $
. Let
![]() $\mathcal {SN}$
be the collection of all strong measure zero sets; it is easy to see that
$\mathcal {SN}$
be the collection of all strong measure zero sets; it is easy to see that
![]() $\mathcal {SN}$
is a proper,
$\mathcal {SN}$
is a proper,
![]() ${\leq }\kappa $
-complete ideal (see also Lemma 8.2) on
${\leq }\kappa $
-complete ideal (see also Lemma 8.2) on
![]() $2^\kappa $
containing all singletons.
$2^\kappa $
containing all singletons.
The Borel Conjecture on
![]() $\kappa $
(BC(
$\kappa $
(BC(
![]() $\kappa $
)) is the statement “a subset of
$\kappa $
)) is the statement “a subset of
![]() $2^\kappa $
is strong measure zero iff it has cardinality
$2^\kappa $
is strong measure zero iff it has cardinality
![]() ${\leq }\kappa $
”. Strong measure zero sets for
${\leq }\kappa $
”. Strong measure zero sets for
![]() $\kappa $
regular uncountable have been studied in [Reference Halko and Shelah11], where the authors have proven that BC(
$\kappa $
regular uncountable have been studied in [Reference Halko and Shelah11], where the authors have proven that BC(
![]() $\kappa $
) is false for successor
$\kappa $
) is false for successor
![]() $\kappa $
satisfying
$\kappa $
satisfying
![]() $\kappa ^{<\kappa } = \kappa $
.
$\kappa ^{<\kappa } = \kappa $
.
Throughout this paper we shall restrict our attention to
![]() $\kappa $
at least inaccessible, thus in particular
$\kappa $
at least inaccessible, thus in particular
![]() $\kappa ^{<\kappa } = \kappa $
. The question of the consistency of BC(
$\kappa ^{<\kappa } = \kappa $
. The question of the consistency of BC(
![]() $\kappa $
) on such
$\kappa $
) on such
![]() $\kappa $
is still open [Reference Khomskii, Laguzzi, Löwe and Sharankou17]. An argument similar to the one in the proof of Theorem 5.1—forgoing the notion of
$\kappa $
is still open [Reference Khomskii, Laguzzi, Löwe and Sharankou17]. An argument similar to the one in the proof of Theorem 5.1—forgoing the notion of
![]() $\kappa ^\kappa $
-bounding and focusing instead directly on encoding coverings within the
$\kappa ^\kappa $
-bounding and focusing instead directly on encoding coverings within the
![]() $\kappa $
-Cohen real—tells us that a
$\kappa $
-Cohen real—tells us that a
![]() $\kappa ^{++}$
-c.c. forcing iteration of length
$\kappa ^{++}$
-c.c. forcing iteration of length
![]() $\kappa ^{++}$
in which
$\kappa ^{++}$
in which
![]() $\kappa $
-Cohen reals are added cofinally will necessarily yield large strong measure zero sets—in fact, the set of ground model
$\kappa $
-Cohen reals are added cofinally will necessarily yield large strong measure zero sets—in fact, the set of ground model
![]() $\kappa $
-reals will become strong measure zero. Unfortunately, by the results in [Reference Khomskii, Koelbing, Laguzzi and Wohofsky16], every Laver-like tree forcing on
$\kappa $
-reals will become strong measure zero. Unfortunately, by the results in [Reference Khomskii, Koelbing, Laguzzi and Wohofsky16], every Laver-like tree forcing on
![]() $\kappa ^\kappa $
necessarily adds a
$\kappa ^\kappa $
necessarily adds a
![]() $\kappa $
-Cohen real. Any treatment of the consistency of BC
$\kappa $
-Cohen real. Any treatment of the consistency of BC
![]() $(\kappa )$
thus cannot be merely a straightforward adaptation of Laver’s results; potentially, a wholly new approach is needed here.
$(\kappa )$
thus cannot be merely a straightforward adaptation of Laver’s results; potentially, a wholly new approach is needed here.
We shall give two proofs establishing the relative consistency of
the first of which is an adaptation of an iteration found in [Reference Goldstern, Judah and Shelah8] and requires
![]() $\kappa $
to be strongly unfoldable (a large cardinal property between weakly compact and Ramsey that is consistent with
$\kappa $
to be strongly unfoldable (a large cardinal property between weakly compact and Ramsey that is consistent with
![]() $V=L$
). The second, somewhat better, proof only requires
$V=L$
). The second, somewhat better, proof only requires
![]() $\kappa $
to be inaccessible and employs the same iteration by establishing minimality of the respective forcing extension, following the approach of Corazza [Reference Corazza4].
$\kappa $
to be inaccessible and employs the same iteration by establishing minimality of the respective forcing extension, following the approach of Corazza [Reference Corazza4].
2 Notation and basic definitions
Let us make some preliminary remarks.
The higher Cantor space
![]() $2^\kappa $
is equipped with the standard
$2^\kappa $
is equipped with the standard
![]() ${<}\kappa $
-box topology, whose base consists of the basic clopen sets
${<}\kappa $
-box topology, whose base consists of the basic clopen sets
for
![]() $\eta \in 2^{<\kappa }$
; for the higher Baire space
$\eta \in 2^{<\kappa }$
; for the higher Baire space
![]() $\kappa ^\kappa $
the topology is defined analogously. The relation
$\kappa ^\kappa $
the topology is defined analogously. The relation
![]() $\eta \lhd \nu $
denotes the extension relation for sequences, i.e.,
$\eta \lhd \nu $
denotes the extension relation for sequences, i.e.,
![]() $\eta = \nu {\restriction } i$
for some
$\eta = \nu {\restriction } i$
for some
![]() $i \leq \operatorname {\mathrm {dom}}(\nu )$
. The relation
$i \leq \operatorname {\mathrm {dom}}(\nu )$
. The relation
![]() $\eta \bot \nu $
denotes incompatibility, i.e.,
$\eta \bot \nu $
denotes incompatibility, i.e.,
![]() $\eta \ntriangleleft \nu $
and
$\eta \ntriangleleft \nu $
and
![]() $\nu \ntriangleleft \eta $
.
$\nu \ntriangleleft \eta $
.
A (
![]() $\kappa $
-) tree is a subset of
$\kappa $
-) tree is a subset of
![]() $\kappa ^{<\kappa }$
closed under initial segments.
$\kappa ^{<\kappa }$
closed under initial segments.
Let
![]() $T \subseteq \kappa ^{<\kappa }$
be a tree and
$T \subseteq \kappa ^{<\kappa }$
be a tree and
![]() $\eta \in T$
. Then we define the following notions:
$\eta \in T$
. Then we define the following notions:
-
• A
 $b \in \kappa ^\kappa $
is a branch of T iff
$b \in \kappa ^\kappa $
is a branch of T iff
 $b {\restriction } i \in T$
for all
$b {\restriction } i \in T$
for all
 $i < \kappa $
. Let
$i < \kappa $
. Let
 $[T]$
denote the set of all branches of T.
$[T]$
denote the set of all branches of T. -
• Denote by
 $\operatorname {\mathrm {succ}}_T(\eta )$
the set of immediate successors of
$\operatorname {\mathrm {succ}}_T(\eta )$
the set of immediate successors of
 $\eta $
in T. Call
$\eta $
in T. Call
 $\eta $
a splitting node of T iff
$\eta $
a splitting node of T iff
 $|\operatorname {\mathrm {succ}}_T(\eta )|> 1$
. Denote the set of all splitting nodes of T as
$|\operatorname {\mathrm {succ}}_T(\eta )|> 1$
. Denote the set of all splitting nodes of T as
 $\operatorname {\mathrm {split}}(T)$
. We will only consider trees in which every node has a successor.
$\operatorname {\mathrm {split}}(T)$
. We will only consider trees in which every node has a successor. -
• T is perfect iff for every
 $\eta \in T$
there is a
$\eta \in T$
there is a
 $\nu $
such that
$\nu $
such that
 $\eta \lhd \nu $
and
$\eta \lhd \nu $
and
 $\nu \in \operatorname {\mathrm {split}}(T)$
. Note that for
$\nu \in \operatorname {\mathrm {split}}(T)$
. Note that for
 $\kappa \neq \omega $
this is not equivalent to
$\kappa \neq \omega $
this is not equivalent to
 $[T]$
containing a homeomorphic copy of
$[T]$
containing a homeomorphic copy of
 $2^\kappa $
, even if every node of the tree lies on a branch (of length
$2^\kappa $
, even if every node of the tree lies on a branch (of length
 $\kappa $
).
$\kappa $
). -
• The splitting height
 ${\mathrm {ht^{s}}}_T(\eta )$
of a node
${\mathrm {ht^{s}}}_T(\eta )$
of a node
 $\eta $
is the order type of the set
$\eta $
is the order type of the set  . Additionally, for
. Additionally, for
 $i < \kappa $
, define
$i < \kappa $
, define  $$\begin{align*}\operatorname{\mathrm{split}}_i(T) := \{ \eta \in \operatorname{\mathrm{split}}(T): {\mathrm{ht^{s}}}_T(\eta) =i \}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{split}}_i(T) := \{ \eta \in \operatorname{\mathrm{split}}(T): {\mathrm{ht^{s}}}_T(\eta) =i \}. \end{align*}$$
-
• As usual, the set of branches of a tree is a closed set and every closed set Y can be represented as the set of branches of the tree
 $T = \{b {\restriction } i:\ i < \kappa \land b \in Y\}$
. However, it may be the case that this tree T necessarily contains dying branches, i.e., T might contain an increasing sequence
$T = \{b {\restriction } i:\ i < \kappa \land b \in Y\}$
. However, it may be the case that this tree T necessarily contains dying branches, i.e., T might contain an increasing sequence
 $(\eta _i)_{i < \lambda }$
with
$(\eta _i)_{i < \lambda }$
with
 $\lambda < \kappa $
whose limit
$\lambda < \kappa $
whose limit
 $\bigcup _{i < \lambda } \eta _i$
is not an element of T
Footnote
1
. This phenomenon is unique to the
$\bigcup _{i < \lambda } \eta _i$
is not an element of T
Footnote
1
. This phenomenon is unique to the
 $\kappa $
-case and has no
$\kappa $
-case and has no
 $\omega $
-equivalent.We say T (or
$\omega $
-equivalent.We say T (or
 $[T]$
) is superclosed iff this does not happen, meaning that whenever
$[T]$
) is superclosed iff this does not happen, meaning that whenever
 $\lambda < \kappa $
is a limit ordinal and
$\lambda < \kappa $
is a limit ordinal and
 $\eta \in \kappa ^\lambda $
, then
$\eta \in \kappa ^\lambda $
, then
 $\eta \in T \Leftrightarrow \forall i < \lambda :\ \eta {\restriction } i \in T$
.
$\eta \in T \Leftrightarrow \forall i < \lambda :\ \eta {\restriction } i \in T$
.
We shall attempt to, wherever feasible, adhere to certain self-imposed notational conventions. In this vein, the letters
![]() $i,j,k,\ell ,m$
will generally refer to ordinals
$i,j,k,\ell ,m$
will generally refer to ordinals
![]() ${<}\kappa $
;
${<}\kappa $
;
![]() $\delta , \lambda $
to limit ordinals
$\delta , \lambda $
to limit ordinals
![]() ${\leq }\kappa $
and
${\leq }\kappa $
and
![]() $\alpha , \beta , \gamma , \zeta $
to ordinals
$\alpha , \beta , \gamma , \zeta $
to ordinals
![]() ${\leq } \kappa ^{++}$
. The letters
${\leq } \kappa ^{++}$
. The letters
![]() $p,q,r,s,t$
denote conditions while
$p,q,r,s,t$
denote conditions while
![]() $\eta , \nu , \rho $
are elements of
$\eta , \nu , \rho $
are elements of
![]() $\kappa ^{<\kappa }$
. The pair
$\kappa ^{<\kappa }$
. The pair
![]() $F,i$
will always fulfil
$F,i$
will always fulfil
![]() $F \in [\alpha ]^{<\kappa }, i < \kappa $
, where
$F \in [\alpha ]^{<\kappa }, i < \kappa $
, where
![]() $\alpha \leq \kappa ^{++}$
is either explicitly given or clear from context.
$\alpha \leq \kappa ^{++}$
is either explicitly given or clear from context.
3 Perfect tree forcing
We are interested in a particular forcing consisting of
![]() ${<}\kappa $
-splitting perfect trees whose splitting is bounded by an
${<}\kappa $
-splitting perfect trees whose splitting is bounded by an
![]() $f \in \kappa ^\kappa $
with
$f \in \kappa ^\kappa $
with
![]() $f(i) \geq 2$
for all
$f(i) \geq 2$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Definition 3.1 Let
![]() $p \in PT_f$
iff:
$p \in PT_f$
iff:
-
(S1)
 $p \subseteq \kappa ^{< \kappa }$
is a nonempty tree.
$p \subseteq \kappa ^{< \kappa }$
is a nonempty tree. -
(S2) p is perfect.
-
(S3)
 $\forall \eta \in p \, \forall i \in \textrm {dom} (\eta ):\ \eta (i) < f(i).$
$\forall \eta \in p \, \forall i \in \textrm {dom} (\eta ):\ \eta (i) < f(i).$
-
(S4) p has full splitting:
 $\forall \eta \in p \colon \vert \operatorname {\mathrm {succ}}_p (\eta ) \vert =1 \vee \operatorname {\mathrm {succ}}_p (\eta )= \{\eta ^\frown j \colon j < f(\textrm {dom}\, \eta )\}.$
$\forall \eta \in p \colon \vert \operatorname {\mathrm {succ}}_p (\eta ) \vert =1 \vee \operatorname {\mathrm {succ}}_p (\eta )= \{\eta ^\frown j \colon j < f(\textrm {dom}\, \eta )\}.$
-
(S5) p is superclosed.
-
(S6) splitting is continuous: If
 $\lambda < \kappa $
is a limit, then
$\lambda < \kappa $
is a limit, then
The significance of (S4) and (S6) lies in ensuring
![]() ${<}\kappa $
-closure of the forcing (see Lemma 3.6). The axioms (S4) and (S5) guarantee that for all
${<}\kappa $
-closure of the forcing (see Lemma 3.6). The axioms (S4) and (S5) guarantee that for all
![]() $\eta \in p$
we have
$\eta \in p$
we have
i.e., there is a branch of p going through
![]() $\eta $
. Under the other axioms, (S2) + (S6) is equivalent to the following statement: whenever
$\eta $
. Under the other axioms, (S2) + (S6) is equivalent to the following statement: whenever
![]() $b \in [p]$
is a branch of p, then
$b \in [p]$
is a branch of p, then
is a club subset of
![]() $\kappa $
.
$\kappa $
.
For
![]() $f \equiv 2$
we have a
$f \equiv 2$
we have a
![]() $\kappa $
-version of Sacks forcing, first studied by Kanamori [Reference Kanamori15]. An overview of variants of familiar forcing notions on higher cardinals can be found in [Reference Friedman, Khomskii and Kulikov7].
$\kappa $
-version of Sacks forcing, first studied by Kanamori [Reference Kanamori15]. An overview of variants of familiar forcing notions on higher cardinals can be found in [Reference Friedman, Khomskii and Kulikov7].
The rest of this section is devoted to proving some regularity properties for
![]() $PT_f$
, generalized straightforwardly from the classical treatment of similar tree forcings on
$PT_f$
, generalized straightforwardly from the classical treatment of similar tree forcings on
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Set
![]() $q \leq _{PT_f} p$
iff
$q \leq _{PT_f} p$
iff
![]() $q \subseteq p$
. For a
$q \subseteq p$
. For a
![]() $PT_f$
-generic filter G define the generic real
$PT_f$
-generic filter G define the generic real
![]() $s_G$
to be the unique real contained in
$s_G$
to be the unique real contained in
![]() $\bigcap _{p \in G} [p]$
.
$\bigcap _{p \in G} [p]$
.
Fact 3.2. For a condition
![]() $p \in PT_f$
the set
$p \in PT_f$
the set
![]() $\operatorname {\mathrm {split}}_i(p)$
is a front in p, i.e., it is an antichain in
$\operatorname {\mathrm {split}}_i(p)$
is a front in p, i.e., it is an antichain in
![]() $(p, \lhd )$
with
$(p, \lhd )$
with
Call it the ith splitting front of p.
Lemma 3.3. Let
![]() $i < \kappa $
and
$i < \kappa $
and
![]() $p \in PT_f$
be a condition. Then
$p \in PT_f$
be a condition. Then
![]() $|\operatorname {\mathrm {split}}_i(p)| < \kappa $
.
$|\operatorname {\mathrm {split}}_i(p)| < \kappa $
.
Proof We proceed by induction on i:
-
•
 $i = 0$
: Trivial.
$i = 0$
: Trivial. -
•
 $i \to i+1$
: The map
$i \to i+1$
: The map
 $\eta \mapsto \min \{\nu \lhd \eta : {\mathrm {ht^{s}}}_p(\nu ) = i+1\}$
is bijection between
$\eta \mapsto \min \{\nu \lhd \eta : {\mathrm {ht^{s}}}_p(\nu ) = i+1\}$
is bijection between
 $\operatorname {\mathrm {split}}_{i+1}(p)$
and
$\operatorname {\mathrm {split}}_{i+1}(p)$
and
 $\bigcup _{\eta \in \operatorname {\mathrm {split}}_i(p)} \operatorname {\mathrm {succ}}_p(\eta )$
. By the inductive hypothesis and the fact that p is
$\bigcup _{\eta \in \operatorname {\mathrm {split}}_i(p)} \operatorname {\mathrm {succ}}_p(\eta )$
. By the inductive hypothesis and the fact that p is
 ${<}\kappa $
-splitting, the latter set has size
${<}\kappa $
-splitting, the latter set has size
 $<\kappa $
.
$<\kappa $
. -
•
 $\lambda $
is a limit: Since every
$\lambda $
is a limit: Since every
 $\eta \in \operatorname {\mathrm {split}}_\lambda (p)$
is the limit of a sequence
$\eta \in \operatorname {\mathrm {split}}_\lambda (p)$
is the limit of a sequence
 $(\eta _j)_{j < \lambda }$
with
$(\eta _j)_{j < \lambda }$
with
 $\eta _j \in \operatorname {\mathrm {split}}_j(p)$
, we have
$\eta _j \in \operatorname {\mathrm {split}}_j(p)$
, we have
 $|\operatorname {\mathrm {split}}_\lambda (p)| \leq |\prod _{j < \lambda } \operatorname {\mathrm {split}}_j(p)| < \kappa $
by the inaccessibility of
$|\operatorname {\mathrm {split}}_\lambda (p)| \leq |\prod _{j < \lambda } \operatorname {\mathrm {split}}_j(p)| < \kappa $
by the inaccessibility of
 $\kappa $
.
$\kappa $
.
Definition 3.4. Let
![]() $(\mathcal {P}, \leq _{\mathcal {P}})$
be a forcing notion and
$(\mathcal {P}, \leq _{\mathcal {P}})$
be a forcing notion and
![]() $(\leq _i)_{i <\kappa }$
be a sequence of reflexive and transitive binary relations on
$(\leq _i)_{i <\kappa }$
be a sequence of reflexive and transitive binary relations on
![]() $\mathcal {P}$
such that
$\mathcal {P}$
such that
Then:
-
1.
 $(p_j)_{j<\delta }$
is a fusion sequence of length
$(p_j)_{j<\delta }$
is a fusion sequence of length
 $\delta \leq \kappa $
iff
$\delta \leq \kappa $
iff
 $\forall j < k < \delta : p_k \leq _j p_j$
.
$\forall j < k < \delta : p_k \leq _j p_j$
. -
2.
 $\mathcal {P}$
has Property B iff:
$\mathcal {P}$
has Property B iff:-
•
 $(\mathcal {P}, \leq _{\mathcal {P}})$
is
$(\mathcal {P}, \leq _{\mathcal {P}})$
is
 ${<}\kappa $
-closed.
${<}\kappa $
-closed. -
• Whenever
 $(p_j)_{j<\delta }, \delta \leq \kappa $
is a fusion sequence in
$(p_j)_{j<\delta }, \delta \leq \kappa $
is a fusion sequence in
 $\mathcal {P}$
, then there exists a fusion limit q with
$\mathcal {P}$
, then there exists a fusion limit q with
 $\forall j < \delta : q \leq _j p_j$
.
$\forall j < \delta : q \leq _j p_j$
. -
• If A is a maximal antichain,
 $p \in \mathcal {P}$
and
$p \in \mathcal {P}$
and
 $i < \kappa $
, then there exists a
$i < \kappa $
, then there exists a
 $q \leq _ i p$
such that
$q \leq _ i p$
such that
 $A {\restriction } q:=\{ r \in A \colon r \parallel q\}$
has size
$A {\restriction } q:=\{ r \in A \colon r \parallel q\}$
has size
 ${<}\kappa $
, where
${<}\kappa $
, where
 $\parallel $
means compatible.
$\parallel $
means compatible.
-
Equivalently, we can demand the third condition to hold for all antichains A, by enlarging them to maximal antichains if necessary. Note that by weakening the third requirement to
![]() $|A {\restriction } q| \leq \kappa $
, we get a
$|A {\restriction } q| \leq \kappa $
, we get a
![]() $\kappa $
-version of Baumgartner’s Axiom A. Property B is thus a variant of Axiom A combined with the notion of being
$\kappa $
-version of Baumgartner’s Axiom A. Property B is thus a variant of Axiom A combined with the notion of being
![]() $\kappa ^\kappa $
-bounding [Reference Bartoszyński and Judah1, Definition 7.2.C]; it is well-known from the countable context that many standard tree forcings, such as Sacks and Silver forcing, have this property.
$\kappa ^\kappa $
-bounding [Reference Bartoszyński and Judah1, Definition 7.2.C]; it is well-known from the countable context that many standard tree forcings, such as Sacks and Silver forcing, have this property.
Lemma 3.5. Property B implies
![]() $\kappa ^\kappa $
-bounding.
$\kappa ^\kappa $
-bounding.
Proof Assume
![]() $p \Vdash \dot {g} \in \kappa ^\kappa $
and
$p \Vdash \dot {g} \in \kappa ^\kappa $
and
![]() $\dot {g}(i)$
is decided by an antichain
$\dot {g}(i)$
is decided by an antichain
![]() $A_{i+1}$
for every
$A_{i+1}$
for every
![]() $i < \kappa $
. Construct a fusion sequence
$i < \kappa $
. Construct a fusion sequence
![]() $(q_{i})_{i < \kappa }$
below p by setting
$(q_{i})_{i < \kappa }$
below p by setting
![]() $q_0 := p$
and finding a
$q_0 := p$
and finding a
![]() $q_{i+1} \leq _i q_i$
with
$q_{i+1} \leq _i q_i$
with
![]() $|A_{i+1} {\restriction } q_{i+1}| < \kappa $
in successor steps. In limit steps
$|A_{i+1} {\restriction } q_{i+1}| < \kappa $
in successor steps. In limit steps
![]() $\lambda $
, set
$\lambda $
, set
![]() $q_\lambda $
to be a fusion limit of
$q_\lambda $
to be a fusion limit of
![]() $(q_i)_{i < \lambda }$
. The fusion limit
$(q_i)_{i < \lambda }$
. The fusion limit
![]() $q_\kappa $
of the whole sequence will force
$q_\kappa $
of the whole sequence will force
![]() $q_\kappa \Vdash \dot {g} \leq \check {h}$
for some
$q_\kappa \Vdash \dot {g} \leq \check {h}$
for some
![]() $h \in \kappa ^\kappa $
in the ground model.
$h \in \kappa ^\kappa $
in the ground model.
Lemma 3.6.
![]() $PT_f$
is
$PT_f$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
Proof If
![]() $(p_i)_{i < \delta }$
with
$(p_i)_{i < \delta }$
with
![]() $\delta < \kappa $
is a decreasing sequence, set
$\delta < \kappa $
is a decreasing sequence, set
![]() $q := \bigcap _{i < \delta } p_i$
. We check that q is a condition; only (S2) is nontrivial, so we assume that all other axioms hold.
$q := \bigcap _{i < \delta } p_i$
. We check that q is a condition; only (S2) is nontrivial, so we assume that all other axioms hold.
Let thus
![]() $\eta \in q$
. For some
$\eta \in q$
. For some
![]() $b \in [q]$
with
$b \in [q]$
with
![]() $\eta \lhd b$
(recall that by (S4) + (S5) such a b exists) consider the sets
$\eta \lhd b$
(recall that by (S4) + (S5) such a b exists) consider the sets
By (S2) and (S6),
![]() $C_i$
is a club subset of
$C_i$
is a club subset of
![]() $\kappa $
. Thus
$\kappa $
. Thus
![]() $\bigcap _{i < \delta } C_i$
is a club and yields a
$\bigcap _{i < \delta } C_i$
is a club and yields a
![]() $\nu $
with
$\nu $
with
![]() $\eta \lhd \nu $
and
$\eta \lhd \nu $
and
![]() $\nu \in \operatorname {\mathrm {split}}(q)$
.
$\nu \in \operatorname {\mathrm {split}}(q)$
.
Remark 3.7. Clearly, the intersection
![]() $\bigcap _{i < \delta } p_i$
in the previous lemma is simultaneously also the greatest lower bound of the decreasing sequence
$\bigcap _{i < \delta } p_i$
in the previous lemma is simultaneously also the greatest lower bound of the decreasing sequence
![]() $(p_i)_{i < \delta }$
,
$(p_i)_{i < \delta }$
,
![]() $\delta < \kappa $
.
$\delta < \kappa $
.
Definition 3.8. For
![]() $p,q \in PT_f$
, define
$p,q \in PT_f$
, define
![]() $q \leq _i p$
iff
$q \leq _i p$
iff
![]() $q \leq _{PT_f} p$
and
$q \leq _{PT_f} p$
and
![]() $\operatorname {\mathrm {split}}_i(p) = \operatorname {\mathrm {split}}_i(q)$
.
$\operatorname {\mathrm {split}}_i(p) = \operatorname {\mathrm {split}}_i(q)$
.
Fact 3.9. The following are equivalent:
-
1.
 $q \leq _i p.$
$q \leq _i p.$
-
2.
 $q \leq _{PT_f} p$
and
$q \leq _{PT_f} p$
and
 $\forall j \leq i: \operatorname {\mathrm {split}}_j(p) = \operatorname {\mathrm {split}}_j(q).$
$\forall j \leq i: \operatorname {\mathrm {split}}_j(p) = \operatorname {\mathrm {split}}_j(q).$
-
3.
 $q \leq _{PT_f} p$
and
$q \leq _{PT_f} p$
and
 $\forall \eta \in p: {\mathrm {ht^{s}}}_p(\eta ) \leq i \Rightarrow \operatorname {\mathrm {succ}}_p(\eta ) \subseteq q.$
$\forall \eta \in p: {\mathrm {ht^{s}}}_p(\eta ) \leq i \Rightarrow \operatorname {\mathrm {succ}}_p(\eta ) \subseteq q.$
-
4.
 $q \leq _{PT_f} p $
and
$q \leq _{PT_f} p $
and
 $\operatorname {\mathrm {split}}_{i+1}(p) \subseteq q.$
$\operatorname {\mathrm {split}}_{i+1}(p) \subseteq q.$
It remains to prove that equipped with these relations,
![]() $PT_f$
has Property B.
$PT_f$
has Property B.
Lemma 3.10. For every fusion sequence
![]() $(p_j)_{j<\delta }$
of length
$(p_j)_{j<\delta }$
of length
![]() $\delta \leq \kappa $
in
$\delta \leq \kappa $
in
![]() $PT_f$
there exists a q with
$PT_f$
there exists a q with
![]() $\forall j < \delta : q \leq _j p_j$
.
$\forall j < \delta : q \leq _j p_j$
.
Proof If
![]() $\delta < \kappa $
, the intersection q from Lemma 3.6 can be seen to also be a fusion limit.
$\delta < \kappa $
, the intersection q from Lemma 3.6 can be seen to also be a fusion limit.
Otherwise once again set
![]() $q = \bigcap _{j < \kappa } p_j$
and follow the proof of Lemma 3.6; along a branch
$q = \bigcap _{j < \kappa } p_j$
and follow the proof of Lemma 3.6; along a branch
![]() $b \in [q]$
again define the sets
$b \in [q]$
again define the sets
By using the fact that
![]() $(p_j)_{j < \kappa }$
is a fusion sequence, one can arrive at
$(p_j)_{j < \kappa }$
is a fusion sequence, one can arrive at
which is enough to conclude that
![]() $\bigcap _{j < \kappa } C_j$
is also a club by the closure of the club filter under diagonal intersections. It can easily be seen that q is a fusion limit.
$\bigcap _{j < \kappa } C_j$
is also a club by the closure of the club filter under diagonal intersections. It can easily be seen that q is a fusion limit.
Before concluding the proof, we first give two definitions which will come in handy later in the iteration context.
Definition 3.11. For a condition
![]() $p \in PT_f$
and
$p \in PT_f$
and
![]() $\eta \in p$
, define
$\eta \in p$
, define
![]() $p^{[\eta ]} := \{\nu \in p: \nu \lhd \eta \vee \eta \lhd \nu \}$
. One can see easily that
$p^{[\eta ]} := \{\nu \in p: \nu \lhd \eta \vee \eta \lhd \nu \}$
. One can see easily that
![]() $p^{[\eta ]}$
is a stronger condition than p and that for any
$p^{[\eta ]}$
is a stronger condition than p and that for any
![]() $i < \kappa $
we have
$i < \kappa $
we have
![]() $p = \bigcup _{\eta \in \operatorname {\mathrm {split}}_i(p)} p^{[\eta ]}$
.
$p = \bigcup _{\eta \in \operatorname {\mathrm {split}}_i(p)} p^{[\eta ]}$
.
Definition 3.12. Let
![]() $p \in PT_f$
be a condition and
$p \in PT_f$
be a condition and
![]() $i < \kappa $
. We say that a condition
$i < \kappa $
. We say that a condition
![]() $s \in PT_f$
is
$s \in PT_f$
is
![]() $(p,i)$
-determined iff
$(p,i)$
-determined iff
![]() $s \leq p$
and
$s \leq p$
and
Lemma 3.13. The set of
![]() $(p,i)$
-determined conditions is dense below p for all i.
$(p,i)$
-determined conditions is dense below p for all i.
Proof For any
![]() $r \leq p$
we may extend the stem of r in the following way: take any branch
$r \leq p$
we may extend the stem of r in the following way: take any branch
![]() $b \in [r] \subseteq [p]$
; since we then know
$b \in [r] \subseteq [p]$
; since we then know
![]() $|b \cap \operatorname {\mathrm {split}}_{i}(p)| = 1$
, we see that there is a unique
$|b \cap \operatorname {\mathrm {split}}_{i}(p)| = 1$
, we see that there is a unique
![]() $\nu $
with
$\nu $
with
![]() $\nu \in b \cap r \cap \operatorname {\mathrm {split}}_i(p)$
. Then
$\nu \in b \cap r \cap \operatorname {\mathrm {split}}_i(p)$
. Then
![]() $r^{[\nu ]}$
is
$r^{[\nu ]}$
is
![]() $(p,i)$
-determined.
$(p,i)$
-determined.
Theorem 3.14.
![]() $PT_f$
has Property B.
$PT_f$
has Property B.
Proof It remains to show the antichain condition. To this end, let A be a maximal antichain,
![]() $p \in PT_f$
and
$p \in PT_f$
and
![]() $i < \kappa $
. Enumerate
$i < \kappa $
. Enumerate
![]() $\operatorname {\mathrm {split}}_{i+1}(p)$
as
$\operatorname {\mathrm {split}}_{i+1}(p)$
as
![]() $(\eta _j)_{j < \delta }$
with
$(\eta _j)_{j < \delta }$
with
![]() $\delta < \kappa $
. We will decompose p into
$\delta < \kappa $
. We will decompose p into
![]() $|\delta |$
many parts, each of which will be thinned out above the
$|\delta |$
many parts, each of which will be thinned out above the
![]() $(i+1)$
th splitting front.
$(i+1)$
th splitting front.
Proceed by finding for each
![]() $j < \delta $
a condition
$j < \delta $
a condition
![]() $s_j \leq p^{[\eta _j]}$
such that
$s_j \leq p^{[\eta _j]}$
such that
![]() $|A {\restriction } s_j| = 1$
. Set
$|A {\restriction } s_j| = 1$
. Set
Then
![]() $q \in PT_f$
is a condition with
$q \in PT_f$
is a condition with
![]() $\operatorname {\mathrm {split}}_{i+1}(p) \subseteq q$
and thus
$\operatorname {\mathrm {split}}_{i+1}(p) \subseteq q$
and thus
![]() $q \leq _i p$
. To prove
$q \leq _i p$
. To prove
![]() $|A {\restriction } q| < \kappa $
, let
$|A {\restriction } q| < \kappa $
, let
![]() $r \in A$
be compatible with q. By the previous lemma we may pick a
$r \in A$
be compatible with q. By the previous lemma we may pick a
![]() $t_r$
that is
$t_r$
that is
![]() $(p,i+1)$
-determined with
$(p,i+1)$
-determined with
![]() $t_r \leq r,q$
and hence
$t_r \leq r,q$
and hence
![]() $t_r \cap \operatorname {\mathrm {split}}_{i+1}(p) = \{\eta _{j_r}\}$
for some
$t_r \cap \operatorname {\mathrm {split}}_{i+1}(p) = \{\eta _{j_r}\}$
for some
![]() $j_r < \delta $
. But since
$j_r < \delta $
. But since
![]() $t_r \leq q$
, we can conclude
$t_r \leq q$
, we can conclude
![]() $t_r \leq s_{j_r}$
and thus
$t_r \leq s_{j_r}$
and thus
![]() $r \parallel s_{j_r}$
. We have thus found a function from
$r \parallel s_{j_r}$
. We have thus found a function from
![]() $A {\restriction } q$
to
$A {\restriction } q$
to
![]() $\delta $
, mapping
$\delta $
, mapping
![]() $r \mapsto j_r$
, which is injective (since
$r \mapsto j_r$
, which is injective (since
![]() $|A {\restriction } s_j| = 1$
for all
$|A {\restriction } s_j| = 1$
for all
![]() $j < \delta $
). The desired conclusion
$j < \delta $
). The desired conclusion
![]() $|A {\restriction } q| < \kappa $
follows.
$|A {\restriction } q| < \kappa $
follows.
4 The iteration
The backbone of our forcing construction will consist of an iteration of
![]() $PT_f$
forcings. Let therefore
$PT_f$
forcings. Let therefore
![]() $\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
be a
$\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
be a
![]() ${\leq }\kappa $
-supported forcing iteration with
${\leq }\kappa $
-supported forcing iteration with
where the sequence
![]() $(f_\alpha )_{\alpha < \kappa ^{++}}$
is in the ground model and
$(f_\alpha )_{\alpha < \kappa ^{++}}$
is in the ground model and
![]() $f_\alpha (i) \geq 2$
for all
$f_\alpha (i) \geq 2$
for all
![]() $i < \kappa $
. Set
$i < \kappa $
. Set
![]() $\mathbb {P} := \mathbb {P}_{\kappa ^{++}}$
.
$\mathbb {P} := \mathbb {P}_{\kappa ^{++}}$
.
As a matter of notation, let
![]() $\dot {G}_\alpha $
for
$\dot {G}_\alpha $
for
![]() $\alpha \leq \kappa ^{++}$
denote the canonical
$\alpha \leq \kappa ^{++}$
denote the canonical
![]() $\mathbb {P}_\alpha $
-name for a
$\mathbb {P}_\alpha $
-name for a
![]() $\mathbb {P}_\alpha $
-generic filter; we also write
$\mathbb {P}_\alpha $
-generic filter; we also write
![]() $\dot {G}$
for
$\dot {G}$
for
![]() $\dot {G}_{\kappa ^{++}}$
. Finally, let
$\dot {G}_{\kappa ^{++}}$
. Finally, let
![]() $\dot {s}_\alpha $
be the canonical name for the
$\dot {s}_\alpha $
be the canonical name for the
![]() $\alpha $
th generic real.
$\alpha $
th generic real.
This section is dedicated to verifying some regularity properties of such iterations. We will observe that:
-
1.
 $\mathbb {P}$
is
$\mathbb {P}$
is
 ${<}\kappa $
-closed,
${<}\kappa $
-closed, -
2.
 $\mathbb {P}$
does not collapse
$\mathbb {P}$
does not collapse
 $\kappa ^+$
,
$\kappa ^+$
, -
3. if
 $V \models |2^\kappa | = \kappa ^+$
, then
$V \models |2^\kappa | = \kappa ^+$
, then
 $\mathbb {P}$
has the
$\mathbb {P}$
has the
 $\kappa ^{++}$
-c.c.,
$\kappa ^{++}$
-c.c.,
thus in aggregate no cardinals are collapsed when forcing with
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Fact 4.1.
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
In the countable case, the favoured tool one would look towards in the endeavour of preserving
![]() $\omega _1$
is the notion of properness. Finding a satisfactory analogue for higher cardinals is a long-standing open problem (see, e.g., [Reference Rosłanowski and Shelah22] and [Reference Friedman, Honzik and Zdomskyy5]). A relatively straightforward generalization that still enjoys many desirable qualities of properness is the following:
$\omega _1$
is the notion of properness. Finding a satisfactory analogue for higher cardinals is a long-standing open problem (see, e.g., [Reference Rosłanowski and Shelah22] and [Reference Friedman, Honzik and Zdomskyy5]). A relatively straightforward generalization that still enjoys many desirable qualities of properness is the following:
Definition 4.2. A forcing
![]() $\mathcal {P}$
is called
$\mathcal {P}$
is called
![]() $\kappa $
-proper iff for every sufficiently large
$\kappa $
-proper iff for every sufficiently large
![]() $\theta $
(e.g.,
$\theta $
(e.g.,
![]() $\theta> \vert 2^{\mathcal {P}}\vert $
) and every elementary submodel
$\theta> \vert 2^{\mathcal {P}}\vert $
) and every elementary submodel
![]() $M \preccurlyeq H(\theta )$
such that
$M \preccurlyeq H(\theta )$
such that
![]() $\mathcal {P} \in M$
,
$\mathcal {P} \in M$
,
![]() $|M| = \kappa $
and
$|M| = \kappa $
and
![]() $^{<\kappa }M \subseteq M$
, and every
$^{<\kappa }M \subseteq M$
, and every
![]() $p \in \mathcal {P} \cap M$
, there exists
$p \in \mathcal {P} \cap M$
, there exists
![]() $q \leq _{\mathcal {P}} p$
such that for every dense
$q \leq _{\mathcal {P}} p$
such that for every dense
![]() $D \in M$
,
$D \in M$
,
![]() $D \cap M$
is predense below q.
$D \cap M$
is predense below q.
Fact 4.3. Forcing notions that are
![]() ${<}\kappa ^+$
-closed or have the
${<}\kappa ^+$
-closed or have the
![]() $\kappa ^+$
-c.c. are
$\kappa ^+$
-c.c. are
![]() $\kappa $
-proper. Furthermore,
$\kappa $
-proper. Furthermore,
![]() $\kappa $
-proper forcing notions do not collapse
$\kappa $
-proper forcing notions do not collapse
![]() $\kappa ^+$
.
$\kappa ^+$
.
Further details on
![]() $\kappa $
-properness can be found in [Reference Friedman, Khomskii and Kulikov7].
$\kappa $
-properness can be found in [Reference Friedman, Khomskii and Kulikov7].
Unfortunately, in stark contrast to the classical setting, there is no preservation theorem for
![]() $\kappa $
-properness in iterations (see [Reference Roslanowski21] for an iteration of
$\kappa $
-properness in iterations (see [Reference Roslanowski21] for an iteration of
![]() $\kappa ^+$
-c.c. forcings whose
$\kappa ^+$
-c.c. forcings whose
![]() $\omega $
-limit collapses
$\omega $
-limit collapses
![]() $\kappa ^+$
). Our strategy for ensuring
$\kappa ^+$
). Our strategy for ensuring
![]() $\kappa $
-properness is to verify an iteration version of Property B. Similar to fusion with countable support, in such cases the correct tool is the following notion:
$\kappa $
-properness is to verify an iteration version of Property B. Similar to fusion with countable support, in such cases the correct tool is the following notion:
Definition 4.4. For
![]() $\zeta \leq \kappa ^{++}$
let
$\zeta \leq \kappa ^{++}$
let
![]() $\langle \mathcal {P}_\alpha , \dot {\mathcal {Q}}_\beta : \alpha \leq \zeta , \beta < \zeta \rangle $
be a
$\langle \mathcal {P}_\alpha , \dot {\mathcal {Q}}_\beta : \alpha \leq \zeta , \beta < \zeta \rangle $
be a
![]() ${\leq }\kappa $
-support iteration with
${\leq }\kappa $
-support iteration with
Let
![]() $F \in [\zeta ]^{<\kappa }$
and
$F \in [\zeta ]^{<\kappa }$
and
![]() $i < \kappa $
. We define
$i < \kappa $
. We define
![]() $ q \leq _{F,i} p$
iff
$ q \leq _{F,i} p$
iff
Then:
-
1. A sequence
 $\langle p_i, F_i: i < \delta \rangle $
of length
$\langle p_i, F_i: i < \delta \rangle $
of length
 $\delta \leq \kappa $
is called a fusion sequence iff:
$\delta \leq \kappa $
is called a fusion sequence iff:-
•
 $\forall j < k < \delta : p_k \leq _{F_j,j} p_j.$
$\forall j < k < \delta : p_k \leq _{F_j,j} p_j.$
-
• The
 $F_j$
are increasing and, if
$F_j$
are increasing and, if
 $\delta = \kappa $
, then
$\delta = \kappa $
, then
 $\bigcup _{j < \delta } \textrm {supp}(p_j) \subseteq \bigcup _{j < \delta } F_j$
.
$\bigcup _{j < \delta } \textrm {supp}(p_j) \subseteq \bigcup _{j < \delta } F_j$
.
-
-
2. We say that
 $\mathcal {P}_{\zeta }$
has Property B* iff:
$\mathcal {P}_{\zeta }$
has Property B* iff:-
• For every fusion sequence
 $\langle p_i, F_i: i < \delta \rangle ,\ \delta \leq \kappa $
there exists a fusion limit q with
$\langle p_i, F_i: i < \delta \rangle ,\ \delta \leq \kappa $
there exists a fusion limit q with
 $\forall j < \delta : q \leq _{F_j,j} p_j$
.
$\forall j < \delta : q \leq _{F_j,j} p_j$
. -
• For every maximal antichain A, every
 $p \in \mathcal {P}_{\zeta }, F \in [\zeta ]^{<\kappa }$
and
$p \in \mathcal {P}_{\zeta }, F \in [\zeta ]^{<\kappa }$
and
 $i<\kappa $
there exists a
$i<\kappa $
there exists a
 $q \leq _{F,i} p$
such that
$q \leq _{F,i} p$
such that
 $|A {\restriction } q| < \kappa $
.
$|A {\restriction } q| < \kappa $
.
-
Hence for iterations we consider fusion sequences pointwise, with the added caveat of being able to delay fusion arbitrarily long in each coordinate. In practice, the auxiliary sets
![]() $F_j$
will almost always be defined by a bookkeeping argument relative to the
$F_j$
will almost always be defined by a bookkeeping argument relative to the
![]() $p_j$
.
$p_j$
.
Fact 4.5. Property B* implies
![]() $\kappa $
-properness and
$\kappa $
-properness and
![]() $\kappa ^\kappa $
-bounding.
$\kappa ^\kappa $
-bounding.
In the definition of Property B*, only the antichain condition is nontrivial. In fact, for such iterations of Property B forcings, fusion limits always exist.
Lemma 4.6. With the notation from the previous definition, every fusion sequence
![]() $\langle p_i, F_i: i < \delta \rangle ,\ \delta \leq \kappa $
in
$\langle p_i, F_i: i < \delta \rangle ,\ \delta \leq \kappa $
in
![]() $\mathcal {P}_{\zeta }$
has a fusion limit q.
$\mathcal {P}_{\zeta }$
has a fusion limit q.
Proof We construct q inductively such that
![]() $\mathcal {P}_\alpha \ni q {\restriction } \alpha $
is a fusion limit of
$\mathcal {P}_\alpha \ni q {\restriction } \alpha $
is a fusion limit of
![]() $\langle p_i {\restriction } \alpha , F_i \cap \alpha : i < \delta \rangle $
for each
$\langle p_i {\restriction } \alpha , F_i \cap \alpha : i < \delta \rangle $
for each
![]() $\alpha \leq \zeta $
.
$\alpha \leq \zeta $
.
Assume
![]() $q {\restriction } \alpha $
has been defined for
$q {\restriction } \alpha $
has been defined for
![]() $\alpha < \zeta $
. To define
$\alpha < \zeta $
. To define
![]() $q(\alpha )$
, distinguish three cases:
$q(\alpha )$
, distinguish three cases:
-
•
 $\alpha \in \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j) \wedge \alpha \in \bigcup _{j < \delta } F_j$
: Find
$\alpha \in \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j) \wedge \alpha \in \bigcup _{j < \delta } F_j$
: Find
 $j^*(\alpha )$
minimal such that
$j^*(\alpha )$
minimal such that
 $\alpha \in F_{j^*(\alpha )}$
. Now
$\alpha \in F_{j^*(\alpha )}$
. Now
 $q {\restriction } \alpha \Vdash " (p_j(\alpha ))_{j \geq j^*(\alpha )} \textrm { is a fusion sequence"}$
, so let
$q {\restriction } \alpha \Vdash " (p_j(\alpha ))_{j \geq j^*(\alpha )} \textrm { is a fusion sequence"}$
, so let
 $q(\alpha )$
be a fusion limit of that sequence.
$q(\alpha )$
be a fusion limit of that sequence. -
•
 $\alpha \in \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j) \wedge \alpha \notin \bigcup _{j < \delta } F_j$
: Note that this case may only occur for
$\alpha \in \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j) \wedge \alpha \notin \bigcup _{j < \delta } F_j$
: Note that this case may only occur for
 $\delta < \kappa $
, thus we may use
$\delta < \kappa $
, thus we may use
 ${<}\kappa $
-closure of
${<}\kappa $
-closure of
 $\dot {\mathcal {Q}}_\alpha $
to construct
$\dot {\mathcal {Q}}_\alpha $
to construct
 $q(\alpha )$
from
$q(\alpha )$
from
 $(p_j(\alpha ))_{j < \delta }$
.
$(p_j(\alpha ))_{j < \delta }$
. -
•
 $\alpha \notin \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j)$
: Set
$\alpha \notin \bigcup _{j < \delta } \operatorname {\mathrm {supp}}(p_j)$
: Set  .
.
To see that
![]() $q {\restriction } \gamma \in \mathcal {P}_\gamma $
for limit
$q {\restriction } \gamma \in \mathcal {P}_\gamma $
for limit
![]() $\gamma $
, merely note
$\gamma $
, merely note
![]() $\operatorname {\mathrm {supp}}(q {\restriction } \gamma ) \subseteq \bigcup _{i < \delta } \operatorname {\mathrm {supp}}(p_i {\restriction } \gamma )$
.
$\operatorname {\mathrm {supp}}(q {\restriction } \gamma ) \subseteq \bigcup _{i < \delta } \operatorname {\mathrm {supp}}(p_i {\restriction } \gamma )$
.
Remark 4.7. Note that the forcings
![]() $\dot {\mathcal {Q}}_\alpha = PT_{f_\alpha }$
fulfil
$\dot {\mathcal {Q}}_\alpha = PT_{f_\alpha }$
fulfil
![]() ${<}\kappa $
-closure and the existence of fusion limits in a particularly strong way: in either case, a canonical weakest lower bound/fusion limit exists. Thus by following the above proof and choosing these canonical conditions, we can see that an iteration of
${<}\kappa $
-closure and the existence of fusion limits in a particularly strong way: in either case, a canonical weakest lower bound/fusion limit exists. Thus by following the above proof and choosing these canonical conditions, we can see that an iteration of
![]() $PT_f$
forcings also fulfils a stronger fusion condition: for every fusion sequence there exists a canonical, weakest fusion limit.
$PT_f$
forcings also fulfils a stronger fusion condition: for every fusion sequence there exists a canonical, weakest fusion limit.
Some work remains to prove the antichain condition for
![]() $\mathbb {P}_\zeta $
, which we do in a rather ad hoc manner by induction on
$\mathbb {P}_\zeta $
, which we do in a rather ad hoc manner by induction on
![]() $\zeta $
. On the way we will introduce some notation that will also come in handy later.
$\zeta $
. On the way we will introduce some notation that will also come in handy later.
First off, let us define the iteration version of Definition 3.12 and the corresponding density lemma.
Definition 4.8. Let
![]() $\zeta \leq \kappa ^{++}, p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
$\zeta \leq \kappa ^{++}, p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
![]() $i < \kappa $
. We say a condition
$i < \kappa $
. We say a condition
![]() $s \in \mathbb {P}_\zeta $
is
$s \in \mathbb {P}_\zeta $
is
![]() $(p,F,i)$
-determined following
$(p,F,i)$
-determined following
![]() $g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
iff
$g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
iff
![]() $s \leq _{\mathbb {P}_\zeta } p$
and
$s \leq _{\mathbb {P}_\zeta } p$
and
 $$ \begin{gather*} \forall \beta \in F \, \exists \eta_\beta \in \kappa^{<\kappa}: \\ s {\restriction} \beta \Vdash s(\beta) \cap \operatorname{\mathrm{split}}_{i}(p(\beta)) = \check{\{\eta_\beta\}} \wedge \operatorname{\mathrm{succ}}_{s(\beta)}(\eta_\beta) = \check{\{g(\beta)\}}. \end{gather*} $$
$$ \begin{gather*} \forall \beta \in F \, \exists \eta_\beta \in \kappa^{<\kappa}: \\ s {\restriction} \beta \Vdash s(\beta) \cap \operatorname{\mathrm{split}}_{i}(p(\beta)) = \check{\{\eta_\beta\}} \wedge \operatorname{\mathrm{succ}}_{s(\beta)}(\eta_\beta) = \check{\{g(\beta)\}}. \end{gather*} $$
We say a condition s is
![]() $(p,F,i)$
-determined iff it is
$(p,F,i)$
-determined iff it is
![]() $(p,F,i)$
-determined following some (unique) g.
$(p,F,i)$
-determined following some (unique) g.
The function g prescribes the choices s makes at the ith splitting front of p; it is completely determined by s.
Lemma 4.9. The set of
![]() $(p,F,i)$
-determined conditions is dense below
$(p,F,i)$
-determined conditions is dense below
![]() $p \in \mathbb {P}_\zeta $
for all
$p \in \mathbb {P}_\zeta $
for all
![]() $p,F,i$
and the set of
$p,F,i$
and the set of
![]() $(p,F,i)$
-determined conditions following g is open for all
$(p,F,i)$
-determined conditions following g is open for all
![]() $p,F,i,g$
.
$p,F,i,g$
.
Proof Enumerate F as an increasing sequence
![]() $(\beta _j)_{j < \delta }$
with
$(\beta _j)_{j < \delta }$
with
![]() $\delta < \kappa $
and set
$\delta < \kappa $
and set
![]() $\beta _\delta := \zeta $
. For an
$\beta _\delta := \zeta $
. For an
![]() $r \leq p$
we will inductively construct a decreasing sequence
$r \leq p$
we will inductively construct a decreasing sequence
![]() $(s_j)_{j \leq \delta }$
below r and a
$(s_j)_{j \leq \delta }$
below r and a
![]() $\subseteq $
-increasing sequence
$\subseteq $
-increasing sequence
![]() $(g_j)_{j \leq \delta }$
with
$(g_j)_{j \leq \delta }$
with
![]() $g_j \in \prod _{\beta \in F \cap \beta _j} \kappa ^{<\kappa }$
such that
$g_j \in \prod _{\beta \in F \cap \beta _j} \kappa ^{<\kappa }$
such that
![]() $s_j \textrm { is } (p, F \cap \beta _j, i) \textrm {-determined}$
following
$s_j \textrm { is } (p, F \cap \beta _j, i) \textrm {-determined}$
following
![]() $g_j$
.
$g_j$
.
-
•
 $j=0$
: Set
$j=0$
: Set
 $s_{0} := r$
.
$s_{0} := r$
. -
•
 $j \to j+1$
: Since
$j \to j+1$
: Since
 $s_j {\restriction } \beta _j \Vdash s_j(\beta _j) \leq _{\dot {\mathbb {Q}}_{\beta _j}} p(\beta _j)$
, we may use Lemma 3.13 to find
$s_j {\restriction } \beta _j \Vdash s_j(\beta _j) \leq _{\dot {\mathbb {Q}}_{\beta _j}} p(\beta _j)$
, we may use Lemma 3.13 to find
 $\mathbb {P}_{\beta _j}$
-names
$\mathbb {P}_{\beta _j}$
-names
 $\dot {t}, \dot {\eta }_{\beta _j}, \dot {\nu }_{\beta _j} $
with and
$\dot {t}, \dot {\eta }_{\beta _j}, \dot {\nu }_{\beta _j} $
with and $$\begin{align*}s_j {\restriction} \beta_j \Vdash \dot{t} \in \mathbb{Q}_{\beta_j} \wedge \dot{t} \leq_{\dot{\mathbb{Q}}_{\beta_j}} s_j(\beta_j) \end{align*}$$
Find a stronger condition
$$\begin{align*}s_j {\restriction} \beta_j \Vdash \dot{t} \in \mathbb{Q}_{\beta_j} \wedge \dot{t} \leq_{\dot{\mathbb{Q}}_{\beta_j}} s_j(\beta_j) \end{align*}$$
Find a stronger condition $$ \begin{gather*} s_j {\restriction} \beta_j \Vdash \dot{t} \cap \operatorname{\mathrm{split}}_i(p) = \{\dot{\eta}_{\beta_j}\} \wedge \operatorname{\mathrm{succ}}_{\dot{t}}(\dot{\eta}_{\beta_j}) = \{\dot{\nu}_{\beta_j}\}. \end{gather*} $$
$$ \begin{gather*} s_j {\restriction} \beta_j \Vdash \dot{t} \cap \operatorname{\mathrm{split}}_i(p) = \{\dot{\eta}_{\beta_j}\} \wedge \operatorname{\mathrm{succ}}_{\dot{t}}(\dot{\eta}_{\beta_j}) = \{\dot{\nu}_{\beta_j}\}. \end{gather*} $$
 $\tilde {s}_j \leq s_j {\restriction } \beta _j$
that decides the names
$\tilde {s}_j \leq s_j {\restriction } \beta _j$
that decides the names
 $\dot {\eta }_{\beta _j}, \dot {\nu }_{\beta _j}$
as
$\dot {\eta }_{\beta _j}, \dot {\nu }_{\beta _j}$
as
 $\eta _{\beta _j}, \nu _{\beta _j}$
. Define
$\eta _{\beta _j}, \nu _{\beta _j}$
. Define
 $s_{j+1} := \tilde {s}_j ^\frown \dot {t} ^\frown (s_j {\restriction } [\beta _j + 1, \zeta ))$
and
$s_{j+1} := \tilde {s}_j ^\frown \dot {t} ^\frown (s_j {\restriction } [\beta _j + 1, \zeta ))$
and
 $g_{j+1} := g_j \cup \{(\beta _j, \nu _{\beta _j})\}$
.
$g_{j+1} := g_j \cup \{(\beta _j, \nu _{\beta _j})\}$
.
-
•
 $\lambda \leq \delta $
is a limit: By
$\lambda \leq \delta $
is a limit: By
 ${<}\kappa $
-closure we can find a lower bound
${<}\kappa $
-closure we can find a lower bound
 $s_\lambda $
of the sequence
$s_\lambda $
of the sequence
 $(s_\ell )_{\ell < \lambda }$
. Define
$(s_\ell )_{\ell < \lambda }$
. Define
 $g_\lambda := \bigcup _{\ell < \lambda } g_\ell $
. Clearly,
$g_\lambda := \bigcup _{\ell < \lambda } g_\ell $
. Clearly,
 $s_\lambda $
is
$s_\lambda $
is
 $(p, F \cap \beta _\lambda , i)$
-determined following
$(p, F \cap \beta _\lambda , i)$
-determined following
 $g_\lambda $
.
$g_\lambda $
.
Now
![]() $s_\delta \leq r$
is
$s_\delta \leq r$
is
![]() $(p,F,i)$
-determined following
$(p,F,i)$
-determined following
![]() $g_\delta $
. Lastly, if s is
$g_\delta $
. Lastly, if s is
![]() $(p,F,i)$
-determined following g, then clearly any
$(p,F,i)$
-determined following g, then clearly any
![]() $s' \leq s$
is as well.
$s' \leq s$
is as well.
Fact 4.10. If
![]() $p' \leq _{F,i} p$
and
$p' \leq _{F,i} p$
and
![]() $s \leq p'$
, then s is
$s \leq p'$
, then s is
![]() $(p,F,i)$
-determined iff it is
$(p,F,i)$
-determined iff it is
![]() $(p', F,i)$
-determined.
$(p', F,i)$
-determined.
Suppose now that
![]() $s \leq _{PT_f} p$
. The extension of p to s may be undertaken in two steps by interpolating on the
$s \leq _{PT_f} p$
. The extension of p to s may be undertaken in two steps by interpolating on the
![]() $\leq _i$
relation. In the first step, we thin out as much as is necessary from p, but only in its ‘upper regions’—say, above the
$\leq _i$
relation. In the first step, we thin out as much as is necessary from p, but only in its ‘upper regions’—say, above the
![]() $(i+1)$
th splitting front—yielding an interpolating condition
$(i+1)$
th splitting front—yielding an interpolating condition
![]() $p^{(s)}$
with
$p^{(s)}$
with
![]() $p^{(s)} \leq _i p$
(above nodes not present in s, p may be left untouched in the extension to
$p^{(s)} \leq _i p$
(above nodes not present in s, p may be left untouched in the extension to
![]() $p^{(s)}$
). In the second step, nodes are removed from
$p^{(s)}$
). In the second step, nodes are removed from
![]() $p^{(s)}$
, but only near the base of the tree, such that whenever
$p^{(s)}$
, but only near the base of the tree, such that whenever
![]() $\eta \in p^{(s)} \backslash s$
, then there is already some initial segment
$\eta \in p^{(s)} \backslash s$
, then there is already some initial segment
![]() $\nu \lhd \eta $
with
$\nu \lhd \eta $
with
![]() $\nu \in p^{(s)} \backslash s$
and
$\nu \in p^{(s)} \backslash s$
and
![]() ${\mathrm {ht^{s}}}_{p^{(s)}}(\nu ) \leq i+1$
. We thus have
${\mathrm {ht^{s}}}_{p^{(s)}}(\nu ) \leq i+1$
. We thus have
This motivates the next lemma.
Lemma 4.11 (Interpolation).
Let
![]() $p \in \mathbb {P}_\zeta $
and s be
$p \in \mathbb {P}_\zeta $
and s be
![]() $(p,F,i)$
-determined following
$(p,F,i)$
-determined following
![]() $g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
for some
$g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
for some
![]() $F \in [\zeta ]^{<\kappa }, i < \kappa $
. Then there exists a condition
$F \in [\zeta ]^{<\kappa }, i < \kappa $
. Then there exists a condition
![]() $p^{(s)} \leq _{F,i} p$
with:
$p^{(s)} \leq _{F,i} p$
with:
-
•
 $s \leq _{\mathbb {P}_\zeta } p^{(s)} \leq _{F,i} p$
and
$s \leq _{\mathbb {P}_\zeta } p^{(s)} \leq _{F,i} p$
and -
• for all
 $(p,F,i)$
-determined conditions
$(p,F,i)$
-determined conditions
 $s'$
following g, whenever
$s'$
following g, whenever
 $s' \leq _{\mathbb {P}_\zeta } p^{(s)}$
, then already
$s' \leq _{\mathbb {P}_\zeta } p^{(s)}$
, then already
 $s' \leq _{\mathbb {P_\zeta }} s$
.
$s' \leq _{\mathbb {P_\zeta }} s$
.
Proof Construct
![]() $p^{(s)}$
by induction such that for each
$p^{(s)}$
by induction such that for each
![]() $\alpha \leq \zeta $
we have
$\alpha \leq \zeta $
we have
![]() $p^{(s)} {\restriction } \alpha \in \mathbb {P}_\alpha $
and
$p^{(s)} {\restriction } \alpha \in \mathbb {P}_\alpha $
and
![]() $p^{(s)} {\restriction } \alpha \leq _{F \cap \alpha , i} p {\restriction } \alpha $
.
$p^{(s)} {\restriction } \alpha \leq _{F \cap \alpha , i} p {\restriction } \alpha $
.
Assume
![]() $p^{(s)} {\restriction } \alpha $
has been defined; to define
$p^{(s)} {\restriction } \alpha $
has been defined; to define
![]() $p^{(s)}(\alpha )$
, there are two cases to distinguish:
$p^{(s)}(\alpha )$
, there are two cases to distinguish:
-
• If
 $\alpha \notin F$
, set
$\alpha \notin F$
, set
 $p^{(s)}(\alpha ) := \begin {cases} s(\alpha ), & \textrm { if } s {\restriction } \alpha \in \dot {G}_\alpha , \\ p(\alpha ), & \textrm { otherwise.} \end {cases}$
$p^{(s)}(\alpha ) := \begin {cases} s(\alpha ), & \textrm { if } s {\restriction } \alpha \in \dot {G}_\alpha , \\ p(\alpha ), & \textrm { otherwise.} \end {cases}$
-
• If
 $\alpha \in F$
, set
$\alpha \in F$
, set
 $p^{(s)}(\alpha ) := \begin {cases} s(\alpha ) \cup (p(\alpha ) \backslash p(\alpha )^{[g(\alpha )]}), & \textrm { if } s {\restriction } \alpha \in \dot {G}_\alpha , \\ p(\alpha ), & \textrm { otherwise.} \end {cases}$
$p^{(s)}(\alpha ) := \begin {cases} s(\alpha ) \cup (p(\alpha ) \backslash p(\alpha )^{[g(\alpha )]}), & \textrm { if } s {\restriction } \alpha \in \dot {G}_\alpha , \\ p(\alpha ), & \textrm { otherwise.} \end {cases}$
Note that we have
 $s {\restriction } \alpha \Vdash g(\alpha ) \in p(\alpha )$
and
$s {\restriction } \alpha \Vdash g(\alpha ) \in p(\alpha )$
and  $$\begin{align*}p^{(s)} {\restriction} \alpha \Vdash p^{(s)}(\alpha) \leq_{i} p(\alpha). \end{align*}$$
$$\begin{align*}p^{(s)} {\restriction} \alpha \Vdash p^{(s)}(\alpha) \leq_{i} p(\alpha). \end{align*}$$
To see that
![]() $p^{(s)} {\restriction } \gamma \in \mathbb {P}_\gamma $
for
$p^{(s)} {\restriction } \gamma \in \mathbb {P}_\gamma $
for
![]() $\gamma $
limit, we note that
$\gamma $
limit, we note that
Furthermore, we clearly have
![]() $s \leq p^{(s)}$
.
$s \leq p^{(s)}$
.
It remains to check the second requirement. Take some
![]() $(p,F,i)$
-determined
$(p,F,i)$
-determined
![]() $s'$
following g with
$s'$
following g with
![]() $s' \leq p^{(s)}$
. Assume inductively that
$s' \leq p^{(s)}$
. Assume inductively that
![]() $s' {\restriction } \alpha \leq s {\restriction } \alpha $
. Since the case
$s' {\restriction } \alpha \leq s {\restriction } \alpha $
. Since the case
![]() $\alpha \notin F$
is trivial, we may restrict our attention to the case
$\alpha \notin F$
is trivial, we may restrict our attention to the case
![]() $\alpha \in F$
. Then we have
$\alpha \in F$
. Then we have
![]() $s' {\restriction } \alpha \Vdash s'(\alpha ) \leq _{\mathbb {Q}_\alpha } p^{(s)}(\alpha ) = s(\alpha ) \cup (p(\alpha ) \backslash p(\alpha )^{[g(\alpha )]})$
. But then we already have
$s' {\restriction } \alpha \Vdash s'(\alpha ) \leq _{\mathbb {Q}_\alpha } p^{(s)}(\alpha ) = s(\alpha ) \cup (p(\alpha ) \backslash p(\alpha )^{[g(\alpha )]})$
. But then we already have
![]() $s' {\restriction } \alpha \Vdash s'(\alpha ) \leq _{\mathbb {Q}_\alpha } s(\alpha )$
. In conclusion,
$s' {\restriction } \alpha \Vdash s'(\alpha ) \leq _{\mathbb {Q}_\alpha } s(\alpha )$
. In conclusion,
![]() $s' \leq s$
, which finishes the proof of the lemma.
$s' \leq s$
, which finishes the proof of the lemma.
Remark 4.12. The above construction yields the following observation: not only is
![]() $p^{(s)}$
an interpolant for
$p^{(s)}$
an interpolant for
![]() $p,s, F$
and i, but we even have that
$p,s, F$
and i, but we even have that
![]() $p^{(s)} {\restriction } \alpha $
is an interpolant for
$p^{(s)} {\restriction } \alpha $
is an interpolant for
![]() $p {\restriction } \alpha , s {\restriction } \alpha , F \cap \alpha $
and i for any
$p {\restriction } \alpha , s {\restriction } \alpha , F \cap \alpha $
and i for any
![]() $\alpha < \zeta $
.
$\alpha < \zeta $
.
In the next lemma, we show that under certain conditions, the forcing
![]() $\mathbb {P}_\zeta $
admits least upper bounds of the form
$\mathbb {P}_\zeta $
admits least upper bounds of the form

Lemma 4.13. Let
![]() $p \in \mathbb {P}_\zeta $
and s be
$p \in \mathbb {P}_\zeta $
and s be
![]() $(p,F,i)$
-determined following
$(p,F,i)$
-determined following
![]() $g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
. Then for every
$g \in \prod _{\beta \in F} \kappa ^{<\kappa }$
. Then for every
![]() $q \leq _{F,i} p^{(s)}$
there exists an
$q \leq _{F,i} p^{(s)}$
there exists an
![]() $\tilde {s} \leq q, s$
that is
$\tilde {s} \leq q, s$
that is
![]() $(q,F,i)$
-determined following g such that for every
$(q,F,i)$
-determined following g such that for every
![]() $s' \leq q$
, if
$s' \leq q$
, if
![]() $s'$
is
$s'$
is
![]() $(q,F,i)$
-determined following g, then
$(q,F,i)$
-determined following g, then
![]() $s' \leq \tilde {s}$
. In other words,
$s' \leq \tilde {s}$
. In other words,
![]() $\tilde {s}$
is the weakest
$\tilde {s}$
is the weakest
![]() $(q,F,i)$
-determined condition following g.
$(q,F,i)$
-determined condition following g.
Proof Construct
![]() $\tilde {s}$
by induction such that for all
$\tilde {s}$
by induction such that for all
![]() $\alpha \leq \zeta $
we have
$\alpha \leq \zeta $
we have
![]() $\tilde {s} {\restriction } \alpha \in \mathbb {P}_\alpha $
,
$\tilde {s} {\restriction } \alpha \in \mathbb {P}_\alpha $
,
![]() $\tilde {s} {\restriction } \alpha \leq q {\restriction } \alpha $
and
$\tilde {s} {\restriction } \alpha \leq q {\restriction } \alpha $
and
![]() $\tilde {s} {\restriction } \alpha $
is
$\tilde {s} {\restriction } \alpha $
is
![]() $(q {\restriction } \alpha , F \cap \alpha , i)$
-determined following
$(q {\restriction } \alpha , F \cap \alpha , i)$
-determined following
![]() $g {\restriction } \alpha $
.
$g {\restriction } \alpha $
.
Assume
![]() $\tilde {s} {\restriction } \alpha $
has been defined; define
$\tilde {s} {\restriction } \alpha $
has been defined; define
![]() $\tilde {s}(\alpha )$
as
$\tilde {s}(\alpha )$
as
 $$\begin{align*}\tilde{s}(\alpha) := \begin{cases} q(\alpha)^{[g(\alpha)]}, & \textrm{ if } \alpha \in F, \\ q(\alpha),& \textrm{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\tilde{s}(\alpha) := \begin{cases} q(\alpha)^{[g(\alpha)]}, & \textrm{ if } \alpha \in F, \\ q(\alpha),& \textrm{ otherwise.} \end{cases} \end{align*}$$
If
![]() $\alpha \notin F$
, there is nothing to prove. For
$\alpha \notin F$
, there is nothing to prove. For
![]() $\alpha \in F$
, observe that since
$\alpha \in F$
, observe that since
![]() $\tilde {s} {\restriction } \alpha \leq q {\restriction } \alpha $
is
$\tilde {s} {\restriction } \alpha \leq q {\restriction } \alpha $
is
![]() $(q {\restriction } \alpha , F \cap \alpha , i)$
-determined following
$(q {\restriction } \alpha , F \cap \alpha , i)$
-determined following
![]() $g {\restriction } \alpha $
and
$g {\restriction } \alpha $
and
![]() $q \leq _{F,i} p^{(s)}$
, so by the above remark we can conclude
$q \leq _{F,i} p^{(s)}$
, so by the above remark we can conclude
![]() $\tilde {s} {\restriction } \alpha \leq s {\restriction } \alpha $
. But
$\tilde {s} {\restriction } \alpha \leq s {\restriction } \alpha $
. But
and
![]() $q {\restriction } \alpha \Vdash \operatorname {\mathrm {split}}_i(p(\alpha )) = \operatorname {\mathrm {split}}_i(q(\alpha ))$
, hence
$q {\restriction } \alpha \Vdash \operatorname {\mathrm {split}}_i(p(\alpha )) = \operatorname {\mathrm {split}}_i(q(\alpha ))$
, hence
![]() $\tilde {s}(\alpha )$
is well-defined. The other two properties follow easily.
$\tilde {s}(\alpha )$
is well-defined. The other two properties follow easily.
If
![]() $\gamma $
is a limit, then we have
$\gamma $
is a limit, then we have
![]() $\operatorname {\mathrm {supp}}(\tilde {s} {\restriction } \gamma ) \subseteq \operatorname {\mathrm {supp}}(q) \cup F$
, hence
$\operatorname {\mathrm {supp}}(\tilde {s} {\restriction } \gamma ) \subseteq \operatorname {\mathrm {supp}}(q) \cup F$
, hence
![]() $\tilde {s} {\restriction } \gamma \in \mathbb {P}_\gamma $
is a condition.
$\tilde {s} {\restriction } \gamma \in \mathbb {P}_\gamma $
is a condition.
Knowing
![]() $\tilde {s}$
to be well-defined, one can easily see that for each
$\tilde {s}$
to be well-defined, one can easily see that for each
![]() $s' \leq q$
that is
$s' \leq q$
that is
![]() $(q,F,i)$
-determined following g we have
$(q,F,i)$
-determined following g we have
![]() $s' \leq \tilde {s}$
.
$s' \leq \tilde {s}$
.
Fact 4.14.
![]() $(\mathbb {P}_\zeta , \leq _{F,i})$
is
$(\mathbb {P}_\zeta , \leq _{F,i})$
is
![]() ${<}\kappa $
-closed for all
${<}\kappa $
-closed for all
![]() $\zeta , F,i$
.
$\zeta , F,i$
.
Let us now introduce two auxiliary “boundedness” properties a
![]() $\mathbb {P}_\zeta $
-condition may exhibit.
$\mathbb {P}_\zeta $
-condition may exhibit.
Definition 4.15. We say a condition
![]() $p \in \mathbb {P}_\zeta $
is
$p \in \mathbb {P}_\zeta $
is
![]() $(F,i)$
-bounded for
$(F,i)$
-bounded for
![]() $F \in [\zeta ]^{<\kappa }, i < \kappa $
iff there exists a
$F \in [\zeta ]^{<\kappa }, i < \kappa $
iff there exists a
![]() $\mu < \kappa $
with
$\mu < \kappa $
with
Fact 4.16. If
![]() $p \in \mathbb {P}_\zeta $
is
$p \in \mathbb {P}_\zeta $
is
![]() $(F,i)$
-bounded and
$(F,i)$
-bounded and
![]() $p' \leq _{F,i} p$
, then
$p' \leq _{F,i} p$
, then
![]() $p'$
is as well.
$p'$
is as well.
Definition 4.17. Let
![]() $\zeta \leq \kappa ^{++}, p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
$\zeta \leq \kappa ^{++}, p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
![]() $i < \kappa $
. Take furthermore a
$i < \kappa $
. Take furthermore a
![]() $D \subseteq \mathbb {P}_\zeta $
that is open dense below p. We say p is
$D \subseteq \mathbb {P}_\zeta $
that is open dense below p. We say p is
![]() $(D,F,i)$
-complete iff there exists a
$(D,F,i)$
-complete iff there exists a
![]() $C \subseteq \prod _{\beta \in F} \kappa ^{<\kappa }, |C| < \kappa $
and a family
$C \subseteq \prod _{\beta \in F} \kappa ^{<\kappa }, |C| < \kappa $
and a family
![]() $(s_g)_{g \in C}$
in D such that:
$(s_g)_{g \in C}$
in D such that:
-
a)
 $s_g$
is
$s_g$
is
 $(p,F,i)$
-determined following g for all
$(p,F,i)$
-determined following g for all
 $g \in C.$
$g \in C.$
-
b) Whenever
 $s \leq p$
is
$s \leq p$
is
 $(p,F,i)$
-determined following a function g and
$(p,F,i)$
-determined following a function g and
 $s \in D$
, then
$s \in D$
, then
 $g \in C$
and
$g \in C$
and
 $s \leq s_g.$
$s \leq s_g.$
Fact 4.18. If
![]() $p \in \mathbb {P}_\zeta $
is
$p \in \mathbb {P}_\zeta $
is
![]() $(D,F,i)$
-complete as witnessed by
$(D,F,i)$
-complete as witnessed by
![]() $(s_g)_{g \in C}$
, then
$(s_g)_{g \in C}$
, then
![]() $(s_g)_{g \in C}$
is a maximal antichain below p.
$(s_g)_{g \in C}$
is a maximal antichain below p.
Lemma 4.19. Let
![]() $p' \leq _{F,i} p$
be
$p' \leq _{F,i} p$
be
![]() $\mathbb {P}_\zeta $
-conditions such that p is
$\mathbb {P}_\zeta $
-conditions such that p is
![]() $(D,F,i)$
-complete and
$(D,F,i)$
-complete and
![]() $p'$
is
$p'$
is
![]() $(D',F,i)$
-complete. Let
$(D',F,i)$
-complete. Let
![]() $(s_g)_{g \in C}$
and
$(s_g)_{g \in C}$
and
![]() $(s^{\prime }_g)_{g \in C'}$
witness this. Then
$(s^{\prime }_g)_{g \in C'}$
witness this. Then
![]() $C' \subseteq C$
. If in addition
$C' \subseteq C$
. If in addition
![]() $D' \subseteq D$
, then we even have
$D' \subseteq D$
, then we even have
![]() $s^{\prime }_g \leq s_g$
for each
$s^{\prime }_g \leq s_g$
for each
![]() $g \in C'$
.
$g \in C'$
.
Proof Assume that
![]() $g \in C'$
and find a
$g \in C'$
and find a
![]() $t \leq s^{\prime }_{g}$
with
$t \leq s^{\prime }_{g}$
with
![]() $t \in D$
(note that
$t \in D$
(note that
![]() $s^{\prime }_g \leq p$
). Then
$s^{\prime }_g \leq p$
). Then
![]() $t \leq p$
is
$t \leq p$
is
![]() $(p,F,i)$
-determined following g by Fact 4.10 and thus
$(p,F,i)$
-determined following g by Fact 4.10 and thus
![]() $g \in C$
and
$g \in C$
and
![]() $t \leq s_g$
by the second requirement in the definition of completeness. If
$t \leq s_g$
by the second requirement in the definition of completeness. If
![]() $D' \subseteq D$
, we may take
$D' \subseteq D$
, we may take
![]() $t = s^{\prime }_{g}$
and get
$t = s^{\prime }_{g}$
and get
![]() $s^{\prime }_{g} \leq s_{g}$
.
$s^{\prime }_{g} \leq s_{g}$
.
In particular we know that the set C in the definition of completeness is completely determined by p. Complete conditions are also going to be playing a major role later in Lemma 7.1.
Our strategy for proving Property B* for all
![]() $\mathbb {P}_\zeta , \zeta \leq \kappa ^{++}$
is by the equivalence of the following four statements:
$\mathbb {P}_\zeta , \zeta \leq \kappa ^{++}$
is by the equivalence of the following four statements:
-
a(ζ):
 $\mathbb {P}_\alpha $
has Property B* for each
$\mathbb {P}_\alpha $
has Property B* for each
 $\alpha < \zeta $
.
$\alpha < \zeta $
. -
b(ζ): The set of
 $(F,i)$
-bounded conditions is
$(F,i)$
-bounded conditions is
 $\leq _{F,i}$
-dense in
$\leq _{F,i}$
-dense in
 $\mathbb {P}_\alpha $
for all
$\mathbb {P}_\alpha $
for all
 $\alpha \leq \zeta $
,
$\alpha \leq \zeta $
,
 $F \in [\alpha ]^{<\kappa }$
and
$F \in [\alpha ]^{<\kappa }$
and
 $i < \kappa $
.
$i < \kappa $
. -
c(ζ): The set of
 $(D,F,i)$
-complete conditions is
$(D,F,i)$
-complete conditions is
 $\leq _{F,i}$
-dense in
$\leq _{F,i}$
-dense in
 $\mathbb {P}_\zeta $
for all
$\mathbb {P}_\zeta $
for all
 $F,i$
and open dense
$F,i$
and open dense
 $D \subseteq \mathbb {P}_\zeta $
.
$D \subseteq \mathbb {P}_\zeta $
. -
d(ζ):
 $\mathbb {P}_\zeta $
has Property B*.
$\mathbb {P}_\zeta $
has Property B*.
The implication a(
![]() $\zeta $
)
$\zeta $
)
![]() $\Rightarrow $
b(
$\Rightarrow $
b(
![]() $\zeta $
) is Lemma 4.21, b(
$\zeta $
) is Lemma 4.21, b(
![]() $\zeta $
)
$\zeta $
)
![]() $\Rightarrow $
c(
$\Rightarrow $
c(
![]() $\zeta $
) is Lemma 4.22, and c(
$\zeta $
) is Lemma 4.22, and c(
![]() $\zeta $
)
$\zeta $
)
![]() $\Rightarrow $
d(
$\Rightarrow $
d(
![]() $\zeta $
) is Lemma 4.23. Thus a(
$\zeta $
) is Lemma 4.23. Thus a(
![]() $\zeta $
)
$\zeta $
)
![]() $\Rightarrow $
d(
$\Rightarrow $
d(
![]() $\zeta $
) establishes an induction by which Property B* is verified for all
$\zeta $
) establishes an induction by which Property B* is verified for all
![]() $\mathbb {P}_\zeta $
.
$\mathbb {P}_\zeta $
.
Corollary 4.20.
![]() $\mathbb {P}_\zeta $
has Property B* for all
$\mathbb {P}_\zeta $
has Property B* for all
![]() $\zeta \leq \kappa ^{++}$
.
$\zeta \leq \kappa ^{++}$
.
Lemma 4.21. Let
![]() $\zeta \leq \kappa ^{++}$
and assume
$\zeta \leq \kappa ^{++}$
and assume
![]() $\mathbb {P}_{\alpha }$
has Property B* for each
$\mathbb {P}_{\alpha }$
has Property B* for each
![]() $\alpha < \zeta $
. Then for each
$\alpha < \zeta $
. Then for each
![]() $\alpha \leq \zeta $
,
$\alpha \leq \zeta $
,
![]() $p \in \mathbb {P}_{\alpha }, F \in [\alpha ]^{<\kappa }$
and
$p \in \mathbb {P}_{\alpha }, F \in [\alpha ]^{<\kappa }$
and
![]() $i < \kappa $
there is a condition
$i < \kappa $
there is a condition
![]() $q \leq _{F,i} p$
that is
$q \leq _{F,i} p$
that is
![]() $(F,i)$
-bounded.
$(F,i)$
-bounded.
Proof We proceed by induction on
![]() $\alpha \leq \zeta $
.
$\alpha \leq \zeta $
.
-
•
 $\alpha = 1$
: Trivial by the inaccessibility of
$\alpha = 1$
: Trivial by the inaccessibility of
 $\kappa $
.
$\kappa $
. -
•
 $\alpha \to \alpha + 1$
: Let
$\alpha \to \alpha + 1$
: Let
 $p \in \mathbb {P}_{\alpha +1}, F \in [\alpha + 1]^{<\kappa }$
and
$p \in \mathbb {P}_{\alpha +1}, F \in [\alpha + 1]^{<\kappa }$
and
 $i< \kappa $
be given. Since
$i< \kappa $
be given. Since
 $\mathbb {P}_\alpha $
is
$\mathbb {P}_\alpha $
is
 ${<}\kappa $
-closed,
${<}\kappa $
-closed,
 $\kappa $
remains inaccessible in
$\kappa $
remains inaccessible in
 $V^{\mathbb {P}_\alpha }$
. Thus and considering
$V^{\mathbb {P}_\alpha }$
. Thus and considering $$\begin{align*}\Vdash_{\mathbb{P}_\alpha} \forall \beta \in F\, \exists \mu_\beta < \kappa:\ \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \mu_\beta^{<\mu_\beta} \end{align*}$$
$$\begin{align*}\Vdash_{\mathbb{P}_\alpha} \forall \beta \in F\, \exists \mu_\beta < \kappa:\ \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \mu_\beta^{<\mu_\beta} \end{align*}$$
 $\sup _{\beta \in F} \mu _\beta $
we can find a name
$\sup _{\beta \in F} \mu _\beta $
we can find a name
 $\dot {\mu }$
for an ordinal less than
$\dot {\mu }$
for an ordinal less than
 $\kappa $
with Let now
$\kappa $
with Let now $$\begin{align*}\Vdash_{\mathbb{P}_\alpha} \forall \beta \in F:\ \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \dot{\mu}^{<\dot{\mu}}. \end{align*}$$
$$\begin{align*}\Vdash_{\mathbb{P}_\alpha} \forall \beta \in F:\ \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \dot{\mu}^{<\dot{\mu}}. \end{align*}$$
 $A \subseteq \mathbb {P}_\alpha $
be a maximal antichain deciding
$A \subseteq \mathbb {P}_\alpha $
be a maximal antichain deciding
 $\dot {\mu }$
; we may find a
$\dot {\mu }$
; we may find a
 $\mathbb {P}_\alpha \ni \hat {q} \leq _{F \cap \alpha ,i} p {\restriction } \alpha $
with
$\mathbb {P}_\alpha \ni \hat {q} \leq _{F \cap \alpha ,i} p {\restriction } \alpha $
with
 $|A {\restriction } \hat {q}| < \kappa $
. Thus for some
$|A {\restriction } \hat {q}| < \kappa $
. Thus for some $$\begin{align*}\hat{q} \Vdash \dot{\mu} < \mu_q \end{align*}$$
$$\begin{align*}\hat{q} \Vdash \dot{\mu} < \mu_q \end{align*}$$
 $\mu _q < \kappa $
and therefore Setting
$\mu _q < \kappa $
and therefore Setting $$\begin{align*}\forall \beta \in F:\ \hat{q} {\restriction} \beta \Vdash \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \mu_q^{<\mu_q}. \end{align*}$$
$$\begin{align*}\forall \beta \in F:\ \hat{q} {\restriction} \beta \Vdash \operatorname{\mathrm{split}}_i(p(\beta)) \subseteq \mu_q^{<\mu_q}. \end{align*}$$
 $q := \hat {q} ^\frown p(\alpha )$
and noting that since
$q := \hat {q} ^\frown p(\alpha )$
and noting that since
 $\hat {q} \leq _{F \cap \alpha , i} p {\restriction } \alpha $
we have
$\hat {q} \leq _{F \cap \alpha , i} p {\restriction } \alpha $
we have
 $q {\restriction } \beta \Vdash \operatorname {\mathrm {split}}(q(\beta )) = \operatorname {\mathrm {split}}(p(\beta ))$
for all
$q {\restriction } \beta \Vdash \operatorname {\mathrm {split}}(q(\beta )) = \operatorname {\mathrm {split}}(p(\beta ))$
for all
 $\beta \in F$
, so it follows that q is
$\beta \in F$
, so it follows that q is
 $(F,i)$
-bounded.
$(F,i)$
-bounded.
-
•
 $\gamma \leq \zeta $
is a limit: Let
$\gamma \leq \zeta $
is a limit: Let
 $p \in \mathbb {P}_{\gamma }, F \in [\gamma ]^{<\kappa }$
and
$p \in \mathbb {P}_{\gamma }, F \in [\gamma ]^{<\kappa }$
and
 $i< \kappa $
be given. Using
$i< \kappa $
be given. Using
 ${<}\kappa $
-closure of
${<}\kappa $
-closure of
 $(\mathbb {P}_\gamma , \leq _{F,i})$
(see Fact 4.14) and the inductive assumption, we can construct a
$(\mathbb {P}_\gamma , \leq _{F,i})$
(see Fact 4.14) and the inductive assumption, we can construct a
 $\leq _{F,i}$
-decreasing sequence
$\leq _{F,i}$
-decreasing sequence
 $(q_\beta )_{\beta \in F}$
in
$(q_\beta )_{\beta \in F}$
in
 $\mathbb {P}_\gamma $
with the following properties:
$\mathbb {P}_\gamma $
with the following properties:-
–
 $\forall \beta \in F\, \forall \beta ' \in F \cap \beta :\ q_\beta \leq _{F,i} q_{\beta '} \leq _{F,i} p.$
$\forall \beta \in F\, \forall \beta ' \in F \cap \beta :\ q_\beta \leq _{F,i} q_{\beta '} \leq _{F,i} p.$
-
–
 $\forall \beta \in F\, \exists \mu _\beta < \kappa \, \forall \beta ' \in F \cap (\beta +1):\ q_\beta {\restriction } \beta ' \Vdash _{\mathbb {P}_{\beta '}} \operatorname {\mathrm {split}}_i(q_\beta (\beta ')) \subseteq \mu _\beta ^{<\mu _\beta }.$
$\forall \beta \in F\, \exists \mu _\beta < \kappa \, \forall \beta ' \in F \cap (\beta +1):\ q_\beta {\restriction } \beta ' \Vdash _{\mathbb {P}_{\beta '}} \operatorname {\mathrm {split}}_i(q_\beta (\beta ')) \subseteq \mu _\beta ^{<\mu _\beta }.$
Again using
 ${<}\kappa $
-closure of
${<}\kappa $
-closure of
 $(\mathbb {P}_\gamma , \leq _{F,i})$
, set q to a
$(\mathbb {P}_\gamma , \leq _{F,i})$
, set q to a
 $\leq _{F,i}$
-lower bound of
$\leq _{F,i}$
-lower bound of
 $(q_\beta )_{\beta \in F}$
and
$(q_\beta )_{\beta \in F}$
and
 $\mu := \sup _{\beta \in F} \mu _\beta $
. Now
$\mu := \sup _{\beta \in F} \mu _\beta $
. Now
 $q \leq _{F,i} p$
and
$q \leq _{F,i} p$
and  $$\begin{align*}\forall \beta \in F:\ q {\restriction} \beta \Vdash \operatorname{\mathrm{split}}_i(q(\beta)) \subseteq \mu^{<\mu}.\\[-34pt] \end{align*}$$
$$\begin{align*}\forall \beta \in F:\ q {\restriction} \beta \Vdash \operatorname{\mathrm{split}}_i(q(\beta)) \subseteq \mu^{<\mu}.\\[-34pt] \end{align*}$$
-
Lemma 4.22. Let
![]() $\zeta \leq \kappa ^{++}, F \in [\zeta ]^{<\kappa }, i < \kappa $
and suppose
$\zeta \leq \kappa ^{++}, F \in [\zeta ]^{<\kappa }, i < \kappa $
and suppose
![]() $p \in \mathbb {P}_{\zeta }$
is
$p \in \mathbb {P}_{\zeta }$
is
![]() $(F,i)$
-bounded. Let furthermore
$(F,i)$
-bounded. Let furthermore
![]() $D \subseteq \mathbb {P}_{\zeta }$
be open dense below p. Then there is a
$D \subseteq \mathbb {P}_{\zeta }$
be open dense below p. Then there is a
![]() $q \leq _{F,i} p$
which is
$q \leq _{F,i} p$
which is
![]() $(D,F,i)$
-complete.
$(D,F,i)$
-complete.
In particular, if the set of
![]() $(F,i)$
-bounded conditions is
$(F,i)$
-bounded conditions is
![]() $\leq _{F,i}$
-dense in
$\leq _{F,i}$
-dense in
![]() $\mathbb {P}_\zeta $
, then for all open dense
$\mathbb {P}_\zeta $
, then for all open dense
![]() $D \subseteq \mathbb {P}_\zeta $
the set of
$D \subseteq \mathbb {P}_\zeta $
the set of
![]() $(D,F,i)$
-complete conditions is
$(D,F,i)$
-complete conditions is
![]() $\leq _{F,i}$
-dense as well.
$\leq _{F,i}$
-dense as well.
Proof By assumption p is
![]() $(F,i)$
-bounded, hence we can find a
$(F,i)$
-bounded, hence we can find a
![]() $\mu $
such that
$\mu $
such that
Our strategy is to consider all possible choices a
![]() $(p,F,i)$
-determined condition might make at the ith splitting front of p and then interpolate on the witnesses of such choices. Since we have a uniform bound
$(p,F,i)$
-determined condition might make at the ith splitting front of p and then interpolate on the witnesses of such choices. Since we have a uniform bound
![]() $\mu $
on the respective splitting fronts, this will require us to only iterate through
$\mu $
on the respective splitting fronts, this will require us to only iterate through
![]() ${<}\kappa $
many possibilities. Set
${<}\kappa $
many possibilities. Set
![]() $\tilde {\mu }_\beta := \sup _{j \leq \mu } f_\beta (j)$
and consider the set
$\tilde {\mu }_\beta := \sup _{j \leq \mu } f_\beta (j)$
and consider the set
 $$\begin{align*}\tilde{C} := \prod_{\beta \in F} \tilde{\mu}_\beta^{\leq \mu}. \end{align*}$$
$$\begin{align*}\tilde{C} := \prod_{\beta \in F} \tilde{\mu}_\beta^{\leq \mu}. \end{align*}$$
Whenever s is
![]() $(p,F,i)$
-determined following some g, then
$(p,F,i)$
-determined following some g, then
![]() $g \in \tilde {C}$
. Enumerate
$g \in \tilde {C}$
. Enumerate
![]() $\tilde {C}$
as
$\tilde {C}$
as
![]() $(g_{j+1})_{j < \delta }$
with
$(g_{j+1})_{j < \delta }$
with
![]() $\delta < \kappa $
. We now construct a
$\delta < \kappa $
. We now construct a
![]() $\leq _{F,i}$
-decreasing sequence
$\leq _{F,i}$
-decreasing sequence
![]() $(t_j)_{j < \delta }$
:
$(t_j)_{j < \delta }$
:
-
•
 $j = 0$
: Set
$j = 0$
: Set
 $t_0 := p$
.
$t_0 := p$
. -
•
 $j \to j+1$
: If there exists an
$j \to j+1$
: If there exists an
 $s \leq t_j$
that is
$s \leq t_j$
that is
 $(p,F,i)$
-determined following
$(p,F,i)$
-determined following
 $g_{j+1}$
, pick an arbitrary such condition from D (this is possible, since D is dense below p) and call it
$g_{j+1}$
, pick an arbitrary such condition from D (this is possible, since D is dense below p) and call it
 $\tilde {s}_{g_{j+1}}$
. Set
$\tilde {s}_{g_{j+1}}$
. Set
 $t_{j+1} := t_j^{(\tilde {s}_{g_{j+1}})}$
. If there is no such s, simply set
$t_{j+1} := t_j^{(\tilde {s}_{g_{j+1}})}$
. If there is no such s, simply set
 $t_{j+1} := t_j$
. In any case we have
$t_{j+1} := t_j$
. In any case we have
 $t_{j+1} \leq _{F,i} t_j$
.
$t_{j+1} \leq _{F,i} t_j$
. -
•
 $\lambda $
is a limit: Set
$\lambda $
is a limit: Set
 $t_\lambda $
to a
$t_\lambda $
to a
 $\leq _{F,i}$
-lower bound of
$\leq _{F,i}$
-lower bound of
 $(t_j)_{j < \lambda }$
(see Fact 4.14).
$(t_j)_{j < \lambda }$
(see Fact 4.14).
Set q to a
![]() $\leq _{F,i}$
-lower bound of
$\leq _{F,i}$
-lower bound of
![]() $(t_j)_{j < \delta }$
. We know
$(t_j)_{j < \delta }$
. We know
![]() $q \leq _{F,i} p$
. Now let
$q \leq _{F,i} p$
. Now let
i.e., C is the set of all
![]() $g_{j+1}$
for which a witness was found in the inductive step
$g_{j+1}$
for which a witness was found in the inductive step
![]() $j \to j+1$
. We have
$j \to j+1$
. We have
![]() $|C| < \kappa $
. Finally, for each
$|C| < \kappa $
. Finally, for each
![]() $g = g_{j+1} \in C$
apply Lemma 4.13 to
$g = g_{j+1} \in C$
apply Lemma 4.13 to
![]() $p = t_j$
,
$p = t_j$
,
![]() $s = \tilde {s}_{g_{j+1}}$
and
$s = \tilde {s}_{g_{j+1}}$
and
![]() $q = q$
to construct the condition
$q = q$
to construct the condition
![]() $s_g$
. We have
$s_g$
. We have
![]() $s_g \in D$
since
$s_g \in D$
since
![]() $s_g \leq \tilde {s}_g \in D$
and D is open.
$s_g \leq \tilde {s}_g \in D$
and D is open.
We verify that q is
![]() $(D,F,i)$
-complete, witnessed by
$(D,F,i)$
-complete, witnessed by
![]() $(s_g)_{g \in C}$
. The first condition in the definition of completeness follows by construction. The second follows immediately from Lemma 4.13 by noting that if
$(s_g)_{g \in C}$
. The first condition in the definition of completeness follows by construction. The second follows immediately from Lemma 4.13 by noting that if
![]() $s \leq q$
is
$s \leq q$
is
![]() $(q,F,i)$
-determined following g, then
$(q,F,i)$
-determined following g, then
![]() $g = g_{j+1}$
for some
$g = g_{j+1}$
for some
![]() $j < \delta $
, and thus a witness was found in the inductive step
$j < \delta $
, and thus a witness was found in the inductive step
![]() $j \to j+1$
; hence
$j \to j+1$
; hence
![]() $g \in C$
.
$g \in C$
.
Lemma 4.23. If the set of
![]() $(D,F,i)$
-complete conditions is
$(D,F,i)$
-complete conditions is
![]() $\leq _{F,i}$
-dense in
$\leq _{F,i}$
-dense in
![]() $\mathbb {P}_\zeta $
for all
$\mathbb {P}_\zeta $
for all
![]() $F,i$
and
$F,i$
and
![]() $D \subseteq \mathbb {P}_\zeta $
open dense, then
$D \subseteq \mathbb {P}_\zeta $
open dense, then
![]() $\mathbb {P}_\zeta $
has Property B*.
$\mathbb {P}_\zeta $
has Property B*.
Proof We have seen in Lemma 4.6 that the fusion condition is always fulfilled. We will now prove that
![]() $\mathbb {P}_{\zeta }$
fulfils the antichain condition: let
$\mathbb {P}_{\zeta }$
fulfils the antichain condition: let
![]() $A \subseteq \mathbb {P}_\zeta $
be a maximal antichain,
$A \subseteq \mathbb {P}_\zeta $
be a maximal antichain,
![]() $p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
$p \in \mathbb {P}_\zeta , F \in [\zeta ]^{<\kappa }$
and
![]() $i < \kappa $
. Find a
$i < \kappa $
. Find a
![]() $q \leq _{F,i} p$
that is
$q \leq _{F,i} p$
that is
![]() $(D,F,i)$
-complete, where
$(D,F,i)$
-complete, where
and let
![]() $(s_g)_{g \in C}$
witness this. Since
$(s_g)_{g \in C}$
witness this. Since
![]() $(s_g)_{g \in C}$
is a maximal antichain below q by Fact 4.18, it is easy to see that
$(s_g)_{g \in C}$
is a maximal antichain below q by Fact 4.18, it is easy to see that
and thus
![]() $|A {\restriction } q| \leq |C| < \kappa $
.
$|A {\restriction } q| \leq |C| < \kappa $
.
From this point onward, assume that
From among our stated goals at the beginning of this section, only one remains to be verified; our interest now turns to the
![]() $\kappa ^{++}$
-chain condition:
$\kappa ^{++}$
-chain condition:
Theorem 4.24.
![]() $\mathbb {P}$
has the
$\mathbb {P}$
has the
![]() $\kappa ^{++}$
-c.c.
$\kappa ^{++}$
-c.c.
This will follow easily from Lemma 4.29 once we have proven that each
![]() $\mathbb {P}_\alpha $
for
$\mathbb {P}_\alpha $
for
![]() $\alpha < \kappa ^{++}$
has a dense subset of size
$\alpha < \kappa ^{++}$
has a dense subset of size
![]() $\kappa ^{+}$
.
$\kappa ^{+}$
.
For the purposes of the next definition, for each
![]() $\alpha < \kappa ^{++}$
fix a
$\alpha < \kappa ^{++}$
fix a
![]() $\mathbb {P}_\alpha $
-name
$\mathbb {P}_\alpha $
-name
![]() $\dot {c}_\alpha $
for a bijection
$\dot {c}_\alpha $
for a bijection
![]() $c_\alpha : (PT_{f_\alpha })^{V^{\mathbb {P_\alpha }}} \to (\mathcal {P}(\kappa ))^{V^{\mathbb {P_\alpha }}}$
such that
$c_\alpha : (PT_{f_\alpha })^{V^{\mathbb {P_\alpha }}} \to (\mathcal {P}(\kappa ))^{V^{\mathbb {P_\alpha }}}$
such that ![]() . Let us also fix a
. Let us also fix a
![]() $\theta $
sufficiently large (e.g.,
$\theta $
sufficiently large (e.g.,
![]() $\theta> |2^{\mathbb {P}}|$
) and a well-ordering
$\theta> |2^{\mathbb {P}}|$
) and a well-ordering
![]() $\preceq $
of
$\preceq $
of
![]() $H(\theta )$
(by which we mean the sets hereditarily of size
$H(\theta )$
(by which we mean the sets hereditarily of size
![]() ${<} \theta $
, not
${<} \theta $
, not
![]() $H_\theta $
as defined below).
$H_\theta $
as defined below).
Definition 4.25. Let
![]() $\alpha < \kappa ^{++}$
.
$\alpha < \kappa ^{++}$
.
-
• A
 $\mathbb {P}_\alpha $
-name
$\mathbb {P}_\alpha $
-name
 $\dot {\tau }$
for a subset of
$\dot {\tau }$
for a subset of
 $\kappa $
is
$\kappa $
is
 $\alpha $
-good iff
$\alpha $
-good iff
 $\dot {\tau }$
is a nice name of the form where
$\dot {\tau }$
is a nice name of the form where $$\begin{align*}\dot{\tau} = \{\{j\} \times A_j: j < \kappa\},\end{align*}$$
$$\begin{align*}\dot{\tau} = \{\{j\} \times A_j: j < \kappa\},\end{align*}$$
 $A_j \subseteq H_\alpha $
and
$A_j \subseteq H_\alpha $
and
 $|A_j| \leq \kappa $
for all
$|A_j| \leq \kappa $
for all
 $j < \kappa $
.
$j < \kappa $
.
-
• A condition
 $p \in \mathbb {P}_\alpha $
is in
$p \in \mathbb {P}_\alpha $
is in
 $\tilde {H}_\alpha $
iff
$\tilde {H}_\alpha $
iff
 $p {\restriction } \beta \in H_\beta $
for each
$p {\restriction } \beta \in H_\beta $
for each
 $\beta < \alpha $
and, if
$\beta < \alpha $
and, if
 $\alpha = \beta + 1$
is a successor, there additionally is a
$\alpha = \beta + 1$
is a successor, there additionally is a
 $\beta $
-good name
$\beta $
-good name
 $\dot {\tau }$
such that
$\dot {\tau }$
such that
 $p {\restriction } \beta \Vdash _{\beta } \dot {c}_{\beta }(p(\beta )) = \dot {\tau }$
and
$p {\restriction } \beta \Vdash _{\beta } \dot {c}_{\beta }(p(\beta )) = \dot {\tau }$
and
 $p(\beta )$
is the
$p(\beta )$
is the
 $\preceq $
-least
$\preceq $
-least
 $\mathbb {P}_\beta $
-name that satisfies this relation for
$\mathbb {P}_\beta $
-name that satisfies this relation for
 $p {\restriction } \beta $
and
$p {\restriction } \beta $
and
 $\dot {\tau }$
. Now let
$\dot {\tau }$
. Now let
 $H_\alpha $
be the closure of
$H_\alpha $
be the closure of
 $\tilde {H}_\alpha $
under canonical fusion limits (see Remark 4.7), where we always choose the pointwise
$\tilde {H}_\alpha $
under canonical fusion limits (see Remark 4.7), where we always choose the pointwise
 $\preceq $
-least name for the canonical fusion limit (i.e., for every
$\preceq $
-least name for the canonical fusion limit (i.e., for every
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $q(\beta )$
is the
$q(\beta )$
is the
 $\preceq $
-least name for the
$\preceq $
-least name for the
 $\beta $
th entry of the canonical fusion limit q of a fusion sequence)Footnote
2
.
$\beta $
th entry of the canonical fusion limit q of a fusion sequence)Footnote
2
.
Remark 4.26. It is easy to see that for
![]() $p \in H_\alpha $
(not only
$p \in H_\alpha $
(not only
![]() $p \in \tilde {H}_\alpha $
) we have
$p \in \tilde {H}_\alpha $
) we have
![]() $p {\restriction } \beta \in H_\beta $
for all
$p {\restriction } \beta \in H_\beta $
for all
![]() $\beta < \alpha $
as well.
$\beta < \alpha $
as well.
Note also that there is a canonical embedding
![]() $H_\beta \hookrightarrow H_{\alpha }$
for
$H_\beta \hookrightarrow H_{\alpha }$
for
![]() $\beta < \alpha $
.
$\beta < \alpha $
.
Remark 4.27.
![]() $H_\alpha $
-conditions and
$H_\alpha $
-conditions and
![]() $\alpha $
-good names appeared first as
$\alpha $
-good names appeared first as
![]() $H_\kappa $
-
$H_\kappa $
-
![]() $\mathbb {P}_\alpha $
-names in [Reference Baumhauer, Goldstern and Shelah2] and are themselves a straightforward generalization of hereditarily countable names as introduced in [Reference Shelah23].
$\mathbb {P}_\alpha $
-names in [Reference Baumhauer, Goldstern and Shelah2] and are themselves a straightforward generalization of hereditarily countable names as introduced in [Reference Shelah23].
Lemma 4.28. For every
![]() $0 < \alpha < \kappa ^{++}$
,
$0 < \alpha < \kappa ^{++}$
,
![]() $F \in [\alpha ]^{<\kappa }$
and
$F \in [\alpha ]^{<\kappa }$
and
![]() $i < \kappa $
,
$i < \kappa $
,
![]() $H_\alpha $
is
$H_\alpha $
is
![]() $\leq _{F,i}$
-dense in
$\leq _{F,i}$
-dense in
![]() $\mathbb {P}_\alpha $
and
$\mathbb {P}_\alpha $
and
![]() $|H_\alpha | = \kappa ^+$
.
$|H_\alpha | = \kappa ^+$
.
Proof We prove the statements by induction on
![]() $\alpha $
.
$\alpha $
.
-
•
 $\alpha =1$
: We have
$\alpha =1$
: We have
 $H_1 = \mathbb {P}_1$
and
$H_1 = \mathbb {P}_1$
and
 $|\mathbb {P}_1| = |PT_{f_0}| = \kappa ^{+}$
.
$|\mathbb {P}_1| = |PT_{f_0}| = \kappa ^{+}$
. -
•
 $\alpha \to \alpha + 1$
: Let
$\alpha \to \alpha + 1$
: Let
 $p \in \mathbb {P}_{\alpha +1}$
,
$p \in \mathbb {P}_{\alpha +1}$
,
 $F \in [\alpha +1]^{<\kappa }$
and
$F \in [\alpha +1]^{<\kappa }$
and
 $i < \kappa $
. Using the inductive hypothesis, we may assume
$i < \kappa $
. Using the inductive hypothesis, we may assume
 $p {\restriction } \alpha \Vdash _\alpha \dot {c}_\alpha (p(\alpha )) = \{\{j\} \times A_j: j < \kappa \}$
with
$p {\restriction } \alpha \Vdash _\alpha \dot {c}_\alpha (p(\alpha )) = \{\{j\} \times A_j: j < \kappa \}$
with
 $A_j \subseteq H_\alpha $
for all
$A_j \subseteq H_\alpha $
for all
 $j < \kappa $
. Additionally using Property B*, construct a fusion sequence
$j < \kappa $
. Additionally using Property B*, construct a fusion sequence
 $\langle q_j, F_j: j < \kappa \rangle $
with:
$\langle q_j, F_j: j < \kappa \rangle $
with:-
–
 $\forall j < \kappa : q_j \in H_\alpha $
and
$\forall j < \kappa : q_j \in H_\alpha $
and
 $|A_j {\restriction } q_j| < \kappa $
,
$|A_j {\restriction } q_j| < \kappa $
, -
–
 $q_0 \leq _{F \cap \alpha , i} p {\restriction } \alpha $
,
$q_0 \leq _{F \cap \alpha , i} p {\restriction } \alpha $
, -
–
 $\forall j < \ell < \kappa : q_\ell \leq _{F_j, i + j} q_j$
and
$\forall j < \ell < \kappa : q_\ell \leq _{F_j, i + j} q_j$
and
 $F \cap \alpha \subseteq F_j$
,
$F \cap \alpha \subseteq F_j$
,
where the
 $F_j$
are constructed using a bookkeeping argument. Let
$F_j$
are constructed using a bookkeeping argument. Let
 $q_\kappa $
be a canonical fusion limit of this sequence that is a member of
$q_\kappa $
be a canonical fusion limit of this sequence that is a member of
 $H_\alpha $
. By the first property of the fusion sequence, is an
$H_\alpha $
. By the first property of the fusion sequence, is an $$\begin{align*}\dot{\tau} = \{\{j\} \times (A_j {\restriction} q_\kappa): j < \kappa\}\end{align*}$$
$$\begin{align*}\dot{\tau} = \{\{j\} \times (A_j {\restriction} q_\kappa): j < \kappa\}\end{align*}$$
 $\alpha $
-good name and
$\alpha $
-good name and
 $q_\kappa \Vdash _\alpha \dot {c}_\alpha (p(\alpha )) = \dot {\tau }$
. Let thus
$q_\kappa \Vdash _\alpha \dot {c}_\alpha (p(\alpha )) = \dot {\tau }$
. Let thus
 $\dot {r}$
be the
$\dot {r}$
be the
 $\preceq $
-least
$\preceq $
-least
 $\mathbb {P}_\alpha $
-name that satisfies
$\mathbb {P}_\alpha $
-name that satisfies
 $q_\kappa \Vdash _\alpha \dot {c}_\alpha (\dot {r}) = \dot {\tau }$
; now we can (pedantically, using Remark 4.26) conclude
$q_\kappa \Vdash _\alpha \dot {c}_\alpha (\dot {r}) = \dot {\tau }$
; now we can (pedantically, using Remark 4.26) conclude
 $H_{\alpha + 1} \ni (q_\kappa \, ^\frown \dot {r}) \leq _{F,i} p$
.Since
$H_{\alpha + 1} \ni (q_\kappa \, ^\frown \dot {r}) \leq _{F,i} p$
.Since
 $|H_\alpha | = \kappa ^+$
and there are only
$|H_\alpha | = \kappa ^+$
and there are only
 $|(\kappa ^+)^\kappa |=\kappa ^+$
many
$|(\kappa ^+)^\kappa |=\kappa ^+$
many
 $\alpha $
-good names for reals, we get
$\alpha $
-good names for reals, we get
 $|\tilde {H}_{\alpha +1}| = \kappa ^+$
and therefore also
$|\tilde {H}_{\alpha +1}| = \kappa ^+$
and therefore also
 $|H_{\alpha +1}| = \kappa ^+$
by standard arguments.
$|H_{\alpha +1}| = \kappa ^+$
by standard arguments.
-
-
•
 $\gamma $
is a limit: If
$\gamma $
is a limit: If
 $\operatorname {\mathrm {cf}}(\gamma ) = \kappa ^+$
, density is trivial and
$\operatorname {\mathrm {cf}}(\gamma ) = \kappa ^+$
, density is trivial and
 $|H_\gamma | \leq |\bigcup _{\beta < \gamma } H_\beta | \leq \kappa ^+$
.
$|H_\gamma | \leq |\bigcup _{\beta < \gamma } H_\beta | \leq \kappa ^+$
.Assume
 $\operatorname {\mathrm {cf}}(\gamma ) = \delta \leq \kappa $
and let furthermore
$\operatorname {\mathrm {cf}}(\gamma ) = \delta \leq \kappa $
and let furthermore
 $p \in \mathbb {P}_{\gamma }$
,
$p \in \mathbb {P}_{\gamma }$
,
 $F \in [\gamma ]^{<\kappa }$
and
$F \in [\gamma ]^{<\kappa }$
and
 $i < \kappa $
be given. For a cofinal sequence
$i < \kappa $
be given. For a cofinal sequence
 $(\beta _j)_{j < \delta }$
construct a fusion sequence
$(\beta _j)_{j < \delta }$
construct a fusion sequence
 $\langle q_j, F_j: j < \delta \rangle $
with:
$\langle q_j, F_j: j < \delta \rangle $
with:-
–
 $\forall j < \delta : F \cap \beta _j \subseteq F_j \subseteq \beta _j$
,
$\forall j < \delta : F \cap \beta _j \subseteq F_j \subseteq \beta _j$
, -
–
 $\forall j < \delta : q_j {\restriction } \beta _j \leq _{F_j, i + j} p {\restriction } \beta _j$
,
$\forall j < \delta : q_j {\restriction } \beta _j \leq _{F_j, i + j} p {\restriction } \beta _j$
, -
–
 $\forall j < \ell < \delta : q_\ell \leq _{F_j, i+j} q_j$
,
$\forall j < \ell < \delta : q_\ell \leq _{F_j, i+j} q_j$
, -
–
 $\forall j < \delta : q_j \in H_\gamma $
, which may be achieved by having
$\forall j < \delta : q_j \in H_\gamma $
, which may be achieved by having
 $q_j {\restriction } \beta _j \in H_{\beta _j}$
and letting
$q_j {\restriction } \beta _j \in H_{\beta _j}$
and letting
 $q_j(\beta )$
be the trivial condition for
$q_j(\beta )$
be the trivial condition for
 $\beta \geq \beta _j$
.
$\beta \geq \beta _j$
.
The
 $F_j$
are again constructed using a bookkeeping argument. Set
$F_j$
are again constructed using a bookkeeping argument. Set
 $q_\delta $
to be a fusion limit contained in
$q_\delta $
to be a fusion limit contained in
 $H_\gamma $
; then we have
$H_\gamma $
; then we have
 $H_\gamma \ni q_\delta \leq _{F,i} p$
. Lastly, using Remark 4.26, we get
$H_\gamma \ni q_\delta \leq _{F,i} p$
. Lastly, using Remark 4.26, we get
 $|H_\gamma | \leq \left | \prod _{j < \delta } H_{\beta _j} \right | \leq \kappa ^+$
.
$|H_\gamma | \leq \left | \prod _{j < \delta } H_{\beta _j} \right | \leq \kappa ^+$
. -
Lemma 4.29. Let
![]() $\langle \mathcal {P}_\alpha , \dot {\mathcal {Q}}_\beta : \alpha \leq \zeta , \beta < \zeta \rangle $
be an iteration such that
$\langle \mathcal {P}_\alpha , \dot {\mathcal {Q}}_\beta : \alpha \leq \zeta , \beta < \zeta \rangle $
be an iteration such that
where
![]() $\theta $
is a regular uncountable cardinal. If
$\theta $
is a regular uncountable cardinal. If
![]() $\mathcal {P}_\zeta $
is a direct limit and, additionally, either
$\mathcal {P}_\zeta $
is a direct limit and, additionally, either
![]() $\operatorname {\mathrm {cf}}(\zeta ) \neq \theta $
or the set
$\operatorname {\mathrm {cf}}(\zeta ) \neq \theta $
or the set
![]() $\{\gamma < \zeta :\ \mathcal {P}_\gamma \textrm { is a direct limit}\}$
is stationary, then
$\{\gamma < \zeta :\ \mathcal {P}_\gamma \textrm { is a direct limit}\}$
is stationary, then
![]() $\mathcal {P}_\zeta $
has the
$\mathcal {P}_\zeta $
has the
![]() $\theta $
-c.c.
$\theta $
-c.c.
Proof See [Reference Jech12, Theorem 16.30].
Proof of Theorem 4.24
By Lemma 4.28, each
![]() $\mathbb {P}_\alpha $
has a dense subset of size
$\mathbb {P}_\alpha $
has a dense subset of size
![]() ${\leq }\kappa ^{+}$
and therefore satisfies the
${\leq }\kappa ^{+}$
and therefore satisfies the
![]() $\kappa ^{++}$
-c.c.; our desired conclusion thus follows easily from Lemma 4.29 and by noting that the set
$\kappa ^{++}$
-c.c.; our desired conclusion thus follows easily from Lemma 4.29 and by noting that the set
![]() $\{\gamma < \kappa ^{++}: \operatorname {\mathrm {cf}}(\gamma ) = \kappa ^{+}\}$
is stationary in
$\{\gamma < \kappa ^{++}: \operatorname {\mathrm {cf}}(\gamma ) = \kappa ^{+}\}$
is stationary in
![]() $\kappa ^{++}$
.
$\kappa ^{++}$
.
As we have remarked at the beginning of this section, we get the following corollary:
Corollary 4.30. Forcing with
![]() $\mathbb {P}_\alpha , \alpha \leq \kappa ^{++}$
does not collapse cardinals.
$\mathbb {P}_\alpha , \alpha \leq \kappa ^{++}$
does not collapse cardinals.
Lemma 4.31. We have:
-
• If
 $\alpha < \kappa ^{++}$
, then
$\alpha < \kappa ^{++}$
, then
 $V^{\mathbb {P}_\alpha } \models |2^\kappa | = \kappa ^+$
.
$V^{\mathbb {P}_\alpha } \models |2^\kappa | = \kappa ^+$
. -
• If
 $\operatorname {\mathrm {cof}}(\alpha )> \kappa $
, then
$\operatorname {\mathrm {cof}}(\alpha )> \kappa $
, then
 $V^{\mathbb {P}_\alpha } \models 2^\kappa = \bigcup _{\beta < \alpha } (2^\kappa \cap V^{\mathbb {P}_\beta })$
.
$V^{\mathbb {P}_\alpha } \models 2^\kappa = \bigcup _{\beta < \alpha } (2^\kappa \cap V^{\mathbb {P}_\beta })$
. -
•
 $V^{\mathbb {P}} \models |2^\kappa | = \kappa ^{++}$
.
$V^{\mathbb {P}} \models |2^\kappa | = \kappa ^{++}$
.
Proof Suppose
![]() $\alpha < \kappa ^{++}$
. Let
$\alpha < \kappa ^{++}$
. Let
![]() $\dot {\tau }$
be a
$\dot {\tau }$
be a
![]() $\mathbb {P}_\alpha $
-name and
$\mathbb {P}_\alpha $
-name and
![]() $p \in \mathbb {P}_\alpha $
force
$p \in \mathbb {P}_\alpha $
force
![]() $\dot {\tau }$
to be a subset of
$\dot {\tau }$
to be a subset of
![]() $\kappa $
. Without loss of generality assume
$\kappa $
. Without loss of generality assume
![]() $\dot {\tau } = \{\{j\} \times A_j: j < \kappa \}$
is a nice name with
$\dot {\tau } = \{\{j\} \times A_j: j < \kappa \}$
is a nice name with
![]() $A_j \subseteq H_\alpha $
for all
$A_j \subseteq H_\alpha $
for all
![]() $j < \kappa $
. Just like in Lemma 4.28, construct a fusion sequence
$j < \kappa $
. Just like in Lemma 4.28, construct a fusion sequence
![]() $\langle q_j, F_j: j < \kappa \rangle $
below p with
$\langle q_j, F_j: j < \kappa \rangle $
below p with
![]() $|A_j {\restriction } q_j| < \kappa $
for all
$|A_j {\restriction } q_j| < \kappa $
for all
![]() $j < \kappa $
. The fusion limit
$j < \kappa $
. The fusion limit
![]() $q_\kappa $
forces
$q_\kappa $
forces
![]() $\dot {\tau }$
to be equal to an
$\dot {\tau }$
to be equal to an
![]() $\alpha $
-good name, of which there are only
$\alpha $
-good name, of which there are only
![]() $\kappa ^+$
many. If we additionally assume
$\kappa ^+$
many. If we additionally assume
![]() $\operatorname {\mathrm {cf}}(\alpha )> \kappa $
, then
$\operatorname {\mathrm {cf}}(\alpha )> \kappa $
, then
![]() $q_\kappa $
forces
$q_\kappa $
forces
![]() $\dot {\tau }$
to be equal to a
$\dot {\tau }$
to be equal to a
![]() $\mathbb {P}_\gamma $
-name for some
$\mathbb {P}_\gamma $
-name for some
![]() $\gamma < \alpha $
. The first two statements thus follow by a density argument.
$\gamma < \alpha $
. The first two statements thus follow by a density argument.
The last point follows immediately from the previous two.
For
![]() $\alpha < \kappa ^{++}$
we can define in
$\alpha < \kappa ^{++}$
we can define in
![]() $V^{\mathbb {P}_\alpha }$
the
$V^{\mathbb {P}_\alpha }$
the
![]() ${\leq }\kappa $
-support tail iteration
${\leq }\kappa $
-support tail iteration
![]() $\langle \tilde {\mathbb {P}}_\gamma , \dot {\tilde {\mathbb {Q}}}_\beta : \gamma \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
such that
$\langle \tilde {\mathbb {P}}_\gamma , \dot {\tilde {\mathbb {Q}}}_\beta : \gamma \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
such that
![]() $\Vdash _{\tilde {\mathbb {P}}_\gamma } \dot {\tilde {\mathbb {Q}}}_\gamma = \dot {\mathbb {Q}}_{\alpha + \gamma }$
. Set
$\Vdash _{\tilde {\mathbb {P}}_\gamma } \dot {\tilde {\mathbb {Q}}}_\gamma = \dot {\mathbb {Q}}_{\alpha + \gamma }$
. Set
![]() $\mathbb {P}_{\alpha , \kappa ^{++}} := \tilde {\mathbb {P}}_{\kappa ^{++}}$
and note that
$\mathbb {P}_{\alpha , \kappa ^{++}} := \tilde {\mathbb {P}}_{\kappa ^{++}}$
and note that
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
has Property B* as well. It follows from standard proper forcing arguments (adapting [Reference Shelah23, Theorem III.3.4] to the case of
$\mathbb {P}_{\alpha , \kappa ^{++}}$
has Property B* as well. It follows from standard proper forcing arguments (adapting [Reference Shelah23, Theorem III.3.4] to the case of
![]() $\kappa $
-properness) that
$\kappa $
-properness) that
![]() $\mathbb {P} \simeq \mathbb {P}_\alpha \star \mathbb {P}/_{\dot {G}_\alpha }$
is densely embedded in
$\mathbb {P} \simeq \mathbb {P}_\alpha \star \mathbb {P}/_{\dot {G}_\alpha }$
is densely embedded in
![]() $\mathbb {P}_\alpha \star \mathbb {P}_{\alpha , \kappa ^{++}}$
.
$\mathbb {P}_\alpha \star \mathbb {P}_{\alpha , \kappa ^{++}}$
.
5 First proof
We are now equipped to present the first proof of the relative consistency of
Starting with a model of
![]() $|2^\kappa | = \kappa ^+$
, we consider a
$|2^\kappa | = \kappa ^+$
, we consider a
![]() ${\leq }\kappa $
-supported forcing iteration
${\leq }\kappa $
-supported forcing iteration
![]() $\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
with
$\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
with
such that
![]() $(f_\alpha )_{\alpha < \kappa ^{++}} \in V$
and each increasing
$(f_\alpha )_{\alpha < \kappa ^{++}} \in V$
and each increasing
![]() $f \in \kappa ^\kappa \cap V$
appears as an
$f \in \kappa ^\kappa \cap V$
appears as an
![]() $f_\alpha $
cofinally often. Set
$f_\alpha $
cofinally often. Set
![]() $\mathbb {P} := \mathbb {P}_{\kappa ^{++}}$
. By Lemma 4.31 we see
$\mathbb {P} := \mathbb {P}_{\kappa ^{++}}$
. By Lemma 4.31 we see
![]() $V^{\mathbb {P}} \models |2^\kappa | = \kappa ^{++}$
.
$V^{\mathbb {P}} \models |2^\kappa | = \kappa ^{++}$
.
By a density argument, the
![]() $\alpha $
th generic real
$\alpha $
th generic real
![]() $\dot {s}_\alpha $
will encode a covering of the ground model reals satisfying the ‘challenge’
$\dot {s}_\alpha $
will encode a covering of the ground model reals satisfying the ‘challenge’
![]() $f_\alpha $
. For this argument it is sufficient that only
$f_\alpha $
. For this argument it is sufficient that only
![]() $f_\alpha $
from some dominating family appear cofinally often; from the perspective of some intermediate model
$f_\alpha $
from some dominating family appear cofinally often; from the perspective of some intermediate model
![]() $V^{\mathbb {P}_\alpha }$
, the tail forcing
$V^{\mathbb {P}_\alpha }$
, the tail forcing
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
fulfils this criterion. Hence the observation can be extended to the set of reals appearing already in some
$\mathbb {P}_{\alpha , \kappa ^{++}}$
fulfils this criterion. Hence the observation can be extended to the set of reals appearing already in some
![]() $V^{\mathbb {P}_\alpha }$
; the following theorem formalizes this.
$V^{\mathbb {P}_\alpha }$
; the following theorem formalizes this.
Theorem 5.1.
![]() $V^{\mathbb {P}} \models \forall \alpha < \kappa ^{++}: 2^\kappa \cap V^{\mathbb {P}_\alpha } \in \mathcal {SN}.$
$V^{\mathbb {P}} \models \forall \alpha < \kappa ^{++}: 2^\kappa \cap V^{\mathbb {P}_\alpha } \in \mathcal {SN}.$
Proof Working within
![]() $V^{\mathbb {P}}$
, take
$V^{\mathbb {P}}$
, take
![]() $\alpha < \kappa ^{++}$
and
$\alpha < \kappa ^{++}$
and
![]() $f \in \kappa ^\kappa $
. Since
$f \in \kappa ^\kappa $
. Since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa ^\kappa $
-bounding by Fact 4.5, we find an
$\kappa ^\kappa $
-bounding by Fact 4.5, we find an
![]() $h \in \kappa ^\kappa \cap V$
with
$h \in \kappa ^\kappa \cap V$
with
![]() $f \leq h$
and
$f \leq h$
and
![]() $\beta> \alpha $
with
$\beta> \alpha $
with
![]() $f_\beta (i) = |2^{h(i)}|$
for all
$f_\beta (i) = |2^{h(i)}|$
for all
![]() $i < \kappa $
. In V we may construct bijections
$i < \kappa $
. In V we may construct bijections
![]() $c_\ell : |2^\ell | \to 2^\ell $
for
$c_\ell : |2^\ell | \to 2^\ell $
for
![]() $\ell < \kappa $
.
$\ell < \kappa $
.
Working now in
![]() $V^{\mathbb {P}_\beta }$
, define the function
$V^{\mathbb {P}_\beta }$
, define the function
![]() $\dot {\sigma }(i) = c_{h(i)}(\dot {s}_\beta (i))$
. For
$\dot {\sigma }(i) = c_{h(i)}(\dot {s}_\beta (i))$
. For
![]() $x \in 2^\kappa \cap V^{\mathbb {P}_\alpha }$
the set
$x \in 2^\kappa \cap V^{\mathbb {P}_\alpha }$
the set
is dense; in fact, it is easy to see that for any
![]() $p \in \mathbb {Q}_\beta $
and
$p \in \mathbb {Q}_\beta $
and
![]() $\eta \in \operatorname {\mathrm {split}}(p), j = \operatorname {\mathrm {dom}}(\eta )$
we have
$\eta \in \operatorname {\mathrm {split}}(p), j = \operatorname {\mathrm {dom}}(\eta )$
we have
![]() $p^{[\eta ^\frown c^{-1}_{h(j)}(x {\restriction } h(j)) ]} \in D_x$
. Here
$p^{[\eta ^\frown c^{-1}_{h(j)}(x {\restriction } h(j)) ]} \in D_x$
. Here
![]() $c^{-1}_{h(j)}(x {\restriction } h(j))$
is well-defined, since
$c^{-1}_{h(j)}(x {\restriction } h(j))$
is well-defined, since
![]() $2^{<\kappa } \cap V = 2^{<\kappa } \cap V^{\mathbb {P}_\beta }$
. Hence
$2^{<\kappa } \cap V = 2^{<\kappa } \cap V^{\mathbb {P}_\beta }$
. Hence
![]() $(\sigma (i))_{i < \kappa }$
provides the required covering for the challenge f and
$(\sigma (i))_{i < \kappa }$
provides the required covering for the challenge f and
![]() $2^\kappa \cap V^{\mathbb {P}_\alpha } \in \mathcal {SN}$
follows.
$2^\kappa \cap V^{\mathbb {P}_\alpha } \in \mathcal {SN}$
follows.
If
![]() $V^{\mathbb {P}} \models X \subseteq 2^\kappa , |X| \leq \kappa ^+$
, then by the
$V^{\mathbb {P}} \models X \subseteq 2^\kappa , |X| \leq \kappa ^+$
, then by the
![]() $\kappa ^{++}$
-c.c., X already appears at some intermediate stage
$\kappa ^{++}$
-c.c., X already appears at some intermediate stage
![]() $V^{\mathbb {P}_\alpha }$
. We thus get one direction of our desired result by the previous theorem.
$V^{\mathbb {P}_\alpha }$
. We thus get one direction of our desired result by the previous theorem.
Theorem 5.2.
![]() $V^{\mathbb {P}} \models [2^\kappa ]^{\leq \kappa ^+} \subseteq \mathcal {SN}$
.
$V^{\mathbb {P}} \models [2^\kappa ]^{\leq \kappa ^+} \subseteq \mathcal {SN}$
.
In order to lift the arguments appearing in [Reference Goldstern, Judah and Shelah8], we require additional large cardinal assumptions on
![]() $\kappa $
. A priori it is sufficient for our purposes for
$\kappa $
. A priori it is sufficient for our purposes for
![]() $\kappa $
to merely be weakly compact, since the only occasion at which a property stronger than inaccessibility is utilized is a crucial invocation of the tree property in Lemma 5.5. However, the aforementioned lemma is invoked not only in V, but also at intermediate stages
$\kappa $
to merely be weakly compact, since the only occasion at which a property stronger than inaccessibility is utilized is a crucial invocation of the tree property in Lemma 5.5. However, the aforementioned lemma is invoked not only in V, but also at intermediate stages
![]() $V^{\mathbb {P}_\alpha }$
; it might be the case that weak compactness of
$V^{\mathbb {P}_\alpha }$
; it might be the case that weak compactness of
![]() $\kappa $
is by that point destroyed.
$\kappa $
is by that point destroyed.
The following large cardinal property was introduced by Villaveces [Reference Villaveces25, Definition 4]:
Definition 5.3. Let
![]() $\theta $
be an ordinal. We say an inaccessible cardinal
$\theta $
be an ordinal. We say an inaccessible cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\theta $
-strongly unfoldable iff for all transitive models M of ZF
$\theta $
-strongly unfoldable iff for all transitive models M of ZF
![]() $^-$
(ZF without the Power Set Axiom) such that
$^-$
(ZF without the Power Set Axiom) such that
![]() $|M| = \kappa , \kappa \in M$
and
$|M| = \kappa , \kappa \in M$
and
![]() ${}^{<\kappa }M \subseteq M$
there exists a transitive model N with
${}^{<\kappa }M \subseteq M$
there exists a transitive model N with
![]() $V_{\theta } \cup \{\theta \} \subseteq N$
and an elementary embedding
$V_{\theta } \cup \{\theta \} \subseteq N$
and an elementary embedding
![]() $j : M \to N$
with critical point
$j : M \to N$
with critical point
![]() $\kappa $
and
$\kappa $
and
![]() $j(\kappa ) \geq \theta $
.
$j(\kappa ) \geq \theta $
.
Furthermore, call
![]() $\kappa $
strongly unfoldable iff it is
$\kappa $
strongly unfoldable iff it is
![]() $\theta $
-strongly unfoldable for all
$\theta $
-strongly unfoldable for all
![]() $\theta $
.
$\theta $
.
Strongly unfoldable cardinals are weakly compact and are downwards absolute to L [Reference Villaveces25]. Villaveces also observed that Ramsey cardinals are strongly unfoldable in L (though they may fail to be such in V). The consistency strength of a strongly unfoldable cardinal thus slots between a weakly compact and Ramsey cardinal, with it being a conservative enough strengthening of weak compactness as to still be consistent with
![]() $V=L$
.
$V=L$
.
Of interest to us is a preservation theorem by Johnstone [Reference Johnstone13].
Theorem 5.4 (Johnstone [Reference Johnstone13]).
For any
![]() $\kappa $
strongly unfoldable there is a forcing extension in which the strong unfoldability of
$\kappa $
strongly unfoldable there is a forcing extension in which the strong unfoldability of
![]() $\kappa $
is indestructible under
$\kappa $
is indestructible under
![]() ${<}\kappa $
-closed,
${<}\kappa $
-closed,
![]() $\kappa $
-proper forcing notions.
$\kappa $
-proper forcing notions.
We stress that the full strength of strong unfoldability is not used in our proof; we merely require it in order to make the weak compactness of
![]() $\kappa $
indestructible by the forcings
$\kappa $
indestructible by the forcings
![]() $\mathbb {P}_\alpha $
.
$\mathbb {P}_\alpha $
.
For a strongly unfoldable
![]() $\kappa $
, after forcing indestructibility using Johnstone’s theorem, we may collapse a potentially blown up
$\kappa $
, after forcing indestructibility using Johnstone’s theorem, we may collapse a potentially blown up
![]() $2^\kappa $
back to
$2^\kappa $
back to
![]() $\kappa ^+$
with a
$\kappa ^+$
with a
![]() ${<}\kappa ^+$
-closed forcingFootnote
3
. Throughout this section we may therefore assume
${<}\kappa ^+$
-closed forcingFootnote
3
. Throughout this section we may therefore assume
 $$ \begin{align*} V \models " |2^\kappa| = \kappa^+ + &\textrm{ the strong unfoldability of } \kappa \textrm{ is indestructible} \\ &\textrm{under } {<}\kappa\text{-}\textrm{closed}, \kappa\textrm{-proper forcing notions".} \end{align*} $$
$$ \begin{align*} V \models " |2^\kappa| = \kappa^+ + &\textrm{ the strong unfoldability of } \kappa \textrm{ is indestructible} \\ &\textrm{under } {<}\kappa\text{-}\textrm{closed}, \kappa\textrm{-proper forcing notions".} \end{align*} $$
We now set out to prove
![]() $V^{\mathbb {P}} \models \mathcal {SN} \subseteq [2^\kappa ]^{\leq \kappa ^+}$
.
$V^{\mathbb {P}} \models \mathcal {SN} \subseteq [2^\kappa ]^{\leq \kappa ^+}$
.
The statement of the next two lemmas takes place in
![]() $V^{\mathbb {P}_\alpha }$
. Recall that
$V^{\mathbb {P}_\alpha }$
. Recall that
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
denotes the tail forcing.
$\mathbb {P}_{\alpha , \kappa ^{++}}$
denotes the tail forcing.
Lemma 5.5. Let
![]() $\alpha < \kappa ^{++}$
be an ordinal,
$\alpha < \kappa ^{++}$
be an ordinal,
![]() $\dot \tau $
a
$\dot \tau $
a
![]() $\mathbb {P}_{\alpha ,\kappa ^{++}}$
-name for a real in
$\mathbb {P}_{\alpha ,\kappa ^{++}}$
-name for a real in
![]() $2^\kappa $
,
$2^\kappa $
,
![]() $F \in [\kappa ^{++} \backslash \alpha ]^{< \kappa }$
and
$F \in [\kappa ^{++} \backslash \alpha ]^{< \kappa }$
and
![]() $i < \kappa $
. Assume furthermore that
$i < \kappa $
. Assume furthermore that
![]() $p \in \mathbb {P}_{\alpha , \kappa ^{++}}$
forces
$p \in \mathbb {P}_{\alpha , \kappa ^{++}}$
forces
![]() $\dot \tau \notin V^{\mathbb {P}_\alpha }$
. Then there exists a
$\dot \tau \notin V^{\mathbb {P}_\alpha }$
. Then there exists a
![]() $\delta <\kappa $
such that
$\delta <\kappa $
such that
We will write
![]() $\delta _{p, F,i}$
for the least such
$\delta _{p, F,i}$
for the least such
![]() $\delta $
.
$\delta $
.
Proof Suppose not. Then we can find
![]() $\alpha , \dot {\tau }, F,i$
and p with
$\alpha , \dot {\tau }, F,i$
and p with
Set
![]() $T:= \{\eta _\delta {\restriction } \ell : \ell \leq \delta < \kappa \}$
. By virtue of the preparation of
$T:= \{\eta _\delta {\restriction } \ell : \ell \leq \delta < \kappa \}$
. By virtue of the preparation of
![]() $\kappa $
,
$\kappa $
,
and therefore, since T is a
![]() ${<}\kappa $
-splitting tree of height
${<}\kappa $
-splitting tree of height
![]() $\kappa $
, it has a branch
$\kappa $
, it has a branch
![]() $b^*$
in
$b^*$
in
![]() $V^{\mathbb {P}_\alpha }$
. Since p forces
$V^{\mathbb {P}_\alpha }$
. Since p forces
![]() $\dot {\tau } \notin V^{\mathbb {P}_\alpha }$
, there is a
$\dot {\tau } \notin V^{\mathbb {P}_\alpha }$
, there is a
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
-name
$\mathbb {P}_{\alpha , \kappa ^{++}}$
-name
![]() $\dot {\ell }$
for an ordinal less than
$\dot {\ell }$
for an ordinal less than
![]() $\kappa $
such that
$\kappa $
such that
![]() $p \Vdash \dot {\tau } {\restriction } \dot {\ell } \neq b^* {\restriction } \dot {\ell }$
. As
$p \Vdash \dot {\tau } {\restriction } \dot {\ell } \neq b^* {\restriction } \dot {\ell }$
. As
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
satisfies Property B*, there is a
$\mathbb {P}_{\alpha , \kappa ^{++}}$
satisfies Property B*, there is a
![]() $q \leq _{F,i} p$
and
$q \leq _{F,i} p$
and
![]() $\ell ^* < \kappa $
with
$\ell ^* < \kappa $
with
![]() $q \Vdash \dot {\ell } < \ell ^*$
.
$q \Vdash \dot {\ell } < \ell ^*$
.
Since
![]() $b^* {\restriction } \ell ^* \in T$
, there is a
$b^* {\restriction } \ell ^* \in T$
, there is a
![]() $\delta \geq \ell ^*$
such that
$\delta \geq \ell ^*$
such that
![]() $b^* {\restriction } \ell ^* = \eta _\delta {\restriction } \ell ^*$
. But this means
$b^* {\restriction } \ell ^* = \eta _\delta {\restriction } \ell ^*$
. But this means
![]() $q \Vdash \dot {\tau } {\restriction } \ell ^* \neq \check {\eta }_\delta {\restriction } \ell ^*$
and therefore
$q \Vdash \dot {\tau } {\restriction } \ell ^* \neq \check {\eta }_\delta {\restriction } \ell ^*$
and therefore
![]() $q \Vdash \eta _\delta \ntriangleleft \dot {\tau }$
, a contradiction.
$q \Vdash \eta _\delta \ntriangleleft \dot {\tau }$
, a contradiction.
In the following we refer to pointwise (everywhere) domination
![]() $\leq $
and not just the eventually dominating relation. For a
$\leq $
and not just the eventually dominating relation. For a
![]() ${<}\kappa $
-closed,
${<}\kappa $
-closed,
![]() $\kappa ^\kappa $
-bounding forcing, the ground model
$\kappa ^\kappa $
-bounding forcing, the ground model
![]() $\kappa $
-reals form a pointwise dominating family.
$\kappa $
-reals form a pointwise dominating family.
Definition 5.6. Let
![]() $D\subseteq \kappa ^\kappa $
be a dominating family. We say that H has index D iff
$D\subseteq \kappa ^\kappa $
be a dominating family. We say that H has index D iff
![]() $H=\{h_f \colon f\in D\}$
and
$H=\{h_f \colon f\in D\}$
and
![]() $\forall i <\kappa \colon h_f (i) \in 2^{f(i)}$
.
$\forall i <\kappa \colon h_f (i) \in 2^{f(i)}$
.
Fact 5.7.
Lemma 5.8. Let
![]() $D \in V$
be a dominating family,
$D \in V$
be a dominating family,
![]() $\alpha < \kappa ^{++}$
and
$\alpha < \kappa ^{++}$
and
![]() $H \in V^{\mathbb {P}_\alpha }$
have index D. Let furthermore
$H \in V^{\mathbb {P}_\alpha }$
have index D. Let furthermore
![]() $\dot {\tau }$
be a name for an element of
$\dot {\tau }$
be a name for an element of
![]() $2^\kappa $
with
$2^\kappa $
with
![]() $\Vdash _{\mathbb {P}_{\alpha , \kappa ^{++}}} \dot {\tau } \notin V^{\mathbb {P}_\alpha }$
. Then we have
$\Vdash _{\mathbb {P}_{\alpha , \kappa ^{++}}} \dot {\tau } \notin V^{\mathbb {P}_\alpha }$
. Then we have
Proof We prove the claim with a density argument, let therefore
![]() $p \in \mathbb {P}_{\alpha , \kappa ^{++}}$
be arbitrary. Working in
$p \in \mathbb {P}_{\alpha , \kappa ^{++}}$
be arbitrary. Working in
![]() $V^{\mathbb {P}_\alpha }$
, we will construct an increasing sequence
$V^{\mathbb {P}_\alpha }$
, we will construct an increasing sequence
![]() $(\delta _i)_{i < \kappa }$
of ordinals less than
$(\delta _i)_{i < \kappa }$
of ordinals less than
![]() $\kappa $
. On the tree
$\kappa $
. On the tree
we shall construct a mapping
![]() $\mathfrak {q}: T \to \mathbb {P}_{\alpha , \kappa ^{++}}$
and a sequence of increasing sets
$\mathfrak {q}: T \to \mathbb {P}_{\alpha , \kappa ^{++}}$
and a sequence of increasing sets
![]() $(F_i)_{i < \kappa }$
such that whenever
$(F_i)_{i < \kappa }$
such that whenever
![]() $b \in \prod _{j < \kappa } 2^{\delta _j}$
is a branch of T in
$b \in \prod _{j < \kappa } 2^{\delta _j}$
is a branch of T in
![]() $V^{\mathbb {P}_\alpha }$
, then
$V^{\mathbb {P}_\alpha }$
, then
is a fusion sequence below p. Each condition
![]() $\mathfrak {q}(g)$
will carry some information about an increasingly long initial segment of
$\mathfrak {q}(g)$
will carry some information about an increasingly long initial segment of
![]() $\dot {\tau }$
. More specifically, we will ensure that for all
$\dot {\tau }$
. More specifically, we will ensure that for all
![]() $i < \kappa $
and
$i < \kappa $
and
![]() $g \in \prod _{j < i} 2^{\delta _j}$
we have
$g \in \prod _{j < i} 2^{\delta _j}$
we have
We define
![]() $\mathfrak {q}(g)$
for
$\mathfrak {q}(g)$
for
![]() $g \in \prod _{j < i} 2^{\delta _j}$
by induction in i.
$g \in \prod _{j < i} 2^{\delta _j}$
by induction in i.
-
•
 $i=0$
: Set
$i=0$
: Set
 $\mathfrak {q}(\emptyset ) := p$
and
$\mathfrak {q}(\emptyset ) := p$
and
 $F_0 := \emptyset $
.
$F_0 := \emptyset $
. -
•
 $i \to i+1$
: Assume
$i \to i+1$
: Assume
 $\mathfrak {q}(g)$
is defined for every
$\mathfrak {q}(g)$
is defined for every
 $g \in \prod _{j < i} 2^{\delta _j}$
. Using Lemma 5.5 we can define
$g \in \prod _{j < i} 2^{\delta _j}$
. Using Lemma 5.5 we can define
 $\delta _{i} := \sup \Big (\{\delta _{\mathfrak {q}(g), F_i, i}: g \in \prod _{j < i} 2^{\delta _j}\} \cup \{\delta _j + 1: j < i\} \Big )$
and for every
$\delta _{i} := \sup \Big (\{\delta _{\mathfrak {q}(g), F_i, i}: g \in \prod _{j < i} 2^{\delta _j}\} \cup \{\delta _j + 1: j < i\} \Big )$
and for every
 $g \in \prod _{j < i} 2^{\delta _j}, \eta _{i} \in 2^{\delta _{i}}$
find a condition
$g \in \prod _{j < i} 2^{\delta _j}, \eta _{i} \in 2^{\delta _{i}}$
find a condition
 $\mathfrak {q}(g ^\frown \eta _{i}) \leq _{F_i,i} \mathfrak {q}(g)$
with Now since
$\mathfrak {q}(g ^\frown \eta _{i}) \leq _{F_i,i} \mathfrak {q}(g)$
with Now since $$\begin{align*}\mathfrak{q}(g ^\frown \eta_{i}) \Vdash \eta_{i} \ntriangleleft \dot{\tau}. \end{align*}$$
$$\begin{align*}\mathfrak{q}(g ^\frown \eta_{i}) \Vdash \eta_{i} \ntriangleleft \dot{\tau}. \end{align*}$$
 $\mathfrak {q}(g ^\frown \eta _{i}) \leq \mathfrak {q}(g)$
, we also have Use a bookkeeping argument to define
$\mathfrak {q}(g ^\frown \eta _{i}) \leq \mathfrak {q}(g)$
, we also have Use a bookkeeping argument to define $$\begin{align*}\mathfrak{q}(g ^\frown \eta_{i}) \Vdash \forall j < i:\ g(j) \ntriangleleft \dot{\tau}. \end{align*}$$
$$\begin{align*}\mathfrak{q}(g ^\frown \eta_{i}) \Vdash \forall j < i:\ g(j) \ntriangleleft \dot{\tau}. \end{align*}$$
 $F_{i+1}$
.
$F_{i+1}$
.
-
•
 $\lambda < \kappa $
is a limit: By construction, for every
$\lambda < \kappa $
is a limit: By construction, for every
 $g \in \prod _{j < \lambda } 2^{\delta _j}$
the sequence
$g \in \prod _{j < \lambda } 2^{\delta _j}$
the sequence
 $(\mathfrak {q}(g {\restriction } j))_{j < \lambda }$
is a fusion sequence. Set
$(\mathfrak {q}(g {\restriction } j))_{j < \lambda }$
is a fusion sequence. Set
 $\mathfrak {q}(g)$
to be a fusion limit of said sequence and
$\mathfrak {q}(g)$
to be a fusion limit of said sequence and
 $F_\lambda := \bigcup _{j < \lambda } F_j$
. Note that we have
$F_\lambda := \bigcup _{j < \lambda } F_j$
. Note that we have  $$\begin{align*}\mathfrak{q}(g) \Vdash \forall j < \lambda:\ g(j) \ntriangleleft \dot{\tau}. \end{align*}$$
$$\begin{align*}\mathfrak{q}(g) \Vdash \forall j < \lambda:\ g(j) \ntriangleleft \dot{\tau}. \end{align*}$$
This concludes the construction of
![]() $\mathfrak {q}$
. Let now
$\mathfrak {q}$
. Let now
![]() $f \in D$
dominate the function
$f \in D$
dominate the function
![]() $i \mapsto \delta _i$
and set
$i \mapsto \delta _i$
and set
![]() $\eta _i := h_f(i) {\restriction } \delta _i$
. Now
$\eta _i := h_f(i) {\restriction } \delta _i$
. Now
![]() $(\mathfrak {q}(g_i))_{i < \kappa }$
with
$(\mathfrak {q}(g_i))_{i < \kappa }$
with
![]() $g_i = (\eta _j)_{j < i}$
is a fusion sequence and has a fusion limit
$g_i = (\eta _j)_{j < i}$
is a fusion sequence and has a fusion limit
![]() $q_\kappa $
. It follows that
$q_\kappa $
. It follows that
for each
![]() $i < \kappa $
and therefore
$i < \kappa $
and therefore
![]() $q_\kappa \Vdash \dot {\tau } \notin \bigcap _{f\in D} \bigcup _{i <\kappa } [h_f(i)]$
. Thus the set of conditions that force
$q_\kappa \Vdash \dot {\tau } \notin \bigcap _{f\in D} \bigcup _{i <\kappa } [h_f(i)]$
. Thus the set of conditions that force
![]() $\dot {\tau } \notin \bigcap _{f\in D} \bigcup _{i <\kappa } [h_f(i)]$
is dense in
$\dot {\tau } \notin \bigcap _{f\in D} \bigcup _{i <\kappa } [h_f(i)]$
is dense in
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
.
$\mathbb {P}_{\alpha , \kappa ^{++}}$
.
We see that every intermediate model
![]() $V^{\mathbb {P}_\alpha }$
believes that a set
$V^{\mathbb {P}_\alpha }$
believes that a set
![]() $X \subseteq 2^\kappa $
which contains a real appearing in a later model will never be strong measure zero with respect to any test conducted in
$X \subseteq 2^\kappa $
which contains a real appearing in a later model will never be strong measure zero with respect to any test conducted in
![]() $V^{\mathbb {P}_\alpha }$
. This essentially gives us our theorem.
$V^{\mathbb {P}_\alpha }$
. This essentially gives us our theorem.
Theorem 5.9.
![]() $V^{\mathbb {P}} \models \mathcal {SN} = [2^\kappa ]^{\leq \kappa ^+}$
.
$V^{\mathbb {P}} \models \mathcal {SN} = [2^\kappa ]^{\leq \kappa ^+}$
.
Proof Since we already saw one inclusion in Theorem 5.2, it suffices to show
![]() $V^{\mathbb {P}} \models \mathcal {SN} \subseteq [2^\kappa ]^{\leq \kappa ^+}$
. Let now
$V^{\mathbb {P}} \models \mathcal {SN} \subseteq [2^\kappa ]^{\leq \kappa ^+}$
. Let now
![]() $X \in V^{\mathbb {P}}$
be of size
$X \in V^{\mathbb {P}}$
be of size
![]() $\kappa ^{++}$
and D be a dominating family in
$\kappa ^{++}$
and D be a dominating family in
![]() $V^{\mathbb {P}}$
which lies in V. We will show that there is no
$V^{\mathbb {P}}$
which lies in V. We will show that there is no
![]() $H \in V^{\mathbb {P}}$
with index D such that
$H \in V^{\mathbb {P}}$
with index D such that
hence X is not strong measure zero by Fact 5.7. Towards a contradiction, assume such an H exists. Note that since D is in V, the set H can have cardinality at most
![]() $\kappa ^+$
; since
$\kappa ^+$
; since
![]() $\mathbb {P}$
fulfils the
$\mathbb {P}$
fulfils the
![]() $\kappa ^{++}$
-c.c., we know H must already appear in some intermediate model
$\kappa ^{++}$
-c.c., we know H must already appear in some intermediate model
![]() $V^{\mathbb {P}_\alpha }$
. But
$V^{\mathbb {P}_\alpha }$
. But
![]() $|X| = \kappa ^{++}$
, thus there must be an
$|X| = \kappa ^{++}$
, thus there must be an
![]() $x \in X$
with
$x \in X$
with
![]() $x \notin V^{\mathbb {P}_\alpha }$
.
$x \notin V^{\mathbb {P}_\alpha }$
.
Working in
![]() $V^{\mathbb {P_\alpha }}$
, let
$V^{\mathbb {P_\alpha }}$
, let
![]() $\dot {x}$
and
$\dot {x}$
and
![]() $\dot {X}$
be
$\dot {X}$
be
![]() $\mathbb {P}_{\alpha , \kappa ^{++}}$
-names for x and X, respectively, so that we have
$\mathbb {P}_{\alpha , \kappa ^{++}}$
-names for x and X, respectively, so that we have
Then by Lemma 5.8 we have
and thus
![]() $X \nsubseteq \bigcap _{f \in D} \bigcup _{i < \kappa } [h_f(i)]$
in
$X \nsubseteq \bigcap _{f \in D} \bigcup _{i < \kappa } [h_f(i)]$
in
![]() $V^{\mathbb {P}}$
, a contradiction.
$V^{\mathbb {P}}$
, a contradiction.
6 Coding of continuous functions
For the reader’s convenience we collect some selected facts about the coding of continuous functions that are going to find use in the next section.
Throughout this section, every tree T is assumed to be a tree on
![]() $2^{<\kappa }$
.
$2^{<\kappa }$
.
Definition 6.1. Let T be a tree and
![]() $(T_\eta )_{\eta \in 2^{<\kappa }}$
a family of trees. Then
$(T_\eta )_{\eta \in 2^{<\kappa }}$
a family of trees. Then
![]() $\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
is a code for a continuous function (or just code) iff:
$\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
is a code for a continuous function (or just code) iff:
-
1. if
 $\eta _1 \lhd \eta _2$
, then
$\eta _1 \lhd \eta _2$
, then
 $[T_{\eta _2}] \subseteq [T_{\eta _1}].$
$[T_{\eta _2}] \subseteq [T_{\eta _1}].$
-
2. if
 $\eta _1 \perp \eta _2$
, then
$\eta _1 \perp \eta _2$
, then
 $[T_{\eta _1}] \cap [T_{\eta _2}] = \emptyset .$
$[T_{\eta _1}] \cap [T_{\eta _2}] = \emptyset .$
-
3.
 $\bigcup _{\eta \in 2^i} [T_\eta ] = [T]$
for each
$\bigcup _{\eta \in 2^i} [T_\eta ] = [T]$
for each
 $i < \kappa $
.
$i < \kappa $
.
Theorem 6.2. If
![]() $\mathcal {P}$
is a
$\mathcal {P}$
is a
![]() ${<}\kappa $
-closed forcing notion, then
${<}\kappa $
-closed forcing notion, then
![]() $\mathbf {\Sigma }^1_1(\kappa )$
properties (i.e., analytic properties in the sense of the projective hierarchy on
$\mathbf {\Sigma }^1_1(\kappa )$
properties (i.e., analytic properties in the sense of the projective hierarchy on
![]() $\kappa ^\kappa $
) are absolute between V and
$\kappa ^\kappa $
) are absolute between V and
![]() $V^{\mathcal {P}}$
.
$V^{\mathcal {P}}$
.
Proof See [Reference Friedman, Khomskii and Kulikov7].
Lemma 6.3. Let
![]() $\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
be a code. Then there exists a unique continuous function
$\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
be a code. Then there exists a unique continuous function
![]() $g_{\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle } : [T] \to 2^\kappa $
such that
$g_{\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle } : [T] \to 2^\kappa $
such that
for all
![]() $\eta \in 2^{<\kappa }$
.
$\eta \in 2^{<\kappa }$
.
Proof If we set
![]() $g(y) := \bigcup \{\eta \in 2^{<\kappa }: y \in [T_\eta ]\}$
, then it is easy to see that
$g(y) := \bigcup \{\eta \in 2^{<\kappa }: y \in [T_\eta ]\}$
, then it is easy to see that
![]() $g : [T] \to 2^\kappa $
is a well-defined continuous function and
$g : [T] \to 2^\kappa $
is a well-defined continuous function and
![]() $g^{-1}([\eta ]) = [T_\eta ]$
for all
$g^{-1}([\eta ]) = [T_\eta ]$
for all
![]() $\eta \in 2^{<\kappa }$
. Since
$\eta \in 2^{<\kappa }$
. Since
![]() $([\eta ])_{\eta \in 2^{<\kappa }}$
forms a clopen basis of
$([\eta ])_{\eta \in 2^{<\kappa }}$
forms a clopen basis of
![]() $2^\kappa $
, uniqueness is given.
$2^\kappa $
, uniqueness is given.
On the other hand, if
![]() $g : Y \to 2^\kappa $
is a continuous function where
$g : Y \to 2^\kappa $
is a continuous function where
![]() $Y \subseteq 2^\kappa $
is closed, then
$Y \subseteq 2^\kappa $
is closed, then
![]() $\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
is a code for g, where T and the
$\langle T, (T_\eta )_{\eta \in 2^{<\kappa }} \rangle $
is a code for g, where T and the
![]() $T_\eta $
’s are trees with
$T_\eta $
’s are trees with
![]() $[T] = Y$
and
$[T] = Y$
and
![]() $[T_\eta ] = g^{-1}([\eta ])$
.
$[T_\eta ] = g^{-1}([\eta ])$
.
Definition 6.4. For codes
![]() $c, c'$
define
$c, c'$
define
![]() $c \preccurlyeq c' :\Leftrightarrow g_c \subseteq g_{c'}$
.
$c \preccurlyeq c' :\Leftrightarrow g_c \subseteq g_{c'}$
.
Clearly
![]() $\preccurlyeq $
is reflexive and transitive.
$\preccurlyeq $
is reflexive and transitive.
Definition 6.5. A function
![]() $g : Y \to Z$
with
$g : Y \to Z$
with
![]() $Y,Z \subseteq 2^\kappa $
is uniformly continuous iff
$Y,Z \subseteq 2^\kappa $
is uniformly continuous iff
The map
![]() $i \mapsto j(i)$
is the modulus of continuity of g.
$i \mapsto j(i)$
is the modulus of continuity of g.
Fact 6.6. The following statements are
![]() $\mathbf {\Pi }_1^1(\kappa )$
and therefore absolute for
$\mathbf {\Pi }_1^1(\kappa )$
and therefore absolute for
![]() ${<}\kappa $
-closed forcing extensions:
${<}\kappa $
-closed forcing extensions:
-
• c is a code for a continuous function.
-
• “
 $[T] = [T']$
” for trees
$[T] = [T']$
” for trees
 $T,T'$
.
$T,T'$
. -
• “
 $c \preccurlyeq c'$
” for codes
$c \preccurlyeq c'$
” for codes
 $c,c'$
.
$c,c'$
. -
• “
 $g_c$
is a total function” for a code c.
$g_c$
is a total function” for a code c. -
• “
 $\operatorname {\mathrm {ran}} (g_c) \subseteq [T]$
” for a code c and a tree
$\operatorname {\mathrm {ran}} (g_c) \subseteq [T]$
” for a code c and a tree
 $T.$
$T.$
-
• “
 $g_c$
is uniformly continuous with modulus of continuity
$g_c$
is uniformly continuous with modulus of continuity
 $i \mapsto j(i)$
” for a code
$i \mapsto j(i)$
” for a code
 $c.$
$c.$
Let now
![]() $Y \subseteq 2^\kappa $
be closed and
$Y \subseteq 2^\kappa $
be closed and
![]() $g: Y \to 2^\kappa $
be continuous. The above thus yields a method to continuously and uniquely extend g to
$g: Y \to 2^\kappa $
be continuous. The above thus yields a method to continuously and uniquely extend g to
![]() $\tilde {g}: Y^{(V^{\mathcal {P}})} \to (2^\kappa )^{(V^{\mathcal {P}})}$
Footnote
4
for a
$\tilde {g}: Y^{(V^{\mathcal {P}})} \to (2^\kappa )^{(V^{\mathcal {P}})}$
Footnote
4
for a
![]() ${<}\kappa $
-closed forcing
${<}\kappa $
-closed forcing
![]() $\mathcal {P}$
. To do so, choose a code c for g and evaluate it in
$\mathcal {P}$
. To do so, choose a code c for g and evaluate it in
![]() $V^{\mathcal {P}}$
. It is easy to prove that
$V^{\mathcal {P}}$
. It is easy to prove that
![]() $\tilde {g} = (g_c)^{V^{\mathcal {P}}}$
is an extension of g; also observe that
$\tilde {g} = (g_c)^{V^{\mathcal {P}}}$
is an extension of g; also observe that
![]() $\tilde {g}$
is independent of the chosen code c, since the statement
$\tilde {g}$
is independent of the chosen code c, since the statement
![]() $c \preccurlyeq c'$
is absolute by the above fact. Furthermore, we note that
$c \preccurlyeq c'$
is absolute by the above fact. Furthermore, we note that
![]() $\tilde {g}$
is the unique continuous extension of g, since Y is dense in
$\tilde {g}$
is the unique continuous extension of g, since Y is dense in
![]() $Y^{V^{\mathcal {P}}}$
.
$Y^{V^{\mathcal {P}}}$
.
In the future we will not be making a notational distinction between g and
![]() $\tilde {g}$
.
$\tilde {g}$
.
7 Second proof
In this section we will construct a model in which every
![]() $X \subseteq 2^\kappa $
of size
$X \subseteq 2^\kappa $
of size
![]() $|2^\kappa |$
can be uniformly continuously mapped onto
$|2^\kappa |$
can be uniformly continuously mapped onto
![]() $2^\kappa $
. The construction closely follows Corazza’s approach [Reference Corazza4].
$2^\kappa $
. The construction closely follows Corazza’s approach [Reference Corazza4].
We will consider the same forcing iteration
![]() $\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
with
$\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\beta : \alpha \leq \kappa ^{++}, \beta < \kappa ^{++} \rangle $
with
![]() ${\leq }\kappa $
-support as in the previous section. Additionally, we also choose
${\leq }\kappa $
-support as in the previous section. Additionally, we also choose
![]() $\dot {\mathbb {Q}}_\alpha $
to be
$\dot {\mathbb {Q}}_\alpha $
to be
![]() $\kappa $
-Sacks forcing (i.e.,
$\kappa $
-Sacks forcing (i.e.,
![]() $f_\alpha \equiv 2$
) for
$f_\alpha \equiv 2$
) for
![]() $\alpha = 0$
and for
$\alpha = 0$
and for
![]() $\alpha $
with cofinality
$\alpha $
with cofinality
![]() $\kappa ^+$
. We still assume
$\kappa ^+$
. We still assume
![]() $V \models |2^\kappa | = \kappa ^+$
, but
$V \models |2^\kappa | = \kappa ^+$
, but
![]() $\kappa $
is only required to be inaccessible this time.
$\kappa $
is only required to be inaccessible this time.
Since the forcing iteration is identical to the one in the previous section, Theorem 5.2 holds and thus
The other direction of the proof hinges on a technical lemma.
Lemma 7.1. Let
![]() $p \in \mathbb {P}, F \in [\kappa ^{++}]^{<\kappa }, i < \kappa $
,
$p \in \mathbb {P}, F \in [\kappa ^{++}]^{<\kappa }, i < \kappa $
,
![]() $Y \in [2^\kappa ]^{<\kappa }$
and a
$Y \in [2^\kappa ]^{<\kappa }$
and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\tau }$
be given such that p forces
$\dot {\tau }$
be given such that p forces
![]() $\dot {\tau } \in 2^\kappa $
and
$\dot {\tau } \in 2^\kappa $
and
![]() $\dot {\tau } \notin V$
. Then we may find an
$\dot {\tau } \notin V$
. Then we may find an
![]() $X \in [2^\kappa ]^{<\kappa }$
and a sequence
$X \in [2^\kappa ]^{<\kappa }$
and a sequence
![]() $(q_j)_{j < \kappa }$
of conditions below p such that:
$(q_j)_{j < \kappa }$
of conditions below p such that:
-
•
 $\forall j_1 < j_2 < \kappa :\ q_{j_2} \leq _{F,i} q_{j_1} \leq _{F,i} p$
,
$\forall j_1 < j_2 < \kappa :\ q_{j_2} \leq _{F,i} q_{j_1} \leq _{F,i} p$
, -
•
 $\forall j < \kappa :\ q_j \Vdash \exists x \in \check {X}:\ \dot {\tau } {\restriction } j = x {\restriction } j$
, and
$\forall j < \kappa :\ q_j \Vdash \exists x \in \check {X}:\ \dot {\tau } {\restriction } j = x {\restriction } j$
, and -
•
 $X \cap Y = \emptyset $
.
$X \cap Y = \emptyset $
.
Proof If necessary, we may strengthen p twice in the following manner:
-
• Firstly, since
 $|Y| < \kappa $
and
$|Y| < \kappa $
and
 $p \Vdash \dot {\tau } \notin \check {Y}$
, we may find a name
$p \Vdash \dot {\tau } \notin \check {Y}$
, we may find a name
 $\dot {\ell }$
for an ordinal less than
$\dot {\ell }$
for an ordinal less than
 $\kappa $
such that Property B* enables us to find a
$\kappa $
such that Property B* enables us to find a $$\begin{align*}p \Vdash \forall y \in \check{Y}:\ \dot{\tau} {\restriction} \dot{\ell} \neq y {\restriction} \dot{\ell}. \end{align*}$$
$$\begin{align*}p \Vdash \forall y \in \check{Y}:\ \dot{\tau} {\restriction} \dot{\ell} \neq y {\restriction} \dot{\ell}. \end{align*}$$
 $p' \leq _{F,i} p$
and
$p' \leq _{F,i} p$
and
 $\ell ^* < \kappa $
with by restricting a maximal antichain deciding
$\ell ^* < \kappa $
with by restricting a maximal antichain deciding $$\begin{align*}\forall y \in Y: p' \Vdash \ \dot{\tau} {\restriction} \ell^* \neq y {\restriction} \ell^* \end{align*}$$
$$\begin{align*}\forall y \in Y: p' \Vdash \ \dot{\tau} {\restriction} \ell^* \neq y {\restriction} \ell^* \end{align*}$$
 $\dot {\ell }$
.
$\dot {\ell }$
.
-
• Secondly, we can find a
 $p" \leq _{F,i} p'$
that is
$p" \leq _{F,i} p'$
that is
 $(F,i)$
-bounded (see Definition 4.15).
$(F,i)$
-bounded (see Definition 4.15).
So without loss of generality assume that p already has both these properties. We construct the sequence
![]() $(q_j)_{j < \kappa }$
inductively:
$(q_j)_{j < \kappa }$
inductively:
-
•
 $j=0$
: Set
$j=0$
: Set
 $q_0 := p$
.
$q_0 := p$
. -
•
 $j \to j+1$
: Since is open dense below
$j \to j+1$
: Since is open dense below $$\begin{align*}D_{j+1} := \{r \leq q_j: r \textrm{ decides } \dot{\tau} {\restriction} (j+1)\} \end{align*}$$
$$\begin{align*}D_{j+1} := \{r \leq q_j: r \textrm{ decides } \dot{\tau} {\restriction} (j+1)\} \end{align*}$$
 $q_j$
, we may apply Lemma 4.22 to
$q_j$
, we may apply Lemma 4.22 to
 $q_j, F,i$
and
$q_j, F,i$
and
 $D_{j+1}$
Footnote
5
to get
$D_{j+1}$
Footnote
5
to get
 $q_{j+1}$
and
$q_{j+1}$
and
 $(s_g^{j+1})_{g \in C_{j+1}}$
such that
$(s_g^{j+1})_{g \in C_{j+1}}$
such that
 $q_{j+1}$
is
$q_{j+1}$
is
 $(D_{j+1},F,i)$
-complete as witnessed by
$(D_{j+1},F,i)$
-complete as witnessed by
 $(s_g^{j+1})_{g \in C_{j+1}}$
. Note that we have
$(s_g^{j+1})_{g \in C_{j+1}}$
. Note that we have
 $q_{j+1} \leq _{F,i} q_j \leq _{F,i} p$
.
$q_{j+1} \leq _{F,i} q_j \leq _{F,i} p$
.
-
•
 $\delta $
is a limit: Find a
$\delta $
is a limit: Find a
 $\leq _{F,i}$
-lower bound
$\leq _{F,i}$
-lower bound
 $\tilde {q}_\delta $
of
$\tilde {q}_\delta $
of
 $(q_\ell )_{\ell < \delta }$
. Just as in the successor step, apply Lemma 4.22 to
$(q_\ell )_{\ell < \delta }$
. Just as in the successor step, apply Lemma 4.22 to
 $\tilde {q_\delta }, F,i$
and to get
$\tilde {q_\delta }, F,i$
and to get $$\begin{align*}D_\delta := \{r \leq \tilde{q_\delta}: r \textrm{ decides } \dot{\tau} {\restriction} \delta\} \end{align*}$$
$$\begin{align*}D_\delta := \{r \leq \tilde{q_\delta}: r \textrm{ decides } \dot{\tau} {\restriction} \delta\} \end{align*}$$
 $q_\delta $
and
$q_\delta $
and
 $(s_g^\delta )_{g \in C_\delta }$
.
$(s_g^\delta )_{g \in C_\delta }$
.
By Lemma 4.19 we know that
![]() $(C_j)_{j < \kappa }$
is a decreasing sequence of non-empty sets of size less than
$(C_j)_{j < \kappa }$
is a decreasing sequence of non-empty sets of size less than
![]() $\kappa $
; as such, the sequence is eventually constant. Let
$\kappa $
; as such, the sequence is eventually constant. Let
![]() $j^*$
be the index at which this happens.
$j^*$
be the index at which this happens.
Now define
For
![]() $g \in C_{j^*}$
the sequence
$g \in C_{j^*}$
the sequence
![]() $(s_g^j)_{j < \kappa }$
is decreasing by Lemma 4.19. Hence each
$(s_g^j)_{j < \kappa }$
is decreasing by Lemma 4.19. Hence each
![]() $g \in C_{j^*}$
successfully interprets
$g \in C_{j^*}$
successfully interprets
![]() $\dot {\tau }$
as some unique
$\dot {\tau }$
as some unique
![]() $x \in X$
, i.e.,
$x \in X$
, i.e.,
Since
![]() $ \forall y \in Y:\ p \Vdash \dot {\tau } {\restriction } \ell ^* \neq y {\restriction } \ell ^*$
, we know that
$ \forall y \in Y:\ p \Vdash \dot {\tau } {\restriction } \ell ^* \neq y {\restriction } \ell ^*$
, we know that
![]() $X \cap Y = \emptyset $
.
$X \cap Y = \emptyset $
.
Suppose now that
![]() $j \geq j^*$
and
$j \geq j^*$
and
![]() $r \leq q_{j}$
. Then r is compatible with
$r \leq q_{j}$
. Then r is compatible with
![]() $s_{g}^j$
for some
$s_{g}^j$
for some
![]() $g \in C_{j} = C_{j^*}$
and we can find a
$g \in C_{j} = C_{j^*}$
and we can find a
![]() $t \leq r, s_{g}^j$
. But then
$t \leq r, s_{g}^j$
. But then
![]() $\exists x \in X:\ t \Vdash \dot {\tau } {\restriction } j = x {\restriction } j$
, so we can conclude
$\exists x \in X:\ t \Vdash \dot {\tau } {\restriction } j = x {\restriction } j$
, so we can conclude
Since
![]() $|Y| < \kappa $
, we may for each
$|Y| < \kappa $
, we may for each
![]() $j < j^*$
pick an arbitrary
$j < j^*$
pick an arbitrary
![]() $x_j \in [\sigma _j] \backslash Y$
, where
$x_j \in [\sigma _j] \backslash Y$
, where
and add those
![]() $x_j$
to X, thereby ensuring that
$x_j$
to X, thereby ensuring that
holds for
![]() $j < j^*$
as well.
$j < j^*$
as well.
We are now preparing to show that every new real
![]() $\dot {\tau }^G \in V^{\mathbb {P}}$
can be mapped onto the first Sacks real
$\dot {\tau }^G \in V^{\mathbb {P}}$
can be mapped onto the first Sacks real
![]() $\dot {s}_0$
via a uniformly continuous ground model function. In what follows we shall slightly abuse notation; for
$\dot {s}_0$
via a uniformly continuous ground model function. In what follows we shall slightly abuse notation; for
![]() $p \in \mathbb {P}$
and a node
$p \in \mathbb {P}$
and a node
![]() $\eta \in p(0)$
denote by
$\eta \in p(0)$
denote by
![]() $p^{[\eta ]}$
the condition that satisfies
$p^{[\eta ]}$
the condition that satisfies
![]() $p^{[\eta ]}(0) = p(0)^{[\eta ]}$
and
$p^{[\eta ]}(0) = p(0)^{[\eta ]}$
and
![]() $p^{[\eta ]}(\beta ) = p(\beta )$
for
$p^{[\eta ]}(\beta ) = p(\beta )$
for
![]() $\beta> 0$
.
$\beta> 0$
.
Lemma 7.2. Let
![]() $p \in \mathbb {P}, F \in [\kappa ^{++}]^{<\kappa }$
and
$p \in \mathbb {P}, F \in [\kappa ^{++}]^{<\kappa }$
and
![]() $i, \ell < \kappa $
. Let furthermore a
$i, \ell < \kappa $
. Let furthermore a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\tau }$
be given such that p forces
$\dot {\tau }$
be given such that p forces
![]() $\dot {\tau } \in 2^\kappa $
and
$\dot {\tau } \in 2^\kappa $
and
![]() $\dot {\tau } \notin V$
. Then we can find a
$\dot {\tau } \notin V$
. Then we can find a
![]() $q \leq _{F,i} p$
, an
$q \leq _{F,i} p$
, an
![]() $\ell ^*> \ell $
and a family
$\ell ^*> \ell $
and a family
![]() $(A_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(p(0))}$
of non-empty, clopen sets with:
$(A_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(p(0))}$
of non-empty, clopen sets with:
-
• if
 $\eta _1 \neq \eta _2$
, then
$\eta _1 \neq \eta _2$
, then
 $A_{\eta _1} \cap A_{\eta _2} = \emptyset $
,
$A_{\eta _1} \cap A_{\eta _2} = \emptyset $
, -
•
 $A_\eta = \bigcup _{\nu \in S_\eta } [\nu ]$
for some
$A_\eta = \bigcup _{\nu \in S_\eta } [\nu ]$
for some
 $S_\eta \subseteq 2^{\ell ^*}$
, and
$S_\eta \subseteq 2^{\ell ^*}$
, and -
•
 $q^{[\eta ]} \Vdash \dot {\tau } \in A_\eta $
.
$q^{[\eta ]} \Vdash \dot {\tau } \in A_\eta $
.
Proof Enumerate
![]() $\operatorname {\mathrm {split}}_i(p(0))$
as
$\operatorname {\mathrm {split}}_i(p(0))$
as
![]() $(\eta _k)_{k < \delta }$
with
$(\eta _k)_{k < \delta }$
with
![]() $\delta < \kappa $
. We inductively construct sequences
$\delta < \kappa $
. We inductively construct sequences
![]() $((t_j^k)_{j < \kappa })_{k < \delta }$
and a sequence of sets
$((t_j^k)_{j < \kappa })_{k < \delta }$
and a sequence of sets
![]() $(X_k)_{k < \delta }$
: assuming that
$(X_k)_{k < \delta }$
: assuming that
![]() $X_m$
has been constructed for
$X_m$
has been constructed for
![]() $m < k$
, apply Lemma 7.1 to
$m < k$
, apply Lemma 7.1 to
![]() $p^{[\eta _k]}$
and
$p^{[\eta _k]}$
and
![]() $Y := \bigcup _{m < k} X_m$
to get a sequence of conditions
$Y := \bigcup _{m < k} X_m$
to get a sequence of conditions
![]() $(t_j^k)_{j < \kappa }$
and a set
$(t_j^k)_{j < \kappa }$
and a set
![]() $X_k$
.
$X_k$
.
Now let
![]() $\ell ^*> \ell $
be an ordinal large enough such that whenever
$\ell ^*> \ell $
be an ordinal large enough such that whenever
![]() $j_1 \neq j_2$
for
$j_1 \neq j_2$
for
![]() $j_1, j_2 < \delta $
and
$j_1, j_2 < \delta $
and
![]() $x_1 \in X_{j_1}, x_2 \in X_{j_2}$
then
$x_1 \in X_{j_1}, x_2 \in X_{j_2}$
then
![]() $x_1 {\restriction } \ell ^* \neq x_2 {\restriction } \ell ^*$
. This is possible, since the
$x_1 {\restriction } \ell ^* \neq x_2 {\restriction } \ell ^*$
. This is possible, since the
![]() $(X_k)_{k < \delta }$
are disjoint and of size less than
$(X_k)_{k < \delta }$
are disjoint and of size less than
![]() $\kappa $
. This allows us to define
$\kappa $
. This allows us to define
Now we glue the conditions
![]() $t^k_{\ell ^*}$
together in the following way: Set
$t^k_{\ell ^*}$
together in the following way: Set
and for
![]() $\beta> 0$
define
$\beta> 0$
define
![]() $q(\beta )$
inductively; assuming
$q(\beta )$
inductively; assuming
![]() $q {\restriction } \beta $
has been defined, set
$q {\restriction } \beta $
has been defined, set
Note that
![]() $(t_{\ell ^*}^k {\restriction } \beta )_{k< \delta }$
is a maximal antichain below
$(t_{\ell ^*}^k {\restriction } \beta )_{k< \delta }$
is a maximal antichain below
![]() $q {\restriction } \beta $
. For limit
$q {\restriction } \beta $
. For limit
![]() $\beta $
observe that
$\beta $
observe that
![]() $\operatorname {\mathrm {supp}}(q {\restriction } \beta ) \subseteq \bigcup _{k < \delta } \operatorname {\mathrm {supp}}(t^k_{\ell ^*} {\restriction } \beta )$
. By Lemma 7.1 we know that
$\operatorname {\mathrm {supp}}(q {\restriction } \beta ) \subseteq \bigcup _{k < \delta } \operatorname {\mathrm {supp}}(t^k_{\ell ^*} {\restriction } \beta )$
. By Lemma 7.1 we know that
![]() $t_{\ell ^*}^k \leq _{F,i} p^{[\eta _k]}$
for each
$t_{\ell ^*}^k \leq _{F,i} p^{[\eta _k]}$
for each
![]() $k < \delta $
, and since
$k < \delta $
, and since
![]() $\operatorname {\mathrm {split}}_i(p(0)) = \{\eta _k : k < \delta \}$
, we can inductively conclude
$\operatorname {\mathrm {split}}_i(p(0)) = \{\eta _k : k < \delta \}$
, we can inductively conclude
![]() $q {\restriction } \beta \leq _{F \cap \beta ,i} p {\restriction } \beta $
for all
$q {\restriction } \beta \leq _{F \cap \beta ,i} p {\restriction } \beta $
for all
![]() $\beta \leq \kappa ^{++}$
.
$\beta \leq \kappa ^{++}$
.
To see the last claim, only note that
![]() $q^{[\eta ]} = t_{\ell ^*}^k$
for some
$q^{[\eta ]} = t_{\ell ^*}^k$
for some
![]() $k < \delta $
, therefore by Lemma 7.1 we have
$k < \delta $
, therefore by Lemma 7.1 we have
![]() $t_{\ell ^*}^k \Vdash \exists x \in \check {X_k}:\ \dot {\tau } {\restriction } \ell ^* = x {\restriction } \ell ^*$
and thus
$t_{\ell ^*}^k \Vdash \exists x \in \check {X_k}:\ \dot {\tau } {\restriction } \ell ^* = x {\restriction } \ell ^*$
and thus
by definition of
![]() $A_\eta $
.
$A_\eta $
.
Remark 7.3. Without loss of generality, we may choose the
![]() $A_\eta $
in the previous lemma to be minimal in the following sense: for each
$A_\eta $
in the previous lemma to be minimal in the following sense: for each
![]() $\nu \in 2^{\ell ^*}$
we have
$\nu \in 2^{\ell ^*}$
we have
![]() $\nu \in S_\eta $
iff there exists a condition
$\nu \in S_\eta $
iff there exists a condition
![]() $r \leq q^{[\eta ]}$
such that
$r \leq q^{[\eta ]}$
such that
![]() $r \Vdash \dot {\tau } \in [\nu ]$
.
$r \Vdash \dot {\tau } \in [\nu ]$
.
Lemma 7.4. Let
![]() $p \in \mathbb {P}$
and a
$p \in \mathbb {P}$
and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {\tau }$
be given such that p forces
$\dot {\tau }$
be given such that p forces
![]() $\dot {\tau } \in 2^\kappa $
and
$\dot {\tau } \in 2^\kappa $
and
![]() $\dot {\tau } \notin V$
. Then there exists a
$\dot {\tau } \notin V$
. Then there exists a
![]() $q \leq p$
, a sequence
$q \leq p$
, a sequence
![]() $(\ell ^*(i))_{i < \kappa }$
and a family
$(\ell ^*(i))_{i < \kappa }$
and a family
![]() $(A_\eta )_{\eta \in \operatorname {\mathrm {split}}(q(0))}$
such that
$(A_\eta )_{\eta \in \operatorname {\mathrm {split}}(q(0))}$
such that
![]() $A_\eta \subseteq 2^\kappa $
are non-empty, clopen and:
$A_\eta \subseteq 2^\kappa $
are non-empty, clopen and:
-
• if
 $\eta _1 \lhd \eta _2$
, then
$\eta _1 \lhd \eta _2$
, then
 $A_{\eta _2} \subseteq A_{\eta _1}$
,
$A_{\eta _2} \subseteq A_{\eta _1}$
, -
• if
 $\eta _1 \perp \eta _2$
, then
$\eta _1 \perp \eta _2$
, then
 $A_{\eta _1} \cap A_{\eta _2} = \emptyset $
,
$A_{\eta _1} \cap A_{\eta _2} = \emptyset $
, -
• if
 $\eta \in \operatorname {\mathrm {split}}_i(q(0))$
, then
$\eta \in \operatorname {\mathrm {split}}_i(q(0))$
, then
 $A_\eta = \bigcup _{\nu \in S_\eta } [\nu ]$
for some
$A_\eta = \bigcup _{\nu \in S_\eta } [\nu ]$
for some
 $S_\eta \subseteq 2^{\ell ^*(i)}$
, and
$S_\eta \subseteq 2^{\ell ^*(i)}$
, and -
•
 $q^{[\eta ]} \Vdash \dot {\tau } \in A_\eta $
.
$q^{[\eta ]} \Vdash \dot {\tau } \in A_\eta $
.
Proof We shall construct a fusion sequence
![]() $\langle q_i, F_i: i < \kappa \rangle $
and a strictly increasing sequence
$\langle q_i, F_i: i < \kappa \rangle $
and a strictly increasing sequence
![]() $(\ell ^*(i))_{i < \kappa }$
of ordinals less than
$(\ell ^*(i))_{i < \kappa }$
of ordinals less than
![]() $\kappa $
such that
$\kappa $
such that
![]() $q_{i+1}$
has the required properties for
$q_{i+1}$
has the required properties for
![]() $(A_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(q_i(0))}$
.
$(A_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(q_i(0))}$
.
-
•
 $i=0$
: Set
$i=0$
: Set
 $q_0 := p$
and
$q_0 := p$
and
 $F_0 := \{0\}$
.
$F_0 := \{0\}$
. -
•
 $i \to i+1$
: Applying Lemma 7.2 to
$i \to i+1$
: Applying Lemma 7.2 to
 $q_i, F_i, i$
and
$q_i, F_i, i$
and
 $\sup _{j < i}\ell ^*(j)$
yields a
$\sup _{j < i}\ell ^*(j)$
yields a
 $\tilde {q} \leq _{F_i,i} q_i$
, an ordinal
$\tilde {q} \leq _{F_i,i} q_i$
, an ordinal
 $\ell ^*(i)$
and a family
$\ell ^*(i)$
and a family
 $(A^i_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(q_i(0))}$
. Set
$(A^i_\eta )_{\eta \in \operatorname {\mathrm {split}}_i(q_i(0))}$
. Set
 $q_{i+1} := \tilde {q}$
. Define
$q_{i+1} := \tilde {q}$
. Define
 $F_{i+1}$
with a bookkeeping argument.
$F_{i+1}$
with a bookkeeping argument. -
•
 $\delta $
is a limit: Set
$\delta $
is a limit: Set
 $q_\delta $
to a fusion limit of
$q_\delta $
to a fusion limit of
 $\langle q_j, F_j: j < \delta \rangle $
and
$\langle q_j, F_j: j < \delta \rangle $
and
 $F_\delta := \bigcup _{j < \delta } F_j$
.
$F_\delta := \bigcup _{j < \delta } F_j$
.
Let now
![]() $q_\kappa $
be a fusion limit of the sequence
$q_\kappa $
be a fusion limit of the sequence
![]() $\langle q_i, F_i: i < \kappa \rangle $
and for
$\langle q_i, F_i: i < \kappa \rangle $
and for
![]() $\eta \in \operatorname {\mathrm {split}}(q_\kappa (0))$
define
$\eta \in \operatorname {\mathrm {split}}(q_\kappa (0))$
define
where
![]() $i(\eta )$
is the unique i with
$i(\eta )$
is the unique i with
![]() $\eta \in \operatorname {\mathrm {split}}_i(q_\kappa (0)) = \operatorname {\mathrm {split}}_i(q_i(0))$
. We claim
$\eta \in \operatorname {\mathrm {split}}_i(q_\kappa (0)) = \operatorname {\mathrm {split}}_i(q_i(0))$
. We claim
![]() $q_\kappa $
has the properties we are looking for:
$q_\kappa $
has the properties we are looking for:
-
• The third property holds by Lemma 7.2.
-
• If we assume the
 $A_\eta ^{i(\eta )}$
have been chosen minimal in each step as in Remark 7.3, then the first property holds. To see this, take
$A_\eta ^{i(\eta )}$
have been chosen minimal in each step as in Remark 7.3, then the first property holds. To see this, take
 $\nu \lhd \eta $
and
$\nu \lhd \eta $
and
 $\eta ' \in S_\eta $
, where
$\eta ' \in S_\eta $
, where
 $S_\eta $
is as stated in Lemma 7.2. By Remark 7.3 there is a condition
$S_\eta $
is as stated in Lemma 7.2. By Remark 7.3 there is a condition
 $r \leq q_{i(\eta ) + 1}^{[\eta ]}$
such that
$r \leq q_{i(\eta ) + 1}^{[\eta ]}$
such that
 $r \Vdash \dot {\tau } \in [\eta ']$
. But then
$r \Vdash \dot {\tau } \in [\eta ']$
. But then
 $r \leq q_{i(\eta ) + 1}^{[\eta ]} \leq q_{i(\nu ) + 1}^{[\nu ]}$
, and thus
$r \leq q_{i(\eta ) + 1}^{[\eta ]} \leq q_{i(\nu ) + 1}^{[\nu ]}$
, and thus
 $\eta ' {\restriction } \ell ^*(i(\nu )) \in S_\nu $
. Hence
$\eta ' {\restriction } \ell ^*(i(\nu )) \in S_\nu $
. Hence
 $A_\eta \subseteq A_\nu $
.
$A_\eta \subseteq A_\nu $
. -
• For the second property, let
 $\eta , \nu \in \operatorname {\mathrm {split}}(q_\kappa (0))$
with
$\eta , \nu \in \operatorname {\mathrm {split}}(q_\kappa (0))$
with
 $\eta \perp \nu $
be given. Without loss of generality assume
$\eta \perp \nu $
be given. Without loss of generality assume
 $i(\nu ) \leq i(\eta )$
and find an
$i(\nu ) \leq i(\eta )$
and find an
 $\eta '$
with
$\eta '$
with
 $\eta ' \lhd \eta $
and
$\eta ' \lhd \eta $
and
 $\eta ' \in \operatorname {\mathrm {split}}_{i(\nu )}(q_\kappa (0))$
; by incompatibility we have
$\eta ' \in \operatorname {\mathrm {split}}_{i(\nu )}(q_\kappa (0))$
; by incompatibility we have
 $\eta ' \neq \nu $
. By the first property we have
$\eta ' \neq \nu $
. By the first property we have
 $A_{\eta } \subseteq A_{\eta '}$
and Lemma 7.2 yields
$A_{\eta } \subseteq A_{\eta '}$
and Lemma 7.2 yields
 $A_{\eta '} \cap A_\nu = \emptyset $
.
$A_{\eta '} \cap A_\nu = \emptyset $
. -
• To see the fourth property, let
 $\eta \in \operatorname {\mathrm {split}}(q_\kappa (0))$
. Then we have
$\eta \in \operatorname {\mathrm {split}}(q_\kappa (0))$
. Then we have
 $q_\kappa ^{[\eta ]} \leq q_{i(\eta )+1}^{[\eta ]}$
and therefore as desired.
$q_\kappa ^{[\eta ]} \leq q_{i(\eta )+1}^{[\eta ]}$
and therefore as desired. $$\begin{align*}q_\kappa^{[\eta]} \Vdash \dot{\tau} \in A_\eta, \end{align*}$$
$$\begin{align*}q_\kappa^{[\eta]} \Vdash \dot{\tau} \in A_\eta, \end{align*}$$
The following lemma substitutes in for Tietze’s Extension Theorem from the countable case in [Reference Corazza4]. Recall the notion of superclosure (page 4) and uniform continuity (Definition 6.5).
Lemma 7.5. Let
![]() $Y,Z \subseteq 2^\kappa $
, where Y is closed and Z is superclosed, and let
$Y,Z \subseteq 2^\kappa $
, where Y is closed and Z is superclosed, and let
![]() $g: Y \to Z$
be uniformly continuous. Then g can be extended to a uniformly continuous function
$g: Y \to Z$
be uniformly continuous. Then g can be extended to a uniformly continuous function
![]() $\tilde {g} : 2^\kappa \to Z$
with the same modulus of continuity as g.
$\tilde {g} : 2^\kappa \to Z$
with the same modulus of continuity as g.
Proof The open set
![]() $2^\kappa \backslash Y$
can be be written as a union of basic open sets
$2^\kappa \backslash Y$
can be be written as a union of basic open sets
![]() $\bigcup _{i < \delta } [\nu _i]$
with
$\bigcup _{i < \delta } [\nu _i]$
with
![]() $\delta \leq \kappa , \nu _i \in 2^{\lambda _i}$
such that the
$\delta \leq \kappa , \nu _i \in 2^{\lambda _i}$
such that the
![]() $\nu _i$
are minimal, i.e.,
$\nu _i$
are minimal, i.e.,
In particular the sets
![]() $[\nu _i]$
are pairwise disjoint. We will define
$[\nu _i]$
are pairwise disjoint. We will define
![]() $\tilde {g}$
to extend g and to be constant on each
$\tilde {g}$
to extend g and to be constant on each
![]() $[\nu _i]$
.
$[\nu _i]$
.
For
![]() $i < \delta $
define
$i < \delta $
define
Clearly
![]() $S(i)$
consists of pairwise
$S(i)$
consists of pairwise
![]() $\lhd $
-compatible elements; furthermore, for each
$\lhd $
-compatible elements; furthermore, for each
![]() $\eta \in S(i)$
we have
$\eta \in S(i)$
we have
![]() $[\eta ] \cap Z \neq \emptyset $
. Since Z is superclosedFootnote
6
, we have
$[\eta ] \cap Z \neq \emptyset $
. Since Z is superclosedFootnote
6
, we have
![]() $Z \cap [\bigcup S(i)] \neq \emptyset $
. We may thus set
$Z \cap [\bigcup S(i)] \neq \emptyset $
. We may thus set
![]() $\tilde {g} {\restriction } [\nu _i]$
to be constant with an arbitrary, fixed value from
$\tilde {g} {\restriction } [\nu _i]$
to be constant with an arbitrary, fixed value from
![]() $Z \cap [\bigcup S(i)]$
.
$Z \cap [\bigcup S(i)]$
.
It remains to check that
![]() $\tilde {g} : 2^\kappa \to Z$
is uniformly continuous with the same modulus of continuity as g. To this end, let
$\tilde {g} : 2^\kappa \to Z$
is uniformly continuous with the same modulus of continuity as g. To this end, let
![]() $i < \kappa $
and
$i < \kappa $
and
![]() $x \in 2^\kappa $
. Consider
$x \in 2^\kappa $
. Consider
![]() $y \in [x {\restriction } j(i)]$
.
$y \in [x {\restriction } j(i)]$
.
-
• If
 $x \in Y$
, the interesting case is
$x \in Y$
, the interesting case is
 $y \notin Y$
, hence
$y \notin Y$
, hence
 $y \in [\nu _\ell ]$
for some
$y \in [\nu _\ell ]$
for some
 $\ell < \delta $
. But then
$\ell < \delta $
. But then
 $j(i) < \lambda _\ell $
and hence by definition
$j(i) < \lambda _\ell $
and hence by definition $$\begin{align*}g"([x {\restriction} j(i)] \cap Y) \subseteq [g(x) {\restriction} i] \cap Z, \end{align*}$$
$$\begin{align*}g"([x {\restriction} j(i)] \cap Y) \subseteq [g(x) {\restriction} i] \cap Z, \end{align*}$$
 $g(x) {\restriction } i \in S(\ell )$
and thus
$g(x) {\restriction } i \in S(\ell )$
and thus
 $\tilde {g}(y) \in [\bigcup S(\ell )] \cap Z \subseteq [\tilde {g}(x) {\restriction } i] \cap Z$
.
$\tilde {g}(y) \in [\bigcup S(\ell )] \cap Z \subseteq [\tilde {g}(x) {\restriction } i] \cap Z$
.
-
• On the other hand, if
 $x \notin Y$
, then x is in
$x \notin Y$
, then x is in
 $[\nu _k]$
for some
$[\nu _k]$
for some
 $k < \delta $
.Now one possibility is
$k < \delta $
.Now one possibility is
 $[x {\restriction } j(i)] \cap Y = \emptyset $
, in which case
$[x {\restriction } j(i)] \cap Y = \emptyset $
, in which case
 $j(i) \geq \lambda _k$
and
$j(i) \geq \lambda _k$
and
 $\tilde {g}$
is constant on
$\tilde {g}$
is constant on
 $[x {\restriction } j(i)]$
, therefore
$[x {\restriction } j(i)]$
, therefore
 $\tilde {g}(y) = \tilde {g}(x) \in [\tilde {g}(x) {\restriction } i] \cap Z$
.
$\tilde {g}(y) = \tilde {g}(x) \in [\tilde {g}(x) {\restriction } i] \cap Z$
.The other possibility is
 $[x {\restriction } j(i)] \cap Y \neq \emptyset $
and thus
$[x {\restriction } j(i)] \cap Y \neq \emptyset $
and thus
 $j(i) < \lambda _k$
, and there once again are two cases to be distinguished:
$j(i) < \lambda _k$
, and there once again are two cases to be distinguished:-
– If
 $y \in Y$
, then
$y \in Y$
, then
 $g(y) {\restriction } i \in S(k)$
and thus
$g(y) {\restriction } i \in S(k)$
and thus  $$\begin{align*}\tilde{g}(y) = g(y) \in [g(y) {\restriction} i] \cap Z = [\tilde{g}(x) {\restriction} i] \cap Z. \end{align*}$$
$$\begin{align*}\tilde{g}(y) = g(y) \in [g(y) {\restriction} i] \cap Z = [\tilde{g}(x) {\restriction} i] \cap Z. \end{align*}$$
-
– On the other hand, if
 $y \notin Y$
, then
$y \notin Y$
, then
 $y \in [\nu _\ell ]$
for some
$y \in [\nu _\ell ]$
for some
 $\ell < \delta $
. Since
$\ell < \delta $
. Since
 $[y {\restriction } j(i)] \cap Y = [x {\restriction } j(i)] \cap Y \neq \emptyset $
, we can also conclude
$[y {\restriction } j(i)] \cap Y = [x {\restriction } j(i)] \cap Y \neq \emptyset $
, we can also conclude
 $j(i) < \lambda _\ell $
. This means that
$j(i) < \lambda _\ell $
. This means that
 $S(k) \cap S(\ell )$
contains an
$S(k) \cap S(\ell )$
contains an
 $\eta $
with
$\eta $
with
 $\operatorname {\mathrm {dom}}(\eta ) = i$
(namely
$\operatorname {\mathrm {dom}}(\eta ) = i$
(namely
 $g(x') {\restriction } i$
for some
$g(x') {\restriction } i$
for some
 $x' \in [x {\restriction } j(i)] \cap Y$
) and thus
$x' \in [x {\restriction } j(i)] \cap Y$
) and thus
 $\tilde {g}(y) \in [\eta ] \cap Z = [\tilde {g}(x) {\restriction } i] \cap Z$
.
$\tilde {g}(y) \in [\eta ] \cap Z = [\tilde {g}(x) {\restriction } i] \cap Z$
.
-
A natural question the inquisitive reader might pose is the validity of Lemma 7.5 in case of the additional “artificial” assumption of superclosure being dropped. Indeed, the statement no longer holds; in [Reference Lücke and Schlicht19] the authors observe, for instance, that the closed subset Y of
![]() $2^\kappa $
consisting of all sequences with finitely many zeroes is not a retract of
$2^\kappa $
consisting of all sequences with finitely many zeroes is not a retract of
![]() $2^\kappa $
(and thus the identity
$2^\kappa $
(and thus the identity
![]() $Y \to Y$
cannot be extended to a continuous function on
$Y \to Y$
cannot be extended to a continuous function on
![]() $2^\kappa $
).
$2^\kappa $
).
Theorem 7.6. Let
![]() $p \in \mathbb {P}$
force
$p \in \mathbb {P}$
force
![]() $\dot {\tau } \in 2^\kappa $
and
$\dot {\tau } \in 2^\kappa $
and
![]() $\dot {\tau } \notin V$
. Then there exists a
$\dot {\tau } \notin V$
. Then there exists a
![]() $q \leq p$
and a uniformly continuous function
$q \leq p$
and a uniformly continuous function
![]() $f^* : 2^\kappa \to [q(0)]$
in V such that
$f^* : 2^\kappa \to [q(0)]$
in V such that
where
![]() $\dot {s}_0$
denotes the first Sacks real.
$\dot {s}_0$
denotes the first Sacks real.
Proof Lemma 7.4 yields a condition
![]() $q \leq p$
, a sequence
$q \leq p$
, a sequence
![]() $(\ell ^*(i))_{i < \kappa }$
and a family
$(\ell ^*(i))_{i < \kappa }$
and a family
![]() $(A_\eta )_{\eta \in \operatorname {\mathrm {split}}(q(0))}$
of clopen sets. This family codesFootnote
7
a continuous function
$(A_\eta )_{\eta \in \operatorname {\mathrm {split}}(q(0))}$
of clopen sets. This family codesFootnote
7
a continuous function
 $$ \begin{align*} f : Y \to [q(0)] \\ y \mapsto \bigcup\{\eta: y \in A_\eta\} \end{align*} $$
$$ \begin{align*} f : Y \to [q(0)] \\ y \mapsto \bigcup\{\eta: y \in A_\eta\} \end{align*} $$
defined on the closed set
![]() $Y = \bigcap _{i < \kappa } \bigcup _{\eta \in \operatorname {\mathrm {split}}_i(q(0))} A_\eta $
Footnote
8
.
$Y = \bigcap _{i < \kappa } \bigcup _{\eta \in \operatorname {\mathrm {split}}_i(q(0))} A_\eta $
Footnote
8
.
We claim that f is in fact uniformly continuous. To see this, let
![]() $i < \kappa $
and
$i < \kappa $
and
![]() $x \in Y$
. Choose
$x \in Y$
. Choose
![]() $\eta $
such that
$\eta $
such that
![]() $x \in A_\eta $
and
$x \in A_\eta $
and
![]() $\eta \in \operatorname {\mathrm {split}}_{i}(q(0))$
. Recall that
$\eta \in \operatorname {\mathrm {split}}_{i}(q(0))$
. Recall that
![]() $A_\eta $
is of the form (see Lemma 7.4)
$A_\eta $
is of the form (see Lemma 7.4)
with
![]() $S_\eta \subseteq 2^{\ell ^*(i)}$
. Therefore we have
$S_\eta \subseteq 2^{\ell ^*(i)}$
. Therefore we have
since
![]() $i \leq \operatorname {\mathrm {dom}}(\eta )$
.
$i \leq \operatorname {\mathrm {dom}}(\eta )$
.
Since the set
![]() $[q(0)]$
is superclosed, we can apply Lemma 7.5 and extend f to a uniformly continuous function
$[q(0)]$
is superclosed, we can apply Lemma 7.5 and extend f to a uniformly continuous function
![]() $f^* : 2^\kappa \to [q(0)]$
. Lastly, we have
$f^* : 2^\kappa \to [q(0)]$
. Lastly, we have
for each
![]() $\eta \in \operatorname {\mathrm {split}}(q(0))$
and thus
$\eta \in \operatorname {\mathrm {split}}(q(0))$
and thus
As in the classical case, every
![]() $\kappa $
-Sacks condition can be decomposed into
$\kappa $
-Sacks condition can be decomposed into
![]() $|2^\kappa |$
many
$|2^\kappa |$
many
![]() $\kappa $
-Sacks conditions in a continuous way. The last auxiliary result we require formalizes this:
$\kappa $
-Sacks conditions in a continuous way. The last auxiliary result we require formalizes this:
Lemma 7.7. Let
![]() $p \in \mathbb {P}$
be a condition. Then there exists a uniformly continuous
$p \in \mathbb {P}$
be a condition. Then there exists a uniformly continuous
![]() $g^* : [p(0)] \to 2^{\kappa }$
Footnote
9
and for each
$g^* : [p(0)] \to 2^{\kappa }$
Footnote
9
and for each
![]() $x \in 2^\kappa \cap V$
a condition
$x \in 2^\kappa \cap V$
a condition
![]() $q_x \leq p$
such that
$q_x \leq p$
such that
Proof First we construct a function
![]() $e = (e_1, e_2) : p(0) \to 2^{<\kappa } \times 2^{<\kappa }$
with the following properties:
$e = (e_1, e_2) : p(0) \to 2^{<\kappa } \times 2^{<\kappa }$
with the following properties:
-
• e is continuous and monotone increasing,
-
•
 $e(\emptyset ) = (\emptyset , \emptyset ),$
$e(\emptyset ) = (\emptyset , \emptyset ),$
-
• if
 $\eta \notin \operatorname {\mathrm {split}}(p(0))$
, then
$\eta \notin \operatorname {\mathrm {split}}(p(0))$
, then
 $e(\eta ^\frown i) = e(\eta ),$
$e(\eta ^\frown i) = e(\eta ),$
-
• if
 $\eta \in \operatorname {\mathrm {split}}_j(p(0))$
and:
$\eta \in \operatorname {\mathrm {split}}_j(p(0))$
and:-
– j is a successor, then
 $e(\eta ^\frown i) = (e_1(\eta )^\frown i, e_2(\eta )),$
$e(\eta ^\frown i) = (e_1(\eta )^\frown i, e_2(\eta )),$
-
–
 $j=0$
or j is a limit, then
$j=0$
or j is a limit, then
 $e(\eta ^\frown i) = (e_1(\eta ), e_2(\eta )^\frown i)$
.
$e(\eta ^\frown i) = (e_1(\eta ), e_2(\eta )^\frown i)$
.
-
Define
![]() $\hat {g} = (\hat {g}_1, \hat {g}_2) : [p(0)] \to 2^{\kappa } \times 2^\kappa $
as
$\hat {g} = (\hat {g}_1, \hat {g}_2) : [p(0)] \to 2^{\kappa } \times 2^\kappa $
as
![]() $\hat {g}_k(b) = \bigcup \{e_k(b {\restriction } i) : i < \kappa \}$
for
$\hat {g}_k(b) = \bigcup \{e_k(b {\restriction } i) : i < \kappa \}$
for
![]() $k=1,2$
. Since
$k=1,2$
. Since
![]() $[p(0)]$
is perfect,
$[p(0)]$
is perfect,
![]() $\hat {g}$
is well-defined. Moreover,
$\hat {g}$
is well-defined. Moreover,
![]() $\hat {g}$
maps the clopen basis
$\hat {g}$
maps the clopen basis
![]() $([\eta ])_{\eta \in \operatorname {\mathrm {split}}(p(0))}$
to a clopen basis of
$([\eta ])_{\eta \in \operatorname {\mathrm {split}}(p(0))}$
to a clopen basis of
![]() $2^\kappa \times 2^\kappa $
, hence it is a homeomorphism.
$2^\kappa \times 2^\kappa $
, hence it is a homeomorphism.
For
![]() $x \in 2^\kappa $
now set
$x \in 2^\kappa $
now set
![]() $q_x(0) := \{\eta \in 2^{<\kappa }:\ \exists y \in \hat {g}^{-1}(\{x\} \times 2^\kappa ):\ \eta \lhd y\}$
and
$q_x(0) := \{\eta \in 2^{<\kappa }:\ \exists y \in \hat {g}^{-1}(\{x\} \times 2^\kappa ):\ \eta \lhd y\}$
and
![]() $q_x(\beta ) = p(\beta )$
for
$q_x(\beta ) = p(\beta )$
for
![]() $\beta> 0$
. We claim that
$\beta> 0$
. We claim that
![]() $q_x$
is a condition; it is sufficient to check that
$q_x$
is a condition; it is sufficient to check that
![]() $q_x(0)$
is. We check (S2), (S5), and (S6); the rest is left as an exercise for the reader.
$q_x(0)$
is. We check (S2), (S5), and (S6); the rest is left as an exercise for the reader.
-
• (S2): Since
 $\hat {g}$
is a homeomorphism, it follows that
$\hat {g}$
is a homeomorphism, it follows that
 $\hat {g}^{-1}\left (\{x\} \times 2^\kappa \right )$
is a perfect set.
$\hat {g}^{-1}\left (\{x\} \times 2^\kappa \right )$
is a perfect set. -
• (S5): Let
 $\left (\eta _j\right )_{j<\delta }$
with
$\left (\eta _j\right )_{j<\delta }$
with
 $\eta _j \in q_x(0)$
be a strictly increasing sequence of length
$\eta _j \in q_x(0)$
be a strictly increasing sequence of length
 $\delta <\kappa $
. Set
$\delta <\kappa $
. Set
 $\eta :=\bigcup _{j<\delta } \eta _j$
. It easily follows that
$\eta :=\bigcup _{j<\delta } \eta _j$
. It easily follows that
 $\nu \in q_x(0) \Leftrightarrow x \in [e_1(\nu )]$
for all
$\nu \in q_x(0) \Leftrightarrow x \in [e_1(\nu )]$
for all
 $\nu \in 2^{<\kappa }$
. As
$\nu \in 2^{<\kappa }$
. As
 $e_1(\eta )=\bigcup \{e_1(\eta _j) : j < \delta \}$
we see that
$e_1(\eta )=\bigcup \{e_1(\eta _j) : j < \delta \}$
we see that
 $x \in [e_1(\eta )]$
, hence
$x \in [e_1(\eta )]$
, hence
 $\eta \in q_x(0)$
.
$\eta \in q_x(0)$
. -
• (S6): Let
 $(\eta _j)_{j<\delta }$
be a strictly increasing sequence of length less than
$(\eta _j)_{j<\delta }$
be a strictly increasing sequence of length less than
 $\kappa $
such that
$\kappa $
such that
 $\eta _j \in \operatorname {\mathrm {split}}(q_x(0))$
. Again, set
$\eta _j \in \operatorname {\mathrm {split}}(q_x(0))$
. Again, set
 $\eta :=\bigcup _{j<\delta } \eta _j$
. It follows that
$\eta :=\bigcup _{j<\delta } \eta _j$
. It follows that
 $\eta \in \operatorname {\mathrm {split}}_\lambda (p(0))$
for some limit
$\eta \in \operatorname {\mathrm {split}}_\lambda (p(0))$
for some limit
 $\lambda $
. But as
$\lambda $
. But as
 $x \in [e_1(\eta )]$
and
$x \in [e_1(\eta )]$
and
 $e_1(\eta )=e_1(\eta ^\frown i)$
, we have
$e_1(\eta )=e_1(\eta ^\frown i)$
, we have
 $\eta ^\frown i \in q_x(0)$
for
$\eta ^\frown i \in q_x(0)$
for
 $i=0,1$
, hence
$i=0,1$
, hence
 $\eta \in \operatorname {\mathrm {split}}(q_x(0))$
.
$\eta \in \operatorname {\mathrm {split}}(q_x(0))$
.
Clearly
![]() $q_x \leq p$
. Now set
$q_x \leq p$
. Now set
![]() $g^* := \hat {g}_1$
. Then
$g^* := \hat {g}_1$
. Then
![]() $g^*$
is uniformly continuous with modulus of continuity
$g^*$
is uniformly continuous with modulus of continuity
Finally, we have
![]() $q_x \Vdash \check {x} = g^*(\dot {s}_0)$
by the definition of
$q_x \Vdash \check {x} = g^*(\dot {s}_0)$
by the definition of
![]() $q_x(0)$
and the absoluteness (see Fact 6.6) of the statement
$q_x(0)$
and the absoluteness (see Fact 6.6) of the statement
Theorem 7.8. In
![]() $V^{\mathbb {P}}$
, every subset X of
$V^{\mathbb {P}}$
, every subset X of
![]() $2^\kappa $
of size
$2^\kappa $
of size
![]() $\kappa ^{++}$
can be uniformly continuously mapped onto
$\kappa ^{++}$
can be uniformly continuously mapped onto
![]() $2^\kappa $
.
$2^\kappa $
.
Proof Assume that
![]() $\dot {X}$
is a
$\dot {X}$
is a
![]() $\mathbb {P}$
-name for a subset of
$\mathbb {P}$
-name for a subset of
![]() $2^\kappa $
such that
$2^\kappa $
such that
We will show
![]() $\exists \alpha ^* < \kappa ^{++}:\ \Vdash _{\mathbb {P}} \dot {X} \subseteq V^{\mathbb {P}_{\alpha ^*}}$
, thus
$\exists \alpha ^* < \kappa ^{++}:\ \Vdash _{\mathbb {P}} \dot {X} \subseteq V^{\mathbb {P}_{\alpha ^*}}$
, thus
![]() $\Vdash _{\mathbb {P}} |\dot {X}| \leq \kappa ^+$
.
$\Vdash _{\mathbb {P}} |\dot {X}| \leq \kappa ^+$
.
By our assumption on
![]() $\dot {X}$
and
$\dot {X}$
and
![]() $\mathbb {P}$
satisfying the
$\mathbb {P}$
satisfying the
![]() $\kappa ^{++}$
-c.c. we get
$\kappa ^{++}$
-c.c. we get
 $$ \begin{align*} \forall \alpha < \kappa^{++}\, \forall& \dot{h}\ \mathbb{P}_\alpha\textrm{-name for a uniformly continuous function } \\ \exists& \beta < \kappa^{++}, \beta \geq \alpha \, \exists y\ \mathbb{P}_\beta\textrm{-name for a real}:\ \Vdash_{\mathbb{P}} \dot{y} \notin \dot{h}" \dot{X}. \end{align*} $$
$$ \begin{align*} \forall \alpha < \kappa^{++}\, \forall& \dot{h}\ \mathbb{P}_\alpha\textrm{-name for a uniformly continuous function } \\ \exists& \beta < \kappa^{++}, \beta \geq \alpha \, \exists y\ \mathbb{P}_\beta\textrm{-name for a real}:\ \Vdash_{\mathbb{P}} \dot{y} \notin \dot{h}" \dot{X}. \end{align*} $$
To increase legibility, let the ellipsis
![]() $(\dots )$
denote the four quantifications in the above statement. By interpreting the name
$(\dots )$
denote the four quantifications in the above statement. By interpreting the name
![]() $\dot {X}$
partially in the intermediate model
$\dot {X}$
partially in the intermediate model
![]() $V^{\mathbb {P}_\beta }$
, i.e., by identifying
$V^{\mathbb {P}_\beta }$
, i.e., by identifying
![]() $\dot {X}$
with a canonical
$\dot {X}$
with a canonical
![]() $\mathbb {P}_\beta $
-name for a
$\mathbb {P}_\beta $
-name for a
![]() $\mathbb {P}_{\beta , \kappa ^{++}}$
-name, we get
$\mathbb {P}_{\beta , \kappa ^{++}}$
-name, we get
Keep in mind that
![]() $\dot {y}, \dot {h}$
are both
$\dot {y}, \dot {h}$
are both
![]() $\mathbb {P}_\beta $
-names, since
$\mathbb {P}_\beta $
-names, since
![]() $\beta \geq \alpha $
.
$\beta \geq \alpha $
.
Without loss of generality assume that the function
![]() $\alpha \mapsto \beta (\alpha )$
maps to the minimal
$\alpha \mapsto \beta (\alpha )$
maps to the minimal
![]() $\beta $
for which the statement holds. Observe that, crucially, since every continuous function
$\beta $
for which the statement holds. Observe that, crucially, since every continuous function
![]() $h : 2^\kappa \to 2^\kappa $
can be coded by an element of
$h : 2^\kappa \to 2^\kappa $
can be coded by an element of
![]() $2^\kappa $
(see Section 6), no new functions of the kind appear at stages of cofinality
$2^\kappa $
(see Section 6), no new functions of the kind appear at stages of cofinality
![]() $>\kappa $
(Lemma 4.31). Therefore we can easily find a fixed point of the function
$>\kappa $
(Lemma 4.31). Therefore we can easily find a fixed point of the function
![]() $\alpha \mapsto \beta (\alpha )$
with cofinality
$\alpha \mapsto \beta (\alpha )$
with cofinality
![]() $\kappa ^+$
; call it
$\kappa ^+$
; call it
![]() $\alpha ^*$
. For
$\alpha ^*$
. For
![]() $\alpha ^*$
we thus know that
$\alpha ^*$
we thus know that
For the remainder of this proof we will be working within
![]() $V^{\mathbb {P}_{\alpha ^*}}$
. We wish to show
$V^{\mathbb {P}_{\alpha ^*}}$
. We wish to show
![]() $\Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \dot {X} \subseteq V^{\mathbb {\mathbb {P}_{\alpha ^*}}}$
.
$\Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \dot {X} \subseteq V^{\mathbb {\mathbb {P}_{\alpha ^*}}}$
.
Let thus
![]() $p \in \mathbb {P}_{\alpha ^*, \kappa ^{++}}$
and
$p \in \mathbb {P}_{\alpha ^*, \kappa ^{++}}$
and
![]() $\dot {\tau }$
be a
$\dot {\tau }$
be a
![]() $\mathbb {P}_{\alpha ^*, \kappa ^{++}}$
-name such that p forces
$\mathbb {P}_{\alpha ^*, \kappa ^{++}}$
-name such that p forces
![]() $\dot {\tau } \in 2^\kappa $
and
$\dot {\tau } \in 2^\kappa $
and
![]() $\dot {\tau } \notin V^{\mathbb {P}_{\alpha ^*}}$
. Theorem 7.6 applied within
$\dot {\tau } \notin V^{\mathbb {P}_{\alpha ^*}}$
. Theorem 7.6 applied within
![]() $V^{\mathbb {P}_{\alpha ^*}}$
(recall that the tail iteration
$V^{\mathbb {P}_{\alpha ^*}}$
(recall that the tail iteration
![]() $\mathbb {P}_{\alpha *, \kappa ^{++}}$
has the same structure as the full iteration) yields a
$\mathbb {P}_{\alpha *, \kappa ^{++}}$
has the same structure as the full iteration) yields a
![]() $q \leq p$
and a uniformly continuous function
$q \leq p$
and a uniformly continuous function
![]() $f^*: 2^\kappa \to [q(0)]$
such that
$f^*: 2^\kappa \to [q(0)]$
such that
![]() $q \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} f^*(\dot {\tau }) = \dot {s_0}$
. Likewise, Lemma 7.7 applied to q gives us a uniformly continuous function
$q \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} f^*(\dot {\tau }) = \dot {s_0}$
. Likewise, Lemma 7.7 applied to q gives us a uniformly continuous function
![]() $g^*: [q(0)] \to 2^\kappa $
and conditions
$g^*: [q(0)] \to 2^\kappa $
and conditions
![]() $(q_x)_{x \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}}$
with
$(q_x)_{x \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}}$
with
![]() $q_x \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \check {x} = g^*(\dot {s_0})$
.
$q_x \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \check {x} = g^*(\dot {s_0})$
.
Now let
![]() $x \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}$
be arbitrary. By construction we have
$x \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}$
be arbitrary. By construction we have
![]() $q_x \Vdash \check {x} = (g^*\circ f^*)(\dot {\tau })$
. For the uniformly continuous function
$q_x \Vdash \check {x} = (g^*\circ f^*)(\dot {\tau })$
. For the uniformly continuous function
![]() $(g^* \circ f^*) : 2^\kappa \to 2^\kappa $
we can by our assumption on
$(g^* \circ f^*) : 2^\kappa \to 2^\kappa $
we can by our assumption on
![]() $\alpha ^*$
find a
$\alpha ^*$
find a
![]() $y \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}$
with
$y \in 2^\kappa \cap V^{\mathbb {P}_{\alpha ^*}}$
with
![]() $\Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \check {y} \notin (g^* \circ f^*)" \dot {X}$
. The condition
$\Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \check {y} \notin (g^* \circ f^*)" \dot {X}$
. The condition
![]() $q_y$
thus forces
$q_y$
thus forces
![]() $\dot {\tau } \notin \dot {X}$
. Since p and
$\dot {\tau } \notin \dot {X}$
. Since p and
![]() $\dot {\tau }$
were arbitrary, we may conclude
$\dot {\tau }$
were arbitrary, we may conclude
Thus we have shown
![]() $V \models \ \Vdash _{\mathbb {P}_{\alpha ^*}} \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \dot {X} \subseteq V^{\mathbb {\mathbb {P}_{\alpha ^*}}}$
, which finishes the proof.
$V \models \ \Vdash _{\mathbb {P}_{\alpha ^*}} \Vdash _{\mathbb {P}_{\alpha ^*, \kappa ^{++}}} \dot {X} \subseteq V^{\mathbb {\mathbb {P}_{\alpha ^*}}}$
, which finishes the proof.
It is easy to see that the uniformly continuous image of a strong measure zero set remains strong measure zero; thus we have shown
Corollary 7.9.
![]() $V^{\mathbb {P}} \models \mathcal {SN} = [2^\kappa ]^{\leq \kappa ^+}$
.
$V^{\mathbb {P}} \models \mathcal {SN} = [2^\kappa ]^{\leq \kappa ^+}$
.
8 Stationary strong measure zero
Finally, let us take a look at the following definition, introduced by Halko [Reference Halko10]:
Definition 8.1. A set
![]() $X \subseteq 2^\kappa $
is called stationary strong measure zero iff
$X \subseteq 2^\kappa $
is called stationary strong measure zero iff
So a set X is stationary strong measure zero iff we can find coverings that cover every point of X stationarily often. To motivate why this definition might be of interest, observe that even for regular strong measure zero sets, we can always find coverings that cover each point at least unboundedly often:
Lemma 8.2. Let
![]() $X \subseteq 2^\kappa $
be strong measure zero. Then
$X \subseteq 2^\kappa $
be strong measure zero. Then
Proof Partition
![]() $\kappa $
into sets
$\kappa $
into sets
![]() $(U_i)_{i < \kappa }$
, where each
$(U_i)_{i < \kappa }$
, where each
![]() $U_i$
has size
$U_i$
has size
![]() $\kappa $
. For a challenge
$\kappa $
. For a challenge
![]() $f \in \kappa ^\kappa $
and every
$f \in \kappa ^\kappa $
and every
![]() $i < \kappa $
we can find coverings
$i < \kappa $
we can find coverings
![]() $(\eta _j^i)_{j \in U_i}$
that satisfy the challenge
$(\eta _j^i)_{j \in U_i}$
that satisfy the challenge
![]() $(f(j))_{j \in U_i}$
. But now
$(f(j))_{j \in U_i}$
. But now
![]() $(\eta _j^i)_{j \in U_i, i < \kappa }$
has the property we are looking for.
$(\eta _j^i)_{j \in U_i, i < \kappa }$
has the property we are looking for.
Lemma 8.3. Let
![]() $\mathcal {P}$
be a
$\mathcal {P}$
be a
![]() $\kappa ^\kappa $
-bounding forcing notion and
$\kappa ^\kappa $
-bounding forcing notion and
![]() $cl \in V^{\mathcal {P}}$
a club subset of
$cl \in V^{\mathcal {P}}$
a club subset of
![]() $\kappa $
. Then there is a club
$\kappa $
. Then there is a club
![]() $cl' \in V$
with
$cl' \in V$
with
![]() $cl' \subseteq cl$
.
$cl' \subseteq cl$
.
Proof In
![]() $V^{\mathcal {P}}$
, let
$V^{\mathcal {P}}$
, let
![]() $h \in \kappa ^\kappa $
enumerate
$h \in \kappa ^\kappa $
enumerate
![]() $cl$
and
$cl$
and
![]() $g \in \kappa ^\kappa \cap V$
dominate h; note that h is a continuous function. Define the functions
$g \in \kappa ^\kappa \cap V$
dominate h; note that h is a continuous function. Define the functions
 $$ \begin{gather*} g'(0) = g(0),\ g'(\alpha + 1) = g(g'(\alpha)) \textrm{ and } g'(\lambda) = \sup_{i < \lambda} g'(i) \textrm{ for limit } \lambda, \\ h'(0) = h(0),\ h'(\alpha + 1) = h(g'(\alpha)) \textrm{ and } h'(\lambda) = \sup_{i < \lambda} h'(i) \textrm{ for limit } \lambda. \end{gather*} $$
$$ \begin{gather*} g'(0) = g(0),\ g'(\alpha + 1) = g(g'(\alpha)) \textrm{ and } g'(\lambda) = \sup_{i < \lambda} g'(i) \textrm{ for limit } \lambda, \\ h'(0) = h(0),\ h'(\alpha + 1) = h(g'(\alpha)) \textrm{ and } h'(\lambda) = \sup_{i < \lambda} h'(i) \textrm{ for limit } \lambda. \end{gather*} $$
Let
![]() $\lambda $
be a limit. Then since
$\lambda $
be a limit. Then since
![]() $h'(\alpha ) \leq g'(\alpha )$
and
$h'(\alpha ) \leq g'(\alpha )$
and
![]() $g'(\alpha ) \leq h'(\alpha + 1)$
, we have
$g'(\alpha ) \leq h'(\alpha + 1)$
, we have
![]() $h'(\lambda ) = g'(\lambda )$
; furthermore we know
$h'(\lambda ) = g'(\lambda )$
; furthermore we know
![]() $h'(\lambda ) \in cl$
and
$h'(\lambda ) \in cl$
and
![]() $g \in V$
, hence
$g \in V$
, hence
![]() $(g'(\lambda ))_{\lambda < \kappa , \lambda \textrm { limit}}$
is a ground model club contained in
$(g'(\lambda ))_{\lambda < \kappa , \lambda \textrm { limit}}$
is a ground model club contained in
![]() $cl$
.
$cl$
.
In the Corazza-type model from Section 7, the notions of strong measure zero and stationary strong measure zero coincide.
Theorem 8.4.
![]() $V^{\mathbb {P}} \models \forall X \subseteq 2^\kappa :\ X \in \mathcal {SN} \Leftrightarrow X \textrm { is stationary strong measure zero}$
.
$V^{\mathbb {P}} \models \forall X \subseteq 2^\kappa :\ X \in \mathcal {SN} \Leftrightarrow X \textrm { is stationary strong measure zero}$
.
Proof Modify the argument in Theorem 5.1 to show
by instead showing the set
to be dense for every
![]() $x \in V^{\mathbb {P}_\alpha }$
and every ground model club
$x \in V^{\mathbb {P}_\alpha }$
and every ground model club
![]() $cl \subseteq \kappa $
, where
$cl \subseteq \kappa $
, where
![]() $\dot {\sigma }$
is as defined in Theorem 5.1. As every club
$\dot {\sigma }$
is as defined in Theorem 5.1. As every club
![]() $cl \in V^{\mathbb {P}}$
contains a ground model club
$cl \in V^{\mathbb {P}}$
contains a ground model club
![]() $cl'$
by Lemma 8.3, this is sufficient. To see that
$cl'$
by Lemma 8.3, this is sufficient. To see that
![]() $D_{x,cl}$
is dense, merely note that for any
$D_{x,cl}$
is dense, merely note that for any
![]() $p \in \mathbb {Q}_\beta $
and
$p \in \mathbb {Q}_\beta $
and
![]() $b \in [p] \cap V^{\mathbb {P}_\beta }$
, the set
$b \in [p] \cap V^{\mathbb {P}_\beta }$
, the set
is a club and thus intersects
![]() $cl$
.
$cl$
.
On the other hand, it follows from
![]() $|2^\kappa | = \kappa ^+$
that there is a strong measure zero set which is not stationary strong measure zero.
$|2^\kappa | = \kappa ^+$
that there is a strong measure zero set which is not stationary strong measure zero.
Theorem 8.5. Under
![]() $|2^\kappa |=\kappa ^+$
there exists an
$|2^\kappa |=\kappa ^+$
there exists an
![]() $X \in \mathcal {SN}$
that is not stationary strong measure zero.
$X \in \mathcal {SN}$
that is not stationary strong measure zero.
Proof First off, let us enumerate all strictly increasing functions in
![]() $\kappa ^\kappa $
as
$\kappa ^\kappa $
as
![]() $(f_\alpha )_{\alpha < \kappa ^+}$
and likewise enumerate the set
$(f_\alpha )_{\alpha < \kappa ^+}$
and likewise enumerate the set
as
![]() $(\sigma _\alpha )_{\alpha < \kappa ^+}$
.
$(\sigma _\alpha )_{\alpha < \kappa ^+}$
.
We shall inductively construct three sequences
![]() $(x_\alpha )_{\alpha < \kappa ^+}$
,
$(x_\alpha )_{\alpha < \kappa ^+}$
,
![]() $(\tau _\alpha )_{\alpha < \kappa ^+}$
, and
$(\tau _\alpha )_{\alpha < \kappa ^+}$
, and
![]() $(cl_\alpha )_{\alpha < \kappa ^+}$
with the following properties:
$(cl_\alpha )_{\alpha < \kappa ^+}$
with the following properties:
-
a)
 $\forall \alpha < \kappa ^+:\ x_\alpha \in 2^\kappa , \tau _\alpha \in (2^{<\kappa })^\kappa $
and
$\forall \alpha < \kappa ^+:\ x_\alpha \in 2^\kappa , \tau _\alpha \in (2^{<\kappa })^\kappa $
and
 $cl_\alpha $
is a club subset of
$cl_\alpha $
is a club subset of
 $\kappa $
.
$\kappa $
. -
b)
 $\forall \alpha < \kappa ^+\, \forall i < \kappa :\ \operatorname {\mathrm {dom}}(\tau _\alpha (i)) = f_\alpha (i)$
.
$\forall \alpha < \kappa ^+\, \forall i < \kappa :\ \operatorname {\mathrm {dom}}(\tau _\alpha (i)) = f_\alpha (i)$
. -
c)
 $\forall \alpha < \kappa ^+ \, \forall i < \kappa :\ \bigcup _{j \geq i} [\tau _\alpha (j)]$
is open dense.
$\forall \alpha < \kappa ^+ \, \forall i < \kappa :\ \bigcup _{j \geq i} [\tau _\alpha (j)]$
is open dense. -
d)
 $\forall \alpha < \kappa ^+\, \forall \beta \leq \alpha :\ x_\beta \in \bigcup _{i < \kappa } [\tau _\alpha (i)]$
.
$\forall \alpha < \kappa ^+\, \forall \beta \leq \alpha :\ x_\beta \in \bigcup _{i < \kappa } [\tau _\alpha (i)]$
. -
e)
 $\forall \beta < \kappa ^+\, \forall \alpha < \beta :\ x_\beta \in \bigcup _{i < \kappa } [\tau _\alpha (i)]$
.
$\forall \beta < \kappa ^+\, \forall \alpha < \beta :\ x_\beta \in \bigcup _{i < \kappa } [\tau _\alpha (i)]$
. -
f)
 $\forall \alpha < \kappa ^+:\ x_\alpha \notin \bigcup _{i \in cl_\alpha } [\sigma _\alpha (i)]$
.
$\forall \alpha < \kappa ^+:\ x_\alpha \notin \bigcup _{i \in cl_\alpha } [\sigma _\alpha (i)]$
.
Setting
![]() $X = \{x_\alpha : \alpha < \kappa ^+\}$
yields a strong measure zero set (by b), d), and e)). However, X is not stationary strong measure zero, since for the challenge
$X = \{x_\alpha : \alpha < \kappa ^+\}$
yields a strong measure zero set (by b), d), and e)). However, X is not stationary strong measure zero, since for the challenge
![]() $g: i \mapsto i+1$
property f) ensures
$g: i \mapsto i+1$
property f) ensures
Suppose now, inductively, that
![]() $(x_\alpha )_{\alpha < \gamma }$
,
$(x_\alpha )_{\alpha < \gamma }$
,
![]() $(\tau _\alpha )_{\alpha < \gamma }$
, and
$(\tau _\alpha )_{\alpha < \gamma }$
, and
![]() $(cl_\alpha )_{\alpha < \gamma }$
have been constructed for
$(cl_\alpha )_{\alpha < \gamma }$
have been constructed for
![]() $\gamma < \kappa ^+$
. We wish to define
$\gamma < \kappa ^+$
. We wish to define
![]() $x_\gamma , \tau _\gamma $
, and
$x_\gamma , \tau _\gamma $
, and
![]() $cl_\gamma $
. To this end, reindex
$cl_\gamma $
. To this end, reindex
![]() $(x_\alpha )_{\alpha < \gamma }$
and
$(x_\alpha )_{\alpha < \gamma }$
and
![]() $(\tau _\alpha )_{\alpha < \gamma }$
as
$(\tau _\alpha )_{\alpha < \gamma }$
as
![]() $(\tilde {x}_{i+1})_{i < \kappa }$
,
$(\tilde {x}_{i+1})_{i < \kappa }$
,
![]() $(\tilde {\tau }_{i+1})_{i < \kappa }$
Footnote
10
and inductively construct
$(\tilde {\tau }_{i+1})_{i < \kappa }$
Footnote
10
and inductively construct
![]() $x_\gamma $
and
$x_\gamma $
and
![]() $cl_\gamma $
by building up partial approximations
$cl_\gamma $
by building up partial approximations
![]() $x_\gamma ^j$
and
$x_\gamma ^j$
and
![]() $cl_\gamma ^j$
for
$cl_\gamma ^j$
for
![]() $j < \kappa $
. Here
$j < \kappa $
. Here
![]() $x_\gamma ^j$
will be a binary sequence of length at least
$x_\gamma ^j$
will be a binary sequence of length at least
![]() $j+1$
.
$j+1$
.
-
•
 $j = 0$
: Set
$j = 0$
: Set
 $cl_\gamma ^0 := 0$
and
$cl_\gamma ^0 := 0$
and
 $x_\gamma ^0 := \langle 1 - \sigma _\gamma (0)(0) \rangle $
.
$x_\gamma ^0 := \langle 1 - \sigma _\gamma (0)(0) \rangle $
. -
•
 $j \to j+1$
: Since by assumption
$j \to j+1$
: Since by assumption
 $\ell \mapsto \operatorname {\mathrm {dom}}(\tilde {\tau }_{j+1}(\ell ))$
is strictly increasing and
$\ell \mapsto \operatorname {\mathrm {dom}}(\tilde {\tau }_{j+1}(\ell ))$
is strictly increasing and
 $\bigcup _{\ell ' \geq \ell } [\tilde {\tau }_{j+1}(\ell ')]$
is open dense for all
$\bigcup _{\ell ' \geq \ell } [\tilde {\tau }_{j+1}(\ell ')]$
is open dense for all
 $\ell < \kappa $
, we can find an
$\ell < \kappa $
, we can find an
 $\ell ^*> cl_\gamma ^j$
with
$\ell ^*> cl_\gamma ^j$
with
 $x_\gamma ^j \lhd \tilde {\tau }_{j+1}(\ell ^*)$
. Set
$x_\gamma ^j \lhd \tilde {\tau }_{j+1}(\ell ^*)$
. Set
 $cl_\gamma ^{j+1} := \operatorname {\mathrm {dom}}(\tilde {\tau }_{j+1}(\ell ^*))$
and
$cl_\gamma ^{j+1} := \operatorname {\mathrm {dom}}(\tilde {\tau }_{j+1}(\ell ^*))$
and
 $x_\gamma ^{j+1} := \tilde {\tau }_{j+1}(\ell ^*) ^\frown (1 - \sigma _\gamma (cl_\gamma ^{j+1})(cl_\gamma ^{j+1}))$
.
$x_\gamma ^{j+1} := \tilde {\tau }_{j+1}(\ell ^*) ^\frown (1 - \sigma _\gamma (cl_\gamma ^{j+1})(cl_\gamma ^{j+1}))$
. -
•
 $\lambda $
is a limit: Set
$\lambda $
is a limit: Set
 $cl_\gamma ^\lambda := \sup _{j < \lambda } cl_\gamma ^j$
and
$cl_\gamma ^\lambda := \sup _{j < \lambda } cl_\gamma ^j$
and
 $x_\gamma ^\lambda := (\bigcup _{j < \lambda } x_\gamma ^j) ^\frown (1 - \sigma _\gamma (cl_\gamma ^\lambda )(cl_\gamma ^\lambda ))$
.
$x_\gamma ^\lambda := (\bigcup _{j < \lambda } x_\gamma ^j) ^\frown (1 - \sigma _\gamma (cl_\gamma ^\lambda )(cl_\gamma ^\lambda ))$
.
Now set
![]() $x_\gamma := \bigcup \{x_\gamma ^j: j < \kappa \}$
and
$x_\gamma := \bigcup \{x_\gamma ^j: j < \kappa \}$
and
![]() $cl_\gamma := \{cl_\gamma ^j: j < \kappa \}$
. In the construction we have ensured
$cl_\gamma := \{cl_\gamma ^j: j < \kappa \}$
. In the construction we have ensured
![]() $x_\gamma \notin \bigcup _{j \in cl_\gamma } [\sigma _\gamma (j)]$
and
$x_\gamma \notin \bigcup _{j \in cl_\gamma } [\sigma _\gamma (j)]$
and
![]() $x_\gamma \in \bigcup _{j < \kappa } [\tilde {\tau }_{i+1}(j)]$
for all
$x_\gamma \in \bigcup _{j < \kappa } [\tilde {\tau }_{i+1}(j)]$
for all
![]() $i < \kappa $
. Finally, it is elementary to construct
$i < \kappa $
. Finally, it is elementary to construct
![]() $\tau _\gamma $
such that b), c), and d) holds.
$\tau _\gamma $
such that b), c), and d) holds.
Acknowledgements
We would like to thank Martin Goldstern for fruitful discussions during the preparation of this paper. We would also like to thank the anonymous referee for their many valuable remarks and suggestions that helped substantially improve the presentation of the paper. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme.
Funding
The second author was generously supported by FWF project I3081.