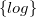1 Introduction
Constraint Logic Programming (CLP) systems can be used for formal software verification. In general, these systems provide untyped languages. Adding prescriptive type systems to CLP languages may help when CLP is used for formal verification because typecheckers are sound and complete.
Prescriptive type checking catch errors at compile time, whereas constraint solving can catch errors at runtime. Catching errors at runtime might not be acceptable in certain contexts – for example, safety-critical systems. In this note, we show how prescriptive type checking and set constraint solving can be combined in CLP to automatically found errors before the program is executed. We do so by defining a type system and implementing a typechecker for
$\{log\}$
(‘setlog’) (Dovier et al. Reference Dovier, Piazza, Pontelli and Rossi2000; Rossi Reference Rossi2008).
$\{log\}$
is a satisfiability solver implementing decision procedures for several expressive fragments of the theory of finite sets and finite set relation algebra. Several in-depth empirical evaluations provide evidence that
$\{log\}$
is able to solve nontrivial problems (Cristiá and Rossi Reference Cristiá, Rossi, Desharnais, Guttmann and Joosten2018; Reference Cristiá and Rossi2020, Reference Cristiá and Rossi2021b, Reference Cristiá, Rossi, Cantone and Pulvirenti2024a; Cristiá et al. Reference Cristiá, Rossi, Frydman, Hierons, Merayo and Bravetti2013); in particular as an automated verifier of security properties (Cristiá and Rossi Reference Cristiá and Rossi2021a; Reference Cristiá and Rossi2021c, Reference Cristiá and Rossi2023). That is,
$\{log\}$
is able to automatically prove that a program or a model verifies some complex properties such as the invariance lemmas arising from the verification of nontrivial state machines. Rooted in CLP and Prolog,
$\{log\}$
essentially provides an untyped language. The lack of types makes it impossible for
$\{log\}$
to find certain classes of errors.
In this note, we show how
$\{log\}$
has been enriched with a (prescriptive) type system.
$\{log\}$
’s type system is an instance of a Hindley–Milner system including parametric polymorphism for function and predicate symbols. Given that in
$\{log\}$
finite sets and set operators are first-class entities of the language, the type system is defined as to provide support for them. That is, there are types for sets, binary relations and their elements, and set and relational operators are typed accordingly. The type system is based on the type system defined for the Z formal notation (Spivey Reference Spivey1992), which in turn is similar to B’s (Abrial Reference Abrial1996). Actually,
$\{log\}$
has been proposed as a prototyping language for B and Z specifications (Cristiá et al. Reference Cristiá, Rossi, Frydman, Hierons, Merayo and Bravetti2013; Cristiá and Rossi Reference Cristiá and Rossi2021c; Reference Cristiá, Rossi, Cantone and Pulvirenti2024a).
Through the combination between type checking and CLP features
$\{log\}$
performs three important tasks: it type checks a program, it runs the program, and it automatically proves properties of the same program. As far as we understand, this is a novel approach concerning tools for set-based languages. There are tools where types are used to guarantee some properties (e.g., Atelier-B (Mentré et al. Reference Pfenning2012), Rodin (Abrial et al. Reference Abrial, Butler, Hallerstede, Hoang, Mehta and Voisin2010) and Zenon Modulo (Bonichon et al. Reference Bonichon, Delahaye, Doligez, Dershowitz and Voronkov2007)), but they do not enjoy CLP properties – for instance, they cannot execute their models. Other tools clearly fit in the CLP paradigm (e.g., ProB (Leuschel and Butler Reference Leuschel, Butler, A.Keijiro, Gnesi and Mandrioli2003)), but they cannot prove properties true of the specification. None of these tools implement decision procedures for set theory as those implemented in
$\{log\}$
. At the same time,
$\{log\}$
provides a language almost at the same level of abstraction of formal notations such as B and Z. These features make
$\{log\}$
to solve real-world problems as shown in Section 5.3.
As a design choice, we allow the typechecker in
$\{log\}$
to be switched on and off by users; when switched off,
$\{log\}$
works as usual. This choice is not only a matter of backward compatibility but the result of understanding that typed and untyped formalisms have their own advantages and disadvantages (Lamport and Paulson Reference Lamport and Paulson1999). Hence, being
$\{log\}$
at the intersection of a specification language, a programming language and an automated verifier, we think that users can decide when they need types.
The contents of this note are rather informal and conceptual. All the technical details can be found in an online document (Cristiá and Rossi Reference Cristiá and Rossi2022).
2 Combining type checking and constraint solving
As we have said,
$\{log\}$
provides an untyped language. For example, if variable X represents the current value of a traffic light it should always be the case that X in {red,yellow,green} holds (where in is interpreted as
$\in$
). However, in a
$\{log\}$
program it is possible for X to be bound to any value, say 2. Then, 2 in {red,yellow,green} will fail making
$\{log\}$
to answer false at runtime – which is potentially dangerous in a safety-critical system.
$\{log\}$
will also answer false if X is bound to green when
X in {red,yellow} holds. Hence, we have two false answers arising from quite different causes: the first one (
X = 2) is clearly a programming error; the second one (X = green) is just a possible, although unsatisfiable, situation. We would like to help the programmer to easily tell these false answers apart. A (prescriptive) typechecker can signal the user with a type error if there is the chance of X being bound to something outside of {red,yellow,green}; the constraint solver can determine whether or not
X in {red,yellow} is satisfiable by discharging a certain proof obligation. Both checks are performed before the program is run, thus avoiding runtime errors.
2.1 Typechecking and formally verifying a simple library system
Consider the following
$\{log\}$
clause concerning a simple library system:
addBook(Books,B,T,Books_) :-
dom(Books,D) & B nin D & Books_ = [B,T] / Books.
where Books is a set of ordered pairs mapping books IDs (BID) onto their titles and Books_ is the state of the library after adding [B,T] to it. In turn, B and T are the book ID and title of a new book being added to the library. Besides, dom/2 is a
$\{log\}$
constraint computing the domain of a function; nin is interpreted as
$\notin$
; and [B,T] / Books is a
$\{log\}$
set term interpreted as
$\{(B,T)\} \cup Books$
, where
$(B,T)$
is an ordered pair. Finally, & stands for conjunction.
Without types, T can be bound to any term (e.g., an ordered pair or a list) which is clearly not the intention. After adding types to
$\{log\}$
we can declare the type of addBook as follows:
dec_p_type(addBook(rel(bid,title),bid,title,rel(bid,title)).
addBook(Books,B,T,Books_) :-
dom(Books,D) & B nin D & Books_ = [B,T] / Books.
That is, the clause is preceded by a dec_p_type fact asserting the type of each argument.Footnote 1 As can be seen, dec_p_type takes one argument corresponding to the head predicate of the clause being declared. In turn, each argument of the predicate inside dec_p_type is a type. In this way, rel(bid,title) is the type of Books, bid is the type of B, etc.
rel(bid,title) corresponds to the type of the binary relations from bid to title, which in turn are basic types. Values of basic type x are of the form x?
$atom$
where
$atom$
is any Prolog atom.
When the file containing addBook/4 is consulted, the typechecker checks the type of addBook/4. Later, users can issue queries involving the clauses declared in the file. In this case, users have to give the types of all the variables involved in the query. For example:
dec(NewBooks,rel(bid,title)) & addBook(,bid?b1,title?aleph,NewBooks)
where dec(NewBooks,rel(bid,title)) declares NewBooks’s type and denotes the empty set. Before executing the query,
$\{log\}$
calls the typechecker to check whether the query is type correct or not. In this case, the typechecker uses the dec_p_type of addBook/4, the dec predicates and the arguments in the query to control that each argument in the query has the right type.
Types ensure that programs “are free from certain kinds of misbehavior” (Pierce Reference Pierce2002). However, types cannot catch all kinds of errors. Concerning the library system, observe that Books is supposed to be a function but its type declaration states that it is a binary relation. Then, this type declaration cannot catch the error of putting in Books two ordered pairs sharing the same BID but different titles.
One may think in a type system where functions are first-class entities. However, in set-based formal notations such as B and Z binary relations are first-class entities, whereas functions are defined as a subclass of binary relations. Hence, in this context, this problem is approached by asking the user to discharge proof obligations ensuring that, for instance, a binary relation is actually a function.
$\{log\}$
follows the same approach. Actually,
$\{log\}$
uses its automated proving power to discharge those proof obligations. Hence,
$\{log\}$
combines type checking and constraint solving to ensure program correctness.
In this way, if we want Books to be a function we can use the pfun constraint in combination with a type declaration: dec(Books,rel(bid,title)) & pfun(Books). pfun is a
$\{log\}$
constraint asserting that its argument is a partial function.
This approach is particularly amenable to work with invariance lemmas. An invariance lemma states that some property, the invariant, is preserved along all program executions. Indeed, one can propose a typing property that cannot be enforced by the type system as a program invariant. Afterwards, one proves that the program preserves that invariant by discharging the corresponding invariance lemma. The obvious problem with this approach is the fact that discharging an invariance lemma requires, in general, a manual proof. However, if the invariance lemma corresponds to a formula belonging to some decidable theory, it can, in principle, be automatically discharged. Here is where
$\{log\}$
constraint solving capabilities come into play.
Example 1. The type system ensures that, for instance, [B,12] cannot be added to Books, but it cannot ensure that Books is a function. On the other hand,
$\{log\}$
(without types) can automatically prove that pfun(Books) is a type invariant for that operation but it cannot check that [B,12] cannot be an element of Books before the program is executed. In order to prove that pfun(Books) is a type invariant the following is (automatically) proved to be unsatisfiable:
dec([Books,Books_],rel(bid,title)) & dec(B,bid) & dec(T,title) &
pfun(Books) & addBook(Books,B,T,Books_) & npfun(Books_)
where npfun is interpreted as
$\lnot$
pfun. We know this can be automatically proved because the formula belongs to a decidable fragment implemented in
$\{log\}$
(see Section 4.1).
Furthermore, types simplify some proof obligations thus further reducing the verification effort. The following is an example.
Example 2. Consider that in the library system
$\texttt{Books} \in \texttt{bid} \shortmid \!\!\!\rightarrow \texttt{title}$
should be an invariant of the system. This invariant can be mathematically rewritten as:
$\textrm{dom} \texttt{Books} \subseteq \texttt{bid} \land \textrm{ran} \texttt{Books} \subseteq \texttt{title} \land \texttt{pfun}(\texttt{Books})$
. With the type declaration dec(Books,rel(bid,title)) the first two conjuncts are proved by the typechecker. Then, pfun(Books) is the only property the constraint solver has to prove.
As set constraint solving is always less efficient than type checking, the combination between type checking and constraint solving makes a better use of the computing resources because type checking finds errors before constraint solving is called.
Once
$\{log\}$
has been used to verify the program, it can also be used to run simulations.
Example 3. The predicate addBook can be called as a normal subroutine.
{log}
$\texttt{=}\gt$
addBook({},bid?b1,title?the_farm,Books_).
Books_
$\texttt{=}$
{[bid?b1,title?the_farm]}
{log}
$\texttt{=}\gt$
addBook({},bid?b1,title?the_farm,Books1)
& addBook(Books1,bid?b2,title?houses,Books_).
Books_
$\texttt{=}$
{[bid?b1,title?the_farm],[bid?b2,title?houses]}
{log}
$\texttt{=}\gt$
addBook ({},bid?b1,title?the_farm,Books1)
& addBook(Books1,bid?b1,title?houses,Books_).
false
We can also define other operations on the library:
dec_p_type(title(rel(bid,title),bid,title)).
title(Books,B,T) :- applyTo(Books,B,T).
where applyTo(F,X,Y) is true when
$F(X) = Y$
. Then we can run the program calling all the operations:
{log}
$\texttt{=}\gt$
addBook({},bid?b1,title?the_farm,Books1)
& addBook(Books1,bid?b2,title?houses,Books_)
& title(Books_,bid?b1,T).
T
$\texttt{=}$
title?the_farm
3 A type system for
$\{log\}$
In this section, we describe the type system defined for
$\{log\}$
. After the introduction of types, every variable, term, and predicate is of or has a type.Footnote
2
The type system includes types for a subclass of Prolog atoms, integer numbers, sum types,Footnote
3
ordered pairs, and sets, which can be recursively combined. This recursion enables the definition of types corresponding to sets of ordered pairs which allow the correct typing of binary relations. Terms of any type can be used to build set terms as long as they are all of the same type, no nesting restrictions being enforced (in particular, membership chains of any finite length can be modeled). In this and the following section we use a more abstract, math-oriented notation, instead of the
$\{log\}$
code shown in the previous section and in Section 5. A fully detailed presentation can be found in the online document (Cristiá and Rossi Reference Cristiá and Rossi2022).
The type system is given by the following grammar:
\begin{align} & \tau ::= \mathsf{int} | b | \mathsf{sum}([\overbrace{C,\dots, C}^{\geq 2}]) | \mathsf{prod}(\tau, \tau ) | \mathsf{set}(\tau ) \\ & C ::= a | a(\tau ) \end{align}
where
$b \in{\mathcal{B}}$
and
$a \in \mathcal{A}$
whereas
$\mathcal{A}$
represent the set of Prolog atoms and
$\mathcal{B}$
is a countable set of type names.
Intuitively,
$\mathsf{int}$
corresponds to the type of integer numbers;
$\mathsf{sum}([C_1,\dots, C_n])$
with
$2 \leq n$
defines a sum type given by all the values that can be built by each constructor
$C_i$
;
$\mathsf{prod}(T_1,T_2)$
defines the product type given by the Cartesian product
$T_1 \times T_2$
; and
$\mathsf{set}(T)$
defines the powerset type of type
$T$
. Each constant
$b \in{\mathcal{B}}$
represents the type name of a basic type interpreted as the set
$\{b ? a | a \in \mathcal{A}\}$
. An example of a sum type is
$\mathsf{sum}([\textbf{nil},\textbf{some}(\mathsf{int})])$
representing the set
$\{\textbf{nil}\} \cup \{\textbf{some}(i) | i \in \mathbb{Z}\}$
. We write
$\mathsf{rel}(\tau _1,\tau _2)$
as a shortcut for
$\mathsf{set}(\mathsf{prod}(\tau _1,\tau _2))$
. Clearly,
$\mathsf{rel}$
represents the type of binary relations. This type system is aligned with those of Z (Spivey Reference Spivey1992) and B (Abrial Reference Abrial1996).
The type of the main
$\{log\}$
function symbols is defined in Figure 1, where:
$dec(v,t)$
is a predicate interpreted as “variable
$v$
is of type
$t$
” a typing context
$\Gamma$
is a set of
$dec$
predicates;
$\Gamma \vdash s:\tau$
can be read as ‘in typing context
$\Gamma$
,
$s$
is of or has type
$\tau$
’
$v \notin \textrm{dom} \Gamma$
means that
$v$
is not one of the variables declared in
$\Gamma$
;
$\tau = \dots \mathsf{sum}([a_1,a_2(\tau _2)])\dots$
asserts that
$\mathsf{sum}([a_1,a_2(\tau _2)])$
is part of the definition of
$\tau$
; and
$\{a_1,a_2\} \parallel (\tau \cup \Gamma )$
asserts that
$\{a_1,a_2\}$
is disjoint w.r.t. the union of the constructors of any other
$\mathsf{sum}$
used in
$\tau$
and
$\Gamma$
(except itself). Symbols
$\{\}$
,
$[\cdot, \cdot ]$
, and
$\{\cdot /\cdot \}$
were introduced in Section 2;
$int(m,n)$
stands for the set
$\{z \in \mathbb{Z} \mid m \leq z \leq n\}$
; and
$\boxplus$
stands for any integer binary operator.
Fig. 1. Type rules for function symbols.
Rule Sum is given for a simple case to keep the presentation manageable; it can be easily extended to any number of constructors. Note that a sum constructor can be used in only one sum type, and that there must be at least two constructors in a sum type.
As can be seen, several function symbols are polymorphic. In particular, the type of a term of the form
$\textsf{u}?a$
is given by its first argument. As terms must have exactly one type, any
$a \in \mathcal{A}$
can be used as the constructor of at most one
$\mathsf{sum}$
in
$\Gamma$
. The type of a variable is the type given in its declaration through the
$dec$
predicate in
$\Gamma$
. With this type system a set such as
$\{\textbf{a}, 1, \{2\}, (5,4)\}$
is ruled out because not all of its elements are of the same type. However, that set can be encoded as
$\{\textbf{a}, \textbf{n}(1), \textbf{s}(\{2\}), \textbf{p}((5,4))\}$
, where
$\textbf{a}$
,
$\textbf{n}$
,
$\textbf{s}$
, and
$\textbf{p}$
are constructors of a
$\mathsf{sum}$
type. If in a
$\mathsf{sum}$
all constructors are nullary terms then we write
$\mathsf{enum}([a_1,\dots, a_n])$
to emphasize the fact that the sum is actually defining an enumeration.
Fig. 2. Type rules for predicate symbols in
$\Pi _C$
.
Example 4. The following are some examples on how terms are typed.
\begin{align*} & \{dec(k,\mathsf{int})\} \cup \Gamma \vdash k + 1: \mathsf{int} \\ & \{dec(A,\mathsf{set}(\mathsf{int}))\} \cup \Gamma \vdash \{4,9 / A\}: \mathsf{set}(\mathsf{int}) \\ & \{dec(m,\mathsf{int}), dec(x,\mathsf{sum}([\textbf{a},\textbf{e}(\mathsf{int})])\} \vdash (\{m\},\textbf{e}(m+1)): \mathsf{prod}(\mathsf{set}(\mathsf{int}),\mathsf{sum}([\textbf{a},\textbf{e}(\mathsf{int})])) \\ & \Gamma \vdash \{\textsf{u}?\textbf{a},\textsf{u}?\textbf{aa},\textsf{u}?\textbf{ab}\}:\mathsf{set}(\textsf{u}) \\ & \{\textsf{u}?\textbf{a},\textsf{v}?\textbf{a}\}: \text{cannot be typed because}\; \textsf{u}?\textbf{a}\; \text{has type}\; \textsf{u}\;\text{and}\;\textsf{v}?\textbf{a}\;\text{has type}\;\textsf{v} \\ & \textsf{u}?10: \text{cannot be typed because}\;10 \notin \mathcal{A} \\ & \{dec(x,\mathsf{sum}([\textbf{a},\textbf{b},\textbf{a}(\textsf{t})]))\} \cup \Gamma \vdash{\dots } \\ &\qquad \text{ is an ill-formed typing context because}\; \textbf{a} \;\text{appears twice} \\ & \{dec(x,\mathsf{prod}(\mathsf{enum}([\textbf{a},\textbf{b}]), \mathsf{sum}([\textbf{q},\textbf{a}(\textsf{t})]))\} \cup \Gamma \vdash{\dots } \\ &\qquad \text{ is an ill-formed typing context because } \textbf{a}\; \text{appears in two different}\;\mathsf{sum} \\ & \{dec(x,\mathsf{enum}([\textbf{a,b}])), dec(y,\mathsf{enum}([\textbf{q},\textbf{a}]))\} \cup \Gamma \vdash{\dots } \\ &\qquad \text{ is an ill-formed typing context because } \textbf{a} \text{appears in two different}\;\mathsf{enum} \end{align*}
In the last three examples the problem is that the terms a, b, and q cannot be typed because no type rule can be applied to infer their types.
The type of each primitive constraint available in
$\{log\}$
is given in Figure 2. If
$\tau _1,\dots, \tau _n$
are types, a type judgment such as
$\Gamma \vdash \pi (\tau _1,\dots, \tau _n)$
can be read as ‘predicate
$\pi$
is correctly typed’. Constraints are interpreted as follows:
$x \mathbin{neq} y$
as
$x \neq y$
;
$x \mathbin{in} A$
as
$x \in A$
;
$x \mathbin{nin} A$
as
$x \notin A$
;
${un}(A,B,C)$
is interpreted as
$C = A \cup B$
;
$disj(A,B)$
as
$A \cap B = \varnothing$
;
$size(A,m)$
as
$\lvert A \rvert = m$
;
${id}(A,R)$
as
$R = \{(x,x) \mid x \in A\}$
, that is the identity relation on set
$A$
;
$inv(R,S)$
as
$S = \{(y,x) \mid (x,y) \in R\}$
, that is the converse of a binary relation; and
$comp(R,S,T)$
as
$T = \{(x,z) \mid \exists y ((x,y) \in R \land (y,z) \in S)\}$
, that is composition of binary relations. Again, several constraints are polymorphic. Besides, it is worth to be noticed that in untyped formalisms a constraint such as
$1 \neq (2,4)$
would usually be deemed as a true proposition while in
$\{log\}$
such a constraint is ill-typed and thus rejected.
In
$\{log\}$
, formulas are built in the usual way by connecting constraints (i.e., predefined predicates) by means of conjunction (
$\land$
), disjunction (
$\lor$
) and negation (
$\lnot$
). Formulas can also contain user-defined predicates (addBook/4 in Section 2 is an example). A well-typed formula is a formula where all its constraints are typed according to the rules given in Figure 2 and user-defined predicates are typed by means of dec_p_type declarations.
Example 5. The following are well-typed
$\{log\}$
formulas:
\begin{align} &{id}(\{x / A\},R) \land{id}(R,A) \land dec(x,\textsf{t}) \land dec(A, \mathsf{set}(\textsf{t})) \land dec(R,\mathsf{rel}(\textsf{t},\textsf{t})) \end{align}
\begin{align} & dec([A,B,C],\mathsf{set}(\mathsf{int})) \land dec([n,k],\mathsf{int}) \land \\ & \qquad{un}(A,B,C) \land n+k \gt 5 \land size(C,n) \land B \neq \{\} \notag \end{align}
\begin{align} & dec(y,\textsf{t}) \land dec(R,\mathsf{rel}(\textsf{t},\mathsf{int})) \land dec([S,T],\mathsf{rel}(\mathsf{int},\textsf{t})) \land dec(x,\mathsf{prod}(\mathsf{int},\textsf{t})) \land \\ & \qquad [y,5] \in R \land [2,\textsf{t}?\textbf{b}] \notin S \land inv(R,S) \land S = \{x / T\} \notag \end{align}
On the contrary,
$dec(x,\textsf{t}) \land dec(y,\mathsf{int}) \land x \mathbin{neq} y$
is not well-typed because
$x \mathbin{neq} y$
cannot be typed as
$neq$
expects arguments of the same type (rule Eq in Figure 2).
Expressiveness. As we have said, Figure 2 presents the type of each
$\{log\}$
primitive constraint. These constraints are used to define a number of integer, set, and relational constraints by means of suitable formulas. Dovier et al. (Reference Dovier, Piazza, Pontelli and Rossi2000) proved that
$un$
,
$\in$
and
$disj$
are enough to define constraints implementing the set operators
$\cap$
,
$\subseteq$
, and
$\setminus$
. For example,
$A \subseteq B$
can be defined by the formula
${un}(A,B,B)$
. In turn, these constraints plus
$id$
,
$inv$
and
$comp$
are as expressive as the class of finite set relation algebras (Cristiá and Rossi Reference Cristiá and Rossi2020). Within this class of algebras it is possible to define many relational operators such as domain, range, domain restriction, relational image, etc. Finally, by adding the
$size$
constraint and integer intervals, it is possible to define operators such as the minimum of a set, the successor function on a set, partition of a set w.r.t. a given number, etc. (Cristiá and Rossi Reference Cristiá and Rossi2024b).
The negated versions of set, relational, and integer operators can be introduced in the same way (Dovier et al. Reference Dovier, Piazza, Pontelli and Rossi2000; Cristiá and Rossi Reference Cristiá and Rossi2020, Reference Cristiá and Rossi2023, Reference Cristiá and Rossi2024b). For example,
$\lnot (A \cup B = C)$
is introduced as:
\begin{equation} nun(A,B,C) \mathbin{\widehat{=}} (n \mathbin{in} C \land n \mathbin{nin} A \land n \mathbin{nin} B) \lor (n \mathbin{in} A \land n \mathbin{nin} C) \lor (n \mathbin{in} B \land n \mathbin{nin} C) \end{equation}
The combination between sum and product types permit to encode arbitrary compound terms. For instance, a term of the form
$\textbf{p}(2,\{4\})$
can be encoded as
$\textbf{p}([2,\{4\}])$
whose type is
$\mathsf{sum}([\textbf{p}(\mathsf{prod}(\mathsf{int},\mathsf{set}(\mathsf{int}))), \dots ])$
.
4 Type safety
The definition of a type system for a CLP language entails to prove that the operational semantics of the language preserves the types of variables and terms as it processes any well-typed formula. This is called type soundness or type safety (Harper Reference Harper2016, Chapter 4). The operational semantics of a CLP language is given primarily by its constraint solving procedure.
4.1
The
$\{log\}$
constraint solver
The constraint solver for
$\{log\}$
with types is the same solver for
$\{log\}$
without types.Footnote 4 In
$\{log\}$
with types, the solver is simply run once the type checking phase has finished successfully and ignores
$dec$
predicates. The solver for
$\{log\}$
without types has been thoroughly studied elsewhere (Dovier et al. Reference Dovier, Piazza, Pontelli and Rossi2000 and Cristiá and Rossi Reference Cristiá and Rossi2020, Reference Cristiá and Rossi2023, Reference Cristiá and Rossi2024b). Several results on the decidability of the satisfiability problem for these languages have been put forward and several empirical studies showing the practical capabilities of
$\{log\}$
have also been reported (Cristiá and Rossi Reference Cristiá and Rossi2021a, Reference Cristiá and Rossi2021c; Cristiá et al. Reference Cristiá, Rossi, Frydman, Hierons, Merayo and Bravetti2013). For this reason here we give only an overview of the
$\{log\}$
solver.
The
$\{log\}$
solver is essentially a rewriting system whose core is a collection of specialized rewriting procedures. Each rewriting procedure applies a few non-deterministic rewrite rules which reduce the syntactic complexity of
$\{log\}$
constraints of one kind.
$\{log\}$
takes as input a formula,
$\Phi$
. In each iteration,
$\{log\}$
rewrites
$\Phi$
into a new formula, called
$\Phi '$
, which becomes the input formula for the next iteration.
As is shown in the aforementioned papers, there are three possible outcomes when
$\{log\}$
is applied to
$\Phi$
:
-
1.
$\{log\}$
returns
$false$
meaning that
$\Phi$
is unsatisfiable. -
2.
$\{log\}$
cannot rewrite
$\Phi '$
anymore and it is not
$false$
, so
$\Phi '$
is returned as it is. Since
$\{log\}$
can open a number of non-deterministic choices, many such
$\Phi '$
can be returned to the user. The disjunction of all these
$\Phi '$
is equivalent to
$\Phi$
. The constraints making these formulas are of a particular kind called irreducible (Dovier et al. Reference Dovier, Piazza, Pontelli and Rossi2000 and Cristiá and Rossi Reference Cristiá and Rossi2020; Reference Cristiá, Luca and Luna2023, Reference Cristiá and Rossi2024b). -
3. If
$\Phi$
belongs to an undecidable fragment of the language supported by
$\{log\}$
, then the above steps will not terminate.
As we have said, the core of
$\{log\}$
is a collection of rewriting procedures which in turn contain a collection of rewrite rules. There are about 60 of such rules which can be found online (Cristiá and Rossi Reference Cristiá and Rossi2019). Figure 3 lists some representative rewrite rules for the reader to have an idea of what they look like. As can be seen, each rule has the form:
$\phi \longrightarrow \Phi _1 \lor \dots \lor \Phi _n$
, where
$\phi$
is a
$\{log\}$
constraint and
$\Phi _i$
,
$i \geq 1$
, are
$\{log\}$
formulas. Besides, each rule is applied depending on some syntactic conditions on the constraint arguments. For example, rule (6) applies only when the first argument is an extensional set and the third is a variable (noted as
$\dot{B}$
); the second argument can be any set term. On the right-hand side of the rules,
$n,n_i,N,N_i$
represent new variables.
Fig. 3. Some rewrite rules implemented by
$\mathit{SAT}_{\{\cdot \}}$
.
Rule (5) is the main rule of set unification (Dovier et al. Reference Dovier, Pontelli and Rossi2006), a concept at the base of
$\{log\}$
. It states when two non-empty, non-variable sets are equal by non-deterministically and recursively computing four cases. As an example, by applying rule (5) to
$\{1\} = \{1,1\}$
we get: (
$1 = 1 \land \{\} = \{1\}) \lor (1 = 1 \land \{1\} = \{1\}) \lor (1 = 1 \land \{\} = \{1,1\}) \lor (\{\} = \{1 / N\} \land \{1 / N\} = \{1\})$
, which turns out to be true (due to the second disjunct).
Rule (6) is one of the main rules for
$un$
constraints. Observe that this rule is based on set unification, as well. It computes two cases:
$x$
does not belong to
$A$
and
$x$
belongs to
$A$
(in which case
$A$
is of the form
$\{x / N_2\}$
for some set
$N_2$
). In the latter case
$x \mathbin{nin} N_2$
prevents
$\{log\}$
from generating infinite terms denoting the same set.
Rule (7) computes the size of any extensional set by counting the elements that belong to it while taking care of avoiding duplicates. This means that, for instance, the first non-deterministic choice for a formula such as
$size(\{1,2,3,1,4\},m)$
will be:
\begin{equation*} 1 \mathbin {nin} \{2,3,1,4\} \land m = 1 + n \land size(\{2,3,1,4\},n) \land 0 \leq n \end{equation*}
which will eventually lead to a failure due to the presence of
$1 \mathbin{nin} \{2,3,1,4\}$
.
4.2 Proving type safety
The theorem stating type safety for
$\{log\}$
follows the guidelines set forth by (Harper Reference Harper2016, Chapter 6). However, due to the peculiarities of CLP we have to introduce some modifications to the theorem. Indeed, most of the foundational work on type systems has been done in a framework where programs are functions (Milner Reference Milner1978; Martin-Löf Reference Martin-Löf1984; Wright and Felleisen Reference Wright and Felleisen1994; Pierce Reference Pierce2002; Barendregt et al. Reference Barendregt, Dekkers and Statman2013), so it is natural to adapt some of its concepts and results to CLP.
Intuitively, Harper’s theorem states that: the type of any given term remains the same during the execution of the program; and if a term is well-typed, either it is a value or it can be further rewritten by the system. The first property is called preservation (or subject reduction), and the second is called progress. This theorem is adapted to our context as follows.
Theorem 1 ({log} is type safe). Consider any
$\{log\}$
constraint
$\pi$
. Let
$t_1:\tau _1, \dots, t_k:\tau _k$
be such that
$\pi (t_1,\dots, t_k)$
is a well-typed constraint. Then (
$\longrightarrow$
denotes any
$\{log\}$
rewrite rule):
-
1. If
$\pi (t_1,\dots, t_k) \longrightarrow \Phi$
, then there exist types
$\tau _1', \dots, \tau _m'$
(
$0 \leq m$
) such that:is a well-typed formula, were
\begin{equation*} dec(n_1,\tau _1') \land \dots \land dec(n_m,\tau _m') \land \Phi \end{equation*}
$n_1,\dots, n_m$
are the new variables of
$\Phi$
.
-
2.
$\pi (t_1,\dots, t_k)$
is irreducible, or there exists
$\Phi$
such that
$\pi (t_1,\dots, t_k) \longrightarrow \Phi$
The proof can be found in an on-line document (Cristiá and Rossi Reference Cristiá and Rossi2022). As Theorem1 suggests, the proof entails to prove that each of the 60 rewrite rules present in
$\{log\}$
are type safe.
5 Implementation
A typechecker for
$\{log\}$
has been implemented in Prolog. The program comprises about 1.1 KLOC of which 200 are devoted to error printing. It uses only basic, standard Prolog predicates. The typechecker can be downloaded from the
$\{log\}$
web site (Rossi Reference Rossi2008, file setlog_tc.pl). As we have pointed out in Section 2, the typechecker can be activated and deactivated by users at their will. If the typechecker is not active
$dec$
predicates are ignored and
$\{log\}$
works as usual.
The typechecker is implemented in four phases (see Figure 4): phase 1, the typechecker analyzes the
$dec$
predicates in the formula; phase 2, the logical structure of the formula is analyzed; phase 3, once we have a conjunction of atomic constraints the typechecker goes to check the type of each atomic constraint using rules in Figure 2; and phase 4, the type of each argument, of a given constraint, is checked using rules in Figure 1.
Fig. 4. Graphical depiction of the four phases implemented by the typechecker.
Going deeply into implementation details, in phase 1,
$dec$
predicates that are found correct by the typechecker are turned into ‘type’ facts of the form type(Var,type), asserting that the type of the variable is the one declared by the user.
Phases 3 and 4 are solved as unification problems. For example, the following clause typechecks
$id$
constraints (i.e., phase 3):
typecheck_constraint(id(X,Y)) :- !,
typecheck_term(X,Tx),
typecheck_term(Y,Ty),
(Tx = set(T), Ty = set(prod(T,T)),!
;
print_type_error(id(X,Y),Tx,Ty)
).
As can be seen, if the inferred types of X and Y cannot be unified in terms of a common type T (as indicated in rule Id of Figure 2), a type error is issued.
5.1 Introducing parametric polymorphism
Consider the following clause:
applyTo(F,X,Y) :- {F = [X,Y] / G} & [X,Y] nin G & comp({[X,X]},G,{}).
It states minimum conditions for applying binary relation F to a given point X whose image is Y. applyTo is meant to be a polymorphic definition in the sense that F is expected to be a binary relation of any rel type, X is expected to be of the domain type of F and Y of the range type. This is usually called parametric polymorphism.
Clauses that are meant to be polymorphic must be preceded by a dec_pp_type fact asserting the type of each argument.Footnote 5 For example, the typed version of applyTo is the following:
dec_pp_type(applyTo(rel(T,U),T,U)).
applyTo(F,X,Y) :- F = [X,Y] / G & [X,Y] nin G & comp([X,X],G,{}).
Differently from dec_p_type declarations, the types written in a dec_pp_type declaration can contain variables (e.g., T).
Users can query polymorphic clauses such as applyTo by giving types unifying with those declared in the corresponding dec_pp_type declarations.
5.2 Dealing with finite types
When working in typechecking mode, the following goal is unsatisfiable:
dec(Z,enum([t,f])) & Z neq t & Z neq f.
because the only two values Z can take are exactly t and f. In this case,
$\{log\}$
automatically transforms that goal into:
Z in {t,f} & Z neq t & Z neq f.
However, if the typechecker is not active, the first given goal is found to be satisfiable because the dec predicate is ignored and Z can take any value beyond t and f.
As another example, consider the following goal:
dec(F,rel(enum([t,f]),int)) & dec([X1,X2,X3],[enum([t,f]),int]) &
pfun(F) & F = X1,X2,X3 & X1 neq X2 & X1 neq X3 & X2 neq X3.
As F is a partial function and given the neq constraints, the first components of X1, X2, and X3 must be different from each other. At the same time, these first components have type enum([t,f]). So at least two of these first components must have the same value. Consequently the goal is unsatisfiable. As with the first goal, when working in typechecking mode,
$\{log\}$
identifies this situation and automatically conjoin suitable membership constraints to make type information available to the constraint solver.
These situations arise when the formula involves variables whose types are finite and entails, in a way or another, “too many” neq constraints. In these situations the constraint solver retrieves the type information generated by the typechecker transforming it into suitable membership constraints. This interplay between these two components is crucial to the correctness of
$\{log\}$
when working in typechecking mode.
5.3 Case studies
The combination between typechecking and constraint solving as presented in this note has been applied to some case studies. Here we briefly present two of them. Both case studies are based on problems, specifications, and verification conditions proposed by others, thus reducing a possible bias towards our method. We use these case studies as benchmarks to empirically evaluate
$\{log\}$
. Each case study shows a
$\{log\}$
program taking the form of a state machine. Transitions of these state machines are encoded as
$\{log\}$
predicates – for example as addBook. In turn, these predicates constitute an executable API from which the program can be run – as shown in Example3. At the same time, these
$\{log\}$
programs behave as specifications over which the verification conditions are automatically discharged – as shown in Example1.
5.3.1 The landing gear system
The first case study is based on the Landing Gear System (LGS) problem (Boniol and Wiels Reference Boniol, Wiels, Boniol, Wiels, Ameur and Schewe2014). Mammar and Laleau (Reference Mammar, Laleau, Boniol, Wiels, Ameur and Schewe2014, Reference Mammar and Laleau2017) developed an Event-B (Abrial Reference Abrial2010) specification formally verified using Rodin (Abrial et al. Reference Abrial, Butler, Hallerstede, Hoang, Mehta and Voisin2010), ProB (Leuschel and Butler Reference Leuschel, Butler, A.Keijiro, Gnesi and Mandrioli2003) and AnimB.Footnote
6
They were able to automatically discharge 72% of the proof obligations by calling Rodin. Hence, we encoded in
$\{log\}$
the entire Event-B specification of the LGS and used
$\{log\}$
to automatically discharge 100% of the proof obligations generated by the Rodin tool in roughly 290 s (Cristiá and Rossi Reference Cristiá, Rossi, Cantone and Pulvirenti2024a). The
$\{log\}$
encoding of the LGSFootnote
7
comprises 7.8 KLOC plus 465 proof obligations. In order to discharge all those proof obligations we used the combination between types and CLP as discussed above. Many proof obligations could be avoided while many others were simpler, due to the combined work between the typechecker and the constraint solver – as shown in Example2; see also (Cristiá and Rossi Reference Cristiá, Rossi, Cantone and Pulvirenti2024a, Section 4.5). The net result is an automatically verified
$\{log\}$
prototype of the LGS.
5.3.2 Android permission system
A model of the Android permission system has been developed and certified in Coq (Betarte et al. Reference Barendregt, Dekkers and Statman2015, Reference Betarte, Campo, Luna, Romano, Leucker, Rueda and Valencia2016; Luna et al. Reference Luna, Betarte, Campo, Sanz, Cristiá and Gorostiaga2018; De Luca and Luna Reference De Luca, Luna, de’Liguoro, Berardi and Altenkirch2020). As with the previous case study, we translated the Coq model into
$\{log\}$
and used it to run all the verification conditions proposed in CoqFootnote 8 Cristiá et al., (Reference Betarte, Campo, Luna and Romano2023).
$\{log\}$
is able to automatically prove 24 of the 27 properties (
$\approx 90\%$
) in approximately 21 m. The 3 properties that cannot be proved by
$\{log\}$
require 500 LOC of Coq proof commands (
$\approx 2\%$
of all proof commands). That is,
$\{log\}$
automatically proves 90% of the properties covering 98% of the proof effort in terms of proof commands. As can be seen, the gain in terms of human effort is considerable. The type system proposed for
$\{log\}$
can encode all the types used in the Coq model. This is important given that Coq is prized by its powerful type system. Then, concerning the Android model, our typechecker can prove the same type properties that are proved by Coq, whereas the constraint solver is able to automatically prove most of the properties that are manually proved in Coq.
6 Discussion and related work
The inclusion of prescriptive type systems in logic programmingFootnote
9
can be traced back to the seminal work of Mycroft and O’Keefe (Reference Mycroft and O’Keefe1984); later on Lakshman and Reddy (Reference Lakshman, Reddy, Saraswat and Ueda1991) define the formal semantics for that type system. At some point in time, these ideas started to be part of different logic programming languages (Hill and Lloyd Reference Hill and Lloyd1994; Schrijvers et al. Reference Schrijvers, Costa, Wielemaker, Demoen, de la Banda and Pontelli2008), and even they made through all the way to functional logic programming languages (Somogyi et al. Reference Somogyi, Henderson and Conway1996; Hanus Reference Hanus, Voronkov and Weidenbach2013). Schrijvers et al. (Reference Schrijvers, Costa, Wielemaker, Demoen, de la Banda and Pontelli2008) propose types to be optional in SWI-Prolog and Yap, as we do for
$\{log\}$
.
Descriptive type systems provide an approximation of the semantics of a given program, usually, as a set of terms greater than (cf. set inclusion) the one provided by the semantics. Answers of a descriptive typechecker are necessarily approximate. These type systems (Zobel Reference Zobel and Lassez1987; Bruynooghe and Janssens Reference Bruynooghe, Janssens, Kowalski and Bowen1988; Fr FC;hwirth et al. Reference Frühwirth, Shapiro, Vardi and Yardeni1991; Dart and Zobel Reference Dart, Zobel and Pfenning1992; Yardeni, Fr FC;hwirth et al. Reference Yardeni, Frühwirth, Shapiro and Pfenning1992; Heintze and Jaffar Reference Heintze, Jaffar and Pfenning1992; Gallagher and de Waal Reference Gallagher, de Waal and Hentenryck1994; Barbosa et al. Reference Barbosa, Florido, Costa, Angelis and Vanhoof2021) have been used in the context of abstract interpretation and program analysis of logic programs (Vaucheret and Bueno Reference Vaucheret, Bueno and Tessier2002; Hermenegildo et al. Reference Hermenegildo, Puebla, Bueno and López-García2005; Pietrzak et al. Reference Pietrzak, Correas, Puebla, Hermenegildo, Glück and de Moor2008).
It is worth to be noted that some other works on program approximation, for example (Heintze and Jaffar Reference Heintze, Jaffar and Allen1990; Talbot et al. Reference Talbot, Tison, Devienne and Hentenryck1997), use a technique called set-based analysis. This is not to be confused with our approach. We use sets and binary relations as the main data structures for programming and specification, while in these other works sets are used to analyze general logic programs. In other words, we use sets and binary relations to write programs, they use sets to analyze them. Descriptive type systems were also applied to CLP, for example as a means to find certain classes of errors in programs (Drabent et al. Reference Drabent, Maluszynski and Pietrzak2002).
Fages and Coquery (Reference Fages and Coquery2001) study a prescriptive type system for CLP programs that is independent from any constraint domain. The authors prove that their type system verifies subject reduction (i.e., type preservation) w.r.t. the abstract execution model of CLP (cf. accumulation of constraints), and w.r.t. an execution model of CLP with substitutions. As far as we understand, Fages and Coquery do not prove progress – cf. Theorem1. Clearly, Fages and Coquery’s preservation result reliefs us of proving that
$\{log\}$
’s CLP engine preserves types because it is just an implementation of the general CLP scheme addressed by these authors. On the other hand, Fages and Coquery’s result depends on the well-typedness of each rewrite rule of the execution model. This is exactly what we prove in Theorem1: that the execution model of our CLP language verifies type safety – that is preservation and progress. However, instead of typing each rewrite rule we prove that they preserve types. We are not aware of previous works in the field of CLP featuring a formulation of type safety like that of Theorem1.
As we have said,
$\{log\}$
’s type system is inspired in the type system of Z and B. Borrowing ideas from these notations is quite natural as
$\{log\}$
is based on a set theory similar to those underlying Z and B. In Z and B type inference, in the sense of deducing the type of some variable from the terms where it participates in, is not allowed; all variables must be declared. Subtyping is also nonexistent in Z and B. So we do in
$\{log\}$
. Differently from Z and B, in
$\{log\}$
elements of basic types have a known form (e.g.,
$\textsf{b}?\textbf{a}$
). This is useful when
$\{log\}$
is used as a programming language because users can give values to input variables of basic types. Obviously, tools for Z and B implement typecheckers similar to ours. Leuschel (Reference Leuschel, Fribourg and Heizmann2020) shows snippets of the Prolog implementation of a B typechecker.
Finally, we use the combination between type checking and constraint solving in a different way compared to works in logic programming. For example, Drabent et al. (Reference Drabent, Maluszynski and Pietrzak2002) or Pietrzak et al. (Reference Pietrzak, Correas, Puebla, Hermenegildo, Glück and de Moor2008) mentioned above, solve a system of constraints (sometimes based on set-analysis) to find out whether or not the program verifies some properties given by means of types. In
$\{log\}$
, type checking is used to rule out wrong programs or specifications, and constraint solving is used as the mechanism of a sort of automated theorem prover. In
$\{log\}$
, programs, specifications and properties are set formulas as in Z and B.
7 Conclusions
We have defined a type system and a typechecker for the CLP tool
$\{log\}$
. Type checking can be activated or not according to the users needs. The type system is based on the type systems of formal notations such as B and Z. We have proved that the operational semantics of
$\{log\}$
is type safe by adapting the type safety theorem of functional programming to the CLP context. Although the typechecker and the constraint solver are mostly independent from each other, they work together when formulas include finite types in order to ensure soundness. It is our understanding that the results presented in this paper show that the combination between a type system and CLP might be a practical approach to software verification. The case studies based on the LGS problem and the Android permission system provide empirical evidence about this claim.
As future work we want to study how the introduction of types may help with the problem of computing the negation of formulas. For example, the negation of
$p(x) \text{ :- } x = (\textbf{a},y)$
yields
$\forall y(x \neq (\textbf{a},y))$
, which lies outside the decision procedures implemented in
$\{log\}$
. However, if types are brought into the game, the negation of
$p(x)$
can be turned into a formula that
$\{log\}$
can solve. In effect,
$x = (\textbf{a},y)$
is type-correct iff
$\textbf{a}$
is part of a sum type, say
$\mathsf{sum}([\textbf{a},\textbf{b}(\mathsf{int})])$
,
$y$
is of some type
$\tau _y$
, and
$x$
is of type
$\mathsf{prod}(\mathsf{sum}([\textbf{a},\textbf{b}(\mathsf{int})]),\tau _y)$
. Then, if
$x$
is different from
$(\textbf{a},y)$
for all
$y$
, it can only be equal to
$(\textbf{b}(z),w)$
for some
$z$
and some
$w$
, because otherwise it would lie outside its type. Therefore,
$\forall y(x \neq (\textbf{a},y))$
can be turned into
$\exists z,w(x = (\textbf{b}(z),w))$
.
$\{log\}$
is able to deal with formulas including the latter, meaning that it would be able to deal with formulas including the negation of
$p(x)$
– something that, without types, could not be achieved. Then, we will work in finding the class of formulas whose negation can be safely computed when type information is available. This would be another area where the interplay between the typechecker and the constraint solver produces good results.
We think that the combination between type checking and constraint solving can be improved through the introduction of subtypes. For example, if
$0 \leq x$
is a type invariant and we have
$x' = x + 3$
we need to prove
$0 \leq x \land x' = x + 3 \implies 0 \leq x'$
. However, by introducing
$\mathsf{nat}$
as a subtype of
$\mathsf{int}$
, typing
$+:\mathsf{nat} \times \mathsf{nat} \rightarrow \mathsf{nat}$
and declaring
$dec([x,x'],\mathsf{nat})$
, it would be possible for the typechecker to automatically discharge the invariant by deciding whether the program is type-correct or not. The greatest gains along this line would be the introduction of a type for functions (say
$\texttt{fun}$
) as a subtype of
$\mathsf{rel}$
and a library of function-based constraints that would typecheck when their arguments are functions. This would make unnecessary the introduction of a number of invariance lemmas ensuring that a given binary relation is indeed a function. For instance, the update or override operator available in B (
$\vartriangleleft \!\!\!\!-$
) and Z (
$\oplus$
) is known to be closed for functions. Hence, a type declaration such as
$\vartriangleleft \!\!\!\!-: \texttt{fun}(T,U) \times \texttt{fun}(T,U) \rightarrow \texttt{fun}(T,U)$
can be added to the system. In this case, many proof obligations that today are passed to a prover could be easily discharged by the typechecker, instead.
Competing interests
The authors declare none.
Open access
